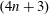Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T20:56:44.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogeneous Einstein Finsler Metrics on $(4n+3)$-dimensional Spheres

Part of: Global differential geometry Local differential geometry

Published online by Cambridge University Press:  09 November 2018

Libing Huang  and
Xiaohuan Mo
Libing Huang
Affiliation:
School of Mathematical Sciences, Nankai University, Tianjin 300071, China Email: huanglb@nankai.edu.cn
Xiaohuan Mo
Affiliation:
Key Laboratory of Pure and Applied Mathematics, School of Mathematical Sciences, Peking University, Beijing 100871, China Email: moxh@pku.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study a class of homogeneous Finsler metrics of vanishing 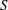$S$-curvature on a 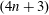$(4n+3)$-dimensional sphere. We find a second order ordinary differential equation that characterizes Einstein metrics with constant Ricci curvature 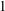$1$ in this class. Using this equation we show that there are infinitely many homogeneous Einstein metrics on 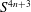$S^{4n+3}$ of constant Ricci curvature 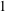$1$ and vanishing 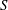$S$-curvature. They contain the canonical metric on 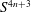$S^{4n+3}$ of constant sectional curvature 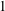$1$ and the Einstein metric of non-constant sectional curvature given by Jensen in 1973.

Keywords

Finsler metrichomogeneous spaceEinstein metric

MSC classification

Primary: 53B40: Finsler spaces and generalizations (areal metrics)
Secondary: 53C60: Finsler spaces and generalizations (areal metrics)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 509 - 523
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author Mo is the corresponding author. Author Huang was supported by the National Natural Science Foundation of China 11301283 and 11571185. Mo was supported by the National Natural Science Foundation of China 11771020.

References

Bao, D. and Robles, C., Ricci and flag curvature . In: A Sampler of Riemann-Finsler geometry , Math. Sci. Res. Inst. Publ., 50, Cambridge University Press, 2004.Google Scholar
Cheng, X., Shen, Z., and Tian, Y., A class of Einstein (𝛼, 𝛽)-metrics . Israel J. Math. 192(2012), 221–249. https://doi.org/10.1007/s11856-012-0036-x.Google Scholar
Chern, S. S., Finsler geometry is just Riemannian geometry without the quadratic restriction . Notices Amer. Math. Soc. 43(1996), 959–963.Google Scholar
Deng, S. and Hou, Z., Invariant Finsler metrics on homogeneous manifolds . J. Phys. A 37(2004), n. 34, 8245–8253. https://doi.org/10.1088/0305-4470/37/34/004.Google Scholar
Huang, L., Einstein Finsler metrics on S 3 with nonconstant flag curvature . Houston J. Math. 37(2011), 1071–1086.Google Scholar
Huang, L., Ricci curvature of left invariant Finsler metrics on Lie groups . Israel J. Math. 207(2015), 783–792. https://doi.org/10.1007/s11856-015-1161-0.Google Scholar
Huang, L., On the fundamental equations of homogeneous Finsler spaces . Diff. Geom. Appl. 40(2015), 187–208. https://doi.org/10.1016/j.difgeo.2014.12.009.Google Scholar
Huang, L., Flag curvatures of homogeneous Finsler spaces . European J. Math. 3(2017), 1000–1029. https://doi.org/10.1007/s40879-017-0157-1.Google Scholar
Jensen, G. R., Einstein metrics on principle fibre bundles . J. Diff. Geom. 8(1973), 599–614.Google Scholar
Milnor, J., Curvatures of left invariant metrics on Lie groups . Adv. Math. 21(1976), 293–329. https://doi.org/10.1016/S0001-8708(76)80002-3.Google Scholar
Mo, X., On the flag curvature of a Finsler space with constant S-curvature . Houston J. Math. 31(2005), 131–144.Google Scholar
Sevim, E. S., Shen, Z., and Zhao, L., On a class of Ricci flat Douglas metrics . Intern. J. Math. 23(2012), 1250046, 15pp. https://doi.org/10.1142/S0129167X12500462.Google Scholar
Shen, Z., Volume comparison and its application in Riemann-Finsler geometry . Adv. Math. 128(1997), 306–328. https://doi.org/10.1006/aima.1997.1630.Google Scholar
Shen, Z., Lectures on Finsler geometry . World Scientific Publishing Co., Singapore, 2001. https://doi.org/10.1142/9789812811622.Google Scholar
Shen, Z. and Yu, C., On a class of Einstein Finsler metrics . Internat. J. Math. 25(2014), 1450030, 18pp. https://doi.org/10.1142/S0129167X1450030X.Google Scholar
Wang, H., Huang, L., and Deng, S., Homogeneous Einstein-Randers metrics on spheres . Nonlinear Anal. 74(2011), 6295–6301. https://doi.org/10.1016/j.na.2011.06.008.Google Scholar
Ziller, W., Homogeneous Einstein metrics on spheres and projective spaces . Math. Ann. 259(1982), 351–358. https://doi.org/10.1007/BF01456947.Google Scholar