Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-27T10:24:34.544Z Has data issue: false hasContentIssue false
  • English
  • Français

The isotrivial case in the Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  13 January 2025

Dragos Ghioca Open the ORCID record for Dragos Ghioca [Opens in a new window]
Dragos Ghioca*
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada
*
e-mail: dghioca@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a semiabelian variety defined over a finite subfield of an algebraically closed field K of prime characteristic. We describe the intersection of a subvariety X of G with a finitely generated subgroup of 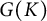$G(K)$.

Keywords

Semiabelian varietiesfinite fieldsMordell–Lang conjecture

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$
Secondary: 14G17: Positive characteristic ground fields
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Corvaja, P., Ghioca, D., Scanlon, T., and Zannier, U., The dynamical Mordell-Lang conjecture for endomorphisms of semiabelian varieties defined over fields of positive characteristic . J. Inst. Math. Jussieu 20(2021), no. 2, 669–698.CrossRefGoogle Scholar
Faltings, G., The general case of S. Lang’s conjecture. In: Barsotti symposium in algebraic geometry (Abano Terme, 1991), Perspectives in Mathematics, 15, Academic Press, San Diego, CA, 1994, 175–182.CrossRefGoogle Scholar
Ghioca, D., The isotrivial case in the Mordell-Lang theorem . Trans. Amer. Math. Soc. 360(2008), no. 7, 3839–3856.CrossRefGoogle Scholar
Ghioca, D. and Yang, S., The Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic . Bull. Aust. Math. Soc. 109(2024), no. 2, 254–264.CrossRefGoogle Scholar
Ginsburg, S. and Spanier, E. H., Semigroups, Presburger Formulas, and Languages . Pac. J. Math. 16(1966), 285–296.CrossRefGoogle Scholar
Hieronymi, P. and Schulz, C., A strong version of Cobham’s theorem. In: STOC’22-Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, ACM, New York, 2022, 1172–1179.CrossRefGoogle Scholar
Hrushovski, E., The Mordell-Lang conjecture for function fields . J. Amer. Math. Soc. 9(1996), no. 3, 667–690.CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles . Invent. Math. 78(1984), 299–327.CrossRefGoogle Scholar
Moosa, R. and Scanlon, T., F-structures and integral points on semiabelian varieties over finite fields . Amer. J. Math. 126(2004), 473–522.CrossRefGoogle Scholar
Skolem, T., Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen. C. r. 8 congr. scand. á Stockholm (1934), 163–188.Google Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. I . Invent. Math. 126(1996), no. 1, 133–181.CrossRefGoogle Scholar