Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mauldin, R.Daniel
and
Ulam, S.M
1987.
Mathematical problems and games.
Advances in Applied Mathematics,
Vol. 8,
Issue. 3,
p.
281.
Miller, Arnold W.
1989.
Infinite combinatorics and definability.
Annals of Pure and Applied Logic,
Vol. 41,
Issue. 2,
p.
179.
Croft, Hallard T.
Falconer, Kenneth J.
and
Guy, Richard K.
1991.
Unsolved Problems in Geometry.
Vol. 2,
Issue. ,
p.
168.
Humke, Paul
and
Laczkovich, Miklós
1998.
A visit to the Erdös problem.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 3,
p.
819.
Conti, Sergio
and
Schweizer, Ben
2006.
A Sharp-Interface Limit for a Two-Well Problem in Geometrically Linear Elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 179,
Issue. 3,
p.
413.
Łaba, Izabella
and
Pramanik, Malabika
2009.
Arithmetic Progressions in Sets of Fractional Dimension.
Geometric and Functional Analysis,
Vol. 19,
Issue. 2,
p.
429.
Bingham, N.H.
and
Ostaszewski, A.J.
2009.
Infinite combinatorics and the foundations of regular variation.
Journal of Mathematical Analysis and Applications,
Vol. 360,
Issue. 2,
p.
518.
Bingham, N.H.
and
Ostaszewski, A.J.
2010.
Regular variation without limits.
Journal of Mathematical Analysis and Applications,
Vol. 370,
Issue. 2,
p.
322.
Bingham, N. H.
and
Ostaszewski, A. J.
2011.
Homotopy and the Kestelman–Borwein–Ditor Theorem.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 1,
p.
12.
Miller, Harry I.
and
Ostaszewski, A.J.
2012.
Group action and shift-compactness.
Journal of Mathematical Analysis and Applications,
Vol. 392,
Issue. 1,
p.
23.
Chan, Vincent
Łaba, Izabella
and
Pramanik, Malabika
2016.
Finite configurations in sparse sets.
Journal d'Analyse Mathématique,
Vol. 128,
Issue. 1,
p.
289.
Miller, H.I.
Miller-Van Wieren, L.
and
Ostaszewski, A.J.
2021.
Beyond Erdős-Kunen-Mauldin: Shift-compactness properties and singular sets.
Topology and its Applications,
Vol. 291,
Issue. ,
p.
107605.
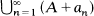 covers the interval. An application of this result is Theorem 3: for any sequence {an} and ε > 0 there is a set H of measure 1 - ε such that for no N and c is {an + c}n ≥ N contained by H.
covers the interval. An application of this result is Theorem 3: for any sequence {an} and ε > 0 there is a set H of measure 1 - ε such that for no N and c is {an + c}n ≥ N contained by H.