Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T01:11:38.818Z Has data issue: false hasContentIssue false
  • English
  • Français

The Milnor–Stasheff Filtration on Spaces and Generalized Cyclic Maps

Published online by Cambridge University Press:  20 November 2018

Norio Iwase ,
Mamoru Mimura ,
Nobuyuki Oda  and
Yeon Soo Yoon
Norio Iwase
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka 819-0395, Japane-mail: iwase@math.kyushu-u.ac.jp
Mamoru Mimura
Affiliation:
Department of Mathematics, Okayama University, Okayama 700-8530, Japane-mail: mimura@math.okayama-u.ac.jp
Nobuyuki Oda
Affiliation:
Department of Applied Mathematics, Fukuoka University, Fukuoka 814-0180, Japane-mail: odanobu@cis.fukuoka-u.ac.jp
Yeon Soo Yoon
Affiliation:
Department of Mathematics Education, Hannam University, Daejeon 306-791, Koreae-mail: yoon@hannam.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

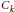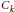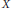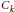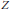The concept of ${{C}_{k}}$-spaces is introduced, situated at an intermediate stage between $H$-spaces and $T$-spaces. The ${{C}_{k}}$-space corresponds to the $k$-th Milnor–Stasheff filtration on spaces. 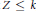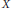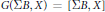It is proved that a space $X$ is a ${{C}_{k}}$-space if and only if the Gottlieb set $G(Z,\,X)\,=\,[Z,\,X]$ for any space $Z$ with cat $Z\,\le \,k$, which generalizes the fact that $X$ is a $T$-space if and only if $G(\sum B,\,X)\,=\,[\sum B,\,X]$ for any space $B$. Some results on the 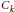${{C}_{k}}$-space are generalized to the 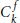$C_{k}^{f}$-space for a map 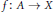$f\,:\,A\,\to \,X$. Projective spaces, lens spaces and spaces with a few cells are studied as examples of 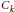${{C}_{k}}$-spaces, and non-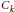${{C}_{k}}$-spaces.

Keywords

55P4555P35Gottlieb sets for mapsL-S categoryT-spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 523 - 536
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Aguadé, J., Decomposable free loop spaces. Canad. J. Math. 39(1987), no. 4, 938–955. http://dx.doi.org/10.4153/CJM-1987-047-9 Google Scholar
[2] Broughton, S. A., The Gottlieb group of finite linear quotients of odd-dimensional spheres. Proc. Amer. Math. Soc. 111(1991), no. 4, 1195–1197.Google Scholar
[3] Ganea, T., Lusternik-Schnirelmann category and strong category. Illionis J. Math. 11(1967), 417–427.Google Scholar
[4] Gottlieb, D. H., A certain subgroup of the fundamental group. Amer. J. Math. 87(1965), 840–856. http://dx.doi.org/10.2307/2373248 Google Scholar
[5] Gottlieb, D. H., Evaluation subgroups of homotopy groups. Amer. J. Math. 91(1969), 729–756. http://dx.doi.org/10.2307/2373349 Google Scholar
[6] Gottlieb, D. H., On the construction of G-spaces and applications to homogeneous spaces. Proc. Cambridge Philos. Soc. 68(1970), 321–327. http://dx.doi.org/10.1017/S0305004100046120 Google Scholar
[7] Haslam, H. B., G-spaces mod F and H-spaces mod F. Duke Math. J. 38(1971), 671–679. http://dx.doi.org/10.1215/S0012-7094-71-03882-8 Google Scholar
[8] Hubbuck, J. R., Hopf structures on Stiefel manifolds. Math. Ann. 262(1983), no. 4, 529–547. http://dx.doi.org/10.1007/BF01456067 Google Scholar
[9] Iwase, N., H-spaces with generating subspaces. Proc. Roy. Soc. Edinburgh Sect. A 111(1989), no. 3-4, 199–211.Google Scholar
[10] Iwase, N., Ganea's conjecture on Lusternik-Schnirelmann category. Bull. London Math. Soc. 30(1998), no. 6, 623–634. http://dx.doi.org/10.1112/S0024609398004548 Google Scholar
[11] Iwase, N., The Ganea conjecture and recent developments on Lusternik-Schnirelmann category. Sugaku Expositions 20(2007), no. 1, 43–63.Google Scholar
[12] Iwase, N., Kono, A. and Mimura, M., Generalized Whitehead spaces with few cells. Publ. Res. Inst. Math. Sci. 28(1992), no. 4, 615–652. http://dx.doi.org/10.2977/prims/1195168211 Google Scholar
[13] Iwase, N. and Oda, N., Splitting off rational parts in homotopy types. Topology Appl. 153(2005), no. 1, 133–140. http://dx.doi.org/10.1016/j.topol.2005.01.027 Google Scholar
[14] James, I. M., On category in the sense of Lusternik-Schnirelmann. Topology 17(1978), no. 4, 331–348. http://dx.doi.org/10.1016/0040-9383(78)90002-2 Google Scholar
[15] Lang, G. E. Jr, Evaluation subgroups of factor spaces. Pacific J. Math. 42(1972), 701–709.Google Scholar
[16] Milnor, J., Construction of universal bundles. I, II. Ann. Math. 63(1956), 272–284, 430–436. http://dx.doi.org/10.2307/1969609 Google Scholar
[17] Oda, N., The homotopy set of the axes of pairings. Canad. J. Math. 17(1990), no. 5, 856–868. http://dx.doi.org/10.4153/CJM-1990-044-3 Google Scholar
[18] Oda, N., Pairings and copairings in the category of topological spaces. Publ. Res. Inst. Math. Sci. 28(1992), no. 1, 83–97. http://dx.doi.org/10.2977/prims/1195168857 Google Scholar
[19] Oprea, J., Finite group actions on spheres and the Gottlieb group. J. Korean Math. Soc. 28(1991), no. 1, 65–78.Google Scholar
[20] Siegel, J., G-spaces, H-spaces andW-spaces. Pacific J. Math. 31(1969), 209–214.Google Scholar
[21] Stasheff, J. D., Homotopy associativity of H-spaces I, II. Trans. Amer. Math. Soc. 108(1963), 275–292, 293–312.Google Scholar
[22] Thomas, E., On functional cup-products and the transgression operator. Arch. Math. (Basel) 12(1961), 435–444.Google Scholar
[23] Varadarajan, K., Generalized Gottlieb groups. J. Indian Math. Soc. 33(1969), 141–164.Google Scholar
[24] Whitehead, G. W., Elements of Homotopy Theory. Graduate Texts in Mathematics 61. Springer-Verlag, New York, 1978.Google Scholar
[25] Woo, M. H. and Kim, J.-R., Certain subgroups of homotopy groups. J. Korean Math. Soc. 21(1984), no. 2, 109–120.Google Scholar
[26] Woo, M. H. and Yoon, Y. S., T-spaces by the Gottlieb groups and duality. J. Austral.Math. Soc. Ser. A 59(1995), no. 2, 193–203. http://dx.doi.org/10.1017/S1446788700038593 Google Scholar
[27] Yoon, Y. S., Generalized Gottlieb groups and generalized Wang homomorphisms. Sci. Math. Jpn. 55(2002), no. 1, 139–148.Google Scholar
[28] Yoon, Y. S., Hf -spaces for maps and their duals. J. Korea Soc. Math. Educ. Ser. B Pure Appl. Math. 14(2007), no. 4, 289–306.Google Scholar
[29] Yoon, Y. S., Lifting T-structures and their duals. J. Chungcheong Math. Soc. 20(2007), 245–259.Google Scholar