Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T11:35:02.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Uniqueness of The Solution to a Generalized Dirichlet Problem

Published online by Cambridge University Press:  20 November 2018

E. L. Koh
E. L. Koh*
Affiliation:
Department of Mathematics, University of Saskatchewan, Regina, Saskatchewan Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is generally known [1] that the singular partial differential equation

may not have a unique solution because of the existence of nontrivial representations of zero.

1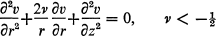

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 4 , 01 December 1974 , pp. 605 - 606
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Colton, David, Applications of a Class of Singular partial Differential Equations to Gegenbauer Series which converge to zero, SIAM J. Math. Anal. Vol. 1 No. 1 (1970), pp. 90-95.Google Scholar
2. Zemanian, A.H., A distributional Hankel transformation, J. Soc. Ind. Appl. Math. 14 (1966), pp. 561-576.Google Scholar
3. Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F.G., Table of integral transformst Vol. II, McGraw-Hill, New York, 1954.Google Scholar
4. Koshlyakov, N. S., Smirnow, M.M., and Gliner, E.B., Differential Equations of Mathematical Physics, North-Holland, Amsterdam, 1964.Google Scholar