Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Skula, Ladislav
1969.
On a reflective subcategory of the category of all topological spaces..
Transactions of the American Mathematical Society,
Vol. 142,
Issue. 0,
p.
37.
Herrlich, Horst
1971.
Categorical topology.
General Topology and its Applications,
Vol. 1,
Issue. 1,
p.
1.
Hoffmann, Rudolf -E.
1974.
Bemerkungen �ber Td- R�ume.
Manuscripta Mathematica,
Vol. 12,
Issue. 2,
p.
195.
Schr�der, J.
1974.
Epi und extremer Mono inT 2a.
Archiv der Mathematik,
Vol. 25,
Issue. 1,
p.
561.
Hoffmann, Rudolf -E.
1975.
Charakterisierung n�chterner R�ume.
Manuscripta Mathematica,
Vol. 15,
Issue. 2,
p.
185.
Hoffmann, Rudolf-E.
1976.
Categorical Topology.
Vol. 540,
Issue. ,
p.
286.
Salbany, Sergio
1976.
Categorical Topology.
Vol. 540,
Issue. ,
p.
548.
Pumpl�n, Dieter
1980.
Initial morphisms and monomorphisms.
Manuscripta Mathematica,
Vol. 32,
Issue. 3-4,
p.
309.
Giuli, Eraldo
1980.
Bases of topological epi-reflections.
Topology and its Applications,
Vol. 11,
Issue. 3,
p.
265.
Brümmer, G. C. L.
1982.
Categorical Aspects of Topology and Analysis.
Vol. 915,
Issue. ,
p.
50.
Pumpl�n, D.
and
R�hrl, H.
1985.
Separated totally convex spaces.
Manuscripta Mathematica,
Vol. 50,
Issue. 1,
p.
145.
Herrlich, H.
Salicrup, G.
and
Strecker, G.E.
1987.
Factorizations, denseness, separation, and relatively compact objects.
Topology and its Applications,
Vol. 27,
Issue. 2,
p.
157.
Dikranjan, Dikran
and
Giuli, Eraldo
1987.
Closure operators I.
Topology and its Applications,
Vol. 27,
Issue. 2,
p.
129.
Lord, Harriet Lazowick
1988.
Factorizations, M-separation, and extremal-epireflective subcategories.
Topology and its Applications,
Vol. 28,
Issue. 3,
p.
241.
ERVYNCK, G.
1988.
A NOTE ON THE FRONT CLOSURE TOPOLOGY.
Quaestiones Mathematicae,
Vol. 11,
Issue. 2,
p.
213.
Nakagawa, Ryosuke
1989.
Topics in General Topology.
Vol. 41,
Issue. ,
p.
563.
Castellini, G.
and
Strecker, G. E.
1990.
GLOBAL CLOSURE OPERATORS VS. SUBCATEGORIES.
Quaestiones Mathematicae,
Vol. 13,
Issue. 3-4,
p.
417.
Castellini, Gabriele
Koslowski, Jürgen
and
Strecker, George E.
1992.
A factorization of the Pumplün-Röhrl connection.
Topology and its Applications,
Vol. 44,
Issue. 1-3,
p.
69.
Alderton, Ian W.
and
Castellini, Gabriele
1993.
Epimorphisms in categories of separated fuzzy topological spaces.
Fuzzy Sets and Systems,
Vol. 56,
Issue. 3,
p.
323.
Castellini, G.
and
Hajek, D.
1994.
Closure operators and connectedness.
Topology and its Applications,
Vol. 55,
Issue. 1,
p.
29.

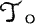
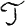 and
and 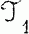 (where
(where 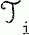 . is the category of T
. is the category of T