Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thompson, R.C.
1970.
The l property for singular values.
Linear Algebra and its Applications,
Vol. 3,
Issue. 2,
p.
179.
Hristev, Anatole P.
1971.
Conformal Charge Conjugation.
Journal of Mathematical Physics,
Vol. 12,
Issue. 1,
p.
118.
Grone, Robert
1994.
A biography of Marvin Marcus.
Linear Algebra and its Applications,
Vol. 201,
Issue. ,
p.
1.


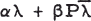 for some αβ ≠ 0 then A is normal. Here
for some αβ ≠ 0 then A is normal. Here 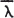 is the conjugate vector of λ. As a companion result they also proved that if the eigenvalues of AA* are
is the conjugate vector of λ. As a companion result they also proved that if the eigenvalues of AA* are  , i = 1, …, n then A is normal.
, i = 1, …, n then A is normal.