Published online by Cambridge University Press: 03 May 2021
Let 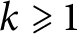 $k\geqslant 1$
be a natural number and
$k\geqslant 1$
be a natural number and 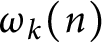 $\omega _k(n)$
denote the number of distinct prime factors of a natural number n with multiplicity k. We estimate the first and second moments of the functions
$\omega _k(n)$
denote the number of distinct prime factors of a natural number n with multiplicity k. We estimate the first and second moments of the functions 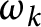 $\omega _k$
with
$\omega _k$
with 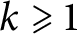 $k\geqslant 1$
. Moreover, we prove that the function
$k\geqslant 1$
. Moreover, we prove that the function 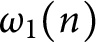 $\omega _1(n)$
has normal order
$\omega _1(n)$
has normal order 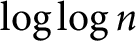 $\log \log n$
and the function
$\log \log n$
and the function 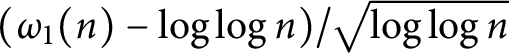 $(\omega _1(n)-\log \log n)/\sqrt {\log \log n}$
has a normal distribution. Finally, we prove that the functions
$(\omega _1(n)-\log \log n)/\sqrt {\log \log n}$
has a normal distribution. Finally, we prove that the functions 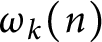 $\omega _k(n)$
with
$\omega _k(n)$
with 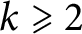 $k\geqslant 2$
do not have normal order
$k\geqslant 2$
do not have normal order 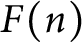 $F(n)$
for any nondecreasing nonnegative function F.
$F(n)$
for any nondecreasing nonnegative function F.