Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gronau, Hans-Dietrich O.H.
1981.
On maximal families of subsets of a finite set.
Discrete Mathematics,
Vol. 34,
Issue. 2,
p.
119.
Katchalski, M.
Klamkin, M. S.
and
Liu, A.
1981.
An Experience in Problem Solving.
The American Mathematical Monthly,
Vol. 88,
Issue. 8,
p.
551.
West, Douglas B.
1982.
Ordered Sets.
p.
473.
Füredi, Zoltán
1987.
The maximum number of balancing sets.
Graphs and Combinatorics,
Vol. 3,
Issue. 1,
p.
251.
Katona, Gyula O.H.
2004.
Strong qualitative independence.
Discrete Applied Mathematics,
Vol. 137,
Issue. 1,
p.
87.
Маренич, Е Е
Marenich, E E
Большакова, Н С
and
Bol'shakova, N S
2007.
Число пересечений графа.
Дискретная математика,
Vol. 19,
Issue. 4,
p.
97.
Marenich, E. E.
and
Bolshakova, N. S.
2007.
On the intersection number of a graph.
Discrete Mathematics and Applications,
Vol. 17,
Issue. 6,
Maltais, Elizabeth
Moura, Lucia
and
Newman, Mike
2017.
Graph-intersecting set systems and LYM inequalities.
Discrete Mathematics,
Vol. 340,
Issue. 3,
p.
379.
Chouraqui, Fabienne
2020.
Developments in Language Theory.
Vol. 12086,
Issue. ,
p.
55.
Arató, M.
Katona, Gy. O. H.
Michaletzky, Gy.
Móri, T. F.
Pintz, J.
Rudas, T.
Székely, G. J.
and
Tusnády, G.
2021.
Rényi 100, Quantitative and qualitative (in)dependence.
Acta Mathematica Hungarica,
Vol. 165,
Issue. 1,
p.
218.


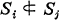 for i≠j, i, j, =1, 2, …, t; and if
for i≠j, i, j, =1, 2, …, t; and if