On Closed Ideals in a Certain Class of Algebras of Holomorphic Functions

Abstract

We recently introduced a weighted Banach algebra 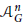$\mathcal{A}_{G}^{n}$ of functions that are holomorphic on the unit disc 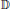$\mathbb{D}$, continuous up to the boundary, and of the class 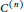${{C}^{\left( n \right)}}$ at all points where the function 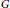$G$ does not vanish. Here, 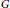$G$ refers to a function of the disc algebra without zeros on 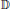$\mathbb{D}$. Then we proved that all closed ideals in 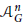$\mathcal{A}_{G}^{n}$ with at most countable hull are standard. In this paper, on the assumption that 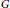$G$ is an outer function in 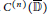${{C}^{\left( n \right)}}\,\left( {\bar{\mathbb{D}}} \right)$ having infinite roots in 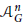$\mathcal{A}_{G}^{n}$ and countable zero set 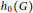${{h}_{o}}\left( G \right)$, we show that all the closed ideals $I$ with hull containing 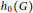${{h}_{o}}\left( G \right)$ are standard.