Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-11T02:27:40.254Z Has data issue: false hasContentIssue false
  • English
  • Français

On Functions Whose Graph is a Hamel Basis, II

Published online by Cambridge University Press:  20 November 2018

Krzysztof Płotka
Krzysztof Płotka*
Affiliation:
Department of Mathematics, University of Scranton, Scranton, PA 18510, USA e-mail: Krzysztof.Plotka@scranton.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We say that a function 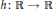$h\,:\,\mathbb{R}\,\to \,\mathbb{R}$ is a Hamel function 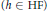$(h\,\in \,\text{HF)}$ if $h$, considered as a subset of 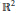${{\mathbb{R}}^{2}},$ is a Hamel basis for 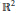${{\mathbb{R}}^{2}}.$ We show that 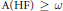$\text{A}\left( \text{HF} \right)\,\ge \,\omega$, i.e., for every finite 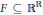$F\,\subseteq \,{{\mathbb{R}}^{\mathbb{R}}}$ there exists 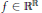$f\,\in \,{{\mathbb{R}}^{\mathbb{R}}}$ such that 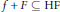$f\,+\,F\,\subseteq \,\text{HF}$. From the previous work of the author it then follows that 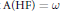$\text{A}\left( \text{HF} \right)\,=\,\omega$.

Keywords

26A2154C4015A0354C30Hamel basisadditiveand Hamel functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 295 - 302
Copyright
Copyright © Canadian Mathematical Society 2009

References

[C] Ciesielski, K., Set theory for the working mathematician. London Mathematical Society Student Texts 39, Cambridge University Press, Cambridge, 1997.Google Scholar
[CM] Ciesielski, K. and Miller, A. W., Cardinal invariants concerning functions whose sum is almost continuous. Real Anal. Exchange 20(1994/95), no. 2, 657–672.Google Scholar
[CN] Ciesielski, K. and Natkaniec, T., Algebraic properties of the class of Sierpi´nski-Zygmund functions. Topology Appl. 79(1997), no. 1, 75–99.Google Scholar
[CR] Ciesielski, K. and Recław, I., Cardinal invariants concerning extendable and peripherally continuous functions. Real Anal. Exchange 21(1995/96), no. 2, 459–472.Google Scholar
[MK] Kuczma, M., An introduction to the theory of functional equations and inequalities. Scientific Publications of the University of Silesia 489, Polish Scientific Publishers, PWN, Warsaw, 1985.Google Scholar
[P] Płotka, K., On functions whose graph is a Hamel basis. Proc. Amer. Math. Soc. 131(2003), no. 4, 1031–1041.Google Scholar
[PR] Płotka, K., and Recław, I., Finitely continuous Hamel functions. Real Anal. Exchange 30(2004/05), no. 2, 867–870.Google Scholar