Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T21:37:47.612Z Has data issue: false hasContentIssue false
  • English
  • Français

On Quantizing Nilpotent and Solvable Basic Algebras

Published online by Cambridge University Press:  20 November 2018

Mark J. Gotay  and
Janusz Grabowski
Mark J. Gotay
Affiliation:
Department of Mathematics University of Hawai‘i 2565 The Mall Honolulu, HI 96822 USA, e-mail: gotay@math.hawaii.edu
Janusz Grabowski
Affiliation:
Institute of Mathematics University of Warsaw ul. Banacha 2 02-097 Warsaw Poland, e-mail: jagrab@mimuw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove an algebraic “no-go theorem” to the effect that a nontrivial Poisson algebra cannot be realized as an associative algebra with the commutator bracket. Using it, we show that there is an obstruction to quantizing the Poisson algebra of polynomials generated by a nilpotent basic algebra on a symplectic manifold. This result generalizes Groenewold’s famous theorem on the impossibility of quantizing the Poisson algebra of polynomials on 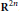${{\mathbf{R}}^{2n}}$. Finally, we explicitly construct a polynomial quantization of a symplectic manifold with a solvable basic algebra, thereby showing that the obstruction in the nilpotent case does not extend to the solvable case.

Keywords

81S9958F06
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 2 , 01 June 2001 , pp. 140 - 149
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Arnal, D., Cortet, J. C., Molin, P., and Pinczon, G., Covariance and geometrical invariance in *-quantization. J. Math. Phys. 24 (1983), 276–283.Google Scholar
[2] Barut, A. O. and Raçzka, R., Theory of Group Representations and Applications. World Scientific, Singapore, 2nd edition, 1986.Google Scholar
[3] Dixmier, J., Enveloping Algebras. North-Holland, Amsterdam, 1977.Google Scholar
[4] Flato, M. and Simon, J., Separate and joint analyticity in Lie groups representations. J. Funct. Anal. 13 (1973), 268–276.Google Scholar
[5] Gotay, M. J., On a full quantization of the torus. In: Quantization, Coherent States and Complex Structures (eds. J.-P. Antoine et al.), Plenum, New York, 1995, 55–62.Google Scholar
[6] Gotay, M. J., On the Groenewold-Van Hove problem for R2n . J. Math. Phys. 40 (1999), 2107–2116.Google Scholar
[7] Gotay, M. J., Obstructions to quantization. In: Mechanics: From Theory to Computation (eds. Journal of Nonlinear Science Editors), Springer, New York, 2000, 171–216.Google Scholar
[8] Gotay, M. J., Grabowski, J. and Grundling, H. B., An obstruction to quantizing compact symplectic manifolds. Proc. Amer.Math. Soc. 28 (2000), 237–243.Google Scholar
[9] Gotay, M. J. and Grundling, H. B., On quantizing T*S1 . Rep. Math. Phys. 40 (1997), 107–123.Google Scholar
[10] Gotay, M. J. and Grundling, H. B., Nonexistence of finite-dimensional quantizations of a noncompact symplectic manifold. In: Differential Geometry and Applications (eds. I. Kolář et al.), Masaryk Univ., Brno, 1999, 593–596.Google Scholar
[11] Grabowski, J., The Lie structure of C* and Poisson algebras. Studia Math. 81 (1985), 259–270.Google Scholar
[12] Grabowski, J., Remarks on nilpotent Lie algebras of vector fields. J. Reine Angew. Math. 406 (1990), 1–4.Google Scholar
[13] Groenewold, H. J., On the principles of elementary quantum mechanics. Physica 12 (1946), 405–460.Google Scholar
[14] Isham, C. J., Topological and global aspects of quantum theory. In: Relativity, Groups, and Topology II (eds. B. S. De Witt and R. Stora), North-Holland, Amsterdam, 1984, 1059–1290.Google Scholar
[15] Joseph, A., Derivations of Lie brackets and canonical quantization. Commun. Math. Phys. 17 (1970), 210–232.Google Scholar
[16] Naimark, M. A. and Štern, A. I., Theory of Group Representations. Springer, New York, 1982.Google Scholar
[17] Pedersen, N. V., Geometric quantization and the universal enveloping algebra of a nilpotent Lie group. Trans. Amer.Math. Soc. 315 (1989), 511–563.Google Scholar
[18] Reed, M. and Simon, B., Functional Analysis II. Academic Press, New York, 1975.Google Scholar
[19] Robert, A., Introduction to the Representation Theory of Compact and Locally Compact Groups. London Math. Soc. Lecture Note Ser. 80, Cambridge Univ. Press, Cambridge, 1983.Google Scholar
[20] Vergne, M., La structure de Poisson sur l’algèbre symmétrique d’une algèbre de Lie nilpotente. Bull. Soc. Math. France 100 (1972), 301–335.Google Scholar
[21] Wildberger, N., Quantization and Harmonic Analysis on Lie Groups. Dissertation, Yale University, 1983.Google Scholar