No CrossRef data available.
Article contents
On Some Functional Equations of Carleman
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The celebrated Fredholm theory of linear integral equations holds if the kernel K(x, y) or one of its iterates K (n) is bounded. Hilbert utilizing his theory of quadratic form was able to extend the theory to the kernels K(x, y) satisfying
a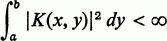
b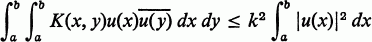
where k is independent of u(x).
These theories were extended considerably by T. Carleman who deleted condition (b) above.
Equations involving this Carleman kernel have been found useful in connection with Hermitian forms, continued fractions, Schroedinger wave equations (see [1], [2]) and more recently in scattering theory in quantum physics, etc. [3]. See also [5] for a variety of applications and extensions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
1.
Carleman, T., La théorie des équations intégrales singulières et ses applications, Ann. Inst. H. Poincaré, 1931.Google Scholar
2.
Carleman, T., Sur les équations singulières ? noyau réel et symétrique, Uppsala Univ. Arsskrift
17, 1923.Google Scholar
3.
Misra, B., Speiser, D., and Targonski, G., Integral operators in the theory of scattering, Helv. Phys. Act. 36.
1963.Google Scholar
5.
Trjitzinsky, W. J., Singular Lebesgue-Stieltjes integral equations, Acta Math.
74 (1942), 197-310.Google Scholar

