Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T10:54:45.055Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Inner Radius of a Nodal Domain

Published online by Cambridge University Press:  20 November 2018

Dan Mangoubi
Dan Mangoubi*
Affiliation:
Department of Mathematics, The Technion, Haifa 32000, Israel e-mail: mangoubi@techunix.technion.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

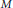Let $M$ be a closed Riemannian manifold. We consider the inner radius of a nodal domain for a large eigenvalue $\text{ }\!\!\lambda\!\!\text{ }.$ We give upper and lower bounds on the inner radius of the type 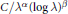$C/{{\lambda }^{\alpha }}{{(\log \lambda )}^{\beta }}.$ Our proof is based on a local behavior of eigenfunctions discovered by Donnelly and Fefferman and a Poincaré type inequality proved by Maz’ya. Sharp lower bounds are known only in dimension two. We give an account of this case too.

Keywords

58J5035P1535P20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 249 - 260
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Ahlfors, L. V., Lectures on Quasiconformal Mappings. Van Nostrand Mathematical Studies 10, Van Nostrand, Toronto, 1966.Google Scholar
[2] Ahlfors, L. V., Conformal Invariants: Topics in Geometric Function Theory. McGraw-Hill, New York, 1973.Google Scholar
[3] Brüning, J., Über Knoten von Eigenfunktionen des Laplace-Beltrami-Operators. Math. Z. 158(1978), no. 1, 15–21.Google Scholar
[4] Brüning, J. and Gromes, D., Über die Länge der Knotenlinien schwingender Membranen. Math. Z. 124(1972), 79–82.Google Scholar
[5] Chanillo, S. and Muckenhoupt, B., Nodal geometry on Riemannian manifolds. J. Differential Geom. 34(1991), no. 1, 85–91.Google Scholar
[6] Chanillo, S. and Wheeden, R. L., Weighted Poincaré and Sobolev inequalities and estimates for weighted Peano maximal functions. Amer. J. Math. 107(1985), no. 5, 1191–1226.Google Scholar
[7] Chavel, I., Eigenvalues in Riemannian geometry. Pure and Applied Mathematics 115, Academic Press, Orlando, FL, 1984.Google Scholar
[8] Donnelly, H. and Fefferman, C., Nodal sets of eigenfunctions on Riemannian manifolds. Invent. Math. 93(1988), no. 1, 161–183.Google Scholar
[9] Donnelly, H. and Fefferman, C., Growth and geometry of eigenfunctions of the Laplacian. In: Analysis and Partial Differential Equations. Lecture Notes in Pure and Appl. Math. 122, Dekker, New York, 1990, pp. 635–655.Google Scholar
[10] Egorov, Y. and Kondratiev, V., On spectral theory of elliptic operators, Operator Theory: Advances and Applications 89, Birkhäuser Verlag, Basel, 1996.Google Scholar
[11] Hayman, W. K., Some bounds for principal frequency. Applicable Anal. 7(1977/78), no. 3, 247–254.Google Scholar
[12] Lieb, E. H., On the lowest eigenvalue of the Laplacian for the intersection of two domains. Invent. Math. 74(1983), no. 3, 441–448.Google Scholar
[13] Lu, G., Covering lemmas and an application to nodal geometry on Riemannian manifolds. Proc. Amer. Math. Soc. 117(1993), no. 4, 971–978.Google Scholar
[14] Maz’ya, V., The Dirichlet problem for elliptic equations of arbitrary order in unbounded domains. Dokl. Akad. Nauk SSSR 150(1963), 1221–1224, translation in Soviet Math. Dokl. 4(1963), no. 3, 860–863.Google Scholar
[15] Maz’ya, V., Sobolev Spaces. Springer Series in Soviet Mathematics, Springer-Verlag, Berlin, 1985.Google Scholar
[16] Maz’ya, V. and Shubin, M., Discreteness of spectrum and positivity criteria for Schrödinger operators. Ann. of Math. 162(2005), no. 2, 919–942.Google Scholar
[17] Maz’ya, V. and Shubin, M., Can one see the fundamental frequency of a drum? Lett. Math. Phys. 74 (2005), no. 2, 135–151.Google Scholar
[18] Nadirashvili, N. S., Metric properties of eigenfunctions of the Laplace operator on manifolds. Ann. Inst. Fourier (Grenoble) 41(1991), no. 1, 259–265.Google Scholar
[19] Nazarov, F., Polterovich, L., and Sodin, M., Sign and area in nodal geometry of Laplace eigenfunctions. Amer. J. Math. 127(2005), no. 4, 879–910.Google Scholar
[20] Osserman, R., A note on Hayman's theorem on the bass note of a drum. Comment. Math. Helv. 52(1977), no. 4, 545–555.Google Scholar
[21] Savo, A., Lower bounds for the nodal length of eigenfunctions of the Laplacian. Ann. Global Anal. Geom. 19(2001), no. 2, 133–151.Google Scholar
[22] Simon, L., Existence of surfaces minimizing the Willmore functional. Comm. Anal. Geom. 1(1993), no. 2, 281–326.Google Scholar
[23] Xu, B., Asymptotic behavior of L 2 -normalized eigenfunctions of the Laplace-Beltrami operator on a closed Riemannian manifold. arXiv:math.SP/0509061, 2005.Google Scholar
[24] Ziemer, W. P.,Weakly differentiable functions. Sobolev spaces and functions of bounded variation. Graduate Texts in Mathematics 120, Springer-Verlag, New York, 1989,Google Scholar