Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T13:44:21.173Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp Inequalities for Differentially Subordinate Harmonic Functions and Martingales

Published online by Cambridge University Press:  20 November 2018

Adam Osękowski
Adam Osękowski*
Affiliation:
Department of Mathematics, Informatics and Mechanics, University of Warsaw, Banacha 2, 02-097 Warsaw, Polande-mail: ados@mimuw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We determine the best constants 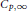${{C}_{p,\infty }}$ and 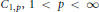${{C}_{1,p}},\,1\,<\,p\,<\,\infty $, for which the following holds. If 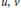$u,v$ are orthogonal harmonic functions on a Euclidean domain such that $v$ is differentially subordinate to $u$, then

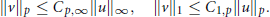$${{\left\| v \right\|}_{p}}\le {{C}_{p}}{{,}_{\infty }}{{\left\| u \right\|}_{\infty }},\,\,\,\,\,\,\,\,\,\,\,{{\left\| v \right\|}_{1}}\le {{C}_{1,p}}{{\left\| u \right\|}_{p}}.$$

In particular, the inequalities are still sharp for the conjugate harmonic functions on the unit disc of 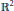${{\mathbb{R}}^{2}}$. Sharp probabilistic versions of these estimates are also studied. As an application, we establish a sharp version of the classical logarithmic inequality of Zygmund.

Keywords

31B0560G4460G40harmonic functionconjugate harmonic functionsorthogonal harmonic functionsmartingaleorthogonal martingalesnorm inequalityoptimal stopping problem
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 597 - 610
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bañuelos, R., and Wang, G., Sharp inequalities for martingales with applications to the Beurling-Ahlfors and Riesz transforms. Duke Math. J. 80(1995), no. 3, 575–600. http://dx.doi.org/10.1215/S0012-7094-95-08020-X Google Scholar
[2] Bañuelos, R., and Wang, G., Orthogonal martingales under differential subordination and application to Riesz transforms. Illinois J. Math. 40(1996), no. 4, 678–691.Google Scholar
[3] Bañuelos, R., and Wang, G., Davis's inequality for orthogonal martingales under differential subordination. Michigan Math. J. 47(2000), no. 1, 109–124. http://dx.doi.org/10.1307/mmj/1030374671 Google Scholar
[4] Burkholder, D. L., Boundary value problems and sharp inequalities for martingale transforms. Ann. Probab. 12(1984), no. 3, 647–702. http://dx.doi.org/10.1214/aop/1176993220 Google Scholar
[5] Burkholder, D. L., Differential subordination of harmonic functions and martingales. In: Harmonic Analysis and Partial Differential Equations. Lecture Notes in Math. 1384, Springer, Berlin, 1989, pp. 1–23.Google Scholar
[6] Choi, C., A weak-type inequality for differentially subordinate harmonic functions. Trans. Amer. Math. Soc. 350(1998), no. 7, 2687–2696. http://dx.doi.org/10.1090/S0002-9947-98-02259-4 Google Scholar
[7] Davis, B., On the weak (1, 1) inequality for conjugate functions Proc. Amer. Math. Soc. 44(1974), 307–311.Google Scholar
[8] Dellacherie, C. and Meyer, P. A., Probabilities and Potential. B. Theory of Martingales. North-Holland Mathematics Studies 72. North-Holland, Amsterdam, 1982.Google Scholar
[9] Essén, M., Shea, D. F. and Stanton, C. S., Sharp L logα inequalities for conjugate functions. Ann. Inst. Fourier (Grenoble) 52(2002), no. 2, 623–659.Google Scholar
[10] Gamelin, T. W., Uniform Algebras and Jensen Measures. London Mathematical Society Lecture Note Series 32. Cambridge University Press, Cambridge, 1978.Google Scholar
[11] Kolmogorov, A. N., Sur les fonctions harmoniques conjugées et les séries de Fourier. Fund. Math. 7(1925), 24–29.Google Scholar
[12] Pichorides, S. K., On the best values of the constants in the theorems of M. Riesz, Zygmund and Kolmogorov. Studia Math. 44(1972), 165–179.Google Scholar
[13] Peskir, G. and Shiryaev, A., Optimal Stopping and Free-Boundary Problems. Lectures in Math. ETH Zürich, Birkhäuser-Verlag, Basel, 2006.Google Scholar
[14] Riesz, M., Sur les fonctions conjugées. Math. Z. 27(1928), no. 1, 218–244. http://dx.doi.org/10.1007/BF01171098 Google Scholar
[15] Revuz, D. and Yor, M., Continuous Martingales and Brownian Motion. 3rd edition. Grundlehren der Mathematischen Wissenschaften 293. Springer-Verlag, Berlin, 1999.Google Scholar
[16] Wang, G., Differential subordination and strong differential subordination for continuous-time martingales and related sharp inequalities. Ann. Probab. 23(1995), no. 2, 522–551. http://dx.doi.org/10.1214/aop/1176988278 Google Scholar
[17] Zygmund, A., Sur les fonctions conjugées. Fund. Math. 13(1929), 284–303.Google Scholar