Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T11:02:15.461Z Has data issue: false hasContentIssue false
  • English
  • Français

Support Points of the Class of Close-to-Convex Functions

Published online by Cambridge University Press:  20 November 2018

E. Grassmann ,
W. Hengartner  and
G. Schober
E. Grassmann
Affiliation:
University of Calgary
W. Hengartner
Affiliation:
Université Laval
G. Schober
Affiliation:
Indiana University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H(U) be the linear space of holomorphic functions on U = {z:|z|<1} endowed with the topology of compact convergence, and denote by H′(U) its topological dual space. Let 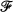be a compact subset of H(U) and ƒ∈F. We say ƒ is a support point of 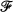if there exists an L∈H'(U), non-constant on 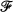, such that 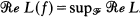On the other hand, ƒ is an extreme point of 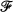if ƒ is not a proper convex combination of two other points of .

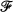Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 2 , 01 June 1976 , pp. 177 - 179
Copyright
Copyright © Canadian Mathematical Society 1976

Footnotes

(1)

This work was supported in part by the National Research Council of Canada.

References

1. Brickman, L., MacGregor, T. H., and Wilken, D. R., Convex hulls of some classical families of univalent functions, Trans. Amer. Math. Soc. 156 (1971), 91–107.CrossRefGoogle Scholar