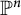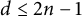Toric degenerations of low-degree hypersurfaces

Abstract

We show that a sufficiently general hypersurface of degree d in $\mathbb {P}^n$ admits a toric Gröbner degeneration after linear change of coordinates if and only if $d\leq 2n-1$.

1 Introduction

When does a projective variety X admit a flat degeneration to a toric variety? Among other applications, such degenerations are used in the mirror-theoretic approach to the classification of Fano varieties [CCG⁺13], the construction of integrable systems [HK15], and in bounding Seshadri constants [Ito14]. The many applications of toric degenerations notwithstanding, there is as of yet no general method for determining if a given variety admits a toric degeneration.

In this note, we will consider the special case of toric degenerations of some $X\subset \mathbb {P}^n$ obtained as the flat limit of X under a $\mathbb {G}_m$ -action on $\mathbb {P}^n$ . In the case that the $\mathbb {G}_m$ -action arises as a one-parameter subgroup of the standard torus on $\mathbb {P}^n$ , the situation may be well understood by studying the Gröbner fan and tropicalization of X [MS15]. However, if we consider arbitrary $\mathbb {G}_m$ -actions on $\mathbb {P}^n$ , the situation becomes more complicated. As a test case, we investigate the existence of such toric degenerations when X is a hypersurface.

In order to state our result, we introduce some notation. Throughout the paper, $\mathbb {K}$ will be an algebraically closed field of characteristic zero. Let $\omega \in \mathbb {R}^{n+1}$ . Consider any polynomial $f\in \mathbb {K}[x_0,\ldots ,x_n]$ , where we write

(1.1) $$ \begin{align} f=\sum_{u\in \mathbb{Z}_{\geq 0}^{n+1}} c_ux^u \end{align} $$

using multi-index notation. The initial term of f with respect to the weight vector $\omega $ is

$$\begin{align*}\operatorname{\mathrm{In}}_\omega(f)=\sum_{u: \langle u,\omega \rangle =\lambda} c_ux^u, \end{align*}$$

where $\lambda $ is the maximum of $\langle u,\omega \rangle $ as u ranges over all $u\in \mathbb {Z}_{\geq 0}$ with $c_u\neq 0$ . For an ideal $J\subset \mathbb {K}[x_0,\ldots ,x_n]$ , its initial ideal with respect to the weight vector $\omega $ is

$$\begin{align*}\operatorname{\mathrm{In}}_\omega(J)=\langle \operatorname{\mathrm{In}}_\omega(f)\ |\ f\in J\rangle. \end{align*}$$

The weight of a monomial $x^u$ with respect to $\omega $ is the scalar product $\langle u,\omega \rangle \in \mathbb {R}$ .

Definition 1.1 Let $X\subset \mathbb {P}^n$ be a projective variety over $\mathbb {K}$ . We say that X admits a toric Gröbner degeneration up to change of coordinates if there exist a $\operatorname {\mathrm {PGL}}(n+1)$ translate $X'$ of X and a weight vector $\omega \in \mathbb {R}^{n+1}$ such that the initial ideal

$$\begin{align*}\operatorname{\mathrm{In}}_\omega (I(X')) \end{align*}$$

of the ideal $I(X')\subseteq \mathbb {K}[x_0,\ldots ,x_n]$ of $X'$ is a prime binomial ideal.

We can now state our result.

Theorem 1.2 Let $d,n\in \mathbb {N}$ . There is a non-empty Zariski open subset U of the linear system of degree d hypersurfaces in $\mathbb {P}^n$ with the property that every hypersurface in U admits a toric Gröbner degeneration up to change of coordinates if and only if $d\leq 2n-1$ .

Before proving this theorem in the following section, we discuss connections to the existing literature.

A common source of toric degenerations of a projective variety $X\subset \mathbb {P}^n$ arises by considering the Rees algebra associated with a full-rank homogeneous valuation $\mathfrak {v}$ on the homogeneous coordinate ring of X [And13]. As long as the homogeneous coordinate ring of X contains a finite set $\mathcal {S}$ whose valuations generate the value semigroup of $\mathfrak {v}$ , one obtains a toric degeneration. Such a set $\mathcal {S}$ is called a finite Khovanskii basis for the coordinate ring of X. This construction is in fact quite general: essentially any $\mathbb {G}_m$ -equivariant degeneration of X over $\mathbb {A}^1$ arises by this construction (see [KMM23, Theorem 1.11] for a precise statement). There has been some work on algorithmically constructing valuations with finite Khovanskii bases (see, e.g., [BLMM17] for applications to degenerations of certain flag varieties), but as of yet, there is no general effective criterion for deciding when such a valuation exists.

Drawing on [KM19] which connects Khovanskii bases and tropical geometry, we may rephrase our results in the language of Khovanskii bases. It is straightforward to show that X admits a toric Gröbner degeneration up to change of coordinates if and only if there is some full-rank homogeneous valuation $\mathfrak {v}$ for which the homogeneous coordinate ring has a finite Khovanskii basis consisting of degree one elements. Thus, our theorem shows the existence of finite Khovanskii bases for general hypersurfaces of degree at most $2n-1$ , and shows that any finite Khovanskii basis for a general hypersurface of larger degree necessarily contains elements of degrees larger than one. In fact, we suspect that a general hypersurface of sufficiently large degree does not admit any finite Khovanskii basis at all.

We note in passing that a general hypersurface of arbitrary degree will admit a toric degeneration in a weaker sense. Indeed, the universal hypersurface over the linear system of degree d hypersurfaces is a flat family, and for any degree d, there is a toric hypersurface of degree d. However, such a degeneration is not $\mathbb {G}_m$ -equivariant.

An interesting comparison of our result can be made with [KMM21], which states that after a generic change of coordinates, any arithmetically Cohen Macaulay variety $X\subset \mathbb {P}^n$ has a Gröbner degeneration to a (potentially non-normal) variety equipped with an effective action of a codimension-one torus. Such varieties, called complexity-one T-varieties, are in a sense one step away from being toric. The hypersurfaces we consider in our main result (Theorem 1.2) are of course arithmetically Cohen Macaulay, so they admit Gröbner degenerations to complexity-one T-varieties. Our result characterizes when we can go one step further and Gröbner degenerate to something toric. When $d\leq 2n-1$ and we are in the range for which this is possible for a generic hypersurface, the change of coordinates required is a special one as opposed to the generic change of coordinates of [KMM21].

2 Proof of the theorem

2.1 Setup

Throughout, we will assume that $d,n>1$ since the theorem is clearly true if $d=1$ or $n=1$ . We will view the coefficients $c_u$ of f in (1.1) as coordinates on affine space $\mathbb {A}^{d+n \choose n}$ . To indicate the dependence of f on the choice of coefficients c, we will often write $f=f_c$ . Let K be the subset of all $u\in \mathbb {Z}_{\geq 0}^{n+1}$ such that $u_0+u_1=d$ , $u_i=0$ for $i>1$ , and $u_1<d$ . We then set

$$\begin{align*}W=V(\langle c_u \rangle_{u\in K})\subset \mathbb{A}^{d+n \choose n}. \end{align*}$$

The family of polynomials parameterized by W consists of all degree d forms such that the only monomial involving only $x_0$ and $x_1$ is $x_1^d$ .

We will be considering the map

$$ \begin{align*} \phi:\operatorname{\mathrm{GL}}(n+1)\times W&\to \mathbb{K}[x_0,\ldots,x_n]_d\\ (A,c)&\mapsto A.f_c, \end{align*} $$

where $A.f_c$ denotes the action of $A\in \operatorname {\mathrm {GL}}(n+1)$ on a polynomial $f_c=\sum c_ux^u$ via linear change of coordinates. We will be especially interested in the differential of $\phi $ at $(e,c)$ , where $e\in \operatorname {\mathrm {GL}}(n+1)$ is the identity. A straightforward computation shows that the image of the differential at $(e,c)$ is generated by

(2.1) $$ \begin{align} \kern2pt x^u\qquad\qquad\qquad\qquad\qquad\qquad\qquad u\notin K, \end{align} $$

(2.2) $$ \begin{align} &\frac{\partial f_c}{\partial x_i} \cdot x_j \qquad &0\leq i,j \leq n. \end{align} $$

The following lemma is the key to our proof.

Lemma 2.1 The differential $\phi $ is surjective at $(e,c)$ for general $c\in W$ if and only if $d\leq 2n-1$ .

Proof Consider the image of the differential of $\phi $ at $(e,c)$ . From (2.1), we obtain the span of all monomials of $\mathbb {K}[x_0,\ldots ,x_n]_d$ with the exceptions of the d monomials $x_0^d,x_0^{d-1}x_1,\ldots ,x_0x_1^{d-1}$ . From (2.2) with $i=1$ and $j=0$ , modulo (2.1), we additionally obtain the monomial $x_0x_1^{d-1}$ . We do not obtain anything new from (2.2) when $i=1$ and $j=1$ , when $i=0$ , or when $j>1$ .

It remains to consider the contributions to the image from (2.2) with $i>1$ and $j=0,1$ . For $2\leq i \leq n$ and $1\leq m\leq d-1$ , let $u(i,m)\in \mathbb {Z}^{n+1}$ be the exponent vector with $u_i=1$ , $u_0=m$ , $u_1=d-m-1$ . Modulo the span of (2.1) and $x_0x_1^{d-1}$ , from (2.2), we obtain

$$ \begin{align*} \frac{\partial f_c}{\partial x_i}\cdot x_0\equiv &c_{u(i,d-1)}x_0^d+c_{u(i,d-2)}x_0^{d-1}x_1+\cdots+c_{u(i,1)}x_0^2x_1^{d-2},\\ \frac{\partial f_c}{\partial x_i}\cdot x_1\equiv &\phantom{c_{u(i,d-1)}x_0^d+}c_{u(i,d-1)}x_0^{d-1}x_1+\cdots+c_{u(i,2)}x_0^2x_1^{d-2}. \end{align*} $$

Varying i from $2$ to n, we obtain $2n-2$ polynomials of degree d. The $(2n-2)\times (d-1)$ matrix of their coefficients has the form

$$\begin{align*}\left(\begin{array}{c c c c c} c_{u(2,d-1)} &c_{u(2,d-2)} &\ldots &c_{u(2,1)}\\ 0 &c_{u(2,d-1)} &\ldots &c_{u(2,2)}\\ c_{u(3,d-1)} &c_{u(3,d-2)} &\ldots &c_{u(3,1)}\\ 0 &c_{u(3,d-1)} &\ldots & c_{u(3,2)}\\ \vdots&\vdots&&\vdots\\ c_{u(n,d-1)}&c_{u(n,d-2)}&\ldots &c_{u(n,1)}\\ 0&c_{u(n,d-1)}&\ldots &c_{u(n,2)} \end{array} \right). \end{align*}$$

Since $c\in W$ is general, this matrix has full rank, that is, its rank is $\min \{d-1, 2n-2\}$ . Hence, the image of the differential of $\phi $ has codimension

$$\begin{align*}d-1-\min\{d-1,2n-2\}, \end{align*}$$

so the differential is surjective if and only if $d\leq 2n-1$ .

We now move on to prove the theorem.

2.2 Existence

We will first show that if $d\leq 2n-1$ , a general degree d hypersurface admits a toric Gröbner degeneration up to change of coordinates. As noted above, the family of polynomials parameterized by W consists of all degree d forms such that the only monomial involving only $x_0$ and $x_1$ is $x_1^d$ . Consider any $\omega \in \mathbb {R}^{n+1}$ such that

$$ \begin{align*} \omega_0>\omega_1>\omega_2>\cdots>\omega_n\qquad (d-1)\omega_0+\omega_2=d\omega_1. \end{align*} $$

For general $c\in W$ , the initial term of $f_{c}$ is

$$\begin{align*}ax_1^d+bx_0^{d-1}x_2 \end{align*}$$

for some $a,b\neq 0$ ; this is a prime binomial. Thus, we will be done with our first claim if we can show that the image of $\phi $ contains a non-empty open subset of $\mathbb {K}[x_0,\ldots ,x_n]_d$ .

To this end, we consider the image of the differential at $(e,c)$ for general $c\in W$ . By Lemma 2.1, we conclude that $\phi $ has surjective differential at $(e,c)$ for general $c\in W$ ; it follows that $\phi $ has surjective differential at a general point of $\operatorname {\mathrm {GL}}(n+1)\times W$ . Thus, the dimension of the image of $\phi $ is the dimension of $\mathbb {K}[x_0,\ldots ,x_n]_d$ , and the image of $\phi $ contains a non-empty open subset of $\mathbb {K}[x_0,\ldots ,x_n]_d$ .

2.3 Nonexistence

Assume now that $d>2n-1$ . We first give an overview of the proof strategy. There are only finitely many prime binomials g of degree d. Likewise, there are only finitely many linear orderings $\prec $ of the variable indices $0,\ldots ,n$ . We say that a weight vector $\omega $ is compatible with $\prec $ and g if whenever $i\prec j$ in the linear ordering, then $\omega _i\geq \omega _j$ , and the two monomials of g have the same weight with respect to $\omega $ .

For fixed g and linear ordering on the variables, we may consider the set S of all polynomials f in $\mathbb {K}[x_0,\ldots ,x_n]_d$ for which there exists a compatible weight vector $\omega \in \mathbb {R}^{n+1}$ such that initial term of f with respect to $\omega $ is g. We will show that up to permutation of the coordinates, this set S can be identified as a subfamily of W. By Lemma 2.1, the map $\phi $ has nowhere surjective differential. Thus, by generic smoothness, the dimension of the image of $\phi $ must be strictly less than the dimension of $\mathbb {K}[x_0,\ldots ,x_n]_d$ . It follows that there cannot be a Zariski-open subset of $\mathbb {K}[x_0,\ldots ,x_n]_d$ such that every hypersurface in this subset admits a toric Gröbner degeneration up to change of coordinates.

To complete the proof, we will fix a prime binomial $g=g'+g''$ of degree d and a linear ordering of the variables. Here, $g'$ and $g''$ are the two terms of g. After permuting the variables and appropriately adapting g, we may assume without loss of generality that the indices are ordered as $0\prec 1 \prec 2 \prec \cdots \prec n$ . The irreducibility of g implies that g involves at least three distinct variables, and no variable appears in both $g'$ and $g''$ . Let p be the smallest index such that $x_p$ appears in g; we denote the corresponding term by $g'$ . Let q be the smallest index such that $x_q$ appears in the term $g''$ .

If $g'$ only involves variables $x_i$ with indices $i<q$ , then any compatible term order $\omega $ must satisfy $\omega _p=\omega _q=\omega _j$ for all $p\leq j \leq q$ . Indeed, if not, the term $g''$ would necessarily have smaller weight. Without loss of generality, we may thus permute indices without changing the set of compatible weight vectors to also assume that $g'$ involves some $x_i$ with $i>q$ . For this, we are using that the irreducibility of g guarantees that at least one of $g'$ and $g''$ is not a dth power.

Consider the set S of polynomials $f_c$ such that there is a compatible weight $\omega $ for which $f_c$ has g as its initial term. We claim that S is a subset of the family parameterized by $W.$ Indeed, since $q>0$ , $g''$ has weight at most equal to the weight of $x_1^d$ . The monomials $x_0^d,x_0^{d-1}x_1,\ldots ,x_0x_1^{d-1}$ all have weight at least as big as the weight of $x_1^d$ , and are not scalar multiples of $g'$ or $g''$ . Hence, none of these monomials can appear in any element of S, and the claim follows.

The proof of the theorem now follows from the argument given above.