Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Henry
and
Sousa, Teresa
2013.
Monochromatic -Decompositions of Graphs.
Electronic Notes in Discrete Mathematics,
Vol. 43,
Issue. ,
p.
121.
Liu, Henry
and
Sousa, Teresa
2014.
Monochromatic Kr‐Decompositions of Graphs.
Journal of Graph Theory,
Vol. 76,
Issue. 2,
p.
89.
Sousa, Teresa
2015.
Dynamics, Games and Science.
Vol. 1,
Issue. ,
p.
735.
Liu, Henry
Pikhurko, Oleg
and
Sousa, Teresa
2015.
Monochromatic Clique Decompositions of Graphs.
Journal of Graph Theory,
Vol. 80,
Issue. 4,
p.
287.
Puleo, Gregory J.
2015.
Tuza’s Conjecture for graphs with maximum average degree less than 7.
European Journal of Combinatorics,
Vol. 49,
Issue. ,
p.
134.
BARON, JACOB D.
and
KAHN, JEFF
2016.
Tuza's Conjecture is Asymptotically Tight for Dense Graphs.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 5,
p.
645.
Szestopalow, Michael
2017.
Fractional
$$K_{4}$$
K
4
-Covers.
Graphs and Combinatorics,
Vol. 33,
Issue. 4,
p.
1055.
Gera, Ralucca
Haynes, Teresa W.
Hedetniemi, Stephen T.
and
Henning, Michael A.
2018.
Graph Theory.
p.
177.
Bennett, Patrick
Dudek, Andrzej
and
Zerbib, Shira
2020.
Large triangle packings and Tuza’s conjecture in sparse random graphs.
Combinatorics, Probability and Computing,
Vol. 29,
Issue. 5,
p.
757.
McDonald, Jessica
Puleo, Gregory J.
and
Tennenhouse, Craig
2020.
Packing and Covering Directed Triangles.
Graphs and Combinatorics,
Vol. 36,
Issue. 4,
p.
1059.
Bennett, Patrick
Cushman, Ryan
and
Dudek, Andrzej
2021.
Closing the Random Graph Gap in Tuza's Conjecture through the Online Triangle Packing Process.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
2145.
Cooper, Jacob W.
Grzesik, Andrzej
Kabela, Adam
and
Král’, Daniel
2022.
Packing and covering directed triangles asymptotically.
European Journal of Combinatorics,
Vol. 101,
Issue. ,
p.
103462.
Tang, Zhongzheng
and
Diao, Zhuo
2022.
Triangle packing and covering in dense random graphs.
Journal of Combinatorial Optimization,
Vol. 44,
Issue. 4,
p.
3153.
Tang, Zhongzheng
Tang, Yucong
and
Diao, Zhuo
2022.
Characterizing 3-uniform linear extremal hypergraphs on feedback vertex number.
Journal of Combinatorial Optimization,
Vol. 44,
Issue. 5,
p.
3310.
Yuster, Raphael
2024.
Packing and Covering a Given Directed Graph in a Directed Graph.
SIAM Journal on Discrete Mathematics,
Vol. 38,
Issue. 1,
p.
43.
Guruswami, Venkatesan
and
Sandeep, Sai
2025.
Approximate Hypergraph Vertex Cover and Generalized Tuza’s Conjecture.
SIAM Journal on Discrete Mathematics,
Vol. 39,
Issue. 2,
p.
1312.
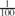 is an absolute constant. This improves upon a previous m(1/4−o(1)) bound which follows from the asymptotic validity of Tuza's conjecture for dense graphs. We conjecture that such graphs have an asymptotically optimal triangle packing of size m(1/3−o(1)).
is an absolute constant. This improves upon a previous m(1/4−o(1)) bound which follows from the asymptotic validity of Tuza's conjecture for dense graphs. We conjecture that such graphs have an asymptotically optimal triangle packing of size m(1/3−o(1)).
