Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T08:13:00.045Z Has data issue: false hasContentIssue false
  • English
  • Français

Birational geometry of the moduli space of quartic 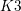$K3$ surfaces

Part of: Families, fibrations Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  02 August 2019

Radu Laza  and
Kieran O’Grady
Radu Laza
Affiliation:
Stony Brook University, Stony Brook, NY 11794, USA email radu.laza@stonybrook.edu
Kieran O’Grady
Affiliation:
‘Sapienza’ Universitá di Roma, Rome, Italy email ogrady@mat.uniroma1.it
Get access Rights & Permissions [Opens in a new window]

Abstract

By work of Looijenga and others, one understands the relationship between Geometric Invariant Theory (GIT) and Baily–Borel compactifications for the moduli spaces of degree-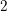$2$ 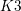$K3$ surfaces, cubic fourfolds, and a few other related examples. The similar-looking cases of degree-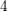$4$ 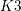$K3$ surfaces and double Eisenbud–Popescu–Walter (EPW) sextics turn out to be much more complicated for arithmetic reasons. In this paper, we refine work of Looijenga in order to handle these cases. Specifically, in analogy with the so-called Hassett–Keel program for the moduli space of curves, we study the variation of log canonical models for locally symmetric varieties of Type IV associated to 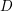$D$-lattices. In particular, for the 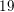$19$-dimensional case, we conjecturally obtain a continuous one-parameter interpolation between the GIT and Baily–Borel compactifications for the moduli of degree-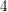$4$ 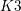$K3$ surfaces. 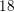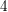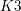The analogous $18$-dimensional case, which corresponds to hyperelliptic degree-$4$ $K3$ surfaces, can be verified by means of Variation of Geometric Invariant Theory (VGIT) quotients.

Keywords

moduliperiodsK3 surfaces

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles
Secondary: 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 9 , September 2019 , pp. 1655 - 1710
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of the first author is supported in part by NSF grants DMS-125481 and DMS-1361143. Research of the second author is supported in part by PRIN 2013.

References

Bergeron, N., Li, Z., Millson, J. and Moeglin, C., The Noether–Lefschetz conjecture and generalizations , Invent. Math. 208 (2017), 501–552.Google Scholar
Borcherds, R. E., Automorphic forms on Os+2, 2(R) and infinite products , Invent. Math. 120 (1995), 161–213.Google Scholar
Borcherds, R. E., Katzarkov, L., Pantev, T. and Shepherd-Barron, N. I., Families of K3 surfaces , J. Algebraic Geom. 7 (1998), 183–193.Google Scholar
Bruinier, J. H., Borcherds products on O(2, l) and Chern classes of Heegner divisors, Lecture Notes in Mathematics, vol. 1780 (Springer, Berlin, 2002).Google Scholar
Casalaina-Martin, S., Jensen, D. and Laza, R., Log canonical models and variation of GIT for genus 4 canonical curves , J. Algebraic Geom. 23 (2014), 727–764.Google Scholar
Friedman, R. and Morgan, J. W., Exceptional groups and del Pezzo surfaces , in Symposium in honor of C. H. Clemens, Contemporary Mathematics, vol. 312 (American Mathematical Society, Providence, RI, 2002), 101–116.Google Scholar
Gritsenko, V. A., Reflective modular forms and their applications , Uspekhi Mat. Nauk 73 (2018), 53–122.Google Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K., The Kodaira dimension of the moduli of K3 surfaces , Invent. Math. 169 (2007), 519–567.Google Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K., Abelianisation of orthogonal groups and the fundamental group of modular varieties , J. Algebra 322 (2009), 463–478.Google Scholar
Hassett, B. and Hyeon, D., Log minimal model program for the moduli space of stable curves: the first flip , Ann. of Math. (2) 177 (2013), 911–968.Google Scholar
Iliev, A., Kapustka, G., Kapustka, M. and Ranestad, K., EPW cubes , J. Reine Angew. Math. 748 (2019), 241–268.Google Scholar
Kirwan, F. C., Moduli spaces of degree d hypersurfaces in P n , Duke Math. J. 58 (1989), 39–78.Google Scholar
Kirwan, F. C. and Lee, R., The cohomology of moduli spaces of K3 surfaces of degree 2. I , Topology 28 (1989), 495–516.Google Scholar
Laza, R., The moduli space of cubic fourfolds via the period map , Ann. of Math. (2) 172 (2010), 673–711.Google Scholar
Laza, R. and O’Grady, K. G., GIT versus Baily–Borel compactification for  $K3\text{'}\mathit{s}$ which are double covers of $\mathbb{P}^{1}\times \mathbb{P}^{1}$ , Preprint (2018), arXiv:1801.04845.Google Scholar
Laza, R. and O’Grady, K. G., GIT versus Baily–Borel compactification for quartic K3 surfaces , in Geometry of moduli—the Abel symposium 2017, Abel Symposia, vol. 14 (Springer, Berlin, 2018), 217–283.Google Scholar
Looijenga, E., New compactifications of locally symmetric varieties , in Proc. 1984 Vancouver conf. in algebraic geometry, CMS Conference Proceedings, vol. 6 (American Mathematical Society, Providence, RI, 1986), 341–364.Google Scholar
Looijenga, E., Compactifications defined by arrangements. I. The ball quotient case , Duke Math. J. 118 (2003), 151–187.Google Scholar
Looijenga, E., Compactifications defined by arrangements. II. Locally symmetric varieties of type IV , Duke Math. J. 119 (2003), 527–588.Google Scholar
Looijenga, E., The period map for cubic fourfolds , Invent. Math. 177 (2009), 213–233.Google Scholar
Mayer, A. L., Families of K-3 surfaces , Nagoya Math. J. 48 (1972), 1–17.Google Scholar
Mongardi, G., On the monodromy of irreducible symplectic manifolds , Algebr. Geom. 3 (2016), 385–391.Google Scholar
Mustaţă, M., Multiplier ideals of hyperplane arrangements , Trans. Amer. Math. Soc. 358 (2006), 5015–5023.Google Scholar
Nikulin, V. V., Integral symmetric bilinear forms and some of their applications , Math. USSR Izv. 43 (1980), 103–167.Google Scholar
O’Grady, K. G., Irreducible symplectic 4-folds and Eisenbud–Popescu–Walter sextics , Duke Math. J. 134 (2006), 99–137.Google Scholar
O’Grady, K. G., Dual double EPW-sextics and their periods , Pure Appl. Math. Q. 4 (2008), 427–468.Google Scholar
O’Grady, K. G., Periods of double EPW-sextics , Math. Z. 280 (2015), 485–524.Google Scholar
O’Grady, K. G., Moduli of double EPW-sextics , Mem. Amer. Math. Soc. 240 (2016), 1–172.Google Scholar
Rapagnetta, A., On the Beauville form of the known irreducible symplectic varieties , Math. Ann. 340 (2008), 77–95.Google Scholar
Shah, J., A complete moduli space for K3 surfaces of degree 2 , Ann. of Math. (2) 112 (1980), 485–510.Google Scholar
Shah, J., Degenerations of K3 surfaces of degree 4 , Trans. Amer. Math. Soc. 263 (1981), 271–308.Google Scholar
Thaddeus, M., Geometric invariant theory and flips , J. Amer. Math. Soc. 9 (1996), 691–723.Google Scholar
Verbitsky, M., Mapping class group and a global Torelli theorem for hyperkähler manifolds , Duke Math. J. 162 (2013), 2929–2986.Google Scholar