Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T08:27:25.232Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fukui–Kurdyka–Paunescu conjecture

Part of: Singularities Theory of singularities and catastrophe theory Local theory

Published online by Cambridge University Press:  11 August 2022

Alexandre Fernandes ,
Zbigniew Jelonek  and
José Edson Sampaio
Alexandre Fernandes
Affiliation:
Departamento de Matemática, Universidade Federal do Ceará, Rua Campus do Pici, s/n, Bloco 914, Pici, 60440-900 Fortaleza-CE, Brazil alex@mat.ufc.br
Zbigniew Jelonek
Affiliation:
Instytut Matematyczny, Polska Akademia Nauk, Śniadeckich 8, 00-656 Warszawa, Poland najelone@cyf-kr.edu.pl
José Edson Sampaio
Affiliation:
Departamento de Matemática, Universidade Federal do Ceará, Rua Campus do Pici, s/n, Bloco 914, Pici, 60440-900 Fortaleza-CE, Brazil edsonsampaio@mat.ufc.br
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the Fukui–Kurdyka–Paunescu conjecture, which says that sub-analytic arc-analytic bi-Lipschitz homeomorphisms preserve the multiplicities of real analytic sets. We also prove several other results on the invariance of the multiplicity (respectively, degree) of real and complex analytic (respectively, algebraic) sets. For instance, still in the real case, we prove a global version of the Fukui–Kurdyka–Paunescu conjecture. In the complex case, one of the results that we prove is the following: if 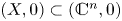$(X,0)\subset (\mathbb {C}^{n},0)$, 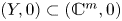$(Y,0)\subset (\mathbb {C}^{m},0)$ are germs of analytic sets and 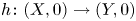$h\colon (X,0)\to (Y,0)$ is a semi-bi-Lipschitz homeomorphism whose graph is a complex analytic set, then the germs 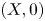$(X,0)$ and 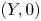$(Y,0)$ have the same multiplicity. One of the results that we prove in the global case is the following: if 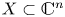$X\subset \mathbb {C}^{n}$, 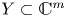$Y\subset \mathbb {C}^{m}$ are algebraic sets and 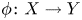$\phi \colon X\to Y$ is a semi-algebraic semi-bi-Lipschitz homeomorphism such that the closure of its graph in 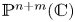$\mathbb {P}^{n+m}(\mathbb {C})$ is an orientable homological cycle, then 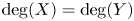${\rm deg}(X)={\rm deg}(Y)$.

Keywords

Zariski's multiplicity conjectureFukui–Kurdyka–Paunescu conjecturearc-analyticbi-Lipschitz homeomorphismdegreemultiplicity

MSC classification

Primary: 14B05: Singularities 32S50: Topological aspects 58K30: Global theory
Secondary: 58K20: Algebraic and analytic properties of mappings
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 6 , June 2022 , pp. 1298 - 1313
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first named author was partially supported by CNPq-Brazil grant 304700/2021-5. The second named author is partially supported by the grant of Narodowe Centrum Nauki number 2019/33/B/ST1/00755. The third named author was partially supported by CNPq-Brazil grant 310438/2021-7. 2021/06/13.

References

Bernig, A. and Lytchak, A., Tangent spaces and Gromov-Hausdorff limits of subanalytic spaces, J. Reine Angew. Math. 608 (2007), 1–15.CrossRefGoogle Scholar
Birbrair, L., Fernandes, A., Lê, D. T. and Sampaio, J. E., Lipschitz regular complex algebraic sets are smooth, Proc. Amer. Math. Soc. 144 (2016), 983–987.CrossRefGoogle Scholar
Birbrair, L., Fernandes, A., Sampaio, J. E. and Verbitsky, M., Multiplicity of singularities is not a bi-Lipschitz invariant, Math. Ann. 377 (2020), 115–121.CrossRefGoogle Scholar
de Bobadilla, J. F., Fernandes, A. and Sampaio, J. E., Multiplicity and degree as bi-Lipschitz invariants for complex sets, J. Topol. 11 (2018), 958–966.CrossRefGoogle Scholar
Chirka, E. M., Complex analytic sets (Kluwer Academic Publishers, 1989).CrossRefGoogle Scholar
Comte, G., Multiplicity of complex analytic sets and bi-Lipschitz maps, in Real analytic and algebraic singularities (Nagoya/Sapporo/Hachioji, 1996), Pitman Research Notes in Mathematics Series, vol. 381 (Addison Wesley Longman Inc., 1998), 182–188.Google Scholar
Eyral, C., Zariski's multiplicity questions – A survey, New Zealand J. Math. 36 (2007), 253–276.Google Scholar
Fernandes, A., Topological equivalence of complex curves and bi-Lipschitz maps, Michigan Math. J. 51 (2003), 593–606.CrossRefGoogle Scholar
Fernandes, A. and Sampaio, J. E., Multiplicity of analytic hypersurface singularities under bi-Lipschitz homeomorphisms, J. Topol. 9 (2016), 927–933.CrossRefGoogle Scholar
Fernandes, A. and Sampaio, J. E., On Lipschitz rigidity of complex analytic sets, J. Geom. Anal. 30 (2020), 706–718.CrossRefGoogle Scholar
Fernandes, A. and Sampaio, J. E., On characterization of smoothness of complex analytic sets, Indiana Univ. Math. J., to appear. Preprint (2022), arXiv:2110.08199 [math.AG].Google Scholar
Fukui, T., Kurdyka, K. and Paunescu, L., An inverse mapping theorem for arc-analytic homeomorphisms, in Geometric singularity theory, Banach Center Publications, vol. 65 (Institute of Mathematics of the Polish Academy of Sciences, Warsaw, 2004), 49–56.CrossRefGoogle Scholar
Greenberg, J., Lectures on algebraic topology, Advanced Book Program (W.A. Benjamin, London, 1966).Google Scholar
Jelonek, Z., On algebraic bi-Lipschitz homeomorphisms, Preprint (2021), arXiv:2104.06894v2 [math.AG].Google Scholar
Kurdyka, K. and Rusek, K., Surjectivity of certain injective semialgebraic transformations of $\mathbb {R}^{n}$, Math. Z. 200 (1988), 141–148.CrossRefGoogle Scholar
Kurdyka, K. and Parusinski, A., Arc-symmetric sets and arc-analytic mappings, in Arcs spaces and additive invariants in real algebraic and analytic geometry, Panoramas et Synthèses, vol. 24 (Sociét ḾathḾatique de France, 2008), 33–67.Google Scholar
Kurdyka, K., Ensembles semi-algébriques symétriques par arcs, Math. Ann. 282 (1988), 445–462.CrossRefGoogle Scholar
Kurdyka, K. and Raby, G., Densité des ensembles sous-analytiques, Ann. Inst. Fourier (Grenoble) 39 (1989), 753–771.CrossRefGoogle Scholar
Lamotke, K., The topology of complex projective varieties after S. Lefschetz, Topology 20 (1981), 15–51.CrossRefGoogle Scholar
Milnor, J., Singular points of complex hypersurfaces (Princeton University Press, 1968).Google Scholar
Narasimhan, R., Introduction to the theory of analytic spaces, Lecture Notes in Mathematics, vol. 25 (Springer, Berlin, Heidelberg, 1966).CrossRefGoogle Scholar
Neumann, W. and Pichon, A., Lipschitz geometry of complex curves, J. Singul. 10 (2014), 225–234.Google Scholar
Parusiński, A., Topology of injective endomorphisms of real algebraic sets, Math. Ann. 328 (2004), 353–372.CrossRefGoogle Scholar
Pawłucki, W., Quasi-regular boundary and Stokes’ formula for a sub-analytic leaf, in Seminar on Deformations, eds Ławrynowicz, J., Lecture Notes in Mathematics, vol. 1165 (Springer, Berlin, Heidelberg, 1985), 235–252.CrossRefGoogle Scholar
Pham, F. and Teissier, B., Fractions lipschitziennes d'une algèbre analytique complexe et saturation de Zariski, Prépublications du Centre de Mathématiques de l'Ecole Polytechnique (Paris), no. M17.0669, June (1969). Available at https://hal.archives-ouvertes.fr/hal-00384928/.Google Scholar
Risler, J.-J., Invariant curves and topological invariants for real plane analytic vector fields, J. Differential Equations 172 (2001), 212–226.CrossRefGoogle Scholar
Sampaio, J. E., Bi-Lipschitz homeomorphic subanalytic sets have bi-Lipschitz homeomorphic tangent cones, Selecta Math. (N.S.) 22 (2016), 553–559.CrossRefGoogle Scholar
Sampaio, J. E., On Zariski's multiplicity problem at infinity, Proc. Amer. Math. Soc. 147 (2019), 1367–1376.Google Scholar
Sampaio, J. E., Multiplicity, regularity and Lipschitz geometry of real analytic hypersurfaces, Israel J. Math. 246 (2021), 371–394.CrossRefGoogle Scholar
Sampaio, J. E., On Lipschitz geometry at infinity of complex analytic sets, Preprint (2021), arXiv:2207.07692 [math.CV].Google Scholar
Sampaio, J. E., Differential invariance of the multiplicity of real and complex analytic sets, Publ. Mat. 66 (2022), 355–368.CrossRefGoogle Scholar
Sampaio, J. E., Multiplicity, regularity and blow-spherical equivalence of real analytic sets, Math. Z. 301 (2022), 385–410.CrossRefGoogle Scholar
Valette, G., Multiplicity mod 2 as a metric invariant, Discrete Comput. Geom. 43 (2010), 663–679.CrossRefGoogle Scholar
Zariski, O., Some open questions in the theory of singularities, Bull. Amer. Math. Soc. 77 (1971), 481–491.CrossRefGoogle Scholar