Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Choudhury, Utsav
and
Gallauer Alves de Souza, Martin
2017.
An isomorphism of motivic Galois groups.
Advances in Mathematics,
Vol. 313,
Issue. ,
p.
470.
Wildeshaus, Jörg
2017.
Intermediate extension of Chow motives of Abelian type.
Advances in Mathematics,
Vol. 305,
Issue. ,
p.
515.
Vaish, Vaibhav
2018.
On weight truncations in the motivic setting.
Advances in Mathematics,
Vol. 338,
Issue. ,
p.
339.
Huber, Annette
and
Kings, Guido
2018.
Polylogarithm for families of commutative group schemes.
Journal of Algebraic Geometry,
Vol. 27,
Issue. 3,
p.
449.
Ivorra, Florian
and
Sebag, Julien
2019.
Artin Motives, Weights, and Motivic Nearby Sheaves.
Michigan Mathematical Journal,
Vol. 68,
Issue. 2,
Vezzani, Alberto
2019.
The Berkovich realization for rigid analytic motives.
Journal of Algebra,
Vol. 527,
Issue. ,
p.
30.
Barbieri-Viale, Luca
Huber, Annette
and
Prest, Mike
2020.
Tensor structure for Nori motives.
Pacific Journal of Mathematics,
Vol. 306,
Issue. 1,
p.
1.
Barbieri-Viale, Luca
and
Prest, Mike
2020.
Tensor product of motives via Künneth formula.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 6,
p.
106267.
Ivorra, Florian
2022.
Some topics in the theory of Tannakian categories and applications to motives and motivic Galois groups.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
45.
Dupont, Clément
and
Juteau, Daniel
2024.
The localization spectral sequence in the motivic setting.
Algebraic & Geometric Topology,
Vol. 24,
Issue. 3,
p.
1431.
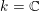 $k=\mathbb{C}$ be the field of complex numbers. In this article we construct Hodge realization functors defined on the triangulated categories of étale motives with rational coefficients. Our construction extends to every smooth quasi-projective
$k=\mathbb{C}$ be the field of complex numbers. In this article we construct Hodge realization functors defined on the triangulated categories of étale motives with rational coefficients. Our construction extends to every smooth quasi-projective 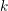 $k$-scheme, the construction done by Nori over a field, and relies on the original version of the basic lemma proved by Beĭlinson. As in the case considered by Nori, the realization functor factors through the bounded derived category of a perverse version of the Abelian category of Nori motives.
$k$-scheme, the construction done by Nori over a field, and relies on the original version of the basic lemma proved by Beĭlinson. As in the case considered by Nori, the realization functor factors through the bounded derived category of a perverse version of the Abelian category of Nori motives.