Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-29T08:47:38.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Theological Question-Begging1

Published online by Cambridge University Press:  13 April 2010

J. J. MacIntosh
J. J. MacIntosh
Affiliation:
University of Calgary
Get access Rights & Permissions [Opens in a new window]

Extract

In the first section of this paper I offer a necessary condition (Moore's maxim) for members of a particular class of arguments to be acceptable as proofs. (Throughout I ignore proofs within formal systems.) In the second section, I point out that a plausible extension of this principle reveals that a number of additional arguments cannot function successfully as proofs. Finally, I note that a number of theological arguments, particularly cosmological and ontological arguments, are suspect in the light of this extended principle. Standardly in the ontological argument, criticism falls on the conditional, modality-enriching premise which involves a move from possibility (or conceivability) to actuality. I offer two defences of this premise, and argue that—as the use of Moore's extended maxim shows—the problem lies with the premise that asserts mere possibility.

Type
Articles
Information
Dialogue: Canadian Philosophical Review / Revue canadienne de philosophie , Volume 30 , Issue 4 , Fall 1991 , pp. 531 - 548
Copyright
Copyright © Canadian Philosophical Association 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Notes

2 Though I have stated the soundness condition in a form that allows arguments with no premises to be sound, in what follows I am interested only in arguments with premises.

3 In “‘P, therefore, P’ without Circularity” (Journal of Philosophy, 88, 5 [1991]: 245–66)Google Scholar, Roy A. Sorenson offers a cumulatively persuasive series of reasons for thinking this general claim to be an overstatement. Had I read his paper before writing this one, I would have phrased these introductiory remarks differently. However, his ingenious counter-examples do not affect my subsequent remarks, directed as they are to a particular set of arguments, and so I content myself here with drawing the reader's attention to them.

4 As, that de Bergerac lived from 1620 to 1655, that Oersted did not isolate aluminium until 1825, and that a substance not available until the nineteenth century could not have been used in the manufacture of seventeenth century artefacts. The very simple arguments which I am considering as proofs may well strike the reader as too simple, since much of the work expended in actual or putative proofs–particularly in theological ones –consists in establishing the premises. However, I am concerned with the state of play after the premises are taken to be established, and at that stage the arguments typically are simple. But though they are simple, there is still a distinction between those which beg the question and those which do not.

5 Walton, Douglas N., Informal Fallacies (Amsterdam: Benjamins, 1987), p. 175CrossRefGoogle Scholar. See also Woods, John and Walton, Douglas, Fallacies: Selected Papers, 1972–1982 (Dordrecht: Foris, 1989)Google Scholar, and Merrill, Kenneth R., “A Modest Defence of ‘Bad Old Logic’;,” New Scholasticism, 56 (1982): 500–12.CrossRefGoogle Scholar

6 Moore, G. E., “Proof of an External World,” in Proceedings of the British Academy, 25 (1939)Google Scholar, reprinted in his Philosophical Papers (London: George Allen & Unwin, 1959), p. 127–50. My references are to the reprint.Google Scholar

7 Penelhum, Terence, Problems of Religious Knowledge (London: Macmillan, 1971), especially chap. 2, “The Nature of Proof.”Google Scholar

8 See, e.g., Topics, 162b34–163a13. For a helpful discussion of the Aristotelian points, and further references, see Woods, John and Walton, Douglas, “The Petitio: Aristotle's Five Ways,” Canadian Journal of Philosophy, 12 (1982): 77–100.CrossRefGoogle Scholar

9 As already noted, I am ignoring proofs in formal systems throughout: they raise interesting and important problems of a kind quite different from those considered here.

10 For the moment I accept Moore's definite description, “the premise,” for ease of exposition, and treat multi-premised arguments as being equivalent to arguments with a single conjunctive premise. Qualifications will follow.

11 Moore explicitly requires validity (the conclusion, he says, must “really follow” from the premise), and gets soundness by means of the epistemological condition (Moore, “Proof,” p. 146).

12 Ibid.

13 Summa Theologiae, 1a2.1.

14 Penelhum, Problems of Religious Knowledge, p. 26. This restatement may in fact change Moore's notion, since he offers the fact that the conclusion may be true while the premise is false in order to make the Leibniz's Law point that the two cannot be identical (Moore, “Proof,” p. 146), but it is worth noting that this feature also separates the two equivalence classes of sentences involved. It ensures, that is, that the conclusion and the premise not be logically equivalent.

15 In his later Cod and Skepticism (Dordrecht: Reidel, 1983)Google Scholar, Penelhum, returning to the question of the nature of theological proof, retains the ‘stating’ criterion without further amplification: “arguments that are offered as proofs of God … are supposed to proceed from premises that can be stated without stating the conclusion they are designed to establish” (p. 96).

16 I take two sentences, A and B, to be logically equivalent IFF ▭(A - B), where ▭ is a necessity operator, and I shall express such logical equivalence by writing A = B. I use A B for ▭(A ⊃ B), but other readings of ‘’ (for example, as a necessitated relevance conditional) may well be compatible with all I have to say. Indeed, they may well provide us with a better account, but here I am interested in seeing what may be done within a classical framework.

17 Woods and Walton, “The Petitio,” p. 80.

18 Ammonius, “In Aristotelis De Interpretatione Commentarius,” Commentaria in Aristotelem Graeca, Vol. IV, Pars V, Berlin, 1897, p. 73, ad de Int., 7, 17a15–17, quoted in Christopher J. Martin, “Negation and Its Consequences” (forthcoming). Martin points out that Boethius was at one with Ammonius on this matter. On this point see further, Calvin Normore, “Mediaeval Connectives, Hellenistic Connections: The Strange Case of Propositional Logic,” forthcoming in Atoms, Pneuma, and Tranquillity: Epicurean and Stoic Themes in European Thought, edited by Osier, M. J. (Cambridge: Cambridge University Press, 1991).Google Scholar

19 Although ‘⊃’ is a notorious problem generator, there are many cases of “if … then” where all that seems to be involved is ‘⊃’. For, after all, all that is required is that, in the given case, the following two moves be acceptable: (i) from ‘not-A orB’ derive ‘if A then B’. (ii) from ‘if, A then B’ derive 'not-A or B'. The first derivation requires allowing (either actually or in effect) particular instances of ‘if A then not-not-A’, disjunctive syllogism, and conditional proof. But these are acceptable in many instances. And the second seems even less problematic (for non-intuitionists), for it requires the move simply from ‘if A then B’ via a consideration of ‘A or not-A’ to get ‘either B or not-A’ and hence ‘either not-A or B’. Even if we are unwilling to allow these moves in general, we may be willing to agree that there are particular cases in which they are acceptable, and that is all that is required: for even in those cases we may want to allow modus ponens as an acceptable proof form, while disallowing simplification. Indeed, even less will do to justify reading ‘if … then hellip; ' materially in a given case. For all that is really needed is the willingness to sanction the following: B is true. Consequently it is true whether or not A is.

That is, it is true if A is true, and it is true if A is not true.

20 Equally, we might think of them as being the Ammonian form of the arguments in question.

21 Aristotle points out in effect that Moore's maxim is by no means a sufficient condition even for Ammonian arguments since it ignores the case where we move from a universally quantified sentence to one of its instantiations (Topics, 163b1). Similarly, I omit discussion of arguments such as:

We could enlarge Moore's maxim to accommodate these points, but, since here I am interested in an application of the maxim that does not require such an enlargement, I omit it. We might notice, though, that the “conjunction of premises” disjunct cuts out some arguments which are otherwise allowable. It eliminates, for example, Hempel's:

(attributed to Hempel by Katz, J. J. in The Problem of Induction and fts Solution [Chicago: University of Chicago Press, 1962], p. 36).Google Scholar

22 Penelhum, Problems of Religious Knowledge, p. 27.

23 Simple, or perhaps better, compressed. Penelhum calls it “degenerate,” but even in the mathematical sense of ‘degenerate’, that seems a bit harsh. Of course a lot of prior argumentation would be required to establish the first premise, but that is another matter.

24 “If anything exists, an absolutely necessary being must also exist. Now I, at least, exist. Therefore an absolutely necessary being exists” (Critique of Pure Reason, A604 = B632).

25 Penelhum, Problems of Religious Knowledge, p. 27.

26 As Kant points out in effect (Critique of Pure Reason, A606 = B634), the conditional premise is established on a priori grounds, and experience appears only minimally in the proof. That, of course, is what makes such proofs cosmological and not physicotheological.

27 It may also be conceptually enlightening and, as we have said, useful within a proof. Thus, for example, we may make use of the fact that (a = b) ▭ (a = b), a = b ├ ▭ (a = b) within an argument to show the impossibility of certain kinds of reincarnation. (See my “Reincarnation and Relativized Identity,” Religious Studies, 25, 2 [June 1989]: 153–65.)

28 It is important, in these cases, that we obtain logical equivalence between the conclusion and the minor (non-conditional) premise. We obtain material equivalence (via the paradoxes of material implication) between the conditional premise and the conclusion in every case of modus ponens since p ⇒ q − (p ⊃ q). Similarly, because of the paradoxes of strong implication, we may get logical equivalence between the conditional premise and the conclusion, when we have a necessity operator prefixing the minor premise, since we have as K4 or KT4 theorems:

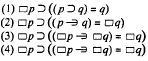
This raises interesting additional points which I shall not now consider, contenting myself here with noting that in the normal case where the non-conditional (minor) premise is unmodalized we obtain logical equivalence between the conclusion and the minor premise (or indeed the major premise) only in certain special, theologically uninteresting cases.

29 Woods and Walton, “The Petitio,” p. 86.

30 James van Cleve writes: “Under what circumstances is an argument viciously circular? I submit that it is so under one circumstance only: a necessary condition of using it to gain knowledge of (or justified belief in) its conclusion is that one already have knowledge of (or justified belief in) its conclusion. Let us say that an argument with this trait is epistemically circular. The most obvious examples of epistemically circular arguments are those in which the conclusion or a mere stylistic variant of it occurs among the premises. More subtle examples are those in which the conclusion, though not occurring in any guise among the premises, is nonetheless epistemically prior to one of the premises, in the sense that one could arrive at knowledge of the premise only via an epistemic route that passed through the conclusion first. In either of these cases we may speak of premise circularity” (van Cleve, James, “Reliability, Justification, and the Problem of Induction,” Midwest Studies in Philosophy, 9 [1984], p. 558)Google Scholar. In these terms we may say that Moore's (extended) maxim rules out cases where, given one of the premises (in the general case, a subset of the premises), one of the remaining premises (premise subsets) suffers from premise circularity.

31 Notice that St. Thomas's thud way, whatever other problems it may have, seems not to violate Moore's maxim, since in the truncated version its conditional premise would read: If anything exists contingently then God exists. and it is of course not the case that we have as a law of logic: If God exists then something exists contingently.

32 In what follows I have been influenced by Peter van Inwagen's excellent article, “Ontological Arguments” (Nous, 11 [1977]: 375–95), though I am not sure either that this influence shows, or that he would agree with what is suggested here. I am following him, as it were, well off to the side.

33 Alternatively, from actuality to necessity: g ▭g. What are the logics in which if we can make one such modal jump we can make the other, in which, for a given p, either both p ▭p and ◊ p p are theses or neither is? In his clear and helpful “The Logical Structure of Anselm's Arguments” (Philosophical Review, 80 [1971]: 28–54), R. M. Adams points out that we can move from ◊p p to p ▭p (and conversely) in normal systems which contain the Brouwer axiom p ⊃ ▭◊P Indeed, in such a system we can move from ◊p q to p ▭q, and the move from ◊p p to p ▭ p is a simple substitution instance of the stronger move. Thus KB has essentially the property that either ◊p⊃ p and p ⊃, ▭ p are both theses, or neither is, which is to say, every normal extension of it also has this property. S5, for example, has this property, while S4 does not. Krister Segerberg and Brian Chellas (to whom I owe the foregoing observations) have proved that the smallest logic with this property is the intersection of D ∩ Verum, where D is the basic deontic logic, axiomatized by ◊T, and Verum, axiomatized by ▭⊥, is the logic in which ▭ A is a thesis, for every A.

34 Adams, “The Structure of Anselm's Arguments,” p. 28.

35 Prior, Arthur, Papers on Time and Tense (Oxford: Clarendon, 1968), p. 70.Google Scholar

36 H = it has always been the case that; G = it is always going to be the case that.

37 Fitch, Frederick B., “A Logical Analysis of Some Value Concepts,” Journal of Symbolic Logic, 28, 2 (1963): 135–42CrossRefGoogle Scholar. I have discussed the Fitch argument in “Fitch's Factives,” Analysis, 44 (1984): 153–58. For a treatment of Fitch's (and relevant other) arguments in depth, see Sorenson, Roy A., Blindspots (Oxford: Oxford University Press, 1988).Google Scholar

38 Where PL and ML refer to simple steps in sentential and modal logic respectively, we have: (1) D(p&-Dp)⊃(Dp&D∼Dp) Distrib.

(2) D-Dp ⊃ ∼Dp Fact

(3) ∼D(p&∼Dp) 1, 2, PL

(4) ▭∼D(p&∼Dp) 3, ML

(5) ∼◊D(p&∼Dp) 4, ML

Bernard Linsky has pointed out that since Fact is only used in its substitution instance D-Dp ⊃ -Dp, we could simply use that as one of our initial theorems, thereby extending the range of acceptable interpretations of D (B. Linsky, “Factives, Blindspots and Some Paradoxes,” Analysis, 46, 1 [1986]: 10–15).

39 Once again the proof is straightforward: (1) (p &∼Dp) ⊃ ◊D(p & -Dp) Poss.

(2) ∼◊D(p&∼Dp) as before

(3) p⊃Dp 1, 2, PL

(4) Dp ⊃p Fact

(5) p-Dp 3, 4, PL

40 See, e.g., Aquinas, Summa Theologiae, 1a22.2.

41 For a highly original discussion of this move from a very different point of view see Tichy, Pavel, “Existence and God,” Journal of Philosophy, 76, 8 (1979): 403–20.CrossRefGoogle Scholar

42 On this point, see both Tichy and the very acute discussion in van Inwagen's already mentioned “Ontological Arguments.” There is a short but helpful discussion of Leibniz's claim (for which see, e.g., Gerhardt 3.443) in Lovejoy, A. O., “Kant's Antithesis of Dogmatism and Criticism,” Mind, 15 (1906): 191–214.CrossRefGoogle Scholar

43 Adams (“Anselm's Arguments,” p. 48) remarks: “although the modal argument for the existence of God helps us to see that the question of possibility is the crucial question about logically necessary divine existence, neither the modal nor the ontological argument provides us with grounds for answering it.”

44 As Penelhum has put it, “if religion is true, why is it not more obviously true?” (“Do Religious Beliefs Need Grounds?,” Nederlands Theologisch Tidschrift, 40, 3 [1986], p. 237).Google Scholar

45 Similarly, if it is possible for God not to exist then, necessarily, God does not exist. In “A Formal Analysis of the Ontological Argument” (American Philosophical Quarterly, 20, 1 [1983], p. 46)Google Scholar, Gerald Pottinger suggested that, since God's necessary nonexistence must be shown, “the atheist has a very tough row to hoe.” In fact, of course, as Pottinger's own arguments clearly reveal, believer and non-believer alike have the same row to hoe, and it is a row to which modality is irrelevant.

46 Nor is it really to the point for us to follow Hume and Kant in allowing weight to the fact that design arguments would, even if successful, succeed in proving a designer merely, and not a deity, for while it is perhaps logically possible to be a designeraccepting but deity-rejecting atheist, this is certainly not the usual stance. Hume and Kant are right about this being the most that the design argument could prove, of course, but their point is not really relevant to the actual psychology of belief and disbelief.