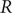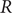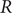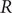Introduction
Since the onset of the coronavirus disease in early 2020 (COVID-19) as a pandemic, mathematical modelling has been widely used to generate policy-relevant evidence. Mathematical modelling provides a framework for simulating the dynamics of the pandemic. When parameterized with and calibrated to data, this can be used to generate projections of future epidemic trajectories as well as to track the current epidemic status. Epidemiological estimates such as the reproduction number
![]() $ R $
derived from models can be useful tools for such epidemic status tracking.
$ R $
derived from models can be useful tools for such epidemic status tracking.
The reproduction number
![]() $ R $
is a measure of the infectious potential of a disease and represents the average number of secondary infections that emerge from one infection [Reference Abbott and Funk1]. At the onset of a new disease, in a naive, fully susceptible population, the basic reproduction number
$ R $
is a measure of the infectious potential of a disease and represents the average number of secondary infections that emerge from one infection [Reference Abbott and Funk1]. At the onset of a new disease, in a naive, fully susceptible population, the basic reproduction number
![]() $ {R}_0 $
represents the average number of secondary infections stemming from an initial case. In contrast to
$ {R}_0 $
represents the average number of secondary infections stemming from an initial case. In contrast to
![]() $ {R}_0 $
,
$ {R}_0 $
,
![]() $ R $
is the reproduction number at any time during an epidemic – often referred to as the effective reproduction number
$ R $
is the reproduction number at any time during an epidemic – often referred to as the effective reproduction number
![]() $ {R}_e $
or temporal reproduction number
$ {R}_e $
or temporal reproduction number
![]() $ {R}_t $
[Reference Abbott2]. It reflects the average number of secondary infections generated from a population consisting of susceptible, exposed, and immune individuals, and potential changes in mixing and the presence of interventions.
$ {R}_t $
[Reference Abbott2]. It reflects the average number of secondary infections generated from a population consisting of susceptible, exposed, and immune individuals, and potential changes in mixing and the presence of interventions.
The growth rate
![]() $ r $
represents the rate at which the epidemic is growing during the exponential phase of epidemic growth. In epidemiological modelling,
$ r $
represents the rate at which the epidemic is growing during the exponential phase of epidemic growth. In epidemiological modelling,
![]() $ r $
and
$ r $
and
![]() $ R $
are related via the generation time distribution
$ R $
are related via the generation time distribution
![]() $ (f(\tau )) $
of the epidemic [Reference Abbott2]. Mathematically, this is expressed as follows:
$ (f(\tau )) $
of the epidemic [Reference Abbott2]. Mathematically, this is expressed as follows:
where
![]() $ \tau $
is the time since infection of an individual and the generation time distribution
$ \tau $
is the time since infection of an individual and the generation time distribution
![]() $ f\left(\tau \right) $
is defined as the probability density function for the time of a subsequent infection made by that individual. The generation time Tg is defined as the mean of the generation time distribution. As evident from this equation, changes in
$ f\left(\tau \right) $
is defined as the probability density function for the time of a subsequent infection made by that individual. The generation time Tg is defined as the mean of the generation time distribution. As evident from this equation, changes in
![]() $ f(\tau ) $
,
$ f(\tau ) $
,
![]() $ r $
, and
$ r $
, and
![]() $ R $
affect each other. Although precise statements depend on the specific shape of
$ R $
affect each other. Although precise statements depend on the specific shape of
![]() $ f(\tau ) $
, broadly speaking, for fixed Tg, r and R increase/decrease in tandem; for fixed r, Tg and R increase/decrease in tandem, while for fixed R, increasing Tg means decreasing r and vice versa.
$ f(\tau ) $
, broadly speaking, for fixed Tg, r and R increase/decrease in tandem; for fixed r, Tg and R increase/decrease in tandem, while for fixed R, increasing Tg means decreasing r and vice versa.
While
![]() $ R $
is reflective of the current strength of transmission,
$ R $
is reflective of the current strength of transmission,
![]() $ r $
is reflective of the transmission speed [Reference Abbott3]. Both provide information about the impact of control measures. For example, if an intervention is imposed and
$ r $
is reflective of the transmission speed [Reference Abbott3]. Both provide information about the impact of control measures. For example, if an intervention is imposed and
![]() $ R $
is consequentially reduced to below the
$ R $
is consequentially reduced to below the
![]() $ R=1 $
threshold, or
$ R=1 $
threshold, or
![]() $ r $
is reduced to below the
$ r $
is reduced to below the
![]() $ 0 $
threshold, this suggests that the intervention has had an impact on reducing onward transmission. However, when providing policy advice during the COVID-19 epidemic,
$ 0 $
threshold, this suggests that the intervention has had an impact on reducing onward transmission. However, when providing policy advice during the COVID-19 epidemic,
![]() $ R $
was used as it is more easily interpretable than
$ R $
was used as it is more easily interpretable than
![]() $ r $
and does not require a conceptual understanding of exponential growth or decay, so it is therefore simpler to explain to the public. Additionally,
$ r $
and does not require a conceptual understanding of exponential growth or decay, so it is therefore simpler to explain to the public. Additionally,
![]() $ R $
at the onset of the epidemic
$ R $
at the onset of the epidemic
![]() $ \left({R}_0\right) $
provides information on the likely level of herd immunity necessary. In a homogeneous population, the herd immunity threshold as a percentage of the population,
$ \left({R}_0\right) $
provides information on the likely level of herd immunity necessary. In a homogeneous population, the herd immunity threshold as a percentage of the population,
![]() $ {I}_c $
, can be calculated as follows:
$ {I}_c $
, can be calculated as follows:
which suggests that the more people that become infected by each individual who has the virus, the higher the proportion of the population that needs to be immune to reach herd immunity [Reference Ackland4]. However, it should be noted that this is subject to large uncertainties due to the difficulty in calculating
![]() $ {R}_0 $
, which leads to differing estimates of
$ {R}_0 $
, which leads to differing estimates of
![]() $ {I}_c $
, and should therefore be used with care [Reference Anderson5, Reference Baguelin6]. Further details on
$ {I}_c $
, and should therefore be used with care [Reference Anderson5, Reference Baguelin6]. Further details on
![]() $ R $
and the differing methodologies for calculating the reproduction number can be found in the Section titled “Outline of epidemiological models used to produce
$ R $
and the differing methodologies for calculating the reproduction number can be found in the Section titled “Outline of epidemiological models used to produce
![]() $ R $
values”.
$ R $
values”.
In the UK, the Scientific Advisory Group for Emergencies (SAGE) is activated in response to emergencies and is made up of several subgroups consisting of experts relating to different scientific fields [Reference Birrell7]. These subgroups are often called upon in order to provide evidence to the UK government relating to key policy questions. One of these groups is the Scientific Pandemic Influenza Group on Modelling-Operational (SPI-M-O), which has been leading the modelling of the COVID-19 epidemic since its onset [Reference Birrell8]. SPI-M-O primarily consists of experts in infectious disease modelling.
In early 2021, a formal collaboration between SPI-M-O and the UK Health Security Agency Epidemiological Ensemble (UKHSA Epi-Ensemble) modelling group was established, which has provided the UK government with weekly estimates of key epidemiological indicators, including the effective reproduction number
![]() $ R $
[Reference Bracher9] throughout 2021–2023. The consensus values were generated as a combined estimate from a set of epidemiological models maintained and run by members of SPI-M-O and the UKHSA Epi-Ensemble and were combined using a random-effects meta-analysis approach with equal weighting applied [Reference Brooks-Pollock10], with visualization implemented using CrystalCast developed by the Defence Science and Technology Laboratory (DSTL) [Reference Burton11]. The combined estimates were agreed in a weekly meeting of the UKHSA Epidemiology Modelling Review Group (EMRG), attended by government modellers and policy stakeholders, as well as academic modellers.
$ R $
[Reference Bracher9] throughout 2021–2023. The consensus values were generated as a combined estimate from a set of epidemiological models maintained and run by members of SPI-M-O and the UKHSA Epi-Ensemble and were combined using a random-effects meta-analysis approach with equal weighting applied [Reference Brooks-Pollock10], with visualization implemented using CrystalCast developed by the Defence Science and Technology Laboratory (DSTL) [Reference Burton11]. The combined estimates were agreed in a weekly meeting of the UKHSA Epidemiology Modelling Review Group (EMRG), attended by government modellers and policy stakeholders, as well as academic modellers.
Generating a combined ensemble estimate in place of a single model truth can lead to improved predictive power [Reference Castillo-Garsow and Castillo-Chavez12], allows an increased robustness of the outcomes, and is a useful tool for policymakers [Reference Chowell13]. Generating a combined estimate from a set of models is not a new concept; they are widely used across many disciplines, such as forecasting the weather [Reference Cori14], hydrology [15], flood losses [Reference Cramer16], cancer prediction [Reference Delamater17] and climate modelling [Reference den Boon18]. Within infectious diseases, combined model estimates have been applied to modelling human immunodeficiency virus (HIV) [Reference Diekmann, Heesterbeek and Roberts19], influenza [Reference Dushoff and Park20], and Ebola [Reference Eaton21, Reference Figueiredo22] transmission and recently for outbreak analysis related to COVID-19 in the United States [Reference Fine, Eames and Heymann23] and Europe [Reference Flaxman24].
While mathematical models have been used to offer informed advice to the scientific community and policymakers throughout the COVID-19 pandemic across a number of countries, the use of modelling has differed. For example, modellers in the United States, in conjunction with the Center for Disease Control and Prevention (CDC), published ensemble forecasts using a wide variety of mathematical models [Reference Chowell13, 25]. These models had focused on forecasting new cases, hospitalizations, and deaths at a national and state level but did not estimate
![]() $ R $
or
$ R $
or
![]() $ r $
specifically. On the other hand, in New Zealand and Italy, modellers advising the government have compared estimates of
$ r $
specifically. On the other hand, in New Zealand and Italy, modellers advising the government have compared estimates of
![]() $ R $
obtained from different models but without producing formal combined estimates [26, 27]. In Norway, multiple data sources including confirmed cases, proportion of COVID-19 attributable hospital admissions, and a national symptom survey were used to estimate
$ R $
obtained from different models but without producing formal combined estimates [26, 27]. In Norway, multiple data sources including confirmed cases, proportion of COVID-19 attributable hospital admissions, and a national symptom survey were used to estimate
![]() $ r $
over the course of the pandemic, but only one model has been used to estimate
$ r $
over the course of the pandemic, but only one model has been used to estimate
![]() $ R $
from these sources [28]. Similarly, the Robert Koch Institute in Germany only used a single model to estimate
$ R $
from these sources [28]. Similarly, the Robert Koch Institute in Germany only used a single model to estimate
![]() $ R, $
which depended on nowcasting estimates of the number of new cases [Reference Fraser29].
$ R, $
which depended on nowcasting estimates of the number of new cases [Reference Fraser29].
As noted above, in the UK, since the onset of the pandemic, a set of mathematical models developed, maintained, and applied by the members of SPI-M-O and the UKHSA Epi-Ensemble have been used to track the epidemic status, including generating
![]() $ R $
and
$ R $
and
![]() $ r $
alongside estimates of incidence and prevalence. The
$ r $
alongside estimates of incidence and prevalence. The
![]() $ R $
value published on the UK Government Dashboard [Reference García-García30] has been generated as a combined value from these models and agreed at the weekly EMRG meeting.
$ R $
value published on the UK Government Dashboard [Reference García-García30] has been generated as a combined value from these models and agreed at the weekly EMRG meeting.
The usefulness in getting a combined estimate from across models and data sets is not just in the averaging of different models’ estimates with weighting but also in the formation of a community that is constantly discussing the outcomes, the assumptions, and the input data identifying the drivers behind the differences across models. This is especially important when generating
![]() $ R $
. While doubling time and
$ R $
. While doubling time and
![]() $ r $
can be thought of as almost features of the data, requiring very few assumptions, the move to
$ r $
can be thought of as almost features of the data, requiring very few assumptions, the move to
![]() $ R $
requires a set of subjective assumptions. This is why there is a need to have multiple groups making different assumptions, leading to heterogeneous outcomes that can be discussed, understood, and combined. When
$ R $
requires a set of subjective assumptions. This is why there is a need to have multiple groups making different assumptions, leading to heterogeneous outcomes that can be discussed, understood, and combined. When
![]() $ R $
can be generated using different data sets, in addition to different models, this is particularly important. The development of the formal collaboration between the modellers at UKHSA Epi-Ensemble and within SPI-M-O, and the weekly technical meetings of the group and the follow-up EMRG meeting, gave a platform for informed discussions of the similarities and the differences across models’ nowcast estimates and provided a place where decisions could be made on whether to include or exclude a given model from the combined estimate.
$ R $
can be generated using different data sets, in addition to different models, this is particularly important. The development of the formal collaboration between the modellers at UKHSA Epi-Ensemble and within SPI-M-O, and the weekly technical meetings of the group and the follow-up EMRG meeting, gave a platform for informed discussions of the similarities and the differences across models’ nowcast estimates and provided a place where decisions could be made on whether to include or exclude a given model from the combined estimate.
This paper outlines the process of this collaboration between government and academia to continually generate estimates for the effective reproduction number in England over the COVID-19 epidemic. Specifically, we outline how a previously established combination method, described in [Reference Brooks-Pollock10], has been applied in the UK throughout the COVID-19 pandemic. We detail our approach of generating a consensus value of
![]() $ R $
from an ensemble of epidemiological models applied to the English epidemic. We illustrate the process, show how a combined
$ R $
from an ensemble of epidemiological models applied to the English epidemic. We illustrate the process, show how a combined
![]() $ R $
estimate has been generated in April 2021 and in September 2021, and explore the robustness of the combined
$ R $
estimate has been generated in April 2021 and in September 2021, and explore the robustness of the combined
![]() $ R $
value on the size and weighting of the models’ combination. By comparing the change in
$ R $
value on the size and weighting of the models’ combination. By comparing the change in
![]() $ R $
with the change in measurable data such as COVID-19 cases, hospitalizations, and deaths, we also explore whether
$ R $
with the change in measurable data such as COVID-19 cases, hospitalizations, and deaths, we also explore whether
![]() $ R $
can be a good indicator of epidemic status.
$ R $
can be a good indicator of epidemic status.
Methodology
Outline of epidemiological models used to produce
 $ R $
values
$ R $
values
Generating an
![]() $ R $
estimate requires a model of some kind with subjective assumptions and information from other sources. Our modelling ensemble comprised mathematical models that were developed, adapted, and used throughout 2020–2022, to model the COVID-19 epidemic in England; to generate epidemic metrics such as
$ R $
estimate requires a model of some kind with subjective assumptions and information from other sources. Our modelling ensemble comprised mathematical models that were developed, adapted, and used throughout 2020–2022, to model the COVID-19 epidemic in England; to generate epidemic metrics such as
![]() $ R $
,
$ R $
,
![]() $ r $
, incidence, and prevalence; and to produce medium-term projections (MTPs) of hospital admissions, hospital bed occupancy, and deaths. The MTPs will be explored separately in a future publication. These models fall into three broad groups, as described in [Reference Georgakakos31] and [Reference Abbott2]: population-based models (PBMs), data-driven models (DDMs), and agent-based models (ABMs). The models in the ensemble can be split further into three broad categories based on the data they primarily used to inform their estimates: case-based models, admission-based models, and models that were fitted to both case data and hospital data. For the purposes of this study, models that were fitted to survey data are categorized as case-based models as they were focused on detecting the incidence of the disease, though there were differing delays associated with models that were fitted to cases and models that were fitted to survey data. There are drawbacks and advantages associated with fitting to either cases or admissions. Case data are highly sensitive to ascertainment biases. For example, an under-ascertainment of cases may be related to weekend/weekday periods, with people with milder symptoms over the weekend less likely to get confirmed than during the weekdays. The scale of these biases has varied greatly over time. Therefore, models that were fitted to case counts or positivity must be interpreted in the context of testing behaviours and policies at the time. However, admission data are not free from bias either, as they depend on input from physicians and other hospital staff, which means that weekend/weekday effects are likely. In addition, the likelihood of being admitted to the hospital varies greatly by age. Hence, without age stratification in the model, it is likely that community transmission is underestimated among younger age groups. Furthermore, the delay between being infected with COVID-19 and being admitted to the hospital is on average far greater than that between infection and receiving a positive test. This presented difficulties when trying to produce timely estimates of community transmission. Table 1 lists these models along with the type of data they were fitted to and whether or not they were run internally by either the UKHSA Epi-Ensemble or a Devolved Administration (DA) Department.
$ r $
, incidence, and prevalence; and to produce medium-term projections (MTPs) of hospital admissions, hospital bed occupancy, and deaths. The MTPs will be explored separately in a future publication. These models fall into three broad groups, as described in [Reference Georgakakos31] and [Reference Abbott2]: population-based models (PBMs), data-driven models (DDMs), and agent-based models (ABMs). The models in the ensemble can be split further into three broad categories based on the data they primarily used to inform their estimates: case-based models, admission-based models, and models that were fitted to both case data and hospital data. For the purposes of this study, models that were fitted to survey data are categorized as case-based models as they were focused on detecting the incidence of the disease, though there were differing delays associated with models that were fitted to cases and models that were fitted to survey data. There are drawbacks and advantages associated with fitting to either cases or admissions. Case data are highly sensitive to ascertainment biases. For example, an under-ascertainment of cases may be related to weekend/weekday periods, with people with milder symptoms over the weekend less likely to get confirmed than during the weekdays. The scale of these biases has varied greatly over time. Therefore, models that were fitted to case counts or positivity must be interpreted in the context of testing behaviours and policies at the time. However, admission data are not free from bias either, as they depend on input from physicians and other hospital staff, which means that weekend/weekday effects are likely. In addition, the likelihood of being admitted to the hospital varies greatly by age. Hence, without age stratification in the model, it is likely that community transmission is underestimated among younger age groups. Furthermore, the delay between being infected with COVID-19 and being admitted to the hospital is on average far greater than that between infection and receiving a positive test. This presented difficulties when trying to produce timely estimates of community transmission. Table 1 lists these models along with the type of data they were fitted to and whether or not they were run internally by either the UKHSA Epi-Ensemble or a Devolved Administration (DA) Department.
Table 1. The UKHSA/SPI-M-O models split by model type and the data to which they fit to

While these models can be broadly stratified into the PBM, DDM, and ABM groups, each model within the group has distinctive characteristics. For example, EpiEstim followed the methodology described in [Reference Gostic32] and therefore assumed a consistent relationship between infections and cases. The estimated
![]() $ R $
was therefore only robust when the ascertainment rate was roughly constant. While GenSur shared this same limitation, Epidemia and OxfordCSML did not make this assumption [33]. Furthermore, renewal equation-based models tend to be semi-mechanistic, that is assuming that the effects of interventions are absorbed into the data to which they fit. In contrast, fully mechanistic models, such as the susceptible–exposed–infected–recovered (SEIR) population-based models and ABMs, explicitly modelled the effects of interventions such as test–trace–isolate strategies and imposing and removing of social distancing measures.
$ R $
was therefore only robust when the ascertainment rate was roughly constant. While GenSur shared this same limitation, Epidemia and OxfordCSML did not make this assumption [33]. Furthermore, renewal equation-based models tend to be semi-mechanistic, that is assuming that the effects of interventions are absorbed into the data to which they fit. In contrast, fully mechanistic models, such as the susceptible–exposed–infected–recovered (SEIR) population-based models and ABMs, explicitly modelled the effects of interventions such as test–trace–isolate strategies and imposing and removing of social distancing measures.
In epidemiological models, the structure of the model determines the method to calculate
![]() $ R $
and depends on the assumptions and data sets used to parameterize and validate the model [Reference Green, Ferguson and Cori34].
$ R $
and depends on the assumptions and data sets used to parameterize and validate the model [Reference Green, Ferguson and Cori34].
In the classic compartmental SEIR model,
![]() $ {R}_0=\beta \ast c/\gamma $
, where
$ {R}_0=\beta \ast c/\gamma $
, where
![]() $ \beta $
is the transmission probability per contact,
$ \beta $
is the transmission probability per contact,
![]() $ c $
is the number of contacts
$ c $
is the number of contacts
![]() $ c $
, and
$ c $
, and
![]() $ 1/\gamma $
is the infectiousness period (average time that an individual is infectious for).
$ 1/\gamma $
is the infectiousness period (average time that an individual is infectious for).
![]() $ R $
is typically calculated from more complex (e.g. multi-group) SEIR models as the largest eigenvalue of the next-generation matrix (NGM), which can be expressed as
$ R $
is typically calculated from more complex (e.g. multi-group) SEIR models as the largest eigenvalue of the next-generation matrix (NGM), which can be expressed as
![]() $ {FV}^{-1} $
, where
$ {FV}^{-1} $
, where
![]() $ F $
represents infection rates and
$ F $
represents infection rates and
![]() $ V $
represents recovery rates [Reference Hinch35, Reference James36].
$ V $
represents recovery rates [Reference Hinch35, Reference James36].
![]() $ R $
can also be estimated using the renewal equation [Reference Keeling37, Reference Kendall38]:
$ R $
can also be estimated using the renewal equation [Reference Keeling37, Reference Kendall38]:
 $$ R(t)=\frac{E[I(t)]}{\int_0^{\mathrm{\infty}}f(\tau )I(t-\tau )d\tau}\hskip1em , $$
$$ R(t)=\frac{E[I(t)]}{\int_0^{\mathrm{\infty}}f(\tau )I(t-\tau )d\tau}\hskip1em , $$
where
![]() $ I(t) $
is number of new infections (i.e. the incidence) at time
$ I(t) $
is number of new infections (i.e. the incidence) at time
![]() $ t $
and
$ t $
and
![]() $ E\left[\right] $
denotes the expected value.
$ E\left[\right] $
denotes the expected value.
Across the dynamical models that comprise sets of differential equations in our ensemble, such as the Manchester or University of Liverpool models,
![]() $ R $
was estimated by inferring the rate of transmission within the model, which was fitted to observed data on cases, hospitalizations, deaths, or their combination. Some more complex dynamical models, such as the one developed by Public Health England (PHE) and Cambridge or the Imperial one (sircovid), explicitly calculated R as the largest eigenvalue of the NGM.
$ R $
was estimated by inferring the rate of transmission within the model, which was fitted to observed data on cases, hospitalizations, deaths, or their combination. Some more complex dynamical models, such as the one developed by Public Health England (PHE) and Cambridge or the Imperial one (sircovid), explicitly calculated R as the largest eigenvalue of the NGM.
There is also a difference in how R was estimated between compartmental and ABMs or individual-based models. In ABMs, such as Covasim, it is possible simply to count exactly how many secondary infections are caused by each primary infection at any stage of the epidemic and hence explicitly calculate
![]() $ R $
.
$ R $
.
A third approach, and a characteristic of the data-driven models in our ensemble, used statistical models to estimate R empirically from the notification data. These methods made minimal structural assumptions about epidemic dynamics and only required users to specify the generation time distribution. A selection of models in this category in the ensemble was formulated based on Equation (1). For example, where the generation time distribution is described by a gamma distribution with shape
![]() $ a $
and rate
$ a $
and rate
![]() $ b $
,
$ b $
,
![]() $ R $
can be expressed in terms of the growth rate
$ R $
can be expressed in terms of the growth rate
![]() $ r $
as follows:
$ r $
as follows:
A high-level description of the methods used to calculate
![]() $ R $
, along with an outline of the main characteristics of each model, is given in Table A1 in the Appendix.
$ R $
, along with an outline of the main characteristics of each model, is given in Table A1 in the Appendix.
Combining model estimates to generate a consensus
 $ R $
$ R $
To generate combined
![]() $ R $
estimates from the ensemble of models, we used the statistical model developed as a collaboration between DSTL, the University of Southampton, and the University of Liverpool with the underlying methodology described in [Reference Brooks-Pollock10]. We present a high-level outline of the method below. Each of the epidemiological models described in Table A1 and calibrated to the data as outlined in Table 1 generated 5th, 25th, 50th, 75th, and 95th percentile estimates for
$ R $
estimates from the ensemble of models, we used the statistical model developed as a collaboration between DSTL, the University of Southampton, and the University of Liverpool with the underlying methodology described in [Reference Brooks-Pollock10]. We present a high-level outline of the method below. Each of the epidemiological models described in Table A1 and calibrated to the data as outlined in Table 1 generated 5th, 25th, 50th, 75th, and 95th percentile estimates for
![]() $ R $
. Using these, a mean and a standard deviation for each model’s
$ R $
. Using these, a mean and a standard deviation for each model’s
![]() $ R $
estimate were generated. The mean of the
$ R $
estimate were generated. The mean of the
![]() $ {i}^{th} $
model,
$ {i}^{th} $
model,
![]() $ {y}_i $
, was initially estimated as the median (or
$ {y}_i $
, was initially estimated as the median (or
![]() $ {50}^{th} $
quantile), and the standard deviation was calculated as follows:
$ {50}^{th} $
quantile), and the standard deviation was calculated as follows:
where
![]() $ {q}_i(x) $
represented the
$ {q}_i(x) $
represented the
![]() $ {x}^{th} $
quantile of the
$ {x}^{th} $
quantile of the
![]() $ {i}^{th} $
model and
$ {i}^{th} $
model and
![]() $ {z}_{95} $
is the z-score for the 90% confidence interval (CI) of the standard normal distribution. Where model estimates were highly skewed, a skewness correction calculation was applied to provide alternative estimates for the mean and the standard error (see [Reference Brooks-Pollock10] for further details). Otherwise, the distribution of the model estimates for
$ {z}_{95} $
is the z-score for the 90% confidence interval (CI) of the standard normal distribution. Where model estimates were highly skewed, a skewness correction calculation was applied to provide alternative estimates for the mean and the standard error (see [Reference Brooks-Pollock10] for further details). Otherwise, the distribution of the model estimates for
![]() $ R $
was assumed to be symmetric.
$ R $
was assumed to be symmetric.
These estimates were then combined using a random-effects model, which allowed for differences in model structure and did not assume that models shared a common effect size. The random-effects statistical model was described as follows:
where the estimated mean for model
![]() $ i $
is denoted by
$ i $
is denoted by
![]() $ {y}_i $
and the standard error is denoted by
$ {y}_i $
and the standard error is denoted by
![]() $ {s}_i=\sqrt{v_i} $
. The model was fitted to provide estimates for
$ {s}_i=\sqrt{v_i} $
. The model was fitted to provide estimates for
![]() $ \mu $
and
$ \mu $
and
![]() $ \tau $
, which are the mean and standard deviation of the true effect size, respectively. The between-model variance,
$ \tau $
, which are the mean and standard deviation of the true effect size, respectively. The between-model variance,
![]() $ {\tau}^2 $
, was estimated using the restricted maximum-likelihood method, and the CI of the mean true overall effect size is estimated using the standard Wald-type method. The models were equally weighted (see next section for more details) and the range of
$ {\tau}^2 $
, was estimated using the restricted maximum-likelihood method, and the CI of the mean true overall effect size is estimated using the standard Wald-type method. The models were equally weighted (see next section for more details) and the range of
![]() $ R $
was rounded out to one decimal place, by using the lower and upper bounds, respectively. Further details of other methods used for calculating the between group errors and CIs are provided in [Reference Kendall39].
$ R $
was rounded out to one decimal place, by using the lower and upper bounds, respectively. Further details of other methods used for calculating the between group errors and CIs are provided in [Reference Kendall39].
Collaborating across government and academia to produce a consensus nowcast
The process of cross-academic and government collaboration to generate consensus
![]() $ R $
was done in several steps. Firstly, the outputs from the models detailed in Table A1 were submitted by the modellers to the UKHSA Epi-Ensemble team weekly. The team then combined the model estimates using CrystalCast to generate a combined estimate for
$ R $
was done in several steps. Firstly, the outputs from the models detailed in Table A1 were submitted by the modellers to the UKHSA Epi-Ensemble team weekly. The team then combined the model estimates using CrystalCast to generate a combined estimate for
![]() $ R $
,
$ R $
,
![]() $ r $
, incidence, and prevalence in England, the English regions and the DAs. The combined estimates, as well as individual model estimates, were discussed at a weekly meeting between the UKHSA Epi-Ensemble and SPI-M modellers, wider SPI-M-O members, and wider representatives from UKHSA and DAs. These meetings gave the modellers the chance to explain their outputs, discuss the model behaviour, and agree on the inclusion or exclusion of any specific models in the ensemble for that week. A model would only be excluded if there was a clear error in its outputs or if it displayed behaviour that could not be justified from an epidemiological perspective. Once a consensus was reached for each of the epidemic metrics, a recommendation was made to the EMRG, who then finally approved and published the consensus outputs.
$ r $
, incidence, and prevalence in England, the English regions and the DAs. The combined estimates, as well as individual model estimates, were discussed at a weekly meeting between the UKHSA Epi-Ensemble and SPI-M modellers, wider SPI-M-O members, and wider representatives from UKHSA and DAs. These meetings gave the modellers the chance to explain their outputs, discuss the model behaviour, and agree on the inclusion or exclusion of any specific models in the ensemble for that week. A model would only be excluded if there was a clear error in its outputs or if it displayed behaviour that could not be justified from an epidemiological perspective. Once a consensus was reached for each of the epidemic metrics, a recommendation was made to the EMRG, who then finally approved and published the consensus outputs.
Sensitivity analysis
Two sensitivity analyses explored the extent to which the combined
![]() $ R $
would have been impacted by the variable weighting of the models within the ensemble and the size of the ensemble. For consistency, no individual models were re-run for these analyses; we used only the original model results submitted at the time the consensus
$ R $
would have been impacted by the variable weighting of the models within the ensemble and the size of the ensemble. For consistency, no individual models were re-run for these analyses; we used only the original model results submitted at the time the consensus
![]() $ R $
was published. This was intentional so that the analysis would serve as a historic record of the combined estimates at the time.
$ R $
was published. This was intentional so that the analysis would serve as a historic record of the combined estimates at the time.
Exploring the impact of model weighting on the combined R
Firstly, we explored the impact of the choice of model weighting on the consensus
![]() $ R $
. The combined estimate
$ R $
. The combined estimate
![]() $ y $
was calculated from the true effect size of each model
$ y $
was calculated from the true effect size of each model
![]() $ {y}_i $
. The true effect size can therefore be weighted. The simplest method is equal weighting, which was used to generate the published consensus
$ {y}_i $
. The true effect size can therefore be weighted. The simplest method is equal weighting, which was used to generate the published consensus
![]() $ R $
over 2020–2022. In this method, each model is assumed to have an equal contribution to the combined estimate under the assumption that all models are equally valid.
$ R $
over 2020–2022. In this method, each model is assumed to have an equal contribution to the combined estimate under the assumption that all models are equally valid.
Another common method of weighting is inverse-variance weighting. In this method, models with a high variance, that is those that are less certain, are penalized more than models with a low variance, that is more certain models. However, individual models have different methods of representing uncertainty, and a model that is more certain is not necessarily more likely to be accurate. Therefore, this method is not applicable here.
An alternative method of model weighting is to group models by either their structure or the data to which they fit. For example, models that may have a different structure but use the same data form a subgroup as described in Table 1. We explored the impact of this on the consensus
![]() $ R $
value by dividing the ensemble into subgroups, so each subgroup represents a homogeneous set of models according to either their structure or the data to which they fit. Models within each subgroup were equally weighted, and then, the contributions from the subgroups were equally weighted to give the overall combined estimate. This had two purposes: firstly, a single data stream or model structure would not have gained a larger weighting in the final combination, meaning that the combination was ‘data-agnostic’ or ‘model-agnostic’ and models such as EpiEstim, with a larger representation in the ensemble, did not bias the final estimates; secondly, it allowed us to compare the difference in trends between admissions and case data and therefore learn about the epidemic dynamics by inspection.
$ R $
value by dividing the ensemble into subgroups, so each subgroup represents a homogeneous set of models according to either their structure or the data to which they fit. Models within each subgroup were equally weighted, and then, the contributions from the subgroups were equally weighted to give the overall combined estimate. This had two purposes: firstly, a single data stream or model structure would not have gained a larger weighting in the final combination, meaning that the combination was ‘data-agnostic’ or ‘model-agnostic’ and models such as EpiEstim, with a larger representation in the ensemble, did not bias the final estimates; secondly, it allowed us to compare the difference in trends between admissions and case data and therefore learn about the epidemic dynamics by inspection.
Similarly, as for the equal weighting model method, a consensus
![]() $ R $
value was derived with this alternative variable weighting method as a range for April and September 2021. We present the results as rounded to two decimal places. However, we note that the range was published to only one decimal place to avoid presenting a false sense of precision. The range published was also rounded out, rather than rounding to the nearest decimal place, in order to increase the uncertainty instead of possibly reducing it.
$ R $
value was derived with this alternative variable weighting method as a range for April and September 2021. We present the results as rounded to two decimal places. However, we note that the range was published to only one decimal place to avoid presenting a false sense of precision. The range published was also rounded out, rather than rounding to the nearest decimal place, in order to increase the uncertainty instead of possibly reducing it.
Exploring the impact of ensemble size on the combined R
The models included within the ensemble varied throughout the pandemic; as new models were developed and introduced, some were phased out and others were updated in response to the changing epidemic. This could hypothetically result in inconsistent estimates through time. Furthermore, as UKHSA moved from a ‘response’ to a ‘business-as-usual’ phase during 2022, a need emerged to reduce the resource dedicated to modelling COVID-19 and hence reduce the number of models in the ensemble. These factors motivated us to explore how the combined
![]() $ R $
may have changed if a different model ensemble was used to generate it.
$ R $
may have changed if a different model ensemble was used to generate it.
We investigated the implications of reducing the size of the ensemble on the combined
![]() $ R $
estimate over the period April 2021–December 2021. UKHSA models are labelled in Table 1 and comprised of internal models, that is run by UKHSA or DA modellers. We re-calculated the combined estimate using the ‘reduced’ ensemble of only internal models and, using equal weighting, compared this to the published consensus
$ R $
estimate over the period April 2021–December 2021. UKHSA models are labelled in Table 1 and comprised of internal models, that is run by UKHSA or DA modellers. We re-calculated the combined estimate using the ‘reduced’ ensemble of only internal models and, using equal weighting, compared this to the published consensus
![]() $ R $
number in England.
$ R $
number in England.
 $ R $
as an epidemic indicator
$ R $
as an epidemic indicator
The
![]() $ R $
time series is a transform of epidemic metrics such as case incidence or hospitalizations. Hence, we expect it would be statistically correlated with the epidemic metrics, but quantifying the degree of correlation with different metrics is interesting.
$ R $
time series is a transform of epidemic metrics such as case incidence or hospitalizations. Hence, we expect it would be statistically correlated with the epidemic metrics, but quantifying the degree of correlation with different metrics is interesting.
We explored the correlation between the consensus
![]() $ R $
as published on the UK Government COVID-19 Dashboard and the key public data sources relating to the COVID-19 pandemic, namely cases, admissions, and deaths. We expect the
$ R $
as published on the UK Government COVID-19 Dashboard and the key public data sources relating to the COVID-19 pandemic, namely cases, admissions, and deaths. We expect the
![]() $ R $
number to be correlated in some way to the rate of change of these three metrics, and we know this relationship is non-linear. Therefore, we used Spearman’s rank correlation coefficient,
$ R $
number to be correlated in some way to the rate of change of these three metrics, and we know this relationship is non-linear. Therefore, we used Spearman’s rank correlation coefficient,
![]() $ \rho $
.
$ \rho $
.
In order to adjust for periodic weekly fluctuations (e.g. weekend/weekday differences in under-ascertainment), each source of data was transformed into a centred weekly moving average. For each date that an
![]() $ R $
number was calculated, the slope of the data was calculated over a centred weekly window. We used the same length and position of windows over which to perform the analysis in order to ensure consistency; otherwise, additional artificial lag would be introduced into the analysis.
$ R $
number was calculated, the slope of the data was calculated over a centred weekly window. We used the same length and position of windows over which to perform the analysis in order to ensure consistency; otherwise, additional artificial lag would be introduced into the analysis.
The correlation between
![]() $ R $
and the weekly rate of change in cases, admissions, or deaths may have an inherent lag due to the fact that it takes time for more severe symptoms to develop. In order to investigate this, we explored how the correlation changed between the
$ R $
and the weekly rate of change in cases, admissions, or deaths may have an inherent lag due to the fact that it takes time for more severe symptoms to develop. In order to investigate this, we explored how the correlation changed between the
![]() $ R $
number, shifted along its time axis by a varying number of days, and the rate of change of new hospital admissions and deaths. This was done by shifting the calculated values of
$ R $
number, shifted along its time axis by a varying number of days, and the rate of change of new hospital admissions and deaths. This was done by shifting the calculated values of
![]() $ R $
we used by 1–20 days and observing how
$ R $
we used by 1–20 days and observing how
![]() $ \rho $
changed with an increasing shift size. Mathematically, we are calculating the following, where the variable
$ \rho $
changed with an increasing shift size. Mathematically, we are calculating the following, where the variable
![]() $ X $
represents the centred weekly rolling average of either the recorded incidence of cases, hospital admissions, or deaths:
$ X $
represents the centred weekly rolling average of either the recorded incidence of cases, hospital admissions, or deaths:
 $$ {\rho}_{\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)}=\frac{\mathrm{Cov}\left[\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)\right]}{\sigma_{\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)}}\hskip1em . $$
$$ {\rho}_{\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)}=\frac{\mathrm{Cov}\left[\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)\right]}{\sigma_{\mathcal{R}\left({R}_{t^{\prime }}\right),\mathcal{R}\left(\dot{X}\right)}}\hskip1em . $$
In the above,
![]() $ \mathcal{R}\left(\cdot \right) $
denotes the ordinal rank and
$ \mathcal{R}\left(\cdot \right) $
denotes the ordinal rank and
![]() $ {R}_{t^{\prime }} $
is the time-shifted
$ {R}_{t^{\prime }} $
is the time-shifted
![]() $ R $
, equal to
$ R $
, equal to
![]() $ R\left(t-{t}_{\mathrm{shift}}\right) $
, where
$ R\left(t-{t}_{\mathrm{shift}}\right) $
, where
![]() $ {t}_{\mathrm{shift}}\in \left(1,20\right) $
.
$ {t}_{\mathrm{shift}}\in \left(1,20\right) $
.
![]() $ \dot{X} $
denotes the rate of change of variable
$ \dot{X} $
denotes the rate of change of variable
![]() $ X $
with respect to time, and all times considered are measured in days. We performed this calculation on data within specific time windows, which correspond to the Delta and Omicron waves, respectively, and shifted the time window for the published
$ X $
with respect to time, and all times considered are measured in days. We performed this calculation on data within specific time windows, which correspond to the Delta and Omicron waves, respectively, and shifted the time window for the published
![]() $ R $
value against the static recorded data. These time windows were 7 May 2021 to 30 July 2021 and 26 November 2021 to 25 February 2022 for the Delta and Omicron waves, respectively.
$ R $
value against the static recorded data. These time windows were 7 May 2021 to 30 July 2021 and 26 November 2021 to 25 February 2022 for the Delta and Omicron waves, respectively.
Results
Generating a consensus
 $ R $
range in April and September 2021 using different weighting methods
$ R $
range in April and September 2021 using different weighting methods
Whisker plots of the 90th CIs of
![]() $ R $
for each model are plotted alongside the resulting combinations from the different methods and shown in Figure 1. We note that because of the delays between new infections and the time they are observed as cases or admissions, the combined R estimates on 21 April 2021 and 29 September 2021 reflect the R values on 6 April 2021 and 14 September 2021.The numerical values for the 90% CIs for each weighting method are given in Table 2.
$ R $
for each model are plotted alongside the resulting combinations from the different methods and shown in Figure 1. We note that because of the delays between new infections and the time they are observed as cases or admissions, the combined R estimates on 21 April 2021 and 29 September 2021 reflect the R values on 6 April 2021 and 14 September 2021.The numerical values for the 90% CIs for each weighting method are given in Table 2.

Figure 1. Model ensemble generated
![]() $ R $
values at two time points of the COVID-19 epidemic in England. The parts of each plot to the left of the dashed line show the median and the 10th and 90th percentiles of the reproduction numbers
$ R $
values at two time points of the COVID-19 epidemic in England. The parts of each plot to the left of the dashed line show the median and the 10th and 90th percentiles of the reproduction numbers
![]() $ R $
from the models included in the model ensemble on 21 April 2021 and 29 September 2021. The
$ R $
from the models included in the model ensemble on 21 April 2021 and 29 September 2021. The
![]() $ R $
values on the right of the dashed line show the 90% CI for the combined
$ R $
values on the right of the dashed line show the 90% CI for the combined
![]() $ R $
value generated with different weighted methods. Because of the delays between new infections and the time they are observed as cases or admissions, the combined R estimates reflect the R values on 6 April 2021 and 14 September 2021.
$ R $
value generated with different weighted methods. Because of the delays between new infections and the time they are observed as cases or admissions, the combined R estimates reflect the R values on 6 April 2021 and 14 September 2021.
Table 2. 90% confidence intervals for combined
![]() $ R $
estimates using different weighting methods
$ R $
estimates using different weighting methods

Using the equal weighting method, and combining the
![]() $ R $
outcomes from the various epidemiological models (a mixture of SEIR-type, agent-based, and data-driven models), we generated combined
$ R $
outcomes from the various epidemiological models (a mixture of SEIR-type, agent-based, and data-driven models), we generated combined
![]() $ R $
estimates of
$ R $
estimates of
![]() $ \left[\mathrm{0.81,0.93}\right] $
in April 2021 and
$ \left[\mathrm{0.81,0.93}\right] $
in April 2021 and
![]() $ \left[\mathrm{0.91,1.07}\right] $
in September 2021. These represent the 90% CI that was published on the UK Government dashboard at the time.
$ \left[\mathrm{0.91,1.07}\right] $
in September 2021. These represent the 90% CI that was published on the UK Government dashboard at the time.
Using a different weighting for the combination of models produces very similar combined
![]() $ R $
values at the two snapshots in time we studied: in April 2021 and in September 2021. Weighting by data resulted in an
$ R $
values at the two snapshots in time we studied: in April 2021 and in September 2021. Weighting by data resulted in an
![]() $ R $
combination of
$ R $
combination of
![]() $ \left[\mathrm{0.82,0.93}\right] $
and
$ \left[\mathrm{0.82,0.93}\right] $
and
![]() $ \left[\mathrm{0.86,1.04}\right] $
for the April 2021 and September 2021 estimates, respectively. Weighting by model structure resulted in a combination of
$ \left[\mathrm{0.86,1.04}\right] $
for the April 2021 and September 2021 estimates, respectively. Weighting by model structure resulted in a combination of
![]() $ \left[\mathrm{0.8,0.94}\right] $
and
$ \left[\mathrm{0.8,0.94}\right] $
and
![]() $ \left[\mathrm{0.9,1.07}\right] $
for the April 2021 and September 2021 estimates, respectively.
$ \left[\mathrm{0.9,1.07}\right] $
for the April 2021 and September 2021 estimates, respectively.
The effect of ensemble size on the combined estimate
Figure 2A compares the unrounded combined
![]() $ R $
number generated from a reduced model ensemble that includes models run by UKHSA and DA teams as outlined in the sectiontitled “Exploring the impact of ensemble size on the combined R”. Our results show that the two combined
$ R $
number generated from a reduced model ensemble that includes models run by UKHSA and DA teams as outlined in the sectiontitled “Exploring the impact of ensemble size on the combined R”. Our results show that the two combined
![]() $ R $
value time series are similar but not identical, with the level of agreement changing over the study period. For most of the study period, the values of the combined
$ R $
value time series are similar but not identical, with the level of agreement changing over the study period. For most of the study period, the values of the combined
![]() $ R $
from the two model ensembles were similar, with the smaller model ensemble increasing the uncertainty in the consensus
$ R $
from the two model ensembles were similar, with the smaller model ensemble increasing the uncertainty in the consensus
![]() $ R $
value (comparing the width of the blue bandwidth and orange bands in Figure 2A). There was a notable difference in the combined
$ R $
value (comparing the width of the blue bandwidth and orange bands in Figure 2A). There was a notable difference in the combined
![]() $ R $
from the two ensembles in July 2021, which is due to a very different number of models constituting the model ensemble. The full ensemble for 14 July 2021 contained thirteen different models, compared to the internal model ensemble, which contained four different models (Figure 2B). On 21 July 2021, the full ensemble had eleven models, while the internal model ensemble contained only two. The two models for 21 July 2021 would not have been sufficient to produce a published combination,Footnote
1 but we have shown the result here for completeness. From August 2021 onwards, the full and internal model-only ensembles show much better agreement, which is due to the latter having a more comparable number of models.
$ R $
from the two ensembles in July 2021, which is due to a very different number of models constituting the model ensemble. The full ensemble for 14 July 2021 contained thirteen different models, compared to the internal model ensemble, which contained four different models (Figure 2B). On 21 July 2021, the full ensemble had eleven models, while the internal model ensemble contained only two. The two models for 21 July 2021 would not have been sufficient to produce a published combination,Footnote
1 but we have shown the result here for completeness. From August 2021 onwards, the full and internal model-only ensembles show much better agreement, which is due to the latter having a more comparable number of models.

Figure 2. The combined
![]() $ R $
number in the period April 2021–December 2021 in England for the full model ensemble and the reduced (internal UKHSA and DA models only) ensemble. Plot A shows the time series of the two
$ R $
number in the period April 2021–December 2021 in England for the full model ensemble and the reduced (internal UKHSA and DA models only) ensemble. Plot A shows the time series of the two
![]() $ R $
values over the study period, while plot B shows the number of models in each ensemble at different time points when the
$ R $
values over the study period, while plot B shows the number of models in each ensemble at different time points when the
![]() $ R $
value was generated.
$ R $
value was generated.
The combined
 $ R $
is a good, but delayed, epidemic indicator
$ R $
is a good, but delayed, epidemic indicator
Figure 3 shows the relationship between the rate of change of the 7-day rolling mean of cases, admissions, and deaths with an optimally time-shifted
![]() $ R $
. Figure 3A shows that
$ R $
. Figure 3A shows that
![]() $ R $
values larger or smaller than 1 (shown in red and blue, respectively) occur when the number of COVID-19 cases is increasing and decreasing. The correlation, calculated as Spearman’s rank coefficient between a time-shifted
$ R $
values larger or smaller than 1 (shown in red and blue, respectively) occur when the number of COVID-19 cases is increasing and decreasing. The correlation, calculated as Spearman’s rank coefficient between a time-shifted
![]() $ R $
and the rate of change of recorded cases (Table 3), is given in the box to the top left of the plot. This is done separately for the Delta and Omicron waves, and the time periods we considered for each wave are demarcated by the vertical dotted lines. Overall, our results show a good positive correlation between epidemic status indicators and a time-shifted
$ R $
and the rate of change of recorded cases (Table 3), is given in the box to the top left of the plot. This is done separately for the Delta and Omicron waves, and the time periods we considered for each wave are demarcated by the vertical dotted lines. Overall, our results show a good positive correlation between epidemic status indicators and a time-shifted
![]() $ R $
across both epidemic waves, confirming that
$ R $
across both epidemic waves, confirming that
![]() $ R $
is following the trends in cases, hospitalizations, and deaths related to COVID-19 over both of the Delta and Omicron epidemic waves, albeit with a delay. Here, we have shown only the maximum correlation obtained from the optimal shift of the
$ R $
is following the trends in cases, hospitalizations, and deaths related to COVID-19 over both of the Delta and Omicron epidemic waves, albeit with a delay. Here, we have shown only the maximum correlation obtained from the optimal shift of the
![]() $ R $
number. The values of
$ R $
number. The values of
![]() $ \rho $
calculated for
$ \rho $
calculated for
![]() $ {R}_{t-{t}_{\mathrm{shift}}} $
where
$ {R}_{t-{t}_{\mathrm{shift}}} $
where
![]() $ {t}_{\mathrm{shift}}\in \left(1,20\right) $
are shown in Figure B1.
$ {t}_{\mathrm{shift}}\in \left(1,20\right) $
are shown in Figure B1.

Figure 3. Plots comparing the published
![]() $ R $
number to data published on the public government COVID-19 dashboard. The plots show the superimposed time series of the 7-day rolling average of the dashboard data for various metrics, on top of the published
$ R $
number to data published on the public government COVID-19 dashboard. The plots show the superimposed time series of the 7-day rolling average of the dashboard data for various metrics, on top of the published
![]() $ R $
number for England. Where the shading is red, the median estimate for the
$ R $
number for England. Where the shading is red, the median estimate for the
![]() $ R $
number was greater than 1. Where it is blue, the median
$ R $
number was greater than 1. Where it is blue, the median
![]() $ R $
was less than 1. For each plot, Spearman’s rank correlation coefficient,
$ R $
was less than 1. For each plot, Spearman’s rank correlation coefficient,
![]() $ \rho $
, was calculated to evaluate the correlation between the rate of change of the rolling 7-day mean of a given epidemic metric (cases, hospital admissions, and deaths) and the median published
$ \rho $
, was calculated to evaluate the correlation between the rate of change of the rolling 7-day mean of a given epidemic metric (cases, hospital admissions, and deaths) and the median published
![]() $ R $
number, where
$ R $
number, where
![]() $ R(t) $
has been shifted along the time axis to maximize the correlation and
$ R(t) $
has been shifted along the time axis to maximize the correlation and
![]() $ t $
is measured in days. The amount of shift is different for each metric and wave. The maximum
$ t $
is measured in days. The amount of shift is different for each metric and wave. The maximum
![]() $ \rho $
is obtained at a shift of 3 days for the Delta wave and 1 day for the Omicron wave for cases; 9 days for the Delta wave and no shift for the Omicron wave for hospital admissions; and 18 days for the Delta wave and 9 days for the Omicron wave for deaths. Only the data within the dotted lines pertaining to the Delta and Omicron waves, respectively, were included in the correlation calculation.
$ \rho $
is obtained at a shift of 3 days for the Delta wave and 1 day for the Omicron wave for cases; 9 days for the Delta wave and no shift for the Omicron wave for hospital admissions; and 18 days for the Delta wave and 9 days for the Omicron wave for deaths. Only the data within the dotted lines pertaining to the Delta and Omicron waves, respectively, were included in the correlation calculation.
Table 3. Spearman’s rank coefficient,
![]() $ \rho $
, and the respective p-values between the time-shifted
$ \rho $
, and the respective p-values between the time-shifted
![]() $ R $
and the rate of change in a given epidemic metric. The coefficient was calculated only on data within the time period shown in the table
$ R $
and the rate of change in a given epidemic metric. The coefficient was calculated only on data within the time period shown in the table

Discussion
This study outlines a collaborative approach across government and academia to generate the combined
![]() $ R $
value for England over the period April 2021 to December 2021 using a previously established combination method [Reference Brooks-Pollock10] and
$ R $
value for England over the period April 2021 to December 2021 using a previously established combination method [Reference Brooks-Pollock10] and
![]() $ R $
estimates from an ensemble of epidemiological models. The combined
$ R $
estimates from an ensemble of epidemiological models. The combined
![]() $ R $
value was used to track the epidemic status over the COVID-19 epidemic in England and was produced by SPI-M-O in 2020 and by the UKHSA Epi-Ensemble modelling team since early 2021.
$ R $
value was used to track the epidemic status over the COVID-19 epidemic in England and was produced by SPI-M-O in 2020 and by the UKHSA Epi-Ensemble modelling team since early 2021.
In this paper, we described the process of cross-academia and government collaboration and outlined the ensemble of epidemiological models used to generate individual
![]() $ R $
values in England, highlighting their key structural characteristics and the data they used, as well as the method to individually derive an
$ R $
values in England, highlighting their key structural characteristics and the data they used, as well as the method to individually derive an
![]() $ R $
value. We also outlined the methodology developed in [Reference Brooks-Pollock10] of combining the individual
$ R $
value. We also outlined the methodology developed in [Reference Brooks-Pollock10] of combining the individual
![]() $ R $
values to generate a combined consensus
$ R $
values to generate a combined consensus
![]() $ R $
value and illustrated this by generating the published
$ R $
value and illustrated this by generating the published
![]() $ R $
values of
$ R $
values of
![]() $ \left[\mathrm{0.81,0.93}\right] $
on 21 April 2021 and
$ \left[\mathrm{0.81,0.93}\right] $
on 21 April 2021 and
![]() $ \left[\mathrm{0.91,1.07}\right] $
on 29 September 2021.
$ \left[\mathrm{0.91,1.07}\right] $
on 29 September 2021.
21 April 2021 and 29 September 2021 were very different epidemic points in time. 21 April 2021 followed the third national lockdown in England imposed to control the transmission of the Alpha variant [Reference Kerr40]. Incidence and prevalence within the population were low and large-scale vaccination against COVID-19 had only started to be rolled out, with roughly half the population having received a first dose and only 8% having received a second dose. Against this mostly homogeneous immunity, susceptibility, and vaccine backdrop, the assumptions within the models would have been similar, producing similar
![]() $ R $
values across models.
$ R $
values across models.
In September 2021, the immunity, susceptibility, and vaccination levels were very different. There was a backdrop of population immunity from either vaccination or previous infection, with a large proportion of the population aged 12 and over either having received two doses of the vaccines or having been infected by the large Delta epidemic wave over the summer of 2021. The COVID-19 case rate remained high with schools just returning, and this period preceded the arrival of the Omicron variant.
Different models would have made different assumptions on the impact of the large Delta wave on population immunity and would have incorporated different assumptions around vaccination and social mixing associated with returning to school. All of these assumptions would impact individual
![]() $ R $
values, illustrated by the varying
$ R $
values, illustrated by the varying
![]() $ R $
values across models at this time.
$ R $
values across models at this time.
Furthermore, different models were fit to different data and this can generate different estimates. For example, the two London School of Hygiene and Tropical Medicine (LSHTM) EpiNow2 models, one that fits to cases and the second that fits to admissions, have vastly different
![]() $ R $
estimates. This difference is also reflected in the combinations from models that fit only to cases (reporting a range of [0.98, 1.15]) and from models that fit only to hospital data (reporting a range of [0.8, 0.93]). If we were only to use models that fit to cases, this would imply that the epidemic was increasing. However, models that fit to hospital data imply that the epidemic was decreasing. Models that fit to both report a central estimate in between the two with larger uncertainty. A more thorough study of different weighting methods and their effects on the combination estimate is out of the scope of this paper; however, this relatively simple example demonstrates that it is important that the ensemble features models that fit to a range of different data sources.
$ R $
estimates. This difference is also reflected in the combinations from models that fit only to cases (reporting a range of [0.98, 1.15]) and from models that fit only to hospital data (reporting a range of [0.8, 0.93]). If we were only to use models that fit to cases, this would imply that the epidemic was increasing. However, models that fit to hospital data imply that the epidemic was decreasing. Models that fit to both report a central estimate in between the two with larger uncertainty. A more thorough study of different weighting methods and their effects on the combination estimate is out of the scope of this paper; however, this relatively simple example demonstrates that it is important that the ensemble features models that fit to a range of different data sources.
We note that the ensemble of models on 21 April 2021 and 29 September 2021 are not identical, and the model ensemble has been changing over time. New models were introduced to the ensemble throughout the epidemic, and models were omitted from or not submitted to the ensemble due to technical issues, such as calibration error or computer outage. Furthermore, in periods of change, such as the introduction of a new variant, some models required extensive development work before re-inclusion into the ensemble. This is an inevitable part of the process when collaborating with various modelling teams across government and academia, who are responsively modelling a fast-changing epidemic.
Reducing the size of the model ensemble to include only models run internally within UKHSA and DAs made a small difference to the combined
![]() $ R $
value, but did increase the width of the 90% CI. Overall, and for the majority of the study period, the values of the combined
$ R $
value, but did increase the width of the 90% CI. Overall, and for the majority of the study period, the values of the combined
![]() $ R $
from the two model ensembles were similar as shown in Figure 2A. There were some differences around the peaks of the Delta epidemic waves in the summer of 2021, when the internal model ensemble (comprising UKHSA and DA-only models) had a very small number of models (Figure 2B) and as a consequence the combined
$ R $
from the two model ensembles were similar as shown in Figure 2A. There were some differences around the peaks of the Delta epidemic waves in the summer of 2021, when the internal model ensemble (comprising UKHSA and DA-only models) had a very small number of models (Figure 2B) and as a consequence the combined
![]() $ R $
had a wider CI. This suggests that our process was robust to changes in the model ensemble, provided there were more than five constituent models going into any combination. This is encouraging for institutions that may be nowcasting future epidemic: an ensemble does not need to be enormous to reap the benefits of model combination.
$ R $
had a wider CI. This suggests that our process was robust to changes in the model ensemble, provided there were more than five constituent models going into any combination. This is encouraging for institutions that may be nowcasting future epidemic: an ensemble does not need to be enormous to reap the benefits of model combination.
The time series of the combined
![]() $ R $
for the duration of the Delta and Omicron waves, respectively, is strongly positively and statistically significantly correlated with the rate of change of cases, hospitalization, and deaths related to COVID-19 (Figure 3). However, this strong positive correlation only occurred for each metric if the time series for
$ R $
for the duration of the Delta and Omicron waves, respectively, is strongly positively and statistically significantly correlated with the rate of change of cases, hospitalization, and deaths related to COVID-19 (Figure 3). However, this strong positive correlation only occurred for each metric if the time series for
![]() $ R $
was shifted along its time axis by a certain optimum number of days, which differs for each wave and metric (Table 3). Exactly what causes the specific lag for each wave and metric is unclear. We acknowledge the limitations of using Spearman’s rank correlation coefficient to show this relationship; however, for this paper we simply wanted to gain an understanding of whether or not the
$ R $
was shifted along its time axis by a certain optimum number of days, which differs for each wave and metric (Table 3). Exactly what causes the specific lag for each wave and metric is unclear. We acknowledge the limitations of using Spearman’s rank correlation coefficient to show this relationship; however, for this paper we simply wanted to gain an understanding of whether or not the
![]() $ R $
number is a valid proxy for epidemic status. Therefore, a more sophisticated regression model, combined with a full investigation of the cause of the lag between epidemic metrics and
$ R $
number is a valid proxy for epidemic status. Therefore, a more sophisticated regression model, combined with a full investigation of the cause of the lag between epidemic metrics and
![]() $ R $
, is left to future work.
$ R $
, is left to future work.
In order to mitigate uncertainty associated with nowcasting, since March 2021, the
![]() $ R $
value from each model was taken on a single day in time 2 weeks before the day on which models were combined.Footnote
2 Incorporating these delays in
$ R $
value from each model was taken on a single day in time 2 weeks before the day on which models were combined.Footnote
2 Incorporating these delays in
![]() $ R $
is important as not all models are always able to report estimates up to the day that they are run as they do not possess the ability to forecast. For example, the simplest model, an application of EpiEstim, uses a delay distribution between infection and the observation to which it is fit, to back-calculate and infer the incidence time series. The
$ R $
is important as not all models are always able to report estimates up to the day that they are run as they do not possess the ability to forecast. For example, the simplest model, an application of EpiEstim, uses a delay distribution between infection and the observation to which it is fit, to back-calculate and infer the incidence time series. The
![]() $ R $
number is then estimated directly from the back-calculated time series for incidence. Therefore, the model is only able to provide estimates lagged to the order of the length of the delay distribution. Even where models are able to estimate current
$ R $
number is then estimated directly from the back-calculated time series for incidence. Therefore, the model is only able to provide estimates lagged to the order of the length of the delay distribution. Even where models are able to estimate current
![]() $ R $
numbers, due to the delay between infection and observation, the infections occurring on a given day correspond to data that will be observed in the future and hence, are, in essence, projections. Due to the difficulty in producing accurate estimates for
$ R $
numbers, due to the delay between infection and observation, the infections occurring on a given day correspond to data that will be observed in the future and hence, are, in essence, projections. Due to the difficulty in producing accurate estimates for
![]() $ R $
without the time delay, and in the light of the above discussion about the lagged correlation, it is vital to use a range of metrics to inform policy decisions around epidemic status. For this reason, the
$ R $
without the time delay, and in the light of the above discussion about the lagged correlation, it is vital to use a range of metrics to inform policy decisions around epidemic status. For this reason, the
![]() $ R $
value estimates were used alongside estimates of three other epidemiological metrics when informing policy decisions: the growth rate,
$ R $
value estimates were used alongside estimates of three other epidemiological metrics when informing policy decisions: the growth rate,
![]() $ r, $
incidence, and prevalence, and the MTPs for hospital admissions, occupancy, and deaths.
$ r, $
incidence, and prevalence, and the MTPs for hospital admissions, occupancy, and deaths.
Future planning and lessons learnt
While combining multiple models, particularly in epidemic modelling, has proven to be very useful during the COVID-19 epidemic, there are lessons from this that should be considered in future.
Firstly, it should be ensured that CIs calculated by each of the models represent the same sources of uncertainty. Do they capture the underlying uncertainty present in the data, the parametric uncertainty or the structural uncertainty? The forecast hub at the CDC treats models primarily as black boxes, though model details are published and models are assessed for accuracy, and there is no explicit treatment of the resulting uncertainty. For future pandemics, there should be a clear definition of uncertainty and what it should represent.
Secondly, the combination method used to generate a consensus
![]() $ R $
is insensitive to the performance of individual models. Whereas for forecasts, model performance can be calculated by comparing model estimates with observed data, the
$ R $
is insensitive to the performance of individual models. Whereas for forecasts, model performance can be calculated by comparing model estimates with observed data, the
![]() $ R $
number is a latent variable and therefore is not observed. We rely on the expertise of modellers to ensure that models fit well to the data and make sound assumptions. In the future, developing an unbiased scoring method for individual models would help in ensuring the robustness and reliability of the individual models before combining them into an ensemble.
$ R $
number is a latent variable and therefore is not observed. We rely on the expertise of modellers to ensure that models fit well to the data and make sound assumptions. In the future, developing an unbiased scoring method for individual models would help in ensuring the robustness and reliability of the individual models before combining them into an ensemble.
Finally, running an ensemble of models is resource-intensive and relies on a significant amount of external expertise. If models are not to be treated as black boxes, specialist expertise of academic groups continues to be required, and developing formal cross-government and academia modelling hubs is necessary for ongoing cross-institutional collaboration.
Data availability statement
The weekly published reproduction number
![]() $ R $
value data are publicly available at https://www.gov.uk/guidance/the-r-value-and-growth-rate. Individual model
$ R $
value data are publicly available at https://www.gov.uk/guidance/the-r-value-and-growth-rate. Individual model
![]() $ R $
values can be requested from the corresponding author, but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available.
$ R $
values can be requested from the corresponding author, but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available.
Acknowledgements
Estimates for
![]() $ R $
have been provided and combined as part of the UK-wide response to COVID-19. We would like to thank members of the SPI-M-O modelling group named as co-authors for continuing to provide estimates. In addition, we also acknowledge Yee-Whye Teh, Robert Hinch and Christophe Fraser (University of Oxford); Michelle Kendall and Louise Dyson (University of Warwick); Axel Gandy and Neil Ferguson (Imperial College London); Robert Moore, Conor Rosato, and Simon Maskell (University of Liverpool); Leon Danon and Ellen Brooks-Pollock (University of Bristol); Sam Abbott and John Edmunds (London School of Hygiene and Tropical Medicine); Robert Shaw, Ewan Wakeman, Nicholas Groves-Kirkby, and Seema Patel (NHS England); and Ross Burton (Cardiff University) for insightful ongoing discussions and input to this modelling work. We would in particular like to thank the SPI-M-O secretariat and Graham Medley (LSHTM and SPI-M-O chair) for their support and continued discussions while conducting this analysis and while producing consensus
$ R $
have been provided and combined as part of the UK-wide response to COVID-19. We would like to thank members of the SPI-M-O modelling group named as co-authors for continuing to provide estimates. In addition, we also acknowledge Yee-Whye Teh, Robert Hinch and Christophe Fraser (University of Oxford); Michelle Kendall and Louise Dyson (University of Warwick); Axel Gandy and Neil Ferguson (Imperial College London); Robert Moore, Conor Rosato, and Simon Maskell (University of Liverpool); Leon Danon and Ellen Brooks-Pollock (University of Bristol); Sam Abbott and John Edmunds (London School of Hygiene and Tropical Medicine); Robert Shaw, Ewan Wakeman, Nicholas Groves-Kirkby, and Seema Patel (NHS England); and Ross Burton (Cardiff University) for insightful ongoing discussions and input to this modelling work. We would in particular like to thank the SPI-M-O secretariat and Graham Medley (LSHTM and SPI-M-O chair) for their support and continued discussions while conducting this analysis and while producing consensus
![]() $ R $
estimates.
$ R $
estimates.
Author contribution
Formal analysis: H.M., J.P., A.S.M., T.B., G.D., J.PG and Nowcasts Model Contribution Group; Validation: H.M., J.P., A.S.M., G.D., T.B., J.PG. and Nowcasts Model Contributing Group; Writing – original draft: H.M., J.P. and J.PG. Writing – review & editing: H.M, J.P, V.B., T.M., T.F., A.C.,N.W., J.H., S.R., J.PG.; Data curation: A.S.M., H.M., J.P., T.B.; Methodology: A.S.M, J.P., G.D., H.M., T.B., J.PG.; Visualization: H.M., L.B., J.P. and J.PG; Investigation: G.D., H.M., T.B., J.P., J.PG; G.M.; Conceptualization: J.PG, S.R., J.P., H.M.; Software: V.B., T.M., H.M., J.P., J.PG.; Supervision: J.PG.; Project administration: H.M., and J.PG.
Code availability
The numerical code used in this analysis can be requested from the corresponding author. Restrictions apply to the availability of the model combining code, which was under collaborative license for the current study and hence is not publicly available.
Appendix
A models used in the ensemble
Table A1. Summary of the epidemiological models used to generate
![]() $ R $
outcomes for the English COVID-19 epidemic. We list the names of the models, their main modelling characteristics, and the data to which they are calibrated against and the method to calculate
$ R $
outcomes for the English COVID-19 epidemic. We list the names of the models, their main modelling characteristics, and the data to which they are calibrated against and the method to calculate
![]() $ R $
$ R $

B Hospital admissions and deaths with a shifted R

Figure B1. Plots A, B, and C show Spearman’s rank correlation coefficient,
![]() $ \rho $
, between
$ \rho $
, between
![]() $ R\left(t-{t}_{\mathrm{shift}}\right) $
and the rate of change in cases, hospital admissions, and deaths, respectively, for a varying
$ R\left(t-{t}_{\mathrm{shift}}\right) $
and the rate of change in cases, hospital admissions, and deaths, respectively, for a varying
![]() $ {t}_{\mathrm{shift}} $
. The maximum value of
$ {t}_{\mathrm{shift}} $
. The maximum value of
![]() $ \rho $
found from this analysis is included in Figure 3. The minimum p-values occurred in each instance for the maximum correlations; hence, the p-values are not included in this plot.
$ \rho $
found from this analysis is included in Figure 3. The minimum p-values occurred in each instance for the maximum correlations; hence, the p-values are not included in this plot.