INTRODUCTION
Hepatitis A virus (HAV) is an RNA virus that replicates in the liver and is shed into the stool, resulting in transmission by the faecal–oral route. Common modes of such transmission include contaminated water and food, and close person-to-person contact that occurs in families, institutions and childcare settings. While there is little evidence to support heterosexual contact as an important mode of HAV transmission, numerous outbreaks of HAV in men who have sex with men (MSM) have been reported worldwide. These outbreaks are probably associated with certain sexual practices including oral-anal and digital-anal sex, and insertive anal intercourse [Reference Gorgos1].
In Australia, as in most developed countries, improvements in public health led to marked declines in hepatitis A notifications in the 1980s and 1990s [Reference Nelson and Murphy2]. The average monthly notification rate for hepatitis A in Australia (as reported by the National Notifiable Diseases Surveillance System) was 11·65/100 000 (s.d. = 2·49) in the period 1991–1999, 2·04/100 000 (s.d. = 0·98) in the period 2000–2009, and since 2011 the average monthly notification rate has been <1/100 000 [3]. Decreased population immunity as a result of these declines is viewed as being responsible for numerous outbreaks of hepatitis A reported in Australia and other countries since the 1980s [Reference Gorgos1, Reference Ferson, Young and Stokes4–Reference Stokes, Ferson and Young6]. During this period a large outbreak of hepatitis A occurred in Sydney between February 1991 and October 1992, primarily in MSM, amounting to 570 notified cases [Reference Stokes, Ferson and Young6]. This outbreak coincided with a slightly smaller and more contained outbreak in Melbourne [Reference Stewart and Crofts5], as well as outbreaks in a number of other major overseas centres including London [Reference Kani7] and San Francisco [Reference Schomer8].
In 1994, an HAV vaccine was licensed in Australia for high-risk individuals including MSM and travellers to countries where HAV is endemic. While the vaccine is provided free to Indigenous children in Queensland, the Northern Territory, South Australia and Western Australia, vaccination for other at-risk individuals is not subsidized and this is a potential barrier to widespread uptake of the vaccine in Australia, particularly among young people who are most at risk. Vaccination is recommended but not funded for other groups at high risk of exposure to HAV including MSM. It is practice at some sexual health clinics in Australia for MSM attendees to be offered the first dose free and this may boost vaccination coverage in this group. An estimate obtained from vaccine sales data for the years 2008–2010 suggests that 1·1–1·7% of the population is vaccinated in Australia each year [Reference Heywood9]. Interestingly, ecological data from the same study show a trend of increasing seropositivity in the Australian population from ~34% in 1988 to ~55% in 2008 despite declining notification rates. This is thought to be due to factors including increasing travel to and immigration from HAV-endemic countries, and vaccine uptake rather than endemic transmission of infection.
Since 1996, no outbreaks of hepatitis A in Australian MSM have been reported, suggesting perhaps that immunity in this population is above the critical threshold beyond which sustained epidemics cannot occur [Reference Anderson and May10]. This threshold has been estimated at 40–60% in children [Reference Gay11], while evidence from implementation of the Indigenous vaccination programme in northern Australia shows near-elimination has been achieved with about 60% coverage of infants in affected communities [Reference Hanna, Hills and Humphreys12–14]. However, the threshold has not been estimated for MSM for whom the primary mode of transmission and contact networks are different. Weerakoon et al. [Reference Weerakoon15] estimated the level of immunity in MSM in Victoria to be 40–50% but lower in younger MSM. It was noted that this may be an underestimate of the level of immunity in the entire Victorian MSM population due to an over-representation of younger MSM in the study population, who were less likely to be HAV seropositive. Data from the Sydney Sexual Health Centre [Reference Ali16] indicate a level of immunity of 60–65% in MSM.
The aim of the study described here was to use the 1991/1992 Sydney outbreak data in conjunction with a mathematical model of HAV transmission in a MSM population to estimate the basic reproduction number (R 0) and the immunity threshold required to prevent sustained outbreaks of hepatitis A in this population [Reference Anderson and May10].
METHODS
Data sources
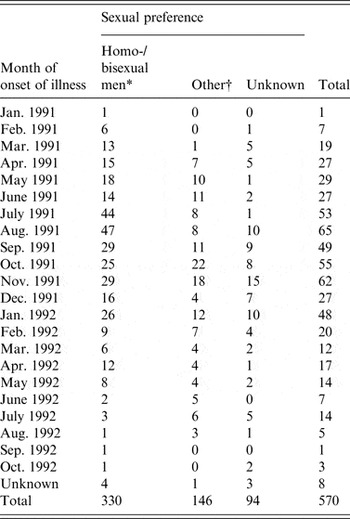
The primary data used in this study were taken from enhanced surveillance of the 1991/1992 Sydney outbreak of hepatitis A, in which a large proportion of infected individuals were MSM. The outbreak is summarized in a paper by Stokes et al. [Reference Stokes, Ferson and Young6] and an unpublished treatise by the same author [Reference Stokes17]. The outbreak was concentrated in young MSM, with sexual contact the most frequently reported mode of transmission in this group. Incident case numbers were reported monthly over the outbreak period and are summarized in Table 1. In the primary analysis we fitted the model to the MSM-only case counts but also conducted fits to the overall data as a test.
Table 1. Hepatitis A cases by month of onset of illness and by sexual preference (adapted from [Reference Stokes17])

* The model was fitted to these case numbers.
† Heterosexual men, women, children.
Description of models
A deterministic (compartmental) mathematical model of HAV transmission in a MSM population was developed. This model was formulated as a system of differential equations [Supplementary Technical Appendix, eqn (A1)] and used to estimate transmission and natural history parameters, including the force of infection (λ) and the basic reproduction number (R 0) [Reference Anderson and May10]. Figure 1 provides a schematic illustration of the model. In this simplified representation of HAV natural history the S state denotes those in the population who have never been infected with HAV and are thus susceptible to infection; the E state denotes those who have been exposed to HAV and are infected but not yet infectious; the I P state denotes those who are infectious but pre-symptomatic; the I S state denotes infectious individuals who develop symptoms including jaundice (the icteric stage of HAV infection); the I A state denotes infectious individuals who do not develop symptoms including jaundice (i.e. remain anicteric); and the R state denotes those who have recovered from HAV infection and have acquired lifetime immunity to re-infection. The model tracks the flow of people between these states over time. We have assumed that those in the symptomatic state (I S) do not engage in sexual activity because of the severity of symptoms (which include anorexia, fever, fatigue, malaise, myalgia, nausea and vomiting [Reference Hollinger, Martin, Knipe and Howley18]) and thus do not contribute to transmission of infection (see Supplementary Technical Appendix). The rate of entry and exit from the modelled population (as specified by the parameter α, see Table 2) implies that individuals remain in the population for a period of 30 years. This value was chosen because 98% of the notified cases in men for the 1991/1992 outbreak were attributed to individuals aged between 20 and 50 years.

Fig. 1. Schematic diagram of model structure. The compartments (S, E, I P, I S, I A, R) represent the natural history of hepatitis A infection as described in the Methods section. The modelled population is distributed across these ‘states’ and flows from one state to another at the rates indicated by the arrows. Descriptions of these rates and their inferred values are given in Table 1. Entry and exit from the modelled population [denoted by α in Table 1 and eqn (1) in the Technical Appendix] are not shown in the diagram. These rates are assumed to be equal in the model to ensure a conserved population size and have negligible bearing on transmission dynamics because the timeframe of the outbreak to which the model is fitted is short (<2 years) relative to the age-span of the population (30 years).
Table 2. Descriptions, fitting constraints and estimated plausible intervals (PIs) for model parameters

* This is equal to the inverse of the average duration an individual will spend in the sexually active population, in this case assumed to be 30 years.
† This is the proportion of the population assumed to be immune to infection prior to the onset of the outbreak due to prior exposure.
‡ This is the initial number of individuals assumed to be in the state (E, I P, I S) at t = 0 when first outbreak cases were observed.
The average duration of time spent in a state is equal to the inverse of the rate of efflux from that state. For example, the average duration of time an individual spends in the E state is constrained to 10–18 days in the fitting procedure.
An analogous event-driven stochastic model [Reference Vynnycky and White19] was derived from the deterministic model, whereby the probability of an event [transition from one model state to another, e.g. susceptible (S) to exposed (E)] occurring is proportional to the rate for that transition as defined in the deterministic model. The time to next event is sampled from an exponential distribution with mean 1/(sum of rates). This model, which accounts for stochastic variation in transmission dynamics, was used to derive attack rate (total number of cases in an epidemic) distributions and to estimate the probability of an epidemic occurring as a function of the proportion of the population that is immune prior to introduction of the pathogen.
The steady state solution for the system of differential equations [see Technical Appendix, eqn (A3)] was derived, allowing calculation of the basic reproduction number R 0 (the average number of secondary infections that will occur on average when an infectious individual is introduced into a wholly susceptible population) as 1/S*, where S* denotes the proportion of the population susceptible to infection at equilibrium [Reference Anderson and May10].
The deterministic and stochastic models were implemented and analysed in Matlab (The Mathworks Inc., USA) and the steady-state solution was derived in Mathematica (Wolfram Research, USA). (All computer codes are available on request.)
Fitting to data
The model was fitted to monthly case data from the 1991/1992 hepatitis A outbreak as described in the Data sources section above and summarized in Table 1.
In order to reduce the number of parameters to be fitted, rates of recovery for symptomatic and asymptomatic individuals were assumed to be equivalent such that the ratio of symptomatic to asymptomatic individuals is constant:
where p S is the proportion of those with pre-symptomatic infection that go on to develop symptomatic infection. This is a parsimonious assumption requiring only a single recovery parameter, γ, to be fitted and is justified on the basis that data to support different recovery rates from symptomatic and asymptomatic infection are not available.
Fitting was conducted in Matlab using the lsqcurvefit constrained least squares algorithm. Briefly, the fitting procedure involved minimizing the sum of the squared differences between the incidence of symptomatic cases predicted by the model at each time point and the case numbers at the respective time points in the outbreak data. Parameters, their descriptions and the upper and lower bounds used in the fitting process are given in Table 2. The published literature does not provide definitive estimates of natural history parameters for HAV infection and these bounds were thus necessarily wide and informed from a range of sources [Reference Hollinger, Martin, Knipe and Howley18, Reference Bauch20–Reference Martin and Lemon27]. We estimated the size of the MSM population in the postcodes that predominated in the 1991 outbreak to be in the range 5000–10 000 [Reference Madeddu28, Reference Poynten29]. However, because our model was simple in structure and did not account for heterogeneity in sexual behaviour (partner acquisition rates in particular), we allowed the population size (N) to be a variable in the fitting procedure in order to estimate an effective population size of exposed individuals. We assumed that prior to onset of the outbreak a proportion of the population (p I) was immune to HAV infection due to previous exposure. In order to inform the range (upper and lower bounds) for this parameter in the fitting procedure we collected data on HAV status in first time attendees identifying as MSM at the Sydney Sexual Health Centre indicating that prior to 1996 it is likely that 30% (vaccination was available in 1996 but not in 1991) or less of the population would have been immune [Reference Ali16]. Upper and lower bounds for this parameter were thus set at 0·5 and 0·1, respectively. The remaining population would have been susceptible to infection (i.e. occupy the S state) prior to the onset of the epidemic other than a small number of individuals, assumed to be in the range 1–20, already in the E, I P and I S/I A states when the first cases were observed.
The model was first fitted using the multistart optimization procedure with 100 000 initial starting points (the initial value for each parameter sampled randomly from the constraints listed in Table 1) in conjunction with lsqcurvefit to obtain an optimized point estimate of R 0. The robustness of the fit was then assessed by applying a parametric bootstrap procedure to add Poisson noise to the epidemic data. This was achieved by setting the observed case numbers as the means of Poisson distributions at each time point and generating 1000 alternate epidemic curves through sampling using the poissrnd routine in Matlab (Fig. A1 of the Technical Appendix shows outbreak data with 95% confidence intervals obtained from the parametric bootstrap procedure and an example dataset). Fitting was then conducted as described above using the multistart optimisation procedure with 100 initial starting points in conjunction with lsqcurvefit for each of these simulated datasets. In this way we were able to specify a 95% plausible interval (PI) for each parameter, this being the interval within which 95% of the estimates obtained for a particular parameter fall. In addition, the PIs for R 0 and the critical immunity threshold (p C) were calculated using the steady-state solution [Technical Appendix, eqn (A3)] and the following relationship [Reference Anderson and May10]:
Outbreak analysis
The event-driven (stochastic) model was then used to derive the distribution of epidemic attack rates with 100 000 simulations performed for immune proportions (p I) varing from 0 to 100% in 5% increments, starting with a single infected individual introduced at time t = 0. The input parameters for these simulations were generated using resampling with replacement from the 1000 parameter sets obtained through the fits to data with added noise, described above. We then used mixture models [Reference McLachlan and Peel30] to characterize the proportion of simulations that led to sustained epidemics at each level of prior immunity and thereby an immunity threshold (p C). In this context, sustained epidemics correspond to simulations in which the epidemic ceases through depletion of susceptible individuals rather than by chance elimination. We used maximum-likelihood estimation (optimization with Matlab routine fminunc) to fit two-component mixtures to the simulated attack rate data (see Technical Appendix for further details).
Sensitivity analysis
Sensitivity analysis was undertaken to assess the relative importance of the parameters in determining model outcomes. Partial rank correlation coefficients (PRCCs) [Reference Saltelli31] were calculated with respect to the goodness of the fit and epidemic potential; mean square error (MSE; mean of the squared differences between the model-predicted symptomatic cases and the outbreak data at each time point) and R 0 were the respective outcomes in this analysis. SaSAT software [Reference Hoare, Regan and Wilson32] was used to generate 10 000 parameter vectors by the method of Latin hypercube sampling [Reference Blower and Dowlatabadi33]. Uniform distributions were specified for all parameters with the same upper and lower bounds as used in the fitting process. The model was run for each parameter vector and the MSE and R 0 calculated for each. PRCCs were then calculated in SaSAT for parameter sets that yielded MSE <500 (n = 2285), MSE <300 (n = 681) and MSE <100 (n = 39).
RESULTS
Figure 2 shows the result of fitting the model to the 1991/1992 outbreak data. The PIs estimated for model parameters through the fitting process are given in Table 2. By fitting the model to simulated data we obtained a 95% PI for R 0 of 1·71–3·67. This corresponds to a 95% PI for the critical immunity threshold, p C, of 0·41–0·73, suggesting that prevention of sustained outbreaks may be possible with immunity as low 40% but would be achieved with high confidence at values >70%. The distributions of all model parameters are shown in Figure A2 of the Technical Appendix.

Fig. 2. Comparison between model fits to data with added Poisson noise and original 1991/1992 hepatitis A outbreak data. Solid lines enclosing grey area indicate 95% plausible intervals for modelled incidence, while the line with symbols (–■–) shows the original monthly incidence time-series.
When the model was fitted to the actual outbreak data using 100 000 multistart iterations, we obtained an optimised point estimate for R 0 of 3·3, corresponding to an immunity threshold of 70%. Similar results were obtained through analysis of the simulated outbreak data, with a threshold of 0·75 and an outbreak probability per initial MSM case of <4% when population immunity was 70%, as illustrated in Figure 3a . We also display the trend in size of these outbreaks in Figure 3b , showing that for an immune proportion <30%, very large outbreaks (>1000 cases) of hepatitis A would be likely in this community, with the mean size of such outbreaks falling below 100 only at an immune proportion >70%. Figure 3c shows the distribution of outbreak sizes as a function of the immune proportion. Additional plots showing the mixture fits to the simulated outbreaks are provided in Figure A4 of the Technical Appendix.

Fig. 3. (a) Probability that an outbreak will occur as a function of the immune proportion, and (b) the mean size (with 95% confidence intervals indicated by dashed lines) of such outbreaks based on mixture-model analysis of the simulated stochastic outbreaks. (c) Distributions of outbreak size as a function of the immune proportion.
Sensitivity analysis
The outbreak data were insufficiently detailed to obtain robust estimates for the values of most model parameters as indicated by PI estimates that did not differ greatly from the fitting constraints (see Table 2). Nonetheless, a sensitivity analysis was conducted and PRCCs were calculated for all model parameters with respect to the MSE of the fit and R 0. A complete listing of PRCCs and associated P values for all model parameters, at the three levels of MSE tested, is provided in Table A2 of the Technical Appendix. In summary, the analysis identified λ and κ as the most important parameters in determining both MSE and R 0. The analysis also identified γ, p S, and p I as important but with slightly different rankings with respect to MSE and R 0.
In the primary analysis, the model was fitted to cases reported in men who identified as homosexual or bisexual (n = 330). However, a further 240 cases (see Table A1, Technical Appendix) were also recorded as heterosexual men/women and children (n = 146) or as unknown (n = 94). It is probable that a proportion of these 240 cases were also MSM as only 53 cases were reported in women. We fitted the model to the total outbreak (n = 570) and while this resulted in a lower point estimate of R 0 (2·63) the PIs for R 0 largely overlapped (1·68–3·27 for the total outbreak and 1·71–3·67 for the MSM cases).
DISCUSSION
In this study we applied a deterministic model of HAV transmission to an epidemic in an MSM population in Sydney in 1991/1992 to estimate the basic reproduction number, R 0, and the critical immunity threshold. Robustness in fitting was assessed by adding Poisson noise to the data, with PIs thus generated for model parameters and for R 0. We obtained an optimized point estimate for R 0 of 3·3 (PI 1·71–3·67) corresponding to an immunity threshold of 70% (PI 41–73). To our knowledge this is the first study to estimate R 0 for an MSM population. We also examined the distribution of attack rates under simulated outbreaks using a stochastic analogue of the deterministic model at varying levels of population immunity. Mixture-model analysis of the simulated outbreaks confirmed our immunity threshold estimate of 70% and thus our estimate of 3·3 for R 0.
In most developed country settings, HAV incidence has declined as a result of improved sanitation and socioeconomic conditions such that infection is more likely to occur at a later age when symptoms are more severe. In this context MSM and travellers are among those at highest risk. A highly effective vaccine is available for HAV and is recommended in Australia for these groups [34, 35], but it has been unclear what level of coverage needs to be achieved in order to obtain herd immunity and prevent major outbreaks. Our study suggests that vaccine coverage in the vicinity of ⩾70% is required for MSM populations. While the outbreak used to estimate this threshold occurred in Sydney, the Gay Periodic Surveys [36] provide strong evidence that MSM populations in major urban centres in Australia share broadly similar behavioural and demographic characteristics. These populations differ in size, Sydney being the largest, and it is possible that the smaller MSM populations (e.g. Adelaide) may not support sustained epidemics. However, as noted in the Introduction, the Sydney outbreak coincided with a smaller outbreak in Melbourne and with outbreaks in San Francisco and London. We therefore consider our estimate for the immune threshold of ~70% to be broadly applicable to MSM populations in most large Western metropolitan centres. However, this threshold may be different for MSM populations in other settings such as South East Asia that have different behavioural and sociodemographic characteristics and different age structures.
Visual inspection of Figure 2 suggests a good fit of the model to the epidemic data. Sensitivity analysis indicated four natural history parameters (λ, κ, γ p S, p I) as being the most important in determining both MSE and R 0. This is unsurprising, as with the exception of p S these completely determine R 0, which is the primary determinant of epidemic shape. However, in respect to the durations of the three infectious periods (E, I P, I S/I A) our estimated PIs are essentially identical to the original fitting constraints suggesting that the data are not informative for estimating these parameters. This is partly a consequence of attempting to fit a large number of parameters with respect to a relatively small number of data points. However, duration of infection is usually estimated from observations of clinical onset in infector–infectee pairs (see e.g. [Reference Donnelly37]), but data of this nature were not available for outbreak studied here.
Other modelling studies have estimated R 0 in the range ~0·4–4 [Reference Gay11, Reference Van Effelterre25, Reference Farrington, Kanaan and Gay38–Reference Martinelli41] for HAV outbreaks in general populations and Gay et al. have estimated the immunity threshold to be 40–60% in children [Reference Gay11], corresponding to R 0 in the range 1·7–2·4. Our estimate of 3·3 (PI 1·71–3·67) is therefore consistent with other estimates but lies towards the high end of the range. This is perhaps not surprising as consideration of a large outbreak in isolation may lead to overestimates in R 0, given that other smaller outbreaks may not have been identified. R 0 is dependent on the contact rate, the transmission probability and the duration of infection [Reference Anderson and May10]. As the duration of infection is the least likely to vary substantially between populations, a relatively high estimate of R 0 can be attributed to a high contact rate and/or a high transmission probability. While in Australia contact rates are generally higher in MSM than in the general population [Reference Grulich42, Reference de Visser43] the transmission probability for this mode (sexual contact) of HAV transmission is unknown. In our model, these two parameters are implicitly contained in the force-of-infection term and we make no attempt to infer their values separately. This is partly because the simple structure we have adopted does not account for heterogeneity in sexual contact rates and therefore an overall estimate of the mean contact rate cannot be inferred.
We assumed that symptoms in the cases of acute hepatitis A infection identified in the 1991/1992 outbreak were severe enough for these cases to seek medical care. While we were not able to identify any published study to support our assumption that those with symptoms are too sick to engage in sexual activity we feel this is a reasonable assumption that is concordant with the expert opinions we sought from clinicians on this matter, including those involved in this study (authors C.K.F. and B.D.). We tested the contrary assumption that those with symptoms do not abstain from sexual activity and while this had some impact on the estimated values of model parameters it had very little impact on the estimation of R 0 (3·26 vs. 3·3 with largely overlapping confidence intervals) and thus on the critical immunity threshold.
We have noted above the difficulty of independently estimating many parameters for a model consisting of a small number of equations and the limitations imposed by the simple contact structure that assumes homogeneous mixing. In addition, we have assumed a single mode of transmission in a closed MSM population. While the outbreak we analysed occurred primarily in MSM, it did not occur exclusively in this subpopulation and it is likely that some transmission should be attributed to settings such as households, workplaces and food outlets. Our model does not account for these other modes of transmission or for interaction between MSM and the wider community. We chose a simple model structure that captures the key features of the 1991/1992 outbreak and enabled us to obtain a credible estimate of R 0. A far more complex model would be required to describe the entire community and its detailed contact structure and would result in much greater uncertainty in the estimates obtained.
In conclusion, we fitted a simple model of HAV transmission to data from a hepatitis A outbreak that occurred in Sydney in 1991/1992, primarily in MSM. We estimate that in order to minimize the likelihood of future outbreaks of sexually transmitted hepatitis A in MSM, around 70% of this population must be immune. HAV is no longer endemic in Australia meaning this level of immunity can only be reached through vaccination. Weerakoon et al. [Reference Weerakoon15] have estimated HAV seroprevalence in MSM in Victoria to be 54% in those aged >30 years, 32% in those aged <30 years and only 19% in those aged <20 years. Furthermore HAV vaccination was only recorded in 49% of the study population. On the other hand, data from Sydney Sexual Health Centre [Reference Ali16] indicate that 60–65% of the MSM population that attended this clinic between 2004 and 2012 were seropositive or reported having been vaccinated and this proportion remained steady over this time interval. These studies suggest that the level of immunity in MSM in Australia may be below the threshold required to prevent major HAV outbreaks. Travel to countries where HAV is endemic is probably the most important risk factor for MSM. There has only been low-key promotion of HAV vaccination for MSM in Australia, primarily through publication of the STI/HIV Testing Guidelines for Asymptomatic MSM [35] and the Australian STI Management Guidelines [44]. There should be greater emphasis on education about the importance of HAV vaccination for young MSM, particularly travellers, and subsidizing immunization in this population should be considered. Other measures such as promoting vaccination at Gay community events [Reference Storholm45] and providing no-cost vaccinations in settings such as sexual health clinics, drug treatment programmes, prisons, universities and other community resource centres that reach high-risk MSM may also help to ensure immunity does not fall to levels where major outbreaks are likely to occur.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0950268815002605.
ACKNOWLEDGEMENTS
D.G.R. is funded by a National Health and Medical Research Council Program Grant (568 971). The Kirby Institute receives funding from the Australian Government Department of Health and Ageing. The views expressed in this publication do not necessarily represent the position of the Australian Government. The Kirby Institute is affiliated with the Faculty of Medicine, University of New South Wales.
DECLARATION OF INTEREST
None.