Inter- and intra-specific exposure to parasites and pathogens via the faecal–oral route: a consequence of behaviour in a patchy environment

Summary

Livestock herbivores are at risk of inter- and intra-specific exposure to parasites/pathogens via the faecal–oral route during grazing. Each contact between livestock and faeces in the environment is a potential parasite/pathogen transmission event. Cattle grazing contact with faeces varies in relation to the species depositing the faeces and the distribution of the faeces. We used a foraging model to simulate the grazing behaviour of beef cattle in two grazing systems to compare the relative inter-specific and intra-specific exposure risks to parasites/pathogens. Overall, there is a greater level of intra- vs. inter-specific risk via the faecal–oral route. However, under certain conditions, particularly for microparasite infections, e.g. paratuberculosis in rabbits and bovine tuberculosis in badgers, wildlife may pose a significant exposure risk to parasites/pathogens. These risks can be enhanced when cattle are first turned out onto pasture and in situations where intra-specific variations in wildlife behaviour result in more dispersed defecation patterns.

INTRODUCTION

Grazing herbivores must make foraging decisions in pastoral environments that are contaminated with faeces. Faeces may contain both macroparasites (e.g. parasitic helminths) and microparasites (e.g. bacterial pathogens) that can be transmitted via the faecal–oral route when grazing [1]. However, herbivores are unable to detect the presence of parasites in the environment, but instead use faeces as a cue for parasites [2]. Thus, herbivores generally avoid grazing near swards contaminated with both their own faeces [3, 4]; and faeces of other species [3, 5, 6]. Additionally, when forced to graze faecally contaminated forage, or pasture spread with slurry, herbivores will modify their behaviour to select the top uncontaminated part of the sward [4, 7–9]. This selective behaviour is believed to have evolved as a method of parasite avoidance [10, 11] and has been shown to significantly reduce the grazing herbivores intake of parasite larvae [12]. However, in both natural systems and agricultural systems, selective grazing to avoid faeces creates a heterogeneous distribution of forage resources consisting of a mosaic of gaps (short, non-contaminated, grazed patches) and tussocks (tall, faecally contaminated, avoided patches) [13, 14]. Nutrient leaching from faecal deposits results in these faecally contaminated tussocks of grass having relatively high nutrient contents [15]. Thus the mosaic represents a nutrition vs. parasitism trade-off in that the faecally contaminated tussocks are localized concentrations of both nutritional resources and parasites [16]. Grazing herbivores must make decisions in relation to this trade-off in order to try and maximize the nutritional benefits and minimize the parasitic cost.

Grazing herbivores share their environment with a number of other host animal species, and will come into contact with their own faeces and faeces of other species. Thus, there is the potential for indirect inter-specific and intra-specific disease transmission via the faecal–oral route during grazing. The faeces of different species pose a risk of a variety of different parasites/pathogens to the grazing herbivore, e.g. cattle are at risk of bovine tuberculosis from badger faeces [17] and paratuberculosis from rabbit faeces [18, 19]. Defecation pattern also varies both between species and within species, from single deposits dispersed throughout the environment, to the accumulation of faeces at latrines. For example, rabbits deposit pellets both randomly within their home range and at latrine sites [20]. Badgers tend to accumulate defecations at latrines, although at low densities there are an increasing number of single defecations throughout their habitat [21]. Faeces are often present at latrines for extended periods of time due to wildlife hosts adding fresh faecal contamination. In contrast, for highly dispersed defecation patterns, the faeces will decay from the contaminated patches at a faster rate. These faecal patterns represent patterns of pathogen distribution in the grazing environment. Each oral contact of a susceptible host with faeces (e.g. a bite) represents a potential transmission event. Smith et al. (unpublished observations) showed in two separate grazing experiments that cattle vary their grazing response to faeces from different species and to different faecal patterns in the environment. Thus, in isolation these two factors affect the contact rate between herbivores and faeces/pathogens in the environment. However, in real grazing environments it is the interaction of these two effects that will determine livestock contact with faeces in the environment and therefore the risk of exposure to parasites and pathogens.

Herbivore grazing behaviour in relation to faeces is also affected by the grazing environment (e.g. nutritional environment) [22], therefore grazing management practices which alter the environment will also affect herbivore contact with faeces. Rotational grazing, a practice to optimize pasture growth and productivity, involves the rotation of livestock around a number of paddocks giving each paddock a period of rest for regrowth. This grazing practice allows the herbivore to graze almost all the available pasture in order to stimulate sward growth during the rest period. The grazing pressure in rotational systems is therefore relatively high compared to set stocking where animals continually graze a set pasture size so that grass growth is approximately equal to animal intake. Grazing systems in which the forage availability may become limiting can result in animals being forced to graze faecally contaminated vegetation and studies have suggested that livestock in rotational systems have increased parasite loads compared with set stocking [23, 24]. Furthermore, farm management practices which intensify the grazing pressure are known to increase livestock contact with badger faeces [5, 6, 25].

The risk of livestock exposure to parasites and pathogens in the environment is therefore driven by the interplay between herbivore grazing behaviour, pattern of contamination in the environment and farm management systems. This paper builds on a modelling framework (whose development started with Marion et al. [26]), which focused on resource use efficiency from the point of view of the animal and the resource manager, using a spatially explicit individual-based stochastic model incorporating grazing and avoidance behaviour. That framework demonstrated the importance of spatial heterogeneity in such systems. A further study used the model to explore the importance of search distance on resource use efficiency using an extension of this earlier model [27]. The modelling framework has since been developed further to explore the impact of spatial heterogeneity and search distance on the risk of contact with faecal contamination [28]. Here we employ this model [28] to simulate beef cattle grazing behaviour in order to determine the impact of these interactions on herbivore contacts with faeces/pathogens in the environment. The first aim of this paper is to simulate the behavioural patterns exhibited by cattle in field experiments (Smith et al., unpublished observations). The subsequent aims are to use the simulation model to quantify the impact on cattle contact with faeces in the environment of: (1) different levels of cattle avoidance of faeces; (2) different faecal defecation patterns of wildlife; and (3) the interaction of these factors in both set-stocking and rotation grazing.

MATERIALS AND METHODS

Model

We used simulation code implementing an extended version of a grazing model [26] (that explicitly captures herbivore contact with faecal contamination in grazing systems, i.e. parasite/pathogen exposure via the faecal–oral rote and thus risk of infection), to address our objectives. The model used in this paper extends that described in Marion et al. [28] which itself builds on an existing framework [26, 27] which primarily addressed issues relating to resource use efficiency. The model [26–28] is based on a series of empirically observed behavioural rules-of-thumb that are used to capture herbivore grazing behaviour in heterogeneous landscapes: (1) herbivores visually assess local neighbourhood to select tall and more nutrient-rich swards over short and nutrient-poor swards [29], and (2) herbivores select non-contaminated swards over faecally contaminated swards [4]. However, herbivores have incomplete knowledge of the local environment. Thus the model describes the grazing system as a grid of spatially configured patches, and the selection behaviour of grazing herbivores is captured using a two-stage process of herbivore grazing in a heterogeneous environment (Fig. 1). Herbivores first select and approach patches based on local visual cues, e.g. sward height and sward nutritional value. The second stage of the selection process is based on patch olfactory cues, e.g. faecal contamination at the patch site. Herbivore grazing decisions (selection or rejection of a patch) are determined by the relative strength of these cues. Previous studies using this model [27], show the importance of limited information and spatial heterogeneity in assessing infection risk, necessitating the introduction of the following novel features: (i) wildlife faecal contamination and associated decay and avoidance parameters; (ii) a model for faecal deposition by livestock; and (iii) measurement of daily grazing and investigative contact rates as indicators of infection risk. Features such as nearest-neighbour search, grass growth, intrinsic bite rate, and avoidance of livestock faeces were introduced in the initial model [26].

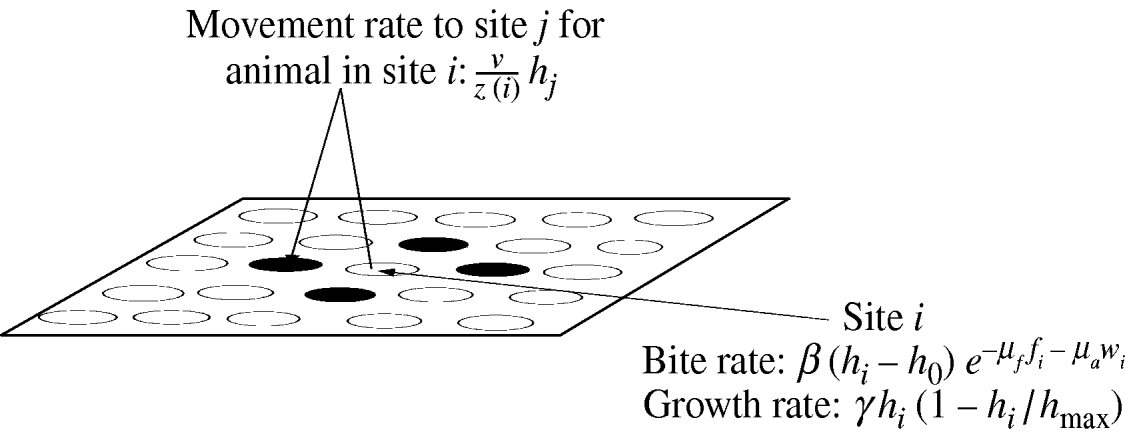
Fig. 1. An overview of the spatially configured model framework. Animals graze in the local patch and search nearest-neighbour patches (patches are denoted by circles) only. Where ν is the intrinsic movement rate; z(i) is the number of nearest-neighbour patches; h _i is the resource available in patch i; h _j is the resource available in patch j; h ₀ is the minimum grazable portion each patch; h _max is the maximum resource available in each patch; γ is the intrinsic growth rate of the sward. The movement rate weights the sward height of each neighbouring patch and is used to determine the actual movement of individual animals. The bite rate at each patch is linear in the sward height (above the minimum grazable portion h ₀) and is reduced exponentially by faecal avoidance exp(−μ_ff _i−μ_aw _i), where μ_f is the level of avoidance of herbivore faeces, μ_a is the level of avoidance of wildlife faeces, and f _i and w _i represent the respective levels of herbivore and wildlife faecal contamination at patch i. Sward growth at each patch is logistic as shown.

The extension and modifications used here are as follows. We introduce a daily intake requirement for the livestock, denoted dR _k for animal k. Within a given day, animal k will continue grazing until the intake accumulated over the current day reaches dR _k, at which point it stops grazing until the following day when this process is repeated. To describe a range of different management practices, such as set-stocking and rotation, the model also allows the animals to be repeatedly removed and returned to the pasture. During the periods when the animals are absent from the system, sward growth and faecal decay continue as before, but grazing and defecation are suspended. When the animals return to the pasture, their accumulated intakes are reset to zero. The search distance of herbivores is currently unknown and extremely difficult to measure [30]. However, it has been demonstrated that in the context of a managed temperate grazing system, such as that considered here, varying the search distance had no significant effect on model-predicted infection risk [27], and therefore here we adopt a nearest-neighbour search model.

The spatially explicit agent-based model, used in this paper to assess infection risk to livestock from inter- and intra-specific faecal contacts, has been previously fully described [28]. However, for completeness a short description is included here. The model state-space represents, at site i, the sward height h _i, the number of animals c _i, and the contamination f _i due to livestock and w _i due to external sources such as wildlife faeces. In addition s _k represents the stomach contents of animal k=1, …, A, where the total number of animals is . All state variables are assumed to be integers. The sward growth rate in each patch, i=1, …, N, is assumed to be logistic γh _i(1−h _i/h _max), where γ is the intrinsic (i.e. without density dependence) growth rate of the sward, h _i is the resource available at patch i and h _max is the maximum resource available in each patch. The grazing rate of each individual animal in patch i at time t, is

(1)

where β is the per capita feeding rate, h ₀ represents the ungrazable portion of the sward, and μ_f and μ_a are the avoidance parameters for livestock and wildlife faeces respectively. When a grazing event occurs the local sward height is reduced, and the stomach contents increased by one unit. The rate of decay of faecal contamination at patch i is λ_ww _i for wildlife faeces and λ_ff _i for livestock faeces. Individuals are assumed to defecate in their current patch at a rate,

(2)

where the Heaviside function Θ(s _k−s ₀), which is unity if s _k>s ₀ and is zero otherwise, ensures that individuals deposit s ₀ units of faeces per deposition event only if they contain at least s ₀ units of forage. This means that intake and livestock faeces are measured in the same units, and the level of faecal contamination would have to be rescaled to allow direct comparison with empirical measurements of deposited faecal mass.

The search distance of herbivores is currently unknown. However, the sensitivity of the modelling framework to changes in the search distance was tested in [28], and it was found that due to the high movement rate of grazing cattle in field sizes typical of agricultural systems, the frequency of cattle contact with faeces is insensitive to search distance. Therefore as previously [26, 27], we assume nearest-neighbour searching at rate

(3)

for each animal at patch i, the z(i) (usually 4 except at the edge of the lattice) nearest neighbours of site i denoted as j∊N _i, where ν is the intrinsic search, or movement rate.

The events and event rates are summarized in Table 1, and subsequently this model is simulated as a stochastic (discrete state-space Markov process) model in which during a given small time-interval from t up to t+δt, written as (t, t+δt), an event of type x with associated rate r _x occurs with probability r _xδt. The total event rate is given by summing the bite, movement and deposition rates in Table 1 across all animals, and the growth and faecal decay rates over all patches. The time-step δt is then chosen such that Rδt is <1 (i.e. all the terms r _xδt<1 can be interpreted as probabilities). For example, see Renshaw [31] for an introduction to Markov process modelling and simulation of biological populations, and Swain et al. [27] for a more detailed description of the above algorithm.

Table 1. Agent-based model of grazing behaviour

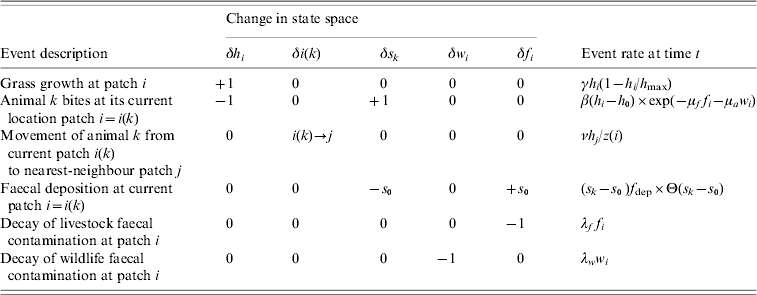
The model is defined in terms of the sward height h _i, the number of animals c _i, and wildlife and livestock faecal contamination, respectively w _i and f _i, in patches i=1, …, N. The sward grows logistically at rate γh _i(1−h _i/h _max), and an individual agent, labelled k, currently at patch i takes bites at rate β(h _i−h ₀) exp(−μ_ff _i−μ_aw _i), moves from patch i to a nearest-neighbour patch j at rate νh _j/z(i), or deposits faeces in patch i at rate (s _k−s ₀)f _dep Θ(s _k−s ₀). Note that in the deposition rate Θ(.) is the Heaviside function and Θ(s _k−s ₀) is unity if the stomach contents s _k exceeds the size of the faecal deposit s ₀, and is zero otherwise. The faecal contamination decays at rates λ_ww _i for wildlife faeces and λ_ff _i for livestock faeces.

Parameterization

The model was parameterized to simulate a grazing situation with three beef cows in a set-stocking scenario, except for the rotational grazing scenario specified below. It was important to ensure the simulations replicated the spatial scale of agricultural systems as parasite/pathogen transmission occurs on a bite by bite basis. Thus, all simulations were carried out in a 70×70 patch lattice, where each patch represented 0·5 m², the approximate area of one cattle faecal pat and the rejected area around it [30] and the whole lattice represented a pasture of 0·25 ha. The simulation size was a compromise between the duration of individual runs of the model and the number of animals in the system. The resources in each patch are defined as the number of bites available per patch. Each cattle bite is approximately 0·01 m² [30], thus the 0·5 m² patch used in these simulations contains 50 bite-areas of forage resource, and the ungrazable portion of each patch is set at 50 units of forage. However each patch starts with an initial sward ‘height’ (h _start) of 200 units of forage resources per patch; and has a maximum sward height (h _max) of 400 units per patch. In the model each single bite event removes one unit of forage. The sward growth rate (γ=0·00004) was calculated to provide a set-stock scenario, i.e. where mean grass height is stable and sward growth is equal to herbivore intake, where herbivore grazing rate (β) represented approximately 30 000 bites of herbage a day (β=0·1) [30], and a herbivore movement rate (ν) represent a cattle step rate of approximately three steps a minute [32] (ν=0·015). At the start of the simulation, cattle were introduced into a pasture free of any cattle faecal contamination [f _i=0 (∀i=1, …, N)] and cattle deposited faeces approximately 10–15 times a day [30] (f _dep=1·0, s ₀=2000·0). Each individual animal's daily intake requirement was not set, allowing the animals to graze the whole day. Cattle faeces had a decay rate, where degradation to approximately 10% of the initial faecal deposit would occur 3 months after deposition [15] (λ_f=0·00001776). Initial response by cattle to their own fresh faeces was set at almost complete avoidance [3] (μ_f=0·0025, corresponding to a bite rate from fresh faecally contaminated patches of <1% of the bite rate from clean patches). Note that the level of avoidance is set by the product μ_f∗f _i which in the case of a fresh faecal deposit equals 5, and corresponds to a reduction in bite rate to <1% of a non-contaminated sward. In order to allow a contrast between levels of inter- and intra-specific contact with faeces, additional faeces were added to the system and were parameterized to represent different scenarios of wildlife faeces as described in the model runs performed. All the simulations were run for 100 days, which for the set-stock scenarios, allowed intake and sward heights to reach equilibrium.

Model runs performed

Cattle avoidance of wildlife faeces

To investigate the impact of varying the level of cattle avoidance of wildlife faeces in isolation, simulations were run varying cattle avoidance for each patch of wildlife faeces. A herbivore's avoidance level of a patch is dependent on the amount of faeces within it. Thus, in all simulations for cattle avoidance of wildlife faeces, there were 150 randomly selected patches contaminated with faeces. Each contaminated patch had 6·67 units of wildlife faeces, giving a total of 1000 units of wildlife faeces in the environment. Six scenarios were modelled with varying levels of cattle avoidance of faeces: (1) μ_a=0 (cattle initially show no avoidance of fresh wildlife faeces, representative of cattle avoidance of rabbit faeces [18]). (2) μ_a=0·15, (3) μ_a=0·30, (4) μ_a=0·45, (5) μ_a=0·60, (6) μ_a=0·75 (cattle initially show almost complete avoidance of fresh wildlife faeces, representative of badger faeces [5]). As noted above the level of avoidance is set by the product μ∗f _i which for the complete avoidance case here is 0·75∗6·67~5 and again this corresponds to a reduction in initial bite rate at a contaminated patch to <1% of a non-contaminated sward. In order to consider cattle avoidance of wildlife faeces in isolation, all wildlife faeces in the environment were set to have no decay (λ_w=0).

Defecation pattern

To investigate defecation pattern in isolation, simulations were run with different defecation patterns and the same total amount of wildlife faeces in the environment (1000 units), varying the number of contaminated patches. Four scenarios were modelled varying the number of wildlife faecally contaminated patches: (1) One wildlife faecally contaminated patch (representative of a latrine-type defecation pattern), (2) 50 wildlife faecally contaminated patches, (3) 100 wildlife faecally contaminated patches, (4) 150 wildlife faecally contaminated patches (representative of single dispersed deposit defecation patterns). In all cases the contaminated patches were selected at random. The initial level of avoidance by cattle of each patch contaminated with wildlife faeces was set to represent ‘almost complete’, i.e. the same degree of avoidance level that cattle show towards their own faeces. As a herbivore's avoidance level of a patch is dependent on the amount of faeces in the contaminated patch, in order to get the same initial level of avoidance μ_a varied for each defecation pattern (1 patch, μ_a=0·005; 50 patches, μ_a=0·25; 100 patches, μ_a=0·50; 150 patches, μ_a=0·75). To investigate the effect of defecation pattern in isolation, all wildlife faeces in the environment were set to have no decay (λ_w=0).

Interaction between level of avoidance behaviour and wildlife defecation pattern

Set-stock grazing

To investigate the interaction between avoidance level and wildlife defecation pattern within a set-stocking context, four scenarios were modelled with two defecation patterns (the same total amount of wildlife faeces in the environment (1000 units), varying the number of contaminated patches) and two levels of cattle avoidance: (1) a single contaminated patch (representing a latrine-type defecation pattern), with no cattle avoidance of wildlife faeces (μ_a=0), (2) a single contaminated patch (latrine-type defecation pattern) and almost complete avoidance (for one patch contaminated μ_a=0·005), (3) 150 contaminated patches (representing a dispersed defecation pattern) and no cattle avoidance of wildlife faeces (μ_a=0), (4) 150 contaminated patches (representing a dispersed defecation pattern) and almost complete avoidance of wildlife faeces (for 150 contaminated patches μ_a=0·75). In order to include the effect of faecal decay, wildlife faecal decay rate was set so that at the end of the simulation (day 100), 10% of the initial wildlife faeces remained in the system (λ_w=0·00001599).

Rotation grazing

The same four scenarios described in the previous section were also used to investigate the interaction effects of defecation pattern and cattle level of avoidance of wildlife faeces within a rotational grazing scenario. For rotational grazing, the set-stock pasture was divided into two pastures and three cattle were rotated round each pasture twice. Only one of the pastures was simulated, thus the simulations were carried out on a 49×50 patch lattice. Each patch represented 0·5 m² and the whole lattice represented a pasture of 0·125 ha, half the size of the set-stock pasture. The rotation was 25 days in the simulated pasture, 25 days out, so that two complete rotations lasted 100 days. To prevent ‘unrealistic’ overgrazing on the first day back in the pasture, the cattle's daily intake requirement was set to the equivalent daily intake of cattle in a set-stock environment (dR _k=9000).

Measurements of forage availability

For the realistic grazing scenarios, i.e. the set-stock and rotation grazing, measurements of grass availability were gathered to ensure the model successfully created a heterogeneous gap and tussock mosaic, and thus presented the grazing cattle with the nutrition vs. parasitism trade-off. The following statistics for grass availability were gathered over the 10 repeated stochastic simulations:

1. (1) The mean forage availability (number of bites available per 0·5 m²) of wildlife faecally contaminated patches with high cattle avoidance. No measurements of forage availability were gathered for wildlife faecally contaminated patches with no cattle avoidance as tussocks would not form at these patches due to non-avoidance of faeces.

2. (2) The mean forage availability (number of bites available per 0·5 m²) of cattle faecally contaminated patches.

3. (3) The mean forage availability (number of bites available per 0·5 m²) of non-contaminated patches.

Measurements of cattle grazing behaviour

The grazing statistics (model outputs) were gathered over 10 repeated stochastic simulations for each scenario described above.

1. (1) Number of bites from wildlife faecally contaminated patches per day.

2. (2) Number of investigations of wildlife faecally contaminated patches per day. An investigation was defined as a visit to a patch with no bites.

3. (3) Number of bites from cattle faecally contaminated patches per day.

4. (4) Number of investigations from cattle faecally contaminated patches per day.

RESULTS

Forage availability in the set-stock and rotation grazing systems

Overall the mean number of bites of forage available in a 0·5 m² patch (i.e. sward height) of wildlife faecally contaminated patches and cattle faecally contaminated patches was greater than the mean number of bites of forage available in a 0. 5 m² patch of clean non-contaminated patches in both set-stock and rotational grazing systems (Fig. 2). In the set-stock system, at the maximum difference in forage availability, wildlife faecally contaminated patches and cattle faecally contaminated patches had 2·6- and 2-fold greater forage availability than the non-contaminated patches, respectively (Fig. 2 a). Similarly, in the rotational grazing system, at the maximum difference in forage availability, wildlife faecally contaminated patches and cattle faecally contaminated patches had 3- and 2·3-fold greater forage availability than the non-contaminated patches, respectively (Fig. 2 b).

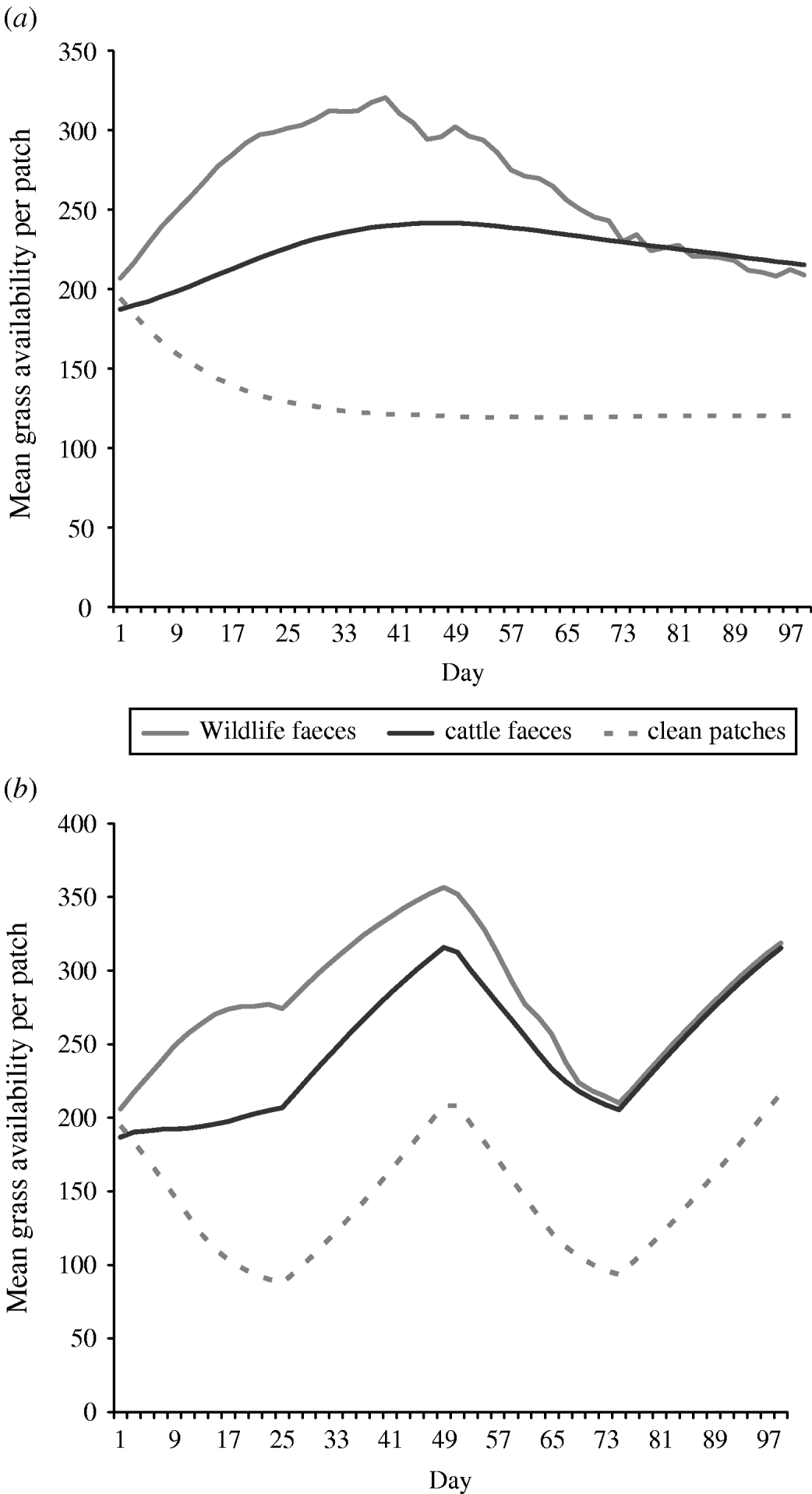
Fig. 2. The mean grass availability of wildlife faecally contaminated patches with high cattle avoidance, cattle faecally contaminated patches and clean non-contaminated patches for (a) set-stock grazing and (b) rotational grazing systems. The mean grass availability per type of patch (e.g. wildlife faeces, cattle faeces, clean patch) showed little difference between each of the scenarios simulated in each grazing system, therefore the values shown are mean number of bites of forage available per 0·5 m² patch type per day averaged over all the scenarios simulated for each grazing system.

Cattle avoidance of wildlife faeces

Increasing cattle avoidance of wildlife faeces is associated with a decrease in the number of cattle bites from wildlife faecally contaminated patches both pre- (days 1–30) and post-system equilibrium (days 31–100). However, post-equilibrium there is no difference in grazing contact levels between the three lowest avoidance levels (e.g. in scenario 1, μ_a=0; scenario 2, μ_a=0·15; scenario 3, μ_a=0·3) (Fig. 3 a). Increasing cattle avoidance of wildlife faeces is associated with an increase in the number of investigations of wildlife faecally contaminated patches both pre- and post-equilibrium (Fig. 3 b). The overall number of bites and number of investigations from cattle faecally contaminated patches is significantly greater than the number of bites/investigations from wildlife faecally contaminated patches (i.e. up to 46 times more bites and up to 14 times more investigations; Fig. 3 a, b).

Fig. 3. Effect of herbivore level of avoidance (μ_a) on (a) number of bites taken and (b) number of investigations taken by cattle from wildlife faecally contaminated patches (left y-axis) and cattle faecally contaminated patches (right y-axis). μ_a values represent the initial level of avoidance of cattle to fresh wildlife faecal patches. μ_a=0 is when cattle initially show no avoidance of fresh wildlife faeces. Avoidance increases with increasing μ_a values up to μ_a=0·75 which is when cattle initially show almost complete avoidance of fresh wildlife faeces. Cattle faecal patches represent faeces in the environment deposited by the cattle during the simulation. Figures are the mean number of bites/number of investigations from wildlife faecally contaminated patches per day averaged over 10 simulations, ±standard deviation. Grazing and investigative contacts with cattle faeces showed little difference between each of the scenarios simulated, therfore the values shown are the mean number of contacts with cattle faeces over all the scenarios simulated.

Defecation pattern

Increasing the number of faecally contaminated patches (i.e. more dispersed faecal contamination patterns) is associated with an increasing number of cattle bites and investigations from wildlife-contaminated patches both pre- (days 1–40) and post-equilibrium (days 41–100) (Fig. 4 a, b). However, the relative numbers of both grazing contacts and investigative contacts are less than commensurate with area. For example, defecation patterns with 150 contaminated patches (scenario 4) lead to only approximately 90 times greater number of bites and 100 times greater number of investigations compared to single contaminated patches (scenario 1). The overall number of bites and number of investigations from cattle-contaminated patches is significantly greater than the number of bites/investigations from wildlife faecally contaminated patches (i.e. up to 4251 times more bites and up to 191 times more investigations; Fig. 4 a, b).

Fig. 4. Effect of defecation pattern on (a) number of bites taken and (b) number of investigations taken by cattle from wildlife faecally contaminated patches (left y-axis) and from cattle faecally contaminated patches (right y-axis). One contaminated patch is representative of latrine-type defecation patterns, and 150 contaminated patches is representative of single dispersed, deposit defecation patterns. Cattle faecal patches represent faeces in the environment deposited by the cattle during the simulation. Figures are the mean number of bites/number of investigations from wildlife faecally contaminated patches per day averaged over 10 simulations, ±standard deviation. Grazing and investigative contacts with cattle faeces showed little difference between each of the scenarios simulated, therefore the values shown are the mean number of contacts with cattle faeces over all the scenarios simulated.

Set-stock grazing

The combined effects of avoidance and defecation pattern demonstrate that level of faecal avoidance has a lesser effect than defecation pattern on the number of cattle contacts with faeces, e.g. dispersed patterns of both avoidance levels have a significantly greater number of grazing contacts and investigative contacts relative to single latrine patches (Fig. 5 a, b). However, this observed increase in contacts with the number of contaminated patches is not commensurate with the area contaminated, e.g. 150 contaminated patches result in only 105 times more bites compared than one contaminated patch (Table 2). There is no significant difference in grazing contacts or investigative contacts between the two different single-patch wildlife-faeces scenarios (e.g. scenarios 1 and 2; Fig. 5 a, b). In contrast, a comparison of the dispersed wildlife-faeces scenarios (scenarios 3 and 4) demonstrates that grazing contacts (Fig. 5 a) are greatest in scenario 3 (dispersed wildlife faeces and no cattle avoidance) pre–equilibrium (days 1–39), and then in scenario 4 (dispersed wildlife faeces and high cattle avoidance) post-equilibrium (days 40–100) (Fig. 5 a). Investigative contacts with dispersed wildlife faeces are highest in scenario 4 (dispersed wildlife faeces and high cattle avoidance) throughout the simulation (Fig. 5 b). The overall number of bites and number of investigations from cattle faecally contaminated patches are significantly greater than the number of bites/investigations from wildlife faecally contaminated patches (up to 379 times more bites and up to 1463 times more investigations; Fig. 5 a, b).

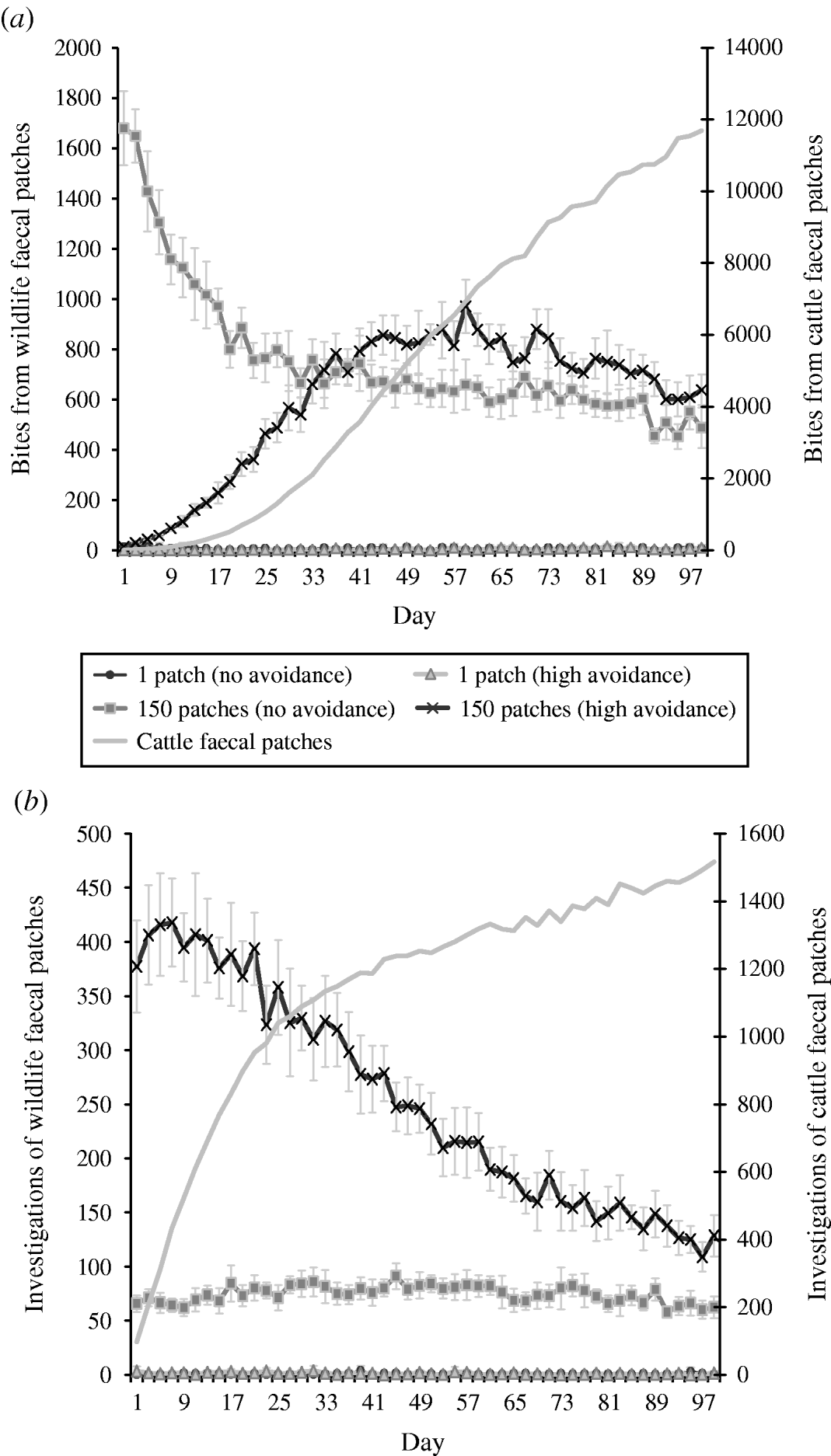
Fig. 5. Effect of defecation pattern and herbivore level of avoidance in a set-stock grazing system, on (a) number of bites taken and (b) number of investigations taken by cattle from wildlife faecally contaminated patches (left y-axis) and from cattle faecally contaminated patches (right y-axis). One contaminated patch is representative of latrine-type defecation patterns, and 150 contaminated patches is representative of single dispersed, deposit defecation patterns. Cattle faecal patches represent faeces in the environment deposited by the cattle during the simulation. Figures are the mean number of bites/number of investigations from wildlife faecally contaminated patches per day averaged over 10 simulations, ±standard deviation. Grazing and investigative contacts with cattle faeces showed little difference between each of the scenarios simulated, therefore the values shown are the mean number of contacts with cattle faeces over all the scenarios simulated.

Table 2. A comparison of the number of bites/number of investigation from dispersed wildlife faeces (150 patches) relative to the number of bites/investigations from latrine wildlife faeces (one patch), for both levels of cattle avoidance in the set-stock and the rotation grazing scenarios

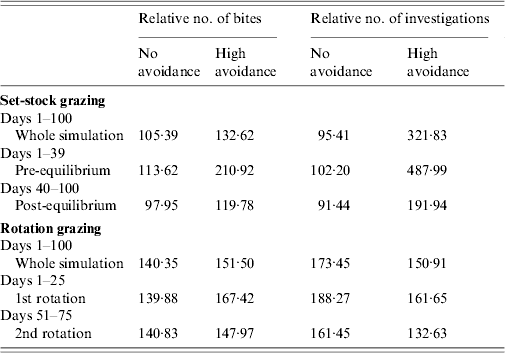
Rotation grazing

Under rotation grazing, the effects of cattle avoidance of faeces and defecation pattern are consistent with the patterns observed in a set-stock environment (Fig. 6 a, b). However, the non-commensurate increase in both grazing contact and investigative contact associated with dispersed defecation patterns (150 contaminated patches) under set-stock conditions does not occur. In the rotational grazing scenario, the increase in grazing and investigative contact is commensurate with the area/number of patches contaminated (Table 2). A comparison of the interaction effects of avoidance and wildlife defecation pattern in a set-stocking (Fig. 5 a, b) and a rotational grazing scenario (Fig. 6 a, b) shows that, per unit time spent in the pasture, there are a greater number of grazing contacts and investigative contacts with wildlife faecally contaminated vegetation in rotational grazing systems compared to set- stock systems. In the rotation grazing, the number of investigative contacts are highest in scenario 4 (dispersed wildlife faeces and high cattle avoidance) during both the first (days 1–25) and second rotation (days 51–75) (Fig. 6 b). In contrast, grazing contacts are not consistent across the first and second rotations. During the first rotation, grazing contacts are greatest in scenario 3 (dispersed wildlife faeces and no cattle avoidance). During the second rotation, the number of grazing contacts is highest in scenario 4 (Fig. 6 a). The overall number of bites and number of investigations (i.e. total grazing contact and total investigation contact over a complete simulation) from cattle faecally contaminated patches are significantly greater than the number of bites/investigations from wildlife faecally contaminated patches (i.e. up to 163 times more bites and up to 1198 times more investigations) (Fig. 6 a, b). However, during the first rotation, there are a greater number of bites from wildlife faeces both in a dispersed defecation pattern with no cattle avoidance, and a dispersed defecation pattern with high cattle avoidance relative to the single-patch faecal patterns. There are also a greater number of investigations of wildlife faeces in a dispersed wildlife defecation pattern with high cattle avoidance relative to the number of bites and investigations from patches contaminated with cattle faeces (Fig. 6 a, b).

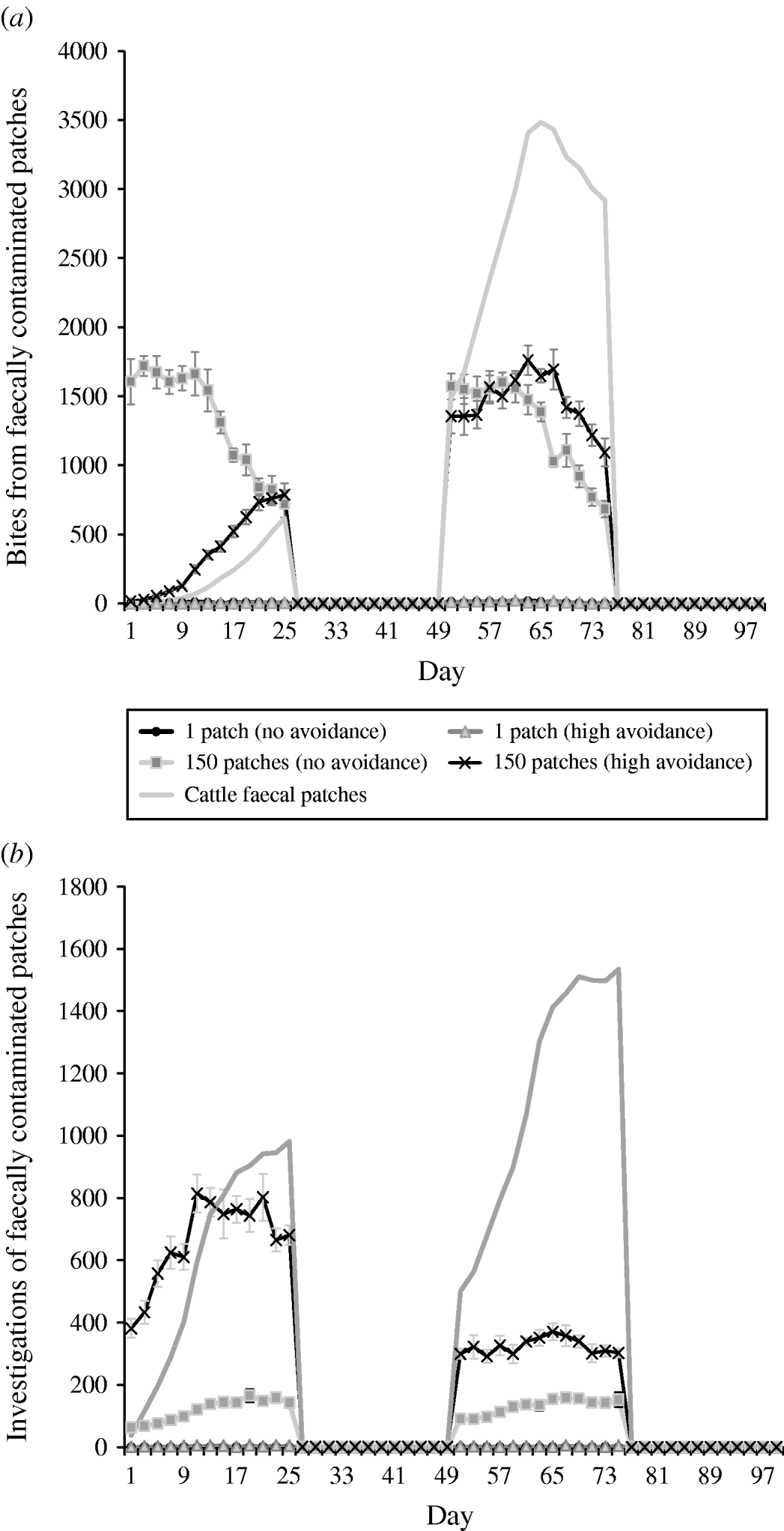
Fig. 6. Effect of defecation pattern and herbivore level of avoidance in a rotational grazing system, on (a) number of bites taken and (b) number of investigations taken by cattle from both wildlife faecally contaminated patches and cattle faecally contaminated patches. One contaminated patch is representative of latrine-type defecation patterns, and 150 contaminated patches is representative of single dispersed, deposit defecation patterns. Cattle faecal patches represent faeces in the environment deposited by the cattle during the simulation. Figures are the mean number of bites/number of investigations from wildlife faecally contaminated patches per day averaged over 10 simulations, ±standard deviation Grazing and investigative contacts with cattle faeces showed little difference between each of the scenarios simulated, therefore the values shown are the mean number of contacts with cattle faeces over all the scenarios simulated.

DISCUSSION

The aim of this study was to determine the interactions between herbivore behaviour and the environment during grazing and their subsequent impact on the contact process between grazing herbivores and faeces/pathogens in the environment. Our generic approach can then be applied to quantify the relative risk of a number of different parasites and pathogens transmitted to livestock via the faecal–oral route. The first step in this study was to determine if the model successfully simulated the heterogeneous sward structure representing the nutrition vs. parasitism trade-off. In both the set-stock and rotational grazing scenarios, the faecally contaminated patches (both wildlife and cattle) had significantly greater mean forage availability (i.e. sward height) relative to the non-contaminated patches. Thus, a heterogeneous sward structure had been created in all the grazing systems, suggesting that the behavioural rules-of-thumb governing herbivore grazing in the model were adequate for representing real environments, i.e. the emergent properties of the model match empirical observation. Furthermore, the costs and benefits of this dynamic system were also similar to actual systems in that faecally contaminated patches provide localized concentrations of both nutritional resources and parasites.

To allow for a comparison between livestock behavioural patterns simulated by the model and those observed in cattle grazing experiments (Smith et al., unpublished observations), the individual effects of cattle avoidance of faeces and faecal defecation pattern were simulated in a simple system with no faecal decay. In order to simulate cattle avoidance of different types (species) of faeces the model was parameterized to simulate a range of different avoidance levels from no initial avoidance (representative of rabbit faeces) to almost complete initial avoidance (representative of badger faeces). Here this step-wise increase in the level of cattle avoidance resulted in fewer grazing contacts with faecally contaminated patches for each level of avoidance, when cattle are first placed in the pasture. Once cattle are in agricultural systems, their grazing behaviour is also influenced by the availability of grass in the system. Due to the initial avoidance of faecally contaminated areas and further contamination of clean pasture, the decreasing amount of clean grass available may force cattle to graze faecally contaminated areas [33]. This has been effectively simulated in the model, with a gradual increase in the number of bites from faecally contaminated patches with time, for all avoidance levels. In contrast, the reduction in bites from faecally contaminated patches with time, under conditions of no faecal avoidance is driven by the reduction of grass availability at the faecally contaminated patches. Thus, the model successfully produced the range of cattle faecal avoidance behaviours as expected. Therefore, cattle avoidance of the faeces of different wildlife hosts can be placed in the context of the model. For example, cattle show strong initial avoidance of both badger faeces and their own faeces; and no avoidance of rabbit faeces (Smith et al., unpublished observations). This will have implications for the contact rates of cattle with the different infectious agents excreted in the faeces by these different species.

The varying defecation pattern scenarios demonstrated that dispersed defecation patterns result in a greater amount of grazing contacts and investigative contacts than latrines. The grazing contact simulated here is consistent with the grazing study by Smith et al. (unpublished observations), in which cattle grazed badger faecally contaminated patches in a more dispersed faecal pattern faster than those concentrated in a single patch (i.e. representative of latrines). Thus, the model has simulated successfully the patterns of grazing contact by cattle shown towards different types of faeces, and different faecal defecation patterns.

In the more realistic set-stock grazing scenarios (the interaction of avoidance and defecation pattern with faecal decay), the effects of avoidance and defecation pattern are similar to the effects of these factors in isolation. However, defecation pattern has a much stronger effect on infection risk than the level of cattle avoidance, with dispersed defecation patterns representing a significantly greater parasite exposure risk in terms of absolute grazing and investigative contact, relative to latrine-type defecation patterns. The risk of exposure to parasites and pathogens via grazing contact is also affected by the phase of the grazing process. In the early phase of set-stock grazing (pre-equilibrium), cattle have the greatest grazing contact with wildlife faeces where these faeces are dispersed and there is no cattle avoidance of them. The dispersed wildlife faeces with no cattle avoidance is representative of rabbit faeces, as cattle show no avoidance of rabbit faeces [19] and they can occur dispersed throughout the pasture [20]. Microparasite numbers (e.g. Mycobacterium) are at their maximum and pose the greatest infection risk when faeces are first deposited in the environment [34]. Rabbit faeces pose a risk of paratuberculosis (Mycobacterium avium subsp. paratuberculosis) as they can contain up to 4×10⁶ c.f.u./g faeces [35]. There will therefore be an enhanced risk of exposure to microparasites via the faecal–oral route when cattle are first placed on a pasture.

The patterns of contact observed in set-stock grazing are similar to those in the rotational grazing scenario. Thus, during the first rotation, when cattle are first placed in the pasture, cattle have the greatest number of grazing contacts when wildlife faeces are dispersed and there is no cattle avoidance (i.e. representative of rabbit faeces and badger urinations). However, under rotation grazing this risk is also amplified relative to the risk in a set-stock environment. The greater levels of contacts in rotation grazing are largely driven by the increased stocking density in this grazing system. Whilst grazing, livestock selectively graze non-contaminated pasture and further contaminate clean areas with their own faeces. Thus, in rotational grazing the cattle are forced to graze fresh faeces faster and therefore increase their exposure to microparasite diseases such as paratuberculosis and bovine tuberculosis.

In all of the grazing scenarios here, cattle have a greater overall number of grazing contacts and investigative contacts with their own faeces relative to the contacts with the wildlife faeces in the system. The simulations indicate that a major factor that drives cattle contact with faeces in grazing systems is the area of pasture that is contaminated. In agricultural systems, often a greater proportion of the pasture is covered by livestock faeces compared to the area covered by wildlife faeces, resulting in livestock contacting their own faeces more often. Furthermore, for the grazing contacts with cattle faeces, there is an initial strong avoidance in the pre-equilibrium stage of the set-stock scenario, and in the first rotation of the rotation grazing scenario. This results in cattle faecally contaminated patches being relatively tall and attractive to the cattle, which drives the increase in grazing contact with faeces post-equilibrium in the set-stock scenario, and in the second rotation of the rotation grazing. Macroparasites take a number of weeks to develop into infective-stage larvae and migrate from the faeces into the surrounding sward, where herbivores can contact the macroparasites [36]. While some wildlife species may harbour macroparasites that can infect cattle, e.g. wild deer have been implicated in the transmission of lungworm (Dictycaulus spp.) to domestic cattle [37, 38], pasture contaminated with wildlife faeces that has a lower level of cattle avoidance (e.g. rabbit and deer faeces) may be grazed before infectious macroparasite larvae can develop. In contrast, the simulations show that in typical cattle grazing systems the levels of avoidance of cattle faeces create a situation where grazing of faecally contaminated patches will occur after 3 weeks (i.e. when the larvae have developed). Thus, due to the temporal pattern of grazing behaviour associated with the faeces of different species, any macroparasite infections arising from rabbit faeces will pose a lesser exposure risk than those associated with cattle faeces.

Contact with a pathogen in the environment and the risk of infection from that pathogen is further complicated by the dose required for an effective transmission event, e.g. infection. Dose–response assessment typically predicts that the probability of infection increases with increasing dose of a pathogen, in the shape of a sigmoid curve. In the simulations here, each contaminated patch in the dispersed faecal patterns contains fewer units of faeces, and therefore may have a lower dose of pathogen per patch. In contrast, at latrine sites it is likely that there will be a far higher dose of pathogens present in the patch. Currently, there are no definitive data to describe the relationship between exposure to pathogens in the environment and infection via the faecal–oral route. However, the infection risk associated with different faecal patterns will be dependent on the dose of the pathogen at a single patch, and the corresponding probability of infection on the dose–response sigmoid curve. If the dose of pathogen present in one dispersed faecal patch falls before the plateau of the sigmoid curve, the corresponding probability of infection for one contact with a dispersed patch will be less than the probability of infection for one contact with a latrine patch, which will have a greater dose of pathogen. In a number of the grazing scenarios simulated here (e.g. set-stock grazing), the overall increase in grazing contact with dispersed faecal patterns relative to the grazing contacts to latrine faecal patterns is less than commensurate to the area of pasture contaminated. Thus, in these situations latrine-type defecation patterns may pose a greater risk of infection compared to dispersed faecal patterns. In contrast, in the rotation grazing scenarios the overall increase in grazing contact with dispersed faecal patterns relative to the grazing contact with the latrine faecal patterns is commensurate with the area of pasture contaminated, indicating that absolute contacts may provide a better indication of pathogen exposure. If the dose from one dispersed faecal patch falls after the plateau of the dose–response sigmoid curve then the corresponding probability of infection for one contact with a dispersed patch will be equal to the probability of infection for one contact with a latrine patch. Thus, the absolute contacts will determine risk of infection and a dispersed defecation pattern will pose a greater risk of infection relative to the latrine faecal patterns. The number of contacts relative to the area contaminated is also affected by the grazing phase. In the pre-equilibrium phase of the set-stock grazing, there is a greater than commensurate increase in both grazing and investigative contacts for dispersed faecal patterns with high cattle avoidance, relative to the area of pasture contaminated. This is of applied significance for the management and prevention of wildlife diseases. For example, in areas where there is bovine tuberculosis in badgers, there may be a greater risk of exposure to Mycobacterium bovis in areas of lower badger density (where faeces are more dispersed) relative to high-density badgers (where faeces are more aggregated at latrine sites) when cattle are first placed on the pasture. Similarly, the risk of exposure to M. bovis may be increased by disturbance of the badger population during culling operations, resulting in a more dispersed defecation pattern.

In conclusion, the contact patterns between grazing cattle and distributions of faeces/parasites in the environment play an important role in the risk of exposure to parasites and pathogens via the faecal–oral route. The results of the simulations, in combination with the often greater amounts of livestock vs. wildlife faeces in the agricultural systems, highlight the far greater risk of intra- vs. inter-specific parasite/pathogen exposure risk via the faecal–oral route. However, under certain conditions, particularly for microparasite infections, wildlife faeces can also pose a significant risk of exposure to pathogens. Our model has quantified how this risk can be modified by different patterns of cattle avoidance behaviour, wildlife faecal deposition in the environment and agricultural grazing systems, with rotation grazing systems posing a greater parasite/pathogen exposure risk to grazing cattle compared to set-stock grazing systems. Further investigations of the relationship between exposure to a specific dose of pathogen in the environment and subsequent infection are required to quantify the risk of infection associated with these behavioural contact patterns for specific disease scenarios.