INTRODUCTION
The causal association between water quality and the occurrence of waterborne diseases [Reference Blum and Feachem1–Reference Jacobsen and Koopman3] is well known and has long been demonstrated. Obviously, the consumption of pathogen-free water implies a reduction in the incidence of waterborne diseases, such as hepatitis A. However, a large proportion of water-communicable diseases, in populations in which these diseases are endemic, is due to the limited amount of water available for domestic consumption and personal hygiene [Reference Cairncross, Drangert, Swiderki and Woodhouse4, Reference Cvjetanovic5]. The potential effects of limited water consumption are less well-known, curtailing personal hygiene even in situations with good-quality drinking water [Reference Cairncross, Drangert, Swiderki and Woodhouse4]. Seeking evidence of the potentially deleterious effects of the lack of adequate household water supplies, Luiz et al. [Reference Luiz6] concluded that limited water consumption is an important factor for the occurrence of hepatitis A, particularly when there is no exposure to a sanitary landfill or an open sewer close to the home.
However, as this is an observational study, despite this association being controlled by a set of analysed covariables, a potential unmeasured confounder (hidden bias) may also account for these findings [Reference Rosenbaum and Rubin7]. For example, individuals who do not have water taps in their homes may have to travel to areas where hepatitis A is endemic far more frequently than individuals who do have water taps in their residence. In this case, the individuals classified as exposed would have more chance of being infected than those who are not exposed, and consequently a higher prevalence of hepatitis A in the group of exposed individuals might reflect only this difference. This variable may be considered as a third non-observed variable that might potentially affect the findings.
According to Greenland [Reference Greenland8], most statistical methods used in epidemiological surveys focus on the assessment of random errors and confounders measured during the data generation process, which are frequently only a fraction of the total error, and rarely the sole important source of uncertainty when estimating a causal effect measurement.
Sensitivity analysis is a statistical technique that allows the quantification of the impact of an unmeasured confounder in an association of interest observed in a specific study. Instead of saying that the association found may not imply causation through the possible presence of an unmeasured confounder in the process, the magnitude of the bias may be assessed, as required, to alter or eliminate the observed association.
Cornfield et al. [Reference Cornfield9] were the first to formally establish a sensitivity analysis for an unmeasured confounder in an observational study dealing with the association between smoking and lung cancer. Marcus [Reference Marcus10], Modan et al. [Reference Modan11] and Leow et al. [Reference Leow12] also used a sensitivity analysis to evaluate the presence of unmeasured variables in their studies. More formally, Rosenbaum [Reference Rosenbaum13] and Greenland [Reference Greenland8] developed two sensitivity analysis methods that allowed analyses of the behaviour of the findings obtained in a study, taking the presence of an unmeasured confounding variable into consideration.
Although developed independently and with different approaches, consideration may be given to merging these two methods in order to use a sensitivity analysis that integrates these two approaches, as both are important for assessing an unmeasured covariable in an observational study.
The purpose of this paper is to assess the impact of a possible unmeasured confounding variable in an association between the effects of access to domestic drinking water and positive results for hepatitis A serology, published by Luiz et al. [Reference Luiz6], through the integrated application of these two sensitivity analysis methods.
MATERIALS AND METHODS
Data and variables
During the preparation of this paper, the data were used from Brazil's Impacts on Health and Quality of Life Assessment Project (PAISQUA; Projeto de Avaliação dos Impactos sobre a Saúde e Qualidade de Vida), which was a sectional study carried out in 1977 by the Collective Health Studies Center (NESC; Núcleo de Estudos de Saúde Coletiva) at the Rio de Janeiro Federal University, for assessing the Guanabara Bay Clean-Up Program (PDBG; Programa de Despoluição da Baía de Guanabara). This study analyses data on access to household water supply, measured by the presence of water taps in the home (exposure variable) and positive hepatitis A serology (variable outcome), obtained through a sample of 3779 individuals in the Duque de Caxias Municipality, Rio de Janeiro, Brazil. The exposure and outcome variables were dichotomized, respectively, as no water tap vs. ⩾1 water taps, and positive hepatitis A serology vs. negative hepatitis A serology. Details of the study in question are presented by Luiz [Reference Luiz14].
Sensitivity analysis
The sensitivity analysis method proposed by Greenland [Reference Greenland8] – also known as the external adjustment method – attempts to quantify the variation in the association observed in a specific study, when ‘adjusted’ by a potential unmeasured confounder in the study. This method considers the classic confounding scheme, meaning the confounder should be associated with the exposure and should be an independent outcome predictor. It consists of simulating various plausible values for the magnitude of the association between the confounder and the outcome of interest and also for the prevalence of the assumed unmeasured confounder in the exposed and non-exposed groups, calculating a new estimate for the association of interest, i.e. the association between the exposure variable and the outcome, adjusted by these values. Thus, by varying the values of the simulated magnitudes, this method allows an assessment of the variations in the observed association of interest, adjusted externally by an unmeasured confounder, for various estimates of this confounder. The values to be used in the assumptions should be based on considerations that are plausible for the study in question, grounded in consultations with specialists, the literature, familiarity with the subject, etc.
The Rosenbaum method [Reference Rosenbaum13] works only with the association between the confounder and the exposure. It determines the magnitude of the association between the unmeasured confounding variable and the exposure, sufficient for this confounding variable to be responsible for the association found between the exposure and the outcome of interest, implicitly considering that the confounder is a near perfect outcome predictor, meaning that it considers that the magnitude of the association between the confounder and the outcome would be sufficient for the confounding to depend only on the association between this confounder and the exposure variable.
For dichotomic variables, the methodology utilizes the odds ratio given by the Mantel–Haenszel statistic, which is based on the number of individuals exposed and presenting the outcome, being a procedure that is frequently used in analyses where a third variable is considered that may ‘mask’ the association found between the exposure and the outcome of interest [Reference Fleiss15]. Under the null hypothesis of there being no effective exposure on the outcome of interest, the Rosenbaum method seeks the lowest value for Γ, the magnitude representing the effects of the unmeasured confounding variable on the exposure variable considered, which makes the Mantel–Haenszel statistic statistically non-significant, through the calculation of the P values of the upper and lower limits of this statistic, with a confidence level of 95%.
Rosenbaum uses an approach that is focused more on statistical criteria, while Greenland adopts an approach grounded more in the epidemiological considerations of the study. As both methods are important for assessing the potential effects of an unmeasured covariable in an observational study, the proposal is to merge them in order to allow a sensitivity analysis that integrates both approaches.
As a path to integration, it is proposed to use the findings produced through the application of the Rosenbaum method as the starting point for the use of the Greenland method, using the minimum value of Γ, which makes the association between the exposure and the outcome statistically non-significant, as the initial value for the set of values to be assumed for the odds ratio (OR) between the unmeasured confounding variable and the outcome of the Greenland method. A description of the methodology proposed for the integration of both methods is presented in Cabral [Reference Cabral16] and a tool to allow the feasibility of applying each of these methods utilizing an electronic spreadsheet in order to make it easier for researches is presented in Cabral & Luiz [Reference Cabral and Luiz17].
The ratio between these two magnitudes is given in equation (1), where PA is the confounder prevalence in the group of exposed individuals and PB is the confounder prevalence in the group of non-exposed individuals, the magnitude of which should also be assumed.
Another magnitude that should also be speculated in the use of the Greenland method is the odds ratio between the unmeasured confounder and the outcome. Through assumptions of all these magnitudes, the magnitude may be estimated for the association between the unmeasured confounder and the outcome considered explicitly in the Rosenbaum method, but which is not quantified.
RESULTS
In order to assess the impact of a possible unmeasured confounding variable on the association of the effects of access to domestic drinking water and positive hepatitis A serology [Reference Luiz6], the data are considered for the group of individuals who do not live close to a sanitary landfill or an open sewer, as the association between access to water and hepatitis A seroprevalence did not prove significant for the group of individuals living close to a sanitary landfill or an open sewer. The findings are presented in Table 1. The association considered in the preparation of this paper is the odds ratio.
Table 1. Effects of access to household water supply on hepatitis A seroprevalence for the group of individuals not residing close to a sanitary landfill or an open sewer
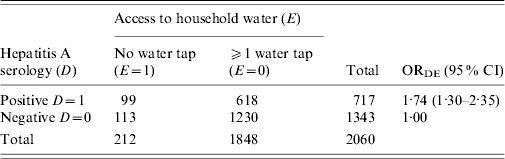
OR, Odds ratio; CI, confidence interval.
Reference population: Duque de Caxias, RJ, Brazil 1997.
According to Table 1, an individual with no water tap in the home is 1·74 times more likely to present positive hepatitis A serology than an individual with one or more water taps in the home.
The application of the sensitivity analysis proposed as the integration of the two methods initially uses the Rosenbaum method, whose findings are presented in Table 2.
Table 2. Sensitivity analysis (Rosenbaum technique) of the association with access to household water supply for individuals not living close to a sanitary landfill or an open sewer, in the presence of an unmeasured variable confounder Z
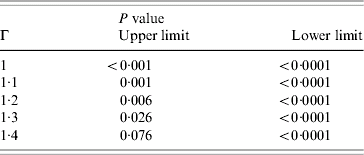
The P value recorded is for the Mantel–Haenszel statistic, based on the number of cases for various possible Γ values.
According to these findings, the lowest Γ value making access to water non-significant for hepatitis A serology is Γ=1·4, meaning that this association is shown to be ‘sensitive’ to a confounder that increases by 40% the odds of exposure with access to household water supply, and would be a near perfect predictor for hepatitis A seroprevalence.
In order to assess the magnitude of the association between the confounder and the outcome of interest (ORZE) and also the variations in the estimates of the exposure odds ratios with the outcome (ORDE) adjusted by the unmeasured confounder, the Greenland method is used, taking as possible ORZE values the values obtained through the Rosenbaum method from 1·4 onwards. This paper assumes that the ORZE values are fixed at 1·4, 2·0, 4·0 and 5·0, with a set of confounder prevalences among exposed individuals (PA) varying between 0·90 and 0·10. The values for PB were calculated in compliance with equation (1). The consideration of a value for ORZE=5·0 means that the confounder increases the odds of an individual being exposed fivefold, which is a value rarely noted in most epidemiological studies.
Table 3 presents the findings of the sensitivity analysis using the Greenland method, based on the findings of the sensitivity analysis obtained by the Rosenbaum method.
Table 3. Sensitivity analysis (Greenland technique) of the association of access to household water supply (dichotomized as no water tap in the home and ⩾1 water taps), hepatitis A seroprevalence for individuals not residing close to a sanitary landfill or an open sewer, in the presence of an unmeasured confounding variable

OR, Odds ratio; CI, confidence interval.
The 95% CI was calculated by the Cornfield method [Reference Fleiss15].
Reference population: Duque de Caxias, RJ, Brazil 1997.
The analysis in Table 3 shows that the adjusted ORDE values are quite different from the ORDE value observed (1·74), mainly when the confounder is an important factor for the occurrence of hepatitis A (ORDZ values from 4 upwards). If the ORDZ value is <4, a stronger association is needed between the confounder and the exposure (ORDZ values also ⩾4), so that the adjusted ORDE values move away from 1·74. According to the Rosenbaum method, for the association observed between access to household water supply and hepatitis A seroprevalence to be due to an unmeasured confounder, it is necessary for this confounder to increase the odds of exposure by 40%, assuming that it is a near perfect outcome predictor. Analysing the findings presented in Table 3, it is clear that for a 40% increase between the confounder and access to water for the odds of exposure to throw doubt on the association found, the odds ratio between this confounder and the outcome should present a value ⩾4, as it is from this value onwards that the adjusted ORDE starts to become statistically non-significant, at a confidence level of 95%. Even if the confounder doubles the odds of an individual being exposed, this alone is not sufficient to negate the observed association of interest. Moreover, the confounder must also present an odds ratio of at least 5, with the outcome variable. The plausibility of the existence of an unmeasured confounder with these characteristics should be assessed carefully. It is difficult to believe that a variable of this importance has not been observed, based on current knowledge of hepatitis A, thus indicating that an association between access to water and positive hepatitis A serology is not likely to be due to an unmeasured confounder in the process.
DISCUSSION
Hepatitis A seroprevalence is generally due to faecal–oral transmission. Personal hygiene, sanitary conditions and population density are risk factors identified for transmission [Reference Moyer, Warwick and Mahoney18]. Serological surveys indicate that the positive hepatitis A serology prevalences vary from 15% to almost 100% among populations in the less-developed countries [19]. It is known that the incidence and prevalence of hepatitis A are directly related to social and economic conditions [Reference Vitral20]. A large proportion of waterborne diseases in populations where they are endemic is due to the limited amounts of water available for domestic consumption and personal hygiene [Reference Cairncross, Drangert, Swiderki and Woodhouse4]. The challenge for epidemiologists is to develop indicators that assess the impact of sanitary upgrade projects.
The work by Luiz et al. [Reference Luiz6] analysed the relationship between access to household water (measured in terms of water taps available in the home) and positive for hepatitis A seroprevalence, as a specific example of the relationship between sanitary conditions and health. These authors concluded that a limited water supply is an important factor for the occurrence of hepatitis A, particularly when there is no exposure to a sanitary landfill or an open sewer close to the home. As this is an observational study, one possibility would be that the association found is the outcome of the presence a confounding variable that is not measured in the study. This paper shows that the association between access to water and positive hepatitis A serology [Reference Luiz6] is relatively insensitive to a non-controlled confounder, meaning the sensitivity analysis used in its assessment suggests that the causality of association hypothesis should not be undermined by the presence of a possible unmeasured confounding variable. However, the fragility of a sectional study is well known when there is a causal assumption, with additional hypotheses being required to assess the causal hypothesis in terms of the prognosis and reverse causality in time.
Considering the current knowledge about hepatitis A, it is unlikely to exist as an unmeasured variable potentially related to the outcome presenting an odds ratio close to 4. Basically, in observational studies, the odds ratio found, once the other variables involved are controlled for, is <2 [Reference Almeida2]. An alternative way to assess the strength of the association of a given risk factor with an outcome is to estimate the exposure intensity necessary for that factor to produce an association of the same magnitude as that of a well-established risk factor or vice versa [Reference Szklo and Nieto21].
As this is an observational study, the association between access to water and hepatitis A serology will be difficult to measure with complete certainty. However, a sensitivity analysis allows the magnitude to be calculated for the association between the unmeasured confounder and the exposure and outcome variables being studied, in order to assess the potential for the observed association being explained by the presence of this confounder. Although a sensitivity analysis neither confirms nor eliminates the presence of an unmeasured confounder, it may be used by the researcher as a quantitative assessment that can be integrated with the analysis carried out during the validation of findings stage, particularly in observational studies. Moreover, this paper discusses the presence of a single unmeasured confounder, when multiple confounders may exist and blend, altering the association of interest and requiring more complex calculations that are beyond the scope of this study. Furthermore, consideration may be given to using a sensitivity analysis for assessing possible classification errors, as the serological tests performed in order to discover whether a person is positive or negative have a certain specificity and sensitivity, and consequently an associated classification error. For more details about this type of sensitivity analysis, see Greenland [Reference Greenland8].
As the most part of epidemiological studies is observational, the models used depend on assumptions that frequently can not be checked by the observed data, meaning that the discussion of causality addresses the study of the validity of the findings obtained in the studies. The sensitivity analysis could be considered an appropriate tool to enhance causal conclusions in observational studies. The integration of the two sensitivity analysis methods presented proved useful, using the Rosenbaum method to reduce and guide the assumptions to be considered for the association between the confounder and the exposure variable (ORZE) in the Greenland method, stipulating values for this association that are equal or greater than the Γ value found (OREZ⩾Γ values), and the Greenland method, in order to calculate the variations in the estimates of the ORDE, arising from the consideration of the various possible distributions of the confounder, as well as determining the magnitude of the near perfect association between the unmeasured confounder and the outcome of interest, implicit but not quantified by the Rosenbaum method. In conclusion, this paper shows that the association between access to water and positive hepatitis A serology found by Luiz et al. [Reference Luiz6] is unlikely to be due to an unmeasured confounder in the study.
DECLARATION OF INTEREST
None.





