No CrossRef data available.
Article contents
The natural extension of the random beta-transformation
Part of:
Random dynamical systems
Probability theory on algebraic and topological structures
Elementary number theory
Published online by Cambridge University Press: 04 November 2022
Abstract
We construct a geometrico-symbolic version of the natural extension of the random 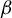 $\beta $-transformation introduced by Dajani and Kraaikamp [Random
$\beta $-transformation introduced by Dajani and Kraaikamp [Random 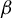 $\beta $-expansions. Ergod. Th. & Dynam. Sys. 23(2) (2003) 461–479]. This construction provides a new proof of the existence of a unique absolutely continuous invariant probability measure for the random
$\beta $-expansions. Ergod. Th. & Dynam. Sys. 23(2) (2003) 461–479]. This construction provides a new proof of the existence of a unique absolutely continuous invariant probability measure for the random 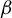 $\beta $-transformation, and an expression for its density. We then prove that this natural extension is a Bernoulli automorphism, generalizing to the random case the result of Smorodinsky [
$\beta $-transformation, and an expression for its density. We then prove that this natural extension is a Bernoulli automorphism, generalizing to the random case the result of Smorodinsky [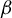 $\beta $-automorphisms are Bernoulli shifts. Acta Math. Acad. Sci. Hungar. 24 (1973), 273–278] about the greedy transformation.
$\beta $-automorphisms are Bernoulli shifts. Acta Math. Acad. Sci. Hungar. 24 (1973), 273–278] about the greedy transformation.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Boyarsky, A. and Góra, P.. Laws of Chaos: Invariant Measures and Dynamical Systems in One Dimension. Birkhäuser, Boston, MA, 1997.CrossRefGoogle Scholar
Bruin, H. and Kalle, C.. Natural extensions for piecewise affine maps via Hofbauer towers. Monatsh. Math. 175(1) (2014), 65–88.CrossRefGoogle Scholar
Dajani, K. and de Vries, M.. Invariant densities for random
 $\beta$
-expansions. J. Eur. Math. Soc. (JEMS) 9(1) (2007), 157–176.CrossRefGoogle Scholar
$\beta$
-expansions. J. Eur. Math. Soc. (JEMS) 9(1) (2007), 157–176.CrossRefGoogle Scholar
Dajani, K. and Kraaikamp, C.. From greedy to lazy expansions and their driving dynamics. Expo. Math. 20(4) (2002), 315–327.10.1016/S0723-0869(02)80010-XCrossRefGoogle Scholar
Dajani, K. and Kraaikamp, C.. Random
 $\beta$
-expansions. Ergod. Th. & Dynam. Sys. 23(2) (2003) 461–479.10.1017/S0143385702001141CrossRefGoogle Scholar
$\beta$
-expansions. Ergod. Th. & Dynam. Sys. 23(2) (2003) 461–479.10.1017/S0143385702001141CrossRefGoogle Scholar
Dajani, K., Kraaikamp, C. and Solomyak, B.. The natural extension of the
 $\beta$
-transformation. Acta Math. Hungar. 73(1–2) (1996), 97–109.CrossRefGoogle Scholar
$\beta$
-transformation. Acta Math. Hungar. 73(1–2) (1996), 97–109.CrossRefGoogle Scholar
Erdős, P., Joó, I. and Komornik, V.. Characterization of the unique expansions
 $1={\sum}_{i=1}^{\infty }{q}^{-{n}_i}$
and related problems. Bull. Soc. Math. France 118(3) (1990), 377–390.10.24033/bsmf.2151CrossRefGoogle Scholar
$1={\sum}_{i=1}^{\infty }{q}^{-{n}_i}$
and related problems. Bull. Soc. Math. France 118(3) (1990), 377–390.10.24033/bsmf.2151CrossRefGoogle Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Ito, S., Murata, H. and Totoki, H.. Remarks on the isomorphism theorems for weak Bernoulli transformations in general case. Publ. Res. Inst. Math. Sci. 7 (1972), 541–580.10.2977/prims/1195193398CrossRefGoogle Scholar
Janvresse, É., Rittaud, B. and de la Rue, T.. Dynamics of
 $\lambda$
-continued fractions and
$\lambda$
-continued fractions and
 $\beta$
-shifts. Discrete Contin. Dyn. Syst. 33(4) (2013), 1477–1498.CrossRefGoogle Scholar
$\beta$
-shifts. Discrete Contin. Dyn. Syst. 33(4) (2013), 1477–1498.CrossRefGoogle Scholar
Kempton, T.. On the invariant density of the random
 $\beta$
-transformation. Acta Math. Hungar. 142(2) (2014), 403–419.10.1007/s10474-013-0377-xCrossRefGoogle Scholar
$\beta$
-transformation. Acta Math. Hungar. 142(2) (2014), 403–419.10.1007/s10474-013-0377-xCrossRefGoogle Scholar
Parry, W.. On the
 $\beta$
-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
$\beta$
-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Rokhlin, V. A.. Exact endomorphism of a Lebesgue space. Izv. Akad. Nauk SSSR, Ser. Mat. 25 (1961), 499–530.Google Scholar
Smorodinsky, M..
 $\beta$
-automorphisms are Bernoulli shifts. Acta Math. Acad. Sci. Hungar. 24 (1973), 273–278.10.1007/BF01958037CrossRefGoogle Scholar
$\beta$
-automorphisms are Bernoulli shifts. Acta Math. Acad. Sci. Hungar. 24 (1973), 273–278.10.1007/BF01958037CrossRefGoogle Scholar
Suzuki, S.. Invariant density functions of random
 $\beta$
-transformations. Ergod. Th. & Dynam. Sys. 39(4) (2019), 1099–1120.CrossRefGoogle Scholar
$\beta$
-transformations. Ergod. Th. & Dynam. Sys. 39(4) (2019), 1099–1120.CrossRefGoogle Scholar
Tierce, Y.. Étude ergodique de bêta-transformations aléatoires. Thesis, Normandie Université, December 2021, https://tel.archives-ouvertes.fr/tel-03516372.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.10.1007/BF02808180CrossRefGoogle Scholar


