Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T23:13:22.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of a class of degenerateelliptic-parabolic operators: a unitary approach

Published online by Cambridge University Press:  20 July 2007

Fabio Paronetto
Fabio Paronetto*
Affiliation:
Dipartimento di Matematica “Ennio De Giorgi”, Università del Salento, via per Arnesano, 73100 Lecce, Italy; fabio.paronetto@unile.it
Get access

Abstract

We study the asymptotic behaviour of a sequence of stronglydegenerate parabolic equations $\partial_t (r_h u) - {\rm div}(a_h \cdot Du)$ 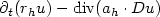with $r_h(x,t) \geq0$ 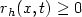, $r_h \in L^{\infty}(\Omega\times (0,T))$ 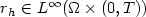.The main problem is the lack of compactness, by-passed via a regularity result.As particular cases, we obtain G-convergence for elliptic operators $(r_h \equiv 0)$ 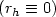,G-convergence for parabolic operators $(r_h \equiv 1)$ 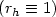, singular perturbationsof an elliptic operator $(a_h \equiv a$ 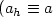and $r_h \to r$ , possibly $r\equiv 0)$ .

Keywords

G-convergencePDE of mixed typelinear elliptic and parabolic equations
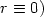Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 4 , October 2007 , pp. 669 - 691
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R.W. Carroll and R.E. Showalter, Singular and Degenerate Cauchy Problems. Academic Press, New York (1976).
V. Chiadò Piat, G. Dal Maso and A. Defranceschi, G-convergence of monotone operators. Ann. Inst. H. Poincaré, Anal. Non Linéaire 7 (1990) 123–160. CrossRef
F. Colombini and S. Spagnolo, Sur la convergence de solutions d'équations paraboliques. J. Math. Pur. Appl. 56 (1977) 263–306.
G. Dal Maso, An introduction to Γ-convergence. Birkhäuser, Boston (1993).
De Giorgi, E. and Spagnolo, S., Sulla convergenza degli integrali dell'energia per operatori ellittici del secondo ordine. Boll. Un. Mat. Ital. 8 (1973) 391–411.
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, USA (1992).
A. Pankov, G-convergence and Homogenization of Nonlinear Partial Differential Operators. Kluwer Academic Publishers, Dordrecht (1997).
F. Paronetto, Existence results for a class of evolution equations of mixed type. J. Funct. Anal. 212 (2004) 324–356.
F. Paronetto, Homogenization of degenerate elliptic-parabolic equations. Asymptotic Anal. 37 (2004) 21–56.
R.E. Showalter, Degenerate parabolic initial-boundary value problems. J. Diff. Eq. 31 (1979) 296–312.
R.E. Showalter, Monotone Operators in Banach Space and Nonlinear Partial Differential Equations. American Mathematical Society (1997).
J. Simon, Compact sets in the space $L^p(0,T;B)$ . Ann. Mat. Pura Appl. 146 (1987) 65–96. CrossRef
S. Spagnolo, Sul limite delle soluzioni di problemi di Cauchy relativi all'equazione del calore. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 21 (1967) 657–699.
S. Spagnolo, Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22 (1968) 571–597.
S. Spagnolo, Convergence of parabolic equations. Boll. Un. Mat. Ital. 14-B (1977) 547–568.
L. Tartar, Convergence d'operateurs defferentiels, Proceedings of the Meeting “Analisi convessa e Applicazioni”. Roma (1974).
L. Tartar, Cours Peccot, Collège de France, 1977. Partially written in: F. Murat, H-convergence - Séminaire d'Analyse Fonctionnelle et Numérique, Université d'Alger, 1977-78. English translation: F. Murat and L. Tartar: H-Convergence, in Topics in the Mathematical Modelling of Composite Materials, A. Cherkaev, R. Kohn, Editors, Birkhäuser, Boston (1997) 21–43.