Article contents
Controlled functional differential equations:approximateand exact asymptotic trackingwith prescribed transient performance
Published online by Cambridge University Press: 19 July 2008
Abstract
A tracking problem is consideredin the context of a class $\mathcal{S}$ 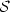 of multi-input,multi-output, nonlinear systems modelled by controlled functionaldifferential equations. The class contains, as a prototype, allfinite-dimensional, linear, m-input, m-output, minimum-phasesystems with sign-definite “high-frequency gain". The first controlobjective is tracking of reference signals r by the output y ofany system in $\mathcal{S}$
of multi-input,multi-output, nonlinear systems modelled by controlled functionaldifferential equations. The class contains, as a prototype, allfinite-dimensional, linear, m-input, m-output, minimum-phasesystems with sign-definite “high-frequency gain". The first controlobjective is tracking of reference signals r by the output y ofany system in $\mathcal{S}$ 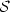 : given $\lambda \geq 0$
: given $\lambda \geq 0$  , construct afeedback strategy which ensures that, for every r (assumed boundedwith essentially bounded derivative) and every system of class $\mathcal{S}$
, construct afeedback strategy which ensures that, for every r (assumed boundedwith essentially bounded derivative) and every system of class $\mathcal{S}$ 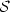 , the tracking error $e = y-r$
, the tracking error $e = y-r$  is such that, in the case $\lambda >0$
is such that, in the case $\lambda >0$ 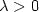 , $\limsup_{t\rightarrow\infty}\|e(t)\|<\lambda$
, $\limsup_{t\rightarrow\infty}\|e(t)\|<\lambda$ 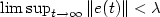 or, inthe case $\lambda=0$
or, inthe case $\lambda=0$ 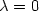 , $\lim_{t\rightarrow\infty}\|e(t)\| = 0$
, $\lim_{t\rightarrow\infty}\|e(t)\| = 0$ 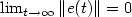 . Thesecond objective is guaranteed output transient performance: theerror is required to evolve within a prescribed performance funnel $\mathcal{F}_\varphi$
. Thesecond objective is guaranteed output transient performance: theerror is required to evolve within a prescribed performance funnel $\mathcal{F}_\varphi$ 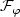 (determined by a function φ). Forsuitably chosen functions α, ν and θ, bothobjectives are achieved via a control structure of the form $u(t)=-\nu (k(t))\theta (e(t))$
(determined by a function φ). Forsuitably chosen functions α, ν and θ, bothobjectives are achieved via a control structure of the form $u(t)=-\nu (k(t))\theta (e(t))$ 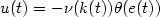 with $k(t)=\alpha (\varphi(t)\|e(t)\|)$
with $k(t)=\alpha (\varphi(t)\|e(t)\|)$ 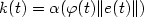 , whilst maintaining boundedness of the control andgain functions u and k. In the case $\lambda=0$
, whilst maintaining boundedness of the control andgain functions u and k. In the case $\lambda=0$ 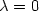 , the feedbackstrategy may be discontinuous: to accommodate this feature, aunifying framework of differential inclusions is adopted in theanalysis of the general case $\lambda \geq 0$
, the feedbackstrategy may be discontinuous: to accommodate this feature, aunifying framework of differential inclusions is adopted in theanalysis of the general case $\lambda \geq 0$  .
.
Keywords
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 4 , October 2009 , pp. 745 - 762
- Copyright
- © EDP Sciences, SMAI, 2008
References
- 12
- Cited by


