Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T16:56:56.960Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogenization of periodic non self-adjoint problemswith large drift and potential

Published online by Cambridge University Press:  20 July 2007

Grégoire Allaire  and
Rafael Orive
Grégoire Allaire
Affiliation:
Centre de Mathématiques Appliquées, École Polytechnique, 91128 Palaiseau Cedex, Paris, France; gregoire.allaire@polytechnique.fr
Rafael Orive
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain; rafael.orive@uam.es
Get access

Abstract

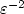We consider the homogenization of both the parabolic and eigenvalue problems for a singularly perturbedconvection-diffusion equation in a periodic medium. All coefficients of the equation may vary both on themacroscopic scale and on the periodic microscopic scale. Denoting by ε the period, the potential or zero-orderterm is scaled as $\varepsilon^{-2}$ and the drift or first-order term is scaled as $\varepsilon^{-1}$ 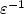. Under a structuralhypothesis on the first cell eigenvalue, which is assumed to admit a unique minimum in the domain withnon-degenerate quadratic behavior, we prove an exponential localization at this minimum point. The homogenizedproblem features a diffusion equation with quadratic potential in the whole space.

Keywords

Homogenizationnon self-adjoint operatorsconvection-diffusionperiodic medium
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 4 , October 2007 , pp. 735 - 749
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allaire, G., Homogenization and two-scale convergence. SIAM J. Math. Anal. 23 (1992) 1482–1518. CrossRef
G. Allaire, Dispersive limits in the homogenization of the wave equation. Annales de la Faculté des Sciences de Toulouse XII (2003) 415–431.
Allaire, G. and Capdeboscq, Y., Homogenization of a spectral problem in neutronic multigroup diffusion. Comput. Methods Appl. Mech. Engrg. 187 (2000) 91–117. CrossRef
Allaire, G. and Conca, C., Bloch wave homogenization and spectral asymptotic analysis. J. Math. Pures Appl. 77 (1998) 153–208. CrossRef
Allaire, G. and Malige, F., Analyse asymptotique spectrale d'un probléme de diffusion neutronique. C. R. Acad. Sci. Paris Sér. I 324 (1997) 939–944. CrossRef
Allaire, G. and Orive, R., On the band gap structure of Hill's equation. J. Math. Anal. Appl. 306 (2005) 462–480. CrossRef
Allaire, G. and Piatnitski, A., Uniform spectral asymptotics for singularly perturbed locally periodic operator. Comm. Partial Differential Equations 27 (2002) 705–725. CrossRef
Allaire, G., Capdeboscq, Y., Piatnitski, A., Siess, V. and Vanninathan, M., Homogenization of periodic systems with large potentials. Arch. Rational Mech. Anal. 174 (2004) 179–220. CrossRef
P.H. Anselone, Collectively compact operator approximation theory and applications to integral equations. Series in Automatic Computation, Prentice-Hall, Inc., Englewood Cliffs, New Jersey (1971).
Benchérif-Madani, A. and Pardoux, É., Locally periodic homogenization. Asymptot. Anal. 39 (2004) 263–279.
A. Benchérif-Madani and É. Pardoux, Homogenization of a diffusion with locally periodic coefficients. Séminaire de Probabilités XXXVIII Lect. Notes Math. 1857 (2005) 363–392.
A. Bensoussan, J.L. Lions and G. Papanicolaou, Asymptotic Analysis for Periodic Structures. North-Holland, Amsterdam (1978).
Capdeboscq, Y., Homogenization of a diffusion equation with drift. C. R. Acad. Sci. Paris Sér. I 327 (1998) 807–812. CrossRef
Capdeboscq, Y., Homogenization of a neutronic critical diffusion problem with drift. Proc. Roy. Soc. Edinburgh Sect. A 132 (2002) 567–594. CrossRef
P. Donato and A. Piatnitski, Averaging of nonstationary parabolic operators with large lower order terms. (2005) (in preparation).
Nguetseng, G., A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20 (1989) 608–623. CrossRef
Piatnitski, A., Asymptotic behaviour of the ground state of singularly perturbed elliptic equations. Commun. Math. Phys. 197 (1998) 527–551. CrossRef
A. Piatnitski, Ground State Asymptotics for Singularly Perturbed Elliptic Problem with Locally Periodic Microstructure. Preprint (2006).
J. Simon, Compact sets in the space $L\sp p(0,T;B)$ . Ann. Mat. Pura Appl. 146 (1987) 65–96.
Sivaji Ganesh, S. and Vanninathan, M., Bloch wave homogenization of scalar elliptic operators. Asymptotic Anal. 39 (2004) 15–44.
Vanninathan, M., Homogenization of eigenvalue problems in perforated domains. Proc. Indian Acad. Sci. Math. Sci. 90 (1981) 239–271. CrossRef