Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T01:14:55.821Z Has data issue: false hasContentIssue false
  • English
  • Français

L∞ -Norm minimal control of the wave equation: on the weakness of the bang-bang principle

Published online by Cambridge University Press:  20 March 2008

Martin Gugat  and
Gunter Leugering
Martin Gugat
Affiliation:
Lehrstuhl 2 für Angewandte Mathematik, Martensstr. 3, 91058 Erlangen, Germany; gugat@am.uni-erlangen.de; leugering@am.uni-erlangen.de
Gunter Leugering
Affiliation:
Lehrstuhl 2 für Angewandte Mathematik, Martensstr. 3, 91058 Erlangen, Germany; gugat@am.uni-erlangen.de; leugering@am.uni-erlangen.de
Get access

Abstract


For optimal control problems with ordinarydifferential equations where the $L^\infty$ 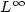-norm of the control isminimized, often bang-bang principles hold. For systems that aregoverned by a hyperbolic partial differential equation, thesituation is different:even if a weak form of the bang-bang principle still holds for the wave equation,it implies no restriction on the form of the optimal control.To illustrate thatfor the Dirichlet boundary control of the wave equation in general not even feasible controlsof bang-bang type exist,we examine the states that can be reached by bang-bang-offcontrols, that is controls that are allowed to attain only threevalues: Their maximum and minimum values and the value zero.We show that for certain control times,the difference between the initial and the terminal state can onlyattain a finite number of values.For the problems of optimal exact and approximate boundary control of the wave equationwhere the $L^\infty$ 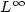-norm of the control is minimized, we introduce dual problems and present the weak form of a bang-bangprinciple, that states that the values of $L^\infty$ 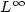-norm minimalcontrols are constrained by the sign of the dual solutions. Sincethese dual solutions are in general given as measures, thisis no restriction on the form of the control function:the dual solution may have a finite support, and when the dual solution vanishes,the control is allowed to attain all values from the intervalbetween the two extremal control values.


Keywords

Optimal control of pdesoptimal boundary controlwaveequationbang-bangbang-bang-offdual problemdual solutions$L^\infty$measures
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 14 , Issue 2 , April 2008 , pp. 254 - 283
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A. Barvinok, A course in convexity. AMS, Providence, Rhode Island (2002).
Bennighof, J.K. and Boucher, R.L., Exact minimum-time control of a distributed system using a traveling wave formulation. J. Optim. Theory Appl 73 (1992) 149–167. CrossRef
F.H. Clarke, Optimization and Nonsmooth Analysis. John Wiley, New York (1983).
Dovretzki, A., Liapunov's, On convexity theorem. Proc. Natl. Acad. Sci 91 (1994) 2145. CrossRef
Drobot, V., An infinte-dimensional version of Liapunov's convexity theorem. Michigan Math. J 17 (1970) 405–408.
C. Fabre, J.-P. Puel and E. Zuazua, Contrôlabilité approchée de l'équation de la chaleur linéaire avec des contrôles de norme $l\sp \infty$ minimale. (Approximate controllability for the linear heat equation with controls of minimal $l\sp \infty$ norm). C. R. Acad. Sci., Paris, Sér. I 316 (1993) 679–684.
C. Fabre, J.-P. Puel and E. Zuazua, Approximate controllability of the semilinear heat equation. Proc. R. Soc. Edinb., Sect. A 125 (1995) 31–61.
Gugat, M., Time-parametric control: Uniform convergence of the optimal value functions of discretized problems. Contr. Cybern 28 (1999) 7–33.
Gugat, M. and Leugering, G., Regularization of $l^\infty$ -optimal control problems for distributed parameter systems. Comput. Optim. Appl 22 (2002) 151–192. CrossRef
Gugat, M., Leugering, G. and Sklyar, G., lp -optimal boundary control for the wave equation. SIAM J. Control Optim 44 (2005) 49–74. CrossRef
H. Hermes and J. Lasalle. Functional analysis and time optimal control. Academic Press (1969).
Kato, T., Linear evolution equations of hyperbolic type. Univ. Tokyo Sec. I 17 (1970) 241–258.
T. Kato, Perturbation theory for linear operators, Corr. printing of the 2nd edn. Springer (1980).
W. Krabs, On moment theory and controllability of one-dimensional vibrating systems and heating processes, Lecture Notes in Control and Information Science 173. Springer-Verlag, Heidelberg (1992).
W. Krabs, Optimal Control of Undamped Linear Vibrations. Heldermann Verlag, Lemgo, Germany (1995).
Lee, C.M. and Roberts, F.D.K., A comparison of algorithms for rational $l_\infty$ approximation. Math. Comp 27 (1973) 111–121.
E.B. Lee and L. Markus, Foundations of Optimal Control Theory. Wiley, New York (1968).
Lions, J.-L., Exact controllability, stabilization and perturbations of distributed systems. SIAM Rev 30 (1988) 1–68. CrossRef
A. Lyapunov, Sur les fonctions-vecteurs complètement additives. Bull. Acad. Sci. URSS, Sér. Math 4 (1940) 465–478.
J. Macki and A. Strauss, Introduction to Optimal Control Theory. Springer-Verlag, New York (1982).
Mizel, V.J. and Seidman, T.I., An abstract bang-bang principle and time-optimal boundary control of the heat equation. SIAM J. Control Optim 35 (1997) 1204–1216. CrossRef
Papageorgiu, N., Measurable multifunctions and their applications to convex integral functionals. Internat. J. Math. Math. Sciences 12 (1989) 175–192. CrossRef
G.K. Pedersen, Analysis Now. Springer-Verlag, New York (1989).
R.T. Rockafellar, Convex Analysis. Princeton University Press (1970).
K. Yosida, Functional Analysis. Springer, Berlin (1965).
Zuazua, E., Optimal and approximate control of finite-difference approximation schemes for the 1d wave equation. Rend. Mat. Appl 24 (2004) 201–237.
Zuazua, E., Propagation, observation. and control of waves approximated by finite difference methods. SIAM Rev 47 (2005) 197–243. CrossRef
E. Zuazua, Controllability of partial differential equations: Some results and open problems, in Handbook of Differential Equations: Evolutionary Differential Equations, C. Dafermos and E. Feireisl Eds., Elsevier Science (2006).