Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T17:40:33.007Z Has data issue: false hasContentIssue false
  • English
  • Français

A regularity result for a convex functionaland bounds for the singularset

Published online by Cambridge University Press:  11 August 2009

Bruno De Maria
Bruno De Maria*
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli” Università di Napoli “Federico II” Via Cintia, 80126 Napoli, Italy. bruno.demaria@dma.unina.it
Get access

Abstract

In this paper we prove a regularityresult for local minimizers of functionals of the Calculus of Variations of thetype

$$\int_{\Omega}f(x, Du)\ {\rm d}x$$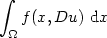

where Ω is a bounded open set in $\mathbb{R}^{n}$ 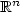, u∈ $W^{1,p}_{\rm loc}$ 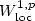(Ω; $\mathbb{R}^{N}$ 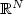), p> 1, n≥ 2 and N≥ 1.We use the technique of difference quotient without the usual assumption on the growth of the second derivatives of the function f. We apply this result to givea bound on the Hausdorff dimension of the singular set of minimizers.

Keywords

Partial regularitysingular setsfractional differentiabilityvariational integrals
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 4 , October 2010 , pp. 1002 - 1017
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., A regularity theorem for minimizers of quasiconvex integrals. Arch. Ration. Mech. Anal. 99 (1987) 261–281. CrossRef
Acerbi, E. and Fusco, N., Regularity of minimizers of non-quadratic functionals: the case $1<p<2$ . J. Math. Anal. Appl. 140 (1989) 115–135. CrossRef
R.A. Adams, Sobolev Spaces. Academic Press, New York (1975).
Carozza, M. and Passarelli di, A. Napoli, A regularity theorem for minimizers of quasiconvex integrals: the case $1<p<2^{\star}$ . Proc. R. Math. Soc. Edinb. A 126 (1996) 1181–1199. CrossRef
Carozza, M. and Passarelli di, A. Napoli, Model problems from nonlinear elasticity: partial regularity results. ESAIM: COCV 13 (2007) 120–134. CrossRef
M. Carozza, N. Fusco and R. Mingione, Partial regularity of minimizers of quasiconvex integrals with subquadratic growth. Annali di matematica pura e applicata (IV) CLXXV (1998) 141–164.
Cupini, G., Fusco, N. and Petti, R., Hölder continuity of local minimizers. J. Math. Anal. Appl. 235 (1999) 578–597. CrossRef
De Giorgi, E., Un esempio di estremali discontinue per un problema variazionale di tipo ellittico. Boll. Un. Mat. It. 1 (1968) 135–137.
Esposito, L., Leonetti, F. and Mingione, G., Higher integrability for minimizers of integral functionals with $(p,q)$ growth. J. Differ. Equ. 157 (1999) 414–438. CrossRef
Esposito, L., Leonetti, F. and Mingione, G., Regularity results for minimizers of irregular integrals with $(p,q)$ growth. Forum Math. 14 (2002) 245–272. CrossRef
Esposito, L., Leonetti, F. and Mingione, G., Sharp regularity for functionals with $(p,q)$ growth. J. Differ. Equ. 204 (2004) 5–55. CrossRef
Evans, L.C., Quasiconvexity and partial regularity in the Calculus of Variations. Arch. Ration. Mech. Anal. 95 (1984) 227–252.
Evans, L.C. and Gariepy, R.F., Blow-up, compactness and partial regularity in the Calculus of Variations. Indiana Univ. Math. J. 36 (1987) 361–371. CrossRef
Fonseca, I. and Fusco, N., Regularity results for anisotropic image segmentation models. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 3 (1997) 463–499.
Fonseca, I., Fusco, N. and Marcellini, P., An existence result for a nonconvex variational problem via regularity. ESAIM: COCV 7 (2002) 69–95. CrossRef
Giaquinta, M. and Modica, G., Remarks on the regularity of minimizers of certain degenerate functionals. Manuscripta Math. 47 (1986) 55–99. CrossRef
E. Giusti, Direct methods in the calculus of variations. World Scientific, River Edge, USA (2003).
John, O., Malý, J. and Stará, J., Nowhere continuous solutions to elliptic systems. Comm. Math. Univ. Carolin. 30 (1989) 33–43.
Kristensen, J. and Mingione, G., Non-differentiable functionals and singular sets of minima. C. R. Acad. Sci. Paris Ser. I Math. 340 (2005) 93–98. CrossRef
Kristensen, J. and Mingione, G., The singular set of minima of integral functionals. Arch. Ration. Mech. Anal. 180 (2006) 331–398. CrossRef
Mingione, G., The singular set of solutions to non differentiable elliptic systems. Arch. Ration. Mech. Anal. 166 (2003) 287–301. CrossRef
Mingione, G., Bounds for the singular set of solutions to non linear elliptic system. Calc. Var. 18 (2003) 373–400. CrossRef
Mingione, G., Regularity of minima: an invitation to the dark side of calculus of variations. Appl. Math. 51 (2006) 355–426. CrossRef
J. Nečas, Example of an irregular solution to a nonlinear elliptic system with analytic coefficients and conditions for regularity, in Theory of nonlinear operators, Proc. Fourth Internat. Summer School, Acad. Sci., Berlin (1975) 197–206.
A. Passarelli di Napoli, A regularity result for a class of polyconvex functionals. Ric. di Matem. XLVIII (1994) 379–393.
Šverák, V. and Yan, X., A singular minimizer of a smooth strongly convex functional in three dimensions. Calc. Var. 10 (2000) 213–221.
Šverák, V. and Yan, X., Non Lipschitz minimizers of smooth strongly convex variational integrals. Proc. Nat. Acad. Sc. USA 99 (2002) 15269–15276. CrossRef