Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T21:46:20.249Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence rates of symplectic Pontryaginapproximations in optimal control theory

Published online by Cambridge University Press:  23 February 2006

Mattias Sandberg  and
Anders Szepessy
Mattias Sandberg
Affiliation:
Institutionen för Matematik, Kungl. Tekniska Högskolan, 100 44 Stockholm, Sweden. mattiass@math.kth.se; szepessy@kth.se
Anders Szepessy
Affiliation:
Institutionen för Matematik, Kungl. Tekniska Högskolan, 100 44 Stockholm, Sweden. mattiass@math.kth.se; szepessy@kth.se
Get access

Abstract

Many inverse problems for differential equationscan be formulated as optimal control problems.It is well known that inverse problems often need tobe regularized to obtain good approximations.This work presents a systematic method to regularizeand to establish error estimates for approximations tosome control problems in high dimension, based on symplectic approximationof the Hamiltonian system for the control problem. In particularthe work derives error estimatesand constructs regularizations for numerical approximations tooptimally controlled ordinary differential equations in ${\mathbb R}^d$ 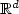,with non smooth control.Though optimal controls in general becomenon smooth,viscosity solutions to the corresponding Hamilton-Jacobi-Bellmanequation provide good theoretical foundation, but poor computational efficiencyin high dimensions.The computational method here uses the adjoint variable and worksefficiently also for high dimensional problems with d >> 1.Controls can be discontinuous due to a lack of regularityin the Hamiltonian or due to colliding backward paths, i.e. shocks.The error analysis, for both these cases, is based on consistency with theHamilton-Jacobi-Bellman equation, in the viscosity solution sense,and a discrete Pontryagin principle:the bi-characteristic Hamiltonian ODE system is solvedwith a C 2 approximate Hamiltonian.
The error analysis leads to estimatesuseful also in high dimensions since the bounds depend on the Lipschitznorms of the Hamiltonian and the gradient of the value functionbut not on d explicitly.Applications to inverse implied volatility estimation, in mathematical finance,and to a topology optimization problem are presented.An advantage with the Pontryagin based method is that the Newton method can be applied to efficientlysolve the discrete nonlinear Hamiltonian system,with a sparse Jacobian that can be calculated explicitly.

Keywords

Optimal controlHamilton-JacobiHamiltonian systemPontryagin principle.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 40 , Issue 1 , January 2006 , pp. 149 - 173
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achdou, Y. and Pironneau, O., Volatility smile by multilevel least square. Int. J. Theor. Appl. Finance 5 (2002) 619–643. CrossRef
G. Barles, Solutions de viscosité des équations de Hamilton-Jacobi. Springer-Verlag, Paris. Math. Appl. (Berlin) 17 (1994).
Barles, G. and Jakobsen, E., On the convergence rate of approximation schemes for Hamilton-Jacobi-Bellman equations. ESAIM: M2AN 36 (2002) 33–54. CrossRef
Barron, E. and Jensen, R., The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations. Trans. Amer. Math. Soc. 298 (1986) 635–641. CrossRef
M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, with appendices by M. Falcone and P. Soravia, Systems and Control: Foundations and Applications. Birkhäuser Boston, Inc., Boston, MA (1997).
Cannarsa, P. and Frankowska, H., Some characterizations of the optimal trajectories in control theory. SIAM J. Control Optim. 29 (1991) 1322–1347. CrossRef
Cannarsa, P., Mennucci, A. and Sinestrari, C., Regularity results for solutions of a class of Hamilton-Jacobi equations. Arch. Rational Mech. Anal. 140 (1997) 197–223. CrossRef
J. Carlsson, M. Sandberg and A. Szepessy, Symplectic Pontryagin approximations for optimal design, preprint www.nada.kth.se/~szepessy.
Crandall, M. and Lions, P.-L., Viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 277 (1983) 1–42. CrossRef
Crandall, M. and Lions, P.-L., Two approximations of solutions of Hamilton-Jacobi equations. Math. Comp. 43 (1984) 1–19. CrossRef
Crandall, M., Evans, L.C. and Lions, P.-L., Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282 (1984) 487–502. CrossRef
B. Dupire, Pricing with a smile. Risk (1994) 18–20.
H. Engl, M. Hanke and A. Neubauer, Regularization of Inverse Problems. Kluwer Academic Publishers Group, Dordrecht. Math. Appl. 375 (1996).
L.C. Evans, Partial Differential Equations. Graduate Studies in Mathematics, 19. American Mathematical Society, Providence, RI (1998).
Falcone, M. and Ferretti, R., Semi-Lagrangian schemes for Hamilton-Jacobi equations, discrete representation formulae and Godunov methods. J. Comput. Phys. 175 (2002) 559–575. CrossRef
Frankowska, H., Contigent cones to reachable sets of control systems. SIAM J. Control Optim. 27 (1989) 170–198. CrossRef
R. Glowinski and J.-L. Lions, Exact and approximate controllability for distributed parameter systems. Acta numerica (1994), 269–378, Acta Numer., Cambridge Univ. Press, Cambridge (1994).
R. Glowinski and J.-L. Lions, Exact and approximate controllability for distributed parameter systems. Acta numerica (1995), 159–333, Acta Numer., Cambridge Univ. Press, Cambridge (1995).
E. Harrier, C. Lubich and G. Wanner, Geometric Numerical Integrators: Structure Preserving Algorithms for Ordinary Differential Equations, Springer (2002).
Lin, C.-T. and Tadmor, E., L 1-stability and error estimates for approximate Hamilton-Jacobi solutions. Numer. Math. 87 (2001) 701–735. CrossRef
B. Mohammadi and O. Pironneau, Applied Shape Optimization for Fluids. Numerical Mathematics and Scientific Computation. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York (2001).
P. Pedregal, Optimization, relaxation and Young measures. Bull. Amer. Math. Soc. (N.S.) 36 (1999) 27–58.
E. Polak, Optimization, Algorithms and Consistent Approximations, Springer-Verlag, New York. Appl. Math. Sci. 124. (1997).
L.S. Pontryagin, V.G. Boltyanskii, R.V. Gamkrelidze and E.F. Mishchenko, The Mathematical Theory of Optimal Processes, Pergamon Press (1964).
M. Sandberg, Convergence rates for Euler approximation of non convex differential inclusions, work in progress.
M. Sandberg, Convergence rates for Symplectic Euler approximations of the Ginzburg-Landau equation, work in progress.
Souganidis, P., Existence of viscosity solutions of Hamilton-Jacobi equations. J. Differential Equations 56 (1985) 345–390. CrossRef
A. Subbotin, Generalized Solutions of First-Order PDEs. The Dynamical Optimization Perspective. Translated from the Russian. Systems & Control: Foundations & Applications. Birkhäuser Boston, Inc., Boston, MA (1995).
C. Vogel, Computational Methods for Inverse Problems. Frontiers in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2002).
L.C. Young, Lectures on the Calculus of Variations and Optimal Control Theory. Saunders Co., Philadelphia-London-Toronto, Ont. (1969).