Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T20:08:47.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical approximation of effective coefficientsin stochastic homogenization of discrete elliptic equations

Published online by Cambridge University Press:  22 July 2011

Antoine Gloria
Antoine Gloria*
Affiliation:
Project-Team SIMPAF, INRIA Lille-Nord Europe, France and Laboratoire Paul Painlevé (UMR CNRS 8524), Université Lille 1, 59655 Villeneuve d'Ascq, France. antoine.gloria@inria.fr
Get access

Abstract

We introduce and analyze a numerical strategy to approximate effective coefficients in stochastic homogenization of discrete ellipticequations. In particular, we consider the simplest case possible: An elliptic equation on the d-dimensional lattice $\mathbb{Z}^d$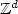with independent and identically distributed conductivities on the associated edges.Recent results by Otto and the author quantify the error made by approximatingthe homogenized coefficient by the averaged energy of a regularizedcorrector (with parameter T) on some box of finite size L. In this article, we replace the regularizedcorrector (which is the solution of a problem posed on $\mathbb{Z}^d$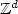) by some practically computable proxy on some box of size R ≥ L, and quantify the associated additional error.In order to improve the convergence, one may also consider N independentrealizations of the computable proxy, and take the empirical average of the associated approximate homogenized coefficients.A natural optimization problem consists in properly choosing T, R, L and N in order toreduce the error at given computational complexity.Our analysis is sharp and sheds some light on this question.In particular, we propose and analyze a numerical algorithm to approximate the homogenized coefficients, taking advantage of the (nearly) optimal scalings of the errorswe derive. The efficiency of the approach is illustrated by a numerical study in dimension 2.

Keywords

Stochastic homogenizationeffective coefficientsdifference operatornumerical method
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 46 , Issue 1 , January 2012 , pp. 1 - 38
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S. Agmon, Lectures on exponential decay of solutions of second-order elliptic equations: bounds on eigenfunctions of N-body Schrödinger operators, Mathematical Notes 29. Princeton University Press, Princeton, NJ (1982).
Alicandro, R., Cicalese, M. and Gloria, A., Integral representation results for energies defined on stochastic lattices and application to nonlinear elasticity. Arch. Ration. Mech. Anal. 200 (2011) 881–943. CrossRef
Bourgeat, A. and Piatnitski, A., Approximations of effective coefficients in stochastic homogenization. Ann. Inst. H. Poincaré 40 (2004) 153–165. CrossRef
Caputo, P. and Ioffe, D., Finite volume approximation of the effective diffusion matrix: the case of independent bond disorder. Ann. Inst. H. Poincaré Probab. Statist. 39 (2003) 505–525. CrossRef
Delmotte, T., Inégalité de Harnack elliptique sur les graphes. Colloq. Math. 72 (1997) 19–37.
Dykhne, A., Conductivity of a two-dimensional two-phase system. Sov. Phys. JETP 32 (1971) 63–65. Russian version: Zh. Eksp. Teor. Fiz. 59 (1970) 110–5.
W. E, P.B. Ming and P.W. Zhang, Analysis of the heterogeneous multiscale method for elliptic homogenization problems. J. Amer. Math. Soc. 18 (2005) 121–156. CrossRef
A. Gloria, Reduction of the resonance error – Part 1: Approximation of homogenized coefficients. Math. Models Methods Appl. Sci., to appear.
Gloria, A. and Otto, F., An optimal variance estimate in stochastic homogenization of discrete elliptic equations. Ann. Probab. 39 (2011) 779–856. CrossRef
A. Gloria and F. Otto, An optimal error estimate in stochastic homogenization of discrete elliptic equations. Ann. Appl. Probab., to appear.
A. Gloria and F. Otto, Quantitative estimates in stochastic homogenization of linear elliptic equations. In preparation.
Hou, T.Y. and Wu, X.H., Multiscale, A finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 134 (1997) 169–189. CrossRef
V.V. Jikov, S.M. Kozlov and O.A. Oleinik, Homogenization of Differential Operators and Integral Functionals. Springer-Verlag, Berlin (1994).
Kanit, T., Forest, S., Galliet, I., Mounoury, V. and Jeulin, D., Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int. J. Sol. Struct. 40 (2003) 3647–3679. CrossRef
Kozlov, S.M., The averaging of random operators. Mat. Sb. (N.S.) 109 (1979) 188–202, 327.
Kozlov, S.M., Averaging of difference schemes. Mat. Sb. 57 (1987) 351–369. CrossRef
Künnemann, R., The diffusion limit for reversible jump processes on $\mathbb{Z}^d$ with ergodic random bond conductivities. Commun. Math. Phys. 90 (1983) 27–68. CrossRef
Meijerink, J.A. and van der Vorst, H.A., An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix. Math. Comp. 31 (1977) 148–162.
A. Naddaf and T. Spencer, Estimates on the variance of some homogenization problems. Preprint (1998).
Owhadi, H., Approximation of the effective conductivity of ergodic media by periodization. Probab. Theory Relat. Fields 125 (2003) 225–258. CrossRef
G.C. Papanicolaou and S.R.S. Varadhan, Boundary value problems with rapidly oscillating random coefficients, in Random fields I, II (Esztergom, 1979), Colloq. Math. Soc. János Bolyai 27. North-Holland, Amsterdam (1981) 835–873.
Yue, X. and The, W. E local microscale problem in the multiscale modeling of strongly heterogeneous media: effects of boundary conditions and cell size. J. Comput. Phys. 222 (2007) 556–572. CrossRef
Yurinskii, V.V., Averaging of symmetric diffusion in random medium. Sibirskii Matematicheskii Zhurnal 27 (1986) 167–180.