Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:13:48.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Probabilistic interpretation and random walkon spheres algorithms for the Poisson-Boltzmann equationin molecular dynamics

Published online by Cambridge University Press:  26 August 2010

Mireille Bossy ,
Nicolas Champagnat ,
Sylvain Maire  and
Denis Talay
Mireille Bossy
Affiliation:
TOSCA project-team, INRIA Sophia Antipolis – Méditerranée, France. Mireille.Bossy@sophia.inria.fr; Nicolas.Champagnat@sophia.inria.fr; Denis.Talay@sophia.inria.fr
Nicolas Champagnat
Affiliation:
TOSCA project-team, INRIA Sophia Antipolis – Méditerranée, France. Mireille.Bossy@sophia.inria.fr; Nicolas.Champagnat@sophia.inria.fr; Denis.Talay@sophia.inria.fr
Sylvain Maire
Affiliation:
IMATH, Université du sud Toulon-Var, France. maire@univ-tln.fr
Denis Talay
Affiliation:
TOSCA project-team, INRIA Sophia Antipolis – Méditerranée, France. Mireille.Bossy@sophia.inria.fr; Nicolas.Champagnat@sophia.inria.fr; Denis.Talay@sophia.inria.fr
Get access

Abstract

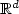Motivated by the development of efficient Monte Carlo methodsfor PDE models in molecular dynamics,we establish a new probabilistic interpretation of a family of divergence formoperators with discontinuous coefficients at the interfaceof two open subsets of $\mathbb{R}^d$ . This family of operators includes the case of thelinearized Poisson-Boltzmann equation used tocompute the electrostatic free energy of a molecule.More precisely, we explicitly construct a Markov process whoseinfinitesimal generator belongs to this family, as the solution of a SDEincluding a non standard local time term related to the interfaceof discontinuity. We then prove an extendedFeynman-Kac formula for the Poisson-Boltzmann equation.This formula allows us to justifyvarious probabilistic numerical methods toapproximate the free energy of a molecule.We analyse the convergence rate of these simulation procedures andnumerically compare them on idealized molecules models.

Keywords

Divergence form operatorPoisson-Boltzmann equationFeynman-Kac formularandom walk on sphere algorithm
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 44 , Issue 5: Special Issue on Probabilistic methods and their applications , September 2010 , pp. 997 - 1048
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aronson, D.G., Bounds for the fundamental solution of a parabolic equation. Bull. Amer. Math. Soc. 73 (1967) 890–896. CrossRef
Baker, N.A., Sept, D., Holst, M.J. and McCammon, J.A., The adaptive multilevel finite element solution of the Poisson-Boltzmann equation on massively parallel computers. IBM J. Res. Dev. 45 (2001) 427–437. CrossRef
N.A. Baker, D. Bashford and D.A. Case, Implicit solvent electrostatics in biomolecular simulation, in New algorithms for macromolecular simulation, Lect. Notes Comput. Sci. Eng. 49, Springer, Berlin (2005) 263–295.
A.N. Borodin and P. Salminen, Handbook of Brownian motion-facts and formulae. Probability and its Applications, 2nd edition, Birkhäuser Verlag, Basel (2002).
H. Brezis, Analyse fonctionnelle : Théorie et applications. Collection Mathématiques Appliquées pour la Maîtrise, Masson, Paris (1983).
R. Dautray and J.-L. Lions, Evolution problems II, Mathematical analysis and numerical methods for science and technology 6. Springer-Verlag, Berlin (1993).
S.N. Ethier and T.G. Kurtz, Markov processes – Characterization and convergence. Wiley Series in Probability and Mathematical Statistics, Probability and Mathematical Statistics, John Wiley & Sons Inc., New York (1986).
M. Fukushima, Y. Ōshima and M. Takeda, Dirichlet forms and symmetric Markov processes, de Gruyter Studies in Mathematics 19. Walter de Gruyter & Co., Berlin (1994).
D. Gilbarg and N.S. Trudinger, Elliptic partial differential equations of second order. Classics in Mathematics, Reprint of the 1998 edition, Springer-Verlag, Berlin (2001).
N. Ikeda and S. Watanabe, Stochastic differential equations and diffusion processes, North-Holland Mathematical Library 24. Second edition, North-Holland Publishing Co., Amsterdam (1989).
I. Karatzas and S.E. Shreve, Brownian motion and stochastic calculus, Graduate Texts in Mathematics 113. Second edition, Springer-Verlag, New York (1991).
O.A. Ladyzhenskaya and N.N. Ural'tseva, Linear and quasilinear elliptic equations. Academic Press, New York (1968).
B. Lapeyre, É. Pardoux and R. Sentis, Introduction to Monte-Carlo methods for transport and diffusion equations, Oxford Texts in Applied and Engineering Mathematics 6. Oxford University Press, Oxford (2003).
J.-F. Le Gall, One-dimensional stochastic differential equations involving the local times of the unknown process, in Stochastic analysis and applications (Swansea, 1983), Lecture Notes Math. 1095, Springer, Berlin (1984) 51–82.
A. Lejay, Méthodes probabilistes pour l'homogénéisation des opérateurs sous forme divergence : Cas linéaires et semi-linéaires. Ph.D. Thesis, Université de Provence, Marseille, France (2000).
Lejay, A. and Maire, S., Simulating diffusions with piecewise constant coefficients using a kinetic approximation. Comput. Meth. Appl. Mech. Eng. 199 (2010) 2014–2023. CrossRef
Lejay, A. and Martinez, M., A scheme for simulating one-dimensional diffusion processes with discontinuous coefficients. Ann. Appl. Probab. 16 (2006) 107–139. CrossRef
N. Limić, Markov jump processes approximating a nonsymmetric generalized diffusion. Preprint, arXiv:0804.0848v4 (2008).
S. Maire, Réduction de variance pour l'intégration numérique et pour le calcul critique en transport neutronique. Ph.D. Thesis, Université de Toulon et du Var, France (2001).
Maire, S. and Talay, D., On a Monte Carlo method for neutron transport criticality computations. IMA J. Numer. Anal. 26 (2006) 657–685. CrossRef
M. Martinez, Interprétations probabilistes d'opérateurs sous forme divergence et analyse des méthodes numériques probabilistes associées. Ph.D. Thesis, Université de Provence, Marseille, France (2004).
Martinez, M. and Talay, D., Discrétisation d'équations différentielles stochastiques unidimensionnelles à générateur sous forme divergence avec coefficient discontinu. C. R. Math. Acad. Sci. Paris 342 (2006) 51–56. CrossRef
Mascagni, M. and Simonov, N.A., Monte Carlo methods for calculating some physical properties of large molecules. SIAM J. Sci. Comput. 26 (2004) 339–357. CrossRef
Portenko, N.I., Diffusion processes with a generalized drift coefficient. Teor. Veroyatnost. i Primenen. 24 (1979) 62–77.
Portenko, N.I., Stochastic differential equations with a generalized drift vector. Teor. Veroyatnost. i Primenen. 24 (1979) 332–347.
P.E. Protter, Stochastic integration and differential equations – Second edition, Version 2.1, Stochastic Modelling and Applied Probability 21. Corrected third printing, Springer-Verlag, Berlin (2005).
D. Revuz and M. Yor, Continuous martingales and Brownian motion, Grundlehren der Mathematischen Wissenschaften 293. Springer-Verlag, Berlin (1991).
L.C.G. Rogers and D. Williams, Foundations, Diffusions, Markov processes, and martingales 1. Reprint of the second edition (1994), Cambridge Mathematical Library, Cambridge University Press, Cambridge (2000).
L.C.G. Rogers and D. Williams, Itô calculus, Diffusions, Markov processes, and martingales 2. Reprint of the second edition (1994), Cambridge Mathematical Library, Cambridge University Press, Cambridge (2000).
Rozkosz, A. and Słomiński, L., Extended convergence of Dirichlet processes. Stochastics Stochastics Rep. 65 (1998) 79–109. CrossRef
K.K. Sabelfeld, Monte Carlo methods in boundary value problems. Springer Series in Computational Physics, Springer-Verlag, Berlin (1991).
Sabelfeld, K.K. and Talay, D., Integral formulation of the boundary value problems and the method of random walk on spheres. Monte Carlo Meth. Appl. 1 (1995) 1–34. CrossRef
N.A. Simonov, Walk-on-spheres algorithm for solving boundary-value problems with continuity flux conditions, in Monte Carlo and quasi-Monte Carlo methods 2006, Springer, Berlin (2008) 633–643.
Simonov, N.A., Mascagni, M. and Fenley, M.O., Monte Carlo-based linear Poisson-Boltzmann approach makes accurate salt-dependent solvation free energy predictions possible. J. Chem. Phys. 127 (2007) 185105. CrossRef
D.W. Stroock, Diffusion semigroups corresponding to uniformly elliptic divergence form operators, in Séminaire de Probabilités, XXII, Lecture Notes in Math. 1321, Springer, Berlin (1988) 316–347.
D.W. Stroock and S.R.S. Varadhan, Multidimensional diffusion processes, Grundlehren der Mathematischen Wissenschaften 233. Springer-Verlag, Berlin (1979).