Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Achdou, Y.
and
Guermond, J. L.
2000.
Convergence Analysis of a Finite Element Projection/Lagrange--Galerkin Method for the Incompressible Navier--Stokes Equations.
SIAM Journal on Numerical Analysis,
Vol. 37,
Issue. 3,
p.
799.
Guermond, J.-L.
and
Quartapelle, L.
2000.
A Projection FEM for Variable Density Incompressible Flows.
Journal of Computational Physics,
Vol. 165,
Issue. 1,
p.
167.
Auteri, F.
Saleri, F.
and
Vigevano, L.
2001.
Incompressible Navier–Stokes solutions by a triangular spectral/p element projection method.
Computer Methods in Applied Mechanics and Engineering,
Vol. 190,
Issue. 51-52,
p.
6927.
Auteri, F.
and
Parolini, N.
2001.
Computational Fluid and Solid Mechanics.
p.
1451.
Guermond, Jean-Luc
and
Shen, Jie
2001.
Quelques résultats nouveaux sur les méthodes de projection.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 333,
Issue. 12,
p.
1111.
Auteri, F.
Guermond, J.-L.
and
Parolini, N.
2001.
Role of the LBB Condition in Weak Spectral Projection Methods.
Journal of Computational Physics,
Vol. 174,
Issue. 1,
p.
405.
Auteri, F.
Parolini, N.
and
Quartapelle, L.
2002.
Numerical Investigation on the Stability of Singular Driven Cavity Flow.
Journal of Computational Physics,
Vol. 183,
Issue. 1,
p.
1.
Auteri, F.
and
Parolini, N.
2002.
A Mixed-Basis Spectral Projection Method.
Journal of Computational Physics,
Vol. 175,
Issue. 1,
p.
1.
Auteri, F.
and
Parolini, N.
2002.
Numerical investigation of the first instabilities in the differentially heated 8:1 cavity.
International Journal for Numerical Methods in Fluids,
Vol. 40,
Issue. 8,
p.
1121.
Guermond, J.
and
Shen, Jie
2003.
On the error estimates for the rotational pressure-correction projection methods.
Mathematics of Computation,
Vol. 73,
Issue. 248,
p.
1719.
Guermond, J.L.
and
Shen, Jie
2003.
A new class of truly consistent splitting schemes for incompressible flows.
Journal of Computational Physics,
Vol. 192,
Issue. 1,
p.
262.
Iannelli, P.
and
Denaro, F. M.
2003.
Analysis of the local truncation error in the pressure‐free projection method for incompressible flows: a new accurate expression of the intermediate boundary conditions.
International Journal for Numerical Methods in Fluids,
Vol. 42,
Issue. 4,
p.
399.
Maria Denaro, Filippo
2003.
On the application of the Helmholtz–Hodge decomposition in projection methods for incompressible flows with general boundary conditions.
International Journal for Numerical Methods in Fluids,
Vol. 43,
Issue. 1,
p.
43.
Glowinski, Roland
2003.
Numerical Methods for Fluids (Part 3).
Vol. 9,
Issue. ,
p.
3.
Marra, A.
Mola, A.
Quartapelle, L.
and
Riviello, L.
2004.
Calculation of impulsively started incompressible viscous flows.
International Journal for Numerical Methods in Fluids,
Vol. 46,
Issue. 8,
p.
877.
Quarteroni, Alfio
and
Formaggia, Luca
2004.
Computational Models for the Human Body.
Vol. 12,
Issue. ,
p.
3.
Denaro, F. M.
2005.
Time‐accurate intermediate boundary conditions for large eddy simulations based on projection methods.
International Journal for Numerical Methods in Fluids,
Vol. 48,
Issue. 8,
p.
869.
Bejanov, B.
Guermond, J.-L.
and
Minev, P. D.
2005.
A locally DIV-free projection scheme for incompressible flows based on non-conforming finite elements.
International Journal for Numerical Methods in Fluids,
Vol. 49,
Issue. 5,
p.
549.
Jobelin, M.
Lapuerta, C.
Latché, J.-C.
Angot, Ph.
and
Piar, B.
2006.
A finite element penalty–projection method for incompressible flows.
Journal of Computational Physics,
Vol. 217,
Issue. 2,
p.
502.
Guermond, J.L.
Minev, P.
and
Shen, Jie
2006.
An overview of projection methods for incompressible flows.
Computer Methods in Applied Mechanics and Engineering,
Vol. 195,
Issue. 44-47,
p.
6011.
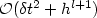 for the velocity in the norm of l 2(L2(Ω)d), where l ≥ 1 isthe polynomial degree of the velocity approximation. It is also shownthat the splitting error of projection schemes based on theincremental pressure correction is of ${\cal O}(\delta t^2)$
for the velocity in the norm of l 2(L2(Ω)d), where l ≥ 1 isthe polynomial degree of the velocity approximation. It is also shownthat the splitting error of projection schemes based on theincremental pressure correction is of ${\cal O}(\delta t^2)$ 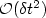 independent of theapproximation order of the velocity time derivative.
independent of theapproximation order of the velocity time derivative. 

