Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T18:22:05.287Z Has data issue: false hasContentIssue false
  • English
  • Français

The Cahn–Hilliard equation with a concentration dependent mobility: motion by minus the Laplacian of the mean curvature

Published online by Cambridge University Press:  26 September 2008

J. W. Cahn ,
C. M. Elliott  and
A. Novick-Cohen
J. W. Cahn
Affiliation:
Materials Science and Engineering Laboratory, NIST, Gaithersburg, MD 20899, USA
C. M. Elliott
Affiliation:
Centre for Mathematical Analysis and its Applications, University of Sussex, Brighton BN1 9QH, UK
A. Novick-Cohen
Affiliation:
Department of Mathematics, Technion-IIT, Haifa, Israel 32000
Get access Rights & Permissions [Opens in a new window]

Abstract

We show by using formal asymptotics that the zero level set of the solution to the Cahn–Hilliard equation with a concentration dependent mobility approximates to lowest order in ɛ. an interface evolving according to the geometric motion,

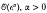(where V is the normal velocity, Δ8 is the surface Laplacian and κ is the mean curvature of the interface), both in the deep quench limit and when the temperature θ is where є2 is the coefficient of gradient energy. Equation (0.1) may be viewed as motion by surface diffusion, and as a higher-order analogue of motion by mean curvature predicted by the bistable reaction-diffusion equation.

Type
Research Article
Information
European Journal of Applied Mathematics , Volume 7 , Issue 3 , June 1996 , pp. 287 - 301
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Cahn, J. W. 1961 On spinodal decomposition. Acta Met. 9, 795–801.CrossRefGoogle Scholar
[2] Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28, 258–267.CrossRefGoogle Scholar
[3] Hilliard, J. E. 1958 Spinodal decomposition, in Phase Transformations, ASM, Cleveland, 1970, Chapt. 12, 497–560.Google Scholar
[4] Novick-Cohen, A. 1989 Non-linear aspects of the Cahn–Hilliard equation. Physica 10D, 277–298.Google Scholar
[5] Elliott, C. M. & Zheng, S. 1986 On the Cahn-Hilliard equation. Arch. Rat. Mech. Anal. 96, 339–357.CrossRefGoogle Scholar
[6] Novick-Cohen, A. 1990 On Cahn–Hilliard type equations. Nonlinear Analysis TMA 15, 797–814.CrossRefGoogle Scholar
[7] Temam, R. 1988 Infinite Dimensional Dynamical Systems in Mechanics and Physics. Applied Mathematical Sciences 68, Springer.CrossRefGoogle Scholar
[8].Elliott, C. M. 1989 The Cahn–Hilliard model for the kinetics of phase separation. In Mathematical Models for Phase Change Problems (Rodrigues, J. F., Ed.), International Series on Numerical Mathematics, Vol. 88, Birkhauser.Google Scholar
[9] Novick-Cohen, A. 1996 The Cahn–Hilliard equation: mathematical and modelling perspectives, in Surveys in Nonlinear Diffusion (Peletier, L. A., Ed.), in preparation.Google Scholar
[10] Novick-Cohen, A. & Peletier, L. A. 1993 Steady states of the one-dimensional Cahn–Hilliard equation. Proc. Roy. Society of Edinburgh, Ser. A 123, 1071–1098.CrossRefGoogle Scholar
[11] Grinfeld, M. & Novick-Cohen, A. 1995 Counting stationary solutions of the Cahn–Hilliard equation by transversality arguments. Proc. Roy. Soc. Edinburgh, Ser. A, 125, 351–370.CrossRefGoogle Scholar
[12] Alikakos, N., Bates, P. W. & Fusco, G. 1991 Slow motion of the Cahn–Hilliard equation in one space dimension. J. Diff. Equations 90, 81–134.CrossRefGoogle Scholar
[13] Cahn, J. W. & Taylor, J. E. 1994 Surface motion by surface diffusion. Acta Met. Mat. 42, 1045–1063.CrossRefGoogle Scholar
[14] Taylor, J. E. & Cahn, J. W. 1993 Linking anisotropic sharp and diffuse surface motion laws via gradient flows. J. Stat. Phys. 11, 183–197.Google Scholar
[15] Elliott, C. M. & Garcke, H. 1994 On the Cahn–Hilliard equation with degenerate mobility. SIAM J. Math. Anal. (to appear).Google Scholar
[16] Mullins, W. W. 1957 Theory of thermal grooving. J. Appl. Phys. 28, 333–339.CrossRefGoogle Scholar
[17] Davi, F. & Gurtin, M. 1990 On the motion of a phase interface by surface diffusion. J. Appl. Math. Phys. (ZAMP) 41, 782–811.CrossRefGoogle Scholar
[18] Elliott, C. M. & Garcke, H. 1994 Existence results for geometric interface models for surface diffusion. CMAIA Research Report 94/22.Google Scholar
[19] Pego, R. 1989 Front migration with the nonlinear Cahn–Hilliard equation. Proc. Roy. Soc. A 422, 261–278.Google Scholar
[20] Alikakos, N., Bates, P. W. & Chen, X. 1994 Convergence of the Cahn–Hilliard equation to the Hele–Shaw model. Arc. Rat. Mech. Anal. 128, 165–205.CrossRefGoogle Scholar
[21] Rubinstein, J., Sternberg, P. & Keller, J. 1989 Fast reaction, slow diffusion, and curve shortening. SIAM Appl. Math. 49, 116–133.CrossRefGoogle Scholar
[22] Allen, S. M. & Cahn, J. W. 1979 A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Met. 27, 1085–1095.CrossRefGoogle Scholar
[23] Taylor, J. E., Cahn, J. W. & Handwerker, C. A. 1992 Geometric models of crystal growth. Acta Metall. Mater. 40, 1443–1474.CrossRefGoogle Scholar
[24] Gurtin, M. E. 1993 Thermomechanics of Evolving Phase Boundaries in the Plane. Oxford University Press.CrossRefGoogle Scholar
[25] Luckhaus, S. & Modica, L. 1989 The Gibbs–Thomson relation within the gradient theory of phase transition. Arch. Rat. Mech. Anal. 107, 71–83.CrossRefGoogle Scholar
[26] Modica, L. 1987 The gradient theory of phase transitions and the minimal interface criterion. Arch. Rat. Mech. Anal. 98, 123–142.CrossRefGoogle Scholar
[27] Sternberg, P. 1988 The effect of a singular perturbation on nonconvex variational problems. Arch. Rat. Mech. Anal. 101, 209–260.CrossRefGoogle Scholar
[28] Blowey, J. F. & Elliott, C. M. 1992 The Cahn–Hilliard gradient theory for phase separation with non-smooth free energy, Part I: Mathematical analysis. Euro. J. Appl. Math. 2, 233–279.CrossRefGoogle Scholar
[29] Elliott, C. M. & Luckhaus, S. 1991 A generalized diffusion equation for phase separation of a multi-component mixture with interfacial free energy. IMA preprint series no. 887.Google Scholar
[30] Blowey, J. F. & Elliott, C. M. 1992 The Cahn–Hilliard gradient theory with non-smooth free energy, Part 11: Numerical analysis. Euro. J. Appl. Math. 3, 147–179.CrossRefGoogle Scholar