Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aquino, M.
Dáger, R.
and
Negreanu, M.
2021.
Uniform Boundedness of Solutions for a Two Species Taxis System with Intraspecific and Interspecific Competition.
Results in Mathematics,
Vol. 76,
Issue. 2,
Ren, Guoqiang
and
Wei, Jinlong
2021.
Analysis of a two-dimensional triply haptotactic model with a fusogenic oncolytic virus and syncytia.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 72,
Issue. 4,
Tao, Xueyan
and
Zhou, Shulin
2022.
Dampening effects on global boundedness and asymptotic behavior in an oncolytic virotherapy model.
Journal of Differential Equations,
Vol. 308,
Issue. ,
p.
57.
Dai, Feng
and
Liu, Bin
2022.
Global weak solutions in a three-dimensional two-species cancer invasion haptotaxis model without cell proliferation.
Journal of Mathematical Physics,
Vol. 63,
Issue. 9,
Bellomo, N.
Outada, N.
Soler, J.
Tao, Y.
and
Winkler, M.
2022.
Chemotaxis and cross-diffusion models in complex environments: Models and analytic problems toward a multiscale vision.
Mathematical Models and Methods in Applied Sciences,
Vol. 32,
Issue. 04,
p.
713.
Zhao, Qian
and
Liu, Bin
2022.
Dampening effects on global boundedness in a quartic haptotactic model with fusogenic oncolytic virus and syncytia.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 73,
Issue. 6,
Wang, Yifu
and
Xu, Chi
2023.
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 153,
Issue. 3,
p.
881.
Youshan, Tao
2023.
A probe into research of complex chemotaxis models.
SCIENTIA SINICA Mathematica,
Dai, Feng
and
Ma, Linjie
2023.
Boundedness in a two-dimensional two-species cancer invasion haptotaxis model without cell proliferation.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 74,
Issue. 2,
Wang, Yifu
and
Xu, Chi
2023.
Asymptotic behavior of a three-dimensional haptotactic cross-diffusion system modeling oncolytic virotherapy.
Mathematical Models and Methods in Applied Sciences,
Vol. 33,
Issue. 11,
p.
2313.
Zheng, Jiashan
and
Ke, Yuanyuan
2023.
Boundedness and large time behavior of solutions of a higher-dimensional haptotactic system modeling oncolytic virotherapy.
Mathematical Models and Methods in Applied Sciences,
Vol. 33,
Issue. 09,
p.
1875.
Wen, Qiang
and
Liu, Bin
2023.
Global boundedness in an oncolytic virotherapy model with generalized logistic source.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 74,
Issue. 1,
Ren, Guoqiang
2024.
Boundedness of solutions to a chemotaxis–haptotaxis model with nonlocal terms.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 31,
Issue. 2,
Tao, Xueyan
and
Zhou, Shulin
2024.
Global boundedness and asymptotic behavior in a double haptotaxis model for oncolytic virotherapy.
Journal of Mathematical Analysis and Applications,
Vol. 539,
Issue. 1,
p.
128522.
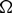 $\Omega$
, we consider the model for oncolytic virotherapy given by
$\Omega$
, we consider the model for oncolytic virotherapy given by  $$\left\{ \begin{array}{l} u_t = \Delta u - \nabla \cdot (u\nabla v) - uz, \\[1mm] v_t = - (u+w)v, \\[1mm] w_t = d_w \Delta w - w + uz, \\[1mm] z_t = d_z \Delta z - z - uz + \beta w, \end{array} \right.$$
$$\left\{ \begin{array}{l} u_t = \Delta u - \nabla \cdot (u\nabla v) - uz, \\[1mm] v_t = - (u+w)v, \\[1mm] w_t = d_w \Delta w - w + uz, \\[1mm] z_t = d_z \Delta z - z - uz + \beta w, \end{array} \right.$$
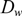 $ D_w $
,
$ D_w $
, 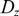 $ D_z $
and
$ D_z $
and 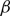 $\beta$
. It is firstly shown that whenever
$\beta$
. It is firstly shown that whenever 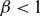 $\beta \lt 1$
, for any choice of
$\beta \lt 1$
, for any choice of 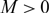 $M \gt 0$
, one can find initial data such that the solution of an associated no-flux initial-boundary value problem, well known to exist globally actually for any choice of
$M \gt 0$
, one can find initial data such that the solution of an associated no-flux initial-boundary value problem, well known to exist globally actually for any choice of 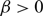 $\beta \gt 0$
, satisfies
$\beta \gt 0$
, satisfies 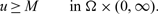 $$u\ge M \qquad \mbox{in } \Omega\times (0,\infty).$$
$$u\ge M \qquad \mbox{in } \Omega\times (0,\infty).$$
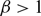 $\beta \gt 1$
, however, then for arbitrary initial data the corresponding is seen to have the property that
$\beta \gt 1$
, however, then for arbitrary initial data the corresponding is seen to have the property that 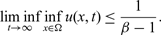 $$\liminf_{t\to\infty} \inf_{x\in\Omega} u(x,t)\le \frac{1}{\beta-1}.$$
$$\liminf_{t\to\infty} \inf_{x\in\Omega} u(x,t)\le \frac{1}{\beta-1}.$$
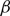 $\beta$
plays the role of a critical virus replication rate with regard to efficiency of the considered virotherapy, with corresponding threshold value given by
$\beta$
plays the role of a critical virus replication rate with regard to efficiency of the considered virotherapy, with corresponding threshold value given by 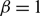 $\beta = 1$
.
$\beta = 1$
.