Article contents
Shock waves and compactons for fifth-order non-linear dispersion equations
Published online by Cambridge University Press: 12 November 2009
Abstract
The following first problem is posed:
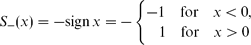 is a correct ‘entropy solution’ of the Cauchy problem for the fifth-order degenerate non-linear dispersion equations (NDEs), same as for the classic Euler one ut + uux = 0,
is a correct ‘entropy solution’ of the Cauchy problem for the fifth-order degenerate non-linear dispersion equations (NDEs), same as for the classic Euler one ut + uux = 0,
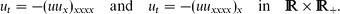 These two quasi-linear degenerate partial differential equations (PDEs) are chosen as typical representatives; so other (2m + 1)th-order NDEs of non-divergent form admit such shocks waves. As a related second problem, the opposite initial shock S+(x) = −S−(x) = sign x is shown to be a non-entropy solution creating a rarefaction wave, which becomes C∞ for any t > 0. Formation of shocks leads to non-uniqueness of any ‘entropy solutions’. Similar phenomena are studied for a fifth-order in time NDE uttttt = (uux)xxxx in normal form.
These two quasi-linear degenerate partial differential equations (PDEs) are chosen as typical representatives; so other (2m + 1)th-order NDEs of non-divergent form admit such shocks waves. As a related second problem, the opposite initial shock S+(x) = −S−(x) = sign x is shown to be a non-entropy solution creating a rarefaction wave, which becomes C∞ for any t > 0. Formation of shocks leads to non-uniqueness of any ‘entropy solutions’. Similar phenomena are studied for a fifth-order in time NDE uttttt = (uux)xxxx in normal form.
On the other hand, related NDEs, such as
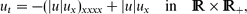 are shown to admit smooth compactons, as oscillatory travelling wave solutions with compact support. The well-known non-negative compactons, which appeared in various applications (first examples by Dey, 1998, Phys. Rev. E, vol. 57, pp. 4733–4738, and Rosenau and Levy, 1999, Phys. Lett. A, vol. 252, pp. 297–306), are non-existent in general and are not robust relative to small perturbations of parameters of the PDE.
are shown to admit smooth compactons, as oscillatory travelling wave solutions with compact support. The well-known non-negative compactons, which appeared in various applications (first examples by Dey, 1998, Phys. Rev. E, vol. 57, pp. 4733–4738, and Rosenau and Levy, 1999, Phys. Lett. A, vol. 252, pp. 297–306), are non-existent in general and are not robust relative to small perturbations of parameters of the PDE.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2009
References
- 5
- Cited by


