Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-27T16:29:35.231Z Has data issue: false hasContentIssue false
  • English
  • Français

Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes

Part of: Partial differential equations, boundary value problems Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  05 January 2023

Ruchi Guo Open the ORCID record for Ruchi Guo [Opens in a new window] ,
Yanping Lin  and
Jun Zou
Ruchi Guo*
Affiliation:
Department of Mathematics, University of California, Irvine, CA 92697, USA
Yanping Lin
Affiliation:
Department of Applied Mathematics, The Hong Kong Polytechnic University, Kowloon, Hong Kong, China
Jun Zou
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong
*
*Correspondence author. Email: ruchig@uci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Finite element methods developed for unfitted meshes have been widely applied to various interface problems. However, many of them resort to non-conforming spaces for approximation, which is a critical obstacle for the extension to 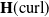$\textbf{H}(\text{curl})$ equations. This essential issue stems from the underlying Sobolev space 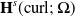$\textbf{H}^s(\text{curl};\,\Omega)$, and even the widely used penalty methodology may not yield the optimal convergence rate. One promising approach to circumvent this issue is to use a conforming test function space, which motivates us to develop a Petrov–Galerkin immersed finite element (PG-IFE) method for 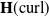$\textbf{H}(\text{curl})$-elliptic interface problems. We establish the Nédélec-type IFE spaces and develop some important properties including their edge degrees of freedom, an exact sequence relating to the 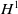$H^1$ IFE space and optimal approximation capabilities. We analyse the inf-sup condition under certain assumptions and show the optimal convergence rate, which is also validated by numerical experiments.

Keywords

Maxwell equationsinterface problemsH(curl)-elliptic equationsNédélec elementsimmersed finite element methodsPetrov–Galerkin formulationexact sequence

MSC classification

Primary: 65N15: Error bounds
Secondary: 35R05: Partial differential equations with discontinuous coefficients or data 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods
Type
Papers
Information
European Journal of Applied Mathematics , Volume 34 , Issue 4 , August 2023 , pp. 774 - 805
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adjerid, S., Babuška, I., Guo, R. & Lin, T. (2023) An enriched immersed finite element method for interface problems with nonhomogeneous jump conditions. Comput. Methods Appl. Mech. Eng. 404.CrossRefGoogle Scholar
Adjerid, S., Chaabane, N. & Lin, T. (in press) An immersed discontinuous finite element method for stokes interface problems. Comput. Methods Appl. Mech. Eng. 293, 170–190.CrossRefGoogle Scholar
Alberti, G. S. (2018) Hölder regularity for Maxwell’s equations under minimal assumptions on the coefficients. Calc. Var. Partial Differ. Equations 57(3), 71.CrossRefGoogle Scholar
Ammari, H., Buffa, A. & Nédélec, J. C. (2000) A justification of eddy currents model for the Maxwell equations. SIAM J. Appl. Math. 60(5), 1805–1823.Google Scholar
Ammari, H., Chen, J., Chen, Z., Volkov, D. & Wang, H. (2015) Detection and classification from electromagnetic induction data. J. Comput. Phys. 301, 201–217.CrossRefGoogle Scholar
Arnold, D. N., Falk, R. S. & Winther, R. (2006) Differential complexes and stability of finite element methods I. The de Rham complex. In: Arnold, D. N., Bochev, P. B., Lehoucq, R. B., Nicolaides, R. A. and Shashkov, M. (editors), Compatible Spatial Discretizations, Springer, New York, pp. 23–46.Google Scholar
Arnold, D. N., Falk, R. S. & Winther, R. (2006) Finite element exterior calculus, homological techniques, and applications. Acta Numerica 15, 1–155.CrossRefGoogle Scholar
Babuška, I. & Aziz, A. K. (1972) Survey lectures on the mathematical foundations of the finite element method with applications. In: The Mathematical Foundations of the Finite Element Method with Applicaions to Partial Differential Equations, pp. 3–359.CrossRefGoogle Scholar
Babuška, I. & Aziz, A. K. (1976) On the angle condition in the finite element method. SIAM J. Numer. Anal. 13(2), 214–226.CrossRefGoogle Scholar
Babuška, I., Caloz, G. & Osborn, J. E. (1994) Special finite element methods for a class of second order elliptic problems with rough coefficients. SIAM J. Numer. Anal. 31(4), 945–981.CrossRefGoogle Scholar
Babuška, I. & Osborn, J. E. (1983) Generalized finite element methods: their performance and their relation to mixed methods. SIAM J. Numer. Anal. 20(3), 510–536.CrossRefGoogle Scholar
Babuška, I. & Osborn, J. E. (2000) Can a finite element method perform arbitrarily badly? Math. Comput. 69(230), 443–462.CrossRefGoogle Scholar
Beck, R., Hiptmair, R., Hoppe, R. H. W. & Wohlmuth, B. (2000) Residual based a posteriori error estimators for eddy current computation. ESAIM M2AN 34(1), 159–182.CrossRefGoogle Scholar
Becker, R., Burman, E. & Hansbo, P. (2009) A Nitsche extended finite element method for incompressible elasticity with discontinuous modulus of elasticity. Comput. Methods Appl. Mech. Eng. 198(41–44), 3352–3360.CrossRefGoogle Scholar
Ben Belgacem, F., Buffa, A. & Maday, Y. (2001) The mortar finite element method for 3d Maxwell equations: first results. SIAM J. Numer. Anal. 39(3), 880–901.CrossRefGoogle Scholar
Brezzi, F. & Fortin, M. (1991) Mixed and Hybrid Finite Element Methods , Springer Series in Computational Mathematics, Vol. 15, Springer-Verlag, New York.Google Scholar
Burman, E., Claus, S., Hansbo, P., Larson, M. G. & Massing, A. (2015) CutFEM: discretizing geometry and partial differential equations. Int. J. Numer. Methods Eng. 104(7), 472–501.CrossRefGoogle Scholar
Cai, Z. & Cao, S. (2015) A recovery-based a posteriori error estimator for H(curl) interface problems. Comput. Methods Appl. Mech. Eng. 296, 169–195.CrossRefGoogle Scholar
Casagrande, R., Hiptmair, R. & Ostrowski, J. (2016) An a priori error estimate for interior penalty discretizations of the Curl-Curl operator on non-conforming meshes. J. Math. Ind. 6(1), 4.CrossRefGoogle Scholar
Casagrande, R., Winkelmann, C., Hiptmair, R. & Ostrowski, J. (2016) DG treatment of non-conforming interfaces in 3D Curl-Curl problems. In: A. Bartel, M. Clemens, M. Günther and E. J. W. Maten (editors), Scientific Computing in Electrical Engineering, Springer International Publishing, Cham, pp. 53–61.Google Scholar
Chan, T. F. & Zou, J. (1996) A convergence theory of multilevel additive schwarz methods on unstructured meshes. Numer. Algorithms 13(2), 365–398.CrossRefGoogle Scholar
Chen, Z., Du, Q. & Zou, J. (2000) Finite element methods with matching and nonmatching meshes for Maxwell equations with discontinuous coefficients. SIAM J. Numer. Anal. 37(5), 1542–1570.CrossRefGoogle Scholar
Chen, Z., Xiao, Y. & Zhang, L. (2009) The adaptive immersed interface finite element method for elliptic and Maxwell interface problems. J. Comput. Phys. 228(14), 5000–5019.CrossRefGoogle Scholar
Chu, C.-C., Graham, I. G. & Hou, T.-Y. (2010) A new multiscale finite element method for high-contrast elliptic interface problems. Math. Comput. 79(272), 1915–1955.CrossRefGoogle Scholar
Ciarlet, P. Jr. & Zou, J. (1999) Fully discrete finite element approaches for time-dependent Maxwell’s equations. Numer. Math. 82(2), 193–219.CrossRefGoogle Scholar
Costabel, M., Dauge, M. & Nicaise, S. (1999) Singularities of Maxwell interface problems. ESAIM Math. Model. Numer. Anal. 33(3), 627–649.CrossRefGoogle Scholar
Dirks, H. K. (1996) Quasi-stationary fields for microelectronic applications. Electr. Eng. 79(2), 145–155.CrossRefGoogle Scholar
Duan, H., Li, S., Tan, R. C. E. & Zheng, W. (2012) A delta-regularization finite element method for a double curl problem with divergence-free constraint. SIAM J. Numer. Anal. 50(6), 3208–3230.CrossRefGoogle Scholar
Duan, H., Qiu, F., Tan, R. C. E. & Zheng, W. (2016) An adaptive FEM for a Maxwell interface problem. J. Sci. Comput. 67(2), 669–704.CrossRefGoogle Scholar
Ern, A. & Guermond, J.-L. (2006) Evaluation of the condition number in linear systems arising in finite element approximations. ESAIM M2AN 40(1), 29–48.CrossRefGoogle Scholar
Gong, Y., Li, B. & Li, Z. (2008) Immersed-interface finite-element methods for elliptic interface problems with nonhomogeneous jump conditions. SIAM J. Numer. Anal. 46(1), 472–495.CrossRefGoogle Scholar
Groß, S. & Reusken, A. (2007) An extended pressure finite element space for two-phase incompressible flows with surface tension. J. Comput. Phys. 224(1), 40–58. Special Issue Dedicated to Professor Piet Wesseling on the occasion of his retirement from Delft University of Technology.CrossRefGoogle Scholar
Guo, R. (2021) Solving parabolic moving interface problems with dynamical immersed spaces on unfitted meshes: fully discrete analysis. SIAM J. Numer. Anal. 2(59), 797–828.CrossRefGoogle Scholar
Guo, R. & Lin, T. (2017) A group of immersed finite element spaces for elliptic interface problems. IMA J. Numer. Anal. 39(1), 482–511.CrossRefGoogle Scholar
Guo, R. & Lin, T. (2019) A higher degree immersed finite element method based on a Cauchy extension. SIAM J. Numer. Anal. 57(4), 1545–1573.CrossRefGoogle Scholar
Guo, R., Lin, T. & Lin, Y. (2020) Error estimates for a partially penalized immersed finite element method for elasticity interface problems. ESAIM Math. Model. Numer. Anal. 54(1), 1–24.CrossRefGoogle Scholar
Guo, R., Lin, Y., Lin, T. & Zhuang, Q. (2021) Error analysis of symmetric linear/bilinear partially penalized immersed finite element methods for Helmholtz interface problems. J. Comput. Appl. Math. 390, 113378.CrossRefGoogle Scholar
He, X., Lin, T. & Lin, Y. (2011) Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions. Int. J. Numer. Anal. Model. 8(2), 284–301.Google Scholar
He, X., Lin, T., Lin, Y. & Zhang, X. (2013) Immersed finite element methods for parabolic equations with moving interface. Numer. Methods Partial Differ. Equations 29(2), 619–646.CrossRefGoogle Scholar
Hiptmair, R. (2002) Finite elements in computational electromagnetism. Acta Numer. 11, 237–339.CrossRefGoogle Scholar
Hiptmair, R., Li, J. & Zou, J. (2012) Convergence analysis of finite element methods for $H(curl; \Omega)$ -elliptic interface problems. Numer. Math. 122(3), 557–578.CrossRefGoogle Scholar
Hiptmair, R. & Pechstein, C. (2017) Discrete regular decompositions of tetrahedral discrete 1-forms. SAM-Report 2017-47, ETH Zurich.Google Scholar
Hiptmair, R. & Pechstein, C. (2019) Regular decompositions of vector fields - continuous, discrete, and structure-preserving. SAM-Report 2019-18, ETH Zurich.Google Scholar
Hou, S., Song, P., Wang, L. & Zhao, H. (2013) A weak formulation for solving elliptic interface problems without body fitted grid. J. Comput. Phys. 249, 80–95.CrossRefGoogle Scholar
Hou, T.-Y., Wu, X. & Zhang, Y. (2004) Removing the cell resonance error in the multiscale finite element method via a Petrov-Galerkin formulation. Commun. Math. Sci. 2(2), 185–205.CrossRefGoogle Scholar
Houston, P., Perugia, I., Schneebeli, A. & Schötzau, D. (2005) Interior penalty method for the indefinite time-harmonic Maxwell equations. Numer. Math. 100(3), 485–518.CrossRefGoogle Scholar
Houston, P., Perugia, I. & Schotzau, D. (2004) Mixed discontinuous Galerkin approximation of the maxwell operator. SIAM J. Numer. Anal. 42(1), 434–459.CrossRefGoogle Scholar
Hu, Q., Shu, S. & Zou, J. (2008) A mortar edge element method with nearly optimal convergence for three-dimensional Maxwell’s equations. Math. Comp. 77.CrossRefGoogle Scholar
Huang, J. & Zou, J. (2007) Uniform a priori estimates for elliptic and static Maxwell interface problems. Disc. Cont. Dynam. Sys. Ser. B 7.Google Scholar
Huang, P., Wu, H. & Xiao, Y. (2017) An unfitted interface penalty finite element method for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 323, 439–460.CrossRefGoogle Scholar
Ji, H., Zhang, Q. & Zhang, B. (2018) Inf-sup stability of Petrov-Galerkin immersed finite element methods for one-dimensional elliptic interface problems. Numer. Methods Partial Differ. Equations 34(6), 1917–1932.CrossRefGoogle Scholar
Li, J., Melenk, J. M., Wohlmuth, B. & Zou, J. (2010) Optimal a priori estimates for higher order finite elements for elliptic interface problems. Appl. Numer. Math. 60(1), 19–37.CrossRefGoogle Scholar
Li, Z., Lin, T., Lin, Y. & Rogers, R. C. (2004) An immersed finite element space and its approximation capability. Numer. Methods Partial Differ. Equations 20(3), 338–367.CrossRefGoogle Scholar
Li, Z. Lin, T. & Wu, X. (2003) New Cartesian grid methods for interface problems using the finite element formulation. Numer. Math. 96(1), 61–98.CrossRefGoogle Scholar
Lin, T., Lin, Y. & Zhang, X. (2015) Partially penalized immersed finite element methods for elliptic interface problems. SIAM J. Numer. Anal. 53(2), 1121–1144.CrossRefGoogle Scholar
Lin, T., Lin, Y. & Zhang, X. (2013) A method of lines based on immersed finite elements for parabolic moving interface problems. Adv. Appl. Math. Mech. 5(4), 548–568.CrossRefGoogle Scholar
Lin, T., Sheen, D. & Zhang, X. (2013) A locking-free immersed finite element method for planar elasticity interface problems. J. Comput. Phys. 247(15), 228–247.CrossRefGoogle Scholar
Liu, H., Zhang, L., Zhang, X. & Zheng, W. (2020) Interface-penalty finite element methods for interface problems in ${H}^1$ , H(curl), and H(div). Comput. Methods Appl. Mech. Eng. 367, 113137.CrossRefGoogle Scholar
Lu, C., Yang, Z., Bai, J., Cao, Y. & He, X. (2019) Three-dimensional immersed finite element method for anisotropic magnetostatic/electrostatic interface problems with non-homogeneous flux jump. Int. J. Numer. Methods Eng.CrossRefGoogle Scholar
Monk, P. (2003) Finite Element Methods for Maxwell’s Equations, Oxford University Press.CrossRefGoogle Scholar
Nedelec, J. C. (1980) Mixed finite elements in $\mathbb{R}^3$ . Numer. Math. 35(3), 315–341.CrossRefGoogle Scholar
Roppert, K., Schoder, S., Toth, F. & Kaltenbacher, M. (2020) Non-conforming Nitsche interfaces for edge elements in curl–curl-type problems. IEEE Trans. Manag. 56(5).Google Scholar
Wang, J., Zhang, X. & Zhuang, Q. (2022) An immersed Crouzeix-Raviart finite element method for Navier-Stokes equations with moving interfaces. Int. J. Numer. Anal. Model. 19(4).Google Scholar
Warburton, T. & Hesthaven, J. S. (2003) On the constants in hp-finite element trace inverse inequalities. Comput. Methods Appl. Mech. Eng. 192(25), 2765–2773.CrossRefGoogle Scholar
Xu, J. & Zhu, Y. (2011) Robust preconditioner for H(curl) interface problems. In: Y. Huang, R. Kornhuber, O. Widlund and J. Xu (editors), Domain Decomposition Methods in Science and Engineering XIX, Springer, Berlin, pp. 173–180.Google Scholar
Zhao, S. & Wei, G. W. (2004) High-order FDTD methods via derivative matching for Maxwell’s equations with material interfaces. J. Comput. Phys. 200(1), 60–103.CrossRefGoogle Scholar