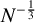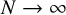1 Introduction
In the 1940s, experiments on the cohesive energy and specific heat of alkali atomsFootnote 1 showed a large discrepancy with theoretical calculations based solely on the Hartree–Fock approximation [Reference Bardeen3], further complicated by the fact that second-order perturbation theory failed because it yielded infinities. Motivated by this unfortunate situation, Bohm and Pines in four seminal papers [Reference Bohm and Pines11, Reference Bohm and Pines12, Reference Bohm and Pines13, Reference Pines32] introduced the random phase approximation (RPA) as a useful tool for studying the properties of a high-density electron gas moving in a background of uniform positive charge, called jellium. In the Bohm–Pines RPA approach, the electron gas could be decoupled into collective plasmon excitations and quasi-electrons that interacted via a screened Coulomb interaction. The latter fact justified the independent particle approach commonly used for many-body fermion systems. Their work was also in good agreement with experimental data, the culmination of which was the experimental detection of plasmons [Reference Watanabe42, Reference Ferrell17].
The microscopic derivation of the RPA has led to notable work by theoretical physicists since the 1950s. In 1957, Gell-Mann and Brueckner [Reference Gell-Mann and Brueckner20] derived the correlation energy of the electron gas in the high density limit by using a formal summation of a particular class of Feynman diagrams. Although each diagram is divergent in itself, it turned out that the sum is finite. This diagrammatic picture further suggested that the main contribution to the ground-state energy came from the interaction of pairs of fermions, one from inside and one from outside the Fermi ball. Shortly thereafter, Sawada [Reference Sawada36] and Sawada–Brueckner–Fukuda–Brout [Reference Sawada, Brueckner, Fukuda and Brout37] interpreted these pairs as bosons and obtained the correlation energy by diagonalizing an effective Hamiltonian which is quadratic with respect to the bosonic particle pairs. Since then, the random phase approximation has become a cornerstone in the physics of condensed matter and nuclear physics [Reference Repko, Kvasil, Nesterenko, Reinhard and Casta-Papiernicka34], also playing a significant role in bosonic field theory [Reference Hansen, Chanfray, Davesne and Schuck26], in the quark-gluon plasma [Reference Walecka41] and especially in computational chemistry and materials science. Although originally proposed for an electron gas, it is applicable to a wide variety of fermionic systems.
The complete derivation of the RPA from first principles, namely from the microscopic Schrödinger equation, has, however, long been a major open problem in mathematical physics. Recently, some rigorous results on the correlation energy have been derived in the mean-field regime for small interaction potentials by Hainzl–Porta–Rexze [Reference Hainzl, Porta and Rexze24] (perturbative results) and by Benedikter–Nam–Porta–Schlein–Seiringer [Reference Benedikter4, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] (non-perturbative results).
The aim of the present paper is to justify the RPA for a large class of interaction potentials in the mean-field regime, addressing not only the ground state energy but also the excitation spectrum. As we will explain below, the correlation structure of Fermi gases can indeed be described correctly by treating appropriate pairs of fermions as bosons. The corresponding bosonic Hamiltonian can be handled by Bogolubov’s diagonalization method, thus putting the description in the physics literature [Reference Gell-Mann and Brueckner20, Reference Sawada36, Reference Sawada, Brueckner, Fukuda and Brout37] on a firm mathematical footing. Although this general point of view has been employed in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], we will provide a new bosonization approach to fermionic systems which enables us to not only extend the study on the ground state energy initiated in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] but also obtain all bosonic elementary excitations predicted in the physics literature, thus justifying the RPA in the mean-field regime. In the long run, we expect that the tools developed in our work will pave the way towards the Coulomb gas in the thermodynamic limit.
1.1 Model
We consider a system of N (spinless) fermions on the torus
![]() $\mathbb {T}^{3}=\left[0,2\pi \right]^{3}$
(with periodic boundary conditions), interacting via a bounded potential
$\mathbb {T}^{3}=\left[0,2\pi \right]^{3}$
(with periodic boundary conditions), interacting via a bounded potential
![]() $V:\mathbb {T}^{3}\rightarrow \mathbb {R}$
. The system is described by the Hamiltonian
$V:\mathbb {T}^{3}\rightarrow \mathbb {R}$
. The system is described by the Hamiltonian
 $$ \begin{align} H_{N}=H_{\text{kin}}+k_{F}^{-1}H_{\text{int}} = \sum_{i=1}^{N} (-\Delta_{i}) + k_F^{-1}\sum_{1\leq i<j\leq N}V\left(x_{i}-x_{j}\right), \end{align} $$
$$ \begin{align} H_{N}=H_{\text{kin}}+k_{F}^{-1}H_{\text{int}} = \sum_{i=1}^{N} (-\Delta_{i}) + k_F^{-1}\sum_{1\leq i<j\leq N}V\left(x_{i}-x_{j}\right), \end{align} $$
which acts on the fermionic space
Here, the coupling constant
![]() $k_F^{-1}>0$
corresponds to the interaction strength. We will focus on the mean-field regime
$k_F^{-1}>0$
corresponds to the interaction strength. We will focus on the mean-field regime
![]() $k_F^{-1}\sim N^{-\frac 1 3}$
, where the kinetic and interaction energies are comparable. More precisely, we assume that
$k_F^{-1}\sim N^{-\frac 1 3}$
, where the kinetic and interaction energies are comparable. More precisely, we assume that
namely, the Fermi ball
![]() $B_F$
is completely filled by N integer points. In this case, the kinetic operator
$B_F$
is completely filled by N integer points. In this case, the kinetic operator
![]() $H_{\text {kin}}$
has a unique, non-degenerate ground state which is the Fermi state
$H_{\text {kin}}$
has a unique, non-degenerate ground state which is the Fermi state
 $$ \begin{align} \psi_{\mathrm{FS}}=\bigwedge_{p\in B_{F}}u_{p}, \quad u_{p} (x )=(2\pi)^{-\frac{3}{2}}e^{ip\cdot x}. \end{align} $$
$$ \begin{align} \psi_{\mathrm{FS}}=\bigwedge_{p\in B_{F}}u_{p}, \quad u_{p} (x )=(2\pi)^{-\frac{3}{2}}e^{ip\cdot x}. \end{align} $$
More generally, the eigenstates of
![]() $H_{\text {kin}}$
can be written explicitly in terms of the plane waves
$H_{\text {kin}}$
can be written explicitly in terms of the plane waves
![]() $\left(u_{p}\right)_{p\in \mathbb {Z}^{3}}$
. However, the spectrum of the interacting operator
$\left(u_{p}\right)_{p\in \mathbb {Z}^{3}}$
. However, the spectrum of the interacting operator
![]() $H_N$
is highly nontrivial, and its computation often requires suitable approximations.
$H_N$
is highly nontrivial, and its computation often requires suitable approximations.
We assume that V is of positive type, namely, its Fourier transform satisfies
![]() $\hat V \ge 0$
with
$\hat V \ge 0$
with
 $$ \begin{align} V (x )=\frac{1}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k}e^{ik\cdot x}\quad\text{with}\quad\hat{V}_{k}=\int_{\mathbb{T}^{3}}V (x )e^{-ik\cdot x}\,dx. \end{align} $$
$$ \begin{align} V (x )=\frac{1}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k}e^{ik\cdot x}\quad\text{with}\quad\hat{V}_{k}=\int_{\mathbb{T}^{3}}V (x )e^{-ik\cdot x}\,dx. \end{align} $$
Under our assumption,
![]() $H_{N}$
is a self-adjoint operator on
$H_{N}$
is a self-adjoint operator on
![]() $\mathcal {H}_{N}$
with domain
$\mathcal {H}_{N}$
with domain
![]() $D\left(H_{N}\right)=D\left(H_{\text {kin}}\right)=\bigwedge ^{N}H^{2}\left(\mathbb {T}^{3}\right).$
Moreover,
$D\left(H_{N}\right)=D\left(H_{\text {kin}}\right)=\bigwedge ^{N}H^{2}\left(\mathbb {T}^{3}\right).$
Moreover,
![]() $H_N$
is bounded from below and has compact resolvent. We are interested in the asymptotic behavior of the low-lying spectrum of
$H_N$
is bounded from below and has compact resolvent. We are interested in the asymptotic behavior of the low-lying spectrum of
![]() $H_N$
when
$H_N$
when
![]() $N\to \infty $
and
$N\to \infty $
and
![]() $k_F\to \infty $
.
$k_F\to \infty $
.
One of the most famous approximations for fermions is the Hartree–Fock theory, where one restricts the states under consideration to the set of all Slater determinants
![]() $g_{1}\wedge g_{2}\cdots \wedge g_{N}$
with
$g_{1}\wedge g_{2}\cdots \wedge g_{N}$
with
![]() $\left\{ g_{i}\right\} _{i=1}^{N}$
orthonormal in
$\left\{ g_{i}\right\} _{i=1}^{N}$
orthonormal in
![]() $L^{2}\left(\mathbb {T}^{3}\right)$
. The precision of the Hartree–Fock energy is an interesting subject, which has been studied for Coulomb systems by Bach [Reference Bach1] and Graf–Solovej [Reference Graf and Solovej22]. In general, the Hartree–Fock minimizer could be different from the Fermi state
$L^{2}\left(\mathbb {T}^{3}\right)$
. The precision of the Hartree–Fock energy is an interesting subject, which has been studied for Coulomb systems by Bach [Reference Bach1] and Graf–Solovej [Reference Graf and Solovej22]. In general, the Hartree–Fock minimizer could be different from the Fermi state
![]() $\psi _{\mathrm {FS}}$
; see [Reference Gontier, Hainzl and Lewin21] for an estimate for Coulomb systems. However, in the mean-field model that we are considering here, the Hartree–Fock minimizer coincides with
$\psi _{\mathrm {FS}}$
; see [Reference Gontier, Hainzl and Lewin21] for an estimate for Coulomb systems. However, in the mean-field model that we are considering here, the Hartree–Fock minimizer coincides with
![]() $\psi _{\mathrm {FS}}$
; see [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Theorem A.1] for a precise statement. Thus, to obtain the correction to the ansatz of plane waves, we have to understand the correlation structure of the system.Footnote
2
$\psi _{\mathrm {FS}}$
; see [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Theorem A.1] for a precise statement. Thus, to obtain the correction to the ansatz of plane waves, we have to understand the correlation structure of the system.Footnote
2
To go beyond the ansatz of plane waves, the first step is the extraction of the energy of the Fermi state. For computational purposes, it is convenient to use the second quantization language. For every
![]() $p\in \mathbb {Z}^3$
, we denote by
$p\in \mathbb {Z}^3$
, we denote by
![]() $c_{p}^{\ast }=c^*(u_p)$
,
$c_{p}^{\ast }=c^*(u_p)$
,
![]() $c_{p}=c(u_p)$
the fermionic creation and annihilation operators associated to the plane-wave state
$c_{p}=c(u_p)$
the fermionic creation and annihilation operators associated to the plane-wave state
![]() $u_{p}$
. These operators act on the fermionic Fock space
$u_{p}$
. These operators act on the fermionic Fock space
 $$ \begin{align} \mathcal{F}^{-}\left(\mathfrak{h}\right)=\bigoplus_{N=0}^{\infty}\bigwedge^{N}\mathfrak{h} \end{align} $$
$$ \begin{align} \mathcal{F}^{-}\left(\mathfrak{h}\right)=\bigoplus_{N=0}^{\infty}\bigwedge^{N}\mathfrak{h} \end{align} $$
and obey the canonical anticommutation relations (CAR)
where
![]() $\left\{ A,B\right\} =AB+BA$
. The Hamiltonian operator
$\left\{ A,B\right\} =AB+BA$
. The Hamiltonian operator
![]() $H_{N}$
in (1.1) can be expressed as
$H_{N}$
in (1.1) can be expressed as
 $$ \begin{align} H_{N}=H_{\text{kin}}+k_{F}^{-1}H_{\text{int}} = \sum_{p\in\mathbb{Z}^{3}}|p|^{2}c_{p}^{\ast}c_{p}+\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\sum_{p,q\in\mathbb{Z}^{3}}\hat{V}_{k}c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p}. \end{align} $$
$$ \begin{align} H_{N}=H_{\text{kin}}+k_{F}^{-1}H_{\text{int}} = \sum_{p\in\mathbb{Z}^{3}}|p|^{2}c_{p}^{\ast}c_{p}+\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\sum_{p,q\in\mathbb{Z}^{3}}\hat{V}_{k}c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p}. \end{align} $$
Thanks to the CAR (1.7), it is straightforward to see that the Fermi state obeys, for all
![]() $p\in \mathbb {Z}^{3}$
,
$p\in \mathbb {Z}^{3}$
,
 $$ \begin{align} c_{p}^{\ast}c_{p}\psi_{\mathrm{FS}}=1_{B_{F}}(p)\psi_{\mathrm{FS}}=\begin{cases} \psi_{\mathrm{FS}} & p\in B_{F}\\ 0 & p\in B_{F}^{c}, \end{cases} \end{align} $$
$$ \begin{align} c_{p}^{\ast}c_{p}\psi_{\mathrm{FS}}=1_{B_{F}}(p)\psi_{\mathrm{FS}}=\begin{cases} \psi_{\mathrm{FS}} & p\in B_{F}\\ 0 & p\in B_{F}^{c}, \end{cases} \end{align} $$
where
![]() $1_{B_{F}}(\cdot )$
denotes the indicator function of the Fermi ball
$1_{B_{F}}(\cdot )$
denotes the indicator function of the Fermi ball
![]() $B_{F}$
. Thus, the kinetic energy of the Fermi state is
$B_{F}$
. Thus, the kinetic energy of the Fermi state is
 $$ \begin{align} \left\langle \psi_{\mathrm{FS}},H_{\text{kin}}\psi_{\mathrm{FS}}\right\rangle =\sum_{p\in\mathbb{Z}^{3}}|p|^{2}\left\langle \psi_{\mathrm{FS}},c_{p}^{\ast}c_{p}\psi_{\mathrm{ FS}}\right\rangle =\sum_{p\in\mathbb{Z}^{3}}1_{B_{F}}(p)|p|^{2}\left\Vert \psi_{\mathrm{ FS}}\right\Vert ^{2}=\sum_{p\in B_{F}}|p|^{2}. \end{align} $$
$$ \begin{align} \left\langle \psi_{\mathrm{FS}},H_{\text{kin}}\psi_{\mathrm{FS}}\right\rangle =\sum_{p\in\mathbb{Z}^{3}}|p|^{2}\left\langle \psi_{\mathrm{FS}},c_{p}^{\ast}c_{p}\psi_{\mathrm{ FS}}\right\rangle =\sum_{p\in\mathbb{Z}^{3}}1_{B_{F}}(p)|p|^{2}\left\Vert \psi_{\mathrm{ FS}}\right\Vert ^{2}=\sum_{p\in B_{F}}|p|^{2}. \end{align} $$
Hence, we can define the localized kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }:D\left(H_{\text {kin}}\right)\subset \mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
by
$H_{\operatorname {\mathrm {kin}}}^{\prime }:D\left(H_{\text {kin}}\right)\subset \mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
by
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}=H_{\text{kin}} - \left\langle \psi_{\mathrm{FS}},H_{\text{kin}}\psi_{\mathrm{FS}}\right\rangle = \sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p}-\sum_{p\in B_{F}}|p|^{2}c_{p}c_{p}^{\ast}. \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}=H_{\text{kin}} - \left\langle \psi_{\mathrm{FS}},H_{\text{kin}}\psi_{\mathrm{FS}}\right\rangle = \sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p}-\sum_{p\in B_{F}}|p|^{2}c_{p}c_{p}^{\ast}. \end{align} $$
We refer to this operator as being ‘localized’ since extracting
![]() $\langle \psi _{\mathrm {FS}} , H_{\mathrm {kin}} \psi _{\mathrm {FS}}\rangle $
in this manner can be seen as changing the point of reference from the vacuum state
$\langle \psi _{\mathrm {FS}} , H_{\mathrm {kin}} \psi _{\mathrm {FS}}\rangle $
in this manner can be seen as changing the point of reference from the vacuum state
![]() $\Omega $
to the Fermi state
$\Omega $
to the Fermi state
![]() $\psi _{\mathrm {FS}}$
, so
$\psi _{\mathrm {FS}}$
, so
![]() $H_{\mathrm {kin}}^\prime $
can be seen as a kind of expansion of
$H_{\mathrm {kin}}^\prime $
can be seen as a kind of expansion of
![]() $ H_{\mathrm {kin}}$
around
$ H_{\mathrm {kin}}$
around
![]() $\psi _{\mathrm {FS}}$
.
$\psi _{\mathrm {FS}}$
.
Note that it is clear from the first identity in (1.11) that
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
is nonnegative since
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
is nonnegative since
![]() $\psi _{\mathrm {FS}}$
is the ground state of
$\psi _{\mathrm {FS}}$
is the ground state of
![]() $H_{\text {kin}}$
. However, the positivity of
$H_{\text {kin}}$
. However, the positivity of
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
is unclear from the second identity in (1.11) since the difference of two operators which are nonnegative may not have a sign. The resolution of this apparent paradox lies in the underlying Hilbert space: in the N-body space
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
is unclear from the second identity in (1.11) since the difference of two operators which are nonnegative may not have a sign. The resolution of this apparent paradox lies in the underlying Hilbert space: in the N-body space
![]() $\mathcal {H}_{N}$
, we always have
$\mathcal {H}_{N}$
, we always have
 $$ \begin{align} N = \sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}} (1- c_{p} c_{p}^{\ast}) +\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}= |B_F|- \sum_{p\in B_{F}}c_{p}c_{p}^{\ast}+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}. \end{align} $$
$$ \begin{align} N = \sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}} (1- c_{p} c_{p}^{\ast}) +\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}= |B_F|- \sum_{p\in B_{F}}c_{p}c_{p}^{\ast}+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}. \end{align} $$
Therefore, the assumption
![]() $|B_F|=N$
implies the particle-hole symmetry
$|B_F|=N$
implies the particle-hole symmetry
 $$ \begin{align} \mathcal{N}_{E}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}\quad\text{on }\mathcal{H}_{N}, \end{align} $$
$$ \begin{align} \mathcal{N}_{E}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}\quad\text{on }\mathcal{H}_{N}, \end{align} $$
namely, the excitation number operator (which counts the number of particles outside the Fermi state) coincides with the hole number operator (which counts the number of holes inside the Fermi state). Consequently, the kinetic operator in (1.11) can be rewritten as
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} =\sum_{p\in B_{F}^{c}}\vert|p|^{2}-\zeta \vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}}\vert|p|^{2}-\zeta\vert\,c_{p}c_{p}^{\ast} \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} =\sum_{p\in B_{F}^{c}}\vert|p|^{2}-\zeta \vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}}\vert|p|^{2}-\zeta\vert\,c_{p}c_{p}^{\ast} \end{align} $$
for any
![]() $\zeta \in [\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}]$
, which is clearly nonnegative.
$\zeta \in [\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}]$
, which is clearly nonnegative.
For the interaction operator, it is convenient to use the factorized form
 $$ \begin{align} H_{\text{int}} &=\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\sum_{p,q\in\mathbb{Z}^{3}}\hat{V}_{k}c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p} \nonumber \\ &=\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k}(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-N), \end{align} $$
$$ \begin{align} H_{\text{int}} &=\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\sum_{p,q\in\mathbb{Z}^{3}}\hat{V}_{k}c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p} \nonumber \\ &=\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k}(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-N), \end{align} $$
where
 $$ \begin{align} \text{d}\Gamma(e^{-ik\cdot x})=\sum_{p,q\in\mathbb{Z}^{3}}\left\langle u_{p},e^{-ik\cdot x}u_{q}\right\rangle c_{p}^{\ast}c_{q}=\sum_{p,q\in\mathbb{Z}^{3}}\delta_{p,q-k}c_{p}^{\ast}c_{q}=\sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p+k}. \end{align} $$
$$ \begin{align} \text{d}\Gamma(e^{-ik\cdot x})=\sum_{p,q\in\mathbb{Z}^{3}}\left\langle u_{p},e^{-ik\cdot x}u_{q}\right\rangle c_{p}^{\ast}c_{q}=\sum_{p,q\in\mathbb{Z}^{3}}\delta_{p,q-k}c_{p}^{\ast}c_{q}=\sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p+k}. \end{align} $$
Note that for any
![]() $k\in \mathbb {Z}_{\ast }^{3}=\mathbb {Z}^{3}\backslash \left\{ 0\right\}$
, we have
$k\in \mathbb {Z}_{\ast }^{3}=\mathbb {Z}^{3}\backslash \left\{ 0\right\}$
, we have
 $$ \begin{align} \text{d}\Gamma(e^{-ik\cdot x})\psi_{\mathrm{FS}}=\sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}}=\sum_{p\in L_{-k}}c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}} \end{align} $$
$$ \begin{align} \text{d}\Gamma(e^{-ik\cdot x})\psi_{\mathrm{FS}}=\sum_{p\in\mathbb{Z}^{3}}c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}}=\sum_{p\in L_{-k}}c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}} \end{align} $$
since the summand
![]() $c_{p}^{\ast }c_{p+k}\psi _{\mathrm {FS}}$
in (1.17) does not vanish if and only if
$c_{p}^{\ast }c_{p+k}\psi _{\mathrm {FS}}$
in (1.17) does not vanish if and only if
![]() $p\in L_{-k}$
, where the lune
$p\in L_{-k}$
, where the lune
will play an important role in our analysis. In particular, using (1.9) and the CAR again, we find that for all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
,
$k\in \mathbb {Z}_{\ast }^{3}$
,
 $$ \begin{align} \left\Vert \text{d}\Gamma(e^{-ik\cdot x})\psi_{\mathrm{FS}}\right\Vert ^{2}=\sum_{p\in L_{-k}}\left\Vert c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}}\right\Vert ^{2}=\sum_{p\in L_{-k}}1=\left|L_{-k}\right|=\left|L_{k}\right|. \end{align} $$
$$ \begin{align} \left\Vert \text{d}\Gamma(e^{-ik\cdot x})\psi_{\mathrm{FS}}\right\Vert ^{2}=\sum_{p\in L_{-k}}\left\Vert c_{p}^{\ast}c_{p+k}\psi_{\mathrm{FS}}\right\Vert ^{2}=\sum_{p\in L_{-k}}1=\left|L_{-k}\right|=\left|L_{k}\right|. \end{align} $$
Thus, the interaction energy of the Fermi state is given by
 $$ \begin{align} \left\langle \psi_{\mathrm{FS}},H_{\text{int}}\psi_{\mathrm{FS}}\right\rangle =\frac{N\left(N-1\right)}{2(2\pi)^{3}}\hat{V}_{0}+\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\left|L_{k}\right|-N\right), \end{align} $$
$$ \begin{align} \left\langle \psi_{\mathrm{FS}},H_{\text{int}}\psi_{\mathrm{FS}}\right\rangle =\frac{N\left(N-1\right)}{2(2\pi)^{3}}\hat{V}_{0}+\frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\left|L_{k}\right|-N\right), \end{align} $$
where we see the direct and exchange energies (involving
![]() $\hat V_0$
and
$\hat V_0$
and
![]() $\{\hat V_k\}_{k\ne 0}$
, respectively). We can define the localized interaction operator
$\{\hat V_k\}_{k\ne 0}$
, respectively). We can define the localized interaction operator
 $$ \begin{align} H_{\text{int}}^{\prime}=H_{\text{int}}- \left\langle \psi_{\mathrm{FS}},H_{\text{int}}\psi_{\mathrm{ FS}}\right\rangle = \frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-\left|L_{k}\right|). \end{align} $$
$$ \begin{align} H_{\text{int}}^{\prime}=H_{\text{int}}- \left\langle \psi_{\mathrm{FS}},H_{\text{int}}\psi_{\mathrm{ FS}}\right\rangle = \frac{1}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-\left|L_{k}\right|). \end{align} $$
In summary, with
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
and
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
and
![]() $H_{\operatorname {\mathrm {int}}}^{\prime }$
defined in (1.11) and (1.21), we can write
$H_{\operatorname {\mathrm {int}}}^{\prime }$
defined in (1.11) and (1.21), we can write
Note that in the prior works [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], the localization procedure was carried out by employing what is known as the particle-hole transformation, which maps the Fermi state
![]() $\psi _{\mathrm {FS}}$
to the vacuum; see, for example, [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Eq. (1.20)] for an analogue of (1.22). However, in the present paper we do not follow this approach since we prefer to work on the N-body Hilbert space.
$\psi _{\mathrm {FS}}$
to the vacuum; see, for example, [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Eq. (1.20)] for an analogue of (1.22). However, in the present paper we do not follow this approach since we prefer to work on the N-body Hilbert space.
1.2 Random phase approximation
In this subsection, we explain the ideas of the bosonization approach to the random phase approximation. On the one hand, in the original approach [Reference Bohm and Pines11, Reference Bohm and Pines12, Reference Bohm and Pines13, Reference Pines32], Bohm and Pines considered fluctuations of density in the momentum representation where the plasma momenta and the effective particle momenta of different wavelengths
![]() $k,l$
are coupled by phases
$k,l$
are coupled by phases
![]() $e^{i(k-l) \cdot x_j}$
, summing over the ‘random’ particle positions
$e^{i(k-l) \cdot x_j}$
, summing over the ‘random’ particle positions
![]() $x_j$
. The assumption that the phases average toward zero for a large number of particles is originally called the ‘random phase approximation’. On the other hand, after the work of Sawada [Reference Sawada36] and Sawada–Brueckner–Fukuda–Brout [Reference Sawada, Brueckner, Fukuda and Brout37], the term RPA has been widely used in the physics literature in the context of a quasi-bosonic Hamiltonian, where a quasi-boson consists of a particle-hole pair. The quasi-bosonic approach is used not only for Coulomb gases but also in a much broader context, especially in nuclear matter (for a standard textbook, see [Reference Fetter and Walecka18, p. 156] for Coulomb gases and [Reference Fetter and Walecka18, pp. 540-543] for nuclear matter).
$x_j$
. The assumption that the phases average toward zero for a large number of particles is originally called the ‘random phase approximation’. On the other hand, after the work of Sawada [Reference Sawada36] and Sawada–Brueckner–Fukuda–Brout [Reference Sawada, Brueckner, Fukuda and Brout37], the term RPA has been widely used in the physics literature in the context of a quasi-bosonic Hamiltonian, where a quasi-boson consists of a particle-hole pair. The quasi-bosonic approach is used not only for Coulomb gases but also in a much broader context, especially in nuclear matter (for a standard textbook, see [Reference Fetter and Walecka18, p. 156] for Coulomb gases and [Reference Fetter and Walecka18, pp. 540-543] for nuclear matter).
In the present paper, we will focus on building a mathematical formulation of the quasi-bosonic approach for general potentials and eventually apply this theory to regular potentials. In the long run, we hope that this general theory will also be helpful for singular potentials, in particular for Coulomb gases where the next-order correction to the bosonization picture matters (in [Reference Christiansen, Hainzl and Nam15], we used the formulation provided in the present paper to find the analogue of the Gell-Mann–Brueckner formula for the mean-field Coulomb gas, which shows how important it is to carry the non-bosonic part in the calculation at least to the leading order).
Now let us explain the bosonization argument in detail. Roughly speaking, the RPA suggests that the fermionic correlation can be described by a Hamiltonian which is quadratic in suitable bosonic creation and annihilation operators. To explain the heuristic bosonization argument, let us decompose further the interaction terms in (1.21) by defining, for every
![]() $k\in \mathbb {Z}_{\ast }^{3}$
,
$k\in \mathbb {Z}_{\ast }^{3}$
,
where
![]() $P_{B_F}$
and
$P_{B_F}$
and
![]() $P_{B_F^c}$
are projections in the one-fermion Hilbert space and
$P_{B_F^c}$
are projections in the one-fermion Hilbert space and
 $$ \begin{align} \tilde{B}_{k}&=\text{d}\Gamma\big(P_{B_{F}}e^{-ik\cdot x}P_{B_{F}^{c}}\big)=\sum_{p,q\in\mathbb{Z}^{3}}\left\langle u_{p}, P_{B_{F}}e^{-ik\cdot x}P_{B_{F}^{c}} u_{q}\right\rangle c_{p}^{\ast}c_{q} = \sum_{p\in L_{k}}c_{p-k}^{\ast}c_{p}, \\ D_k &= \text{d}\Gamma\big(P_{B_{F}}e^{-ik\cdot x}P_{B_{F}}\big) + \text{d}\Gamma\big(P_{B_{F}^c}e^{-ik\cdot x}P_{B_{F}^{c}}\big) = \sum_{p\in B_F \cap (B_F+k)} c_{p-k}^{\ast}c_{p} + \sum_{p\in B_F^c \cap (B_F^c+k) } c_{p-k}^{\ast}c_{p}. \nonumber \end{align} $$
$$ \begin{align} \tilde{B}_{k}&=\text{d}\Gamma\big(P_{B_{F}}e^{-ik\cdot x}P_{B_{F}^{c}}\big)=\sum_{p,q\in\mathbb{Z}^{3}}\left\langle u_{p}, P_{B_{F}}e^{-ik\cdot x}P_{B_{F}^{c}} u_{q}\right\rangle c_{p}^{\ast}c_{q} = \sum_{p\in L_{k}}c_{p-k}^{\ast}c_{p}, \\ D_k &= \text{d}\Gamma\big(P_{B_{F}}e^{-ik\cdot x}P_{B_{F}}\big) + \text{d}\Gamma\big(P_{B_{F}^c}e^{-ik\cdot x}P_{B_{F}^{c}}\big) = \sum_{p\in B_F \cap (B_F+k)} c_{p-k}^{\ast}c_{p} + \sum_{p\in B_F^c \cap (B_F^c+k) } c_{p-k}^{\ast}c_{p}. \nonumber \end{align} $$
Note that for all
![]() $k\in \mathbb {Z}^3_{*}$
, we have
$k\in \mathbb {Z}^3_{*}$
, we have
![]() $D_k^*=D_{-k}$
and
$D_k^*=D_{-k}$
and
which can be seen from the identity
![]() $[\mathrm {d} \Gamma (X),\mathrm {d} \Gamma (Y) ] = \mathrm {d} \Gamma ([X,Y])$
and (1.24). Due to the symmetry between k and
$[\mathrm {d} \Gamma (X),\mathrm {d} \Gamma (Y) ] = \mathrm {d} \Gamma ([X,Y])$
and (1.24). Due to the symmetry between k and
![]() $-k$
, it is convenient to introduce the setFootnote
3
$-k$
, it is convenient to introduce the setFootnote
3
such that
Using this notation and the assumption
![]() $\hat V_k=\hat V_{-k}$
, we can rewrite the interaction operator in (1.21) as
$\hat V_k=\hat V_{-k}$
, we can rewrite the interaction operator in (1.21) as
 $$ \begin{align} k_{F}^{-1} H_{\text{int}}^{\prime} & =\frac{k_F^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}} \hat{V}_{k}\left(\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}+D_{k}\right)^{\ast}\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}+D_{k}\right)-\left|L_{k}\right|\right) \nonumber\\ & = \sum_{k\in\mathbb{Z}_{+}^{3}}\left(H_{\text{int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) +\frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right) , \end{align} $$
$$ \begin{align} k_{F}^{-1} H_{\text{int}}^{\prime} & =\frac{k_F^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}} \hat{V}_{k}\left(\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}+D_{k}\right)^{\ast}\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}+D_{k}\right)-\left|L_{k}\right|\right) \nonumber\\ & = \sum_{k\in\mathbb{Z}_{+}^{3}}\left(H_{\text{int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) +\frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right) , \end{align} $$
where for each
![]() $k\in \mathbb {Z}_{+}^{3}$
, we denote
$k\in \mathbb {Z}_{+}^{3}$
, we denote
 $$ \begin{align} H_{\text{int}}^{k} & =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}\right)^{\ast}\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}\right)+\left(\tilde{B}_{-k}+\tilde{B}_{k}^{\ast}\right)^{\ast}\left(\tilde{B}_{-k}+\tilde{B}_{k}^{\ast}\right)\right) \nonumber \\ & =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}} \left( \{ \tilde{B}_{k}^{\ast}, \tilde{B}_{k}\} + \{\tilde{B}_{-k}^{\ast}, \tilde{B}_{-k}\} + 2 \tilde{B}_{k}^{\ast} \tilde{B}_{-k}^{\ast} +2 \tilde{B}_{-k} \tilde{B}_{k} \right). \end{align} $$
$$ \begin{align} H_{\text{int}}^{k} & =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}\right)^{\ast}\left(\tilde{B}_{k}+\tilde{B}_{-k}^{\ast}\right)+\left(\tilde{B}_{-k}+\tilde{B}_{k}^{\ast}\right)^{\ast}\left(\tilde{B}_{-k}+\tilde{B}_{k}^{\ast}\right)\right) \nonumber \\ & =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}} \left( \{ \tilde{B}_{k}^{\ast}, \tilde{B}_{k}\} + \{\tilde{B}_{-k}^{\ast}, \tilde{B}_{-k}\} + 2 \tilde{B}_{k}^{\ast} \tilde{B}_{-k}^{\ast} +2 \tilde{B}_{-k} \tilde{B}_{k} \right). \end{align} $$
Now let us introduce the quasi-bosonicity. From the CAR (1.7), it is straightforward to see that
 $$ \begin{align} \left[\tilde{B}_{k},\tilde{B}_{l}\right]=\left[\tilde{B}_{k}^{\ast},\tilde{B}_{l}^{\ast}\right]=0,\quad \left[\tilde{B}_{k},\tilde{B}_{l}^{\ast}\right]= \left|L_{k}\right|\delta_{k,l}-\sum_{p\in L_{k}\cap L_{l}}c_{p-l}c_{p-k}^{\ast}-\sum_{p\in L_{k}\cap\left(L_{l}-l+k\right)}c_{p-k+l}^{\ast}c_{p} \end{align} $$
$$ \begin{align} \left[\tilde{B}_{k},\tilde{B}_{l}\right]=\left[\tilde{B}_{k}^{\ast},\tilde{B}_{l}^{\ast}\right]=0,\quad \left[\tilde{B}_{k},\tilde{B}_{l}^{\ast}\right]= \left|L_{k}\right|\delta_{k,l}-\sum_{p\in L_{k}\cap L_{l}}c_{p-l}c_{p-k}^{\ast}-\sum_{p\in L_{k}\cap\left(L_{l}-l+k\right)}c_{p-k+l}^{\ast}c_{p} \end{align} $$
for all
![]() $k,l\in \mathbb {Z}^3_{*}$
, where
$k,l\in \mathbb {Z}^3_{*}$
, where
![]() $[A,B]= AB-BA$
. Hence, on states with few excitations (e.g., the expectation value of
$[A,B]= AB-BA$
. Hence, on states with few excitations (e.g., the expectation value of
![]() $\mathcal {N}_E$
is much smaller than
$\mathcal {N}_E$
is much smaller than
![]() $|L_k| \sim \min \{|k| k_F^2,k_F^3\}$
), the rescaled operators
$|L_k| \sim \min \{|k| k_F^2,k_F^3\}$
), the rescaled operators
![]() $\tilde {B}_{k}^{\prime }=\left|L_{k}\right|^{-\frac {1}{2}}\tilde {B}_{k}$
obey the commutation relations
$\tilde {B}_{k}^{\prime }=\left|L_{k}\right|^{-\frac {1}{2}}\tilde {B}_{k}$
obey the commutation relations
for all
![]() $k,l\in \mathbb {Z}_{\ast }^{3}$
, in direct analogy with the canonical commutation relations (CCR) obeyed by a set of bosonic creation and annihilation operators
$k,l\in \mathbb {Z}_{\ast }^{3}$
, in direct analogy with the canonical commutation relations (CCR) obeyed by a set of bosonic creation and annihilation operators
![]() $a_{k}^{\ast }$
,
$a_{k}^{\ast }$
,
![]() $a_{k}$
indexed by
$a_{k}$
indexed by
![]() $\mathbb {Z}_{\ast }^{3}$
,
$\mathbb {Z}_{\ast }^{3}$
,
Since the relation
![]() $[\tilde {B}_{k}^{\prime }, (\tilde {B}_{l}^{\prime })^{\ast }] \approx \delta _{k,l}$
is only approximate, we call these operators quasi-bosonic.
$[\tilde {B}_{k}^{\prime }, (\tilde {B}_{l}^{\prime })^{\ast }] \approx \delta _{k,l}$
is only approximate, we call these operators quasi-bosonic.
In view of the quasi-bosonicity of these operators, in the form (1.28) of
![]() $H_{\text {int}}^{\prime }$
, we call the first sum on the right-hand side of this equation the bosonizable terms, while the second sum constitutes the non-bosonizable terms which are regarded as error terms. The bosonizable part
$H_{\text {int}}^{\prime }$
, we call the first sum on the right-hand side of this equation the bosonizable terms, while the second sum constitutes the non-bosonizable terms which are regarded as error terms. The bosonizable part
![]() $H_{\text {int}}^{k}$
can be viewed as a quadratic Hamiltonian in the bosonic setting, which can be diagonalized by Bogolubov transformations. This is the spirit of what we will do, but there is a catch: the kinetic operator
$H_{\text {int}}^{k}$
can be viewed as a quadratic Hamiltonian in the bosonic setting, which can be diagonalized by Bogolubov transformations. This is the spirit of what we will do, but there is a catch: the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
cannot be written in terms of
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
cannot be written in terms of
![]() $\tilde {B}_{k}$
. The solution is to further decompose the operators
$\tilde {B}_{k}$
. The solution is to further decompose the operators
![]() $\tilde {B}_{k}$
by defining the excitation operators
$\tilde {B}_{k}$
by defining the excitation operators
The name is due to the fact that the action of
![]() $b_{k,p}^{\ast }$
is to create a state at momentum
$b_{k,p}^{\ast }$
is to create a state at momentum
![]() $p\in B_{F}^{c}$
and annihilate a state at momentum
$p\in B_{F}^{c}$
and annihilate a state at momentum
![]() $p-k\in B_{F}$
.
$p-k\in B_{F}$
.
Since
![]() $H_{\text {int}}^{k}$
is quadratic in terms of
$H_{\text {int}}^{k}$
is quadratic in terms of
![]() $\tilde {B}_{k}$
, it is also quadratic in terms of
$\tilde {B}_{k}$
, it is also quadratic in terms of
![]() $b_{k,p}^{\ast }$
, namely,
$b_{k,p}^{\ast }$
, namely,
 $$ \begin{align} H_{\text{int}}^{k} & =\sum_{p,q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{k,p}^{\ast}b_{k,q}+b_{k,q}b_{k,p}^{\ast}\big)+\sum_{p,q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{-k,p}^{\ast}b_{-k,q}+b_{-k,q}b_{-k,p}^{\ast}\big)\nonumber \\ &\quad +\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{k,p}^{\ast}b_{-k,q}^{\ast}+b_{-k,q}b_{k,p}\big)+\sum_{p\in L_{-k}}\sum_{q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{-k,p}^{\ast}b_{k,q}^{\ast}+b_{k,q}b_{-k,p}\big). \end{align} $$
$$ \begin{align} H_{\text{int}}^{k} & =\sum_{p,q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{k,p}^{\ast}b_{k,q}+b_{k,q}b_{k,p}^{\ast}\big)+\sum_{p,q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{-k,p}^{\ast}b_{-k,q}+b_{-k,q}b_{-k,p}^{\ast}\big)\nonumber \\ &\quad +\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{k,p}^{\ast}b_{-k,q}^{\ast}+b_{-k,q}b_{k,p}\big)+\sum_{p\in L_{-k}}\sum_{q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\big(b_{-k,p}^{\ast}b_{k,q}^{\ast}+b_{k,q}b_{-k,p}\big). \end{align} $$
The reason that the operators
![]() $b_{k,p}$
are preferable to the operators
$b_{k,p}$
are preferable to the operators
![]() $\tilde {B}_{k}$
is that they satisfy the following commutation relation with the kinetic operator (see (1.74) below)
$\tilde {B}_{k}$
is that they satisfy the following commutation relation with the kinetic operator (see (1.74) below)
Note that
![]() $\lambda _{k,p}\ge \frac {1}{2}$
(first,
$\lambda _{k,p}\ge \frac {1}{2}$
(first,
![]() $\lambda _{k,p}>0$
since
$\lambda _{k,p}>0$
since
![]() $p\in L_k$
; moreover,
$p\in L_k$
; moreover,
![]() $|p|^2- |p-k|^2$
is an integer as
$|p|^2- |p-k|^2$
is an integer as
![]() $p,k\in \mathbb {Z}^3$
). This is to be compared with the bosonic setting: if the operators
$p,k\in \mathbb {Z}^3$
). This is to be compared with the bosonic setting: if the operators
![]() $a_{k}$
obey the CCR (1.32), then
$a_{k}$
obey the CCR (1.32), then
 $$ \begin{align} \left[\sum_{l}\varepsilon_{l}a_{l}^{\ast}a_{l},a_{k}^{\ast}\right]=\varepsilon_{k}a_{k}^{\ast}. \end{align} $$
$$ \begin{align} \left[\sum_{l}\varepsilon_{l}a_{l}^{\ast}a_{l},a_{k}^{\ast}\right]=\varepsilon_{k}a_{k}^{\ast}. \end{align} $$
Therefore, viewing
![]() $b_{k,p}^{\ast }$
as being analogous to a bosonic creation operator, we get
$b_{k,p}^{\ast }$
as being analogous to a bosonic creation operator, we get
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}\approx \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}} 2 \lambda_{k,p} b_{k,p}^{\ast}b_{k,p} =\sum_{k\in\mathbb{Z}_{+}^{3}} \Big( \sum_{p\in L_{k}} 2 \lambda_{k,p} b_{k,p}^{\ast}b_{k,p} + \sum_{p\in L_{-k}} 2 \lambda_{-k,p} b_{-k,p}^{\ast}b_{-k,p} \Big). \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}\approx \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}} 2 \lambda_{k,p} b_{k,p}^{\ast}b_{k,p} =\sum_{k\in\mathbb{Z}_{+}^{3}} \Big( \sum_{p\in L_{k}} 2 \lambda_{k,p} b_{k,p}^{\ast}b_{k,p} + \sum_{p\in L_{-k}} 2 \lambda_{-k,p} b_{-k,p}^{\ast}b_{-k,p} \Big). \end{align} $$
Combining (1.34) and (1.37), we arrive at a Hamiltonian quadratic in terms of the operators
![]() $b_{k,p}$
, which could be treated in the bosonic interpretation. Note that
$b_{k,p}$
, which could be treated in the bosonic interpretation. Note that
![]() $b_{k,p}\psi _{\mathrm { FS}}=0$
for all
$b_{k,p}\psi _{\mathrm { FS}}=0$
for all
![]() $k\in \mathbb {Z}_{*}^3,p\in L_k$
, and hence, the Fermi state plays the role of the bosonic vacuum.
$k\in \mathbb {Z}_{*}^3,p\in L_k$
, and hence, the Fermi state plays the role of the bosonic vacuum.
Overview of the heuristic assumptions behind the random phase approximation
In the physics literature [Reference Sawada36, Reference Sawada, Brueckner, Fukuda and Brout37], the RPA entails two assumptions:
1. That the excitation operators
![]() $b_{k,p}^{\ast }$
,
$b_{k,p}^{\ast }$
,
![]() $b_{k,p}$
in (1.33) can be treated as bosonic creation and annihilation operators, and that the operators
$b_{k,p}$
in (1.33) can be treated as bosonic creation and annihilation operators, and that the operators
![]() $b_{k,p}$
and
$b_{k,p}$
and
![]() $b_{l,q}$
with
$b_{l,q}$
with
![]() $k\neq l$
can be considered as acting on independent Fock spaces. Mathematically, we thus expect that the approximate canonical commutation relations (CCR)
$k\neq l$
can be considered as acting on independent Fock spaces. Mathematically, we thus expect that the approximate canonical commutation relations (CCR)
should hold in an appropriate sense.
2. That the operator in (1.22) can be approximated by an effective Hamiltonian which is quadratic in terms of
![]() $b_{k,p}^{\ast }$
and
$b_{k,p}^{\ast }$
and
![]() $b_{k,p}$
. This is already true for the interaction part
$b_{k,p}$
. This is already true for the interaction part
![]() $\sum _{k\in \mathbb {Z}_{+}^{3}}H_{\text {int}}^{k}$
in (1.34), and in the RPA, the non-bosonizable terms
$\sum _{k\in \mathbb {Z}_{+}^{3}}H_{\text {int}}^{k}$
in (1.34), and in the RPA, the non-bosonizable terms
 $$ \begin{align} \frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right) \end{align} $$
$$ \begin{align} \frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right) \end{align} $$
are simply dropped. Moreover, the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
is not exactly of the desired form, but it can be replaced by the right side of (1.37). All this leads to the effective Hamiltonian
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
is not exactly of the desired form, but it can be replaced by the right side of (1.37). All this leads to the effective Hamiltonian
 $$ \begin{align} \sum_{k\in\mathbb{Z}_{+}^{3}}H_{\text{Bog},k}=\sum_{k\in\mathbb{Z}_{+}^{3}}\left(2\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}+2\sum_{p\in L_{-k}}\lambda_{-k,p}b_{-k,p}^{\ast}b_{-k,p}+H_{\text{int}}^{k} - \frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| \right) \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}_{+}^{3}}H_{\text{Bog},k}=\sum_{k\in\mathbb{Z}_{+}^{3}}\left(2\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}+2\sum_{p\in L_{-k}}\lambda_{-k,p}b_{-k,p}^{\ast}b_{-k,p}+H_{\text{int}}^{k} - \frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| \right) \end{align} $$
acting on the bosonic Fock space
![]() $\bigoplus _{k\in \mathbb {Z}_{+}^{3}}\mathcal {F}^{+}\left(\ell ^{2}\left(L_{k}\cup L_{-k}\right)\right)$
.
$\bigoplus _{k\in \mathbb {Z}_{+}^{3}}\mathcal {F}^{+}\left(\ell ^{2}\left(L_{k}\cup L_{-k}\right)\right)$
.
Consequently, since the operators
![]() $b_{k,p}$
and
$b_{k,p}$
and
![]() $b_{l,q}$
with
$b_{l,q}$
with
![]() $k\neq l$
are considered as acting independently, we can diagonalize separately each quadratic bosonic Hamiltonian
$k\neq l$
are considered as acting independently, we can diagonalize separately each quadratic bosonic Hamiltonian
![]() $H_{\text {Bog},k}$
by a Bogolubov transformation
$H_{\text {Bog},k}$
by a Bogolubov transformation
![]() $\mathcal {U}_{k}$
on
$\mathcal {U}_{k}$
on
![]() $\mathcal {F}^{+}\left(\ell ^{2}\left(L_{k}\cup L_{-k}\right)\right)$
such that
$\mathcal {F}^{+}\left(\ell ^{2}\left(L_{k}\cup L_{-k}\right)\right)$
such that
 $$ \begin{align} \mathcal{U}_{k}H_{\text{Bog},k}\mathcal{U}_{k}^{\ast} =2\,\text{tr}\left(\widetilde{E}_{k}-h_{k}\right) - \frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| +2\sum_{p\in L_{k}\cup L_{-k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
$$ \begin{align} \mathcal{U}_{k}H_{\text{Bog},k}\mathcal{U}_{k}^{\ast} =2\,\text{tr}\left(\widetilde{E}_{k}-h_{k}\right) - \frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| +2\sum_{p\in L_{k}\cup L_{-k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
where for every
![]() $k\in \mathbb {Z}_{\ast }^{3}$
, we denote the following quantities on
$k\in \mathbb {Z}_{\ast }^{3}$
, we denote the following quantities on
![]() $\ell ^{2}(L_{k})$
:
$\ell ^{2}(L_{k})$
:
 $$ \begin{align} \widetilde{E}_{k}= (h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}})^{\frac{1}{2}}, \quad h_{k}e_{p}=\lambda_{k,p}e_{p}, \quad P_{v_k} =|v_{k} \rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \end{align} $$
$$ \begin{align} \widetilde{E}_{k}= (h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}})^{\frac{1}{2}}, \quad h_{k}e_{p}=\lambda_{k,p}e_{p}, \quad P_{v_k} =|v_{k} \rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \end{align} $$
with
![]() $(e_{p})_{p\in L_{k}}$
the standard orthonormal basis of
$(e_{p})_{p\in L_{k}}$
the standard orthonormal basis of
![]() $\ell ^{2}(L_{k})$
.
$\ell ^{2}(L_{k})$
.
Summing over k, we obtain the correlation energy (see Proposition 7.1)
 $$ \begin{align} E_{\mathrm{corr}} = \sum_{k\in \mathbb{Z}^3_+} \left( \text{tr}\left(\widetilde{E}_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right| \right)=\sum_{k\in \mathbb{Z}^3_{*}} \frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt, \end{align} $$
$$ \begin{align} E_{\mathrm{corr}} = \sum_{k\in \mathbb{Z}^3_+} \left( \text{tr}\left(\widetilde{E}_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right| \right)=\sum_{k\in \mathbb{Z}^3_{*}} \frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt, \end{align} $$
where
![]() $F (x )=\log \left(1+x\right)-x$
. All in all, the RPA thus suggests that up to a unitary transformation, we expect that
$F (x )=\log \left(1+x\right)-x$
. All in all, the RPA thus suggests that up to a unitary transformation, we expect that
 $$ \begin{align} H_{N} \approx E_{\mathrm{FS}} + E_{\mathrm{corr}} +2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,p}, \end{align} $$
$$ \begin{align} H_{N} \approx E_{\mathrm{FS}} + E_{\mathrm{corr}} +2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,p}, \end{align} $$
at least on states with few excitations.
Prediction of the correlation energy and the excitation spectrum
Equation (1.44) leads immediately to the following approximation for the ground state energy
which coincides with [Reference Sawada, Brueckner, Fukuda and Brout37, Eq. (34)],Footnote 4 where the authors derived it from the effective operator of equation (1.40) and also explained the connection to the original work of Gell-Mann–Brueckner [Reference Gell-Mann and Brueckner20]. See also [Reference Raimes35, Eq. (9.54)] and [Reference Fetter and Walecka18, Eq. (12.53)] for this expression of the ground state energy.
More importantly, (1.44) also suggests that the excitation spectrum of
![]() $H_{N}$
could be described in terms of the eigenvalues of
$H_{N}$
could be described in terms of the eigenvalues of
![]() $2\widetilde {E}_{k}$
, which correspond to the bosonic elementary excitations and can be explicitly computed.
$2\widetilde {E}_{k}$
, which correspond to the bosonic elementary excitations and can be explicitly computed.
Indeed, for every eigenvalue
![]() $\epsilon $
of
$\epsilon $
of
![]() $\widetilde {E}_{k}$
, we may find an eigenvector
$\widetilde {E}_{k}$
, we may find an eigenvector
![]() $w\in \ell ^{2}(L_{k})$
such that
$w\in \ell ^{2}(L_{k})$
such that
But either
![]() $\epsilon $
is also an eigenvalue of
$\epsilon $
is also an eigenvalue of
![]() $h_{k}$
or
$h_{k}$
or
![]() $\epsilon ^{2}-h_{k}^{2}$
is invertible. In the latter case, we can write
$\epsilon ^{2}-h_{k}^{2}$
is invertible. In the latter case, we can write
and taking the inner product with
![]() $h_{k}^{\frac {1}{2}}v_{k}$
and cancelling the factors of
$h_{k}^{\frac {1}{2}}v_{k}$
and cancelling the factors of
![]() $\langle h_{k}^{\frac {1}{2}}v_{k},w\rangle $
yields
$\langle h_{k}^{\frac {1}{2}}v_{k},w\rangle $
yields
 $$ \begin{align} 1=2\langle v_{k},h_{k}(\epsilon^{2}-h_{k}^{2})^{-1}v_{k}\rangle=\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\epsilon^{2}-\lambda_{k,p}^{2}}, \end{align} $$
$$ \begin{align} 1=2\langle v_{k},h_{k}(\epsilon^{2}-h_{k}^{2})^{-1}v_{k}\rangle=\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\epsilon^{2}-\lambda_{k,p}^{2}}, \end{align} $$
which appears in [Reference Sawada, Brueckner, Fukuda and Brout37, Eq. (6)]. The sum can be rewritten as
 $$ \begin{align} 1=\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in B_{F}}\frac{|k|^{2}}{\left(\epsilon-k\cdot p\right)^{2}-\left(\frac{1}{2}|k|^2\right)^{2}}. \end{align} $$
$$ \begin{align} 1=\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in B_{F}}\frac{|k|^{2}}{\left(\epsilon-k\cdot p\right)^{2}-\left(\frac{1}{2}|k|^2\right)^{2}}. \end{align} $$
The formula (1.49) allows to compute all eigenvalues of
![]() $\widetilde {E}_{k}$
outside the spectrum of
$\widetilde {E}_{k}$
outside the spectrum of
![]() $h_k$
.
$h_k$
.
In the physically relevant case of the Coulomb potential where
![]() $\hat {V}_{k}k_{F}^{-1}$
is replaced by
$\hat {V}_{k}k_{F}^{-1}$
is replaced by
![]() $4\pi e^{2}|k|^{-2}$
, one can immediately derive the famous plasmon frequency from (1.49): for
$4\pi e^{2}|k|^{-2}$
, one can immediately derive the famous plasmon frequency from (1.49): for
![]() $|k|\ll k_F^{1/2}$
, the largest eigenvalue
$|k|\ll k_F^{1/2}$
, the largest eigenvalue
![]() $\epsilon $
is proportional to
$\epsilon $
is proportional to
![]() $k_F^{3/2}$
(see [Reference Christiansen, Hainzl and Nam14, Eq. (2.27)–(2.54)] for a detailed explanation), and its leading order behavior can be computed easily in the thermodynamic limit (including also a factor of
$k_F^{3/2}$
(see [Reference Christiansen, Hainzl and Nam14, Eq. (2.27)–(2.54)] for a detailed explanation), and its leading order behavior can be computed easily in the thermodynamic limit (including also a factor of
![]() $2$
for the electron spin states)
$2$
for the electron spin states)
 $$ \begin{align} \epsilon^{2}=\frac{4\pi e^{2}}{(2\pi)^{3}}\int_{\overline{B}(0,k_{F})}\frac{\epsilon^{2}}{\left(\epsilon-k\cdot p\right)^{2}-\left(\frac{1}{2}|k|^2\right)^{2}}\,dp\approx\frac{2e^{2}}{(2\pi)^{2}}\text{Vol}(\overline{B}(0,k_{F}))=\frac{2e^{2}}{3\pi}k_{F}^{3}=2\pi ne^{2}, \end{align} $$
$$ \begin{align} \epsilon^{2}=\frac{4\pi e^{2}}{(2\pi)^{3}}\int_{\overline{B}(0,k_{F})}\frac{\epsilon^{2}}{\left(\epsilon-k\cdot p\right)^{2}-\left(\frac{1}{2}|k|^2\right)^{2}}\,dp\approx\frac{2e^{2}}{(2\pi)^{2}}\text{Vol}(\overline{B}(0,k_{F}))=\frac{2e^{2}}{3\pi}k_{F}^{3}=2\pi ne^{2}, \end{align} $$
where
![]() $n=\frac {N}{\mathcal {V}}=\frac {1}{3\pi ^{2}}k_{F}^{3}$
is the number density of the system. Recalling that the relevant operator is
$n=\frac {N}{\mathcal {V}}=\frac {1}{3\pi ^{2}}k_{F}^{3}$
is the number density of the system. Recalling that the relevant operator is
![]() $2\widetilde {E}_{k}$
rather than
$2\widetilde {E}_{k}$
rather than
![]() $\widetilde {E}_{k}$
and that
$\widetilde {E}_{k}$
and that
![]() $\frac {\hbar ^{2}}{2m}=1$
, this yields an excitation energy of
$\frac {\hbar ^{2}}{2m}=1$
, this yields an excitation energy of
 $$ \begin{align} 2\epsilon\approx2\sqrt{2\pi ne^{2}}=\hbar\sqrt{\frac{4\pi ne^{2}}{m}} = \hbar \omega_{\text{plasmon}}, \end{align} $$
$$ \begin{align} 2\epsilon\approx2\sqrt{2\pi ne^{2}}=\hbar\sqrt{\frac{4\pi ne^{2}}{m}} = \hbar \omega_{\text{plasmon}}, \end{align} $$
where
![]() $\omega _{\text {plasmon}}=\sqrt { {4\pi ne^{2}}m^{-1}}$
is called the plasmon frequency in [Reference Pines33, Eq. (3-90)] and [Reference Fetter and Walecka18, Eq. (15.16) - (15.18)]. Note that the Coulomb potential is special as it makes the right-hand side of (1.51) independent of k. See also [Reference Benedikter4, Reference Christiansen, Hainzl and Nam14] where (1.51) was discussed.
$\omega _{\text {plasmon}}=\sqrt { {4\pi ne^{2}}m^{-1}}$
is called the plasmon frequency in [Reference Pines33, Eq. (3-90)] and [Reference Fetter and Walecka18, Eq. (15.16) - (15.18)]. Note that the Coulomb potential is special as it makes the right-hand side of (1.51) independent of k. See also [Reference Benedikter4, Reference Christiansen, Hainzl and Nam14] where (1.51) was discussed.
Establishing the above heuristic computation is a longstanding problem in mathematical physics. In the present paper, we will give a rigorous formulation for the operator approximation (1.44) and then use this to justify the prediction of the correlation energy and the bosonic elementary excitations for a wide class of bounded potentials in the mean-field regime.
1.3 Main results
Our first result is the following rigorous formulation of the operator approximation (1.44).
Theorem 1.1 (Operator formulation of the RPA).
Let
![]() $V:\mathbb {T}^{3}\rightarrow \mathbb {R}$
obey
$V:\mathbb {T}^{3}\rightarrow \mathbb {R}$
obey
![]() $\hat {V}_{k}\geq 0$
and
$\hat {V}_{k}\geq 0$
and
![]() $\hat {V}_{-k}=\hat {V}_{k}$
for all
$\hat {V}_{-k}=\hat {V}_{k}$
for all
![]() $k\in \mathbb {Z}^{3}$
, and assume furthermore that
$k\in \mathbb {Z}^{3}$
, and assume furthermore that
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Consider the Hamiltonian
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Consider the Hamiltonian
![]() $H_N$
given in (1.1) with
$H_N$
given in (1.1) with
![]() $N=|B_F|$
. Let the operators
$N=|B_F|$
. Let the operators
![]() $H_{\mathrm {kin}}'$
,
$H_{\mathrm {kin}}'$
,
![]() $\mathcal {N}_E$
,
$\mathcal {N}_E$
,
![]() $\widetilde {E}_{k}-h_k$
be defined in (1.11), (1.13), (1.42). Let the energies
$\widetilde {E}_{k}-h_k$
be defined in (1.11), (1.13), (1.42). Let the energies
![]() $E_{\mathrm {FS}}$
,
$E_{\mathrm {FS}}$
,
![]() $E_{\mathrm {corr}}$
be defined in (1.22), (1.43). Then there exists a unitary transformation
$E_{\mathrm {corr}}$
be defined in (1.22), (1.43). Then there exists a unitary transformation
![]() $\mathcal {U}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
such that
$\mathcal {U}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
such that
where the effective operator
![]() $H_{\text {eff}}: \mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
is
$H_{\text {eff}}: \mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
is
 $$ \begin{align} H_{\mathrm{eff}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in\mathbb{Z}^{3}_{*} }\sum_{p,q\in L_{k}}\left\langle e_{p},(\widetilde{E}_{k}-h_{k})e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q} \end{align} $$
$$ \begin{align} H_{\mathrm{eff}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in\mathbb{Z}^{3}_{*} }\sum_{p,q\in L_{k}}\left\langle e_{p},(\widetilde{E}_{k}-h_{k})e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q} \end{align} $$
and the error operator
![]() $\mathcal {E}_{\mathcal {U}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
obeys the operator inequality: for every constant
$\mathcal {E}_{\mathcal {U}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
obeys the operator inequality: for every constant
![]() $\epsilon>0$
,
$\epsilon>0$
,
The unitary operator in Theorem 1.1 is given explicitly as
![]() $\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, where
$\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, where
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {J}$
are given in (1.78) and (1.85), respectively (the transformations
$\mathcal {J}$
are given in (1.78) and (1.85), respectively (the transformations
![]() $e^{\mathcal {K}}$
and
$e^{\mathcal {K}}$
and
![]() $e^{\mathcal {J}}$
are studied in detail in Sections 5 and 9).
$e^{\mathcal {J}}$
are studied in detail in Sections 5 and 9).
Remark 1.1. The operator
![]() $\mathcal {N}_E H_{\mathrm {kin}}'$
on the right-hand side of (1.54) is nothing but the ‘bosonic kinetic operator’, due to the following remarkable identity (see Proposition 10.1):
$\mathcal {N}_E H_{\mathrm {kin}}'$
on the right-hand side of (1.54) is nothing but the ‘bosonic kinetic operator’, due to the following remarkable identity (see Proposition 10.1):
 $$ \begin{align} 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
Thus, in Theorem 1.1, we control the error in the random phase approximation using only the fermionic and bosonic kinetic operators, which is very natural.
Remark 1.2. In the expansion (1.52),
![]() $E_{\mathrm {FS}}$
is of order
$E_{\mathrm {FS}}$
is of order
![]() $k_F^5$
, and
$k_F^5$
, and
![]() $E_{\mathrm {corr}}$
is of order
$E_{\mathrm {corr}}$
is of order
![]() $k_F$
. As we will argue below, when we apply this to the low-lying eigenstates with energy
$k_F$
. As we will argue below, when we apply this to the low-lying eigenstates with energy
![]() $E_{\mathrm {FS}}+ O(k_F)$
, the expectation of the effective Hamiltonian
$E_{\mathrm {FS}}+ O(k_F)$
, the expectation of the effective Hamiltonian
![]() $H_{\mathrm {eff}}$
in (1.53) is of order
$H_{\mathrm {eff}}$
in (1.53) is of order
![]() $k_F$
, while the error term
$k_F$
, while the error term
![]() $\mathcal {E}_{\mathcal {U}}$
in (1.54) is of order
$\mathcal {E}_{\mathcal {U}}$
in (1.54) is of order
![]() $O(k_F^{1-\frac 1 {94}+\epsilon })=o(k_F)$
.
$O(k_F^{1-\frac 1 {94}+\epsilon })=o(k_F)$
.
In order to put Theorem 1.1 to good use, we need some a priori estimate on the low-lying eigenstates of the Hamiltonian
![]() $H_N$
. We have the following:
$H_N$
. We have the following:
Theorem 1.2 (A priori estimate for eigenstates).
Let V and
![]() $\mathcal {U}$
be as in Theorem 1.1. Let
$\mathcal {U}$
be as in Theorem 1.1. Let
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be a normalized eigenstate of
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be a normalized eigenstate of
![]() $H_{N}$
with energy
$H_{N}$
with energy
![]() $\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + \kappa k_F$
for some constant
$\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + \kappa k_F$
for some constant
![]() $\kappa>0$
independent of
$\kappa>0$
independent of
![]() $k_F$
. Then,
$k_F$
. Then,
for a constant
![]() $C>0$
depending only on V. The same bound holds with
$C>0$
depending only on V. The same bound holds with
![]() $\Psi $
replaced by
$\Psi $
replaced by
![]() $\mathcal {U} \Psi $
.
$\mathcal {U} \Psi $
.
Remark 1.3. Thanks to the inequality
![]() $\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
(see [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Lemma 2.4] and also Proposition 2.1 below), Theorem 1.2 implies that for an eigenstate
$\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
(see [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Lemma 2.4] and also Proposition 2.1 below), Theorem 1.2 implies that for an eigenstate
![]() $\Psi $
of
$\Psi $
of
![]() $H_{N}$
with energy
$H_{N}$
with energy
![]() $\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + O(k_F)$
, we have
$\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + O(k_F)$
, we have
Thus, the number of excitations is much smaller than the total number of particles (
![]() $k_F\sim N^{1/3}\ll N$
). While (1.56) has been derived in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] for every state with energy
$k_F\sim N^{1/3}\ll N$
). While (1.56) has been derived in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] for every state with energy
![]() $\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + O(k_F)$
(at least for a class of potentials V), the improved bound in Theorem 1.2 is deeper, and the eigenstate assumption plays a crucial role in the proof.
$\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + O(k_F)$
(at least for a class of potentials V), the improved bound in Theorem 1.2 is deeper, and the eigenstate assumption plays a crucial role in the proof.
From Theorems 1.1 and 1.2, we can deduce immediately the asymptotic formula (1.45) on the ground state energy up to an error
![]() $o(k_F)$
. Indeed, the energy upper bound is given by the trial state
$o(k_F)$
. Indeed, the energy upper bound is given by the trial state
![]() $\mathcal {U}^* \psi _{\mathrm {FS}}$
, while the energy lower bound follows from the obvious operator inequality
$\mathcal {U}^* \psi _{\mathrm {FS}}$
, while the energy lower bound follows from the obvious operator inequality
![]() $\widetilde {E}_{k} \ge h_k$
. Moreover, our approach is quantitative, and we can derive (1.45) with explicit error estimates.
$\widetilde {E}_{k} \ge h_k$
. Moreover, our approach is quantitative, and we can derive (1.45) with explicit error estimates.
Theorem 1.3 (Ground state energy).
Let V be as in Theorem 1.1. Then for all
![]() $\epsilon>0$
,
$\epsilon>0$
,
Here are some remarks concerning Theorem 1.3.
Remark 1.4. The method of our proof can be adapted to give the upper bound under the weaker condition
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}^{2}|k|<\infty $
(see [Reference Benedikter, Porta, Schlein and Seiringer8, Appendix A] for a derivation of the upper bound under this weaker condition). Additionally, under this condition it can be shown that
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}^{2}|k|<\infty $
(see [Reference Benedikter, Porta, Schlein and Seiringer8, Appendix A] for a derivation of the upper bound under this weaker condition). Additionally, under this condition it can be shown that
 $$ \begin{align} \frac{1}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt=\frac{k_{F}}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }|k|\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}}{(2\pi)^{2}}I (t )\right)dt+o\left(k_{F}\right), \end{align} $$
$$ \begin{align} \frac{1}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt=\frac{k_{F}}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }|k|\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}}{(2\pi)^{2}}I (t )\right)dt+o\left(k_{F}\right), \end{align} $$
where
![]() $F (x )=\log \left(1+x\right)-x$
and
$F (x )=\log \left(1+x\right)-x$
and
![]() $I (t )=1-t\tan ^{-1}\left(t^{-1}\right)$
(this essentially amounts to replacing the Riemann sum by the integral and can be done by following either the proof of [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Eq. (5.15)] or the analysis in Appendix A; the condition
$I (t )=1-t\tan ^{-1}\left(t^{-1}\right)$
(this essentially amounts to replacing the Riemann sum by the integral and can be done by following either the proof of [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Eq. (5.15)] or the analysis in Appendix A; the condition
![]() $\sum \hat {V}_{k}^{2}|k|<\infty $
ensures that the main contribution comes from
$\sum \hat {V}_{k}^{2}|k|<\infty $
ensures that the main contribution comes from
![]() $|k|\sim O(1)$
). Hence, Theorem 1.3 implies that
$|k|\sim O(1)$
). Hence, Theorem 1.3 implies that
 $$ \begin{align} \inf\sigma\left(H_{N}\right)= E_{\mathrm{FS}} +\frac{k_{F}}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }|k|\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}}{(2\pi)^{2}}I (t )\right)dt+o\left(k_{F}\right). \end{align} $$
$$ \begin{align} \inf\sigma\left(H_{N}\right)= E_{\mathrm{FS}} +\frac{k_{F}}{\pi}\sum_{k\in\mathbb{Z}^{3}_{*} }|k|\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}}{(2\pi)^{2}}I (t )\right)dt+o\left(k_{F}\right). \end{align} $$
A result similar to ours, namely, the bound (1.58) for all potentials satisfying
![]() $\sum _k \hat V_k |k|<\infty $
, has been independently obtained in [Reference Benedikter, Porta, Schlein and Seiringer8], based on a refinement of the method in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6].Footnote
5
The bound (1.58) was proved earlier in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], under the additional assumption that the Fourier coefficients
$\sum _k \hat V_k |k|<\infty $
, has been independently obtained in [Reference Benedikter, Porta, Schlein and Seiringer8], based on a refinement of the method in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6].Footnote
5
The bound (1.58) was proved earlier in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], under the additional assumption that the Fourier coefficients
![]() $\hat {V}_{k}$
be finitely supported and that
$\hat {V}_{k}$
be finitely supported and that
![]() $\Vert \hat {V}\Vert _{\ell ^{1}}$
be sufficiently small. For small
$\Vert \hat {V}\Vert _{\ell ^{1}}$
be sufficiently small. For small
![]() $\hat {V}_{k}$
, the logarithm of equation (1.58) can be expanded for
$\hat {V}_{k}$
, the logarithm of equation (1.58) can be expanded for
 $$ \begin{align} \sigma\left(H_{N}\right)= E_{\mathrm{FS}} -\frac{1 - \log\left(2\right)}{6(2\pi)^{4}}k_{F}\sum_{k\in\mathbb{Z}^{3}_{*} }\hat{V}_{k}^{2}|k|\left(1+O\left(\hat{V}_{k}\right)\right)+o\left(k_{F}\right), \end{align} $$
$$ \begin{align} \sigma\left(H_{N}\right)= E_{\mathrm{FS}} -\frac{1 - \log\left(2\right)}{6(2\pi)^{4}}k_{F}\sum_{k\in\mathbb{Z}^{3}_{*} }\hat{V}_{k}^{2}|k|\left(1+O\left(\hat{V}_{k}\right)\right)+o\left(k_{F}\right), \end{align} $$
which was first proved in [Reference Hainzl, Porta and Rexze24].
Remark 1.5. A further refinement of our method allows a derivation of a rigorous energy upper bound for all potentials satisfying
![]() $\sum _{k\ne 0} \hat V_k^2<\infty $
; see [Reference Christiansen, Hainzl and Nam15]. This covers the case of the Coulomb potential
$\sum _{k\ne 0} \hat V_k^2<\infty $
; see [Reference Christiansen, Hainzl and Nam15]. This covers the case of the Coulomb potential
![]() $\hat {V}_{k} = 4\pi e^2 |k|^{-2}$
, where the correlation energy is given by the left-hand side of (1.57) which is of order
$\hat {V}_{k} = 4\pi e^2 |k|^{-2}$
, where the correlation energy is given by the left-hand side of (1.57) which is of order
![]() $k_F \log k_{F}$
plus a correlation exchange correction of order
$k_F \log k_{F}$
plus a correlation exchange correction of order
![]() $k_F$
(the correlation exchange contribution comes from the fact that the purely bosonic picture is not exact; it is different from the exchange energy which is part of
$k_F$
(the correlation exchange contribution comes from the fact that the purely bosonic picture is not exact; it is different from the exchange energy which is part of
![]() $E_{\mathrm {FS}}$
). In particular, for the Coulomb potential, the right-hand side of (1.57) diverges, whereas the left-hand side does not, and hence the discrete form in (1.57) is arguably more fundamental than the continuous form. It is interesting that in our method the discrete version of the correlation energy always appears naturally.
$E_{\mathrm {FS}}$
). In particular, for the Coulomb potential, the right-hand side of (1.57) diverges, whereas the left-hand side does not, and hence the discrete form in (1.57) is arguably more fundamental than the continuous form. It is interesting that in our method the discrete version of the correlation energy always appears naturally.
Besides containing the information of the ground state energy, another decisive consequence of the operator statement in Theorem 1.1 is that it allows us to obtain all bosonic elementary excitations predicted in the physics literature. We have the following:
Theorem 1.4 (Bosonic elementary excitations).
Let V and
![]() $\mathcal {U}$
be as in Theorem 1.1. Let
$\mathcal {U}$
be as in Theorem 1.1. Let
![]() $\Psi \in \mathcal {H}_{N}$
be a normalized wave function such that
$\Psi \in \mathcal {H}_{N}$
be a normalized wave function such that
![]() $ \mathcal {N}_{E} \Psi = \Psi $
and
$ \mathcal {N}_{E} \Psi = \Psi $
and
![]() $\langle \Psi , H_{\operatorname {\mathrm {kin}}}^{\prime } \Psi \rangle = O(k_F)$
. Then for all
$\langle \Psi , H_{\operatorname {\mathrm {kin}}}^{\prime } \Psi \rangle = O(k_F)$
. Then for all
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
where
 $$ \begin{align} \left.H_{\mathrm{eff}}\right|_{\mathcal{N}_{E}=1}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q} = \tilde{U} \left( \bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}2\widetilde{E}_{k} \right) \tilde{U}^{\ast} \end{align} $$
$$ \begin{align} \left.H_{\mathrm{eff}}\right|_{\mathcal{N}_{E}=1}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q} = \tilde{U} \left( \bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}2\widetilde{E}_{k} \right) \tilde{U}^{\ast} \end{align} $$
on the space
![]() $\left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi \right\}$
, and
$\left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi \right\}$
, and
 $$ \begin{align} \tilde{U}:\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}L^{2}(L_{k})\rightarrow\left\{ \Psi\in\mathcal{H}_{N}\mid\mathcal{N}_{E}\Psi=\Psi\right\} \end{align} $$
$$ \begin{align} \tilde{U}:\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}L^{2}(L_{k})\rightarrow\left\{ \Psi\in\mathcal{H}_{N}\mid\mathcal{N}_{E}\Psi=\Psi\right\} \end{align} $$
is a unitary isomorphism defined by
 $$ \begin{align} \tilde{U}\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}\varphi_{k}=\sum_{k\in\mathbb{Z}_{\ast}^{3}}b_{k}^{\ast}\left(\varphi_{k}\right)\psi_{\mathrm{FS}} = \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_k} \langle e_p, \varphi_k\rangle b_{k,p}^{\ast}\psi_{\mathrm{ FS}}. \end{align} $$
$$ \begin{align} \tilde{U}\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}\varphi_{k}=\sum_{k\in\mathbb{Z}_{\ast}^{3}}b_{k}^{\ast}\left(\varphi_{k}\right)\psi_{\mathrm{FS}} = \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_k} \langle e_p, \varphi_k\rangle b_{k,p}^{\ast}\psi_{\mathrm{ FS}}. \end{align} $$
Recall that all eigenvalues of
![]() $\widetilde {E}_{k}$
can be computed explicitly from the spectrum of
$\widetilde {E}_{k}$
can be computed explicitly from the spectrum of
![]() $h_k$
and (1.49). From Theorem 1.1 and Theorem 1.4, we may say that up to the unitary transformation
$h_k$
and (1.49). From Theorem 1.1 and Theorem 1.4, we may say that up to the unitary transformation
![]() $\mathcal {U}$
, the RPA is exact for the
$\mathcal {U}$
, the RPA is exact for the
![]() $\{\mathcal {N}_{E}=1\}$
eigenspace of the effective Hamiltonian
$\{\mathcal {N}_{E}=1\}$
eigenspace of the effective Hamiltonian
![]() $H_{\mathrm {eff}}$
. To our knowledge, this is the first rigorous derivation of the bosonic elementary excitations from first principles.
$H_{\mathrm {eff}}$
. To our knowledge, this is the first rigorous derivation of the bosonic elementary excitations from first principles.
Remark 1.6. For every fixed
![]() $k\in \mathbb {Z}^3_{*}$
, in the limit
$k\in \mathbb {Z}^3_{*}$
, in the limit
![]() $k_F\to \infty $
, most eigenvalues of
$k_F\to \infty $
, most eigenvalues of
![]() $\widetilde {E}_{k}$
are of order
$\widetilde {E}_{k}$
are of order
![]() $k_F$
, but the lowest eigenvalue of
$k_F$
, but the lowest eigenvalue of
![]() $\widetilde {E}_{k}$
is of order
$\widetilde {E}_{k}$
is of order
![]() $o(k_F)$
. This absence of a one-body spectral gap corresponds to the expected fact that the excitation spectrum of
$o(k_F)$
. This absence of a one-body spectral gap corresponds to the expected fact that the excitation spectrum of
![]() $k_F^{-1}H_N$
becomes continuous in the limit
$k_F^{-1}H_N$
becomes continuous in the limit
![]() $k_F\to \infty $
. Therefore, in principle, it is very difficult to extract useful information by analyzing the full spectrum of
$k_F\to \infty $
. Therefore, in principle, it is very difficult to extract useful information by analyzing the full spectrum of
![]() $H_N$
. The significance of Theorem 1.4 is to offer a nontrivial statement on the bosonic excitations by analyzing exactly the spectrum of the effective Hamiltonian instead of looking directly at the spectrum of
$H_N$
. The significance of Theorem 1.4 is to offer a nontrivial statement on the bosonic excitations by analyzing exactly the spectrum of the effective Hamiltonian instead of looking directly at the spectrum of
![]() $H_N$
.
$H_N$
.
Remark 1.7. In Theorem 1.4, the restriction to the
![]() $\mathcal {N}_{E}=1$
eigenspace is important. Obviously, the effective Hamiltonian (1.53) does not coincide with that in the heuristic formula (1.44). Hence, it is natural to ask what to make of the assumption of the RPA that the effective Hamiltonian should behave like a diagonalized bosonic Hamiltonian. To approach this question, we note that using (1.55), we can rewrite the effective Hamiltonian in (1.53) as
$\mathcal {N}_{E}=1$
eigenspace is important. Obviously, the effective Hamiltonian (1.53) does not coincide with that in the heuristic formula (1.44). Hence, it is natural to ask what to make of the assumption of the RPA that the effective Hamiltonian should behave like a diagonalized bosonic Hamiltonian. To approach this question, we note that using (1.55), we can rewrite the effective Hamiltonian in (1.53) as
 $$ \begin{align} H_{\text{eff}}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}-\left(\mathcal{N}_{E}-1\right)H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} H_{\text{eff}}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}-\left(\mathcal{N}_{E}-1\right)H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
Since this operator commutes with
![]() $\mathcal {N}_{E}$
, we can restrict
$\mathcal {N}_{E}$
, we can restrict
![]() $H_{\text {eff}}$
to the eigenspaces of
$H_{\text {eff}}$
to the eigenspaces of
![]() $\mathcal {N}_{E}$
. Doing so, we see that the trivial eigenspace
$\mathcal {N}_{E}$
. Doing so, we see that the trivial eigenspace
![]() $\left\{ \mathcal {N}_{E}=0\right\} =\operatorname {\mathrm {span}}\left(\psi _{\mathrm { FS}}\right)$
exactly corresponds to the ground state energy which is already addressed in Theorem 1.3. For the first nontrivial eigenspace
$\left\{ \mathcal {N}_{E}=0\right\} =\operatorname {\mathrm {span}}\left(\psi _{\mathrm { FS}}\right)$
exactly corresponds to the ground state energy which is already addressed in Theorem 1.3. For the first nontrivial eigenspace
![]() $\{\mathcal {N}_{E}=1\}$
, we do indeed obtain the expected operator
$\{\mathcal {N}_{E}=1\}$
, we do indeed obtain the expected operator
 $$ \begin{align} \left.H_{\text{eff}}\right|_{\mathcal{N}_{E}=1}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
$$ \begin{align} \left.H_{\text{eff}}\right|_{\mathcal{N}_{E}=1}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
as in the heuristic formula (1.44). Moreover, the second identity in (1.60) tells us that
![]() $\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=1}$
can be diagonalized explicitly on
$\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=1}$
can be diagonalized explicitly on
![]() $\{\mathcal {N}_{E}=1\}$
, which is important for applications.
$\{\mathcal {N}_{E}=1\}$
, which is important for applications.
More generally, we can also consider the higher excitation sectors
![]() $\left\{ \mathcal {N}_{E}=M\right\} $
for
$\left\{ \mathcal {N}_{E}=M\right\} $
for
![]() $M\in \mathbb {N}$
.
$M\in \mathbb {N}$
.
Theorem 1.5 (Higher excitations).
Let V and
![]() $\mathcal {U}$
be as in Theorem 1.1. Let
$\mathcal {U}$
be as in Theorem 1.1. Let
![]() $1\le M\le O(k_F)$
. Let
$1\le M\le O(k_F)$
. Let
![]() $\Psi \in \mathcal {H}_{N}$
be a normalized wave function such that
$\Psi \in \mathcal {H}_{N}$
be a normalized wave function such that
![]() $ \mathcal {N}_{E} \Psi = M\Psi $
and
$ \mathcal {N}_{E} \Psi = M\Psi $
and
![]() $\langle \Psi , H_{\operatorname {\mathrm {kin}}}^{\prime } \Psi \rangle \le O(k_F)$
. Then for all
$\langle \Psi , H_{\operatorname {\mathrm {kin}}}^{\prime } \Psi \rangle \le O(k_F)$
. Then for all
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
where
 $$ \begin{align*} \left.H_{\mathrm{{eff}}}\right|_{\mathcal{N}_{E}=M}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},(\widetilde{E}_{k}-(1-M^{-1})h_{k})e_{q}\rangle b_{k,p}^{\ast}b_{k,q}. \end{align*} $$
$$ \begin{align*} \left.H_{\mathrm{{eff}}}\right|_{\mathcal{N}_{E}=M}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},(\widetilde{E}_{k}-(1-M^{-1})h_{k})e_{q}\rangle b_{k,p}^{\ast}b_{k,q}. \end{align*} $$
Remark 1.8. For
![]() $M\ge 2$
, the operator
$M\ge 2$
, the operator
![]() $\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=M}$
in Theorem 1.5 cannot be diagonalized explicitly as in (1.60). The quasi-bosonic property is insufficient to guarantee that it is diagonalizable, even approximately. Understanding the behaviour of
$\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=M}$
in Theorem 1.5 cannot be diagonalized explicitly as in (1.60). The quasi-bosonic property is insufficient to guarantee that it is diagonalizable, even approximately. Understanding the behaviour of
![]() $H_{\text {eff}}$
on higher eigenspaces and reconciling the RPA thus appears to be an interesting but nontrivial task. Some progress in this direction was done in [Reference Christiansen, Hainzl and Nam14] where the norm
$H_{\text {eff}}$
on higher eigenspaces and reconciling the RPA thus appears to be an interesting but nontrivial task. Some progress in this direction was done in [Reference Christiansen, Hainzl and Nam14] where the norm
![]() $\|(H_{\mathrm {{eff}}} - M \epsilon ) \Psi \|$
was estimated for suitable trial states.
$\|(H_{\mathrm {{eff}}} - M \epsilon ) \Psi \|$
was estimated for suitable trial states.
1.4 Proof strategy
Now let us explain some key ingredients of the proof. Following [Reference Sawada, Brueckner, Fukuda and Brout37], our approach consists of studying pair-excitations
![]() $b_{k,p}^{\ast }=c_{p}^{\ast }c_{p-k}$
, where
$b_{k,p}^{\ast }=c_{p}^{\ast }c_{p-k}$
, where
![]() $c_{p-k}$
annihilates a particle with momentum
$c_{p-k}$
annihilates a particle with momentum
![]() $p-k$
(i.e., creates a hole in the Fermi ball), and
$p-k$
(i.e., creates a hole in the Fermi ball), and
![]() $c_{p}^{\ast }$
creates a particle outside the Fermi ball. These operators
$c_{p}^{\ast }$
creates a particle outside the Fermi ball. These operators
![]() $b_{k,p}$
,
$b_{k,p}$
,
![]() $b_{k,p}^{\ast }$
satisfy the bosonic commutation relations in an appropriate sense. This enables the use of a quasi-bosonic Bogolubov transformation to diagonalize the original fermionic operator. A main achievement of the present work is the analytical elaboration of this bosonic picture.
$b_{k,p}^{\ast }$
satisfy the bosonic commutation relations in an appropriate sense. This enables the use of a quasi-bosonic Bogolubov transformation to diagonalize the original fermionic operator. A main achievement of the present work is the analytical elaboration of this bosonic picture.
In [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], a different, collective bosonization approach was developed by averaging the pair-excitations
![]() $b_{k,p}^{\ast }$
on ‘patches’ near the surface of the Fermi ball, thus realizing strengthened versions of the bosonic commutation relations which make the comparison with the purely bosonic computation significantly easier. In the present paper, we show that the bosonization idea can be implemented directly for pairs of fermions without such an averaging procedure. In our opinion, this new approach is conceptually closer to the physics of the problem and more transparent for applications. In particular, it allows us to obtain all bosonic elementary excitations as in Theorem 1.4. Moreover, the new method is potentially applicable to Coulomb systems, where the correlation exchange correction to the purely bosonic computation plays an important role; see [Reference Christiansen, Hainzl and Nam15] for a rigorous ground state energy upper bound.
$b_{k,p}^{\ast }$
on ‘patches’ near the surface of the Fermi ball, thus realizing strengthened versions of the bosonic commutation relations which make the comparison with the purely bosonic computation significantly easier. In the present paper, we show that the bosonization idea can be implemented directly for pairs of fermions without such an averaging procedure. In our opinion, this new approach is conceptually closer to the physics of the problem and more transparent for applications. In particular, it allows us to obtain all bosonic elementary excitations as in Theorem 1.4. Moreover, the new method is potentially applicable to Coulomb systems, where the correlation exchange correction to the purely bosonic computation plays an important role; see [Reference Christiansen, Hainzl and Nam15] for a rigorous ground state energy upper bound.
In the context of interacting Bose gases, Bogolubov transformations based on another approximate CCR have been used to study the excitation spectrum; see, for example, [Reference Seiringer38, Reference Grech and Seiringer23, Reference Boccato, Brennecke, Cenatiempo and Schlein9, Reference Hainzl, Schlein and Triay25]. However, for the fermionic problem considered in the present paper, the approximate CCR holds in a very different setting and requires distinct estimation techniques.
Now let us provide further details.
Bosonization method
The driving concept of the random phase approximation is the bosonization of fermionic pairs. We must therefore argue why the excitation operators
obey an approximate CCR. Consider for simplicity the case
![]() $k=l$
: then computation shows that for any
$k=l$
: then computation shows that for any
![]() $p,q\in L_{k}$
,
$p,q\in L_{k}$
,
![]() $[b_{k,p},b_{k,q}]=[b_{k,p}^{\ast },b_{k,q}^{\ast }]=0$
, but
$[b_{k,p},b_{k,q}]=[b_{k,p}^{\ast },b_{k,q}^{\ast }]=0$
, but
In general, thanks to Pauli’s exclusion principle (
![]() $c_{p}^{\ast }c_{p},\,c_{p}c_{p}^{\ast }\leq 1$
), the error term in (1.66) satisfies the simple bound
$c_{p}^{\ast }c_{p},\,c_{p}c_{p}^{\ast }\leq 1$
), the error term in (1.66) satisfies the simple bound
![]() $\delta _{p,q}(c_{p}^{\ast }c_{p}+c_{p-k}c_{p-k}^{\ast })\leq 2\delta _{p,q}$
, but this is even bigger than the leading term
$\delta _{p,q}(c_{p}^{\ast }c_{p}+c_{p-k}c_{p-k}^{\ast })\leq 2\delta _{p,q}$
, but this is even bigger than the leading term
![]() $\delta _{p,q}$
. The key observation is that although these errors terms can not be considered to be small individually, they are so on average. For instance,
$\delta _{p,q}$
. The key observation is that although these errors terms can not be considered to be small individually, they are so on average. For instance,
where
![]() $\mathcal {N}_{E}$
is the ‘excitation number operator’ defined in (1.13). Thus, for states where the expectation value of
$\mathcal {N}_{E}$
is the ‘excitation number operator’ defined in (1.13). Thus, for states where the expectation value of
![]() $\mathcal {N}_{E}$
is much smaller than
$\mathcal {N}_{E}$
is much smaller than
![]() $\sum _{p,q\in L_{k}}\delta _{p,q}=\left|L_{k}\right| \sim \min \{|k| k_F^2,k_F^3\}$
, one may expect that the contribution of the non-bosonic error terms are also smaller than the leading bosonic behaviour. Justifying this idea rigorously is one of the main results of this paper.
$\sum _{p,q\in L_{k}}\delta _{p,q}=\left|L_{k}\right| \sim \min \{|k| k_F^2,k_F^3\}$
, one may expect that the contribution of the non-bosonic error terms are also smaller than the leading bosonic behaviour. Justifying this idea rigorously is one of the main results of this paper.
Note that unlike the works [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], we do not employ the ‘particle-hole transformation’ R, which maps
![]() $\psi _{\mathrm {FS}}$
to the vacuum, so that we always work directly on the space
$\psi _{\mathrm {FS}}$
to the vacuum, so that we always work directly on the space
![]() $\mathcal {H}_{N}$
.
$\mathcal {H}_{N}$
.
A priori estimates
As explained above, to apply the bosonization method, we need to show that the expectation of
![]() $\mathcal {N}_E$
against low-lying eigenstates of
$\mathcal {N}_E$
against low-lying eigenstates of
![]() $H_N$
is much smaller than
$H_N$
is much smaller than
![]() $\left|L_{k}\right|\sim \min \left\{ k_{F}^{2}|k|,k_{F}^{3}\right\}$
.
$\left|L_{k}\right|\sim \min \left\{ k_{F}^{2}|k|,k_{F}^{3}\right\}$
.
Using the condition
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
and a variant of Onsager’s lemma, we can prove that
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
and a variant of Onsager’s lemma, we can prove that
Consequently, if
![]() $\Psi $
is any eigenstate for
$\Psi $
is any eigenstate for
![]() $H_N$
satisfying
$H_N$
satisfying
![]() $\left\langle \Psi ,H_{N}\Psi \right\rangle \leq E_{\mathrm {FS}} +Ck_{F}$
, then
$\left\langle \Psi ,H_{N}\Psi \right\rangle \leq E_{\mathrm {FS}} +Ck_{F}$
, then
Since
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }\ge \mathcal {N}_{E}$
, which was already explained in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], this implies that
$H_{\operatorname {\mathrm {kin}}}^{\prime }\ge \mathcal {N}_{E}$
, which was already explained in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], this implies that
![]() $\langle \Psi , \mathcal {N}_E \Psi \rangle \le Ck_F \ll |L_k|$
. For V sufficiently small, this bound was first proved in [Reference Hainzl, Porta and Rexze24] (by a different method), and it was also used in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. In practice, we will also need a stronger a priori estimate, namely,
$\langle \Psi , \mathcal {N}_E \Psi \rangle \le Ck_F \ll |L_k|$
. For V sufficiently small, this bound was first proved in [Reference Hainzl, Porta and Rexze24] (by a different method), and it was also used in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. In practice, we will also need a stronger a priori estimate, namely,
as stated in Theorem 1.2. This we will obtain by employing a bootstrapping argument for eigenstates, inspired by the ‘improved condensation’ in the context of Bose gases in [Reference Seiringer38, Reference Grech and Seiringer23, Reference Nam29, Reference Nam and Napiórkowski30]. In [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], an analogue of equation (1.70) was proved for a modified ground state by using a ‘localization in Fock space’ technique. In comparison, our estimate of equation (1.70) is obtained in a far more direct fashion and yields a uniform bound for all low-lying eigenstates. In particular, thanks to (1.69) and (1.70), the operator estimate in Theorem 1.1 leads to direct consequences on the ground state energy and the excitation spectrum of
![]() $H_N$
.
$H_N$
.
Removing the non-bosonizable terms
An important ingredient of the RPA is that the non-bosonizable terms
 $$ \begin{align} \frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(2\,\mathrm{ Re}\left(\tilde{B}_{k}^{\ast}+\tilde{B}_{-k}\right)D_{k}+D_{k}^{\ast}D_{k}\right) \end{align} $$
$$ \begin{align} \frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(2\,\mathrm{ Re}\left(\tilde{B}_{k}^{\ast}+\tilde{B}_{-k}\right)D_{k}+D_{k}^{\ast}D_{k}\right) \end{align} $$
are negligible to the leading order of the correlation energy. Here, we offer a direct estimate for these terms, which is simpler than the strategy proposed in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6] and does not require a smallness condition on V. More precisely, in Theorem 2.4, we will prove that the non-bosonizable terms are bounded by
![]() $o(1) (k_F^{-1}\mathcal {N}_E H_{\operatorname {\mathrm {kin}}}' + H_{\operatorname {\mathrm {kin}}}'+k_F)$
, and hence, the expectation against the low-lying eigenstates of
$o(1) (k_F^{-1}\mathcal {N}_E H_{\operatorname {\mathrm {kin}}}' + H_{\operatorname {\mathrm {kin}}}'+k_F)$
, and hence, the expectation against the low-lying eigenstates of
![]() $H_N$
is of order
$H_N$
is of order
![]() $o(k_F)$
due to the a priori estimates mentioned before.
$o(k_F)$
due to the a priori estimates mentioned before.
Bosonization of the kinetic operator and the excitation number operator
Concerning the bosonizable terms, while the interaction terms can be interpreted directly as a quadratic Hamiltonian in the quasi-bosonic picture as in (1.34), the treatment of the kinetic operator is more subtle. In fact, (1.37) does not hold as a direct operator approximation. Instead, we will justify it by appealing to the commutator relation
 $$ \begin{align} \left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{l,q}^{\ast}\right]\approx\left[2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p},b_{l,q}^{\ast}\right]. \end{align} $$
$$ \begin{align} \left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{l,q}^{\ast}\right]\approx\left[2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p},b_{l,q}^{\ast}\right]. \end{align} $$
This commutator relation ensures that the difference
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} \end{align} $$
is essentially invariant under the Bogolubov transformations introduced later, which is sufficient for our purpose. The approximation (1.72) is a consequence of the exact commutation relation (1.35): For every
![]() $p\in L_k= B_F^c \cap (B_F+k)$
, by the CAR, we have
$p\in L_k= B_F^c \cap (B_F+k)$
, by the CAR, we have
 $$ \begin{align} \left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{k,p}^{\ast}\right] &= \sum_{q\in B_{F}^{c}} \left|q\right|^{2} \left[c_{q}^{\ast}c_{q},c_{p}^* c_{p-k} \right] - \sum_{q\in B_{F}}\left|q\right|^{2} \left[c_{q}c_{q}^{\ast}, c_{p}^* c_{p-k} \right] \nonumber\\ &=\sum_{q\in B_{F}^{c}} \left|q\right|^{2} \left[c_{q}^{\ast}c_{q},c_{p}^*\right] c_{p-k} - \sum_{q\in B_{F}}\left|q\right|^{2} c_{p}^* \left[c_{q}c_{q}^{\ast}, c_{p-k} \right] \nonumber \\ &=\sum_{q\in B_{F}^{c}} \left|q\right|^{2} \delta_{q,p} c_{q}^{\ast} c_{p-k} - \sum_{q\in B_{F}}\left|q\right|^{2} \delta_{q,p-k} c_{p}^* c_{p-k} \nonumber \\ & =|p|^{2} c_{p}^{\ast} c_{p-k} - |p-k|^{2} c_{p}^* c_{p-k} = \left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}. \end{align} $$
$$ \begin{align} \left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{k,p}^{\ast}\right] &= \sum_{q\in B_{F}^{c}} \left|q\right|^{2} \left[c_{q}^{\ast}c_{q},c_{p}^* c_{p-k} \right] - \sum_{q\in B_{F}}\left|q\right|^{2} \left[c_{q}c_{q}^{\ast}, c_{p}^* c_{p-k} \right] \nonumber\\ &=\sum_{q\in B_{F}^{c}} \left|q\right|^{2} \left[c_{q}^{\ast}c_{q},c_{p}^*\right] c_{p-k} - \sum_{q\in B_{F}}\left|q\right|^{2} c_{p}^* \left[c_{q}c_{q}^{\ast}, c_{p-k} \right] \nonumber \\ &=\sum_{q\in B_{F}^{c}} \left|q\right|^{2} \delta_{q,p} c_{q}^{\ast} c_{p-k} - \sum_{q\in B_{F}}\left|q\right|^{2} \delta_{q,p-k} c_{p}^* c_{p-k} \nonumber \\ & =|p|^{2} c_{p}^{\ast} c_{p-k} - |p-k|^{2} c_{p}^* c_{p-k} = \left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}. \end{align} $$
A similar strategy was used in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], although the analysis there is more complicated due to the averaging technique of the ‘patches’. In particular, the operators on ‘patches’ in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6] do not obey the exact commutator relation
![]() $[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k,p}^{\ast }]=2\lambda _{k,p}b_{k,p}^{\ast }$
, and so the kinetic operator has to be handled by an additional linearization argument.
$[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k,p}^{\ast }]=2\lambda _{k,p}b_{k,p}^{\ast }$
, and so the kinetic operator has to be handled by an additional linearization argument.
Note that in the same manner of the dispersion relation in (1.74), we also have
 $$ \begin{align} \big[\mathcal{N}_{E},b_{k,p}\big] & =\sum_{q\in B_{F}^{c}}\big[c_{q}^{\ast}c_{q},c_{p-k}^{\ast}c_{p}\big]=\sum_{q\in B_{F}^{c}}\big(c_{q}^{\ast}\big[c_{q},c_{p-k}^{\ast}c_{p}\big]+\big[c_{q}^{\ast},c_{p-k}^{\ast}c_{p}\big]c_{q}\big)\nonumber\\ & =\sum_{q\in B_{F}^{c}}\big(c_{q}^{\ast}\big(-c_{p-k}^{\ast}\big\{ c_{q},c_{p}\big\} +\big\{ c_{q},c_{p-k}^{\ast}\big\} c_{p}\big)+\big(-c_{p-k}^{\ast}\big\{ c_{q}^{\ast},c_{p}\big\} +\big\{ c_{q}^{\ast},c_{p-k}^{\ast}\big\} c_{p}\big)c_{q}\big)\nonumber \\ & =-\sum_{q\in B_{F}^{c}}\big(\delta_{q,p}c_{p-k}^{\ast}\big)c_{q}=-c_{p-k}^{\ast}c_{p}=-b_{k,p}\end{align} $$
$$ \begin{align} \big[\mathcal{N}_{E},b_{k,p}\big] & =\sum_{q\in B_{F}^{c}}\big[c_{q}^{\ast}c_{q},c_{p-k}^{\ast}c_{p}\big]=\sum_{q\in B_{F}^{c}}\big(c_{q}^{\ast}\big[c_{q},c_{p-k}^{\ast}c_{p}\big]+\big[c_{q}^{\ast},c_{p-k}^{\ast}c_{p}\big]c_{q}\big)\nonumber\\ & =\sum_{q\in B_{F}^{c}}\big(c_{q}^{\ast}\big(-c_{p-k}^{\ast}\big\{ c_{q},c_{p}\big\} +\big\{ c_{q},c_{p-k}^{\ast}\big\} c_{p}\big)+\big(-c_{p-k}^{\ast}\big\{ c_{q}^{\ast},c_{p}\big\} +\big\{ c_{q}^{\ast},c_{p-k}^{\ast}\big\} c_{p}\big)c_{q}\big)\nonumber \\ & =-\sum_{q\in B_{F}^{c}}\big(\delta_{q,p}c_{p-k}^{\ast}\big)c_{q}=-c_{p-k}^{\ast}c_{p}=-b_{k,p}\end{align} $$
for all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and
$k\in \mathbb {Z}_{\ast }^{3}$
and
![]() $p\in L_{k}$
. This means that
$p\in L_{k}$
. This means that
![]() $\mathcal {N}_{E}$
plays the same role as the number operator in the bosonic picture.
$\mathcal {N}_{E}$
plays the same role as the number operator in the bosonic picture.
Bogolubov transformation I
We will estimate the contribution of high momenta separately and only diagonalize the effective operator in (1.40) for low momenta. For this reason, we define a cutoff set
where
![]() $\gamma \in (0,1]$
will be optimized later. For a given
$\gamma \in (0,1]$
will be optimized later. For a given
![]() $k_{F}$
, we then diagonalize only
$k_{F}$
, we then diagonalize only
 $$ \begin{align} H_{\text{eff}}^{\prime}=\sum_{k\in S_{C}}\left(2\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}+2\sum_{p\in L_{-k}}\lambda_{-k,p}b_{-k,p}^{\ast}b_{-k,p}+H_{\text{int}}^{k}\right) \end{align} $$
$$ \begin{align} H_{\text{eff}}^{\prime}=\sum_{k\in S_{C}}\left(2\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}+2\sum_{p\in L_{-k}}\lambda_{-k,p}b_{-k,p}^{\ast}b_{-k,p}+H_{\text{int}}^{k}\right) \end{align} $$
and treat the remaining terms with
![]() $k\in \mathbb {Z}_{+}^{3}\backslash S_{C}$
as an error term. As
$k\in \mathbb {Z}_{+}^{3}\backslash S_{C}$
as an error term. As
![]() $\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
forms an exhaustion of
$\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
forms an exhaustion of
![]() $\mathbb {Z}_{+}^{3}$
, all terms are thus nonetheless diagonalized in the limit
$\mathbb {Z}_{+}^{3}$
, all terms are thus nonetheless diagonalized in the limit
![]() $k_{F}\rightarrow \infty $
.
$k_{F}\rightarrow \infty $
.
Inspired by the exact bosonic diagonalization (see Theorem 3.1 for details), we take the diagonalizing Bogolubov transformation to be of the form
![]() $e^{\mathcal {K}}$
for a generator
$e^{\mathcal {K}}$
for a generator
![]() $\mathcal {K}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
defined by
$\mathcal {K}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
defined by
 $$ \begin{align} \mathcal{K}=\sum_{k\in S_{C}}\left(\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\left\langle e_{p},K_{k}e_{-q}\right\rangle \left(b_{k,p}b_{-k,q}-b_{-k,q}^{\ast}b_{k,p}^{\ast}\right)\right), \end{align} $$
$$ \begin{align} \mathcal{K}=\sum_{k\in S_{C}}\left(\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\left\langle e_{p},K_{k}e_{-q}\right\rangle \left(b_{k,p}b_{-k,q}-b_{-k,q}^{\ast}b_{k,p}^{\ast}\right)\right), \end{align} $$
where the transformation kernels
![]() $K_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
,
$K_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
,
![]() $k\in \mathbb {Z}_{+}^{3}$
, are defined by
$k\in \mathbb {Z}_{+}^{3}$
, are defined by
 $$ \begin{align} K_{k}=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\left(h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right) \end{align} $$
$$ \begin{align} K_{k}=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\left(h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right) \end{align} $$
with
![]() $h_{k},P_{v_{k}}$
as defined in equation (1.42). With this choice, we find that
$h_{k},P_{v_{k}}$
as defined in equation (1.42). With this choice, we find that
 $$ \begin{align} e^{\mathcal{K}}H_{\text{eff}}^{\prime}e^{-\mathcal{K}}\approx\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\left(\text{tr}\left(E_{k}-h_{k}\right)+2\sum_{p,q\in L_{k}}\left\langle e_{p},E_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right) \end{align} $$
$$ \begin{align} e^{\mathcal{K}}H_{\text{eff}}^{\prime}e^{-\mathcal{K}}\approx\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\left(\text{tr}\left(E_{k}-h_{k}\right)+2\sum_{p,q\in L_{k}}\left\langle e_{p},E_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right) \end{align} $$
for
and by the commutation relation of equation (1.72), that
 $$ \begin{align} e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}\right)e^{-\mathcal{K}}\approx H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} \end{align} $$
$$ \begin{align} e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}\right)e^{-\mathcal{K}}\approx H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} \end{align} $$
so by the equations (1.77), (1.80) and (1.82), noting also that
![]() $\left\langle e_{p},h_{k}e_{q}\right\rangle =\delta _{p,q}\lambda _{k,p}$
,
$\left\langle e_{p},h_{k}e_{q}\right\rangle =\delta _{p,q}\lambda _{k,p}$
,
 $$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}\cup\left(-S_{C}\right)}H_{\text{int}}^{k}\right)e^{-\mathcal{K}} \nonumber\\ &\quad \approx H_{\operatorname{\mathrm{kin}}}^{\prime} +\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\left(\text{tr}\left(E_{k}-h_{k}\right)+2\sum_{p,q\in L_{k}}\left\langle e_{p},\left(E_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right).\end{align} $$
$$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}\cup\left(-S_{C}\right)}H_{\text{int}}^{k}\right)e^{-\mathcal{K}} \nonumber\\ &\quad \approx H_{\operatorname{\mathrm{kin}}}^{\prime} +\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\left(\text{tr}\left(E_{k}-h_{k}\right)+2\sum_{p,q\in L_{k}}\left\langle e_{p},\left(E_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right).\end{align} $$
On the right side of (1.83), the constant
![]() $\sum _{k\in S_{C}\cup \left(-S_{C}\right)}\text {tr}\left(E_{k}-h_{k}\right)$
captures correctly the leading order of the correlation energy
$\sum _{k\in S_{C}\cup \left(-S_{C}\right)}\text {tr}\left(E_{k}-h_{k}\right)$
captures correctly the leading order of the correlation energy
![]() $E_{\mathrm {corr}}$
. However, although
$E_{\mathrm {corr}}$
. However, although
![]() $E_{k}$
is isospectral to
$E_{k}$
is isospectral to
 $$ \begin{align} \widetilde{E}_k=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\left(h_{k}^{\frac{1}{2}}(h_{k}+2P_{v_{k}})h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}\geq h_{k}, \end{align} $$
$$ \begin{align} \widetilde{E}_k=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\left(h_{k}^{\frac{1}{2}}(h_{k}+2P_{v_{k}})h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}\geq h_{k}, \end{align} $$
the operator
![]() $E_{k}-h_{k}$
is not non-negative. Thus the term
$E_{k}-h_{k}$
is not non-negative. Thus the term
![]() $2\sum _{p,q\in L_{k}}\left\langle e_{p},\left(E_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast }b_{k,q}$
– a kind of second quantization of
$2\sum _{p,q\in L_{k}}\left\langle e_{p},\left(E_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast }b_{k,q}$
– a kind of second quantization of
![]() $E_{k}-h_{k}$
– cannot be ignored for the lower bound.
$E_{k}-h_{k}$
– cannot be ignored for the lower bound.
The Bogolubov transformation used in this part is analogous to that of [Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. It was proved in [Reference Benedikter, Nam, Porta, Schlein and Seiringer6] that if V is small, then the quantization of
![]() $E_{k}-h_{k}$
can be controlled by
$E_{k}-h_{k}$
can be controlled by
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
, leading to the desired lower bound on the ground state energy. In order to treat an arbitrary potential, we will instead utilize a second Bogolubov transformation which effectively replaces
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
, leading to the desired lower bound on the ground state energy. In order to treat an arbitrary potential, we will instead utilize a second Bogolubov transformation which effectively replaces
![]() $E_k$
by
$E_k$
by
![]() $\widetilde {E}_k$
in (1.83).
$\widetilde {E}_k$
in (1.83).
Bogolubov transformation II
We define the second Bogolubov transformation
![]() $e^{\mathcal {J}}$
for a generator
$e^{\mathcal {J}}$
for a generator
![]() $\mathcal {J}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
defined by
$\mathcal {J}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
defined by
 $$ \begin{align} \mathcal{J}=\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p,q\in L_{k}}\left\langle e_{p},J_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
$$ \begin{align} \mathcal{J}=\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p,q\in L_{k}}\left\langle e_{p},J_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
where
![]() $J_{k}=\log \left(U_{k}\right)$
denotes the (principal) logarithm of the unitary transformation
$J_{k}=\log \left(U_{k}\right)$
denotes the (principal) logarithm of the unitary transformation
![]() $U_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
defined by
$U_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
defined by
 $$ \begin{align} U_{k}=\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}e^{K_{k}}. \end{align} $$
$$ \begin{align} U_{k}=\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}e^{K_{k}}. \end{align} $$
This is precisely the unitary transformation which satisfies
 $$ \begin{align} U_{k}E_{k}U_{k}^{\ast}=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\left(h_{k}^{\frac{1}{2}}(h_{k}+2P_{v_{k}})h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}} = \widetilde{E}_k, \end{align} $$
$$ \begin{align} U_{k}E_{k}U_{k}^{\ast}=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\left(h_{k}^{\frac{1}{2}}(h_{k}+2P_{v_{k}})h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}} = \widetilde{E}_k, \end{align} $$
as is easily verified. This transformation acts such that
 $$ \begin{align} e^{\mathcal{J}}\left(\sum_{p,q\in L_{k}}\left\langle e_{p},E_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right)e^{-\mathcal{J}}\approx\sum_{p,q\in L_{k}}\left\langle e_{p},\widetilde{E}_k e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
$$ \begin{align} e^{\mathcal{J}}\left(\sum_{p,q\in L_{k}}\left\langle e_{p},E_{k}e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}\right)e^{-\mathcal{J}}\approx\sum_{p,q\in L_{k}}\left\langle e_{p},\widetilde{E}_k e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align} $$
and thanks to the relation of equation (1.72), also
 $$ \begin{align} e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}\right)e^{-\mathcal{J}}\approx H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}, \end{align} $$
$$ \begin{align} e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}\right)e^{-\mathcal{J}}\approx H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}, \end{align} $$
so all in all,
 $$ \begin{align} & e^{\mathcal{J}}e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}\cup\left(-S_{C}\right)}H_{\text{int}}^{k}\right)e^{-\mathcal{K}}e^{-\mathcal{J}} \nonumber\\ &\quad\approx\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\text{tr}\left(E_{k}-h_{k}\right)+H_{\operatorname{\mathrm{kin}}}^{\prime} +\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p,q\in L_{k}}\left\langle e_{p},(\widetilde{E}_k - h_k) e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}.\end{align} $$
$$ \begin{align} & e^{\mathcal{J}}e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}\cup\left(-S_{C}\right)}H_{\text{int}}^{k}\right)e^{-\mathcal{K}}e^{-\mathcal{J}} \nonumber\\ &\quad\approx\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\text{tr}\left(E_{k}-h_{k}\right)+H_{\operatorname{\mathrm{kin}}}^{\prime} +\sum_{k\in S_{C}\cup\left(-S_{C}\right)}\sum_{p,q\in L_{k}}\left\langle e_{p},(\widetilde{E}_k - h_k) e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}.\end{align} $$
As
![]() $\widetilde {E}_k-h_{k}\geq 0$
, the last term can now be dropped and the energy lower bound concluded. The cutoff
$\widetilde {E}_k-h_{k}\geq 0$
, the last term can now be dropped and the energy lower bound concluded. The cutoff
![]() $S_C$
can be removed at the end without serious difficulties. On the technical level, the second Bogolubov transformation is an important new tool to remove the smallness condition of [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], thus enabling us to work with a significantly larger class of interaction potentials. In the independent work [Reference Benedikter, Porta, Schlein and Seiringer8], the idea of using the second Bogolubov transformation has also been introduced to refine the method in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6].
$S_C$
can be removed at the end without serious difficulties. On the technical level, the second Bogolubov transformation is an important new tool to remove the smallness condition of [Reference Benedikter, Nam, Porta, Schlein and Seiringer6], thus enabling us to work with a significantly larger class of interaction potentials. In the independent work [Reference Benedikter, Porta, Schlein and Seiringer8], the idea of using the second Bogolubov transformation has also been introduced to refine the method in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6].
Elementary excitations
The key ingredient to obtain all bosonic elementary excitations is the formula (1.60) in Theorem 1.4. To prove this, note that
![]() $\left.H_{\mathrm {eff}}\right|_{\mathcal {N}_{E}=1}$
commutes with
$\left.H_{\mathrm {eff}}\right|_{\mathcal {N}_{E}=1}$
commutes with
![]() $\mathcal {N}_{E}$
and the total momentum
$\mathcal {N}_{E}$
and the total momentum
![]() $P= \sum _{p\in \mathbb {Z}^3_{*}} p c_p^* c_p$
, so we may restrict
$P= \sum _{p\in \mathbb {Z}^3_{*}} p c_p^* c_p$
, so we may restrict
![]() $H_{\text {eff}}$
to the simultanous eigenspaces of
$H_{\text {eff}}$
to the simultanous eigenspaces of
![]() $\mathcal {N}_{E}$
and P, which are
$\mathcal {N}_{E}$
and P, which are
It turns out that the mapping
![]() $U_k:L^{2}(L_{k})\rightarrow \left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi ,\,P\Psi =k\Psi \right\} $
defined by
$U_k:L^{2}(L_{k})\rightarrow \left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi ,\,P\Psi =k\Psi \right\} $
defined by
is a unitary isomorphism with the property that
Summing over different momenta k’s, we obtain the transformation
![]() $\tilde {U}$
introduced in (1.62).
$\tilde {U}$
introduced in (1.62).
In summary, our approach is different from the previous works [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] in many aspects. On the conceptual level, our direct bosonization method (i.e., working directly with the operators
![]() $b_{k,p}$
instead of averaging them on ‘patches’) allows us to stick closely to the heuristic argument of the physics literature and to obtain not only the ground state energy but also all bosonic elementary excitations, thus leading to the first complete justification of the RPA in the mean-field regime.
$b_{k,p}$
instead of averaging them on ‘patches’) allows us to stick closely to the heuristic argument of the physics literature and to obtain not only the ground state energy but also all bosonic elementary excitations, thus leading to the first complete justification of the RPA in the mean-field regime.
Although our general ideas are very transparent, to realize the whole procedure on a rigorous basis, we will need to develop several new estimates to justify all of the approximations made. In the rest of the paper, we will show how to implement the proof strategy rigorously.
Outline of the paper. In Section 2, we prove some general estimates involving the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}$
and bound the non-bosonizable terms. In Section 3, we review the theory of bosonic Bogolubov transformations; in particular, we review how one may explicitly define a Bogolubov transformation which diagonalizes a given positive-definite quadratic Hamiltonian. We then apply the bosonic theory to our study of the Fermi gas where we implement the diagonalization procedure in the quasi-bosonic framework. This is done by introducing the quasi-bosonic quadratic Hamiltonian in Section 4 and the quasi-bosonic Bogolubov transformation
$H_{\operatorname {\mathrm {kin}}}$
and bound the non-bosonizable terms. In Section 3, we review the theory of bosonic Bogolubov transformations; in particular, we review how one may explicitly define a Bogolubov transformation which diagonalizes a given positive-definite quadratic Hamiltonian. We then apply the bosonic theory to our study of the Fermi gas where we implement the diagonalization procedure in the quasi-bosonic framework. This is done by introducing the quasi-bosonic quadratic Hamiltonian in Section 4 and the quasi-bosonic Bogolubov transformation
![]() $e^{\mathcal {K}}$
in Section 5 (these notations mirror the exact bosonic ones as closely as possible such that the bosonic theory is easily transferred to the quasi-bosonic setting). In this way, the quasi-bosonic analysis reduces to that of a collection of exact bosonic quadratic Hamiltonians plus correlation exchange terms – error terms which arise due to the deviation from the exact CCR. In Section 6, we estimate the exchange terms, reducing the analysis of these to the associated one-body operators of the bosonic problem. The one-body operators are studied separately in Section 7. In this part, we will need several estimates of Riemann sums, which are collected in the Appendix. We complete the analysis of the transformation
$e^{\mathcal {K}}$
in Section 5 (these notations mirror the exact bosonic ones as closely as possible such that the bosonic theory is easily transferred to the quasi-bosonic setting). In this way, the quasi-bosonic analysis reduces to that of a collection of exact bosonic quadratic Hamiltonians plus correlation exchange terms – error terms which arise due to the deviation from the exact CCR. In Section 6, we estimate the exchange terms, reducing the analysis of these to the associated one-body operators of the bosonic problem. The one-body operators are studied separately in Section 7. In this part, we will need several estimates of Riemann sums, which are collected in the Appendix. We complete the analysis of the transformation
![]() $e^{\mathcal {K}}$
in Section 8, where we prove that
$e^{\mathcal {K}}$
in Section 8, where we prove that
![]() $H_{\operatorname {\mathrm {kin}}}'$
and
$H_{\operatorname {\mathrm {kin}}}'$
and
![]() $\mathcal {N}_E$
are stable under the transformation
$\mathcal {N}_E$
are stable under the transformation
![]() $e^{\mathcal {K}}$
. In Section 9, we introduce the second unitary transformation
$e^{\mathcal {K}}$
. In Section 9, we introduce the second unitary transformation
![]() $e^{\mathcal {J}}$
. The analysis of this transformation is essentially similar to the first one, except that we require new one-body operator estimates which are somewhat more difficult. Finally, we conclude the proofs of the main theorems in Section 10.
$e^{\mathcal {J}}$
. The analysis of this transformation is essentially similar to the first one, except that we require new one-body operator estimates which are somewhat more difficult. Finally, we conclude the proofs of the main theorems in Section 10.
2 Removal of the non-bosonizable terms
In this section, we collect several basic estimates concerning the operator
![]() $H_N$
which can be obtained without using Bogolubov transformations. Recall the decomposition (1.22)
$H_N$
which can be obtained without using Bogolubov transformations. Recall the decomposition (1.22)
We will bound the interaction operator
![]() $H_{\operatorname {\mathrm {int}}}^{\prime }$
in terms of the kinetic operator
$H_{\operatorname {\mathrm {int}}}^{\prime }$
in terms of the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
and then prove a priori estimates for eigenstates of
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
and then prove a priori estimates for eigenstates of
![]() $H_N$
which are parts of Theorem 1.2.
$H_N$
which are parts of Theorem 1.2.
Recall the following result from [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Lemma 2.4] concerning the kinetic operator
![]() $H_{\mathrm {kin}}'$
in (1.11).
$H_{\mathrm {kin}}'$
in (1.11).
Proposition 2.1. We have
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime } \ge \mathcal {N}_{E}$
with
$H_{\operatorname {\mathrm {kin}}}^{\prime } \ge \mathcal {N}_{E}$
with
![]() $\mathcal {N}_{E}$
given in (1.13).
$\mathcal {N}_{E}$
given in (1.13).
Proof. Since
![]() $|p|^2$
is an integer for
$|p|^2$
is an integer for
![]() $p\in \mathbb {Z}^3$
, our assumption
$p\in \mathbb {Z}^3$
, our assumption
![]() $|B_F|=N$
implies that
$|B_F|=N$
implies that
Therefore, in (1.14), we can choose
![]() $\zeta $
such that
$\zeta $
such that
![]() $\vert |p|^{2}-\zeta \vert \,\geq 1/2$
for all
$\vert |p|^{2}-\zeta \vert \,\geq 1/2$
for all
![]() $p\in \mathbb {Z}^3$
.
$p\in \mathbb {Z}^3$
.
Next, we consider the bosonizable terms in
![]() $H_{\operatorname {\mathrm {int}}}^{\prime }$
. The following result is a minor extension of [Reference Hainzl, Porta and Rexze24, Lemma 4.7] (see also [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Appendix B] for a simplified proof).
$H_{\operatorname {\mathrm {int}}}^{\prime }$
. The following result is a minor extension of [Reference Hainzl, Porta and Rexze24, Lemma 4.7] (see also [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Appendix B] for a simplified proof).
Proposition 2.2. For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
, the operator
$k\in \mathbb {Z}_{\ast }^{3}$
, the operator
![]() $\tilde {B}_{k}$
in (1.24) satisfies that
$\tilde {B}_{k}$
in (1.24) satisfies that
where the constant
![]() $C>0$
is independent of k and
$C>0$
is independent of k and
![]() $k_{F}$
.
$k_{F}$
.
Proof. As argued in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer6], for any
![]() $\Psi \in \mathcal {H}_{N}$
, it follows from the triangle and Cauchy-Schwarz inequalities that
$\Psi \in \mathcal {H}_{N}$
, it follows from the triangle and Cauchy-Schwarz inequalities that
 $$ \begin{align} \left\Vert \tilde{B}_{k}\Psi\right\Vert =\left\Vert \sum_{p\in L_{k}}c_{p-k}^{\ast}c_{p}\Psi\right\Vert \leq\sum_{p\in L_{k}}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}}\lambda_{k,p}^{-1}}\sqrt{\sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}}, \end{align} $$
$$ \begin{align} \left\Vert \tilde{B}_{k}\Psi\right\Vert =\left\Vert \sum_{p\in L_{k}}c_{p-k}^{\ast}c_{p}\Psi\right\Vert \leq\sum_{p\in L_{k}}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}}\lambda_{k,p}^{-1}}\sqrt{\sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}}, \end{align} $$
where
![]() $\lambda _{k,p}=\frac {1}{2}(|p|^{2}-|p-k|^{2})$
. Using (1.14) and Pauli’s exclusion principle
$\lambda _{k,p}=\frac {1}{2}(|p|^{2}-|p-k|^{2})$
. Using (1.14) and Pauli’s exclusion principle
![]() $\|c_p\|_{\mathrm {op}}\le 1$
,
$\|c_p\|_{\mathrm {op}}\le 1$
,
![]() $\|c^*_p\|_{\mathrm {op}}\le 1$
, we find that
$\|c^*_p\|_{\mathrm {op}}\le 1$
, we find that
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2} & =\frac{1}{2}\sum_{p\in L_{k}}\left(\vert|p|^{2}-\zeta\vert+\vert|p-k|^{2}-\zeta\vert\right)\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}\\ & \leq\frac{1}{2}\sum_{p\in L_{k}}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}\Psi\right\Vert ^{2}+\frac{1}{2}\sum_{p\in L_{k}}\vert|p-k|^{2}-\zeta\vert\left\Vert c_{p-k}^{\ast}\Psi\right\Vert ^{2}\nonumber \\ & \leq \frac{1}{2}\sum_{p\in B_F^c}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}\Psi\right\Vert ^{2}+\frac{1}{2}\sum_{p\in B_F}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}^{\ast}\Psi\right\Vert ^{2}\nonumber =\frac{1}{2}\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle. \nonumber \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2} & =\frac{1}{2}\sum_{p\in L_{k}}\left(\vert|p|^{2}-\zeta\vert+\vert|p-k|^{2}-\zeta\vert\right)\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}\\ & \leq\frac{1}{2}\sum_{p\in L_{k}}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}\Psi\right\Vert ^{2}+\frac{1}{2}\sum_{p\in L_{k}}\vert|p-k|^{2}-\zeta\vert\left\Vert c_{p-k}^{\ast}\Psi\right\Vert ^{2}\nonumber \\ & \leq \frac{1}{2}\sum_{p\in B_F^c}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}\Psi\right\Vert ^{2}+\frac{1}{2}\sum_{p\in B_F}\vert|p|^{2}-\zeta\vert\left\Vert c_{p}^{\ast}\Psi\right\Vert ^{2}\nonumber =\frac{1}{2}\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle. \nonumber \end{align} $$
Thus, it remains to show that
![]() $\sum _{p\in L_{k}}\lambda _{k,p}^{-1}\leq Ck_{F}$
. For
$\sum _{p\in L_{k}}\lambda _{k,p}^{-1}\leq Ck_{F}$
. For
![]() $|k|\sim O(1)$
, this bound was already proved in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. For completeness, we will establish this bound for all
$|k|\sim O(1)$
, this bound was already proved in [Reference Hainzl, Porta and Rexze24, Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. For completeness, we will establish this bound for all
![]() $k\in \mathbb {Z}^3_{*}$
in the Appendix (Proposition A.2). Thus, in summary,
$k\in \mathbb {Z}^3_{*}$
in the Appendix (Proposition A.2). Thus, in summary,
 $$ \begin{align} \tilde{B}_{k}^{\ast}\tilde{B}_{k}\leq\frac{1}{2}\left(\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right)H_{\operatorname{\mathrm{kin}}}^{\prime} \le Ck_{F}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} \tilde{B}_{k}^{\ast}\tilde{B}_{k}\leq\frac{1}{2}\left(\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right)H_{\operatorname{\mathrm{kin}}}^{\prime} \le Ck_{F}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
Then the bound for
![]() $\tilde {B}_{k}\tilde {B}_{k}^{\ast }$
follows from the fact that
$\tilde {B}_{k}\tilde {B}_{k}^{\ast }$
follows from the fact that
In the last estimate, we used
![]() $\left|L_{k}\right|\leq Ck_{F}^{2}|k|$
for all
$\left|L_{k}\right|\leq Ck_{F}^{2}|k|$
for all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
(see Proposition A.1 for details).
$k\in \mathbb {Z}_{\ast }^{3}$
(see Proposition A.1 for details).
For the non-bosonizable terms in
![]() $H_{\operatorname {\mathrm {int}}}^{\prime }$
, it was proved in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Eq. (5.1)] that
$H_{\operatorname {\mathrm {int}}}^{\prime }$
, it was proved in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Eq. (5.1)] that
However, this bound is not optimal for low-lying eigenfunctions (for which
![]() $\mathcal {N}_{E}\sim k_F$
). In order to remove the non-bosonizable terms completely, we need the following improvement.
$\mathcal {N}_{E}\sim k_F$
). In order to remove the non-bosonizable terms completely, we need the following improvement.
Proposition 2.3. For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and any
$k\in \mathbb {Z}_{\ast }^{3}$
and any
![]() $0<\lambda \le \frac {1}{6}k_F^2$
, the operator
$0<\lambda \le \frac {1}{6}k_F^2$
, the operator
![]() $D_k$
in (1.23) satisfies
$D_k$
in (1.23) satisfies
 $$\begin{align*}D_{k}^{\ast}D_{k}\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)(\lambda +|k|) \mathcal{N}_{E}+C\lambda^{-\frac{1}{2}}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} \end{align*}$$
$$\begin{align*}D_{k}^{\ast}D_{k}\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)(\lambda +|k|) \mathcal{N}_{E}+C\lambda^{-\frac{1}{2}}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} \end{align*}$$
for a constant
![]() $C>0$
independent of k,
$C>0$
independent of k,
![]() $k_{F}$
and
$k_{F}$
and
![]() $\lambda $
.
$\lambda $
.
In applications, we will eventually choose
![]() $\lambda =k_F^{2\gamma }/|k|^{4}$
for some constant
$\lambda =k_F^{2\gamma }/|k|^{4}$
for some constant
![]() $\gamma \in (0,1/9)$
.
$\gamma \in (0,1/9)$
.
Proof. For
![]() $k\in \mathbb {Z}_{\ast }^{3}$
, we write
$k\in \mathbb {Z}_{\ast }^{3}$
, we write
![]() $D_{k}=D_{k}^{1}+D_{k}^{2}$
as in (1.24), namely,
$D_{k}=D_{k}^{1}+D_{k}^{2}$
as in (1.24), namely,
 $$ \begin{align} D_{k}^{1}=\sum_{q\in B_{F}\cap\left(B_{F}+k\right)}c_{q-k}^{\ast}c_{q},\quad D_{k}^{2}= \sum_{q\in B_{F}^c \cap\left(B_{F}^c+k\right)}c_{q-k}^{\ast}c_{q}. \end{align} $$
$$ \begin{align} D_{k}^{1}=\sum_{q\in B_{F}\cap\left(B_{F}+k\right)}c_{q-k}^{\ast}c_{q},\quad D_{k}^{2}= \sum_{q\in B_{F}^c \cap\left(B_{F}^c+k\right)}c_{q-k}^{\ast}c_{q}. \end{align} $$
By the Cauchy–Schwarz inequality,
We will estimate
![]() $(D_{k}^{1})^{\ast }D_{k}^{1}$
in detail, with the estimate of
$(D_{k}^{1})^{\ast }D_{k}^{1}$
in detail, with the estimate of
![]() $(D_{k}^{2})^{\ast }D_{k}^{2}$
being similar. We have
$(D_{k}^{2})^{\ast }D_{k}^{2}$
being similar. We have
 $$ \begin{align} (D_{k}^{1})^{\ast}D_{k}^{1} &=\sum_{p,q\in B_{F}\cap\left(B_{F}+k\right)} c_p^* c_{p-k} c_{q-k}^{\ast} c_{q} =\sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( \delta_{p,q}c_{p-k}c_{p-k}^{\ast} - c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} ) \nonumber \\ &= \sum_{p \in B_{F}\cap\left(B_{F}+k\right)} c_{p-k}c_{p-k}^{\ast} - \frac{1}{2}\sum_{p,q\in B_{F}\cap\left(B_{F}+k\right)} ( c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} + h.c.). \end{align} $$
$$ \begin{align} (D_{k}^{1})^{\ast}D_{k}^{1} &=\sum_{p,q\in B_{F}\cap\left(B_{F}+k\right)} c_p^* c_{p-k} c_{q-k}^{\ast} c_{q} =\sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( \delta_{p,q}c_{p-k}c_{p-k}^{\ast} - c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} ) \nonumber \\ &= \sum_{p \in B_{F}\cap\left(B_{F}+k\right)} c_{p-k}c_{p-k}^{\ast} - \frac{1}{2}\sum_{p,q\in B_{F}\cap\left(B_{F}+k\right)} ( c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} + h.c.). \end{align} $$
Here, we used
![]() $k\ne 0$
so that
$k\ne 0$
so that
![]() $c_{p-k}$
and
$c_{p-k}$
and
![]() $c^*_p$
anti-commute. By the definition of
$c^*_p$
anti-commute. By the definition of
![]() $\mathcal {N}_E$
in (1.13),
$\mathcal {N}_E$
in (1.13),
Moreover, by the Cauchy–Schwarz inequality, for all
![]() $\epsilon _p>0$
, we get
$\epsilon _p>0$
, we get
 $$ \begin{align} &\pm \frac{1}{2}\sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} + h.c. ) \nonumber\\ & \le \frac{1}{2} \sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} (\epsilon_p c_{p-k}c_{q} c_q^* c_{p-k}^* + \epsilon_p^{-1} c_{q-k} c_p c_{p}^{\ast}c_{q-k}^{\ast}) \nonumber\\ & \le \frac{1}{2} \sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( \epsilon_p c_{p-k}c_{p-k}^* c_{q} c_q^* + \epsilon_p^{-1} c_{q-k} c_{q-k}^{\ast} c_p c_{p}^{\ast}) \nonumber\\ &\le \frac{1}{2} \sum_{p \in B_{F}\cap\left(B_{F}+k\right)} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \mathcal{N}_E . \end{align} $$
$$ \begin{align} &\pm \frac{1}{2}\sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( c_{p-k}c_{q}c_{p}^{\ast}c_{q-k}^{\ast} + h.c. ) \nonumber\\ & \le \frac{1}{2} \sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} (\epsilon_p c_{p-k}c_{q} c_q^* c_{p-k}^* + \epsilon_p^{-1} c_{q-k} c_p c_{p}^{\ast}c_{q-k}^{\ast}) \nonumber\\ & \le \frac{1}{2} \sum_{p,q \in B_{F}\cap\left(B_{F}+k\right)} ( \epsilon_p c_{p-k}c_{p-k}^* c_{q} c_q^* + \epsilon_p^{-1} c_{q-k} c_{q-k}^{\ast} c_p c_{p}^{\ast}) \nonumber\\ &\le \frac{1}{2} \sum_{p \in B_{F}\cap\left(B_{F}+k\right)} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \mathcal{N}_E . \end{align} $$
By taking
![]() $\epsilon _p\equiv 1$
, we obtain immediately
$\epsilon _p\equiv 1$
, we obtain immediately
![]() $(D_{k}^{1})^{\ast }D_{k}^{1} \le \mathcal {N}_E^2$
, which, together with a similar bound for
$(D_{k}^{1})^{\ast }D_{k}^{1} \le \mathcal {N}_E^2$
, which, together with a similar bound for
![]() $D_{k}^{2}$
, leads to (2.7). To improve on this, we have to choose
$D_{k}^{2}$
, leads to (2.7). To improve on this, we have to choose
![]() $\epsilon _p$
differently.
$\epsilon _p$
differently.
Recall that in (1.14) we can choose
![]() $\zeta \in [\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}]$
such that
$\zeta \in [\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}]$
such that
![]() $\vert |p|^{2}-\zeta \vert \,\geq 1/2$
for all
$\vert |p|^{2}-\zeta \vert \,\geq 1/2$
for all
![]() $p\in \mathbb {Z}^3$
. For any
$p\in \mathbb {Z}^3$
. For any
![]() $\lambda>0$
, we can split
$\lambda>0$
, we can split
where
 $$ \begin{align} S_{k,\lambda}^{1} &=\left\{ p\in B_{F}\cap\left(B_{F}+k\right)\mid \max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} <\lambda\right\} ,\nonumber\\ S_{k,\geq\lambda}^{1} &=\left\{ p\in B_{F}\cap\left(B_{F}+k\right)\mid\max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} \geq\lambda\right\} . \end{align} $$
$$ \begin{align} S_{k,\lambda}^{1} &=\left\{ p\in B_{F}\cap\left(B_{F}+k\right)\mid \max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} <\lambda\right\} ,\nonumber\\ S_{k,\geq\lambda}^{1} &=\left\{ p\in B_{F}\cap\left(B_{F}+k\right)\mid\max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} \geq\lambda\right\} . \end{align} $$
Choosing
![]() $\epsilon _p=1$
for
$\epsilon _p=1$
for
![]() $p\in S_{k,\lambda }^{1}$
and using
$p\in S_{k,\lambda }^{1}$
and using
![]() $\|c_p^*\|_{\mathrm {op}} \le 1$
, we get
$\|c_p^*\|_{\mathrm {op}} \le 1$
, we get
 $$ \begin{align} \frac 1 2\sum_{p \in S_{k,\lambda}^{1}} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \le |S_{k,\lambda}^{1}|. \end{align} $$
$$ \begin{align} \frac 1 2\sum_{p \in S_{k,\lambda}^{1}} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \le |S_{k,\lambda}^{1}|. \end{align} $$
Choosing
![]() $\epsilon _p = \sqrt { | |p-k|^{2}-\zeta |} / \sqrt { | |p|^2 -\zeta |} $
for
$\epsilon _p = \sqrt { | |p-k|^{2}-\zeta |} / \sqrt { | |p|^2 -\zeta |} $
for
![]() $p\in S_{k,\geq \lambda }^{1}$
, we have
$p\in S_{k,\geq \lambda }^{1}$
, we have
 $$ \begin{align} & \sum_{p \in S_{k,\geq\lambda}^{1}} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \nonumber\\ &\quad = \sum_{p \in S_{k,\geq\lambda}^{1}} \frac{1}{ \sqrt{| |p|^2 -\zeta| \cdot | |p-k|^{2}-\zeta| }}( | |p-k|^{2}-\zeta| c_{p-k}c_{p-k}^* + | |p|^2 -\zeta| c_p c_{p}^{\ast} ) \nonumber\\ &\quad \le \sum_{p \in S_{k,\geq\lambda}^{1}} \frac{1}{ \sqrt{\lambda/2} }( | |p-k|^{2}-\zeta| c_{p-k}c_{p-k}^* + | |p|^2 -\zeta| c_p c_{p}^{\ast} ) \le \frac{2\sqrt{2}}{\sqrt{\lambda}} H_{\mathrm{kin}}'. \end{align} $$
$$ \begin{align} & \sum_{p \in S_{k,\geq\lambda}^{1}} ( \epsilon_p c_{p-k}c_{p-k}^* + \epsilon_p^{-1}c_p c_{p}^{\ast} ) \nonumber\\ &\quad = \sum_{p \in S_{k,\geq\lambda}^{1}} \frac{1}{ \sqrt{| |p|^2 -\zeta| \cdot | |p-k|^{2}-\zeta| }}( | |p-k|^{2}-\zeta| c_{p-k}c_{p-k}^* + | |p|^2 -\zeta| c_p c_{p}^{\ast} ) \nonumber\\ &\quad \le \sum_{p \in S_{k,\geq\lambda}^{1}} \frac{1}{ \sqrt{\lambda/2} }( | |p-k|^{2}-\zeta| c_{p-k}c_{p-k}^* + | |p|^2 -\zeta| c_p c_{p}^{\ast} ) \le \frac{2\sqrt{2}}{\sqrt{\lambda}} H_{\mathrm{kin}}'. \end{align} $$
Here, we used that among two factors
![]() $| |p|^2 -\zeta |$
and
$| |p|^2 -\zeta |$
and
![]() $| |p-k|^{2}-\zeta | $
, there is at least one
$| |p-k|^{2}-\zeta | $
, there is at least one
![]() $\ge \lambda $
due to the assumption
$\ge \lambda $
due to the assumption
![]() $p\in S_{k,\geq \lambda }^{1}$
, and the other one is trivially
$p\in S_{k,\geq \lambda }^{1}$
, and the other one is trivially
![]() $\ge 1/2$
. In summary,
$\ge 1/2$
. In summary,
Similarly, we have
where
The desired conclusion of
![]() $D_k^* D_k$
follows from the bound
$D_k^* D_k$
follows from the bound
 $$ \begin{align} |S_{k,\lambda}^{1}|+|S_{k,\lambda}^{2}|\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda +|k|\right) \end{align} $$
$$ \begin{align} |S_{k,\lambda}^{1}|+|S_{k,\lambda}^{2}|\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda +|k|\right) \end{align} $$
whose proof can be found in Proposition A.4 in the Appendix.
2.1 Estimation of the non-bosonizable terms
Now we are ready to remove the non-bosonizable terms, namely, the terms involving operators
![]() $D_k$
in the decomposition (1.28) of the interaction operator:
$D_k$
in the decomposition (1.28) of the interaction operator:
 $$ \begin{align} k_{F}^{-1} H_{\text{int}}^{\prime} = \sum_{k\in\mathbb{Z}_{+}^{3}}\left(H_{\text{int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) +\frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right), \end{align} $$
$$ \begin{align} k_{F}^{-1} H_{\text{int}}^{\prime} = \sum_{k\in\mathbb{Z}_{+}^{3}}\left(H_{\text{int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) +\frac{k_{F}^{-1}}{(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k}+\frac{1}{2}D_{k}^{\ast}D_{k}\right), \end{align} $$
where
![]() $H_{\text {int}}^{k}$
is defined in (1.29). Moreover, for technical reasons, we will also impose a momentum cutoff in the bosonizable terms. Recall the set
$H_{\text {int}}^{k}$
is defined in (1.29). Moreover, for technical reasons, we will also impose a momentum cutoff in the bosonizable terms. Recall the set
![]() $S_C$
in (1.76). Define
$S_C$
in (1.76). Define
 $$ \begin{align} \mathcal{E}_{\mathrm{NB}} = k_{F}^{-1} H_{\text{int}}^{\prime} - \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right). \end{align} $$
$$ \begin{align} \mathcal{E}_{\mathrm{NB}} = k_{F}^{-1} H_{\text{int}}^{\prime} - \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right). \end{align} $$
Proposition 2.4. Let
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Then for all
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Then for all
![]() $\gamma \in (0,1/9)$
in
$\gamma \in (0,1/9)$
in
![]() $S_C$
, we have
$S_C$
, we have
Here, the constant
![]() $C>0$
depends only on V (in particular, it is independent of
$C>0$
depends only on V (in particular, it is independent of
![]() $k,k_F$
and
$k,k_F$
and
![]() $\lambda $
).
$\lambda $
).
We write
![]() $\pm X\le Y$
for two operator inequalities
$\pm X\le Y$
for two operator inequalities
![]() $X\le Y$
and
$X\le Y$
and
![]() $-X\le Y$
.
$-X\le Y$
.
Proof. For the bosonizable terms, by (2.6), Proposition 2.2 and Proposition 2.1, we can bound
 $$ \begin{align} \pm ( \{\tilde{B}_{k}^{\ast},\tilde{B}_{k}\} - |L_k| ) = \pm \left( 2 \tilde{B}_{k}^{\ast}\tilde{B}_{k} - \sum_{p\in L_{k}}c_{p}^{\ast}c_{p}-\sum_{p\in L_{k}}c_{p-k}c_{p-k}^{\ast} \right) \le 2 \tilde{B}_{k}^{\ast}\tilde{B}_{k} + \mathcal{N}_E\le C k_F H_{\mathrm{kin}}' \end{align} $$
$$ \begin{align} \pm ( \{\tilde{B}_{k}^{\ast},\tilde{B}_{k}\} - |L_k| ) = \pm \left( 2 \tilde{B}_{k}^{\ast}\tilde{B}_{k} - \sum_{p\in L_{k}}c_{p}^{\ast}c_{p}-\sum_{p\in L_{k}}c_{p-k}c_{p-k}^{\ast} \right) \le 2 \tilde{B}_{k}^{\ast}\tilde{B}_{k} + \mathcal{N}_E\le C k_F H_{\mathrm{kin}}' \end{align} $$
for all
![]() $k\in \mathbb {Z}^3_{*}$
. Moreover, by the Cauchy–Schwarz inequality,
$k\in \mathbb {Z}^3_{*}$
. Moreover, by the Cauchy–Schwarz inequality,
for all
![]() $k\in \mathbb {Z}^3_{*}$
. Combining (2.23) and (2.24), we find that
$k\in \mathbb {Z}^3_{*}$
. Combining (2.23) and (2.24), we find that
 $$ \begin{align} \pm \sum_{k \in \mathbb{Z}_{+}^{3} \backslash S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) &\le C (H_{\mathrm{kin}}' + k_F) \sum_{k \in \mathbb{Z}_{+}^{3} \backslash S_C} \hat V_k |k|^{1/2}\nonumber\\ & \le C (H_{\mathrm{kin}}' + k_F) k_F^{-\gamma/2} \sum_{k \in \mathbb{Z}^{3}} \hat V_k |k|. \end{align} $$
$$ \begin{align} \pm \sum_{k \in \mathbb{Z}_{+}^{3} \backslash S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) &\le C (H_{\mathrm{kin}}' + k_F) \sum_{k \in \mathbb{Z}_{+}^{3} \backslash S_C} \hat V_k |k|^{1/2}\nonumber\\ & \le C (H_{\mathrm{kin}}' + k_F) k_F^{-\gamma/2} \sum_{k \in \mathbb{Z}^{3}} \hat V_k |k|. \end{align} $$
For the non-bosonizable terms, by the Cauchy–Schwarz inequality and Proposition 2.2, we have
and hence,
 $$ \begin{align} \pm \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} \left( \tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k} + D_{k}^{\ast} D_{k} \right) \le C k_F^{1-\gamma/2} H_{\mathrm{kin}}' + \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} ( k_F^{\gamma/2} |k|^{-1} +1 ) D_{k}^{\ast} D_{k}. \end{align} $$
$$ \begin{align} \pm \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} \left( \tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k} + D_{k}^{\ast} D_{k} \right) \le C k_F^{1-\gamma/2} H_{\mathrm{kin}}' + \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} ( k_F^{\gamma/2} |k|^{-1} +1 ) D_{k}^{\ast} D_{k}. \end{align} $$
Let us decompose the sum on the right-hand side of (2.27) into the high-momenta
![]() $|k|> k_F^{\gamma /2}$
and the low-momenta
$|k|> k_F^{\gamma /2}$
and the low-momenta
![]() $|k|\le k_F^{\gamma /2}$
. For the high-momenta, from the simple bound (2.7), we get
$|k|\le k_F^{\gamma /2}$
. For the high-momenta, from the simple bound (2.7), we get
 $$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|> k_F^{\gamma/2}}\hat{V}_{k} ( k_F^{\gamma/2} |k|^{-1} +1 ) D_{k}^{\ast} D_{k} \le C k_F^{-\gamma/2} \mathcal{N}_E^2 \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k|. \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|> k_F^{\gamma/2}}\hat{V}_{k} ( k_F^{\gamma/2} |k|^{-1} +1 ) D_{k}^{\ast} D_{k} \le C k_F^{-\gamma/2} \mathcal{N}_E^2 \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k|. \end{align} $$
For the low-momenta, using Proposition 2.3 with
![]() $\lambda =k_F^{\gamma }/|k|^{2}$
, we have
$\lambda =k_F^{\gamma }/|k|^{2}$
, we have
and hence,
 $$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|\le k_F^{\gamma/2}}\hat{V}_{k} D_{k}^{\ast}D_{k} &\le C \left( \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k| \right) \left( k_F^{(3+\frac 2 3) \frac \gamma 2+ \frac 2 3} (\log k_F)^{\frac 2 3} \mathcal{N}_E + k_F^{-\frac \gamma 2} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \nonumber\\ &\le C k_F^{-\gamma/2} \left( k_F \mathcal{N}_E +\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|\le k_F^{\gamma/2}}\hat{V}_{k} D_{k}^{\ast}D_{k} &\le C \left( \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k| \right) \left( k_F^{(3+\frac 2 3) \frac \gamma 2+ \frac 2 3} (\log k_F)^{\frac 2 3} \mathcal{N}_E + k_F^{-\frac \gamma 2} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \nonumber\\ &\le C k_F^{-\gamma/2} \left( k_F \mathcal{N}_E +\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \end{align} $$
for all
![]() $\gamma \in (0,1/7)$
. Moreover, using Proposition 2.3 with
$\gamma \in (0,1/7)$
. Moreover, using Proposition 2.3 with
![]() $\lambda =k_F^{2\gamma }/|k|^{4}$
, we have
$\lambda =k_F^{2\gamma }/|k|^{4}$
, we have
 $$ \begin{align} k_F^{\gamma/2} |k|^{-1} D_{k}^{\ast}D_{k} &\leq C\left( k_F^{4\gamma} + k_F^{(2+\frac 1 2)\gamma} (\log k_F)^{\frac 2 3} k_F^{2/3} + k_F^{\frac \gamma 2}|k|^{2+2/3} (\log k_F)^{\frac 2 3} k_F^{2/3}\right) |k|\mathcal{N}_E \nonumber\\ &\qquad +Ck_F^{-\gamma/2} |k| \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \end{align} $$
$$ \begin{align} k_F^{\gamma/2} |k|^{-1} D_{k}^{\ast}D_{k} &\leq C\left( k_F^{4\gamma} + k_F^{(2+\frac 1 2)\gamma} (\log k_F)^{\frac 2 3} k_F^{2/3} + k_F^{\frac \gamma 2}|k|^{2+2/3} (\log k_F)^{\frac 2 3} k_F^{2/3}\right) |k|\mathcal{N}_E \nonumber\\ &\qquad +Ck_F^{-\gamma/2} |k| \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \end{align} $$
and hence,
 $$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|\le k_F^{\gamma/2}}\hat{V}_{k} k_F^{\gamma/2} |k|^{-1} D_{k}^{\ast}D_{k} &\le C \left( \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k| \right) \left( k_F^{(2+\frac 1 2) \gamma + \frac 2 3} (\log k_F)^{\frac 2 3} \mathcal{N}_E + k_F^{-\frac \gamma 2} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \nonumber\\ &\le C k_F^{-\gamma/2} \left( k_F \mathcal{N}_E +\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \end{align} $$
$$ \begin{align} \sum_{k\in\mathbb{Z}_{\ast}^{3}, |k|\le k_F^{\gamma/2}}\hat{V}_{k} k_F^{\gamma/2} |k|^{-1} D_{k}^{\ast}D_{k} &\le C \left( \sum_{k\in\mathbb{Z}^{3}}\hat{V}_{k} |k| \right) \left( k_F^{(2+\frac 1 2) \gamma + \frac 2 3} (\log k_F)^{\frac 2 3} \mathcal{N}_E + k_F^{-\frac \gamma 2} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \nonumber\\ &\le C k_F^{-\gamma/2} \left( k_F \mathcal{N}_E +\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\right) \end{align} $$
for all
![]() $\gamma \in (0,1/9)$
. Inserting (2.28), (2.30) and (2.32) in (2.27) and using Proposition 2.1, we conclude that
$\gamma \in (0,1/9)$
. Inserting (2.28), (2.30) and (2.32) in (2.27) and using Proposition 2.1, we conclude that
 $$ \begin{align} \pm \frac{k_{F}^{-1}}{(2\pi)^{3}} \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} \left( \tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k} + D_{k}^{\ast} D_{k} \right) \le C k_F^{-\gamma/2} \Big( H_{\mathrm{kin}}' + k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} \Big) \end{align} $$
$$ \begin{align} \pm \frac{k_{F}^{-1}}{(2\pi)^{3}} \sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k} \left( \tilde{B}_{k}^{\ast}D_{k}+D_{k}^{\ast}\tilde{B}_{k} + D_{k}^{\ast} D_{k} \right) \le C k_F^{-\gamma/2} \Big( H_{\mathrm{kin}}' + k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} \Big) \end{align} $$
for all
![]() $\gamma \in (0,1/9)$
. The conclusion follows from (2.25) and (2.33).
$\gamma \in (0,1/9)$
. The conclusion follows from (2.25) and (2.33).
3 Overview of bosonic Bogolubov transformations
In this section, we review the general theory of quadratic Hamiltonians and Bogolubov transformations in the exact bosonic setting. Later, in the remainder of the paper, the analysis here will be adapted to handle the quasi-bosonic case where error terms have to be estimated carefully.
The study of bosonic quadratic Hamiltonians goes back to Bogolubov’s 1947 paper [Reference Bogolubov10] where he proposed an effective Hamiltonian to describe the excitation spectrum of weakly interacting Bose gases. An important property of quadratic Hamiltonians is that they can be diagonalized by suitable Bogolubov transformations; see, for example, [Reference Bach and Bru2, Reference Nam, Napiórkowski and Solovej31, Reference Dereziński16] for recent results in the infinite dimensional cases. For our application, we will only focus on the situation where the one-body Hilbert space is real and finite dimensional. Historically, the diagonalization problem in finite dimensions can be solved abstractly by using Williamson’s theorem [Reference Williamson43]. We refer to [Reference Hörmander27] and [Reference Dereziński16, Section 2] for systematic discussions on the finite dimensional case.
In the present paper, we will need an explicit construction of the diagonalizing transformations so that we can adapt this to the quasi-bosonic operators. Such an explicit construction can be found in [Reference Grech and Seiringer23], which was also used in the fermionic context in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6] and will be recalled below. Here, we will offer a slightly different treatment of Bogolubov transformations, in that we will view quadratic operators on Fock spaces as the fundamental object of study rather than the creation and annihilation operators.
Notation. We will denote by V a finite-dimensional real Hilbert space and let
![]() $n=\dim \left(V\right)$
. The bosonic Fock space associated to V is
$n=\dim \left(V\right)$
. The bosonic Fock space associated to V is
 $$ \begin{align} \mathcal{F}^{+}\left(V\right)=\bigoplus_{N=0}^{\infty}\bigotimes_{\text{Sym}}^{N}V, \end{align} $$
$$ \begin{align} \mathcal{F}^{+}\left(V\right)=\bigoplus_{N=0}^{\infty}\bigotimes_{\text{Sym}}^{N}V, \end{align} $$
where
![]() $\bigotimes _{\text {Sym}}^{N}V$
denotes the space of symmetric N-fold tensor products of V. To any element
$\bigotimes _{\text {Sym}}^{N}V$
denotes the space of symmetric N-fold tensor products of V. To any element
![]() $\varphi \in V$
, there are associated two operators on
$\varphi \in V$
, there are associated two operators on
![]() $\mathcal {F}^{+}\left(V\right)$
: the annihilation operator
$\mathcal {F}^{+}\left(V\right)$
: the annihilation operator
![]() $a(\varphi )$
and the creation operator
$a(\varphi )$
and the creation operator
![]() $a^{\ast }(\varphi )$
. These are (formal) adjoints of one another and obey the canonical commutation relations (CCR): for any
$a^{\ast }(\varphi )$
. These are (formal) adjoints of one another and obey the canonical commutation relations (CCR): for any
![]() $\varphi ,\psi \in V$
,
$\varphi ,\psi \in V$
,
Additionally, the mappings
![]() $\varphi \mapsto a(\varphi )$
,
$\varphi \mapsto a(\varphi )$
,
![]() $\varphi \mapsto a^{\ast }(\varphi )$
are linear.Footnote
6
$\varphi \mapsto a^{\ast }(\varphi )$
are linear.Footnote
6
3.1 Quadratic Hamiltonians
Similarly to how we can to any
![]() $\varphi \in V$
associate the two operators
$\varphi \in V$
associate the two operators
![]() $a(\varphi )$
and
$a(\varphi )$
and
![]() $a^{\ast }(\varphi )$
, we may also associate two types of symmetric operators on
$a^{\ast }(\varphi )$
, we may also associate two types of symmetric operators on
![]() $\mathcal {F}^{+}\left(V\right)$
to any symmetric operator on V. For the definition, we let
$\mathcal {F}^{+}\left(V\right)$
to any symmetric operator on V. For the definition, we let
![]() $(e_{i})_{i=1}^{n}$
denote an orthonormal basis of V. Given any symmetric operator
$(e_{i})_{i=1}^{n}$
denote an orthonormal basis of V. Given any symmetric operator
![]() $A:V\rightarrow V$
, we then define the operator
$A:V\rightarrow V$
, we then define the operator
![]() $Q_{1}(A)$
on
$Q_{1}(A)$
on
![]() $\mathcal {F}^{+}\left(V\right)$
by
$\mathcal {F}^{+}\left(V\right)$
by
 $$ \begin{align} Q_{1}(A)=\sum_{i,j=1}^{n}\left\langle e_{i},Ae_{j}\right\rangle \left(a^{\ast}(e_{i})a(e_{j})+a(e_{j})a^{\ast}(e_{i})\right), \end{align} $$
$$ \begin{align} Q_{1}(A)=\sum_{i,j=1}^{n}\left\langle e_{i},Ae_{j}\right\rangle \left(a^{\ast}(e_{i})a(e_{j})+a(e_{j})a^{\ast}(e_{i})\right), \end{align} $$
and likewise, for any symmetric operator
![]() $B:V\rightarrow V$
, we define the operator
$B:V\rightarrow V$
, we define the operator
![]() $Q_{2}(B)$
by
$Q_{2}(B)$
by
 $$ \begin{align} Q_{2}(B)=\sum_{i,j=1}^{n}\left\langle e_{i},Be_{j}\right\rangle \left(a^{\ast}(e_{i})a^{\ast}(e_{j})+a(e_{j})a(e_{i})\right). \end{align} $$
$$ \begin{align} Q_{2}(B)=\sum_{i,j=1}^{n}\left\langle e_{i},Be_{j}\right\rangle \left(a^{\ast}(e_{i})a^{\ast}(e_{j})+a(e_{j})a(e_{i})\right). \end{align} $$
These definitions are independent of the basis chosen, and we can write equivalently
 $$ \begin{align} Q_{1}(A) & =\sum_{i=1}^{n}\left(a^{\ast}(Ae_{i})a(e_{i})+a(e_{i})a^{\ast}(Ae_{i})\right)\\ Q_{2}(B) & =\sum_{i=1}^{n}\left(a^{\ast}\left(Be_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(Be_{i}\right)\right).\nonumber \end{align} $$
$$ \begin{align} Q_{1}(A) & =\sum_{i=1}^{n}\left(a^{\ast}(Ae_{i})a(e_{i})+a(e_{i})a^{\ast}(Ae_{i})\right)\\ Q_{2}(B) & =\sum_{i=1}^{n}\left(a^{\ast}\left(Be_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(Be_{i}\right)\right).\nonumber \end{align} $$
Thus, for real, symmetric
![]() $A,B:V\rightarrow V$
, we can define a quadratic Hamiltonian on
$A,B:V\rightarrow V$
, we can define a quadratic Hamiltonian on
![]() $\mathcal {F}^{+}\left(V\right)$
by
$\mathcal {F}^{+}\left(V\right)$
by
Note that by the CCR, we may express
![]() $Q_{1}(A)$
as
$Q_{1}(A)$
as
 $$ \begin{align} Q_{1}(A) =2\sum_{i,j=1}^{n}\left\langle e_{i},Ae_{j}\right\rangle a^{\ast}(e_{i})a(e_{j})+\text{tr}(A)=2\,\text{d}\Gamma(A)+\text{tr}(A), \end{align} $$
$$ \begin{align} Q_{1}(A) =2\sum_{i,j=1}^{n}\left\langle e_{i},Ae_{j}\right\rangle a^{\ast}(e_{i})a(e_{j})+\text{tr}(A)=2\,\text{d}\Gamma(A)+\text{tr}(A), \end{align} $$
where
![]() $\text {d}\Gamma (A)$
denotes the second quantization of
$\text {d}\Gamma (A)$
denotes the second quantization of
![]() $A:V\rightarrow V$
. Sometimes in the literature, in particular in infinite dimensions, quadratic Hamiltonians are defined by
$A:V\rightarrow V$
. Sometimes in the literature, in particular in infinite dimensions, quadratic Hamiltonians are defined by
![]() $\text {d}\Gamma (A)+Q_{2}(B)$
, which is the same to our definition up to the constant
$\text {d}\Gamma (A)+Q_{2}(B)$
, which is the same to our definition up to the constant
![]() $\text {tr}(A)$
. Here, we prefer to use
$\text {tr}(A)$
. Here, we prefer to use
![]() $Q_1(A)$
instead of
$Q_1(A)$
instead of
![]() $\text {d}\Gamma (\cdot )$
; the reason for this is that the relations of Proposition 3.4 below are symmetric in the Q’s.
$\text {d}\Gamma (\cdot )$
; the reason for this is that the relations of Proposition 3.4 below are symmetric in the Q’s.
Note that the basis-independence is a nice property of the real space setting. In general, if V is a complex Hilbert space and B is symmetric, then the definition of
![]() $Q_{2}(B)$
in (3.4) may depend on the basis. In fact, we can obtain a basis-independent formulation in the complex case, but the mapping
$Q_{2}(B)$
in (3.4) may depend on the basis. In fact, we can obtain a basis-independent formulation in the complex case, but the mapping
![]() $B\mapsto Q_{2}(B)$
is not to be defined for symmetric linear operators B, but rather symmetric anti-linear operators B to make up for the fact that in the complex case the assignment
$B\mapsto Q_{2}(B)$
is not to be defined for symmetric linear operators B, but rather symmetric anti-linear operators B to make up for the fact that in the complex case the assignment
![]() $\varphi \mapsto a(\varphi )$
is also anti-linear. This is unimportant for our application, which is why we only consider real Hilbert spaces in this section, for the sake of simplicity.
$\varphi \mapsto a(\varphi )$
is also anti-linear. This is unimportant for our application, which is why we only consider real Hilbert spaces in this section, for the sake of simplicity.
3.2 Bogolubov transformations
In this subsection, we review an explicit construction of a Bogolubov transformation
![]() $\mathcal {U}:\mathcal {F}^{+}\left(V\right)\rightarrow \mathcal {F}^{+}\left(V\right)$
that diagonalizes the quadratic Hamiltonian
$\mathcal {U}:\mathcal {F}^{+}\left(V\right)\rightarrow \mathcal {F}^{+}\left(V\right)$
that diagonalizes the quadratic Hamiltonian
![]() $H= Q_1(A)+Q_2(B)$
, namely,
$H= Q_1(A)+Q_2(B)$
, namely,
for a real, symmetric operator
![]() $E:V\rightarrow V$
. Such a construction is well known; see, for example, [Reference Dereziński16] for a recent review. We consider a unitary transformation
$E:V\rightarrow V$
. Such a construction is well known; see, for example, [Reference Dereziński16] for a recent review. We consider a unitary transformation
![]() $\mathcal {U}=e^{\mathcal {K}}$
where
$\mathcal {U}=e^{\mathcal {K}}$
where
![]() $\mathcal {K}$
is an anti-symmetric operator on
$\mathcal {K}$
is an anti-symmetric operator on
![]() $\mathcal {F}^{+}\left(V\right)$
of the following form:
$\mathcal {F}^{+}\left(V\right)$
of the following form:
 $$ \begin{align} \mathcal{K}=\frac{1}{2}\sum_{i,j=1}^{n}\langle e_{i},Ke_{j}\rangle \left(a(e_{i})a(e_{j})-a^{\ast}(e_{j})a^{\ast}(e_{i})\right)=\frac{1}{2}\sum_{i=1}^{n}\left(a(Ke_{i})a(e_{i})-a^{\ast}(e_{i})a^{\ast}(Ke_{i})\right). \end{align} $$
$$ \begin{align} \mathcal{K}=\frac{1}{2}\sum_{i,j=1}^{n}\langle e_{i},Ke_{j}\rangle \left(a(e_{i})a(e_{j})-a^{\ast}(e_{j})a^{\ast}(e_{i})\right)=\frac{1}{2}\sum_{i=1}^{n}\left(a(Ke_{i})a(e_{i})-a^{\ast}(e_{i})a^{\ast}(Ke_{i})\right). \end{align} $$
Here,
![]() $K:V\rightarrow V$
is a symmetric operator (called the transformation kernel) and
$K:V\rightarrow V$
is a symmetric operator (called the transformation kernel) and
![]() $(e_{i})_{i=1}^{n}$
denotes any orthonormal basis of V (as with
$(e_{i})_{i=1}^{n}$
denotes any orthonormal basis of V (as with
![]() $Q_{1}(\cdot )$
and
$Q_{1}(\cdot )$
and
![]() $Q_{2}(\cdot )$
this definition is independent of the basis).
$Q_{2}(\cdot )$
this definition is independent of the basis).
In this subsection, we discuss the following:
Theorem 3.1. Let
![]() $A,B:V\rightarrow V$
be real, symmetric operators such that
$A,B:V\rightarrow V$
be real, symmetric operators such that
![]() $A\pm B>0$
(namely,
$A\pm B>0$
(namely,
![]() $A+B>0$
and
$A+B>0$
and
![]() $A-B>0$
). Consider the Bogolubov transformation
$A-B>0$
). Consider the Bogolubov transformation
![]() $e^{\mathcal {K}}$
where
$e^{\mathcal {K}}$
where
![]() $\mathcal {K}$
is given in (3.9) with
$\mathcal {K}$
is given in (3.9) with
 $$\begin{align*}K=-\frac{1}{2}\log\left((A-B)^{-\frac{1}{2}}\left((A-B)^{\frac{1}{2}}(A+B)(A-B)^{\frac{1}{2}}\right)^{\frac{1}{2}}(A-B)^{-\frac{1}{2}}\right). \end{align*}$$
$$\begin{align*}K=-\frac{1}{2}\log\left((A-B)^{-\frac{1}{2}}\left((A-B)^{\frac{1}{2}}(A+B)(A-B)^{\frac{1}{2}}\right)^{\frac{1}{2}}(A-B)^{-\frac{1}{2}}\right). \end{align*}$$
Then
where
Moreover, the diagonalizing K is uniquely determined by this.
In the following, we will prove Theorem 3.1 by using a generalization and simplification of the argument used in [Reference Grech and Seiringer23, Reference Benedikter, Nam, Porta, Schlein and Seiringer5]. We will first discuss the action of the Bogolubov transformation with a general kernel K and then explain where the diagonalization condition comes from.
Let us start with some basic properties of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Proposition 3.2. For any symmetric operator
![]() $K:V\rightarrow V$
, the operator
$K:V\rightarrow V$
, the operator
![]() $\mathcal {K}$
defined by (3.9) is an anti-symmetric operator on
$\mathcal {K}$
defined by (3.9) is an anti-symmetric operator on
![]() $\mathcal {F}^{+}\left(V\right)$
and obeys the commutators
$\mathcal {F}^{+}\left(V\right)$
and obeys the commutators
Thus,
![]() $\left[\mathcal {K},\cdot \right]$
acts on the creation and annihilation operators by ‘swapping’ each type into the other and applying the operator K to their arguments. From this, one can now deduce that the unitary transformation
$\left[\mathcal {K},\cdot \right]$
acts on the creation and annihilation operators by ‘swapping’ each type into the other and applying the operator K to their arguments. From this, one can now deduce that the unitary transformation
![]() $e^{\mathcal {K}}$
acts on the creation and annihilation operators according to
$e^{\mathcal {K}}$
acts on the creation and annihilation operators according to
 $$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right)\\ e^{\mathcal{K}}a^{\ast}(\varphi )e^{-\mathcal{K}} & =a^{\ast}\left(\cosh\left(K\right)\varphi\right)+a\left(\sinh\left(K\right)\varphi\right),\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right)\\ e^{\mathcal{K}}a^{\ast}(\varphi )e^{-\mathcal{K}} & =a^{\ast}\left(\cosh\left(K\right)\varphi\right)+a\left(\sinh\left(K\right)\varphi\right),\nonumber \end{align} $$
since by the Baker-Campbell-Hausdorff formula,
 $$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a(\varphi )+\frac{1}{1!}\left[\mathcal{K},a(\varphi )\right]+\frac{1}{2!}\left[\mathcal{K},\left[\mathcal{K},a(\varphi )\right]\right]+\frac{1}{3!}\left[\mathcal{K},\left[\mathcal{K},\left[\mathcal{K},a(\varphi )\right]\right]\right]+\cdots\nonumber \\ & =a(\varphi )+\frac{1}{1!}a^{\ast}\left(K\varphi\right)+\frac{1}{2!}a\left(K^{2}\varphi\right)+\frac{1}{3!}a^{\ast}\left(K^{3}\varphi\right)+\cdots\\ & =a\left(\varphi+\frac{1}{2!}K^{2}\varphi+\cdots\right)+a^{\ast}\left(\frac{1}{1!}K\varphi+\frac{1}{3!}K^{3}\varphi+\cdots\right)\nonumber \\ & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right),\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a(\varphi )+\frac{1}{1!}\left[\mathcal{K},a(\varphi )\right]+\frac{1}{2!}\left[\mathcal{K},\left[\mathcal{K},a(\varphi )\right]\right]+\frac{1}{3!}\left[\mathcal{K},\left[\mathcal{K},\left[\mathcal{K},a(\varphi )\right]\right]\right]+\cdots\nonumber \\ & =a(\varphi )+\frac{1}{1!}a^{\ast}\left(K\varphi\right)+\frac{1}{2!}a\left(K^{2}\varphi\right)+\frac{1}{3!}a^{\ast}\left(K^{3}\varphi\right)+\cdots\\ & =a\left(\varphi+\frac{1}{2!}K^{2}\varphi+\cdots\right)+a^{\ast}\left(\frac{1}{1!}K\varphi+\frac{1}{3!}K^{3}\varphi+\cdots\right)\nonumber \\ & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right),\nonumber \end{align} $$
and the identity for
![]() $e^{\mathcal {K}}a^{\ast }(\varphi )e^{-\mathcal {K}}$
then follows immediately by taking the adjoint.
$e^{\mathcal {K}}a^{\ast }(\varphi )e^{-\mathcal {K}}$
then follows immediately by taking the adjoint.
Now let us consider
![]() $e^{\mathcal {K}}Q_{1}(\cdot )e^{-\mathcal {K}}$
and
$e^{\mathcal {K}}Q_{1}(\cdot )e^{-\mathcal {K}}$
and
![]() $e^{\mathcal {K}}Q_{2}(\cdot )e^{-\mathcal {K}}$
. For this, we will first make an observation on their structure which will greatly simplify computations: namely, we note that the operators
$e^{\mathcal {K}}Q_{2}(\cdot )e^{-\mathcal {K}}$
. For this, we will first make an observation on their structure which will greatly simplify computations: namely, we note that the operators
![]() $Q_{1}(A)$
and
$Q_{1}(A)$
and
![]() $Q_{2}(B)$
are both of a ‘trace-form’ in the sense that we can write, say,
$Q_{2}(B)$
are both of a ‘trace-form’ in the sense that we can write, say,
![]() $Q_{1}(A)=\sum _{i=1}^{n}q\left(e_{i},Ae_{i}\right)$
, where
$Q_{1}(A)=\sum _{i=1}^{n}q\left(e_{i},Ae_{i}\right)$
, where
defines a bilinear mapping from
![]() $V\times V$
into the space of operators on
$V\times V$
into the space of operators on
![]() $\mathcal {F}^{+}\left(V\right)$
, similar to how the trace of an operator T is
$\mathcal {F}^{+}\left(V\right)$
, similar to how the trace of an operator T is
![]() $\text {tr}(T)=\sum _{i=1}^{n}q\left(e_{i},Te_{i}\right)$
for
$\text {tr}(T)=\sum _{i=1}^{n}q\left(e_{i},Te_{i}\right)$
for
![]() $q\left(x,y\right)=\left\langle x,y\right\rangle $
. This abstract viewpoint is worth noting because all such expressions are both basis-independent and obey an additional property, which for the trace is just the familiar cyclicity property. Since we will encounter such ‘trace-form’ expressions repeatedly during computations throughout this paper, we state this property in full generality. In the following, we take sesquilinear to mean anti-linear in the first argument and linear in the second (we note that in the present real case a sesquilinear mapping is of course just a bilinear mapping, but stating it in this generality will prove useful later).
$q\left(x,y\right)=\left\langle x,y\right\rangle $
. This abstract viewpoint is worth noting because all such expressions are both basis-independent and obey an additional property, which for the trace is just the familiar cyclicity property. Since we will encounter such ‘trace-form’ expressions repeatedly during computations throughout this paper, we state this property in full generality. In the following, we take sesquilinear to mean anti-linear in the first argument and linear in the second (we note that in the present real case a sesquilinear mapping is of course just a bilinear mapping, but stating it in this generality will prove useful later).
Lemma 3.3. Let
![]() $\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
be an n-dimensional Hilbert space and let
$\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
be an n-dimensional Hilbert space and let
![]() $q:V\times V\rightarrow W$
be a sesquilinear mapping into a vector space W. Let
$q:V\times V\rightarrow W$
be a sesquilinear mapping into a vector space W. Let
![]() $(e_{i})_{i=1}^{n}$
be an orthonormal basis for V. Then for any linear operators
$(e_{i})_{i=1}^{n}$
be an orthonormal basis for V. Then for any linear operators
![]() $S,T:V\rightarrow V$
, it holds that
$S,T:V\rightarrow V$
, it holds that
 $$\begin{align*}\sum_{i=1}^{n}q\left(Se_{i},Te_{i}\right)=\sum_{i=1}^{n}q\left(ST^{\ast}e_{i},e_{i}\right). \end{align*}$$
$$\begin{align*}\sum_{i=1}^{n}q\left(Se_{i},Te_{i}\right)=\sum_{i=1}^{n}q\left(ST^{\ast}e_{i},e_{i}\right). \end{align*}$$
As a consequence, the expression
![]() $\sum _{i=1}^{n}q\left(e_{i},e_{i}\right)$
is independent of the chosen basis.
$\sum _{i=1}^{n}q\left(e_{i},e_{i}\right)$
is independent of the chosen basis.
Proof. By orthonormal expansion, we find that
 $$ \begin{align} \sum_{i=1}^{n}q\left(Se_{i},Te_{i}\right) & =\sum_{i=1}^{n}q\left(Se_{i},\sum_{j=1}^{n}\left\langle e_{j},Te_{i}\right\rangle e_{j}\right) =\sum_{j=1}^{n}q\left(\sum_{i=1}^{n}\left\langle Te_{i},e_{j}\right\rangle Se_{i},e_{j}\right) \nonumber\\ & =\sum_{j=1}^{n}q\left(S\sum_{i=1}^{n}\left\langle e_{i},T^{\ast}e_{j}\right\rangle e_{i},e_{j}\right)=\sum_{i=1}^{n}q\left(ST^{\ast}e_{i},e_{i}\right). \end{align} $$
$$ \begin{align} \sum_{i=1}^{n}q\left(Se_{i},Te_{i}\right) & =\sum_{i=1}^{n}q\left(Se_{i},\sum_{j=1}^{n}\left\langle e_{j},Te_{i}\right\rangle e_{j}\right) =\sum_{j=1}^{n}q\left(\sum_{i=1}^{n}\left\langle Te_{i},e_{j}\right\rangle Se_{i},e_{j}\right) \nonumber\\ & =\sum_{j=1}^{n}q\left(S\sum_{i=1}^{n}\left\langle e_{i},T^{\ast}e_{j}\right\rangle e_{i},e_{j}\right)=\sum_{i=1}^{n}q\left(ST^{\ast}e_{i},e_{i}\right). \end{align} $$
The basis independence follows from the fact that for all unitary transformation
![]() $U:V\rightarrow V$
,
$U:V\rightarrow V$
,
 $$ \begin{align} \sum_{i=1}^{n}q\left(Ue_{i},Ue_{i}\right)=\sum_{i=1}^{n}q\left(UU^{\ast}e_{i},e_{i}\right)=\sum_{i=1}^{n}q\left(e_{i},e_{i}\right). \end{align} $$
$$ \begin{align} \sum_{i=1}^{n}q\left(Ue_{i},Ue_{i}\right)=\sum_{i=1}^{n}q\left(UU^{\ast}e_{i},e_{i}\right)=\sum_{i=1}^{n}q\left(e_{i},e_{i}\right). \end{align} $$
The lemma thus allows us to move a mapping from one argument to the other when under a sum, which will be immensely useful when simplifying expressions. As mentioned, this can indeed be seen as a generalization of the cyclicity property of the trace, since the lemma implies
 $$ \begin{align} \text{tr}\left(ST\right)=\sum_{i=1}^{n}\left\langle e_{i},STe_{i}\right\rangle =\sum_{i=1}^{n}\left\langle S^{\ast}e_{i},Te_{i}\right\rangle =\sum_{i=1}^{n}\left\langle S^{\ast}T^{\ast}e_{i},e_{i}\right\rangle =\sum_{i=1}^{n}\left\langle e_{i},TSe_{i}\right\rangle =\text{tr}\left(TS\right), \end{align} $$
$$ \begin{align} \text{tr}\left(ST\right)=\sum_{i=1}^{n}\left\langle e_{i},STe_{i}\right\rangle =\sum_{i=1}^{n}\left\langle S^{\ast}e_{i},Te_{i}\right\rangle =\sum_{i=1}^{n}\left\langle S^{\ast}T^{\ast}e_{i},e_{i}\right\rangle =\sum_{i=1}^{n}\left\langle e_{i},TSe_{i}\right\rangle =\text{tr}\left(TS\right), \end{align} $$
but it is important to note that cyclicity is not a general property of trace-form sums; the assignments
![]() $A\mapsto Q_{1}(A)$
and
$A\mapsto Q_{1}(A)$
and
![]() $B\mapsto Q_{2}(B)$
do not obey such a property.
$B\mapsto Q_{2}(B)$
do not obey such a property.
With the lemma, we can now easily derive the commutator of
![]() $\mathcal {K}$
with
$\mathcal {K}$
with
![]() $Q_{1}(\cdot )$
and
$Q_{1}(\cdot )$
and
![]() $Q_{2}(\cdot )$
:
$Q_{2}(\cdot )$
:
Proposition 3.4. For any real, symmetric operators
![]() $A,B,K:V\rightarrow V$
, the operator
$A,B,K:V\rightarrow V$
, the operator
![]() $\mathcal {K}$
defined by equation (3.9) obeys the following commutators on
$\mathcal {K}$
defined by equation (3.9) obeys the following commutators on
![]() $\mathcal {F}^+(V)$
:
$\mathcal {F}^+(V)$
:
 $$ \begin{align*} \left[\mathcal{K},Q_{1}(A)\right] & =Q_{2}\left(\left\{ K,A\right\} \right)\\ \left[\mathcal{K},Q_{2}(B)\right] & =Q_{1}\left(\left\{ K,B\right\} \right). \end{align*} $$
$$ \begin{align*} \left[\mathcal{K},Q_{1}(A)\right] & =Q_{2}\left(\left\{ K,A\right\} \right)\\ \left[\mathcal{K},Q_{2}(B)\right] & =Q_{1}\left(\left\{ K,B\right\} \right). \end{align*} $$
Proof. We compute using the commutators of Proposition 3.2 that
 $$ \begin{align} \left[\mathcal{K},Q_{1}(A)\right] & =\sum_{i=1}^{n}\left(\left[\mathcal{K},a^{\ast}(Ae_{i})a(e_{i})\right]+\left[\mathcal{K},a(e_{i})a^{\ast}(Ae_{i})\right]\right)\nonumber\\ & =\sum_{i=1}^{n}(a^{\ast}(Ae_{i})\left[\mathcal{K},a(e_{i})\right] \nonumber \\ &\quad +\left[\mathcal{K},a^{\ast}(Ae_{i})\right]a(e_{i})+a(e_{i})\left[\mathcal{K},a^{\ast}(Ae_{i})\right]+\left[\mathcal{K},a(e_{i})\right]a^{\ast}(Ae_{i}))\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}(Ae_{i})a^{\ast}(Ke_{i})+a(KAe_{i})a(e_{i})+a(e_{i})a(KAe_{i})+a^{\ast}(Ke_{i})a^{\ast}(Ae_{i})\right). \end{align} $$
$$ \begin{align} \left[\mathcal{K},Q_{1}(A)\right] & =\sum_{i=1}^{n}\left(\left[\mathcal{K},a^{\ast}(Ae_{i})a(e_{i})\right]+\left[\mathcal{K},a(e_{i})a^{\ast}(Ae_{i})\right]\right)\nonumber\\ & =\sum_{i=1}^{n}(a^{\ast}(Ae_{i})\left[\mathcal{K},a(e_{i})\right] \nonumber \\ &\quad +\left[\mathcal{K},a^{\ast}(Ae_{i})\right]a(e_{i})+a(e_{i})\left[\mathcal{K},a^{\ast}(Ae_{i})\right]+\left[\mathcal{K},a(e_{i})\right]a^{\ast}(Ae_{i}))\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}(Ae_{i})a^{\ast}(Ke_{i})+a(KAe_{i})a(e_{i})+a(e_{i})a(KAe_{i})+a^{\ast}(Ke_{i})a^{\ast}(Ae_{i})\right). \end{align} $$
As the assignments
![]() $\varphi ,\psi \mapsto a(\varphi )a(\psi ),a^{\ast }(\varphi )a^{\ast }(\psi )$
are bilinear, we can apply Lemma 3.3 to see that
$\varphi ,\psi \mapsto a(\varphi )a(\psi ),a^{\ast }(\varphi )a^{\ast }(\psi )$
are bilinear, we can apply Lemma 3.3 to see that
 $$ \begin{align} \left[\mathcal{K},Q_{1}(A)\right] & =\sum_{i=1}^{n}\left(a^{\ast}\left(AK^{\ast}e_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(\left(KA\right)^{\ast}e_{i}\right)+a(e_{i})a(KAe_{i})+a^{\ast}\left(KA^{\ast}e_{i}\right)a^{\ast}(e_{i})\right)\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}\left(AKe_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(AKe_{i}\right)+a(e_{i})a(KAe_{i})+a^{\ast}(KAe_{i})a^{\ast}(e_{i})\right)\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}\left((AK+KA)e_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left((AK+KA)e_{i}\right)\right)=Q_{2}\left(\left\{ K,A\right\} \right), \end{align} $$
$$ \begin{align} \left[\mathcal{K},Q_{1}(A)\right] & =\sum_{i=1}^{n}\left(a^{\ast}\left(AK^{\ast}e_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(\left(KA\right)^{\ast}e_{i}\right)+a(e_{i})a(KAe_{i})+a^{\ast}\left(KA^{\ast}e_{i}\right)a^{\ast}(e_{i})\right)\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}\left(AKe_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left(AKe_{i}\right)+a(e_{i})a(KAe_{i})+a^{\ast}(KAe_{i})a^{\ast}(e_{i})\right)\nonumber \\ & =\sum_{i=1}^{n}\left(a^{\ast}\left((AK+KA)e_{i}\right)a^{\ast}(e_{i})+a(e_{i})a\left((AK+KA)e_{i}\right)\right)=Q_{2}\left(\left\{ K,A\right\} \right), \end{align} $$
where we also used that A and K are symmetric. The computation of
![]() $\left[\mathcal {K},Q_{2}(B)\right]$
is similar.
$\left[\mathcal {K},Q_{2}(B)\right]$
is similar.
Note the similarity between this result and that of Proposition 3.2. Again we see that that
![]() $\left[\mathcal {K},\cdot \right]$
acts by ‘swapping the types and applying K to the argument’, although now the relevant types are
$\left[\mathcal {K},\cdot \right]$
acts by ‘swapping the types and applying K to the argument’, although now the relevant types are
![]() $Q_{1}(\cdot )$
, and
$Q_{1}(\cdot )$
, and
![]() $Q_{2}(\cdot )$
and the application of K is taking the anticommutator.
$Q_{2}(\cdot )$
and the application of K is taking the anticommutator.
We can now appeal to the Baker-Campbell-Hausdorff formula again to conclude that
 $$ \begin{align} &e^{\mathcal{K}}Q_{1}(A)e^{-\mathcal{K}} =Q_{1}(A)+\frac{1}{1!}\left[\mathcal{K},Q_{1}(A)\right]+\frac{1}{2!}\left[\mathcal{K},\left[\mathcal{K},Q_{1}(A)\right]\right]+\frac{1}{3!}\left[\mathcal{K},\left[\mathcal{K},\left[\mathcal{K},Q_{1}(A)\right]\right]\right]+\cdots \nonumber\\ & =Q_{1}(A)+\frac{1}{1!}Q_{2}\left(\left\{ K,A\right\} \right)+\frac{1}{2!}Q_{1}\left(\left\{ K,\left\{ K,A\right\} \right\} \right)+\frac{1}{3!}Q_{2}\left(\left\{ K,\left\{ K,\left\{ K,A\right\} \right\} \right\} \right)+\cdots \nonumber\\ & =Q_{1}\left(A+\frac{1}{2!}\left\{ K,\left\{ K,A\right\} \right\} +\cdots\right)+Q_{2}\left(\frac{1}{1!}\left\{ K,A\right\} +\frac{1}{3!}\left\{ K,\left\{ K,\left\{ K,A\right\} \right\} \right\} +\cdots\right), \end{align} $$
$$ \begin{align} &e^{\mathcal{K}}Q_{1}(A)e^{-\mathcal{K}} =Q_{1}(A)+\frac{1}{1!}\left[\mathcal{K},Q_{1}(A)\right]+\frac{1}{2!}\left[\mathcal{K},\left[\mathcal{K},Q_{1}(A)\right]\right]+\frac{1}{3!}\left[\mathcal{K},\left[\mathcal{K},\left[\mathcal{K},Q_{1}(A)\right]\right]\right]+\cdots \nonumber\\ & =Q_{1}(A)+\frac{1}{1!}Q_{2}\left(\left\{ K,A\right\} \right)+\frac{1}{2!}Q_{1}\left(\left\{ K,\left\{ K,A\right\} \right\} \right)+\frac{1}{3!}Q_{2}\left(\left\{ K,\left\{ K,\left\{ K,A\right\} \right\} \right\} \right)+\cdots \nonumber\\ & =Q_{1}\left(A+\frac{1}{2!}\left\{ K,\left\{ K,A\right\} \right\} +\cdots\right)+Q_{2}\left(\frac{1}{1!}\left\{ K,A\right\} +\frac{1}{3!}\left\{ K,\left\{ K,\left\{ K,A\right\} \right\} \right\} +\cdots\right), \end{align} $$
but to succeed, we must identify the sums of these iterated anticommutators. First, we note that we can rephrase this in a manner closer to that of equation (3.10) for
![]() $e^{\mathcal {K}}a(\varphi )e^{-\mathcal {K}}$
. One may view the anticommutator with K as a linear mapping
$e^{\mathcal {K}}a(\varphi )e^{-\mathcal {K}}$
. One may view the anticommutator with K as a linear mapping
![]() $A\mapsto \left\{ K,A\right\} $
on the space of operators on V,
$A\mapsto \left\{ K,A\right\} $
on the space of operators on V,
![]() $\mathcal {B}\left(V\right)$
– denote this mapping by
$\mathcal {B}\left(V\right)$
– denote this mapping by
![]() $\mathcal {A}_{K}:\mathcal {B}\left(V\right)\rightarrow \mathcal {B}\left(V\right)$
(i.e.,
$\mathcal {A}_{K}:\mathcal {B}\left(V\right)\rightarrow \mathcal {B}\left(V\right)$
(i.e.,
![]() $\mathcal {A}_{K}(\cdot )=\left\{ K,\cdot \right\} $
). Then we may phrase the above identity as
$\mathcal {A}_{K}(\cdot )=\left\{ K,\cdot \right\} $
). Then we may phrase the above identity as
and likewise
so that the arguments again involve hyperbolic functions of linear operators, but now acting on
![]() $\mathcal {B}\left(V\right)$
rather than V itself. We then note the following ‘anticommutator Baker-Campbell-Hausdorff formula’:
$\mathcal {B}\left(V\right)$
rather than V itself. We then note the following ‘anticommutator Baker-Campbell-Hausdorff formula’:
Proposition 3.5. Let
![]() $\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
be an n-dimensional Hilbert space, let
$\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
be an n-dimensional Hilbert space, let
![]() $K:V\rightarrow V$
be a self-adjoint operator and let
$K:V\rightarrow V$
be a self-adjoint operator and let
![]() $\mathcal {A}_{K}(\cdot )=\left\{ K,\cdot \right\} :\mathcal {B}\left(V\right)\rightarrow \mathcal {B}\left(V\right)$
denote the anticommutator with K. Then for any linear operator
$\mathcal {A}_{K}(\cdot )=\left\{ K,\cdot \right\} :\mathcal {B}\left(V\right)\rightarrow \mathcal {B}\left(V\right)$
denote the anticommutator with K. Then for any linear operator
![]() $T:V\rightarrow V$
,
$T:V\rightarrow V$
,
 $$\begin{align*}e^{\mathcal{A}_{K}}(T)=\sum_{m=0}^{\infty}\frac{1}{m!}\mathcal{A}_{K}^{m}(T)=e^{K}Te^{K}. \end{align*}$$
$$\begin{align*}e^{\mathcal{A}_{K}}(T)=\sum_{m=0}^{\infty}\frac{1}{m!}\mathcal{A}_{K}^{m}(T)=e^{K}Te^{K}. \end{align*}$$
Consequently,
 $$ \begin{align*} \cosh\left(\mathcal{A}_{K}\right)(T) & =\frac{1}{2}(e^{K}Te^{K}+e^{-K}Te^{-K}),\\ \sinh(\mathcal{A}_{K})(T) & =\frac{1}{2}(e^{K}Te^{K}-e^{-K}Te^{-K}). \end{align*} $$
$$ \begin{align*} \cosh\left(\mathcal{A}_{K}\right)(T) & =\frac{1}{2}(e^{K}Te^{K}+e^{-K}Te^{-K}),\\ \sinh(\mathcal{A}_{K})(T) & =\frac{1}{2}(e^{K}Te^{K}-e^{-K}Te^{-K}). \end{align*} $$
Proof. Let
![]() $(x_{i})_{i=1}^{n}$
be an eigenbasis for K with associated eigenvalues
$(x_{i})_{i=1}^{n}$
be an eigenbasis for K with associated eigenvalues
![]() $\left(\lambda _{i}\right)_{i=1}^{n}$
. Denote
$\left(\lambda _{i}\right)_{i=1}^{n}$
. Denote
![]() $P_{i,j}=|x_j\rangle \langle x_i|$
, namely,
$P_{i,j}=|x_j\rangle \langle x_i|$
, namely,
![]() $P_{i,j}x=\left\langle x_{i},x\right\rangle x_{j}$
for all
$P_{i,j}x=\left\langle x_{i},x\right\rangle x_{j}$
for all
![]() $x\in V$
. It is well known that for any orthonormal basis
$x\in V$
. It is well known that for any orthonormal basis
![]() $(x_{i})_{i=1}^{n}$
of V, the collection
$(x_{i})_{i=1}^{n}$
of V, the collection
![]() $\left(P_{i,j}\right)_{i,j=1}^{n}$
form an orthonormal basis for
$\left(P_{i,j}\right)_{i,j=1}^{n}$
form an orthonormal basis for
![]() $\left(\mathcal {B}\left(V\right),\left\langle \cdot ,\cdot \right\rangle _{\text {HS}}\right)$
. Moreover, for any
$\left(\mathcal {B}\left(V\right),\left\langle \cdot ,\cdot \right\rangle _{\text {HS}}\right)$
. Moreover, for any
![]() $x\in V$
and
$x\in V$
and
![]() $1\leq i,j\leq n$
, by self-adjointness of K,
$1\leq i,j\leq n$
, by self-adjointness of K,
 $$ \begin{align} \mathcal{A}_{K}\left(P_{i,j}\right)x & =\left\{ K,P_{i,j}\right\} x=\left\langle x_{i},x\right\rangle Kx_{j}+\left\langle x_{i},Kx\right\rangle x_{j}=\left\langle x_{i},x\right\rangle \lambda_{j}x_{j}+\left\langle \lambda_{i}x_{i},x\right\rangle x_{j}\\ & =\left(\lambda_{i}+\lambda_{j}\right)\left\langle x_{i},x\right\rangle x_{j}=\left(\lambda_{i}+\lambda_{j}\right)P_{i,j}x.\nonumber \end{align} $$
$$ \begin{align} \mathcal{A}_{K}\left(P_{i,j}\right)x & =\left\{ K,P_{i,j}\right\} x=\left\langle x_{i},x\right\rangle Kx_{j}+\left\langle x_{i},Kx\right\rangle x_{j}=\left\langle x_{i},x\right\rangle \lambda_{j}x_{j}+\left\langle \lambda_{i}x_{i},x\right\rangle x_{j}\\ & =\left(\lambda_{i}+\lambda_{j}\right)\left\langle x_{i},x\right\rangle x_{j}=\left(\lambda_{i}+\lambda_{j}\right)P_{i,j}x.\nonumber \end{align} $$
Thus,
![]() $\{P_{i,j}\}_{i,j=1}^n$
an eigenbasis for
$\{P_{i,j}\}_{i,j=1}^n$
an eigenbasis for
![]() $\mathcal {A}_{K}$
with associated eigenvalues
$\mathcal {A}_{K}$
with associated eigenvalues
![]() $\left(\lambda _{i}+\lambda _{j}\right)_{i,j=1}^{n}$
.
$\left(\lambda _{i}+\lambda _{j}\right)_{i,j=1}^{n}$
.
Hence, it suffices to verify the identity
![]() $e^{\mathcal {A}_{K}}(T)=e^{K}Te^{K}$
with the eigenbasis
$e^{\mathcal {A}_{K}}(T)=e^{K}Te^{K}$
with the eigenbasis
![]() $\left(P_{i,j}\right)_{i,j=1}^{n}$
:
$\left(P_{i,j}\right)_{i,j=1}^{n}$
:
 $$ \begin{align} e^{\mathcal{A}_{K}}\left(P_{i,j}\right) x & =e^{\lambda_{i}+\lambda_{j}}P_{i,j}=e^{\lambda_{i}+\lambda_{j}}\left\langle x_{i},x\right\rangle x_{j}=\left\langle e^{\lambda_{i}}x_{i},x\right\rangle e^{\lambda_{j}}x_{j}=\left\langle e^{K}x_{i},x\right\rangle e^{K}x_{j}\\ & =\left\langle x_{i},e^{K}x\right\rangle e^{K}x_{j}=e^{K}P_{i,j}e^{K}x.\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{A}_{K}}\left(P_{i,j}\right) x & =e^{\lambda_{i}+\lambda_{j}}P_{i,j}=e^{\lambda_{i}+\lambda_{j}}\left\langle x_{i},x\right\rangle x_{j}=\left\langle e^{\lambda_{i}}x_{i},x\right\rangle e^{\lambda_{j}}x_{j}=\left\langle e^{K}x_{i},x\right\rangle e^{K}x_{j}\\ & =\left\langle x_{i},e^{K}x\right\rangle e^{K}x_{j}=e^{K}P_{i,j}e^{K}x.\nonumber \end{align} $$
The statements regarding
![]() $\cosh \left(\mathcal {A}_{K}\right)$
and
$\cosh \left(\mathcal {A}_{K}\right)$
and
![]() $\sinh \left(\mathcal {A}_{K}\right)$
follow from the identities
$\sinh \left(\mathcal {A}_{K}\right)$
follow from the identities
By these formulas, we thus deduce the quadratic operator analogue of equation (3.10):
 $$ \begin{align} e^{\mathcal{K}}Q_{1}(A)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}(e^{K}Ae^{K}+e^{-K}Ae^{-K})+\frac{1}{2}Q_{2}(e^{K}Ae^{K}-e^{-K}Ae^{-K}) \nonumber\\ e^{\mathcal{K}}Q_{2}(B)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}(e^{K}Be^{K}-e^{-K}Be^{-K})+\frac{1}{2}Q_{2}(e^{K}Be^{K}+e^{-K}Be^{-K}). \end{align} $$
$$ \begin{align} e^{\mathcal{K}}Q_{1}(A)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}(e^{K}Ae^{K}+e^{-K}Ae^{-K})+\frac{1}{2}Q_{2}(e^{K}Ae^{K}-e^{-K}Ae^{-K}) \nonumber\\ e^{\mathcal{K}}Q_{2}(B)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}(e^{K}Be^{K}-e^{-K}Be^{-K})+\frac{1}{2}Q_{2}(e^{K}Be^{K}+e^{-K}Be^{-K}). \end{align} $$
Diagonalization condition
We can now finally describe how to diagonalize a quadratic Hamiltonian using a Bogolubov transformation of the form
![]() $e^{\mathcal {K}}$
. By the transformation identities above, we find that under
$e^{\mathcal {K}}$
. By the transformation identities above, we find that under
![]() $e^{\mathcal {K}}$
, the quadratic Hamiltonian
$e^{\mathcal {K}}$
, the quadratic Hamiltonian
![]() $H=Q_{1}(A)+Q_{2}(B)$
transforms as
$H=Q_{1}(A)+Q_{2}(B)$
transforms as
 $$ \begin{align} e^{\mathcal{K}}He^{-\mathcal{K}} &=\frac{1}{2}Q_{1}(e^{K}Ae^{K}+e^{-K}Ae^{-K})+\frac{1}{2}Q_{2}(e^{K}Ae^{K}-e^{-K}Ae^{-K})\nonumber \\ &\quad +\frac{1}{2}Q_{1}(e^{K}Be^{K}-e^{-K}Be^{-K})+\frac{1}{2}Q_{2}(e^{K}Be^{K}+e^{-K}Be^{-K})\nonumber\\ & =\frac{1}{2}Q_{1}(e^{K}(A+B)e^{K}+e^{-K}(A-B)e^{-K})+\frac{1}{2}Q_{2}(e^{K}(A+B)e^{K}-e^{-K}(A-B)e^{-K}). \end{align} $$
$$ \begin{align} e^{\mathcal{K}}He^{-\mathcal{K}} &=\frac{1}{2}Q_{1}(e^{K}Ae^{K}+e^{-K}Ae^{-K})+\frac{1}{2}Q_{2}(e^{K}Ae^{K}-e^{-K}Ae^{-K})\nonumber \\ &\quad +\frac{1}{2}Q_{1}(e^{K}Be^{K}-e^{-K}Be^{-K})+\frac{1}{2}Q_{2}(e^{K}Be^{K}+e^{-K}Be^{-K})\nonumber\\ & =\frac{1}{2}Q_{1}(e^{K}(A+B)e^{K}+e^{-K}(A-B)e^{-K})+\frac{1}{2}Q_{2}(e^{K}(A+B)e^{K}-e^{-K}(A-B)e^{-K}). \end{align} $$
Therefore, the diagonalization condition on K is
If we can find such a K, then
where
There remains the question of existence and uniqueness of such a K:
Conclusion of the proof of Theorem 3.1 .
Write
![]() $A_{\pm }=A\pm B>0$
for brevity. Then we may write the diagonalization condition as
$A_{\pm }=A\pm B>0$
for brevity. Then we may write the diagonalization condition as
Multiplying by
![]() $A_{-}^{\frac {1}{2}}$
on both sides yields
$A_{-}^{\frac {1}{2}}$
on both sides yields
which is equivalent to
This implies the existence and uniqueness of the diagonalizing K as the operator exponential is a bijection between the real, symmetric operators and the real, symmetric, positive-definite operators.
4 The quasi-bosonic quadratic Hamiltonian
Now we turn to the quasi-bosonic setting. We start by casting the bosonizable terms
![]() $ H_{\operatorname {\mathrm {kin}}}^{\prime } + \sum _{k\in S_C} H^k_{\mathrm {int}}$
, which we encountered in Section 2.1, into a form which closely mirrors the form of the bosonic quadratic Hamiltonians that we considered in the preceding section.
$ H_{\operatorname {\mathrm {kin}}}^{\prime } + \sum _{k\in S_C} H^k_{\mathrm {int}}$
, which we encountered in Section 2.1, into a form which closely mirrors the form of the bosonic quadratic Hamiltonians that we considered in the preceding section.
4.1 Quadratic Hamiltonian
Let us define the pair excitation operators
We remark that in contrast to the bosonic case, the fermionic creation and annihilation operators are bounded (in fact,
![]() $\Vert c_{p,\sigma }\Vert _{\text {Op}}=\Vert c_{p,\sigma }^{\ast }\Vert _{\text {Op}}=1$
), and therefore so are the operators
$\Vert c_{p,\sigma }\Vert _{\text {Op}}=\Vert c_{p,\sigma }^{\ast }\Vert _{\text {Op}}=1$
), and therefore so are the operators
![]() $b_{k,p}^{\ast }$
,
$b_{k,p}^{\ast }$
,
![]() $b_{k,p}$
.
$b_{k,p}$
.
Then
![]() $H_{\text {int}}^{k}$
in (1.34) is exactly given by
$H_{\text {int}}^{k}$
in (1.34) is exactly given by
 $$ \begin{align} H_{\text{int}}^{k} & =\sum_{p,q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{k,p}^{\ast}b_{k,q}+b_{k,q}b_{k,p}^{\ast}\right)+\sum_{p,q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{-k,p}^{\ast}b_{-k,q}+b_{-k,q}b_{-k,p}^{\ast}\right)\nonumber \\ &\quad +\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{k,p}^{\ast}b_{-k,q}^{\ast}+b_{-k,q}b_{k,p}\right) \nonumber \\ &\quad +\sum_{p\in L_{-k}}\sum_{q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{-k,p}^{\ast}b_{k,q}^{\ast}+b_{k,q}b_{-k,p}\right). \end{align} $$
$$ \begin{align} H_{\text{int}}^{k} & =\sum_{p,q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{k,p}^{\ast}b_{k,q}+b_{k,q}b_{k,p}^{\ast}\right)+\sum_{p,q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{-k,p}^{\ast}b_{-k,q}+b_{-k,q}b_{-k,p}^{\ast}\right)\nonumber \\ &\quad +\sum_{p\in L_{k}}\sum_{q\in L_{-k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{k,p}^{\ast}b_{-k,q}^{\ast}+b_{-k,q}b_{k,p}\right) \nonumber \\ &\quad +\sum_{p\in L_{-k}}\sum_{q\in L_{k}}\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left(b_{-k,p}^{\ast}b_{k,q}^{\ast}+b_{k,q}b_{-k,p}\right). \end{align} $$
Thus, the natural one-body Hilbert space associated to
![]() $H_{\text {int}}^{k}$
is
$H_{\text {int}}^{k}$
is
![]() $\ell ^2 (L_k \cup L_{-k})$
. To free us from having to explicitly write sums over
$\ell ^2 (L_k \cup L_{-k})$
. To free us from having to explicitly write sums over
![]() $L_{k}$
and
$L_{k}$
and
![]() $L_{-k}$
separately, we introduce some more notation. First, we will denote this union of lunes by
$L_{-k}$
separately, we introduce some more notation. First, we will denote this union of lunes by
Here, we used the fact that
![]() $L_{k}\cap L_{-k}=\emptyset $
for any
$L_{k}\cap L_{-k}=\emptyset $
for any
![]() $k\in \mathbb {Z}_{+}^{3}$
, since if
$k\in \mathbb {Z}_{+}^{3}$
, since if
![]() $p\in L_{k}\cap L_{-k}$
, then
$p\in L_{k}\cap L_{-k}$
, then
which is a contradiction. It is also convenient to introduce the ‘bar-notation’
 $$ \begin{align} \overline{k,p}=\begin{cases} k,p & p\in L_{k}\\ -k,p & p\in L_{-k} \end{cases},\quad\overline{p-k}=\begin{cases} p-k & p\in L_{k}\\ p+k & p\in L_{-k} \end{cases} \end{align} $$
$$ \begin{align} \overline{k,p}=\begin{cases} k,p & p\in L_{k}\\ -k,p & p\in L_{-k} \end{cases},\quad\overline{p-k}=\begin{cases} p-k & p\in L_{k}\\ p+k & p\in L_{-k} \end{cases} \end{align} $$
to automatically encode the appropriate sign of k depending on
![]() $p\in L_{k}^{\pm }=L_{k}\cup L_{-k}$
(this will allow us to avoid expanding all our terms on a case-by-case basis when this is irrelevant).
$p\in L_{k}^{\pm }=L_{k}\cup L_{-k}$
(this will allow us to avoid expanding all our terms on a case-by-case basis when this is irrelevant).
In analogy with the definitions (3.3) and (3.4) we now define, for any
![]() $k\in \mathbb {Z}_{+}^{3}$
and symmetric operators
$k\in \mathbb {Z}_{+}^{3}$
and symmetric operators
![]() $A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, the quadratic operators
$A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, the quadratic operators
![]() $Q_{1}^{k}(A),Q_{2}^{k}(B):\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
by
$Q_{1}^{k}(A),Q_{2}^{k}(B):\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
by
 $$ \begin{align} Q_{1}^{k}(A) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},Ae_{q}\right\rangle \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}+b_{\overline{k,q}}b_{\overline{k,p}}^{\ast}\right),\nonumber\\ Q_{2}^{k}(B) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},Be_{q}\right\rangle \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right). \end{align} $$
$$ \begin{align} Q_{1}^{k}(A) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},Ae_{q}\right\rangle \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}+b_{\overline{k,q}}b_{\overline{k,p}}^{\ast}\right),\nonumber\\ Q_{2}^{k}(B) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},Be_{q}\right\rangle \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right). \end{align} $$
In order to cast
![]() $H_{\text {int}}^{k}$
as given by equation (4.2) into this form, we must identify the relevant operators A and B. Define the (un-normalized) rank-one projection
$H_{\text {int}}^{k}$
as given by equation (4.2) into this form, we must identify the relevant operators A and B. Define the (un-normalized) rank-one projection
![]() $P_{v_k}: \ell ^2(L_k)\to \ell ^2(L_k)$
by
$P_{v_k}: \ell ^2(L_k)\to \ell ^2(L_k)$
by
 $$ \begin{align} P_{v_k} =|v_k\rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \in \ell^2(L_k), \end{align} $$
$$ \begin{align} P_{v_k} =|v_k\rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \in \ell^2(L_k), \end{align} $$
where
![]() $(e_{p})_{p\in L_{k}}$
denotes the standard orthonormal basis of
$(e_{p})_{p\in L_{k}}$
denotes the standard orthonormal basis of
![]() $\ell ^{2}(L_{k})$
. Put differently, the matrix elements of
$\ell ^{2}(L_{k})$
. Put differently, the matrix elements of
![]() $P_{v_k}$
are
$P_{v_k}$
are
![]() $\left\langle e_{p},P_{v_{k}}e_{q}\right\rangle =\frac {1}{2\left(2\pi \right)^{3}} \hat {V}_{k}k_{F}^{-1}$
for all
$\left\langle e_{p},P_{v_{k}}e_{q}\right\rangle =\frac {1}{2\left(2\pi \right)^{3}} \hat {V}_{k}k_{F}^{-1}$
for all
![]() $p,q\in L_{k}$
. Next, we define the operators
$p,q\in L_{k}$
. Next, we define the operators
 $$ \begin{align} A_{k}^{\oplus},B_{k}^{\oplus}:\ell^{2}\left(L_{k}^{\pm}\right)\rightarrow\ell^{2}\left(L_{k}^{\pm}\right), \quad A_{k}^{\oplus}=\left(\begin{array}{cc} P_{v_{k}} & 0\\ 0 & P_{v_{k}} \end{array}\right),\quad B_{k}^{\oplus}=\left(\begin{array}{cc} 0 & P_{v_{k}}\\ P_{v_{k}} & 0 \end{array}\right) \end{align} $$
$$ \begin{align} A_{k}^{\oplus},B_{k}^{\oplus}:\ell^{2}\left(L_{k}^{\pm}\right)\rightarrow\ell^{2}\left(L_{k}^{\pm}\right), \quad A_{k}^{\oplus}=\left(\begin{array}{cc} P_{v_{k}} & 0\\ 0 & P_{v_{k}} \end{array}\right),\quad B_{k}^{\oplus}=\left(\begin{array}{cc} 0 & P_{v_{k}}\\ P_{v_{k}} & 0 \end{array}\right) \end{align} $$
with respect to the decomposition
![]() $\ell ^{2}(L_{k}^{\pm })=\ell ^{2}(L_{k})\oplus \ell ^{2}(L_{-k})$
and the identification
$\ell ^{2}(L_{k}^{\pm })=\ell ^{2}(L_{k})\oplus \ell ^{2}(L_{-k})$
and the identification
![]() $\ell ^{2}(L_{k})\cong \ell ^{2}(L_{-k})$
(under
$\ell ^{2}(L_{k})\cong \ell ^{2}(L_{-k})$
(under
![]() $e_{p}\mapsto e_{-p}$
).
$e_{p}\mapsto e_{-p}$
).
Thus, the operator
![]() $H_{\text {int}}^{k}$
is concisely expressed as
$H_{\text {int}}^{k}$
is concisely expressed as
It remains to consider the kinetic operator. The equality (1.74) bids us to think of
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
as it were
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
as it were
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} &\sim \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p} \nonumber\\ &= \sum_{k\in\mathbb{Z}_{+}^{3}} \left(\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p}+\sum_{p\in L_{-k}}\left(|p|^{2}-\left|p+k\right|^{2}\right)b_{-k,p}^{\ast}b_{-k,p}\right) \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} &\sim \sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p} \nonumber\\ &= \sum_{k\in\mathbb{Z}_{+}^{3}} \left(\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p}+\sum_{p\in L_{-k}}\left(|p|^{2}-\left|p+k\right|^{2}\right)b_{-k,p}^{\ast}b_{-k,p}\right) \end{align} $$
in an appropriate sense. To put this in the same framework as
![]() $H_{\mathrm {int}}^k$
, let us introduce (for every
$H_{\mathrm {int}}^k$
, let us introduce (for every
![]() $k\in \mathbb {Z}_{+}^{3}$
) the operator
$k\in \mathbb {Z}_{+}^{3}$
) the operator
![]() $h_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
by
$h_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
by
Using again the identification
![]() $\ell ^{2}(L_{k})\cong \ell ^{2}(L_{-k})$
(under
$\ell ^{2}(L_{k})\cong \ell ^{2}(L_{-k})$
(under
![]() $e_{p}\mapsto e_{-p}$
), we define the operators
$e_{p}\mapsto e_{-p}$
), we define the operators
![]() $h_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
$h_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
 $$ \begin{align} h_{k}^{\oplus}=\left(\begin{array}{cc} h_{{k}} & 0\\ 0 & h_{{k}} \end{array}\right). \end{align} $$
$$ \begin{align} h_{k}^{\oplus}=\left(\begin{array}{cc} h_{{k}} & 0\\ 0 & h_{{k}} \end{array}\right). \end{align} $$
Then we can rewrite (4.9) as
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} \sim \sum_{k\in\mathbb{Z}_{+}^{3}} \Big( Q_1^k (h_k^{\oplus}) - 2\,\mathrm{tr} (h_k)\Big). \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} \sim \sum_{k\in\mathbb{Z}_{+}^{3}} \Big( Q_1^k (h_k^{\oplus}) - 2\,\mathrm{tr} (h_k)\Big). \end{align} $$
Recall that
![]() $S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
for an exponent
$S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
for an exponent
![]() $1\ge \gamma>0$
which is to be optimized over at the end. As far as the lower bound is concerned, we may replace
$1\ge \gamma>0$
which is to be optimized over at the end. As far as the lower bound is concerned, we may replace
![]() $\sum _{k\in \mathbb {Z}_+}$
by
$\sum _{k\in \mathbb {Z}_+}$
by
![]() $\sum _{k\in S_C}$
(the upper bound is easier and will be explained separately). In summary, we arrive at the following quasi-bosonic expression for the bosonizable terms:
$\sum _{k\in S_C}$
(the upper bound is easier and will be explained separately). In summary, we arrive at the following quasi-bosonic expression for the bosonizable terms:
 $$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} + \sum_{k\in S_C} H_{\mathrm{int}}^k \sim \sum_{k\in S_C} \Big( Q_1^k (h_k^{\oplus} + A_k^{\oplus}) + Q_2^k (B_k^{\oplus}) - 2\,\mathrm{tr}(h_k)\Big). \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{kin}}}^{\prime} + \sum_{k\in S_C} H_{\mathrm{int}}^k \sim \sum_{k\in S_C} \Big( Q_1^k (h_k^{\oplus} + A_k^{\oplus}) + Q_2^k (B_k^{\oplus}) - 2\,\mathrm{tr}(h_k)\Big). \end{align} $$
Note that unlike the bosonic case, the operators on the right side of (4.13) are bounded.
4.2 Generalized pair operators
For every
![]() $k\in \mathbb {Z}_{+}^{3}$
and
$k\in \mathbb {Z}_{+}^{3}$
and
![]() $\varphi \in \ell ^2(L_k^{\pm })$
, we define the operators
$\varphi \in \ell ^2(L_k^{\pm })$
, we define the operators
 $$ \begin{align} b_{k}(\varphi )=\sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}},\quad b_{k}^{\ast}(\varphi )=\sum_{p\in L_{k}^{\pm}}\left\langle e_{p},\varphi\right\rangle b_{\overline{k,p}}^{\ast}. \end{align} $$
$$ \begin{align} b_{k}(\varphi )=\sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}},\quad b_{k}^{\ast}(\varphi )=\sum_{p\in L_{k}^{\pm}}\left\langle e_{p},\varphi\right\rangle b_{\overline{k,p}}^{\ast}. \end{align} $$
They obey the quasi-bosonic commutation relations (for
![]() $k,l\in \mathbb {Z}_{+}^{3}$
and
$k,l\in \mathbb {Z}_{+}^{3}$
and
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
![]() $\psi \in \ell ^{2}\left(L_{l}^{\pm }\right)$
)
$\psi \in \ell ^{2}\left(L_{l}^{\pm }\right)$
)
 $$ \begin{align} \left[b_{k}(\varphi ),b_{l}\left(\psi\right)\right] & =\left[b_{k}^{\ast}(\varphi ),b_{l}^{\ast}\left(\psi\right)\right]=0, \nonumber\\ \left[b_{k}(\varphi ),b_{l}^{\ast}\left(\psi\right)\right] & =\delta_{k,l}\left\langle \varphi,\psi\right\rangle +\varepsilon_{k,l}\left(\varphi;\psi\right), \end{align} $$
$$ \begin{align} \left[b_{k}(\varphi ),b_{l}\left(\psi\right)\right] & =\left[b_{k}^{\ast}(\varphi ),b_{l}^{\ast}\left(\psi\right)\right]=0, \nonumber\\ \left[b_{k}(\varphi ),b_{l}^{\ast}\left(\psi\right)\right] & =\delta_{k,l}\left\langle \varphi,\psi\right\rangle +\varepsilon_{k,l}\left(\varphi;\psi\right), \end{align} $$
where the correction term is
 $$ \begin{align} \varepsilon_{k,l}\left(\varphi;\psi\right) & =\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\psi\right\rangle \varepsilon\left(\overline{k,p};\overline{l,q}\right), \nonumber\\ \varepsilon\left(\overline{k,p};\overline{l,q}\right) & =-\left(\delta_{p,q}c_{\overline{q-l}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-l}}c_{q}^{\ast}c_{p}\right). \end{align} $$
$$ \begin{align} \varepsilon_{k,l}\left(\varphi;\psi\right) & =\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\psi\right\rangle \varepsilon\left(\overline{k,p};\overline{l,q}\right), \nonumber\\ \varepsilon\left(\overline{k,p};\overline{l,q}\right) & =-\left(\delta_{p,q}c_{\overline{q-l}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-l}}c_{q}^{\ast}c_{p}\right). \end{align} $$
We simply have
![]() $b_{k}(e_{p})=b_{\overline {k,p}}$
and the quadratic operators in (4.5) can be expressed as
$b_{k}(e_{p})=b_{\overline {k,p}}$
and the quadratic operators in (4.5) can be expressed as
 $$ \begin{align} Q_{1}^{k}(A) & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+b_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right) \nonumber\\ Q_{2}^{k}(B) & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(Be_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(Be_{p}\right)\right) \end{align} $$
$$ \begin{align} Q_{1}^{k}(A) & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+b_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right) \nonumber\\ Q_{2}^{k}(B) & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(Be_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(Be_{p}\right)\right) \end{align} $$
in analogy with equation (3.5). In order to justify the quasi-bosonic interpretation, we need rigorous estimates for the correction term in (4.16). Let us start with the following:
Proposition 4.1. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
and
$k\in \mathbb {Z}_{+}^{3}$
and
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
, it holds that
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
, it holds that
![]() $\varepsilon _{k,k}\left(\varphi ,\varphi \right)\leq 0$
, namely,
$\varepsilon _{k,k}\left(\varphi ,\varphi \right)\leq 0$
, namely,
Note that the observation of the error term
![]() $\varepsilon _{k,k}$
being non-positive also appeared in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Proof of Lemma 4.2] in the context of different bosonic operators.
$\varepsilon _{k,k}$
being non-positive also appeared in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Proof of Lemma 4.2] in the context of different bosonic operators.
Proof. We expand the term
 $$ \begin{align} \varepsilon_{k,k}\left(\varphi;\varphi\right) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle \varepsilon\left(\overline{k,p};\overline{k,q}\right) \nonumber\\ &=-\sum_{p,q\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle \left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{\overline{p-k}}c_{\overline{p-k}}^{\ast}-\sum_{p,q\in L_{k}^{\pm}}\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p} \\ &\le - \sum_{p,q\in L_{k}^{\pm}}\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}.\nonumber \end{align} $$
$$ \begin{align} \varepsilon_{k,k}\left(\varphi;\varphi\right) & =\sum_{p,q\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle \varepsilon\left(\overline{k,p};\overline{k,q}\right) \nonumber\\ &=-\sum_{p,q\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle \left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{\overline{p-k}}c_{\overline{p-k}}^{\ast}-\sum_{p,q\in L_{k}^{\pm}}\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p} \\ &\le - \sum_{p,q\in L_{k}^{\pm}}\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}.\nonumber \end{align} $$
We treat the terms of the last sum on a case-by-case basis according to which of
![]() $L_{k}$
and
$L_{k}$
and
![]() $L_{-k}$
, p and q lie in: if p and q lie in the same lune, then
$L_{-k}$
, p and q lie in: if p and q lie in the same lune, then
![]() $\delta _{\overline {p-k},\overline {q-k}}=\delta _{p\mp k,q\mp k}=\delta _{p,q}$
and so
$\delta _{\overline {p-k},\overline {q-k}}=\delta _{p\mp k,q\mp k}=\delta _{p,q}$
and so
 $$ \begin{align} A =\left(\sum_{p,q\in L_{k}}+\sum_{p,q\in L_{-k}}\right)\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}=\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{p}^{\ast}c_{p} \ge 0. \end{align} $$
$$ \begin{align} A =\left(\sum_{p,q\in L_{k}}+\sum_{p,q\in L_{-k}}\right)\delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}=\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{p}^{\ast}c_{p} \ge 0. \end{align} $$
However, by the Cauchy–Schwarz inequality,
 $$ \begin{align} &\pm \left( \sum_{p\in L_{k}}\sum_{q\in L_{-k}} + \sum_{p\in L_{-k}}\sum_{q\in L_{k}} \right) \delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}\nonumber\\ &\le \left( \sum_{p\in L_{k}}\sum_{q\in L_{-k}} + \sum_{p\in L_{-k}}\sum_{q\in L_{k}} \right) \frac{1}{2}\Big( \delta_{\overline{p-k},\overline{q-k}} |\left\langle \varphi,e_{p}\right\rangle|^2 c_p^* c_p + |\left\langle e_{q},\varphi\right\rangle|^2 c_{q}^{\ast}c_{q} \Big) \\ &\le \sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{p}^{\ast}c_{p} = A. \nonumber \end{align} $$
$$ \begin{align} &\pm \left( \sum_{p\in L_{k}}\sum_{q\in L_{-k}} + \sum_{p\in L_{-k}}\sum_{q\in L_{k}} \right) \delta_{\overline{p-k},\overline{q-k}}\left\langle \varphi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle c_{q}^{\ast}c_{p}\nonumber\\ &\le \left( \sum_{p\in L_{k}}\sum_{q\in L_{-k}} + \sum_{p\in L_{-k}}\sum_{q\in L_{k}} \right) \frac{1}{2}\Big( \delta_{\overline{p-k},\overline{q-k}} |\left\langle \varphi,e_{p}\right\rangle|^2 c_p^* c_p + |\left\langle e_{q},\varphi\right\rangle|^2 c_{q}^{\ast}c_{q} \Big) \\ &\le \sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi\right\rangle \right|^{2}c_{p}^{\ast}c_{p} = A. \nonumber \end{align} $$
We thus conclude that
![]() $\varepsilon _{k,k}\left(\varphi ,\varphi \right)\leq 0$
as claimed.
$\varepsilon _{k,k}\left(\varphi ,\varphi \right)\leq 0$
as claimed.
Next, we have the following:
Proposition 4.2. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
,
$k\in \mathbb {Z}_{+}^{3}$
,
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
and
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
The bounds here are similar to [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Lemma 4.2]. Recall that in our quasi-bosonic setting the excitation number operator
 $$ \begin{align} \mathcal{N}_{E}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast} \end{align} $$
$$ \begin{align} \mathcal{N}_{E}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast} \end{align} $$
plays the role that the usual number operator
![]() $\mathcal {N}$
does in the exact bosonic case. Thus, Proposition 4.2 is the analogue of the well-known bosonic estimate
$\mathcal {N}$
does in the exact bosonic case. Thus, Proposition 4.2 is the analogue of the well-known bosonic estimate
Proof. By the Cauchy-Schwarz inequality,
 $$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert & = \left\Vert \sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\nonumber \\ & \leq\left\Vert \varphi\right\Vert \sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert c_{p}\Psi\right\Vert ^{2}}\leq\left\Vert \varphi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }. \end{align} $$
$$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert & = \left\Vert \sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\nonumber \\ & \leq\left\Vert \varphi\right\Vert \sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert c_{p}\Psi\right\Vert ^{2}}\leq\left\Vert \varphi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }. \end{align} $$
The second bound follows from the first and Proposition 4.1.
We remark that the above estimate is also valid for
![]() $\Psi \in \mathcal {H}_{M}$
when
$\Psi \in \mathcal {H}_{M}$
when
![]() $M\neq N$
, provided
$M\neq N$
, provided
![]() $\mathcal {N}_{E}$
is understood as
$\mathcal {N}_{E}$
is understood as
![]() $\sum _{p\in B_{F}^{c}}c_{p}^{\ast }c_{p}$
acting on
$\sum _{p\in B_{F}^{c}}c_{p}^{\ast }c_{p}$
acting on
![]() $\mathcal {H}_{M}$
(in (4.23) we used
$\mathcal {H}_{M}$
(in (4.23) we used
![]() $L_k^{\pm } \subset B_F^c$
). One must be precise here as the identity
$L_k^{\pm } \subset B_F^c$
). One must be precise here as the identity
![]() $\mathcal {N}_{E}=\sum _{p\in B_{F}}c_{p}c_{p}^{\ast }$
does not hold on
$\mathcal {N}_{E}=\sum _{p\in B_{F}}c_{p}c_{p}^{\ast }$
does not hold on
![]() $\mathcal {H}_{M}$
. In fact, the estimate also holds if
$\mathcal {H}_{M}$
. In fact, the estimate also holds if
![]() $\mathcal {N}_{E}$
is understood as
$\mathcal {N}_{E}$
is understood as
![]() $\sum _{p\in B_{F}}c_{p}c_{p}^{\ast }$
, up to an additional factor of
$\sum _{p\in B_{F}}c_{p}c_{p}^{\ast }$
, up to an additional factor of
![]() $\sqrt {2}$
due to the necessary overcounting of the holes,Footnote
7
namely, from
$\sqrt {2}$
due to the necessary overcounting of the holes,Footnote
7
namely, from
![]() $\left\Vert b_{\overline {k,p}}\Psi \right\Vert =\left\Vert c_{\overline {p-k}}^{\ast }c_{p}\Psi \right\Vert \leq \left\Vert c_{\overline {p-k}}^{\ast }\Psi \right\Vert $
with
$\left\Vert b_{\overline {k,p}}\Psi \right\Vert =\left\Vert c_{\overline {p-k}}^{\ast }c_{p}\Psi \right\Vert \leq \left\Vert c_{\overline {p-k}}^{\ast }\Psi \right\Vert $
with
![]() $\overline {p-k} \in B_F$
, we get
$\overline {p-k} \in B_F$
, we get
 $$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert \leq\left\Vert \varphi\right\Vert \sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert c_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2}}\leq\sqrt{2}\left\Vert \varphi\right\Vert \sqrt{\left\langle \Psi,\left(\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}\right)\Psi\right\rangle }. \end{align} $$
$$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert \leq\left\Vert \varphi\right\Vert \sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert c_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2}}\leq\sqrt{2}\left\Vert \varphi\right\Vert \sqrt{\left\langle \Psi,\left(\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}\right)\Psi\right\rangle }. \end{align} $$
This is a point that we must consider, since below we will also encounter expressions such as
![]() $\left\Vert b_{k}(\varphi )c_{p}\Psi \right\Vert $
for
$\left\Vert b_{k}(\varphi )c_{p}\Psi \right\Vert $
for
![]() $\Psi \in \mathcal {H}_{N}$
(so that
$\Psi \in \mathcal {H}_{N}$
(so that
![]() $c_{p}\Psi \in \mathcal {H}_{N-1}$
). For this, we denote by
$c_{p}\Psi \in \mathcal {H}_{N-1}$
). For this, we denote by
![]() $\mathcal {N}_{E}^{\left(-1\right)}:\mathcal {H}_{N-1}\rightarrow \mathcal {H}_{N-1}$
and
$\mathcal {N}_{E}^{\left(-1\right)}:\mathcal {H}_{N-1}\rightarrow \mathcal {H}_{N-1}$
and
![]() $\mathcal {N}_{E}^{\left(+1\right)}:\mathcal {H}_{N+1}\rightarrow \mathcal {H}_{N+1}$
the operators
$\mathcal {N}_{E}^{\left(+1\right)}:\mathcal {H}_{N+1}\rightarrow \mathcal {H}_{N+1}$
the operators
 $$ \begin{align} \mathcal{N}_{E}^{\left(-1\right)}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p},\quad\mathcal{N}_{E}^{\left(+1\right)}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}. \end{align} $$
$$ \begin{align} \mathcal{N}_{E}^{\left(-1\right)}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p},\quad\mathcal{N}_{E}^{\left(+1\right)}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}. \end{align} $$
This choice is motivated by the following identities:
Lemma 4.3. For all
![]() $p\in B_{F}^{c}$
and
$p\in B_{F}^{c}$
and
![]() $q\in B_{F}$
, it holds that
$q\in B_{F}$
, it holds that
 $$ \begin{align*} \mathcal{N}_{E}c_{p}^{\ast} &=c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}+c_{p}^{\ast}, \quad c_p\mathcal{N}_{E}^{(-1)}c_{p}^{\ast} \le \mathcal{N}_E,\\ \mathcal{N}_{E}c_{q} &=c_{q}\mathcal{N}_{E}^{\left(+1\right)}+c_{q}, \quad c_{q}^{\ast}\mathcal{N}_{E}^{\left(+1\right)} c_{q} \le \mathcal{N}_E. \end{align*} $$
$$ \begin{align*} \mathcal{N}_{E}c_{p}^{\ast} &=c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}+c_{p}^{\ast}, \quad c_p\mathcal{N}_{E}^{(-1)}c_{p}^{\ast} \le \mathcal{N}_E,\\ \mathcal{N}_{E}c_{q} &=c_{q}\mathcal{N}_{E}^{\left(+1\right)}+c_{q}, \quad c_{q}^{\ast}\mathcal{N}_{E}^{\left(+1\right)} c_{q} \le \mathcal{N}_E. \end{align*} $$
Consequently,
 $$\begin{align*}\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}c_{p}=\mathcal{N}_{E}^{2}-\mathcal{N}_{E}=\sum_{p\in B_{F}}c_{p}\mathcal{N}_{E}^{\left(+1\right)}c_{p}^{\ast}. \end{align*}$$
$$\begin{align*}\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}c_{p}=\mathcal{N}_{E}^{2}-\mathcal{N}_{E}=\sum_{p\in B_{F}}c_{p}\mathcal{N}_{E}^{\left(+1\right)}c_{p}^{\ast}. \end{align*}$$
Proof. This follows directly by the CAR, as for all
![]() $p\in B_{F}^{c}$
,
$p\in B_{F}^{c}$
,
 $$ \begin{align} \mathcal{N}_{E}c_{p}^{\ast}=\sum_{q\in B_{F}^{c}}c_{q}^{\ast}c_{q}c_{p}^{\ast}=\sum_{q\in B_{F}^{c}}c_{p}^{\ast}c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}^{c}}\left(c_{q}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{q}^{\ast},c_{p}^{\ast}\right\} c_{q}\right)=c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}+c_{p}^{\ast}. \end{align} $$
$$ \begin{align} \mathcal{N}_{E}c_{p}^{\ast}=\sum_{q\in B_{F}^{c}}c_{q}^{\ast}c_{q}c_{p}^{\ast}=\sum_{q\in B_{F}^{c}}c_{p}^{\ast}c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}^{c}}\left(c_{q}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{q}^{\ast},c_{p}^{\ast}\right\} c_{q}\right)=c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}+c_{p}^{\ast}. \end{align} $$
Consequently, using
![]() $\|c_p\|_{\mathrm {Op}}=1$
and
$\|c_p\|_{\mathrm {Op}}=1$
and
![]() $[\mathcal {N}_{E},c_{p}^{\ast }c_p]=0$
, we have
$[\mathcal {N}_{E},c_{p}^{\ast }c_p]=0$
, we have
Likewise, for all
![]() $q\in B_{F}$
,
$q\in B_{F}$
,
 $$ \begin{align} \mathcal{N}_{E}c_{q}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}c_{q}=\sum_{p\in B_{F}}c_{q}c_{p}c_{p}^{\ast}+\sum_{p\in B_{F}}\left(c_{p}\left\{ c_{p}^{\ast},c_{q}\right\} -\left\{ c_{p},c_{q}\right\} c_{p}^{\ast}\right)=c_{q}\mathcal{N}_{E}^{\left(+1\right)}+c_{q}, \end{align} $$
$$ \begin{align} \mathcal{N}_{E}c_{q}=\sum_{p\in B_{F}}c_{p}c_{p}^{\ast}c_{q}=\sum_{p\in B_{F}}c_{q}c_{p}c_{p}^{\ast}+\sum_{p\in B_{F}}\left(c_{p}\left\{ c_{p}^{\ast},c_{q}\right\} -\left\{ c_{p},c_{q}\right\} c_{p}^{\ast}\right)=c_{q}\mathcal{N}_{E}^{\left(+1\right)}+c_{q}, \end{align} $$
and hence,
![]() $\mathcal {N}_{E} \ge c_{q}^{\ast }\mathcal {N}_{E}^{\left(+1\right)} c_{q}$
. Moreover,
$\mathcal {N}_{E} \ge c_{q}^{\ast }\mathcal {N}_{E}^{\left(+1\right)} c_{q}$
. Moreover,
 $$ \begin{align} \sum_{p\in B_{F}^{c}}c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}c_{p} &=\sum_{p\in B_{F}^{c}}\left(\mathcal{N}_{E}c_{p}^{\ast}-c_{p}^{\ast}\right)c_{p}=\mathcal{N}_{E}^{2}-\mathcal{N}_{E}=\sum_{p\in B_{F}}\left(\mathcal{N}_{E}c_{p}-c_{p}\right)c_{p}^{\ast}\nonumber \\ &=\sum_{p\in B_{F}}c_{p}\mathcal{N}_{E}^{\left(+1\right)}c_{p}^{\ast}. \end{align} $$
$$ \begin{align} \sum_{p\in B_{F}^{c}}c_{p}^{\ast}\mathcal{N}_{E}^{\left(-1\right)}c_{p} &=\sum_{p\in B_{F}^{c}}\left(\mathcal{N}_{E}c_{p}^{\ast}-c_{p}^{\ast}\right)c_{p}=\mathcal{N}_{E}^{2}-\mathcal{N}_{E}=\sum_{p\in B_{F}}\left(\mathcal{N}_{E}c_{p}-c_{p}\right)c_{p}^{\ast}\nonumber \\ &=\sum_{p\in B_{F}}c_{p}\mathcal{N}_{E}^{\left(+1\right)}c_{p}^{\ast}. \end{align} $$
In some cases, it is important to refine error estimates by using the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
rather than
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
rather than
![]() $\mathcal {N}_{E}$
. We can implement the kinetic estimate of Proposition 2.2 in the generalized setting:
$\mathcal {N}_{E}$
. We can implement the kinetic estimate of Proposition 2.2 in the generalized setting:
Proposition 4.4. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
,
$k\in \mathbb {Z}_{+}^{3}$
,
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
and
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
Proof. We start by applying the Cauchy-Schwarz inequality
 $$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert =\left\Vert \sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}. \end{align} $$
$$ \begin{align} \left\Vert b_{k}(\varphi )\Psi\right\Vert =\left\Vert \sum_{p\in L_{k}^{\pm}}\left\langle \varphi,e_{p}\right\rangle b_{\overline{k,p}}\Psi\right\Vert \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}. \end{align} $$
As the vectors
![]() $(e_{p})_{p\in L_{k}^{\pm }}$
obey
$(e_{p})_{p\in L_{k}^{\pm }}$
obey
![]() $h_{k}^{\oplus }e_{p}=\lambda _{\overline {k,p}}e_{p}$
, we recognize the first sum on the right-hand side as
$h_{k}^{\oplus }e_{p}=\lambda _{\overline {k,p}}e_{p}$
, we recognize the first sum on the right-hand side as
 $$ \begin{align} \sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}=\left\langle \varphi,\left(h_{k}^{\oplus}\right)^{-1}\varphi\right\rangle =\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert ^{2}. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left|\left\langle \varphi,e_{p}\right\rangle \right|^{2}=\left\langle \varphi,\left(h_{k}^{\oplus}\right)^{-1}\varphi\right\rangle =\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert ^{2}. \end{align} $$
For the second sum, we have by equation (2.4) that
 $$ \begin{align} \sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}=\sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}+\sum_{p\in L_{-k}}\lambda_{-k,p}\left\Vert c_{p+k}^{\ast}c_{p}\Psi\right\Vert ^{2}\leq\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}=\sum_{p\in L_{k}}\lambda_{k,p}\left\Vert c_{p-k}^{\ast}c_{p}\Psi\right\Vert ^{2}+\sum_{p\in L_{-k}}\lambda_{-k,p}\left\Vert c_{p+k}^{\ast}c_{p}\Psi\right\Vert ^{2}\leq\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle, \end{align} $$
which implies the first claim. The second bound follows from the first and Proposition 4.1:
 $$ \begin{align} \left\Vert b_{k}^{\ast}(\varphi )\Psi\right\Vert \leq\sqrt{\left\langle \Psi,\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert ^{2}H_{\operatorname{\mathrm{kin}}}^{\prime}+\left\Vert \varphi\right\Vert ^{2}\right)\Psi\right\rangle }\leq\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert \sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }+\left\Vert \varphi\right\Vert \left\Vert \Psi\right\Vert. \end{align} $$
$$ \begin{align} \left\Vert b_{k}^{\ast}(\varphi )\Psi\right\Vert \leq\sqrt{\left\langle \Psi,\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert ^{2}H_{\operatorname{\mathrm{kin}}}^{\prime}+\left\Vert \varphi\right\Vert ^{2}\right)\Psi\right\rangle }\leq\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\varphi\right\Vert \sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }+\left\Vert \varphi\right\Vert \left\Vert \Psi\right\Vert. \end{align} $$
4.3 Preliminary estimates for quadratic operators
In this subsection, we provide some basic bounds on the quadratic operators
![]() $Q_{1}^{k}(A)$
and
$Q_{1}^{k}(A)$
and
![]() $Q_{1}^{k}(B)$
defined in (4.5) for any
$Q_{1}^{k}(B)$
defined in (4.5) for any
![]() $k\in \mathbb {Z}_{+}^{3}$
. First, for
$k\in \mathbb {Z}_{+}^{3}$
. First, for
![]() $Q_{1}^{k}(A)$
, we can normal order as follows:
$Q_{1}^{k}(A)$
, we can normal order as follows:
 $$ \begin{align} Q_{1}^{k}(A) & =\sum_{p\in L_{k}^{\pm}}\left(2\,b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+\left[b_{k}(e_{p}),b_{k}^{\ast}(Ae_{p})\right]\right)\nonumber \\ & =2\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+\sum_{p\in L_{k}^{\pm}}\left\langle e_{p},Ae_{p}\right\rangle +\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};Ae_{p}\right)\\ & =2\,\tilde{Q}_{1}^{k}(A)+\text{tr}(A)+\varepsilon_{k}(A)\nonumber, \end{align} $$
$$ \begin{align} Q_{1}^{k}(A) & =\sum_{p\in L_{k}^{\pm}}\left(2\,b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+\left[b_{k}(e_{p}),b_{k}^{\ast}(Ae_{p})\right]\right)\nonumber \\ & =2\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})+\sum_{p\in L_{k}^{\pm}}\left\langle e_{p},Ae_{p}\right\rangle +\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};Ae_{p}\right)\\ & =2\,\tilde{Q}_{1}^{k}(A)+\text{tr}(A)+\varepsilon_{k}(A)\nonumber, \end{align} $$
where for brevity, we have defined the notation
 $$ \begin{align} \tilde{Q}_{1}^{k}(A)=\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}(Ae_{p})b_{k}(e_{p}),\quad\varepsilon_{k}(A)=\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};Ae_{p}\right). \end{align} $$
$$ \begin{align} \tilde{Q}_{1}^{k}(A)=\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}(Ae_{p})b_{k}(e_{p}),\quad\varepsilon_{k}(A)=\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};Ae_{p}\right). \end{align} $$
The term
![]() $\tilde {Q}_{1}^{k}(A)$
plays the same role of
$\tilde {Q}_{1}^{k}(A)$
plays the same role of
![]() $\text {d}\Gamma (A)$
in the exact bosonic case, whereas
$\text {d}\Gamma (A)$
in the exact bosonic case, whereas
![]() $\varepsilon _{k}(A)$
is a correction term in the quasi-bosonic case.
$\varepsilon _{k}(A)$
is a correction term in the quasi-bosonic case.
Proposition 4.5. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
 $$ \begin{align*} \left|\left\langle \Psi,\tilde{Q}_{1}^{k}(A)\Psi\right\rangle \right| &\leq \left\Vert A\right\Vert _{\operatorname{\mathrm{Op}}}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle ,\\ \left|\left\langle \Psi,\varepsilon_{k}(A)\Psi\right\rangle \right| &\leq 3\left\Vert A\right\Vert _{\operatorname{\mathrm{Op}}}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*} $$
$$ \begin{align*} \left|\left\langle \Psi,\tilde{Q}_{1}^{k}(A)\Psi\right\rangle \right| &\leq \left\Vert A\right\Vert _{\operatorname{\mathrm{Op}}}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle ,\\ \left|\left\langle \Psi,\varepsilon_{k}(A)\Psi\right\rangle \right| &\leq 3\left\Vert A\right\Vert _{\operatorname{\mathrm{Op}}}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*} $$
If furthermore,
![]() $A\geq 0$
, then also
$A\geq 0$
, then also
![]() $\tilde {Q}_{1}^{k}(A)\geq 0$
.
$\tilde {Q}_{1}^{k}(A)\geq 0$
.
Proof. Let
![]() $(x_{i})_i$
be an eigenbasis for A with eigenvalues
$(x_{i})_i$
be an eigenbasis for A with eigenvalues
![]() $\left(\lambda _{i}\right)_i$
. Noting that the mapping
$\left(\lambda _{i}\right)_i$
. Noting that the mapping
![]() $x,y\mapsto b_{k}^{\ast }\left(Ax\right)b_{k}\left(y\right)$
is bilinear, we may invoke Lemma 3.3 (the part of basis independence) to write
$x,y\mapsto b_{k}^{\ast }\left(Ax\right)b_{k}\left(y\right)$
is bilinear, we may invoke Lemma 3.3 (the part of basis independence) to write
Clearly, if
![]() $A\ge 0$
, then all
$A\ge 0$
, then all
![]() $\lambda _i\ge 0$
, and hence,
$\lambda _i\ge 0$
, and hence,
![]() $\tilde {Q}_{1}^{k}(A)\ge 0$
. In general, we always have
$\tilde {Q}_{1}^{k}(A)\ge 0$
. In general, we always have
![]() $|\lambda _i | \le \left\Vert A\right\Vert _{\operatorname {\mathrm {Op}}}$
for all i. Hence, using Lemma 3.3 again and
$|\lambda _i | \le \left\Vert A\right\Vert _{\operatorname {\mathrm {Op}}}$
for all i. Hence, using Lemma 3.3 again and
![]() $b_{\overline {k,p}}^* b_{\overline {k,p}} \le c_p^* c_p$
, we have
$b_{\overline {k,p}}^* b_{\overline {k,p}} \le c_p^* c_p$
, we have
 $$ \begin{align} \pm \tilde{Q}_{1}^{k}(A) \le \left\Vert A\right\Vert _{\text{Op}} \sum_{i}b_{k}^{\ast}(x_{i})b_{k}(x_{i})= \left\Vert A\right\Vert _{\text{Op}} \sum_{p\in L_{k}^{\pm}}b_{\overline{k,p}}^{\ast}b_{\overline{k,p}} \le \left\Vert A\right\Vert _{\text{Op}} \sum_{p\in L_{k}^{\pm}} c_p^* c_p \le \left\Vert A\right\Vert _{\text{Op}} \mathcal{N}_{E}. \end{align} $$
$$ \begin{align} \pm \tilde{Q}_{1}^{k}(A) \le \left\Vert A\right\Vert _{\text{Op}} \sum_{i}b_{k}^{\ast}(x_{i})b_{k}(x_{i})= \left\Vert A\right\Vert _{\text{Op}} \sum_{p\in L_{k}^{\pm}}b_{\overline{k,p}}^{\ast}b_{\overline{k,p}} \le \left\Vert A\right\Vert _{\text{Op}} \sum_{p\in L_{k}^{\pm}} c_p^* c_p \le \left\Vert A\right\Vert _{\text{Op}} \mathcal{N}_{E}. \end{align} $$
Similarly,
 $$ \begin{align} \pm \varepsilon_{k}(A)&= \pm \sum_{i}\varepsilon_{k,k}\left(x_{i};Ax_{i}\right)= \pm \sum_{i}\lambda_{i}\varepsilon_{k,k}\left(x_{i};x_{i}\right) \nonumber\\ &\le - \|A\|_{\mathrm{Op}}\sum_{i} \varepsilon_{k,k}\left(x_{i};x_{i}\right) = - \|A\|_{\mathrm{Op}} \sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};e_{p}\right), \end{align} $$
$$ \begin{align} \pm \varepsilon_{k}(A)&= \pm \sum_{i}\varepsilon_{k,k}\left(x_{i};Ax_{i}\right)= \pm \sum_{i}\lambda_{i}\varepsilon_{k,k}\left(x_{i};x_{i}\right) \nonumber\\ &\le - \|A\|_{\mathrm{Op}}\sum_{i} \varepsilon_{k,k}\left(x_{i};x_{i}\right) = - \|A\|_{\mathrm{Op}} \sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};e_{p}\right), \end{align} $$
where in the first inequality we used the fact that
![]() $\varepsilon _{k,k}\left(x_{i};x_{i}\right)\le 0$
as shown in the proof of Proposition 4.1. Using
$\varepsilon _{k,k}\left(x_{i};x_{i}\right)\le 0$
as shown in the proof of Proposition 4.1. Using
![]() $\varepsilon _{k,k}(e_{p};e_{p})=\varepsilon (\overline {k,p};\overline {l,q})$
and the definition (4.16), we get
$\varepsilon _{k,k}(e_{p};e_{p})=\varepsilon (\overline {k,p};\overline {l,q})$
and the definition (4.16), we get
 $$ \begin{align} - \sum_{p\in L_{k}^{\pm}}\varepsilon\left(\overline{k,p};\overline{k,p}\right) &=\sum_{p\in L_{k}^{\pm}}\left(c_{\overline{p-k}}c_{\overline{p-k}}^{\ast}+c_{p}^{\ast}c_{p}\right) \leq 2 \sum_{p\in B_{F}} c_{p}c_{p}^{\ast} +\sum_{p\in B_{F}^{c}} c_{p}^{\ast}c_{p} =3 \mathcal{N}_{E}, \end{align} $$
$$ \begin{align} - \sum_{p\in L_{k}^{\pm}}\varepsilon\left(\overline{k,p};\overline{k,p}\right) &=\sum_{p\in L_{k}^{\pm}}\left(c_{\overline{p-k}}c_{\overline{p-k}}^{\ast}+c_{p}^{\ast}c_{p}\right) \leq 2 \sum_{p\in B_{F}} c_{p}c_{p}^{\ast} +\sum_{p\in B_{F}^{c}} c_{p}^{\ast}c_{p} =3 \mathcal{N}_{E}, \end{align} $$
which implies the desired claim.
From these results and equation (4.34), we immediately obtain the following:
Proposition 4.6. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
Next, we turn to
![]() $Q_{2}^{k}(B)$
.
$Q_{2}^{k}(B)$
.
Proposition 4.7. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
Proof. We have (using that the
![]() $b_{k}$
operators commute)
$b_{k}$
operators commute)
 $$ \begin{align} \left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle &=\sum_{p\in L_{k}^{\pm}}\left\langle \Psi,\left(b_{k}^{\ast}\left(Be_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(Be_{p}\right)\right)\Psi\right\rangle \nonumber\\ &=2\sum_{p\in L_{k}^{\pm}}\mathrm{Re} \left\langle b_{k}^{\ast}\left(Be_{p}\right)\Psi,b_{k}(e_{p})\Psi\right\rangle, \end{align} $$
$$ \begin{align} \left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle &=\sum_{p\in L_{k}^{\pm}}\left\langle \Psi,\left(b_{k}^{\ast}\left(Be_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(Be_{p}\right)\right)\Psi\right\rangle \nonumber\\ &=2\sum_{p\in L_{k}^{\pm}}\mathrm{Re} \left\langle b_{k}^{\ast}\left(Be_{p}\right)\Psi,b_{k}(e_{p})\Psi\right\rangle, \end{align} $$
so using the estimates of Proposition 4.2 and the Cauchy-Schwarz inequality, we conclude that
 $$ \begin{align} \left|\left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle \right| &\leq 2\sum_{p\in L_{k}^{\pm}}\left\Vert b_{k}^{\ast}\left(Be_{p}\right)\Psi\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert \leq2\sqrt{\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle }\sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{\overline{k,p}}\Psi\right\Vert \nonumber\\ & \leq2\sqrt{\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle }\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}} \nonumber \\ &\leq2\left\Vert B\right\Vert _{\text{HS}}\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle, \end{align} $$
$$ \begin{align} \left|\left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle \right| &\leq 2\sum_{p\in L_{k}^{\pm}}\left\Vert b_{k}^{\ast}\left(Be_{p}\right)\Psi\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert \leq2\sqrt{\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle }\sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{\overline{k,p}}\Psi\right\Vert \nonumber\\ & \leq2\sqrt{\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle }\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}} \nonumber \\ &\leq2\left\Vert B\right\Vert _{\text{HS}}\left\langle \Psi,\left(1+\mathcal{N}_{E}\right)\Psi\right\rangle, \end{align} $$
where we again used that
![]() $\left\Vert b_{\overline {k,p}}\Psi \right\Vert \leq \left\Vert c_{p}\Psi \right\Vert $
.
$\left\Vert b_{\overline {k,p}}\Psi \right\Vert \leq \left\Vert c_{p}\Psi \right\Vert $
.
Kinetic estimates for quadratic operators
Finally, let us improve the estimates in this subsection by using the kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
instead of the number operator
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
instead of the number operator
![]() $\mathcal {N}_E$
.
$\mathcal {N}_E$
.
Proposition 4.8. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
Proof. Let
![]() $(x_{i})_{i}$
be an eigenbasis for
$(x_{i})_{i}$
be an eigenbasis for
![]() $(h_{k}^{\oplus })^{-\frac {1}{2}}A(h_{k}^{\oplus })^{-\frac {1}{2}}$
with eigenvalues
$(h_{k}^{\oplus })^{-\frac {1}{2}}A(h_{k}^{\oplus })^{-\frac {1}{2}}$
with eigenvalues
![]() $\left(\mu _{i}\right)_i$
. By Lemma 3.3, we then see that we may write
$\left(\mu _{i}\right)_i$
. By Lemma 3.3, we then see that we may write
![]() $\tilde {Q}_{1}^{k}(A)$
as
$\tilde {Q}_{1}^{k}(A)$
as
 $$ \begin{align} \tilde{Q}_{1}^{k}(A) & =\sum_{i}b_{k}^{\ast}\left(Ax_{i}\right)b_{k}(x_{i})=\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}(x_{i})\nonumber \\ & =\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\\ & =\sum_{i}\mu_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right),\nonumber \end{align} $$
$$ \begin{align} \tilde{Q}_{1}^{k}(A) & =\sum_{i}b_{k}^{\ast}\left(Ax_{i}\right)b_{k}(x_{i})=\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}(x_{i})\nonumber \\ & =\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\\ & =\sum_{i}\mu_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right),\nonumber \end{align} $$
and so we can estimate
 $$ \begin{align} \left|\left\langle \Psi,\tilde{Q}_{1}^{k}(A)\Psi\right\rangle \right| &\leq\left(\max_{1\leq i\leq\left|L_{k}^{\pm}\right|}\left|\mu_{i}\right|\right)\sum_{i}\left\langle \Psi,b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\Psi\right\rangle \\ & =\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \Psi,\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\Psi\right\rangle .\nonumber \end{align} $$
$$ \begin{align} \left|\left\langle \Psi,\tilde{Q}_{1}^{k}(A)\Psi\right\rangle \right| &\leq\left(\max_{1\leq i\leq\left|L_{k}^{\pm}\right|}\left|\mu_{i}\right|\right)\sum_{i}\left\langle \Psi,b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\Psi\right\rangle \\ & =\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}A\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \Psi,\sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)\Psi\right\rangle .\nonumber \end{align} $$
Applying Lemma 3.3 again, we also see that
 $$ \begin{align} \sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right) &=\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}e_{p}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}e_{p}\right)\nonumber \\ &=\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}b_{\overline{k,p}}^{\ast}b_{\overline{k,p}}, \end{align} $$
$$ \begin{align} \sum_{i}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}x_{i}\right) &=\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}e_{p}\right)b_{k}\left(\left(h_{k}^{\oplus}\right)^{\frac{1}{2}}e_{p}\right)\nonumber \\ &=\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}b_{\overline{k,p}}^{\ast}b_{\overline{k,p}}, \end{align} $$
so by equation (4.32), we obtain the desired bound of
Next are the
![]() $\varepsilon _{k}(A)$
terms. These we cannot estimate in terms of
$\varepsilon _{k}(A)$
terms. These we cannot estimate in terms of
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
, but for A of diagonal form, we can still control them strongly:
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
, but for A of diagonal form, we can still control them strongly:
Proposition 4.9. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
 $A^{\oplus }=\left(\begin {array}{cc} A & 0\\ 0 & A \end {array}\right):\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$A^{\oplus }=\left(\begin {array}{cc} A & 0\\ 0 & A \end {array}\right):\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
 $$\begin{align*}\left|\left\langle \Psi,\varepsilon_{k}\left(A^{\oplus}\right)\Psi\right\rangle \right|\leq3\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*}$$
$$\begin{align*}\left|\left\langle \Psi,\varepsilon_{k}\left(A^{\oplus}\right)\Psi\right\rangle \right|\leq3\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*}$$
Proof. By the assumed form of
![]() $A^{\oplus }$
, we may write
$A^{\oplus }$
, we may write
![]() $\varepsilon _{k}\left(A^{\oplus }\right)$
as
$\varepsilon _{k}\left(A^{\oplus }\right)$
as
 $$ \begin{align} \varepsilon_{k}\left(A^{\oplus}\right) & =\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};A^{\oplus}e_{p}\right)=\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{q},A^{\oplus}e_{p}\right\rangle \varepsilon_{k,k}\left(\overline{k,p};\overline{k,q}\right)\nonumber \\ & =-\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{q},A^{\oplus}e_{p}\right\rangle \left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p,q\in L_{k}}\left\langle e_{q},Ae_{p}\right\rangle \left(\delta_{p,q}c_{q-k}c_{p-k}^{\ast}+\delta_{p-k,q-k}c_{q}^{\ast}c_{p}\right)\\ &\quad -\sum_{p,q\in L_{-k}}\left\langle e_{-q},Ae_{-p}\right\rangle \left(\delta_{p,q}c_{q+k}c_{p+k}^{\ast}+\delta_{p+k,q+k}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p\in L_{k}}\left\langle e_{p},Ae_{p}\right\rangle \left(c_{p-k}c_{p-k}^{\ast}+c_{p}^{\ast}c_{p}\right)-\sum_{p\in L_{-k}}\left\langle e_{-p},Ae_{-p}\right\rangle \left(c_{p+k}c_{p+k}^{\ast}+c_{p}^{\ast}c_{p}\right)\nonumber \end{align} $$
$$ \begin{align} \varepsilon_{k}\left(A^{\oplus}\right) & =\sum_{p\in L_{k}^{\pm}}\varepsilon_{k,k}\left(e_{p};A^{\oplus}e_{p}\right)=\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{q},A^{\oplus}e_{p}\right\rangle \varepsilon_{k,k}\left(\overline{k,p};\overline{k,q}\right)\nonumber \\ & =-\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{q},A^{\oplus}e_{p}\right\rangle \left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p,q\in L_{k}}\left\langle e_{q},Ae_{p}\right\rangle \left(\delta_{p,q}c_{q-k}c_{p-k}^{\ast}+\delta_{p-k,q-k}c_{q}^{\ast}c_{p}\right)\\ &\quad -\sum_{p,q\in L_{-k}}\left\langle e_{-q},Ae_{-p}\right\rangle \left(\delta_{p,q}c_{q+k}c_{p+k}^{\ast}+\delta_{p+k,q+k}c_{q}^{\ast}c_{p}\right)\nonumber \\ & =-\sum_{p\in L_{k}}\left\langle e_{p},Ae_{p}\right\rangle \left(c_{p-k}c_{p-k}^{\ast}+c_{p}^{\ast}c_{p}\right)-\sum_{p\in L_{-k}}\left\langle e_{-p},Ae_{-p}\right\rangle \left(c_{p+k}c_{p+k}^{\ast}+c_{p}^{\ast}c_{p}\right)\nonumber \end{align} $$
since the terms with
![]() $p\in L_{k},q\in L_{-k}$
or
$p\in L_{k},q\in L_{-k}$
or
![]() $p\in L_{-k},q\in L_{k}$
vanish (because
$p\in L_{-k},q\in L_{k}$
vanish (because
![]() $L_k\cap L_{-k}=\emptyset $
and there are
$L_k\cap L_{-k}=\emptyset $
and there are
![]() $\delta _{p,q}$
,
$\delta _{p,q}$
,
![]() $\delta _{p-k,q-k}$
in the summand). We can thus estimate
$\delta _{p-k,q-k}$
in the summand). We can thus estimate
 $$ \begin{align} \left|\left\langle \Psi,\varepsilon_{k}\left(A^{\oplus}\right)\Psi\right\rangle \right| & \leq\sum_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\left\langle \Psi,\left(c_{p-k}c_{p-k}^{\ast}+c_{p}^{\ast}c_{p}\right)\Psi\right\rangle \nonumber \\ &\quad +\sum_{p\in L_{-k}}\left|\left\langle e_{-p},Ae_{-p}\right\rangle \right|\left\langle \Psi,\left(c_{p+k}c_{p+k}^{\ast}+c_{p}^{\ast}c_{p}\right)\Psi\right\rangle \\ & \leq\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\left(\sum_{p\in L_{k}^{\pm}}c_{p}^{\ast}c_{p}+\sum_{p\in L_{k}-k}c_{p}c_{p}^{\ast}+\sum_{p\in L_{-k}+k}c_{p}c_{p}^{\ast}\right)\Psi\right\rangle \nonumber \\ & \leq3\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle .\nonumber \end{align} $$
$$ \begin{align} \left|\left\langle \Psi,\varepsilon_{k}\left(A^{\oplus}\right)\Psi\right\rangle \right| & \leq\sum_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\left\langle \Psi,\left(c_{p-k}c_{p-k}^{\ast}+c_{p}^{\ast}c_{p}\right)\Psi\right\rangle \nonumber \\ &\quad +\sum_{p\in L_{-k}}\left|\left\langle e_{-p},Ae_{-p}\right\rangle \right|\left\langle \Psi,\left(c_{p+k}c_{p+k}^{\ast}+c_{p}^{\ast}c_{p}\right)\Psi\right\rangle \\ & \leq\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\left(\sum_{p\in L_{k}^{\pm}}c_{p}^{\ast}c_{p}+\sum_{p\in L_{k}-k}c_{p}c_{p}^{\ast}+\sum_{p\in L_{-k}+k}c_{p}c_{p}^{\ast}\right)\Psi\right\rangle \nonumber \\ & \leq3\left(\max_{p\in L_{k}}\left|\left\langle e_{p},Ae_{p}\right\rangle \right|\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle .\nonumber \end{align} $$
Lastly, we consider the
![]() $Q_{2}^{k}(B)$
terms:
$Q_{2}^{k}(B)$
terms:
Proposition 4.10. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
Proof. By the Cauchy-Schwarz inequality and Proposition 4.4, we have
 $$ \begin{align} & \left|\left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle \right| =\left|2\sum_{p\in L_{k}^{\pm}}\mathrm{ Re}\left(\left\langle \Psi,b_{k}\left(Be_{p}\right)b_{k}(e_{p})\Psi\right\rangle \right)\right|\leq2\sum_{p\in L_{k}^{\pm}}\left\Vert b_{k}^{\ast}\left(Be_{p}\right)\Psi\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert \nonumber \\ & \leq2\sum_{p\in L_{k}^{\pm}}\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }+\left\Vert Be_{p}\right\Vert \left\Vert \Psi\right\Vert \right)\left\Vert b_{k}(e_{p})\Psi\right\Vert \\ & \leq2\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert +2\left\Vert \Psi\right\Vert \sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert .\nonumber \end{align} $$
$$ \begin{align} & \left|\left\langle \Psi,Q_{2}^{k}(B)\Psi\right\rangle \right| =\left|2\sum_{p\in L_{k}^{\pm}}\mathrm{ Re}\left(\left\langle \Psi,b_{k}\left(Be_{p}\right)b_{k}(e_{p})\Psi\right\rangle \right)\right|\leq2\sum_{p\in L_{k}^{\pm}}\left\Vert b_{k}^{\ast}\left(Be_{p}\right)\Psi\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert \nonumber \\ & \leq2\sum_{p\in L_{k}^{\pm}}\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }+\left\Vert Be_{p}\right\Vert \left\Vert \Psi\right\Vert \right)\left\Vert b_{k}(e_{p})\Psi\right\Vert \\ & \leq2\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert +2\left\Vert \Psi\right\Vert \sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert .\nonumber \end{align} $$
For the first sum, we can again apply the Cauchy-Schwarz inequality and (4.32):
 $$ \begin{align} \sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\\ & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}B\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}e_{p}\right\Vert ^{2}}\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\nonumber \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\\ & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}B\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}e_{p}\right\Vert ^{2}}\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\nonumber \end{align} $$
and we likewise estimate the second sum as
 $$ \begin{align} \sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left\Vert Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\\ & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert B\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}e_{p}\right\Vert ^{2}}\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }.\nonumber \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}^{\pm}}\left\Vert Be_{p}\right\Vert \left\Vert b_{k}(e_{p})\Psi\right\Vert & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}^{-1}\left\Vert Be_{p}\right\Vert ^{2}}\sqrt{\sum_{p\in L_{k}^{\pm}}\lambda_{\overline{k,p}}\left\Vert b_{\overline{k,p}}\Psi\right\Vert ^{2}}\\ & \leq\sqrt{\sum_{p\in L_{k}^{\pm}}\left\Vert B\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}e_{p}\right\Vert ^{2}}\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }.\nonumber \end{align} $$
The claim now follows by recognizing the Hilbert-Schmidt norms.
5 The quasi-bosonic Bogolubov transformation
Now we are prepared to define the quasi-bosonic Bogolubov transformation that will approximately diagonalize the Hamiltonian in (4.13),
where
![]() $h_k^{\oplus }$
,
$h_k^{\oplus }$
,
![]() $A_k^{\oplus }$
,
$A_k^{\oplus }$
,
![]() $B_k^{\oplus }$
are defined in (4.11) and (4.7).
$B_k^{\oplus }$
are defined in (4.11) and (4.7).
We define the generator
![]() $\mathcal {K}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
of the Bogolubov transformation as follows. Let
$\mathcal {K}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
of the Bogolubov transformation as follows. Let
![]() $(K_{k}^{\oplus })_{k\in S_{C}}$
be a collection of symmetric operators
$(K_{k}^{\oplus })_{k\in S_{C}}$
be a collection of symmetric operators
![]() $K_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
. Then we define
$K_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
. Then we define
 $$ \begin{align} \mathcal{K} & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},K_{k}^{\oplus}e_{q}\right\rangle \left(b_{\overline{k,p}}b_{\overline{k,q}}-b_{\overline{k,q}}^{\ast}b_{\overline{k,p}}^{\ast}\right)\\ & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})-b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)\right)\nonumber \end{align} $$
$$ \begin{align} \mathcal{K} & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},K_{k}^{\oplus}e_{q}\right\rangle \left(b_{\overline{k,p}}b_{\overline{k,q}}-b_{\overline{k,q}}^{\ast}b_{\overline{k,p}}^{\ast}\right)\\ & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})-b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)\right)\nonumber \end{align} $$
in analogy with equation (3.9). As in the bosonic case,
![]() $\mathcal {K}$
is seen to be a skew-symmetric operator.Footnote
8
Moreover, unlike the bosonic case,
$\mathcal {K}$
is seen to be a skew-symmetric operator.Footnote
8
Moreover, unlike the bosonic case,
![]() $\mathcal {K}$
is now a bounded operator by the same argument that
$\mathcal {K}$
is now a bounded operator by the same argument that
![]() $Q_{1}^{k}(\cdot )$
and
$Q_{1}^{k}(\cdot )$
and
![]() $Q_{2}^{k}(\cdot )$
are. Therefore,
$Q_{2}^{k}(\cdot )$
are. Therefore,
![]() $\mathcal {K}$
generates a unitary transformation
$\mathcal {K}$
generates a unitary transformation
![]() $e^{\mathcal {K}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
, which is the quasi-bosonic Bogolubov transformation.
$e^{\mathcal {K}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
, which is the quasi-bosonic Bogolubov transformation.
The specific kernels
![]() $K_k^\oplus $
we will use are those which diagonalize the corresponding bosonic Hamiltonian exactly, but first we will consider the action of
$K_k^\oplus $
we will use are those which diagonalize the corresponding bosonic Hamiltonian exactly, but first we will consider the action of
![]() $e^{\mathcal {K}}$
on quadratic operators and the localized kinetic operator more generally.
$e^{\mathcal {K}}$
on quadratic operators and the localized kinetic operator more generally.
5.1 Transformation of quadratic operators
By exploiting the similarity of our quasi-bosonic definitions with the exact bosonic case, we can now easily deduce the analogues of Propositions 3.2 and 3.4:
Proposition 5.1. For all
![]() $k\in S_{C}$
,
$k\in S_{C}$
,
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
and symmetric operators
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
and symmetric operators
![]() $(K_{l}^{\oplus })_{l\in S_{C}}$
, it holds that
$(K_{l}^{\oplus })_{l\in S_{C}}$
, it holds that
 $$ \begin{align*} \left[\mathcal{K},b_{k}(\varphi )\right] & =b_{k}^{\ast}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi ),\\ \left[\mathcal{K},b_{k}^{\ast}(\varphi )\right] & =b_{k}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi )^{\ast}, \end{align*} $$
$$ \begin{align*} \left[\mathcal{K},b_{k}(\varphi )\right] & =b_{k}^{\ast}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi ),\\ \left[\mathcal{K},b_{k}^{\ast}(\varphi )\right] & =b_{k}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi )^{\ast}, \end{align*} $$
where
 $$\begin{align*}\mathcal{E}_{k}(\varphi )=\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right\}. \end{align*}$$
$$\begin{align*}\mathcal{E}_{k}(\varphi )=\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right\}. \end{align*}$$
Proof. We calculate using the commutation relations of (4.15) that
 $$ \begin{align} \left[\mathcal{K},b_{k}(\varphi )\right] & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\left[b_{l}\left(K_{l}^{\oplus}e_{q}\right)b_{l}(e_{p}),b_{k}(\varphi )\right]-\left[b_{l}^{\ast}\left(e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),b_{k}(\varphi )\right]\right)\nonumber \\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}\left(e_{q}\right)\left[b_{k}(\varphi ),b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right]+\left[b_{k}(\varphi ),b_{l}^{\ast}\left(e_{q}\right)\right]b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right)\nonumber \\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}b_{l}^{\ast}\left(e_{q}\right)\left(\delta_{k,l}\left\langle \varphi,K_{l}^{\oplus}e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;K_{l}^{\oplus}e_{q}\right)\right)\nonumber\\ &\quad +\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\delta_{k,l}\left\langle \varphi,e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\nonumber \\ & =\frac{1}{2}b_{k}^{\ast}\left(\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,K_{k}^{\oplus}e_{q}\right\rangle e_{q}\right)+\frac{1}{2}b_{k}^{\ast}\left(K_{k}^{\oplus}\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle e_{q}\right)+\mathcal{E}_{k}(\varphi )\nonumber \\ & =b_{k}^{\ast}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi ) \end{align} $$
$$ \begin{align} \left[\mathcal{K},b_{k}(\varphi )\right] & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\left[b_{l}\left(K_{l}^{\oplus}e_{q}\right)b_{l}(e_{p}),b_{k}(\varphi )\right]-\left[b_{l}^{\ast}\left(e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),b_{k}(\varphi )\right]\right)\nonumber \\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}\left(e_{q}\right)\left[b_{k}(\varphi ),b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right]+\left[b_{k}(\varphi ),b_{l}^{\ast}\left(e_{q}\right)\right]b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right)\nonumber \\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}b_{l}^{\ast}\left(e_{q}\right)\left(\delta_{k,l}\left\langle \varphi,K_{l}^{\oplus}e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;K_{l}^{\oplus}e_{q}\right)\right)\nonumber\\ &\quad +\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\delta_{k,l}\left\langle \varphi,e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\nonumber \\ & =\frac{1}{2}b_{k}^{\ast}\left(\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,K_{k}^{\oplus}e_{q}\right\rangle e_{q}\right)+\frac{1}{2}b_{k}^{\ast}\left(K_{k}^{\oplus}\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle e_{q}\right)+\mathcal{E}_{k}(\varphi )\nonumber \\ & =b_{k}^{\ast}\left(K_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}(\varphi ) \end{align} $$
for
![]() $\mathcal {E}_{k}(\varphi )$
given by
$\mathcal {E}_{k}(\varphi )$
given by
 $$ \begin{align} \mathcal{E}_{k}(\varphi ) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}\left(e_{q}\right)\varepsilon_{k,l}\left(\varphi;K_{l}^{\oplus}e_{q}\right)+\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right)\nonumber\\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right\} , \end{align} $$
$$ \begin{align} \mathcal{E}_{k}(\varphi ) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}\left(e_{q}\right)\varepsilon_{k,l}\left(\varphi;K_{l}^{\oplus}e_{q}\right)+\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right)\nonumber\\ & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(\varphi;e_{q}\right)\right\} , \end{align} $$
where we used Lemma 3.3 to simplify the expression (as
![]() $x,y\mapsto b_{l}^{\ast } (x )\varepsilon _{k,l}\left(\varphi ;y\right)$
is bilinear for fixed
$x,y\mapsto b_{l}^{\ast } (x )\varepsilon _{k,l}\left(\varphi ;y\right)$
is bilinear for fixed
![]() $\varphi $
and
$\varphi $
and
![]() $K_{k}^{\oplus }$
is symmetric). The commutator
$K_{k}^{\oplus }$
is symmetric). The commutator
![]() $\left[\mathcal {K},b_{k}^{\ast }(\varphi )\right]$
follows by taking the adjoint.
$\left[\mathcal {K},b_{k}^{\ast }(\varphi )\right]$
follows by taking the adjoint.
From this, we easily deduce the commutator of
![]() $\mathcal {K}$
with quadratic operators:
$\mathcal {K}$
with quadratic operators:
Proposition 5.2. For all
![]() $k\in S_{C}$
and symmetric operators
$k\in S_{C}$
and symmetric operators
![]() $A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
$A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
 $$ \begin{align*} \left[\mathcal{K},Q_{1}^{k}(A)\right] & =Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\mathcal{E}_{1}^{k}(A)\\ \left[\mathcal{K},Q_{2}^{k}(B)\right] & =Q_{1}^{k}\left(\left\{ K_{k}^{\oplus},B\right\} \right)+\mathcal{E}_{2}^{k}(B), \end{align*} $$
$$ \begin{align*} \left[\mathcal{K},Q_{1}^{k}(A)\right] & =Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\mathcal{E}_{1}^{k}(A)\\ \left[\mathcal{K},Q_{2}^{k}(B)\right] & =Q_{1}^{k}\left(\left\{ K_{k}^{\oplus},B\right\} \right)+\mathcal{E}_{2}^{k}(B), \end{align*} $$
where
 $$ \begin{align*} \mathcal{E}_{1}^{k}(A) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}(e_{p};e_{q})\right\} \right\} \right.\\ & \quad\left.+\left\{ \left\{ \varepsilon_{l,k}\left(e_{q};e_{p}\right),b_{l}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}(Ae_{p})\right\} \right)\\ \mathcal{E}_{2}^{k}(B) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}\left(Be_{p}\right),\left\{ b_{l}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{l,k}\left(e_{q};e_{p}\right)\right\} \right\} \right.\\ & \quad \left.+\left\{ \left\{ \varepsilon_{k,l}(e_{p};e_{q}),b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}\left(Be_{p}\right)\right\} \right). \end{align*} $$
$$ \begin{align*} \mathcal{E}_{1}^{k}(A) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}(e_{p};e_{q})\right\} \right\} \right.\\ & \quad\left.+\left\{ \left\{ \varepsilon_{l,k}\left(e_{q};e_{p}\right),b_{l}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}(Ae_{p})\right\} \right)\\ \mathcal{E}_{2}^{k}(B) & =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}\left(Be_{p}\right),\left\{ b_{l}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{l,k}\left(e_{q};e_{p}\right)\right\} \right\} \right.\\ & \quad \left.+\left\{ \left\{ \varepsilon_{k,l}(e_{p};e_{q}),b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}\left(Be_{p}\right)\right\} \right). \end{align*} $$
Proof. We compute using the commutators of the previous proposition (and Lemma 3.3, to simplify the resulting expressions) that
 $$ \begin{align} \left[\mathcal{K},Q_{1}^{k}(A)\right] & =\sum_{p\in L_{k}^{\pm}}\left(\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})\right]+\left[\mathcal{K},b_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right]\right)\nonumber \\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left[\mathcal{K},b_{k}(e_{p})\right]+\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})\right]b_{k}(e_{p})\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}(e_{p})\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})\right]+\left[\mathcal{K},b_{k}(e_{p})\right]b_{k}^{\ast}(Ae_{p})\right)\nonumber\\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left(b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}(e_{p})\right)+\left(b_{k}\left(K_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}(Ae_{p})^{\ast}\right)b_{k}(e_{p})\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}(e_{p})\left(b_{k}\left(K_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}(Ae_{p})^{\ast}\right)+\left(b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}(e_{p})\right)b_{k}^{\ast}(Ae_{p})\right)\nonumber \\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(\left(AK_{k}^{\oplus}+K_{k}^{\oplus}A\right)e_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(\left(K_{k}^{\oplus}A+K_{k}^{\oplus}A\right)e_{p}\right)\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\mathcal{E}_{k}(e_{p})+\mathcal{E}_{k}(e_{p})^{\ast}b_{k}(Ae_{p})+b_{k}(Ae_{p})\mathcal{E}_{k}(e_{p})^{\ast}+\mathcal{E}_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right)\nonumber \\ & =Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\sum_{p\in L_{k}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\mathcal{E}_{k}(e_{p})\right\} +\left\{ \mathcal{E}_{k}(e_{p})^{\ast},b_{k}(Ae_{p})\right\} \right) \end{align} $$
$$ \begin{align} \left[\mathcal{K},Q_{1}^{k}(A)\right] & =\sum_{p\in L_{k}^{\pm}}\left(\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})\right]+\left[\mathcal{K},b_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right]\right)\nonumber \\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left[\mathcal{K},b_{k}(e_{p})\right]+\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})\right]b_{k}(e_{p})\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}(e_{p})\left[\mathcal{K},b_{k}^{\ast}(Ae_{p})\right]+\left[\mathcal{K},b_{k}(e_{p})\right]b_{k}^{\ast}(Ae_{p})\right)\nonumber\\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left(b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}(e_{p})\right)+\left(b_{k}\left(K_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}(Ae_{p})^{\ast}\right)b_{k}(e_{p})\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}(e_{p})\left(b_{k}\left(K_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}(Ae_{p})^{\ast}\right)+\left(b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}(e_{p})\right)b_{k}^{\ast}(Ae_{p})\right)\nonumber \\ & =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(\left(AK_{k}^{\oplus}+K_{k}^{\oplus}A\right)e_{p}\right)b_{k}^{\ast}(e_{p})+b_{k}(e_{p})b_{k}\left(\left(K_{k}^{\oplus}A+K_{k}^{\oplus}A\right)e_{p}\right)\right)\nonumber \\ &\quad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\mathcal{E}_{k}(e_{p})+\mathcal{E}_{k}(e_{p})^{\ast}b_{k}(Ae_{p})+b_{k}(Ae_{p})\mathcal{E}_{k}(e_{p})^{\ast}+\mathcal{E}_{k}(e_{p})b_{k}^{\ast}(Ae_{p})\right)\nonumber \\ & =Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\sum_{p\in L_{k}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\mathcal{E}_{k}(e_{p})\right\} +\left\{ \mathcal{E}_{k}(e_{p})^{\ast},b_{k}(Ae_{p})\right\} \right) \end{align} $$
and
 $$ \begin{align} & \sum_{p\in L_{k}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\mathcal{E}_{k}(e_{p})\right\} +\left\{ \mathcal{E}_{k}(e_{p})^{\ast},b_{k}(Ae_{p})\right\} \right)\nonumber \\ &\quad =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}(e_{p};e_{q})\right\} \right\} \right.\\ & \qquad\left.+\left\{ \left\{ \varepsilon_{l,k}\left(e_{q};e_{p}\right),b_{l}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}(Ae_{p})\right\} \right)=\mathcal{E}_{1}^{k}(A) \nonumber \end{align} $$
$$ \begin{align} & \sum_{p\in L_{k}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\mathcal{E}_{k}(e_{p})\right\} +\left\{ \mathcal{E}_{k}(e_{p})^{\ast},b_{k}(Ae_{p})\right\} \right)\nonumber \\ &\quad =\frac{1}{2}\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\left(\left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}(e_{p};e_{q})\right\} \right\} \right.\\ & \qquad\left.+\left\{ \left\{ \varepsilon_{l,k}\left(e_{q};e_{p}\right),b_{l}\left(K_{l}^{\oplus}e_{q}\right)\right\} ,b_{k}(Ae_{p})\right\} \right)=\mathcal{E}_{1}^{k}(A) \nonumber \end{align} $$
as
![]() $\varepsilon _{k,l}(e_{p};e_{q})^{\ast }=\varepsilon _{l,k}\left(e_{q};e_{p}\right)$
. The computation of
$\varepsilon _{k,l}(e_{p};e_{q})^{\ast }=\varepsilon _{l,k}\left(e_{q};e_{p}\right)$
. The computation of
![]() $Q_{2}^{k}(B)$
is similar.
$Q_{2}^{k}(B)$
is similar.
Action of
 $e^{\mathcal {K}}$
on quadratic operators
$e^{\mathcal {K}}$
on quadratic operators
With the commutators calculated, we are now ready to determine the full action of
![]() $e^{\mathcal {K}}$
on the quadratic operators
$e^{\mathcal {K}}$
on the quadratic operators
![]() $Q_{1}^{k}(\cdot )$
and
$Q_{1}^{k}(\cdot )$
and
![]() $Q_{2}^{k}(\cdot )$
. Rather than appeal to the Baker-Campbell-Hausdorff formula, which would also require describing the commutators
$Q_{2}^{k}(\cdot )$
. Rather than appeal to the Baker-Campbell-Hausdorff formula, which would also require describing the commutators
![]() $\left[\mathcal {K},\mathcal {E}_{1}^{k}(A)\right]$
, etc., we will employ a ‘Duhamel-type’ argument which allows us to more selectively expand the operator
$\left[\mathcal {K},\mathcal {E}_{1}^{k}(A)\right]$
, etc., we will employ a ‘Duhamel-type’ argument which allows us to more selectively expand the operator
![]() $e^{\mathcal {K}}$
.
$e^{\mathcal {K}}$
.
As in Section 3, we use the notation
![]() $\mathcal {A}_{K_{k}^{\oplus }}=\left\{ K_{k}^{\oplus },\cdot \right\}$
for anticommutators with
$\mathcal {A}_{K_{k}^{\oplus }}=\left\{ K_{k}^{\oplus },\cdot \right\}$
for anticommutators with
![]() $K_{k}^{\oplus }$
.
$K_{k}^{\oplus }$
.
Before stating the proposition, we must make a remark. To use these identities, we will need to take limits, and to justify those limits, we need some general estimates on operators of the form
![]() $Q_{1}^{k}(\cdot ),Q_{2}^{k}(\cdot ),\mathcal {E}_{1}^{k}(\cdot ),\mathcal {E}_{2}^{k}(\cdot )$
. The Propositions 4.6, 4.7 establish these for
$Q_{1}^{k}(\cdot ),Q_{2}^{k}(\cdot ),\mathcal {E}_{1}^{k}(\cdot ),\mathcal {E}_{2}^{k}(\cdot )$
. The Propositions 4.6, 4.7 establish these for
![]() $Q_{1}^{k}(\cdot )$
and
$Q_{1}^{k}(\cdot )$
and
![]() $Q_{2}^{k}(\cdot )$
, while Proposition 6.4 will establish these for
$Q_{2}^{k}(\cdot )$
, while Proposition 6.4 will establish these for
![]() $\mathcal {E}_{1}^{k}(\cdot )$
and
$\mathcal {E}_{1}^{k}(\cdot )$
and
![]() $\mathcal {E}_{2}^{k}(\cdot )$
.
$\mathcal {E}_{2}^{k}(\cdot )$
.
The statement follows:
Proposition 5.3. For all
![]() $k\in S_{C}$
and symmetric
$k\in S_{C}$
and symmetric
![]() $A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
$A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
 $$ \begin{align*} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(A)\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(A)\right)\right)e^{-t\mathcal{K}}\,dt\\ e^{\mathcal{K}}Q_{2}^{k}(B)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Be^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Be^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}Be^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Be^{-K_{k}^{\oplus}}\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(B)\right)+\mathcal{E}_{2}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(B)\right)\right)e^{-t\mathcal{K}}\,dt, \end{align*} $$
$$ \begin{align*} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(A)\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(A)\right)\right)e^{-t\mathcal{K}}\,dt\\ e^{\mathcal{K}}Q_{2}^{k}(B)e^{-\mathcal{K}} & =\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Be^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Be^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}Be^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Be^{-K_{k}^{\oplus}}\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(B)\right)+\mathcal{E}_{2}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)(B)\right)\right)e^{-t\mathcal{K}}\,dt, \end{align*} $$
the integrals being Riemann integrals of bounded operators.
Proof. We consider
![]() $e^{\mathcal {K}}Q_{1}^{k}(A)e^{-\mathcal {K}}$
, with the argument for
$e^{\mathcal {K}}Q_{1}^{k}(A)e^{-\mathcal {K}}$
, with the argument for
![]() $e^{\mathcal {K}}Q_{2}^{k}(B)e^{-\mathcal {K}}$
being similar. We first claim that for any
$e^{\mathcal {K}}Q_{2}^{k}(B)e^{-\mathcal {K}}$
being similar. We first claim that for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} &=Q_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m}(A)\right)+Q_{2}^{k}\left(\sum_{m=0}^{n_{2}}\frac{1}{\left(2m+1\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m+1}(A)\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{2m}(A)\right)+\mathcal{E}_{2}^{k}\left(\sum_{m=0}^{n_{2}}\frac{1}{\left(2m+1\right)!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{2m+1}(A)\right)\right)e^{-t\mathcal{K}}\,dt\nonumber \\ &\quad +\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}(1-t)^{n-1}\,dt,\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} &=Q_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m}(A)\right)+Q_{2}^{k}\left(\sum_{m=0}^{n_{2}}\frac{1}{\left(2m+1\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m+1}(A)\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{2m}(A)\right)+\mathcal{E}_{2}^{k}\left(\sum_{m=0}^{n_{2}}\frac{1}{\left(2m+1\right)!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{2m+1}(A)\right)\right)e^{-t\mathcal{K}}\,dt\nonumber \\ &\quad +\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}(1-t)^{n-1}\,dt,\nonumber \end{align} $$
where, for brevity,
![]() $\overline {n-1}=n-1\ \mod 2$
and
$\overline {n-1}=n-1\ \mod 2$
and
![]() $n_{1},n_{2}$
are the largest integers such that
$n_{1},n_{2}$
are the largest integers such that
![]() $2n_{1}<n$
and
$2n_{1}<n$
and
![]() $2n_{2}+1<n$
, respectively.
$2n_{2}+1<n$
, respectively.
We proceed by induction. For
![]() $n=1$
, we find by the fundamental theorem of calculus that
$n=1$
, we find by the fundamental theorem of calculus that
 $$ \begin{align} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} & =Q_{1}^{k}(A)+\int_{0}^{1}\frac{d}{dt}\left(e^{t\mathcal{K}}Q_{1}^{k}(A)e^{-t\mathcal{K}}\right)\,dt=Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},Q_{1}^{k}(A)\right]e^{-t\mathcal{K}}\,dt\nonumber \\ & =Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\left(Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\mathcal{E}_{1}^{k}(A)\right)e^{-t\mathcal{K}}\,dt\\ & =Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{1}^{k}(A)e^{-t\mathcal{K}}\,dt+\int_{0}^{1}e^{t\mathcal{K}}Q_{2}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}(A)\right)e^{-t\mathcal{K}}\,dt\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}Q_{1}^{k}(A)e^{-\mathcal{K}} & =Q_{1}^{k}(A)+\int_{0}^{1}\frac{d}{dt}\left(e^{t\mathcal{K}}Q_{1}^{k}(A)e^{-t\mathcal{K}}\right)\,dt=Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},Q_{1}^{k}(A)\right]e^{-t\mathcal{K}}\,dt\nonumber \\ & =Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\left(Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},A\right\} \right)+\mathcal{E}_{1}^{k}(A)\right)e^{-t\mathcal{K}}\,dt\\ & =Q_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{1}^{k}(A)e^{-t\mathcal{K}}\,dt+\int_{0}^{1}e^{t\mathcal{K}}Q_{2}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}(A)\right)e^{-t\mathcal{K}}\,dt\nonumber \end{align} $$
by the commutator of Proposition 5.2, which is the statement for
![]() $n=1$
(in this case,
$n=1$
(in this case,
![]() $n_1=0$
and
$n_1=0$
and
![]() $n_2=-1$
, so
$n_2=-1$
, so
![]() $\sum _{m=0}^{n_1}$
contains one term and
$\sum _{m=0}^{n_1}$
contains one term and
![]() $\sum _{m=0}^{n_2}$
is empty).
$\sum _{m=0}^{n_2}$
is empty).
For the inductive step, we now assume that case n holds. Integrating the last term of equation (5.7) by parts, we find that
 $$ \begin{align} & \frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}(1-t)^{n-1}dt\nonumber \\ &\quad =\frac{1}{(n-1)!}\left[e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}\left(-\frac{(1-t)^{n}}{n}\right)\right]_{0}^{1}\nonumber \\ &\qquad -\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)\right]e^{-t\mathcal{K}}\left(-\frac{(1-t)^{n}}{n}\right)dt\\ &\quad =\frac{1}{n!}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)+\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{K}}\left(Q_{\overline{n}}^{k}\left(\left\{ K_{k}^{\oplus},\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right\} \right)+\mathcal{E}_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)\right)e^{-t\mathcal{K}}(1-t)^{n}dt\nonumber \\ &\quad =Q_{\overline{n-1}}^{k}\left(\frac{1}{n!}\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)+\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{\overline{n-1}}^{k}\left(\frac{1}{n!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}\,dt\nonumber \\ &\qquad +\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n+1}(A)\right)e^{-t\mathcal{K}}(1-t)^{n}dt,\nonumber \end{align} $$
$$ \begin{align} & \frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}(1-t)^{n-1}dt\nonumber \\ &\quad =\frac{1}{(n-1)!}\left[e^{t\mathcal{K}}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}\left(-\frac{(1-t)^{n}}{n}\right)\right]_{0}^{1}\nonumber \\ &\qquad -\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)\right]e^{-t\mathcal{K}}\left(-\frac{(1-t)^{n}}{n}\right)dt\\ &\quad =\frac{1}{n!}Q_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)+\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{K}}\left(Q_{\overline{n}}^{k}\left(\left\{ K_{k}^{\oplus},\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right\} \right)+\mathcal{E}_{\overline{n-1}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)\right)e^{-t\mathcal{K}}(1-t)^{n}dt\nonumber \\ &\quad =Q_{\overline{n-1}}^{k}\left(\frac{1}{n!}\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\right)+\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{\overline{n-1}}^{k}\left(\frac{1}{n!}\mathcal{A}_{(1-t)K_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{K}}\,dt\nonumber \\ &\qquad +\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{K}}Q_{\overline{n}}^{k}\left(\mathcal{A}_{K_{k}^{\oplus}}^{n+1}(A)\right)e^{-t\mathcal{K}}(1-t)^{n}dt,\nonumber \end{align} $$
where we also used that
Inserting this into (5.7) and collecting like terms yields the statement for case
![]() $n+1$
.
$n+1$
.
We now deduce the statement from (5.7) by taking
![]() $n\to \infty $
. Recall the identities
$n\to \infty $
. Recall the identities
 $$ \begin{align} \cosh\big(\mathcal{A}_{K_{k}^{\oplus}}\big)(T) & =\frac{1}{2}\big(e^{K_{k}^{\oplus}}Te^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Te^{-K_{k}^{\oplus}}\big) \\ \sinh\big(\mathcal{A}_{K_{k}^{\oplus}}\big)(T) & =\frac{1}{2}\big(e^{K_{k}^{\oplus}}Te^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Te^{-K_{k}^{\oplus}}\big)\nonumber \end{align} $$
$$ \begin{align} \cosh\big(\mathcal{A}_{K_{k}^{\oplus}}\big)(T) & =\frac{1}{2}\big(e^{K_{k}^{\oplus}}Te^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Te^{-K_{k}^{\oplus}}\big) \\ \sinh\big(\mathcal{A}_{K_{k}^{\oplus}}\big)(T) & =\frac{1}{2}\big(e^{K_{k}^{\oplus}}Te^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}Te^{-K_{k}^{\oplus}}\big)\nonumber \end{align} $$
from Proposition 3.5 and note that
![]() $\left((n-1)!\right)^{-1}\mathcal {A}_{K_{k}^{\oplus }}^{n}(A)\to 0$
as
$\left((n-1)!\right)^{-1}\mathcal {A}_{K_{k}^{\oplus }}^{n}(A)\to 0$
as
![]() $n\to \infty $
. By Proposition 4.6,
$n\to \infty $
. By Proposition 4.6,
 $$ \begin{align*}Q_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m}(A)\right)\to \frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right) \end{align*} $$
$$ \begin{align*}Q_{1}^{k}\left(\sum_{m=0}^{n_{1}}\frac{1}{\left(2m\right)!}\mathcal{A}_{K_{k}^{\oplus}}^{2m}(A)\right)\to \frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}Ae^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}Ae^{-K_{k}^{\oplus}}\right) \end{align*} $$
and
 $$ \begin{align*}\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{1}^{k}\big(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\big)e^{-t\mathcal{K}}(1-t)^{n-1}\,dt \to 0. \end{align*} $$
$$ \begin{align*}\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{K}}Q_{1}^{k}\big(\mathcal{A}_{K_{k}^{\oplus}}^{n}(A)\big)e^{-t\mathcal{K}}(1-t)^{n-1}\,dt \to 0. \end{align*} $$
Similar convergence for
![]() $Q_2$
is justified by Proposition 4.7. The convergence for
$Q_2$
is justified by Proposition 4.7. The convergence for
![]() $\mathcal {E}_{1}^{k}$
and
$\mathcal {E}_{1}^{k}$
and
![]() $\mathcal {E}_{2}^{k}$
follows from Proposition 6.4.
$\mathcal {E}_{2}^{k}$
follows from Proposition 6.4.
Remark on the transformation of excitation operators
Let us make a quick remark on why we choose to approach the Bogolubov transformation from the point of view of quadratic operators rather than the usual creation and annihilation operator approach. Recall that in the exact bosonic case the creation and annihilation operators transformed under a Bogolubov transformation as
 $$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right)\\ e^{\mathcal{K}}a^{\ast}(\varphi )e^{-\mathcal{K}} & =a^{\ast}\left(\cosh\left(K\right)\varphi\right)+a\left(\sinh\left(K\right)\varphi\right).\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}a(\varphi )e^{-\mathcal{K}} & =a\left(\cosh\left(K\right)\varphi\right)+a^{\ast}\left(\sinh\left(K\right)\varphi\right)\\ e^{\mathcal{K}}a^{\ast}(\varphi )e^{-\mathcal{K}} & =a^{\ast}\left(\cosh\left(K\right)\varphi\right)+a\left(\sinh\left(K\right)\varphi\right).\nonumber \end{align} $$
In the quasi-bosonic setting, we can use the commutators of Proposition 5.1 and a similar Duhamel-type argument to what we just applied to conclude that
 $$ \begin{align} e^{\mathcal{K}}b_{k}(\varphi )e^{-\mathcal{K}} & =b_{k}\left(\cosh\left(K_{k}^{\oplus}\right)\varphi\right)+b_{k}^{\ast}\left(\sinh\left(K_{k}^{\oplus}\right)\varphi\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{k}\left(\cosh\left((1-t)K_{k}^{\oplus}\right)\varphi\right)+\mathcal{E}_{k}\left(\sinh\left((1-t)K_{k}^{\oplus}\right)\varphi\right)^{\ast}\right)e^{-t\mathcal{K}}\,dt\nonumber \end{align} $$
$$ \begin{align} e^{\mathcal{K}}b_{k}(\varphi )e^{-\mathcal{K}} & =b_{k}\left(\cosh\left(K_{k}^{\oplus}\right)\varphi\right)+b_{k}^{\ast}\left(\sinh\left(K_{k}^{\oplus}\right)\varphi\right)\\ &\quad +\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{k}\left(\cosh\left((1-t)K_{k}^{\oplus}\right)\varphi\right)+\mathcal{E}_{k}\left(\sinh\left((1-t)K_{k}^{\oplus}\right)\varphi\right)^{\ast}\right)e^{-t\mathcal{K}}\,dt\nonumber \end{align} $$
with a similar expression for
![]() $e^{\mathcal {K}}b_{k}^{\ast }(\varphi )e^{-\mathcal {K}}$
. This is a more cumbersome expression to work with, and if we were to describe
$e^{\mathcal {K}}b_{k}^{\ast }(\varphi )e^{-\mathcal {K}}$
. This is a more cumbersome expression to work with, and if we were to describe
![]() $e^{\mathcal {K}}Q_{1}^{k}(A)e^{-\mathcal {K}}$
by transforming the individual terms of
$e^{\mathcal {K}}Q_{1}^{k}(A)e^{-\mathcal {K}}$
by transforming the individual terms of
![]() $Q_{1}^{k}(A)$
like this rather than transforming
$Q_{1}^{k}(A)$
like this rather than transforming
![]() $Q_{1}^{k}(A)$
as a whole, the error terms would not only go from being under a single integral to involving the product of two integrals, it would also involve cross terms between the bosonic terms and the error terms of equation (5.13). These cross terms, in particular, would severely reduce the quality of the final error estimate. Hence, we prefer the quadratic operator approach in the quasi-bosonic setting.
$Q_{1}^{k}(A)$
as a whole, the error terms would not only go from being under a single integral to involving the product of two integrals, it would also involve cross terms between the bosonic terms and the error terms of equation (5.13). These cross terms, in particular, would severely reduce the quality of the final error estimate. Hence, we prefer the quadratic operator approach in the quasi-bosonic setting.
5.2 Transformation of the kinetic operator
There remains the task of describing the action of
![]() $e^{\mathcal {K}}$
on the localized kinetic operator
$e^{\mathcal {K}}$
on the localized kinetic operator
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
. For this, we must first formulate
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
. For this, we must first formulate
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
– or rather the commutator
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
– or rather the commutator
![]() $[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k,p}^{\ast }]$
calculated in (1.74) – within the general framework that we have introduced in this section. Recalling the operators
$[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k,p}^{\ast }]$
calculated in (1.74) – within the general framework that we have introduced in this section. Recalling the operators
![]() $h_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
in (4.11), then by (1.74) and linearity it follows that
$h_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
in (4.11), then by (1.74) and linearity it follows that
for all
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
. (The factor of
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
. (The factor of
![]() $2$
is introduced here because in the analogy of equation (4.9),
$2$
is introduced here because in the analogy of equation (4.9),
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
appears like a
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
appears like a
![]() $\text {d}\Gamma (\cdot )=\frac {1}{2}Q_{1}(\cdot )-\frac {1}{2}\text {tr}(\cdot )$
term rather than a pure
$\text {d}\Gamma (\cdot )=\frac {1}{2}Q_{1}(\cdot )-\frac {1}{2}\text {tr}(\cdot )$
term rather than a pure
![]() $Q_{1}(\cdot )$
term.)
$Q_{1}(\cdot )$
term.)
We now calculate
![]() $\left[\mathcal {K},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]$
as follows:
$\left[\mathcal {K},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]$
as follows:
Proposition 5.4.
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
obeys
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
obeys
Proof. We compute, using the commutators of equation (5.14) and Lemma 3.3, that
 $$ \begin{align} \left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}\right] & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(\left[b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}),H_{\operatorname{\mathrm{kin}}}^{\prime}\right]-\left[b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right),H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\right)\nonumber \\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(h_{k}^{\oplus}K_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(h_{k}^{\oplus}e_{p}\right)b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)\right)\\ &\quad +\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}\left(h_{k}^{\oplus}e_{p}\right)+b_{k}\left(h_{k}^{\oplus}K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)\nonumber \\ & =\sum_{k\in S_{C}}Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right).\nonumber \end{align} $$
$$ \begin{align} \left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}\right] & =\frac{1}{2}\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(\left[b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}),H_{\operatorname{\mathrm{kin}}}^{\prime}\right]-\left[b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right),H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\right)\nonumber \\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(h_{k}^{\oplus}K_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(h_{k}^{\oplus}e_{p}\right)b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)\right)\\ &\quad +\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}\left(h_{k}^{\oplus}e_{p}\right)+b_{k}\left(h_{k}^{\oplus}K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)\nonumber \\ & =\sum_{k\in S_{C}}Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right).\nonumber \end{align} $$
Note that because the commutator
![]() $\left[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k}^{\ast }(\varphi )\right]=2\,b_{k}^{\ast }\left(h_{k}^{\oplus }\varphi \right)$
exactly mirrors the bosonic case (in that there is no additional error term), the commutator
$\left[H_{\operatorname {\mathrm {kin}}}^{\prime },b_{k}^{\ast }(\varphi )\right]=2\,b_{k}^{\ast }\left(h_{k}^{\oplus }\varphi \right)$
exactly mirrors the bosonic case (in that there is no additional error term), the commutator
![]() $\left[\mathcal {K},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]$
is likewise ‘purely bosonic’, being simply a sum of
$\left[\mathcal {K},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]$
is likewise ‘purely bosonic’, being simply a sum of
![]() $Q_{2}^{k}(\cdot )$
terms without error terms such as those appearing in the statement of Proposition 5.2. With the groundwork laid, we can now easily deduce the following:
$Q_{2}^{k}(\cdot )$
terms without error terms such as those appearing in the statement of Proposition 5.2. With the groundwork laid, we can now easily deduce the following:
Proposition 5.5.
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
obeys
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
obeys
 $$ \begin{align*} & e^{\mathcal{K}}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}\\ & +\sum_{k\in S_{C}}\left(\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)\right)\\ & +\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)-h_{k}^{\oplus}\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)\right)e^{-t\mathcal{K}}\,dt. \end{align*} $$
$$ \begin{align*} & e^{\mathcal{K}}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}\\ & +\sum_{k\in S_{C}}\left(\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)\right)\\ & +\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)-h_{k}^{\oplus}\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)\right)e^{-t\mathcal{K}}\,dt. \end{align*} $$
Proof. By adding and subtracting, we have
 $$ \begin{align} e^{\mathcal{K}}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{-\mathcal{K}}=\sum_{k\in S_{C}}e^{\mathcal{K}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-\mathcal{K}}+e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{K}}, \end{align} $$
$$ \begin{align} e^{\mathcal{K}}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{-\mathcal{K}}=\sum_{k\in S_{C}}e^{\mathcal{K}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-\mathcal{K}}+e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{K}}, \end{align} $$
and the first term on the right-hand side is by Proposition 5.3,
 $$ \begin{align} &\sum_{k\in S_{C}}e^{\mathcal{K}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-\mathcal{K}} \\ &\quad =\sum_{k\in S_{C}}\left(\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)\right) \nonumber\\ &\qquad +\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)\right)e^{-t\mathcal{K}}\,dt,\nonumber \end{align} $$
$$ \begin{align} &\sum_{k\in S_{C}}e^{\mathcal{K}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-\mathcal{K}} \\ &\quad =\sum_{k\in S_{C}}\left(\frac{1}{2}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)+\frac{1}{2}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}h_{k}^{\oplus}e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}h_{k}^{\oplus}e^{-K_{k}^{\oplus}}\right)\right) \nonumber\\ &\qquad +\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)+\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{(1-t)K_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}\right)\right)\right)e^{-t\mathcal{K}}\,dt,\nonumber \end{align} $$
while the second is calculated using the commutators of the Propositions 5.2 and 5.4 to be
 $$ \begin{align} &e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{K}} - \left( H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right) \right) \nonumber\\ &\quad =\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right]e^{-t\mathcal{K}}\,dt = -\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{K}}\,dt , \end{align} $$
$$ \begin{align} &e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{K}} - \left( H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right) \right) \nonumber\\ &\quad =\int_{0}^{1}e^{t\mathcal{K}}\left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{k\in S_{C}}Q_{1}^{k}\left(h_{k}^{\oplus}\right)\right]e^{-t\mathcal{K}}\,dt = -\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{K}}\mathcal{E}_{1}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{K}}\,dt , \end{align} $$
which yields the claim.
5.3 Fixing the transformation kernels
With all the transformation identities determined, we now choose the transformation kernels
![]() $(K_{k}^{\oplus })_{k\in S_{C}}$
such that
$(K_{k}^{\oplus })_{k\in S_{C}}$
such that
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_{C}}H_{\text {int}}^{k}$
is diagonalized. For any choice of
$H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_{C}}H_{\text {int}}^{k}$
is diagonalized. For any choice of
![]() $(K_{k}^{\oplus })_{k\in S_{C}}$
, the Propositions 5.3 and 5.5 imply that
$(K_{k}^{\oplus })_{k\in S_{C}}$
, the Propositions 5.3 and 5.5 imply that
 $$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\text{int}}^{k}\right)e^{-\mathcal{K}} \nonumber\\ &\quad =\frac{1}{2}\sum_{k\in S_{C}}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)\nonumber \\ &\qquad +\frac{1}{2}\sum_{k\in S_{C}}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}\right)+H_{\operatorname{\mathrm{kin}}}^{\prime}+\text{error terms}. \end{align} $$
$$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\text{int}}^{k}\right)e^{-\mathcal{K}} \nonumber\\ &\quad =\frac{1}{2}\sum_{k\in S_{C}}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)\nonumber \\ &\qquad +\frac{1}{2}\sum_{k\in S_{C}}Q_{2}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}-e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}\right)+H_{\operatorname{\mathrm{kin}}}^{\prime}+\text{error terms}. \end{align} $$
In analogy with the bosonic case, we consider this expression to be diagonalized provided the
![]() $Q_{2}^{k}(\cdot )$
terms vanish, whence the diagonalization condition is that
$Q_{2}^{k}(\cdot )$
terms vanish, whence the diagonalization condition is that
which we note is the same as the diagonalization condition (equation (3.26)) of the exact bosonic quadratic Hamiltonian
Recalling the definitions of
![]() $h_k^{\oplus }$
,
$h_k^{\oplus }$
,
![]() $A_k^{\oplus }$
and
$A_k^{\oplus }$
and
![]() $B_k^{\oplus }$
from (4.11) and (4.7), we have
$B_k^{\oplus }$
from (4.11) and (4.7), we have
 $$ \begin{align*} h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus} =\left(\begin{array}{cc} h_k+P_{v_k} & \pm P_{v_{k}}\\ \pm P_k & h_k + P_{v_{k}}\\ \end{array}\right)>0. \end{align*} $$
$$ \begin{align*} h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus} =\left(\begin{array}{cc} h_k+P_{v_k} & \pm P_{v_{k}}\\ \pm P_k & h_k + P_{v_{k}}\\ \end{array}\right)>0. \end{align*} $$
So by Theorem 3.1, the choice
 $$ \begin{align*} K_{k}^{\oplus} & =-\frac{1}{2}\log\left(\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{\frac{1}{2}}\right)^{\frac{1}{2}}\right.\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\;\left.\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{-\frac{1}{2}}\right) \end{align*} $$
$$ \begin{align*} K_{k}^{\oplus} & =-\frac{1}{2}\log\left(\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{\frac{1}{2}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{\frac{1}{2}}\right)^{\frac{1}{2}}\right.\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\;\left.\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)^{-\frac{1}{2}}\right) \end{align*} $$
is the unique diagonalizing kernel for the Hamiltonian. In this form, it is, however, not easy to see how
![]() $K_{k}^{\oplus }$
acts, so we will proceed slightly differently: we define
$K_{k}^{\oplus }$
acts, so we will proceed slightly differently: we define
![]() $K_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
$K_{k}^{\oplus }:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
 $$ \begin{align} K_{k}^{\oplus}=\left(\begin{array}{cc} 0 & K_{k}\\ K_{k} & 0 \end{array}\right), \end{align} $$
$$ \begin{align} K_{k}^{\oplus}=\left(\begin{array}{cc} 0 & K_{k}\\ K_{k} & 0 \end{array}\right), \end{align} $$
where the operator
![]() $K_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
is given by
$K_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
is given by
 $$ \begin{align} K_{k}=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\Big(h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}}\Big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right)=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\Big(h_{k}^{2}+2P_{h_{k}^{\frac{1}{2}}v_{k}}\Big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right). \end{align} $$
$$ \begin{align} K_{k}=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\Big(h_{k}^{\frac{1}{2}}\left(h_{k}+2P_{v_{k}}\right)h_{k}^{\frac{1}{2}}\Big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right)=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\Big(h_{k}^{2}+2P_{h_{k}^{\frac{1}{2}}v_{k}}\Big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right). \end{align} $$
A kernel similar to
![]() $K_k$
also appeared in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. Note that
$K_k$
also appeared in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5, Reference Benedikter, Nam, Porta, Schlein and Seiringer6]. Note that
![]() $K_{k}$
is precisely the diagonalizer of Theorem 3.1 for the exact bosonic quadratic Hamiltonian
$K_{k}$
is precisely the diagonalizer of Theorem 3.1 for the exact bosonic quadratic Hamiltonian
rather than that of equation (5.21). Now we can verify that this
![]() $K_{k}^{\oplus }$
is, in fact, equal to the diagonalizing kernel:
$K_{k}^{\oplus }$
is, in fact, equal to the diagonalizing kernel:
Proposition 5.6. The operator
![]() $K_{k}^{\oplus }$
defined by the equations (5.22) and (5.23) satisfies
$K_{k}^{\oplus }$
defined by the equations (5.22) and (5.23) satisfies
 $$\begin{align*}e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}=e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}=\left(\begin{array}{cc} E_{k} & 0\\ 0 & E_{k} \end{array}\right) \end{align*}$$
$$\begin{align*}e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}=e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}=\left(\begin{array}{cc} E_{k} & 0\\ 0 & E_{k} \end{array}\right) \end{align*}$$
for
![]() $E_{k}=e^{-K_{k}}h_{k}e^{-K_{k}}$
.
$E_{k}=e^{-K_{k}}h_{k}e^{-K_{k}}$
.
Proof. It is easily verified that
![]() $e^{\pm K_{k}^{\oplus }}$
is given by
$e^{\pm K_{k}^{\oplus }}$
is given by
 $$ \begin{align} e^{\pm K_{k}^{\oplus}}=\left(\begin{array}{cc} \cosh\left(K_{k}\right) & \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right), \end{align} $$
$$ \begin{align} e^{\pm K_{k}^{\oplus}}=\left(\begin{array}{cc} \cosh\left(K_{k}\right) & \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right), \end{align} $$
and so
 $$ \begin{align} & e^{\pm K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus}\right)e^{\pm K_{k}^{\oplus}}\nonumber\\ &\quad =\left(\begin{array}{cc} \cosh\left(K_{k}\right) &\quad \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right)\left(\begin{array}{cc} h_{k}+P_{v_{k}} & \pm P_{v_{k}}\\ \pm P_{v_{k}} & h_{k}+P_{v_{k}} \end{array}\right)\left(\begin{array}{cc} \cosh\left(K_{k}\right) & \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right)\nonumber \\ &\quad =\frac{1}{2}\left(\begin{array}{cc} e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}+e^{-K_{k}}h_{k}e^{-K_{k}} & \pm\left(e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}-e^{-K_{k}}h_{k}e^{-K_{k}}\right)\\ \pm\left(e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}-e^{-K_{k}}h_{k}e^{-K_{k}}\right) & e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}+e^{-K_{k}}h_{k}e^{-K_{k}} \end{array}\right). \end{align} $$
$$ \begin{align} & e^{\pm K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus}\right)e^{\pm K_{k}^{\oplus}}\nonumber\\ &\quad =\left(\begin{array}{cc} \cosh\left(K_{k}\right) &\quad \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right)\left(\begin{array}{cc} h_{k}+P_{v_{k}} & \pm P_{v_{k}}\\ \pm P_{v_{k}} & h_{k}+P_{v_{k}} \end{array}\right)\left(\begin{array}{cc} \cosh\left(K_{k}\right) & \pm\sinh\left(K_{k}\right)\\ \pm\sinh\left(K_{k}\right) & \cosh\left(K_{k}\right) \end{array}\right)\nonumber \\ &\quad =\frac{1}{2}\left(\begin{array}{cc} e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}+e^{-K_{k}}h_{k}e^{-K_{k}} & \pm\left(e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}-e^{-K_{k}}h_{k}e^{-K_{k}}\right)\\ \pm\left(e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}-e^{-K_{k}}h_{k}e^{-K_{k}}\right) & e^{K_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{K_{k}}+e^{-K_{k}}h_{k}e^{-K_{k}} \end{array}\right). \end{align} $$
The condition
thus holds if and only if
which is the diagonalization condition for the bosonic Hamiltonian of equation (5.24). Theorem 3.1 asserts that this condition is satisfied for our choice of
![]() $K_{k}$
, and the claim follows.
$K_{k}$
, and the claim follows.
5.4 Full transformation of the bosonizable terms
With the above choice of transformation kernels, we thus conclude that
 $$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\text{int}}^{k}\right)e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+\text{error terms}\nonumber \\ &\qquad +\frac{1}{2}\sum_{k\in S_{C}}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)\nonumber\\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k}\left(\begin{array}{cc} E_{k}-h_{k} & 0\\ 0 & E_{k}-h_{k} \end{array}\right)+\text{error terms}, \end{align} $$
$$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\text{int}}^{k}\right)e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+\text{error terms}\nonumber \\ &\qquad +\frac{1}{2}\sum_{k\in S_{C}}Q_{1}^{k}\left(e^{K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}+B_{k}^{\oplus}\right)e^{K_{k}^{\oplus}}+e^{-K_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}-B_{k}^{\oplus}\right)e^{-K_{k}^{\oplus}}-2h_{k}^{\oplus}\right)\nonumber\\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k}\left(\begin{array}{cc} E_{k}-h_{k} & 0\\ 0 & E_{k}-h_{k} \end{array}\right)+\text{error terms}, \end{align} $$
and so we have succeeded in diagonalizing
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_{C}}H_{\text {int}}^{k}$
while simultanously decoupling the spaces
$H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_{C}}H_{\text {int}}^{k}$
while simultanously decoupling the spaces
![]() $\ell ^{2}\left(L_{\pm k}\right)\subset \ell ^{2}(L_{k}^{\pm })$
in a symmetric fashion. We still need to determine the exact form of the error terms, which we record in the following proposition:
$\ell ^{2}\left(L_{\pm k}\right)\subset \ell ^{2}(L_{k}^{\pm })$
in a symmetric fashion. We still need to determine the exact form of the error terms, which we record in the following proposition:
Proposition 5.7. Let
![]() $S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
$S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
![]() $\gamma \in (0,1]$
. Then the unitary transformation
$\gamma \in (0,1]$
. Then the unitary transformation
![]() $e^{\mathcal {K}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
with
$e^{\mathcal {K}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
with
![]() $\mathcal {K}$
defined by (5.2), (5.22), (5.23) satisfies
$\mathcal {K}$
defined by (5.2), (5.22), (5.23) satisfies
 $$ \begin{align*} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\operatorname{\mathrm{int}}}^{k}\right)e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k} (E_k^{\oplus} - h_k^{\oplus})\\ &\quad +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k}(A_k^\oplus(t))+\mathcal{E}_{2}^{k} (B_k^\oplus(t))\right)e^{-(1-t)\mathcal{K}}\,dt, \end{align*} $$
$$ \begin{align*} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\operatorname{\mathrm{int}}}^{k}\right)e^{-\mathcal{K}}=H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k} (E_k^{\oplus} - h_k^{\oplus})\\ &\quad +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k}(A_k^\oplus(t))+\mathcal{E}_{2}^{k} (B_k^\oplus(t))\right)e^{-(1-t)\mathcal{K}}\,dt, \end{align*} $$
where
![]() $\mathcal {E}_1(\cdot )$
,
$\mathcal {E}_1(\cdot )$
,
![]() $\mathcal {E}_2(\cdot )$
are defined in Proposition 5.2 and
$\mathcal {E}_2(\cdot )$
are defined in Proposition 5.2 and
 $$ \begin{align*}E_k^{\oplus} - h_k^{\oplus}= \left(\begin{array}{cc} E_{k}-h_{k} & 0\\ 0 & E_{k}-h_{k} \end{array}\right),\,\, A_{k}^\oplus (t) = \left(\begin{array}{cc} A_{k} (t ) & 0\\ 0 & A_{k} (t ) \end{array}\right),\,\, B_{k}^\oplus (t) = \left(\begin{array}{cc} 0 & B_{k} (t )\\ B_{k} (t ) & 0 \end{array}\right) \end{align*} $$
$$ \begin{align*}E_k^{\oplus} - h_k^{\oplus}= \left(\begin{array}{cc} E_{k}-h_{k} & 0\\ 0 & E_{k}-h_{k} \end{array}\right),\,\, A_{k}^\oplus (t) = \left(\begin{array}{cc} A_{k} (t ) & 0\\ 0 & A_{k} (t ) \end{array}\right),\,\, B_{k}^\oplus (t) = \left(\begin{array}{cc} 0 & B_{k} (t )\\ B_{k} (t ) & 0 \end{array}\right) \end{align*} $$
with
![]() $E_k= e^{-K_k} h_k e^{-K_k}$
and the operators
$E_k= e^{-K_k} h_k e^{-K_k}$
and the operators
![]() $A_{k} (t ),B_{k} (t ):\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
defined by
$A_{k} (t ),B_{k} (t ):\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
defined by
 $$ \begin{align*} A_{k} (t ) & =\frac{1}{2}\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}}\right)-h_{k}\\ B_{k} (t ) & =\frac{1}{2}\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right). \end{align*} $$
$$ \begin{align*} A_{k} (t ) & =\frac{1}{2}\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}}\right)-h_{k}\\ B_{k} (t ) & =\frac{1}{2}\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right). \end{align*} $$
Proof. By the Propositions 5.3 and 5.5, the error terms are
 $$ \begin{align*} & \sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}\right)+\sinh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(B_{k}^{\oplus}\right)-h_{k}^{\oplus}\right)\right)e^{-(1-t)\mathcal{K}}\,dt\\ &\quad +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}\right)+\cosh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(B_{k}^{\oplus}\right)\right)\right)e^{-(1-t)\mathcal{K}}\,dt, \end{align*} $$
$$ \begin{align*} & \sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k}\left(\cosh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}\right)+\sinh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(B_{k}^{\oplus}\right)-h_{k}^{\oplus}\right)\right)e^{-(1-t)\mathcal{K}}\,dt\\ &\quad +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{2}^{k}\left(\sinh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(h_{k}^{\oplus}+A_{k}^{\oplus}\right)+\cosh\left(\mathcal{A}_{tK_{k}^{\oplus}}\right)\left(B_{k}^{\oplus}\right)\right)\right)e^{-(1-t)\mathcal{K}}\,dt, \end{align*} $$
where we have reparametrized the integral by
![]() $t\mapsto 1-t$
to simplify the arguments of the
$t\mapsto 1-t$
to simplify the arguments of the
![]() $\mathcal {E}_{1}^{k}(\cdot )$
and
$\mathcal {E}_{1}^{k}(\cdot )$
and
![]() $\mathcal {E}_{2}^{k}(\cdot )$
operators. By (5.11), the arguments of
$\mathcal {E}_{2}^{k}(\cdot )$
operators. By (5.11), the arguments of
![]() $\mathcal {E}_{1}^{k}$
and
$\mathcal {E}_{1}^{k}$
and
![]() $\mathcal {E}_{2}^{k}$
in each term above equal
$\mathcal {E}_{2}^{k}$
in each term above equal
and
respectively. By the same identities that we used in the preceding proposition, it holds that
 $$ \begin{align} & e^{\pm tK_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus}\right)e^{\pm tK_{k}^{\oplus}}\\ &\quad =\frac{1}{2}\left(\begin{array}{cc} e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}} & \pm\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right)\\ \pm\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right) & e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}} \end{array}\right)\nonumber, \end{align} $$
$$ \begin{align} & e^{\pm tK_{k}^{\oplus}}\left(h_{k}^{\oplus}+A_{k}^{\oplus}\pm B_{k}^{\oplus}\right)e^{\pm tK_{k}^{\oplus}}\\ &\quad =\frac{1}{2}\left(\begin{array}{cc} e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}} & \pm\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right)\\ \pm\left(e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}\right) & e^{tK_{k}}\left(h_{k}+2P_{v_{k}}\right)e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}} \end{array}\right)\nonumber, \end{align} $$
and the claim follows.
6 Analysis of the exchange terms
In the preceding section, we accomplished a major qualitative goal of this paper, which was diagonalizing the bosonizable terms
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_C}H_{\text {int}}^{k}$
in an explicit, quasi-bosonic fashion. In this section, we begin the quantitative study of the quasi-bosonic expression in Proposition 5.7.
$H_{\operatorname {\mathrm {kin}}}^{\prime }+\sum _{k\in S_C}H_{\text {int}}^{k}$
in an explicit, quasi-bosonic fashion. In this section, we begin the quantitative study of the quasi-bosonic expression in Proposition 5.7.
The aim of this section is to estimate the
![]() $\mathcal {E}_{1}^{k}(\cdot )$
,
$\mathcal {E}_{1}^{k}(\cdot )$
,
![]() $\mathcal {E}_{2}^{k}(\cdot )$
operators, which enter in the error terms due to the presence of the exchange correction
$\mathcal {E}_{2}^{k}(\cdot )$
operators, which enter in the error terms due to the presence of the exchange correction
![]() $\varepsilon _{k,l}(\varphi ;\psi )$
in the quasi-bosonic commutation relations. We will therefore refer to them as exchange terms. Since these expressions are complicated, we thus devote three subsections to the analysis of them. In the first, we carry out a reduction procedure, in which we systematically consider the type of terms that can appear in the sums defining
$\varepsilon _{k,l}(\varphi ;\psi )$
in the quasi-bosonic commutation relations. We will therefore refer to them as exchange terms. Since these expressions are complicated, we thus devote three subsections to the analysis of them. In the first, we carry out a reduction procedure, in which we systematically consider the type of terms that can appear in the sums defining
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
for given
$\mathcal {E}_{2}^{k}(B)$
for given
![]() $A,B$
, and reduce these to simpler expressions, or schematic forms. In doing so, we will see that every term appearing in
$A,B$
, and reduce these to simpler expressions, or schematic forms. In doing so, we will see that every term appearing in
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
can for the purpose of estimation be sorted into one of four schematic forms. In the second subsection, we provide some basic commutator estimates associated with the four schematic forms, and in the final subsection we then carry out the quantitative analysis of these four forms to obtain the desired estimates of
$\mathcal {E}_{2}^{k}(B)$
can for the purpose of estimation be sorted into one of four schematic forms. In the second subsection, we provide some basic commutator estimates associated with the four schematic forms, and in the final subsection we then carry out the quantitative analysis of these four forms to obtain the desired estimates of
![]() $\mathcal {E}_{1}^{k}(\cdot )$
and
$\mathcal {E}_{1}^{k}(\cdot )$
and
![]() $\mathcal {E}_{2}^{k}(\cdot )$
.
$\mathcal {E}_{2}^{k}(\cdot )$
.
6.1 Reduction to simpler expressions
Recall that for
![]() $k\in S_C$
and symmetric operators
$k\in S_C$
and symmetric operators
![]() $A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, we already defined
$A,B:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, we already defined
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
in Proposition 5.2. Since these expressions are complicated, it is helpful to discuss the general structure of
$\mathcal {E}_{2}^{k}(B)$
in Proposition 5.2. Since these expressions are complicated, it is helpful to discuss the general structure of
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
. Consider the first term of
$\mathcal {E}_{2}^{k}(B)$
. Consider the first term of
![]() $\mathcal {E}_{1}^{k}(A)$
, which upon expansion is
$\mathcal {E}_{1}^{k}(A)$
, which upon expansion is
 $$ \begin{align} & \left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} \right\} \nonumber \\ &\quad =b_{k}^{\ast}(Ae_{p})\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} +\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} b_{k}^{\ast}(Ae_{p})\\ &\quad =b_{k}^{\ast}(Ae_{p})b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\varepsilon_{k,l}\left(e_{p},e_{q}\right)+b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\nonumber \\ &\qquad +b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{k}^{\ast}(Ae_{p})+\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)b_{k}^{\ast}(Ae_{p}),\nonumber \end{align} $$
$$ \begin{align} & \left\{ b_{k}^{\ast}(Ae_{p}),\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} \right\} \nonumber \\ &\quad =b_{k}^{\ast}(Ae_{p})\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} +\left\{ b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right),\varepsilon_{k,l}\left(e_{p},e_{q}\right)\right\} b_{k}^{\ast}(Ae_{p})\\ &\quad =b_{k}^{\ast}(Ae_{p})b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\varepsilon_{k,l}\left(e_{p},e_{q}\right)+b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\nonumber \\ &\qquad +b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{k}^{\ast}(Ae_{p})+\varepsilon_{k,l}\left(e_{p},e_{q}\right)b_{l}^{\ast}\left(K_{l}^{\oplus}e_{q}\right)b_{k}^{\ast}(Ae_{p}),\nonumber \end{align} $$
which we may expand further using
and then removing the delta on a case-by-case basis. This causes the sums over
![]() $p\in L_{k}^{\pm }$
and
$p\in L_{k}^{\pm }$
and
![]() $q\in L_{l}^{\pm }$
of any of these terms to reduce to one of the schematic forms
$q\in L_{l}^{\pm }$
of any of these terms to reduce to one of the schematic forms
 $$ \begin{align} &\sum_{p\in S}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}},\quad\sum_{p\in S}b_{k}^{\natural}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right),\quad \nonumber\\ & \quad \sum_{p\in S}\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right) \end{align} $$
$$ \begin{align} &\sum_{p\in S}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}},\quad\sum_{p\in S}b_{k}^{\natural}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right),\quad \nonumber\\ & \quad \sum_{p\in S}\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right) \end{align} $$
subject to the following: S is a subset of
![]() $L_{k}^{\pm }\cap L_{l}^{\pm }$
,
$L_{k}^{\pm }\cap L_{l}^{\pm }$
,
![]() $b_{k}^{\natural }$
can denote either
$b_{k}^{\natural }$
can denote either
![]() $b_{k}$
or
$b_{k}$
or
![]() $b_{k}^{\ast }$
,
$b_{k}^{\ast }$
,
![]() $\varepsilon _{k,l}(e_{p},e_{q})$
may instead be
$\varepsilon _{k,l}(e_{p},e_{q})$
may instead be
![]() $\varepsilon _{l,k}(e_{q},e_{p})=\varepsilon _{k,l}(e_{p},e_{q})^{\ast }$
, T denotes either A or B, the terms
$\varepsilon _{l,k}(e_{q},e_{p})=\varepsilon _{k,l}(e_{p},e_{q})^{\ast }$
, T denotes either A or B, the terms
![]() $b_{k}^{\natural }(Te_{p})$
and
$b_{k}^{\natural }(Te_{p})$
and
![]() $b_{l}^{\natural }(K_{l}^{\oplus }e_{q})$
may be interchanged, the notation
$b_{l}^{\natural }(K_{l}^{\oplus }e_{q})$
may be interchanged, the notation
 $$ \begin{align} \tilde{c}_{p}=\begin{cases} c_{p} & p\in B_{F}^{c}\\ c_{p}^{\ast} & p\in B_{F} \end{cases} \end{align} $$
$$ \begin{align} \tilde{c}_{p}=\begin{cases} c_{p} & p\in B_{F}^{c}\\ c_{p}^{\ast} & p\in B_{F} \end{cases} \end{align} $$
encodes the correct type of creation/annihilation operator depending on whether p corresponds to a hole state or an excited state, and
![]() $p_{1},p_{2},p_{3},p_{4}$
denote indices which depend on p.
$p_{1},p_{2},p_{3},p_{4}$
denote indices which depend on p.
The same decomposition holds for every term appearing in either
![]() $\mathcal {E}_{1}^{k}(A)$
or
$\mathcal {E}_{1}^{k}(A)$
or
![]() $\mathcal {E}_{2}^{k}(B)$
, so we must consider the forms of (6.3).
$\mathcal {E}_{2}^{k}(B)$
, so we must consider the forms of (6.3).
The only important feature of the dependency that the
![]() $p_{i}$
have with respect to p is that regardless of the term, when summing over
$p_{i}$
have with respect to p is that regardless of the term, when summing over
![]() $p\in S$
,
$p\in S$
,
![]() $p_{i}$
ranges either exclusively over excited states (i.e.,
$p_{i}$
ranges either exclusively over excited states (i.e.,
![]() $p_{i}\in L_{k}^{\pm }$
) or exclusively over hole states (i.e.,
$p_{i}\in L_{k}^{\pm }$
) or exclusively over hole states (i.e.,
![]() $p_{i}\in \left(L_{k}-k\right)\cup \left(L_{-k}+k\right)$
or the analogous set for
$p_{i}\in \left(L_{k}-k\right)\cup \left(L_{-k}+k\right)$
or the analogous set for
![]() $L_{l}^{\pm }$
), and that the assignments
$L_{l}^{\pm }$
), and that the assignments
![]() $p\mapsto p_{i}$
(for a given term) are injective. (Additionally,
$p\mapsto p_{i}$
(for a given term) are injective. (Additionally,
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
will always be excited states.)
$p_{2}$
will always be excited states.)
Therefore, when estimating, we can always expand the sum to either all of
![]() $B_{F}$
or all of
$B_{F}$
or all of
![]() $B_{F}^{c}$
, which is why the exact identities of S and the
$B_{F}^{c}$
, which is why the exact identities of S and the
![]() $p_{i}$
are of no importance to the estimation. For example,
$p_{i}$
are of no importance to the estimation. For example,
 $$ \begin{align} \left|\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}\Psi\right\rangle \right| \leq\sum_{p\in S}\left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \leq\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert ^{2}} \le \left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle \end{align} $$
$$ \begin{align} \left|\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}\Psi\right\rangle \right| \leq\sum_{p\in S}\left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \leq\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert ^{2}} \le \left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle \end{align} $$
independently of S,
![]() $p_{3}$
and
$p_{3}$
and
![]() $p_{4}$
. Here, the two situations when both
$p_{4}$
. Here, the two situations when both
![]() $p_{3}$
and
$p_{3}$
and
![]() $p_{4}$
range over excited states, and when both
$p_{4}$
range over excited states, and when both
![]() $p_{3}$
and
$p_{3}$
and
![]() $p_{4}$
range over hole states, can be treated similarly thanks to the particle-hole symmetry (1.13).
$p_{4}$
range over hole states, can be treated similarly thanks to the particle-hole symmetry (1.13).
Discussion of estimation strategy
We conclude that both
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
reduce to sums over
$\mathcal {E}_{2}^{k}(B)$
reduce to sums over
![]() $l\in S_{C}$
of finitely many terms of the schematic forms of equation (6.3), so it suffices to estimate these. To this end, we must first perform some additional algebraic manipulation.
$l\in S_{C}$
of finitely many terms of the schematic forms of equation (6.3), so it suffices to estimate these. To this end, we must first perform some additional algebraic manipulation.
To motivate our goal, let us first derive a simple but insufficent estimate for one of these terms:
Using
![]() $\left\Vert c_{p}\right\Vert _{\text {Op}}=1$
, Proposition 4.4 and the Cauchy–Schwarz inequality, we find that
$\left\Vert c_{p}\right\Vert _{\text {Op}}=1$
, Proposition 4.4 and the Cauchy–Schwarz inequality, we find that
 $$ \begin{align} & \sum_{p\in S}\left|\left\langle \Psi,b_{k}^{\ast}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\Psi\right\rangle \right| \leq\sum_{p\in S}\left\Vert b_{k}\left(Te_{p_{1}}\right)\Psi\right\Vert \left\Vert b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\Psi\right\Vert \\ &\quad \leq\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \leq\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}T\right\Vert _{\operatorname{\mathrm{HS}}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \nonumber \end{align} $$
$$ \begin{align} & \sum_{p\in S}\left|\left\langle \Psi,b_{k}^{\ast}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{4}}b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\Psi\right\rangle \right| \leq\sum_{p\in S}\left\Vert b_{k}\left(Te_{p_{1}}\right)\Psi\right\Vert \left\Vert b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\Psi\right\Vert \\ &\quad \leq\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \leq\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}T\right\Vert _{\operatorname{\mathrm{HS}}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \nonumber \end{align} $$
for any
![]() $\Psi \in \mathcal {H}_{N}$
. To get a feeling for the quality of this estimate, we must know what to expect of the quantities on the right-hand side. We will see in the next sections that
$\Psi \in \mathcal {H}_{N}$
. To get a feeling for the quality of this estimate, we must know what to expect of the quantities on the right-hand side. We will see in the next sections that
![]() $\big\Vert (h_{l}^{\oplus })^{-\frac {1}{2}}K_{l}^{\oplus }\big\Vert _{\operatorname {\mathrm {HS}}} \leq O(k_{F}^{-\frac {1}{3} + \epsilon })$
. In general, what will take the place of T will be the
$\big\Vert (h_{l}^{\oplus })^{-\frac {1}{2}}K_{l}^{\oplus }\big\Vert _{\operatorname {\mathrm {HS}}} \leq O(k_{F}^{-\frac {1}{3} + \epsilon })$
. In general, what will take the place of T will be the
![]() $A_{k} (t )$
and
$A_{k} (t )$
and
![]() $B_{k} (t )$
operators we defined in the last section, but as a simple example we consider
$B_{k} (t )$
operators we defined in the last section, but as a simple example we consider
 $$ \begin{align} T= \left(\begin{array}{cc} P_{v_{k}} & 0\\ 0 & P_{v_{k}} \end{array}\right),\quad P_{v_{k}} = |v_k\rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \in \ell^{2}(L_{k}) \end{align} $$
$$ \begin{align} T= \left(\begin{array}{cc} P_{v_{k}} & 0\\ 0 & P_{v_{k}} \end{array}\right),\quad P_{v_{k}} = |v_k\rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p} \in \ell^{2}(L_{k}) \end{align} $$
for which
 $$ \begin{align} \left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}T\right\Vert _{\operatorname{\mathrm{HS}}} & =2\left\Vert h_{k}^{-\frac{1}{2}}P_{v_{k}}\right\Vert _{\operatorname{\mathrm{HS}}}=2\sqrt{\operatorname{\mathrm{tr}}\left(P_{v_{k}}h_{k}^{-1}P_{v_{k}}\right)}\\ & =2\left\Vert v_{k}\right\Vert \sqrt{\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle }=\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|^{\frac 1 2} \sqrt{\sum_{p\in L_{k}}\lambda_{k,p}^{-1}}\leq O\big(k_{F}^{\frac{1}{2}} \big)\nonumber \end{align} $$
$$ \begin{align} \left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}T\right\Vert _{\operatorname{\mathrm{HS}}} & =2\left\Vert h_{k}^{-\frac{1}{2}}P_{v_{k}}\right\Vert _{\operatorname{\mathrm{HS}}}=2\sqrt{\operatorname{\mathrm{tr}}\left(P_{v_{k}}h_{k}^{-1}P_{v_{k}}\right)}\\ & =2\left\Vert v_{k}\right\Vert \sqrt{\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle }=\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|^{\frac 1 2} \sqrt{\sum_{p\in L_{k}}\lambda_{k,p}^{-1}}\leq O\big(k_{F}^{\frac{1}{2}} \big)\nonumber \end{align} $$
when
![]() $|k|\sim 1$
. Here, we used
$|k|\sim 1$
. Here, we used
![]() $|L_k|\le C|k| k_F^2$
and the bound
$|L_k|\le C|k| k_F^2$
and the bound
![]() $\sum _{p\in L_{k}}\lambda _{k,p}^{-1}\leq Ck_{F}$
from Proposition A.2. Thus, for any state satisfying
$\sum _{p\in L_{k}}\lambda _{k,p}^{-1}\leq Ck_{F}$
from Proposition A.2. Thus, for any state satisfying
![]() $\left\langle \Psi ,H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F)$
(c.f. Theorem 1.2), the overall estimate for the right side of (6.7) is
$\left\langle \Psi ,H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F)$
(c.f. Theorem 1.2), the overall estimate for the right side of (6.7) is
![]() $O(k_{F}^{\frac {7}{6} + \epsilon })$
which is insufficient as the correlation energy is of order
$O(k_{F}^{\frac {7}{6} + \epsilon })$
which is insufficient as the correlation energy is of order
![]() $k_F$
.
$k_F$
.
The technical issue with the estimation in (6.7) lies in only using that
![]() $\left\Vert c_{p}\right\Vert _{\text {Op}}=1$
, for we may get better bounds by using
$\left\Vert c_{p}\right\Vert _{\text {Op}}=1$
, for we may get better bounds by using
![]() $\left\langle \Psi ,\mathcal {N}_{E} H^{\prime }_{\mathrm {kin}}\Psi \right\rangle $
instead of
$\left\langle \Psi ,\mathcal {N}_{E} H^{\prime }_{\mathrm {kin}}\Psi \right\rangle $
instead of
![]() $\left\langle \Psi ,H^{\prime }_{\mathrm {kin}}\Psi \right\rangle $
. For example,
$\left\langle \Psi ,H^{\prime }_{\mathrm {kin}}\Psi \right\rangle $
. For example,
 $$ \begin{align} &=\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\ast}\left(Te_{p_{1}}\right)b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{p\in S}\left\Vert b_{k}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle } \end{align} $$
$$ \begin{align} &=\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\ast}\left(Te_{p_{1}}\right)b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{p\in S}\left\Vert b_{k}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle } \end{align} $$
 $$\begin{align*} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\sqrt{\sum_{p\in S}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{q}\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle }\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\nonumber \\ & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\sqrt{\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\end{align*}$$
$$\begin{align*} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\sqrt{\sum_{p\in S}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{q}\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}H_{\operatorname{\mathrm{kin}}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle }\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\nonumber \\ & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\sqrt{\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\end{align*}$$
where we used that
![]() $\left[\tilde {c}_{p},b_{k}(\cdot )\right]=0$
(as we will see in Proposition 6.1 below) and momentarily looked ahead to the definition (6.30) for
$\left[\tilde {c}_{p},b_{k}(\cdot )\right]=0$
(as we will see in Proposition 6.1 below) and momentarily looked ahead to the definition (6.30) for
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime \left(\pm 1\right)}$
and Lemma 6.6 (we take supremum over
$H_{\operatorname {\mathrm {kin}}}^{\prime \left(\pm 1\right)}$
and Lemma 6.6 (we take supremum over
![]() $p_4$
and sum over
$p_4$
and sum over
![]() $p_3$
to get the second inequality). Considering again the example in (6.8), we find
$p_3$
to get the second inequality). Considering again the example in (6.8), we find
 $$ \begin{align} \max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert =\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\left\Vert h_{k}^{-\frac{1}{2}}v_{k}\right\Vert =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sqrt{\sum_{k\in L_{k}}\lambda_{k,p}^{-1}}\leq O(k_{F}^{-\frac{1}{2}}). \end{align} $$
$$ \begin{align} \max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert =\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\left\Vert h_{k}^{-\frac{1}{2}}v_{k}\right\Vert =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sqrt{\sum_{k\in L_{k}}\lambda_{k,p}^{-1}}\leq O(k_{F}^{-\frac{1}{2}}). \end{align} $$
Thus, for any state satisfying
![]() $\left\langle \Psi ,H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F)$
and
$\left\langle \Psi ,H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F)$
and
![]() $\left\langle \Psi ,\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F^2)$
(c.f. Theorem 1.2), the right side of (6.10) is thus bounded by
$\left\langle \Psi ,\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi \right\rangle \le O(k_F^2)$
(c.f. Theorem 1.2), the right side of (6.10) is thus bounded by
![]() $O(k_{F}^{ \frac {2}{3} + \epsilon })$
, which is much smaller than the correlation energy.
$O(k_{F}^{ \frac {2}{3} + \epsilon })$
, which is much smaller than the correlation energy.
Our goal is, therefore, to reduce the schematic forms of equation (6.3) to those of the form
![]() $\sum _{p\in S}\tilde {c}_{p_{3}}^{\ast }b_{k}^{\natural }(Te_{p_{1}})b_{l}^{\natural }(K_{l}^{\oplus }e_{p_{2}})\tilde {c}_{p_{4}}$
, which we may then estimate as above. While
$\sum _{p\in S}\tilde {c}_{p_{3}}^{\ast }b_{k}^{\natural }(Te_{p_{1}})b_{l}^{\natural }(K_{l}^{\oplus }e_{p_{2}})\tilde {c}_{p_{4}}$
, which we may then estimate as above. While
![]() $\left[\tilde {c}_{p},b_{k}(\cdot )\right]=0$
, it is generally the case that
$\left[\tilde {c}_{p},b_{k}(\cdot )\right]=0$
, it is generally the case that
![]() $\left[\tilde {c}_{p},b_{k}^{\ast }(\cdot )\right]\neq 0$
, so this will also introduce additional commutator terms which we must then estimate separately.
$\left[\tilde {c}_{p},b_{k}^{\ast }(\cdot )\right]\neq 0$
, so this will also introduce additional commutator terms which we must then estimate separately.
Taking into account whether
![]() $b_{k}^{\natural }=b_{k}$
or
$b_{k}^{\natural }=b_{k}$
or
![]() $b_{k}^{\natural }=b_{k}^{\ast }$
, the schematic forms of equation (6.3) are either of the form (supressing the summation, the arguments and the subscripts for brevity)
$b_{k}^{\natural }=b_{k}^{\ast }$
, the schematic forms of equation (6.3) are either of the form (supressing the summation, the arguments and the subscripts for brevity)
or reduce to one of these by taking the adjoint, which as we will estimate,
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
as bilinear forms does not matter. Using that commutators of the form
$\mathcal {E}_{2}^{k}(B)$
as bilinear forms does not matter. Using that commutators of the form
![]() $\left[b,\tilde {c}\right]$
,
$\left[b,\tilde {c}\right]$
,
![]() $\left[b^{\ast },\tilde {c}^{\ast }\right]$
and
$\left[b^{\ast },\tilde {c}^{\ast }\right]$
and
![]() $\left[b,\left[b,\tilde {c}^{\ast }\right]\right]$
vanish (verified below), these schematic forms reduce to
$\left[b,\left[b,\tilde {c}^{\ast }\right]\right]$
vanish (verified below), these schematic forms reduce to
 $$ \begin{align} b^{\ast}b^{\ast}\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}b^{\ast}b^{\ast}\tilde{c} ,\nonumber \\ b^{\ast}b\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}b^{\ast}b\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c}+\left[b^{\ast},\left[b,\tilde{c}^{\ast}\right]\right]\tilde{c},\nonumber \\ bb^{\ast}\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}bb^{\ast}\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c},\nonumber \\ bb\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}bb\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c},\\ b^{\ast}\tilde{c}^{\ast}\tilde{c}b & =\tilde{c}^{\ast}b^{\ast}b\tilde{c},\nonumber \\ b\tilde{c}^{\ast}\tilde{c}b & =\tilde{c}^{\ast}bb\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c},\nonumber \\ b\tilde{c}^{\ast}\tilde{c}b^{\ast} & =\tilde{c}^{\ast}bb^{\ast}\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c}+\tilde{c}^{\ast}b\left[\tilde{c},b^{\ast}\right]+\left[b,\tilde{c}^{\ast}\right]\left[\tilde{c},b^{\ast}\right].\nonumber \end{align} $$
$$ \begin{align} b^{\ast}b^{\ast}\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}b^{\ast}b^{\ast}\tilde{c} ,\nonumber \\ b^{\ast}b\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}b^{\ast}b\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c}+\left[b^{\ast},\left[b,\tilde{c}^{\ast}\right]\right]\tilde{c},\nonumber \\ bb^{\ast}\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}bb^{\ast}\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c},\nonumber \\ bb\tilde{c}^{\ast}\tilde{c} & =\tilde{c}^{\ast}bb\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c},\\ b^{\ast}\tilde{c}^{\ast}\tilde{c}b & =\tilde{c}^{\ast}b^{\ast}b\tilde{c},\nonumber \\ b\tilde{c}^{\ast}\tilde{c}b & =\tilde{c}^{\ast}bb\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b\tilde{c},\nonumber \\ b\tilde{c}^{\ast}\tilde{c}b^{\ast} & =\tilde{c}^{\ast}bb^{\ast}\tilde{c}+\left[b,\tilde{c}^{\ast}\right]b^{\ast}\tilde{c}+\tilde{c}^{\ast}b\left[\tilde{c},b^{\ast}\right]+\left[b,\tilde{c}^{\ast}\right]\left[\tilde{c},b^{\ast}\right].\nonumber \end{align} $$
Reintroducing the
![]() $b^{\natural }$
notation outside the commutators and using once more our freedom to take adjoints, we find that every term on the right-hand sides of the two equations above takes one of the four schematic forms
$b^{\natural }$
notation outside the commutators and using once more our freedom to take adjoints, we find that every term on the right-hand sides of the two equations above takes one of the four schematic forms
These are the final forms which we will explicitly estimate.
6.2 Preliminary commutator estimates
In addition to the general estimates which we derived at the start of this section, we will also need estimates on the commutator terms which appear in the schematic forms of equation (6.23), which we now derive. First, we must, however, verify that the commutators
![]() $\left[b,\tilde {c}\right]$
,
$\left[b,\tilde {c}\right]$
,
![]() $\left[b^{\ast },\tilde {c}^{\ast }\right]$
and
$\left[b^{\ast },\tilde {c}^{\ast }\right]$
and
![]() $\left[b,\left[b,\tilde {c}^{\ast }\right]\right]$
vanish, which we relied upon in our reduction procedure:
$\left[b,\left[b,\tilde {c}^{\ast }\right]\right]$
vanish, which we relied upon in our reduction procedure:
Proposition 6.1. For all
![]() $k,l\in \mathbb {Z}_{+}^{3}$
,
$k,l\in \mathbb {Z}_{+}^{3}$
,
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
![]() $\psi \in \ell ^{2}\left(L_{l}^{\pm }\right)$
and
$\psi \in \ell ^{2}\left(L_{l}^{\pm }\right)$
and
![]() $p\in \mathbb {Z}^{3}$
it holds that
$p\in \mathbb {Z}^{3}$
it holds that
Proof. We compute from the definitions that for any
![]() $q\in L_{k}^{\pm }$
,
$q\in L_{k}^{\pm }$
,
 $$ \begin{align} \left[b_{\overline{k,q}},\tilde{c}_{p}\right] & =\left[c_{\overline{q-k}}^{\ast}c_{q},\tilde{c}_{p}\right]=c_{\overline{q-k}}^{\ast}\left\{ c_{q},\tilde{c}_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},\tilde{c}_{p}\right\} c_{q}\nonumber \\ & =\begin{cases} c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}\right\} c_{q} ,& p\in B_{F}^{c}\nonumber\\ c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}^{\ast}\right\} c_{q} ,& p\in B_{F} \end{cases}\\ & =0 \end{align} $$
$$ \begin{align} \left[b_{\overline{k,q}},\tilde{c}_{p}\right] & =\left[c_{\overline{q-k}}^{\ast}c_{q},\tilde{c}_{p}\right]=c_{\overline{q-k}}^{\ast}\left\{ c_{q},\tilde{c}_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},\tilde{c}_{p}\right\} c_{q}\nonumber \\ & =\begin{cases} c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}\right\} c_{q} ,& p\in B_{F}^{c}\nonumber\\ c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}^{\ast}\right\} c_{q} ,& p\in B_{F} \end{cases}\\ & =0 \end{align} $$
as all anticommutators on the second line vanish either directly by the CAR or by disjointness of
![]() $B_{F}$
and
$B_{F}$
and
![]() $B_{F}^{c}$
. By linearity,
$B_{F}^{c}$
. By linearity,
![]() $\left[b_{k}(\varphi ),\tilde {c}_{p}\right]=0$
, and
$\left[b_{k}(\varphi ),\tilde {c}_{p}\right]=0$
, and
![]() $\left[b_{k}^{\ast }(\varphi ),\tilde {c}_{p}^{\ast }\right]=-\left[b_{k}(\varphi ),\tilde {c}_{p}\right]^{\ast }=0$
.
$\left[b_{k}^{\ast }(\varphi ),\tilde {c}_{p}^{\ast }\right]=-\left[b_{k}(\varphi ),\tilde {c}_{p}\right]^{\ast }=0$
.
For the double commutator, we first compute
![]() $[b_{\overline {k,q}},\tilde {c}_{p}^{\ast }]$
. As above, we find
$[b_{\overline {k,q}},\tilde {c}_{p}^{\ast }]$
. As above, we find
 $$\begin{align*}\left[b_{\overline{k,q}},\tilde{c}_{p}^{\ast}\right] =\begin{cases} c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}^{\ast}\right\} c_{q} ,& p\in B_{F}^{c}\\ c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}\right\} c_{q}, & p\in B_{F} \end{cases} =\begin{cases} \delta_{q,p}\tilde{c}_{\overline{q-k}} ,& p\in B_{F}^{c}\\ -\delta_{\overline{q-k},p}\tilde{c}_{q}, & p\in B_{F} \end{cases}\end{align*}$$
$$\begin{align*}\left[b_{\overline{k,q}},\tilde{c}_{p}^{\ast}\right] =\begin{cases} c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}^{\ast}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}^{\ast}\right\} c_{q} ,& p\in B_{F}^{c}\\ c_{\overline{q-k}}^{\ast}\left\{ c_{q},c_{p}\right\} -\left\{ c_{\overline{q-k}}^{\ast},c_{p}\right\} c_{q}, & p\in B_{F} \end{cases} =\begin{cases} \delta_{q,p}\tilde{c}_{\overline{q-k}} ,& p\in B_{F}^{c}\\ -\delta_{\overline{q-k},p}\tilde{c}_{q}, & p\in B_{F} \end{cases}\end{align*}$$
so
 $$ \begin{align} \left[b_{k}(\varphi ),\tilde{c}_{p}^{\ast}\right] & =\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle \left[b_{\overline{k,q}},\tilde{c}_{p}^{\ast}\right]=\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle \begin{cases} \delta_{q,p}\tilde{c}_{\overline{q-k}} & p\in B_{F}^{c} \nonumber\\ -\delta_{\overline{q-k},p}\tilde{c}_{q} & p\in B_{F} \end{cases}\\ & =1_{L_{k}^{\pm}}(p)\left\langle \varphi,e_{p}\right\rangle \tilde{c}_{\overline{p-k}}-1_{L_{k}-k}(p)\left\langle \varphi,e_{p+k}\right\rangle \tilde{c}_{p+k}-1_{L_{k}+k}(p)\left\langle \varphi,e_{p-k}\right\rangle \tilde{c}_{p-k}, \end{align} $$
$$ \begin{align} \left[b_{k}(\varphi ),\tilde{c}_{p}^{\ast}\right] & =\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle \left[b_{\overline{k,q}},\tilde{c}_{p}^{\ast}\right]=\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,e_{q}\right\rangle \begin{cases} \delta_{q,p}\tilde{c}_{\overline{q-k}} & p\in B_{F}^{c} \nonumber\\ -\delta_{\overline{q-k},p}\tilde{c}_{q} & p\in B_{F} \end{cases}\\ & =1_{L_{k}^{\pm}}(p)\left\langle \varphi,e_{p}\right\rangle \tilde{c}_{\overline{p-k}}-1_{L_{k}-k}(p)\left\langle \varphi,e_{p+k}\right\rangle \tilde{c}_{p+k}-1_{L_{k}+k}(p)\left\langle \varphi,e_{p-k}\right\rangle \tilde{c}_{p-k}, \end{align} $$
where
![]() $1_{S}(\cdot )$
denotes the indicator function of a set S. Observing that
$1_{S}(\cdot )$
denotes the indicator function of a set S. Observing that
![]() $\left[b_{k}(\varphi ),\tilde {c}_{p}^{\ast }\right]$
is a linear combination of
$\left[b_{k}(\varphi ),\tilde {c}_{p}^{\ast }\right]$
is a linear combination of
![]() $\tilde {c}_{p}$
terms, we conclude that
$\tilde {c}_{p}$
terms, we conclude that
![]() $\left[b_{l}(\psi ),\left[b_{k}(\varphi ),\tilde {c}_{p}^{\ast }\right]\right]=0$
by the first part.
$\left[b_{l}(\psi ),\left[b_{k}(\varphi ),\tilde {c}_{p}^{\ast }\right]\right]=0$
by the first part.
We now move into the estimation of the nonvanishing commutators. We begin with the single commutator; we state the estimate and make a remark:
Proposition 6.2. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, sequences
$k\in \mathbb {Z}_{+}^{3}$
, sequences
![]() $\left(\varphi _{p}\right)_{p\in \mathbb {Z}^{3}}\in \ell ^{2}(L_{k}^{\pm })$
and
$\left(\varphi _{p}\right)_{p\in \mathbb {Z}^{3}}\in \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
 $$ \begin{align*} \sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} & \leq3\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}\\ \sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{k}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} & \leq4\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*} $$
$$ \begin{align*} \sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} & \leq3\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}\\ \sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{k}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} & \leq4\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*} $$
Remark 6.1. The statement may appear overly general in that it involves general sequences
![]() $(\varphi_{p})_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}(L_{k}^{\pm })$
rather than the explicit vectors
$(\varphi_{p})_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}(L_{k}^{\pm })$
rather than the explicit vectors
![]() $(Te_{p_{1}})_{p\in S}\subset \ell ^{2}(L_{k}^{\pm })$
that we must consider. The point of the generality is, however, only to avoid having to explicitly state the dependencies of the set S and the
$(Te_{p_{1}})_{p\in S}\subset \ell ^{2}(L_{k}^{\pm })$
that we must consider. The point of the generality is, however, only to avoid having to explicitly state the dependencies of the set S and the
![]() $p_{i}$
’s of each possible schematic form, as independently of these it is easy to see that a sum such as
$p_{i}$
’s of each possible schematic form, as independently of these it is easy to see that a sum such as
![]() $\sum _{p\in S}\left\Vert [\tilde {c}_{p_{3}},b_{k}^{\ast }(Te_{p_{1}})]\Psi \right\Vert ^{2}$
can always be cast into the form in the statement.
$\sum _{p\in S}\left\Vert [\tilde {c}_{p_{3}},b_{k}^{\ast }(Te_{p_{1}})]\Psi \right\Vert ^{2}$
can always be cast into the form in the statement.
Proof. Taking the adjoint of equation (6.17) yields
and so we can for any
![]() $\Psi \in \mathcal {H}_{N}$
estimate by the (squared) triangle inequality, using also that
$\Psi \in \mathcal {H}_{N}$
estimate by the (squared) triangle inequality, using also that
![]() $L_{k}^{\pm }$
and
$L_{k}^{\pm }$
and
![]() $\left(L_{k}-k\right)\cap \left(L_{-k}+k\right)$
are disjoint and
$\left(L_{k}-k\right)\cap \left(L_{-k}+k\right)$
are disjoint and
![]() $\left\Vert \tilde {c}_{p}^{\ast }\right\Vert _{\text {Op}}=1$
, that
$\left\Vert \tilde {c}_{p}^{\ast }\right\Vert _{\text {Op}}=1$
, that
 $$ \begin{align} &\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} \nonumber \\ &\leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2} +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p+k}^{\ast}\Psi\right\Vert ^{2} +2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p-k}^{\ast}\Psi\right\Vert ^{2}\nonumber \\ & \leq\left(\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}+2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}+2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2} \nonumber\\ & \leq\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}+2\sum_{p\in L_{k}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}+2\sum_{p\in L_{-k}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}\nonumber \\ & =3\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}, \end{align} $$
$$ \begin{align} &\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} \nonumber \\ &\leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2} +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p+k}^{\ast}\Psi\right\Vert ^{2} +2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p-k}^{\ast}\Psi\right\Vert ^{2}\nonumber \\ & \leq\left(\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}+2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}+2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2} \nonumber\\ & \leq\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}+2\sum_{p\in L_{k}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}+2\sum_{p\in L_{-k}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}\nonumber \\ & =3\left(\sum_{p\in L_{k}^{\pm}}\max_{q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\Vert \Psi\right\Vert ^{2}, \end{align} $$
which implies the first estimate. For the second estimate, we find in a similar manner (now directly from equation (6.17)) that
 $$ \begin{align} &\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{k}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} \leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{\overline{p-k}}\Psi\right\Vert ^{2} +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p+k}\Psi\right\Vert ^{2} \nonumber \\ &\qquad +2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p-k}\Psi\right\Vert ^{2} \nonumber\\ &\quad \leq\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert \tilde{c}_{\overline{p-k}}\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}-k}\left\Vert \tilde{c}_{p+k}\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}+k}\left\Vert \tilde{c}_{p-k}\Psi\right\Vert ^{2}\right)\nonumber \\ &\quad =\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert c_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}}\left\Vert c_{p}\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}}\left\Vert c_{p}\Psi\right\Vert ^{2}\right)\nonumber \\ &\quad \leq4\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align} $$
$$ \begin{align} &\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{k}\left(\varphi_{p}\right)\right]\Psi\right\Vert ^{2} \leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{\overline{p-k}}\Psi\right\Vert ^{2} +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p+k}\Psi\right\Vert ^{2} \nonumber \\ &\qquad +2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \tilde{c}_{p-k}\Psi\right\Vert ^{2} \nonumber\\ &\quad \leq\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert \tilde{c}_{\overline{p-k}}\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}-k}\left\Vert \tilde{c}_{p+k}\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}+k}\left\Vert \tilde{c}_{p-k}\Psi\right\Vert ^{2}\right)\nonumber \\ &\quad =\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert c_{\overline{p-k}}^{\ast}\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}}\left\Vert c_{p}\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}}\left\Vert c_{p}\Psi\right\Vert ^{2}\right)\nonumber \\ &\quad \leq4\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align} $$
Lastly, we estimate the double commutator:
Proposition 6.3. For all
![]() $k,l\in \mathbb {Z}_{+}^{3}$
, sequences
$k,l\in \mathbb {Z}_{+}^{3}$
, sequences
![]() $\left(\varphi _{p}\right)_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}(L_{k}^{\pm })$
and
$\left(\varphi _{p}\right)_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}(L_{k}^{\pm })$
and
![]() $\left(\psi _{p}\right)_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}\left(L_{l}^{\pm }\right)$
, and
$\left(\psi _{p}\right)_{p\in \mathbb {Z}^{3}}\subset \ell ^{2}\left(L_{l}^{\pm }\right)$
, and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
 $$\begin{align*}\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\leq12\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\psi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*}$$
$$\begin{align*}\sum_{p\in\mathbb{Z}^{3}}\left\Vert \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\leq12\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\psi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align*}$$
Proof. From (6.18), we have that
 $$ \begin{align} \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right] & =1_{L_{k}^{\pm}}(p)\left\langle e_{p},\varphi\right\rangle \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]-1_{L_{k}-k}(p)\left\langle e_{p+k},\varphi\right\rangle \left[\tilde{c}_{p+k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\\ &\quad -1_{L_{k}+k}(p)\left\langle e_{p-k},\varphi\right\rangle \left[\tilde{c}_{p-k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\nonumber, \end{align} $$
$$ \begin{align} \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right] & =1_{L_{k}^{\pm}}(p)\left\langle e_{p},\varphi\right\rangle \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]-1_{L_{k}-k}(p)\left\langle e_{p+k},\varphi\right\rangle \left[\tilde{c}_{p+k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\\ &\quad -1_{L_{k}+k}(p)\left\langle e_{p-k},\varphi\right\rangle \left[\tilde{c}_{p-k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\nonumber, \end{align} $$
and so, by the triangle inequality and the second estimate of Proposition 6.2,
 $$ \begin{align} & \sum_{p\in\mathbb{Z}^{n}}\left\Vert \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\nonumber \\ &\qquad +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{p+k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{p-k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\nonumber \\ &\quad \leq\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{l}\left(\psi_{p-k}\right)\right]\Psi\right\Vert ^{2}\right.\nonumber \\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.+2\sum_{p\in L_{-k}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{l}\left(\psi_{p+k}\right)\right]\Psi\right\Vert ^{2}\right) \nonumber\\ &\quad \leq12\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\psi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align} $$
$$ \begin{align} & \sum_{p\in\mathbb{Z}^{n}}\left\Vert \left[\left[\tilde{c}_{p},b_{k}^{\ast}\left(\varphi_{p}\right)\right],b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\leq\sum_{p\in L_{k}^{\pm}}\left|\left\langle e_{p},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\nonumber \\ &\qquad +2\sum_{p\in L_{k}-k}\left|\left\langle e_{p+k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{p+k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}+2\sum_{p\in L_{-k}+k}\left|\left\langle e_{p-k},\varphi_{p}\right\rangle \right|^{2}\left\Vert \left[\tilde{c}_{p-k}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}\nonumber \\ &\quad \leq\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\sum_{p\in L_{k}^{\pm}}\left\Vert \left[\tilde{c}_{\overline{p-k}}^{\ast},b_{l}\left(\psi_{p}\right)\right]\Psi\right\Vert ^{2}+2\sum_{p\in L_{k}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{l}\left(\psi_{p-k}\right)\right]\Psi\right\Vert ^{2}\right.\nonumber \\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.+2\sum_{p\in L_{-k}}\left\Vert \left[\tilde{c}_{p}^{\ast},b_{l}\left(\psi_{p+k}\right)\right]\Psi\right\Vert ^{2}\right) \nonumber\\ &\quad \leq12\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\varphi_{q}\right\rangle \right|^{2}\right)\left(\max_{p\in L_{k}^{\pm},q\in\mathbb{Z}^{3}}\left|\left\langle e_{p},\psi_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \end{align} $$
6.3 Final estimation of the exchange terms
Now we are ready to derive bounds for the exchange terms
![]() $\mathcal {E}_{1}^{k}(A)$
and
$\mathcal {E}_{1}^{k}(A)$
and
![]() $\mathcal {E}_{2}^{k}(B)$
defined in Proposition 5.2. Recall that we have reduced the estimation of these complicated operators to the task of obtaining a uniform estimate for the four explicit forms
$\mathcal {E}_{2}^{k}(B)$
defined in Proposition 5.2. Recall that we have reduced the estimation of these complicated operators to the task of obtaining a uniform estimate for the four explicit forms
 $$ \begin{align} & \sum_{l\in S_{C}}\sum_{p\in S}\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}},\qquad\quad\;\;\sum_{l\in S_{C}}\sum_{p\in S}\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}} \nonumber\\ & \sum_{l\in S_{C}}\sum_{p\in S}\left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]^{\ast}\tilde{c}_{p_{4}},\quad\sum_{l\in S_{C}}\sum_{p\in S}\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}\left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right], \end{align} $$
$$ \begin{align} & \sum_{l\in S_{C}}\sum_{p\in S}\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}},\qquad\quad\;\;\sum_{l\in S_{C}}\sum_{p\in S}\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}} \nonumber\\ & \sum_{l\in S_{C}}\sum_{p\in S}\left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]^{\ast}\tilde{c}_{p_{4}},\quad\sum_{l\in S_{C}}\sum_{p\in S}\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}\left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right], \end{align} $$
subject to the following rules:
![]() $b_{k}^{\natural }$
denotes either
$b_{k}^{\natural }$
denotes either
![]() $b_{k}$
or
$b_{k}$
or
![]() $b_{k}^{\ast }$
, T denotes either A or B, and
$b_{k}^{\ast }$
, T denotes either A or B, and
![]() $b_{k}^{\natural }\left(Te_{p_{1}}\right)$
and
$b_{k}^{\natural }\left(Te_{p_{1}}\right)$
and
![]() $b_{l}^{\natural }(K_{l}^{\oplus }e_{p_{2}})$
may be interchanged. Furthermore, the notation
$b_{l}^{\natural }(K_{l}^{\oplus }e_{p_{2}})$
may be interchanged. Furthermore, the notation
![]() $\tilde {c}_{p}$
denotes either
$\tilde {c}_{p}$
denotes either
![]() $c_{p}$
or
$c_{p}$
or
![]() $c_{p}^{\ast }$
as appropriate for p, and the set S is such that the assignments
$c_{p}^{\ast }$
as appropriate for p, and the set S is such that the assignments
![]() $p\mapsto p_{1},p_{2},p_{3},p_{4}$
are injective and map exclusively into
$p\mapsto p_{1},p_{2},p_{3},p_{4}$
are injective and map exclusively into
![]() $B_{F}$
or
$B_{F}$
or
![]() $B_{F}^{c}$
.
$B_{F}^{c}$
.
Let us start by giving estimates in terms of
![]() $\mathcal {N}_E^2$
. For the statement, we define the
$\mathcal {N}_E^2$
. For the statement, we define the
![]() $\left\Vert \cdot \right\Vert _{\infty ,2}$
-norm of an operator
$\left\Vert \cdot \right\Vert _{\infty ,2}$
-norm of an operator
![]() $T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
$T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
 $$ \begin{align} \left\Vert T\right\Vert _{\infty,2}=\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}}. \end{align} $$
$$ \begin{align} \left\Vert T\right\Vert _{\infty,2}=\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}}. \end{align} $$
This is a minor but necessary detail, as unlike the simple estimate of equation (6.10), we cannot take the maximum outside the sum for all schematic terms, so we need this slightly stronger norm. Note that
Now the estimate the follows.
Proposition 6.4. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in \mathcal {H}_{N}$
, it holds that
$\Psi \in \mathcal {H}_{N}$
, it holds that
 $$\begin{align*}\left|\left\langle \Psi,\mathcal{E}_{i}^{k}(T)\Psi\right\rangle \right|\leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,\left(1+\mathcal{N}_{E}^{2}\right)\Psi\right\rangle \end{align*}$$
$$\begin{align*}\left|\left\langle \Psi,\mathcal{E}_{i}^{k}(T)\Psi\right\rangle \right|\leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,\left(1+\mathcal{N}_{E}^{2}\right)\Psi\right\rangle \end{align*}$$
with
![]() $i=1,2$
, for a constant
$i=1,2$
, for a constant
![]() $C>0$
independent of all relevant quantities.
$C>0$
independent of all relevant quantities.
Proof. We estimate each schematic form of (6.23) using the estimates of the Propositions 4.2, 6.2, 6.3 and Lemma 4.3, as well as the Cauchy-Schwarz inequality. First is
![]() $\tilde {c}^{\ast }b^{\natural }b^{\natural }\tilde {c}$
:
$\tilde {c}^{\ast }b^{\natural }b^{\natural }\tilde {c}$
:
 $$ \begin{align} & \qquad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}^\sharp \left(Te_{p_{1}}\right)^\ast\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq C\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\\ & \leq C\max_{p\in L_{k}^{\pm}}\left\Vert Te_{p}\right\Vert \sum_{l\in S_{C}}\max_{q\in L_{l}^{\pm}}\left\Vert K_{l}^{\oplus}e_{q}\right\Vert \sqrt{\sum_{p\in S}\left\langle \Psi,\left(\tilde{c}_{p_{3}}^{\ast}\mathcal{N}_{E}^{\left(\pm1\right)}\tilde{c}_{p_{3}}+\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{3}}\right)\Psi\right\rangle }\nonumber \\ & \quad\;\cdot\sqrt{\sum_{p\in S}\left\langle \Psi,\left(\tilde{c}_{p_{4}}^{\ast}\mathcal{N}_{E}^{\left(\pm1\right)}\tilde{c}_{p_{4}}+\tilde{c}_{p_{4}}^{\ast}\tilde{c}_{p_{4}}\right)\Psi\right\rangle }\leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle. \nonumber \end{align} $$
$$ \begin{align} & \qquad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}^\sharp \left(Te_{p_{1}}\right)^\ast\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq C\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\\ & \leq C\max_{p\in L_{k}^{\pm}}\left\Vert Te_{p}\right\Vert \sum_{l\in S_{C}}\max_{q\in L_{l}^{\pm}}\left\Vert K_{l}^{\oplus}e_{q}\right\Vert \sqrt{\sum_{p\in S}\left\langle \Psi,\left(\tilde{c}_{p_{3}}^{\ast}\mathcal{N}_{E}^{\left(\pm1\right)}\tilde{c}_{p_{3}}+\tilde{c}_{p_{3}}^{\ast}\tilde{c}_{p_{3}}\right)\Psi\right\rangle }\nonumber \\ & \quad\;\cdot\sqrt{\sum_{p\in S}\left\langle \Psi,\left(\tilde{c}_{p_{4}}^{\ast}\mathcal{N}_{E}^{\left(\pm1\right)}\tilde{c}_{p_{4}}+\tilde{c}_{p_{4}}^{\ast}\tilde{c}_{p_{4}}\right)\Psi\right\rangle }\leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle. \nonumber \end{align} $$
Then,
![]() $\left[\tilde {c},b^{\ast }\right]^{\ast }b^{\natural }\tilde {c}$
:
$\left[\tilde {c},b^{\ast }\right]^{\ast }b^{\natural }\tilde {c}$
:
 $$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right| \nonumber\\ &\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq C\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & \leq C\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\\ & \leq C\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\sqrt{\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle }\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\Vert \Psi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle }.\nonumber \end{align} $$
$$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right| \nonumber\\ &\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq C\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & \leq C\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \tilde{c}_{p_{4}}\Psi,\left(1+\mathcal{N}_{E}^{\left(\pm1\right)}\right)\tilde{c}_{p_{4}}\Psi\right\rangle }\\ & \leq C\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\sqrt{\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle }\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\Vert \Psi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}^{2}\Psi\right\rangle }.\nonumber \end{align} $$
Now,
![]() $\left[\left[\tilde {c},b^{\ast }\right],b\right]^{\ast }\tilde {c}$
:
$\left[\left[\tilde {c},b^{\ast }\right],b\right]^{\ast }\tilde {c}$
:
 $$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]^{\ast}\tilde{c}_{p_{4}}\Psi\right\rangle \right|\nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert ^{2}}\\ & \leq C\sum_{l\in S_{C}}\sqrt{\left(\max_{p,q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\right)\left(\max_{p,q\in L_{l}^{\pm}}\left|\left\langle e_{p},K_{l}^{\oplus}e_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }\sqrt{\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \nonumber \end{align} $$
$$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]^{\ast}\tilde{c}_{p_{4}}\Psi\right\rangle \right|\nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left[\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right],b_{l}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert ^{2}}\\ & \leq C\sum_{l\in S_{C}}\sqrt{\left(\max_{p,q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\right)\left(\max_{p,q\in L_{l}^{\pm}}\left|\left\langle e_{p},K_{l}^{\oplus}e_{q}\right\rangle \right|^{2}\right)\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }\sqrt{\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle }\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\left\langle \Psi,\mathcal{N}_{E}\Psi\right\rangle. \nonumber \end{align} $$
And finally,
![]() $\left[\tilde {c},b^{\ast }\right]^{\ast }\left[\tilde {c},b^{\ast }\right]$
:
$\left[\tilde {c},b^{\ast }\right]^{\ast }\left[\tilde {c},b^{\ast }\right]$
:
 $$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}\left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\rangle \right|\nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert \left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert ^{2}}\\ & \leq C\sum_{l\in S_{C}}\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\sqrt{\sum_{p\in L_{l}^{\pm}}\max_{q\in L_{l}^{\pm}}\left|\left\langle e_{p},K_{l}^{\oplus}e_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\left\Vert \Psi\right\Vert ^{2}.\nonumber \end{align} $$
$$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]^{\ast}\left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\rangle \right|\nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert \left\Vert \left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{3}},b_{k}^{\ast}\left(Te_{p_{1}}\right)\right]\Psi\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\Vert \left[\tilde{c}_{p_{4}},b_{l}^{\ast}\left(K_{l}^{\oplus}e_{p_{2}}\right)\right]\Psi\right\Vert ^{2}}\\ & \leq C\sum_{l\in S_{C}}\sqrt{\sum_{p\in L_{k}^{\pm}}\max_{q\in L_{k}^{\pm}}\left|\left\langle e_{p},Te_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\sqrt{\sum_{p\in L_{l}^{\pm}}\max_{q\in L_{l}^{\pm}}\left|\left\langle e_{p},K_{l}^{\oplus}e_{q}\right\rangle \right|^{2}\left\Vert \Psi\right\Vert ^{2}}\nonumber \\ & \leq C\left\Vert T\right\Vert _{\infty,2}\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\left\Vert \Psi\right\Vert ^{2}.\nonumber \end{align} $$
Now we derive a kinetic bound.
Proposition 6.5. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$T:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
,
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
,
 $$ \begin{align*} \left|\left\langle \Psi,\mathcal{E}_{i}^{k}(T)\Psi\right\rangle \right| &\le C \sum_{l\in S_{C}}\left(\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}+\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right) \\ &\quad \times \Bigg[ \left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\\ &\quad +\left\Vert T\right\Vert _{\infty,2} \left(\left\langle \Psi,\left(1+H_{\operatorname{\mathrm{kin}}}^{\prime}\right)\Psi\right\rangle +\left\Vert \Psi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\right) \Bigg] \end{align*} $$
$$ \begin{align*} \left|\left\langle \Psi,\mathcal{E}_{i}^{k}(T)\Psi\right\rangle \right| &\le C \sum_{l\in S_{C}}\left(\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}+\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right) \\ &\quad \times \Bigg[ \left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\\ &\quad +\left\Vert T\right\Vert _{\infty,2} \left(\left\langle \Psi,\left(1+H_{\operatorname{\mathrm{kin}}}^{\prime}\right)\Psi\right\rangle +\left\Vert \Psi\right\Vert \sqrt{\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\right) \Bigg] \end{align*} $$
for
![]() $i=1,2$
, for a constant
$i=1,2$
, for a constant
![]() $C>0$
independent of all relevant quantities.
$C>0$
independent of all relevant quantities.
As a technical preparation, let us observe that from (1.14) we may associate to
![]() $H_{\mathrm {kin}}'$
the operators
$H_{\mathrm {kin}}'$
the operators
 $$ \begin{align} H_{\text{kin}}^{\prime\left(\pm1\right)}=\sum_{p\in B_{F}^{c}}\vert|p|^{2}-\zeta\vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}}\vert|p|^{2}-\zeta\vert\,c_{p}c_{p}^{\ast} \end{align} $$
$$ \begin{align} H_{\text{kin}}^{\prime\left(\pm1\right)}=\sum_{p\in B_{F}^{c}}\vert|p|^{2}-\zeta\vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}}\vert|p|^{2}-\zeta\vert\,c_{p}c_{p}^{\ast} \end{align} $$
acting on
![]() $\mathcal {H}_{N\pm 1}$
(the expressions of
$\mathcal {H}_{N\pm 1}$
(the expressions of
![]() $H_{\text {kin}}^{\prime \left(+1\right)}$
and
$H_{\text {kin}}^{\prime \left(+1\right)}$
and
![]() $H_{\text {kin}}^{\prime \left(-1\right)}$
are the same, but the domains are different). With this interpretation, we have the following lemma (c.f. Lemma 4.3):
$H_{\text {kin}}^{\prime \left(-1\right)}$
are the same, but the domains are different). With this interpretation, we have the following lemma (c.f. Lemma 4.3):
Lemma 6.6. It holds that
for all
![]() $p\in \mathbb {Z}^{3}$
and
$p\in \mathbb {Z}^{3}$
and
 $$\begin{align*}\sum_{p\in B_{F}^{c}}c_{p}^{\ast}H_{\operatorname{\mathrm{kin}}}^{\prime\left(-1\right)}c_{p} \le \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \quad \sum_{p\in B_{F}}c_{p}H_{\operatorname{\mathrm{kin}}}^{\prime\left(+1\right)}c_{p}^{\ast}\leq\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align*}$$
$$\begin{align*}\sum_{p\in B_{F}^{c}}c_{p}^{\ast}H_{\operatorname{\mathrm{kin}}}^{\prime\left(-1\right)}c_{p} \le \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \quad \sum_{p\in B_{F}}c_{p}H_{\operatorname{\mathrm{kin}}}^{\prime\left(+1\right)}c_{p}^{\ast}\leq\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align*}$$
Proof. By the CAR, we have that
 $$ \begin{align} & \quad\quad\sum_{p\in B_{F}^{c}}c_{p}^{\ast}H_{\text{kin}}^{\prime\left(-1\right)}c_{p}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\left(\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}c_{q}^{\ast}\right)c_{p}\nonumber\\ & =\left(\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\right)\left(\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}c_{q}^{\ast}\right)+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\left[\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q},c_{p}\right]\nonumber \\ & =\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{p,q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,\delta_{p,q}c_{p}^{\ast}c_{q} \leq\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \end{align} $$
$$ \begin{align} & \quad\quad\sum_{p\in B_{F}^{c}}c_{p}^{\ast}H_{\text{kin}}^{\prime\left(-1\right)}c_{p}=\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\left(\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}c_{q}^{\ast}\right)c_{p}\nonumber\\ & =\left(\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\right)\left(\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q}+\sum_{q\in B_{F}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}c_{q}^{\ast}\right)+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}\left[\sum_{q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,c_{q}^{\ast}c_{q},c_{p}\right]\nonumber \\ & =\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}-\sum_{p,q\in B_{F}^{c}}\vert\left|q\right|^{2}-\zeta_{0}\vert\,\delta_{p,q}c_{p}^{\ast}c_{q} \leq\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}, \end{align} $$
and the inequality for
![]() $c_{p}H_{\text {kin}}^{\prime \left(+1\right)}c_{p}^{\ast }$
can be derived similarly. That
$c_{p}H_{\text {kin}}^{\prime \left(+1\right)}c_{p}^{\ast }$
can be derived similarly. That
![]() $\tilde {c}_{p}^{\ast }H_{\text {kin}}^{\prime \left(\pm 1\right)}\tilde {c}_{p}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
follows exactly as the inequality
$\tilde {c}_{p}^{\ast }H_{\text {kin}}^{\prime \left(\pm 1\right)}\tilde {c}_{p}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
follows exactly as the inequality
![]() $\tilde {c}_{p}^{\ast }\mathcal {N}_{E}^{\left(\pm 1\right)}\tilde {c}_{p}\leq \mathcal {N}_{E}$
did in Lemma 4.3.
$\tilde {c}_{p}^{\ast }\mathcal {N}_{E}^{\left(\pm 1\right)}\tilde {c}_{p}\leq \mathcal {N}_{E}$
did in Lemma 4.3.
Now we are ready to give the
Proof of Proposition 6.5.
For all schematic forms except
we can use the estimates derived in Proposition 6.4, specifically the equations (6.27) through (6.29), and the fact that
![]() $\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
. For the schematic form in (6.32), we can by Proposition 4.4 estimate that
$\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
. For the schematic form in (6.32), we can by Proposition 4.4 estimate that
 $$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}^{\natural}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle }\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber\\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \sqrt{\left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & =:A_{1}+A_{2}+A_{3}+A_{4}. \end{align} $$
$$ \begin{align} & \quad\,\sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\natural}\left(Te_{p_{1}}\right)b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}^{\natural}\left(Te_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}^{\natural}\left(K_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle }\left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber\\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \sqrt{\left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ & +\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert Te_{p_{1}}\right\Vert \left\Vert K_{l}^{\oplus}e_{p_{2}}\right\Vert \left\Vert \tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert \tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ & =:A_{1}+A_{2}+A_{3}+A_{4}. \end{align} $$
The terms
![]() $A_{1}$
through
$A_{1}$
through
![]() $A_{4}$
can be estimated by the Cauchy-Schwarz inequality, Lemma 6.6, the inequality
$A_{4}$
can be estimated by the Cauchy-Schwarz inequality, Lemma 6.6, the inequality
![]() $\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
and the fact that
$\mathcal {N}_{E}\leq H_{\operatorname {\mathrm {kin}}}^{\prime }$
and the fact that
![]() $\max _{p\in L_{k}^{\pm }}\left\Vert Te_{p}\right\Vert \leq \left\Vert T\right\Vert _{\infty ,2}$
as
$\max _{p\in L_{k}^{\pm }}\left\Vert Te_{p}\right\Vert \leq \left\Vert T\right\Vert _{\infty ,2}$
as
 $$ \begin{align} A_{1} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\nonumber \\ A_{2} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\\ A_{3} & \leq\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \nonumber, \\ A_{4} & \leq\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle ,\nonumber \end{align} $$
$$ \begin{align} A_{1} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\nonumber \\ A_{2} & \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Te_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle },\\ A_{3} & \leq\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}K_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \nonumber, \\ A_{4} & \leq\left\Vert T\right\Vert _{\infty,2}\left(\sum_{l\in S_{C}}\left\Vert K_{l}^{\oplus}\right\Vert _{\infty,2}\right)\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle ,\nonumber \end{align} $$
all of which are also accounted for by the statement.
7 Analysis of the one-body operators K,
 $A (t )$
and
$A (t )$
and
 $B (t )$
$B (t )$
In this section, we study the one-body operators on
![]() $\ell ^2(L_k)$
defined in Section 5, including
$\ell ^2(L_k)$
defined in Section 5, including
![]() $K_k$
introduced in (5.23) and
$K_k$
introduced in (5.23) and
![]() $A_k,B_k$
defined in Proposition 5.7:
$A_k,B_k$
defined in Proposition 5.7:
 $$ \begin{align} K_{k}&=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\big(h_{k}^{2}+2P_{h_{k}^{\frac{1}{2}}v_{k}}\big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right), \nonumber\\ A_{k} (t ) & =\frac{1}{2}(e^{tK_{k}}(h_{k}+2P_{v_{k}})e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}})-h_{k},\nonumber\\ B_{k} (t ) & =\frac{1}{2}(e^{tK_{k}}(h_{k}+2P_{v_{k}})e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}) , \end{align} $$
$$ \begin{align} K_{k}&=-\frac{1}{2}\log\left(h_{k}^{-\frac{1}{2}}\big(h_{k}^{2}+2P_{h_{k}^{\frac{1}{2}}v_{k}}\big)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}\right), \nonumber\\ A_{k} (t ) & =\frac{1}{2}(e^{tK_{k}}(h_{k}+2P_{v_{k}})e^{tK_{k}}+e^{-tK_{k}}h_{k}e^{-tK_{k}})-h_{k},\nonumber\\ B_{k} (t ) & =\frac{1}{2}(e^{tK_{k}}(h_{k}+2P_{v_{k}})e^{tK_{k}}-e^{-tK_{k}}h_{k}e^{-tK_{k}}) , \end{align} $$
where
 $$ \begin{align} h_{k}e_{p} =\lambda_{k,p}e_{p},\quad\;\;\lambda_{k,p}=\frac{1}{2}\left(|p|^{2}-|p-k|^{2}\right), \quad P_{v_{k}} = |v_k \rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p}, \end{align} $$
$$ \begin{align} h_{k}e_{p} =\lambda_{k,p}e_{p},\quad\;\;\lambda_{k,p}=\frac{1}{2}\left(|p|^{2}-|p-k|^{2}\right), \quad P_{v_{k}} = |v_k \rangle \langle v_k|, \quad v_{k}=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sum_{p\in L_{k}}e_{p}, \end{align} $$
and
![]() $(e_{p})_{p\in L_{k}}$
is the standard orthonormal basis of
$(e_{p})_{p\in L_{k}}$
is the standard orthonormal basis of
![]() $\ell ^{2}(L_{k})$
. We will need precise estimates on these operators to control the quasi-bosonic Bogolubov transformation
$\ell ^{2}(L_{k})$
. We will need precise estimates on these operators to control the quasi-bosonic Bogolubov transformation
![]() $e^{\mathcal {K}}$
diagonalizing the bosonizable terms. In particular, we will prove the following bounds.
$e^{\mathcal {K}}$
diagonalizing the bosonizable terms. In particular, we will prove the following bounds.
Proposition 7.1 (Trace formulas).
For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
, it holds that
$k\in \mathbb {Z}_{\ast }^{3}$
, it holds that
![]() $K_k\le 0$
and
$K_k\le 0$
and
 $$ \begin{align*}\operatorname{\mathrm{tr}}\left(K_{k}\right) = -\frac{1}{4}\log\left(1+2\hat{V}_{k}\left(\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right) \right) \ge - C\hat{V}_{k}. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{tr}}\left(K_{k}\right) = -\frac{1}{4}\log\left(1+2\hat{V}_{k}\left(\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right) \right) \ge - C\hat{V}_{k}. \end{align*} $$
Moreover, with
![]() $E_k= e^{-K_k} h_k e^{-K_k}$
, we have
$E_k= e^{-K_k} h_k e^{-K_k}$
, we have
 $$\begin{align*}\operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|=\frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt, \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|=\frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt, \end{align*}$$
with
![]() $F (x )=\log \left(1+x\right)-x$
, and
$F (x )=\log \left(1+x\right)-x$
, and
 $$\begin{align*}\left|\operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right|\leq Ck_{F}\hat{V}_{k}^{2}|k|,\quad k_{F}\rightarrow\infty. \end{align*}$$
$$\begin{align*}\left|\operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right|\leq Ck_{F}\hat{V}_{k}^{2}|k|,\quad k_{F}\rightarrow\infty. \end{align*}$$
Here,
![]() $C>0$
is a constant independent of k and
$C>0$
is a constant independent of k and
![]() $k_{F}$
.
$k_{F}$
.
Proposition 7.2 (Matrix element estimates).
For all
![]() $k\in \overline {B}\left(0,2k_{F}\right)\cap \mathbb {Z}_{\ast }^{3}$
, it holds that
$k\in \overline {B}\left(0,2k_{F}\right)\cap \mathbb {Z}_{\ast }^{3}$
, it holds that
and for all
![]() $t\in \left[0,1\right]$
, that
$t\in \left[0,1\right]$
, that
Moreover, with
![]() $E_k= e^{-K_k} h_k e^{-K_k}$
, we have
$E_k= e^{-K_k} h_k e^{-K_k}$
, we have
Here,
![]() $C>0$
is a constant independent of k and
$C>0$
is a constant independent of k and
![]() $k_{F}$
.
$k_{F}$
.
Proposition 7.3 (Kinetic estimates).
For all
![]() $k\in \overline {B}\left(0,2k_{F}\right)$
, it holds as
$k\in \overline {B}\left(0,2k_{F}\right)$
, it holds as
![]() $k_{F}\rightarrow \infty $
that
$k_{F}\rightarrow \infty $
that
 $$ \begin{align*} \left\Vert h_{k}^{-\frac{1}{2}}K_{k}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k}|k|^{3+\frac{2}{3}}\\ \left\Vert \left\{ K_{k},h_{k}\right\} h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq Ck_{F}^{\frac{1}{2}}\hat{V}_{k}|k|^{\frac{1}{2}}\\ \left\Vert h_{k}^{-\frac{1}{2}}\left\{ K_{k},h_{k}\right\} h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C\hat{V}_{k}, \end{align*} $$
$$ \begin{align*} \left\Vert h_{k}^{-\frac{1}{2}}K_{k}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k}|k|^{3+\frac{2}{3}}\\ \left\Vert \left\{ K_{k},h_{k}\right\} h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq Ck_{F}^{\frac{1}{2}}\hat{V}_{k}|k|^{\frac{1}{2}}\\ \left\Vert h_{k}^{-\frac{1}{2}}\left\{ K_{k},h_{k}\right\} h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C\hat{V}_{k}, \end{align*} $$
and for all
![]() $t\in \left[0,1\right]$
,
$t\in \left[0,1\right]$
,
 $$\begin{align*}\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}A_{k} (t )e_{p}\right\Vert ,\,\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}B_{k} (t )e_{p}\right\Vert \leq Ck_{F}^{-\frac{1}{2}}\hat{V}_{k}\left(1+\hat{V}_{k}^{2}\right). \end{align*}$$
$$\begin{align*}\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}A_{k} (t )e_{p}\right\Vert ,\,\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}B_{k} (t )e_{p}\right\Vert \leq Ck_{F}^{-\frac{1}{2}}\hat{V}_{k}\left(1+\hat{V}_{k}^{2}\right). \end{align*}$$
Here,
![]() $C>0$
is a constant independent of k and
$C>0$
is a constant independent of k and
![]() $k_{F}$
.
$k_{F}$
.
Notation. In order to simplify the notation, we will throughout this section let
![]() $h:V\rightarrow V$
denote any positive self-adjoint operator acting on an n-dimensional Hilbert space V, let
$h:V\rightarrow V$
denote any positive self-adjoint operator acting on an n-dimensional Hilbert space V, let
![]() $(x_{i})_{i=1}^{n}$
be an eigenbasis for h with eigenvalues
$(x_{i})_{i=1}^{n}$
be an eigenbasis for h with eigenvalues
![]() $\left(\lambda _{i}\right)_{i=1}^{n}$
and let
$\left(\lambda _{i}\right)_{i=1}^{n}$
and let
![]() $v\in V$
be any vector satisfying
$v\in V$
be any vector satisfying
![]() $\left\langle x_{i},v\right\rangle \geq 0$
for all
$\left\langle x_{i},v\right\rangle \geq 0$
for all
![]() $1\leq i\leq n$
. We will establish general results for the operators (c.f. (7.1))
$1\leq i\leq n$
. We will establish general results for the operators (c.f. (7.1))
 $$ \begin{align} K&=-\frac{1}{2}\log\big(h^{-\frac{1}{2}}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}}h^{-\frac{1}{2}}\big),\\ A\big(t\big) & =\frac{1}{2}\big(e^{tK}\big(h+2P_{v}\big)e^{tK}+e^{-tK}he^{-tK}\big)-h,\nonumber\\ B\big(t\big) & =\frac{1}{2}\big(e^{tK}\big(h+2P_{v}\big)e^{tK}-e^{-tK}he^{-tK}\big)\nonumber \end{align} $$
$$ \begin{align} K&=-\frac{1}{2}\log\big(h^{-\frac{1}{2}}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}}h^{-\frac{1}{2}}\big),\\ A\big(t\big) & =\frac{1}{2}\big(e^{tK}\big(h+2P_{v}\big)e^{tK}+e^{-tK}he^{-tK}\big)-h,\nonumber\\ B\big(t\big) & =\frac{1}{2}\big(e^{tK}\big(h+2P_{v}\big)e^{tK}-e^{-tK}he^{-tK}\big)\nonumber \end{align} $$
and then at the end insert the specific choice (7.2) to get explicit estimates.
We will prove the trace formulas first. Then we derive general estimates for the matrix elements of the operators
![]() $e^{-2K}$
and
$e^{-2K}$
and
![]() $e^{2K}$
in terms of a single, simpler operator T. This allows us to show that all matrix elements of K are non-negative, which in turn implies that all matrix elements of
$e^{2K}$
in terms of a single, simpler operator T. This allows us to show that all matrix elements of K are non-negative, which in turn implies that all matrix elements of
![]() $e^{-tK}$
,
$e^{-tK}$
,
![]() $\sinh \left(-tK\right)$
and
$\sinh \left(-tK\right)$
and
![]() $\cosh \left(-tK\right)$
are convex with respect to t. With these estimates, we can then obtain the desired estimates of K,
$\cosh \left(-tK\right)$
are convex with respect to t. With these estimates, we can then obtain the desired estimates of K,
![]() $A(t)$
and
$A(t)$
and
![]() $B(t)$
.
$B(t)$
.
7.1 Trace formulas
In this section, we prove Proposition 7.1. We will prove some general results using the notation in (7.3), and then we insert the special choice of
![]() $h_k$
,
$h_k$
,
![]() $v_k$
in (7.2) to conclude. Let us start with the following:
$v_k$
in (7.2) to conclude. Let us start with the following:
Proposition 7.4. The operator K in (7.3) satisfies
![]() $K\le 0$
and
$K\le 0$
and
Proof. Since
![]() $h^{2}+2P_{h^{\frac {1}{2}}v} \ge h^2>0$
and
$h^{2}+2P_{h^{\frac {1}{2}}v} \ge h^2>0$
and
![]() $A\mapsto A^{\frac {1}{2}}$
is operator monotone, we find that
$A\mapsto A^{\frac {1}{2}}$
is operator monotone, we find that
Hence, K is well defined and
![]() $K\le 0$
. By the identity
$K\le 0$
. By the identity
![]() $\text {tr}\left(\log (A)\right)=\log \left(\det (A)\right)$
and multiplicativity of the determinant, we find
$\text {tr}\left(\log (A)\right)=\log \left(\det (A)\right)$
and multiplicativity of the determinant, we find
 $$ \begin{align} \text{tr}\big(K\big) & =-\frac{1}{2}\log\big(\det\big(h^{-\frac{1}{2}}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}}h^{-\frac{1}{2}}\big)\big)\nonumber\\ &=-\frac{1}{4}\log\big(\det\big(h\big)^{-1}\det\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)\det\big(h\big)^{-1}\big)\nonumber \\ & =-\frac{1}{4}\log\big(\det\big(h^{-1}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)h^{-1}\big)\big)=-\frac{1}{4}\log\big(\det\big(1+2P_{h^{-\frac{1}{2}}v}\big)\big), \end{align} $$
$$ \begin{align} \text{tr}\big(K\big) & =-\frac{1}{2}\log\big(\det\big(h^{-\frac{1}{2}}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}}h^{-\frac{1}{2}}\big)\big)\nonumber\\ &=-\frac{1}{4}\log\big(\det\big(h\big)^{-1}\det\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)\det\big(h\big)^{-1}\big)\nonumber \\ & =-\frac{1}{4}\log\big(\det\big(h^{-1}\big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)h^{-1}\big)\big)=-\frac{1}{4}\log\big(\det\big(1+2P_{h^{-\frac{1}{2}}v}\big)\big), \end{align} $$
and by Sylvester’s determinant theorem [Reference Sylvester40],
![]() $\det \left(1+\alpha P_{x}\right)=1+\alpha \left\Vert x\right\Vert ^{2}$
for any
$\det \left(1+\alpha P_{x}\right)=1+\alpha \left\Vert x\right\Vert ^{2}$
for any
![]() $\alpha \in \mathbb {C}$
; hence,
$\alpha \in \mathbb {C}$
; hence,
Another exact trace formula which we will need is the following integral representation of the square root of a rank one perturbation, first presented in [Reference Benedikter, Nam, Porta, Schlein and Seiringer5].
Proposition 7.5. Let
![]() $\left(H,\left\langle \cdot ,\cdot \right\rangle \right)$
be a Hilbert space and let
$\left(H,\left\langle \cdot ,\cdot \right\rangle \right)$
be a Hilbert space and let
![]() $A:H\rightarrow H$
be a positive self-adjoint operator. Then for any
$A:H\rightarrow H$
be a positive self-adjoint operator. Then for any
![]() $x\in H$
and
$x\in H$
and
![]() $g\in \mathbb {R}$
such that
$g\in \mathbb {R}$
such that
![]() $A+gP_{x}>0$
, it holds that
$A+gP_{x}>0$
, it holds that
 $$\begin{align*}\left(A+gP_{x}\right)^{\frac{1}{2}}=A^{\frac{1}{2}}+\frac{2g}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+g\left\langle x,\left(A+t^{2}\right)^{-1}x\right\rangle }P_{\left(A+t^{2}\right)^{-1}x}\,dt \end{align*}$$
$$\begin{align*}\left(A+gP_{x}\right)^{\frac{1}{2}}=A^{\frac{1}{2}}+\frac{2g}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+g\left\langle x,\left(A+t^{2}\right)^{-1}x\right\rangle }P_{\left(A+t^{2}\right)^{-1}x}\,dt \end{align*}$$
and
 $$\begin{align*}\operatorname{\mathrm{tr}}\left(\left(A+gP_{x}\right)^{\frac{1}{2}}\right)=\operatorname{\mathrm{tr}}\left(A^{\frac{1}{2}}\right)+\frac{1}{\pi}\int_{0}^{\infty}\log\left(1+g\left\langle x,\left(A+t^{2}\right)^{-1}x\right\rangle \right)dt. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}\left(\left(A+gP_{x}\right)^{\frac{1}{2}}\right)=\operatorname{\mathrm{tr}}\left(A^{\frac{1}{2}}\right)+\frac{1}{\pi}\int_{0}^{\infty}\log\left(1+g\left\langle x,\left(A+t^{2}\right)^{-1}x\right\rangle \right)dt. \end{align*}$$
Note that Proposition 7.5 follows from the Sherman–Morrison formula [Reference Sherman and Morrison39]
with
![]() $P_{x,y}= |y\rangle \langle x| = \left\langle x,\cdot \right\rangle y$
, and the functional calculus
$P_{x,y}= |y\rangle \langle x| = \left\langle x,\cdot \right\rangle y$
, and the functional calculus
 $$ \begin{align} \sqrt{A}=\frac{2}{\pi}\int_{0}^{\infty}\frac{A}{A+t^{2}}\,dt=\frac{2}{\pi}\int_{0}^{\infty}\left(1-\frac{t^{2}}{A+t^{2}}\right)dt \end{align} $$
$$ \begin{align} \sqrt{A}=\frac{2}{\pi}\int_{0}^{\infty}\frac{A}{A+t^{2}}\,dt=\frac{2}{\pi}\int_{0}^{\infty}\left(1-\frac{t^{2}}{A+t^{2}}\right)dt \end{align} $$
for every self-adjoint non-negative operator A. Using this, we conclude the following:
Proposition 7.6. The trace of
![]() $E-h$
where
$E-h$
where
![]() $E=e^{-K}he^{-K}$
is given by
$E=e^{-K}he^{-K}$
is given by
 $$\begin{align*}\operatorname{\mathrm{tr}}\left(E-h\right)=\frac{1}{\pi}\int_{0}^{\infty}\log\left(1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle \right)dt. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}\left(E-h\right)=\frac{1}{\pi}\int_{0}^{\infty}\log\left(1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle \right)dt. \end{align*}$$
Proof. By cyclicity of the trace and the definition of K,
 $$ \begin{align} \text{tr}\left(e^{-K}he^{-K}\right)=\text{tr}\left(he^{-2K}\right)=\text{tr}\left(h\left(h^{-\frac{1}{2}}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}h^{-\frac{1}{2}}\right)\right)=\text{tr}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}, \end{align} $$
$$ \begin{align} \text{tr}\left(e^{-K}he^{-K}\right)=\text{tr}\left(he^{-2K}\right)=\text{tr}\left(h\left(h^{-\frac{1}{2}}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}h^{-\frac{1}{2}}\right)\right)=\text{tr}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}, \end{align} $$
so applying Proposition 7.5 with
![]() $A=h^{2}$
,
$A=h^{2}$
,
![]() $x=h^{\frac {1}{2}}v$
and
$x=h^{\frac {1}{2}}v$
and
![]() $g=2$
, we get the claim.
$g=2$
, we get the claim.
Proof of Proposition 7.1.
By inserting
![]() $h_{k}$
and
$h_{k}$
and
![]() $v_{k}$
in Proposition 7.4, we get
$v_{k}$
in Proposition 7.4, we get
![]() $K_k\le 0$
and
$K_k\le 0$
and
With the choice of
![]() $h_{k}$
and
$h_{k}$
and
![]() $v_{k}$
in (7.2), we have
$v_{k}$
in (7.2), we have
 $$ \begin{align} 0\le \left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},h_{k}^{-1}e_{q}\right\rangle =\frac{\hat{V}_{k} k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1} \le C \hat V_k, \end{align} $$
$$ \begin{align} 0\le \left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle =\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},h_{k}^{-1}e_{q}\right\rangle =\frac{\hat{V}_{k} k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1} \le C \hat V_k, \end{align} $$
where the last inequality is taken from Proposition A.2 in the Appendix. Combining with the bound
![]() $ \log (1+x) \le x $
with
$ \log (1+x) \le x $
with
![]() $x>0$
, we find that
$x>0$
, we find that
 $$ \begin{align} \operatorname{\mathrm{tr}}\left(K_k\right)=-\frac{1}{4}\log\left(1+2 \hat{V}_{k}\left(\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right) \right) \ge - C \hat V_k. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{tr}}\left(K_k\right)=-\frac{1}{4}\log\left(1+2 \hat{V}_{k}\left(\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\lambda_{k,p}^{-1}\right) \right) \ge - C \hat V_k. \end{align} $$
Next, using Proposition 7.6 and the identity (c.f. (7.8))
 $$ \begin{align} \left|L_{k}\right|=\sum_{p\in L_{k}}1=\frac{2}{\pi}\int_{0}^{\infty}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\,dt, \end{align} $$
$$ \begin{align} \left|L_{k}\right|=\sum_{p\in L_{k}}1=\frac{2}{\pi}\int_{0}^{\infty}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\,dt, \end{align} $$
we conclude that
 $$ \begin{align} \operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|=\frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt \end{align} $$
$$ \begin{align} \operatorname{\mathrm{tr}}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|=\frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt \end{align} $$
with
![]() $F (x )=\log \left(1+x\right)-x$
. Since
$F (x )=\log \left(1+x\right)-x$
. Since
![]() $\left|F (x )\right|\leq \frac {1}{2}x^{2}$
, we have
$\left|F (x )\right|\leq \frac {1}{2}x^{2}$
, we have
 $$ \begin{align} \left|\text{tr}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right| & \leq\frac{1}{\pi}\int_{0}^{\infty}\frac{1}{2}\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)^{2}dt\\ & =\frac{\hat{V}_{k}^{2}k_{F}^{-2}}{(2\pi)^{7}}\sum_{p,q\in L_{k}}\int_{0}^{\infty}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\frac{\lambda_{k,q}}{\lambda_{k,q}^{2}+t^{2}}\,dt\nonumber, \end{align} $$
$$ \begin{align} \left|\text{tr}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right| & \leq\frac{1}{\pi}\int_{0}^{\infty}\frac{1}{2}\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)^{2}dt\\ & =\frac{\hat{V}_{k}^{2}k_{F}^{-2}}{(2\pi)^{7}}\sum_{p,q\in L_{k}}\int_{0}^{\infty}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\frac{\lambda_{k,q}}{\lambda_{k,q}^{2}+t^{2}}\,dt\nonumber, \end{align} $$
and by the integral identity
it holds that
 $$ \begin{align} \sum_{p,q\in L_{k}}\int_{0}^{\infty}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\frac{\lambda_{k,q}}{\lambda_{k,q}^{2}+t^{2}}\,dt &=\frac{\pi}{2}\sum_{p,q\in L_{k}}\frac{1}{\lambda_{k,p}+\lambda_{k,q}}\leq\frac{\pi}{2}\sum_{p,q\in L_{k}}\frac{1}{\sqrt{\lambda_{k,p}}\sqrt{\lambda_{k,q}}} \nonumber \\ &=\frac{\pi}{2}\left(\sum_{p\in L_{k}}\lambda_{k,p}^{-\frac{1}{2}}\right)^{2}. \end{align} $$
$$ \begin{align} \sum_{p,q\in L_{k}}\int_{0}^{\infty}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\frac{\lambda_{k,q}}{\lambda_{k,q}^{2}+t^{2}}\,dt &=\frac{\pi}{2}\sum_{p,q\in L_{k}}\frac{1}{\lambda_{k,p}+\lambda_{k,q}}\leq\frac{\pi}{2}\sum_{p,q\in L_{k}}\frac{1}{\sqrt{\lambda_{k,p}}\sqrt{\lambda_{k,q}}} \nonumber \\ &=\frac{\pi}{2}\left(\sum_{p\in L_{k}}\lambda_{k,p}^{-\frac{1}{2}}\right)^{2}. \end{align} $$
By Proposition A.1, we have for any
![]() $k\in \mathbb {Z}_{\ast }^{3}$
that
$k\in \mathbb {Z}_{\ast }^{3}$
that
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{-\frac{1}{2}}\leq C\begin{cases} k_{F}^{\frac{3}{2}}\sqrt{|k|} & |k|<2k_{F}\\ k_{F}^{3}|k|^{-1} & |k|\geq2k_{F} \end{cases}\leq Ck_{F}^{\frac{3}{2}}\sqrt{|k|},\quad k_{F}\rightarrow\infty \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{-\frac{1}{2}}\leq C\begin{cases} k_{F}^{\frac{3}{2}}\sqrt{|k|} & |k|<2k_{F}\\ k_{F}^{3}|k|^{-1} & |k|\geq2k_{F} \end{cases}\leq Ck_{F}^{\frac{3}{2}}\sqrt{|k|},\quad k_{F}\rightarrow\infty \end{align} $$
for a constant
![]() $C>0$
independent of k and
$C>0$
independent of k and
![]() $k_{F}$
, so we get the desired bound
$k_{F}$
, so we get the desired bound
 $$ \begin{align} \left|\text{tr}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right|\leq C\hat{V}_{k}^{2}k_{F}^{-2}\left(k_{F}^{\frac{3}{2}}\sqrt{|k|}\right)^{2}=Ck_{F}\hat{V}_{k}^{2}|k|. \end{align} $$
$$ \begin{align} \left|\text{tr}\left(E_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|\right|\leq C\hat{V}_{k}^{2}k_{F}^{-2}\left(k_{F}^{\frac{3}{2}}\sqrt{|k|}\right)^{2}=Ck_{F}\hat{V}_{k}^{2}|k|. \end{align} $$
7.2 Preliminary estimates for
 $e^{-2K}$
and
$e^{-2K}$
and
 $e^{2K}$
$e^{2K}$
The square root formula also yields the following exact representations of
![]() $e^{-2K}$
and
$e^{-2K}$
and
![]() $e^{2K}$
:
$e^{2K}$
:
Proposition 7.7. The operator K in (7.3) satisfies
 $$ \begin{align*} e^{-2K} & =1+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h \left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\\ e^{2K} & =1-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt. \end{align*} $$
$$ \begin{align*} e^{-2K} & =1+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h \left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\\ e^{2K} & =1-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt. \end{align*} $$
Proof. Let us consider
first. Applying Proposition 7.5 with
![]() $A=h^{2}$
,
$A=h^{2}$
,
![]() $x=h^{\frac {1}{2}}v$
and
$x=h^{\frac {1}{2}}v$
and
![]() $g=2$
, again we find
$g=2$
, again we find
 $$ \begin{align} \big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}} & =(h^{2})^{\frac{1}{2}}+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\langle h^{\frac{1}{2}}v,(h^{2}+t^{2})^{-1}h^{\frac{1}{2}}v\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}h^{\frac{1}{2}}v}\,dt \nonumber\\ & =h+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\langle v,h(h^{2}+t^{2})^{-1}v\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{2}\right)^{-1}v}\,dt \end{align} $$
$$ \begin{align} \big(h^{2}+2P_{h^{\frac{1}{2}}v}\big)^{\frac{1}{2}} & =(h^{2})^{\frac{1}{2}}+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\langle h^{\frac{1}{2}}v,(h^{2}+t^{2})^{-1}h^{\frac{1}{2}}v\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}h^{\frac{1}{2}}v}\,dt \nonumber\\ & =h+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\langle v,h(h^{2}+t^{2})^{-1}v\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{2}\right)^{-1}v}\,dt \end{align} $$
whence
 $$ \begin{align} e^{-2K} & =h^{-\frac{1}{2}}\left(h+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)h^{-\frac{1}{2}}\nonumber\\ & =1+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
$$ \begin{align} e^{-2K} & =h^{-\frac{1}{2}}\left(h+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)h^{-\frac{1}{2}}\nonumber\\ & =1+\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
For
![]() $e^{2K}=h^{\frac {1}{2}}\big(h^{2}+2P_{h^{\frac {1}{2}}v}\big)^{-\frac {1}{2}}h^{\frac {1}{2}}$
, we first use (7.7) to write
$e^{2K}=h^{\frac {1}{2}}\big(h^{2}+2P_{h^{\frac {1}{2}}v}\big)^{-\frac {1}{2}}h^{\frac {1}{2}}$
, we first use (7.7) to write
 $$ \begin{align} (h^{2}+2P_{h^{\frac{1}{2}}v})^{-1} &=(h^{2})^{-1}-\frac{2}{1+2\left\langle h^{\frac{1}{2}}v,\left(h^{2}\right)^{-1}h^{\frac{1}{2}}v\right\rangle }P_{\left(h^{2}\right)^{-1}h^{\frac{1}{2}}v} \nonumber \\ &=h^{-2}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}v}. \end{align} $$
$$ \begin{align} (h^{2}+2P_{h^{\frac{1}{2}}v})^{-1} &=(h^{2})^{-1}-\frac{2}{1+2\left\langle h^{\frac{1}{2}}v,\left(h^{2}\right)^{-1}h^{\frac{1}{2}}v\right\rangle }P_{\left(h^{2}\right)^{-1}h^{\frac{1}{2}}v} \nonumber \\ &=h^{-2}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}v}. \end{align} $$
As this is an equality, the right-hand side is, in fact, positive (as the left-hand side is), so we may apply Proposition 7.5 with
![]() $A=h^{-2}$
,
$A=h^{-2}$
,
![]() $x=h^{-\frac {3}{2}}v$
and
$x=h^{-\frac {3}{2}}v$
and
![]() $g=-2\left(1+2\left\langle v,h^{-1}v\right\rangle \right)^{-1}$
for
$g=-2\left(1+2\left\langle v,h^{-1}v\right\rangle \right)^{-1}$
for
 $$ \begin{align} & \quad\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{-\frac{1}{2}}=\left(h^{-2}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}v}\right)^{\frac{1}{2}}\nonumber \\ & =\left(h^{-2}\right)^{\frac{1}{2}}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }\frac{2}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }\left\langle h^{-\frac{3}{2}}v,\left(h^{-2}+t^{2}\right)^{-1}h^{-\frac{3}{2}}v\right\rangle }P_{\left(h^{-2}+t^{2}\right)^{-1}h^{-\frac{3}{2}}v}\,dt\nonumber \\ & =h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}v\right\rangle -2\left\langle v,h^{-3}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt\nonumber\\ & =h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
$$ \begin{align} & \quad\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{-\frac{1}{2}}=\left(h^{-2}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}v}\right)^{\frac{1}{2}}\nonumber \\ & =\left(h^{-2}\right)^{\frac{1}{2}}-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }\frac{2}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1-\frac{2}{1+2\left\langle v,h^{-1}v\right\rangle }\left\langle h^{-\frac{3}{2}}v,\left(h^{-2}+t^{2}\right)^{-1}h^{-\frac{3}{2}}v\right\rangle }P_{\left(h^{-2}+t^{2}\right)^{-1}h^{-\frac{3}{2}}v}\,dt\nonumber \\ & =h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}v\right\rangle -2\left\langle v,h^{-3}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle }P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt\nonumber\\ & =h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
Hence,
 $$ \begin{align} e^{2K} & =h^{\frac{1}{2}}\left(h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt\right)h^{\frac{1}{2}}\\ & =1-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt.\nonumber \end{align} $$
$$ \begin{align} e^{2K} & =h^{\frac{1}{2}}\left(h^{-1}-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-\frac{3}{2}}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt\right)h^{\frac{1}{2}}\\ & =1-\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v\right\rangle t^{2}}P_{h^{-1}\left(h^{-2}+t^{2}\right)^{-1}v}\,dt.\nonumber \end{align} $$
These exact formulas now allow us to derive some simple estimates for
![]() $e^{-2K}-1$
and
$e^{-2K}-1$
and
![]() $1-e^{2K}$
. To state these estimates, we first define a new operator T on
$1-e^{2K}$
. To state these estimates, we first define a new operator T on
![]() $\ell ^2 (L_k)$
with matrix elements
$\ell ^2 (L_k)$
with matrix elements
 $$ \begin{align} \left\langle x_{i},T x_{j}\right\rangle =2\frac{\left\langle x_{i},v \right\rangle \left\langle v, x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}},\quad \forall 1\le i,j \le n. \end{align} $$
$$ \begin{align} \left\langle x_{i},T x_{j}\right\rangle =2\frac{\left\langle x_{i},v \right\rangle \left\langle v, x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}},\quad \forall 1\le i,j \le n. \end{align} $$
Recall that
![]() $(x_i)_{i=1}^n$
are an eigenbasis of h with eigenvalues
$(x_i)_{i=1}^n$
are an eigenbasis of h with eigenvalues
![]() $\lambda _{i}$
’s and
$\lambda _{i}$
’s and
![]() $\langle x_i,v\rangle \ge 0$
for all
$\langle x_i,v\rangle \ge 0$
for all
![]() $1\le i\le n$
.
$1\le i\le n$
.
Proposition 7.8. For K in (7.3) and T in (7.26), we have both the operator estimates
 $$ \begin{align*} 0&\leq e^{-2K} -1 \le T \leq ( 1+2\langle v ,h^{-1}v\rangle ) (e^{-2K}-1),\\ 0&\leq 1- e^{2K} \le T \leq ( 1+2\langle v ,h^{-1}v\rangle ) (1-e^{2K}), \end{align*} $$
$$ \begin{align*} 0&\leq e^{-2K} -1 \le T \leq ( 1+2\langle v ,h^{-1}v\rangle ) (e^{-2K}-1),\\ 0&\leq 1- e^{2K} \le T \leq ( 1+2\langle v ,h^{-1}v\rangle ) (1-e^{2K}), \end{align*} $$
and for all
![]() $1\le i,j \le n$
, the elementwise estimates
$1\le i,j \le n$
, the elementwise estimates
 $$ \begin{align*} 0&\leq \langle x_{i}, (e^{-2K} -1) x_j \rangle \le \langle x_{i}, T x_j \rangle \le ( 1+2\langle v ,h^{-1}v\rangle ) \langle x_{i},(e^{-2K}-1)x_{j}\rangle,\\ 0&\leq \langle x_{i}, (1-e^{2K}) x_j \rangle \le \langle x_{i}, T x_j \rangle \le ( 1+2\langle v ,h^{-1}v\rangle ) \langle x_{i},( 1-e^{2K})x_{j}\rangle. \end{align*} $$
$$ \begin{align*} 0&\leq \langle x_{i}, (e^{-2K} -1) x_j \rangle \le \langle x_{i}, T x_j \rangle \le ( 1+2\langle v ,h^{-1}v\rangle ) \langle x_{i},(e^{-2K}-1)x_{j}\rangle,\\ 0&\leq \langle x_{i}, (1-e^{2K}) x_j \rangle \le \langle x_{i}, T x_j \rangle \le ( 1+2\langle v ,h^{-1}v\rangle ) \langle x_{i},( 1-e^{2K})x_{j}\rangle. \end{align*} $$
Proof. We first prove the bound
![]() $0\le e^{-2K}-1\leq T$
. Obviously,
$0\le e^{-2K}-1\leq T$
. Obviously,
![]() $0\le e^{-2K}-1$
since
$0\le e^{-2K}-1$
since
![]() $K\le 0$
. Noting that
$K\le 0$
. Noting that
![]() $\langle v,h(h^{2}+t^{2})^{-1}v\rangle \geq 0$
and
$\langle v,h(h^{2}+t^{2})^{-1}v\rangle \geq 0$
and
![]() $P_{\left(h^{2}+t^{2}\right)^{-1}v}\geq 0$
for all
$P_{\left(h^{2}+t^{2}\right)^{-1}v}\geq 0$
for all
![]() $t\in \left[0,\infty \right)$
, we have by the first identity of Proposition 7.7 that
$t\in \left[0,\infty \right)$
, we have by the first identity of Proposition 7.7 that
 $$ \begin{align} e^{-2K}-1=\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\leq\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
$$ \begin{align} e^{-2K}-1=\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\leq\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt. \end{align} $$
We claim that the right-hand side is precisely T. To see this, we compute the matrix elements with respect to
![]() $(x_{i})_{i=1}^{n}$
: For any
$(x_{i})_{i=1}^{n}$
: For any
![]() $1\leq i,j\leq n$
, we have
$1\leq i,j\leq n$
, we have
 $$ \begin{align} & \left\langle x_{i},\left(\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)x_{j}\right\rangle =\frac{4}{\pi}\int_{0}^{\infty}t^{2}\left\langle x_{i},\left(h^{2}+t^{2}\right)^{-1}v\right\rangle \left\langle \left(h^{2}+t^{2}\right)^{-1}v,x_{j}\right\rangle dt\nonumber \\ & =\frac{4}{\pi}\int_{0}^{\infty}t^{2}\frac{\left\langle x_{i},v\right\rangle }{\lambda_{i}^{2}+t^{2}}\frac{\left\langle v,x_{j}\right\rangle }{\lambda_{j}^{2}+t^{2}}\,dt=\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)\nonumber\\ & =\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\frac{\pi}{2}\frac{1}{\lambda_{i}+\lambda_{j}}\right)=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},Tx_{j}\right\rangle , \end{align} $$
$$ \begin{align} & \left\langle x_{i},\left(\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)x_{j}\right\rangle =\frac{4}{\pi}\int_{0}^{\infty}t^{2}\left\langle x_{i},\left(h^{2}+t^{2}\right)^{-1}v\right\rangle \left\langle \left(h^{2}+t^{2}\right)^{-1}v,x_{j}\right\rangle dt\nonumber \\ & =\frac{4}{\pi}\int_{0}^{\infty}t^{2}\frac{\left\langle x_{i},v\right\rangle }{\lambda_{i}^{2}+t^{2}}\frac{\left\langle v,x_{j}\right\rangle }{\lambda_{j}^{2}+t^{2}}\,dt=\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)\nonumber\\ & =\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\frac{\pi}{2}\frac{1}{\lambda_{i}+\lambda_{j}}\right)=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},Tx_{j}\right\rangle , \end{align} $$
where we used that
![]() $(x_{i})_{i=1}^{n}$
is an eigenbasis for h as well as the integral identity (7.16).
$(x_{i})_{i=1}^{n}$
is an eigenbasis for h as well as the integral identity (7.16).
The lower bound
![]() $T\leq \left(1+2\left\langle v,h^{-1}v\right\rangle \right) (e^{-2K}-1)$
follows by the same argument as
$T\leq \left(1+2\left\langle v,h^{-1}v\right\rangle \right) (e^{-2K}-1)$
follows by the same argument as
for all
![]() $t\in \left[0,\infty \right)$
, so
$t\in \left[0,\infty \right)$
, so
 $$ \begin{align} e^{-2K}-1\geq\frac{1}{1+2\left\langle v,h^{-1}v\right\rangle }\left(\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)=\frac{1}{1+2\left\langle v,h^{-1}v\right\rangle }T. \end{align} $$
$$ \begin{align} e^{-2K}-1\geq\frac{1}{1+2\left\langle v,h^{-1}v\right\rangle }\left(\frac{4}{\pi}\int_{0}^{\infty}t^{2}P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt\right)=\frac{1}{1+2\left\langle v,h^{-1}v\right\rangle }T. \end{align} $$
The bounds
follow by exactly the same argument, starting from the second identity of Proposition 7.7, using that
for all
![]() $t\in \left[0,\infty \right)$
as well as the integral identity (7.16).
$t\in \left[0,\infty \right)$
as well as the integral identity (7.16).
The matrix element estimates likewise follow by the same argument as, for example,
 $$ \begin{align} 0&\le \;\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle =\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }\frac{\left\langle x_{i},v\right\rangle }{\lambda_{i}^{2}+t^{2}}\frac{\left\langle v,x_{j}\right\rangle }{\lambda_{j}^{2}+t^{2}}\,dt\nonumber \\ & =\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{1}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)\\ & \leq\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},Tx_{j}\right\rangle \nonumber \end{align} $$
$$ \begin{align} 0&\le \;\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle =\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }\frac{\left\langle x_{i},v\right\rangle }{\lambda_{i}^{2}+t^{2}}\frac{\left\langle v,x_{j}\right\rangle }{\lambda_{j}^{2}+t^{2}}\,dt\nonumber \\ & =\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{1}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)\\ & \leq\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left(\frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{\left(\lambda_{i}^{2}+t^{2}\right)\left(\lambda_{j}^{2}+t^{2}\right)}\,dt\right)=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},Tx_{j}\right\rangle \nonumber \end{align} $$
by the assumption that the inner products
![]() $\left\langle x_{i},v\right\rangle $
and
$\left\langle x_{i},v\right\rangle $
and
![]() $\left\langle v,x_{j}\right\rangle $
are non-negative.
$\left\langle v,x_{j}\right\rangle $
are non-negative.
Remark 7.1 (Optimality of the estimates).
We may observe that the estimates for
![]() $e^{-2K}$
,
$e^{-2K}$
,
![]() $e^{2K}$
are, in general, optimal. To see this, let us add a small parameter
$e^{2K}$
are, in general, optimal. To see this, let us add a small parameter
![]() $g\geq 0$
to the problem by substituting
$g\geq 0$
to the problem by substituting
![]() $\sqrt {g}v$
for v in equation (7.3) – that is, defining
$\sqrt {g}v$
for v in equation (7.3) – that is, defining
Then the general bounds of the corollary read for
![]() $K_{g}$
that
$K_{g}$
that
 $$ \begin{align} \frac{1}{1+2g\left\langle v,h^{-1}v\right\rangle }T_{g}\leq-2K_{g}\leq T_{g}. \end{align} $$
$$ \begin{align} \frac{1}{1+2g\left\langle v,h^{-1}v\right\rangle }T_{g}\leq-2K_{g}\leq T_{g}. \end{align} $$
Hence,
 $$ \begin{align} 0\geq-2K_{g}-T_{g}\geq-\left(1-\frac{1}{1+2g\left\langle v,h^{-1}v\right\rangle }\right)T_{g}=-\left(\frac{2\left\langle v,h^{-1}v\right\rangle }{1+2g\left\langle v,h^{-1}v\right\rangle }T\right)g^{2}\geq-Cg^{2}, \end{align} $$
$$ \begin{align} 0\geq-2K_{g}-T_{g}\geq-\left(1-\frac{1}{1+2g\left\langle v,h^{-1}v\right\rangle }\right)T_{g}=-\left(\frac{2\left\langle v,h^{-1}v\right\rangle }{1+2g\left\langle v,h^{-1}v\right\rangle }T\right)g^{2}\geq-Cg^{2}, \end{align} $$
which by self-adjointness of the operators involved implies that
with respect to, say, operator norm. This shows that the operator
![]() $T_{g}=gT$
is, in fact, the first-order expansion of
$T_{g}=gT$
is, in fact, the first-order expansion of
![]() $K_{g}$
with respect to the parameter g, which is then also the case for
$K_{g}$
with respect to the parameter g, which is then also the case for
![]() $e^{-2K_{g}}-1$
,
$e^{-2K_{g}}-1$
,
![]() $1-e^{2K_{g}}$
as, for example,
$1-e^{2K_{g}}$
as, for example,
![]() $e^{-2K_{g}}-1=-2K_{g}+O\left(g^{2}\right)=T_{g}+O\left(g^{2}\right)$
. The estimate
$e^{-2K_{g}}-1=-2K_{g}+O\left(g^{2}\right)=T_{g}+O\left(g^{2}\right)$
. The estimate
is therefore (asymptotically) optimal since
![]() $T_{g}$
is precisely the small g limit of
$T_{g}$
is precisely the small g limit of
![]() $e^{-2K_{g}}-1$
.
$e^{-2K_{g}}-1$
.
This is relevant for our application, for although we do not have an explicit parameter g to consider, we do have
![]() $\hat V_k$
as an effective one. More precisely, the summability condition of
$\hat V_k$
as an effective one. More precisely, the summability condition of
![]() $\hat V_k$
ensures that essentially all but finitely many coefficients
$\hat V_k$
ensures that essentially all but finitely many coefficients
![]() $\hat {V}_{k}$
are small, even when the coefficients
$\hat {V}_{k}$
are small, even when the coefficients
![]() $(\hat {V}_{k})_{k\in \mathbb {Z}^{3}}$
are not finitely supported.
$(\hat {V}_{k})_{k\in \mathbb {Z}^{3}}$
are not finitely supported.
7.3 Matrix element estimates for K,
 $A(t)$
,
$A(t)$
,
 $B(t)$
$B(t)$
In this section, we prove Proposition 7.1. As before, we will prove some general results using the notation from (7.3), and then we insert
![]() $h_k$
,
$h_k$
,
![]() $v_k$
from (7.2) at the end. Recall that
$v_k$
from (7.2) at the end. Recall that
![]() $(x_i)_{i}$
is an eigenbasis of h. We start with the following:
$(x_i)_{i}$
is an eigenbasis of h. We start with the following:
Proposition 7.9. For all
![]() $1\leq i,j\leq n$
, we have
$1\leq i,j\leq n$
, we have
![]() $\langle x_i, -K x_j \rangle \ge 0$
and the functions
$\langle x_i, -K x_j \rangle \ge 0$
and the functions
are non-negative and convex for
![]() $t\in \left[0,\infty \right)$
.
$t\in \left[0,\infty \right)$
.
Proof. By Proposition 7.8, the operator
![]() $S=1-e^{2K}$
satisfies that
$S=1-e^{2K}$
satisfies that
![]() $0\le S<1$
and
$0\le S<1$
and
![]() $\langle x_i, S x_j\rangle \ge 0$
for all
$\langle x_i, S x_j\rangle \ge 0$
for all
![]() $1\le i,j\le n$
. By writing
$1\le i,j\le n$
. By writing
we find that
![]() $-2K$
also has non-negative matrix elements. By using the series expansion again, we see that for any
$-2K$
also has non-negative matrix elements. By using the series expansion again, we see that for any
![]() $1\leq i,j\leq n$
and
$1\leq i,j\leq n$
and
![]() $t\in \left[0,\infty \right)$
,
$t\in \left[0,\infty \right)$
,
 $$ \begin{align} \big\langle x_{i},\big(e^{-tK}-1\big)x_{j}\big\rangle & =\sum_{m=1}^{\infty}\frac{\big\langle x_{i},(-K)^{m}x_{j}\big\rangle }{m!}t^{m}\geq0,\nonumber\\ \frac{d^{2}}{dt^{2}}\big\langle x_{i},\big(e^{-tK}-1\big)x_{j}\big\rangle & =\sum_{m=3}^{\infty}\frac{\big\langle x_{i},(-K)^{m}x_{j}\big\rangle }{\left(m-2\right)!}t^{m-2}\geq0, \end{align} $$
$$ \begin{align} \big\langle x_{i},\big(e^{-tK}-1\big)x_{j}\big\rangle & =\sum_{m=1}^{\infty}\frac{\big\langle x_{i},(-K)^{m}x_{j}\big\rangle }{m!}t^{m}\geq0,\nonumber\\ \frac{d^{2}}{dt^{2}}\big\langle x_{i},\big(e^{-tK}-1\big)x_{j}\big\rangle & =\sum_{m=3}^{\infty}\frac{\big\langle x_{i},(-K)^{m}x_{j}\big\rangle }{\left(m-2\right)!}t^{m-2}\geq0, \end{align} $$
yielding the claim for
![]() $t\mapsto \left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle $
. The functions
$t\mapsto \left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle $
. The functions
![]() $ t\mapsto \left\langle x_{i},\sinh \left(-tK\right)x_{j}\right\rangle $
and
$ t\mapsto \left\langle x_{i},\sinh \left(-tK\right)x_{j}\right\rangle $
and
![]() $t\mapsto \left\langle x_{i},\left(\cosh \left(-tK\right)-1\right)x_{j}\right\rangle $
can be treated similarly.
$t\mapsto \left\langle x_{i},\left(\cosh \left(-tK\right)-1\right)x_{j}\right\rangle $
can be treated similarly.
Next, we have the key matrix element bounds.
Proposition 7.10. For all
![]() $1\leq i,j\leq n$
and
$1\leq i,j\leq n$
and
![]() $t\in \left[0,1\right]$
, we have the elementwise estimates
$t\in \left[0,1\right]$
, we have the elementwise estimates
 $$ \begin{align*} & \left|\left\langle x_{i},Kx_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(1-e^{tK}\right)x_{j}\right\rangle \right|,\\ & \qquad\;\;\left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\leq \frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*} $$
$$ \begin{align*} & \left|\left\langle x_{i},Kx_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(1-e^{tK}\right)x_{j}\right\rangle \right|,\\ & \qquad\;\;\left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\leq \frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*} $$
Proof. The arguments for
![]() $e^{-tK}-1$
,
$e^{-tK}-1$
,
![]() $\sinh \left(-tK\right)$
and
$\sinh \left(-tK\right)$
and
![]() $\cosh \left(-tK\right)-1$
are again the same, so we focus on
$\cosh \left(-tK\right)-1$
are again the same, so we focus on
![]() $e^{-tK}-1$
. By the convexity of Proposition 7.9 and the elementwise estimate of Proposition 7.8, we find for all
$e^{-tK}-1$
. By the convexity of Proposition 7.9 and the elementwise estimate of Proposition 7.8, we find for all
![]() $t\in \left[0,1\right]$
that
$t\in \left[0,1\right]$
that
 $$ \begin{align} 0 & \leq\left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle \leq\left(1-\frac{t}{2}\right)\left\langle x_{i},\left(e^{-0\cdot K}-1\right)x_{j}\right\rangle +\frac{t}{2}\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \nonumber\\ & =\frac{t}{2}\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \leq\frac{1}{2}\left|\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \right|\leq\frac{1}{2}\left\langle x_{i},Tx_{j}\right\rangle =\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align} $$
$$ \begin{align} 0 & \leq\left\langle x_{i},\left(e^{-tK}-1\right)x_{j}\right\rangle \leq\left(1-\frac{t}{2}\right)\left\langle x_{i},\left(e^{-0\cdot K}-1\right)x_{j}\right\rangle +\frac{t}{2}\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \nonumber\\ & =\frac{t}{2}\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \leq\frac{1}{2}\left|\left\langle x_{i},\left(e^{-2K}-1\right)x_{j}\right\rangle \right|\leq\frac{1}{2}\left\langle x_{i},Tx_{j}\right\rangle =\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align} $$
This also gives us the estimate for K as
 $$ \begin{align} 0\leq\left\langle x_{i},\left(-K\right)x_{j}\right\rangle \leq\sum_{m=1}^{\infty}\frac{1}{m!}\left\langle x_{i},\left(-K\right)^{m}x_{j}\right\rangle =\left\langle x_{i},\left(e^{-K}-1\right)x_{j}\right\rangle \leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}, \end{align} $$
$$ \begin{align} 0\leq\left\langle x_{i},\left(-K\right)x_{j}\right\rangle \leq\sum_{m=1}^{\infty}\frac{1}{m!}\left\langle x_{i},\left(-K\right)^{m}x_{j}\right\rangle =\left\langle x_{i},\left(e^{-K}-1\right)x_{j}\right\rangle \leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}, \end{align} $$
where we used again the positivity of
![]() $\langle x_i, -K x_j\rangle $
from Proposition 7.9. Finally, the estimate for
$\langle x_i, -K x_j\rangle $
from Proposition 7.9. Finally, the estimate for
![]() $1-e^{-tK}$
is deduced from that of
$1-e^{-tK}$
is deduced from that of
![]() $\sinh \left(-tK\right)$
and
$\sinh \left(-tK\right)$
and
![]() $\cosh \left(-tK\right)-1$
as
$\cosh \left(-tK\right)-1$
as
 $$ \begin{align} |\langle x_{i},(1-e^{tK})x_{j}\rangle | & =\left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle -\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\nonumber\\ & \leq\max\left\{ \left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle \right|,\left|\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\right\} \leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} , \end{align} $$
$$ \begin{align} |\langle x_{i},(1-e^{tK})x_{j}\rangle | & =\left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle -\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\nonumber\\ & \leq\max\left\{ \left|\left\langle x_{i},\sinh\left(-tK\right)x_{j}\right\rangle \right|,\left|\left\langle x_{i},\left(\cosh\left(-tK\right)-1\right)x_{j}\right\rangle \right|\right\} \leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} , \end{align} $$
where we also used the positivity of
![]() $\left\langle x_{i},\left(\cosh \left(-tK\right)-1\right)x_{j}\right\rangle $
and
$\left\langle x_{i},\left(\cosh \left(-tK\right)-1\right)x_{j}\right\rangle $
and
![]() $\left\langle x_{i},\sinh \left(-tK\right)x_{j}\right\rangle $
from Proposition 7.9 to justify the first inequality.
$\left\langle x_{i},\sinh \left(-tK\right)x_{j}\right\rangle $
from Proposition 7.9 to justify the first inequality.
As a simple application of these estimates, we can easily obtain the following:
Proposition 7.11. It holds that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
Proof. We estimate using Proposition 7.10 that
 $$ \begin{align} \left\Vert K\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left(\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right)^{2} \nonumber\\ & \leq\left(\max_{1\leq j\leq n}\left|\left\langle v,x_{j}\right\rangle \right|^{2}\right)\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{2}}=\alpha^{2}\left\langle v,h^{-2}v\right\rangle. \end{align} $$
$$ \begin{align} \left\Vert K\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left(\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right)^{2} \nonumber\\ & \leq\left(\max_{1\leq j\leq n}\left|\left\langle v,x_{j}\right\rangle \right|^{2}\right)\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{2}}=\alpha^{2}\left\langle v,h^{-2}v\right\rangle. \end{align} $$
Now we consider
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
, which can be written as
$B (t )$
, which can be written as
for
 $$ \begin{align} A_{h} (t ) & =\frac{1}{2}\left(e^{tK}he^{tK}+e^{-tK}he^{-tK}\right)-h\nonumber \\ & =\cosh\left(-tK\right)h\cosh\left(-tK\right)+\sinh\left(-tK\right)h\sinh\left(-tK\right)-h \nonumber\\ & =\sinh\left(-tK\right)h\sinh\left(-tK\right)+\left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)+\left\{ h,\cosh\left(-tK\right)-1\right\} \end{align} $$
$$ \begin{align} A_{h} (t ) & =\frac{1}{2}\left(e^{tK}he^{tK}+e^{-tK}he^{-tK}\right)-h\nonumber \\ & =\cosh\left(-tK\right)h\cosh\left(-tK\right)+\sinh\left(-tK\right)h\sinh\left(-tK\right)-h \nonumber\\ & =\sinh\left(-tK\right)h\sinh\left(-tK\right)+\left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)+\left\{ h,\cosh\left(-tK\right)-1\right\} \end{align} $$
and
 $$ \begin{align} B_{h} (t ) & =\frac{1}{2}\left(e^{tK}he^{tK}-e^{-tK}he^{-tK}\right)\nonumber \\ & =-\left(\cosh\left(-tK\right)h\sinh\left(-tK\right)+\sinh\left(-tK\right)h\cosh\left(-tK\right)\right) \nonumber\\ & =-\left(\left(\cosh\left(-tK\right)-1\right)h\sinh\left(-tK\right)+\sinh\left(-tK\right)h\left(\cosh\left(-tK\right)-1\right)+\left\{ h,\sinh\left(-tK\right)\right\} \right). \end{align} $$
$$ \begin{align} B_{h} (t ) & =\frac{1}{2}\left(e^{tK}he^{tK}-e^{-tK}he^{-tK}\right)\nonumber \\ & =-\left(\cosh\left(-tK\right)h\sinh\left(-tK\right)+\sinh\left(-tK\right)h\cosh\left(-tK\right)\right) \nonumber\\ & =-\left(\left(\cosh\left(-tK\right)-1\right)h\sinh\left(-tK\right)+\sinh\left(-tK\right)h\left(\cosh\left(-tK\right)-1\right)+\left\{ h,\sinh\left(-tK\right)\right\} \right). \end{align} $$
Specifically, we must estimate the
![]() $\left\Vert \cdot \right\Vert _{\infty ,2}$
norms of
$\left\Vert \cdot \right\Vert _{\infty ,2}$
norms of
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
with respect to
$B (t )$
with respect to
![]() $(x_{i})_{i=1}^{n}$
. We begin with the
$(x_{i})_{i=1}^{n}$
. We begin with the
![]() $e^{tK}P_{v}e^{tK}$
term:
$e^{tK}P_{v}e^{tK}$
term:
Proposition 7.12. It holds for all
![]() $t\in \left[0,1\right]$
that
$t\in \left[0,1\right]$
that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
Proof. We first observe that
 $$ \begin{align} \left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},e^{tK}P_{v}e^{tK}x_{j}\right\rangle \right|^{2}=\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},e^{tK}v\right\rangle \right|^{2}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2} \nonumber\\ & =\left(\max_{1\leq j\leq n}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2}\right)\left\Vert e^{tK}v\right\Vert ^{2}\leq\left(\max_{1\leq j\leq n}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2}\right)\left\Vert v\right\Vert ^{2} , \end{align} $$
$$ \begin{align} \left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},e^{tK}P_{v}e^{tK}x_{j}\right\rangle \right|^{2}=\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},e^{tK}v\right\rangle \right|^{2}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2} \nonumber\\ & =\left(\max_{1\leq j\leq n}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2}\right)\left\Vert e^{tK}v\right\Vert ^{2}\leq\left(\max_{1\leq j\leq n}\left|\left\langle v,e^{tK}x_{j}\right\rangle \right|^{2}\right)\left\Vert v\right\Vert ^{2} , \end{align} $$
where we used that by monotonicity of
![]() $e^{x}$
and the fact that
$e^{x}$
and the fact that
![]() $K\leq 0$
,
$K\leq 0$
,
![]() $\left\Vert e^{tK}v\right\Vert ^{2}=\left\langle v,e^{2tK}v\right\rangle \leq \left\Vert v\right\Vert ^{2}$
. For the remaining factor, we first write
$\left\Vert e^{tK}v\right\Vert ^{2}=\left\langle v,e^{2tK}v\right\rangle \leq \left\Vert v\right\Vert ^{2}$
. For the remaining factor, we first write
 $$ \begin{align} \left\langle v,e^{tK}x_{j}\right\rangle =\left\langle v,x_{j}\right\rangle +\left\langle v,\left(e^{tK}-1\right)x_{j}\right\rangle =\left\langle v,x_{j}\right\rangle +\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle ,\quad1\leq j\leq n \end{align} $$
$$ \begin{align} \left\langle v,e^{tK}x_{j}\right\rangle =\left\langle v,x_{j}\right\rangle +\left\langle v,\left(e^{tK}-1\right)x_{j}\right\rangle =\left\langle v,x_{j}\right\rangle +\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle ,\quad1\leq j\leq n \end{align} $$
and estimate using Proposition 7.10 that
 $$ \begin{align} \left|\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right| & \leq\sum_{i=1}^{n}\left|\left\langle v,x_{i}\right\rangle \right|\left|\left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right|\leq\sum_{i=1}^{n}\left|\left\langle v,x_{i}\right\rangle \right|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\nonumber \\ & \leq\left\langle v,x_{j}\right\rangle \sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}=\left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle ,\quad1\leq j\leq n. \end{align} $$
$$ \begin{align} \left|\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right| & \leq\sum_{i=1}^{n}\left|\left\langle v,x_{i}\right\rangle \right|\left|\left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right|\leq\sum_{i=1}^{n}\left|\left\langle v,x_{i}\right\rangle \right|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\nonumber \\ & \leq\left\langle v,x_{j}\right\rangle \sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}=\left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle ,\quad1\leq j\leq n. \end{align} $$
Hence,
 $$ \begin{align} \left|\left\langle v,e^{tK}x_{j}\right\rangle \right|\leq\left\langle v,x_{j}\right\rangle +\left|\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right|\leq\left\langle v,x_{j}\right\rangle \left(1+\left\langle v,h^{-1}v\right\rangle \right),\quad1\leq j\leq n, \end{align} $$
$$ \begin{align} \left|\left\langle v,e^{tK}x_{j}\right\rangle \right|\leq\left\langle v,x_{j}\right\rangle +\left|\sum_{i=1}^{n}\left\langle v,x_{i}\right\rangle \left\langle x_{i},\left(e^{tK}-1\right)x_{j}\right\rangle \right|\leq\left\langle v,x_{j}\right\rangle \left(1+\left\langle v,h^{-1}v\right\rangle \right),\quad1\leq j\leq n, \end{align} $$
so returning to equation (7.48), we conclude that
 $$ \begin{align} \left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty}^{2}\leq\left(\max_{1\leq j\leq n}\left|\left\langle v,x_{j}\right\rangle \left(1+\left\langle v,h^{-1}v\right\rangle \right)\right|^{2}\right)\left\Vert v\right\Vert ^{2}=\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\Vert v\right\Vert ^{2}, \end{align} $$
$$ \begin{align} \left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty}^{2}\leq\left(\max_{1\leq j\leq n}\left|\left\langle v,x_{j}\right\rangle \left(1+\left\langle v,h^{-1}v\right\rangle \right)\right|^{2}\right)\left\Vert v\right\Vert ^{2}=\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\Vert v\right\Vert ^{2}, \end{align} $$
implying the claim.
For
![]() $A_{h} (t )$
and
$A_{h} (t )$
and
![]() $B_{h} (t )$
, we estimate the matrix elements of the operators appearing in the equations (7.46) and (7.47):
$B_{h} (t )$
, we estimate the matrix elements of the operators appearing in the equations (7.46) and (7.47):
Proposition 7.13. It holds for all
![]() $1\leq i,j\leq n$
and
$1\leq i,j\leq n$
and
![]() $t\in \left[0,1\right]$
that, for
$t\in \left[0,1\right]$
that, for
![]() $C_{t}=\cosh \left(-tK\right)-1$
and
$C_{t}=\cosh \left(-tK\right)-1$
and
![]() $S_{t}=\sinh \left(-tK\right)$
,
$S_{t}=\sinh \left(-tK\right)$
,
and
Proof. The arguments for the elements of the two groups are the same, so we focus on particular representatives. For the first, we have by the estimates of Proposition 7.10 that
 $$ \begin{align} \left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right),x_{j}\right\rangle \right| & =\left|\sum_{k=1}^{n}\lambda_{k}\left\langle x_{i},\sinh\left(-tK\right),x_{k}\right\rangle \left\langle x_{k},\sinh\left(-tK\right),x_{j}\right\rangle \right|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\nonumber \\ & \leq\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}} = \left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right),x_{j}\right\rangle \right| & =\left|\sum_{k=1}^{n}\lambda_{k}\left\langle x_{i},\sinh\left(-tK\right),x_{k}\right\rangle \left\langle x_{k},\sinh\left(-tK\right),x_{j}\right\rangle \right|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\nonumber \\ & \leq\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}} = \left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle \end{align} $$
and for the second, that
 $$ \begin{align} \left|\left\langle x_{i},\left\{ h,\sinh\left(-tK\right)\right\} ,x_{j}\right\rangle \right| & =\left(\lambda_{i}+\lambda_{j}\right)\left|\left\langle x_{i},\sinh\left(-tK\right),x_{j}\right\rangle \right| \nonumber\\ & \leq\left(\lambda_{i}+\lambda_{j}\right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle . \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},\left\{ h,\sinh\left(-tK\right)\right\} ,x_{j}\right\rangle \right| & =\left(\lambda_{i}+\lambda_{j}\right)\left|\left\langle x_{i},\sinh\left(-tK\right),x_{j}\right\rangle \right| \nonumber\\ & \leq\left(\lambda_{i}+\lambda_{j}\right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}=\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle . \end{align} $$
We can now obtain the desired estimate:
Proposition 7.14. It holds for all
![]() $t\in \left[0,1\right]$
that
$t\in \left[0,1\right]$
that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
Proof. Again, the arguments for
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
are the same, so we focus on
$B (t )$
are the same, so we focus on
![]() $A (t )$
. Using that
$A (t )$
. Using that
![]() $\left\Vert \cdot \right\Vert _{\infty ,2}$
is indeed a norm, and hence obeys the triangle inequality, we have for any
$\left\Vert \cdot \right\Vert _{\infty ,2}$
is indeed a norm, and hence obeys the triangle inequality, we have for any
![]() $t\in \left[0,1\right]$
that
$t\in \left[0,1\right]$
that
 $$ \begin{align} \left\Vert A (t )\right\Vert _{\infty,2} & \leq\left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}+\left\Vert A_{h} (t )\right\Vert _{\infty,2} \nonumber \\ &\leq\left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}+\left\Vert \sinh\left(-tK\right)h\sinh\left(-tK\right)\right\Vert _{\infty,2}\nonumber \\ &\quad +\left\Vert \left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)\right\Vert _{\infty,2}+\left\Vert \left\{ h,\cosh\left(-tK\right)-1\right\} \right\Vert _{\infty,2}. \end{align} $$
$$ \begin{align} \left\Vert A (t )\right\Vert _{\infty,2} & \leq\left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}+\left\Vert A_{h} (t )\right\Vert _{\infty,2} \nonumber \\ &\leq\left\Vert e^{tK}P_{v}e^{tK}\right\Vert _{\infty,2}+\left\Vert \sinh\left(-tK\right)h\sinh\left(-tK\right)\right\Vert _{\infty,2}\nonumber \\ &\quad +\left\Vert \left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)\right\Vert _{\infty,2}+\left\Vert \left\{ h,\cosh\left(-tK\right)-1\right\} \right\Vert _{\infty,2}. \end{align} $$
We estimate
![]() $\left\Vert \sinh \left(-tK\right)h\sinh \left(-tK\right)\right\Vert _{\infty ,2}$
using Proposition 7.13 as
$\left\Vert \sinh \left(-tK\right)h\sinh \left(-tK\right)\right\Vert _{\infty ,2}$
using Proposition 7.13 as
 $$ \begin{align} \left\Vert \sinh\left(-tK\right)h\sinh\left(-tK\right)\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle \right|^{2}\\ & =\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}=\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\left\Vert v\right\Vert ^{2},\nonumber \end{align} $$
$$ \begin{align} \left\Vert \sinh\left(-tK\right)h\sinh\left(-tK\right)\right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \left\langle v,h^{-1}v\right\rangle \right|^{2}\\ & =\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}=\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\left\Vert v\right\Vert ^{2},\nonumber \end{align} $$
the same bound holding also for
![]() $\left\Vert \left(\cosh \left(-tK\right)-1\right)h\left(\cosh \left(-tK\right)-1\right)\right\Vert _{\infty ,2}^{2}$
. We likewise find
$\left\Vert \left(\cosh \left(-tK\right)-1\right)h\left(\cosh \left(-tK\right)-1\right)\right\Vert _{\infty ,2}^{2}$
. We likewise find
 $$ \begin{align} \left\Vert \left\{ h,\cosh\left(-tK\right)-1\right\} \right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\rangle \right|^{2}\\ & \leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2}=\alpha^{2}\left\Vert v\right\Vert ^{2},\nonumber \end{align} $$
$$ \begin{align} \left\Vert \left\{ h,\cosh\left(-tK\right)-1\right\} \right\Vert _{\infty,2}^{2} & =\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\rangle \right|^{2}\\ & \leq\sum_{i=1}^{n}\max_{1\leq j\leq n}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2}=\alpha^{2}\left\Vert v\right\Vert ^{2},\nonumber \end{align} $$
so recalling the estimate of Proposition 7.12, we conclude that
Now we come to the last ingredient of Proposition 7.1.
Proposition 7.15. Let
![]() $E=e^{-K}he^{-K}$
. For all
$E=e^{-K}he^{-K}$
. For all
![]() $1\leq i,j\leq n$
, it holds that
$1\leq i,j\leq n$
, it holds that
Proof. Using the identity
we can write
We can apply Proposition 7.10 to estimate the first term of this equation as
 $$ \begin{align} \big|\big(\lambda_{i}+\lambda_{j}\big)\big\langle x_{i},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\leq\big(\lambda_{i}+\lambda_{j}\big)\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{i}+\lambda_{j}}=\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \end{align} $$
$$ \begin{align} \big|\big(\lambda_{i}+\lambda_{j}\big)\big\langle x_{i},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\leq\big(\lambda_{i}+\lambda_{j}\big)\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{i}+\lambda_{j}}=\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \end{align} $$
and the second term as
 $$ \begin{align} \big|\big\langle x_{i},\big(e^{-K}-1\big)h\big(e^{-K}-1\big)x_{j}\big\rangle \big| & =\left|\sum_{k=1}^{n}\lambda_{k}\big\langle x_{i},\big(e^{-K}-1\big)x_{k}\big\rangle \big\langle x_{k},\big(e^{-K}-1\big)x_{j}\big\rangle \right|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{k}\big\rangle }{\lambda_{i}+\lambda_{k}}\frac{\big\langle x_{k},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{k}+\lambda_{j}}\\ & \leq\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \sum_{k=1}^{n}\frac{\big|\big\langle x_{k},v\big\rangle \big|^{2}}{\lambda_{k}}=\big\langle v,h^{-1}v\big\rangle \big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \nonumber, \end{align} $$
$$ \begin{align} \big|\big\langle x_{i},\big(e^{-K}-1\big)h\big(e^{-K}-1\big)x_{j}\big\rangle \big| & =\left|\sum_{k=1}^{n}\lambda_{k}\big\langle x_{i},\big(e^{-K}-1\big)x_{k}\big\rangle \big\langle x_{k},\big(e^{-K}-1\big)x_{j}\big\rangle \right|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{k}\big\rangle }{\lambda_{i}+\lambda_{k}}\frac{\big\langle x_{k},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{k}+\lambda_{j}}\\ & \leq\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \sum_{k=1}^{n}\frac{\big|\big\langle x_{k},v\big\rangle \big|^{2}}{\lambda_{k}}=\big\langle v,h^{-1}v\big\rangle \big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \nonumber, \end{align} $$
which implies the claim.
Proof of Proposition 7.2.
Now we insert
![]() $h_{k}$
and
$h_{k}$
and
![]() $v_{k}$
to conclude. Using Proposition 7.11, and noting that ‘
$v_{k}$
to conclude. Using Proposition 7.11, and noting that ‘
![]() $\alpha $
’ of our problem is simply the constant
$\alpha $
’ of our problem is simply the constant
 $$ \begin{align} \max_{p\in L_{k}}\left\langle v_{k},e_{p}\right\rangle =\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}, \end{align} $$
$$ \begin{align} \max_{p\in L_{k}}\left\langle v_{k},e_{p}\right\rangle =\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}, \end{align} $$
we find that
 $$ \begin{align} \left\Vert K_{k}\right\Vert _{\infty,2} &\leq\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sqrt{\left\langle v_{k},h_{k}^{-2}v_{k}\right\rangle }=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}}} \nonumber\\ &\leq C\hat{V}_{k}k_{F}^{-1}\sqrt{\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}}}. \end{align} $$
$$ \begin{align} \left\Vert K_{k}\right\Vert _{\infty,2} &\leq\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sqrt{\left\langle v_{k},h_{k}^{-2}v_{k}\right\rangle }=\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}}} \nonumber\\ &\leq C\hat{V}_{k}k_{F}^{-1}\sqrt{\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}}}. \end{align} $$
The desired upper bound
then follows from an estimate from Proposition A.3 in the Appendix:
 $$\begin{align*}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}} \leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}},\quad k_{F}\rightarrow\infty. \end{align*}$$
$$\begin{align*}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}^{2}} \leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}},\quad k_{F}\rightarrow\infty. \end{align*}$$
However, by Proposition 7.14 and (7.11), we conclude that
 $$ \begin{align} \left\Vert A_{k} (t )\right\Vert _{\infty,2},\,\left\Vert B_{k} (t )\right\Vert _{\infty,2} & \leq3\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|} \nonumber\\ & \leq C\hat{V}_{k}k_{F}^{-1}\sqrt{\left|L_{k}\right|}\left(1+\hat{V}_{k}k_{F}^{-1}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}}\right) \leq C\hat{V}_{k}|k|^{\frac{1}{2}}\left(1+\hat{V}_{k}\right) , \end{align} $$
$$ \begin{align} \left\Vert A_{k} (t )\right\Vert _{\infty,2},\,\left\Vert B_{k} (t )\right\Vert _{\infty,2} & \leq3\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}}\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)\sqrt{\frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}}\left|L_{k}\right|} \nonumber\\ & \leq C\hat{V}_{k}k_{F}^{-1}\sqrt{\left|L_{k}\right|}\left(1+\hat{V}_{k}k_{F}^{-1}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}}\right) \leq C\hat{V}_{k}|k|^{\frac{1}{2}}\left(1+\hat{V}_{k}\right) , \end{align} $$
where we used
 $$ \begin{align} |L_k| \le C|k| k_F^2, \quad \sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}} \le C k_F \end{align} $$
$$ \begin{align} |L_k| \le C|k| k_F^2, \quad \sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}} \le C k_F \end{align} $$
from Proposition A.1 and Proposition A.2. Finally, from Proposition 7.15, we have
 $$ \begin{align} \max_{p\in L_{k}} \left|\left\langle e_p,\left(E_k-h_k\right)e_p\right\rangle \right| & \leq \left(1+\left\langle v_k,h_k^{-1}v_k\right\rangle \right) \sup_{p\in L_k} |\left\langle e_p,v\right\rangle|^2 \nonumber\\ &= \left(1+\hat{V}_{k}k_{F}^{-1}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}}\right) \frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}} \le Ck_{F}^{-1}\hat{V}_{k}\left(1+\hat{V}_{k}\right) , \end{align} $$
$$ \begin{align} \max_{p\in L_{k}} \left|\left\langle e_p,\left(E_k-h_k\right)e_p\right\rangle \right| & \leq \left(1+\left\langle v_k,h_k^{-1}v_k\right\rangle \right) \sup_{p\in L_k} |\left\langle e_p,v\right\rangle|^2 \nonumber\\ &= \left(1+\hat{V}_{k}k_{F}^{-1}\sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}}\right) \frac{\hat{V}_{k}k_{F}^{-1}}{2(2\pi)^{3}} \le Ck_{F}^{-1}\hat{V}_{k}\left(1+\hat{V}_{k}\right) , \end{align} $$
7.4 Kinetic estimates
Now we prove Proposition 7.3. Again, let us start with the notation (7.3). We have the following:
Proposition 7.16. Under the notation (7.3), it holds that
 $$ \begin{align*} \left\Vert h^{-\frac{1}{2}}K\right\Vert _{\operatorname{\mathrm{HS}}} & \leq\left\langle v,h^{-\frac{3}{2}}v\right\rangle ,\\ \left\Vert \left\{ K,h\right\} h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq2\left\Vert v\right\Vert \sqrt{\left\langle v,h^{-1}v\right\rangle },\\ \left\Vert h^{-\frac{1}{2}}\left\{ K,h\right\} h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq2\left\langle v,h^{-1}v\right\rangle. \end{align*} $$
$$ \begin{align*} \left\Vert h^{-\frac{1}{2}}K\right\Vert _{\operatorname{\mathrm{HS}}} & \leq\left\langle v,h^{-\frac{3}{2}}v\right\rangle ,\\ \left\Vert \left\{ K,h\right\} h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq2\left\Vert v\right\Vert \sqrt{\left\langle v,h^{-1}v\right\rangle },\\ \left\Vert h^{-\frac{1}{2}}\left\{ K,h\right\} h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq2\left\langle v,h^{-1}v\right\rangle. \end{align*} $$
Proof. Using Proposition 7.10, we estimate
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}K\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\leq\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{3}{2}}}\right)^{2}=\left\langle v,h^{-\frac{3}{2}}v\right\rangle ^{2}, \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}K\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\leq\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{3}{2}}}\right)^{2}=\left\langle v,h^{-\frac{3}{2}}v\right\rangle ^{2}, \end{align} $$
and for
![]() $\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}$
use that
$\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}$
use that
![]() $\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}\leq \left\Vert Kh^{\frac {1}{2}}\right\Vert _{\text {HS}}+\left\Vert hKh^{-\frac {1}{2}}\right\Vert _{\text {HS}}$
to estimate
$\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}\leq \left\Vert Kh^{\frac {1}{2}}\right\Vert _{\text {HS}}+\left\Vert hKh^{-\frac {1}{2}}\right\Vert _{\text {HS}}$
to estimate
 $$ \begin{align} \left\Vert Kh^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} & =\sum_{i,j=1}^{n}\lambda_{j}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}=\left\Vert v\right\Vert ^{2}\left\langle v,h^{-1}v\right\rangle \nonumber\\ \left\Vert hKh^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2} & =\sum_{i,j=1}^{n}\frac{\lambda_{i}^{2}}{\lambda_{j}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}=\left\Vert v\right\Vert ^{2}\left\langle v,h^{-1}v\right\rangle \end{align} $$
$$ \begin{align} \left\Vert Kh^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} & =\sum_{i,j=1}^{n}\lambda_{j}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}=\left\Vert v\right\Vert ^{2}\left\langle v,h^{-1}v\right\rangle \nonumber\\ \left\Vert hKh^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2} & =\sum_{i,j=1}^{n}\frac{\lambda_{i}^{2}}{\lambda_{j}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}=\left\Vert v\right\Vert ^{2}\left\langle v,h^{-1}v\right\rangle \end{align} $$
for the claimed
![]() $\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}\leq 2\left\Vert v\right\Vert \sqrt {\left\langle v,h^{-1}v\right\rangle }$
. We likewise have that
$\left\Vert \left\{ K,h\right\} h^{-\frac {1}{2}}\right\Vert _{\text {HS}}\leq 2\left\Vert v\right\Vert \sqrt {\left\langle v,h^{-1}v\right\rangle }$
. We likewise have that
so the bound
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}Kh^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\frac{\lambda_{i}}{\lambda_{j}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{2}=\left\langle v,h^{-1}v\right\rangle ^{2} \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}Kh^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\frac{\lambda_{i}}{\lambda_{j}}\left|\left\langle x_{i},Kx_{j}\right\rangle \right|^{2}\leq\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{2}=\left\langle v,h^{-1}v\right\rangle ^{2} \end{align} $$
implies the final claim.
For
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
, we recall the decompositions (7.45)-(7.47). Recall also that
$B (t )$
, we recall the decompositions (7.45)-(7.47). Recall also that
![]() $(x_i)_i$
is an eigenbasis of h and
$(x_i)_i$
is an eigenbasis of h and
![]() $\langle x_i,v\rangle \ge 0$
for all
$\langle x_i,v\rangle \ge 0$
for all
![]() $1\le i\le n$
. We first estimate the
$1\le i\le n$
. We first estimate the
![]() $e^{tK}P_{v}e^{tK}$
term:
$e^{tK}P_{v}e^{tK}$
term:
Proposition 7.17. For all
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
Proof. We write
![]() $e^{tK}P_{v}e^{tK}$
as
$e^{tK}P_{v}e^{tK}$
as
and estimate each term separately. By the definition of
![]() $P_{v}$
, the first term is simply
$P_{v}$
, the first term is simply
For the remaining terms, we use Proposition 7.10 to estimate that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left(e^{tK}-1\right)P_{v}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(e^{tK}-1\right)x_{k}\right\rangle \left\langle x_{k},P_{v}x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2}\qquad\qquad\qquad\qquad \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left(e^{tK}-1\right)P_{v}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(e^{tK}-1\right)x_{k}\right\rangle \left\langle x_{k},P_{v}x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2}\qquad\qquad\qquad\qquad \end{align} $$
 $$ \begin{align} \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{3}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{3}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}P_{v}\left(e^{tK}-1\right)x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},P_{v}x_{k}\right\rangle \left\langle x_{k},\left(e^{tK}-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{3}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}\nonumber \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}P_{v}\left(e^{tK}-1\right)x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},P_{v}x_{k}\right\rangle \left\langle x_{k},\left(e^{tK}-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{3}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}\nonumber \end{align} $$
and
 $$ \begin{align} & \,\,\left\Vert h^{-\frac{1}{2}}\left(e^{tK}-1\right)P_{v}\left(e^{tK}-1\right)x_{j}\right\Vert ^{2}\nonumber\\ &=\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\left\langle x_{i},\left(e^{tK}-1\right)x_{k}\right\rangle \left\langle x_{k},P_{v}x_{l}\right\rangle \left\langle x_{l},\left(e^{tK}-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{5}\nonumber, \end{align} $$
$$ \begin{align} & \,\,\left\Vert h^{-\frac{1}{2}}\left(e^{tK}-1\right)P_{v}\left(e^{tK}-1\right)x_{j}\right\Vert ^{2}\nonumber\\ &=\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\left\langle x_{i},\left(e^{tK}-1\right)x_{k}\right\rangle \left\langle x_{k},P_{v}x_{l}\right\rangle \left\langle x_{l},\left(e^{tK}-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{5}\nonumber, \end{align} $$
which imply the claim.
Finally, the full estimates on
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
are now easily obtained:
$B (t )$
are now easily obtained:
Proposition 7.18. It holds for all
![]() $t\in \left[0,1\right]$
that
$t\in \left[0,1\right]$
that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
.
Proof. The estimates for
![]() $A (t )$
and
$A (t )$
and
![]() $B (t )$
are similar, so we focus on
$B (t )$
are similar, so we focus on
![]() $A (t )$
. We have
$A (t )$
. We have
 $$ \begin{align} &\left\Vert h^{-\frac{1}{2}}A (t )x_{j}\right\Vert \nonumber\\ &\quad \leq\left\Vert h^{-\frac{1}{2}}\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}\left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)x_{j}\right\Vert \nonumber\\ &\qquad +\left\Vert h^{-\frac{1}{2}}\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}e^{tK}P_{v}e^{tK}x_{j}\right\Vert , \end{align} $$
$$ \begin{align} &\left\Vert h^{-\frac{1}{2}}A (t )x_{j}\right\Vert \nonumber\\ &\quad \leq\left\Vert h^{-\frac{1}{2}}\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}\left(\cosh\left(-tK\right)-1\right)h\left(\cosh\left(-tK\right)-1\right)x_{j}\right\Vert \nonumber\\ &\qquad +\left\Vert h^{-\frac{1}{2}}\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}e^{tK}P_{v}e^{tK}x_{j}\right\Vert , \end{align} $$
and by Proposition 7.13, we can estimate that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\rangle \right|^{2}\nonumber\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\sinh\left(-tK\right)h\sinh\left(-tK\right)x_{j}\right\rangle \right|^{2}\nonumber\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left\langle v,h^{-1}v\right\rangle ^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
the same estimate holding also for
![]() $\left\Vert h^{-\frac {1}{2}}\left(\cosh \left(-tK\right)-1\right)h\left(\cosh \left(-tK\right)-1\right)x_{j}\right\Vert $
, and
$\left\Vert h^{-\frac {1}{2}}\left(\cosh \left(-tK\right)-1\right)h\left(\cosh \left(-tK\right)-1\right)x_{j}\right\Vert $
, and
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\rangle \right|^{2}\nonumber\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle . \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\left\{ h,\cosh\left(-tK\right)-1\right\} x_{j}\right\rangle \right|^{2}\nonumber\\ & \leq\left|\left\langle v,x_{j}\right\rangle \right|^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq\alpha^{2}\left\langle v,h^{-1}v\right\rangle . \end{align} $$
Inserting also the estimate of Proposition 7.17, we thus obtain
 $$ \begin{align} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}A (t )x_{j}\right\Vert & \leq2\alpha\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}+\alpha\sqrt{\left\langle v,h^{-1}v\right\rangle }+\alpha(1+\left\langle v,h^{-1}v\right\rangle )^{2}\sqrt{\left\langle v,h^{-1}v\right\rangle }\\ & \leq2\alpha(1+\langle v,h^{-1}v\rangle )^{2}\sqrt{\langle v,h^{-1}v\rangle }.\nonumber \end{align} $$
$$ \begin{align} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}A (t )x_{j}\right\Vert & \leq2\alpha\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}+\alpha\sqrt{\left\langle v,h^{-1}v\right\rangle }+\alpha(1+\left\langle v,h^{-1}v\right\rangle )^{2}\sqrt{\left\langle v,h^{-1}v\right\rangle }\\ & \leq2\alpha(1+\langle v,h^{-1}v\rangle )^{2}\sqrt{\langle v,h^{-1}v\rangle }.\nonumber \end{align} $$
Proof of Proposition 7.3.
The desired bounds follow from applying the general estimates of this section to
![]() $h_k$
and
$h_k$
and
![]() $v_k$
, plus using the uniform bound on
$v_k$
, plus using the uniform bound on
![]() $\alpha $
in (7.65) and the estimates
$\alpha $
in (7.65) and the estimates
which hold for all
![]() $k\in \overline {B}\left(0,2k_{F}\right)$
due to Propositions A.1, A.2, and A.3.
$k\in \overline {B}\left(0,2k_{F}\right)$
due to Propositions A.1, A.2, and A.3.
8 Gronwall estimates for the Bogolubov transformation
In the previous sections, we have bounded several error terms using the operators
![]() $H_{\mathrm {kin}}'$
and
$H_{\mathrm {kin}}'$
and
![]() $\mathcal {N}_E$
. In this section, we control the propagation of these operators under the Bogolubov transformation
$\mathcal {N}_E$
. In this section, we control the propagation of these operators under the Bogolubov transformation
![]() $e^{-\mathcal {K}}$
defined in Section 5. We have the following Gronwall-type estimates.
$e^{-\mathcal {K}}$
defined in Section 5. We have the following Gronwall-type estimates.
Proposition 8.1. Let
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Then for all
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
. Then for all
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
![]() $\left|t\right|\leq 1$
, it holds that
$\left|t\right|\leq 1$
, it holds that
 $$ \begin{align*} \left\langle e^{-t\mathcal{K}}\Psi, (H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) e^{-t\mathcal{K}}\Psi\right\rangle &\leq C \left\langle \Psi, ( H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi\right\rangle,\\ \left\langle e^{-t\mathcal{K}}\Psi, (k_F^{-1} \mathcal{N}_E H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) e^{-t\mathcal{K}}\Psi\right\rangle &\leq C\left\langle \Psi,(k_F^{-1} \mathcal{N}_E H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi\right\rangle \end{align*} $$
$$ \begin{align*} \left\langle e^{-t\mathcal{K}}\Psi, (H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) e^{-t\mathcal{K}}\Psi\right\rangle &\leq C \left\langle \Psi, ( H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi\right\rangle,\\ \left\langle e^{-t\mathcal{K}}\Psi, (k_F^{-1} \mathcal{N}_E H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) e^{-t\mathcal{K}}\Psi\right\rangle &\leq C\left\langle \Psi,(k_F^{-1} \mathcal{N}_E H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi\right\rangle \end{align*} $$
for a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $k_{F}$
.
$k_{F}$
.
As a preparation, let us first prove the following:
Lemma 8.2. Let
![]() $X,Y,Z$
be self-adjoint operators on a Hilbert space such that
$X,Y,Z$
be self-adjoint operators on a Hilbert space such that
Then,
Proof of Lemma 8.2 .
Using (7.8), we can write
 $$ \begin{align} \left[Y,\sqrt{X}\right]=\frac{2}{\pi}\int_{0}^{\infty} \left[Y, \frac{X}{X+t^{2}}\right]\,dt= \frac{2}{\pi}\int_{0}^{\infty} \left[Y, \frac{-t^2}{X+t^{2}}\right]\,dt = \frac{2}{\pi}\int_{0}^{\infty} \frac{1}{X+t^{2}} \left[Y, X\right] \frac{1}{X+t^{2}}\, t^2 dt, \end{align} $$
$$ \begin{align} \left[Y,\sqrt{X}\right]=\frac{2}{\pi}\int_{0}^{\infty} \left[Y, \frac{X}{X+t^{2}}\right]\,dt= \frac{2}{\pi}\int_{0}^{\infty} \left[Y, \frac{-t^2}{X+t^{2}}\right]\,dt = \frac{2}{\pi}\int_{0}^{\infty} \frac{1}{X+t^{2}} \left[Y, X\right] \frac{1}{X+t^{2}}\, t^2 dt, \end{align} $$
and applying this identity twice, we get
 $$ \begin{align} \left[\left[Y,\sqrt{X}\right],\sqrt{X}\right] = \left(\frac{2}{\pi} \right)^2 \int_{0}^{\infty} \int_0^\infty \frac{1}{X+t^{2}} \frac{1}{X+s^{2}} \left[\left[Y, X\right],X \right] \frac{1}{X+s^{2}} \frac{1}{X+t^{2}}\, s^2 t^2 ds dt. \end{align} $$
$$ \begin{align} \left[\left[Y,\sqrt{X}\right],\sqrt{X}\right] = \left(\frac{2}{\pi} \right)^2 \int_{0}^{\infty} \int_0^\infty \frac{1}{X+t^{2}} \frac{1}{X+s^{2}} \left[\left[Y, X\right],X \right] \frac{1}{X+s^{2}} \frac{1}{X+t^{2}}\, s^2 t^2 ds dt. \end{align} $$
Therefore, the assumptions
![]() $\pm \left[\left[Y,X\right],X\right] \le Z$
and
$\pm \left[\left[Y,X\right],X\right] \le Z$
and
![]() $[X,Z]=0$
imply that
$[X,Z]=0$
imply that
 $$ \begin{align} \pm \left[\left[Y,\sqrt{X}\right],\sqrt{X}\right] \le \left(\frac{2}{\pi} \right)^2 \int_{0}^{\infty} \int_0^\infty \frac{1}{X+t^{2}} \frac{1}{X+s^{2}} Z \frac{1}{X+s^{2}} \frac{1}{X+t^{2}}\, s^2 t^2 ds dt = \frac{Z}{4X}. \end{align} $$
$$ \begin{align} \pm \left[\left[Y,\sqrt{X}\right],\sqrt{X}\right] \le \left(\frac{2}{\pi} \right)^2 \int_{0}^{\infty} \int_0^\infty \frac{1}{X+t^{2}} \frac{1}{X+s^{2}} Z \frac{1}{X+s^{2}} \frac{1}{X+t^{2}}\, s^2 t^2 ds dt = \frac{Z}{4X}. \end{align} $$
Now we give the following:
Proof of Proposition 8.1 .
Write
![]() $\Psi _{t}=e^{t\mathcal {K}} \Psi $
for brevity. Recalling Proposition 5.4, we see that
$\Psi _{t}=e^{t\mathcal {K}} \Psi $
for brevity. Recalling Proposition 5.4, we see that
 $$ \begin{align} \frac{d}{dt}\left\langle \Psi_{t},(H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F)\Psi_{t}\right\rangle =\left\langle \Psi_{t},\left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle =\sum_{k\in S_{C}}\left\langle \Psi_{t},Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right)\Psi_{t}\right\rangle. \end{align} $$
$$ \begin{align} \frac{d}{dt}\left\langle \Psi_{t},(H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F)\Psi_{t}\right\rangle =\left\langle \Psi_{t},\left[\mathcal{K},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle =\sum_{k\in S_{C}}\left\langle \Psi_{t},Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right)\Psi_{t}\right\rangle. \end{align} $$
The right-hand side can be bounded by using Propositions 4.10 and 7.3 as
 $$ \begin{align} & \sum_{k\in S_{C}}\left|\left\langle \Psi_{t},Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right)\Psi_{t}\right\rangle \right| \leq2\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{HS}}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle \nonumber \\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad+2\sum_{k\in S_{C}}\left\Vert \left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{HS}}\sqrt{\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle }\left\Vert \Psi_{t}\right\Vert \nonumber \\ & \leq C\left(\sum_{k\in S_{C}}\hat{V}_{k}\right)\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle +Ck_{F}^{\frac{1}{2}}\left(\sum_{k\in S_{C}}\hat{V}_{k}|k|^{\frac{1}{2}}\right)\sqrt{\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle }\left\Vert \Psi_t\right\Vert \nonumber \\ & \leq C\left\langle \Psi_{t}, (H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi_{t}\right\rangle, \end{align} $$
$$ \begin{align} & \sum_{k\in S_{C}}\left|\left\langle \Psi_{t},Q_{2}^{k}\left(\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \right)\Psi_{t}\right\rangle \right| \leq2\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{HS}}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle \nonumber \\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad+2\sum_{k\in S_{C}}\left\Vert \left\{ K_{k}^{\oplus},h_{k}^{\oplus}\right\} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{HS}}\sqrt{\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle }\left\Vert \Psi_{t}\right\Vert \nonumber \\ & \leq C\left(\sum_{k\in S_{C}}\hat{V}_{k}\right)\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle +Ck_{F}^{\frac{1}{2}}\left(\sum_{k\in S_{C}}\hat{V}_{k}|k|^{\frac{1}{2}}\right)\sqrt{\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle }\left\Vert \Psi_t\right\Vert \nonumber \\ & \leq C\left\langle \Psi_{t}, (H_{\operatorname{\mathrm{kin}}}^{\prime} + k_F) \Psi_{t}\right\rangle, \end{align} $$
where we also used the Cauchy–Schwarz inequality in the last step. Thus, the first estimate of Proposition 8.1 follows by Gronwall’s lemma. For the second bound of Proposition 8.1, let us denote
Note that
![]() $Y_1,Y_2$
are symmetric since
$Y_1,Y_2$
are symmetric since
![]() $X_1,X_2$
are symmetric and
$X_1,X_2$
are symmetric and
![]() $\mathcal {K}$
is skew-symmetric. Moreover, since
$\mathcal {K}$
is skew-symmetric. Moreover, since
![]() $[X_1,X_2]=0$
,
$[X_1,X_2]=0$
,
![]() $[\mathcal {K}, X_1X_2]$
is also symmetric, and we can write
$[\mathcal {K}, X_1X_2]$
is also symmetric, and we can write
 $$ \begin{align} 2[\mathcal{K}, X_1 X_2] &= 2\Big( X_1 [\mathcal{K}, X_2] + [\mathcal{K}, X_1] X_2\Big) = 2( X_1 Y_1+ Y_2X_2) \nonumber\\ &= \sum_{i=1}^2 ( X_i Y_i+ Y_iX_i) = \sum_{i=1}^2 \left( 2 \sqrt{X_i} Y_i \sqrt{X_i} + [[ Y_i, \sqrt{X_i}], \sqrt{X_i}] \right). \end{align} $$
$$ \begin{align} 2[\mathcal{K}, X_1 X_2] &= 2\Big( X_1 [\mathcal{K}, X_2] + [\mathcal{K}, X_1] X_2\Big) = 2( X_1 Y_1+ Y_2X_2) \nonumber\\ &= \sum_{i=1}^2 ( X_i Y_i+ Y_iX_i) = \sum_{i=1}^2 \left( 2 \sqrt{X_i} Y_i \sqrt{X_i} + [[ Y_i, \sqrt{X_i}], \sqrt{X_i}] \right). \end{align} $$
For
![]() $i=1$
, arguing similarly to (8.4) and (8.5), we have
$i=1$
, arguing similarly to (8.4) and (8.5), we have
Here, we used
![]() $[X_1,X_2]=0$
in the last estimate. To apply Lemma 8.2, let us compute
$[X_1,X_2]=0$
in the last estimate. To apply Lemma 8.2, let us compute
![]() $[[Y_1, X_1], X_1]$
. Note that for every symmetric operator B on
$[[Y_1, X_1], X_1]$
. Note that for every symmetric operator B on
![]() $\ell ^2(L_k^{\pm })$
, we deduce from (1.75) that
$\ell ^2(L_k^{\pm })$
, we deduce from (1.75) that
 $$ \begin{align} \left[ Q_{2}^{k}(B) ,\mathcal{N}_E\right] & = 2 \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right), \nonumber\\ \left[ \left[ Q_{2}^{k}(B) ,\mathcal{N}_E\right],\mathcal{N}_E\right] &= 4 \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left( b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right) = 4 Q_{2}^{k}(B). \end{align} $$
$$ \begin{align} \left[ Q_{2}^{k}(B) ,\mathcal{N}_E\right] & = 2 \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right), \nonumber\\ \left[ \left[ Q_{2}^{k}(B) ,\mathcal{N}_E\right],\mathcal{N}_E\right] &= 4 \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left( b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right) = 4 Q_{2}^{k}(B). \end{align} $$
Using (8.9) and (8.8), we have
which implies by Lemma 8.2 that
Next, we consider the terms of
![]() $i=2$
in (8.7). Let us compute the commutator
$i=2$
in (8.7). Let us compute the commutator
![]() $Y_2=\left[\mathcal {K},\mathcal {N}_{E}\right]$
. By linearity, we deduce from (1.75) that
$Y_2=\left[\mathcal {K},\mathcal {N}_{E}\right]$
. By linearity, we deduce from (1.75) that
![]() $\left[b_{k}(\varphi ),\mathcal {N}_{E}\right]=b_{k}(\varphi )$
for any
$\left[b_{k}(\varphi ),\mathcal {N}_{E}\right]=b_{k}(\varphi )$
for any
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
, and hence from the definition of
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
, and hence from the definition of
![]() $\mathcal {K}$
in (5.2),
$\mathcal {K}$
in (5.2),
 $$ \begin{align} Y_2=\left[\mathcal{K},\mathcal{N}_{E}\right] =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)=\sum_{k\in S_{C}}Q_{2}^{k}\left(K_{k}^{\oplus}\right). \end{align} $$
$$ \begin{align} Y_2=\left[\mathcal{K},\mathcal{N}_{E}\right] =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(e_{p})b_{k}^{\ast}\left(K_{k}^{\oplus}e_{p}\right)+b_{k}\left(K_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)=\sum_{k\in S_{C}}Q_{2}^{k}\left(K_{k}^{\oplus}\right). \end{align} $$
Note that
 $$ \begin{align} K_{k}^{\oplus}= \left(\begin{array}{cc} 0 & K_{k}\\ K_{k} & 0 \end{array}\right)=\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right)\left(\begin{array}{cc} K_{k} & 0\\ 0 & -K_{k} \end{array}\right)\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right), \end{align} $$
$$ \begin{align} K_{k}^{\oplus}= \left(\begin{array}{cc} 0 & K_{k}\\ K_{k} & 0 \end{array}\right)=\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right)\left(\begin{array}{cc} K_{k} & 0\\ 0 & -K_{k} \end{array}\right)\left(\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right), \end{align} $$
and hence by Proposition 7.1, we obtain
Therefore, by Proposition 4.7,
 $$ \begin{align} \pm Y_2 \leq2\left(\sum_{k\in S_{C}}\left\Vert K_{k}^{\oplus}\right\Vert _{\text{HS}}\right) \left(1+\mathcal{N}_{E}\right) \le C X_1, \quad \pm \sqrt{X_2} Y_2 \sqrt{X_2} \le C X_1 X_2. \end{align} $$
$$ \begin{align} \pm Y_2 \leq2\left(\sum_{k\in S_{C}}\left\Vert K_{k}^{\oplus}\right\Vert _{\text{HS}}\right) \left(1+\mathcal{N}_{E}\right) \le C X_1, \quad \pm \sqrt{X_2} Y_2 \sqrt{X_2} \le C X_1 X_2. \end{align} $$
Finally, consider
For every symmetric operator B on
![]() $\ell ^2(L_k^{\pm })$
, by (1.74), we compute
$\ell ^2(L_k^{\pm })$
, by (1.74), we compute
 $$ \begin{align} \left[ Q_{2}^{k}(B) , H_{\operatorname{\mathrm{kin}}}' \right] & = \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left[ \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right),H_{\operatorname{\mathrm{kin}}}' \right] \nonumber\\ &= \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} ) \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right), \nonumber \\ \left[ \left[ Q_{2}^{k}(B) ,H_{\operatorname{\mathrm{kin}}}' \right],H_{\operatorname{\mathrm{kin}}}' \right] & = \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} ) \left[ \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right) , H_{\operatorname{\mathrm{kin}}}' \right] \nonumber \\ &= \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} )^2 \left( b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right). \end{align} $$
$$ \begin{align} \left[ Q_{2}^{k}(B) , H_{\operatorname{\mathrm{kin}}}' \right] & = \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle \left[ \left(b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right),H_{\operatorname{\mathrm{kin}}}' \right] \nonumber\\ &= \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} ) \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right), \nonumber \\ \left[ \left[ Q_{2}^{k}(B) ,H_{\operatorname{\mathrm{kin}}}' \right],H_{\operatorname{\mathrm{kin}}}' \right] & = \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} ) \left[ \left(- b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right) , H_{\operatorname{\mathrm{kin}}}' \right] \nonumber \\ &= \sum_{p,q\in L_{k}^{\pm}} \left\langle e_{p},Be_{q}\right\rangle (\lambda_{\overline{k,p}} +\lambda_{ \overline{k,q}} )^2 \left( b_{\overline{k,p}}^{\ast}b_{\overline{k,q}}^{\ast}+b_{\overline{k,q}}b_{\overline{k,p}}\right). \end{align} $$
By the Cauchy–Schwarz inequality, we can estimate
 $$ \begin{align} \pm \left[ \left[ Q_{2}^{k}(B) ,H_{\operatorname{\mathrm{kin}}}' \right],H_{\operatorname{\mathrm{kin}}}' \right] \le \sum_{p,q\in L_{k}^{\pm}} \left( \epsilon \Big( \lambda_{\overline{k,p}} +\lambda_{\overline{k,q}} \Big)^4 b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} + \epsilon^{-1} |\left\langle e_{p},Be_{q}\right\rangle|^2 \right) \end{align} $$
$$ \begin{align} \pm \left[ \left[ Q_{2}^{k}(B) ,H_{\operatorname{\mathrm{kin}}}' \right],H_{\operatorname{\mathrm{kin}}}' \right] \le \sum_{p,q\in L_{k}^{\pm}} \left( \epsilon \Big( \lambda_{\overline{k,p}} +\lambda_{\overline{k,q}} \Big)^4 b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} + \epsilon^{-1} |\left\langle e_{p},Be_{q}\right\rangle|^2 \right) \end{align} $$
for all
![]() $\epsilon>0$
. From Propositions 4.5, 4.8 and the commutation relations (1.74), (1.75), we have
$\epsilon>0$
. From Propositions 4.5, 4.8 and the commutation relations (1.74), (1.75), we have
 $$ \begin{align} 0&\le \sum_{p,q\in L_k^{\pm}} \lambda_{\overline{k,p}} b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} \le \sum_{p\in L_k^{\pm}} \lambda_{\overline{k,p}} b_{\overline{k,p}}^{\ast} \mathcal{N}_E b_{\overline{k,p}} \le H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E, \nonumber\\ 0&\le \sum_{p,q\in L_k^{\pm}} \lambda_{\overline{k,q}} b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} \le \sum_{p\in L_k^{\pm}} b_{\overline{k,p}}^{\ast} H_{\operatorname{\mathrm{kin}}}' b_{\overline{k,p}} \le H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E. \end{align} $$
$$ \begin{align} 0&\le \sum_{p,q\in L_k^{\pm}} \lambda_{\overline{k,p}} b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} \le \sum_{p\in L_k^{\pm}} \lambda_{\overline{k,p}} b_{\overline{k,p}}^{\ast} \mathcal{N}_E b_{\overline{k,p}} \le H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E, \nonumber\\ 0&\le \sum_{p,q\in L_k^{\pm}} \lambda_{\overline{k,q}} b_{\overline{k,p}}^{\ast} b_{\overline{k,q}}^{\ast} b_{\overline{k,q}} b_{\overline{k,p}} \le \sum_{p\in L_k^{\pm}} b_{\overline{k,p}}^{\ast} H_{\operatorname{\mathrm{kin}}}' b_{\overline{k,p}} \le H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E. \end{align} $$
Moreover, when
![]() $k\in S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
$k\in S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
![]() $1\ge \gamma>0$
, we have
$1\ge \gamma>0$
, we have
Hence, we conclude from (8.18) that
for all
![]() $\epsilon>0$
. Optimizing over
$\epsilon>0$
. Optimizing over
![]() $\epsilon $
gives
$\epsilon $
gives
for all symmetric operators B on
![]() $\ell ^2(L_k^{\pm })$
. Inserting this in (8.16) and using
$\ell ^2(L_k^{\pm })$
. Inserting this in (8.16) and using
(which is similar to (8.14)), we find that
 $$ \begin{align} \pm [[Y_1, X_2], X_2] = \pm \sum_{k\in S_{C}} \left[ \left[ Q_{2}^{k}\left(K_{k}^{\oplus} \right), H_{\operatorname{\mathrm{kin}}}' \right], H_{\operatorname{\mathrm{kin}}}'\right] \le C k_F \Big( H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E + k_F^2 \Big) \le C X_1 X_2^2. \end{align} $$
$$ \begin{align} \pm [[Y_1, X_2], X_2] = \pm \sum_{k\in S_{C}} \left[ \left[ Q_{2}^{k}\left(K_{k}^{\oplus} \right), H_{\operatorname{\mathrm{kin}}}' \right], H_{\operatorname{\mathrm{kin}}}'\right] \le C k_F \Big( H_{\operatorname{\mathrm{kin}}}' \mathcal{N}_E + k_F^2 \Big) \le C X_1 X_2^2. \end{align} $$
Applying Lemma 8.2, we obtain
Putting together (8.8), (8.11), (8.15) and (8.25), we conclude from (8.7) that
Thus,
 $$ \begin{align} \left|\frac{d}{dt}\left\langle \Psi_{t},X_1X_2 \Psi_{t}\right\rangle \right| =\left| \left\langle \Psi_{t}, [\mathcal{K}, X_1X_2] \Psi_{t}\right\rangle \right| \le C \left\langle \Psi_{t},X_1X_2 \Psi_{t}\right\rangle. \end{align} $$
$$ \begin{align} \left|\frac{d}{dt}\left\langle \Psi_{t},X_1X_2 \Psi_{t}\right\rangle \right| =\left| \left\langle \Psi_{t}, [\mathcal{K}, X_1X_2] \Psi_{t}\right\rangle \right| \le C \left\langle \Psi_{t},X_1X_2 \Psi_{t}\right\rangle. \end{align} $$
By Gronwall’s lemma, we have
This implies the desired bound since
![]() $\frac {1}{2}X_1X_2 \le \mathcal {N}_E H_{\operatorname {\mathrm {kin}}}^{\prime } + k_F H_{\operatorname {\mathrm {kin}}}^{\prime } + k_F^2 \le X_1X_2$
. Here, we used again Proposition 2.1.
$\frac {1}{2}X_1X_2 \le \mathcal {N}_E H_{\operatorname {\mathrm {kin}}}^{\prime } + k_F H_{\operatorname {\mathrm {kin}}}^{\prime } + k_F^2 \le X_1X_2$
. Here, we used again Proposition 2.1.
9 The second Bogolubov transformation
Recall that after the conjugation by
![]() $e^{\mathcal {K}}$
, up to negligible error terms, we obtain the correlation energy and the operator
$e^{\mathcal {K}}$
, up to negligible error terms, we obtain the correlation energy and the operator
In the bosonic analogy, where we informally consider
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }\sim 2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
, this expression would be manifestly non-negative as
$H_{\operatorname {\mathrm {kin}}}^{\prime }\sim 2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
, this expression would be manifestly non-negative as
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
cancels the negative terms
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
cancels the negative terms
![]() $2\sum _{k\in S_{C}}\tilde {Q}_{1}^{k}(-h_{k}^{\oplus })$
(and
$2\sum _{k\in S_{C}}\tilde {Q}_{1}^{k}(-h_{k}^{\oplus })$
(and
![]() $E_{k}^{\oplus }>0$
as
$E_{k}^{\oplus }>0$
as
![]() $E_{k}=e^{-K_{k}}h_{k}e^{-K_{k}}>0$
), so this term could be neglected for the lower bound. This analogy is only formal, however. One might still hope that
$E_{k}=e^{-K_{k}}h_{k}e^{-K_{k}}>0$
), so this term could be neglected for the lower bound. This analogy is only formal, however. One might still hope that
![]() $E_{k}^{\oplus }-h_{k}^{\oplus }\geq 0$
since
$E_{k}^{\oplus }-h_{k}^{\oplus }\geq 0$
since
![]() $E_{k}$
is isospectral to
$E_{k}$
is isospectral to
![]() $\widetilde {E}_k$
and
$\widetilde {E}_k$
and
![]() $\widetilde {E}_k\ge h_k$
, but this fails too; it can be shown that
$\widetilde {E}_k\ge h_k$
, but this fails too; it can be shown that
![]() $E_{k}-h_{k}$
is indefinite. While these two ideas – the bosonic analogy and the fact that
$E_{k}-h_{k}$
is indefinite. While these two ideas – the bosonic analogy and the fact that
![]() $E_k-h_{k}\geq 0$
– fail on their own, we will overcome this issue by combining them. In this section, we will carry out another unitary transformation which effectively replaces
$E_k-h_{k}\geq 0$
– fail on their own, we will overcome this issue by combining them. In this section, we will carry out another unitary transformation which effectively replaces
![]() $E_k$
by
$E_k$
by
![]() $\widetilde {E}_k$
in (9.1).
$\widetilde {E}_k$
in (9.1).
Consider the unitary transformation
![]() $e^{\mathcal {J}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
, where
$e^{\mathcal {J}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
, where
![]() $\mathcal {J}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
is now of the form
$\mathcal {J}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
is now of the form
 $$ \begin{align} \mathcal{J}=\sum_{k\in S_{C}}\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},J_{k}^{\oplus}e_{q}\right\rangle b_{k}^{\ast}(e_{p})b_{k}\left(e_{q}\right)=\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}), \end{align} $$
$$ \begin{align} \mathcal{J}=\sum_{k\in S_{C}}\sum_{p,q\in L_{k}^{\pm}}\left\langle e_{p},J_{k}^{\oplus}e_{q}\right\rangle b_{k}^{\ast}(e_{p})b_{k}\left(e_{q}\right)=\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}), \end{align} $$
where
![]() $S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
$S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
![]() $1\ge \gamma>0$
and
$1\ge \gamma>0$
and
 $$ \begin{align} J_{k}^{\oplus}=\left(\begin{array}{cc} J_{k} & 0\\ 0 & J_{k} \end{array}\right), \quad J_{k}=\log\left(U_{k}\right), \quad U_{k}=\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}e^{K_{k}}. \end{align} $$
$$ \begin{align} J_{k}^{\oplus}=\left(\begin{array}{cc} J_{k} & 0\\ 0 & J_{k} \end{array}\right), \quad J_{k}=\log\left(U_{k}\right), \quad U_{k}=\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}h_{k}^{-\frac{1}{2}}e^{K_{k}}. \end{align} $$
Here,
![]() $U_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
is the unitary transformation which takes
$U_{k}:\ell ^{2}(L_{k})\rightarrow \ell ^{2}(L_{k})$
is the unitary transformation which takes
![]() $E_{k}$
to
$E_{k}$
to
![]() $\widetilde E_k$
, namely,
$\widetilde E_k$
, namely,
 $$ \begin{align} U_{k} E_{k}U_{k}^{\ast} =\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\widetilde E_k, \end{align} $$
$$ \begin{align} U_{k} E_{k}U_{k}^{\ast} =\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}\left(h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}\right)^{\frac{1}{2}}=h_{k}^{\frac{1}{2}}e^{-2K_{k}}h_{k}^{\frac{1}{2}}=\widetilde E_k, \end{align} $$
and
![]() $J_k$
is the (principal) logarithm of
$J_k$
is the (principal) logarithm of
![]() $U_{k}$
, so that
$U_{k}$
, so that
![]() $e^{J_k}= U_k$
. Since
$e^{J_k}= U_k$
. Since
![]() $J_k$
is skew-symmetric, so are
$J_k$
is skew-symmetric, so are
![]() $J_{k}^{\oplus }$
and
$J_{k}^{\oplus }$
and
![]() $\mathcal {J}$
, and hence,
$\mathcal {J}$
, and hence,
![]() $e^{\mathcal {J}}$
is a unitary operator on
$e^{\mathcal {J}}$
is a unitary operator on
![]() $\mathcal {H}_{N}$
.
$\mathcal {H}_{N}$
.
In the exact bosonic case, it is not difficult to see that for every skew-symmetric operator
![]() $J: V\to V$
, the unitary operator
$J: V\to V$
, the unitary operator
![]() $e^{\mathcal {J}}$
with
$e^{\mathcal {J}}$
with
![]() $\mathcal {J}= \text {d}\Gamma \left(J\right) = \sum _{i} a^{\ast }\left(Je_{i}\right)a(e_{i})$
is a Bogolubov transformation on
$\mathcal {J}= \text {d}\Gamma \left(J\right) = \sum _{i} a^{\ast }\left(Je_{i}\right)a(e_{i})$
is a Bogolubov transformation on
![]() $\mathcal {F}^+(V)$
which acts on a second-quantized operator as
$\mathcal {F}^+(V)$
which acts on a second-quantized operator as
Returning to the quasi-bosonic case, we will show that
 $$ \begin{align} \quad\;e^{\mathcal{J}} \left( \sum_{k\in S_{C}}\tilde{Q}_{1}^{k} ( E_{k}^{\oplus} ) \right)e^{-\mathcal{J}} \approx \sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}}E_{k}^{\oplus}e^{-J_{k}^{\oplus}}\right) = \sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde {E}_{k}^{\oplus}\right) \end{align} $$
$$ \begin{align} \quad\;e^{\mathcal{J}} \left( \sum_{k\in S_{C}}\tilde{Q}_{1}^{k} ( E_{k}^{\oplus} ) \right)e^{-\mathcal{J}} \approx \sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}}E_{k}^{\oplus}e^{-J_{k}^{\oplus}}\right) = \sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde {E}_{k}^{\oplus}\right) \end{align} $$
up to error terms which are similar to the exchange terms coming from the first transformation. Moreover, although
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime } \sim 2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
does not hold precisely, it is valid from the point of view of commutators as explained in (1.72), which results in
$H_{\operatorname {\mathrm {kin}}}^{\prime } \sim 2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
does not hold precisely, it is valid from the point of view of commutators as explained in (1.72), which results in
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }-2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
being essentially invariant under the Bogolubov transformation
$H_{\operatorname {\mathrm {kin}}}^{\prime }-2\sum _{k\in \mathbb {Z}_{+}^{3}}\tilde {Q}_{1}^{k}(h_{k}^{\oplus })$
being essentially invariant under the Bogolubov transformation
![]() $e^{\mathcal {J}}$
. The overall transformation then takes the form
$e^{\mathcal {J}}$
. The overall transformation then takes the form
 $$ \begin{align} e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \approx H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\widetilde {E}_{k}^{\oplus}-h_{k}^{\oplus}\right), \end{align} $$
$$ \begin{align} e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \approx H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\widetilde {E}_{k}^{\oplus}-h_{k}^{\oplus}\right), \end{align} $$
and we now have the desired non-negative operator
![]() $\widetilde {E}_{k}^{\oplus }-h_{k}^{\oplus }\ge 0$
on the right-hand side.
$\widetilde {E}_{k}^{\oplus }-h_{k}^{\oplus }\ge 0$
on the right-hand side.
While the error terms in (9.7) are similar to those coming from the first transformation, they are in practice more difficult to estimate, for although we derived simple, optimal estimates for the transformation kernels
![]() $\left(K_{k}\right)_{k\in S_{C}}$
in Section 7, we cannot obtain the same for the transformation kernels
$\left(K_{k}\right)_{k\in S_{C}}$
in Section 7, we cannot obtain the same for the transformation kernels
![]() $\left(J_{k}\right)_{k\in S_{C}}$
. The justification that the second transformation works as claimed will therefore take more effort than was needed for the first transformation.
$\left(J_{k}\right)_{k\in S_{C}}$
. The justification that the second transformation works as claimed will therefore take more effort than was needed for the first transformation.
9.1 Actions on the bosonizable terms
The first step of justifying (9.7) is to prove the following exact equality.
Proposition 9.1. The unitary transformation
![]() $e^{\mathcal {J}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
given in (9.2)-(9.3) satisfies
$e^{\mathcal {J}}:\mathcal {H}_{N}\rightarrow \mathcal {H}_{N}$
given in (9.2)-(9.3) satisfies
 $$ \begin{align*} &e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \\ & =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) +2\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t))e^{-(1-t)\mathcal{J}}dt, \end{align*} $$
$$ \begin{align*} &e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \\ & =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) +2\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t))e^{-(1-t)\mathcal{J}}dt, \end{align*} $$
where for all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and
$k\in \mathbb {Z}_{\ast }^{3}$
and
![]() $t\in \left[0,1\right]$
, we defined the operator
$t\in \left[0,1\right]$
, we defined the operator
![]() $F_{k}^{\oplus }(t):\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
$F_{k}^{\oplus }(t):\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
by
 $$\begin{align*}F_{k}^{\oplus} (t) = \left(\begin{array}{cc} e^{tJ_{k}} E_{k}e^{-tJ_{k}} - h_k & 0\\ 0 & e^{tJ_{k}}E_{k}e^{-tJ_{k}} - h_k \end{array}\right), \end{align*}$$
$$\begin{align*}F_{k}^{\oplus} (t) = \left(\begin{array}{cc} e^{tJ_{k}} E_{k}e^{-tJ_{k}} - h_k & 0\\ 0 & e^{tJ_{k}}E_{k}e^{-tJ_{k}} - h_k \end{array}\right), \end{align*}$$
and for symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, we defined the new exchange operator
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, we defined the new exchange operator
 $$ \begin{align*} \mathcal{E}_{3}^{k}(A) & =2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}(e_{p};e_{q})b_{l}(J_{l}^{\oplus}e_{q})\right)\\ & =2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)b_{l}(J_{l}^{\oplus}e_{q})\right).\nonumber \end{align*} $$
$$ \begin{align*} \mathcal{E}_{3}^{k}(A) & =2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}(e_{p};e_{q})b_{l}(J_{l}^{\oplus}e_{q})\right)\\ & =2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\left(\delta_{p,q}c_{\overline{q-k}}c_{\overline{p-k}}^{\ast}+\delta_{\overline{p-k},\overline{q-k}}c_{q}^{\ast}c_{p}\right)b_{l}(J_{l}^{\oplus}e_{q})\right).\nonumber \end{align*} $$
We will follow the same strategy as we did when we considered the action of the quasi-bosonic Bogolubov transformation on the
![]() $Q_{1}^{k}(A)$
and
$Q_{1}^{k}(A)$
and
![]() $Q_{2}^{k}(B)$
terms. First, we calculate the commutator:
$Q_{2}^{k}(B)$
terms. First, we calculate the commutator:
Proposition 9.2. For all
![]() $k\in S_{C}$
and symmetric
$k\in S_{C}$
and symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
Proof. We first calculate, using the commutation relations of the excitation operators
![]() $b_{k}(\varphi )$
and
$b_{k}(\varphi )$
and
![]() $b_{k}^{\ast }(\varphi )$
, that for any
$b_{k}^{\ast }(\varphi )$
, that for any
![]() $k\in S_{C}$
and
$k\in S_{C}$
and
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
,
 $$ \begin{align} \left[\mathcal{J},b_{k}(\varphi )\right] & =-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}(J_{l}^{\oplus}e_{q})\left[b_{k}(\varphi ),b_{l}\left(e_{q}\right)\right]+\left[b_{k}(\varphi ),b_{l}^{\ast}(J_{l}^{\oplus}e_{q})\right]b_{l}\left(e_{q}\right)\right)\nonumber \\ & =-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\delta_{k,l}\left\langle \varphi,J_{l}^{\oplus}e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;J_{l}^{\oplus}e_{q}\right)\right)b_{l}\left(e_{q}\right)\\ & =-\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,J_{k}^{\oplus}e_{q}\right\rangle b_{k}\left(e_{q}\right)-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;J_{l}^{\oplus}e_{q}\right)b_{l}\left(e_{q}\right)\nonumber \\ & =\sum_{q\in L_{k}^{\pm}}\left\langle J_{k}^{\oplus}\varphi,e_{q}\right\rangle b_{k}\left(e_{q}\right)+\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}(J_{l}^{\oplus}e_{q})\nonumber \\ & =b_{k}\left(J_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}^{\mathcal{J}}(\varphi )\nonumber \end{align} $$
$$ \begin{align} \left[\mathcal{J},b_{k}(\varphi )\right] & =-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(b_{l}^{\ast}(J_{l}^{\oplus}e_{q})\left[b_{k}(\varphi ),b_{l}\left(e_{q}\right)\right]+\left[b_{k}(\varphi ),b_{l}^{\ast}(J_{l}^{\oplus}e_{q})\right]b_{l}\left(e_{q}\right)\right)\nonumber \\ & =-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\left(\delta_{k,l}\left\langle \varphi,J_{l}^{\oplus}e_{q}\right\rangle +\varepsilon_{k,l}\left(\varphi;J_{l}^{\oplus}e_{q}\right)\right)b_{l}\left(e_{q}\right)\\ & =-\sum_{q\in L_{k}^{\pm}}\left\langle \varphi,J_{k}^{\oplus}e_{q}\right\rangle b_{k}\left(e_{q}\right)-\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;J_{l}^{\oplus}e_{q}\right)b_{l}\left(e_{q}\right)\nonumber \\ & =\sum_{q\in L_{k}^{\pm}}\left\langle J_{k}^{\oplus}\varphi,e_{q}\right\rangle b_{k}\left(e_{q}\right)+\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}(J_{l}^{\oplus}e_{q})\nonumber \\ & =b_{k}\left(J_{k}^{\oplus}\varphi\right)+\mathcal{E}_{k}^{\mathcal{J}}(\varphi )\nonumber \end{align} $$
for
 $$ \begin{align} \mathcal{E}_{k}^{\mathcal{J}}(\varphi )=\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}(J_{l}^{\oplus}e_{q}), \end{align} $$
$$ \begin{align} \mathcal{E}_{k}^{\mathcal{J}}(\varphi )=\sum_{l\in S_{C}}\sum_{q\in L_{l}^{\pm}}\varepsilon_{k,l}\left(\varphi;e_{q}\right)b_{l}(J_{l}^{\oplus}e_{q}), \end{align} $$
where we used the skew-symmetry of
![]() $J_{k}^{\oplus }$
, anti-linearity of
$J_{k}^{\oplus }$
, anti-linearity of
![]() $\varphi \mapsto b_{k}(\varphi )$
, and Lemma 3.3. Consequently, we compute for
$\varphi \mapsto b_{k}(\varphi )$
, and Lemma 3.3. Consequently, we compute for
![]() $\tilde {Q}_{1}^{k}(A)$
that
$\tilde {Q}_{1}^{k}(A)$
that
 $$ \begin{align} &\left[\mathcal{J},\tilde{Q}_{1}^{k}(A)\right] =\sum_{p\in L_{k}^{\pm}}\left[\mathcal{J},b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})\right] \nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left[\mathcal{J},b_{k}(e_{p})\right]+\left[\mathcal{J},b_{k}(Ae_{p})\right]^{\ast}b_{k}(e_{p})\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left(b_{k}\left(J_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}^{\mathcal{J}}(e_{p})\right)+\left(b_{k}\left(J_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}^{\mathcal{J}}(Ae_{p})\right)^{\ast}b_{k}(e_{p})\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})b_{k}\left(J_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(J_{k}^{\oplus}Ae_{p}\right)b_{k}(e_{p})\right)\\ &\qquad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\mathcal{E}_{k}^{\mathcal{J}}(e_{p})+\left(b_{k}^{\ast}(e_{p})\mathcal{E}_{k}^{\mathcal{J}}(Ae_{p})\right)^{\ast}\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(J_{k}^{\oplus}A-AJ_{k}^{\oplus}\right)e_{p}\right)b_{k}(e_{p})+2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}(e_{p};e_{q})b_{l}(J_{l}^{\oplus}e_{q})\right)\nonumber \\ &\quad =\tilde{Q}_{1}^{k}([J_{k}^{\oplus},A])+\mathcal{E}_{3}^{k}(A).\nonumber \end{align} $$
$$ \begin{align} &\left[\mathcal{J},\tilde{Q}_{1}^{k}(A)\right] =\sum_{p\in L_{k}^{\pm}}\left[\mathcal{J},b_{k}^{\ast}(Ae_{p})b_{k}(e_{p})\right] \nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left[\mathcal{J},b_{k}(e_{p})\right]+\left[\mathcal{J},b_{k}(Ae_{p})\right]^{\ast}b_{k}(e_{p})\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\left(b_{k}\left(J_{k}^{\oplus}e_{p}\right)+\mathcal{E}_{k}^{\mathcal{J}}(e_{p})\right)+\left(b_{k}\left(J_{k}^{\oplus}Ae_{p}\right)+\mathcal{E}_{k}^{\mathcal{J}}(Ae_{p})\right)^{\ast}b_{k}(e_{p})\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})b_{k}\left(J_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(J_{k}^{\oplus}Ae_{p}\right)b_{k}(e_{p})\right)\\ &\qquad +\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}(Ae_{p})\mathcal{E}_{k}^{\mathcal{J}}(e_{p})+\left(b_{k}^{\ast}(e_{p})\mathcal{E}_{k}^{\mathcal{J}}(Ae_{p})\right)^{\ast}\right)\nonumber \\ &\quad =\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(J_{k}^{\oplus}A-AJ_{k}^{\oplus}\right)e_{p}\right)b_{k}(e_{p})+2\sum_{l\in S_{C}}\sum_{p\in L_{k}^{\pm}}\sum_{q\in L_{l}^{\pm}}\mathrm{ Re}\left(b_{k}^{\ast}(Ae_{p})\varepsilon_{k,l}(e_{p};e_{q})b_{l}(J_{l}^{\oplus}e_{q})\right)\nonumber \\ &\quad =\tilde{Q}_{1}^{k}([J_{k}^{\oplus},A])+\mathcal{E}_{3}^{k}(A).\nonumber \end{align} $$
To derive an expression for
![]() $e^{\mathcal {J}}\tilde {Q}_{1}^{k}(A)e^{-\mathcal {J}}$
, we will use the Baker-Campbell-Hausdorff formula
$e^{\mathcal {J}}\tilde {Q}_{1}^{k}(A)e^{-\mathcal {J}}$
, we will use the Baker-Campbell-Hausdorff formula
 $$ \begin{align} \exp\left(\mathcal{C}_{J_{k}^{\oplus}}\right)(A)=\sum_{m=0}^{\infty}\frac{1}{m!}\mathcal{C}_{J_{k}^{\oplus}}^{m}(A)=e^{J_{k}^{\oplus}}Ae^{-J_{k}^{\oplus}},\quad \text{with } \mathcal{C}_{J_{k}^{\oplus}}(A)=\left[J_{k}^{\oplus},A\right]. \end{align} $$
$$ \begin{align} \exp\left(\mathcal{C}_{J_{k}^{\oplus}}\right)(A)=\sum_{m=0}^{\infty}\frac{1}{m!}\mathcal{C}_{J_{k}^{\oplus}}^{m}(A)=e^{J_{k}^{\oplus}}Ae^{-J_{k}^{\oplus}},\quad \text{with } \mathcal{C}_{J_{k}^{\oplus}}(A)=\left[J_{k}^{\oplus},A\right]. \end{align} $$
Imitating the proof of Proposition 5.3, we deduce the following:
Proposition 9.3. For all
![]() $k\in S_{C}$
and symmetric
$k\in S_{C}$
and symmetric
![]() $A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
$A:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
, it holds that
 $$\begin{align*}e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}}=\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}}Ae^{-J_{k}^{\oplus}}\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{(1-t)J_{k}^{\oplus}}Ae^{-(1-t)J_{k}^{\oplus}}\right)e^{-t\mathcal{J}}dt, \end{align*}$$
$$\begin{align*}e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}}=\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}}Ae^{-J_{k}^{\oplus}}\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{(1-t)J_{k}^{\oplus}}Ae^{-(1-t)J_{k}^{\oplus}}\right)e^{-t\mathcal{J}}dt, \end{align*}$$
the integrals being Riemann integrals of bounded operators.
Proof. We claim that for any
![]() $n\in \mathbb {N}$
, it holds that
$n\in \mathbb {N}$
, it holds that
 $$ \begin{align} e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}} & =\tilde{Q}_{1}^{k}\left(\sum_{m=0}^{n-1}\frac{1}{m!}\mathcal{C}_{J_{k}^{\oplus}}^{m}(A)\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(\sum_{m=0}^{n-1}\frac{1}{m!}\mathcal{C}_{(1-t)J_{k}^{\oplus}}^{m}(A)\right)e^{-t\mathcal{J}}dt \nonumber\\ &\quad +\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}(1-t)^{n-1}dt. \end{align} $$
$$ \begin{align} e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}} & =\tilde{Q}_{1}^{k}\left(\sum_{m=0}^{n-1}\frac{1}{m!}\mathcal{C}_{J_{k}^{\oplus}}^{m}(A)\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(\sum_{m=0}^{n-1}\frac{1}{m!}\mathcal{C}_{(1-t)J_{k}^{\oplus}}^{m}(A)\right)e^{-t\mathcal{J}}dt \nonumber\\ &\quad +\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}(1-t)^{n-1}dt. \end{align} $$
We proceed by induction. For
![]() $n=1$
, we have by the fundamental theorem of calculus and Proposition 9.2 that
$n=1$
, we have by the fundamental theorem of calculus and Proposition 9.2 that
 $$ \begin{align} e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}} & =\tilde{Q}_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},\tilde{Q}_{1}^{k}(A)\right]e^{-t\mathcal{J}}\,dt \nonumber\\ & =\tilde{Q}_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}([J_{k}^{\oplus},A])e^{-t\mathcal{J}}\,dt+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}(A)e^{-t\mathcal{J}}\,dt, \end{align} $$
$$ \begin{align} e^{\mathcal{J}}\tilde{Q}_{1}^{k}(A)e^{-\mathcal{J}} & =\tilde{Q}_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},\tilde{Q}_{1}^{k}(A)\right]e^{-t\mathcal{J}}\,dt \nonumber\\ & =\tilde{Q}_{1}^{k}(A)+\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}([J_{k}^{\oplus},A])e^{-t\mathcal{J}}\,dt+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}(A)e^{-t\mathcal{J}}\,dt, \end{align} $$
which is the claim. For the inductive step, we assume that case n holds and integrate the last term of equation (9.12) by parts:
 $$ \begin{align} & \frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}(1-t)^{n-1}dt\nonumber \\ &\quad =\frac{1}{(n-1)!}\left[e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}\left(-\frac{(1-t)^{n}}{n}\right)\right]_{0}^{1}\nonumber \\ &\qquad -\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)\right]e^{-t\mathcal{J}}\left(-\frac{(1-t)^{n}}{n}\right)dt\\ &\quad =\frac{1}{n!}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)+\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{J}}\left(\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right]\right)+\mathcal{E}_{3}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)\right)e^{-t\mathcal{J}}(1-t)^{n}dt\nonumber \\ &\quad =\tilde{Q}_{1}^{k}\left(\frac{1}{n!}\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(\frac{1}{n!}\mathcal{C}_{(1-t)J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}\,dt \nonumber\\ &\qquad +\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{J}} \tilde{Q}_1^k \left( \mathcal{C}_{J_{k}^{\oplus}}^{n+1}(A) \right)e^{-t\mathcal{J}}(1-t)^{n}dt.\nonumber \end{align} $$
$$ \begin{align} & \frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}(1-t)^{n-1}dt\nonumber \\ &\quad =\frac{1}{(n-1)!}\left[e^{t\mathcal{J}}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}\left(-\frac{(1-t)^{n}}{n}\right)\right]_{0}^{1}\nonumber \\ &\qquad -\frac{1}{(n-1)!}\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)\right]e^{-t\mathcal{J}}\left(-\frac{(1-t)^{n}}{n}\right)dt\\ &\quad =\frac{1}{n!}\tilde{Q}_{1}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)+\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{J}}\left(\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right]\right)+\mathcal{E}_{3}^{k}\left(\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)\right)e^{-t\mathcal{J}}(1-t)^{n}dt\nonumber \\ &\quad =\tilde{Q}_{1}^{k}\left(\frac{1}{n!}\mathcal{C}_{J_{k}^{\oplus}}^{n}(A)\right)+\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(\frac{1}{n!}\mathcal{C}_{(1-t)J_{k}^{\oplus}}^{n}(A)\right)e^{-t\mathcal{J}}\,dt \nonumber\\ &\qquad +\frac{1}{n!}\int_{0}^{1}e^{t\mathcal{J}} \tilde{Q}_1^k \left( \mathcal{C}_{J_{k}^{\oplus}}^{n+1}(A) \right)e^{-t\mathcal{J}}(1-t)^{n}dt.\nonumber \end{align} $$
Insertion of this identity into equation (9.12) yields the statement for case
![]() $n+1$
, so our claim (9.12) holds. We can now take
$n+1$
, so our claim (9.12) holds. We can now take
![]() $n\rightarrow \infty $
and appeal to equation (9.11) to get the claim.
$n\rightarrow \infty $
and appeal to equation (9.11) to get the claim.
Proposition 9.2 also allows us to describe the action of
![]() $e^{\mathcal {J}}$
on
$e^{\mathcal {J}}$
on
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
:
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
:
Proposition 9.4. It holds that
 $$\begin{align*}e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}}=H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)-2\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{J}}dt. \end{align*}$$
$$\begin{align*}e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}}=H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)-2\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{J}}dt. \end{align*}$$
Proof. By the fundemental theorem of calculus and the fact that
![]() $\partial _t (e^{tA}B e^{-tA})= e^{tA}[A,B]e^{-tA}$
, the left side is equal to
$\partial _t (e^{tA}B e^{-tA})= e^{tA}[A,B]e^{-tA}$
, the left side is equal to
 $$\begin{align*} H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right) +\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]e^{-t\mathcal{J}}dt. \end{align*}$$
$$\begin{align*} H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right) +\int_{0}^{1}e^{t\mathcal{J}}\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]e^{-t\mathcal{J}}dt. \end{align*}$$
Recalling (1.74), we may compute using Lemma 3.3 that
 $$ \begin{align} \left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right] & =-\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right]\nonumber \\ &\quad -2\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(-b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}\left(h_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(h_{k}^{\oplus}J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right) \nonumber\\ & =2\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(J_{k}^{\oplus}h_{k}^{\oplus}-h_{k}^{\oplus}J_{k}^{\oplus}\right)e_{p}\right)b_{k}(e_{p})=2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right). \end{align} $$
$$ \begin{align} \left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right] & =-\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left[H_{\operatorname{\mathrm{kin}}}^{\prime},b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right]\nonumber \\ &\quad -2\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(-b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}\left(h_{k}^{\oplus}e_{p}\right)+b_{k}^{\ast}\left(h_{k}^{\oplus}J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right) \nonumber\\ & =2\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}b_{k}^{\ast}\left(\left(J_{k}^{\oplus}h_{k}^{\oplus}-h_{k}^{\oplus}J_{k}^{\oplus}\right)e_{p}\right)b_{k}(e_{p})=2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right). \end{align} $$
Combining with Proposition 9.2, we have that
 $$ \begin{align} \left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]=\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]-2\sum_{k\in S_{C}}\left[\mathcal{J},\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]=-2\sum_{k\in S_{C}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right), \end{align} $$
$$ \begin{align} \left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]=\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]-2\sum_{k\in S_{C}}\left[\mathcal{J},\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)\right]=-2\sum_{k\in S_{C}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right), \end{align} $$
which implies the claim.
We can now conclude:
Proof of Proposition 9.1 .
By the Propositions 9.3 and 9.4, we see that
 $$ \begin{align} & e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}- 2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( h_{k}^{\oplus}\right) + 2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}\right)\right)e^{-\mathcal{J}}\nonumber \\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)-2\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{J}}\,dt \nonumber\\ &\qquad +2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}} E_{k}^{\oplus}e^{-J_{k}^{\oplus}}\right)+2\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{(1-t)J_{k}^{\oplus}} E_{k}^{\oplus}e^{-(1-t)J_{k}^{\oplus}}\right)e^{-t\mathcal{J}}dt\nonumber \\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}} E_{k}^{\oplus}e^{-J_{k}^{\oplus}}-h_{k}^{\oplus}\right)+2\int_{0}^{1}e^{(1-t)\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{tJ_{k}^{\oplus}} E_{k}^{\oplus}e^{-tJ_{k}^{\oplus}}-h_{k}^{\oplus}\right)e^{-(1-t)\mathcal{J}}dt, \end{align} $$
$$ \begin{align} & e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}- 2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( h_{k}^{\oplus}\right) + 2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( E_{k}^{\oplus}\right)\right)e^{-\mathcal{J}}\nonumber \\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}-2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(h_{k}^{\oplus}\right)-2\sum_{k\in S_{C}}\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(h_{k}^{\oplus}\right)e^{-t\mathcal{J}}\,dt \nonumber\\ &\qquad +2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}} E_{k}^{\oplus}e^{-J_{k}^{\oplus}}\right)+2\int_{0}^{1}e^{t\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{(1-t)J_{k}^{\oplus}} E_{k}^{\oplus}e^{-(1-t)J_{k}^{\oplus}}\right)e^{-t\mathcal{J}}dt\nonumber \\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(e^{J_{k}^{\oplus}} E_{k}^{\oplus}e^{-J_{k}^{\oplus}}-h_{k}^{\oplus}\right)+2\int_{0}^{1}e^{(1-t)\mathcal{J}}\mathcal{E}_{3}^{k}\left(e^{tJ_{k}^{\oplus}} E_{k}^{\oplus}e^{-tJ_{k}^{\oplus}}-h_{k}^{\oplus}\right)e^{-(1-t)\mathcal{J}}dt, \end{align} $$
where we also reparametrized the integral. From the choice of
![]() $J_k^{\oplus }$
in (9.3), we have
$J_k^{\oplus }$
in (9.3), we have
 $$ \begin{align} e^{tJ_{k}^{\oplus}} E_{k}^{\oplus}e^{-tJ_{k}^{\oplus}} - h_k^{\oplus} = \left(\begin{array}{cc} e^{tJ_{k}} E_k e^{-tJ_k} - h_k & 0\\ 0 & e^{tJ_{k}} E_k e^{-tJ_k} -h_k \end{array}\right) ={E}_k^{\oplus}(t) \end{align} $$
$$ \begin{align} e^{tJ_{k}^{\oplus}} E_{k}^{\oplus}e^{-tJ_{k}^{\oplus}} - h_k^{\oplus} = \left(\begin{array}{cc} e^{tJ_{k}} E_k e^{-tJ_k} - h_k & 0\\ 0 & e^{tJ_{k}} E_k e^{-tJ_k} -h_k \end{array}\right) ={E}_k^{\oplus}(t) \end{align} $$
for all
![]() $t\in [0,1]$
. Moreover, using
$t\in [0,1]$
. Moreover, using
![]() $e^{J_k}=U_k$
and (9.4), we get
$e^{J_k}=U_k$
and (9.4), we get
![]() $e^{J_{k}^{\oplus }} E_{k}^{\oplus }e^{-tJ_{k}^{\oplus }}=\widetilde {E}_k^{\oplus }$
.
$e^{J_{k}^{\oplus }} E_{k}^{\oplus }e^{-tJ_{k}^{\oplus }}=\widetilde {E}_k^{\oplus }$
.
9.2 Estimates for the exchange terms
Now we estimate the new exchange term
![]() $\mathcal {E}_3$
in Proposition 9.1. We have the following:
$\mathcal {E}_3$
in Proposition 9.1. We have the following:
Proposition 9.5. For all
![]() $k\in \mathbb {Z}_{+}^{3}$
, symmetric
$k\in \mathbb {Z}_{+}^{3}$
, symmetric
![]() $E:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
$E:\ell ^{2}(L_{k}^{\pm })\rightarrow \ell ^{2}(L_{k}^{\pm })$
and
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
, it holds that
 $$\begin{align*}\left|\left\langle \Psi,\mathcal{E}_{3}^{k}(E)\Psi\right\rangle \right|\leq C\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle } \end{align*}$$
$$\begin{align*}\left|\left\langle \Psi,\mathcal{E}_{3}^{k}(E)\Psi\right\rangle \right|\leq C\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle } \end{align*}$$
for a constant
![]() $C>0$
independent of all quantities.
$C>0$
independent of all quantities.
Proof of Proposition 9.5 .
We can follow the analysis in Section 6. In particular, the same reduction in Section 6.1 applies to
![]() $\mathcal {E}_{3}^{k}(E)$
, but in this case, it is significantly simpler. By definition, up to taking adjoints, every term of
$\mathcal {E}_{3}^{k}(E)$
, but in this case, it is significantly simpler. By definition, up to taking adjoints, every term of
![]() $\mathcal {E}_{3}^{k}(E)$
immediately reduces to the schematic form
$\mathcal {E}_{3}^{k}(E)$
immediately reduces to the schematic form
and recalling that commutators of the forms
![]() $\left[\tilde {c}_{p},b_{k}(\varphi )\right]$
and
$\left[\tilde {c}_{p},b_{k}(\varphi )\right]$
and
![]() $\left[\tilde {c}_{p}^{\ast },b_{k}^{\ast }(\varphi )\right]$
also vanish, we may normal-order this schematic form without introducing additional terms. Controlling
$\left[\tilde {c}_{p}^{\ast },b_{k}^{\ast }(\varphi )\right]$
also vanish, we may normal-order this schematic form without introducing additional terms. Controlling
![]() $\mathcal {E}_{3}^{k}(E)$
thus reduces entirely to the estimation of the single schematic form
$\mathcal {E}_{3}^{k}(E)$
thus reduces entirely to the estimation of the single schematic form
We estimate the schematic form of equation (9.20) using Proposition 4.4, Lemma 6.6 and the Cauchy-Schwarz inequality:
 $$ \begin{align} & \sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\ast}\left(Ee_{p_{1}}\right)b_{l}\left(J_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}\left(Ee_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}\left(J_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ &\quad \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle } \nonumber\\ & \quad\leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p}\right\Vert \right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}e_{p_{2}}\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{4}}^{\ast}H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ &\quad \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p_{1}}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }. \end{align} $$
$$ \begin{align} & \sum_{l\in S_{C}}\sum_{p\in S}\left|\left\langle \Psi,\tilde{c}_{p_{3}}^{\ast}b_{k}^{\ast}\left(Ee_{p_{1}}\right)b_{l}\left(J_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\rangle \right|\leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert b_{k}\left(Ee_{p_{1}}\right)\tilde{c}_{p_{3}}\Psi\right\Vert \left\Vert b_{l}\left(J_{l}^{\oplus}e_{p_{2}}\right)\tilde{c}_{p_{4}}\Psi\right\Vert \nonumber \\ &\quad \leq\sum_{l\in S_{C}}\sum_{p\in S}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p_{1}}\right\Vert \left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}e_{p_{2}}\right\Vert \sqrt{\left\langle \tilde{c}_{p_{3}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{3}}\Psi\right\rangle \left\langle \tilde{c}_{p_{4}}\Psi,H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle } \nonumber\\ & \quad\leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p}\right\Vert \right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }\sum_{l\in S_{C}}\sqrt{\sum_{p\in S}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}e_{p_{2}}\right\Vert ^{2}}\sqrt{\sum_{p\in S}\left\langle \Psi,\tilde{c}_{p_{4}}^{\ast}H_{\text{kin}}^{\prime\left(\pm1\right)}\tilde{c}_{p_{4}}\Psi\right\rangle }\nonumber \\ &\quad \leq\left(\max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}Ee_{p_{1}}\right\Vert \right)\left(\sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\text{HS}}\right)\sqrt{\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle }. \end{align} $$
9.3 One-body operator estimates
In this subsection, we derive estimates on the one-body quantities
 $$ \begin{align} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t )e_{p}\right\Vert ,\quad\left\Vert h_{k}^{-\frac{1}{2}}J_{k}\right\Vert_{\text{HS}},\quad \quad\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert_{\text{HS}}, \quad \mathrm{tr} ( h_k^{-1/2} (\widetilde{E}_k - h_k) h_k^{-1/2}). \end{align} $$
$$ \begin{align} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t )e_{p}\right\Vert ,\quad\left\Vert h_{k}^{-\frac{1}{2}}J_{k}\right\Vert_{\text{HS}},\quad \quad\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert_{\text{HS}}, \quad \mathrm{tr} ( h_k^{-1/2} (\widetilde{E}_k - h_k) h_k^{-1/2}). \end{align} $$
The first two quantities arise from the analysis of the exchange terms in the previous subsection, while the third quantity will be needed in order to derive Gronwall-type estimates for the kinetic operator. The last one is useful to remove the cutoff
![]() $S_C$
on the right-hand side of (9.7) at the end. The estimates we will establish are the following:
$S_C$
on the right-hand side of (9.7) at the end. The estimates we will establish are the following:
Proposition 9.6. Assume
![]() $\sum _{k\in \mathbb {Z}^3_{*}}\hat V_k |k|<\infty $
. Then for all
$\sum _{k\in \mathbb {Z}^3_{*}}\hat V_k |k|<\infty $
. Then for all
![]() $k\in \mathbb {Z}^3_{*}$
, we have
$k\in \mathbb {Z}^3_{*}$
, we have
Moreover, if
![]() $k\in \overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{\ast }^{3}$
,
$k\in \overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{\ast }^{3}$
,
![]() $0<\gamma <\frac {1}{47}$
and
$0<\gamma <\frac {1}{47}$
and
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
 $$ \begin{align*} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t ) e_{p}\right\Vert & \leq Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right),\\ \left\Vert h_{k}^{-\frac{1}{2}}J_{k}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k},\\ \left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C\hat{V}_{k}. \end{align*} $$
$$ \begin{align*} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t ) e_{p}\right\Vert & \leq Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right),\\ \left\Vert h_{k}^{-\frac{1}{2}}J_{k}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k},\\ \left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}} & \leq C\hat{V}_{k}. \end{align*} $$
Here, the constant
![]() $C>0$
is independent of k and
$C>0$
is independent of k and
![]() $k_{F}$
.
$k_{F}$
.
Proposition 9.6 is the main source of the technical restriction
![]() $\gamma <\frac 1 {47}$
which comes from the use of the first bound in Proposition A.3 (we need
$\gamma <\frac 1 {47}$
which comes from the use of the first bound in Proposition A.3 (we need
![]() $\gamma <\frac {4+3\beta }{8-3\beta }$
with
$\gamma <\frac {4+3\beta }{8-3\beta }$
with
![]() $\beta =-\frac 5 4$
).
$\beta =-\frac 5 4$
).
As in Section 7, in order to simplify the notation, let
![]() $h:V\rightarrow V$
denote a self-adjoint operator acting on an n-dimensional Hilbert space V, let
$h:V\rightarrow V$
denote a self-adjoint operator acting on an n-dimensional Hilbert space V, let
![]() $(x_{i})_{i=1}^{n}$
denote an eigenbasis for h with eigenvalues
$(x_{i})_{i=1}^{n}$
denote an eigenbasis for h with eigenvalues
![]() $\left(\lambda _{i}\right)_{i=1}^{n}$
, and let
$\left(\lambda _{i}\right)_{i=1}^{n}$
, and let
![]() $v\in V$
be any vector such that
$v\in V$
be any vector such that
![]() $\left\langle v,x_{i}\right\rangle \geq 0$
for all
$\left\langle v,x_{i}\right\rangle \geq 0$
for all
![]() $1\leq i\leq n$
. As before, we take
$1\leq i\leq n$
. As before, we take
 $$ \begin{align} K=-\frac{1}{2}\log\left(h^{-\frac{1}{2}}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}h^{-\frac{1}{2}}\right). \end{align} $$
$$ \begin{align} K=-\frac{1}{2}\log\left(h^{-\frac{1}{2}}\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{2}}h^{-\frac{1}{2}}\right). \end{align} $$
We will establish general estimates for the operators
and then at the end insert the explicit choice (7.2) to get the desired estimates.
Unlike the case in Section 7, we will now also take V to be a complex Hilbert space. This is not a strictly necessary assumption, but it allows us to streamline the presentation significantly, as it implies that the unitary operator U is diagonalizable and so lets us describe the operators
![]() $J=\log (U)$
and
$J=\log (U)$
and
![]() $e^{tJ}$
solely in terms of eigenvectors of U.
$e^{tJ}$
solely in terms of eigenvectors of U.
The main difficulty of the proof of Proposition 9.6 is that we cannot extend the argument leading to matrix element estimates for
![]() $e^{-2K}-1$
and
$e^{-2K}-1$
and
![]() $1-e^{2K}$
in Section 7 to handle the operators J and
$1-e^{2K}$
in Section 7 to handle the operators J and
![]() $e^{tJ}$
. Instead, we will utilize a technique which effectively lets us replace relevant quantities of J by these of
$e^{tJ}$
. Instead, we will utilize a technique which effectively lets us replace relevant quantities of J by these of
![]() $U-1$
, by exploiting the diagonalizability of U.
$U-1$
, by exploiting the diagonalizability of U.
We start with the easy part of Proposition 9.6.
Proposition 9.7. With
![]() $\widetilde {E} = \left(h^{2}+2P_{h^{\frac {1}{2}}v}\right)^{\frac {1}{2}}$
, we have
$\widetilde {E} = \left(h^{2}+2P_{h^{\frac {1}{2}}v}\right)^{\frac {1}{2}}$
, we have
Proof. Using (7.21) for
![]() $\widetilde {E} = \left(h^{2}+2P_{h^{\frac {1}{2}}v}\right)^{\frac {1}{2}}$
, we can write
$\widetilde {E} = \left(h^{2}+2P_{h^{\frac {1}{2}}v}\right)^{\frac {1}{2}}$
, we can write
 $$ \begin{align} h^{-1/2} (\widetilde{E} - h) h^{-1/2} = \frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt \le \frac{4}{\pi}\int_{0}^{\infty} P_{\left(h^{2}+t^{2}\right)^{-1}v} t^2\,dt. \end{align} $$
$$ \begin{align} h^{-1/2} (\widetilde{E} - h) h^{-1/2} = \frac{4}{\pi}\int_{0}^{\infty}\frac{t^{2}}{1+2\left\langle v,h\left(h^{2}+t^{2}\right)^{-1}v\right\rangle }P_{\left(h^{2}+t^{2}\right)^{-1}v}\,dt \le \frac{4}{\pi}\int_{0}^{\infty} P_{\left(h^{2}+t^{2}\right)^{-1}v} t^2\,dt. \end{align} $$
Taking the trace and using (7.8), we complete the proof.
Estimates for U
Let us consider the unitary operator
![]() $U:V\rightarrow V$
defined by
$U:V\rightarrow V$
defined by
First, the analysis of
![]() $(h^{2}+2P_{h^{\frac {1}{2}}v})^{\frac {1}{2}}$
in Section 7 can be extended to
$(h^{2}+2P_{h^{\frac {1}{2}}v})^{\frac {1}{2}}$
in Section 7 can be extended to
![]() $(h^{2}+2P_{h^{\frac {1}{2}}v})^{\frac {1}{4}}$
. We have the following:
$(h^{2}+2P_{h^{\frac {1}{2}}v})^{\frac {1}{4}}$
. We have the following:
Proposition 9.8. For all
![]() $1\leq i,j\leq n$
, it holds that
$1\leq i,j\leq n$
, it holds that
 $$\begin{align*}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \right|\leq\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*}$$
$$\begin{align*}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \right|\leq\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*}$$
Note that by using the integral identity
 $$ \begin{align} A^{\frac{1}{4}}=\frac{2\sqrt{2}}{\pi}\int_{0}^{\infty}\left(1-\frac{t^{4}}{A+t^{4}}\right)dt \end{align} $$
$$ \begin{align} A^{\frac{1}{4}}=\frac{2\sqrt{2}}{\pi}\int_{0}^{\infty}\left(1-\frac{t^{4}}{A+t^{4}}\right)dt \end{align} $$
for every self-adjoint non-negative operator A instead of (7.8), we obtain the following analogue of Proposition 7.5:
Proposition 9.9. Let
![]() $\left(H,\left\langle \cdot ,\cdot \right\rangle \right)$
be a Hilbert space and let
$\left(H,\left\langle \cdot ,\cdot \right\rangle \right)$
be a Hilbert space and let
![]() $A:H\rightarrow H$
be a positive self-adjoint operator. Then for any
$A:H\rightarrow H$
be a positive self-adjoint operator. Then for any
![]() $x\in H$
and
$x\in H$
and
![]() $g\in \mathbb {R}$
such that
$g\in \mathbb {R}$
such that
![]() $A+gP_{x}>0$
, it holds that
$A+gP_{x}>0$
, it holds that
 $$\begin{align*}\left(A+gP_{x}\right)^{\frac{1}{4}}=A^{\frac{1}{4}}+\frac{2\sqrt{2}g}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+g\left\langle v,\left(A+t^{4}\right)^{-1}v\right\rangle }P_{\left(A+t^{4}\right)^{-1}v}\,dt. \end{align*}$$
$$\begin{align*}\left(A+gP_{x}\right)^{\frac{1}{4}}=A^{\frac{1}{4}}+\frac{2\sqrt{2}g}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+g\left\langle v,\left(A+t^{4}\right)^{-1}v\right\rangle }P_{\left(A+t^{4}\right)^{-1}v}\,dt. \end{align*}$$
Proof of Proposition 9.8 .
Applying Proposition 9.9 with
![]() $A=h^{2}$
,
$A=h^{2}$
,
![]() $x=h^{\frac {1}{2}}v$
and
$x=h^{\frac {1}{2}}v$
and
![]() $g=2$
, we find
$g=2$
, we find
 $$ \begin{align} \left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}} & =\left(h^{2}\right)^{\frac{1}{4}}+\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle h^{\frac{1}{2}}v,\left(h^{2}+t^{4}\right)^{-1}h^{\frac{1}{2}}v\right\rangle }P_{\left(h^{2}+t^{4}\right)^{-1}h^{\frac{1}{2}}v}\,dt\\ & =h^{\frac{1}{2}}+\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{4}\right)^{-1}v}\,dt,\nonumber \end{align} $$
$$ \begin{align} \left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}} & =\left(h^{2}\right)^{\frac{1}{4}}+\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle h^{\frac{1}{2}}v,\left(h^{2}+t^{4}\right)^{-1}h^{\frac{1}{2}}v\right\rangle }P_{\left(h^{2}+t^{4}\right)^{-1}h^{\frac{1}{2}}v}\,dt\\ & =h^{\frac{1}{2}}+\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }P_{h^{\frac{1}{2}}\left(h^{2}+t^{4}\right)^{-1}v}\,dt,\nonumber \end{align} $$
and so we can estimate that
 $$ \begin{align} 0 & \le \left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \nonumber \\ & =\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }\left\langle x_{i},P_{h^{\frac{1}{2}}\left(h^{2}+t^{4}\right)^{-1}v}x_{j}\right\rangle dt\nonumber \\ & =\frac{4\sqrt{2}}{\pi}\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }\frac{\sqrt{\lambda_{i}}}{\lambda_{i}^{2}+t^{4}}\frac{\sqrt{\lambda_{j}}}{\lambda_{j}^{2}+t^{4}}\,dt\\ & \leq\frac{4\sqrt{2}}{\pi}\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \int_{0}^{\infty}\frac{\sqrt{\lambda_{i}}}{\lambda_{i}^{2}+t^{4}}\frac{\sqrt{\lambda_{j}}}{\lambda_{j}^{2}+t^{4}}t^{4}\,dt=\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}},\nonumber \end{align} $$
$$ \begin{align} 0 & \le \left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \nonumber \\ & =\frac{4\sqrt{2}}{\pi}\int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }\left\langle x_{i},P_{h^{\frac{1}{2}}\left(h^{2}+t^{4}\right)^{-1}v}x_{j}\right\rangle dt\nonumber \\ & =\frac{4\sqrt{2}}{\pi}\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \int_{0}^{\infty}\frac{t^{4}}{1+2\left\langle v,h\left(h^{2}+t^{4}\right)^{-1}v\right\rangle }\frac{\sqrt{\lambda_{i}}}{\lambda_{i}^{2}+t^{4}}\frac{\sqrt{\lambda_{j}}}{\lambda_{j}^{2}+t^{4}}\,dt\\ & \leq\frac{4\sqrt{2}}{\pi}\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \int_{0}^{\infty}\frac{\sqrt{\lambda_{i}}}{\lambda_{i}^{2}+t^{4}}\frac{\sqrt{\lambda_{j}}}{\lambda_{j}^{2}+t^{4}}t^{4}\,dt=\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}},\nonumber \end{align} $$
where we also applied the integral identity
 $$ \begin{align} \int_{0}^{\infty}\frac{\sqrt{a}}{a^{2}+t^{4}}\frac{\sqrt{b}}{b^{2}+t^{4}}t^{4}\,dt=\frac{\pi}{2\sqrt{2}}\frac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\frac{1}{a+b},\quad a,b>0. \end{align} $$
$$ \begin{align} \int_{0}^{\infty}\frac{\sqrt{a}}{a^{2}+t^{4}}\frac{\sqrt{b}}{b^{2}+t^{4}}t^{4}\,dt=\frac{\pi}{2\sqrt{2}}\frac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\frac{1}{a+b},\quad a,b>0. \end{align} $$
We may then conclude the following:
Proposition 9.10. For all
![]() $1\leq i,j\leq n$
, it holds that
$1\leq i,j\leq n$
, it holds that
 $$\begin{align*}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(U^{\ast}-1\right)x_{j}\right\rangle \right|\leq3\left(1+\left\langle v,h^{-1}v\right\rangle \right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*}$$
$$\begin{align*}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},\left(U^{\ast}-1\right)x_{j}\right\rangle \right|\leq3\left(1+\left\langle v,h^{-1}v\right\rangle \right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align*}$$
Proof. As
![]() $\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|=\left|\left\langle x_{j},\left(U^{\ast }-1\right)x_{i}\right\rangle \right|$
and the claimed estimate is symmetric with respect to i and j, it suffices to consider
$\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|=\left|\left\langle x_{j},\left(U^{\ast }-1\right)x_{i}\right\rangle \right|$
and the claimed estimate is symmetric with respect to i and j, it suffices to consider
![]() $U-1$
. We write
$U-1$
. We write
 $$ \begin{align} U-1 & =\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}h^{-\frac{1}{2}}e^{K}-1=\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}e^{K}+e^{K}-1\\ & =e^{K}-1+\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}+\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}\left(e^{K}-1\right)\nonumber \end{align} $$
$$ \begin{align} U-1 & =\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}h^{-\frac{1}{2}}e^{K}-1=\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}e^{K}+e^{K}-1\\ & =e^{K}-1+\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}+\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}\left(e^{K}-1\right)\nonumber \end{align} $$
and estimate each term separately. The first is directly covered by Proposition 7.10, with
 $$ \begin{align} \left|\left\langle x_{i},\left(e^{K}-1\right)x_{j}\right\rangle \right|\leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},\left(e^{K}-1\right)x_{j}\right\rangle \right|\leq\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}. \end{align} $$
For the second term, we can by Proposition 9.8 estimate that
 $$ \begin{align} \left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}x_{j}\right\rangle \right| & =\frac{1}{\sqrt{\lambda_{j}}}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \right|\\ & \leq\frac{1}{\sqrt{\lambda_{j}}}\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\leq2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}.\nonumber \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}x_{j}\right\rangle \right| & =\frac{1}{\sqrt{\lambda_{j}}}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)x_{j}\right\rangle \right|\\ & \leq\frac{1}{\sqrt{\lambda_{j}}}\frac{2\sqrt{\lambda_{i}\lambda_{j}}}{\sqrt{\lambda_{i}}+\sqrt{\lambda_{j}}}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\leq2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}.\nonumber \end{align} $$
For the final term, we carry out an orthonormal expansion and apply the previous two estimates to see that
 $$ \begin{align} & \left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}\left(e^{K}-1\right)x_{j}\right\rangle \right|\nonumber \\ &\quad \leq\sum_{k=1}^{n}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}x_{k}\right\rangle \right|\left|\left\langle x_{k},\left(e^{K}-1\right)x_{j}\right\rangle \right| \nonumber\\ & \quad\leq2\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\sum_{k=1}^{n}\frac{\lambda_{i}+\lambda_{j}}{\left(\lambda_{i}+\lambda_{k}\right)\left(\lambda_{k}+\lambda_{j}\right)}\left|\left\langle x_{k},v\right\rangle \right|^{2}\nonumber \\ &\quad \leq2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}=2\left\langle v,h^{-1}v\right\rangle \frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} , \end{align} $$
$$ \begin{align} & \left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}\left(e^{K}-1\right)x_{j}\right\rangle \right|\nonumber \\ &\quad \leq\sum_{k=1}^{n}\left|\left\langle x_{i},\left(\left(h^{2}+2P_{h^{\frac{1}{2}}v}\right)^{\frac{1}{4}}-h^{\frac{1}{2}}\right)h^{-\frac{1}{2}}x_{k}\right\rangle \right|\left|\left\langle x_{k},\left(e^{K}-1\right)x_{j}\right\rangle \right| \nonumber\\ & \quad\leq2\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}=2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\sum_{k=1}^{n}\frac{\lambda_{i}+\lambda_{j}}{\left(\lambda_{i}+\lambda_{k}\right)\left(\lambda_{k}+\lambda_{j}\right)}\left|\left\langle x_{k},v\right\rangle \right|^{2}\nonumber \\ &\quad \leq2\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}=2\left\langle v,h^{-1}v\right\rangle \frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} , \end{align} $$
where we also applied the elementary inequality
Combining the estimates now yields the claim.
Estimates for J
Recall that we defined
![]() $J:V\rightarrow V$
to be the principal logarithm of U. Since U is a unitary operator on the finite-dimensional complex Hilbert space V, by the spectral theorem it is diagonalizable – that is, there exists an orthonormal basis
$J:V\rightarrow V$
to be the principal logarithm of U. Since U is a unitary operator on the finite-dimensional complex Hilbert space V, by the spectral theorem it is diagonalizable – that is, there exists an orthonormal basis
![]() $(w_{j})_{j=1}^{n}$
for V of eigenstates of U with eigenvalues
$(w_{j})_{j=1}^{n}$
for V of eigenstates of U with eigenvalues
![]() $\left(e^{i\theta _{j}}\right)_{j=1}^{n}$
,
$\left(e^{i\theta _{j}}\right)_{j=1}^{n}$
,
![]() $\left(\theta _{j}\right)_{j=1}^{n}\subset \left(-\pi ,\pi \right]$
, (i.e.,
$\left(\theta _{j}\right)_{j=1}^{n}\subset \left(-\pi ,\pi \right]$
, (i.e.,
![]() $Uw_{j}=e^{i\theta _{j}}w_{j}$
for all
$Uw_{j}=e^{i\theta _{j}}w_{j}$
for all
![]() $1\leq j\leq n$
). Thus, J can be explicitly written as
$1\leq j\leq n$
). Thus, J can be explicitly written as
To estimate the quantity
![]() $\left\Vert h^{-\frac {1}{2}}J\right\Vert _{\text {HS}}$
, we will apply the following:
$\left\Vert h^{-\frac {1}{2}}J\right\Vert _{\text {HS}}$
, we will apply the following:
Proposition 9.11. It holds that
Proof. We note the elementary inequality
which can be deduced from the fact that
![]() $x\mapsto \left|e^{ix}-1\right|$
is an even function and concave on
$x\mapsto \left|e^{ix}-1\right|$
is an even function and concave on
![]() $x\in \left[0,\pi \right]$
. As the eigenbasis
$x\in \left[0,\pi \right]$
. As the eigenbasis
![]() $(w_{j})_{j=1}^{n}$
obeys
$(w_{j})_{j=1}^{n}$
obeys
we can for any
![]() $w\in V$
perform an orthonormal expansion in terms of
$w\in V$
perform an orthonormal expansion in terms of
![]() $(w_{j})_{j=1}^{n}$
to see that
$(w_{j})_{j=1}^{n}$
to see that
 $$ \begin{align} \left\langle w,JJ^{\ast}w\right\rangle & =\left\Vert J^{\ast}w\right\Vert ^{2}=\sum_{j=1}^{n}\left|\theta_{j}\right|^{2}\left|\left\langle w_{j},w\right\rangle \right|^{2}\leq\sum_{j=1}^{n}\left(\frac{\pi}{2}\left|e^{i\theta_{j}}-1\right|\right)^{2}\left|\left\langle w_{j},w\right\rangle \right|^{2} \nonumber\\ & =\frac{\pi^{2}}{4}\sum_{j=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)w_{j},w\right\rangle \right|^{2}=\frac{\pi^{2}}{4}\left\Vert \left(U-1\right)w\right\Vert ^{2}=\frac{\pi^{2}}{4}\left\langle w,\left(U-1\right)^{\ast}\left(U-1\right)w\right\rangle , \end{align} $$
$$ \begin{align} \left\langle w,JJ^{\ast}w\right\rangle & =\left\Vert J^{\ast}w\right\Vert ^{2}=\sum_{j=1}^{n}\left|\theta_{j}\right|^{2}\left|\left\langle w_{j},w\right\rangle \right|^{2}\leq\sum_{j=1}^{n}\left(\frac{\pi}{2}\left|e^{i\theta_{j}}-1\right|\right)^{2}\left|\left\langle w_{j},w\right\rangle \right|^{2} \nonumber\\ & =\frac{\pi^{2}}{4}\sum_{j=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)w_{j},w\right\rangle \right|^{2}=\frac{\pi^{2}}{4}\left\Vert \left(U-1\right)w\right\Vert ^{2}=\frac{\pi^{2}}{4}\left\langle w,\left(U-1\right)^{\ast}\left(U-1\right)w\right\rangle , \end{align} $$
which is the claim.
Corollary 9.12. There exists a universal constant
![]() $C>0$
such that
$C>0$
such that
Proof. By cyclicity of the trace and the estimate of the previous proposition, we have that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}J\right\Vert _{\text{HS}}^{2} & =\text{tr}\left(J^{\ast}h^{-1}J\right)=\text{tr}\left(h^{-\frac{1}{2}}JJ^{\ast}h^{-\frac{1}{2}}\right) \nonumber\\ & \leq\frac{\pi^{2}}{4}\text{tr}\left(h^{-\frac{1}{2}}\left(U-1\right)^{\ast}\left(U-1\right)h^{-\frac{1}{2}}\right)=\frac{\pi^{2}}{4}\left\Vert \left(U-1\right)h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2}, \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}J\right\Vert _{\text{HS}}^{2} & =\text{tr}\left(J^{\ast}h^{-1}J\right)=\text{tr}\left(h^{-\frac{1}{2}}JJ^{\ast}h^{-\frac{1}{2}}\right) \nonumber\\ & \leq\frac{\pi^{2}}{4}\text{tr}\left(h^{-\frac{1}{2}}\left(U-1\right)^{\ast}\left(U-1\right)h^{-\frac{1}{2}}\right)=\frac{\pi^{2}}{4}\left\Vert \left(U-1\right)h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2}, \end{align} $$
and by the matrix element estimate of Proposition 9.10,
 $$ \begin{align} & \quad\;\left\Vert \left(U-1\right)h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)h^{-\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}^{\frac{3}{4}}\lambda_{j}^{\frac{1}{4}}}\right|^{2}\nonumber \\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{j}^{\frac{3}{2}}}\right)^{2}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{3}{2}}v\right\rangle ^{2}, \end{align} $$
$$ \begin{align} & \quad\;\left\Vert \left(U-1\right)h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2}=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)h^{-\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}^{\frac{3}{4}}\lambda_{j}^{\frac{1}{4}}}\right|^{2}\nonumber \\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{j}^{\frac{3}{2}}}\right)^{2}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{3}{2}}v\right\rangle ^{2}, \end{align} $$
which gives the claim.
Next, consider
![]() $\Vert h^{-\frac {1}{2}}[J,h]h^{-\frac {1}{2}}\Vert _{\text {HS}}$
. By the triangle inequality, it suffices to bound
$\Vert h^{-\frac {1}{2}}[J,h]h^{-\frac {1}{2}}\Vert _{\text {HS}}$
. By the triangle inequality, it suffices to bound
![]() $\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}$
. Unlike
$\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}$
. Unlike
![]() $\Vert h^{-\frac {1}{2}}J\Vert _{\text {HS}}$
, this is more involved as the presence of factors of h on both sides of J prevents us from combining J and
$\Vert h^{-\frac {1}{2}}J\Vert _{\text {HS}}$
, this is more involved as the presence of factors of h on both sides of J prevents us from combining J and
![]() $J^{\ast }$
in
$J^{\ast }$
in
![]() $\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}^{2}=\text {tr}(J^{\ast }h^{-1}Jh)$
, and so we need to proceed differently. First, we note the following elementary estimate:
$\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}^{2}=\text {tr}(J^{\ast }h^{-1}Jh)$
, and so we need to proceed differently. First, we note the following elementary estimate:
Lemma 9.13. There exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$\begin{align*}\left|i\theta-\frac{1}{2}\left(e^{i\theta}-e^{-i\theta}\right)\right|\leq C\left|e^{i\theta}-1\right|^{3},\quad\theta\in\left[-\pi,\pi\right]. \end{align*}$$
$$\begin{align*}\left|i\theta-\frac{1}{2}\left(e^{i\theta}-e^{-i\theta}\right)\right|\leq C\left|e^{i\theta}-1\right|^{3},\quad\theta\in\left[-\pi,\pi\right]. \end{align*}$$
Proof. The left-hand side is
![]() $|\theta -\sin (\theta )|=O(|\theta |^3)$
, while
$|\theta -\sin (\theta )|=O(|\theta |^3)$
, while
![]() $ |\theta | \ge \left|e^{i\theta }-1\right| \ge C^{-1}\theta $
.
$ |\theta | \ge \left|e^{i\theta }-1\right| \ge C^{-1}\theta $
.
Proposition 9.14. There exists a universal constant
![]() $C>0$
such that
$C>0$
such that
 $$\begin{align*}\left\Vert h^{-\frac{1}{2}}\left[J,h\right]h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\langle v,h^{-1}v\right\rangle +\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}\right). \end{align*}$$
$$\begin{align*}\left\Vert h^{-\frac{1}{2}}\left[J,h\right]h^{-\frac{1}{2}}\right\Vert _{\operatorname{\mathrm{HS}}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\langle v,h^{-1}v\right\rangle +\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}\right). \end{align*}$$
Proof. It suffices to bound
![]() $\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}$
. By writing
$\Vert h^{-\frac {1}{2}}Jh^{\frac {1}{2}}\Vert _{\text {HS}}$
. By writing
we see by the triangle inequality that
By Proposition 9.10, we have
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},h^{-\frac{1}{2}}\left(U-1\right)h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\frac{\lambda_{j}}{\lambda_{i}}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{\lambda_{j}}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\nonumber \\ &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{2} \nonumber\\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{2} \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}\left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},h^{-\frac{1}{2}}\left(U-1\right)h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\frac{\lambda_{j}}{\lambda_{i}}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\frac{\lambda_{j}}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\nonumber \\ &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\right)^{2} \nonumber\\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{2} \end{align} $$
and likewise for
![]() $\Vert h^{-\frac {1}{2}}(1-U^{\ast })h^{\frac {1}{2}}\Vert _{\text {HS}}^{2}$
. For
$\Vert h^{-\frac {1}{2}}(1-U^{\ast })h^{\frac {1}{2}}\Vert _{\text {HS}}^{2}$
. For
![]() $h^{-\frac {1}{2}}\widetilde {J} h^{\frac {1}{2}}$
, we instead apply Lemma 9.13 and the Cauchy-Schwarz inequality to see that for any
$h^{-\frac {1}{2}}\widetilde {J} h^{\frac {1}{2}}$
, we instead apply Lemma 9.13 and the Cauchy-Schwarz inequality to see that for any
![]() $1\leq i,j\leq n$
,
$1\leq i,j\leq n$
,
 $$ \begin{align} \left|\left\langle x_{i},h^{-\frac{1}{2}} \widetilde{J} h^{\frac{1}{2}}x_{j}\right\rangle \right|^2 & =\left|\sum_{k=1}^{n}\left(i\theta_{k}-\frac{1}{2}\left(e^{i\theta_{k}}-e^{-i\theta_{k}}\right)\right)\left\langle h^{-\frac{1}{2}}x_{i},w_{k}\right\rangle \left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^2 \nonumber \\ & \leq C \left( \sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{3}\left|\left\langle h^{-\frac{1}{2}}x_{i},w_{k}\right\rangle \right|\left|\left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right| \right)^2 \nonumber\\ & \leq C \left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{4}\left|\left\langle w_{k},h^{-\frac{1}{2}}x_{i}\right\rangle \right|^{2}\right) \left( \sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2}\left|\left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2} \right)\nonumber \\ & =C \left( \sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)^{2}w_{k},h^{-\frac{1}{2}}x_{i}\right\rangle \right|^{2} \right) \left( \sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2} \right) \nonumber \\ & =C\left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}x_{i}\right\Vert^2 \left\Vert \left(U-1\right)h^{\frac{1}{2}}x_{j}\right\Vert^2. \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},h^{-\frac{1}{2}} \widetilde{J} h^{\frac{1}{2}}x_{j}\right\rangle \right|^2 & =\left|\sum_{k=1}^{n}\left(i\theta_{k}-\frac{1}{2}\left(e^{i\theta_{k}}-e^{-i\theta_{k}}\right)\right)\left\langle h^{-\frac{1}{2}}x_{i},w_{k}\right\rangle \left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^2 \nonumber \\ & \leq C \left( \sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{3}\left|\left\langle h^{-\frac{1}{2}}x_{i},w_{k}\right\rangle \right|\left|\left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right| \right)^2 \nonumber\\ & \leq C \left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{4}\left|\left\langle w_{k},h^{-\frac{1}{2}}x_{i}\right\rangle \right|^{2}\right) \left( \sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2}\left|\left\langle w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2} \right)\nonumber \\ & =C \left( \sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)^{2}w_{k},h^{-\frac{1}{2}}x_{i}\right\rangle \right|^{2} \right) \left( \sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)w_{k},h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2} \right) \nonumber \\ & =C\left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}x_{i}\right\Vert^2 \left\Vert \left(U-1\right)h^{\frac{1}{2}}x_{j}\right\Vert^2. \end{align} $$
Summing over
![]() $i,j$
, we obtain
$i,j$
, we obtain
We can now again apply Proposition 9.10 to estimate that
 $$ \begin{align} \left\Vert \left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\lambda_{j}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\lambda_{j}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\lambda_{j}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}^{\frac{1}{4}}\lambda_{j}^{\frac{3}{4}}}\right|^{2}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2} \end{align} $$
$$ \begin{align} \left\Vert \left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)h^{\frac{1}{2}}x_{j}\right\rangle \right|^{2}=\sum_{i,j=1}^{n}\lambda_{j}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\lambda_{j}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i,j=1}^{n}\lambda_{j}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}^{\frac{1}{4}}\lambda_{j}^{\frac{3}{4}}}\right|^{2}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2} \end{align} $$
and
 $$ \begin{align} \left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)^{2}h^{-\frac{1}{2}}x_{j}\right\rangle \right|^{2}\nonumber \\ & =\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(U-1\right)x_{k}\right\rangle \left\langle x_{k},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left(\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right)^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}\left(\sum_{k=1}^{n}\frac{\left\langle v,x_{k}\right\rangle }{\lambda_{i}^{\frac{5}{8}}\lambda_{k}^{\frac{3}{8}}}\frac{\left\langle x_{k},v\right\rangle }{\lambda_{k}^{\frac{7}{8}}\lambda_{j}^{\frac{1}{8}}}\right)^{2}\nonumber \\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{5}{4}}}\right)^{4}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{4} \end{align} $$
$$ \begin{align} \left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}\right\Vert _{\text{HS}}^{2} &=\sum_{i,j=1}^{n}\left|\left\langle x_{i},\left(U-1\right)^{2}h^{-\frac{1}{2}}x_{j}\right\rangle \right|^{2}\nonumber \\ & =\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(U-1\right)x_{k}\right\rangle \left\langle x_{k},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{j}}\left(\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right)^{2} \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\frac{\left|\left\langle x_{j},v\right\rangle \right|^{2}}{\lambda_{j}}\left(\sum_{k=1}^{n}\frac{\left\langle v,x_{k}\right\rangle }{\lambda_{i}^{\frac{5}{8}}\lambda_{k}^{\frac{3}{8}}}\frac{\left\langle x_{k},v\right\rangle }{\lambda_{k}^{\frac{7}{8}}\lambda_{j}^{\frac{1}{8}}}\right)^{2}\nonumber \\ & =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left(\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{5}{4}}}\right)^{4}=C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{4} \end{align} $$
so
Combining the estimates yields the claim.
Remark 9.1 (Remarks on the estimation technique).
As we will use the same approach to obtain estimates on
![]() $E (t )$
, let us consider the technique of the proof in detail. The idea is that, as we have a good estimate for the matrix elements of
$E (t )$
, let us consider the technique of the proof in detail. The idea is that, as we have a good estimate for the matrix elements of
![]() $U-1$
and
$U-1$
and
![]() $U^{\ast }-1$
, we should attempt to express our operator solely in terms of these. The first step is therefore to decompose J as in (9.42). The error term
$U^{\ast }-1$
, we should attempt to express our operator solely in terms of these. The first step is therefore to decompose J as in (9.42). The error term
![]() $\widetilde {J}=J-\frac {1}{2}\left(U-U^{\ast }\right) $
cannot be simplified further in terms of U but by orthonormal expansion and Lemma 9.13, we can nonetheless estimate it solely in terms of
$\widetilde {J}=J-\frac {1}{2}\left(U-U^{\ast }\right) $
cannot be simplified further in terms of U but by orthonormal expansion and Lemma 9.13, we can nonetheless estimate it solely in terms of
![]() $U-1$
, despite being unable to apply an operator inequality, as we did for
$U-1$
, despite being unable to apply an operator inequality, as we did for
![]() $\| h^{-\frac {1}{2}}J\|_{\text {HS}}$
, to ‘substitute’
$\| h^{-\frac {1}{2}}J\|_{\text {HS}}$
, to ‘substitute’
![]() $U-1$
for J directly. The utility of the estimate (9.46) is thus that it allows us to replace the unknown error operator with factors of
$U-1$
for J directly. The utility of the estimate (9.46) is thus that it allows us to replace the unknown error operator with factors of
![]() $U-1$
, which we can estimate well. The downside to this is that it simultanously ‘decouples’ the
$U-1$
, which we can estimate well. The downside to this is that it simultanously ‘decouples’ the
![]() $h^{-\frac {1}{2}}$
and
$h^{-\frac {1}{2}}$
and
![]() $h^{\frac {1}{2}}$
factors, which prevents us from exploiting the cancellation between these.
$h^{\frac {1}{2}}$
factors, which prevents us from exploiting the cancellation between these.
This decoupling is also the reason why it is important that in (9.46) we distribute two factors of
![]() $U-1$
to
$U-1$
to
![]() $h^{-\frac {1}{2}}$
rather than only one. One can by the same argument estimate that
$h^{-\frac {1}{2}}$
rather than only one. One can by the same argument estimate that
 $$ \begin{align} \big\Vert h^{-\frac{1}{2}} \widetilde{J} h^{\frac{1}{2}}\big\Vert _{\text{HS}} & \leq C\big\Vert \big(U-1\big)h^{-\frac{1}{2}}\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)^{2}h^{\frac{1}{2}}\big\Vert _{\text{HS}} \nonumber\\ & \leq C\big(1+\big\langle v,h^{-3}v\big\rangle \big)^{3}\big\langle v,h^{-\frac{3}{4}}v\big\rangle ^{2}\big\langle v,h^{-\frac{3}{2}}v\big\rangle , \end{align} $$
$$ \begin{align} \big\Vert h^{-\frac{1}{2}} \widetilde{J} h^{\frac{1}{2}}\big\Vert _{\text{HS}} & \leq C\big\Vert \big(U-1\big)h^{-\frac{1}{2}}\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)^{2}h^{\frac{1}{2}}\big\Vert _{\text{HS}} \nonumber\\ & \leq C\big(1+\big\langle v,h^{-3}v\big\rangle \big)^{3}\big\langle v,h^{-\frac{3}{4}}v\big\rangle ^{2}\big\langle v,h^{-\frac{3}{2}}v\big\rangle , \end{align} $$
but in Proposition A.3, we only have the good estimates
![]() $\big\langle v_{k},h_{k}^{\alpha }v_{k}\big\rangle \sim Ck_{F}^{1+\alpha }$
for
$\big\langle v_{k},h_{k}^{\alpha }v_{k}\big\rangle \sim Ck_{F}^{1+\alpha }$
for
![]() $\alpha>-\frac {4}{3}$
, which makes (9.50) a worse estimate due to the
$\alpha>-\frac {4}{3}$
, which makes (9.50) a worse estimate due to the
![]() $\big\langle v,h^{-\frac {3}{2}}v\big\rangle $
factor. There is therefore a limit to how low the exponent
$\big\langle v,h^{-\frac {3}{2}}v\big\rangle $
factor. There is therefore a limit to how low the exponent
![]() $\alpha $
can be without affecting our estimates, and so it is advantageous to distribute the factors of
$\alpha $
can be without affecting our estimates, and so it is advantageous to distribute the factors of
![]() $U-1$
such that the overall minimal exponent is not too small.
$U-1$
such that the overall minimal exponent is not too small.
Estimation of
 $E (t )$
$E (t )$
We now estimate
![]() $\max _{j}\Vert h^{-\frac {1}{2}}E (t )x_{j}\Vert $
using the technique outlined above. First, we decompose
$\max _{j}\Vert h^{-\frac {1}{2}}E (t )x_{j}\Vert $
using the technique outlined above. First, we decompose
and using the algebraic identity
with
![]() $A=e^{tJ}$
,
$A=e^{tJ}$
,
![]() $B=h$
and
$B=h$
and
![]() $C=e^{-tJ}$
further decompose
$C=e^{-tJ}$
further decompose
![]() $E_{1} (t )$
as
$E_{1} (t )$
as
 $$ \begin{align} E_{1} (t )=e^{tJ}he^{-tJ}-h & =\big(\big(e^{tJ}-1\big)h+h\big(e^{-tJ}-1\big)\big)+\big(e^{tJ}-1\big)h\big(e^{-tJ}-1\big) \nonumber\\ & =:E_{1,1} (t )+E_{1,2} (t ). \end{align} $$
$$ \begin{align} E_{1} (t )=e^{tJ}he^{-tJ}-h & =\big(\big(e^{tJ}-1\big)h+h\big(e^{-tJ}-1\big)\big)+\big(e^{tJ}-1\big)h\big(e^{-tJ}-1\big) \nonumber\\ & =:E_{1,1} (t )+E_{1,2} (t ). \end{align} $$
Defining
![]() $E_{0}=E\big(0\big)=e^{-K}he^{-K}-h$
, we likewise decompose
$E_{0}=E\big(0\big)=e^{-K}he^{-K}-h$
, we likewise decompose
![]() $E_{2} (t )$
according to
$E_{2} (t )$
according to
 $$ \begin{align} E_{2} (t )=e^{tJ}E_{0}e^{-tJ} & =E_{0}+\big(\big(e^{tJ}-1\big)E_{0}+E_{0}\big(e^{-tJ}-1\big)\big)+\big(e^{tJ}-1\big)E_{0}\big(e^{-tJ}-1\big) \nonumber\\ & =:E_{0}+E_{2,1} (t )+E_{2,2} (t ). \end{align} $$
$$ \begin{align} E_{2} (t )=e^{tJ}E_{0}e^{-tJ} & =E_{0}+\big(\big(e^{tJ}-1\big)E_{0}+E_{0}\big(e^{-tJ}-1\big)\big)+\big(e^{tJ}-1\big)E_{0}\big(e^{-tJ}-1\big) \nonumber\\ & =:E_{0}+E_{2,1} (t )+E_{2,2} (t ). \end{align} $$
The
![]() $E_{1,1} (t )$
,
$E_{1,1} (t )$
,
![]() $E_{1,2} (t )$
and
$E_{1,2} (t )$
and
![]() $E_{2,1} (t )$
,
$E_{2,1} (t )$
,
![]() $E_{2,2} (t )$
terms differ only in replacing the operator h by
$E_{2,2} (t )$
terms differ only in replacing the operator h by
![]() $E_{0}$
. We can therefore estimate these terms similarly, provided we have an estimate on
$E_{0}$
. We can therefore estimate these terms similarly, provided we have an estimate on
![]() $E_{0}$
. This is given by the following:
$E_{0}$
. This is given by the following:
Proposition 9.15. For all
![]() $1\leq i,j\leq n$
, it holds that
$1\leq i,j\leq n$
, it holds that
Consequently,
where
![]() $\alpha =\max _{1\leq j\leq n}\big\langle v,x_{j}\big\rangle $
.
$\alpha =\max _{1\leq j\leq n}\big\langle v,x_{j}\big\rangle $
.
Proof. Using the identity of equation (9.52) with
![]() $A=e^{-K}=C$
and
$A=e^{-K}=C$
and
![]() $B=h$
, we have that
$B=h$
, we have that
Hence,
We can apply Proposition 7.10 to estimate the first term of this equation as
 $$ \begin{align} \big|\big(\lambda_{i}+\lambda_{j}\big)\big\langle x_{i},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\leq\big(\lambda_{i}+\lambda_{j}\big)\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{i}+\lambda_{j}}=\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \end{align} $$
$$ \begin{align} \big|\big(\lambda_{i}+\lambda_{j}\big)\big\langle x_{i},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\leq\big(\lambda_{i}+\lambda_{j}\big)\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{i}+\lambda_{j}}=\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \end{align} $$
and the second term as
 $$ \begin{align} \big|\big\langle x_{i},\big(e^{-K}-1\big)h\big(e^{-K}-1\big)x_{j}\big\rangle \big| & =\big|\sum_{k=1}^{n}\lambda_{k}\big\langle x_{i},\big(e^{-K}-1\big)x_{k}\big\rangle \big\langle x_{k},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{k}\big\rangle }{\lambda_{i}+\lambda_{k}}\frac{\big\langle x_{k},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{k}+\lambda_{j}} \nonumber\\ & \leq\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \sum_{k=1}^{n}\frac{\big|\big\langle x_{k},v\big\rangle \big|^{2}}{\lambda_{k}}=\big\langle v,h^{-1}v\big\rangle \big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle , \end{align} $$
$$ \begin{align} \big|\big\langle x_{i},\big(e^{-K}-1\big)h\big(e^{-K}-1\big)x_{j}\big\rangle \big| & =\big|\sum_{k=1}^{n}\lambda_{k}\big\langle x_{i},\big(e^{-K}-1\big)x_{k}\big\rangle \big\langle x_{k},\big(e^{-K}-1\big)x_{j}\big\rangle \big|\nonumber \\ & \leq\sum_{k=1}^{n}\lambda_{k}\frac{\big\langle x_{i},v\big\rangle \big\langle v,x_{k}\big\rangle }{\lambda_{i}+\lambda_{k}}\frac{\big\langle x_{k},v\big\rangle \big\langle v,x_{j}\big\rangle }{\lambda_{k}+\lambda_{j}} \nonumber\\ & \leq\big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle \sum_{k=1}^{n}\frac{\big|\big\langle x_{k},v\big\rangle \big|^{2}}{\lambda_{k}}=\big\langle v,h^{-1}v\big\rangle \big\langle x_{i},v\big\rangle \big\langle v,x_{j}\big\rangle , \end{align} $$
which implies the first claim. Consequently,
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{0}x_{j}\right\Vert ^{2} &=\sum_{i=1}^{n}\left|\left\langle x_{i},h^{-\frac{1}{2}}\left(e^{-K}he^{-K}-h\right)x_{j}\right\rangle \right|^{2}=\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\left(e^{-K}he^{-K}-h\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \leq\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle. \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{0}x_{j}\right\Vert ^{2} &=\sum_{i=1}^{n}\left|\left\langle x_{i},h^{-\frac{1}{2}}\left(e^{-K}he^{-K}-h\right)x_{j}\right\rangle \right|^{2}=\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},\left(e^{-K}he^{-K}-h\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \leq\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle. \end{align} $$
Now it remains to consider the operators
![]() $e^{tJ}-1$
and
$e^{tJ}-1$
and
![]() $e^{-tJ}-1=\left(e^{tJ}-1\right)^{\ast }$
. To implement the above estimation technique, from the following analogue of Lemma 9.13,
$e^{-tJ}-1=\left(e^{tJ}-1\right)^{\ast }$
. To implement the above estimation technique, from the following analogue of Lemma 9.13,
 $$ \begin{align} \left|\big(e^{it\theta}-1\big)-t\big(e^{i\theta}-1\big)+\frac{t(1-t)}{2}\big(e^{i\theta}+e^{-i\theta}-2\big)\right|\leq C\left|e^{i\theta}-1\right|^{3},\quad t\in\left[0,1\right],\,\theta\in\left[-\pi,\pi\right], \end{align} $$
$$ \begin{align} \left|\big(e^{it\theta}-1\big)-t\big(e^{i\theta}-1\big)+\frac{t(1-t)}{2}\big(e^{i\theta}+e^{-i\theta}-2\big)\right|\leq C\left|e^{i\theta}-1\right|^{3},\quad t\in\left[0,1\right],\,\theta\in\left[-\pi,\pi\right], \end{align} $$
we are motivated in approximating
![]() $e^{tJ}-1$
by
$e^{tJ}-1$
by
with the error term being cubic with respect to
![]() $U-1$
. We then have the following bounds for
$U-1$
. We then have the following bounds for
![]() $F_{t}$
and the associated error terms:
$F_{t}$
and the associated error terms:
Proposition 9.16. For any
![]() $T:V\rightarrow V$
,
$T:V\rightarrow V$
,
![]() $x\in V$
,
$x\in V$
,
![]() $m\in \left\{ 1,2\right\} $
and
$m\in \left\{ 1,2\right\} $
and
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
and for all
![]() $1\leq i,j\leq n$
,
$1\leq i,j\leq n$
,
![]() $t\in \left[0,1\right]$
,
$t\in \left[0,1\right]$
,
 $$\begin{align*}\left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},F_{t}^{\ast}x_{j}\right\rangle \right|\leq C\big(1+\left\langle v,h^{-1}v\right\rangle \big)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} \end{align*}$$
$$\begin{align*}\left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right|,\,\left|\left\langle x_{i},F_{t}^{\ast}x_{j}\right\rangle \right|\leq C\big(1+\left\langle v,h^{-1}v\right\rangle \big)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} \end{align*}$$
for a constant
![]() $C>0$
independent of all quantities.
$C>0$
independent of all quantities.
Proof. Recall that
![]() $(w_{j})_{j=1}^{n}$
is an orthonormal eigenbasis of J, namely,
$(w_{j})_{j=1}^{n}$
is an orthonormal eigenbasis of J, namely,
![]() $e^{tJ}w_{j}=e^{it\theta _{j}} w_j$
for all
$e^{tJ}w_{j}=e^{it\theta _{j}} w_j$
for all
![]() $1\leq j\leq n$
. Using (9.60) and the Cauchy-Schwarz inequality, we have that
$1\leq j\leq n$
. Using (9.60) and the Cauchy-Schwarz inequality, we have that
 $$ \begin{align} & \left\Vert T\left(e^{tJ}-1-F_{t}\right)x\right\Vert ^{2}=\sum_{j=1}^{n}\left|\left\langle w_{j},T\left(e^{tJ}-1-F_{t}\right)x\right\rangle \right|^{2}\nonumber \\ &\quad =\sum_{j=1}^{n}\left|\sum_{k=1}^{n}\left(\left(e^{it\theta_{k}}-1\right)-t\left(e^{i\theta_{k}}-1\right)+\frac{t(1-t)}{2}\left(e^{i\theta_{k}}+e^{-i\theta_{k}}-2\right)\right)\left\langle w_{j},Tw_{k}\right\rangle \left\langle w_{k},x\right\rangle \right|^{2}\nonumber \\ &\quad \leq C\sum_{j=1}^{n}\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{3}\left|\left\langle w_{j},Tw_{k}\right\rangle \right|\left|\left\langle w_{k},x\right\rangle \right|\right)^{2}\nonumber\\ &\quad \leq C\sum_{j=1}^{n}\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2m}\left|\left\langle w_{j},Tw_{k}\right\rangle \right|^{2}\right)\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2\left(3-m\right)}\left|\left\langle w_{k},x\right\rangle \right|^{2}\right)\nonumber \\ &\quad =C\left(\sum_{j,k=1}^{n}\left|\left\langle w_{j},T\left(U-1\right)^{m}w_{k}\right\rangle \right|^{2}\right)\left(\sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)^{3-m}w_{k},x\right\rangle \right|^{2}\right)\nonumber \\ &\quad =C\left\Vert T\left(U-1\right)^{m}\right\Vert _{\text{HS}}^{2}\left\Vert \left(U-1\right)^{3-m}x\right\Vert ^{2}, \end{align} $$
$$ \begin{align} & \left\Vert T\left(e^{tJ}-1-F_{t}\right)x\right\Vert ^{2}=\sum_{j=1}^{n}\left|\left\langle w_{j},T\left(e^{tJ}-1-F_{t}\right)x\right\rangle \right|^{2}\nonumber \\ &\quad =\sum_{j=1}^{n}\left|\sum_{k=1}^{n}\left(\left(e^{it\theta_{k}}-1\right)-t\left(e^{i\theta_{k}}-1\right)+\frac{t(1-t)}{2}\left(e^{i\theta_{k}}+e^{-i\theta_{k}}-2\right)\right)\left\langle w_{j},Tw_{k}\right\rangle \left\langle w_{k},x\right\rangle \right|^{2}\nonumber \\ &\quad \leq C\sum_{j=1}^{n}\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{3}\left|\left\langle w_{j},Tw_{k}\right\rangle \right|\left|\left\langle w_{k},x\right\rangle \right|\right)^{2}\nonumber\\ &\quad \leq C\sum_{j=1}^{n}\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2m}\left|\left\langle w_{j},Tw_{k}\right\rangle \right|^{2}\right)\left(\sum_{k=1}^{n}\left|e^{i\theta_{k}}-1\right|^{2\left(3-m\right)}\left|\left\langle w_{k},x\right\rangle \right|^{2}\right)\nonumber \\ &\quad =C\left(\sum_{j,k=1}^{n}\left|\left\langle w_{j},T\left(U-1\right)^{m}w_{k}\right\rangle \right|^{2}\right)\left(\sum_{k=1}^{n}\left|\left\langle \left(U^{\ast}-1\right)^{3-m}w_{k},x\right\rangle \right|^{2}\right)\nonumber \\ &\quad =C\left\Vert T\left(U-1\right)^{m}\right\Vert _{\text{HS}}^{2}\left\Vert \left(U-1\right)^{3-m}x\right\Vert ^{2}, \end{align} $$
the same estimate holding also for
![]() $\left\Vert T\left(e^{-tJ}-1-F_{t}^{\ast }\right)x\right\Vert $
. For the matrix element estimate of
$\left\Vert T\left(e^{-tJ}-1-F_{t}^{\ast }\right)x\right\Vert $
. For the matrix element estimate of
![]() $F_{t}$
, we have by Proposition 9.10 that
$F_{t}$
, we have by Proposition 9.10 that
 $$ \begin{align} \left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right| & =\left|\left\langle x_{i},\left(\frac{t\left(1+t\right)}{2}\left(U-1\right)-\frac{t(1-t)}{2}\left(U^{\ast}-1\right)\right)x_{j}\right\rangle \right|\nonumber \\ & \leq\frac{t\left(1+t\right)}{2}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|+\frac{t(1-t)}{2}\left|\left\langle x_{i},\left(U^{\ast}-1\right)x_{j}\right\rangle \right| \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} \end{align} $$
$$ \begin{align} \left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right| & =\left|\left\langle x_{i},\left(\frac{t\left(1+t\right)}{2}\left(U-1\right)-\frac{t(1-t)}{2}\left(U^{\ast}-1\right)\right)x_{j}\right\rangle \right|\nonumber \\ & \leq\frac{t\left(1+t\right)}{2}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|+\frac{t(1-t)}{2}\left|\left\langle x_{i},\left(U^{\ast}-1\right)x_{j}\right\rangle \right| \nonumber\\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}} \end{align} $$
as we only consider
![]() $t\in \left[0,1\right]$
, and likewise for
$t\in \left[0,1\right]$
, and likewise for
![]() $\left|\left\langle x_{i},F_{t}^{\ast }x_{j}\right\rangle \right|$
.
$\left|\left\langle x_{i},F_{t}^{\ast }x_{j}\right\rangle \right|$
.
Estimation of
 $E_{1} (t )$
$E_{1} (t )$
We are now ready to estimate
![]() $E_{1} (t )=E_{1,1} (t )+E_{1,2} (t )$
, starting with
$E_{1} (t )=E_{1,1} (t )+E_{1,2} (t )$
, starting with
![]() $E_{1,1} (t )=\left(e^{tJ}-1\right)h+h\left(e^{-tJ}-1\right)$
. Recall that
$E_{1,1} (t )=\left(e^{tJ}-1\right)h+h\left(e^{-tJ}-1\right)$
. Recall that
![]() $(x_i)_i$
are an eigenbasis of h with
$(x_i)_i$
are an eigenbasis of h with
![]() $\langle x_i, v\rangle \ge 0$
for all
$\langle x_i, v\rangle \ge 0$
for all
![]() $1\le i\le n$
.
$1\le i\le n$
.
Proposition 9.17. For all
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
 $$ \begin{align*} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{1,1} (t )x_j\right\Vert & \leq C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)\sqrt{\left\langle v,h^{-1}v\right\rangle }\\ &\quad + C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\Vert v\right\Vert \left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}+\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\right), \end{align*} $$
$$ \begin{align*} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{1,1} (t )x_j\right\Vert & \leq C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)\sqrt{\left\langle v,h^{-1}v\right\rangle }\\ &\quad + C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\Vert v\right\Vert \left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}+\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\right), \end{align*} $$
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
![]() $C>0$
is a constant independent of all quantities.
$C>0$
is a constant independent of all quantities.
Proof. We write
so that for any
![]() $1\leq j\leq n$
, we can estimate by Proposition 9.16
$1\leq j\leq n$
, we can estimate by Proposition 9.16
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{1,1} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}hx_{j}\right\Vert +\left\Vert h^{\frac{1}{2}}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hx_{j}\right\Vert \nonumber\\ &\quad +C\left\Vert h^{\frac{1}{2}}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert . \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{1,1} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}hx_{j}\right\Vert +\left\Vert h^{\frac{1}{2}}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hx_{j}\right\Vert \nonumber\\ &\quad +C\left\Vert h^{\frac{1}{2}}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert . \end{align} $$
We consider each term above for the following. By Proposition 9.16, we see that independently of
![]() $1\leq j\leq n$
,
$1\leq j\leq n$
,
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}hx_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{\lambda_{j}^{2}}{\lambda_{i}}\left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\lambda_{j}^{2}}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\nonumber \\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ,\nonumber \\ \left\Vert h^{\frac{1}{2}}F^*_{t}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\lambda_{i}\left|\left\langle x_{i},F^*_{t}x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\lambda_{i}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle . \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}hx_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\frac{\lambda_{j}^{2}}{\lambda_{i}}\left|\left\langle x_{i},F_{t}x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\lambda_{j}^{2}}{\lambda_{i}}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2}\nonumber \\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ,\nonumber \\ \left\Vert h^{\frac{1}{2}}F^*_{t}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\lambda_{i}\left|\left\langle x_{i},F^*_{t}x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\lambda_{i}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle . \end{align} $$
For the remaining terms of equation (9.65), we recall that we already estimated
![]() $\big\Vert h^{-\frac {1}{2}}\big(U-1\big)^{2}\big\Vert _{\text {HS}}$
and
$\big\Vert h^{-\frac {1}{2}}\big(U-1\big)^{2}\big\Vert _{\text {HS}}$
and
![]() $\big\Vert h^{\frac {1}{2}}\big(U-1\big)\big\Vert _{\text {HS}}$
in the equations (9.47) and (9.48) to be
$\big\Vert h^{\frac {1}{2}}\big(U-1\big)\big\Vert _{\text {HS}}$
in the equations (9.47) and (9.48) to be
 $$ \begin{align} \left\Vert h^{\frac{1}{2}}\left(U-1\right)\right\Vert _{\text{HS}} & =\left\Vert \left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)\left\langle v,h^{-\frac{1}{2}}v\right\rangle , \\ \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}} & =\left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}\right\Vert _{\text{HS}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2},\nonumber \end{align} $$
$$ \begin{align} \left\Vert h^{\frac{1}{2}}\left(U-1\right)\right\Vert _{\text{HS}} & =\left\Vert \left(U-1\right)h^{\frac{1}{2}}\right\Vert _{\text{HS}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)\left\langle v,h^{-\frac{1}{2}}v\right\rangle , \\ \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}} & =\left\Vert \left(U-1\right)^{2}h^{-\frac{1}{2}}\right\Vert _{\text{HS}}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2},\nonumber \end{align} $$
the equalities holding by normality of U. The only unknown quantities are thus
![]() $\left\Vert \left(U-1\right)hx_{j}\right\Vert $
and
$\left\Vert \left(U-1\right)hx_{j}\right\Vert $
and
![]() $\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert $
, which we estimate using Proposition 9.10 as
$\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert $
, which we estimate using Proposition 9.10 as
 $$ \begin{align} \left\Vert \left(U-1\right)hx_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\lambda_{j}^{2}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\lambda_{j}^{2}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\Vert v\right\Vert ^{2}, \end{align} $$
$$ \begin{align} \left\Vert \left(U-1\right)hx_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\lambda_{j}^{2}\left|\left\langle x_{i},\left(U-1\right)x_{j}\right\rangle \right|^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\lambda_{j}^{2}\left|\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{i}+\lambda_{j}}\right|^{2} \nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\Vert v\right\Vert ^{2}, \end{align} $$
 $$ \begin{align} \left\Vert \left(U-1\right)^{2}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(U-1\right)x_{k}\right\rangle \left\langle x_{k},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \qquad\qquad\qquad\qquad\nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{2}{3}}\lambda_{k}^{\frac{4}{3}}}\right)^{2}\nonumber \\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{3}. \end{align} $$
$$ \begin{align} \left\Vert \left(U-1\right)^{2}x_{j}\right\Vert ^{2} & =\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\left\langle x_{i},\left(U-1\right)x_{k}\right\rangle \left\langle x_{k},\left(U-1\right)x_{j}\right\rangle \right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \qquad\qquad\qquad\qquad\nonumber\\ & \leq C\left|\left\langle v,x_{j}\right\rangle \right|^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{2}{3}}\lambda_{k}^{\frac{4}{3}}}\right)^{2}\nonumber \\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{3}. \end{align} $$
Thus,
 $$ \begin{align} \big\Vert h^{-\frac{1}{2}}\big(U-1\big)^{2}\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)hx_{j}\big\Vert & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\Vert v\big\Vert \big\langle v,h^{-\frac{5}{4}}h\big\rangle ^{2} \nonumber\\ \big\Vert h^{\frac{1}{2}}\big(U-1\big)\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)^{2}x_{j}\big\Vert & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\langle v,h^{-\frac{1}{2}}v\big\rangle \big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}, \end{align} $$
$$ \begin{align} \big\Vert h^{-\frac{1}{2}}\big(U-1\big)^{2}\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)hx_{j}\big\Vert & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\Vert v\big\Vert \big\langle v,h^{-\frac{5}{4}}h\big\rangle ^{2} \nonumber\\ \big\Vert h^{\frac{1}{2}}\big(U-1\big)\big\Vert _{\text{HS}}\big\Vert \big(U-1\big)^{2}x_{j}\big\Vert & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\langle v,h^{-\frac{1}{2}}v\big\rangle \big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}, \end{align} $$
which, upon combination with the estimates of equation (9.66), imply the claim.
Proposition 9.18. For all
![]() $t\in \big[0,1\big]$
, it holds that
$t\in \big[0,1\big]$
, it holds that
 $$ \begin{align*} & \left(C\alpha\right)^{-1}\max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{1,2} (t )x_{j}\right\Vert \\ &\quad \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}+\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left(\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right), \end{align*} $$
$$ \begin{align*} & \left(C\alpha\right)^{-1}\max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{1,2} (t )x_{j}\right\Vert \\ &\quad \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}+\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}h\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left(\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right), \end{align*} $$
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
![]() $C>0$
is a constant independent of all quantities.
$C>0$
is a constant independent of all quantities.
Proof. We write
![]() $E_{1,2} (t )=\left(e^{tJ}-1\right)h\left(e^{-tJ}-1\right)$
as
$E_{1,2} (t )=\left(e^{tJ}-1\right)h\left(e^{-tJ}-1\right)$
as
and see by Proposition 9.16 that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{1,2} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}hF_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert .\nonumber \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{1,2} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}hF_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert .\nonumber \end{align} $$
We estimate by Propositions 9.10 and 9.16 that
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}hF_{t}^{\ast}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}hF_{t}^{\ast}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} & \left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} & \left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{4}}\lambda_{j}^{\frac{1}{4}}\lambda_{k}^{\frac{1}{2}}}\right)^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{4}. \end{align} $$
$$ \begin{align} & \left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\sum_{k=1}^{n}\lambda_{k}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{4}}\lambda_{j}^{\frac{1}{4}}\lambda_{k}^{\frac{1}{2}}}\right)^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{4}. \end{align} $$
Combining these with the estimates of the equations (9.67) and (9.69) yields
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert & \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}},\nonumber \\ \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert & \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2} \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert & \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}},\nonumber \\ \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)hF_{t}^{\ast}x_{j}\right\Vert & \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2} \end{align} $$
and
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber\\ &\quad \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)h\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber\\ &\quad \leq C\alpha\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}, \end{align} $$
which imply the claim.
Estimation of
 $E_{2} (t )$
$E_{2} (t )$
We now repeat the same steps for
![]() $E_{2} (t )=E_{0}+E_{2,1} (t )+E_{2,2} (t )$
where
$E_{2} (t )=E_{0}+E_{2,1} (t )+E_{2,2} (t )$
where
Proposition 9.19. For all
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
 $$ \begin{align*} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{2,1} (t )x\right\Vert &\leq C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}} \\ &\quad + C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\\ &\quad +C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}, \end{align*} $$
$$ \begin{align*} \max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E_{2,1} (t )x\right\Vert &\leq C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}} \\ &\quad + C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\\ &\quad +C\alpha \left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}, \end{align*} $$
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
![]() $C>0$
is a constant independent of all quantities.
$C>0$
is a constant independent of all quantities.
Proof. By Proposition 9.16, we can estimate that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{2,1} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}E_{0}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert. \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{2,1} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}x_{j}\right\Vert +\left\Vert h^{-\frac{1}{2}}E_{0}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert. \end{align} $$
Then let us consider each term separately. By the Propositions 9.10, 9.15, 9.16, we have that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}x_{j}\right\Vert ^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}\nonumber\\ & =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}x_{j}\right\Vert ^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}\nonumber\\ & =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}E_{0}F_{t}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ & \quad\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}E_{0}F_{t}x_{j}\right\Vert ^{2}\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2} \nonumber\\ & \quad\leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\right)^{2}=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-1}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} \left\Vert \left(U-1\right)E_{0}x_{j}\right\Vert ^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\right)^{2}\nonumber\\ &=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} \left\Vert \left(U-1\right)E_{0}x_{j}\right\Vert ^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\sum_{k=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle \right|^{2} \nonumber\\ & \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\right)^{2}\nonumber\\ &=C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2}\nonumber\\ & =C(1+\langle v,h^{-1}v\rangle )^{4}\langle v,h^{-1}v\rangle \langle v,h^{-\frac{2}{3}}v\rangle ^{3}. \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} &\leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k=1}^{n}\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle \frac{\left\langle x_{k},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{k}+\lambda_{j}}\right|^{2}\nonumber \\ & \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2}\nonumber\\ & =C(1+\langle v,h^{-1}v\rangle )^{4}\langle v,h^{-1}v\rangle \langle v,h^{-\frac{2}{3}}v\rangle ^{3}. \end{align} $$
Combining these with our prior estimates that
 $$ \begin{align} \big\Vert h^{-\frac{1}{2}}\big(U-1\big)^{2}\big\Vert _{\text{HS}} & \leq C\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{2}\big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}, \nonumber\\ \big\Vert \big(U-1\big)^{2}x_{j}\big\Vert _{\text{HS}} & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{2}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}, \end{align} $$
$$ \begin{align} \big\Vert h^{-\frac{1}{2}}\big(U-1\big)^{2}\big\Vert _{\text{HS}} & \leq C\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{2}\big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}, \nonumber\\ \big\Vert \big(U-1\big)^{2}x_{j}\big\Vert _{\text{HS}} & \leq C\alpha\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{2}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}, \end{align} $$
we obtain the claim.
Proposition 9.20. For all
![]() $t\in \big[0,1\big]$
, it holds that
$t\in \big[0,1\big]$
, it holds that
 $$ \begin{align*} & \big(C\alpha\big)^{-1}\max_{1\leq j\leq n}\big\Vert h^{-\frac{1}{2}}E_{2,2} (t )x_{j}\big\Vert \\ &\quad \leq\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\langle v,h^{-1}v\big\rangle ^{\frac{5}{2}}+\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{7}\big\langle v,h^{-\frac{2}{3}}\big\rangle ^{3}\big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}\\ &\qquad +\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{5} \big\langle v,h^{-\frac{2}{3}}v\big\rangle ^{\frac{3}{2}} \big(\big\langle v,h^{-1}v\big\rangle ^{\frac{3}{2}}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}+\big\langle v,h^{-1}v\big\rangle \big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}\big), \end{align*} $$
$$ \begin{align*} & \big(C\alpha\big)^{-1}\max_{1\leq j\leq n}\big\Vert h^{-\frac{1}{2}}E_{2,2} (t )x_{j}\big\Vert \\ &\quad \leq\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{3}\big\langle v,h^{-1}v\big\rangle ^{\frac{5}{2}}+\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{7}\big\langle v,h^{-\frac{2}{3}}\big\rangle ^{3}\big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}\\ &\qquad +\big(1+\big\langle v,h^{-1}v\big\rangle \big)^{5} \big\langle v,h^{-\frac{2}{3}}v\big\rangle ^{\frac{3}{2}} \big(\big\langle v,h^{-1}v\big\rangle ^{\frac{3}{2}}\big\langle v,h^{-\frac{4}{3}}v\big\rangle ^{\frac{3}{2}}+\big\langle v,h^{-1}v\big\rangle \big\langle v,h^{-\frac{5}{4}}v\big\rangle ^{2}\big), \end{align*} $$
where
![]() $\alpha =\max _{1\leq j\leq n}\big\langle v,x_{j}\big\rangle $
and
$\alpha =\max _{1\leq j\leq n}\big\langle v,x_{j}\big\rangle $
and
![]() $C>0$
is a constant independent of all quantities.
$C>0$
is a constant independent of all quantities.
Proof. We decompose
![]() $E_{2,2} (t )=\big(e^{tJ}-1\big)E_{0}\big(e^{-tJ}-1\big)$
as
$E_{2,2} (t )=\big(e^{tJ}-1\big)E_{0}\big(e^{-tJ}-1\big)$
as
and estimate by Proposition 9.16 that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{2,2} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}F_{t}^{\ast}x_{j}\right\Vert \nonumber\\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert . \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}E_{2,2} (t )x_{j}\right\Vert & \leq\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}F_{t}^{\ast}x_{j}\right\Vert +C\left\Vert h^{-\frac{1}{2}}F_{t}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert \nonumber \\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}F_{t}^{\ast}x_{j}\right\Vert \nonumber\\ &\quad +C\left\Vert h^{-\frac{1}{2}}\left(U-1\right)^{2}\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)E_{0}\left(U-1\right)\right\Vert _{\text{HS}}\left\Vert \left(U-1\right)^{2}x_{j}\right\Vert . \end{align} $$
We estimate as in the previous proposition that
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}F_{t}^{\ast}x_{j}\right\Vert ^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2} \nonumber\\ &\quad =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{5}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}F_{t}^{\ast}x_{j}\right\Vert ^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left(\sum_{k=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2} \nonumber\\ &\quad =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{5}, \end{align} $$
and
 $$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2}\nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{3}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert h^{-\frac{1}{2}}F_{t}E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\frac{1}{\lambda_{i}}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\frac{\left|\left\langle x_{i},v\right\rangle \right|^{2}}{\lambda_{i}}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{k}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right)^{2}\nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{3}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
and
 $$ \begin{align} & \left\Vert \left(U-1\right)E_{0}F_{t}^{\ast}x_{j}\right\Vert ^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2} \nonumber\\ &\quad =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{2}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
$$ \begin{align} & \left\Vert \left(U-1\right)E_{0}F_{t}^{\ast}x_{j}\right\Vert ^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left(\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}}\right)^{2} \nonumber\\ &\quad =C\alpha^{2}\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-1}v\right\rangle ^{2}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}, \end{align} $$
and finally that
 $$ \begin{align} & \left\Vert \left(U-1\right)E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left|\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right|^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{2}{3}}\right\rangle ^{6}. \end{align} $$
$$ \begin{align} & \left\Vert \left(U-1\right)E_{0}\left(U-1\right)\right\Vert _{\text{HS}}^{2} \nonumber\\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\left|\sum_{k,l=1}^{n}\frac{\left\langle x_{i},v\right\rangle \left\langle v,x_{k}\right\rangle }{\lambda_{i}+\lambda_{k}}\left\langle x_{k},v\right\rangle \left\langle v,x_{l}\right\rangle \frac{\left\langle x_{l},v\right\rangle \left\langle v,x_{j}\right\rangle }{\lambda_{l}+\lambda_{j}}\right|^{2}\nonumber \\ &\quad \leq C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\sum_{i,j=1}^{n}\left|\left\langle x_{i},v\right\rangle \right|^{2}\left|\left\langle x_{j},v\right\rangle \right|^{2}\left|\sum_{k,l=1}^{n}\frac{\left|\left\langle x_{k},v\right\rangle \right|^{2}}{\lambda_{i}^{\frac{1}{3}}\lambda_{k}^{\frac{2}{3}}}\frac{\left|\left\langle x_{l},v\right\rangle \right|^{2}}{\lambda_{l}^{\frac{2}{3}}\lambda_{j}^{\frac{1}{3}}}\right|^{2} \nonumber\\ &\quad =C\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{2}{3}}\right\rangle ^{6}. \end{align} $$
Combining these bounds with equation (9.85) yields the claim.
Combining the estimates from Proposition 9.17 through 9.20 and the last bound of Proposition 9.15, we obtain
 $$ \begin{align} & \left(C\alpha\right)^{-1}\max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E (t )x_{j}\right\Vert \nonumber\\ &\quad \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)\sqrt{\left\langle v,h^{-1}v\right\rangle }+\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}} \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\langle v,h^{-1}v\right\rangle ^{\frac{5}{2}}+\left\Vert v\right\Vert \left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}+\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\right) \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4} \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}} \left(\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right) \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{5} \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}} \left(\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-1}v\right\rangle \left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right)\nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}} \nonumber\\ & \qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{7}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}. \end{align} $$
$$ \begin{align} & \left(C\alpha\right)^{-1}\max_{1\leq j\leq n}\left\Vert h^{-\frac{1}{2}}E (t )x_{j}\right\Vert \nonumber\\ &\quad \leq\left(1+\left\langle v,h^{-1}v\right\rangle \right)\sqrt{\left\langle v,h^{-1}v\right\rangle }+\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{2}\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}} \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{3}\left(\left\langle v,h^{-1}v\right\rangle ^{\frac{5}{2}}+\left\Vert v\right\Vert \left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}+\left\langle v,h^{-\frac{1}{2}}v\right\rangle \left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}\right) \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{4} \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}} \left(\sqrt{\left\langle v,h^{-1}v\right\rangle }\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right) \nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{5} \left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{\frac{3}{2}} \left(\left\langle v,h^{-1}v\right\rangle ^{\frac{3}{2}}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}+\left\langle v,h^{-1}v\right\rangle \left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\right)\nonumber\\ &\qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{6}\left\langle v,h^{-\frac{1}{2}}v\right\rangle ^{2}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}} \nonumber\\ & \qquad +\left(1+\left\langle v,h^{-1}v\right\rangle \right)^{7}\left\langle v,h^{-\frac{2}{3}}v\right\rangle ^{3}\left\langle v,h^{-\frac{5}{4}}v\right\rangle ^{2}\left\langle v,h^{-\frac{4}{3}}v\right\rangle ^{\frac{3}{2}}. \end{align} $$
The right hand can be simplified further using the Hölder estimates
All this gives the following:
Proposition 9.21. For all
![]() $t\in \left[0,1\right]$
, it holds that
$t\in \left[0,1\right]$
, it holds that
where
![]() $\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
$\alpha =\max _{1\leq j\leq n}\left\langle v,x_{j}\right\rangle $
and
![]() $C>0$
is a constant independent of all quantities.
$C>0$
is a constant independent of all quantities.
Conclusion of Proposition 9.6: Inserting
![]() $h_k$
and
$h_k$
and
![]() $v_k$
in Proposition 9.7 and (7.11), we have immediately
$v_k$
in Proposition 9.7 and (7.11), we have immediately
Next, consider the corresponding expressions on the right-hand side of Proposition 9.21. Recall that
![]() $\alpha _{k}=\max _{p\in L_{k}}\left\langle v_{k},e_{p}\right\rangle \le C(\hat {V}_{k})^{\frac {1}{2}}k_{F}^{-\frac {1}{2}}$
. Moreover, by Propositions A.1, A.2 and A.3, we get
$\alpha _{k}=\max _{p\in L_{k}}\left\langle v_{k},e_{p}\right\rangle \le C(\hat {V}_{k})^{\frac {1}{2}}k_{F}^{-\frac {1}{2}}$
. Moreover, by Propositions A.1, A.2 and A.3, we get
 $$ \begin{align} \left\langle v_k, h_k^{\beta} v_k\right\rangle &\le C \hat V_k k_F^{-1} \sum_{p\in L_k} \lambda_{k,p}^{\beta} \le C \hat V_k (|k| k_F)^{1+\beta}, \quad 0\ge \beta\ge -\frac 5 4, \nonumber\\ \left\langle v_{k},h_{k}^{\beta}v_{k}\right\rangle^{\frac 3 2} & \le C(\hat{V}_{k})^{\frac 3 2} \left(|k|k_{F}\right)^{-\frac{1}{2}} |k|^{6}\log\left(k_{F}\right),\quad \beta\le -\frac 4 3. \end{align} $$
$$ \begin{align} \left\langle v_k, h_k^{\beta} v_k\right\rangle &\le C \hat V_k k_F^{-1} \sum_{p\in L_k} \lambda_{k,p}^{\beta} \le C \hat V_k (|k| k_F)^{1+\beta}, \quad 0\ge \beta\ge -\frac 5 4, \nonumber\\ \left\langle v_{k},h_{k}^{\beta}v_{k}\right\rangle^{\frac 3 2} & \le C(\hat{V}_{k})^{\frac 3 2} \left(|k|k_{F}\right)^{-\frac{1}{2}} |k|^{6}\log\left(k_{F}\right),\quad \beta\le -\frac 4 3. \end{align} $$
Putting these bounds together, we deduce from Proposition 9.21 that
 $$ \begin{align} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t )e_{p}\right\Vert & \leq C(\hat{V}_{k})^{\frac{1}{2}}k_{F}^{-\frac{1}{2}} \left(1+\hat{V}_{k}\right)^8 \left( (\hat V_k)^{\frac 1 2} + (\hat V_k)^{\frac 5 2}\right) \left( 1 + \hat V_k^2 |k|^6 \log k_F\right) \nonumber \\ & \leq Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right) \end{align} $$
$$ \begin{align} \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}E_{k} (t )e_{p}\right\Vert & \leq C(\hat{V}_{k})^{\frac{1}{2}}k_{F}^{-\frac{1}{2}} \left(1+\hat{V}_{k}\right)^8 \left( (\hat V_k)^{\frac 1 2} + (\hat V_k)^{\frac 5 2}\right) \left( 1 + \hat V_k^2 |k|^6 \log k_F\right) \nonumber \\ & \leq Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right) \end{align} $$
for
![]() $|k|\leq k_{F}^{\gamma }$
, as claimed. Similarly, inserting (9.95) in Corollary 9.12 and Proposition 9.14, we see that
$|k|\leq k_{F}^{\gamma }$
, as claimed. Similarly, inserting (9.95) in Corollary 9.12 and Proposition 9.14, we see that
 $$ \begin{align} \left\Vert h^{-\frac{1}{2}}J\right\Vert _{\text{HS}} &\leq C\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)\left\langle v_{k},h_{k}^{-\frac{3}{2}}v_{k}\right\rangle \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k}\left(1+\hat{V}_{k}\right)|k|^{3+\frac{2}{3}}, \nonumber\\ \left\Vert h^{-\frac{1}{2}}\left[J,h\right]h^{-\frac{1}{2}}\right\Vert _{\text{HS}} & \leq C\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)^{3}\left(\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle +\left\langle v_{k},h_{k}^{-\frac{1}{2}}v_{k}\right\rangle \left\langle v_{k},h_{k}^{-\frac{5}{4}}v_{k}\right\rangle ^{2}\right)\nonumber \\ & \leq C\left(1+\hat{V}_{k}\right)^{3}\left(\hat{V}_{k}+\hat{V}_{k}\left(|k|k_{F}\right)^{\frac{1}{2}}\left(\hat{V}_{k}\left(|k|k_{F}\right)^{-\frac{1}{4}}\right)^{2}\right) \leq C\hat{V}_{k}. \end{align} $$
$$ \begin{align} \left\Vert h^{-\frac{1}{2}}J\right\Vert _{\text{HS}} &\leq C\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)\left\langle v_{k},h_{k}^{-\frac{3}{2}}v_{k}\right\rangle \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\hat{V}_{k}\left(1+\hat{V}_{k}\right)|k|^{3+\frac{2}{3}}, \nonumber\\ \left\Vert h^{-\frac{1}{2}}\left[J,h\right]h^{-\frac{1}{2}}\right\Vert _{\text{HS}} & \leq C\left(1+\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle \right)^{3}\left(\left\langle v_{k},h_{k}^{-1}v_{k}\right\rangle +\left\langle v_{k},h_{k}^{-\frac{1}{2}}v_{k}\right\rangle \left\langle v_{k},h_{k}^{-\frac{5}{4}}v_{k}\right\rangle ^{2}\right)\nonumber \\ & \leq C\left(1+\hat{V}_{k}\right)^{3}\left(\hat{V}_{k}+\hat{V}_{k}\left(|k|k_{F}\right)^{\frac{1}{2}}\left(\hat{V}_{k}\left(|k|k_{F}\right)^{-\frac{1}{4}}\right)^{2}\right) \leq C\hat{V}_{k}. \end{align} $$
Here, we also note that
![]() $\hat V_k$
is uniformly bounded, and hence, the constant C may depend on V, but it is still independent of k and
$\hat V_k$
is uniformly bounded, and hence, the constant C may depend on V, but it is still independent of k and
![]() $k_F$
.
$k_F$
.
9.4 Gronwall estimates for the kinetic operator
We now come to the kinetic Gronwall estimates for the transformation
![]() $e^{\mathcal {J}}$
. We have the following:
$e^{\mathcal {J}}$
. We have the following:
Proposition 9.22. Assume
![]() $\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
and
$\sum _{k\in \mathbb {Z}^{3}}\hat {V}_{k}|k|<\infty $
and
![]() $S_C=\mathbb {Z}^3_+ \cap \overline {B}\left(0,k_{F}^{\gamma }\right)$
with
$S_C=\mathbb {Z}^3_+ \cap \overline {B}\left(0,k_{F}^{\gamma }\right)$
with
![]() $0<\gamma <\frac {1}{47}$
. Then for all
$0<\gamma <\frac {1}{47}$
. Then for all
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
![]() $\left|t\right|\leq 1$
, it holds that
$\left|t\right|\leq 1$
, it holds that
 $$ \begin{align*} \left\langle e^{t\mathcal{J}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}e^{t\mathcal{J}}\Psi\right\rangle & \leq C\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \\ \left\langle e^{t\mathcal{J}}\Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{t\mathcal{J}}\Psi\right\rangle & \leq C\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \end{align*} $$
$$ \begin{align*} \left\langle e^{t\mathcal{J}}\Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}e^{t\mathcal{J}}\Psi\right\rangle & \leq C\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \\ \left\langle e^{t\mathcal{J}}\Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}e^{t\mathcal{J}}\Psi\right\rangle & \leq C\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle \end{align*} $$
for a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $k_{F}$
.
$k_{F}$
.
Proof. Write
![]() $\Psi _{t}=e^{t\mathcal {J}}\Psi $
for brevity. By the commutator in (9.15), we have
$\Psi _{t}=e^{t\mathcal {J}}\Psi $
for brevity. By the commutator in (9.15), we have
 $$ \begin{align} -\frac{d}{dt}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle =\left\langle \Psi_{t},\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle =2\sum_{k\in S_{C}}\left\langle \Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \end{align} $$
$$ \begin{align} -\frac{d}{dt}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle =\left\langle \Psi_{t},\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle =2\sum_{k\in S_{C}}\left\langle \Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \end{align} $$
with
![]() $\tilde {Q}_{1}^{k}$
defined in (4.35). Moreover, Proposition 4.8 allows us to estimate
$\tilde {Q}_{1}^{k}$
defined in (4.35). Moreover, Proposition 4.8 allows us to estimate
 $$ \begin{align} \sum_{k\in S_{C}}\left|\left\langle \Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \right|\leq\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle. \end{align} $$
$$ \begin{align} \sum_{k\in S_{C}}\left|\left\langle \Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \right|\leq\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle. \end{align} $$
Since
 $$ \begin{align} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}=\left(\begin{array}{cc} h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}} & 0\\ 0 & h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}} \end{array}\right), \end{align} $$
$$ \begin{align} \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}=\left(\begin{array}{cc} h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}} & 0\\ 0 & h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}} \end{array}\right), \end{align} $$
by Proposition 9.6 we can estimate further that
 $$ \begin{align} \sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}} & =\sum_{k\in S_{C}}\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\text{Op}}\leq\sum_{k\in S_{C}}\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\text{HS}}\nonumber \\ & \leq C\sum_{k\in S_C}\hat{V}_{k}\leq C. \end{align} $$
$$ \begin{align} \sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}} & =\sum_{k\in S_{C}}\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\text{Op}}\leq\sum_{k\in S_{C}}\left\Vert h_{k}^{-\frac{1}{2}}\left[J_{k},h_{k}\right]h_{k}^{-\frac{1}{2}}\right\Vert _{\text{HS}}\nonumber \\ & \leq C\sum_{k\in S_C}\hat{V}_{k}\leq C. \end{align} $$
Hence,
![]() $\left|\frac {d}{dt}\left\langle \Psi _{t},H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle \right|\leq C\left\langle \Psi _{t},H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle $
, so by Gronwall’s lemma
$\left|\frac {d}{dt}\left\langle \Psi _{t},H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle \right|\leq C\left\langle \Psi _{t},H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle $
, so by Gronwall’s lemma
For
![]() $\left\langle \Psi _{t},\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle $
, besides the commutator in (9.15), we also note that
$\left\langle \Psi _{t},\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }\Psi _{t}\right\rangle $
, besides the commutator in (9.15), we also note that
 $$ \begin{align} \left[\mathcal{J},\mathcal{N}_{E}\right] & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left[b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}),\mathcal{N}_{E}\right]\nonumber \\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)\left[b_{k}(e_{p}),\mathcal{N}_{E}\right]+\left[b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right),\mathcal{N}_{E}\right]b_{k}(e_{p})\right)\\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})-b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)=0.\nonumber \end{align} $$
$$ \begin{align} \left[\mathcal{J},\mathcal{N}_{E}\right] & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left[b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p}),\mathcal{N}_{E}\right]\nonumber \\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)\left[b_{k}(e_{p}),\mathcal{N}_{E}\right]+\left[b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right),\mathcal{N}_{E}\right]b_{k}(e_{p})\right)\\ & =\sum_{k\in S_{C}}\sum_{p\in L_{k}^{\pm}}\left(b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})-b_{k}^{\ast}\left(J_{k}^{\oplus}e_{p}\right)b_{k}(e_{p})\right)=0.\nonumber \end{align} $$
Here again, we used
![]() $\left[\mathcal {N}_{E},b_{k}(\varphi )\right]=-b_{k}$
for all
$\left[\mathcal {N}_{E},b_{k}(\varphi )\right]=-b_{k}$
for all
![]() $\varphi \in \ell ^{2}(L_{k}^{\pm })$
, which follows from (1.75) and linearity. Hence,
$\varphi \in \ell ^{2}(L_{k}^{\pm })$
, which follows from (1.75) and linearity. Hence,
 $$\begin{align*} -\frac{d}{dt}\left\langle \Psi_{t},\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle =\left\langle \Psi_{t},\mathcal{N}_{E}\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle=2\sum_{k\in S_{C}}\left\langle \Psi_{t},\mathcal{N}_{E}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle. \end{align*}$$
$$\begin{align*} -\frac{d}{dt}\left\langle \Psi_{t},\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle =\left\langle \Psi_{t},\mathcal{N}_{E}\left[\mathcal{J},H_{\operatorname{\mathrm{kin}}}^{\prime}\right]\Psi_{t}\right\rangle=2\sum_{k\in S_{C}}\left\langle \Psi_{t},\mathcal{N}_{E}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle. \end{align*}$$
Now, it holds that
![]() $[\mathcal {N}_{E},\tilde {Q}_{1}^{k}([J_{k}^{\oplus },h_{k}^{\oplus }])]=0$
(as can be seen by a computation similar to that of equation (9.103)), so we may estimate as above for
$[\mathcal {N}_{E},\tilde {Q}_{1}^{k}([J_{k}^{\oplus },h_{k}^{\oplus }])]=0$
(as can be seen by a computation similar to that of equation (9.103)), so we may estimate as above for
 $$ \begin{align} &\sum_{k\in S_{C}}\left|\left\langle \Psi_{t},\mathcal{N}_{E}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \right| =\sum_{k\in S_{C}}\left|\left\langle \mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t}\right\rangle \right|\nonumber\\ &\quad \leq\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t}\right\rangle \leq C\left\langle \Psi_{t},\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle , \end{align} $$
$$ \begin{align} &\sum_{k\in S_{C}}\left|\left\langle \Psi_{t},\mathcal{N}_{E}\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\Psi_{t}\right\rangle \right| =\sum_{k\in S_{C}}\left|\left\langle \mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t},\tilde{Q}_{1}^{k}\left(\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\right)\mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t}\right\rangle \right|\nonumber\\ &\quad \leq\sum_{k\in S_{C}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left[J_{k}^{\oplus},h_{k}^{\oplus}\right]\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}\left\langle \mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t},H_{\operatorname{\mathrm{kin}}}^{\prime}\mathcal{N}_{E}^{\frac{1}{2}}\Psi_{t}\right\rangle \leq C\left\langle \Psi_{t},\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_{t}\right\rangle , \end{align} $$
where we also used that
![]() $[\mathcal {N}_{E},H_{\operatorname {\mathrm {kin}}}^{\prime }]=0$
. The second claim now follows.
$[\mathcal {N}_{E},H_{\operatorname {\mathrm {kin}}}^{\prime }]=0$
. The second claim now follows.
10 Conclusion of the main results
Now we are ready to provide the proof of the main theorems stated in the introduction.
10.1 Proof of Theorem 1.1
The proof follows almost immediately by the analysis we have performed throughout the paper, for we will simply take
![]() $\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
where
$\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
where
![]() $e^{\mathcal {K}}$
is the quasi-bosonic Bogolubov transformation
$e^{\mathcal {K}}$
is the quasi-bosonic Bogolubov transformation
![]() $e^{\mathcal {K}}$
of Section 4 and
$e^{\mathcal {K}}$
of Section 4 and
![]() $e^{\mathcal {J}}$
is the second transformation of Section 9.
$e^{\mathcal {J}}$
is the second transformation of Section 9.
Step 1: Let us start from the decomposition (1.22):
 $$ \begin{align} H_N - E_{\mathrm{FS}} = H_{\operatorname{\mathrm{kin}}}' + k_F^{-1} H_{\mathrm{int}}' = H_{\operatorname{\mathrm{kin}}}' + \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) + \mathcal{E}_{\mathrm{NB}}, \end{align} $$
$$ \begin{align} H_N - E_{\mathrm{FS}} = H_{\operatorname{\mathrm{kin}}}' + k_F^{-1} H_{\mathrm{int}}' = H_{\operatorname{\mathrm{kin}}}' + \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) + \mathcal{E}_{\mathrm{NB}}, \end{align} $$
where
![]() $H_{\text {int}}^{k}$
is given in (1.29),
$H_{\text {int}}^{k}$
is given in (1.29),
![]() $\mathcal {E}_{\mathrm {NB}}$
is given in (2.22), and
$\mathcal {E}_{\mathrm {NB}}$
is given in (2.22), and
![]() $S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
$S_{C}=\overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{+}^{3}$
with
![]() $0<\gamma < \frac 1 {47}$
. From Proposition 2.4, the non-bosonizable term
$0<\gamma < \frac 1 {47}$
. From Proposition 2.4, the non-bosonizable term
![]() $\mathcal {E}_{\mathrm {NB}}$
is estimated as
$\mathcal {E}_{\mathrm {NB}}$
is estimated as
By the Gronwall estimates of Propositions 8.1, 9.22 and the choice
![]() $\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, we have
$\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, we have
Thus, it remains to apply the transformations
![]() $e^{\mathcal K}$
and
$e^{\mathcal K}$
and
![]() $e^{\mathcal J}$
to the bosonizable terms.
$e^{\mathcal J}$
to the bosonizable terms.
Step 2: Now we apply the transformation
![]() $e^{\mathcal K}$
. By Proposition 5.7, we have
$e^{\mathcal K}$
. By Proposition 5.7, we have
 $$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\operatorname{\mathrm{int}}}^{k}\right)e^{-\mathcal{K}}\nonumber\\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k} (E_k^\oplus - h_k^\oplus) +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}} \left(\mathcal{E}_{1}^{k} (A_k^{\oplus}(t)) +\mathcal{E}_{2}^{k} (B_k^\oplus(t))\right)e^{-(1-t)\mathcal{K}}\,dt. \end{align} $$
$$ \begin{align} & e^{\mathcal{K}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}H_{\operatorname{\mathrm{int}}}^{k}\right)e^{-\mathcal{K}}\nonumber\\ &\quad =H_{\operatorname{\mathrm{kin}}}^{\prime}+\sum_{k\in S_{C}}Q_{1}^{k} (E_k^\oplus - h_k^\oplus) +\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{K}} \left(\mathcal{E}_{1}^{k} (A_k^{\oplus}(t)) +\mathcal{E}_{2}^{k} (B_k^\oplus(t))\right)e^{-(1-t)\mathcal{K}}\,dt. \end{align} $$
We will use the kinetic estimate of Proposition 6.5 and the Gronwall estimates of Proposition 8.1 to bound the exchange terms in (10.4). Thanks to the one-body estimates in Propositions 7.3, 7.2 and our assumption
![]() $\sum _{k\in S_{C}}\hat {V}_{k}|k|<\infty $
, we get
$\sum _{k\in S_{C}}\hat {V}_{k}|k|<\infty $
, we get
 $$ \begin{align} \sum_{k\in S_{C}}\max_{t\in\left[0,1\right]}\left\{ \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}A_{k}^{\oplus} (t )e_{p}\right\Vert ,\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}B_{k}^{\oplus} (t )e_{p}\right\Vert \right\} &\leq C\sum_{k\in S_{C}}k_{F}^{-\frac{1}{2}}\hat{V}_{k}\left(1+\hat{V}_{k}^{2}\right)\leq Ck_{F}^{-\frac{1}{2}}, \nonumber\\ \sum_{k\in S_{C}}\max_{t\in\left[0,1\right]}\left\{ \left\Vert A_{k}^{\oplus} (t )\right\Vert _{\infty,2},\left\Vert B_{k}^{\oplus} (t )\right\Vert _{\infty,2}\right\} \leq C\sum_{k\in S_{C}}&\hat{V}_{k}|k|^{\frac{1}{2}}\left(1+\hat{V}_{k}\right)\leq C, \nonumber\\ \sum_{k\in S_{C}}\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}K_{k}^{\oplus}\right\Vert _{\text{HS}}+\left\Vert K_{k}^{\oplus}\right\Vert _{\infty,2}\right) \leq C(\log k_{F})^{\frac{2}{3}}& k_{F}^{-\frac{1}{3}}\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}. \end{align} $$
$$ \begin{align} \sum_{k\in S_{C}}\max_{t\in\left[0,1\right]}\left\{ \max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}A_{k}^{\oplus} (t )e_{p}\right\Vert ,\max_{p\in L_{k}}\left\Vert h_{k}^{-\frac{1}{2}}B_{k}^{\oplus} (t )e_{p}\right\Vert \right\} &\leq C\sum_{k\in S_{C}}k_{F}^{-\frac{1}{2}}\hat{V}_{k}\left(1+\hat{V}_{k}^{2}\right)\leq Ck_{F}^{-\frac{1}{2}}, \nonumber\\ \sum_{k\in S_{C}}\max_{t\in\left[0,1\right]}\left\{ \left\Vert A_{k}^{\oplus} (t )\right\Vert _{\infty,2},\left\Vert B_{k}^{\oplus} (t )\right\Vert _{\infty,2}\right\} \leq C\sum_{k\in S_{C}}&\hat{V}_{k}|k|^{\frac{1}{2}}\left(1+\hat{V}_{k}\right)\leq C, \nonumber\\ \sum_{k\in S_{C}}\left(\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}K_{k}^{\oplus}\right\Vert _{\text{HS}}+\left\Vert K_{k}^{\oplus}\right\Vert _{\infty,2}\right) \leq C(\log k_{F})^{\frac{2}{3}}& k_{F}^{-\frac{1}{3}}\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}. \end{align} $$
All this gives that for every state
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
![]() $\Psi _t=e^{-(1-t)\mathcal {K}}\Psi $
,
$\Psi _t=e^{-(1-t)\mathcal {K}}\Psi $
,
 $$ \begin{align} & \sum_{k\in S_{C}}\int_{0}^{1}\left|\left\langle \Psi_t,\left(\mathcal{E}_{1}^{k} (A^{\oplus}_k(t) )+\mathcal{E}_{2}^{k} (B^{\oplus}_k(t) )\right) \Psi_t \right\rangle \right|dt \leq C(\log k_{F})^{\frac{2}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\nonumber\\ &\quad \times\left(k_{F}^{-\frac{5}{6}}\max_{t\in\left[0,1\right]}\sqrt{\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle \left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle }\right.\nonumber\\ &\quad\left. +\ k_{F}^{-\frac{1}{3}}\max_{t\in\left[0,1\right]}\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle +k_{F}^{-\frac{1}{3}}\max_{t\in\left[0,1\right]}\sqrt{\left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle }\right)\nonumber \\ & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left(\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle +k_{F}^{-1}\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle +k_{F}\left\Vert \Psi\right\Vert ^{2}\right), \end{align} $$
$$ \begin{align} & \sum_{k\in S_{C}}\int_{0}^{1}\left|\left\langle \Psi_t,\left(\mathcal{E}_{1}^{k} (A^{\oplus}_k(t) )+\mathcal{E}_{2}^{k} (B^{\oplus}_k(t) )\right) \Psi_t \right\rangle \right|dt \leq C(\log k_{F})^{\frac{2}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\nonumber\\ &\quad \times\left(k_{F}^{-\frac{5}{6}}\max_{t\in\left[0,1\right]}\sqrt{\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle \left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle }\right.\nonumber\\ &\quad\left. +\ k_{F}^{-\frac{1}{3}}\max_{t\in\left[0,1\right]}\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle +k_{F}^{-\frac{1}{3}}\max_{t\in\left[0,1\right]}\sqrt{\left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle }\right)\nonumber \\ & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left(\left\langle \Psi,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle +k_{F}^{-1}\left\langle \Psi,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi\right\rangle +k_{F}\left\Vert \Psi\right\Vert ^{2}\right), \end{align} $$
where we also used the Cauchy–Schwarz inequality to split the square roots at the end. Thus, the exchange terms in (10.4) can be estimated as
 $$ \begin{align} &\pm \sum_{k\in S_{C}}\int_{0}^{1} e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k} (A^{\oplus}_k(t) )+\mathcal{E}_{2}^{k} (B^{\oplus}_k(t) )\right) e^{-(1-t)\mathcal{K}} dt \nonumber\\ & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
$$ \begin{align} &\pm \sum_{k\in S_{C}}\int_{0}^{1} e^{(1-t)\mathcal{K}}\left(\mathcal{E}_{1}^{k} (A^{\oplus}_k(t) )+\mathcal{E}_{2}^{k} (B^{\oplus}_k(t) )\right) e^{-(1-t)\mathcal{K}} dt \nonumber\\ & \leq C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
It remains to consider the main term
![]() $Q_1(E_k^{\oplus } - h_k^{\oplus })$
on the right side of (10.4). We use the normal order form in (4.34):
$Q_1(E_k^{\oplus } - h_k^{\oplus })$
on the right side of (10.4). We use the normal order form in (4.34):
By Propositions 4.9, 7.2 and 2.1,
Moreover, by Proposition 7.1, we have
 $$ \begin{align} \sum_{k\in S_C} \left( 2\operatorname{\mathrm{tr}}\left({E}_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| \right) & = \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt \end{align} $$
$$ \begin{align} \sum_{k\in S_C} \left( 2\operatorname{\mathrm{tr}}\left({E}_{k}-h_{k}\right)-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right| \right) & = \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt \end{align} $$
with
![]() $F (x )=\log \left(1+x\right)-x$
. Thus in summary, we conclude from (10.4) that
$F (x )=\log \left(1+x\right)-x$
. Thus in summary, we conclude from (10.4) that
 $$ \begin{align} & e^{\mathcal{K}} \left( H_{\operatorname{\mathrm{kin}}}' + \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) \right) e^{-\mathcal{K}} \nonumber\\ &= H_{\operatorname{\mathrm{kin}}}^{\prime}+ 2\sum_{k\in S_{C}} \widetilde Q_{1}^{k} (E_{k}^{\oplus}-h_{k}^{\oplus}) + \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal K}, \end{align} $$
$$ \begin{align} & e^{\mathcal{K}} \left( H_{\operatorname{\mathrm{kin}}}' + \sum_{k\in S_C} \left(H_{\mathrm{ int}}^{k}-\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\left|L_{k}\right|\right) \right) e^{-\mathcal{K}} \nonumber\\ &= H_{\operatorname{\mathrm{kin}}}^{\prime}+ 2\sum_{k\in S_{C}} \widetilde Q_{1}^{k} (E_{k}^{\oplus}-h_{k}^{\oplus}) + \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal K}, \end{align} $$
where
 $$ \begin{align} \pm \mathcal{E}_{\mathcal K} \le C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
$$ \begin{align} \pm \mathcal{E}_{\mathcal K} \le C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
Step 3: Next, we apply the transformation
![]() $e^{\mathcal J}$
to the right-hand side of (10.11). From (10.12) and the Gronwall estimates of Proposition 9.22, we have
$e^{\mathcal J}$
to the right-hand side of (10.11). From (10.12) and the Gronwall estimates of Proposition 9.22, we have
 $$ \begin{align} \pm e^{\mathcal{J}} \mathcal{E}_{\mathcal K} e^{-\mathcal{J}} \le C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
$$ \begin{align} \pm e^{\mathcal{J}} \mathcal{E}_{\mathcal K} e^{-\mathcal{J}} \le C(\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}\left(\sum_{k\in S_C}\hat{V}_{k}|k|^{3+\frac{2}{3}}\right)\left( H_{\operatorname{\mathrm{kin}}}^{\prime}+k_{F}^{-1} \mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} +k_{F}\right). \end{align} $$
For the main terms, by Proposition 9.1,
 $$ \begin{align} &e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \\ & =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) +2\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) e^{-(1-t)\mathcal{J}}dt .\nonumber \end{align} $$
$$ \begin{align} &e^{\mathcal{J}}\left(H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left(E_{k}^{\oplus}-h_{k}^{\oplus}\right)\right)e^{-\mathcal{J}} \\ & =H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) +2\sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) e^{-(1-t)\mathcal{J}}dt .\nonumber \end{align} $$
Let us bound the exchange term
![]() $\mathcal {E}_3(\cdot )$
. For all
$\mathcal {E}_3(\cdot )$
. For all
![]() $k\in \overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{\ast }^{3}$
with
$k\in \overline {B}\left(0,k_{F}^{\gamma }\right)\cap \mathbb {Z}_{\ast }^{3}$
with
![]() $0<\gamma <\frac {1}{47}$
and
$0<\gamma <\frac {1}{47}$
and
![]() $t\in [0,1]$
, by Proposition 9.6, we have
$t\in [0,1]$
, by Proposition 9.6, we have
 $$ \begin{align} \max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}E_k(t) e_{p}\right\Vert &\le Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right) \le Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{3} k_F^{\frac 3 {47}}\log\left(k_{F}\right)\right) ,\nonumber\\ \sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}} &\le C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}} \sum_{l\in S_{C}} \hat{V}_{l}\left(1+\hat{V}_{l}\right) \le C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}. \end{align} $$
$$ \begin{align} \max_{p\in L_{k}^{\pm}}\left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}E_k(t) e_{p}\right\Vert &\le Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{6}\log\left(k_{F}\right)\right) \le Ck_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{3} k_F^{\frac 3 {47}}\log\left(k_{F}\right)\right) ,\nonumber\\ \sum_{l\in S_{C}}\left\Vert \left(h_{l}^{\oplus}\right)^{-\frac{1}{2}}J_{l}^{\oplus}\right\Vert _{\operatorname{\mathrm{HS}}} &\le C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}} \sum_{l\in S_{C}} \hat{V}_{l}\left(1+\hat{V}_{l}\right) \le C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}}. \end{align} $$
Hence, using the kinetic estimate of Proposition 9.5, Gronwall’s bounds of Proposition 9.22 and the assumption
![]() $\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| <\infty $
, we find that for every state
$\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| <\infty $
, we find that for every state
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
and
![]() $\Psi _t=e^{-(1-t)\mathcal {J}}\Psi $
,
$\Psi _t=e^{-(1-t)\mathcal {J}}\Psi $
,
 $$ \begin{align} &\sum_{k\in S_{C}}\int_{0}^{1} \left| \langle \Psi_t, {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) \Psi_t\rangle \right| dt \\ &\le \sum_{k\in S_{C}} C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}} k_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{3}k_F^{\frac 3 {47}}\log\left(k_{F}\right)\right) \max_{t\in [0,1]} \sqrt{\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle \left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t \right\rangle} \nonumber\\ &\le C(\log k_F)^{\frac 5 3} k_F^{-\frac{1}{3}} \left\langle \Psi, ( k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F ) \Psi \right\rangle. \nonumber \end{align} $$
$$ \begin{align} &\sum_{k\in S_{C}}\int_{0}^{1} \left| \langle \Psi_t, {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) \Psi_t\rangle \right| dt \\ &\le \sum_{k\in S_{C}} C (\log k_{F})^{\frac{2}{3}}k_{F}^{-\frac{1}{3}} k_{F}^{-\frac{1}{2}}\left(\hat{V}_{k}+\hat{V}_{k}^{3}|k|^{3}k_F^{\frac 3 {47}}\log\left(k_{F}\right)\right) \max_{t\in [0,1]} \sqrt{\left\langle \Psi_t,H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t\right\rangle \left\langle \Psi_t,\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\Psi_t \right\rangle} \nonumber\\ &\le C(\log k_F)^{\frac 5 3} k_F^{-\frac{1}{3}} \left\langle \Psi, ( k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F ) \Psi \right\rangle. \nonumber \end{align} $$
Here, we used
![]() $\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k^3 |k|^3 \le \left( \sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| \right)^3 <\infty $
. Consequently,
$\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k^3 |k|^3 \le \left( \sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| \right)^3 <\infty $
. Consequently,
 $$ \begin{align} \pm \sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) e^{-(1-t)\mathcal{J}}dt \le C (\log k_F)^{\frac 5 3} k_F^{-\frac{1}{3}} (k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F ). \end{align} $$
$$ \begin{align} \pm \sum_{k\in S_{C}}\int_{0}^{1}e^{(1-t)\mathcal{J}} {\mathcal{E}}_{3}^{k}(F_{k}^{\oplus}(t)) e^{-(1-t)\mathcal{J}}dt \le C (\log k_F)^{\frac 5 3} k_F^{-\frac{1}{3}} (k_F^{-1}\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime} + H_{\operatorname{\mathrm{kin}}}^{\prime}+k_F ). \end{align} $$
In summary, we have for
![]() $\mathcal {U}= e^{\mathcal {J}} e^{\mathcal {K}}$
and
$\mathcal {U}= e^{\mathcal {J}} e^{\mathcal {K}}$
and
![]() $0<\gamma <\frac 1 {47}$
,
$0<\gamma <\frac 1 {47}$
,
 $$ \begin{align} \mathcal{U} H_N \mathcal{U}^* = E_{\mathrm{FS}} + H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) + \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal J}, \end{align} $$
$$ \begin{align} \mathcal{U} H_N \mathcal{U}^* = E_{\mathrm{FS}} + H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in S_{C}}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) + \sum_{k\in S_C} \frac{2}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal J}, \end{align} $$
where the error term is collected from (10.3), (10.13), (10.17) which satisfies
Step 4: Finally, let us remove the cutoff
![]() $S_C= \mathbb {Z}_{+}^{3}\cap \overline {B}\left(0,k_{F}^{\gamma }\right) $
on the right-hand side of (10.18). By Proposition 7.1, we can bound
$S_C= \mathbb {Z}_{+}^{3}\cap \overline {B}\left(0,k_{F}^{\gamma }\right) $
on the right-hand side of (10.18). By Proposition 7.1, we can bound
 $$ \begin{align} \left|\frac{1}{\pi}\sum_{k\in\mathbb{Z}_{\ast}^{3}\backslash S_C}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt\right|\leq Ck_{F}\sum_{k\in\mathbb{Z}_{\ast}^{3}\backslash S_C}\hat{V}_{k}^{2}|k| \le C k_F^{1 - \gamma}. \end{align} $$
$$ \begin{align} \left|\frac{1}{\pi}\sum_{k\in\mathbb{Z}_{\ast}^{3}\backslash S_C}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt\right|\leq Ck_{F}\sum_{k\in\mathbb{Z}_{\ast}^{3}\backslash S_C}\hat{V}_{k}^{2}|k| \le C k_F^{1 - \gamma}. \end{align} $$
Here, we used
![]() $\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k^2 |k|^2 \le \left( \sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| \right)^2 <\infty $
. Moreover, by Propositions 4.8 and 9.6 (together with the fact that the trace norm dominates the operator norm), we can bound
$\sum _{k\in \mathbb {Z}^3_{*}} \hat V_k^2 |k|^2 \le \left( \sum _{k\in \mathbb {Z}^3_{*}} \hat V_k |k| \right)^2 <\infty $
. Moreover, by Propositions 4.8 and 9.6 (together with the fact that the trace norm dominates the operator norm), we can bound
 $$ \begin{align} \pm\tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) &\leq \left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right)\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}H_{\operatorname{\mathrm{kin}}}^{\prime} \nonumber\\ &= \left\Vert h_{k}^{-\frac{1}{2}}\left(\widetilde{E}_{k} -h_{k} \right) h_{k}^{-\frac{1}{2}}\right\Vert _{\text{Op}}H_{\operatorname{\mathrm{kin}}}^{\prime} \le C \hat V_k H_{\operatorname{\mathrm{kin}}}^{\prime} \end{align} $$
$$ \begin{align} \pm\tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) &\leq \left\Vert \left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right)\left(h_{k}^{\oplus}\right)^{-\frac{1}{2}}\right\Vert _{\text{Op}}H_{\operatorname{\mathrm{kin}}}^{\prime} \nonumber\\ &= \left\Vert h_{k}^{-\frac{1}{2}}\left(\widetilde{E}_{k} -h_{k} \right) h_{k}^{-\frac{1}{2}}\right\Vert _{\text{Op}}H_{\operatorname{\mathrm{kin}}}^{\prime} \le C \hat V_k H_{\operatorname{\mathrm{kin}}}^{\prime} \end{align} $$
for all
![]() $k\in \mathbb {Z}^3_+$
, and hence,
$k\in \mathbb {Z}^3_+$
, and hence,
 $$ \begin{align} \pm \sum_{k\in \mathbb{Z}^3_+\backslash S_C} \tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) \le C \left( \sum_{k\in \mathbb{Z}^3_+\backslash S_C} \hat V_k \right) H_{\operatorname{\mathrm{kin}}}^{\prime} \le C k_F^{-\gamma}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} \pm \sum_{k\in \mathbb{Z}^3_+\backslash S_C} \tilde{Q}_{1}^{k}\left(\widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) \le C \left( \sum_{k\in \mathbb{Z}^3_+\backslash S_C} \hat V_k \right) H_{\operatorname{\mathrm{kin}}}^{\prime} \le C k_F^{-\gamma}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
Therefore, we can deduce from (10.18) that for
![]() $\mathcal {U}= e^{\mathcal {J}} e^{\mathcal {K}}$
and
$\mathcal {U}= e^{\mathcal {J}} e^{\mathcal {K}}$
and
![]() $0<\gamma <\frac 1 {47}$
,
$0<\gamma <\frac 1 {47}$
,
 $$ \begin{align} \mathcal{U} H_N \mathcal{U}^* =E_{\mathrm{FS}} + H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in \mathbb{Z}^3_+}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) + \sum_{k\in \mathbb{Z}^3_{*}} \frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal U}, \end{align} $$
$$ \begin{align} \mathcal{U} H_N \mathcal{U}^* =E_{\mathrm{FS}} + H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in \mathbb{Z}^3_+}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) + \sum_{k\in \mathbb{Z}^3_{*}} \frac{1}{\pi}\int_{0}^{\infty}F\left(\frac{\hat{V}_{k}k_{F}^{-1}}{(2\pi)^{3}}\sum_{p\in L_{k}}\frac{\lambda_{k,p}}{\lambda_{k,p}^{2}+t^{2}}\right)dt + \mathcal{E}_{\mathcal U}, \end{align} $$
where
The statement of Theorem 1.1 follows by recognizing the identity
 $$ \begin{align*}2\sum_{k\in \mathbb{Z}^3_+}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) = 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align*} $$
$$ \begin{align*}2\sum_{k\in \mathbb{Z}^3_+}\tilde{Q}_{1}^{k}\left( \widetilde{E}_{k}^{\oplus}-h_{k}^{\oplus}\right) = 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}, \end{align*} $$
which follows from the definition of
![]() $\tilde {Q}_{1}^{k}$
in (4.35).
$\tilde {Q}_{1}^{k}$
in (4.35).
10.2 Proof of Theorem 1.2
Let
![]() $\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be a normalized eigenstate of
$\Psi \in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be a normalized eigenstate of
![]() $H_{N}$
with energy
$H_{N}$
with energy
![]() $\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + \kappa k_F$
for some
$\left\langle \Psi ,H_{N}\Psi \right\rangle \le E_{\mathrm {FS}} + \kappa k_F$
for some
![]() $\kappa>0$
. Denoting
$\kappa>0$
. Denoting
![]() $\tilde {H}_{N}=H_{N}- E_{\mathrm {FS}}$
, we have
$\tilde {H}_{N}=H_{N}- E_{\mathrm {FS}}$
, we have
![]() $\tilde {H}_{N}\Psi =E'\Psi $
with
$\tilde {H}_{N}\Psi =E'\Psi $
with
![]() $E' \le \kappa k_F$
. Using (1.22) and the obvious inequality
$E' \le \kappa k_F$
. Using (1.22) and the obvious inequality
![]() $A^*A\ge 0$
, we obtain the Onsager-type estimate
$A^*A\ge 0$
, we obtain the Onsager-type estimate
 $$ \begin{align} \tilde{H}_{N} - H_{\operatorname{\mathrm{kin}}}^{\prime} &= \frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-\left|L_{k}\right|\right)\\ & \geq -\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left|L_{k}\right| \ge - Ck_{F} \sum_{k\in \mathbb{Z}^3} |k| \hat V_k.\nonumber \end{align} $$
$$ \begin{align} \tilde{H}_{N} - H_{\operatorname{\mathrm{kin}}}^{\prime} &= \frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left(\text{d}\Gamma(e^{-ik\cdot x})^{\ast}\text{d}\Gamma(e^{-ik\cdot x})-\left|L_{k}\right|\right)\\ & \geq -\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}_{\ast}^{3}}\hat{V}_{k}\left|L_{k}\right| \ge - Ck_{F} \sum_{k\in \mathbb{Z}^3} |k| \hat V_k.\nonumber \end{align} $$
Here, we used
![]() $\left|L_{k}\right|\leq Ck_{F}^{2}|k|$
for all
$\left|L_{k}\right|\leq Ck_{F}^{2}|k|$
for all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
(see Proposition A.1). From (10.25) and the assumption
$k\in \mathbb {Z}_{\ast }^{3}$
(see Proposition A.1). From (10.25) and the assumption
![]() $\tilde {H}_{N}\Psi =E'\Psi $
with
$\tilde {H}_{N}\Psi =E'\Psi $
with
![]() $E' \le \kappa k_F$
, we deduce immediately that
$E' \le \kappa k_F$
, we deduce immediately that
To prove the bound for
![]() $\mathcal {N}_E H_{\mathrm {kin}}'$
, we use the operator inequality
$\mathcal {N}_E H_{\mathrm {kin}}'$
, we use the operator inequality
 $$ \begin{align} \mathcal{N}_{E}^{2}H_{\operatorname{\mathrm{kin}}}^{\prime}&=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\mathcal{N}_{E}\leq\mathcal{N}_{E}\tilde{H}_{N}\mathcal{N}_{E}+Ck_{F}\mathcal{N}_{E}^{2} \nonumber\\ &= \frac{1}{2}\left(\mathcal{N}_{E}^{2}\tilde{H}_{N}+\tilde{H}_{N}\mathcal{N}_{E}^{2}-\left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right]\right)+Ck_{F}\mathcal{N}_{E}^{2}, \end{align} $$
$$ \begin{align} \mathcal{N}_{E}^{2}H_{\operatorname{\mathrm{kin}}}^{\prime}&=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}\mathcal{N}_{E}\leq\mathcal{N}_{E}\tilde{H}_{N}\mathcal{N}_{E}+Ck_{F}\mathcal{N}_{E}^{2} \nonumber\\ &= \frac{1}{2}\left(\mathcal{N}_{E}^{2}\tilde{H}_{N}+\tilde{H}_{N}\mathcal{N}_{E}^{2}-\left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right]\right)+Ck_{F}\mathcal{N}_{E}^{2}, \end{align} $$
which follows from (10.25) and the fact that
![]() $\left[\mathcal {N}_{E},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]=0$
. Thanks to the eigenvalue equation
$\left[\mathcal {N}_{E},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]=0$
. Thanks to the eigenvalue equation
![]() $\tilde {H}_{N}\Psi =E'\Psi $
with
$\tilde {H}_{N}\Psi =E'\Psi $
with
![]() $E'\le \kappa k_F$
, we deduce that
$E'\le \kappa k_F$
, we deduce that
Using
![]() $\mathcal {N}_{E} = \sum _{s\in B_F^c} c_{s}^* c_s$
and
$\mathcal {N}_{E} = \sum _{s\in B_F^c} c_{s}^* c_s$
and
we deduce from (1.8) that
 $$ \begin{align} \left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right] =\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}} \sum_{p,q\in\mathbb{Z}^{3}} \hat{V}_{k} c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p} \Big( \sum_{s\in B_F^c} (\delta_{s,p+k} + \delta_{s,q-k}- \delta_{s,q}- \delta_{s,p}) \Big)^2. \end{align} $$
$$ \begin{align} \left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right] =\frac{k_{F}^{-1}}{2(2\pi)^{3}}\sum_{k\in\mathbb{Z}^{3}} \sum_{p,q\in\mathbb{Z}^{3}} \hat{V}_{k} c_{p+k}^{\ast}c_{q-k}^{\ast}c_{q}c_{p} \Big( \sum_{s\in B_F^c} (\delta_{s,p+k} + \delta_{s,q-k}- \delta_{s,q}- \delta_{s,p}) \Big)^2. \end{align} $$
Using the obvious bound
 $$ \begin{align} 0\le \Big( \sum_{s\in B_F^c} (\delta_{s,p+k} + \delta_{s,q-k}- \delta_{s,q}- \delta_{s,p}) \Big)^2 \le 4 \end{align} $$
$$ \begin{align} 0\le \Big( \sum_{s\in B_F^c} (\delta_{s,p+k} + \delta_{s,q-k}- \delta_{s,q}- \delta_{s,p}) \Big)^2 \le 4 \end{align} $$
and the Cauchy–Schwarz inequality, we estimate
 $$ \begin{align} &\left| \left\langle \Psi,\left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right]\Psi\right\rangle \right| \le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \sum_{p,q\in\mathbb{Z}^{3}} \hat V_k \| c_{p+k} c_{q-k} \Psi\| \|c_{q}c_{p} \Psi\| \nonumber \\ &\le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \hat V_k \sum_{p,q\in\mathbb{Z}^{3}} ( \| c_{p+k} c_{q-k} \Psi\|^2 + \|c_{q}c_{p} \Psi\|^2) \le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \hat V_k \langle \Psi, \mathcal{N}_E^2 \Psi\rangle. \end{align} $$
$$ \begin{align} &\left| \left\langle \Psi,\left[\mathcal{N}_{E},\left[\mathcal{N}_{E},\tilde{H}_{N}\right]\right]\Psi\right\rangle \right| \le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \sum_{p,q\in\mathbb{Z}^{3}} \hat V_k \| c_{p+k} c_{q-k} \Psi\| \|c_{q}c_{p} \Psi\| \nonumber \\ &\le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \hat V_k \sum_{p,q\in\mathbb{Z}^{3}} ( \| c_{p+k} c_{q-k} \Psi\|^2 + \|c_{q}c_{p} \Psi\|^2) \le C k_F^{-1} \sum_{k\in\mathbb{Z}^{3}} \hat V_k \langle \Psi, \mathcal{N}_E^2 \Psi\rangle. \end{align} $$
Since
![]() $\hat V$
is summable, (10.28) and (10.32) imply that
$\hat V$
is summable, (10.28) and (10.32) imply that
Combining with the inequality
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime } \ge \mathcal {N}_{E}$
from Proposition 2.1, we deduce by Hölder’s inequality
$H_{\operatorname {\mathrm {kin}}}^{\prime } \ge \mathcal {N}_{E}$
from Proposition 2.1, we deduce by Hölder’s inequality
which implies that
![]() $\left\langle \Psi ,\mathcal {N}_{E}^{2} \Psi \right\rangle \le C (\kappa +1)^2k_F^2$
, and hence by (10.33) again,
$\left\langle \Psi ,\mathcal {N}_{E}^{2} \Psi \right\rangle \le C (\kappa +1)^2k_F^2$
, and hence by (10.33) again,
The bound
![]() $\left\langle \Psi ,\mathcal {N}_{E} H_{\operatorname {\mathrm {kin}}}' \Psi \right\rangle \le C(\kappa +1)^2k_F^2$
follows from (10.26) and (10.35). In summary, we have
$\left\langle \Psi ,\mathcal {N}_{E} H_{\operatorname {\mathrm {kin}}}' \Psi \right\rangle \le C(\kappa +1)^2k_F^2$
follows from (10.26) and (10.35). In summary, we have
By the Gronwall estimates of Propositions 8.1, 9.22 and the choice
![]() $\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, we also obtain
$\mathcal {U}=e^{\mathcal {J}}e^{\mathcal {K}}$
, we also obtain
10.3 Proof of Theorem 1.2
Taking the expectation against
![]() $\Psi _{\mathrm {FS}}$
of the operator estimate in Theorem 1.1, we have
$\Psi _{\mathrm {FS}}$
of the operator estimate in Theorem 1.1, we have
Here, we used the bound on
![]() $\mathcal {E}_U$
from Theorem 1.1 and the identities
$\mathcal {E}_U$
from Theorem 1.1 and the identities
![]() $H_{\operatorname {\mathrm {kin}}}' \Psi _{\mathrm {FS}} = H_{\mathrm {eff}} \Psi _{\mathrm {FS}} =0$
.
$H_{\operatorname {\mathrm {kin}}}' \Psi _{\mathrm {FS}} = H_{\mathrm {eff}} \Psi _{\mathrm {FS}} =0$
.
To see the lower bound, let
![]() $\Psi _{\mathrm {GS}}\in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be the normalized ground state of
$\Psi _{\mathrm {GS}}\in D\left(H_{\operatorname {\mathrm {kin}}}^{\prime }\right)$
be the normalized ground state of
![]() $H_{N}$
. By the definition of
$H_{N}$
. By the definition of
![]() $\Psi _{\mathrm {GS}}$
and the above upper bound, we have
$\Psi _{\mathrm {GS}}$
and the above upper bound, we have
and hence, Theorem 1.2 implies that the state
![]() $\Psi _{\mathrm {GS}}'= \mathcal {U} \Psi _{\mathrm { GS}}$
satisfies
$\Psi _{\mathrm {GS}}'= \mathcal {U} \Psi _{\mathrm { GS}}$
satisfies
Taking the expectation against
![]() $\Psi _{\mathrm {GS}}'$
of the operator estimate in Theorem 1.1, we conclude that
$\Psi _{\mathrm {GS}}'$
of the operator estimate in Theorem 1.1, we conclude that
 $$ \begin{align} \inf \sigma(H_N) &= \left\langle \Psi_{\mathrm{GS}},H_{N} \Psi_{\mathrm{GS}} \right\rangle = \left\langle \Psi_{\mathrm{GS}}',\mathcal{U} H_{N} \mathcal{U} ^* \Psi_{\mathrm{GS}}' \right\rangle\\ &=E_{\mathrm{FS}} + E_{\mathrm{corr}} + \left\langle \Psi_{\mathrm{GS}}', \left( H_{\operatorname{\mathrm{kin}}}^{\prime}+ H_{\mathrm{eff}} +\mathcal{E}_{\mathcal U} \right) \Psi_{\mathrm{GS}}' \right\rangle \ge E_{\mathrm{FS}} + E_{\mathrm{corr}} + O(k_F^{1-\frac{1}{94}+\epsilon}). \nonumber \end{align} $$
$$ \begin{align} \inf \sigma(H_N) &= \left\langle \Psi_{\mathrm{GS}},H_{N} \Psi_{\mathrm{GS}} \right\rangle = \left\langle \Psi_{\mathrm{GS}}',\mathcal{U} H_{N} \mathcal{U} ^* \Psi_{\mathrm{GS}}' \right\rangle\\ &=E_{\mathrm{FS}} + E_{\mathrm{corr}} + \left\langle \Psi_{\mathrm{GS}}', \left( H_{\operatorname{\mathrm{kin}}}^{\prime}+ H_{\mathrm{eff}} +\mathcal{E}_{\mathcal U} \right) \Psi_{\mathrm{GS}}' \right\rangle \ge E_{\mathrm{FS}} + E_{\mathrm{corr}} + O(k_F^{1-\frac{1}{94}+\epsilon}). \nonumber \end{align} $$
Here, we used the operator inequalities
and the a priori estimate (10.40). This completes the proof of Theorem 1.3.
10.4 Proof of Theorems 1.4 and 1.5
In this subsection, we study the effective operator
![]() $H_{\mathrm {eff}}$
in Theorem 1.1 in more detail. First, we prove the following remarkable fact.
$H_{\mathrm {eff}}$
in Theorem 1.1 in more detail. First, we prove the following remarkable fact.
Proposition 10.1. We have the operator identity on
![]() $D(H_{\operatorname {\mathrm {kin}}}^{\prime })$
:
$D(H_{\operatorname {\mathrm {kin}}}^{\prime })$
:
 $$\begin{align*}2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align*}$$
$$\begin{align*}2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align*}$$
Proof of Proposition 10.1 .
The idea is simply to interchange the summation on
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and
$k\in \mathbb {Z}_{\ast }^{3}$
and
![]() $p\in L_{k}$
. By rephrasing the condition that
$p\in L_{k}$
. By rephrasing the condition that
![]() $p\in L_{k}$
, we have the equivalences
$p\in L_{k}$
, we have the equivalences
 $$ \begin{align} \left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(p\in L_{k}\right) & \Leftrightarrow\left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(|p-k|\leq k_{F}<|p|\right)\nonumber \\ & \Leftrightarrow\left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(k\in\overline{B}\left(p,k_{F}\right)\right)\wedge\left(p\in B_{F}^{c}\right)\\ & \Leftrightarrow\left(p\in B_{F}^{c}\right)\wedge\left(k\in\overline{B}\left(p,k_{F}\right)\cap\mathbb{Z}^{3}\right),\nonumber \end{align} $$
$$ \begin{align} \left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(p\in L_{k}\right) & \Leftrightarrow\left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(|p-k|\leq k_{F}<|p|\right)\nonumber \\ & \Leftrightarrow\left(k\in\mathbb{Z}_{\ast}^{3}\right)\wedge\left(k\in\overline{B}\left(p,k_{F}\right)\right)\wedge\left(p\in B_{F}^{c}\right)\\ & \Leftrightarrow\left(p\in B_{F}^{c}\right)\wedge\left(k\in\overline{B}\left(p,k_{F}\right)\cap\mathbb{Z}^{3}\right),\nonumber \end{align} $$
where we could replace
![]() $\mathbb {Z}_{\ast }^{3}$
by
$\mathbb {Z}_{\ast }^{3}$
by
![]() $\mathbb {Z}^{3}$
in the last line as the conditions
$\mathbb {Z}^{3}$
in the last line as the conditions
![]() $p\in B_{F}^{c}=\mathbb {Z}^{3}\backslash \overline {B}(0,k_{F})$
and
$p\in B_{F}^{c}=\mathbb {Z}^{3}\backslash \overline {B}(0,k_{F})$
and
![]() $k\in \overline {B}\left(p,k_{F}\right)$
exclude
$k\in \overline {B}\left(p,k_{F}\right)$
exclude
![]() $k=0$
automatically. Recognizing that
$k=0$
automatically. Recognizing that
![]() $\overline {B}\left(p,k_{F}\right)\cap \mathbb {Z}^{3}=B_{F}+p$
, we can now write
$\overline {B}\left(p,k_{F}\right)\cap \mathbb {Z}^{3}=B_{F}+p$
, we can now write
 $$ \begin{align} 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} & =\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p}\\ & =\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}b_{k,p}^{\ast}b_{k,p}-\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}b_{k,p}^{\ast}b_{k,p},\nonumber \end{align} $$
$$ \begin{align} 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} & =\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\left(|p|^{2}-|p-k|^{2}\right)b_{k,p}^{\ast}b_{k,p}\\ & =\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}b_{k,p}^{\ast}b_{k,p}-\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}b_{k,p}^{\ast}b_{k,p},\nonumber \end{align} $$
and by expanding the excitation operators, we find for the first sum that
 $$ \begin{align} \sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}b_{k,p}^{\ast}b_{k,p} & =\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}c_{p}^{\ast}c_{p-k}c_{p-k}^{\ast}c_{p} \nonumber \\ &=\sum_{p\in B_{F}^{c}}\left(\sum_{k\in\left(B_{F}+p\right)}c_{p-k}c_{p-k}^{\ast}\right)|p|^{2}c_{p}^{\ast}c_{p}\nonumber \\ & =\sum_{p\in B_{F}^{c}}\left(\sum_{k\in B_{F}}c_{-k}c_{-k}^{\ast}\right)|p|^{2}c_{p}^{\ast}c_{p}=\mathcal{N}_{E}\sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p} \end{align} $$
$$ \begin{align} \sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}b_{k,p}^{\ast}b_{k,p} & =\sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p|^{2}c_{p}^{\ast}c_{p-k}c_{p-k}^{\ast}c_{p} \nonumber \\ &=\sum_{p\in B_{F}^{c}}\left(\sum_{k\in\left(B_{F}+p\right)}c_{p-k}c_{p-k}^{\ast}\right)|p|^{2}c_{p}^{\ast}c_{p}\nonumber \\ & =\sum_{p\in B_{F}^{c}}\left(\sum_{k\in B_{F}}c_{-k}c_{-k}^{\ast}\right)|p|^{2}c_{p}^{\ast}c_{p}=\mathcal{N}_{E}\sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p} \end{align} $$
as
![]() $\sum _{k\in B_{F}}c_{-k}c_{-k}^{\ast }=\sum _{k\in B_{F}}c_{k}c_{k}^{\ast }=\mathcal {N}_{E}$
by the particle-hole symmetry, and similarly,
$\sum _{k\in B_{F}}c_{-k}c_{-k}^{\ast }=\sum _{k\in B_{F}}c_{k}c_{k}^{\ast }=\mathcal {N}_{E}$
by the particle-hole symmetry, and similarly,
 $$ \begin{align} \sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}b_{k,p}^{\ast}b_{k,p} & =\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}c_{p-k}c_{p-k}^{\ast}\\ & =\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in B_{F}}|k|^{2}c_{k}c_{k}^{\ast}=\mathcal{N}_{E}\sum_{k\in B_{F}}|k|^{2}c_{k}c_{k}^{\ast}\nonumber \end{align} $$
$$ \begin{align} \sum_{p\in B_{F}^{c}}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}b_{k,p}^{\ast}b_{k,p} & =\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in\left(B_{F}+p\right)}|p-k|^{2}c_{p-k}c_{p-k}^{\ast}\\ & =\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in B_{F}}|k|^{2}c_{k}c_{k}^{\ast}=\mathcal{N}_{E}\sum_{k\in B_{F}}|k|^{2}c_{k}c_{k}^{\ast}\nonumber \end{align} $$
for the claimed equality of
 $$ \begin{align} T= 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}\left(\sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p}-\sum_{p\in B_{F}}|p|^{2}c_{p}c_{p}^{\ast}\right)=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} T= 2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p}=\mathcal{N}_{E}\left(\sum_{p\in B_{F}^{c}}|p|^{2}c_{p}^{\ast}c_{p}-\sum_{p\in B_{F}}|p|^{2}c_{p}c_{p}^{\ast}\right)=\mathcal{N}_{E}H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
To complete the proof, let us show that the relevant operators are well defined on the domain
![]() $D(H_{\mathrm {kin}}')$
. This is clear for
$D(H_{\mathrm {kin}}')$
. This is clear for
![]() $\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }$
since
$\mathcal {N}_{E}H_{\operatorname {\mathrm {kin}}}^{\prime }$
since
![]() $\mathcal {N}_{E}$
is a bounded operator (
$\mathcal {N}_{E}$
is a bounded operator (
![]() $0\le \mathcal {N}_E\le N$
on
$0\le \mathcal {N}_E\le N$
on
![]() $\mathcal {H}_N$
). For T, we can interchange the summations of k and p using the same observation in (10.43). This gives the quadratic form estimate
$\mathcal {H}_N$
). For T, we can interchange the summations of k and p using the same observation in (10.43). This gives the quadratic form estimate
 $$ \begin{align} T&=2\sum_{k\in \mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} =\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\vert|p|^{2}-\zeta\vert\,b_{k,p}^{\ast}b_{k,p}+\sum_{k\in \mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\vert|p-k|^{2}-\zeta\vert\,b_{k,p}^{\ast}b_{k,p} \nonumber\\ &\le \sum_{p\in B_{F}^{c}}\left(\sum_{k\in B_{F}}c_{k}c_{k}^{\ast}\right)\vert|p|^{2}-\zeta\vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in B_{F}}\vert|k|^{2}-\zeta\vert\,c_{k}c_{k}^{\ast}\le \mathcal{N}_E H_{\mathrm{kin}}', \end{align} $$
$$ \begin{align} T&=2\sum_{k\in \mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\lambda_{k,p}b_{k,p}^{\ast}b_{k,p} =\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\vert|p|^{2}-\zeta\vert\,b_{k,p}^{\ast}b_{k,p}+\sum_{k\in \mathbb{Z}_{\ast}^{3}}\sum_{p\in L_{k}}\vert|p-k|^{2}-\zeta\vert\,b_{k,p}^{\ast}b_{k,p} \nonumber\\ &\le \sum_{p\in B_{F}^{c}}\left(\sum_{k\in B_{F}}c_{k}c_{k}^{\ast}\right)\vert|p|^{2}-\zeta\vert\,c_{p}^{\ast}c_{p}+\sum_{p\in B_{F}^{c}}c_{p}^{\ast}c_{p}\sum_{k\in B_{F}}\vert|k|^{2}-\zeta\vert\,c_{k}c_{k}^{\ast}\le \mathcal{N}_E H_{\mathrm{kin}}', \end{align} $$
where
![]() $\zeta>0$
is the constant in (1.14). Moreover, it is easily seen that T commutes with both
$\zeta>0$
is the constant in (1.14). Moreover, it is easily seen that T commutes with both
![]() $\mathcal {N}_E$
and
$\mathcal {N}_E$
and
![]() $H_{\operatorname {\mathrm {kin}}}^{\prime }$
. Therefore, the above quadratic form estimate also implies the stronger estimate
$H_{\operatorname {\mathrm {kin}}}^{\prime }$
. Therefore, the above quadratic form estimate also implies the stronger estimate
which justifies that
![]() $D(T)\subset D(\mathcal {N}_{E}H^{\prime }_{\operatorname {\mathrm {kin}}}) \subset D(H_{\operatorname {\mathrm {kin}}}^{\prime })$
.
$D(T)\subset D(\mathcal {N}_{E}H^{\prime }_{\operatorname {\mathrm {kin}}}) \subset D(H_{\operatorname {\mathrm {kin}}}^{\prime })$
.
Now we are ready to give the
Proof of Theorem 1.5.
Thanks to Proposition 10.1 and the identity
![]() $\langle e_p, h_k e_q\rangle =\lambda _{k,p}\delta _{p,q}$
, we have
$\langle e_p, h_k e_q\rangle =\lambda _{k,p}\delta _{p,q}$
, we have
 $$ \begin{align} H_{\text{eff}}&=H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in\mathbb{Z}^{3}_{*} }\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q} \nonumber\\ &=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}-\left(\mathcal{N}_{E}-1\right)H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
$$ \begin{align} H_{\text{eff}}&=H_{\operatorname{\mathrm{kin}}}^{\prime}+2\sum_{k\in\mathbb{Z}^{3}_{*} }\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q} \nonumber\\ &=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\langle e_{p},\widetilde{E}_{k}e_{q}\rangle b_{k,p}^{\ast}b_{k,q}-\left(\mathcal{N}_{E}-1\right)H_{\operatorname{\mathrm{kin}}}^{\prime}. \end{align} $$
Since
![]() $\left[H_{\text {eff}},\mathcal {N}_{E}\right]=0$
, we can restrict
$\left[H_{\text {eff}},\mathcal {N}_{E}\right]=0$
, we can restrict
![]() $H_{\text {eff}}$
to the eigenspaces of
$H_{\text {eff}}$
to the eigenspaces of
![]() $\mathcal {N}_{E}$
: for every
$\mathcal {N}_{E}$
: for every
![]() $M=\{1,2,...\}$
, we can write the restriction to
$M=\{1,2,...\}$
, we can write the restriction to
![]() $\left\{ \mathcal {N}_{E}=M\right\} $
for
$\left\{ \mathcal {N}_{E}=M\right\} $
for
![]() $M\in \mathbb {N}$
in the quasi-bosonic form
$M\in \mathbb {N}$
in the quasi-bosonic form
 $$ \begin{align} \left.H_{\text{eff}}\right|_{\mathcal{N}_{E}=M}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-\left(1-M^{-1}\right)h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}. \end{align} $$
$$ \begin{align} \left.H_{\text{eff}}\right|_{\mathcal{N}_{E}=M}=2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\left(\widetilde{E}_{k}-\left(1-M^{-1}\right)h_{k}\right)e_{q}\right\rangle b_{k,p}^{\ast}b_{k,q}. \end{align} $$
Proof of Theorem 1.4.
We only need to verify the statement on the effective operator
![]() $\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=M}$
with
$\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=M}$
with
![]() $M=1$
. In this case, it is convenient to introduce the total momentum
$M=1$
. In this case, it is convenient to introduce the total momentum
![]() $P=\left(P_{1},P_{2},P_{3}\right)$
, where each
$P=\left(P_{1},P_{2},P_{3}\right)$
, where each
![]() $P_{j}$
is given by
$P_{j}$
is given by
![]() $P_{j}=\sum _{p\in \mathbb {Z}^{3}}p_{j}c_{p}^{\ast }c_{p}.$
It is easily checked that
$P_{j}=\sum _{p\in \mathbb {Z}^{3}}p_{j}c_{p}^{\ast }c_{p}.$
It is easily checked that
![]() $P_{j}$
obeys the commutators
$P_{j}$
obeys the commutators
and additionally
![]() $\left[P_{j},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]=0$
, whence the effective Hamiltonian
$\left[P_{j},H_{\operatorname {\mathrm {kin}}}^{\prime }\right]=0$
, whence the effective Hamiltonian
![]() $H_{\text {eff}}$
also commutes with
$H_{\text {eff}}$
also commutes with
![]() $P_{j}$
,
$P_{j}$
,
![]() $j=1,2,3$
. It also holds that
$j=1,2,3$
. It also holds that
![]() $\left[\mathcal {N}_{E},P_{j}\right]=0$
, so we may restrict
$\left[\mathcal {N}_{E},P_{j}\right]=0$
, so we may restrict
![]() $H_{\text {eff}}$
to the simultanous eigenspaces of
$H_{\text {eff}}$
to the simultanous eigenspaces of
![]() $\mathcal {N}_{E}$
and P. It follows from
$\mathcal {N}_{E}$
and P. It follows from
![]() $\left[P_{j},b_{k,p}^{\ast }\right]=k_{j}b_{k,p}^{\ast }$
that this simultaneous eigenspace is precisely
$\left[P_{j},b_{k,p}^{\ast }\right]=k_{j}b_{k,p}^{\ast }$
that this simultaneous eigenspace is precisely
In fact, the mapping
![]() $U:\varphi \mapsto b_{k}^{\ast }(\varphi )\psi _{\mathrm {FS}}$
is an isomorphism. To see that, we compute, using the commutation relations of the excitation operators and the fact that
$U:\varphi \mapsto b_{k}^{\ast }(\varphi )\psi _{\mathrm {FS}}$
is an isomorphism. To see that, we compute, using the commutation relations of the excitation operators and the fact that
![]() $b_{k}(\phi )\psi _{\mathrm { FS}}=0=\varepsilon _{k,k}(\phi ;\varphi )\psi _{\mathrm {FS}}$
for any
$b_{k}(\phi )\psi _{\mathrm { FS}}=0=\varepsilon _{k,k}(\phi ;\varphi )\psi _{\mathrm {FS}}$
for any
![]() $\phi ,\varphi \in L^{2}(L_{k})$
, that
$\phi ,\varphi \in L^{2}(L_{k})$
, that
 $$ \begin{align} \left\langle U\phi,U\varphi\right\rangle & =\left\langle b_{k}^{\ast}(\phi )\psi_{\mathrm{ FS}},b_{k}^{\ast}(\varphi )\psi_{\mathrm{FS}}\right\rangle =\left\langle \psi_{\mathrm{ FS}},\left(b_{k}^{\ast}(\varphi )b_{k}(\phi )+\left\langle \phi,\varphi\right\rangle +\varepsilon_{k,k}\left(\phi;\varphi\right)\right)\psi_{\mathrm{FS}}\right\rangle \\ & =\left\langle \phi,\varphi\right\rangle \left\langle \psi_{\mathrm{FS}},\psi_{\mathrm{FS}}\right\rangle =\left\langle \phi,\varphi\right\rangle ,\nonumber \end{align} $$
$$ \begin{align} \left\langle U\phi,U\varphi\right\rangle & =\left\langle b_{k}^{\ast}(\phi )\psi_{\mathrm{ FS}},b_{k}^{\ast}(\varphi )\psi_{\mathrm{FS}}\right\rangle =\left\langle \psi_{\mathrm{ FS}},\left(b_{k}^{\ast}(\varphi )b_{k}(\phi )+\left\langle \phi,\varphi\right\rangle +\varepsilon_{k,k}\left(\phi;\varphi\right)\right)\psi_{\mathrm{FS}}\right\rangle \\ & =\left\langle \phi,\varphi\right\rangle \left\langle \psi_{\mathrm{FS}},\psi_{\mathrm{FS}}\right\rangle =\left\langle \phi,\varphi\right\rangle ,\nonumber \end{align} $$
so U is a unitary embedding of
![]() $L^{2}(L_{k})$
into
$L^{2}(L_{k})$
into
![]() $\left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi ,\,P\Psi =k\Psi \right\} $
and hence an isomorphism for dimensional reasons.
$\left\{ \Psi \in \mathcal {H}_{N}\mid \mathcal {N}_{E}\Psi =\Psi ,\,P\Psi =k\Psi \right\} $
and hence an isomorphism for dimensional reasons.
Similarly, we find as
![]() $\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=1}=2\sum _{l\in \mathbb {Z}_{\ast }^{3}}\sum _{p,q\in L_{l}}\left\langle e_{p},\widetilde {E}_{l}e_{q}\right\rangle b_{l,p}^{\ast }b_{l,q}$
that for any
$\left.H_{\text {eff}}\right|_{\mathcal {N}_{E}=1}=2\sum _{l\in \mathbb {Z}_{\ast }^{3}}\sum _{p,q\in L_{l}}\left\langle e_{p},\widetilde {E}_{l}e_{q}\right\rangle b_{l,p}^{\ast }b_{l,q}$
that for any
![]() $\phi ,\varphi \in L^{2}(L_{k})$
,
$\phi ,\varphi \in L^{2}(L_{k})$
,
 $$ \begin{align} \left\langle U\phi,H_{\text{eff}}U\varphi\right\rangle & =2\sum_{l\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{l}}\left\langle e_{p},\widetilde{E}_{l}e_{q}\right\rangle \left\langle b_{l,p}b_{k}^{\ast}(\phi )\psi_{\mathrm{FS}},b_{l,q}b_{k}^{\ast}(\varphi )\psi_{\mathrm{ FS}}\right\rangle \\ & =2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\widetilde{E}_{l}e_{q}\right\rangle \delta_{k,l}\left\langle \phi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle =2\left\langle \phi,\widetilde{E}_{k}\varphi\right\rangle, \nonumber \end{align} $$
$$ \begin{align} \left\langle U\phi,H_{\text{eff}}U\varphi\right\rangle & =2\sum_{l\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{l}}\left\langle e_{p},\widetilde{E}_{l}e_{q}\right\rangle \left\langle b_{l,p}b_{k}^{\ast}(\phi )\psi_{\mathrm{FS}},b_{l,q}b_{k}^{\ast}(\varphi )\psi_{\mathrm{ FS}}\right\rangle \\ & =2\sum_{k\in\mathbb{Z}_{\ast}^{3}}\sum_{p,q\in L_{k}}\left\langle e_{p},\widetilde{E}_{l}e_{q}\right\rangle \delta_{k,l}\left\langle \phi,e_{p}\right\rangle \left\langle e_{q},\varphi\right\rangle =2\left\langle \phi,\widetilde{E}_{k}\varphi\right\rangle, \nonumber \end{align} $$
whence
![]() $U^{\ast }H_{\mathrm {eff}}U=2\widetilde E_{k}$
. By elaborating the above argument slightly, one finds that the mapping
$U^{\ast }H_{\mathrm {eff}}U=2\widetilde E_{k}$
. By elaborating the above argument slightly, one finds that the mapping
 $$ \begin{align} \tilde{U}:\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}L^{2}(L_{k})\rightarrow\left\{ \Psi\in\mathcal{H}_{N}\mid\mathcal{N}_{E}\Psi=\Psi\right\} \end{align} $$
$$ \begin{align} \tilde{U}:\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}L^{2}(L_{k})\rightarrow\left\{ \Psi\in\mathcal{H}_{N}\mid\mathcal{N}_{E}\Psi=\Psi\right\} \end{align} $$
defined by
 $$ \begin{align} \tilde{U}\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}\varphi_{k}=\sum_{k\in\mathbb{Z}_{\ast}^{3}}b_{k}^{\ast}\left(\varphi_{k}\right)\psi_{\mathrm{ FS}} \end{align} $$
$$ \begin{align} \tilde{U}\bigoplus_{k\in\mathbb{Z}_{\ast}^{3}}\varphi_{k}=\sum_{k\in\mathbb{Z}_{\ast}^{3}}b_{k}^{\ast}\left(\varphi_{k}\right)\psi_{\mathrm{ FS}} \end{align} $$
is likewise a unitary isomorphism under which
![]() $\tilde {U}^{\ast }H_{\text {eff}}\tilde {U}=\bigoplus _{k\in \mathbb {Z}_{\ast }^{3}} \widetilde E_{k}$
.
$\tilde {U}^{\ast }H_{\text {eff}}\tilde {U}=\bigoplus _{k\in \mathbb {Z}_{\ast }^{3}} \widetilde E_{k}$
.
A Appendix: Lattice estimates and Riemann sums
In this appendix, we collect several useful estimates for the lattice points and Riemann sums. In particular, we want to obtain estimates on the sum
![]() $\sum _{p\in L_k} \lambda _{k,p}^{\beta }$
, where
$\sum _{p\in L_k} \lambda _{k,p}^{\beta }$
, where
![]() $\beta \le 0$
and
$\beta \le 0$
and
It is natural to expect the sum to be approximated by the corresponding integrals – that is,
 $$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p})\sim\int_{\overline{B}\left(k,k_{F}\right)\backslash\overline{B}(0,k_{F})}f\left(k\cdot p-\frac{1}{2}|k|^{2}\right)\,dp, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p})\sim\int_{\overline{B}\left(k,k_{F}\right)\backslash\overline{B}(0,k_{F})}f\left(k\cdot p-\frac{1}{2}|k|^{2}\right)\,dp, \end{align} $$
with
![]() $f(t)=t^{\beta }$
. Indeed, when
$f(t)=t^{\beta }$
. Indeed, when
![]() $-1<\beta \le 0$
, the Riemann sum is well behaved, and using general estimation methods based on (A.1), we have the following:
$-1<\beta \le 0$
, the Riemann sum is well behaved, and using general estimation methods based on (A.1), we have the following:
Proposition A.1. For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and
$k\in \mathbb {Z}_{\ast }^{3}$
and
![]() $-1<\beta \leq 0$
, it holds that
$-1<\beta \leq 0$
, it holds that
 $$ \begin{align*} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq C\begin{cases} k_{F}^{2+\beta}|k|^{1+\beta} & |k|<2k_{F}\\ k_{F}^{3}|k|^{2\beta} & |k|\geq2k_{F} \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq C\begin{cases} k_{F}^{2+\beta}|k|^{1+\beta} & |k|<2k_{F}\\ k_{F}^{3}|k|^{2\beta} & |k|\geq2k_{F} \end{cases} \end{align*} $$
for a constant
![]() $C>0$
depending only on
$C>0$
depending only on
![]() $\beta $
.
$\beta $
.
For
![]() $\beta \leq -1$
, the summands are, however, too divergent to obtain good estimates using only general methods. For example, when
$\beta \leq -1$
, the summands are, however, too divergent to obtain good estimates using only general methods. For example, when
![]() $\beta =-1$
, using standard estimates based on (A.1), we obtain
$\beta =-1$
, using standard estimates based on (A.1), we obtain
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{-1} \leq C\begin{cases} \left(1+|k|^{-1}\log\left(k_{F}\right)\right)k_{F} & |k|<2k_{F}\\ k_{F}^{3}|k|^{-2} & |k|\geq2k_{F}, \end{cases} \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{-1} \leq C\begin{cases} \left(1+|k|^{-1}\log\left(k_{F}\right)\right)k_{F} & |k|<2k_{F}\\ k_{F}^{3}|k|^{-2} & |k|\geq2k_{F}, \end{cases} \end{align} $$
which is non-optimal when
![]() $|k|<2k_F$
. To obtain good estimates on the sums
$|k|<2k_F$
. To obtain good estimates on the sums
![]() $\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
for more singular f, we will instead derive a summation formula which reduces the
$\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
for more singular f, we will instead derive a summation formula which reduces the
![]() $3$
-dimensional Riemann sum to two
$3$
-dimensional Riemann sum to two
![]() $1$
-dimensional Riemann sums plus an error term. The utility of this summation formula, apart from reducing the dimensionality of the sums, is that the
$1$
-dimensional Riemann sums plus an error term. The utility of this summation formula, apart from reducing the dimensionality of the sums, is that the
![]() $1$
-dimensional Riemann sums contain weighting factors which explicitly cancel the divergent behaviour of the summands. To derive this summation formula, we need to carry out a detailed analysis of the structure of the lunes
$1$
-dimensional Riemann sums contain weighting factors which explicitly cancel the divergent behaviour of the summands. To derive this summation formula, we need to carry out a detailed analysis of the structure of the lunes
![]() $L_{k}$
, which is related to a lattice point counting problem in the plane and can be handled by classical results from analytic number theory.
$L_{k}$
, which is related to a lattice point counting problem in the plane and can be handled by classical results from analytic number theory.
With the summation formula at our disposal, we can improve (A.2) to the following:
Proposition A.2. For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
, it holds that
$k\in \mathbb {Z}_{\ast }^{3}$
, it holds that
for a constant
![]() $C>0$
independent of k and
$C>0$
independent of k and
![]() $k_{F}$
.
$k_{F}$
.
We refer to [Reference Hainzl, Porta and Rexze24, Lemma 4.7] and [Reference Benedikter, Nam, Porta, Schlein and Seiringer6, Eq. B.1] for results similar to Proposition A.2. However, the k-independence of the constant C was not completely clear in these previous results.
For more singular functions, we have the following:
Proposition A.3. For
![]() $-\frac {4}{3}<\beta <-1$
and
$-\frac {4}{3}<\beta <-1$
and
![]() $k\in \overline {B}\left(0,k_{F}^{\gamma }\right)$
with
$k\in \overline {B}\left(0,k_{F}^{\gamma }\right)$
with
![]() $0<\gamma <\frac {4+3\beta }{8-3\beta }$
, we have
$0<\gamma <\frac {4+3\beta }{8-3\beta }$
, we have
Moreover, for
![]() $\beta \leq -\frac {4}{3}$
and
$\beta \leq -\frac {4}{3}$
and
![]() $k\in \overline {B}\left(0,2k_{F}\right)$
, we have
$k\in \overline {B}\left(0,2k_{F}\right)$
, we have
 $$\begin{align*}\sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}},\quad k_{F}\rightarrow\infty. \end{align*}$$
$$\begin{align*}\sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}},\quad k_{F}\rightarrow\infty. \end{align*}$$
Here, the constant
![]() $C>0$
is independent of k and
$C>0$
is independent of k and
![]() $k_{F}$
.
$k_{F}$
.
In Proposition A.3, the first bound is optimal in terms of both
![]() $k_F^{2+\beta }$
and
$k_F^{2+\beta }$
and
![]() $|k|^\beta $
. The second bound is unlikely to be optimal but is sufficient in applications if
$|k|^\beta $
. The second bound is unlikely to be optimal but is sufficient in applications if
![]() $|k|$
is relatively small.
$|k|$
is relatively small.
Finally, for the kinetic estimate in Proposition 2.3, we need the following proposition, which can be obtained by the same argument of the above results.
Proposition A.4. Let
![]() $S_{k,\lambda }^{1},S_{k,\lambda }^{2}$
as in (2.14), (2.19) with
$S_{k,\lambda }^{1},S_{k,\lambda }^{2}$
as in (2.14), (2.19) with
![]() $k\in \overline {B}(0,k_{F})\cap \mathbb {Z}_{\ast }^{3}$
and
$k\in \overline {B}(0,k_{F})\cap \mathbb {Z}_{\ast }^{3}$
and
![]() $0<\lambda =\lambda \left(k_{F},k\right)\leq \frac {1}{6}k_{F}^{2}$
. Then there exists a constant
$0<\lambda =\lambda \left(k_{F},k\right)\leq \frac {1}{6}k_{F}^{2}$
. Then there exists a constant
![]() $C>0$
independent of k,
$C>0$
independent of k,
![]() $k_{F}$
,
$k_{F}$
,
![]() $\lambda $
such that
$\lambda $
such that
 $$\begin{align*}|S_{k,\lambda}^{1}|+|S_{k,\lambda}^{2}|\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda+|k|\right),\quad k_{F}\rightarrow\infty. \end{align*}$$
$$\begin{align*}|S_{k,\lambda}^{1}|+|S_{k,\lambda}^{2}|\leq C\left(|k|^{-1}\lambda +|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda+|k|\right),\quad k_{F}\rightarrow\infty. \end{align*}$$
In the rest of the appendix, we will discuss some preliminary results in Sections A.1 and A.2 and then turn to the proofs of Propositions A.1, A.2, A.3 and A.4.
A.1 Some lattice concepts
Let V be a real n-dimensional vector space. The lattice
![]() $\Lambda \subset V$
generated by
$\Lambda \subset V$
generated by
![]() $\left(v_{i}\right)_{i=1}^{n}$
is
$\left(v_{i}\right)_{i=1}^{n}$
is
 $$ \begin{align} \Lambda=\Lambda(v_1, \cdots ,v_n) =\left\{ \sum_{i=1}^{n}m_{i}v_{i}\mid m_{1},\ldots,m_{n}\in\mathbb{Z}\right\}. \end{align} $$
$$ \begin{align} \Lambda=\Lambda(v_1, \cdots ,v_n) =\left\{ \sum_{i=1}^{n}m_{i}v_{i}\mid m_{1},\ldots,m_{n}\in\mathbb{Z}\right\}. \end{align} $$
Given two bases
![]() $\left(v_{i}\right)_{i=1}^{n}$
and
$\left(v_{i}\right)_{i=1}^{n}$
and
![]() $\left(w_{i}\right)_{i=1}^{n}$
, it may happen that
$\left(w_{i}\right)_{i=1}^{n}$
, it may happen that
![]() $\Lambda (v_{1},\ldots ,v_{n}) =\Lambda (w_{1},\ldots ,w_{n})$
even if the bases are not equal. The following is well known (see, for example, [Reference Micciancio and Goldwasser28, p. 4])
$\Lambda (v_{1},\ldots ,v_{n}) =\Lambda (w_{1},\ldots ,w_{n})$
even if the bases are not equal. The following is well known (see, for example, [Reference Micciancio and Goldwasser28, p. 4])
Proposition A.5. Let
![]() $\left(v_{i}\right)_{i=1}^{n}$
and
$\left(v_{i}\right)_{i=1}^{n}$
and
![]() $\left(w_{i}\right)_{i=1}^{n}$
be bases of V. Then
$\left(w_{i}\right)_{i=1}^{n}$
be bases of V. Then
![]() $\Lambda (v_{1},\ldots ,v_{n}) =\Lambda (w_{1},\ldots ,w_{n})$
if and only if the transition matrix
$\Lambda (v_{1},\ldots ,v_{n}) =\Lambda (w_{1},\ldots ,w_{n})$
if and only if the transition matrix
![]() $T=\left(T_{i,j}\right)_{i,j=1}^{n}$
defined by
$T=\left(T_{i,j}\right)_{i,j=1}^{n}$
defined by
 $$\begin{align*}w_{i}=\sum_{j=1}^{n}T_{i,j}v_{j},\quad1\leq i\leq n \end{align*}$$
$$\begin{align*}w_{i}=\sum_{j=1}^{n}T_{i,j}v_{j},\quad1\leq i\leq n \end{align*}$$
has integer entries and determinant
![]() $\pm 1$
.
$\pm 1$
.
This result has an important consequence when V is endowed with an inner product.
Proposition A.6. Let
![]() $\Lambda $
be a lattice in
$\Lambda $
be a lattice in
![]() $\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
and let
$\left(V,\left\langle \cdot ,\cdot \right\rangle \right)$
and let
![]() $\left(v_{i}\right)_{i=1}^{n}$
generate
$\left(v_{i}\right)_{i=1}^{n}$
generate
![]() $\Lambda $
. Then the quantity
$\Lambda $
. Then the quantity
 $$\begin{align*}d\left(\Lambda\right)=\left|\det\left(\begin{array}{ccc} \left\langle e_{1},v_{1}\right\rangle & \cdots & \left\langle e_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},v_{n}\right\rangle & \cdots & \left\langle e_{n},v_{n}\right\rangle \end{array}\right)\right|=\sqrt{\det\left(\begin{array}{ccc} \left\langle v_{1},v_{1}\right\rangle & \cdots & \left\langle v_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle v_{1},v_{n}\right\rangle & \cdots & \left\langle v_{n},v_{n}\right\rangle \end{array}\right)} \end{align*}$$
$$\begin{align*}d\left(\Lambda\right)=\left|\det\left(\begin{array}{ccc} \left\langle e_{1},v_{1}\right\rangle & \cdots & \left\langle e_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},v_{n}\right\rangle & \cdots & \left\langle e_{n},v_{n}\right\rangle \end{array}\right)\right|=\sqrt{\det\left(\begin{array}{ccc} \left\langle v_{1},v_{1}\right\rangle & \cdots & \left\langle v_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle v_{1},v_{n}\right\rangle & \cdots & \left\langle v_{n},v_{n}\right\rangle \end{array}\right)} \end{align*}$$
is independent of the choice of generators
![]() $\left(v_{i}\right)_{i=1}^{n}$
. Here,
$\left(v_{i}\right)_{i=1}^{n}$
. Here,
![]() $(e_{i})_{i=1}^{n}$
is any orthonormal basis for V.
$(e_{i})_{i=1}^{n}$
is any orthonormal basis for V.
Here,
![]() $d(\Lambda )$
is referred to as the covolume (or simply determinant) of
$d(\Lambda )$
is referred to as the covolume (or simply determinant) of
![]() $\Lambda $
. The fact that
$\Lambda $
. The fact that
![]() $d(\Lambda )$
is independent of
$d(\Lambda )$
is independent of
![]() $(e_{i})_{i=1}^{n}$
follows by a standard orthonormal expansion, while the fact that
$(e_{i})_{i=1}^{n}$
follows by a standard orthonormal expansion, while the fact that
![]() $d(\Lambda )$
is independent of
$d(\Lambda )$
is independent of
![]() $\left(v_{i}\right)_{i=1}^{n}$
follows from the previous proposition: if
$\left(v_{i}\right)_{i=1}^{n}$
follows from the previous proposition: if
![]() $\left(v_{i}\right)_{i=1}^{n}$
and
$\left(v_{i}\right)_{i=1}^{n}$
and
![]() $\left(w_{i}\right)_{i=1}^{n}$
are two bases with transition matrix T, then
$\left(w_{i}\right)_{i=1}^{n}$
are two bases with transition matrix T, then
 $$ \begin{align} \left|\det\left(\begin{array}{ccc} \left\langle e_{1},w_{1}\right\rangle & \cdots & \left\langle e_{n},w_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},w_{n}\right\rangle & \cdots & \left\langle e_{n},w_{n}\right\rangle \end{array}\right)\right|=\left|\det(T)\right|\left|\det\left(\begin{array}{ccc} \left\langle e_{1},v_{1}\right\rangle & \cdots & \left\langle e_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},v_{n}\right\rangle & \cdots & \left\langle e_{n},v_{n}\right\rangle \end{array}\right)\right|. \end{align} $$
$$ \begin{align} \left|\det\left(\begin{array}{ccc} \left\langle e_{1},w_{1}\right\rangle & \cdots & \left\langle e_{n},w_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},w_{n}\right\rangle & \cdots & \left\langle e_{n},w_{n}\right\rangle \end{array}\right)\right|=\left|\det(T)\right|\left|\det\left(\begin{array}{ccc} \left\langle e_{1},v_{1}\right\rangle & \cdots & \left\langle e_{n},v_{1}\right\rangle \\ \vdots & \ddots & \vdots\\ \left\langle e_{1},v_{n}\right\rangle & \cdots & \left\langle e_{n},v_{n}\right\rangle \end{array}\right)\right|. \end{align} $$
Given a lattice
![]() $\Lambda $
in an n-dimensional inner product space V, one defines the successive minima
$\Lambda $
in an n-dimensional inner product space V, one defines the successive minima
![]() $\left(\lambda _{i}\right)_{i=1}^{n}$
(relative to the closed unit ball
$\left(\lambda _{i}\right)_{i=1}^{n}$
(relative to the closed unit ball
![]() $\overline {B}\left(0,1\right)$
) by
$\overline {B}\left(0,1\right)$
) by
A well-known theorem due to Minkowski provides an inequality relating the successive minima of a lattice
![]() $\Lambda $
to its covolume:
$\Lambda $
to its covolume:
Theorem A.7 (Minkowski’s second theorem).
Let
![]() $\Lambda $
be a lattice in an n-dimensional inner product space V. Then it holds that
$\Lambda $
be a lattice in an n-dimensional inner product space V. Then it holds that
 $$\begin{align*}\frac{2^{n}d(\Lambda)}{n!\operatorname{\mathrm{Vol}}(\overline{B}(0,1))}\leq\lambda_{1}\cdots\lambda_{n}\leq\frac{2^{n}d(\Lambda)}{\operatorname{\mathrm{Vol}}(\overline{B}(0,1))}. \end{align*}$$
$$\begin{align*}\frac{2^{n}d(\Lambda)}{n!\operatorname{\mathrm{Vol}}(\overline{B}(0,1))}\leq\lambda_{1}\cdots\lambda_{n}\leq\frac{2^{n}d(\Lambda)}{\operatorname{\mathrm{Vol}}(\overline{B}(0,1))}. \end{align*}$$
Note that although
![]() $\overline {B}\left(0,\lambda _{n}\right)\cap \Lambda $
contains n linearly independent vectors, it is not ensured that these n vectors can be chosen to generate
$\overline {B}\left(0,\lambda _{n}\right)\cap \Lambda $
contains n linearly independent vectors, it is not ensured that these n vectors can be chosen to generate
![]() $\Lambda $
. For
$\Lambda $
. For
![]() $n=2$
, this is nonetheless the case:
$n=2$
, this is nonetheless the case:
Corollary A.8. Let
![]() $\Lambda $
be a lattice in a
$\Lambda $
be a lattice in a
![]() $2$
-dimensional inner product space V. Then there exist vectors
$2$
-dimensional inner product space V. Then there exist vectors
![]() $v_{1},v_{2}\in \Lambda $
which generate
$v_{1},v_{2}\in \Lambda $
which generate
![]() $\Lambda $
such that
$\Lambda $
such that
Proof. By definition of
![]() $\lambda _{2}$
, there exists linearly independent vectors
$\lambda _{2}$
, there exists linearly independent vectors
![]() $v_{1},v_{2}\in \Lambda $
such that
$v_{1},v_{2}\in \Lambda $
such that
![]() $|v_{1}|,|v_{2}|\leq \lambda _{2}$
and by Minkowski’s second theorem
$|v_{1}|,|v_{2}|\leq \lambda _{2}$
and by Minkowski’s second theorem
![]() $|v_{1}||v_{2}|\leq \frac {4}{\pi }d(\Lambda )$
. We argue that
$|v_{1}||v_{2}|\leq \frac {4}{\pi }d(\Lambda )$
. We argue that
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
must necessarily generate
$v_{2}$
must necessarily generate
![]() $\Lambda $
. Suppose otherwise (i.e., that there exists a
$\Lambda $
. Suppose otherwise (i.e., that there exists a
![]() $v\in \Lambda $
such that
$v\in \Lambda $
such that
![]() $v\neq m_{1}v_{1}+m_{2}v_{2}$
for
$v\neq m_{1}v_{1}+m_{2}v_{2}$
for
![]() $m_{1},m_{2}\in \mathbb {Z}$
). As
$m_{1},m_{2}\in \mathbb {Z}$
). As
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
are linearly independent and
$v_{2}$
are linearly independent and
![]() $\dim \left(V\right)=2$
, these do nonetheless span V (i.e., there must exist
$\dim \left(V\right)=2$
, these do nonetheless span V (i.e., there must exist
![]() $c_{1},c_{2}\in \mathbb {R}$
such that
$c_{1},c_{2}\in \mathbb {R}$
such that
![]() $v=c_{1}v_{1}+c_{2}v_{2}$
).
$v=c_{1}v_{1}+c_{2}v_{2}$
).
Now we can assume that
![]() $\left|c_{1}\right|,\left|c_{2}\right|\leq \frac {1}{2}$
, since as
$\left|c_{1}\right|,\left|c_{2}\right|\leq \frac {1}{2}$
, since as
![]() $\Lambda $
is a lattice and
$\Lambda $
is a lattice and
![]() $v_{1},v_{2},v\in \Lambda $
, we may subtract multiples of
$v_{1},v_{2},v\in \Lambda $
, we may subtract multiples of
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
from v until this is the case. Then, since
$v_{2}$
from v until this is the case. Then, since
![]() $\left|\left\langle v_{1},v_{2}\right\rangle \right|<|v_{1}||v_{2}|$
by the Cauchy-Schwarz inequality (strict inequality being a consequence of the linear independence of
$\left|\left\langle v_{1},v_{2}\right\rangle \right|<|v_{1}||v_{2}|$
by the Cauchy-Schwarz inequality (strict inequality being a consequence of the linear independence of
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
), we can estimate that
$v_{2}$
), we can estimate that
 $$ \begin{align} \left|v\right|^{2} & =|v_{1}|^{2}c_{1}^{2}+|v_{2}|^{2}c_{2}^{2}+2\left\langle v_{1},v_{2}\right\rangle c_{1}c_{2}<|v_{1}|^{2}c_{1}^{2}+|v_{2}|^{2}c_{2}^{2}+2|v_{1}||v_{2}|\left|c_{1}\right|\left|c_{2}\right|\\ & =\left(\left|c_{1}\right||v_{1}|+\left|c_{2}\right||v_{2}|\right)^{2}\leq\left(\frac{1}{2}\lambda_{2}+\frac{1}{2}\lambda_{2}\right)^{2}=\lambda_{2}^{2},\nonumber \end{align} $$
$$ \begin{align} \left|v\right|^{2} & =|v_{1}|^{2}c_{1}^{2}+|v_{2}|^{2}c_{2}^{2}+2\left\langle v_{1},v_{2}\right\rangle c_{1}c_{2}<|v_{1}|^{2}c_{1}^{2}+|v_{2}|^{2}c_{2}^{2}+2|v_{1}||v_{2}|\left|c_{1}\right|\left|c_{2}\right|\\ & =\left(\left|c_{1}\right||v_{1}|+\left|c_{2}\right||v_{2}|\right)^{2}\leq\left(\frac{1}{2}\lambda_{2}+\frac{1}{2}\lambda_{2}\right)^{2}=\lambda_{2}^{2},\nonumber \end{align} $$
or
![]() $\left|v\right|<\lambda _{2}$
. But this contradicts the minimality of
$\left|v\right|<\lambda _{2}$
. But this contradicts the minimality of
![]() $\lambda _{2}$
as
$\lambda _{2}$
as
![]() $v\neq 0$
, and at least one of
$v\neq 0$
, and at least one of
![]() $\left\{ v_{1},v\right\} $
and
$\left\{ v_{1},v\right\} $
and
![]() $\left\{ v_{2},v\right\} $
must be a linearly independent set, so such a v cannot exist.
$\left\{ v_{2},v\right\} $
must be a linearly independent set, so such a v cannot exist.
The sublattice orthogonal to a vector
 $k\in \mathbb {Z}^{3}$
$k\in \mathbb {Z}^{3}$
Consider
![]() $\mathbb {Z}^{3}$
as a lattice in
$\mathbb {Z}^{3}$
as a lattice in
![]() $\mathbb {R}^{3}$
endowed with the usual dot product. Let
$\mathbb {R}^{3}$
endowed with the usual dot product. Let
![]() $k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be arbitrary and write
$k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be arbitrary and write
![]() $\hat {k}=|k|^{-1}k$
. Now we consider the set
$\hat {k}=|k|^{-1}k$
. Now we consider the set
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
, namely, the sublattice orthogonal to k. Let us recall the following well-known result.
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
, namely, the sublattice orthogonal to k. Let us recall the following well-known result.
Theorem A.9. For
![]() $\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
and
$\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
and
![]() $c\in \mathbb {Z}$
, the linear Diophantine equation
$c\in \mathbb {Z}$
, the linear Diophantine equation
is solvable with
![]() $\left(m_{1},m_{2},m_{3}\right)\in \mathbb {Z}^{3}$
if and only if c is a multiple of
$\left(m_{1},m_{2},m_{3}\right)\in \mathbb {Z}^{3}$
if and only if c is a multiple of
![]() $\gcd \left(k_{1},k_{2},k_{3}\right)$
. Moreover, in this case, there exist linearly independent vectors
$\gcd \left(k_{1},k_{2},k_{3}\right)$
. Moreover, in this case, there exist linearly independent vectors
![]() $v_{1},v_{2}\in \mathbb {Z}^{3}$
, which do not depend on c, such that if
$v_{1},v_{2}\in \mathbb {Z}^{3}$
, which do not depend on c, such that if
![]() $\left(m_{1}^{\ast },m_{2}^{\ast },m_{3}^{\ast }\right)$
is any particular solution of the equation, then all solutions are given by
$\left(m_{1}^{\ast },m_{2}^{\ast },m_{3}^{\ast }\right)$
is any particular solution of the equation, then all solutions are given by
Note that the second part of the proposition states that (up to translation by a particular solution) the solution set of a linear Diophantine equation forms a lattice, much as the solution set of a real-variable linear equation forms a linear subspace. This result implies the following:
Proposition A.10. Let
![]() $k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be given. Then with
$k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be given. Then with
![]() $l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
, the following disjoint union of nonempty sets holds:
$l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
, the following disjoint union of nonempty sets holds:
Additionally, there exist linearly independent vectors
![]() $v_{1},v_{2}\in \mathbb {Z}^{3}$
, which span
$v_{1},v_{2}\in \mathbb {Z}^{3}$
, which span
![]() $\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
, such that for any
$\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
, such that for any
![]() $m\in \mathbb {Z}$
, it holds for all
$m\in \mathbb {Z}$
, it holds for all
![]() $q\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
that
$q\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
that
Proof. Clearly,
![]() $\mathbb {Z}^{3}=\bigcup _{t\in \mathbb {R}}\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=t\right\} $
, so we must determine for which values of t it holds that
$\mathbb {Z}^{3}=\bigcup _{t\in \mathbb {R}}\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=t\right\} $
, so we must determine for which values of t it holds that
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=t\right\} \neq \emptyset $
. The equation
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=t\right\} \neq \emptyset $
. The equation
![]() $\hat {k}\cdot p=t$
is equivalent to
$\hat {k}\cdot p=t$
is equivalent to
where
![]() $p=\left(p_{1},p_{2},p_{3}\right)\in \mathbb {Z}^{3}$
, and as the left-hand side is an integer, we must have
$p=\left(p_{1},p_{2},p_{3}\right)\in \mathbb {Z}^{3}$
, and as the left-hand side is an integer, we must have
![]() $t=|k|^{-1}c$
for some
$t=|k|^{-1}c$
for some
![]() $c\in \mathbb {Z}$
. Theorem A.9 now furthermore implies that
$c\in \mathbb {Z}$
. Theorem A.9 now furthermore implies that
![]() $c=\gcd \left(k_{1},k_{2},k_{3}\right)\cdot m$
for some
$c=\gcd \left(k_{1},k_{2},k_{3}\right)\cdot m$
for some
![]() $m\in \mathbb {Z}$
, so that
$m\in \mathbb {Z}$
, so that
![]() $t=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)\cdot m=lm$
, and as p was arbitrary, we see that
$t=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)\cdot m=lm$
, and as p was arbitrary, we see that
![]() $\mathbb {Z}^{3}=\bigcup _{m\in \mathbb {Z}}\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
as claimed.
$\mathbb {Z}^{3}=\bigcup _{m\in \mathbb {Z}}\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
as claimed.
That all the sets
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
,
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
,
![]() $m\in \mathbb {Z}$
, are also nonempty similarly follows from the ‘only if’ part of Theorem A.9, and the representation
$m\in \mathbb {Z}$
, are also nonempty similarly follows from the ‘only if’ part of Theorem A.9, and the representation
for linearly independent
![]() $v_{1},v_{2}\in \mathbb {Z}^{3}$
is likewise a simple restatement of the second part of the theorem. Finally, that
$v_{1},v_{2}\in \mathbb {Z}^{3}$
is likewise a simple restatement of the second part of the theorem. Finally, that
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
span
$v_{2}$
span
![]() $\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
follows by noting that
$\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
follows by noting that
![]() $q=\left(0,0,0\right)$
is a particular solution of
$q=\left(0,0,0\right)$
is a particular solution of
![]() $\hat {k}\cdot p=0$
, whence by the previous part
$\hat {k}\cdot p=0$
, whence by the previous part
so we find that
![]() $\text {span}\left(\left\{ v_{1},v_{2}\right\} \right)=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
by linear independence of
$\text {span}\left(\left\{ v_{1},v_{2}\right\} \right)=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
by linear independence of
![]() $\left\{ v_{1},v_{2}\right\} $
and dimensionality consideration.
$\left\{ v_{1},v_{2}\right\} $
and dimensionality consideration.
Proposition A.10 implies that
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
is a lattice in
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
is a lattice in
![]() $\{k\}^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
. Since
$\{k\}^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
. Since
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
is a lattice, it has a well-defined covolume
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
is a lattice, it has a well-defined covolume
 $$ \begin{align} \sqrt{\det\left(\begin{array}{cc} v_{1}\cdot v_{1} & v_{2}\cdot v_{1}\\ v_{1}\cdot v_{2} & v_{2}\cdot v_{2} \end{array}\right)}=\sqrt{|v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2}} \end{align} $$
$$ \begin{align} \sqrt{\det\left(\begin{array}{cc} v_{1}\cdot v_{1} & v_{2}\cdot v_{1}\\ v_{1}\cdot v_{2} & v_{2}\cdot v_{2} \end{array}\right)}=\sqrt{|v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2}} \end{align} $$
for any choice of generators
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
. This covolume is explicitly given by the following:
$v_{2}$
. This covolume is explicitly given by the following:
Proposition A.11. For any
![]() $v_{1},v_{2}\in \mathbb {Z}^{3}$
generating
$v_{1},v_{2}\in \mathbb {Z}^{3}$
generating
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
, it holds that
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
, it holds that
with
![]() $l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
. Additionally,
$l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
. Additionally,
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
can be chosen such that
$v_{2}$
can be chosen such that
![]() $ |v_{1}|^{2}+|v_{2}|^{2}\leq \frac {8}{\pi ^2 l^2}. $
$ |v_{1}|^{2}+|v_{2}|^{2}\leq \frac {8}{\pi ^2 l^2}. $
Proof. Let
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
generate
$v_{2}$
generate
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
and let
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
and let
![]() $w\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=l\right\} $
be arbitrary. By linearity, it holds that
$w\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=l\right\} $
be arbitrary. By linearity, it holds that
so by the Proposition A.10,
(i.e.,
![]() $\left(v_{1},v_{2},w\right)$
is a set of generators for
$\left(v_{1},v_{2},w\right)$
is a set of generators for
![]() $\mathbb {Z}^{3}$
). Now, let
$\mathbb {Z}^{3}$
). Now, let
![]() $\{k\}^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
be the orthogonal complement of
$\{k\}^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\}$
be the orthogonal complement of
![]() $\left\{ k\right\}$
. Let
$\left\{ k\right\}$
. Let
![]() $\left(e_{1},e_{2}\right)$
be an orthonormal basis for
$\left(e_{1},e_{2}\right)$
be an orthonormal basis for
![]() $\{k\}^{\perp }$
so that
$\{k\}^{\perp }$
so that
![]() $\left(e_{1},e_{2},\hat {k}\right)$
forms an orthonormal basis for
$\left(e_{1},e_{2},\hat {k}\right)$
forms an orthonormal basis for
![]() $\mathbb {R}^{3}$
. Then
$\mathbb {R}^{3}$
. Then
![]() $d\left(\mathbb {Z}^{3}\right)$
is equal to
$d\left(\mathbb {Z}^{3}\right)$
is equal to
 $$ \begin{align} & \left|\det\left(\begin{array}{ccc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1} & \hat{k}\cdot v_{1}\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} & \hat{k}\cdot v_{2}\\ e_{1}\cdot w & e_{2}\cdot w & \hat{k}\cdot w \end{array}\right)\right|=\left|\det\left(\begin{array}{ccc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1} & 0\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} & 0\\ e_{1}\cdot w & e_{2}\cdot w & l \end{array}\right)\right|=l\left|\det\left(\begin{array}{cc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1}\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} \end{array}\right)\right|\nonumber \\ & =l\sqrt{\det\left(\begin{array}{cc} v_{1}\cdot v_{1} & v_{2}\cdot v_{1}\\ v_{1}\cdot v_{2} & v_{2}\cdot v_{2} \end{array}\right)}=l\sqrt{|v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2}}, \end{align} $$
$$ \begin{align} & \left|\det\left(\begin{array}{ccc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1} & \hat{k}\cdot v_{1}\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} & \hat{k}\cdot v_{2}\\ e_{1}\cdot w & e_{2}\cdot w & \hat{k}\cdot w \end{array}\right)\right|=\left|\det\left(\begin{array}{ccc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1} & 0\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} & 0\\ e_{1}\cdot w & e_{2}\cdot w & l \end{array}\right)\right|=l\left|\det\left(\begin{array}{cc} e_{1}\cdot v_{1} & e_{2}\cdot v_{1}\\ e_{1}\cdot v_{2} & e_{2}\cdot v_{2} \end{array}\right)\right|\nonumber \\ & =l\sqrt{\det\left(\begin{array}{cc} v_{1}\cdot v_{1} & v_{2}\cdot v_{1}\\ v_{1}\cdot v_{2} & v_{2}\cdot v_{2} \end{array}\right)}=l\sqrt{|v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2}}, \end{align} $$
but it is also clear that
![]() $d\left(\mathbb {Z}^{3}\right)=1$
, so the first result follows. From this result, (A.10) and Corollary A.8, we deduce that there exist generators
$d\left(\mathbb {Z}^{3}\right)=1$
, so the first result follows. From this result, (A.10) and Corollary A.8, we deduce that there exist generators
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
such that
$v_{2}$
such that
Since
![]() $v_1,v_2\in \mathbb {Z}^{3}\backslash \left\{ 0\right\}$
, we have
$v_1,v_2\in \mathbb {Z}^{3}\backslash \left\{ 0\right\}$
, we have
![]() $|v_1|,|v_2|\ge 1$
, and hence,
$|v_1|,|v_2|\ge 1$
, and hence,
A.2 Plane decomposition of
 $L_{k}$
and the summation formula
$L_{k}$
and the summation formula
Now we turn to consider the lune
![]() $L_{k}=\left\{ p\in \mathbb {Z}^{3}\mid |p-k|\leq k_{F}<|p|\right\} $
. Throughout this subsection, we let
$L_{k}=\left\{ p\in \mathbb {Z}^{3}\mid |p-k|\leq k_{F}<|p|\right\} $
. Throughout this subsection, we let
![]() $k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be fixed and write
$k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\} $
be fixed and write
![]() $\hat {k}=|k|^{-1}k$
and
$\hat {k}=|k|^{-1}k$
and
![]() $l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
for the sake of brevity. The integrands of the Riemann sums we must consider only depend on the quantity
$l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
for the sake of brevity. The integrands of the Riemann sums we must consider only depend on the quantity
![]() $\lambda _{k,p}=k\cdot p-\frac {1}{2}|k|^{2}=|k|\left(\hat {k}\cdot p-\frac {1}{2}|k|\right)$
, so we begin by decomposing
$\lambda _{k,p}=k\cdot p-\frac {1}{2}|k|^{2}=|k|\left(\hat {k}\cdot p-\frac {1}{2}|k|\right)$
, so we begin by decomposing
![]() $L_{k}$
along the
$L_{k}$
along the
![]() $\hat {k}\cdot p=\text {constant}$
planes. By the definition of
$\hat {k}\cdot p=\text {constant}$
planes. By the definition of
![]() $L_{k}$
, it easily follows that
$L_{k}$
, it easily follows that
 $$ \begin{align} L_{k}\subset\left\{ p\in\mathbb{R}^{3}\mid\frac{1}{2}|k|<\hat{k}\cdot p\leq k_{F}+|k|\right\}. \end{align} $$
$$ \begin{align} L_{k}\subset\left\{ p\in\mathbb{R}^{3}\mid\frac{1}{2}|k|<\hat{k}\cdot p\leq k_{F}+|k|\right\}. \end{align} $$
Letting
![]() $m^{\ast }$
be the least integer and
$m^{\ast }$
be the least integer and
![]() $M^{\ast }$
the greatest integer such that
$M^{\ast }$
the greatest integer such that
we see that the lune
![]() $L_{k}$
can be expressed as the disjoint union
$L_{k}$
can be expressed as the disjoint union
 $$ \begin{align} L_{k}=\bigcup_{m=m^{\ast}}^{M^{\ast}}L_{k}^{m}, \quad L_{k}^{m}=\left\{ p\in L_{k}\mid\hat{k}\cdot p=lm\right\}. \end{align} $$
$$ \begin{align} L_{k}=\bigcup_{m=m^{\ast}}^{M^{\ast}}L_{k}^{m}, \quad L_{k}^{m}=\left\{ p\in L_{k}\mid\hat{k}\cdot p=lm\right\}. \end{align} $$
So for any function
![]() $f:\mathbb {R}\to \mathbb {R}$
, we may express a sum of the form
$f:\mathbb {R}\to \mathbb {R}$
, we may express a sum of the form
![]() $\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
as
$\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
as
 $$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p})=\sum_{m=m^{\ast}}^{M^{\ast}}\sum_{p\in L_{k}^{m}}f\left(|k|\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)\right)=\sum_{m=m^{\ast}}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)|L_{k}^{m}|. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p})=\sum_{m=m^{\ast}}^{M^{\ast}}\sum_{p\in L_{k}^{m}}f\left(|k|\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)\right)=\sum_{m=m^{\ast}}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)|L_{k}^{m}|. \end{align} $$
Rewriting
 $L_{k}^{m}$
$L_{k}^{m}$
To proceed, we must analyze
![]() $|L_{k}^{m}|$
, the number of points contained in
$|L_{k}^{m}|$
, the number of points contained in
![]() $L_{k}^{m}$
. For this we first rewrite
$L_{k}^{m}$
. For this we first rewrite
Now let
![]() $P_{\perp }:\mathbb {R}^{3}\rightarrow \{k\}^{\perp }$
denote the orthogonal projection onto
$P_{\perp }:\mathbb {R}^{3}\rightarrow \{k\}^{\perp }$
denote the orthogonal projection onto
![]() $\{k\}^{\perp }$
. Then for any
$\{k\}^{\perp }$
. Then for any
![]() $p\in \mathbb {R}^{3}$
,
$p\in \mathbb {R}^{3}$
,
![]() $|p|^{2}=\left|P_{\perp }p\right|^{2}+\left(\hat {k}\cdotp p\right)^{2}$
, whence
$|p|^{2}=\left|P_{\perp }p\right|^{2}+\left(\hat {k}\cdotp p\right)^{2}$
, whence
 $$ \begin{align} L_{k} & =\left\{ p\in\mathbb{Z}^{3}\mid k_{F}^{2}-\left(\hat{k}\cdotp p\right)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-|k|^{2}+2k\cdot p-\left(\hat{k}\cdotp p\right)^{2}\right\} \nonumber\\ & =\left\{ p\in\mathbb{Z}^{3}\mid k_{F}^{2}-\left(\hat{k}\cdotp p\right)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-\left(\hat{k}\cdotp p-|k|\right)^{2}\right\} , \end{align} $$
$$ \begin{align} L_{k} & =\left\{ p\in\mathbb{Z}^{3}\mid k_{F}^{2}-\left(\hat{k}\cdotp p\right)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-|k|^{2}+2k\cdot p-\left(\hat{k}\cdotp p\right)^{2}\right\} \nonumber\\ & =\left\{ p\in\mathbb{Z}^{3}\mid k_{F}^{2}-\left(\hat{k}\cdotp p\right)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-\left(\hat{k}\cdotp p-|k|\right)^{2}\right\} , \end{align} $$
and so the sets
![]() $L_{k}^{m}=L_{k}\cap \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdotp p=lm\right\} $
may be written as
$L_{k}^{m}=L_{k}\cap \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdotp p=lm\right\} $
may be written as
 $$ \begin{align} L_{k}^{m} & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdotp p=lm,\,k_{F}^{2}-(lm)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-\left(lm-|k|\right)^{2}\right\} \nonumber\\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdotp p=lm,\,\left(R_{1}^{m}\right)^{2}<\left|P_{\perp}p\right|^{2}\leq\left(R_{2}^{m}\right)^{2}\right\} , \end{align} $$
$$ \begin{align} L_{k}^{m} & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdotp p=lm,\,k_{F}^{2}-(lm)^{2}<\left|P_{\perp}p\right|^{2}\leq k_{F}^{2}-\left(lm-|k|\right)^{2}\right\} \nonumber\\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdotp p=lm,\,\left(R_{1}^{m}\right)^{2}<\left|P_{\perp}p\right|^{2}\leq\left(R_{2}^{m}\right)^{2}\right\} , \end{align} $$
where the real numbers
![]() $R_{1}^{m}$
and
$R_{1}^{m}$
and
![]() $R_{2}^{m}$
are
$R_{2}^{m}$
are
which are well defined by definition of
![]() $m^{\ast }$
and
$m^{\ast }$
and
![]() $M^{\ast }$
.
$M^{\ast }$
.
Now by Proposition A.10, we can find the generators
![]() $v_{1},v_{2}\in \mathbb {Z}^{3}$
of
$v_{1},v_{2}\in \mathbb {Z}^{3}$
of
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
. Moreover, a fixed
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=0\right\} $
. Moreover, a fixed
![]() $m^{\ast }\leq m\leq M^{\ast }$
, there exists
$m^{\ast }\leq m\leq M^{\ast }$
, there exists
![]() $q\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
, and any
$q\in \left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
, and any
![]() $p\in \mathbb {Z}^{3}$
is an element of
$p\in \mathbb {Z}^{3}$
is an element of
![]() $\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
if and only if it can be written as
$\left\{ p\in \mathbb {Z}^{3}\mid \hat {k}\cdot p=lm\right\} $
if and only if it can be written as
for some
![]() $a_{1},a_{2}\in \mathbb {Z}$
. Since
$a_{1},a_{2}\in \mathbb {Z}$
. Since
![]() $P_{\perp }q\in \{k\}^{\perp }$
by definition and the proposition likewise asserts that
$P_{\perp }q\in \{k\}^{\perp }$
by definition and the proposition likewise asserts that
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
span
$v_{2}$
span
![]() $\{k\}^{\perp }$
, there must also exist
$\{k\}^{\perp }$
, there must also exist
![]() $b_{1},b_{2}\in \mathbb {R}$
such that
$b_{1},b_{2}\in \mathbb {R}$
such that
![]() $P_{\perp }q=b_{1}v_{1}+b_{2}v_{2}$
. Consequently,
$P_{\perp }q=b_{1}v_{1}+b_{2}v_{2}$
. Consequently,
![]() $P_{\perp }p$
for our arbitrary element p takes the form
$P_{\perp }p$
for our arbitrary element p takes the form
whence
so by equation (A.22) we conclude that
 $$ \begin{align} |L_{k}^{m}| &= \Big|\Big\{ \left(a_{1},a_{2}\right)\in\mathbb{Z}^{2}\mid\left(R_{1}^{m}\right)^{2}<\left(a_{1}+b_{1}\right)^{2}|v_{1}|^{2}+\left(a_{2}+b_{2}\right)^{2}|v_{2}|^{2}\nonumber \\ &\quad +2\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)\left(v_{1}\cdot v_{2}\right)\leq\left(R_{2}^{m}\right)^{2}\Big\} \Big|\nonumber \\ & =\left|\left(E_{2}^{m}\backslash E_{1}^{m}-\left(b_{1},b_{2}\right)\right)\cap\mathbb{Z}^{2}\right|, \end{align} $$
$$ \begin{align} |L_{k}^{m}| &= \Big|\Big\{ \left(a_{1},a_{2}\right)\in\mathbb{Z}^{2}\mid\left(R_{1}^{m}\right)^{2}<\left(a_{1}+b_{1}\right)^{2}|v_{1}|^{2}+\left(a_{2}+b_{2}\right)^{2}|v_{2}|^{2}\nonumber \\ &\quad +2\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)\left(v_{1}\cdot v_{2}\right)\leq\left(R_{2}^{m}\right)^{2}\Big\} \Big|\nonumber \\ & =\left|\left(E_{2}^{m}\backslash E_{1}^{m}-\left(b_{1},b_{2}\right)\right)\cap\mathbb{Z}^{2}\right|, \end{align} $$
where the sets
![]() $E_{1}^{m}$
and
$E_{1}^{m}$
and
![]() $E_{2}^{m}$
, defined by
$E_{2}^{m}$
, defined by
are seen to be (the closed interiors of) ellipses. The analysis of
![]() $|L_{k}^{m}|$
thus reduces to the estimation of the number of lattice points enclosed by these.
$|L_{k}^{m}|$
thus reduces to the estimation of the number of lattice points enclosed by these.
Lattice point estimation
To estimate
![]() $|L_{k}^{m}|=\left|\left(E_{2}^{m}\backslash E_{1}^{m} - \left(b_{1},b_{2}\right)\right)\cap \mathbb {Z}^{2}\right|$
, we will use the following result on the number of lattice points contained in compact, strictly convex regions in the plane:
$|L_{k}^{m}|=\left|\left(E_{2}^{m}\backslash E_{1}^{m} - \left(b_{1},b_{2}\right)\right)\cap \mathbb {Z}^{2}\right|$
, we will use the following result on the number of lattice points contained in compact, strictly convex regions in the plane:
Theorem A.12 [Reference Gel’fond and Linnik19].
Let
![]() $K\subset \mathbb {R}^{2}$
be a compact, strictly convex set with
$K\subset \mathbb {R}^{2}$
be a compact, strictly convex set with
![]() $C^{2}$
boundary and let
$C^{2}$
boundary and let
![]() $\partial K$
have minimal and maximal radii of curvature
$\partial K$
have minimal and maximal radii of curvature
![]() $0<r_{1}\leq r_{2}$
. If
$0<r_{1}\leq r_{2}$
. If
![]() $r_{2}\geq 1$
, then
$r_{2}\geq 1$
, then
for a constant
![]() $C>0$
independent of K,
$C>0$
independent of K,
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
.
$r_{2}$
.
This result follows from the techniques of Chapter 8 of [Reference Gel’fond and Linnik19].
From the theorem, we deduce the following practical corollary:
Corollary A.13. Let
![]() $E\subset \mathbb {R}^{2}$
be an ellipse with radii of curvature
$E\subset \mathbb {R}^{2}$
be an ellipse with radii of curvature
![]() $0<r_{1}\leq r_{2}$
. Then,
$0<r_{1}\leq r_{2}$
. Then,
 $$\begin{align*}\left|\left|E\cap\mathbb{Z}^{2}\right|-\operatorname{\mathrm{Area}}(E)\right|\leq C\left(1+\frac{r_{2}}{r_{1}}r_{2}^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2}\right)^{\frac{2}{3}}\right) \end{align*}$$
$$\begin{align*}\left|\left|E\cap\mathbb{Z}^{2}\right|-\operatorname{\mathrm{Area}}(E)\right|\leq C\left(1+\frac{r_{2}}{r_{1}}r_{2}^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2}\right)^{\frac{2}{3}}\right) \end{align*}$$
for a constant
![]() $C>0$
independent of E,
$C>0$
independent of E,
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
.
$r_{2}$
.
Proof. The theorem gives the case that
![]() $r_{2}\geq 1$
. If
$r_{2}\geq 1$
. If
![]() $r_{2}<1$
, then we can circumscribe some disk D of radius
$r_{2}<1$
, then we can circumscribe some disk D of radius
![]() $1$
around E, and trivially
$1$
around E, and trivially
as the right-hand side is seen to be bounded irrespective of the exact position of D.
This corollary lets us estimate that
 $$ \begin{align} |L_{k}^{m}|=\text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)+O\left(1+\frac{r_{2}}{r_{1}}r_{2}^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2}\right)^{\frac{2}{3}}+\frac{r_{2}^{\prime}}{r_{1}^{\prime}}\left(r_{2}^{\prime}\right)^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2'}\right)^{\frac{2}{3}}\right), \end{align} $$
$$ \begin{align} |L_{k}^{m}|=\text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)+O\left(1+\frac{r_{2}}{r_{1}}r_{2}^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2}\right)^{\frac{2}{3}}+\frac{r_{2}^{\prime}}{r_{1}^{\prime}}\left(r_{2}^{\prime}\right)^{\frac{2}{3}}\log\left(1+2\sqrt{2 r_2'}\right)^{\frac{2}{3}}\right), \end{align} $$
where
![]() $r_{i}$
and
$r_{i}$
and
![]() $r_{i}^{\prime }$
,
$r_{i}^{\prime }$
,
![]() $i=1,2$
denote the radii of curvature of
$i=1,2$
denote the radii of curvature of
![]() $E_{1}^{m}$
and
$E_{1}^{m}$
and
![]() $E_{2}^{m}$
, as the translation by
$E_{2}^{m}$
, as the translation by
![]() $\left(b_{1},b_{2}\right)$
affects neither the areas nor the radii of curvature of the ellipses.
$\left(b_{1},b_{2}\right)$
affects neither the areas nor the radii of curvature of the ellipses.
To proceed, we must obtain some information on the geometry of the ellipses
![]() $E_{i}^{m}$
. By the definition (A.28), the semi-axes
$E_{i}^{m}$
. By the definition (A.28), the semi-axes
![]() $a_{i}\geq b_{i}>0$
of
$a_{i}\geq b_{i}>0$
of
![]() $E_{i}^{m}$
are given by
$E_{i}^{m}$
are given by
 $$ \begin{align} a_{i} & =\sqrt{2}R_{i}^{m}\left(|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{-\frac{1}{2}}, \nonumber\\ b_{i} & =\sqrt{2}R_{i}^{m}\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{-\frac{1}{2}}. \end{align} $$
$$ \begin{align} a_{i} & =\sqrt{2}R_{i}^{m}\left(|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{-\frac{1}{2}}, \nonumber\\ b_{i} & =\sqrt{2}R_{i}^{m}\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{-\frac{1}{2}}. \end{align} $$
We can now describe the geometry of the ellipses
![]() $E_{i}^{m}$
in terms of k and m:
$E_{i}^{m}$
in terms of k and m:
Proposition A.14. If
![]() $|k|\leq 2k_{F}$
, then
$|k|\leq 2k_{F}$
, then
 $$\begin{align*}\operatorname{\mathrm{Area}}\left(E_{2}^{m}\backslash E_{1}^{m}\right)=\begin{cases} 2\pi|k|\left(lm-\frac{1}{2}|k|\right)l & \text{ if } \, lm^{\ast}\leq lm\leq k_{F},\\ \pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l & \text{ if } \, k_{F}<lm\leq lM^{\ast}, \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Area}}\left(E_{2}^{m}\backslash E_{1}^{m}\right)=\begin{cases} 2\pi|k|\left(lm-\frac{1}{2}|k|\right)l & \text{ if } \, lm^{\ast}\leq lm\leq k_{F},\\ \pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l & \text{ if } \, k_{F}<lm\leq lM^{\ast}, \end{cases} \end{align*}$$
and the radii of curvature
![]() $0<r_{1}\leq r_{2}$
of both
$0<r_{1}\leq r_{2}$
of both
![]() $E_{1}^{m}$
,
$E_{1}^{m}$
,
![]() $E_{2}^{m}$
obey
$E_{2}^{m}$
obey
for a constant
![]() $C>0$
independent of k and m.
$C>0$
independent of k and m.
(The condition
![]() $|k|\leq 2k_{F}$
ensures that the lune does not degenerate into a ball, in which case the area formula must be modified.)
$|k|\leq 2k_{F}$
ensures that the lune does not degenerate into a ball, in which case the area formula must be modified.)
Proof. Let
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
be the generators given by Proposition A.11. The area enclosed by an ellipse with semi-axes a and b is
$v_{2}$
be the generators given by Proposition A.11. The area enclosed by an ellipse with semi-axes a and b is
![]() $\pi ab$
, so as
$\pi ab$
, so as
![]() $E_{1}^{m}\subset E_{2}^{m}$
for any
$E_{1}^{m}\subset E_{2}^{m}$
for any
![]() $m^{\ast }\leq m\leq M^{\ast }$
and
$m^{\ast }\leq m\leq M^{\ast }$
and
![]() $E_{1}^{m}\neq \emptyset $
when
$E_{1}^{m}\neq \emptyset $
when
![]() $lm\leq k_{F}$
, we find in this case that
$lm\leq k_{F}$
, we find in this case that
 $$ \begin{align} \text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right) & =\pi\left(a_{2}b_{2}-a_{1}b_{1}\right)=\frac{2\pi\left(\left(R_{2}^{m}\right)^{2}-\left(R_{1}^{m}\right)^{2}\right)}{\sqrt{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)}}\nonumber \\ & =\frac{2\pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}-\left(k_{F}^{2}-(lm)^{2}\right)\right)}{\sqrt{4|v_{1}|^{2}|v_{2}|^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}} =2\pi|k|\left(lm-\frac{1}{2}|k|\right)l \end{align} $$
$$ \begin{align} \text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right) & =\pi\left(a_{2}b_{2}-a_{1}b_{1}\right)=\frac{2\pi\left(\left(R_{2}^{m}\right)^{2}-\left(R_{1}^{m}\right)^{2}\right)}{\sqrt{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)}}\nonumber \\ & =\frac{2\pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}-\left(k_{F}^{2}-(lm)^{2}\right)\right)}{\sqrt{4|v_{1}|^{2}|v_{2}|^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}} =2\pi|k|\left(lm-\frac{1}{2}|k|\right)l \end{align} $$
and similarly in the case
![]() $k_{F}<lm$
that
$k_{F}<lm$
that
 $$ \begin{align} \text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)=\text{Area}\left(E_{2}^{m}\right)=\pi a_{2}b_{2}=\frac{2\pi\left(R_{2}^{m}\right)^{2}}{2l^{-1}}=\pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l. \end{align} $$
$$ \begin{align} \text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)=\text{Area}\left(E_{2}^{m}\right)=\pi a_{2}b_{2}=\frac{2\pi\left(R_{2}^{m}\right)^{2}}{2l^{-1}}=\pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l. \end{align} $$
For the radii of curvature, we note that for an ellipse with semi-axes
![]() $a\geq b>0$
, these are given by
$a\geq b>0$
, these are given by
![]() $r_{1}=a^{-1}b^{2}$
and
$r_{1}=a^{-1}b^{2}$
and
![]() $r_{2}=b^{-1}a^{2}$
, respectively, so for the ratio
$r_{2}=b^{-1}a^{2}$
, respectively, so for the ratio
![]() $r_{1}^{-1}r_{2}$
, we can for either of
$r_{1}^{-1}r_{2}$
, we can for either of
![]() $E_{1}^{m}$
and
$E_{1}^{m}$
and
![]() $E_{2}^{m}$
estimate using equation (A.31) that
$E_{2}^{m}$
estimate using equation (A.31) that
 $$ \begin{align} \frac{r_{2}}{r_{1}} & =\left(\frac{a_{i}}{b_{i}}\right)^{3}=\left(\frac{|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}{|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}\right)^{\frac{3}{2}}\nonumber \\ & =\left(\frac{\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{2}}{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)}\right)^{\frac{3}{2}} \nonumber\\ & \le \left( \frac{\left( 2( |v_{1}|^{2}+|v_{2}|^{2}) \right)^2}{4( |v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2} )} \right)^{\frac{3}{2}} \le \left( \frac{(Cl^{-2})^2}{l^2}\right)^{3/2} \leq Cl^{-3} \end{align} $$
$$ \begin{align} \frac{r_{2}}{r_{1}} & =\left(\frac{a_{i}}{b_{i}}\right)^{3}=\left(\frac{|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}{|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}\right)^{\frac{3}{2}}\nonumber \\ & =\left(\frac{\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{2}}{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)}\right)^{\frac{3}{2}} \nonumber\\ & \le \left( \frac{\left( 2( |v_{1}|^{2}+|v_{2}|^{2}) \right)^2}{4( |v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2} )} \right)^{\frac{3}{2}} \le \left( \frac{(Cl^{-2})^2}{l^2}\right)^{3/2} \leq Cl^{-3} \end{align} $$
and likewise estimate for
![]() $r_{2}$
that
$r_{2}$
that
 $$ \begin{align} r_{2} & =\frac{a_{i}^{2}}{b_{i}}=\sqrt{2}R_{i}^{m}\frac{\sqrt{|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}}{|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}\nonumber \\ & =\sqrt{2}R_{i}^{m}\frac{\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{\frac{3}{2}}}{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)} \nonumber\\ & \leq\sqrt{2}R_{i}^{m}\frac{\left(2\left(|v_{1}|^{2}+|v_{2}|^{2}\right)\right)^{\frac{3}{2}}}{4( |v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2} )} \leq\left(Cl^{-2}\right)^{\frac{3}{2}}l^{2}R_{i}^{m}\leq Cl^{-1}k_{F} . \end{align} $$
$$ \begin{align} r_{2} & =\frac{a_{i}^{2}}{b_{i}}=\sqrt{2}R_{i}^{m}\frac{\sqrt{|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}}{|v_{1}|^{2}+|v_{2}|^{2}-\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}}\nonumber \\ & =\sqrt{2}R_{i}^{m}\frac{\left(|v_{1}|^{2}+|v_{2}|^{2}+\sqrt{\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}}\right)^{\frac{3}{2}}}{\left(|v_{1}|^{2}+|v_{2}|^{2}\right)^{2}-\left(\left(|v_{1}|^{2}-|v_{2}|^{2}\right)^{2}+4\left(v_{1}\cdot v_{2}\right)^{2}\right)} \nonumber\\ & \leq\sqrt{2}R_{i}^{m}\frac{\left(2\left(|v_{1}|^{2}+|v_{2}|^{2}\right)\right)^{\frac{3}{2}}}{4( |v_{1}|^{2}|v_{2}|^{2}-\left(v_{1}\cdot v_{2}\right)^{2} )} \leq\left(Cl^{-2}\right)^{\frac{3}{2}}l^{2}R_{i}^{m}\leq Cl^{-1}k_{F} . \end{align} $$
Here, we also used that
![]() $R_{1}^{m},R_{2}^{m}\leq k_{F}$
for all
$R_{1}^{m},R_{2}^{m}\leq k_{F}$
for all
![]() $m^{\ast }\leq m\leq M^{\ast }$
.
$m^{\ast }\leq m\leq M^{\ast }$
.
The summation formula
We can now present the summation formula that we will use to estimate the sums
![]() $\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
. Noting that the quantity
$\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
. Noting that the quantity
![]() $l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
obeys the lower bound
$l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
obeys the lower bound
![]() $l\geq |k|^{-1}$
independently of k, we can by equation (A.30) and Proposition A.14 estimate (provided
$l\geq |k|^{-1}$
independently of k, we can by equation (A.30) and Proposition A.14 estimate (provided
![]() $|k|\leq 2k_{F}$
) that
$|k|\leq 2k_{F}$
) that
 $$ \begin{align} \left||L_{k}^{m}|-\text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)\right| & \leq C\left(1+l^{-3}\left(l^{-1}k_{F}\right)^{\frac{2}{3}}\log\left(1+2\sqrt{2}\left(l^{-1}k_{F}\right)^{\frac{1}{2}}\right)^{\frac{2}{3}}\right) \nonumber\\ & \leq C\left(1+|k|^{3+\frac{2}{3}}k_{F}^{\frac{2}{3}}\log\left(1+\sqrt{|k|k_{F}}\right)^{\frac{2}{3}}\right)\leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}} \end{align} $$
$$ \begin{align} \left||L_{k}^{m}|-\text{Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)\right| & \leq C\left(1+l^{-3}\left(l^{-1}k_{F}\right)^{\frac{2}{3}}\log\left(1+2\sqrt{2}\left(l^{-1}k_{F}\right)^{\frac{1}{2}}\right)^{\frac{2}{3}}\right) \nonumber\\ & \leq C\left(1+|k|^{3+\frac{2}{3}}k_{F}^{\frac{2}{3}}\log\left(1+\sqrt{|k|k_{F}}\right)^{\frac{2}{3}}\right)\leq C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}} \end{align} $$
as
![]() $k_{F}\rightarrow \infty $
, for a constant
$k_{F}\rightarrow \infty $
, for a constant
![]() $C>0$
independent of k and m. Inserting the expression for
$C>0$
independent of k and m. Inserting the expression for
![]() $\text {Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)$
that we determined in Proposition A.14, we then have
$\text {Area}\left(E_{2}^{m}\backslash E_{1}^{m}\right)$
that we determined in Proposition A.14, we then have
 $$ \begin{align} |L_{k}^{m}|=\begin{cases} 2\pi|k|\left(lm-\frac{1}{2}|k|\right)l & lm^{\ast}\leq lm\leq k_{F}\\ \pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l & k_{F}<lm\leq lM^{\ast} \end{cases}+O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right). \end{align} $$
$$ \begin{align} |L_{k}^{m}|=\begin{cases} 2\pi|k|\left(lm-\frac{1}{2}|k|\right)l & lm^{\ast}\leq lm\leq k_{F}\\ \pi\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l & k_{F}<lm\leq lM^{\ast} \end{cases}+O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right). \end{align} $$
Letting M denote the greatest integer such that
![]() $lM\leq k_{F}$
, it now follows from equation (A.19) that for any
$lM\leq k_{F}$
, it now follows from equation (A.19) that for any
![]() $f:\left(0,\infty \right)\rightarrow \mathbb {R}$
, it holds that
$f:\left(0,\infty \right)\rightarrow \mathbb {R}$
, it holds that
 $$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p}) & =2\pi|k|\sum_{m=m^{\ast}}^{M}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(lm-\frac{1}{2}|k|\right)l\nonumber \\ &\quad +\pi\sum_{m=M+1}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l \nonumber\\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left|f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\right|\right), \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}f(\lambda_{k,p}) & =2\pi|k|\sum_{m=m^{\ast}}^{M}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(lm-\frac{1}{2}|k|\right)l\nonumber \\ &\quad +\pi\sum_{m=M+1}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-\left(lm-|k|\right)^{2}\right)l \nonumber\\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left|f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\right|\right), \end{align} $$
so the
![]() $3$
-dimensional Riemann sum
$3$
-dimensional Riemann sum
![]() $\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
has been reduced to two
$\sum _{p\in L_{k}}f\left(\lambda _{k,p}\right)$
has been reduced to two
![]() $1$
-dimensional Riemann sums plus an error term. In fact, these two
$1$
-dimensional Riemann sums plus an error term. In fact, these two
![]() $1$
-dimensional Riemann sums are just what one would expect, since by 3D integrating along the
$1$
-dimensional Riemann sums are just what one would expect, since by 3D integrating along the
![]() $\hat {k}$
axis it is not difficult to show that, in general,
$\hat {k}$
axis it is not difficult to show that, in general,
 $$ \begin{align} \int_{\overline{B}\left(k,k_{F}\right)\backslash\overline{B}(0,k_{F})}f\left(k\cdot p-\frac{1}{2}|k|^{2}\right)dp & =2\pi|k|\int_{\frac{1}{2}|k|}^{k_{F}}f\left(|k|\left(t-\frac{1}{2}|k|\right)\right)\left(t-\frac{1}{2}|k|\right)dt \nonumber\\ &\quad +\pi\int_{k_{F}}^{k_{F}+|k|}f\left(|k|\left(t-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-\left(t-|k|\right)^{2}\right)dt, \end{align} $$
$$ \begin{align} \int_{\overline{B}\left(k,k_{F}\right)\backslash\overline{B}(0,k_{F})}f\left(k\cdot p-\frac{1}{2}|k|^{2}\right)dp & =2\pi|k|\int_{\frac{1}{2}|k|}^{k_{F}}f\left(|k|\left(t-\frac{1}{2}|k|\right)\right)\left(t-\frac{1}{2}|k|\right)dt \nonumber\\ &\quad +\pi\int_{k_{F}}^{k_{F}+|k|}f\left(|k|\left(t-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-\left(t-|k|\right)^{2}\right)dt, \end{align} $$
and the two Riemann sums of equation (A.38) are seen to be Riemann sums for the two
![]() $1$
-dimensional integrals above.
$1$
-dimensional integrals above.
In the statement in the following proposition, we make a minor adjustment: We expand the factor
![]() $k_{F}^{2}-\left(lm-|k|\right)^{2}$
as
$k_{F}^{2}-\left(lm-|k|\right)^{2}$
as
 $$ \begin{align} k_{F}^{2}-\left(lm-|k|\right)^{2}=k_{F}^{2}-(lm)^{2}-|k|^{2}+2|k|lm=\left(k_{F}^{2}-(lm)^{2}\right)+2|k|\left(lm-\frac{1}{2}|k|\right) \end{align} $$
$$ \begin{align} k_{F}^{2}-\left(lm-|k|\right)^{2}=k_{F}^{2}-(lm)^{2}-|k|^{2}+2|k|lm=\left(k_{F}^{2}-(lm)^{2}\right)+2|k|\left(lm-\frac{1}{2}|k|\right) \end{align} $$
and collect the
![]() $2|k|(lm-\frac {1}{2}|k|)$
terms in the first sum. We have the summation formula:
$2|k|(lm-\frac {1}{2}|k|)$
terms in the first sum. We have the summation formula:
Proposition A.15. Let
![]() $k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\}$
with
$k=\left(k_{1},k_{2},k_{3}\right)\in \mathbb {Z}^{3}\backslash \left\{ 0\right\}$
with
![]() $|k|\leq 2k_{F}$
,
$|k|\leq 2k_{F}$
,
![]() $f:\left(0,\infty \right)\rightarrow \mathbb {R}$
. Let
$f:\left(0,\infty \right)\rightarrow \mathbb {R}$
. Let
![]() $l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
and
$l=|k|^{-1}\gcd \left(k_{1},k_{2},k_{3}\right)$
and
![]() $m^{\ast }$
is the least integer and M,
$m^{\ast }$
is the least integer and M,
![]() $M^{\ast }$
the greatest integers for which
$M^{\ast }$
the greatest integers for which
Then for all functions
![]() $f: (0,\infty )\to \mathbb {R}$
, it holds that
$f: (0,\infty )\to \mathbb {R}$
, it holds that
 $$ \begin{align*} \sum_{p\in L_{k}}f(\lambda_{k,p}) & =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(lm-\frac{1}{2}|k|\right)l\\ &\quad +\pi\sum_{m=M+1}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-(lm)^{2}\right)l\\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left|f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\right|\right),\quad k_{F}\rightarrow\infty. \end{align*} $$
$$ \begin{align*} \sum_{p\in L_{k}}f(\lambda_{k,p}) & =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(lm-\frac{1}{2}|k|\right)l\\ &\quad +\pi\sum_{m=M+1}^{M^{\ast}}f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\left(k_{F}^{2}-(lm)^{2}\right)l\\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left|f\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)\right|\right),\quad k_{F}\rightarrow\infty. \end{align*} $$
A.3 Proof of Proposition A.1
Now we prove Proposition A.1 and (A.2). In this part, we do not use Proposition A.15.
Some Riemann sum estimation techniques
We must first establish some preliminary Riemann sum estimation results. Let
![]() $S\subset \mathbb {R}^{n}$
,
$S\subset \mathbb {R}^{n}$
,
![]() $n\in \mathbb {N}$
, be given, define for
$n\in \mathbb {N}$
, be given, define for
![]() $k\in \mathbb {Z}^{n}$
the translated unit cube
$k\in \mathbb {Z}^{n}$
the translated unit cube
![]() $\mathcal {C}_{k}$
by
$\mathcal {C}_{k}$
by
and let
![]() $\mathcal {C}_{S}=\bigcup _{k\in S\cap \mathbb {Z}^{n}}\mathcal {C}_{k}$
denote the union of the cubes centered at the lattice points contained in S. The first result we will establish is that for a convex function f, the integral
$\mathcal {C}_{S}=\bigcup _{k\in S\cap \mathbb {Z}^{n}}\mathcal {C}_{k}$
denote the union of the cubes centered at the lattice points contained in S. The first result we will establish is that for a convex function f, the integral
![]() $\int _{\mathcal {C}_{S}}f(p)dp$
always yields an upper bound to the Riemann sum
$\int _{\mathcal {C}_{S}}f(p)dp$
always yields an upper bound to the Riemann sum
![]() $\sum _{k\in S\cap \mathbb {Z}^{n}}f(k)$
:
$\sum _{k\in S\cap \mathbb {Z}^{n}}f(k)$
:
Proposition A.16. Let
![]() $f\in C\left(\mathcal {C}_{S}\right)$
be a function which is convex on
$f\in C\left(\mathcal {C}_{S}\right)$
be a function which is convex on
![]() $\mathcal {C}_{k}$
for all
$\mathcal {C}_{k}$
for all
![]() $k\in S\cap \mathbb {Z}^{n}$
. Then,
$k\in S\cap \mathbb {Z}^{n}$
. Then,
 $$\begin{align*}\sum_{k\in S\cap\mathbb{Z}^{n}}f(k)\leq\int_{\mathcal{C}_{S}}f(p)dp. \end{align*}$$
$$\begin{align*}\sum_{k\in S\cap\mathbb{Z}^{n}}f(k)\leq\int_{\mathcal{C}_{S}}f(p)dp. \end{align*}$$
Proof. As a convex function admits a supporting hyperplane at every interior point of its domain, we see that for every
![]() $k\in S\cap \mathbb {Z}^{n}$
, there exists a
$k\in S\cap \mathbb {Z}^{n}$
, there exists a
![]() $c\in \mathbb {R}^{n}$
such that
$c\in \mathbb {R}^{n}$
such that
which upon integration over
![]() $\mathcal {C}_{k}$
yields
$\mathcal {C}_{k}$
yields
as
![]() $\int _{\mathcal {C}_{S}}f(k)dp=f(k)$
since
$\int _{\mathcal {C}_{S}}f(k)dp=f(k)$
since
![]() $\text {Vol}\left(\mathcal {C}_{k}\right)=1$
and
$\text {Vol}\left(\mathcal {C}_{k}\right)=1$
and
![]() $\int _{\mathcal {C}_{S}}c\cdot \left(p-k\right)dp=0$
, as
$\int _{\mathcal {C}_{S}}c\cdot \left(p-k\right)dp=0$
, as
![]() $\mathcal {C}_{k}$
is symmetric with respect to k but the integrand
$\mathcal {C}_{k}$
is symmetric with respect to k but the integrand
![]() $p\mapsto c\cdot \left(p-k\right)$
is antisymmetric. Consequently,
$p\mapsto c\cdot \left(p-k\right)$
is antisymmetric. Consequently,
 $$ \begin{align} \sum_{k\in S\cap\mathbb{Z}^{n}}f(k)\leq\sum_{k\in S\cap\mathbb{Z}^{n}}\int_{\mathcal{C}_{k}}f(p)dp=\int_{\mathcal{C}_{S}}f(p)dp. \end{align} $$
$$ \begin{align} \sum_{k\in S\cap\mathbb{Z}^{n}}f(k)\leq\sum_{k\in S\cap\mathbb{Z}^{n}}\int_{\mathcal{C}_{k}}f(p)dp=\int_{\mathcal{C}_{S}}f(p)dp. \end{align} $$
This proposition lets us replace the sum by an integral but over an integration domain
![]() $\mathcal {C}_{S}$
which will generally be complicated. An exception is the
$\mathcal {C}_{S}$
which will generally be complicated. An exception is the
![]() $n=1$
case which we record in the following (generalizing also the statement to any lattice spacing l):
$n=1$
case which we record in the following (generalizing also the statement to any lattice spacing l):
Proposition A.17. Let
![]() $a,b\in \mathbb {Z}$
,
$a,b\in \mathbb {Z}$
,
![]() $l>0$
, and
$l>0$
, and
![]() $f\in C\left(\left[la-\frac {1}{2}l,lb+\frac {1}{2}l\right]\right)$
be a convex function. Then,
$f\in C\left(\left[la-\frac {1}{2}l,lb+\frac {1}{2}l\right]\right)$
be a convex function. Then,
 $$\begin{align*}\sum_{m=a}^{b}f(lm)l\leq\int_{la-\frac{1}{2}l}^{lb+\frac{1}{2}l}f (x )dx. \end{align*}$$
$$\begin{align*}\sum_{m=a}^{b}f(lm)l\leq\int_{la-\frac{1}{2}l}^{lb+\frac{1}{2}l}f (x )dx. \end{align*}$$
For
![]() $n\neq 1$
, we instead require an additional result that lets us replace
$n\neq 1$
, we instead require an additional result that lets us replace
![]() $\mathcal {C}_{S}$
by a simpler integration domain. We define a subset
$\mathcal {C}_{S}$
by a simpler integration domain. We define a subset
![]() $S_{+}\subset \mathbb {R}^{n}$
by
$S_{+}\subset \mathbb {R}^{n}$
by
 $$ \begin{align} S_{+} = \left\{ p\in\mathbb{R}^{n}\mid\inf_{q\in S}\left|p-q\right|\leq\frac{\sqrt{n}}{2}\right\} \end{align} $$
$$ \begin{align} S_{+} = \left\{ p\in\mathbb{R}^{n}\mid\inf_{q\in S}\left|p-q\right|\leq\frac{\sqrt{n}}{2}\right\} \end{align} $$
and observe the following:
Proposition A.18. It holds that
![]() $\mathcal {C}_{S}\subset S_{+}$
. Consequently,
$\mathcal {C}_{S}\subset S_{+}$
. Consequently,
Proof. We first note that for any
![]() $p\in \mathbb {R}^{n}$
, every point of the translated cube
$p\in \mathbb {R}^{n}$
, every point of the translated cube
![]() $\left(\left[-2^{-1},2^{-1}\right]+p\right)^{n}$
is a distance of at most
$\left(\left[-2^{-1},2^{-1}\right]+p\right)^{n}$
is a distance of at most
![]() $\frac {\sqrt {n}}{2}$
separated from p itself. Now, let
$\frac {\sqrt {n}}{2}$
separated from p itself. Now, let
![]() $p\in \mathcal {C}_{S}$
. Then by definition of
$p\in \mathcal {C}_{S}$
. Then by definition of
![]() $\mathcal {C}_{S}$
and the previous observation, there exists some
$\mathcal {C}_{S}$
and the previous observation, there exists some
![]() $k\in S\cap \mathbb {Z}^{n}$
such that
$k\in S\cap \mathbb {Z}^{n}$
such that
![]() $|p-k|\leq \frac {\sqrt {n}}{2}$
, and hence,
$|p-k|\leq \frac {\sqrt {n}}{2}$
, and hence,
![]() $p\in S_{+}$
since
$p\in S_{+}$
since
Clearly,
![]() $\left|S\cap \mathbb {Z}^{n}\right|=\sum _{k\in S\cap \mathbb {Z}^{n}}1=\sum _{k\in S\cap \mathbb {Z}^{n}}\text {Vol}\left(\mathcal {C}_{k}\right)=\text {Vol}\left(\mathcal {C}_{S}\right)$
, so the inclusion
$\left|S\cap \mathbb {Z}^{n}\right|=\sum _{k\in S\cap \mathbb {Z}^{n}}1=\sum _{k\in S\cap \mathbb {Z}^{n}}\text {Vol}\left(\mathcal {C}_{k}\right)=\text {Vol}\left(\mathcal {C}_{S}\right)$
, so the inclusion
![]() $\mathcal {C}_{S}\subset S_{+}$
immediately implies that
$\mathcal {C}_{S}\subset S_{+}$
immediately implies that
![]() $\left|S\cap \mathbb {Z}^{n}\right|\leq \operatorname {\mathrm {Vol}}\left(S_{+}\right)$
.
$\left|S\cap \mathbb {Z}^{n}\right|\leq \operatorname {\mathrm {Vol}}\left(S_{+}\right)$
.
Lune geometry
Returning to Proposition A.1 and (A.2), we now let
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and
$k\in \mathbb {Z}_{\ast }^{3}$
and
![]() $-1\leq \beta \leq 0$
be fixed. The Riemann sum ranges over
$-1\leq \beta \leq 0$
be fixed. The Riemann sum ranges over
![]() $p\in L_{k}=(\overline {B}(k,k_{F})\backslash \overline {B}(0,k_{F}))\cap \mathbb {Z}^{3}$
, so in the notation of the above discussion we must consider
$p\in L_{k}=(\overline {B}(k,k_{F})\backslash \overline {B}(0,k_{F}))\cap \mathbb {Z}^{3}$
, so in the notation of the above discussion we must consider
![]() $S=\overline {B}(k,k_{F})\backslash \overline {B}(0,k_{F})$
. The relevant integrand,
$S=\overline {B}(k,k_{F})\backslash \overline {B}(0,k_{F})$
. The relevant integrand,
 $$ \begin{align} p\mapsto\lambda_{k,p}^{\beta}=\left(\frac{1}{2}\left(|p|^{2}-|p-k|^{2}\right)\right)^{\beta}=|k|^{\beta}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}, \end{align} $$
$$ \begin{align} p\mapsto\lambda_{k,p}^{\beta}=\left(\frac{1}{2}\left(|p|^{2}-|p-k|^{2}\right)\right)^{\beta}=|k|^{\beta}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}, \end{align} $$
is convex on
![]() $\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p>\frac {1}{2}|k|\} $
but singular at
$\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p>\frac {1}{2}|k|\} $
but singular at
![]() $\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=\frac {1}{2}|k|\} $
. For this reason, we must introduce a cutoff to the Riemann sum
$\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=\frac {1}{2}|k|\} $
. For this reason, we must introduce a cutoff to the Riemann sum
![]() $\sum _{p\in L_{k}}\lambda _{k,p}^{\beta }$
. We write
$\sum _{p\in L_{k}}\lambda _{k,p}^{\beta }$
. We write
![]() $S=S^{1}\cup S^{2}$
$S=S^{1}\cup S^{2}$
 $$ \begin{align} S^{1}=\left\{ p\in S\mid\hat{k}\cdot p\leq\frac{1}{2}|k|+\frac{2+\sqrt{3}}{2}\right\} ,\quad S^{2}=\left\{ p\in S\mid\hat{k}\cdot p>\frac{1}{2}|k|+\frac{2+\sqrt{3}}{2}\right\}, \end{align} $$
$$ \begin{align} S^{1}=\left\{ p\in S\mid\hat{k}\cdot p\leq\frac{1}{2}|k|+\frac{2+\sqrt{3}}{2}\right\} ,\quad S^{2}=\left\{ p\in S\mid\hat{k}\cdot p>\frac{1}{2}|k|+\frac{2+\sqrt{3}}{2}\right\}, \end{align} $$
so that likewise,
![]() $L_{k}=L_{k}^{1}\cup L_{k}^{2}$
where
$L_{k}=L_{k}^{1}\cup L_{k}^{2}$
where
![]() $L_k^1=L_k\cap S^1$
,
$L_k^1=L_k\cap S^1$
,
![]() $L_k^2=L_k\cap S^2$
. Hence, by Proposition A.18,
$L_k^2=L_k\cap S^2$
. Hence, by Proposition A.18,
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} =\sum_{p\in L_{k}^{1}}\lambda_{k,p}^{\beta}+\sum_{p\in L_{k}^{2}}\lambda_{k,p}^{\beta}& \leq\left(\inf_{p\in L_{k}}\lambda_{k,p}\right)^{\beta}\left|L_{k}^{1}\right|+\int_{\mathcal{C}_{S^{2}}}|k|^{\beta}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp \nonumber\\ & \leq\left(\inf_{p\in L_{k}}\lambda_{k,p}\right)^{\beta}\text{Vol}\left(S_{+}^{1}\right)+|k|^{\beta}\int_{S_{+}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} =\sum_{p\in L_{k}^{1}}\lambda_{k,p}^{\beta}+\sum_{p\in L_{k}^{2}}\lambda_{k,p}^{\beta}& \leq\left(\inf_{p\in L_{k}}\lambda_{k,p}\right)^{\beta}\left|L_{k}^{1}\right|+\int_{\mathcal{C}_{S^{2}}}|k|^{\beta}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp \nonumber\\ & \leq\left(\inf_{p\in L_{k}}\lambda_{k,p}\right)^{\beta}\text{Vol}\left(S_{+}^{1}\right)+|k|^{\beta}\int_{S_{+}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp, \end{align} $$
where we also used that
![]() $p\mapsto (\hat {k}\cdot p-\frac {1}{2}|k|)^{\beta }$
is non-negative to expand the integration range of the integral. In order to apply this inequality, we will again replace the sets
$p\mapsto (\hat {k}\cdot p-\frac {1}{2}|k|)^{\beta }$
is non-negative to expand the integration range of the integral. In order to apply this inequality, we will again replace the sets
![]() $S_{+}^{1}$
,
$S_{+}^{1}$
,
![]() $S_{+}^{2}$
by ones which are easier to work with. We have the following:
$S_{+}^{2}$
by ones which are easier to work with. We have the following:
Proposition A.19. For all
![]() $k\in \mathbb {Z}^{3}$
, it holds that
$k\in \mathbb {Z}^{3}$
, it holds that
 $$ \begin{align*} S_{+}&=\left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S} =\overline{B}\left(k,k_{F}+\frac{\sqrt{3}}{2}\right)\backslash B\left(0,k_{F}-\frac{\sqrt{3}}{2}\right),\\ S_{+}^{1}&=\left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S^{1}}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S}^{1} =\left\{ p\in\widetilde{S}\mid-\frac{\sqrt{3}}{2}\leq\hat{k}\cdot p-\frac{1}{2}|k|\leq1+\sqrt{3}\right\} , \nonumber\\ S_{+}^{2} &= \left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S^{2}}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S}^{2}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\geq1\right\}.\nonumber \end{align*} $$
$$ \begin{align*} S_{+}&=\left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S} =\overline{B}\left(k,k_{F}+\frac{\sqrt{3}}{2}\right)\backslash B\left(0,k_{F}-\frac{\sqrt{3}}{2}\right),\\ S_{+}^{1}&=\left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S^{1}}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S}^{1} =\left\{ p\in\widetilde{S}\mid-\frac{\sqrt{3}}{2}\leq\hat{k}\cdot p-\frac{1}{2}|k|\leq1+\sqrt{3}\right\} , \nonumber\\ S_{+}^{2} &= \left\{ p\in\mathbb{R}^{3}\mid\inf_{q\in S^{2}}\left|p-q\right|\leq\frac{\sqrt{3}}{2}\right\} \subset \widetilde{S}^{2}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\geq1\right\}.\nonumber \end{align*} $$
Proof. We first show that
![]() $S_+\subset \widetilde {S}$
. For every
$S_+\subset \widetilde {S}$
. For every
![]() $p\in S_{+}$
by the triangle inequality, we can estimate
$p\in S_{+}$
by the triangle inequality, we can estimate
 $$ \begin{align} |p| & \geq \sup_{q\in S} \Big( \left|q\right|-\left|p-q\right| \Big)>k_{F}- \inf_{q\in S}\left|p-q\right| \ge k_F - \frac{\sqrt{3}}{2},\\ |p-k| & \leq \inf_{q\in S} \Big( \left|q-k\right|+\left|p-q\right| \Big) \leq k_{F}+ \inf_{q\in S}\left|p-q\right| \le k_F + \frac{\sqrt{3}}{2},\nonumber \end{align} $$
$$ \begin{align} |p| & \geq \sup_{q\in S} \Big( \left|q\right|-\left|p-q\right| \Big)>k_{F}- \inf_{q\in S}\left|p-q\right| \ge k_F - \frac{\sqrt{3}}{2},\\ |p-k| & \leq \inf_{q\in S} \Big( \left|q-k\right|+\left|p-q\right| \Big) \leq k_{F}+ \inf_{q\in S}\left|p-q\right| \le k_F + \frac{\sqrt{3}}{2},\nonumber \end{align} $$
and hence,
![]() $p\in \widetilde {S}$
. Next, we prove
$p\in \widetilde {S}$
. Next, we prove
![]() $S_{+}^{1}\subset \widetilde {S}^{1}$
: for every
$S_{+}^{1}\subset \widetilde {S}^{1}$
: for every
![]() $p\in S_{+}^{1}$
, we have
$p\in S_{+}^{1}$
, we have
 $$ \begin{align} \hat{k}\cdot p-\frac{1}{2}|k| &= \inf_{q\in S^1} \Big( \hat{k}\cdot q-\frac{1}{2}|k|+\hat{k}\cdot\left(p-q\right) \Big) \leq\frac{2+\sqrt{3}}{2}+ \inf_{q\in S^1}\left|p-q\right| \le 1 +\sqrt{3},\end{align} $$
$$ \begin{align} \hat{k}\cdot p-\frac{1}{2}|k| &= \inf_{q\in S^1} \Big( \hat{k}\cdot q-\frac{1}{2}|k|+\hat{k}\cdot\left(p-q\right) \Big) \leq\frac{2+\sqrt{3}}{2}+ \inf_{q\in S^1}\left|p-q\right| \le 1 +\sqrt{3},\end{align} $$
 $$ \begin{align} \hat{k}\cdot p-\frac{1}{2}|k| &= \sup_{q\in S^1}\Big( \hat{k}\cdot q-\frac{1}{2}|k|+\hat{k}\cdot\left(p-q\right) \Big) \ge - \inf_{q\in S^1}\left|p-q\right| \ge -\frac {\sqrt 3} 2\end{align} $$
$$ \begin{align} \hat{k}\cdot p-\frac{1}{2}|k| &= \sup_{q\in S^1}\Big( \hat{k}\cdot q-\frac{1}{2}|k|+\hat{k}\cdot\left(p-q\right) \Big) \ge - \inf_{q\in S^1}\left|p-q\right| \ge -\frac {\sqrt 3} 2\end{align} $$
and hence,
![]() $p\in \widetilde {S}^{1}$
. Here, we used the definition of
$p\in \widetilde {S}^{1}$
. Here, we used the definition of
![]() $S^{1}$
and
$S^{1}$
and
![]() $S^{1}\subset S\subset \left\{ q\in \mathbb {R}^{3}\mid \hat {k}\cdot q>\frac {1}{2}|k|\right\} $
. That
$S^{1}\subset S\subset \left\{ q\in \mathbb {R}^{3}\mid \hat {k}\cdot q>\frac {1}{2}|k|\right\} $
. That
![]() $p\in S_{+}^{2}$
implies
$p\in S_{+}^{2}$
implies
![]() $\hat {k}\cdot p-\frac {1}{2}|k|\geq 1$
follows by the same argument.
$\hat {k}\cdot p-\frac {1}{2}|k|\geq 1$
follows by the same argument.
Thanks to the simple bound
![]() $\lambda _{k,p}\geq \frac {1}{2}$
for all
$\lambda _{k,p}\geq \frac {1}{2}$
for all
![]() $p\in L_k$
, we can now conclude the inequality
$p\in L_k$
, we can now conclude the inequality
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}(\widetilde{S}^{1})+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}(\widetilde{S}^{1})+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp. \end{align} $$
Hence, we need only consider the sets
![]() $\widetilde {S}^{1}$
and
$\widetilde {S}^{1}$
and
![]() $\widetilde {S}^{2}$
, which consist of ‘slices’ of
$\widetilde {S}^{2}$
, which consist of ‘slices’ of
![]() $\widetilde {S}$
:
$\widetilde {S}$
:
Recalling the definition of
![]() $\widetilde {S}$
from Proposition A.19 and using elementary trigonometry, we can show that
$\widetilde {S}$
from Proposition A.19 and using elementary trigonometry, we can show that
 $$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) & =\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right)-\pi\left(\left(k_{F}-\frac{\sqrt{3}}{2}\right)^{2}-\left|t\right|^{2}\right) \nonumber\\ & =\pi\left(2\sqrt{3}k_{F}-\left(|k|^{2}-2|k|t\right)\right)=2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right) \end{align} $$
$$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) & =\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right)-\pi\left(\left(k_{F}-\frac{\sqrt{3}}{2}\right)^{2}-\left|t\right|^{2}\right) \nonumber\\ & =\pi\left(2\sqrt{3}k_{F}-\left(|k|^{2}-2|k|t\right)\right)=2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right) \end{align} $$
for
![]() $|k|/2-\sqrt {3}/2 \leq t\leq k_{F}-\sqrt {3}/2$
, and that
$|k|/2-\sqrt {3}/2 \leq t\leq k_{F}-\sqrt {3}/2$
, and that
 $$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) & =\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right)=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t^{2}-2|k|\left(t-\frac{1}{2}|k|\right)\right)\right)\nonumber \\ & =2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)+\pi\left(\left(k_{F}-\frac{\sqrt{3}}{2}\right)^{2}-t^{2}\right) \nonumber\\ &\leq2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right) \end{align} $$
$$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) & =\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right)=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t^{2}-2|k|\left(t-\frac{1}{2}|k|\right)\right)\right)\nonumber \\ & =2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)+\pi\left(\left(k_{F}-\frac{\sqrt{3}}{2}\right)^{2}-t^{2}\right) \nonumber\\ &\leq2\pi\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right) \end{align} $$
for
![]() $k_{F}-\sqrt {3}/2\leq t\leq k_{F}+\sqrt {3}/2+|k|$
.
$k_{F}-\sqrt {3}/2\leq t\leq k_{F}+\sqrt {3}/2+|k|$
.
With these formulas, we can now give the following:
Proof of the
 $|k|<2k_{F}$
case of Proposition A.1 and (A.2).
$|k|<2k_{F}$
case of Proposition A.1 and (A.2).
By equation (A.53), we have
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}(\widetilde{S}^{1})+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}(\widetilde{S}^{1})+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp, \end{align} $$
and we can estimate
 $$ \begin{align} \text{Vol}(\widetilde{S}^{1}) & =\int_{\frac{1}{2}|k|-\frac{\sqrt{3}}{2}}^{\frac{1}{2}|k|+1+\sqrt{3}}\text{Area}(\widetilde{S}_{t})dt=2\pi\int_{\frac{1}{2}|k|-\frac{\sqrt{3}}{2}}^{\frac{1}{2}|k|+1+\sqrt{3}}\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)dt\\ & =2\pi\int_{-\frac{\sqrt{3}}{2}}^{1+\sqrt{3}}\left(|k|t+\sqrt{3}k_{F}\right)dt\leq C\left(|k|+k_{F}\right)\leq Ck_{F} = O\left(k_{F}^{2+\beta}|k|^{1+\beta}\right),\nonumber \end{align} $$
$$ \begin{align} \text{Vol}(\widetilde{S}^{1}) & =\int_{\frac{1}{2}|k|-\frac{\sqrt{3}}{2}}^{\frac{1}{2}|k|+1+\sqrt{3}}\text{Area}(\widetilde{S}_{t})dt=2\pi\int_{\frac{1}{2}|k|-\frac{\sqrt{3}}{2}}^{\frac{1}{2}|k|+1+\sqrt{3}}\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)dt\\ & =2\pi\int_{-\frac{\sqrt{3}}{2}}^{1+\sqrt{3}}\left(|k|t+\sqrt{3}k_{F}\right)dt\leq C\left(|k|+k_{F}\right)\leq Ck_{F} = O\left(k_{F}^{2+\beta}|k|^{1+\beta}\right),\nonumber \end{align} $$
for all
![]() $-1\leq \beta \leq 0$
, and
$-1\leq \beta \leq 0$
, and
 $$ \begin{align} & \int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp =\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt\nonumber \\ &\quad \leq2\pi\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)dt\nonumber \\ &\quad =2\pi\left(|k|\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{1+\beta}\,dt+\sqrt{3}k_{F}\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{\beta}\,dt\right)\nonumber\\ & \quad\leq2\pi\left(\frac{|k|}{2+\beta}\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)^{2+\beta}+\frac{\sqrt{3}}{1+\beta}k_{F}\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)^{1+\beta}\right) \leq Ck_{F}^{2+\beta}|k| \end{align} $$
$$ \begin{align} & \int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp =\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt\nonumber \\ &\quad \leq2\pi\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\left(|k|\left(t-\frac{1}{2}|k|\right)+\sqrt{3}k_{F}\right)dt\nonumber \\ &\quad =2\pi\left(|k|\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{1+\beta}\,dt+\sqrt{3}k_{F}\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{\beta}\,dt\right)\nonumber\\ & \quad\leq2\pi\left(\frac{|k|}{2+\beta}\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)^{2+\beta}+\frac{\sqrt{3}}{1+\beta}k_{F}\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)^{1+\beta}\right) \leq Ck_{F}^{2+\beta}|k| \end{align} $$
for
![]() $-1<\beta \leq 0$
, and
$-1<\beta \leq 0$
, and
 $$ \begin{align} \int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{-1}dp &\leq2\pi\left(|k|\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}1\,dt+\sqrt{3}k_{F}\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{-1}\,dt\right) \nonumber\\ & \leq C\left(|k|k_{F}+k_{F}\log\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)\right) \leq C|k|\left(1+|k|^{-1}\log\left(k_{F}\right)\right)k_{F} \end{align} $$
$$ \begin{align} \int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{-1}dp &\leq2\pi\left(|k|\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}1\,dt+\sqrt{3}k_{F}\int_{1}^{k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|}t^{-1}\,dt\right) \nonumber\\ & \leq C\left(|k|k_{F}+k_{F}\log\left(k_{F}+\frac{\sqrt{3}}{2}+\frac{1}{2}|k|\right)\right) \leq C|k|\left(1+|k|^{-1}\log\left(k_{F}\right)\right)k_{F} \end{align} $$
for
![]() $\beta =-1$
. Combining the estimates yields the claim.
$\beta =-1$
. Combining the estimates yields the claim.
Proof of the
 $|k| \geq 2k_{F}$
case of Proposition A.1.
$|k| \geq 2k_{F}$
case of Proposition A.1.
For
![]() $|k|\geq 2k_{F}$
, the lune
$|k|\geq 2k_{F}$
, the lune
![]() $S=\overline {B}\left(k,k_{F}\right)\backslash \overline {B}(0,k_{F})$
degenerates into a ball, and so we must adapt our argument. Now it is simply the case that
$S=\overline {B}\left(k,k_{F}\right)\backslash \overline {B}(0,k_{F})$
degenerates into a ball, and so we must adapt our argument. Now it is simply the case that
 $$ \begin{align} S_{+}=\widetilde{S}=\overline{B}\left(k,k_{F}+\frac{\sqrt{3}}{2}\right). \end{align} $$
$$ \begin{align} S_{+}=\widetilde{S}=\overline{B}\left(k,k_{F}+\frac{\sqrt{3}}{2}\right). \end{align} $$
If
![]() $\frac {1}{2}|k|\geq k_{F}+\frac {2+\sqrt {3}}{2}$
, then every
$\frac {1}{2}|k|\geq k_{F}+\frac {2+\sqrt {3}}{2}$
, then every
![]() $p\in \widetilde {S}$
satisfies
$p\in \widetilde {S}$
satisfies
![]() $\hat {k}\cdot p-\frac {1}{2}|k|\geq 1$
and the cutoff set
$\hat {k}\cdot p-\frac {1}{2}|k|\geq 1$
and the cutoff set
![]() $\widetilde {S}^{1}$
is unnecessary. Otherwise, the equation (A.53),
$\widetilde {S}^{1}$
is unnecessary. Otherwise, the equation (A.53),
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}\left(\widetilde{S}^{1}\right)+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}\,dp, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq2^{-\beta}\,\text{Vol}\left(\widetilde{S}^{1}\right)+|k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}\,dp, \end{align} $$
still holds for
 $$ \begin{align} \widetilde{S}^{1}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\leq1+\sqrt{3}\right\} ,\quad\widetilde{S}^{2}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\geq+1\right\} , \end{align} $$
$$ \begin{align} \widetilde{S}^{1}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\leq1+\sqrt{3}\right\} ,\quad\widetilde{S}^{2}=\left\{ p\in\widetilde{S}\mid\hat{k}\cdot p-\frac{1}{2}|k|\geq+1\right\} , \end{align} $$
where we simplified the description for
![]() $\widetilde {S}^{1}$
using that
$\widetilde {S}^{1}$
using that
![]() $\hat {k}\cdot p-\frac {1}{2}|k|\geq -\frac {\sqrt {3}}{2}$
holds for all
$\hat {k}\cdot p-\frac {1}{2}|k|\geq -\frac {\sqrt {3}}{2}$
holds for all
![]() $p\in \widetilde {S}$
when
$p\in \widetilde {S}$
when
![]() $|k|\geq 2k_{F}$
. We can then easily estimate
$|k|\geq 2k_{F}$
. We can then easily estimate
![]() $\text {Vol}\left(\widetilde {S}_{1}\right)$
, as it is now seen to be a spherical cap of radius
$\text {Vol}\left(\widetilde {S}_{1}\right)$
, as it is now seen to be a spherical cap of radius
![]() $k_{F}+\frac {\sqrt {3}}{2}$
and height
$k_{F}+\frac {\sqrt {3}}{2}$
and height
 $$ \begin{align} \left(\frac{1}{2}|k|+1+\sqrt{3}\right)-\left(|k|-k_{F}-\frac{\sqrt{3}}{2}\right)\leq k_{F}-\frac{1}{2}|k|+\frac{2+3\sqrt{3}}{2}\leq\frac{2+3\sqrt{3}}{2}, \end{align} $$
$$ \begin{align} \left(\frac{1}{2}|k|+1+\sqrt{3}\right)-\left(|k|-k_{F}-\frac{\sqrt{3}}{2}\right)\leq k_{F}-\frac{1}{2}|k|+\frac{2+3\sqrt{3}}{2}\leq\frac{2+3\sqrt{3}}{2}, \end{align} $$
whence
 $$ \begin{align} \text{Vol}\left(\widetilde{S}^{1}\right)\leq\frac{\pi}{3}\left(\frac{2+3\sqrt{3}}{2}\right)^{2}\left(3\left(k_{F}+\frac{\sqrt{3}}{2}\right)-\frac{2+3\sqrt{3}}{2}\right)\leq Ck_{F}, \end{align} $$
$$ \begin{align} \text{Vol}\left(\widetilde{S}^{1}\right)\leq\frac{\pi}{3}\left(\frac{2+3\sqrt{3}}{2}\right)^{2}\left(3\left(k_{F}+\frac{\sqrt{3}}{2}\right)-\frac{2+3\sqrt{3}}{2}\right)\leq Ck_{F}, \end{align} $$
so as
![]() $k_{F}=O\left(k_{F}^{3}|k|^{2\beta }\right)$
for all
$k_{F}=O\left(k_{F}^{3}|k|^{2\beta }\right)$
for all
![]() $-1\leq \beta \leq 0$
when
$-1\leq \beta \leq 0$
when
![]() $2k_{F}\leq |k|\leq 2k_{F}+\frac {\sqrt {3}}{2}$
, this is again negligible.
$2k_{F}\leq |k|\leq 2k_{F}+\frac {\sqrt {3}}{2}$
, this is again negligible.
We estimate the integrals to conclude the following:
Proof of the second part of Proposition A.1 .
We again note that the area of the slice
![]() $\widetilde {S}_{t}$
is given by
$\widetilde {S}_{t}$
is given by
 $$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right)=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right), \end{align} $$
$$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right)=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(t-|k|\right)^{2}\right), \end{align} $$
now for
![]() $|k|-k_{F}-\frac {\sqrt {3}}{2}\leq t\leq |k|+k_{F}+\frac {\sqrt {3}}{2}$
. If
$|k|-k_{F}-\frac {\sqrt {3}}{2}\leq t\leq |k|+k_{F}+\frac {\sqrt {3}}{2}$
. If
![]() $|k|\leq 2k_{F}+1+\sqrt {3}$
, we just saw that the contribution coming from the cutoff set
$|k|\leq 2k_{F}+1+\sqrt {3}$
, we just saw that the contribution coming from the cutoff set
![]() $\widetilde {S}^{1}$
is negligible, while the integral term is
$\widetilde {S}^{1}$
is negligible, while the integral term is
 $$ \begin{align} |k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp=|k|^{\beta}\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt\leq Ck_{F}^{2+\beta}|k|^{1+\beta} \end{align} $$
$$ \begin{align} |k|^{\beta}\int_{\widetilde{S}^{2}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp=|k|^{\beta}\int_{\frac{1}{2}|k|+1}^{k_{F}+\frac{\sqrt{3}}{2}+|k|}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt\leq Ck_{F}^{2+\beta}|k|^{1+\beta} \end{align} $$
as calculated in equation (A.59), which is
![]() $O\left(k_{F}^{3}|k|^{2\beta }\right)$
for
$O\left(k_{F}^{3}|k|^{2\beta }\right)$
for
![]() $2k_{F}\leq |k|\leq 2k_{F}+1+\sqrt {3}$
(here we also use that for
$2k_{F}\leq |k|\leq 2k_{F}+1+\sqrt {3}$
(here we also use that for
![]() $\beta =-1$
, the logarithmic term in the estimate of equation (A.60) is negligible when
$\beta =-1$
, the logarithmic term in the estimate of equation (A.60) is negligible when
![]() $|k|\geq 2k_{F}$
due to the additional factor of
$|k|\geq 2k_{F}$
due to the additional factor of
![]() $|k|^{-1}$
).
$|k|^{-1}$
).
If
![]() $|k|>2k_{F}+\frac {2+\sqrt {3}}{2}$
, we simply have
$|k|>2k_{F}+\frac {2+\sqrt {3}}{2}$
, we simply have
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq|k|^{\beta}\int_{\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp=|k|^{\beta}\int_{|k|-k_{F}-\frac{\sqrt{3}}{2}}^{|k|+k_{F}+\frac{\sqrt{3}}{2}}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq|k|^{\beta}\int_{\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp=|k|^{\beta}\int_{|k|-k_{F}-\frac{\sqrt{3}}{2}}^{|k|+k_{F}+\frac{\sqrt{3}}{2}}\left(t-\frac{1}{2}|k|\right)^{\beta}\text{Area}\left(\widetilde{S}_{t}\right)dt, \end{align} $$
and by writing
![]() $\left(t-|k|\right)^{2}=\left(t-\frac {1}{2}|k|\right)^{2}-|k|\left(t-\frac {1}{2}|k|\right)+\frac {1}{4}|k|^{2}$
, we can furthermore estimate that
$\left(t-|k|\right)^{2}=\left(t-\frac {1}{2}|k|\right)^{2}-|k|\left(t-\frac {1}{2}|k|\right)+\frac {1}{4}|k|^{2}$
, we can furthermore estimate that
 $$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) &=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(\left(t-\frac{1}{2}|k|\right)^{2}-|k|\left(t-\frac{1}{2}|k|\right)+\frac{1}{4}|k|^{2}\right)\right)\nonumber\\ & =\pi\left(|k|\left(t-\frac{1}{2}|k|\right)-\left(\frac{1}{4}|k|^{2}-\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}\right)-\left(t-\frac{1}{2}|k|\right)^{2}\right)\leq\pi|k|\left(t-\frac{1}{2}|k|\right), \end{align} $$
$$ \begin{align} \text{Area}\left(\widetilde{S}_{t}\right) &=\pi\left(\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}-\left(\left(t-\frac{1}{2}|k|\right)^{2}-|k|\left(t-\frac{1}{2}|k|\right)+\frac{1}{4}|k|^{2}\right)\right)\nonumber\\ & =\pi\left(|k|\left(t-\frac{1}{2}|k|\right)-\left(\frac{1}{4}|k|^{2}-\left(k_{F}+\frac{\sqrt{3}}{2}\right)^{2}\right)-\left(t-\frac{1}{2}|k|\right)^{2}\right)\leq\pi|k|\left(t-\frac{1}{2}|k|\right), \end{align} $$
so
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq\pi|k|^{1+\beta}\int_{|k|-k_{F}-\frac{\sqrt{3}}{2}}^{|k|+k_{F}+\frac{\sqrt{3}}{2}}\left(t-\frac{1}{2}|k|\right)^{1+\beta}dt\nonumber \\ & =\frac{\pi|k|^{1+\beta}}{2+\beta}\left(\left(\frac{1}{2} |k|+k_{F}+\frac{\sqrt{3}}{2}\right)^{2+\beta}-\left(\frac{1}{2} |k|-k_{F}-\frac{\sqrt{3}}{2}\right)^{2+\beta}\right) \nonumber\\ & \leq C|k|^{1+\beta}\left(\frac{1}{2} |k|+k_{F}+\frac{\sqrt{3}}{2}\right)^{2+\beta}\leq C|k|^{3+2\beta}. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq\pi|k|^{1+\beta}\int_{|k|-k_{F}-\frac{\sqrt{3}}{2}}^{|k|+k_{F}+\frac{\sqrt{3}}{2}}\left(t-\frac{1}{2}|k|\right)^{1+\beta}dt\nonumber \\ & =\frac{\pi|k|^{1+\beta}}{2+\beta}\left(\left(\frac{1}{2} |k|+k_{F}+\frac{\sqrt{3}}{2}\right)^{2+\beta}-\left(\frac{1}{2} |k|-k_{F}-\frac{\sqrt{3}}{2}\right)^{2+\beta}\right) \nonumber\\ & \leq C|k|^{1+\beta}\left(\frac{1}{2} |k|+k_{F}+\frac{\sqrt{3}}{2}\right)^{2+\beta}\leq C|k|^{3+2\beta}. \end{align} $$
If additionally
![]() $|k|\leq 3k_{F}$
(say), then this is again
$|k|\leq 3k_{F}$
(say), then this is again
![]() $O\left(k_{F}^{3}|k|^{2\beta }\right)$
. If this is not the case, however, then we can instead trivially estimate that
$O\left(k_{F}^{3}|k|^{2\beta }\right)$
. If this is not the case, however, then we can instead trivially estimate that
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq|k|^{\beta}\int_{\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp\leq|k|^{\beta}\left(\inf_{p\in\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)\right)^{\beta}\int_{\widetilde{S}}1\,dp\nonumber \\ & \leq \left| k \right|^{\beta} \left(\frac{1}{2}|k|-k_{F}-\frac{\sqrt{3}}{2}\right)^{\beta}\text{Vol}\left(\overline{B}\left(0,k_{F}+\frac{\sqrt{3}}{2}\right)\right) \nonumber\\ & \leq Ck_{F}^{3}|k|^{\beta}\left(\frac{1}{2}|k|-\frac{1}{3}|k|-\frac{\sqrt{3}}{2}\right)^{\beta}\leq Ck_{F}^{3}|k|^{2\beta}. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta} & \leq|k|^{\beta}\int_{\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)^{\beta}dp\leq|k|^{\beta}\left(\inf_{p\in\widetilde{S}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)\right)^{\beta}\int_{\widetilde{S}}1\,dp\nonumber \\ & \leq \left| k \right|^{\beta} \left(\frac{1}{2}|k|-k_{F}-\frac{\sqrt{3}}{2}\right)^{\beta}\text{Vol}\left(\overline{B}\left(0,k_{F}+\frac{\sqrt{3}}{2}\right)\right) \nonumber\\ & \leq Ck_{F}^{3}|k|^{\beta}\left(\frac{1}{2}|k|-\frac{1}{3}|k|-\frac{\sqrt{3}}{2}\right)^{\beta}\leq Ck_{F}^{3}|k|^{2\beta}. \end{align} $$
A.4 Proof of Proposition A.2
In the cases
![]() $|k| \ge 2k_F$
and
$|k| \ge 2k_F$
and
![]() $2k_F\ge |k| \ge \log (k_F)$
, the claim has been proved. Thus, it remains to consider the case
$2k_F\ge |k| \ge \log (k_F)$
, the claim has been proved. Thus, it remains to consider the case
![]() $|k|\le \log (k_F)$
, for which we will apply the summation formula in Proposition A.15 to improve (A.2). By Proposition A.15, we have
$|k|\le \log (k_F)$
, for which we will apply the summation formula in Proposition A.15 to improve (A.2). By Proposition A.15, we have
 $$ \begin{align} \sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}} & =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}\frac{lm-\frac{1}{2}|k|}{|k|\left(lm-\frac{1}{2}|k|\right)}l+\pi\sum_{m=M+1}^{M^{\ast}}\frac{k_{F}^{2}-(lm)^{2}}{|k|\left(lm-\frac{1}{2}|k|\right)}l\nonumber \\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{|k|\left(lm-\frac{1}{2}|k|\right)}\right) \nonumber\\ & \leq2\pi\sum_{m=m^{\ast}}^{M^{\ast}}l+O\left(|k|^{2+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|}\right),\quad k_{F}\rightarrow\infty, \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\frac{1}{\lambda_{k,p}} & =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}\frac{lm-\frac{1}{2}|k|}{|k|\left(lm-\frac{1}{2}|k|\right)}l+\pi\sum_{m=M+1}^{M^{\ast}}\frac{k_{F}^{2}-(lm)^{2}}{|k|\left(lm-\frac{1}{2}|k|\right)}l\nonumber \\ &\quad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{|k|\left(lm-\frac{1}{2}|k|\right)}\right) \nonumber\\ & \leq2\pi\sum_{m=m^{\ast}}^{M^{\ast}}l+O\left(|k|^{2+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|}\right),\quad k_{F}\rightarrow\infty, \end{align} $$
where we used that by definition of M,
![]() $(k_{F}^{2}-(lm)^{2})<0$
for all
$(k_{F}^{2}-(lm)^{2})<0$
for all
![]() $m\geq M+1$
. As
$m\geq M+1$
. As
![]() $|k|\leq 2k_{F}$
,
$|k|\leq 2k_{F}$
,
 $$ \begin{align} \sum_{m=m^{\ast}}^{M^{\ast}}l=l\left(M^{\ast}-m^{\ast}+1\right)\leq k_{F}+|k|+l\leq Ck_{F},\quad k_{F}\rightarrow\infty, \end{align} $$
$$ \begin{align} \sum_{m=m^{\ast}}^{M^{\ast}}l=l\left(M^{\ast}-m^{\ast}+1\right)\leq k_{F}+|k|+l\leq Ck_{F},\quad k_{F}\rightarrow\infty, \end{align} $$
where we also used that
 $$ \begin{align} l=|k|^{-1}\gcd\left(k_{1},k_{2},k_{3}\right)\leq\frac{\max\left(\left|k_{1}\right|,\left|k_{2}\right|,\left|k_{3}\right|\right)}{\sqrt{k_{1}^{2}+k_{2}^{2}+k_{3}^{2}}}\leq1. \end{align} $$
$$ \begin{align} l=|k|^{-1}\gcd\left(k_{1},k_{2},k_{3}\right)\leq\frac{\max\left(\left|k_{1}\right|,\left|k_{2}\right|,\left|k_{3}\right|\right)}{\sqrt{k_{1}^{2}+k_{2}^{2}+k_{3}^{2}}}\leq1. \end{align} $$
We now consider the sum
![]() $\sum _{m=m^{\ast }}^{M^{\ast }} \Big ( lm-\frac {1}{2}|k| \Big )^{-1}$
. To apply Proposition A.17, we must estimate the
$\sum _{m=m^{\ast }}^{M^{\ast }} \Big ( lm-\frac {1}{2}|k| \Big )^{-1}$
. To apply Proposition A.17, we must estimate the
![]() $m=m^{\ast }$
term separately, so that the integration range does not cross the point
$m=m^{\ast }$
term separately, so that the integration range does not cross the point
![]() $x=\frac {1}{2}|k|$
, where the integrand diverges. Note that using
$x=\frac {1}{2}|k|$
, where the integrand diverges. Note that using
![]() $ \lambda _{k,p}\geq \frac {1}{2} $
for all
$ \lambda _{k,p}\geq \frac {1}{2} $
for all
![]() $p\in L_k$
, we have
$p\in L_k$
, we have
 $$ \begin{align} lm^{\ast}-\frac{1}{2}|k|=\min_{p\in L_{k}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)=|k|^{-1}\left(\min_{p\in L_{k}}\left(k\cdot p-\frac{1}{2}|k|^{2}\right)\right)\geq\frac{1}{2}|k|^{-1}. \end{align} $$
$$ \begin{align} lm^{\ast}-\frac{1}{2}|k|=\min_{p\in L_{k}}\left(\hat{k}\cdot p-\frac{1}{2}|k|\right)=|k|^{-1}\left(\min_{p\in L_{k}}\left(k\cdot p-\frac{1}{2}|k|^{2}\right)\right)\geq\frac{1}{2}|k|^{-1}. \end{align} $$
Therefore,
 $$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|} \le 2|k| + \sum_{m=m^{\ast}+1}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|} \leq 2|k| +|k|\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\frac{1}{x-\frac{1}{2}|k|}\,dx\nonumber \\ &\quad \leq C|k|\left(1+\log\left(\frac{lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|}{lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|}\right)\right)\leq C|k|\left(1+\log\left(\frac{k_{F}+|k|+\frac{1}{2}l-\frac{1}{2}|k|}{\frac{1}{2}l}\right)\right) \nonumber\\ & \quad \leq C|k|\left(1+\log\left(|k|k_{F}\right)\right)\leq C|k|\log\left(k_{F}\right),\quad k_{F}\rightarrow\infty, \end{align} $$
$$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|} \le 2|k| + \sum_{m=m^{\ast}+1}^{M^{\ast}}\frac{1}{lm-\frac{1}{2}|k|} \leq 2|k| +|k|\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\frac{1}{x-\frac{1}{2}|k|}\,dx\nonumber \\ &\quad \leq C|k|\left(1+\log\left(\frac{lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|}{lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|}\right)\right)\leq C|k|\left(1+\log\left(\frac{k_{F}+|k|+\frac{1}{2}l-\frac{1}{2}|k|}{\frac{1}{2}l}\right)\right) \nonumber\\ & \quad \leq C|k|\left(1+\log\left(|k|k_{F}\right)\right)\leq C|k|\log\left(k_{F}\right),\quad k_{F}\rightarrow\infty, \end{align} $$
yielding the total bound when
![]() $|k|\le \log (k_F)$
$|k|\le \log (k_F)$
 $$ \begin{align} \sum_{p\in L_{k}} \frac{1}{\lambda_{k,p}} \leq C\left( k_F +|k|^{3+\frac{2}{3}}\log\left(k_{F}\right)^{\frac{5}{3}}k_{F}^{\frac{2}{3}}\right) \le Ck_F. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}} \frac{1}{\lambda_{k,p}} \leq C\left( k_F +|k|^{3+\frac{2}{3}}\log\left(k_{F}\right)^{\frac{5}{3}}k_{F}^{\frac{2}{3}}\right) \le Ck_F. \end{align} $$
A.5 Proof of Proposition A.3
First, consider the case
![]() $-\frac 4 3 \le \beta <-1$
and
$-\frac 4 3 \le \beta <-1$
and
![]() $k \in \overline {B}(0,2k_F)$
. By Proposition A.15, we can estimate using the argument leading to (A.77) that
$k \in \overline {B}(0,2k_F)$
. By Proposition A.15, we can estimate using the argument leading to (A.77) that
 $$ \begin{align} &\sum_{p\in L_{k}}\lambda_{k,p}^{\beta} =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\left(lm-\frac{1}{2}|k|\right)l\nonumber \\ & \qquad +\pi\sum_{m=M+1}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\left(k_{F}^{2}-(lm)^{2}\right)l \nonumber\\ & \qquad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\right)\nonumber \\ & \quad \leq2\pi|k|^{1+\beta}\sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l+O\left(|k|^{3+\frac{2}{3}+\beta}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}\right). \end{align} $$
$$ \begin{align} &\sum_{p\in L_{k}}\lambda_{k,p}^{\beta} =2\pi|k|\sum_{m=m^{\ast}}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\left(lm-\frac{1}{2}|k|\right)l\nonumber \\ & \qquad +\pi\sum_{m=M+1}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\left(k_{F}^{2}-(lm)^{2}\right)l \nonumber\\ & \qquad +O\left(|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left(|k|\left(lm-\frac{1}{2}|k|\right)\right)^{\beta}\right)\nonumber \\ & \quad \leq2\pi|k|^{1+\beta}\sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l+O\left(|k|^{3+\frac{2}{3}+\beta}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}\right). \end{align} $$
Applying Proposition A.17 and A.75, again we have
 $$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l=\left(lm^{\ast}-\frac{1}{2}|k|\right)^{1+\beta}l+\sum_{m=m^{\ast}+1}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l\nonumber \\ &\quad \leq\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}+\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}dx \nonumber\\ &\quad =\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}+\frac{1}{2+\beta}\left(\left(lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{2+\beta}-\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{2+\beta}\right)\nonumber \\ & \quad \leq C\left(|k|^{-(1+\beta)} + \left(k_{F}+\frac{1}{2}l+\frac{1}{2}|k|\right)^{2+\beta}\right)\leq Ck_{F}^{2+\beta},\quad k_{F}\rightarrow\infty, \end{align} $$
$$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l=\left(lm^{\ast}-\frac{1}{2}|k|\right)^{1+\beta}l+\sum_{m=m^{\ast}+1}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}l\nonumber \\ &\quad \leq\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}+\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\left(lm-\frac{1}{2}|k|\right)^{1+\beta}dx \nonumber\\ &\quad =\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}+\frac{1}{2+\beta}\left(\left(lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{2+\beta}-\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{2+\beta}\right)\nonumber \\ & \quad \leq C\left(|k|^{-(1+\beta)} + \left(k_{F}+\frac{1}{2}l+\frac{1}{2}|k|\right)^{2+\beta}\right)\leq Ck_{F}^{2+\beta},\quad k_{F}\rightarrow\infty, \end{align} $$
and likewise,
 $$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}=\left(lm^{\ast}-\frac{1}{2}|k|\right)^{\beta}+l^{-1}\sum_{m=m^{\ast}+1}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}l\nonumber \\ &\quad \leq\left(\frac{1}{2}|k|^{-1}\right)^{\beta}+|k|\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\left(lm-\frac{1}{2}|k|\right)^{\beta}dx \nonumber\\ &\quad =2^{-\beta}|k|^{-\beta}+\frac{|k|}{1+\beta}\left(\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}-\left(lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}\right)\nonumber \\ &\quad \leq C\left(|k|^{-\beta}+|k|\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}\right)\geq C\left(|k|^{-\beta}+|k|\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}\right)\leq C|k|^{-\beta}. \end{align} $$
$$ \begin{align} & \sum_{m=m^{\ast}}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}=\left(lm^{\ast}-\frac{1}{2}|k|\right)^{\beta}+l^{-1}\sum_{m=m^{\ast}+1}^{M^{\ast}}\left(lm-\frac{1}{2}|k|\right)^{\beta}l\nonumber \\ &\quad \leq\left(\frac{1}{2}|k|^{-1}\right)^{\beta}+|k|\int_{lm^{\ast}+\frac{1}{2}l}^{lM^{\ast}+\frac{1}{2}l}\left(lm-\frac{1}{2}|k|\right)^{\beta}dx \nonumber\\ &\quad =2^{-\beta}|k|^{-\beta}+\frac{|k|}{1+\beta}\left(\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}-\left(lM^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}\right)\nonumber \\ &\quad \leq C\left(|k|^{-\beta}+|k|\left(lm^{\ast}+\frac{1}{2}l-\frac{1}{2}|k|\right)^{1+\beta}\right)\geq C\left(|k|^{-\beta}+|k|\left(\frac{1}{2}|k|^{-1}\right)^{1+\beta}\right)\leq C|k|^{-\beta}. \end{align} $$
Combining these, we find that for all
![]() $-\frac 4 3 \le \beta <-1$
and
$-\frac 4 3 \le \beta <-1$
and
![]() $k\in \overline {B}(0,2k_F)$
,
$k\in \overline {B}(0,2k_F)$
,
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C\left(k_{F}^{2+\beta}|k|^{1+\beta}+|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right),\quad k_{F}\rightarrow\infty. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C\left(k_{F}^{2+\beta}|k|^{1+\beta}+|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right),\quad k_{F}\rightarrow\infty. \end{align} $$
Consequently, if
![]() $\beta \le -\frac 4 3$
and
$\beta \le -\frac 4 3$
and
![]() $k\in \overline {B}(0,2k_F)$
, then using
$k\in \overline {B}(0,2k_F)$
, then using
![]() $\lambda _{k,p}\ge \frac 1 2$
, we have
$\lambda _{k,p}\ge \frac 1 2$
, we have
 $$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C \sum_{p\in L_{k}}\lambda_{k,p}^{- \frac 4 3} \le C |k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}. \end{align} $$
$$ \begin{align} \sum_{p\in L_{k}}\lambda_{k,p}^{\beta}\leq C \sum_{p\in L_{k}}\lambda_{k,p}^{- \frac 4 3} \le C |k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}. \end{align} $$
Moreover, if
![]() $-\frac {4}{3}<\beta <-1$
and
$-\frac {4}{3}<\beta <-1$
and
![]() $|k|\leq k_{F}^{\gamma }$
with
$|k|\leq k_{F}^{\gamma }$
with
![]() $\gamma <\frac {4+3\beta }{8-3\beta }$
, then the right-hand side of (A.81) can be simplified to
$\gamma <\frac {4+3\beta }{8-3\beta }$
, then the right-hand side of (A.81) can be simplified to
![]() $C k_{F}^{2+\beta }|k|^{1+\beta }.$
$C k_{F}^{2+\beta }|k|^{1+\beta }.$
A.6 Proof of Proposition A.4
In this subsection, we prove Proposition A.4. We first establish a simple upper bound:
Proposition A.20. For all
![]() $k\in \mathbb {Z}_{\ast }^{3}$
and any
$k\in \mathbb {Z}_{\ast }^{3}$
and any
![]() $\lambda>0$
, it holds that
$\lambda>0$
, it holds that
![]() $\left|S_{k,\lambda }^{1}\right|+\left|S_{k,\lambda }^{2}\right|\leq \left|S_{k,\lambda }\right|$
, where
$\left|S_{k,\lambda }^{1}\right|+\left|S_{k,\lambda }^{2}\right|\leq \left|S_{k,\lambda }\right|$
, where
 $$\begin{align*}S_{k,\lambda}=\left\{ p\in\mathbb{Z}^{3}\mid\vert|p|^{2}-\zeta\vert<\lambda \,\, \text{ and }\,\, \left|\hat{k}\cdot p-\frac{1}{2}|k|\right|<\frac{1}{2}|k|^{-1}\lambda\right\}. \end{align*}$$
$$\begin{align*}S_{k,\lambda}=\left\{ p\in\mathbb{Z}^{3}\mid\vert|p|^{2}-\zeta\vert<\lambda \,\, \text{ and }\,\, \left|\hat{k}\cdot p-\frac{1}{2}|k|\right|<\frac{1}{2}|k|^{-1}\lambda\right\}. \end{align*}$$
Proof. As
![]() $S_{k,\lambda }^{1}\cap S_{k,\lambda }^{2}=\emptyset $
, the claim will follow if we can show that
$S_{k,\lambda }^{1}\cap S_{k,\lambda }^{2}=\emptyset $
, the claim will follow if we can show that
![]() $S_{k,\lambda }^{1},S_{k,\lambda }^{2}\subset S_{k,\lambda }$
. Consider an arbitrary
$S_{k,\lambda }^{1},S_{k,\lambda }^{2}\subset S_{k,\lambda }$
. Consider an arbitrary
![]() $p\in S_{k,\lambda }^{1}.$
By definition of
$p\in S_{k,\lambda }^{1}.$
By definition of
![]() $S_{k,\lambda }^{1}$
,
$S_{k,\lambda }^{1}$
,
so the first condition for
![]() $S_{k,\lambda }$
is satisfied. For the other, we note that
$S_{k,\lambda }$
is satisfied. For the other, we note that
 $$ \begin{align} \left|2k\cdot p-|k|^{2}\right| & =\left||p|^{2}-|p-k|^{2}\right|=\left|\vert|p|^{2}-\zeta\vert-\vert|p-k|^{2}-\zeta\vert\right|\\ & \leq\max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} <\lambda\nonumber, \end{align} $$
$$ \begin{align} \left|2k\cdot p-|k|^{2}\right| & =\left||p|^{2}-|p-k|^{2}\right|=\left|\vert|p|^{2}-\zeta\vert-\vert|p-k|^{2}-\zeta\vert\right|\\ & \leq\max\left\{ \vert|p|^{2}-\zeta\vert,\vert|p-k|^{2}-\zeta\vert\right\} <\lambda\nonumber, \end{align} $$
where in the second equality we used that both
![]() $p,\left(p-k\right)\in B_{F}$
if
$p,\left(p-k\right)\in B_{F}$
if
![]() $p\in S_{k,\lambda }$
. This now implies that
$p\in S_{k,\lambda }$
. This now implies that
![]() $p\in S_{k,\lambda }$
, so indeed,
$p\in S_{k,\lambda }$
, so indeed,
![]() $S_{k,\lambda }^{1}\subset S_{k,\lambda }$
. The inclusion
$S_{k,\lambda }^{1}\subset S_{k,\lambda }$
. The inclusion
![]() $S_{k,\lambda }^{2}\subset S_{k,\lambda }$
follows similarly.
$S_{k,\lambda }^{2}\subset S_{k,\lambda }$
follows similarly.
The quantity
![]() $\left|S_{k,\lambda }\right|$
can in turn be estimated with exactly the same techniques which we used for the estimation of Riemann sums in the previous subsections. Let us start by using the arguments from Proposition A.10. Now, the condition that
$\left|S_{k,\lambda }\right|$
can in turn be estimated with exactly the same techniques which we used for the estimation of Riemann sums in the previous subsections. Let us start by using the arguments from Proposition A.10. Now, the condition that
![]() $\vert |p|^{2}-\zeta \vert <\lambda $
is equivalent with
$\vert |p|^{2}-\zeta \vert <\lambda $
is equivalent with
![]() $\zeta -\lambda <|p|^{2}<\zeta +\lambda $
, and writing
$\zeta -\lambda <|p|^{2}<\zeta +\lambda $
, and writing
![]() $|p|^{2}= (\hat {k}\cdot p )^{2}+\left|P_{\perp }p\right|^{2}$
(where
$|p|^{2}= (\hat {k}\cdot p )^{2}+\left|P_{\perp }p\right|^{2}$
(where
![]() $P_{\perp }:\mathbb {R}^{3}\rightarrow \mathbb {R}^{3}$
denotes the orthogonal projection onto
$P_{\perp }:\mathbb {R}^{3}\rightarrow \mathbb {R}^{3}$
denotes the orthogonal projection onto
![]() $\left\{ k\right\} ^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
), this is equivalent with
$\left\{ k\right\} ^{\perp }=\left\{ p\in \mathbb {R}^{3}\mid \hat {k}\cdot p=0\right\} $
), this is equivalent with
Consequently, if we let
![]() $m_{-}$
and
$m_{-}$
and
![]() $m_{+}$
be the least and greatest integers, respectively, such that
$m_{+}$
be the least and greatest integers, respectively, such that
it follows that we can decompose
![]() $S_{k,\lambda }=\bigcup _{m=m_{-}}^{m_{+}}S_{k,\lambda }^{m}$
, where
$S_{k,\lambda }=\bigcup _{m=m_{-}}^{m_{+}}S_{k,\lambda }^{m}$
, where
 $$ \begin{align} S_{k,\lambda}^{m} & =S_{k,\lambda}\cap\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm\right\} =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\vert|p|^{2}-\zeta\vert<\lambda\right\} \nonumber \\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\,\zeta-(lm)^{2}-\lambda<\left|P_{\perp}p\right|^{2}<\zeta-(lm)^{2}+\lambda\right\} \\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\,(R_{-}^{m})^{2}<\left|P_{\perp}p\right|^{2}<(R_{-}^{m})^{2}\right\} \nonumber \end{align} $$
$$ \begin{align} S_{k,\lambda}^{m} & =S_{k,\lambda}\cap\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm\right\} =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\vert|p|^{2}-\zeta\vert<\lambda\right\} \nonumber \\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\,\zeta-(lm)^{2}-\lambda<\left|P_{\perp}p\right|^{2}<\zeta-(lm)^{2}+\lambda\right\} \\ & =\left\{ p\in\mathbb{Z}^{3}\mid\hat{k}\cdot p=lm,\,(R_{-}^{m})^{2}<\left|P_{\perp}p\right|^{2}<(R_{-}^{m})^{2}\right\} \nonumber \end{align} $$
for
We see that the sets
![]() $S_{k,\lambda }^{m}$
are of the same form as the sets
$S_{k,\lambda }^{m}$
are of the same form as the sets
![]() $L_{k}^{m}$
which we considered in Section A.2. The arguments which we used to estimate
$L_{k}^{m}$
which we considered in Section A.2. The arguments which we used to estimate
![]() $|L_{k}^{m}|$
thus immediately carry over, provided we can establish some basic estimates on
$|L_{k}^{m}|$
thus immediately carry over, provided we can establish some basic estimates on
![]() $R_{-}^{m}$
and
$R_{-}^{m}$
and
![]() $R_{+}^{m}$
. We have the following:
$R_{+}^{m}$
. We have the following:
Proposition A.21. For all
![]() $k\in \overline {B}(0,k_{F})\cap \mathbb {Z}_{\ast }^{3}$
and
$k\in \overline {B}(0,k_{F})\cap \mathbb {Z}_{\ast }^{3}$
and
![]() $0<\lambda =\lambda \left(k_{F},k\right)\leq \frac {1}{6}k_{F}^{2}$
, it holds that
$0<\lambda =\lambda \left(k_{F},k\right)\leq \frac {1}{6}k_{F}^{2}$
, it holds that
as
![]() $k_{F}\rightarrow \infty $
for a constant
$k_{F}\rightarrow \infty $
for a constant
![]() $C>0$
independent of k,
$C>0$
independent of k,
![]() $k_{F}$
and
$k_{F}$
and
![]() $\lambda $
.
$\lambda $
.
Proof. First, recall that
![]() $\zeta $
is the midpoint of the interval
$\zeta $
is the midpoint of the interval
![]() $I=\left[\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}\right]$
. Since
$I=\left[\sup _{p\in B_{F}}|p|^{2},\inf _{p\in B_{F}^{c}}|p|^{2}\right]$
. Since
![]() $k_{F}^{2}\in I$
by definition of the Fermi ball, we can bound
$k_{F}^{2}\in I$
by definition of the Fermi ball, we can bound
 $$ \begin{align} |\zeta-k_F^2|\le \frac{|I|}{2}=\frac{1}{2}\left( \inf_{q\in B_{F}^{c}}|p|^{2}-\sup_{q\in B_{F}}|p|^{2} \right) \le k_F+1. \end{align} $$
$$ \begin{align} |\zeta-k_F^2|\le \frac{|I|}{2}=\frac{1}{2}\left( \inf_{q\in B_{F}^{c}}|p|^{2}-\sup_{q\in B_{F}}|p|^{2} \right) \le k_F+1. \end{align} $$
Here, the last inequality can be seen by taking the trial points
![]() $p_{-}=\left(\left\lfloor k_{F}\right\rfloor ,0,0\right) \in B_F$
and
$p_{-}=\left(\left\lfloor k_{F}\right\rfloor ,0,0\right) \in B_F$
and
![]() $p_{+}=\left(\left\lfloor k_{F}\right\rfloor +1,0,0\right) \in B_F^c$
. Combining (A.90), the definitions of
$p_{+}=\left(\left\lfloor k_{F}\right\rfloor +1,0,0\right) \in B_F^c$
. Combining (A.90), the definitions of
![]() $m_{-}$
,
$m_{-}$
,
![]() $m_{+}$
and the assumptions of the statement, we may estimate independently of m that
$m_{+}$
and the assumptions of the statement, we may estimate independently of m that
 $$ \begin{align} (R_{-}^{m})^{2}&\geq\zeta-\max\left\{ \left(lm_{-}\right)^{2},\left(lm_{+}\right)^{2}\right\} -\lambda\nonumber \\ & \geq\zeta-\frac{1}{4}\left(\left(|k|-|k|^{-1}\lambda\right)^{2}+\left(|k|+|k|^{-1}\lambda\right)^{2}\right)-\lambda\\ & \geq\zeta-\frac{1}{2}\left(|k|^{2}+|k|^{-2}\lambda\right)-\lambda\geq\zeta-\frac{1}{2}k_{F}^{2}-\frac{3}{2}\lambda\geq\frac{1}{4}k_{F}^{2}-k_{F}-1,\nonumber \end{align} $$
$$ \begin{align} (R_{-}^{m})^{2}&\geq\zeta-\max\left\{ \left(lm_{-}\right)^{2},\left(lm_{+}\right)^{2}\right\} -\lambda\nonumber \\ & \geq\zeta-\frac{1}{4}\left(\left(|k|-|k|^{-1}\lambda\right)^{2}+\left(|k|+|k|^{-1}\lambda\right)^{2}\right)-\lambda\\ & \geq\zeta-\frac{1}{2}\left(|k|^{2}+|k|^{-2}\lambda\right)-\lambda\geq\zeta-\frac{1}{2}k_{F}^{2}-\frac{3}{2}\lambda\geq\frac{1}{4}k_{F}^{2}-k_{F}-1,\nonumber \end{align} $$
and
This allows us to estimate
![]() $|S_{k,\lambda }^{m}|$
with the same error term as that of
$|S_{k,\lambda }^{m}|$
with the same error term as that of
![]() $|L_{k}^{m}|$
, which is to say
$|L_{k}^{m}|$
, which is to say
![]() $C|k|^{3+\frac {2}{3}}(\log k_{F})^{\frac {2}{3}}k_{F}^{\frac {2}{3}}$
. We can now give the following:
$C|k|^{3+\frac {2}{3}}(\log k_{F})^{\frac {2}{3}}k_{F}^{\frac {2}{3}}$
. We can now give the following:
Proof of Proposition A.4.
By Proposition A.21 and the above arguments, we can estimate
 $$ \begin{align} \left|S_{k,\lambda}^{m}\right| &\leq\frac{2\pi\left((R_{+}^{m})^{2}-(R_{-}^{m})^{2}\right)}{2l^{-1}}+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\nonumber\\ &=2\pi\lambda\left(k_{F},k\right)l+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}} \end{align} $$
$$ \begin{align} \left|S_{k,\lambda}^{m}\right| &\leq\frac{2\pi\left((R_{+}^{m})^{2}-(R_{-}^{m})^{2}\right)}{2l^{-1}}+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\nonumber\\ &=2\pi\lambda\left(k_{F},k\right)l+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}} \end{align} $$
for
![]() $m_{-}\leq m\leq m_{+}$
. By the decomposition
$m_{-}\leq m\leq m_{+}$
. By the decomposition
![]() $S_{k,\lambda }=\bigcup _{m=m_{-}}^{m_{+}}S_{k,\lambda }^{m}$
, we can then estimate further
$S_{k,\lambda }=\bigcup _{m=m_{-}}^{m_{+}}S_{k,\lambda }^{m}$
, we can then estimate further
 $$ \begin{align} \left|S_{k,\lambda}\right| & =\sum_{m=m_{-}}^{m_{+}}\left|S_{k,\lambda}^{m}\right|\leq2\pi\lambda\sum_{m=m_{-}}^{m_{+}}l+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m_{-}}^{m_{+}}1\nonumber \\ & \le C\left(\lambda+|k|^{4+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(lm_{+}-lm_{-}+l\right)\\ & \leq C\left(\lambda+|k|^{4+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\frac{1}{2}\left(|k|+|k|^{-1}\lambda\right)-\frac{1}{2}\left(|k|-|k|^{-1}\lambda\right)+l\right)\nonumber \\ & \leq C\left(|k|^{-1}\lambda+|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda+|k|\right)\nonumber, \end{align} $$
$$ \begin{align} \left|S_{k,\lambda}\right| & =\sum_{m=m_{-}}^{m_{+}}\left|S_{k,\lambda}^{m}\right|\leq2\pi\lambda\sum_{m=m_{-}}^{m_{+}}l+C|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\sum_{m=m_{-}}^{m_{+}}1\nonumber \\ & \le C\left(\lambda+|k|^{4+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(lm_{+}-lm_{-}+l\right)\\ & \leq C\left(\lambda+|k|^{4+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\frac{1}{2}\left(|k|+|k|^{-1}\lambda\right)-\frac{1}{2}\left(|k|-|k|^{-1}\lambda\right)+l\right)\nonumber \\ & \leq C\left(|k|^{-1}\lambda+|k|^{3+\frac{2}{3}}(\log k_{F})^{\frac{2}{3}}k_{F}^{\frac{2}{3}}\right)\left(\lambda+|k|\right)\nonumber, \end{align} $$
where we also applied the estimate
![]() $|k|^{-1}\leq l\leq 1$
.
$|k|^{-1}\leq l\leq 1$
.
Acknowledgements
PTN thanks Niels Benedikter, Marcello Porta, Benjamin Schlein and Robert Seiringer for helpful discussions. We thank the referees for constructive remarks and suggestions. MRC and PTN acknowledge the support from the Deutsche Forschungsgemeinschaft (DFG project Nr. 426365943).
Competing interest
The authors have no competing interest to declare.