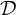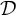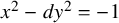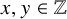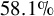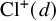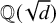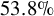1 Introduction
In recent years, much progress has been made in the study of the distribution of
![]() $2$
-parts of class groups of quadratic number fields, most notably by Fouvry and Klüners [Reference Fouvry and Klüners4, Reference Fouvry and Klüners5] and Smith [Reference Smith18]. One way to test the robustness of new methods in this subject is to study their applications to a conjecture of Stevenhagen [Reference Stevenhagen19] concerning the solvability over
$2$
-parts of class groups of quadratic number fields, most notably by Fouvry and Klüners [Reference Fouvry and Klüners4, Reference Fouvry and Klüners5] and Smith [Reference Smith18]. One way to test the robustness of new methods in this subject is to study their applications to a conjecture of Stevenhagen [Reference Stevenhagen19] concerning the solvability over
![]() $\mathbb {Z}$
of the negative Pell equation
$\mathbb {Z}$
of the negative Pell equation
Here and henceforth, we take d to be a positive squarefree integer. Equation (1.1) is solvable over
![]() $\mathbb {Z}$
if and only if the ordinary and narrow class groups of the quadratic field
$\mathbb {Z}$
if and only if the ordinary and narrow class groups of the quadratic field
![]() $\mathbb {Q}(\sqrt {d})$
, denoted by
$\mathbb {Q}(\sqrt {d})$
, denoted by
![]() $\operatorname {\mathrm {Cl}}(d)$
and
$\operatorname {\mathrm {Cl}}(d)$
and
![]() $\operatorname {\mathrm {Cl}}^+(d)$
, respectively, coincide. As the odd parts of
$\operatorname {\mathrm {Cl}}^+(d)$
, respectively, coincide. As the odd parts of
![]() $\operatorname {\mathrm {Cl}}(d)$
and
$\operatorname {\mathrm {Cl}}(d)$
and
![]() $\operatorname {\mathrm {Cl}}^+(d)$
are isomorphic, the frequency of solvability of equation (1.1) is intimately related to the joint distribution of the
$\operatorname {\mathrm {Cl}}^+(d)$
are isomorphic, the frequency of solvability of equation (1.1) is intimately related to the joint distribution of the
![]() $2$
-primary parts of
$2$
-primary parts of
![]() $\operatorname {\mathrm {Cl}}(d)$
and
$\operatorname {\mathrm {Cl}}(d)$
and
![]() $\operatorname {\mathrm {Cl}}^+(d)$
. We note that
$\operatorname {\mathrm {Cl}}^+(d)$
. We note that
![]() $\operatorname {\mathrm {Cl}}(d)/2\operatorname {\mathrm {Cl}}(d) \cong \operatorname {\mathrm {Cl}}^+(d)/2\operatorname {\mathrm {Cl}}^+(d)$
if and only if d is in the set
$\operatorname {\mathrm {Cl}}(d)/2\operatorname {\mathrm {Cl}}(d) \cong \operatorname {\mathrm {Cl}}^+(d)/2\operatorname {\mathrm {Cl}}^+(d)$
if and only if d is in the set
which we occasionally refer to as the Pell family. As
![]() $\mathcal {D}$
has natural density
$\mathcal {D}$
has natural density
![]() $0$
in the set of all squarefree integers, it is more meaningful to study density questions concerning the solvability of equation (1.1) relative to
$0$
in the set of all squarefree integers, it is more meaningful to study density questions concerning the solvability of equation (1.1) relative to
![]() $\mathcal {D}$
than relative to the set of all squarefree integers.
$\mathcal {D}$
than relative to the set of all squarefree integers.
One of the main conjectures in [Reference Stevenhagen19] is that
where
and
 $$\begin{align*}\alpha = \prod_{j \text{ odd}}(1 - 2^{-j}) = \prod_{j = 1}^{\infty}(1 + 2^{-j})^{-1} = 0.41942\ldots. \end{align*}$$
$$\begin{align*}\alpha = \prod_{j \text{ odd}}(1 - 2^{-j}) = \prod_{j = 1}^{\infty}(1 + 2^{-j})^{-1} = 0.41942\ldots. \end{align*}$$
We remark that the constant
![]() $\alpha $
already appears in the work of Cremona–Odoni [Reference Cremona and Odoni3], namely as the constant
$\alpha $
already appears in the work of Cremona–Odoni [Reference Cremona and Odoni3], namely as the constant
![]() $\lambda _\infty $
. These authors studied the negative Pell equation when the number of prime divisors is fixed, which is traditionally viewed as a simpler problem.
$\lambda _\infty $
. These authors studied the negative Pell equation when the number of prime divisors is fixed, which is traditionally viewed as a simpler problem.
Until now, the best bounds in the direction of Stevenhagen’s conjecture are due to Fouvry and Klüners [Reference Fouvry and Klüners6, Reference Fouvry and Klüners7], who used the methods they developed in [Reference Fouvry and Klüners5] to prove that
By incorporating the methods developed by Smith [Reference Smith18], we can improve the lower bound.
Theorem 1.1. With
![]() $\mathcal {D}(X)$
,
$\mathcal {D}(X)$
,
![]() $\mathcal {D}^-(X)$
and
$\mathcal {D}^-(X)$
and
![]() $\alpha $
defined as above, we have
$\alpha $
defined as above, we have
where
 $$\begin{align*}\beta = \sum_{n = 0}^{\infty}2^{-n(n+3)/2} = 1.28326\ldots. \end{align*}$$
$$\begin{align*}\beta = \sum_{n = 0}^{\infty}2^{-n(n+3)/2} = 1.28326\ldots. \end{align*}$$
We note that
![]() $\beta>5/4$
. To the nearest tenth of a percent, Stevenhagen’s conjecture states that the density of
$\beta>5/4$
. To the nearest tenth of a percent, Stevenhagen’s conjecture states that the density of
![]() $d\in \mathcal {D}$
for which (1.1) is solvable over
$d\in \mathcal {D}$
for which (1.1) is solvable over
![]() $\mathbb {Z}$
is
$\mathbb {Z}$
is
![]() $58.1\%$
. Fouvry and Klüners proved that the lower density is at least
$58.1\%$
. Fouvry and Klüners proved that the lower density is at least
![]() $52.4\%$
, and we prove that the lower density is at least
$52.4\%$
, and we prove that the lower density is at least
![]() $53.8\%$
.
$53.8\%$
.
For a finite abelian group G and an integer
![]() $k\geq 1$
, we let
$k\geq 1$
, we let
![]() $\operatorname {\mathrm {rk}}_{2^k}G = \dim _{\mathbb {F}_2}(2^{k-1}G/2^kG)$
; this is called the
$\operatorname {\mathrm {rk}}_{2^k}G = \dim _{\mathbb {F}_2}(2^{k-1}G/2^kG)$
; this is called the
![]() $2^k$
-rank of G. The nonincreasing sequence of nonnegative integers
$2^k$
-rank of G. The nonincreasing sequence of nonnegative integers
![]() $\{\operatorname {\mathrm {rk}}_{2^k}G\}_k$
determines the isomorphism class of the
$\{\operatorname {\mathrm {rk}}_{2^k}G\}_k$
determines the isomorphism class of the
![]() $2$
-primary part of G. Hence
$2$
-primary part of G. Hence
The lower bound in (1.2) comes from proving that the density of
![]() $d\in \mathcal {D}$
such that
$d\in \mathcal {D}$
such that
is equal to
![]() $\alpha $
and the density of
$\alpha $
and the density of
![]() $d\in \mathcal {D}$
such that
$d\in \mathcal {D}$
such that
is equal to
![]() $\alpha /4$
. We obtain our lower bound by proving that the density of
$\alpha /4$
. We obtain our lower bound by proving that the density of
![]() $d\in \mathcal {D}$
such that
$d\in \mathcal {D}$
such that
is equal to
![]() $2^{-n(n + 3)/2}\alpha $
. In fact, we will prove more. Define
$2^{-n(n + 3)/2}\alpha $
. In fact, we will prove more. Define
![]() $P(r|n)$
to be the probability that a uniformly chosen r by r symmetric matrix with coefficients in
$P(r|n)$
to be the probability that a uniformly chosen r by r symmetric matrix with coefficients in
![]() $\mathbb {F}_2$
has rank
$\mathbb {F}_2$
has rank
![]() $r - n$
and define
$r - n$
and define
![]() $Q(n|m)$
to be the probability that a uniformly chosen
$Q(n|m)$
to be the probability that a uniformly chosen
![]() $(n + 1) \times n$
matrix with coefficients in
$(n + 1) \times n$
matrix with coefficients in
![]() $\mathbb {F}_2$
has a bottom row consisting of all zeroes and rank
$\mathbb {F}_2$
has a bottom row consisting of all zeroes and rank
![]() $n - m$
.
$n - m$
.
Theorem 1.2. Let
![]() $\mathcal {D}(X)$
and
$\mathcal {D}(X)$
and
![]() $\alpha $
be as above, and, for integers
$\alpha $
be as above, and, for integers
![]() $n\geq m\geq 0$
, let
$n\geq m\geq 0$
, let
Then
 $$\begin{align*}\lim_{X\rightarrow\infty}\frac{|\mathcal{D}_{n, m}(X)|}{|\mathcal{D}(X)|} = Q(n|m) \cdot \lim_{r \rightarrow \infty} P(r|n) = \alpha\cdot 2^{-n(n+1)}\frac{\prod_{j = m+1}^n(2^n - 2^{n-j})}{\prod_{k = 1}^m(2^k-1)\prod_{l = 1}^{n-m}(2^l-1)}. \end{align*}$$
$$\begin{align*}\lim_{X\rightarrow\infty}\frac{|\mathcal{D}_{n, m}(X)|}{|\mathcal{D}(X)|} = Q(n|m) \cdot \lim_{r \rightarrow \infty} P(r|n) = \alpha\cdot 2^{-n(n+1)}\frac{\prod_{j = m+1}^n(2^n - 2^{n-j})}{\prod_{k = 1}^m(2^k-1)\prod_{l = 1}^{n-m}(2^l-1)}. \end{align*}$$
It is the first equality that we shall prove in Section 6. The second equality is a straightforward computation but has the nice feature that it makes immediately visible how Theorem 1.2 implies Theorem 1.1. We note that our proof of Theorem 1.2 gives an alternative proof of [Reference Fouvry and Klüners5, Theorem 2] and [Reference Fouvry and Klüners7, Theorem 2].
The major novel difficulty with working in the Pell family is that the integers
![]() $d \in \mathcal {D}$
have the remarkable property that the sets
$d \in \mathcal {D}$
have the remarkable property that the sets
and
coincide, where
![]() $(\cdot , \cdot )$
denotes the Hilbert symbol. However, for Smith’s method to work, it is essential that these spaces typically intersect trivially. For instance, this is used in [Reference Smith18, p.76] to argue that most assignments a are generic. This is not the case for the Pell family, and all the integers
$(\cdot , \cdot )$
denotes the Hilbert symbol. However, for Smith’s method to work, it is essential that these spaces typically intersect trivially. For instance, this is used in [Reference Smith18, p.76] to argue that most assignments a are generic. This is not the case for the Pell family, and all the integers
![]() $d \in \mathcal {D}$
end up in the error term in Smith’s proof. It is therefore of utmost importance to extend Smith’s algebraic results.
$d \in \mathcal {D}$
end up in the error term in Smith’s proof. It is therefore of utmost importance to extend Smith’s algebraic results.
We introduce a different notion of genericity in equations (6.1) and (6.2) to circumvent this. This necessitates new algebraic results, which can be found in Section 2. These algebraic results essentially rely on the fact that we are working with the 8-rank, which brings manipulations with Rédei symbols into play; see [Reference Stevenhagen20] for an extensive treatment of Rédei symbols. Note that this approach is inspired by Smith’s first paper [Reference Smith17]. However, the result in [Reference Smith17] assumes GRH, which we avoid by borrowing from the ideas that Smith introduced in his breakthrough paper [Reference Smith18].
In Section 4, we give more direct proofs of the results that appear in [Reference Smith18, Section 5] and concern the typical distribution of prime divisors of a squarefree integer. Of course, we once again adapt these results to d coming from the Pell family
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
2 Algebraic results
We start this section by introducing the Rédei symbol, which will play a prominent role throughout the paper. Then we prove several identities on the sum of four Rédei symbols, which serve as the algebraic input for our analytic machinery.
2.1 Rédei symbols
We shall review the fundamental properties of Rédei symbols. Our main reference is Stevenhagen’s recent work [Reference Stevenhagen20]. Fix a separable closure
![]() $\mathbb {Q}^{\text {sep}}$
of
$\mathbb {Q}^{\text {sep}}$
of
![]() $\mathbb {Q}$
. All our number fields are implicitly taken inside this fixed separable closure. If K is a number field, we write
$\mathbb {Q}$
. All our number fields are implicitly taken inside this fixed separable closure. If K is a number field, we write
![]() $G_K := \operatorname {\mathrm {Gal}}(\mathbb {Q}^{\text {sep}}/K)$
for its absolute Galois group.
$G_K := \operatorname {\mathrm {Gal}}(\mathbb {Q}^{\text {sep}}/K)$
for its absolute Galois group.
Definition 2.1. Write
![]() $\Omega $
for the collection of the places of
$\Omega $
for the collection of the places of
![]() $\mathbb {Q}$
. For a place v in
$\mathbb {Q}$
. For a place v in
![]() $\Omega $
, we write
$\Omega $
, we write
![]() $(-,-)_v$
for the Hilbert symbol. If
$(-,-)_v$
for the Hilbert symbol. If
![]() $K/\mathbb {Q}$
is a finite extension, write
$K/\mathbb {Q}$
is a finite extension, write
![]() $\Delta _K$
for the discriminant of
$\Delta _K$
for the discriminant of
![]() $K/\mathbb {Q}$
.
$K/\mathbb {Q}$
.
Definition 2.2. Let
![]() $a, b \in \mathbb {Q}^{*}/(\mathbb {Q}^{*})^2$
. If a is nontrivial, write
$a, b \in \mathbb {Q}^{*}/(\mathbb {Q}^{*})^2$
. If a is nontrivial, write
![]() $\chi _a$
for the unique character
$\chi _a$
for the unique character
![]() $\chi _a: G_{\mathbb {Q}}\rightarrow \mathbb {F}_2$
with kernel
$\chi _a: G_{\mathbb {Q}}\rightarrow \mathbb {F}_2$
with kernel
![]() $G_{\mathbb {Q}(\sqrt {a})}$
. We say that
$G_{\mathbb {Q}(\sqrt {a})}$
. We say that
![]() $(a, b)$
is acceptable if we have that
$(a, b)$
is acceptable if we have that
![]() $(a, b)_v=1$
for each
$(a, b)_v=1$
for each
![]() $v \in \Omega $
.
$v \in \Omega $
.
In case one of
![]() $a, b$
is trivial, then
$a, b$
is trivial, then
![]() $(a, b)$
is clearly acceptable. Now suppose a and b are both nontrivial. Then
$(a, b)$
is clearly acceptable. Now suppose a and b are both nontrivial. Then
![]() $(a, b)$
is acceptable if and only if there exists a Galois extension
$(a, b)$
is acceptable if and only if there exists a Galois extension
![]() $L/\mathbb {Q}$
containing
$L/\mathbb {Q}$
containing
![]() $\mathbb {Q}(\sqrt {a},\sqrt {b})$
, with
$\mathbb {Q}(\sqrt {a},\sqrt {b})$
, with
![]() $\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {ab}))$
cyclic of order
$\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {ab}))$
cyclic of order
![]() $4$
, and such that every element
$4$
, and such that every element
![]() $\sigma \in \operatorname {\mathrm {Gal}}(L/\mathbb {Q})$
with
$\sigma \in \operatorname {\mathrm {Gal}}(L/\mathbb {Q})$
with
![]() $\chi _a(\sigma )\neq \chi _b(\sigma )$
must be an involution: that is,
$\chi _a(\sigma )\neq \chi _b(\sigma )$
must be an involution: that is,
![]() $\sigma ^2=\text {id}$
.
$\sigma ^2=\text {id}$
.
If
![]() $a=b$
, we are simply requiring
$a=b$
, we are simply requiring
![]() $L/\mathbb {Q}$
to be a cyclic extension of degree
$L/\mathbb {Q}$
to be a cyclic extension of degree
![]() $4$
of
$4$
of
![]() $\mathbb {Q}$
containing
$\mathbb {Q}$
containing
![]() $\mathbb {Q}(\sqrt {a})$
. If
$\mathbb {Q}(\sqrt {a})$
. If
![]() $a \neq b$
, we are requiring
$a \neq b$
, we are requiring
![]() $L/\mathbb {Q}$
to be dihedral of degree
$L/\mathbb {Q}$
to be dihedral of degree
![]() $8$
with
$8$
with
![]() $\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {ab}))$
cyclic of order
$\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {ab}))$
cyclic of order
![]() $4$
. When
$4$
. When
![]() $a, b$
are both nontrivial and
$a, b$
are both nontrivial and
![]() $(a, b)$
is acceptable, denote by
$(a, b)$
is acceptable, denote by
![]() $\mathcal {F}_{a, b}$
the collection of fields
$\mathcal {F}_{a, b}$
the collection of fields
![]() $L/\mathbb {Q}$
described above.
$L/\mathbb {Q}$
described above.
Write
![]() $\Gamma _{\mathbb {F}_2}(\mathbb {Q}):=\text {Hom}_{\text {top.gr.}}(G_{\mathbb {Q}},\mathbb {F}_2)$
. For
$\Gamma _{\mathbb {F}_2}(\mathbb {Q}):=\text {Hom}_{\text {top.gr.}}(G_{\mathbb {Q}},\mathbb {F}_2)$
. For
![]() $\chi \in \Gamma _{\mathbb {F}_2}(\mathbb {Q})$
, write
$\chi \in \Gamma _{\mathbb {F}_2}(\mathbb {Q})$
, write
![]() $\mathbb {Q}(\chi ):=(\mathbb {Q}^{\text {sep}})^{\text {ker}(\chi )}$
. We put
$\mathbb {Q}(\chi ):=(\mathbb {Q}^{\text {sep}})^{\text {ker}(\chi )}$
. We put
![]() $\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\}):=\frac {\Gamma _{\mathbb {F}_2}(\mathbb {Q})}{\langle \{\chi _a,\chi _b\} \rangle }$
. Note that the set
$\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\}):=\frac {\Gamma _{\mathbb {F}_2}(\mathbb {Q})}{\langle \{\chi _a,\chi _b\} \rangle }$
. Note that the set
![]() $\mathcal {F}_{a, b}$
is equipped with a difference, which is a map
$\mathcal {F}_{a, b}$
is equipped with a difference, which is a map
![]() $-:\mathcal {F}_{a, b} \times \mathcal {F}_{a, b} \to \Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
such that for all
$-:\mathcal {F}_{a, b} \times \mathcal {F}_{a, b} \to \Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
such that for all
![]() $L_1,L_2,L_3 \in \mathcal {F}_{a, b}$
,
$L_1,L_2,L_3 \in \mathcal {F}_{a, b}$
,
and
![]() $L_2-L_1=0$
if and only if
$L_2-L_1=0$
if and only if
![]() $L_1=L_2$
. Indeed, for
$L_1=L_2$
. Indeed, for
![]() $L_1,L_2 \in \mathcal {F}_{a, b}$
, we define
$L_1,L_2 \in \mathcal {F}_{a, b}$
, we define
![]() $L_2 - L_1$
to be the unique
$L_2 - L_1$
to be the unique
![]() $\chi \in \Gamma _{\mathbb {F}_2}(\mathbb {Q}, \{a, b\})$
such that
$\chi \in \Gamma _{\mathbb {F}_2}(\mathbb {Q}, \{a, b\})$
such that
![]() $\mathbb {Q}(\chi )\cdot L_2 \supseteq L_1$
.
$\mathbb {Q}(\chi )\cdot L_2 \supseteq L_1$
.
Therefore each
![]() $L \in \mathcal {F}_{a, b}$
induces an explicit bijection between
$L \in \mathcal {F}_{a, b}$
induces an explicit bijection between
![]() $\mathcal {F}_{a, b}$
and
$\mathcal {F}_{a, b}$
and
![]() $\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
. For any subgroup
$\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
. For any subgroup
![]() $H \leq \Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
, we say that
$H \leq \Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
, we say that
![]() $S \subseteq \mathcal {F}_{a, b}$
is a H-coset if there exists some
$S \subseteq \mathcal {F}_{a, b}$
is a H-coset if there exists some
![]() $s_0 \in S$
such that
$s_0 \in S$
such that
![]() $S=\{s \in \mathcal {F}_{a, b}:s-s_0 \in H\}$
.
$S=\{s \in \mathcal {F}_{a, b}:s-s_0 \in H\}$
.
Now let
![]() $(a, b)$
be an acceptable pair such that a and b are not divisible by any prime congruent to
$(a, b)$
be an acceptable pair such that a and b are not divisible by any prime congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
. Write
$4$
. Write
![]() $a=t_a\prod _{l \mid a} l$
and
$a=t_a\prod _{l \mid a} l$
and
![]() $b=t_b\prod _{l' \mid b} l'$
, where the products run over all odd primes
$b=t_b\prod _{l' \mid b} l'$
, where the products run over all odd primes
![]() $l\mid a$
and
$l\mid a$
and
![]() $l'\mid b$
. Define
$l'\mid b$
. Define
![]() $\Gamma _{\mathbb {F}_2}^{\text {unr}}(\mathbb {Q},\{a, b\})$
to be the subgroup of
$\Gamma _{\mathbb {F}_2}^{\text {unr}}(\mathbb {Q},\{a, b\})$
to be the subgroup of
![]() $\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
generated by the set
$\Gamma _{\mathbb {F}_2}(\mathbb {Q},\{a, b\})$
generated by the set
![]() $\{\chi _p:p \mid a\} \cup \{\chi _p:p \mid b\} \cup \{\chi _{t_a},\chi _{t_b}\}$
. One calls an element
$\{\chi _p:p \mid a\} \cup \{\chi _p:p \mid b\} \cup \{\chi _{t_a},\chi _{t_b}\}$
. One calls an element
![]() $L \in \mathcal {F}_{a, b}$
minimally ramified (see [Reference Stevenhagen20, Definition 7.4]) if
$L \in \mathcal {F}_{a, b}$
minimally ramified (see [Reference Stevenhagen20, Definition 7.4]) if
-
○
 $L/\mathbb {Q}(\sqrt {a},\sqrt {b})$
does not ramify above any odd, finite place
$L/\mathbb {Q}(\sqrt {a},\sqrt {b})$
does not ramify above any odd, finite place
 $v\nmid \gcd (\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})})$
;
$v\nmid \gcd (\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})})$
; -
○
 $L/\mathbb {Q}(\sqrt {a}, \sqrt {b})$
is unramified at
$L/\mathbb {Q}(\sqrt {a}, \sqrt {b})$
is unramified at
 $2$
if
$2$
if
 $\Delta _{\mathbb {Q}(\sqrt {a})} \Delta _{\mathbb {Q}(\sqrt {b})}$
is odd or if one of the discriminants is
$\Delta _{\mathbb {Q}(\sqrt {a})} \Delta _{\mathbb {Q}(\sqrt {b})}$
is odd or if one of the discriminants is
 $1$
modulo
$1$
modulo
 $8$
;
$8$
; -
○ if
 $\{\Delta _{\mathbb {Q}(\sqrt {a})}, \Delta _{\mathbb {Q}(\sqrt {b})}\}$
is the set
$\{\Delta _{\mathbb {Q}(\sqrt {a})}, \Delta _{\mathbb {Q}(\sqrt {b})}\}$
is the set
 $\{4, 5\}$
modulo
$\{4, 5\}$
modulo
 $8$
, then we ask that
$8$
, then we ask that
 $L/\mathbb {Q}(\sqrt {ab})$
is
$L/\mathbb {Q}(\sqrt {ab})$
is
 $2$
-minimally ramified; see [Reference Stevenhagen20, Definition 7.3].
$2$
-minimally ramified; see [Reference Stevenhagen20, Definition 7.3].
We denote by
![]() $\mathcal {F}_{a, b}^{\text {unr}}$
the subset of
$\mathcal {F}_{a, b}^{\text {unr}}$
the subset of
![]() $\mathcal {F}_{a, b}$
consisting of minimally ramified elements. As it is shown in [Reference Stevenhagen20, Lemma 7.5], the set
$\mathcal {F}_{a, b}$
consisting of minimally ramified elements. As it is shown in [Reference Stevenhagen20, Lemma 7.5], the set
![]() $\mathcal {F}_{a, b}^{\text {unr}}$
is a
$\mathcal {F}_{a, b}^{\text {unr}}$
is a
![]() $\Gamma ^{\text {unr}}(\mathbb {Q},\{a, b\})$
-coset (which in particular implies that it is nonempty).
$\Gamma ^{\text {unr}}(\mathbb {Q},\{a, b\})$
-coset (which in particular implies that it is nonempty).
Definition 2.3. Let
![]() $(a, b, c)$
be a triple with
$(a, b, c)$
be a triple with
![]() $ a, b, c \in (\mathbb {Q}^{*})/(\mathbb {Q}^{*})^2$
. We say that
$ a, b, c \in (\mathbb {Q}^{*})/(\mathbb {Q}^{*})^2$
. We say that
![]() $(a, b, c)$
is jointly unramified if
$(a, b, c)$
is jointly unramified if
We say that
![]() $(a, b, c)$
is admissible if all
$(a, b, c)$
is admissible if all
![]() $(a, b),(a, c),(b, c)$
are acceptable pairs; a, b and c are not divisible by any prime congruent to
$(a, b),(a, c),(b, c)$
are acceptable pairs; a, b and c are not divisible by any prime congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
; and
$4$
; and
![]() $(a, b, c)$
is jointly unramified.
$(a, b, c)$
is jointly unramified.
Observe that if a triple is admissible, then so is any permutation of it.
Definition 2.4. For any admissible triple
![]() $(a, b, c)$
, define the Rédei symbol
$(a, b, c)$
, define the Rédei symbol
![]() $[a, b, c] \in \mathbb {F}_2$
as follows.Footnote
1
If any of
$[a, b, c] \in \mathbb {F}_2$
as follows.Footnote
1
If any of
![]() $a, b, c$
is trivial, set
$a, b, c$
is trivial, set
![]() $[a, b, c] := 0$
. Assuming
$[a, b, c] := 0$
. Assuming
![]() $a, b, c$
are all nontrivial, choose
$a, b, c$
are all nontrivial, choose
![]() $L \in \mathcal {F}_{a, b}^{\mathrm {unr}}$
and
$L \in \mathcal {F}_{a, b}^{\mathrm {unr}}$
and
![]() $\mathfrak {c}$
an integral ideal of norm
$\mathfrak {c}$
an integral ideal of norm
![]() $|c|$
in the ring of integers of
$|c|$
in the ring of integers of
![]() $\mathbb {Q}(\sqrt {ab})$
; existence of
$\mathbb {Q}(\sqrt {ab})$
; existence of
![]() $\mathfrak {c}$
follows from admissibility of
$\mathfrak {c}$
follows from admissibility of
![]() $(a, b, c)$
. Define
$(a, b, c)$
. Define
 $$\begin{align*}[a, b, c]:= \begin{cases} \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{c}}\right] &\mathrm{if}\ c>0 \\ \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{c}\tilde{\infty}}\right]&\mathrm{if}\ c<0, \end{cases} \end{align*}$$
$$\begin{align*}[a, b, c]:= \begin{cases} \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{c}}\right] &\mathrm{if}\ c>0 \\ \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{c}\tilde{\infty}}\right]&\mathrm{if}\ c<0, \end{cases} \end{align*}$$
where
![]() $\tilde {\infty }$
is any choice of infinite prime in
$\tilde {\infty }$
is any choice of infinite prime in
![]() $\mathbb {Q}(\sqrt {ab})$
. We identify the Artin symbol with its image under the isomorphism
$\mathbb {Q}(\sqrt {ab})$
. We identify the Artin symbol with its image under the isomorphism
![]() $\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {a},\sqrt {b}))\cong \mathbb {F}_2$
.
$\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {a},\sqrt {b}))\cong \mathbb {F}_2$
.
A priori, the resulting symbol would depend on the choices of L and
![]() $\mathfrak {c}$
, so the notation should reflect this dependency. However, the following theorem shows in particular that the symbol does not depend on any of the choices. For a proof, see [Reference Stevenhagen20, Theorem 7.7].
$\mathfrak {c}$
, so the notation should reflect this dependency. However, the following theorem shows in particular that the symbol does not depend on any of the choices. For a proof, see [Reference Stevenhagen20, Theorem 7.7].
Theorem 2.5 (Rédei reciprocity)
Let
![]() $(a, b, c)$
be an admissible triple. Then
$(a, b, c)$
be an admissible triple. Then
![]() $[a, b, c]$
does not depend on the choice of L and
$[a, b, c]$
does not depend on the choice of L and
![]() $\mathfrak {c}$
. Furthermore,
$\mathfrak {c}$
. Furthermore,
As a consequence of Rédei reciprocity, the following proposition shows that the Rédei symbol is linear in every entry.
Proposition 2.6. Let
![]() $(a, b, c)$
,
$(a, b, c)$
,
![]() $(a, b', c)$
be two admissible triples. Then
$(a, b', c)$
be two admissible triples. Then
![]() $(a, bb', c)$
is also an admissible triple, and furthermore,
$(a, bb', c)$
is also an admissible triple, and furthermore,
Since admissibility and the Rédei symbol do not depend on the order of
![]() $a, b, c$
in the triple, the corresponding statements hold for all three entries.
$a, b, c$
in the triple, the corresponding statements hold for all three entries.
Proof. It follows from
![]() $(a, b)_v=(a, b')_v=1$
for all
$(a, b)_v=(a, b')_v=1$
for all
![]() $v \in \Omega $
and the bilinearity of Hilbert symbols that
$v \in \Omega $
and the bilinearity of Hilbert symbols that
![]() $(a, bb')_v=1$
for all
$(a, bb')_v=1$
for all
![]() $v \in \Omega $
. Therefore
$v \in \Omega $
. Therefore
![]() $(a, bb')$
is acceptable, and similarly
$(a, bb')$
is acceptable, and similarly
![]() $(bb', c)$
. Since
$(bb', c)$
. Since
![]() $(a, b, c)$
or
$(a, b, c)$
or
![]() $(a, b', c)$
are jointly ramified, we have
$(a, b', c)$
are jointly ramified, we have
 $$ \begin{align*} \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b})}\Delta_{\mathbb{Q}(\sqrt{b'})}, &\Delta_{\mathbb{Q}(\sqrt{c})}) = \\ &\quad \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b})}, \Delta_{\mathbb{Q}(\sqrt{c})}) \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b'})}, \Delta_{\mathbb{Q}(\sqrt{c})}) =1. \end{align*} $$
$$ \begin{align*} \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b})}\Delta_{\mathbb{Q}(\sqrt{b'})}, &\Delta_{\mathbb{Q}(\sqrt{c})}) = \\ &\quad \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b})}, \Delta_{\mathbb{Q}(\sqrt{c})}) \gcd(\Delta_{\mathbb{Q}(\sqrt{a})}, \Delta_{\mathbb{Q}(\sqrt{b'})}, \Delta_{\mathbb{Q}(\sqrt{c})}) =1. \end{align*} $$
Observe that
![]() $\Delta _{\mathbb {Q}(\sqrt {bb'})}\mid \Delta _{\mathbb {Q}(\sqrt {b})}\Delta _{\mathbb {Q}(\sqrt {b'})}$
. Hence
$\Delta _{\mathbb {Q}(\sqrt {bb'})}\mid \Delta _{\mathbb {Q}(\sqrt {b})}\Delta _{\mathbb {Q}(\sqrt {b'})}$
. Hence
![]() $(a, bb', c)$
is jointly unramified. It follows that
$(a, bb', c)$
is jointly unramified. It follows that
![]() $(a, bb', c)$
is an admissible triple.
$(a, bb', c)$
is an admissible triple.
Now the desired identity follows from Theorem 2.5 and the linearity of the last entry.
We need a final fact that will be crucial in the proof of Theorem 2.10. We thank Professor Stevenhagen for showing us this fact.
Proposition 2.7. Let
![]() $(a, b, c)$
be an admissible triple such that
$(a, b, c)$
be an admissible triple such that
![]() $a, b>0$
and
$a, b>0$
and
Then
![]() $(a, b,-abc)$
is also admissible and
$(a, b,-abc)$
is also admissible and
Proof. Assume that
![]() $a, b$
are both nontrivial; otherwise, the statement is immediate.
$a, b$
are both nontrivial; otherwise, the statement is immediate.
We first show that
![]() $(a, b,-ab)$
is admissible. The condition of being jointly unramified follows immediately from the assumption that
$(a, b,-ab)$
is admissible. The condition of being jointly unramified follows immediately from the assumption that
![]() $\Delta _{\mathbb {Q}(\sqrt {a})}$
and
$\Delta _{\mathbb {Q}(\sqrt {a})}$
and
![]() $\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime. Since
$\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime. Since
![]() $(a, -a)$
and
$(a, -a)$
and
![]() $(b, -b)$
are always acceptable and
$(b, -b)$
are always acceptable and
![]() $(a, b)$
is acceptable by assumption, we conclude that
$(a, b)$
is acceptable by assumption, we conclude that
![]() $(a, b,-ab)$
is admissible.
$(a, b,-ab)$
is admissible.
We claim that
![]() $[a, b,-ab]=0$
. Let us pick L in
$[a, b,-ab]=0$
. Let us pick L in
![]() $\mathcal {F}_{a, b}^{\text {unr}}$
. Since
$\mathcal {F}_{a, b}^{\text {unr}}$
. Since
![]() $\gcd (\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})})=1$
, it follows that
$\gcd (\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})})=1$
, it follows that
![]() $L/\mathbb {Q}(\sqrt {ab})$
is unramified at all odd, finite places. At the prime
$L/\mathbb {Q}(\sqrt {ab})$
is unramified at all odd, finite places. At the prime
![]() $2$
, we use that
$2$
, we use that
![]() $a> 0$
and admissibility to deduce that
$a> 0$
and admissibility to deduce that
![]() $\Delta _{\mathbb {Q}(\sqrt {a})}$
is never
$\Delta _{\mathbb {Q}(\sqrt {a})}$
is never
![]() $4$
modulo
$4$
modulo
![]() $8$
. Then we see that
$8$
. Then we see that
![]() $2 \mid \Delta _{\mathbb {Q}(\sqrt {a})}$
implies that
$2 \mid \Delta _{\mathbb {Q}(\sqrt {a})}$
implies that
![]() $\Delta _{\mathbb {Q}(\sqrt {b})}$
is odd by our coprimality condition and hence
$\Delta _{\mathbb {Q}(\sqrt {b})}$
is odd by our coprimality condition and hence
![]() $1$
modulo
$1$
modulo
![]() $8$
, since otherwise
$8$
, since otherwise
![]() $(a, b)$
is not acceptable. We conclude that we are always in the second case in the definition of minimally ramified, and we conclude that
$(a, b)$
is not acceptable. We conclude that we are always in the second case in the definition of minimally ramified, and we conclude that
![]() $L/\mathbb {Q}(\sqrt {ab})$
is also unramified at
$L/\mathbb {Q}(\sqrt {ab})$
is also unramified at
![]() $2$
.
$2$
.
Furthermore,
![]() $L/\mathbb {Q}(\sqrt {ab})$
is a cyclic degree
$L/\mathbb {Q}(\sqrt {ab})$
is a cyclic degree
![]() $4$
extension. On the other hand, the principal ideal
$4$
extension. On the other hand, the principal ideal
![]() $(\sqrt {ab})$
generates the kernel of the natural surjection
$(\sqrt {ab})$
generates the kernel of the natural surjection
![]() $\text {Cl}^{+}(\mathbb {Q}(\sqrt {ab})) \twoheadrightarrow \text {Cl}(\mathbb {Q}(\sqrt {ab}))$
. The extension
$\text {Cl}^{+}(\mathbb {Q}(\sqrt {ab})) \twoheadrightarrow \text {Cl}(\mathbb {Q}(\sqrt {ab}))$
. The extension
![]() $L/\mathbb {Q}(\sqrt {ab})$
is totally real if and only if this kernel acts trivially on L via the Artin map. Therefore
$L/\mathbb {Q}(\sqrt {ab})$
is totally real if and only if this kernel acts trivially on L via the Artin map. Therefore
 $$\begin{align*}\left[\frac{L/\mathbb{Q}(\sqrt{ab})}{(\sqrt{ab})}\right] = \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\tilde{\infty}}\right]. \end{align*}$$
$$\begin{align*}\left[\frac{L/\mathbb{Q}(\sqrt{ab})}{(\sqrt{ab})}\right] = \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\tilde{\infty}}\right]. \end{align*}$$
Hence
![]() $[a, b,-ab]=0$
. By Proposition 2.6, we have that
$[a, b,-ab]=0$
. By Proposition 2.6, we have that
![]() $(a, b,-abc)$
is also admissible and
$(a, b,-abc)$
is also admissible and
as desired.
2.2 Reflection principles
We begin by recalling the connection between Rédei symbols and
![]() $8$
-rank pairings. Throughout this subsection, D is a positive squarefree integer with no prime divisors
$8$
-rank pairings. Throughout this subsection, D is a positive squarefree integer with no prime divisors
![]() $3$
modulo
$3$
modulo
![]() $4$
.
$4$
.
Recall that
![]() $\operatorname {\mathrm {Cl}}^+(D)[2]$
is generated by the primes above the rational primes ramifying in
$\operatorname {\mathrm {Cl}}^+(D)[2]$
is generated by the primes above the rational primes ramifying in
![]() $\mathbb {Q}(\sqrt {D})/\mathbb {Q}$
. For each positive
$\mathbb {Q}(\sqrt {D})/\mathbb {Q}$
. For each positive
![]() $b \mid D$
, we define
$b \mid D$
, we define
![]() $\mathfrak {B}_D(b)$
to be the unique integral ideal of
$\mathfrak {B}_D(b)$
to be the unique integral ideal of
![]() $\mathcal {O}_{\mathbb {Q}(\sqrt {D})}$
having norm equal to b. If
$\mathcal {O}_{\mathbb {Q}(\sqrt {D})}$
having norm equal to b. If
![]() $b < 0$
, we instead put
$b < 0$
, we instead put
![]() $\mathfrak {B}_D(b) := \mathfrak {B}_D(|b|) \cdot (\sqrt {D})$
. Recall that
$\mathfrak {B}_D(b) := \mathfrak {B}_D(|b|) \cdot (\sqrt {D})$
. Recall that
![]() $\mathfrak {B}_D(b) \in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
if and only if
$\mathfrak {B}_D(b) \in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
if and only if
![]() $(b, D)$
forms an acceptable pair: that is,
$(b, D)$
forms an acceptable pair: that is,
![]() $(b, D)_v=1$
for all
$(b, D)_v=1$
for all
![]() $v \in \Omega $
.
$v \in \Omega $
.
We now define the dual class group
![]() $\operatorname {\mathrm {Cl}}^+(D)^{\vee } = \text {Hom}(\operatorname {\mathrm {Cl}}^+(D), \mathbb {Q}/\mathbb {Z})$
. Then recall that
$\operatorname {\mathrm {Cl}}^+(D)^{\vee } = \text {Hom}(\operatorname {\mathrm {Cl}}^+(D), \mathbb {Q}/\mathbb {Z})$
. Then recall that
![]() $\operatorname {\mathrm {Cl}}^+(D)^{\vee }[2]$
is generated by the characters
$\operatorname {\mathrm {Cl}}^+(D)^{\vee }[2]$
is generated by the characters
![]() $\chi _p$
with p a prime dividing D. There is precisely one relation among these characters, which comes from the fact that
$\chi _p$
with p a prime dividing D. There is precisely one relation among these characters, which comes from the fact that
![]() $\chi _D$
is the trivial character when restricted to
$\chi _D$
is the trivial character when restricted to
![]() $\mathbb {Q}(\sqrt {D})$
. For a positive divisor
$\mathbb {Q}(\sqrt {D})$
. For a positive divisor
![]() $a \mid D$
, we have that
$a \mid D$
, we have that
![]() $\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(D)^{\vee }[4]$
if and only if
$\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(D)^{\vee }[4]$
if and only if
![]() $(a,-D)$
is an acceptable pair: that is,
$(a,-D)$
is an acceptable pair: that is,
![]() $(a,-D)_v=1$
for all
$(a,-D)_v=1$
for all
![]() $v \in \Omega $
.
$v \in \Omega $
.
Since D is not divisible by any primes congruent to
![]() $3 \bmod 4$
, we have for any positive
$3 \bmod 4$
, we have for any positive
![]() $a\mid D$
that
$a\mid D$
that
![]() $(a,D)_v=(a,-D)_v$
. In particular, we have for any positive
$(a,D)_v=(a,-D)_v$
. In particular, we have for any positive
![]() $a\mid D$
$a\mid D$
Now let
![]() $a, b\mid \Delta _{\mathbb {Q}(\sqrt {D})}$
such that
$a, b\mid \Delta _{\mathbb {Q}(\sqrt {D})}$
such that
![]() $\chi _a \in 2\operatorname {\mathrm {Cl}}^+(D)^{\vee }[4]$
and
$\chi _a \in 2\operatorname {\mathrm {Cl}}^+(D)^{\vee }[4]$
and
![]() $\mathfrak {B}_D(b) \in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
. Then for all cyclic degree
$\mathfrak {B}_D(b) \in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
. Then for all cyclic degree
![]() $4$
extensions
$4$
extensions
![]() $L/\mathbb {Q}(\sqrt {D})$
unramified at all finite places and containing
$L/\mathbb {Q}(\sqrt {D})$
unramified at all finite places and containing
![]() $\mathbb {Q}(\sqrt {a},\sqrt {D})$
, the Artin symbol
$\mathbb {Q}(\sqrt {a},\sqrt {D})$
, the Artin symbol
![]() $[\frac {L/\mathbb {Q}(\sqrt {D})}{\mathfrak {B}_D(b)}]$
always lands in the unique cyclic subgroup of order
$[\frac {L/\mathbb {Q}(\sqrt {D})}{\mathfrak {B}_D(b)}]$
always lands in the unique cyclic subgroup of order
![]() $2$
of
$2$
of
![]() $\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {D}))$
, since
$\operatorname {\mathrm {Gal}}(L/\mathbb {Q}(\sqrt {D}))$
, since
![]() $\mathfrak {B}_D(b)\in \operatorname {\mathrm {Cl}}^+(D)[2]$
. Furthermore, for a fixed a, the value of the symbol does not depend on the choice of L, since
$\mathfrak {B}_D(b)\in \operatorname {\mathrm {Cl}}^+(D)[2]$
. Furthermore, for a fixed a, the value of the symbol does not depend on the choice of L, since
![]() $\mathfrak {B}_D(b)\in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
. In this statement, we are implicitly identifying any two groups of size
$\mathfrak {B}_D(b)\in 2\operatorname {\mathrm {Cl}}^+(D)[4]$
. In this statement, we are implicitly identifying any two groups of size
![]() $2$
in the unique possible way. The value of this symbol is by definition
$2$
in the unique possible way. The value of this symbol is by definition
and we shall refer to it as the Artin pairing between
![]() $\chi _a$
and b. The two crucial features of this pairing are that it can be computed using Rédei symbols and that it determines
$\chi _a$
and b. The two crucial features of this pairing are that it can be computed using Rédei symbols and that it determines
![]() $4\operatorname {\mathrm {Cl}}^+(D)[8]$
and
$4\operatorname {\mathrm {Cl}}^+(D)[8]$
and
![]() $4\operatorname {\mathrm {Cl}}^+(D)^\vee [8]$
(namely, they are respectively the right and the left kernel of the pairing).
$4\operatorname {\mathrm {Cl}}^+(D)^\vee [8]$
(namely, they are respectively the right and the left kernel of the pairing).
Proposition 2.8. Let
![]() $(a, b)$
be a pair with
$(a, b)$
be a pair with
![]() $a, b \in \mathbb {Q}^{*}/(\mathbb {Q}^{*})^2$
and such that
$a, b \in \mathbb {Q}^{*}/(\mathbb {Q}^{*})^2$
and such that
![]() $\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime. Furthermore, assume that
$\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime. Furthermore, assume that
![]() $a, b> 0$
are not divisible by any prime congruent to
$a, b> 0$
are not divisible by any prime congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
. Let c be a squarefree divisor of
$4$
. Let c be a squarefree divisor of
![]() $\Delta _{\mathbb {Q}(\sqrt {ab})}$
, not necessarily positive. Assume that
$\Delta _{\mathbb {Q}(\sqrt {ab})}$
, not necessarily positive. Assume that
![]() $\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(ab)^{\vee }[4]$
and
$\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(ab)^{\vee }[4]$
and
![]() $\mathfrak {B}_{ab}(c) \in 2\operatorname {\mathrm {Cl}}^+(ab)[4]$
. Then the triple
$\mathfrak {B}_{ab}(c) \in 2\operatorname {\mathrm {Cl}}^+(ab)[4]$
. Then the triple
![]() $(a, b, c)$
is admissible, and we have that
$(a, b, c)$
is admissible, and we have that
Proof. Observe that
![]() $(a, b)$
and
$(a, b)$
and
![]() $(ab, c)$
are acceptable since
$(ab, c)$
are acceptable since
![]() $\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(ab)^{\vee }[4]$
and
$\chi _{a} \in 2\operatorname {\mathrm {Cl}}^+(ab)^{\vee }[4]$
and
![]() $\mathfrak {B}_{ab}(c) \in 2\operatorname {\mathrm {Cl}}^+(ab)[4]$
.
$\mathfrak {B}_{ab}(c) \in 2\operatorname {\mathrm {Cl}}^+(ab)[4]$
.
We claim that
![]() $(a, c)$
is acceptable. A similar argument shows that
$(a, c)$
is acceptable. A similar argument shows that
![]() $(b, c)$
is acceptable. Firstly,
$(b, c)$
is acceptable. Firstly,
![]() $a>0$
implies
$a>0$
implies
![]() $(a, c)_{\infty }=1$
. Now we check that
$(a, c)_{\infty }=1$
. Now we check that
![]() $(a, c)_{v}=1$
for all
$(a, c)_{v}=1$
for all
![]() $v \in \Omega $
finite and odd. If
$v \in \Omega $
finite and odd. If
![]() $v \nmid ac$
, we trivially have
$v \nmid ac$
, we trivially have
![]() $(a, c)_v=1$
. If v divides only a but not c, we have that
$(a, c)_v=1$
. If v divides only a but not c, we have that
![]() $(a, c)_v = (ab, c)_v = 1$
. If v divides only c but not a, we have that
$(a, c)_v = (ab, c)_v = 1$
. If v divides only c but not a, we have that
![]() $(a, c)_v = (a, ab)_v = 1$
. Now assume that v divides both a and c. Since
$(a, c)_v = (a, ab)_v = 1$
. Now assume that v divides both a and c. Since
![]() $\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime, we must have
$\Delta _{\mathbb {Q}(\sqrt {a})},\Delta _{\mathbb {Q}(\sqrt {b})}$
are coprime, we must have
![]() $v \nmid b$
. Also, by assumption,
$v \nmid b$
. Also, by assumption,
![]() $v^2$
cannot divide a or c, so
$v^2$
cannot divide a or c, so
![]() $(b, ac)_v=1$
. Therefore
$(b, ac)_v=1$
. Therefore
Since
![]() $(a, b)$
and
$(a, b)$
and
![]() $(ab, c)$
are acceptable, we have
$(ab, c)$
are acceptable, we have
so
![]() $(ab, ac)_v=1$
, as required. The remaining case
$(ab, ac)_v=1$
, as required. The remaining case
![]() $v=2$
follows from Hilbert reciprocity. This shows that
$v=2$
follows from Hilbert reciprocity. This shows that
![]() $(a, c)$
and similarly
$(a, c)$
and similarly
![]() $(b, c)$
are acceptable pairs.
$(b, c)$
are acceptable pairs.
Since
![]() $a, b$
are coprime and not divisible by any prime congruent to
$a, b$
are coprime and not divisible by any prime congruent to
![]() $3\bmod 4$
, we conclude that
$3\bmod 4$
, we conclude that
![]() $\gcd (\Delta _{\mathbb {Q}(\sqrt {a})}, \Delta _{\mathbb {Q}(\sqrt {b})}, \Delta _{\mathbb {Q}(\sqrt {c})})=1$
. Therefore the triple
$\gcd (\Delta _{\mathbb {Q}(\sqrt {a})}, \Delta _{\mathbb {Q}(\sqrt {b})}, \Delta _{\mathbb {Q}(\sqrt {c})})=1$
. Therefore the triple
![]() $(a, b, c)$
is admissible. Now observe that any
$(a, b, c)$
is admissible. Now observe that any
![]() $L \in \mathcal {F}_{a, b}^{\text {unr}}$
gives a cyclic degree
$L \in \mathcal {F}_{a, b}^{\text {unr}}$
gives a cyclic degree
![]() $4$
extension of
$4$
extension of
![]() $\mathbb {Q}(\sqrt {ab})$
that is unramified at all finite places and contains
$\mathbb {Q}(\sqrt {ab})$
that is unramified at all finite places and contains
![]() $\mathbb {Q}(\sqrt {a},\sqrt {b})$
. Therefore
$\mathbb {Q}(\sqrt {a},\sqrt {b})$
. Therefore
 $$ \begin{align*}\langle \chi_a, c \rangle_{ab} = \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{B}_{ab}(c)}\right] = [a, b, c] \end{align*} $$
$$ \begin{align*}\langle \chi_a, c \rangle_{ab} = \left[\frac{L/\mathbb{Q}(\sqrt{ab})}{\mathfrak{B}_{ab}(c)}\right] = [a, b, c] \end{align*} $$
as was to be shown.
We are now ready to prove our main algebraic results.
Theorem 2.9. Let
![]() $d \in \mathcal {D}$
. Let
$d \in \mathcal {D}$
. Let
![]() $p_1, p_2, q_1, q_2$
be primes that are
$p_1, p_2, q_1, q_2$
be primes that are
![]() $1$
modulo 4 and coprime to d. Let a be a positive divisor of d, and let b be any (possibly negative) divisor of d. Assume that
$1$
modulo 4 and coprime to d. Let a be a positive divisor of d, and let b be any (possibly negative) divisor of d. Assume that
-
1. Suppose
Then $$\begin{align*}\chi_a \in 2\operatorname{\mathrm{Cl}}^+(p_iq_jd)^\vee[4] \ \mathrm{for \ all} \ (i, j) \in i, j \in \{1, 2\}. \end{align*}$$
(2.3)
$$\begin{align*}\chi_a \in 2\operatorname{\mathrm{Cl}}^+(p_iq_jd)^\vee[4] \ \mathrm{for \ all} \ (i, j) \in i, j \in \{1, 2\}. \end{align*}$$
(2.3) $$ \begin{align} \langle \chi_a, b \rangle_{p_1q_1d} + \langle \chi_a, b \rangle_{p_1q_2d} + \langle \chi_a, b \rangle_{p_2q_1d} + \langle \chi_a, b \rangle_{p_2q_2d} = 0. \end{align} $$
$$ \begin{align} \langle \chi_a, b \rangle_{p_1q_1d} + \langle \chi_a, b \rangle_{p_1q_2d} + \langle \chi_a, b \rangle_{p_2q_1d} + \langle \chi_a, b \rangle_{p_2q_2d} = 0. \end{align} $$
-
2. Suppose instead
Then the triple $$\begin{align*}\chi_{p_ia} \in 2\operatorname{\mathrm{Cl}}^+(p_iq_jd)^\vee[4] \ \mathrm{for \ all}\ (i, j) \in i, j \in \{1, 2\}. \end{align*}$$
$$\begin{align*}\chi_{p_ia} \in 2\operatorname{\mathrm{Cl}}^+(p_iq_jd)^\vee[4] \ \mathrm{for \ all}\ (i, j) \in i, j \in \{1, 2\}. \end{align*}$$
 $(p_1p_2,q_1q_2, b)$
is admissible and (2.4)
$(p_1p_2,q_1q_2, b)$
is admissible and (2.4) $$ \begin{align} \langle \chi_{p_1a}, b \rangle_{p_1q_1d} + \langle \chi_{p_1a}, b \rangle_{p_1q_2d} + \langle \chi_{p_2a}, b \rangle_{p_2q_1d} + \langle \chi_{p_2a}, b \rangle_{p_2q_2d} = [p_1p_2, q_1q_2, b]. \end{align} $$
$$ \begin{align} \langle \chi_{p_1a}, b \rangle_{p_1q_1d} + \langle \chi_{p_1a}, b \rangle_{p_1q_2d} + \langle \chi_{p_2a}, b \rangle_{p_2q_1d} + \langle \chi_{p_2a}, b \rangle_{p_2q_2d} = [p_1p_2, q_1q_2, b]. \end{align} $$
Proof.
![]() $(\mathrm{i})$
By Proposition 2.8, we obtain that the four triples
$(\mathrm{i})$
By Proposition 2.8, we obtain that the four triples
![]() $(a,p_1q_1 \frac {d}{a}, b)$
,
$(a,p_1q_1 \frac {d}{a}, b)$
,
![]() $(a,p_1q_2\frac {d}{a}, b)$
,
$(a,p_1q_2\frac {d}{a}, b)$
,
![]() $(a,p_2q_1\frac {d}{a}, b)$
and
$(a,p_2q_1\frac {d}{a}, b)$
and
![]() $(a,p_2q_2\frac {d}{a}, b)$
are all admissible and the left-hand side of (2.3) equals
$(a,p_2q_2\frac {d}{a}, b)$
are all admissible and the left-hand side of (2.3) equals
 $$\begin{align*}\left[a,p_1q_1 \frac{d}{a}, b\right]+\left[a,p_1q_2\frac{d}{a}, b\right]+\left[a,p_2q_1\frac{d}{a}, b\right]+\left[a,p_2q_2\frac{d}{a}, b\right]. \end{align*}$$
$$\begin{align*}\left[a,p_1q_1 \frac{d}{a}, b\right]+\left[a,p_1q_2\frac{d}{a}, b\right]+\left[a,p_2q_1\frac{d}{a}, b\right]+\left[a,p_2q_2\frac{d}{a}, b\right]. \end{align*}$$
By Proposition 2.6, this sum equals
![]() $(\mathrm{ii})$
By Proposition 2.8, we know that the triples
$(\mathrm{ii})$
By Proposition 2.8, we know that the triples
![]() $(p_1a,q_1 \frac {d}{a}, b),(p_1a,q_2\frac {d}{a}, b),(p_2a,q_1\frac {d}{a}, b)$
and
$(p_1a,q_1 \frac {d}{a}, b),(p_1a,q_2\frac {d}{a}, b),(p_2a,q_1\frac {d}{a}, b)$
and
![]() $(p_2a,q_2\frac {d}{a}, b)$
are all admissible and that the left-hand side of (2.4) equals
$(p_2a,q_2\frac {d}{a}, b)$
are all admissible and that the left-hand side of (2.4) equals
 $$\begin{align*}\left[p_1a,q_1 \frac{d}{a}, b\right]+\left[p_1a,q_2\frac{d}{a}, b\right]+\left[p_2a,q_1\frac{d}{a}, b\right]+\left[p_2a,q_2\frac{d}{a}, b\right]. \end{align*}$$
$$\begin{align*}\left[p_1a,q_1 \frac{d}{a}, b\right]+\left[p_1a,q_2\frac{d}{a}, b\right]+\left[p_2a,q_1\frac{d}{a}, b\right]+\left[p_2a,q_2\frac{d}{a}, b\right]. \end{align*}$$
Applying Proposition 2.6, we find that
![]() $(p_1a,q_1q_2, b)$
and
$(p_1a,q_1q_2, b)$
and
![]() $(p_2a,q_1q_2, b)$
are also admissible and this sum equals
$(p_2a,q_1q_2, b)$
are also admissible and this sum equals
Another application of Proposition 2.6 shows that
![]() $(p_1p_2,q_1q_2, b)$
is admissible and the above sum is
$(p_1p_2,q_1q_2, b)$
is admissible and the above sum is
![]() $[p_1p_2,q_1q_2, b]$
, completing the proof.
$[p_1p_2,q_1q_2, b]$
, completing the proof.
We remark that it is possible to prove Proposition 2.6 without using Rédei reciprocity. It is precisely this approach that works in the generality of [Reference Smith18, Theorem 2.8]. The resulting argument is substantially more involved, so for brevity, we opted to use the proofs with Rédei reciprocity. Note that Theorem 2.10, Theorem 2.11 and Theorem 2.12 have no analogues in [Reference Smith18].
Theorem 2.10. Let
![]() $d \in \mathcal {D}$
. Take primes
$d \in \mathcal {D}$
. Take primes
![]() $p_1, p_2, q_1, q_2$
that are
$p_1, p_2, q_1, q_2$
that are
![]() $1$
modulo 4 and coprime to d. Let a be a positive divisor of d. We assume that
$1$
modulo 4 and coprime to d. Let a be a positive divisor of d. We assume that
Then we have
Moreover, the triple
![]() $(p_1p_2,q_1q_2,p_1p_2)$
is admissible and
$(p_1p_2,q_1q_2,p_1p_2)$
is admissible and
Proof. By equation (2.2),
![]() $\mathfrak {B}_{p_iq_jd}(p_ia) \in 2\operatorname {\mathrm {Cl}}^+(p_iq_jd)[4]$
implies that
$\mathfrak {B}_{p_iq_jd}(p_ia) \in 2\operatorname {\mathrm {Cl}}^+(p_iq_jd)[4]$
implies that
![]() $\chi _{p_ia} \in 2\operatorname {\mathrm {Cl}}^+(p_iq_jd)^{\vee }[4]$
for each
$\chi _{p_ia} \in 2\operatorname {\mathrm {Cl}}^+(p_iq_jd)^{\vee }[4]$
for each
![]() $i,j \in \{1,2\}$
.
$i,j \in \{1,2\}$
.
By Proposition 2.8, we conclude that
![]() $(p_1a,q_1\frac {d}{a},p_1a)$
,
$(p_1a,q_1\frac {d}{a},p_1a)$
,
![]() $(p_1a,q_2\frac {d}{a},p_1a)$
,
$(p_1a,q_2\frac {d}{a},p_1a)$
,
![]() $(p_2a,q_1\frac {d}{a},p_2a)$
and
$(p_2a,q_1\frac {d}{a},p_2a)$
and
![]() $(p_2a,q_2\frac {d}{a},p_2a)$
are all admissible, and furthermore that the left-hand side of (2.5) is
$(p_2a,q_2\frac {d}{a},p_2a)$
are all admissible, and furthermore that the left-hand side of (2.5) is
 $$\begin{align*}\left[p_1a,q_1\frac{d}{a},p_1a\right]+\left[p_1a,q_2\frac{d}{a},p_1a\right]+\left[p_2a,q_1\frac{d}{a},p_2a\right]+\left[p_2a,q_2\frac{d}{a},p_2a\right]. \end{align*}$$
$$\begin{align*}\left[p_1a,q_1\frac{d}{a},p_1a\right]+\left[p_1a,q_2\frac{d}{a},p_1a\right]+\left[p_2a,q_1\frac{d}{a},p_2a\right]+\left[p_2a,q_2\frac{d}{a},p_2a\right]. \end{align*}$$
Using Proposition 2.6, we have that
![]() $(p_1a,q_1q_2,p_1a)$
and
$(p_1a,q_1q_2,p_1a)$
and
![]() $(p_2a,q_1q_2,p_2a)$
are admissible triples, and the sum becomes
$(p_2a,q_1q_2,p_2a)$
are admissible triples, and the sum becomes
Next, since
![]() $p_1a,q_1q_2$
are coprime and
$p_1a,q_1q_2$
are coprime and
![]() $p_2a,q_1q_2$
are coprime, Proposition 2.7 implies that
$p_2a,q_1q_2$
are coprime, Proposition 2.7 implies that
![]() $(p_1a,q_1q_2,-q_1q_2)$
and
$(p_1a,q_1q_2,-q_1q_2)$
and
![]() $(p_2a,q_1q_2,-q_1q_2)$
are admissible, and the above sum is
$(p_2a,q_1q_2,-q_1q_2)$
are admissible, and the above sum is
By Proposition 2.6,
![]() $(p_1p_2,q_1q_2,-q_1q_2)$
is admissible, and the above sum is
$(p_1p_2,q_1q_2,-q_1q_2)$
is admissible, and the above sum is
Since
![]() $p_1p_2,q_1q_2$
are coprime, applying Proposition 2.7 again shows that
$p_1p_2,q_1q_2$
are coprime, applying Proposition 2.7 again shows that
![]() $(p_1p_2,q_1q_2,p_1p_2)$
is admissible and
$(p_1p_2,q_1q_2,p_1p_2)$
is admissible and
which gives the desired result.
Theorem 2.11. Let
![]() $d \in \mathcal {D}$
. Let
$d \in \mathcal {D}$
. Let
![]() $p_1, p_2, q_1, q_2$
be distinct primes that are
$p_1, p_2, q_1, q_2$
be distinct primes that are
![]() $1$
modulo 4 and coprime to d. Let
$1$
modulo 4 and coprime to d. Let
![]() $a, b$
be a positive divisors of d. We assume that
$a, b$
be a positive divisors of d. We assume that
Then we have that
Furthermore, we have that
 $$\begin{align*}\sum_{i,j \in \{1,2\}}\langle \chi_{p_ia}, b \rangle_{p_iq_jd}+\langle \chi_{b},p_ia \rangle_{p_iq_jd}=0. \end{align*}$$
$$\begin{align*}\sum_{i,j \in \{1,2\}}\langle \chi_{p_ia}, b \rangle_{p_iq_jd}+\langle \chi_{b},p_ia \rangle_{p_iq_jd}=0. \end{align*}$$
Proof. The first assertion follows from equation (2.2). By Proposition 2.8,
![]() $(p_ia,\frac {d}{a}q_j, b)$
and
$(p_ia,\frac {d}{a}q_j, b)$
and
![]() $(b,\frac {d}{b}p_iq_j, ap_i)$
are admissible for all choices of
$(b,\frac {d}{b}p_iq_j, ap_i)$
are admissible for all choices of
![]() $i,j$
in
$i,j$
in
![]() $\{1,2\}$
. Therefore the sum of the pairings in this proposition can be rewritten as
$\{1,2\}$
. Therefore the sum of the pairings in this proposition can be rewritten as
 $$\begin{align*}\sum_{i,j\in\{1,2\}}\left[p_ia,\frac{d}{a}q_j, b\right] +\left[b,\frac{d}{b}p_iq_j, ap_i\right]. \end{align*}$$
$$\begin{align*}\sum_{i,j\in\{1,2\}}\left[p_ia,\frac{d}{a}q_j, b\right] +\left[b,\frac{d}{b}p_iq_j, ap_i\right]. \end{align*}$$
Applying Proposition 2.6, we can rewrite this as
The first equality follows from Proposition 2.6, and the last equality follows from applying Theorem 2.5.
Theorem 2.12. Let
![]() $d \in \mathcal {D}$
. Let
$d \in \mathcal {D}$
. Let
![]() $p_1, p_2, q_1, q_2$
be distinct primes that are
$p_1, p_2, q_1, q_2$
be distinct primes that are
![]() $1$
modulo 4 and coprime to d. Let
$1$
modulo 4 and coprime to d. Let
![]() $a, b$
be positive divisors of d. We assume that
$a, b$
be positive divisors of d. We assume that
Then we have that
In addition, the triple
![]() $(p_1p_2,q_1q_2,-1)$
is admissible and
$(p_1p_2,q_1q_2,-1)$
is admissible and
 $$ \begin{align} \sum_{i, j \in \{1,2\}} \langle \chi_{p_ia}, q_jb \rangle_{p_iq_jd} + \langle \chi_{q_jb},p_ia \rangle_{p_iq_jd}= [p_1p_2, q_1q_2, -1]. \end{align} $$
$$ \begin{align} \sum_{i, j \in \{1,2\}} \langle \chi_{p_ia}, q_jb \rangle_{p_iq_jd} + \langle \chi_{q_jb},p_ia \rangle_{p_iq_jd}= [p_1p_2, q_1q_2, -1]. \end{align} $$
Proof. The first assertion follows as usual. By Proposition 2.8, we have that the triples
![]() $(p_ia,\frac {d}{a}q_j,q_jb),(q_jb,\frac {d}{b}p_i,p_ia)$
are admissible for each choice of
$(p_ia,\frac {d}{a}q_j,q_jb),(q_jb,\frac {d}{b}p_i,p_ia)$
are admissible for each choice of
![]() $i,j$
in
$i,j$
in
![]() $\{1,2\}$
, and the left-hand side of equation (2.6) equals
$\{1,2\}$
, and the left-hand side of equation (2.6) equals
 $$\begin{align*}\sum_{i,j \in \{1,2\}}\left[p_ia,\frac{d}{a}q_j,q_jb\right]+\left[q_jb,\frac{d}{b}p_i,p_ia\right]. \end{align*}$$
$$\begin{align*}\sum_{i,j \in \{1,2\}}\left[p_ia,\frac{d}{a}q_j,q_jb\right]+\left[q_jb,\frac{d}{b}p_i,p_ia\right]. \end{align*}$$
By Proposition 2.6, we can rewrite this sum of Rédei symbols as
 $$\begin{align*}\left[p_1p_2,\frac{d}{a}q_1, bq_1\right]+\left[p_1p_2,\frac{d}{a}q_2, bq_2\right]+\left[q_1q_2,\frac{d}{b}p_1, ap_1\right]+\left[q_1q_2,\frac{d}{b}p_2, ap_2\right]. \end{align*}$$
$$\begin{align*}\left[p_1p_2,\frac{d}{a}q_1, bq_1\right]+\left[p_1p_2,\frac{d}{a}q_2, bq_2\right]+\left[q_1q_2,\frac{d}{b}p_1, ap_1\right]+\left[q_1q_2,\frac{d}{b}p_2, ap_2\right]. \end{align*}$$
One readily checks that
![]() $p_i\frac {d}{b}$
is coprime to
$p_i\frac {d}{b}$
is coprime to
![]() $q_1q_2$
and
$q_1q_2$
and
![]() $q_j\frac {d}{a}$
is coprime to
$q_j\frac {d}{a}$
is coprime to
![]() $p_1p_2$
. Therefore, we can apply Proposition 2.7 to each of the terms in the above sum to obtain
$p_1p_2$
. Therefore, we can apply Proposition 2.7 to each of the terms in the above sum to obtain
 $$\begin{align*} & \left[p_1p_2,\frac{d}{a}q_1,-dabp_1p_2\right] +\left[p_1p_2,\frac{d}{a}q_2,-dabp_1p_2\right] +\left[q_1q_2,\frac{d}{b}p_1,-dabq_1q_2\right]+\left[q_1q_2,\frac{d}{b}p_2,-dabq_1q_2\right]. \end{align*}$$
$$\begin{align*} & \left[p_1p_2,\frac{d}{a}q_1,-dabp_1p_2\right] +\left[p_1p_2,\frac{d}{a}q_2,-dabp_1p_2\right] +\left[q_1q_2,\frac{d}{b}p_1,-dabq_1q_2\right]+\left[q_1q_2,\frac{d}{b}p_2,-dabq_1q_2\right]. \end{align*}$$
Applying Proposition 2.6, we can further simplify this and get
Since
![]() $p_1p_2$
and
$p_1p_2$
and
![]() $q_1q_2$
are coprime, we can apply Proposition 2.7 and get that
$q_1q_2$
are coprime, we can apply Proposition 2.7 and get that
![]() $(p_1p_2,q_1q_2,-1)$
is admissible and the above Rédei symbol equals
$(p_1p_2,q_1q_2,-1)$
is admissible and the above Rédei symbol equals
![]() $[p_1p_2,q_1q_2,-1]$
as required.
$[p_1p_2,q_1q_2,-1]$
as required.
3 A combinatorial result
Let
![]() $X_1, \ldots , X_m$
be finite, nonempty sets, and let
$X_1, \ldots , X_m$
be finite, nonempty sets, and let
![]() $X := X_1 \times \ldots \times X_m$
. Put
$X := X_1 \times \ldots \times X_m$
. Put
Given two elements
![]() $x_1, x_2 \in X$
and
$x_1, x_2 \in X$
and
![]() $\mathbf {v} \in \{1, 2\}^m$
, we define
$\mathbf {v} \in \{1, 2\}^m$
, we define
![]() $\mathbf {v}(x_1, x_2)$
to be the unique element
$\mathbf {v}(x_1, x_2)$
to be the unique element
![]() $y \in X$
such that
$y \in X$
such that
![]() $\pi _j(y) = \pi _j(x_{\pi _j(\mathbf {v})})$
. Let
$\pi _j(y) = \pi _j(x_{\pi _j(\mathbf {v})})$
. Let
![]() $d: V \rightarrow W$
be the linear map given by
$d: V \rightarrow W$
be the linear map given by
We define
![]() $\mathcal {A}(X) := \operatorname {\mathrm {im}}(d)$
.
$\mathcal {A}(X) := \operatorname {\mathrm {im}}(d)$
.
Lemma 3.1. We have that
 $$\begin{align*}\dim_{\mathbb{F}_2} \mathcal{A}(X) = \prod_{i = 1}^m \left(|X_i| - 1\right). \end{align*}$$
$$\begin{align*}\dim_{\mathbb{F}_2} \mathcal{A}(X) = \prod_{i = 1}^m \left(|X_i| - 1\right). \end{align*}$$
Proof. See Proposition 9.3 of Koymans and Pagano [Reference Koymans and Pagano13].
Definition 3.2. Let
![]() $\epsilon> 0$
be given. We say that F is
$\epsilon> 0$
be given. We say that F is
![]() $\epsilon $
-bad if
$\epsilon $
-bad if
 $$\begin{align*}\left|F^{-1}(0) - \frac{|X|}{2}\right| \geq \epsilon |X|. \end{align*}$$
$$\begin{align*}\left|F^{-1}(0) - \frac{|X|}{2}\right| \geq \epsilon |X|. \end{align*}$$
We say that
![]() $g \in \mathcal {A}(X)$
is
$g \in \mathcal {A}(X)$
is
![]() $\epsilon $
-bad if there is
$\epsilon $
-bad if there is
![]() $\epsilon $
-bad F such that
$\epsilon $
-bad F such that
![]() $dF = g$
.
$dF = g$
.
In our application, we shall be able to prove distributional properties of g by using the Chebotarev density theorem. However, we have no direct control over F itself. Nevertheless, the following theorem will allow us to prove the desired equidistribution for F. Note the similarity to Proposition 4.3 in Smith [Reference Smith18]. Since we are dealing with the
![]() $8$
-rank, we shall not need the more complicated Proposition 4.4 in Smith [Reference Smith18].
$8$
-rank, we shall not need the more complicated Proposition 4.4 in Smith [Reference Smith18].
Theorem 3.3. Let
![]() $\epsilon> 0$
be given. Then we have
$\epsilon> 0$
be given. Then we have
Proof. Hoeffding’s inequality shows that the proportion of F that are
![]() $\epsilon $
-bad is at most
$\epsilon $
-bad is at most
Define
 $$\begin{align*}a := |X| - \prod_{i = 1}^m \left(|X_i| - 1\right). \end{align*}$$
$$\begin{align*}a := |X| - \prod_{i = 1}^m \left(|X_i| - 1\right). \end{align*}$$
By Lemma 3.1, we see that the kernel of d is an a-dimensional vector space. Combining this with equation (3.1), we infer that
which is the theorem.
4 Prime divisors
In [Reference Smith18, Section 5], Smith proved that several properties pertaining to the spacing of prime divisors of integers in the set
![]() $\{1\leq n\leq N:\ \omega (n) = r,\ p \mid n \Rightarrow p> D\}$
occur frequently. Using different methods, we will obtain similar results on squarefree integers with no prime factor congruent to
$\{1\leq n\leq N:\ \omega (n) = r,\ p \mid n \Rightarrow p> D\}$
occur frequently. Using different methods, we will obtain similar results on squarefree integers with no prime factor congruent to
![]() $3 \bmod 4$
.
$3 \bmod 4$
.
Define
![]() $S(N) := \{1 \leq n < N: p\mid n \Rightarrow p \not \equiv 3\bmod 4,\ n\text { squarefree}\}$
,
$S(N) := \{1 \leq n < N: p\mid n \Rightarrow p \not \equiv 3\bmod 4,\ n\text { squarefree}\}$
,
![]() $S_r(N) := \{n \in S(N): \omega (n)=r\}$
and
$S_r(N) := \{n \in S(N): \omega (n)=r\}$
and
![]() $\mu := \frac {1}{2}\log \log N$
. A classical result by Landau [Reference Landau14] shows that
$\mu := \frac {1}{2}\log \log N$
. A classical result by Landau [Reference Landau14] shows that
 $$\begin{align*}\Phi(N) := |S(N)| = \frac{CN}{\sqrt{\log N}} + o\left(\frac{N}{\sqrt{\log N}}\right) \end{align*}$$
$$\begin{align*}\Phi(N) := |S(N)| = \frac{CN}{\sqrt{\log N}} + o\left(\frac{N}{\sqrt{\log N}}\right) \end{align*}$$
for some constant
![]() $C> 0$
. We recall the prime number theorem for arithmetic progressions
$C> 0$
. We recall the prime number theorem for arithmetic progressions
Write
![]() $\Phi _r(N) := |S_r(N)|$
. Then following the proof of the Sathé–Selberg theorem [Reference Selberg16], one can deduce that there exists a constant
$\Phi _r(N) := |S_r(N)|$
. Then following the proof of the Sathé–Selberg theorem [Reference Selberg16], one can deduce that there exists a constant
![]() $A> 0$
such that for all
$A> 0$
such that for all
![]() $r < 10\mu $
and all
$r < 10\mu $
and all
![]() $N \geq A$
,
$N \geq A$
,
 $$ \begin{align} \frac{A^{-1}N}{\log N} \frac{\left(\frac{1}{2}\log\log N\right)^{r - 1}}{(r - 1)!} \leq \Phi_r(N) \leq \frac{AN}{\log N} \frac{\left(\frac{1}{2}\log\log N\right)^{r - 1}}{(r - 1)!}. \end{align} $$
$$ \begin{align} \frac{A^{-1}N}{\log N} \frac{\left(\frac{1}{2}\log\log N\right)^{r - 1}}{(r - 1)!} \leq \Phi_r(N) \leq \frac{AN}{\log N} \frac{\left(\frac{1}{2}\log\log N\right)^{r - 1}}{(r - 1)!}. \end{align} $$
We can easily bound the number of integers with more than, say,
![]() $10\mu $
prime divisors by computing the average number of divisors. Then by standard bounds for the tail of the Poisson distribution, it follows that
$10\mu $
prime divisors by computing the average number of divisors. Then by standard bounds for the tail of the Poisson distribution, it follows that
 $$ \begin{align} \frac{|\{n \in S(N) : |\omega(n) - \mu|> \mu^{2/3}\}|}{|S(N)|} \ll \exp\left(-\frac{1}{3}\mu^{1/3}\right). \end{align} $$
$$ \begin{align} \frac{|\{n \in S(N) : |\omega(n) - \mu|> \mu^{2/3}\}|}{|S(N)|} \ll \exp\left(-\frac{1}{3}\mu^{1/3}\right). \end{align} $$
In the following, for any
![]() $n\in S(N)$
, write
$n\in S(N)$
, write
![]() $r=\omega (n)$
and list the distinct prime factors of n as
$r=\omega (n)$
and list the distinct prime factors of n as
![]() $p_1<p_2<\dots <p_r$
. We will prove that almost all
$p_1<p_2<\dots <p_r$
. We will prove that almost all
![]() $n\in S_r(N)$
have three particular types of spacing.
$n\in S_r(N)$
have three particular types of spacing.
Theorem 4.1. Let
![]() $\epsilon>0$
. Take
$\epsilon>0$
. Take
![]() $y_1>3$
and
$y_1>3$
and
![]() $\eta>1$
. Assume
$\eta>1$
. Assume
Then
-
1. other than
 $\ll _\epsilon \Phi _r(N)\left ((\log y_1)^{-1}+(\log x)^{-1/2+\epsilon }\right )$
exceptions, all
$\ll _\epsilon \Phi _r(N)\left ((\log y_1)^{-1}+(\log x)^{-1/2+\epsilon }\right )$
exceptions, all
 $n\in S_r(N)$
are comfortably spaced above
$n\in S_r(N)$
are comfortably spaced above
 $y_1$
:
$y_1$
:
 $2y_1<p_i<p_{i+1}/2$
for any
$2y_1<p_i<p_{i+1}/2$
for any
 $p_i>y_1$
;
$p_i>y_1$
; -
2. other than
 $\ll \Phi _r(N)\exp (-k\eta )$
exceptions, where k is an absolute constant, all
$\ll \Phi _r(N)\exp (-k\eta )$
exceptions, where k is an absolute constant, all
 $n\in S_r(N)$
are
$n\in S_r(N)$
are
 $\eta $
-regularly spaced:
$\eta $
-regularly spaced:  $$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|<\eta ^{1/5}\max\{i,\eta \}^{4/5} \ \mathrm{for \ all} \ i<\frac{1}{3}r; \end{align*}$$
$$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|<\eta ^{1/5}\max\{i,\eta \}^{4/5} \ \mathrm{for \ all} \ i<\frac{1}{3}r; \end{align*}$$
-
3. other than
 $\ll _\epsilon \Phi _r(N)\exp \left (-(\log \log \log N)^{1/3-\epsilon }\right )$
exceptions, all
$\ll _\epsilon \Phi _r(N)\exp \left (-(\log \log \log N)^{1/3-\epsilon }\right )$
exceptions, all
 $n\in S_r(N)$
are extravagantly spaced:
$n\in S_r(N)$
are extravagantly spaced:  $$\begin{align*}\log p_i\geq (\log\log p_i)^2\cdot \log\log \log N\cdot \sum_{j=1}^{i-1}\log p_j \ \mathrm{for \ some} \ \frac{1}{2}r^{1/2}<i<\frac{1}{2}r. \end{align*}$$
$$\begin{align*}\log p_i\geq (\log\log p_i)^2\cdot \log\log \log N\cdot \sum_{j=1}^{i-1}\log p_j \ \mathrm{for \ some} \ \frac{1}{2}r^{1/2}<i<\frac{1}{2}r. \end{align*}$$
4.1 Some estimates
4.1.1 Upper bound for rough numbers
Mertens’ theorem shows that there exist constants
![]() $c,M>0$
such that for any
$c,M>0$
such that for any
![]() $N>2$
,
$N>2$
,
 $$\begin{align*}\sum_{\substack{p\leq N\\p\not\equiv 3\bmod 4}}\frac{1}{p} =\frac{1}{2}\log\log N+M+O\left(\exp\left(-c\sqrt{\log N}\right)\right). \end{align*}$$
$$\begin{align*}\sum_{\substack{p\leq N\\p\not\equiv 3\bmod 4}}\frac{1}{p} =\frac{1}{2}\log\log N+M+O\left(\exp\left(-c\sqrt{\log N}\right)\right). \end{align*}$$
Fixing some large enough absolute constant
![]() $B_1>0$
, we have for any
$B_1>0$
, we have for any
![]() $N>2$
$N>2$
 $$\begin{align*}\frac{1}{2}\log\log N- B_1\leq \sum_{\substack{p\leq N\\p\not\equiv 3\bmod 4}}\frac{1}{p} \leq \frac{1}{2}\log\log N+ B_1. \end{align*}$$
$$\begin{align*}\frac{1}{2}\log\log N- B_1\leq \sum_{\substack{p\leq N\\p\not\equiv 3\bmod 4}}\frac{1}{p} \leq \frac{1}{2}\log\log N+ B_1. \end{align*}$$
For any set of primes E, define
 $$\begin{align*}E(N) := \sum_{\substack{p\leq N\\ p\in E}} \frac{1}{p}. \end{align*}$$
$$\begin{align*}E(N) := \sum_{\substack{p\leq N\\ p\in E}} \frac{1}{p}. \end{align*}$$
We also define
![]() $\omega _E(n)$
to be the number of prime divisors of n that are in E. We will apply the following theorem by Tudesq [Reference Tudesq21, Theorem 2].
$\omega _E(n)$
to be the number of prime divisors of n that are in E. We will apply the following theorem by Tudesq [Reference Tudesq21, Theorem 2].
Theorem 4.2. There exists an absolute constant
![]() $B_2>0$
such that
$B_2>0$
such that
 $$\begin{align*}|\{n\leq N: \omega_{E_j}(n)=k_j \ \mathrm{for} \ 0\leq j\leq l\}| \ll N\exp\,\left(-\sum_{j=0}^l E_j(N)\right) \prod_{j=0}^l\frac{\left(E_j(N)+B_2\right)^{k_j}}{k_j!} \end{align*}$$
$$\begin{align*}|\{n\leq N: \omega_{E_j}(n)=k_j \ \mathrm{for} \ 0\leq j\leq l\}| \ll N\exp\,\left(-\sum_{j=0}^l E_j(N)\right) \prod_{j=0}^l\frac{\left(E_j(N)+B_2\right)^{k_j}}{k_j!} \end{align*}$$
for all
![]() $N\geq 1$
,
$N\geq 1$
,
![]() $l\geq 0$
,
$l\geq 0$
,
![]() $E_j$
pairwise disjoint sets of primes,
$E_j$
pairwise disjoint sets of primes,
![]() $k_j\geq 0$
.
$k_j\geq 0$
.
In our application, we will take
![]() $E_0$
to be the set of primes congruent to
$E_0$
to be the set of primes congruent to
![]() $3\bmod 4$
and
$3\bmod 4$
and
![]() $E_0,E_1,\ldots ,E_l$
to be pairwise disjoint sets of primes so that
$E_0,E_1,\ldots ,E_l$
to be pairwise disjoint sets of primes so that
![]() $\cup _{j=0}^l E_j$
contains all primes. Also take
$\cup _{j=0}^l E_j$
contains all primes. Also take
![]() $k_0=0$
and
$k_0=0$
and
![]() $k_1+\cdots +k_l=r$
. Then
$k_1+\cdots +k_l=r$
. Then
 $$\begin{align*}|\{n\in S_r(N): \omega_{E_j}(n)=k_j,\ 1\leq j\leq l\}| \ll \frac{N}{\log N}\prod_{j=1}^l\frac{\left(E_j(N)+B_2\right)^{k_j}}{k_j!}. \end{align*}$$
$$\begin{align*}|\{n\in S_r(N): \omega_{E_j}(n)=k_j,\ 1\leq j\leq l\}| \ll \frac{N}{\log N}\prod_{j=1}^l\frac{\left(E_j(N)+B_2\right)^{k_j}}{k_j!}. \end{align*}$$
We set
![]() $B := \max (B_1 + B_2, 100)$
, where
$B := \max (B_1 + B_2, 100)$
, where
![]() $B_2$
is the absolute constant from Theorem 4.2.
$B_2$
is the absolute constant from Theorem 4.2.
4.1.2 Upper bound for smooth numbers
Define
so that
![]() $|\Psi _r(N, y)|$
is the size of the set of y-smooth numbers in
$|\Psi _r(N, y)|$
is the size of the set of y-smooth numbers in
![]() $S_r(N)$
.
$S_r(N)$
.
We will need an upper bound for smooth numbers for small
![]() $u:=\log N/\log y$
. There are works treating the number of prime factors of smooth numbers [Reference Alladi1, Reference Hensley10, Reference Hildebrand11], but none of them explicitly give a formula for the range of small u we are interested in. We prove an upper bound here that is sufficient for our application, although more work could be done to obtain a more precise estimate.
$u:=\log N/\log y$
. There are works treating the number of prime factors of smooth numbers [Reference Alladi1, Reference Hensley10, Reference Hildebrand11], but none of them explicitly give a formula for the range of small u we are interested in. We prove an upper bound here that is sufficient for our application, although more work could be done to obtain a more precise estimate.
Lemma 4.3. Fix some
![]() $\epsilon \in (0, 1)$
. There exists some large enough
$\epsilon \in (0, 1)$
. There exists some large enough
![]() $A>0$
such that the following holds. Take
$A>0$
such that the following holds. Take
![]() $N>y>2$
and some integer
$N>y>2$
and some integer
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $\frac {1}{2}k<\frac {1}{2}\log \log y<2k$
and
$\frac {1}{2}k<\frac {1}{2}\log \log y<2k$
and
![]() $u:=\frac {\log N}{\log y}<(\log N)^{1-\epsilon }$
, and assume
$u:=\frac {\log N}{\log y}<(\log N)^{1-\epsilon }$
, and assume
![]() $u>A$
. Then
$u>A$
. Then
 $$\begin{align*}\Psi_k(N,y)\leq\frac{u^{-u}N}{\log y}\cdot\frac{(\frac{1}{2}\log\log y)^{k-1}}{(k-1)!}. \end{align*}$$
$$\begin{align*}\Psi_k(N,y)\leq\frac{u^{-u}N}{\log y}\cdot\frac{(\frac{1}{2}\log\log y)^{k-1}}{(k-1)!}. \end{align*}$$
Proof. We have
 $$ \begin{align} (\log N)\Psi_k(N,y)=\sum_{n\in\Psi_k(N,y)}\log n+\sum_{n\in\Psi_k(N,y)}\log \frac{N}{n}. \end{align} $$
$$ \begin{align} (\log N)\Psi_k(N,y)=\sum_{n\in\Psi_k(N,y)}\log n+\sum_{n\in\Psi_k(N,y)}\log \frac{N}{n}. \end{align} $$
We first treat the first term, which is the main contribution. Factoring each
![]() $n\in \Psi _k(N,y)$
gives
$n\in \Psi _k(N,y)$
gives
 $$ \begin{align} \sum_{n\in\Psi_k(N,y)}\log n \leq \sum_{m\in \Psi_{k-1}(N,y)}\sum_{\substack{p<\min\left\{\frac{N}{m},y\right\}\\ p\not\equiv 3\bmod 4}} \log p. \end{align} $$
$$ \begin{align} \sum_{n\in\Psi_k(N,y)}\log n \leq \sum_{m\in \Psi_{k-1}(N,y)}\sum_{\substack{p<\min\left\{\frac{N}{m},y\right\}\\ p\not\equiv 3\bmod 4}} \log p. \end{align} $$
Indeed, for every
![]() $n \in \Psi _k(N, y)$
and every prime divisor p of n, we see that the pair
$n \in \Psi _k(N, y)$
and every prime divisor p of n, we see that the pair
![]() $(n/p, p)$
contributes
$(n/p, p)$
contributes
![]() $\log p$
to the sum on the RHS of equation (4.5) so that the total contribution of n is
$\log p$
to the sum on the RHS of equation (4.5) so that the total contribution of n is
![]() $\log n$
. Now, taking any
$\log n$
. Now, taking any
![]() $0<\sigma <1$
, we have
$0<\sigma <1$
, we have
 $$\begin{align*}\sum_{\substack{p<\min\left\{\frac{N}{m},y\right\}\\ p\not\equiv 3\bmod 4}} \log p\ll \min\left\{\frac{N}{m},y\right\}\leq \left( \frac{N}{m}\right)^{\sigma}y^{1-\sigma}. \end{align*}$$
$$\begin{align*}\sum_{\substack{p<\min\left\{\frac{N}{m},y\right\}\\ p\not\equiv 3\bmod 4}} \log p\ll \min\left\{\frac{N}{m},y\right\}\leq \left( \frac{N}{m}\right)^{\sigma}y^{1-\sigma}. \end{align*}$$
Then, writing
![]() $\frac {1}{m}=\prod _{p\mid m}\frac {1}{p}$
, equation (4.5) becomes
$\frac {1}{m}=\prod _{p\mid m}\frac {1}{p}$
, equation (4.5) becomes
 $$\begin{align*}\sum_{n\in\Psi_k(N,y)}\log n\ll N^{\sigma}y^{1-\sigma}\sum_{m\in \Psi_{k-1}\left(N,y\right)} \frac{1}{m^{\sigma}}\ll \frac{N^{\sigma}y^{1-\sigma}}{(k-1)!}\left(\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}\right)^{k-1}. \end{align*}$$
$$\begin{align*}\sum_{n\in\Psi_k(N,y)}\log n\ll N^{\sigma}y^{1-\sigma}\sum_{m\in \Psi_{k-1}\left(N,y\right)} \frac{1}{m^{\sigma}}\ll \frac{N^{\sigma}y^{1-\sigma}}{(k-1)!}\left(\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}\right)^{k-1}. \end{align*}$$
Take
![]() $\sigma =1-\frac {\log (u\log u)}{\log y}$
, which is positive and tends to
$\sigma =1-\frac {\log (u\log u)}{\log y}$
, which is positive and tends to
![]() $1$
since
$1$
since
![]() $u<(\log N)^{1-\epsilon }$
. Then
$u<(\log N)^{1-\epsilon }$
. Then
![]() $N^{\sigma }=\frac {N}{(u\log u)^u}$
and
$N^{\sigma }=\frac {N}{(u\log u)^u}$
and
![]() $y^{1-\sigma }=u\log u$
. Noting that
$y^{1-\sigma }=u\log u$
. Noting that
![]() $\operatorname {\mathrm {Li}}(t)=\frac {t}{\log t}+O(\frac {t}{(\log t)^2})$
and
$\operatorname {\mathrm {Li}}(t)=\frac {t}{\log t}+O(\frac {t}{(\log t)^2})$
and
![]() $\operatorname {\mathrm {Ei}}(1/t)=-\log t+O(1)$
as
$\operatorname {\mathrm {Ei}}(1/t)=-\log t+O(1)$
as
![]() $t \rightarrow \infty $
, we have
$t \rightarrow \infty $
, we have
 $$\begin{align*}\int_{e<t<y}\frac{dt}{t^{\sigma}\log t} =\operatorname{\mathrm{Li}}(u\log u)-\operatorname{\mathrm{Ei}}\left(\frac{\log(u\log u)}{\log y}\right) =\log\log y+u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right). \end{align*}$$
$$\begin{align*}\int_{e<t<y}\frac{dt}{t^{\sigma}\log t} =\operatorname{\mathrm{Li}}(u\log u)-\operatorname{\mathrm{Ei}}\left(\frac{\log(u\log u)}{\log y}\right) =\log\log y+u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right). \end{align*}$$
Therefore, evaluating the Stieltjes integral
![]() $\int _{t<y}\frac {d\pi (t)}{2t^{\sigma }}$
gives
$\int _{t<y}\frac {d\pi (t)}{2t^{\sigma }}$
gives
 $$\begin{align*}\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}=\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right). \end{align*}$$
$$\begin{align*}\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}=\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right). \end{align*}$$
Putting the above together, we obtain
 $$\begin{align*}\sum_{n\in\Psi_k(N,y)}\log n \ll \frac{N}{(u\log u)^{u-1}}\cdot\frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}}{(k-1)!}. \end{align*}$$
$$\begin{align*}\sum_{n\in\Psi_k(N,y)}\log n \ll \frac{N}{(u\log u)^{u-1}}\cdot\frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}}{(k-1)!}. \end{align*}$$
The second sum in equation (4.4) is at most
 $$\begin{align*}\frac{N^\sigma}{\sigma} \sum_{n\in \Psi_k(N,y)}\frac{1}{n^\sigma} \leq \frac{N^\sigma}{\sigma \cdot k!} \left(\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}\right)^k \ll \frac{N}{(u\log u)^u}\cdot \frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^k}{k!}. \end{align*}$$
$$\begin{align*}\frac{N^\sigma}{\sigma} \sum_{n\in \Psi_k(N,y)}\frac{1}{n^\sigma} \leq \frac{N^\sigma}{\sigma \cdot k!} \left(\sum_{\substack{p<y\\ p\not\equiv 3\bmod 4}}\frac{1}{p^{\sigma}}\right)^k \ll \frac{N}{(u\log u)^u}\cdot \frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^k}{k!}. \end{align*}$$
Since
![]() $\log \log y/2k$
is bounded, putting back in equation (4.4) yields
$\log \log y/2k$
is bounded, putting back in equation (4.4) yields
 $$ \begin{align*} \Psi_k(N,y) \ll \frac{1}{(u\log u)^{u-1}}\cdot \frac{N}{\log N}\cdot \frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}}{(k-1)!}. \end{align*} $$
$$ \begin{align*} \Psi_k(N,y) \ll \frac{1}{(u\log u)^{u-1}}\cdot \frac{N}{\log N}\cdot \frac{\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}}{(k-1)!}. \end{align*} $$
We have
 $$ \begin{align*} &\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1} = \left(\frac{1}{2}\log\log y\right)^{k - 1} \cdot \left(1 + \frac{u}{\log \log y}\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}. \end{align*} $$
$$ \begin{align*} &\left(\frac{1}{2}\log\log y+\frac{1}{2}u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1} = \left(\frac{1}{2}\log\log y\right)^{k - 1} \cdot \left(1 + \frac{u}{\log \log y}\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{k-1}. \end{align*} $$
Since
![]() $k < \log \log y$
, we get that this is at most
$k < \log \log y$
, we get that this is at most
 $$\begin{align*}\left(1 + \frac{u}{\log \log y}\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{\log \log y} \leq e^{u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)}. \end{align*}$$
$$\begin{align*}\left(1 + \frac{u}{\log \log y}\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)\right)^{\log \log y} \leq e^{u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)}. \end{align*}$$
Because
 $$\begin{align*}\frac{e^{u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)}}{(u \log u)^{u - 1}} \ll u^{-u + 1} = u^{-u} \cdot \frac{\log N}{\log y} \end{align*}$$
$$\begin{align*}\frac{e^{u\left(1+O\left(\frac{\log\log u}{\log u}\right)\right)}}{(u \log u)^{u - 1}} \ll u^{-u + 1} = u^{-u} \cdot \frac{\log N}{\log y} \end{align*}$$
for sufficiently large u, this implies that
 $$\begin{align*}\Psi_k(N,y) \ll u^{-u} \cdot\frac{N}{\log y}\cdot\frac{\left(\frac{1}{2}\log\log y\right)^{k-1}}{(k-1)!} \end{align*}$$
$$\begin{align*}\Psi_k(N,y) \ll u^{-u} \cdot\frac{N}{\log y}\cdot\frac{\left(\frac{1}{2}\log\log y\right)^{k-1}}{(k-1)!} \end{align*}$$
as desired.
4.2 Proof of Theorem 4.1
4.2.1 Proof of Theorem 4.11
The number of
![]() $n\in S_r(N)$
for which
$n\in S_r(N)$
for which
is bounded by
 $$\begin{align*}\sum_{\substack{y_1<p_i<2y_1\\p\equiv 1\bmod 4}}\Phi_{r-1}\left(\frac{N}{p}\right) +\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p\equiv 1\bmod 4}}\Phi_{r-2}\left(\frac{N}{pq}\right) .\end{align*}$$
$$\begin{align*}\sum_{\substack{y_1<p_i<2y_1\\p\equiv 1\bmod 4}}\Phi_{r-1}\left(\frac{N}{p}\right) +\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p\equiv 1\bmod 4}}\Phi_{r-2}\left(\frac{N}{pq}\right) .\end{align*}$$
Split the sum into the cases
![]() $p<N^{1/4}$
and
$p<N^{1/4}$
and
![]() $p>N^{1/4}$
. First, bound the sum
$p>N^{1/4}$
. First, bound the sum
![]() $p<N^{1/4}$
and assume
$p<N^{1/4}$
and assume
![]() $y_1<N^{1/4}$
; otherwise the sum is zero. Using equation (4.1), we see that the sum is bounded by
$y_1<N^{1/4}$
; otherwise the sum is zero. Using equation (4.1), we see that the sum is bounded by
 $$\begin{align*}\ll \Phi_r(N)\sum_{\substack{y_1<p<2y_1\\p\equiv 1\bmod 4}}\frac{1}{p} +\Phi_r(N)\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p\equiv 1\bmod 4}}\frac{1}{pq} \ll\frac{\Phi_r(N)}{\log y_1}. \end{align*}$$
$$\begin{align*}\ll \Phi_r(N)\sum_{\substack{y_1<p<2y_1\\p\equiv 1\bmod 4}}\frac{1}{p} +\Phi_r(N)\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p\equiv 1\bmod 4}}\frac{1}{pq} \ll\frac{\Phi_r(N)}{\log y_1}. \end{align*}$$
The sum
![]() $p>N^{1/4}$
is similarly bounded by
$p>N^{1/4}$
is similarly bounded by
 $$\begin{align*}N \sum_{\substack{y_1<p<2y_1\\p>N^{1/4}\\p\equiv 1\bmod 4}}\frac{1}{p}+N\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p>N^{1/4}\\p\equiv 1\bmod 4}}\frac{1}{pq} \ll \frac{N}{\log N} \ll_\epsilon \frac{\Phi_r(N)}{(\log{N})^{1/2-\epsilon}}, \end{align*}$$
$$\begin{align*}N \sum_{\substack{y_1<p<2y_1\\p>N^{1/4}\\p\equiv 1\bmod 4}}\frac{1}{p}+N\sum_{\substack{y_1<q<\sqrt{N}\\q\equiv 1\bmod 4}}\sum_{\substack{q<p<2q\\p>N^{1/4}\\p\equiv 1\bmod 4}}\frac{1}{pq} \ll \frac{N}{\log N} \ll_\epsilon \frac{\Phi_r(N)}{(\log{N})^{1/2-\epsilon}}, \end{align*}$$
completing the proof of part (i).
4.2.2 Proof of Theorem 4.12
Recall that
![]() $B = \max (B_1 + B_2, 100)$
.
$B = \max (B_1 + B_2, 100)$
.
Lemma 4.4. Then there exist some
![]() $A>0$
such that the following holds. Assume r satisfies equation (4.3), and take
$A>0$
such that the following holds. Assume r satisfies equation (4.3), and take
![]() $1\leq i\leq \frac {1}{2} r$
. Let
$1\leq i\leq \frac {1}{2} r$
. Let
![]() $\max \{200B,i^{4/5}\} \leq \lambda < \frac {1}{3}r$
. For all
$\max \{200B,i^{4/5}\} \leq \lambda < \frac {1}{3}r$
. For all
![]() $N>A$
,
$N>A$
,
 $$\begin{align*}\left|\left\{n \in S_r(N) : \left|\frac{1}{2}\log\log p_i-i\right|>\lambda\right\}\right| \ll \Phi_r(N) \exp\left(-\frac{\lambda^2}{100(i+\lambda)}\right). \end{align*}$$
$$\begin{align*}\left|\left\{n \in S_r(N) : \left|\frac{1}{2}\log\log p_i-i\right|>\lambda\right\}\right| \ll \Phi_r(N) \exp\left(-\frac{\lambda^2}{100(i+\lambda)}\right). \end{align*}$$
Proof. We apply Theorem 4.2 with
![]() $E_0$
the set of primes that are
$E_0$
the set of primes that are
![]() $3$
modulo
$3$
modulo
![]() $4$
,
$4$
,
![]() $E_1$
the set of primes p with
$E_1$
the set of primes p with
![]() $\frac {1}{2} \log \log p < i + \lambda $
and
$\frac {1}{2} \log \log p < i + \lambda $
and
![]() $E_2$
the set of primes p with
$E_2$
the set of primes p with
![]() $i + \lambda \leq \frac {1}{2} \log \log p \leq \mu $
. We take
$i + \lambda \leq \frac {1}{2} \log \log p \leq \mu $
. We take
![]() $k_0 = 0$
,
$k_0 = 0$
,
![]() $k_1 < i$
and
$k_1 < i$
and
![]() $k_1 + k_2 = r$
. Then the number of
$k_1 + k_2 = r$
. Then the number of
![]() $n\in S_r(N)$
such that
$n\in S_r(N)$
such that
![]() $\frac {1}{2} \,\log \, \log p_i>i+\lambda $
is at most
$\frac {1}{2} \,\log \, \log p_i>i+\lambda $
is at most
 $$ \begin{align} \frac{N}{\log N}\sum_{l=0}^{i-1} \frac{\left(i+\lambda+B\right)^{l}}{l!}\frac{\left(\mu-(i+\lambda)+B\right)^{r-l}}{(r-l)!} \ll \Phi_r(N) \sum_{l=0}^{i-1} \binom{r}{l} \left(\frac{i+\lambda}{\mu}\right)^{l} \left(1-\frac{i+\lambda}{\mu}\right)^{r-l} \hspace{-0.4cm}, \end{align} $$
$$ \begin{align} \frac{N}{\log N}\sum_{l=0}^{i-1} \frac{\left(i+\lambda+B\right)^{l}}{l!}\frac{\left(\mu-(i+\lambda)+B\right)^{r-l}}{(r-l)!} \ll \Phi_r(N) \sum_{l=0}^{i-1} \binom{r}{l} \left(\frac{i+\lambda}{\mu}\right)^{l} \left(1-\frac{i+\lambda}{\mu}\right)^{r-l} \hspace{-0.4cm}, \end{align} $$
where the second inequality uses equation (4.1) and the inequality
 $$\begin{align*}\left(1+ \frac{B} {i+\lambda} \right)^{l} \left(1+ \frac{B} {\mu-(i+\lambda)} \right)^{r-l} \leq \exp\left(\frac{iB} {i+\lambda} + \frac{rB} {\mu-(i+\lambda)} \right) \leq \exp(7B). \end{align*}$$
$$\begin{align*}\left(1+ \frac{B} {i+\lambda} \right)^{l} \left(1+ \frac{B} {\mu-(i+\lambda)} \right)^{r-l} \leq \exp\left(\frac{iB} {i+\lambda} + \frac{rB} {\mu-(i+\lambda)} \right) \leq \exp(7B). \end{align*}$$
Let
![]() $X_1, \ldots , X_n$
be independent random variables taking values in
$X_1, \ldots , X_n$
be independent random variables taking values in
![]() $\{0, 1\}$
. If X denotes their sum and
$\{0, 1\}$
. If X denotes their sum and
![]() $M = \mathbb {E}[X]$
, then the lower tail Chernoff bound states that for any
$M = \mathbb {E}[X]$
, then the lower tail Chernoff bound states that for any
![]() $0 \leq \delta \leq 1$
,
$0 \leq \delta \leq 1$
,
See [Reference Alon and Spencer2, Theorem A.1.13] for a reference in a slightly different form. We warn the reader that the X there corresponds to our
![]() $X - M$
. Then we bound equation (4.6) as
$X - M$
. Then we bound equation (4.6) as
 $$ \begin{align*} \Phi_r(N) \exp\left(-\frac{r\mu}{2(i+\lambda)}\left(\frac{i+\lambda}{\mu}-\frac{i}{r}\right)^2\right) &\leq \Phi_r(N) \exp\left(-\frac{1-\mu^{-1/3}}{2(i+\lambda)}\left(i+\lambda-\frac{i}{1-\mu^{-1/3}}\right)^2\right)\\ &\leq \Phi_r(N) \exp\left(-\frac{1-\mu^{-1/3}}{2(i+\lambda)}\left(\lambda-i^{2/3}\right)^2\right)\\ &\leq \Phi_r(N) \exp\left(-\frac{\lambda^2}{4(i+\lambda)}\right). \end{align*} $$
$$ \begin{align*} \Phi_r(N) \exp\left(-\frac{r\mu}{2(i+\lambda)}\left(\frac{i+\lambda}{\mu}-\frac{i}{r}\right)^2\right) &\leq \Phi_r(N) \exp\left(-\frac{1-\mu^{-1/3}}{2(i+\lambda)}\left(i+\lambda-\frac{i}{1-\mu^{-1/3}}\right)^2\right)\\ &\leq \Phi_r(N) \exp\left(-\frac{1-\mu^{-1/3}}{2(i+\lambda)}\left(\lambda-i^{2/3}\right)^2\right)\\ &\leq \Phi_r(N) \exp\left(-\frac{\lambda^2}{4(i+\lambda)}\right). \end{align*} $$
If
![]() $n\in S_r(N)$
satisfies
$n\in S_r(N)$
satisfies
![]() $\frac {1}{2}\log \log p_i<i-\lambda $
, then certainly
$\frac {1}{2}\log \log p_i<i-\lambda $
, then certainly
![]() $\lambda < i$
. Another application of Theorem 4.2 yields the bound
$\lambda < i$
. Another application of Theorem 4.2 yields the bound
 $$ \begin{align*} \frac{N}{\log N} \sum_{l=i}^{r} \frac{\left(i-\lambda+B\right)^{l}}{l!}\frac{\left(\mu-(i-\lambda)+B\right)^{r-l}}{(r-l)!} \ll \Phi_r(N) \sum_{l=i}^{r} \binom{r}{l} \left(\frac{i-\lambda+B}{\mu}\right)^{l} \left(1-\frac{i-\lambda+B}{\mu}\right)^{r-l}, \end{align*} $$
$$ \begin{align*} \frac{N}{\log N} \sum_{l=i}^{r} \frac{\left(i-\lambda+B\right)^{l}}{l!}\frac{\left(\mu-(i-\lambda)+B\right)^{r-l}}{(r-l)!} \ll \Phi_r(N) \sum_{l=i}^{r} \binom{r}{l} \left(\frac{i-\lambda+B}{\mu}\right)^{l} \left(1-\frac{i-\lambda+B}{\mu}\right)^{r-l}, \end{align*} $$
where the last inequality uses that
 $$\begin{align*}\left(\frac{\mu - i + \lambda + B}{\mu - i + \lambda - B}\right)^{r - l} = \left(1 + \frac{2B}{\mu - (i - \lambda) - B}\right)^{r - l} \leq \exp\left(\frac{2B(r - l)}{\mu - i + \lambda - B}\right) \leq \exp(4B). \end{align*}$$
$$\begin{align*}\left(\frac{\mu - i + \lambda + B}{\mu - i + \lambda - B}\right)^{r - l} = \left(1 + \frac{2B}{\mu - (i - \lambda) - B}\right)^{r - l} \leq \exp\left(\frac{2B(r - l)}{\mu - i + \lambda - B}\right) \leq \exp(4B). \end{align*}$$
We now apply the upper tail Chernoff bound
with
![]() $(1 + \delta )M = i$
. In case
$(1 + \delta )M = i$
. In case
![]() $\delta \leq 1$
, the computation proceeds among the same lines as before. If instead
$\delta \leq 1$
, the computation proceeds among the same lines as before. If instead
![]() $\delta> 1$
, we use that
$\delta> 1$
, we use that
so we have
![]() $\exp (-i/6)$
. Since
$\exp (-i/6)$
. Since
![]() $\delta> 1$
implies that
$\delta> 1$
implies that
![]() $\lambda> \frac {i}{3}$
, this finishes the proof.
$\lambda> \frac {i}{3}$
, this finishes the proof.
We are now ready to prove part (ii). The theorem is trivial when
![]() $\eta> 2r$
, so assume
$\eta> 2r$
, so assume
![]() $\eta < 2r$
. Take
$\eta < 2r$
. Take
![]() $\tilde {\eta }=\frac {1}{6}\eta $
so that
$\tilde {\eta }=\frac {1}{6}\eta $
so that
![]() $\tilde {\eta }<\frac {1}{3}r$
, and apply Lemma 4.4 with
$\tilde {\eta }<\frac {1}{3}r$
, and apply Lemma 4.4 with
![]() $\lambda =\tilde {\eta }^{1/5}\max \{i,\tilde {\eta }\}^{4/5}$
for every i between
$\lambda =\tilde {\eta }^{1/5}\max \{i,\tilde {\eta }\}^{4/5}$
for every i between
![]() $1$
to
$1$
to
![]() $\frac {1}{3}r$
. We get that the number of
$\frac {1}{3}r$
. We get that the number of
![]() $n\in S_r(N)$
such that
$n\in S_r(N)$
such that
 $$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|>\eta ^{1/5}\max\{i,\eta \}^{4/5}>\tilde{\eta }^{1/5}\max\{i,\tilde{\eta }\}^{4/5} \text{ for some } i<\frac{1}{3}r \end{align*}$$
$$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|>\eta ^{1/5}\max\{i,\eta \}^{4/5}>\tilde{\eta }^{1/5}\max\{i,\tilde{\eta }\}^{4/5} \text{ for some } i<\frac{1}{3}r \end{align*}$$
is bounded by
 $$ \begin{align*} \Phi_r(N) \sum_{i = 1}^{\lfloor\frac{1}{3}r\rfloor} \exp\left(-\frac{\tilde{\eta }^{2/5}\max\{i, \tilde{\eta }\}^{8/5}}{100(i+\tilde{\eta }^{1/5}\max\{i,\tilde{\eta }\}^{4/5})}\right) &\ll\Phi_r(N)\exp\left(-\frac{\tilde{\eta}}{200}\right) \\ &= \Phi_r(N)\exp\left(-\frac{\eta}{1200}\right) \end{align*} $$
$$ \begin{align*} \Phi_r(N) \sum_{i = 1}^{\lfloor\frac{1}{3}r\rfloor} \exp\left(-\frac{\tilde{\eta }^{2/5}\max\{i, \tilde{\eta }\}^{8/5}}{100(i+\tilde{\eta }^{1/5}\max\{i,\tilde{\eta }\}^{4/5})}\right) &\ll\Phi_r(N)\exp\left(-\frac{\tilde{\eta}}{200}\right) \\ &= \Phi_r(N)\exp\left(-\frac{\eta}{1200}\right) \end{align*} $$
when
![]() $\tilde {\eta }>200B$
.
$\tilde {\eta }>200B$
.
4.2.3 Proof of Theorem 4.13
Fix
![]() $\kappa>\frac {2}{3}$
. We will show that other than
$\kappa>\frac {2}{3}$
. We will show that other than
![]() $\ll _\epsilon \Phi _r(N)\exp \left (-(\log \mu )^{1-\kappa (1+\epsilon )}\right )$
exceptions, we have
$\ll _\epsilon \Phi _r(N)\exp \left (-(\log \mu )^{1-\kappa (1+\epsilon )}\right )$
exceptions, we have
 $$\begin{align*}\max_{\frac{1}{2}\sqrt{r}<i<\frac{1}{2}r} \log\log p_i-\log\left(\sum_{j=1}^{i-1}\log p_j\right) - 2\log \log\log p_i>(3\kappa-1)\log\log\mu -2. \end{align*}$$
$$\begin{align*}\max_{\frac{1}{2}\sqrt{r}<i<\frac{1}{2}r} \log\log p_i-\log\left(\sum_{j=1}^{i-1}\log p_j\right) - 2\log \log\log p_i>(3\kappa-1)\log\log\mu -2. \end{align*}$$
First, remove
![]() $n\in S_r(N)$
for which
$n\in S_r(N)$
for which
 $$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|>i^{4/5} \text{ for some } \frac{1}{2}\sqrt{r}<i<\frac{1}{2}r. \end{align*}$$
$$\begin{align*}\left|\frac{1}{2}\log\log p_i-i\right|>i^{4/5} \text{ for some } \frac{1}{2}\sqrt{r}<i<\frac{1}{2}r. \end{align*}$$
For each i with
![]() $\frac {1}{2}\sqrt {r} < i < \frac {1}{2}r$
, we apply Lemma 4.4 with
$\frac {1}{2}\sqrt {r} < i < \frac {1}{2}r$
, we apply Lemma 4.4 with
![]() $\lambda =i^{4/5}$
to deduce that there are at most
$\lambda =i^{4/5}$
to deduce that there are at most
![]() $\Phi _r(N)\exp \left (-\frac {1}{200}i^{3/5}\right )$
such n. Summing over
$\Phi _r(N)\exp \left (-\frac {1}{200}i^{3/5}\right )$
such n. Summing over
![]() $\frac {1}{2}\sqrt {r}<i<\frac {1}{2}r$
gives
$\frac {1}{2}\sqrt {r}<i<\frac {1}{2}r$
gives
 $$\begin{align*}\ll \Phi_r(N)\exp\left(-\frac{1}{400}\mu^{3/10}\right). \end{align*}$$
$$\begin{align*}\ll \Phi_r(N)\exp\left(-\frac{1}{400}\mu^{3/10}\right). \end{align*}$$
The remaining
![]() $n\in S_r(N)$
satisfy
$n\in S_r(N)$
satisfy
 $$ \begin{align} \left|\frac{1}{2}\log\log p_i-i\right|<i^{4/5} \text{ for every } \frac{1}{2}\sqrt{r}<i<\frac{1}{2}r. \end{align} $$
$$ \begin{align} \left|\frac{1}{2}\log\log p_i-i\right|<i^{4/5} \text{ for every } \frac{1}{2}\sqrt{r}<i<\frac{1}{2}r. \end{align} $$
Let
![]() $m=\lceil \frac {1}{2}\sqrt {r}\rceil -1$
and
$m=\lceil \frac {1}{2}\sqrt {r}\rceil -1$
and
![]() $k=\lfloor \frac {1}{2}r\rfloor -1$
, so
$k=\lfloor \frac {1}{2}r\rfloor -1$
, so
![]() $p_1\cdots p_k\leq \sqrt {N}$
. We first bound the number of
$p_1\cdots p_k\leq \sqrt {N}$
. We first bound the number of
![]() $n\in S_r(N)$
for which
$n\in S_r(N)$
for which
![]() $p_i< p_{i+1}\leq p_i^{a_i}$
for all
$p_i< p_{i+1}\leq p_i^{a_i}$
for all
![]() $m \leq i < k$
, where
$m \leq i < k$
, where
![]() $a_i=(i+1)^2(\log \mu )^{2\kappa }$
. Apply Theorem 4.2 with the set
$a_i=(i+1)^2(\log \mu )^{2\kappa }$
. Apply Theorem 4.2 with the set
![]() $E_1$
containing the primes less than
$E_1$
containing the primes less than
![]() $p_m$
and
$p_m$
and
![]() $E_2$
containing the primes greater than
$E_2$
containing the primes greater than
![]() $p_k$
and on numbers up to
$p_k$
and on numbers up to
![]() $\frac {N}{p_m \cdot \ldots \cdot p_k}$
. We let
$\frac {N}{p_m \cdot \ldots \cdot p_k}$
. We let
![]() $\mathcal {T}$
be the set of tuples
$\mathcal {T}$
be the set of tuples
![]() $(p_m, \dots , p_k)$
all consisting of primes not congruent to
$(p_m, \dots , p_k)$
all consisting of primes not congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
such that
$4$
such that
![]() $p_i < p_{i + 1} \leq p_i^{a_i}$
for all
$p_i < p_{i + 1} \leq p_i^{a_i}$
for all
![]() $m \leq i < k$
. Then the number of
$m \leq i < k$
. Then the number of
![]() $n\in S_r(N)$
for which
$n\in S_r(N)$
for which
![]() $p_i< p_{i+1}\leq p_i^{a_i}$
for all
$p_i< p_{i+1}\leq p_i^{a_i}$
for all
![]() $m \leq i < k$
is at most
$m \leq i < k$
is at most
 $$\begin{align*}\ll \frac{N}{\log N}\sum_{(p_m, \dots, p_k) \in \mathcal{T}} \frac{1}{p_m \cdots p_k}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_{k}+B\right)^{r-k}}{(r-k)!}\cdot \frac{\left(\frac{1}{2}\log\log p_{m}+B\right)^{m - 1}}{(m - 1)!}. \end{align*}$$
$$\begin{align*}\ll \frac{N}{\log N}\sum_{(p_m, \dots, p_k) \in \mathcal{T}} \frac{1}{p_m \cdots p_k}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_{k}+B\right)^{r-k}}{(r-k)!}\cdot \frac{\left(\frac{1}{2}\log\log p_{m}+B\right)^{m - 1}}{(m - 1)!}. \end{align*}$$
Now, fixing some
![]() $m\leq i < k$
, we obtain by partial summation on
$m\leq i < k$
, we obtain by partial summation on
![]() $\frac {1}{p_{i + 1}}$
and the prime number theorem that
$\frac {1}{p_{i + 1}}$
and the prime number theorem that
 $$ \begin{align*} \sum_{\substack{p_{i}<p_{i+1}\leq p_{i}^{a_{i}}\\p_{i + 1}\not\equiv 3\bmod 4}} \frac{1}{p_{i+1}} &\frac{\left(\frac{1}{2}\log\log p_{i+1}\right)^{r-i-1}}{(r-i-1)!} \\ &\qquad = \frac{\left(\frac{1}{2}\log\log p_i + \frac{1}{2}\log a_{i}\right)^{r-i}}{(r-i)!} - \frac{\left(\frac{1}{2}\log\log p_{i}\right)^{r-i}}{(r-i)!} + O\left(\exp(-c\sqrt{\log p_i})\right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{p_{i}<p_{i+1}\leq p_{i}^{a_{i}}\\p_{i + 1}\not\equiv 3\bmod 4}} \frac{1}{p_{i+1}} &\frac{\left(\frac{1}{2}\log\log p_{i+1}\right)^{r-i-1}}{(r-i-1)!} \\ &\qquad = \frac{\left(\frac{1}{2}\log\log p_i + \frac{1}{2}\log a_{i}\right)^{r-i}}{(r-i)!} - \frac{\left(\frac{1}{2}\log\log p_{i}\right)^{r-i}}{(r-i)!} + O\left(\exp(-c\sqrt{\log p_i})\right). \end{align*} $$
Hence we deduce
 $$ \begin{align*} &\sum_{\substack{p_{i}<p_{i+1}\leq p_{i}^{a_{i}}\\p_{i + 1}\not\equiv 3\bmod 4}} \frac{1}{p_{i+1}} \frac{\left(\mu-\frac{1}{2}\log\log p_{i+1}+B\right)^{r-i-1}}{(r-i-1)!} \\ &\quad =\frac{\left(\mu-\frac{1}{2}\log\log p_{i}+B\right)^{r-i}}{(r-i)!}-\frac{\left(\mu-\frac{1}{2}\log\log p_{i}-\frac{1}{2}\log a_{i}+B\right)^{r-i}}{(r-i)!}+O\left(\exp(-c\sqrt{\log p_i})\right) \\ &\quad =\frac{\left(\mu-\frac{1}{2}\log\log p_{i}+B\right)^{r-i}}{(r-i)!} \left(1- \left(1-\frac{\frac{1}{2}\log a_{i}}{\mu-\frac{1}{2}\log\log p_{i}+B}\right)^{r-i}\right)+O\left(\exp(-c\sqrt{\log p_i})\right). \end{align*} $$
$$ \begin{align*} &\sum_{\substack{p_{i}<p_{i+1}\leq p_{i}^{a_{i}}\\p_{i + 1}\not\equiv 3\bmod 4}} \frac{1}{p_{i+1}} \frac{\left(\mu-\frac{1}{2}\log\log p_{i+1}+B\right)^{r-i-1}}{(r-i-1)!} \\ &\quad =\frac{\left(\mu-\frac{1}{2}\log\log p_{i}+B\right)^{r-i}}{(r-i)!}-\frac{\left(\mu-\frac{1}{2}\log\log p_{i}-\frac{1}{2}\log a_{i}+B\right)^{r-i}}{(r-i)!}+O\left(\exp(-c\sqrt{\log p_i})\right) \\ &\quad =\frac{\left(\mu-\frac{1}{2}\log\log p_{i}+B\right)^{r-i}}{(r-i)!} \left(1- \left(1-\frac{\frac{1}{2}\log a_{i}}{\mu-\frac{1}{2}\log\log p_{i}+B}\right)^{r-i}\right)+O\left(\exp(-c\sqrt{\log p_i})\right). \end{align*} $$
Furthermore, we have the lower bound
 $$\begin{align*}\left(1-\frac{\frac{1}{2}\log a_{i}}{\mu-\frac{1}{2}\log\log p_{i}+B} \right)^{r-i} \geq a_i^{-\frac{1}{2}-2\mu^{-1/5}}. \end{align*}$$
$$\begin{align*}\left(1-\frac{\frac{1}{2}\log a_{i}}{\mu-\frac{1}{2}\log\log p_{i}+B} \right)^{r-i} \geq a_i^{-\frac{1}{2}-2\mu^{-1/5}}. \end{align*}$$
Applying this repeatedly for
![]() $i=k - 1, k - 2, \dots , m$
, we obtain the upper bound
$i=k - 1, k - 2, \dots , m$
, we obtain the upper bound
 $$\begin{align*}\Phi_r(N) \prod_{m\leq i<k} \left(1-\frac{1}{((i + 1) \cdot (\log \mu)^{\kappa})^{1+4\mu^{-1/5}}}\right) \ll_\epsilon \Phi_r(N)\exp\left(-(\log \mu)^{1-\kappa(1+\epsilon)}\right). \end{align*}$$
$$\begin{align*}\Phi_r(N) \prod_{m\leq i<k} \left(1-\frac{1}{((i + 1) \cdot (\log \mu)^{\kappa})^{1+4\mu^{-1/5}}}\right) \ll_\epsilon \Phi_r(N)\exp\left(-(\log \mu)^{1-\kappa(1+\epsilon)}\right). \end{align*}$$
It follows that other than
![]() $\ll _\epsilon \Phi _r(N)\exp \left (-(\log \mu )^{1-\kappa (1+\epsilon )}\right )$
exceptions, we have
$\ll _\epsilon \Phi _r(N)\exp \left (-(\log \mu )^{1-\kappa (1+\epsilon )}\right )$
exceptions, we have
For the remaining
![]() $n\in S_r(N)$
, we have equations (4.7) and (4.8), which implies
$n\in S_r(N)$
, we have equations (4.7) and (4.8), which implies
It remains to remove
![]() $n\in S_r(N)$
for which there exists some
$n\in S_r(N)$
for which there exists some
![]() $\frac {1}{2}\sqrt {r}\leq i<\frac {1}{2}r$
such that
$\frac {1}{2}\sqrt {r}\leq i<\frac {1}{2}r$
such that
![]() $p_i^{a_i}<p_{i+1}$
and
$p_i^{a_i}<p_{i+1}$
and
 $$\begin{align*}\sum_{j=1}^{i}\log p_j>(\log \mu)^{1-\kappa}\log p_i. \end{align*}$$
$$\begin{align*}\sum_{j=1}^{i}\log p_j>(\log \mu)^{1-\kappa}\log p_i. \end{align*}$$
Rewrite the second condition as
![]() $p_i^u<p_1\cdots p_{i-1}$
, where
$p_i^u<p_1\cdots p_{i-1}$
, where
![]() $u:=(\log \mu )^{1-\kappa }-1$
. We wish to bound
$u:=(\log \mu )^{1-\kappa }-1$
. We wish to bound
 $$ \begin{align} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} &\sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \sum_{\substack{p_i^{a_i}<p_{i+1}<\dots<p_r\\ p_{i+1}\cdots p_r<\frac{N}{p_1\cdots p_i}\\p_j\not\equiv 3\bmod 4}} 1 \notag \\ &\qquad\ll \frac{N}{\log N}\sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{\left(\mu-\frac{1}{2}\log\log p_i-\frac{1}{2}\log a_i+B\right)^{r-i}}{p_i(r-i)!} \sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}}. \end{align} $$
$$ \begin{align} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} &\sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \sum_{\substack{p_i^{a_i}<p_{i+1}<\dots<p_r\\ p_{i+1}\cdots p_r<\frac{N}{p_1\cdots p_i}\\p_j\not\equiv 3\bmod 4}} 1 \notag \\ &\qquad\ll \frac{N}{\log N}\sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{\left(\mu-\frac{1}{2}\log\log p_i-\frac{1}{2}\log a_i+B\right)^{r-i}}{p_i(r-i)!} \sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}}. \end{align} $$
Fix a given
![]() $p_i$
with
$p_i$
with
![]() $\left |\frac {1}{2}\log \log p_i-i\right |<i^{4/5}$
, and fix x with
$\left |\frac {1}{2}\log \log p_i-i\right |<i^{4/5}$
, and fix x with
![]() $p_i^{u}<x<\min \{p_i^{i - 1},N\}$
. By Lemma 4.3, we have
$p_i^{u}<x<\min \{p_i^{i - 1},N\}$
. By Lemma 4.3, we have
 $$\begin{align*}\sum_{\substack{p_1<\dots<p_{i-1}<p_i\\x<p_1\cdots p_{i-1}\leq 2x\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}} \leq \frac{1}{x}|\Psi_{i-1}(2x,p_i)| \ll \frac{v^{-v}}{\log p_i}\cdot\frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!},\end{align*}$$
$$\begin{align*}\sum_{\substack{p_1<\dots<p_{i-1}<p_i\\x<p_1\cdots p_{i-1}\leq 2x\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}} \leq \frac{1}{x}|\Psi_{i-1}(2x,p_i)| \ll \frac{v^{-v}}{\log p_i}\cdot\frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!},\end{align*}$$
where
![]() $v:=\log x/\log p_i$
. To deal with final part of the sum in equation (4.9), split
$v:=\log x/\log p_i$
. To deal with final part of the sum in equation (4.9), split
![]() $(p_i^u,p_i^{i-1})$
into dyadic intervals of the form
$(p_i^u,p_i^{i-1})$
into dyadic intervals of the form
![]() $(x,2x]$
; then
$(x,2x]$
; then
 $$ \begin{align*} \sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}} &\ll \frac{1}{\log p_i}\cdot\frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \sum_{\substack{k\geq 0\\x=2^kp_i^u}}v^{-v}\\ &\ll \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!}\int_{v>u} v^{-v}dv \ll u^{-u}\frac{\left(\frac{1}{2}\log \log p_i\right)^{i-1}}{(i-1)!}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{p_1<\dots<p_i\\p_1\cdots p_{i-1}>p_i^{u}\\p_j\not\equiv 3\bmod 4}} \frac{1}{p_1\cdots p_{i-1}} &\ll \frac{1}{\log p_i}\cdot\frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \sum_{\substack{k\geq 0\\x=2^kp_i^u}}v^{-v}\\ &\ll \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!}\int_{v>u} v^{-v}dv \ll u^{-u}\frac{\left(\frac{1}{2}\log \log p_i\right)^{i-1}}{(i-1)!}. \end{align*} $$
Therefore, equation (4.9) becomes
 $$ \begin{align*} &\ll \frac{Nu^{-u}}{\log N} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{1}{p_i}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_i\right)^{r-i}}{(r-i)!} \cdot \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \left(1-\frac{\frac{1}{2}\log a_i}{\mu-\frac{1}{2}\log\log p_i+B}\right)^{r-i} \\ &\qquad \ll \frac{N}{\log N} \cdot \frac{u^{-u}}{a_i^{1/2+2\mu^{-1/5}}} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{1}{p_i}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_i\right)^{r-i}}{(r-i)!} \cdot \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \ll \frac{u^{-u}\Phi_r(N)}{a_i^{1/2+2\mu^{-1/5}}}. \end{align*} $$
$$ \begin{align*} &\ll \frac{Nu^{-u}}{\log N} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{1}{p_i}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_i\right)^{r-i}}{(r-i)!} \cdot \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \left(1-\frac{\frac{1}{2}\log a_i}{\mu-\frac{1}{2}\log\log p_i+B}\right)^{r-i} \\ &\qquad \ll \frac{N}{\log N} \cdot \frac{u^{-u}}{a_i^{1/2+2\mu^{-1/5}}} \sum_{\substack{p_i\equiv 1\bmod 4\\ (4.7)}} \frac{1}{p_i}\cdot \frac{\left(\mu-\frac{1}{2}\log\log p_i\right)^{r-i}}{(r-i)!} \cdot \frac{(\frac{1}{2}\log\log p_i)^{i-1}}{(i-1)!} \ll \frac{u^{-u}\Phi_r(N)}{a_i^{1/2+2\mu^{-1/5}}}. \end{align*} $$
Summing over
![]() $\frac {1}{2}\sqrt {r}<i<\frac {1}{2}r$
, the total number of such n is
$\frac {1}{2}\sqrt {r}<i<\frac {1}{2}r$
, the total number of such n is
 $$\begin{align*}\ll \Phi_r(N)\exp\left(-2(\log \mu)^{1-\kappa}\right)\sum_{\frac{1}{2}r^{1/2}<i<\frac{1}{2}r}\frac{1}{i} \ll \Phi_r(N)\exp\left(-(\log \mu)^{1-\kappa}\right), \end{align*}$$
$$\begin{align*}\ll \Phi_r(N)\exp\left(-2(\log \mu)^{1-\kappa}\right)\sum_{\frac{1}{2}r^{1/2}<i<\frac{1}{2}r}\frac{1}{i} \ll \Phi_r(N)\exp\left(-(\log \mu)^{1-\kappa}\right), \end{align*}$$
which completes the proof of the theorem.
5 Equidistribution of Legendre symbol matrices
We will use the two following propositions from Section 6 of Smith [Reference Smith18].
Proposition 5.1. Suppose
![]() $L/\mathbb {Q}$
is Galois of degree d and
$L/\mathbb {Q}$
is Galois of degree d and
![]() $K/\mathbb {Q}$
is an elementary abelian extension, and
$K/\mathbb {Q}$
is an elementary abelian extension, and
![]() $\gcd (\Delta _L,\Delta _K)=1$
. Let
$\gcd (\Delta _L,\Delta _K)=1$
. Let
![]() $K_0$
be a quadratic subfield of K with maximal discriminant
$K_0$
be a quadratic subfield of K with maximal discriminant
![]() $|\Delta _{K_0}|$
. Let
$|\Delta _{K_0}|$
. Let
![]() $G:=\operatorname {\mathrm {Gal}}(KL/\mathbb {Q})$
be a
$G:=\operatorname {\mathrm {Gal}}(KL/\mathbb {Q})$
be a
![]() $2$
-group. Take
$2$
-group. Take
![]() $F:G\rightarrow [-1,1]$
to be a class function with average
$F:G\rightarrow [-1,1]$
to be a class function with average
![]() $0$
over G. Then there exists an absolute constant
$0$
over G. Then there exists an absolute constant
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*} \sum_{p\leq x} F\left(\left(\frac{KL/\mathbb{Q}}{p}\right)\right) \log p \ll x^{\beta}|G| +x|G|(d^2\log |x\Delta_{K_0}\Delta_L|)^4 \exp\left(\frac{-cd^{-4}\log x}{\sqrt{\log x}+3d\log |\Delta_{K_0}\Delta_L|}\right) \end{align*} $$
$$ \begin{align*} \sum_{p\leq x} F\left(\left(\frac{KL/\mathbb{Q}}{p}\right)\right) \log p \ll x^{\beta}|G| +x|G|(d^2\log |x\Delta_{K_0}\Delta_L|)^4 \exp\left(\frac{-cd^{-4}\log x}{\sqrt{\log x}+3d\log |\Delta_{K_0}\Delta_L|}\right) \end{align*} $$
for
![]() $x\geq 3$
, where
$x\geq 3$
, where
![]() $\beta $
is the maximal real zero of any Artin L-function defined for G.
$\beta $
is the maximal real zero of any Artin L-function defined for G.
Proof. This follows from the Chebotarev density theorem; see [Reference Smith18, Proposition 6.5].
Proposition 5.2. Let
![]() $X_1$
and
$X_1$
and
![]() $X_2$
be disjoint sets of odd primes with its elements bounded by
$X_2$
be disjoint sets of odd primes with its elements bounded by
![]() $t_1$
and
$t_1$
and
![]() $t_2$
, respectively. Then for any
$t_2$
, respectively. Then for any
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
 $$\begin{align*}\sum_{x_1\in X_1}\left|\sum_{x_2\in X_2}\left(\frac{x_1}{x_2}\right)\right|\ll_{\epsilon} t_1t_2^{3/4+\epsilon}+t_2t_1^{3/4+\epsilon}.\end{align*}$$
$$\begin{align*}\sum_{x_1\in X_1}\left|\sum_{x_2\in X_2}\left(\frac{x_1}{x_2}\right)\right|\ll_{\epsilon} t_1t_2^{3/4+\epsilon}+t_2t_1^{3/4+\epsilon}.\end{align*}$$
Proof. This is an easy consequence of the large sieve inequality stated in the work of Jutila [Reference Jutila12, Lemma 3]; see Proposition 6.6 in Smith [Reference Smith18].
We shall not work with all squarefree integers simultaneously but instead work with more restricted sets of squarefree integers that have extra combinatorial structure. In our next definition, we define this combinatorial structure, which we call preboxes.
Definition 5.3. Take a sequence of real numbers
Take
![]() $P, X_1,\dots , X_r$
to be disjoint sets of primes not congruent to
$P, X_1,\dots , X_r$
to be disjoint sets of primes not congruent to
![]() $3 \bmod 4$
so that
$3 \bmod 4$
so that
![]() $X_i\subset (s_i,t_i)$
. Define
$X_i\subset (s_i,t_i)$
. Define
![]() $X := X_1\times \dots \times X_r$
. We call the pair
$X := X_1\times \dots \times X_r$
. We call the pair
![]() $(X, P)$
a prebox.
$(X, P)$
a prebox.
The goal of this section is to prove a weak equidistribution statement regarding matrices of Jacobi symbols associated to each
![]() $x \in X$
. To make sense of this, we first need to define how we attach a matrix of Jacobi symbols to each
$x \in X$
. To make sense of this, we first need to define how we attach a matrix of Jacobi symbols to each
![]() $x \in X$
, which we shall do now. We will often implicitly identify
$x \in X$
, which we shall do now. We will often implicitly identify
![]() $\mathbb {F}_2$
with
$\mathbb {F}_2$
with
![]() $\{\pm 1\}$
in this section. We use
$\{\pm 1\}$
in this section. We use
![]() $\sqcup $
to denote disjoint union and
$\sqcup $
to denote disjoint union and
![]() $[r]$
to denote the set
$[r]$
to denote the set
![]() $\{1, \dots , r\}$
.
$\{1, \dots , r\}$
.
Definition 5.4. Let
![]() $(X, P)$
be a prebox. Take
$(X, P)$
be a prebox. Take
![]() $\mathcal {M}\subseteq \{(i,j):1\leq i< j\leq r\}$
and
$\mathcal {M}\subseteq \{(i,j):1\leq i< j\leq r\}$
and
![]() $\mathcal {N}\subseteq P\times [r]$
. Define
$\mathcal {N}\subseteq P\times [r]$
. Define
![]() $M: X\rightarrow \mathbb {F}_2^{\mathcal {M}\sqcup \mathcal {N}}$
as follows:
$M: X\rightarrow \mathbb {F}_2^{\mathcal {M}\sqcup \mathcal {N}}$
as follows:
 $$\begin{align*}M(x_1,\dots,x_r):\mathcal{M}\sqcup\mathcal{N}\rightarrow\{\pm 1\}\qquad M(x_1,\dots,x_r)(\mathbf{m})= \begin{cases} \left(\frac{x_i}{x_j}\right)&\text{ if }\mathbf{m}=(i,j)\in\mathcal{M}\\ \left(\frac{p}{x_j}\right)&\text{ if }\mathbf{m}=(p,j)\in\mathcal{N}. \end{cases} \end{align*}$$
$$\begin{align*}M(x_1,\dots,x_r):\mathcal{M}\sqcup\mathcal{N}\rightarrow\{\pm 1\}\qquad M(x_1,\dots,x_r)(\mathbf{m})= \begin{cases} \left(\frac{x_i}{x_j}\right)&\text{ if }\mathbf{m}=(i,j)\in\mathcal{M}\\ \left(\frac{p}{x_j}\right)&\text{ if }\mathbf{m}=(p,j)\in\mathcal{N}. \end{cases} \end{align*}$$
Denote
![]() $\mathcal {N}_{j}:={\{(p,j)\in \mathcal {N} : p \in P\}}$
. Let
$\mathcal {N}_{j}:={\{(p,j)\in \mathcal {N} : p \in P\}}$
. Let
![]() $M_j:X_j\rightarrow \mathbb {F}_2^{\mathcal {N}_{j}}$
be the function defined by
$M_j:X_j\rightarrow \mathbb {F}_2^{\mathcal {N}_{j}}$
be the function defined by
 $$\begin{align*}M_j(x_j):\mathcal{N}_{j}\rightarrow\{\pm 1\}\qquad M_j(x_j)(p,j)= \left(\frac{p}{x_j}\right). \end{align*}$$
$$\begin{align*}M_j(x_j):\mathcal{N}_{j}\rightarrow\{\pm 1\}\qquad M_j(x_j)(p,j)= \left(\frac{p}{x_j}\right). \end{align*}$$
For any
![]() $a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, define
$a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, define
and
![]() $X_j(a,P):=\{x_j\in X_j: M_j(x_j)=a\restriction _{\mathcal {N}_{j}}\}$
, where
$X_j(a,P):=\{x_j\in X_j: M_j(x_j)=a\restriction _{\mathcal {N}_{j}}\}$
, where
![]() $\restriction $
is restriction of functions. Let
$\restriction $
is restriction of functions. Let
![]() $Y \subseteq X$
be a subset, let
$Y \subseteq X$
be a subset, let
![]() $S \subseteq [r]$
, and let
$S \subseteq [r]$
, and let
![]() $Q \in \prod _{i \in S} X_i$
. We put
$Q \in \prod _{i \in S} X_i$
. We put
We shall slightly abuse notation by writing
![]() $X(a, Q)$
for
$X(a, Q)$
for
![]() $X(a)(Q)$
.
$X(a)(Q)$
.
Ideally, we would like to prove that
![]() $X(a)$
is of the expected size: that is,
$X(a)$
is of the expected size: that is,
Instead, we shall prove a weaker equidistribution statement that allows for permutations of the first few rows and columns.
Definition 5.5. Let
![]() $\mathcal {P}(r)$
denote the set of permutations of
$\mathcal {P}(r)$
denote the set of permutations of
![]() $[r]$
. For any
$[r]$
. For any
![]() $\sigma \in \mathcal {P}(r)$
, any prebox
$\sigma \in \mathcal {P}(r)$
, any prebox
![]() $(X,P)$
and any
$(X,P)$
and any
![]() $a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, define
$a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, define
where
![]() $\sigma (x)=\sigma (x_1,\dots ,x_r)=(x_{\sigma (1)},\dots ,x_{\sigma (r)})$
.
$\sigma (x)=\sigma (x_1,\dots ,x_r)=(x_{\sigma (1)},\dots ,x_{\sigma (r)})$
.
Finally, there is the well-known problem of Siegel zeroes that we need to take care of. This prompts the following definition.
Definition 5.6. For
![]() $c> 0$
, take
$c> 0$
, take
![]() $\mathcal {S}(c)$
to be the set of (possibly negative) squarefree integers d so that
$\mathcal {S}(c)$
to be the set of (possibly negative) squarefree integers d so that
List the elements in
![]() $\mathcal {S}(c)$
as
$\mathcal {S}(c)$
as
![]() $|d_1| \leq |d_2| \leq \cdots $
. By Landau’s theorem, fix an absolute c sufficiently small so that
$|d_1| \leq |d_2| \leq \cdots $
. By Landau’s theorem, fix an absolute c sufficiently small so that
![]() $d_i^2 \leq |d_{i + 1}|$
for all
$d_i^2 \leq |d_{i + 1}|$
for all
![]() $i \geq 1$
. We say that a prebox
$i \geq 1$
. We say that a prebox
![]() $(X,P)$
is Siegel-less above t if
$(X,P)$
is Siegel-less above t if
 $$\begin{align*}\left\{\epsilon \prod_{i \in S} \pi_i(x) \prod_{p\in \tilde{P}} p : x \in X, \epsilon \in \{\pm 1\}, \tilde{P}\subseteq P, S \subseteq [r], \left|\epsilon \prod_{i \in S} \pi_i(x) \prod_{p\in \tilde{P}} p\right|> t\right\}\cap \mathcal{S}(c) = \varnothing. \end{align*}$$
$$\begin{align*}\left\{\epsilon \prod_{i \in S} \pi_i(x) \prod_{p\in \tilde{P}} p : x \in X, \epsilon \in \{\pm 1\}, \tilde{P}\subseteq P, S \subseteq [r], \left|\epsilon \prod_{i \in S} \pi_i(x) \prod_{p\in \tilde{P}} p\right|> t\right\}\cap \mathcal{S}(c) = \varnothing. \end{align*}$$
We are now ready to prove our first proposition, which shows that
![]() $X(a)$
is of the expected size for sufficiently regular preboxes
$X(a)$
is of the expected size for sufficiently regular preboxes
![]() $(X, P)$
and sufficiently nice
$(X, P)$
and sufficiently nice
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
. It is directly based on Proposition 6.3 in Smith [Reference Smith18].
$\mathcal {N}$
. It is directly based on Proposition 6.3 in Smith [Reference Smith18].
Proposition 5.7. Fix positive constants
![]() $c_1,\dots , c_6$
such that
$c_1,\dots , c_6$
such that
![]() $c_2c_3+2c_4+c_5< \frac {1}{4}$
and
$c_2c_3+2c_4+c_5< \frac {1}{4}$
and
![]() $c_6>3$
. Take
$c_6>3$
. Take
![]() $\delta>0$
satisfying
$\delta>0$
satisfying
![]() $2\delta <\frac {1}{4}-c_2c_3-2c_4-c_5$
; then the following holds for any large enough
$2\delta <\frac {1}{4}-c_2c_3-2c_4-c_5$
; then the following holds for any large enough
![]() $D_1$
. Let
$D_1$
. Let
![]() $(X, P)$
be a prebox with parameters
$(X, P)$
be a prebox with parameters
![]() $D_1<s_1<t_1<s_2<t_2<\dots <s_r<t_r$
. Take
$D_1<s_1<t_1<s_2<t_2<\dots <s_r<t_r$
. Take
![]() $1\leq k\leq r$
. Let
$1\leq k\leq r$
. Let
![]() $\mathcal {M}\subseteq \{(i,j):1\leq i< j\leq r\}$
and
$\mathcal {M}\subseteq \{(i,j):1\leq i< j\leq r\}$
and
![]() $\mathcal {N}\subseteq P\times \{k+1,\dots ,r\}$
. Suppose that
$\mathcal {N}\subseteq P\times \{k+1,\dots ,r\}$
. Suppose that
Assume
-
1.
 $(X,P)$
is Siegel-less above
$(X,P)$
is Siegel-less above
 $D_1$
;
$D_1$
; -
2.
 $|P|\leq \log t_i-i$
for all
$|P|\leq \log t_i-i$
for all
 $1\leq i\leq r$
and
$1\leq i\leq r$
and
 $p \in P$
implies
$p \in P$
implies
 $p < s_1$
;
$p < s_1$
; -
3.
 $\log t_{k+1}>\max \{(\log t_1)^{c_6},D_1^{c_1}\}$
if
$\log t_{k+1}>\max \{(\log t_1)^{c_6},D_1^{c_1}\}$
if
 $k<r$
, and
$k<r$
, and
 $\log t_k<t_1^{c_2}$
;
$\log t_k<t_1^{c_2}$
; -
4.
 $|X_i|\geq e^it_i(\log t_i)^{-c_3}$
for all
$|X_i|\geq e^it_i(\log t_i)^{-c_3}$
for all
 $1\leq i\leq r$
;
$1\leq i\leq r$
; -
5.
 $r<t_1^{c_4}$
;
$r<t_1^{c_4}$
; -
6. for each
 $1\leq i\leq r$
,
$1\leq i\leq r$
,
 $j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
$j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
 $j_1> k$
, and
$j_1> k$
, and
 $\log t_{j_i}>(\log t_i)^{c_6}$
if
$\log t_{j_i}>(\log t_i)^{c_6}$
if
 $j_i\leq r$
.
$j_i\leq r$
.
Then for all
![]() $a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
,
$a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
,
Proof. Let
![]() $\kappa :=c_4+\delta $
. Since
$\kappa :=c_4+\delta $
. Since
![]() $r<t_1^{c_4}$
, it suffices to show that
$r<t_1^{c_4}$
, it suffices to show that
We proceed by induction on r. Define
 $$\begin{align*}X_j(a,x_1):=\left\{x_j\in X_j: \left(\frac{x_1}{x_j}\right)=a(1,j)\text{ if }(1,j)\in\mathcal{M}\right\}. \end{align*}$$
$$\begin{align*}X_j(a,x_1):=\left\{x_j\in X_j: \left(\frac{x_1}{x_j}\right)=a(1,j)\text{ if }(1,j)\in\mathcal{M}\right\}. \end{align*}$$
First consider
![]() $(1,j)\in \mathcal {M}$
, where
$(1,j)\in \mathcal {M}$
, where
![]() $j> k$
. Apply Proposition 5.1 to
$j> k$
. Apply Proposition 5.1 to
and
 $$\begin{align*}F:\sigma\mapsto \begin{cases} 1-2^{-|P|-2} &\text{if } \sigma=\left(\frac{KL/\mathbb{Q}}{x_j}\right)\text{ for some }x_j\in X_j(a,x_1),\\ \hfil -2^{-|P|-2} &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}F:\sigma\mapsto \begin{cases} 1-2^{-|P|-2} &\text{if } \sigma=\left(\frac{KL/\mathbb{Q}}{x_j}\right)\text{ for some }x_j\in X_j(a,x_1),\\ \hfil -2^{-|P|-2} &\text{otherwise.} \end{cases} \end{align*}$$
Notice that
![]() $\left (\frac {KL/\mathbb {Q}}{x_j}\right )$
is independent of the choice
$\left (\frac {KL/\mathbb {Q}}{x_j}\right )$
is independent of the choice
![]() $x_j\in X_j(a,x_1)$
. By Siegel’s theorem, for
$x_j\in X_j(a,x_1)$
. By Siegel’s theorem, for
![]() $D_1$
sufficiently large, we have
$D_1$
sufficiently large, we have
![]() $1-\beta>D_1^{-c_1/6}$
if
$1-\beta>D_1^{-c_1/6}$
if
![]() $\beta $
is an exceptional real zero of
$\beta $
is an exceptional real zero of
![]() $L(s,\chi _d)$
with
$L(s,\chi _d)$
with
![]() $|d|<D_1$
. Then
$|d|<D_1$
. Then
We have the bounds
and
Since
![]() $c_6>3$
, we have by a double application of Proposition 5.1 and partial summation
$c_6>3$
, we have by a double application of Proposition 5.1 and partial summation
 $$\begin{align*}\left|\sum_{s_j < p < t_j}F\left(\left(\frac{KL/\mathbb{Q}}{p}\right)\right)\right| \leq t_j\exp\left(-(\log t_j)^{1/3}\right) \end{align*}$$
$$\begin{align*}\left|\sum_{s_j < p < t_j}F\left(\left(\frac{KL/\mathbb{Q}}{p}\right)\right)\right| \leq t_j\exp\left(-(\log t_j)^{1/3}\right) \end{align*}$$
for sufficiently large
![]() $D_1$
. Repeating this for the field
$D_1$
. Repeating this for the field
![]() $K/\mathbb {Q}$
, we get after possibly enlarging
$K/\mathbb {Q}$
, we get after possibly enlarging
![]() $D_1$
$D_1$
 $$\begin{align*}\left||X_j(a,x_1)|-\frac{1}{2}|X_j|\right|\leq 2t_j\exp\left(-(\log t_j)^{1/3}\right)<t_1^{-1}|X_j|. \end{align*}$$
$$\begin{align*}\left||X_j(a,x_1)|-\frac{1}{2}|X_j|\right|\leq 2t_j\exp\left(-(\log t_j)^{1/3}\right)<t_1^{-1}|X_j|. \end{align*}$$
Next consider
![]() $(1,j)\in \mathcal {M}$
, where
$(1,j)\in \mathcal {M}$
, where
![]() $j\leq k$
. Note that
$j\leq k$
. Note that
![]() $\frac {1}{4}-c_2c_3-c_5-2\kappa> 0$
by assumption, so we can fix a positive constant
$\frac {1}{4}-c_2c_3-c_5-2\kappa> 0$
by assumption, so we can fix a positive constant
![]() $\epsilon $
such that
$\epsilon $
such that
![]() $2\epsilon <\frac {1}{4}-c_2c_3-c_5-2\kappa $
. The large sieve in Proposition 5.2 gives
$2\epsilon <\frac {1}{4}-c_2c_3-c_5-2\kappa $
. The large sieve in Proposition 5.2 gives
 $$\begin{align*}\sum_{x_1\in X_1}\left|\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)\right|\ll_{\epsilon} t_jt_1^{3/4+\epsilon}. \end{align*}$$
$$\begin{align*}\sum_{x_1\in X_1}\left|\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)\right|\ll_{\epsilon} t_jt_1^{3/4+\epsilon}. \end{align*}$$
From the identity
 $$\begin{align*}|X_j(a,x_1)|=\frac{1}{2}\sum_{x_j\in X_j}\left(a(1,j)\left(\frac{x_1}{x_j}\right)+1\right) =\frac{a(1,j)}{2}\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)+\frac{1}{2}|X_j|, \end{align*}$$
$$\begin{align*}|X_j(a,x_1)|=\frac{1}{2}\sum_{x_j\in X_j}\left(a(1,j)\left(\frac{x_1}{x_j}\right)+1\right) =\frac{a(1,j)}{2}\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)+\frac{1}{2}|X_j|, \end{align*}$$
we deduce that for sufficiently large
![]() $D_1$
,
$D_1$
,
 $$\begin{align*}\sum_{x_1\in X_1}\left| |X_j(a,x_1)| -\frac{1}{2}|X_j| \right| =\frac{1}{2}\sum_{x_1\in X_1}\left|\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)\right| \leq t_1^{-\frac{1}{4}+c_2c_3+\epsilon}|X_1||X_j|.\end{align*}$$
$$\begin{align*}\sum_{x_1\in X_1}\left| |X_j(a,x_1)| -\frac{1}{2}|X_j| \right| =\frac{1}{2}\sum_{x_1\in X_1}\left|\sum_{x_j\in X_j}\left(\frac{x_1}{x_j}\right)\right| \leq t_1^{-\frac{1}{4}+c_2c_3+\epsilon}|X_1||X_j|.\end{align*}$$
Let
![]() $B_1:=c_5+\kappa $
and
$B_1:=c_5+\kappa $
and
![]() $B_2:=\kappa +\epsilon $
; then
$B_2:=\kappa +\epsilon $
; then
![]() $B_1+B_2< \frac {1}{4}-c_2c_3-\epsilon $
. We conclude that
$B_1+B_2< \frac {1}{4}-c_2c_3-\epsilon $
. We conclude that
 $$\begin{align*}\left| |X_j(a,x_1)|-\frac{1}{2}|X_j| \right|<t_1^{-B_2}|X_j| \text{ for all }(1,j)\in\mathcal{M}\text{ and }j\leq k \end{align*}$$
$$\begin{align*}\left| |X_j(a,x_1)|-\frac{1}{2}|X_j| \right|<t_1^{-B_2}|X_j| \text{ for all }(1,j)\in\mathcal{M}\text{ and }j\leq k \end{align*}$$
holds with at most
![]() $kt_1^{-B_1}|X_1|$
exceptions
$kt_1^{-B_1}|X_1|$
exceptions
![]() $x_1 \in X$
. Call the set of exceptions
$x_1 \in X$
. Call the set of exceptions
![]() $X_1^{\text {bad}}(a)$
.
$X_1^{\text {bad}}(a)$
.
We bound the size of the set of exceptions
![]() $X^{\text {bad}}(a)=X(a)\cap \pi _1^{-1}(X_1^{\text {bad}}(a))$
in X. First, fix some
$X^{\text {bad}}(a)=X(a)\cap \pi _1^{-1}(X_1^{\text {bad}}(a))$
in X. First, fix some
![]() $x_1\in X_1$
and move
$x_1\in X_1$
and move
![]() $x_1$
to P. Apply the induction hypothesis to
$x_1$
to P. Apply the induction hypothesis to
Let us briefly explain the value of k to which we apply the induction hypothesis. Let
![]() $k_{\text {old}}$
be the current value of k, and let
$k_{\text {old}}$
be the current value of k, and let
![]() $k_{\text {new}}$
be the value of k to which we apply the induction hypothesis. We choose
$k_{\text {new}}$
be the value of k to which we apply the induction hypothesis. We choose
![]() $k_{\text {new}}$
as the smallest integer satisfying
$k_{\text {new}}$
as the smallest integer satisfying
and we choose
![]() $k_{\text {new}} = r - 1$
if there is no such integer.
$k_{\text {new}} = r - 1$
if there is no such integer.
Since
![]() $t_1> r^{c_4}$
with
$t_1> r^{c_4}$
with
![]() $c_4 < \frac {1}{8}$
, we get
$c_4 < \frac {1}{8}$
, we get
 $$\begin{align*}|X(a)\cap \pi_1^{-1}(x_1)| \leq \left(1 + \frac{2}{t_1}\right)^r \cdot 2^{-|\mathcal{M}|+k}\frac{|X|}{|X_1|} \leq 2^{-|\mathcal{M}|+k+1}\frac{|X|}{|X_1|} \end{align*}$$
$$\begin{align*}|X(a)\cap \pi_1^{-1}(x_1)| \leq \left(1 + \frac{2}{t_1}\right)^r \cdot 2^{-|\mathcal{M}|+k}\frac{|X|}{|X_1|} \leq 2^{-|\mathcal{M}|+k+1}\frac{|X|}{|X_1|} \end{align*}$$
and hence
For
![]() $x_1\notin X^{\text {bad}}(a)$
, we look at
$x_1\notin X^{\text {bad}}(a)$
, we look at
Then we obtain
 $$ \begin{align*} |X(a)\setminus X^{\text{bad}}(a)| &=\sum_{x_1\in X_1\setminus X_1^{\text{bad}}(a)}|X(a)\cap \pi_1^{-1}(x_1)| \\ &=\sum_{x_1\in X_1\setminus X_1^{\text{bad}}(a)}|(X_2(a,x_1)\times\dots\times X_r(a,x_1))(a)|, \end{align*} $$
$$ \begin{align*} |X(a)\setminus X^{\text{bad}}(a)| &=\sum_{x_1\in X_1\setminus X_1^{\text{bad}}(a)}|X(a)\cap \pi_1^{-1}(x_1)| \\ &=\sum_{x_1\in X_1\setminus X_1^{\text{bad}}(a)}|(X_2(a,x_1)\times\dots\times X_r(a,x_1))(a)|, \end{align*} $$
which lies between
 $$\begin{align*}\left(1\pm \frac{2}{t_1}\right)^r\left(1\pm \frac{2}{t_1^{B_2}}\right)^k \left(1 \pm(r-1)t_1^{-\kappa}\right)\cdot 2^{-|\mathcal{M}|}|X| \end{align*}$$
$$\begin{align*}\left(1\pm \frac{2}{t_1}\right)^r\left(1\pm \frac{2}{t_1^{B_2}}\right)^k \left(1 \pm(r-1)t_1^{-\kappa}\right)\cdot 2^{-|\mathcal{M}|}|X| \end{align*}$$
by the induction hypothesis. Since
![]() $r<t_1^{c_4}<t_1^{\kappa }$
,
$r<t_1^{c_4}<t_1^{\kappa }$
,
![]() $1-c_4>\kappa $
and
$1-c_4>\kappa $
and
![]() $B_2>\kappa $
, we have
$B_2>\kappa $
, we have
 $$ \begin{align*} \left(1+ \frac{2}{t_1}\right)^r &\left(1+ \frac{2}{t_1^{B_2}}\right)^k \frac{1+(r-1)t_1^{-\kappa}}{1 +(r-\frac{1}{2})t_1^{-\kappa}} = \left(1+ \frac{2}{t_1}\right)^r\left(1+ \frac{2}{t_1^{B_2}}\right)^k \left(1- \frac{ \frac{1}{2}t_1^{-\kappa}}{1 + (r - \frac{1}{2})t_1^{-\kappa}}\right)\\ &\qquad\qquad <\exp\left(2rt_1^{-1}+2kt_1^{-B_2}-\frac{1}{4}t_1^{-\kappa}\right)< \exp\left(2t_1^{-(1-c_4)} +2c_5t_1^{-B_2}\log t_1 -\frac{1}{4}t_1^{-\kappa}\right) <1 \end{align*} $$
$$ \begin{align*} \left(1+ \frac{2}{t_1}\right)^r &\left(1+ \frac{2}{t_1^{B_2}}\right)^k \frac{1+(r-1)t_1^{-\kappa}}{1 +(r-\frac{1}{2})t_1^{-\kappa}} = \left(1+ \frac{2}{t_1}\right)^r\left(1+ \frac{2}{t_1^{B_2}}\right)^k \left(1- \frac{ \frac{1}{2}t_1^{-\kappa}}{1 + (r - \frac{1}{2})t_1^{-\kappa}}\right)\\ &\qquad\qquad <\exp\left(2rt_1^{-1}+2kt_1^{-B_2}-\frac{1}{4}t_1^{-\kappa}\right)< \exp\left(2t_1^{-(1-c_4)} +2c_5t_1^{-B_2}\log t_1 -\frac{1}{4}t_1^{-\kappa}\right) <1 \end{align*} $$
and similarly
 $$\begin{align*}\left(1- \frac{2}{t_1}\right)^r\left(1- \frac{2}{t_1^{B_2}}\right)^k \frac{1 -(r-1)t_1^{-\kappa}}{1 - (r-\frac{1}{2})t_1^{-\kappa}} = \left(1- \frac{2}{t_1}\right)^r \hspace{-0.1cm} \left(1- \frac{2}{t_1^{B_2}}\right)^k \hspace{-0.1cm} \left(1+ \frac{ \frac{1}{2}t_1^{-\kappa}}{1 - (r - \frac{1}{2})t_1^{-\kappa}}\right)>1. \end{align*}$$
$$\begin{align*}\left(1- \frac{2}{t_1}\right)^r\left(1- \frac{2}{t_1^{B_2}}\right)^k \frac{1 -(r-1)t_1^{-\kappa}}{1 - (r-\frac{1}{2})t_1^{-\kappa}} = \left(1- \frac{2}{t_1}\right)^r \hspace{-0.1cm} \left(1- \frac{2}{t_1^{B_2}}\right)^k \hspace{-0.1cm} \left(1+ \frac{ \frac{1}{2}t_1^{-\kappa}}{1 - (r - \frac{1}{2})t_1^{-\kappa}}\right)>1. \end{align*}$$
We conclude that the sum lies between
 $$ \begin{align} \left(1 \pm\left(r-\frac{1}{2}\right)t_1^{-\kappa}\right)\cdot 2^{-|\mathcal{M}|}|X|. \end{align} $$
$$ \begin{align} \left(1 \pm\left(r-\frac{1}{2}\right)t_1^{-\kappa}\right)\cdot 2^{-|\mathcal{M}|}|X|. \end{align} $$
Adding the contributions from equations (5.1) and (5.2) completes the inductive step.
The condition
![]() $\mathcal {N}\subseteq P\times \{k+1,\dots ,r\}$
in Proposition 5.7 turns out to be too restrictive for us. It is, however, not so straightforward to remove this condition. Hence we shall only prove a weaker equidistribution statement that allows for permutations of the first few columns. This weaker equidistribution statement will fall as a consequence of Proposition 5.7 and the following combinatorial proposition, which is Proposition 6.7 of Smith [Reference Smith18].
$\mathcal {N}\subseteq P\times \{k+1,\dots ,r\}$
in Proposition 5.7 turns out to be too restrictive for us. It is, however, not so straightforward to remove this condition. Hence we shall only prove a weaker equidistribution statement that allows for permutations of the first few columns. This weaker equidistribution statement will fall as a consequence of Proposition 5.7 and the following combinatorial proposition, which is Proposition 6.7 of Smith [Reference Smith18].
Proposition 5.8. Let
![]() $(X,P)$
be a prebox. Let
$(X,P)$
be a prebox. Let
![]() $\mathcal {M}= \{(i,j):1\leq i< j\leq r\}$
and
$\mathcal {M}= \{(i,j):1\leq i< j\leq r\}$
and
![]() $\mathcal {N}= P\times [r]$
. Take
$\mathcal {N}= P\times [r]$
. Take
![]() $0\leq k_0\leq k_1\leq k_2\leq r$
so that
$0\leq k_0\leq k_1\leq k_2\leq r$
so that
Let
![]() $\sigma \in \mathcal {P}(r)$
. Define
$\sigma \in \mathcal {P}(r)$
. Define
Let
![]() $m:=|S(\sigma )|=k_1|P|+\frac {1}{2}k_0(k_0-1)+k_0(k_1-k_0)$
. If
$m:=|S(\sigma )|=k_1|P|+\frac {1}{2}k_0(k_0-1)+k_0(k_1-k_0)$
. If
![]() $a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, we put
$a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
, we put
For any
![]() $x\in X$
, define
$x\in X$
, define
Then we have
 $$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}}\left| |W(x, a)|-2^{-m}\cdot k_2!\right| \leq \left(\frac{2^{|P|+k_0+1}}{k_2}\right)^{1/2}k_1\cdot 2^{-m + |\mathcal{M}\sqcup\mathcal{N}|} \cdot k_2!. \end{align*}$$
$$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}}\left| |W(x, a)|-2^{-m}\cdot k_2!\right| \leq \left(\frac{2^{|P|+k_0+1}}{k_2}\right)^{1/2}k_1\cdot 2^{-m + |\mathcal{M}\sqcup\mathcal{N}|} \cdot k_2!. \end{align*}$$
Proof. Fix some
![]() $x\in X$
, and write
$x\in X$
, and write
![]() $W(a):=W(x, a)$
. We will show that
$W(a):=W(x, a)$
. We will show that
 $$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}}\left(|W(a)|-2^{-m}\cdot k_2!\right)^2 \leq \frac{2^{|P|+k_0+1} k_1^2}{k_2}\cdot 2^{-2m+|\mathcal{M}\sqcup\mathcal{N}|}(k_2!)^2 .\end{align*}$$
$$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}}\left(|W(a)|-2^{-m}\cdot k_2!\right)^2 \leq \frac{2^{|P|+k_0+1} k_1^2}{k_2}\cdot 2^{-2m+|\mathcal{M}\sqcup\mathcal{N}|}(k_2!)^2 .\end{align*}$$
Then the proposition follows from the Cauchy-Schwarz inequality.
The average of
![]() $|W(a)|$
over a is
$|W(a)|$
over a is
![]() $2^{-m}\cdot k_2!$
, since
$2^{-m}\cdot k_2!$
, since
![]() $|\mathcal {P}(k_2)|=k_2!$
and there are m Legendre symbol conditions to satisfy. Now
$|\mathcal {P}(k_2)|=k_2!$
and there are m Legendre symbol conditions to satisfy. Now
We have
![]() $\sum _{a\in \mathbb {F}_2^{\mathcal {M}\sqcup \mathcal {N}}}|W(a)|^2=\sum _{\sigma _1,\sigma _2\in \mathcal {P}(k_2)}|W(\sigma _1,\sigma _2)|$
, where
$\sum _{a\in \mathbb {F}_2^{\mathcal {M}\sqcup \mathcal {N}}}|W(a)|^2=\sum _{\sigma _1,\sigma _2\in \mathcal {P}(k_2)}|W(\sigma _1,\sigma _2)|$
, where
We fix some
![]() $\sigma _1,\sigma _2\in \mathcal {P}(k_2)$
and bound
$\sigma _1,\sigma _2\in \mathcal {P}(k_2)$
and bound
![]() $|W(\sigma _1,\sigma _2)|$
. Let
$|W(\sigma _1,\sigma _2)|$
. Let
![]() $ d:=|\{i\in [k_2]:\sigma _1(i)\leq k_1,\ \sigma _2(i)\leq k_1\}|$
. We have
$ d:=|\{i\in [k_2]:\sigma _1(i)\leq k_1,\ \sigma _2(i)\leq k_1\}|$
. We have
 $$ \begin{align*} |S(\sigma_1)\cap S(\sigma_2)| &=|\left\{(i,j)\in\mathcal{M}: (\sigma_1(i),\sigma_1(j)),\ (\sigma_2(i),\sigma_2(j))\in ([k_0]\times[k_1])\cup ([k_1]\times[k_0])\right\}| \\ &\qquad\qquad\qquad\qquad\qquad +|\left\{(p,j)\in\mathcal{N}:\sigma_1(j),\ \sigma_2(j)\in [k_1] \right\}| \leq d(|P|+k_0). \end{align*} $$
$$ \begin{align*} |S(\sigma_1)\cap S(\sigma_2)| &=|\left\{(i,j)\in\mathcal{M}: (\sigma_1(i),\sigma_1(j)),\ (\sigma_2(i),\sigma_2(j))\in ([k_0]\times[k_1])\cup ([k_1]\times[k_0])\right\}| \\ &\qquad\qquad\qquad\qquad\qquad +|\left\{(p,j)\in\mathcal{N}:\sigma_1(j),\ \sigma_2(j)\in [k_1] \right\}| \leq d(|P|+k_0). \end{align*} $$
Therefore the conditions fix at least
![]() $2m-d(|P|+k_0)$
arguments of
$2m-d(|P|+k_0)$
arguments of
![]() $a\in W(\sigma _1,\sigma _2)$
. Then
$a\in W(\sigma _1,\sigma _2)$
. Then
Given some
![]() $d\leq k_1$
, we bound the number of
$d\leq k_1$
, we bound the number of
![]() $(\sigma _1,\sigma _2)\in \mathcal {P}(k_2)\times \mathcal {P}(k_2)$
that gives the same d. There are
$(\sigma _1,\sigma _2)\in \mathcal {P}(k_2)\times \mathcal {P}(k_2)$
that gives the same d. There are
![]() $\binom {k_2}{d}$
ways to pick the indices that map to
$\binom {k_2}{d}$
ways to pick the indices that map to
![]() $[k_1]$
under
$[k_1]$
under
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
. Then there are at most
$\sigma _2$
. Then there are at most
![]() $(\frac {k_1!}{(k_1-d)!}(k_2-d)!)^2$
ways to pick a pair of
$(\frac {k_1!}{(k_1-d)!}(k_2-d)!)^2$
ways to pick a pair of
![]() $(\sigma _1,\sigma _2)$
in such a way. Hence the total number is bounded by
$(\sigma _1,\sigma _2)$
in such a way. Hence the total number is bounded by
 $$\begin{align*}\binom{k_2}{d}\left(\frac{k_1!}{(k_1-d)!}(k_2-d)!\right)^2\leq (k_2!)^2\left(\frac{k_1!}{(k_1-d)!}\right)^2\frac{ (k_2-d)!}{k_2!} \leq (k_2!)^2\left(\frac{k_1^2}{k_2}\right)^d .\end{align*}$$
$$\begin{align*}\binom{k_2}{d}\left(\frac{k_1!}{(k_1-d)!}(k_2-d)!\right)^2\leq (k_2!)^2\left(\frac{k_1!}{(k_1-d)!}\right)^2\frac{ (k_2-d)!}{k_2!} \leq (k_2!)^2\left(\frac{k_1^2}{k_2}\right)^d .\end{align*}$$
The average of
![]() $|W(a)|^2$
is bounded by
$|W(a)|^2$
is bounded by
 $$\begin{align*}(k_2!)^2\sum_{d\geq 0}\left(\frac{k_1^2}{k_2}\right)^d \cdot 2^{-2m+d(|P|+k_0)} =\frac{k_2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2. \end{align*}$$
$$\begin{align*}(k_2!)^2\sum_{d\geq 0}\left(\frac{k_1^2}{k_2}\right)^d \cdot 2^{-2m+d(|P|+k_0)} =\frac{k_2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2. \end{align*}$$
Then the variance of
![]() $|W(a)|$
is bounded by
$|W(a)|$
is bounded by
 $$ \begin{align*} \frac{k_2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2-(2^{-m}\cdot k_2!)^2 &=\frac{2^{|P|+k_0}k_1^2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2 \\ &\leq \frac{2^{|P|+k_0+1}k_1^2}{k_2}\cdot 2^{-2m}(k_2!)^2 .\end{align*} $$
$$ \begin{align*} \frac{k_2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2-(2^{-m}\cdot k_2!)^2 &=\frac{2^{|P|+k_0}k_1^2}{k_2-2^{|P|+k_0}k_1^2}\cdot 2^{-2m}(k_2!)^2 \\ &\leq \frac{2^{|P|+k_0+1}k_1^2}{k_2}\cdot 2^{-2m}(k_2!)^2 .\end{align*} $$
Multiplying by
![]() $2^{|\mathcal {M}\sqcup \mathcal {N}|}$
gives the required estimate.
$2^{|\mathcal {M}\sqcup \mathcal {N}|}$
gives the required estimate.
We are now ready to prove our weak equidistribution result for
![]() $|X(a)|$
, which is very similar to Theorem 6.4 in Smith [Reference Smith18]. We define
$|X(a)|$
, which is very similar to Theorem 6.4 in Smith [Reference Smith18]. We define
![]() $a(i, j) := a(j, i)$
in case
$a(i, j) := a(j, i)$
in case
![]() $i> j$
.
$i> j$
.
Theorem 5.9. Take positive constants
![]() $c_1,\dots , c_8$
, where
$c_1,\dots , c_8$
, where
![]() $c_2c_3+2c_4+c_5< \frac {1}{4}$
,
$c_2c_3+2c_4+c_5< \frac {1}{4}$
,
![]() $c_6>3$
and
$c_6>3$
and
![]() $c_8<c_7<\frac {1}{2}$
. Let
$c_8<c_7<\frac {1}{2}$
. Let
![]() $(X, P)$
be a prebox, and suppose that for all
$(X, P)$
be a prebox, and suppose that for all
![]() $1\leq j\leq r$
,
$1\leq j\leq r$
,
The following holds for any large enough
![]() $D_1$
. Choose integers
$D_1$
. Choose integers
![]() $0 \leq k_0 < k_1 < k_2 \leq r$
, and assume
$0 \leq k_0 < k_1 < k_2 \leq r$
, and assume
![]() $t_{k_0+1}>D_1$
and
$t_{k_0+1}>D_1$
and
![]() $k_2>D_1$
. Assume
$k_2>D_1$
. Assume
-
1.
 $\log k_1< c_8\log k_2$
;
$\log k_1< c_8\log k_2$
; -
2.
 $(|P|+k_0)\log 2< (1-2c_7)\log k_2$
.
$(|P|+k_0)\log 2< (1-2c_7)\log k_2$
.
Further assume
-
1.
 $(X,P)$
is Siegel-less above
$(X,P)$
is Siegel-less above
 $D_1$
;
$D_1$
; -
2.
 $|P|\leq \log t_i-i$
for all
$|P|\leq \log t_i-i$
for all
 $k_0 < i\leq r$
and
$k_0 < i\leq r$
and
 $p \in P$
implies
$p \in P$
implies
 $p < s_{k_0 + 1}$
;
$p < s_{k_0 + 1}$
; -
3.
 $\log t_{k_1+1}>\max \{(\log t_{k_0 + 1})^{c_6},D_1^{c_1}\}$
and
$\log t_{k_1+1}>\max \{(\log t_{k_0 + 1})^{c_6},D_1^{c_1}\}$
and
 $\log t_{k_1}<t_1^{c_2}$
;
$\log t_{k_1}<t_1^{c_2}$
; -
4.
 $|X_i|\geq 2^{|P|}e^{i}k_2^{c_7}t_i(\log t_i)^{-c_3}$
for all
$|X_i|\geq 2^{|P|}e^{i}k_2^{c_7}t_i(\log t_i)^{-c_3}$
for all
 $k_0 < i\leq r$
;
$k_0 < i\leq r$
; -
5.
 $r<t_{k_0+1}^{c_4}$
;
$r<t_{k_0+1}^{c_4}$
; -
6. for each
 $k_0 < i\leq r$
,
$k_0 < i\leq r$
,
 $j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
$j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
 $j_{k_0+1}> k_1$
, and
$j_{k_0+1}> k_1$
, and
 $\log t_{j_i}>(\log t_i)^{c_6}$
if
$\log t_{j_i}>(\log t_i)^{c_6}$
if
 $j_i\leq r$
.
$j_i\leq r$
.
Take
![]() $\delta _1<c_7-c_8$
and
$\delta _1<c_7-c_8$
and
![]() $2\delta _2 <\frac {1}{4}-c_2c_3-3c_4-c_5$
. Then for any
$2\delta _2 <\frac {1}{4}-c_2c_3-3c_4-c_5$
. Then for any
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
, we have
$\mathcal {N}$
, we have
 $$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left|2^{-|\mathcal{M}\sqcup\mathcal{N}|}\cdot k_2!\cdot |X|-\sum_{\sigma\in\mathcal{P}(k_2)}|X(\sigma, a)|\right| \leq (k_2^{-\delta_1}+t_{k_0 + 1}^{-\delta_2})\cdot k_2!\cdot |X|. \end{align*}$$
$$\begin{align*}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left|2^{-|\mathcal{M}\sqcup\mathcal{N}|}\cdot k_2!\cdot |X|-\sum_{\sigma\in\mathcal{P}(k_2)}|X(\sigma, a)|\right| \leq (k_2^{-\delta_1}+t_{k_0 + 1}^{-\delta_2})\cdot k_2!\cdot |X|. \end{align*}$$
Proof. Without loss of generality, assume that
![]() $\mathcal {M}= \{(i,j):1\leq i < j\leq r\}$
and
$\mathcal {M}= \{(i,j):1\leq i < j\leq r\}$
and
![]() $\mathcal {N}= P\times [r]$
,
$\mathcal {N}= P\times [r]$
,
![]() $X_i=\{x_i\}$
for
$X_i=\{x_i\}$
for
![]() $i\leq k_0$
. Let
$i\leq k_0$
. Let
![]() $m:=k_1|P|+\frac {1}{2}k_0(k_0-1)+k_0(k_1-k_0)$
as in Proposition 5.8. Apply the triangle inequality to the sum we wish to bound,
$m:=k_1|P|+\frac {1}{2}k_0(k_0-1)+k_0(k_1-k_0)$
as in Proposition 5.8. Apply the triangle inequality to the sum we wish to bound,
 $$ \begin{align} 2^{-|\mathcal{M}\sqcup\mathcal{N}|}&\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left|k_2!\cdot |X|- 2^m\sum_{\sigma\in\mathcal{P}(k_2)}|X_S(\sigma, a)|\right| \notag\\ &\qquad\qquad\qquad\quad \ + 2^{-|\mathcal{M}\sqcup\mathcal{N}|+m}\sum_{\sigma\in\mathcal{P}(k_2)}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left||X_S(\sigma, a)|-2^{|\mathcal{M}\sqcup\mathcal{N}|-m}|X(\sigma, a)|\right|. \end{align} $$
$$ \begin{align} 2^{-|\mathcal{M}\sqcup\mathcal{N}|}&\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left|k_2!\cdot |X|- 2^m\sum_{\sigma\in\mathcal{P}(k_2)}|X_S(\sigma, a)|\right| \notag\\ &\qquad\qquad\qquad\quad \ + 2^{-|\mathcal{M}\sqcup\mathcal{N}|+m}\sum_{\sigma\in\mathcal{P}(k_2)}\sum_{a\in\mathbb{F}_2^{\mathcal{M}\sqcup\mathcal{N}}} \left||X_S(\sigma, a)|-2^{|\mathcal{M}\sqcup\mathcal{N}|-m}|X(\sigma, a)|\right|. \end{align} $$
For the first sum in equation (5.3), noting that
we obtain by Proposition 5.8 an upper bound
 $$\begin{align*}\left(\frac{2^{|P|+k_0+1}}{k_2}\right)^{1/2} k_1\cdot k_2!\cdot |X|<k_2^{-\delta_1}\cdot k_2!\cdot |X|.\end{align*}$$
$$\begin{align*}\left(\frac{2^{|P|+k_0+1}}{k_2}\right)^{1/2} k_1\cdot k_2!\cdot |X|<k_2^{-\delta_1}\cdot k_2!\cdot |X|.\end{align*}$$
Now consider the second sum of equation (5.3). For each
![]() $\sigma \in \mathcal {P}(k_2)$
, we can partition X into
$\sigma \in \mathcal {P}(k_2)$
, we can partition X into
![]() $2^m$
sets according to
$2^m$
sets according to
![]() $\tilde {a}:S(\sigma )\rightarrow \{\pm 1\}$
as follows:
$\tilde {a}:S(\sigma )\rightarrow \{\pm 1\}$
as follows:
where
![]() $\tilde {P}=\{x_1\}\cup \dots \cup \{x_{k_0}\}\cup P$
and
$\tilde {P}=\{x_1\}\cup \dots \cup \{x_{k_0}\}\cup P$
and
![]() $X_i(\tilde {a},\tilde {P})$
is the subset of those
$X_i(\tilde {a},\tilde {P})$
is the subset of those
![]() $q \in X_i$
satisfying
$q \in X_i$
satisfying
 $$\begin{align*}\left(\frac{q}{x_j}\right) = \widetilde{a}(\sigma^{-1}(i), \sigma^{-1}(j)) \text{ for } j \in [k_0] \text{ and } \left(\frac{q}{p}\right) = \widetilde{a}(p, \sigma^{-1}(i)) \text{ for } p \in P. \end{align*}$$
$$\begin{align*}\left(\frac{q}{x_j}\right) = \widetilde{a}(\sigma^{-1}(i), \sigma^{-1}(j)) \text{ for } j \in [k_0] \text{ and } \left(\frac{q}{p}\right) = \widetilde{a}(p, \sigma^{-1}(i)) \text{ for } p \in P. \end{align*}$$
We first bound the contribution of
![]() $\sigma \in \mathcal {P}(k_2)$
with
$\sigma \in \mathcal {P}(k_2)$
with
![]() $|X_i(\tilde {a},\tilde {P})|< 2^{-|\tilde {P}|}k_2^{-c_7}|X_i|$
for some
$|X_i(\tilde {a},\tilde {P})|< 2^{-|\tilde {P}|}k_2^{-c_7}|X_i|$
for some
![]() $\tilde {a}:S(\sigma )\rightarrow \{\pm 1\}$
and some
$\tilde {a}:S(\sigma )\rightarrow \{\pm 1\}$
and some
![]() $k_0< i\leq k_1$
in the sum. For each
$k_0< i\leq k_1$
in the sum. For each
![]() $\sigma \in \mathcal {P}(k_2)$
and
$\sigma \in \mathcal {P}(k_2)$
and
![]() $k_0<i\leq k_1$
, we have the upper bound
$k_0<i\leq k_1$
, we have the upper bound
 $$\begin{align*}\sum_{\tilde{a}:|X_i(\tilde{a},\tilde{P})|\leq 2^{-|\tilde{P}|}k_2^{-c_7} |X_i|}\left|X_S(\sigma,\tilde{a})\right| \leq k_2^{-c_7}|X|. \end{align*}$$
$$\begin{align*}\sum_{\tilde{a}:|X_i(\tilde{a},\tilde{P})|\leq 2^{-|\tilde{P}|}k_2^{-c_7} |X_i|}\left|X_S(\sigma,\tilde{a})\right| \leq k_2^{-c_7}|X|. \end{align*}$$
For each
![]() $\tilde {a}$
, there are
$\tilde {a}$
, there are
![]() $2^{|\mathcal {M}\sqcup \mathcal {N}|-m}$
many a satisfying
$2^{|\mathcal {M}\sqcup \mathcal {N}|-m}$
many a satisfying
![]() $a\restriction _{S(\sigma )}=\tilde {a}$
, so the contribution of such a is bounded by
$a\restriction _{S(\sigma )}=\tilde {a}$
, so the contribution of such a is bounded by
 $$\begin{align*}\sum_{\sigma\in\mathcal{P}(k_2)}\sum_{k_0<i\leq k_1}\sum_{\tilde{a}:|X_i(\tilde{a},\tilde{P})|\leq 2^{-|\tilde{P}|}\cdot k_2^{-c_7}\cdot |X_i| } |X_S(\sigma,\tilde{a})| \leq k_1 k_2^{-c_7}\cdot k_2!\cdot |X| < k_2^{-\delta_1}\cdot k_2! \cdot |X|. \end{align*}$$
$$\begin{align*}\sum_{\sigma\in\mathcal{P}(k_2)}\sum_{k_0<i\leq k_1}\sum_{\tilde{a}:|X_i(\tilde{a},\tilde{P})|\leq 2^{-|\tilde{P}|}\cdot k_2^{-c_7}\cdot |X_i| } |X_S(\sigma,\tilde{a})| \leq k_1 k_2^{-c_7}\cdot k_2!\cdot |X| < k_2^{-\delta_1}\cdot k_2! \cdot |X|. \end{align*}$$
For the remaining terms, we have
![]() $|X_i(\tilde {a},\tilde {P})| \geq 2^{-|\tilde {P}|} k_2^{-c_7} |X_i|$
for all
$|X_i(\tilde {a},\tilde {P})| \geq 2^{-|\tilde {P}|} k_2^{-c_7} |X_i|$
for all
![]() $k_0< i\leq r$
. Bound each summand by Proposition 5.7
$k_0< i\leq r$
. Bound each summand by Proposition 5.7
then summing over
![]() $\sigma $
and a gives the required estimate.
$\sigma $
and a gives the required estimate.
There is a final technical proposition that will be of key importance in our next section. First we need a definition.
Definition 5.10. Let
![]() $(X, P)$
be a prebox, and let
$(X, P)$
be a prebox, and let
![]() $S \subseteq [r]$
. If
$S \subseteq [r]$
. If
![]() $j \not \in S$
, we define for a subset
$j \not \in S$
, we define for a subset
![]() $Z \subseteq \prod _{i \in S} X_i$
$Z \subseteq \prod _{i \in S} X_i$
 $$\begin{align*}X_j(a, Z) := X_j(a, P) \cap \left\{x \in X_j : \ \mathrm{for \ all} \ i \in S, Q \in Z \ \mathrm{we \ have} \ \left(\frac{x}{\pi_i(Q)}\right) = a(i, j)\right\}. \end{align*}$$
$$\begin{align*}X_j(a, Z) := X_j(a, P) \cap \left\{x \in X_j : \ \mathrm{for \ all} \ i \in S, Q \in Z \ \mathrm{we \ have} \ \left(\frac{x}{\pi_i(Q)}\right) = a(i, j)\right\}. \end{align*}$$
Note that this is a natural generalisation of
![]() $X_j(a, P)$
as defined in Definition 5.4.
$X_j(a, P)$
as defined in Definition 5.4.
Proposition 5.11. Fix positive constants
![]() $c_1,\dots , c_6$
such that
$c_1,\dots , c_6$
such that
![]() $c_2c_3+2c_4+c_5< \frac {1}{4}$
and
$c_2c_3+2c_4+c_5< \frac {1}{4}$
and
![]() $c_6>3$
. Take
$c_6>3$
. Take
![]() $\delta>0$
satisfying
$\delta>0$
satisfying
![]() $2\delta <\frac {1}{4}-c_2c_3-2c_4-c_5$
; then the following holds for any large enough
$2\delta <\frac {1}{4}-c_2c_3-2c_4-c_5$
; then the following holds for any large enough
![]() $D_1$
. Take P to be a set of prime numbers, none of them congruent to
$D_1$
. Take P to be a set of prime numbers, none of them congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
, and take
$4$
, and take
![]() $1\leq k\leq r$
. Suppose
$1\leq k\leq r$
. Suppose
![]() $\mathcal {M} = \{(i,j):1\leq i< j\leq r\}$
and
$\mathcal {M} = \{(i,j):1\leq i< j\leq r\}$
and
![]() $\mathcal {N} = P \times \{k + 1, \dots , r\}$
. Let
$\mathcal {N} = P \times \{k + 1, \dots , r\}$
. Let
![]() $(X, P)$
be a prebox with parameters
$(X, P)$
be a prebox with parameters
![]() $D_1<s_1<t_1<s_2<t_2<\dots <s_r<t_r$
such that
$D_1<s_1<t_1<s_2<t_2<\dots <s_r<t_r$
such that
Let
![]() $U, V \subseteq [r]$
be disjoint subsets such that
$U, V \subseteq [r]$
be disjoint subsets such that
![]() $U \cup V = [l]$
for some l. Further assume
$U \cup V = [l]$
for some l. Further assume
-
1.
 $(X, P)$
is Siegel-less above
$(X, P)$
is Siegel-less above
 $D_1$
;
$D_1$
; -
2.
 $|P|\leq \log t_i-i$
for all
$|P|\leq \log t_i-i$
for all
 $1\leq i\leq r$
and
$1\leq i\leq r$
and
 $p \in P$
implies
$p \in P$
implies
 $p < s_1$
;
$p < s_1$
; -
3.
 $\log t_{k+1}>\max \{(\log t_1)^{c_6},D_1^{c_1}\}$
if
$\log t_{k+1}>\max \{(\log t_1)^{c_6},D_1^{c_1}\}$
if
 $k<r$
, and
$k<r$
, and
 $\log t_k<t_1^{c_2}$
;
$\log t_k<t_1^{c_2}$
; -
4.
 $|X_i|\geq e^it_i(\log t_i)^{-c_3}$
for all
$|X_i|\geq e^it_i(\log t_i)^{-c_3}$
for all
 $1\leq i\leq r$
;
$1\leq i\leq r$
; -
5.
 $r<t_1^{c_4}$
;
$r<t_1^{c_4}$
; -
6. for each
 $1\leq i\leq r$
,
$1\leq i\leq r$
,
 $j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
$j_i:= 1+i+\lfloor c_5 \log t_i\rfloor $
satisfy
 $j_1> k$
and
$j_1> k$
and
 $\log t_{j_i}>(\log t_i)^{c_6}$
if
$\log t_{j_i}>(\log t_i)^{c_6}$
if
 $j_i\leq r$
;
$j_i\leq r$
; -
7.
 $c_5 \log t_u> r + 10$
and
$c_5 \log t_u> r + 10$
and
 $u> k$
for all
$u> k$
for all
 $u \in U$
.
$u \in U$
.
We say that
![]() $Q \in \pi _V(X)$
is poor if there is
$Q \in \pi _V(X)$
is poor if there is
![]() $u \in U$
such that
$u \in U$
such that
 $$\begin{align*}\left||X_u(a, Q)| - \frac{|X_u|}{2^{|V|}}\right|> t_1^{-c_4 - \delta} |V| |X_u|. \end{align*}$$
$$\begin{align*}\left||X_u(a, Q)| - \frac{|X_u|}{2^{|V|}}\right|> t_1^{-c_4 - \delta} |V| |X_u|. \end{align*}$$
Then for all
![]() $a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
,
$a:\mathcal {M}\sqcup \mathcal {N}\rightarrow \{\pm 1\}$
,
 $$\begin{align*}\sum_{Q \in \pi_V(X) \ \mathrm{ poor }} |X(a, Q)| \leq r \cdot t_1^{-c_4 - \delta} \cdot \frac{|X|}{2^{|\mathcal{M}|}}. \end{align*}$$
$$\begin{align*}\sum_{Q \in \pi_V(X) \ \mathrm{ poor }} |X(a, Q)| \leq r \cdot t_1^{-c_4 - \delta} \cdot \frac{|X|}{2^{|\mathcal{M}|}}. \end{align*}$$
Proof. We proceed by induction on
![]() $|V|$
. The case
$|V|$
. The case
![]() $|V| = 0$
is trivial. Let v be the smallest element in V. Define
$|V| = 0$
is trivial. Let v be the smallest element in V. Define
![]() $\tilde {k}$
to be the k from the proposition if
$\tilde {k}$
to be the k from the proposition if
![]() $v = 1$
, and define
$v = 1$
, and define
![]() $\tilde {k}$
to be r if
$\tilde {k}$
to be r if
![]() $v \neq 1$
. Fix some
$v \neq 1$
. Fix some
![]() $x \in X_v$
. Put
$x \in X_v$
. Put
![]() $B_1 := c_4 + c_5 + \delta $
and
$B_1 := c_4 + c_5 + \delta $
and
![]() $B_2 := c_4 + \delta $
. Following the proof of Proposition 5.7, we get that
$B_2 := c_4 + \delta $
. Following the proof of Proposition 5.7, we get that
 $$\begin{align*}\left||X_j(a, x)| - \frac{1}{2} |X_j| \right| < t_1^{-B_2} |X_j| \text{ for all } 1 \leq j \leq \tilde{k} \text{ with } j \neq v \end{align*}$$
$$\begin{align*}\left||X_j(a, x)| - \frac{1}{2} |X_j| \right| < t_1^{-B_2} |X_j| \text{ for all } 1 \leq j \leq \tilde{k} \text{ with } j \neq v \end{align*}$$
holds for
![]() $x \in X_v$
with at most
$x \in X_v$
with at most
![]() $\tilde {k} t_1^{-B_1} |X_v|$
exceptions, while for
$\tilde {k} t_1^{-B_1} |X_v|$
exceptions, while for
![]() $j> \tilde {k}$
, we always get
$j> \tilde {k}$
, we always get
 $$\begin{align*}\left||X_j(a, x)| - \frac{1}{2} |X_j| \right| < t_1^{-1} |X_j|. \end{align*}$$
$$\begin{align*}\left||X_j(a, x)| - \frac{1}{2} |X_j| \right| < t_1^{-1} |X_j|. \end{align*}$$
Just as in the proof of Proposition 5.7, define
![]() $X_v^{\text {bad}}(a)$
to be the set of exceptions. We split the sum in the proposition as
$X_v^{\text {bad}}(a)$
to be the set of exceptions. We split the sum in the proposition as
 $$ \begin{align} \sum_{Q \in \pi_V(X) \ \mathrm{ poor }} |X(a, Q)| &= \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \not \in X_v^{\text{bad}}(a)}} |X(a, Q)| + \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \in X_v^{\text{bad}}(a)}} |X(a, Q)| \nonumber \\ &\leq \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \not \in X_v^{\text{bad}}(a)}} |X(a, Q)| + \sum_{\substack{Q \in \pi_V(X) \\ \pi_v(Q) \in X_v^{\text{bad}}(a)}} |X(a, Q)|. \end{align} $$
$$ \begin{align} \sum_{Q \in \pi_V(X) \ \mathrm{ poor }} |X(a, Q)| &= \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \not \in X_v^{\text{bad}}(a)}} |X(a, Q)| + \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \in X_v^{\text{bad}}(a)}} |X(a, Q)| \nonumber \\ &\leq \sum_{\substack{Q \in \pi_V(X) \ \mathrm{ poor } \\ \pi_v(Q) \not \in X_v^{\text{bad}}(a)}} |X(a, Q)| + \sum_{\substack{Q \in \pi_V(X) \\ \pi_v(Q) \in X_v^{\text{bad}}(a)}} |X(a, Q)|. \end{align} $$
We first treat the latter sum in equation (5.4). In the case
![]() $v = 1$
, we apply Proposition 5.7 to the prebox
$v = 1$
, we apply Proposition 5.7 to the prebox
for
![]() $x \in X_1^{\text {bad}}(a)$
and the natural restrictions of a, U, V,
$x \in X_1^{\text {bad}}(a)$
and the natural restrictions of a, U, V,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
. Then the latter sum is bounded by
$\mathcal {N}$
. Then the latter sum is bounded by
 $$\begin{align*}\sum_{\substack{Q \in \pi_V(X) \\ \pi_1(Q) \in X_1^{\text{bad}}(a)}} |X(a, Q)| = \sum_{x \in X_1^{\text{bad}}(a)} |X(a) \cap \pi_1^{-1}(x)| \leq |X_1^{\text{bad}}(a)| \cdot 2^{-|\mathcal{M}| + k + 1} \frac{|X|}{|X_1|}. \end{align*}$$
$$\begin{align*}\sum_{\substack{Q \in \pi_V(X) \\ \pi_1(Q) \in X_1^{\text{bad}}(a)}} |X(a, Q)| = \sum_{x \in X_1^{\text{bad}}(a)} |X(a) \cap \pi_1^{-1}(x)| \leq |X_1^{\text{bad}}(a)| \cdot 2^{-|\mathcal{M}| + k + 1} \frac{|X|}{|X_1|}. \end{align*}$$
A small computation shows that this is at most
for sufficiently large
![]() $D_1$
. Now suppose that
$D_1$
. Now suppose that
![]() $v \neq 1$
so that
$v \neq 1$
so that
![]() $1 \in U$
. Then apply Proposition 5.7 with
$1 \in U$
. Then apply Proposition 5.7 with
![]() $k = r - 1$
, the prebox
$k = r - 1$
, the prebox
and the natural restrictions of a, U, V,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
. Crucially, we have that this choice of k satisfies the requirements of Proposition 5.7 for sufficiently large
$\mathcal {N}$
. Crucially, we have that this choice of k satisfies the requirements of Proposition 5.7 for sufficiently large
![]() $D_1$
due to our assumption
$D_1$
due to our assumption
![]() $c_5 \log t_u> r + 10$
for all
$c_5 \log t_u> r + 10$
for all
![]() $u \in U$
. Then a similar computation shows that the latter sum is again at most
$u \in U$
. Then a similar computation shows that the latter sum is again at most
It remains to bound the former sum in equation (5.4). We first treat the case
![]() $v = 1$
. Take a poor
$v = 1$
. Take a poor
![]() $Q \in \pi _V(X)$
with
$Q \in \pi _V(X)$
with
![]() $x := \pi _1(Q) \not \in X_1^{\text {bad}}(a)$
. Then we claim that
$x := \pi _1(Q) \not \in X_1^{\text {bad}}(a)$
. Then we claim that
![]() $\pi _{V - \{1\}}(Q)$
is poor for the prebox
$\pi _{V - \{1\}}(Q)$
is poor for the prebox
Suppose that
![]() $\pi _{V - \{1\}}(Q)$
is not poor. Then we get for all
$\pi _{V - \{1\}}(Q)$
is not poor. Then we get for all
![]() $u \in U$
that
$u \in U$
that
 $$\begin{align*}\left||X_u(a, Q)| - \frac{|X_u(a, x)|}{2^{|V| - 1}}\right| \leq t_2^{-B_2} (|V| - 1) |X_u|. \end{align*}$$
$$\begin{align*}\left||X_u(a, Q)| - \frac{|X_u(a, x)|}{2^{|V| - 1}}\right| \leq t_2^{-B_2} (|V| - 1) |X_u|. \end{align*}$$
But from this, we deduce that for all
![]() $u \in U$
,
$u \in U$
,
 $$ \begin{align*} \left||X_u(a, Q)| - \frac{|X_u|}{2^{|V|}}\right| &\leq \left||X_u(a, Q)| - \frac{|X_u(a, x)|}{2^{|V| - 1}}\right| + \left|\frac{|X_u(a, x)|}{2^{|V| - 1}} - \frac{|X_u|}{2^{|V|}}\right| \\ &\leq t_2^{-B_2} (|V| - 1) |X_u| + t_1^{-B_2} |X_u| \leq t_1^{-B_2} |V| |X_u|, \end{align*} $$
$$ \begin{align*} \left||X_u(a, Q)| - \frac{|X_u|}{2^{|V|}}\right| &\leq \left||X_u(a, Q)| - \frac{|X_u(a, x)|}{2^{|V| - 1}}\right| + \left|\frac{|X_u(a, x)|}{2^{|V| - 1}} - \frac{|X_u|}{2^{|V|}}\right| \\ &\leq t_2^{-B_2} (|V| - 1) |X_u| + t_1^{-B_2} |X_u| \leq t_1^{-B_2} |V| |X_u|, \end{align*} $$
establishing the claim. Now we can easily bound the former sum in equation (5.4) using the induction hypothesis. Finally, we deal with the case that
![]() $v \neq 1$
so that
$v \neq 1$
so that
![]() $1 \in U$
. In this case, we apply the induction hypothesis to the prebox
$1 \in U$
. In this case, we apply the induction hypothesis to the prebox
with
![]() $k = r - 1$
.
$k = r - 1$
.
As alluded to earlier, the squarefree integers play a crucial role in our analysis. It turns out to be more convenient to work with squarefree integers with a fixed number of prime divisors, and this naturally leads to the following definition.
We now define special preboxes that we call boxes. These boxes provide a natural way to study distributional properties
![]() $S_r(N)$
, as we shall see in the coming proposition, which is based on Proposition 6.9 in Smith [Reference Smith18].
$S_r(N)$
, as we shall see in the coming proposition, which is based on Proposition 6.9 in Smith [Reference Smith18].
Definition 5.12. Suppose
![]() $0 \leq k\leq r$
. For any
$0 \leq k\leq r$
. For any
![]() $\mathbf {t}=(p_1,\dots ,p_k,s_{k+1},\dots ,s_r)$
such that
$\mathbf {t}=(p_1,\dots ,p_k,s_{k+1},\dots ,s_r)$
such that
-
1.
 $p_1<p_2<\dots <p_k<D_1$
is a sequence of primes not congruent to
$p_1<p_2<\dots <p_k<D_1$
is a sequence of primes not congruent to
 $3\bmod 4$
,
$3\bmod 4$
, -
2.
 $D_1<s_{k+1}<t_{k+1}<s_{k+2}<t_{k+2}<\dots <s_r<t_r$
is a sequence of real numbers where
$D_1<s_{k+1}<t_{k+1}<s_{k+2}<t_{k+2}<\dots <s_r<t_r$
is a sequence of real numbers where  $$\begin{align*}t_i=\left(1+\frac{1}{e^{i-k}\log D_1}\right)s_i, \end{align*}$$
$$\begin{align*}t_i=\left(1+\frac{1}{e^{i-k}\log D_1}\right)s_i, \end{align*}$$
we define
![]() $X(\mathbf {t}):=X_1\times \dots \times X_r$
with
$X(\mathbf {t}):=X_1\times \dots \times X_r$
with
 $$\begin{align*}X_i:= \begin{cases} \hfil\{p_i\}&\text{if }i\leq k,\\ \{p\in (s_i,t_i)\ \mathrm{ prime} \ : p\equiv 1\bmod 4\}&\text{if }i>k.\end{cases} \end{align*}$$
$$\begin{align*}X_i:= \begin{cases} \hfil\{p_i\}&\text{if }i\leq k,\\ \{p\in (s_i,t_i)\ \mathrm{ prime} \ : p\equiv 1\bmod 4\}&\text{if }i>k.\end{cases} \end{align*}$$
We call X a box if
![]() $X=X(\mathbf {t})$
for some
$X=X(\mathbf {t})$
for some
![]() $\mathbf {t}$
. There is a bijection from X to a subset of
$\mathbf {t}$
. There is a bijection from X to a subset of
![]() $S_r(\infty )$
. By abuse of notation, denote this subset by X.
$S_r(\infty )$
. By abuse of notation, denote this subset by X.
Theorem 5.13. Take
![]() $N\geq D_1\geq 3$
with
$N\geq D_1\geq 3$
with
![]() $\log N\geq (\log D_1)^2$
. Suppose that r satisfies equation (4.3). Let
$\log N\geq (\log D_1)^2$
. Suppose that r satisfies equation (4.3). Let
![]() $W\subseteq S_r(N)$
be a set of comfortably spaced elements above
$W\subseteq S_r(N)$
be a set of comfortably spaced elements above
![]() $D_1$
such that
$D_1$
such that
for some constant
![]() $\epsilon>0$
. Let
$\epsilon>0$
. Let
![]() $V\subseteq S_r(N)$
, and suppose that there exists some constant
$V\subseteq S_r(N)$
, and suppose that there exists some constant
![]() $\delta>0$
such that
$\delta>0$
such that
for any box
![]() $X\subseteq S_r(N)$
satisfying
$X\subseteq S_r(N)$
satisfying
![]() $X\cap W\neq \varnothing $
. Then there exists an absolute constant
$X\cap W\neq \varnothing $
. Then there exists an absolute constant
![]() $C> 0$
such that
$C> 0$
such that
 $$\begin{align*}|V|-\delta\Phi_r(N)\ll \epsilon\Phi_r(N) + \left(\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right)\right). \end{align*}$$
$$\begin{align*}|V|-\delta\Phi_r(N)\ll \epsilon\Phi_r(N) + \left(\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right)\right). \end{align*}$$
Proof. Define
![]() $\mathcal {T}_k=\{\mathbf {t}:X(\mathbf {t}) \subseteq S_r(N) \text { and } X(\mathbf {t})\cap W\neq \varnothing \}$
. Our aim is to estimate
$\mathcal {T}_k=\{\mathbf {t}:X(\mathbf {t}) \subseteq S_r(N) \text { and } X(\mathbf {t})\cap W\neq \varnothing \}$
. Our aim is to estimate
![]() $|V|$
in terms of
$|V|$
in terms of
where
![]() $dp_i$
is
$dp_i$
is
![]() $1$
if
$1$
if
![]() $p_i\equiv 1\bmod 4$
is prime and
$p_i\equiv 1\bmod 4$
is prime and
![]() $0$
otherwise.
$0$
otherwise.
Consider
![]() $n=(q_1,\dots ,q_r)\in S_r(N)$
with exactly k prime factors less than
$n=(q_1,\dots ,q_r)\in S_r(N)$
with exactly k prime factors less than
![]() $D_1$
. Then
$D_1$
. Then
![]() $n\in X(\mathbf {t})$
if and only if
$n\in X(\mathbf {t})$
if and only if
![]() $q_i=p_i$
for
$q_i=p_i$
for
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
 $$\begin{align*}s_i<q_i<\left(1+\frac{1}{e^{i-k}\log D_1}\right)s_i \text{ for }k<i\leq r.\end{align*}$$
$$\begin{align*}s_i<q_i<\left(1+\frac{1}{e^{i-k}\log D_1}\right)s_i \text{ for }k<i\leq r.\end{align*}$$
If
![]() $n\in W$
and
$n\in W$
and
 $$ \begin{align} n\prod_{i=k+1}^r \left(1+\frac{1}{e^{i-k}\log D_1}\right)<N, \end{align} $$
$$ \begin{align} n\prod_{i=k+1}^r \left(1+\frac{1}{e^{i-k}\log D_1}\right)<N, \end{align} $$
then
 $$ \begin{align*} \begin{aligned} \int_{\substack{\mathbf{t}\in\mathcal{T}_k:\\n\in X(\mathbf{t})}}\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} &=\int_{q_{k+1}\left(1+\frac{1}{e\log D_1}\right)^{-1}}^{q_{k+1}}\cdots\int_{q_r\left(1+\frac{1}{e^{r-k}\log D_1}\right)^{-1}}^{q_r}\frac{ds_{k+1}\cdots ds_r}{s_{k+1}\dots s_r} \\ &=\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right) .\end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\substack{\mathbf{t}\in\mathcal{T}_k:\\n\in X(\mathbf{t})}}\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} &=\int_{q_{k+1}\left(1+\frac{1}{e\log D_1}\right)^{-1}}^{q_{k+1}}\cdots\int_{q_r\left(1+\frac{1}{e^{r-k}\log D_1}\right)^{-1}}^{q_r}\frac{ds_{k+1}\cdots ds_r}{s_{k+1}\dots s_r} \\ &=\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right) .\end{aligned} \end{align*} $$
If equation (5.5) does not hold or
![]() $n\notin W$
, then
$n\notin W$
, then
 $$\begin{align*}\int_{\substack{\mathbf{t}\in\mathcal{T}_k:\\n\in X(\mathbf{t})}}\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} \leq\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right). \end{align*}$$
$$\begin{align*}\int_{\substack{\mathbf{t}\in\mathcal{T}_k:\\n\in X(\mathbf{t})}}\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} \leq\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right). \end{align*}$$
There exists some constant
![]() $C>0$
such that any n that does not satisfy equation (5.5) lies in
$C>0$
such that any n that does not satisfy equation (5.5) lies in
 $$\begin{align*}N\left(1-\frac{C}{\log D_1}\right) \leq N\prod_{i=k+1}^r\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1}\leq n\leq N, \end{align*}$$
$$\begin{align*}N\left(1-\frac{C}{\log D_1}\right) \leq N\prod_{i=k+1}^r\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1}\leq n\leq N, \end{align*}$$
which we bound by
 $$\begin{align*}\Phi_r(N)-\Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right). \end{align*}$$
$$\begin{align*}\Phi_r(N)-\Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right). \end{align*}$$
Then
 $$\begin{align*}\sum_{k=0}^{\infty}\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1}\int_{\mathcal{T}_k}|V\cap X(\mathbf{t})|\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} \end{align*}$$
$$\begin{align*}\sum_{k=0}^{\infty}\prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1}\int_{\mathcal{T}_k}|V\cap X(\mathbf{t})|\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r}{s_{k+1}\cdots s_r} \end{align*}$$
is bounded above by
![]() $|V|$
and below by
$|V|$
and below by
 $$ \begin{align*} & |V\cap W| + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right)= \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad |V| + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right) + O\left(\epsilon \Phi_r(N)\right). \end{align*} $$
$$ \begin{align*} & |V\cap W| + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right)= \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad |V| + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right) + O\left(\epsilon \Phi_r(N)\right). \end{align*} $$
Similarly,
 $$ \begin{align*} \sum_{k=0}^{\infty} \prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1} &\int_{\mathcal{T}_k}|X(\mathbf{t})|\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r} {s_{k+1}\cdots s_r}\\ & =\Phi_r(N) + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right) + O\left(\epsilon \Phi_r(N)\right). \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{\infty} \prod_{i=k+1}^r \log\left(1+\frac{1}{e^{i-k}\log D_1}\right)^{-1} &\int_{\mathcal{T}_k}|X(\mathbf{t})|\frac{dp_1\cdots dp_kds_{k+1}\cdots ds_r} {s_{k+1}\cdots s_r}\\ & =\Phi_r(N) + O\left(\Phi_r(N) - \Phi_r\left(N\left(1-\frac{C}{\log D_1}\right)\right)\right) + O\left(\epsilon \Phi_r(N)\right). \end{align*} $$
The result follows from the estimate
![]() $|V\cap X(\mathbf {t})|=(\delta +O(\epsilon ))|X(\mathbf {t})|$
for
$|V\cap X(\mathbf {t})|=(\delta +O(\epsilon ))|X(\mathbf {t})|$
for
![]() $\mathbf {t} \in \mathcal {T}_k$
.
$\mathbf {t} \in \mathcal {T}_k$
.
With some extra work, it is possible to prove that
 $$\begin{align*}\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right) \ll \frac{\Phi_r(N)}{\log D_1}, \end{align*}$$
$$\begin{align*}\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right) \ll \frac{\Phi_r(N)}{\log D_1}, \end{align*}$$
which ensures that the error term in Theorem 5.13 is smaller than the main term. However, in our applications, we work with all values of r simultaneously so that the trivial bound
 $$\begin{align*}\sum_r \left(\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right)\right) \ll \frac{\Phi(N)}{\log D_1} \end{align*}$$
$$\begin{align*}\sum_r \left(\Phi_r(N) - \Phi_r\left(N\left(1 - \frac{C}{\log D_1}\right)\right)\right) \ll \frac{\Phi(N)}{\log D_1} \end{align*}$$
suffices for our purposes. Our next proposition deals with boxes that are not Siegel-less. It is directly based on Proposition 6.10 in Smith [Reference Smith18].
Theorem 5.14. Let
![]() $d_1,d_2,\dots $
be a sequence of distinct squarefree integers greater than
$d_1,d_2,\dots $
be a sequence of distinct squarefree integers greater than
![]() $D_1$
satisfying
$D_1$
satisfying
![]() $d_i^2<d_{i+1}$
. Take
$d_i^2<d_{i+1}$
. Take
![]() $N\geq D_1\geq 3$
satisfying
$N\geq D_1\geq 3$
satisfying
![]() $\log N\geq (\log D_1)^4$
, and suppose that r satisfies equation (4.3). Define
$\log N\geq (\log D_1)^4$
, and suppose that r satisfies equation (4.3). Define
Then
Proof. Suppose we have some box
![]() $X\subseteq V_i$
and
$X\subseteq V_i$
and
![]() $d_i=p_1\cdots p_m$
. For any element
$d_i=p_1\cdots p_m$
. For any element
![]() $x\in X$
, there are prime factors
$x\in X$
, there are prime factors
![]() $q_1,\dots ,q_m$
of x such that
$q_1,\dots ,q_m$
of x such that
If
![]() $d_i<N^{2/3}$
, we deduce from equation (4.1) that there exists some constant
$d_i<N^{2/3}$
, we deduce from equation (4.1) that there exists some constant
![]() $C>0$
with
$C>0$
with
 $$\begin{align*}\begin{aligned} |V_i|& \leq \Phi_{r-m}\left(\frac{2^m N}{d_i}\right) \cdot\prod_{p_i\geq D_1}\left|\left\{q_i\text{ prime}:\frac{1}{2}p_i<q_i<2p_i,\ q_i\equiv 1\bmod 4\right\}\right|\\ &\leq \Phi_r(N)\cdot \frac{C^m }{d_i}\prod_{p_i\geq D_1}\frac{p_i}{\log p_i} \ll\frac{\Phi_r(N)}{\log d_i}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} |V_i|& \leq \Phi_{r-m}\left(\frac{2^m N}{d_i}\right) \cdot\prod_{p_i\geq D_1}\left|\left\{q_i\text{ prime}:\frac{1}{2}p_i<q_i<2p_i,\ q_i\equiv 1\bmod 4\right\}\right|\\ &\leq \Phi_r(N)\cdot \frac{C^m }{d_i}\prod_{p_i\geq D_1}\frac{p_i}{\log p_i} \ll\frac{\Phi_r(N)}{\log d_i}. \end{aligned} \end{align*}$$
Notice that
![]() $d_i>D_1^{2^{i-1}}$
. Then
$d_i>D_1^{2^{i-1}}$
. Then
 $$\begin{align*}\left|\bigcup_{d_i<N^{2/3}}V_i\right| \ll\Phi_r(N)\sum_{i\geq 1}\frac{1}{2^{i-1}\log D_1} \ll\frac{\Phi_r(N)}{\log D_1}. \end{align*}$$
$$\begin{align*}\left|\bigcup_{d_i<N^{2/3}}V_i\right| \ll\Phi_r(N)\sum_{i\geq 1}\frac{1}{2^{i-1}\log D_1} \ll\frac{\Phi_r(N)}{\log D_1}. \end{align*}$$
If
![]() $d_i\geq N^{2/3}$
, then
$d_i\geq N^{2/3}$
, then
![]() $d_{i+1}\geq N^{4/3}>N$
. Therefore there is at most one i such that
$d_{i+1}\geq N^{4/3}>N$
. Therefore there is at most one i such that
![]() $d_i\geq N^{2/3}$
and
$d_i\geq N^{2/3}$
and
![]() $V_i$
is not empty. Then for sufficiently large
$V_i$
is not empty. Then for sufficiently large
![]() $D_1$
,
$D_1$
,
 $$ \begin{align*} |V_i|&\leq \left|\left\{x\in S_r(N):d_i\mid x\right\}\right|\cdot\prod_{p_i\geq D_1}\left|\left\{q_i\text{ prime}:\frac{1}{2}p_i<q_i<2p_i,\ q_i\equiv 1\bmod 4\right\}\right|\\ &\leq \frac{N}{d_i}\prod_{p_i\geq D_1}\frac{2p_i}{\log p_i} \ll \frac{N}{\log d_i} \ll \frac{N}{\log N}, \end{align*} $$
$$ \begin{align*} |V_i|&\leq \left|\left\{x\in S_r(N):d_i\mid x\right\}\right|\cdot\prod_{p_i\geq D_1}\left|\left\{q_i\text{ prime}:\frac{1}{2}p_i<q_i<2p_i,\ q_i\equiv 1\bmod 4\right\}\right|\\ &\leq \frac{N}{d_i}\prod_{p_i\geq D_1}\frac{2p_i}{\log p_i} \ll \frac{N}{\log d_i} \ll \frac{N}{\log N}, \end{align*} $$
which fits into the error bound.
Definition 5.15. Fix some constants
![]() $c_{9}, c_{10}>0$
. We call a box X of
$c_{9}, c_{10}>0$
. We call a box X of
![]() $S_r(N)$
acceptable if it
$S_r(N)$
acceptable if it
-
1. contains a comfortably spaced element above
 $D_1=\exp \left (\left (\frac {1}{2}\log \log N\right )^{c_{9}}\right )$
,
$D_1=\exp \left (\left (\frac {1}{2}\log \log N\right )^{c_{9}}\right )$
, -
2. contains a
 $(c_{10}\log \log \log N)$
-regular element, and
$(c_{10}\log \log \log N)$
-regular element, and -
3. is Siegel-less above
 $D_1$
.
$D_1$
.
Given any integer
![]() $x \in \mathcal {D}$
, let
$x \in \mathcal {D}$
, let
![]() $p_1<\dots <p_n$
be the distinct prime factors of x, and call the matrix
$p_1<\dots <p_n$
be the distinct prime factors of x, and call the matrix
![]() $(c_{ij})_{1\leq i,j\leq n}$
defined by
$(c_{ij})_{1\leq i,j\leq n}$
defined by
 $$\begin{align*}(-1)^{c_{ij}}= \begin{cases} \hfil \left(\frac{p_i}{p_j}\right)&\text{ if }i\neq j\\ \prod_{l\neq j} \left(\frac{p_l}{p_j}\right)&\text{ if }i=j \end{cases}\end{align*}$$
$$\begin{align*}(-1)^{c_{ij}}= \begin{cases} \hfil \left(\frac{p_i}{p_j}\right)&\text{ if }i\neq j\\ \prod_{l\neq j} \left(\frac{p_l}{p_j}\right)&\text{ if }i=j \end{cases}\end{align*}$$
the Rédei matrix of x. This is a symmetric matrix with column (and row) sum zero due to our assumption
![]() $x \in \mathcal {D}$
. We are now ready to reprove a well-known result due to Fouvry and Klüners [Reference Fouvry and Klüners6]. Note that unlike the work of Fouvry and Klüners, our theorem has the benefit of providing an error term.
$x \in \mathcal {D}$
. We are now ready to reprove a well-known result due to Fouvry and Klüners [Reference Fouvry and Klüners6]. Note that unlike the work of Fouvry and Klüners, our theorem has the benefit of providing an error term.
Theorem 5.16. There exists a constant
![]() $c>0$
such that for all integers
$c>0$
such that for all integers
![]() $k \geq 0$
,
$k \geq 0$
,
 $$\begin{align*}\left|\frac{|\{d\in\mathcal{D}(N) : \operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(d)=k\}|}{|\mathcal{D}(N)|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll (\log\log N)^{-c}. \end{align*}$$
$$\begin{align*}\left|\frac{|\{d\in\mathcal{D}(N) : \operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(d)=k\}|}{|\mathcal{D}(N)|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll (\log\log N)^{-c}. \end{align*}$$
Proof. By our Erdős–Kac result – that is, equation (4.2) – it suffices to show that
 $$\begin{align*}\left|\frac{|\{d\in S_r(N) : \operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(d)=k\}|}{|S_r(N)|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll (\log\log N)^{-c} \end{align*}$$
$$\begin{align*}\left|\frac{|\{d\in S_r(N) : \operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(d)=k\}|}{|S_r(N)|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll (\log\log N)^{-c} \end{align*}$$
for any r satisfying equation (4.3). We can find some
![]() $W\subseteq S_r(N)$
that is comfortably spaced above
$W\subseteq S_r(N)$
that is comfortably spaced above
![]() $D_1$
and
$D_1$
and
![]() $(c_{10}\log \log \log N)$
-regular by Theorem 4.1 and Siegel-less above
$(c_{10}\log \log \log N)$
-regular by Theorem 4.1 and Siegel-less above
![]() $D_1$
by Proposition 5.14 so that
$D_1$
by Proposition 5.14 so that
for some absolute constant
![]() $c> 0$
. Then, applying Theorem 5.13, we see that we can restrict to acceptable boxes by introducing an error
$c> 0$
. Then, applying Theorem 5.13, we see that we can restrict to acceptable boxes by introducing an error
![]() $\ll (\log \log N)^{-c}$
. In other words, it suffices to show that we have for any acceptable box
$\ll (\log \log N)^{-c}$
. In other words, it suffices to show that we have for any acceptable box
![]() $X \subseteq S_r(N)$
$X \subseteq S_r(N)$
 $$ \begin{align} \left|\frac{|\{x\in X :\operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(x)=k\}|}{|X|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll(\log\log N)^{-c}. \end{align} $$
$$ \begin{align} \left|\frac{|\{x\in X :\operatorname{\mathrm{rk}}_4 \operatorname{\mathrm{Cl}}^+(x)=k\}|}{|X|}-\lim_{n\rightarrow\infty} P(n|k)\right|\ll(\log\log N)^{-c}. \end{align} $$
Take X to be an acceptable box. Then one can check that there exist constants that satisfy the requirements in Theorem 5.9 applied to the prebox
![]() $(X_1\times \dots \times X_r, \varnothing )$
. Then Theorem 5.9 shows that the Rédei matrices of
$(X_1\times \dots \times X_r, \varnothing )$
. Then Theorem 5.9 shows that the Rédei matrices of
![]() $x\in X$
are equidistributed amongst all
$x\in X$
are equidistributed amongst all
![]() $r \times r$
symmetric matrices over
$r \times r$
symmetric matrices over
![]() $\mathbb {F}_2$
with column sum zero, up to reordering some columns and rows, with an error within the statement. Since reordering columns and rows does not change the rank, we can assume that the Rédei matrix is a random
$\mathbb {F}_2$
with column sum zero, up to reordering some columns and rows, with an error within the statement. Since reordering columns and rows does not change the rank, we can assume that the Rédei matrix is a random
![]() $r \times r$
symmetric matrix over
$r \times r$
symmetric matrix over
![]() $\mathbb {F}_2$
with column sum zero.
$\mathbb {F}_2$
with column sum zero.
Let A be the matrix obtained from the Rédei matrix after removing a column and a row. It is a classical fact that
![]() $\operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}^+(x)$
is equal to the corank of A. But A is a random
$\operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}^+(x)$
is equal to the corank of A. But A is a random
![]() $(r - 1) \times (r - 1)$
symmetric matrix. By [Reference MacWilliams15, Theorem 2], we have for all
$(r - 1) \times (r - 1)$
symmetric matrix. By [Reference MacWilliams15, Theorem 2], we have for all
![]() $n \geq k \geq 0$
$n \geq k \geq 0$
 $$ \begin{align*} P(n|k) &= \frac{N(n, n - k)}{2^{\frac{n(n + 1)}{2}}} = \frac{1}{2^{\frac{n(n + 1)}{2}}} \prod_{i = 1}^{\frac{n - k}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (2^{n - i} - 1) \\ &= \frac{1}{2^{\frac{k(k + 1)}{2}}} \prod_{i = 1}^{\frac{n - k}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (1 - 2^{i - n}) \end{align*} $$
$$ \begin{align*} P(n|k) &= \frac{N(n, n - k)}{2^{\frac{n(n + 1)}{2}}} = \frac{1}{2^{\frac{n(n + 1)}{2}}} \prod_{i = 1}^{\frac{n - k}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (2^{n - i} - 1) \\ &= \frac{1}{2^{\frac{k(k + 1)}{2}}} \prod_{i = 1}^{\frac{n - k}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (1 - 2^{i - n}) \end{align*} $$
if
![]() $n - k \equiv 0 \bmod 2$
and
$n - k \equiv 0 \bmod 2$
and
 $$ \begin{align*} P(n|k) &= \frac{N(n, n - k)}{2^{\frac{n(n + 1)}{2}}} = \frac{1}{2^{\frac{n(n + 1)}{2}}} \prod_{i = 1}^{\frac{n - k - 1}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (2^{n - i} - 1) \\ &= \frac{1}{2^{\frac{k(k + 1)}{2}}} \prod_{i = 1}^{\frac{n - k - 1}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (1 - 2^{i - n}) \end{align*} $$
$$ \begin{align*} P(n|k) &= \frac{N(n, n - k)}{2^{\frac{n(n + 1)}{2}}} = \frac{1}{2^{\frac{n(n + 1)}{2}}} \prod_{i = 1}^{\frac{n - k - 1}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (2^{n - i} - 1) \\ &= \frac{1}{2^{\frac{k(k + 1)}{2}}} \prod_{i = 1}^{\frac{n - k - 1}{2}} \frac{2^{2i}}{2^{2i} - 1} \cdot \prod_{i = 0}^{n - k - 1} (1 - 2^{i - n}) \end{align*} $$
if
![]() $n - k \equiv 1 \bmod 2$
, where
$n - k \equiv 1 \bmod 2$
, where
![]() $N(n, k)$
denotes the number of symmetric
$N(n, k)$
denotes the number of symmetric
![]() $n \times n$
-matrices with coefficients in
$n \times n$
-matrices with coefficients in
![]() $\mathbb {F}_2$
and rank k. Using this, one directly bounds the difference
$\mathbb {F}_2$
and rank k. Using this, one directly bounds the difference
![]() $P(r - 1|k) - \lim _{n\rightarrow \infty } P(n|k)$
, completing the proof.
$P(r - 1|k) - \lim _{n\rightarrow \infty } P(n|k)$
, completing the proof.
Gerth [Reference Gerth8, Theorem 2.2] also studied the difference
![]() $P(r - 1|k) - \lim _{n\rightarrow \infty } P(n|k)$
but without giving a rate of convergence. It is for this reason that we appeal to the work [Reference MacWilliams15] instead.
$P(r - 1|k) - \lim _{n\rightarrow \infty } P(n|k)$
but without giving a rate of convergence. It is for this reason that we appeal to the work [Reference MacWilliams15] instead.
6 Proof of main theorems
Recall from the introduction that
We also define
In this section, we prove the following theorem.
Theorem 6.1. There are
![]() $A, N_0> 0$
such that for all
$A, N_0> 0$
such that for all
![]() $N> N_0$
and all integers
$N> N_0$
and all integers
![]() $n_2 \geq n_3 \geq 0$
, we have
$n_2 \geq n_3 \geq 0$
, we have
Theorem 5.16 and Theorem 6.1 together imply Theorem 1.2. Hence it remains to prove Theorem 6.1. Our first step is to reduce to sufficiently nice boxes X. We formalise this in our next definition.
Definition 6.2. Let
![]() $r \geq 1$
be an integer, let
$r \geq 1$
be an integer, let
![]() $X = X_1 \times \ldots \times X_r$
be a box, and let
$X = X_1 \times \ldots \times X_r$
be a box, and let
![]() $N \geq 10^{10^{10}}$
be a real number. Put
$N \geq 10^{10^{10}}$
be a real number. Put
We let W be the maximal subset of
![]() $S_r(N)$
that is comfortably spaced above
$S_r(N)$
that is comfortably spaced above
![]() $D_1$
,
$D_1$
,
![]() $\eta $
-regular and disjoint from the sets
$\eta $
-regular and disjoint from the sets
![]() $V_i$
in Proposition 5.14. We call X a nice box for N if
$V_i$
in Proposition 5.14. We call X a nice box for N if
![]() $X \subseteq S_r(N)$
,
$X \subseteq S_r(N)$
,
![]() $X \cap W \neq \varnothing $
and r satisfies equation (4.3).
$X \cap W \neq \varnothing $
and r satisfies equation (4.3).
Proposition 6.3. There are
![]() $A, N_0> 0$
such that for all
$A, N_0> 0$
such that for all
![]() $N> N_0$
, all nice boxes X for N and all integers
$N> N_0$
, all nice boxes X for N and all integers
![]() $n_2 \geq n_3 \geq 0$
, we have
$n_2 \geq n_3 \geq 0$
, we have
Proof that Proposition 6.3 implies Theorem 6.1
From Erdős—Kac (see equation (4.2)), it follows that we only need to consider r satisfying equation (4.3). For each such r, we apply Proposition 5.13 with W as in Definition 6.2; the required lower bound for
![]() $|W|$
follows from the material in Section 4 and Proposition 5.14.
$|W|$
follows from the material in Section 4 and Proposition 5.14.
Given a box X and
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
, our next step is to reduce to
$a:\mathcal {M} \rightarrow \{\pm 1\}$
, our next step is to reduce to
![]() $X(a)$
. However, it turns out that we cannot prove equidistribution for all
$X(a)$
. However, it turns out that we cannot prove equidistribution for all
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
, but only if a is generic in the following sense.
$a:\mathcal {M} \rightarrow \{\pm 1\}$
, but only if a is generic in the following sense.
Definition 6.4. For a field K and for integers
![]() $a, b \geq 0$
, we denote by
$a, b \geq 0$
, we denote by
![]() $\operatorname {\mathrm {Mat}}(K, a, b)$
the set of
$\operatorname {\mathrm {Mat}}(K, a, b)$
the set of
![]() $a \times b$
-matrices with coefficients in K. Let
$a \times b$
-matrices with coefficients in K. Let
![]() $\iota $
be the unique group isomorphism between
$\iota $
be the unique group isomorphism between
![]() $\{\pm 1\}$
and
$\{\pm 1\}$
and
![]() $\mathbb {F}_2$
. For the rest of the paper, we will use
$\mathbb {F}_2$
. For the rest of the paper, we will use
Given
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
, we associate a symmetric matrix
$a:\mathcal {M} \rightarrow \{\pm 1\}$
, we associate a symmetric matrix
![]() $A \in \operatorname {\mathrm {Mat}}(\mathbb {F}_2, r, r)$
by setting for all
$A \in \operatorname {\mathrm {Mat}}(\mathbb {F}_2, r, r)$
by setting for all
![]() $i < j$
$i < j$
and finally
 $$\begin{align*}A(i, i) = \iota \circ \prod_{j = 1}^r a(i, j). \end{align*}$$
$$\begin{align*}A(i, i) = \iota \circ \prod_{j = 1}^r a(i, j). \end{align*}$$
Think of
![]() $\mathbb {F}_2^r$
as column vectors. We define the vector space
$\mathbb {F}_2^r$
as column vectors. We define the vector space
Let
![]() $R := (1, \ldots , 1)$
so that
$R := (1, \ldots , 1)$
so that
![]() $R \in \mathcal {V}_{a,2}$
. Put
$R \in \mathcal {V}_{a,2}$
. Put
![]() $n_2(a) := -1 + \dim _{\mathbb {F}_2} \mathcal {V}_{a,2}$
.
$n_2(a) := -1 + \dim _{\mathbb {F}_2} \mathcal {V}_{a,2}$
.
Let N be a large real, and let
![]() $X = X_1 \times \ldots \times X_r$
be a nice box for N. Choose an index
$X = X_1 \times \ldots \times X_r$
be a nice box for N. Choose an index
![]() $k_{\mathrm {gap}}$
such that the extravagant spacing of X is between
$k_{\mathrm {gap}}$
such that the extravagant spacing of X is between
![]() $k_{\mathrm {gap}}$
and
$k_{\mathrm {gap}}$
and
![]() $k_{\mathrm {gap}} + 1$
. Set
$k_{\mathrm {gap}} + 1$
. Set
We say that
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X if
$a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X if
![]() $n_2(a) \leq n_{\mathrm {max}}$
, and furthermore we have for all
$n_2(a) \leq n_{\mathrm {max}}$
, and furthermore we have for all
![]() $S \in \mathcal {V}_{a,2} \setminus \langle R \rangle $
and all
$S \in \mathcal {V}_{a,2} \setminus \langle R \rangle $
and all
![]() $i \in \mathbb {F}_2$
that
$i \in \mathbb {F}_2$
that
 $$ \begin{align} \left|\left|\left\{j \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq j \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_j(S) = i\right\}\right| - \frac{k_{\mathrm{gap}}}{4}\right| \leq 2^{-10n_{\mathrm{max}}} \cdot k_{\mathrm{gap}} \end{align} $$
$$ \begin{align} \left|\left|\left\{j \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq j \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_j(S) = i\right\}\right| - \frac{k_{\mathrm{gap}}}{4}\right| \leq 2^{-10n_{\mathrm{max}}} \cdot k_{\mathrm{gap}} \end{align} $$
and
 $$ \begin{align} \left|\left|\left\{j \in [r] : k_{\mathrm{gap}} < j \leq 2k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_j(S) = i\right\}\right| - \frac{k_{\mathrm{gap}}}{2}\right| \leq 2^{-10n_{\mathrm{max}}} \cdot k_{\mathrm{gap}}. \end{align} $$
$$ \begin{align} \left|\left|\left\{j \in [r] : k_{\mathrm{gap}} < j \leq 2k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_j(S) = i\right\}\right| - \frac{k_{\mathrm{gap}}}{2}\right| \leq 2^{-10n_{\mathrm{max}}} \cdot k_{\mathrm{gap}}. \end{align} $$
We shall prove that the Artin pairing
![]() $\text {Art}_2$
is equidistributed in
$\text {Art}_2$
is equidistributed in
![]() $X(a)$
under favorable circumstances. For this reason, we make the following definition.
$X(a)$
under favorable circumstances. For this reason, we make the following definition.
Definition 6.5. We say that a bilinear pairing
is valid if the right kernel contains
![]() $(1, \ldots , 1)$
. Fix a basis
$(1, \ldots , 1)$
. Fix a basis
![]() $w_1, \ldots w_{n_2}, R$
for
$w_1, \ldots w_{n_2}, R$
for
![]() $\mathcal {V}_{a,2}$
. Using this basis, we may identify
$\mathcal {V}_{a,2}$
. Using this basis, we may identify
![]() $\operatorname {\mathrm {Art}}_2$
with a
$\operatorname {\mathrm {Art}}_2$
with a
![]() $(n_2 + 1) \times (n_2 + 1)$
matrix with coefficients in
$(n_2 + 1) \times (n_2 + 1)$
matrix with coefficients in
![]() $\mathbb {F}_2$
. Since
$\mathbb {F}_2$
. Since
![]() $(1, \ldots , 1)$
is in the right kernel, we may also naturally identify
$(1, \ldots , 1)$
is in the right kernel, we may also naturally identify
![]() $\operatorname {\mathrm {Art}}_2$
with a
$\operatorname {\mathrm {Art}}_2$
with a
![]() $(n_2 + 1) \times n_2$
matrix. Finally, define for a box X
$(n_2 + 1) \times n_2$
matrix. Finally, define for a box X
Here one defines the Artin pairing of x as follows:
 $$\begin{align*}\mathrm{Art}_2(x)(i, j) := \left\langle \sum_{a \in [r]} \pi_a(w_j) \chi_{\pi_a(x)}, \prod_{b \in [r]} \pi_b(x)^{\pi_b(w_i)}\right\rangle_x, \end{align*}$$
$$\begin{align*}\mathrm{Art}_2(x)(i, j) := \left\langle \sum_{a \in [r]} \pi_a(w_j) \chi_{\pi_a(x)}, \prod_{b \in [r]} \pi_b(x)^{\pi_b(w_i)}\right\rangle_x, \end{align*}$$
where
![]() $w_i$
and
$w_i$
and
![]() $w_j$
are allowed to be equal to R and
$w_j$
are allowed to be equal to R and
![]() $\langle \cdot , \cdot \rangle _x$
is the pairing defined in Section 2. We recall that
$\langle \cdot , \cdot \rangle _x$
is the pairing defined in Section 2. We recall that
![]() $\operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}(x) = \operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}^+(x)$
if and only if
$\operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}(x) = \operatorname {\mathrm {rk}}_4 \operatorname {\mathrm {Cl}}^+(x)$
if and only if
![]() $(1, \dots , 1)$
is in the left kernel of
$(1, \dots , 1)$
is in the left kernel of
![]() $\mathrm {Art}_2(x)$
. Furthermore, the dimension of the left kernel of
$\mathrm {Art}_2(x)$
. Furthermore, the dimension of the left kernel of
![]() $\mathrm {Art}_2(x)$
is precisely one more than the dimension of
$\mathrm {Art}_2(x)$
is precisely one more than the dimension of
![]() $4\operatorname {\mathrm {Cl}}^+(x)[8]$
.
$4\operatorname {\mathrm {Cl}}^+(x)[8]$
.
If
![]() $X = X_1 \times \dots \times X_r$
is a box with
$X = X_1 \times \dots \times X_r$
is a box with
![]() $D_1$
sufficiently large, we recall that k is the largest index such that
$D_1$
sufficiently large, we recall that k is the largest index such that
![]() $|X_k| = 1$
.
$|X_k| = 1$
.
Proposition 6.6. There are
![]() $A, N_0> 0$
such that for all
$A, N_0> 0$
such that for all
![]() $N> N_0$
, all nice boxes X for N, all integers
$N> N_0$
, all nice boxes X for N, all integers
![]() $n_2 \geq 0$
, all generic
$n_2 \geq 0$
, all generic
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
for X with
$a:\mathcal {M} \rightarrow \{\pm 1\}$
for X with
![]() $n_2(a) = n_2$
and
$n_2(a) = n_2$
and
for all
![]() $k < j \leq r$
, and all valid Artin pairings
$k < j \leq r$
, and all valid Artin pairings
![]() $\operatorname {\mathrm {Art}}_2$
, we have
$\operatorname {\mathrm {Art}}_2$
, we have
Here we write
![]() $x_1, \ldots , x_k$
for the unique elements of
$x_1, \ldots , x_k$
for the unique elements of
![]() $X_1, \ldots , X_k$
.
$X_1, \ldots , X_k$
.
Proof that Proposition 6.6 implies Proposition 6.3
Take N to be a large integer, and take X to be a nice box for N. If N is sufficiently large and
![]() $n_2> n_{\text {max}}$
, we have
$n_2> n_{\text {max}}$
, we have
 $$\begin{align*}\lim_{k \rightarrow \infty} P(k|n_2) = O\left(\frac{1}{\log \log \log \log N}\right). \end{align*}$$
$$\begin{align*}\lim_{k \rightarrow \infty} P(k|n_2) = O\left(\frac{1}{\log \log \log \log N}\right). \end{align*}$$
Then it follows from equation (5.6) that
for a sufficiently large constant
![]() $A> 0$
. From now on, suppose that
$A> 0$
. From now on, suppose that
![]() $n_2 \leq n_{\text {max}}$
. We deduce from Hoeffding’s inequality that the proportion of S in
$n_2 \leq n_{\text {max}}$
. We deduce from Hoeffding’s inequality that the proportion of S in
![]() $\mathbb {F}_2^r$
failing equation (6.1) or equation (6.2) is bounded by
$\mathbb {F}_2^r$
failing equation (6.1) or equation (6.2) is bounded by
Given
![]() $S \not \in \langle R \rangle $
, the proportion of
$S \not \in \langle R \rangle $
, the proportion of
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
with
$a:\mathcal {M} \rightarrow \{\pm 1\}$
with
![]() $S \in \mathcal {V}_{a,2}$
is
$S \in \mathcal {V}_{a,2}$
is
![]() $O(0.5^r)$
. Taking the union over all S in
$O(0.5^r)$
. Taking the union over all S in
![]() $\mathbb {F}_2^r$
failing equation (6.1) or equation (6.2) proves that the proportion of nongeneric a is at most
$\mathbb {F}_2^r$
failing equation (6.1) or equation (6.2) proves that the proportion of nongeneric a is at most
Put
![]() $k_2 := \lfloor 0.25k_{\text {gap}}\rfloor $
. Then we have for all
$k_2 := \lfloor 0.25k_{\text {gap}}\rfloor $
. Then we have for all
![]() $\sigma \in \mathcal {P}(k_2)$
that
$\sigma \in \mathcal {P}(k_2)$
that
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic if and only if
$a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic if and only if
![]() $\sigma (a)$
is generic, where
$\sigma (a)$
is generic, where
![]() $\sigma (a)$
is defined in the natural way. Theorem 5.9 implies that
$\sigma (a)$
is defined in the natural way. Theorem 5.9 implies that
 $$\begin{align*}\sum_{a:\mathcal{M} \rightarrow \{\pm 1\}} \left|2^{-|\mathcal{M}|} \cdot |X| - \frac{1}{k_2!} \sum_{\sigma \in \mathcal{P}(k_2)} |X(\sigma(a))|\right| \leq (k_2^{-\delta_1} + t_{k + 1}^{\prime -\delta_2}) \cdot |X|, \end{align*}$$
$$\begin{align*}\sum_{a:\mathcal{M} \rightarrow \{\pm 1\}} \left|2^{-|\mathcal{M}|} \cdot |X| - \frac{1}{k_2!} \sum_{\sigma \in \mathcal{P}(k_2)} |X(\sigma(a))|\right| \leq (k_2^{-\delta_1} + t_{k + 1}^{\prime -\delta_2}) \cdot |X|, \end{align*}$$
where
![]() $\delta _1$
and
$\delta _1$
and
![]() $\delta _2$
are small, positive absolute constants. Restricting this sum to the nongeneric a shows that the union of
$\delta _2$
are small, positive absolute constants. Restricting this sum to the nongeneric a shows that the union of
![]() $X(a)$
over all nongeneric a is within the error term of Proposition 6.3. We now deal with the
$X(a)$
over all nongeneric a is within the error term of Proposition 6.3. We now deal with the
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
that fail equation (6.3). Let j be an integer satisfying
$a:\mathcal {M} \rightarrow \{\pm 1\}$
that fail equation (6.3). Let j be an integer satisfying
![]() $k < j \leq r$
. We say that
$k < j \leq r$
. We say that
![]() $a, a': \mathcal {M} \rightarrow \{\pm 1\}$
are equivalent at j, which we write as
$a, a': \mathcal {M} \rightarrow \{\pm 1\}$
are equivalent at j, which we write as
![]() $a \sim _j a'$
, if
$a \sim _j a'$
, if
![]() $a(i, j) = a'(i, j)$
for all
$a(i, j) = a'(i, j)$
for all
![]() $1 \leq i \leq k$
. Since our box is
$1 \leq i \leq k$
. Since our box is
![]() $\eta $
-regular, we see that k is roughly equal to
$\eta $
-regular, we see that k is roughly equal to
![]() $\log \log D_1$
. In particular, if N is sufficiently large, we get
$\log \log D_1$
. In particular, if N is sufficiently large, we get
Then there are at most
![]() $2^{\frac {1}{5} \log \log \log N}$
equivalence classes. Furthermore, if
$2^{\frac {1}{5} \log \log \log N}$
equivalence classes. Furthermore, if
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
is such that equation (6.3) fails for some fixed j, we have that
$a:\mathcal {M} \rightarrow \{\pm 1\}$
is such that equation (6.3) fails for some fixed j, we have that
 $$\begin{align*}\left|\bigcup_{a': a \sim_j a'} X(a')\right| \leq \frac{1}{(\log t_{k + 1})^{100}} \cdot |X|, \end{align*}$$
$$\begin{align*}\left|\bigcup_{a': a \sim_j a'} X(a')\right| \leq \frac{1}{(\log t_{k + 1})^{100}} \cdot |X|, \end{align*}$$
where the union is over all
![]() $a':\mathcal {M} \rightarrow \{\pm 1\}$
equivalent to
$a':\mathcal {M} \rightarrow \{\pm 1\}$
equivalent to
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
at j. Summing this over all choices of j and all equivalence classes, we stay within the error term of Proposition 6.3. So far, we have shown
$a:\mathcal {M} \rightarrow \{\pm 1\}$
at j. Summing this over all choices of j and all equivalence classes, we stay within the error term of Proposition 6.3. So far, we have shown
 $$ \begin{align*} &\left|\left|X \cap \mathcal{D}_{n_2, n_3}(N)\right| - Q(n_2|n_3) \cdot \left|X \cap \mathcal{D}_{n_2}(N)\right|\right| \\ &\qquad\qquad\qquad\quad \leq \sum_{\substack{a \text{ generic} \\ a \text{ sat. eq. } (6.3) \\ n_2(a) = n_2}} \sum_{\substack{\text{rk}(\text{Art}_2) = n_2 - n_3 \\ \text{Art}_2 \text{ valid}}} \left||X(a, \operatorname{\mathrm{Art}}_2)| - 2^{-n_2(n_2 + 1)}|X(a)|\right| + \frac{A|X|}{\log \log \log \log N}. \end{align*} $$
$$ \begin{align*} &\left|\left|X \cap \mathcal{D}_{n_2, n_3}(N)\right| - Q(n_2|n_3) \cdot \left|X \cap \mathcal{D}_{n_2}(N)\right|\right| \\ &\qquad\qquad\qquad\quad \leq \sum_{\substack{a \text{ generic} \\ a \text{ sat. eq. } (6.3) \\ n_2(a) = n_2}} \sum_{\substack{\text{rk}(\text{Art}_2) = n_2 - n_3 \\ \text{Art}_2 \text{ valid}}} \left||X(a, \operatorname{\mathrm{Art}}_2)| - 2^{-n_2(n_2 + 1)}|X(a)|\right| + \frac{A|X|}{\log \log \log \log N}. \end{align*} $$
Note that we could have further restricted the sum over Artin pairings to only those with bottom row identically
![]() $0$
. However, the displayed inequality suffices for our purposes. We now apply Proposition 6.6 for every generic
$0$
. However, the displayed inequality suffices for our purposes. We now apply Proposition 6.6 for every generic
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
for X such that it satisfies equation (6.3) and
$a:\mathcal {M} \rightarrow \{\pm 1\}$
for X such that it satisfies equation (6.3) and
![]() $n_2(a) = n_2$
, and all valid Artin pairings
$n_2(a) = n_2$
, and all valid Artin pairings
![]() $\text {Art}_2$
with
$\text {Art}_2$
with
![]() $\text {rk}(\text {Art}_2) = n_2 - n_3$
. Since there are at most
$\text {rk}(\text {Art}_2) = n_2 - n_3$
. Since there are at most
valid Artin pairings, we get
 $$\begin{align*}\sum_{\substack{a \text{ generic} \\ a \text{ sat. eq. } (6.3) \\ n_2(a) = n_2}} \hspace{-0.1cm} \sum_{\substack{\text{rk}(\text{Art}_2) = n_2 - n_3 \\ \text{Art}_2 \text{ valid}}} \hspace{-0.1cm} \left||X(a, \operatorname{\mathrm{Art}}_2)| - 2^{-n_2(n_2 + 1)}|X(a)|\right| \leq 2^{n_{\text{max}}(n_{\text{max}} + 1)} \frac{A|X|}{(\log \log \log \log N)^4} \end{align*}$$
$$\begin{align*}\sum_{\substack{a \text{ generic} \\ a \text{ sat. eq. } (6.3) \\ n_2(a) = n_2}} \hspace{-0.1cm} \sum_{\substack{\text{rk}(\text{Art}_2) = n_2 - n_3 \\ \text{Art}_2 \text{ valid}}} \hspace{-0.1cm} \left||X(a, \operatorname{\mathrm{Art}}_2)| - 2^{-n_2(n_2 + 1)}|X(a)|\right| \leq 2^{n_{\text{max}}(n_{\text{max}} + 1)} \frac{A|X|}{(\log \log \log \log N)^4} \end{align*}$$
as desired.
In our next definition, we introduce the notion of variable indices, which are by definition certain subsets S of
![]() $[r]$
. At the very end of this section, we will reduce to the case where we have chosen one element
$[r]$
. At the very end of this section, we will reduce to the case where we have chosen one element
![]() $x_i \in X_i$
for all
$x_i \in X_i$
for all
![]() $i \in [r] - S$
, whence the terminology.
$i \in [r] - S$
, whence the terminology.
Definition 6.7. Let
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
. Recall that we fixed a basis
$a:\mathcal {M} \rightarrow \{\pm 1\}$
. Recall that we fixed a basis
![]() $w_1, \ldots w_{n_2}, R$
for
$w_1, \ldots w_{n_2}, R$
for
![]() $\mathcal {V}_{a,2}$
in Definition 6.5. Let
$\mathcal {V}_{a,2}$
in Definition 6.5. Let
![]() $1 \leq j_1 \leq n_2 + 1$
, and let
$1 \leq j_1 \leq n_2 + 1$
, and let
![]() $1 \leq j_2 \leq n_2$
. Let
$1 \leq j_2 \leq n_2$
. Let
![]() $E_{j_1, j_2}$
be the
$E_{j_1, j_2}$
be the
![]() $(n_2 + 1) \times n_2$
-matrix with
$(n_2 + 1) \times n_2$
-matrix with
![]() $E_{j_1, j_2}(j_1, j_2) = 1$
and
$E_{j_1, j_2}(j_1, j_2) = 1$
and
![]() $0$
otherwise, and let
$0$
otherwise, and let
![]() $F_{j_1, j_2}$
be the dual basis. Any nonzero multiplicative character
$F_{j_1, j_2}$
be the dual basis. Any nonzero multiplicative character
![]() $F: \operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2) \rightarrow \{\pm 1\}$
can be written as
$F: \operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2) \rightarrow \{\pm 1\}$
can be written as
 $$\begin{align*}F = \iota^{-1} \circ \sum_{\substack{1 \leq j_1 \leq n_2 + 1 \\ 1 \leq j_2 \leq n_2}} c_{j_1, j_2} F_{j_1, j_2} \end{align*}$$
$$\begin{align*}F = \iota^{-1} \circ \sum_{\substack{1 \leq j_1 \leq n_2 + 1 \\ 1 \leq j_2 \leq n_2}} c_{j_1, j_2} F_{j_1, j_2} \end{align*}$$
with not all
![]() $c_{j_1, j_2}$
zero. A set
$c_{j_1, j_2}$
zero. A set
![]() $S \subseteq [r]$
is called a set of variable indices for F if there are
$S \subseteq [r]$
is called a set of variable indices for F if there are
![]() $i_1(F), i_2(F) \in S$
such that
$i_1(F), i_2(F) \in S$
such that
and
-
○ if
 $c_{n_2 + 1, j_2} = 0$
for all
$c_{n_2 + 1, j_2} = 0$
for all
 $1 \leq j_2 \leq n_2$
and
$1 \leq j_2 \leq n_2$
and
 $c_{j_1, j_1} = 0$
for all
$c_{j_1, j_1} = 0$
for all
 $1 \leq j_1 \leq n_2$
and
$1 \leq j_1 \leq n_2$
and
 $c_{j_1, j_2} = 0$
implies
$c_{j_1, j_2} = 0$
implies
 $c_{j_2, j_1} = 0$
for all
$c_{j_2, j_1} = 0$
for all
 $1 \leq j_1, j_2 \leq n_2$
, we choose any pair
$1 \leq j_1, j_2 \leq n_2$
, we choose any pair
 $(j_1, j_2)$
such that
$(j_1, j_2)$
such that
 $c_{j_1, j_2} = 1$
. Furthermore, choose
$c_{j_1, j_2} = 1$
. Furthermore, choose
 $|S(F)| = 2$
, and
$|S(F)| = 2$
, and $$\begin{align*}i_1(F) \in \bigcap_{i \neq j_1} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_1}) = 1\} \end{align*}$$
$$\begin{align*}i_1(F) \in \bigcap_{i \neq j_1} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_1}) = 1\} \end{align*}$$
 $$\begin{align*}i_2(F) \in \bigcap_{i \neq j_2} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_2}) = 1\}; \end{align*}$$
$$\begin{align*}i_2(F) \in \bigcap_{i \neq j_2} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_2}) = 1\}; \end{align*}$$
-
○ if there are
 $1 \leq j_1, j_2 \leq n_2$
such that
$1 \leq j_1, j_2 \leq n_2$
such that
 $c_{j_1, j_2} = 1$
and
$c_{j_1, j_2} = 1$
and
 $c_{j_2, j_1} = 0$
, choose such a pair
$c_{j_2, j_1} = 0$
, choose such a pair
 $(j_1, j_2)$
. Next choose
$(j_1, j_2)$
. Next choose
 $|S(F)| = 3$
and and
$|S(F)| = 3$
and and $$\begin{align*}S(F) \subseteq \bigcap_{i \not \in \{j_1, j_2\}} \{j \in [r] : \pi_j(w_i) = 0\} \end{align*}$$
and
$$\begin{align*}S(F) \subseteq \bigcap_{i \not \in \{j_1, j_2\}} \{j \in [r] : \pi_j(w_i) = 0\} \end{align*}$$
and $$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_1}) = 1, \pi_j(w_{j_2}) = 0\} = \{i_1(F)\} \end{align*}$$
and
$$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_1}) = 1, \pi_j(w_{j_2}) = 0\} = \{i_1(F)\} \end{align*}$$
and $$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_2}) = 1, \pi_j(w_{j_1}) = 0\} = \{i_2(F)\} \end{align*}$$
$$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_2}) = 1, \pi_j(w_{j_1}) = 0\} = \{i_2(F)\} \end{align*}$$
 $$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_1}) = 1, \pi_j(w_{j_2}) = 1\} = \varnothing; \end{align*}$$
$$\begin{align*}S(F) \cap \{j \in [r] : \pi_j(w_{j_1}) = 1, \pi_j(w_{j_2}) = 1\} = \varnothing; \end{align*}$$
-
○ in all other cases, choose a pair
 $(j_2, j_2)$
such that
$(j_2, j_2)$
such that
 $c_{j_2, j_2} = 1$
or choose a pair
$c_{j_2, j_2} = 1$
or choose a pair
 $(n_2 + 1, j_2)$
such that
$(n_2 + 1, j_2)$
such that
 $c_{n_2 + 1, j_2} = 1$
. We pick
$c_{n_2 + 1, j_2} = 1$
. We pick
 $|S(F)| = 2$
and and
$|S(F)| = 2$
and and $$\begin{align*}i_1(F) \in \bigcap_{i \neq j_2} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_2}) = 1\} \end{align*}$$
$$\begin{align*}i_1(F) \in \bigcap_{i \neq j_2} \{j \in [r] : \pi_j(w_i) = 0\} \cap \{j \in [r] : \pi_j(w_{j_2}) = 1\} \end{align*}$$
 $$\begin{align*}i_2(F) \in \bigcap_{i = 1}^{n_2} \{j \in [r] : \pi_j(w_i) = 0\}. \end{align*}$$
$$\begin{align*}i_2(F) \in \bigcap_{i = 1}^{n_2} \{j \in [r] : \pi_j(w_i) = 0\}. \end{align*}$$
If
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X, we will now show that one can find variable indices provided that r is sufficiently large. Our essential tool is the following combinatorial lemma.
$a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X, we will now show that one can find variable indices provided that r is sufficiently large. Our essential tool is the following combinatorial lemma.
Lemma 6.8. Assume that
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X. If
$a:\mathcal {M} \rightarrow \{\pm 1\}$
is generic for X. If
![]() $w_1, \ldots , w_d, R \in \mathcal {V}_{a,2}$
are linearly independent, then we have for all
$w_1, \ldots , w_d, R \in \mathcal {V}_{a,2}$
are linearly independent, then we have for all
![]() $\mathbf {v} \in \mathbb {F}_2^d$
$\mathbf {v} \in \mathbb {F}_2^d$
 $$\begin{align*}\left|\left|\left\{i \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq i \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_i(w_j) = \pi_j(\mathbf{v}) \ \mathrm{ for \ all } \ 1 \leq j \leq d\right\}\right| - \frac{k_{\mathrm{gap}}}{2^{d + 1}}\right| \leq \frac{3^d \cdot k_{\mathrm{gap}}}{2^{10n_{\mathrm{max}}}}. \end{align*}$$
$$\begin{align*}\left|\left|\left\{i \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq i \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_i(w_j) = \pi_j(\mathbf{v}) \ \mathrm{ for \ all } \ 1 \leq j \leq d\right\}\right| - \frac{k_{\mathrm{gap}}}{2^{d + 1}}\right| \leq \frac{3^d \cdot k_{\mathrm{gap}}}{2^{10n_{\mathrm{max}}}}. \end{align*}$$
Proof. We proceed by induction on d. The base case
![]() $d = 1$
follows immediately from equation (6.1). Now suppose that
$d = 1$
follows immediately from equation (6.1). Now suppose that
![]() $d> 1$
. We define for
$d> 1$
. We define for
![]() $\mathbf {w} \in \mathbb {F}_2^d$
$\mathbf {w} \in \mathbb {F}_2^d$
 $$\begin{align*}g(\mathbf{w}) = \left|\left\{i \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq i \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_i(w_j) = \pi_j(\mathbf{w}) \ \mathrm{ for \ all } \ 1 \leq j \leq d\right\}\right|. \end{align*}$$
$$\begin{align*}g(\mathbf{w}) = \left|\left\{i \in [r] : \frac{k_{\mathrm{gap}}}{2} \leq i \leq k_{\mathrm{gap}} \ \mathrm{ and } \ \pi_i(w_j) = \pi_j(\mathbf{w}) \ \mathrm{ for \ all } \ 1 \leq j \leq d\right\}\right|. \end{align*}$$
Let
![]() $\mathbf {v} \in \mathbb {F}_2^d$
be given. Let
$\mathbf {v} \in \mathbb {F}_2^d$
be given. Let
![]() $\mathbf {v}_1, \mathbf {v}_2, \mathbf {v}_3$
be the three unique pairwise distinct vectors such that
$\mathbf {v}_1, \mathbf {v}_2, \mathbf {v}_3$
be the three unique pairwise distinct vectors such that
![]() $\pi _{d - 2}(\mathbf {v}_i) = \pi _{d - 2}(\mathbf {v})$
and
$\pi _{d - 2}(\mathbf {v}_i) = \pi _{d - 2}(\mathbf {v})$
and
![]() $\mathbf {v}_i \neq \mathbf {v}$
. We have
$\mathbf {v}_i \neq \mathbf {v}$
. We have
 $$ \begin{align*} 2\left|g(\mathbf{v}) - \frac{k_{\mathrm{gap}}}{2^{d + 1}}\right| &\leq \left|3g(\mathbf{v}) + \sum_{i = 1}^3 g(\mathbf{v}_i) - \frac{3k_{\mathrm{gap}}}{2^d}\right| + \left|\frac{k_{\mathrm{gap}}}{2^{d - 1}} - g(\mathbf{v}) - \sum_{i = 1}^3 g(\mathbf{v}_i)\right| \\ &\leq \sum_{i = 1}^3 \left|g(\mathbf{v}) + g(\mathbf{v}_i) - \frac{k_{\mathrm{gap}}}{2^d}\right| + \left|\frac{k_{\mathrm{gap}}}{2^{d - 1}} - g(\mathbf{v}) - \sum_{i = 1}^3 g(\mathbf{v}_i)\right|. \end{align*} $$
$$ \begin{align*} 2\left|g(\mathbf{v}) - \frac{k_{\mathrm{gap}}}{2^{d + 1}}\right| &\leq \left|3g(\mathbf{v}) + \sum_{i = 1}^3 g(\mathbf{v}_i) - \frac{3k_{\mathrm{gap}}}{2^d}\right| + \left|\frac{k_{\mathrm{gap}}}{2^{d - 1}} - g(\mathbf{v}) - \sum_{i = 1}^3 g(\mathbf{v}_i)\right| \\ &\leq \sum_{i = 1}^3 \left|g(\mathbf{v}) + g(\mathbf{v}_i) - \frac{k_{\mathrm{gap}}}{2^d}\right| + \left|\frac{k_{\mathrm{gap}}}{2^{d - 1}} - g(\mathbf{v}) - \sum_{i = 1}^3 g(\mathbf{v}_i)\right|. \end{align*} $$
Now apply the induction hypothesis.
With this lemma, it is straightforward to find variable indices provided that a is generic for X and r is sufficiently large. We can now formulate our next reduction step. For a subset
![]() $T \subseteq [r]$
, a point
$T \subseteq [r]$
, a point
![]() $P \in \prod _{i \in T} X_i$
and
$P \in \prod _{i \in T} X_i$
and
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
, we say that P is consistent with a if
$a:\mathcal {M} \rightarrow \{\pm 1\}$
, we say that P is consistent with a if
 $$\begin{align*}\left(\frac{\pi_i(P)}{\pi_j(P)}\right) = a(i, j) \end{align*}$$
$$\begin{align*}\left(\frac{\pi_i(P)}{\pi_j(P)}\right) = a(i, j) \end{align*}$$
for all distinct
![]() $i, j \in T$
with
$i, j \in T$
with
![]() $i < j$
.
$i < j$
.
Proposition 6.9. There are
![]() $A, N_0> 0$
such that for all
$A, N_0> 0$
such that for all
![]() $N> N_0$
, all nice boxes X for N, all integers
$N> N_0$
, all nice boxes X for N, all integers
![]() $n_2 \geq 0$
, all generic
$n_2 \geq 0$
, all generic
![]() $a:\mathcal {M} \rightarrow \{\pm 1\}$
for X with
$a:\mathcal {M} \rightarrow \{\pm 1\}$
for X with
![]() $n_2(a) = n_2$
, all nonzero multiplicative characters F from
$n_2(a) = n_2$
, all nonzero multiplicative characters F from
![]() $\operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2)$
to
$\operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2)$
to
![]() $\{\pm 1\}$
, all sets of variable indices S for F and all
$\{\pm 1\}$
, all sets of variable indices S for F and all
![]() $Q \in \prod _{i \in [k_{\mathrm {gap}}] - S} X_i$
consistent with a such that
$Q \in \prod _{i \in [k_{\mathrm {gap}}] - S} X_i$
consistent with a such that
for all
![]() $j \in S$
, we have
$j \in S$
, we have
 $$\begin{align*}\left|\sum_{x \in X(a, Q)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|X(a, Q)|}{(\log \log \log \log N)^4}. \end{align*}$$
$$\begin{align*}\left|\sum_{x \in X(a, Q)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|X(a, Q)|}{(\log \log \log \log N)^4}. \end{align*}$$
Proof that Proposition 6.9 implies Proposition 6.6
Let F be a nonzero multiplicative character from
![]() $\operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2)$
to
$\operatorname {\mathrm {Mat}}(\mathbb {F}_2, n_2 + 1, n_2)$
to
![]() $\{\pm 1\}$
. We claim that there exist absolute constants
$\{\pm 1\}$
. We claim that there exist absolute constants
![]() $A', N_0'> 0$
such that for all
$A', N_0'> 0$
such that for all
![]() $N> N_0'$
$N> N_0'$
 $$ \begin{align} \left|\sum_{x \in X(a)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A'|X(a)|}{(\log \log \log \log N)^{4}}. \end{align} $$
$$ \begin{align} \left|\sum_{x \in X(a)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A'|X(a)|}{(\log \log \log \log N)^{4}}. \end{align} $$
Once we establish equation (6.5), Proposition 6.6 follows easily. Take a set of variable indices S for F. We split the sum in equation (6.5) over all
![]() $Q \in \prod _{i \in [k_{\text {gap}}] - S} X_i$
consistent with a. If Q satisfies equation (6.4) for all
$Q \in \prod _{i \in [k_{\text {gap}}] - S} X_i$
consistent with a. If Q satisfies equation (6.4) for all
![]() $j \in S$
, we apply Proposition 6.9 with this S. It remains to bound
$j \in S$
, we apply Proposition 6.9 with this S. It remains to bound
 $$ \begin{align} \sum_{\substack{Q \in \prod_{i \in [k_{\text{gap}}] - S} X_i \\ Q \text{ consistent with } a \\ Q \text{ fails eq. } (6.4)}} |X(a, Q)|. \end{align} $$
$$ \begin{align} \sum_{\substack{Q \in \prod_{i \in [k_{\text{gap}}] - S} X_i \\ Q \text{ consistent with } a \\ Q \text{ fails eq. } (6.4)}} |X(a, Q)|. \end{align} $$
But this follows quickly from an application of Proposition 5.11 with the prebox
where P is the union of
![]() $x_1, \dots , x_k$
. Note that we make crucial usage of equation (6.3) to validate the fourth condition of Proposition 5.11.
$x_1, \dots , x_k$
. Note that we make crucial usage of equation (6.3) to validate the fourth condition of Proposition 5.11.
It remains to prove Proposition 6.9, which we shall do now.
Proof of Proposition 6.9
Put
Define
and
Also set
![]() $R := \lfloor \exp \left (\exp \left (0.2k_{\text {gap}}\right )\right )\rfloor $
. We let
$R := \lfloor \exp \left (\exp \left (0.2k_{\text {gap}}\right )\right )\rfloor $
. We let
![]() $Z_{\text {var}}^1, \ldots , Z_{\text {var}}^t$
be a longest sequence of subsets of
$Z_{\text {var}}^1, \ldots , Z_{\text {var}}^t$
be a longest sequence of subsets of
![]() $X'$
satisfying
$X'$
satisfying
-
○ we have for all
 $1 \leq s \leq t$
the equality for some subset
$1 \leq s \leq t$
the equality for some subset $$\begin{align*}Z_{\text{var}}^s = \prod_{i \in S'} Z_i^s \end{align*}$$
$$\begin{align*}Z_{\text{var}}^s = \prod_{i \in S'} Z_i^s \end{align*}$$
 $Z_i^s$
of
$Z_i^s$
of
 $X_i(a, Q)$
with cardinality M;
$X_i(a, Q)$
with cardinality M;
-
○ we have
 $Z_{\text {var}}^s \subseteq Y$
and every
$Z_{\text {var}}^s \subseteq Y$
and every
 $y \in Y$
is in at most R different
$y \in Y$
is in at most R different
 $Z_{\text {var}}^s$
;
$Z_{\text {var}}^s$
; -
○ for all distinct
 $1 \leq s, s' \leq t$
, we have
$1 \leq s, s' \leq t$
, we have
 $\left |Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}\right | \leq 1$
.
$\left |Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}\right | \leq 1$
.
Define
![]() $Y_{\text {bad}}$
as
$Y_{\text {bad}}$
as
and let
![]() $\delta $
be the density of
$\delta $
be the density of
![]() $Y_{\text {bad}}$
in
$Y_{\text {bad}}$
in
![]() $X'$
. With a greedy algorithm, we can construct a subset W of
$X'$
. With a greedy algorithm, we can construct a subset W of
![]() $Y_{\text {bad}}$
of density at least
$Y_{\text {bad}}$
of density at least
![]() $\delta /RM^m$
such that
$\delta /RM^m$
such that
![]() $|W \cap Z_{\text {var}}^s| \leq 1$
for all s. If there were to be subsets
$|W \cap Z_{\text {var}}^s| \leq 1$
for all s. If there were to be subsets
![]() $Z_i \subseteq X_i(a, Q)$
for each
$Z_i \subseteq X_i(a, Q)$
for each
![]() $i \in S'$
satisfying
$i \in S'$
satisfying
![]() $|Z_i| = M$
and
$|Z_i| = M$
and
we could extend our sequence
![]() $Z_{\text {var}}^1, \ldots , Z_{\text {var}}^t$
to a longer sequence. Hence we may apply the contrapositive of Proposition 4.1 of Smith [Reference Smith18] to infer
$Z_{\text {var}}^1, \ldots , Z_{\text {var}}^t$
to a longer sequence. Hence we may apply the contrapositive of Proposition 4.1 of Smith [Reference Smith18] to infer
 $$\begin{align*}M> \frac{\exp(0.3k_{\text{gap}})}{5 \log(RM^m/\delta)}, \end{align*}$$
$$\begin{align*}M> \frac{\exp(0.3k_{\text{gap}})}{5 \log(RM^m/\delta)}, \end{align*}$$
since
![]() $|X_i(a, Q)| \geq \exp (\exp (0.3k_{\text {gap}}))$
for sufficiently large N thanks to equation (6.4) and the regular spacing. This yields
$|X_i(a, Q)| \geq \exp (\exp (0.3k_{\text {gap}}))$
for sufficiently large N thanks to equation (6.4) and the regular spacing. This yields
 $$ \begin{align} \delta < \frac{RM^m}{\exp\left(\frac{\exp(0.3k_{\text{gap}})}{5M}\right)} \leq \exp(-0.25\exp(k_{\text{gap}})) \end{align} $$
$$ \begin{align} \delta < \frac{RM^m}{\exp\left(\frac{\exp(0.3k_{\text{gap}})}{5M}\right)} \leq \exp(-0.25\exp(k_{\text{gap}})) \end{align} $$
if N is sufficiently large. An application of the Chebotarev density theorem (see Theorem 5.1) shows that for
![]() $i> k_{\text {gap}}$
$i> k_{\text {gap}}$
where we made use of the extravagant spacing of
![]() $k_{\text {gap}}$
. We can deal with a potential exceptional zero due to our Siegel-less assumption on X and the famous theorem of Heilbronn [Reference Heilbronn9]. Then Proposition 5.7 implies that for each
$k_{\text {gap}}$
. We can deal with a potential exceptional zero due to our Siegel-less assumption on X and the famous theorem of Heilbronn [Reference Heilbronn9]. Then Proposition 5.7 implies that for each
![]() $y \in Y$
the quantity
$y \in Y$
the quantity
![]() $|X(a, Q \times \{y\})|$
is of the expected size. Hence equation (6.7) implies that
$|X(a, Q \times \{y\})|$
is of the expected size. Hence equation (6.7) implies that
 $$\begin{align*}\left|\sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \in Y_{\text{bad}}}} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \in Y_{\text{bad}}}} 1 \end{align*}$$
$$\begin{align*}\left|\sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \in Y_{\text{bad}}}} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \in Y_{\text{bad}}}} 1 \end{align*}$$
is easily within the error of our proposition. Given
![]() $Z_{\text {var}}^s$
, we define
$Z_{\text {var}}^s$
, we define
 $$\begin{align*}\text{Hull}(Z_{\text{var}}^s) := \{Q\} \times Z_{\text{var}}^s \times \prod_{j \in [r] - [k_{\text{gap}}]} X_j(a, Q \times Z_{\text{var}}^s). \end{align*}$$
$$\begin{align*}\text{Hull}(Z_{\text{var}}^s) := \{Q\} \times Z_{\text{var}}^s \times \prod_{j \in [r] - [k_{\text{gap}}]} X_j(a, Q \times Z_{\text{var}}^s). \end{align*}$$
For each
![]() $x \in X(a, Q)$
with
$x \in X(a, Q)$
with
![]() $\pi _{S'}(x) \not \in Y_{\text {bad}}$
, we define the counting function
$\pi _{S'}(x) \not \in Y_{\text {bad}}$
, we define the counting function
We shall compute the first and second moment of
![]() $\Lambda (x)$
. Since the second moment will turn out to be approximately the square of the first moment, we see that the value of
$\Lambda (x)$
. Since the second moment will turn out to be approximately the square of the first moment, we see that the value of
![]() $\Lambda (x)$
is roughly constant. Then we shall use this to reduce to spaces of the shape
$\Lambda (x)$
is roughly constant. Then we shall use this to reduce to spaces of the shape
![]() $\text {Hull}(Z_{\text {var}}^s) \cap X(a, Q)$
.
$\text {Hull}(Z_{\text {var}}^s) \cap X(a, Q)$
.
We start by computing the first moment as follows:
 $$ \begin{align*} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \not \in Y_{\text{bad}}}} \Lambda(x) &= \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} \\ &= \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{1 \leq s \leq t} \left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \pi_{S'}^{-1}(y)\right|. \end{align*} $$
$$ \begin{align*} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \not \in Y_{\text{bad}}}} \Lambda(x) &= \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} \\ &= \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{1 \leq s \leq t} \left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \pi_{S'}^{-1}(y)\right|. \end{align*} $$
The last expression is obviously
![]() $0$
if
$0$
if
![]() $y \not \in Z_{\text {var}}^s$
. If
$y \not \in Z_{\text {var}}^s$
. If
![]() $y \in Z_{\text {var}}^s$
, we make an appeal to equation (6.8) and Proposition 5.7 to deduce
$y \in Z_{\text {var}}^s$
, we make an appeal to equation (6.8) and Proposition 5.7 to deduce
 $$\begin{align*}\left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \pi_{S'}^{-1}(y)\right| = \frac{\left|X(a, Q) \cap \pi_{S'}^{-1}(y)\right|}{2^{(M - 1) m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*}$$
$$\begin{align*}\left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \pi_{S'}^{-1}(y)\right| = \frac{\left|X(a, Q) \cap \pi_{S'}^{-1}(y)\right|}{2^{(M - 1) m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*}$$
Since there are precisely R values of s such that
![]() $y \in Z_{\text {var}}^s$
, we conclude that the first moment of
$y \in Z_{\text {var}}^s$
, we conclude that the first moment of
![]() $\Lambda (x)$
is equal to
$\Lambda (x)$
is equal to
To compute the second moment, we expand
![]() $\Lambda (x)^2$
as
$\Lambda (x)^2$
as
 $$\begin{align*}\sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \not \in Y_{\text{bad}}}} \Lambda(x)^2 = \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \sum_{1 \leq s' \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^{s'})}, \end{align*}$$
$$\begin{align*}\sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) \not \in Y_{\text{bad}}}} \Lambda(x)^2 = \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \sum_{1 \leq s' \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^{s'})}, \end{align*}$$
which we split as
 $$\begin{align*}\sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} + \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{\substack{1 \leq s, s' \leq t \\ s \neq s'}} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'})}. \end{align*}$$
$$\begin{align*}\sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{1 \leq s \leq t} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s)} + \sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{x \in X(a, Q) \\ \pi_{S'}(x) = y}} \sum_{\substack{1 \leq s, s' \leq t \\ s \neq s'}} \mathbf{1}_{x \in \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'})}. \end{align*}$$
We have already seen how to deal with the first sum. To treat the second sum, we first rewrite it as
 $$\begin{align*}\sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{1 \leq s, s' \leq t \\ s \neq s'}} \left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'}) \cap \pi_{S'}^{-1}(y)\right|. \end{align*}$$
$$\begin{align*}\sum_{y \in Y \setminus Y_{\text{bad}}} \sum_{\substack{1 \leq s, s' \leq t \\ s \neq s'}} \left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'}) \cap \pi_{S'}^{-1}(y)\right|. \end{align*}$$
Next observe that the above sum is zero if
![]() $y \not \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
. If
$y \not \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
. If
![]() $y \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
, we have, again due to the Chebotarev density theorem and Proposition 5.7, that
$y \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
, we have, again due to the Chebotarev density theorem and Proposition 5.7, that
 $$\begin{align*}\left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'}) \cap \pi_{S'}^{-1}(y)\right| = \frac{\left|X(a, Q) \cap \pi_{S'}^{-1}(y)\right|}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*}$$
$$\begin{align*}\left|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s) \cap \text{Hull}(Z_{\text{var}}^{s'}) \cap \pi_{S'}^{-1}(y)\right| = \frac{\left|X(a, Q) \cap \pi_{S'}^{-1}(y)\right|}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*}$$
There are precisely
![]() $R^2 - R$
pairs of
$R^2 - R$
pairs of
![]() $(s, s')$
such that
$(s, s')$
such that
![]() $y \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
and
$y \in Z_{\text {var}}^s \cap Z_{\text {var}}^{s'}$
and
![]() $s \neq s'$
. Hence the second moment equals
$s \neq s'$
. Hence the second moment equals
 $$ \begin{align*} \left(\frac{R^2 - R}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}} + \frac{R}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\right) &\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right) =\frac{R^2}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*} $$
$$ \begin{align*} \left(\frac{R^2 - R}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}} + \frac{R}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\right) &\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right) =\frac{R^2}{2^{2(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\left(1 + O\left(e^{-k_{\text{gap}}}\right)\right). \end{align*} $$
Having computed the first and second moment, we apply Chebyshev’s inequality to deduce that outside a set of density
![]() $O\left (e^{-0.5k_{\text {gap}}}\right )$
in the subset of those
$O\left (e^{-0.5k_{\text {gap}}}\right )$
in the subset of those
![]() $x \in X(a, Q)$
satisfying
$x \in X(a, Q)$
satisfying
![]() $\pi _{S'}(x) \not \in Y_{\text {bad}}$
, we have that
$\pi _{S'}(x) \not \in Y_{\text {bad}}$
, we have that
 $$\begin{align*}\left|\Lambda(x) - \frac{R}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\right| \leq \frac{Re^{-0.25k_{\text{gap}}}}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}. \end{align*}$$
$$\begin{align*}\left|\Lambda(x) - \frac{R}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}\right| \leq \frac{Re^{-0.25k_{\text{gap}}}}{2^{(M - 1)m \cdot |[r] - [k_{\text{gap}}]|}}. \end{align*}$$
From this, we easily deduce that it suffices to prove that
 $$\begin{align*}\left|\sum_{x \in X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s)|}{(\log \log \log \log N)^4}. \end{align*}$$
$$\begin{align*}\left|\sum_{x \in X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s)} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|X(a, Q) \cap \text{Hull}(Z_{\text{var}}^s)|}{(\log \log \log \log N)^4}. \end{align*}$$
Since we are only dealing with one
![]() $Z_{\text {var}}^s$
at a time, we will abbreviate it as Z. If
$Z_{\text {var}}^s$
at a time, we will abbreviate it as Z. If
![]() $m = 2$
, we will also write
$m = 2$
, we will also write
![]() $Z = Z_1 \times Z_2$
with
$Z = Z_1 \times Z_2$
with
![]() $i_1(F) \in Z_1$
.
$i_1(F) \in Z_1$
.
We will now define a field L depending on the shape of F as in Definition 6.7. If we are in the first case, we have
![]() $m = 1$
, and we set
$m = 1$
, and we set
Here we construct the fields
![]() $\phi _{p_1p_2, -1}$
as follows. First pick
$\phi _{p_1p_2, -1}$
as follows. First pick
![]() $p_1 \in Z$
arbitrary and choose fields
$p_1 \in Z$
arbitrary and choose fields
![]() $\phi _{p_1p_j, -1}$
in
$\phi _{p_1p_j, -1}$
in
![]() $\mathcal {F}_{p_1p_j, -1}^{\text {unr}}$
for all
$\mathcal {F}_{p_1p_j, -1}^{\text {unr}}$
for all
![]() $p_j \neq p_1$
. Then we define
$p_j \neq p_1$
. Then we define
![]() $\phi _{p_ip_j, -1}$
to be the unique element of
$\phi _{p_ip_j, -1}$
to be the unique element of
![]() $\mathcal {F}_{p_ip_j, -1}^{\text {unr}}$
contained in the compositum
$\mathcal {F}_{p_ip_j, -1}^{\text {unr}}$
contained in the compositum
![]() $\phi _{p_1p_i, -1} \phi _{p_1p_j, -1}$
. If we are instead in the second case, we have
$\phi _{p_1p_i, -1} \phi _{p_1p_j, -1}$
. If we are instead in the second case, we have
![]() $m = 2$
, and we define
$m = 2$
, and we define
In this case, we pick
![]() $p_1 \in Z_1$
,
$p_1 \in Z_1$
,
![]() $q_1 \in Z_2$
arbitrary, and we choose fields
$q_1 \in Z_2$
arbitrary, and we choose fields
![]() $\phi _{p_1p_i, q_1q_k}$
in
$\phi _{p_1p_i, q_1q_k}$
in
![]() $\mathcal {F}_{p_1p_i, q_1q_k}^{\text {unr}}$
for all
$\mathcal {F}_{p_1p_i, q_1q_k}^{\text {unr}}$
for all
![]() $p_i \neq p_1$
and all
$p_i \neq p_1$
and all
![]() $q_k \neq q_1$
. Then we define
$q_k \neq q_1$
. Then we define
![]() $\phi _{p_ip_j, q_kq_l}$
to be the unique element of
$\phi _{p_ip_j, q_kq_l}$
to be the unique element of
![]() $\mathcal {F}_{p_ip_j, q_kq_l}^{\text {unr}}$
contained in the compositum
$\mathcal {F}_{p_ip_j, q_kq_l}^{\text {unr}}$
contained in the compositum
![]() $\phi _{p_1p_i, q_1q_k} \phi _{p_1p_j, q_1q_k} \phi _{p_1p_i, q_1q_l} \phi _{p_1p_j, q_1q_l}$
.
$\phi _{p_1p_i, q_1q_k} \phi _{p_1p_j, q_1q_k} \phi _{p_1p_i, q_1q_l} \phi _{p_1p_j, q_1q_l}$
.
Finally, if we are in the third case, we have
![]() $m = 1$
again, and we put
$m = 1$
again, and we put
where
Let K be the largest multiquadratic extension of
![]() $\mathbb {Q}$
inside L. In each case, we have a natural isomorphism
$\mathbb {Q}$
inside L. In each case, we have a natural isomorphism
In the first case, this isomorphism is given by
where
![]() $\pi _{(p_1, p_2)}$
is the natural quotient map
$\pi _{(p_1, p_2)}$
is the natural quotient map
![]() $\operatorname {\mathrm {Gal}}(L/K ) \rightarrow \operatorname {\mathrm {Gal}}(K\phi _{p_1p_2, -1}/K) \cong \mathbb {F}_2$
. In the second and third cases, we have similar isomorphisms.
$\operatorname {\mathrm {Gal}}(L/K ) \rightarrow \operatorname {\mathrm {Gal}}(K\phi _{p_1p_2, -1}/K) \cong \mathbb {F}_2$
. In the second and third cases, we have similar isomorphisms.
Note that any prime
![]() $p \in X_j(a, Q)$
splits completely in K by construction. Given
$p \in X_j(a, Q)$
splits completely in K by construction. Given
![]() $\sigma \in \operatorname {\mathrm {Gal}}(L/K)$
, we define
$\sigma \in \operatorname {\mathrm {Gal}}(L/K)$
, we define
![]() $X_j(a, Q \times Z, \sigma )$
be the subset of primes
$X_j(a, Q \times Z, \sigma )$
be the subset of primes
![]() $p \in X_j(a, Q \times Z)$
that map to
$p \in X_j(a, Q \times Z)$
that map to
![]() $\sigma $
under Frobenius. Then Lemma 3.1 and Proposition 5.1 yield
$\sigma $
under Frobenius. Then Lemma 3.1 and Proposition 5.1 yield
Proposition 5.11 shows that for almost all choices of
![]() $Q_{\text {gap}} \in \prod _{[r] - [k_{\text {gap}}] - i_2(F)} X_j(a, Q \times Z)$
consistent with a, we have that
$Q_{\text {gap}} \in \prod _{[r] - [k_{\text {gap}}] - i_2(F)} X_j(a, Q \times Z)$
consistent with a, we have that
![]() $|X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)|$
is of the expected size and furthermore
$|X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)|$
is of the expected size and furthermore
for all
![]() $\sigma \in \operatorname {\mathrm {Gal}}(L/K)$
. By construction, we have that
$\sigma \in \operatorname {\mathrm {Gal}}(L/K)$
. By construction, we have that
so it suffices to prove that
 $$ \begin{align} \left|\sum_{x \in Z_{\text{final}}} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|Z_{\text{final}}|}{(\log \log \log \log N)^4}. \end{align} $$
$$ \begin{align} \left|\sum_{x \in Z_{\text{final}}} F(\operatorname{\mathrm{Art}}_2(x))\right| \leq \frac{A|Z_{\text{final}}|}{(\log \log \log \log N)^4}. \end{align} $$
Now pick
We formally apply Theorem 3.3 to
![]() $Z \times [M]$
. We see that Theorem 3.3 guarantees the existence of
$Z \times [M]$
. We see that Theorem 3.3 guarantees the existence of
![]() $g_{\text {spec}} \in \mathcal {A}(Z \times [M])$
such that
$g_{\text {spec}} \in \mathcal {A}(Z \times [M])$
such that
![]() $g_{\text {spec}}$
is not
$g_{\text {spec}}$
is not
![]() $\epsilon $
-bad. Now pick any
$\epsilon $
-bad. Now pick any
![]() $x_1, \ldots , x_M \in X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
. Then we can define a map
$x_1, \ldots , x_M \in X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
. Then we can define a map
![]() $[M] \times [M] \rightarrow \operatorname {\mathrm {Gal}}(L/K)$
by
$[M] \times [M] \rightarrow \operatorname {\mathrm {Gal}}(L/K)$
by
which we can naturally view as a map
![]() $[M] \times [M] \rightarrow \mathcal {A}(Z)$
due to the isomorphism in equation (6.9). Hence g naturally becomes an element of
$[M] \times [M] \rightarrow \mathcal {A}(Z)$
due to the isomorphism in equation (6.9). Hence g naturally becomes an element of
![]() $\mathcal {A}(Z \times [M])$
.
$\mathcal {A}(Z \times [M])$
.
We claim that we can find disjoint ordered subsets
![]() $A_1, \ldots , A_k$
of
$A_1, \ldots , A_k$
of
![]() $X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
whose union is the whole set
$X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
whose union is the whole set
![]() $X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
except for a small remainder such that defining g as above for each
$X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
except for a small remainder such that defining g as above for each
![]() $A_1, \ldots , A_k$
, we get
$A_1, \ldots , A_k$
, we get
![]() $g_{\text {spec}}$
under the natural identifications.
$g_{\text {spec}}$
under the natural identifications.
Let
![]() $g^{\prime }_{\text {spec}} : [M] \times [M] \rightarrow \operatorname {\mathrm {Gal}}(L/K)$
be the map that is sent to
$g^{\prime }_{\text {spec}} : [M] \times [M] \rightarrow \operatorname {\mathrm {Gal}}(L/K)$
be the map that is sent to
![]() $g_{\text {spec}}$
under the natural identifications. Suppose that elements
$g_{\text {spec}}$
under the natural identifications. Suppose that elements
![]() $x_1, \ldots , x_M \in X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
are given. Now look at the equation
$x_1, \ldots , x_M \in X_{i_2(F)}(a, Q \times Q_{\text {gap}} \times Z)$
are given. Now look at the equation
We see that one can freely choose
![]() $x_1$
, and then all the
$x_1$
, and then all the
![]() $\operatorname {\mathrm {Frob}}_{L/K}(x_j)$
for
$\operatorname {\mathrm {Frob}}_{L/K}(x_j)$
for
![]() $j> 1$
are uniquely determined by
$j> 1$
are uniquely determined by
![]() $g^{\prime }_{\text {spec}}(i, j)$
and
$g^{\prime }_{\text {spec}}(i, j)$
and
![]() $\operatorname {\mathrm {Frob}}_{L/K}(x_1)$
. Now an appeal to equation (6.10) finishes the proof of our claim.
$\operatorname {\mathrm {Frob}}_{L/K}(x_1)$
. Now an appeal to equation (6.10) finishes the proof of our claim.
Now pick one of the
![]() $A_i$
and suppose that
$A_i$
and suppose that
![]() $A_i = \{x_1, \ldots , x_M\}$
. Let
$A_i = \{x_1, \ldots , x_M\}$
. Let
![]() $\widetilde {F}: Z_{\text {final}} \rightarrow \mathbb {F}_2$
be the map that sends x to
$\widetilde {F}: Z_{\text {final}} \rightarrow \mathbb {F}_2$
be the map that sends x to
![]() $\iota \circ F(\text {Art}_2(x))$
. We can restrict
$\iota \circ F(\text {Art}_2(x))$
. We can restrict
![]() $\widetilde {F}$
to
$\widetilde {F}$
to
![]() $A_i$
and then naturally view
$A_i$
and then naturally view
![]() $\widetilde {F}$
as a map from
$\widetilde {F}$
as a map from
![]() $Z \times [M]$
to
$Z \times [M]$
to
![]() $\mathbb {F}_2$
. Theorem 3.3 then implies equation (6.11) and therefore Proposition 6.9, provided that we can verify the identity
$\mathbb {F}_2$
. Theorem 3.3 then implies equation (6.11) and therefore Proposition 6.9, provided that we can verify the identity
![]() $d\widetilde {F} = g^{\prime }_{\text {spec}}$
.
$d\widetilde {F} = g^{\prime }_{\text {spec}}$
.
We distinguish three cases depending on the type of F as in Definition 6.7. In the first case, we apply Theorem 2.11 and Theorem 2.12. Let
![]() $(j_1, j_2)$
be the entry as chosen in Definition 6.7, so that
$(j_1, j_2)$
be the entry as chosen in Definition 6.7, so that
![]() $c_{j_1, j_2} = c_{j_2, j_1} = 1$
. Theorem 2.12 gives
$c_{j_1, j_2} = c_{j_2, j_1} = 1$
. Theorem 2.12 gives
where
![]() $\widetilde {F}_{j_1, j_2}$
is obtained from
$\widetilde {F}_{j_1, j_2}$
is obtained from
![]() $F_{j_1, j_2}$
in the same way as
$F_{j_1, j_2}$
in the same way as
![]() $\widetilde {F}$
was obtained from F. Now consider any
$\widetilde {F}$
was obtained from F. Now consider any
![]() $(j_3, j_4)$
not equal to
$(j_3, j_4)$
not equal to
![]() $(j_1, j_2)$
, with
$(j_1, j_2)$
, with
![]() $1 \leq j_3 \leq n_2 + 1$
,
$1 \leq j_3 \leq n_2 + 1$
,
![]() $1 \leq j_4 \leq n_2$
and
$1 \leq j_4 \leq n_2$
and
![]() $c_{j_3, j_4} = 1$
. Then we have
$c_{j_3, j_4} = 1$
. Then we have
![]() $j_3 \leq n_2$
and
$j_3 \leq n_2$
and
![]() $c_{j_4, j_3} = 1$
. Hence Theorem 2.11 implies
$c_{j_4, j_3} = 1$
. Hence Theorem 2.11 implies
Altogether, we conclude that
![]() $d\widetilde {F} = g^{\prime }_{\text {spec}}$
.
$d\widetilde {F} = g^{\prime }_{\text {spec}}$
.
We now deal with the second case. Once more let
![]() $(j_1, j_2)$
be the entry as chosen in Definition 6.7, so that
$(j_1, j_2)$
be the entry as chosen in Definition 6.7, so that
![]() $1 \leq j_1, j_2 \leq n_2$
,
$1 \leq j_1, j_2 \leq n_2$
,
![]() $c_{j_1, j_2} = 1$
and
$c_{j_1, j_2} = 1$
and
![]() $c_{j_2, j_1} = 0$
. Two applications of part (ii) of Theorem 2.9 show that
$c_{j_2, j_1} = 0$
. Two applications of part (ii) of Theorem 2.9 show that
Two applications of Theorem 2.10 show that for all
![]() $1 \leq j_2 \leq n_2$
,
$1 \leq j_2 \leq n_2$
,
while two applications of part (i) of Theorem 2.9 imply
for all
![]() $1 \leq j_3 \leq n_2 + 1$
,
$1 \leq j_3 \leq n_2 + 1$
,
![]() $1 \leq j_4 \leq n_2$
such that
$1 \leq j_4 \leq n_2$
such that
![]() $(j_1, j_2) \not \in \{(j_3, j_4), (j_4, j_3)\}$
and
$(j_1, j_2) \not \in \{(j_3, j_4), (j_4, j_3)\}$
and
![]() $j_3 \neq j_4$
. This finishes the proof of the second case.
$j_3 \neq j_4$
. This finishes the proof of the second case.
It remains to treat the third case, which follows from an application of Theorem 2.9 and Theorem 2.10.
Acknowledgements
We would like to thank Andrew Granville for his support throughout this project. We wish to thank Peter Stevenhagen for some very helpful discussions at the beginning of the project. We are grateful to Alexander Smith for answering questions about his paper and for several conversations on the challenges of this project. We are also grateful to Mark Watkins for pointing out a small error in a previous version. We would also like to thank Kevin Ford, Andrew Granville and Sam Porritt for their useful suggestions in writing some of the proofs in Section 4.
Conflicts of Interest
None.
Funding statement
The first and third authors were supported by the European Research Council grant agreement No. 670239. The second and fourth author are grateful to the Max Planck Institute for Mathematics in Bonn for its financial support.