Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T13:02:57.914Z Has data issue: false hasContentIssue false
  • English
  • Français

AN 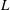$L$-FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM

Part of: Multiplicative number theory Additive number theory; partitions

Published online by Cambridge University Press:  04 November 2014

XUANCHENG SHAO
XUANCHENG SHAO*
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK; Xuancheng.Shao@maths.ox.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a new proof of Vinogradov’s three primes theorem, which asserts that all sufficiently large odd positive integers can be written as the sum of three primes. Existing proofs rely on the theory of 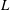$L$-functions, either explicitly or implicitly. Our proof is sieve theoretical and uses a transference principle, the idea of which was first developed by Green [Ann. of Math. (2) 161 (3) (2005), 1609–1636] and used in the proof of Green and Tao’s theorem [Ann. of Math. (2) 167 (2) (2008), 481–547]. To make our argument work, we also develop an additive combinatorial result concerning popular sums, which may be of independent interest.

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes 11N35: Sieves
Secondary: 11P70: Inverse problems of additive number theory, including sumsets
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e27
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2014

References

Bourgain, J., ‘On 𝛬(p)-subsets of squares’, Israel J. Math. 67(3) (1989), 291–311.Google Scholar
Chen, J. R. and Wang, T. Z., ‘On the Goldbach problem’, Acta Math. Sin. 32(5) (1989), 702–718.Google Scholar
Davenport, H., Multiplicative Number Theory, 3rd edn, Graduate Texts in Mathematics, 74 (Springer, New York, 2000), revised and with a preface by H. L. Montgomery.Google Scholar
Eberhard, S., Green, B. and Manners, F., ‘Sets of integers with no large sum-free subset’, Ann. of Math. (2) 180(2) (2014), 621–652.Google Scholar
Freiman, G. A., ‘Inverse problems in additive number theory VI. On the addition of finite sets III’, Izv. Vyssh. Uchebn. Zaved. Mat. 3(28) (1962), 151–157 (in Russian).Google Scholar
Friedlander, J. and Iwaniec, H., ‘The polynomial X 2 + Y 4 captures its primes’, Ann. of Math. (2) 148(3) (1998), 945–1040.Google Scholar
Friedlander, J. and Iwaniec, H., Opera de Cribro, American Mathematical Society Colloquium Publications, 57 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Granville, A., ‘Different approaches to the distribution of primes’, Milan J. Math. 78(1) (2010), 65–84.CrossRefGoogle Scholar
Green, B., ‘Roth’s theorem in the primes’, Ann. of Math. (2) 161(3) (2005), 1609–1636.Google Scholar
Green, B. and Ruzsa, I. Z., ‘Sum-free sets in abelian groups’, Israel J. Math. 147 (2005), 157–188.CrossRefGoogle Scholar
Green, B. and Tao, T., ‘Restriction theory of the Selberg sieve, with applications’, J. Théor. Nombres Bordeaux 18(1) (2006), 147–182.CrossRefGoogle Scholar
Green, B. and Tao, T., ‘The primes contain arbitrarily long arithmetic progressions’, Ann. of Math. (2) 167(2) (2008), 481–547.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘The ternary Goldbach problem’, Rev. Mat. Iberoam. 1(1) (1985), 45–59.CrossRefGoogle Scholar
Helfgott, H. A., ‘The ternary Goldbach conjecture is true’, Preprint (2013), arXiv:1312.7748.Google Scholar
Helfgott, H. A. and de Roton, A., ‘Improving Roth’s theorem in the primes’, Int. Math. Res. Not. IMRN 2011(4) (2011), 767–783.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Koukoulopoulos, D., ‘Pretentious multiplicative functions and the prime number theorem for arithmetic progressions’, Compositio Math. 149(7) (2013), 1129–1149.CrossRefGoogle Scholar
Lev, V. F. and Smeliansky, P. Y., ‘On addition of two distinct sets of integers’, Acta Arith. 70(1) (1995), 85–91.Google Scholar
Li, H. and Pan, H., ‘A density version of Vinogradov’s three primes theorem’, Forum Math. 22(4) (2010), 699–714.CrossRefGoogle Scholar
Liu, M.-Ch. and Wang, T., ‘On the Vinogradov bound in the three primes Goldbach conjecture’, Acta Arith. 105(2) (2002), 133–175.Google Scholar
Naslund, E., ‘On improving Roth’s theorem in the primes’, Mathematika, to appear.Google Scholar
Naslund, E., ‘A density increment approach to Roth’s theorem in the primes’, Preprint (2014), arXiv:1409.3595.Google Scholar
Nathanson, M. B., Additive Number Theory, The Classical Bases, Graduate Texts in Mathematics, 164 (Springer, New York, 1996).Google Scholar
Ramaré, O., ‘On Šnirel’man’s constant’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 22(4) (1995), 645–706.Google Scholar
Ramaré, O. and Ruzsa, I. Z., ‘Additive properties of dense subsets of sifted sequences’, J. Théor. Nombres Bordeaux 13(2) (2001), 559–581.CrossRefGoogle Scholar
Selberg, A., ‘An elementary proof of the prime-number theorem for arithmetic progressions’, Canad. J. Math. 2 (1950), 66–78.CrossRefGoogle Scholar
Shao, X., ‘A density version of the Vinogradov three primes theorem’, Duke Math. J. 163(3) (2014), 489–512.CrossRefGoogle Scholar
Tao, T. and Vu, V., Additive Combinatorics, Cambridge Studies in Advanced Mathematics, 105 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Vinogradov, I. M., ‘The representation of an odd number as a sum of three primes’, Dokl. Akad. Nauk. SSSR 16 (1937), 139–142.Google Scholar