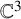1 Introduction
1.1 Quasi-BPS categories
In [Reference Pădurariu and TodaPTa, Reference PădurariuPăda, Reference PădurariuPăd23], we studied quasi-BPS (named after Bogomol'nyi–Prasad–Sommerfield states) categories
![]() $\mathbb {S}(d)_w$
for
$\mathbb {S}(d)_w$
for
![]() $d\in \mathbb {N}$
(length) and
$d\in \mathbb {N}$
(length) and
![]() $w\in \mathbb {Z}$
(weight) in relation to categorical Donaldson–Thomas (DT) theory and to categorical Hall algebras (of surfaces and of quivers with potentials). They are defined to be full subcategories of the category of matrix factorizations
$w\in \mathbb {Z}$
(weight) in relation to categorical Donaldson–Thomas (DT) theory and to categorical Hall algebras (of surfaces and of quivers with potentials). They are defined to be full subcategories of the category of matrix factorizations
where
![]() $\mathbb {M}(d)_w$
is a twisted noncommutative resolution first considered by Špenko–Van den Bergh [Reference Špenko and Van den BerghŠdB17]; see Subsection 2.6 for more details. Here, the stack
$\mathbb {M}(d)_w$
is a twisted noncommutative resolution first considered by Špenko–Van den Bergh [Reference Špenko and Van den BerghŠdB17]; see Subsection 2.6 for more details. Here, the stack
![]() $\mathcal {X}(d)$
and the regular function
$\mathcal {X}(d)$
and the regular function
![]() $\mathop {\mathrm {Tr}}\nolimits W_d$
are given by
$\mathop {\mathrm {Tr}}\nolimits W_d$
are given by
where V is a d-dimensional vector space.
There is also a graded quasi-BPS category
![]() $\mathbb {S}^{\mathrm {gr}}(d)_v$
, which is equivalent (via Koszul duality) to a subcategory
$\mathbb {S}^{\mathrm {gr}}(d)_v$
, which is equivalent (via Koszul duality) to a subcategory
where
![]() $\mathscr {C}(d)$
is the derived moduli stack of zero-dimensional sheaves on
$\mathscr {C}(d)$
is the derived moduli stack of zero-dimensional sheaves on
![]() $\mathbb {C}^2$
with length d. We will also consider T-equivariant versions of these categories, where
$\mathbb {C}^2$
with length d. We will also consider T-equivariant versions of these categories, where
![]() $T=(\mathbb {C}^{*})^2$
is the Calabi–Yau torus of
$T=(\mathbb {C}^{*})^2$
is the Calabi–Yau torus of
![]() $\mathbb {C}^3$
. We denote by
$\mathbb {C}^3$
. We denote by
![]() $\mathbb {K}=K(BT)=\mathbb {Z}[q_1^{\pm 1}, q_2^{\pm 1}]$
and by
$\mathbb {K}=K(BT)=\mathbb {Z}[q_1^{\pm 1}, q_2^{\pm 1}]$
and by
![]() $\mathbb {F}$
the fractional field of
$\mathbb {F}$
the fractional field of
![]() $\mathbb {K}$
. The (T-equivariant or not) Grothendieck groups of
$\mathbb {K}$
. The (T-equivariant or not) Grothendieck groups of
![]() $\mathbb {S}(d)_w$
and
$\mathbb {S}(d)_w$
and
![]() $\mathbb {S}^{\mathrm {gr}}(d)_w\cong \mathbb {T}(d)_w$
are isomorphic.
$\mathbb {S}^{\mathrm {gr}}(d)_w\cong \mathbb {T}(d)_w$
are isomorphic.
The purpose of this paper is to prove several properties of quasi-BPS categories analogous to BPS sheaves in cohomological DT theory and use these properties to compute the T-equivariant K-theory of quasi-BPS categories.
1.2 Semiorthogonal decompositions
We briefly review semiorthogonal decompositions with summands given by quasi-BPS categories proved in [Reference Pădurariu and TodaPTa, Reference PădurariuPăda].
In our previous paper [Reference Pădurariu and TodaPTa], we constructed a semiorthogonal decomposition of the categorification
![]() $\mathcal {DT}(d)$
of the DT invariant
$\mathcal {DT}(d)$
of the DT invariant
![]() $\mathrm {DT}_d$
, which is a virtual count of zero-dimensional closed subschemes in
$\mathrm {DT}_d$
, which is a virtual count of zero-dimensional closed subschemes in
![]() $\mathbb {C}^3$
. The category
$\mathbb {C}^3$
. The category
![]() $\mathcal {DT}(d)$
is defined by
$\mathcal {DT}(d)$
is defined by
see [Reference Pădurariu and TodaPTa, Subsection 1.5]. Here,
![]() $\text {NHilb}(d)$
is the noncommutative Hilbert scheme of points
$\text {NHilb}(d)$
is the noncommutative Hilbert scheme of points
More precisely, in [Reference Pădurariu and TodaPTa, Theorem 1.1] we showed that there is a semiorthogonal decomposition
 $$ \begin{align} \mathcal{DT}(d)= \left\langle \boxtimes_{i=1}^k \mathbb{S}(d_i)_{v_i+d_i\left(\sum_{i>j}d_j-\sum_{j>i}d_j\right)} \,\bigg|\, \begin{array}{c} 0\leqslant v_1/d_1 < \cdots < v_k/d_k<1 \\ d_1+\cdots+d_k=d \end{array} \right\rangle.\end{align} $$
$$ \begin{align} \mathcal{DT}(d)= \left\langle \boxtimes_{i=1}^k \mathbb{S}(d_i)_{v_i+d_i\left(\sum_{i>j}d_j-\sum_{j>i}d_j\right)} \,\bigg|\, \begin{array}{c} 0\leqslant v_1/d_1 < \cdots < v_k/d_k<1 \\ d_1+\cdots+d_k=d \end{array} \right\rangle.\end{align} $$
There is also a semiorthogonal decomposition of
![]() $D^b(\mathscr {C}(d))$
in graded quasi-BPS categories; see [Reference PădurariuPăda, Theorem 1.1]:
$D^b(\mathscr {C}(d))$
in graded quasi-BPS categories; see [Reference PădurariuPăda, Theorem 1.1]:
 $$ \begin{align} D^b\left(\mathscr{C}(d)\right)=\left\langle \boxtimes_{i=1}^k \mathbb{T}(d_i)_{v_i} \,\bigg|\, \begin{array}{c} v_1/d_1 < \cdots < v_k/d_k \\ d_1+\cdots+d_k=d \end{array} \right\rangle. \end{align} $$
$$ \begin{align} D^b\left(\mathscr{C}(d)\right)=\left\langle \boxtimes_{i=1}^k \mathbb{T}(d_i)_{v_i} \,\bigg|\, \begin{array}{c} v_1/d_1 < \cdots < v_k/d_k \\ d_1+\cdots+d_k=d \end{array} \right\rangle. \end{align} $$
1.3 Numerical and cohomological BPS invariants
It is expected that, for any smooth Calabi–Yau threefold X, there are certain deformation invariant integers called BPS invariants which determine the DT and Gromov–Witten invariants of X; see [Reference Pandharipande and ThomasPT14, Section 2 and a half]. Denote by
![]() $\Omega _d$
the BPS invariants of
$\Omega _d$
the BPS invariants of
![]() $\mathbb {C}^3$
for
$\mathbb {C}^3$
for
![]() $d\geqslant 1$
. Then
$d\geqslant 1$
. Then
The wall-crossing formula for the DT invariants of
![]() $\mathbb {C}^3$
, see [Reference Joyce and SongJS12, Section 6.3], [Reference TodaTod10, Remark 5.14], says that
$\mathbb {C}^3$
, see [Reference Joyce and SongJS12, Section 6.3], [Reference TodaTod10, Remark 5.14], says that
 $$ \begin{align} \sum_{d \geqslant 0} \mathrm{DT}_{d}q^d= \prod_{d\geqslant 1}(1-(-q)^d)^{d \Omega_d}=\prod_{d\geqslant 1}\frac{1}{\left(1-(-q)^d\right)^d}; \end{align} $$
$$ \begin{align} \sum_{d \geqslant 0} \mathrm{DT}_{d}q^d= \prod_{d\geqslant 1}(1-(-q)^d)^{d \Omega_d}=\prod_{d\geqslant 1}\frac{1}{\left(1-(-q)^d\right)^d}; \end{align} $$
see [Reference Pădurariu and TodaPTa, Subsection 1.6] for more details.
Davison–Meinhardt [Reference Davison and MeinhardtDM20] constructed a perverse sheaf
![]() $\mathcal {B}PS_d$
on
$\mathcal {B}PS_d$
on
![]() $\mathrm {Sym}^d(\mathbb {C}^3)$
, called BPS sheaf, whose Euler characteristic recovers the BPS invariant
$\mathrm {Sym}^d(\mathbb {C}^3)$
, called BPS sheaf, whose Euler characteristic recovers the BPS invariant
![]() $\Omega _d$
. Davison [Reference DavisonDavb, Theorem 5.1] showed that
$\Omega _d$
. Davison [Reference DavisonDavb, Theorem 5.1] showed that
where
![]() $\Delta \colon \mathbb {C}^3\hookrightarrow \mathrm {Sym}^d(\mathbb {C}^3)$
is the small diagonal. Davison [Reference DavisonDavb, Lemma 4.1] also proved restrictions on the support of BPS sheaves for tripled quivers with potentials and used [Reference DavisonDavb, Lemma 4.1] to prove purity results about stacks of representations of preprojective algebras [Reference DavisonDavb, Theorem A]. We refer to Equation (1.7) as Davison’s support lemma. The (cohomological) BPS spaces are the cohomology of the BPS sheaf.
$\Delta \colon \mathbb {C}^3\hookrightarrow \mathrm {Sym}^d(\mathbb {C}^3)$
is the small diagonal. Davison [Reference DavisonDavb, Lemma 4.1] also proved restrictions on the support of BPS sheaves for tripled quivers with potentials and used [Reference DavisonDavb, Lemma 4.1] to prove purity results about stacks of representations of preprojective algebras [Reference DavisonDavb, Theorem A]. We refer to Equation (1.7) as Davison’s support lemma. The (cohomological) BPS spaces are the cohomology of the BPS sheaf.
Properties (and computations in special cases) of BPS sheaves have applications in the study of Hodge theory of various cohomological DT spaces (in particular, in proving purity of the Borel-Moore homology of moduli of objects in K
![]() $3$
categories [Reference DavisonDavc]) and in the study of Cohomological Hall algebras [Reference DavisonDava, Reference Kapranov and VasserotKV].
$3$
categories [Reference DavisonDavc]) and in the study of Cohomological Hall algebras [Reference DavisonDava, Reference Kapranov and VasserotKV].
Our point of view is that the semiorthogonal decomposition (1.3) may be regarded as a categorification of the wall-crossing formula (1.6) and the category
![]() $\mathbb {S}(d)_w$
may be regarded as a categorical analogue of the BPS invariant (1.5) or BPS sheaf (1.7). In this paper, we make the above heuristic more rigorous. Let
$\mathbb {S}(d)_w$
may be regarded as a categorical analogue of the BPS invariant (1.5) or BPS sheaf (1.7). In this paper, we make the above heuristic more rigorous. Let
![]() $(d, w)\in \mathbb {N}\times \mathbb {Z}$
be integers with
$(d, w)\in \mathbb {N}\times \mathbb {Z}$
be integers with
![]() $\gcd (d, w)=1$
. We first prove a categorical analogue of Equation (1.7), namely any object of
$\gcd (d, w)=1$
. We first prove a categorical analogue of Equation (1.7), namely any object of
![]() $\mathbb {S}(d)_w$
is supported over the small diagonal in
$\mathbb {S}(d)_w$
is supported over the small diagonal in
![]() $\mathrm {Sym}^d(\mathbb {C}^3)$
. Further, for
$\mathrm {Sym}^d(\mathbb {C}^3)$
. Further, for
![]() $n\in \mathbb {N}$
, we define a K-theoretic analogue of the cohomological BPS space:
$n\in \mathbb {N}$
, we define a K-theoretic analogue of the cohomological BPS space:
and show that
![]() $\mathrm {P}(nd)_{nw,\mathbb {F}}:=\mathrm {P}(nd)_{nw}\otimes _{\mathbb {K}}\mathbb {F}$
is a one-dimensional
$\mathrm {P}(nd)_{nw,\mathbb {F}}:=\mathrm {P}(nd)_{nw}\otimes _{\mathbb {K}}\mathbb {F}$
is a one-dimensional
![]() $\mathbb {F}$
-vector space, compare with Equation (1.5).
$\mathbb {F}$
-vector space, compare with Equation (1.5).
1.4 Support of matrix factorizations in quasi-BPS categories
We prove a version of the support lemma (1.7) for categories
![]() $\mathbb {S}(d)_w$
with
$\mathbb {S}(d)_w$
with
![]() $\gcd (d, w)=1$
. We consider the quotient stack
$\gcd (d, w)=1$
. We consider the quotient stack
![]() $\mathcal {X}(d)$
defined in Equation (1.2) together with its good moduli space
$\mathcal {X}(d)$
defined in Equation (1.2) together with its good moduli space
Consider the diagram

where
![]() $\mathcal {C}oh(\mathbb {C}^3, d)$
is the stack of sheaves with zero-dimensional support and length d on
$\mathcal {C}oh(\mathbb {C}^3, d)$
is the stack of sheaves with zero-dimensional support and length d on
![]() $\mathbb {C}^3$
. In Section 3, we prove the following (see Theorem 3.1 for a more precise statement):
$\mathbb {C}^3$
. In Section 3, we prove the following (see Theorem 3.1 for a more precise statement):
Theorem 1.1 (Theorem 3.1).
For a pair
![]() $(d, w) \in \mathbb {N}\times \mathbb {Z}$
with
$(d, w) \in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, w)=1$
, any object in
$\gcd (d, w)=1$
, any object in
![]() $\mathbb {S}(d)_w$
is supported on
$\mathbb {S}(d)_w$
is supported on
![]() $\pi ^{-1}(\Delta )$
.
$\pi ^{-1}(\Delta )$
.
The categorical support restriction in Theorem 1.1 implies a strong constraint on T-equivariant K-theory classes of objects of quasi-BPS categories. Let
![]() $\Theta $
be the forget-the-potential map
$\Theta $
be the forget-the-potential map
see [Reference PădurariuPăd22, Proposition 3.6]. In Lemma 4.1, we show that if a complex
![]() $\mathcal {F}$
is supported on
$\mathcal {F}$
is supported on
![]() $\pi ^{-1}(\Delta )$
, then
$\pi ^{-1}(\Delta )$
, then
![]() $\Theta ([\mathcal {F}])$
is divisible by the element
$\Theta ([\mathcal {F}])$
is divisible by the element
In [Reference Pădurariu and TodaPTa], we introduced certain complexes
![]() $\mathcal {E}_{d, w}\in \mathbb {T}(d)_w$
using a derived stack of pairs of commuting matrices, both of which have spectrum of cardinality one and have an explicit shuffle description (2.38). In particular, Lemma 4.1 applies to
$\mathcal {E}_{d, w}\in \mathbb {T}(d)_w$
using a derived stack of pairs of commuting matrices, both of which have spectrum of cardinality one and have an explicit shuffle description (2.38). In particular, Lemma 4.1 applies to
![]() $\mathcal {E}_{d,w}$
for
$\mathcal {E}_{d,w}$
for
![]() $\gcd (d, w)=1$
. We remark that the divisibility by Equation (1.9) is not obvious from the shuffle description of
$\gcd (d, w)=1$
. We remark that the divisibility by Equation (1.9) is not obvious from the shuffle description of
![]() $\Theta ([\mathcal {E}_{d,w}])$
.
$\Theta ([\mathcal {E}_{d,w}])$
.
1.5 Integral generator of K-theory of quasi-BPS categories
In [Reference Pădurariu and TodaPTa, Theorem 1.2], we showed that the localized (i.e., taking
![]() $\otimes _{\mathbb {K}} \mathbb {F}$
) T-equivariant K-theory of
$\otimes _{\mathbb {K}} \mathbb {F}$
) T-equivariant K-theory of
![]() $\mathbb {T}(d)_{w}$
(and thus of
$\mathbb {T}(d)_{w}$
(and thus of
![]() $\mathbb {S}(d)_{w}$
) is generated by monomials in
$\mathbb {S}(d)_{w}$
) is generated by monomials in
![]() $[\mathcal {E}_{d', w'}]$
for
$[\mathcal {E}_{d', w'}]$
for
![]() $d'\leqslant d$
and
$d'\leqslant d$
and
![]() $\frac {w}{d}=\frac {w'}{d'}$
. The divisibility by Equation (1.9) will be useful to compute the T-equivariant K-theory of quasi-BPS categories without localization. For a
$\frac {w}{d}=\frac {w'}{d'}$
. The divisibility by Equation (1.9) will be useful to compute the T-equivariant K-theory of quasi-BPS categories without localization. For a
![]() $\mathbb {K}$
-module M, we will use the notation
$\mathbb {K}$
-module M, we will use the notation
![]() $M':=M/(\mathbb {K}\text {-torsion})$
. Using Lemma 4.1 and Theorem 1.1, we show that:
$M':=M/(\mathbb {K}\text {-torsion})$
. Using Lemma 4.1 and Theorem 1.1, we show that:
Theorem 1.2 (Theorem 4.4).
Let
![]() $(d, w) \in \mathbb {N}\times \mathbb {Z}$
with
$(d, w) \in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, w)=1$
. The
$\gcd (d, w)=1$
. The
![]() $\mathbb {K}$
-module
$\mathbb {K}$
-module
![]() $K_T\left (\mathbb {S}(d)_w\right )'$
is free of rank one with generator
$K_T\left (\mathbb {S}(d)_w\right )'$
is free of rank one with generator
![]() $\left [\mathcal {E}_{d, w}\right ]$
.
$\left [\mathcal {E}_{d, w}\right ]$
.
For
![]() $(d, w)\in \mathbb {N}\times \mathbb {Z}$
with
$(d, w)\in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, w)=1$
, we believe the category
$\gcd (d, w)=1$
, we believe the category
![]() $\mathbb {T}(d)_w$
is generated by
$\mathbb {T}(d)_w$
is generated by
![]() $\mathcal {E}_{d,w}$
, which in particular implies Theorem 1.2. Further, for
$\mathcal {E}_{d,w}$
, which in particular implies Theorem 1.2. Further, for
![]() $\ast \in \{\emptyset , T\}$
, we suspect there are equivalences
$\ast \in \{\emptyset , T\}$
, we suspect there are equivalences
![]() $\mathbb {T}_{\ast }(1)_0\xrightarrow {\sim } \mathbb {T}_{\ast }(d)_w$
, but we do not have much evidence supporting this belief.
$\mathbb {T}_{\ast }(1)_0\xrightarrow {\sim } \mathbb {T}_{\ast }(d)_w$
, but we do not have much evidence supporting this belief.
1.6 The coproduct
For the reminder of the introduction, we consider a pair
![]() $(d,v)\in \mathbb {N}\times \mathbb {Z}$
with
$(d,v)\in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, v)=1$
. The Grothendieck group of the category
$\gcd (d, v)=1$
. The Grothendieck group of the category
![]() $\mathbb {T}(nd)_{nv}$
for
$\mathbb {T}(nd)_{nv}$
for
![]() $n>1$
contains a contribution from partitions
$n>1$
contains a contribution from partitions
![]() $a+b=n$
because the Hall product restricts to a functor
$a+b=n$
because the Hall product restricts to a functor
for
![]() $a, b\geqslant 1$
with
$a, b\geqslant 1$
with
![]() $a+b=n$
; see [Reference Pădurariu and TodaPTa, Lemma 4.8]. The category
$a+b=n$
; see [Reference Pădurariu and TodaPTa, Lemma 4.8]. The category
is thus monoidal. For
![]() $n=a+b$
, there is a coproduct
$n=a+b$
, there is a coproduct
see also [Reference PădurariuPăda, Section 5]. The construction also provides a T-equivariant version. In Section 5, we prove that the Hall product is compatible with the above coproduct:
Theorem 1.3 (Corollary 5.6).
Let
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime, let
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime, let
![]() $a, b, c, e, n\in \mathbb {N}$
such that
$a, b, c, e, n\in \mathbb {N}$
such that
![]() $a+b=c+e=n$
, and let S be the set of tuples
$a+b=c+e=n$
, and let S be the set of tuples
![]() $(f_1, f_2, f_3, f_4)$
such that
$(f_1, f_2, f_3, f_4)$
such that
![]() $a=f_1+f_2$
,
$a=f_1+f_2$
,
![]() $b=f_3+f_4$
,
$b=f_3+f_4$
,
![]() $c=f_1+f_3$
,
$c=f_1+f_3$
,
![]() $e=f_2+f_4$
. The following diagram commutes:
$e=f_2+f_4$
. The following diagram commutes:

where we have used the shorthand notations
![]() $\Delta :=\bigoplus _S \Delta _{f_1, f_2}\otimes \Delta _{f_3, f_4}$
and
$\Delta :=\bigoplus _S \Delta _{f_1, f_2}\otimes \Delta _{f_3, f_4}$
and
![]() $m':=\bigoplus _S (m\otimes m)(1\otimes \text {sw}_{f_2, f_3}\otimes 1)$
.
$m':=\bigoplus _S (m\otimes m)(1\otimes \text {sw}_{f_2, f_3}\otimes 1)$
.
In the proof, we first construct a version of
![]() $\Delta _{a, b}$
for the subcategories
$\Delta _{a, b}$
for the subcategories
![]() $\mathbb {M}(nd)_{nv}\subset D^b(\mathcal {X}(nd))_{nv}$
; see Equation (1.1). We then construct the functor (1.11) by applying matrix factorizations and using the Koszul equivalence.
$\mathbb {M}(nd)_{nv}\subset D^b(\mathcal {X}(nd))_{nv}$
; see Equation (1.1). We then construct the functor (1.11) by applying matrix factorizations and using the Koszul equivalence.
In Propositions 5.7 and 5.8, we show that the product and the coproduct on
![]() $K_T(\mathcal {D}_{d,v})'$
are commutative and cocommutative. We then obtain an isomorphism
$K_T(\mathcal {D}_{d,v})'$
are commutative and cocommutative. We then obtain an isomorphism
where
![]() $\Lambda _{\mathbb {F}}$
is the
$\Lambda _{\mathbb {F}}$
is the
![]() $\mathbb {F}$
-algebra of symmetric functions; see Subsection 2.12 for its definition. The elementary functions
$\mathbb {F}$
-algebra of symmetric functions; see Subsection 2.12 for its definition. The elementary functions
![]() $e_n\in \Lambda _{\mathbb {F}}$
are sent, up to a factor in
$e_n\in \Lambda _{\mathbb {F}}$
are sent, up to a factor in
![]() $\mathbb {F}$
, to
$\mathbb {F}$
, to
![]() $\mathcal {E}_{nd, nv}$
.
$\mathcal {E}_{nd, nv}$
.
1.7 K-theoretic BPS spaces
We define the K-theoretic BPS space to be the space of primitive elements of
![]() $K_T(\mathbb {T}(nd)_{nv})$
with respect to the above coproduct:
$K_T(\mathbb {T}(nd)_{nv})$
with respect to the above coproduct:
 $$ \begin{align} \mathrm{P}(nd)_{nv}:=\mathrm{ker}\left(\bigoplus_{\substack{a+b=n\\a, b\geqslant 1}}\Delta_{a, b}: K_T\left(\mathbb{T}(nd)_{nv}\right)\to \bigoplus_{\substack{a+b=n\\a, b\geqslant 1}}K_T\left(\mathbb{T}(ad)_{av}\otimes \mathbb{T}(bd)_{bv}\right)\right). \end{align} $$
$$ \begin{align} \mathrm{P}(nd)_{nv}:=\mathrm{ker}\left(\bigoplus_{\substack{a+b=n\\a, b\geqslant 1}}\Delta_{a, b}: K_T\left(\mathbb{T}(nd)_{nv}\right)\to \bigoplus_{\substack{a+b=n\\a, b\geqslant 1}}K_T\left(\mathbb{T}(ad)_{av}\otimes \mathbb{T}(bd)_{bv}\right)\right). \end{align} $$
We show that the dimension over
![]() $\mathbb {F}$
of localized K-theoretic BPS spaces for all pairs
$\mathbb {F}$
of localized K-theoretic BPS spaces for all pairs
![]() $(nd, nv)\in \mathbb {N}\times \mathbb {Z}$
is the same as the (numerical) BPS invariants (1.5) up to a sign:
$(nd, nv)\in \mathbb {N}\times \mathbb {Z}$
is the same as the (numerical) BPS invariants (1.5) up to a sign:
Proposition 1.4 (Corollary 5.11).
The
![]() $\mathbb {F}$
-vector space
$\mathbb {F}$
-vector space
![]() $\mathrm {P}(nd)_{nv, \mathbb {F}}$
is one-dimensional.
$\mathrm {P}(nd)_{nv, \mathbb {F}}$
is one-dimensional.
Using the above proposition and [Reference Pădurariu and TodaPTa, Theorem 1.1], we obtain a K-theoretic analogue of the wall-crossing formula (1.6); see Subsection 5.5 and [Reference Pădurariu and TodaPTa, Subsection 1.6] for more details.
Corollary 1.5 (Corollary 5.13).
There is an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {F}$
-vector spaces:
$\mathbb {F}$
-vector spaces:
 $$ \begin{align} \bigoplus_{d\geqslant 0}K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant v<d \\ \gcd(d,v)=1}} \left(\bigotimes_{n\geqslant 1}\mathrm{Sym}\big(\mathrm{P}(nd)_{nv, \mathbb{F}}\big)\right). \end{align} $$
$$ \begin{align} \bigoplus_{d\geqslant 0}K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant v<d \\ \gcd(d,v)=1}} \left(\bigotimes_{n\geqslant 1}\mathrm{Sym}\big(\mathrm{P}(nd)_{nv, \mathbb{F}}\big)\right). \end{align} $$
We conjecture an integral version of Proposition 1.4, which is a version of Theorem 1.2 for pairs
![]() $(nd, nv)$
for all
$(nd, nv)$
for all
![]() $n\in \mathbb {N}$
:
$n\in \mathbb {N}$
:
Conjecture 1.6. The
![]() $\mathbb {K}$
-module
$\mathbb {K}$
-module
![]() $\mathrm {P}(nd)_{nv}$
is free of rank one.
$\mathrm {P}(nd)_{nv}$
is free of rank one.
The torsion-free version of the above conjecture for
![]() $(d,v)=(1,0)$
and
$(d,v)=(1,0)$
and
![]() $n=2$
follows from the discussion in Subsection 4.3. We finally conjecture an analogue of Theorem 1.1 for all
$n=2$
follows from the discussion in Subsection 4.3. We finally conjecture an analogue of Theorem 1.1 for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Conjecture 1.7. The subspace
![]() $\mathrm {P}(nd)_{nv}\subset K_T(\mathbb {T}(nd)_{nv})\cong K_T(\mathbb {S}(nd)_{nv})$
is supported over
$\mathrm {P}(nd)_{nv}\subset K_T(\mathbb {T}(nd)_{nv})\cong K_T(\mathbb {S}(nd)_{nv})$
is supported over
![]() $\pi ^{-1}(\Delta )$
, alternatively, the following composition is zero:
$\pi ^{-1}(\Delta )$
, alternatively, the following composition is zero:
2 Preliminaries
2.1 Notations
The spaces considered in this paper are defined over the complex field
![]() $\mathbb {C}$
, and they are quotient stacks
$\mathbb {C}$
, and they are quotient stacks
![]() $\mathcal {X}=A/G$
, where A is a dg scheme, the derived zero locus of a section s of a finite rank bundle vector bundle
$\mathcal {X}=A/G$
, where A is a dg scheme, the derived zero locus of a section s of a finite rank bundle vector bundle
![]() $\mathcal {E}$
on a finite type separated scheme X over
$\mathcal {E}$
on a finite type separated scheme X over
![]() $\mathbb {C}$
, and G is a reductive group. For such a dg scheme A, let
$\mathbb {C}$
, and G is a reductive group. For such a dg scheme A, let
![]() $\dim A:=\dim X-\text {rank}(\mathcal {E})$
, let
$\dim A:=\dim X-\text {rank}(\mathcal {E})$
, let
![]() $A^{\mathrm {cl}}:=Z(s)\subset X$
be the (classical) zero locus, and let
$A^{\mathrm {cl}}:=Z(s)\subset X$
be the (classical) zero locus, and let
![]() $\mathcal {X}^{\mathrm {cl}}:=A^{\mathrm {cl}}/G$
. We denote by
$\mathcal {X}^{\mathrm {cl}}:=A^{\mathrm {cl}}/G$
. We denote by
![]() $\mathcal {O}_{\mathcal {X}}$
or
$\mathcal {O}_{\mathcal {X}}$
or
![]() $\mathcal {O}_A$
the structure sheaf of
$\mathcal {O}_A$
the structure sheaf of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
For G a reductive group and A a dg scheme as above, denote by
![]() $A/G$
the corresponding quotient stack and by
$A/G$
the corresponding quotient stack and by
![]() $A/\!\!/ G$
the quotient dg scheme with dg-ring of regular functions
$A/\!\!/ G$
the quotient dg scheme with dg-ring of regular functions
![]() $\mathcal {O}_A^G$
.
$\mathcal {O}_A^G$
.
For a classical stack
![]() $\mathcal {X}$
with a morphism
$\mathcal {X}$
with a morphism
![]() $\mathcal {X} \to X$
to a scheme X and for a closed point
$\mathcal {X} \to X$
to a scheme X and for a closed point
![]() $p\in X$
, we denote by
$p\in X$
, we denote by
![]() $\mathcal {X}_p$
its formal fiber
$\mathcal {X}_p$
its formal fiber
![]() $\mathcal {X}_p := \mathcal {X} \times _X \operatorname {Spec} \widehat {\mathcal {O}}_{X, p}$
.
$\mathcal {X}_p := \mathcal {X} \times _X \operatorname {Spec} \widehat {\mathcal {O}}_{X, p}$
.
For a (derived) stack
![]() $\mathcal {X}$
with an action of a torus T, we denote by
$\mathcal {X}$
with an action of a torus T, we denote by
![]() $D^b_T(\mathcal {X})$
the bounded derived category of T-equivariant coherent sheaves on
$D^b_T(\mathcal {X})$
the bounded derived category of T-equivariant coherent sheaves on
![]() $\mathcal {X}$
and by
$\mathcal {X}$
and by
![]() $G_T(\mathcal {X})$
its Grothendieck group. We denote by
$G_T(\mathcal {X})$
its Grothendieck group. We denote by
![]() $\mathrm {Perf}_T(\mathcal {X})$
the subcategory of T-equivariant perfect complexes and by
$\mathrm {Perf}_T(\mathcal {X})$
the subcategory of T-equivariant perfect complexes and by
![]() $K_T(\mathcal {X})$
its Grothendieck group. When T is trivial, we drop T from the notation of the above Grothendieck groups. We introduce more notations for categories and K-theory in Subsection 2.6.2.
$K_T(\mathcal {X})$
its Grothendieck group. When T is trivial, we drop T from the notation of the above Grothendieck groups. We introduce more notations for categories and K-theory in Subsection 2.6.2.
Consider the two-dimensional torus
The isomorphism above is given by
![]() $(t_1, t_2) \mapsto (t_1, t_2, t_1^{-1} t_2^{-1})$
. We denote by
$(t_1, t_2) \mapsto (t_1, t_2, t_1^{-1} t_2^{-1})$
. We denote by
![]() $\mathbb {K}:=K_T(\mathrm {pt})=\mathbb {Z}[q_1^{\pm 1}, q_2^{\pm 1}]$
and let
$\mathbb {K}:=K_T(\mathrm {pt})=\mathbb {Z}[q_1^{\pm 1}, q_2^{\pm 1}]$
and let
![]() $\mathbb {F}$
be the fraction field of
$\mathbb {F}$
be the fraction field of
![]() $\mathbb {K}$
. For V a
$\mathbb {K}$
. For V a
![]() $\mathbb {K}$
-module, we use the notations
$\mathbb {K}$
-module, we use the notations
![]() $V':=V/(\mathbb {K}\text {-torsion})$
and
$V':=V/(\mathbb {K}\text {-torsion})$
and
![]() $V_{\mathbb {F}}:=V\otimes _{\mathbb {K}}\mathbb {F}$
.
$V_{\mathbb {F}}:=V\otimes _{\mathbb {K}}\mathbb {F}$
.
For a dg-category
![]() $\mathcal {D}$
, a full dg-subcategory
$\mathcal {D}$
, a full dg-subcategory
![]() $\mathcal {C} \subset \mathcal {D}$
is called dense if any object in
$\mathcal {C} \subset \mathcal {D}$
is called dense if any object in
![]() $\mathcal {D}$
is a direct summand of an object in
$\mathcal {D}$
is a direct summand of an object in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
2.2 Weights and partitions
2.2.1
For
![]() $d\in \mathbb {N}$
, let V be a
$d\in \mathbb {N}$
, let V be a
![]() $\mathbb {C}$
-vector space of dimension d, and let
$\mathbb {C}$
-vector space of dimension d, and let
![]() $\mathfrak {g}=\mathfrak {gl}(V):=\text {End}(V)$
. When the dimension is clear from the context, we drop d from its notation. Let
$\mathfrak {g}=\mathfrak {gl}(V):=\text {End}(V)$
. When the dimension is clear from the context, we drop d from its notation. Let
Alternatively,
![]() $\mathcal {X}(d)$
is the stack of representations of dimension d of the quiver Q with one vertex and three loops
$\mathcal {X}(d)$
is the stack of representations of dimension d of the quiver Q with one vertex and three loops
![]() $\{x, y, z\}$
:
$\{x, y, z\}$
:

Consider the superpotential
![]() $W=x[y, z]$
of Q and the regular function
$W=x[y, z]$
of Q and the regular function
where
![]() $(A, B, C)\in \mathfrak {gl}(V)^{\oplus 3}$
.
$(A, B, C)\in \mathfrak {gl}(V)^{\oplus 3}$
.
Fix the maximal torus
![]() $T(d)\subset GL(d)$
to be consisting of diagonal matrices. Denote by
$T(d)\subset GL(d)$
to be consisting of diagonal matrices. Denote by
![]() $M=\oplus _{i=1}^d \mathbb {Z} \beta _i$
the weight space of
$M=\oplus _{i=1}^d \mathbb {Z} \beta _i$
the weight space of
![]() $T(d)$
, and let
$T(d)$
, and let
![]() $M(d)_{\mathbb {R}}:=M(d)\otimes _{\mathbb {Z}}\mathbb {R}$
, where
$M(d)_{\mathbb {R}}:=M(d)\otimes _{\mathbb {Z}}\mathbb {R}$
, where
![]() $\beta _1,\ldots , \beta _d$
is the set of simple roots. A weight
$\beta _1,\ldots , \beta _d$
is the set of simple roots. A weight
![]() $\chi =\sum _{i=1}^d c_i\beta _i$
is dominant if
$\chi =\sum _{i=1}^d c_i\beta _i$
is dominant if
We denote by
![]() $M^+\subset M$
and
$M^+\subset M$
and
![]() $M^+_{\mathbb {R}}\subset M_{\mathbb {R}}$
the dominant chambers. When we want to emphasize the dimension vector, we write
$M^+_{\mathbb {R}}\subset M_{\mathbb {R}}$
the dominant chambers. When we want to emphasize the dimension vector, we write
![]() $M(d)$
and so on. Denote by N the coweight lattice of
$M(d)$
and so on. Denote by N the coweight lattice of
![]() $T(d)$
and by
$T(d)$
and by
![]() $N_{\mathbb {R}}:=N\otimes _{\mathbb {Z}}\mathbb {R}$
. Let
$N_{\mathbb {R}}:=N\otimes _{\mathbb {Z}}\mathbb {R}$
. Let
![]() $\langle \,,\,\rangle $
be the natural pairing between
$\langle \,,\,\rangle $
be the natural pairing between
![]() $N_{\mathbb {R}}$
and
$N_{\mathbb {R}}$
and
![]() $M_{\mathbb {R}}$
.
$M_{\mathbb {R}}$
.
Let
![]() $W=\mathfrak {S}_d$
be the Weyl group of
$W=\mathfrak {S}_d$
be the Weyl group of
![]() $GL(d)$
. For
$GL(d)$
. For
![]() $\chi \in M(d)^+$
, let
$\chi \in M(d)^+$
, let
![]() $\Gamma _{GL(d)}(\chi )$
be the irreducible representation of
$\Gamma _{GL(d)}(\chi )$
be the irreducible representation of
![]() $GL(d)$
of highest weight
$GL(d)$
of highest weight
![]() $\chi $
. We drop
$\chi $
. We drop
![]() $GL(d)$
from the notation if the dimension vector d is clear from the context. Let
$GL(d)$
from the notation if the dimension vector d is clear from the context. Let
![]() $w*\chi :=w(\chi +\rho )-\rho $
be the Weyl-shifted action of
$w*\chi :=w(\chi +\rho )-\rho $
be the Weyl-shifted action of
![]() $w\in W$
on
$w\in W$
on
![]() $\chi \in M(d)_{\mathbb {R}}$
. We denote by
$\chi \in M(d)_{\mathbb {R}}$
. We denote by
![]() $\ell (w)$
the length of
$\ell (w)$
the length of
![]() $w\in W$
.
$w\in W$
.
Denote by
![]() $\mathcal {W}$
the multiset of
$\mathcal {W}$
the multiset of
![]() $T(d)$
-weights of
$T(d)$
-weights of
![]() $R(d)$
. If there is a natural action of a torus T on
$R(d)$
. If there is a natural action of a torus T on
![]() $R(d)$
, we abuse notation and write
$R(d)$
, we abuse notation and write
![]() $\mathcal {W}$
for the multiset of
$\mathcal {W}$
for the multiset of
![]() $(T\times T(d))$
-weights of
$(T\times T(d))$
-weights of
![]() $R(d)$
. For
$R(d)$
. For
![]() $\lambda $
a cocharacter of
$\lambda $
a cocharacter of
![]() $T(d)$
, we denote by
$T(d)$
, we denote by
![]() $N^{\lambda>0}$
the sum of weights
$N^{\lambda>0}$
the sum of weights
![]() $\beta $
in
$\beta $
in
![]() $\mathcal {W}$
such that
$\mathcal {W}$
such that
![]() $\langle \lambda , \beta \rangle>0$
.
$\langle \lambda , \beta \rangle>0$
.
2.2.2
We denote by
![]() $\rho $
half the sum of positive roots of
$\rho $
half the sum of positive roots of
![]() $GL(d)$
. In our convention of the dominant chamber, it is given by
$GL(d)$
. In our convention of the dominant chamber, it is given by
 $$ \begin{align*} \rho=\frac{1}{2}\sum_{j<i}(\beta_i-\beta_j). \end{align*} $$
$$ \begin{align*} \rho=\frac{1}{2}\sum_{j<i}(\beta_i-\beta_j). \end{align*} $$
We denote by
![]() $1_d:=z\cdot \text {Id}$
the diagonal cocharacter of
$1_d:=z\cdot \text {Id}$
the diagonal cocharacter of
![]() $T(d)$
. Define the weights
$T(d)$
. Define the weights
 $$ \begin{align*} \sigma_d:=\sum_{j=1}^d\beta_j\in M,\ \tau_d:=\frac{\sigma_d}{d}\in M_{\mathbb{R}}. \end{align*} $$
$$ \begin{align*} \sigma_d:=\sum_{j=1}^d\beta_j\in M,\ \tau_d:=\frac{\sigma_d}{d}\in M_{\mathbb{R}}. \end{align*} $$
2.2.3
Let G be a reductive group (in this paper, G will be a Levi subgroup of
![]() $GL(d)$
for some positive integer d), let
$GL(d)$
for some positive integer d), let
![]() $T_G$
be a maximal torus of G, let X be a G-representation and let
$T_G$
be a maximal torus of G, let X be a G-representation and let
be the corresponding quotient stack. Let
![]() $\mathcal {W}$
be the multiset of
$\mathcal {W}$
be the multiset of
![]() $T_G$
-weights of X. For
$T_G$
-weights of X. For
![]() $\lambda $
a cocharacter of
$\lambda $
a cocharacter of
![]() $T_G$
, let
$T_G$
, let
![]() $X^{\lambda }\subset X$
be the subspace generated by weights
$X^{\lambda }\subset X$
be the subspace generated by weights
![]() $\beta \in \mathcal {W}$
such that
$\beta \in \mathcal {W}$
such that
![]() $\langle \lambda , \beta \rangle =0$
, let
$\langle \lambda , \beta \rangle =0$
, let
![]() $X^{\lambda \geqslant 0}\subset X$
be the subspace generated by weights
$X^{\lambda \geqslant 0}\subset X$
be the subspace generated by weights
![]() $\beta \in \mathcal {W}$
such that
$\beta \in \mathcal {W}$
such that
![]() $\langle \lambda , \beta \rangle \geqslant 0$
and let
$\langle \lambda , \beta \rangle \geqslant 0$
and let
![]() $G^{\lambda }$
and
$G^{\lambda }$
and
![]() $G^{\lambda \geqslant 0}$
be the Levi and parabolic groups associated to
$G^{\lambda \geqslant 0}$
be the Levi and parabolic groups associated to
![]() $\lambda $
. Consider the fixed and attracting stacks
$\lambda $
. Consider the fixed and attracting stacks
with maps
Define the integer
2.2.4
Let
![]() $d\in \mathbb {N}$
, and recall the definition of
$d\in \mathbb {N}$
, and recall the definition of
![]() $\mathcal {X}(d)$
from Subsection 2.2.1. For a cocharacter
$\mathcal {X}(d)$
from Subsection 2.2.1. For a cocharacter
![]() $\lambda :\mathbb {C}^{*}\to T(d)$
, consider the maps of fixed and attracting loci
$\lambda :\mathbb {C}^{*}\to T(d)$
, consider the maps of fixed and attracting loci
We say that two cocharacters
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda '$
are equivalent and write
$\lambda '$
are equivalent and write
![]() $\lambda \sim \lambda '$
if
$\lambda \sim \lambda '$
if
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda '$
have the same fixed and attracting stacks as above.
$\lambda '$
have the same fixed and attracting stacks as above.
We call
![]() $\underline {d}:=(d_i)_{i=1}^k$
a partition of d if
$\underline {d}:=(d_i)_{i=1}^k$
a partition of d if
![]() $d_i\in \mathbb {N}$
are all nonzero and
$d_i\in \mathbb {N}$
are all nonzero and
![]() $\sum _{i=1}^k d_i=d$
. In Section 5, we allow partitions
$\sum _{i=1}^k d_i=d$
. In Section 5, we allow partitions
![]() $\underline {d}=(d_i)_{i=1}^k$
to have terms
$\underline {d}=(d_i)_{i=1}^k$
to have terms
![]() $d_i$
equal to zero. We similarly define partitions of
$d_i$
equal to zero. We similarly define partitions of
![]() $(d,w)\in \mathbb {N}\times \mathbb {Z}$
. For a cocharacter
$(d,w)\in \mathbb {N}\times \mathbb {Z}$
. For a cocharacter
![]() $\lambda $
of
$\lambda $
of
![]() $T(d)$
, there is an associated partition
$T(d)$
, there is an associated partition
![]() $(d_i)_{i=1}^k$
such that
$(d_i)_{i=1}^k$
such that
Define the length
![]() $\ell (\lambda ):=k$
.
$\ell (\lambda ):=k$
.
Equivalence classes of antidominant cocharacters are in bijection with ordered partitions
![]() $(d_i)_{i=1}^k$
of d. For an ordered partition
$(d_i)_{i=1}^k$
of d. For an ordered partition
![]() $\underline {d}=(d_i)_{i=1}^k$
of d, fix a corresponding antidominant cocharacter
$\underline {d}=(d_i)_{i=1}^k$
of d, fix a corresponding antidominant cocharacter
![]() $\lambda =\lambda _{\underline {d}}$
of
$\lambda =\lambda _{\underline {d}}$
of
![]() $T(d)$
which induces the maps
$T(d)$
which induces the maps
We also use the notations
![]() $p_{\lambda }=p_{\underline {d}}$
,
$p_{\lambda }=p_{\underline {d}}$
,
![]() $q_{\lambda }=q_{\underline {d}}$
. The categorical Hall algebra is given by the functor
$q_{\lambda }=q_{\underline {d}}$
. The categorical Hall algebra is given by the functor
![]() $p_{\lambda *}q_{\lambda }^{*}=p_{\underline {d}*}q_{\underline {d}}^{*}$
:
$p_{\lambda *}q_{\lambda }^{*}=p_{\underline {d}*}q_{\underline {d}}^{*}$
:
We may drop the subscript
![]() $\lambda $
or
$\lambda $
or
![]() $\underline {d}$
in the functors
$\underline {d}$
in the functors
![]() $p_*$
and
$p_*$
and
![]() $q^{*}$
when the cocharacter
$q^{*}$
when the cocharacter
![]() $\lambda $
or the partition
$\lambda $
or the partition
![]() $\underline {d}$
is clear. We also use the notation
$\underline {d}$
is clear. We also use the notation
![]() $\ast $
for the Hall product.
$\ast $
for the Hall product.
2.2.5
Let
![]() $(d_i)_{i=1}^k$
be a partition of d. There is an identification
$(d_i)_{i=1}^k$
be a partition of d. There is an identification
 $$\begin{align*}\bigoplus_{i=1}^k M(d_i)\cong M(d),\end{align*}$$
$$\begin{align*}\bigoplus_{i=1}^k M(d_i)\cong M(d),\end{align*}$$
where the simple roots
![]() $\beta _j$
in
$\beta _j$
in
![]() $M(d_1)$
correspond to the first
$M(d_1)$
correspond to the first
![]() $d_1$
simple roots
$d_1$
simple roots
![]() $\beta _j$
of d etc.
$\beta _j$
of d etc.
2.2.6
Let
![]() $\underline {e}=(e_i)_{i=1}^l$
and
$\underline {e}=(e_i)_{i=1}^l$
and
![]() $\underline {d}=(d_i)_{i=1}^k$
be two partitions of
$\underline {d}=(d_i)_{i=1}^k$
be two partitions of
![]() $d\in \mathbb {N}$
. We write
$d\in \mathbb {N}$
. We write
![]() $\underline {e}\geqslant \underline {d}$
if there exist integers
$\underline {e}\geqslant \underline {d}$
if there exist integers
such that for any
![]() $0\leqslant j\leqslant k-1$
, we have
$0\leqslant j\leqslant k-1$
, we have
 $$\begin{align*}\sum_{i=a_{j}+1}^{a_{j+1}} e_i=d_{j+1}.\end{align*}$$
$$\begin{align*}\sum_{i=a_{j}+1}^{a_{j+1}} e_i=d_{j+1}.\end{align*}$$
We say
![]() $\underline {e}$
is a refinement of
$\underline {e}$
is a refinement of
![]() $\underline {d}$
. There is a similarly defined order on pairs
$\underline {d}$
. There is a similarly defined order on pairs
![]() $(d, w)\in \mathbb {N}\times \mathbb {Z}$
.
$(d, w)\in \mathbb {N}\times \mathbb {Z}$
.
2.2.7
Let A be a partition
![]() $(d_i, w_i)_{i=1}^k$
of
$(d_i, w_i)_{i=1}^k$
of
![]() $(d, w)$
, and consider its corresponding antidominant cocharacter
$(d, w)$
, and consider its corresponding antidominant cocharacter
![]() $\lambda $
. Define the weights
$\lambda $
. Define the weights
 $$ \begin{align*} \chi_A:=\sum_{i=1}^k w_i\tau_{d_i},\ \chi^{\prime}_A:=\chi_A+\mathfrak{g}^{\lambda>0}. \end{align*} $$
$$ \begin{align*} \chi_A:=\sum_{i=1}^k w_i\tau_{d_i},\ \chi^{\prime}_A:=\chi_A+\mathfrak{g}^{\lambda>0}. \end{align*} $$
Consider weights
![]() $\chi ^{\prime }_i\in M(d_i)_{\mathbb {R}}$
such that
$\chi ^{\prime }_i\in M(d_i)_{\mathbb {R}}$
such that
 $$\begin{align*}\chi^{\prime}_A=\sum_{i=1}^k \chi^{\prime}_i.\end{align*}$$
$$\begin{align*}\chi^{\prime}_A=\sum_{i=1}^k \chi^{\prime}_i.\end{align*}$$
Let
![]() $v_i$
be the sum of coefficients of
$v_i$
be the sum of coefficients of
![]() $\chi ^{\prime }_i$
for
$\chi ^{\prime }_i$
for
![]() $1\leqslant i\leqslant k$
; alternatively,
$1\leqslant i\leqslant k$
; alternatively,
![]() $v_i:=\langle 1_{d_i}, \chi ^{\prime }_i\rangle $
. We denote the above transformation by
$v_i:=\langle 1_{d_i}, \chi ^{\prime }_i\rangle $
. We denote the above transformation by
Explicitly, the weights
![]() $v_i$
for
$v_i$
for
![]() $1\leqslant i\leqslant k$
are given by
$1\leqslant i\leqslant k$
are given by
 $$ \begin{align} v_i=w_i+d_i\left(\sum_{j>i}d_j -\sum_{j<i}d_j \right). \end{align} $$
$$ \begin{align} v_i=w_i+d_i\left(\sum_{j>i}d_j -\sum_{j<i}d_j \right). \end{align} $$
2.3 Polytopes
The polytope
![]() $\textbf {W}(d)$
is defined as
$\textbf {W}(d)$
is defined as
where the Minkowski sum is after all
![]() $1\leqslant i, j\leqslant d$
. For
$1\leqslant i, j\leqslant d$
. For
![]() $w\in \mathbb {Z}$
, consider the hyperplane
$w\in \mathbb {Z}$
, consider the hyperplane
For
![]() $r>0$
and
$r>0$
and
![]() $\lambda $
a cocharacter of
$\lambda $
a cocharacter of
![]() $T(d)$
, let
$T(d)$
, let
![]() $F_r(\lambda )$
be the face of the polytope
$F_r(\lambda )$
be the face of the polytope
![]() $2r\textbf {W}(d)$
corresponding to the cocharacter
$2r\textbf {W}(d)$
corresponding to the cocharacter
![]() $\lambda $
, so the set of weights
$\lambda $
, so the set of weights
![]() $\chi $
in
$\chi $
in
![]() $M(d)_{\mathbb {R}}$
such that
$M(d)_{\mathbb {R}}$
such that
When
![]() $r=\frac {1}{2}$
, we use the notations
$r=\frac {1}{2}$
, we use the notations
![]() $F(\lambda )$
. For
$F(\lambda )$
. For
![]() $\chi \in M(d)^+_{\mathbb {R}}$
, its r-invariant
$\chi \in M(d)^+_{\mathbb {R}}$
, its r-invariant
![]() $r(\chi )$
is the smallest real number r such that
$r(\chi )$
is the smallest real number r such that
For a cocharacter
![]() $\lambda $
of
$\lambda $
of
![]() $T(d)$
, denote by
$T(d)$
, denote by
where the sum is after all weights
![]() $1\leqslant i, j\leqslant d$
such that
$1\leqslant i, j\leqslant d$
such that
![]() $\langle \lambda , \beta _i-\beta _j\rangle =0$
.
$\langle \lambda , \beta _i-\beta _j\rangle =0$
.
2.4 A corollary of the Borel–Weyl–Bott theorem
For future reference, we state a result from [Reference Halpern-Leistner and SamHLS20, Section 3.2]. We continue with the notations from Subsection 2.2.3. Let M be the weight lattice of
![]() $T_G$
. We assume that X is a symmetric G-representation, meaning that for any weight
$T_G$
. We assume that X is a symmetric G-representation, meaning that for any weight
![]() $\beta $
of X, the weights
$\beta $
of X, the weights
![]() $\beta $
and
$\beta $
and
![]() $-\beta $
appear with the same multiplicity in X. Let
$-\beta $
appear with the same multiplicity in X. Let
![]() $\chi $
be a weight in M. Let
$\chi $
be a weight in M. Let
![]() $\chi ^+$
be the dominant Weyl-shifted conjugate of
$\chi ^+$
be the dominant Weyl-shifted conjugate of
![]() $\chi $
if it exists and zero otherwise. For a multiset
$\chi $
if it exists and zero otherwise. For a multiset
![]() $J\subset \mathcal {W}$
, let
$J\subset \mathcal {W}$
, let
 $$\begin{align*}\sigma_J:=\sum_{\beta\in J}\beta.\end{align*}$$
$$\begin{align*}\sigma_J:=\sum_{\beta\in J}\beta.\end{align*}$$
Let w be the element of the Weyl group of minimal length such that
![]() $w*(\chi -\sigma _J)$
is dominant or zero. We let
$w*(\chi -\sigma _J)$
is dominant or zero. We let
![]() $\ell (J):=\ell (w)$
.
$\ell (J):=\ell (w)$
.
Proposition 2.1. Let X be a symmetric G-representation, and let
![]() $\lambda $
be an antidominant cocharacter of
$\lambda $
be an antidominant cocharacter of
![]() $T_G$
. Recall the fixed and attracting stacks and the corresponding maps
$T_G$
. Recall the fixed and attracting stacks and the corresponding maps
For a weight
![]() $\chi $
in M, there is a quasi-isomorphism
$\chi $
in M, there is a quasi-isomorphism
 $$\begin{align*}\left(\bigoplus_{J}\mathcal{O}_{X}\otimes \Gamma_{G}\left((\chi-\sigma_J)^+\right)\left[|J|-\ell(J)\right], d\right)\xrightarrow{\sim}p_{\lambda*}q_{\lambda}^{*}\left(\mathcal{O}_{X^{\lambda}}\otimes\Gamma_{G^{\lambda}}(\chi)\right),\end{align*}$$
$$\begin{align*}\left(\bigoplus_{J}\mathcal{O}_{X}\otimes \Gamma_{G}\left((\chi-\sigma_J)^+\right)\left[|J|-\ell(J)\right], d\right)\xrightarrow{\sim}p_{\lambda*}q_{\lambda}^{*}\left(\mathcal{O}_{X^{\lambda}}\otimes\Gamma_{G^{\lambda}}(\chi)\right),\end{align*}$$
where the complex on the left-hand side has terms (shifted) vector bundles for all multisets
![]() $J\subset \{\beta \in \mathcal {W} \mid \langle \lambda , \beta \rangle <0\}$
.
$J\subset \{\beta \in \mathcal {W} \mid \langle \lambda , \beta \rangle <0\}$
.
2.5 Matrix factorizations
In the notations from Subsection 2.2.1, we denote by
the dg-category of matrix factorizations of the regular function
![]() $\mathop {\mathrm {Tr}}\nolimits W_d$
on the smooth stack
$\mathop {\mathrm {Tr}}\nolimits W_d$
on the smooth stack
![]() $\mathcal {X}(d)$
. Its objects consist of tuples
$\mathcal {X}(d)$
. Its objects consist of tuples
where
![]() $F, G \in \operatorname {Coh}(\mathcal {X}(d))$
; see [Reference Pădurariu and TodaPTa, Subsection 2.6] for details. For an object
$F, G \in \operatorname {Coh}(\mathcal {X}(d))$
; see [Reference Pădurariu and TodaPTa, Subsection 2.6] for details. For an object
![]() $\mathcal {F} \in \mathrm {MF}(\mathcal {X}(d), \mathop {\mathrm {Tr}}\nolimits W_d)$
, its internal homomorphism
$\mathcal {F} \in \mathrm {MF}(\mathcal {X}(d), \mathop {\mathrm {Tr}}\nolimits W_d)$
, its internal homomorphism
![]() $R\mathcal {H}om (\mathcal {F}, \mathcal {F})$
is an object of the
$R\mathcal {H}om (\mathcal {F}, \mathcal {F})$
is an object of the
![]() $\mathbb {Z}/2$
-graded derived category of
$\mathbb {Z}/2$
-graded derived category of
![]() $\operatorname {Coh}(\mathcal {X}(d))$
. The support of
$\operatorname {Coh}(\mathcal {X}(d))$
. The support of
![]() $\mathcal {F}$
$\mathcal {F}$
is defined to be the support of
![]() $R\mathcal {H}om(\mathcal {F}, \mathcal {F})$
, which is a closed substack of
$R\mathcal {H}om(\mathcal {F}, \mathcal {F})$
, which is a closed substack of
![]() $\mathcal {X}(d)$
. Alternatively, it is the smallest closed substack
$\mathcal {X}(d)$
. Alternatively, it is the smallest closed substack
![]() $\mathcal {Z} \subset \mathcal {X}(d)$
such that
$\mathcal {Z} \subset \mathcal {X}(d)$
such that
![]() $\mathcal {F}|_{\mathcal {X}(d) \setminus \mathcal {Z}} \cong 0$
in
$\mathcal {F}|_{\mathcal {X}(d) \setminus \mathcal {Z}} \cong 0$
in
![]() $\mathrm {MF}(\mathcal {X}(d) \setminus \mathcal {Z}, \mathop {\mathrm {Tr}}\nolimits W_d)$
.
$\mathrm {MF}(\mathcal {X}(d) \setminus \mathcal {Z}, \mathop {\mathrm {Tr}}\nolimits W_d)$
.
Similarly to Equation (2.5), for
![]() $d=d_1+d_2$
we have the categorical Hall product
$d=d_1+d_2$
we have the categorical Hall product
see [Reference PădurariuPăd22] for details. We sometimes write
![]() $a\ast b$
instead of
$a\ast b$
instead of
![]() $m(a, b)$
.
$m(a, b)$
.
We also consider equivariant and graded matrix factorizations for the regular function (2.2); see [Reference Pădurariu and TodaPTa, Subsection 2.6.2] for details. The group
![]() $(\mathbb {C}^{\ast })^3$
acts on the linear maps corresponding to the edges
$(\mathbb {C}^{\ast })^3$
acts on the linear maps corresponding to the edges
![]() $(x, y, z)$
of the quiver Q by scalar multiplication. Consider the two-dimensional subtorus
$(x, y, z)$
of the quiver Q by scalar multiplication. Consider the two-dimensional subtorus
which preserves the superpotential
![]() $W=x[y, z]$
; see Equation (2.1). Then T acts on
$W=x[y, z]$
; see Equation (2.1). Then T acts on
![]() $\mathcal {X}(d)$
and preserves
$\mathcal {X}(d)$
and preserves
![]() $\mathop {\mathrm {Tr}}\nolimits W$
. We will also consider graded matrix factorizations, where the grading is given by scaling with weight
$\mathop {\mathrm {Tr}}\nolimits W$
. We will also consider graded matrix factorizations, where the grading is given by scaling with weight
![]() $2$
the space
$2$
the space
![]() $\mathfrak {gl}(V)$
for V a vector space. For example, we can choose an edge
$\mathfrak {gl}(V)$
for V a vector space. For example, we can choose an edge
![]() $e\in \{x, y, z\}$
of Q and let
$e\in \{x, y, z\}$
of Q and let
![]() $\mathbb {C}^{*}$
scale with weight
$\mathbb {C}^{*}$
scale with weight
![]() $2$
the linear map corresponding to e. Contrary to the T-action, the regular function
$2$
the linear map corresponding to e. Contrary to the T-action, the regular function
![]() $\mathop {\mathrm {Tr}}\nolimits W$
has weight
$\mathop {\mathrm {Tr}}\nolimits W$
has weight
![]() $2$
with respect to such a grading. The corresponding categories of matrix factorizations are denoted by
$2$
with respect to such a grading. The corresponding categories of matrix factorizations are denoted by
2.6 Quasi-BPS categories
2.6.1
For
![]() $w \in \mathbb {Z}$
, we denote by
$w \in \mathbb {Z}$
, we denote by
![]() $D^b(\mathcal {X}(d))_w$
the subcategory of
$D^b(\mathcal {X}(d))_w$
the subcategory of
![]() $D^b(\mathcal {X}(d))$
consisting of objects of weight w with respect to the diagonal cocharacter
$D^b(\mathcal {X}(d))$
consisting of objects of weight w with respect to the diagonal cocharacter
![]() $1_d$
of
$1_d$
of
![]() $T(d)$
. We have the direct sum decomposition
$T(d)$
. We have the direct sum decomposition
We define the dg subcategories
to be generated by the vector bundles
![]() $\mathcal {O}_{\mathcal {X}(d)}\otimes \Gamma _{GL(d)}(\chi )$
, where
$\mathcal {O}_{\mathcal {X}(d)}\otimes \Gamma _{GL(d)}(\chi )$
, where
![]() $\chi $
is a dominant weight of
$\chi $
is a dominant weight of
![]() $T(d)$
such that
$T(d)$
such that
Note that
![]() $\mathbb {M}(d)$
decomposes into the direct sum of
$\mathbb {M}(d)$
decomposes into the direct sum of
![]() $\mathbb {M}(d)_w$
for
$\mathbb {M}(d)_w$
for
![]() $w \in \mathbb {Z}$
. The following is an alternative description of the category
$w \in \mathbb {Z}$
. The following is an alternative description of the category
![]() $\mathbb {M}(d)_w$
:
$\mathbb {M}(d)_w$
:
Lemma 2.2 [Reference Halpern-Leistner and SamHLS20, Lemma 2.9].
The category
![]() $\mathbb {M}(d)_w$
is generated by the vector bundles
$\mathbb {M}(d)_w$
is generated by the vector bundles
![]() $\mathcal {O}_{\mathcal {X}(d)} \otimes \Gamma $
for
$\mathcal {O}_{\mathcal {X}(d)} \otimes \Gamma $
for
![]() $\Gamma $
a
$\Gamma $
a
![]() $GL(d)$
-representation such that the
$GL(d)$
-representation such that the
![]() $T(d)$
-weights of
$T(d)$
-weights of
![]() $\Gamma $
are contained in the set
$\Gamma $
are contained in the set
![]() $\nabla _w$
defined by
$\nabla _w$
defined by
 $$ \begin{align*} \nabla_{w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n_{\lambda} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n_{\lambda} \mbox{ for all } \lambda \colon \mathbb{C}^{\ast} \to T(d) \right\} +w\tau_d. \end{align*} $$
$$ \begin{align*} \nabla_{w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n_{\lambda} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n_{\lambda} \mbox{ for all } \lambda \colon \mathbb{C}^{\ast} \to T(d) \right\} +w\tau_d. \end{align*} $$
For a partition
![]() $A=(d_i, w_i)_{i=1}^k$
of
$A=(d_i, w_i)_{i=1}^k$
of
![]() $(d, w)$
, define
$(d, w)$
, define
2.6.2
Recall the regular function (2.2). We define the subcategory
to be the subcategory of matrix factorizations
![]() $\left (\alpha \colon F\rightleftarrows G\colon \beta \right )$
with F and G in
$\left (\alpha \colon F\rightleftarrows G\colon \beta \right )$
with F and G in
![]() $\mathbb {M}(d)$
. It decomposes into the direct sum of
$\mathbb {M}(d)$
. It decomposes into the direct sum of
![]() $\mathbb {S}(d)_w$
for
$\mathbb {S}(d)_w$
for
![]() $w \in \mathbb {Z}$
, where
$w \in \mathbb {Z}$
, where
![]() $\mathbb {S}(d)_w$
is defined similarly to
$\mathbb {S}(d)_w$
is defined similarly to
![]() $\mathbb {S}(d)$
using
$\mathbb {S}(d)$
using
![]() $\mathbb {M}(d)_w$
.
$\mathbb {M}(d)_w$
.
We also consider subcategories for
![]() $\ast \in \{\emptyset , T\}$
,
$\ast \in \{\emptyset , T\}$
,
![]() $\bullet \in \{\emptyset , \text {gr}\}$
defined in a similar way
$\bullet \in \{\emptyset , \text {gr}\}$
defined in a similar way
The subcategory
![]() $\mathbb {S}^{\bullet }_{\ast }(d)_w$
is also defined in a similar way. For a partition
$\mathbb {S}^{\bullet }_{\ast }(d)_w$
is also defined in a similar way. For a partition
![]() $A=(d_i, w_i)_{i=1}^k$
of
$A=(d_i, w_i)_{i=1}^k$
of
![]() $(d, w)$
, the category
$(d, w)$
, the category
![]() $\mathbb {S}_{\ast , A}^{\bullet }$
is also defined similarly to Equation (2.11). We denote the Grothendieck group of
$\mathbb {S}_{\ast , A}^{\bullet }$
is also defined similarly to Equation (2.11). We denote the Grothendieck group of
![]() $\mathbb {S}^{\bullet }_{\ast }(d)_w$
by
$\mathbb {S}^{\bullet }_{\ast }(d)_w$
by
By [Reference TodaTod23, Corollary 3.13], there are natural isomorphisms (which hold for all graded matrix factorizations as in Subsection 2.5):
2.7 Complexes in quasi-BPS categories
Let V be a d-dimensional complex vector space, and recall that we denote by
![]() $\mathfrak {g}=\operatorname {Hom}(V, V)$
the Lie algebra of
$\mathfrak {g}=\operatorname {Hom}(V, V)$
the Lie algebra of
![]() $GL(V)$
. We set
$GL(V)$
. We set
where
![]() $GL(V)$
acts on
$GL(V)$
acts on
![]() $\mathfrak {g}$
by conjugation. The stack
$\mathfrak {g}$
by conjugation. The stack
![]() $\mathcal {Y}(d)$
is the moduli stack of representations of dimension d of the quiver with one vertex and two loops. Let s be the morphism
$\mathcal {Y}(d)$
is the moduli stack of representations of dimension d of the quiver with one vertex and two loops. Let s be the morphism
The morphism s induces a map of vector bundles
![]() $\partial : \mathfrak {g}^{\vee }\otimes \mathcal {O}_{\mathfrak {g}^{\oplus 2}}\to \mathcal {O}_{\mathfrak {g}^{\oplus 2}}$
. Let
$\partial : \mathfrak {g}^{\vee }\otimes \mathcal {O}_{\mathfrak {g}^{\oplus 2}}\to \mathcal {O}_{\mathfrak {g}^{\oplus 2}}$
. Let
![]() $s^{-1}(0)$
be the derived scheme with the dg-ring of regular functions
$s^{-1}(0)$
be the derived scheme with the dg-ring of regular functions
where the differential
![]() $d_s$
is induced by the map
$d_s$
is induced by the map
![]() $\partial $
. Consider the (derived) stack
$\partial $
. Consider the (derived) stack
For a smooth variety X, we denote by
![]() $\mathscr {C}oh(X, d)$
the derived moduli stack of zero-dimensional sheaves on X with length d and by
$\mathscr {C}oh(X, d)$
the derived moduli stack of zero-dimensional sheaves on X with length d and by
![]() $\mathcal {C}oh(X, d)$
the classical truncation of
$\mathcal {C}oh(X, d)$
the classical truncation of
![]() $\mathscr {C}oh(X, d)$
. Then
$\mathscr {C}oh(X, d)$
. Then
![]() $\mathscr {C}(d)$
is equivalent to
$\mathscr {C}(d)$
is equivalent to
![]() $\mathscr {C}oh(\mathbb {C}^2, d)$
.
$\mathscr {C}oh(\mathbb {C}^2, d)$
.
For a decomposition
![]() $d=d_1+\cdots +d_k$
, let
$d=d_1+\cdots +d_k$
, let
![]() $\mathscr {C}(d_1, \ldots , d_k)$
be the derived moduli stack of filtrations of coherent sheaves on
$\mathscr {C}(d_1, \ldots , d_k)$
be the derived moduli stack of filtrations of coherent sheaves on
![]() $\mathbb {C}^2$
:
$\mathbb {C}^2$
:
such that each subquotient
![]() $Q_i/Q_{i-1}$
is a zero-dimensional sheaf on
$Q_i/Q_{i-1}$
is a zero-dimensional sheaf on
![]() $\mathbb {C}^2$
with length
$\mathbb {C}^2$
with length
![]() $d_i$
. There exist evaluation morphisms
$d_i$
. There exist evaluation morphisms
where p is proper and q is quasi-smooth. The above diagram for
![]() $k=2$
defines the categorical Hall product
$k=2$
defines the categorical Hall product
which is a special case of the product of categorical Hall algebras for surfaces defined by Porta–Sala [Reference Porta and SalaPS23].
Let T be the two-dimensional torus in Equation (2.1) which acts on
![]() $\mathbb {C}^2$
by
$\mathbb {C}^2$
by
![]() $(t_1, t_2) \cdot (x, y)=(t_1 x, t_2 y)$
. It naturally induces an action on
$(t_1, t_2) \cdot (x, y)=(t_1 x, t_2 y)$
. It naturally induces an action on
![]() $\mathscr {C}(d)$
. There is also a T-equivariant Hall product
$\mathscr {C}(d)$
. There is also a T-equivariant Hall product
Here, the box product is taken over
![]() $BT$
. In what follows, whenever we take a box-product in the T-equivariant setting, we take it over
$BT$
. In what follows, whenever we take a box-product in the T-equivariant setting, we take it over
![]() $BT$
. We also use the notation
$BT$
. We also use the notation
![]() $\ast $
for the Hall product.
$\ast $
for the Hall product.
2.8 Subcategories
 $\mathbb {T}(d)_v$
$\mathbb {T}(d)_v$
Let
be the natural closed immersion. Define the full triangulated subcategory
generated by the vector bundles
![]() $\mathcal {O}_{\mathcal {Y}(d)}\otimes \Gamma _{GL(d)}(\chi )$
for a dominant weight
$\mathcal {O}_{\mathcal {Y}(d)}\otimes \Gamma _{GL(d)}(\chi )$
for a dominant weight
![]() $\chi $
satisfying
$\chi $
satisfying
Define the full triangulated subcategory
with objects
![]() $\mathcal {E}$
such that
$\mathcal {E}$
such that
![]() $i_{\ast }\mathcal {E}$
is in
$i_{\ast }\mathcal {E}$
is in
![]() $\widetilde {\mathbb {T}}(d)_v$
. In [Reference Pădurariu and TodaPTa, Lemma 4.8], we showed that the Hall product restricts to functors
$\widetilde {\mathbb {T}}(d)_v$
. In [Reference Pădurariu and TodaPTa, Lemma 4.8], we showed that the Hall product restricts to functors
for
![]() $(d, v)=(d_1, v_1)+(d_2, v_2)$
and
$(d, v)=(d_1, v_1)+(d_2, v_2)$
and
![]() $\frac {v_1}{d_1}=\frac {v_2}{d_2}$
. Also, there is a semiorthogonal decomposition; see [Reference PădurariuPăd23, Corollary 3.3]:
$\frac {v_1}{d_1}=\frac {v_2}{d_2}$
. Also, there is a semiorthogonal decomposition; see [Reference PădurariuPăd23, Corollary 3.3]:
 $$ \begin{align} D^b(\mathscr{C}(d))=\left\langle \mathbb{T}(d_1)_{v_1} \boxtimes \cdots \boxtimes \mathbb{T}(d_k)_{v_k} \,\bigg|\, \begin{array}{c} v_1/d_1 < \cdots < v_k/d_k \\ d_1+\cdots+d_k=d \end{array} \right\rangle. \end{align} $$
$$ \begin{align} D^b(\mathscr{C}(d))=\left\langle \mathbb{T}(d_1)_{v_1} \boxtimes \cdots \boxtimes \mathbb{T}(d_k)_{v_k} \,\bigg|\, \begin{array}{c} v_1/d_1 < \cdots < v_k/d_k \\ d_1+\cdots+d_k=d \end{array} \right\rangle. \end{align} $$
In the above, each fully faithful functor
is given by the categorical Hall product (2.17).
Consider the grading induced by the action of
![]() $\mathbb {C}^{*}$
on
$\mathbb {C}^{*}$
on
![]() $\mathcal {X}(d)$
scaling the linear map corresponding to Z with weight
$\mathcal {X}(d)$
scaling the linear map corresponding to Z with weight
![]() $2$
. The Koszul duality equivalence, also called dimensional reduction in the literature, gives the following equivalence [Reference IsikIsi13, Reference HiranoHir17, Reference TodaToda]:
$2$
. The Koszul duality equivalence, also called dimensional reduction in the literature, gives the following equivalence [Reference IsikIsi13, Reference HiranoHir17, Reference TodaToda]:
Under this equivalence, we have that
![]() $\Phi \colon \mathbb {T}(d)_v\stackrel {\sim }{\to } \mathbb {S}^{\mathrm {gr}}(d)_v$
.
$\Phi \colon \mathbb {T}(d)_v\stackrel {\sim }{\to } \mathbb {S}^{\mathrm {gr}}(d)_v$
.
2.9 Constructions of objects in
 $\mathbb {T}(d)_v$
$\mathbb {T}(d)_v$
Here, we review the construction of objects
![]() $\mathcal {E}_{d, v} \in \mathbb {T}(d)_v$
(which also produces an object in
$\mathcal {E}_{d, v} \in \mathbb {T}(d)_v$
(which also produces an object in
![]() $\mathbb {T}_T(d)_v$
) following [Reference Pădurariu and TodaPTa, Subsection 4.3]. Let
$\mathbb {T}_T(d)_v$
) following [Reference Pădurariu and TodaPTa, Subsection 4.3]. Let
![]() $\mathcal {Z} \subset \mathscr {C}(1, 1, \ldots , 1)$
be the closed substack defined as follows. Let
$\mathcal {Z} \subset \mathscr {C}(1, 1, \ldots , 1)$
be the closed substack defined as follows. Let
![]() $\lambda $
be the cocharacter
$\lambda $
be the cocharacter
The attracting stack of
![]() $\mathcal {Y}(d)$
with respect to
$\mathcal {Y}(d)$
with respect to
![]() $\lambda $
is given by
$\lambda $
is given by
where
![]() $GL(V)^{\lambda \geqslant 0} \subset GL(V)$
is the subgroup of upper triangular matrices. Then the morphism (2.13) restricts to the morphism
$GL(V)^{\lambda \geqslant 0} \subset GL(V)$
is the subgroup of upper triangular matrices. Then the morphism (2.13) restricts to the morphism
whose derived zero locus
![]() $\mathscr {C}(d)^{\lambda \geqslant 0}$
is equivalent to
$\mathscr {C}(d)^{\lambda \geqslant 0}$
is equivalent to
![]() $\mathscr {C}(1, \ldots , 1)$
. Let
$\mathscr {C}(1, \ldots , 1)$
. Let
![]() $X=(x_{i,j})$
and
$X=(x_{i,j})$
and
![]() $Y=(y_{i,j})$
be elements of
$Y=(y_{i,j})$
be elements of
![]() $\mathfrak {g}^{\lambda \geqslant 0}$
for
$\mathfrak {g}^{\lambda \geqslant 0}$
for
![]() $1\leqslant i, j\leqslant d$
, where
$1\leqslant i, j\leqslant d$
, where
![]() $x_{i,j}=y_{i,j}=0$
for
$x_{i,j}=y_{i,j}=0$
for
![]() $i>j$
. Then the equation
$i>j$
. Then the equation
![]() $s^{\lambda \geqslant 0}(X, Y)=0$
is equivalent to the equations
$s^{\lambda \geqslant 0}(X, Y)=0$
is equivalent to the equations
for each
![]() $(i, j)$
with
$(i, j)$
with
![]() $i\leqslant j$
. We call the above equation
$i\leqslant j$
. We call the above equation
![]() $\mathbb {E}_{i, j}$
. The equation
$\mathbb {E}_{i, j}$
. The equation
![]() $\mathbb {E}_{i, i}$
is
$\mathbb {E}_{i, i}$
is
![]() $x_{i, i} y_{i, i}-y_{i, i} x_{i, i}=0$
, which always holds but imposes a nontrivial derived structure on
$x_{i, i} y_{i, i}-y_{i, i} x_{i, i}=0$
, which always holds but imposes a nontrivial derived structure on
![]() $\mathscr {C}(1, \ldots , 1)$
. The equation
$\mathscr {C}(1, \ldots , 1)$
. The equation
![]() $\mathbb {E}_{i, i+1}$
is
$\mathbb {E}_{i, i+1}$
is
The above equation is satisfied if the following equation
![]() $\mathbb {F}_{i, i+1}$
is satisfied:
$\mathbb {F}_{i, i+1}$
is satisfied:
We define the closed derived substack
to be the derived zero locus of the equations
![]() $\mathbb {F}_{i, i+1}$
for all i and
$\mathbb {F}_{i, i+1}$
for all i and
![]() $\mathbb {E}_{i, j}$
for all
$\mathbb {E}_{i, j}$
for all
![]() $i+2 \leqslant j$
. We usually drop d from the notation if the dimension is clear from the context. Then
$i+2 \leqslant j$
. We usually drop d from the notation if the dimension is clear from the context. Then
![]() $\mathcal {Z}$
is a closed substack of
$\mathcal {Z}$
is a closed substack of
![]() $\mathscr {C}(d)^{\lambda \geqslant 0}=\mathscr {C}(1, \ldots , 1)$
. Note that, set theoretically, the closed substack
$\mathscr {C}(d)^{\lambda \geqslant 0}=\mathscr {C}(1, \ldots , 1)$
. Note that, set theoretically, the closed substack
![]() $\mathcal {Z}$
corresponds to filtrations (2.16) such that each
$\mathcal {Z}$
corresponds to filtrations (2.16) such that each
![]() $Q_i/Q_{i-1}$
is isomorphic to
$Q_i/Q_{i-1}$
is isomorphic to
![]() $\mathcal {O}_x$
for some
$\mathcal {O}_x$
for some
![]() $x \in \mathbb {C}^2$
independent of i.
$x \in \mathbb {C}^2$
independent of i.
We have the diagram of attracting loci
where p is a proper morphism. We set
 $$ \begin{align} m_i :=\left\lceil \frac{vi}{d} \right\rceil -\left\lceil \frac{v(i-1)}{d} \right\rceil +\delta_i^d -\delta_i^1 \in \mathbb{Z}, \end{align} $$
$$ \begin{align} m_i :=\left\lceil \frac{vi}{d} \right\rceil -\left\lceil \frac{v(i-1)}{d} \right\rceil +\delta_i^d -\delta_i^1 \in \mathbb{Z}, \end{align} $$
where
![]() $\delta ^j_i$
is the Kronecker delta function defined by
$\delta ^j_i$
is the Kronecker delta function defined by
![]() $\delta ^j_i=1$
if
$\delta ^j_i=1$
if
![]() $i=j$
and
$i=j$
and
![]() $\delta ^j_i=0$
otherwise. For a weight
$\delta ^j_i=0$
otherwise. For a weight
![]() $\chi =\sum _{i=1}^d n_i \beta _i$
with
$\chi =\sum _{i=1}^d n_i \beta _i$
with
![]() $n_i \in \mathbb {Z}$
, we denote by
$n_i \in \mathbb {Z}$
, we denote by
![]() $\mathbb {C}(\chi )$
the one-dimensional
$\mathbb {C}(\chi )$
the one-dimensional
![]() $GL(V)^{\lambda \geqslant 0}$
-representation given by
$GL(V)^{\lambda \geqslant 0}$
-representation given by
where the first morphism is the projection.
Definition 2.3 [Reference Pădurariu and TodaPTa, Definition 4.2].
We define the complex
![]() $\mathcal {E}_{d, v}$
by
$\mathcal {E}_{d, v}$
by
The construction above is T-equivariant, so we also obtain an object
![]() $\mathcal {E}_{d, v}\in D^b_T(\mathscr {C}(d))_v$
.
$\mathcal {E}_{d, v}\in D^b_T(\mathscr {C}(d))_v$
.
In [Reference Pădurariu and TodaPTa, Lemma 4.3], we showed that
![]() $\mathcal {E}_{d, v}$
is an object of
$\mathcal {E}_{d, v}$
is an object of
![]() $\mathbb {T}(d)_v$
and
$\mathbb {T}(d)_v$
and
![]() $\mathbb {T}_T(d)_v$
.
$\mathbb {T}_T(d)_v$
.
2.10 Shuffle algebras
2.10.1
Consider the
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {K}$
-module:
$\mathbb {K}$
-module:
We define a shuffle product on
![]() $\mathcal {S}h$
as follows. Let
$\mathcal {S}h$
as follows. Let
![]() $\xi (x)$
be defined by
$\xi (x)$
be defined by
 $$ \begin{align*} \xi(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)(1-q^{-1}x^{-1})}{1-x}, \end{align*} $$
$$ \begin{align*} \xi(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)(1-q^{-1}x^{-1})}{1-x}, \end{align*} $$
where
![]() $q:=q_1 q_2$
. For
$q:=q_1 q_2$
. For
![]() $f \in \mathbb {K}\left [z_1^{\pm }, \ldots , z_a^{\pm }\right ]$
and
$f \in \mathbb {K}\left [z_1^{\pm }, \ldots , z_a^{\pm }\right ]$
and
![]() $g \in \mathbb {K}\left [z_{a+1}^{\pm }, \ldots , z_{a+b}^{\pm }\right ]$
, we set
$g \in \mathbb {K}\left [z_{a+1}^{\pm }, \ldots , z_{a+b}^{\pm }\right ]$
, we set
 $$ \begin{align} f \ast g:=\frac{1}{a! b!} \mathrm{Sym}\left(fg \cdot \prod_{\substack{1\leqslant i\leqslant a,\\ a<j\leqslant a+b}} \xi(z_i z_j^{-1})\right), \end{align} $$
$$ \begin{align} f \ast g:=\frac{1}{a! b!} \mathrm{Sym}\left(fg \cdot \prod_{\substack{1\leqslant i\leqslant a,\\ a<j\leqslant a+b}} \xi(z_i z_j^{-1})\right), \end{align} $$
where we denote by
![]() $\mathrm {Sym}(h(z_1, \ldots , z_d))$
the sum of
$\mathrm {Sym}(h(z_1, \ldots , z_d))$
the sum of
![]() $h(z_{\sigma (1)}, \ldots , z_{\sigma (d)})$
after all permutations
$h(z_{\sigma (1)}, \ldots , z_{\sigma (d)})$
after all permutations
![]() $\sigma \in \mathfrak {S}_d$
. Let
$\sigma \in \mathfrak {S}_d$
. Let
![]() $\mathcal {S}\subset \mathcal {S}h$
be the subalgebra generated by
$\mathcal {S}\subset \mathcal {S}h$
be the subalgebra generated by
![]() $z_1^l$
for
$z_1^l$
for
![]() $l\in \mathbb {Z}$
. Let
$l\in \mathbb {Z}$
. Let
![]() $\mathcal {S}_{\mathbb {F}}:=\mathcal {S}\otimes _{\mathbb {K}}\mathbb {F}$
. It is proved in [Reference NeguţNeg23, Theorem 4.6] that there is an isomorphism
$\mathcal {S}_{\mathbb {F}}:=\mathcal {S}\otimes _{\mathbb {K}}\mathbb {F}$
. It is proved in [Reference NeguţNeg23, Theorem 4.6] that there is an isomorphism
The above isomorphism is induced by the algebra homomorphism which will be defined in Equation (2.37).
2.10.2
Let
be the
![]() $\mathbb {K}$
-subalgebra generated by elements of the form
$\mathbb {K}$
-subalgebra generated by elements of the form
 $$ \begin{align} A^{\prime}_{k_{\bullet}}:= \mathrm{Sym}\left(\frac{z_1^{k_1} \cdots z_d^{k_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}w(z_i z_j^{-1}) \right) \end{align} $$
$$ \begin{align} A^{\prime}_{k_{\bullet}}:= \mathrm{Sym}\left(\frac{z_1^{k_1} \cdots z_d^{k_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}w(z_i z_j^{-1}) \right) \end{align} $$
for various
![]() $(k_1, \ldots , k_d) \in \mathbb {Z}^d$
and
$(k_1, \ldots , k_d) \in \mathbb {Z}^d$
and
![]() $d\geqslant 1$
, for the shuffle product (2.29) where we replace
$d\geqslant 1$
, for the shuffle product (2.29) where we replace
![]() $\xi (x)$
with
$\xi (x)$
with
![]() $w(x)$
defined by
$w(x)$
defined by
 $$ \begin{align*} w(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)}{(1-x)(1-q^{-1}x)}. \end{align*} $$
$$ \begin{align*} w(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)}{(1-x)(1-q^{-1}x)}. \end{align*} $$
Let
![]() $\mathcal {S}^{\prime }_{\mathbb {F}}:=\mathcal {S}'\otimes _{\mathbb {K}}\mathbb {F}$
. Consider the morphism
$\mathcal {S}^{\prime }_{\mathbb {F}}:=\mathcal {S}'\otimes _{\mathbb {K}}\mathbb {F}$
. Consider the morphism
defined by
Then Equation (2.32) induces an algebra homomorphism
![]() $\mathcal {S}\to \mathcal {S}'$
. There is an isomorphism
$\mathcal {S}\to \mathcal {S}'$
. There is an isomorphism
see [Reference Pădurariu and TodaPTa, Proof of Lemma 4.11]. For
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
, we set
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
, we set
![]() $A^{\prime }_{d, v}$
to be
$A^{\prime }_{d, v}$
to be
![]() $A^{\prime }_{m_{\bullet }}$
for the choice of
$A^{\prime }_{m_{\bullet }}$
for the choice of
![]() $m_{\bullet }$
in Equation (2.27). By [Reference NeguţNeg22, Equation (2.12)], we have the following isomorphism of
$m_{\bullet }$
in Equation (2.27). By [Reference NeguţNeg22, Equation (2.12)], we have the following isomorphism of
![]() $\mathbb {K}$
-modules:
$\mathbb {K}$
-modules:
where the tuples
![]() $(d_i, v_i)_{i=1}^k$
appearing above are unordered for subtuples
$(d_i, v_i)_{i=1}^k$
appearing above are unordered for subtuples
![]() $(d_i, v_i)_{i=a}^b$
with
$(d_i, v_i)_{i=a}^b$
with
![]() $v_a/d_a=\cdots =v_b/d_b$
. We also define
$v_a/d_a=\cdots =v_b/d_b$
. We also define
 $$ \begin{align} A_{d, v}:=\mathrm{Sym}\left(\frac{z_1^{m_1} \cdots z_d^{m_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1}) \right), \end{align} $$
$$ \begin{align} A_{d, v}:=\mathrm{Sym}\left(\frac{z_1^{m_1} \cdots z_d^{m_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1}) \right), \end{align} $$
where the exponents
![]() $m_i$
for
$m_i$
for
![]() $1\leqslant i\leqslant d$
are given by Equation (2.27).
$1\leqslant i\leqslant d$
are given by Equation (2.27).
2.10.3
The T-equivariant Hall product (2.18) induces an associative algebra structure
Let
![]() $i \colon \mathscr {C}(d) \hookrightarrow \mathcal {Y}(d)$
be the closed immersion. The pull-back via
$i \colon \mathscr {C}(d) \hookrightarrow \mathcal {Y}(d)$
be the closed immersion. The pull-back via
![]() $\mathcal {Y}(d) \to BGL(d)$
gives the isomorphism
$\mathcal {Y}(d) \to BGL(d)$
gives the isomorphism
Therefore, the push-forward by i induces a morphism
The product (2.36) is compatible with a shuffle product defined on the right-hand side of Equation (2.37); see [Reference Pădurariu and TodaPTa, Subsection 4.5]. In [Reference Pădurariu and TodaPTa, Lemma 4.11], we showed that
2.11 Compatibility of the Hall product under the Koszul equivalence
In this subsection, we denote by m the Hall product (2.17) and by
![]() $\widetilde {m}$
the Hall product for the quiver with potential
$\widetilde {m}$
the Hall product for the quiver with potential
![]() $(Q, W)$
from Subsection 2.2.1. Using the results in [Reference TodaToda, Section 2.4], Koszul duality equivalences are compatible with the Hall products by the following commutative diagram (see [Reference PădurariuPăd23, Proposition 3.1]):
$(Q, W)$
from Subsection 2.2.1. Using the results in [Reference TodaToda, Section 2.4], Koszul duality equivalences are compatible with the Hall products by the following commutative diagram (see [Reference PădurariuPăd23, Proposition 3.1]):

where the left arrow
![]() $\widetilde {\Phi }$
is the composition of Koszul duality equivalences (2.22) with the tensor product of
$\widetilde {\Phi }$
is the composition of Koszul duality equivalences (2.22) with the tensor product of
The cocharacter
![]() $\nu \colon \mathbb {C}^{\ast } \to T(d)$
is
$\nu \colon \mathbb {C}^{\ast } \to T(d)$
is
 $\nu (t)=(\overbrace {t, \ldots , t}^{d_1}, \overbrace {1, \ldots , 1}^{d_2})$
, the vector spaces
$\nu (t)=(\overbrace {t, \ldots , t}^{d_1}, \overbrace {1, \ldots , 1}^{d_2})$
, the vector spaces
![]() $V_i$
have
$V_i$
have
![]() $\dim V_i=d_i$
for
$\dim V_i=d_i$
for
![]() $i=1, 2$
and
$i=1, 2$
and
![]() $(1)$
is a twist by the weight one
$(1)$
is a twist by the weight one
![]() $\mathbb {C}^{\ast }$
-character, which is isomorphic to the shift functor
$\mathbb {C}^{\ast }$
-character, which is isomorphic to the shift functor
![]() $[1]$
of the category of graded matrix factorizations.
$[1]$
of the category of graded matrix factorizations.
2.12 Symmetric polynomials
Let
![]() $\Lambda $
be the
$\Lambda $
be the
![]() $\mathbb {Z}$
-algebra of symmetric polynomials [Reference MacDonaldMac79, Chapter I, Section 2], [Reference SchiffmannSch12, Subsection 2.4]:
$\mathbb {Z}$
-algebra of symmetric polynomials [Reference MacDonaldMac79, Chapter I, Section 2], [Reference SchiffmannSch12, Subsection 2.4]:
with multiplication defined by
and comultiplication induced by the restriction map
Alternatively,
![]() $\Lambda $
is isomorphic to the Grothendieck group of the monoidal category
$\Lambda $
is isomorphic to the Grothendieck group of the monoidal category
where
![]() $\text {Rep}(\mathfrak {S}_n)$
is the abelian category of finite-dimensional
$\text {Rep}(\mathfrak {S}_n)$
is the abelian category of finite-dimensional
![]() $\mathfrak {S}_n$
-representations, multiplication is given by the induction functor
$\mathfrak {S}_n$
-representations, multiplication is given by the induction functor
and comultiplication is given by the restriction functor
The isomorphism
![]() $\mathcal {R} \stackrel {\cong }{\to } \Lambda $
is given by sending an irreducible
$\mathcal {R} \stackrel {\cong }{\to } \Lambda $
is given by sending an irreducible
![]() $\mathfrak {S}_n$
-representation
$\mathfrak {S}_n$
-representation
![]() $W_{\lambda }$
corresponding to a partition
$W_{\lambda }$
corresponding to a partition
![]() $\lambda $
of n to the Schur function
$\lambda $
of n to the Schur function
![]() $s_{\lambda }$
, see [Reference MacDonaldMac79, Chapter I, Equation (7.5)].
$s_{\lambda }$
, see [Reference MacDonaldMac79, Chapter I, Equation (7.5)].
For R a ring with a map
![]() $\mathbb {Z}\to R$
, denote by
$\mathbb {Z}\to R$
, denote by
![]() $\Lambda _R:=R\otimes _{\mathbb {Z}}\Lambda $
the R-algebra with multiplication and comultiplication induced from those of
$\Lambda _R:=R\otimes _{\mathbb {Z}}\Lambda $
the R-algebra with multiplication and comultiplication induced from those of
![]() $\Lambda $
. Consider the elementary symmetric functions
$\Lambda $
. Consider the elementary symmetric functions
and the power sum functions
We also denote by
![]() $e_n$
and
$e_n$
and
![]() $p_n$
the images of these symmetric functions in
$p_n$
the images of these symmetric functions in
![]() $\Lambda _R$
. Let t be a formal variable. These functions are connected via the identity
$\Lambda _R$
. Let t be a formal variable. These functions are connected via the identity
 $$ \begin{align} \sum_{n\geqslant 0}e_nt^n=\text{exp}\left(\sum_{n\geqslant 1}\frac{(-1)^{n+1}}{n}p_nt^n\right).\end{align} $$
$$ \begin{align} \sum_{n\geqslant 0}e_nt^n=\text{exp}\left(\sum_{n\geqslant 1}\frac{(-1)^{n+1}}{n}p_nt^n\right).\end{align} $$
There are isomorphisms (see [Reference MacDonaldMac79, Chapter I, Equations (2.4), (2.14)]):
For
![]() $n\geqslant 1$
, let
$n\geqslant 1$
, let
![]() $P(n)$
be the free one-dimensional
$P(n)$
be the free one-dimensional
![]() $\mathbb {Z}$
-module with generator
$\mathbb {Z}$
-module with generator
![]() $p_n$
. By Equation (2.42), there is an isomorphism of
$p_n$
. By Equation (2.42), there is an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {Q}$
-vector spaces
$\mathbb {Q}$
-vector spaces
3 The support of complexes in quasi-BPS categories
Recall the regular function (2.2). Consider the commutative diagram

where the vertical arrows are good moduli space morphisms and the horizontal arrows are closed immersions. The left vertical arrow sends a zero-dimensional sheaf to its support. Let
![]() $\Delta \colon \mathbb {C}^3 \subset \mathrm {Sym}^d(\mathbb {C}^3)$
be the small diagonal
$\Delta \colon \mathbb {C}^3 \subset \mathrm {Sym}^d(\mathbb {C}^3)$
be the small diagonal
We abuse notation and denote the image of
![]() $\Delta $
also by
$\Delta $
also by
![]() $\Delta \cong \mathbb {C}^3$
. We consider the pull-back
$\Delta \cong \mathbb {C}^3$
. We consider the pull-back
![]() $\pi ^{-1}(\Delta ) \subset \mathcal {C}oh(\mathbb {C}^3, d)$
, which is a closed substack of
$\pi ^{-1}(\Delta ) \subset \mathcal {C}oh(\mathbb {C}^3, d)$
, which is a closed substack of
![]() $\mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d) \subset \mathcal {X}(d)$
. Davison [Reference DavisonDavb, Theorem 5.1] showed that the BPS sheaf for the moduli stack of degree d sheaves on
$\mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d) \subset \mathcal {X}(d)$
. Davison [Reference DavisonDavb, Theorem 5.1] showed that the BPS sheaf for the moduli stack of degree d sheaves on
![]() $\mathbb {C}^3$
is
$\mathbb {C}^3$
is
Recall the notations involving formal completions from Subsection 2.1. The following is the main result of this section, which will be proved in Subsection 3.1:
Theorem 3.1. Consider a pair
![]() $(d, w)\in \mathbb {N}\times \mathbb {Z}$
, and let
$(d, w)\in \mathbb {N}\times \mathbb {Z}$
, and let
![]() $\mathcal {F}$
be an object in
$\mathcal {F}$
be an object in
![]() $\mathbb {S}(d)_w$
. Assume there exists
$\mathbb {S}(d)_w$
. Assume there exists
![]() $p\in \mathrm {Sym}^d(\mathbb {C}^3)\setminus \Delta $
such that the support of
$p\in \mathrm {Sym}^d(\mathbb {C}^3)\setminus \Delta $
such that the support of
![]() $\mathcal {F}$
intersects
$\mathcal {F}$
intersects
![]() $\pi ^{-1}(p)$
. Write
$\pi ^{-1}(p)$
. Write
![]() $p=\sum _{i=1}^l p^{(i)}$
,
$p=\sum _{i=1}^l p^{(i)}$
,
![]() $p^{(i)}=d^{(i)}x^{(i)}$
,
$p^{(i)}=d^{(i)}x^{(i)}$
,
![]() $d^{(i)}\in \mathbb {Z}_{>0}$
,
$d^{(i)}\in \mathbb {Z}_{>0}$
,
![]() $x^{(i)}\neq x^{(i')}$
for
$x^{(i)}\neq x^{(i')}$
for
![]() $i\neq i'$
and
$i\neq i'$
and
![]() $l\geqslant 2$
. Then there exist nonzero objects
$l\geqslant 2$
. Then there exist nonzero objects
![]() $\mathcal {F}_i \in \mathrm {MF}(\mathcal {X}_{p^{(i)}}(d^{(i)}), \mathop {\mathrm {Tr}}\nolimits W_{d^{(i)}})_{w^{(i)}}$
for
$\mathcal {F}_i \in \mathrm {MF}(\mathcal {X}_{p^{(i)}}(d^{(i)}), \mathop {\mathrm {Tr}}\nolimits W_{d^{(i)}})_{w^{(i)}}$
for
![]() $1\leqslant i\leqslant l$
with
$1\leqslant i\leqslant l$
with
and
![]() $w^{(1)}+\cdots +w^{(l)}=w$
. In particular, if
$w^{(1)}+\cdots +w^{(l)}=w$
. In particular, if
![]() $\gcd (d, w)=1$
, then any object in
$\gcd (d, w)=1$
, then any object in
![]() $\mathbb {S}(d)_w$
is supported on
$\mathbb {S}(d)_w$
is supported on
![]() $\pi ^{-1}(\Delta )$
. The same result holds for the categories
$\pi ^{-1}(\Delta )$
. The same result holds for the categories
![]() $\mathbb {S}^{\bullet }_{\ast }(d)_w$
introduced in Subsection 2.6.2.
$\mathbb {S}^{\bullet }_{\ast }(d)_w$
introduced in Subsection 2.6.2.
In Subsection 4.1, we discuss divisibility properties of complexes supported on
![]() $\pi ^{-1}(\Delta )$
; see Lemma 4.1. In Subsection 4.2, we use Theorem 3.1 and Lemma 4.1 to show that
$\pi ^{-1}(\Delta )$
; see Lemma 4.1. In Subsection 4.2, we use Theorem 3.1 and Lemma 4.1 to show that
![]() $K_T(\mathbb {S}(d)_w)'$
is a free
$K_T(\mathbb {S}(d)_w)'$
is a free
![]() $\mathbb {K}$
-module with generator
$\mathbb {K}$
-module with generator
![]() $[\mathcal {E}_{d,w}]$
when
$[\mathcal {E}_{d,w}]$
when
![]() $\gcd (d, w)=1$
.
$\gcd (d, w)=1$
.
3.1 Proof of the main result
Proof of Theorem 3.1.
Suppose that an object
![]() $\mathcal {F} \in \mathbb {S}(d)_w$
has support not contained in
$\mathcal {F} \in \mathbb {S}(d)_w$
has support not contained in
![]() $\pi ^{-1}(\Delta )$
. Then there is
$\pi ^{-1}(\Delta )$
. Then there is
![]() $p \in \mathrm {Sym}^d(\mathbb {C}^3) \setminus \Delta $
such that
$p \in \mathrm {Sym}^d(\mathbb {C}^3) \setminus \Delta $
such that
![]() $\mathcal {F}|_{\mathcal {X}_p(d)} \neq 0$
in
$\mathcal {F}|_{\mathcal {X}_p(d)} \neq 0$
in
![]() $\mathrm {MF}(\mathcal {X}_p(d), \mathop {\mathrm {Tr}}\nolimits W_d)$
, where
$\mathrm {MF}(\mathcal {X}_p(d), \mathop {\mathrm {Tr}}\nolimits W_d)$
, where
![]() $\mathcal {X}_p(d)$
is the formal fiber of p along the good moduli space morphism
$\mathcal {X}_p(d)$
is the formal fiber of p along the good moduli space morphism
![]() $\mathcal {X}(d) \to X(d)$
. Since
$\mathcal {X}(d) \to X(d)$
. Since
![]() $p \notin \Delta $
, it is written as
$p \notin \Delta $
, it is written as
 $$ \begin{align*} p=\sum_{i=1}^l p^{(i)}, \ p^{(i)}=d^{(i)}x^{(i)}, \ d^{(i)} \in \mathbb{Z}_{>0}, \ x^{(i)} \neq x^{(i')} \mbox{ for } i \neq i', \ l\geqslant 2. \end{align*} $$
$$ \begin{align*} p=\sum_{i=1}^l p^{(i)}, \ p^{(i)}=d^{(i)}x^{(i)}, \ d^{(i)} \in \mathbb{Z}_{>0}, \ x^{(i)} \neq x^{(i')} \mbox{ for } i \neq i', \ l\geqslant 2. \end{align*} $$
The unique closed point in
![]() $\pi ^{-1}(p)$
corresponds to the semisimple Q-representation
$\pi ^{-1}(p)$
corresponds to the semisimple Q-representation
 $$ \begin{align*} R=\bigoplus_{i=1}^l V^{(i)} \otimes R^{(i)}, \end{align*} $$
$$ \begin{align*} R=\bigoplus_{i=1}^l V^{(i)} \otimes R^{(i)}, \end{align*} $$
where
![]() $R^{(i)}$
is the one-dimensional Q-representation corresponding to
$R^{(i)}$
is the one-dimensional Q-representation corresponding to
![]() $\mathcal {O}_{x^{(i)}}$
and
$\mathcal {O}_{x^{(i)}}$
and
![]() $V^{(i)}$
is a
$V^{(i)}$
is a
![]() $d^{(i)}$
-dimensional vector space such that
$d^{(i)}$
-dimensional vector space such that
![]() $d^{(1)}+\cdots +d^{(l)}=d$
. Below we write a basis of
$d^{(1)}+\cdots +d^{(l)}=d$
. Below we write a basis of
![]() $V^{(i)}$
as
$V^{(i)}$
as
![]() $\beta _1^{(i)}, \ldots , \beta _{d^{(i)}}^{(i)}$
and set
$\beta _1^{(i)}, \ldots , \beta _{d^{(i)}}^{(i)}$
and set
The étale slice theorem implies that
where
![]() $G_p=\mathrm {Aut}(R)=\prod _{i=1}^l GL(V^{(i)})$
and
$G_p=\mathrm {Aut}(R)=\prod _{i=1}^l GL(V^{(i)})$
and
![]() $\widehat {\operatorname {Ext}}^1_Q(R, R)$
is the formal fiber of the origin along the morphism
$\widehat {\operatorname {Ext}}^1_Q(R, R)$
is the formal fiber of the origin along the morphism
![]() $\operatorname {Ext}^1_Q(R, R) \to \operatorname {Ext}_Q^1(R, R)/\!\!/G_p$
. By Lemma 3.2, the Ext-group
$\operatorname {Ext}^1_Q(R, R) \to \operatorname {Ext}_Q^1(R, R)/\!\!/G_p$
. By Lemma 3.2, the Ext-group
![]() $\operatorname {Ext}^1_Q(R, R)$
is computed as follows:
$\operatorname {Ext}^1_Q(R, R)$
is computed as follows:
 $$ \begin{align} \operatorname{Ext}_Q^1(R, R)=\bigoplus_{i=1}^l \mathrm{End}(V^{(i)}, V^{(i)})^{\oplus 3} \oplus \bigoplus_{i \neq j} \operatorname{Hom}(V^{(i)}, V^{(j)})^{\oplus 2}. \end{align} $$
$$ \begin{align} \operatorname{Ext}_Q^1(R, R)=\bigoplus_{i=1}^l \mathrm{End}(V^{(i)}, V^{(i)})^{\oplus 3} \oplus \bigoplus_{i \neq j} \operatorname{Hom}(V^{(i)}, V^{(j)})^{\oplus 2}. \end{align} $$
Note that the maximal torus
![]() $T(d) \subset GL(V)$
is contained in
$T(d) \subset GL(V)$
is contained in
![]() $G_p$
.
$G_p$
.
We define
to be the full subcategory generated by matrix factorizations whose entries are of the form
![]() $\Gamma _{G_p}(\chi ) \otimes \mathcal {O}$
, where
$\Gamma _{G_p}(\chi ) \otimes \mathcal {O}$
, where
![]() $\chi $
is a
$\chi $
is a
![]() $G_p$
-dominant
$G_p$
-dominant
![]() $T(d)$
-weight satisfying
$T(d)$
-weight satisfying
Here,
![]() $\rho _p$
is half the sum of positive roots of
$\rho _p$
is half the sum of positive roots of
![]() $G_p$
and
$G_p$
and
![]() $\textbf {W}_p(d)_{w}$
is defined as in Equation (2.9) for the
$\textbf {W}_p(d)_{w}$
is defined as in Equation (2.9) for the
![]() $G_p$
-representation
$G_p$
-representation
![]() $\operatorname {Ext}_Q^1(R, R)$
$\operatorname {Ext}_Q^1(R, R)$
where the Minkowski sum is after all weights
![]() $\beta $
in
$\beta $
in
![]() $\operatorname {Ext}_Q^1(R, R)$
. By Lemma 3.5, we have
$\operatorname {Ext}_Q^1(R, R)$
. By Lemma 3.5, we have
![]() $\mathcal {F}|_{\mathcal {X}_p(d)} \in \mathbb {S}_p(d)_w$
, in particular
$\mathcal {F}|_{\mathcal {X}_p(d)} \in \mathbb {S}_p(d)_w$
, in particular
![]() $\mathbb {S}_p(d)_{w} \neq 0$
.
$\mathbb {S}_p(d)_{w} \neq 0$
.
Below, in order to simplify the notation, we treat the case
![]() $l=2$
. Since any zero-dimensional sheaf Q on
$l=2$
. Since any zero-dimensional sheaf Q on
![]() $\mathbb {C}^3$
supported on p decomposes into
$\mathbb {C}^3$
supported on p decomposes into
![]() $Q^{(1)} \oplus Q^{(2)}$
, where
$Q^{(1)} \oplus Q^{(2)}$
, where
![]() $Q^{(i)}$
is supported on
$Q^{(i)}$
is supported on
![]() $x^{(i)}$
, we have
$x^{(i)}$
, we have
Here,
![]() $\widehat {\mathcal {C}oh}_p(\mathbb {C}^3, d)$
is the formal fiber of the left vertical arrow in Equation (3.1) at p. Indeed, by Lemma 3.3, we can show that, by replacing the isomorphism (3.2) if necessary, the regular function
$\widehat {\mathcal {C}oh}_p(\mathbb {C}^3, d)$
is the formal fiber of the left vertical arrow in Equation (3.1) at p. Indeed, by Lemma 3.3, we can show that, by replacing the isomorphism (3.2) if necessary, the regular function
![]() $\mathop {\mathrm {Tr}}\nolimits W_d$
restricted to
$\mathop {\mathrm {Tr}}\nolimits W_d$
restricted to
![]() $\mathcal {X}_p(d)$
is written as
$\mathcal {X}_p(d)$
is written as
Here,
![]() $\mathop {\mathrm {Tr}}\nolimits W_{d^{(i)}}$
is the regular function (2.2) on
$\mathop {\mathrm {Tr}}\nolimits W_{d^{(i)}}$
is the regular function (2.2) on
![]() $\mathcal {X}(d^{(i)})$
restricted to
$\mathcal {X}(d^{(i)})$
restricted to
![]() $\mathcal {X}_{p^{(i)}}(d^{(i)})$
and q is a nondegenerate
$\mathcal {X}_{p^{(i)}}(d^{(i)})$
and q is a nondegenerate
![]() $G_p$
-invariant quadratic form on
$G_p$
-invariant quadratic form on
![]() $U\oplus U^{\vee }$
given by
$U\oplus U^{\vee }$
given by
![]() $q(u, v)=\langle u, v \rangle $
, where U is the following self-dual
$q(u, v)=\langle u, v \rangle $
, where U is the following self-dual
![]() $G_p$
-representation
$G_p$
-representation
The decomposition (3.6) in particular implies Equation (3.5).
We have the following diagram

where
![]() $\mathcal {U}$
is the vector bundle on
$\mathcal {U}$
is the vector bundle on
![]() $\mathcal {X}_{p^{(1)}}(d^{(1)}) \times \mathcal {X}_{p^{(2)}}(d^{(2)})$
determined by the
$\mathcal {X}_{p^{(1)}}(d^{(1)}) \times \mathcal {X}_{p^{(2)}}(d^{(2)})$
determined by the
![]() $G_p$
-representation U, i is the closed immersion
$G_p$
-representation U, i is the closed immersion
![]() $x \mapsto (x, 0)$
, and j is the natural morphism induced by the formal completion which induces the isomorphism on critical loci of
$x \mapsto (x, 0)$
, and j is the natural morphism induced by the formal completion which induces the isomorphism on critical loci of
![]() $\mathop {\mathrm {Tr}}\nolimits W_d$
. We have the following functors
$\mathop {\mathrm {Tr}}\nolimits W_d$
. We have the following functors
 $$ \begin{align} \Psi := j^{\ast}i_{\ast}p^{\ast} \colon \mathrm{MF}(\mathcal{X}_{p^{(1)}}(d^{(1)}), \mathop{\mathrm{Tr}}\nolimits W_{d^{(1)}}) &\boxtimes \mathrm{MF}(\mathcal{X}_{p^{(2)}}(d^{(2)}), \mathop{\mathrm{Tr}}\nolimits W_{d^{(2)}}) \\ \notag &\stackrel{\sim}{\to}\mathrm{MF}(\mathcal{U} \oplus \mathcal{U}^{\vee}, \mathop{\mathrm{Tr}}\nolimits W_d) \stackrel{j^{\ast}}{\hookrightarrow} \mathrm{MF}(\mathcal{X}_p(d), \mathop{\mathrm{Tr}}\nolimits W_d). \end{align} $$
$$ \begin{align} \Psi := j^{\ast}i_{\ast}p^{\ast} \colon \mathrm{MF}(\mathcal{X}_{p^{(1)}}(d^{(1)}), \mathop{\mathrm{Tr}}\nolimits W_{d^{(1)}}) &\boxtimes \mathrm{MF}(\mathcal{X}_{p^{(2)}}(d^{(2)}), \mathop{\mathrm{Tr}}\nolimits W_{d^{(2)}}) \\ \notag &\stackrel{\sim}{\to}\mathrm{MF}(\mathcal{U} \oplus \mathcal{U}^{\vee}, \mathop{\mathrm{Tr}}\nolimits W_d) \stackrel{j^{\ast}}{\hookrightarrow} \mathrm{MF}(\mathcal{X}_p(d), \mathop{\mathrm{Tr}}\nolimits W_d). \end{align} $$
Here, the first arrow is an equivalence by Knörrer periodicity (see [Reference HiranoHir17, Theorem 4.2]), and the second arrow is fully faithful with dense image (see [Reference TodaTodb, Lemma 6.4]). By Lemma 3.4, the above functor restricts to the fully faithful functor
 $$ \begin{align} \bigoplus_{\begin{subarray}{c}w^{(1)}+w^{(2)}=w \\ w^{(1)}/d^{(1)}=w^{(2)}/d^{(2)} \end{subarray}} \mathbb{S}_{p^{(1)}}(d^{(1)})_{w^{(1)}} \boxtimes \mathbb{S}_{p^{(2)}}(d^{(2)})_{w^{(2)}} \to \mathbb{S}_{p}(d)_w. \end{align} $$
$$ \begin{align} \bigoplus_{\begin{subarray}{c}w^{(1)}+w^{(2)}=w \\ w^{(1)}/d^{(1)}=w^{(2)}/d^{(2)} \end{subarray}} \mathbb{S}_{p^{(1)}}(d^{(1)})_{w^{(1)}} \boxtimes \mathbb{S}_{p^{(2)}}(d^{(2)})_{w^{(2)}} \to \mathbb{S}_{p}(d)_w. \end{align} $$
Below, we show that the above functor (3.8) has dense image, and thus the conclusion follows. By the semiorthogonal decomposition (2.21) together with Equation (2.39), we have
 $$ \begin{align} &\mathrm{MF}(\mathcal{X}(d), \mathop{\mathrm{Tr}}\nolimits W_d) \\ \notag & \quad = \left\langle \ast_{i=1}^k \mathbb{S}(d_i)_{v_i+d_i(\sum_{i>j}d_j-\sum_{j>i}d_j)}\,\bigg|\, \frac{v_1}{d_1}<\cdots<\frac{v_k}{d_k}, d_1+\cdots+d_k=d\right\rangle. \end{align} $$
$$ \begin{align} &\mathrm{MF}(\mathcal{X}(d), \mathop{\mathrm{Tr}}\nolimits W_d) \\ \notag & \quad = \left\langle \ast_{i=1}^k \mathbb{S}(d_i)_{v_i+d_i(\sum_{i>j}d_j-\sum_{j>i}d_j)}\,\bigg|\, \frac{v_1}{d_1}<\cdots<\frac{v_k}{d_k}, d_1+\cdots+d_k=d\right\rangle. \end{align} $$
The weights
![]() $w_i:=v_i+d_i(\sum _{i>j}d_j-\sum _{j>i}d_j)$
are computed as in Equation (2.7):
$w_i:=v_i+d_i(\sum _{i>j}d_j-\sum _{j>i}d_j)$
are computed as in Equation (2.7):
 $$ \begin{align} \sum_{i=1}^k w_i \tau_{d_i}=\sum_{i=1}^k v_i \tau_{d_i} -\mathfrak{g}^{\lambda>0}, \end{align} $$
$$ \begin{align} \sum_{i=1}^k w_i \tau_{d_i}=\sum_{i=1}^k v_i \tau_{d_i} -\mathfrak{g}^{\lambda>0}, \end{align} $$
where
![]() $\mathfrak {g}$
is the Lie algebra of
$\mathfrak {g}$
is the Lie algebra of
![]() $GL(d)$
and
$GL(d)$
and
![]() $\lambda $
is the antidominant cocharacter corresponding to the decomposition
$\lambda $
is the antidominant cocharacter corresponding to the decomposition
![]() $d=d_1+\cdots +d_k$
:
$d=d_1+\cdots +d_k$
:
 $$ \begin{align} \lambda(t)=(\overbrace{t^k, \ldots, t^k}^{d_1}, \overbrace{t^{k-1}, \ldots, t^{k-1}}^{d_2}, \ldots, \overbrace{t, \ldots, t}^{d_k}). \end{align} $$
$$ \begin{align} \lambda(t)=(\overbrace{t^k, \ldots, t^k}^{d_1}, \overbrace{t^{k-1}, \ldots, t^{k-1}}^{d_2}, \ldots, \overbrace{t, \ldots, t}^{d_k}). \end{align} $$
For
![]() $x \in \mathbb {C}^3$
, let
$x \in \mathbb {C}^3$
, let
![]() $q=d[x]:=(x,\ldots , x) \in \mathrm {Sym}^d(\mathbb {C}^3)$
. Since
$q=d[x]:=(x,\ldots , x) \in \mathrm {Sym}^d(\mathbb {C}^3)$
. Since
![]() $G_q=GL(V)$
and
$G_q=GL(V)$
and
![]() $\mathcal {X}_q(d)\cong \mathfrak {g}^{\oplus 3}_{d[0]}/GL(V)$
, the argument showing Equation (3.9) applies verbatim to show the semiorthogonal decomposition
$\mathcal {X}_q(d)\cong \mathfrak {g}^{\oplus 3}_{d[0]}/GL(V)$
, the argument showing Equation (3.9) applies verbatim to show the semiorthogonal decomposition
 $$ \begin{align} &\mathrm{MF}(\mathcal{X}_q(d), \mathop{\mathrm{Tr}}\nolimits W_d) \\ \notag &= \left\langle \ast_{i=1}^k \mathbb{S}_q(d_i)_{v_i+d_i(\sum_{i>j}d_j-\sum_{j>i}d_j)}\,\bigg|\, \frac{v_1}{d_1}<\cdots<\frac{v_k}{d_k}, d_1+\cdots+d_k=d\right\rangle. \end{align} $$
$$ \begin{align} &\mathrm{MF}(\mathcal{X}_q(d), \mathop{\mathrm{Tr}}\nolimits W_d) \\ \notag &= \left\langle \ast_{i=1}^k \mathbb{S}_q(d_i)_{v_i+d_i(\sum_{i>j}d_j-\sum_{j>i}d_j)}\,\bigg|\, \frac{v_1}{d_1}<\cdots<\frac{v_k}{d_k}, d_1+\cdots+d_k=d\right\rangle. \end{align} $$
From Equation (3.12), the left-hand side of Equation (3.7) admits a semiorthogonal decomposition S whose summands are of the form
Here, the left-hand side in Equation (3.8) comes to the rightmost part of the semiorthogonal decomposition S,
![]() $p_i^{(j)}=d_i^{(j)}x^{(j)}$
, the integers
$p_i^{(j)}=d_i^{(j)}x^{(j)}$
, the integers
![]() $d_i^{(j)}$
satisfy
$d_i^{(j)}$
satisfy
and we have the inequalities
 $$ \begin{align*} \frac{v_1^{(1)}}{d_1^{(1)}}<\cdots< \frac{v_a^{(1)}}{d_a^{(1)}}, \ \frac{v_1^{(2)}}{d_1^{(2)}}<\cdots< \frac{v_b^{(2)}}{d_b^{(2)}}. \end{align*} $$
$$ \begin{align*} \frac{v_1^{(1)}}{d_1^{(1)}}<\cdots< \frac{v_a^{(1)}}{d_a^{(1)}}, \ \frac{v_1^{(2)}}{d_1^{(2)}}<\cdots< \frac{v_b^{(2)}}{d_b^{(2)}}. \end{align*} $$
We write
 $$ \begin{align*} \left\{ \frac{v_1^{(1)}}{d_1^{(1)}}, \ldots, \frac{v_a^{(1)}}{d_a^{(1)}}, \ldots, \frac{v_1^{(2)}}{d_1^{(2)}}, \ldots, \frac{v_b^{(2)}}{d_b^{(2)}} \right\}= \{\mu_1<\cdots<\mu_k\}, \end{align*} $$
$$ \begin{align*} \left\{ \frac{v_1^{(1)}}{d_1^{(1)}}, \ldots, \frac{v_a^{(1)}}{d_a^{(1)}}, \ldots, \frac{v_1^{(2)}}{d_1^{(2)}}, \ldots, \frac{v_b^{(2)}}{d_b^{(2)}} \right\}= \{\mu_1<\cdots<\mu_k\}, \end{align*} $$
where k is the number of distinct elements in the left-hand side. For
![]() $1\leqslant i\leqslant k$
, we replace
$1\leqslant i\leqslant k$
, we replace
![]() $(d_i^{(j)}, v_i^{(j)})$
by
$(d_i^{(j)}, v_i^{(j)})$
by
 $$ \begin{align*} (d_i^{(j)}, v_i^{(j)}) \mapsto \begin{cases} (d_l^{(j)}, v_l^{(j)}), & \mbox{ if } \mu_i=v_l^{(j)}/d_l^{(j)} \mbox{ for some }l, \\ (0, 0), & \mbox{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} (d_i^{(j)}, v_i^{(j)}) \mapsto \begin{cases} (d_l^{(j)}, v_l^{(j)}), & \mbox{ if } \mu_i=v_l^{(j)}/d_l^{(j)} \mbox{ for some }l, \\ (0, 0), & \mbox{ otherwise}. \end{cases} \end{align*} $$
The subcategory (3.13) of Equation (3.8) is unchanged under the above replacement. Therefore, we may assume that
![]() $a=b=k$
and, by setting
$a=b=k$
and, by setting
![]() $(d_i, v_i)=(d_i^{(1)}, v_i^{(1)}) +(d_i^{(2)}, v_i^{(2)})$
, we have
$(d_i, v_i)=(d_i^{(1)}, v_i^{(1)}) +(d_i^{(2)}, v_i^{(2)})$
, we have
 $$ \begin{align*} \frac{v_i}{d_i}=\frac{v_i^{(j)}}{d_i^{(j)}}, \ \frac{v_1}{d_1}< \cdots< \frac{v_k}{d_k}. \end{align*} $$
$$ \begin{align*} \frac{v_i}{d_i}=\frac{v_i^{(j)}}{d_i^{(j)}}, \ \frac{v_1}{d_1}< \cdots< \frac{v_k}{d_k}. \end{align*} $$
Here, the first identity holds whenever
![]() $(d_i^{(j)}, v_i^{(j)}) \neq (0, 0)$
.
$(d_i^{(j)}, v_i^{(j)}) \neq (0, 0)$
.
Let us take decompositions
![]() $V^{(j)}=\oplus _{i=1}^k V_i^{(j)}$
with
$V^{(j)}=\oplus _{i=1}^k V_i^{(j)}$
with
![]() $\dim V_i^{(j)}=d_i^{(j)}$
and a cocharacter as in Equation (3.11)
$\dim V_i^{(j)}=d_i^{(j)}$
and a cocharacter as in Equation (3.11)
which acts on
![]() $V_i^{(j)}$
with weight
$V_i^{(j)}$
with weight
![]() $k+1-i$
. The diagrams of attracting loci with respect to
$k+1-i$
. The diagrams of attracting loci with respect to
![]() $\lambda $
give the commutative diagram; see [Reference TodaTodb, Proposition 2.5]:
$\lambda $
give the commutative diagram; see [Reference TodaTodb, Proposition 2.5]:

Here, the vertical arrows are categorical Hall products determined by
![]() $\lambda $
,
$\lambda $
,
![]() $p_i:=p_i^{(1)}+p_i^{(2)}$
, the bottom horizontal arrow is Equation (3.7), and the top horizontal arrow is the composition of the Knörrer periodicity equivalences with the tensor product of (a shift of)
$p_i:=p_i^{(1)}+p_i^{(2)}$
, the bottom horizontal arrow is Equation (3.7), and the top horizontal arrow is the composition of the Knörrer periodicity equivalences with the tensor product of (a shift of)
 $$ \begin{align*} \det \left((U^{\lambda>0})^{\vee}\right)= \bigotimes_{i=1}^k\left( (\det V_i^{(1)})^{\sum_{i>j}d_j^{(2)}-\sum_{j>i}d_j^{(2)}} \otimes (\det V_i^{(2)})^{\sum_{i>j}d_j^{(1)}-\sum_{j>i}d_j^{(1)}}\right). \end{align*} $$
$$ \begin{align*} \det \left((U^{\lambda>0})^{\vee}\right)= \bigotimes_{i=1}^k\left( (\det V_i^{(1)})^{\sum_{i>j}d_j^{(2)}-\sum_{j>i}d_j^{(2)}} \otimes (\det V_i^{(2)})^{\sum_{i>j}d_j^{(1)}-\sum_{j>i}d_j^{(1)}}\right). \end{align*} $$
By the above commutative diagram together with the fact that Equation (3.7) restricts to the functor (3.8), the functor (3.7) sends Equation (3.13) to
Let us take a decomposition
where
![]() $w_i$
is given in Equation (3.10). Then by Lemma 3.6, the subcategory (3.15) for
$w_i$
is given in Equation (3.10). Then by Lemma 3.6, the subcategory (3.15) for
![]() $k\geqslant 2$
is right orthogonal to
$k\geqslant 2$
is right orthogonal to
![]() $\mathbb {S}_p(d)_w$
. Together with the semiorthogonal decomposition
$\mathbb {S}_p(d)_w$
. Together with the semiorthogonal decomposition
![]() $\mathrm {S}$
with summands (3.13), we conclude that the functor (3.8) has dense image. Indeed, for an object
$\mathrm {S}$
with summands (3.13), we conclude that the functor (3.8) has dense image. Indeed, for an object
![]() $A \in \mathbb {S}_p(d)_w$
, there is a distinguished triangle
$A \in \mathbb {S}_p(d)_w$
, there is a distinguished triangle
where
![]() $A_1$
is a direct summand of an object
$A_1$
is a direct summand of an object
![]() $\Psi (B_1)$
for some
$\Psi (B_1)$
for some
![]() $B_1$
in the left-hand side of Equation (3.8) and
$B_1$
in the left-hand side of Equation (3.8) and
![]() $A_2$
is a direct summand of an object
$A_2$
is a direct summand of an object
![]() $\Psi (B_2)$
for some
$\Psi (B_2)$
for some
![]() $B_2$
in Equation (3.13) for
$B_2$
in Equation (3.13) for
![]() $a=b\geqslant 2$
. Then
$a=b\geqslant 2$
. Then
![]() $\Psi (B_2)$
is an object of Equation (3.15) for
$\Psi (B_2)$
is an object of Equation (3.15) for
![]() $k\geqslant 2$
, hence
$k\geqslant 2$
, hence
![]() $\beta $
is a zero map by Lemma 3.6. So
$\beta $
is a zero map by Lemma 3.6. So
![]() $\alpha $
is an isomorphism, hence the functor (3.8) has dense image.
$\alpha $
is an isomorphism, hence the functor (3.8) has dense image.
We have postponed several lemmas, which are given below:
Lemma 3.2. The
![]() $\operatorname {Ext}$
-group
$\operatorname {Ext}$
-group
![]() $\operatorname {Ext}_Q^1(R, R)$
is computed as Equation (3.3).
$\operatorname {Ext}_Q^1(R, R)$
is computed as Equation (3.3).
Proof. By the Euler pairing computation, we have
![]() $\chi _Q(R^{(i)}, R^{(j)})=-2$
. Since
$\chi _Q(R^{(i)}, R^{(j)})=-2$
. Since
![]() $\operatorname {Hom}(R^{(i)}, R^{(j)})=\mathbb {C} \delta _{ij}$
, we have
$\operatorname {Hom}(R^{(i)}, R^{(j)})=\mathbb {C} \delta _{ij}$
, we have
 $$ \begin{align*} \operatorname{Ext}_Q^1(R^{(i)}, R^{(j)})=\begin{cases} \mathbb{C}^2, & i \neq j, \\ \mathbb{C}^3, & i=j. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{Ext}_Q^1(R^{(i)}, R^{(j)})=\begin{cases} \mathbb{C}^2, & i \neq j, \\ \mathbb{C}^3, & i=j. \end{cases} \end{align*} $$
Therefore, Equation (3.3) holds.
Proof. We may assume
![]() $x^{(1)}=(0, 0, 1)$
and
$x^{(1)}=(0, 0, 1)$
and
![]() $x^{(2)}=(0, 0, 0)$
. We write an element of
$x^{(2)}=(0, 0, 0)$
. We write an element of
![]() $\operatorname {Ext}_Q^1(R, R)$
as
$\operatorname {Ext}_Q^1(R, R)$
as
where
![]() $X^{(i)} \in \mathrm {End}(V^{(i)})$
and
$X^{(i)} \in \mathrm {End}(V^{(i)})$
and
![]() $A^{(ij)} \in \operatorname {Hom}(V^{(i)}, V^{(j)})$
. We have the morphism of algebraic stacks
$A^{(ij)} \in \operatorname {Hom}(V^{(i)}, V^{(j)})$
. We have the morphism of algebraic stacks
which sends Equation (3.17) to
 $$ \begin{align*} \left( \begin{pmatrix} X^{(1)} & A^{(12)} \\ A^{(21)} & X^{(2)} \\ \end{pmatrix}, \ \begin{pmatrix} Y^{(1)} & B^{(12)} \\ B^{(21)} & Y^{(2)} \\ \end{pmatrix}, \ \begin{pmatrix} Z^{(1)}+I & 0 \\ 0 & Z^{(2)} \\ \end{pmatrix} \right) \in \mathfrak{g}^{\oplus 3}. \end{align*} $$
$$ \begin{align*} \left( \begin{pmatrix} X^{(1)} & A^{(12)} \\ A^{(21)} & X^{(2)} \\ \end{pmatrix}, \ \begin{pmatrix} Y^{(1)} & B^{(12)} \\ B^{(21)} & Y^{(2)} \\ \end{pmatrix}, \ \begin{pmatrix} Z^{(1)}+I & 0 \\ 0 & Z^{(2)} \\ \end{pmatrix} \right) \in \mathfrak{g}^{\oplus 3}. \end{align*} $$
Indeed, the above correspondence is
![]() $GL(V)$
-equivariant using the embedding
$GL(V)$
-equivariant using the embedding
![]() $G_p \subset GL(V)$
, so it determines a morphism
$G_p \subset GL(V)$
, so it determines a morphism
![]() $\nu $
. Note that
$\nu $
. Note that
![]() $\nu (0)$
corresponds to the polystable Q-representation
$\nu (0)$
corresponds to the polystable Q-representation
![]() $R=(V^{(1)} \otimes R^{(1)}) \oplus (V^{(2)} \otimes R^{(2)})$
, where
$R=(V^{(1)} \otimes R^{(1)}) \oplus (V^{(2)} \otimes R^{(2)})$
, where
![]() $R^{(i)}$
corresponds to
$R^{(i)}$
corresponds to
![]() $\mathcal {O}_{x^{(i)}}$
.
$\mathcal {O}_{x^{(i)}}$
.
We now explain that the morphism
![]() $\nu $
is étale at
$\nu $
is étale at
![]() $\nu (0)$
. The tangent complex of
$\nu (0)$
. The tangent complex of
![]() $\mathcal {X}(d)$
at
$\mathcal {X}(d)$
at
![]() $\nu (0)$
is
$\nu (0)$
is
 $$ \begin{align*} \mathbb{T}_{\mathcal{X}(d)}|_{\nu(0)}= \left(\mathrm{End}(V) \to \mathrm{End}(V)^{\oplus 3} \right), \ \alpha \mapsto (0, 0, [\alpha, u]), \ u=\begin{pmatrix} I & 0 \\ 0 & 0 \\ \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \mathbb{T}_{\mathcal{X}(d)}|_{\nu(0)}= \left(\mathrm{End}(V) \to \mathrm{End}(V)^{\oplus 3} \right), \ \alpha \mapsto (0, 0, [\alpha, u]), \ u=\begin{pmatrix} I & 0 \\ 0 & 0 \\ \end{pmatrix}. \end{align*} $$
The kernel of the above map is
![]() $\mathrm {End}(V^{(1)}) \oplus \mathrm {End}(V^{(2)})$
, and the cokernel is
$\mathrm {End}(V^{(1)}) \oplus \mathrm {End}(V^{(2)})$
, and the cokernel is
![]() $\operatorname {Ext}_Q^1(R, R)$
, so the morphism
$\operatorname {Ext}_Q^1(R, R)$
, so the morphism
![]() $\nu $
induces a quasi-isomorphism on tangent complexes at
$\nu $
induces a quasi-isomorphism on tangent complexes at
![]() $\nu (0)$
.
$\nu (0)$
.
A straightforward computation shows that
 $$ \begin{align*} \nu^{\ast} \mathop{\mathrm{Tr}}\nolimits W_d &= \mathrm{Tr}(Z^{(1)}[X^{(1)}, Y^{(1)}]) + \mathrm{Tr}(Z^{(2)}[X^{(2)}, Y^{(2)}]) \\& \quad +\mathrm{Tr}(A^{(12)}(B^{(21)}+B^{(21)}Z^{(1)}-Z^{(2)}B^{(21)})) \\&\quad +\mathrm{Tr}(B^{(12)}(Z^{(2)}A^{(21)}-A^{(21)}Z^{(1)}-A^{(21)})). \end{align*} $$
$$ \begin{align*} \nu^{\ast} \mathop{\mathrm{Tr}}\nolimits W_d &= \mathrm{Tr}(Z^{(1)}[X^{(1)}, Y^{(1)}]) + \mathrm{Tr}(Z^{(2)}[X^{(2)}, Y^{(2)}]) \\& \quad +\mathrm{Tr}(A^{(12)}(B^{(21)}+B^{(21)}Z^{(1)}-Z^{(2)}B^{(21)})) \\&\quad +\mathrm{Tr}(B^{(12)}(Z^{(2)}A^{(21)}-A^{(21)}Z^{(1)}-A^{(21)})). \end{align*} $$
By the following
![]() $G_p$
-equivariant variable change
$G_p$
-equivariant variable change
we obtain the identity (3.6).
Proof (cf. the proof of [Reference Koseki and TodaKT21, Theorem 2.7]).
For a cocharacter
![]() $\lambda \colon \mathbb {C}^{\ast } \to T(d)$
, let
$\lambda \colon \mathbb {C}^{\ast } \to T(d)$
, let
 $$ \begin{align*} n_{\lambda, p} :=\left\langle \lambda, \mathbb{L}^{\lambda>0}_{\mathcal{X}_p(d)}\big|_{0} \right\rangle, \ n_{\lambda, p}':=\left\langle \lambda, \mathbb{L}^{\lambda>0}_{\mathcal{X}_{p^{(1)}}(d^{(1)}) \times \mathcal{X}_{p^{(2)}}(d^{(2)})}\big|_{0} \right\rangle. \end{align*} $$
$$ \begin{align*} n_{\lambda, p} :=\left\langle \lambda, \mathbb{L}^{\lambda>0}_{\mathcal{X}_p(d)}\big|_{0} \right\rangle, \ n_{\lambda, p}':=\left\langle \lambda, \mathbb{L}^{\lambda>0}_{\mathcal{X}_{p^{(1)}}(d^{(1)}) \times \mathcal{X}_{p^{(2)}}(d^{(2)})}\big|_{0} \right\rangle. \end{align*} $$
Define the sets of weights
 $$ \begin{align*} \nabla_{p, w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n_{\lambda, p} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n_{\lambda, p} \mbox{ for all } \lambda \right\} +w\tau_d, \\ \nabla^{\prime}_{p, w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n^{\prime}_{\lambda, p} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n^{\prime}_{\lambda, p} \mbox{ for all } \lambda \right\}+w\tau_d. \end{align*} $$
$$ \begin{align*} \nabla_{p, w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n_{\lambda, p} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n_{\lambda, p} \mbox{ for all } \lambda \right\} +w\tau_d, \\ \nabla^{\prime}_{p, w} &:= \left\{\chi \in M_{\mathbb{R}} \,\bigg|\, -\frac{1}{2} n^{\prime}_{\lambda, p} \leqslant \langle \lambda, \chi \rangle \leqslant \frac{1}{2}n^{\prime}_{\lambda, p} \mbox{ for all } \lambda \right\}+w\tau_d. \end{align*} $$
Then an object in the right- (resp. left-) hand side of Equation (3.7) lies in the right- (resp. left-) hand side of Equation (3.8) if and only if its
![]() $T(d)$
-weights are contained in
$T(d)$
-weights are contained in
![]() $\nabla _{p, w}$
(resp.
$\nabla _{p, w}$
(resp.
![]() $\nabla _{p, w}^{\prime }$
); see [Reference Halpern-Leistner and SamHLS20, Lemma 2.9]. Let
$\nabla _{p, w}^{\prime }$
); see [Reference Halpern-Leistner and SamHLS20, Lemma 2.9]. Let
![]() $\mathcal {E}$
be an object in the left-hand side of Equation (3.8). Using a Koszul resolution, the complex
$\mathcal {E}$
be an object in the left-hand side of Equation (3.8). Using a Koszul resolution, the complex
![]() $\Psi (\mathcal {E})$
is generated by
$\Psi (\mathcal {E})$
is generated by
![]() $p^{\ast }(\mathcal {E})\otimes \wedge ^{\bullet }U$
. Let
$p^{\ast }(\mathcal {E})\otimes \wedge ^{\bullet }U$
. Let
![]() $\chi $
be a
$\chi $
be a
![]() $T(d)$
-weight of
$T(d)$
-weight of
![]() $p^{\ast }(\mathcal {E})\otimes \wedge ^{\bullet }U$
. We then have that
$p^{\ast }(\mathcal {E})\otimes \wedge ^{\bullet }U$
. We then have that
Since U is self-dual, we have
![]() $\langle \lambda , U^{\lambda <0}\rangle = -\langle \lambda , U^{\lambda>0}\rangle $
. Moreover, from Equation (3.3), it is easy to see that
$\langle \lambda , U^{\lambda <0}\rangle = -\langle \lambda , U^{\lambda>0}\rangle $
. Moreover, from Equation (3.3), it is easy to see that
Therefore,
![]() $\Psi (\mathcal {E})$
is an object of the right-hand side of Equation (3.8).
$\Psi (\mathcal {E})$
is an object of the right-hand side of Equation (3.8).
Lemma 3.5. If a
![]() $T(d)$
-weight
$T(d)$
-weight
![]() $\chi $
satisfies Equation (3.4), then
$\chi $
satisfies Equation (3.4), then
Conversely if a
![]() $GL(V)$
-dominant
$GL(V)$
-dominant
![]() $T(d)$
-weight
$T(d)$
-weight
![]() $\chi $
satisfies Equation (3.18), then it satisfies Equation (3.4).
$\chi $
satisfies Equation (3.18), then it satisfies Equation (3.4).
Proof. If a
![]() $T(d)$
-weight
$T(d)$
-weight
![]() $\chi $
satisfies Equation (3.4), it is written as
$\chi $
satisfies Equation (3.4), it is written as
 $$ \begin{align} \chi+\rho_p=\sum_{i, j, a} c_{ij}^{(a)}(\beta_i^{(a)}-\beta_j^{(a)}) +\sum_{i, j, a \neq b} c_{ij}^{(ab)}(\beta_i^{(a)}-\beta_j^{(b)}), \end{align} $$
$$ \begin{align} \chi+\rho_p=\sum_{i, j, a} c_{ij}^{(a)}(\beta_i^{(a)}-\beta_j^{(a)}) +\sum_{i, j, a \neq b} c_{ij}^{(ab)}(\beta_i^{(a)}-\beta_j^{(b)}), \end{align} $$
where
![]() $0\leqslant c_{ij}^{(a)} \leqslant 3/2$
and
$0\leqslant c_{ij}^{(a)} \leqslant 3/2$
and
![]() $0\leqslant c_{ij}^{(ab)} \leqslant 1$
. Since we have
$0\leqslant c_{ij}^{(ab)} \leqslant 1$
. Since we have
 $$ \begin{align} \rho-\rho_p=\frac{1}{2}\sum_{i, j, a<b}(\beta_i^{(b)}-\beta_j^{(a)}), \end{align} $$
$$ \begin{align} \rho-\rho_p=\frac{1}{2}\sum_{i, j, a<b}(\beta_i^{(b)}-\beta_j^{(a)}), \end{align} $$
the weight
![]() $\chi +\rho $
satisfies Equation (3.18). Conversely, if
$\chi +\rho $
satisfies Equation (3.18). Conversely, if
![]() $\chi $
is a
$\chi $
is a
![]() $GL(V)$
-dominant
$GL(V)$
-dominant
![]() $T(d)$
-weight satisfying Equation (3.18), from [Reference Pădurariu and TodaPTa, Proposition 3.5] it is written as
$T(d)$
-weight satisfying Equation (3.18), from [Reference Pădurariu and TodaPTa, Proposition 3.5] it is written as
for
![]() $0\leqslant c_{ij} \leqslant 3/2$
. Therefore, from Equation (3.20), the weight
$0\leqslant c_{ij} \leqslant 3/2$
. Therefore, from Equation (3.20), the weight
![]() $\chi +\rho _p$
is written as Equation (3.19).
$\chi +\rho _p$
is written as Equation (3.19).
Lemma 3.6. The subcategory (3.15) for
![]() $k\geqslant 2$
is right orthogonal to
$k\geqslant 2$
is right orthogonal to
![]() $\mathbb {S}_p(d)_{w}$
for
$\mathbb {S}_p(d)_{w}$
for
![]() $w=w_1+ \cdots +w_k$
, where
$w=w_1+ \cdots +w_k$
, where
![]() $w_i$
is given in Equation (3.10).
$w_i$
is given in Equation (3.10).
Proof. Recall that
![]() $w_i=v_i+d_i(\sum _{i>j}d_j-\sum _{j>i}d_j)$
. Choose weights
$w_i=v_i+d_i(\sum _{i>j}d_j-\sum _{j>i}d_j)$
. Choose weights
![]() $\psi _i \in \textbf {W}_{p_i}(d_i)_{0}$
for
$\psi _i \in \textbf {W}_{p_i}(d_i)_{0}$
for
![]() $1\leqslant i\leqslant k$
. From the proof of semiorthogonality in [Reference PădurariuPăda, Proposition 4.3], it is enough to show that the r-invariant of the weight
$1\leqslant i\leqslant k$
. From the proof of semiorthogonality in [Reference PădurariuPăda, Proposition 4.3], it is enough to show that the r-invariant of the weight
 $$ \begin{align} \sum_{i=1}^k \psi_i+ \sum_{i=1}^k w_i \tau_{d_i}-\sum_{i=1}^k \rho_{p_i}+\rho_p \end{align} $$
$$ \begin{align} \sum_{i=1}^k \psi_i+ \sum_{i=1}^k w_i \tau_{d_i}-\sum_{i=1}^k \rho_{p_i}+\rho_p \end{align} $$
with respect to the polytope
![]() $\textbf {W}_p(d)$
is bigger than
$\textbf {W}_p(d)$
is bigger than
![]() $1/2$
. Here, the polytope
$1/2$
. Here, the polytope
![]() $\textbf {W}_p(d)$
is defined as follows:
$\textbf {W}_p(d)$
is defined as follows:
where the sum is after all weights in
![]() $\operatorname {Ext}_Q^1(R, R)$
.
$\operatorname {Ext}_Q^1(R, R)$
.
Suppose the contrary, that is, the weight (3.21) lies in
![]() $\textbf {W}_p(d)_{w}$
. Let
$\textbf {W}_p(d)_{w}$
. Let
![]() $\lambda $
be the cocharacter as in Equation (3.14), and write it as
$\lambda $
be the cocharacter as in Equation (3.14), and write it as
![]() $\lambda =(\lambda ^{(1)}, \lambda ^{(2)})$
, where
$\lambda =(\lambda ^{(1)}, \lambda ^{(2)})$
, where
![]() $\lambda ^{(j)}$
is the cocharacter of
$\lambda ^{(j)}$
is the cocharacter of
![]() $GL(V^{(j)})$
. We set
$GL(V^{(j)})$
. We set
![]() $\mathfrak {g}=\mathrm {End}(V)$
and
$\mathfrak {g}=\mathrm {End}(V)$
and
![]() $\mathfrak {g}^{(j)}=\mathrm {End}(V^{(j)})$
. The weight (3.21) is written as
$\mathfrak {g}^{(j)}=\mathrm {End}(V^{(j)})$
. The weight (3.21) is written as
 $$ \begin{align*} \sum_{i=1}^k \psi_i+ \sum_{i=1}^k v_i \tau_{d_i} -\mathfrak{g}^{\lambda>0}-\frac{1}{2}(\mathfrak{g}^{(1)})^{\lambda^{(1)}>0} -\frac{1}{2}(\mathfrak{g}^{(2)})^{\lambda^{(2)}>0}. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^k \psi_i+ \sum_{i=1}^k v_i \tau_{d_i} -\mathfrak{g}^{\lambda>0}-\frac{1}{2}(\mathfrak{g}^{(1)})^{\lambda^{(1)}>0} -\frac{1}{2}(\mathfrak{g}^{(2)})^{\lambda^{(2)}>0}. \end{align*} $$
By the assumption, the above weight is an element of
![]() $\textbf {W}_p(d)_w$
. Then using an argument as in the proof of Lemma 3.5, we have that
$\textbf {W}_p(d)_w$
. Then using an argument as in the proof of Lemma 3.5, we have that
 $$ \begin{align} \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} \in \textbf{W}(d)_w. \end{align} $$
$$ \begin{align} \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} \in \textbf{W}(d)_w. \end{align} $$
Note that we have
 $$ \begin{align*} \left\langle \lambda, \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} -w \tau_d \right\rangle =\sum_{i=1}^k (k+1-i)d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right) -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align*} $$
$$ \begin{align*} \left\langle \lambda, \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} -w \tau_d \right\rangle =\sum_{i=1}^k (k+1-i)d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right) -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align*} $$
For
![]() $1\leqslant i\leqslant k$
, define
$1\leqslant i\leqslant k$
, define
 $$\begin{align*}\tilde{v}_i:=d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right).\end{align*}$$
$$\begin{align*}\tilde{v}_i:=d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right).\end{align*}$$
Then
![]() $\tilde {v}_1+\cdots +\tilde {v}_k=0$
and
$\tilde {v}_1+\cdots +\tilde {v}_k=0$
and
![]() $\tilde {v}_1+\cdots +\tilde {v}_l<0$
for
$\tilde {v}_1+\cdots +\tilde {v}_l<0$
for
![]() $1\leqslant l<k$
. Therefore,
$1\leqslant l<k$
. Therefore,
 $$ \begin{align*} \sum_{i=1}^k (k+1-i)d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right) =\sum_{l=1}^k \left(\sum_{i=1}^l \tilde{v}_i \right)<0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^k (k+1-i)d_i\left(\frac{v_i}{d_i}-\frac{w}{d}\right) =\sum_{l=1}^k \left(\sum_{i=1}^l \tilde{v}_i \right)<0. \end{align*} $$
It follows that
 $$ \begin{align} \left\langle \lambda, \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} -w \tau_d \right\rangle <-\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align} $$
$$ \begin{align} \left\langle \lambda, \sum_{i=1}^k \psi_i+\sum_{i=1}^k v_i \tau_{d_i}-\frac{3}{2}\mathfrak{g}^{\lambda>0} -w \tau_d \right\rangle <-\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align} $$
On the other hand, we claim that for any weight
![]() $\chi \in \textbf {W}(d)_{0}$
, we have that
$\chi \in \textbf {W}(d)_{0}$
, we have that
 $$ \begin{align} \langle \lambda, \chi\rangle \geqslant -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align} $$
$$ \begin{align} \langle \lambda, \chi\rangle \geqslant -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle. \end{align} $$
We thus obtain a contradiction with Equations (3.23) and (3.22). To prove Equation (3.24), write
![]() $\chi =\sum _{i, j}c_{ij}(\beta _i-\beta _j)$
with
$\chi =\sum _{i, j}c_{ij}(\beta _i-\beta _j)$
with
![]() $0\leqslant c_{ij} \leqslant 3/2$
. Then
$0\leqslant c_{ij} \leqslant 3/2$
. Then
 $$ \begin{align*} \langle \lambda, \chi \rangle \geqslant \sum_{\langle \lambda, \beta_i-\beta_j \rangle<0} c_{ij}\langle \lambda, \beta_i-\beta_j \rangle \geqslant \frac{3}{2}\sum_{\langle \lambda, \beta_i-\beta_j \rangle<0} \langle \lambda, \beta_i-\beta_j \rangle= -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle.\\[-48pt] \end{align*} $$
$$ \begin{align*} \langle \lambda, \chi \rangle \geqslant \sum_{\langle \lambda, \beta_i-\beta_j \rangle<0} c_{ij}\langle \lambda, \beta_i-\beta_j \rangle \geqslant \frac{3}{2}\sum_{\langle \lambda, \beta_i-\beta_j \rangle<0} \langle \lambda, \beta_i-\beta_j \rangle= -\left\langle \lambda, \frac{3}{2}\mathfrak{g}^{\lambda>0} \right\rangle.\\[-48pt] \end{align*} $$
4 Integral generator of equivariant K-theory of quasi-BPS categories
Recall the graded quasi-BPS category
![]() $\mathbb {S}^{\mathrm {gr}}(d)_v$
, which is equivalent via Koszul duality to
$\mathbb {S}^{\mathrm {gr}}(d)_v$
, which is equivalent via Koszul duality to
In [Reference Pădurariu and TodaPTa], we proved that the monomials
![]() $[\mathcal {E}_{d_1, v_1}] \ast \cdots \ast [\mathcal {E}_{d_k, v_k}]$
for
$[\mathcal {E}_{d_1, v_1}] \ast \cdots \ast [\mathcal {E}_{d_k, v_k}]$
for
![]() $v_i/d_i=v/d$
give a basis of the
$v_i/d_i=v/d$
give a basis of the
![]() $\mathbb {F}$
-vector space
$\mathbb {F}$
-vector space
![]() $K_T(\mathbb {T}(d)_v)\otimes _{\mathbb {K}} \mathbb {F}$
. In this section, we consider the torsion-free equivariant K-theory defined by
$K_T(\mathbb {T}(d)_v)\otimes _{\mathbb {K}} \mathbb {F}$
. In this section, we consider the torsion-free equivariant K-theory defined by
It is conjectured by Schiffmann–Vasserot [Reference Schiffmann and VasserotSV13, Conjecture 7.13] that
![]() $K_T(\mathscr {C}(d))$
is torsion free as a
$K_T(\mathscr {C}(d))$
is torsion free as a
![]() $\mathbb {K}$
-module, so conjecturally
$\mathbb {K}$
-module, so conjecturally
![]() $K_T(\mathbb {T}(d)_v)'$
is isomorphic to
$K_T(\mathbb {T}(d)_v)'$
is isomorphic to
![]() $K_T(\mathbb {T}(d)_v)$
. We compute
$K_T(\mathbb {T}(d)_v)$
. We compute
![]() $K_T(\mathbb {T}(d)_v)'$
when
$K_T(\mathbb {T}(d)_v)'$
when
![]() $\gcd (d, v)=1$
, and when
$\gcd (d, v)=1$
, and when
![]() $(d, v)=(2, 0)$
. Theorem 3.1 plays a key role in the case of
$(d, v)=(2, 0)$
. Theorem 3.1 plays a key role in the case of
![]() $\gcd (d, v)=1$
.
$\gcd (d, v)=1$
.
4.1 Sheaves supported over the small diagonal
Let
be the
![]() $(-1)$
-shifted cotangent of
$(-1)$
-shifted cotangent of
![]() $\mathscr {C}(d)$
. An object
$\mathscr {C}(d)$
. An object
![]() $\mathcal {E} \in D^b(\mathscr {C}(d))$
has singular support [Reference Arinkin and GaitsgoryAG15]:
$\mathcal {E} \in D^b(\mathscr {C}(d))$
has singular support [Reference Arinkin and GaitsgoryAG15]:
We identify the right-hand side with
![]() $\mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d) \subset \mathcal {X}(d)$
, which is isomorphic to the moduli stack of zero-dimensional coherent sheaves on
$\mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d) \subset \mathcal {X}(d)$
, which is isomorphic to the moduli stack of zero-dimensional coherent sheaves on
![]() $\mathbb {C}^3$
of length d. Under the Koszul duality equivalence (2.22), we have by [Reference TodaToda, Proposition 2.3.9] that
$\mathbb {C}^3$
of length d. Under the Koszul duality equivalence (2.22), we have by [Reference TodaToda, Proposition 2.3.9] that
In the following lemma, we show that the K-theory class of an object in
![]() $D^b_T(\mathscr {C}(d))$
with singular support contained in
$D^b_T(\mathscr {C}(d))$
with singular support contained in
![]() $\pi ^{-1}(\Delta )$
has a certain divisibility property. The proof is inspired by the proof of wheel conditions in [Reference ZhaoZha, Theorem 2.9, Corollary 2.10], [Reference NeguţNeg23, Proposition 2.11]
$\pi ^{-1}(\Delta )$
has a certain divisibility property. The proof is inspired by the proof of wheel conditions in [Reference ZhaoZha, Theorem 2.9, Corollary 2.10], [Reference NeguţNeg23, Proposition 2.11]
Lemma 4.1. For any
![]() $\mathcal {E} \in D^b_T(\mathscr {C}(d))$
whose singular support is contained in
$\mathcal {E} \in D^b_T(\mathscr {C}(d))$
whose singular support is contained in
![]() $\pi ^{-1}(\Delta )$
, the element
$\pi ^{-1}(\Delta )$
, the element
![]() $i_{\ast }[\mathcal {E}] \in K_T(\mathcal {Y}(d))= \mathbb {K}[z_1^{\pm }, \ldots , z_d^{\pm 1}]^{\mathfrak {S}_d}$
is divisible by
$i_{\ast }[\mathcal {E}] \in K_T(\mathcal {Y}(d))= \mathbb {K}[z_1^{\pm }, \ldots , z_d^{\pm 1}]^{\mathfrak {S}_d}$
is divisible by
Proof. By [Reference Pădurariu and TodaPTa, Lemma 4.9], it is enough to show that, for
![]() $\mathcal {F} \in \mathrm {MF}_T(\mathcal {X}(d), \mathop {\mathrm {Tr}}\nolimits W)$
supported on
$\mathcal {F} \in \mathrm {MF}_T(\mathcal {X}(d), \mathop {\mathrm {Tr}}\nolimits W)$
supported on
![]() $\pi ^{-1}(\Delta )$
, its image under the forget-the-potential map (1.8):
$\pi ^{-1}(\Delta )$
, its image under the forget-the-potential map (1.8):
is divisible by
![]() $(q_1-1)^{d-1}(q_2-1)^{d-1}(q_1 q_2-1)^{d-1}$
. We consider the morphism
$(q_1-1)^{d-1}(q_2-1)^{d-1}(q_1 q_2-1)^{d-1}$
. We consider the morphism
 $$ \begin{align*} h \colon \mathbb{C}^{d-1} \setminus \{0\} &\to \mathrm{Crit}(\mathop{\mathrm{Tr}}\nolimits W_d) \subset \mathfrak{g}^{\oplus 3}\\ (t_1, \ldots, t_{d-1}) &\mapsto \left(0, 0, (t_1, \ldots, t_{d-1}, 0) \right), \end{align*} $$
$$ \begin{align*} h \colon \mathbb{C}^{d-1} \setminus \{0\} &\to \mathrm{Crit}(\mathop{\mathrm{Tr}}\nolimits W_d) \subset \mathfrak{g}^{\oplus 3}\\ (t_1, \ldots, t_{d-1}) &\mapsto \left(0, 0, (t_1, \ldots, t_{d-1}, 0) \right), \end{align*} $$
where
![]() $(t_1, \ldots , t_{d-1}, 0)$
is the diagonal matrix. Let
$(t_1, \ldots , t_{d-1}, 0)$
is the diagonal matrix. Let
![]() $T=(\mathbb {C}^{\ast })^2$
act on
$T=(\mathbb {C}^{\ast })^2$
act on
![]() $\mathbb {C}^{d-1}$
with weight
$\mathbb {C}^{d-1}$
with weight
![]() $q_1^{-1}q_2^{-1}$
, and let the maximal torus
$q_1^{-1}q_2^{-1}$
, and let the maximal torus
![]() $T(d) \subset GL(d)$
act on
$T(d) \subset GL(d)$
act on
![]() $\mathbb {C}^{d-1}$
trivially. Then the above morphism h is
$\mathbb {C}^{d-1}$
trivially. Then the above morphism h is
![]() $T \times T(d)$
-equivariant, so it induces a morphism
$T \times T(d)$
-equivariant, so it induces a morphism
By the localization sequence
we have an isomorphism
Note that we have
in particular the image of h does not intersect
![]() $\pi ^{-1}(\Delta ) \subset \mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d)$
. We thus have that
$\pi ^{-1}(\Delta ) \subset \mathrm {Crit}(\mathop {\mathrm {Tr}}\nolimits W_d)$
. We thus have that
Therefore, the element (4.2) is divisible by
![]() $(q_1 q_2-1)^{d-1}$
. By replacing h with
$(q_1 q_2-1)^{d-1}$
. By replacing h with
 $$ \begin{align*} (t_1, \ldots, t_{d-1}) &\mapsto (0, (t_1, \ldots, t_{d-1}, 0), 0), \\ (t_1, \ldots, t_{d-1}) & \mapsto ((t_1, \ldots, t_{d-1}, 0), 0, 0), \end{align*} $$
$$ \begin{align*} (t_1, \ldots, t_{d-1}) &\mapsto (0, (t_1, \ldots, t_{d-1}, 0), 0), \\ (t_1, \ldots, t_{d-1}) & \mapsto ((t_1, \ldots, t_{d-1}, 0), 0, 0), \end{align*} $$
the element (4.2) is also divisible by
![]() $(q_1-1)^{d-1}$
,
$(q_1-1)^{d-1}$
,
![]() $(q_2-1)^{d-1}$
, respectively.
$(q_2-1)^{d-1}$
, respectively.
By combining the above lemma with Theorem 3.1, we obtain the following:
Corollary 4.2. For any object
![]() $\mathcal {E} \in \mathbb {T}_T(d)_v$
with
$\mathcal {E} \in \mathbb {T}_T(d)_v$
with
![]() $\gcd (d, v)=1$
, the element
$\gcd (d, v)=1$
, the element
is divisible by Equation (4.1). In particular, the element
![]() $i_{\ast }[\mathcal {E}_{d, v}]$
in Equation (2.38) for
$i_{\ast }[\mathcal {E}_{d, v}]$
in Equation (2.38) for
![]() $\gcd (d, v)=1$
is divisible by Equation (4.1).
$\gcd (d, v)=1$
is divisible by Equation (4.1).
Remark 4.3. It is not clear from the expression (2.38) that
![]() $i_{\ast }[\mathcal {E}_{d, v}]$
is divisible by Equation (4.1) when
$i_{\ast }[\mathcal {E}_{d, v}]$
is divisible by Equation (4.1) when
![]() $\gcd (d, v)=1$
. Further, the condition
$\gcd (d, v)=1$
. Further, the condition
![]() $\gcd (d, v)=1$
is necessary for the above divisibility. Indeed, for
$\gcd (d, v)=1$
is necessary for the above divisibility. Indeed, for
![]() $d=2$
, a direct computation shows that
$d=2$
, a direct computation shows that
 $$ \begin{align*} i_{\ast}[\mathcal{E}_{2, 0}]&= (1-q_1^{-1})(1-q_2^{-1})(1-q_1^{-1}-q_2^{-1}-q_1^{-1}q_2^{-1}+z_1^{-1}z_2+z_1 z_2^{-1}), \\ i_{\ast}[\mathcal{E}_{2, 1}]&= (1-q_1^{-1})(1-q_2^{-1})(1-q_1^{-1}q_2^{-1})(z_1+z_2). \end{align*} $$
$$ \begin{align*} i_{\ast}[\mathcal{E}_{2, 0}]&= (1-q_1^{-1})(1-q_2^{-1})(1-q_1^{-1}-q_2^{-1}-q_1^{-1}q_2^{-1}+z_1^{-1}z_2+z_1 z_2^{-1}), \\ i_{\ast}[\mathcal{E}_{2, 1}]&= (1-q_1^{-1})(1-q_2^{-1})(1-q_1^{-1}q_2^{-1})(z_1+z_2). \end{align*} $$
The element
![]() $i_{\ast }[\mathcal {E}_{2, 0}]$
is not divisible by Equation (4.1). In particular, the singular support of
$i_{\ast }[\mathcal {E}_{2, 0}]$
is not divisible by Equation (4.1). In particular, the singular support of
![]() $\mathcal {E}_{2, 0}$
is not included in
$\mathcal {E}_{2, 0}$
is not included in
![]() $\pi ^{-1}(\Delta )$
.
$\pi ^{-1}(\Delta )$
.
4.2 Integral generator for the coprime case
Recall that
![]() $K_T(\mathbb {T}(d)_v)$
is expected to be torsion free as a
$K_T(\mathbb {T}(d)_v)$
is expected to be torsion free as a
![]() $\mathbb {K}$
-module. We also expect that
$\mathbb {K}$
-module. We also expect that
![]() $K_T(\mathbb {T}(d)_v)$
is freely generated by
$K_T(\mathbb {T}(d)_v)$
is freely generated by
![]() $[\mathcal {E}_{d, v}]$
if
$[\mathcal {E}_{d, v}]$
if
![]() $\gcd (d, v)=1$
. The following theorem, which is an application of Corollary 4.2, gives evidence towards this expectation.
$\gcd (d, v)=1$
. The following theorem, which is an application of Corollary 4.2, gives evidence towards this expectation.
Theorem 4.4. Consider a pair
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
with
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, v)=1$
. There is an isomorphism of
$\gcd (d, v)=1$
. There is an isomorphism of
![]() $\mathbb {K}$
-modules:
$\mathbb {K}$
-modules:
Proof. By the isomorphism (2.30), the
![]() $\mathbb {K}$
-module
$\mathbb {K}$
-module
![]() $K_T(\mathbb {T}(d)_v)'$
is isomorphic to the image of
$K_T(\mathbb {T}(d)_v)'$
is isomorphic to the image of
It is enough to show that the image of the above morphism is generated by
![]() $i_{\ast }[\mathcal {E}_{d, v}]$
as a
$i_{\ast }[\mathcal {E}_{d, v}]$
as a
![]() $\mathbb {K}$
-module. By Corollary 4.2, we have
$\mathbb {K}$
-module. By Corollary 4.2, we have
Moreover,
![]() $\mathrm {Im}(i_{\ast })\otimes _{\mathbb {K}} \mathbb {F}$
is generated by
$\mathrm {Im}(i_{\ast })\otimes _{\mathbb {K}} \mathbb {F}$
is generated by
![]() $i_{\ast }[\mathcal {E}_{d, v}]$
over
$i_{\ast }[\mathcal {E}_{d, v}]$
over
![]() $\mathbb {F}$
by [Reference Pădurariu and TodaPTa, Theorem 4.12]. It is thus enough to show that
$\mathbb {F}$
by [Reference Pădurariu and TodaPTa, Theorem 4.12]. It is thus enough to show that
![]() $i_{\ast }[\mathcal {E}_{d, v}]$
is written as
$i_{\ast }[\mathcal {E}_{d, v}]$
is written as
where E is not divisible by a nonunit element in
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
By Equation (2.38), we have that
 $$ \begin{align} \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_d^{m_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1})\right)=(q_1 q_2-1)^{d-1} \cdot E. \end{align} $$
$$ \begin{align} \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_d^{m_d}}{(1-q^{-1}z_1^{-1}z_2)\cdots (1-q^{-1}z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1})\right)=(q_1 q_2-1)^{d-1} \cdot E. \end{align} $$
By setting
 $$ \begin{align} f_d(z_1, \ldots, z_d):=\prod_{i=1}^{d-1}(z_{i+1}-q_1^{-1}z_i)&(z_{i+1}-q_2^{-1}z_i) \cdot \\&\prod_{j>i+1}(z_j-q_1^{-1}z_i)(z_j-q_2^{-1}z_i)(z_j-q z_i),\nonumber \end{align} $$
$$ \begin{align} f_d(z_1, \ldots, z_d):=\prod_{i=1}^{d-1}(z_{i+1}-q_1^{-1}z_i)&(z_{i+1}-q_2^{-1}z_i) \cdot \\&\prod_{j>i+1}(z_j-q_1^{-1}z_i)(z_j-q_2^{-1}z_i)(z_j-q z_i),\nonumber \end{align} $$
we can write Equation (4.3) as
 $$ \begin{align} (-q)^{-\frac{1}{2}(d-1)(d-2)}(z_1 \cdots z_d)^{2-d} \cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\cdots z_{d-1}^{m_{d-1}}z_d^{m_d-1} f_d(z_1, \ldots, z_d)}{\prod_{j>i}(z_j-z_i)} \right). \end{align} $$
$$ \begin{align} (-q)^{-\frac{1}{2}(d-1)(d-2)}(z_1 \cdots z_d)^{2-d} \cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\cdots z_{d-1}^{m_{d-1}}z_d^{m_d-1} f_d(z_1, \ldots, z_d)}{\prod_{j>i}(z_j-z_i)} \right). \end{align} $$
Plug in
![]() $z_i=q_1^i$
for
$z_i=q_1^i$
for
![]() $1\leqslant i\leqslant d$
in the formula (4.5). The only nonzero term in the sum above corresponds to the identity permutation. The factors of this term not in
$1\leqslant i\leqslant d$
in the formula (4.5). The only nonzero term in the sum above corresponds to the identity permutation. The factors of this term not in
![]() $\mathbb {K}^{*}$
divide
$\mathbb {K}^{*}$
divide
Next, plug in
![]() $z_i=q_2^i$
for
$z_i=q_2^i$
for
![]() $1\leqslant i\leqslant d$
in the formula (4.5). The only nonzero term in the sum of Equation (4.5) corresponds to the identity permutation. The factors of this term not in
$1\leqslant i\leqslant d$
in the formula (4.5). The only nonzero term in the sum of Equation (4.5) corresponds to the identity permutation. The factors of this term not in
![]() $\mathbb {K}^{*}$
divide
$\mathbb {K}^{*}$
divide
The only factors which divide terms in both sets (4.6) and (4.7) are
![]() $q_1-q_2$
and
$q_1-q_2$
and
![]() $q_1q_2-1$
. The factor
$q_1q_2-1$
. The factor
![]() $q_1q_2-1$
appears with multiplicity
$q_1q_2-1$
appears with multiplicity
![]() $d-1$
as it corresponds to
$d-1$
as it corresponds to
![]() $z_{i+1}-q_2^{-1}z_i$
for
$z_{i+1}-q_2^{-1}z_i$
for
![]() $1\leqslant i\leqslant d-1$
.
$1\leqslant i\leqslant d-1$
.
It suffices to show that
![]() $q_1-q_2$
does not divide Equation (4.5). We will be using computations from [Reference NeguţNeg22, Section 2]. Note that
$q_1-q_2$
does not divide Equation (4.5). We will be using computations from [Reference NeguţNeg22, Section 2]. Note that
![]() $q_1, q_2, q$
from our paper correspond to
$q_1, q_2, q$
from our paper correspond to
![]() $q_1^{-1}, q_2^{-1}, q^{-1}$
in loc. cit. Further, the weight
$q_1^{-1}, q_2^{-1}, q^{-1}$
in loc. cit. Further, the weight
![]() $v\in \mathbb {Z}$
corresponds to
$v\in \mathbb {Z}$
corresponds to
![]() $k\in \mathbb {Z}$
in loc. cit. By [Reference NeguţNeg22, Equation (2.35)], the equality
$k\in \mathbb {Z}$
in loc. cit. By [Reference NeguţNeg22, Equation (2.35)], the equality
![]() $P_{d, k}=E_{d, k}$
for
$P_{d, k}=E_{d, k}$
for
![]() $\gcd (d, k)=1$
in loc. cit. (see [Reference NeguţNeg22, Equations (2.6) and (2.35)]) and the isomorphism between shuffle algebras
$\gcd (d, k)=1$
in loc. cit. (see [Reference NeguţNeg22, Equations (2.6) and (2.35)]) and the isomorphism between shuffle algebras
![]() $\mathcal {S}_{\mathbb {F}}\xrightarrow {\sim }\mathcal {S}^{\prime }_{\mathbb {F}}$
, we can write
$\mathcal {S}_{\mathbb {F}}\xrightarrow {\sim }\mathcal {S}^{\prime }_{\mathbb {F}}$
, we can write
 $$\begin{align*}(q_1q_2-1)^{d-1}\cdot E=y+t \text{ in }\mathcal{S}\otimes_{\mathbb{K}}\mathbb{K}\left[\frac{1}{1-q_2^{-1}}, \frac{1}{1-q^{-1}}\right] \end{align*}$$
$$\begin{align*}(q_1q_2-1)^{d-1}\cdot E=y+t \text{ in }\mathcal{S}\otimes_{\mathbb{K}}\mathbb{K}\left[\frac{1}{1-q_2^{-1}}, \frac{1}{1-q^{-1}}\right] \end{align*}$$
for t a
![]() $\mathbb {K}$
-torsion element and
$\mathbb {K}$
-torsion element and
 $$ \begin{align} y:=\frac{(1-q_2^{-1})(1-q)^v}{(1-q_2^{-1})^v(1-q^{-1})}\cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_d^{m_d}}{(1-q_2z_1^{-1}z_2)\cdots (1-q_2z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1})\right). \end{align} $$
$$ \begin{align} y:=\frac{(1-q_2^{-1})(1-q)^v}{(1-q_2^{-1})^v(1-q^{-1})}\cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_d^{m_d}}{(1-q_2z_1^{-1}z_2)\cdots (1-q_2z_{d-1}^{-1}z_d)} \cdot \prod_{j>i}\xi(z_i z_j^{-1})\right). \end{align} $$
It suffices to show that
![]() $q_1-q_2$
does not divide y. By setting
$q_1-q_2$
does not divide y. By setting
 $$ \begin{align} g_d(z_1, \ldots, z_d):=\prod_{i=1}^{d-1}(z_{i+1}-q_1^{-1}z_i)&(z_{i+1}-qz_i) \cdot \\&\prod_{j>i+1}(z_j-q_1^{-1}z_i)(z_j-q_2^{-1}z_i)(z_j-q z_i),\nonumber\end{align} $$
$$ \begin{align} g_d(z_1, \ldots, z_d):=\prod_{i=1}^{d-1}(z_{i+1}-q_1^{-1}z_i)&(z_{i+1}-qz_i) \cdot \\&\prod_{j>i+1}(z_j-q_1^{-1}z_i)(z_j-q_2^{-1}z_i)(z_j-q z_i),\nonumber\end{align} $$
we can write the
![]() $\mathrm {Sym}(-)$
term of y as
$\mathrm {Sym}(-)$
term of y as
 $$ \begin{align} (-q_2)^{-\frac{1}{2}(d-1)(d-2)}(z_1 \cdots z_d)^{2-d} \cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_{d-1}^{m_{d-1}}z_d^{m_d-1} g_d(z_1, \ldots, z_d)}{\prod_{j>i}(z_j-z_i)} \right). \end{align} $$
$$ \begin{align} (-q_2)^{-\frac{1}{2}(d-1)(d-2)}(z_1 \cdots z_d)^{2-d} \cdot \mathrm{Sym}\left(\frac{z_1^{m_1}\ldots z_{d-1}^{m_{d-1}}z_d^{m_d-1} g_d(z_1, \ldots, z_d)}{\prod_{j>i}(z_j-z_i)} \right). \end{align} $$
It suffices to show that
![]() $q_1-q_2$
does not divide Equation (4.10). Let
$q_1-q_2$
does not divide Equation (4.10). Let
![]() $z_i=q^{-i}$
for
$z_i=q^{-i}$
for
![]() $1\leqslant i\leqslant d$
. The only nonzero term in the sum of Equation (4.10) corresponds to the identity permutation. The factors of this term not in
$1\leqslant i\leqslant d$
. The only nonzero term in the sum of Equation (4.10) corresponds to the identity permutation. The factors of this term not in
![]() $\mathbb {K}^{*}$
divide
$\mathbb {K}^{*}$
divide
None of these polynomials is divisible by
![]() $q_1-q_2$
, and the conclusion thus follows.
$q_1-q_2$
, and the conclusion thus follows.
4.3 Integral generator for
 $K_T(\mathbb {T}(2)_0)'$
$K_T(\mathbb {T}(2)_0)'$
The computation of
![]() $K_T(\mathbb {T}(d)_v)'$
is more subtle when
$K_T(\mathbb {T}(d)_v)'$
is more subtle when
![]() $\gcd (d, v)>1$
, since the monomials
$\gcd (d, v)>1$
, since the monomials
![]() $[\mathcal {E}_{d_1, v_1}] \ast \cdots \ast [\mathcal {E}_{d_k, v_k}]$
for
$[\mathcal {E}_{d_1, v_1}] \ast \cdots \ast [\mathcal {E}_{d_k, v_k}]$
for
![]() $v_i/d_i=v/d$
do not generate it over
$v_i/d_i=v/d$
do not generate it over
![]() $\mathbb {K}$
; see Remark 4.8. We need to find other objects giving
$\mathbb {K}$
; see Remark 4.8. We need to find other objects giving
![]() $\mathbb {K}$
-basis of
$\mathbb {K}$
-basis of
![]() $K_T(\mathbb {T}(d)_v)'$
. Here, we give a computation for
$K_T(\mathbb {T}(d)_v)'$
. Here, we give a computation for
![]() $(d, v)=(2, 0)$
.
$(d, v)=(2, 0)$
.
Let V be a two-dimensional vector space, and let
![]() $\mathfrak {sl} \subset \mathfrak {g}=\mathrm {End}(V)$
be its traceless part. Note that
$\mathfrak {sl} \subset \mathfrak {g}=\mathrm {End}(V)$
be its traceless part. Note that
The structure sheaf of the classical truncation
![]() $\mathscr {C}(2)^{\mathrm {cl}}$
fits into the exact sequence
$\mathscr {C}(2)^{\mathrm {cl}}$
fits into the exact sequence
Here, over
![]() $(X, Y) \in \mathfrak {g}^{\oplus 2}$
, the maps A, B are given by
$(X, Y) \in \mathfrak {g}^{\oplus 2}$
, the maps A, B are given by
We set
![]() $M_1:=\mathcal {O}_{\mathscr {C}(2)^{\mathrm {cl}}}(q_1 q_2)$
. We also define a coherent sheaf
$M_1:=\mathcal {O}_{\mathscr {C}(2)^{\mathrm {cl}}}(q_1 q_2)$
. We also define a coherent sheaf
![]() $M_2$
on
$M_2$
on
![]() $\mathscr {C}(2)^{\mathrm {cl}}$
by the exact sequence
$\mathscr {C}(2)^{\mathrm {cl}}$
by the exact sequence
The sequences (4.11), (4.12) are the Eagon–Northcott complex and the Buchsbaum–Rim complex associated with
![]() $A^{\vee } \colon \mathfrak {sl} \otimes \mathcal {O}_{\mathcal {Y}(2)} \to \mathcal {O}_{\mathcal {Y}(2)}(q_1) \oplus \mathcal {O}_{\mathcal {Y}(2)}(q_2)$
, respectively. In particular they are exact; see [Reference EisenbudEis95, Theorem A2.10]. From the exact sequences (4.11), (4.12), we have
$A^{\vee } \colon \mathfrak {sl} \otimes \mathcal {O}_{\mathcal {Y}(2)} \to \mathcal {O}_{\mathcal {Y}(2)}(q_1) \oplus \mathcal {O}_{\mathcal {Y}(2)}(q_2)$
, respectively. In particular they are exact; see [Reference EisenbudEis95, Theorem A2.10]. From the exact sequences (4.11), (4.12), we have
![]() $M_1, M_2 \in \mathbb {T}(2)_0$
.
$M_1, M_2 \in \mathbb {T}(2)_0$
.
Proposition 4.5. As a
![]() $\mathbb {K}$
-module, we have
$\mathbb {K}$
-module, we have
Proof. It is enough to show that the image of
is generated by
![]() $i_{\ast }M_1$
,
$i_{\ast }M_1$
,
![]() $i_{\ast }M_2$
and that
$i_{\ast }M_2$
and that
![]() $i_{\ast }M_1, i_{\ast }M_2$
are linearly independent over
$i_{\ast }M_1, i_{\ast }M_2$
are linearly independent over
![]() $\mathbb {F}$
. Below, we omit
$\mathbb {F}$
. Below, we omit
![]() $i_{\ast }$
from the notation
$i_{\ast }$
from the notation
![]() $i_{\ast }M_j$
. From the exact sequences (4.11), (4.12), we have
$i_{\ast }M_j$
. From the exact sequences (4.11), (4.12), we have
A direct computation shows that
 $$ \begin{align} [\mathcal{E}_{1, 0} \ast \mathcal{E}_{1, 0}]&= 1+q_1^{-1}+q_2^{-1}+q_1^{-1}q_2^{-2}+q_1^{-2}q_2^{-1}+q_1^{-2}q_2^{-2}-2\mathfrak{sl} q_1^{-1}q_2^{-1} \\ \notag &=q_1^{-1}q_2^{-1}([M_1]+[M_2]), \\ \notag [\mathcal{E}_{2, 0}]&= (1-q_1^{-1})(1-q_2^{-1})(\mathfrak{sl}-q_1^{-1}-q_2^{-1}-q_1^{-1}q_2^{-1}) \\ \notag &=(q_1^{-1}+q_2^{-1})[M_1]-(q_1^{-1}q_2^{-1}+1)[M_2]. \end{align} $$
$$ \begin{align} [\mathcal{E}_{1, 0} \ast \mathcal{E}_{1, 0}]&= 1+q_1^{-1}+q_2^{-1}+q_1^{-1}q_2^{-2}+q_1^{-2}q_2^{-1}+q_1^{-2}q_2^{-2}-2\mathfrak{sl} q_1^{-1}q_2^{-1} \\ \notag &=q_1^{-1}q_2^{-1}([M_1]+[M_2]), \\ \notag [\mathcal{E}_{2, 0}]&= (1-q_1^{-1})(1-q_2^{-1})(\mathfrak{sl}-q_1^{-1}-q_2^{-1}-q_1^{-1}q_2^{-1}) \\ \notag &=(q_1^{-1}+q_2^{-1})[M_1]-(q_1^{-1}q_2^{-1}+1)[M_2]. \end{align} $$
Here,
![]() $[\mathcal {E}_{1, 0} \ast \mathcal {E}_{1, 0}]$
is computed from Equation (2.29) and
$[\mathcal {E}_{1, 0} \ast \mathcal {E}_{1, 0}]$
is computed from Equation (2.29) and
![]() $[\mathcal {E}_{2, 0}]$
is computed from Equation (2.38). Therefore, we have
$[\mathcal {E}_{2, 0}]$
is computed from Equation (2.38). Therefore, we have
Since we have
 $$ \begin{align} \det \begin{pmatrix} q_1^{-1}q_2^{-1} & q_1^{-1} q_2^{-1} \\[4pt] q_1^{-1}+q_2^{-1} & -(q_1^{-1}q_2^{-1}+1) \\ \end{pmatrix} =-q_1^{-1}q_2^{-1}(1+q_1^{-1})(1+q_2^{-1}) \in \mathbb{K} \setminus \{0\}, \end{align} $$
$$ \begin{align} \det \begin{pmatrix} q_1^{-1}q_2^{-1} & q_1^{-1} q_2^{-1} \\[4pt] q_1^{-1}+q_2^{-1} & -(q_1^{-1}q_2^{-1}+1) \\ \end{pmatrix} =-q_1^{-1}q_2^{-1}(1+q_1^{-1})(1+q_2^{-1}) \in \mathbb{K} \setminus \{0\}, \end{align} $$
the embedding (4.17) is an isomorphism after taking
![]() $\otimes _{\mathbb {K}} \mathbb {F}$
. In particular,
$\otimes _{\mathbb {K}} \mathbb {F}$
. In particular,
![]() $[M_1]$
,
$[M_1]$
,
![]() $[M_2]$
are linearly independent over
$[M_2]$
are linearly independent over
![]() $\mathbb {F}$
.
$\mathbb {F}$
.
By the above argument, we have
where the first isomorphism is proved in [Reference Pădurariu and TodaPTa, Theorem 4.12]. It follows that any element in the image of Equation (4.14) is written as
![]() $a_1[M_1]+a_2[M_2]$
for
$a_1[M_1]+a_2[M_2]$
for
![]() $a_1, a_2 \in \mathbb {F}$
. As it lies in
$a_1, a_2 \in \mathbb {F}$
. As it lies in
![]() $\mathbb {K}[z_1^{\pm 1}, z_2^{\pm 1}]$
, from Equation (4.15) we have
$\mathbb {K}[z_1^{\pm 1}, z_2^{\pm 1}]$
, from Equation (4.15) we have
By solving the above equation, there exist
![]() $b, c \in \mathbb {K}$
such that
$b, c \in \mathbb {K}$
such that
where
![]() $\Delta $
is given by
$\Delta $
is given by
 $$ \begin{align*} \Delta &:=q_1^{-1}+q_2^{-1}+q_1q_2-q_1-q_2-q_1^{-1} q_2^{-1} \\ &=q_1^{-1}q_2^{-1}(q_1-1)(q_2-1)(q_1 q_2-1). \end{align*} $$
$$ \begin{align*} \Delta &:=q_1^{-1}+q_2^{-1}+q_1q_2-q_1-q_2-q_1^{-1} q_2^{-1} \\ &=q_1^{-1}q_2^{-1}(q_1-1)(q_2-1)(q_1 q_2-1). \end{align*} $$
It is enough to show that b is divisible by
![]() $\Delta $
. If
$\Delta $
. If
![]() $a_1, a_2$
are given by Equation (4.19), then
$a_1, a_2$
are given by Equation (4.19), then
![]() $a_1[M_1]+a_2[M_2]=b+c[M_2]$
. As we assumed that
$a_1[M_1]+a_2[M_2]=b+c[M_2]$
. As we assumed that
![]() $a_1[M_1]+a_2[M_2]$
lies in the image of Equation (4.14), by the wheel condition [Reference NeguţNeg23, Proposition 2.11] we have
$a_1[M_1]+a_2[M_2]$
lies in the image of Equation (4.14), by the wheel condition [Reference NeguţNeg23, Proposition 2.11] we have
unless
![]() $i=j=k$
; see Remark 4.6. By setting
$i=j=k$
; see Remark 4.6. By setting
![]() $i=k=1$
and
$i=k=1$
and
![]() $j=2$
, we obtain
$j=2$
, we obtain
![]() $b|_{q_1 q_2=1}=0$
. Similarly, we also obtain
$b|_{q_1 q_2=1}=0$
. Similarly, we also obtain
![]() $b|_{q_1=1}=b|_{q_2=1}=0$
, so b is divisible by
$b|_{q_1=1}=b|_{q_2=1}=0$
, so b is divisible by
![]() $\Delta $
.
$\Delta $
.
Remark 4.6. In [Reference NeguţNeg23, Proposition 2.11], it is assumed that i, j and k are pairwise distinct for the identity (4.20), but the proof in loc. cit. works unless
![]() $i=j=k$
. Indeed, using the notation in loc. cit., let
$i=j=k$
. Indeed, using the notation in loc. cit., let
![]() $\phi _e=(x_{ij})$
for
$\phi _e=(x_{ij})$
for
![]() $x_{bc} \neq 0$
,
$x_{bc} \neq 0$
,
![]() $x_{ij}=0$
for
$x_{ij}=0$
for
![]() $(i, j) \neq (b, c)$
,
$(i, j) \neq (b, c)$
,
![]() $\phi _{e}^{\ast }=(y_{ij})$
for
$\phi _{e}^{\ast }=(y_{ij})$
for
![]() $y_{ab} \neq 0$
,
$y_{ab} \neq 0$
,
![]() $y_{ij}=0$
for
$y_{ij}=0$
for
![]() $(i, j) \neq (a, b)$
. Then
$(i, j) \neq (a, b)$
. Then
![]() $\phi _e^{\ast } \phi _e$
is concentrated on
$\phi _e^{\ast } \phi _e$
is concentrated on
![]() $(a, c)$
with value
$(a, c)$
with value
![]() $y_{ab}x_{bc} \neq 0$
,
$y_{ab}x_{bc} \neq 0$
,
![]() $\phi _e \phi _e^{\ast }$
is concentrated on
$\phi _e \phi _e^{\ast }$
is concentrated on
![]() $(b, b)$
(either zero or nonzero). Therefore, if
$(b, b)$
(either zero or nonzero). Therefore, if
![]() $[\phi _e, \phi _e^{\ast }]=0$
holds, then we must have
$[\phi _e, \phi _e^{\ast }]=0$
holds, then we must have
![]() $a=b=c$
. Unless
$a=b=c$
. Unless
![]() $a=b=c$
, we have
$a=b=c$
, we have
![]() $\mu _n^{-1}(0) \cap V_e=\emptyset $
in the notation of the proof of [Reference NeguţNeg23, Proposition 2.11]. The rest of the argument is verbatim.
$\mu _n^{-1}(0) \cap V_e=\emptyset $
in the notation of the proof of [Reference NeguţNeg23, Proposition 2.11]. The rest of the argument is verbatim.
Remark 4.7. Note that
where R is the determinantal variety of
![]() $(3 \times 2)$
-matrices, and
$(3 \times 2)$
-matrices, and
![]() $M_1 \oplus M_2$
gives a noncommutative resolution of
$M_1 \oplus M_2$
gives a noncommutative resolution of
![]() $R \times \mathbb {C}^2$
by [Reference Buchweitz, Leuschke and Van den BerghBLdB10, Theorem A].
$R \times \mathbb {C}^2$
by [Reference Buchweitz, Leuschke and Van den BerghBLdB10, Theorem A].
Remark 4.8. Since Equation (4.18) is not invertible in
![]() $\mathbb {K}$
, the inclusion (4.17) is not an isomorphism if we do not take
$\mathbb {K}$
, the inclusion (4.17) is not an isomorphism if we do not take
![]() $\otimes _{\mathbb {K}} \mathbb {F}$
.
$\otimes _{\mathbb {K}} \mathbb {F}$
.
Remark 4.9. For
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
with
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
with
![]() $\gcd (d, v)=1$
and
$\gcd (d, v)=1$
and
![]() $n\geqslant 1$
, let
$n\geqslant 1$
, let
![]() $P_{nd, nv}$
be defined as in [Reference NeguţNeg14, Equation (1.2)]:
$P_{nd, nv}$
be defined as in [Reference NeguţNeg14, Equation (1.2)]:
 $$ \begin{align} P_{nd,nv}&:= \frac{(q_1^{-1}-1)^{nd}(q_2^{-1}-1)^{nd}}{(q_1^{-n}-1)(q_2^{-n}-1)}\cdot \\& \quad\text{Sym}\left( \frac{\prod_{i=1}^{nd} z_i^{\big\lfloor \frac{iv}{d}\big\rfloor-\big\lfloor \frac{(i-1)v}{d}\big\rfloor}}{\prod_{i=1}^{nd-1}\left(1-q^{-1}z_{i+1}z_i^{-1}\right)}\sum_{s=0}^{n-1}q^{-s}\frac{z_{d(n-1)+1}\ldots z_{d(n-s)+1}}{z_{d(n-1)}\ldots z_{d(n-s)}}\prod_{i<j}\xi\left(\frac{z_i}{z_j}\right) \right). \nonumber\end{align} $$
$$ \begin{align} P_{nd,nv}&:= \frac{(q_1^{-1}-1)^{nd}(q_2^{-1}-1)^{nd}}{(q_1^{-n}-1)(q_2^{-n}-1)}\cdot \\& \quad\text{Sym}\left( \frac{\prod_{i=1}^{nd} z_i^{\big\lfloor \frac{iv}{d}\big\rfloor-\big\lfloor \frac{(i-1)v}{d}\big\rfloor}}{\prod_{i=1}^{nd-1}\left(1-q^{-1}z_{i+1}z_i^{-1}\right)}\sum_{s=0}^{n-1}q^{-s}\frac{z_{d(n-1)+1}\ldots z_{d(n-s)+1}}{z_{d(n-1)}\ldots z_{d(n-s)}}\prod_{i<j}\xi\left(\frac{z_i}{z_j}\right) \right). \nonumber\end{align} $$
Then we have
Together with (4.16), we have
with cokernel
![]() $\mathbb {Z}/2$
. The inclusion (4.23) is an isomorphism after
$\mathbb {Z}/2$
. The inclusion (4.23) is an isomorphism after
![]() $\otimes _{\mathbb {Z}} \mathbb {Q}$
.
$\otimes _{\mathbb {Z}} \mathbb {Q}$
.
More generally, we expect that
More details will be discussed in [Reference Pădurariu and TodaPTb].
5 The coproduct on quasi-BPS categories and K-theoretic BPS spaces
Recall that Q is the quiver with one vertex and three edges
![]() $x, y, z$
. Recall the regular function (2.2) induced from the superpotential
$x, y, z$
. Recall the regular function (2.2) induced from the superpotential
![]() $W:=x[y, z]$
. We will denote by
$W:=x[y, z]$
. We will denote by
![]() $\widetilde {m}$
the Hall product (2.5) of
$\widetilde {m}$
the Hall product (2.5) of
![]() $(Q, W)$
and by m the Hall product (2.17).
$(Q, W)$
and by m the Hall product (2.17).
In Subsection 5.1, we define the coproduct
![]() $\widetilde {\Delta }$
for the categories
$\widetilde {\Delta }$
for the categories
![]() $\mathbb {S}^{\bullet }_{\ast }(d)_w$
. In Subsection 5.2, we prove the compatibility of the product and coproduct for the quasi-BPS categories
$\mathbb {S}^{\bullet }_{\ast }(d)_w$
. In Subsection 5.2, we prove the compatibility of the product and coproduct for the quasi-BPS categories
![]() $\mathbb {S}^{\bullet }_T(d)_w$
; see Theorem 5.2. In Subsection 5.3, we use the Koszul equivalence to define the coproduct
$\mathbb {S}^{\bullet }_T(d)_w$
; see Theorem 5.2. In Subsection 5.3, we use the Koszul equivalence to define the coproduct
![]() $\Delta $
for the categories
$\Delta $
for the categories
![]() $\mathbb {T}_{\ast }(d)_v$
and to check the compatibility between the product and the coproduct for the quasi-BPS categories
$\mathbb {T}_{\ast }(d)_v$
and to check the compatibility between the product and the coproduct for the quasi-BPS categories
![]() $\mathbb {T}_T(d)_v.$
$\mathbb {T}_T(d)_v.$
Recall the definition of
![]() $\mathcal {D}_{d,v}$
for
$\mathcal {D}_{d,v}$
for
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
for
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
for
![]() $\gcd (d, v)=1$
from Equation (1.10). In Subsection 5.4, we show that
$\gcd (d, v)=1$
from Equation (1.10). In Subsection 5.4, we show that
![]() $K(\mathcal {D}_{d,v})_{\mathbb {F}}$
is isomorphic to the
$K(\mathcal {D}_{d,v})_{\mathbb {F}}$
is isomorphic to the
![]() $\mathbb {F}$
-algebra of symmetric polynomials; see Proposition 5.11. Further, we consider the space of primitive elements
$\mathbb {F}$
-algebra of symmetric polynomials; see Proposition 5.11. Further, we consider the space of primitive elements
which we regard as an analogue of cohomological BPS spaces in K-theory; see Proposition 5.11 and the equality (1.5).
Note that the definition of Hall multiplication involves attracting stacks of antidominant cocharacters. The definition of the coproduct is through attracting stacks of dominant cocharacters. In this section, we will use dominant cocharacters.
5.1 Preliminaries
Let
![]() $d\in \mathbb {N}$
. Recall the stack of representation of Q of dimension d:
$d\in \mathbb {N}$
. Recall the stack of representation of Q of dimension d:
In this section, we allow partitions which have terms equal to zero. For
![]() $w\in \mathbb {Z}$
, let
$w\in \mathbb {Z}$
, let
![]() $H_{d, w}$
be the set of partitions
$H_{d, w}$
be the set of partitions
![]() $(d_i, w_i)_{i=1}^k$
of
$(d_i, w_i)_{i=1}^k$
of
![]() $(d, w)$
with
$(d, w)$
with
![]() $d_i\geqslant 1$
for
$d_i\geqslant 1$
for
![]() $i\in \{1,\ldots , k\}$
such that, for
$i\in \{1,\ldots , k\}$
such that, for
![]() $v_i:=w_i-d_i\left (\sum _{i>j}d_j-\sum _{j>i}d_j\right )$
for
$v_i:=w_i-d_i\left (\sum _{i>j}d_j-\sum _{j>i}d_j\right )$
for
![]() $i\in \{1,\ldots , k\}$
, we have
$i\in \{1,\ldots , k\}$
, we have
For a partition
![]() $A=(d_i, w_i)_{i=1}^k$
with terms possibly equal to zero, let
$A=(d_i, w_i)_{i=1}^k$
with terms possibly equal to zero, let
![]() $I\subset \{1,\ldots , k\}$
be the subset of i with
$I\subset \{1,\ldots , k\}$
be the subset of i with
![]() $d_i\geqslant 1$
, and define the partition of
$d_i\geqslant 1$
, and define the partition of
![]() $(d, w)$
with nonzero terms
$(d, w)$
with nonzero terms
![]() $\overline {A}:=(d_i, w_i)_{i\in I}$
.
$\overline {A}:=(d_i, w_i)_{i\in I}$
.
5.1.1
For
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
two cocharacters, let
$\mu $
two cocharacters, let
![]() $A_{\lambda }$
be the set of
$A_{\lambda }$
be the set of
![]() $(T(d)\times T)$
-weights
$(T(d)\times T)$
-weights
![]() $\beta $
of
$\beta $
of
![]() $R(d)$
such that
$R(d)$
such that
![]() $\langle \lambda , \beta \rangle>0$
, let
$\langle \lambda , \beta \rangle>0$
, let
![]() $I^{\mu }_{\lambda }\subset A_{\lambda }$
be the set of weights such that
$I^{\mu }_{\lambda }\subset A_{\lambda }$
be the set of weights such that
![]() $\langle \mu , \beta \rangle <0$
and let
$\langle \mu , \beta \rangle <0$
and let
![]() $A^{\mu }_{\lambda }\subset A_{\lambda }$
be the set of weights such that
$A^{\mu }_{\lambda }\subset A_{\lambda }$
be the set of weights such that
![]() $\langle \mu , \beta \rangle =0$
. Let
$\langle \mu , \beta \rangle =0$
. Let
![]() $J^{\mu }_{\lambda }$
be the set of weights
$J^{\mu }_{\lambda }$
be the set of weights
![]() $\beta $
of
$\beta $
of
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $\langle \lambda , \beta \rangle>0$
and
$\langle \lambda , \beta \rangle>0$
and
![]() $\langle \mu , \beta \rangle <0$
. Define the weights
$\langle \mu , \beta \rangle <0$
. Define the weights
 $$ \begin{align*} N^{\mu}_{\lambda}:=\sum_{I^{\mu}_{\lambda}}\beta,\ \mathfrak{g}^{\mu}_{\lambda}:=\sum_{J^{\mu}_{\lambda}}\beta. \end{align*} $$
$$ \begin{align*} N^{\mu}_{\lambda}:=\sum_{I^{\mu}_{\lambda}}\beta,\ \mathfrak{g}^{\mu}_{\lambda}:=\sum_{J^{\mu}_{\lambda}}\beta. \end{align*} $$
5.1.2
Let
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
be dominant cocharacters of
$\mu $
be dominant cocharacters of
![]() $T(d)$
with associated partitions
$T(d)$
with associated partitions
![]() $A=(d_i)_{i=1}^k$
and
$A=(d_i)_{i=1}^k$
and
![]() $B=(e_i)_{i=1}^s$
, respectively. Let
$B=(e_i)_{i=1}^s$
, respectively. Let
![]() $W\cong \mathfrak {S}_d$
be the Weyl group of
$W\cong \mathfrak {S}_d$
be the Weyl group of
![]() $GL(d)$
, let
$GL(d)$
, let
![]() $W^{\lambda }\cong \times _{i=1}^k \mathfrak {S}_{d_i}$
be the Weyl group of
$W^{\lambda }\cong \times _{i=1}^k \mathfrak {S}_{d_i}$
be the Weyl group of
![]() $GL(d)^{\lambda }$
and let
$GL(d)^{\lambda }$
and let
![]() $W^{\mu }$
be the Weyl group of
$W^{\mu }$
be the Weyl group of
![]() $GL(d)^{\mu }$
. Define the set of cosets
$GL(d)^{\mu }$
. Define the set of cosets
A coset
![]() $C\in S^{\mu }_{\lambda }$
corresponds to partitions
$C\in S^{\mu }_{\lambda }$
corresponds to partitions
![]() $(f_{ij})$
for
$(f_{ij})$
for
![]() $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
![]() $1\leqslant j\leqslant s$
such that
$1\leqslant j\leqslant s$
such that
 $$ \begin{align*} \sum_{j=1}^s f_{ij}=d_i\mbox{ for }1\leqslant i\leqslant k, \ \sum_{i=1}^k f_{ij}=e_j\mbox{ for }1\leqslant j\leqslant s. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^s f_{ij}=d_i\mbox{ for }1\leqslant i\leqslant k, \ \sum_{i=1}^k f_{ij}=e_j\mbox{ for }1\leqslant j\leqslant s. \end{align*} $$
Let
![]() $\nu $
be a dominant cocharacter corresponding to the partition
$\nu $
be a dominant cocharacter corresponding to the partition
and let
![]() $\kappa $
be a dominant cocharacter corresponding to the partition
$\kappa $
be a dominant cocharacter corresponding to the partition
Consider the permutation w of
![]() $\mathfrak {S}_d$
of minimal length which permutes blocks of consecutive integers
$\mathfrak {S}_d$
of minimal length which permutes blocks of consecutive integers
 $$ \begin{align} w&=w_C\colon (f_{11},\cdots, f_{1s}, f_{21},\cdots, f_{2s}, \cdots, f_{k1},\cdots, f_{ks})\mapsto \\&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(f_{11},\cdots, f_{k1}, f_{12},\cdots, f_{k2}, \cdots, f_{1s},\cdots, f_{ks}). \nonumber\end{align} $$
$$ \begin{align} w&=w_C\colon (f_{11},\cdots, f_{1s}, f_{21},\cdots, f_{2s}, \cdots, f_{k1},\cdots, f_{ks})\mapsto \\&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(f_{11},\cdots, f_{k1}, f_{12},\cdots, f_{k2}, \cdots, f_{1s},\cdots, f_{ks}). \nonumber\end{align} $$
Consider the partition
where
![]() $f_{ij}$
are ordered as on Equation (5.2), and assume that
$f_{ij}$
are ordered as on Equation (5.2), and assume that
![]() $\overline {D}$
is in
$\overline {D}$
is in
![]() $H_{d,w}$
. Then there also exists a partition E with terms
$H_{d,w}$
. Then there also exists a partition E with terms
![]() $(f_{ij}, \widetilde {u}_{ij})$
where
$(f_{ij}, \widetilde {u}_{ij})$
where
![]() $f_{ij}$
are ordered as on Equation (5.3) such that
$f_{ij}$
are ordered as on Equation (5.3) such that
![]() $\overline {E}$
is in
$\overline {E}$
is in
![]() $H_{d, w}$
. Consider the order
$H_{d, w}$
. Consider the order
![]() $1\leqslant l\leqslant ks$
of the pairs
$1\leqslant l\leqslant ks$
of the pairs
![]() $(i, j)$
as on the first line on Equation (5.4). Define the functor
$(i, j)$
as on the first line on Equation (5.4). Define the functor
 $$ \begin{align} \text{sw}_C: \boxtimes_{l=1}^{ks} \mathbb{M}(f_{l})_{u_{l}}&\to \boxtimes_{l=1}^{ks}\mathbb{M}(f_{w(l)})_{\widetilde{u}_{w(l)}}, \\ \notag\boxtimes_{l=1}^{ks} \mathcal{A}_{l} &\mapsto \boxtimes_{l=1}^{ks} \mathcal{A}_{w(l)} \end{align} $$
$$ \begin{align} \text{sw}_C: \boxtimes_{l=1}^{ks} \mathbb{M}(f_{l})_{u_{l}}&\to \boxtimes_{l=1}^{ks}\mathbb{M}(f_{w(l)})_{\widetilde{u}_{w(l)}}, \\ \notag\boxtimes_{l=1}^{ks} \mathcal{A}_{l} &\mapsto \boxtimes_{l=1}^{ks} \mathcal{A}_{w(l)} \end{align} $$
which permutes the factors as in Equation (5.4). Define
 $$ \begin{align*} \widetilde{\text{sw}}_C\colon \boxtimes_{i=1}^k \boxtimes_{j=1}^s \mathbb{M}(f_{ij})_{u_{ij}}&\to \boxtimes_{j=1}^s \boxtimes_{i=1}^k \mathbb{M}(f_{ij})_{\widetilde{u}_{ij}},\\ \mathcal{A}&\mapsto \mathrm{sw}_{C}\left( \mathcal{A}\otimes \mathcal{O}(-N^{w^{-1}\mu}_{\lambda}+\mathfrak{g}^{w^{-1}\mu}_{\lambda})[|I^{w^{-1}\mu}_{\lambda}|-|J^{w^{-1}\mu}_{\lambda}|] \right), \end{align*} $$
$$ \begin{align*} \widetilde{\text{sw}}_C\colon \boxtimes_{i=1}^k \boxtimes_{j=1}^s \mathbb{M}(f_{ij})_{u_{ij}}&\to \boxtimes_{j=1}^s \boxtimes_{i=1}^k \mathbb{M}(f_{ij})_{\widetilde{u}_{ij}},\\ \mathcal{A}&\mapsto \mathrm{sw}_{C}\left( \mathcal{A}\otimes \mathcal{O}(-N^{w^{-1}\mu}_{\lambda}+\mathfrak{g}^{w^{-1}\mu}_{\lambda})[|I^{w^{-1}\mu}_{\lambda}|-|J^{w^{-1}\mu}_{\lambda}|] \right), \end{align*} $$
where
![]() $\mathcal {O}(-N^{w^{-1}\mu }_{\lambda }+\mathfrak {g}^{w^{-1}\mu }_{\lambda })$
is a one-dimensional representation of
$\mathcal {O}(-N^{w^{-1}\mu }_{\lambda }+\mathfrak {g}^{w^{-1}\mu }_{\lambda })$
is a one-dimensional representation of
![]() $G^{\nu }\cong G^{\kappa }$
. Consider the maps
$G^{\nu }\cong G^{\kappa }$
. Consider the maps
Finally, define
There are analogous such functors for categories of (equivariant and/ or graded) matrix factorizations
5.1.3
We introduce some more maps and functors needed in the rest of this section. Let
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
be dominant cocharacters, and let
$\mu $
be dominant cocharacters, and let
![]() $\nu $
be a dominant cocharacter corresponding to a partition in
$\nu $
be a dominant cocharacter corresponding to a partition in
![]() $S^{\mu }_{\lambda }$
. The map
$S^{\mu }_{\lambda }$
. The map
![]() $p_{\lambda ^{-1}}$
factors as
$p_{\lambda ^{-1}}$
factors as
![]() $p_{\lambda ^{-1}}=\pi _{\lambda ^{-1}} \iota _{\lambda ^{-1}}$
, where
$p_{\lambda ^{-1}}=\pi _{\lambda ^{-1}} \iota _{\lambda ^{-1}}$
, where
 $$ \begin{align*} \pi_{\lambda^{-1}}&: R(d)/G(d)^{\lambda^{-1}\geqslant 0}\to R(d)/G(d),\\ \iota_{\lambda^{-1}}&: R(d)^{\lambda^{-1}\geqslant 0}/G(d)^{{\lambda^{-1}}\geqslant 0}\to R(d)/G(d)^{{\lambda^{-1}}\geqslant 0}. \end{align*} $$
$$ \begin{align*} \pi_{\lambda^{-1}}&: R(d)/G(d)^{\lambda^{-1}\geqslant 0}\to R(d)/G(d),\\ \iota_{\lambda^{-1}}&: R(d)^{\lambda^{-1}\geqslant 0}/G(d)^{{\lambda^{-1}}\geqslant 0}\to R(d)/G(d)^{{\lambda^{-1}}\geqslant 0}. \end{align*} $$
There are similarly defined maps
 $$ \begin{align*} \pi_{\kappa^{-1}\mu}&: R(d)^{\mu}/\left(G(d)^{\mu}\right)^{{\kappa^{-1}}\geqslant 0}\to R(d)^{\mu}/G(d)^{\mu},\\ \iota_{\kappa^{-1}\mu}&: \left(R(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}/\left(G(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}\to R(d)^{\mu}/\left(G(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}. \end{align*} $$
$$ \begin{align*} \pi_{\kappa^{-1}\mu}&: R(d)^{\mu}/\left(G(d)^{\mu}\right)^{{\kappa^{-1}}\geqslant 0}\to R(d)^{\mu}/G(d)^{\mu},\\ \iota_{\kappa^{-1}\mu}&: \left(R(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}/\left(G(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}\to R(d)^{\mu}/\left(G(d)^{\mu}\right)^{\kappa^{-1}\geqslant 0}. \end{align*} $$
5.1.4
Let
![]() $\mu $
be a dominant cocharacter of
$\mu $
be a dominant cocharacter of
![]() $T(d)$
, let
$T(d)$
, let
![]() $b\in \mathbb {Z}$
and let
$b\in \mathbb {Z}$
and let
![]() $D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )_{\leqslant b}$
be the subcategory of
$D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )_{\leqslant b}$
be the subcategory of
![]() $D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )$
generated by complexes
$D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )$
generated by complexes
![]() $q_{\mu }^{*}\mathcal {A}$
for
$q_{\mu }^{*}\mathcal {A}$
for
![]() $\mathcal {A}\in D^b\left (\mathcal {X}(d)^{\mu }\right )_i$
and
$\mathcal {A}\in D^b\left (\mathcal {X}(d)^{\mu }\right )_i$
and
![]() $i\leqslant b$
. There is a semiorthogonal decomposition
$i\leqslant b$
. There is a semiorthogonal decomposition
and there are equivalences
![]() $q_{\mu }^{*}: D^b\left (\mathcal {X}(d)^{\mu }\right )_{b}\xrightarrow {\sim } D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )_{b}$
. We define the functor
$q_{\mu }^{*}: D^b\left (\mathcal {X}(d)^{\mu }\right )_{b}\xrightarrow {\sim } D^b\left (\mathcal {X}(d)^{\mu \geqslant 0}\right )_{b}$
. We define the functor
to be the projection with respect to the above semiorthogonal decomposition.
5.1.5
Let
![]() $B=(d_i, w_i)_{i=1}^k$
be a partition of
$B=(d_i, w_i)_{i=1}^k$
be a partition of
![]() $(d, w)$
in
$(d, w)$
in
![]() $H_{d, w}$
. Let
$H_{d, w}$
. Let
![]() $\mu $
be a dominant cocharacter for the partition
$\mu $
be a dominant cocharacter for the partition
![]() $(d_i)_{i=1}^k$
, and let
$(d_i)_{i=1}^k$
, and let
![]() $b:=\frac {n_{\mu }}{2}=\langle \mu , \mathfrak {g}^{\mu>0} \rangle $
; see Equation (2.3) for the definition of
$b:=\frac {n_{\mu }}{2}=\langle \mu , \mathfrak {g}^{\mu>0} \rangle $
; see Equation (2.3) for the definition of
![]() $n_{\lambda }$
.
$n_{\lambda }$
.
Lemma 5.1. There is a functor
Proof. First, note that the image of
![]() $p_{\mu }^{*}\left (\mathbb {M}(d)_w\right )$
is in
$p_{\mu }^{*}\left (\mathbb {M}(d)_w\right )$
is in
![]() $D^b(\mathcal {X}(d)^{\mu \geqslant 0})_{\leqslant b}$
from the description of the category
$D^b(\mathcal {X}(d)^{\mu \geqslant 0})_{\leqslant b}$
from the description of the category
![]() $\mathbb {M}(d)_w$
in Lemma 2.2. Thus, the image of
$\mathbb {M}(d)_w$
in Lemma 2.2. Thus, the image of
![]() $\widetilde {\Delta }_B$
is in
$\widetilde {\Delta }_B$
is in
![]() $D^b(\mathcal {X}(d)^{\mu })_b$
. Also, note that the category
$D^b(\mathcal {X}(d)^{\mu })_b$
. Also, note that the category
![]() $\mathbb {M}_B$
is a subcategory of
$\mathbb {M}_B$
is a subcategory of
![]() $D^b(\mathcal {X}(d)^{\mu })_b$
because
$D^b(\mathcal {X}(d)^{\mu })_b$
because
![]() $B=(d_i, w_i)_{i=1}^k$
is in
$B=(d_i, w_i)_{i=1}^k$
is in
![]() $H_{d,w}$
.
$H_{d,w}$
.
Let
![]() $\chi $
be a dominant weight of
$\chi $
be a dominant weight of
![]() $T(d)$
such that
$T(d)$
such that
![]() $\chi +\rho \in \textbf {W}(d)_{w}$
. If
$\chi +\rho \in \textbf {W}(d)_{w}$
. If
![]() $\chi +\rho $
is not on the face
$\chi +\rho $
is not on the face
![]() $F(\mu )$
of the polytope
$F(\mu )$
of the polytope
![]() $\textbf {W}(d)$
, then
$\textbf {W}(d)$
, then
If
![]() $\chi +\rho $
is on the face
$\chi +\rho $
is on the face
![]() $F(\mu )$
, then by [Reference PădurariuPăda, Corollary 3.4] we can write
$F(\mu )$
, then by [Reference PădurariuPăda, Corollary 3.4] we can write
 $$ \begin{align} \chi+\rho-w\tau_d=\frac{1}{2}N^{\mu>0}+\sum_{i=1}^k\left(\psi_i+\rho_i\right), \end{align} $$
$$ \begin{align} \chi+\rho-w\tau_d=\frac{1}{2}N^{\mu>0}+\sum_{i=1}^k\left(\psi_i+\rho_i\right), \end{align} $$
where
![]() $\psi _i \in M(d_i)$
and
$\psi _i \in M(d_i)$
and
![]() $\psi _i+\rho _i\in \textbf {W}(d_i)_0$
. In particular, we have that
$\psi _i+\rho _i\in \textbf {W}(d_i)_0$
. In particular, we have that
 $$\begin{align*}\chi=\sum_{i=1}^k \psi_i +\mathfrak{g}^{\mu>0}+w\tau_d.\end{align*}$$
$$\begin{align*}\chi=\sum_{i=1}^k \psi_i +\mathfrak{g}^{\mu>0}+w\tau_d.\end{align*}$$
Write
![]() $\chi =\sum _{i=1}^k \chi _i$
. We have
$\chi =\sum _{i=1}^k \chi _i$
. We have
Further, we have that
![]() $\chi _i=\psi _i+w_i\tau _{d_i}$
, so
$\chi _i=\psi _i+w_i\tau _{d_i}$
, so
![]() $\chi _i+\rho _i\in \textbf {W}(d_i)_{w_i}$
. Therefore, we have
$\chi _i+\rho _i\in \textbf {W}(d_i)_{w_i}$
. Therefore, we have
Let
![]() $\chi $
be a dominant weight with
$\chi $
be a dominant weight with
![]() $\chi +\rho \in \textbf {W}(d)$
. Note that
$\chi +\rho \in \textbf {W}(d)$
. Note that
 $$ \begin{align} \widetilde{\Delta}_B\left(\mathcal{O}_{\mathcal{X}(d)}\otimes \Gamma_{GL(d)}(\chi)\right)= \begin{cases} \mathcal{O}_{\mathcal{X}(d)^{\mu}}\otimes \Gamma_{GL(d)^{\mu}}(\chi),\text{ if }\chi\in F(\mu),\\ 0,\text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \widetilde{\Delta}_B\left(\mathcal{O}_{\mathcal{X}(d)}\otimes \Gamma_{GL(d)}(\chi)\right)= \begin{cases} \mathcal{O}_{\mathcal{X}(d)^{\mu}}\otimes \Gamma_{GL(d)^{\mu}}(\chi),\text{ if }\chi\in F(\mu),\\ 0,\text{ otherwise}. \end{cases} \end{align} $$
The functor (5.7) induces a functor
Let
![]() $A=(d_i, w_i)_{i=1}^k$
and
$A=(d_i, w_i)_{i=1}^k$
and
![]() $C=(f_i, u_i)_{i=1}^{l}$
be partitions in
$C=(f_i, u_i)_{i=1}^{l}$
be partitions in
![]() $H_{d,w}$
such that C is a refinement of A; see Subsection 2.2.6. One can analogously define functors
$H_{d,w}$
such that C is a refinement of A; see Subsection 2.2.6. One can analogously define functors
for categories
![]() $\mathbb {S}^{\bullet }_{\ast }$
as in Subsection 2.6.2.
$\mathbb {S}^{\bullet }_{\ast }$
as in Subsection 2.6.2.
5.2 Compatibility between the product and the coproduct
In this section, we show that
![]() $\widetilde {m}$
and
$\widetilde {m}$
and
![]() $\widetilde {\Delta }$
are compatible. Recall the forget-the-potential map (1.8):
$\widetilde {\Delta }$
are compatible. Recall the forget-the-potential map (1.8):
Recall that
![]() $K_T(\mathbb {S}_A)_{\mathbb {F}}\hookrightarrow K_T(\mathbb {M}_A)_{\mathbb {F}}$
; see [Reference Pădurariu and TodaPTa, Theorem 4.12 and Equation (4.36)]. Let
$K_T(\mathbb {S}_A)_{\mathbb {F}}\hookrightarrow K_T(\mathbb {M}_A)_{\mathbb {F}}$
; see [Reference Pădurariu and TodaPTa, Theorem 4.12 and Equation (4.36)]. Let
Theorem 5.2. Consider a pair
![]() $(d, w)\in \mathbb {N}\times \mathbb {Z}$
. Let
$(d, w)\in \mathbb {N}\times \mathbb {Z}$
. Let
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
be dominant cocharacters with associated partitions
$\mu $
be dominant cocharacters with associated partitions
![]() $A=(d_i, w_i)_{i=1}^k$
and
$A=(d_i, w_i)_{i=1}^k$
and
![]() $B=(e_i, v_i)_{i=1}^s$
in
$B=(e_i, v_i)_{i=1}^s$
in
![]() $H_{d, w}$
. Let
$H_{d, w}$
. Let
![]() $S^B_A\subset S^{\mu }_{\lambda }$
be the set of partitions
$S^B_A\subset S^{\mu }_{\lambda }$
be the set of partitions
![]() $C=(f_i, u_i)_{i=1}^l$
with
$C=(f_i, u_i)_{i=1}^l$
with
![]() $l=ks$
with
$l=ks$
with
![]() $\overline {C}$
in
$\overline {C}$
in
![]() $H_{d,w}$
and such that
$H_{d,w}$
and such that
 $$ \begin{align*} f_{(i-1)s+1}+f_{(i-1)s+2}+\ldots+f_{is}&=d_i\text{ for }1\leqslant i\leqslant k,\\ f_j+f_{s+j}+\ldots+f_{(k-1)s+j}&=e_j\text{ for }1\leqslant j\leqslant s. \end{align*} $$
$$ \begin{align*} f_{(i-1)s+1}+f_{(i-1)s+2}+\ldots+f_{is}&=d_i\text{ for }1\leqslant i\leqslant k,\\ f_j+f_{s+j}+\ldots+f_{(k-1)s+j}&=e_j\text{ for }1\leqslant j\leqslant s. \end{align*} $$
Then the following diagram commutes:

Theorem 5.2 is a T-equivariant version of [Reference PădurariuPăda, Theorem 5.2], and the same proof works to show this statement. However, we present an alternative proof which first proves a categorical statement about complexes in
![]() $D^b(\mathcal {X}(d)^{\mu })$
which is stronger than the results in loc. cit. and is of independent interest for computations in categorical Hall algebras.
$D^b(\mathcal {X}(d)^{\mu })$
which is stronger than the results in loc. cit. and is of independent interest for computations in categorical Hall algebras.
Note that the compatibility of the product and coproduct for localized K-theory, either in the above setting or in the setting of Corollary 5.6, follows by a direct computation and Propositions 5.7 and 5.8.
Proposition 5.3. Let
![]() $A, B$
be as in Theorem 5.2. For
$A, B$
be as in Theorem 5.2. For
![]() $1\leqslant i\leqslant k$
, let
$1\leqslant i\leqslant k$
, let
![]() $\chi _i$
be a dominant weight of
$\chi _i$
be a dominant weight of
![]() $T(d_i)$
for
$T(d_i)$
for
![]() $1\leqslant i\leqslant k$
such that
$1\leqslant i\leqslant k$
such that
![]() $\chi _i+\rho _i\in \mathbf {W}(d_i)$
. Let
$\chi _i+\rho _i\in \mathbf {W}(d_i)$
. Let
![]() $\chi :=\sum _{i=1}^k \chi _i$
. For any
$\chi :=\sum _{i=1}^k \chi _i$
. For any
![]() $C\in S^B_A$
, there are natural maps,
$C\in S^B_A$
, there are natural maps,
such that there is an isomorphism
 $$ \begin{align} \bigoplus_{C\in S^B_A} \widehat{m}_{CB}\widetilde{\Delta}_{AC}\left( \mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi)\right)\xrightarrow{\sim} \widetilde{\Delta}_B \widetilde{m}_A\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi)\right). \end{align} $$
$$ \begin{align} \bigoplus_{C\in S^B_A} \widehat{m}_{CB}\widetilde{\Delta}_{AC}\left( \mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi)\right)\xrightarrow{\sim} \widetilde{\Delta}_B \widetilde{m}_A\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi)\right). \end{align} $$
Proof of Theorem 5.2.
By Proposition 5.3, the following diagram commutes:

The maps
![]() $\widetilde {m}$
and
$\widetilde {m}$
and
![]() $\widetilde {\Delta }$
are compatible with the forget-the-potential map (1.8) by [Reference PădurariuPăd22, Proposition 3.6] and [Reference PădurariuPăda, Proposition 5.1], respectively. The conclusion thus follows.
$\widetilde {\Delta }$
are compatible with the forget-the-potential map (1.8) by [Reference PădurariuPăd22, Proposition 3.6] and [Reference PădurariuPăda, Proposition 5.1], respectively. The conclusion thus follows.
Proof of Proposition 5.3.
The argument follows closely the proof of [Reference PădurariuPădb, Theorem 5.2]. We give an overview of the proof. We use a Koszul resolution to compute
![]() $\widetilde {m}_A\left (\mathcal {O}_{\mathcal {X}(d)^{\lambda }}\otimes \Gamma _{GL(d)^{\lambda }}(\chi )\right )$
in terms of
$\widetilde {m}_A\left (\mathcal {O}_{\mathcal {X}(d)^{\lambda }}\otimes \Gamma _{GL(d)^{\lambda }}(\chi )\right )$
in terms of
![]() $\mathcal {O}\otimes \Gamma _{GL(d)}(\theta )$
, where
$\mathcal {O}\otimes \Gamma _{GL(d)}(\theta )$
, where
![]() $\theta =(\chi -\sigma _I)^+$
for
$\theta =(\chi -\sigma _I)^+$
for
![]() $\sigma _I$
a partial sum of weights pairing positively with
$\sigma _I$
a partial sum of weights pairing positively with
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mathcal {O}\otimes \Gamma _{GL(d)}(\theta )$
be a vector bundle appearing in the Koszul resolution with nonzero
$\mathcal {O}\otimes \Gamma _{GL(d)}(\theta )$
be a vector bundle appearing in the Koszul resolution with nonzero
![]() $\widetilde {\Delta }_B$
. Then the weight
$\widetilde {\Delta }_B$
. Then the weight
![]() $\theta $
is on a face of
$\theta $
is on a face of
![]() $\textbf {W}(d)$
; see Equation (5.9). We use Proposition 5.4 to characterize the highest weights
$\textbf {W}(d)$
; see Equation (5.9). We use Proposition 5.4 to characterize the highest weights
![]() $\theta $
on a face of
$\theta $
on a face of
![]() $\textbf {W}(d)$
in terms of partitions
$\textbf {W}(d)$
in terms of partitions
![]() $C\in S^B_A$
. The proof then follows from a direct comparison with the right-hand side of Equation (5.12). Let
$C\in S^B_A$
. The proof then follows from a direct comparison with the right-hand side of Equation (5.12). Let
![]() $\sigma _I$
be a sum such that
$\sigma _I$
be a sum such that
![]() $\chi -\sigma _I$
is on a face of
$\chi -\sigma _I$
is on a face of
![]() $\textbf {W}(d)$
corresponding to
$\textbf {W}(d)$
corresponding to
![]() $C\in S^B_A$
with associated permutation w; see Equation (5.4). The swap morphism appears because conjugating
$C\in S^B_A$
with associated permutation w; see Equation (5.4). The swap morphism appears because conjugating
![]() $\chi -\sigma _I$
to
$\chi -\sigma _I$
to
![]() $\theta =(\chi -\sigma _I)^+$
first requires to act by w.
$\theta =(\chi -\sigma _I)^+$
first requires to act by w.
The multiplication
![]() $\widetilde {m}_A$
is defined as
$\widetilde {m}_A$
is defined as
![]() $\widetilde {m}_A=p_{\lambda ^{-1}*}q_{\lambda ^{-1}}^{*}$
. Let
$\widetilde {m}_A=p_{\lambda ^{-1}*}q_{\lambda ^{-1}}^{*}$
. Let
![]() $\chi :=\sum _{i=1}^k \chi _i$
. Consider the Koszul resolution
$\chi :=\sum _{i=1}^k \chi _i$
. Consider the Koszul resolution
 $$ \begin{align*} \widetilde{m}_A\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right)&= \pi_{\lambda^{-1}*}\iota_{\lambda^{-1}*}q_{\lambda^{-1}}^{*}\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right)\\ &\cong \pi_{\lambda^{-1}*}\left(\bigoplus_{I\subset A_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi-\sigma_I)[|I|], d\right); \end{align*} $$
$$ \begin{align*} \widetilde{m}_A\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right)&= \pi_{\lambda^{-1}*}\iota_{\lambda^{-1}*}q_{\lambda^{-1}}^{*}\left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right)\\ &\cong \pi_{\lambda^{-1}*}\left(\bigoplus_{I\subset A_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi-\sigma_I)[|I|], d\right); \end{align*} $$
see Proposition 2.1 for the notation. The differential d is induced by multiplication with generators
![]() $(e_i)_{i=1}^t$
of the polynomial ring
$(e_i)_{i=1}^t$
of the polynomial ring
![]() $\mathbb {C}\left [R(d)^{\lambda <0}\right ]\cong \mathbb {C}[e_1,\ldots , e_t]$
. Fix
$\mathbb {C}\left [R(d)^{\lambda <0}\right ]\cong \mathbb {C}[e_1,\ldots , e_t]$
. Fix
![]() $C\in S^B_A$
, consider the associated dominant cocharacters
$C\in S^B_A$
, consider the associated dominant cocharacters
![]() $\nu $
and
$\nu $
and
![]() $\kappa $
and let
$\kappa $
and let
![]() $w=w_C\in \mathfrak {S}_d$
as in Equation (5.4). Let
$w=w_C\in \mathfrak {S}_d$
as in Equation (5.4). Let
![]() $\varphi :=w^{-1}\mu $
. There are natural maps of complexes
$\varphi :=w^{-1}\mu $
. There are natural maps of complexes
 $$ \begin{align} \pi_{\lambda^{-1} *} &\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes\mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [\lvert I^{\varphi}_{\lambda} \rvert+\lvert J \rvert], d \right) \to\\&\qquad\qquad\qquad\pi_{\lambda^{-1} *}\left(\bigoplus_{I\subset A_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi)\otimes \mathcal{O}(-\sigma_I)[|I|], d\right)\nonumber \end{align} $$
$$ \begin{align} \pi_{\lambda^{-1} *} &\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes\mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [\lvert I^{\varphi}_{\lambda} \rvert+\lvert J \rvert], d \right) \to\\&\qquad\qquad\qquad\pi_{\lambda^{-1} *}\left(\bigoplus_{I\subset A_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi)\otimes \mathcal{O}(-\sigma_I)[|I|], d\right)\nonumber \end{align} $$
induced by the inclusion of sets
The differential d of the complex on the first line is induced by multiplication with generators of the polynomial ring
![]() $\mathbb {C}\left [\left (R(d)^{\varphi }\right )^{\lambda <0}\right ]$
. For
$\mathbb {C}\left [\left (R(d)^{\varphi }\right )^{\lambda <0}\right ]$
. For
![]() $C, C'$
different elements in
$C, C'$
different elements in
![]() $S^B_A$
, we have that
$S^B_A$
, we have that
![]() $I_C\cap I_{C'}=\emptyset $
. If
$I_C\cap I_{C'}=\emptyset $
. If
![]() $\sigma \in \{\sigma _I \mid I\subset A_{\lambda }\}\setminus \left (\bigcup _{C\in S^B_A}I_C\right )$
, then
$\sigma \in \{\sigma _I \mid I\subset A_{\lambda }\}\setminus \left (\bigcup _{C\in S^B_A}I_C\right )$
, then
![]() $\mathcal {O}_{R(d)}\otimes \Gamma _{GL(d)^{\lambda \leqslant 0}}(\chi )\otimes \mathcal {O}(-\sigma _I)$
has
$\mathcal {O}_{R(d)}\otimes \Gamma _{GL(d)^{\lambda \leqslant 0}}(\chi )\otimes \mathcal {O}(-\sigma _I)$
has
![]() $u\mu $
-weights strictly less than
$u\mu $
-weights strictly less than
![]() $\frac {n_{\mu }}{2}=\langle \mu , \mathfrak {g}^{\mu>0}\rangle $
for all
$\frac {n_{\mu }}{2}=\langle \mu , \mathfrak {g}^{\mu>0}\rangle $
for all
![]() $u\in \mathfrak {S}_d$
; see Proposition 5.4. It follows that
$u\in \mathfrak {S}_d$
; see Proposition 5.4. It follows that
for such sums
![]() $\sigma $
; see Equation (5.9). It suffices to show that, for
$\sigma $
; see Equation (5.9). It suffices to show that, for
![]() $C\in S^B_A$
, we have natural isomorphisms of complexes
$C\in S^B_A$
, we have natural isomorphisms of complexes
 $$ \begin{align} \widetilde{\Delta}_B\pi_{\lambda^{-1}*} &\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes\mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right)\\&\qquad\qquad\qquad\qquad\qquad\qquad\cong \widehat{m}_{CB}\widetilde{\Delta}_{AC} \left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right).\nonumber \end{align} $$
$$ \begin{align} \widetilde{\Delta}_B\pi_{\lambda^{-1}*} &\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes\mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right)\\&\qquad\qquad\qquad\qquad\qquad\qquad\cong \widehat{m}_{CB}\widetilde{\Delta}_{AC} \left(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes\Gamma_{GL(d)^{\lambda}}(\chi)\right).\nonumber \end{align} $$
Using Equation (5.13), we obtain the natural maps (5.11), and further we obtain the isomorphism (5.12) using the vanishing (5.14).
For
![]() $J\subset A^{\varphi }_{\lambda }$
, we have that
$J\subset A^{\varphi }_{\lambda }$
, we have that
see Proposition 5.4. Let
![]() $\widetilde {w}_J\in \mathfrak {S}_{d}$
be the element of minimal length such that
$\widetilde {w}_J\in \mathfrak {S}_{d}$
be the element of minimal length such that
![]() $\widetilde {w}_J*\left (\chi -N^{\varphi }_{\lambda }-\sigma _J\right )$
is dominant or zero. Observe that
$\widetilde {w}_J*\left (\chi -N^{\varphi }_{\lambda }-\sigma _J\right )$
is dominant or zero. Observe that
![]() $\widetilde {w}_{\emptyset }=w$
. However, for general J, we have that
$\widetilde {w}_{\emptyset }=w$
. However, for general J, we have that
![]() $\widetilde {w}_J=u_J\circ w$
for a permutation
$\widetilde {w}_J=u_J\circ w$
for a permutation
![]() $u_J$
in
$u_J$
in
![]() $\times _{i=1}^s\mathfrak {S}_{e_i}\cong W^{\mu }$
and
$\times _{i=1}^s\mathfrak {S}_{e_i}\cong W^{\mu }$
and
![]() $\ell (\widetilde {w}_J)=\ell (w)+\ell (u_J)$
. By the Borel–Bott–Weyl theorem, there is a natural isomorphism
$\ell (\widetilde {w}_J)=\ell (w)+\ell (u_J)$
. By the Borel–Bott–Weyl theorem, there is a natural isomorphism
 $$ \begin{align*} &\pi_{\lambda^{-1}*}\left( \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) \right)\cong\\ &\pi_{\lambda^{-1}*}\left( \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right)[-|J^{\varphi}_{\lambda}|] \right) \end{align*} $$
$$ \begin{align*} &\pi_{\lambda^{-1}*}\left( \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) \right)\cong\\ &\pi_{\lambda^{-1}*}\left( \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right)[-|J^{\varphi}_{\lambda}|] \right) \end{align*} $$
and further there are natural isomorphisms
 $$ \begin{align} & \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\\notag& \quad \cong \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [|I^{\varphi}_{\lambda}|-|J^{\varphi}_{\lambda}|+|J|], d \right) \\\notag&\quad \cong \pi_{\kappa^{-1}\mu*}\left(\bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)^{\mu}}\otimes\Gamma_{(GL(d)^{\mu})^{\kappa\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [|I^{\varphi}_{\lambda}|-|J^{\varphi}_{\lambda}|+|J|], d \right). \end{align} $$
$$ \begin{align} & \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\\notag& \quad \cong \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [|I^{\varphi}_{\lambda}|-|J^{\varphi}_{\lambda}|+|J|], d \right) \\\notag&\quad \cong \pi_{\kappa^{-1}\mu*}\left(\bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)^{\mu}}\otimes\Gamma_{(GL(d)^{\mu})^{\kappa\leqslant 0}}\left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [|I^{\varphi}_{\lambda}|-|J^{\varphi}_{\lambda}|+|J|], d \right). \end{align} $$
We have that
For a weight
![]() $\theta $
of
$\theta $
of
![]() $T(d)$
, denote by
$T(d)$
, denote by
For a subset
![]() $J\subset A^{\varphi }_{\lambda }$
, let
$J\subset A^{\varphi }_{\lambda }$
, let
![]() $J'=\{w\beta \mid \beta \in J\}$
be the corresponding subset of
$J'=\{w\beta \mid \beta \in J\}$
be the corresponding subset of
![]() $I_{\kappa \mu }:=\{\beta \text { weight of }R(d)^{\mu } \mid \langle \kappa , \beta \rangle>0\}$
; see Proposition 5.5. There is an isomorphism
$I_{\kappa \mu }:=\{\beta \text { weight of }R(d)^{\mu } \mid \langle \kappa , \beta \rangle>0\}$
; see Proposition 5.5. There is an isomorphism
 $$ \begin{align} \mathcal{O}_{(\mathcal{X}(d)^{\mu})^{\kappa\leqslant 0}}\otimes \Gamma_{(GL(d)^{\mu})^{\kappa\leqslant 0}} \left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [-|J^{\varphi}_{\lambda}|] \cong\\ \notag q_{\kappa^{-1}\mu}^{*} \left(\Psi \left(\mathcal{O}_{\mathcal{X}(d)^{\nu}}\otimes\Gamma_{GL(d)^{\nu}} \left(\chi-N^{\varphi}_{\lambda}\right) [-|J^{\varphi}_{\lambda}|]\right)\otimes\mathcal{O}(-\sigma_{J'})\right).\end{align} $$
$$ \begin{align} \mathcal{O}_{(\mathcal{X}(d)^{\mu})^{\kappa\leqslant 0}}\otimes \Gamma_{(GL(d)^{\mu})^{\kappa\leqslant 0}} \left(w*(\chi-N^{\varphi}_{\lambda}-\sigma_J)\right) [-|J^{\varphi}_{\lambda}|] \cong\\ \notag q_{\kappa^{-1}\mu}^{*} \left(\Psi \left(\mathcal{O}_{\mathcal{X}(d)^{\nu}}\otimes\Gamma_{GL(d)^{\nu}} \left(\chi-N^{\varphi}_{\lambda}\right) [-|J^{\varphi}_{\lambda}|]\right)\otimes\mathcal{O}(-\sigma_{J'})\right).\end{align} $$
For
![]() $\mathcal {B}$
a complex in
$\mathcal {B}$
a complex in
![]() $D^b(\mathcal {X}(d)^{\nu })$
, by the definition of
$D^b(\mathcal {X}(d)^{\nu })$
, by the definition of
![]() $\widetilde {\text {sw}}_C$
we have that
$\widetilde {\text {sw}}_C$
we have that
We next want to use Proposition 2.1 for the map
![]() $\iota _{\kappa ^{-1}\mu }$
. For this, it is convenient to use the following notation
$\iota _{\kappa ^{-1}\mu }$
. For this, it is convenient to use the following notation
for
![]() $\theta $
a dominant weight of
$\theta $
a dominant weight of
![]() $T(d)$
. We consider the Koszul resolution
$T(d)$
. We consider the Koszul resolution
 $$ \begin{align} &\iota_{\kappa^{-1}\mu*}q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes\Gamma_{GL(d)^{\kappa}}(\chi)\right)\right)\cong \\&\qquad\qquad\left(\bigoplus_{J'\subset I_{\kappa\mu}} \mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes\Gamma_{GL(d)^{\kappa}}(\chi)\right)\right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right),\nonumber\end{align} $$
$$ \begin{align} &\iota_{\kappa^{-1}\mu*}q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes\Gamma_{GL(d)^{\kappa}}(\chi)\right)\right)\cong \\&\qquad\qquad\left(\bigoplus_{J'\subset I_{\kappa\mu}} \mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes\Gamma_{GL(d)^{\kappa}}(\chi)\right)\right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right),\nonumber\end{align} $$
where the differential d is induced by multiplication with generators of the polynomial ring
![]() $\mathbb {C}\left [\left (R(d)^{\mu }\right )^{\kappa <0}\right ]$
. Rewrite Equation (5.16) using Equations (5.18), (5.19), (5.20):
$\mathbb {C}\left [\left (R(d)^{\mu }\right )^{\kappa <0}\right ]$
. Rewrite Equation (5.16) using Equations (5.18), (5.19), (5.20):
 $$ \begin{align} & \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\\notag&\quad \cong \pi_{\kappa^{-1}\mu*} \left(\bigoplus_{J'\subset I_{\kappa\mu}}\mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)) \right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right)\right). \end{align} $$
$$ \begin{align} & \widetilde{\Delta}_B\pi_{\lambda^{-1}*}\left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes\Gamma_{GL(d)^{\lambda\leqslant 0}}\left(\chi-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\\notag&\quad \cong \pi_{\kappa^{-1}\mu*} \left(\bigoplus_{J'\subset I_{\kappa\mu}}\mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)) \right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right)\right). \end{align} $$
There are isomorphisms
 $$ \begin{align*} &\widetilde{\Delta}_B \pi_{\lambda^{-1}*} \left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes \Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes \mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\&\quad\overset{(1)}{\cong} \pi_{\kappa^{-1}\mu*} \left(\bigoplus_{J'\subset I_{\kappa\mu}}\mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi) \right)\right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right)\\&\quad\overset{(2)}{\cong}\pi_{\kappa^{-1}\mu*} \iota_{\kappa^{-1}\mu*} q_{\kappa^{-1}\mu}^{*} \left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)\right) \right) \\&\quad\overset{(3)}{\cong}\widetilde{m}_{CB} \left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)\right) \right)\\&\quad\overset{(4)}{\cong}\widetilde{m}_{CB} \left(\widetilde{\text{sw}}_{C} \left(\widetilde{\Delta}_{AC}(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi))\right) \right). \end{align*} $$
$$ \begin{align*} &\widetilde{\Delta}_B \pi_{\lambda^{-1}*} \left( \bigoplus_{J\subset A^{\varphi}_{\lambda}} \mathcal{O}_{R(d)}\otimes \Gamma_{GL(d)^{\lambda\leqslant 0}}(\chi) \otimes \mathcal{O}\left(-N^{\varphi}_{\lambda}-\sigma_J\right) [|I^{\varphi}_{\lambda}|+|J|], d \right) \\&\quad\overset{(1)}{\cong} \pi_{\kappa^{-1}\mu*} \left(\bigoplus_{J'\subset I_{\kappa\mu}}\mathrm{F} q_{\kappa^{-1}\mu}^{*}\left(\widetilde{\text{sw}}_{C}\left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi) \right)\right)\otimes \mathcal{O}(-\sigma_{J'})[|J'|], d\right)\\&\quad\overset{(2)}{\cong}\pi_{\kappa^{-1}\mu*} \iota_{\kappa^{-1}\mu*} q_{\kappa^{-1}\mu}^{*} \left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)\right) \right) \\&\quad\overset{(3)}{\cong}\widetilde{m}_{CB} \left(\widetilde{\text{sw}}_{C} \left(\mathcal{O}_{\mathcal{X}(d)^{\kappa}}\otimes \Gamma_{GL(d)^{\kappa}}(\chi)\right) \right)\\&\quad\overset{(4)}{\cong}\widetilde{m}_{CB} \left(\widetilde{\text{sw}}_{C} \left(\widetilde{\Delta}_{AC}(\mathcal{O}_{\mathcal{X}(d)^{\lambda}}\otimes \Gamma_{GL(d)^{\lambda}}(\chi))\right) \right). \end{align*} $$
Recall that
![]() $\widetilde {m}_{\kappa \mu }=\widetilde {m}_{CB}$
and
$\widetilde {m}_{\kappa \mu }=\widetilde {m}_{CB}$
and
![]() $\widetilde {\Delta }_{\nu \lambda }=\widetilde {\Delta }_{AC}$
. The isomorphism (1) is the isomorphism (5.22), and it respects the differentials. The isomorphism (2) follows from Equation (5.21). The isomorphism (3) follows from the definition of
$\widetilde {\Delta }_{\nu \lambda }=\widetilde {\Delta }_{AC}$
. The isomorphism (1) is the isomorphism (5.22), and it respects the differentials. The isomorphism (2) follows from Equation (5.21). The isomorphism (3) follows from the definition of
![]() $\widetilde {m}_{CB}$
. The isomorphism (4) follows from Equation (5.17) and the equality
$\widetilde {m}_{CB}$
. The isomorphism (4) follows from Equation (5.17) and the equality
Proposition 5.4. Let
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
be dominant cocharacters of
$\mu $
be dominant cocharacters of
![]() $GL(d)$
, and let
$GL(d)$
, and let
![]() $w\in W$
. Assume that
$w\in W$
. Assume that
![]() $\chi $
is a dominant weight with
$\chi $
is a dominant weight with
![]() $\chi +\rho \in F(\lambda )$
and that
$\chi +\rho \in F(\lambda )$
and that
![]() $I\subset A_{\lambda }$
such that
$I\subset A_{\lambda }$
such that
![]() $w*(\chi -\sigma _I)+\rho \in F(\mu )$
. Let
$w*(\chi -\sigma _I)+\rho \in F(\mu )$
. Let
![]() $\varphi :=w^{-1}\mu $
. Then
$\varphi :=w^{-1}\mu $
. Then
for a subset
![]() $J\subset A^{\varphi }_{\lambda }$
.
$J\subset A^{\varphi }_{\lambda }$
.
Conversely, for all
![]() $I\subset A_{\lambda }$
as in Equation (5.23), we have
$I\subset A_{\lambda }$
as in Equation (5.23), we have
![]() $w*(\chi -\sigma _I)+\rho \in F(\mu )$
.
$w*(\chi -\sigma _I)+\rho \in F(\mu )$
.
Proof. For two cocharacters
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
, we use the notations
$\tau '$
, we use the notations
 $$\begin{align*}N^{\tau>0}:=\sum_{A_{\tau}}\beta,\ N^{\tau'=0, \tau>0}=\sum_{A^{\tau'}_{\tau}}\beta.\end{align*}$$
$$\begin{align*}N^{\tau>0}:=\sum_{A_{\tau}}\beta,\ N^{\tau'=0, \tau>0}=\sum_{A^{\tau'}_{\tau}}\beta.\end{align*}$$
Let
![]() $v=\langle 1_d, \chi \rangle $
. Write
$v=\langle 1_d, \chi \rangle $
. Write
 $$ \begin{align*} \chi-v\tau_d+\rho&=\frac{1}{2}N^{\lambda>0}+\psi,\\ w*(\chi-v\tau_d-\sigma_I)+\rho&=\frac{1}{2}N^{\mu>0}+\phi',\\ \chi-v\tau_d-\sigma_I+\rho&=\frac{1}{2}N^{\varphi>0}+\phi, \end{align*} $$
$$ \begin{align*} \chi-v\tau_d+\rho&=\frac{1}{2}N^{\lambda>0}+\psi,\\ w*(\chi-v\tau_d-\sigma_I)+\rho&=\frac{1}{2}N^{\mu>0}+\phi',\\ \chi-v\tau_d-\sigma_I+\rho&=\frac{1}{2}N^{\varphi>0}+\phi, \end{align*} $$
where
![]() $\psi \in \textbf {W}(\lambda )_0$
and
$\psi \in \textbf {W}(\lambda )_0$
and
![]() $\phi \in \textbf {W}(\varphi )_0$
; see [Reference PădurariuPăd23, Proposition 3.4]. Then
$\phi \in \textbf {W}(\varphi )_0$
; see [Reference PădurariuPăd23, Proposition 3.4]. Then
 $$ \begin{align} \sigma_I=N_{\lambda}^{\varphi}+\left(\frac{1}{2}N^{\varphi=0, \lambda>0}-\phi\right)+\left(\psi-\frac{1}{2}N^{\lambda=0, \varphi>0}\right). \end{align} $$
$$ \begin{align} \sigma_I=N_{\lambda}^{\varphi}+\left(\frac{1}{2}N^{\varphi=0, \lambda>0}-\phi\right)+\left(\psi-\frac{1}{2}N^{\lambda=0, \varphi>0}\right). \end{align} $$
The weight
![]() $\widetilde {\phi }:=\frac {1}{2}N^{\varphi =0, \lambda>0}-\phi $
is a sum with nonnegative coefficients of weights
$\widetilde {\phi }:=\frac {1}{2}N^{\varphi =0, \lambda>0}-\phi $
is a sum with nonnegative coefficients of weights
![]() $\beta $
such that
$\beta $
such that
![]() $\langle \varphi , \beta \rangle =0$
and
$\langle \varphi , \beta \rangle =0$
and
![]() $\langle \lambda , \beta \rangle>0$
and weights
$\langle \lambda , \beta \rangle>0$
and weights
![]() $\beta '$
such that
$\beta '$
such that
![]() $\langle \varphi , \beta '\rangle =\langle \lambda , \beta '\rangle =0$
. The weight
$\langle \varphi , \beta '\rangle =\langle \lambda , \beta '\rangle =0$
. The weight
![]() $\widetilde {\psi }:=\psi -\frac {1}{2}N^{\lambda =0, \varphi>0}$
is a sum with nonnegative coefficients of weights
$\widetilde {\psi }:=\psi -\frac {1}{2}N^{\lambda =0, \varphi>0}$
is a sum with nonnegative coefficients of weights
![]() $\beta $
such that
$\beta $
such that
![]() $\langle \lambda , \beta \rangle =0$
and
$\langle \lambda , \beta \rangle =0$
and
![]() $\langle \varphi , \beta \rangle <0$
and weights
$\langle \varphi , \beta \rangle <0$
and weights
![]() $\beta '$
such that
$\beta '$
such that
![]() $\langle \varphi , \beta '\rangle =\langle \lambda , \beta '\rangle =0$
. We denote by
$\langle \varphi , \beta '\rangle =\langle \lambda , \beta '\rangle =0$
. We denote by
![]() $\sigma ^{\lambda +}_{\varphi 0}$
a sum with nonnegative coefficients of weights
$\sigma ^{\lambda +}_{\varphi 0}$
a sum with nonnegative coefficients of weights
![]() $\beta $
such that
$\beta $
such that
![]() $\langle \lambda , \beta \rangle>0$
and
$\langle \lambda , \beta \rangle>0$
and
![]() $\langle \varphi , \beta \rangle =0$
etc. Then we can write
$\langle \varphi , \beta \rangle =0$
etc. Then we can write
where all the sums on the right-hand side are further partial sums of weights in
![]() $A_{\lambda }$
. We can rewrite Equation (5.24) as
$A_{\lambda }$
. We can rewrite Equation (5.24) as
The
![]() $\varphi $
-weight of the left-hand side is nonnegative, while the
$\varphi $
-weight of the left-hand side is nonnegative, while the
![]() $\varphi $
-weight of the right-hand side is nonpositive. Thus,
$\varphi $
-weight of the right-hand side is nonpositive. Thus,
![]() $\sigma ^{\lambda +}_{\varphi +}=n^{\lambda +}_{\varphi -}=\widetilde {\psi }^{\lambda 0}_{\varphi -}=0$
. In particular, Equation (5.25) becomes
$\sigma ^{\lambda +}_{\varphi +}=n^{\lambda +}_{\varphi -}=\widetilde {\psi }^{\lambda 0}_{\varphi -}=0$
. In particular, Equation (5.25) becomes
which implies the first direction. The converse follows in a similar way.
Proposition 5.5. For a subset
![]() $J\subset A^{\varphi }_{\lambda }$
, the set
$J\subset A^{\varphi }_{\lambda }$
, the set
![]() $J'=\{w\beta \mid \beta \in J\}$
is a subset of
$J'=\{w\beta \mid \beta \in J\}$
is a subset of
![]() $I_{\kappa \mu }:=\{\beta \text { weight of }R(d)^{\mu }\mid \langle \kappa , \beta \rangle>0\}$
. This transformation induces a bijection of sets
$I_{\kappa \mu }:=\{\beta \text { weight of }R(d)^{\mu }\mid \langle \kappa , \beta \rangle>0\}$
. This transformation induces a bijection of sets
![]() $A^{\varphi }_{\lambda }\xrightarrow {\sim } I_{\kappa \mu }$
.
$A^{\varphi }_{\lambda }\xrightarrow {\sim } I_{\kappa \mu }$
.
Proof. It suffices to check the first claim. To construct an inverse of this transformation, send
![]() $L\subset I_{\kappa \mu }$
to
$L\subset I_{\kappa \mu }$
to
![]() $L^{\circ }=\{w^{-1}\beta \mid \beta \in L\}$
.
$L^{\circ }=\{w^{-1}\beta \mid \beta \in L\}$
.
Let
![]() $\beta \in A^{\varphi }_{\lambda }$
. Recall that
$\beta \in A^{\varphi }_{\lambda }$
. Recall that
![]() $\varphi =w^{-1}\mu $
, so we have that
$\varphi =w^{-1}\mu $
, so we have that
![]() $\langle w^{-1}\mu , \beta \rangle =0$
, and thus
$\langle w^{-1}\mu , \beta \rangle =0$
, and thus
![]() $\langle \mu , w\beta \rangle =0$
.
$\langle \mu , w\beta \rangle =0$
.
It suffices to show that if a weight
![]() $\beta _i-\beta _j$
is in
$\beta _i-\beta _j$
is in
![]() $A^{\varphi }_{\lambda }$
, then
$A^{\varphi }_{\lambda }$
, then
![]() $\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
. For simplicity, we discuss the case when
$\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
. For simplicity, we discuss the case when
![]() $k=s=2$
. Rename
$k=s=2$
. Rename
![]() $f_{11}=f_1$
,
$f_{11}=f_1$
,
![]() $f_{12}=f_2$
,
$f_{12}=f_2$
,
![]() $f_{21}=f_3$
,
$f_{21}=f_3$
,
![]() $f_{22}=f_4$
. The permutation w is
$f_{22}=f_4$
. The permutation w is
 $$ \begin{align*} w(i)=\begin{cases} i+f_3,\text{ if }f_1+1\leqslant i\leqslant f_1+f_2,\\ i-f_2,\text{ if }f_1+f_2+1\leqslant i\leqslant f_1+f_2+f_3,\\ i,\text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} w(i)=\begin{cases} i+f_3,\text{ if }f_1+1\leqslant i\leqslant f_1+f_2,\\ i-f_2,\text{ if }f_1+f_2+1\leqslant i\leqslant f_1+f_2+f_3,\\ i,\text{ otherwise}. \end{cases} \end{align*} $$
We have that
so one of two possibilities happens:
 $$ \begin{align*} (1)\, & f_1+f_2+f_3+1\leqslant i\leqslant f_1+f_2+f_3+f_4\text{ and }f_1+1\leqslant j\leqslant f_1+f_2,\\ (2)\, & f_1+f_2+1\leqslant i\leqslant f_1+f_2+f_3\text{ and }1\leqslant j\leqslant f_1. \end{align*} $$
$$ \begin{align*} (1)\, & f_1+f_2+f_3+1\leqslant i\leqslant f_1+f_2+f_3+f_4\text{ and }f_1+1\leqslant j\leqslant f_1+f_2,\\ (2)\, & f_1+f_2+1\leqslant i\leqslant f_1+f_2+f_3\text{ and }1\leqslant j\leqslant f_1. \end{align*} $$
In case (1), we have that
![]() $i=w(i)$
and
$i=w(i)$
and
![]() $f_1+f_3+1\leqslant w(j)\leqslant f_1+f_3+f_2$
, and then
$f_1+f_3+1\leqslant w(j)\leqslant f_1+f_3+f_2$
, and then
![]() $\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
. In case (2), we have that
$\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
. In case (2), we have that
![]() $f_1+1\leqslant w(i)\leqslant f_1+f_3$
and
$f_1+1\leqslant w(i)\leqslant f_1+f_3$
and
![]() $j=w(j)$
, and then
$j=w(j)$
, and then
![]() $\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
.
$\langle \kappa , \beta _{w(i)}-\beta _{w(j)}\rangle>0$
.
5.3 The bialgebra structure under the Koszul equivalence
Let
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime integers. For
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime integers. For
![]() $n\in \mathbb {N}$
, denote by
$n\in \mathbb {N}$
, denote by
![]() $R_n$
the set of ordered partitions
$R_n$
the set of ordered partitions
![]() $A=(n_i)_{i=1}^k$
of n with
$A=(n_i)_{i=1}^k$
of n with
![]() $n_i\geqslant 1$
. For each such partition A of n, denote also by A the partition
$n_i\geqslant 1$
. For each such partition A of n, denote also by A the partition
![]() $(n_id, n_iv)_{i=1}^k$
of
$(n_id, n_iv)_{i=1}^k$
of
![]() $(nd, nv)$
. Let
$(nd, nv)$
. Let
![]() $\gamma _i$
be the weights of T for
$\gamma _i$
be the weights of T for
![]() $i\in \{1, 2\}$
with
$i\in \{1, 2\}$
with
![]() $q^{\gamma _i}=q_i\in \mathbb {K}$
. Let
$q^{\gamma _i}=q_i\in \mathbb {K}$
. Let
![]() $\gamma =\gamma _1+\gamma _2$
, and let
$\gamma =\gamma _1+\gamma _2$
, and let
![]() $q^{\gamma }=q_1q_2$
. For simplicity, we will denote
$q^{\gamma }=q_1q_2$
. For simplicity, we will denote
![]() $q^{\gamma }$
just by q.
$q^{\gamma }$
just by q.
5.3.1
The coproduct (5.10) induces coproduct maps
for C a refinement of A as follows. Recall the Koszul equivalence
for all pairs
![]() $(e, v)\in \mathbb {N}\times \mathbb {Z}$
. Let
$(e, v)\in \mathbb {N}\times \mathbb {Z}$
. Let
![]() $A=(n_id, w_i)_{i=1}^k$
be a partition of
$A=(n_id, w_i)_{i=1}^k$
be a partition of
![]() $(nd, nv)$
with associated prime partition
$(nd, nv)$
with associated prime partition
![]() $A'=(n_id, n_iv)_{i=1}^k$
; see Subsection 2.2.7. Let
$A'=(n_id, n_iv)_{i=1}^k$
; see Subsection 2.2.7. Let
![]() $\mathbb {T}_A:=\otimes _{i=1}^k \mathbb {T}(n_id)_{n_iv}$
. There is a Koszul equivalence
$\mathbb {T}_A:=\otimes _{i=1}^k \mathbb {T}(n_id)_{n_iv}$
. There is a Koszul equivalence
Let
![]() $\Phi _A^{-1}$
be its inverse. For V a vector space of dimension
$\Phi _A^{-1}$
be its inverse. For V a vector space of dimension
![]() $nd$
, let
$nd$
, let
![]() $\mathfrak {l}:=\mathrm {End}(V)^{\lambda _A}$
. Let
$\mathfrak {l}:=\mathrm {End}(V)^{\lambda _A}$
. Let
![]() $\lambda _C$
be the antidominant cocharacter of
$\lambda _C$
be the antidominant cocharacter of
![]() $T(nd)\subset GL(nd)^{\lambda _A}$
corresponding to C; let
$T(nd)\subset GL(nd)^{\lambda _A}$
corresponding to C; let
![]() $\omega _{AC}:=\det \left ( (\mathfrak {l}^{\lambda _C>0})^{\vee }\right )[-\dim \mathfrak {l}^{\lambda _C>0}] $
, where T acts on
$\omega _{AC}:=\det \left ( (\mathfrak {l}^{\lambda _C>0})^{\vee }\right )[-\dim \mathfrak {l}^{\lambda _C>0}] $
, where T acts on
![]() $\mathfrak {l}$
with weight
$\mathfrak {l}$
with weight
![]() $\gamma :=\gamma _1+\gamma _2$
. Note that
$\gamma :=\gamma _1+\gamma _2$
. Note that
![]() $\det \left ( (\mathfrak {l}^{\lambda _C>0})^{\vee }\right )$
is a character of
$\det \left ( (\mathfrak {l}^{\lambda _C>0})^{\vee }\right )$
is a character of
![]() $GL(d)^{\lambda _C}$
; hence, it determines a line bundle on
$GL(d)^{\lambda _C}$
; hence, it determines a line bundle on
![]() $\mathcal {X}(nd)^{\lambda _C}$
. We define the functor
$\mathcal {X}(nd)^{\lambda _C}$
. We define the functor
by the commutative diagram

When
![]() $A=(nd, nv)$
and C is a two term partition
$A=(nd, nv)$
and C is a two term partition
![]() $(n_id, n_iv)_{i=1}^2$
, the term
$(n_id, n_iv)_{i=1}^2$
, the term
![]() $\omega _{n_1,n_2}:=\omega _{AC}$
is Equation (2.40) for
$\omega _{n_1,n_2}:=\omega _{AC}$
is Equation (2.40) for
![]() $\dim V_i=n_id$
for
$\dim V_i=n_id$
for
![]() $i\in \{1, 2\}$
. For these partitions, we let
$i\in \{1, 2\}$
. For these partitions, we let
![]() $\Delta _{n_1 n_2}:=\Delta _{AC}$
. For such partitions A and C, consider the
$\Delta _{n_1 n_2}:=\Delta _{AC}$
. For such partitions A and C, consider the
![]() $(T\times T(d))$
-weight
$(T\times T(d))$
-weight
 $$ \begin{align*} \nu_{n_1, n_2}:=\sum_{i>n_1d\geqslant j}(\beta_i-\beta_j-\gamma). \end{align*} $$
$$ \begin{align*} \nu_{n_1, n_2}:=\sum_{i>n_1d\geqslant j}(\beta_i-\beta_j-\gamma). \end{align*} $$
Then
![]() $\omega _{n_1, n_2}=(-1)^{(n_1d)\cdot (n_2d)}q^{\nu _{n_1, n_2}}$
. Alternatively,
$\omega _{n_1, n_2}=(-1)^{(n_1d)\cdot (n_2d)}q^{\nu _{n_1, n_2}}$
. Alternatively,
![]() $\omega _{n_1, n_2}$
measures a ratio (called renormalized twist in [Reference Varagnolo and VasserotVV22, Proof of Lemma 2.3.7]) constructed from the shuffle product for
$\omega _{n_1, n_2}$
measures a ratio (called renormalized twist in [Reference Varagnolo and VasserotVV22, Proof of Lemma 2.3.7]) constructed from the shuffle product for
![]() $\widetilde {m}$
with kernel
$\widetilde {m}$
with kernel
 $$\begin{align*}\xi'(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)(1-qx)}{1-x},\end{align*}$$
$$\begin{align*}\xi'(x):=\frac{(1-q_1^{-1}x)(1-q_2^{-1}x)(1-qx)}{1-x},\end{align*}$$
and the shuffle product for m with kernel
![]() $\xi (x)$
; see the computation in [Reference Pădurariu and TodaPTa, Proof of Lemma 4.9].
$\xi (x)$
; see the computation in [Reference Pădurariu and TodaPTa, Proof of Lemma 4.9].
5.3.2
Let
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime integers, and let
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
be coprime integers, and let
![]() $n\in \mathbb {N}$
. Consider partitions
$n\in \mathbb {N}$
. Consider partitions
![]() $A=(d_i)_{i=1}^k$
and
$A=(d_i)_{i=1}^k$
and
![]() $B=(e_i)_{i=1}^s$
of n. Let
$B=(e_i)_{i=1}^s$
of n. Let
![]() $S^B_A$
be the set of partitions
$S^B_A$
be the set of partitions
![]() $C=(f_{i})_{i=1}^{l}$
of n with
$C=(f_{i})_{i=1}^{l}$
of n with
![]() $l=ks$
such that
$l=ks$
such that
 $$ \begin{align*} f_{(i-1)s+1}+f_{(i-1)s+2}+\ldots+f_{is}&=d_i\text{ for }1\leqslant i\leqslant k,\\ f_j+f_{s+j}+\ldots+f_{(k-1)s+j}&=e_j\text{ for }1\leqslant j\leqslant s. \end{align*} $$
$$ \begin{align*} f_{(i-1)s+1}+f_{(i-1)s+2}+\ldots+f_{is}&=d_i\text{ for }1\leqslant i\leqslant k,\\ f_j+f_{s+j}+\ldots+f_{(k-1)s+j}&=e_j\text{ for }1\leqslant j\leqslant s. \end{align*} $$
Let D be the partition on n constructed as in Equation (5.5). Define
![]() $m^{\prime }_{BC}:=m_{BC}\circ \text {sw}_{C}$
, for
$m^{\prime }_{BC}:=m_{BC}\circ \text {sw}_{C}$
, for
![]() $\text {sw}_{C}$
as in Equation (5.6). Theorem 5.2 implies the following:
$\text {sw}_{C}$
as in Equation (5.6). Theorem 5.2 implies the following:
Corollary 5.6. In the above setting, the following diagram commutes:

Proof. For simplicity of notation, we assume that
![]() $k=l=2$
, that A is the partition
$k=l=2$
, that A is the partition
![]() $a+b=n$
, and that B is the partition
$a+b=n$
, and that B is the partition
![]() $c+e=n$
. Then
$c+e=n$
. Then
![]() $S:=S^B_A$
is the set of partitions
$S:=S^B_A$
is the set of partitions
![]() $C=(f_i)_{i=1}^4\in \mathbb {N}^4$
such that
$C=(f_i)_{i=1}^4\in \mathbb {N}^4$
such that
Note that, for such a partition C, the partition D is
![]() $(f_1, f_3, f_2, f_4)$
. The swap morphism is
$(f_1, f_3, f_2, f_4)$
. The swap morphism is
 $$ \begin{align*} \text{sw}_{ab}: K_T\left(\mathbb{T}(ad)_{av}\right)'\otimes K_T\left(\mathbb{T}(bd)_{bv}\right)' &\to K_T\left(\mathbb{T}(bd)_{bv}\right)'\otimes K_T\left(\mathbb{T}(ad)_{av}\right)',\\ x\otimes y&\mapsto y\otimes x. \end{align*} $$
$$ \begin{align*} \text{sw}_{ab}: K_T\left(\mathbb{T}(ad)_{av}\right)'\otimes K_T\left(\mathbb{T}(bd)_{bv}\right)' &\to K_T\left(\mathbb{T}(bd)_{bv}\right)'\otimes K_T\left(\mathbb{T}(ad)_{av}\right)',\\ x\otimes y&\mapsto y\otimes x. \end{align*} $$
We abuse notation and write
![]() $m_{ab}$
instead of
$m_{ab}$
instead of
![]() $m_{ad, bd}$
and so on. We then need to show that the following diagram commutes:
$m_{ad, bd}$
and so on. We then need to show that the following diagram commutes:

where
![]() $m':=\bigoplus _S \left (m_{f_1f_3}\otimes m_{f_2 f_4}\right )\left ( 1\otimes \text {sw}_{f_2f_3}\otimes 1\right )$
and
$m':=\bigoplus _S \left (m_{f_1f_3}\otimes m_{f_2 f_4}\right )\left ( 1\otimes \text {sw}_{f_2f_3}\otimes 1\right )$
and
![]() $\Delta :=\bigoplus _S \Delta _{f_1f_2}\otimes \Delta _{f_3f_4}$
.
$\Delta :=\bigoplus _S \Delta _{f_1f_2}\otimes \Delta _{f_3f_4}$
.
For
![]() $m\in \mathbb {N}$
, recall that
$m\in \mathbb {N}$
, recall that
![]() $\sigma _m:=m\tau _m=\sum _{i=1}^m \beta _i$
. Then
$\sigma _m:=m\tau _m=\sum _{i=1}^m \beta _i$
. Then
![]() $\sigma _{ad}=\sigma _{f_1d}+\sigma _{f_2d}$
and so on. In this proof, we will use the notation
$\sigma _{ad}=\sigma _{f_1d}+\sigma _{f_2d}$
and so on. In this proof, we will use the notation
![]() $z:=q^{-\gamma }$
instead of
$z:=q^{-\gamma }$
instead of
![]() $q^{-1}$
to reduce the use of the letter q. We use the notation
$q^{-1}$
to reduce the use of the letter q. We use the notation
![]() $\Phi _n$
for the Koszul equivalence (5.27) for
$\Phi _n$
for the Koszul equivalence (5.27) for
![]() $(nd, nv)$
. Then
$(nd, nv)$
. Then
Fix a tuplet
![]() $C=(f_i)_{i=1}^4$
as above, and let
$C=(f_i)_{i=1}^4$
as above, and let
![]() $w=w_C\in \mathfrak {S}_{nd}$
be its corresponding Weyl element as in Subsection 5.1.2. Let
$w=w_C\in \mathfrak {S}_{nd}$
be its corresponding Weyl element as in Subsection 5.1.2. Let
![]() $x_m\in K_T\left (\mathbb {T}(md)_{mv}\right )$
for
$x_m\in K_T\left (\mathbb {T}(md)_{mv}\right )$
for
![]() $m\in \{f_i, a, b, n\mid 1\leqslant i\leqslant 4\}$
. By the discussions in Subsections 2.11 and 5.3.1, we have that
$m\in \{f_i, a, b, n\mid 1\leqslant i\leqslant 4\}$
. By the discussions in Subsections 2.11 and 5.3.1, we have that
 $$ \begin{align*} m_{ab}(x_a\boxtimes x_b)&= \Phi_n^{-1} \widetilde{m}_{ab} \left( \Phi_a(x_a)q^{-bd\sigma_{ad}}\boxtimes \Phi_b(x_b)q^{ad\sigma_{bd}}(-z)^{d^2ab}\right),\\ \Delta_{ab}(x_n)&= \Phi_a^{-1}\boxtimes\Phi^{-1}_b \left( \left(\widetilde{\Delta}_{ab}\Phi_n(x_n)\right)q^{bd\sigma_{ad}}q^{-ad\sigma_{bd}}(-z)^{-d^2ab} \right),\\ \widetilde{\text{sw}}_{C}\left(x_{f_1}\boxtimes x_{f_2}\boxtimes x_{f_3}\boxtimes x_{f_4}\right)&= x_{f_1}\boxtimes \left(x_{f_3}q^{2f_3\sigma_{f_2}}\right)\boxtimes \left(x_{f_2}q^{-2f_2\sigma_{f_3}}\right)\boxtimes x_{f_4}. \end{align*} $$
$$ \begin{align*} m_{ab}(x_a\boxtimes x_b)&= \Phi_n^{-1} \widetilde{m}_{ab} \left( \Phi_a(x_a)q^{-bd\sigma_{ad}}\boxtimes \Phi_b(x_b)q^{ad\sigma_{bd}}(-z)^{d^2ab}\right),\\ \Delta_{ab}(x_n)&= \Phi_a^{-1}\boxtimes\Phi^{-1}_b \left( \left(\widetilde{\Delta}_{ab}\Phi_n(x_n)\right)q^{bd\sigma_{ad}}q^{-ad\sigma_{bd}}(-z)^{-d^2ab} \right),\\ \widetilde{\text{sw}}_{C}\left(x_{f_1}\boxtimes x_{f_2}\boxtimes x_{f_3}\boxtimes x_{f_4}\right)&= x_{f_1}\boxtimes \left(x_{f_3}q^{2f_3\sigma_{f_2}}\right)\boxtimes \left(x_{f_2}q^{-2f_2\sigma_{f_3}}\right)\boxtimes x_{f_4}. \end{align*} $$
We use the shorthand notations
![]() $\text {sw}_{23}=1\boxtimes \text {sw}_{f_2 f_3}\boxtimes 1$
,
$\text {sw}_{23}=1\boxtimes \text {sw}_{f_2 f_3}\boxtimes 1$
,
![]() $\widetilde {m}_{13}=\widetilde {m}_{f_1f_3}$
,
$\widetilde {m}_{13}=\widetilde {m}_{f_1f_3}$
,
![]() $\widetilde {m}_C:=\widetilde {m}_{13}\boxtimes \widetilde {m}_{24}$
and so on in what follows. We compute, by ignoring the z factor for simplicity of notation,
$\widetilde {m}_C:=\widetilde {m}_{13}\boxtimes \widetilde {m}_{24}$
and so on in what follows. We compute, by ignoring the z factor for simplicity of notation,
 $$ \begin{align} &\Delta_{ce}m_{ab}(x_a\boxtimes x_b)\\&\quad=\Phi_c^{-1}\boxtimes\Phi_e^{-1}\left(\widetilde{\Delta}_{cf}\left(\widetilde{m}_{ab}(\Phi_a(x_a)q^{-bd\sigma_{ad}}\boxtimes \Phi_b(x_b)q^{ad\sigma_{bd}})\right)q^{ed\sigma_{cd}}q^{-cd\sigma_{ed}}\right)\nonumber\\&\quad=\Phi_c^{-1}\boxtimes \Phi_e^{-1} \sum_{S} \widetilde{m}_{C}\left(\widetilde{\text{sw}}_{C}\left( \widetilde{\Delta}_{12}(\Phi_a(x_a)q^{-bd\sigma_{ad}})\boxtimes \widetilde{\Delta}_{34}(\Phi_b(x_b)q^{ad\sigma_{bd}}) \right)\right)q^{ed\sigma_{cd}}q^{-cd\sigma_{ed}}.\nonumber \end{align} $$
$$ \begin{align} &\Delta_{ce}m_{ab}(x_a\boxtimes x_b)\\&\quad=\Phi_c^{-1}\boxtimes\Phi_e^{-1}\left(\widetilde{\Delta}_{cf}\left(\widetilde{m}_{ab}(\Phi_a(x_a)q^{-bd\sigma_{ad}}\boxtimes \Phi_b(x_b)q^{ad\sigma_{bd}})\right)q^{ed\sigma_{cd}}q^{-cd\sigma_{ed}}\right)\nonumber\\&\quad=\Phi_c^{-1}\boxtimes \Phi_e^{-1} \sum_{S} \widetilde{m}_{C}\left(\widetilde{\text{sw}}_{C}\left( \widetilde{\Delta}_{12}(\Phi_a(x_a)q^{-bd\sigma_{ad}})\boxtimes \widetilde{\Delta}_{34}(\Phi_b(x_b)q^{ad\sigma_{bd}}) \right)\right)q^{ed\sigma_{cd}}q^{-cd\sigma_{ed}}.\nonumber \end{align} $$
We next compute
 $$ \begin{align} &\sum_S m'\Delta(x_a\boxtimes x_b)\\&\quad =\Phi_c^{-1}\boxtimes\Phi_e^{-1} \sum_{S} \left(\widetilde{m}_{13}\boxtimes \widetilde{m}_{24}\right)\left(q^{-f_3d\sigma_{f_1d}}\boxtimes q^{f_1d\sigma_{f_3d}}\boxtimes q^{-f_4d\sigma_{f_2d}}\boxtimes q^{f_2d\sigma_{f_4d}}\right)\nonumber \\&\qquad \times \text{sw}_{23} \left(\left(\widetilde{\Delta}_{12}(\Phi_a(x_a))q^{f_2d\sigma_{f_1d}}q^{-f_1d\sigma_{f_2d}}\right) \boxtimes \left(\widetilde{\Delta}_{34}(\Phi_b(x_b))q^{f_4d\sigma_{f_3d}}q^{-f_3d\sigma_{f_4d}}\right)\right).\nonumber \end{align} $$
$$ \begin{align} &\sum_S m'\Delta(x_a\boxtimes x_b)\\&\quad =\Phi_c^{-1}\boxtimes\Phi_e^{-1} \sum_{S} \left(\widetilde{m}_{13}\boxtimes \widetilde{m}_{24}\right)\left(q^{-f_3d\sigma_{f_1d}}\boxtimes q^{f_1d\sigma_{f_3d}}\boxtimes q^{-f_4d\sigma_{f_2d}}\boxtimes q^{f_2d\sigma_{f_4d}}\right)\nonumber \\&\qquad \times \text{sw}_{23} \left(\left(\widetilde{\Delta}_{12}(\Phi_a(x_a))q^{f_2d\sigma_{f_1d}}q^{-f_1d\sigma_{f_2d}}\right) \boxtimes \left(\widetilde{\Delta}_{34}(\Phi_b(x_b))q^{f_4d\sigma_{f_3d}}q^{-f_3d\sigma_{f_4d}}\right)\right).\nonumber \end{align} $$
We claim that the expressions (5.28) and (5.29) are equal. We only match the coefficients in
![]() $\mathbb {K}$
corresponding to
$\mathbb {K}$
corresponding to
![]() $f_1$
and
$f_1$
and
![]() $f_2$
as the computations for
$f_2$
as the computations for
![]() $f_3$
and
$f_3$
and
![]() $f_4$
are similar:
$f_4$
are similar:
 $$ \begin{align*} q^{(f_2+f_4)d\sigma_{f_1d}}q^{-(f_3+f_4)d\sigma_{f_1d}}&=q^{f_2d\sigma_{f_1d}}q^{-f_3d\sigma_{f_1d}},\\ q^{-(f_1+f_3)d\sigma_{f_2d}}q^{-(f_3+f_4)d\sigma_{f_2d}}\cdot q^{2f_3d\sigma_{f_2d}}&=q^{-f_1d\sigma_{f_2d}}q^{-f_4d\sigma_{f_2d}}. \end{align*} $$
$$ \begin{align*} q^{(f_2+f_4)d\sigma_{f_1d}}q^{-(f_3+f_4)d\sigma_{f_1d}}&=q^{f_2d\sigma_{f_1d}}q^{-f_3d\sigma_{f_1d}},\\ q^{-(f_1+f_3)d\sigma_{f_2d}}q^{-(f_3+f_4)d\sigma_{f_2d}}\cdot q^{2f_3d\sigma_{f_2d}}&=q^{-f_1d\sigma_{f_2d}}q^{-f_4d\sigma_{f_2d}}. \end{align*} $$
Finally, the z factors in
![]() $\Delta _{ce}m_{ab}$
and
$\Delta _{ce}m_{ab}$
and
![]() $m'\Delta $
are equal because
$m'\Delta $
are equal because
5.4 The localized bialgebra
Recall that for V a
![]() $\mathbb {K}$
-module, we let
$\mathbb {K}$
-module, we let
![]() $V_{\mathbb {F}}:=V\otimes _{\mathbb {K}}\mathbb {F}$
. Recall that
$V_{\mathbb {F}}:=V\otimes _{\mathbb {K}}\mathbb {F}$
. Recall that
![]() $(d, v)\in \mathbb {N}\times \mathbb {Z}$
are coprime. Consider the
$(d, v)\in \mathbb {N}\times \mathbb {Z}$
are coprime. Consider the
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {F}$
-vector space
$\mathbb {F}$
-vector space
We next explain that the operations m and
![]() $\Delta $
endow V with the structure of a commutative and cocommutative
$\Delta $
endow V with the structure of a commutative and cocommutative
![]() $\mathbb {F}$
-bialgebra. We show this by an explicit computation using the generators of these vector spaces; see Equations (2.34) and (2.33). Recall the complex
$\mathbb {F}$
-bialgebra. We show this by an explicit computation using the generators of these vector spaces; see Equations (2.34) and (2.33). Recall the complex
![]() $\mathcal {E}_{e, v}$
from Definition 2.3 and the shuffle elements
$\mathcal {E}_{e, v}$
from Definition 2.3 and the shuffle elements
![]() $A^{\prime }_{e,v}$
and
$A^{\prime }_{e,v}$
and
![]() $A_{e, v}$
from Equations (2.31) and (2.35) for a pair
$A_{e, v}$
from Equations (2.31) and (2.35) for a pair
![]() $(e, v)\in \mathbb {N}\times \mathbb {Z}$
.
$(e, v)\in \mathbb {N}\times \mathbb {Z}$
.
Proposition 5.7. Let
![]() $a, b\in \mathbb {N}$
with
$a, b\in \mathbb {N}$
with
![]() $a+b=n$
. Then
$a+b=n$
. Then
![]() $[\mathcal {E}_{ad, av}]\cdot [\mathcal {E}_{bd, bv}]=[\mathcal {E}_{bd, bv}]\cdot [\mathcal {E}_{ad, av}]$
in
$[\mathcal {E}_{ad, av}]\cdot [\mathcal {E}_{bd, bv}]=[\mathcal {E}_{bd, bv}]\cdot [\mathcal {E}_{ad, av}]$
in
![]() $K_T\left (\mathbb {T}(nd)_{nv}\right )$
.
$K_T\left (\mathbb {T}(nd)_{nv}\right )$
.
Proof. By Equations (2.34) and (2.33), it suffices to check the statement for
![]() $A_{ad, aw}$
and
$A_{ad, aw}$
and
![]() $A_{bd, bw}$
or, alternatively, for
$A_{bd, bw}$
or, alternatively, for
![]() $A^{\prime }_{ad, aw}$
and
$A^{\prime }_{ad, aw}$
and
![]() $A^{\prime }_{bd, bw}$
for
$A^{\prime }_{bd, bw}$
for
![]() $a, b\in \mathbb {N}$
. Any two such elements commute because they are in the subalgebra of
$a, b\in \mathbb {N}$
. Any two such elements commute because they are in the subalgebra of
![]() $\mathcal {S}^{\prime }_{\mathbb {F}}\cong \mathcal {S}_{\mathbb {F}}$
generated by elements
$\mathcal {S}^{\prime }_{\mathbb {F}}\cong \mathcal {S}_{\mathbb {F}}$
generated by elements
![]() $A^{\prime }_{e, v}$
of fixed slope
$A^{\prime }_{e, v}$
of fixed slope
![]() $\frac {v}{e}$
, and such algebra are commutative; see, for example, [Reference NeguţNeg19, Subsection 3.2].
$\frac {v}{e}$
, and such algebra are commutative; see, for example, [Reference NeguţNeg19, Subsection 3.2].
For the following proposition, it is convenient to introduce the element
 $$\begin{align*}\hat{A}_{nd, nv}:=\left(-q^{-1}\right)^{n-1}A_{nd, nv}= \frac{\left(-q^{-1}\right)^{n-1}}{(1-q_1^{-1})^{nd-1}(1-q_2^{-1})^{nd-1}}[\mathcal{E}_{nd, nv}]\in K_T(\mathbb{T}(nd)_{nv})_{\mathbb{F}}.\end{align*}$$
$$\begin{align*}\hat{A}_{nd, nv}:=\left(-q^{-1}\right)^{n-1}A_{nd, nv}= \frac{\left(-q^{-1}\right)^{n-1}}{(1-q_1^{-1})^{nd-1}(1-q_2^{-1})^{nd-1}}[\mathcal{E}_{nd, nv}]\in K_T(\mathbb{T}(nd)_{nv})_{\mathbb{F}}.\end{align*}$$
Proposition 5.8. Let
![]() $a, b, n\in \mathbb {N}$
be such that
$a, b, n\in \mathbb {N}$
be such that
![]() $a+b=n$
. Then
$a+b=n$
. Then
For
![]() $d, v, n$
as above, let
$d, v, n$
as above, let
![]() $O_n$
and
$O_n$
and
![]() $L_n$
be the following sets of
$L_n$
be the following sets of
![]() $(T\times T(d))$
-weights:
$(T\times T(d))$
-weights:
 $$ \begin{align*} O_n&:=\{\beta_j-\beta_i+\gamma \mid \,i>j+1\}, \\ L_n&:=\{\beta_i-\beta_j+\gamma_l \mid \,i>j,\, 1\leqslant l\leqslant 2\}\sqcup O_n. \end{align*} $$
$$ \begin{align*} O_n&:=\{\beta_j-\beta_i+\gamma \mid \,i>j+1\}, \\ L_n&:=\{\beta_i-\beta_j+\gamma_l \mid \,i>j,\, 1\leqslant l\leqslant 2\}\sqcup O_n. \end{align*} $$
For a subset
![]() $I\subset L_n$
, let
$I\subset L_n$
, let
![]() $\sigma _I$
be the sum of the corresponding
$\sigma _I$
be the sum of the corresponding
![]() $T(d)$
-weights in I, let
$T(d)$
-weights in I, let
![]() $\gamma _I$
be the sum of the weights of the corresponding T-weights in I and let
$\gamma _I$
be the sum of the weights of the corresponding T-weights in I and let
![]() $q_I:=q^{\gamma _I}$
. Let
$q_I:=q^{\gamma _I}$
. Let
![]() $\ell (I)$
be the length of the minimal Weyl element such that
$\ell (I)$
be the length of the minimal Weyl element such that
![]() $w*(\chi -\sigma _I)$
is dominant or zero. Let
$w*(\chi -\sigma _I)$
is dominant or zero. Let
 $$\begin{align*}\chi_n:=\sum_{i=1}^{nd-1}\left(\frac{vi}{d}+1-\Big\lceil\frac{vi}{d}\Big\rceil\right)(\beta_{i+1}-\beta_i)+\frac{v}{d}\sum_{i=1}^{nd}\beta_i\in M(nd).\end{align*}$$
$$\begin{align*}\chi_n:=\sum_{i=1}^{nd-1}\left(\frac{vi}{d}+1-\Big\lceil\frac{vi}{d}\Big\rceil\right)(\beta_{i+1}-\beta_i)+\frac{v}{d}\sum_{i=1}^{nd}\beta_i\in M(nd).\end{align*}$$
The element
![]() $A_{nd, nv}\in K_T\left (\mathcal {X}(nd)\right )$
from Equation (2.35) can be written as
$A_{nd, nv}\in K_T\left (\mathcal {X}(nd)\right )$
from Equation (2.35) can be written as
Recall the framework on Subsection 5.3.1. Consider the composition of the Koszul equivalence (2.22) and the forget-the-potential map (1.8):
Using Equation (2.38) and the computation in [Reference Pădurariu and TodaPTa, Lemma 4.3], we have that
Remark 5.9. Note that
![]() $\Psi \left (\hat {A}_{nd, nv}\right )$
equals the shuffle element
$\Psi \left (\hat {A}_{nd, nv}\right )$
equals the shuffle element
![]() $E_{k, d}$
considered by Neguţ in [Reference NeguţNeg18, Equation 2.10], where q, k, d in loc. cit. correspond to
$E_{k, d}$
considered by Neguţ in [Reference NeguţNeg18, Equation 2.10], where q, k, d in loc. cit. correspond to
![]() $q^{-1}$
,
$q^{-1}$
,
![]() $nd$
and
$nd$
and
![]() $nv$
, respectively, in our paper.
$nv$
, respectively, in our paper.
Proof of Proposition 5.8.
By the definition of
![]() $\Delta $
from Subsection 5.3.1, it suffices to show that
$\Delta $
from Subsection 5.3.1, it suffices to show that
where we are using
![]() $\widetilde {\Delta }_{ab}$
instead of
$\widetilde {\Delta }_{ab}$
instead of
![]() $\widetilde {\Delta }_{ad, bd}$
. Let
$\widetilde {\Delta }_{ad, bd}$
. Let
![]() $I\subset L_n$
. Then
$I\subset L_n$
. Then
 $$\begin{align*}\chi_n-\sigma_I+\rho=\sum_{i>j}d_{ij}(\beta_i-\beta_j)+\frac{v}{d}\sum_{i=1}^{nd}\beta_i,\end{align*}$$
$$\begin{align*}\chi_n-\sigma_I+\rho=\sum_{i>j}d_{ij}(\beta_i-\beta_j)+\frac{v}{d}\sum_{i=1}^{nd}\beta_i,\end{align*}$$
where
Let
![]() $\lambda $
be the antidominant cocharacter associated to the partition
$\lambda $
be the antidominant cocharacter associated to the partition
![]() $(ad, bd)$
of
$(ad, bd)$
of
![]() $nd$
. Assume such a weight is on a wall
$nd$
. Assume such a weight is on a wall
![]() $F\left (w\lambda \right )$
for some
$F\left (w\lambda \right )$
for some
![]() $w\in \mathfrak {S}_{nd}$
. Then there exists a partition
$w\in \mathfrak {S}_{nd}$
. Then there exists a partition
![]() $E\sqcup C=\{1,\cdots , nd \}$
with
$E\sqcup C=\{1,\cdots , nd \}$
with
![]() $|C|=ad$
and
$|C|=ad$
and
 $$ \begin{align} d_{ij}=\begin{cases} \frac{3}{2}\text{ for }i\in E, j\in C\text{ and }i>j,\\ -\frac{3}{2}\text{ for }i\in E, j\in C\text{ and }i<j; \end{cases} \end{align} $$
$$ \begin{align} d_{ij}=\begin{cases} \frac{3}{2}\text{ for }i\in E, j\in C\text{ and }i>j,\\ -\frac{3}{2}\text{ for }i\in E, j\in C\text{ and }i<j; \end{cases} \end{align} $$
see [Reference Halpern-Leistner and SamHLS20, Lemma 3.12], [Reference PădurariuPăda, Proposition 3.2]. We claim that
![]() $C=\{1,\ldots , ad\}$
. Otherwise, there exists
$C=\{1,\ldots , ad\}$
. Otherwise, there exists
![]() $1\leqslant j\leqslant ad$
with
$1\leqslant j\leqslant ad$
with
![]() $j\in E$
and
$j\in E$
and
![]() $j+1\in C$
. Then
$j+1\in C$
. Then
![]() $d_{j+1, j}>-\frac {3}{2}$
, and this contradicts Equation (5.32). Then
$d_{j+1, j}>-\frac {3}{2}$
, and this contradicts Equation (5.32). Then
![]() $d_{ij}=-\frac {3}{2}$
for
$d_{ij}=-\frac {3}{2}$
for
![]() $i>ad\geqslant j$
. Further, we have
$i>ad\geqslant j$
. Further, we have
and I does not contain any weights
![]() $\beta _i-\beta _j-\gamma _l$
for
$\beta _i-\beta _j-\gamma _l$
for
![]() $i>ad\geqslant j$
and
$i>ad\geqslant j$
and
![]() $l\in \{1, 2\}$
. Define
$l\in \{1, 2\}$
. Define
![]() $L_a$
and
$L_a$
and
![]() $L_b$
similarly to
$L_b$
similarly to
![]() $L_n$
, using the weights
$L_n$
, using the weights
![]() $\beta _i$
with
$\beta _i$
with
![]() $1\leqslant i\leqslant ad$
for
$1\leqslant i\leqslant ad$
for
![]() $L_a$
and
$L_a$
and
![]() $\beta _i$
with
$\beta _i$
with
![]() $ad<i\leqslant nd$
for
$ad<i\leqslant nd$
for
![]() $L_b$
. We can thus write
$L_b$
. We can thus write
![]() $I=Q\sqcup I_a\sqcup I_b$
, where
$I=Q\sqcup I_a\sqcup I_b$
, where
![]() $I_a\subset L_a$
and
$I_a\subset L_a$
and
![]() $I_b\subset L_b$
. Let
$I_b\subset L_b$
. Let
![]() $\mathcal {I}$
be the set of such sets
$\mathcal {I}$
be the set of such sets
![]() $I\subset L_n$
. We have that (see Equation (5.9))
$I\subset L_n$
. We have that (see Equation (5.9))
 $$ \begin{align} \widetilde{\Delta}_{ab} \left(A_{nd, nv}\right)=\widetilde{\Delta}_{ab}\left(\sum_{I\in\mathcal{I}} (-1)^{|I|-\ell(I)}q_I^{-1}\left[\Gamma_{GL(nd)}\left((\chi_n-\sigma_I)^+\right)\otimes\mathcal{O}_{\mathcal{X}(nd)}\right]\right). \end{align} $$
$$ \begin{align} \widetilde{\Delta}_{ab} \left(A_{nd, nv}\right)=\widetilde{\Delta}_{ab}\left(\sum_{I\in\mathcal{I}} (-1)^{|I|-\ell(I)}q_I^{-1}\left[\Gamma_{GL(nd)}\left((\chi_n-\sigma_I)^+\right)\otimes\mathcal{O}_{\mathcal{X}(nd)}\right]\right). \end{align} $$
Write
![]() $I=Q\sqcup I_a\sqcup I_b$
with
$I=Q\sqcup I_a\sqcup I_b$
with
![]() $I_a\subset L_a$
and
$I_a\subset L_a$
and
![]() $I_b\subset L_b$
. A direct computation shows that
$I_b\subset L_b$
. A direct computation shows that
 $$\begin{align*}\chi_n-\sigma_I+\rho=\sum_{i>ad\geqslant j}\frac{3}{2}(\beta_i-\beta_j)-(d^2ab-1)\gamma + (\chi_a-\sigma_{I_a}+\rho_a)+(\chi_b-\sigma_{I_b}+\rho_b).\end{align*}$$
$$\begin{align*}\chi_n-\sigma_I+\rho=\sum_{i>ad\geqslant j}\frac{3}{2}(\beta_i-\beta_j)-(d^2ab-1)\gamma + (\chi_a-\sigma_{I_a}+\rho_a)+(\chi_b-\sigma_{I_b}+\rho_b).\end{align*}$$
Let
![]() $w\in \mathfrak {S}_{nd}$
be the Weyl element of minimal length such that
$w\in \mathfrak {S}_{nd}$
be the Weyl element of minimal length such that
![]() $w*(\chi _n-\sigma _I)$
is dominant, and let
$w*(\chi _n-\sigma _I)$
is dominant, and let
![]() $w_a\in \mathfrak {S}_{na}$
and
$w_a\in \mathfrak {S}_{na}$
and
![]() $w_b\in \mathfrak {S}_{nb}$
be the Weyl elements of minimal length such that
$w_b\in \mathfrak {S}_{nb}$
be the Weyl elements of minimal length such that
![]() $w_a*(\chi _a-\sigma _{I_a})$
and
$w_a*(\chi _a-\sigma _{I_a})$
and
![]() $w_b*(\chi _b-\sigma _{I_b})$
are dominant. Then
$w_b*(\chi _b-\sigma _{I_b})$
are dominant. Then
![]() $w=w_a w_b$
, therefore
$w=w_a w_b$
, therefore
We have that
![]() $|Q|=d^2ab-1$
, and
$|Q|=d^2ab-1$
, and
For
![]() $m\in \{a, b, n\}$
, let
$m\in \{a, b, n\}$
, let
The coproduct (5.33) thus simplifies to
The conclusion thus follows.
Corollary 5.10. The operations m and
![]() $\Delta $
endow V with the structure of an
$\Delta $
endow V with the structure of an
![]() $\mathbb {N}$
-graded commutative and cocommutative
$\mathbb {N}$
-graded commutative and cocommutative
![]() $\mathbb {F}$
-bialgebra.
$\mathbb {F}$
-bialgebra.
5.5 Primitive elements
Let
![]() $R^{\prime }_n\subset R_n$
be the complement of the trivial partition n. For
$R^{\prime }_n\subset R_n$
be the complement of the trivial partition n. For
![]() $A=(n_i)_{i=1}^k$
, let
$A=(n_i)_{i=1}^k$
, let
![]() $\mathbb {T}_A:=\otimes _{i=1}^k \mathbb {T}(n_id)_{n_iv}$
. Define
$\mathbb {T}_A:=\otimes _{i=1}^k \mathbb {T}(n_id)_{n_iv}$
. Define
 $$\begin{align*}\mathrm{P}(nd)_{nv}:=\text{ker}\left(\bigoplus_{A\in R^{\prime}_n} \Delta_A: K_T\left(\mathbb{T}(nd)_{nv}\right)\to \bigoplus_{A\in R^{\prime}_n} K_T\left(\mathbb{T}_A\right)\right).\end{align*}$$
$$\begin{align*}\mathrm{P}(nd)_{nv}:=\text{ker}\left(\bigoplus_{A\in R^{\prime}_n} \Delta_A: K_T\left(\mathbb{T}(nd)_{nv}\right)\to \bigoplus_{A\in R^{\prime}_n} K_T\left(\mathbb{T}_A\right)\right).\end{align*}$$
Let
![]() $\mathrm {P}(nd)_{nv, \mathbb {F}}:=\mathrm {P}(nd)_{nv}\otimes _{\mathbb {K}}\mathbb {F}$
. Corollary 5.10 can be rephrased as follows; see the isomorphism (2.43):
$\mathrm {P}(nd)_{nv, \mathbb {F}}:=\mathrm {P}(nd)_{nv}\otimes _{\mathbb {K}}\mathbb {F}$
. Corollary 5.10 can be rephrased as follows; see the isomorphism (2.43):
Corollary 5.11. Recall the bialgebra
![]() $\Lambda _{\mathbb {F}}:=\lambda \otimes _{\mathbb {Z}}\mathbb {F}$
from Subsection (2.12). There exists an isomorphism of bialgebras
$\Lambda _{\mathbb {F}}:=\lambda \otimes _{\mathbb {Z}}\mathbb {F}$
from Subsection (2.12). There exists an isomorphism of bialgebras
 $$ \begin{align*} \Phi \colon \Lambda_{\mathbb{F}}&\cong V,\\ e_n&\mapsto\widehat{A}_{nd, nv}. \end{align*} $$
$$ \begin{align*} \Phi \colon \Lambda_{\mathbb{F}}&\cong V,\\ e_n&\mapsto\widehat{A}_{nd, nv}. \end{align*} $$
In particular, the
![]() $\mathbb {F}$
-vector space
$\mathbb {F}$
-vector space
![]() $\mathrm {P}(nd)_{nv, \mathbb {F}}$
is one-dimensional.
$\mathrm {P}(nd)_{nv, \mathbb {F}}$
is one-dimensional.
Proof. Both
![]() $\Lambda _{\mathbb {F}}$
and V are commutative and cocommutative, and
$\Lambda _{\mathbb {F}}$
and V are commutative and cocommutative, and
![]() $\Phi $
is a morphism of algebras by construction. The coproduct is respected by Proposition 5.8. Finally,
$\Phi $
is a morphism of algebras by construction. The coproduct is respected by Proposition 5.8. Finally,
![]() $\Phi $
is an isomorphism of
$\Phi $
is an isomorphism of
![]() $\mathbb {N}$
-graded vector spaces by [Reference Pădurariu and TodaPTa, Theorem 4.12], so the conclusion follows.
$\mathbb {N}$
-graded vector spaces by [Reference Pădurariu and TodaPTa, Theorem 4.12], so the conclusion follows.
Remark 5.12. The isomorphism
![]() $\Phi $
sends
$\Phi $
sends
![]() $e_n$
to
$e_n$
to
![]() $\widehat {A}_{nd, nv}$
. Since
$\widehat {A}_{nd, nv}$
. Since
![]() $\widehat {A}_{nd, nv}$
is not contained in the integral part
$\widehat {A}_{nd, nv}$
is not contained in the integral part
![]() $K_T(\mathbb {T}(nd)_{nv})$
, it does not restrict to a morphism
$K_T(\mathbb {T}(nd)_{nv})$
, it does not restrict to a morphism
![]() $\Lambda _{\mathbb {K}} \to K_T(\mathcal {D}_{d, v})$
. On the other hand, we expect the existence of a McKay-type functor
$\Lambda _{\mathbb {K}} \to K_T(\mathcal {D}_{d, v})$
. On the other hand, we expect the existence of a McKay-type functor
![]() $\mathrm {MF}^{\mathrm {gr}}([\mathbb {C}^{3d}/\mathfrak {S}_d], 0) \to \mathbb {T}(nd)_{nv}$
which may induce an isomorphism
$\mathrm {MF}^{\mathrm {gr}}([\mathbb {C}^{3d}/\mathfrak {S}_d], 0) \to \mathbb {T}(nd)_{nv}$
which may induce an isomorphism
For a full understanding of
![]() $K_T(\mathbb {T}(nd)_{nv})$
, we thus need to construct an isomorphism different from the one in Corollary 5.11. Such an isomorphism will be discussed in [Reference Pădurariu and TodaPTb].
$K_T(\mathbb {T}(nd)_{nv})$
, we thus need to construct an isomorphism different from the one in Corollary 5.11. Such an isomorphism will be discussed in [Reference Pădurariu and TodaPTb].
Finally, we prove Corollary 1.5:
Corollary 5.13. There is an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {F}$
-vector spaces
$\mathbb {F}$
-vector spaces
 $$ \begin{align*} \bigoplus_{d\geqslant 0}K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant v<d \\ \gcd(d,v)=1}} \left(\bigotimes_{n\geqslant 1}\mathrm{Sym}\big(\mathrm{P}(nd)_{nv, \mathbb{F}}\big)\right). \end{align*} $$
$$ \begin{align*} \bigoplus_{d\geqslant 0}K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant v<d \\ \gcd(d,v)=1}} \left(\bigotimes_{n\geqslant 1}\mathrm{Sym}\big(\mathrm{P}(nd)_{nv, \mathbb{F}}\big)\right). \end{align*} $$
Proof. For
![]() $\bullet \in \{\emptyset , \mathrm {gr}\}$
, there are equivalences
$\bullet \in \{\emptyset , \mathrm {gr}\}$
, there are equivalences
![]() $\mathbb {S}^{\bullet }_T(d)_w\xrightarrow {\sim }\mathbb {S}^{\bullet }_T(d)_{d+w}$
. By [Reference Pădurariu and TodaPTa, Theorem 1.1], there is an isomorphism
$\mathbb {S}^{\bullet }_T(d)_w\xrightarrow {\sim }\mathbb {S}^{\bullet }_T(d)_{d+w}$
. By [Reference Pădurariu and TodaPTa, Theorem 1.1], there is an isomorphism
 $$ \begin{align} K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigoplus_{\substack{0\leqslant v_1/d_1<\ldots<v_k/d_k<1\\d_1+\ldots+d_k=d}} \bigotimes_{i=1}^k K_T\left(\mathbb{S}(d_i)_{v_i}\right)_{\mathbb{F}}. \end{align} $$
$$ \begin{align} K_T(\mathcal{DT}(d))_{\mathbb{F}}\cong \bigoplus_{\substack{0\leqslant v_1/d_1<\ldots<v_k/d_k<1\\d_1+\ldots+d_k=d}} \bigotimes_{i=1}^k K_T\left(\mathbb{S}(d_i)_{v_i}\right)_{\mathbb{F}}. \end{align} $$
Further, there are isomorphisms of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {F}$
-vector spaces
$\mathbb {F}$
-vector spaces
 $$ \begin{align} \bigoplus_{\substack{0\leqslant v_1/d_1<\ldots<v_k/d_k<1}} \bigotimes_{i=1}^k K_T\left(\mathbb{S}(d_i)_{v_i}\right)_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant \mu<1 \\ \mu=a/b, \ \gcd(a, b)=1}}\left(\bigoplus_{n\ge 1}K_T\left(\mathbb{S}(nb)_{na}\right)_{\mathbb{F}}\right). \end{align} $$
$$ \begin{align} \bigoplus_{\substack{0\leqslant v_1/d_1<\ldots<v_k/d_k<1}} \bigotimes_{i=1}^k K_T\left(\mathbb{S}(d_i)_{v_i}\right)_{\mathbb{F}}\cong \bigotimes_{\substack{0\leqslant \mu<1 \\ \mu=a/b, \ \gcd(a, b)=1}}\left(\bigoplus_{n\ge 1}K_T\left(\mathbb{S}(nb)_{na}\right)_{\mathbb{F}}\right). \end{align} $$
For each coprime
![]() $(a, b) \in \mathbb {Z} \times \mathbb {N}$
, by Corollary 5.11 and the isomorphism (2.43), we obtain the isomorphism
$(a, b) \in \mathbb {Z} \times \mathbb {N}$
, by Corollary 5.11 and the isomorphism (2.43), we obtain the isomorphism
We obtain the conclusion by combining the isomorphisms (5.34), (5.35), (5.36).
We explain how the above isomorphism categorifies Equation (1.6) up to a sign. We use the same computation as in [Reference Pădurariu and TodaPTa, Subsection 4.7]. Let
![]() $a_d:=\dim _{\mathbb {F}} K_T(\mathcal {DT}(d))_{\mathbb {F}}$
. We have that
$a_d:=\dim _{\mathbb {F}} K_T(\mathcal {DT}(d))_{\mathbb {F}}$
. We have that
![]() $\dim _{\mathbb {F}} \mathrm {P}(nb)_{na, \mathbb {F}}=1$
for any
$\dim _{\mathbb {F}} \mathrm {P}(nb)_{na, \mathbb {F}}=1$
for any
![]() $(a,b)$
with
$(a,b)$
with
![]() $\gcd (a,b)=1$
and
$\gcd (a,b)=1$
and
![]() $n\in \mathbb {Z}_{\geqslant 1}$
. For each
$n\in \mathbb {Z}_{\geqslant 1}$
. For each
![]() $d \in \mathbb {Z}_{\geqslant 1}$
, there is a bijection
$d \in \mathbb {Z}_{\geqslant 1}$
, there is a bijection
given by
![]() $(n, a, b) \mapsto na$
. In particular, the number of the elements of the left-hand side equals to d. We compute
$(n, a, b) \mapsto na$
. In particular, the number of the elements of the left-hand side equals to d. We compute
 $$\begin{align*}\sum_{d\geqslant 0} a_d q^d= \prod_{\begin{subarray}{c} 0\leqslant \mu<1 \\ \mu=a/b, \ \gcd(a, b)=1 \end{subarray} } \prod_{n\geqslant 1}\frac{1}{1-q^{bn}}=\prod_{d\geqslant 1}\frac{1}{\left(1-q^d\right)^d}.\end{align*}$$
$$\begin{align*}\sum_{d\geqslant 0} a_d q^d= \prod_{\begin{subarray}{c} 0\leqslant \mu<1 \\ \mu=a/b, \ \gcd(a, b)=1 \end{subarray} } \prod_{n\geqslant 1}\frac{1}{1-q^{bn}}=\prod_{d\geqslant 1}\frac{1}{\left(1-q^d\right)^d}.\end{align*}$$
Compare with the wall-crossing formula for DT invariants (1.6).
Acknowledgements
We thank Tasuki Kinjo, Davesh Maulik, Andrei Neguţ, Raphaël Rouquier, Christopher Ryba, Olivier Schiffmann, Špela Špenko, Eric Vasserot and Yu Zhao for discussions related to this work. We thank the referee for useful suggestions. Y. T. is supported by World Premier International Research Center Initiative (WPI initiative), MEXT, Japan and Grant-in Aid for Scientific Research grant (No. 19H01779) from MEXT, Japan.
Competing interests
None.