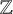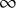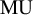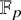1 Introduction
Whatever it is that animates anima and breathes life into higher algebra, this something leaves its trace in the structure of a Dirac ring on the homotopy groups of a commutative algebra in spectra. Dirac geometry is built from Dirac rings in the same way as algebraic geometry is built from commutative rings. In the prequel to this paper, we developed the commutative algebra of Dirac rings and defined the category of Dirac schemes. Here, we first embed this category in the larger
![]() $\infty $
-category of Dirac stacks, which also contains formal Dirac schemes. We next develop the coherent cohomology of Dirac stacks, which amounts to a functor that to a Dirac stack X assigns a presentably symmetric monoidal stable
$\infty $
-category of Dirac stacks, which also contains formal Dirac schemes. We next develop the coherent cohomology of Dirac stacks, which amounts to a functor that to a Dirac stack X assigns a presentably symmetric monoidal stable
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)$
of quasi-coherent
${\mathrm {QCoh}}(X)$
of quasi-coherent
![]() $\mathcal {O}_X$
-modules together with a symmetric monoidal subcategory
$\mathcal {O}_X$
-modules together with a symmetric monoidal subcategory
![]() ${\mathrm {QCoh}}(X)_{\geq 0} \subset {\mathrm {QCoh}}(X)$
, which is the connective part of a t-structure. As applications of the general theory to stable homotopy theory, we use Quillen’s theorem on complex cobordism and Milnor’s theorem on the dual Steenrod algebra to identify the Dirac stacks corresponding to
${\mathrm {QCoh}}(X)_{\geq 0} \subset {\mathrm {QCoh}}(X)$
, which is the connective part of a t-structure. As applications of the general theory to stable homotopy theory, we use Quillen’s theorem on complex cobordism and Milnor’s theorem on the dual Steenrod algebra to identify the Dirac stacks corresponding to
![]() $\operatorname {MU}$
and
$\operatorname {MU}$
and
![]() $\mathbb {F}_p$
in terms of their functors of points. Finally, in an appendix, we develop a rudimentary theory of accessible presheaves of anima on coaccessible
$\mathbb {F}_p$
in terms of their functors of points. Finally, in an appendix, we develop a rudimentary theory of accessible presheaves of anima on coaccessible
![]() $\infty $
-categories.
$\infty $
-categories.
To develop the theory of Dirac stacks and their coherent cohomology, we follow Lurie in [Reference Lurie23]. The category
![]() $\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is the opposite of the category
$\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is the opposite of the category
![]() $\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
of Dirac rings. The category of Dirac rings
$\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
of Dirac rings. The category of Dirac rings
![]() $\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
and the
$\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
and the
![]() $\infty $
-category of anima
$\infty $
-category of anima
![]() ${\mathcal {S}}$
are both presentable, and we define the
${\mathcal {S}}$
are both presentable, and we define the
![]() $\infty $
-category of Dirac prestacks to be the
$\infty $
-category of Dirac prestacks to be the
![]() $\infty $
-category of accessible presheaves of anima on
$\infty $
-category of accessible presheaves of anima on
![]() $\operatorname {\mathrm {Aff}}$
,
$\operatorname {\mathrm {Aff}}$
,
We show in Appendix A that this
![]() $\infty $
-category has excellent categorical properties and that it admits a number of equivalent descriptions. If
$\infty $
-category has excellent categorical properties and that it admits a number of equivalent descriptions. If
![]() $\kappa $
is a small regular cardinal, then we let
$\kappa $
is a small regular cardinal, then we let
![]() ${\mathrm {Aff}}_{\kappa } \subset \operatorname {\mathrm {Aff}}$
be the full subcategory spanned by the affine Dirac schemes of cardinality
${\mathrm {Aff}}_{\kappa } \subset \operatorname {\mathrm {Aff}}$
be the full subcategory spanned by the affine Dirac schemes of cardinality
![]() $< \kappa $
. Since it is essentially small, the
$< \kappa $
. Since it is essentially small, the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}({\mathrm {Aff}}_{\kappa })$
of presheaves of anima on
${\mathcal {P}}({\mathrm {Aff}}_{\kappa })$
of presheaves of anima on
![]() ${\mathrm {Aff}}_{\kappa }$
is presentable, and we show that
${\mathrm {Aff}}_{\kappa }$
is presentable, and we show that
It follows that the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
admits all small colimits and limits, both of which are calculated pointwise. We also show that the Yoneda embedding restricts to a fully faithful functor
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
admits all small colimits and limits, both of which are calculated pointwise. We also show that the Yoneda embedding restricts to a fully faithful functor
and that this functor exhibits the target as the cocompletion of the source.
The flat topology on
![]() $\operatorname {\mathrm {Aff}}$
is the Grothendieck topology, where a sieve
$\operatorname {\mathrm {Aff}}$
is the Grothendieck topology, where a sieve
![]() $j \colon U \to h(S)$
is a covering sieve if there exists a finite family of maps
$j \colon U \to h(S)$
is a covering sieve if there exists a finite family of maps
![]() $(T_i \to S)_{i \in I}$
such that the induced map
$(T_i \to S)_{i \in I}$
such that the induced map
![]() $T \simeq \coprod _{i \in I} T_i \to S$
is faithfully flat and such that each
$T \simeq \coprod _{i \in I} T_i \to S$
is faithfully flat and such that each
![]() $h(T_i) \to h(S)$
factors through j.
$h(T_i) \to h(S)$
factors through j.
Definition 1.1. The
![]() $\infty $
-category of Dirac stacks is the full subcategory
$\infty $
-category of Dirac stacks is the full subcategory
spanned by the sheaves for the flat topology.
It is not immediately clear that there exists a ‘sheafification’ functor, left adjoint to the canonical inclusion of sheaves in presheaves. That this is nevertheless the case is a consequence of a theorem of Waterhouse [Reference Waterhouse35, Theorem 5.1], which is perhaps not as well known as it deserves. It shows that the flat topology is well-behaved. What is not well-behaved is the
![]() $\infty $
-category of all presheaves on
$\infty $
-category of all presheaves on
![]() $\operatorname {\mathrm {Aff}}$
; once we limit ourselves to considering accessible presheaves only, the supposed problems with the flat topology disappear. In the Dirac context, Waterhouse’s theorem is the following statement, and the essential ingredient in its proof is the Dirac analogue of the equational criterion for faithful flatness, which we proved in [Reference Hesselholt and Pstrągowski12, Addendum 3.9].
$\operatorname {\mathrm {Aff}}$
; once we limit ourselves to considering accessible presheaves only, the supposed problems with the flat topology disappear. In the Dirac context, Waterhouse’s theorem is the following statement, and the essential ingredient in its proof is the Dirac analogue of the equational criterion for faithful flatness, which we proved in [Reference Hesselholt and Pstrągowski12, Addendum 3.9].
Theorem 1.2 (Waterhouse’s theorem).
Let
![]() $\kappa < \kappa '$
be small regular cardinals. In this situation, the left Kan extension along the canonical inclusion
$\kappa < \kappa '$
be small regular cardinals. In this situation, the left Kan extension along the canonical inclusion
preserves sheaves with respect to the flat topology.
As we have already mentioned, an important consequence of Theorem 1.2 is the existence of a left exact ‘sheafification’ functor
left adjoint to the canonical inclusion functor. Indeed, if we replace
![]() $\operatorname {\mathrm {Aff}}$
by the essentially small
$\operatorname {\mathrm {Aff}}$
by the essentially small
![]() ${\mathrm {Aff}}_{\kappa }$
, then Lurie has proved in [Reference Lurie20, Proposition 6.2.2.7] that a left exact sheafification functor exists, and Theorem 1.2 and [Reference Lurie17, Tag 02FV] show that these left adjoint functors assemble to give the stated left adjoint functor.
${\mathrm {Aff}}_{\kappa }$
, then Lurie has proved in [Reference Lurie20, Proposition 6.2.2.7] that a left exact sheafification functor exists, and Theorem 1.2 and [Reference Lurie17, Tag 02FV] show that these left adjoint functors assemble to give the stated left adjoint functor.
We can now deduce from [Reference Lurie20, Theorem 6.1.0.6] that the
![]() $\infty $
-category of Dirac stacks satisfies the
$\infty $
-category of Dirac stacks satisfies the
![]() $\infty $
-categorical Giraud axioms, except that it not presentable.
$\infty $
-categorical Giraud axioms, except that it not presentable.
Theorem 1.3 (Giraud’s axioms for Dirac stacks).
The
![]() $\infty $
-category
$\infty $
-category
![]() $\,\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of Dirac stacks has the following properties:
$\,\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of Dirac stacks has the following properties:
-
(i) It is complete and cocomplete, and it is generated under small colimits by the essential image of the Yoneda embedding
 $h \colon \operatorname {\mathrm {Aff}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which consists of
$h \colon \operatorname {\mathrm {Aff}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which consists of
 $\omega _1$
-compact objects and is coaccessible.
$\omega _1$
-compact objects and is coaccessible. -
(ii) Colimits in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal. -
(iii) Coproducts in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint. -
(iv) Every groupoid in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is effective.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is effective.
The
![]() $\infty $
-category of Dirac stacks is close enough to being an
$\infty $
-category of Dirac stacks is close enough to being an
![]() $\infty $
-topos that it retains the important property of
$\infty $
-topos that it retains the important property of
![]() $\infty $
-topoi that the contravariant functor
$\infty $
-topoi that the contravariant functor
that to X assigns the slice
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
takes colimits of Dirac stacks to limits of
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
takes colimits of Dirac stacks to limits of
![]() $\infty $
-categories. This statement is the source of all descent statements in the paper. In typical situations, we wish to show that flat descent holds for the full subcategory
$\infty $
-categories. This statement is the source of all descent statements in the paper. In typical situations, we wish to show that flat descent holds for the full subcategory
spanned by the maps
![]() $f \colon Y \to X$
that have some property P. But this follows from the fundamental descent statement, once we prove that the property P satisfies descent for the flat topology in the sense that for every effective epimorphism
$f \colon Y \to X$
that have some property P. But this follows from the fundamental descent statement, once we prove that the property P satisfies descent for the flat topology in the sense that for every effective epimorphism
![]() $f \colon X' \to X$
, the diagram of
$f \colon X' \to X$
, the diagram of
![]() $\infty $
-categories
$\infty $
-categories

is cartesian. For example, we define a functor that to a Dirac stack X assigns the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {FGroup}}(X)$
of formal groups over X and use this strategy to show that it descends along effective epimorphisms.
$\operatorname {\mathrm {FGroup}}(X)$
of formal groups over X and use this strategy to show that it descends along effective epimorphisms.
It follows from Grothendieck’s faithfully flat descent for graded modules, which we proved in [Reference Hesselholt and Pstrągowski12, Theorem 1.5], that the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
is subcanonical. Here, we prove that, more generally, the category of Dirac schemes, which we defined in [Reference Hesselholt and Pstrągowski12, Definition 2.29], embeds fully faithfully into the
$\operatorname {\mathrm {Aff}}$
is subcanonical. Here, we prove that, more generally, the category of Dirac schemes, which we defined in [Reference Hesselholt and Pstrągowski12, Definition 2.29], embeds fully faithfully into the
![]() $\infty $
-category of Dirac stacks.
$\infty $
-category of Dirac stacks.
Theorem 1.4 (Schemes are stacks).
Dirac schemes are Dirac stacks:
-
(1) If X is a Dirac scheme, then the functor
 $h(X) \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
that to an affine scheme S assigns
$h(X) \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
that to an affine scheme S assigns
 $\operatorname {\mathrm {Map}}(S,X)$
is accessible and a sheaf for the flat topology.
$\operatorname {\mathrm {Map}}(S,X)$
is accessible and a sheaf for the flat topology. -
(2) The resulting functor
 $h \colon \operatorname {\mathrm {Sch}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is fully faithful.
$h \colon \operatorname {\mathrm {Sch}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is fully faithful.
This result is the starting point for the definition following Toën–Vezzosi [Reference Toën and Vezzosi33] and Lurie [Reference Lurie18] of the property of a map of Dirac stacks
![]() $f \colon Y \to X$
of being geometric. Informally, the geometric maps span the smallest full subcategory
$f \colon Y \to X$
of being geometric. Informally, the geometric maps span the smallest full subcategory
that contains the maps
![]() $f \colon Y \to X$
that, locally on X, are equivalent to maps of Dirac schemes, and that is closed under the formation of the geometric realization of groupoids with flat face maps.Footnote
1
However, the formal definition, which we give in Section 2.3 below, is more complicated, because the notions of being geometric and being flat must be defined recursively together. The property of being geometric is well-behaved: it is preserved under composition and base-change, it is local on the target, and maps in
$f \colon Y \to X$
that, locally on X, are equivalent to maps of Dirac schemes, and that is closed under the formation of the geometric realization of groupoids with flat face maps.Footnote
1
However, the formal definition, which we give in Section 2.3 below, is more complicated, because the notions of being geometric and being flat must be defined recursively together. The property of being geometric is well-behaved: it is preserved under composition and base-change, it is local on the target, and maps in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}^{\operatorname {\mathrm {geom}}}$
are automatically geometric.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}^{\operatorname {\mathrm {geom}}}$
are automatically geometric.
We now explain the theory of coherent cohomology of Dirac stacks, which we develop following Lurie [Reference Lurie23, Chapter 6]. It consists of the following data:
-
(Q1) A functor
 ${\mathrm {QCoh}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {op}}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
; it assigns to map of Dirac stacks
${\mathrm {QCoh}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {op}}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
; it assigns to map of Dirac stacks
 $f \colon Y \to X$
a symmetric monoidal adjunction between presentably symmetric monoidal stable
$f \colon Y \to X$
a symmetric monoidal adjunction between presentably symmetric monoidal stable
 $\infty $
-categories.
$\infty $
-categories.
-
(Q2) For every Dirac stack X, a symmetric monoidal adjunction
such that i is the fully faithful inclusion of the connective part of a t-structure, and such that for every map of Dirac stacks
 $f \colon Y \to X$
, the functor
$f \colon Y \to X$
, the functor
 $f^*$
is right t-exact, or equivalently, the functor
$f^*$
is right t-exact, or equivalently, the functor
 $f_*$
is left t-exact.
$f_*$
is left t-exact.
First, to produce the functor (Q1), we begin with the functor that to an affine Dirac scheme
![]() $S \simeq \operatorname {\mathrm {Spec}}(A)$
assigns the presentably symmetric monoidal category
$S \simeq \operatorname {\mathrm {Spec}}(A)$
assigns the presentably symmetric monoidal category
of graded A-modules. It promotes via animation to a functor that to S assigns the presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
of animated graded A-modules, which, in turn, promotes via stabilization to a functor that to S assigns the presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
of spectra in animated graded A-modules. Following Grothendieck, we show that this functor is a sheaf for the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
, a fact, which, in homotopy theory, was first observed and exploited by Hopkins [Reference Hopkins14]. This gives us (Q1):
$\operatorname {\mathrm {Aff}}$
, a fact, which, in homotopy theory, was first observed and exploited by Hopkins [Reference Hopkins14]. This gives us (Q1):
Theorem 1.5 (Faithfully flat descent for quasi-coherent modules).
The right Kan extension of the functor
![]() ${\mathrm {QCoh}} \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
along
${\mathrm {QCoh}} \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
along
![]() $h \colon \operatorname {\mathrm {Aff}} \to {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
admits a unique factorization
$h \colon \operatorname {\mathrm {Aff}} \to {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
admits a unique factorization
through the sheafification functor.
To spell out this definition of
![]() ${\mathrm {QCoh}}(X)$
, if we choose a regular cardinal
${\mathrm {QCoh}}(X)$
, if we choose a regular cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $X \in \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is the left Kan extension of
$X \in \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is the left Kan extension of
![]() $X_{\kappa } \in \operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\kappa })$
, then
$X_{\kappa } \in \operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\kappa })$
, then
where the limit is indexed by
![]() $(({\mathrm {Aff}}_{\kappa })_{/X})^{\operatorname {\mathrm {op}}}$
and is calculated in
$(({\mathrm {Aff}}_{\kappa })_{/X})^{\operatorname {\mathrm {op}}}$
and is calculated in
![]() $\operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
.Footnote
2
$\operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
.Footnote
2
Second, to produce the symmetric monoidal adjunction (Q2), we show that for an affine Dirac scheme S, the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(S)_{\geq 0}$
is Grothendieck prestable in the sense of [Reference Lurie23, Definition C.1.4.2]. Thus, the symmetric monoidal adjunction
${\mathrm {QCoh}}(S)_{\geq 0}$
is Grothendieck prestable in the sense of [Reference Lurie23, Definition C.1.4.2]. Thus, the symmetric monoidal adjunction
is the connective part of a t-structure, and we obtain (Q2) by right Kan extension. More concretely, if X is a Dirac stack, then
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
is connective if and only if
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
is connective if and only if
![]() $\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is connective for every map
$\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is connective for every map
![]() $\eta \colon S \to X$
with S affine. It is also true that if
$\eta \colon S \to X$
with S affine. It is also true that if
![]() $\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is coconnective for every map
$\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is coconnective for every map
![]() $\eta \colon S \to X$
with S affine, then
$\eta \colon S \to X$
with S affine, then
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
is coconnective, but the converse is false. In particular, the tensor unit
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
is coconnective, but the converse is false. In particular, the tensor unit
![]() $\mathcal {O}_X$
belongs to the heart of the t-structure.
$\mathcal {O}_X$
belongs to the heart of the t-structure.
In general, the t-structure on
![]() ${\mathrm {QCoh}}(X)$
is not left complete or right complete, and the coconnective part is next to impossible to understand. However, for geometric Dirac stacks, including Dirac schemes, the situation improves:
${\mathrm {QCoh}}(X)$
is not left complete or right complete, and the coconnective part is next to impossible to understand. However, for geometric Dirac stacks, including Dirac schemes, the situation improves:
Theorem 1.6 (Geometric stacks and t-structure).
If X is a geometric Dirac stack, then the t-structure on
![]() ${\mathrm {QCoh}}(X)$
is left and right complete and the coconnective part is closed under filtered colimits. Moreover, if
${\mathrm {QCoh}}(X)$
is left and right complete and the coconnective part is closed under filtered colimits. Moreover, if
![]() $\eta \colon S \to X$
is submersive with S affine, then
$\eta \colon S \to X$
is submersive with S affine, then
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
is coconnective if and only if
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
is coconnective if and only if
![]() $\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is so.
$\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)$
is so.
We let
![]() $\pi _i^{\heartsuit }(\mathcal {F}) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
be the ith homotopy
$\pi _i^{\heartsuit }(\mathcal {F}) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
be the ith homotopy
![]() $\mathcal {O}_X$
-module of
$\mathcal {O}_X$
-module of
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
with respect to the canonical t-structure. We refer to i as the ‘animated’ degree to separate it from the ‘spin’ degree intrinsic to Dirac geometry. If
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
with respect to the canonical t-structure. We refer to i as the ‘animated’ degree to separate it from the ‘spin’ degree intrinsic to Dirac geometry. If
![]() $f \colon Y \to X$
is a map of Dirac stacks, then the ‘correct’ relative coherent cohomology
$f \colon Y \to X$
is a map of Dirac stacks, then the ‘correct’ relative coherent cohomology
![]() $\mathcal {O}_X$
-modules of the
$\mathcal {O}_X$
-modules of the
![]() $\mathcal {O}_Y$
-module
$\mathcal {O}_Y$
-module
![]() $\mathcal {G} \in {\mathrm {QCoh}}(Y)$
are given by
$\mathcal {G} \in {\mathrm {QCoh}}(Y)$
are given by
This functor can generally not be calculated as the derived functor of the left-exact functor between abelian categories
![]() $f_*^{\heartsuit }$
induced by the left t-exact functor
$f_*^{\heartsuit }$
induced by the left t-exact functor
![]() $f_*$
.
$f_*$
.
Another special class of Dirac stacks that we consider are the formal Dirac schemes. If
![]() $\eta \colon S \to X$
is a closed immersion of Dirac schemes, whose defining quasi-coherent ideal
$\eta \colon S \to X$
is a closed immersion of Dirac schemes, whose defining quasi-coherent ideal
![]() $\mathcal {I} \subset \mathcal {O}_X$
is of finite type, then we define the formal completion of X along S to be the colimit in Dirac stacks
$\mathcal {I} \subset \mathcal {O}_X$
is of finite type, then we define the formal completion of X along S to be the colimit in Dirac stacks
of the infinitesimal thickenings
![]() $\eta ^{(m)} \colon S^{(m)} \to X$
. The map j is not geometric, but if the closed immersion
$\eta ^{(m)} \colon S^{(m)} \to X$
. The map j is not geometric, but if the closed immersion
![]() $\eta \colon S \to X$
is regular in the sense that, locally on X, it is defined by a regular sequence, then it behaves as an open and affine immersion of a tubular neighborhood of S in X, as envisioned by Grothendieck.
$\eta \colon S \to X$
is regular in the sense that, locally on X, it is defined by a regular sequence, then it behaves as an open and affine immersion of a tubular neighborhood of S in X, as envisioned by Grothendieck.
Theorem 1.7 (Formal completion and recollement).
Let X be a Dirac scheme and let
![]() $\eta \colon S \to X$
be a regular closed immersion. Let
$\eta \colon S \to X$
be a regular closed immersion. Let
![]() $j \colon Y \to X$
be the formal completion of X along S and let
$j \colon Y \to X$
be the formal completion of X along S and let
![]() $i \colon U \simeq X \smallsetminus S \to X$
be the inclusion of the open complement of S. In this situation, there is a stable recollement
$i \colon U \simeq X \smallsetminus S \to X$
be the inclusion of the open complement of S. In this situation, there is a stable recollement

and, in addition, the functor
![]() $j_*$
is t-exact.
$j_*$
is t-exact.
The formal schemes that we will consider are the formal affine spaces, defined as follows. If S is a Dirac scheme and
![]() $\mathcal {E} \in {\mathrm {QCoh}}(S)^{\heartsuit }$
an
$\mathcal {E} \in {\mathrm {QCoh}}(S)^{\heartsuit }$
an
![]() $\mathcal {O}_S$
-module locally free of finite rank, then the affine space associated with
$\mathcal {O}_S$
-module locally free of finite rank, then the affine space associated with
![]() $\mathcal {E}$
is the affine map
$\mathcal {E}$
is the affine map
and the formal affine space associated with
![]() $\mathcal {E}$
is its formal completion
$\mathcal {E}$
is its formal completion
along the zero section. We define a map of Dirac stacks
![]() $q \colon Y \to X$
to be a formal hyperplane if its base change along any map
$q \colon Y \to X$
to be a formal hyperplane if its base change along any map
![]() $\eta \colon S \to X$
from an affine Dirac scheme is equivalent to a formal affine space. This property is stable under base change, but it does not descend along effective epimorphisms in general, even if X is a Dirac scheme.Footnote
3
However, if we fix a section, then it does. We consider a formal affine space to be pointed by the zero section.
$\eta \colon S \to X$
from an affine Dirac scheme is equivalent to a formal affine space. This property is stable under base change, but it does not descend along effective epimorphisms in general, even if X is a Dirac scheme.Footnote
3
However, if we fix a section, then it does. We consider a formal affine space to be pointed by the zero section.
Definition 1.8. A pointed Dirac stack

is a pointed formal hyperplane if its base change along any map
![]() $\eta \colon S \to X$
from an affine Dirac scheme is equivalent to a pointed formal affine space.
$\eta \colon S \to X$
from an affine Dirac scheme is equivalent to a pointed formal affine space.
By definition, the
![]() $\infty $
-category of pointed formal hyperplanes over a Dirac stack is the full subcategory of the
$\infty $
-category of pointed formal hyperplanes over a Dirac stack is the full subcategory of the
![]() $\infty $
-category of pointed Dirac stacks
$\infty $
-category of pointed Dirac stacks
spanned by the pointed formal hyperplanes. We show that it is equivalent to a
![]() $1$
-category and that the property of being a pointed formal hyperplane descends along effective epimorphisms of Dirac stacks
$1$
-category and that the property of being a pointed formal hyperplane descends along effective epimorphisms of Dirac stacks
![]() $f \colon X' \to X$
in the sense that
$f \colon X' \to X$
in the sense that

is a cartesian diagram of
![]() $\infty $
-categories. So by Theorem 1.3, the
$\infty $
-categories. So by Theorem 1.3, the
![]() $\infty $
-category of pointed formal hyperplanes satisfies descent along effective epimorphisms:
$\infty $
-category of pointed formal hyperplanes satisfies descent along effective epimorphisms:
Theorem 1.9 (Flat descent for pointed formal hyperplanes).
If
![]() $f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then the canonical maps
$f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then the canonical maps
are equivalences of
![]() $\infty $
-categories.
$\infty $
-categories.
We recall from [Reference Hesselholt and Pstrągowski12, Proposition A.1] that the right-hand map in Theorem 1.9 is an equivalence, because the
![]() $\infty $
-category of pointed formal hyperplanes is equivalent to a
$\infty $
-category of pointed formal hyperplanes is equivalent to a
![]() $1$
-category, and moreover, the right-hand term is equivalent to the
$1$
-category, and moreover, the right-hand term is equivalent to the
![]() $1$
-category of pointed formal hyperplanes over
$1$
-category of pointed formal hyperplanes over
![]() $X'$
with descent data along
$X'$
with descent data along
![]() $f \colon X' \to X$
.
$f \colon X' \to X$
.
Let
![]() $\mathcal {C}$
be an
$\mathcal {C}$
be an
![]() $\infty $
-category which admits finite products. Following Lawvere, we let
$\infty $
-category which admits finite products. Following Lawvere, we let
![]() $\operatorname {\mathrm {Lat}}$
be the category of finitely generated free abelian groups and define the
$\operatorname {\mathrm {Lat}}$
be the category of finitely generated free abelian groups and define the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Ab}}(\mathcal {C})$
of abelian group objects in the
$\operatorname {\mathrm {Ab}}(\mathcal {C})$
of abelian group objects in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
to be the full subcategory
$\mathcal {C}$
to be the full subcategory
spanned by the functors that preserve finite products.
Definition 1.10. The
![]() $\infty $
-category of formal groups over a Dirac stack X is the
$\infty $
-category of formal groups over a Dirac stack X is the
![]() $\infty $
-category
$\infty $
-category
of abelian group objects in the
![]() $\infty $
-category of formal hyperplanes over X.
$\infty $
-category of formal hyperplanes over X.
The
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {FGroup}}(X)$
is equivalent to a
$\operatorname {\mathrm {FGroup}}(X)$
is equivalent to a
![]() $1$
-category. If
$1$
-category. If
![]() $\mathcal {G}$
is a formal group over X, then the underlying hyperplane
$\mathcal {G}$
is a formal group over X, then the underlying hyperplane
![]() $\mathcal {G}(\mathbb {Z})$
is pointed by the zero section
$\mathcal {G}(\mathbb {Z})$
is pointed by the zero section
![]() $\mathcal {G}(0) \to \mathcal {G}(\mathbb {Z})$
. Therefore, by Theorem 1.9, if
$\mathcal {G}(0) \to \mathcal {G}(\mathbb {Z})$
. Therefore, by Theorem 1.9, if
![]() $f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then the canonical map
$f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then the canonical map
is an equivalence of
![]() $\infty $
-categories, and the target
$\infty $
-categories, and the target
![]() $\infty $
-category is equivalent to the
$\infty $
-category is equivalent to the
![]() $1$
-category of formal groups over
$1$
-category of formal groups over
![]() $X'$
with descent data along
$X'$
with descent data along
![]() $f \colon X' \to X$
. Moreover, if
$f \colon X' \to X$
. Moreover, if
![]() $\mathcal {G}$
is a formal group over X, then we define its Lie algebra to be the vector bundle
$\mathcal {G}$
is a formal group over X, then we define its Lie algebra to be the vector bundle
associated with the conormal sheaf at the zero section. Since
![]() $\mathcal {G}$
is abelian, the Lie bracket on this vector bundle will be zero, so we do not take the trouble to define it.
$\mathcal {G}$
is abelian, the Lie bracket on this vector bundle will be zero, so we do not take the trouble to define it.
We end with a number of applications of Dirac geometry to algebraic topology, which we encode as a six-functor formalism on the
![]() $\infty $
-category of anima following the general theory of Liu–Zheng [Reference Liu and Zheng16] and Mann [Reference Mann24, Appendix A.5]. The definition of this six-functor formalism is informed by the fact that anima are ‘discrete’ objects, as opposed to ‘continuous’ objects. So we declare that every map of anima
$\infty $
-category of anima following the general theory of Liu–Zheng [Reference Liu and Zheng16] and Mann [Reference Mann24, Appendix A.5]. The definition of this six-functor formalism is informed by the fact that anima are ‘discrete’ objects, as opposed to ‘continuous’ objects. So we declare that every map of anima
![]() $f \colon T \to S$
is a local isomorphism and that a map of anima
$f \colon T \to S$
is a local isomorphism and that a map of anima
![]() $f \colon T \to S$
is proper if its fibers are equivalent to finite sets, including the empty set. By [Reference Mann24, Proposition A.5.10], this determines a six-functor formalism on
$f \colon T \to S$
is proper if its fibers are equivalent to finite sets, including the empty set. By [Reference Mann24, Proposition A.5.10], this determines a six-functor formalism on
![]() $\mathcal {S}$
that to an anima S assigns the functor
$\mathcal {S}$
that to an anima S assigns the functor
![]() $\infty $
-category
$\infty $
-category
and that to a map of anima
![]() $f \colon T \to S$
assigns the adjoint functors
$f \colon T \to S$
assigns the adjoint functors

where
![]() $f^! \simeq f^*$
is the restriction along f, and
$f^! \simeq f^*$
is the restriction along f, and
![]() $f_!$
and
$f_!$
and
![]() $f_*$
are the left and right Kan extensions along f.
$f_*$
are the left and right Kan extensions along f.
Given a commutative algebra in spectra E and a group in anima G, we apply the general theory to construct a formal Dirac scheme
over
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
with
$S \simeq \operatorname {\mathrm {Spec}}(R)$
with
![]() $R \simeq \pi _*(E)$
, and we will consider situations in which q is a formal hyperplane. By varying G, we will obtain formal groups, and by varying E, we will obtain formal groups over geometric Dirac stacks, which we characterize by exhibiting their functors of points.
$R \simeq \pi _*(E)$
, and we will consider situations in which q is a formal hyperplane. By varying G, we will obtain formal groups, and by varying E, we will obtain formal groups over geometric Dirac stacks, which we characterize by exhibiting their functors of points.
To this end, we recall from [Reference Lurie19, Theorem 5.6.2.10] that every group in anima G is the loop group
![]() $\Omega BG$
of a pointed
$\Omega BG$
of a pointed
![]() $1$
-connective anima
$1$
-connective anima
and we apply the general theory to the unique map
The
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Sp}}^{BG}$
is the
$\operatorname {\mathrm {Sp}}^{BG}$
is the
![]() $\infty $
-category of spectra with G-action, and
$\infty $
-category of spectra with G-action, and
![]() $p_!$
and
$p_!$
and
![]() $p_*$
are the functors that to a spectrum with G-action Y assign its homotopy orbit spectrum
$p_*$
are the functors that to a spectrum with G-action Y assign its homotopy orbit spectrum
![]() $p_!(Y) \simeq Y_{hG}$
and its homotopy fixed point spectrum
$p_!(Y) \simeq Y_{hG}$
and its homotopy fixed point spectrum
![]() $p_*(Y) \simeq Y^{hG}$
, respectively, whereas
$p_*(Y) \simeq Y^{hG}$
, respectively, whereas
![]() $p^*$
is the functor that to a spectrum X assigns the spectrum with trivial G-action
$p^*$
is the functor that to a spectrum X assigns the spectrum with trivial G-action
![]() $Y \simeq p^*(X)$
. We only consider spectra with trivial G-action.
$Y \simeq p^*(X)$
. We only consider spectra with trivial G-action.
Given a commutative algebra in spectra E, the spectrum
promotes to a commutative algebra in spectra, and the unit maps
promote to maps of commutative algebras in spectra. Hence, if
![]() $R \simeq \pi _*(E)$
and
$R \simeq \pi _*(E)$
and
![]() $A \simeq \pi _*(p_*p^*(E))$
are the respective Dirac rings of homotopy groups, then these maps give A the structure of an augmented R-algebra. We now define
$A \simeq \pi _*(p_*p^*(E))$
are the respective Dirac rings of homotopy groups, then these maps give A the structure of an augmented R-algebra. We now define
to be the formal completion of
![]() $X \simeq \operatorname {\mathrm {Spec}}(A)$
along the closed immersion
$X \simeq \operatorname {\mathrm {Spec}}(A)$
along the closed immersion
defined by the augmentation.
First, we let G be the Pontryagin dual
![]() $\widehat {L} \simeq \operatorname {\mathrm {Hom}}(L,U(1))$
of
$\widehat {L} \simeq \operatorname {\mathrm {Hom}}(L,U(1))$
of
![]() $L \in \operatorname {\mathrm {Lat}}$
. If E is complex orientable, then the formal scheme
$L \in \operatorname {\mathrm {Lat}}$
. If E is complex orientable, then the formal scheme
is a formal hyperplane, and as L varies, this defines the Quillen formal group
associated with E. Moreover, by considering the Postnikov filtration of E, we obtain a canonical isomorphism of line bundles
from the spin-
![]() $1$
affine line over S to the Lie algebra of the Quillen formal group. We now let E vary through the tensor powers of the commutative algebra in spectra
$1$
affine line over S to the Lie algebra of the Quillen formal group. We now let E vary through the tensor powers of the commutative algebra in spectra
![]() $\operatorname {MU}$
representing complex cobordism. In this way, we obtain a simplicial formal group
$\operatorname {MU}$
representing complex cobordism. In this way, we obtain a simplicial formal group
that to
![]() $[n]$
assigns the Quillen formal group associated with
$[n]$
assigns the Quillen formal group associated with
![]() $\operatorname {MU}^{\otimes [n]}$
. Its geometric realization is a formal group
$\operatorname {MU}^{\otimes [n]}$
. Its geometric realization is a formal group
![]() $\mathcal {G}^Q$
over the geometric Dirac stack
$\mathcal {G}^Q$
over the geometric Dirac stack
equipped with a trivialization
![]() $\phi ^Q$
of its Lie algebra. We show that Quillen’s theorem on complex cobordism, [Reference Quillen31, Theorem 2], implies and is implied by the statement that
$\phi ^Q$
of its Lie algebra. We show that Quillen’s theorem on complex cobordism, [Reference Quillen31, Theorem 2], implies and is implied by the statement that
![]() $(\mathcal {G}^Q,\phi ^Q)$
is the universal
$(\mathcal {G}^Q,\phi ^Q)$
is the universal
![]() $1$
-dimensional spin-
$1$
-dimensional spin-
![]() $1$
formal group equipped with a trivialization of its Lie algebra.
$1$
formal group equipped with a trivialization of its Lie algebra.
Theorem 1.11 (Quillen’s theorem).
Let T be a Dirac stack. The functor that to
![]() $f \colon T \to X^Q$
assigns the pair
$f \colon T \to X^Q$
assigns the pair
![]() $(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence of anima from
$(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence of anima from
![]() $X^Q(T)$
to the groupoid of pairs
$X^Q(T)$
to the groupoid of pairs
![]() $(\mathcal {G},\phi )$
of a formal group
$(\mathcal {G},\phi )$
of a formal group
![]() $\mathcal {G}$
over T and an isomorphism
$\mathcal {G}$
over T and an isomorphism
of line bundles over T from the spin-
![]() $1$
affine line.
$1$
affine line.
We also show that if T is an affine Dirac scheme and
![]() $(\mathcal {G},\phi ) \in X^Q(T)$
, then the trivialization
$(\mathcal {G},\phi ) \in X^Q(T)$
, then the trivialization
![]() $\phi $
lifts to a spin-
$\phi $
lifts to a spin-
![]() $1$
global coordinate on the formal group
$1$
global coordinate on the formal group
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Second, we let p be an odd prime number and let G be the p-torsion subgroup
of the Pontryagin dual of
![]() $L \in \operatorname {\mathrm {Lat}}$
. If
$L \in \operatorname {\mathrm {Lat}}$
. If
![]() $k \simeq \mathbb {F}_p$
, then for every commutative k-algebra in spectra E,
$k \simeq \mathbb {F}_p$
, then for every commutative k-algebra in spectra E,
is a formal hyperplane, and as L varies, this defines the Milnor formal group
associated with E. The canonical inclusion i induces a map of formal groups
to the Quillen formal group. It is surjective, and its kernel
is again a formal group over S. This filtration gives rise to a grading of the Lie algebra
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M)$
, which we refer to as the ‘charge’ grading.Footnote
4
Moreover, from the Postnikov filtration of E, we obtain a canonical isomorphism of graded vector bundles over S,
$\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M)$
, which we refer to as the ‘charge’ grading.Footnote
4
Moreover, from the Postnikov filtration of E, we obtain a canonical isomorphism of graded vector bundles over S,
where e has spin ![]() and charge
and charge
![]() $1$
and where
$1$
and where
![]() $\gamma $
has spin
$\gamma $
has spin
![]() $1$
and charge
$1$
and charge
![]() $0$
.
$0$
.
Letting E vary through the tensor powers of k, we obtain a simplicial filtered formal group that to
![]() $[n] \in \Delta ^{\operatorname {\mathrm {op}}}$
assigns the Milnor formal group associated with
$[n] \in \Delta ^{\operatorname {\mathrm {op}}}$
assigns the Milnor formal group associated with
![]() $k^{\otimes [n]}$
with the filtration defined by the map to the Quillen formal group. Its geometric realization is a filtered formal group
$k^{\otimes [n]}$
with the filtration defined by the map to the Quillen formal group. Its geometric realization is a filtered formal group
![]() $\operatorname {\mathrm {Fil}}\mathcal {G}^M$
over the geometric Dirac stack
$\operatorname {\mathrm {Fil}}\mathcal {G}^M$
over the geometric Dirac stack
equipped with a trivialization
![]() $\phi ^M$
of its graded Lie algebra. We show that Milnor’s theorem [Reference Milnor29] on the structure of the dual Steenrod algebra implies and is implied by the following statement.
$\phi ^M$
of its graded Lie algebra. We show that Milnor’s theorem [Reference Milnor29] on the structure of the dual Steenrod algebra implies and is implied by the following statement.
Theorem 1.12 (Milnor’s theorem).
Let
![]() $S \simeq \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p odd and let T be an S-Dirac stack. The functor that to a map of S-Dirac stacks
$S \simeq \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p odd and let T be an S-Dirac stack. The functor that to a map of S-Dirac stacks
![]() $f \colon T \to X^M$
assigns the pair
$f \colon T \to X^M$
assigns the pair
![]() $(f^*\operatorname {\mathrm {Fil}}\mathcal {G}^M,f^*\phi ^M)$
is an equivalence from
$(f^*\operatorname {\mathrm {Fil}}\mathcal {G}^M,f^*\phi ^M)$
is an equivalence from
![]() $X^M(T)$
to the groupoid of pairs
$X^M(T)$
to the groupoid of pairs
![]() $(\operatorname {\mathrm {Fil}}\mathcal {G},\phi )$
of a filtered formal group
$(\operatorname {\mathrm {Fil}}\mathcal {G},\phi )$
of a filtered formal group
![]() $\operatorname {\mathrm {Fil}}\mathcal {G}$
over T, locally isomorphic to a filtered additive formal group, and an isomorphism of graded vector bundles over T,
$\operatorname {\mathrm {Fil}}\mathcal {G}$
over T, locally isomorphic to a filtered additive formal group, and an isomorphism of graded vector bundles over T,
where e has spin ![]() and charge
and charge
![]() $1$
and where
$1$
and where
![]() $\gamma $
has spin
$\gamma $
has spin
![]() $1$
and charge
$1$
and charge
![]() $0$
.
$0$
.
Since
![]() $k \simeq \mathbb {F}_p$
is a prime field, the face maps
$k \simeq \mathbb {F}_p$
is a prime field, the face maps
![]() $d_0,d_1 \colon S_{k^{\otimes [1]}} \to S_{k^{\otimes [0]}}$
are equal, so the groupoid Dirac scheme
$d_0,d_1 \colon S_{k^{\otimes [1]}} \to S_{k^{\otimes [0]}}$
are equal, so the groupoid Dirac scheme
![]() $S_{k^{\otimes [-]}}$
is, in fact, a group Dirac scheme
$S_{k^{\otimes [-]}}$
is, in fact, a group Dirac scheme
![]() $G^M$
and
$G^M$
and
is its classifying Dirac stack. The dual Steenrod algebra is the Hopf algebra in Dirac k-vector spaces corresponding to
![]() $G^M$
.
$G^M$
.
Finally, we express the method of descent, which goes back to Adams [Reference Adams1], in Dirac geometric terms. Given a map of commutative algebras in spectra
![]() $\phi \colon k \to E$
, we may form the Dirac stack
$\phi \colon k \to E$
, we may form the Dirac stack
This Dirac stack and its coherent cohomology is particularly useful if the face maps in the simplicial Dirac scheme are flat, in which case, we construct a functor
that to a k-module in spectra V assigns a quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {F}(V)$
. This functor gives rise to an Adams filtration of V, and the associated spectral sequence is the Adams or descent spectral sequence
$\mathcal {F}(V)$
. This functor gives rise to an Adams filtration of V, and the associated spectral sequence is the Adams or descent spectral sequence
It starts from the coherent cohomology of X with coefficients in the half-integer Serre twists of
![]() $\mathcal {F}(V)$
, and it converges conditionally to the homotopy groups of the completion of V with respect to the Adams filtration. A particularly understandable application of this method was given by Liu–Wang [Reference Liu and Wang15] in the situation of the base-change map in topological Hochschild homology
$\mathcal {F}(V)$
, and it converges conditionally to the homotopy groups of the completion of V with respect to the Adams filtration. A particularly understandable application of this method was given by Liu–Wang [Reference Liu and Wang15] in the situation of the base-change map in topological Hochschild homology
where the descent spectral sequence is concentrated on the lines
![]() $-1 \leq i \leq 0$
and therefore degenerates for degree-reasons.
$-1 \leq i \leq 0$
and therefore degenerates for degree-reasons.
Terminology. We write
![]() $\operatorname {\mathrm {Ab}}$
for the symmetric monoidal category of
$\operatorname {\mathrm {Ab}}$
for the symmetric monoidal category of
![]() $\mathbb {Z}$
-graded abelian groups with the Koszul sign in the symmetry isomorphism, and we define the category of Dirac rings to be the category
$\mathbb {Z}$
-graded abelian groups with the Koszul sign in the symmetry isomorphism, and we define the category of Dirac rings to be the category
![]() $\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
of commutative algebras therein. We use the terminology of Clausen–Jansen [Reference Clausen and Jansen8, Theorem 2.19] and say that a map
$\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
of commutative algebras therein. We use the terminology of Clausen–Jansen [Reference Clausen and Jansen8, Theorem 2.19] and say that a map
![]() $f \colon L \to K$
between small
$f \colon L \to K$
between small
![]() $\infty $
-categories is a
$\infty $
-categories is a
![]() $\smash { \varinjlim }$
-equivalence if for every diagram
$\smash { \varinjlim }$
-equivalence if for every diagram
![]() $X \colon K \to \mathcal {C}$
, the induced map
$X \colon K \to \mathcal {C}$
, the induced map
is an equivalence. These maps are referred to as cofinal in [Reference Lurie20, Section 4.1].
2 Dirac stacks
We wish to define a Dirac stack to be a presheaf
![]() $X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
of anima on the category of affine Dirac schemes, which is well behaved in the sense that
$X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
of anima on the category of affine Dirac schemes, which is well behaved in the sense that
-
(1) X to be determined by a small amount of data, and
-
(2) X to be determined by local data,
and both of these conditions require some care.
In the case of
![]() $(1)$
, the category
$(1)$
, the category
![]() $\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is not small, so not every presheaf of anima on
$\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is not small, so not every presheaf of anima on
![]() $\operatorname {\mathrm {Aff}}$
can be written as a small colimit of representable presheaves. Our solution, which is similar to the one used by Clausen–Scholze [Reference Clausen and Scholze9], is to only consider the presheaves which can be expressed as small colimits of representable presheaves. We show in Appendix A that this condition is equivalent to the functor X being accessible and that it leads to an excellent theory.
$\operatorname {\mathrm {Aff}}$
can be written as a small colimit of representable presheaves. Our solution, which is similar to the one used by Clausen–Scholze [Reference Clausen and Scholze9], is to only consider the presheaves which can be expressed as small colimits of representable presheaves. We show in Appendix A that this condition is equivalent to the functor X being accessible and that it leads to an excellent theory.
In the case of (2), this leads us to consider presheaves which satisfy the sheaf condition with respect to some Grothendieck topology. We would like to use the fpqc-topology, which is very strong but still subcanonical. In general, the category of fpqc-covering sieves of a fixed affine Dirac scheme does not have a small cofinal subcategory, and hence, it is not clear that a sheafication functor exists. We extend the work of Waterhouse [Reference Waterhouse35] to show our solution to (1) also solves (2) in that an accessible presheaf admits a sheafification which is again accessible.
Remark 2.1. We will show that there exists a fully faithful embedding
of the category of Dirac schemes, which we defined in [Reference Hesselholt and Pstrągowski12, Definition 2.29], into the
![]() $\infty $
-category of Dirac stacks defined according to the above principles.
$\infty $
-category of Dirac stacks defined according to the above principles.
2.1 The flat topology
The category
![]() $\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is not small, but it is coaccessible in the sense that its opposite category
$\operatorname {\mathrm {Aff}}$
of affine Dirac schemes is not small, but it is coaccessible in the sense that its opposite category
![]() $\operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \simeq \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
is accessible. We show in Proposition A.2 that a presheaf
$\operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \simeq \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
is accessible. We show in Proposition A.2 that a presheaf
is an accessible functor if and only if it is a small colimit of representable presheaves.
Definition 2.2. The
![]() $\infty $
-category of Dirac prestacks is the full subcategory
$\infty $
-category of Dirac prestacks is the full subcategory
spanned by the accessible presheaves.
We show in Theorem A.10 that
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is complete and cocomplete and that it satisfies the Giraud axioms, with the exception that it is not presentable. We also show that the Yoneda embedding factors through a fully faithful functor
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is complete and cocomplete and that it satisfies the Giraud axioms, with the exception that it is not presentable. We also show that the Yoneda embedding factors through a fully faithful functor
and that this functor exhibits
![]() $\mathcal {P}(\operatorname {\mathrm {Aff}})$
as the cocompletion of
$\mathcal {P}(\operatorname {\mathrm {Aff}})$
as the cocompletion of
![]() $\operatorname {\mathrm {Aff}}$
.
$\operatorname {\mathrm {Aff}}$
.
We proceed to define the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
and to show that it gives rise to a well-behaved subcategory
$\operatorname {\mathrm {Aff}}$
and to show that it gives rise to a well-behaved subcategory
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of accessible flat sheaves. We recall the general notions of sieves and Grothendieck topologies in Appendix B.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of accessible flat sheaves. We recall the general notions of sieves and Grothendieck topologies in Appendix B.
Definition 2.3. A sieve
![]() $j \colon U \to h(S)$
on an affine Dirac scheme S is a covering sieve for the flat topology if there exists a finite family
$j \colon U \to h(S)$
on an affine Dirac scheme S is a covering sieve for the flat topology if there exists a finite family
![]() $(f_i \colon T_i \to S)_{i \in I}$
of maps of affine Dirac schemes such that the induced map
$(f_i \colon T_i \to S)_{i \in I}$
of maps of affine Dirac schemes such that the induced map
is faithfully flat and such that each
![]() $h(f_i) \colon h(T_i) \to h(S)$
factors through j.
$h(f_i) \colon h(T_i) \to h(S)$
factors through j.
Proposition 2.4. The collection of covering sieves for the flat topology forms a finitary Grothendieck topology on
![]() $\operatorname {\mathrm {Aff}}$
.
$\operatorname {\mathrm {Aff}}$
.
Proof. The assumptions of [Reference Lurie23, Proposition A.3.2.1] are satisfied, since coproducts in
![]() $\operatorname {\mathrm {Aff}}$
are universal and since flat maps in
$\operatorname {\mathrm {Aff}}$
are universal and since flat maps in
![]() $\operatorname {\mathrm {Aff}}$
are stable under composition and under base-change along arbitrary maps.
$\operatorname {\mathrm {Aff}}$
are stable under composition and under base-change along arbitrary maps.
Proposition 2.5. A presheaf
![]() $X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
is a sheaf for the flat topology if and only if it has the following properties:
$X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
is a sheaf for the flat topology if and only if it has the following properties:
-
(i) For every finite family
 $(S_i)_{i \in I}$
of objects in
$(S_i)_{i \in I}$
of objects in
 $\operatorname {\mathrm {Aff}}$
, the induced map is an equivalence of anima.
$\operatorname {\mathrm {Aff}}$
, the induced map is an equivalence of anima.
-
(ii) For every faithfully flat map
 $f \colon T \to S$
in
$f \colon T \to S$
in
 $\operatorname {\mathrm {Aff}}$
, the induced map is an equivalence of anima.
$\operatorname {\mathrm {Aff}}$
, the induced map is an equivalence of anima.
Proof. This is [Reference Lurie23, Proposition A.3.3.1].
Definition 2.6. The
![]() $\infty $
-category of Dirac stacks is the full subcategory
$\infty $
-category of Dirac stacks is the full subcategory
spanned by the sheaves for the flat topology.
Let us emphasize that for a presheaf
![]() $X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
to be a Dirac stack, it must be both accessible and a sheaf for the flat topology. The former is the case if and only if the equivalent conditions of Proposition A.2 are satisfied, and the latter is the case if and only if the conditions of Proposition 2.5 are satisfied.
$X \colon \operatorname {\mathrm {Aff}}^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
to be a Dirac stack, it must be both accessible and a sheaf for the flat topology. The former is the case if and only if the equivalent conditions of Proposition A.2 are satisfied, and the latter is the case if and only if the conditions of Proposition 2.5 are satisfied.
Remark 2.7. We will only consider sheaves on
![]() $\operatorname {\mathrm {Aff}}$
for the flat topology. However, it is also possible to consider sheaves for the étale topology, whose covering sieves are defined by substituting étale for flat in Definition 2.3. Since étale maps in
$\operatorname {\mathrm {Aff}}$
for the flat topology. However, it is also possible to consider sheaves for the étale topology, whose covering sieves are defined by substituting étale for flat in Definition 2.3. Since étale maps in
![]() $\operatorname {\mathrm {Aff}}$
are flat by [Reference Hesselholt and Pstrągowski12, Theorem 1.9], the flat topology is finer than the étale topology.
$\operatorname {\mathrm {Aff}}$
are flat by [Reference Hesselholt and Pstrągowski12, Theorem 1.9], the flat topology is finer than the étale topology.
A priori, it is not clear that the inclusion
![]() $\iota \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
admits a left adjoint ‘sheafification’ functor. However, we now show that, by an argument of Waterhouse [Reference Waterhouse35, Theorem 5.1], such a functor does indeed exist. It will be convenient to work with Dirac rings instead of affine Dirac schemes, and we will use the following notion throughout the proof.
$\iota \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
admits a left adjoint ‘sheafification’ functor. However, we now show that, by an argument of Waterhouse [Reference Waterhouse35, Theorem 5.1], such a functor does indeed exist. It will be convenient to work with Dirac rings instead of affine Dirac schemes, and we will use the following notion throughout the proof.
Definition 2.8. A subextension of a map of Dirac rings
![]() $f \colon A \to B$
is a diagram of rings of the form
$f \colon A \to B$
is a diagram of rings of the form

with i and j inclusions of sub-Dirac rings. The subextensions of
![]() $f \colon A \to B$
form a partially ordered set
$f \colon A \to B$
form a partially ordered set
![]() $\operatorname {\mathrm {SubExt}}(f)$
.
$\operatorname {\mathrm {SubExt}}(f)$
.
Remark 2.9. The partially ordered set
![]() $\operatorname {\mathrm {SubExt}}(f)$
of
$\operatorname {\mathrm {SubExt}}(f)$
of
![]() $f \colon A \to B$
is equivalent to the full subcategory of
$f \colon A \to B$
is equivalent to the full subcategory of
![]() $\operatorname {\mathrm {Fun}}(\Delta ^1,\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}}))_{/f}$
spanned by the monomorphisms.
$\operatorname {\mathrm {Fun}}(\Delta ^1,\operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}}))_{/f}$
spanned by the monomorphisms.
Lemma 2.10. Let
![]() $\kappa $
be an uncountable cardinal, let
$\kappa $
be an uncountable cardinal, let
![]() $f \colon A \to B$
be a faithfully flat map of Dirac rings, and let
$f \colon A \to B$
be a faithfully flat map of Dirac rings, and let
![]() $g' \colon C' \to D'$
be a subextension of
$g' \colon C' \to D'$
be a subextension of
![]() $f \colon A \to B$
such that
$f \colon A \to B$
such that
![]() $C'$
and
$C'$
and
![]() $D'$
are
$D'$
are
![]() $\kappa $
-small. There exists a subextension
$\kappa $
-small. There exists a subextension
![]() $g \colon C \to D$
of
$g \colon C \to D$
of
![]() $f \colon A \to B$
such that
$f \colon A \to B$
such that
![]() $g' \colon C' \to D'$
is a subextension of
$g' \colon C' \to D'$
is a subextension of
![]() $g \colon C \to D$
, such that C and D are
$g \colon C \to D$
, such that C and D are
![]() $\kappa $
-small, and such that
$\kappa $
-small, and such that
![]() $g \colon C \to D$
is faithfully flat.
$g \colon C \to D$
is faithfully flat.
Proof. In the case of ordinary rings, this is proved in [Reference Waterhouse35, Lemma 3.1]. We recall the argument for the convenience of the reader and to verify that that it works without much change in the Dirac setting.
We first recall the necessary commutative algebra. By the equational criterion for flatness [Reference Hesselholt and Pstrągowski12, Theorem 3.8], a map of Dirac rings
![]() $f \colon A \to B$
is flat if and only if for every system of linear equations
$f \colon A \to B$
is flat if and only if for every system of linear equations
where the
![]() $c_{ki}$
are homogeneous elements of A, every solution
$c_{ki}$
are homogeneous elements of A, every solution
![]() $(y_k)_{1 \leq k \leq n}$
, consisting of homogeneous elements of B, is a linear combination
$(y_k)_{1 \leq k \leq n}$
, consisting of homogeneous elements of B, is a linear combination
where the
![]() $b_j$
are homogeneous elements of B, of solutions
$b_j$
are homogeneous elements of B, of solutions
![]() $(z_{jk})_{1 \leq k \leq n}$
to (2.11) consisting of homogeneous elements
$(z_{jk})_{1 \leq k \leq n}$
to (2.11) consisting of homogeneous elements
![]() $z_{jk}$
of A.
$z_{jk}$
of A.
By the equational criterion for faithful flatness, which we proved in [Reference Hesselholt and Pstrągowski12, Addendum 3.9], a flat map of Dirac rings
![]() $f \colon A \to B$
is faithfully flat if and only if it is a monomorphism and for every solution
$f \colon A \to B$
is faithfully flat if and only if it is a monomorphism and for every solution
![]() $(y_k)_{1 \leq k \leq n}$
consisting of homogeneous elements of B to a system of linear equations
$(y_k)_{1 \leq k \leq n}$
consisting of homogeneous elements of B to a system of linear equations
where the
![]() $c_{ki}$
and
$c_{ki}$
and
![]() $d_i$
are homogeneous elements of A, there exists a solution
$d_i$
are homogeneous elements of A, there exists a solution
![]() $(x_k)_{1 \leq k \leq n}$
consisting of homogeneous elements of A.
$(x_k)_{1 \leq k \leq n}$
consisting of homogeneous elements of A.
Now, in order to prove the lemma, we let
![]() $f \colon A \to B$
and
$f \colon A \to B$
and
![]() $g' \colon C' \to D'$
be as in the statement. We note that, as a consequence of [Reference Hesselholt and Pstrągowski12, Addendum 3.23], the map
$g' \colon C' \to D'$
be as in the statement. We note that, as a consequence of [Reference Hesselholt and Pstrągowski12, Addendum 3.23], the map
![]() $f \colon A \to B$
necessarily is a monomorphism, and therefore, we may assume that it is the inclusion of a sub-Dirac ring.
$f \colon A \to B$
necessarily is a monomorphism, and therefore, we may assume that it is the inclusion of a sub-Dirac ring.
We will define subextensions
![]() $g_n \colon C_n \to D_n$
of
$g_n \colon C_n \to D_n$
of
![]() $f \colon A \to B$
recursively for
$f \colon A \to B$
recursively for
![]() $n \geq 0$
. We define
$n \geq 0$
. We define
![]() $g_0 = g'$
, and assuming that
$g_0 = g'$
, and assuming that
![]() $g_n$
has been defined for
$g_n$
has been defined for
![]() $n < r$
, we define
$n < r$
, we define
![]() $g_r$
as follows: We consider all systems of equations of the form (2.11) and (2.12) with
$g_r$
as follows: We consider all systems of equations of the form (2.11) and (2.12) with
![]() $c_{ki}$
and
$c_{ki}$
and
![]() $d_i$
homogeneous elements in
$d_i$
homogeneous elements in
![]() $C_{r-1}$
. Since
$C_{r-1}$
. Since
![]() $f \colon A \to B$
is flat, every solution
$f \colon A \to B$
is flat, every solution
![]() $(y_k)$
, consisting of homogeneous elements of B, to such a system of equations of the first kind can be written as a linear combination
$(y_k)$
, consisting of homogeneous elements of B, to such a system of equations of the first kind can be written as a linear combination
![]() $y_k = \sum b_jz_{jk}$
with the
$y_k = \sum b_jz_{jk}$
with the
![]() $b_j$
and
$b_j$
and
![]() $z_{jk}$
homogeneous elements of B and A, respectively. Similarly, since
$z_{jk}$
homogeneous elements of B and A, respectively. Similarly, since
![]() $f \colon A \to B$
is faithfully flat, for every solution
$f \colon A \to B$
is faithfully flat, for every solution
![]() $(y_k)$
, consisting of homogeneous elements of B, to a system of equations of the second kind, there exists a solution
$(y_k)$
, consisting of homogeneous elements of B, to a system of equations of the second kind, there exists a solution
![]() $(x_k)$
to the same system of equations consisting of homogeneous elements of A. We now define
$(x_k)$
to the same system of equations consisting of homogeneous elements of A. We now define
![]() $D_r \subset B$
to be the sub-Dirac ring obtained by adjoining to
$D_r \subset B$
to be the sub-Dirac ring obtained by adjoining to
![]() $D_{r-1}$
all the homogeneous elements
$D_{r-1}$
all the homogeneous elements
![]() $b_j$
,
$b_j$
,
![]() $z_{jk}$
, and
$z_{jk}$
, and
![]() $x_k$
of B obtained in this way and define
$x_k$
of B obtained in this way and define
![]() $g_r \colon C_r \to D_r$
to be the inclusion of
$g_r \colon C_r \to D_r$
to be the inclusion of
![]() $C_r = A \cap D_r$
. This completes the definition of the subextensions
$C_r = A \cap D_r$
. This completes the definition of the subextensions
![]() $g_n \colon C_n \to D_n$
for
$g_n \colon C_n \to D_n$
for
![]() $n \geq 0$
.
$n \geq 0$
.
We claim that their union
![]() $g \colon C \to D$
is the desired subextension of
$g \colon C \to D$
is the desired subextension of
![]() $f \colon A \to B$
. Indeed, it is faithfully flat as both the above criteria hold for it by construction, and since
$f \colon A \to B$
. Indeed, it is faithfully flat as both the above criteria hold for it by construction, and since
![]() $\kappa $
is uncountable, the Dirac rings C and D are
$\kappa $
is uncountable, the Dirac rings C and D are
![]() $\kappa $
-small.
$\kappa $
-small.
Corollary 2.13. Let
![]() $f \colon A \to B$
be a faithfully flat map of Dirac rings and
$f \colon A \to B$
be a faithfully flat map of Dirac rings and
![]() $\kappa $
an uncountable regular cardinal. Let
$\kappa $
an uncountable regular cardinal. Let
![]() $\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
be the poset of those subextensions
$\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
be the poset of those subextensions
![]() $g \colon C \to D$
such that both C and D are
$g \colon C \to D$
such that both C and D are
![]() $\kappa $
-small, and let
$\kappa $
-small, and let
![]() $\operatorname {\mathrm {SubExt}}^{{\operatorname {f}\!\operatorname {f}}}_{\kappa }(f)$
be the subposet of those
$\operatorname {\mathrm {SubExt}}^{{\operatorname {f}\!\operatorname {f}}}_{\kappa }(f)$
be the subposet of those
![]() $g \colon C \to D$
that, in addition, are faithfully flat. In this situation, the inclusion
$g \colon C \to D$
that, in addition, are faithfully flat. In this situation, the inclusion
is cofinal. In particular, the partially ordered set
![]() $\operatorname {\mathrm {SubExt}}^{{\operatorname {f}\!\operatorname {f}}}_{\kappa }(f)$
is
$\operatorname {\mathrm {SubExt}}^{{\operatorname {f}\!\operatorname {f}}}_{\kappa }(f)$
is
![]() $\kappa $
-filtered.
$\kappa $
-filtered.
Proof. The first part is a restatement of Lemma 2.10. The second part is a consequence of the first part, since
![]() $\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
is
$\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
is
![]() $\kappa $
-filtered as it is a poset which admits
$\kappa $
-filtered as it is a poset which admits
![]() $\kappa $
-small upper bounds.
$\kappa $
-small upper bounds.
Lemma 2.14. Let
![]() $f \colon A \to B$
be a faithfully flat map of Dirac rings, let
$f \colon A \to B$
be a faithfully flat map of Dirac rings, let
![]() $\kappa $
be an uncountable regular cardinal, and let
$\kappa $
be an uncountable regular cardinal, and let
![]() $[n] \in \Delta _{+}$
. The map
$[n] \in \Delta _{+}$
. The map
from the poset of
![]() $\kappa $
-small subextensions of f to the category of
$\kappa $
-small subextensions of f to the category of
![]() $\kappa $
-small Dirac rings over
$\kappa $
-small Dirac rings over
![]() $B^{\otimes _{A} [n]}$
that to
$B^{\otimes _{A} [n]}$
that to
![]() $g \colon C \to D$
assigns the induced map
$g \colon C \to D$
assigns the induced map
is a
![]() $\varinjlim $
-equivalence as a functor of
$\varinjlim $
-equivalence as a functor of
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. Using Joyal’s version of Quillen’s Theorem A, [Reference Clausen and Jansen8, Theorem 2.19], we must show that for any
![]() $k \colon R \to B^{\otimes _{A} [n]}$
with R a
$k \colon R \to B^{\otimes _{A} [n]}$
with R a
![]() $\kappa $
-small Dirac ring, the slice category
$\kappa $
-small Dirac ring, the slice category
is weakly contractible. Explicitly, the objects of this category are pairs
of a
![]() $\kappa $
-small subextension of
$\kappa $
-small subextension of
![]() $f \colon A \to B$
and a map h such that the composite
$f \colon A \to B$
and a map h such that the composite
coincides with k. Maps are inclusions of subextensions that commute with the given maps from R. In particular, the category in question is a poset. We will show that it is a
![]() $\kappa $
-filtered, which implies that it is weakly contractible.
$\kappa $
-filtered, which implies that it is weakly contractible.
Since we are considering a poset, it suffices to show that every subset
indexed by a
![]() $\kappa $
-small index set I has an upper bound. By first choosing an upper bound
$\kappa $
-small index set I has an upper bound. By first choosing an upper bound
![]() $g \colon C \to D$
of the subset
$g \colon C \to D$
of the subset
we can assume that
![]() $C_i = C$
and
$C_i = C$
and
![]() $D_i = D$
for all
$D_i = D$
for all
![]() $i \in I$
.
$i \in I$
.
With this accomplished, we consider the canonical comparison map
where the colimits are indexed by the partially ordered set
![]() $\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
. Since this partially ordered set is
$\operatorname {\mathrm {SubExt}}_{\kappa }(f)$
. Since this partially ordered set is
![]() $\kappa $
-filtered, and since I is
$\kappa $
-filtered, and since I is
![]() $\kappa $
-small, the map in question is an equivalence by [Reference Lurie20, Proposition 5.3.3.3]. Similarly, the map
$\kappa $
-small, the map in question is an equivalence by [Reference Lurie20, Proposition 5.3.3.3]. Similarly, the map
is an equivalence, because R is
![]() $\kappa $
-small, and therefore a
$\kappa $
-small, and therefore a
![]() $\kappa $
-compact object in the category of Dirac rings. Finally, the map
$\kappa $
-compact object in the category of Dirac rings. Finally, the map
is an equivalence since
![]() $A \simeq \varinjlim C$
and
$A \simeq \varinjlim C$
and
![]() $B \simeq \varinjlim D$
and since relative tensor products preserve filtered colimits in all three variables.
$B \simeq \varinjlim D$
and since relative tensor products preserve filtered colimits in all three variables.
Considering the composite of these maps, we conclude that there exists a
![]() $\kappa $
-small subextension
$\kappa $
-small subextension
![]() $g' \colon C' \to D'$
of
$g' \colon C' \to D'$
of
![]() $f \colon A \to B$
that contains
$f \colon A \to B$
that contains
![]() $g \colon C \to D$
as a subextension and a map of Dirac rings
$g \colon C \to D$
as a subextension and a map of Dirac rings
![]() $h \colon R \to D'{}^{\otimes _{C'}[n]}$
such that for all
$h \colon R \to D'{}^{\otimes _{C'}[n]}$
such that for all
![]() $i \in I$
, the map
$i \in I$
, the map
is equal to the map h. Thus, the pair
![]() $(g' \colon C' \to D', h \colon R \to D'{}^{\otimes _{C'}[n]})$
is the desired upper bound of the subset S.
$(g' \colon C' \to D', h \colon R \to D'{}^{\otimes _{C'}[n]})$
is the desired upper bound of the subset S.
For every infinite cardinal
![]() $\kappa $
, the flat topology on
$\kappa $
, the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
induces a topology on the full subcategory
$\operatorname {\mathrm {Aff}}$
induces a topology on the full subcategory
![]() ${\mathrm {Aff}}_{\kappa } \subset \operatorname {\mathrm {Aff}}$
. A presheaf
${\mathrm {Aff}}_{\kappa } \subset \operatorname {\mathrm {Aff}}$
. A presheaf
![]() $X \colon {\mathrm {Aff}}_{\kappa }^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
is a sheaf for this topology if and only if the conditions (i)–(ii) of Proposition 2.5 hold for all finite families
$X \colon {\mathrm {Aff}}_{\kappa }^{\operatorname {\mathrm {op}}} \to {\mathcal {S}}$
is a sheaf for this topology if and only if the conditions (i)–(ii) of Proposition 2.5 hold for all finite families
![]() $(S_i)_{i \in I}$
of objects in
$(S_i)_{i \in I}$
of objects in
![]() ${\mathrm {Aff}}_{\kappa }$
and for all faithfully flat maps
${\mathrm {Aff}}_{\kappa }$
and for all faithfully flat maps
![]() $f \colon T \to S$
in
$f \colon T \to S$
in
![]() ${\mathrm {Aff}}_{\kappa }$
, respectively.
${\mathrm {Aff}}_{\kappa }$
, respectively.
Theorem 2.15. For every uncountable regular cardinal
![]() $\lambda $
, the left Kan extension
$\lambda $
, the left Kan extension
preserves sheaves with respect to the flat topology.
Proof. We extend Waterhouse’s argument in [Reference Waterhouse35, Theorem 5.1] to the case of sheaves of anima. So we wish to show that if
![]() $X \in {\mathcal {P}}({\mathrm {Aff}}_{\lambda })$
satisfies the hypotheses (i)–(ii) of Proposition 2.5, then so does
$X \in {\mathcal {P}}({\mathrm {Aff}}_{\lambda })$
satisfies the hypotheses (i)–(ii) of Proposition 2.5, then so does
![]() $i_!(X) \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
.
$i_!(X) \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
.
First, if X satisfies (i), then by [Reference Lurie20, Lemma 5.5.8.14], it can be written as a sifted colimit of representable presheaves. Moreover, since
![]() $i_!$
preserves colimits and takes representable presheaves to representable presheaves, we deduce that also
$i_!$
preserves colimits and takes representable presheaves to representable presheaves, we deduce that also
![]() $i_!(X)$
can be written as a sifted colimit of representable presheaves and hence preserves finite products by [Reference Lurie20, Proposition 5.5.8.10].
$i_!(X)$
can be written as a sifted colimit of representable presheaves and hence preserves finite products by [Reference Lurie20, Proposition 5.5.8.10].
Second, suppose that X satisfies (ii) and let
![]() $f \colon A \to B$
be a faithfully flat map of Dirac rings. We must show that the induced map of anima
$f \colon A \to B$
be a faithfully flat map of Dirac rings. We must show that the induced map of anima
is an equivalence. Now, for any
![]() $[n] \in \Delta _+$
, the left Kan extension is given by
$[n] \in \Delta _+$
, the left Kan extension is given by
where the colimit is indexed by
![]() $R \to B^{\otimes _A[n]}$
in
$R \to B^{\otimes _A[n]}$
in
![]() $(({\mathrm {Aff}}_{\lambda })^{\operatorname {\mathrm {op}}})_{/B^{\otimes _A[n]}}$
, and a combination of Corollary 2.13 and Lemma 2.14 shows that the functor
$(({\mathrm {Aff}}_{\lambda })^{\operatorname {\mathrm {op}}})_{/B^{\otimes _A[n]}}$
, and a combination of Corollary 2.13 and Lemma 2.14 shows that the functor
that to the subextension
![]() $g \colon C \to D$
of
$g \colon C \to D$
of
![]() $f \colon A \to B$
assigns
$f \colon A \to B$
assigns
![]() $D^{\otimes _C[n]} \to B^{\otimes _A[n]}$
is a
$D^{\otimes _C[n]} \to B^{\otimes _A[n]}$
is a
![]() $\smash { \varinjlim }$
-equivalence. Hence, we can identify the map in question with the map
$\smash { \varinjlim }$
-equivalence. Hence, we can identify the map in question with the map
with the colimits indexed by
![]() $\operatorname {\mathrm {SubExt}}_{\lambda }^{{\operatorname {f}\!\operatorname {f}}}(f)$
. Since the latter is
$\operatorname {\mathrm {SubExt}}_{\lambda }^{{\operatorname {f}\!\operatorname {f}}}(f)$
. Since the latter is
![]() $\lambda $
-filtered, and since
$\lambda $
-filtered, and since
![]() $\lambda $
is uncountable, we can commute the limit past the colimit, and therefore, it will suffice to show that the map
$\lambda $
is uncountable, we can commute the limit past the colimit, and therefore, it will suffice to show that the map
is an equivalence. However, since every
![]() $g \colon C \to D$
in
$g \colon C \to D$
in
![]() $\operatorname {\mathrm {SubExt}}_{\lambda }^{{\operatorname {f}\!\operatorname {f}}}(f)$
is faithfully flat, and since X satisfies (ii), this map is a colimit of equivalences and hence is itself an equivalence. This shows that
$\operatorname {\mathrm {SubExt}}_{\lambda }^{{\operatorname {f}\!\operatorname {f}}}(f)$
is faithfully flat, and since X satisfies (ii), this map is a colimit of equivalences and hence is itself an equivalence. This shows that
![]() $i_!(X)$
also satisfies (ii) as desired.
$i_!(X)$
also satisfies (ii) as desired.
Remark 2.16. Let
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\kappa }) \subset {\mathcal {P}}({\mathrm {Aff}}_{\kappa })$
be the full subcategory spanned by the sheaves for the flat topology. Theorem 2.15 shows that the canonical map
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\kappa }) \subset {\mathcal {P}}({\mathrm {Aff}}_{\kappa })$
be the full subcategory spanned by the sheaves for the flat topology. Theorem 2.15 shows that the canonical map
from the colimit indexed by the large partially ordered set of uncountable regular cardinals
![]() $\lambda $
in the universe of discourse of the large
$\lambda $
in the universe of discourse of the large
![]() $\infty $
-categories
$\infty $
-categories
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
to the large
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
to the large
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of accessible stacks on
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of accessible stacks on
![]() $\operatorname {\mathrm {Aff}}$
is an equivalence.
$\operatorname {\mathrm {Aff}}$
is an equivalence.
Corollary 2.17. The inclusion of the full subcategory spanned by the sheaves for the flat topology admits a left adjoint sheafification functor,
and the sheafification functor L preserves finite limits.
Proof. Given
![]() $X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, by Proposition A.2, we can write
$X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, by Proposition A.2, we can write
![]() $X \simeq i_!(X_0)$
for some cardinal
$X \simeq i_!(X_0)$
for some cardinal
![]() $\lambda $
and
$\lambda $
and
![]() $X_0 \in {\mathcal {P}}({\mathrm {Aff}}_{\lambda })$
. Since
$X_0 \in {\mathcal {P}}({\mathrm {Aff}}_{\lambda })$
. Since
![]() ${\mathrm {Aff}}_{\lambda }$
is essentially small, the inclusion
${\mathrm {Aff}}_{\lambda }$
is essentially small, the inclusion
admits a left adjoint sheafification functor
![]() $L_{\lambda } \colon {\mathcal {P}}({\mathrm {Aff}}_{\lambda }) \to \operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
because its domain and target are both presentable. Now, we claim that the map
$L_{\lambda } \colon {\mathcal {P}}({\mathrm {Aff}}_{\lambda }) \to \operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
because its domain and target are both presentable. Now, we claim that the map
is a sheafification. Indeed, by Theorem 2.15, the target is the underlying presheaf of a sheaf, and for every
![]() $Y \in \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we have
$Y \in \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we have
 $$ \begin{align*}\begin{aligned} {} & \operatorname{\mathrm{Map}}(i_!\iota_{\lambda}L_{\lambda}(X_0),\iota(Y)) \simeq \operatorname{\mathrm{Map}}(\iota_{\lambda}L_{\lambda}(X_0),i^*\iota(Y)) \cr {} & \quad \simeq \operatorname{\mathrm{Map}}(\iota_{\lambda}L_{\lambda}(X_0),\iota_{\lambda}i^*(Y)) \simeq \operatorname{\mathrm{Map}}(L_{\lambda}(X_0),i^*(Y)) \simeq \operatorname{\mathrm{Map}}(X_0,\iota_{\lambda}i^*(Y)) \cr {} & \quad \simeq \operatorname{\mathrm{Map}}(X_0,i^*\iota(Y)) \simeq \operatorname{\mathrm{Map}}(i_!(X_0),\iota(Y)) \simeq \operatorname{\mathrm{Map}}(X,\iota(Y)), \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} {} & \operatorname{\mathrm{Map}}(i_!\iota_{\lambda}L_{\lambda}(X_0),\iota(Y)) \simeq \operatorname{\mathrm{Map}}(\iota_{\lambda}L_{\lambda}(X_0),i^*\iota(Y)) \cr {} & \quad \simeq \operatorname{\mathrm{Map}}(\iota_{\lambda}L_{\lambda}(X_0),\iota_{\lambda}i^*(Y)) \simeq \operatorname{\mathrm{Map}}(L_{\lambda}(X_0),i^*(Y)) \simeq \operatorname{\mathrm{Map}}(X_0,\iota_{\lambda}i^*(Y)) \cr {} & \quad \simeq \operatorname{\mathrm{Map}}(X_0,i^*\iota(Y)) \simeq \operatorname{\mathrm{Map}}(i_!(X_0),\iota(Y)) \simeq \operatorname{\mathrm{Map}}(X,\iota(Y)), \cr \end{aligned}\end{align*} $$
as desired. Hence, we conclude from [Reference Lurie17, Tag 02FV] that the desired left adjoint functor L exists. It preserves finite limits because each
![]() $L_{\lambda }$
does so.
$L_{\lambda }$
does so.
Remark 2.18. The sheafification functor
![]() $L \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a localization with respect to the large set W consisting of the following colimit-interchange maps:
$L \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a localization with respect to the large set W consisting of the following colimit-interchange maps:
-
(i) For every finite family
 $(S_i)_{i \in I}$
of objects in
$(S_i)_{i \in I}$
of objects in
 $\operatorname {\mathrm {Aff}}$
, the map where
$\operatorname {\mathrm {Aff}}$
, the map where
 $h \colon \operatorname {\mathrm {Aff}} \hookrightarrow {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is the Yoneda embedding.
$h \colon \operatorname {\mathrm {Aff}} \hookrightarrow {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is the Yoneda embedding.
-
(ii) For every faithfully flat map
 $f \colon T \to S$
in
$f \colon T \to S$
in
 $\operatorname {\mathrm {Aff}}$
, the map
$\operatorname {\mathrm {Aff}}$
, the map 
Indeed, this follows from Proposition 2.5.
We now show that the
![]() $\infty $
-category of Dirac stacks satisfies the following variant on the
$\infty $
-category of Dirac stacks satisfies the following variant on the
![]() $\infty $
-categorical Giraud axioms.
$\infty $
-categorical Giraud axioms.
Theorem 2.19. The
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has the following properties:
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has the following properties:
-
(i) It is complete and cocomplete, and it is generated under small colimits by the essential image of the Yoneda embedding
 $h \colon \operatorname {\mathrm {Aff}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which consists of
$h \colon \operatorname {\mathrm {Aff}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which consists of
 $\omega _1$
-compact objects and is coaccessible.
$\omega _1$
-compact objects and is coaccessible. -
(ii) Colimits in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal. -
(iii) Coproducts in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint. -
(iv) Every groupoid in
 $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is effective.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is effective.
Proof. Corollary 2.17 shows that
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a left exact localization of
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a left exact localization of
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, so completeness, cocompletness, the fact that
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, so completeness, cocompletness, the fact that
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is generated under small colimits by the Yoneda image, and parts (ii)–(iv) follow from Theorem A.10. It remains to prove that if S is an affine Dirac scheme, then
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is generated under small colimits by the Yoneda image, and parts (ii)–(iv) follow from Theorem A.10. It remains to prove that if S is an affine Dirac scheme, then
![]() $h(S)$
is
$h(S)$
is
![]() $\omega _1$
-compact. Now, for every Dirac stack X, we have
$\omega _1$
-compact. Now, for every Dirac stack X, we have
so the claim that
![]() $h(S)$
is
$h(S)$
is
![]() $\omega _1$
-compact is equivalent to the statement that
$\omega _1$
-compact is equivalent to the statement that
![]() $\omega _1$
-filtered colimits in
$\omega _1$
-filtered colimits in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are calculated pointwise. By Proposition A.9, all small colimits in
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are calculated pointwise. By Proposition A.9, all small colimits in
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
are calculated pointwise, so it suffices to show that
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
are calculated pointwise, so it suffices to show that
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is closed under
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
is closed under
![]() $\omega _1$
-filtered colimits. But by Proposition 2.5, the sheaf condition is expressed in terms of
$\omega _1$
-filtered colimits. But by Proposition 2.5, the sheaf condition is expressed in terms of
![]() $\omega _1$
-small limits, so the pointwise colimit of an
$\omega _1$
-small limits, so the pointwise colimit of an
![]() $\omega _1$
-filtered diagram of sheaves is again a sheaf because
$\omega _1$
-filtered diagram of sheaves is again a sheaf because
![]() $\omega _1$
-small limits and
$\omega _1$
-small limits and
![]() $\omega _1$
-filtered colimits of anima commute by [Reference Lurie20, Proposition 5.3.3.3], as
$\omega _1$
-filtered colimits of anima commute by [Reference Lurie20, Proposition 5.3.3.3], as
![]() $\omega _1$
is a regular cardinal.
$\omega _1$
is a regular cardinal.
Remark 2.20. In the language of Question A.20, part (i) of Theorem 2.19 would be phrased as saying that
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is an
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is an
![]() $\omega _1$
-macropresentable
$\omega _1$
-macropresentable
![]() $\infty $
-category.
$\infty $
-category.
We next deduce from [Reference Lurie20, Theorem 6.1.3.9] the following fundamental descent theorem. We will use later to prove that
![]() $\infty $
-categories of Dirac formal groups over Dirac stacks descend along effective epimorphisms.
$\infty $
-categories of Dirac formal groups over Dirac stacks descend along effective epimorphisms.
Theorem 2.21. The slice
![]() $\infty $
-category functor
$\infty $
-category functor
preserves small limits.
Proof. Suppose that
![]() $X \simeq \varinjlim _{k \in K}X_k$
is a colimit of a small diagram in
$X \simeq \varinjlim _{k \in K}X_k$
is a colimit of a small diagram in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. We wish to prove that the canonical map
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. We wish to prove that the canonical map
is an equivalence. As in Remark 2.16, we may write
as the filtered colimit indexed by the partially ordered set L consisting of the small uncountable regular cardinals
![]() $\lambda $
for which the diagram in equation factors through
$\lambda $
for which the diagram in equation factors through
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda }) \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. Now, for every
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda }) \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. Now, for every
![]() $\lambda \in L$
,
$\lambda \in L$
,
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an
![]() $\infty $
-topos, so
$\infty $
-topos, so
is an equivalence by [Reference Lurie20, Theorem 6.1.3.9]. Therefore, also the induced map of colimits
is an equivalence, so it remains to argue that the canonical map
is an equivalence. But there exists a regular cardinal
![]() $\kappa $
such that K is
$\kappa $
such that K is
![]() $\kappa $
-small and L is
$\kappa $
-small and L is
![]() $\kappa $
-filtered, so this follows from [Reference Lurie20, Proposition 5.3.3.3] by the same argument as in the proof of [Reference Lurie23, Lemma 4.5.3.1].
$\kappa $
-filtered, so this follows from [Reference Lurie20, Proposition 5.3.3.3] by the same argument as in the proof of [Reference Lurie23, Lemma 4.5.3.1].
2.2 Dirac schemes as stacks
We show that that the category of Dirac schemes embeds fully faithfully into the
![]() $\infty $
-category of Dirac stacks.
$\infty $
-category of Dirac stacks.
Definition 2.22. The restricted Yoneda embedding is the composition
of the Yoneda embedding and the restriction along the canonical inclusion.
If X is a Dirac scheme, then we write
![]() $h(X)$
for its image by the restricted Yoneda embedding. We proceed to show that
$h(X)$
for its image by the restricted Yoneda embedding. We proceed to show that
![]() $h(X)$
is a Dirac stack.
$h(X)$
is a Dirac stack.
Lemma 2.23. If X is affine, then the presheaf
![]() $h(X)$
is a Dirac stack.
$h(X)$
is a Dirac stack.
Proof. The presheaf
![]() $h(X)$
is representable, and hence accessible, as the
$h(X)$
is representable, and hence accessible, as the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Aff}}$
is coaccessible. The fact that
$\operatorname {\mathrm {Aff}}$
is coaccessible. The fact that
![]() $h(X)$
is a sheaf for flat topology is a restatement of faithfully flat descent, which we proved in [Reference Hesselholt and Pstrągowski12, Addendum 3.23].
$h(X)$
is a sheaf for flat topology is a restatement of faithfully flat descent, which we proved in [Reference Hesselholt and Pstrągowski12, Addendum 3.23].
Proposition 2.24. If X is a Dirac scheme, then the presheaf
![]() $h(X)$
is a sheaf for the flat topology.
$h(X)$
is a sheaf for the flat topology.
Proof. We must verify that
![]() $h(X)$
satisfies conditions (i) and (ii) of Proposition 2.5. In the case of (i), there is nothing to prove, and in the case of (ii), we must show that if
$h(X)$
satisfies conditions (i) and (ii) of Proposition 2.5. In the case of (i), there is nothing to prove, and in the case of (ii), we must show that if
![]() $h \colon T \to S$
is a faithfully flat map of affine Dirac schemes, then
$h \colon T \to S$
is a faithfully flat map of affine Dirac schemes, then
is an equivalence of anima. Now, since the presheaf
![]() $h(X)$
takes values in the full subcategory
$h(X)$
takes values in the full subcategory
![]() ${\mathcal {S}}_{\leq 0} \subset {\mathcal {S}}$
of
${\mathcal {S}}_{\leq 0} \subset {\mathcal {S}}$
of
![]() $0$
-truncated anima, the restriction
$0$
-truncated anima, the restriction
is an equivalence by [Reference Hesselholt and Pstrągowski12, Proposition A.1]. So it suffices to show that

is a limit diagram of sets.
We first verify that
![]() $h^*$
is injective. So we let
$h^*$
is injective. So we let
![]() $f_1, f_2 \colon S \to X$
be maps of Dirac schemes with
$f_1, f_2 \colon S \to X$
be maps of Dirac schemes with
![]() $f_1h = f_2h \colon T \to X$
. Since h induces a surjective map of underlying topological spaces by [Reference Hesselholt and Pstrągowski12, Proposition 3.15], we deduce that
$f_1h = f_2h \colon T \to X$
. Since h induces a surjective map of underlying topological spaces by [Reference Hesselholt and Pstrągowski12, Proposition 3.15], we deduce that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
have the same underlying map
$f_2$
have the same underlying map
![]() $p \colon |S| \to |X|$
of topological spaces. So we have
$p \colon |S| \to |X|$
of topological spaces. So we have
![]() $f_i = (p,\phi _i)$
and wish to show that the maps
$f_i = (p,\phi _i)$
and wish to show that the maps
![]() $\phi _1, \phi _2 \colon p^*\mathcal {O}_{X} \to \mathcal {O}_S$
of sheaves of Dirac rings coincide. This can be checked stalkwise. So we write
$\phi _1, \phi _2 \colon p^*\mathcal {O}_{X} \to \mathcal {O}_S$
of sheaves of Dirac rings coincide. This can be checked stalkwise. So we write
![]() $h = (q,\psi )$
, let
$h = (q,\psi )$
, let
![]() $s \in |X|$
with
$s \in |X|$
with
![]() $x = p(x)$
and choose
$x = p(x)$
and choose
![]() $t \in |T|$
such that
$t \in |T|$
such that
![]() $s = q(t)$
, where we use that
$s = q(t)$
, where we use that
![]() $q \colon |T| \to |S|$
is surjective. Now, by the assumption that
$q \colon |T| \to |S|$
is surjective. Now, by the assumption that
![]() $f_1h = f_2h$
, the two composites
$f_1h = f_2h$
, the two composites
coincide. But the latter map is a flat local homomorphism of local Dirac rings, and therefore, it is injective by [Reference Hesselholt and Pstrągowski12, Proposition 3.16]. This shows that
![]() $\phi _{1,x} = \phi _{2,x}$
and hence that
$\phi _{1,x} = \phi _{2,x}$
and hence that
![]() $f_1 = f_2$
, as desired.
$f_1 = f_2$
, as desired.
Next, we show that
![]() $g \colon T \to X$
with
$g \colon T \to X$
with
![]() $gd_0 = gd_1 \colon T \times _ST \to X$
factors through a map
$gd_0 = gd_1 \colon T \times _ST \to X$
factors through a map
![]() $f \colon S \to X$
. Such a factorization is necessarily unique, by what was proved above. We choose a covering
$f \colon S \to X$
. Such a factorization is necessarily unique, by what was proved above. We choose a covering
![]() $(W_i)_{i \in I}$
of X by affine open subschemes and consider the covering
$(W_i)_{i \in I}$
of X by affine open subschemes and consider the covering
![]() $(V_i)_{i \in I}$
of T by the open subschemes
$(V_i)_{i \in I}$
of T by the open subschemes
![]() $V_i \simeq T \times _XW_i \to T$
. Since
$V_i \simeq T \times _XW_i \to T$
. Since
we conclude from [Reference Hesselholt and Pstrągowski12, Proposition 3.24] that there exists a unique covering
![]() $(U_i)_{i \in I}$
of S by open subschemes such that
$(U_i)_{i \in I}$
of S by open subschemes such that
![]() $V_i \simeq T \times _SU_i \to T$
for all
$V_i \simeq T \times _SU_i \to T$
for all
![]() $i \in I$
. We observe that any
$i \in I$
. We observe that any
![]() $f \colon S \to X$
with the desired property necessarily will satisfy
$f \colon S \to X$
with the desired property necessarily will satisfy
![]() $f(U_i) \subset W_i$
. Thus, it suffices to show that for every
$f(U_i) \subset W_i$
. Thus, it suffices to show that for every
![]() $i \in I$
, there exists a map of Dirac schemes
$i \in I$
, there exists a map of Dirac schemes
![]() $f_i \colon U_i \to W_i$
with the property that the composite map
$f_i \colon U_i \to W_i$
with the property that the composite map
is equal to
![]() $g|_{V_i} \colon V_i \to X$
.
$g|_{V_i} \colon V_i \to X$
.
Now, for every
![]() $i \in I$
, we choose a covering
$i \in I$
, we choose a covering
![]() $(U_{i,j})_{j \in J_i}$
of
$(U_{i,j})_{j \in J_i}$
of
![]() $U_i$
by affine open subschemes and note that also
$U_i$
by affine open subschemes and note that also
![]() $(V_{i,j})_{j \in J_i}$
with
$(V_{i,j})_{j \in J_i}$
with
![]() $V_{i,j} \simeq T \times _SU_{i,j} \to T$
is a covering of
$V_{i,j} \simeq T \times _SU_{i,j} \to T$
is a covering of
![]() $V_i$
by affine open subschemes. Moreover, the map
$V_i$
by affine open subschemes. Moreover, the map
![]() $h|_{V_{i,j}} \colon V_{i,j} \to U_{i,j}$
is a faithfully flat map of affine Dirac schemes, and we have a map
$h|_{V_{i,j}} \colon V_{i,j} \to U_{i,j}$
is a faithfully flat map of affine Dirac schemes, and we have a map
with the property its restriction along the two projections
coincide. As everything is affine, we conclude from Lemma 2.23 that
![]() $g|_{V_{i,j}}$
admits a unique factorization through a map
$g|_{V_{i,j}}$
admits a unique factorization through a map
![]() $f_{i,j} \colon U_{i,j} \to W_i$
. By uniqueness, the maps
$f_{i,j} \colon U_{i,j} \to W_i$
. By uniqueness, the maps
![]() $f_{i,j} \colon U_{i,j} \to W_i$
glue to give the desired
$f_{i,j} \colon U_{i,j} \to W_i$
glue to give the desired
![]() $f_i \colon U_i \to W_i$
. This completes the proof.
$f_i \colon U_i \to W_i$
. This completes the proof.
Lemma 2.25. Let X be a Dirac scheme and let
![]() $\mathfrak {B}$
be a basis for the topology on its underlying space
$\mathfrak {B}$
be a basis for the topology on its underlying space
![]() $|X|$
such that if
$|X|$
such that if
![]() $U,V \in \mathfrak {B}$
, then
$U,V \in \mathfrak {B}$
, then
![]() $U \cap V \in \mathfrak {B}$
. If
$U \cap V \in \mathfrak {B}$
. If
![]() $h(U)$
is accessible for all
$h(U)$
is accessible for all
![]() $U \in \mathfrak {B}$
, then so is
$U \in \mathfrak {B}$
, then so is
![]() $h(X)$
.
$h(X)$
.
Proof. We know from Proposition 2.24 that
![]() $h(X) \in \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Aff}}^{\mathrm {op}},{\mathcal {S}})$
is a sheaf for the flat topology, and we wish to prove that it belongs to the full subcategory
$h(X) \in \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Aff}}^{\mathrm {op}},{\mathcal {S}})$
is a sheaf for the flat topology, and we wish to prove that it belongs to the full subcategory
Since the inclusions
![]() $i_{\kappa } \colon {\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
exhibit
$i_{\kappa } \colon {\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
exhibit
![]() $\operatorname {\mathrm {Aff}}$
as a colimit of the
$\operatorname {\mathrm {Aff}}$
as a colimit of the
![]() ${\mathrm {Aff}}_{\kappa }$
, it suffices to show that there exists a
${\mathrm {Aff}}_{\kappa }$
, it suffices to show that there exists a
![]() $\lambda $
such that for all
$\lambda $
such that for all
![]() $\kappa \geq \lambda $
, the diagram
$\kappa \geq \lambda $
, the diagram

exhibits
![]() $i_{\kappa }^*h(X)$
as a left Kan extension of
$i_{\kappa }^*h(X)$
as a left Kan extension of
![]() $i_{\lambda }^*h(X)$
. Now, each
$i_{\lambda }^*h(X)$
. Now, each
![]() $h(U)$
is accessible and
$h(U)$
is accessible and
![]() $\mathfrak {B}$
is small, so we can find a
$\mathfrak {B}$
is small, so we can find a
![]() $\lambda $
such that for all
$\lambda $
such that for all
![]() $\kappa \geq \lambda $
, the diagram
$\kappa \geq \lambda $
, the diagram

exhibits
![]() $i_{\kappa }^*h(U)$
as a left Kan extension of
$i_{\kappa }^*h(U)$
as a left Kan extension of
![]() $i_{\lambda }^*h(U)$
. Since left Kan extension preserves sheaves by Theorem 2.15, we conclude that it will suffice to show that the map
$i_{\lambda }^*h(U)$
. Since left Kan extension preserves sheaves by Theorem 2.15, we conclude that it will suffice to show that the map
in
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an equivalence.
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an equivalence.
To prove that this is so, let us write
![]() $h_{\lambda } \simeq i_{\lambda }^*h$
. Since, locally on S, every map
$h_{\lambda } \simeq i_{\lambda }^*h$
. Since, locally on S, every map
![]() $\eta \colon S \to X$
from an affine Dirac scheme factors through some
$\eta \colon S \to X$
from an affine Dirac scheme factors through some
![]() $U \in \mathfrak {B}$
, the map
$U \in \mathfrak {B}$
, the map
in
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an effective epimorphism. Therefore, it will suffice to show that the base-change
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an effective epimorphism. Therefore, it will suffice to show that the base-change
of the map in question along the map induced by the open immersion of any
![]() $U_0 \in \mathfrak {B}$
into X is an equivalence. Since colimits in
$U_0 \in \mathfrak {B}$
into X is an equivalence. Since colimits in
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
are universal, and since the Yoneda embedding preserves limits, the canonical map
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
are universal, and since the Yoneda embedding preserves limits, the canonical map
in
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an equivalence. Hence, we wish to show that the map of colimits
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{\lambda })$
is an equivalence. Hence, we wish to show that the map of colimits
induced by the functor
![]() $- \times _XU_0 \colon \mathfrak {B} \to \mathfrak {B}_{/U_0}$
, which exists by our assumption that the basis
$- \times _XU_0 \colon \mathfrak {B} \to \mathfrak {B}_{/U_0}$
, which exists by our assumption that the basis
![]() $\mathfrak {B}$
is closed under finite intersections, is an equivalence. In fact, we claim that this functor is a
$\mathfrak {B}$
is closed under finite intersections, is an equivalence. In fact, we claim that this functor is a
![]() $\varinjlim $
-equivalence. Indeed, by [Reference Lurie20, Theorem 4.1.3.1], it suffices to show that
$\varinjlim $
-equivalence. Indeed, by [Reference Lurie20, Theorem 4.1.3.1], it suffices to show that
is weakly contractible for every
![]() $V \in \mathfrak {B}_{/U_0}$
. But we can identify this category with the poset
$V \in \mathfrak {B}_{/U_0}$
. But we can identify this category with the poset
![]() $\mathfrak {B}_{V/}$
, which has V as a minimal element, so its classifying anima is contractible, as required.
$\mathfrak {B}_{V/}$
, which has V as a minimal element, so its classifying anima is contractible, as required.
Proposition 2.26. If X is a Dirac scheme, then the presheaf
![]() $h(X)$
is accessible.
$h(X)$
is accessible.
Proof. The statement holds for affine Dirac schemes by Lemma 2.23, and we now use Lemma 2.25 to bootstrap our way to general Dirac schemes.
First, if X admits an open immersion
![]() $j \colon X \to S$
into an affine Dirac scheme, then we take
$j \colon X \to S$
into an affine Dirac scheme, then we take
![]() $\mathfrak {B}$
to be the poset consisting of the open subschemes
$\mathfrak {B}$
to be the poset consisting of the open subschemes
![]() $U \subset X$
with the property that
$U \subset X$
with the property that
![]() $j(U) = S_f \subset S$
is a distinguished open subscheme. This
$j(U) = S_f \subset S$
is a distinguished open subscheme. This
![]() $\mathfrak {B}$
is a basis for the topology on
$\mathfrak {B}$
is a basis for the topology on
![]() $|X|$
, it is stable under finite intersection, and
$|X|$
, it is stable under finite intersection, and
![]() $h(U)$
is accessible for every
$h(U)$
is accessible for every
![]() $U \in \mathfrak {B}$
, because
$U \in \mathfrak {B}$
, because
![]() $S_f$
is affine. So
$S_f$
is affine. So
![]() $h(X)$
is accessible by Lemma 2.25.
$h(X)$
is accessible by Lemma 2.25.
Finally, if X is any Dirac scheme, then we take
![]() $\mathfrak {B}$
to be the poset of open subschemes
$\mathfrak {B}$
to be the poset of open subschemes
![]() $U \subset X$
with the property that U admits an open immersion into some affine Dirac scheme. Again, this
$U \subset X$
with the property that U admits an open immersion into some affine Dirac scheme. Again, this
![]() $\mathfrak {B}$
is a basis for the topology on
$\mathfrak {B}$
is a basis for the topology on
![]() $|X|$
, it is stable under finite intersection, and by the case considered above
$|X|$
, it is stable under finite intersection, and by the case considered above
![]() $h(U)$
is accessible for all
$h(U)$
is accessible for all
![]() $U \in \mathfrak {B}$
. So Lemma 2.25 shows that
$U \in \mathfrak {B}$
. So Lemma 2.25 shows that
![]() $h(X)$
is accessible.
$h(X)$
is accessible.
Theorem 2.27. The restricted Yoneda embedding defines a fully faithful functor
from the category of Dirac schemes to the
![]() $\infty $
-category of Dirac stacks.
$\infty $
-category of Dirac stacks.
Proof. It follows from Proposition 2.24 and Proposition 2.26 that the restricted Yoneda embedding from Definition 2.22 takes values in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Aff}}^{\mathrm {op}},{\mathcal {S}})$
. So we get the desired functor and must prove that it is fully faithful. We let X and Y be Dirac schemes and wish to prove that the canonical map
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}}) \subset \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Aff}}^{\mathrm {op}},{\mathcal {S}})$
. So we get the desired functor and must prove that it is fully faithful. We let X and Y be Dirac schemes and wish to prove that the canonical map
is an equivalence of anima. (In fact, the domain and target of this map are both
![]() $0$
-truncated anima.) If Y is affine, then this follows from the Yoneda lemma.
$0$
-truncated anima.) If Y is affine, then this follows from the Yoneda lemma.
In general, if
![]() $\mathfrak {B}$
is a basis for the topology on the underlying space
$\mathfrak {B}$
is a basis for the topology on the underlying space
![]() $|Y|$
, which is stable under finite intersection, then the canonical map of Dirac schemes
$|Y|$
, which is stable under finite intersection, then the canonical map of Dirac schemes
is an equivalence by [Reference Hesselholt and Pstrągowski12, Theorem 2.32], and the canonical map of Dirac stacks
is an equivalence by the proof of Lemma 2.25. Thus, we can bootstrap our way from affine Dirac schemes to general Dirac schemes in the same way as we did in the proof of Proposition 2.26.
A small diagram
![]() $X \colon K \to \operatorname {\mathrm {Sch}}$
may not admit a colimit, and even if it does, then the colimit is generally not meaningful. Instead, it is the colimit of the composite diagram
$X \colon K \to \operatorname {\mathrm {Sch}}$
may not admit a colimit, and even if it does, then the colimit is generally not meaningful. Instead, it is the colimit of the composite diagram
![]() $h(X) \colon K \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which always exists, that is meaningful. We show, however, that if K is static, then the two colimits do agree.
$h(X) \colon K \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, which always exists, that is meaningful. We show, however, that if K is static, then the two colimits do agree.
Addendum 2.28. The functor
![]() $h \colon \operatorname {\mathrm {Sch}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
preserves coproducts.
$h \colon \operatorname {\mathrm {Sch}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
preserves coproducts.
Proof. The functor in question preserves finite coproducts, so it suffices to show that for a small family of Dirac schemes
![]() $(X_k)_{k \in K}$
, the canonical map
$(X_k)_{k \in K}$
, the canonical map
where the colimits range over the filtered category of finite subsets
![]() $I \subset K$
, is an equivalence. We claim that the left-hand colimit is calculated pointwise. Indeed, this claim is equivalent to the statement that the presheaf given by pointwise colimit satisfies the sheaf condition. But the flat topology on
$I \subset K$
, is an equivalence. We claim that the left-hand colimit is calculated pointwise. Indeed, this claim is equivalent to the statement that the presheaf given by pointwise colimit satisfies the sheaf condition. But the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
if finitary and the diagram in question takes values in
$\operatorname {\mathrm {Aff}}$
if finitary and the diagram in question takes values in
![]() ${\mathcal {S}}_{\leq 0}$
-valued presheaves, so by [Reference Hesselholt and Pstrągowski12, Proposition A.1], the sheaf condition amounts to the requirement that certain finite diagrams in
${\mathcal {S}}_{\leq 0}$
-valued presheaves, so by [Reference Hesselholt and Pstrągowski12, Proposition A.1], the sheaf condition amounts to the requirement that certain finite diagrams in
![]() ${\mathcal {S}}$
are limit diagrams. Hence, the claim follows from the fact that finite limits and filtered colimits of anima commute. Finally, given
${\mathcal {S}}$
are limit diagrams. Hence, the claim follows from the fact that finite limits and filtered colimits of anima commute. Finally, given
![]() $T \in \operatorname {\mathrm {Aff}}$
, the canonical map
$T \in \operatorname {\mathrm {Aff}}$
, the canonical map
is an equivalence since T is quasi-compact.
2.3 Geometric maps
The
![]() $\infty $
-category of all Dirac stacks is quite large, and in practice, one is often interested in the smaller subcategory of geometric Dirac stacks, which, informally, is the closure of the full subcategory of Dirac schemes under quotients by flat groupoids. The precise definition, however, is more delicate and follows Lurie [Reference Lurie18, Chapter 26] and Töen–Vezzosi [Reference Toën and Vezzosi33]. Geometric Dirac stacks are formally similar to Artin stacks, the main differences being the following:
$\infty $
-category of all Dirac stacks is quite large, and in practice, one is often interested in the smaller subcategory of geometric Dirac stacks, which, informally, is the closure of the full subcategory of Dirac schemes under quotients by flat groupoids. The precise definition, however, is more delicate and follows Lurie [Reference Lurie18, Chapter 26] and Töen–Vezzosi [Reference Toën and Vezzosi33]. Geometric Dirac stacks are formally similar to Artin stacks, the main differences being the following:
-
1. We consider sheaves of anima, as opposed to sheaves of groupoids.
-
2. We consider sheaves on affine Dirac schemes, as opposed to affine schemes.
-
3. We allow quotients by flat groupoids, as opposed to only smooth grouoids.
More generally, we define the relative notion of a geometric map between Dirac stacks. We follow Lurie [Reference Lurie18, Chapter 26], who sets up the analogous theory in derived algebraic geometry. The definition is recursive.
Definition 2.29. Let
![]() $f \colon Y \to X$
be a map of Dirac stacks.
$f \colon Y \to X$
be a map of Dirac stacks.
-
(1) The map
 $f \colon Y \to X$
is
$f \colon Y \to X$
is
 $0$
-geometric if for every map
$0$
-geometric if for every map
 $\eta \colon S \to X$
from a Dirac scheme, the base-change
$\eta \colon S \to X$
from a Dirac scheme, the base-change
 $f_S \colon Y_S \to S$
of f along
$f_S \colon Y_S \to S$
of f along
 $\eta $
is equivalent to a map of Dirac schemes.
$\eta $
is equivalent to a map of Dirac schemes. -
(2) The map
 $f \colon Y \to X$
is
$f \colon Y \to X$
is
 $0$
-submersive if for every map
$0$
-submersive if for every map
 $\eta \colon S \to X$
from a Dirac scheme, the base-change
$\eta \colon S \to X$
from a Dirac scheme, the base-change
 $f_S \colon Y_S \to S$
of f along
$f_S \colon Y_S \to S$
of f along
 $\eta $
is an effective epimorphism and equivalent to a flat map of Dirac schemes.
$\eta $
is an effective epimorphism and equivalent to a flat map of Dirac schemes.
Remark 2.30 (Affine source suffices).
In Definition 2.29, it suffices to consider maps
![]() $\eta \colon S \to X$
with S an affine Dirac scheme. However, the source of the base-change
$\eta \colon S \to X$
with S an affine Dirac scheme. However, the source of the base-change
![]() $f_S \colon Y_S \to S$
will typically not be an affine Dirac scheme, even if S is affine.
$f_S \colon Y_S \to S$
will typically not be an affine Dirac scheme, even if S is affine.
Remark 2.31 (Effective epimorphisms).
It follows from Proposition B.6 that a map of Dirac stacks
![]() $p \colon Y \to X$
is an effective epimorphism if and only if for every map
$p \colon Y \to X$
is an effective epimorphism if and only if for every map
![]() $\eta \colon S \to X$
from an affine Dirac scheme, there exists a diagram
$\eta \colon S \to X$
from an affine Dirac scheme, there exists a diagram

where q is a faithfully flat map of affine Dirac schemes. So
![]() $p \colon Y \to X$
is an effective epimorphism if and only if, locally for the flat topology on the source, every map
$p \colon Y \to X$
is an effective epimorphism if and only if, locally for the flat topology on the source, every map
![]() $\eta \colon S \to X$
from an affine Dirac scheme admits a factorization through f.
$\eta \colon S \to X$
from an affine Dirac scheme admits a factorization through f.
Remark 2.32 (Submersive maps of Dirac schemes).
Let
![]() $f \colon Y \to X$
be a map of Dirac schemes. The map f is automatically
$f \colon Y \to X$
be a map of Dirac schemes. The map f is automatically
![]() $0$
-geometric because the embedding of Dirac schemes in Dirac stacks preserves fiber products, and Remark 2.31 shows that f is
$0$
-geometric because the embedding of Dirac schemes in Dirac stacks preserves fiber products, and Remark 2.31 shows that f is
![]() $0$
-submersive if and only if it is an
$0$
-submersive if and only if it is an
![]() $\operatorname {\mathrm {fpqc}}$
-covering in the sense that f is flat and for every affine open
$\operatorname {\mathrm {fpqc}}$
-covering in the sense that f is flat and for every affine open
![]() $U \subset X$
, there exists a quasi-compact open
$U \subset X$
, there exists a quasi-compact open
![]() $V \subset f^{-1}(U)$
such that
$V \subset f^{-1}(U)$
such that
![]() $f|_V \colon V \to U$
is surjective. This is the analogue for Dirac schemes of the definition of an
$f|_V \colon V \to U$
is surjective. This is the analogue for Dirac schemes of the definition of an
![]() $\operatorname {\mathrm {fpqc}}$
-covering given in [32, Tag 022B].
$\operatorname {\mathrm {fpqc}}$
-covering given in [32, Tag 022B].
Definition 2.33. Let
![]() $f \colon Y \to X$
be a map of Dirac stacks and
$f \colon Y \to X$
be a map of Dirac stacks and
![]() $n \geq 1$
an integer.
$n \geq 1$
an integer.
-
(1) The map
 $f \colon Y \to X$
is n-geometric if for every base-change
$f \colon Y \to X$
is n-geometric if for every base-change
 $f_S \colon Y_S \to S$
along a map
$f_S \colon Y_S \to S$
along a map
 $\eta \colon S \to X$
from a Dirac scheme, there exists an
$\eta \colon S \to X$
from a Dirac scheme, there exists an
 $(n-1)$
-submersive map
$(n-1)$
-submersive map
 $p \colon T \to Y_S$
from a Dirac scheme.
$p \colon T \to Y_S$
from a Dirac scheme. -
(2) The map
 $f \colon Y \to X$
is n-submersive if for every base-change
$f \colon Y \to X$
is n-submersive if for every base-change
 $f_S \colon Y_S \to S$
along a map
$f_S \colon Y_S \to S$
along a map
 $\eta \colon S \to X$
from a Dirac scheme, there exists an
$\eta \colon S \to X$
from a Dirac scheme, there exists an
 $(n-1)$
-submersive map
$(n-1)$
-submersive map
 $p \colon T \to Y_S$
from a Dirac scheme such that the composite map is
$p \colon T \to Y_S$
from a Dirac scheme such that the composite map is
 $0$
-submersive.
$0$
-submersive.
The map
![]() $f \colon Y \to X$
is geometric if it is n-geometric for some
$f \colon Y \to X$
is geometric if it is n-geometric for some
![]() $n \geq 0$
, and it is submersive if it is n-submersive for some
$n \geq 0$
, and it is submersive if it is n-submersive for some
![]() $n \geq 0$
.
$n \geq 0$
.
Remark 2.34 (Stability under base-change).
In Definition 2.33, it suffices to consider maps
![]() $\eta \colon S \to X$
with S an affine Dirac scheme. The properties of being n-geometric and being n-submersive are preserved under base-change along any map.
$\eta \colon S \to X$
with S an affine Dirac scheme. The properties of being n-geometric and being n-submersive are preserved under base-change along any map.
Warning 2.35 (The value of n is irrelevant).
Contrary to what Definition 2.33 might suggest, it is the properties of a map of Dirac stacks of being geometric or submersive that are important, whereas the particular n for which the map in question is n-geometric or n-submersive is of little relevance. However, the recursive nature of the definitions is useful for making inductive proofs.
Lemma 2.36. Let
![]() $f \colon Y \to X$
be a map of Dirac stacks and let
$f \colon Y \to X$
be a map of Dirac stacks and let
![]() $n \geq 0$
be an integer. If f is n-geometric, then f is also
$n \geq 0$
be an integer. If f is n-geometric, then f is also
![]() $(n+1)$
-geometric. If f is n-submersive, then f is also
$(n+1)$
-geometric. If f is n-submersive, then f is also
![]() $(n+1)$
-submersive.
$(n+1)$
-submersive.
Proof. We argue by induction on
![]() $n \geq 0$
. If f is
$n \geq 0$
. If f is
![]() $0$
-geometric, then, by definition, the base-change
$0$
-geometric, then, by definition, the base-change
![]() $f_S \colon Y_S \to S$
of f along any map
$f_S \colon Y_S \to S$
of f along any map
![]() $\eta \colon S \to X$
from a Dirac scheme is equivalent to a map of Dirac schemes. Since the identity map
$\eta \colon S \to X$
from a Dirac scheme is equivalent to a map of Dirac schemes. Since the identity map
![]() $\operatorname {\mathrm {id}} \colon Y_S \to Y_S$
is a
$\operatorname {\mathrm {id}} \colon Y_S \to Y_S$
is a
![]() $0$
-submersive map from a Dirac scheme, we conclude that f is
$0$
-submersive map from a Dirac scheme, we conclude that f is
![]() $1$
-geometric.
$1$
-geometric.
So we let
![]() $n \geq 1$
and assume inductively that the statement has been proved for
$n \geq 1$
and assume inductively that the statement has been proved for
![]() $k < n$
. If f is n-geometric, then for every base-change
$k < n$
. If f is n-geometric, then for every base-change
![]() $f_S \colon Y_S \to S$
of f along a map
$f_S \colon Y_S \to S$
of f along a map
![]() $\eta \colon S \to X$
from a Dirac scheme S, there exits an
$\eta \colon S \to X$
from a Dirac scheme S, there exits an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $p \colon T \to Y_S$
from a Dirac scheme. By the inductive hypothesis, the map p is also n-submersive, which shows that f is
$p \colon T \to Y_S$
from a Dirac scheme. By the inductive hypothesis, the map p is also n-submersive, which shows that f is
![]() $(n+1)$
-geometric. The same argument shows that if f is n-submersive, then it is
$(n+1)$
-geometric. The same argument shows that if f is n-submersive, then it is
![]() $(n+1)$
-submersive.
$(n+1)$
-submersive.
Proposition 2.37. If a map of Dirac stacks
![]() $f \colon Y \to X$
is n-submersive for some
$f \colon Y \to X$
is n-submersive for some
![]() $n \geq 0$
, then it is an effective epimorphism.
$n \geq 0$
, then it is an effective epimorphism.
Proof. Since
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is generated under small colimits by the image of the Yoneda embedding, and since the property of being an effective epimorphism is local on the base, we may assume that X is affine. We proceed by induction on
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is generated under small colimits by the image of the Yoneda embedding, and since the property of being an effective epimorphism is local on the base, we may assume that X is affine. We proceed by induction on
![]() $n \geq 0$
, the case
$n \geq 0$
, the case
![]() $n = 0$
being trivial, because a
$n = 0$
being trivial, because a
![]() $0$
-submersive map is an effective epimorphism by definition. So we let
$0$
-submersive map is an effective epimorphism by definition. So we let
![]() $n \geq 1$
and inductively assume the statement for
$n \geq 1$
and inductively assume the statement for
![]() $k < n$
. Since
$k < n$
. Since
![]() $f \colon Y \to X$
is n-submersive and X affine, there exists a factorization
$f \colon Y \to X$
is n-submersive and X affine, there exists a factorization
with p an
![]() $(n-1)$
-submersive map from a Dirac scheme such that
$(n-1)$
-submersive map from a Dirac scheme such that
![]() $fp$
is
$fp$
is
![]() $0$
-submersive. Now, by the inductive hypothesis, both p and
$0$
-submersive. Now, by the inductive hypothesis, both p and
![]() $fp$
are effective epimorphisms, so we conclude from [Reference Lurie20, Corollary 6.2.3.12] that also f is an effective epimorphism.
$fp$
are effective epimorphisms, so we conclude from [Reference Lurie20, Corollary 6.2.3.12] that also f is an effective epimorphism.
Proposition 2.38. Let
![]() $g \colon Z \to Y$
and
$g \colon Z \to Y$
and
![]() $f \colon Y \to X$
be maps of Dirac stacks and let
$f \colon Y \to X$
be maps of Dirac stacks and let
![]() $n \geq 0$
. If f and g are both n-geometric or both n-submersive, then so is
$n \geq 0$
. If f and g are both n-geometric or both n-submersive, then so is
![]() $fg$
.
$fg$
.
Proof. We argue by induction on
![]() $n \geq 0$
. The geometric part of case
$n \geq 0$
. The geometric part of case
![]() $n = 0$
follows from definitions, and the submersive part follows from the fact that both effective epimorphisms and flat maps of Dirac schemes are closed under composition. So we let
$n = 0$
follows from definitions, and the submersive part follows from the fact that both effective epimorphisms and flat maps of Dirac schemes are closed under composition. So we let
![]() $n \geq 1$
and assume inductively that the statements have been proved for
$n \geq 1$
and assume inductively that the statements have been proved for
![]() $k < n$
. To prove the induction step, we consider the diagram
$k < n$
. To prove the induction step, we consider the diagram

with S a Dirac scheme and the squares cartesian. Suppose first that f and g are n-geometric. We first choose an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $p \colon U \to Y_S$
from a Dirac scheme. Since g is n-geometric, so is
$p \colon U \to Y_S$
from a Dirac scheme. Since g is n-geometric, so is
![]() $g_U$
, and hence, we may choose an
$g_U$
, and hence, we may choose an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $q \colon V \to Z_U$
from a Dirac scheme. By the inductive hypothesis, the composition of the
$q \colon V \to Z_U$
from a Dirac scheme. By the inductive hypothesis, the composition of the
![]() $(n-1)$
-submersive maps
$(n-1)$
-submersive maps
![]() $p'$
and q is
$p'$
and q is
![]() $(n-1)$
-submersive. This shows that
$(n-1)$
-submersive. This shows that
![]() $fg$
is n-geometric. If f and g are n-submersive, then we may choose the maps p and q such that
$fg$
is n-geometric. If f and g are n-submersive, then we may choose the maps p and q such that
![]() $f_Sp$
and
$f_Sp$
and
![]() $g_Uq$
are
$g_Uq$
are
![]() $0$
-submersive. But then also
$0$
-submersive. But then also
is
![]() $0$
-submersive, so we conclude that
$0$
-submersive, so we conclude that
![]() $fg$
is n-submersive.
$fg$
is n-submersive.
Lemma 2.39. If
![]() $f \colon Y \to X$
is an effective epimorphism of Dirac stacks, then for every map
$f \colon Y \to X$
is an effective epimorphism of Dirac stacks, then for every map
![]() $\eta \colon V \to X$
from a Dirac scheme, there exists a diagram
$\eta \colon V \to X$
from a Dirac scheme, there exists a diagram

with
![]() $p \colon W \to V$
a
$p \colon W \to V$
a
![]() $0$
-submersion from a Dirac scheme W.
$0$
-submersion from a Dirac scheme W.
Proof. Let
![]() $(S_i)_{i \in I}$
be a family with
$(S_i)_{i \in I}$
be a family with
![]() $S_i \subset V$
affine open and
$S_i \subset V$
affine open and
![]() $\bigcup _{i \in I}|S_i| = |V|$
. It follows from Remark 2.32 and Addendum 2.28 that the induced map
$\bigcup _{i \in I}|S_i| = |V|$
. It follows from Remark 2.32 and Addendum 2.28 that the induced map
is
![]() $0$
-submersive. Applying Remark 2.31 to each
$0$
-submersive. Applying Remark 2.31 to each
![]() $S_i$
separately, we find
$S_i$
separately, we find
![]() $0$
-submersive maps
$0$
-submersive maps
![]() $q_i \colon T_i \to S_i$
with
$q_i \colon T_i \to S_i$
with
![]() $T_i$
affine and factorizations of the composite maps
$T_i$
affine and factorizations of the composite maps
through
![]() $f \colon Y \to X$
. Thus, we obtain the desired diagram with
$f \colon Y \to X$
. Thus, we obtain the desired diagram with
![]() $W \simeq \coprod _{i \in I}T_i$
.
$W \simeq \coprod _{i \in I}T_i$
.
Proposition 2.40. Let
![]() $g \colon Z \to Y$
and
$g \colon Z \to Y$
and
![]() $f \colon Y \to X$
be morphisms of Dirac stacks and
$f \colon Y \to X$
be morphisms of Dirac stacks and
![]() $n \geq 0$
.
$n \geq 0$
.
-
(a) Let g be n-submersive. If
 $fg$
is
$fg$
is
 $(n+1)$
-geometric, then so is f.
$(n+1)$
-geometric, then so is f. -
(b) Let f be
 $(n+2)$
-geometric. If
$(n+2)$
-geometric. If
 $fg$
is
$fg$
is
 $(n+1)$
-geometric, so is g.
$(n+1)$
-geometric, so is g.
Proof. For part (a), we consider the diagram

with S a Dirac scheme and the squares cartesian. Since
![]() $fg$
is
$fg$
is
![]() $(n+1)$
-geometric, we can find an n-submersive map q from a Dirac scheme, and since g is n-submersive, so is its base-change
$(n+1)$
-geometric, we can find an n-submersive map q from a Dirac scheme, and since g is n-submersive, so is its base-change
![]() $g_S$
and the composite map
$g_S$
and the composite map
![]() $g_Sq$
by Proposition 2.38. Hence,
$g_Sq$
by Proposition 2.38. Hence,
![]() $g_Sq$
is the required n-submersive map to
$g_Sq$
is the required n-submersive map to
![]() $Y_S$
.
$Y_S$
.
For part (b), we consider the diagram

with S a Dirac scheme and with the squares cartesian. The maps p and q are an
![]() $(n+1)$
-submersive map from a Dirac scheme U and an n-submersive map from a Dirac scheme V, and they exist by the assumption that f and
$(n+1)$
-submersive map from a Dirac scheme U and an n-submersive map from a Dirac scheme V, and they exist by the assumption that f and
![]() $fg$
be respectively
$fg$
be respectively
![]() $(n+2)$
-geometric and
$(n+2)$
-geometric and
![]() $(n+1)$
-geometric. Now, Proposition 2.37 shows that p is an effective epimorphism, so by Lemma 2.39, we can find a
$(n+1)$
-geometric. Now, Proposition 2.37 shows that p is an effective epimorphism, so by Lemma 2.39, we can find a
![]() $0$
-submersive map of Dirac schemes
$0$
-submersive map of Dirac schemes
![]() $h \colon W \to V$
together with the indicated factorization of
$h \colon W \to V$
together with the indicated factorization of
![]() $g_S q h$
through p.
$g_S q h$
through p.
Since h is
![]() $0$
-submersive, it is n-submersive by Lemma 2.36, and since also q is n-submersive, it follows from Proposition 2.38 that
$0$
-submersive, it is n-submersive by Lemma 2.36, and since also q is n-submersive, it follows from Proposition 2.38 that
![]() $qh$
is n-submersive. Similarly, since k is
$qh$
is n-submersive. Similarly, since k is
![]() $0$
-geometric, it is
$0$
-geometric, it is
![]() $(n+1)$
-geometric by Lemma 2.36, and since also p is
$(n+1)$
-geometric by Lemma 2.36, and since also p is
![]() $(n+1)$
-geometric, it follows from another application of Proposition 2.38 that
$(n+1)$
-geometric, it follows from another application of Proposition 2.38 that
![]() $pk$
is
$pk$
is
![]() $(n+1)$
-geometric. So part (a) shows that
$(n+1)$
-geometric. So part (a) shows that
![]() $g_S$
is
$g_S$
is
![]() $(n+1)$
-geometric, as desired.
$(n+1)$
-geometric, as desired.
Proposition 2.41. Let
![]() $f \colon Y \to X$
be a map of Dirac stacks and let
$f \colon Y \to X$
be a map of Dirac stacks and let
![]() $f' \colon Y' \to X'$
be the base-change of f along an effective epimorphism
$f' \colon Y' \to X'$
be the base-change of f along an effective epimorphism
![]() $p \colon X' \to X$
.
$p \colon X' \to X$
.
-
(a) If
 $f'$
is n-geometric with
$f'$
is n-geometric with
 $n \geq 1$
, then so is f.
$n \geq 1$
, then so is f. -
(b) If
 $f'$
is n-submersive with
$f'$
is n-submersive with
 $n \geq 1$
, then so is f.
$n \geq 1$
, then so is f.
Proof. Let
![]() $\eta \colon S \to X$
be a Dirac scheme and let
$\eta \colon S \to X$
be a Dirac scheme and let
![]() $f_S \colon Y_S \to S$
be the base-change of f along
$f_S \colon Y_S \to S$
be the base-change of f along
![]() $\eta $
. We wish to find an
$\eta $
. We wish to find an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $U \to Y_S$
from a Dirac scheme. Using Lemma 2.39, we can find the left-hand square
$U \to Y_S$
from a Dirac scheme. Using Lemma 2.39, we can find the left-hand square

with q a
![]() $0$
-submersive map of Dirac schemes. Since
$0$
-submersive map of Dirac schemes. Since
![]() $f'$
is n-geometric, we can find an
$f'$
is n-geometric, we can find an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $r \colon U \to Y_T'$
from a Dirac scheme. But then
$r \colon U \to Y_T'$
from a Dirac scheme. But then
is
![]() $(n-1)$
-submersive. Indeed, the map
$(n-1)$
-submersive. Indeed, the map
![]() $q_Y$
is the base-change of the
$q_Y$
is the base-change of the
![]() $0$
-submersive map q and hence
$0$
-submersive map q and hence
![]() $0$
-submersive, so by Lemma 2.36, it is also
$0$
-submersive, so by Lemma 2.36, it is also
![]() $(n-1)$
-submersive, and finally, the composite map is
$(n-1)$
-submersive, and finally, the composite map is
![]() $(n-1)$
-submersive by Proposition 2.38. This completes the proof of (a), and the proof of (b) is analogous.
$(n-1)$
-submersive by Proposition 2.38. This completes the proof of (a), and the proof of (b) is analogous.
Warning 2.42. The statement of Proposition 2.41 does not hold for
![]() $n = 0$
since the property of being a Dirac scheme is not local for the flat topology. In fact, there exists an algebraic space
$n = 0$
since the property of being a Dirac scheme is not local for the flat topology. In fact, there exists an algebraic space
![]() $f \colon Y \to X$
over a scheme X and an étale surjection
$f \colon Y \to X$
over a scheme X and an étale surjection
![]() $p \colon Y' \to Y$
such that
$p \colon Y' \to Y$
such that
![]() $Y'$
is a scheme, but Y is not; see [Reference Vistoli34, §4.4.2].
$Y'$
is a scheme, but Y is not; see [Reference Vistoli34, §4.4.2].
Lemma 2.43. If a map of Dirac schemes
![]() $f \colon T \to S$
is n-submersive for some
$f \colon T \to S$
is n-submersive for some
![]() $n \geq 0$
, then it is
$n \geq 0$
, then it is
![]() $0$
-submersive.
$0$
-submersive.
Proof. We proceed by induction on
![]() $n \geq 0$
, the case
$n \geq 0$
, the case
![]() $n = 0$
being trivial. So we let
$n = 0$
being trivial. So we let
![]() $n \geq 1$
and assume that the statement has been proved for
$n \geq 1$
and assume that the statement has been proved for
![]() $k < n$
. Since
$k < n$
. Since
![]() $f \colon T \to S$
is n-submersive, there exists, by definition, a scheme V and an
$f \colon T \to S$
is n-submersive, there exists, by definition, a scheme V and an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $p \colon V \to T$
such that the composite map
$p \colon V \to T$
such that the composite map
is
![]() $0$
-submersive. By the inductive hypothesis, the map p is
$0$
-submersive. By the inductive hypothesis, the map p is
![]() $0$
-submersive, and since both
$0$
-submersive, and since both
![]() $fp$
and p are flat, we deduce that f is flat as well. Similarly, since both
$fp$
and p are flat, we deduce that f is flat as well. Similarly, since both
![]() $fp$
and p are effective epimorphisms, so is f. Hence, f is a
$fp$
and p are effective epimorphisms, so is f. Hence, f is a
![]() $0$
-submersion.
$0$
-submersion.
Proposition 2.44. Let
![]() $f \colon Y \to X$
be an n-geometric map of Dirac stacks. If f is m-submersive for some
$f \colon Y \to X$
be an n-geometric map of Dirac stacks. If f is m-submersive for some
![]() $m \geq 0$
, then f is n-submersive.
$m \geq 0$
, then f is n-submersive.
Proof. Using Lemma 2.36 and downward induction, it suffices to show that if f is n-geometric and
![]() $(n+1)$
-submersive, then it is n-submersive. Since both properties are detected after base-change to a Dirac scheme, we may assume that X is a Dirac scheme. If
$(n+1)$
-submersive, then it is n-submersive. Since both properties are detected after base-change to a Dirac scheme, we may assume that X is a Dirac scheme. If
![]() $n = 0$
, then there is nothing to prove, so we assume that
$n = 0$
, then there is nothing to prove, so we assume that
![]() $n \geq 1$
. Since f is n-geometric, and since X is a Dirac scheme, there exists an
$n \geq 1$
. Since f is n-geometric, and since X is a Dirac scheme, there exists an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $p \colon U \to Y$
from a Dirac scheme. We claim that the composite map
$p \colon U \to Y$
from a Dirac scheme. We claim that the composite map
is a
![]() $0$
-submersive map of Dirac schemes, so that f is also n-submersive.
$0$
-submersive map of Dirac schemes, so that f is also n-submersive.
To prove the claim, we consider the diagram

with q an n-submersive map from a Dirac scheme and the square cartesian. The map q exists, because f is
![]() $(n+1)$
-submersive. The base-change
$(n+1)$
-submersive. The base-change
![]() $q_U$
is also n-submersive, so we can find the
$q_U$
is also n-submersive, so we can find the
![]() $(n-1)$
-submersive map r from a Dirac scheme such that
$(n-1)$
-submersive map r from a Dirac scheme such that
![]() $q_Ur$
is
$q_Ur$
is
![]() $0$
-submersive. The composite map
$0$
-submersive. The composite map
![]() $(fp)(q_Ur)$
is an n-submersive map between Dirac schemes and hence
$(fp)(q_Ur)$
is an n-submersive map between Dirac schemes and hence
![]() $0$
-submersive by Lemma 2.43. Thus,
$0$
-submersive by Lemma 2.43. Thus,
![]() $(fp)(q_Ur)$
and
$(fp)(q_Ur)$
and
![]() $q_Ur$
are both flat maps of Dirac schemes, so
$q_Ur$
are both flat maps of Dirac schemes, so
![]() $fp$
is flat, and
$fp$
is flat, and
![]() $(fp)(q_Ur)$
and
$(fp)(q_Ur)$
and
![]() $q_Ur$
are both effective epimorphisms, so
$q_Ur$
are both effective epimorphisms, so
![]() $fp$
is an effective epimorphism. This proves the claim.
$fp$
is an effective epimorphism. This proves the claim.
We have now established the notions of maps of Dirac schemes being geometric and submersive and proved that both are stable under composition and base-change as well as local on the base for the flat topology, so we proceed to specialize and consider the absolute notion of a geometric Dirac stack.
Definition 2.45. A Dirac stack X is n-geometric if the unique map
is n-geometric. It is geometric if it is n-geometric for some
![]() $n \geq 0$
.
$n \geq 0$
.
Remark 2.46. In our definition, a Dirac stack is
![]() $0$
-geometric if and only if it is represented by a Dirac scheme. Different choices are possible, but as we explained in Warning 2.35, it is the property of being geometric that is important and not the property of being n-geometric for a particular
$0$
-geometric if and only if it is represented by a Dirac scheme. Different choices are possible, but as we explained in Warning 2.35, it is the property of being geometric that is important and not the property of being n-geometric for a particular
![]() $n \geq 0$
.
$n \geq 0$
.
We record some basic stability properties of geometric Dirac stacks.
Proposition 2.47. Let
![]() $f \colon Y \to X$
be a map of Dirac stacks and let
$f \colon Y \to X$
be a map of Dirac stacks and let
![]() $n \geq 0$
.
$n \geq 0$
.
-
(a) Suppose that f is n-geometric. If X is n-geometric, then so is Y.
-
(b) Suppose that f is n-submersive. If Y is
 $(n+1)$
-geometric, then so is X.
$(n+1)$
-geometric, then so is X. -
(c) Suppose that X is
 $(n+2)$
-geometric. If Y is
$(n+2)$
-geometric. If Y is
 $(n+1)$
-geometric, then so is f.
$(n+1)$
-geometric, then so is f.
In particular, all maps between geometric Dirac stacks are geometric.
Proposition 2.48. The full subcategory
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
spanned by the geometric stacks is closed under finite limits. More precisely, the final Dirac stack is
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
spanned by the geometric stacks is closed under finite limits. More precisely, the final Dirac stack is
![]() $0$
-geometric, and given a cartesian square of Dirac stacks
$0$
-geometric, and given a cartesian square of Dirac stacks

with
![]() $X'$
, X and
$X'$
, X and
![]() $Y n$
-geometric, also
$Y n$
-geometric, also
![]() $Y'$
is n-geometric.
$Y'$
is n-geometric.
Proof. Only the claim concerning fiber products needs proof. If
![]() $n = 0$
, then X,
$n = 0$
, then X,
![]() $X'$
and Y are Dirac schemes, and hence, so is
$X'$
and Y are Dirac schemes, and hence, so is
![]() $Y'$
. If
$Y'$
. If
![]() $n \geq 1$
, then by Proposition 2.47 (c), the map f is n-geometric, and therefore, so is
$n \geq 1$
, then by Proposition 2.47 (c), the map f is n-geometric, and therefore, so is
![]() $f'$
. Thus, Proposition 2.47 (a) implies that
$f'$
. Thus, Proposition 2.47 (a) implies that
![]() $Y'$
is n-geometric as stated.
$Y'$
is n-geometric as stated.
Theorem 2.49. The full subcategory
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
spanned by the geometric Dirac stacks has the following properties:
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
spanned by the geometric Dirac stacks has the following properties:
-
(1) It contains all small coproducts of affine Dirac schemes.
-
(2) It is closed under colimits of groupoids with submersive face maps.
Moreover, it is minimal with these properties.
Proof. We first show that
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
satisfies (1) and (2). For (1), we recall from Addendum 2.28 that a small coproduct of affine Dirac schemes is a Dirac scheme – hence, a geometric Dirac stack. For (2), we let
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
satisfies (1) and (2). For (1), we recall from Addendum 2.28 that a small coproduct of affine Dirac schemes is a Dirac scheme – hence, a geometric Dirac stack. For (2), we let
![]() $S \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
be a groupoid with colimit X. By Theorem 2.19, S is effective in the sense that the square
$S \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
be a groupoid with colimit X. By Theorem 2.19, S is effective in the sense that the square

is cartesian. In this situation, we wish to show that if
![]() $d_0$
is a submersive map between geometric Dirac stacks, then X is geometric. If we choose an
$d_0$
is a submersive map between geometric Dirac stacks, then X is geometric. If we choose an
![]() $n \geq 0$
such that both
$n \geq 0$
such that both
![]() $S_0$
and
$S_0$
and
![]() $S_1$
are n-geometric, then Proposition 2.47 (c) shows that
$S_1$
are n-geometric, then Proposition 2.47 (c) shows that
![]() $d_0$
is n-geometric, and thus Proposition 2.44 shows that
$d_0$
is n-geometric, and thus Proposition 2.44 shows that
![]() $d_0$
is n-submersive. Since (the horizontal) f is an effective epimorphism, we conclude from Proposition 2.41 and from the fact that
$d_0$
is n-submersive. Since (the horizontal) f is an effective epimorphism, we conclude from Proposition 2.41 and from the fact that
![]() $d_0$
is n-submersive that (the vertical) f is n-submersive. But then Proposition 2.47 (b) shows that X is
$d_0$
is n-submersive that (the vertical) f is n-submersive. But then Proposition 2.47 (b) shows that X is
![]() $(n+1)$
-geometric, as desired.
$(n+1)$
-geometric, as desired.
Finally, we let
![]() $\mathcal {C} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
be a full subcategory satisfying (1) and (2) and show, by induction on
$\mathcal {C} \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
be a full subcategory satisfying (1) and (2) and show, by induction on
![]() $n \geq 0$
, that
$n \geq 0$
, that
![]() $\mathcal {C}$
contains all n-geometric Dirac stacks. For
$\mathcal {C}$
contains all n-geometric Dirac stacks. For
![]() $n = 0$
, we must show that
$n = 0$
, we must show that
![]() $\mathcal {C}$
contains every Dirac scheme X. We first suppose that
$\mathcal {C}$
contains every Dirac scheme X. We first suppose that
![]() $X \simeq \coprod _{i \in I}X_i$
is a coproduct of Dirac schemes, each of which can be embedded as an open subscheme
$X \simeq \coprod _{i \in I}X_i$
is a coproduct of Dirac schemes, each of which can be embedded as an open subscheme
![]() $X_i \subset S_i$
of an affine Dirac scheme. We can write each
$X_i \subset S_i$
of an affine Dirac scheme. We can write each
![]() $X_i$
as the union of a family
$X_i$
as the union of a family
![]() $(T_{i,j})_{j \in J_i}$
of distinguished open subschemes
$(T_{i,j})_{j \in J_i}$
of distinguished open subschemes
![]() $T_{i,j} \subset S_i$
, and therefore, it follows from Addendum 2.28 that the canonical map
$T_{i,j} \subset S_i$
, and therefore, it follows from Addendum 2.28 that the canonical map
is
![]() $0$
-submersive. Now, since p is an effective epimorphism, its Čech nerve
$0$
-submersive. Now, since p is an effective epimorphism, its Čech nerve
is a colimit diagram, and since coproducts in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint, we have
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are disjoint, we have
for
![]() $k \geq 0$
. But each summand is an affine Dirac scheme, since distinguished open subschemes of an affine Dirac scheme are closed under finite intersections, so we conclude from properties (1) and (2) that X is contained in
$k \geq 0$
. But each summand is an affine Dirac scheme, since distinguished open subschemes of an affine Dirac scheme are closed under finite intersections, so we conclude from properties (1) and (2) that X is contained in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Next, if X is a general Dirac scheme, then we choose a family
![]() $(S_i)_{i \in I}$
of affine open subschemes such that
$(S_i)_{i \in I}$
of affine open subschemes such that
![]() $\bigcup _{i \in I}|S_i| = |X|$
. In this case, the canonical map
$\bigcup _{i \in I}|S_i| = |X|$
. In this case, the canonical map
is an effective epimorphism, and its Čech nerve
![]() $V \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has the property that for all
$V \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has the property that for all
![]() $k \geq 0$
, the Dirac scheme
$k \geq 0$
, the Dirac scheme
![]() $V_k$
is a coproduct of open subschemes of affine Dirac schemes. Hence, each
$V_k$
is a coproduct of open subschemes of affine Dirac schemes. Hence, each
![]() $V_k$
is contained in
$V_k$
is contained in
![]() $\mathcal {C}$
by what was proved in the previous paragraph, and therefore, so is X. This proves the case
$\mathcal {C}$
by what was proved in the previous paragraph, and therefore, so is X. This proves the case
![]() $n = 0$
.
$n = 0$
.
Finally, we let
![]() $n \geq 1$
and assume, inductively, that
$n \geq 1$
and assume, inductively, that
![]() $\mathcal {C}$
contains all
$\mathcal {C}$
contains all
![]() $(n-1)$
-geometric Dirac stacks. Given an n-geometric Dirac stack X, we choose an
$(n-1)$
-geometric Dirac stacks. Given an n-geometric Dirac stack X, we choose an
![]() $(n-1)$
-submersive map
$(n-1)$
-submersive map
![]() $p \colon V_0 \to X$
from a Dirac scheme and consider its Čech nerve
$p \colon V_0 \to X$
from a Dirac scheme and consider its Čech nerve
Since p is
![]() $(n-1)$
-submersive and
$(n-1)$
-submersive and
![]() $V|_{\Delta ^{\mathrm {op}}}$
an effective groupoid, we conclude that all face maps in
$V|_{\Delta ^{\mathrm {op}}}$
an effective groupoid, we conclude that all face maps in
![]() $V|_{\Delta ^{\mathrm {op}}}$
are
$V|_{\Delta ^{\mathrm {op}}}$
are
![]() $(n-1)$
-submersive – hence, by Proposition 2.38, so is every iterated face map
$(n-1)$
-submersive – hence, by Proposition 2.38, so is every iterated face map
![]() $V_k \to V_0$
. But
$V_k \to V_0$
. But
![]() $V_0$
is
$V_0$
is
![]() $(n-1)$
-geometric, being a Dirac scheme, so Proposition 2.47 shows that
$(n-1)$
-geometric, being a Dirac scheme, so Proposition 2.47 shows that
![]() $V_k$
is
$V_k$
is
![]() $(n-1)$
-geometric for all
$(n-1)$
-geometric for all
![]() $k \geq 0$
. By the inductive hypothesis,
$k \geq 0$
. By the inductive hypothesis,
![]() $V|_{\Delta ^{\mathrm {op}}}$
is a groupoid in
$V|_{\Delta ^{\mathrm {op}}}$
is a groupoid in
![]() $\mathcal {C}$
with submersive face maps, so we conclude from property (2) that X is contained in
$\mathcal {C}$
with submersive face maps, so we conclude from property (2) that X is contained in
![]() $\mathcal {C}$
, as desired.
$\mathcal {C}$
, as desired.
Remark 2.50 (Flat maps).
The notion of a flat map of Dirac schemes may be generalized to the notion of a flat map of Dirac stacks as follows. A map of Dirac stacks
![]() $f \colon Y \to X$
is flat if, in every diagram of the form
$f \colon Y \to X$
is flat if, in every diagram of the form

with S and T Dirac schemes and with
![]() $p \colon S \to X$
and
$p \colon S \to X$
and
![]() $(g,h) \colon T \to Y_S$
submersive, the map of Dirac schemes
$(g,h) \colon T \to Y_S$
submersive, the map of Dirac schemes
![]() $g \colon T \to S$
is flat. One can show that a map of Dirac stacks is submersive if and only if it is a flat effective epimorphism. In particular, if a flat map of Dirac stacks admits a section, then it is submersive. It follows that, in Theorem 2.49, the property (2) is equivalent to the following:
$g \colon T \to S$
is flat. One can show that a map of Dirac stacks is submersive if and only if it is a flat effective epimorphism. In particular, if a flat map of Dirac stacks admits a section, then it is submersive. It follows that, in Theorem 2.49, the property (2) is equivalent to the following:
-
(2’) It is closed under colimits of groupoids with flat face maps.
Thus, the theorem shows that the full subcategory spanned by the geometric Dirac stacks is precisely the closure under colimits of groupoids with flat face maps of the full subcategory spanned by the Dirac schemes.
3 Coherent cohomology
In this section, we construct the functor that to a Dirac stack X assigns the presentably symmetric monoidal stable
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)$
of a quasi-coherent
${\mathrm {QCoh}}(X)$
of a quasi-coherent
![]() $\mathcal {O}_X$
-modules that we outlined in the introduction.
$\mathcal {O}_X$
-modules that we outlined in the introduction.
3.1 Quasi-coherent
 $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
We first define the functor that to an affine Dirac scheme S assigns its presentably symmetric monoidal stable
![]() $\infty $
-category of quasi-coherent
$\infty $
-category of quasi-coherent
![]() $\mathcal {O}_S$
-modules. The definition uses animation, which we first recall following [Reference Lurie20, Section 5.5.8] and [Reference Cesnavicius and Scholze6].
$\mathcal {O}_S$
-modules. The definition uses animation, which we first recall following [Reference Lurie20, Section 5.5.8] and [Reference Cesnavicius and Scholze6].
Let
![]() $\mathcal {C}$
be a presentable
$\mathcal {C}$
be a presentable
![]() $1$
-category. An object
$1$
-category. An object
![]() $P \in \mathcal {C}$
is compact
$P \in \mathcal {C}$
is compact
![]() $1$
-projective if the map
$1$
-projective if the map
![]() $\operatorname {\mathrm {Map}}(P,-) \colon \mathcal {C} \to \operatorname {\mathrm {Set}}$
corepresented by P preserves small sifted colimits, and we write
$\operatorname {\mathrm {Map}}(P,-) \colon \mathcal {C} \to \operatorname {\mathrm {Set}}$
corepresented by P preserves small sifted colimits, and we write
![]() $\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
for the inclusion of the full subcategory spanned by the compact
$\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
for the inclusion of the full subcategory spanned by the compact
![]() $1$
-projective objects. Now, if
$1$
-projective objects. Now, if
![]() $\mathcal {C}$
is generated under small sifted colimits by
$\mathcal {C}$
is generated under small sifted colimits by
![]() $\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
, then its animation is defined to be the initial map
$\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
, then its animation is defined to be the initial map
to an
![]() $\infty $
-category that admits small sifted colimits. So any map
$\infty $
-category that admits small sifted colimits. So any map
![]() $f_0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {D}$
to an
$f_0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {D}$
to an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}$
that admits small sifted colimits admits a unique factorization
$\mathcal {D}$
that admits small sifted colimits admits a unique factorization

such that f preserves sifted colimits. The
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}^{\operatorname {\mathrm {an}}}$
is presentable and the map
$\mathcal {C}^{\operatorname {\mathrm {an}}}$
is presentable and the map
![]() $h \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}^{\operatorname {\mathrm {an}}}$
preserves finite coproducts. Moreover, if also
$h \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}^{\operatorname {\mathrm {an}}}$
preserves finite coproducts. Moreover, if also
![]() $\mathcal {D}$
admits all small colimits and if
$\mathcal {D}$
admits all small colimits and if
![]() $f_0$
preserves finite coproducts, then f preserves all small colimits. In particular, the inclusion
$f_0$
preserves finite coproducts, then f preserves all small colimits. In particular, the inclusion
![]() $\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
factors uniquely as
$\pi _0 \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
factors uniquely as

and the map
![]() $\bar {\pi } \colon \tau _{\leq 0}(\mathcal {C}^{\operatorname {\mathrm {an}}}) \to \mathcal {C}$
induced by
$\bar {\pi } \colon \tau _{\leq 0}(\mathcal {C}^{\operatorname {\mathrm {an}}}) \to \mathcal {C}$
induced by
![]() $\pi $
is an equivalence, so that the right adjoint of
$\pi $
is an equivalence, so that the right adjoint of
![]() $\pi $
can be identified with the inclusion
$\pi $
can be identified with the inclusion
![]() $s \colon \mathcal {C} \to \mathcal {C}^{\operatorname {\mathrm {an}}}$
of the full subcategory spanned by the
$s \colon \mathcal {C} \to \mathcal {C}^{\operatorname {\mathrm {an}}}$
of the full subcategory spanned by the
![]() $0$
-truncated objects.
$0$
-truncated objects.
Lemma 3.1. If R is a Dirac ring, then the animation
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {an}}}$
of the abelian category
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {an}}}$
of the abelian category
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
exists and is a complete Grothendieck prestable
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
exists and is a complete Grothendieck prestable
![]() $\infty $
-category.
$\infty $
-category.
Proof. The compact
![]() $1$
-projective objects in the abelian category
$1$
-projective objects in the abelian category
![]() $\mathcal {C} \simeq \operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
are the graded R-modules which are finitely generated and projective, so
$\mathcal {C} \simeq \operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
are the graded R-modules which are finitely generated and projective, so
![]() $\mathcal {C}^{\operatorname {\mathrm {cp}}} \subset \mathcal {C}$
generates
$\mathcal {C}^{\operatorname {\mathrm {cp}}} \subset \mathcal {C}$
generates
![]() $\mathcal {C}$
under sifted colimits. Therefore, the animation
$\mathcal {C}$
under sifted colimits. Therefore, the animation
![]() $i \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
exists and agrees, by [Reference Lurie20, Proposition 5.5.8.15], with the Yoneda embedding
$i \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to \mathcal {C}$
exists and agrees, by [Reference Lurie20, Proposition 5.5.8.15], with the Yoneda embedding
![]() $h \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to {\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
into the full subcategory
$h \colon \mathcal {C}^{\operatorname {\mathrm {cp}}} \to {\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
into the full subcategory
![]() ${\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}}) \subset {\mathcal {P}}(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
spanned by the functors
${\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}}) \subset {\mathcal {P}}(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
spanned by the functors
![]() $(\mathcal {C}^{\operatorname {\mathrm {cp}}})^{\mathrm {op}} \to {\mathcal {S}}$
that preserve finite products. Moreover, since
$(\mathcal {C}^{\operatorname {\mathrm {cp}}})^{\mathrm {op}} \to {\mathcal {S}}$
that preserve finite products. Moreover, since
![]() $\mathcal {C}^{\operatorname {\mathrm {cp}}}$
is additive,
$\mathcal {C}^{\operatorname {\mathrm {cp}}}$
is additive,
![]() ${\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
is complete Grothendieck prestable by [Reference Lurie23, Proposition C.1.5.7 and Remark C.1.5.9].
${\mathcal {P}}_{\Sigma }(\mathcal {C}^{\operatorname {\mathrm {cp}}})$
is complete Grothendieck prestable by [Reference Lurie23, Proposition C.1.5.7 and Remark C.1.5.9].
Definition 3.2. If
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac stack, then
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac stack, then
is the animation of the abelian category of graded R-modules, and
is its stabilization.
Warning 3.3. While the inclusion
![]() $i \colon {\mathrm {QCoh}}(S)_{\geq 0 } \to {\mathrm {QCoh}}(S)$
is a stabilization for affine Dirac schemes, this will not be true for general Dirac stacks.
$i \colon {\mathrm {QCoh}}(S)_{\geq 0 } \to {\mathrm {QCoh}}(S)$
is a stabilization for affine Dirac schemes, this will not be true for general Dirac stacks.
To assure the reader that the definition in terms of animation is very natural, we record two equivalent definitions. For (3) below, we recall from [Reference Hesselholt and Pstrągowski12, §2.1] that the abelian category of graded abelian groups is equivalent (as a symmetric monoidal category) to the heart of the Beilinson t-structure on graded spectra, so that any Dirac ring determines a commutative algebra in graded spectra.
Proposition 3.4. If
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the following
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the following
![]() $\infty $
-categories are canonically equivalent:
$\infty $
-categories are canonically equivalent:
-
(1) The
 $\infty $
-category
$\infty $
-category
 ${\mathrm {QCoh}}(X) \simeq \operatorname {\mathrm {Sp}}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {an}}})$
.
${\mathrm {QCoh}}(X) \simeq \operatorname {\mathrm {Sp}}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {an}}})$
. -
(2) The derived
 $\infty $
-category
$\infty $
-category
 $\mathcal {D}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}}))$
of the Grothendieck abelian category of R-modules in graded abelian groups.
$\mathcal {D}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}}))$
of the Grothendieck abelian category of R-modules in graded abelian groups. -
(3) The
 $\infty $
-category
$\infty $
-category
 $\operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Fun}}(\mathbb {Z},\operatorname {\mathrm {Sp}}))$
of R-modules in
$\operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Fun}}(\mathbb {Z},\operatorname {\mathrm {Sp}}))$
of R-modules in
 $\mathbb {Z}$
-graded spectra.
$\mathbb {Z}$
-graded spectra.
Proof. The
![]() $\infty $
-categories (1)–(3) are all presentable and stable and equipped with right complete t-structures. So it suffices to compare connective parts, and by the universal property of animation, it suffices to verify that (2) and (3) are generated under sifted colimits by the subcategories spanned by compact projective objects, which coincide with
$\infty $
-categories (1)–(3) are all presentable and stable and equipped with right complete t-structures. So it suffices to compare connective parts, and by the universal property of animation, it suffices to verify that (2) and (3) are generated under sifted colimits by the subcategories spanned by compact projective objects, which coincide with
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}}}$
. In the case of (2), this is [Reference Lurie19, Proposition 1.3.3.14], and in the case of (3), the heart of the Beilinson t-structure is given by
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}}}$
. In the case of (2), this is [Reference Lurie19, Proposition 1.3.3.14], and in the case of (3), the heart of the Beilinson t-structure is given by
and the connective part
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Fun}}(\mathbb {Z},\operatorname {\mathrm {Sp}})_{\geq 0}$
is generated under sifted colimits by subcategory spanned by the compact projective objects in the heart, which precisely is
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Fun}}(\mathbb {Z},\operatorname {\mathrm {Sp}})_{\geq 0}$
is generated under sifted colimits by subcategory spanned by the compact projective objects in the heart, which precisely is
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}}}$
.
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}}}$
.
The symmetric monoidal structure on
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
restricts to one on the full subcategory spanned by the compact 1-projective objects, which, in turn, gives rise to symmetric monoidal structures on
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})$
restricts to one on the full subcategory spanned by the compact 1-projective objects, which, in turn, gives rise to symmetric monoidal structures on
![]() ${\mathrm {QCoh}}(S)_{\geq 0}$
and
${\mathrm {QCoh}}(S)_{\geq 0}$
and
![]() ${\mathrm {QCoh}}(S)$
, as well as on the Yoneda embedding h and on the canonical inclusion i.
${\mathrm {QCoh}}(S)$
, as well as on the Yoneda embedding h and on the canonical inclusion i.
Lemma 3.5. If
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the functors
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the functors
promote uniquely to symmetric monoidal functors such that the tensor products on the middle and right-hand terms preserve colimits in each variable.
Proof. This is [Reference Lurie19, Propositions 4.8.1.10 and 2.2.1.9].
The symmetric monoidal category of compact 1-projective R-modules in graded abelian groups is covariantly functorial in R through extension of scalars, and it follows from [Reference Lurie19, Proposition 4.8.1.10] that this gives rise to a functor
that to S assigns the symmetric monoidal functor
provided by Lemma 3.5. Since we were unable to find this argument spelled out in detail in the literature, we take this opportunity to do so here.
Construction 3.6. Let
![]() ${\widehat {\mathrm {Cat}}}_{\infty }^{\Sigma }, {\widehat {\mathrm {Cat}}}_{\infty }^L \subset {\widehat {\mathrm {Cat}}}_{\infty }$
be the subcategories spanned by the (possibly large)
${\widehat {\mathrm {Cat}}}_{\infty }^{\Sigma }, {\widehat {\mathrm {Cat}}}_{\infty }^L \subset {\widehat {\mathrm {Cat}}}_{\infty }$
be the subcategories spanned by the (possibly large)
![]() $\infty $
-categories that admit finite coproducts and small colimits, respectively, and the functors between them that preserve the colimits in question. We recall from [Reference Lurie19, Corollary 4.8.1.4] that the canonical inclusion
$\infty $
-categories that admit finite coproducts and small colimits, respectively, and the functors between them that preserve the colimits in question. We recall from [Reference Lurie19, Corollary 4.8.1.4] that the canonical inclusion
promotes to a lax symmetric monoidal functor such that the induced map
is the canonical inclusion of the
![]() $\infty $
-category of symmetric monoidal
$\infty $
-category of symmetric monoidal
![]() $\infty $
-categories, whose underlying
$\infty $
-categories, whose underlying
![]() $\infty $
-categories admit small colimits and whose tensor products preserve small colimits in each variable, in the
$\infty $
-categories admit small colimits and whose tensor products preserve small colimits in each variable, in the
![]() $\infty $
-category of symmetric monoidal
$\infty $
-category of symmetric monoidal
![]() $\infty $
-categories, whose underlying
$\infty $
-categories, whose underlying
![]() $\infty $
-categories admit finite coproducts and whose tensor products preserve finite coproducts in each variable. In this situation, it follows from [Reference Lurie19, Proposition 4.8.1.10] that the diagram
$\infty $
-categories admit finite coproducts and whose tensor products preserve finite coproducts in each variable. In this situation, it follows from [Reference Lurie19, Proposition 4.8.1.10] that the diagram

is left adjointable. If
![]() $\mathcal {C}$
is small, then the left adjoint of the bottom horizontal map takes
$\mathcal {C}$
is small, then the left adjoint of the bottom horizontal map takes
![]() $\mathcal {C}$
to the
$\mathcal {C}$
to the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {P}_{\Sigma }(\mathcal {C})$
of finite product-preserving presheaves of small anima, which by [Reference Lurie20, Theorem 5.5.1.1], is presentable. Thus, the left adjoint of the top horizontal map restricts to a map
$\mathcal {P}_{\Sigma }(\mathcal {C})$
of finite product-preserving presheaves of small anima, which by [Reference Lurie20, Theorem 5.5.1.1], is presentable. Thus, the left adjoint of the top horizontal map restricts to a map
from the
![]() $\infty $
-category of small symmetric monoidal
$\infty $
-category of small symmetric monoidal
![]() $\infty $
-categories, whose underlying
$\infty $
-categories, whose underlying
![]() $\infty $
-categories admit finite coproducts and whose tensor products preserve finite coproducts in each variable, to the
$\infty $
-categories admit finite coproducts and whose tensor products preserve finite coproducts in each variable, to the
![]() $\infty $
-category of presentably symmetric monoidal
$\infty $
-category of presentably symmetric monoidal
![]() $\infty $
-categories. It follows that the composition
$\infty $
-categories. It follows that the composition
of the functor that to
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
assigns
$S \simeq \operatorname {\mathrm {Spec}}(R)$
assigns
![]() $\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}},\otimes }$
and the restricted left adjoint is a functor that to S assigns
$\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}})^{\operatorname {\mathrm {cp}},\otimes }$
and the restricted left adjoint is a functor that to S assigns
![]() ${\mathrm {QCoh}}(S)_{\geq 0}^{\otimes }$
. Finally, the map
${\mathrm {QCoh}}(S)_{\geq 0}^{\otimes }$
. Finally, the map
is given by tensor product with
![]() $\operatorname {\mathrm {Sp}} \in {\operatorname {LPr}}$
because
$\operatorname {\mathrm {Sp}} \in {\operatorname {LPr}}$
because
![]() ${\mathrm {QCoh}}(S)_{\geq 0}$
is presentable and therefore is functorial.
${\mathrm {QCoh}}(S)_{\geq 0}$
is presentable and therefore is functorial.
We recall from Remark A.4 that the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of Dirac prestacks is the free cocompletion of the
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of Dirac prestacks is the free cocompletion of the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Aff}}$
of affine Dirac schemes. Therefore, the following definition is meaningful.
$\operatorname {\mathrm {Aff}}$
of affine Dirac schemes. Therefore, the following definition is meaningful.
Definition 3.7. The unique small limit-preserving extension

of the functor provided by Construction 3.6 is said to be the functor that to a Dirac prestack X assigns its presentably symmetric monoidal
![]() $\infty $
-category of quasi-coherent
$\infty $
-category of quasi-coherent
![]() $\mathcal {O}_X$
-modules.
$\mathcal {O}_X$
-modules.
If
![]() $f \colon Y \to X$
is a map of Dirac prestacks, then we write
$f \colon Y \to X$
is a map of Dirac prestacks, then we write

for the adjoint functors provided by Definition 3.7. We call
![]() $f^*$
and
$f^*$
and
![]() $f_*$
the inverse image and the direct image, respectively. In fact, Definition 3.7 promotes
$f_*$
the inverse image and the direct image, respectively. In fact, Definition 3.7 promotes
![]() $f^*$
to a symmetric monoidal functor, and therefore, by [Reference Lurie19, Corollary 7.3.2.7], it also promotes
$f^*$
to a symmetric monoidal functor, and therefore, by [Reference Lurie19, Corollary 7.3.2.7], it also promotes
![]() $f_*$
to a lax symmetric monoidal functor.
$f_*$
to a lax symmetric monoidal functor.
Warning 3.8. We will often abuse notation and simply write
![]() ${\mathrm {QCoh}}(X)$
both for the presentably symmetric monoidal
${\mathrm {QCoh}}(X)$
both for the presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)^{\otimes }$
and for its underlying presentable
${\mathrm {QCoh}}(X)^{\otimes }$
and for its underlying presentable
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)$
.
${\mathrm {QCoh}}(X)$
.
Let X be a Dirac prestack and let
![]() $p \colon X \to \operatorname {\mathrm {Spec}}(\mathbb {Z})$
be the unique map. Since the inverse image
$p \colon X \to \operatorname {\mathrm {Spec}}(\mathbb {Z})$
be the unique map. Since the inverse image
![]() $p^*$
is symmetric monoidal, it follows in particular that
$p^*$
is symmetric monoidal, it follows in particular that
is the tensor unit of
![]() ${\mathrm {QCoh}}(X)$
. More generally, its spin-s Serre twist defined by
${\mathrm {QCoh}}(X)$
. More generally, its spin-s Serre twist defined by
is a tensor-invertible object of
![]() ${\mathrm {QCoh}}(X)$
.
${\mathrm {QCoh}}(X)$
.
Definition 3.9. Let X be a Dirac prestack, let
![]() $p \colon X \to \operatorname {\mathrm {Spec}}(\mathbb {Z})$
be the unique map, and let s be a half-integer. The spin-s Serre twist of a quasi-coherent
$p \colon X \to \operatorname {\mathrm {Spec}}(\mathbb {Z})$
be the unique map, and let s be a half-integer. The spin-s Serre twist of a quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {F}$
is the quasi-coherent
$\mathcal {F}$
is the quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
Remark 3.10. We may describe
![]() ${\mathrm {QCoh}}(X)$
for a Dirac prestack X more concretely as follows. By Proposition A.2, we may write any prestack
${\mathrm {QCoh}}(X)$
for a Dirac prestack X more concretely as follows. By Proposition A.2, we may write any prestack
![]() $X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
as the colimit of the diagram given by the composite map
$X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
as the colimit of the diagram given by the composite map
for some small cardinal
![]() $\kappa $
. Hence, by definition, we can identify
$\kappa $
. Hence, by definition, we can identify
![]() ${\mathrm {QCoh}}(X)$
with the limit of the diagram given by the composite map
${\mathrm {QCoh}}(X)$
with the limit of the diagram given by the composite map
Remark 3.11. Let
![]() $f \colon Y \to X$
be a map of Dirac prestack, such that the induced map of Dirac stacks
$f \colon Y \to X$
be a map of Dirac prestack, such that the induced map of Dirac stacks
![]() $L(f) \colon L(Y) \to L(X)$
is an equivalence. We will show in Theorem 3.24 below that the
$L(f) \colon L(Y) \to L(X)$
is an equivalence. We will show in Theorem 3.24 below that the
![]() $f^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is an equivalence.
$f^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is an equivalence.
3.2 The canonical t-structure
We showed in Lemma 3.1 that if
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is an affine Dirac scheme, then the
![]() $\infty $
-category
$\infty $
-category
is complete Grothendieck prestable. So by [Reference Lurie23, Proposition C.1.2.9], its stabilization
![]() ${\mathrm {QCoh}}(S)$
has a canonical t-structure, which is both left complete and right complete. Moreover, its connective part is the essential image of the fully faithful functor
${\mathrm {QCoh}}(S)$
has a canonical t-structure, which is both left complete and right complete. Moreover, its connective part is the essential image of the fully faithful functor
and its coconnective part is stable under filtered colimits.
Remark 3.12. Under the equivalence
![]() ${\mathrm {QCoh}}(S) \simeq \mathcal {D}(\operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Ab}}))$
from Proposition 3.4, the canonical t-structure corresponds to the t-structure on the derived
${\mathrm {QCoh}}(S) \simeq \mathcal {D}(\operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Ab}}))$
from Proposition 3.4, the canonical t-structure corresponds to the t-structure on the derived
![]() $\infty $
-category with
$\infty $
-category with
![]() $\mathcal {F}$
connective if and only if
$\mathcal {F}$
connective if and only if
![]() $\pi _i(\mathcal {F}) \in \operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Ab}})$
is zero for all
$\pi _i(\mathcal {F}) \in \operatorname {\mathrm {Mod}}_{R}(\operatorname {\mathrm {Ab}})$
is zero for all
![]() $i < 0$
.
$i < 0$
.
Proposition 3.13. Let
![]() $X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
be a Dirac prestack.
$X \in {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
be a Dirac prestack.
-
(1) There exists a unique t-structure on
 ${\mathrm {QCoh}}(X)$
such that
${\mathrm {QCoh}}(X)$
such that
 $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
if and only if
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
if and only if
 $\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)_{\geq 0}$
for every map
$\eta ^*(\mathcal {F}) \in {\mathrm {QCoh}}(S)_{\geq 0}$
for every map
 $\eta \colon S \to X$
with S affine.
$\eta \colon S \to X$
with S affine. -
(2) If
 $\mathcal {G} \in {\mathrm {QCoh}}(X)$
and
$\mathcal {G} \in {\mathrm {QCoh}}(X)$
and
 $\eta ^*(\mathcal {G}) \in {\mathrm {QCoh}}(S)_{\leq 0}$
for every map
$\eta ^*(\mathcal {G}) \in {\mathrm {QCoh}}(S)_{\leq 0}$
for every map
 $\eta \colon S \to X$
with S affine, then
$\eta \colon S \to X$
with S affine, then
 $\mathcal {G} \in {\mathrm {QCoh}}(X)_{\leq 0}$
.
$\mathcal {G} \in {\mathrm {QCoh}}(X)_{\leq 0}$
. -
(3) For every half-integer s,
 $\mathcal {O}_{X}(s) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
.
$\mathcal {O}_{X}(s) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
.
Proof. To prove (1), we use Proposition A.2 to write X as a colimit of a small diagram
![]() $S \colon K \to {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of affine Dirac stacks. Hence,
$S \colon K \to {\mathcal {P}}(\operatorname {\mathrm {Aff}})$
of affine Dirac stacks. Hence,
and we wish to show that
is the connective part of a t-structure. But
![]() ${\mathrm {QCoh}}(X)_{\geq 0}$
and
${\mathrm {QCoh}}(X)_{\geq 0}$
and
![]() ${\mathrm {QCoh}}(X)$
are both presentable, and therefore, it suffices by [Reference Lurie19, Proposition 1.4.4.11] to show that
${\mathrm {QCoh}}(X)$
are both presentable, and therefore, it suffices by [Reference Lurie19, Proposition 1.4.4.11] to show that
is closed under small colimits and extensions, which is clear. This proves (1).
To prove (2), given
![]() $\mathcal {G} \in {\mathrm {QCoh}}(X)$
be as in the statement, we must show that for every
$\mathcal {G} \in {\mathrm {QCoh}}(X)$
be as in the statement, we must show that for every
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
, the mapping anima
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
, the mapping anima
![]() $\operatorname {\mathrm {Map}}(\mathcal {F},\mathcal {G})$
is
$\operatorname {\mathrm {Map}}(\mathcal {F},\mathcal {G})$
is
![]() $0$
-truncated. We again write
$0$
-truncated. We again write
![]() $X \simeq \varinjlim _KS$
as a colimit of a small diagram
$X \simeq \varinjlim _KS$
as a colimit of a small diagram
![]() $S \colon K \to \operatorname {\mathrm {Aff}}$
of affine Dirac stacks, and for
$S \colon K \to \operatorname {\mathrm {Aff}}$
of affine Dirac stacks, and for
![]() $k \in K$
, we write
$k \in K$
, we write
![]() $\eta _k \colon S_k \to X$
be the canonical map. This exhibits the mapping anima in question as a limit
$\eta _k \colon S_k \to X$
be the canonical map. This exhibits the mapping anima in question as a limit
of anima, each of which is
![]() $0$
-truncated, by assumption. But then also the limit is
$0$
-truncated, by assumption. But then also the limit is
![]() $0$
-truncated since the inclusion
$0$
-truncated since the inclusion
![]() ${\mathcal {S}}_{\leq 0} \to {\mathcal {S}}$
preserves limits. This proves (2).
${\mathcal {S}}_{\leq 0} \to {\mathcal {S}}$
preserves limits. This proves (2).
Finally, we observe that (3) holds because
![]() $\eta ^*(\mathcal {O}_X(s)) \simeq \mathcal {O}_S(s) \in {\mathrm {QCoh}}(S)^{\heartsuit }$
for every map
$\eta ^*(\mathcal {O}_X(s)) \simeq \mathcal {O}_S(s) \in {\mathrm {QCoh}}(S)^{\heartsuit }$
for every map
![]() $\eta \colon S \to X$
with S affine.
$\eta \colon S \to X$
with S affine.
Remark 3.14. The opposite implication of (2) in Proposition 3.13 fails in general. Indeed, the inverse image functor
![]() $\eta ^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(S)$
need not in general preserve coconnectivity, even if both S and X are affine.
$\eta ^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(S)$
need not in general preserve coconnectivity, even if both S and X are affine.
We recall that an exact functor
![]() $F \colon \mathcal {C} \to \mathcal {D}$
between stable
$F \colon \mathcal {C} \to \mathcal {D}$
between stable
![]() $\infty $
-categories with t-structures is defined to be right t-exact, if
$\infty $
-categories with t-structures is defined to be right t-exact, if
![]() $F(\mathcal {C}_{\geq 0}) \subset \mathcal {D}_{\geq 0}$
, and to be left t-exact, if
$F(\mathcal {C}_{\geq 0}) \subset \mathcal {D}_{\geq 0}$
, and to be left t-exact, if
![]() $F(\mathcal {C}_{\leq 0}) \subset \mathcal {D}_{\leq 0}$
. It is t-exact, if it is both left t-exact and right t-exact.
$F(\mathcal {C}_{\leq 0}) \subset \mathcal {D}_{\leq 0}$
. It is t-exact, if it is both left t-exact and right t-exact.
Addendum 3.15. If
![]() $f \colon Y \to X$
is a map of Dirac stacks, then the extension of scalars functor and the restriction of scalars functor
$f \colon Y \to X$
is a map of Dirac stacks, then the extension of scalars functor and the restriction of scalars functor

are right t-exact and left t-exact, respectively.
Proof. Since
![]() $f^*$
and
$f^*$
and
![]() $f_*$
are adjoint, the statement that the former is right t-exact is equivalent to the statement that the latter is left t-exact. To show that
$f_*$
are adjoint, the statement that the former is right t-exact is equivalent to the statement that the latter is left t-exact. To show that
![]() $f^*$
is right t-exact, we let
$f^*$
is right t-exact, we let
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
and wish to show that
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
and wish to show that
![]() $f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\geq 0}$
. But if
$f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\geq 0}$
. But if
![]() $\eta \colon S \to Y$
is map from an affine Dirac scheme, then so is
$\eta \colon S \to Y$
is map from an affine Dirac scheme, then so is
![]() $f \circ \eta \colon S \to X$
, so
$f \circ \eta \colon S \to X$
, so
since
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
.
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\geq 0}$
.
Remark 3.16 (Comparison with derived
 $\infty $
-category).
$\infty $
-category).
If X is any Dirac prestack, then there is a canonical exact functor
from the bounded derived
![]() $\infty $
-category of the abelian category of quasi-coherent
$\infty $
-category of the abelian category of quasi-coherent
![]() $\mathcal {O}_X$
-modules. In this generality, the functor and the bounded derived
$\mathcal {O}_X$
-modules. In this generality, the functor and the bounded derived
![]() $\infty $
-category are constructed in [Reference Bunke, Cisinski, Kasprowski and Winges4, Corollary 7.59]. However, it may not be fully faithful, even for qcqs schemes, as Verdier’s counterexample in [36, Exposé II, Appendice I] shows. In fact, in general, the
$\infty $
-category are constructed in [Reference Bunke, Cisinski, Kasprowski and Winges4, Corollary 7.59]. However, it may not be fully faithful, even for qcqs schemes, as Verdier’s counterexample in [36, Exposé II, Appendice I] shows. In fact, in general, the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}^b({\mathrm {QCoh}}(X)^{\heartsuit })$
may not even be locally small, unlike the presentable
$\mathcal {D}^b({\mathrm {QCoh}}(X)^{\heartsuit })$
may not even be locally small, unlike the presentable
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)$
.
${\mathrm {QCoh}}(X)$
.
Remark 3.17. If
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then the canonical t-structure on
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then the canonical t-structure on
![]() ${\mathrm {QCoh}}(S) \simeq \mathcal {D}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}}))$
is compatible with filtered colimits by [Reference Lurie19, Proposition 1.3.5.21]. We will show that this is true, more generally, if X is geometric in the sense of Definition 2.45. In particular, for X geometric, the
${\mathrm {QCoh}}(S) \simeq \mathcal {D}(\operatorname {\mathrm {Mod}}_R(\operatorname {\mathrm {Ab}}))$
is compatible with filtered colimits by [Reference Lurie19, Proposition 1.3.5.21]. We will show that this is true, more generally, if X is geometric in the sense of Definition 2.45. In particular, for X geometric, the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(X)_{\geq 0}$
is Grothendieck prestable in the sense of [Reference Lurie23, Definition C.1.4.2].
${\mathrm {QCoh}}(X)_{\geq 0}$
is Grothendieck prestable in the sense of [Reference Lurie23, Definition C.1.4.2].
3.3 Descent for quasi-coherent
 $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
We proceed to show that the functor
![]() ${\mathrm {QCoh}}$
of Definition 3.7 admits a factorization through the sheafification functor
${\mathrm {QCoh}}$
of Definition 3.7 admits a factorization through the sheafification functor
![]() $L \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, and we begin with the following lemma.
$L \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, and we begin with the following lemma.
Lemma 3.18. Given a cartesian square of affine Dirac schemes

in which either f or g or both are flat, the diagram

is right adjointable in the sense that the canonical map
is an equivalence.
Proof. We write
![]() $S \simeq \operatorname {\mathrm {Spec}}(A)$
,
$S \simeq \operatorname {\mathrm {Spec}}(A)$
,
![]() $S' \simeq \operatorname {\mathrm {Spec}}(A')$
,
$S' \simeq \operatorname {\mathrm {Spec}}(A')$
,
![]() $T \simeq \operatorname {\mathrm {Spec}}(B)$
and
$T \simeq \operatorname {\mathrm {Spec}}(B)$
and
![]() $T' \simeq \operatorname {\mathrm {Spec}}(B')$
. The right adjoints
$T' \simeq \operatorname {\mathrm {Spec}}(B')$
. The right adjoints
![]() $g_*$
and
$g_*$
and
![]() $g_*'$
exist, and since we consider affine Dirac schemes only, they are given by restriction of scalars, and hence, they preserve small colimits. Therefore, it suffices to show that for the generator
$g_*'$
exist, and since we consider affine Dirac schemes only, they are given by restriction of scalars, and hence, they preserve small colimits. Therefore, it suffices to show that for the generator
![]() $A'$
of the presentable stable
$A'$
of the presentable stable
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {QCoh}}(S')$
, the map
${\mathrm {QCoh}}(S')$
, the map
![]() $f^*g_*(A') \to g_*'f'{}^*(A')$
is an equivalence. But this map is given by the canonical projection
$f^*g_*(A') \to g_*'f'{}^*(A')$
is an equivalence. But this map is given by the canonical projection
which is an equivalence by the assumption that either f or g or both are flat.
Remark 3.19. If we built animated Dirac geometry by replacing Dirac rings by animated Dirac rings, then the analogue of Lemma 3.18 would hold without any flatness assumptions.
The following generalization to the relatively affine case will be useful later. Here, given a morphism
![]() $f \colon Y \rightarrow X$
of Dirac stacks, we say it is flat affine if for any map
$f \colon Y \rightarrow X$
of Dirac stacks, we say it is flat affine if for any map
![]() $\eta : S \rightarrow X$
from an affine scheme, the pullback
$\eta : S \rightarrow X$
from an affine scheme, the pullback
![]() $Y \times _{X} S$
is an affine scheme and the induced morphism
$Y \times _{X} S$
is an affine scheme and the induced morphism
![]() $Y \times _{X} S \rightarrow S$
is flat.
$Y \times _{X} S \rightarrow S$
is flat.
Proposition 3.20. If
![]() $f \colon Y \to X$
is a flat affine map of Dirac stacks, then the following hold:
$f \colon Y \to X$
is a flat affine map of Dirac stacks, then the following hold:
-
(1) The functor
 $f_* \colon {\mathrm {QCoh}}(Y) \to {\mathrm {QCoh}}(X)$
is t-exact and admits a right adjoint.
$f_* \colon {\mathrm {QCoh}}(Y) \to {\mathrm {QCoh}}(X)$
is t-exact and admits a right adjoint. -
(2) If
 $g \colon X' \to X$
is any map of Dirac stacks and if
$g \colon X' \to X$
is any map of Dirac stacks and if
 $f' \colon Y' \to X'$
is the base-change of f along g, then is right adjointable in the sense that the base-change map
$f' \colon Y' \to X'$
is the base-change of f along g, then is right adjointable in the sense that the base-change map is an equivalence.
is an equivalence.
Proof. We first prove (1). Since
![]() $f \colon Y \to X$
is affine, we have an adjunction
$f \colon Y \to X$
is affine, we have an adjunction
with u given by composition with f and v given by base-change along f. A counit p of the adjunction induces a natural transformation
of functors from
![]() $({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
$({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
![]() $\operatorname {\mathrm {Cat}}_{\infty }$
given by extension of scalars along the canonical projection
$\operatorname {\mathrm {Cat}}_{\infty }$
given by extension of scalars along the canonical projection
![]() $p \colon S \times _X Y \to S$
, and we have a commutative diagram
$p \colon S \times _X Y \to S$
, and we have a commutative diagram

with the top horizontal map and the right-hand slanted map the maps of limits induced by
![]() $u^{\mathrm {op}}$
and
$u^{\mathrm {op}}$
and
![]() $v^{\mathrm {op}}$
, respectively. Moreover, the latter map is an equivalence. Indeed, this follows from [Reference Lurie20, Example 2.21] since v admits a left adjoint and hence is a
$v^{\mathrm {op}}$
, respectively. Moreover, the latter map is an equivalence. Indeed, this follows from [Reference Lurie20, Example 2.21] since v admits a left adjoint and hence is a
![]() $\smash { \varinjlim }$
-equivalence. Hence, to prove that
$\smash { \varinjlim }$
-equivalence. Hence, to prove that
![]() $f_*$
admits a right adjoint, we may instead prove that
$f_*$
admits a right adjoint, we may instead prove that
![]() $p^*$
admits a right adjoint
$p^*$
admits a right adjoint
![]() $p_*$
which itself admits a further right adjoint.
$p_*$
which itself admits a further right adjoint.
We may view
![]() $p^*$
as a map in
$p^*$
as a map in
![]() ${\operatorname {LPr}}$
, so it is clear that it has a right adjoint
${\operatorname {LPr}}$
, so it is clear that it has a right adjoint
![]() $p_*$
, and to understand
$p_*$
, and to understand
![]() $p_*$
, we employ [Reference Lurie19, Proposition 4.7.4.19]. The assumption (*) in loc. cit. that for every map
$p_*$
, we employ [Reference Lurie19, Proposition 4.7.4.19]. The assumption (*) in loc. cit. that for every map
![]() $h \colon T \to S $
in
$h \colon T \to S $
in
![]() ${\mathrm {Aff}}_{/X}$
, the square
${\mathrm {Aff}}_{/X}$
, the square

be right adjointable holds by Lemma 3.18 since
![]() $f \colon Y \to X$
is flat affine. So we conclude that
$f \colon Y \to X$
is flat affine. So we conclude that
![]() $p_*$
is the map of limits induced by a natural transformation
$p_*$
is the map of limits induced by a natural transformation
of functors from
![]() $({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
$({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
![]() ${\widehat {\mathrm {Cat}}}_{\infty }$
.
${\widehat {\mathrm {Cat}}}_{\infty }$
.
Now, for every
![]() $(S,S \to X)$
, we may identify
$(S,S \to X)$
, we may identify
![]() $(p_{S})_{*}$
with the restriction of scalars along a map of Dirac rings, and hence, it is right t-exact. This implies that the induced map of limits
$(p_{S})_{*}$
with the restriction of scalars along a map of Dirac rings, and hence, it is right t-exact. This implies that the induced map of limits
![]() $p_*$
is right t-exact, which shows that
$p_*$
is right t-exact, which shows that
![]() $f_*$
is right t-exact. But by Addendum 3.15,
$f_*$
is right t-exact. But by Addendum 3.15,
![]() $f_*$
is also left t-exact, so we conclude that
$f_*$
is also left t-exact, so we conclude that
![]() $f_*$
is t-exact.
$f_*$
is t-exact.
Similarly, for every
![]() $(S,S \to X)$
, the functor
$(S,S \to X)$
, the functor
![]() $(p_S)_*$
admits a right adjoint given by coextension of scalars. Therefore, we may view
$(p_S)_*$
admits a right adjoint given by coextension of scalars. Therefore, we may view
![]() $(p_S)_*$
as a natural transformation of functors from
$(p_S)_*$
as a natural transformation of functors from
![]() $({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
$({\mathrm {Aff}}_{/X})^{\mathrm {op}}$
to
![]() ${\operatorname {LPr}}$
, and since the forgetful functor
${\operatorname {LPr}}$
, and since the forgetful functor
preserves limits, we conclude that
![]() $p_*$
admits a right adjoint.Footnote
5
So
$p_*$
admits a right adjoint.Footnote
5
So
![]() $f_*$
admits a right adjoint, which completes the proof of (1).
$f_*$
admits a right adjoint, which completes the proof of (1).
It remains to prove (2). First, if
![]() $X'$
is affine, then with notation as in the proof of (1) above, we may equivalently prove that the diagram
$X'$
is affine, then with notation as in the proof of (1) above, we may equivalently prove that the diagram

is right adjointable. But this follows from [Reference Lurie19, Proposition 4.7.4.19], since for every
![]() $\eta \colon S \to X$
and
$\eta \colon S \to X$
and
![]() $h \colon T \to S$
with S and T affine, the diagram
$h \colon T \to S$
with S and T affine, the diagram

is right adjointable by Lemma 3.18.
In general, we use that a map in
![]() ${\mathrm {QCoh}}(X')$
is an equivalence if and only if its image by the inverse image
${\mathrm {QCoh}}(X')$
is an equivalence if and only if its image by the inverse image
![]() $h^* \colon {\mathrm {QCoh}}(X') \to {\mathrm {QCoh}}(X" )$
is an equivalence for every map
$h^* \colon {\mathrm {QCoh}}(X') \to {\mathrm {QCoh}}(X" )$
is an equivalence for every map
![]() $h \colon X" \to X'$
with
$h \colon X" \to X'$
with
![]() $X" $
affine. So we consider the diagram
$X" $
affine. So we consider the diagram

with
![]() $f'$
the base-change of f along g and
$f'$
the base-change of f along g and
![]() $f" $
the base-change of
$f" $
the base-change of
![]() $f'$
along h. Since
$f'$
along h. Since
![]() $X" $
is affine, both the outer square and the bottom square are right adjointable by what was already proved. Thus, in the diagram of canonical maps
$X" $
is affine, both the outer square and the bottom square are right adjointable by what was already proved. Thus, in the diagram of canonical maps

the two slanted maps are equivalences, and hence, so is the top horizontal map. Therefore, we conclude that the canonical map
is an equivalence, as we wanted to prove.
Remark 3.21. A useful way to interpret the second part of Proposition 3.20 is that if f is flat affine, then
![]() $f_*$
can be calculated locally on the target.
$f_*$
can be calculated locally on the target.
Remark 3.22. A consequence of Proposition 3.20 is that coherent cohomology can be calculated by means of ‘relative injective’ resolutions in the situation

with f affine flat and an effective epimorphism, with Y affine, and with
![]() $S \simeq \operatorname {\mathrm {Spec}}(\mathbb {Z})$
. The direct image
$S \simeq \operatorname {\mathrm {Spec}}(\mathbb {Z})$
. The direct image
![]() $q_*$
is t-exact because q is a map between affine Dirac schemes, and
$q_*$
is t-exact because q is a map between affine Dirac schemes, and
![]() $f_*$
is t-exact, by Proposition 3.20. Therefore, given a resolution
$f_*$
is t-exact, by Proposition 3.20. Therefore, given a resolution
in the abelian category
![]() ${\mathrm {QCoh}}(X)^{\heartsuit }$
such that the terms
${\mathrm {QCoh}}(X)^{\heartsuit }$
such that the terms
![]() $\mathcal {G}^n$
belong to the essential image of
$\mathcal {G}^n$
belong to the essential image of
![]() $f_* \colon {\mathrm {QCoh}}(Y)^{\heartsuit } \to {\mathrm {QCoh}}(X)^{\heartsuit }$
, the coherent cohomology
$f_* \colon {\mathrm {QCoh}}(Y)^{\heartsuit } \to {\mathrm {QCoh}}(X)^{\heartsuit }$
, the coherent cohomology
is represented by the complex
in the abelian category
![]() ${\mathrm {QCoh}}(S)^{\heartsuit } \simeq \operatorname {\mathrm {Ab}}$
. In the homotopy theory literature, the objects in the essential image of
${\mathrm {QCoh}}(S)^{\heartsuit } \simeq \operatorname {\mathrm {Ab}}$
. In the homotopy theory literature, the objects in the essential image of
![]() $f_* \colon {\mathrm {QCoh}}(Y)^{\heartsuit } \to {\mathrm {QCoh}}(X)^{\heartsuit }$
are referred to as relative injective objects.
$f_* \colon {\mathrm {QCoh}}(Y)^{\heartsuit } \to {\mathrm {QCoh}}(X)^{\heartsuit }$
are referred to as relative injective objects.
We now proceed to show that the
![]() $\infty $
-category of quasi-coherent
$\infty $
-category of quasi-coherent
![]() $\mathcal {O}_X$
-modules descends along effective epimorphisms.
$\mathcal {O}_X$
-modules descends along effective epimorphisms.
Proposition 3.23. If
![]() $f \colon T \to S$
is a faithfully flat map of affine Dirac schemes, then the diagram
$f \colon T \to S$
is a faithfully flat map of affine Dirac schemes, then the diagram
![]() ${\mathrm {QCoh}}(T^{\times _S[-]}) \colon \Delta _+ \to {\operatorname {LPr}}$
is a limit diagram.
${\mathrm {QCoh}}(T^{\times _S[-]}) \colon \Delta _+ \to {\operatorname {LPr}}$
is a limit diagram.
Proof. We let
![]() $U \simeq T^{\times _S[-]} \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Aff}}$
be the Čech nerve of f and wish to show that
$U \simeq T^{\times _S[-]} \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Aff}}$
be the Čech nerve of f and wish to show that
![]() ${\mathrm {QCoh}}(U) \colon \Delta _+ \to {\operatorname {LPr}}$
is a limit diagram. By [Reference Lurie20, Lemma 6.2.3.7], we may instead show that its restriction
${\mathrm {QCoh}}(U) \colon \Delta _+ \to {\operatorname {LPr}}$
is a limit diagram. By [Reference Lurie20, Lemma 6.2.3.7], we may instead show that its restriction
![]() ${\mathrm {QCoh}}(U)|_{\Delta _{s+}} \colon \Delta _{s+} \to {\operatorname {LPr}}$
along the inclusion of the (nonfull) subcategory
${\mathrm {QCoh}}(U)|_{\Delta _{s+}} \colon \Delta _{s+} \to {\operatorname {LPr}}$
along the inclusion of the (nonfull) subcategory
![]() $\Delta _{s+} \subset \Delta _+$
spanned by the injective order-preserving maps is a limit diagram. The advantage of restricting to
$\Delta _{s+} \subset \Delta _+$
spanned by the injective order-preserving maps is a limit diagram. The advantage of restricting to
![]() $\Delta _{s+} \subset \Delta _+$
is that, in the diagram
$\Delta _{s+} \subset \Delta _+$
is that, in the diagram
![]() $U|_{\Delta _{s+}} \colon \Delta _{s+}^{\mathrm {op}} \to \operatorname {\mathrm {Aff}}$
, every map is a base-change of f and hence flat. So by Proposition 3.20, for every map
$U|_{\Delta _{s+}} \colon \Delta _{s+}^{\mathrm {op}} \to \operatorname {\mathrm {Aff}}$
, every map is a base-change of f and hence flat. So by Proposition 3.20, for every map
![]() $\theta \colon [n] \to [m]$
in
$\theta \colon [n] \to [m]$
in
![]() $\Delta _{s+}$
, we have a diagram
$\Delta _{s+}$
, we have a diagram

in which the rows are semi-orthogonal decompositions. It follows that the retractions r define a map of diagrams from
![]() ${\mathrm {QCoh}}(U)|_{\Delta _{s+}}$
to the limit of the diagrams
${\mathrm {QCoh}}(U)|_{\Delta _{s+}}$
to the limit of the diagrams
and this map is an equivalence, by the definition of
![]() ${\mathrm {QCoh}}(U)$
as the stabilization of
${\mathrm {QCoh}}(U)$
as the stabilization of
![]() ${\mathrm {QCoh}}(U)_{\geq 0}$
. Therefore, since limits commute with limits, it will suffice to show that the diagram
${\mathrm {QCoh}}(U)_{\geq 0}$
. Therefore, since limits commute with limits, it will suffice to show that the diagram
![]() ${\mathrm {QCoh}}(U)_{\geq 0}|_{\Delta _{s+}} \colon \Delta _{s+} \to {\operatorname {LPr}}$
, or equivalently, the diagram
${\mathrm {QCoh}}(U)_{\geq 0}|_{\Delta _{s+}} \colon \Delta _{s+} \to {\operatorname {LPr}}$
, or equivalently, the diagram
is a limit diagram. To this end, we use that by (the dual of) Barr–Beck–Lurie theorem [Reference Lurie19, Theorem 4.7.5.3], it suffices to verify the following:
-
(1) The functor
 $f^* \colon {\mathrm {QCoh}}(U_{-1})_{\geq 0} \to {\mathrm {QCoh}}(U_{0})_{\geq 0}$
is comonadic.
$f^* \colon {\mathrm {QCoh}}(U_{-1})_{\geq 0} \to {\mathrm {QCoh}}(U_{0})_{\geq 0}$
is comonadic. -
(2) For every map
 $\theta \colon [m] \to n$
in
$\theta \colon [m] \to n$
in
 $\Delta _+$
, the diagram is right adjointable.
$\Delta _+$
, the diagram is right adjointable.
But (1) holds by [Reference Lurie23, Proposition D.6.4.6] since the map
![]() $f \colon T \to S$
is faithfully flat, and (2) holds by Lemma 3.18 because the map
$f \colon T \to S$
is faithfully flat, and (2) holds by Lemma 3.18 because the map
![]() $d_0 \colon U_m \to U_{m+1}$
is flat.
$d_0 \colon U_m \to U_{m+1}$
is flat.
Theorem 3.24. Up to contractible choice, there exists a unique factorization

through the sheafification functor L, and moreover, the functor
takes small colimits of Dirac stacks to limits of symmetric monoidal
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. We must show that the functor
![]() ${\mathrm {QCoh}} \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
takes the colimit-interchange maps in Remark 2.18 to equivalences of
${\mathrm {QCoh}} \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
takes the colimit-interchange maps in Remark 2.18 to equivalences of
![]() $\infty $
-categories, and since the forgetful functor
$\infty $
-categories, and since the forgetful functor
![]() $\operatorname {\mathrm {CAlg}}({\operatorname {LPr}}) \to {\operatorname {LPr}}$
preserves and reflects limits, it suffices to show that the functor
$\operatorname {\mathrm {CAlg}}({\operatorname {LPr}}) \to {\operatorname {LPr}}$
preserves and reflects limits, it suffices to show that the functor
![]() ${\mathrm {QCoh}} \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to {\operatorname {LPr}}$
does so. Thus, we must show that for every faithfully flat map
${\mathrm {QCoh}} \colon {\mathcal {P}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to {\operatorname {LPr}}$
does so. Thus, we must show that for every faithfully flat map
![]() $f \colon T \to S$
of affine Dirac schemes, the map
$f \colon T \to S$
of affine Dirac schemes, the map
is an equivalence, and that for every pair
![]() $(S_1,S_2)$
of affine Dirac schemes, the map
$(S_1,S_2)$
of affine Dirac schemes, the map
is an equivalence. The former statement follows from Proposition 3.23, whereas the latter statement follows from the idempotent decomposition of graded modules over a product of two graded rings.
Remark 3.25. We note that Theorem 3.24 is equivalent to the statement that for every Dirac prestack X, the map induced by unit of the sheafification adjunction
is an equivalence. In homotopy theory, this fact was first observed by Hopkins [Reference Hopkins14].
Corollary 3.26. If
![]() $p \colon Y \to X$
is an effective epimorphism in
$p \colon Y \to X$
is an effective epimorphism in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, then the following hold:
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, then the following hold:
-
(1) The diagram
 ${\mathrm {QCoh}}(Y^{\times _X[-]}) \colon \Delta _+ \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
is a limit diagram.
${\mathrm {QCoh}}(Y^{\times _X[-]}) \colon \Delta _+ \to \operatorname {\mathrm {CAlg}}({\operatorname {LPr}})$
is a limit diagram. -
(2) The inverse image
 $p^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is conservative.
$p^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is conservative.
Proof. That
![]() $p \colon Y \to X$
is an effective epimorphism means, by definition, that the diagram
$p \colon Y \to X$
is an effective epimorphism means, by definition, that the diagram
![]() $Y^{\times _X[-]} \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a colimit diagram. Thus, the assertion (1) follows from Theorem 3.24. The assertion (2) follows from (1) and from the folklore fact, which we prove in [Reference Hesselholt and Pstrągowski12, Lemma B.1], that if
$Y^{\times _X[-]} \colon \Delta _+^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a colimit diagram. Thus, the assertion (1) follows from Theorem 3.24. The assertion (2) follows from (1) and from the folklore fact, which we prove in [Reference Hesselholt and Pstrągowski12, Lemma B.1], that if
![]() $\mathcal {C} \colon \Delta \to \operatorname {\mathrm {Cat}}_{\infty }$
is a cosimplicial
$\mathcal {C} \colon \Delta \to \operatorname {\mathrm {Cat}}_{\infty }$
is a cosimplicial
![]() $\infty $
-category, then the canonical map
$\infty $
-category, then the canonical map
![]() $\varprojlim _{\,\Delta } \mathcal {C} \to \mathcal {C}^0$
is conservative.
$\varprojlim _{\,\Delta } \mathcal {C} \to \mathcal {C}^0$
is conservative.
3.4 Quasi-coherent
 $\mathcal {O}_X$
-modules on geometric stacks
$\mathcal {O}_X$
-modules on geometric stacks
An advantage of geometric Dirac stacks is that the t-structure on the stable
![]() $\infty $
-category of quasi-coherent
$\infty $
-category of quasi-coherent
![]() $\mathcal {O}_X$
-modules is particularly well-behaved, as we now show.
$\mathcal {O}_X$
-modules is particularly well-behaved, as we now show.
Theorem 3.27. If X is a geometric Dirac stack, then the following hold:
-
(1) The canonical t-structure on the presentable stable
 $\infty $
-category
$\infty $
-category
 ${\mathrm {QCoh}}(X)$
is left complete, right complete, and compatible with filtered colimits.
${\mathrm {QCoh}}(X)$
is left complete, right complete, and compatible with filtered colimits. -
(2) The presentable
 $\infty $
-category
$\infty $
-category
 ${\mathrm {QCoh}}(X)_{\geq 0}$
is complete Grothendieck prestable, and the inclusion
${\mathrm {QCoh}}(X)_{\geq 0}$
is complete Grothendieck prestable, and the inclusion
 $i \colon {\mathrm {QCoh}}(X)_{\geq 0} \to {\mathrm {QCoh}}(X)$
is a stabilization.
$i \colon {\mathrm {QCoh}}(X)_{\geq 0} \to {\mathrm {QCoh}}(X)$
is a stabilization. -
(3) For
 $\mathcal {F} \in {\mathrm {QCoh}}(X)$
, the following are equivalent:
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
, the following are equivalent:-
(a)
 $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
.
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
. -
(b) There exists a submersion
 $p \colon V \to X$
, where V is a small coproduct of affine Dirac schemes, such that
$p \colon V \to X$
, where V is a small coproduct of affine Dirac schemes, such that
 $p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
.
$p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
. -
(c) For every submersion
 $p \colon V \to X$
, where V is a small coproduct of affine Dirac schemes, we have
$p \colon V \to X$
, where V is a small coproduct of affine Dirac schemes, we have
 $p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
.
$p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
.
-
Proof. We note (1) and (2) are equivalent by [Reference Lurie23, Corollary C.3.1.4]. To prove the theorem, let us say that a geometric stack X is good if the statements (1)–(3) hold for X. So we wish to prove that all geometric stacks are good, and by the minimality part of Theorem 2.49, it suffices to verify the following:
-
(i) If
 $X \simeq \coprod _{\alpha } U_{\alpha }$
is a small coproduct of affine Dirac schemes, then X is good.
$X \simeq \coprod _{\alpha } U_{\alpha }$
is a small coproduct of affine Dirac schemes, then X is good. -
(ii) If
 $X \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a groupoid in good geometric stacks with submersive face maps, then the colimit
$X \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
is a groupoid in good geometric stacks with submersive face maps, then the colimit
 $\varinjlim _{[n] \in \Delta ^{\mathrm {op}}} X_n$
is good.
$\varinjlim _{[n] \in \Delta ^{\mathrm {op}}} X_n$
is good.
To verify (i), we let
![]() $X \simeq \coprod _{\alpha } U_{\alpha }$
be a small coproduct of affine Dirac schemes and first show X satisfies (1) in the statement. By the definition of
$X \simeq \coprod _{\alpha } U_{\alpha }$
be a small coproduct of affine Dirac schemes and first show X satisfies (1) in the statement. By the definition of
![]() ${\mathrm {QCoh}}$
, we have
${\mathrm {QCoh}}$
, we have
and by definition of the canonical t-structure, we have
Moreover, since a product of anima is contractible if and only if all of its factors are so, the coconnective part of the canonical t-structure is given by
By Proposition 3.4, for
![]() $U_{\alpha } \simeq \operatorname {\mathrm {Spec}}(R_{\alpha })$
, we have an equivalence
$U_{\alpha } \simeq \operatorname {\mathrm {Spec}}(R_{\alpha })$
, we have an equivalence
with the derived
![]() $\infty $
-category of an abelian category with enough projectives, and hence, by [Reference Lurie19, Propositions 1.3.3.16, 1.3.5.21, and 1.3.5.24], the canonical t-structure on
$\infty $
-category of an abelian category with enough projectives, and hence, by [Reference Lurie19, Propositions 1.3.3.16, 1.3.5.21, and 1.3.5.24], the canonical t-structure on
![]() ${\mathrm {QCoh}}(U_{\alpha })$
is left and right complete and compatible with filtered colimits. But the properties of being left and right complete are expressed in terms of limits and hence are stable under products of
${\mathrm {QCoh}}(U_{\alpha })$
is left and right complete and compatible with filtered colimits. But the properties of being left and right complete are expressed in terms of limits and hence are stable under products of
![]() $\infty $
-categories, as is compatibility with filtered colimits by [Reference Lurie23, Proposition C.3.2.4]. This shows that (1) holds for X.
$\infty $
-categories, as is compatibility with filtered colimits by [Reference Lurie23, Proposition C.3.2.4]. This shows that (1) holds for X.
To prove that (3) holds for X, let
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
. It is clear that (c) implies (b), so we proceed to prove that (a) implies (c) and that (b) implies (a). We first assume that
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
. It is clear that (c) implies (b), so we proceed to prove that (a) implies (c) and that (b) implies (a). We first assume that
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
and let
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
and let
![]() $p \colon V \to X$
be a submersion with
$p \colon V \to X$
be a submersion with
![]() $V \simeq \coprod _{\beta } V_{\beta }$
a small coproduct of affine Dirac schemes. We wish to show that
$V \simeq \coprod _{\beta } V_{\beta }$
a small coproduct of affine Dirac schemes. We wish to show that
![]() $p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
, or equivalently, that
$p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
, or equivalently, that
![]() $p_{\beta }^*(\mathcal {F}) \in {\mathrm {QCoh}}(V_{\beta })_{\leq 0}$
for all
$p_{\beta }^*(\mathcal {F}) \in {\mathrm {QCoh}}(V_{\beta })_{\leq 0}$
for all
![]() $\beta $
, where
$\beta $
, where
![]() $j_{\beta } \colon V_{\beta } \to V$
the canonical open immersion and
$j_{\beta } \colon V_{\beta } \to V$
the canonical open immersion and
![]() $p_{\beta } = pj_{\beta }$
. Since
$p_{\beta } = pj_{\beta }$
. Since
![]() $V_{\beta }$
is quasi-compact, the map
$V_{\beta }$
is quasi-compact, the map
![]() $p_{\beta } \colon V_{\beta } \to X$
factors as
$p_{\beta } \colon V_{\beta } \to X$
factors as
![]() $p_{\beta } = i_{\beta }q_{\beta }$
with
$p_{\beta } = i_{\beta }q_{\beta }$
with
![]() $i_{\beta } \colon X_{\beta } \to X$
the canonical open immersion of some finite sub-coproduct
$i_{\beta } \colon X_{\beta } \to X$
the canonical open immersion of some finite sub-coproduct
![]() $X_{\beta } = \coprod _{\alpha \in I_{\beta }} U_{\alpha }$
. So we have a diagram of Dirac schemes
$X_{\beta } = \coprod _{\alpha \in I_{\beta }} U_{\alpha }$
. So we have a diagram of Dirac schemes

with p a submersion and with
![]() $j_{\beta }$
and
$j_{\beta }$
and
![]() $i_{\beta }$
open immersions. Now, we conclude from Lemma 2.43 that p is flat, and hence, so is
$i_{\beta }$
open immersions. Now, we conclude from Lemma 2.43 that p is flat, and hence, so is
![]() $pj_{\beta } \simeq i_{\beta }q_{\beta }$
. Since
$pj_{\beta } \simeq i_{\beta }q_{\beta }$
. Since
![]() $i_{\beta }$
is an open immersion, it follows that
$i_{\beta }$
is an open immersion, it follows that
![]() $q_{\beta }$
is flat. Since
$q_{\beta }$
is flat. Since
![]() $q_{\beta }$
is a flat map between affine Dirac schemes, we conclude that
$q_{\beta }$
is a flat map between affine Dirac schemes, we conclude that
![]() $q_{\beta }^*$
is t-exact. But
$q_{\beta }^*$
is t-exact. But
![]() $i_{\beta }^*$
is also t-exact because
$i_{\beta }^*$
is also t-exact because
![]() $i_{\beta }$
is the inclusion of a summand, and hence, so is
$i_{\beta }$
is the inclusion of a summand, and hence, so is
![]() $p_{\beta }^* \simeq q_{\beta }^*i_{\beta }^*$
. We conclude that
$p_{\beta }^* \simeq q_{\beta }^*i_{\beta }^*$
. We conclude that
![]() $p_{\beta }^*(\mathcal {F}) \in {\mathrm {QCoh}}(V_{\beta })_{\leq 0}$
, as we wanted to prove. This shows that (a) implies (c).
$p_{\beta }^*(\mathcal {F}) \in {\mathrm {QCoh}}(V_{\beta })_{\leq 0}$
, as we wanted to prove. This shows that (a) implies (c).
Finally, to prove that (b) implies (a), we let
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
and let
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
and let
![]() $p \colon V \to X$
be a submersion with
$p \colon V \to X$
be a submersion with
![]() $\smash { V \simeq \coprod _{\beta } V_{\beta } }$
a small coproduct of affine Dirac schemes such that
$\smash { V \simeq \coprod _{\beta } V_{\beta } }$
a small coproduct of affine Dirac schemes such that
![]() $p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
. Now, for every
$p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
. Now, for every
![]() $\alpha $
, we conclude from Lemma 2.43 and Remark 2.31 that we have a diagram
$\alpha $
, we conclude from Lemma 2.43 and Remark 2.31 that we have a diagram

with
![]() $i_{\alpha }$
and
$i_{\alpha }$
and
![]() $j_{\alpha }$
open immersions and with
$j_{\alpha }$
open immersions and with
![]() $q_{\beta }$
a faithfully flat map between affine Dirac schemes. Hence, in the diagram
$q_{\beta }$
a faithfully flat map between affine Dirac schemes. Hence, in the diagram

the top horizontal map is an equivalence, and the bottom horizontal map preserves (connectivity and) coconnectivity, whereas the right-hand vertical map preserves and reflects (connectivity and) coconnectivity. Since
![]() $p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
, we find that
$p^*(\mathcal {F}) \in {\mathrm {QCoh}}(V)_{\leq 0}$
, we find that
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
, as desired. This shows that (b) implies (a), which completes the proof of (i).
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
, as desired. This shows that (b) implies (a), which completes the proof of (i).
It remains to prove (ii). We claim that if
![]() $f \colon Y \to X$
is any submersion of good geometric Dirac stacks and if
$f \colon Y \to X$
is any submersion of good geometric Dirac stacks and if
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
, then
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
, then
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
if and only
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
if and only
![]() $f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\leq 0}$
. Indeed, if we choose a submersion
$f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\leq 0}$
. Indeed, if we choose a submersion
![]() $p \colon V \to Y$
with V a small coproduct of affine Dirac stacks, then also
$p \colon V \to Y$
with V a small coproduct of affine Dirac stacks, then also
![]() $q \simeq f p \colon V \to X$
is a submersion, so (3) shows that
$q \simeq f p \colon V \to X$
is a submersion, so (3) shows that
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
if and only if
$\mathcal {F} \in {\mathrm {QCoh}}(X)_{\leq 0}$
if and only if
![]() $q^*(\mathcal {F}) \simeq p^*(f^*(\mathcal {F})) \in {\mathrm {QCoh}}(V)_{\leq 0}$
if and only if
$q^*(\mathcal {F}) \simeq p^*(f^*(\mathcal {F})) \in {\mathrm {QCoh}}(V)_{\leq 0}$
if and only if
![]() $f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\leq 0}$
, as claimed.
$f^*(\mathcal {F}) \in {\mathrm {QCoh}}(Y)_{\leq 0}$
, as claimed.
Now, to prove (ii), we let
![]() $X \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
be groupoid in good geometric stacks, whose face maps are submersions, and show that
$X \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
be groupoid in good geometric stacks, whose face maps are submersions, and show that
is good. Here,
![]() $\Delta _s \subset \Delta $
is the subcategory spanned by the injective order-preserving maps, and the right-hand equivalence follows from [Reference Lurie20, Lemma 6.5.3.7]. The claim that we proved above shows that the diagram
$\Delta _s \subset \Delta $
is the subcategory spanned by the injective order-preserving maps, and the right-hand equivalence follows from [Reference Lurie20, Lemma 6.5.3.7]. The claim that we proved above shows that the diagram
![]() ${\mathrm {QCoh}}(X)_{\geq 0} \colon \Delta _s \to {\operatorname {LPr}}$
admits a factorization through the canonical inclusion
${\mathrm {QCoh}}(X)_{\geq 0} \colon \Delta _s \to {\operatorname {LPr}}$
admits a factorization through the canonical inclusion
of the (nonfull) subcategory spanned by the Grothendieck prestable
![]() $\infty $
-categories and the functors between them that preserve small colimits and finite limits. But Lurie proves in [Reference Lurie23, Proposition C.3.2.4] that this subcategory is closed under small limits, so we conclude that the
$\infty $
-categories and the functors between them that preserve small colimits and finite limits. But Lurie proves in [Reference Lurie23, Proposition C.3.2.4] that this subcategory is closed under small limits, so we conclude that the
![]() $\infty $
-category
$\infty $
-category
is Grothendieck prestable. It is also complete, since completeness is a property expressed in terms of limits and truncations, both of which are preserved by limits along left-exact functors, and it follows from [Reference Lurie23, Corollary C.3.2.5] that
is a stabilization. This shows that (2), or equivalently (1), holds for
![]() $|X|$
.
$|X|$
.
Finally, to see that also (3) holds for
![]() $|X|$
, let
$|X|$
, let
![]() $p \colon V \to |X|$
be a submersion with V a small coproduct of affine Dirac schemes. Since
$p \colon V \to |X|$
be a submersion with V a small coproduct of affine Dirac schemes. Since
![]() $f \colon X_0 \to |X|$
is an effective epimorphism, we may use Lemma 2.39 to obtain a diagram
$f \colon X_0 \to |X|$
is an effective epimorphism, we may use Lemma 2.39 to obtain a diagram

where both g and q are submersions from a small coproduct of affine Dirac schemes. Since
![]() $X_{0}$
and V are good, we conclude that in the diagram
$X_{0}$
and V are good, we conclude that in the diagram

the maps
![]() $g^*$
and
$g^*$
and
![]() $q^*$
preserve and reflect coconnectivity, and so does
$q^*$
preserve and reflect coconnectivity, and so does
![]() $f^*$
, being the stabilization of a cocontinuous left-exact functor between prestable
$f^*$
, being the stabilization of a cocontinuous left-exact functor between prestable
![]() $\infty $
-categories. Therefore, also
$\infty $
-categories. Therefore, also
![]() $p^*$
preserves and reflect coconnectivity, which shows that (3) holds for
$p^*$
preserves and reflect coconnectivity, which shows that (3) holds for
![]() $|X|$
. This completes the proof of (ii), and hence, of the theorem.
$|X|$
. This completes the proof of (ii), and hence, of the theorem.
Remark 3.28. As outlined in Remark 2.50, it is possible to generalize the notion of a flat map from Dirac schemes to geometric Dirac stacks. Moreover, one may show that if
![]() $f \colon Y \to X$
is a flat map between geometric Dirac stacks, then the inverse image functor
$f \colon Y \to X$
is a flat map between geometric Dirac stacks, then the inverse image functor
![]() $f^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is t-exact.
$f^* \colon {\mathrm {QCoh}}(X) \to {\mathrm {QCoh}}(Y)$
is t-exact.
3.5 Affine maps and vector bundles
We discuss the relationship between quasi-coherent
![]() $\mathcal {O}_X$
-modules and affine maps of stacks, which we now define.
$\mathcal {O}_X$
-modules and affine maps of stacks, which we now define.
Definition 3.29. A map of Dirac stacks
![]() $f \colon Y \to X$
is affine if the domain of its base-change
$f \colon Y \to X$
is affine if the domain of its base-change
![]() $f_S \colon Y_S \to S$
along every map
$f_S \colon Y_S \to S$
along every map
![]() $\eta \colon S \to X$
from an affine Dirac scheme is an affine Dirac scheme.
$\eta \colon S \to X$
from an affine Dirac scheme is an affine Dirac scheme.
We write
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}^{\operatorname {\mathrm {aff}}}$
for the full subcategory
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}^{\operatorname {\mathrm {aff}}}$
for the full subcategory
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
spanned by the affine maps
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
spanned by the affine maps
![]() $f \colon Y \to X$
.
$f \colon Y \to X$
.
Example 3.30. A map of Dirac stacks
![]() $f \colon Y \to S$
to an affine Dirac scheme is affine if and only if Y is an affine Dirac scheme. Hence, the Dirac spectrum functor
$f \colon Y \to S$
to an affine Dirac scheme is affine if and only if Y is an affine Dirac scheme. Hence, the Dirac spectrum functor
is an equivalence of
![]() $\infty $
-categories.
$\infty $
-categories.
It is clear that the property of being affine is preserved under base-change, and we now prove that it is local on the base.
Proposition 3.31. If
![]() $p \colon X' \to X$
is an effective epimorphism of Dirac stacks, then
$p \colon X' \to X$
is an effective epimorphism of Dirac stacks, then

is a cartesian diagram of
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. We first suppose that
![]() $p \colon X' \to X$
is a faithfully flat map
$p \colon X' \to X$
is a faithfully flat map
![]() $q \colon T \to S$
of affine Dirac schemes and consider the expanded diagram
$q \colon T \to S$
of affine Dirac schemes and consider the expanded diagram

The right-hand square is cartesian since the property of being affine is preserved under base-change, and the left horizontal maps are both equivalences. Indeed, for the bottom map, this follows from Theorem 2.21, and for the top map, it follows from faithfully flat descent for modules [Reference Hesselholt and Pstrągowski12, Proposition 1.4] and Example 3.30.
Next, in the general case, we must show that if
![]() $f \colon Y \to X$
is a map of Dirac stacks with the property that its base-change
$f \colon Y \to X$
is a map of Dirac stacks with the property that its base-change
![]() $f' \colon Y' \to X'$
along p is affine, then f is affine. So we let
$f' \colon Y' \to X'$
along p is affine, then f is affine. So we let
![]() $\eta \colon S \to X$
be a map from an affine Dirac stack and must show that the base-change
$\eta \colon S \to X$
be a map from an affine Dirac stack and must show that the base-change
![]() $f_S \colon Y_S \to X$
of f along
$f_S \colon Y_S \to X$
of f along
![]() $\eta $
is affine. Since p is an effective epimorphism, we conclude from Proposition B.6 that there exists a diagram
$\eta $
is affine. Since p is an effective epimorphism, we conclude from Proposition B.6 that there exists a diagram

with q a faithfully flat map of affine Dirac schemes. By what was already proved, it suffices to show that the base-change
![]() $f_T \colon Y_T \to T$
of f along
$f_T \colon Y_T \to T$
of f along
![]() $\eta q$
is affine. But
$\eta q$
is affine. But
![]() $f_T$
is also the base-change of
$f_T$
is also the base-change of
![]() $f'$
along
$f'$
along
![]() $\xi $
, and since
$\xi $
, and since
![]() $f'$
is affine, so is
$f'$
is affine, so is
![]() $f_T$
.
$f_T$
.
Example 3.32. A geometric Dirac stack X admits an effective epimorphism
from a coproduct in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of a family of affine Dirac schemes. Since coproducts in
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of a family of affine Dirac schemes. Since coproducts in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal, Proposition 3.31 shows that
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal, Proposition 3.31 shows that
![]() $f \colon Y \to X$
is affine if and only if its base-change
$f \colon Y \to X$
is affine if and only if its base-change
![]() $f_i' \colon Y_{S_i} \to S_i$
along
$f_i' \colon Y_{S_i} \to S_i$
along
![]() $p_i \colon S_i \to X$
is affine for all
$p_i \colon S_i \to X$
is affine for all
![]() $i \in I$
.
$i \in I$
.
Let X be a Dirac stack and let
![]() $\kappa $
be a regular cardinal such that X is a left Kan extension along
$\kappa $
be a regular cardinal such that X is a left Kan extension along
![]() ${\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
. Theorem 1.3 shows that the canonical map
${\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
. Theorem 1.3 shows that the canonical map
to the limit indexed by
![]() $\eta \colon S \to X$
in
$\eta \colon S \to X$
in
![]() $(({\mathrm {Aff}}_{\kappa })_{/X})^{\mathrm {op}}$
is an equivalence, and it follows directly from Definition 3.29 that this equivalence restricts to an equivalence of the respective full subcategories spanned by the affine maps.
$(({\mathrm {Aff}}_{\kappa })_{/X})^{\mathrm {op}}$
is an equivalence, and it follows directly from Definition 3.29 that this equivalence restricts to an equivalence of the respective full subcategories spanned by the affine maps.
Definition 3.33. Let X be a Dirac stack. The Dirac spectrum relative to X is the left-hand vertical map in the essentially unique diagram

whose right-hand vertical map is provided by the Yoneda embedding.
Remark 3.34. In Definition 3.33, the right-hand vertical and bottom maps are equivalence. The top horizontal map is a right adjoint, and therefore, so is the Dirac spectrum relative to X. Its left adjoint takes an affine map
![]() $f \colon Y \to X$
to the quasi-coherent
$f \colon Y \to X$
to the quasi-coherent
![]() $\mathcal {O}_X$
-algebra
$\mathcal {O}_X$
-algebra
![]() $f_*^{\heartsuit }\mathcal {O}_Y \simeq f_*\mathcal {O}_Y$
.
$f_*^{\heartsuit }\mathcal {O}_Y \simeq f_*\mathcal {O}_Y$
.
Warning 3.35. In general, the Dirac spectrum relative to X, or equivalently, the top horizontal map in Definition 3.33 is not an equivalence. If it were, then
would take colimits of Dirac stacks to limits of categories. To see that this is not the case, we let k be a commutative ring and let X be the Dirac stack obtained by gluing two copies of the affine line
![]() $\mathbb {A}_k^1$
along the origin. Let
$\mathbb {A}_k^1$
along the origin. Let
![]() $f \colon X \to X'$
be the unique map to the corresponding pushout in the category of Dirac schemes. It follows from [Reference Lurie23, Theorem 16.2.0.2] that the map
$f \colon X \to X'$
be the unique map to the corresponding pushout in the category of Dirac schemes. It follows from [Reference Lurie23, Theorem 16.2.0.2] that the map
is an equivalence, and therefore, so is the induced map of hearts. Thus, it suffices to show that the diagram of categories

is not cartesian. If it were, then for every
![]() $k[x,y]/(xy)$
-algebra A, the diagram
$k[x,y]/(xy)$
-algebra A, the diagram
would be a limit diagram. But for
![]() $A = k[x,y]/(xy,x-y) = k[t]/t^2$
, this becomes
$A = k[x,y]/(xy,x-y) = k[t]/t^2$
, this becomes
which is not a limit diagram.
Theorem 3.36. If X is a geometric Dirac stack, then
is an equivalence.
Proof. Let
![]() $\mathcal {C} \subseteq \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
be the full subcategory spanned by the geometric Dirac stacks X for which the Dirac spectrum relative to X is an equivalence. To show that
$\mathcal {C} \subseteq \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
be the full subcategory spanned by the geometric Dirac stacks X for which the Dirac spectrum relative to X is an equivalence. To show that
![]() $\mathcal {C} = \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
, it suffices by Theorem 2.49 to show that
$\mathcal {C} = \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\operatorname {\mathrm {geom}}}$
, it suffices by Theorem 2.49 to show that
-
(1)
 $\mathcal {C}$
contains all small coproducts of affine Dirac stacks, and that
$\mathcal {C}$
contains all small coproducts of affine Dirac stacks, and that -
(2)
 $\mathcal {C}$
closed under colimits of groupoids with submersive face maps.
$\mathcal {C}$
closed under colimits of groupoids with submersive face maps.
For (1), we observe that the source and target of the Dirac spectrum relative to X both take coproducts of Dirac stacks to products of
![]() $\infty $
-categories. Since the Dirac spectrum relative to an affine Dirac stack is an equivalence by Example 3.30, we conclude that (1) holds. For (2), we let
$\infty $
-categories. Since the Dirac spectrum relative to an affine Dirac stack is an equivalence by Example 3.30, we conclude that (1) holds. For (2), we let
![]() $X \simeq \varinjlim _{\Delta ^{\mathrm {op}}}S$
be a colimit of a groupoid in
$X \simeq \varinjlim _{\Delta ^{\mathrm {op}}}S$
be a colimit of a groupoid in
![]() $\mathcal {C}$
with submersive face maps and consider the diagram
$\mathcal {C}$
with submersive face maps and consider the diagram

Now, the left-hand vertical map is an equivalence by Theorem 3.27, the right-hand vertical map is an equivalence by Theorem 2.21 and Proposition 3.31, and the lower horizontal map is an equivalence by assumption. Hence, also the top horizontal map is an equivalence, which shows that X is contained in
![]() $\mathcal {C}$
. So (2) holds.
$\mathcal {C}$
. So (2) holds.
Finally, we define the
![]() $\infty $
-category of vector bundles on a Dirac stack. To this end, we consider the composition
$\infty $
-category of vector bundles on a Dirac stack. To this end, we consider the composition
of the symmetric algebra and the relative Dirac spectrum functors. We write
for the affine map given by the image of the quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {F}$
under this composite functor and call it the affine space associated with
$\mathcal {F}$
under this composite functor and call it the affine space associated with
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
The symmetric algebra has a natural grading, which gives rise to an action of the multiplicative group
![]() $\mathbb {G}_m$
on the affine space functor. It follows that the affine space functor promotes to a functor
$\mathbb {G}_m$
on the affine space functor. It follows that the affine space functor promotes to a functor
that takes values in the
![]() $\infty $
-category of affine Dirac stacks over X with a left action by the underlying
$\infty $
-category of affine Dirac stacks over X with a left action by the underlying
![]() $\mathbf {E}_1$
-group of
$\mathbf {E}_1$
-group of
![]() $\mathbb {G}_m$
. The functor
$\mathbb {G}_m$
. The functor
![]() $V_X'$
admits a left adjoint that to an affine map with
$V_X'$
admits a left adjoint that to an affine map with
![]() $\mathbb {G}_m$
-action
$\mathbb {G}_m$
-action
![]() $p \colon V \to X$
assigns the degree
$p \colon V \to X$
assigns the degree
![]() $1$
part of the quasi-coherent
$1$
part of the quasi-coherent
![]() $\mathcal {O}_X$
-algebra
$\mathcal {O}_X$
-algebra
![]() $p_*\mathcal {O}_V$
. It is fully faithful if X is geometric, but not in general.
$p_*\mathcal {O}_V$
. It is fully faithful if X is geometric, but not in general.
Definition 3.37. Let X be a Dirac stack. A quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {E}$
is locally free of finite rank if for every map
$\mathcal {E}$
is locally free of finite rank if for every map
![]() $\eta \colon S \to X$
with S affine,
$\eta \colon S \to X$
with S affine,
![]() $\eta ^*(\mathcal {E}) \in {\mathrm {QCoh}}(S)$
is compact and in the heart of the t-structure.
$\eta ^*(\mathcal {E}) \in {\mathrm {QCoh}}(S)$
is compact and in the heart of the t-structure.
If a quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {E}$
is locally free of finite rank, then we also say that
$\mathcal {E}$
is locally free of finite rank, then we also say that
![]() $\mathcal {E}$
is perfect with
$\mathcal {E}$
is perfect with
![]() $\operatorname {\mathrm {Tor}}$
-amplitude in
$\operatorname {\mathrm {Tor}}$
-amplitude in
![]() $[0,0]$
, and we write
$[0,0]$
, and we write
for the full subcategory spanned by the quasi-coherent
![]() $\mathcal {O}_X$
-modules that are locally free of finite rank. It is contained in the heart of the t-structure.
$\mathcal {O}_X$
-modules that are locally free of finite rank. It is contained in the heart of the t-structure.
Example 3.38. If
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then
$S \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then
![]() ${\mathrm {QCoh}}(S)^{\operatorname {\mathrm {loc}}}$
is canonically equivalent to the category of finitely generated projective graded R-modules.
${\mathrm {QCoh}}(S)^{\operatorname {\mathrm {loc}}}$
is canonically equivalent to the category of finitely generated projective graded R-modules.
Let X be a Dirac stack. If we write
![]() $X \simeq \varinjlim _{\,\alpha } S_{\alpha }$
as a small colimit of affine Dirac schemes, then, by Definition 3.37, the canonical map
$X \simeq \varinjlim _{\,\alpha } S_{\alpha }$
as a small colimit of affine Dirac schemes, then, by Definition 3.37, the canonical map
is an equivalence. It follows that the difficulties appearing in comparing affine maps and quasi-coherent
![]() $\mathcal {O}_X$
-modules outlined in Warning 3.35 do not occur in the locally free of finite rank case, so that the functor
$\mathcal {O}_X$
-modules outlined in Warning 3.35 do not occur in the locally free of finite rank case, so that the functor
![]() $V_X'$
restricts to a fully faithful functor
$V_X'$
restricts to a fully faithful functor
Definition 3.39. The
![]() $\infty $
-category of vector bundles on X is the full subcategory
$\infty $
-category of vector bundles on X is the full subcategory
given by the essential image of the functor
![]() $V_X$
.
$V_X$
.
Remark 3.40. Since
![]() ${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
![]() $\operatorname {\mathrm {Vect}}(X)$
are canonically anti-equivalent, they are both equivalent to
$\operatorname {\mathrm {Vect}}(X)$
are canonically anti-equivalent, they are both equivalent to
![]() $1$
-categories. The inverse of
$1$
-categories. The inverse of
![]() $V_X$
assigns to a vector bundle
$V_X$
assigns to a vector bundle
![]() $(p \colon V \to X, \mu \colon \mathbb {G}_m \times V \to V)$
the degree
$(p \colon V \to X, \mu \colon \mathbb {G}_m \times V \to V)$
the degree
![]() $1$
part of the graded
$1$
part of the graded
![]() $\mathcal {O}_X$
-algebra
$\mathcal {O}_X$
-algebra
![]() $p_*^{\heartsuit }\mathcal {O}_V$
.
$p_*^{\heartsuit }\mathcal {O}_V$
.
Remark 3.41. The full subcategory
![]() ${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}} \subset {\mathrm {QCoh}}(X)^{\heartsuit }$
agrees with the full subcategory of dualizable
${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}} \subset {\mathrm {QCoh}}(X)^{\heartsuit }$
agrees with the full subcategory of dualizable
![]() $\mathcal {O}_X$
-modules. In particular, it is canonically selfdual, so it is possible to identify
$\mathcal {O}_X$
-modules. In particular, it is canonically selfdual, so it is possible to identify
![]() ${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
![]() $\operatorname {\mathrm {Vect}}(X)$
via the covariant equivalence
$\operatorname {\mathrm {Vect}}(X)$
via the covariant equivalence
However, we will follow Grothendieck [Reference Grothendieck11, Definition 1.7.8] and use the contravariant equivalence
![]() $V_X$
between
$V_X$
between
![]() ${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
${\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
and
![]() $\operatorname {\mathrm {Vect}}(X)$
, which, among other things, leads to the correct geometric interpretation of the Lie algebra of a formal group.
$\operatorname {\mathrm {Vect}}(X)$
, which, among other things, leads to the correct geometric interpretation of the Lie algebra of a formal group.
4 Formal stacks and formal groups
We extend the definition of formal groups to the setting of Dirac stacks. To do so, we follow Lurie [Reference Lurie21, Reference Lurie22] and define the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {FGroup}}(X)$
of formal groups over a Dirac stack X to the
$\operatorname {\mathrm {FGroup}}(X)$
of formal groups over a Dirac stack X to the
![]() $\infty $
-category of abelian group objects in the
$\infty $
-category of abelian group objects in the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Hyp}}(X)$
of formal hyperplanes over X, which we define first. We show that the
$\operatorname {\mathrm {Hyp}}(X)$
of formal hyperplanes over X, which we define first. We show that the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {FGroup}}(X)$
descends along effective epimorphisms
$\operatorname {\mathrm {FGroup}}(X)$
descends along effective epimorphisms
![]() $f \colon X' \to X$
.
$f \colon X' \to X$
.
4.1 Formal completion and quasi-coherent
 $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
We define the formal completion of a Dirac scheme along a closed immersion and prove that, in the case of a regular closed immersion, the
![]() $\infty $
-category of quasi-coherent modules on the formal completion participates in a ‘local cohomology’ stable recollement.
$\infty $
-category of quasi-coherent modules on the formal completion participates in a ‘local cohomology’ stable recollement.
Definition 4.1. Let
![]() $g \colon Z \to X$
be a closed immersion of Dirac schemes defined by a quasi-coherent ideal
$g \colon Z \to X$
be a closed immersion of Dirac schemes defined by a quasi-coherent ideal
![]() $\mathcal {I} \subset \mathcal {O}_X$
. For each
$\mathcal {I} \subset \mathcal {O}_X$
. For each
![]() $m \geq 0$
, the m-th infinitesimal neighbourhood is the Dirac scheme given by
$m \geq 0$
, the m-th infinitesimal neighbourhood is the Dirac scheme given by
The formal completion of X along g is the map of Dirac stacks
from the colimit in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of the infinitesimal neighborhoods.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of the infinitesimal neighborhoods.
Remark 4.2. The colimit in Definition 4.1 agrees with the colimit calculated in the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, or equivalently, the latter colimit is automatically a sheaf for the flat topology on
${\mathcal {P}}(\operatorname {\mathrm {Aff}})$
, or equivalently, the latter colimit is automatically a sheaf for the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
. Indeed, since the Dirac stacks
$\operatorname {\mathrm {Aff}}$
. Indeed, since the Dirac stacks
![]() $Z^{(m)}$
are N-truncated for a fixed N (namely,
$Z^{(m)}$
are N-truncated for a fixed N (namely,
![]() $N = 0$
) and since the flat topology on
$N = 0$
) and since the flat topology on
![]() $\operatorname {\mathrm {Aff}}$
is finitary, the sheaf condition amounts to the statement that a finite diagram is a limit diagram. But this condition is preserved under filtered colimits by [Reference Lurie20, Proposition 5.3.3.3].
$\operatorname {\mathrm {Aff}}$
is finitary, the sheaf condition amounts to the statement that a finite diagram is a limit diagram. But this condition is preserved under filtered colimits by [Reference Lurie20, Proposition 5.3.3.3].
In Grothendieck’s philosophy, the formal completion of X along
![]() $g \colon Z \to X$
plays the role of the nonexisting tubular neighborhood of Z in X. So we should expect that
$g \colon Z \to X$
plays the role of the nonexisting tubular neighborhood of Z in X. So we should expect that
![]() $j \colon Y \to X$
behaves as an open and affine immersion with
$j \colon Y \to X$
behaves as an open and affine immersion with
![]() $i \colon U \simeq X \smallsetminus Z \to X$
as its complement. The following result bears out this expectation.
$i \colon U \simeq X \smallsetminus Z \to X$
as its complement. The following result bears out this expectation.
Theorem 4.3. Let X be a Dirac scheme and let
![]() $\eta \colon Z \to X$
be a regular closed immersion. Let
$\eta \colon Z \to X$
be a regular closed immersion. Let
![]() $j \colon Y \to X$
be the formal completion of X along
$j \colon Y \to X$
be the formal completion of X along
![]() $\eta \colon Z \to X$
and let
$\eta \colon Z \to X$
and let
![]() $i \colon U \simeq X \smallsetminus Z \to X$
be the inclusion of the open complement of S. In this situation, there is a stable recollement
$i \colon U \simeq X \smallsetminus Z \to X$
be the inclusion of the open complement of S. In this situation, there is a stable recollement

and, in addition, the functor
![]() $j_*$
is t-exact.
$j_*$
is t-exact.
Proof. We will prove the statement in detail in the case where X is affine and
![]() $\eta \colon Z \to X$
is a closed immersion defined by a regular sequence
$\eta \colon Z \to X$
is a closed immersion defined by a regular sequence
![]() $(f_1,\dots ,f_d)$
of homogeneous global sections. To reduce the general case to this special case, we will admit the following base-change result, the proof of which is similar to that of [Reference Lurie23, Corollary 3.4.2.2]: If
$(f_1,\dots ,f_d)$
of homogeneous global sections. To reduce the general case to this special case, we will admit the following base-change result, the proof of which is similar to that of [Reference Lurie23, Corollary 3.4.2.2]: If
![]() $f \colon U \to X$
is a qcqs and flat map of Dirac schemes, and if
$f \colon U \to X$
is a qcqs and flat map of Dirac schemes, and if
![]() $f' \colon U' \to X'$
is the base-change of f along any map
$f' \colon U' \to X'$
is the base-change of f along any map
![]() $g \colon X' \to X$
of Dirac schemes, then the square
$g \colon X' \to X$
of Dirac schemes, then the square

is right adjointable in the sense that the base-change map
is an equivalence. The open immersion
![]() $i \colon U \to X$
is flat, and we claim that it is qcqs. Indeed, the property of being qcqs is local on the target, so we assume that X is affine and that
$i \colon U \to X$
is flat, and we claim that it is qcqs. Indeed, the property of being qcqs is local on the target, so we assume that X is affine and that
![]() $\eta \colon Z \to X$
is defined by a regular sequence of global section
$\eta \colon Z \to X$
is defined by a regular sequence of global section
![]() $(f_1,\dots ,f_d)$
. But then
$(f_1,\dots ,f_d)$
. But then
![]() $i \colon U = X_{f_1} \cup \dots \cup X_{f_d} \to X$
is the open immersion of a finite union of distinguished open subsets and hence is quasi-compact, and it is also quasi-separated because the diagonal
$i \colon U = X_{f_1} \cup \dots \cup X_{f_d} \to X$
is the open immersion of a finite union of distinguished open subsets and hence is quasi-compact, and it is also quasi-separated because the diagonal
![]() $\Delta \colon U \to U \times _XU$
is an isomorphism.
$\Delta \colon U \to U \times _XU$
is an isomorphism.
We now suppose that
![]() $\mathfrak {B}$
is a basis for the topology of
$\mathfrak {B}$
is a basis for the topology of
![]() $|X|$
, which is closed under finite intersections, and that the statement has been proved for all
$|X|$
, which is closed under finite intersections, and that the statement has been proved for all
![]() $V \in \mathfrak {B}$
. The proof of Lemma 2.25 shows that
$V \in \mathfrak {B}$
. The proof of Lemma 2.25 shows that
is an equivalence. A stable recollement is determined uniquely by a functor
![]() $i_* \simeq i_!$
with the property that it is fully faithful and admits both a left adjoint
$i_* \simeq i_!$
with the property that it is fully faithful and admits both a left adjoint
![]() $i^*$
and a right adjoint
$i^*$
and a right adjoint
![]() $i^!$
. The base-change property above implies, by [Reference Lurie19, Proposition 4.7.4.19], that the
$i^!$
. The base-change property above implies, by [Reference Lurie19, Proposition 4.7.4.19], that the
![]() $\mathfrak {B}$
-indexed family of functors
$\mathfrak {B}$
-indexed family of functors
promotes to a map of
![]() $\mathfrak {B}^{\triangleleft }$
-indexed limit diagrams in
$\mathfrak {B}^{\triangleleft }$
-indexed limit diagrams in
![]() ${\operatorname {LPr}}$
. In particular, the map of limits
${\operatorname {LPr}}$
. In particular, the map of limits
is a map in
![]() ${\operatorname {LPr}}$
and hence admits a right adjoint
${\operatorname {LPr}}$
and hence admits a right adjoint
![]() $i^!$
, as desired. It is also fully faithful since this property is preserved under limits. Moreover, the fiber of
$i^!$
, as desired. It is also fully faithful since this property is preserved under limits. Moreover, the fiber of
![]() $i^!$
is identified with
$i^!$
is identified with
![]() $j_* \colon {\mathrm {QCoh}}(Y) \to \mathrm {QCoh}(X)$
since limits commute, and
$j_* \colon {\mathrm {QCoh}}(Y) \to \mathrm {QCoh}(X)$
since limits commute, and
![]() $j_*$
is t-exact since it is left t-exact and since the property of being right t-exact can be tested after base-change to
$j_*$
is t-exact since it is left t-exact and since the property of being right t-exact can be tested after base-change to
![]() $V \in \mathfrak {B}$
.
$V \in \mathfrak {B}$
.
Now, for a general X, we take
![]() $\mathfrak {B}$
to be the poset of open subschemes
$\mathfrak {B}$
to be the poset of open subschemes
![]() $V \subset X$
that admit an open immersion in an affine Dirac scheme. And if X admits an open immersion
$V \subset X$
that admit an open immersion in an affine Dirac scheme. And if X admits an open immersion
![]() $j \colon X \to S$
in an affine Dirac scheme, then we take
$j \colon X \to S$
in an affine Dirac scheme, then we take
![]() $\mathfrak {B}$
to be poset of open subschemes
$\mathfrak {B}$
to be poset of open subschemes
![]() $V \subset X$
with the property that
$V \subset X$
with the property that
![]() $j(V) \subset S$
is a distinguished open subscheme. This reduces us to the special case where
$j(V) \subset S$
is a distinguished open subscheme. This reduces us to the special case where
![]() $X \simeq \operatorname {\mathrm {Spec}}(A)$
is affine and where the graded ideal
$X \simeq \operatorname {\mathrm {Spec}}(A)$
is affine and where the graded ideal
![]() $I \subset A$
that defines
$I \subset A$
that defines
![]() $\eta \colon Z \to X$
is generated by a regular sequence
$\eta \colon Z \to X$
is generated by a regular sequence
![]() $(f_1,\dots ,f_d)$
of homogeneous elements. In this case, we find as in [Reference Lurie23, Chapter 7] that there are semi-orthogonal decompositions
$(f_1,\dots ,f_d)$
of homogeneous elements. In this case, we find as in [Reference Lurie23, Chapter 7] that there are semi-orthogonal decompositions


with
![]() $i_* \simeq i_!$
and that the composite adjoint functors
$i_* \simeq i_!$
and that the composite adjoint functors

are equivalences. Moreover, one proves as in [Reference Lurie23, Proposition 7.2.3.1] that
is fully faithful and that its essential image is the full subcategory spanned by the I-local A-modules. So we must prove that the functor
is fully faithful and that its essential image is the full subcategory spanned by the I-complete A-modules. The functor
![]() $j_*$
factors as
$j_*$
factors as
and since the full subcategory spanned by the I-complete A-modules is closed under small limits, the functor G admits a left adjoint functor
It follows from the definition of I-completeness that the unit map
is an equivalence. By the triangle identities, this, in turn, implies that the natural transformation
![]() $GFG \to G$
induced by the counit is an equivalence, so it remains to prove that G is conservative. The functor G takes a compatible family
$GFG \to G$
induced by the counit is an equivalence, so it remains to prove that G is conservative. The functor G takes a compatible family
![]() $(M_m)_{m \geq 1}$
with
$(M_m)_{m \geq 1}$
with
![]() $M_m \in \operatorname {\mathrm {Mod}}_{A/I^{m+1}}(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
to the limit
$M_m \in \operatorname {\mathrm {Mod}}_{A/I^{m+1}}(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
to the limit
![]() $M \simeq \varprojlim _mM_m \in \operatorname {\mathrm {Mod}}_A(\mathcal {D}(\operatorname {\mathrm {Ab}}))^{\operatorname {\mathrm {Cpl}}(I)}$
, and we must show that if
$M \simeq \varprojlim _mM_m \in \operatorname {\mathrm {Mod}}_A(\mathcal {D}(\operatorname {\mathrm {Ab}}))^{\operatorname {\mathrm {Cpl}}(I)}$
, and we must show that if
![]() $M \simeq 0$
, then
$M \simeq 0$
, then
![]() $M_m \simeq 0$
for all
$M_m \simeq 0$
for all
![]() $m \geq 1$
.
$m \geq 1$
.
To do so, we rewrite the limit in question. We write P for the set of positive integers considered as a category with a single map
![]() $i \to j$
if
$i \to j$
if
![]() $i \geq j$
and recall from [Reference Lurie20, Proposition 5.3.1.20] that the diagonal
$i \geq j$
and recall from [Reference Lurie20, Proposition 5.3.1.20] that the diagonal
![]() $\Delta \colon P \to P^d$
is a
$\Delta \colon P \to P^d$
is a
![]() $\varprojlim $
-equivalence. Given
$\varprojlim $
-equivalence. Given
![]() $e = (e_1,\dots ,e_d) \in P^d$
, we let
$e = (e_1,\dots ,e_d) \in P^d$
, we let
![]() $I_e = (f_1^{e_1},\dots ,f_d^{e_d}) \subset A$
and observe that
$I_e = (f_1^{e_1},\dots ,f_d^{e_d}) \subset A$
and observe that
![]() $I_{\Delta (m)} \subset I^m \subset I_{\Delta ([m/d])}$
. It follows that the canonical maps define equivalences
$I_{\Delta (m)} \subset I^m \subset I_{\Delta ([m/d])}$
. It follows that the canonical maps define equivalences
 $$ \begin{align*}\begin{aligned} {\mathrm{QCoh}}(Y) {} & \simeq \textstyle{ \varprojlim_{m \in P} \operatorname{\mathrm{Mod}}_{A/I^m}(\mathcal{D}(\operatorname{\mathrm{Ab}})) } \cr {} & \simeq \textstyle{ \varprojlim_{m \in P} \operatorname{\mathrm{Mod}}_{A/I_{\Delta(m)}}(\mathcal{D}(\operatorname{\mathrm{Ab}})) } \cr {} & \simeq \textstyle{ \varprojlim_{e \in P^d} \operatorname{\mathrm{Mod}}_{A/I_e}(\mathcal{D}(\operatorname{\mathrm{Ab}})). } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} {\mathrm{QCoh}}(Y) {} & \simeq \textstyle{ \varprojlim_{m \in P} \operatorname{\mathrm{Mod}}_{A/I^m}(\mathcal{D}(\operatorname{\mathrm{Ab}})) } \cr {} & \simeq \textstyle{ \varprojlim_{m \in P} \operatorname{\mathrm{Mod}}_{A/I_{\Delta(m)}}(\mathcal{D}(\operatorname{\mathrm{Ab}})) } \cr {} & \simeq \textstyle{ \varprojlim_{e \in P^d} \operatorname{\mathrm{Mod}}_{A/I_e}(\mathcal{D}(\operatorname{\mathrm{Ab}})). } \cr \end{aligned}\end{align*} $$
Hence, given a compatible family
![]() $(M_e)_{e \in P^d}$
with
$(M_e)_{e \in P^d}$
with
![]() $M_e \in \operatorname {\mathrm {Mod}}_{A/I_e}(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
, we must prove that if
$M_e \in \operatorname {\mathrm {Mod}}_{A/I_e}(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
, we must prove that if
![]() $M \simeq \varprojlim _eM_e \simeq 0$
, then
$M \simeq \varprojlim _eM_e \simeq 0$
, then
![]() $M_e \simeq 0$
for all
$M_e \simeq 0$
for all
![]() $e \in P^d$
, and to do so, we proceed by induction on
$e \in P^d$
, and to do so, we proceed by induction on
![]() $d \geq 1$
. We first consider the case
$d \geq 1$
. We first consider the case
![]() $d = 1$
, where we abbreviate
$d = 1$
, where we abbreviate
![]() $f = f_1$
and
$f = f_1$
and
![]() $e = e_1$
. Given any
$e = e_1$
. Given any
![]() $N \in \operatorname {\mathrm {Mod}}_A(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
, we write
$N \in \operatorname {\mathrm {Mod}}_A(\mathcal {D}(\operatorname {\mathrm {Ab}}))$
, we write
![]() $N/f^e$
for the cofiber of
$N/f^e$
for the cofiber of
![]() $f^e \cdot \operatorname {\mathrm {id}} \colon N \to N$
. Since
$f^e \cdot \operatorname {\mathrm {id}} \colon N \to N$
. Since
![]() $f \in A$
is a non-zero-divisor, the canonical map
$f \in A$
is a non-zero-divisor, the canonical map
![]() $A/f^e \to A/(f^e)$
is an equivalence. Hence, the cofiber
$A/f^e \to A/(f^e)$
is an equivalence. Hence, the cofiber
![]() $A/f^e$
has a ring structure. We observe that
$A/f^e$
has a ring structure. We observe that
 $$ \begin{align*}\begin{aligned} M_e/f {} & \simeq M_e \otimes_{A/(f^e)}((A/f^e)/f) \simeq M_e \otimes_{A/(f^e)}((A/f)/f^e) \cr {} & \simeq M_e \otimes_{A/(f^e)}(A/f \oplus A/f[1]) \simeq M_1 \oplus M_1[1] \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} M_e/f {} & \simeq M_e \otimes_{A/(f^e)}((A/f^e)/f) \simeq M_e \otimes_{A/(f^e)}((A/f)/f^e) \cr {} & \simeq M_e \otimes_{A/(f^e)}(A/f \oplus A/f[1]) \simeq M_1 \oplus M_1[1] \cr \end{aligned}\end{align*} $$
and that, under this equivalence, the map
![]() $M_e \to M_{e-1}$
induces the identity map on the first summand and the zero map on the second summand. It follows that
$M_e \to M_{e-1}$
induces the identity map on the first summand and the zero map on the second summand. It follows that
So if
![]() $M \simeq 0$
, then
$M \simeq 0$
, then
![]() $M_1 \simeq 0$
, which implies that
$M_1 \simeq 0$
, which implies that
![]() $M_e \simeq 0$
for all
$M_e \simeq 0$
for all
![]() $e \in P$
by dévissage. This proves the case
$e \in P$
by dévissage. This proves the case
![]() $d = 1$
. So we assume that the statement holds for
$d = 1$
. So we assume that the statement holds for
![]() $d = r$
and proceed to prove that it holds for
$d = r$
and proceed to prove that it holds for
![]() $d = r+1$
. We assume that
$d = r+1$
. We assume that
![]() $M \simeq \varprojlim _eM_e \simeq 0$
and must show that
$M \simeq \varprojlim _eM_e \simeq 0$
and must show that
![]() $M_e \simeq 0$
for all
$M_e \simeq 0$
for all
![]() $e \in P^{r+1}$
. We first write
$e \in P^{r+1}$
. We first write
By the inductive hypothesis, it will suffice to show that
![]() $N_{e_{r+1}} \simeq 0$
for all
$N_{e_{r+1}} \simeq 0$
for all
![]() $e_{r+1} \in P$
. But the A-module structure on
$e_{r+1} \in P$
. But the A-module structure on
![]() $N_{e_{r+1}}$
extends to a structure of module over the completed Dirac ring
$N_{e_{r+1}}$
extends to a structure of module over the completed Dirac ring
and the image of
![]() $f_{r+1}$
in
$f_{r+1}$
in
![]() $\smash { \widehat {A} }$
is a non-zero-divisor. Indeed, it follows from [Reference Matsumura27, Theorem 16.1] that the image of
$\smash { \widehat {A} }$
is a non-zero-divisor. Indeed, it follows from [Reference Matsumura27, Theorem 16.1] that the image of
![]() $f_{r+1}$
in
$f_{r+1}$
in
![]() $A/(f_1^{e_1},\dots ,f_r^{e_r})$
is a non-zero-divisor for all
$A/(f_1^{e_1},\dots ,f_r^{e_r})$
is a non-zero-divisor for all
![]() $(e_1,\dots ,e_r) \in P^r$
. Therefore, the same argument as in the case
$(e_1,\dots ,e_r) \in P^r$
. Therefore, the same argument as in the case
![]() $d = 1$
shows that
$d = 1$
shows that
![]() $N_{e_{r+1}} \simeq 0$
for all
$N_{e_{r+1}} \simeq 0$
for all
![]() $e_{r+1} \in P$
, as desired. This establishes the two semi-orthogonal decompositions.
$e_{r+1} \in P$
, as desired. This establishes the two semi-orthogonal decompositions.
Finally, we know that
![]() $j_*$
is left t-exact and must prove that it is also right t-exact, or equivalently, that it restricts to a functor
$j_*$
is left t-exact and must prove that it is also right t-exact, or equivalently, that it restricts to a functor
But this follows from the Milnor sequence and from the fact that the maps
induce surjections on
![]() $\pi _0$
.
$\pi _0$
.
4.2 Formal hyperplanes
We define a map of Dirac stacks
![]() $q \colon Y \to X$
to be a formal hyperplane if, locally on X, it is isomorphic to the formal affine space associated with a locally free
$q \colon Y \to X$
to be a formal hyperplane if, locally on X, it is isomorphic to the formal affine space associated with a locally free
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {E}$
. In older literature, including [Reference Goerss10, Reference Messing28], formal hyperplanes are called formal Lie varieties.
$\mathcal {E}$
. In older literature, including [Reference Goerss10, Reference Messing28], formal hyperplanes are called formal Lie varieties.
Let S be a Dirac scheme and let
![]() $\mathcal {E}$
be an
$\mathcal {E}$
be an
![]() $\mathcal {O}_S$
-module locally free of finite rank. The rank is locally constant, and we do not require that it be constant. We define the associated affine space over S to be the Dirac S-scheme
$\mathcal {O}_S$
-module locally free of finite rank. The rank is locally constant, and we do not require that it be constant. We define the associated affine space over S to be the Dirac S-scheme
and we define the zero section
to be the map induced by the unique map of
![]() $\mathcal {O}_S$
-modules
$\mathcal {O}_S$
-modules
![]() $\mathcal {E} \to 0$
. Finally, we define the formal affine space over S associated with
$\mathcal {E} \to 0$
. Finally, we define the formal affine space over S associated with
![]() $\mathcal {E}$
to be the formal completion
$\mathcal {E}$
to be the formal completion
of the affine space
![]() $p \colon \mathbb {A}_S(\mathcal {E}) \to S$
along the zero section.
$p \colon \mathbb {A}_S(\mathcal {E}) \to S$
along the zero section.
Definition 4.4. Let X be a Dirac stack. A map of Dirac stacks
![]() $q \colon Y \to X$
is a formal hyperplane over X if for every map
$q \colon Y \to X$
is a formal hyperplane over X if for every map
![]() $\eta \colon S \to X$
from an affine Dirac stack S, its base-change along
$\eta \colon S \to X$
from an affine Dirac stack S, its base-change along
![]() $\eta $
is equivalent to a formal affine space.
$\eta $
is equivalent to a formal affine space.
We write
![]() $\operatorname {\mathrm {Hyp}}(X) \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
for the full subcategory spanned by the formal hyperplanes over X. It is a priori an
$\operatorname {\mathrm {Hyp}}(X) \subset \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
for the full subcategory spanned by the formal hyperplanes over X. It is a priori an
![]() $\infty $
-category, but we now show that it is, in fact, equivalent to a
$\infty $
-category, but we now show that it is, in fact, equivalent to a
![]() $1$
-category.
$1$
-category.
Lemma 4.5. If
![]() $q \colon Y \to X$
is a formal hyperplane, then for any map of Dirac stacks
$q \colon Y \to X$
is a formal hyperplane, then for any map of Dirac stacks
![]() $\eta \colon Z \to X$
, the mapping anima
$\eta \colon Z \to X$
, the mapping anima
![]() $\operatorname {\mathrm {Map}}(Z,Y)$
calculated in
$\operatorname {\mathrm {Map}}(Z,Y)$
calculated in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
is
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
is
![]() $0$
-truncated. In particular, the
$0$
-truncated. In particular, the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Hyp}}(X)$
is equivalent to a
$\operatorname {\mathrm {Hyp}}(X)$
is equivalent to a
![]() $1$
-category.
$1$
-category.
Proof. The inclusion
![]() ${\mathcal {S}}_{\leq 0} \to {\mathcal {S}}$
of
${\mathcal {S}}_{\leq 0} \to {\mathcal {S}}$
of
![]() $0$
-truncated anima preserves limits, and it also preserves filtered colimits. In particular, by writing Z as a colimit of affine Dirac schemes, we may assume that
$0$
-truncated anima preserves limits, and it also preserves filtered colimits. In particular, by writing Z as a colimit of affine Dirac schemes, we may assume that
![]() $Z \simeq S$
is affine. Since q is a formal hyperplane, its base-change
$Z \simeq S$
is affine. Since q is a formal hyperplane, its base-change
![]() $q_S \colon Y_S \to S$
along
$q_S \colon Y_S \to S$
along
![]() $\eta \colon S \to X$
is equivalent to the formal affine space associated with some locally free
$\eta \colon S \to X$
is equivalent to the formal affine space associated with some locally free
![]() $\mathcal {O}_S$
-module of finite rank
$\mathcal {O}_S$
-module of finite rank
![]() $\mathcal {E}$
. Hence, we have
$\mathcal {E}$
. Hence, we have
where the latter equivalence follows from Remark 4.2. The right-hand side is a filtered colimit of
![]() $0$
-truncated anima and hence is itself
$0$
-truncated anima and hence is itself
![]() $0$
-truncated.
$0$
-truncated.
It follows immediately from the definition that if
![]() $f \colon X' \to X$
is any map of Dirac stacks, then the base-change along f restricts to a functor
$f \colon X' \to X$
is any map of Dirac stacks, then the base-change along f restricts to a functor
There functors are part of the functor
which classifies the cartesian fibration
given by the restriction of the target map
![]() $\operatorname {\mathrm {Fun}}(\Delta ^{1}, \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})) \rightarrow \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
to the full subcategory spanned by the formal hyperplanes; see [Reference Lurie20, Notation 6.1.3.4].
$\operatorname {\mathrm {Fun}}(\Delta ^{1}, \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})) \rightarrow \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
to the full subcategory spanned by the formal hyperplanes; see [Reference Lurie20, Notation 6.1.3.4].
Warning 4.6. The
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Hyp}}(X)$
of formal hyperplanes over X does generally not descend along effective epimorphisms, even if X is a Dirac scheme. We refer to [Reference Lurie22, Warning 1.1.22] for an instructive counterexample.
$\operatorname {\mathrm {Hyp}}(X)$
of formal hyperplanes over X does generally not descend along effective epimorphisms, even if X is a Dirac scheme. We refer to [Reference Lurie22, Warning 1.1.22] for an instructive counterexample.
We proceed to show that for pointed formal hyperplanes, the above descent issue goes away. As far as formal groups are concerned, it makes no difference if we work with formal hyperplanes or pointed formal hyperplanes. By definition, the
![]() $\infty $
-category of pointed Dirac stacks over X is the slice category
$\infty $
-category of pointed Dirac stacks over X is the slice category
Its objects are diagrams
![]() $\sigma \colon \Delta ^{2} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of the form
$\sigma \colon \Delta ^{2} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
of the form

and we view q as a structure map and
![]() $\eta $
as a section thereof.
$\eta $
as a section thereof.
Definition 4.7. Let X be a Dirac stack. A pointed Dirac stack over X is a pointed formal hyperplane if its base-change along every map
![]() $\eta \colon S \to X$
from an affine Dirac scheme is equivalent to
$\eta \colon S \to X$
from an affine Dirac scheme is equivalent to

for some locally free
![]() $\mathcal {O}_S$
-module of finite rank
$\mathcal {O}_S$
-module of finite rank
![]() $\mathcal {E}$
. Here,
$\mathcal {E}$
. Here,
![]() $\eta $
is the zero section.
$\eta $
is the zero section.
We will show that a pointed formal hyperplane admits a canonical exhaustive filtration. A map of Dirac stacks
![]() $f \colon Z \to X$
is
$f \colon Z \to X$
is
![]() $(-1)$
-truncated if and only if the map of anima
$(-1)$
-truncated if and only if the map of anima
![]() $f_S \colon Z(S) \to X(S)$
is
$f_S \colon Z(S) \to X(S)$
is
![]() $(-1)$
-truncated for all affine Dirac schemes S. By [Reference Lurie20, Proposition 6.2.3.17], the property of being
$(-1)$
-truncated for all affine Dirac schemes S. By [Reference Lurie20, Proposition 6.2.3.17], the property of being
![]() $(-1)$
-truncated is preserved by base-change along arbitrary maps and descends along effective epimorphisms. Also, if
$(-1)$
-truncated is preserved by base-change along arbitrary maps and descends along effective epimorphisms. Also, if
![]() $f \colon Z \to X$
is
$f \colon Z \to X$
is
![]() $(-1)$
-truncated and
$(-1)$
-truncated and
![]() $\eta \colon Y \to X$
any map, then the anima of lifts
$\eta \colon Y \to X$
any map, then the anima of lifts

is
![]() $(-1)$
-truncated so that for
$(-1)$
-truncated so that for
![]() $\eta $
to factor through f is a property. We now extend the definition of infinitesimal neighborhoods to Dirac stacks as follows.
$\eta $
to factor through f is a property. We now extend the definition of infinitesimal neighborhoods to Dirac stacks as follows.
Definition 4.8. Let
![]() $g \colon Z \to X$
be a
$g \colon Z \to X$
be a
![]() $(-1)$
-truncated map of Dirac stacks and let
$(-1)$
-truncated map of Dirac stacks and let
![]() $m \geq 0$
be an integer. The mth infinitesimal neighbourhood of Z in X is the essentially unique
$m \geq 0$
be an integer. The mth infinitesimal neighbourhood of Z in X is the essentially unique
![]() $(-1)$
-truncated map of Dirac stacks
$(-1)$
-truncated map of Dirac stacks
such that a map
![]() $\eta \colon S \to X$
from an affine Dirac scheme factors through
$\eta \colon S \to X$
from an affine Dirac scheme factors through
![]() $g^{(m)}$
if and only if there exists an effective epimorphism
$g^{(m)}$
if and only if there exists an effective epimorphism
![]() $p \colon T' \to S$
from an affine Dirac scheme and a closed immersion
$p \colon T' \to S$
from an affine Dirac scheme and a closed immersion
![]() $i \colon T \to T'$
defined by a quasi-coherent ideal, whose
$i \colon T \to T'$
defined by a quasi-coherent ideal, whose
![]() $(m+1)$
th power is zero, such that
$(m+1)$
th power is zero, such that
![]() $\eta |_T \colon T \to X$
factors through g.
$\eta |_T \colon T \to X$
factors through g.
We will often abbreviate and write
![]() $g^{(m)} \colon Z^{(m)} \to X$
for the mth infinitesimal neighborhood of Z in X. Definition 4.8 implicitly contains the assertion that
$g^{(m)} \colon Z^{(m)} \to X$
for the mth infinitesimal neighborhood of Z in X. Definition 4.8 implicitly contains the assertion that
![]() $Z^{(m)}$
is a Dirac stack. We now verify that this is indeed the case.
$Z^{(m)}$
is a Dirac stack. We now verify that this is indeed the case.
Proposition 4.9. Let
![]() $g \colon Z \to X$
be a
$g \colon Z \to X$
be a
![]() $(-1)$
-truncated map of Dirac stacks and let
$(-1)$
-truncated map of Dirac stacks and let
![]() $g^{(m)} \colon Z^{(m)} \to X$
be its mth infinitesimal neighborhood with
$g^{(m)} \colon Z^{(m)} \to X$
be its mth infinitesimal neighborhood with
![]() $m \geq 0$
. In this situation, the presheaf
$m \geq 0$
. In this situation, the presheaf
![]() $Z^{(m)} \colon \operatorname {\mathrm {Aff}}^{\mathrm {op}} \to {\mathcal {S}}$
is a Dirac stack.
$Z^{(m)} \colon \operatorname {\mathrm {Aff}}^{\mathrm {op}} \to {\mathcal {S}}$
is a Dirac stack.
Proof. We must show that the presheaf
![]() $Z^{(m)}$
is accessible and that it is a sheaf for the flat topology. To this end, we define
$Z^{(m)}$
is accessible and that it is a sheaf for the flat topology. To this end, we define
![]() $g^{(m)}{}' \colon Z^{(m)}{}' \to X$
to be the essentially unique
$g^{(m)}{}' \colon Z^{(m)}{}' \to X$
to be the essentially unique
![]() $(-1)$
-truncated map of presheaves such that a map
$(-1)$
-truncated map of presheaves such that a map
![]() $\eta \colon S \to X$
from an affine Dirac scheme factors through
$\eta \colon S \to X$
from an affine Dirac scheme factors through
![]() $g^{(m)}{}'$
if and only if there exists a closed immersion
$g^{(m)}{}'$
if and only if there exists a closed immersion
![]() $i \colon S' \to S$
defined by a quasi-coherent ideal, whose
$i \colon S' \to S$
defined by a quasi-coherent ideal, whose
![]() $(m+1)$
th power is zero, such that
$(m+1)$
th power is zero, such that
![]() $\eta |_{S'} \colon S' \to X$
factors through g. By definition, the inclusion
$\eta |_{S'} \colon S' \to X$
factors through g. By definition, the inclusion
![]() $Z^{(m)}{}' \to Z^{(m)}$
is a sheafification for the flat topology, so in order to show that
$Z^{(m)}{}' \to Z^{(m)}$
is a sheafification for the flat topology, so in order to show that
![]() $Z^{(m)}$
is a Dirac stack, it will suffice to show that
$Z^{(m)}$
is a Dirac stack, it will suffice to show that
![]() $Z^{(m)}{}'$
is accessible.
$Z^{(m)}{}'$
is accessible.
There exists a regular cardinal
![]() $\kappa $
such that X and Z are
$\kappa $
such that X and Z are
![]() $\kappa $
-accessible in the sense that they agree with the left Kan extensions of their restrictions along the inclusion
$\kappa $
-accessible in the sense that they agree with the left Kan extensions of their restrictions along the inclusion
![]() $i \colon {\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
of the full subcategory of
$i \colon {\mathrm {Aff}}_{\kappa } \to \operatorname {\mathrm {Aff}}$
of the full subcategory of
![]() $\kappa $
-small affine Dirac schemes. We claim that also
$\kappa $
-small affine Dirac schemes. We claim that also
![]() $Z^{(m)}{}'$
is
$Z^{(m)}{}'$
is
![]() $\kappa $
-accessible.
$\kappa $
-accessible.
To prove the claim, we consider the diagram

with the colimits indexed by
![]() $p \colon S \to T$
in
$p \colon S \to T$
in
![]() $({\mathrm {Aff}}_{\kappa })_{S/}$
. The bottom horizontal map is an equivalence, by the assumption that X is
$({\mathrm {Aff}}_{\kappa })_{S/}$
. The bottom horizontal map is an equivalence, by the assumption that X is
![]() $\kappa $
-accessible, and we wish to show the same for the top horizontal map. The right-hand vertical map is
$\kappa $
-accessible, and we wish to show the same for the top horizontal map. The right-hand vertical map is
![]() $(-1)$
-truncated by definition, and the left-hand vertical map is
$(-1)$
-truncated by definition, and the left-hand vertical map is
![]() $(-1)$
-truncated since it is a filtered colimit of
$(-1)$
-truncated since it is a filtered colimit of
![]() $(-1)$
-truncated maps. Indeed, by Lemma A.1, the category
$(-1)$
-truncated maps. Indeed, by Lemma A.1, the category
![]() $({\mathrm {Aff}}_{\kappa })_{S/}$
is
$({\mathrm {Aff}}_{\kappa })_{S/}$
is
![]() $\kappa $
-filtered and hence filtered. We conclude that also the top horizontal map is
$\kappa $
-filtered and hence filtered. We conclude that also the top horizontal map is
![]() $(-1)$
-truncated, so it remains to show that it is essentially surjective.
$(-1)$
-truncated, so it remains to show that it is essentially surjective.
Let us switch to ring notation. Given a point x of
![]() $Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A))$
, we must show that there exists a map of Dirac rings
$Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A))$
, we must show that there exists a map of Dirac rings
![]() $B \to A$
such that B is
$B \to A$
such that B is
![]() $\kappa $
-small and such that x is in the essential image of
$\kappa $
-small and such that x is in the essential image of
![]() $Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(B)) \to Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A))$
. By definition, we can identify x with a point of
$Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(B)) \to Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A))$
. By definition, we can identify x with a point of
![]() $X(\operatorname {\mathrm {Spec}}(A))$
with the property that there exists an ideal
$X(\operatorname {\mathrm {Spec}}(A))$
with the property that there exists an ideal
![]() $I \subset A$
with
$I \subset A$
with
![]() $I^{m+1} = 0$
such that the image of x by
$I^{m+1} = 0$
such that the image of x by
belongs to
![]() $Z(\operatorname {\mathrm {Spec}}(A/I))$
. If we write A as the
$Z(\operatorname {\mathrm {Spec}}(A/I))$
. If we write A as the
![]() $\kappa $
-filtered colimit
$\kappa $
-filtered colimit
![]() $A \simeq \varinjlim B$
of its
$A \simeq \varinjlim B$
of its
![]() $\kappa $
-small sub-Dirac rings
$\kappa $
-small sub-Dirac rings
![]() $B \subset A$
, then also
$B \subset A$
, then also
![]() $A/I \simeq \varinjlim B/(B \cap I)$
. Moreover, since X and Z are assumed to be
$A/I \simeq \varinjlim B/(B \cap I)$
. Moreover, since X and Z are assumed to be
![]() $\kappa $
-accessible, they preserve
$\kappa $
-accessible, they preserve
![]() $\kappa $
-filtered colimits, so we conclude that there exists a
$\kappa $
-filtered colimits, so we conclude that there exists a
![]() $\kappa $
-small sub-Dirac ring
$\kappa $
-small sub-Dirac ring
![]() $A_0 \subset A$
such that x lifts to a point
$A_0 \subset A$
such that x lifts to a point
![]() $x_0$
of
$x_0$
of
![]() $X(\operatorname {\mathrm {Spec}}(A_0))$
with the property that its image by
$X(\operatorname {\mathrm {Spec}}(A_0))$
with the property that its image by
belongs to
![]() $Z(\operatorname {\mathrm {Spec}}(A_0/(A_0 \cap I)))$
. But we have
$Z(\operatorname {\mathrm {Spec}}(A_0/(A_0 \cap I)))$
. But we have
![]() $(A_0 \cap I)^{m+1} = 0$
as an ideal of
$(A_0 \cap I)^{m+1} = 0$
as an ideal of
![]() $A_0$
because
$A_0$
because
![]() $I^{m+1} = 0$
and because
$I^{m+1} = 0$
and because
![]() $A_0 \subset A$
is a sub-Dirac ring, so we conclude that the point
$A_0 \subset A$
is a sub-Dirac ring, so we conclude that the point
![]() $x_0$
belongs to
$x_0$
belongs to
![]() $Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A_0))$
as desired.
$Z^{(m)}{}'(\operatorname {\mathrm {Spec}}(A_0))$
as desired.
Remark 4.10 (Base-change for infinitesimal neighbourhoods).
Let
![]() $g \colon Z \to X$
be a
$g \colon Z \to X$
be a
![]() $(-1)$
-truncated map of Dirac stacks, let
$(-1)$
-truncated map of Dirac stacks, let
![]() $m \geq 0$
be an integer and let
$m \geq 0$
be an integer and let
![]() $f \colon X' \to X$
be any map of Dirac stacks. In this situation, the base-change
$f \colon X' \to X$
be any map of Dirac stacks. In this situation, the base-change
![]() $g' \colon Z' \to X'$
of g along f is
$g' \colon Z' \to X'$
of g along f is
![]() $(-1)$
-truncated, and
$(-1)$
-truncated, and
![]() $g'{}^{(m)} \colon Z'{}^{(m)} \to X'$
is the base-change of
$g'{}^{(m)} \colon Z'{}^{(m)} \to X'$
is the base-change of
![]() $g^{(m)} \colon Z^{(m)} \to X$
along f.
$g^{(m)} \colon Z^{(m)} \to X$
along f.
We also verify that the notion of infinitesimal neighborhoods for Dirac stacks of Definition 4.8 extends the notion of infinitesimal neighborhoods of a closed embedding Dirac schemes introduced in Definition 4.1.
Lemma 4.11. Let
![]() $g \colon Z \to X$
be a closed immersion of Dirac schemes. The induced map
$g \colon Z \to X$
be a closed immersion of Dirac schemes. The induced map
![]() $h(g) \colon h(Z) \to h(X)$
of Dirac stacks is
$h(g) \colon h(Z) \to h(X)$
of Dirac stacks is
![]() $(-1)$
-truncated and the canonical map
$(-1)$
-truncated and the canonical map
is an equivalence for every
![]() $m \geq 0$
.
$m \geq 0$
.
Proof. It is clear that the map in the statement exists and is
![]() $(-1)$
-truncated, so only the essential surjectivity of this map is at issue. So we let
$(-1)$
-truncated, so only the essential surjectivity of this map is at issue. So we let
![]() $\eta \colon S \to X$
be a map from an affine Dirac scheme such that
$\eta \colon S \to X$
be a map from an affine Dirac scheme such that
![]() $h(\eta )$
factors through
$h(\eta )$
factors through
![]() $h(g)^{(m)}$
and wish to show that
$h(g)^{(m)}$
and wish to show that
![]() $\eta $
factors
$\eta $
factors
![]() $g^{(m)}$
.
$g^{(m)}$
.
Since
![]() $h(\eta )$
factors through
$h(\eta )$
factors through
![]() $h(g)^{(m)}$
, there exists, by definition, a faithfully flat map
$h(g)^{(m)}$
, there exists, by definition, a faithfully flat map
![]() $p \colon T' \to S$
from an affine Dirac scheme and a closed immersion
$p \colon T' \to S$
from an affine Dirac scheme and a closed immersion
![]() $i \colon T \to T'$
defined by a quasi-coherent ideal of
$i \colon T \to T'$
defined by a quasi-coherent ideal of
![]() $\mathcal {O}_{T'}$
, whose
$\mathcal {O}_{T'}$
, whose
![]() $(m+1)$
th power is zero, such that
$(m+1)$
th power is zero, such that
![]() $\eta |_T \colon T \to X$
factors through g. We now consider the diagram
$\eta |_T \colon T \to X$
factors through g. We now consider the diagram

with all squares cartesian. Since
![]() $g^{(m)}$
is a monomorphism, the statement that
$g^{(m)}$
is a monomorphism, the statement that
![]() $\eta $
factors through
$\eta $
factors through
![]() $g^{(m)}$
, which we wish to prove, is equivalent to the statement that the base-change of
$g^{(m)}$
, which we wish to prove, is equivalent to the statement that the base-change of
![]() $g^{(m)}$
along
$g^{(m)}$
along
![]() $\eta $
is an isomorphism. And since p is faithfully flat, the common statement, in turn, is equivalent to the statement that the base-change of
$\eta $
is an isomorphism. And since p is faithfully flat, the common statement, in turn, is equivalent to the statement that the base-change of
![]() $g^{(m)}$
along
$g^{(m)}$
along
![]() $\eta \circ p$
is an isomorphism. By the same reasoning, the assumption that
$\eta \circ p$
is an isomorphism. By the same reasoning, the assumption that
![]() $\eta |_T$
factors through
$\eta |_T$
factors through
![]() $g \simeq g^{(m)}h_m$
implies that the base-changes of both
$g \simeq g^{(m)}h_m$
implies that the base-changes of both
![]() $g^{(m)}$
and
$g^{(m)}$
and
![]() $h_m$
along
$h_m$
along
![]() $\eta \circ p \circ i$
are isomorphisms.
$\eta \circ p \circ i$
are isomorphisms.
We now consider the two left-hand columns in the diagram above together with the horizontal maps between them. The maps in this part of the diagram all induce homeomorphisms of underlying spaces, and moreover, the maps in the left-hand column are isomorphisms. Hence, if
![]() $I,J \subset \mathcal {O}_{T'}$
are the quasi-coherent ideals that define
$I,J \subset \mathcal {O}_{T'}$
are the quasi-coherent ideals that define
![]() $g_{T'}$
and i, respectively, then
$g_{T'}$
and i, respectively, then
![]() $I \subset J$
. But then
$I \subset J$
. But then
![]() $I^{m+1} \subset J^{m+1} = 0$
, which shows that the base-change of
$I^{m+1} \subset J^{m+1} = 0$
, which shows that the base-change of
![]() $g^{(m)}$
along
$g^{(m)}$
along
![]() $\eta \circ p$
is an isomorphism, as desired.
$\eta \circ p$
is an isomorphism, as desired.
Definition 4.12. Let
![]() $g \colon Z \to X$
be a
$g \colon Z \to X$
be a
![]() $(-1)$
-truncated map of Dirac stacks. The formal completion of X along g is the induced
$(-1)$
-truncated map of Dirac stacks. The formal completion of X along g is the induced
![]() $(-1)$
-truncated map
$(-1)$
-truncated map
from the colimit of the infinitesimal neighborhoods of Z in X. The Dirac stack X is formally complete along g if the map j is an equivalence.
We next show that the formal completion along a
![]() $(-1)$
-truncated map of Dirac stacks is an idempotent operation in the following precise sense.
$(-1)$
-truncated map of Dirac stacks is an idempotent operation in the following precise sense.
Proposition 4.13. Let
![]() $g \colon Z \to X$
be a
$g \colon Z \to X$
be a
![]() $(-1)$
-truncated map of Dirac stacks, let
$(-1)$
-truncated map of Dirac stacks, let
![]() $j \colon Y \to X$
be the formal completion of X along g and let
$j \colon Y \to X$
be the formal completion of X along g and let
![]() $h \colon Z \to Y$
be the unique map such that
$h \colon Z \to Y$
be the unique map such that
![]() $g \simeq j \circ h$
. In this situation, the map j induces an equivalence
$g \simeq j \circ h$
. In this situation, the map j induces an equivalence
for all
![]() $m \geq 0$
. In particular, the Dirac stack Y is formally complete along h.
$m \geq 0$
. In particular, the Dirac stack Y is formally complete along h.
Proof. It is clear that the map in the statement exists and is
![]() $(-1)$
-truncated. So we let
$(-1)$
-truncated. So we let
![]() $\eta \colon S \to X$
be a map from an affine Dirac scheme and assume that
$\eta \colon S \to X$
be a map from an affine Dirac scheme and assume that
![]() $\eta $
factors through
$\eta $
factors through
![]() $g^{(m)}$
. In particular, it factors through j, so that
$g^{(m)}$
. In particular, it factors through j, so that
![]() $\eta \simeq j \circ \eta '$
for a unique map
$\eta \simeq j \circ \eta '$
for a unique map
![]() $\eta ' \colon S \to Y$
, and we wish to show that
$\eta ' \colon S \to Y$
, and we wish to show that
![]() $\eta '$
factors through
$\eta '$
factors through
![]() $h^{(m)}$
. Now, since
$h^{(m)}$
. Now, since
![]() $\eta $
factors through g, there exists, by definition, a faithfully flat map
$\eta $
factors through g, there exists, by definition, a faithfully flat map
![]() $p \colon T' \to S$
with
$p \colon T' \to S$
with
![]() $T'$
affine and a closed immersion
$T'$
affine and a closed immersion
![]() $i \colon T \to T'$
defined by a quasi-coherent ideal, whose
$i \colon T \to T'$
defined by a quasi-coherent ideal, whose
![]() $(m+1)$
th power is zero, such that
$(m+1)$
th power is zero, such that
![]() $\eta |_T$
factors through
$\eta |_T$
factors through
![]() $g \simeq j \circ h$
. Since j is
$g \simeq j \circ h$
. Since j is
![]() $(-1)$
-truncated, this implies that
$(-1)$
-truncated, this implies that
![]() $\eta '|_T$
factors through h, so
$\eta '|_T$
factors through h, so
![]() $\eta '$
factors, by definition, through
$\eta '$
factors, by definition, through
![]() $h^{(m)}$
, as we wanted to prove.
$h^{(m)}$
, as we wanted to prove.
We now specialize to the case of the
![]() $(-1)$
-truncated map of Dirac stacks given by the zero section of a pointed formal hyperplane.
$(-1)$
-truncated map of Dirac stacks given by the zero section of a pointed formal hyperplane.
Corollary 4.14. Let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
.
$\eta \colon X \to Y$
.
-
(1) The Dirac stack Y is formally complete along
 $\eta $
.
$\eta $
. -
(2) The composite map
 $q_m \simeq q \circ \eta ^{(m)} \colon X_{\eta }^{(m)} \to X$
is finite affine for all
$q_m \simeq q \circ \eta ^{(m)} \colon X_{\eta }^{(m)} \to X$
is finite affine for all
 $m \geq 0$
, and it is flat for
$m \geq 0$
, and it is flat for
 $0 \leq m \leq 1$
.
$0 \leq m \leq 1$
.
Proof. The statement (1) is a special case of Proposition 4.13. The statement (2) can be verified after base-change along any map from an affine Dirac scheme, so it suffices to consider the case where
![]() $q \colon Y \simeq {\hat {\mathbb {A}}}_S(\mathcal {E}) \to S$
is the formal affine space associated with a locally free
$q \colon Y \simeq {\hat {\mathbb {A}}}_S(\mathcal {E}) \to S$
is the formal affine space associated with a locally free
![]() $\mathcal {O}_S$
-module
$\mathcal {O}_S$
-module
![]() $\mathcal {E}$
and where
$\mathcal {E}$
and where
![]() $\eta \colon S \to Y$
is the zero section. In this case, Proposition 4.13 identifies
$\eta \colon S \to Y$
is the zero section. In this case, Proposition 4.13 identifies
from which (2) follows.
Warning 4.15. We note that, in the presence of sections of half-integer spin, the symmetric powers
![]() $\operatorname {\mathrm {Sym}}^d_{\mathcal {O}_S}(\mathcal {E})$
of a locally free
$\operatorname {\mathrm {Sym}}^d_{\mathcal {O}_S}(\mathcal {E})$
of a locally free
![]() $\mathcal {O}_S$
-module of finite rank
$\mathcal {O}_S$
-module of finite rank
![]() $\mathcal {E}$
are not necessarily flat for
$\mathcal {E}$
are not necessarily flat for
![]() $d \geq 2$
. For instance,
$d \geq 2$
. For instance,

is not a flat
![]() $\mathbb {Z}$
-module for
$\mathbb {Z}$
-module for
![]() $d \geq 2$
.
$d \geq 2$
.
Remark 4.16. If
![]() $q \colon Y \to S$
is the formal affine space associated with a locally free
$q \colon Y \to S$
is the formal affine space associated with a locally free
![]() $\mathcal {O}_S$
-module
$\mathcal {O}_S$
-module
![]() $\mathcal {E}$
of finite rank pointed by the zero section
$\mathcal {E}$
of finite rank pointed by the zero section
![]() $\eta \colon S \to Y$
, then, by the proof of Corollary 4.14, there is a cofiber sequence of quasi-coherent
$\eta \colon S \to Y$
, then, by the proof of Corollary 4.14, there is a cofiber sequence of quasi-coherent
![]() $\mathcal {O}_S$
-modules
$\mathcal {O}_S$
-modules
In particular, the cofiber of the left-hand map is a locally free
![]() $\mathcal {O}_S$
-module.
$\mathcal {O}_S$
-module.
The following definition globalizes this observation.
Definition 4.17. Let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
.
$\eta \colon X \to Y$
.
-
(1) The conormal sheaf of
 $q \colon Y \to X$
at
$q \colon Y \to X$
at
 $\eta \colon X \to Y$
is the cofiber
$\eta \colon X \to Y$
is the cofiber  $$ \begin{align*}\mathcal{N}_{X/Y} \simeq \operatorname{\mathrm{cof}}(\mathcal{O}_X \to q_{1*}\mathcal{O}_{X_{\eta}^{(1)}}) \in {\mathrm{QCoh}}(X).\end{align*} $$
$$ \begin{align*}\mathcal{N}_{X/Y} \simeq \operatorname{\mathrm{cof}}(\mathcal{O}_X \to q_{1*}\mathcal{O}_{X_{\eta}^{(1)}}) \in {\mathrm{QCoh}}(X).\end{align*} $$
-
(2) The tangent space of
 $q \colon Y \to X$
at
$q \colon Y \to X$
at
 $\eta \colon X \to Y$
is the vector bundle
$\eta \colon X \to Y$
is the vector bundle  $$ \begin{align*}T_{Y/X,\eta} \simeq V_X(\mathcal{N}_{X/Y}) \in \operatorname{\mathrm{Vect}}(X).\end{align*} $$
$$ \begin{align*}T_{Y/X,\eta} \simeq V_X(\mathcal{N}_{X/Y}) \in \operatorname{\mathrm{Vect}}(X).\end{align*} $$
The assignment of the conormal sheaf defines a functor
or equivalently, the assignment of the tangent space defines a functor
Proposition 4.18. Let
![]() $f \colon X' \to X$
be a map of Dirac stacks, let
$f \colon X' \to X$
be a map of Dirac stacks, let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
and let
$\eta \colon X \to Y$
and let
![]() $q' \colon Y' \to X'$
be the base-change of q along f pointed by
$q' \colon Y' \to X'$
be the base-change of q along f pointed by
![]() $\eta ' \simeq (\eta ,\operatorname {\mathrm {id}})$
. In this situation, the canonical map
$\eta ' \simeq (\eta ,\operatorname {\mathrm {id}})$
. In this situation, the canonical map
is an equivalence.
Proof. Since
![]() $f^* \colon {\mathrm {QCoh}}(X) \rightarrow {\mathrm {QCoh}}(X')$
is exact and
$f^* \colon {\mathrm {QCoh}}(X) \rightarrow {\mathrm {QCoh}}(X')$
is exact and
![]() $f^* \mathcal {O}_{X} \simeq \mathcal {O}_{X'}$
, it will suffice to show that in the cartesian diagram
$f^* \mathcal {O}_{X} \simeq \mathcal {O}_{X'}$
, it will suffice to show that in the cartesian diagram

the base-change map
![]() $f^*q_{1*} \to q_{1*}'f'{}^*$
is an equivalence. But this follows from Proposition 3.20 since
$f^*q_{1*} \to q_{1*}'f'{}^*$
is an equivalence. But this follows from Proposition 3.20 since
![]() $q_1$
is affine flat by Corollary 4.14.
$q_1$
is affine flat by Corollary 4.14.
Corollary 4.19. If
![]() $q \colon Y \to X$
is a formal hyperplane pointed at
$q \colon Y \to X$
is a formal hyperplane pointed at
![]() $\eta \colon X \to Y$
, then the conormal sheaf
$\eta \colon X \to Y$
, then the conormal sheaf
![]() $\mathcal {N}_{X/Y}$
is a locally free
$\mathcal {N}_{X/Y}$
is a locally free
![]() $\mathcal {O}_X$
-module of finite rank.
$\mathcal {O}_X$
-module of finite rank.
Proof. By Proposition 4.18, we can assume that X is affine, in which case the statement follows from Remark 4.16.
If
![]() $q \colon Y \to X$
is a formal hyperplane, then so is its base-change
$q \colon Y \to X$
is a formal hyperplane, then so is its base-change
![]() $q' \colon Y' \to Y$
along itself, and moreover, the formal hyperplane
$q' \colon Y' \to Y$
along itself, and moreover, the formal hyperplane
![]() $q' \colon Y' \to Y$
is canonically pointed by the diagonal
$q' \colon Y' \to Y$
is canonically pointed by the diagonal
![]() $\Delta \colon Y \to Y'$
.
$\Delta \colon Y \to Y'$
.
Definition 4.20. Let
![]() $q \colon Y \to X$
be a formal hyperplane.
$q \colon Y \to X$
be a formal hyperplane.
-
(1) The
 $\mathcal {O}_Y$
-module of differentials of
$\mathcal {O}_Y$
-module of differentials of
 $q \colon Y \to X$
is the conormal sheaf of the base-change
$q \colon Y \to X$
is the conormal sheaf of the base-change $$ \begin{align*}\Omega_{Y/X}^1 \simeq \mathcal{N}_{Y/Y'} \in {\mathrm{QCoh}}(Y)\end{align*} $$
$$ \begin{align*}\Omega_{Y/X}^1 \simeq \mathcal{N}_{Y/Y'} \in {\mathrm{QCoh}}(Y)\end{align*} $$
 $q' \colon Y' \to Y$
of q along itself pointed by the diagonal.
$q' \colon Y' \to Y$
of q along itself pointed by the diagonal.
-
(2) The tangent bundle of
 $q \colon Y \to X$
is the vector bundle
$q \colon Y \to X$
is the vector bundle  $$ \begin{align*}T_{Y/X} \simeq V_Y(\Omega_{Y/X}^1) \in \operatorname{\mathrm{Vect}}(Y).\end{align*} $$
$$ \begin{align*}T_{Y/X} \simeq V_Y(\Omega_{Y/X}^1) \in \operatorname{\mathrm{Vect}}(Y).\end{align*} $$
Remark 4.21. Let
![]() $q \colon Y \to X$
be a formal hyperplane and let
$q \colon Y \to X$
be a formal hyperplane and let
![]() $q' \colon Y' \to Y$
be the base-change of q along itself, pointed by the diagonal
$q' \colon Y' \to Y$
be the base-change of q along itself, pointed by the diagonal
![]() $\Delta \colon Y \to Y'$
. If
$\Delta \colon Y \to Y'$
. If
![]() $\eta \colon X \to Y$
is a point of
$\eta \colon X \to Y$
is a point of
![]() $q \colon Y \to X$
, then the base-change of
$q \colon Y \to X$
, then the base-change of
![]() $q' \colon Y' \to Y$
pointed by
$q' \colon Y' \to Y$
pointed by
![]() $\Delta \colon Y \to Y'$
along
$\Delta \colon Y \to Y'$
along
![]() $\eta \colon X \to Y$
is canonically identified with
$\eta \colon X \to Y$
is canonically identified with
![]() $q \colon Y \to X$
pointed by
$q \colon Y \to X$
pointed by
![]() $\eta \colon X \to Y$
,
$\eta \colon X \to Y$
,

so Proposition 4.18 shows that
![]() $\mathcal {N}_{X/Y} \simeq \eta ^*\Omega _{Y/X}^1$
and
$\mathcal {N}_{X/Y} \simeq \eta ^*\Omega _{Y/X}^1$
and
![]() $T_{Y/X,\eta } \simeq \eta ^*T_{Y/X}$
.
$T_{Y/X,\eta } \simeq \eta ^*T_{Y/X}$
.
Remark 4.22. Our definition of the tangent bundle is provisional. In [Reference Hesselholt and Pstrągowski13], we will define the cotangent complex
![]() $L_{Y/X}$
of a formal hyperplane
$L_{Y/X}$
of a formal hyperplane
![]() $q \colon Y \to X$
and prove that it is a locally free
$q \colon Y \to X$
and prove that it is a locally free
![]() $\mathcal {O}_Y$
-module isomorphic to
$\mathcal {O}_Y$
-module isomorphic to
![]() $\Omega _{Y/X}^1$
.
$\Omega _{Y/X}^1$
.
If
![]() $q \colon Y \to X$
is a formal hyperplane pointed by
$q \colon Y \to X$
is a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
, then the rank of the conormal sheaf
$\eta \colon X \to Y$
, then the rank of the conormal sheaf
![]() $\mathcal {N}_{X/Y}$
is locally constant in the sense that for every map
$\mathcal {N}_{X/Y}$
is locally constant in the sense that for every map
![]() $f \colon S \to X$
from a Dirac scheme, the rank of the locally free
$f \colon S \to X$
from a Dirac scheme, the rank of the locally free
![]() $\mathcal {O}_S$
-module
$\mathcal {O}_S$
-module
![]() $f^*\mathcal {N}_{X/Y}$
is a locally constant function on the underlying topological space
$f^*\mathcal {N}_{X/Y}$
is a locally constant function on the underlying topological space
![]() $|S|$
.
$|S|$
.
Definition 4.23. The dimension of a pointed formal hyperplane is the rank of its conormal sheaf.
Warning 4.24. It is tempting to also define the spin of a pointed formal hyperplane as the spin of local generators of its conormal sheaf. But said spin is not well defined, so this is not possible. For example, if k is the Dirac field
![]() $\mathbb {F}_2[x^{\pm 1}]$
with x of spin
$\mathbb {F}_2[x^{\pm 1}]$
with x of spin ![]() , then as a k-vector space, k is generated by
, then as a k-vector space, k is generated by
![]() $x^d$
for any integer d.
$x^d$
for any integer d.
Remark 4.25. If X is an affine Dirac scheme, then Remark 4.16 shows that every pointed formal hyperplane over X is isomorphic to the formal affine space of its conormal sheaf pointed by the zero section. However, such an isomorphism is highly noncanonical, and if X is not affine, then it may not exist.
4.3 Automorphisms of pointed formal hyperplanes and descent
Given a formal hyperplane
![]() $q \colon Y \to X$
, a point
$q \colon Y \to X$
, a point
![]() $\eta \colon X \to Y$
determines by Corollary 4.14 an exhaustive increasing filtration of Y by the infinitesimal neighborhoods of X in Y. This filtration, in turn, induces a filtration of the automorphism group, which we proceed to describe. We first promote the automorphism group to a group stack.
$\eta \colon X \to Y$
determines by Corollary 4.14 an exhaustive increasing filtration of Y by the infinitesimal neighborhoods of X in Y. This filtration, in turn, induces a filtration of the automorphism group, which we proceed to describe. We first promote the automorphism group to a group stack.
We show in Theorem A.14 that the
![]() $\infty $
-categories of accessible sheaves of anima have the same functoriality as do
$\infty $
-categories of accessible sheaves of anima have the same functoriality as do
![]() $\infty $
-topoi. So, given a map
$\infty $
-topoi. So, given a map
![]() $f \colon Y \to X$
in
$f \colon Y \to X$
in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we have adjoint functors
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we have adjoint functors

with
![]() $f_!$
given by composition with f and
$f_!$
given by composition with f and
![]() $f^*$
given by base-change along f. Moreover, the base-change formula holds in the sense that given a cartesian square
$f^*$
given by base-change along f. Moreover, the base-change formula holds in the sense that given a cartesian square

in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, the base-change maps
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, the base-change maps
![]() $f_!'\,j'{}^* \to j^*f_!$
and
$f_!'\,j'{}^* \to j^*f_!$
and
![]() $j^*f_* \to f_*'\,j'{}^*$
are equivalences. This has the following consequence:
$j^*f_* \to f_*'\,j'{}^*$
are equivalences. This has the following consequence:
Proposition 4.26. The slice
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
is cartesian closed.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
is cartesian closed.
Proof. Suppose that
![]() $f \colon Y \to X$
and
$f \colon Y \to X$
and
![]() $g \colon Z \to X$
are two objects of the slice category, and let
$g \colon Z \to X$
are two objects of the slice category, and let
![]() $\mathrm {id}_{X} \colon X \to X$
be the terminal object. We claim that internal mapping object
$\mathrm {id}_{X} \colon X \to X$
be the terminal object. We claim that internal mapping object
![]() $\operatorname {\mathrm {Hom}}(f, g)$
is given by
$\operatorname {\mathrm {Hom}}(f, g)$
is given by
![]() $f_*f^*g_!g^*\mathrm {id}_{X} $
. To see this, note that for any
$f_*f^*g_!g^*\mathrm {id}_{X} $
. To see this, note that for any
![]() $h \colon R \rightarrow X$
,
$h \colon R \rightarrow X$
,
where the mapping spaces and the product
![]() $f \times h$
are calculated in the slice category
$f \times h$
are calculated in the slice category
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
.
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
.
Remark 4.27. Given an object
![]() $f \colon Y \to X$
in
$f \colon Y \to X$
in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
, the internal mapping object
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
, the internal mapping object
![]() $\operatorname {\mathrm {Hom}}(f,f)$
canonically promotes to an
$\operatorname {\mathrm {Hom}}(f,f)$
canonically promotes to an
![]() $\mathbf {E}_1$
-monoid
$\mathbf {E}_1$
-monoid
![]() $\operatorname {\mathrm {End}}(f)$
in
$\operatorname {\mathrm {End}}(f)$
in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. We denote its maximal sub-
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. We denote its maximal sub-
![]() $\mathbf {E}_1$
-group by
$\mathbf {E}_1$
-group by
![]() $\operatorname {\mathrm {Aut}}(f)$
and refer to it as the classifying stack for automorphisms of f.
$\operatorname {\mathrm {Aut}}(f)$
and refer to it as the classifying stack for automorphisms of f.
Remark 4.28. Suppose that
![]() $\sigma \in (\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
is a pointed object in
$\sigma \in (\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
is a pointed object in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. In a similar manner, we have a classifying stack
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. In a similar manner, we have a classifying stack
for automorphisms of
![]() $\sigma $
as a pointed object. Writing
$\sigma $
as a pointed object. Writing
![]() $\sigma $
as a diagram
$\sigma $
as a diagram

in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we also use the notation
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, we also use the notation
![]() $\operatorname {\mathrm {Aut}}_{\eta }(Y/X)$
instead of
$\operatorname {\mathrm {Aut}}_{\eta }(Y/X)$
instead of
![]() $\operatorname {\mathrm {Aut}}(\sigma )$
.
$\operatorname {\mathrm {Aut}}(\sigma )$
.
Let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
. The infinitesimal neighborhoods of X in Y define a filtered object in
$\eta \colon X \to Y$
. The infinitesimal neighborhoods of X in Y define a filtered object in
![]() $(\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
with
$(\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
with

as its mth term.
Definition 4.29. Let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
and let
$\eta \colon X \to Y$
and let
![]() $G \simeq \operatorname {\mathrm {Aut}}_{\eta }(Y/X)$
be its classifying stack for automorphisms. The canonical filtration of G is the filtered object in
$G \simeq \operatorname {\mathrm {Aut}}_{\eta }(Y/X)$
be its classifying stack for automorphisms. The canonical filtration of G is the filtered object in
![]() $\operatorname {\mathrm {Grp}}_{\mathbf {E}_1}(\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})$
with
$\operatorname {\mathrm {Grp}}_{\mathbf {E}_1}(\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})$
with
Remark 4.30. We recall from Corollary 4.14 that, in the situation of Definition 4.29, the Dirac stack Y is formally complete along
![]() $\eta \colon X \to Y$
. Thus, the canonical filtration of G is complete in the sense that
$\eta \colon X \to Y$
. Thus, the canonical filtration of G is complete in the sense that
Since
![]() $q_m \colon X_{\eta }^{(m)} \to X$
is affine, it is in particular
$q_m \colon X_{\eta }^{(m)} \to X$
is affine, it is in particular
![]() $0$
-truncated. This implies that also the
$0$
-truncated. This implies that also the
![]() $\mathbf {E}_1$
-group
$\mathbf {E}_1$
-group
![]() $G^{\hspace {.5pt}m}$
is
$G^{\hspace {.5pt}m}$
is
![]() $0$
-truncated, or equivalently, that it represents a functor taking values in ordinary groups.
$0$
-truncated, or equivalently, that it represents a functor taking values in ordinary groups.
Remark 4.31. Given
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
, we similarly have a classifying stack
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
, we similarly have a classifying stack
that represents the functor
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X} \to \operatorname {\mathrm {Grp}}_{\mathbf {E}_1}({\mathcal {S}})$
that to
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X} \to \operatorname {\mathrm {Grp}}_{\mathbf {E}_1}({\mathcal {S}})$
that to
![]() $j \colon X' \to X$
assigns the
$j \colon X' \to X$
assigns the
![]() $\mathbf {E}_1$
-group of automorphisms of
$\mathbf {E}_1$
-group of automorphisms of
![]() $j^*(\mathcal {F}) \in {\mathrm {QCoh}}(X')$
. Indeed, this functor descends along effective epimorphisms because
$j^*(\mathcal {F}) \in {\mathrm {QCoh}}(X')$
. Indeed, this functor descends along effective epimorphisms because
![]() ${\mathrm {QCoh}}(X)$
does so, and one may show that it is accessible.
${\mathrm {QCoh}}(X)$
does so, and one may show that it is accessible.
Remark 4.32. If
![]() $\mathcal {E} \in {\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
is a locally free
$\mathcal {E} \in {\mathrm {QCoh}}(X)^{\operatorname {\mathrm {loc}}}$
is a locally free
![]() $\mathcal {O}_X$
-module with corresponding vector bundle
$\mathcal {O}_X$
-module with corresponding vector bundle
![]() $V \simeq V_X(\mathcal {E}) \in \operatorname {\mathrm {Vect}}(X)$
, then the
$V \simeq V_X(\mathcal {E}) \in \operatorname {\mathrm {Vect}}(X)$
, then the
![]() $\mathbf {E}_1$
-group
$\mathbf {E}_1$
-group
represents the functor
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X} \to \operatorname {\mathrm {Grp}}_{\mathbf {E}_1}({\mathcal {S}})$
that to the map
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X} \to \operatorname {\mathrm {Grp}}_{\mathbf {E}_1}({\mathcal {S}})$
that to the map
![]() $j \colon X' \to X$
assigns the
$j \colon X' \to X$
assigns the
![]() $\mathbf {E}_1$
-group of automorphisms of
$\mathbf {E}_1$
-group of automorphisms of
![]() $j^*(V) \in \operatorname {\mathrm {Vect}}(X')$
.
$j^*(V) \in \operatorname {\mathrm {Vect}}(X')$
.
Let
![]() $q \colon Y \to X$
be a formal hyperplane pointed by
$q \colon Y \to X$
be a formal hyperplane pointed by
![]() $\eta \colon X \to Y$
. Taking the tangent space at
$\eta \colon X \to Y$
. Taking the tangent space at
![]() $\eta $
defines a map of classifying stacks for automorphisms
$\eta $
defines a map of classifying stacks for automorphisms
that to an automorphism f assigns its derivative
![]() $df_{\eta }$
at
$df_{\eta }$
at
![]() $\eta $
.
$\eta $
.
Lemma 4.33. The derivative at
![]() $\eta $
factors through an equivalence
$\eta $
factors through an equivalence
Proof. We must show that the induced map of functors represented by the map in the statement is an equivalence pointwise for all
![]() $j \colon X' \to X$
. It will suffice to consider the case where
$j \colon X' \to X$
. It will suffice to consider the case where
![]() $X' \simeq \operatorname {\mathrm {Spec}}(A)$
is affine. Indeed, we show in Appendix A that the Yoneda embedding extends to an equivalence
$X' \simeq \operatorname {\mathrm {Spec}}(A)$
is affine. Indeed, we show in Appendix A that the Yoneda embedding extends to an equivalence
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{/X}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. In this case, the statement follows from the well-known fact that the map
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{/X}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
. In this case, the statement follows from the well-known fact that the map
that to an A-algebra
![]() $q_1 \colon A \to B$
augmented by
$q_1 \colon A \to B$
augmented by
![]() $\eta _1 \colon B \to A$
assigns the cokernel of
$\eta _1 \colon B \to A$
assigns the cokernel of
![]() $q_1$
is an equivalence of categories.
$q_1$
is an equivalence of categories.
Lemma 4.34. For all
![]() $m \geq 2$
, the following hold:
$m \geq 2$
, the following hold:
-
(1) The canonical map
 $G^{\hspace {.5pt}m} \to G^{\hspace {.5pt}m-1}$
is an effective epimorphism.
$G^{\hspace {.5pt}m} \to G^{\hspace {.5pt}m-1}$
is an effective epimorphism. -
(2) If
 $j \colon X' \to X$
has
$j \colon X' \to X$
has
 $X' \simeq \operatorname {\mathrm {Spec}}(A)$
affine, then with
$X' \simeq \operatorname {\mathrm {Spec}}(A)$
affine, then with $$ \begin{align*}\ker(G^{\hspace{.5pt}m} \to G^{\hspace{.5pt}m-1})(X' \to X) \simeq \operatorname{\mathrm{Hom}}_A(P,\operatorname{\mathrm{Sym}}_A^m(P))\end{align*} $$
$$ \begin{align*}\ker(G^{\hspace{.5pt}m} \to G^{\hspace{.5pt}m-1})(X' \to X) \simeq \operatorname{\mathrm{Hom}}_A(P,\operatorname{\mathrm{Sym}}_A^m(P))\end{align*} $$
 $P \simeq \mathcal {N}_{Y/X}(X' \to X)$
. In particular, the kernel is an abelian group.
$P \simeq \mathcal {N}_{Y/X}(X' \to X)$
. In particular, the kernel is an abelian group.
Proof. (1) We claim that the map is a
![]() $\pi _0$
-surjection pointwise for every
$\pi _0$
-surjection pointwise for every
![]() $j \colon X' \to X$
with
$j \colon X' \to X$
with
![]() $X'$
affine. Granting this, the lemma follows because the Yoneda embedding extends to an equivalence
$X'$
affine. Granting this, the lemma follows because the Yoneda embedding extends to an equivalence
![]() $\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{/X}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
by Appendix A. To prove the claim, we write
$\operatorname {\mathrm {Shv}}({\mathrm {Aff}}_{/X}) \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X}$
by Appendix A. To prove the claim, we write
![]() $X' \simeq \operatorname {\mathrm {Spec}}(A)$
and
$X' \simeq \operatorname {\mathrm {Spec}}(A)$
and
![]() $Y' \simeq \operatorname {\mathrm {Spf}}(\operatorname {\mathrm {Sym}}_A(P))$
for some finitely generated projective A-module P. We let
$Y' \simeq \operatorname {\mathrm {Spf}}(\operatorname {\mathrm {Sym}}_A(P))$
for some finitely generated projective A-module P. We let
![]() $q \colon A \to \operatorname {\mathrm {Sym}}_A(P)$
and
$q \colon A \to \operatorname {\mathrm {Sym}}_A(P)$
and
![]() $\eta \colon \operatorname {\mathrm {Sym}}_A(P) \to A$
be the structure map and the augmentation, respectively, and let
$\eta \colon \operatorname {\mathrm {Sym}}_A(P) \to A$
be the structure map and the augmentation, respectively, and let
![]() $I \subset \operatorname {\mathrm {Sym}}_A(P)$
be the augmentation ideal. We wish to prove that the canonical map
$I \subset \operatorname {\mathrm {Sym}}_A(P)$
be the augmentation ideal. We wish to prove that the canonical map
is surjective. By the universal property of the symmetric algebra, an endomorphism of the augmented A-algebra
![]() $\operatorname {\mathrm {Sym}}_A(P)/I^{m+1}$
determines and is determined by an A-linear map
$\operatorname {\mathrm {Sym}}_A(P)/I^{m+1}$
determines and is determined by an A-linear map
![]() $P \to I/I^{m+1}$
. Since P is projective, any A-linear map
$P \to I/I^{m+1}$
. Since P is projective, any A-linear map
![]() $P \to I/I^m$
factors through the projection
$P \to I/I^m$
factors through the projection
![]() $I/I^{m+1} \to I/I^m$
, so
$I/I^{m+1} \to I/I^m$
, so
is surjective. But an endomorphism of the augmented A-algebra
![]() $\operatorname {\mathrm {Sym}}_A(P)/I^{m+1}$
is an automorphism if and only if the induced map of the associated graded for the I-adic filtration is an isomorphism if and only if the induced A-linear map
$\operatorname {\mathrm {Sym}}_A(P)/I^{m+1}$
is an automorphism if and only if the induced map of the associated graded for the I-adic filtration is an isomorphism if and only if the induced A-linear map
is an isomorphism. This proves the claim.
(2) The proof of (1) shows that
and
![]() $I^m/I^{m+1} \simeq \operatorname {\mathrm {Sym}}_A^m(P)$
, as we wanted to show.
$I^m/I^{m+1} \simeq \operatorname {\mathrm {Sym}}_A^m(P)$
, as we wanted to show.
We return to our purpose in this section of showing that the
![]() $\infty $
-category of pointed formal hyperplanes descends along effective epimorphisms.
$\infty $
-category of pointed formal hyperplanes descends along effective epimorphisms.
Lemma 4.35. If
![]() $f \colon S' \to S$
is a faithfully flat map of affine Dirac stacks, then
$f \colon S' \to S$
is a faithfully flat map of affine Dirac stacks, then

is a cartesian square of
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. By definition, pointed formal hyperplanes are preserved under base-change, so the square exists. Thus, to complete the proof, we must show that if
![]() $\sigma $
is a pointed Dirac stack over S, whose base-change
$\sigma $
is a pointed Dirac stack over S, whose base-change
![]() $\sigma '$
along
$\sigma '$
along
![]() $f \colon S' \to S$
is a pointed formal hyperplane, then
$f \colon S' \to S$
is a pointed formal hyperplane, then
![]() $\sigma $
is itself a pointed formal hyperplane. We write
$\sigma $
is itself a pointed formal hyperplane. We write
![]() $q \colon Y \to S$
and
$q \colon Y \to S$
and
![]() $\eta \colon S \to Y$
for the structure map and point of
$\eta \colon S \to Y$
for the structure map and point of
![]() $\sigma $
, and similarly for
$\sigma $
, and similarly for
![]() $\sigma '$
.
$\sigma '$
.
We claim that Y is formally complete along S. Indeed, the canonical map
is an equivalence because its base-change
along the effective epimorphism f is so. We also claim that
![]() $q_1 \colon S^{(1)} \to S$
is affine flat. Indeed, its base-change
$q_1 \colon S^{(1)} \to S$
is affine flat. Indeed, its base-change
![]() $q_1'$
along f is affine flat by Corollary 4.14, and the property of being affine flat descends along effective epimorphisms. Now, the cofiber
$q_1'$
along f is affine flat by Corollary 4.14, and the property of being affine flat descends along effective epimorphisms. Now, the cofiber
is a candidate for the conormal sheaf
![]() $\mathcal {N}_{S/Y}$
of
$\mathcal {N}_{S/Y}$
of
![]() $\sigma $
as in Definition 4.17, except that we do not yet know that
$\sigma $
as in Definition 4.17, except that we do not yet know that
![]() $\sigma $
is a pointed formal hyperplane. Since
$\sigma $
is a pointed formal hyperplane. Since
is a locally free
![]() $\mathcal {O}_{S'}$
-module of finite rank, and since the property of being locally free of finite rank descends along effective epimorphisms, we conclude that
$\mathcal {O}_{S'}$
-module of finite rank, and since the property of being locally free of finite rank descends along effective epimorphisms, we conclude that
![]() $\mathcal {E}$
is a locally free
$\mathcal {E}$
is a locally free
![]() $\mathcal {O}_S$
-module of finite rank.
$\mathcal {O}_S$
-module of finite rank.
To complete the proof, we will show that there exists an equivalence
of pointed Dirac stacks over S from the formal affine space associated with
![]() $\mathcal {E}$
pointed by the zero section
$\mathcal {E}$
pointed by the zero section
![]() $\zeta \colon S \to Z$
. Since both Y and Z are formally complete along S, it will suffice to show that there exists a compatible sequence of equivalences
$\zeta \colon S \to Z$
. Since both Y and Z are formally complete along S, it will suffice to show that there exists a compatible sequence of equivalences
for all
![]() $m \geq 0$
. The case
$m \geq 0$
. The case
![]() $m = 0$
is trivial, and the case
$m = 0$
is trivial, and the case
![]() $m = 1$
follows from the definition of
$m = 1$
follows from the definition of
![]() $\mathcal {E}$
. So we let
$\mathcal {E}$
. So we let
![]() $m \geq 2$
and show that an equivalence
$m \geq 2$
and show that an equivalence
![]() $h^{(m-1)}$
admits an extension to an equivalence
$h^{(m-1)}$
admits an extension to an equivalence
![]() $h^{(m)}$
. To this end, we let
$h^{(m)}$
. To this end, we let
![]() $\mathcal {F}^{\,m}$
be the sheaf on
$\mathcal {F}^{\,m}$
be the sheaf on
![]() ${\mathrm {Aff}}_{/S}^{\hspace {.5pt}\flat }$
that to
${\mathrm {Aff}}_{/S}^{\hspace {.5pt}\flat }$
that to
![]() $g \colon U \to S$
affine flat assigns the anima of diagrams
$g \colon U \to S$
affine flat assigns the anima of diagrams

with
![]() $h_U^{(m)}$
an equivalence. The sheaf
$h_U^{(m)}$
an equivalence. The sheaf
![]() $\mathcal {F}^{\,m}$
is naturally a torsor for the
$\mathcal {F}^{\,m}$
is naturally a torsor for the
![]() $\mathbf {E}_1$
-group
$\mathbf {E}_1$
-group
of automorphisms of
![]() $S_{\eta }^{(m)}$
that extend the identity on
$S_{\eta }^{(m)}$
that extend the identity on
![]() $S_{\eta }^{(m-1)}$
. The isomorphism classes of such torsors are parametrized by the sheaf cohomology group
$S_{\eta }^{(m-1)}$
. The isomorphism classes of such torsors are parametrized by the sheaf cohomology group
![]() $H^1(S,\mathcal {K}^{\hspace {.5pt}m})$
. But Lemma 4.34 identifies this group with a coherent cohomology group of the affine Dirac scheme S, and therefore, it is zero. Hence, the torsor
$H^1(S,\mathcal {K}^{\hspace {.5pt}m})$
. But Lemma 4.34 identifies this group with a coherent cohomology group of the affine Dirac scheme S, and therefore, it is zero. Hence, the torsor
![]() $\mathcal {F}^{\,m}$
is trivial, so it admits a global section, which is the desired equivalence
$\mathcal {F}^{\,m}$
is trivial, so it admits a global section, which is the desired equivalence
![]() $h^{(m)}$
.
$h^{(m)}$
.
Theorem 4.36. The functor
![]() $\operatorname {\mathrm {Hyp}}_{*} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to {\widehat {\mathrm {Cat}}}_{\infty }$
preserves small limits.
$\operatorname {\mathrm {Hyp}}_{*} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to {\widehat {\mathrm {Cat}}}_{\infty }$
preserves small limits.
Proof. Suppose that
![]() $X \simeq \varinjlim _{\alpha }X_{\alpha }$
is a colimit of a small diagram in
$X \simeq \varinjlim _{\alpha }X_{\alpha }$
is a colimit of a small diagram in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. We consider the diagram
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
. We consider the diagram

and wish to prove that the top horizontal map is an equivalence. We claim that the bottom horizontal map is an equivalence. By Theorem 2.21, the map
is an equivalence, so it suffices to show that the canonical map
is an equivalence, which follows from the adjunctions
Here, the bottom left-hand map is the inclusion of the (nonfull) subcategory spanned by the
![]() $\infty $
-categories that admit a final object and the maps that preserve final objects, and the top right-hand map is the inclusion of the full subcategory spanned by the pointed
$\infty $
-categories that admit a final object and the maps that preserve final objects, and the top right-hand map is the inclusion of the full subcategory spanned by the pointed
![]() $\infty $
-categories. The former is a right adjoint, by (the dual of) [Reference Lurie20, Corollary 5.3.6.10], and therefore, it preserves limits. Moreover, the latter admits a right adjoint that to an
$\infty $
-categories. The former is a right adjoint, by (the dual of) [Reference Lurie20, Corollary 5.3.6.10], and therefore, it preserves limits. Moreover, the latter admits a right adjoint that to an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
that admits a final object assigns the
$\mathcal {C}$
that admits a final object assigns the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}_* \simeq \mathcal {C}_{1/}$
of pointed objects in
$\mathcal {C}_* \simeq \mathcal {C}_{1/}$
of pointed objects in
![]() $\mathcal {C}$
. This proves the claim.
$\mathcal {C}$
. This proves the claim.
Now, in the diagram at the beginning of the proof, the vertical maps are fully faithful, so the claim shows that the top horizontal map is fully faithful. It remains to prove that it is essentially surjective. So we fix
![]() $\sigma \in (\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
such that
$\sigma \in (\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})_{/X})_*$
such that
![]() $i_{\alpha }^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(X_{\alpha })$
for all
$i_{\alpha }^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(X_{\alpha })$
for all
![]() $\alpha $
and proceed to show that
$\alpha $
and proceed to show that
![]() $\sigma \in \operatorname {\mathrm {Hyp}}_*(X)$
.
$\sigma \in \operatorname {\mathrm {Hyp}}_*(X)$
.
First, we consider the special case, where
![]() $T \simeq \coprod _{\alpha }T_{\alpha }$
is a finite coproduct of affine Dirac schemes. In this case, the desired statement follows from that the fact that for a locally free
$T \simeq \coprod _{\alpha }T_{\alpha }$
is a finite coproduct of affine Dirac schemes. In this case, the desired statement follows from that the fact that for a locally free
![]() $\mathcal {O}_T$
-module of finite rank
$\mathcal {O}_T$
-module of finite rank
![]() $\mathcal {E}$
, the
$\mathcal {E}$
, the
![]() $\mathcal {O}_{T_{\alpha }}$
-modules
$\mathcal {O}_{T_{\alpha }}$
-modules
![]() $\mathcal {E}_{\alpha } \simeq i_{\alpha }^*(\mathcal {E})$
are locally free of finite rank, and the diagram
$\mathcal {E}_{\alpha } \simeq i_{\alpha }^*(\mathcal {E})$
are locally free of finite rank, and the diagram

is cartesian with the horizontal maps equivalences.
Next, in the general case, we must show that for
![]() $\eta \colon S \to X$
with S affine,
$\eta \colon S \to X$
with S affine,
![]() $\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(S)$
. By Lemma 4.35, if suffices to show that there exists a faithfully flat map of affine Dirac schemes
$\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(S)$
. By Lemma 4.35, if suffices to show that there exists a faithfully flat map of affine Dirac schemes
![]() $g \colon T \to S$
such that
$g \colon T \to S$
such that
![]() $g^*\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(T)$
. To this end, we consider the canonical map of presheaves
$g^*\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(T)$
. To this end, we consider the canonical map of presheaves
It becomes an equivalence and therefore an effective epimorphism after sheafification, so it follows from Proposition B.6 that there exists a diagram of presheaves

with
![]() $(g_i \colon T_i \to S)_{i \in I}$
a finite covering family. Moreover, since colimits of presheaves are calculated pointwise, each
$(g_i \colon T_i \to S)_{i \in I}$
a finite covering family. Moreover, since colimits of presheaves are calculated pointwise, each
![]() $\tilde {\eta }_i$
factors through some
$\tilde {\eta }_i$
factors through some
![]() $\iota (X_{\alpha _i})$
, so
$\iota (X_{\alpha _i})$
, so
for all
![]() $i \in I$
. Now, the coproduct
$i \in I$
. Now, the coproduct
![]() $g \colon T \to S$
of the
$g \colon T \to S$
of the
![]() $g_i \colon T_i \to S$
is a faithfully flat map of affine Dirac schemes, and the special case that we considered above shows that
$g_i \colon T_i \to S$
is a faithfully flat map of affine Dirac schemes, and the special case that we considered above shows that
![]() $g^*\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(T)$
, as desired. This completes the proof.
$g^*\eta ^*(\sigma ) \in \operatorname {\mathrm {Hyp}}_*(T)$
, as desired. This completes the proof.
Corollary 4.37. If
![]() $f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then
$f \colon X' \to X$
is an effective epimorphism of Dirac stacks, then
is an equivalence of
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. This is a special case of Theorem 4.36.
Corollary 4.38. For every Dirac stack X,
![]() $\operatorname {\mathrm {Hyp}}_*(X)$
is essentially small.
$\operatorname {\mathrm {Hyp}}_*(X)$
is essentially small.
Proof. If
![]() $X \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then the cardinality of the set of equivalence classes of formal hyperplanes over X is equal, by Remark 4.16, to that of isomorphism classes of finitely generated projective graded R-modules, which is small. In general, we can write
$X \simeq \operatorname {\mathrm {Spec}}(R)$
is affine, then the cardinality of the set of equivalence classes of formal hyperplanes over X is equal, by Remark 4.16, to that of isomorphism classes of finitely generated projective graded R-modules, which is small. In general, we can write
![]() $X \simeq \varinjlim X_{\alpha }$
as a small colimit of affine Dirac schemes, and since
$X \simeq \varinjlim X_{\alpha }$
as a small colimit of affine Dirac schemes, and since
![]() $\operatorname {\mathrm {Hyp}}_{*}(X) \simeq \varprojlim \operatorname {\mathrm {Hyp}}_{*}(X_{\alpha })$
by Theorem 4.36, the corollary follows.
$\operatorname {\mathrm {Hyp}}_{*}(X) \simeq \varprojlim \operatorname {\mathrm {Hyp}}_{*}(X_{\alpha })$
by Theorem 4.36, the corollary follows.
4.4 Formal groups
In this section, we define the groupoid of formal groups over a Dirac stack and show that it descends along effective epimorphisms.
Definition 4.39. Let
![]() $\operatorname {\mathrm {Lat}}$
be the category of finitely generated free abelian groups. If
$\operatorname {\mathrm {Lat}}$
be the category of finitely generated free abelian groups. If
![]() $\mathcal {C}$
is an
$\mathcal {C}$
is an
![]() $\infty $
-category, which admits finite products, then the
$\infty $
-category, which admits finite products, then the
![]() $\infty $
-category of abelian group objects in
$\infty $
-category of abelian group objects in
![]() $\mathcal {C}$
is the full subcategory
$\mathcal {C}$
is the full subcategory
spanned by the functors that preserve finite products.
Remark 4.40. We note that the full subcategory
![]() $\operatorname {\mathrm {Ab}}(\mathcal {C}) \subset \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Lat}}^{\mathrm {op}}, \mathcal {C})$
is closed under sifted colimits and limits by [Reference Lurie20, Proposition 5.5.8.10]. Therefore, it follows from [Reference Lurie20, Corollary 5.1.2.3] that small limits and small sifted colimits in
$\operatorname {\mathrm {Ab}}(\mathcal {C}) \subset \operatorname {\mathrm {Fun}}(\operatorname {\mathrm {Lat}}^{\mathrm {op}}, \mathcal {C})$
is closed under sifted colimits and limits by [Reference Lurie20, Proposition 5.5.8.10]. Therefore, it follows from [Reference Lurie20, Corollary 5.1.2.3] that small limits and small sifted colimits in
![]() $\operatorname {\mathrm {Ab}}(\mathcal {C})$
are calculated pointwise.
$\operatorname {\mathrm {Ab}}(\mathcal {C})$
are calculated pointwise.
By Corollary 4.38, the functor
![]() $\operatorname {\mathrm {Hyp}}_*$
takes values in the
$\operatorname {\mathrm {Hyp}}_*$
takes values in the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Cat}}_{\infty }$
of small
$\operatorname {\mathrm {Cat}}_{\infty }$
of small
![]() $\infty $
-categories. In fact, it takes values in the subcategory
$\infty $
-categories. In fact, it takes values in the subcategory
![]() $\operatorname {\mathrm {Cat}}_{\infty }^{\Pi } \subset \operatorname {\mathrm {Cat}}_{\infty }$
spanned by the
$\operatorname {\mathrm {Cat}}_{\infty }^{\Pi } \subset \operatorname {\mathrm {Cat}}_{\infty }$
spanned by the
![]() $\infty $
-categories that admit finite products and the finite product preserving functors, and hence, we may compose it with the functor
$\infty $
-categories that admit finite products and the finite product preserving functors, and hence, we may compose it with the functor
that to
![]() $\mathcal {C}$
assigns
$\mathcal {C}$
assigns
![]() $\operatorname {\mathrm {Ab}}(\mathcal {C}) \simeq \operatorname {\mathrm {Fun}}^{\Sigma }(\operatorname {\mathrm {Lat}}^{\mathrm {op}},\mathcal {C})$
.
$\operatorname {\mathrm {Ab}}(\mathcal {C}) \simeq \operatorname {\mathrm {Fun}}^{\Sigma }(\operatorname {\mathrm {Lat}}^{\mathrm {op}},\mathcal {C})$
.
Definition 4.41 (Formal groups).
The functor that to a Dirac stack X assigns the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {FGroup}}(X)$
of formal groups over X is the composite functor
$\operatorname {\mathrm {FGroup}}(X)$
of formal groups over X is the composite functor
Example 4.42 (Formal additive groups).
Let X be a Dirac stack and let
![]() $\mathcal {E}$
be a locally free
$\mathcal {E}$
be a locally free
![]() $\mathcal {O}_X$
-module of finite rank. The functor
$\mathcal {O}_X$
-module of finite rank. The functor
![]() $\smash { {\hat {\mathbb {G}}_a}(\mathcal {E}) \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X) }$
that to L assigns
$\smash { {\hat {\mathbb {G}}_a}(\mathcal {E}) \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X) }$
that to L assigns
![]() $q_L \colon {\hat {\mathbb {A}}}_X(L \otimes _{\mathbb {Z}} \mathcal {E}) \to X$
is a formal group over X, which we call the formal additive group associated with
$q_L \colon {\hat {\mathbb {A}}}_X(L \otimes _{\mathbb {Z}} \mathcal {E}) \to X$
is a formal group over X, which we call the formal additive group associated with
![]() $\mathcal {E}$
. Its dimension is equal to the rank of
$\mathcal {E}$
. Its dimension is equal to the rank of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Proposition 4.43. The functor
![]() $\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
takes small colimits of Dirac stacks to limits of
$\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
takes small colimits of Dirac stacks to limits of
![]() $\infty $
-categories.
$\infty $
-categories.
Proof. Indeed, this is a consequence of Theorem 4.36 and from the fact, which is proved in (the dual of) [Reference Lurie20, Corollary 5.3.6.10], that
![]() $\operatorname {\mathrm {Cat}}_{\infty }^{\Pi } \subset \operatorname {\mathrm {Cat}}_{\infty }$
is closed under limits.
$\operatorname {\mathrm {Cat}}_{\infty }^{\Pi } \subset \operatorname {\mathrm {Cat}}_{\infty }$
is closed under limits.
Remark 4.44 (Formal groups and formal group laws).
We spell out the definition of a formal group in more concrete terms. So let
![]() $\mathcal {G} \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X)$
be a formal group over X and let
$\mathcal {G} \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X)$
be a formal group over X and let
![]() $q \colon Y \to X$
be its underlying formal hyperplane
$q \colon Y \to X$
be its underlying formal hyperplane
![]() $\mathcal {G}(\mathbb {Z})$
. The canonical inclusions
$\mathcal {G}(\mathbb {Z})$
. The canonical inclusions
![]() $\mathbb {Z} \to \mathbb {Z} \oplus \mathbb {Z}$
induce an equivalence
$\mathbb {Z} \to \mathbb {Z} \oplus \mathbb {Z}$
induce an equivalence
and a composition of an inverse of this equivalence and the map induced by the diagonal map
![]() $\mathbb {Z} \to \mathbb {Z} \oplus \mathbb {Z}$
defines the addition
$\mathbb {Z} \to \mathbb {Z} \oplus \mathbb {Z}$
defines the addition
in the formal group. Similarly, the unique map
![]() $\mathbb {Z} \to 0$
defines the zero section
$\mathbb {Z} \to 0$
defines the zero section
Conversely, a formal hyperplane
![]() $q \colon Y \to X$
together with maps
$q \colon Y \to X$
together with maps
![]() $+ \colon Y \times _XY \to Y$
and
$+ \colon Y \times _XY \to Y$
and
![]() $\eta \colon X \to Y$
satisfying the abelian group axioms determine a formal group
$\eta \colon X \to Y$
satisfying the abelian group axioms determine a formal group
![]() $\mathcal {G} \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X)$
, which is unique up to contractible choice.
$\mathcal {G} \colon \operatorname {\mathrm {Lat}}^{\mathrm {op}} \to \operatorname {\mathrm {Hyp}}(X)$
, which is unique up to contractible choice.
Suppose that
![]() $X \simeq \operatorname {\mathrm {Spec}}(R)$
and
$X \simeq \operatorname {\mathrm {Spec}}(R)$
and
![]() $Y \simeq \operatorname {\mathrm {Spf}}(A)$
with
$Y \simeq \operatorname {\mathrm {Spf}}(A)$
with
![]() $I \subset A$
the ideal that defines the zero section
$I \subset A$
the ideal that defines the zero section
![]() $\eta \colon X \to Y$
. The map
$\eta \colon X \to Y$
. The map
![]() $+ \colon Y \times _XY \to Y$
is a point of the anima
$+ \colon Y \times _XY \to Y$
is a point of the anima
which is
![]() $0$
-truncated. Moreover, Zariski locally on X, we may choose homogeneous coordinates
$0$
-truncated. Moreover, Zariski locally on X, we may choose homogeneous coordinates
![]() $x_1,\dots ,x_d \in A$
such that the family
$x_1,\dots ,x_d \in A$
such that the family
![]() $(x_1,\dots ,x_d)$
generates
$(x_1,\dots ,x_d)$
generates
![]() $I \subset A$
and such that the family
$I \subset A$
and such that the family
![]() $(x_1+I^2,\dots ,x_d+I^2)$
is a basis of the R-module
$(x_1+I^2,\dots ,x_d+I^2)$
is a basis of the R-module
![]() $I/I^2$
. In terms of these coordinates, the map
$I/I^2$
. In terms of these coordinates, the map
![]() $+ \colon Y \times _XY \to Y$
determines and is determined by a family
$+ \colon Y \times _XY \to Y$
determines and is determined by a family
![]() $f(y,z) = (f_s(y,z))$
of d power series in
$f(y,z) = (f_s(y,z))$
of d power series in
![]() $2d$
variables,
$2d$
variables,
such that
Moreover, the map
![]() $+ \colon Y \times _XY \to Y$
defines a structure of formal group on the formal hyperplane
$+ \colon Y \times _XY \to Y$
defines a structure of formal group on the formal hyperplane
![]() $q \colon Y \to X$
with zero section
$q \colon Y \to X$
with zero section
![]() $\eta \colon X \to Y$
defined by
$\eta \colon X \to Y$
defined by
![]() $I \subset A$
if and only if the following identities among families of power series hold.
$I \subset A$
if and only if the following identities among families of power series hold.
-
(a)
 $f(x,0) = x = f(0,x)$
$f(x,0) = x = f(0,x)$
-
(b)
 $f(f(x,y),z) = f(x,f(y,z))$
$f(f(x,y),z) = f(x,f(y,z))$
-
(c)
 $f(x,y) = f(y,x)$
$f(x,y) = f(y,x)$
A family of power series satisfying these conditions is classically known as a formal group law; the above discussion implies that any formal group is locally described (in a noncanonical way) by a formal group law.
We remark that the above three axioms imply the existence and uniqueness of an inverse with respect to addition. Indeed, a map
![]() $- \colon Y \to Y$
determines and is determined by a family
$- \colon Y \to Y$
determines and is determined by a family
![]() $i(x) = (i_s(x))$
of d power series in d variables,
$i(x) = (i_s(x))$
of d power series in d variables,
such that
![]() $\deg (i_s) = \deg (x_s)$
, and the map
$\deg (i_s) = \deg (x_s)$
, and the map
![]() $- \colon Y \to Y$
is an inverse with respect to addition if and only if the following identity holds.
$- \colon Y \to Y$
is an inverse with respect to addition if and only if the following identity holds.
-
(d)
 $f(x,i(x)) = 0 = f(i(x),x)$
$f(x,i(x)) = 0 = f(i(x),x)$
But it follows from (a) that this system of equations admits a unique solution.
Example 4.45. Let R be a Dirac ring and let M be a free R-module. If we choose a basis
![]() $(x_1,\dots ,x_d)$
of M that consists of homogeneous elements, then the additive formal group
$(x_1,\dots ,x_d)$
of M that consists of homogeneous elements, then the additive formal group
![]() ${\hat {\mathbb {G}}_a}(M)$
associated with M determines and is determined by the family of power series
${\hat {\mathbb {G}}_a}(M)$
associated with M determines and is determined by the family of power series
![]() $f(y,z) = y + z$
with
$f(y,z) = y + z$
with
![]() $f_s(y,z) = y_s+z_s$
.
$f_s(y,z) = y_s+z_s$
.
Definition 4.46. Let X be a Dirac stack. The Lie algebra is the functor
that to a formal group
![]() $\mathcal {G}$
assigns the tangent space
$\mathcal {G}$
assigns the tangent space
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G}) \simeq T_{Y/X,\eta }$
of its underlying formal hyperplane
$\operatorname {\mathrm {Lie}}(\mathcal {G}) \simeq T_{Y/X,\eta }$
of its underlying formal hyperplane
![]() $q \colon Y \to X$
at the zero section
$q \colon Y \to X$
at the zero section
![]() $\eta \colon X \to Y$
.
$\eta \colon X \to Y$
.
Since
![]() $\mathcal {G}$
is abelian, it serves no purpose to define a Lie bracket on the vector bundle
$\mathcal {G}$
is abelian, it serves no purpose to define a Lie bracket on the vector bundle
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G})$
because it will turn out to be zero.
$\operatorname {\mathrm {Lie}}(\mathcal {G})$
because it will turn out to be zero.
The functor
![]() $\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
classifies a cartesian fibration
$\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
classifies a cartesian fibration
and we refer to its domain, which by abuse of notation we also denote by
![]() $\operatorname {\mathrm {FGroup}}$
, as the
$\operatorname {\mathrm {FGroup}}$
, as the
![]() $\infty $
-category of formal groups. Its objects are formal groups
$\infty $
-category of formal groups. Its objects are formal groups
![]() $\mathcal {G}$
over varying base Dirac stacks. A map
$\mathcal {G}$
over varying base Dirac stacks. A map
![]() $f \colon \mathcal {G}' \to \mathcal {G}$
in
$f \colon \mathcal {G}' \to \mathcal {G}$
in
![]() $\operatorname {\mathrm {FGroup}}$
determines a diagram
$\operatorname {\mathrm {FGroup}}$
determines a diagram

in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, where q and
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
, where q and
![]() $q'$
are the underlying formal hyperplanes of
$q'$
are the underlying formal hyperplanes of
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {G}'$
, respectively, and the map f is p-cartesian if and only if this diagram of Dirac stacks is cartesian. We recall that a functor
$\mathcal {G}'$
, respectively, and the map f is p-cartesian if and only if this diagram of Dirac stacks is cartesian. We recall that a functor
![]() $\mathcal {G} \colon K \to \operatorname {\mathrm {FGroup}}$
is said to be cartesian if it takes every map
$\mathcal {G} \colon K \to \operatorname {\mathrm {FGroup}}$
is said to be cartesian if it takes every map
![]() $\alpha \colon k' \to k$
in K to a cartesian map in
$\alpha \colon k' \to k$
in K to a cartesian map in
![]() $\operatorname {\mathrm {FGroup}}$
.
$\operatorname {\mathrm {FGroup}}$
.
Proposition 4.47. Let
![]() $\mathcal {G} \colon K \to \operatorname {\mathrm {FGroup}}$
be a cartesian diagram in the
$\mathcal {G} \colon K \to \operatorname {\mathrm {FGroup}}$
be a cartesian diagram in the
![]() $\infty $
-category of formal groups. There exists an essentially unique pair of a cartesian diagram
$\infty $
-category of formal groups. There exists an essentially unique pair of a cartesian diagram
and an equivalence
![]() $\bar {\mathcal {G}}|_K \simeq \mathcal {G}$
. Moreover, the diagram
$\bar {\mathcal {G}}|_K \simeq \mathcal {G}$
. Moreover, the diagram
![]() $\bar {\mathcal {G}}(\mathbb {Z}) \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\Delta ^1}$
of underlying formal hyperplanes is a colimit diagram.
$\bar {\mathcal {G}}(\mathbb {Z}) \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\Delta ^1}$
of underlying formal hyperplanes is a colimit diagram.
Proof. We consider the following diagram of
![]() $\infty $
-categories:
$\infty $
-categories:

where
![]() $p_K$
is the base-change of p along
$p_K$
is the base-change of p along
![]() $X \simeq p \circ \mathcal {G}$
. Since p is a cartesian fibration, so is
$X \simeq p \circ \mathcal {G}$
. Since p is a cartesian fibration, so is
![]() $p_K$
, and since
$p_K$
, and since
![]() $\mathcal {G}$
is a cartesian functor, so is the induced section
$\mathcal {G}$
is a cartesian functor, so is the induced section
![]() $\mathcal {G}_K$
of
$\mathcal {G}_K$
of
![]() $p_K$
. We fix a pair of a colimit diagram
$p_K$
. We fix a pair of a colimit diagram
![]() $\bar {X} \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
and an equivalence
$\bar {X} \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
and an equivalence
![]() $\bar {X}|_K \simeq X$
and consider the diagram
$\bar {X}|_K \simeq X$
and consider the diagram

where
![]() $p_{K^{\triangleright }}$
is the base-change of p along
$p_{K^{\triangleright }}$
is the base-change of p along
![]() $\bar {X}$
. We proved in Proposition 4.43 that the functor
$\bar {X}$
. We proved in Proposition 4.43 that the functor
![]() $\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
takes colimits of Dirac stacks to limits of
$\operatorname {\mathrm {FGroup}} \colon \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\mathrm {op}} \to \operatorname {\mathrm {Cat}}_{\infty }$
takes colimits of Dirac stacks to limits of
![]() $\infty $
-categories. Therefore, it follows from [Reference Lurie20, Proposition 3.3.3.1] that a cartesian section
$\infty $
-categories. Therefore, it follows from [Reference Lurie20, Proposition 3.3.3.1] that a cartesian section
![]() $\mathcal {G}_K$
of
$\mathcal {G}_K$
of
![]() $p_K$
extends essentially uniquely to a cartesian section
$p_K$
extends essentially uniquely to a cartesian section
![]() $\mathcal {G}_{K^{\triangleright }}$
of
$\mathcal {G}_{K^{\triangleright }}$
of
![]() $p_{K^{\triangleright }}$
. This determines a cartesian functor
$p_{K^{\triangleright }}$
. This determines a cartesian functor
![]() $\smash { \bar {\mathcal {G}} \colon K^{\triangleright } \to \operatorname {\mathrm {FGroup}} }$
and an equivalence
$\smash { \bar {\mathcal {G}} \colon K^{\triangleright } \to \operatorname {\mathrm {FGroup}} }$
and an equivalence
![]() $\smash { \bar {\mathcal {G}}|_K \simeq \mathcal {G} }$
, as desired.
$\smash { \bar {\mathcal {G}}|_K \simeq \mathcal {G} }$
, as desired.
It remains to prove that
![]() $\bar {\mathcal {G}}(\mathbb {Z}) \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\Delta ^1}$
is a colimit diagram. Let us write
$\bar {\mathcal {G}}(\mathbb {Z}) \colon K^{\triangleright } \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})^{\Delta ^1}$
is a colimit diagram. Let us write
![]() $q_k \colon Y_k \to X_k$
for the value of
$q_k \colon Y_k \to X_k$
for the value of
![]() $\bar {\mathcal {G}}(\mathbb {Z})$
at
$\bar {\mathcal {G}}(\mathbb {Z})$
at
![]() $k \in K^{\triangleright }$
and let
$k \in K^{\triangleright }$
and let
![]() $\infty \in K^{\triangleright }$
be the cone point. Since
$\infty \in K^{\triangleright }$
be the cone point. Since
![]() $\bar {\mathcal {G}} \colon K^{\triangleright } \to \operatorname {\mathrm {FGroup}}$
is a cartesian functor, the diagram
$\bar {\mathcal {G}} \colon K^{\triangleright } \to \operatorname {\mathrm {FGroup}}$
is a cartesian functor, the diagram

is cartesian, for all
![]() $k \in K$
, and since colimits in
$k \in K$
, and since colimits in
![]() $\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal, so is
$\operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
are universal, so is

But the lower horizontal map is an equivalence, and hence, so is the top horizontal map.
5 Stable homotopy theory
The purpose of this final section is to demonstrate that Dirac geometry is the natural geometric framework in which to formulate various statements in stable homotopy theory.
5.1 The descent spectral sequence
Suppose that
![]() $\eta \colon k \to E$
is a map of commutative algebras in spectra.Footnote
6
We may form the augmented cosimplicial object in the
$\eta \colon k \to E$
is a map of commutative algebras in spectra.Footnote
6
We may form the augmented cosimplicial object in the
![]() $\infty $
-category of k-modules in spectra
$\infty $
-category of k-modules in spectra
which is known as the cobar construction of
![]() $\eta $
. We recall that
$\eta $
. We recall that
![]() $[n] = \{0,1,\dots ,n\}$
so that
$[n] = \{0,1,\dots ,n\}$
so that
![]() $E^{\otimes _k[n]}$
is an
$E^{\otimes _k[n]}$
is an
![]() $(n+1)$
-fold tensor power of E over k. Given a k-module in spectra V, the restriction
$(n+1)$
-fold tensor power of E over k. Given a k-module in spectra V, the restriction
along the inclusion
![]() $\Delta \subset \Delta _+$
is known as the
$\Delta \subset \Delta _+$
is known as the
![]() $\eta $
-nilpotent completion of V. It is typically not a particularly well-behaved operation, but it has the advantage that its target can be analyzed by means of the descent spectral sequence, which we now explain.
$\eta $
-nilpotent completion of V. It is typically not a particularly well-behaved operation, but it has the advantage that its target can be analyzed by means of the descent spectral sequence, which we now explain.
We let
![]() $\Delta ^{\leq n} \subset \Delta $
be the full subcategory spanned by the objects
$\Delta ^{\leq n} \subset \Delta $
be the full subcategory spanned by the objects
![]() $[m]$
with
$[m]$
with
![]() $m \leq n$
and recall that Lurie’s
$m \leq n$
and recall that Lurie’s
![]() $\infty $
-categorical Dold–Kan correspondence
$\infty $
-categorical Dold–Kan correspondence
from [Reference Lurie19, Theorem 1.2.4.1] takes the cosimplicial k-module in spectra
![]() $V \otimes _kE^{\otimes _k[-]}$
to the filtered k-module in spectra
$V \otimes _kE^{\otimes _k[-]}$
to the filtered k-module in spectra
![]() $\operatorname {\mathrm {Fil}}_{\eta }(V)$
that to n assigns
$\operatorname {\mathrm {Fil}}_{\eta }(V)$
that to n assigns
The descent spectral sequence is the associated spectral sequence
which converges conditionally in the sense of Boardman [Reference Boardman3] to the homotopy groups of the
![]() $\eta $
-nilpotent completion of V. We recall the following result concerning the convergence of the descent spectral sequence.
$\eta $
-nilpotent completion of V. We recall the following result concerning the convergence of the descent spectral sequence.
Lemma 5.1. Let
![]() $\eta \colon k \to E$
be a map of commutative algebra in spectra, let I be the k-module in spectra given by the fiber of
$\eta \colon k \to E$
be a map of commutative algebra in spectra, let I be the k-module in spectra given by the fiber of
![]() $\eta $
and let V be any k-module in spectra. In this situation, there is a fiber sequence of k-modules in spectra
$\eta $
and let V be any k-module in spectra. In this situation, there is a fiber sequence of k-modules in spectra
for all
![]() $n \geq 0$
. In particular, if k is connective,
$n \geq 0$
. In particular, if k is connective,
![]() $\eta$
is 1-connective and V is right bounded, then the completion map
$\eta$
is 1-connective and V is right bounded, then the completion map
![]() $V \to \widehat {V}$
is an equivalence.
$V \to \widehat {V}$
is an equivalence.
Proof. This is proved in [Reference Mathew, Nauman and Noel26, Proposition 2.14].
The proof of the
![]() $\infty $
-categorical Dold–Kan correspondence identifies
$\infty $
-categorical Dold–Kan correspondence identifies
with the normalized cochain complex associated with the cosimplicial
![]() $\pi _0(k)$
-module
$\pi _0(k)$
-module
![]() $\smash { \pi _j(V \otimes _kE^{\otimes _k[-]}) }$
. It follows that the descent spectral sequence takes the form
$\smash { \pi _j(V \otimes _kE^{\otimes _k[-]}) }$
. It follows that the descent spectral sequence takes the form
and we proceed to identify the
![]() $E^2$
-term in Dirac geometric terms.
$E^2$
-term in Dirac geometric terms.
The map
![]() $\eta \colon k \to E$
of commutative algebra in spectra gives rise to the groupoid
$\eta \colon k \to E$
of commutative algebra in spectra gives rise to the groupoid
in affine Dirac schemes, so we may form the Dirac stack given by the colimit
in Dirac stacks. We henceforth assume that the groupoid S has flat face maps so that, by Theorem 2.49, the Dirac stack X is geometric.Footnote 7
Construction 5.2. In this situation, we define a pair
![]() $(\mathcal {F},\partial )$
of a functor
$(\mathcal {F},\partial )$
of a functor
that to a k-module in spectra V assigns a quasi-coherent
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {F}(V)$
and a natural isomorphism of quasi-coherent
$\mathcal {F}(V)$
and a natural isomorphism of quasi-coherent
![]() $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
which is a homology theory in the sense of [Reference Patchkoria and Pstrągowski30, Definition 2.8]. To this end, we let
be the cartesian fibration classified by the functor
![]() $\operatorname {\mathrm {Aff}}^{\mathrm {op}} \to {\widehat {\mathrm {Cat}}}_{\infty }$
that to an affine Dirac scheme T assigns the abelian category
$\operatorname {\mathrm {Aff}}^{\mathrm {op}} \to {\widehat {\mathrm {Cat}}}_{\infty }$
that to an affine Dirac scheme T assigns the abelian category
![]() ${\mathrm {QCoh}}(T)^{\heartsuit }$
. Now, we have a lift
${\mathrm {QCoh}}(T)^{\heartsuit }$
. Now, we have a lift

defined by
and it takes injective maps in
![]() $\Delta $
to p-cartesian maps in
$\Delta $
to p-cartesian maps in
![]() ${\mathrm {QCoh}}^{\heartsuit }$
by the assumption that S takes injective maps in
${\mathrm {QCoh}}^{\heartsuit }$
by the assumption that S takes injective maps in
![]() $\Delta $
to flat maps in
$\Delta $
to flat maps in
![]() $\operatorname {\mathrm {Aff}}$
. So let
$\operatorname {\mathrm {Aff}}$
. So let
![]() $\Delta _s \subset \Delta $
be the subcategory spanned by the injective maps. It follows from Corollary 3.26 and by [Reference Lurie20, Corollary 3.3.3.2] that the canonical maps
$\Delta _s \subset \Delta $
be the subcategory spanned by the injective maps. It follows from Corollary 3.26 and by [Reference Lurie20, Corollary 3.3.3.2] that the canonical maps
are equivalences and from Theorem 3.27 that the composite map restricts to an equivalence
By [Reference Lurie20, Corollary 3.3.3.2], the cartesian lift
![]() $\widetilde {S}(V)$
defines a point on the right-hand side, and we define
$\widetilde {S}(V)$
defines a point on the right-hand side, and we define
![]() $\mathcal {F}(V) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
to be the essentially unique corresponding point on the left-hand side.
$\mathcal {F}(V) \in {\mathrm {QCoh}}(X)^{\heartsuit }$
to be the essentially unique corresponding point on the left-hand side.
It is clear that the cartesian lift
![]() $\widetilde {S}(V)$
– and hence, the point
$\widetilde {S}(V)$
– and hence, the point
![]() $\mathcal {F}(V)$
– is functorial in V, so we obtain the desired functor
$\mathcal {F}(V)$
– is functorial in V, so we obtain the desired functor
![]() $\mathcal {F}$
. Moreover, the natural isomorphism
$\mathcal {F}$
. Moreover, the natural isomorphism
from [Reference Hesselholt and Pstrągowski12, Example 2.4] induces the natural isomorphism ![]() .
.
Remark 5.3. Let
![]() $\eta \colon k \to E$
be a map of commutative algebras in spectra with the property that the groupoid
$\eta \colon k \to E$
be a map of commutative algebras in spectra with the property that the groupoid
![]() $S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps and let
$S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps and let
![]() $X \simeq |S|$
. Since
$X \simeq |S|$
. Since
![]() $f_n \colon S_n \to X$
is a submersion, Theorem 3.27 implies that
$f_n \colon S_n \to X$
is a submersion, Theorem 3.27 implies that
![]() $f_n^*$
is t-exact, so we may consider the composition
$f_n^*$
is t-exact, so we may consider the composition
We note that the definition of
![]() $\mathcal {F}$
in Construction 5.2 provides an equivalence between this composite functor and the functor that to V assigns
$\mathcal {F}$
in Construction 5.2 provides an equivalence between this composite functor and the functor that to V assigns
![]() $\pi _*(V \otimes _kE^{\otimes _k[n]})$
.
$\pi _*(V \otimes _kE^{\otimes _k[n]})$
.
Definition 5.4. Let
![]() $\eta \colon k \to E$
be a map of commutative algebras in spectra such that the groupoid
$\eta \colon k \to E$
be a map of commutative algebras in spectra such that the groupoid
![]() $S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps. The homology theory associated with
$S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps. The homology theory associated with
![]() $\eta $
is the pair
$\eta $
is the pair
![]() $(\mathcal {F},\partial )$
defined in Construction 5.2.
$(\mathcal {F},\partial )$
defined in Construction 5.2.
Theorem 5.5. Let
![]() $\eta \colon k \to E$
be a map of commutative algebras in spectra such that the groupoid in affine Dirac schemes
$\eta \colon k \to E$
be a map of commutative algebras in spectra such that the groupoid in affine Dirac schemes
![]() $S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps and let
$S \simeq \operatorname {\mathrm {Spec}}(\pi _*(E^{\otimes _k[-]}))$
has flat face maps and let
![]() $X \simeq |S|$
be the geometric Dirac stack given by its geometric realization. The descent spectral sequence for a k-module in spectra V takes the form
$X \simeq |S|$
be the geometric Dirac stack given by its geometric realization. The descent spectral sequence for a k-module in spectra V takes the form
where
![]() $(\mathcal {F},\partial )$
is the homology theory associated with
$(\mathcal {F},\partial )$
is the homology theory associated with
![]() $\eta $
.
$\eta $
.
Proof. Let
![]() $p \colon X \to 1$
be the unique map to the final Dirac stack
$p \colon X \to 1$
be the unique map to the final Dirac stack
![]() $1 \simeq \operatorname {\mathrm {Spec}}(\mathbb {Z})$
. The coherent cohomology of any
$1 \simeq \operatorname {\mathrm {Spec}}(\mathbb {Z})$
. The coherent cohomology of any
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)$
is defined by
$\mathcal {F} \in {\mathrm {QCoh}}(X)$
is defined by
and we first explain how to use the affine submersion
![]() $f_0 \colon S_0 \to X$
to understand its structure. To this end, we consider the diagram
$f_0 \colon S_0 \to X$
to understand its structure. To this end, we consider the diagram

and observe that the canonical map
is an equivalence. Indeed, for any
![]() $\mathcal {G} \in {\mathrm {QCoh}}(X)$
, we have a diagram of anima
$\mathcal {G} \in {\mathrm {QCoh}}(X)$
, we have a diagram of anima

where the left-hand vertical map is an equivalence because the canonical map
is an equivalence of
![]() $\infty $
-categories. Since also the right-hand vertical map and the lower horizontal maps are equivalences, we conclude that the top horizontal map is an equivalence, as desired. It follows that the canonical map
$\infty $
-categories. Since also the right-hand vertical map and the lower horizontal maps are equivalences, we conclude that the top horizontal map is an equivalence, as desired. It follows that the canonical map
is an equivalence. Hence, we find that
 $$ \begin{align*}\begin{aligned} H^{-i}(X,\mathcal{F}) {} & \simeq \pi_0\operatorname{\mathrm{Map}}(\mathcal{O}_1,\Sigma^{-i}p_*(\mathcal{F})) \simeq \pi_i\operatorname{\mathrm{map}}(\mathcal{O}_1,p_*(\mathcal{F})) \cr {} & \simeq \textstyle{ \pi_i(\varprojlim_{[n] \in \Delta}\operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F})). } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} H^{-i}(X,\mathcal{F}) {} & \simeq \pi_0\operatorname{\mathrm{Map}}(\mathcal{O}_1,\Sigma^{-i}p_*(\mathcal{F})) \simeq \pi_i\operatorname{\mathrm{map}}(\mathcal{O}_1,p_*(\mathcal{F})) \cr {} & \simeq \textstyle{ \pi_i(\varprojlim_{[n] \in \Delta}\operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F})). } \cr \end{aligned}\end{align*} $$
Now, suppose that
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
. Since
$\mathcal {F} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
. Since
![]() $f_n \colon S_n \to X$
is a submersion from an affine Dirac stack, Theorem 3.27 shows that
$f_n \colon S_n \to X$
is a submersion from an affine Dirac stack, Theorem 3.27 shows that
![]() $f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(S_n)^{\heartsuit }$
, and since
$f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(S_n)^{\heartsuit }$
, and since
![]() $p_n$
is affine flat, Proposition 3.20 further shows that
$p_n$
is affine flat, Proposition 3.20 further shows that
![]() $p_{n*}f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(1)^{\heartsuit }$
. Thus, the mapping spectrum
$p_{n*}f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(1)^{\heartsuit }$
. Thus, the mapping spectrum
![]() $\operatorname {\mathrm {map}}(\mathcal {O}_1,p_{n*}f_n^*(\mathcal {F}))$
is the Eilenberg–MacLane spectrum given by the degree
$\operatorname {\mathrm {map}}(\mathcal {O}_1,p_{n*}f_n^*(\mathcal {F}))$
is the Eilenberg–MacLane spectrum given by the degree
![]() $0$
part
$0$
part
![]() $p_{n*}f_n^*(\mathcal {F})_0$
of the graded abelian group
$p_{n*}f_n^*(\mathcal {F})_0$
of the graded abelian group
![]() $p_{n*}f_n^*(\mathcal {F})$
. It follows that the Bousfield–Kan spectral sequence
$p_{n*}f_n^*(\mathcal {F})$
. It follows that the Bousfield–Kan spectral sequence
 $$ \begin{align*}\begin{aligned} E_{s,t}^2 & = \pi^{-s}([n] \mapsto \pi_t\operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F}))) \cr {} & \Rightarrow \textstyle{ \pi_{s+t}(\varprojlim_{[n] \in \Delta} \operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F}))) } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} E_{s,t}^2 & = \pi^{-s}([n] \mapsto \pi_t\operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F}))) \cr {} & \Rightarrow \textstyle{ \pi_{s+t}(\varprojlim_{[n] \in \Delta} \operatorname{\mathrm{map}}(\mathcal{O}_1,p_{n*}f_n^*(\mathcal{F}))) } \cr \end{aligned}\end{align*} $$
is concentrated on the line
![]() $t = 0$
, and therefore, it collapses to an isomorphism
$t = 0$
, and therefore, it collapses to an isomorphism
Hence, for
![]() $\mathcal {F} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
, its coherent cohomology is given by
$\mathcal {F} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
, its coherent cohomology is given by
and more generally, the coherent cohomology of ![]() is given by
is given by
Finally, if
![]() $\mathcal {F} \simeq \mathcal {F}(V)$
, then
$\mathcal {F} \simeq \mathcal {F}(V)$
, then
![]() $f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(S_n)^{\heartsuit }$
is the graded
$f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(S_n)^{\heartsuit }$
is the graded
![]() $\pi _*(E^{\otimes _k[n]})$
-module
$\pi _*(E^{\otimes _k[n]})$
-module
![]() $\pi _*(V \otimes _kE^{\otimes _k[n]})$
, and
$\pi _*(V \otimes _kE^{\otimes _k[n]})$
, and
![]() $p_{n*}f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(1)^{\heartsuit }$
is its underlying graded abelian group, and therefore, we conclude that
$p_{n*}f_n^*(\mathcal {F}) \in {\mathrm {QCoh}}(1)^{\heartsuit }$
is its underlying graded abelian group, and therefore, we conclude that
as we wanted to prove.
Remark 5.6. In the situation of Theorem 5.5, the descent spectral sequence does not depend on the map of commutative algebras in spectra
![]() $\eta \colon k \to E$
, but only on its associated homology theory
$\eta \colon k \to E$
, but only on its associated homology theory
![]() $(\mathcal {F},\eta )$
. We refer to [Reference Patchkoria and Pstrągowski30, Construction 2.24] for the construction in these terms, but we show below that the homology theory
$(\mathcal {F},\eta )$
. We refer to [Reference Patchkoria and Pstrągowski30, Construction 2.24] for the construction in these terms, but we show below that the homology theory
![]() $(\mathcal {F},\partial )$
is indeed adapted in the sense of [Reference Patchkoria and Pstrągowski30, Definition 2.19], as the construction requires.
$(\mathcal {F},\partial )$
is indeed adapted in the sense of [Reference Patchkoria and Pstrągowski30, Definition 2.19], as the construction requires.
In the situation of Theorem 5.5, the counit of the adjunction

given by the extension of scalars along
![]() $\eta $
and the restriction of scalars along
$\eta $
and the restriction of scalars along
![]() $\eta $
induces a map of graded
$\eta $
induces a map of graded
![]() $\pi _*(E)$
-modules
$\pi _*(E)$
-modules
![]() $\pi _*(\eta ^*\eta _*(W)) \to \pi _*(W)$
, or equivalently, a map
$\pi _*(\eta ^*\eta _*(W)) \to \pi _*(W)$
, or equivalently, a map
![]() $f_0^*\mathcal {F}(\eta _*(W)) \to \mathcal {G}(W)$
in
$f_0^*\mathcal {F}(\eta _*(W)) \to \mathcal {G}(W)$
in
![]() ${\mathrm {QCoh}}(S_0)^{\heartsuit }$
, the mate of which is a natural map
${\mathrm {QCoh}}(S_0)^{\heartsuit }$
, the mate of which is a natural map
in
![]() ${\mathrm {QCoh}}(X)^{\heartsuit }$
.
${\mathrm {QCoh}}(X)^{\heartsuit }$
.
Proof. Since
![]() ${\mathrm {QCoh}}(X) \simeq \varprojlim _{[n] \in \Delta } {\mathrm {QCoh}}(S_n)$
, it suffices to show that the map
${\mathrm {QCoh}}(X) \simeq \varprojlim _{[n] \in \Delta } {\mathrm {QCoh}}(S_n)$
, it suffices to show that the map
induced by the map in the statement is an equivalence for all
![]() $n \geq 0$
. In fact, it suffices to consider the case
$n \geq 0$
. In fact, it suffices to consider the case
![]() $n = 0$
, but the argument becomes more transparent by considering all
$n = 0$
, but the argument becomes more transparent by considering all
![]() $n \geq 0$
. We consider the diagram of finite ordinals
$n \geq 0$
. We consider the diagram of finite ordinals

The induced diagram of commutative algebras in spectra

is cocartesian, and the induced diagram of Dirac stacks

is cartesian because S is a groupoid. Since
![]() $f_0$
is affine flat, Proposition 3.20 shows that the base-change map associated with the latter square is an equivalence, so it suffices to show that the composition
$f_0$
is affine flat, Proposition 3.20 shows that the base-change map associated with the latter square is an equivalence, so it suffices to show that the composition
of the map in question with the base-change map is an equivalence for all
![]() $n \geq 0$
. Changing to graded module notation, we have a diagram
$n \geq 0$
. Changing to graded module notation, we have a diagram

of graded
![]() $\pi _*(E^{\otimes _k[n]})$
-modules, and we wish to prove that the top map is an equivalence. The left-hand slanted map is the base-change map associated with the above cocartesian square of commutative algebras in spectra, so it is an isomorphism, and the right-hand slanted map is the Künneth map, which is an isomorphism because
$\pi _*(E^{\otimes _k[n]})$
-modules, and we wish to prove that the top map is an equivalence. The left-hand slanted map is the base-change map associated with the above cocartesian square of commutative algebras in spectra, so it is an isomorphism, and the right-hand slanted map is the Künneth map, which is an isomorphism because
![]() $\pi _*(\eta _n')$
is a flat map of Dirac rings by the assumption that S has flat face maps.
$\pi _*(\eta _n')$
is a flat map of Dirac rings by the assumption that S has flat face maps.
Proposition 5.8. In the situation of Theorem 5.5, the homology theory
![]() $(\mathcal {F},\partial )$
associated with
$(\mathcal {F},\partial )$
associated with
![]() $\eta \colon k \to E$
is adapted.
$\eta \colon k \to E$
is adapted.
Proof. We recall that, by [Reference Patchkoria and Pstrągowski30, Definition 2.19], the homotopy theory
![]() $(\mathcal {F},\partial )$
is adapted if for every injective object
$(\mathcal {F},\partial )$
is adapted if for every injective object
![]() $\mathcal {I} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
, there is an isomorphism
$\mathcal {I} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
, there is an isomorphism
![]() $\phi \colon \mathcal {F}(I) \to \mathcal {I}$
with
$\phi \colon \mathcal {F}(I) \to \mathcal {I}$
with
![]() $I \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
such that for every
$I \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
such that for every
![]() $V \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
, the composite map
$V \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
, the composite map
is an isomorphism. We notice that the class of injective objects
![]() $\mathcal {I} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
for which such an isomorphism
$\mathcal {I} \in {\mathrm {QCoh}}(X)^{\heartsuit }$
for which such an isomorphism
![]() $\phi \colon \mathcal {F}(I) \to \mathcal {I}$
exists is closed under retracts.
$\phi \colon \mathcal {F}(I) \to \mathcal {I}$
exists is closed under retracts.
Now, since
![]() $f \simeq f_0 \colon S_0 \to X$
is affine flat, both functors in the adjunction
$f \simeq f_0 \colon S_0 \to X$
is affine flat, both functors in the adjunction

are t-exact, so they restrict to an adjunction

with both functors exact. Moreover, the unit
![]() $\eta \colon \mathcal {F} \to f_*f^*(\mathcal {F})$
is a monomorphism because
$\eta \colon \mathcal {F} \to f_*f^*(\mathcal {F})$
is a monomorphism because
![]() $f \colon S_0 \to X$
is an effective epimorphism. Thus, every injective object on the left-hand side is a retract of an injective object of the essential image of
$f \colon S_0 \to X$
is an effective epimorphism. Thus, every injective object on the left-hand side is a retract of an injective object of the essential image of
![]() $f_*$
.
$f_*$
.
So we let
![]() $\mathcal {I} \simeq f_*(\mathcal {J})$
with
$\mathcal {I} \simeq f_*(\mathcal {J})$
with
![]() $\mathcal {J} \in {\mathrm {QCoh}}(S_0)^{\heartsuit }$
injective and proceed to find an isomorphism
$\mathcal {J} \in {\mathrm {QCoh}}(S_0)^{\heartsuit }$
injective and proceed to find an isomorphism
![]() $\phi \colon \mathcal {F}(I) \to \mathcal {I}$
with
$\phi \colon \mathcal {F}(I) \to \mathcal {I}$
with
![]() $I \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
with the required property. It follows from Brown representability, [Reference Lurie19, Theorem 1.4.1.2], that the functor
$I \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
with the required property. It follows from Brown representability, [Reference Lurie19, Theorem 1.4.1.2], that the functor
with
![]() $\mathcal {G} \colon \operatorname {\mathrm {Mod}}_E(\operatorname {\mathrm {Sp}}) \to {\mathrm {QCoh}}(S_0)^{\heartsuit }$
as in Lemma 5.7 is representable. Therefore, we obtain a map
$\mathcal {G} \colon \operatorname {\mathrm {Mod}}_E(\operatorname {\mathrm {Sp}}) \to {\mathrm {QCoh}}(S_0)^{\heartsuit }$
as in Lemma 5.7 is representable. Therefore, we obtain a map
![]() $\psi \colon \mathcal {G}(J) \to \mathcal {J}$
with
$\psi \colon \mathcal {G}(J) \to \mathcal {J}$
with
![]() $J \in \operatorname {\mathrm {Mod}}_E(\operatorname {\mathrm {Sp}})$
such that the composite map
$J \in \operatorname {\mathrm {Mod}}_E(\operatorname {\mathrm {Sp}})$
such that the composite map
is a natural isomorphism, and since
![]() ${\mathrm {QCoh}}(S_0)^{\heartsuit }$
has a family of generators contained in the essential image of
${\mathrm {QCoh}}(S_0)^{\heartsuit }$
has a family of generators contained in the essential image of
![]() $\mathcal {G}$
, we conclude that the map
$\mathcal {G}$
, we conclude that the map
![]() $\psi $
is an isomorphism. Accordingly, we let
$\psi $
is an isomorphism. Accordingly, we let
![]() $I \simeq \eta _*(J)$
and define
$I \simeq \eta _*(J)$
and define
![]() $\phi \colon \mathcal {F}(I) \to \mathcal {I} \simeq f_*(\mathcal {J})$
to be the composition
$\phi \colon \mathcal {F}(I) \to \mathcal {I} \simeq f_*(\mathcal {J})$
to be the composition
of the isomorphism provided by Lemma 5.7 and the isomorphism induced by
![]() $\psi $
. Since the composite
$\psi $
. Since the composite
is an isomorphism for all
![]() $V \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
, we conclude that the composite map
$V \in \operatorname {\mathrm {Mod}}_k(\operatorname {\mathrm {Sp}})$
, we conclude that the composite map
is an isomorphism, as desired. This completes the proof.
Remark 5.9. We briefly discuss the second author’s categorification of the descent spectral sequence associated with
![]() $\eta \colon k \to E$
. By Proposition 5.8, the homology theory
$\eta \colon k \to E$
. By Proposition 5.8, the homology theory
![]() $(\mathcal {F},\partial )$
associated with
$(\mathcal {F},\partial )$
associated with
![]() $\eta \colon k \to E$
is adapted, so [Reference Patchkoria and Pstrągowski30, Theorem 6.40] exhibits the homological functor
$\eta \colon k \to E$
is adapted, so [Reference Patchkoria and Pstrągowski30, Theorem 6.40] exhibits the homological functor
![]() $\mathcal {F}$
as the
$\mathcal {F}$
as the
![]() $0$
th truncation
$0$
th truncation

of a fully faithful embedding as a reflexive subcategory in a Grothendieck prestable
![]() $\infty $
-category.Footnote
8
Moreover, if we exhibit
$\infty $
-category.Footnote
8
Moreover, if we exhibit
![]() $\mathcal {D}(\mathcal {F})_{\geq 0}$
as the connective part of a presentable stable
$\mathcal {D}(\mathcal {F})_{\geq 0}$
as the connective part of a presentable stable
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}(\mathcal {F})$
with a t-structure compatible with filtered colimits, then [Reference Patchkoria and Pstrągowski30, Theorem 5.60] identifies the descent spectral sequence in Theorem 5.5 with the spectral sequence associated to the filtered spectrumFootnote
9
$\mathcal {D}(\mathcal {F})$
with a t-structure compatible with filtered colimits, then [Reference Patchkoria and Pstrągowski30, Theorem 5.60] identifies the descent spectral sequence in Theorem 5.5 with the spectral sequence associated to the filtered spectrumFootnote
9
with structure maps given by the colimit interchange maps
![]() $\tau \colon \Sigma \nu (W) \to \nu (\Sigma W)$
. However, the Grothendieck prestable
$\tau \colon \Sigma \nu (W) \to \nu (\Sigma W)$
. However, the Grothendieck prestable
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}(\mathcal {F})_{\geq 0}$
encodes a great deal more information than does the descent spectral sequence, whence its usefulness.
$\mathcal {D}(\mathcal {F})_{\geq 0}$
encodes a great deal more information than does the descent spectral sequence, whence its usefulness.
Remark 5.10. In Construction 5.2, we used the equivalences
where, in the middle term, it is important that we use the truncated extension of scalars maps
![]() $\theta _{\heartsuit }^*$
associated with
$\theta _{\heartsuit }^*$
associated with
![]() $\theta \colon S_m \to S_n$
because not every such map
$\theta \colon S_m \to S_n$
because not every such map
![]() $\theta $
is flat. Since the diagram
$\theta $
is flat. Since the diagram
![]() ${\mathrm {QCoh}}(S)^{\heartsuit }$
is a diagram of
${\mathrm {QCoh}}(S)^{\heartsuit }$
is a diagram of
![]() $1$
-categories, we conclude from [Reference Hesselholt and Pstrągowski12, Proposition A.1] that the restriction map
$1$
-categories, we conclude from [Reference Hesselholt and Pstrągowski12, Proposition A.1] that the restriction map
is an equivalence. An object of the right-hand side, in turn, is a pair
![]() $(\mathcal {F}_0,\epsilon )$
of an object
$(\mathcal {F}_0,\epsilon )$
of an object
![]() $\mathcal {F}_0 \in {\mathrm {QCoh}}(S_0)^{\heartsuit }$
and a ‘descent structure’ mapFootnote
10
$\mathcal {F}_0 \in {\mathrm {QCoh}}(S_0)^{\heartsuit }$
and a ‘descent structure’ mapFootnote
10
in
![]() ${\mathrm {QCoh}}(S_1)^{\heartsuit }$
that makes the diagrams
${\mathrm {QCoh}}(S_1)^{\heartsuit }$
that makes the diagrams


in
![]() ${\mathrm {QCoh}}(S_0)^{\heartsuit }$
and
${\mathrm {QCoh}}(S_0)^{\heartsuit }$
and
![]() ${\mathrm {QCoh}}(S_2)^{\heartsuit }$
commute. The equality signs indicate the various unique isomorphisms. We say that
${\mathrm {QCoh}}(S_2)^{\heartsuit }$
commute. The equality signs indicate the various unique isomorphisms. We say that
![]() $(\mathcal {F}_0,\epsilon )$
is a quasi-coherent
$(\mathcal {F}_0,\epsilon )$
is a quasi-coherent
![]() $\mathcal {O}_{S_0}$
-module with descent structure along
$\mathcal {O}_{S_0}$
-module with descent structure along
![]() $f \colon S_0 \to X$
, and we refer to the fact that the map
$f \colon S_0 \to X$
, and we refer to the fact that the map
![]() $\epsilon $
makes these diagrams commute by saying that it satisfies the cocycle condition. A map
$\epsilon $
makes these diagrams commute by saying that it satisfies the cocycle condition. A map
![]() $\alpha \colon (\mathcal {F}_0,\epsilon ) \to (\mathcal {F}_0',\epsilon ')$
of quasi-coherent
$\alpha \colon (\mathcal {F}_0,\epsilon ) \to (\mathcal {F}_0',\epsilon ')$
of quasi-coherent
![]() $\mathcal {O}_{S_0}$
-modules with descent structure along the map
$\mathcal {O}_{S_0}$
-modules with descent structure along the map
![]() $f \colon S_0 \to X$
is a map
$f \colon S_0 \to X$
is a map
![]() $\alpha \colon \mathcal {F}_0 \to \mathcal {F}_0'$
in
$\alpha \colon \mathcal {F}_0 \to \mathcal {F}_0'$
in
![]() ${\mathrm {QCoh}}(S_0)^{\heartsuit }$
that makes the diagram
${\mathrm {QCoh}}(S_0)^{\heartsuit }$
that makes the diagram

in
![]() ${\mathrm {QCoh}}(S_1)^{\heartsuit }$
commute.
${\mathrm {QCoh}}(S_1)^{\heartsuit }$
commute.
Remark 5.11. Suppose that
![]() $(\mathcal {F}_0,\epsilon )$
is a quasi-coherent
$(\mathcal {F}_0,\epsilon )$
is a quasi-coherent
![]() $\mathcal {O}_{S_0}$
-module with descent data along
$\mathcal {O}_{S_0}$
-module with descent data along
![]() $f \colon S_0 \to X$
as in Remark 5.10. The map of quasi-coherent
$f \colon S_0 \to X$
as in Remark 5.10. The map of quasi-coherent
![]() $\mathcal {O}_{S_1}$
-modules
$\mathcal {O}_{S_1}$
-modules
determines and is determined by the map of quasi-coherent
![]() $\mathcal {O}_{S_0}$
-modules
$\mathcal {O}_{S_0}$
-modules
given by its mate. The cocycle condition for
![]() $\epsilon $
translates to a Leibniz rule for the map
$\epsilon $
translates to a Leibniz rule for the map
![]() $\nabla _{\epsilon }$
, which behaves as a connection.Footnote
11
$\nabla _{\epsilon }$
, which behaves as a connection.Footnote
11
5.2 Quillen’s theorem
Given a commutative algebra in spectra E and a group in anima G, we defined, in the introduction, a formal Dirac scheme
over
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
with
$S \simeq \operatorname {\mathrm {Spec}}(R)$
with
![]() $R \simeq \pi _*(E)$
. We consider the case where
$R \simeq \pi _*(E)$
. We consider the case where
is the Pontryagin dual of a finitely generated free abelian group L. The Postnikov filtration of E defines the Atiyah–Hirzebruch spectral sequence converging to
and since the integral cohomology groups of
![]() $BG$
are free, it takes the form
$BG$
are free, it takes the form
We define
![]() $I \subset A$
to be the kernel of the edge homomorphism
$I \subset A$
to be the kernel of the edge homomorphism
![]() $\theta \colon A \to R$
and recall that E is said to be complex orientable if the canonical map
$\theta \colon A \to R$
and recall that E is said to be complex orientable if the canonical map
is an isomorphism. In this case, all differentials in the spectral sequence are necessarily zero, so we conclude that
![]() $q \colon Y \to S$
is a formal hyperplane.
$q \colon Y \to S$
is a formal hyperplane.
Definition 5.12. Let E be a complex orientable commutative algebra in spectra. The Quillen formal group associated with E is the functor
that to L assigns the formal hyperplane
![]() $q \colon Y_{E,\widehat {L}} \to S$
.
$q \colon Y_{E,\widehat {L}} \to S$
.
Remark 5.13. Let E be a complex orientable commutative algebra in spectra. The canonical isomorphism
![]() $I/I^2 \to R(1)$
provided by the Atiyah–Hirzebruch spectral sequence in the case
$I/I^2 \to R(1)$
provided by the Atiyah–Hirzebruch spectral sequence in the case
![]() $L = \mathbb {Z}$
defines a canonical isomorphism
$L = \mathbb {Z}$
defines a canonical isomorphism
of line bundles over S. This isomorphism provides a canonical trivialization of the Lie algebra, which we defined in Definition 4.46, of the Quillen formal group. In particular, the Quillen formal group
![]() $\mathcal {G}_E^Q$
is
$\mathcal {G}_E^Q$
is
![]() $1$
-dimensional and spin-
$1$
-dimensional and spin-
![]() $1$
over S.
$1$
over S.
We now let
![]() $E \simeq \operatorname {MU}^{\otimes [n]}$
be a tensor power of the commutative algebra in spectra representing complex cobordism. It is proved in [Reference Adams2, Lemma 4.5 and Theorem 8.1] that the homotopy groups of E are concentrated in even degrees, so E is complex orientable. Therefore, the Quillen formal group provides the simplicial formal group
$E \simeq \operatorname {MU}^{\otimes [n]}$
be a tensor power of the commutative algebra in spectra representing complex cobordism. It is proved in [Reference Adams2, Lemma 4.5 and Theorem 8.1] that the homotopy groups of E are concentrated in even degrees, so E is complex orientable. Therefore, the Quillen formal group provides the simplicial formal group
whose value at
![]() $L \in \operatorname {\mathrm {Lat}}$
is the simplicial formal hyperplane
$L \in \operatorname {\mathrm {Lat}}$
is the simplicial formal hyperplane
It satisfies the hypotheses of Proposition 4.47, so the geometric realization
exists and its value at
![]() $L \in \operatorname {\mathrm {Lat}}$
is the formal hyperplane
$L \in \operatorname {\mathrm {Lat}}$
is the formal hyperplane
We write X for the Dirac stack on the right-hand side so that
![]() $\mathcal {G}^Q \in \operatorname {\mathrm {FGroup}}(X)$
. By the descent of modules along effective epimorphisms, the canonical trivializations of Remark 5.13 determine a canonical isomorphism of line bundles over X,
$\mathcal {G}^Q \in \operatorname {\mathrm {FGroup}}(X)$
. By the descent of modules along effective epimorphisms, the canonical trivializations of Remark 5.13 determine a canonical isomorphism of line bundles over X,
We now use Quillen’s theorem to show that
![]() $(\mathcal {G}^Q,\phi ^Q)$
is the universal
$(\mathcal {G}^Q,\phi ^Q)$
is the universal
![]() $1$
-dimensional spin-
$1$
-dimensional spin-
![]() $1$
formal group equipped with a trivialization of its Lie algebra in the following sense.
$1$
formal group equipped with a trivialization of its Lie algebra in the following sense.
Theorem 5.14. Let T be a Dirac stack. The functor that to
![]() $f \colon T \to X$
assigns the pair
$f \colon T \to X$
assigns the pair
![]() $(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence from
$(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence from
![]() $\operatorname {\mathrm {Map}}(T, X)$
to the groupoid of pairs
$\operatorname {\mathrm {Map}}(T, X)$
to the groupoid of pairs
![]() $(\mathcal {G},\phi )$
of a formal group
$(\mathcal {G},\phi )$
of a formal group
![]() $\mathcal {G}$
over T and an isomorphism
$\mathcal {G}$
over T and an isomorphism
![]() $\phi \colon \mathbb {A}_T(1) \to \operatorname {\mathrm {Lie}}(\mathcal {G})$
of line bundles over T.
$\phi \colon \mathbb {A}_T(1) \to \operatorname {\mathrm {Lie}}(\mathcal {G})$
of line bundles over T.
Proof. We let
![]() $p_n \colon Y_n \to S_n$
be the underlying formal hyperplane of the Quillen formal group associated with
$p_n \colon Y_n \to S_n$
be the underlying formal hyperplane of the Quillen formal group associated with
![]() $\operatorname {MU}^{\otimes [n]}$
and note that a complex orientation of
$\operatorname {MU}^{\otimes [n]}$
and note that a complex orientation of
![]() $\operatorname {MU}$
determines and is determined by an isomorphism
$\operatorname {MU}$
determines and is determined by an isomorphism

of pointed formal hyperplanes over
![]() $S_0$
such that the diagram
$S_0$
such that the diagram

of line bundles over
![]() $S_0$
commutes. Here,
$S_0$
commutes. Here,
![]() $\phi _{\operatorname {MU}}^Q$
and
$\phi _{\operatorname {MU}}^Q$
and
![]() $\alpha $
are the canonical trivializations provided by Remark 5.13 and Proposition 4.13. Moreover, under the identification provided by a choice of complex orientation h, the Quillen formal group
$\alpha $
are the canonical trivializations provided by Remark 5.13 and Proposition 4.13. Moreover, under the identification provided by a choice of complex orientation h, the Quillen formal group
![]() $\mathcal {G}_{\operatorname {MU}}^Q$
is encoded by a formal group law
$\mathcal {G}_{\operatorname {MU}}^Q$
is encoded by a formal group law
![]() $f(y,z) \in \pi _*(MU)[[y,z]]$
, which, in turn, determines and is determined by a map of affine Dirac schemes
$f(y,z) \in \pi _*(MU)[[y,z]]$
, which, in turn, determines and is determined by a map of affine Dirac schemes
with L the Lazard ring. Quillen shows in [Reference Quillen31, Theorem 2] that
![]() $\theta $
is an isomorphism; see also [Reference Adams2, Theorem II.8.2] for a purely homotopy theoretic proof of this fact.
$\theta $
is an isomorphism; see also [Reference Adams2, Theorem II.8.2] for a purely homotopy theoretic proof of this fact.
Next, we note that the face maps
![]() $d_0,d_1 \colon Y_1 \to Y_0$
and the complex orientation
$d_0,d_1 \colon Y_1 \to Y_0$
and the complex orientation
![]() $h \colon Y \to {\hat {\mathbb {A}}}_{S_0}(1)$
of
$h \colon Y \to {\hat {\mathbb {A}}}_{S_0}(1)$
of
![]() $\operatorname {MU}$
give rise to two complex orientations of
$\operatorname {MU}$
give rise to two complex orientations of
![]() $\operatorname {MU}^{\otimes [1]}$
,
$\operatorname {MU}^{\otimes [1]}$
,

The composite map
![]() $g \simeq h_0 \circ h_1^{-1}$
is an automorphism of the pointed spin-
$g \simeq h_0 \circ h_1^{-1}$
is an automorphism of the pointed spin-
![]() $1$
formal affine line
$1$
formal affine line
![]() ${\hat {\mathbb {A}}}_{S_1}(1)$
that induces the identity automorphism on conormal sheaves. It defines an
${\hat {\mathbb {A}}}_{S_1}(1)$
that induces the identity automorphism on conormal sheaves. It defines an
![]() $S_1$
-valued point g of the affine group scheme
$S_1$
-valued point g of the affine group scheme
![]() $G'$
of automorphisms of the pointed spin-
$G'$
of automorphisms of the pointed spin-
![]() $1$
formal affine line
$1$
formal affine line
![]() ${\hat {\mathbb {A}}}_{\mathbb {Z}}(1)$
which induce the identity map of tangent spaces at the zero section.Footnote
12
Quillen shows that the map of affine Dirac schemes
${\hat {\mathbb {A}}}_{\mathbb {Z}}(1)$
which induce the identity map of tangent spaces at the zero section.Footnote
12
Quillen shows that the map of affine Dirac schemes
is an isomorphism. Moreover, there are commutative diagrams

where the action map
![]() $\mu $
is given as follows. Let
$\mu $
is given as follows. Let
![]() $T = \operatorname {\mathrm {Spec}}(B)$
be any affine Dirac scheme. A T-valued point of
$T = \operatorname {\mathrm {Spec}}(B)$
be any affine Dirac scheme. A T-valued point of
![]() $S_0$
determines and is determined by a formal group law
$S_0$
determines and is determined by a formal group law
![]() $f = f(y,z) \in B[[y,z]]$
, and a T-valued point of
$f = f(y,z) \in B[[y,z]]$
, and a T-valued point of
![]() $G'$
determines and is determined by a power series
$G'$
determines and is determined by a power series
![]() $g = g(t) \in B[[t]]$
with
$g = g(t) \in B[[t]]$
with
![]() $g(0) = 0$
and
$g(0) = 0$
and
![]() $g'(0) = 1$
. Here, the generators y, z and t are all spin-
$g'(0) = 1$
. Here, the generators y, z and t are all spin-
![]() $1$
, and f and g are also required to be spin-
$1$
, and f and g are also required to be spin-
![]() $1$
. Now, the image of
$1$
. Now, the image of
![]() $(f,g)$
by
$(f,g)$
by
![]() $\mu $
is the formal group law
$\mu $
is the formal group law
![]() $g(f(g^{-1}(y),g^{-1}(z)))$
. It follows, in particular, that the groupoid
$g(f(g^{-1}(y),g^{-1}(z)))$
. It follows, in particular, that the groupoid
![]() $S \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has flat face maps, so by Theorem 2.49, its geometric realization
$S \colon \Delta ^{\mathrm {op}} \to \operatorname {\mathrm {Shv}}(\operatorname {\mathrm {Aff}})$
has flat face maps, so by Theorem 2.49, its geometric realization
![]() $X \simeq \lvert S \rvert $
is a geometric stack.
$X \simeq \lvert S \rvert $
is a geometric stack.
Let
![]() $X'(T)$
be the groupoid consisting of pairs
$X'(T)$
be the groupoid consisting of pairs
![]() $(\mathcal {G},\phi )$
of a formal group
$(\mathcal {G},\phi )$
of a formal group
![]() $\mathcal {G}$
over T and an isomorphism
$\mathcal {G}$
over T and an isomorphism
![]() $\phi \colon \mathbb {A}_T(1) \to \operatorname {\mathrm {Lie}}(\mathcal {G})$
of vector bundles over T. We wish to prove that the functor
$\phi \colon \mathbb {A}_T(1) \to \operatorname {\mathrm {Lie}}(\mathcal {G})$
of vector bundles over T. We wish to prove that the functor
that to
![]() $f \colon T \to X$
assigns
$f \colon T \to X$
assigns
![]() $(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence. To this end, we consider the colimit
$(f^*\mathcal {G}^Q,f^*\phi ^Q)$
is an equivalence. To this end, we consider the colimit
calculated in presheaves, so that X is the sheafification of
![]() $X" $
. As colimits of presheaves are calculated pointwise, we have
$X" $
. As colimits of presheaves are calculated pointwise, we have
![]() $X" (T) \simeq \lvert S(T) \rvert \in {\mathcal {S}}$
, and Quillen’s theorem shows that the functor
$X" (T) \simeq \lvert S(T) \rvert \in {\mathcal {S}}$
, and Quillen’s theorem shows that the functor
that to
![]() $f \colon T \to X" $
assigns
$f \colon T \to X" $
assigns
![]() $(f^*\mathcal {G}" ,f^*\phi" )$
is fully faithful and that its essential image is the subgroupoid spanned by the pairs
$(f^*\mathcal {G}" ,f^*\phi" )$
is fully faithful and that its essential image is the subgroupoid spanned by the pairs
![]() $(\mathcal {G},\phi )$
such that
$(\mathcal {G},\phi )$
such that
![]() $\mathcal {G}$
admits a global coordinate in the sense that
$\mathcal {G}$
admits a global coordinate in the sense that
![]() $\mathcal {G}(\mathbb {Z})$
is isomorphic as a formal hyperplane over T to the spin-
$\mathcal {G}(\mathbb {Z})$
is isomorphic as a formal hyperplane over T to the spin-
![]() $1$
formal affine line. Hence, to prove that
$1$
formal affine line. Hence, to prove that
![]() $X(T) \to X'(T)$
is an equivalence, we must show that the presheaf
$X(T) \to X'(T)$
is an equivalence, we must show that the presheaf
![]() $X'$
is a sheaf. But this is precisely flat descent for formal groups, which we have proved in Proposition 4.43.
$X'$
is a sheaf. But this is precisely flat descent for formal groups, which we have proved in Proposition 4.43.
5.3 Milnor’s theorem
We next let p be an odd prime number and let
be the p-torsion subgroup of the Pontryagin dual of a finitely generated free abelian group L. We claim that if
![]() $\eta \colon \mathbb {F}_p \to E$
is a map of commutative algebras in spectra,Footnote
13
then the formal Dirac scheme
$\eta \colon \mathbb {F}_p \to E$
is a map of commutative algebras in spectra,Footnote
13
then the formal Dirac scheme
over
![]() $S \simeq \operatorname {\mathrm {Spec}}(R)$
with
$S \simeq \operatorname {\mathrm {Spec}}(R)$
with
![]() $R \simeq \pi _*(E)$
, which we defined in the introduction, is a formal hyperplane. Since p is odd, the
$R \simeq \pi _*(E)$
, which we defined in the introduction, is a formal hyperplane. Since p is odd, the
![]() $\mathbb {F}_p$
-cohomology of
$\mathbb {F}_p$
-cohomology of
![]() $BC_p$
is a free Dirac
$BC_p$
is a free Dirac
![]() $\mathbb {F}_p$
-algebra on a spin-
$\mathbb {F}_p$
-algebra on a spin-![]() generator e and a spin-
generator e and a spin-
![]() $1$
generator
$1$
generator
![]() $\gamma $
. It follows that the Atiyah–Hirzebruch spectral sequence converging to
$\gamma $
. It follows that the Atiyah–Hirzebruch spectral sequence converging to
takes the form
and we claim that all differentials are zero. Indeed, the spectral sequence is a spectral sequence of R-algebras, and the generators of the symmetric Dirac R-algebra are all defined over
![]() $\mathbb {F}_p$
, where the differentials vanish for degree-reasons. This proves our claim that
$\mathbb {F}_p$
, where the differentials vanish for degree-reasons. This proves our claim that
![]() $q \colon Y \to S$
is a formal hyperplane.
$q \colon Y \to S$
is a formal hyperplane.
Definition 5.15. Let E be a commutative
![]() $\mathbb {F}_p$
-algebra in spectra, where p is an odd prime number. The Milnor formal group associated with E is the functor
$\mathbb {F}_p$
-algebra in spectra, where p is an odd prime number. The Milnor formal group associated with E is the functor
that to L assigns the formal hyperplane
![]() $q \colon Y_{E,\widehat {L}[p]} \to S$
.
$q \colon Y_{E,\widehat {L}[p]} \to S$
.
Remark 5.16. The Milnor formal group associated with a commutative
![]() $\mathbb {F}_p$
-algebra in spectra E is additive in the sense that, as a formal group over S, it is noncanonically isomorphic to an additive formal group.
$\mathbb {F}_p$
-algebra in spectra E is additive in the sense that, as a formal group over S, it is noncanonically isomorphic to an additive formal group.
If E is a commutative
![]() $\mathbb {F}_p$
-algebra in spectra with p odd, then
$\mathbb {F}_p$
-algebra in spectra with p odd, then
![]() $i \colon \widehat {L}[p] \to \widehat {L}$
induces a map of formal groups from the
$i \colon \widehat {L}[p] \to \widehat {L}$
induces a map of formal groups from the
![]() $2$
-dimensional Milnor formal group to the
$2$
-dimensional Milnor formal group to the
![]() $1$
-dimensional Quillen formal group,
$1$
-dimensional Quillen formal group,
This map is surjective and its kernel
is again a formal group over S. This filtration gives rise to a grading of the Lie algebra
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M)$
, which we refer to as the grading by charge. The Atiyah–Hirzebruch spectral sequence determines a canonical isomorphism of graded vector bundles
$\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M)$
, which we refer to as the grading by charge. The Atiyah–Hirzebruch spectral sequence determines a canonical isomorphism of graded vector bundles
where e has charge
![]() $1$
and
$1$
and
![]() $\gamma $
has charge
$\gamma $
has charge
![]() $0$
. As in Remark 4.27, we have a classifying stack
$0$
. As in Remark 4.27, we have a classifying stack
for automorphisms of the Milnor formal group associated with E that preserve the canonical filtration and induce the identity map on
![]() $\operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M))$
.
$\operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}_E^M))$
.
Proposition 5.17. Let
![]() $S_0 \simeq \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p prime. The classifying stack
$S_0 \simeq \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p prime. The classifying stack
is an affine Dirac group
![]() $S_0$
-scheme represented by the Hopf algebra
$S_0$
-scheme represented by the Hopf algebra
with
![]() $\tau _i$
and
$\tau _i$
and
![]() $\xi _i$
generators of spin
$\xi _i$
generators of spin ![]() and
and
![]() $p^i - 1$
, respectively, and with comultiplication given by
$p^i - 1$
, respectively, and with comultiplication given by
 $$ \begin{align*}\begin{aligned} \psi(\tau_i) & = \textstyle{ \tau_i \otimes 1 + \sum_{0 \leq j \leq i} \xi_{i-j}^{p^j} \otimes \tau_j } \cr \psi(\xi_i) & = \textstyle{ \sum_{0 \leq j \leq i} \xi_{i-j}^{p^j} \otimes \xi_j, } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \psi(\tau_i) & = \textstyle{ \tau_i \otimes 1 + \sum_{0 \leq j \leq i} \xi_{i-j}^{p^j} \otimes \tau_j } \cr \psi(\xi_i) & = \textstyle{ \sum_{0 \leq j \leq i} \xi_{i-j}^{p^j} \otimes \xi_j, } \cr \end{aligned}\end{align*} $$
where
![]() $\xi _0 = 1$
by convention.
$\xi _0 = 1$
by convention.
Proof. Let
![]() $\mathcal {G}_0$
be the Milnor formal group associated with
$\mathcal {G}_0$
be the Milnor formal group associated with
![]() $\mathbb {F}_p$
and let
$\mathbb {F}_p$
and let
![]() $q_0 \colon Y_0 \to S_0$
be its underlying hyperplane
$q_0 \colon Y_0 \to S_0$
be its underlying hyperplane
![]() $\mathcal {G}_0(\mathbb {Z})$
. So
$\mathcal {G}_0(\mathbb {Z})$
. So
![]() $Y_0 \simeq \operatorname {\mathrm {Spf}}(A_0)$
with
$Y_0 \simeq \operatorname {\mathrm {Spf}}(A_0)$
with
![]() $A_0 = \mathbb {F}_p[e,\gamma ]$
and with the zero section defined by the graded ideal
$A_0 = \mathbb {F}_p[e,\gamma ]$
and with the zero section defined by the graded ideal
![]() $I_0 = (e,\gamma )$
. Now, given any Dirac
$I_0 = (e,\gamma )$
. Now, given any Dirac
![]() $\mathbb {F}_p$
-algebra R, we have
$\mathbb {F}_p$
-algebra R, we have
 $$ \begin{align*}\begin{aligned} \operatorname{\mathrm{Hom}}_{S_0}(Y_0,Y_0)(R) & \simeq \operatorname{\mathrm{Hom}}_R(\operatorname{\mathrm{Spf}}(A_0 \otimes_{\mathbb{F}_p}R),\operatorname{\mathrm{Spf}}(A_0 \otimes_{\mathbb{F}_p}R)) \cr {} & \simeq \operatorname{\mathrm{Hom}}_R(R[e,\gamma],R[[e,\gamma]]), \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \operatorname{\mathrm{Hom}}_{S_0}(Y_0,Y_0)(R) & \simeq \operatorname{\mathrm{Hom}}_R(\operatorname{\mathrm{Spf}}(A_0 \otimes_{\mathbb{F}_p}R),\operatorname{\mathrm{Spf}}(A_0 \otimes_{\mathbb{F}_p}R)) \cr {} & \simeq \operatorname{\mathrm{Hom}}_R(R[e,\gamma],R[[e,\gamma]]), \end{aligned}\end{align*} $$
so
![]() $f \in \operatorname {\mathrm {Hom}}_{S_0}(Y_0,Y_0)(R)$
determines and is determined by the two power series
$f \in \operatorname {\mathrm {Hom}}_{S_0}(Y_0,Y_0)(R)$
determines and is determined by the two power series
 $$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ \sum_{i \geq 0}(a_i + c_ie)\gamma^i } \cr f(\gamma) & = \textstyle{ \sum_{i \geq 0}(b_i + d_ie)\gamma^i } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ \sum_{i \geq 0}(a_i + c_ie)\gamma^i } \cr f(\gamma) & = \textstyle{ \sum_{i \geq 0}(b_i + d_ie)\gamma^i } \cr \end{aligned}\end{align*} $$
with
![]() $a_i \in R_{2i-1}$
,
$a_i \in R_{2i-1}$
,
![]() $b_i \in R_{2i-2}$
,
$b_i \in R_{2i-2}$
,
![]() $c_i \in R_{2i}$
and
$c_i \in R_{2i}$
and
![]() $d_i \in R_{2i-1}$
. Now, let
$d_i \in R_{2i-1}$
. Now, let
![]() $T \simeq \operatorname {\mathrm {Spec}}(R)$
and
$T \simeq \operatorname {\mathrm {Spec}}(R)$
and
![]() $Y_{0,T} \simeq Y_0 \times _{S_0}T$
. The statement that f is a map of formal groups is equivalent to the statement that the diagram
$Y_{0,T} \simeq Y_0 \times _{S_0}T$
. The statement that f is a map of formal groups is equivalent to the statement that the diagram

commutes. Each of the two composites in the diagram are elements of
and by comparing the images of e and
![]() $\gamma $
by the two composites, we see that the diagram commutes if and only if the following equations hold:
$\gamma $
by the two composites, we see that the diagram commutes if and only if the following equations hold:
 $$ \begin{align*}\begin{aligned} \textstyle{ \sum_{i \geq 0} (a_i + c_i(e_1 + e_2))(\gamma_1 + \gamma_2)^i } & = \textstyle{ \sum_{i \geq 0} (a_i + c_ie_1)\gamma_1^i + \sum_{i \geq 0}(a_i + c_ie_2)\gamma_2^i, } \cr \textstyle{ \sum_{i \geq 0} (b_i + d_i(e_1 + e_2))(\gamma_1 + \gamma_2)^i } & = \textstyle{ \sum_{i \geq 0} (b_i + d_ie_1)\gamma_1^i + \sum_{i \geq 0}(b_i + d_ie_2)\gamma_2^i. } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \textstyle{ \sum_{i \geq 0} (a_i + c_i(e_1 + e_2))(\gamma_1 + \gamma_2)^i } & = \textstyle{ \sum_{i \geq 0} (a_i + c_ie_1)\gamma_1^i + \sum_{i \geq 0}(a_i + c_ie_2)\gamma_2^i, } \cr \textstyle{ \sum_{i \geq 0} (b_i + d_i(e_1 + e_2))(\gamma_1 + \gamma_2)^i } & = \textstyle{ \sum_{i \geq 0} (b_i + d_ie_1)\gamma_1^i + \sum_{i \geq 0}(b_i + d_ie_2)\gamma_2^i. } \cr \end{aligned}\end{align*} $$
These are satisfied if and only if
![]() $c_i$
and
$c_i$
and
![]() $d_i$
are zero for all
$d_i$
are zero for all
![]() $i> 0$
and
$i> 0$
and
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are zero for all
$b_i$
are zero for all
![]() $i \geq 0$
that are not a power of p. Moreover, the map f preserves the canonical filtration of the Milnor formal group if and only if
$i \geq 0$
that are not a power of p. Moreover, the map f preserves the canonical filtration of the Milnor formal group if and only if
![]() $d_0 = 0$
, and, finally, the induced map of
$d_0 = 0$
, and, finally, the induced map of
![]() $\operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}_0))$
is the identity map if and only if
$\operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}_0))$
is the identity map if and only if
![]() $c_0 = 1$
and
$c_0 = 1$
and
![]() $b_1 = 1$
. Hence, a choice of e and
$b_1 = 1$
. Hence, a choice of e and
![]() $\gamma $
determines an identification of the set of R-valued points of
$\gamma $
determines an identification of the set of R-valued points of
![]() $\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
and the set of pairs of power series of the form
$\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
and the set of pairs of power series of the form
 $$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ e + \sum_{i \geq 0}a_i\gamma^{p^i} } \cr f(\gamma) & = \gamma + \textstyle{ \sum_{i \geq 1}b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ e + \sum_{i \geq 0}a_i\gamma^{p^i} } \cr f(\gamma) & = \gamma + \textstyle{ \sum_{i \geq 1}b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
with
![]() $a_i \in R_{2p^i-1}$
and
$a_i \in R_{2p^i-1}$
and
![]() $b_i \in R_{2p^i-2}$
. This shows that the underlying
$b_i \in R_{2p^i-2}$
. This shows that the underlying
![]() $S_0$
-stack of the
$S_0$
-stack of the
![]() $\mathbf {E}_1$
-group
$\mathbf {E}_1$
-group
![]() $\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is represented by the stated Dirac
$\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is represented by the stated Dirac
![]() $\mathbb {F}_p$
-algebra C, so in particular, we conclude that
$\mathbb {F}_p$
-algebra C, so in particular, we conclude that
![]() $\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is an affine Dirac group
$\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is an affine Dirac group
![]() $S_0$
-scheme.
$S_0$
-scheme.
The multiplication in the Dirac group
![]() $S_0$
-scheme
$S_0$
-scheme
![]() $\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is given, on R-valued points, by the composition of maps
$\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
is given, on R-valued points, by the composition of maps
So let
![]() $(f,g)$
be a pair of maps with f given by
$(f,g)$
be a pair of maps with f given by
 $$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ e + \sum_{i \geq 0}a_i\gamma^{p^i} } \cr f(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1}b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} f(e) & = \textstyle{ e + \sum_{i \geq 0}a_i\gamma^{p^i} } \cr f(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1}b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
and with g given by
 $$ \begin{align*}\begin{aligned} g(e) & = \textstyle{ e + \sum_{i \geq 0}c_i\gamma^{p^i} } \cr g(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1}d_i\gamma^{p^i}. } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} g(e) & = \textstyle{ e + \sum_{i \geq 0}c_i\gamma^{p^i} } \cr g(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1}d_i\gamma^{p^i}. } \cr \end{aligned}\end{align*} $$
Since
![]() $\operatorname {\mathrm {Spf}}$
is contravariant, we have
$\operatorname {\mathrm {Spf}}$
is contravariant, we have
 $$ \begin{align*}\begin{aligned} (f \circ g)(e) & = \textstyle{ g(f(e)) = g(e + \sum_{i \geq 0}a_i\gamma^{p^i}) = g(e) + g(\sum_{i \geq 0}a_i\gamma^{p^i}) } \cr {} & = \textstyle{ e + \sum_{i \geq 0}c_i\gamma^{p^i} + \sum_{i,j \geq 0} a_i^{p^j}d_j\gamma^{p^{i+j}} } \cr (f \circ g)(\gamma) & = \textstyle{ g(\sum_{i \geq 0}b_i\gamma^{p^i}) = \sum_{i,j \geq 0} b_i^{p^j}d_j\gamma^{p^{i+j}} } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} (f \circ g)(e) & = \textstyle{ g(f(e)) = g(e + \sum_{i \geq 0}a_i\gamma^{p^i}) = g(e) + g(\sum_{i \geq 0}a_i\gamma^{p^i}) } \cr {} & = \textstyle{ e + \sum_{i \geq 0}c_i\gamma^{p^i} + \sum_{i,j \geq 0} a_i^{p^j}d_j\gamma^{p^{i+j}} } \cr (f \circ g)(\gamma) & = \textstyle{ g(\sum_{i \geq 0}b_i\gamma^{p^i}) = \sum_{i,j \geq 0} b_i^{p^j}d_j\gamma^{p^{i+j}} } \cr \end{aligned}\end{align*} $$
with
![]() $b_0 = d_0 = 1$
. This shows that the comultiplication on C is as stated.
$b_0 = d_0 = 1$
. This shows that the comultiplication on C is as stated.
We recall Milnor’s calculation of the dual Steenrod algebra at an odd prime. To this end, we consider the groupoid
![]() $S \colon \Delta ^{\mathrm {op}} \to {\mathrm {Aff}}_{/S_0}$
defined by
$S \colon \Delta ^{\mathrm {op}} \to {\mathrm {Aff}}_{/S_0}$
defined by
Since its face maps are flat, the geometric realization
is a geometric Dirac
![]() $S_0$
-stack. Moreover, the face maps
$S_0$
-stack. Moreover, the face maps
![]() $d_0,d_1 \colon S_1 \to S_0$
are necessarily equal because
$d_0,d_1 \colon S_1 \to S_0$
are necessarily equal because
![]() $\mathbb {F}_p$
is a prime field, so we conclude that X is the classifying stack
$\mathbb {F}_p$
is a prime field, so we conclude that X is the classifying stack
of the affine Dirac
![]() $S_0$
-group G corepresented by the dual Steenrod algebra
$S_0$
-group G corepresented by the dual Steenrod algebra
![]() $\smash { A \simeq \pi _*(\mathbb {F}_p^{\,\otimes [1]}) }$
. The geometric realization of the simplicial Milnor formal group
$\smash { A \simeq \pi _*(\mathbb {F}_p^{\,\otimes [1]}) }$
. The geometric realization of the simplicial Milnor formal group
comes equipped with a canonical filtration and a canonical isomorphism of graded vector bundles
We now use Milnor’s theorem to determine the structure of the pair
![]() $(\operatorname {\mathrm {Fil}}(\mathcal {G}^M),\phi ^M)$
.
$(\operatorname {\mathrm {Fil}}(\mathcal {G}^M),\phi ^M)$
.
Theorem 5.18. Let
![]() $S_0 = \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p an odd prime and let T be a Dirac
$S_0 = \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
with p an odd prime and let T be a Dirac
![]() $S_0$
-stack. The functor that to
$S_0$
-stack. The functor that to
![]() $f \colon T \to X$
assigns the pair
$f \colon T \to X$
assigns the pair
![]() $(f^*\operatorname {\mathrm {Fil}}(\mathcal {G}^M),f^*\phi ^M)$
is an equivalence from
$(f^*\operatorname {\mathrm {Fil}}(\mathcal {G}^M),f^*\phi ^M)$
is an equivalence from
![]() $X(T)$
to the groupoid
$X(T)$
to the groupoid
![]() $X'(T)$
of pairs
$X'(T)$
of pairs
![]() $(\operatorname {\mathrm {Fil}}(\mathcal {G}),\phi )$
of a filtered formal group
$(\operatorname {\mathrm {Fil}}(\mathcal {G}),\phi )$
of a filtered formal group
![]() $\operatorname {\mathrm {Fil}}(\mathcal {G})$
over T that is locally isomorphic to a filtered additive formal group and an isomorphism
$\operatorname {\mathrm {Fil}}(\mathcal {G})$
over T that is locally isomorphic to a filtered additive formal group and an isomorphism
![]() $\phi \colon \mathbb {A}_X(e,\gamma ) \to \operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}))$
of graded vector bundles over T.
$\phi \colon \mathbb {A}_X(e,\gamma ) \to \operatorname {\mathrm {gr}}(\operatorname {\mathrm {Lie}}(\mathcal {G}))$
of graded vector bundles over T.
Proof. By definition, we have
![]() $X' \simeq BG'$
, where
$X' \simeq BG'$
, where
![]() $G' \simeq \operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
. Moreover, the map of Dirac
$G' \simeq \operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Fil}}\mathcal {G}_0)$
. Moreover, the map of Dirac
![]() $S_0$
-stacks
$S_0$
-stacks
![]() $h \colon X \to X'$
in the statement determines and is determined by a map of Dirac
$h \colon X \to X'$
in the statement determines and is determined by a map of Dirac
![]() $S_0$
-groups
$S_0$
-groups
![]() $\rho \colon G \to G'$
. It follows from Proposition 5.17 that the latter map determines and is determined by the power series
$\rho \colon G \to G'$
. It follows from Proposition 5.17 that the latter map determines and is determined by the power series
of the form
 $$ \begin{align*}\begin{aligned} \rho(e) & = \textstyle{ e + \sum_{i \geq 0} a_i\gamma^{p^i} } \cr \rho(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1} b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \rho(e) & = \textstyle{ e + \sum_{i \geq 0} a_i\gamma^{p^i} } \cr \rho(\gamma) & = \textstyle{ \gamma + \sum_{i \geq 1} b_i\gamma^{p^i} } \cr \end{aligned}\end{align*} $$
with
![]() $a_i \in \pi _{2p^i-1}(\mathbb {F}_p^{\otimes [1]})$
and
$a_i \in \pi _{2p^i-1}(\mathbb {F}_p^{\otimes [1]})$
and
![]() $b_i \in \pi _{2p^i-2}(\mathbb {F}_p^{\otimes [1]})$
. Now, the statement that
$b_i \in \pi _{2p^i-2}(\mathbb {F}_p^{\otimes [1]})$
. Now, the statement that
![]() $\rho $
is an isomorphism of Dirac
$\rho $
is an isomorphism of Dirac
![]() $S_0$
-group schemes is equivalent to the statement that all
$S_0$
-group schemes is equivalent to the statement that all
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are nonzero. But this is precisely the statement of [Reference Milnor29, Lemma 6].
$b_i$
are nonzero. But this is precisely the statement of [Reference Milnor29, Lemma 6].
A Accessible presheaves
In the body of the paper, we have occasion to consider presheaves of anima on the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Aff}}$
of affine Dirac schemes. The
$\operatorname {\mathrm {Aff}}$
of affine Dirac schemes. The
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {\mathrm {Aff}}$
is not small, but it is coaccessible in the sense that
$\operatorname {\mathrm {Aff}}$
is not small, but it is coaccessible in the sense that
![]() $\operatorname {\mathrm {Aff}}^{\mathrm {op}} \simeq \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
is accessible. In this context, it is natural to only consider accessible presheaves. We will show that, in general, the
$\operatorname {\mathrm {Aff}}^{\mathrm {op}} \simeq \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Ab}})$
is accessible. In this context, it is natural to only consider accessible presheaves. We will show that, in general, the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on a coaccessible
${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on a coaccessible
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
has the following properties:
$\mathcal {C}$
has the following properties:
-
(1) The Yoneda embedding restricts to a fully faithful functor
 $h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
, which exhibits
$h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
, which exhibits
 ${\mathcal {P}}(\mathcal {C})$
as the cocompletion of
${\mathcal {P}}(\mathcal {C})$
as the cocompletion of
 $\mathcal {C}$
.
$\mathcal {C}$
. -
(2) The
 $\infty $
-category
$\infty $
-category
 ${\mathcal {P}}(\mathcal {C})$
satisfies the Giraud axioms, with the exception that, in general, it is not presentable.
${\mathcal {P}}(\mathcal {C})$
satisfies the Giraud axioms, with the exception that, in general, it is not presentable. -
(3) If
 $\mathcal {C}$
admits pullbacks, then there are adjoint functors associated with every map
$\mathcal {C}$
admits pullbacks, then there are adjoint functors associated with every map
 $f \colon Y \to X$
in
$f \colon Y \to X$
in
 ${\mathcal {P}}(\mathcal {C})$
, where
${\mathcal {P}}(\mathcal {C})$
, where
 $f_!$
is given by restriction along f and where
$f_!$
is given by restriction along f and where
 $f^*$
given by base-change along f.
$f^*$
given by base-change along f.
This appendix does not go as far as one would want. We expect that there is a larger and more systematic theory of
![]() $\infty $
-categories which behave as
$\infty $
-categories which behave as
![]() $\infty $
-categories of accessible presheaves on coaccessible
$\infty $
-categories of accessible presheaves on coaccessible
![]() $\infty $
-categories. However, this is not the place to develop such a theory, but to encourage work in this direction, we end with a list of properties that we expect such a theory to have; see Question A.20.
$\infty $
-categories. However, this is not the place to develop such a theory, but to encourage work in this direction, we end with a list of properties that we expect such a theory to have; see Question A.20.
We now proceed to prove the properties (1)–(3) of accessible presheaves listed above. We recall from [Reference Lurie20, Definition A.2.6.3] that the relation
![]() $\lambda \ll \kappa $
among regular cardinals indicates that for every
$\lambda \ll \kappa $
among regular cardinals indicates that for every
![]() $\kappa _0 < \kappa $
and
$\kappa _0 < \kappa $
and
![]() $\lambda _0 < \lambda $
, we have
$\lambda _0 < \lambda $
, we have
![]() $\smash { \kappa _0^{\lambda _0} < \kappa }$
.
$\smash { \kappa _0^{\lambda _0} < \kappa }$
.
Lemma A.1. Let
![]() $\kappa \gg \lambda $
be regular cardinals. If
$\kappa \gg \lambda $
be regular cardinals. If
![]() $\mathcal {D}$
is a
$\mathcal {D}$
is a
![]() $\lambda $
-accessible
$\lambda $
-accessible
![]() $\infty $
-category, then the slice category
$\infty $
-category, then the slice category
![]() $(\mathcal {D}^{\kappa })_{/d}$
is
$(\mathcal {D}^{\kappa })_{/d}$
is
![]() $\kappa $
-filtered for all
$\kappa $
-filtered for all
![]() $d \in \mathcal {D}$
.
$d \in \mathcal {D}$
.
Proof. Given a diagram
![]() $p \colon K \to (\mathcal {D}^{\kappa })_{/d}$
with the property that K is
$p \colon K \to (\mathcal {D}^{\kappa })_{/d}$
with the property that K is
![]() $\kappa $
-small, we must produce a diagram
$\kappa $
-small, we must produce a diagram
![]() $\bar {p} \colon K^{\triangleright } \to (\mathcal {D}^{\kappa })_{/d}$
and an equivalence
$\bar {p} \colon K^{\triangleright } \to (\mathcal {D}^{\kappa })_{/d}$
and an equivalence
![]() $\bar {p}|_K \simeq p$
. We identify
$\bar {p}|_K \simeq p$
. We identify
with the full subcategory of presheaves of anima on
![]() $\mathcal {D}^{\lambda }$
generated under
$\mathcal {D}^{\lambda }$
generated under
![]() $\lambda $
-filtered colimits by the full subcategory of representable presheaves. In these terms, we can identify p with a pair
$\lambda $
-filtered colimits by the full subcategory of representable presheaves. In these terms, we can identify p with a pair
![]() $(q,g)$
of a diagram
$(q,g)$
of a diagram
![]() $q \colon K \to \mathcal {D}^{\kappa } \subset \mathcal {P}(\mathcal {D}^{\lambda })$
and a map
$q \colon K \to \mathcal {D}^{\kappa } \subset \mathcal {P}(\mathcal {D}^{\lambda })$
and a map
from the colimit calculated in
![]() ${\mathcal {P}}(\mathcal {D}^{\lambda })$
, and we must show that g factors through an object of
${\mathcal {P}}(\mathcal {D}^{\lambda })$
, and we must show that g factors through an object of
![]() $\mathcal {D}^{\kappa }$
. We recall from [Reference Lurie20, Proposition 5.4.2.11] that since
$\mathcal {D}^{\kappa }$
. We recall from [Reference Lurie20, Proposition 5.4.2.11] that since
![]() $\kappa \gg \lambda $
, every
$\kappa \gg \lambda $
, every
![]() $\lambda $
-accessible
$\lambda $
-accessible
![]() $\infty $
-category is
$\infty $
-category is
![]() $\kappa $
-accessible. So we can write
$\kappa $
-accessible. So we can write
![]() $d \in \mathcal {D}$
as a
$d \in \mathcal {D}$
as a
![]() $\kappa $
-filtered colimit
$\kappa $
-filtered colimit
with
![]() $d_{\alpha } \in \mathcal {D}^{\kappa } \subset \mathcal {D}$
, and the proof of loc.cit. shows that we can arrange that each of the
$d_{\alpha } \in \mathcal {D}^{\kappa } \subset \mathcal {D}$
, and the proof of loc.cit. shows that we can arrange that each of the
![]() $d_{\alpha }$
is a colimit of a
$d_{\alpha }$
is a colimit of a
![]() $\kappa $
-small
$\kappa $
-small
![]() $\lambda $
-filtered diagram in
$\lambda $
-filtered diagram in
![]() $\mathcal {D}^{\lambda } \subset \mathcal {D}$
. Accordingly, each of the
$\mathcal {D}^{\lambda } \subset \mathcal {D}$
. Accordingly, each of the
![]() $d_{\alpha }$
is also
$d_{\alpha }$
is also
![]() $\kappa $
-compact as an object of
$\kappa $
-compact as an object of
![]() ${\mathcal {P}}(\mathcal {D}^{\lambda })$
. Now, the inclusion
${\mathcal {P}}(\mathcal {D}^{\lambda })$
. Now, the inclusion
![]() $\mathcal {D} \subset {\mathcal {P}}(\mathcal {D}^{\lambda })$
preserves
$\mathcal {D} \subset {\mathcal {P}}(\mathcal {D}^{\lambda })$
preserves
![]() $\lambda $
-filtered colimits, so, in particular, it preserves
$\lambda $
-filtered colimits, so, in particular, it preserves
![]() $\kappa $
-filtered colimits. Therefore, we also have
$\kappa $
-filtered colimits. Therefore, we also have
with the colimit calculated in
![]() ${\mathcal {P}}(\mathcal {D}^{\lambda })$
. Since the domain of the map g in question is a
${\mathcal {P}}(\mathcal {D}^{\lambda })$
. Since the domain of the map g in question is a
![]() $\kappa $
-small colimit of
$\kappa $
-small colimit of
![]() $\kappa $
-compact objects in
$\kappa $
-compact objects in
![]() ${\mathcal {P}}(\mathcal {D}^{\lambda })$
, it is itself
${\mathcal {P}}(\mathcal {D}^{\lambda })$
, it is itself
![]() $\kappa $
-compact, and therefore, we conclude that g factors through some
$\kappa $
-compact, and therefore, we conclude that g factors through some
![]() $d_{\alpha }$
, as we wanted to prove.
$d_{\alpha }$
, as we wanted to prove.
Notation. If
![]() $\kappa $
is a regular cardinal and if
$\kappa $
is a regular cardinal and if
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\kappa $
-coaccessible
$\kappa $
-coaccessible
![]() $\infty $
-category, then we write
$\infty $
-category, then we write
![]() $\mathcal {C}_{\kappa } \subset \mathcal {C}$
for the full subcategory spanned by the
$\mathcal {C}_{\kappa } \subset \mathcal {C}$
for the full subcategory spanned by the
![]() $\kappa $
-cocompact objects. The
$\kappa $
-cocompact objects. The
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}_{\kappa }$
is essentially small, and
$\mathcal {C}_{\kappa }$
is essentially small, and
![]() $\mathcal {C} \simeq \operatorname {\mathrm {Pro}}_{\kappa }(\mathcal {C}_{\kappa })$
is its completion under small
$\mathcal {C} \simeq \operatorname {\mathrm {Pro}}_{\kappa }(\mathcal {C}_{\kappa })$
is its completion under small
![]() $\kappa $
-cofiltered limits.
$\kappa $
-cofiltered limits.
Proposition A.2. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category. For a functor
$\infty $
-category. For a functor
![]() $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
, the following conditions are equivalent:
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
, the following conditions are equivalent:
-
(1) The functor
 $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is accessible.
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is accessible. -
(2) The functor
 $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is the left Kan extension of a functor
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is the left Kan extension of a functor
 $Y \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to {\mathcal {S}}$
along the canonical inclusion
$Y \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to {\mathcal {S}}$
along the canonical inclusion
 $i \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to \mathcal {C}^{\mathrm {op}}$
for some regular cardinal
$i \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to \mathcal {C}^{\mathrm {op}}$
for some regular cardinal
 $\kappa $
.
$\kappa $
. -
(3) The functor
 $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is a colimit in
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is a colimit in
 $\operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
of a small diagram of representable functors.
$\operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
of a small diagram of representable functors.
Proof. To prove that (1) implies (2), we first choose a regular carcinal
![]() $\lambda $
such
$\lambda $
such
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\lambda $
-coaccessible and such that
$\lambda $
-coaccessible and such that
![]() $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is
![]() $\lambda $
-accessible. We next choose a regular cardinal
$\lambda $
-accessible. We next choose a regular cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\kappa \gg \lambda $
. We claim that the counit map
$\kappa \gg \lambda $
. We claim that the counit map
is an equivalence. The value of
![]() $i_!i^*(X)$
at
$i_!i^*(X)$
at
![]() $c \in \mathcal {C}^{\mathrm {op}}$
is the colimit of the diagram
$c \in \mathcal {C}^{\mathrm {op}}$
is the colimit of the diagram
Now, by Lemma A.1, the slice category on the left is
![]() $\kappa $
-filtered, and since X preserves
$\kappa $
-filtered, and since X preserves
![]() $\lambda $
-filtered and hence
$\lambda $
-filtered and hence
![]() $\kappa $
-filtered colimits, we conclude that the counit map
$\kappa $
-filtered colimits, we conclude that the counit map
is an equivalence, which shows that (2) holds with
![]() $Y \simeq i^*(X)$
.
$Y \simeq i^*(X)$
.
To prove that (2) implies (3), we assume that
![]() $X \simeq i_!(Y)$
with
$X \simeq i_!(Y)$
with
![]() $Y \in \operatorname {\mathrm {Fun}}(\mathcal {C}_{\kappa }^{\mathrm {op}},{\mathcal {S}})$
. Since
$Y \in \operatorname {\mathrm {Fun}}(\mathcal {C}_{\kappa }^{\mathrm {op}},{\mathcal {S}})$
. Since
![]() $\mathcal {C}_{\kappa }$
is essentially small, we can identify Y with a small colimit of representable functors. But left Kan extension preserves colimits and takes representable functors to representable functors, so we conclude that (3) holds.
$\mathcal {C}_{\kappa }$
is essentially small, we can identify Y with a small colimit of representable functors. But left Kan extension preserves colimits and takes representable functors to representable functors, so we conclude that (3) holds.
Finally, to see that (3) implies (1), we note that, since
![]() $\mathcal {C}^{\mathrm {op}}$
is accessible, every representable functor
$\mathcal {C}^{\mathrm {op}}$
is accessible, every representable functor
![]() $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is accessible. Hence, given a small diagram of representable functors
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
is accessible. Hence, given a small diagram of representable functors
![]() $X_{\alpha }$
, we can find a small cardinal
$X_{\alpha }$
, we can find a small cardinal
![]() $\lambda $
such that each of the
$\lambda $
such that each of the
![]() $X_{\alpha }$
preserves
$X_{\alpha }$
preserves
![]() $\lambda $
-filtered colimits. Since colimits commute with colimits, their levelwise colimit again preserves
$\lambda $
-filtered colimits. Since colimits commute with colimits, their levelwise colimit again preserves
![]() $\lambda $
-filtered colimits and hence is accessible.
$\lambda $
-filtered colimits and hence is accessible.
Definition A.3. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category. The
$\infty $
-category. The
![]() $\infty $
-category of accessible presheaves of anima on
$\infty $
-category of accessible presheaves of anima on
![]() $\mathcal {C}$
is the full subcategory
$\mathcal {C}$
is the full subcategory
spanned by the functors that satisfy the equivalent conditions of Proposition A.2.
Remark A.4 (Universal property of accessible presheaves).
If
![]() $\mathcal {C}$
is a coaccessible
$\mathcal {C}$
is a coaccessible
![]() $\infty $
-category, then the Yoneda embedding factors through a functor
$\infty $
-category, then the Yoneda embedding factors through a functor
which, by abuse of language, we also refer to as the Yoneda embedding. It follows from Proposition A.2 that this functor is characterized by the following universal property: If
![]() $\mathcal {D}$
is any
$\mathcal {D}$
is any
![]() $\infty $
-category, which admits small colimits, then composition with the Yoneda embedding gives rise to an equivalence
$\infty $
-category, which admits small colimits, then composition with the Yoneda embedding gives rise to an equivalence
from the full subcategory
![]() $\operatorname {\mathrm {Fun}}^L({\mathcal {P}}(\mathcal {C}),\mathcal {D}) \subset \operatorname {\mathrm {Fun}}({\mathcal {P}}(\mathcal {C}),\mathcal {D})$
spanned by the functors that preserve small colimits. An inverse takes
$\operatorname {\mathrm {Fun}}^L({\mathcal {P}}(\mathcal {C}),\mathcal {D}) \subset \operatorname {\mathrm {Fun}}({\mathcal {P}}(\mathcal {C}),\mathcal {D})$
spanned by the functors that preserve small colimits. An inverse takes
![]() $F \colon \mathcal {C} \to \mathcal {D}$
to its left Kan extension
$F \colon \mathcal {C} \to \mathcal {D}$
to its left Kan extension
![]() $h_!(F) \colon {\mathcal {P}}(\mathcal {C}) \to \mathcal {D}$
, which exists because every accessible presheaf is a small colimit of representables and
$h_!(F) \colon {\mathcal {P}}(\mathcal {C}) \to \mathcal {D}$
, which exists because every accessible presheaf is a small colimit of representables and
![]() $\mathcal {D}$
is cocomplete; see also [Reference Lurie20, Remark 5.3.5.9].
$\mathcal {D}$
is cocomplete; see also [Reference Lurie20, Remark 5.3.5.9].
Warning A.5. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category. We write
$\infty $
-category. We write
![]() $h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
for its cocompletion. If
$h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
for its cocompletion. If
![]() $\mathcal {C}$
is small, then [Reference Lurie20, Corollary 5.4.3.6] shows that its cocompletion agrees with the Yoneda embedding
$\mathcal {C}$
is small, then [Reference Lurie20, Corollary 5.4.3.6] shows that its cocompletion agrees with the Yoneda embedding
![]() $h \colon \mathcal {C} \to \operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
to the functor
$h \colon \mathcal {C} \to \operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
to the functor
![]() $\infty $
-category. In general, however, the functor
$\infty $
-category. In general, however, the functor
![]() $\infty $
-category is larger and pathological. For example, we show in Lemma A.7 that
$\infty $
-category is larger and pathological. For example, we show in Lemma A.7 that
![]() ${\mathcal {P}}(\mathcal {C})$
is locally small, but this is generally not true for the functor
${\mathcal {P}}(\mathcal {C})$
is locally small, but this is generally not true for the functor
![]() $\infty $
-category.
$\infty $
-category.
Remark A.6. We recall from [Reference Lurie20, Corollary 5.4.3.6] that a small
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
is accessible if and only if it is idempotent complete. However, if
$\mathcal {C}$
is accessible if and only if it is idempotent complete. However, if
![]() $j \colon \mathcal {C} \to \mathcal {C}'$
is an idempotent completion of
$j \colon \mathcal {C} \to \mathcal {C}'$
is an idempotent completion of
![]() $\mathcal {C}$
, then
$\mathcal {C}$
, then
![]() $\mathcal {C}'$
is again small and
$\mathcal {C}'$
is again small and
![]() $j_! \colon {\mathcal {P}}(\mathcal {C}) \to {\mathcal {P}}(\mathcal {C}')$
is an equivalence. Thus, the theory of accessible presheaves on coaccessible
$j_! \colon {\mathcal {P}}(\mathcal {C}) \to {\mathcal {P}}(\mathcal {C}')$
is an equivalence. Thus, the theory of accessible presheaves on coaccessible
![]() $\infty $
-categories is a strict generalization of the theory of presheaves on small
$\infty $
-categories is a strict generalization of the theory of presheaves on small
![]() $\infty $
-categories.
$\infty $
-categories.
Lemma A.7. Let
![]() $\mathcal {C}$
be coaccessible
$\mathcal {C}$
be coaccessible
![]() $\infty $
-category. The
$\infty $
-category. The
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on
${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on
![]() $\mathcal {C}$
is locally small.
$\mathcal {C}$
is locally small.
Proof. Given
![]() $X,Y \in {\mathcal {P}}(\mathcal {C})$
, the mapping anima
$X,Y \in {\mathcal {P}}(\mathcal {C})$
, the mapping anima
![]() $\operatorname {\mathrm {Map}}(Y,X)$
is potentially large. We must show that it is small. By Proposition A.2, we may write
$\operatorname {\mathrm {Map}}(Y,X)$
is potentially large. We must show that it is small. By Proposition A.2, we may write
![]() $Y \simeq \varinjlim _{\alpha } h(c_{\alpha })$
as a small colimit of representable functors. Thus, the anima
$Y \simeq \varinjlim _{\alpha } h(c_{\alpha })$
as a small colimit of representable functors. Thus, the anima
is a small limit of small anima, and hence, it is indeed small.
Lemma A.8. Suppose that
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\lambda $
-coaccessible and let
$\lambda $
-coaccessible and let
![]() $\lambda \ll \kappa \leq \kappa '$
be infinite regular cardinals. In this situation, the left Kan extension
$\lambda \ll \kappa \leq \kappa '$
be infinite regular cardinals. In this situation, the left Kan extension
along the inclusion
![]() $i \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to (\mathcal {C}_{\kappa '})^{\mathrm {op}}$
preserves all colimits and
$i \colon (\mathcal {C}_{\kappa })^{\mathrm {op}} \to (\mathcal {C}_{\kappa '})^{\mathrm {op}}$
preserves all colimits and
![]() $\kappa $
-small limits.
$\kappa $
-small limits.
Proof. Since left Kan extension is a left adjoint, it preserves colimits. For limits, we note that if
![]() $X \in {\mathcal {P}}(\mathcal {C}_{\kappa })$
and
$X \in {\mathcal {P}}(\mathcal {C}_{\kappa })$
and
![]() $c \in (\mathcal {C}_{\kappa '})^{\mathrm {op}}$
, then
$c \in (\mathcal {C}_{\kappa '})^{\mathrm {op}}$
, then
![]() $i_!(X)(c)$
is the colimit of the diagram
$i_!(X)(c)$
is the colimit of the diagram
where p is the projection. Thus, the statement follows from Lemma A.1 and from the fact proved in [Reference Lurie20, Proposition 5.3.3.3] that
![]() $\kappa $
-filtered colimits and
$\kappa $
-filtered colimits and
![]() $\kappa $
-small limits of anima commute.
$\kappa $
-small limits of anima commute.
Proposition A.9. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category. The
$\infty $
-category. The
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on
${\mathcal {P}}(\mathcal {C})$
of accessible presheaves of anima on
![]() $\mathcal {C}$
admits all small limits and colimits, and both are calculated pointwise.
$\mathcal {C}$
admits all small limits and colimits, and both are calculated pointwise.
Proof. We claim that
![]() ${\mathcal {P}}(\mathcal {C}) \subset \operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
is closed under small limits and colimits. This is clear from condition (3) of Proposition A.2 in the case of colimits. To prove the claim for limits, we fix a diagram
${\mathcal {P}}(\mathcal {C}) \subset \operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
is closed under small limits and colimits. This is clear from condition (3) of Proposition A.2 in the case of colimits. To prove the claim for limits, we fix a diagram
![]() $p \colon K \to {\mathcal {P}}(\mathcal {C})$
with K small. We can choose a cardinal
$p \colon K \to {\mathcal {P}}(\mathcal {C})$
with K small. We can choose a cardinal
![]() $\kappa $
such that
$\kappa $
such that
-
1.
 $\mathcal {C}$
is
$\mathcal {C}$
is
 $\kappa $
-coaccessible,
$\kappa $
-coaccessible, -
2. for every
 $k \in K$
,
$k \in K$
,
 $p(k) \colon \mathcal {C}^{op} \to {\mathcal {S}}$
preserves
$p(k) \colon \mathcal {C}^{op} \to {\mathcal {S}}$
preserves
 $\kappa $
-filtered colimits, and
$\kappa $
-filtered colimits, and -
3. K is
 $\kappa $
-small.
$\kappa $
-small.
With this choice, the limit of p calculated in
![]() $\operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
preserves
$\operatorname {\mathrm {Fun}}(\mathcal {C}^{\mathrm {op}},{\mathcal {S}})$
preserves
![]() $\kappa $
-filtered colimits, and therefore, condition (1) of Proposition A.2 shows that it belongs to
$\kappa $
-filtered colimits, and therefore, condition (1) of Proposition A.2 shows that it belongs to
![]() ${\mathcal {P}}(\mathcal {C})$
.
${\mathcal {P}}(\mathcal {C})$
.
Theorem A.10. The
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\mathcal {C})$
of accessible presheaves on a coaccessible
${\mathcal {P}}(\mathcal {C})$
of accessible presheaves on a coaccessible
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
enjoys the following properties:
$\mathcal {C}$
enjoys the following properties:
-
(i) It is cocomplete, complete and generated under small colimits by the essential image of
 $h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
, which consists of compact objects and is coaccessible.
$h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
, which consists of compact objects and is coaccessible. -
(ii) Colimits in
 ${\mathcal {P}}(\mathcal {C})$
are universal.
${\mathcal {P}}(\mathcal {C})$
are universal. -
(iii) Coproducts in
 ${\mathcal {P}}(\mathcal {C})$
are disjoint.
${\mathcal {P}}(\mathcal {C})$
are disjoint. -
(iv) Every groupoid in
 ${\mathcal {P}}(\mathcal {C})$
is effective.
${\mathcal {P}}(\mathcal {C})$
is effective.
Proof. Since colimits in
![]() ${\mathcal {P}}(\mathcal {C})$
are pointwise, we conclude that all representable presheaves are compact. Moreover, Proposition A.2 shows that
${\mathcal {P}}(\mathcal {C})$
are pointwise, we conclude that all representable presheaves are compact. Moreover, Proposition A.2 shows that
![]() ${\mathcal {P}}(\mathcal {C})$
is generated under small colimits by the representable presheaves, and Proposition A.9 shows that
${\mathcal {P}}(\mathcal {C})$
is generated under small colimits by the representable presheaves, and Proposition A.9 shows that
![]() ${\mathcal {P}}(\mathcal {C})$
is complete and cocomplete. This proves (i). The statements (ii)–(iv) concern the interaction of limits and colimits in
${\mathcal {P}}(\mathcal {C})$
is complete and cocomplete. This proves (i). The statements (ii)–(iv) concern the interaction of limits and colimits in
![]() ${\mathcal {P}}(\mathcal {C})$
, and since both are calculated pointwise, these statements follow from the corresponding statements about the
${\mathcal {P}}(\mathcal {C})$
, and since both are calculated pointwise, these statements follow from the corresponding statements about the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {S}}$
of anima, which are proved in [Reference Lurie20, Theorem 6.1.0.6].
${\mathcal {S}}$
of anima, which are proved in [Reference Lurie20, Theorem 6.1.0.6].
We proceed to discuss localization. We recall that if
![]() $\mathcal {C}$
is small, then for every presheaf
$\mathcal {C}$
is small, then for every presheaf
![]() $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
, there is a canonical equivalence
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
, there is a canonical equivalence
with
![]() $j \colon \mathcal {C}_{/X} \to \mathcal {C}$
the base-change of
$j \colon \mathcal {C}_{/X} \to \mathcal {C}$
the base-change of
![]() $p \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})$
along
$p \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})$
along
![]() $h \colon \mathcal {C} \to \mathcal {P}(\mathcal {C})$
. There is an essentially unique diagram
$h \colon \mathcal {C} \to \mathcal {P}(\mathcal {C})$
. There is an essentially unique diagram

with
![]() $j_!$
cocontinuous, and
$j_!$
cocontinuous, and
![]() $j_!$
factors through an equivalence as stated. We wish to show that there is an analogous picture in the case, where
$j_!$
factors through an equivalence as stated. We wish to show that there is an analogous picture in the case, where
![]() $\mathcal {C}$
is coaccessible.
$\mathcal {C}$
is coaccessible.
Lemma A.11. Suppose that
![]() $\mathcal {C}$
is a coaccessible
$\mathcal {C}$
is a coaccessible
![]() $\infty $
-category. Let
$\infty $
-category. Let
![]() $X \in {\mathcal {P}}(\mathcal {C})$
and let
$X \in {\mathcal {P}}(\mathcal {C})$
and let
![]() $j \colon \mathcal {C}_{/X} \to \mathcal {C}$
be the base-change of
$j \colon \mathcal {C}_{/X} \to \mathcal {C}$
be the base-change of
![]() $p \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})$
along
$p \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})$
along
![]() $h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
. In this situation, the slice
$h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
. In this situation, the slice
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}_{/X}$
and the functor
$\mathcal {C}_{/X}$
and the functor
![]() $j \colon \mathcal {C}_{/X} \to \mathcal {C}$
are coaccessible.
$j \colon \mathcal {C}_{/X} \to \mathcal {C}$
are coaccessible.
Proof. The functor
![]() $j^{\mathrm {op}} \colon (\mathcal {C}_{/X})^{\mathrm {op}} \to \mathcal {C}^{\mathrm {op}}$
is the left fibration classified by the functor
$j^{\mathrm {op}} \colon (\mathcal {C}_{/X})^{\mathrm {op}} \to \mathcal {C}^{\mathrm {op}}$
is the left fibration classified by the functor
![]() $X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
. So there is a cartesian diagram of
$X \colon \mathcal {C}^{\mathrm {op}} \to {\mathcal {S}}$
. So there is a cartesian diagram of
![]() $\infty $
-categories
$\infty $
-categories

with the right-hand vertical map given by the universal left fibration, which is the canonical projection
![]() $p \colon {\mathcal {S}}_* \simeq {\mathcal {S}}_{/1} \to {\mathcal {S}}$
. Since p and X both are accessible functors between accessible
$p \colon {\mathcal {S}}_* \simeq {\mathcal {S}}_{/1} \to {\mathcal {S}}$
. Since p and X both are accessible functors between accessible
![]() $\infty $
-categories, we conclude from [Reference Lurie20, Proposition 5.4.6.6] that the same is true for
$\infty $
-categories, we conclude from [Reference Lurie20, Proposition 5.4.6.6] that the same is true for
![]() $j^{\mathrm {op}}$
.
$j^{\mathrm {op}}$
.
Remark A.12. In the context of Lemma A.11,
![]() $j \colon \mathcal {C}_{/X} \to \mathcal {C}$
is a right fibration. Since every
$j \colon \mathcal {C}_{/X} \to \mathcal {C}$
is a right fibration. Since every
![]() $\kappa $
-cofiltered
$\kappa $
-cofiltered
![]() $\infty $
-category is weakly contractible, it follows from [Reference Lurie17, Tag 02KS] that if
$\infty $
-category is weakly contractible, it follows from [Reference Lurie17, Tag 02KS] that if
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\kappa $
-coaccessible, then
$\kappa $
-coaccessible, then
![]() $\mathcal {C}_{/X}$
admits
$\mathcal {C}_{/X}$
admits
![]() $\kappa $
-cofiltered limits and j preserves and reflects them. This does not necessarily mean that
$\kappa $
-cofiltered limits and j preserves and reflects them. This does not necessarily mean that
![]() $\mathcal {C}_{/X}$
is
$\mathcal {C}_{/X}$
is
![]() $\kappa $
-coaccessible, since it may not be generated under
$\kappa $
-coaccessible, since it may not be generated under
![]() $\kappa $
-cofiltered limits by
$\kappa $
-cofiltered limits by
![]() $\kappa $
-cocompact objects.
$\kappa $
-cocompact objects.
Proposition A.13. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category, and
$\infty $
-category, and
![]() $X \in {\mathcal {P}}(\mathcal {C})$
. In this situation, the Yoneda embedding induces an equivalence
$X \in {\mathcal {P}}(\mathcal {C})$
. In this situation, the Yoneda embedding induces an equivalence
Proof. Since
![]() $\mathcal {C}_{/X}$
is coaccessible by Lemma A.11, and since
$\mathcal {C}_{/X}$
is coaccessible by Lemma A.11, and since
![]() ${\mathcal {P}}(\mathcal {C})_{/X}$
admits small colimits by Proposition A.9, the map
${\mathcal {P}}(\mathcal {C})_{/X}$
admits small colimits by Proposition A.9, the map
![]() $h_{/X} \colon \mathcal {C}_{/X} \to {\mathcal {P}}(\mathcal {C})_{/X}$
induced by the Yoneda embedding extends essentially uniquely to the map in the statement. We may view this map as the restriction of the corresponding map
$h_{/X} \colon \mathcal {C}_{/X} \to {\mathcal {P}}(\mathcal {C})_{/X}$
induced by the Yoneda embedding extends essentially uniquely to the map in the statement. We may view this map as the restriction of the corresponding map
between the
![]() $\infty $
-categories of presheaves of large anima. The latter is an equivalence because
$\infty $
-categories of presheaves of large anima. The latter is an equivalence because
![]() $\mathcal {C}$
is small with respect to this larger universe, so we conclude that the map in the statement is fully faithful. It remains to show that it is essentially surjective. Given
$\mathcal {C}$
is small with respect to this larger universe, so we conclude that the map in the statement is fully faithful. It remains to show that it is essentially surjective. Given
![]() $(Y,f \colon Y \to X)$
in
$(Y,f \colon Y \to X)$
in
![]() ${\mathcal {P}}(\mathcal {C})_{/X}$
, we can find a diagram
${\mathcal {P}}(\mathcal {C})_{/X}$
, we can find a diagram

with K small such that
![]() $\bar {p}$
is a colimit diagram, whose value at the cone point is Y. Thus, the maps
$\bar {p}$
is a colimit diagram, whose value at the cone point is Y. Thus, the maps
![]() $\bar {p}$
and f determine a diagram
$\bar {p}$
and f determine a diagram
![]() $q \colon K \to \mathcal {C}_{/X}$
, and the map in the statement takes the colimit of the composite map
$q \colon K \to \mathcal {C}_{/X}$
, and the map in the statement takes the colimit of the composite map
to the given object
![]() $(Y,f \colon Y \to X)$
, as desired.
$(Y,f \colon Y \to X)$
, as desired.
We recall from [Reference Lurie20, Lemma 6.1.1.1] that a map
![]() $f \colon Y \to X$
in an
$f \colon Y \to X$
in an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}$
that admits pullbacks gives rise to an adjoint pair of functors
$\mathcal {D}$
that admits pullbacks gives rise to an adjoint pair of functors

and from [Reference Lurie20, Lemma 4.4.2.1] that given a cartesian diagram

in
![]() $\mathcal {D}$
, the composite ‘base-change’ map
$\mathcal {D}$
, the composite ‘base-change’ map
is an equivalence. If
![]() $\mathcal {D} \simeq {\mathcal {P}}(\mathcal {C})$
with
$\mathcal {D} \simeq {\mathcal {P}}(\mathcal {C})$
with
![]() $\mathcal {C}$
coaccessible, then Theorem A.10 shows that
$\mathcal {C}$
coaccessible, then Theorem A.10 shows that
![]() $f^*$
preserves small colimits. However, since
$f^*$
preserves small colimits. However, since
![]() ${\mathcal {P}}(\mathcal {C})$
may not be presentable, we cannot invoke the adjoint functor theorem to conclude that
${\mathcal {P}}(\mathcal {C})$
may not be presentable, we cannot invoke the adjoint functor theorem to conclude that
![]() $f^*$
admits a right adjoint
$f^*$
admits a right adjoint
![]() $f_*$
. We will prove that this is nevertheless the case, under the assumption that
$f_*$
. We will prove that this is nevertheless the case, under the assumption that
![]() $\mathcal {C}$
admits pullbacks. We do not know if this assumption is necessary.
$\mathcal {C}$
admits pullbacks. We do not know if this assumption is necessary.
Theorem A.14. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $f \colon Y \to X$
be a map in the
$f \colon Y \to X$
be a map in the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal {P}}(\mathcal {C})$
of accessible presheaves on
${\mathcal {P}}(\mathcal {C})$
of accessible presheaves on
![]() $\mathcal {C}$
. If
$\mathcal {C}$
. If
![]() $\mathcal {C}$
admits pullbacks, then the functor
$\mathcal {C}$
admits pullbacks, then the functor
![]() $f^* \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})_{/Y}$
admits a right adjoint
$f^* \colon {\mathcal {P}}(\mathcal {C})_{/X} \to {\mathcal {P}}(\mathcal {C})_{/Y}$
admits a right adjoint
![]() $f_* \colon {\mathcal {P}}(\mathcal {C})_{/Y} \to {\mathcal {P}}(\mathcal {C})_{/X}$
.
$f_* \colon {\mathcal {P}}(\mathcal {C})_{/Y} \to {\mathcal {P}}(\mathcal {C})_{/X}$
.
Before we begin the proof of Theorem A.14, which will occupy the remainder of this appendix, we give an example to demonstrate the subtleties of the situation.
Example A.15. Under the equivalence of Proposition A.13, we can identify the functor
![]() $f^*$
in Theorem A.14 with the functor
$f^*$
in Theorem A.14 with the functor
![]() $f^* \colon {\mathcal {P}}(\mathcal {C}_{/X}) \to {\mathcal {P}}(\mathcal {C}_{/Y})$
given by restriction along
$f^* \colon {\mathcal {P}}(\mathcal {C}_{/X}) \to {\mathcal {P}}(\mathcal {C}_{/Y})$
given by restriction along
![]() $f_! \colon \mathcal {C}_{/Y} \to \mathcal {C}_{/X}$
. Thus, one might expect that for every coaccessible functor
$f_! \colon \mathcal {C}_{/Y} \to \mathcal {C}_{/X}$
. Thus, one might expect that for every coaccessible functor
![]() $f \colon \mathcal {D} \to \mathcal {C}$
between coaccessible
$f \colon \mathcal {D} \to \mathcal {C}$
between coaccessible
![]() $\infty $
-categories, the functor
$\infty $
-categories, the functor
given by restriction along f admits a right adjoint. Surprisingly, this is not the case in general! For an explicit counterexample, we consider the functor
that to the unique object assigns the set
![]() $\{0,1\}$
. In this case, the functor
$\{0,1\}$
. In this case, the functor
takes an accessible functor
![]() $X \colon {\mathcal {S}} \to {\mathcal {S}}$
to its value at
$X \colon {\mathcal {S}} \to {\mathcal {S}}$
to its value at
![]() $\{0,1\}$
. We claim that this functor
$\{0,1\}$
. We claim that this functor
![]() $f^*$
does not admit a right adjoint
$f^*$
does not admit a right adjoint
![]() $f_*$
. If it did, then we would have
$f_*$
. If it did, then we would have
but this functor is not accessible, since any accessible functor
![]() $X \colon {\mathcal {S}} \to {\mathcal {S}}$
preserves
$X \colon {\mathcal {S}} \to {\mathcal {S}}$
preserves
![]() $\kappa $
-compact objects for some
$\kappa $
-compact objects for some
![]() $\kappa $
.
$\kappa $
.
Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $f \colon Y \to X$
be a map of accessible presheaves on
$f \colon Y \to X$
be a map of accessible presheaves on
![]() $\mathcal {C}$
. We consider the composite functor
$\mathcal {C}$
. We consider the composite functor
and compose it with the functor represented by
![]() $Z \in {\mathcal {P}}(\mathcal {C})$
to obtain a functor
$Z \in {\mathcal {P}}(\mathcal {C})$
to obtain a functor
which takes values in the
![]() $\infty $
-category of small anima because
$\infty $
-category of small anima because
![]() ${\mathcal {P}}(\mathcal {C})$
is locally small, as we proved in Lemma A.7.
${\mathcal {P}}(\mathcal {C})$
is locally small, as we proved in Lemma A.7.
Lemma A.16. Let
![]() $\kappa $
be a regular cardinal and let
$\kappa $
be a regular cardinal and let
![]() $\mathcal {C}$
be a
$\mathcal {C}$
be a
![]() $\kappa $
-coaccessible
$\kappa $
-coaccessible
![]() $\infty $
-category which admits pullbacks. Let
$\infty $
-category which admits pullbacks. Let
![]() $f \colon Y \to X$
be a map of accessible presheaves on
$f \colon Y \to X$
be a map of accessible presheaves on
![]() $\mathcal {C}$
with X a representable presheaf and with Y a
$\mathcal {C}$
with X a representable presheaf and with Y a
![]() $\kappa $
-small colimit of representable presheaves and let Z be a
$\kappa $
-small colimit of representable presheaves and let Z be a
![]() $\kappa $
-accessible presheaf on
$\kappa $
-accessible presheaf on
![]() $\mathcal {C}$
. In this situation, the functor
$\mathcal {C}$
. In this situation, the functor
preserves
![]() $\kappa $
-filtered colimits.
$\kappa $
-filtered colimits.
Proof. We note that by Remark A.12, the slice
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}_{/X}$
admits
$\mathcal {C}_{/X}$
admits
![]() $\kappa $
-cofiltered limits. If we write
$\kappa $
-cofiltered limits. If we write
![]() $\smash { Y \simeq \varinjlim _{\alpha }Y_{\alpha } }$
as a
$\smash { Y \simeq \varinjlim _{\alpha }Y_{\alpha } }$
as a
![]() $\kappa $
-small colimit of representable presheaves and let
$\kappa $
-small colimit of representable presheaves and let
![]() $f_{\alpha } \colon h(b_{\alpha }) \to X$
be the restriction of f along
$f_{\alpha } \colon h(b_{\alpha }) \to X$
be the restriction of f along
![]() $Y_{\alpha } \to Y$
, then
$Y_{\alpha } \to Y$
, then
 $$ \begin{align*}\begin{aligned} { F_{f,Z}(c,h(c) \to X) } & \simeq \operatorname{\mathrm{Map}}(Y \times_Xh(c),Z) \simeq \textstyle{ \operatorname{\mathrm{Map}}(\varinjlim_{\alpha} Y_{\alpha} \times_Xh(c),Z) } \cr {} & \simeq \textstyle{ \varprojlim_{\alpha} \operatorname{\mathrm{Map}}(Y_{\alpha} \times_X h(c),Z) \simeq \varprojlim_{\alpha} F_{f_{\alpha},Z}(c,h(c) \to X), } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} { F_{f,Z}(c,h(c) \to X) } & \simeq \operatorname{\mathrm{Map}}(Y \times_Xh(c),Z) \simeq \textstyle{ \operatorname{\mathrm{Map}}(\varinjlim_{\alpha} Y_{\alpha} \times_Xh(c),Z) } \cr {} & \simeq \textstyle{ \varprojlim_{\alpha} \operatorname{\mathrm{Map}}(Y_{\alpha} \times_X h(c),Z) \simeq \varprojlim_{\alpha} F_{f_{\alpha},Z}(c,h(c) \to X), } \cr \end{aligned}\end{align*} $$
and since
![]() $\kappa $
-small limits and
$\kappa $
-small limits and
![]() $\kappa $
-filtered colimits of anima commute, we may assume that Y is representable.
$\kappa $
-filtered colimits of anima commute, we may assume that Y is representable.
So we write
![]() $X \simeq h(x)$
and
$X \simeq h(x)$
and
![]() $Y \simeq h(y)$
and suppose that
$Y \simeq h(y)$
and suppose that
![]() $(c,h(c) \to X)$
is the limit of a
$(c,h(c) \to X)$
is the limit of a
![]() $\kappa $
-cofiltered diagram
$\kappa $
-cofiltered diagram
![]() $(c_{\alpha },h(c_{\alpha }) \to X)$
in
$(c_{\alpha },h(c_{\alpha }) \to X)$
in
![]() $\mathcal {C}_{/X}$
. We conclude from Remark A.12 that c is the limit of the underlying diagram
$\mathcal {C}_{/X}$
. We conclude from Remark A.12 that c is the limit of the underlying diagram
![]() $(c_{\alpha })$
in
$(c_{\alpha })$
in
![]() $\mathcal {C}$
. Since the Yoneda embedding preserves all limits that exist in
$\mathcal {C}$
. Since the Yoneda embedding preserves all limits that exist in
![]() $\mathcal {C}$
, we have
$\mathcal {C}$
, we have
Therefore, since Z is
![]() $\kappa $
-accessible, we have
$\kappa $
-accessible, we have
 $$ \begin{align*}\begin{aligned} { F_{f,Z}(c,h(c) \to X) } & \simeq \operatorname{\mathrm{Map}}(Y \times_Xh(c),Z) \simeq \textstyle{ Z(\varprojlim_{\alpha} y\times_xc_{\alpha}) } \cr {} & \simeq \textstyle{ \varinjlim_{\alpha} Z(y\times_xc_{\alpha}) \simeq \varinjlim_{\alpha} F_{f,Z}(c_{\alpha},h(c_{\alpha}) \to X), } \cr \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} { F_{f,Z}(c,h(c) \to X) } & \simeq \operatorname{\mathrm{Map}}(Y \times_Xh(c),Z) \simeq \textstyle{ Z(\varprojlim_{\alpha} y\times_xc_{\alpha}) } \cr {} & \simeq \textstyle{ \varinjlim_{\alpha} Z(y\times_xc_{\alpha}) \simeq \varinjlim_{\alpha} F_{f,Z}(c_{\alpha},h(c_{\alpha}) \to X), } \cr \end{aligned}\end{align*} $$
as we wanted to prove.
We will need the following notion.
Definition A.17. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $\kappa $
be a regular cardinal. A map
$\kappa $
be a regular cardinal. A map
![]() $f \colon Y \to X$
of accessible presheaves on
$f \colon Y \to X$
of accessible presheaves on
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\kappa $
-compact if for every map
$\kappa $
-compact if for every map
![]() $g \colon h(c) \to X$
from a representable presheaf on
$g \colon h(c) \to X$
from a representable presheaf on
![]() $\mathcal {C}$
, the domain
$\mathcal {C}$
, the domain
![]() $Y'$
of the base-change
$Y'$
of the base-change
![]() $f' \colon Y' \to h(c)$
of f along g can be written as a
$f' \colon Y' \to h(c)$
of f along g can be written as a
![]() $\kappa $
-small colimit of representable presheaves on
$\kappa $
-small colimit of representable presheaves on
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma A.18. If
![]() $\mathcal {C}$
is a coaccessible
$\mathcal {C}$
is a coaccessible
![]() $\infty $
-category which admits pullbacks, then every map
$\infty $
-category which admits pullbacks, then every map
![]() $f \colon Y \to X$
of accessible presheaves on
$f \colon Y \to X$
of accessible presheaves on
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\kappa $
-compact for some
$\kappa $
-compact for some
![]() $\kappa $
.
$\kappa $
.
Proof. Suppose first that
![]() $X \simeq h(x)$
is representable. We can write
$X \simeq h(x)$
is representable. We can write
![]() $Y \simeq \varinjlim _{\alpha } h(y_{\alpha })$
as a
$Y \simeq \varinjlim _{\alpha } h(y_{\alpha })$
as a
![]() $\kappa $
-small colimit of representable presheaves for some regular cardinal
$\kappa $
-small colimit of representable presheaves for some regular cardinal
![]() $\kappa $
. Now, for any map
$\kappa $
. Now, for any map
![]() $g \colon h(c) \to X$
from a representable presheaf, we find that
$g \colon h(c) \to X$
from a representable presheaf, we find that
which is a
![]() $\kappa $
-small colimit of representable presheaves on
$\kappa $
-small colimit of representable presheaves on
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
In general, we write
![]() $\smash { X \simeq \varinjlim _{\alpha }X_{\alpha } }$
as a small colimit of representable presheaves, and we let
$\smash { X \simeq \varinjlim _{\alpha }X_{\alpha } }$
as a small colimit of representable presheaves, and we let
![]() $f_{\alpha } \colon Y_{\alpha } \to X_{\alpha }$
be the base-change of f along
$f_{\alpha } \colon Y_{\alpha } \to X_{\alpha }$
be the base-change of f along
![]() $X_{\alpha } \to X$
. Since colimits in
$X_{\alpha } \to X$
. Since colimits in
![]() ${\mathcal {P}}(\mathcal {C})$
are calculated pointwise, any map
${\mathcal {P}}(\mathcal {C})$
are calculated pointwise, any map
![]() $g \colon h(c) \to X$
from a representable presheaf will factor through
$g \colon h(c) \to X$
from a representable presheaf will factor through
![]() $X_{\alpha } \to X$
for some
$X_{\alpha } \to X$
for some
![]() $\alpha $
. Moreover, by the special case that we considered above, we find that
$\alpha $
. Moreover, by the special case that we considered above, we find that
is
![]() $\kappa _{\alpha }$
-compact for some regular cardinal
$\kappa _{\alpha }$
-compact for some regular cardinal
![]() $\kappa _{\alpha }$
. Thus, if we choose a regular cardinal
$\kappa _{\alpha }$
. Thus, if we choose a regular cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\kappa \geq \kappa _{\alpha }$
for all
$\kappa \geq \kappa _{\alpha }$
for all
![]() $\alpha $
, then f is
$\alpha $
, then f is
![]() $\kappa $
-compact.
$\kappa $
-compact.
We now improve Lemma A.16 to the general case.
Lemma A.19. Let
![]() $\mathcal {C}$
be a coaccessible
$\mathcal {C}$
be a coaccessible
![]() $\infty $
-category which admits pullbacks, let
$\infty $
-category which admits pullbacks, let
![]() $f \colon Y \to X$
be a map of accessible presheaves on
$f \colon Y \to X$
be a map of accessible presheaves on
![]() $\mathcal {C}$
and let Z be an accessible presheaf on
$\mathcal {C}$
and let Z be an accessible presheaf on
![]() $\mathcal {C}$
. In this situation, the functor
$\mathcal {C}$
. In this situation, the functor
is accessible.
Proof. Using Lemma A.18, we can choose a regular cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\kappa $
-coaccessible, f is
$\kappa $
-coaccessible, f is
![]() $\kappa $
-compact and Z is
$\kappa $
-compact and Z is
![]() $\kappa $
-accessible. We proceed to show that for this
$\kappa $
-accessible. We proceed to show that for this
![]() $\kappa $
, the functor
$\kappa $
, the functor
![]() $F_{j, Z}$
preserves
$F_{j, Z}$
preserves
![]() $\kappa $
-filtered colimits. Here, we use Remark A.12 to conclude that
$\kappa $
-filtered colimits. Here, we use Remark A.12 to conclude that
![]() $\mathcal {C}_{/X}$
admits
$\mathcal {C}_{/X}$
admits
![]() $\kappa $
-cofiltered limits.
$\kappa $
-cofiltered limits.
So we fix a diagram
![]() $p \colon K \to \mathcal {C}_{/X}$
, where K is
$p \colon K \to \mathcal {C}_{/X}$
, where K is
![]() $\kappa $
-cofiltered, and we wish to prove that the canonical map of anima
$\kappa $
-cofiltered, and we wish to prove that the canonical map of anima
is an equivalence. For any
![]() $k \in K$
, the projection
$k \in K$
, the projection
![]() $j \colon K_{/k} \to K$
is a
$j \colon K_{/k} \to K$
is a
![]() $\varprojlim $
-equivalence, and therefore, by replacing p by
$\varprojlim $
-equivalence, and therefore, by replacing p by
![]() $pj$
, if necessary, we may assume that K has a final object. So let
$pj$
, if necessary, we may assume that K has a final object. So let
![]() $1 \in K$
be final and let
$1 \in K$
be final and let
![]() $(d,g \colon h(d) \to X)$
be its value under p. In this situation, the functor
$(d,g \colon h(d) \to X)$
be its value under p. In this situation, the functor
![]() $p \colon K \to \mathcal {C}_{/X}$
factors canonically as
$p \colon K \to \mathcal {C}_{/X}$
factors canonically as

and, by base-change, we have a diagram

with
![]() $f' \colon Y' \to h(c)$
the base-change of f along g. Since
$f' \colon Y' \to h(c)$
the base-change of f along g. Since
![]() $g_!$
preserves
$g_!$
preserves
![]() $\kappa $
-cofiltered limits by Remark A.12, it suffices to show that the canonical map
$\kappa $
-cofiltered limits by Remark A.12, it suffices to show that the canonical map
is an equivalence. But
![]() $Y'$
is a
$Y'$
is a
![]() $\kappa $
-small colimit of representable presheaves because f is
$\kappa $
-small colimit of representable presheaves because f is
![]() $\kappa $
-compact, so this follows from Lemma A.16.
$\kappa $
-compact, so this follows from Lemma A.16.
We now give the proof of the main result of this section.
Proof of Theorem A.14.
By [Reference Lurie17, Tag 02FV], it will suffice to show that for every object
![]() $g \colon Z \to Y$
in
$g \colon Z \to Y$
in
![]() ${\mathcal {P}}(\mathcal {C})_{/Y}$
, the functor
${\mathcal {P}}(\mathcal {C})_{/Y}$
, the functor
given by the composition of
![]() $f^*$
and the functor represented by g is representable. As we already remarked, the functor
$f^*$
and the functor represented by g is representable. As we already remarked, the functor
![]() $f^*$
preserves colimits because colimits in
$f^*$
preserves colimits because colimits in
![]() ${\mathcal {P}}(\mathcal {C})$
are universal, so
${\mathcal {P}}(\mathcal {C})$
are universal, so
![]() $R_g$
preserves limits. Hence, since the canonical map
$R_g$
preserves limits. Hence, since the canonical map
is an equivalence by Proposition A.13, it suffices to show that the restriction
of
![]() $R_g$
along the Yoneda embedding is an accessible functor. Indeed, if so, then the image of
$R_g$
along the Yoneda embedding is an accessible functor. Indeed, if so, then the image of
![]() $r_g$
by the equivalence above is the object
$r_g$
by the equivalence above is the object
![]() $f_*(g)$
that represents
$f_*(g)$
that represents
![]() $R_g$
.
$R_g$
.
Let
![]() $q \colon Y \to 1$
be the unique map to the final object. The adjunction
$q \colon Y \to 1$
be the unique map to the final object. The adjunction
is comonadic, and hence, the cobar construction of
![]() $g \colon Z \to Y$
, which is constructed in [Reference Lurie19, Example 4.7.2.7], is a limit diagram
$g \colon Z \to Y$
, which is constructed in [Reference Lurie19, Example 4.7.2.7], is a limit diagram
whose value at
![]() $[n]$
is the
$[n]$
is the
![]() $(n+1)$
th iterate of
$(n+1)$
th iterate of
![]() $q^*q_!$
applied to g. It follows that
$q^*q_!$
applied to g. It follows that
and since accessible presheaves are closed under small limits, it suffices to show that
![]() $r_g$
is accessible in the case, where
$r_g$
is accessible in the case, where
![]() $g \simeq q^*(W)$
for some
$g \simeq q^*(W)$
for some
![]() $W \in {\mathcal {P}}(\mathcal {C})$
. But
$W \in {\mathcal {P}}(\mathcal {C})$
. But
which is accessible by Lemma A.19. This completes the proof.
Question A.20. Let us say that an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}$
is the following:Footnote
14
$\mathcal {D}$
is the following:Footnote
14
-
1. macroaccessible, if it can be written as
 $\mathcal {D} \simeq \operatorname {\mathrm {Ind}}_{\kappa }(\mathcal {C})$
for some regular cardinal
$\mathcal {D} \simeq \operatorname {\mathrm {Ind}}_{\kappa }(\mathcal {C})$
for some regular cardinal
 $\kappa $
and some coaccessible
$\kappa $
and some coaccessible
 $\infty $
-category
$\infty $
-category
 $\mathcal {C}$
.
$\mathcal {C}$
. -
2. macropresentable, if it is macroaccessible and cocomplete.
-
3. a macrotopos, if it is macropresentable and satisfies Giraud’s axioms (ii)–(iv).
We expect that the following questions have affirmative answers:
-
1. If
 $\mathcal {D}$
is macroaccessible, then for every regular cardinal
$\mathcal {D}$
is macroaccessible, then for every regular cardinal
 $\kappa $
, is the full subcategory
$\kappa $
, is the full subcategory
 $\mathcal {D}^{\kappa } \subset \mathcal {D}$
spanned by the
$\mathcal {D}^{\kappa } \subset \mathcal {D}$
spanned by the
 $\kappa $
-compact objects coaccessible?
$\kappa $
-compact objects coaccessible? -
2. If
 $\mathcal {D}$
is macropresentable, then is it automatically complete?
$\mathcal {D}$
is macropresentable, then is it automatically complete? -
3. Is it possible to formula an adjoint functor theorem that characterizes left adjoint functors between macropresentable
 $\infty $
-categories?
$\infty $
-categories? -
4. Does there exist a good theory of localizations of macroaccessible categories, and if so, then can the properties of being macropresentable and of being a macrotopos be characterized in terms of being a suitable localization of an
 $\infty $
-category of accessible presheaves?
$\infty $
-category of accessible presheaves? -
5. Are macropresentable
 $\infty $
-categories and macrotopoi closed under the formation of slice categories, limits, etc.?
$\infty $
-categories and macrotopoi closed under the formation of slice categories, limits, etc.?
B Effective epimorphisms of sheaves
In this appendix, we spell out some folklore results on effective epimorphisms of sheaves for which we have not been able to find a suitable reference.
Let
![]() $\mathcal {C}$
be a small
$\mathcal {C}$
be a small
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
be the Yoneda embedding into the
$h \colon \mathcal {C} \to {\mathcal {P}}(\mathcal {C})$
be the Yoneda embedding into the
![]() $\infty $
-category of presheaves of anima on
$\infty $
-category of presheaves of anima on
![]() $\mathcal {C}$
. A sieve on
$\mathcal {C}$
. A sieve on
![]() $S \in \mathcal {C}$
is an equivalence class of
$S \in \mathcal {C}$
is an equivalence class of
![]() $(-1)$
-truncated maps
$(-1)$
-truncated maps
![]() $j \colon U \to h(S)$
in
$j \colon U \to h(S)$
in
![]() ${\mathcal {P}}(\mathcal {C})$
. It determines and is determined by the full subcategory
${\mathcal {P}}(\mathcal {C})$
. It determines and is determined by the full subcategory
![]() $\mathcal {C}_{/S}(U) \subset \mathcal {C}_{/S}$
spanned by the maps
$\mathcal {C}_{/S}(U) \subset \mathcal {C}_{/S}$
spanned by the maps
![]() $g \colon S' \to S$
with the property that
$g \colon S' \to S$
with the property that
![]() $h(g)$
factors through j.
$h(g)$
factors through j.
Example B.1. If
![]() $f \colon T \to S$
is a map in
$f \colon T \to S$
is a map in
![]() $\mathcal {C}$
, then [Reference Lurie20, Proposition 6.2.3.4] shows that the colimit of its Čech nerve provides the essentially unique factorization
$\mathcal {C}$
, then [Reference Lurie20, Proposition 6.2.3.4] shows that the colimit of its Čech nerve provides the essentially unique factorization
of
![]() $h(f)$
as the composition of a
$h(f)$
as the composition of a
![]() $(-1)$
-connected map and a
$(-1)$
-connected map and a
![]() $(-1)$
-truncated map. Therefore, a map
$(-1)$
-truncated map. Therefore, a map
![]() $g \colon S' \to S$
in
$g \colon S' \to S$
in
![]() $\mathcal {C}$
factors through f if and only if the map
$\mathcal {C}$
factors through f if and only if the map
![]() $h(g)$
in
$h(g)$
in
![]() ${\mathcal {P}}(\mathcal {C})$
factors through j. In particular, the full subcategory of
${\mathcal {P}}(\mathcal {C})$
factors through j. In particular, the full subcategory of
![]() $\mathcal {C}_{/S}(U) \subset \mathcal {C}_{/S}$
spanned by the maps with this property is closed under coproducts.
$\mathcal {C}_{/S}(U) \subset \mathcal {C}_{/S}$
spanned by the maps with this property is closed under coproducts.
Example B.2. If
![]() $(f_i \colon T_i \to S)_{i \in I}$
is a family of maps in
$(f_i \colon T_i \to S)_{i \in I}$
is a family of maps in
![]() $\mathcal {C}$
, then there is a smallest sieve
$\mathcal {C}$
, then there is a smallest sieve
![]() $j \colon U \to h(S)$
with the property that
$j \colon U \to h(S)$
with the property that
![]() $h(f_i)$
factors through j for all
$h(f_i)$
factors through j for all
![]() $i \in I$
. We say that
$i \in I$
. We say that
![]() $j \colon U \to h(S)$
is the sieve generated by
$j \colon U \to h(S)$
is the sieve generated by
![]() $(f_i \colon T_i \to S)_{i \in I}$
.
$(f_i \colon T_i \to S)_{i \in I}$
.
Definition B.3. Let
![]() $\mathcal {C}$
be a small
$\mathcal {C}$
be a small
![]() $\infty $
-category. A Grothendieck topology on
$\infty $
-category. A Grothendieck topology on
![]() $\mathcal {C}$
is an assignment to every S in
$\mathcal {C}$
is an assignment to every S in
![]() $\mathcal {C}$
of a set
$\mathcal {C}$
of a set
![]() $J(S)$
of sieves on S, called the covering sieves on S, such that the following hold:
$J(S)$
of sieves on S, called the covering sieves on S, such that the following hold:
-
(1) The class of
 $\operatorname {\mathrm {id}}_{h(S)} \colon h(S) \to h(S)$
is a covering sieve for every S in
$\operatorname {\mathrm {id}}_{h(S)} \colon h(S) \to h(S)$
is a covering sieve for every S in
 $\mathcal {C}$
.
$\mathcal {C}$
. -
(2) If
 $j \colon U \to h(S)$
is a covering sieve on S, and if
$j \colon U \to h(S)$
is a covering sieve on S, and if
 $f \colon T \to S$
is any map in
$f \colon T \to S$
is any map in
 $\mathcal {C}$
, then the base-change
$\mathcal {C}$
, then the base-change
 $j' \colon U' \to h(T)$
of j along
$j' \colon U' \to h(T)$
of j along
 $h(f)$
is a covering sieve on T.
$h(f)$
is a covering sieve on T. -
(3) Let
 $j \colon U \to h(S)$
and
$j \colon U \to h(S)$
and
 $k \colon V \to h(S)$
be sieves on S. If k is a covering sieve, and if for every
$k \colon V \to h(S)$
be sieves on S. If k is a covering sieve, and if for every
 $f \colon T \to S$
with the property that
$f \colon T \to S$
with the property that
 $h(f)$
factors through k, the base-change
$h(f)$
factors through k, the base-change
 $j' \colon U' \to h(T)$
of j along
$j' \colon U' \to h(T)$
of j along
 $h(f)$
is a covering sieve on T, then j is a covering sieve on S.
$h(f)$
is a covering sieve on T, then j is a covering sieve on S.
A family
![]() $(f_i \colon T_i \to S)_{i \in I}$
of maps in
$(f_i \colon T_i \to S)_{i \in I}$
of maps in
![]() $\mathcal {C}$
is a covering family if the sieve
$\mathcal {C}$
is a covering family if the sieve
![]() $j \colon U \to h(S)$
that it generates is a covering sieve. A Grothendieck topology is finitary if every covering sieve contains a finite covering family.
$j \colon U \to h(S)$
that it generates is a covering sieve. A Grothendieck topology is finitary if every covering sieve contains a finite covering family.
Remark B.4. Let
![]() $\mathcal {C}$
be a small
$\mathcal {C}$
be a small
![]() $\infty $
-category equipped with a Grothendieck topology. We claim that if
$\infty $
-category equipped with a Grothendieck topology. We claim that if
![]() $j \colon U \to h(S)$
is a sieve on S, which contains a covering sieve in the sense that there exists a covering sieve
$j \colon U \to h(S)$
is a sieve on S, which contains a covering sieve in the sense that there exists a covering sieve
![]() $k \colon V \to h(S)$
such that k factors through j, then j is a covering sieve. Indeed, if
$k \colon V \to h(S)$
such that k factors through j, then j is a covering sieve. Indeed, if
![]() $f \colon T \to S$
has the property that
$f \colon T \to S$
has the property that
![]() $h(f)$
factors through k, then
$h(f)$
factors through k, then
![]() $h(f)$
also factors through j, and hence, the base-change
$h(f)$
also factors through j, and hence, the base-change
![]() $j' \colon U' \to h(T)$
of j along
$j' \colon U' \to h(T)$
of j along
![]() $h(f)$
is a
$h(f)$
is a
![]() $(-1)$
-truncated map, which admits a section. But then
$(-1)$
-truncated map, which admits a section. But then
![]() $j'$
is equivalent to the identity map and hence is a covering sieve by (1), so we conclude from (3) that j is a covering sieve, as claimed.
$j'$
is equivalent to the identity map and hence is a covering sieve by (1), so we conclude from (3) that j is a covering sieve, as claimed.
Definition B.5. Let
![]() $\mathcal {C}$
is a small
$\mathcal {C}$
is a small
![]() $\infty $
-category equipped with a Grothendieck topology, let
$\infty $
-category equipped with a Grothendieck topology, let
![]() $f \colon Y \to X$
be map of presheaves of anima on
$f \colon Y \to X$
be map of presheaves of anima on
![]() $\mathcal {C}$
and let
$\mathcal {C}$
and let
![]() $j \colon U \to X$
be the canonical map from the colimit of its Čech nerve. The map
$j \colon U \to X$
be the canonical map from the colimit of its Čech nerve. The map
![]() $f \colon Y \to X$
is a local epimorphism if the base-change
$f \colon Y \to X$
is a local epimorphism if the base-change
![]() $j_S \colon Y_S \to h(S)$
of j along any map
$j_S \colon Y_S \to h(S)$
of j along any map
![]() $\eta \colon h(S) \to X$
with S in
$\eta \colon h(S) \to X$
with S in
![]() $\mathcal {C}$
is a covering sieve.
$\mathcal {C}$
is a covering sieve.
Proposition B.6. Let
![]() $\mathcal {C}$
be a small
$\mathcal {C}$
be a small
![]() $\infty $
-category equipped with a Grothendieck topology and let
$\infty $
-category equipped with a Grothendieck topology and let
![]() $f \colon Y \to X$
be a map of presheaves of anima on
$f \colon Y \to X$
be a map of presheaves of anima on
![]() $\mathcal {C}$
. The following are equivalent:
$\mathcal {C}$
. The following are equivalent:
-
(1) The map
 $L(f) \colon L(Y) \to L(X)$
in
$L(f) \colon L(Y) \to L(X)$
in
 $\operatorname {\mathrm {Shv}}(\mathcal {C})$
is an effective epimorphism.
$\operatorname {\mathrm {Shv}}(\mathcal {C})$
is an effective epimorphism. -
(2) The map
 $f \colon Y \to X$
is a local epimorphism.
$f \colon Y \to X$
is a local epimorphism. -
(3) For every S in
 $\mathcal {C}$
and every S-valued point
$\mathcal {C}$
and every S-valued point
 $\eta \in X(S)$
, there exists a diagram with
$\eta \in X(S)$
, there exists a diagram with
 $(g_i \colon T_i \to S)_{i \in I}$
a covering family. If the Grothendieck topology is finitary, then said covering family can be taken to be finite.
$(g_i \colon T_i \to S)_{i \in I}$
a covering family. If the Grothendieck topology is finitary, then said covering family can be taken to be finite.
Proof. We recall from [Reference Lurie20, Proposition 6.2.3.4] that
is the essentially unique factorization of f as the composition of a
![]() $(-1)$
-connected map and a
$(-1)$
-connected map and a
![]() $(-1)$
-truncated map. Now, to prove that (1) and (2) are equivalent, let us say that
$(-1)$
-truncated map. Now, to prove that (1) and (2) are equivalent, let us say that
![]() $\eta \colon X' \to X$
is good if the base-change
$\eta \colon X' \to X$
is good if the base-change
![]() $j' \colon U' \to X'$
of j along
$j' \colon U' \to X'$
of j along
![]() $\eta $
is a covering sieve, or equivalently, if
$\eta $
is a covering sieve, or equivalently, if
![]() $L(j') \colon L(U') \to L(X')$
is an equivalence. So (1) is the statement that the identity map
$L(j') \colon L(U') \to L(X')$
is an equivalence. So (1) is the statement that the identity map
![]() $\operatorname {\mathrm {id}}_X \colon X \to X$
is good, whereas (2) is the statement that every map
$\operatorname {\mathrm {id}}_X \colon X \to X$
is good, whereas (2) is the statement that every map
![]() $\eta \colon S \to X$
from a representable presheaf is good. Now, if
$\eta \colon S \to X$
from a representable presheaf is good. Now, if
![]() $\eta \colon X' \to X$
is good, and if
$\eta \colon X' \to X$
is good, and if
![]() $g \colon X" \to X'$
is any map, then
$g \colon X" \to X'$
is any map, then
![]() $\eta g \colon X" \to X$
is good, so (1) implies (2). And the full subcategory of
$\eta g \colon X" \to X$
is good, so (1) implies (2). And the full subcategory of
![]() ${\mathcal {P}}(\mathcal {C})_{/X}$
spanned by the good maps
${\mathcal {P}}(\mathcal {C})_{/X}$
spanned by the good maps
![]() $\eta \colon X' \to X$
is closed under colimits, so (2) implies (1).
$\eta \colon X' \to X$
is closed under colimits, so (2) implies (1).
Finally, to prove that (2) and (3) are equivalent, we note that (2) is the statement that for every S in
![]() $\mathcal {C}$
and every
$\mathcal {C}$
and every
![]() $\eta \in X(S)$
, the base-change
$\eta \in X(S)$
, the base-change
![]() $j_S$
of j along
$j_S$
of j along
![]() $\eta $
is a covering sieve. But the sieve
$\eta $
is a covering sieve. But the sieve
![]() $j_S$
is a covering sieve if and only if there exists a covering family
$j_S$
is a covering sieve if and only if there exists a covering family
![]() $(g_i \colon T_i \to S)_{i \in I}$
and a diagram
$(g_i \colon T_i \to S)_{i \in I}$
and a diagram

Moreover, this diagram exists if and only if the diagram in (3) exists, so we have proved that (2) and (3) are indeed equivalent.
If a covering family
![]() $(g_i \colon T_i \to S)_{i \in I}$
consists of a single map
$(g_i \colon T_i \to S)_{i \in I}$
consists of a single map
![]() $g \colon T \to S$
, then we will also say that the map
$g \colon T \to S$
, then we will also say that the map
![]() $g \colon T \to S$
is a covering.
$g \colon T \to S$
is a covering.
Corollary B.7. Let
![]() $\mathcal {C}$
be a small
$\mathcal {C}$
be a small
![]() $\infty $
-category equipped with a finitary Grothendieck topology and suppose that
$\infty $
-category equipped with a finitary Grothendieck topology and suppose that
![]() $\mathcal {C}$
admits finite coproducts. A map
$\mathcal {C}$
admits finite coproducts. A map
![]() $f \colon Y \to X$
of sheaves of anima on
$f \colon Y \to X$
of sheaves of anima on
![]() $\mathcal {C}$
is an effective epimorphism if and only if for every S in
$\mathcal {C}$
is an effective epimorphism if and only if for every S in
![]() $\mathcal {C}$
and every map
$\mathcal {C}$
and every map
![]() $\eta \colon h(S) \to X$
, there exists a diagram
$\eta \colon h(S) \to X$
, there exists a diagram

with
![]() $g \colon T \to S$
a covering.
$g \colon T \to S$
a covering.
Proof. Proposition B.6 shows that
![]() $f \colon Y \to X$
is an effective epimorphism of sheaves on
$f \colon Y \to X$
is an effective epimorphism of sheaves on
![]() $\mathcal {C}$
if and only if for every
$\mathcal {C}$
if and only if for every
![]() $\eta \colon h(S) \to X$
with S in
$\eta \colon h(S) \to X$
with S in
![]() $\mathcal {C}$
, there exists a diagram
$\mathcal {C}$
, there exists a diagram

with
![]() $(g_i \colon T_i \to S)_{i \in I}$
a finite covering family. But Y preserves finite products, so the map
$(g_i \colon T_i \to S)_{i \in I}$
a finite covering family. But Y preserves finite products, so the map
![]() $\tilde {\eta }$
factors essentially uniquely through the canonical map
$\tilde {\eta }$
factors essentially uniquely through the canonical map
and since
![]() $(g_i \colon T_i \to S$
) is a covering family, we conclude from Remark B.4 that the induced map
$(g_i \colon T_i \to S$
) is a covering family, we conclude from Remark B.4 that the induced map
![]() $g \colon T \simeq \coprod _{i \in I} T_i \to S$
is a covering.
$g \colon T \simeq \coprod _{i \in I} T_i \to S$
is a covering.
Acknowledgements
It is a pleasure to thank Maxime Ramzi for carefully reading a first draft of Appendix 1 and for several helpful suggestions. The second author also would like to thank Kazuhiro Fujiwara and Nagoya University, and Takeshi Saito and the University of Tokyo, for their support and hospitality during his visit to Japan, where part of this paper was written. Finally, we thank an anonymous referee for helpful comments.
Competing interests
The authors have no competing interest to declare.
Funding statement
Both authors were supported by the Danish National Research Foundation through the Copenhagen Center for Geometry and Topology (DNRF151). Lars Hesselholt received support from JSPS Grant-in-Aid for Scientific Research number 21K03161 and from a grant from the Institute for Advanced Study School of Mathematics, and Piotr Pstrągowski received support from NSF Grant #DMS-1926686 and Deutsche Forschungsgemeinschaft #EXC-2047/1 – 390685813.