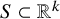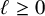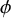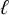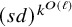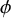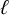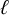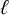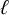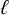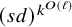1 Introduction
1.1 Background
Let
![]() $\mathrm {R}$
be a real closed field and
$\mathrm {R}$
be a real closed field and
![]() $\mathrm {D}$
an ordered domain contained in
$\mathrm {D}$
an ordered domain contained in
![]() $\mathrm {R}$
.
$\mathrm {R}$
.
The problem of effective computation of topological properties of semialgebraic subsets of
![]() $\mathrm {R}^k$
has a long history. Semialgebraic subsets of
$\mathrm {R}^k$
has a long history. Semialgebraic subsets of
![]() $\mathrm {R}^k$
are subsets defined by first-order formulas in the language of ordered fields (with parameters in
$\mathrm {R}^k$
are subsets defined by first-order formulas in the language of ordered fields (with parameters in
![]() $\mathrm {R}$
). Since the first-order theory of real closed fields admits quantifier-elimination, we can assume that each semialgebraic subset
$\mathrm {R}$
). Since the first-order theory of real closed fields admits quantifier-elimination, we can assume that each semialgebraic subset
![]() $S \subset \mathrm {R}^k$
is defined by some quantifier-free formula
$S \subset \mathrm {R}^k$
is defined by some quantifier-free formula
![]() $\phi $
. A quantifier-free formula
$\phi $
. A quantifier-free formula
![]() $\phi (X_1,\ldots ,X_k)$
in the language of ordered fields with parameters in
$\phi (X_1,\ldots ,X_k)$
in the language of ordered fields with parameters in
![]() $\mathrm {D}$
, is a formula with atoms of the form
$\mathrm {D}$
, is a formula with atoms of the form
![]() $P = 0, P> 0, P < 0$
,
$P = 0, P> 0, P < 0$
,
![]() $P \in \mathrm {D}[X_1,\ldots ,X_k]$
.
$P \in \mathrm {D}[X_1,\ldots ,X_k]$
.
Semialgebraic subsets of
![]() $\mathrm {R}^k$
have tame topology. In particular, closed and bounded semialgebraic subsets of
$\mathrm {R}^k$
have tame topology. In particular, closed and bounded semialgebraic subsets of
![]() $\mathrm {R}^k$
are semialgebraically triangulable (see, for example, [Reference Basu, Pollack and Roy4, Chapter 5]). This means that there exists a finite simplicial complex K, whose geometric realization,
$\mathrm {R}^k$
are semialgebraically triangulable (see, for example, [Reference Basu, Pollack and Roy4, Chapter 5]). This means that there exists a finite simplicial complex K, whose geometric realization,
![]() $|K|$
, considered as a subset of
$|K|$
, considered as a subset of
![]() $\mathrm {R}^N$
for some
$\mathrm {R}^N$
for some
![]() $N>0$
, is semialgebraically homeomorphic to S. The semialgebraic homeomorphism
$N>0$
, is semialgebraically homeomorphic to S. The semialgebraic homeomorphism
![]() $|K| \rightarrow S$
is called a semialgebraic triangulation of S. All topological properties of S are then encoded in the finite data of the simplicial complex K.
$|K| \rightarrow S$
is called a semialgebraic triangulation of S. All topological properties of S are then encoded in the finite data of the simplicial complex K.
For instance, taking
![]() $\mathrm {R} = \mathbb {R}$
, the (singular) homology groups,
$\mathrm {R} = \mathbb {R}$
, the (singular) homology groups,
![]() $\mathrm {H}_*(S)$
, of S are isomorphic to the simplicial homology groups of the simplicial chain complex
$\mathrm {H}_*(S)$
, of S are isomorphic to the simplicial homology groups of the simplicial chain complex
![]() $\mathrm {C}_{\bullet }(K)$
of the simplicial complex K, and the latter is a complex of free
$\mathrm {C}_{\bullet }(K)$
of the simplicial complex K, and the latter is a complex of free
![]() $\mathbb {Z}$
-modules having finite ranks (here and elsewhere in the paper, unless stated otherwise, all homology and cohomology groups are with coefficients in
$\mathbb {Z}$
-modules having finite ranks (here and elsewhere in the paper, unless stated otherwise, all homology and cohomology groups are with coefficients in
![]() $\mathbb {Z}$
).
$\mathbb {Z}$
).
The problem of designing an efficient algorithm for obtaining semialgebraic triangulations has attracted a lot of attention over the years. One reason behind this is that once we have such a triangulation, we can then compute discrete topological invariants, such as the ranks of the homology groups (i.e., the Betti numbers) of the given semialgebraic set with just some added linear algebra over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
There exists a classical algorithm which takes as input a quantifier-free formula defining a semialgebraic set S and produces as output a semialgebraic triangulation of S (see for instance [Reference Basu, Pollack and Roy4, Chapter 5]). However, this algorithm is based on the technique of cylindrical algebraic decomposition, and hence the complexity of this algorithm is prohibitively expensive, being doubly exponential in k. More precisely, given a description by a quantifier-free formula involving s polynomials of degree at most d, of a closed and bounded semialgebraic subset of
![]() $S \subset \mathrm {R}^k$
, there exists an algorithm computing a semialgebraic triangulation of
$S \subset \mathrm {R}^k$
, there exists an algorithm computing a semialgebraic triangulation of
![]() $h: |K| \rightarrow S$
, whose complexity is bounded by
$h: |K| \rightarrow S$
, whose complexity is bounded by
![]() $(s d)^{2^{O(k)}}$
. Moreover, the size of the simplicial complex K (measured by the number of simplices) is also bounded by
$(s d)^{2^{O(k)}}$
. Moreover, the size of the simplicial complex K (measured by the number of simplices) is also bounded by
![]() $(s d)^{2^{O(k)}}$
.
$(s d)^{2^{O(k)}}$
.
1.1.1 Doubly exponential versus singly exponential
One can ask whether the doubly exponential behavior for the semialgebraic triangulation problem is intrinsic to the problem. One reason to think that it is not so comes from the fact that the ranks of the homology groups of S (following the same notation as in the previous paragraph), and so in particular those of the simplicial complex K, is bounded by
![]() $(O(sd))^k$
(see for instance [Reference Basu, Pollack and Roy4, Chapter 7]), which is singly exponential in k. So it is natural to ask if this singly exponential upper bound on
$(O(sd))^k$
(see for instance [Reference Basu, Pollack and Roy4, Chapter 7]), which is singly exponential in k. So it is natural to ask if this singly exponential upper bound on
![]() $\mathrm {rank}(\mathrm {H}_*(S))$
is ‘witnessed’ by an efficient semialgebraic triangulation of small (i.e., singly exponential) size. This is not known.
$\mathrm {rank}(\mathrm {H}_*(S))$
is ‘witnessed’ by an efficient semialgebraic triangulation of small (i.e., singly exponential) size. This is not known.
In fact, designing an algorithm with a singly exponential complexity for computing a semialgebraic triangulation of a given semialgebraic set has remained a holy grail in the field of algorithmic real algebraic geometry and little progress has been made over the last 30 years on this problem (at least for general semialgebraic sets). We note here that designing algorithms with singly exponential complexity has being a leit motif in the research in algorithmic semialgebraic geometry over the past decades – starting from the so-called ‘critical-point method’ which resulted in algorithms for testing emptiness, connectivity, computing the Euler–Poincaré characteristic, as well as for the first few Betti numbers of semialgebraic sets (see [Reference Basu2] for a history of these developments and contributions of many authors). More recently, such algorithms has also been developed in other (more numerical) models of computations [Reference Bürgisser, Cucker and Lairez10, Reference Bürgisser, Cucker and Tonelli-Cueto12, Reference Bürgisser, Cucker and Tonelli-Cueto11] (we discuss the connection of these works with the results presented in this paper in Section 2.4).
1.1.2 Triangulation versus simplicial replacement
While the problem of designing an algorithm with singly exponential complexity for the problem of semialgebraic triangulation is completely open, there has been some progress in designing efficient algorithms for certain related problems. As mentioned above, a semialgebraic triangulation of a closed and bounded semialgebraic set S produces a finite simplicial complex, which encodes all topological properties (i.e., which are homeomorphism invariants) of S. It is well known that homeomorphism invariants are notoriously difficult to compute (for instance, it is an undecidable problem to determine whether two simplicial complexes are homeomorphic [Reference Markov18]). What is much more computable are the homology groups of semialgebraic sets. Homology groups are in fact homotopy (rather than homeomorphism) invariants. Homotopy equivalence is a much weaker equivalence relation compared to homeomorphism. In the absence of a singly exponential complexity triangulation of semialgebraic sets, it is reasonable to ask for an algorithm which given a semialgebraic set
![]() $S \subset \mathrm {R}^k$
described by a quantifier-free formula involving s polynomials of degrees bounded by d, computes a simplicial complex K, such that its geometric realization
$S \subset \mathrm {R}^k$
described by a quantifier-free formula involving s polynomials of degrees bounded by d, computes a simplicial complex K, such that its geometric realization
![]() $|K|$
is homotopy equivalent to S having complexity bounded by
$|K|$
is homotopy equivalent to S having complexity bounded by
![]() $(sd)^{k^{O(1)}}$
. We will call such a simplicial complex a simplicial replacement of the semialgebraic set S.
$(sd)^{k^{O(1)}}$
. We will call such a simplicial complex a simplicial replacement of the semialgebraic set S.
The main results of this paper can be summarized as follows. The precise statements appear in the next section after the necessary definitions of various objects some of which are a bit technical.
1.2 Summary of results
In the statements below,
![]() $\ell \in \mathbb {Z}_{\geq 0}$
is a fixed constant.
$\ell \in \mathbb {Z}_{\geq 0}$
is a fixed constant.
Theorem (cf. Theorems 1 and 1′ below).
Given any closed semialgebraic subset of
![]() $S \subset \mathrm {R}^k$
, there exists a simplicial complex K homologically
$S \subset \mathrm {R}^k$
, there exists a simplicial complex K homologically
![]() $\ell $
-equivalent to S whose size is bounded singly exponentially in k (as a function of the number and degrees of polynomials appearing in the description of S). If
$\ell $
-equivalent to S whose size is bounded singly exponentially in k (as a function of the number and degrees of polynomials appearing in the description of S). If
![]() $\mathrm {R} = \mathbb {R}$
, then K is
$\mathrm {R} = \mathbb {R}$
, then K is
![]() $\ell $
-equivalent to S. Moreover, there exists an algorithm (Algorithm 3) which computes the complex K given S, and whose complexity is bounded singly exponentially in k.
$\ell $
-equivalent to S. Moreover, there exists an algorithm (Algorithm 3) which computes the complex K given S, and whose complexity is bounded singly exponentially in k.
The problem of designing efficient (symbolic and exact) algorithms for computing the Betti numbers of semialgebraic sets have been considered before, and algorithms with singly exponential complexity was given for computing the first (resp. the first
![]() $\ell $
for any fixed
$\ell $
for any fixed
![]() $\ell $
) Betti numbers in [Reference Basu, Pollack and Roy5] (resp. [Reference Basu1]). The algorithm given in the [Reference Basu, Pollack and Roy5] (resp. [Reference Basu1]) computes a complex of vector spaces having isomorphic homology (with coefficients in
$\ell $
) Betti numbers in [Reference Basu, Pollack and Roy5] (resp. [Reference Basu1]). The algorithm given in the [Reference Basu, Pollack and Roy5] (resp. [Reference Basu1]) computes a complex of vector spaces having isomorphic homology (with coefficients in
![]() $\mathbb {Q}$
) up to dimension one (resp.
$\mathbb {Q}$
) up to dimension one (resp.
![]() $\ell $
) as that of the given semialgebraic set. However, information with regards to homotopy is lost. The algorithm implicit in the theorem stated above produces a simplicial complex having the same homotopy type up to dimension
$\ell $
) as that of the given semialgebraic set. However, information with regards to homotopy is lost. The algorithm implicit in the theorem stated above produces a simplicial complex having the same homotopy type up to dimension
![]() $\ell $
as the given semialgebraic set. Thus, the above theorem can be viewed as a homotopy-theoretic generalization of the results in [Reference Basu, Pollack and Roy5] and [Reference Basu1].
$\ell $
as the given semialgebraic set. Thus, the above theorem can be viewed as a homotopy-theoretic generalization of the results in [Reference Basu, Pollack and Roy5] and [Reference Basu1].
The above theorem can be used for the problem of computing the homotopy groups of semialgebraic sets. Homotopy groups are much finer invariants than homology groups but are also more difficult to compute. In fact, the problem of deciding whether the first homotopy group (i.e., the fundamental group) of a semialgebraic set defined over
![]() $\mathbb {R}$
is trivial or not is an undecidable problem. Nevertheless, using the above theorem we have the following corollary which gives an algorithmic reduction having singly exponential complexity of the problem of computing the first
$\mathbb {R}$
is trivial or not is an undecidable problem. Nevertheless, using the above theorem we have the following corollary which gives an algorithmic reduction having singly exponential complexity of the problem of computing the first
![]() $\ell $
homotopy groups of a given closed semialgebraic set to a purely combinatorial problem.
$\ell $
homotopy groups of a given closed semialgebraic set to a purely combinatorial problem.
Corollary (cf. Corollaries 1 and 2 below).
Let
![]() $\mathrm {R} = \mathbb {R}$
. There exists a reduction having singly exponential complexity, of the problem of computing the first
$\mathrm {R} = \mathbb {R}$
. There exists a reduction having singly exponential complexity, of the problem of computing the first
![]() $\ell $
homotopy groups of any given closed semialgebraic subset
$\ell $
homotopy groups of any given closed semialgebraic subset
![]() $S \subset \mathrm {R}^k$
, to the problem of computing the first
$S \subset \mathrm {R}^k$
, to the problem of computing the first
![]() $\ell $
homotopy groups of a finite simplicial complex. This implies that there exists an algorithm with singly exponential complexity which given as input a closed semialgebraic set
$\ell $
homotopy groups of a finite simplicial complex. This implies that there exists an algorithm with singly exponential complexity which given as input a closed semialgebraic set
![]() $S \subset \mathbb {R}^k$
guaranteed to be simply connected, outputs the description of the first
$S \subset \mathbb {R}^k$
guaranteed to be simply connected, outputs the description of the first
![]() $\ell $
homotopy groups of S (in terms of generators and relations).
$\ell $
homotopy groups of S (in terms of generators and relations).
The algorithmic results mentioned above are consequences of a topological construction which can be interpreted as a generalization of the classical ‘nerve lemma’ in topology. We state it here informally.
Assume that there exists a ‘black box’ that given as input any closed semialgebraic set
![]() $S \subset \mathrm {R}^k$
, produces as output a cover of S by closed semialgebraic subsets of S which are homologically
$S \subset \mathrm {R}^k$
, produces as output a cover of S by closed semialgebraic subsets of S which are homologically
![]() $\ell $
-connected.
$\ell $
-connected.
Theorem (cf. Theorem 2 below).
Given a black box as above, there exists for every closed semialgebraic set S a poset
![]() $\mathbf {P}(S)$
(see Definition 3.3 below) which depends on the given black box, of controlled complexity (both in terms of the description of S and the complexity of the black box), such that the geometric realization of the order-complex of
$\mathbf {P}(S)$
(see Definition 3.3 below) which depends on the given black box, of controlled complexity (both in terms of the description of S and the complexity of the black box), such that the geometric realization of the order-complex of
![]() $\mathbf {P}(S)$
is homologically
$\mathbf {P}(S)$
is homologically
![]() $\ell $
-equivalent to S.
$\ell $
-equivalent to S.
Remark 1.1. In the results stated above, we make the assumption that the input semialgebraic sets are closed. Gabrielov and Vorobjov [Reference Gabrielov and Vorobjov15] gave a construction for replacing an arbitrary semialgebraic subset of
![]() $\mathbb {R}^k$
by a closed and bounded one having homology and homotopy groups isomorphic to the given semialgebraic set. Even though Gabrielov and Vorobjov proved their result over
$\mathbb {R}^k$
by a closed and bounded one having homology and homotopy groups isomorphic to the given semialgebraic set. Even though Gabrielov and Vorobjov proved their result over
![]() $\mathbb {R}$
, the construction was extended to arbitrary real closed fields (with the approximating set defined over a real closed extension of the ground field). It is proved in [Reference Basu, Pollack and Roy4] (Theorem 7.45), that the approximating set is in fact semialgebraically homotopy equivalent to the (extension of the) given set. Using this latter result, one could remove the assumption of being closed and bounded in Theorems 1 and 1′
. We choose not to do this in this paper in order not to add yet another layer of technical complication involving a new set of infinitesimals.
$\mathbb {R}$
, the construction was extended to arbitrary real closed fields (with the approximating set defined over a real closed extension of the ground field). It is proved in [Reference Basu, Pollack and Roy4] (Theorem 7.45), that the approximating set is in fact semialgebraically homotopy equivalent to the (extension of the) given set. Using this latter result, one could remove the assumption of being closed and bounded in Theorems 1 and 1′
. We choose not to do this in this paper in order not to add yet another layer of technical complication involving a new set of infinitesimals.
The rest of the paper is organized as follows. In Section 2, we give precise statements of the main results summarized above after introducing the necessary definitions regarding the different notions of topological equivalence that we use in the paper and also the definition of complexity of algorithms that we use. In Section 3, we define the key mathematical object (namely, a poset that we associate to any closed covering of a semialgebraic set) and prove its main properties (Theorems 2 and 2′ ). In Section 4, we describe algorithms for computing efficient simplicial replacements of semialgebraic sets thereby proving Theorems 1 and 1′ . Finally, in Section 5 we state some open questions and directions for future work in this area.
2 Precise statements of the main results
In this section, we will describe in full detail the main results summarized in the previous section. We first introduce certain preliminary definitions and notation.
2.1 Definitions of topological equivalence and complexity
We begin with the precise definitions of the two kinds of topological equivalence that we are going to use in this paper.
2.1.1 Topological equivalences
Definition 2.1 (
 $\ell $
-equivalences).
$\ell $
-equivalences).
We say that a map
![]() $f:X \rightarrow Y$
between two topological spaces is an
$f:X \rightarrow Y$
between two topological spaces is an
![]() $\ell $
-equivalence, if the induced homomorphisms between the homotopy groups
$\ell $
-equivalence, if the induced homomorphisms between the homotopy groups
![]() $f_*: \pi _i(X) \rightarrow \pi _i(Y)$
are isomorphisms for
$f_*: \pi _i(X) \rightarrow \pi _i(Y)$
are isomorphisms for
![]() $0 \leq i \leq \ell $
[Reference Novikov20, page 68].
$0 \leq i \leq \ell $
[Reference Novikov20, page 68].
Remark 2.1. Note that our definition of
![]() $\ell $
-equivalence deviates a little from the standard one which requires that homomorphisms between the homotopy groups
$\ell $
-equivalence deviates a little from the standard one which requires that homomorphisms between the homotopy groups
![]() $f_*: \pi _i(X) \rightarrow \pi _i(Y)$
are isomorphisms for
$f_*: \pi _i(X) \rightarrow \pi _i(Y)$
are isomorphisms for
![]() $0 \leq i \leq \ell -1$
, and only an epimorphism for
$0 \leq i \leq \ell -1$
, and only an epimorphism for
![]() $i=\ell $
. An
$i=\ell $
. An
![]() $\ell $
-equivalence in our sense is an
$\ell $
-equivalence in our sense is an
![]() $\ell $
-equivalence in the traditional sense.
$\ell $
-equivalence in the traditional sense.
The relation of
![]() $\ell $
-equivalence as defined above is not an equivalence relation since it is not symmetric. In order to make it symmetric, one needs to ‘formally invert’
$\ell $
-equivalence as defined above is not an equivalence relation since it is not symmetric. In order to make it symmetric, one needs to ‘formally invert’
![]() $\ell $
-equivalences.
$\ell $
-equivalences.
Definition 2.2 (
 $\ell $
-equivalent and homologically
$\ell $
-equivalent and homologically
 $\ell $
-equivalent).
$\ell $
-equivalent).
We will say that X is
![]() $\ell $
-equivalent to Y (denoted
$\ell $
-equivalent to Y (denoted
![]() $X \sim _{\ell } Y$
), if and only if there exists spaces,
$X \sim _{\ell } Y$
), if and only if there exists spaces,
![]() $X=X_0,X_1,\ldots ,X_n=Y$
and
$X=X_0,X_1,\ldots ,X_n=Y$
and
![]() $\ell $
-equivalences
$\ell $
-equivalences
![]() $f_1,\ldots ,f_{n}$
as shown below:
$f_1,\ldots ,f_{n}$
as shown below:

It is clear that
![]() $\sim _{\ell }$
is an equivalence relation.
$\sim _{\ell }$
is an equivalence relation.
By replacing the homotopy groups,
![]() $\pi _i(\cdot )$
with homology groups
$\pi _i(\cdot )$
with homology groups
![]() $\mathrm {H}_i(\cdot )$
(resp. cohomology groups
$\mathrm {H}_i(\cdot )$
(resp. cohomology groups
![]() $\mathrm {H}^i(\cdot )$
with arrows reversed) in Definitions 2.1 and 2.2, we get the notion of two topological spaces
$\mathrm {H}^i(\cdot )$
with arrows reversed) in Definitions 2.1 and 2.2, we get the notion of two topological spaces
![]() $X,Y$
being homologically
$X,Y$
being homologically
![]() $\ell $
-equivalent (denoted
$\ell $
-equivalent (denoted
![]() $X \overset {h}{\sim }_{\ell } Y$
) (resp. cohomologically
$X \overset {h}{\sim }_{\ell } Y$
) (resp. cohomologically
![]() $\ell $
-equivalent (denoted
$\ell $
-equivalent (denoted
![]() $X \overset {ch}{\sim }_{\ell } Y$
)).
$X \overset {ch}{\sim }_{\ell } Y$
)).
This is a strictly weaker equivalence relation, since there are spaces X for which
![]() $\mathrm {H}_1(X) = 0$
, but
$\mathrm {H}_1(X) = 0$
, but
![]() $\pi _1(X) \neq 0$
.
$\pi _1(X) \neq 0$
.
We extend the above definitions to
![]() $\ell = -1$
by using the convention that
$\ell = -1$
by using the convention that
![]() $X \sim _{-1} Y$
(resp.
$X \sim _{-1} Y$
(resp.
![]() $X \overset {h}{\sim }_{-1} Y$
,
$X \overset {h}{\sim }_{-1} Y$
,
![]() $X \overset {ch}{\sim }_{-1} Y$
), if and only if
$X \overset {ch}{\sim }_{-1} Y$
), if and only if
![]() $X,Y$
are both nonempty or both empty.
$X,Y$
are both nonempty or both empty.
Definition 2.3 (
 $\ell $
-connected and homologically
$\ell $
-connected and homologically
 $\ell $
-connected).
$\ell $
-connected).
We say that a topological space X is
![]() $\ell $
-connected, for
$\ell $
-connected, for
![]() $\ell \geq 0$
, if X is connected and
$\ell \geq 0$
, if X is connected and
![]() $\pi _i(X) = 0$
for
$\pi _i(X) = 0$
for
![]() $0 < i \leq \ell $
. We will say that X is
$0 < i \leq \ell $
. We will say that X is
![]() $(-1$
)-connected if X is nonempty. We say that X is homologically
$(-1$
)-connected if X is nonempty. We say that X is homologically
![]() $\ell $
-connected if X is connected and
$\ell $
-connected if X is connected and
![]() $\mathrm {H}_i(X) = 0$
for
$\mathrm {H}_i(X) = 0$
for
![]() $0 < i \leq \ell $
.
$0 < i \leq \ell $
.
Definition 2.4 (Diagrams of topological spaces).
A diagram of topological spaces is a functor,
![]() $X:J \rightarrow \mathbf {Top}$
, from a small category J to
$X:J \rightarrow \mathbf {Top}$
, from a small category J to
![]() $\mathbf {Top}$
.
$\mathbf {Top}$
.
We extend Definition 2.1 to diagrams of topological spaces. We denote by
![]() $\mathbf {Top}$
the category of topological spaces.
$\mathbf {Top}$
the category of topological spaces.
Definition 2.5 (
 $\ell $
-equivalence between diagrams of topological spaces).
$\ell $
-equivalence between diagrams of topological spaces).
Let J be a small category, and
![]() $X,Y: J \rightarrow \mathbf {Top}$
be two functors. We say a natural transformation
$X,Y: J \rightarrow \mathbf {Top}$
be two functors. We say a natural transformation
![]() $f:X \rightarrow Y$
is an
$f:X \rightarrow Y$
is an
![]() $\ell $
equivalence, if the induced maps,
$\ell $
equivalence, if the induced maps,
are isomorphisms for all
![]() $j \in J$
and
$j \in J$
and
![]() $0 \leq i \leq \ell $
.
$0 \leq i \leq \ell $
.
We will say that a diagram
![]() $X:J \rightarrow \mathbf {Top}$
is
$X:J \rightarrow \mathbf {Top}$
is
![]() $\ell $
-equivalent to the diagram
$\ell $
-equivalent to the diagram
![]() $Y:J \rightarrow \mathbf {Top}$
(denoted as before by
$Y:J \rightarrow \mathbf {Top}$
(denoted as before by
![]() $X \sim _{\ell } Y$
), if and only if there exist diagrams
$X \sim _{\ell } Y$
), if and only if there exist diagrams
![]() $X=X_0,X_1,\ldots ,X_n=Y:J \rightarrow \mathbf {Top}$
and
$X=X_0,X_1,\ldots ,X_n=Y:J \rightarrow \mathbf {Top}$
and
![]() $\ell $
-equivalences
$\ell $
-equivalences
![]() $f_1,\ldots ,f_{n}$
as shown below:
$f_1,\ldots ,f_{n}$
as shown below:

It is clear that
![]() $\sim _{\ell }$
is an equivalence relation.
$\sim _{\ell }$
is an equivalence relation.
In the above definition, by replacing the homotopy groups with homology (resp. cohomology) groups we obtain the notion of homological (resp. cohomological)
![]() $\ell $
-equivalence between diagrams, which we will denote as before by
$\ell $
-equivalence between diagrams, which we will denote as before by
![]() $\overset {h}{\sim }_{\ell }$
(resp.
$\overset {h}{\sim }_{\ell }$
(resp.
![]() $\overset {ch}{\sim }_{\ell }$
).
$\overset {ch}{\sim }_{\ell }$
).
One particular diagram will be important in what follows.
Notation 2.1 (Diagram of various unions of a finite number of subspaces).
Let J be a finite set, A a topological space, and
![]() $\mathcal {A} = (A_j)_{j \in J}$
a tuple of subspaces of A indexed by J.
$\mathcal {A} = (A_j)_{j \in J}$
a tuple of subspaces of A indexed by J.
For any subset
![]() $J' \subset J$
, Footnote
1
we denote
$J' \subset J$
, Footnote
1
we denote
 $$ \begin{align*} \mathcal{A}^{J'} &= \bigcup_{j' \in J'} A_{j'}, \\ \mathcal{A}_{J'} &= \bigcap_{j' \in J'} A_{j'}. \end{align*} $$
$$ \begin{align*} \mathcal{A}^{J'} &= \bigcup_{j' \in J'} A_{j'}, \\ \mathcal{A}_{J'} &= \bigcap_{j' \in J'} A_{j'}. \end{align*} $$
We consider
![]() $2^J$
as a category whose objects are elements of
$2^J$
as a category whose objects are elements of
![]() $2^J$
and whose only morphisms are given by:
$2^J$
and whose only morphisms are given by:
 $$ \begin{align*} 2^J(J',J") &= \emptyset \mbox{ if } J' \not\subset J", \\ 2^J(J',J") &= \{\iota_{J',J"}\} \mbox{ if } J' \subset J". \end{align*} $$
$$ \begin{align*} 2^J(J',J") &= \emptyset \mbox{ if } J' \not\subset J", \\ 2^J(J',J") &= \{\iota_{J',J"}\} \mbox{ if } J' \subset J". \end{align*} $$
We denote by
![]() $\mathbf {Simp}^J(\mathcal {A}):2^J \rightarrow \mathbf {Top}$
the functor (or the diagram) defined by
$\mathbf {Simp}^J(\mathcal {A}):2^J \rightarrow \mathbf {Top}$
the functor (or the diagram) defined by
and
![]() $\mathbf {Simp}^J(\mathcal {A})(\iota _{J',J"})$
is the inclusion map
$\mathbf {Simp}^J(\mathcal {A})(\iota _{J',J"})$
is the inclusion map
![]() $\mathcal {A}^{J'} \hookrightarrow \mathcal {A}^{J"}$
.
$\mathcal {A}^{J'} \hookrightarrow \mathcal {A}^{J"}$
.
2.1.2 Definition of complexity of algorithms
We will use the following notion of ‘complexity of an algorithm’ in this paper. We follow the same definition as used in the book [Reference Basu, Pollack and Roy4].
Definition 2.6 (Complexity of algorithms).
In our algorithms, we will take as input quantifier-free first-order formulas whose terms are polynomials with coefficients belonging to an ordered domain
![]() $\mathrm {D}$
contained in a real closed field
$\mathrm {D}$
contained in a real closed field
![]() $\mathrm {R}$
. By complexity of an algorithm, we will mean the number of arithmetic operations and comparisons in the domain
$\mathrm {R}$
. By complexity of an algorithm, we will mean the number of arithmetic operations and comparisons in the domain
![]() $\mathrm {D}$
. If
$\mathrm {D}$
. If
![]() $\mathrm {D} = \mathbb {R}$
, then the complexity of our algorithm will agree with the Blum–Shub–Smale notion of real number complexity [Reference Blum, Cucker, Shub and Smale9]. In case,
$\mathrm {D} = \mathbb {R}$
, then the complexity of our algorithm will agree with the Blum–Shub–Smale notion of real number complexity [Reference Blum, Cucker, Shub and Smale9]. In case,
![]() $\mathrm {D} = \mathbb {Z}$
, then we are able to deduce the bit-complexity of our algorithms in terms of the bit-sizes of the coefficients of the input polynomials, and this will agree with the classical (Turing) notion of complexity.
$\mathrm {D} = \mathbb {Z}$
, then we are able to deduce the bit-complexity of our algorithms in terms of the bit-sizes of the coefficients of the input polynomials, and this will agree with the classical (Turing) notion of complexity.
Remark 2.2 (Separation of complexity into algebraic and combinatorial partsFootnote 2 ).
In the definition of complexity given above, we are counting only arithmetic operations involving elements of the ring generated by the coefficients of the input formulas. Many algorithms in semialgebraic geometry have the following feature. After a certain number of operations involving elements of the coefficient ring
![]() $\mathrm {D}$
, the problem is reduced to solving a combinatorial or a linear algebra problem defined over
$\mathrm {D}$
, the problem is reduced to solving a combinatorial or a linear algebra problem defined over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
A typical example is an algorithm for computing the Betti numbers of a semialgebraic set via computing a semialgebraic triangulation. Once a simplicial complex whose geometric realization is semialgebraically homeomorphic to the given semialgebraic set has been computed, the problem of computing the Betti numbers of the given semialgebraic set is reduced to linear algebra over
![]() $\mathbb {Z}$
. Usually, this separation of the cost of an algorithm into a part that involves arithmetic operations over
$\mathbb {Z}$
. Usually, this separation of the cost of an algorithm into a part that involves arithmetic operations over
![]() $\mathrm {D}$
, and a part that is independent of
$\mathrm {D}$
, and a part that is independent of
![]() $\mathrm {D}$
, is not very important since often the complexity of the second part is subsumed by that of the first part. However, in this paper the fact that we are only counting arithmetic operations in
$\mathrm {D}$
, is not very important since often the complexity of the second part is subsumed by that of the first part. However, in this paper the fact that we are only counting arithmetic operations in
![]() $\mathrm {D}$
is more significant. In one application that we discuss, namely that of computing the homotopy groups of a given semialgebraic set (see Corollary 1), we give a reduction (having single exponential complexity) to a problem whose definition is independent of
$\mathrm {D}$
is more significant. In one application that we discuss, namely that of computing the homotopy groups of a given semialgebraic set (see Corollary 1), we give a reduction (having single exponential complexity) to a problem whose definition is independent of
![]() $\mathrm {D}$
, namely computing the homotopy groups of a simplicial complex. Note that the problem of deciding whether the first homotopy group of a simplicial complex is trivial or not is an undecidable problem (this fact follows from the undecidability of the word problem for groups [Reference Novikov20]).
$\mathrm {D}$
, namely computing the homotopy groups of a simplicial complex. Note that the problem of deciding whether the first homotopy group of a simplicial complex is trivial or not is an undecidable problem (this fact follows from the undecidability of the word problem for groups [Reference Novikov20]).
2.1.3
 $\mathcal {P}$
-formulas and
$\mathcal {P}$
-formulas and
 $\mathcal {P}$
-semialgebraic sets
$\mathcal {P}$
-semialgebraic sets
Notation 2.2 (Realizations,
 $\mathcal {P}$
-,
$\mathcal {P}$
-,
 $\mathcal {P}$
-closed semialgebraic sets).
$\mathcal {P}$
-closed semialgebraic sets).
For any finite set of polynomials
![]() $\mathcal {P} \subset \mathrm {R} [ X_{1} , \ldots ,X_{k} ]$
, we call any quantifier-free first-order formula
$\mathcal {P} \subset \mathrm {R} [ X_{1} , \ldots ,X_{k} ]$
, we call any quantifier-free first-order formula
![]() $\phi $
with atoms,
$\phi $
with atoms,
![]() $P =0, P < 0, P>0, P \in \mathcal {P}$
, to be a
$P =0, P < 0, P>0, P \in \mathcal {P}$
, to be a
![]() $\mathcal {P}$
-formula. Given any semialgebraic subset
$\mathcal {P}$
-formula. Given any semialgebraic subset
![]() $Z \subset \mathrm {R}^k$
, we call the realization of
$Z \subset \mathrm {R}^k$
, we call the realization of
![]() $\phi $
in Z, namely the semialgebraic set
$\phi $
in Z, namely the semialgebraic set
a
![]() $\mathcal {P}$
-semialgebraic subset of Z.
$\mathcal {P}$
-semialgebraic subset of Z.
If
![]() $Z = \mathrm {R}^k$
, we often denote the realization of
$Z = \mathrm {R}^k$
, we often denote the realization of
![]() $\phi $
in
$\phi $
in
![]() $\mathrm {R}^k$
by
$\mathrm {R}^k$
by
![]() ${\mathcal R}(\phi )$
.
${\mathcal R}(\phi )$
.
If
![]() $\Phi = (\phi _j)_{j \in J}$
is a tuple of formulas indexed by a finite set J,
$\Phi = (\phi _j)_{j \in J}$
is a tuple of formulas indexed by a finite set J,
![]() $Z \subset \mathrm {R}^k$
a semialgebraic subset, we will denote by
$Z \subset \mathrm {R}^k$
a semialgebraic subset, we will denote by
![]() ${\mathcal R}(\Phi ,Z)$
the tuple
${\mathcal R}(\Phi ,Z)$
the tuple
![]() $({\mathcal R}(\phi _j,Z))_{j \in J}$
, and call it the realization of
$({\mathcal R}(\phi _j,Z))_{j \in J}$
, and call it the realization of
![]() $\Phi $
in Z. For
$\Phi $
in Z. For
![]() $J \subset J'$
, we will denote by
$J \subset J'$
, we will denote by
![]() $\Phi |_{J'}$
the tuple
$\Phi |_{J'}$
the tuple
![]() $(\phi _j)_{j \in J'}$
.
$(\phi _j)_{j \in J'}$
.
We say that a quantifier-free formula
![]() $\phi $
is closed if it is a formula in disjunctive normal form with no negations and with atoms of the form
$\phi $
is closed if it is a formula in disjunctive normal form with no negations and with atoms of the form
![]() $P \geq 0, P \leq 0$
(resp.
$P \geq 0, P \leq 0$
(resp.
![]() $P> 0, P < 0$
), where
$P> 0, P < 0$
), where
![]() $P \in \mathrm {D}[X_1,\ldots ,X_k]$
. If the set of polynomials appearing in a closed (resp. open) formula is contained in a finite set
$P \in \mathrm {D}[X_1,\ldots ,X_k]$
. If the set of polynomials appearing in a closed (resp. open) formula is contained in a finite set
![]() $\mathcal {P}$
, we will call such a formula a
$\mathcal {P}$
, we will call such a formula a
![]() $\mathcal {P}$
-closed formula, and we call the realization,
$\mathcal {P}$
-closed formula, and we call the realization,
![]() ${\mathcal R} \left (\phi \right )$
, a
${\mathcal R} \left (\phi \right )$
, a
![]() $\mathcal {P}$
-closed semialgebraic set. We say that a formula
$\mathcal {P}$
-closed semialgebraic set. We say that a formula
![]() $\phi $
is a closed-formula if
$\phi $
is a closed-formula if
![]() $\phi $
is a
$\phi $
is a
![]() $\mathcal {P}$
-closed formula for some finite set of polynomials
$\mathcal {P}$
-closed formula for some finite set of polynomials
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
We will also use the following notation.
Notation 2.3. For
![]() $n \in \mathbb {Z}$
, we denote by
$n \in \mathbb {Z}$
, we denote by
![]() $[n] = \{0,\ldots ,n\}$
. In particular,
$[n] = \{0,\ldots ,n\}$
. In particular,
![]() $[-1] = \emptyset $
.
$[-1] = \emptyset $
.
Finally, we are able to state the main results proved in this paper.
2.2 Efficient simplicial replacements of semialgebraic sets
Theorem 1. There exists an algorithm that takes as input
-
A. a
 $\mathcal {P}$
-closed formula
$\mathcal {P}$
-closed formula
 $\phi $
for some finite set
$\phi $
for some finite set
 $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
;
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
; -
B.
 $\ell , 0 \leq \ell \leq k$
;
$\ell , 0 \leq \ell \leq k$
;
and produces as output a simplicial complex
![]() $\Delta _{\ell }(\phi )$
such that
$\Delta _{\ell }(\phi )$
such that
![]() $|\Delta _{\ell }(\phi )| \overset {h}{\sim }_{\ell } {\mathcal R}(\phi )$
. The complexity of the algorithm is bounded by
$|\Delta _{\ell }(\phi )| \overset {h}{\sim }_{\ell } {\mathcal R}(\phi )$
. The complexity of the algorithm is bounded by
![]() $(s d)^{k^{O(\ell )}}$
, where
$(s d)^{k^{O(\ell )}}$
, where
![]() $s = \mathrm {card}(\mathcal {P})$
and
$s = \mathrm {card}(\mathcal {P})$
and
![]() $d = \max _{P \in \mathcal {P}} \deg (P)$
.
$d = \max _{P \in \mathcal {P}} \deg (P)$
.
More generally, there exists an algorithm that takes as input
-
A. a tuple
 $\Phi = (\phi _0,\ldots ,\phi _{N})$
of
$\Phi = (\phi _0,\ldots ,\phi _{N})$
of
 $\mathcal {P}$
-closed formulas for some finite set
$\mathcal {P}$
-closed formulas for some finite set
 $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
;
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
; -
B.
 $\ell , 0 \leq \ell \leq k$
$\ell , 0 \leq \ell \leq k$
and produces as output a simplicial complex
![]() $\Delta _{\ell }(\Phi )$
, and for each
$\Delta _{\ell }(\Phi )$
, and for each
![]() $J \subset [N]$
a subcomplex
$J \subset [N]$
a subcomplex
![]() $\Delta _{\ell }(\Phi |_{J})$
, such that
$\Delta _{\ell }(\Phi |_{J})$
, such that
The complexity of the algorithm is bounded by
![]() $(N s d)^{k^{O(\ell )}}$
, where
$(N s d)^{k^{O(\ell )}}$
, where
![]() $s = \mathrm {card}(\mathcal {P})$
and
$s = \mathrm {card}(\mathcal {P})$
and
![]() $d = \max _{P \in \mathcal {P}} \deg (P)$
.
$d = \max _{P \in \mathcal {P}} \deg (P)$
.
Theorem 1 is valid over arbitrary real closed fields. In the special case of
![]() $\mathrm {R} = \mathbb {R}$
, we have the following stronger version of Theorem 1, where we are able to replace homological
$\mathrm {R} = \mathbb {R}$
, we have the following stronger version of Theorem 1, where we are able to replace homological
![]() $\ell $
-equivalence by
$\ell $
-equivalence by
![]() $\ell $
-equivalence.
$\ell $
-equivalence.
Theorem 1′. Let
![]() $\mathrm {R} =\mathbb {R}$
. There exists an algorithm that takes as input
$\mathrm {R} =\mathbb {R}$
. There exists an algorithm that takes as input
-
A. a
 $\mathcal {P}$
-closed formula
$\mathcal {P}$
-closed formula
 $\phi $
for some finite set
$\phi $
for some finite set
 $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
;
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
; -
B.
 $\ell , 0 \leq \ell \leq k$
$\ell , 0 \leq \ell \leq k$
and produces as output a simplicial complex
![]() $\Delta _{\ell }(\phi )$
such that
$\Delta _{\ell }(\phi )$
such that
![]() $|\Delta _{\ell }(\phi )| \sim _{\ell } {\mathcal R}(\phi )$
. The complexity of the algorithm is bounded by
$|\Delta _{\ell }(\phi )| \sim _{\ell } {\mathcal R}(\phi )$
. The complexity of the algorithm is bounded by
![]() $(s d)^{k^{O(\ell )}}$
, where
$(s d)^{k^{O(\ell )}}$
, where
![]() $s = \mathrm {card}(\mathcal {P})$
and
$s = \mathrm {card}(\mathcal {P})$
and
![]() $d = \max _{P \in \mathcal {P}} \deg (P)$
.
$d = \max _{P \in \mathcal {P}} \deg (P)$
.
More generally, there exists an algorithm that takes as input
-
A. a tuple
 $\Phi = (\phi _0,\ldots ,\phi _{N})$
of
$\Phi = (\phi _0,\ldots ,\phi _{N})$
of
 $\mathcal {P}$
-closed formulas for some finite set
$\mathcal {P}$
-closed formulas for some finite set
 $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
;
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
; -
B.
 $\ell , 0 \leq \ell \leq k$
$\ell , 0 \leq \ell \leq k$
and produces as output a simplicial complex
![]() $\Delta _{\ell }(\Phi )$
, and for each
$\Delta _{\ell }(\Phi )$
, and for each
![]() $J \subset [N]$
a subcomplex
$J \subset [N]$
a subcomplex
![]() $\Delta _{\ell }(\Phi |_{J})$
such that
$\Delta _{\ell }(\Phi |_{J})$
such that
The complexity of the algorithm is bounded by
![]() $ (N s d)^{k^{O(\ell )}}$
, where
$ (N s d)^{k^{O(\ell )}}$
, where
![]() $s = \mathrm {card}(\mathcal {P})$
and
$s = \mathrm {card}(\mathcal {P})$
and
![]() $d = \max _{P \in \mathcal {P}} \deg (P)$
.
$d = \max _{P \in \mathcal {P}} \deg (P)$
.
Remark 2.3. One main tool that we use is the Vietoris–Begle theorem (see proofs of Claims 3.1, 3.2). Since there are many versions of the Vietoris–Begle theorem in the literature, we make precise what we use below.
It follows from [Reference Smale21, Main Theorem] that if
![]() $X \subset \mathbb {R}^m, Y \subset \mathbb {R}^n$
are compact semialgebraic subsets (and so are locally contractible), and
$X \subset \mathbb {R}^m, Y \subset \mathbb {R}^n$
are compact semialgebraic subsets (and so are locally contractible), and
![]() $f:X \rightarrow Y$
is a semialgebraic continuous map such that for every
$f:X \rightarrow Y$
is a semialgebraic continuous map such that for every
![]() $y \in Y$
,
$y \in Y$
,
![]() $f^{-1}(y)$
is
$f^{-1}(y)$
is
![]() $\ell $
-connected, then f is an
$\ell $
-connected, then f is an
![]() $\ell $
-equivalence. We will refer to this version of the Vietoris–Begle theorem as the homotopy version of the Vietoris–Begle theorem. Since,
$\ell $
-equivalence. We will refer to this version of the Vietoris–Begle theorem as the homotopy version of the Vietoris–Begle theorem. Since,
![]() $\ell $
-equivalence implies homological
$\ell $
-equivalence implies homological
![]() $\ell $
-equivalence (see, for example, [Reference Ya. Viro, Fuchs and Shaddock26, pp. 124, §4.1B]), f is a homological
$\ell $
-equivalence (see, for example, [Reference Ya. Viro, Fuchs and Shaddock26, pp. 124, §4.1B]), f is a homological
![]() $\ell $
-equivalence as well.
$\ell $
-equivalence as well.
Alternatively, if we assume that
![]() $f^{-1}(y)$
is only homologically
$f^{-1}(y)$
is only homologically
![]() $\ell $
-connected for each
$\ell $
-connected for each
![]() $y \in Y$
, then we can conclude that f is a homological
$y \in Y$
, then we can conclude that f is a homological
![]() $\ell $
-equivalence (see, for example, the statement of the Vietoris–Begle theorem in [Reference Ferry14]). This latter theorem is also valid for semialgebraic maps between closed and bounded semialgebraic sets over arbitrary real closed fields, once we know it for maps between compact semialgebraic subsets over
$\ell $
-equivalence (see, for example, the statement of the Vietoris–Begle theorem in [Reference Ferry14]). This latter theorem is also valid for semialgebraic maps between closed and bounded semialgebraic sets over arbitrary real closed fields, once we know it for maps between compact semialgebraic subsets over
![]() $\mathbb {R}$
. This follows from a standard argument using the Tarski–Seidenberg transfer principle and the fact that homology groups of closed bounded semialgebraic sets can be defined in terms of finite triangulations. We will refer to this version of the Vietoris–Begle theorem as the homological version of the Vietoris–Begle theorem.
$\mathbb {R}$
. This follows from a standard argument using the Tarski–Seidenberg transfer principle and the fact that homology groups of closed bounded semialgebraic sets can be defined in terms of finite triangulations. We will refer to this version of the Vietoris–Begle theorem as the homological version of the Vietoris–Begle theorem.
2.3 Application to computing homotopy groups of semialgebraic sets
One important new contribution of the current paper compared to previous algorithms for computing topological invariants of semialgebraic sets [Reference Basu, Pollack and Roy5, Reference Basu1] is that for any given semialgebraic subset
![]() $S \subset \mathbb {R}^k$
, our algorithms give information on not just the homology groups but the homotopy groups of S as well.
$S \subset \mathbb {R}^k$
, our algorithms give information on not just the homology groups but the homotopy groups of S as well.
Computing homotopy groups of semialgebraic sets is a considerably harder problem than computing homology groups. There is no algorithm to decide whether the fundamental group of a finite simplicial complex is trivial [Reference Novikov20]. As such, the problem of deciding whether the fundamental group of any semialgebraic subset
![]() $S \subset \mathbb {R}^k$
is trivial or not is an undecidable problem.
$S \subset \mathbb {R}^k$
is trivial or not is an undecidable problem.
On the other hand, algorithms for computing topological invariants of a given semialgebraic set
![]() $S \subset \mathrm {R}^k$
, defined by a
$S \subset \mathrm {R}^k$
, defined by a
![]() $\mathcal {P}$
-formula where
$\mathcal {P}$
-formula where
![]() $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
, usually involve two kinds of operations.
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
, usually involve two kinds of operations.
-
(a) Arithmetic operations and comparisons amongst elements of the ring
 $\mathrm {D}$
;
$\mathrm {D}$
; -
(b) Operations that do not involve elements of
 $\mathrm {D}$
.
$\mathrm {D}$
.
In our complexity bounds, we only count the first kind of operations (i.e., those which involve elements of
![]() $\mathrm {D}$
).
$\mathrm {D}$
).
From this point of view, it makes sense to ask for any algorithmic problem involving formulas defined over
![]() $\mathrm {D}$
if there is a reduction to another problem whose input is independent of
$\mathrm {D}$
if there is a reduction to another problem whose input is independent of
![]() $\mathrm {D}$
. Theorem 1′
gives precisely such a reduction for computing the first
$\mathrm {D}$
. Theorem 1′
gives precisely such a reduction for computing the first
![]() $\ell $
homotopy groups of any given semialgebraic set defined by a formula involving coefficients from any fixed subring
$\ell $
homotopy groups of any given semialgebraic set defined by a formula involving coefficients from any fixed subring
![]() $\mathrm {D} \subset \mathbb {R}$
.
$\mathrm {D} \subset \mathbb {R}$
.
Corollary 1. For every fixed
![]() $\ell $
and an ordered domain
$\ell $
and an ordered domain
![]() $\mathrm {D} \subset \mathbb {R}$
, there exists a a reduction of the problem of computing the first
$\mathrm {D} \subset \mathbb {R}$
, there exists a a reduction of the problem of computing the first
![]() $\ell $
homotopy groups of a semialgebraic set defined by a quantifier-free formula with coefficients in
$\ell $
homotopy groups of a semialgebraic set defined by a quantifier-free formula with coefficients in
![]() $\mathrm {D}$
, to that of the problem of computing the first
$\mathrm {D}$
, to that of the problem of computing the first
![]() $\ell $
homotopy groups of a finite simplicial complex. The complexity of this reduction is bounded singly exponentially in the size of the input.
$\ell $
homotopy groups of a finite simplicial complex. The complexity of this reduction is bounded singly exponentially in the size of the input.
While the problem of computing the fundamental group as well as the higher homotopy groups of a finite simplicial complex is clearly an extremely challenging problem, there has been recent breakthroughs. If a simplicial complex K is
![]() $1$
-connected, then Čadek et al. [Reference Čadek, Krčál, Matoušek, Vokřínek and Wagner25] has given an algorithm for computing a description of the homotopy groups
$1$
-connected, then Čadek et al. [Reference Čadek, Krčál, Matoušek, Vokřínek and Wagner25] has given an algorithm for computing a description of the homotopy groups
![]() $\pi _i(|K|)$
,
$\pi _i(|K|)$
,
![]() $2 \leq i \leq \ell $
, which has complexity polynomially bounded in the size of the simplicial complex K for every fixed
$2 \leq i \leq \ell $
, which has complexity polynomially bounded in the size of the simplicial complex K for every fixed
![]() $\ell $
. This result coupled with Theorem 1′
gives the following corollary.
$\ell $
. This result coupled with Theorem 1′
gives the following corollary.
Corollary 2. Let
![]() $\mathrm {R} =\mathbb {R}, \mathrm {D} \subset \mathrm {R}$
and
$\mathrm {R} =\mathbb {R}, \mathrm {D} \subset \mathrm {R}$
and
![]() $\ell \geq 2$
. There exists an algorithm that takes as input
$\ell \geq 2$
. There exists an algorithm that takes as input
-
A. a
 $\mathcal {P}$
-closed formula
$\mathcal {P}$
-closed formula
 $\phi $
for some finite set
$\phi $
for some finite set
 $\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
;
$\mathcal {P} \subset \mathrm {D}[X_1,\ldots ,X_k]$
; -
B.
 $\ell , 0 \leq \ell \leq k$
$\ell , 0 \leq \ell \leq k$
such that
![]() ${\mathcal R}(\phi )$
is simply connected and outputs descriptions of the abelian groups
${\mathcal R}(\phi )$
is simply connected and outputs descriptions of the abelian groups
![]() $\pi _i({\mathcal R}(\phi ))$
,
$\pi _i({\mathcal R}(\phi ))$
,
![]() $2\leq i \leq \ell $
in terms of generators and relations.
$2\leq i \leq \ell $
in terms of generators and relations.
The complexity of the algorithm is bounded by
![]() $(s d)^{k^{O(\ell )}}$
, where
$(s d)^{k^{O(\ell )}}$
, where
![]() $s = \mathrm {card}(\mathcal {P})$
and
$s = \mathrm {card}(\mathcal {P})$
and
![]() $d = \max _{P \in \mathcal {P}} \deg (P)$
.
$d = \max _{P \in \mathcal {P}} \deg (P)$
.
Remark 2.4. Note that we do not have an effective algorithm for checking the hypothesis that the given semialgebraic set is simply connected.
2.4 Comparison with prior and related results
As stated previously, there is no algorithm known for computing the Betti numbers of semialgebraic sets having singly exponential complexity. However, algorithms with singly exponential complexity are known for computing certain (small) Betti numbers. The zero-th Betti number of a semialgebraic set is just the number of its semialgebraically connected components. Counting the number of semialgebraically connected components of a given semialgebraic set is a well-studied problem, and algorithms with singly exponential complexity are known for solving this problem [Reference Basu, Pollack and Roy3, Reference Grigoriev and Vorobjov16, Reference Canny13]. In [Reference Basu, Pollack and Roy5], a singly exponential complexity algorithm is given for computing the first Betti number of semialgebraic sets, and this was extended to the first
![]() $\ell $
(for any fixed constant
$\ell $
(for any fixed constant
![]() $\ell $
) Betti numbers in [Reference Basu1]. These algorithms do not produce a simplicial complex homotopy equivalent (or
$\ell $
) Betti numbers in [Reference Basu1]. These algorithms do not produce a simplicial complex homotopy equivalent (or
![]() $\ell $
-equivalent) to the given semialgebraic set.
$\ell $
-equivalent) to the given semialgebraic set.
In [Reference Bürgisser, Cucker and Lairez10, Reference Bürgisser, Cucker and Tonelli-Cueto12, Reference Bürgisser, Cucker and Tonelli-Cueto11], the authors take a different approach. Working over
![]() $\mathbb {R}$
and given a well-conditioned semialgebraic subset
$\mathbb {R}$
and given a well-conditioned semialgebraic subset
![]() $S\subset \mathbb {R}^k$
, they compute a witness complex whose geometric realization is k-equivalent to S. The size of this witness complex is bounded singly exponentially in k. However, the complexity depends on the condition number of the input (and so this bound is not uniform), and the algorithm will fail for ill-conditioned input when the condition number becomes infinite. This is unlike the kind of algorithms we consider in the current paper, which are supposed to work for all inputs and with uniform complexity upper bounds. So these approaches are not comparable.
$S\subset \mathbb {R}^k$
, they compute a witness complex whose geometric realization is k-equivalent to S. The size of this witness complex is bounded singly exponentially in k. However, the complexity depends on the condition number of the input (and so this bound is not uniform), and the algorithm will fail for ill-conditioned input when the condition number becomes infinite. This is unlike the kind of algorithms we consider in the current paper, which are supposed to work for all inputs and with uniform complexity upper bounds. So these approaches are not comparable.
While the approaches in [Reference Basu, Pollack and Roy5, Reference Basu1] and those in [Reference Bürgisser, Cucker and Lairez10, Reference Bürgisser, Cucker and Tonelli-Cueto12, Reference Bürgisser, Cucker and Tonelli-Cueto11] are not comparable, since the meaning of what constitutes an algorithm and the notion of complexity are different, there is a common connection between the results of these papers and those in the current paper which we elucidate below.
2.4.1 Covers
A standard method in algebraic topology for computing homology/cohomology of a space X is by means of an appropriately chosen cover,
![]() $(V_{\alpha } \subset X)_{\alpha \in I}$
, of X by open or closed subsets. Suppose that
$(V_{\alpha } \subset X)_{\alpha \in I}$
, of X by open or closed subsets. Suppose that
![]() $X \subset \mathbb {R}^k$
is a closed or open semialgebraic set. Let
$X \subset \mathbb {R}^k$
is a closed or open semialgebraic set. Let
![]() $\mathcal {V} = (V_{\alpha } \subset X)_{\alpha \in I}$
be a finite cover of X by open or closed semialgebraic subsets such that for each nonempty subset
$\mathcal {V} = (V_{\alpha } \subset X)_{\alpha \in I}$
be a finite cover of X by open or closed semialgebraic subsets such that for each nonempty subset
![]() $J \subset I$
, the intersection
$J \subset I$
, the intersection
![]() $V_J = \bigcap _{\alpha \in J} V_{\alpha }$
is either empty or contractible. We will say that such covers have the Leray property and refer to them as Leray covers. One can then associate to the cover
$V_J = \bigcap _{\alpha \in J} V_{\alpha }$
is either empty or contractible. We will say that such covers have the Leray property and refer to them as Leray covers. One can then associate to the cover
![]() $\mathcal {V}$
, a simplicial complex,
$\mathcal {V}$
, a simplicial complex,
![]() $\mathcal {N}(\mathcal {V})$
, the nerve of
$\mathcal {N}(\mathcal {V})$
, the nerve of
![]() $\mathcal {V}$
defined as follows.
$\mathcal {V}$
defined as follows.
The set of p-simplices of
![]() $\mathcal {N}(\mathcal {V})$
is defined by
$\mathcal {N}(\mathcal {V})$
is defined by
It follows from a classical result of algebraic topology that the geometric realization
![]() $|\mathcal {N}(\mathcal {V})|$
is homotopy equivalent to X, and moreover for each
$|\mathcal {N}(\mathcal {V})|$
is homotopy equivalent to X, and moreover for each
![]() $\ell \geq 0$
, the geometric realization of the
$\ell \geq 0$
, the geometric realization of the
![]() $(\ell +1)$
-st skeleton of
$(\ell +1)$
-st skeleton of
![]() $\mathcal {N}(\mathcal {V})$
,
$\mathcal {N}(\mathcal {V})$
,
is homologically
![]() $\ell $
-equivalent (resp.
$\ell $
-equivalent (resp.
![]() $\ell $
-equivalent) to X (resp. when
$\ell $
-equivalent) to X (resp. when
![]() $\mathrm {R} = \mathbb {R}$
).
$\mathrm {R} = \mathbb {R}$
).
The algorithms for computing the Betti numbers in [Reference Bürgisser, Cucker and Lairez10, Reference Bürgisser, Cucker and Tonelli-Cueto12, Reference Bürgisser, Cucker and Tonelli-Cueto11] proceeds by computing the k-skeleton of the nerve of a cover having the Leray property whose size is bounded singly exponentially in k and computing the simplicial homology groups of this complex. However, the bound on the size of the cover is not uniform but depends on a real valued parameter – namely the condition number of the input – and hence the size of the cover can become infinite. In fact, computing a singly exponential sized cover by semialgebraic subsets having the Leray property of an arbitrary semialgebraic sets is an open problem. If one solves this problem, then one would also solve immediately the problem of designing an algorithm for computing all the Betti numbers of arbitrary semialgebraic sets with singly exponential complexity in full generality.
The algorithms in [Reference Basu, Pollack and Roy5, Reference Basu1] which are able to compute some of the Betti numbers in dimensions
![]() $>0$
also depends on the existence of small covers having size bounded singly exponentially, albeit satisfying a much weaker property than the Leray property. The weaker property is that only the sets
$>0$
also depends on the existence of small covers having size bounded singly exponentially, albeit satisfying a much weaker property than the Leray property. The weaker property is that only the sets
![]() $V_{\alpha }, \alpha \in I$
(i.e., the elements of the cover) are contractible. No assumption is made on the nontrivial finite intersections amongst the sets of the cover. Covers satisfying this weaker property can indeed be computed with singly exponential complexity (this is one of the main results of [Reference Basu, Pollack and Roy5] but see Remark 3.2), and using this fact one is able to compute the first
$V_{\alpha }, \alpha \in I$
(i.e., the elements of the cover) are contractible. No assumption is made on the nontrivial finite intersections amongst the sets of the cover. Covers satisfying this weaker property can indeed be computed with singly exponential complexity (this is one of the main results of [Reference Basu, Pollack and Roy5] but see Remark 3.2), and using this fact one is able to compute the first
![]() $\ell $
Betti numbers of semialgebraic subsets of
$\ell $
Betti numbers of semialgebraic subsets of
![]() $\mathrm {R}^k$
for every fixed
$\mathrm {R}^k$
for every fixed
![]() $\ell $
with singly exponential complexity. The algorithms in [Reference Basu, Pollack and Roy5] and [Reference Basu1] do not construct a simplicial complex homotopy equivalent or
$\ell $
with singly exponential complexity. The algorithms in [Reference Basu, Pollack and Roy5] and [Reference Basu1] do not construct a simplicial complex homotopy equivalent or
![]() $\ell $
-equivalent to the given semialgebraic set S unlike the algorithm in [Reference Bürgisser, Cucker and Lairez10].
$\ell $
-equivalent to the given semialgebraic set S unlike the algorithm in [Reference Bürgisser, Cucker and Lairez10].
2.4.2 Main technical contribution
The main technical result that underlies the algorithmic result of the current paper is the following. Fix
![]() $0 \leq \ell \leq k$
. Suppose for every closed and bounded semialgebraic set S one has a covering of S by closed and bounded semialgebraic subsets which are
$0 \leq \ell \leq k$
. Suppose for every closed and bounded semialgebraic set S one has a covering of S by closed and bounded semialgebraic subsets which are
![]() $\ell $
-connected (see Definition 2.3) and which has singly exponentially bounded complexity (meaning that the number of sets in the cover, the number of polynomials used in the quantifier-free formulas defining these sets and their degrees are all bounded singly exponentially in k). Moreover, since it is clear that contractible covers with singly exponential complexity exists, this is not a vacuous assumption. Using
$\ell $
-connected (see Definition 2.3) and which has singly exponentially bounded complexity (meaning that the number of sets in the cover, the number of polynomials used in the quantifier-free formulas defining these sets and their degrees are all bounded singly exponentially in k). Moreover, since it is clear that contractible covers with singly exponential complexity exists, this is not a vacuous assumption. Using
![]() $\ell $
-connected covers repeatedly we build a simplicial complex of size bounded singly exponentially which is
$\ell $
-connected covers repeatedly we build a simplicial complex of size bounded singly exponentially which is
![]() $\ell $
-equivalent to the given semialgebraic set. The definition of this simplicial complex is a bit involved (much more involved than the nerve complex of a Leray cover) and appears in Section 3. Its main properties are encapsulated in Theorem 2.
$\ell $
-equivalent to the given semialgebraic set. The definition of this simplicial complex is a bit involved (much more involved than the nerve complex of a Leray cover) and appears in Section 3. Its main properties are encapsulated in Theorem 2.
Two remarks are in order.
Remark 2.5.
-
1. Firstly, the Leray property can be weakened to require that for every t-wise intersection,
 $V_J, \mathrm {card}(J) = t$
is either empty or
$V_J, \mathrm {card}(J) = t$
is either empty or
 $(\ell -t+1)$
-connected [Reference Björner, Graham, Grotschel and Lovasz7]. We call this the
$(\ell -t+1)$
-connected [Reference Björner, Graham, Grotschel and Lovasz7]. We call this the
 $\ell $
-Leray property. The nerve complex,
$\ell $
-Leray property. The nerve complex,
 $\mathcal {N}(\mathcal {V})$
is then
$\mathcal {N}(\mathcal {V})$
is then
 $\ell $
-equivalent to X [Reference Björner, Graham, Grotschel and Lovasz7]. However, the property that we use is much weaker – namely that only the elements of the cover are
$\ell $
-equivalent to X [Reference Björner, Graham, Grotschel and Lovasz7]. However, the property that we use is much weaker – namely that only the elements of the cover are
 $\ell $
-connected and we make no assumptions on the connectivity of the intersections of two or more sets of the cover. This is due to the fact that controlling the connectivity of the intersections is very difficult, and we do not know of any algorithm with singly exponential complexity for computing covers having the
$\ell $
-connected and we make no assumptions on the connectivity of the intersections of two or more sets of the cover. This is due to the fact that controlling the connectivity of the intersections is very difficult, and we do not know of any algorithm with singly exponential complexity for computing covers having the
 $\ell $
-Leray property for
$\ell $
-Leray property for
 $\ell \geq 1$
.
$\ell \geq 1$
. -
2. Secondly, note that to be
 $\ell $
-connected is a weaker property than being contractible. Unfortunately, at present we do not know of algorithms for computing
$\ell $
-connected is a weaker property than being contractible. Unfortunately, at present we do not know of algorithms for computing
 $\ell $
-connected covers, for
$\ell $
-connected covers, for
 $\ell> 0$
that has much better complexity asymptotically than the algorithm in [Reference Basu, Pollack and Roy5] for computing covers by contractible semialgebraic sets. However, it is still possible that there could be algorithms with much better complexity for computing
$\ell> 0$
that has much better complexity asymptotically than the algorithm in [Reference Basu, Pollack and Roy5] for computing covers by contractible semialgebraic sets. However, it is still possible that there could be algorithms with much better complexity for computing
 $\ell $
-connected covers (at least for small
$\ell $
-connected covers (at least for small
 $\ell $
) compared to computing contractible covers.
$\ell $
) compared to computing contractible covers.
3 Simplicial replacement in an abstract setting
We now arrive at the technical core of the paper. Given a finite set J, a tuple,
![]() $\Phi = (\phi _j)_{j \in J}$
, of closed formulas with k free variables and numbers
$\Phi = (\phi _j)_{j \in J}$
, of closed formulas with k free variables and numbers
![]() $i,m \geq 0$
, we will describe the construction of a poset, that we denote by
$i,m \geq 0$
, we will describe the construction of a poset, that we denote by
![]() $\mathbf {P}_{m,i}(\Phi )$
. We will assume that the realizations,
$\mathbf {P}_{m,i}(\Phi )$
. We will assume that the realizations,
![]() ${\mathcal R}(\phi _j), j \in J$
, of the formulas in the tuple are homologically
${\mathcal R}(\phi _j), j \in J$
, of the formulas in the tuple are homologically
![]() $\ell $
-connected semialgebraic subsets of
$\ell $
-connected semialgebraic subsets of
![]() $\mathrm {R}^k$
for some
$\mathrm {R}^k$
for some
![]() $\ell \geq 0$
. In case
$\ell \geq 0$
. In case
![]() $\mathrm {R} = \mathbb {R}$
, substitute ‘
$\mathrm {R} = \mathbb {R}$
, substitute ‘
![]() $\ell $
-connected” for “homologically
$\ell $
-connected” for “homologically
![]() $\ell $
-connected’. The poset
$\ell $
-connected’. The poset
![]() $\mathbf {P}_{m,i}(\Phi )$
will have the property that the geometric realization of its order complex,
$\mathbf {P}_{m,i}(\Phi )$
will have the property that the geometric realization of its order complex,
![]() $\Delta (\mathbf {P}_{m,i}(\Phi ))$
, is homologically
$\Delta (\mathbf {P}_{m,i}(\Phi ))$
, is homologically
![]() $(m-1)$
-equivalent (
$(m-1)$
-equivalent (
![]() $(m-1)$
-equivalent if
$(m-1)$
-equivalent if
![]() $\mathrm {R} = \mathbb {R}$
) to
$\mathrm {R} = \mathbb {R}$
) to
![]() ${\mathcal R}(\Phi )^J$
. More generally, for each
${\mathcal R}(\Phi )^J$
. More generally, for each
![]() $J' \subset J$
,
$J' \subset J$
,
![]() $\mathbf {P}_{m,i}(\Phi |_{J'})$
can be identified as a subposet of
$\mathbf {P}_{m,i}(\Phi |_{J'})$
can be identified as a subposet of
![]() $\mathbf {P}_{m,i}(\Phi )$
, and the diagram of inclusions of the corresponding geometric realizations is homologically
$\mathbf {P}_{m,i}(\Phi )$
, and the diagram of inclusions of the corresponding geometric realizations is homologically
![]() $(m-1)$
-equivalent to the diagram
$(m-1)$
-equivalent to the diagram
![]() $\mathbf {Simp}^J({\mathcal R}(\Phi ))$
(
$\mathbf {Simp}^J({\mathcal R}(\Phi ))$
(
![]() $(m-1)$
-equivalent if
$(m-1)$
-equivalent if
![]() $\mathrm {R} = \mathbb {R}$
) (cf. Theorems 2 and 2′
). The poset
$\mathrm {R} = \mathbb {R}$
) (cf. Theorems 2 and 2′
). The poset
![]() $\mathbf {P}_{m,i}(\Phi )$
will then encode in a finite combinatorial way information which determines the first m homotopy groups of
$\mathbf {P}_{m,i}(\Phi )$
will then encode in a finite combinatorial way information which determines the first m homotopy groups of
![]() ${\mathcal R}(\Phi )^{J'}$
for all
${\mathcal R}(\Phi )^{J'}$
for all
![]() $J' \subset J$
and the morphisms
$J' \subset J$
and the morphisms
![]() $\pi _h({\mathcal R}(\Phi )^{J'}) \rightarrow \pi _h({\mathcal R}(\Phi )^{J"})$
induced by inclusions, for
$\pi _h({\mathcal R}(\Phi )^{J'}) \rightarrow \pi _h({\mathcal R}(\Phi )^{J"})$
induced by inclusions, for
![]() $0 \leq h \leq m-1$
and
$0 \leq h \leq m-1$
and
![]() $J' \subset J" \subset J$
. (The significance of the subscript i in the notation
$J' \subset J" \subset J$
. (The significance of the subscript i in the notation
![]() $\mathbf {P}_{m,i}(\Phi )$
will become clear later.)
$\mathbf {P}_{m,i}(\Phi )$
will become clear later.)
Remark 3.1. Note that the idea that a topological space is homotopy equivalent to the geometric realization of the order complex of the poset of inclusions of certain covers of the space has appeared before (see, for example, [Reference McCord19, Reference Weil28]). But the connectivity restrictions on the cover are stricter than the ones we consider in this paper. Also, these prior results are infinitary in nature, while in this paper it is important for us to prove uniform upper bounds on the size of the poset we construct.
3.1 Outline of the main idea
We begin with an outline explaining the main ideas behind the construction. First, observe that if the realizations of the sets in the given tuple, in addition to being
![]() $\ell $
-connected, satisfies the
$\ell $
-connected, satisfies the
![]() $\ell $
-Leray property (i.e., each t-wise intersection amongst them is
$\ell $
-Leray property (i.e., each t-wise intersection amongst them is
![]() $(\ell -t +1)$
-connected), then it follows from [Reference Björner, Graham, Grotschel and Lovasz7] that the poset of the nonempty intersections (with the poset relation being canonical inclusions) satisfies the property that the geometric realization of its order complex (see Definition 3.1) is
$(\ell -t +1)$
-connected), then it follows from [Reference Björner, Graham, Grotschel and Lovasz7] that the poset of the nonempty intersections (with the poset relation being canonical inclusions) satisfies the property that the geometric realization of its order complex (see Definition 3.1) is
![]() $\ell $
-equivalent to
$\ell $
-equivalent to
![]() ${\mathcal R}(\Phi )^J$
. The same is true for all the subposets obtained by restricting the intersections to only amongst those indexed by some subset
${\mathcal R}(\Phi )^J$
. The same is true for all the subposets obtained by restricting the intersections to only amongst those indexed by some subset
![]() $J' \subset J$
. However, if the
$J' \subset J$
. However, if the
![]() $\ell $
-Leray property fails to hold then the poset of canonical inclusions may fail to have the desired property.
$\ell $
-Leray property fails to hold then the poset of canonical inclusions may fail to have the desired property.
Consider for example, the tuple
where
 $$ \begin{align*} \phi_0 &:= (X_1^2 + X_2^2 -1 = 0) \wedge (X_2 \geq 0), \\ \phi_1 &:= (X_1^2 + X_2^2 -1 = 0) \wedge (X_2 \leq 0). \end{align*} $$
$$ \begin{align*} \phi_0 &:= (X_1^2 + X_2^2 -1 = 0) \wedge (X_2 \geq 0), \\ \phi_1 &:= (X_1^2 + X_2^2 -1 = 0) \wedge (X_2 \leq 0). \end{align*} $$
The realizations
![]() ${\mathcal R}(\phi _0), {\mathcal R}(\phi _1)$
are the upper and lower semicircles covering the unit circle in the plane.
${\mathcal R}(\phi _0), {\mathcal R}(\phi _1)$
are the upper and lower semicircles covering the unit circle in the plane.
The intersection
![]() ${\mathcal R}(\phi _0) \cap {\mathcal R}(\phi _1) = {\mathcal R}(\phi _0 \wedge \phi _1)$
is the disjoint union of two points. The Hasse diagram of the poset of canonical inclusions of the sets defined by
${\mathcal R}(\phi _0) \cap {\mathcal R}(\phi _1) = {\mathcal R}(\phi _0 \wedge \phi _1)$
is the disjoint union of two points. The Hasse diagram of the poset of canonical inclusions of the sets defined by
![]() $\phi _0$
,
$\phi _0$
,
![]() $\phi _1$
, and
$\phi _1$
, and
![]() $\phi _0 \wedge \phi _1$
is:
$\phi _0 \wedge \phi _1$
is:

and the order complex of the poset is the simplicial complex shown in Figure 1. The geometric realization of the order complex is clearly not homotopy equivalent to the
which is equal to the unit circle. This is not surprising since the cover of the circle by the two closed semicircle is not a Leray cover (and in fact not
![]() $\ell $
-Leray for any
$\ell $
-Leray for any
![]() $\ell \geq 0$
).
$\ell \geq 0$
).

Figure 1 Order complex for non-Leray cover.
One way of repairing this situation is to go one step further and choose a good (in this case
![]() $\infty $
-connected) cover for the intersection
$\infty $
-connected) cover for the intersection
![]() ${\mathcal R}(\phi _0) \cap {\mathcal R}(\phi _1)$
defined by
${\mathcal R}(\phi _0) \cap {\mathcal R}(\phi _1)$
defined by
![]() $\psi _0,\psi _1$
, where
$\psi _0,\psi _1$
, where
 $$ \begin{align*} \psi_0 &:= (X_1+1 = 0) \wedge (X_2 = 0), \\ \psi_1 &:= (X_1-1=0) \wedge (X_2 = 0 ). \end{align*} $$
$$ \begin{align*} \psi_0 &:= (X_1+1 = 0) \wedge (X_2 = 0), \\ \psi_1 &:= (X_1-1=0) \wedge (X_2 = 0 ). \end{align*} $$
The Hasse diagram of the poset of canonical inclusions of the sets defined by
![]() $\phi _0$
,
$\phi _0$
,
![]() $\phi _1$
,
$\phi _1$
,
![]() $\psi _0$
, and
$\psi _0$
, and
![]() $\psi _1$
$\psi _1$

and the order complex of the poset is shown in Figure 2. It is easily seen to have the same homotopy type (homeomorphism type even in this case) to the circle.

Figure 2 Order complex for modified poset.
The very simple example given above motivates the definition of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
in general. We assume that we have available not just the given tuple of sets, and the nonempty intersections amongst them, but also that we can cover any given nonempty intersections that arise in our construction using
$\mathbf {P}_{m,i}(\Phi )$
in general. We assume that we have available not just the given tuple of sets, and the nonempty intersections amongst them, but also that we can cover any given nonempty intersections that arise in our construction using
![]() $\ell $
-connected closed (resp. open) semialgebraic sets (we do not assume that these covers satisfy the stronger
$\ell $
-connected closed (resp. open) semialgebraic sets (we do not assume that these covers satisfy the stronger
![]() $\ell $
-Leray property). The poset we define depends on the choice of these covers and not just on the formulas in the tuple
$\ell $
-Leray property). The poset we define depends on the choice of these covers and not just on the formulas in the tuple
![]() $\Phi $
(unlike the standard nerve complex of the tuple
$\Phi $
(unlike the standard nerve complex of the tuple
![]() ${\mathcal R}(\Phi )$
). The choices that we make are encapsulated in the functions
${\mathcal R}(\Phi )$
). The choices that we make are encapsulated in the functions
![]() $\mathcal {I}_{k,i}$
and
$\mathcal {I}_{k,i}$
and
![]() $\mathcal {C}_{k,i}$
below. In practice, they would correspond to some effective algorithm for computing well-connected covers of semialgebraic sets.
$\mathcal {C}_{k,i}$
below. In practice, they would correspond to some effective algorithm for computing well-connected covers of semialgebraic sets.
Remark 3.2. There is one technical detail that serves to obscure a little the clarity of the construction. It arises due to the fact that the only algorithm with single exponential complexity that exists in the literature for computing well-connected (
![]() $\infty $
-connected or equivalently contractible) covers is the one in [Reference Basu, Pollack and Roy5]. However, the algorithm requires that the polynomials describing the given set S be in strong general position (see Definition 4.1). In order to satisfy this requirement, one needs to initially perturb the given polynomials and replace the given set by another one, say
$\infty $
-connected or equivalently contractible) covers is the one in [Reference Basu, Pollack and Roy5]. However, the algorithm requires that the polynomials describing the given set S be in strong general position (see Definition 4.1). In order to satisfy this requirement, one needs to initially perturb the given polynomials and replace the given set by another one, say
![]() $S'$
, which is infinitesimally larger but has the same homotopy type as the given set S (see Lemma 3.1). The algorithm then computes closed formulas whose realizations cover
$S'$
, which is infinitesimally larger but has the same homotopy type as the given set S (see Lemma 3.1). The algorithm then computes closed formulas whose realizations cover
![]() $S'$
and moreover are each semialgebraically contractible. While there is a semialgebraic retraction from
$S'$
and moreover are each semialgebraically contractible. While there is a semialgebraic retraction from
![]() $S'$
to S, this retraction is not guaranteed to restrict to the elements of the cover. Our poset construction is designed to be compatible with the fact that the covers we assume to exist actually are covers of infinitesimally larger sets (i.e., that of
$S'$
to S, this retraction is not guaranteed to restrict to the elements of the cover. Our poset construction is designed to be compatible with the fact that the covers we assume to exist actually are covers of infinitesimally larger sets (i.e., that of
![]() $S'$
instead of S following the notation of the previous sentence). This necessitates the use of iterated Puiseux extensions in what follows.
$S'$
instead of S following the notation of the previous sentence). This necessitates the use of iterated Puiseux extensions in what follows.
Of course, the introduction of infinitesimals could be avoided by choosing sufficiently small positive elements in the field
![]() $\mathrm {R}$
itself and thus avoid making extensions. This would be more difficult to visualize, and so we prefer to use the language of infinitesimal extensions. In the special case when
$\mathrm {R}$
itself and thus avoid making extensions. This would be more difficult to visualize, and so we prefer to use the language of infinitesimal extensions. In the special case when
![]() $\mathrm {R} = \mathbb {R}$
, we prefer not to make non-Archimedean extensions, since we discuss homotopy groups, so we take the alternative approach. However, we believe that the infinitesimal language is conceptually easier to grasp, and so we use it in the general case.
$\mathrm {R} = \mathbb {R}$
, we prefer not to make non-Archimedean extensions, since we discuss homotopy groups, so we take the alternative approach. However, we believe that the infinitesimal language is conceptually easier to grasp, and so we use it in the general case.
Before giving the definition of the poset, we first need to introduce some mathematical preliminaries and notation.
3.2 Real closed extensions and Puiseux series
We will need some properties of Puiseux series with coefficients in a real closed field. We refer the reader to [Reference Basu, Pollack and Roy4] for further details.
Notation 3.1. For
![]() $\mathrm {R}$
a real closed field, we denote by
$\mathrm {R}$
a real closed field, we denote by
![]() $\mathrm {R} \left \langle {\varepsilon } \right \rangle $
the real closed field of algebraic Puiseux series in
$\mathrm {R} \left \langle {\varepsilon } \right \rangle $
the real closed field of algebraic Puiseux series in
![]() ${\varepsilon }$
with coefficients in
${\varepsilon }$
with coefficients in
![]() $\mathrm {R}$
. We use the notation
$\mathrm {R}$
. We use the notation
![]() $\mathrm {R} \left \langle {\varepsilon }_{1}, \ldots , {\varepsilon }_{m} \right \rangle $
to denote the real closed field
$\mathrm {R} \left \langle {\varepsilon }_{1}, \ldots , {\varepsilon }_{m} \right \rangle $
to denote the real closed field
![]() $\mathrm {R} \left \langle {\varepsilon }_{1} \right \rangle \left \langle {\varepsilon }_{2} \right \rangle \cdots \left \langle {\varepsilon }_{m} \right \rangle $
. Note that in the unique ordering of the field
$\mathrm {R} \left \langle {\varepsilon }_{1} \right \rangle \left \langle {\varepsilon }_{2} \right \rangle \cdots \left \langle {\varepsilon }_{m} \right \rangle $
. Note that in the unique ordering of the field
![]() $\mathrm {R} \left \langle {\varepsilon }_{1}, \ldots , {\varepsilon }_{m} \right \rangle $
,
$\mathrm {R} \left \langle {\varepsilon }_{1}, \ldots , {\varepsilon }_{m} \right \rangle $
,
![]() $0< {\varepsilon }_{m} \ll {\varepsilon }_{m-1} \ll \cdots \ll {\varepsilon }_{1} \ll 1$
.
$0< {\varepsilon }_{m} \ll {\varepsilon }_{m-1} \ll \cdots \ll {\varepsilon }_{1} \ll 1$
.
If
![]() $\bar {\varepsilon }$
denotes the (possibly infinite) sequence
$\bar {\varepsilon }$
denotes the (possibly infinite) sequence
![]() $({\varepsilon }_1,{\varepsilon }_2,\ldots )$
, we will denote by
$({\varepsilon }_1,{\varepsilon }_2,\ldots )$
, we will denote by
![]() $\mathrm {R}{\langle }\bar {\varepsilon }{\rangle }$
the real closed field
$\mathrm {R}{\langle }\bar {\varepsilon }{\rangle }$
the real closed field
![]() $\bigcup _{m\geq 0} \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }$
.
$\bigcup _{m\geq 0} \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }$
.
Finally, given a finite sequence
![]() $(\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m)$
we will denote by
$(\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m)$
we will denote by
![]() $\mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }$
the real closed field
$\mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }$
the real closed field
![]() $\mathrm {R} \left \langle \bar {\varepsilon }_{1} \right \rangle \left \langle \bar {\varepsilon }_{2} \right \rangle \cdots \left \langle \bar {\varepsilon }_{m} \right \rangle $
.
$\mathrm {R} \left \langle \bar {\varepsilon }_{1} \right \rangle \left \langle \bar {\varepsilon }_{2} \right \rangle \cdots \left \langle \bar {\varepsilon }_{m} \right \rangle $
.
Notation 3.2. For elements
![]() $x \in \mathrm {R} \left \langle {\varepsilon } \right \rangle $
which are bounded over
$x \in \mathrm {R} \left \langle {\varepsilon } \right \rangle $
which are bounded over
![]() $\mathrm {R}$
, we denote by
$\mathrm {R}$
, we denote by
![]() $\lim _{{\varepsilon }} x$
to be the image in
$\lim _{{\varepsilon }} x$
to be the image in
![]() $\mathrm {R}$
under the usual map that sets
$\mathrm {R}$
under the usual map that sets
![]() ${\varepsilon }$
to
${\varepsilon }$
to
![]() $0$
in the Puiseux series x.
$0$
in the Puiseux series x.
Notation 3.3. If
![]() $\mathrm {R}'$
is a real closed extension of a real closed field
$\mathrm {R}'$
is a real closed extension of a real closed field
![]() $\mathrm {R}$
and
$\mathrm {R}$
and
![]() $S \subset \mathrm {R}^{k}$
is a semialgebraic set defined by a first-order formula with coefficients in
$S \subset \mathrm {R}^{k}$
is a semialgebraic set defined by a first-order formula with coefficients in
![]() $\mathrm {R}$
, then we will denote by
$\mathrm {R}$
, then we will denote by
![]() $\mathrm {ext}(S, \mathrm {R}') \subset \mathrm {R}^{\prime k}$
the semialgebraic subset of
$\mathrm {ext}(S, \mathrm {R}') \subset \mathrm {R}^{\prime k}$
the semialgebraic subset of
![]() $\mathrm {R}^{\prime k}$
defined by the same formula. Footnote
3
It is well known that
$\mathrm {R}^{\prime k}$
defined by the same formula. Footnote
3
It is well known that
![]() $\mathrm {ext}(S, \mathrm {R}')$
does not depend on the choice of the formula defining S [Reference Basu, Pollack and Roy4, Proposition 2.87].
$\mathrm {ext}(S, \mathrm {R}')$
does not depend on the choice of the formula defining S [Reference Basu, Pollack and Roy4, Proposition 2.87].
Notation 3.4. Suppose
![]() $\mathrm {R}$
is a real closed field, and let
$\mathrm {R}$
is a real closed field, and let
![]() $X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
$X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
![]() $X^+ \subset \mathrm {R}{\langle }{\varepsilon }{\rangle }^k$
be a semialgebraic subset bounded over
$X^+ \subset \mathrm {R}{\langle }{\varepsilon }{\rangle }^k$
be a semialgebraic subset bounded over
![]() $\mathrm {R}$
. Let for
$\mathrm {R}$
. Let for
![]() $t \in \mathrm {R}, t>0$
,
$t \in \mathrm {R}, t>0$
,
![]() $\widetilde {X}^+_{t} \subset \mathrm {R}^k$
denote the semialgebraic subset obtained by replacing
$\widetilde {X}^+_{t} \subset \mathrm {R}^k$
denote the semialgebraic subset obtained by replacing
![]() ${\varepsilon }$
in the formula defining
${\varepsilon }$
in the formula defining
![]() $X^+$
by t, and it is clear that for
$X^+$
by t, and it is clear that for
![]() $0 < t \ll 1$
,
$0 < t \ll 1$
,
![]() $\widetilde {X}^+_t$
does not depend on the formula chosen. We say that
$\widetilde {X}^+_t$
does not depend on the formula chosen. We say that
![]() $X^+$
is monotonically decreasing to X and denote
$X^+$
is monotonically decreasing to X and denote
![]() $X^+ \searrow X$
if the following conditions are satisfied.
$X^+ \searrow X$
if the following conditions are satisfied.
-
(a) for all
 $0 < t < t' \ll 1$
,
$0 < t < t' \ll 1$
,
 $\widetilde {X}^+_{t} \subset \widetilde {X}^+_{t'}$
;
$\widetilde {X}^+_{t} \subset \widetilde {X}^+_{t'}$
; -
(b)
 $$\begin{align*}\bigcap_{t> 0} \widetilde{X}^+_{t} = X; \end{align*}$$
$$\begin{align*}\bigcap_{t> 0} \widetilde{X}^+_{t} = X; \end{align*}$$
or equivalently
 $\lim _{\varepsilon } X^+ = X$
.
$\lim _{\varepsilon } X^+ = X$
.
More generally, if
![]() $X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
$X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
![]() $X^+ \subset \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }^k$
a semialgebraic subset bounded over
$X^+ \subset \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }^k$
a semialgebraic subset bounded over
![]() $\mathrm {R}$
, we will say
$\mathrm {R}$
, we will say
![]() $X^+ \searrow X$
if and only if
$X^+ \searrow X$
if and only if
where for
![]() $i=1,\ldots , m$
,
$i=1,\ldots , m$
,
![]() $X^+_i = \lim _{{\varepsilon }_i} X^+_{i+1}$
.
$X^+_i = \lim _{{\varepsilon }_i} X^+_{i+1}$
.
Note that if
![]() $\bar {\varepsilon }= ({\varepsilon }_1,{\varepsilon }_2,\ldots )$
is an infinite sequence and
$\bar {\varepsilon }= ({\varepsilon }_1,{\varepsilon }_2,\ldots )$
is an infinite sequence and
![]() $X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }{\rangle }^k$
is a semialgebraic subset bounded over
$X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }{\rangle }^k$
is a semialgebraic subset bounded over
![]() $\mathrm {R}$
, then there exists
$\mathrm {R}$
, then there exists
![]() $m \geq 1$
, and semialgebraic subset
$m \geq 1$
, and semialgebraic subset
![]() $X^+_m \subset \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }^k$
closed and bounded over
$X^+_m \subset \mathrm {R}{\langle }{\varepsilon }_1,\ldots ,{\varepsilon }_m{\rangle }^k$
closed and bounded over
![]() $\mathrm {R}$
such that
$\mathrm {R}$
such that
![]() $X^+ = \mathrm {ext}(X^+_m,\mathrm {R}{\langle }\bar {\varepsilon }{\rangle })$
.
$X^+ = \mathrm {ext}(X^+_m,\mathrm {R}{\langle }\bar {\varepsilon }{\rangle })$
.
In this case, if
![]() $X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset, we will say
$X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset, we will say
![]() $X^+ \searrow X$
if and only if
$X^+ \searrow X$
if and only if
where for
![]() $i=1,\ldots , m$
,
$i=1,\ldots , m$
,
![]() $X^+_i = \lim _{{\varepsilon }_i} X^+_{i+1}$
.
$X^+_i = \lim _{{\varepsilon }_i} X^+_{i+1}$
.
Finally, if
![]() $\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m$
are sequences (possibly infinite),
$\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m$
are sequences (possibly infinite),
![]() $X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
$X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
![]() $X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }^k$
a semialgebraic subset bounded over
$X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }^k$
a semialgebraic subset bounded over
![]() $\mathrm {R}$
, we will say
$\mathrm {R}$
, we will say
![]() $X^+ \searrow X$
if and only if
$X^+ \searrow X$
if and only if
where for
![]() $i=1,\ldots , m$
,
$i=1,\ldots , m$
,
![]() $X^+_i = \lim _{\bar {\varepsilon }_i} X^+_{i+1}$
.
$X^+_i = \lim _{\bar {\varepsilon }_i} X^+_{i+1}$
.
The following lemma will be useful later.
Lemma 3.1. Let
![]() $X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
$X \subset \mathrm {R}^k$
be a closed and bounded semialgebraic subset and
![]() $X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }^k$
a semi-algebraic subset bounded over
$X^+ \subset \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle }^k$
a semi-algebraic subset bounded over
![]() $\mathrm {R}$
such that
$\mathrm {R}$
such that
![]() $X^+ \searrow X$
. Then,
$X^+ \searrow X$
. Then,
![]() $\mathrm {ext}(X,\mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle })$
is semialgebraic deformation retract of
$\mathrm {ext}(X,\mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_m{\rangle })$
is semialgebraic deformation retract of
![]() $X^+$
.
$X^+$
.
Proof. See proof of Lemma 16.17 in [Reference Basu, Pollack and Roy4].
Notation 3.5. For
![]() $x \in \mathrm {R}^{k}$
and
$x \in \mathrm {R}^{k}$
and
![]() $R \in \mathrm {R}$
,
$R \in \mathrm {R}$
,
![]() $R>0$
, we will denote by
$R>0$
, we will denote by
![]() $B_{k} (0,R)$
the open Euclidean ball centered at
$B_{k} (0,R)$
the open Euclidean ball centered at
![]() $0$
of radius R. We will denote by
$0$
of radius R. We will denote by
![]() $\overline {B_k(0,R)}$
the closed Euclidean ball centered at
$\overline {B_k(0,R)}$
the closed Euclidean ball centered at
![]() $0$
of radius R. If
$0$
of radius R. If
![]() $\mathrm {R}'$
is a real closed extension of the real closed field
$\mathrm {R}'$
is a real closed extension of the real closed field
![]() $\mathrm {R}$
and when the context is clear, we will continue to denote by
$\mathrm {R}$
and when the context is clear, we will continue to denote by
![]() $B_{k} (0,R)$
the extension
$B_{k} (0,R)$
the extension
![]() $\mathrm {ext}(B_{k} (0,R) , \mathrm {R}')$
and similarly for
$\mathrm {ext}(B_{k} (0,R) , \mathrm {R}')$
and similarly for
![]() $\overline {B_k(0,R)}$
. This should not cause any confusion. Similarly, we will denote by
$\overline {B_k(0,R)}$
. This should not cause any confusion. Similarly, we will denote by
![]() $\mathbf {S}^{k-1}(0,R)$
the sphere of dimension
$\mathbf {S}^{k-1}(0,R)$
the sphere of dimension
![]() $k-1$
in
$k-1$
in
![]() $\mathrm {R}^k$
centered at
$\mathrm {R}^k$
centered at
![]() $0$
of radius R.
$0$
of radius R.
We refer the reader to [Reference Basu, Pollack and Roy4, Chapter 6] for the definitions of homology and cohomology groups of semialgebraic sets over arbitrary real closed fields.
3.3 Definition of the poset
 $\mathbf {P}_{m,i}(\Phi )$
$\mathbf {P}_{m,i}(\Phi )$
3.3.1 Simplified view of the definition of the poset
 $\mathbf {P}_{m,i}(\Phi )$
$\mathbf {P}_{m,i}(\Phi )$
Before giving a precise definition of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
, we first give a simplified version. We make the following two simplifications in order to illustrate the key idea.
$\mathbf {P}_{m,i}(\Phi )$
, we first give a simplified version. We make the following two simplifications in order to illustrate the key idea.
-
(a) We ignore the role of the index i in what follows. The necessity of the extra parameter i is due to the fact that the hypothesis we assume (Hypothesis 3.1 in the following paragraph) is slightly stronger than we are able to assume for designing effective algorithms for computing the poset (see Remark 3.2). The actual hypothesis that we use is encapsulated in Property 3.2 below.
-
(b) Secondly, in order to keep a geometric view of the construction, we will talk about tuples
 $\mathcal {S} = (S_j)_{j \in J}$
of semialgebraic sets, instead of tuples of formulas
$\mathcal {S} = (S_j)_{j \in J}$
of semialgebraic sets, instead of tuples of formulas
 $\Phi = (\phi _j)_{j \in J}$
defining them. As above, in order to give an effective algorithms and analyzing its complexity, we need to describe the poset in terms of formulas rather than sets, which we do in the precise definition that follows this simplified version.
$\Phi = (\phi _j)_{j \in J}$
defining them. As above, in order to give an effective algorithms and analyzing its complexity, we need to describe the poset in terms of formulas rather than sets, which we do in the precise definition that follows this simplified version.
We make the following hypothesis.
Hypothesis 3.1 (Black-box hypothesis).
There exists a black box (or algorithm) that, given a closed and bounded semialgebraic set
![]() $S \subset \mathbb {R}^k$
as input, produces a cover
$S \subset \mathbb {R}^k$
as input, produces a cover
![]() $(S_{\alpha })_{\alpha \in \mathcal {C}(S)}$
of S by closed and bounded
$(S_{\alpha })_{\alpha \in \mathcal {C}(S)}$
of S by closed and bounded
![]() $\ell $
-connected semialgebraic sets.
$\ell $
-connected semialgebraic sets.
Definition 3.1 (The order complex of a poset).
Let
![]() $(\mathbf {P},\preceq )$
be a poset. We denote by
$(\mathbf {P},\preceq )$
be a poset. We denote by
![]() $\Delta (\mathbf {P})$
the simplicial complex whose simplices are chains of
$\Delta (\mathbf {P})$
the simplicial complex whose simplices are chains of
![]() $\mathbf {P}$
.
$\mathbf {P}$
.
Suppose
![]() $\mathcal {S} = (S_j)_{j \in J}$
is a finite tuple of
$\mathcal {S} = (S_j)_{j \in J}$
is a finite tuple of
![]() $\ell $
-connected closed semialgebraic subsets of
$\ell $
-connected closed semialgebraic subsets of
![]() $\mathbb {R}^k$
.
$\mathbb {R}^k$
.
Our goal is to define a poset
![]() $\mathbf {P}_{m}(\mathcal {S})$
such that:
$\mathbf {P}_{m}(\mathcal {S})$
such that:
Property 3.1.
(see Definition 3.1). We will say that the poset
![]() $\mathbf {P}_{m}(\mathcal {S})$
satisfies Property 3.1 for the pair
$\mathbf {P}_{m}(\mathcal {S})$
satisfies Property 3.1 for the pair
![]() $(m,\mathcal {S})$
.
$(m,\mathcal {S})$
.
Remark 3.3. We use cohomological m-equivalence in Property 3.1. In the final construction, we will lose a dimension while passing from cohomological equivalence to (homological or homotopical) equivalence because of the use of the universal coefficients theorem (see the proof of Claim 3.5 inside the proof of Theorem 2), and we will end up with
The main idea is to approximate homotopically the diagram of sets
(see Notation 2.1), and the inclusion maps
by a corresponding diagram of (the geometric realizations of the order complexes of) posets
(where the poset
![]() $\mathbf {P}_{m - \mathrm {card}(I)+1,I}$
corresponds to
$\mathbf {P}_{m - \mathrm {card}(I)+1,I}$
corresponds to
![]() $\mathcal {S}_I$
) and poset inclusions
$\mathcal {S}_I$
) and poset inclusions
The construction is by induction on m (we call this the global induction below).
-
1. (Base case of the global induction,
 $m=-1$
.) Suppose
$m=-1$
.) Suppose
 $\mathcal {S} = (S_j)_{j \in J}$
is a finite tuple of
$\mathcal {S} = (S_j)_{j \in J}$
is a finite tuple of
 $\ell $
-connected closed and bounded semialgebraic subsets of
$\ell $
-connected closed and bounded semialgebraic subsets of
 $\mathbb {R}^k$
. We define the poset
$\mathbb {R}^k$
. We define the poset
 $\mathbf {P}_{-1}(\mathcal {S})$
to be just the index set J, with no nontrivial order relations. It is depicted in Figure 3(a). It is clear that
$\mathbf {P}_{-1}(\mathcal {S})$
to be just the index set J, with no nontrivial order relations. It is depicted in Figure 3(a). It is clear that
 $\mathbf {P}_{-1}(\mathcal {S})$
satisfies Property 3.1 for the pair
$\mathbf {P}_{-1}(\mathcal {S})$
satisfies Property 3.1 for the pair
 $(-1, \mathcal {S})$
.
$(-1, \mathcal {S})$
.
Figure 3 A simple illustration of the simplified view of the poset.
-
2. (Induction hypothesis of the global induction.) We assume that for each
 $m', -1 \leq m' < m$
, and each finite tuple
$m', -1 \leq m' < m$
, and each finite tuple
 $\mathcal {S} = (S_j)_{j \in J}$
of
$\mathcal {S} = (S_j)_{j \in J}$
of
 $\ell $
-connected closed and bounded semialgebraic subsets of
$\ell $
-connected closed and bounded semialgebraic subsets of
 $\mathbb {R}^k$
, we have defined a poset
$\mathbb {R}^k$
, we have defined a poset
 $\mathbf {P}_{m'}(\mathcal {S})$
satisfying Property 3.1 for the pair
$\mathbf {P}_{m'}(\mathcal {S})$
satisfying Property 3.1 for the pair
 $(m',\mathcal {S})$
.
$(m',\mathcal {S})$
. -
3. (Inductive step of the global induction, going from
 $<m$
to m.) Using the inductive hypothesis, we now define a poset
$<m$
to m.) Using the inductive hypothesis, we now define a poset
 $\mathbf {P}_{m}(\mathcal {S})$
satisfying Property 3.1 for the pair
$\mathbf {P}_{m}(\mathcal {S})$
satisfying Property 3.1 for the pair
 $(m,\mathcal {S})$
, for any tuple
$(m,\mathcal {S})$
, for any tuple
 $\mathcal {S}$
of
$\mathcal {S}$
of
 $\ell $
-connected closed and bounded semialgebraic subsets of
$\ell $
-connected closed and bounded semialgebraic subsets of
 $\mathbb {R}^k$
.
$\mathbb {R}^k$
.Fix a finite tuple
 $\mathcal {S} = (S_j)_{j \in J}$
of
$\mathcal {S} = (S_j)_{j \in J}$
of
 $\ell $
-connected closed and bounded semialgebraic subsets of
$\ell $
-connected closed and bounded semialgebraic subsets of
 $\mathbb {R}^k$
. We will define
$\mathbb {R}^k$
. We will define
 $\mathbf {P}_m(\mathcal {S})$
below in steps. The poset
$\mathbf {P}_m(\mathcal {S})$
below in steps. The poset
 $\mathbf {P}_m(\mathcal {S})$
as a set will be a disjoint union of the index set J, and certain subposets
$\mathbf {P}_m(\mathcal {S})$
as a set will be a disjoint union of the index set J, and certain subposets
 $\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
, where I where
$\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
, where I where
 $I \subset J, 2 \leq \mathrm {card}(I) \leq m+2$
. We define the subposets
$I \subset J, 2 \leq \mathrm {card}(I) \leq m+2$
. We define the subposets
 $\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
by downward induction (we call this the local induction below) on
$\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
by downward induction (we call this the local induction below) on
 $\mathrm {card}(I)$
, starting from the base case,
$\mathrm {card}(I)$
, starting from the base case,
 $\mathrm {card}(I) = m+2$
.
$\mathrm {card}(I) = m+2$
.-
(a) (Base case of the local induction,
 $\mathrm {card}(I) = m+2$
.) We first consider the semialgebraic sets
$\mathrm {card}(I) = m+2$
.) We first consider the semialgebraic sets
 $\mathcal {S}_I, \mathrm {card}(I)= m+2$
. Associated to each such I, we define a poset, which we denoted by
$\mathcal {S}_I, \mathrm {card}(I)= m+2$
. Associated to each such I, we define a poset, which we denoted by
 $\mathbf {P}_{-1,I}$
as follows: Using Hypothesis 3.1 applied to the semialgebraic set
$\mathbf {P}_{-1,I}$
as follows: Using Hypothesis 3.1 applied to the semialgebraic set
 $\mathcal {S}_I$
, we obtain a cover
$\mathcal {S}_I$
, we obtain a cover
 $(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
$(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
 $\mathcal {S}_I$
by closed and bounded
$\mathcal {S}_I$
by closed and bounded
 $\ell $
-connected semialgebraic sets. We define
$\ell $
-connected semialgebraic sets. We define  $$\begin{align*}\mathbf{P}_{-1,I} = \mathbf{P}_{-1}((\mathcal{S}_{I,\alpha})_{\alpha \in \mathcal{C}(\mathcal{S}_I)}) = \mathcal{C}(\mathcal{S}_I) \end{align*}$$
$$\begin{align*}\mathbf{P}_{-1,I} = \mathbf{P}_{-1}((\mathcal{S}_{I,\alpha})_{\alpha \in \mathcal{C}(\mathcal{S}_I)}) = \mathcal{C}(\mathcal{S}_I) \end{align*}$$
with no nontrivial order relation. It is depicted in Figure 3(a). It is clear that
 $\mathbf {P}_{-1,I}$
satisfies Property 3.1 for the pair
$\mathbf {P}_{-1,I}$
satisfies Property 3.1 for the pair
 $(-1, (\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)})$
.
$(-1, (\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)})$
. -
(b) (Going from
 $m+2$
to
$m+2$
to
 $m+1$
.) Next, we consider subsets I of cardinality
$m+1$
.) Next, we consider subsets I of cardinality
 $m+1$
. For each such subset, we construct a poset
$m+1$
. For each such subset, we construct a poset
 $\mathbf {P}_{0,I}$
satisfying two conditions:
$\mathbf {P}_{0,I}$
satisfying two conditions:-
(i) For each set
 $I'$
, with
$I'$
, with
 $\mathrm {card}(I') = \mathrm {card}(I)+1$
, and
$\mathrm {card}(I') = \mathrm {card}(I)+1$
, and
 $I \subset I'$
, the poset
$I \subset I'$
, the poset
 $\mathbf {P}_{-1,I'}$
already defined is isomorphic to a subposet of
$\mathbf {P}_{-1,I'}$
already defined is isomorphic to a subposet of
 $\mathbf {P}_{0,I}$
;
$\mathbf {P}_{0,I}$
; -
(ii)
 $|\Delta (\mathbf {P}_{0,I})|$
is cohomologically
$|\Delta (\mathbf {P}_{0,I})|$
is cohomologically
 $0$
-equivalent to
$0$
-equivalent to
 $\mathcal {S}_I$
.
$\mathcal {S}_I$
.
We apply Hypothesis 3.1 to the semialgebraic set
 $\mathcal {S}_I$
as input and obtain a cover
$\mathcal {S}_I$
as input and obtain a cover
 $(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
$(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
 $\mathcal {S}_I$
by closed and bounded
$\mathcal {S}_I$
by closed and bounded
 $\ell $
-connected semialgebraic sets. We let
$\ell $
-connected semialgebraic sets. We let  $$\begin{align*}\mathbf{P}_{-1,I} = \mathbf{P}_{-1}((\mathcal{S}_{I,\alpha})_{\alpha \in \mathcal{C}(\mathcal{S}_I)}). \end{align*}$$
$$\begin{align*}\mathbf{P}_{-1,I} = \mathbf{P}_{-1}((\mathcal{S}_{I,\alpha})_{\alpha \in \mathcal{C}(\mathcal{S}_I)}). \end{align*}$$
Let
 $J_I$
be the union of the indexing set
$J_I$
be the union of the indexing set
 $\mathcal {C}(\mathcal {S}_I)$
, with the posets
$\mathcal {C}(\mathcal {S}_I)$
, with the posets
 $\mathbf {P}_{-1,I'}$
for each
$\mathbf {P}_{-1,I'}$
for each
 $I'$
with
$I'$
with
 $I \subset I', \mathrm {card}(I') = \mathrm {card}(I) + 1$
. Notice that for each
$I \subset I', \mathrm {card}(I') = \mathrm {card}(I) + 1$
. Notice that for each
 $\alpha \in J_I$
, there is an
$\alpha \in J_I$
, there is an
 $\ell $
-connected closed and bounded semialgebraic set associated to it. Denote this set by
$\ell $
-connected closed and bounded semialgebraic set associated to it. Denote this set by
 $D(\alpha )$
.For every pair
$D(\alpha )$
.For every pair
 $\alpha ,\beta \in J_I$
, we again apply Hypothesis 3.1 to obtain a cover of
$\alpha ,\beta \in J_I$
, we again apply Hypothesis 3.1 to obtain a cover of
 $D(\alpha ) \cap D(\beta )$
by
$D(\alpha ) \cap D(\beta )$
by
 $\ell $
-connected closed and bounded semialgebraic sets,
$\ell $
-connected closed and bounded semialgebraic sets,
 $(S_{I,\alpha ,\beta ,\gamma })_{\gamma \in I_{\alpha ,\beta }}$
, where
$(S_{I,\alpha ,\beta ,\gamma })_{\gamma \in I_{\alpha ,\beta }}$
, where
 $I_{\alpha ,\beta } = \mathcal {C}(D(\alpha ) \cap D(\beta ))$
. The poset
$I_{\alpha ,\beta } = \mathcal {C}(D(\alpha ) \cap D(\beta ))$
. The poset
 $\mathbf {P}_{0,I}$
is defined to be the set
$\mathbf {P}_{0,I}$
is defined to be the set
 $J_I \cup \bigcup _{\alpha ,\beta \in J_I} I_{\alpha ,\beta }$
, and the nontrivial order relations are
$J_I \cup \bigcup _{\alpha ,\beta \in J_I} I_{\alpha ,\beta }$
, and the nontrivial order relations are
 $\gamma \prec \alpha ,\beta $
for each
$\gamma \prec \alpha ,\beta $
for each
 $\gamma \in I_{\alpha ,\beta }$
. It is depicted in Figure 3(b).
$\gamma \in I_{\alpha ,\beta }$
. It is depicted in Figure 3(b). -
-
(c) (Local induction hypothesis.) We assume that we have already defined the posets
 $\mathbf {P}_{m-\mathrm {card}(I')+1,I'}$
, with
$\mathbf {P}_{m-\mathrm {card}(I')+1,I'}$
, with
 $\mathrm {card}(I')> \mathrm {card}(I)$
.
$\mathrm {card}(I')> \mathrm {card}(I)$
. -
(d) (Inductive step in general for the local induction.) We construct the poset
 $\mathbf {P}_{m-\mathrm {card}(I)+1,I}$
as follows. We apply Hypothesis 3.1 with the semialgebraic set
$\mathbf {P}_{m-\mathrm {card}(I)+1,I}$
as follows. We apply Hypothesis 3.1 with the semialgebraic set
 $\mathcal {S}_I$
as input and obtain a cover
$\mathcal {S}_I$
as input and obtain a cover
 $(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
$(\mathcal {S}_{I,\alpha })_{\alpha \in \mathcal {C}(\mathcal {S}_I)}$
of
 $\mathcal {S}_I$
by closed and bounded
$\mathcal {S}_I$
by closed and bounded
 $\ell $
-connected semialgebraic sets. Let
$\ell $
-connected semialgebraic sets. Let
 $J_I$
be the union of the indexing set
$J_I$
be the union of the indexing set
 $\mathcal {C}(\mathcal {S}_I)$
, with the posets
$\mathcal {C}(\mathcal {S}_I)$
, with the posets
 $\mathbf {P}_{m-\mathrm {card}(I')+1,I'}$
for each
$\mathbf {P}_{m-\mathrm {card}(I')+1,I'}$
for each
 $I'$
with
$I'$
with
 $I \subset I', \mathrm {card}(I') = \mathrm {card}(I) + 1$
. Notice that for each
$I \subset I', \mathrm {card}(I') = \mathrm {card}(I) + 1$
. Notice that for each
 $\alpha \in J_I$
, there is an
$\alpha \in J_I$
, there is an
 $\ell $
-connected closed and bounded semialgebraic set associated to it. Denote this set by
$\ell $
-connected closed and bounded semialgebraic set associated to it. Denote this set by
 $D(\alpha )$
.
$D(\alpha )$
.We define the poset
 $\mathbf {P}_{m - \mathrm {card}(I) + 1,I}$
using the global induction hypothesis. The global inductive hypothesis gives us that for any finite tuple of
$\mathbf {P}_{m - \mathrm {card}(I) + 1,I}$
using the global induction hypothesis. The global inductive hypothesis gives us that for any finite tuple of
 $\ell $
-connected closed and bounded semialgebraic set (in particular, the tuple of sets
$\ell $
-connected closed and bounded semialgebraic set (in particular, the tuple of sets
 $(D(\alpha ))_{\alpha \in J_I}$
) we have defined a poset
$(D(\alpha ))_{\alpha \in J_I}$
) we have defined a poset
 $\mathbf {P}_{m - \mathrm {card}(I)+1}((D(\alpha ))_{\alpha \in J_I})$
, which satisfies Property 3.1 for the pair
$\mathbf {P}_{m - \mathrm {card}(I)+1}((D(\alpha ))_{\alpha \in J_I})$
, which satisfies Property 3.1 for the pair
 $(m - \mathrm {card}(I)+1, (D(\alpha ))_{\alpha \in J_I})$
(since
$(m - \mathrm {card}(I)+1, (D(\alpha ))_{\alpha \in J_I})$
(since
 $m - \mathrm {card}(I) +1 < m$
).
$m - \mathrm {card}(I) +1 < m$
).We define
This finishes the local induction, and we have defined $$\begin{align*}\mathbf{P}_{m -\mathrm{card}(I)+1,I} = \mathbf{P}_{m - \mathrm{card}(I)+1}((D(\alpha))_{\alpha \in J_I}). \end{align*}$$
$$\begin{align*}\mathbf{P}_{m -\mathrm{card}(I)+1,I} = \mathbf{P}_{m - \mathrm{card}(I)+1}((D(\alpha))_{\alpha \in J_I}). \end{align*}$$
 $\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
, for each
$\mathbf {P}_{m - \mathrm {card}(I) +1,I}$
, for each
 $I \subset J, 2 \leq \mathrm {card}(I) \leq m+2$
.
$I \subset J, 2 \leq \mathrm {card}(I) \leq m+2$
.
Finally, we define
(3.1) $$ \begin{align} \mathbf{P}_{m}(\mathcal{S}) = J \cup \bigcup_{I \subset J, 2 \leq \mathrm{card}(I) \leq m+2} \mathbf{P}_{m -\mathrm{card}(I) +1, I}. \end{align} $$
$$ \begin{align} \mathbf{P}_{m}(\mathcal{S}) = J \cup \bigcup_{I \subset J, 2 \leq \mathrm{card}(I) \leq m+2} \mathbf{P}_{m -\mathrm{card}(I) +1, I}. \end{align} $$
The partial order in the poset
 $\mathbf {P}_{m}(\mathcal {S})$
is specified as follows. By the local induction, each of the poset
$\mathbf {P}_{m}(\mathcal {S})$
is specified as follows. By the local induction, each of the poset
 $\mathbf {P}_{m -\mathrm {card}(I) +1, I}$
comes with a partial order. We extend these orders as follows:
$\mathbf {P}_{m -\mathrm {card}(I) +1, I}$
comes with a partial order. We extend these orders as follows:-
(a) For each
 $I \subset I' \subset J$
, with
$I \subset I' \subset J$
, with
 $2 \leq \mathrm {card}(I)\leq \mathrm {card}(I') \leq m+2$
, there is a subposet of
$2 \leq \mathrm {card}(I)\leq \mathrm {card}(I') \leq m+2$
, there is a subposet of
 $\mathbf {P}_{m - \mathrm {card}(I)+1,I}$
canonically isomorphic to the poset
$\mathbf {P}_{m - \mathrm {card}(I)+1,I}$
canonically isomorphic to the poset
 $\mathbf {P}_{m - \mathrm {card}(I')+1,I'}$
. For each element
$\mathbf {P}_{m - \mathrm {card}(I')+1,I'}$
. For each element
 $\alpha $
of the former and the corresponding element
$\alpha $
of the former and the corresponding element
 $\alpha '$
of the latter, we set
$\alpha '$
of the latter, we set
 $\alpha ' \prec \alpha $
.
$\alpha ' \prec \alpha $
. -
(b) For each
 $j \in J$
and
$j \in J$
and
 $\alpha \in \mathbf {P}_{m -\mathrm {card}(I)+1,I}, j \in I$
, we set the element
$\alpha \in \mathbf {P}_{m -\mathrm {card}(I)+1,I}, j \in I$
, we set the element
 $\alpha \prec j$
.
$\alpha \prec j$
.
This ends the definition of the poset
 $\mathbf {P}_m(\mathcal {S})$
completing the global induction. Figure 3(c) depicts
$\mathbf {P}_m(\mathcal {S})$
completing the global induction. Figure 3(c) depicts
 $\mathbf {P}_{m}(\mathcal {S})$
in terms of subposets
$\mathbf {P}_{m}(\mathcal {S})$
in terms of subposets
 $\mathbf {P}_{m -\mathrm {card}(I)+1,I}$
. In Claim 3.11, we will show that the height of the poset
$\mathbf {P}_{m -\mathrm {card}(I)+1,I}$
. In Claim 3.11, we will show that the height of the poset
 $\mathbf {P}_{m}(\mathcal {S})$
is bounded by
$\mathbf {P}_{m}(\mathcal {S})$
is bounded by
 $2m+2$
.
$2m+2$
.Notice that for any chain
 $\alpha _k \prec \alpha _{k-1} \prec \ldots \prec \alpha _0$
of elements in
$\alpha _k \prec \alpha _{k-1} \prec \ldots \prec \alpha _0$
of elements in
 $\mathbf {P}_{m}(\mathcal {S})$
, we have a sequence of inclusion maps of semialgebraic sets
$\mathbf {P}_{m}(\mathcal {S})$
, we have a sequence of inclusion maps of semialgebraic sets
 $D(\alpha _k) \hookrightarrow D(\alpha _{k-1}) \hookrightarrow \ldots \hookrightarrow D(\alpha _0)$
. It is depicted in Figure 4 for a hypothetical space with four elements in the initial covering.
$D(\alpha _k) \hookrightarrow D(\alpha _{k-1}) \hookrightarrow \ldots \hookrightarrow D(\alpha _0)$
. It is depicted in Figure 4 for a hypothetical space with four elements in the initial covering.
Figure 4 Poset
 $\mathbf {P}_m(\mathcal {S})$
such that
$\mathbf {P}_m(\mathcal {S})$
such that
 $|\Delta (\mathbf {P}_m(\mathcal {S}))|$
is m-equivalent to
$|\Delta (\mathbf {P}_m(\mathcal {S}))|$
is m-equivalent to
 $ \bigcup _{j \in J} S_j$
with
$ \bigcup _{j \in J} S_j$
with
 $m=2$
,
$m=2$
,
 $J = \{1,2,3,4\}$
.
$J = \{1,2,3,4\}$
. -
The following two examples are illustrative.
Example 3.1. Let
![]() $\ell = \infty , m \geq 2$
,
$\ell = \infty , m \geq 2$
,
![]() $\mathcal {S} = (S_1,S_2)$
, where
$\mathcal {S} = (S_1,S_2)$
, where
![]() $S_1, S_2$
are the closed upper and lower hemispheres of the unit sphere in
$S_1, S_2$
are the closed upper and lower hemispheres of the unit sphere in
![]() $\mathbb {R}^3$
(see Figure 5(a)).
$\mathbb {R}^3$
(see Figure 5(a)).

Figure 5 (a) The ideal situation, (b)
![]() $D_{m,i}'(\Phi )(.)$
and (c)
$D_{m,i}'(\Phi )(.)$
and (c)
![]() $D_{m,i}(\Phi )(.)$
.
$D_{m,i}(\Phi )(.)$
.
Using equation (3.1), we get
Let
![]() $\mathcal {C}(\mathcal {S}_{\{1,2\}})$
be the cover of
$\mathcal {C}(\mathcal {S}_{\{1,2\}})$
be the cover of
![]() $\mathcal {S}_{\{1,2\}}$
by two closed semicircles
$\mathcal {S}_{\{1,2\}}$
by two closed semicircles
![]() $T_3, T_4$
, and let
$T_3, T_4$
, and let
![]() $\mathcal {T} = (T_3,T_4)$
.
$\mathcal {T} = (T_3,T_4)$
.
Note that
![]() $T_3 \cap T_4$
is a set containing two points
$T_3 \cap T_4$
is a set containing two points
![]() $W_5,W_6$
(say), and the only possibility for
$W_5,W_6$
(say), and the only possibility for
![]() $\mathcal {C}(T_3 \cap T_4)$
, is the tuple
$\mathcal {C}(T_3 \cap T_4)$
, is the tuple
![]() $\mathcal {W} = (W_5,W_6)$
. Then,
$\mathcal {W} = (W_5,W_6)$
. Then,
and the subposet
![]() $\mathbf {P}_{m - 2, \{3,4\}}$
is isomorphic to the poset
$\mathbf {P}_{m - 2, \{3,4\}}$
is isomorphic to the poset
Substituting equation (3.4) into equation (3.3) and equation (3.3) into equation (3.2), we finally obtain that the Hasse diagram of the poset
![]() $\mathbf {P}_m(\mathcal {S})$
is
$\mathbf {P}_m(\mathcal {S})$
is

The order complex of this poset is homotopy equivalent (in fact, in this case is homeomorphic) to the sphere.
Example 3.2. Now, let
![]() $\ell = m = 2$
,
$\ell = m = 2$
,
![]() $\mathcal {S} = (S_1,S_2)$
, where
$\mathcal {S} = (S_1,S_2)$
, where
![]() $S_1, S_2$
are the closed upper and lower hemispheres of the unit sphere in
$S_1, S_2$
are the closed upper and lower hemispheres of the unit sphere in
![]() $\mathbb {R}^k$
,
$\mathbb {R}^k$
,
![]() $k> 5$
. That is,
$k> 5$
. That is,
![]() $S_1$
(resp.
$S_1$
(resp.
![]() $S_2$
) is the intersection of the unit sphere in
$S_2$
) is the intersection of the unit sphere in
![]() $\mathrm {R}^k$
, with the set defined by
$\mathrm {R}^k$
, with the set defined by
![]() $X_k \geq 0$
(resp.
$X_k \geq 0$
(resp.
![]() $X_k \leq 0$
).
$X_k \leq 0$
).
Using equation (3.1), we get
Let
![]() $\mathcal {C}(\mathcal {S}_{\{1,2\}})$
be the cover of
$\mathcal {C}(\mathcal {S}_{\{1,2\}})$
be the cover of
![]() $\mathcal {S}_{\{1,2\}}$
by two closed semispheres
$\mathcal {S}_{\{1,2\}}$
by two closed semispheres
![]() $T_3, T_4$
, (i.e.,
$T_3, T_4$
, (i.e.,
![]() $T_3$
(resp.
$T_3$
(resp.
![]() $T_4$
) is the intersection of
$T_4$
) is the intersection of
![]() $\mathcal {S}_{\{1,2\}}$
with
$\mathcal {S}_{\{1,2\}}$
with
![]() $X_{k-1} \geq 0$
(resp.
$X_{k-1} \geq 0$
(resp.
![]() $X_{k-1} \leq 0$
), and let
$X_{k-1} \leq 0$
), and let
![]() $\mathcal {T} = (T_3,T_4)$
.
$\mathcal {T} = (T_3,T_4)$
.
Note that
![]() $W_5 = T_3 \cap T_4$
is a
$W_5 = T_3 \cap T_4$
is a
![]() $(k-3)$
-dimensional sphere, and since
$(k-3)$
-dimensional sphere, and since
![]() $k> 5$
,
$k> 5$
,
![]() $W_5$
is
$W_5$
is
![]() $2$
-connected and we can take
$2$
-connected and we can take
![]() $\mathcal {C}(W_5) = (W_5)$
.
$\mathcal {C}(W_5) = (W_5)$
.
with Hasse diagram

Finally we obtain that the Hasse diagram of the poset
![]() $\mathbf {P}_2(\mathcal {S})$
is
$\mathbf {P}_2(\mathcal {S})$
is

The order complex of this poset is contractible and is
![]() $2$
-equivalent (but in this case not homotopy equivalent) to
$2$
-equivalent (but in this case not homotopy equivalent) to
![]() $\mathbf {S}^{k-1}$
for
$\mathbf {S}^{k-1}$
for
![]() $k>5$
.
$k>5$
.
With the definition of the poset
![]() $\mathbf {P}_m(\mathcal {S})$
, it is possible to prove the following theorem. We do not include a proof of this theorem since it is subsumed by Theorem 2′
.
$\mathbf {P}_m(\mathcal {S})$
, it is possible to prove the following theorem. We do not include a proof of this theorem since it is subsumed by Theorem 2′
.
Theorem. With the same notation as in the Definition of
![]() $\mathbf {P}_m(\mathcal {S})$
defined above:
$\mathbf {P}_m(\mathcal {S})$
defined above:
 $$ \begin{align*} |\Delta(\mathbf{P}_{m}(\mathcal{S}))| {\sim}_{m-1} \bigcup_{j \in J} S_j. \end{align*} $$
$$ \begin{align*} |\Delta(\mathbf{P}_{m}(\mathcal{S}))| {\sim}_{m-1} \bigcup_{j \in J} S_j. \end{align*} $$
More generally, we have the diagrammatic homological
![]() $(m-1)$
-equivalence
$(m-1)$
-equivalence
where
![]() $\mathcal {S}|_{J'} = (S_j)_{j \in J'}$
.
$\mathcal {S}|_{J'} = (S_j)_{j \in J'}$
.
We now return to the precise definition of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
that we are going to the use.
$\mathbf {P}_{m,i}(\Phi )$
that we are going to the use.
3.3.2 Precise definition of
 $\mathbf {P}_{m,i}(\Phi )$
$\mathbf {P}_{m,i}(\Phi )$
We begin with a few useful notation that we will use in the construction.
Notation 3.6. We will denote by
![]() $\mathcal {F}_{\mathrm {R},k}$
the set of quantifier-free formulas with coefficients in
$\mathcal {F}_{\mathrm {R},k}$
the set of quantifier-free formulas with coefficients in
![]() $\mathrm {R}$
and k variables, whose realizations are closed in
$\mathrm {R}$
and k variables, whose realizations are closed in
![]() $\mathrm {R}^k$
.
$\mathrm {R}^k$
.
We also use the following convenient notation.
Notation 3.7 (The relation
 $\subset _{\leq n}$
).
$\subset _{\leq n}$
).
For any
![]() $n \in \mathbb {Z}_{\geq 0}$
and sets
$n \in \mathbb {Z}_{\geq 0}$
and sets
![]() $A,B$
, we will write
$A,B$
, we will write
![]() $A \subset _{\leq n} B$
to mean
$A \subset _{\leq n} B$
to mean
![]() $A \subset B$
and
$A \subset B$
and
![]() $0 < \mathrm {card}(A) \leq n$
.
$0 < \mathrm {card}(A) \leq n$
.
We are now in a position to define a poset associated to a given finite tuple of formulas that will play the key technical role in the rest of the paper.
We first fix the following.
-
A. Let
 $\mathrm {R} = \mathrm {R}_0 \subset \mathrm {R}_1 \subset \mathrm {R}_2 \subset \cdots $
be a sequence of extensions of real closed fields.
$\mathrm {R} = \mathrm {R}_0 \subset \mathrm {R}_1 \subset \mathrm {R}_2 \subset \cdots $
be a sequence of extensions of real closed fields. -
B. We also fix two sequences of functions,
 $$\begin{align*}\mathcal{I}_{i,k}: \mathcal{F}_{\mathrm{R}_i,k} \rightarrow \mathbb{Z}_{\geq -1}, \end{align*}$$
$$\begin{align*}\mathcal{I}_{i,k}: \mathcal{F}_{\mathrm{R}_i,k} \rightarrow \mathbb{Z}_{\geq -1}, \end{align*}$$
and
 $$\begin{align*}\mathcal{C}_{i,k}: \mathcal{F}_{\mathrm{R}_i,k} \rightarrow \bigcup_{p \geq 0}(\mathcal{F}_{\mathrm{R}_{i+1},k})^{[p]}. \end{align*}$$
$$\begin{align*}\mathcal{C}_{i,k}: \mathcal{F}_{\mathrm{R}_i,k} \rightarrow \bigcup_{p \geq 0}(\mathcal{F}_{\mathrm{R}_{i+1},k})^{[p]}. \end{align*}$$
Remark 3.4. The definition of the poset
![]() $\mathbf {P}_{m,i}(\cdot )$
given below does not depend on any specific properties of the functions
$\mathbf {P}_{m,i}(\cdot )$
given below does not depend on any specific properties of the functions
![]() $\mathcal {I}_{i,k}(\cdot )$
and
$\mathcal {I}_{i,k}(\cdot )$
and
![]() $\mathcal {C}_{i,k}(\cdot )$
. Later, we will prove key topological properties of
$\mathcal {C}_{i,k}(\cdot )$
. Later, we will prove key topological properties of
![]() $\mathbf {P}_{m,i}(\cdot )$
(see Theorems 2 and 2′
below) under certain assumptions on
$\mathbf {P}_{m,i}(\cdot )$
(see Theorems 2 and 2′
below) under certain assumptions on
![]() $\mathcal {I}_{i,k}(\cdot )$
and
$\mathcal {I}_{i,k}(\cdot )$
and
![]() $\mathcal {C}_{i,k}(\cdot )$
(see Properties 3.2 and 3.2′
below).
$\mathcal {C}_{i,k}(\cdot )$
(see Properties 3.2 and 3.2′
below).
For each
![]() $i \geq 0$
and
$i \geq 0$
and
![]() $-1 \leq m \leq k$
, a nonempty finite set J, and
$-1 \leq m \leq k$
, a nonempty finite set J, and
![]() $\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
, we define a poset
$\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
, we define a poset
![]() $(\mathbf {P}_{m,i}(\Phi ), \prec )$
.
$(\mathbf {P}_{m,i}(\Phi ), \prec )$
.
We first need an auxilliary definition which will be used in the definition of the underlying set,
![]() $\mathbf {P}_{m,i}(\Phi )$
, of the poset
$\mathbf {P}_{m,i}(\Phi )$
, of the poset
![]() $(\mathbf {P}_{m,i}(\Phi ), \prec )$
.
$(\mathbf {P}_{m,i}(\Phi ), \prec )$
.
Definition 3.2. Let J be a nonempty finite set, and
![]() $\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
. We first define for each subset
$\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
. We first define for each subset
![]() $I \subset _{\leq m+2} J$
, a set
$I \subset _{\leq m+2} J$
, a set
![]() $J_{m,i,I,\Phi }$
, and an element
$J_{m,i,I,\Phi }$
, and an element
![]() $\Phi _{m,i,I,J} \in (\mathcal {F}_{\mathrm {R}_{i+1},k})^{J_{m,i,I,\Phi }}$
(using downward induction on
$\Phi _{m,i,I,J} \in (\mathcal {F}_{\mathrm {R}_{i+1},k})^{J_{m,i,I,\Phi }}$
(using downward induction on
![]() $\mathrm {card}(I)$
).
$\mathrm {card}(I)$
).
Base case (
![]() $\mathrm {card}(I) = m+2$
): In this case, we define
$\mathrm {card}(I) = m+2$
): In this case, we define
 $$ \begin{align} J_{m,i, I,\Phi} = \{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j))], \end{align} $$
$$ \begin{align} J_{m,i, I,\Phi} = \{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j))], \end{align} $$
and for
![]() $(I,p) \in J_{m,i,I,\Phi }$
,
$(I,p) \in J_{m,i,I,\Phi }$
,
 $$\begin{align*}\Phi_{m,i, I,J}((I,p)) = \mathcal{C}_{i,k}( \bigwedge_{j \in I} \Phi(j))(p). \end{align*}$$
$$\begin{align*}\Phi_{m,i, I,J}((I,p)) = \mathcal{C}_{i,k}( \bigwedge_{j \in I} \Phi(j))(p). \end{align*}$$
Inductive step: Suppose we have defined
![]() $J_{m,i,I',\Phi }$
and
$J_{m,i,I',\Phi }$
and
![]() $\Phi _{m,i, I',J}$
for all
$\Phi _{m,i, I',J}$
for all
![]() $I'$
with
$I'$
with
![]() $\mathrm {card}(I') = \mathrm {card}(I) +1$
. We define
$\mathrm {card}(I') = \mathrm {card}(I) +1$
. We define
 $$ \begin{align} J_{m,i,I,\Phi} = \left(\{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j)] \right) \cup \bigcup_{I \subset I' \subset J, \mathrm{card}(I') = \mathrm{card}(I)+1} J_{m,i,I',\Phi}, \end{align} $$
$$ \begin{align} J_{m,i,I,\Phi} = \left(\{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j)] \right) \cup \bigcup_{I \subset I' \subset J, \mathrm{card}(I') = \mathrm{card}(I)+1} J_{m,i,I',\Phi}, \end{align} $$
and
 $$ \begin{align*} \Phi_{m,i,I,J}(\alpha) &= \mathcal{C}_{i,k}( \bigwedge_{j \in I} \Phi(j))(p), \mbox{ if } \alpha =(I,p) \in \{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j))], \\ &=\Phi_{m,i,I',J}(\alpha), \mbox{ if } \alpha \in J_{m,i,I',\Phi} \text{ for some } I' \supset I, \text{with} \\ & \hspace{2.1cm} \mathrm{card}(I') = \mathrm{card}(I)+1. \end{align*} $$
$$ \begin{align*} \Phi_{m,i,I,J}(\alpha) &= \mathcal{C}_{i,k}( \bigwedge_{j \in I} \Phi(j))(p), \mbox{ if } \alpha =(I,p) \in \{I\} \times [ \mathcal{I}_{i,k}( \bigwedge_{j \in I} \Phi(j))], \\ &=\Phi_{m,i,I',J}(\alpha), \mbox{ if } \alpha \in J_{m,i,I',\Phi} \text{ for some } I' \supset I, \text{with} \\ & \hspace{2.1cm} \mathrm{card}(I') = \mathrm{card}(I)+1. \end{align*} $$
The following properties of
![]() $J_{m,i,I,\Phi }$
and
$J_{m,i,I,\Phi }$
and
![]() $\Phi _{m,i,I,J}$
are obvious from the above definition. Using the same notation as in Definition 3.2:
$\Phi _{m,i,I,J}$
are obvious from the above definition. Using the same notation as in Definition 3.2:
Lemma 3.2.
-
(a)
 $\mathrm {card}(J_{m,i,I,\Phi }) < \infty $
for each
$\mathrm {card}(J_{m,i,I,\Phi }) < \infty $
for each
 $I \subset _{\leq m+2} J$
;
$I \subset _{\leq m+2} J$
; -
(b) For
 $I,I' \subset J$
with
$I,I' \subset J$
with
 $\mathrm {card}(I \cup I') \leq m+2$
,
$\mathrm {card}(I \cup I') \leq m+2$
,  $$\begin{align*}J_{m,i, I \cup I',\Phi}\subset J_{m,i,I,\Phi}\cap J_{m,i,I',\Phi}. \end{align*}$$
$$\begin{align*}J_{m,i, I \cup I',\Phi}\subset J_{m,i,I,\Phi}\cap J_{m,i,I',\Phi}. \end{align*}$$
-
(c) If
 $I'\subset I \subset _{\leq m+2} J \subset J'$
, then
$I'\subset I \subset _{\leq m+2} J \subset J'$
, then
 $J_{m,i,I,\Phi } \subset J^{\prime }_{m,i,I',\Phi }$
, and for
$J_{m,i,I,\Phi } \subset J^{\prime }_{m,i,I',\Phi }$
, and for
 $\alpha \in J_{m,i,I,\Phi }$
,
$\alpha \in J_{m,i,I,\Phi }$
,
 $\Phi _{m,i,I,J}(\alpha ) = \Phi _{m,i,I',J'}(\alpha )$
.
$\Phi _{m,i,I,J}(\alpha ) = \Phi _{m,i,I',J'}(\alpha )$
.
Proof. Follows directly from Definition 3.2.
We now define the set
![]() $\mathbf {P}_{m,i}(\Phi )$
.
$\mathbf {P}_{m,i}(\Phi )$
.
Definition 3.3 (The underlying set of the poset
 $(\mathbf {P}_{m,i}(\Phi ), \prec )$
).
$(\mathbf {P}_{m,i}(\Phi ), \prec )$
).
We define the set
![]() $\mathbf {P}_{m,i}(\Phi )$
using induction on m.
$\mathbf {P}_{m,i}(\Phi )$
using induction on m.
Base case (
![]() $m=-1$
): For each finite set J and
$m=-1$
): For each finite set J and
![]() $\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
, we define
$\Phi \in (\mathcal {F}_{\mathrm {R}_i,k})^J$
, we define
 $$\begin{align*}\mathbf{P}_{-1,i}(\Phi) = \bigcup_{j \in J} \{\{j\}\} \times \{\emptyset \}. \end{align*}$$
$$\begin{align*}\mathbf{P}_{-1,i}(\Phi) = \bigcup_{j \in J} \{\{j\}\} \times \{\emptyset \}. \end{align*}$$
Inductive step: Suppose we have defined the sets
![]() $(\mathbf {P}_{m',i'}(\Phi '),\prec )$
for all
$(\mathbf {P}_{m',i'}(\Phi '),\prec )$
for all
![]() $m'$
with
$m'$
with
![]() $-1 \leq m' < m$
,
$-1 \leq m' < m$
,
![]() $i' \geq 0$
, for all nonempty finite sets
$i' \geq 0$
, for all nonempty finite sets
![]() $J'$
and all
$J'$
and all
![]() $\Phi ' \in (\mathcal {F}_{\mathrm {R}_{i'},k})^{J'}$
.
$\Phi ' \in (\mathcal {F}_{\mathrm {R}_{i'},k})^{J'}$
.
We complete the inductive step by defining:
 $$ \begin{align} \mathbf{P}_{m,i}(\Phi) = \bigcup_{j \in J} \{\{j\}\} \times \{\emptyset\} \cup \bigcup_{I \subset J, 1 < \mathrm{card}(I) \leq m+2} \{I\} \times \mathbf{P}_{m -\mathrm{card}(I) +1,i+1}(\Phi_{m,i,I,J}). \end{align} $$
$$ \begin{align} \mathbf{P}_{m,i}(\Phi) = \bigcup_{j \in J} \{\{j\}\} \times \{\emptyset\} \cup \bigcup_{I \subset J, 1 < \mathrm{card}(I) \leq m+2} \{I\} \times \mathbf{P}_{m -\mathrm{card}(I) +1,i+1}(\Phi_{m,i,I,J}). \end{align} $$
We now specify the partial order on
![]() $\mathbf {P}_{m,i}(\Phi )$
. For this, it will be useful to have the following alternative characterization of the elements of the poset
$\mathbf {P}_{m,i}(\Phi )$
. For this, it will be useful to have the following alternative characterization of the elements of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
as tuples of sets. This characterization follows simply by unravelling the inductive definition of the set
$\mathbf {P}_{m,i}(\Phi )$
as tuples of sets. This characterization follows simply by unravelling the inductive definition of the set
![]() $\mathbf {P}_{m,i}(\Phi )$
given above.
$\mathbf {P}_{m,i}(\Phi )$
given above.
3.3.3 Characterization of the elements of the poset
 $\mathbf {P}_{m,i}(\Phi )$
as tuples of sets
$\mathbf {P}_{m,i}(\Phi )$
as tuples of sets
The elements of
![]() $\mathbf {P}_{m,i}(\Phi )$
are all finite tuples of sets (of varying lengths)
$\mathbf {P}_{m,i}(\Phi )$
are all finite tuples of sets (of varying lengths)
satisfying the following conditions.
-
1.
 $I_0$
is a subset of
$I_0$
is a subset of
 $J_0= J$
,
$J_0= J$
,
 $\mathrm {card}(I_0) = 1$
if
$\mathrm {card}(I_0) = 1$
if
 $r = 0$
and
$r = 0$
and
 $2 \leq \mathrm {card}(I_0) \leq m+2$
otherwise.
$2 \leq \mathrm {card}(I_0) \leq m+2$
otherwise. -
2.
 $I_1$
is a subset of
$I_1$
is a subset of
 $J_1 = \left (J_0\right )_{m_0,i_0,I_0,\Phi _0}$
(see equation (3.6), Definition 3.3) with
$J_1 = \left (J_0\right )_{m_0,i_0,I_0,\Phi _0}$
(see equation (3.6), Definition 3.3) with  $$ \begin{align*} m_0 &= m,\\ i_0 &= i, \\ \Phi_0 &= \Phi, \end{align*} $$
$$ \begin{align*} m_0 &= m,\\ i_0 &= i, \\ \Phi_0 &= \Phi, \end{align*} $$
and
 $$\begin{align*}2 \leq \mathrm{card}(I_1) \leq (m_0 - \mathrm{card}(I_0) + 1) +2. \end{align*}$$
$$\begin{align*}2 \leq \mathrm{card}(I_1) \leq (m_0 - \mathrm{card}(I_0) + 1) +2. \end{align*}$$
-
3.
 $I_2$
is a subset of
$I_2$
is a subset of
 $J_2 = \left (J_1 \right )_{m_1,i_1,I_1, \Phi _{1}}$
, where
$J_2 = \left (J_1 \right )_{m_1,i_1,I_1, \Phi _{1}}$
, where  $$ \begin{align*} m_1 &= m_0 - \mathrm{card}(I_0) + 1,\\ i_1 &= i_0+1, \\ \Phi_{1} &= (\Phi_0)_{m_0,i_0,I_0, J_0}, \end{align*} $$
$$ \begin{align*} m_1 &= m_0 - \mathrm{card}(I_0) + 1,\\ i_1 &= i_0+1, \\ \Phi_{1} &= (\Phi_0)_{m_0,i_0,I_0, J_0}, \end{align*} $$
and
 $$\begin{align*}2 \leq \mathrm{card}(I_2) \leq (m_1- \mathrm{card}(I_1) +1) + 2. \end{align*}$$
$$\begin{align*}2 \leq \mathrm{card}(I_2) \leq (m_1- \mathrm{card}(I_1) +1) + 2. \end{align*}$$
-
4. Continuing in the above fashion,
(3.8) $$ \begin{align} I_{r-1} \subset J_{r-1} = \left(J_{r-2} \right)_{m_{r-2},i_{r-2}, I_{r-2}, \Phi_{r-2}}, \end{align} $$
$$ \begin{align} I_{r-1} \subset J_{r-1} = \left(J_{r-2} \right)_{m_{r-2},i_{r-2}, I_{r-2}, \Phi_{r-2}}, \end{align} $$
where
 $$ \begin{align*} m_{r-2} &= m_{r-3} - \mathrm{card}(I_{r-3}) + 1, \\ i_{r-2} &= i_{r-3}+1, \\ \Phi_{r-2} &= (\Phi_{r-3})_{m_{r-3},i_{r-3},I_{r-3}, J_{r-3}}, \end{align*} $$
$$ \begin{align*} m_{r-2} &= m_{r-3} - \mathrm{card}(I_{r-3}) + 1, \\ i_{r-2} &= i_{r-3}+1, \\ \Phi_{r-2} &= (\Phi_{r-3})_{m_{r-3},i_{r-3},I_{r-3}, J_{r-3}}, \end{align*} $$
and
(3.9) $$ \begin{align} 2 \leq \mathrm{card}(I_{r-1}) \leq m_{r-2} +2 = (m +r -1 - \sum_{j=0}^{r-2}\mathrm{card}(I_j)) + 2. \end{align} $$
$$ \begin{align} 2 \leq \mathrm{card}(I_{r-1}) \leq m_{r-2} +2 = (m +r -1 - \sum_{j=0}^{r-2}\mathrm{card}(I_j)) + 2. \end{align} $$
-
5. Finally,
 $$\begin{align*}I_{r} \subset J_{r} =\left(J_{r-1} \right)_{m_{r-1},i_{r-1},I_{r-1}, \Phi_{r -1}}, \end{align*}$$
$$\begin{align*}I_{r} \subset J_{r} =\left(J_{r-1} \right)_{m_{r-1},i_{r-1},I_{r-1}, \Phi_{r -1}}, \end{align*}$$
where
 $$\begin{align*}\Phi_{r -1} = (\Phi_{r -2})_{m_{r-2},i_{r-2},I_{r -2},J_{r-2}}, \end{align*}$$
$$\begin{align*}\Phi_{r -1} = (\Phi_{r -2})_{m_{r-2},i_{r-2},I_{r -2},J_{r-2}}, \end{align*}$$
and
 $$\begin{align*}\mathrm{card}(I_r) = 1. \end{align*}$$
$$\begin{align*}\mathrm{card}(I_r) = 1. \end{align*}$$
(We show later (see Claim 3.8) that for tuples
![]() $(I_0,\ldots ,I_r,\emptyset )$
satisfying the above conditions,
$(I_0,\ldots ,I_r,\emptyset )$
satisfying the above conditions,
![]() $r \leq m+1$
.)
$r \leq m+1$
.)
Definition 3.4 (Partial order on
 $\mathbf {P}_{m,i}(\Phi )$
).
$\mathbf {P}_{m,i}(\Phi )$
).
The partial order
![]() $\prec $
on
$\prec $
on
![]() $\mathbf {P}_{m,i}(\Phi )$
is defined as follows.
$\mathbf {P}_{m,i}(\Phi )$
is defined as follows.
For
![]() $\alpha = (I^{\alpha }_0,\ldots ,I^{\alpha }_{r_{\alpha }},\emptyset ),\beta = (I^{\beta }_0,\ldots ,I^{\beta }_{r_{\beta }},\emptyset ) \in \mathbf {P}_{m,i}(\Phi ),$
$\alpha = (I^{\alpha }_0,\ldots ,I^{\alpha }_{r_{\alpha }},\emptyset ),\beta = (I^{\beta }_0,\ldots ,I^{\beta }_{r_{\beta }},\emptyset ) \in \mathbf {P}_{m,i}(\Phi ),$
3.4 Main properties of the poset
 $\mathbf {P}_{m,i}(\Phi )$
$\mathbf {P}_{m,i}(\Phi )$
We will now state and prove the important properties of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
that motivates its definition.
$\mathbf {P}_{m,i}(\Phi )$
that motivates its definition.
Lemma 3.3. For each
![]() $J' \subset J" \subset J$
, and
$J' \subset J" \subset J$
, and
![]() $-1 \leq m' \leq m" \leq m$
, we have a poset inclusion,
$-1 \leq m' \leq m" \leq m$
, we have a poset inclusion,
We now state a lemma which will be useful later, that states a key property of the partial order relation in
![]() $\mathbf {P}_{m,i}(\Phi )$
. Using the same notation as in Definition 3.3:
$\mathbf {P}_{m,i}(\Phi )$
. Using the same notation as in Definition 3.3:
Lemma 3.4. Suppose that
![]() $I' \subset I \subset J$
.
$I' \subset I \subset J$
.
-
(a) The poset
 $ \mathbf {P}_{m -\mathrm {card}(I) +1,i+1}(\Phi _{m,i,I,J}) $
is a subposet of
$ \mathbf {P}_{m -\mathrm {card}(I) +1,i+1}(\Phi _{m,i,I,J}) $
is a subposet of
 $ \mathbf {P}_{m -\mathrm {card}(I') +1,i+1}(\Phi _{m,i,I',J}) $
.
$ \mathbf {P}_{m -\mathrm {card}(I') +1,i+1}(\Phi _{m,i,I',J}) $
. -
(b) For each
 $\alpha ,\alpha ' \in \mathbf {P}_{m -\mathrm {card}(I) +1,i+1}(\Phi _{m,i,I,J})$
,
$\alpha ,\alpha ' \in \mathbf {P}_{m -\mathrm {card}(I) +1,i+1}(\Phi _{m,i,I,J})$
,  $$\begin{align*}\alpha \prec_{\mathbf{P}_{m -\mathrm{card}(I) +1,i+1}(\Phi_{m,i,I,J})} \alpha' \Leftrightarrow (I,\alpha) \prec_{\mathbf{P}_{m,i}(\Phi)} (I',\alpha'). \end{align*}$$
$$\begin{align*}\alpha \prec_{\mathbf{P}_{m -\mathrm{card}(I) +1,i+1}(\Phi_{m,i,I,J})} \alpha' \Leftrightarrow (I,\alpha) \prec_{\mathbf{P}_{m,i}(\Phi)} (I',\alpha'). \end{align*}$$
Proof. Part (a) follows from the fact that
![]() $J_{m,i,I,\Phi } \subset J_{m,i,I',\Phi }$
,
$J_{m,i,I,\Phi } \subset J_{m,i,I',\Phi }$
,
![]() $m -\mathrm {card}(I) +1 \leq m -\mathrm {card}(I') +1$
and Lemma 3.3.
$m -\mathrm {card}(I) +1 \leq m -\mathrm {card}(I') +1$
and Lemma 3.3.
Part (b) follows immediately from the definition of the partial order on
![]() $\mathbf {P}_{m,i}(\Phi )$
(see Definition 3.4).
$\mathbf {P}_{m,i}(\Phi )$
(see Definition 3.4).
Let
![]() $\mathrm {R}$
be a real closed field and
$\mathrm {R}$
be a real closed field and
![]() $R \in \mathrm {R}, R> 0$
. We say that the tuple
$R \in \mathrm {R}, R> 0$
. We say that the tuple
satisfies the homological
![]() $\ell $
-connectivity property over
$\ell $
-connectivity property over
![]() $\mathrm {R}$
if it satisfies the following conditions.
$\mathrm {R}$
if it satisfies the following conditions.
Property 3.2.
-
1. For each
 $i \geq 0$
,
$i \geq 0$
,
 $\mathrm {R}_i = \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_i{\rangle }$
, where for
$\mathrm {R}_i = \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_i{\rangle }$
, where for
 $j=1,\ldots ,i$
,
$j=1,\ldots ,i$
,
 $\bar {{\varepsilon }}_j$
denotes the sequence
$\bar {{\varepsilon }}_j$
denotes the sequence
 ${\varepsilon }_{j,1},{\varepsilon }_{j,2},\ldots $
.
${\varepsilon }_{j,1},{\varepsilon }_{j,2},\ldots $
. -
2. For each
 $\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
:
$\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
:-
(a) If
 ${\mathcal R}(\phi , \overline {B_k(0,R)})$
is empty, then
${\mathcal R}(\phi , \overline {B_k(0,R)})$
is empty, then
 $\mathcal {I}_{i,k}(\phi ) = -1$
.
$\mathcal {I}_{i,k}(\phi ) = -1$
. -
(b)
 $$\begin{align*}\left(\bigcup_{j \in [\mathcal{I}_{i,k}(\phi)]} {\mathcal R}(\mathcal{C}_{i,k}(\phi)(j), \overline{B_k(0,R)})) \right) \searrow \left({\mathcal R}(\phi, \overline{B_k(0,R)})\right) \end{align*}$$
$$\begin{align*}\left(\bigcup_{j \in [\mathcal{I}_{i,k}(\phi)]} {\mathcal R}(\mathcal{C}_{i,k}(\phi)(j), \overline{B_k(0,R)})) \right) \searrow \left({\mathcal R}(\phi, \overline{B_k(0,R)})\right) \end{align*}$$
(see Notation 3.4). Notice that, in the case
 ${\mathcal R}(\phi , \overline {B_k(0,R)})$
is empty,
${\mathcal R}(\phi , \overline {B_k(0,R)})$
is empty,
 $\mathcal {I}_{i,k}(\phi )= -1$
, hence
$\mathcal {I}_{i,k}(\phi )= -1$
, hence
 $[\mathcal {I}_{i,k}(\phi )] = \emptyset $
, and so
$[\mathcal {I}_{i,k}(\phi )] = \emptyset $
, and so
 $\bigcup _{j \in [\mathcal {I}_{i,k}(\phi )]} {\mathcal R}(\mathcal {C}_{i,k}(\phi )(j),\overline {B_k(0,R)})$
is an empty union and is thus empty as well.
$\bigcup _{j \in [\mathcal {I}_{i,k}(\phi )]} {\mathcal R}(\mathcal {C}_{i,k}(\phi )(j),\overline {B_k(0,R)})$
is an empty union and is thus empty as well. -
(a) For
 $j \in [\mathcal {I}_{i,k}(\phi )]$
,
$j \in [\mathcal {I}_{i,k}(\phi )]$
,
 ${\mathcal R}(\mathcal {C}_{i,k}(\phi )(j), \overline {B_k(0,R)})) $
is homologically
${\mathcal R}(\mathcal {C}_{i,k}(\phi )(j), \overline {B_k(0,R)})) $
is homologically
 $\ell $
-connected.
$\ell $
-connected.
-
Notation 3.8. Let
![]() $\phi $
be a quantifier-free formula with coefficients in
$\phi $
be a quantifier-free formula with coefficients in
![]() $\mathrm {R}[\bar {\varepsilon }]$
. Then
$\mathrm {R}[\bar {\varepsilon }]$
. Then
![]() $\phi $
is defined over
$\phi $
is defined over
![]() $\mathrm {R}[\bar {\varepsilon }_1',\bar {\varepsilon }^{\prime }_2,\ldots ,\bar {\varepsilon }_i']$
, where
$\mathrm {R}[\bar {\varepsilon }_1',\bar {\varepsilon }^{\prime }_2,\ldots ,\bar {\varepsilon }_i']$
, where
![]() $\bar {\varepsilon }_j'$
is a finite subsequence of the sequence
$\bar {\varepsilon }_j'$
is a finite subsequence of the sequence
![]() $\bar {\varepsilon }_j$
. For
$\bar {\varepsilon }_j$
. For
![]() $\bar {t} = (\bar {t}_1,\ldots , \bar {t}_i)$
, where for
$\bar {t} = (\bar {t}_1,\ldots , \bar {t}_i)$
, where for
![]() $1 \leq j \leq i$
,
$1 \leq j \leq i$
,
![]() $\bar {t}_j$
is a tuple of elements of
$\bar {t}_j$
is a tuple of elements of
![]() $\mathbb {R}$
of the same length as
$\mathbb {R}$
of the same length as
![]() $\bar {\varepsilon }_j'$
, we will denote by
$\bar {\varepsilon }_j'$
, we will denote by
![]() $\phi _{\bar {t}}$
the formula defined over
$\phi _{\bar {t}}$
the formula defined over
![]() $\mathbb {R}$
obtained by replacing
$\mathbb {R}$
obtained by replacing
![]() $\bar {\varepsilon }^{\prime }_j$
by
$\bar {\varepsilon }^{\prime }_j$
by
![]() $\bar {t}_j$
in the formula
$\bar {t}_j$
in the formula
![]() $\phi $
.
$\phi $
.
For any finite sequence
![]() $\bar {t} = (t_1,\ldots ,t_N)$
, by the phrase ‘for all sufficiently small and positive
$\bar {t} = (t_1,\ldots ,t_N)$
, by the phrase ‘for all sufficiently small and positive
![]() $\bar {t}$
’we will mean‘for all sufficiently small
$\bar {t}$
’we will mean‘for all sufficiently small
![]() $t_1 \in \mathbb {R}_{> 0}$
, and having chosen
$t_1 \in \mathbb {R}_{> 0}$
, and having chosen
![]() $t_1$
, for all sufficiently small
$t_1$
, for all sufficiently small
![]() $t_2 \in \mathbb {R}_{> 0}$
, …’.
$t_2 \in \mathbb {R}_{> 0}$
, …’.
We will say that
satisfies the
![]() $\ell $
-connectivity property over
$\ell $
-connectivity property over
![]() $\mathrm {R} = \mathbb {R}$
if it satisfies the following conditions.
$\mathrm {R} = \mathbb {R}$
if it satisfies the following conditions.
Property 3.2′.
-
1.
 $\mathrm {R}_0 = \mathbb {R}$
and for each,
$\mathrm {R}_0 = \mathbb {R}$
and for each,
 $i> 0$
,
$i> 0$
,
 $\mathrm {R}_i = \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_i{\rangle }$
.
$\mathrm {R}_i = \mathrm {R}{\langle }\bar {\varepsilon }_1,\ldots ,\bar {\varepsilon }_i{\rangle }$
. -
2. For each
 $\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
:
$\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
:-
(a) If
 ${\mathcal R}(\phi ,\overline {B_k(0,R)})$
is empty, then
${\mathcal R}(\phi ,\overline {B_k(0,R)})$
is empty, then
 $\mathcal {I}_{i,k}(\phi ) = -1$
.
$\mathcal {I}_{i,k}(\phi ) = -1$
. -
(b)
 $$\begin{align*}\left(\bigcup_{j \in [\mathcal{I}_{i,k}(\phi)]} {\mathcal R}(\mathcal{C}_{i,k}(\phi)(j), \overline{B_k(0,R)})) \right) \searrow \left({\mathcal R}(\phi, \overline{B_k(0,R)})\right). \end{align*}$$
$$\begin{align*}\left(\bigcup_{j \in [\mathcal{I}_{i,k}(\phi)]} {\mathcal R}(\mathcal{C}_{i,k}(\phi)(j), \overline{B_k(0,R)})) \right) \searrow \left({\mathcal R}(\phi, \overline{B_k(0,R)})\right). \end{align*}$$
-
(c) For
 $j \in [\mathcal {I}_{i,k}(\phi )]$
, and all sufficiently small and positive
$j \in [\mathcal {I}_{i,k}(\phi )]$
, and all sufficiently small and positive
 $\bar {t}$
,
$\bar {t}$
,  $$\begin{align*}{\mathcal R}(\mathcal{C}_{i,k}(\phi)(j)_{\bar{t}}, \overline{B_k(0,R)})) \end{align*}$$
$$\begin{align*}{\mathcal R}(\mathcal{C}_{i,k}(\phi)(j)_{\bar{t}}, \overline{B_k(0,R)})) \end{align*}$$
is
 $\ell $
-connected.
$\ell $
-connected.
-
The following two theorems give the important topological properties of the posets defined above that will be useful for us.
Theorem 2. Suppose that the tuple
satisfies the homological
![]() $\ell $
-connectivity property over
$\ell $
-connectivity property over
![]() $\mathrm {R}$
(see Property 3.2). Then, for
$\mathrm {R}$
(see Property 3.2). Then, for
![]() $-1 \leq m \leq \ell $
, every finite set J, and
$-1 \leq m \leq \ell $
, every finite set J, and
![]() $\Phi \in (\mathcal {F}_{k,\mathrm {R}_i})^J$
such that for each
$\Phi \in (\mathcal {F}_{k,\mathrm {R}_i})^J$
such that for each
![]() $j \in J$
,
$j \in J$
,
![]() ${\mathcal R}(\Phi (j),\overline {B_k(0,R)})$
is homologically
${\mathcal R}(\Phi (j),\overline {B_k(0,R)})$
is homologically
![]() $\ell $
-connected,
$\ell $
-connected,
More generally, we have the diagrammatic homological
![]() $(m-1)$
-equivalence
$(m-1)$
-equivalence
In the case
![]() $\mathrm {R} = \mathbb {R}$
, we can derive a stronger conclusion from a stronger assumption.
$\mathrm {R} = \mathbb {R}$
, we can derive a stronger conclusion from a stronger assumption.
Theorem 2′. Suppose that
satisfies the
![]() $\ell $
-connectivity property over
$\ell $
-connectivity property over
![]() $\mathrm {R} = \mathbb {R}$
(cf. Property 3.2′
).
$\mathrm {R} = \mathbb {R}$
(cf. Property 3.2′
).
Then, for
![]() $-1 \leq m \leq \ell $
, each finite set J, and
$-1 \leq m \leq \ell $
, each finite set J, and
![]() $\Phi \in (\mathcal {F}_{\mathrm {R},k})^J$
such that for each
$\Phi \in (\mathcal {F}_{\mathrm {R},k})^J$
such that for each
![]() $j \in J$
,
$j \in J$
,
![]() ${\mathcal R}(\Phi (j),\overline {B_k(0,R)})$
is
${\mathcal R}(\Phi (j),\overline {B_k(0,R)})$
is
![]() $\ell $
-connected,
$\ell $
-connected,
More generally, we have the diagrammatic
![]() $(m-1)$
-equivalence:
$(m-1)$
-equivalence:
3.5 Example of the sphere
 $\mathbf {S}^2$
in
$\mathbf {S}^2$
in
 $\mathrm {R}^3$
$\mathrm {R}^3$
In order to illustrate the main ideas behind the definition of the poset,
![]() $\mathbf {P}_{m,i}(\Phi )$
, defined above we discuss a very simple example. Starting from a cover of the two-dimensional unit sphere in
$\mathbf {P}_{m,i}(\Phi )$
, defined above we discuss a very simple example. Starting from a cover of the two-dimensional unit sphere in
![]() $\mathbb {R}^3$
by two closed hemispheres, we show how we construct the associated poset. We will assume that there is an algorithm available as a black box which given any closed formula
$\mathbb {R}^3$
by two closed hemispheres, we show how we construct the associated poset. We will assume that there is an algorithm available as a black box which given any closed formula
![]() $\phi $
such that
$\phi $
such that
![]() ${\mathcal R}(\phi )$
is bounded, produces a tuple of quantifier-free closed formulas as output such that
${\mathcal R}(\phi )$
is bounded, produces a tuple of quantifier-free closed formulas as output such that
-
(a) the realization of each formula in the tuple is contractible;
-
(b) the union of the realizations is a semialgebraic set infinitesimally larger than
 ${\mathcal R}(\phi ) $
, and such that
${\mathcal R}(\phi ) $
, and such that
 ${\mathcal R}(\phi )$
is a semi-algebraic deformation retract of the union.
${\mathcal R}(\phi )$
is a semi-algebraic deformation retract of the union.
Therefore, at each step of our construction the cover by contractible sets that we consider is actually a cover of a semialgebraic set which is infinitesimally larger than that but with the same homotopy type as the original set. As a result, the inclusion property – namely, that each element of the cover is included in the set that it is part of a cover of – which is expected from the elements of a cover will not hold.
We first describe the situation in the case when Part (b) above is replaced with:
(b
![]() $^{\prime }$
) the union of the realizations is equal to
$^{\prime }$
) the union of the realizations is equal to
![]() ${\mathcal R}(\phi )$
.
${\mathcal R}(\phi )$
.
We call this the ideal situation. Figure 5(a) displays three levels of the construction in the ideal situation for the sphere. In the first step, we have two closed contractible hemispheres that cover the whole sphere. The intersection of the two hemispheres is a circle, and the next level shows the two closed semicircles as its cover. The bottom level consists of two points which is the intersection of these semicircles. Clearly, the inclusion property holds in this case.
Unfortunately, as mentioned before we cannot assume that we are in the ideal situation. This is because the only algorithm with a singly exponential complexity that is currently known for computing covers by contractible sets, satisfies Property (b) rather than the ideal Property (b
![]() $^{\prime }$
). In the nonideal situation, we will obtain in the first step a cover of an infinitesimally thickened sphere by two thickened hemispheres where the thickening is in terms of some infinitesimal
$^{\prime }$
). In the nonideal situation, we will obtain in the first step a cover of an infinitesimally thickened sphere by two thickened hemispheres where the thickening is in terms of some infinitesimal
![]() ${\varepsilon }_0, 0 < {\varepsilon }_0 \ll 1$
. The intersection of these two thickened hemispheres is a thickened circle and which is covered by two thickened semicircles whose union is infinitesimally larger than the thickened circle. The new infinitesimal is
${\varepsilon }_0, 0 < {\varepsilon }_0 \ll 1$
. The intersection of these two thickened hemispheres is a thickened circle and which is covered by two thickened semicircles whose union is infinitesimally larger than the thickened circle. The new infinitesimal is
![]() ${\varepsilon }_1$
and
${\varepsilon }_1$
and
![]() $0 < {\varepsilon }_1 \ll {\varepsilon }_0 \ll 1$
. Finally, in the next level, the intersection of the two thickened semicircles is covered by two thickened points involving a third infinitesimal
$0 < {\varepsilon }_1 \ll {\varepsilon }_0 \ll 1$
. Finally, in the next level, the intersection of the two thickened semicircles is covered by two thickened points involving a third infinitesimal
![]() ${\varepsilon }_2$
such that
${\varepsilon }_2$
such that
![]() $0 < {\varepsilon }_2 \ll {\varepsilon }_1 \ll {\varepsilon }_0 \ll 1$
.
$0 < {\varepsilon }_2 \ll {\varepsilon }_1 \ll {\varepsilon }_0 \ll 1$
.
We associate to each element
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
two semialgebraic sets
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
two semialgebraic sets
![]() $D_{m,i}(\Phi )(\alpha )$
,
$D_{m,i}(\Phi )(\alpha )$
,
![]() $D^{\prime }_{m,i}(\Phi )(\alpha )$
. The association
$D^{\prime }_{m,i}(\Phi )(\alpha )$
. The association
![]() $D_{m,i}(\Phi )(\cdot )$
is functorial in the sense that if
$D_{m,i}(\Phi )(\cdot )$
is functorial in the sense that if
![]() $\alpha , \beta \in \mathbf {P}_{m,i}(\Phi )$
, then
$\alpha , \beta \in \mathbf {P}_{m,i}(\Phi )$
, then
![]() $\alpha \preceq \beta \Leftrightarrow D_{m,i}(\Phi )(\alpha ) \subset D_{m,i}(\Phi )(\beta )$
. This functoriality is important since it allows us to define the homotopy colimit of the functor
$\alpha \preceq \beta \Leftrightarrow D_{m,i}(\Phi )(\alpha ) \subset D_{m,i}(\Phi )(\beta )$
. This functoriality is important since it allows us to define the homotopy colimit of the functor
![]() $D_{m,i}(\Phi )$
. The association
$D_{m,i}(\Phi )$
. The association
![]() $\alpha \mapsto D^{\prime }_{m,i}(\Phi )(\alpha )$
does not have the functorial property. However, it follows directly from its definition that
$\alpha \mapsto D^{\prime }_{m,i}(\Phi )(\alpha )$
does not have the functorial property. However, it follows directly from its definition that
![]() $D^{\prime }_{m,i}(\Phi )$
is contractible (or
$D^{\prime }_{m,i}(\Phi )$
is contractible (or
![]() $\ell $
-connected in the more general setting). Finally, we are able to show that
$\ell $
-connected in the more general setting). Finally, we are able to show that
![]() $D^{\prime }_{m,i}(\Phi )(\alpha )$
is homotopy equivalent to
$D^{\prime }_{m,i}(\Phi )(\alpha )$
is homotopy equivalent to
![]() $D_{m,i}(\Phi )(\alpha )$
for each
$D_{m,i}(\Phi )(\alpha )$
for each
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
, and thus the functor
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
, and thus the functor
![]() $D_{m,i}(\Phi )$
has the advantage of being functorial as well as satisfying the connectivity property.
$D_{m,i}(\Phi )$
has the advantage of being functorial as well as satisfying the connectivity property.
In this example, we display
![]() $D_{m,i}'(\Phi )(\alpha )$
and
$D_{m,i}'(\Phi )(\alpha )$
and
![]() $D_{m,i}(\Phi )(\alpha )$
for all different
$D_{m,i}(\Phi )(\alpha )$
for all different
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
in Figures 5(b) and 5(c).
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
in Figures 5(b) and 5(c).
For the rest of this example, we assume the covers of sphere are in the ideal situation. This assumption will not change the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
that we construct.
$\mathbf {P}_{m,i}(\Phi )$
that we construct.
In order to reconcile with the notation used in the definition of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
, we will assume that the different covers described above (which are not Leray but
$\mathbf {P}_{m,i}(\Phi )$
, we will assume that the different covers described above (which are not Leray but
![]() $\infty $
-connected) correspond to the values of the maps
$\infty $
-connected) correspond to the values of the maps
![]() $\mathcal {I}_{i,3}$
and
$\mathcal {I}_{i,3}$
and
![]() $\mathcal {C}_{i,3}$
evaluated at the corresponding formulas which we describe more precisely below.
$\mathcal {C}_{i,3}$
evaluated at the corresponding formulas which we describe more precisely below.
-
Step 1. Let
 $a,b$
denote the closed upper and lower hemispheres of the sphere
$a,b$
denote the closed upper and lower hemispheres of the sphere
 $\mathbf {S}^2(0,1) \subset \mathbb {R}^3$
, defined by formulas
$\mathbf {S}^2(0,1) \subset \mathbb {R}^3$
, defined by formulas  $$ \begin{align*} \phi_a &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 \geq 0), \\ \phi_b &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 \leq 0). \end{align*} $$
$$ \begin{align*} \phi_a &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 \geq 0), \\ \phi_b &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 \leq 0). \end{align*} $$
Let
 $J = J_0 = \{a,b\}$
, and
$J = J_0 = \{a,b\}$
, and
 $\Phi \in \mathcal {F}_{\mathbb {R},3}^J$
be defined by
$\Phi \in \mathcal {F}_{\mathbb {R},3}^J$
be defined by
 $\Phi (a) = \phi _a, \Phi (b) = \phi _b$
. Moreover, since
$\Phi (a) = \phi _a, \Phi (b) = \phi _b$
. Moreover, since
 $\mathrm {card}(J)=2$
,
$\mathrm {card}(J)=2$
,  $$\begin{align*}\mathbf{P}_{3,0}(\Phi) = \{(\{a\}, \emptyset),(\{b\},\emptyset)\} \cup \bigcup_{I_0 \subset J, \mathrm{card}(I_0)=2} \{I_0\}\times \mathbf{P}_{2,1}(\Phi_{3,0,I_0,J_0}). \end{align*}$$
$$\begin{align*}\mathbf{P}_{3,0}(\Phi) = \{(\{a\}, \emptyset),(\{b\},\emptyset)\} \cup \bigcup_{I_0 \subset J, \mathrm{card}(I_0)=2} \{I_0\}\times \mathbf{P}_{2,1}(\Phi_{3,0,I_0,J_0}). \end{align*}$$
Following the notation used in Definition 3.3, let
 $I_0 = J_0 = J = \{a,b\}$
.
$I_0 = J_0 = J = \{a,b\}$
. -
Step 2. We suppose that
 $\mathcal {I}_{0,3}(\phi _a \wedge \phi _b) = 1$
, and
$\mathcal {I}_{0,3}(\phi _a \wedge \phi _b) = 1$
, and
 $\mathcal {C}_{0,3}(\phi _a \wedge \phi _b)(0) = \phi _c$
,
$\mathcal {C}_{0,3}(\phi _a \wedge \phi _b)(0) = \phi _c$
,
 $\mathcal {C}_{0,3}(\phi _a \wedge \phi _b)(1) = \phi _d$
, where
$\mathcal {C}_{0,3}(\phi _a \wedge \phi _b)(1) = \phi _d$
, where  $$ \begin{align*} \phi_c &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 \geq 0), \\ \phi_d &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 \leq 0), \end{align*} $$
$$ \begin{align*} \phi_c &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 \geq 0), \\ \phi_d &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 \leq 0), \end{align*} $$
denote the two semicircles.
 $$ \begin{gather*} J_1 = J_{3,0,I_0,\Phi} = \{I_0\} \times [1] = \{ (I_0,0), (I_0,1)\}, \\ \Phi_1 = \Phi_{3,0,I_0,J_0}, \\ \Phi_{1}((I_0,0)) = \phi_c, \\ \Phi_{1}((I_0,1)) = \phi_d. \end{gather*} $$
$$ \begin{gather*} J_1 = J_{3,0,I_0,\Phi} = \{I_0\} \times [1] = \{ (I_0,0), (I_0,1)\}, \\ \Phi_1 = \Phi_{3,0,I_0,J_0}, \\ \Phi_{1}((I_0,0)) = \phi_c, \\ \Phi_{1}((I_0,1)) = \phi_d. \end{gather*} $$
 $$\begin{align*}\mathbf{P}_{2,1}(\Phi_{1}) = \{(\{(I_0, 0)\}, \emptyset), (\{(I_0, 1)\}, \emptyset)\} \cup \bigcup_{I_1 \subset J_1, \mathrm{card}(I_1)=2} \{I_1 \}\times \mathbf{P}_{1,2}((\Phi_1)_{2,1,I_1,J_1}). \end{align*}$$
$$\begin{align*}\mathbf{P}_{2,1}(\Phi_{1}) = \{(\{(I_0, 0)\}, \emptyset), (\{(I_0, 1)\}, \emptyset)\} \cup \bigcup_{I_1 \subset J_1, \mathrm{card}(I_1)=2} \{I_1 \}\times \mathbf{P}_{1,2}((\Phi_1)_{2,1,I_1,J_1}). \end{align*}$$
Now, let
 $I_1 = J_1$
.
$I_1 = J_1$
. -
Step 3. Suppose that
 $\mathcal {I}_{1,3}(\phi _c \wedge \phi _d) = 1$
and
$\mathcal {I}_{1,3}(\phi _c \wedge \phi _d) = 1$
and
 $\mathcal {C}_{1,3}(\phi _c \wedge \phi _d)(0) = \phi _e$
,
$\mathcal {C}_{1,3}(\phi _c \wedge \phi _d)(0) = \phi _e$
, $\mathcal {C}_{1,3}(\phi _c \wedge \phi _d)(1) = \phi _f$
, where
$\mathcal {C}_{1,3}(\phi _c \wedge \phi _d)(1) = \phi _f$
, where  $$ \begin{align*} \phi_e &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 = 0) \wedge (X_1 + 1 = 0), \\ \phi_f&:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 = 0) \wedge (X_1 - 1 = 0). \end{align*} $$
$$ \begin{align*} \phi_e &:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 = 0) \wedge (X_1 + 1 = 0), \\ \phi_f&:= (X_1^2 + X_2^2 + X_3^2 - 1 = 0) \wedge (X_3 = 0) \wedge (X_2 = 0) \wedge (X_1 - 1 = 0). \end{align*} $$
 $$ \begin{gather*} J_2 = (J_1)_{2,1,I_1,\Phi_1} = \{I_1\} \times [1] = \{ (I_1,0), (I_1,1)\}, \\ \Phi_2 = (\Phi_1)_{2,1,I_1,J_1} \\ \Phi_{2}((I_1,0)) = \phi_e, \\ \Phi_{2}((I_1,1)) = \phi_f. \end{gather*} $$
$$ \begin{gather*} J_2 = (J_1)_{2,1,I_1,\Phi_1} = \{I_1\} \times [1] = \{ (I_1,0), (I_1,1)\}, \\ \Phi_2 = (\Phi_1)_{2,1,I_1,J_1} \\ \Phi_{2}((I_1,0)) = \phi_e, \\ \Phi_{2}((I_1,1)) = \phi_f. \end{gather*} $$
 $$\begin{align*}\mathbf{P}_{1,2}(\Phi_{2}) = \{(\{(I_1, 0)\}, \emptyset), (\{(I_1, 1)\}, \emptyset)\} \cup \bigcup_{I_2 \subset J_2, \mathrm{card}(I_2)=2} \{I_2 \}\times \mathbf{P}_{0, 3}((\Phi_2)_{1,2,I_2,J_2}). \end{align*}$$
$$\begin{align*}\mathbf{P}_{1,2}(\Phi_{2}) = \{(\{(I_1, 0)\}, \emptyset), (\{(I_1, 1)\}, \emptyset)\} \cup \bigcup_{I_2 \subset J_2, \mathrm{card}(I_2)=2} \{I_2 \}\times \mathbf{P}_{0, 3}((\Phi_2)_{1,2,I_2,J_2}). \end{align*}$$
Let
 $I_2 = J_2$
.
$I_2 = J_2$
. -
Step 4. Since
 $\mathcal {I}_{2,3}(\phi _e \wedge \phi _f) = -1$
, hence
$\mathcal {I}_{2,3}(\phi _e \wedge \phi _f) = -1$
, hence
 $\mathbf {P}_{0,3}((\Phi _2)_{1,2,I_2,J_2}) = \emptyset $
, and from Step 3
$\mathbf {P}_{0,3}((\Phi _2)_{1,2,I_2,J_2}) = \emptyset $
, and from Step 3  $$\begin{align*}\mathbf{P}_{1,2}(\Phi_{2}) = \{(\{(I_1, 0)\}, \emptyset), (\{(I_1, 1)\}, \emptyset)\}. \end{align*}$$
$$\begin{align*}\mathbf{P}_{1,2}(\Phi_{2}) = \{(\{(I_1, 0)\}, \emptyset), (\{(I_1, 1)\}, \emptyset)\}. \end{align*}$$
-
Step 5. With these choices of the values of
 $\mathcal {I}_{\cdot ,3}$
and
$\mathcal {I}_{\cdot ,3}$
and
 $\mathcal {C}_{\cdot ,3}$
for the specific formulas described above, and
$\mathcal {C}_{\cdot ,3}$
for the specific formulas described above, and
 $\ell = \infty $
, from Step 2 and Step 4, the Hasse diagram of the poset
$\ell = \infty $
, from Step 2 and Step 4, the Hasse diagram of the poset
 $\mathbf {P}_{2,1}(\Phi _{1})$
is as follows.
$\mathbf {P}_{2,1}(\Phi _{1})$
is as follows. 
-
Step 6. Finally, from Step 1 and Step 5, the Hasse diagram of the poset
 $\mathbf {P}_{3,0}(\Phi )$
is shown below.
$\mathbf {P}_{3,0}(\Phi )$
is shown below. 
The order complex
![]() $\Delta (\mathbf {P}_{3,0}(\Phi ))$
is displayed below, and clearly
$\Delta (\mathbf {P}_{3,0}(\Phi ))$
is displayed below, and clearly
![]() $|\Delta (\mathbf {P}_{3,0}(\Phi ))|$
is homeomorphic to
$|\Delta (\mathbf {P}_{3,0}(\Phi ))|$
is homeomorphic to
![]() $\mathbf {S}^2(0,1)$
.
$\mathbf {S}^2(0,1)$
.

Figure 6 The order complex,
![]() $\Delta (\mathbf {P}_{3,0}(\Phi ))$
.
$\Delta (\mathbf {P}_{3,0}(\Phi ))$
.
3.6 Proofs of Theorems 2 and 2′
In this section, we prove Theorem 2 as well as Theorem 2′ . We first give an outline of the proof of Theorem 2.
3.6.1 Outline of the proof of Theorem 2
In order to prove that
![]() $|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
is homologically
$|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
is homologically
![]() $(m-1)$
-equivalent to
$(m-1)$
-equivalent to
![]() ${\mathcal R}(\Phi )^J$
, we give two homological
${\mathcal R}(\Phi )^J$
, we give two homological
![]() $(m-1)$
-equivalences. The source of both these maps is a semialgebraic set which is defined as the homotopy colimit of a certain functor
$(m-1)$
-equivalences. The source of both these maps is a semialgebraic set which is defined as the homotopy colimit of a certain functor
![]() $D_{m,i}$
from the poset category
$D_{m,i}$
from the poset category
![]() $\mathbf {P}_{m,i}(\Phi )$
to
$\mathbf {P}_{m,i}(\Phi )$
to
![]() $\mathbf {Top}$
taking its values in semialgebraic subsets of
$\mathbf {Top}$
taking its values in semialgebraic subsets of
![]() $\mathrm {R}^k_{i+m+1}$
. The targets are
$\mathrm {R}^k_{i+m+1}$
. The targets are
![]() $|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
and
$|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
and
![]() ${\mathcal R}(\Phi )^J$
. Taken together these two homological
${\mathcal R}(\Phi )^J$
. Taken together these two homological
![]() $(m-1)$
-equivalences imply that
$(m-1)$
-equivalences imply that
![]() $|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
and
$|\Delta (\mathbf {P}_{m,i}(\Phi ))|$
and
![]() ${\mathcal R}(\Phi )^J$
are homologically
${\mathcal R}(\Phi )^J$
are homologically
![]() $(m-1)$
-equivalent.
$(m-1)$
-equivalent.
In what follows, we first define the functor
![]() $D_{m,i}$
as well as an associated map
$D_{m,i}$
as well as an associated map
![]() $D^{\prime }_{m,i}$
, also taking values in semialgebraic sets and prove the main properties of these objects that we are going to need in the proof of Theorem 2.
$D^{\prime }_{m,i}$
, also taking values in semialgebraic sets and prove the main properties of these objects that we are going to need in the proof of Theorem 2.
3.6.2 Definition of
 $D_{m,i},D^{\prime }_{m,i}$
$D_{m,i},D^{\prime }_{m,i}$
We now define for each
![]() $\alpha = (I_0,\ldots ,I_{r},\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
, a closed semialgebraic subset
$\alpha = (I_0,\ldots ,I_{r},\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
, a closed semialgebraic subset
![]() $D_{m,i}(\alpha ) \subset \overline {B_k(0,R)} \subset \mathrm {R}_{i+m+ 1}^k$
and also a semialgebraic set
$D_{m,i}(\alpha ) \subset \overline {B_k(0,R)} \subset \mathrm {R}_{i+m+ 1}^k$
and also a semialgebraic set
![]() $D^{\prime }_{m,i}(\alpha ) \subset \mathrm {R}_{i+r}^k$
.
$D^{\prime }_{m,i}(\alpha ) \subset \mathrm {R}_{i+r}^k$
.
We define
![]() $D_{m,i},D^{\prime }_{m,i}$
by induction on m. For
$D_{m,i},D^{\prime }_{m,i}$
by induction on m. For
![]() $m=-1$
, we define for
$m=-1$
, we define for
![]() $j \in J$
,
$j \in J$
,
We now define
![]() $D_{m,i}(\Phi ), D^{\prime }_{m,i}(\Phi ): \mathbf {P}_{m,i}(\Phi ) \rightarrow \mathbf {Top} $
, using the fact that they are already defined for all
$D_{m,i}(\Phi ), D^{\prime }_{m,i}(\Phi ): \mathbf {P}_{m,i}(\Phi ) \rightarrow \mathbf {Top} $
, using the fact that they are already defined for all
![]() $-1 \leq m' < m$
. We define:
$-1 \leq m' < m$
. We define:
 $$ \begin{align*} D_{m,i}(\Phi)((\{j\},\emptyset)) &= \mathrm{ext}({\mathcal R}(\Phi(j),\overline{B_k(0,R)}), \mathrm{R}_{i+m+1}) \cup \\ &\bigcup_{(I,\alpha) \in \mathbf{P}_{m,i}(\Phi), j \in I} \mathrm{ext}(D_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J})(\alpha),\mathrm{R}_{i+m+1}), \\ D_{m,i}(\Phi)((I,\alpha)) &= \mathrm{ext}(D_{m - \mathrm{card}(I) +1, i+1}(\Phi_{m,i,I,J})(\alpha),\mathrm{R}_{i+m+1}), \\ &I \subset_{\leq m+2} J, \mathrm{card}(I)> 1, \alpha \in \mathbf{P}_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J}), \end{align*} $$
$$ \begin{align*} D_{m,i}(\Phi)((\{j\},\emptyset)) &= \mathrm{ext}({\mathcal R}(\Phi(j),\overline{B_k(0,R)}), \mathrm{R}_{i+m+1}) \cup \\ &\bigcup_{(I,\alpha) \in \mathbf{P}_{m,i}(\Phi), j \in I} \mathrm{ext}(D_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J})(\alpha),\mathrm{R}_{i+m+1}), \\ D_{m,i}(\Phi)((I,\alpha)) &= \mathrm{ext}(D_{m - \mathrm{card}(I) +1, i+1}(\Phi_{m,i,I,J})(\alpha),\mathrm{R}_{i+m+1}), \\ &I \subset_{\leq m+2} J, \mathrm{card}(I)> 1, \alpha \in \mathbf{P}_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J}), \end{align*} $$
and
for
![]() $I \subset _{\leq m+2} J, \mathrm {card}(I)> 1$
,
$I \subset _{\leq m+2} J, \mathrm {card}(I)> 1$
,
![]() $\alpha \in \mathbf {P}_{m-\mathrm {card}(I)+1,i+1}(\Phi _{m,i,I,J})$
.
$\alpha \in \mathbf {P}_{m-\mathrm {card}(I)+1,i+1}(\Phi _{m,i,I,J})$
.
The following lemma is obvious from the definition of
![]() $D_{m,i}(\alpha )$
given above.
$D_{m,i}(\alpha )$
given above.
Lemma 3.5. For each
![]() $\alpha , \beta \in \mathbf {P}_{m,i}(\Phi )$
with
$\alpha , \beta \in \mathbf {P}_{m,i}(\Phi )$
with
![]() $\alpha \preceq \beta $
, the morphism
$\alpha \preceq \beta $
, the morphism
![]() $D_{m,i}(\Phi )(\alpha \preceq \beta ): D_{m,i}(\Phi )(\alpha ) \rightarrow D_{m,i}(\Phi )(\beta )$
is an inclusion. So,
$D_{m,i}(\Phi )(\alpha \preceq \beta ): D_{m,i}(\Phi )(\alpha ) \rightarrow D_{m,i}(\Phi )(\beta )$
is an inclusion. So,
![]() $D_{m,i}(\Phi )$
is a functor from the poset category
$D_{m,i}(\Phi )$
is a functor from the poset category
![]() $(\mathbf {P}_{m,i}(\Phi ), \prec )$
to
$(\mathbf {P}_{m,i}(\Phi ), \prec )$
to
![]() $\mathbf {Top}$
.
$\mathbf {Top}$
.
Remark 3.5. Unlike
![]() $D_{m,i}$
,
$D_{m,i}$
,
![]() $D^{\prime }_{m,i}$
is not necessarily a functor.
$D^{\prime }_{m,i}$
is not necessarily a functor.
Lemma 3.6. For each
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
,
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
,
Proof. Let
with
![]() $I_h^{\alpha } \subset J_h^{\alpha }, 0 \leq h \leq r_{\alpha }$
following the same notation as in Section 3.3.3 (with an added superscript
$I_h^{\alpha } \subset J_h^{\alpha }, 0 \leq h \leq r_{\alpha }$
following the same notation as in Section 3.3.3 (with an added superscript
![]() ${}^{\alpha }$
).
${}^{\alpha }$
).
First, observe that
 $$ \begin{align} D_{m,i}(\Phi)(\alpha) = \mathrm{ext}(D^{\prime}_{m,i}(\Phi)(\alpha), \mathrm{R}_{i+m+1}) \cup \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta). \end{align} $$
$$ \begin{align} D_{m,i}(\Phi)(\alpha) = \mathrm{ext}(D^{\prime}_{m,i}(\Phi)(\alpha), \mathrm{R}_{i+m+1}) \cup \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta). \end{align} $$
We now prove that for each
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
:
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
:
and
 $$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta) \searrow \bigcup_{\beta \prec \alpha} \lim_{\bar{\varepsilon}_{i+r_{\alpha}+1}} D_{m,i}'(\Phi)(\beta) \subset D^{\prime}_{m,i}(\Phi)(\alpha). \end{align} $$
$$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta) \searrow \bigcup_{\beta \prec \alpha} \lim_{\bar{\varepsilon}_{i+r_{\alpha}+1}} D_{m,i}'(\Phi)(\beta) \subset D^{\prime}_{m,i}(\Phi)(\alpha). \end{align} $$
The proof is by induction on the maximum length,
![]() $\mathrm {length}(\alpha )$
, of any chain with
$\mathrm {length}(\alpha )$
, of any chain with
![]() $\alpha $
as the maximal element.
$\alpha $
as the maximal element.
We first note that if
![]() $\mathrm {R}' = \mathrm {R}{\langle }\bar {\varepsilon }{\rangle }$
, and
$\mathrm {R}' = \mathrm {R}{\langle }\bar {\varepsilon }{\rangle }$
, and
![]() $X \subset \mathrm {R}^k$
is a semialgebraic subset, then
$X \subset \mathrm {R}^k$
is a semialgebraic subset, then
This follows easily from the definition of
![]() $\mathrm {ext}(X,\mathrm {R}')$
and standard properties of
$\mathrm {ext}(X,\mathrm {R}')$
and standard properties of
![]() $\lim _{\bar {\varepsilon }}$
. In particular, if X is a closed semialgebraic set, then
$\lim _{\bar {\varepsilon }}$
. In particular, if X is a closed semialgebraic set, then
Base case of the induction,
![]() $\mathrm {length}(\alpha ) = 1$
: It follows from equation (3.15) and the fact that that
$\mathrm {length}(\alpha ) = 1$
: It follows from equation (3.15) and the fact that that
![]() $D^{\prime }_{m,i}(\Phi )(\alpha )$
is a closed semialgebraic set, that equation (3.16) holds if
$D^{\prime }_{m,i}(\Phi )(\alpha )$
is a closed semialgebraic set, that equation (3.16) holds if
![]() $\alpha $
is a minimal element of the poset
$\alpha $
is a minimal element of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
(and so
$\mathbf {P}_{m,i}(\Phi )$
(and so
![]() $\mathrm {length}(\alpha ) = 1$
). In this case, equation (3.17) is trivially true.
$\mathrm {length}(\alpha ) = 1$
). In this case, equation (3.17) is trivially true.
Induction hypothesis: We assume now that equations (3.16) and (3.17) are true for all
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
, with
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
, with
![]() $\mathrm {length}(\alpha ) < t$
.
$\mathrm {length}(\alpha ) < t$
.
Inductive step: Suppose that
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
, with
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
, with
![]() $\mathrm {length}(\alpha ) = t$
. The inductive hypothesis implies that equations (3.16) and (3.17) both hold with
$\mathrm {length}(\alpha ) = t$
. The inductive hypothesis implies that equations (3.16) and (3.17) both hold with
![]() $\alpha $
replaced by
$\alpha $
replaced by
![]() $\alpha '$
for all
$\alpha '$
for all
![]() $\alpha ' \prec \alpha $
.
$\alpha ' \prec \alpha $
.
Using the fact that
![]() $D^{\prime }_{m,i}(\Phi )(\alpha )$
is closed, it is easy to check that equation (3.17) implies equation (3.16). So we need to prove only equation (3.17). Using the induction hypothesis, we have for each
$D^{\prime }_{m,i}(\Phi )(\alpha )$
is closed, it is easy to check that equation (3.17) implies equation (3.16). So we need to prove only equation (3.17). Using the induction hypothesis, we have for each
![]() $\beta \prec \alpha $
$\beta \prec \alpha $
 $$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta) \searrow \bigcup_{\beta \prec \alpha} D_{m,i}'(\Phi)(\beta). \end{align} $$
$$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}(\Phi)(\beta) \searrow \bigcup_{\beta \prec \alpha} D_{m,i}'(\Phi)(\beta). \end{align} $$
Now, observe that for any
![]() $\beta \in \mathbf {P}_{m,i}(\Phi )$
,
$\beta \in \mathbf {P}_{m,i}(\Phi )$
,
![]() $\beta \prec \alpha $
if and only if there exist
$\beta \prec \alpha $
if and only if there exist
![]() $j_{\alpha }' \in I_{r_{\alpha } -1}^{\alpha }, j_{\alpha }' \neq j_{\alpha }$
and
$j_{\alpha }' \in I_{r_{\alpha } -1}^{\alpha }, j_{\alpha }' \neq j_{\alpha }$
and
![]() $j_{\alpha }" \in (J_{r_{\alpha }}^{\alpha })_{m^{\alpha }_{r_{\alpha }}, i^{\alpha }_{r_{\alpha }},\{j_{\alpha },j_{\alpha }'\},\Phi _{r_{\alpha }}}$
such that
$j_{\alpha }" \in (J_{r_{\alpha }}^{\alpha })_{m^{\alpha }_{r_{\alpha }}, i^{\alpha }_{r_{\alpha }},\{j_{\alpha },j_{\alpha }'\},\Phi _{r_{\alpha }}}$
such that
where we assume that
![]() $I_{-1}^{\alpha } = J$
.
$I_{-1}^{\alpha } = J$
.
Using the above observation, we have that
 $$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}'(\Phi)(\beta) = \bigcup_{j_{\alpha}' \in I^{\alpha}_{r_{\alpha} -1}, j_{\alpha}' \neq j_{\alpha}} \bigcup_{j_{\alpha}" \in (J_{r_{\alpha}}^{\alpha})_{m^{\alpha}_{r_{\alpha}}, i^{\alpha}_{r_{\alpha}},\{j_{\alpha},j_{\alpha}'\},\Phi_{r_{\alpha}}}} \left( \bigcup_{\beta \preceq \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \right), \end{align} $$
$$ \begin{align} \bigcup_{\beta \prec \alpha} D_{m,i}'(\Phi)(\beta) = \bigcup_{j_{\alpha}' \in I^{\alpha}_{r_{\alpha} -1}, j_{\alpha}' \neq j_{\alpha}} \bigcup_{j_{\alpha}" \in (J_{r_{\alpha}}^{\alpha})_{m^{\alpha}_{r_{\alpha}}, i^{\alpha}_{r_{\alpha}},\{j_{\alpha},j_{\alpha}'\},\Phi_{r_{\alpha}}}} \left( \bigcup_{\beta \preceq \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \right), \end{align} $$
where
Applying hypothesis (3.17), we have that
 $$ \begin{align} \left( \bigcup_{\beta \prec \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \right) \searrow \lim_{\bar{\varepsilon}_{i+r+2}} \bigcup_{\beta \prec \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \subset D^{\prime}_{m,i}(\Phi)(\gamma(j_{\alpha}")). \end{align} $$
$$ \begin{align} \left( \bigcup_{\beta \prec \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \right) \searrow \lim_{\bar{\varepsilon}_{i+r+2}} \bigcup_{\beta \prec \gamma(j_{\alpha}")} D^{\prime}_{m,i}(\Phi)(\beta) \subset D^{\prime}_{m,i}(\Phi)(\gamma(j_{\alpha}")). \end{align} $$
Also, observe that
 $$ \begin{align} \left( \bigcup_{j_{\alpha}" \in J_{m,i,\{j_{\alpha},j_{\alpha}'\},\Phi}} D^{\prime}_{m,i}(\Phi)(\gamma(j_{\alpha}")) \right) \searrow \left(D^{\prime}_{m,i}(\Phi)(\alpha) \cap D^{\prime}_{m,i}(\Phi)(\alpha') \right) \subset D^{\prime}_{m,i}(\Phi)(\alpha), \end{align} $$
$$ \begin{align} \left( \bigcup_{j_{\alpha}" \in J_{m,i,\{j_{\alpha},j_{\alpha}'\},\Phi}} D^{\prime}_{m,i}(\Phi)(\gamma(j_{\alpha}")) \right) \searrow \left(D^{\prime}_{m,i}(\Phi)(\alpha) \cap D^{\prime}_{m,i}(\Phi)(\alpha') \right) \subset D^{\prime}_{m,i}(\Phi)(\alpha), \end{align} $$
where
Finally, equation (3.17) now follows from equations (3.18), (3.19), (3.20) and (3.21).
Lemma 3.7.
 $$\begin{align*}\left( \bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) \right) \searrow {\mathcal R}(\Phi, \overline{B_k(0,R)})^J. \end{align*}$$
$$\begin{align*}\left( \bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) \right) \searrow {\mathcal R}(\Phi, \overline{B_k(0,R)})^J. \end{align*}$$
In particular,
![]() $\mathrm {ext}({\mathcal R}(\Phi , \overline {B_k(0,R)})^J, \mathrm {R}_i)$
is a semialgebraic deformation retract of
$\mathrm {ext}({\mathcal R}(\Phi , \overline {B_k(0,R)})^J, \mathrm {R}_i)$
is a semialgebraic deformation retract of
![]() $\bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} D_{m,i}(\Phi )(\alpha ) $
.
$\bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} D_{m,i}(\Phi )(\alpha ) $
.
Proof. First, note that for each
![]() $j \in J$
,
$j \in J$
,
![]() $(\{j\},\emptyset )$
is a maximal element of the poset
$(\{j\},\emptyset )$
is a maximal element of the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
. It now follows from Lemma 3.5 that
$\mathbf {P}_{m,i}(\Phi )$
. It now follows from Lemma 3.5 that
 $$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) = \bigcup_{j \in J} D_{m,i}(\Phi)((\{j\},\emptyset)). \end{align*}$$
$$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) = \bigcup_{j \in J} D_{m,i}(\Phi)((\{j\},\emptyset)). \end{align*}$$
Notation 3.9. We will denote the deformation retraction
 $$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) \rightarrow \mathrm{ext}({\mathcal R}(\Phi, \overline{B_k(0,R)})^J, \mathrm{R}_i) \end{align*}$$
$$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha) \rightarrow \mathrm{ext}({\mathcal R}(\Phi, \overline{B_k(0,R)})^J, \mathrm{R}_i) \end{align*}$$
in Lemma 3.7 by
![]() $r_{m,i}(\Phi )$
.
$r_{m,i}(\Phi )$
.
In the proof of Theorem 2, we need the notion of the homotopy colimit of a functor which we define below.
We fix a real closed field
![]() $\mathrm {R}$
in the following definition.
$\mathrm {R}$
in the following definition.
Definition 3.5 (The topological standard n-simplex).
We denote by
 $$\begin{align*}|\Delta^n | = \{ (t_0, \ldots, t_n) \in \mathrm{R}^{n+1}_{\geq 0} | \sum_{i=0}^n t_i = 1 \} \end{align*}$$
$$\begin{align*}|\Delta^n | = \{ (t_0, \ldots, t_n) \in \mathrm{R}^{n+1}_{\geq 0} | \sum_{i=0}^n t_i = 1 \} \end{align*}$$
the standard n-simplex defined over
![]() $\mathrm {R}$
. For
$\mathrm {R}$
. For
![]() $0 \leq i \leq n$
, we define the face operators,
$0 \leq i \leq n$
, we define the face operators,
by
Definition 3.6 (Homotopy colimit).
Let
![]() $(\mathbf {P}, \prec )$
be a poset category and
$(\mathbf {P}, \prec )$
be a poset category and
a functor taking its values in closed and bounded semialgebraic subsets of
![]() $\mathrm {R}^k$
and such that the morphisms
$\mathrm {R}^k$
and such that the morphisms
![]() $D(\alpha \preceq \beta )$
are inclusion maps. The homotopy colimit of D is the quotient space Footnote
4
$D(\alpha \preceq \beta )$
are inclusion maps. The homotopy colimit of D is the quotient space Footnote
4
 $$\begin{align*}\mathrm{hocolim}(D) = \left(\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \right) \Big/ \hspace{-.1cm} \sim \ , \end{align*}$$
$$\begin{align*}\mathrm{hocolim}(D) = \left(\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \right) \Big/ \hspace{-.1cm} \sim \ , \end{align*}$$
where the equivalence relation
![]() $\sim $
is defined as follows.
$\sim $
is defined as follows.
For a chain
![]() $\sigma = (\alpha _0 \prec \cdots \prec \alpha _p)$
,
$\sigma = (\alpha _0 \prec \cdots \prec \alpha _p)$
,
![]() $t \in |\Delta ^p|$
and
$t \in |\Delta ^p|$
and
![]() $x \in D(\alpha _0)$
, we denote by
$x \in D(\alpha _0)$
, we denote by
![]() $(t,x)_{\sigma }$
the image of
$(t,x)_{\sigma }$
the image of
![]() $(t,x)$
under the canonical inclusion of
$(t,x)$
under the canonical inclusion of
![]() $|\Delta ^p| \times D(\alpha _0)$
(corresponding to the chain
$|\Delta ^p| \times D(\alpha _0)$
(corresponding to the chain
![]() $\sigma $
) in the disjoint union
$\sigma $
) in the disjoint union
![]() $\coprod _{\alpha _0 \prec \cdots \prec \alpha _p} |\Delta ^p| \times D(\alpha _0)$
.
$\coprod _{\alpha _0 \prec \cdots \prec \alpha _p} |\Delta ^p| \times D(\alpha _0)$
.
Using the above notation, the equivalence relation
![]() $\sim $
is defined by:
$\sim $
is defined by:
for
![]() $x \in D(\alpha _0)$
and
$x \in D(\alpha _0)$
and
![]() $t \in |\Delta ^{p-1}|$
, where
$t \in |\Delta ^{p-1}|$
, where
![]() $\sigma = (\alpha _0 \prec \cdots \prec \alpha _p)$
and
$\sigma = (\alpha _0 \prec \cdots \prec \alpha _p)$
and
 $$ \begin{align*} \sigma' = \left\{ \begin{array}{ll} (\alpha_1 \prec \cdots \prec \alpha_p) & \text{ if } i =0, \\ (\alpha_0 \prec \cdots \alpha_{i-1} \prec \alpha_{i+1} \prec \cdots \prec \alpha_p) & \text{ if } 0 < i < p, \\ (\alpha_0 \prec \cdots \prec \alpha_{p-1}) & \text{ if } i = p. \end{array} \right. \end{align*} $$
$$ \begin{align*} \sigma' = \left\{ \begin{array}{ll} (\alpha_1 \prec \cdots \prec \alpha_p) & \text{ if } i =0, \\ (\alpha_0 \prec \cdots \alpha_{i-1} \prec \alpha_{i+1} \prec \cdots \prec \alpha_p) & \text{ if } 0 < i < p, \\ (\alpha_0 \prec \cdots \prec \alpha_{p-1}) & \text{ if } i = p. \end{array} \right. \end{align*} $$
We denote by
![]() $\pi ^D_1: \mathrm {hocolim}(D) \rightarrow |\Delta (\mathbf {P})|$
,
$\pi ^D_1: \mathrm {hocolim}(D) \rightarrow |\Delta (\mathbf {P})|$
,
![]() $\pi ^D_2: \mathrm {hocolim}(D) \rightarrow \mathrm {colim}(D)$
the canonical maps, where
$\pi ^D_2: \mathrm {hocolim}(D) \rightarrow \mathrm {colim}(D)$
the canonical maps, where
![]() $|\Delta (\mathbf {P})|$
is the geometric realization of the order complex of
$|\Delta (\mathbf {P})|$
is the geometric realization of the order complex of
![]() $\mathbf {P}$
(see Definition 3.1). More precisely,
$\mathbf {P}$
(see Definition 3.1). More precisely,
![]() $\pi ^D_1$
is the map induced from the projection map
$\pi ^D_1$
is the map induced from the projection map
 $$\begin{align*}\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \rightarrow \coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \end{align*}$$
$$\begin{align*}\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \rightarrow \coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \end{align*}$$
after taking the quotient by
![]() $\sim $
, and
$\sim $
, and
![]() $\pi ^D_2$
is the composition of the map induced by the projection
$\pi ^D_2$
is the composition of the map induced by the projection
 $$\begin{align*}\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \rightarrow \coprod_{\alpha_0 \prec \cdots \prec \alpha_p} D(\alpha_0) \end{align*}$$
$$\begin{align*}\coprod_{\alpha_0 \prec \cdots \prec \alpha_p} |\Delta^p| \times D(\alpha_0) \rightarrow \coprod_{\alpha_0 \prec \cdots \prec \alpha_p} D(\alpha_0) \end{align*}$$
and the canonical map to the colimit of the functor D, which in this case is simply the union
![]() $\bigcup _{\alpha \in \mathbf {P}} D(\alpha )$
.
$\bigcup _{\alpha \in \mathbf {P}} D(\alpha )$
.
The following example illustrates the definition given above.
Example 3.3. Consider the poset
![]() $\mathbf {P} = \{a,b,c\}$
, with three elements with
$\mathbf {P} = \{a,b,c\}$
, with three elements with
![]() $c \prec a, c \prec b$
as the only nontrivial ordering relation (Hasse diagram shown below).
$c \prec a, c \prec b$
as the only nontrivial ordering relation (Hasse diagram shown below).

Let
![]() $D:\mathbf {P} \rightarrow \mathbf {Top}$
be the functor, with
$D:\mathbf {P} \rightarrow \mathbf {Top}$
be the functor, with
 $$ \begin{align*} D(a) &= {\mathcal R}((X_1^2 + X_2^2 - 4 =0) \wedge (X_2 \geq 0)), \\ D(b) &= {\mathcal R}((X_1^2 + X_2^2 - 4 =0) \wedge (X_2 \leq 0)), \\ D(c) &= D(a) \cap D(b) \\ &= \{(-2,0), (2,0)\}. \end{align*} $$
$$ \begin{align*} D(a) &= {\mathcal R}((X_1^2 + X_2^2 - 4 =0) \wedge (X_2 \geq 0)), \\ D(b) &= {\mathcal R}((X_1^2 + X_2^2 - 4 =0) \wedge (X_2 \leq 0)), \\ D(c) &= D(a) \cap D(b) \\ &= \{(-2,0), (2,0)\}. \end{align*} $$
The homotopy colimit of the functor D is then the quotient of the disjoint union of the spaces
 $$ \begin{align*} \Delta^0 &\times D(a), \Delta^0 \times D(b), \Delta^0 \times D(c), \\ &\ \ \Delta^1 \times D(c), \Delta^1 \times D(c) \end{align*} $$
$$ \begin{align*} \Delta^0 &\times D(a), \Delta^0 \times D(b), \Delta^0 \times D(c), \\ &\ \ \Delta^1 \times D(c), \Delta^1 \times D(c) \end{align*} $$
corresponding to the chains
![]() $(a), (b), (c), (c \prec a), (c \prec b)$
by the equivalence relation defined in equation (3.22). The nontrivial identifications induced by the quotienting are given by (following the notation introduced in Definition 3.6)
$(a), (b), (c), (c \prec a), (c \prec b)$
by the equivalence relation defined in equation (3.22). The nontrivial identifications induced by the quotienting are given by (following the notation introduced in Definition 3.6)
 $$ \begin{align*} ((0,1), (-2,0))_{(c \prec a)} &\sim ((1), (-2,0))_{(c)}, \\ ((0,1), (2,0))_{(c \prec a)} &\sim ((1), (2,0))_{(c)}, \\ ((1,0), (-2,0))_{(c \prec a)} &\sim ((1), (-2,0))_{(a)}, \\ ((1,0), (2,0))_{(c \prec a)} &\sim ((1), (2,0))_{(a)}, \\ ((0,1), (-2,0))_{(c \prec b)} &\sim ((1), (-2,0))_{(c)}, \\ ((0,1), (2,0))_{(c \prec b)} &\sim ((1), (2,0))_{(c)}, \\ ((1,0), (-2,0))_{(c \prec b)} &\sim ((1), (-2,0))_{(b)}, \\ ((1,0), (2,0))_{(c \prec b)} &\sim ((1), (2,0))_{(b)}. \end{align*} $$
$$ \begin{align*} ((0,1), (-2,0))_{(c \prec a)} &\sim ((1), (-2,0))_{(c)}, \\ ((0,1), (2,0))_{(c \prec a)} &\sim ((1), (2,0))_{(c)}, \\ ((1,0), (-2,0))_{(c \prec a)} &\sim ((1), (-2,0))_{(a)}, \\ ((1,0), (2,0))_{(c \prec a)} &\sim ((1), (2,0))_{(a)}, \\ ((0,1), (-2,0))_{(c \prec b)} &\sim ((1), (-2,0))_{(c)}, \\ ((0,1), (2,0))_{(c \prec b)} &\sim ((1), (2,0))_{(c)}, \\ ((1,0), (-2,0))_{(c \prec b)} &\sim ((1), (-2,0))_{(b)}, \\ ((1,0), (2,0))_{(c \prec b)} &\sim ((1), (2,0))_{(b)}. \end{align*} $$
The quotient space (as a semialgebraic set) is shown below in Figure 7.

Figure 7 Homotopy colimit of the functor D in Example 3.3.
Proof of Theorem 2.
The theorem will follow from the following two claims.
Claim 3.1. The map
![]() $\pi _1^{D_{m,i}(\Phi )}:\mathrm {hocolim}(D_{m,i}(\Phi )) \rightarrow |\Delta (\mathbf {P}_{m,i}(\Phi ))| $
is a homological
$\pi _1^{D_{m,i}(\Phi )}:\mathrm {hocolim}(D_{m,i}(\Phi )) \rightarrow |\Delta (\mathbf {P}_{m,i}(\Phi ))| $
is a homological
![]() $\ell $
-equivalence (and so a homological
$\ell $
-equivalence (and so a homological
![]() $(m-1)$
-equivalence).
$(m-1)$
-equivalence).
Claim 3.2. The map
is a homological
![]() $(m-1)$
-equivalence.
$(m-1)$
-equivalence.
We first deduce the proof of the theorem from these two claims. The homological
![]() $(m-1)$
-equivalence in equation (3.11) now follows from Claims 3.1, 3.2 and Lemma 3.7.
$(m-1)$
-equivalence in equation (3.11) now follows from Claims 3.1, 3.2 and Lemma 3.7.
The diagrammatic homological
![]() $(m-1)$
-equivalence in equation (3.12) follows from the commutativity of the following diagrams of maps.
$(m-1)$
-equivalence in equation (3.12) follows from the commutativity of the following diagrams of maps.
For each pair
![]() $J',J" \subset J$
, with
$J',J" \subset J$
, with
![]() $J' \subset J"$
, we have the following commutative diagram, where the vertical arrows are inclusions and the slanted arrows induce isomorphisms in the homology groups up to dimension
$J' \subset J"$
, we have the following commutative diagram, where the vertical arrows are inclusions and the slanted arrows induce isomorphisms in the homology groups up to dimension
![]() $m-1$
.
$m-1$
.

This implies that we have the following diagram of morphisms where both arrows are homological
![]() $(m-1)$
-equivalences:
$(m-1)$
-equivalences:

This proves that the diagrams
and
are homologically
![]() $(m-1)$
-equivalent.
$(m-1)$
-equivalent.
We now proceed to prove Claims 3.1 and 3.2.
Proof of Claim 3.1.
Let
![]() $t \in |\Delta (\mathbf {P}_{m,i}(\Phi ))|$
. Then there exists a unique simplex
$t \in |\Delta (\mathbf {P}_{m,i}(\Phi ))|$
. Then there exists a unique simplex
![]() $\sigma $
of the simplicial complex
$\sigma $
of the simplicial complex
![]() $\Delta (\mathbf {P}_{m,i}(\Phi ))$
of the smallest possible dimension such that
$\Delta (\mathbf {P}_{m,i}(\Phi ))$
of the smallest possible dimension such that
![]() $t \in |\sigma |$
. Let
$t \in |\sigma |$
. Let
![]() $\alpha _0 \prec \cdots \prec \alpha _p$
be the chain in
$\alpha _0 \prec \cdots \prec \alpha _p$
be the chain in
![]() $\mathbf {P}_{m,i}(\Phi )$
corresponding to
$\mathbf {P}_{m,i}(\Phi )$
corresponding to
![]() $\sigma $
. Then,
$\sigma $
. Then,
It is clear from its definition that
![]() $D^{\prime }_{m,i}(\Phi )(\alpha )$
is homologically
$D^{\prime }_{m,i}(\Phi )(\alpha )$
is homologically
![]() $\ell $
-connected. From Lemma 3.6, it follows that so is
$\ell $
-connected. From Lemma 3.6, it follows that so is
![]() $D_{m,i}(\Phi )(\alpha )$
. It now follows from the homological version of the Vietoris–Begle theorem (see Remark 2.3) that
$D_{m,i}(\Phi )(\alpha )$
. It now follows from the homological version of the Vietoris–Begle theorem (see Remark 2.3) that
![]() $\pi ^{D_{m,i}(\Phi )}_1$
is a homological
$\pi ^{D_{m,i}(\Phi )}_1$
is a homological
![]() $\ell $
-equivalence.
$\ell $
-equivalence.
Proof of Claim 3.2.
The claim will follow from the following claims. Let
We will prove that the fiber
![]() $(F_{m,i}(\Phi ))^{-1}(x)$
is homologically
$(F_{m,i}(\Phi ))^{-1}(x)$
is homologically
![]() $(m-1)$
-connected which will suffice to prove that
$(m-1)$
-connected which will suffice to prove that
![]() $F_{m,i}(\Phi )$
is a homological
$F_{m,i}(\Phi )$
is a homological
![]() $(m-1)$
-equivalence by the homological version of Vietoris–Begle theorem (see Remark 2.3).
$(m-1)$
-equivalence by the homological version of Vietoris–Begle theorem (see Remark 2.3).
In order to study the fiber
![]() $(F_{m,i}(\Phi ))^{-1}(x)$
, we define for each
$(F_{m,i}(\Phi ))^{-1}(x)$
, we define for each
![]() $I \subset _{\leq m+2} J$
the following posets of
$I \subset _{\leq m+2} J$
the following posets of
![]() $\mathbf {P}_{m,i}(\Phi )$
.
$\mathbf {P}_{m,i}(\Phi )$
.
We define
 $$ \begin{align*} \mathbf{P}_I(x) &= \{(I,\alpha) \in \{I\} \times \mathbf{P}_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J}) \mid \\ & x \in \lim_{\bar{\varepsilon}} D_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J})(\alpha)\} \subset \mathbf{P}_{m,i}(\Phi), \end{align*} $$
$$ \begin{align*} \mathbf{P}_I(x) &= \{(I,\alpha) \in \{I\} \times \mathbf{P}_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J}) \mid \\ & x \in \lim_{\bar{\varepsilon}} D_{m-\mathrm{card}(I)+1,i+1}(\Phi_{m,i,I,J})(\alpha)\} \subset \mathbf{P}_{m,i}(\Phi), \end{align*} $$
and
The motivation behind the definition of the posets
![]() $\mathbf {P}_I(x), \mathbf {Q}_I(x)$
is as follows. First, observe that
$\mathbf {P}_I(x), \mathbf {Q}_I(x)$
is as follows. First, observe that
 $$ \begin{align} (F_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J} \Delta(\mathbf{Q}_{\{j\}}(x))\right|, \end{align} $$
$$ \begin{align} (F_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J} \Delta(\mathbf{Q}_{\{j\}}(x))\right|, \end{align} $$
and
 $$ \begin{align} \bigcap_{j \in I} \mathbf{Q}_{\{j\}}(x) = \mathbf{Q}_I(x). \end{align} $$
$$ \begin{align} \bigcap_{j \in I} \mathbf{Q}_{\{j\}}(x) = \mathbf{Q}_I(x). \end{align} $$
Our strategy for proving the homological
![]() $(m-1)$
-connectedness of
$(m-1)$
-connectedness of
![]() $(F_{m,i}(\Phi ))^{-1}(x)$
is to use the closed covering provided by equation (3.23) and then use the cohomological Mayer–Vietoris spectral sequence to reduce the problem to studying the connectivity of the various
$(F_{m,i}(\Phi ))^{-1}(x)$
is to use the closed covering provided by equation (3.23) and then use the cohomological Mayer–Vietoris spectral sequence to reduce the problem to studying the connectivity of the various
![]() $\left |\Delta (\mathbf {Q}_I(x))\right |$
using equation (3.24). Finally, we prove (see Claim 3.5) that, for each I,
$\left |\Delta (\mathbf {Q}_I(x))\right |$
using equation (3.24). Finally, we prove (see Claim 3.5) that, for each I,
![]() $|\Delta (\mathbf {P}_I(x))|$
is homologically equivalent to
$|\Delta (\mathbf {P}_I(x))|$
is homologically equivalent to
![]() $|\Delta (\mathbf {Q}_I(x))|$
. This last fact allows us to use induction on the cardinality of I to prove the required connectivity statement for the corresponding
$|\Delta (\mathbf {Q}_I(x))|$
. This last fact allows us to use induction on the cardinality of I to prove the required connectivity statement for the corresponding
![]() $|\Delta (\mathbf {Q}_I(x))|$
.
$|\Delta (\mathbf {Q}_I(x))|$
.
We now return to the proof of Claim 3.2. Since, for each
![]() $I'$
, with
$I'$
, with
![]() $I \subset I' \subset _{\leq m+2} J$
,
$I \subset I' \subset _{\leq m+2} J$
,
there is an injective map,
Thus, there is a map
defined by
for each
![]() $(I',\alpha ) \in \mathbf {Q}_I(x),$
where
$(I',\alpha ) \in \mathbf {Q}_I(x),$
where
![]() $I \subset I' \subset _{\leq m+2} J$
.
$I \subset I' \subset _{\leq m+2} J$
.
It is obvious from the above definition and the definition of the partial order in
![]() $\mathbf {P}_{m,i}(\Phi )$
, that the map
$\mathbf {P}_{m,i}(\Phi )$
, that the map
![]() $\theta _I(x)$
is a map of posets (i.e., a map respecting the partial orders of the two posets).
$\theta _I(x)$
is a map of posets (i.e., a map respecting the partial orders of the two posets).
Claim 3.3. The map
![]() $\theta _I(x)$
induces a simplicial map
$\theta _I(x)$
induces a simplicial map
![]() $\Theta _I(x): \Delta (\mathbf {Q}_I(x))\rightarrow \Delta (\mathbf {P}_I(x))$
. Moreover, the corresponding map
$\Theta _I(x): \Delta (\mathbf {Q}_I(x))\rightarrow \Delta (\mathbf {P}_I(x))$
. Moreover, the corresponding map
![]() $|\Theta _I(x)| : |\Delta (\mathbf {Q}_I(x))| \rightarrow |\Delta (\mathbf {P}_I(x))|$
, between the geometric realizations, is a homological equivalence.
$|\Theta _I(x)| : |\Delta (\mathbf {Q}_I(x))| \rightarrow |\Delta (\mathbf {P}_I(x))|$
, between the geometric realizations, is a homological equivalence.
Proof. Since the map
![]() $\theta _i(x)$
is a poset map, it carries a chain of
$\theta _i(x)$
is a poset map, it carries a chain of
![]() $\mathbf {Q}_I(x)$
to a chain of
$\mathbf {Q}_I(x)$
to a chain of
![]() $\mathbf {P}_I(x)$
. This implies that
$\mathbf {P}_I(x)$
. This implies that
![]() $\theta _I(x)$
induces a simplicial map
$\theta _I(x)$
induces a simplicial map
![]() $\Theta _I(x): \Delta (\mathbf {Q}_I(x))\rightarrow \Delta (\mathbf {P}_I(x))$
.
$\Theta _I(x): \Delta (\mathbf {Q}_I(x))\rightarrow \Delta (\mathbf {P}_I(x))$
.
We now prove the second half of the claim. We are going to use the poset fiber theorem proved in [Reference Sturmfels and Ziegler23, Lemma 3.2] (also [Reference Björner, Wachs and Welker8, Corollary 3.4]).
For
![]() $n \geq 0$
, we denote by
$n \geq 0$
, we denote by
![]() $\mathcal {B}_n$
the complete Boolean lattice on a set with n elements. It is a well-known fact (see, for example, [Reference Wachs27]) that
$\mathcal {B}_n$
the complete Boolean lattice on a set with n elements. It is a well-known fact (see, for example, [Reference Wachs27]) that
![]() $|\Delta (\mathcal {B}_n)|$
is homeomorphic to
$|\Delta (\mathcal {B}_n)|$
is homeomorphic to
![]() $[0,1]^n$
and is thus contractible.
$[0,1]^n$
and is thus contractible.
Let
![]() $(I,\alpha ) \in \mathbf {P}_I(x)$
, and
$(I,\alpha ) \in \mathbf {P}_I(x)$
, and
![]() $I' \subset _{\leq m+2} J$
be the unique maximal subset of J such that
$I' \subset _{\leq m+2} J$
be the unique maximal subset of J such that
![]() $(I', \alpha ) \in \mathbf {P}_{I'}(x)$
(see the schematic diagram in Figure 8 which depicts a subposet of the poset shown in Figure 4).
$(I', \alpha ) \in \mathbf {P}_{I'}(x)$
(see the schematic diagram in Figure 8 which depicts a subposet of the poset shown in Figure 4).

Figure 8
![]() $\theta _I(x)^{-1}((I,\alpha ))$
with
$\theta _I(x)^{-1}((I,\alpha ))$
with
![]() $I = \{1,2\}$
and
$I = \{1,2\}$
and
![]() $I' = \{1,2,3, 4\}$
.
$I' = \{1,2,3, 4\}$
.
Then,
Hence, the poset
![]() $\theta _I(x)^{-1}((I,\alpha ))$
is isomorphic as a poset to
$\theta _I(x)^{-1}((I,\alpha ))$
is isomorphic as a poset to
![]() $\mathcal {B}_{\mathrm {card}(I') - \mathrm {card}(I)}$
. Thus,
$\mathcal {B}_{\mathrm {card}(I') - \mathrm {card}(I)}$
. Thus,
![]() $|\Delta (\theta _I(x)^{-1}((I,\alpha )))|$
is contractible.
$|\Delta (\theta _I(x)^{-1}((I,\alpha )))|$
is contractible.
Moreover, for each
![]() $(I",\alpha ) \in \theta _I(x)^{-1}((I,\alpha ))$
,
$(I",\alpha ) \in \theta _I(x)^{-1}((I,\alpha ))$
,
and hence
![]() $\theta _I(x)^{-1}((I,\alpha ))_{\succ (I",\alpha )}$
is isomorphic to
$\theta _I(x)^{-1}((I,\alpha ))_{\succ (I",\alpha )}$
is isomorphic to
![]() $\mathcal {B}_{\mathrm {card}(I") - \mathrm {card}(I)}$
. This proves that
$\mathcal {B}_{\mathrm {card}(I") - \mathrm {card}(I)}$
. This proves that
![]() $|\Delta (\theta _I(x)^{-1}((I,\alpha ))_{\succ (I",\alpha )})|$
is contractible for each
$|\Delta (\theta _I(x)^{-1}((I,\alpha ))_{\succ (I",\alpha )})|$
is contractible for each
![]() $(I",\alpha ) \in \theta _I(x)^{-1}((I,\alpha ))$
.
$(I",\alpha ) \in \theta _I(x)^{-1}((I,\alpha ))$
.
It now follows from the poset fiber theorem [Reference Sturmfels and Ziegler23, Lemma 3.2] (also [Reference Björner, Wachs and Welker8, Corollary 3.4]) that the poset map
![]() $\theta _I(x)$
induces a homological equivalence
$\theta _I(x)$
induces a homological equivalence
![]() $|\Theta _I(x)| : |\Delta (\mathbf {Q}_I(x))| \rightarrow |\Delta (\mathbf {P}_I(x))|$
.
$|\Theta _I(x)| : |\Delta (\mathbf {Q}_I(x))| \rightarrow |\Delta (\mathbf {P}_I(x))|$
.
Observe that Claim 3.3 implies in particular that if
![]() $\mathrm {card}(I) = 1$
, then
$\mathrm {card}(I) = 1$
, then
![]() $|\mathbf {Q}_I(x)|$
is contractible if nonempty.
$|\mathbf {Q}_I(x)|$
is contractible if nonempty.
Claim 3.4. For
![]() $ x \in \mathrm {ext}({\mathcal R}(\Phi ,\overline {B_k(0,R)})^{J"},\mathrm {R}_i) = \lim _{\bar {\varepsilon }}\bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} D_{m,i}(\Phi )(\alpha ), $
$ x \in \mathrm {ext}({\mathcal R}(\Phi ,\overline {B_k(0,R)})^{J"},\mathrm {R}_i) = \lim _{\bar {\varepsilon }}\bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} D_{m,i}(\Phi )(\alpha ), $
 $$ \begin{align} \mathrm{H}^j((F_{m,i}(\Phi))^{-1}(x)) &\cong \mathbb{Z}, \mbox{ for } j =0,\\ \nonumber &= 0, \mbox{ for } 0 < j \leq m. \end{align} $$
$$ \begin{align} \mathrm{H}^j((F_{m,i}(\Phi))^{-1}(x)) &\cong \mathbb{Z}, \mbox{ for } j =0,\\ \nonumber &= 0, \mbox{ for } 0 < j \leq m. \end{align} $$
Proof. The proof is by induction on m starting with the case
![]() $m=0$
. The case
$m=0$
. The case
![]() $m=-1$
is trivial.
$m=-1$
is trivial.
Base case (
![]() $m=0$
). We need to show that, for
$m=0$
). We need to show that, for
 $$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},\mathrm{R}_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{0,i}(\Phi)} D_{0,i}(\Phi)(\alpha), \end{align*}$$
$$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},\mathrm{R}_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{0,i}(\Phi)} D_{0,i}(\Phi)(\alpha), \end{align*}$$
![]() $(F_{0,i}(\Phi ))^{-1}(x)$
is connected.
$(F_{0,i}(\Phi ))^{-1}(x)$
is connected.
First, note that
and
![]() $r_{0,i}(\Phi )$
is a semialgebraic deformation retraction. Hence,
$r_{0,i}(\Phi )$
is a semialgebraic deformation retraction. Hence,
![]() $r_{0,i}(\Phi )^{-1}(x)$
is closed and semialgebraically connected (in fact contractible).
$r_{0,i}(\Phi )^{-1}(x)$
is closed and semialgebraically connected (in fact contractible).
Let
![]() $J(x) = \{j \in J \mid D_{0,i}(\Phi )((\{j\},\emptyset )) \cap r_{0,i}(\Phi )^{-1}(x) \neq \emptyset \}$
. Since the sets
$J(x) = \{j \in J \mid D_{0,i}(\Phi )((\{j\},\emptyset )) \cap r_{0,i}(\Phi )^{-1}(x) \neq \emptyset \}$
. Since the sets
![]() $D_{0,i}(\Phi )((\{j\},\emptyset )), j \in J(x)$
is a covering of the closed and semialgebraically connected set
$D_{0,i}(\Phi )((\{j\},\emptyset )), j \in J(x)$
is a covering of the closed and semialgebraically connected set
![]() $r_{0,i}(\Phi )^{-1}(x)$
by closed sets, it follows that the union
$r_{0,i}(\Phi )^{-1}(x)$
by closed sets, it follows that the union
 $$\begin{align*}\bigcup_{j \in J(x)} D_{0,i}(\Phi)((\{j\},\emptyset)) \end{align*}$$
$$\begin{align*}\bigcup_{j \in J(x)} D_{0,i}(\Phi)((\{j\},\emptyset)) \end{align*}$$
is semialgebraically connected as well. It follows that, given any
![]() $j,j' \in J(x)$
, there exists a sequence
$j,j' \in J(x)$
, there exists a sequence
![]() $j=j_0,j_1,\ldots ,j_N = j'$
such that, for each
$j=j_0,j_1,\ldots ,j_N = j'$
such that, for each
![]() $h, 0 \leq h \leq N-1$
,
$h, 0 \leq h \leq N-1$
,
So there exists for each
![]() $h, 0 \leq h \leq N-1$
$h, 0 \leq h \leq N-1$
![]() $j" = (\{j_h,j_{h+1}\},p) \in J_{0,i,\{j_h,j_{h+1}\},\Phi }$
such that
$j" = (\{j_h,j_{h+1}\},p) \in J_{0,i,\{j_h,j_{h+1}\},\Phi }$
such that
So there exists
![]() $\alpha = (\{j"\},\emptyset ) \in \mathbf {P}_{-1,i+1}(\Phi _{\{j_h,_{h+1}\}})$
such that
$\alpha = (\{j"\},\emptyset ) \in \mathbf {P}_{-1,i+1}(\Phi _{\{j_h,_{h+1}\}})$
such that
and so
Moreover,
(using Lemma 3.4). This implies that
![]() $(\{j_h\},\emptyset ), (\{j_{h+1}\},\emptyset )$
, and thus every pair of the form
$(\{j_h\},\emptyset ), (\{j_{h+1}\},\emptyset )$
, and thus every pair of the form
![]() $(\{j\},\emptyset ), (\{j'\},\emptyset )$
in
$(\{j\},\emptyset ), (\{j'\},\emptyset )$
in
![]() $(F_{0,i}(\Phi ))^{-1}(x)$
belongs to the same connected component of
$(F_{0,i}(\Phi ))^{-1}(x)$
belongs to the same connected component of
![]() $(F_{0,i}(\Phi ))^{-1}(x)$
. Since, for every element of the form
$(F_{0,i}(\Phi ))^{-1}(x)$
. Since, for every element of the form
![]() $(\{j_h,j_{h+1}\},\alpha ) \in (F_{0,i}(\Phi ))^{-1}(x)$
, we have
$(\{j_h,j_{h+1}\},\alpha ) \in (F_{0,i}(\Phi ))^{-1}(x)$
, we have
![]() $(\{j_h,j_{h+1}\},\alpha )$
belong to the same connected component of
$(\{j_h,j_{h+1}\},\alpha )$
belong to the same connected component of
![]() $(F_{0,i}(\Phi ))^{-1}(x)$
as
$(F_{0,i}(\Phi ))^{-1}(x)$
as
as well. Together, these facts imply that
![]() $(F_{0,i}(\Phi ))^{-1}(x)$
is connected. This proves the claim in the base case.
$(F_{0,i}(\Phi ))^{-1}(x)$
is connected. This proves the claim in the base case.
Inductive step. Suppose we have proved the theorem for all
![]() $m', 0 \leq m' < m$
,
$m', 0 \leq m' < m$
,
![]() $i \geq 0$
, all finite
$i \geq 0$
, all finite
![]() $J'$
, and
$J'$
, and
![]() $\Phi ' \in (\mathcal {F}_{k,\mathrm {R}_i})^{J'}$
. We now prove it for
$\Phi ' \in (\mathcal {F}_{k,\mathrm {R}_i})^{J'}$
. We now prove it for
![]() $m,i,J,\Phi $
.
$m,i,J,\Phi $
.
 $$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},R_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha). \end{align*}$$
$$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},R_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha). \end{align*}$$
Recall from equation (3.23) that
 $$\begin{align*}(F_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J} \Delta(\mathbf{Q}_{\{j\}}(x))\right|. \end{align*}$$
$$\begin{align*}(F_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J} \Delta(\mathbf{Q}_{\{j\}}(x))\right|. \end{align*}$$
Let
So
 $$\begin{align*}(F_{m,i}(\Phi))^{-1}(x) = |\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))|. \end{align*}$$
$$\begin{align*}(F_{m,i}(\Phi))^{-1}(x) = |\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))|. \end{align*}$$
It follows from the Mayer–Vietoris exact sequence in cohomology for closed subspaces (see, for example, [Reference Iversen17, page 148]) that there exists a spectral sequence
 $$\begin{align*}E_r^{p,q} \Rightarrow \mathrm{H}^{p+q}\left(\left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right) \end{align*}$$
$$\begin{align*}E_r^{p,q} \Rightarrow \mathrm{H}^{p+q}\left(\left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right) \end{align*}$$
whose
![]() $E_1$
term is given by
$E_1$
term is given by
 $$\begin{align*}E_1^{p,q} = \bigoplus_{I \subset J', \mathrm{card}(I) = p+1} \mathrm{H}^q\left(\left|\bigcap_{j \in I} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right). \end{align*}$$
$$\begin{align*}E_1^{p,q} = \bigoplus_{I \subset J', \mathrm{card}(I) = p+1} \mathrm{H}^q\left(\left|\bigcap_{j \in I} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right). \end{align*}$$
Notice that
 $$\begin{align*}\bigcap_{j \in I} \mathbf{Q}_{\{j\}}(x) = \mathbf{Q}_I(x), \end{align*}$$
$$\begin{align*}\bigcap_{j \in I} \mathbf{Q}_{\{j\}}(x) = \mathbf{Q}_I(x), \end{align*}$$
and it follows from Claim 3.3 that
![]() $ |\Delta (\mathbf {Q}_I(x))| $
is homotopy equivalent to
$ |\Delta (\mathbf {Q}_I(x))| $
is homotopy equivalent to
![]() $ |\Delta (\mathbf {P}_I(x))| $
.
$ |\Delta (\mathbf {P}_I(x))| $
.
So we get
Now, for I, with
![]() $\mathrm {card}(I)> 1$
, we can apply the induction hypothesis to deduce that
$\mathrm {card}(I)> 1$
, we can apply the induction hypothesis to deduce that
 $$ \begin{align*} \mathrm{H}^j(|\Delta(\mathbf{P}_I(x))|) &\cong \mathbb{Z}, \mbox{ for } j =0, \\ &= 0, \mbox{ for } 0 < j \leq m -\mathrm{card}(I)+1. \end{align*} $$
$$ \begin{align*} \mathrm{H}^j(|\Delta(\mathbf{P}_I(x))|) &\cong \mathbb{Z}, \mbox{ for } j =0, \\ &= 0, \mbox{ for } 0 < j \leq m -\mathrm{card}(I)+1. \end{align*} $$
We can deduce from this that
 $$ \begin{align*} E_1^{p,0} &\cong \bigoplus_{I \subset J', \mathrm{card}(I) = p+1} \mathbb{Z}, \\ E_1^{p,q} & \cong 0, \mbox{ for } 0 < q \leq m - p. \end{align*} $$
$$ \begin{align*} E_1^{p,0} &\cong \bigoplus_{I \subset J', \mathrm{card}(I) = p+1} \mathbb{Z}, \\ E_1^{p,q} & \cong 0, \mbox{ for } 0 < q \leq m - p. \end{align*} $$
It follows that
 $$ \begin{align*} E_2^{0,0} &\cong \mathbb{Z}, \\ E_2^{p,0} &\cong 0, p> 0 \\ E_2^{p,q} & \cong 0, \mbox{ for } p \geq 0, 0 < q \leq m-p.\\[-38pt] \end{align*} $$
$$ \begin{align*} E_2^{0,0} &\cong \mathbb{Z}, \\ E_2^{p,0} &\cong 0, p> 0 \\ E_2^{p,q} & \cong 0, \mbox{ for } p \geq 0, 0 < q \leq m-p.\\[-38pt] \end{align*} $$
Note that it follows from Claim 3.5 and the Mayer–Vietoris spectral sequence argument used in its proof that for any
 $$ \begin{align} \mathrm{H}^j\left(\left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right) &\cong \mathbb{Z}, \mbox{ for } j =0,\\ \nonumber &= 0, \mbox{ for } 0 < j \leq m. \end{align} $$
$$ \begin{align} \mathrm{H}^j\left(\left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|\right) &\cong \mathbb{Z}, \mbox{ for } j =0,\\ \nonumber &= 0, \mbox{ for } 0 < j \leq m. \end{align} $$
Claim 3.5. For
 $$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},\mathrm{R}_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha), \end{align*}$$
$$\begin{align*}x \in \mathrm{ext}({\mathcal R}(\Phi,\overline{B_k(0,R)})^{J},\mathrm{R}_i) = \lim_{\bar{\varepsilon}}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} D_{m,i}(\Phi)(\alpha), \end{align*}$$
![]() $(F_{m,i}(\Phi ))^{-1}(x)$
is homologically
$(F_{m,i}(\Phi ))^{-1}(x)$
is homologically
![]() $(m-1)$
-connected.
$(m-1)$
-connected.
Proof. Let
![]() $X=F_{m,i}(\Phi )^{-1}(x)$
. It follows from [Reference Spanier22, Theorem 12, page 248] that there exists a short exact sequence:
$X=F_{m,i}(\Phi )^{-1}(x)$
. It follows from [Reference Spanier22, Theorem 12, page 248] that there exists a short exact sequence:
Thus, for each
![]() $q>0$
$q>0$
implies that
![]() $\mathrm {H}_{q}((F_{m,i}(\Phi ))^{-1}(x)) = 0$
.
$\mathrm {H}_{q}((F_{m,i}(\Phi ))^{-1}(x)) = 0$
.
The claim now follows from equation (3.25).
Claim 3.2 now follows from Claim 3.5 and the homological version of the Vietoris-Begle theorem (see Remark 2.3).
This completes the proof of Theorem 2.
Proof of Theorem 2′ .
Since the proof closely mirrors that of the proof of Theorem 2, we only point out the places where it differs. For each
![]() $\alpha \in \mathbf {P}_{m,i}(\Phi )$
, we replace the infinitesimals
$\alpha \in \mathbf {P}_{m,i}(\Phi )$
, we replace the infinitesimals
![]() $\bar {{\varepsilon }}_0,\ldots ,\bar {{\varepsilon }}_m$
, by sequences of appropriately small enough positive elements
$\bar {{\varepsilon }}_0,\ldots ,\bar {{\varepsilon }}_m$
, by sequences of appropriately small enough positive elements
![]() $\bar {t}_0,\ldots ,\bar {t}_m$
of
$\bar {t}_0,\ldots ,\bar {t}_m$
of
![]() $ \mathbb {R}$
, in the formula defining the set
$ \mathbb {R}$
, in the formula defining the set
![]() $D_{m,i}(\Phi )(\alpha )$
and denote the set defined by the new formula (which are semialgebraic subset of
$D_{m,i}(\Phi )(\alpha )$
and denote the set defined by the new formula (which are semialgebraic subset of
![]() $\mathbb {R}^k$
) by
$\mathbb {R}^k$
) by
![]() $\widetilde {D}_{m,i}(\Phi )(\alpha )$
. Similarly, we will denote the retraction
$\widetilde {D}_{m,i}(\Phi )(\alpha )$
. Similarly, we will denote the retraction
 $$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} \widetilde{D}_{m,i}(\Phi)(\alpha) \rightarrow {\mathcal R}(\Phi, \overline{B_k(0,R)})^J \end{align*}$$
$$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} \widetilde{D}_{m,i}(\Phi)(\alpha) \rightarrow {\mathcal R}(\Phi, \overline{B_k(0,R)})^J \end{align*}$$
by
![]() $\widetilde {r}_{m,i}(\Phi )$
and the composition
$\widetilde {r}_{m,i}(\Phi )$
and the composition
by
![]() $\widetilde {F}_{m,i}(\Phi )$
.
$\widetilde {F}_{m,i}(\Phi )$
.
Claims 3.1 and 3.2 are replaced by:
Claim 3.1′.
The map
![]() $\pi _1^{\widetilde {D}_{m,i}(\Phi )}:\mathrm {hocolim}(\widetilde {D}_{m,i}(\Phi )) \rightarrow |\Delta (\mathbf {P}_{m,i}(\Phi ))| $
is an
$\pi _1^{\widetilde {D}_{m,i}(\Phi )}:\mathrm {hocolim}(\widetilde {D}_{m,i}(\Phi )) \rightarrow |\Delta (\mathbf {P}_{m,i}(\Phi ))| $
is an
![]() $\ell $
-equivalence (and so an
$\ell $
-equivalence (and so an
![]() $(m-1)$
-equivalence).
$(m-1)$
-equivalence).
Claim 3.2′.
The map
is an
![]() $(m-1)$
-equivalence.
$(m-1)$
-equivalence.
The proof of Claim 3.1′
is the same as the proof of Claim 3.1 replacing homologically
![]() $\ell $
-connected by just
$\ell $
-connected by just
![]() $\ell $
-connected and using the homotopy version of the Vietoris–Begle theorem (see Remark 2.3).
$\ell $
-connected and using the homotopy version of the Vietoris–Begle theorem (see Remark 2.3).
For the proof of Claim 3.2′
, we need an extra argument to deduce the
![]() $(m-1)$
-connectivity of the fibers of the map
$(m-1)$
-connectivity of the fibers of the map
![]() $\widetilde {F}_{m,i}(\Phi )$
from the fact that they are homologically
$\widetilde {F}_{m,i}(\Phi )$
from the fact that they are homologically
![]() $(m-1)$
-connected which is already proved in Claim 3.5. In order to do this, we apply Hurewicz’s isomorphism theorem which requires simple connectivity of the fibers
$(m-1)$
-connected which is already proved in Claim 3.5. In order to do this, we apply Hurewicz’s isomorphism theorem which requires simple connectivity of the fibers
![]() $(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
, which is the content of the following claim.
$(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
, which is the content of the following claim.
Claim 3.6. For
![]() $x \in {\mathcal R}(\Phi , \overline {B_k(0,R)})^J$
and
$x \in {\mathcal R}(\Phi , \overline {B_k(0,R)})^J$
and
![]() $m \geq 1$
,
$m \geq 1$
,
![]() $(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is simply connected. In other words,
$(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is simply connected. In other words,
![]() $(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is connected, and
$(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is connected, and
Proof. Let
So
 $$\begin{align*}(\widetilde{F}_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|. \end{align*}$$
$$\begin{align*}(\widetilde{F}_{m,i}(\Phi))^{-1}(x) = \left|\bigcup_{j \in J'} \Delta(\mathbf{Q}_{\{j\}}(x))\right|. \end{align*}$$
We prove the stronger statement that, for all nonempty subsets
![]() $J" \subset J'$
,
$J" \subset J'$
,
 $$\begin{align*}\left|\bigcup_{j \in J"} \Delta(\mathbf{Q}_{\{j\}}(x))\right| \end{align*}$$
$$\begin{align*}\left|\bigcup_{j \in J"} \Delta(\mathbf{Q}_{\{j\}}(x))\right| \end{align*}$$
is simply connected.
We argue using induction on
![]() $\mathrm {card}(J")$
. If
$\mathrm {card}(J")$
. If
![]() $\mathrm {card}(J") = 1$
, then
$\mathrm {card}(J") = 1$
, then
![]() $\Delta (\mathbf {Q}_{\{j\}}(x))$
, where
$\Delta (\mathbf {Q}_{\{j\}}(x))$
, where
![]() $J" = \{j\}$
, is a cone and so
$J" = \{j\}$
, is a cone and so
![]() $|\Delta (\mathbf {Q}_{\{j\}}(x))|$
is contractible and hence simply connected.
$|\Delta (\mathbf {Q}_{\{j\}}(x))|$
is contractible and hence simply connected.
Suppose we have already proved that the claim holds for all subsets of
![]() $J'$
of cardinality strictly smaller than that of
$J'$
of cardinality strictly smaller than that of
![]() $J"$
. Let
$J"$
. Let
![]() $j" \in J"$
. Then, by the induction hypothesis, we have that
$j" \in J"$
. Then, by the induction hypothesis, we have that
![]() $\left |\bigcup _{j' \in J" - \{j"\}} \Delta (\mathbf {Q}_{\{j'\}}(x))\right |$
is simply connected.
$\left |\bigcup _{j' \in J" - \{j"\}} \Delta (\mathbf {Q}_{\{j'\}}(x))\right |$
is simply connected.
We first show that
 $$\begin{align*}|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \left|\bigcup_{j' \in J" - \{j"\}} \Delta(\mathbf{Q}_{\{j'\}}(x))\right| \end{align*}$$
$$\begin{align*}|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \left|\bigcup_{j' \in J" - \{j"\}} \Delta(\mathbf{Q}_{\{j'\}}(x))\right| \end{align*}$$
is connected, which is equivalent to proving that
 $$\begin{align*}\mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \cong \mathbb{Z}. \end{align*}$$
$$\begin{align*}\mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \cong \mathbb{Z}. \end{align*}$$
The Mayer–Vietoris exact sequence in cohomology gives the following exact sequence:
 $$ \begin{align*} &\mathrm{H}^0(\bigcup_{j' \in J"} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))|) \oplus \mathrm{H}^0(\bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \\ &\qquad \mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \mathrm{H}^1(\bigcup_{j' \in J"} |\Delta(\mathbf{Q}_{\{j'\}}(x))|). \end{align*} $$
$$ \begin{align*} &\mathrm{H}^0(\bigcup_{j' \in J"} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))|) \oplus \mathrm{H}^0(\bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \\ &\qquad \mathrm{H}^0(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|) \rightarrow \mathrm{H}^1(\bigcup_{j' \in J"} |\Delta(\mathbf{Q}_{\{j'\}}(x))|). \end{align*} $$
Applying equation (3.26), we have an exact sequence
 $$\begin{align*}\mathbb{Z} \rightarrow \mathbb{Z}\oplus\mathbb{Z} \rightarrow \mathrm{H}^0\left(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|\right) \rightarrow 0, \end{align*}$$
$$\begin{align*}\mathbb{Z} \rightarrow \mathbb{Z}\oplus\mathbb{Z} \rightarrow \mathrm{H}^0\left(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|\right) \rightarrow 0, \end{align*}$$
where the first map is the diagonal embedding. This implies that
 $$\begin{align*}\mathrm{H}^0\left(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|\right) \cong \mathbb{Z}. \end{align*}$$
$$\begin{align*}\mathrm{H}^0\left(|\Delta(\mathbf{Q}_{\{j"\}}(x))| \cap \bigcup_{j' \in J" - \{j"\}} |\Delta(\mathbf{Q}_{\{j'\}}(x))|\right) \cong \mathbb{Z}. \end{align*}$$
Finally, using the fact that
![]() $|\Delta (\mathbf {Q}_{\{j"\}}(x))|$
is simply connected, it follows from the Seifert-van Kampen’s theorem [Reference Spanier22, page 151] that
$|\Delta (\mathbf {Q}_{\{j"\}}(x))|$
is simply connected, it follows from the Seifert-van Kampen’s theorem [Reference Spanier22, page 151] that
![]() $\left |\bigcup _{j \in J"} \Delta (\mathbf {Q}_{\{j\}}(x))\right |$
is simply connected.
$\left |\bigcup _{j \in J"} \Delta (\mathbf {Q}_{\{j\}}(x))\right |$
is simply connected.
We also have the obvious analog of Lemma 3.7.
Lemma 3.7′. The semialgebraic set
![]() ${\mathcal R}(\Phi ,\overline {B_k(0,R)})^J$
is a semialgebraic deformation retract of
${\mathcal R}(\Phi ,\overline {B_k(0,R)})^J$
is a semialgebraic deformation retract of
 $$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} \widetilde{D}_{m,i}(\Phi)(\alpha), \end{align*}$$
$$\begin{align*}\bigcup_{\alpha \in \mathbf{P}_{m,i}(\Phi)} \widetilde{D}_{m,i}(\Phi)(\alpha), \end{align*}$$
and hence
![]() ${\mathcal R}(\Phi ,\overline {B_k(0,R)})^J$
and
${\mathcal R}(\Phi ,\overline {B_k(0,R)})^J$
and
![]() $ \bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} \widetilde {D}_{m,i}(\Phi )(\alpha ) $
are semialgebraically homotopy equivalent.
$ \bigcup _{\alpha \in \mathbf {P}_{m,i}(\Phi )} \widetilde {D}_{m,i}(\Phi )(\alpha ) $
are semialgebraically homotopy equivalent.
Proof. Similar to the proof of Lemma 3.7 and omitted.
Proof of Claim 3.2′ .
It follows from Claim 3.5, Claim 3.6 and Hurewicz isomorphism theorem [Reference Spanier22, Theorem 5, page 398], that, for
and
![]() $m \geq 1$
,
$m \geq 1$
,
![]() $(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is
$(\widetilde {F}_{m,i}(\Phi ))^{-1}(x)$
is
![]() $(m-1)$
-connected. Claim 3.2′
now follows from the previous statement and the homotopy version of the Vietoris–Begle theorem (see Remark 2.3).
$(m-1)$
-connected. Claim 3.2′
now follows from the previous statement and the homotopy version of the Vietoris–Begle theorem (see Remark 2.3).
Finally, Theorem 2′ follows from Claims 3.1′ , 3.2′ and Lemma 3.7′ .
3.7 Upper bound on the size of the simplicial complex
 $\Delta (\mathbf {P}_{m,i}(\Phi ))$
$\Delta (\mathbf {P}_{m,i}(\Phi ))$
We now prove an upper bound on the size of the simplicial complex
![]() $\Delta (\mathbf {P}_{m,i}(\Phi ))$
assuming a ‘singly exponential’ upper bound on the function
$\Delta (\mathbf {P}_{m,i}(\Phi ))$
assuming a ‘singly exponential’ upper bound on the function
![]() $\mathcal {I}_{i,k}(\cdot )$
and
$\mathcal {I}_{i,k}(\cdot )$
and
![]() $\mathcal {C}_{i,k}(\cdot )$
.
$\mathcal {C}_{i,k}(\cdot )$
.
Definition 3.7. For any closed formula
![]() $\phi $
with coefficients in a real closed field
$\phi $
with coefficients in a real closed field
![]() $\mathrm {R}$
, let the size of
$\mathrm {R}$
, let the size of
![]() $\phi $
,
$\phi $
,
![]() $\mathbf {size}(\phi )$
be the product of the number of polynomials appearing in the formula
$\mathbf {size}(\phi )$
be the product of the number of polynomials appearing in the formula
![]() $\phi $
and the maximum amongst the degrees of these polynomials. Similarly, if J is any finite set and
$\phi $
and the maximum amongst the degrees of these polynomials. Similarly, if J is any finite set and
![]() $\Phi \in (\mathcal {F}_{\mathrm {R},k})^J$
, we denote by
$\Phi \in (\mathcal {F}_{\mathrm {R},k})^J$
, we denote by
![]() $\mathbf {size}(\Phi )$
the product of the total number of polynomials appearing in the formulas
$\mathbf {size}(\Phi )$
the product of the total number of polynomials appearing in the formulas
![]() $\Phi (j), j \in J$
, and the maximum amongst the degrees of these polynomials.
$\Phi (j), j \in J$
, and the maximum amongst the degrees of these polynomials.
Theorem 3. Suppose that there exists
![]() $c>0$
such that for each
$c>0$
such that for each
![]() $\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
,
$\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
,
 $$ \begin{align}\nonumber \mathcal{I}_{i,k}(\phi) &\leq \left(\mathbf{size}(\phi)\right)^{k^c}, \\ \max_{j \in [\mathcal{I}_{i,k}(\phi)]} \mathbf{size}(\mathcal{C}_{i,k}(\phi) (j)) &\leq \left(\mathbf{size}(\phi)\right)^{k^c}. \end{align} $$
$$ \begin{align}\nonumber \mathcal{I}_{i,k}(\phi) &\leq \left(\mathbf{size}(\phi)\right)^{k^c}, \\ \max_{j \in [\mathcal{I}_{i,k}(\phi)]} \mathbf{size}(\mathcal{C}_{i,k}(\phi) (j)) &\leq \left(\mathbf{size}(\phi)\right)^{k^c}. \end{align} $$
Let J be a finite set and
![]() $\Phi \in \left (\mathcal {F}_{\mathrm {R}_i,k}\right )^J$
. Then the number of simplices in
$\Phi \in \left (\mathcal {F}_{\mathrm {R}_i,k}\right )^J$
. Then the number of simplices in
![]() $\Delta (\mathbf {P}_{m,i}(\Phi ))$
is bounded by
$\Delta (\mathbf {P}_{m,i}(\Phi ))$
is bounded by
where
Proof. Recall that the elements of
![]() $\mathbf {P}_{m,i}(\Phi )$
are finite tuples
$\mathbf {P}_{m,i}(\Phi )$
are finite tuples
where for each,
![]() $h, 0 \leq h\leq r$
,
$h, 0 \leq h\leq r$
,
![]() $I_h$
is a subset of a certain set
$I_h$
is a subset of a certain set
![]() $J_h$
defined in Section 3.3.3.
$J_h$
defined in Section 3.3.3.
We first bound the cardinalities of the various
![]() $J_{h}$
’s occurring in the sequence above.
$J_{h}$
’s occurring in the sequence above.
Claim 3.7. For any
![]() $i' \geq 0$
,
$i' \geq 0$
,
![]() $m' \geq -1$
, finite set
$m' \geq -1$
, finite set
![]() $J'$
,
$J'$
,
![]() $I' \subset _{m'+2} J'$
and
$I' \subset _{m'+2} J'$
and
![]() $\Phi ' \in (\mathcal {F}_{\mathrm {R}_{i'},k})^{J'}$
,
$\Phi ' \in (\mathcal {F}_{\mathrm {R}_{i'},k})^{J'}$
,
Proof of Claim 3.7.
Let for each fixed
![]() $i,k$
$i,k$
 $$\begin{align*}F(M',N',m',D') = \max_{\substack{J', \mathrm{card}(J') = N', \\ I' \subset_{m'+2} J', \mathrm{card}(I') = M',\\ \Phi' \in \mathcal{F}_{\mathrm{R}_i,k}, \mathbf{size}(\Phi') =D'}} \mathrm{card}(J^{\prime}_{m',i,I',\Phi'}). \end{align*}$$
$$\begin{align*}F(M',N',m',D') = \max_{\substack{J', \mathrm{card}(J') = N', \\ I' \subset_{m'+2} J', \mathrm{card}(I') = M',\\ \Phi' \in \mathcal{F}_{\mathrm{R}_i,k}, \mathbf{size}(\Phi') =D'}} \mathrm{card}(J^{\prime}_{m',i,I',\Phi'}). \end{align*}$$
Using equations (3.5) and (3.6) and equation (3.27), we obtain:
 $$ \begin{align*} F(m'+2,N',D') &\leq D^{\prime k^c}, \\ F(M',N,D') &\leq D^{\prime k^c} + (N'-M') F(M'+1,N',D'), \mbox{ for } 1 < M' < m'+2. \end{align*} $$
$$ \begin{align*} F(m'+2,N',D') &\leq D^{\prime k^c}, \\ F(M',N,D') &\leq D^{\prime k^c} + (N'-M') F(M'+1,N',D'), \mbox{ for } 1 < M' < m'+2. \end{align*} $$
It follows that
 $$ \begin{align*} F(M',N',D') &\leq D^{\prime k^c}(1 + N' + N^{\prime 2} +\cdots+ N^{\prime m'+2 - M'}) \\ &\leq D^{\prime k^c} N^{\prime m'+1} \mbox{ for } 1 < M' \leq m'+2. \end{align*} $$
$$ \begin{align*} F(M',N',D') &\leq D^{\prime k^c}(1 + N' + N^{\prime 2} +\cdots+ N^{\prime m'+2 - M'}) \\ &\leq D^{\prime k^c} N^{\prime m'+1} \mbox{ for } 1 < M' \leq m'+2. \end{align*} $$
The claim follows from the above inequality.
Claim 3.8. For
![]() $(I_0,\ldots ,I_r,\phi ) \in \mathbf {P}_{m,i}(\Phi )$
,
$(I_0,\ldots ,I_r,\phi ) \in \mathbf {P}_{m,i}(\Phi )$
,
![]() $r \leq m+1$
.
$r \leq m+1$
.
Proof of Claim 3.8.
The claim follows from the fact that
![]() $\mathrm {card}(I_0), \ldots ,\mathrm {card}(I_{r-1}) \geq 2$
, and hence it follows from equation (3.9) that
$\mathrm {card}(I_0), \ldots ,\mathrm {card}(I_{r-1}) \geq 2$
, and hence it follows from equation (3.9) that
 $$\begin{align*}2 r \leq \sum_{0 \leq j < r} \mathrm{card}(I_j) \leq m+ (r-1) + 2. \end{align*}$$
$$\begin{align*}2 r \leq \sum_{0 \leq j < r} \mathrm{card}(I_j) \leq m+ (r-1) + 2. \end{align*}$$
It follows that
Claim 3.9. For every tuple
![]() $(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
,
$(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
,
![]() $0 \leq h \leq r$
,
$0 \leq h \leq r$
,
 $$ \begin{align*} \mathbf{size}(\Phi_h(\alpha)) &\leq D^{k^{c h}}, \mbox{ for } \alpha \in J_h,\\ \mathrm{card}(J_{h}) &\leq N^{(m+1)^{h}} D^{(k(m+1))^{c h}}, \end{align*} $$
$$ \begin{align*} \mathbf{size}(\Phi_h(\alpha)) &\leq D^{k^{c h}}, \mbox{ for } \alpha \in J_h,\\ \mathrm{card}(J_{h}) &\leq N^{(m+1)^{h}} D^{(k(m+1))^{c h}}, \end{align*} $$
where
![]() $J_h,\Phi _h, 0 \leq j \leq r$
are defined in equation (3.8), and
$J_h,\Phi _h, 0 \leq j \leq r$
are defined in equation (3.8), and
![]() $N = \mathrm {card}(J)$
.
$N = \mathrm {card}(J)$
.
Proof of Claim 3.9.
The claim is obviously true for
![]() $h=0$
. Also, note that for each
$h=0$
. Also, note that for each
![]() $h, 0\leq h \leq r$
,
$h, 0\leq h \leq r$
,
The claim now follows by induction on h, using the inductive definitions of
![]() $J_h,\Phi _h$
(see equation (3.8)), equation (3.27) and Claim 3.7.
$J_h,\Phi _h$
(see equation (3.8)), equation (3.27) and Claim 3.7.
Claim 3.10.
Proof of Claim 3.10.
In order to bound the cardinality of
![]() $\mathbf {P}_{m,i}(\Phi )$
, we bound the number of possible choices of
$\mathbf {P}_{m,i}(\Phi )$
, we bound the number of possible choices of
![]() $I_0,\ldots ,I_r$
for
$I_0,\ldots ,I_r$
for
![]() $(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
.
$(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
.
It follows from equation (3.9) that, for each
![]() $h, 0 \leq h \leq r$
,
$h, 0 \leq h \leq r$
,
 $$ \begin{align*} \mathrm{card}(I_h) &\leq m - \sum_{t=0}^{h-1} \mathrm{card}(I_t) + h + 2 \\ &\leq m - 2h +h +2 \; (\mbox{since } \mathrm{card}(I_t) \geq 2, 0 \leq t < r) \\ &\leq m - h +2 \\ &\leq m+2. \end{align*} $$
$$ \begin{align*} \mathrm{card}(I_h) &\leq m - \sum_{t=0}^{h-1} \mathrm{card}(I_t) + h + 2 \\ &\leq m - 2h +h +2 \; (\mbox{since } \mathrm{card}(I_t) \geq 2, 0 \leq t < r) \\ &\leq m - h +2 \\ &\leq m+2. \end{align*} $$
Since by Claim 3.9 for
![]() $0 \leq h \leq r$
,
$0 \leq h \leq r$
,
the number of choices for
![]() $I_h$
is clearly bounded by
$I_h$
is clearly bounded by
 $$\begin{align*}\sum_{t=2}^{m+2} \binom{N^{(m+1)^{h}} D^{(k(m+1))^{c h}}}{h} \leq N^{m^{O(h)}} D^{k^{O(h)}}, \end{align*}$$
$$\begin{align*}\sum_{t=2}^{m+2} \binom{N^{(m+1)^{h}} D^{(k(m+1))^{c h}}}{h} \leq N^{m^{O(h)}} D^{k^{O(h)}}, \end{align*}$$
noting that
![]() $m \leq k$
. The above inequality, together with the fact that
$m \leq k$
. The above inequality, together with the fact that
![]() $r \leq m+1$
(by Claim 3.8), proves the claim.
$r \leq m+1$
(by Claim 3.8), proves the claim.
Claim 3.11. The length of any chain in
![]() $\mathbf {P}_{m,i}(\Phi )$
is bounded by
$\mathbf {P}_{m,i}(\Phi )$
is bounded by
![]() $2 m+2$
.
$2 m+2$
.
Proof of Claim 3.11.
Suppose that
![]() $\alpha = (I_0^{\alpha },\ldots ,I_{r_{\alpha }}^{\alpha },\emptyset ), \beta = (I_0^{\beta },\ldots , I_{r_{\beta }}^{\beta },\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
,
$\alpha = (I_0^{\alpha },\ldots ,I_{r_{\alpha }}^{\alpha },\emptyset ), \beta = (I_0^{\beta },\ldots , I_{r_{\beta }}^{\beta },\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
,
![]() $\beta \prec \alpha $
and
$\beta \prec \alpha $
and
![]() $\alpha \neq \beta $
.
$\alpha \neq \beta $
.
It follows from equation (3.10) that
In particular, this implies that
![]() $0 < \sum _{h=0}^{r_{\alpha }} \mathrm {card}(I_h^{\alpha }) < \sum _{h=0}^{r_{\beta }} \mathrm {card}(I_h^{\beta })$
. Since for any
$0 < \sum _{h=0}^{r_{\alpha }} \mathrm {card}(I_h^{\alpha }) < \sum _{h=0}^{r_{\beta }} \mathrm {card}(I_h^{\beta })$
. Since for any
![]() $(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
, we have that
$(I_0,\ldots ,I_r,\emptyset ) \in \mathbf {P}_{m,i}(\Phi )$
, we have that
and
it follows immediately that the length of a chain in
![]() $\mathbf {P}_{m,i}(\Phi )$
is bounded by
$\mathbf {P}_{m,i}(\Phi )$
is bounded by
![]() $2m+2$
.
$2m+2$
.
4 Simplicial replacement: algorithm
We begin with some mathematical and algorithmic preliminaries.
4.1 Mathematical preliminaries
4.1.1 Making closed
We need to take care of the following technical issue. The output of Algorithm 1 (covering by contractible sets) described below, consists of a tuple of formulas whose realizations are closed and semialgebraically contractible semialgebraic sets, but the formulas themselves need not be closed. However, in the recursive Algorithm 2 (computing the poset
![]() $\mathbf {P}_{m,i}(\Phi )$
) we need to assume that the input formulas are closed. We get around this problem by a construction which allows us to replace a formula (not necessarily closed) defining a closed and bounded semialgebraic set S by another closed formula defining a semialgebraic set
$\mathbf {P}_{m,i}(\Phi )$
) we need to assume that the input formulas are closed. We get around this problem by a construction which allows us to replace a formula (not necessarily closed) defining a closed and bounded semialgebraic set S by another closed formula defining a semialgebraic set
![]() $S'$
such that
$S'$
such that
![]() $S' \searrow S$
. The construction is quite similar (but not identical) to the one by Gabrielov and Vorobjov [Reference Gabrielov and Vorobjov15]. In the construction given in [Reference Gabrielov and Vorobjov15], the original set is not necessarily a deformation retract of the new one. By using the extra property that we assume, namely that the given set is closed (albeit without a closed description), we are able to ensure that it is a retract of the new one defined by a closed formula.
$S' \searrow S$
. The construction is quite similar (but not identical) to the one by Gabrielov and Vorobjov [Reference Gabrielov and Vorobjov15]. In the construction given in [Reference Gabrielov and Vorobjov15], the original set is not necessarily a deformation retract of the new one. By using the extra property that we assume, namely that the given set is closed (albeit without a closed description), we are able to ensure that it is a retract of the new one defined by a closed formula.
We remark here that the algorithmic problem of obtaining a closed description of a given closed semialgebraic set (described by a not formula which is not necessarily closed) is a difficult problem for which no algorithm with singly exponential complexity is known in general. We do not solve this general problem, because the closed description that we obtain does not describe the original set, but a closed (infinitesimal) neighborhood of it.
The key result of this section is Lemma 4.1.
Let
![]() $\mathcal {P} = \{P_1,\ldots ,P_s\} \subset \mathrm {R}[X_1,\ldots ,X_k]$
be a finite set of polynomials, and let
$\mathcal {P} = \{P_1,\ldots ,P_s\} \subset \mathrm {R}[X_1,\ldots ,X_k]$
be a finite set of polynomials, and let
![]() $B \subset \mathrm {R}^k$
a closed euclidean ball.
$B \subset \mathrm {R}^k$
a closed euclidean ball.
Notation 4.1. For
![]() $\sigma \in \{0,1,-1\}^{\mathcal {P}}$
, let
$\sigma \in \{0,1,-1\}^{\mathcal {P}}$
, let

Notation 4.2. For
![]() $c,d \in \mathrm {R}, 0< d < c$
, and
$c,d \in \mathrm {R}, 0< d < c$
, and
![]() $\sigma \in \{0,1,-1\}^{\mathcal {P}}$
, let
$\sigma \in \{0,1,-1\}^{\mathcal {P}}$
, let
![]() $\overline {\sigma }(c,d)$
denote the closed formula
$\overline {\sigma }(c,d)$
denote the closed formula
Notation 4.3. For a
![]() $\mathcal {P}$
-formula
$\mathcal {P}$
-formula
![]() $\phi $
, we denote
$\phi $
, we denote
 $$\begin{align*}\Sigma_{\phi} = \{ \sigma \in \{0,1,-1\}^{\mathcal{P}} \mid \left(\bigwedge_{P \in \mathcal{P}} (\mathrm{sign}(P) = \sigma(P))\right) \Rightarrow \phi \}, \end{align*}$$
$$\begin{align*}\Sigma_{\phi} = \{ \sigma \in \{0,1,-1\}^{\mathcal{P}} \mid \left(\bigwedge_{P \in \mathcal{P}} (\mathrm{sign}(P) = \sigma(P))\right) \Rightarrow \phi \}, \end{align*}$$
where ‘
![]() $\Rightarrow $
’ denotes logical implication.
$\Rightarrow $
’ denotes logical implication.
Let
denoting by
![]() $\bar \eta $
the sequence
$\bar \eta $
the sequence
![]() $\mu _s,\nu _s, \ldots , \mu _0, \nu _0$
.
$\mu _s,\nu _s, \ldots , \mu _0, \nu _0$
.
Notation 4.4. We denote
 $$\begin{align*}\mathcal{P}^*(\bar{\mu},\bar{\nu}) = \bigcup_{P \in \mathcal{P}} \bigcup_{j = 0}^{s} \{P \pm \mu_j, P\pm \nu_j\} \subset \mathrm{R}'[X_1,\ldots,X_k]. \end{align*}$$
$$\begin{align*}\mathcal{P}^*(\bar{\mu},\bar{\nu}) = \bigcup_{P \in \mathcal{P}} \bigcup_{j = 0}^{s} \{P \pm \mu_j, P\pm \nu_j\} \subset \mathrm{R}'[X_1,\ldots,X_k]. \end{align*}$$
Finally,

Notation 4.5. We denote by
![]() $\phi ^*(\bar {\mu },\bar {\nu })$
the
$\phi ^*(\bar {\mu },\bar {\nu })$
the
![]() $\mathcal {P}^*(\bar {\mu },\bar {\nu })$
-closed formula
$\mathcal {P}^*(\bar {\mu },\bar {\nu })$
-closed formula
 $$\begin{align*}\bigvee_{\sigma \in \Sigma_{\phi}} \overline{\sigma}(\mu_{\mathrm{level}(\sigma)},\nu_{\mathrm{level}(\sigma)}) \end{align*}$$
$$\begin{align*}\bigvee_{\sigma \in \Sigma_{\phi}} \overline{\sigma}(\mu_{\mathrm{level}(\sigma)},\nu_{\mathrm{level}(\sigma)}) \end{align*}$$
Following the notation introduced above, we have:
Lemma 4.1. Let
![]() $R> 0, B = \overline {B_k(0,R)}$
, and suppose that
$R> 0, B = \overline {B_k(0,R)}$
, and suppose that
![]() $S = {\mathcal R}(\phi ,B)$
is closed. Then,
$S = {\mathcal R}(\phi ,B)$
is closed. Then,
where
![]() $S' = {\mathcal R}(\phi ^*(\bar {\mu },\bar {\nu }),\mathrm {ext}(B,\mathrm {R}'))$
. In particular,
$S' = {\mathcal R}(\phi ^*(\bar {\mu },\bar {\nu }),\mathrm {ext}(B,\mathrm {R}'))$
. In particular,
![]() $\mathrm {ext}(S,\mathrm {R}')$
is a semialgebraic deformation retract of
$\mathrm {ext}(S,\mathrm {R}')$
is a semialgebraic deformation retract of
![]() $S'$
.
$S'$
.
Proof. See Appendix A.
Remark 4.1. It is necessary to use multiple infinitesimals in the construction given above. As a warning, consider the following example.
Example 4.1. Let
![]() $k=1,s=2, B = [-2,2]$
, and
$k=1,s=2, B = [-2,2]$
, and
 $$ \begin{align*} P_1 &= X^2(X-1), \\ P_2 &= X. \end{align*} $$
$$ \begin{align*} P_1 &= X^2(X-1), \\ P_2 &= X. \end{align*} $$
Let
![]() $\sigma _1,\sigma _2$
be defined by
$\sigma _1,\sigma _2$
be defined by
 $$ \begin{align*} \sigma_1(P_1) &=1, \sigma_1(P_2) = 1, \\ \sigma_2(P_1) &=0, \sigma_2(P_2) = 1. \end{align*} $$
$$ \begin{align*} \sigma_1(P_1) &=1, \sigma_1(P_2) = 1, \\ \sigma_2(P_1) &=0, \sigma_2(P_2) = 1. \end{align*} $$
Let
![]() $\phi $
be the unique formula such that
$\phi $
be the unique formula such that
![]() $\Sigma _{\phi } = \{\sigma _1,\sigma _2\}$
. Then,
$\Sigma _{\phi } = \{\sigma _1,\sigma _2\}$
. Then,
![]() ${\mathcal R}(\phi ,B) = [1,2]$
is a closed semialgebraic set, but
${\mathcal R}(\phi ,B) = [1,2]$
is a closed semialgebraic set, but
![]() $\phi $
is not a closed formula.
$\phi $
is not a closed formula.
However, if we take the closed formula
![]() $\phi ^*(\mu _0,\ldots ,\mu _0)$
(i.e., using only one infinitesimal), then
$\phi ^*(\mu _0,\ldots ,\mu _0)$
(i.e., using only one infinitesimal), then
However, it is easy to verify that
4.1.2 Strong general position
We need the following notion of ‘strong general position’ of a finite set of polynomials. It is a required property for the input to Algorithm 1.
Definition 4.1. Let
![]() $\mathcal {P} \subset \mathrm {R} [X_{1} , \ldots ,X_{k} ]$
be a finite set. We say that
$\mathcal {P} \subset \mathrm {R} [X_{1} , \ldots ,X_{k} ]$
be a finite set. We say that
![]() $\mathcal {P}$
is in
$\mathcal {P}$
is in
![]() $\ell $
-general position if no more than
$\ell $
-general position if no more than
![]() $\ell $
polynomials belonging to
$\ell $
polynomials belonging to
![]() $\mathcal {P}$
have a common zero in
$\mathcal {P}$
have a common zero in
![]() $\mathrm {R}^{k}$
. The set
$\mathrm {R}^{k}$
. The set
![]() $\mathcal {P}$
is in strong
$\mathcal {P}$
is in strong
![]() $\ell $
-general position if moreover any
$\ell $
-general position if moreover any
![]() $\ell $
polynomials belonging to
$\ell $
polynomials belonging to
![]() $\mathcal {P}$
have at most a finite number of common zeros in
$\mathcal {P}$
have at most a finite number of common zeros in
![]() $\mathrm {R}^{k}$
.
$\mathrm {R}^{k}$
.
Using the same notation as in Lemma 4.1, we have:
Lemma 4.2. The set
is in strong k-general position.
Proof. The claim follows easily from the fact that
![]() $\mu _0,\ldots ,\mu _s,\nu _0,\ldots ,\nu _s$
are algebraically independent over
$\mu _0,\ldots ,\mu _s,\nu _0,\ldots ,\nu _s$
are algebraically independent over
![]() $\mathrm {R}$
and semialgebraic Sard’s theorem [Reference Basu, Pollack and Roy4, Theorem 5.56].
$\mathrm {R}$
and semialgebraic Sard’s theorem [Reference Basu, Pollack and Roy4, Theorem 5.56].
We now describe some preliminary algorithms that we will need.
4.2 Algorithmic preliminaries
The following algorithm is described in [Reference Basu, Pollack and Roy4]. We briefly recall the input, output and complexity. We made a small and harmless modification to the input by requiring that the closed semialgebraic of which the covering is being computed is contained in the closed ball of radius R centered at the origin, rather than in the sphere of radius R. This is done to avoid complicating notation down the road and is not significant since the algorithm can be easily modified to accommodate this change without any change in the complexity estimates.
Remark 4.2. Note that the last claim in the complexity of Algorithm 1, namely that each polynomial appearing in any of the formulas
![]() $\theta _{\alpha }$
depends on at most
$\theta _{\alpha }$
depends on at most
![]() $m(k+1)^2$
of
$m(k+1)^2$
of
![]() ${\varepsilon }_i$
’s, and on at most one of the
${\varepsilon }_i$
’s, and on at most one of the
![]() $\zeta _i$
’s, does not appear explicitly in [Reference Basu, Pollack and Roy4] but is evident on a close examination of the algorithm. It is also reflected in the fact that the combinatorial part (i.e., the part depending on
$\zeta _i$
’s, does not appear explicitly in [Reference Basu, Pollack and Roy4] but is evident on a close examination of the algorithm. It is also reflected in the fact that the combinatorial part (i.e., the part depending on
![]() $\mathrm {card}(\mathcal {P})$
) of the complexity of Algorithm 16.14 in [Reference Basu, Pollack and Roy4] is bounded by
$\mathrm {card}(\mathcal {P})$
) of the complexity of Algorithm 16.14 in [Reference Basu, Pollack and Roy4] is bounded by
![]() $\mathrm {card}(\mathcal {P})^{(k+1)^2}$
. This is because the Algorithm 16.14 in [Reference Basu, Pollack and Roy4] has a ‘local property’, namely that all computations involve at most a small number (in this case
$\mathrm {card}(\mathcal {P})^{(k+1)^2}$
. This is because the Algorithm 16.14 in [Reference Basu, Pollack and Roy4] has a ‘local property’, namely that all computations involve at most a small number (in this case
![]() $(k+1)^2$
) polynomials in the input at a time.
$(k+1)^2$
) polynomials in the input at a time.
4.3 Algorithm for computing simplicial replacement
We now describe an algorithm that given a tuple of formula
![]() $\Phi $
and
$\Phi $
and
![]() $m,i \geq 0$
, computes the corresponding poset
$m,i \geq 0$
, computes the corresponding poset
![]() $\mathbf {P}_{m,i}(\Phi )$
, using Algorithm 1 to compute
$\mathbf {P}_{m,i}(\Phi )$
, using Algorithm 1 to compute
![]() $\mathcal {I}_{j,k}(\phi )$
and
$\mathcal {I}_{j,k}(\phi )$
and
![]() $\mathcal {C}_{j,k}(\phi )$
for different j and
$\mathcal {C}_{j,k}(\phi )$
for different j and
![]() $\phi $
which arise in the course of the execution of the algorithm.
$\phi $
which arise in the course of the execution of the algorithm.
Proof of correctness.
The algorithm follows Definition 3.3. The correctness of the algorithm follows from Lemma 4.1, Lemma 4.2 and the correctness of Algorithm 1.
Complexity analysis.
The bound on
![]() $\mathrm {card}(\mathbf {P}_{m,i}(\Phi ))$
is a consequence of Theorem 3. The complexity of the algorithm follows from the complexity of the Algorithm 1 and an argument as in the proof of Theorem 3.
$\mathrm {card}(\mathbf {P}_{m,i}(\Phi ))$
is a consequence of Theorem 3. The complexity of the algorithm follows from the complexity of the Algorithm 1 and an argument as in the proof of Theorem 3.
There is one additional point to note that in the recursive calls algorithm the arithmetic operations take place in a larger ring, namely -
![]() $\mathrm {D}[\bar {\varepsilon }_0,\ldots ,\bar {\varepsilon }_{m+2}]$
.
$\mathrm {D}[\bar {\varepsilon }_0,\ldots ,\bar {\varepsilon }_{m+2}]$
.
It follows from the complexity of Algorithm 1 that the number of different infinitesimals occurring in each polynomial that is computed in the course of Algorithm 2 is bounded by
![]() $k^{O(m)}$
, and these infinitesimals occur with degrees bounded by
$k^{O(m)}$
, and these infinitesimals occur with degrees bounded by
![]() $d^{k^{O(m)}}$
. Hence, each arithmetic operation involving the coefficients with these polynomials costs
$d^{k^{O(m)}}$
. Hence, each arithmetic operation involving the coefficients with these polynomials costs
![]() $\left (d^{k^{O(m)}}\right )^{k^{O(m)}} = d^{k^{O(m)}}$
arithmetic operations in the ring
$\left (d^{k^{O(m)}}\right )^{k^{O(m)}} = d^{k^{O(m)}}$
arithmetic operations in the ring
![]() $\mathrm {D}$
. This does not affect the asymptotics of the complexity, where we measure arithmetic operations in the ring
$\mathrm {D}$
. This does not affect the asymptotics of the complexity, where we measure arithmetic operations in the ring
![]() $\mathrm {D}$
.
$\mathrm {D}$
.
Remark 4.3. Suppose we define (following the same notation as in Properties 3.2 and 3.2′
and Algorithm 2) for
![]() $\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
,
$\phi \in \mathcal {F}_{\mathrm {R}_i,k}$
,
 $$ \begin{align*} \mathcal{I}_{i,k}(\phi) &= \mathrm{card}(I) -1, \\ \mathcal{C}_{i,k}(\phi) &= (\theta_{\alpha})_{\alpha \in I}, \end{align*} $$
$$ \begin{align*} \mathcal{I}_{i,k}(\phi) &= \mathrm{card}(I) -1, \\ \mathcal{C}_{i,k}(\phi) &= (\theta_{\alpha})_{\alpha \in I}, \end{align*} $$
where
![]() $(\theta _{\alpha })_{\alpha \in I}$
is the output of Algorithm 1 with input the set of polynomials appearing in the definition of
$(\theta _{\alpha })_{\alpha \in I}$
is the output of Algorithm 1 with input the set of polynomials appearing in the definition of
![]() $\phi ^*(\bar {\mu },\bar {\nu })$
(see Notation 4.5), the closed formula
$\phi ^*(\bar {\mu },\bar {\nu })$
(see Notation 4.5), the closed formula
![]() $\phi ^*(\bar {\mu },\bar {\nu })$
and R set to
$\phi ^*(\bar {\mu },\bar {\nu })$
and R set to
![]() $1/r$
(as in Line 10 of Algorithm 2).
$1/r$
(as in Line 10 of Algorithm 2).
Then it follows from the correctness of Algorithm 1 that (denoting by
![]() $\mathrm {R}_i = \mathrm {R}{\langle }\bar {{\varepsilon }}_0,\ldots ,\bar {{\varepsilon }}_i {\rangle }$
as in Algorithm 2) the tuple
$\mathrm {R}_i = \mathrm {R}{\langle }\bar {{\varepsilon }}_0,\ldots ,\bar {{\varepsilon }}_i {\rangle }$
as in Algorithm 2) the tuple
satisfies the homological
![]() $\ell $
-connectivity property over
$\ell $
-connectivity property over
![]() $\mathrm {R}$
(resp.
$\mathrm {R}$
(resp.
![]() $\ell $
-connectivity property if
$\ell $
-connectivity property if
![]() $\mathrm {R} = \mathbb {R}$
) for every
$\mathrm {R} = \mathbb {R}$
) for every
![]() $\ell \geq 0$
(see Property 3.2 and Property 3.2′
.
$\ell \geq 0$
(see Property 3.2 and Property 3.2′
.
Proof of correctness.
Observe that the image of the realization of each of the formulas
![]() $\phi _{i,j}$
obtained in Line 5 under the
$\phi _{i,j}$
obtained in Line 5 under the
![]() $\lim _{\bar \eta }$
map is contained in
$\lim _{\bar \eta }$
map is contained in
![]() $\overline {B_k(0,1/2\delta )}$
. This implies that the realization of each of the formulas
$\overline {B_k(0,1/2\delta )}$
. This implies that the realization of each of the formulas
![]() $\phi _{i,j}$
is contained in
$\phi _{i,j}$
is contained in
![]() $\overline {B_k(0,\delta )}$
. Thus, in the call to Algorithm 2 in Line 14, the input satisfies property (d) of the input specification of Algorithm 2 with
$\overline {B_k(0,\delta )}$
. Thus, in the call to Algorithm 2 in Line 14, the input satisfies property (d) of the input specification of Algorithm 2 with
![]() $r = \delta $
.
$r = \delta $
.
The correctness of the algorithm now follows from Lemma 4.1, Lemma 4.2, the correctness of Algorithm 2, Remark 4.3 and Theorems 2 and 2′ .
5 Future work and open problems
We conclude by stating some open problems and possible future directions of research in this area.
-
1. It is an interesting problem to try to make the poset
 $\mathbf {P}_{m,i}(\Phi )$
in Theorem 2 smaller in size and more efficiently computable. For instance, in Theorem 3 one should be able to improve the dependence on
$\mathbf {P}_{m,i}(\Phi )$
in Theorem 2 smaller in size and more efficiently computable. For instance, in Theorem 3 one should be able to improve the dependence on
 $\mathrm {card}(J)$
.
$\mathrm {card}(J)$
. -
2. There are some recent work in algorithmic semialgebraic geometry where algorithms have been developed for computing the first few Betti numbers of semialgebraic subsets of
 $\mathrm {R}^k$
having special properties. For example, in [Reference Basu and Riener6] the authors give an algorithm to compute the first
$\mathrm {R}^k$
having special properties. For example, in [Reference Basu and Riener6] the authors give an algorithm to compute the first
 $\ell $
Betti numbers of semialgebraic subsets of
$\ell $
Betti numbers of semialgebraic subsets of
 $\mathrm {R}^k$
defined by symmetric polynomials of degrees bounded by some constant d. The complexity of the algorithm is doubly exponential in both d and
$\mathrm {R}^k$
defined by symmetric polynomials of degrees bounded by some constant d. The complexity of the algorithm is doubly exponential in both d and
 $\ell $
(though polynomial in k for fixed d and
$\ell $
(though polynomial in k for fixed d and
 $\ell $
). This algorithm uses semialgebraic triangulations which leads to the doubly exponential complexity. It is an interesting problem to investigate whether applying the efficient simplicial replacement of the current paper the dependence on d and
$\ell $
). This algorithm uses semialgebraic triangulations which leads to the doubly exponential complexity. It is an interesting problem to investigate whether applying the efficient simplicial replacement of the current paper the dependence on d and
 $\ell $
can be improved.
$\ell $
can be improved.
A Proof of Lemma 4.1
Proof of Lemma 4.1.
We will denote for
![]() $0 \leq i \le s$
$0 \leq i \le s$
 $$ \begin{align*} \mathrm{R}_i' &= \mathrm{R}{\langle}\mu_s,\nu_s, \ldots, \mu_i{\rangle}, \\ \mathrm{R}_i &= \mathrm{R}{\langle}\mu_s,\nu_s, \ldots, \mu_i,\nu_i{\rangle}. \end{align*} $$
$$ \begin{align*} \mathrm{R}_i' &= \mathrm{R}{\langle}\mu_s,\nu_s, \ldots, \mu_i{\rangle}, \\ \mathrm{R}_i &= \mathrm{R}{\langle}\mu_s,\nu_s, \ldots, \mu_i,\nu_i{\rangle}. \end{align*} $$
Note that
For
![]() $0 \leq i \leq s$
, we define inductively:
$0 \leq i \leq s$
, we define inductively:
and for
![]() $i> 0$
,
$i> 0$
,
 $$ \begin{align*} S_i^- &= \lim_{\nu_i} S_i,\\ S_{i+1} &= \lim_{\mu_i} S_i \;\;(= \lim_{\mu_i} S_i^-). \end{align*} $$
$$ \begin{align*} S_i^- &= \lim_{\nu_i} S_i,\\ S_{i+1} &= \lim_{\mu_i} S_i \;\;(= \lim_{\mu_i} S_i^-). \end{align*} $$
The lemma will follow from the following two claims.
Claim A.1. For each
![]() $i, 0 \leq i \leq s$
,
$i, 0 \leq i \leq s$
,
Proof. Easy.
Claim A.2. For each
![]() $i, 0 \leq i \leq s$
,
$i, 0 \leq i \leq s$
,
Proof. We will prove that
which suffices to prove the claim.
It is obvious that
We now show that
Define,
 $$ \begin{align*} S_{i+1}^{(<i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) < i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})),\\ S_{i+1}^{(=i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) = i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})),\\ S_{i+1}^{(>i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) > i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})). \end{align*} $$
$$ \begin{align*} S_{i+1}^{(<i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) < i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})),\\ S_{i+1}^{(=i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) = i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})),\\ S_{i+1}^{(>i)} &= \bigcup_{\sigma \in \Sigma_{\phi}, \mathrm{level}(\sigma) > i}\lim_{\mu_i} {\mathcal R}(\overline{\sigma}, \mathrm{ ext}(B,\mathrm{R}_{i+1})). \end{align*} $$
It is easy to see that
 $$ \begin{align*} \mathrm{ext}(S_{i+1}^{(<i)}, \mathrm{R}_i') &\subset S_i^-, \\ \mathrm{ext}(S_{i+1}^{(>i)}, \mathrm{R}_i') &\subset S_i^-. \end{align*} $$
$$ \begin{align*} \mathrm{ext}(S_{i+1}^{(<i)}, \mathrm{R}_i') &\subset S_i^-, \\ \mathrm{ext}(S_{i+1}^{(>i)}, \mathrm{R}_i') &\subset S_i^-. \end{align*} $$
It remains to prove that
Let
![]() $\sigma \in \Sigma _{\phi }$
,
$\sigma \in \Sigma _{\phi }$
,
![]() $\mathrm {level}(\sigma ) = i$
and
$\mathrm {level}(\sigma ) = i$
and
![]() $x_0 \in \lim _{\mu _i} {\mathcal R}(\overline {\sigma }, \mathrm {ext}(B,\mathrm {R}_{i+1}))$
.
$x_0 \in \lim _{\mu _i} {\mathcal R}(\overline {\sigma }, \mathrm {ext}(B,\mathrm {R}_{i+1}))$
.
Let
![]() $\mathcal {P}_0 = \{P \in \mathcal {P} \mid \lim _{\mu _i} P(x_0) = 0\}$
. If
$\mathcal {P}_0 = \{P \in \mathcal {P} \mid \lim _{\mu _i} P(x_0) = 0\}$
. If
![]() $\mathrm {card}(\mathcal {P}_0) = i$
, then
$\mathrm {card}(\mathcal {P}_0) = i$
, then
![]() $x_0 \in S_i^-$
and we are done.
$x_0 \in S_i^-$
and we are done.
Otherwise,
![]() $\sigma _0 = \mathrm {sign}(\mathcal {P}(x_0)) \in \Sigma _{\phi }$
(using the fact that S is closed). Let
$\sigma _0 = \mathrm {sign}(\mathcal {P}(x_0)) \in \Sigma _{\phi }$
(using the fact that S is closed). Let
![]() $x_1 = \lim _{\mu _{\mathrm {level}(\sigma _0)}} x_0$
,
$x_1 = \lim _{\mu _{\mathrm {level}(\sigma _0)}} x_0$
,
![]() $\sigma _1 = \mathrm {sign}(\mathcal {P}(x_1))$
. If
$\sigma _1 = \mathrm {sign}(\mathcal {P}(x_1))$
. If
![]() $\sigma _1 \neq \sigma _0$
, then define
$\sigma _1 \neq \sigma _0$
, then define
![]() $x_2 = \lim _{\mu _{\mathrm {level}(\sigma _1)}} x_1$
. Continue in this way, and define
$x_2 = \lim _{\mu _{\mathrm {level}(\sigma _1)}} x_1$
. Continue in this way, and define
![]() $x_0,x_1,x_2, \ldots $
, till
$x_0,x_1,x_2, \ldots $
, till
![]() $\sigma _j = \sigma _{j+1}$
. Notice that
$\sigma _j = \sigma _{j+1}$
. Notice that
![]() $\sigma _0, \ldots ,\sigma _j \in \Sigma _{\phi }$
. Consider the point
$\sigma _0, \ldots ,\sigma _j \in \Sigma _{\phi }$
. Consider the point
![]() $x_j$
. Then,
$x_j$
. Then,
![]() $x_j = \lim _{\mu _{\mathrm {level}(\sigma _{j-1})}} x_0$
, and
$x_j = \lim _{\mu _{\mathrm {level}(\sigma _{j-1})}} x_0$
, and
since
![]() $\sigma _j \in \Sigma _{\phi }$
. This ends the proof of the claim.
$\sigma _j \in \Sigma _{\phi }$
. This ends the proof of the claim.
It follows from Claims A.1 and A.2 that
![]() $S' \searrow \lim _{\mu _{s}} S' = S_{s+1}$
. Now, it is obvious from the definition of
$S' \searrow \lim _{\mu _{s}} S' = S_{s+1}$
. Now, it is obvious from the definition of
![]() $\bar \sigma $
that, for each
$\bar \sigma $
that, for each
![]() $\sigma \in \Sigma _{\phi }$
,
$\sigma \in \Sigma _{\phi }$
,
It follows that
Finally, since
![]() $S' \searrow S_{s+1} \subset \mathrm {R}^k$
, it follows that
$S' \searrow S_{s+1} \subset \mathrm {R}^k$
, it follows that
![]() $S' \cap \mathrm {R}^{k} = S_{s+1}$
, and hence
$S' \cap \mathrm {R}^{k} = S_{s+1}$
, and hence
![]() $S_{s+1} = S$
. This implies that
$S_{s+1} = S$
. This implies that
![]() $S' \searrow S$
.
$S' \searrow S$
.
Finally, it follows from Lemma 3.1 that
![]() $\mathrm {ext}(S,\mathrm {R}')$
is a semialgebraic deformation retract of
$\mathrm {ext}(S,\mathrm {R}')$
is a semialgebraic deformation retract of
![]() $S'$
.
$S'$
.
Acknowledgements
The authors are grateful to the referees for their detailed reading and many helpful comments and corrections. In particular, we thank one of the referees for pointing out an error in an example in the previous version of the paper. The example has been omitted in this version.
Competing interests
The authors have no conflicting interests to declare.
Funding statement
This research was supported by the following grants from the National Science Foundation: CCF-1618918; DMS-1620271; CCF-1910441.