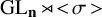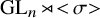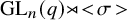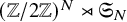1 Introduction
1.1 Mixed Hodge polynomial
The E-polynomial of a complex algebraic variety encodes a part of the dimensional information of its mixed Hodge structure. Mirror partners are expected to have the same E-polynomial, with the caveat that one must suitably modify its definition to include the contribution of singularities. Therefore, it is an important invariant in the study of mirror symmetry. See [Reference Hausel and ThaddeusHT03].
According to Deligne ([Reference DeligneDel71], [Reference DeligneDel74]), to any possibly singular and not necessarily projective complex algebraic variety X, we can associate a mixed Hodge structure on each of its rational cohomology groups
![]() $H^j(X,\mathbb {Q})$
in a functorial manner. The mixed Hodge structure consists of the following data:
$H^j(X,\mathbb {Q})$
in a functorial manner. The mixed Hodge structure consists of the following data:
-
(1) a weight filtration
 $W_{\bullet }$
on
$W_{\bullet }$
on
 $H^j(X,\mathbb {Q})$
:
$H^j(X,\mathbb {Q})$
:  $$ \begin{align*}\{0\}=W_{-1}\subset W_0\subset\cdots\subset W_{2j}=H^j(X,\mathbb{Q}); \end{align*} $$
$$ \begin{align*}\{0\}=W_{-1}\subset W_0\subset\cdots\subset W_{2j}=H^j(X,\mathbb{Q}); \end{align*} $$
-
(2) a Hodge filtration
 $F^{\bullet }$
on
$F^{\bullet }$
on
 $H^j(X,\mathbb {C})$
:
$H^j(X,\mathbb {C})$
:  $$ \begin{align*}H^j(X,\mathbb{C})=F^0\supset F^1\supset\cdots\supset F^m=\{0\}. \end{align*} $$
$$ \begin{align*}H^j(X,\mathbb{C})=F^0\supset F^1\supset\cdots\supset F^m=\{0\}. \end{align*} $$
On each complexified graded space
![]() $(W_i/W_{i-1})\otimes _{\mathbb {Q}}\mathbb {C}$
, the Hodge filtration induces a pure Hodge structure of weight i. Similarly, one can also define a mixed Hodge structure on each compactly supported cohomology group
$(W_i/W_{i-1})\otimes _{\mathbb {Q}}\mathbb {C}$
, the Hodge filtration induces a pure Hodge structure of weight i. Similarly, one can also define a mixed Hodge structure on each compactly supported cohomology group
![]() $H^j_c(X,\mathbb {Q})$
.
$H^j_c(X,\mathbb {Q})$
.
The generating series of the dimensions of the graded spaces of the mixed Hodge structure on the compactly supported cohomology groups is called the mixed Hodge polynomial. More concretely, for any nonnegative integers p, q and j, put
where
![]() $\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i:=W_i/W_{i-1}$
and
$\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i:=W_i/W_{i-1}$
and
![]() $\operatorname {\mathrm {Gr}}^{F^{\bullet }}_j\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i:=F_j\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i/F_{j+1}\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i$
for any i and j. Then the mixed Hodge polynomial of X is defined by
$\operatorname {\mathrm {Gr}}^{F^{\bullet }}_j\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i:=F_j\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i/F_{j+1}\operatorname {\mathrm {Gr}}^{W_{\bullet }}_i$
for any i and j. Then the mixed Hodge polynomial of X is defined by
and the E-polynomial of X is defined by
According to a theorem of Katz [Reference Hausel and Rodriguez-VillegasHRV08], in many cases, the E-polynomial of X can be computed by counting points over finite fields. This means the following. Suppose that there is a ring
![]() $R\subset \mathbb {C}$
and a scheme
$R\subset \mathbb {C}$
and a scheme
![]() $\mathfrak {X}$
over R such that the base change of
$\mathfrak {X}$
over R such that the base change of
![]() $\mathfrak {X}$
to
$\mathfrak {X}$
to
![]() $\mathbb {C}$
is isomorphic to X. Then for any homomorphism
$\mathbb {C}$
is isomorphic to X. Then for any homomorphism
![]() $\phi :R\rightarrow \mathbb {F}_q$
to a finite field, we consider the base change of
$\phi :R\rightarrow \mathbb {F}_q$
to a finite field, we consider the base change of
![]() $\mathfrak {X}$
via
$\mathfrak {X}$
via
![]() $\phi $
, which is a variety
$\phi $
, which is a variety
![]() $X_{\phi }$
over
$X_{\phi }$
over
![]() $\mathbb {F}_q$
. Suppose that there is a polynomial
$\mathbb {F}_q$
. Suppose that there is a polynomial
![]() $P_X(t)\in \mathbb {Z}[t]$
such that
$P_X(t)\in \mathbb {Z}[t]$
such that
![]() $|X_{\phi }(\mathbb {F}_q)|=P_X(q)$
, which is independent of
$|X_{\phi }(\mathbb {F}_q)|=P_X(q)$
, which is independent of
![]() $\phi $
. Then we have
$\phi $
. Then we have
It happens that character varieties satisfy these assumptions, and the first application of this theorem of Katz is [Reference Hausel and Rodriguez-VillegasHRV08].
1.2 The conjecture of Hausel-Letellier-Rodriguez-Villegas
Let
![]() $\Sigma $
be a Riemann surface of genus g with
$\Sigma $
be a Riemann surface of genus g with
![]() $k>0$
punctures. Let
$k>0$
punctures. Let
![]() $n\in \mathbb {Z}_{>0}$
and let
$n\in \mathbb {Z}_{>0}$
and let
![]() $\mathcal {C}=(C_j)_{1\le j\le k}$
be a tuple of semi-simple conjugacy classes of
$\mathcal {C}=(C_j)_{1\le j\le k}$
be a tuple of semi-simple conjugacy classes of
![]() $\operatorname {\mathrm {GL}}_n$
. In [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11], the authors studied the character variety
$\operatorname {\mathrm {GL}}_n$
. In [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11], the authors studied the character variety
 $$ \begin{align*}\mathcal{M}_{\mathcal{C}}:=\left\{(A_i,B_i)_i(X_j)_j\in \operatorname{\mathrm{GL}}_n^{2g}\times \prod_{j=1}^k C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^kX_j=1\right\}\!/\mkern-2mu/\mkern-2mu\operatorname{\mathrm{GL}}_n, \end{align*} $$
$$ \begin{align*}\mathcal{M}_{\mathcal{C}}:=\left\{(A_i,B_i)_i(X_j)_j\in \operatorname{\mathrm{GL}}_n^{2g}\times \prod_{j=1}^k C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^kX_j=1\right\}\!/\mkern-2mu/\mkern-2mu\operatorname{\mathrm{GL}}_n, \end{align*} $$
where the bracket denotes the commutator and the quotient is with respect to conjugation. Their work led to a conjectural formula for the mixed Hodge polynomial
![]() $H_c(\mathcal {M}_{\mathcal {C}};x,y,t)$
. We recall their conjectural formula below, which involves Macdonald polynomials. In this article, we will call Macdonald polynomials what are usually called modified Macdonald polynomials in the literature, since only this version of Macdonald polynomial appears.
$H_c(\mathcal {M}_{\mathcal {C}};x,y,t)$
. We recall their conjectural formula below, which involves Macdonald polynomials. In this article, we will call Macdonald polynomials what are usually called modified Macdonald polynomials in the literature, since only this version of Macdonald polynomial appears.
Denote by
![]() $\mathcal {P}$
the set of all partitions, including the empty one. For any
$\mathcal {P}$
the set of all partitions, including the empty one. For any
![]() $\lambda \in \mathcal {P}$
, denote by
$\lambda \in \mathcal {P}$
, denote by
![]() $H_{\lambda }(\mathbf {z};z,w)$
the Macdonald polynomial. It lives in the ring
$H_{\lambda }(\mathbf {z};z,w)$
the Macdonald polynomial. It lives in the ring
![]() $\operatorname {\mathrm {Sym}}[\mathbf {z}]$
of symmetric functions over the field
$\operatorname {\mathrm {Sym}}[\mathbf {z}]$
of symmetric functions over the field
![]() $\mathbb {Q}(z,w)$
of rational functions in z and w. This ring is equipped with an inner product
$\mathbb {Q}(z,w)$
of rational functions in z and w. This ring is equipped with an inner product
![]() $\langle -,-\rangle $
, called the Hall inner product. It can be deformed into another inner product
$\langle -,-\rangle $
, called the Hall inner product. It can be deformed into another inner product
![]() $\langle -,-\rangle _{z,w}$
. Denote by
$\langle -,-\rangle _{z,w}$
. Denote by
the self-pairing of a Macdonald polynomial for the deformed inner product. We will also need a deformation of it:
![]() $N_{\lambda }(u,z,w)$
, with
$N_{\lambda }(u,z,w)$
, with
![]() $N_{\lambda }(1,z,w)=N_{\lambda }(z,w)$
. It is defined by an explicit formula (See §8.1.)
$N_{\lambda }(1,z,w)=N_{\lambda }(z,w)$
. It is defined by an explicit formula (See §8.1.)
The core of the conjecture of Hausel-Letellier-Rodriguez-Villegas is a mysterious generating series, the shape of which suggests a topological field theory behind. For any
![]() $g\ge 0$
and
$g\ge 0$
and
![]() $k>0$
, define
$k>0$
, define
 $$ \begin{align} \Omega_{HLRV,g,k}(z,w):=\sum_{\lambda\in\mathcal{P}}\frac{N_{\lambda}(zw,z^2,w^2)^g}{N_{\lambda}(z^2,w^2)}\prod_{j=1}^{k}\tilde{H}_{\lambda}(\mathbf{z}_j;z^2,w^2), \end{align} $$
$$ \begin{align} \Omega_{HLRV,g,k}(z,w):=\sum_{\lambda\in\mathcal{P}}\frac{N_{\lambda}(zw,z^2,w^2)^g}{N_{\lambda}(z^2,w^2)}\prod_{j=1}^{k}\tilde{H}_{\lambda}(\mathbf{z}_j;z^2,w^2), \end{align} $$
where
![]() $\{\mathbf {z}_1,\ldots ,\mathbf {z}_k\}$
are independent variables. We may omit g and k from the notation if their values are clear from the context. For each
$\{\mathbf {z}_1,\ldots ,\mathbf {z}_k\}$
are independent variables. We may omit g and k from the notation if their values are clear from the context. For each
![]() $1\le j\le k$
, let
$1\le j\le k$
, let
![]() $\mu _j$
be the partition of n that encodes the multiplicities of the eigenvalues of
$\mu _j$
be the partition of n that encodes the multiplicities of the eigenvalues of
![]() $C_j$
. Write
$C_j$
. Write
![]() $\boldsymbol{\mu} =(\mu _1,\ldots ,\mu _k)$
. Define a rational function
$\boldsymbol{\mu} =(\mu _1,\ldots ,\mu _k)$
. Define a rational function
![]() $\mathbb {H}_{\boldsymbol{\mu} }(z,w)$
by taking the Hall inner product
$\mathbb {H}_{\boldsymbol{\mu} }(z,w)$
by taking the Hall inner product
 $$ \begin{align} \mathbb{H}_{\boldsymbol\mu}(z,w):=(z^2-1)(1-w^2)\left\langle\operatorname{\mathrm{Log}}\Omega_{HLRV}(z,w),\prod_{j=1}^kh_{\mu_j}\right\rangle, \end{align} $$
$$ \begin{align} \mathbb{H}_{\boldsymbol\mu}(z,w):=(z^2-1)(1-w^2)\left\langle\operatorname{\mathrm{Log}}\Omega_{HLRV}(z,w),\prod_{j=1}^kh_{\mu_j}\right\rangle, \end{align} $$
where
![]() $h_{\mu _j}$
is the complete symmetric function and
$h_{\mu _j}$
is the complete symmetric function and
![]() $\operatorname {\mathrm {Log}}$
is the plethystic
$\operatorname {\mathrm {Log}}$
is the plethystic
![]() $\operatorname {\mathrm {Log}}$
operator as defined in [Reference Hausel and Rodriguez-VillegasHRV08].
$\operatorname {\mathrm {Log}}$
operator as defined in [Reference Hausel and Rodriguez-VillegasHRV08].
Let
![]() $d_{\boldsymbol{\mu} }$
be the dimension of
$d_{\boldsymbol{\mu} }$
be the dimension of
![]() $\mathcal {M}_{\mathcal {C}}$
, which only depends on
$\mathcal {M}_{\mathcal {C}}$
, which only depends on
![]() $\boldsymbol{\mu} $
, g and n.
$\boldsymbol{\mu} $
, g and n.
Conjecture 1.1 [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11]
Suppose that
![]() $\mathcal {C}$
is generic in the sense of [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11, Definition 2.1.1]. Then the following statements are true.
$\mathcal {C}$
is generic in the sense of [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11, Definition 2.1.1]. Then the following statements are true.
-
(i) The rational function
 $\mathbb {H}_{\mu }(z,w)$
is a polynomial. It has degree
$\mathbb {H}_{\mu }(z,w)$
is a polynomial. It has degree
 $d_{\mu }$
in each variable and
$d_{\mu }$
in each variable and
 $\mathbb {H}_{\mu }(-z,w)$
has nonnegative integer coefficients.
$\mathbb {H}_{\mu }(-z,w)$
has nonnegative integer coefficients. -
(ii) The mixed Hodge polynomial
 $H_c(\mathcal {M}_{\mathcal {C}};x,y,t)$
is a polynomial in
$H_c(\mathcal {M}_{\mathcal {C}};x,y,t)$
is a polynomial in
 $q:=xy$
and t.
$q:=xy$
and t. -
(iii) The mixed Hodge polynomial is given by
In particular, it only depends on $$ \begin{align*}H_c(\mathcal{M}_{\mathcal{C}};q,t)=(t\sqrt{q})^{d_{\boldsymbol\mu}}\mathbb{H}_{\boldsymbol\mu}(-t\sqrt{q},\frac{1}{\sqrt{q}}).\end{align*} $$
$$ \begin{align*}H_c(\mathcal{M}_{\mathcal{C}};q,t)=(t\sqrt{q})^{d_{\boldsymbol\mu}}\mathbb{H}_{\boldsymbol\mu}(-t\sqrt{q},\frac{1}{\sqrt{q}}).\end{align*} $$
 $\boldsymbol{\mu} $
, and not on the generic eigenvalues of
$\boldsymbol{\mu} $
, and not on the generic eigenvalues of
 $\mathcal {C}$
.
$\mathcal {C}$
.
1.3 Around the mixed Hodge polynomial
The case where
![]() $k=1$
and
$k=1$
and
![]() $C_1$
is central was studied in [Reference Hausel and Rodriguez-VillegasHRV08]. Since the character variety
$C_1$
is central was studied in [Reference Hausel and Rodriguez-VillegasHRV08]. Since the character variety
![]() $\mathcal {M}_{\mathcal {C}}$
can be defined over a subring of
$\mathcal {M}_{\mathcal {C}}$
can be defined over a subring of
![]() $\mathbb {C}$
that is of finite type over
$\mathbb {C}$
that is of finite type over
![]() $\mathbb {Z}$
, it admits base changes to finite fields. As mentioned above, a theorem of Katz reduces the computation of the E-polynomial to counting points over finite fields. The computation is implemented using the character table of
$\mathbb {Z}$
, it admits base changes to finite fields. As mentioned above, a theorem of Katz reduces the computation of the E-polynomial to counting points over finite fields. The computation is implemented using the character table of
![]() $\operatorname {\mathrm {GL}}_n(q)$
. The general case of arbitrary
$\operatorname {\mathrm {GL}}_n(q)$
. The general case of arbitrary
![]() $k>0$
was studied in [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11]. The resulting E-polynomials led to the conjecture that we have just recalled.
$k>0$
was studied in [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11]. The resulting E-polynomials led to the conjecture that we have just recalled.
In [Reference Hausel and Rodriguez-VillegasHRV08], a symmetry in the conjectural mixed Hodge polynomial was observed, which is called the curious Poincaré duality. Hausel and Rodriguez-Villegas further conjectured that this symmetry can be upgraded to a symmetry in the mixed Hodge structure, which they call the curious Hard Lefschetz.
Then a remarkable observation was made by de Cataldo, Hausel and Migliorini, that the curious Hard Lefschetz for character varieties resembles the relative Hard Lefschetz for Hitchin fibrations. This led to the P=W conjecture [Reference de Cataldo, Hausel and MigliorinidCHM12], claiming that the perverse filtration on the cohomology of Dolbeault moduli space coincides with the weight filtration on the cohomology of character variety under the non-abelian Hodge correspondence. This conjecture has recently been settled by Maulik-Shen [Reference Maulik and ShenMS22] and Hausel-Mellit-Minets-Schiffmann [Reference Hausel, Mellit, Minets and SchiffmannHMMS22] independently.
The assertion in part (i) of Conjecture 1.1 concerning the polynomial property of
![]() $\mathbb {H}_{\boldsymbol{\mu} }(z,w)$
has been proved by Mellit in [Reference MellitMel18]. Part (ii) of Conjecture 1.1 has been proved by Mellit in [Reference MellitMel19]. The specialisation of part (iii) to Poincaré polynomials has been proved by Mellit and Schiffmann by counting Higgs bundles over finite fields. See [Reference MellitMel20b], [Reference MellitMel20a] and [Reference SchiffmannSch16].
$\mathbb {H}_{\boldsymbol{\mu} }(z,w)$
has been proved by Mellit in [Reference MellitMel18]. Part (ii) of Conjecture 1.1 has been proved by Mellit in [Reference MellitMel19]. The specialisation of part (iii) to Poincaré polynomials has been proved by Mellit and Schiffmann by counting Higgs bundles over finite fields. See [Reference MellitMel20b], [Reference MellitMel20a] and [Reference SchiffmannSch16].
The goal of this article is to study the mixed Hodge polynomial of a new family of character varieties.
1.4
 $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character Varieties
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character Varieties
We study character varieties that are unitary in the global sense. This is what we call
![]() $\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma {>}$
-character varieties. We will avoid calling them unitary character varieties since in the community of character variety, they often refer to character varieties with structure group
$\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma {>}$
-character varieties. We will avoid calling them unitary character varieties since in the community of character variety, they often refer to character varieties with structure group
![]() $\operatorname {\mathrm {U}}_n(\mathbb {R})$
.
$\operatorname {\mathrm {U}}_n(\mathbb {R})$
.
Let
![]() $\sigma $
be an order 2 exterior automorphism of
$\sigma $
be an order 2 exterior automorphism of
![]() $\operatorname {\mathrm {GL}}_n$
. We will denote by
$\operatorname {\mathrm {GL}}_n$
. We will denote by
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
the semi-direct product
$\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
the semi-direct product
![]() $\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!$
. Let
$\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!$
. Let
![]() $p':\tilde {\Sigma }'\rightarrow \Sigma '$
be a double covering of compact Riemann surfaces that is branched at
$p':\tilde {\Sigma }'\rightarrow \Sigma '$
be a double covering of compact Riemann surfaces that is branched at
![]() $2k$
-points, with
$2k$
-points, with
![]() $k>0$
. Let
$k>0$
. Let
![]() $p:\tilde {\Sigma }\rightarrow \Sigma $
be the restriction of
$p:\tilde {\Sigma }\rightarrow \Sigma $
be the restriction of
![]() $p'$
to its unbranched part, so that the punctures of
$p'$
to its unbranched part, so that the punctures of
![]() $\Sigma $
are exactly the branch points in
$\Sigma $
are exactly the branch points in
![]() $\Sigma '$
. Denote by g the genus of
$\Sigma '$
. Denote by g the genus of
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a tuple of semi-simple conjugacy classes contained in
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a tuple of semi-simple conjugacy classes contained in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
. Our
$\operatorname {\mathrm {GL}}_n\sigma $
. Our
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character variety is defined by
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character variety is defined by
 $$ \begin{align*}\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\Sigma):=\left\{(A_i,B_i)_i(X_j)_j\in \operatorname{\mathrm{GL}}_n^{2g}\times \prod_{j=1}^{2k} C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\!/\mkern-2mu/\mkern-2mu\operatorname{\mathrm{GL}}_n. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\Sigma):=\left\{(A_i,B_i)_i(X_j)_j\in \operatorname{\mathrm{GL}}_n^{2g}\times \prod_{j=1}^{2k} C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\!/\mkern-2mu/\mkern-2mu\operatorname{\mathrm{GL}}_n. \end{align*} $$
This is the moduli space of the homomorphisms
![]() $\rho $
that fit into the following commutative diagram:
$\rho $
that fit into the following commutative diagram:

where
![]() $\operatorname {\mathrm {Gal}}(\tilde {\Sigma }/\Sigma )\cong \mathbb {Z}/2\mathbb {Z}$
is the group of covering transformations,
$\operatorname {\mathrm {Gal}}(\tilde {\Sigma }/\Sigma )\cong \mathbb {Z}/2\mathbb {Z}$
is the group of covering transformations,
![]() $q_1$
is the quotient by
$q_1$
is the quotient by
![]() $\pi _1(\tilde {\Sigma })$
, and
$\pi _1(\tilde {\Sigma })$
, and
![]() $q_2$
is the quotient by the identity component. Of course, the monodromy of
$q_2$
is the quotient by the identity component. Of course, the monodromy of
![]() $\rho $
at the punctures must lie in the given conjugacy classes.
$\rho $
at the punctures must lie in the given conjugacy classes.
The character variety
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}(\Sigma )$
, via the non-abelian Hodge theory,Footnote
1
corresponds to the moduli space of (parabolic) unitary Higgs bundles – that is, torsors under the unitary group scheme over
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}(\Sigma )$
, via the non-abelian Hodge theory,Footnote
1
corresponds to the moduli space of (parabolic) unitary Higgs bundles – that is, torsors under the unitary group scheme over
![]() $\Sigma $
equipped with a Higgs field. Torsors under the unitary group scheme can alternatively be described as vector bundles
$\Sigma $
equipped with a Higgs field. Torsors under the unitary group scheme can alternatively be described as vector bundles
![]() $\mathcal {E}$
on the the covering space
$\mathcal {E}$
on the the covering space
![]() $\tilde {\Sigma }$
equipped with an isomorphism
$\tilde {\Sigma }$
equipped with an isomorphism
![]() $\mathcal {E}\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\tau ^{\ast }\mathcal {E}^{\vee }$
, where
$\mathcal {E}\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\tau ^{\ast }\mathcal {E}^{\vee }$
, where
![]() $\mathcal {E}^{\vee }$
is the dual vector bundle and
$\mathcal {E}^{\vee }$
is the dual vector bundle and
![]() $\tau $
is the nontrivial covering transformation. Recent interests in this kind of moduli spaces grew out its connection to representation theory (e.g., the work of Laumon and Ngô [Reference Laumon and NgôLN08] on the fundamental lemma, where they work with étale coverings of curves). We insist on branched coverings. As we will see, the most interesting phenomenon (i.e., insertion of wreath Macdonald polynomial) arises from the branch points.
$\tau $
is the nontrivial covering transformation. Recent interests in this kind of moduli spaces grew out its connection to representation theory (e.g., the work of Laumon and Ngô [Reference Laumon and NgôLN08] on the fundamental lemma, where they work with étale coverings of curves). We insist on branched coverings. As we will see, the most interesting phenomenon (i.e., insertion of wreath Macdonald polynomial) arises from the branch points.
This character variety also appears as a special case of the twisted character varieties studied by Boalch and Yamakawa [Reference Boalch and YamakawaBY15].
1.5 Wreath Macdonald polynomials
In [Reference HaimanHai03], Haiman conjectured the existence of a family of symmetric functions that are called wreath Macdonald polynomials. Their symmetry is the wreath product
![]() $(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
, with
$(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
, with
![]() $r>0$
, generalising the symmetric group
$r>0$
, generalising the symmetric group
![]() $\mathfrak {S}_n$
for Macdonald polynomials. The existence and Schur-positivity of these symmetric functions were proved by Bezrukavnikov and Finkelberg in [Reference Bezrukavnikov and FinkelbergBF14]. Let
$\mathfrak {S}_n$
for Macdonald polynomials. The existence and Schur-positivity of these symmetric functions were proved by Bezrukavnikov and Finkelberg in [Reference Bezrukavnikov and FinkelbergBF14]. Let
![]() $\mathbf {x}=(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
be two independent sets of infinitely many variables and write
$\mathbf {x}=(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
be two independent sets of infinitely many variables and write
with coefficients in the ring
![]() $\mathbb {Q}(z,w)$
of rational functions. In this article,
$\mathbb {Q}(z,w)$
of rational functions. In this article,
![]() $r=2$
, and the wreath Macdonald polynomials live in
$r=2$
, and the wreath Macdonald polynomials live in
![]() $\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
. Below, we explain some essence of wreath Macdonald polynomials and introduce some notations.
$\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
. Below, we explain some essence of wreath Macdonald polynomials and introduce some notations.
A 2-core is a partition of the form
![]() $(d,d-1,\ldots ,1,0)$
for some
$(d,d-1,\ldots ,1,0)$
for some
![]() $d\in \mathbb {Z}_{\ge 0}$
. A 2-partition is simply an element of
$d\in \mathbb {Z}_{\ge 0}$
. A 2-partition is simply an element of
![]() $\mathcal {P}^2=\mathcal {P}\times \mathcal {P}$
. Any partition determines a 2-core, and a 2-partition which is called its 2-quotient, and these data determine the original partition. For any
$\mathcal {P}^2=\mathcal {P}\times \mathcal {P}$
. Any partition determines a 2-core, and a 2-partition which is called its 2-quotient, and these data determine the original partition. For any
![]() $\boldsymbol{\alpha} =(\alpha ^{(0)},\alpha ^{(1)})\in \mathcal {P}^2$
, its size is defined to be
$\boldsymbol{\alpha} =(\alpha ^{(0)},\alpha ^{(1)})\in \mathcal {P}^2$
, its size is defined to be
![]() $|\alpha ^{(0)}|+|\alpha ^{(1)}|$
. If
$|\alpha ^{(0)}|+|\alpha ^{(1)}|$
. If
![]() $\lambda _c$
and
$\lambda _c$
and
![]() $\boldsymbol{\lambda} _q$
are the 2-core and 2-quotient of
$\boldsymbol{\lambda} _q$
are the 2-core and 2-quotient of
![]() $\lambda $
, respectively, then we have
$\lambda $
, respectively, then we have
![]() $|\lambda |=|\lambda _c|+2|\boldsymbol{\lambda} _q|$
. Fixing a 2-core of size m and an integer
$|\lambda |=|\lambda _c|+2|\boldsymbol{\lambda} _q|$
. Fixing a 2-core of size m and an integer
![]() $n>m$
, we have a bijection
$n>m$
, we have a bijection
This bijection induces from the set of partitions an order on the set of 2-partitions. Wreath Macdonald polynomials are uniquely determined by two triangularity conditions and one normalisation condition. The order used in the triangularity conditions is the one induced from partitions. Different 2-cores may induce different orders on
![]() $\mathcal {P}^2$
, and so define different wreath Macdonald polynomials.
$\mathcal {P}^2$
, and so define different wreath Macdonald polynomials.
In this article, only the 2-cores
![]() $(0)$
and
$(0)$
and
![]() $(1)$
appear. For any
$(1)$
appear. For any
![]() $\boldsymbol{\alpha} \in \mathcal {P}^2$
, we will denote by
$\boldsymbol{\alpha} \in \mathcal {P}^2$
, we will denote by
![]() $\{\boldsymbol{\alpha} \}_0$
(resp.
$\{\boldsymbol{\alpha} \}_0$
(resp.
![]() $\{\boldsymbol{\alpha} \}_1$
) the partition which has
$\{\boldsymbol{\alpha} \}_1$
) the partition which has
![]() $\boldsymbol{\alpha} $
as its 2-quotient, and has
$\boldsymbol{\alpha} $
as its 2-quotient, and has
![]() $(0)$
(resp.
$(0)$
(resp.
![]() $(1)$
) as its 2-core. With a fixed 2-core, we will denote by
$(1)$
) as its 2-core. With a fixed 2-core, we will denote by
![]() $\tilde {H}_{\boldsymbol{\alpha} }(\mathbf {x};z,w)$
the wreath Macdonald polynomial associated to
$\tilde {H}_{\boldsymbol{\alpha} }(\mathbf {x};z,w)$
the wreath Macdonald polynomial associated to
![]() $\boldsymbol{\alpha} \in \mathcal {P}^2$
. We will denote by
$\boldsymbol{\alpha} \in \mathcal {P}^2$
. We will denote by
the self-pairing of wreath Macdonald polynomials for the deformed inner product. We will also need a deformed version
![]() $\tilde {N}_{\boldsymbol{\alpha} }(u,z,w)$
, with
$\tilde {N}_{\boldsymbol{\alpha} }(u,z,w)$
, with
![]() $\tilde {N}_{\boldsymbol{\alpha} }(1,z,w)=\tilde {N}_{\boldsymbol{\alpha} }(z,w)$
. (See §8.2.2.)
$\tilde {N}_{\boldsymbol{\alpha} }(1,z,w)=\tilde {N}_{\boldsymbol{\alpha} }(z,w)$
. (See §8.2.2.)
1.6 From character varieties to wreath Macdonald polynomials
Let q be a prime power. Macdonald polynomials appear in the conjectural formula for the mixed Hodge polynomials of
![]() $\operatorname {\mathrm {GL}}_n$
-character varieties. The first step towards the mixed Hodge polynomial is to compute the E-polynomial by counting points over finite fields. In counting points, the representation theory of
$\operatorname {\mathrm {GL}}_n$
-character varieties. The first step towards the mixed Hodge polynomial is to compute the E-polynomial by counting points over finite fields. In counting points, the representation theory of
![]() $\operatorname {\mathrm {GL}}_n(q)$
provides the necessary combinatorial context in which the connection to the Macdonald polynomials can be observed. Each unipotent character of
$\operatorname {\mathrm {GL}}_n(q)$
provides the necessary combinatorial context in which the connection to the Macdonald polynomials can be observed. Each unipotent character of
![]() $\operatorname {\mathrm {GL}}_n(q)$
is a linear combination of Deligne-Lusztig characters, and the coefficients are given by an irreducible character of the symmetric group
$\operatorname {\mathrm {GL}}_n(q)$
is a linear combination of Deligne-Lusztig characters, and the coefficients are given by an irreducible character of the symmetric group
![]() $\mathfrak {S}_n$
, which is the Weyl group of
$\mathfrak {S}_n$
, which is the Weyl group of
![]() $\operatorname {\mathrm {GL}}_n$
. These Weyl group characters parametrise unipotent characters of
$\operatorname {\mathrm {GL}}_n$
. These Weyl group characters parametrise unipotent characters of
![]() $\operatorname {\mathrm {GL}}_n(q)$
. The computation of a Deligne-Lusztig character is reduced to the Green functions, and the Green functions are the bridge to symmetric functions. In our problem, we use the irreducible characters of
$\operatorname {\mathrm {GL}}_n(q)$
. The computation of a Deligne-Lusztig character is reduced to the Green functions, and the Green functions are the bridge to symmetric functions. In our problem, we use the irreducible characters of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
, which will be described in terms of Deligne-Lusztig characters of nonconnected groups. The bridge to symmetric functions is again provided by Green functions, using Shoji’s results. In [Reference ShojiSho01], Shoji gives a description of Green functions, or rather, Kostka polynomials, associated to symplectic groups and orthogonal groups, in terms of symmetric functions in
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
, which will be described in terms of Deligne-Lusztig characters of nonconnected groups. The bridge to symmetric functions is again provided by Green functions, using Shoji’s results. In [Reference ShojiSho01], Shoji gives a description of Green functions, or rather, Kostka polynomials, associated to symplectic groups and orthogonal groups, in terms of symmetric functions in
![]() $\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
$\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
Regard
![]() $\operatorname {\mathrm {GL}}_n$
as an algebraic group over
$\operatorname {\mathrm {GL}}_n$
as an algebraic group over
![]() $\bar {\mathbb {F}}_q$
, equipped with the Frobenius endomorphism F that sends each entry of a matrix to its q-th power. Then the finite group
$\bar {\mathbb {F}}_q$
, equipped with the Frobenius endomorphism F that sends each entry of a matrix to its q-th power. Then the finite group
![]() $\operatorname {\mathrm {GL}}_n(q)$
consists of the fixed points of F. Let
$\operatorname {\mathrm {GL}}_n(q)$
consists of the fixed points of F. Let
![]() $T_1$
be the maximal torus consisting of diagonal matrices and let
$T_1$
be the maximal torus consisting of diagonal matrices and let
![]() $W\cong \mathfrak {S}_n$
be the Weyl group of
$W\cong \mathfrak {S}_n$
be the Weyl group of
![]() $\operatorname {\mathrm {GL}}_n$
defined by
$\operatorname {\mathrm {GL}}_n$
defined by
![]() $T_1$
. The automorphism
$T_1$
. The automorphism
![]() $\sigma $
induces an automorphism of W. (See §3 for the precise definition of
$\sigma $
induces an automorphism of W. (See §3 for the precise definition of
![]() $\sigma $
.) Denote by
$\sigma $
.) Denote by
![]() $W^{\sigma }$
the fixed points of
$W^{\sigma }$
the fixed points of
![]() $\sigma $
. In fact, we have
$\sigma $
. In fact, we have
with
![]() $N=[n/2]$
. For each
$N=[n/2]$
. For each
![]() $w\in W^{\sigma }$
, we have the generalised Deligne-Lusztig character
$w\in W^{\sigma }$
, we have the generalised Deligne-Lusztig character
![]() $R_{T_w\sigma }\mathbf {1}$
, as defined in [Reference Digne and MichelDM94], which is a function on
$R_{T_w\sigma }\mathbf {1}$
, as defined in [Reference Digne and MichelDM94], which is a function on
![]() $\operatorname {\mathrm {GL}}_n(q)\sigma $
invariant under conjugation by
$\operatorname {\mathrm {GL}}_n(q)\sigma $
invariant under conjugation by
![]() $\operatorname {\mathrm {GL}}_n(q)$
.
$\operatorname {\mathrm {GL}}_n(q)$
.
The clue that eventually leads to wreath Macdonald polynomials is the following theorem of Digne and Michel, which was a conjecture of Malle in [Reference MalleMal93].
Theorem 1.2 [Reference Digne and MichelDM94, Théorème 5.2]
Let
![]() $\lambda $
be a partition of n and denote by m the size of the 2-core of
$\lambda $
be a partition of n and denote by m the size of the 2-core of
![]() $\lambda $
. Suppose that
$\lambda $
. Suppose that
![]() $m\le 1$
. Then, the extension
Footnote
2
to
$m\le 1$
. Then, the extension
Footnote
2
to
![]() $\operatorname {\mathrm {GL}}_n(q)\sigma $
of the unipotent character of
$\operatorname {\mathrm {GL}}_n(q)\sigma $
of the unipotent character of
![]() $\operatorname {\mathrm {GL}}_n(q)$
corresponding to
$\operatorname {\mathrm {GL}}_n(q)$
corresponding to
![]() $\lambda $
is given by
$\lambda $
is given by
where
![]() $\varphi $
is the irreducible character of
$\varphi $
is the irreducible character of
![]() $W^{\sigma }$
corresponding to the 2-quotient of
$W^{\sigma }$
corresponding to the 2-quotient of
![]() $\lambda $
.
$\lambda $
.
This theorem was then extended to quadratic-unipotent characters by Waldspurger in [Reference WaldspurgerWal06]. In fact, Waldspurger’s theorem imposes no restriction on the 2-cores. It says if the 2-core is larger than
![]() $(1)$
, then the above expression would be a linear combination of inductions of cuspidal functions on Levi subgroups that are not tori.Footnote
3
Then a theorem in [Reference Digne and MichelDM15] shows that they must vanish on semi-simple conjugacy classes. Therefore, only the partitions with 2-core
$(1)$
, then the above expression would be a linear combination of inductions of cuspidal functions on Levi subgroups that are not tori.Footnote
3
Then a theorem in [Reference Digne and MichelDM15] shows that they must vanish on semi-simple conjugacy classes. Therefore, only the partitions with 2-core
![]() $(0)$
or
$(0)$
or
![]() $(1)$
have nontrivial contributions to the point counting of character varieties.
$(1)$
have nontrivial contributions to the point counting of character varieties.
The full character table of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
has been completely determined in [Reference ShuShu22], using the main theorem of [Reference WaldspurgerWal06]. Unlike
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
has been completely determined in [Reference ShuShu22], using the main theorem of [Reference WaldspurgerWal06]. Unlike
![]() $\operatorname {\mathrm {GL}}_n(q)$
, the irreducible characters of
$\operatorname {\mathrm {GL}}_n(q)$
, the irreducible characters of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
may not be a linear combination of Deligne-Lusztig characters. Because of this, the determination of the irreducible characters is much more difficult than
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
may not be a linear combination of Deligne-Lusztig characters. Because of this, the determination of the irreducible characters is much more difficult than
![]() $\operatorname {\mathrm {GL}}_n(q)$
and uses character sheaves on nonconnected groups developed by Lusztig. The results of [Reference ShuShu22] will eventually allow us to compute the E-polynomial of
$\operatorname {\mathrm {GL}}_n(q)$
and uses character sheaves on nonconnected groups developed by Lusztig. The results of [Reference ShuShu22] will eventually allow us to compute the E-polynomial of
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties.
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties.
1.7 The generating series
The main discovery of this article is the following infinite series that are built out of Macdonald polynomials, wreath Macdonald polynomials and their self-pairings. They are expected to dominate the mixed Hodge polynomials of
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties.
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties.
For
![]() $e\in \{0,1\}$
, define
$e\in \{0,1\}$
, define
 $$ \begin{align*} \Omega_{e}(z,w):= &\sum_{\boldsymbol\alpha\in\mathcal{P}^2} \frac{N_{\{\boldsymbol\alpha\}_e}(zw,z^2,w^2)^{g+k-1}}{\tilde{N}_{\boldsymbol\alpha}(z^2,w^2) \tilde{N}_{\boldsymbol\alpha}(zw,z^2,w^2)^{k-1}}\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z^2,w^2),\\ \Omega_{\ast}(z,w): =\ &\sum_{\alpha\in\mathcal{P}} \frac{N_{\alpha}(zw,z^2,w^2)^{2g+k-1}}{N_{\alpha}(z^2,w^2)} \prod_{j=1}^{2k}H_{\alpha}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2). \end{align*} $$
$$ \begin{align*} \Omega_{e}(z,w):= &\sum_{\boldsymbol\alpha\in\mathcal{P}^2} \frac{N_{\{\boldsymbol\alpha\}_e}(zw,z^2,w^2)^{g+k-1}}{\tilde{N}_{\boldsymbol\alpha}(z^2,w^2) \tilde{N}_{\boldsymbol\alpha}(zw,z^2,w^2)^{k-1}}\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z^2,w^2),\\ \Omega_{\ast}(z,w): =\ &\sum_{\alpha\in\mathcal{P}} \frac{N_{\alpha}(zw,z^2,w^2)^{2g+k-1}}{N_{\alpha}(z^2,w^2)} \prod_{j=1}^{2k}H_{\alpha}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2). \end{align*} $$
Beware that in
![]() $\Omega _e$
, the wreath Macdonald polynomials and the (deformed) self-pairings are subordinate to the 2-core
$\Omega _e$
, the wreath Macdonald polynomials and the (deformed) self-pairings are subordinate to the 2-core
![]() $(e)$
. In
$(e)$
. In
![]() $\Omega _{\ast }$
, the symmetric functions involved are Macdonald polynomials in the variable
$\Omega _{\ast }$
, the symmetric functions involved are Macdonald polynomials in the variable
![]() $\mathbf {x}^{(0)}+\mathbf {x}^{(1)}:=\mathbf {x}^{(0)}\sqcup \mathbf {x}^{(1)}$
.
$\mathbf {x}^{(0)}+\mathbf {x}^{(1)}:=\mathbf {x}^{(0)}\sqcup \mathbf {x}^{(1)}$
.
Remark 1.3. The series
![]() $\Omega _0$
and
$\Omega _0$
and
![]() $\Omega _1$
have their origin in the quadratic-unipotent characters of
$\Omega _1$
have their origin in the quadratic-unipotent characters of
![]() $\operatorname {\mathrm {GL}}_n(q)$
.
$\operatorname {\mathrm {GL}}_n(q)$
.
Remark 1.4. Note that
where
![]() $\tilde {g}=2g+k-1$
is the genus of
$\tilde {g}=2g+k-1$
is the genus of
![]() $\tilde {\Sigma }$
.
$\tilde {\Sigma }$
.
Remark 1.5. If there are further
![]() $k'$
unbranched punctures, then each summand of the above series should be multiplied by
$k'$
unbranched punctures, then each summand of the above series should be multiplied by
 $$ \begin{align*}\prod^{k'}_{j=1}H_{\{\boldsymbol\alpha\}_0}(\mathbf{z}_j;z^2,w^2),\quad\prod^{k'}_{j=1}H_{\{\boldsymbol\alpha\}_1}(\mathbf{z}_j;z^2,w^2),\quad\prod^{k'}_{j=1}H_{\alpha}(\mathbf{z}_j;z^2,w^2)^2,\end{align*} $$
$$ \begin{align*}\prod^{k'}_{j=1}H_{\{\boldsymbol\alpha\}_0}(\mathbf{z}_j;z^2,w^2),\quad\prod^{k'}_{j=1}H_{\{\boldsymbol\alpha\}_1}(\mathbf{z}_j;z^2,w^2),\quad\prod^{k'}_{j=1}H_{\alpha}(\mathbf{z}_j;z^2,w^2)^2,\end{align*} $$
respectively, where each
![]() $\mathbf {z}_j$
is an independent family of variables. In this article, we will not introduce unbranched punctures.
$\mathbf {z}_j$
is an independent family of variables. In this article, we will not introduce unbranched punctures.
1.8 The conjectural mixed Hodge polynomial
The infinite series that we have defined only depends on g and k, and not on the conjugacy classes. Now we introduce the symmetric functions associated to the conjugacy classes.
At the end of §3, we will define the set
![]() $\tilde {\mathfrak {T}}_s$
of certain combinatorial data, called types, encoding the multiplicities of the ‘eigenvalues’ of semi-simple conjugacy classes in
$\tilde {\mathfrak {T}}_s$
of certain combinatorial data, called types, encoding the multiplicities of the ‘eigenvalues’ of semi-simple conjugacy classes in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
. Given a tuple of semi-simple conjugacy classes
$\operatorname {\mathrm {GL}}_n\sigma $
. Given a tuple of semi-simple conjugacy classes
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
contained in
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
contained in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
, let
$\operatorname {\mathrm {GL}}_n\sigma $
, let
![]() $\boldsymbol{\beta} _j$
be the type of
$\boldsymbol{\beta} _j$
be the type of
![]() $C_j$
and let
$C_j$
and let
![]() $h_{\boldsymbol{\beta} _j^{\ast }}(\mathbf {x}_j)$
be the symmetric function associated to the dual
$h_{\boldsymbol{\beta} _j^{\ast }}(\mathbf {x}_j)$
be the symmetric function associated to the dual
![]() $\boldsymbol{\beta} _j^{\ast }$
(see §6.4), which is essentially the complete symmetric function. Write
$\boldsymbol{\beta} _j^{\ast }$
(see §6.4), which is essentially the complete symmetric function. Write
![]() $\mathbf {B}=(\boldsymbol{\beta} _j)_{1\le j\le 2k}$
. Let
$\mathbf {B}=(\boldsymbol{\beta} _j)_{1\le j\le 2k}$
. Let
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
be the
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
be the
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma{>}$
-character variety associated to
$\operatorname {\mathrm {GL}}_n\!<\!\sigma{>}$
-character variety associated to
![]() $\mathcal {C}$
. Denote by d the dimension of
$\mathcal {C}$
. Denote by d the dimension of
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
, which only depends on
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
, which only depends on
![]() $\mathbf {B}$
, g and n.
$\mathbf {B}$
, g and n.
The summand in
![]() $\Omega _{\ast }$
corresponding to the empty partition is equal to 1; therefore, we can apply the formal expansion
$\Omega _{\ast }$
corresponding to the empty partition is equal to 1; therefore, we can apply the formal expansion
 $$ \begin{align*}\frac{1}{1+x}=\sum_{m\ge 0}(-1)^mx^m\end{align*} $$
$$ \begin{align*}\frac{1}{1+x}=\sum_{m\ge 0}(-1)^mx^m\end{align*} $$
to
![]() $1+x=\Omega _{\ast }$
. Define the rational functions in z and w:
$1+x=\Omega _{\ast }$
. Define the rational functions in z and w:
 $$ \begin{align} \mathbb{H}_{\mathbf{B}}(z,w):=\ &~\left\langle\frac{\Omega_{1}(z,w)\Omega_{0}(z,w)}{\Omega_{\ast}(z,w)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is odd,} \end{align} $$
$$ \begin{align} \mathbb{H}_{\mathbf{B}}(z,w):=\ &~\left\langle\frac{\Omega_{1}(z,w)\Omega_{0}(z,w)}{\Omega_{\ast}(z,w)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is odd,} \end{align} $$
 $$ \begin{align} \mathbb{H}_{\mathbf{B}}(z,w):=\ &~\left\langle\frac{\Omega_{0}(z,w)^2}{\Omega_{\ast}(z,w)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is even.} \end{align} $$
$$ \begin{align} \mathbb{H}_{\mathbf{B}}(z,w):=\ &~\left\langle\frac{\Omega_{0}(z,w)^2}{\Omega_{\ast}(z,w)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is even.} \end{align} $$
Remark 1.6. A peculiar feature of these expressions is the absence of plethystic exponential or logarithm, which is by far ubiquitous in counting Higgs bundles and quiver representations.
Conjecture 1.7. Let
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a strongly generic tuple of semi-simple conjugacy classes contained in
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a strongly generic tuple of semi-simple conjugacy classes contained in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
which satisfies (CCL).Footnote
4
Then
$\operatorname {\mathrm {GL}}_n\sigma $
which satisfies (CCL).Footnote
4
Then
-
(i) The rational function
 $\mathbb {H}_{\mathbf {B}}(z,w)$
is a polynomial. It has degree d in each variable, and each monomial in it has even degree. Moreover,
$\mathbb {H}_{\mathbf {B}}(z,w)$
is a polynomial. It has degree d in each variable, and each monomial in it has even degree. Moreover,
 $\mathbb {H}_{\mathbf {B}}(-z,w)$
has nonnegative integer coefficients.
$\mathbb {H}_{\mathbf {B}}(-z,w)$
has nonnegative integer coefficients. -
(ii) The mixed Hodge polynomial
 $H_c(\operatorname {\mathrm {Ch}}_{\mathcal {C}};x,y,t)$
is a polynomial in
$H_c(\operatorname {\mathrm {Ch}}_{\mathcal {C}};x,y,t)$
is a polynomial in
 $q:=xy$
and t.
$q:=xy$
and t. -
(iii) The mixed Hodge polynomial is given by the following formula:
In particular, it only depends on $$ \begin{align*} H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,t)=(t\sqrt{q})^d\mathbb{H}_{\mathbf{B}}(-t\sqrt{q},\frac{1}{\sqrt{q}}). \end{align*} $$
$$ \begin{align*} H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,t)=(t\sqrt{q})^d\mathbb{H}_{\mathbf{B}}(-t\sqrt{q},\frac{1}{\sqrt{q}}). \end{align*} $$
 $\mathbf {B}$
and not on the generic eigenvalues of
$\mathbf {B}$
and not on the generic eigenvalues of
 $\mathcal {C}$
.
$\mathcal {C}$
.
Part (i) is a sufficient condition for the formula in part (iii) to be a polynomial in q and t with non negative integer coefficients. Part (ii) says that the mixed Hodge structure is Hodge-Tate.
Remark 1.8. In this article, we only need wreath Macdonald polynomials associated to the wreath product
![]() $W^{\sigma }$
, which is the Weyl group of the centraliser of
$W^{\sigma }$
, which is the Weyl group of the centraliser of
![]() $\sigma $
. Since wreath products
$\sigma $
. Since wreath products
![]() $(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
with
$(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
with
![]() $r>2$
are not the Weyl groups of any algebraic groups, their corresponding wreath Macdonald polynomials play no role in any character varieties. It is interesting to see if there are some imaginary mixed Hodge polynomials dominated by more general wreath Macdonald polynomials. Then the purely combinatorial part (i) of the conjecture may have a generalisation.
$r>2$
are not the Weyl groups of any algebraic groups, their corresponding wreath Macdonald polynomials play no role in any character varieties. It is interesting to see if there are some imaginary mixed Hodge polynomials dominated by more general wreath Macdonald polynomials. Then the purely combinatorial part (i) of the conjecture may have a generalisation.
Remark 1.9. We may also consider a cyclic Galois covering
![]() $\tilde {\Sigma }'\rightarrow \Sigma '$
of degree
$\tilde {\Sigma }'\rightarrow \Sigma '$
of degree
![]() $r>2$
and take for
$r>2$
and take for
![]() $\sigma $
an order r exterior automorphism of
$\sigma $
an order r exterior automorphism of
![]() $\operatorname {\mathrm {GL}}_n$
. The ramification index at a branch point determines which connected component of
$\operatorname {\mathrm {GL}}_n$
. The ramification index at a branch point determines which connected component of
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
the local monodromy around that point lies in. The representation theory on a connected component
$\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
the local monodromy around that point lies in. The representation theory on a connected component
![]() $\operatorname {\mathrm {GL}}_n\sigma ^i$
is controlled by
$\operatorname {\mathrm {GL}}_n\sigma ^i$
is controlled by
![]() $\mathfrak {S}_n$
or
$\mathfrak {S}_n$
or
![]() $\mathfrak {W}_N$
, according to the parity of i, or rather, whether
$\mathfrak {W}_N$
, according to the parity of i, or rather, whether
![]() $\sigma ^i$
is inner or exterior. The combinatorial consequence of such a dichotomy of Weyl groups is the different symmetric functions inserted at this point - the usual Macdonald polynomial or the wreath Macdonald polynomial. We expect that essentially no new phenomenon arises when
$\sigma ^i$
is inner or exterior. The combinatorial consequence of such a dichotomy of Weyl groups is the different symmetric functions inserted at this point - the usual Macdonald polynomial or the wreath Macdonald polynomial. We expect that essentially no new phenomenon arises when
![]() $r>2$
. We do not study cyclic coverings of higher degrees because the character table of
$r>2$
. We do not study cyclic coverings of higher degrees because the character table of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
is only written down in the case
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
is only written down in the case
![]() $r=2$
.
$r=2$
.
Part (iii) of the above conjecture, combined with some fundamental symmetries in Macdonald polynomials and wreath Macdonald polynomials, implies the following.
Conjecture 1.10 (Curious Poincaré Duality)
We have
This is the starting point of the Curious Hard Lefschetz conjecture and the P=W conjecture.
1.9 Main theorem and evidences of the conjecture
Our main theorem gives a formula for the E-polynomial, which is a main evidence of Conjecture 1.7.
Theorem 1.11. The
![]() $t=-1$
specialisation of part (iii) of Conjecture 1.7 holds:
$t=-1$
specialisation of part (iii) of Conjecture 1.7 holds:
Then the following theorem follows from this formula.
Theorem 1.12. The
![]() $t=-1$
specialisation of Conjecture 1.10 holds:
$t=-1$
specialisation of Conjecture 1.10 holds:
Other than the E-polynomial, we also have the following evidences. When
![]() $n=1$
, the character variety is simply the torus
$n=1$
, the character variety is simply the torus
![]() $(\mathbb {C}^{\ast })^{2(g+k-1)}$
, and we can confirm our conjecture in this case. When
$(\mathbb {C}^{\ast })^{2(g+k-1)}$
, and we can confirm our conjecture in this case. When
![]() $n=2$
, we do not know how to compute the mixed Hodge polynomial. However, we find a simple relation between
$n=2$
, we do not know how to compute the mixed Hodge polynomial. However, we find a simple relation between
![]() $\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties and
$\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties and
![]() $\operatorname {\mathrm {GL}}_2$
-character varieties, for any g and k. We then prove that under this relation, the conjecture of Hausel-Letellier-Rodriguez-Villegas and our conjecture predict the same mixed Hodge polynomial.
$\operatorname {\mathrm {GL}}_2$
-character varieties, for any g and k. We then prove that under this relation, the conjecture of Hausel-Letellier-Rodriguez-Villegas and our conjecture predict the same mixed Hodge polynomial.
When
![]() $n>2$
, we are unable to say anything about the mixed Hodge polynomial, but we can focus on part (i) of Conjecture 1.7, which is purely combinatorial and nontrivial. To be precise, we have computed
$n>2$
, we are unable to say anything about the mixed Hodge polynomial, but we can focus on part (i) of Conjecture 1.7, which is purely combinatorial and nontrivial. To be precise, we have computed
![]() $\mathbb {H}_{\mathbf {B}}(z,w)$
in the following situations:Footnote
5
$\mathbb {H}_{\mathbf {B}}(z,w)$
in the following situations:Footnote
5
-
○
 $n=3$
$n=3$
 $$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma (\text{i.e., conjugacy class of } \sigma) \end{align*} $$
$$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma (\text{i.e., conjugacy class of } \sigma) \end{align*} $$
-
○
 $n=4$
$n=4$
 $$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary};\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,b^{-1},b^{-1})\sigma\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma;\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,b^{-1},b^{-1})\sigma, C_3=C_4\sim\sigma \end{align*} $$
$$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary};\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,b^{-1},b^{-1})\sigma\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma;\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,b^{-1},b^{-1})\sigma, C_3=C_4\sim\sigma \end{align*} $$
-
○
 $n=5$
$n=5$
 $$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary};\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,1,b^{-1},b^{-1})\sigma\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma;\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,1,b^{-1},b^{-1})\sigma, C_3=C_4\sim\sigma \end{align*} $$
$$ \begin{align*} g=1, &k=1, \mathcal{C}=(C_1,C_2)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary};\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,1,b^{-1},b^{-1})\sigma\\ g=0, &k=2, \mathcal{C}=(C_1,C_2,C_3,C_4)\\ &C_1 \text{ regular}, C_2 \text{ arbitrary}, C_3=C_4\sim\sigma;\\ &C_1\sim\operatorname{\mathrm{diag}}(a,1,1,1,a^{-1})\sigma), C_2\sim\operatorname{\mathrm{diag}}(b,b,1,b^{-1},b^{-1})\sigma, C_3=C_4\sim\sigma \end{align*} $$
and part (i) of Conjecture 1.7 is always true.
Organisation of the article
In Sections 2, 3 and 4, we recall and prove some results concerning character varieties and the representation theory of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
that will be used later on. These sections contain three main ingredients in computing the E-polynomial:
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
that will be used later on. These sections contain three main ingredients in computing the E-polynomial:
-
(1) Formula (2.7.1.1) that reduces the point-counting problem to the evaluation of irreducible characters
 $\tilde {\chi }$
.
$\tilde {\chi }$
. -
(2) Formula (3.4.7.1) that expresses
 $\tilde {\chi }$
as a linear combination of Deligne-Lusztig characters
$\tilde {\chi }$
as a linear combination of Deligne-Lusztig characters
 $R^{G\sigma }_{T_{w_1,\mathbf {w}}\sigma }\tilde {\theta }_{w_1,\mathbf {w}}$
.
$R^{G\sigma }_{T_{w_1,\mathbf {w}}\sigma }\tilde {\theta }_{w_1,\mathbf {w}}$
. -
(3) Formula (3.3.2.1) that reduces the computation of
 $R^{G\sigma }_{T_{w_1,\mathbf {w}}\sigma }\tilde {\theta }_{w_1,\mathbf {w}}$
to the Green function
$R^{G\sigma }_{T_{w_1,\mathbf {w}}\sigma }\tilde {\theta }_{w_1,\mathbf {w}}$
to the Green function
 $\smash {Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)}$
and the linear character
$\smash {Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)}$
and the linear character
 $\tilde {\theta }_{w_1,\mathbf {w}}$
.
$\tilde {\theta }_{w_1,\mathbf {w}}$
.
Section 5 contains some technical lemmas. We prove that with strongly generic conjugacy classes, only a small subset of the characters of
![]() $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma {>}$
can have nontrivial contributions to the E-polynomial. This section also contains a computation of linear characters
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma {>}$
can have nontrivial contributions to the E-polynomial. This section also contains a computation of linear characters
![]() $\tilde {\theta }_{w_1,\mathbf {w}}$
using Möbius inversion function. In Section 6, we recall the essence of symmetric functions associated to wreath products, notably the works of Shoji, and prepare some lemmas. In particular, we relate the Green function in formula (3.3.2.1) to symmetric functions. In Section 7, we compute the E-polynomial, combining results from all previous sections. We also make some sample computations by directly using the irreducible characters of
$\tilde {\theta }_{w_1,\mathbf {w}}$
using Möbius inversion function. In Section 6, we recall the essence of symmetric functions associated to wreath products, notably the works of Shoji, and prepare some lemmas. In particular, we relate the Green function in formula (3.3.2.1) to symmetric functions. In Section 7, we compute the E-polynomial, combining results from all previous sections. We also make some sample computations by directly using the irreducible characters of
![]() $\operatorname {\mathrm {GL}}_2(q)\!<\!\sigma \!>\!$
and
$\operatorname {\mathrm {GL}}_2(q)\!<\!\sigma \!>\!$
and
![]() $\operatorname {\mathrm {GL}}_3(q)\!<\!\sigma \!>\!$
. From these computations, we extract a conjecture on the numbers of connected components of
$\operatorname {\mathrm {GL}}_3(q)\!<\!\sigma \!>\!$
. From these computations, we extract a conjecture on the numbers of connected components of
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties. In Section 8, some basic aspects of (wreath) Macdonald polynomials are recalled. Then we prove that the specialisation of the conjectural formula indeed agrees with our computation of the E-polynomial, concluding the proof of Theorem 1.11. Appendix A gives the explicit expressions of wreath Macdonald polynomials of degree 1 and degree 2 in terms of Schur functions. These formulae will be used in Appendix B and Appendix C. The reader will also observe some key features of wreath Macdonald polynomials. In Appendix B, we verify our conjecture in the cases
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties. In Section 8, some basic aspects of (wreath) Macdonald polynomials are recalled. Then we prove that the specialisation of the conjectural formula indeed agrees with our computation of the E-polynomial, concluding the proof of Theorem 1.11. Appendix A gives the explicit expressions of wreath Macdonald polynomials of degree 1 and degree 2 in terms of Schur functions. These formulae will be used in Appendix B and Appendix C. The reader will also observe some key features of wreath Macdonald polynomials. In Appendix B, we verify our conjecture in the cases
![]() $n=1$
and
$n=1$
and
![]() $n=2$
, admitting the conjecture of Hausel-Letellier-Rodriguez-Villegas. To prove that our claims about
$n=2$
, admitting the conjecture of Hausel-Letellier-Rodriguez-Villegas. To prove that our claims about
![]() $\mathbb {H}_{\mathbf {B}}(z,w)$
in §1.9 are not bluffing, we give two sample computations in Appendix C.
$\mathbb {H}_{\mathbf {B}}(z,w)$
in §1.9 are not bluffing, we give two sample computations in Appendix C.
2 Preliminaries
2.1 General notations and terminology
The 2-element group will be denoted by
![]() $\boldsymbol{\mu} _2$
. If G is a finite group, we will denote by
$\boldsymbol{\mu} _2$
. If G is a finite group, we will denote by
![]() $\operatorname {\mathrm {Irr}}(G)$
the set of irreducible complex characters of G. If
$\operatorname {\mathrm {Irr}}(G)$
the set of irreducible complex characters of G. If ![]() is a given algebraically closed field of characteristic different from 2, we will denote by
is a given algebraically closed field of characteristic different from 2, we will denote by
![]() $\mathfrak {i}$
a chosen square root of
$\mathfrak {i}$
a chosen square root of
![]() $-1$
. In most parts of the article, n will denote the rank of our ambient group
$-1$
. In most parts of the article, n will denote the rank of our ambient group
![]() $\operatorname {\mathrm {GL}}_n$
, and N will denote
$\operatorname {\mathrm {GL}}_n$
, and N will denote
![]() $[n/2]$
.
$[n/2]$
.
Given an abstract group G and an automorphism
![]() $\sigma $
of G, we will denote by
$\sigma $
of G, we will denote by
![]() $G^{\sigma }$
the subgroup of the fixed points of
$G^{\sigma }$
the subgroup of the fixed points of
![]() $\sigma $
. If G is abelian, then
$\sigma $
. If G is abelian, then
![]() $[G,\sigma ]:=\{g\sigma (g^{-1})\mid g\in G\}$
is also a subgroup of G. A
$[G,\sigma ]:=\{g\sigma (g^{-1})\mid g\in G\}$
is also a subgroup of G. A
![]() $\sigma $
-conjugacy class of G is an orbit in G under the action
$\sigma $
-conjugacy class of G is an orbit in G under the action
![]() $g:x\mapsto gx\sigma (g)^{-1}$
, for any g,
$g:x\mapsto gx\sigma (g)^{-1}$
, for any g,
![]() $x\in G$
. If
$x\in G$
. If
![]() $X\subset G$
is a subset, then we say that X is
$X\subset G$
is a subset, then we say that X is
![]() $\sigma $
-stable if
$\sigma $
-stable if
![]() $\sigma (X)=X$
.
$\sigma (X)=X$
.
If
![]() $X\subset G$
is a subset and
$X\subset G$
is a subset and
![]() $H\subset G$
is a subgroup, we will denote by
$H\subset G$
is a subgroup, we will denote by
![]() $C_H(X)$
the centraliser of X in H. If H, X and Y are subsets of G, we will denote by
$C_H(X)$
the centraliser of X in H. If H, X and Y are subsets of G, we will denote by
![]() $N_H(X)$
the normaliser of X in H and by
$N_H(X)$
the normaliser of X in H and by
![]() $N_H(X,Y)=N_H(X)\cap N_H(Y)$
the subset of H that simultaneously normalises X and Y. The centre of a group G will be denoted by
$N_H(X,Y)=N_H(X)\cap N_H(Y)$
the subset of H that simultaneously normalises X and Y. The centre of a group G will be denoted by
![]() $Z_G$
.
$Z_G$
.
If
![]() $G_0\subset G$
is a subgroup and
$G_0\subset G$
is a subgroup and
![]() $G_1\subset G$
is a subset that is normalised by
$G_1\subset G$
is a subset that is normalised by
![]() $G_0$
, then by a
$G_0$
, then by a
![]() $G_0$
-conjugacy class in
$G_0$
-conjugacy class in
![]() $G_1$
, we mean a subset of the form
$G_1$
, we mean a subset of the form
![]() $\{gxg^{-1}\mid g\in G_0\}$
for some
$\{gxg^{-1}\mid g\in G_0\}$
for some
![]() $x\in G_1$
. Similarly, we can talk about a
$x\in G_1$
. Similarly, we can talk about a
![]() $G_0$
-conjugate of an element or a subset of G. When G is an algebraic group, the above notions make sense in the obvious way. If G is an algebraic group, we will denote by
$G_0$
-conjugate of an element or a subset of G. When G is an algebraic group, the above notions make sense in the obvious way. If G is an algebraic group, we will denote by
![]() $G^{\circ }$
its identity component. The subgroup
$G^{\circ }$
its identity component. The subgroup
![]() $G_0$
as above is typically
$G_0$
as above is typically
![]() $G^{\circ }$
or a finite subgroup of G.
$G^{\circ }$
or a finite subgroup of G.
2.2 Partitions
2.2.1
For any
![]() $n\in \mathbb {Z}_{>0}$
, we denote by
$n\in \mathbb {Z}_{>0}$
, we denote by
![]() $\mathfrak {S}_n$
the group of permutations of the set
$\mathfrak {S}_n$
the group of permutations of the set
Each permutation
![]() $\tau \in \mathfrak {S}_n$
can be decomposed into a product of cycles
$\tau \in \mathfrak {S}_n$
can be decomposed into a product of cycles
![]() $c_{I_1}\cdots c_{I_l}$
, where the disjoint subsets
$c_{I_1}\cdots c_{I_l}$
, where the disjoint subsets
![]() $I_r\subset \mathbb {I}(n)$
form a partition of
$I_r\subset \mathbb {I}(n)$
form a partition of
![]() $\mathbb {I}(n)$
and
$\mathbb {I}(n)$
and
![]() $c_{I_r}$
is a circular permutation on
$c_{I_r}$
is a circular permutation on
![]() $I_r$
. For each
$I_r$
. For each
![]() $1\le r\le l$
, put
$1\le r\le l$
, put
![]() $\tau _r=|c_{I_r}|$
, the size of
$\tau _r=|c_{I_r}|$
, the size of
![]() $I_r$
, and then the conjugacy class of
$I_r$
, and then the conjugacy class of
![]() $\tau $
is determined by the partition
$\tau $
is determined by the partition
![]() $(\tau _1,\ldots ,\tau _l)$
.
$(\tau _1,\ldots ,\tau _l)$
.
Let
![]() $n\in \mathbb {Z}_{\ge 0}$
. A partition of n will often be written as a nonincreasing sequence of nonnegative integers
$n\in \mathbb {Z}_{\ge 0}$
. A partition of n will often be written as a nonincreasing sequence of nonnegative integers
![]() $\lambda =(\lambda _1\ge \lambda _2\ge \cdots )$
such that
$\lambda =(\lambda _1\ge \lambda _2\ge \cdots )$
such that
![]() $n=\sum _k\lambda _k$
, and
$n=\sum _k\lambda _k$
, and
![]() $0$
only has the empty partition
$0$
only has the empty partition
![]() $(0,0,\ldots )$
. The length of
$(0,0,\ldots )$
. The length of
![]() $\lambda $
will be denoted by
$\lambda $
will be denoted by
![]() $l(\lambda )$
, and n is called the size of
$l(\lambda )$
, and n is called the size of
![]() $\lambda $
. For each partition
$\lambda $
. For each partition
![]() $\lambda $
, we define the integer
$\lambda $
, we define the integer
![]() $n(\lambda ):=\sum _i(i-1)\lambda _i$
. The dual of a partition
$n(\lambda ):=\sum _i(i-1)\lambda _i$
. The dual of a partition
![]() $\lambda $
will be denoted by
$\lambda $
will be denoted by
![]() $\lambda ^{\ast }$
. The set of partitions of n will be denoted by
$\lambda ^{\ast }$
. The set of partitions of n will be denoted by
![]() $\mathcal {P}(n)$
. Write
$\mathcal {P}(n)$
. Write
![]() $\mathcal {P}=\sqcup _{n\in \mathbb {Z}_{\ge 0}}\mathcal {P}(n)$
. The irreducible characters and the conjugacy classes of
$\mathcal {P}=\sqcup _{n\in \mathbb {Z}_{\ge 0}}\mathcal {P}(n)$
. The irreducible characters and the conjugacy classes of
![]() $\mathfrak {S}_n$
are both parametrised by
$\mathfrak {S}_n$
are both parametrised by
![]() $\mathcal {P}(n)$
. For any
$\mathcal {P}(n)$
. For any
![]() $\lambda \in \mathcal {P}(n)$
, we will denote by
$\lambda \in \mathcal {P}(n)$
, we will denote by
![]() $\chi ^{\lambda }$
the corresponding irreducible character, and by
$\chi ^{\lambda }$
the corresponding irreducible character, and by
![]() $\chi ^{\lambda }_{\mu }$
the value of this character on the conjugacy class corresponding to
$\chi ^{\lambda }_{\mu }$
the value of this character on the conjugacy class corresponding to
![]() $\mu \in \mathcal {P}(n)$
.
$\mu \in \mathcal {P}(n)$
.
Write
![]() $\mathcal {P}^2=\mathcal {P}\times \mathcal {P}$
. The elements of
$\mathcal {P}^2=\mathcal {P}\times \mathcal {P}$
. The elements of
![]() $\mathcal {P}^2$
will be called 2-partitions. For any
$\mathcal {P}^2$
will be called 2-partitions. For any
![]() $\boldsymbol{\lambda} =(\lambda ^{(0)},\lambda ^{(1)})\in \mathcal {P}^2$
, its size is defined by
$\boldsymbol{\lambda} =(\lambda ^{(0)},\lambda ^{(1)})\in \mathcal {P}^2$
, its size is defined by
![]() $|\boldsymbol{\lambda} |:=|\lambda ^{(0)}|+|\lambda ^{(1)}|$
, and its length is defined by
$|\boldsymbol{\lambda} |:=|\lambda ^{(0)}|+|\lambda ^{(1)}|$
, and its length is defined by
![]() $l(\boldsymbol{\lambda} ):=l(\lambda ^{(0)})+l(\lambda ^{(1)})$
. The dual of a 2-partition
$l(\boldsymbol{\lambda} ):=l(\lambda ^{(0)})+l(\lambda ^{(1)})$
. The dual of a 2-partition
![]() $\boldsymbol{\lambda} =(\lambda ^{(0)},\lambda ^{(1)})$
is defined by
$\boldsymbol{\lambda} =(\lambda ^{(0)},\lambda ^{(1)})$
is defined by
![]() $\boldsymbol{\lambda} ^{\ast }:=(\lambda ^{(1)\ast },\lambda ^{(0)\ast })$
. The set of 2-partitions of size n will be denoted by
$\boldsymbol{\lambda} ^{\ast }:=(\lambda ^{(1)\ast },\lambda ^{(0)\ast })$
. The set of 2-partitions of size n will be denoted by
![]() $\mathcal {P}^2(n)$
.
$\mathcal {P}^2(n)$
.
2.2.2
Given a partition
![]() $\lambda =(\lambda _1,\lambda _2,\ldots )$
of size n, we take
$\lambda =(\lambda _1,\lambda _2,\ldots )$
of size n, we take
![]() $r\ge l(\lambda )$
, and we put
$r\ge l(\lambda )$
, and we put
Let
![]() $(2y_1>\cdots >2y_{l_0})$
and
$(2y_1>\cdots >2y_{l_0})$
and
![]() $(2y_1'+1>\cdots >2y^{\prime }_{l_1}+1)$
be the even parts and the odd parts of
$(2y_1'+1>\cdots >2y^{\prime }_{l_1}+1)$
be the even parts and the odd parts of
![]() $\lambda +\delta _r$
, where the sum is taken term by term. Denote by
$\lambda +\delta _r$
, where the sum is taken term by term. Denote by
![]() $\lambda '$
the partition that has as its parts the numbers
$\lambda '$
the partition that has as its parts the numbers
![]() $2s+t$
,
$2s+t$
,
![]() $0\le s\le l_t-1$
,
$0\le s\le l_t-1$
,
![]() $t=0,1$
. We have
$t=0,1$
. We have
![]() $l(\lambda ')=l(\lambda )$
. The 2-core of
$l(\lambda ')=l(\lambda )$
. The 2-core of
![]() $\lambda $
is the partition defined by
$\lambda $
is the partition defined by
![]() $(\lambda ^{\prime }_k-l(\lambda )+k)_{1\le k\le l(\lambda )}$
. It is independent of r and necessarily of the form
$(\lambda ^{\prime }_k-l(\lambda )+k)_{1\le k\le l(\lambda )}$
. It is independent of r and necessarily of the form
![]() $(d,d-1,\ldots ,2,1,0)$
, for some
$(d,d-1,\ldots ,2,1,0)$
, for some
![]() $d\in \mathbb {Z}_{\ge 0}$
. Denote by
$d\in \mathbb {Z}_{\ge 0}$
. Denote by
![]() $\smash {\lambda ^{(0)}}$
the partition defined by
$\smash {\lambda ^{(0)}}$
the partition defined by
![]() $\smash {\lambda ^{(0)}_k}=y_k-l_0+k$
and denote by
$\smash {\lambda ^{(0)}_k}=y_k-l_0+k$
and denote by
![]() $\smash {\lambda ^{(1)}}$
the partition defined by
$\smash {\lambda ^{(1)}}$
the partition defined by
![]() $\smash {\lambda ^{(1)}_k}=y^{\prime }_k-l_1+k$
. Then
$\smash {\lambda ^{(1)}_k}=y^{\prime }_k-l_1+k$
. Then
![]() $(\lambda ^{(0)},\lambda ^{(1)})_r$
is a 2-partition that depends on the parity of r, which we call the 2-quotient of
$(\lambda ^{(0)},\lambda ^{(1)})_r$
is a 2-partition that depends on the parity of r, which we call the 2-quotient of
![]() $\lambda $
. Changing the parity of r will permute
$\lambda $
. Changing the parity of r will permute
![]() $\lambda ^{(0)}$
and
$\lambda ^{(0)}$
and
![]() $\lambda ^{(1)}$
. We make the convention that
$\lambda ^{(1)}$
. We make the convention that
![]() $r\equiv 1\quad\mod 2$
if the 2-core is
$r\equiv 1\quad\mod 2$
if the 2-core is
![]() $(0)$
and
$(0)$
and
![]() $r\equiv 0\quad\mod 2$
if the 2-core is
$r\equiv 0\quad\mod 2$
if the 2-core is
![]() $(1)$
.
$(1)$
.
Remark 2.2.1. In [Reference HaimanHai03], the 2-quotient is defined in terms of the residues of the contents of the boxes. The two definitions of 2-quotient agree when the 2-core is
![]() $(0)$
, but not when the 2-core is
$(0)$
, but not when the 2-core is
![]() $(1)$
. In fact, Haiman’s definition is equivalent to setting
$(1)$
. In fact, Haiman’s definition is equivalent to setting
![]() $r\equiv 1\quad\mod 2$
in all cases. For example, let
$r\equiv 1\quad\mod 2$
in all cases. For example, let
![]() $\lambda =(3)$
. Then our definition gives the 2-quotient
$\lambda =(3)$
. Then our definition gives the 2-quotient
![]() $((1),\varnothing )$
, while Haiman’s definition gives
$((1),\varnothing )$
, while Haiman’s definition gives
![]() $(\varnothing ,(1))$
. Our convention is coherent with Theorem 1.2, where the trivial character of
$(\varnothing ,(1))$
. Our convention is coherent with Theorem 1.2, where the trivial character of
![]() $W^{\sigma }$
corresponds to the trivial character of W.
$W^{\sigma }$
corresponds to the trivial character of W.
The above constructions give a bijection
 $$ \begin{align} \left\{\begin{array}{c}\text{Partitions of } n\\ \text{with 2-core } (d,d-1,\ldots,1,0)\end{array}\right\} \longleftrightarrow\left\{\text{2-partitions of } \frac{1}{2}(n-\frac{d(d+1)}{2})\right\}. \end{align} $$
$$ \begin{align} \left\{\begin{array}{c}\text{Partitions of } n\\ \text{with 2-core } (d,d-1,\ldots,1,0)\end{array}\right\} \longleftrightarrow\left\{\text{2-partitions of } \frac{1}{2}(n-\frac{d(d+1)}{2})\right\}. \end{align} $$
We call this bijection the quotient-core decomposition of partitions.
2.3 Wreath products
2.3.1
Given a finite group
![]() $\Gamma $
and a positive integer m, the symmetric group
$\Gamma $
and a positive integer m, the symmetric group
![]() $\mathfrak {S}_m$
acts on the direct product
$\mathfrak {S}_m$
acts on the direct product
![]() $\Gamma ^m$
of m copies of
$\Gamma ^m$
of m copies of
![]() $\Gamma $
by permuting the factors. This defines a semi-direct product
$\Gamma $
by permuting the factors. This defines a semi-direct product
![]() $\Gamma ^m\rtimes \mathfrak {S}_m$
, called a wreath product. We will denote by
$\Gamma ^m\rtimes \mathfrak {S}_m$
, called a wreath product. We will denote by
![]() $\mathfrak {W}_m$
the wreath product defined by
$\mathfrak {W}_m$
the wreath product defined by
![]() $\Gamma =\mathbb {Z}/2\mathbb {Z}$
. It is the Weyl group of
$\Gamma =\mathbb {Z}/2\mathbb {Z}$
. It is the Weyl group of
![]() $\operatorname {\mathrm {Sp}}_{2m}$
and
$\operatorname {\mathrm {Sp}}_{2m}$
and
![]() $\operatorname {\mathrm {SO}}_{2m+1}$
. More general wreath products
$\operatorname {\mathrm {SO}}_{2m+1}$
. More general wreath products
![]() $(\mathbb {Z}/r\mathbb {Z})^m\rtimes \mathfrak {S}_m$
for
$(\mathbb {Z}/r\mathbb {Z})^m\rtimes \mathfrak {S}_m$
for
![]() $r>2$
cannot be realised as the Weyl groups of any algebraic groups. We will always identify
$r>2$
cannot be realised as the Weyl groups of any algebraic groups. We will always identify
![]() $\mathbb {Z}/2\mathbb {Z}$
with
$\mathbb {Z}/2\mathbb {Z}$
with
![]() $\boldsymbol{\mu} _2$
and write its elements in the multiplicative form.
$\boldsymbol{\mu} _2$
and write its elements in the multiplicative form.
2.3.2
Denote by
![]() $w_0$
the permutation
$w_0$
the permutation
![]() $(1,-1)(2,-2)\cdots (m,-m)$
of the set
$(1,-1)(2,-2)\cdots (m,-m)$
of the set
We can identify
![]() $\mathfrak {W}_m$
as the subgroup of the group of permutations on
$\mathfrak {W}_m$
as the subgroup of the group of permutations on
![]() $\bar {\mathbb {I}}(m)$
consisting of elements commuting with
$\bar {\mathbb {I}}(m)$
consisting of elements commuting with
![]() $w_0$
. Then each element
$w_0$
. Then each element
![]() $\tau \in \mathfrak {S}_m\subset \mathfrak {W}_m$
is identified with the permutation
$\tau \in \mathfrak {S}_m\subset \mathfrak {W}_m$
is identified with the permutation
and for any
![]() $i\in \{1,\ldots ,m\}$
, the element
$i\in \{1,\ldots ,m\}$
, the element
![]() $(e_1,\ldots ,e_m)\in (\mathbb {Z}/2\mathbb {Z})^m\subset \mathfrak {W}_m$
, with
$(e_1,\ldots ,e_m)\in (\mathbb {Z}/2\mathbb {Z})^m\subset \mathfrak {W}_m$
, with
![]() $e_i=-1$
and
$e_i=-1$
and
![]() $e_j=1$
if
$e_j=1$
if
![]() $j\ne i$
, is identified with the permutation
$j\ne i$
, is identified with the permutation
![]() $(i,-i)$
.
$(i,-i)$
.
2.3.3
Let
![]() $w=((e_1,\ldots ,e_m),\tau )\in (\mathbb {Z}/2\mathbb {Z})^m\rtimes \mathfrak {S}_m$
. Then
$w=((e_1,\ldots ,e_m),\tau )\in (\mathbb {Z}/2\mathbb {Z})^m\rtimes \mathfrak {S}_m$
. Then
![]() $\tau $
can be written as
$\tau $
can be written as
![]() $\tau =c_{I_1}\cdots c_{I_l}$
as in §2.2.1. For each
$\tau =c_{I_1}\cdots c_{I_l}$
as in §2.2.1. For each
![]() $1\le r\le l$
, put
$1\le r\le l$
, put
![]() $\bar {e}_r=\prod _{k\in I_r}e_k$
. For any
$\bar {e}_r=\prod _{k\in I_r}e_k$
. For any
![]() $1\le r\le l$
, we will call
$1\le r\le l$
, we will call
![]() $((e_r)_{r\in I_r},c_{I_r})$
a positive (resp. negative) cycle in w if
$((e_r)_{r\in I_r},c_{I_r})$
a positive (resp. negative) cycle in w if
![]() $\bar {e}_r=1$
(resp.
$\bar {e}_r=1$
(resp.
![]() $\bar {e}_r=-1$
), so that w is a product of signed cycles. The size of a signed cycle in w is defined as the size of the corresponding cycle in
$\bar {e}_r=-1$
), so that w is a product of signed cycles. The size of a signed cycle in w is defined as the size of the corresponding cycle in
![]() $\tau $
. Define the permutations
$\tau $
. Define the permutations
so that
![]() $\tau =\tau ^{(0)}\tau ^{(1)}$
. Also denote by
$\tau =\tau ^{(0)}\tau ^{(1)}$
. Also denote by
![]() $\tau ^{(0)}$
and
$\tau ^{(0)}$
and
![]() $\tau ^{(1)}$
the associated partitions by abuse of notation. We then have a 2-partition
$\tau ^{(1)}$
the associated partitions by abuse of notation. We then have a 2-partition
![]() $(\tau ^{(0)},\tau ^{(1)})$
, which is sometimes called a signed partition of m. This 2-partition determines the conjugacy class of w. The conjugacy classes and irreducible characters of
$(\tau ^{(0)},\tau ^{(1)})$
, which is sometimes called a signed partition of m. This 2-partition determines the conjugacy class of w. The conjugacy classes and irreducible characters of
![]() $\mathfrak {W}_m$
are both parametrised by
$\mathfrak {W}_m$
are both parametrised by
![]() $\mathcal {P}^2(m)$
. For any
$\mathcal {P}^2(m)$
. For any
![]() $\boldsymbol{\lambda} \in \mathcal {P}^2(m)$
, we will denote by
$\boldsymbol{\lambda} \in \mathcal {P}^2(m)$
, we will denote by
![]() $\chi ^{\boldsymbol{\lambda} }$
the corresponding irreducible character, and by
$\chi ^{\boldsymbol{\lambda} }$
the corresponding irreducible character, and by
![]() $\chi ^{\boldsymbol{\lambda} }_{\boldsymbol{\mu} }$
the value of this character on the conjugacy class corresponding to
$\chi ^{\boldsymbol{\lambda} }_{\boldsymbol{\mu} }$
the value of this character on the conjugacy class corresponding to
![]() $\boldsymbol{\mu} \in \mathcal {P}^2(m)$
.
$\boldsymbol{\mu} \in \mathcal {P}^2(m)$
.
Regarded as a permutation on the set
![]() $\bar {\mathbb {I}}(m)$
, an element w such that
$\bar {\mathbb {I}}(m)$
, an element w such that
![]() $\tau =\tau ^{(0)}=(1,2,\ldots ,m)$
is typically of the form
$\tau =\tau ^{(0)}=(1,2,\ldots ,m)$
is typically of the form

and an element w such that
![]() $\tau =\tau ^{(1)}=(1,2,\ldots ,m)$
is typically of the form
$\tau =\tau ^{(1)}=(1,2,\ldots ,m)$
is typically of the form

2.4 Springer correspondence and symbols
2.4.1
Let G be a connected reductive group and let W be the Weyl group of G defined by a maximal torus. Denote by
![]() $\mathscr {N}$
the set consisting of pairs
$\mathscr {N}$
the set consisting of pairs
![]() $(C,\phi )$
, where
$(C,\phi )$
, where
![]() $C\subset G$
is a unipotent conjugacy class and
$C\subset G$
is a unipotent conjugacy class and
![]() $\phi $
is an irreducible character of
$\phi $
is an irreducible character of
![]() $C_G(u)/C_G(u)^{\circ }$
for some
$C_G(u)/C_G(u)^{\circ }$
for some
![]() $u\in C$
. The Springer correspondence is an injection ([Reference ShojiSho87, §4])
$u\in C$
. The Springer correspondence is an injection ([Reference ShojiSho87, §4])
There is an equivalence relation on
![]() $\mathscr {N}$
that identifies
$\mathscr {N}$
that identifies
![]() $(C_1,\phi _1)$
and
$(C_1,\phi _1)$
and
![]() $(C_2,\phi _2)$
whenever
$(C_2,\phi _2)$
whenever
![]() $C_1=C_2$
, in which case we say
$C_1=C_2$
, in which case we say
![]() $(C_1,\phi _1)$
and
$(C_1,\phi _1)$
and
![]() $(C_2,\phi _2)$
are similar. Such an equivalence class is called a similarity class.
$(C_2,\phi _2)$
are similar. Such an equivalence class is called a similarity class.
Symbols are certain combinatorial data that are in bijection with the image of (2.4.1.1). If
![]() $G=\operatorname {\mathrm {Sp}}_{2m}$
or
$G=\operatorname {\mathrm {Sp}}_{2m}$
or
![]() $\operatorname {\mathrm {SO}}_{2m+1}$
, then
$\operatorname {\mathrm {SO}}_{2m+1}$
, then
![]() $\operatorname {\mathrm {Irr}}(W)$
is in bijection with
$\operatorname {\mathrm {Irr}}(W)$
is in bijection with
![]() $\mathcal {P}^2(m)$
. Therefore, the symbols are also in bijection with
$\mathcal {P}^2(m)$
. Therefore, the symbols are also in bijection with
![]() $\mathcal {P}^2(m)$
. Similarity classes in
$\mathcal {P}^2(m)$
. Similarity classes in
![]() $\mathcal {P}^2(m)$
or in the set of symbols are induced from
$\mathcal {P}^2(m)$
or in the set of symbols are induced from
![]() $\mathscr {N}$
. If
$\mathscr {N}$
. If
![]() $\boldsymbol{\alpha} $
is a 2-partition, we will denote by
$\boldsymbol{\alpha} $
is a 2-partition, we will denote by
![]() $\boldsymbol{\Lambda} (\boldsymbol{\alpha} )$
the corresponding symbol. In this article, we do not need the notion of symbols in an essential way. We use them only to match the notations in [Reference ShojiSho01].
$\boldsymbol{\Lambda} (\boldsymbol{\alpha} )$
the corresponding symbol. In this article, we do not need the notion of symbols in an essential way. We use them only to match the notations in [Reference ShojiSho01].
2.4.2
For any symbol
![]() $\boldsymbol{\Lambda }$
, let
$\boldsymbol{\Lambda }$
, let
![]() $a(\boldsymbol{\Lambda })$
be the integer defined by [Reference ShojiSho01, (1.2.2)]. This is the analogue of
$a(\boldsymbol{\Lambda })$
be the integer defined by [Reference ShojiSho01, (1.2.2)]. This is the analogue of
![]() $n(\lambda )$
for partitions. Its value is constant on the similarity classes of symbols. If we denote by u an element of the unipotent conjugacy class corresponding to
$n(\lambda )$
for partitions. Its value is constant on the similarity classes of symbols. If we denote by u an element of the unipotent conjugacy class corresponding to
![]() $\boldsymbol{\Lambda }$
, then
$\boldsymbol{\Lambda }$
, then
where
![]() $\mathcal {B}_u$
is the Springer fiber over u. For any 2-partition
$\mathcal {B}_u$
is the Springer fiber over u. For any 2-partition
![]() $\boldsymbol{\alpha} $
, we define
$\boldsymbol{\alpha} $
, we define
![]() $a(\boldsymbol{\alpha }):=a(\boldsymbol{\Lambda }(\boldsymbol{\alpha }))$
. We will fix once and for all a total order
$a(\boldsymbol{\alpha }):=a(\boldsymbol{\Lambda }(\boldsymbol{\alpha }))$
. We will fix once and for all a total order
![]() $\prec $
on the set of symbols in such a way that if
$\prec $
on the set of symbols in such a way that if
![]() $C_1$
(resp.
$C_1$
(resp.
![]() $C_2$
) is the unipotent class corresponding to
$C_2$
) is the unipotent class corresponding to
![]() $\boldsymbol{\Lambda} _1$
(resp.
$\boldsymbol{\Lambda} _1$
(resp.
![]() $\boldsymbol{\Lambda} _2$
), then
$\boldsymbol{\Lambda} _2$
), then
![]() $\boldsymbol{\Lambda} _2\prec \boldsymbol{\Lambda} _1$
if
$\boldsymbol{\Lambda} _2\prec \boldsymbol{\Lambda} _1$
if
![]() $C_2\subset \bar {C}_1$
, and each similarity class forms an interval. We will write
$C_2\subset \bar {C}_1$
, and each similarity class forms an interval. We will write
![]() $\boldsymbol{\Lambda} _1\sim \boldsymbol{\Lambda} _2$
if
$\boldsymbol{\Lambda} _1\sim \boldsymbol{\Lambda} _2$
if
![]() $\boldsymbol{\Lambda} _1$
and
$\boldsymbol{\Lambda} _1$
and
![]() $\boldsymbol{\Lambda} _2$
are similar. Note that
$\boldsymbol{\Lambda} _2$
are similar. Note that
![]() $a(\boldsymbol{\Lambda} _1)\le a(\boldsymbol{\Lambda} _2)$
whenever
$a(\boldsymbol{\Lambda} _1)\le a(\boldsymbol{\Lambda} _2)$
whenever
![]() $\boldsymbol{\Lambda} _2\prec \boldsymbol{\Lambda} _1$
. The set of 2-partitions acquires a total order via the bijection with symbols, so that
$\boldsymbol{\Lambda} _2\prec \boldsymbol{\Lambda} _1$
. The set of 2-partitions acquires a total order via the bijection with symbols, so that
![]() $a(\boldsymbol{\alpha })\le a(\boldsymbol{\beta })$
whenever
$a(\boldsymbol{\alpha })\le a(\boldsymbol{\beta })$
whenever
![]() $\boldsymbol{\beta }\prec \boldsymbol{\alpha }$
. In particular, the element
$\boldsymbol{\beta }\prec \boldsymbol{\alpha }$
. In particular, the element
![]() $\boldsymbol{\alpha }_0:=(\varnothing ,(1^n))$
corresponding to the the identity of the finite classical group is minimal, and it is alone in its similarity class.
$\boldsymbol{\alpha }_0:=(\varnothing ,(1^n))$
corresponding to the the identity of the finite classical group is minimal, and it is alone in its similarity class.
2.5 Nonconnected algebraic groups
2.5.1
Let G be a not necessarily connected linear algebraic group over an algebraically closed field ![]() . We say that G is reductive if
. We say that G is reductive if
![]() $G^{\circ }$
is reductive. Let
$G^{\circ }$
is reductive. Let
![]() $B\subset G^{\circ }$
be a Borel subgroup and let
$B\subset G^{\circ }$
be a Borel subgroup and let
![]() $T\subset B$
be a maximal torus. Then
$T\subset B$
be a maximal torus. Then
![]() $\bar {T}:=N_G(T,B)$
has nonempty intersection with every connected component of G, since the conjugation by any element of G sends T and B to some other maximal torus and Borel subgroup, which are conjugate to T and B by an element of
$\bar {T}:=N_G(T,B)$
has nonempty intersection with every connected component of G, since the conjugation by any element of G sends T and B to some other maximal torus and Borel subgroup, which are conjugate to T and B by an element of
![]() $G^{\circ }$
. An element of G is called quasi-semi-simple if it lies in
$G^{\circ }$
. An element of G is called quasi-semi-simple if it lies in
![]() $\bar {T}$
for some
$\bar {T}$
for some
![]() $T\subset B$
. It is known that semi-simple elements are always quasi-semi-simple ([Reference SteinbergSte68, Theorem 7.5]). We will always assume that
$T\subset B$
. It is known that semi-simple elements are always quasi-semi-simple ([Reference SteinbergSte68, Theorem 7.5]). We will always assume that ![]() . Under this assumption, all unipotent elements of G are contained in
. Under this assumption, all unipotent elements of G are contained in
![]() $G^{\circ }$
and all quasi-semi-simple elements are semi-simple ([Reference Digne and MichelDM94, Remarque 2.7]).
$G^{\circ }$
and all quasi-semi-simple elements are semi-simple ([Reference Digne and MichelDM94, Remarque 2.7]).
2.5.2
Let
![]() $G^1$
be a connected component of G and let
$G^1$
be a connected component of G and let
![]() $\sigma \in G^1$
be a semi-simple element. Let
$\sigma \in G^1$
be a semi-simple element. Let
![]() $T\subset G^{\circ }$
be a maximal torus that is normalised by
$T\subset G^{\circ }$
be a maximal torus that is normalised by
![]() $\sigma $
. Denote by
$\sigma $
. Denote by
![]() $W=W_{G^{\circ }}(T)$
the Weyl group of
$W=W_{G^{\circ }}(T)$
the Weyl group of
![]() $G^{\circ }$
defined by T. Then
$G^{\circ }$
defined by T. Then
![]() $\sigma $
induces an action on W. Denote by
$\sigma $
induces an action on W. Denote by
![]() $W^{\sigma }$
the subgroup of
$W^{\sigma }$
the subgroup of
![]() $\sigma $
-fixed points. The subtori
$\sigma $
-fixed points. The subtori
![]() $(T^{\sigma })^{\circ }$
and
$(T^{\sigma })^{\circ }$
and
![]() $[T,\sigma ]$
are preserved by the action of
$[T,\sigma ]$
are preserved by the action of
![]() $W^{\sigma }$
on T.
$W^{\sigma }$
on T.
Proposition 2.5.1 ([Reference Digne and MichelDM18][Proposition 1.16])
Every semi-simple
![]() $G^{\circ }$
-conjugacy class in
$G^{\circ }$
-conjugacy class in
![]() $G^1$
has a representative in
$G^1$
has a representative in
![]() $(T^{\sigma })^{\circ }\sigma $
. Two elements
$(T^{\sigma })^{\circ }\sigma $
. Two elements
![]() $t\sigma $
and
$t\sigma $
and
![]() $t'\sigma $
with t,
$t'\sigma $
with t,
![]() $t'\in (T^{\sigma })^{\circ }$
, represent the same class if and only if t and
$t'\in (T^{\sigma })^{\circ }$
, represent the same class if and only if t and
![]() $t'$
, when passing to the quotient
$t'$
, when passing to the quotient
![]() $(T^{\sigma })^{\circ }/(T^{\sigma })^{\circ }\cap [T,\sigma ]$
, belong to the same
$(T^{\sigma })^{\circ }/(T^{\sigma })^{\circ }\cap [T,\sigma ]$
, belong to the same
![]() $W^{\sigma }$
-orbit.
$W^{\sigma }$
-orbit.
A semi-simple element
![]() $\sigma $
is quasi-central in
$\sigma $
is quasi-central in
![]() $G^1$
if there is no element
$G^1$
if there is no element
![]() $g\in G^{\circ }$
such that
$g\in G^{\circ }$
such that
![]() $\dim C_{G^{\circ }}(\sigma )^{\circ }<\dim C_{G^{\circ }}(g\sigma )^{\circ }.$
$\dim C_{G^{\circ }}(\sigma )^{\circ }<\dim C_{G^{\circ }}(g\sigma )^{\circ }.$
Theorem 2.5.2 [Reference Digne and MichelDM94, Théorème 1.15]
A semi-simple element
![]() $\sigma \in G^1$
is quasi-central if and only if for every
$\sigma \in G^1$
is quasi-central if and only if for every
![]() $\sigma $
-stable maximal torus T contained in a
$\sigma $
-stable maximal torus T contained in a
![]() $\sigma $
-stable Borel subgroup of
$\sigma $
-stable Borel subgroup of
![]() $G^{\circ }$
, every
$G^{\circ }$
, every
![]() $\sigma $
-stable element of
$\sigma $
-stable element of
![]() $N_{G^{\circ }}(T)/T$
has a representative in
$N_{G^{\circ }}(T)/T$
has a representative in
![]() $C_{G^{\circ }}(\sigma )^{\circ }$
.
$C_{G^{\circ }}(\sigma )^{\circ }$
.
2.5.3
A closed subgroup of G is a parabolic subgroup if
![]() $G/P$
is proper. According to [Reference SpringerSpr98, Lemma 6.2.4], a subgroup
$G/P$
is proper. According to [Reference SpringerSpr98, Lemma 6.2.4], a subgroup
![]() $P\subset G$
is parabolic if and only if
$P\subset G$
is parabolic if and only if
![]() $P^{\circ }$
is parabolic in
$P^{\circ }$
is parabolic in
![]() $G^{\circ }$
. For example, if P is a parabolic subgroup of
$G^{\circ }$
. For example, if P is a parabolic subgroup of
![]() $G^{\circ }$
, then P and
$G^{\circ }$
, then P and
![]() $N_G(P)$
are both parabolic subgroups of G. It is obvious that the intersection of
$N_G(P)$
are both parabolic subgroups of G. It is obvious that the intersection of
![]() $N_G(P)$
with any connected component of G is isomorphic to P if it is nonempty. We want to determine which connected components of G have nonempty intersection with
$N_G(P)$
with any connected component of G is isomorphic to P if it is nonempty. We want to determine which connected components of G have nonempty intersection with
![]() $N_G(P)$
.
$N_G(P)$
.
There is a well-defined action of
![]() $G/G^{\circ }$
on the set of
$G/G^{\circ }$
on the set of
![]() $G^{\circ }$
-conjugacy classes of parabolic subgroups of
$G^{\circ }$
-conjugacy classes of parabolic subgroups of
![]() $G^{\circ }$
, induced by the conjugation action of G. Let
$G^{\circ }$
, induced by the conjugation action of G. Let
![]() $G^1\subset G$
be a connected component and
$G^1\subset G$
be a connected component and
![]() $P\subset G^{\circ }$
a parabolic subgroup. Then
$P\subset G^{\circ }$
a parabolic subgroup. Then
![]() $N_G(P)$
meets
$N_G(P)$
meets
![]() $G^1$
if and only if the
$G^1$
if and only if the
![]() $G^{\circ }$
-conjugacy class of P is
$G^{\circ }$
-conjugacy class of P is
![]() $G^1$
-stable. Let
$G^1$
-stable. Let
![]() $L\subset P$
be a Levi factor. If
$L\subset P$
be a Levi factor. If
![]() $N_G(P)$
meets a connected component
$N_G(P)$
meets a connected component
![]() $G^1$
of G, then
$G^1$
of G, then
![]() $N_G(L,P)$
also meets
$N_G(L,P)$
also meets
![]() $G^1$
, since any two Levi factors of P are conjugate under P.
$G^1$
, since any two Levi factors of P are conjugate under P.
Fix a semi-simple element
![]() $\sigma \in G^1$
. Then by [Reference Digne and MichelDM94, Proposition 1.6] and the above discussions,
$\sigma \in G^1$
. Then by [Reference Digne and MichelDM94, Proposition 1.6] and the above discussions,
![]() $N_G(P)$
meets
$N_G(P)$
meets
![]() $G^1$
if and only if there exists a
$G^1$
if and only if there exists a
![]() $G^{\circ }$
-conjugate of P that is
$G^{\circ }$
-conjugate of P that is
![]() $\sigma $
-stable, and
$\sigma $
-stable, and
![]() $N_G(L,P)$
meets
$N_G(L,P)$
meets
![]() $G^1$
if and only if there exists a
$G^1$
if and only if there exists a
![]() $G^{\circ }$
-conjugate of the pair
$G^{\circ }$
-conjugate of the pair
![]() $(L,P)$
that is
$(L,P)$
that is
![]() $\sigma $
-stable. The following propositions describe the set of
$\sigma $
-stable. The following propositions describe the set of
![]() $\sigma $
-stable parabolic subgroups and the set of
$\sigma $
-stable parabolic subgroups and the set of
![]() $\sigma $
-stable Levi factors of
$\sigma $
-stable Levi factors of
![]() $\sigma $
-stable parabolic subgroups.
$\sigma $
-stable parabolic subgroups.
Proposition 2.5.3 [Reference Digne and MichelDM94, Proposition 1.11 (ii)]
Let
![]() $s\in G$
be semi-simple. Let L be an s-stable Levi factor of an s-stable parabolic subgroup
$s\in G$
be semi-simple. Let L be an s-stable Levi factor of an s-stable parabolic subgroup
![]() $P\subset G^{\circ }$
. Then
$P\subset G^{\circ }$
. Then
![]() $(P^s)^{\circ }\subset (G^s)^{\circ }$
is a parabolic subgroup and
$(P^s)^{\circ }\subset (G^s)^{\circ }$
is a parabolic subgroup and
![]() $(L^s)^{\circ }\subset (P^s)^{\circ }$
is a Levi factor.
$(L^s)^{\circ }\subset (P^s)^{\circ }$
is a Levi factor.
Proposition 2.5.4 [Reference Digne and MichelDM94, Corollaire 1.25]
Let
![]() $\sigma \in G$
be quasi-central.
$\sigma \in G$
be quasi-central.
-
(1) The map
 $P\mapsto (P^{\sigma })^{\circ }$
defines a bijection between the
$P\mapsto (P^{\sigma })^{\circ }$
defines a bijection between the
 $\sigma $
-stable parabolic subgroups of
$\sigma $
-stable parabolic subgroups of
 $G^{\circ }$
and the parabolic subgroups of
$G^{\circ }$
and the parabolic subgroups of
 $(G^{\sigma })^{\circ }$
.
$(G^{\sigma })^{\circ }$
. -
(2) Then map
 $L\mapsto (L^{\sigma })^{\circ }$
defines a bijection between the
$L\mapsto (L^{\sigma })^{\circ }$
defines a bijection between the
 $\sigma $
-stable Levi factors of
$\sigma $
-stable Levi factors of
 $\sigma $
-stable parabolic subgroups of
$\sigma $
-stable parabolic subgroups of
 $G^{\circ }$
and the Levi subgroups of
$G^{\circ }$
and the Levi subgroups of
 $(G^{\sigma })^{\circ }$
. The inverse is given by
$(G^{\sigma })^{\circ }$
. The inverse is given by
 $L'\mapsto C_{G^{\circ }}(Z^{\circ }_{L'})$
for
$L'\mapsto C_{G^{\circ }}(Z^{\circ }_{L'})$
for
 $L'\subset (G^{\sigma })^{\circ }$
.
$L'\subset (G^{\sigma })^{\circ }$
.
2.5.4
The following proposition will be used via its corollaries.
Proposition 2.5.5. Let
![]() $s\in G$
be semi-simple and let L be an s-stable Levi factor of an s-stable parabolic subgroup of
$s\in G$
be semi-simple and let L be an s-stable Levi factor of an s-stable parabolic subgroup of
![]() $G^{\circ }$
. Suppose that
$G^{\circ }$
. Suppose that
![]() $L=C_{G^{\circ }}(Z^{\circ }_{(L^s)^{\circ }})$
. Then
$L=C_{G^{\circ }}(Z^{\circ }_{(L^s)^{\circ }})$
. Then
![]() $N_{(G^{s})^{\circ }}((L^{s})^{\circ })$
is contained in
$N_{(G^{s})^{\circ }}((L^{s})^{\circ })$
is contained in
![]() $N_{G^{\circ }}(L)$
. Moreover, each connected component of
$N_{G^{\circ }}(L)$
. Moreover, each connected component of
![]() $N_{G^{\circ }}(L)$
contains exactly one connected component of
$N_{G^{\circ }}(L)$
contains exactly one connected component of
![]() $N_{(G^{s})^{\circ }}((L^{s})^{\circ })$
.
$N_{(G^{s})^{\circ }}((L^{s})^{\circ })$
.
Proof. The inclusion
![]() $N_{(G^{s})^{\circ }}((L^{s})^{\circ })\subset N_{G^{\circ }}(L)$
follows from the assumption on L and s. To prove the second part, it suffices to prove that
$N_{(G^{s})^{\circ }}((L^{s})^{\circ })\subset N_{G^{\circ }}(L)$
follows from the assumption on L and s. To prove the second part, it suffices to prove that
![]() $N_{(G^{s})^{\circ }}((L^{s})^{\circ })\cap L=(L^{s})^{\circ }$
. This is achieved by considering the conjugation action of
$N_{(G^{s})^{\circ }}((L^{s})^{\circ })\cap L=(L^{s})^{\circ }$
. This is achieved by considering the conjugation action of
![]() $\xi \in N_{(G^{s})^{\circ }}((L^{s})^{\circ })\cap L$
on
$\xi \in N_{(G^{s})^{\circ }}((L^{s})^{\circ })\cap L$
on
![]() $Z_{(L^{s})^{\circ }}^{\circ }$
.
$Z_{(L^{s})^{\circ }}^{\circ }$
.
We have
![]() $(Z_L^{s})^{\circ }=Z_{(L^{s})^{\circ }}^{\circ }$
. The inclusion
$(Z_L^{s})^{\circ }=Z_{(L^{s})^{\circ }}^{\circ }$
. The inclusion
![]() $(Z_L^{s})^{\circ }\subset Z_{(L^{s})^{\circ }}^{\circ }$
is obvious. Inclusion in the other direction follows again from the assumption on L and s. Since
$(Z_L^{s})^{\circ }\subset Z_{(L^{s})^{\circ }}^{\circ }$
is obvious. Inclusion in the other direction follows again from the assumption on L and s. Since
![]() $\xi $
lies in L, the conjugation action of
$\xi $
lies in L, the conjugation action of
![]() $\xi $
on
$\xi $
on
![]() $(Z_L^{s})^{\circ }$
must be trivial.
$(Z_L^{s})^{\circ }$
must be trivial.
It is well known that if M is a Levi subgroup of a connected reductive group H, then
![]() $M=C_H(Z^{\circ }_M)$
. By Proposition 2.5.3,
$M=C_H(Z^{\circ }_M)$
. By Proposition 2.5.3,
![]() $(L^{s})^{\circ }$
is a Levi subgroup of
$(L^{s})^{\circ }$
is a Levi subgroup of
![]() $(G^{s})^{\circ }$
. We conclude that
$(G^{s})^{\circ }$
. We conclude that
![]() $\xi $
must lie in
$\xi $
must lie in
![]() $(L^{\sigma })^{\circ }$
.
$(L^{\sigma })^{\circ }$
.
With the notion of isolated elements, the following two corollaries could be integrated into one uniform result. But we prefer not to introduce more notions.
Corollary 2.5.6. Let
![]() $\sigma \in G$
be quasi-central and let L be a
$\sigma \in G$
be quasi-central and let L be a
![]() $\sigma $
-stable Levi factor of a
$\sigma $
-stable Levi factor of a
![]() $\sigma $
-stable parabolic subgroup of
$\sigma $
-stable parabolic subgroup of
![]() $G^{\circ }$
. Write
$G^{\circ }$
. Write
Then there is a natural injective map
Proof. By [Reference Digne and MichelDM94, Proposition 1.23], L and
![]() $\sigma $
satisfy the assumption on L and s in Proposition 2.5.5. The image is automatically contained in the
$\sigma $
satisfy the assumption on L and s in Proposition 2.5.5. The image is automatically contained in the
![]() $\sigma $
-fixed part.
$\sigma $
-fixed part.
Corollary 2.5.7. Let
![]() $\sigma \in G$
be quasi-central. Let
$\sigma \in G$
be quasi-central. Let
![]() $T\subset G^{\circ }$
be a
$T\subset G^{\circ }$
be a
![]() $\sigma $
-stable maximal torus and let
$\sigma $
-stable maximal torus and let
![]() $s\in T$
. Write
$s\in T$
. Write
Then there is a natural injective map
Proof. We have
![]() $T^{s\sigma }=T^{\sigma }$
. Thus, by Proposition 2.5.4, T and
$T^{s\sigma }=T^{\sigma }$
. Thus, by Proposition 2.5.4, T and
![]() $s\sigma $
satisfy the assumption on L and s in Proposition 2.5.5. It is easy to see that the image is contained in the
$s\sigma $
satisfy the assumption on L and s in Proposition 2.5.5. It is easy to see that the image is contained in the
![]() $\sigma $
-fixed part.
$\sigma $
-fixed part.
Remark 2.5.8. The special case where
![]() $L=T$
is a maximal torus implies that the condition in Theorem 2.5.2 is equivalent to
$L=T$
is a maximal torus implies that the condition in Theorem 2.5.2 is equivalent to
![]() $W_{(G^{\sigma })^{\circ }}((T^{\sigma })^{\circ })\cong W_{G^{\circ }}(T)^{\sigma }$
.
$W_{(G^{\sigma })^{\circ }}((T^{\sigma })^{\circ })\cong W_{G^{\circ }}(T)^{\sigma }$
.
2.6 Algebraic groups defined over a finite field
Let q be a power of a prime number. In this section, ![]() denotes an algebraic closure of
denotes an algebraic closure of
![]() $\mathbb {F}_q$
.
$\mathbb {F}_q$
.
2.6.1
An algebraic group G over ![]() is defined over
is defined over
![]() $\mathbb {F}_q$
if there is an algebraic group
$\mathbb {F}_q$
if there is an algebraic group
![]() $G_0$
over
$G_0$
over
![]() $\mathbb {F}_q$
such that
$\mathbb {F}_q$
such that ![]() . Given
. Given
![]() $G_0$
, the geometric Frobenius endomorphism on G is denoted by F. The set of fixed points of F, denoted by
$G_0$
, the geometric Frobenius endomorphism on G is denoted by F. The set of fixed points of F, denoted by
![]() $G^F$
, is a finite group, which we will sometimes write as
$G^F$
, is a finite group, which we will sometimes write as
![]() $G(q)$
. If
$G(q)$
. If
![]() $X\subset G$
is a subvariety, then we say that X is F-stable if
$X\subset G$
is a subvariety, then we say that X is F-stable if
![]() $F(X)=X$
.
$F(X)=X$
.
2.6.2
Let G be a connected reductive group defined over
![]() $\mathbb {F}_q$
. Let
$\mathbb {F}_q$
. Let
![]() $T\subset G$
be an F-stable maximal torus. Then F-acts naturally on
$T\subset G$
be an F-stable maximal torus. Then F-acts naturally on
![]() $W_G(T)$
, and so we can talk about the F-conjugacy classes in
$W_G(T)$
, and so we can talk about the F-conjugacy classes in
![]() $W_G(T)$
as defined in §2.1. The
$W_G(T)$
as defined in §2.1. The
![]() $G^F$
-conjugacy classes of F-stable maximal tori are in bijection with the F-conjugacy classes of
$G^F$
-conjugacy classes of F-stable maximal tori are in bijection with the F-conjugacy classes of
![]() $W_G(T)$
. This bijection is described as follows. Given
$W_G(T)$
. This bijection is described as follows. Given
![]() $w\in W_G(T)$
, let
$w\in W_G(T)$
, let
![]() $\dot {w}\in G$
be a representative of w. By Lang-Steinberg theorem, there exists
$\dot {w}\in G$
be a representative of w. By Lang-Steinberg theorem, there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $g^{-1}F(g)=\dot {w}$
. Then
$g^{-1}F(g)=\dot {w}$
. Then
![]() $gTg^{-1}$
is again an F-stable maximal torus, and its
$gTg^{-1}$
is again an F-stable maximal torus, and its
![]() $G^F$
-conjugacy class only depends on the F-conjugacy class of w. Conversely, if
$G^F$
-conjugacy class only depends on the F-conjugacy class of w. Conversely, if
![]() $gTg^{-1}$
is an F-stable maximal torus for some
$gTg^{-1}$
is an F-stable maximal torus for some
![]() $g\in G$
, then
$g\in G$
, then
![]() $g^{-1}F(g)$
normalises T and so defines an element of
$g^{-1}F(g)$
normalises T and so defines an element of
![]() $W_G(T)$
. The two constructions are inverse to each other.
$W_G(T)$
. The two constructions are inverse to each other.
Fix an F-stable maximal torus T and a Borel subgroup B containing T. Let
![]() $\Delta =\Delta (T,B)$
be the set of simple roots defined by T and B. The parabolic subgroups containing B, called standard parabolic subgroups, are parametrised by the set of the subsets of
$\Delta =\Delta (T,B)$
be the set of simple roots defined by T and B. The parabolic subgroups containing B, called standard parabolic subgroups, are parametrised by the set of the subsets of
![]() $\Delta $
. For any
$\Delta $
. For any
![]() $I\subset \Delta $
, denote by
$I\subset \Delta $
, denote by
![]() $P_I$
the corresponding standard parabolic subgroup. Its unique Levi factor containing T is called a standard Levi subgroup, denoted by
$P_I$
the corresponding standard parabolic subgroup. Its unique Levi factor containing T is called a standard Levi subgroup, denoted by
![]() $L_I$
. Every Levi subgroup of G is conjugate to a standard Levi subgroup. Fix
$L_I$
. Every Levi subgroup of G is conjugate to a standard Levi subgroup. Fix
![]() $I\subset \Delta $
. The
$I\subset \Delta $
. The
![]() $G^F$
-conjugacy classes of the G-conjugates of
$G^F$
-conjugacy classes of the G-conjugates of
![]() $L_I$
are in bijection with the F-conjugacy classes of
$L_I$
are in bijection with the F-conjugacy classes of
![]() $N_G(L_I)/L_I$
. The construction of this correspondence resembles the case of maximal tori.
$N_G(L_I)/L_I$
. The construction of this correspondence resembles the case of maximal tori.
2.6.3
Suppose that G is a reductive group defined over
![]() $\mathbb {F}_q$
and that
$\mathbb {F}_q$
and that
![]() $G/G^{\circ }$
is a cyclic group. Let
$G/G^{\circ }$
is a cyclic group. Let
![]() $\sigma \in G$
be an F-stable quasi-central element such that
$\sigma \in G$
be an F-stable quasi-central element such that
![]() $G/G^{\circ }$
is generated by the component of
$G/G^{\circ }$
is generated by the component of
![]() $\sigma $
.
$\sigma $
.
Proposition 2.6.1 [Reference Digne and MichelDM94, Proposition 1.40]
The
![]() $G^F$
-conjugacy classes of the F-stable subgroups
$G^F$
-conjugacy classes of the F-stable subgroups
![]() $\bar {L}=N_G(L,P)$
defined by some F-stable Levi factor L of some parabolic subgroup
$\bar {L}=N_G(L,P)$
defined by some F-stable Levi factor L of some parabolic subgroup
![]() $P\subset G^{\circ }$
, satisfying
$P\subset G^{\circ }$
, satisfying
![]() $\bar {L}\cap G^{\circ }\sigma \ne \emptyset $
, are in bijection with the
$\bar {L}\cap G^{\circ }\sigma \ne \emptyset $
, are in bijection with the
![]() $((G^{\sigma })^{\circ })^F$
-conjugacy classes of the F-stable Levi subgroups of
$((G^{\sigma })^{\circ })^F$
-conjugacy classes of the F-stable Levi subgroups of
![]() $(G^{\sigma })^{\circ }$
in the following manner. Each
$(G^{\sigma })^{\circ }$
in the following manner. Each
![]() $\bar {L}$
has a
$\bar {L}$
has a
![]() $G^F$
-conjugate
$G^F$
-conjugate
![]() $\bar {L}_1$
containing
$\bar {L}_1$
containing
![]() $\sigma $
, and the bijection associates the
$\sigma $
, and the bijection associates the
![]() $((G^{\sigma })^{\circ })^F$
-class of
$((G^{\sigma })^{\circ })^F$
-class of
![]() $((\bar {L}_1)^{\sigma })^{\circ }$
to the
$((\bar {L}_1)^{\sigma })^{\circ }$
to the
![]() $G^F$
-class of
$G^F$
-class of
![]() $\bar {L}$
.
$\bar {L}$
.
We give a more concrete description of this correspondence. Fix an F-stable and
![]() $\sigma $
-stable maximal torus T and a
$\sigma $
-stable maximal torus T and a
![]() $\sigma $
-stable Borel subgroup
$\sigma $
-stable Borel subgroup
![]() $B\subset G^{\circ }$
that contains T. Let I be a subset of the set of simple roots defined by
$B\subset G^{\circ }$
that contains T. Let I be a subset of the set of simple roots defined by
![]() $(T,B)$
. Let
$(T,B)$
. Let
![]() $L_I$
be the standard Levi subgroup with respect to
$L_I$
be the standard Levi subgroup with respect to
![]() $(T,B)$
. Suppose that I is
$(T,B)$
. Suppose that I is
![]() $\sigma $
-stable and so
$\sigma $
-stable and so
![]() $(L_I^{\sigma })^{\circ }$
is a standard Levi subgroup of
$(L_I^{\sigma })^{\circ }$
is a standard Levi subgroup of
![]() $(G^{\sigma })^{\circ }$
with respect to
$(G^{\sigma })^{\circ }$
with respect to
![]() $((T^{\sigma })^{\circ },(B^{\sigma })^{\circ })$
. Then the
$((T^{\sigma })^{\circ },(B^{\sigma })^{\circ })$
. Then the
![]() $((G^{\sigma })^{\circ })^F$
-conjugacy classes of the
$((G^{\sigma })^{\circ })^F$
-conjugacy classes of the
![]() $(G^{\sigma })^{\circ }$
-conjugates of
$(G^{\sigma })^{\circ }$
-conjugates of
![]() $(L_I^{\sigma })^{\circ }$
are in bijection with the F-conjugacy classes in
$(L_I^{\sigma })^{\circ }$
are in bijection with the F-conjugacy classes in
![]() $W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
. For any
$W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
. For any
![]() $w\in W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
, the procedure of §2.6.2 gives an F-stable Levi factor
$w\in W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
, the procedure of §2.6.2 gives an F-stable Levi factor
![]() $L^{\prime }_{I,w}$
of some parabolic subgroup
$L^{\prime }_{I,w}$
of some parabolic subgroup
![]() $P^{\prime }_{I,w}\subset (G^{\sigma })^{\circ }$
, which is
$P^{\prime }_{I,w}\subset (G^{\sigma })^{\circ }$
, which is
![]() $(G^{\sigma })^{\circ }$
-conjugate to
$(G^{\sigma })^{\circ }$
-conjugate to
![]() $(L_I^{\sigma })^{\circ }$
and whose
$(L_I^{\sigma })^{\circ }$
and whose
![]() $((G^{\sigma })^{\circ })^F$
-conjugacy class corresponds to the F-conjugacy class of w. By Proposition 2.5.4, the pair
$((G^{\sigma })^{\circ })^F$
-conjugacy class corresponds to the F-conjugacy class of w. By Proposition 2.5.4, the pair
![]() $(L^{\prime }_{I,w},P^{\prime }_{I,w})$
determines an F-stable and
$(L^{\prime }_{I,w},P^{\prime }_{I,w})$
determines an F-stable and
![]() $\sigma $
-stable Levi factor
$\sigma $
-stable Levi factor
![]() $L_{I,w}$
of a
$L_{I,w}$
of a
![]() $\sigma $
-stable parabolic subgroup
$\sigma $
-stable parabolic subgroup
![]() $P_{I,w}$
. In fact, if
$P_{I,w}$
. In fact, if
![]() $\dot {w}$
,
$\dot {w}$
,
![]() $g\in (G^{\sigma })^{\circ }$
are as in §2.6.2, then
$g\in (G^{\sigma })^{\circ }$
are as in §2.6.2, then
![]() $L_{I,w}=gL_Ig^{-1}$
. Put
$L_{I,w}=gL_Ig^{-1}$
. Put
It is F-stable and meets the connected component
![]() $G^{\circ }\sigma $
. By Proposition 2.6.1, such groups for varying I and w exploit all
$G^{\circ }\sigma $
. By Proposition 2.6.1, such groups for varying I and w exploit all
![]() $G^F$
-conjugacy classes of F-stable subgroups of the form
$G^F$
-conjugacy classes of F-stable subgroups of the form
![]() $\bar {L}$
that meet
$\bar {L}$
that meet
![]() $G^{\circ }\sigma $
. This implies, in particular, that the
$G^{\circ }\sigma $
. This implies, in particular, that the
![]() $G^F$
-conjugacy classes of the F-stable subgroups
$G^F$
-conjugacy classes of the F-stable subgroups
![]() $N_G(T',B')$
, defined by an F-stable maximal torus
$N_G(T',B')$
, defined by an F-stable maximal torus
![]() $T'$
contained in a Borel subgroup
$T'$
contained in a Borel subgroup
![]() $B'\subset G^{\circ }$
, are parametrised by the F-conjugacy classes of
$B'\subset G^{\circ }$
, are parametrised by the F-conjugacy classes of
![]() $W_{G^{\circ }}(T)^{\sigma }$
(see Remark 2.5.8).
$W_{G^{\circ }}(T)^{\sigma }$
(see Remark 2.5.8).
Define another Frobenius
![]() $F_w:=\operatorname {\mathrm {ad}}\dot {w}\circ F$
on G. Then there is a commutative diagram
$F_w:=\operatorname {\mathrm {ad}}\dot {w}\circ F$
on G. Then there is a commutative diagram

We will simply say that
![]() $(L_I,F_w)$
is isomorphic to
$(L_I,F_w)$
is isomorphic to
![]() $(L_{I,w},F)$
via
$(L_{I,w},F)$
via
![]() $\operatorname {\mathrm {ad}} g$
.
$\operatorname {\mathrm {ad}} g$
.
2.7 Frobenius formula
2.7.1
Let H be a finite group and let
![]() $H_0\lhd H$
be a normal subgroup of index 2. Let
$H_0\lhd H$
be a normal subgroup of index 2. Let
![]() $\sigma $
be an element of
$\sigma $
be an element of
![]() $H\setminus H_0$
. Then
$H\setminus H_0$
. Then
![]() $\sigma $
defines an involution on
$\sigma $
defines an involution on
![]() $\operatorname {\mathrm {Irr}}(H_0)$
by composing a character with the conjugation by
$\operatorname {\mathrm {Irr}}(H_0)$
by composing a character with the conjugation by
![]() $\sigma $
. This involution does not depend on the choice of
$\sigma $
. This involution does not depend on the choice of
![]() $\sigma $
in
$\sigma $
in
![]() $H\setminus H_0$
. Denote by
$H\setminus H_0$
. Denote by
![]() $\operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
the subset of
$\operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
the subset of
![]() $\sigma $
-fixed elements. By Clifford theory, each element
$\sigma $
-fixed elements. By Clifford theory, each element
![]() $\chi \in \operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
admits an extension to H (i.e., some
$\chi \in \operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
admits an extension to H (i.e., some
![]() $\chi _H\in \operatorname {\mathrm {Irr}}(H)$
such that
$\chi _H\in \operatorname {\mathrm {Irr}}(H)$
such that
![]() $(\chi _H)|_{H_0}=\chi $
). Moreover, there are precisely two such extensions, and they differ by
$(\chi _H)|_{H_0}=\chi $
). Moreover, there are precisely two such extensions, and they differ by
![]() $-1$
on
$-1$
on
![]() $H\setminus H_0$
. For every
$H\setminus H_0$
. For every
![]() $\chi \in \operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
, we choose a preferred extension, denoted by
$\chi \in \operatorname {\mathrm {Irr}}(H_0)^{\sigma }$
, we choose a preferred extension, denoted by
![]() $\tilde {\chi }$
. If the restriction of
$\tilde {\chi }$
. If the restriction of
![]() $\chi _H\in \operatorname {\mathrm {Irr}}(H)$
to
$\chi _H\in \operatorname {\mathrm {Irr}}(H)$
to
![]() $H_0$
is not irreducible (or rather,
$H_0$
is not irreducible (or rather,
![]() $\chi _H$
is not an extension of any
$\chi _H$
is not an extension of any
![]() $\chi \in \operatorname {\mathrm {Irr}}(H_0)$
), then
$\chi \in \operatorname {\mathrm {Irr}}(H_0)$
), then
![]() $\chi _H$
must vanish on
$\chi _H$
must vanish on
![]() $H\setminus H_0$
.
$H\setminus H_0$
.
Proposition 2.7.1. Let
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
be an arbitrary
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
be an arbitrary
![]() $2k$
-tuple of
$2k$
-tuple of
![]() $H_0$
-conjugacy classes contained in
$H_0$
-conjugacy classes contained in
![]() $H\setminus H_0$
. Then we have the following counting formula:
$H\setminus H_0$
. Then we have the following counting formula:
 $$ \begin{align} \begin{aligned} &\#\left\{((A_i,B_i)_{1\le i\le g},(X_j)_{1\le j\le 2k})\in H_0^{2g}\times \prod_{j=1}^{2k}C_j\Big\arrowvert\prod_{i=1}^{g}[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\\ =\ &|H_0|\sum_{\chi\in\operatorname{\mathrm{Irr}}(H_0)^{\sigma}}\Big(\frac{|H_0|}{\chi(1)}\Big)^{2g-2}\prod_{i=1}^{2k} \frac{|C_i|\tilde{\chi}(C_i)}{\chi(1)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\#\left\{((A_i,B_i)_{1\le i\le g},(X_j)_{1\le j\le 2k})\in H_0^{2g}\times \prod_{j=1}^{2k}C_j\Big\arrowvert\prod_{i=1}^{g}[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\\ =\ &|H_0|\sum_{\chi\in\operatorname{\mathrm{Irr}}(H_0)^{\sigma}}\Big(\frac{|H_0|}{\chi(1)}\Big)^{2g-2}\prod_{i=1}^{2k} \frac{|C_i|\tilde{\chi}(C_i)}{\chi(1)}. \end{aligned} \end{align} $$
Note that the value of the counting formula is independent of the choices of
![]() $\tilde {\chi }$
due to the product of
$\tilde {\chi }$
due to the product of
![]() $2k$
terms. The proof is given below.
$2k$
terms. The proof is given below.
2.7.2
Let us prepare some notations of finite groups.
Denote by
![]() $\mathcal {C}(H)$
the vector space of complex valued class functions on H. Put
$\mathcal {C}(H)$
the vector space of complex valued class functions on H. Put
![]() $\hat {H}=\operatorname {\mathrm {Irr}}(H)$
. Denote by
$\hat {H}=\operatorname {\mathrm {Irr}}(H)$
. Denote by
![]() $\mathcal {C}(\hat {H})$
the vector space of linear combinations
$\mathcal {C}(\hat {H})$
the vector space of linear combinations
![]() $\sum _{\chi \in \hat {H}}a_{\chi }\chi $
of irreducible characters, which is the same as
$\sum _{\chi \in \hat {H}}a_{\chi }\chi $
of irreducible characters, which is the same as
![]() $\mathcal {C}(H)$
but will be equipped with a different product operation.
$\mathcal {C}(H)$
but will be equipped with a different product operation.
The convolution product
![]() $\ast $
in
$\ast $
in
![]() $\mathcal {C}(H)$
is defined by
$\mathcal {C}(H)$
is defined by
The dot product
![]() $\cdot $
in
$\cdot $
in
![]() $\mathcal {C}(\hat {H})$
is defined by
$\mathcal {C}(\hat {H})$
is defined by
(i.e., the coefficient of
![]() $\chi $
in the product is the product of the coefficients of
$\chi $
in the product is the product of the coefficients of
![]() $\chi $
).
$\chi $
).
The Fourier transform
![]() $\mathcal {F}:\mathcal {C}(H)\rightarrow \mathcal {C}(\hat {H})$
is defined by
$\mathcal {F}:\mathcal {C}(H)\rightarrow \mathcal {C}(\hat {H})$
is defined by
 $$ \begin{align} \mathcal{F}(f)(\chi)=\sum_{h\in H}\frac{f(h)\chi(h)}{\chi(1)},\quad f\in\mathcal{C}(H). \end{align} $$
$$ \begin{align} \mathcal{F}(f)(\chi)=\sum_{h\in H}\frac{f(h)\chi(h)}{\chi(1)},\quad f\in\mathcal{C}(H). \end{align} $$
We also have the transform
![]() $\mathbb {F}:\mathcal {C}(\hat {H})\rightarrow \mathcal {C}(H)$
defined by
$\mathbb {F}:\mathcal {C}(\hat {H})\rightarrow \mathcal {C}(H)$
defined by
 $$ \begin{align} \mathbb{F}(F)(h)=\sum_{\chi\in\hat{H}}F(\chi)\chi(1)\overline{\chi(h)}. \end{align} $$
$$ \begin{align} \mathbb{F}(F)(h)=\sum_{\chi\in\hat{H}}F(\chi)\chi(1)\overline{\chi(h)}. \end{align} $$
We have
They are compatible with the product operations
From the equality
![]() $\mathbb {F}\circ \mathcal {F}=|H|\cdot \operatorname {\mathrm {Id}}_{\mathcal {C}(H)}$
and the definition of the transforms, we deduce that
$\mathbb {F}\circ \mathcal {F}=|H|\cdot \operatorname {\mathrm {Id}}_{\mathcal {C}(H)}$
and the definition of the transforms, we deduce that
 $$ \begin{align} f(1)=\frac{1}{|H|}\sum_{\chi\in\hat{H}}\chi(1)^2\mathcal{F}(f)(\chi) \end{align} $$
$$ \begin{align} f(1)=\frac{1}{|H|}\sum_{\chi\in\hat{H}}\chi(1)^2\mathcal{F}(f)(\chi) \end{align} $$
for any class function f.
2.7.3
We define the function
![]() $\mathfrak {n}^g:H\rightarrow \mathbb {C}$
by
$\mathfrak {n}^g:H\rightarrow \mathbb {C}$
by
 $$ \begin{align} \mathfrak{n}^g(x)=\#\left\{(A_1,B_1,\cdots,A_g,B_g)\in H_0^{2g}\Big\arrowvert\prod_{i=1}^g[A_i,B_i]=x\right\}. \end{align} $$
$$ \begin{align} \mathfrak{n}^g(x)=\#\left\{(A_1,B_1,\cdots,A_g,B_g)\in H_0^{2g}\Big\arrowvert\prod_{i=1}^g[A_i,B_i]=x\right\}. \end{align} $$
We find that
![]() $\mathfrak {n}^g\in \mathcal {C}(H)$
(identically zero on
$\mathfrak {n}^g\in \mathcal {C}(H)$
(identically zero on
![]() $H\setminus H_0$
) and that
$H\setminus H_0$
) and that
![]() $\mathfrak {n}^g=\mathfrak {n}^1\ast \cdots \ast \mathfrak {n}^1$
. Denote by
$\mathfrak {n}^g=\mathfrak {n}^1\ast \cdots \ast \mathfrak {n}^1$
. Denote by
![]() $1_{C_i}$
the characteristic function of the class
$1_{C_i}$
the characteristic function of the class
![]() $C_i$
. Then
$C_i$
. Then
 $$ \begin{align} \begin{aligned} &\#\left\{((A_i,B_i)_{1\le i\le g},(X_j)_{1\le j\le 2k})\in H_0^{2g}\times \prod_{j=1}^{2k}C_j\Big\arrowvert\prod_{i=1}^{g}[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\\ =\ &(\mathfrak{n}^g\ast 1_{C_1}\ast\cdots\ast 1_{C_{2k}})(1). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\#\left\{((A_i,B_i)_{1\le i\le g},(X_j)_{1\le j\le 2k})\in H_0^{2g}\times \prod_{j=1}^{2k}C_j\Big\arrowvert\prod_{i=1}^{g}[A_i,B_i]\prod_{j=1}^{2k}X_j=1\right\}\\ =\ &(\mathfrak{n}^g\ast 1_{C_1}\ast\cdots\ast 1_{C_{2k}})(1). \end{aligned} \end{align} $$
By (2.7.2.6) and (2.7.2.7), we have
 $$ \begin{align} \begin{aligned} &(\mathfrak{n}^g\ast 1_{C_1}\ast\cdots\ast 1_{C_{2k}})(1)\\ =\ &\frac{1}{|H|}\sum_{\chi\in\operatorname{\mathrm{Irr}}(H)}\chi(1)^2(\mathcal{F}(\mathfrak{n}^1)(\chi))^g\prod_{i=1}^{2k}\frac{|C_i|\chi(C_i)}{\chi(1)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &(\mathfrak{n}^g\ast 1_{C_1}\ast\cdots\ast 1_{C_{2k}})(1)\\ =\ &\frac{1}{|H|}\sum_{\chi\in\operatorname{\mathrm{Irr}}(H)}\chi(1)^2(\mathcal{F}(\mathfrak{n}^1)(\chi))^g\prod_{i=1}^{2k}\frac{|C_i|\chi(C_i)}{\chi(1)}. \end{aligned} \end{align} $$
It is known ([Reference Hausel, Letellier and Rodriguez-VillegasHLRV11, Lemma 3.1.3]) that
Therefore,
 $$ \begin{align} \begin{aligned} &\frac{1}{|H|}\sum_{\chi_H\in\operatorname{\mathrm{Irr}}(H)}\chi_H(1)^2(\mathcal{F}(\mathfrak{n}^1)(\chi_H))^g\prod_{i=1}^{2k}\frac{|C_i|\chi_H(C_i)}{\chi_H(1)}\\ =\ &|H_0|\sum_{\chi\in\operatorname{\mathrm{Irr}}(H_0)^{\sigma}}\left(\frac{|H_0|}{\chi(1)}\right)^{2g-2}\prod_{i=1}^{2k}\frac{|C_i|\tilde{\chi}(C_i)}{\chi(1)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{|H|}\sum_{\chi_H\in\operatorname{\mathrm{Irr}}(H)}\chi_H(1)^2(\mathcal{F}(\mathfrak{n}^1)(\chi_H))^g\prod_{i=1}^{2k}\frac{|C_i|\chi_H(C_i)}{\chi_H(1)}\\ =\ &|H_0|\sum_{\chi\in\operatorname{\mathrm{Irr}}(H_0)^{\sigma}}\left(\frac{|H_0|}{\chi(1)}\right)^{2g-2}\prod_{i=1}^{2k}\frac{|C_i|\tilde{\chi}(C_i)}{\chi(1)}, \end{aligned} \end{align} $$
where we have used the fact that
![]() $\chi _H$
vanishes on
$\chi _H$
vanishes on
![]() $H\setminus H_0$
if it is not an extension of any element of
$H\setminus H_0$
if it is not an extension of any element of
![]() $\operatorname {\mathrm {Irr}}(H_0)$
. This completes the proof of Proposition 2.7.1.
$\operatorname {\mathrm {Irr}}(H_0)$
. This completes the proof of Proposition 2.7.1.
3 The group
 $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
In the rest of the article, we will write
![]() $G=\operatorname {\mathrm {GL}}_n$
. We will denote by T the maximal torus of diagonal matrices and by B the Borel subgroup of upper triangular matrices. The Weyl group of G defined by T will be denoted by
$G=\operatorname {\mathrm {GL}}_n$
. We will denote by T the maximal torus of diagonal matrices and by B the Borel subgroup of upper triangular matrices. The Weyl group of G defined by T will be denoted by
![]() $W=W_G(T)$
. We understand that standard Levi subgroups are defined with respect to T and B. Recall that
$W=W_G(T)$
. We understand that standard Levi subgroups are defined with respect to T and B. Recall that
![]() $N=[n/2]$
.
$N=[n/2]$
.
3.1 The group
 $\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
over
$\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
over 
In this subsection, we work over an algebraically closed field ![]() .
.
3.1.1
Denote by
![]() $J_n$
the matrix
$J_n$
the matrix

If n is even, put
![]() $t_0=\operatorname {\mathrm {diag}}(a_1,\ldots ,a_n)$
with
$t_0=\operatorname {\mathrm {diag}}(a_1,\ldots ,a_n)$
with
![]() $a_i=1$
if
$a_i=1$
if
![]() $i\le N$
and
$i\le N$
and
![]() $a_i=-1$
otherwise. Put
$a_i=-1$
otherwise. Put
![]() $J^{\prime }_n=t_0J_n$
. Write
$J^{\prime }_n=t_0J_n$
. Write
 $$ \begin{align} \mathscr{J}_n:= \begin{cases} J^{\prime}_n & \text{if } n \text{ is even}\\ J_n & \text{if } n \text{ is odd} \end{cases}, \quad \mathscr{J}^{\prime}_n:=J_n \text{ if } n \text{ is even}. \end{align} $$
$$ \begin{align} \mathscr{J}_n:= \begin{cases} J^{\prime}_n & \text{if } n \text{ is even}\\ J_n & \text{if } n \text{ is odd} \end{cases}, \quad \mathscr{J}^{\prime}_n:=J_n \text{ if } n \text{ is even}. \end{align} $$
Define
![]() $\sigma \in \operatorname {\mathrm {Aut}} G$
as sending g to
$\sigma \in \operatorname {\mathrm {Aut}} G$
as sending g to
![]() $\mathscr {J}_ng^{-t}\mathscr {J}^{-1}_n$
, where
$\mathscr {J}_ng^{-t}\mathscr {J}^{-1}_n$
, where
![]() $g^{-t}$
is the transpose-inverse of g, and define
$g^{-t}$
is the transpose-inverse of g, and define
![]() $\sigma '\in \operatorname {\mathrm {Aut}} G$
by replacing
$\sigma '\in \operatorname {\mathrm {Aut}} G$
by replacing
![]() $\mathscr {J}_n$
with
$\mathscr {J}_n$
with
![]() $\mathscr {J}^{\prime }_n$
in the definition of
$\mathscr {J}^{\prime }_n$
in the definition of
![]() $\sigma $
. They are exterior involutions of G. Their fixed points in G are described as follows:
$\sigma $
. They are exterior involutions of G. Their fixed points in G are described as follows:
 $$ \begin{align} \text{ if } n=2N, \text{ then } \begin{cases} (G^{\sigma})^{\circ}\cong\operatorname{\mathrm{Sp}}_{2N}\\ (G^{\sigma'})^{\circ}\cong\operatorname{\mathrm{SO}}_{2N} \end{cases}\!\!\!\!\!\!\!,\quad \text{ if } n=2N+1, \text{ then } (G^{\sigma})^{\circ}\cong\operatorname{\mathrm{SO}}_{2N+1}. \end{align} $$
$$ \begin{align} \text{ if } n=2N, \text{ then } \begin{cases} (G^{\sigma})^{\circ}\cong\operatorname{\mathrm{Sp}}_{2N}\\ (G^{\sigma'})^{\circ}\cong\operatorname{\mathrm{SO}}_{2N} \end{cases}\!\!\!\!\!\!\!,\quad \text{ if } n=2N+1, \text{ then } (G^{\sigma})^{\circ}\cong\operatorname{\mathrm{SO}}_{2N+1}. \end{align} $$
We say that an automorphism is of symplectic type or orthogonal type according to the type of its centraliser.
3.1.2
An involution
![]() $\tau $
of G defines a semi-direct product
$\tau $
of G defines a semi-direct product
![]() $G\rtimes \!<\!\tau \!>\!$
. When n is even, there are two
$G\rtimes \!<\!\tau \!>\!$
. When n is even, there are two
![]() $\operatorname {\mathrm {PGL}}_n$
-conjugacy classes of exterior involutions in
$\operatorname {\mathrm {PGL}}_n$
-conjugacy classes of exterior involutions in
![]() $\operatorname {\mathrm {Aut}} G$
, represented by
$\operatorname {\mathrm {Aut}} G$
, represented by
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
, respectively ([Reference Liebeck and SeitzLS12, Lemma 2.9]). We will write
$\sigma '$
, respectively ([Reference Liebeck and SeitzLS12, Lemma 2.9]). We will write ![]() and
and ![]() , in order to indicate that the type of the defining automorphism is symplectic or orthogonal. These two semi-direct products are not isomorphic over any field of characteristic different from
, in order to indicate that the type of the defining automorphism is symplectic or orthogonal. These two semi-direct products are not isomorphic over any field of characteristic different from
![]() $2$
(This follows from [Reference ShuShu23, Theorem 1.12]). It is convenient to regard
$2$
(This follows from [Reference ShuShu23, Theorem 1.12]). It is convenient to regard
![]() $\sigma $
also as an element of
$\sigma $
also as an element of ![]() , identified with
, identified with
![]() $t_0\sigma '$
, since
$t_0\sigma '$
, since
![]() $\sigma $
and
$\sigma $
and
![]() $t_0\sigma '$
induce the same automorphism of G. Note, however, that in
$t_0\sigma '$
induce the same automorphism of G. Note, however, that in ![]() , we have
, we have
![]() $\sigma ^2=-1$
. Therefore, we write
$\sigma ^2=-1$
. Therefore, we write
![]() $G\!<\!\sigma \!>\!$
instead of
$G\!<\!\sigma \!>\!$
instead of
![]() $G\rtimes \!<\!\sigma '\!>\!$
. We will write
$G\rtimes \!<\!\sigma '\!>\!$
. We will write
![]() $\bar {G}=G\!<\!\sigma \!>\!$
if n is odd or if there is no need to distinguish
$\bar {G}=G\!<\!\sigma \!>\!$
if n is odd or if there is no need to distinguish ![]() and
and ![]() .
.
Since
![]() $\sigma $
normalises T and B, it is semi-simple as an element of
$\sigma $
normalises T and B, it is semi-simple as an element of
![]() $\bar {G}$
. Moreover, according to [Reference Digne and MichelDM94, Proposition 1.22],
$\bar {G}$
. Moreover, according to [Reference Digne and MichelDM94, Proposition 1.22],
![]() $\sigma $
is a quasi-central element of
$\sigma $
is a quasi-central element of
![]() $\bar {G}$
. It is easy to see that the action of
$\bar {G}$
. It is easy to see that the action of
![]() $\sigma $
on G commutes with F, and so F can be extended to
$\sigma $
on G commutes with F, and so F can be extended to
![]() $\bar {G}$
in such a way that
$\bar {G}$
in such a way that
![]() $\sigma $
is an F-stable element.
$\sigma $
is an F-stable element.
3.1.3
Now suppose ![]() . For the moment, we do not distinguish
. For the moment, we do not distinguish ![]() and
and ![]() . We apply Proposition 2.5.1 to the connected component
. We apply Proposition 2.5.1 to the connected component
![]() $G^1=G\sigma $
.
$G^1=G\sigma $
.
The subtorus
![]() $(T^{\sigma })^{\circ }$
consists of the matrices
$(T^{\sigma })^{\circ }$
consists of the matrices
with ![]() for all i, and the commutator
for all i, and the commutator
![]() $[T,\sigma ]$
consists of the matrices
$[T,\sigma ]$
consists of the matrices
with ![]() for all i. So the elements of
for all i. So the elements of
![]() $[T,\sigma ]\cap (T^{\sigma })^{\circ }$
are the matrices
$[T,\sigma ]\cap (T^{\sigma })^{\circ }$
are the matrices
with
![]() $e_i=\pm 1$
for all i.
$e_i=\pm 1$
for all i.
The parametrisation of semi-simple conjugacy classes in
![]() $G\sigma $
is then given as follows. Denote by
$G\sigma $
is then given as follows. Denote by ![]() the set of
the set of
![]() $(\boldsymbol{\mu} _2\times \boldsymbol{\mu} _2)$
-orbits in
$(\boldsymbol{\mu} _2\times \boldsymbol{\mu} _2)$
-orbits in ![]() for the action
for the action
Then the semi-simple conjugacy classes in
![]() $G\sigma $
are parametrised by the
$G\sigma $
are parametrised by the
![]() $\mathfrak {S}_N$
-orbits in
$\mathfrak {S}_N$
-orbits in ![]() , or rather, the N-tuples
, or rather, the N-tuples
![]() $(\hat {a}_1,\ldots ,\hat {a}_N)$
,
$(\hat {a}_1,\ldots ,\hat {a}_N)$
, ![]() , up to permutation, whether
, up to permutation, whether
![]() $n=2N$
or
$n=2N$
or
![]() $n=2N+1$
. We thus regard the elements of
$n=2N+1$
. We thus regard the elements of ![]() as the eigenvalues of a semi-simple element. For example, we may say that
as the eigenvalues of a semi-simple element. For example, we may say that
![]() $\sigma $
has eigenvalues
$\sigma $
has eigenvalues
![]() $(\hat {1},\ldots ,\hat {1})$
. Beware that the eigenvalues depend on the choice of
$(\hat {1},\ldots ,\hat {1})$
. Beware that the eigenvalues depend on the choice of
![]() $\sigma $
in Proposition 2.5.1. For example, if n is even and if we had used
$\sigma $
in Proposition 2.5.1. For example, if n is even and if we had used
![]() $\sigma '$
in Proposition 2.5.1, then
$\sigma '$
in Proposition 2.5.1, then
![]() $\sigma $
would have eigenvalues
$\sigma $
would have eigenvalues
![]() $(\hat {\mathfrak {i}},\ldots ,\hat {\mathfrak {i}})$
. In the rest of the article, we will always use
$(\hat {\mathfrak {i}},\ldots ,\hat {\mathfrak {i}})$
. In the rest of the article, we will always use
![]() $\sigma \in G^1$
when we specify a semi-simple element in terms of elements of
$\sigma \in G^1$
when we specify a semi-simple element in terms of elements of ![]() .
.
Lemma 3.1.1. If
![]() $C\subset G\sigma $
is a G-conjugacy class, we write
$C\subset G\sigma $
is a G-conjugacy class, we write
![]() $C^2=\{g^2\mid g\in C\}$
, which is a well-defined conjugacy class in G. Then,
$C^2=\{g^2\mid g\in C\}$
, which is a well-defined conjugacy class in G. Then,
-
(i) C is semi-simple if and only if
 $C^2$
is semi-simple;
$C^2$
is semi-simple; -
(ii) The map
 $C\mapsto C^2$
defines an injection from the set of semi-simple G-conjugacy classes in
$C\mapsto C^2$
defines an injection from the set of semi-simple G-conjugacy classes in
 $G\sigma $
to the set of
$G\sigma $
to the set of
 $\sigma $
-stable semi-simple conjugacy classes in G.
$\sigma $
-stable semi-simple conjugacy classes in G.
Proof. Part (i) is true for characteristic reason. Part (ii) follows from the above parametrisation.
3.1.4
Let
![]() $P\subset G$
be a parabolic subgroup and let
$P\subset G$
be a parabolic subgroup and let
![]() $L\subset P$
be a Levi factor. We will be interested in those
$L\subset P$
be a Levi factor. We will be interested in those
![]() $L\subset P$
such that
$L\subset P$
such that
![]() $N_{\bar {G}}(L,P)$
meets the connected component
$N_{\bar {G}}(L,P)$
meets the connected component
![]() $G\sigma $
. According to §2.5.3, this is to consider the
$G\sigma $
. According to §2.5.3, this is to consider the
![]() $\sigma $
-stable Levi factors of
$\sigma $
-stable Levi factors of
![]() $\sigma $
-stable parabolic subgroups. If P is a
$\sigma $
-stable parabolic subgroups. If P is a
![]() $\sigma $
-stable standard parabolic subgroup with respect to B, then its unique Levi factor containing T is of the form
$\sigma $
-stable standard parabolic subgroup with respect to B, then its unique Levi factor containing T is of the form

, where
![]() $L_i\cong \operatorname {\mathrm {GL}}_{n_i}$
, for some integers
$L_i\cong \operatorname {\mathrm {GL}}_{n_i}$
, for some integers
![]() $n_i$
,
$n_i$
,
![]() $1\le i\le s$
. Therefore, up to the conjugation by G, we only need to consider these Levi subgroups. Note that for these groups,
$1\le i\le s$
. Therefore, up to the conjugation by G, we only need to consider these Levi subgroups. Note that for these groups,
![]() $N_{\bar {G}}(L,P)=L\sqcup L\sigma $
.
$N_{\bar {G}}(L,P)=L\sqcup L\sigma $
.
3.2 The group
 $\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
over
$\operatorname {\mathrm {GL}}_n\!<\!\sigma \!>\!$
over
 $\mathbb {F}_q$
$\mathbb {F}_q$
In the the rest of this section, we will fix an odd prime power q, ![]() will denote an algebraic closure of
will denote an algebraic closure of
![]() $\mathbb {F}_q$
and
$\mathbb {F}_q$
and
![]() $G=\operatorname {\mathrm {GL}}_n$
over
$G=\operatorname {\mathrm {GL}}_n$
over ![]() is equipped with the Frobenius endomorphism F that sends each entry of a matrix to its q-th power. Taking the fixed points of F in
is equipped with the Frobenius endomorphism F that sends each entry of a matrix to its q-th power. Taking the fixed points of F in
![]() $G\!<\!\sigma \!>\!$
, we get a finite group
$G\!<\!\sigma \!>\!$
, we get a finite group
![]() $G(q)\!<\!\sigma \!>\!$
. Note that F acts trivially on
$G(q)\!<\!\sigma \!>\!$
. Note that F acts trivially on
![]() $N_G(L)/L$
if L is a Levi subgroup containing T; in particular, it acts trivially on W.
$N_G(L)/L$
if L is a Levi subgroup containing T; in particular, it acts trivially on W.
3.2.1
By the theorem of Lang-Steinberg, a G-conjugacy class in
![]() $G\sigma $
contains an element of
$G\sigma $
contains an element of
![]() $G^F\sigma $
if and only if it is F-stable. Let
$G^F\sigma $
if and only if it is F-stable. Let
![]() $C\subset G\sigma $
be a semi-simple conjugacy class with a representative
$C\subset G\sigma $
be a semi-simple conjugacy class with a representative
![]() $t\sigma \in (T^{\sigma })^{\circ }\sigma $
. According to the parametrisation of semi-simple conjugacy classes, C is F-stable if and only if there exist
$t\sigma \in (T^{\sigma })^{\circ }\sigma $
. According to the parametrisation of semi-simple conjugacy classes, C is F-stable if and only if there exist
![]() $w\in W^{\sigma }$
and
$w\in W^{\sigma }$
and
![]() $s\in [T,\sigma ]\cap (T^{\sigma })^{\circ }$
such that
$s\in [T,\sigma ]\cap (T^{\sigma })^{\circ }$
such that
![]() $F(t)=wtw^{-1}s$
(see §3.1.3). We will, however, only be concerned with those semi-simple conjugacy classes that have representatives in
$F(t)=wtw^{-1}s$
(see §3.1.3). We will, however, only be concerned with those semi-simple conjugacy classes that have representatives in
![]() $(T^{\sigma })^{\circ F}\sigma $
; that is,
$(T^{\sigma })^{\circ F}\sigma $
; that is,
![]() $w=1$
and
$w=1$
and
![]() $s=1$
in the above equation. Now let C be such a class with representative
$s=1$
in the above equation. Now let C be such a class with representative
![]() $t\sigma \in (T^{\sigma })^{\circ F}\sigma $
. If we represent C by the N-tuple
$t\sigma \in (T^{\sigma })^{\circ F}\sigma $
. If we represent C by the N-tuple
![]() $(\hat {a}_1,\ldots ,\hat {a}_N)$
,
$(\hat {a}_1,\ldots ,\hat {a}_N)$
, ![]() , then
, then
![]() $a_i\in \mathbb {F}_q^{\ast }$
for all
$a_i\in \mathbb {F}_q^{\ast }$
for all
![]() $1\le i\le N$
.
$1\le i\le N$
.
Lemma 3.2.1 [Reference ShuShu22, Lemma 6.2.1]
Denote by
![]() $N_+$
(resp.
$N_+$
(resp.
![]() $N_-$
) the multiplicity of
$N_-$
) the multiplicity of
![]() $\hat {1}$
(resp.
$\hat {1}$
(resp.
![]() $\hat {\mathfrak {i}}$
) in
$\hat {\mathfrak {i}}$
) in
![]() $(\hat {a}_1,\ldots ,\hat {a}_N)$
. Then the centraliser of
$(\hat {a}_1,\ldots ,\hat {a}_N)$
. Then the centraliser of
![]() $t\sigma $
in G is isomorphic to
$t\sigma $
in G is isomorphic to
 $$ \begin{align*} \operatorname{\mathrm{Sp}}_{2N_+}\times\operatorname{\mathrm{O}}_{2N_-}\times\prod_i\operatorname{\mathrm{GL}}_{n_i} &\text{ if } n \text{ is even and,}\\ \operatorname{\mathrm{O}}_{2N_++1}\times\operatorname{\mathrm{Sp}}_{2N_-}\times\prod_i\operatorname{\mathrm{GL}}_{n_i} &\text{ if } n \text{ is odd,} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sp}}_{2N_+}\times\operatorname{\mathrm{O}}_{2N_-}\times\prod_i\operatorname{\mathrm{GL}}_{n_i} &\text{ if } n \text{ is even and,}\\ \operatorname{\mathrm{O}}_{2N_++1}\times\operatorname{\mathrm{Sp}}_{2N_-}\times\prod_i\operatorname{\mathrm{GL}}_{n_i} &\text{ if } n \text{ is odd,} \end{align*} $$
for some integers
![]() $n_i$
.
$n_i$
.
In general,
![]() $C^F$
is not a single
$C^F$
is not a single
![]() $G^F$
-conjugacy class. By [Reference Digne and MichelDM20, Proposition 4.2.14], the number of
$G^F$
-conjugacy class. By [Reference Digne and MichelDM20, Proposition 4.2.14], the number of
![]() $G^F$
-conjugacy classes contained in
$G^F$
-conjugacy classes contained in
![]() $C^F$
is equal to the number of connected components of
$C^F$
is equal to the number of connected components of
![]() $C_G(t\sigma )$
. If n is odd, then
$C_G(t\sigma )$
. If n is odd, then
![]() $C_G(t\sigma )$
always has two connected components. The
$C_G(t\sigma )$
always has two connected components. The
![]() $G^F$
-class of
$G^F$
-class of
![]() $t\sigma $
has a representative of the form
$t\sigma $
has a representative of the form
with every
![]() $a_i\in \mathbb {F}_q$
, while the other
$a_i\in \mathbb {F}_q$
, while the other
![]() $G^F$
-class in
$G^F$
-class in
![]() $C^F$
is represented by
$C^F$
is represented by
with
![]() $b\in \mathbb {F}_q^{\ast }\setminus (\mathbb {F}_q^{\ast })^2$
.
$b\in \mathbb {F}_q^{\ast }\setminus (\mathbb {F}_q^{\ast })^2$
.
3.2.2
Let I be a subset of
![]() $\Delta (T,B)$
and let
$\Delta (T,B)$
and let
![]() $L_I$
be the corresponding standard Levi subgroup. There are positive integers
$L_I$
be the corresponding standard Levi subgroup. There are positive integers
![]() $\{n_i\mid i\in \Gamma _I\}$
indexed by a finite set
$\{n_i\mid i\in \Gamma _I\}$
indexed by a finite set
![]() $\Gamma _I$
, such that
$\Gamma _I$
, such that
![]() $L_I\cong \prod _{i\in \Gamma _I}\operatorname {\mathrm {GL}}_{n_i}$
. Then
$L_I\cong \prod _{i\in \Gamma _I}\operatorname {\mathrm {GL}}_{n_i}$
. Then
![]() $Z_{L_I}\cong \mathbb {G}_m^{\Gamma _I}$
(i.e., direct product of copies of
$Z_{L_I}\cong \mathbb {G}_m^{\Gamma _I}$
(i.e., direct product of copies of
![]() $\mathbb {G}_m$
indexed by
$\mathbb {G}_m$
indexed by
![]() $\Gamma _I$
). For any
$\Gamma _I$
). For any
![]() $r\in \mathbb {Z}_{>0}$
, put
$r\in \mathbb {Z}_{>0}$
, put
![]() $\Gamma _{I,r}=\{i\in \Gamma _I\mid n_i=r\}$
and put
$\Gamma _{I,r}=\{i\in \Gamma _I\mid n_i=r\}$
and put
![]() $N_r=|\Gamma _{I,r}|$
. Then the G-conjugacy class of
$N_r=|\Gamma _{I,r}|$
. Then the G-conjugacy class of
![]() $L_I$
is uniquely determined by the sequence
$L_I$
is uniquely determined by the sequence
![]() $(N_r)_{r\in \mathbb {Z}_{>0}}$
, and
$(N_r)_{r\in \mathbb {Z}_{>0}}$
, and
![]() $W_G(L_I)\cong \prod _r\mathfrak {S}_{N_r}$
.
$W_G(L_I)\cong \prod _r\mathfrak {S}_{N_r}$
.
Suppose that I is
![]() $\sigma $
-stable, so that the associated
$\sigma $
-stable, so that the associated
![]() $\sigma $
-stable standard Levi subgroup
$\sigma $
-stable standard Levi subgroup
![]() $L_I$
is of the form (3.1.4.1). Now the action of
$L_I$
is of the form (3.1.4.1). Now the action of
![]() $\sigma $
on
$\sigma $
on
![]() $Z_{L_I}$
induces an involution on
$Z_{L_I}$
induces an involution on
![]() $\Gamma _I$
. There is at most one element of
$\Gamma _I$
. There is at most one element of
![]() $\Gamma _I$
fixed by
$\Gamma _I$
fixed by
![]() $\sigma $
, and we denote it by
$\sigma $
, and we denote it by
![]() $0$
so that it corresponds to the direct factor
$0$
so that it corresponds to the direct factor
![]() $\operatorname {\mathrm {GL}}_{n_0}$
in (3.1.4.1). In case no element of
$\operatorname {\mathrm {GL}}_{n_0}$
in (3.1.4.1). In case no element of
![]() $\Gamma _I$
is fixed by
$\Gamma _I$
is fixed by
![]() $\sigma $
, we define
$\sigma $
, we define
![]() $n_0=0$
. For any
$n_0=0$
. For any
![]() $r\in \mathbb {Z}_{>0}$
, put
$r\in \mathbb {Z}_{>0}$
, put
![]() $N_r'=N_r/2$
if
$N_r'=N_r/2$
if
![]() $n_0\ne r$
and
$n_0\ne r$
and
![]() $N_r'=(N_r-1)/2$
if
$N_r'=(N_r-1)/2$
if
![]() $n_0=r$
. Then
$n_0=r$
. Then
![]() $W_{G}(L_I)^{\sigma }\cong \prod _r\mathfrak {W}_{N_r'}$
.
$W_{G}(L_I)^{\sigma }\cong \prod _r\mathfrak {W}_{N_r'}$
.
The action of an element of
![]() $W_{G}(L_I)^{\sigma }$
on
$W_{G}(L_I)^{\sigma }$
on
![]() $L_I$
(up to an inner automorphism of
$L_I$
(up to an inner automorphism of
![]() $L_I$
) can be easily visualised. Let
$L_I$
) can be easily visualised. Let
![]() $r\in \mathbb {Z}_{>0}$
and let
$r\in \mathbb {Z}_{>0}$
and let
![]() $\tau $
be a signed cycle of size d in
$\tau $
be a signed cycle of size d in
![]() $\mathfrak {W}_{N_r'}$
. Then it acts on a subgroup of
$\mathfrak {W}_{N_r'}$
. Then it acts on a subgroup of
![]() $L_I$
that is isomorphic to
$L_I$
that is isomorphic to
![]() $(\operatorname {\mathrm {GL}}_r\times \operatorname {\mathrm {GL}}_r)^d$
. Depending on whether
$(\operatorname {\mathrm {GL}}_r\times \operatorname {\mathrm {GL}}_r)^d$
. Depending on whether
![]() $\tau $
is a positive cycle or a negative cycle (see §2.3.3), its action can be schematically described as
$\tau $
is a positive cycle or a negative cycle (see §2.3.3), its action can be schematically described as

, respectively. If
![]() $r=n_0$
, then
$r=n_0$
, then
![]() $\tau $
simply ignores the component
$\tau $
simply ignores the component
![]() $\operatorname {\mathrm {GL}}_{n_0}$
.
$\operatorname {\mathrm {GL}}_{n_0}$
.
For each
![]() $w\in W_{G}(L_I)^{\sigma }$
, there exists
$w\in W_{G}(L_I)^{\sigma }$
, there exists
![]() $\dot {w}\in (G^{\sigma })^{\circ }$
that represents w. For example, it is easy to see that in (3.2.2.1), one can find explicit matrices in
$\dot {w}\in (G^{\sigma })^{\circ }$
that represents w. For example, it is easy to see that in (3.2.2.1), one can find explicit matrices in
![]() $\operatorname {\mathrm {GL}}_{2rd}$
fixed by
$\operatorname {\mathrm {GL}}_{2rd}$
fixed by
![]() $\sigma $
representing the corresponding cycles in
$\sigma $
representing the corresponding cycles in
![]() $\mathfrak {W}_{N_r'}$
. This implies that the inclusion
$\mathfrak {W}_{N_r'}$
. This implies that the inclusion
is, in fact, an isomorphism. Now the groups
![]() $L_{I,w}$
defined for
$L_{I,w}$
defined for
![]() $w\in W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
in §2.6.3 make sense if we regard w as an element of
$w\in W_{(G^{\sigma })^{\circ }}((L_I^{\sigma })^{\circ })$
in §2.6.3 make sense if we regard w as an element of
![]() $W_{G}(L_I)^{\sigma }$
. The discussions in §2.6.3 give the following:
$W_{G}(L_I)^{\sigma }$
. The discussions in §2.6.3 give the following:
Proposition 3.2.2. The
![]() $G^F$
-conjugacy classes of the F-stable G-conjugates of
$G^F$
-conjugacy classes of the F-stable G-conjugates of
![]() $L_I\!<\!\sigma \!>\!$
are in bijection with the conjugacy classes of
$L_I\!<\!\sigma \!>\!$
are in bijection with the conjugacy classes of
![]() $W_{G}(L_I)^{\sigma }$
.
$W_{G}(L_I)^{\sigma }$
.
3.3 Deligne-Lusztig inductions
3.3.1
Let H be a connected reductive group defined over
![]() $\mathbb {F}_q$
equipped with a geometric Frobenius endomorphism F. Let
$\mathbb {F}_q$
equipped with a geometric Frobenius endomorphism F. Let
![]() $L\subset H$
be an F-stable Levi subgroup. The Deligne-Lusztig induction
$L\subset H$
be an F-stable Levi subgroup. The Deligne-Lusztig induction
![]() $R^H_L$
([Reference Digne and MichelDM20, §9.1]) is a
$R^H_L$
([Reference Digne and MichelDM20, §9.1]) is a
![]() $\bar {\mathbb {Q}}_{\ell }$
-linear map from the set of
$\bar {\mathbb {Q}}_{\ell }$
-linear map from the set of
![]() $L^F$
-invariant functions on
$L^F$
-invariant functions on
![]() $L^F$
to the set of
$L^F$
to the set of
![]() $H^F$
-invariant functions on
$H^F$
-invariant functions on
![]() $H^F$
(invariant for the conjugation actions).
$H^F$
(invariant for the conjugation actions).
Let
![]() $T_H$
be an F-stable maximal torus of H. Denote by
$T_H$
be an F-stable maximal torus of H. Denote by
![]() $W_H$
the Weyl group of H defined by
$W_H$
the Weyl group of H defined by
![]() $T_H$
. By §2.6.2, to each
$T_H$
. By §2.6.2, to each
![]() $w\in W_H$
, we can associate an F-stable maximal torus
$w\in W_H$
, we can associate an F-stable maximal torus
![]() $T_w\subset H$
in such a way that
$T_w\subset H$
in such a way that
![]() $T_H$
is associated to
$T_H$
is associated to
![]() $1\in W_H$
. For any
$1\in W_H$
. For any
![]() $w\in W_H$
, we denote by
$w\in W_H$
, we denote by
![]() $\mathbf {1}$
the trivial character of
$\mathbf {1}$
the trivial character of
![]() $T_w^F$
. Then the Green function is an
$T_w^F$
. Then the Green function is an
![]() $H^F$
-invariant function on the subset
$H^F$
-invariant function on the subset
![]() $H^F_u\subset H^F$
of unipotent elements, defined by
$H^F_u\subset H^F$
of unipotent elements, defined by
Such a function only depends on the
![]() $H^F$
-conjugacy class of
$H^F$
-conjugacy class of
![]() $T_w$
, or rather, the F-conjugacy class of w.
$T_w$
, or rather, the F-conjugacy class of w.
Let
![]() $\tau $
be an automorphism of finite order of H that commutes with F and let
$\tau $
be an automorphism of finite order of H that commutes with F and let
![]() $L\subset H$
be an F-stable and
$L\subset H$
be an F-stable and
![]() $\tau $
-stable Levi factor of a
$\tau $
-stable Levi factor of a
![]() $\tau $
-stable parabolic subgroup
$\tau $
-stable parabolic subgroup
![]() $P\subset H$
. Then
$P\subset H$
. Then
![]() $N_{H\!<\!\tau \!>\!}(L,P)=L\!<\!\tau \!>\!$
. The generalised Deligne-Lusztig induction
$N_{H\!<\!\tau \!>\!}(L,P)=L\!<\!\tau \!>\!$
. The generalised Deligne-Lusztig induction
![]() $R^{H\tau }_{L\tau }$
([Reference Digne and MichelDM94, §2]) is a
$R^{H\tau }_{L\tau }$
([Reference Digne and MichelDM94, §2]) is a
![]() $\bar {\mathbb {Q}}_{\ell }$
-linear map from the set of
$\bar {\mathbb {Q}}_{\ell }$
-linear map from the set of
![]() $L^F$
-invariant functions on
$L^F$
-invariant functions on
![]() $L^F\tau $
to the set of
$L^F\tau $
to the set of
![]() $H^F$
-invariant functions on
$H^F$
-invariant functions on
![]() $H^F\tau $
.
$H^F\tau $
.
3.3.2
By §2.6.3 and Remark 2.5.8, to each
![]() $w\in W^{\sigma }$
, we can associate an F-stable and
$w\in W^{\sigma }$
, we can associate an F-stable and
![]() $\sigma $
-stable maximal torus
$\sigma $
-stable maximal torus
![]() $T_w$
contained in a
$T_w$
contained in a
![]() $\sigma $
-stable Borel subgroup of G, in such a way that T is associated to
$\sigma $
-stable Borel subgroup of G, in such a way that T is associated to
![]() $1\in W^{\sigma }$
. If
$1\in W^{\sigma }$
. If
![]() $B_w\subset G$
is some
$B_w\subset G$
is some
![]() $\sigma $
-stable Borel subgroup containing
$\sigma $
-stable Borel subgroup containing
![]() $T_w$
, then
$T_w$
, then
![]() $\bar {T}_w:=N_{\bar {G}}(T_w,B_w)=T_w\sqcup T_w\sigma $
and the
$\bar {T}_w:=N_{\bar {G}}(T_w,B_w)=T_w\sqcup T_w\sigma $
and the
![]() $G^F$
-conjugacy class of
$G^F$
-conjugacy class of
![]() $\bar {T}_w$
is determined by the conjugacy class of
$\bar {T}_w$
is determined by the conjugacy class of
![]() $w\in W^{\sigma }$
. Let
$w\in W^{\sigma }$
. Let
![]() $\theta \in \operatorname {\mathrm {Irr}}(T_w^F)^{\sigma }$
and denote by
$\theta \in \operatorname {\mathrm {Irr}}(T_w^F)^{\sigma }$
and denote by
![]() $\tilde {\theta }\in \operatorname {\mathrm {Irr}}(T_w^F\!<\!\sigma \!>\!)$
an extension of
$\tilde {\theta }\in \operatorname {\mathrm {Irr}}(T_w^F\!<\!\sigma \!>\!)$
an extension of
![]() $\theta $
. By abuse of notation, we may also denote by
$\theta $
. By abuse of notation, we may also denote by
![]() $\tilde {\theta }$
its restriction on
$\tilde {\theta }$
its restriction on
![]() $T_w^F\sigma $
. Computation of Deligne-Lusztig inductions is reduced to Green functions according to the character formula below.
$T_w^F\sigma $
. Computation of Deligne-Lusztig inductions is reduced to Green functions according to the character formula below.
Proposition 3.3.1. [Reference Digne and MichelDM94, Proposition 2.6]
Let
![]() $s\sigma \in G^F\sigma $
be semi-simple and let
$s\sigma \in G^F\sigma $
be semi-simple and let
![]() $u\in C_G(s\sigma )^{\circ F}$
. Then
$u\in C_G(s\sigma )^{\circ F}$
. Then
 $$ \begin{align} R^{G\sigma}_{T_w\sigma}\tilde{\theta}(us\sigma)=\frac{|(T_w^{\sigma})^{\circ F}|}{|T_w^F|\cdot|C_G(s\sigma)^{\circ F}|}\sum_{\{h\in G^{F}\mid hs\sigma h^{-1}\in T_w\sigma\}}Q^{C_G(s\sigma)^{\circ}}_{C_{h^{-1}T_wh}(s\sigma)^{\circ}}(u)\tilde{\theta}(hs\sigma h^{-1}), \end{align} $$
$$ \begin{align} R^{G\sigma}_{T_w\sigma}\tilde{\theta}(us\sigma)=\frac{|(T_w^{\sigma})^{\circ F}|}{|T_w^F|\cdot|C_G(s\sigma)^{\circ F}|}\sum_{\{h\in G^{F}\mid hs\sigma h^{-1}\in T_w\sigma\}}Q^{C_G(s\sigma)^{\circ}}_{C_{h^{-1}T_wh}(s\sigma)^{\circ}}(u)\tilde{\theta}(hs\sigma h^{-1}), \end{align} $$
where
![]() $Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)$
is the Green function associated to the connected reductive group
$Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)$
is the Green function associated to the connected reductive group
![]() $C_G(s\sigma )^{\circ }$
and its F-stable maximal torus
$C_G(s\sigma )^{\circ }$
and its F-stable maximal torus
![]() $C_{h^{-1}T_wh}(s\sigma )^{\circ }$
.
$C_{h^{-1}T_wh}(s\sigma )^{\circ }$
.
Remark 3.3.2. The extra factor
![]() $|(T_w^{\sigma })^{\circ F}|$
compared with [Reference Digne and MichelDM94, Proposition 2.6] is due to different normalisations of the Green functions
$|(T_w^{\sigma })^{\circ F}|$
compared with [Reference Digne and MichelDM94, Proposition 2.6] is due to different normalisations of the Green functions
![]() $Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)$
.
$Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_wh}(s\sigma )^{\circ }}(u)$
.
An invariant function on
![]() $G^F\sigma $
is called uniform if it is a linear combination of
$G^F\sigma $
is called uniform if it is a linear combination of
![]() $R_{T_w\sigma }^{G\sigma }\tilde {\theta }$
for various w and
$R_{T_w\sigma }^{G\sigma }\tilde {\theta }$
for various w and
![]() $\tilde {\theta }$
.
$\tilde {\theta }$
.
Proposition 3.3.3. [Reference Digne and MichelDM15, Proposition 6.4]
The characteristic function of a semi-simple conjugacy class in
![]() $G^F\sigma $
is uniform.
$G^F\sigma $
is uniform.
3.3.3
Fix semi-simple element
![]() $s\sigma \in G^F\sigma $
and write
$s\sigma \in G^F\sigma $
and write
![]() $L':=C_G(s\sigma )^{\circ }$
. Let
$L':=C_G(s\sigma )^{\circ }$
. Let
![]() $\tau \in W^{\sigma }$
. Write
$\tau \in W^{\sigma }$
. Write
If
![]() $A^F_{\tau }$
is nonempty, we may assume that
$A^F_{\tau }$
is nonempty, we may assume that
![]() $s\sigma \in T_{\tau }\sigma $
, since the problem we will consider is not affected by conjugation by
$s\sigma \in T_{\tau }\sigma $
, since the problem we will consider is not affected by conjugation by
![]() $G^F$
. So, in particular,
$G^F$
. So, in particular,
![]() $A^F_{\tau }$
contains the unit
$A^F_{\tau }$
contains the unit
![]() $1$
. For any
$1$
. For any
![]() $h\in A_{\tau }^F$
,
$h\in A_{\tau }^F$
,
![]() $C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
is an F-stable maximal torus of
$C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
is an F-stable maximal torus of
![]() $L'$
by Proposition 2.5.3. In particular,
$L'$
by Proposition 2.5.3. In particular,
![]() $T^{\prime }_{\tau }:=C_{T_{\tau }}(s\sigma )^{\circ }$
is an F-stable maximal torus of
$T^{\prime }_{\tau }:=C_{T_{\tau }}(s\sigma )^{\circ }$
is an F-stable maximal torus of
![]() $L'$
. The
$L'$
. The
![]() $L^{\prime F}$
-conjugacy classes of the F-stable maximal tori of
$L^{\prime F}$
-conjugacy classes of the F-stable maximal tori of
![]() $L'$
are parametrised by the F-conjugacy classes of
$L'$
are parametrised by the F-conjugacy classes of
![]() $W':=W_{L'}(T_{\tau }')$
. Then the map
$W':=W_{L'}(T_{\tau }')$
. Then the map
![]() $h\mapsto C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
induces a map from
$h\mapsto C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
induces a map from
![]() $A_{\tau }^F$
to the set of F-conjugacy classes of
$A_{\tau }^F$
to the set of F-conjugacy classes of
![]() $W'$
. Denote by
$W'$
. Denote by
![]() $B_{\tau }$
the image of this map so that we have a surjection
$B_{\tau }$
the image of this map so that we have a surjection
![]() $A_{\tau }^F\rightarrow B_{\tau }$
. Let
$A_{\tau }^F\rightarrow B_{\tau }$
. Let
![]() $\nu \in W'$
represent an F-conjugacy class of
$\nu \in W'$
represent an F-conjugacy class of
![]() $W'$
and denote by
$W'$
and denote by
![]() $A^F_{\tau ,\nu }$
the inverse image in
$A^F_{\tau ,\nu }$
the inverse image in
![]() $A_{\tau }^F$
of this F-conjugacy class.
$A_{\tau }^F$
of this F-conjugacy class.
We will fix
![]() $g_{\tau }$
such that
$g_{\tau }$
such that
![]() $T_{\tau }=g_{\tau }Tg^{-1}_{\tau }$
. Write
$T_{\tau }=g_{\tau }Tg^{-1}_{\tau }$
. Write
![]() $\dot {\tau }=g_{\tau }^{-1}F(g_{\tau })$
and
$\dot {\tau }=g_{\tau }^{-1}F(g_{\tau })$
and
![]() $s_0\sigma =g_{\tau }^{-1}s\sigma g_{\tau }$
and
$s_0\sigma =g_{\tau }^{-1}s\sigma g_{\tau }$
and
![]() $L^{\prime }_0=C_G(s_0\sigma )^{\circ }$
. Let
$L^{\prime }_0=C_G(s_0\sigma )^{\circ }$
. Let
![]() $W^{\prime }_0$
denote the Weyl group of
$W^{\prime }_0$
denote the Weyl group of
![]() $L^{\prime }_0$
defined by
$L^{\prime }_0$
defined by
![]() $C_T(s_0\sigma )^{\circ }$
. Then the F-conjugacy classes of
$C_T(s_0\sigma )^{\circ }$
. Then the F-conjugacy classes of
![]() $W'$
are in natural bijection with the
$W'$
are in natural bijection with the
![]() $\tau $
-conjugacy classes of
$\tau $
-conjugacy classes of
![]() $W^{\prime }_0$
. We will therefore regard
$W^{\prime }_0$
. We will therefore regard
![]() $B_{\tau }$
as a set of
$B_{\tau }$
as a set of
![]() $\tau $
-conjugacy classes of
$\tau $
-conjugacy classes of
![]() $W^{\prime }_0$
. By Corollary 2.5.7,
$W^{\prime }_0$
. By Corollary 2.5.7,
![]() $W^{\prime }_0$
is naturally a subgroup of
$W^{\prime }_0$
is naturally a subgroup of
![]() $W^{\sigma }$
.
$W^{\sigma }$
.
3.3.4
We will need the following results.
Lemma 3.3.4. There is a natural isomorphism:
Proof. Since
![]() $T\sigma T\sigma = T$
, we have
$T\sigma T\sigma = T$
, we have
![]() $N_G(T\sigma )\subset N_G(T)$
. It is easy to see that
$N_G(T\sigma )\subset N_G(T)$
. It is easy to see that
![]() $\xi T\sigma \xi ^{-1}=T\sigma $
is equivalent to
$\xi T\sigma \xi ^{-1}=T\sigma $
is equivalent to
![]() $\xi \sigma (\xi )^{-1}\in T$
for any
$\xi \sigma (\xi )^{-1}\in T$
for any
![]() $\xi \in N_G(T)$
.
$\xi \in N_G(T)$
.
Lemma 3.3.5. We have
Proof. Since
![]() $xs_0\sigma x^{-1}$
lies in
$xs_0\sigma x^{-1}$
lies in
![]() $T\sigma $
, it normalises T and besides,
$T\sigma $
, it normalises T and besides,
By Proposition 2.5.3,
![]() $T'$
is a maximal torus of
$T'$
is a maximal torus of
![]() $L'$
. Now
$L'$
. Now
![]() $s\sigma $
normalises
$s\sigma $
normalises
![]() $x^{-1}Tx$
and so
$x^{-1}Tx$
and so
![]() $C_{x^{-1}Tx}(s_0\sigma )^{\circ }$
is also a maximal torus of
$C_{x^{-1}Tx}(s_0\sigma )^{\circ }$
is also a maximal torus of
![]() $L'$
. There exists
$L'$
. There exists
![]() $l\in L'$
such that
$l\in L'$
such that
![]() $C_{x^{-1}Tx}(s_0\sigma )^{\circ }=lT'l^{-1}$
. Note that
$C_{x^{-1}Tx}(s_0\sigma )^{\circ }=lT'l^{-1}$
. Note that
We deduce that
![]() $xl$
normalises
$xl$
normalises
![]() $T'$
and thus normalises T by Proposition 2.5.4. Write
$T'$
and thus normalises T by Proposition 2.5.4. Write
![]() $\xi =xl$
. From the relation
$\xi =xl$
. From the relation
![]() $xs_0\sigma x^{-1}\in T\sigma $
, we see that
$xs_0\sigma x^{-1}\in T\sigma $
, we see that
![]() $\sigma (\xi )\in \xi T$
. By the proof of Lemma 3.3.4, we have
$\sigma (\xi )\in \xi T$
. By the proof of Lemma 3.3.4, we have
![]() $\xi \in N_G(T\sigma )$
. Therefore,
$\xi \in N_G(T\sigma )$
. Therefore,
![]() $x\in N_G(T\sigma )L'$
. Conversely, it is easy to see that every element
$x\in N_G(T\sigma )L'$
. Conversely, it is easy to see that every element
![]() $x\in N_G(T\sigma )L'$
satisfies
$x\in N_G(T\sigma )L'$
satisfies
![]() $xs_0\sigma x^{-1}\in T\sigma $
.
$xs_0\sigma x^{-1}\in T\sigma $
.
Proposition 3.3.6. [Reference ShuShu22, Proposition 10.2.13 (ii)]
We have
where
![]() $\mathfrak {z}_{\tau }$
is the cardinality of the centraliser of
$\mathfrak {z}_{\tau }$
is the cardinality of the centraliser of
![]() $\tau $
in
$\tau $
in
![]() $W^{\sigma }$
and
$W^{\sigma }$
and
![]() $\mathfrak {z}_{\nu }$
is the cardinality of the stabiliser of an element of the
$\mathfrak {z}_{\nu }$
is the cardinality of the stabiliser of an element of the
![]() $\tau $
-conjugacy class
$\tau $
-conjugacy class
![]() $\nu $
under the
$\nu $
under the
![]() $\tau $
-twisted action.
$\tau $
-twisted action.
3.4 Irreducible characters of
 $\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
$\operatorname {\mathrm {GL}}_n(q)\!<\!\sigma \!>\!$
3.4.1
Let
![]() $H=\prod _i\operatorname {\mathrm {GL}}_{n_i}$
for some positive integers
$H=\prod _i\operatorname {\mathrm {GL}}_{n_i}$
for some positive integers
![]() $n_i$
and suppose that H is defined over
$n_i$
and suppose that H is defined over
![]() $\mathbb {F}_q$
equipped with a Frobenius F. Fix an F-stable maximal torus
$\mathbb {F}_q$
equipped with a Frobenius F. Fix an F-stable maximal torus
![]() $T_H\subset H$
and denote by
$T_H\subset H$
and denote by
![]() $W_H$
the Weyl group of H defined by
$W_H$
the Weyl group of H defined by
![]() $T_H$
. By §2.6.2, to each
$T_H$
. By §2.6.2, to each
![]() $w\in W_H$
, we can associate an F-stable maximal torus
$w\in W_H$
, we can associate an F-stable maximal torus
![]() $T_w$
of H in such a way that
$T_w$
of H in such a way that
![]() $T_H$
is associated to
$T_H$
is associated to
![]() $1\in W$
. The
$1\in W$
. The
![]() $H^F$
-conjugacy class of
$H^F$
-conjugacy class of
![]() $T_w$
is determined by the F-conjugacy class of
$T_w$
is determined by the F-conjugacy class of
![]() $w\in W_H$
. The natural action of F on
$w\in W_H$
. The natural action of F on
![]() $W_H$
induces an action on
$W_H$
induces an action on
![]() $\operatorname {\mathrm {Irr}}(W_H)$
. Denote by
$\operatorname {\mathrm {Irr}}(W_H)$
. Denote by
![]() $\operatorname {\mathrm {Irr}}(W_H)^F$
the set of F-stable irreducible characters of
$\operatorname {\mathrm {Irr}}(W_H)^F$
the set of F-stable irreducible characters of
![]() $W_H$
. Let
$W_H$
. Let
![]() $\varphi \in \operatorname {\mathrm {Irr}}(W_H)^F$
. Then it can be extended to
$\varphi \in \operatorname {\mathrm {Irr}}(W_H)^F$
. Then it can be extended to
![]() $\tilde {\varphi }\in \operatorname {\mathrm {Irr}}(W_H\rtimes \!<\! F\!>\!)$
. Such an extension is not unique. We choose such an extension and put
$\tilde {\varphi }\in \operatorname {\mathrm {Irr}}(W_H\rtimes \!<\! F\!>\!)$
. Such an extension is not unique. We choose such an extension and put
where
![]() $\mathbf {1}$
is the trivial character of
$\mathbf {1}$
is the trivial character of
![]() $T_w^F$
.
$T_w^F$
.
Theorem 3.4.1. [Reference Lusztig and SrinivasanLS77, Theorem 2.2]
For any
![]() $\varphi \in \operatorname {\mathrm {Irr}}(W_H)^F$
and some choice of
$\varphi \in \operatorname {\mathrm {Irr}}(W_H)^F$
and some choice of
![]() $\tilde {\varphi }$
, the virtual character
$\tilde {\varphi }$
, the virtual character
![]() $R^H_{\varphi }\mathbf {1}$
is an irreducible character of
$R^H_{\varphi }\mathbf {1}$
is an irreducible character of
![]() $H^F$
, and
$H^F$
, and
![]() $R^H_{\varphi }\mathbf {1}\ne R^H_{\varphi '}\mathbf {1}$
if
$R^H_{\varphi }\mathbf {1}\ne R^H_{\varphi '}\mathbf {1}$
if
![]() $\varphi \ne \varphi '$
.
$\varphi \ne \varphi '$
.
Let
![]() $\theta \in \operatorname {\mathrm {Hom}}(H^F,\bar {\mathbb {Q}}_{\ell }^{\ast })$
(i.e., a linear character of
$\theta \in \operatorname {\mathrm {Hom}}(H^F,\bar {\mathbb {Q}}_{\ell }^{\ast })$
(i.e., a linear character of
![]() $H^F$
). Then
$H^F$
). Then
![]() $\theta \otimes R^H_{\varphi }\mathbf {1}$
is also an irreducible character of
$\theta \otimes R^H_{\varphi }\mathbf {1}$
is also an irreducible character of
![]() $H^F$
. Denote by
$H^F$
. Denote by
![]() $\theta _{T_w}$
the restriction of
$\theta _{T_w}$
the restriction of
![]() $\theta $
to
$\theta $
to
![]() $T_w^F$
for any
$T_w^F$
for any
![]() $w\in W_H$
. Then
$w\in W_H$
. Then
3.4.2
Let
![]() $M\subset G$
be an F-stable Levi subgroup of G. Fix an F-stable maximal torus
$M\subset G$
be an F-stable Levi subgroup of G. Fix an F-stable maximal torus
![]() $T_M\subset M$
and let
$T_M\subset M$
and let
![]() $T_w$
,
$T_w$
,
![]() $w\in W_M$
be defined as in the previous paragraph. Denote by
$w\in W_M$
be defined as in the previous paragraph. Denote by
![]() $\operatorname {\mathrm {Irr}}_{reg}(M^F)$
the set of regular linear characters of
$\operatorname {\mathrm {Irr}}_{reg}(M^F)$
the set of regular linear characters of
![]() $M^F$
(see [Reference Lusztig and SrinivasanLS77, §3.1 (a), (b)]). Concretely, if we choose an isomorphism
$M^F$
(see [Reference Lusztig and SrinivasanLS77, §3.1 (a), (b)]). Concretely, if we choose an isomorphism
![]() $M^F\cong \prod _i\operatorname {\mathrm {GL}}_{n_i}(q^{d_i})$
for some positive intergers
$M^F\cong \prod _i\operatorname {\mathrm {GL}}_{n_i}(q^{d_i})$
for some positive intergers
![]() $n_i$
,
$n_i$
,
![]() $d_i$
and write a linear character
$d_i$
and write a linear character
![]() $\theta \in \operatorname {\mathrm {Irr}}(M^F)$
as
$\theta \in \operatorname {\mathrm {Irr}}(M^F)$
as
![]() $(\theta _i)_i$
for some
$(\theta _i)_i$
for some
![]() $\theta _i\in \operatorname {\mathrm {Hom}}(\operatorname {\mathrm {GL}}_{n_i}(q^{d_i}),\bar {\mathbb {Q}}_{\ell }^{\ast })$
, then
$\theta _i\in \operatorname {\mathrm {Hom}}(\operatorname {\mathrm {GL}}_{n_i}(q^{d_i}),\bar {\mathbb {Q}}_{\ell }^{\ast })$
, then
![]() $\theta $
is regular if and only if
$\theta $
is regular if and only if
![]() $\theta _i\ne \theta _j$
whenever
$\theta _i\ne \theta _j$
whenever
![]() $i\ne j$
and
$i\ne j$
and
![]() $\theta _i^{q^r}\ne \theta _i$
for any
$\theta _i^{q^r}\ne \theta _i$
for any
![]() $1\le r< d_i$
and any i.
$1\le r< d_i$
and any i.
For any connected reductive group H defined over
![]() $\mathbb {F}_q$
, define
$\mathbb {F}_q$
, define
![]() $\epsilon _H:=(-1)^{rk_H}$
where
$\epsilon _H:=(-1)^{rk_H}$
where
![]() $rk_H$
is the
$rk_H$
is the
![]() $\mathbb {F}_q$
-rank of H. For any
$\mathbb {F}_q$
-rank of H. For any
![]() $\varphi \in \operatorname {\mathrm {Irr}}(W_M)^F$
and
$\varphi \in \operatorname {\mathrm {Irr}}(W_M)^F$
and
![]() $\theta \in \operatorname {\mathrm {Hom}}(M^F,\bar {\mathbb {Q}}_{\ell }^{\ast })$
, choose an extension
$\theta \in \operatorname {\mathrm {Hom}}(M^F,\bar {\mathbb {Q}}_{\ell }^{\ast })$
, choose an extension
![]() $\tilde {\varphi }\in \operatorname {\mathrm {Irr}}(W_M\rtimes \!<\! F\!>\!)$
and put
$\tilde {\varphi }\in \operatorname {\mathrm {Irr}}(W_M\rtimes \!<\! F\!>\!)$
and put
Note that
![]() $R_{\varphi }^G\theta =\epsilon _G\epsilon _MR^G_M(R^M_{\varphi }\theta )$
([Reference Digne and MichelDM20, Proposition 9.1.8]).
$R_{\varphi }^G\theta =\epsilon _G\epsilon _MR^G_M(R^M_{\varphi }\theta )$
([Reference Digne and MichelDM20, Proposition 9.1.8]).
Theorem 3.4.2. [Reference Lusztig and SrinivasanLS77, Theorem 3.2]
If
![]() $\theta $
lies in
$\theta $
lies in
![]() $\operatorname {\mathrm {Irr}}_{reg}(M^F)$
, then for some choice of
$\operatorname {\mathrm {Irr}}_{reg}(M^F)$
, then for some choice of
![]() $\tilde {\varphi }$
, the virtual character
$\tilde {\varphi }$
, the virtual character
![]() $R^G_{\varphi }\theta $
is an irreducible character of
$R^G_{\varphi }\theta $
is an irreducible character of
![]() $G^F$
. Moreover, all irreducible characters of
$G^F$
. Moreover, all irreducible characters of
![]() $G^F$
are of the form
$G^F$
are of the form
![]() $R^G_{\varphi }\theta $
for a triple
$R^G_{\varphi }\theta $
for a triple
![]() $(M,\varphi ,\theta )$
as above. The characters associated to the triples
$(M,\varphi ,\theta )$
as above. The characters associated to the triples
![]() $(M,\varphi ,\theta )$
and
$(M,\varphi ,\theta )$
and
![]() $(M',\varphi ',\theta ')$
are distinct if and only if one of the following conditions is satisfied:
$(M',\varphi ',\theta ')$
are distinct if and only if one of the following conditions is satisfied:
-
-
 $(M,\theta )$
and
$(M,\theta )$
and
 $(M',\theta ')$
are not
$(M',\theta ')$
are not
 $G^F$
-conjuguate;
$G^F$
-conjuguate; -
-
 $(M,\theta )=(M',\theta ')$
and
$(M,\theta )=(M',\theta ')$
and
 $\varphi \ne \varphi '$
.
$\varphi \ne \varphi '$
.
3.4.3
Let
![]() $n_0\in \mathbb {Z}_{>0}$
, and let
$n_0\in \mathbb {Z}_{>0}$
, and let
![]() $n_+$
,
$n_+$
,
![]() $n_-\in \mathbb {Z}_{\ge 0}$
be such that
$n_-\in \mathbb {Z}_{\ge 0}$
be such that
![]() $n_++n_-=n_0$
. Let F be the Frobenius of
$n_++n_-=n_0$
. Let F be the Frobenius of
![]() $\operatorname {\mathrm {GL}}_{n_0}$
that sends each entry of a matrix to its q-th power. Let
$\operatorname {\mathrm {GL}}_{n_0}$
that sends each entry of a matrix to its q-th power. Let
![]() $M_{00}\subset \operatorname {\mathrm {GL}}_{n_0}$
be a standard Levi subgroup isomorphic to
$M_{00}\subset \operatorname {\mathrm {GL}}_{n_0}$
be a standard Levi subgroup isomorphic to
![]() $\operatorname {\mathrm {GL}}_{n_+}\times \operatorname {\mathrm {GL}}_{n_-}$
; that is,
$\operatorname {\mathrm {GL}}_{n_+}\times \operatorname {\mathrm {GL}}_{n_-}$
; that is,

With respect to the isomorphism
![]() $M_{00}^F\cong \operatorname {\mathrm {GL}}_{n_+}(q)\times \operatorname {\mathrm {GL}}_{n_-}(q)$
, we define a linear character
$M_{00}^F\cong \operatorname {\mathrm {GL}}_{n_+}(q)\times \operatorname {\mathrm {GL}}_{n_-}(q)$
, we define a linear character
![]() $\theta \in \operatorname {\mathrm {Irr}}(M_{00}^F)$
to be
$\theta \in \operatorname {\mathrm {Irr}}(M_{00}^F)$
to be
![]() $(\mathbf {1}\circ \det ,\eta \circ \det )$
, where
$(\mathbf {1}\circ \det ,\eta \circ \det )$
, where
![]() $\mathbf {1}$
is the trivial character of
$\mathbf {1}$
is the trivial character of
![]() $\mathbb {F}_q^{\ast }$
and
$\mathbb {F}_q^{\ast }$
and
![]() $\eta $
is the order 2 irreducible character of
$\eta $
is the order 2 irreducible character of
![]() $\mathbb {F}_q^{\ast }$
. Now
$\mathbb {F}_q^{\ast }$
. Now
![]() $W_{M_{00}}$
is isomorphic to
$W_{M_{00}}$
is isomorphic to
![]() $\mathfrak {S}_{n_+}\times \mathfrak {S}_{n_-}$
and so
$\mathfrak {S}_{n_+}\times \mathfrak {S}_{n_-}$
and so
![]() $\operatorname {\mathrm {Irr}}(W_{M_{00}})$
is in bijection with
$\operatorname {\mathrm {Irr}}(W_{M_{00}})$
is in bijection with
![]() $\mathcal {P}(n_+)\times \mathcal {P}(n_-)$
. By Theorem 3.4.2, each
$\mathcal {P}(n_+)\times \mathcal {P}(n_-)$
. By Theorem 3.4.2, each
![]() $(\mu _+,\mu _-)\in \mathcal {P}(n_+)\times \mathcal {P}(n_-)$
defines an irreducible character of
$(\mu _+,\mu _-)\in \mathcal {P}(n_+)\times \mathcal {P}(n_-)$
defines an irreducible character of
![]() $\operatorname {\mathrm {GL}}_{n_0}(q)$
, called a quadratic-unipotent character. By [Reference ShuShu22, Lemma 5.2.1], this character is
$\operatorname {\mathrm {GL}}_{n_0}(q)$
, called a quadratic-unipotent character. By [Reference ShuShu22, Lemma 5.2.1], this character is
![]() $\sigma $
-stable (Here,
$\sigma $
-stable (Here,
![]() $\sigma $
is the automorphism of
$\sigma $
is the automorphism of
![]() $\operatorname {\mathrm {GL}}_{n_0}$
defined in the same way as it is defined for
$\operatorname {\mathrm {GL}}_{n_0}$
defined in the same way as it is defined for
![]() $\operatorname {\mathrm {GL}}_n$
).
$\operatorname {\mathrm {GL}}_n$
).
3.4.4
Let
![]() $M\subset G$
be a Levi subgroup of the form
$M\subset G$
be a Levi subgroup of the form
![]() $L_{I,w}$
as defined in §2.6.3, which is an F-stable and
$L_{I,w}$
as defined in §2.6.3, which is an F-stable and
![]() $\sigma $
-stable Levi factor of some
$\sigma $
-stable Levi factor of some
![]() $\sigma $
-stable parabolic subgroup
$\sigma $
-stable parabolic subgroup
![]() $P\subset G$
. It can be written as
$P\subset G$
. It can be written as
![]() $M_0\times M_1$
with
$M_0\times M_1$
with
![]() $M_0\cong \operatorname {\mathrm {GL}}_{n_0}$
and
$M_0\cong \operatorname {\mathrm {GL}}_{n_0}$
and
![]() $M_1\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
following the notations of §3.1.4. The actions of F and
$M_1\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
following the notations of §3.1.4. The actions of F and
![]() $\sigma $
respect the isomorphism
$\sigma $
respect the isomorphism
![]() $M\cong M_0\times M_1$
, and we will also denote by F and
$M\cong M_0\times M_1$
, and we will also denote by F and
![]() $\sigma $
their restrictions to
$\sigma $
their restrictions to
![]() $M_0$
or
$M_0$
or
![]() $M_1$
.
$M_1$
.
Let
![]() $T_M\subset M$
be an F-stable and
$T_M\subset M$
be an F-stable and
![]() $\sigma $
-stable maximal torus. Then we can write
$\sigma $
-stable maximal torus. Then we can write
![]() $T_M=T_0\times T_1$
with
$T_M=T_0\times T_1$
with
![]() $T_0\subset M_0$
and
$T_0\subset M_0$
and
![]() $T_1\subset M_1$
. Denote by
$T_1\subset M_1$
. Denote by
![]() $W_0$
(resp.
$W_0$
(resp.
![]() $W_1$
) the Weyl group of
$W_1$
) the Weyl group of
![]() $M_0$
(resp.
$M_0$
(resp.
![]() $M_1$
) defined by
$M_1$
) defined by
![]() $T_0$
(resp.
$T_0$
(resp.
![]() $T_1$
). Then
$T_1$
). Then
![]() $\sigma $
induces an action on
$\sigma $
induces an action on
![]() $W_1$
and so an action on
$W_1$
and so an action on
![]() $\operatorname {\mathrm {Irr}}(W_1)$
. Let
$\operatorname {\mathrm {Irr}}(W_1)$
. Let
![]() $\varphi \in \operatorname {\mathrm {Irr}}(W_1)^F\cap \operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
and denote by
$\varphi \in \operatorname {\mathrm {Irr}}(W_1)^F\cap \operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
and denote by
![]() $\tilde {\varphi }$
an extension of
$\tilde {\varphi }$
an extension of
![]() $\varphi $
to
$\varphi $
to
![]() $W_1\rtimes \!<\! F\!>\!$
. Let
$W_1\rtimes \!<\! F\!>\!$
. Let
![]() $\theta $
be a linear character of
$\theta $
be a linear character of
![]() $M_1^F$
that is
$M_1^F$
that is
![]() $\sigma $
-stable. Then
$\sigma $
-stable. Then
![]() $\chi _1:=R^{M_1}_{\varphi }\theta $
as defined in §3.4.1 is a
$\chi _1:=R^{M_1}_{\varphi }\theta $
as defined in §3.4.1 is a
![]() $\sigma $
-stable irreducible character of
$\sigma $
-stable irreducible character of
![]() $M_1^F$
. Let
$M_1^F$
. Let
![]() $\chi _0$
be a quadratic-unipotent character of
$\chi _0$
be a quadratic-unipotent character of
![]() $M_0^F$
. It is induced from a Levi subgroup
$M_0^F$
. It is induced from a Levi subgroup
![]() $M_{00}$
of
$M_{00}$
of
![]() $M_0$
as in §3.4.3.
$M_0$
as in §3.4.3.
Theorem 3.4.3. [Reference ShuShu22, Proposition 5.2.2, Proposition 5.2.3]
Suppose that
![]() $\mathbf {1}\boxtimes \eta \boxtimes \theta $
is a regular linear character of
$\mathbf {1}\boxtimes \eta \boxtimes \theta $
is a regular linear character of
![]() $M_{00}^F\times M_1^F$
. Then
$M_{00}^F\times M_1^F$
. Then
![]() $\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
is a
$\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
is a
![]() $\sigma $
-stable irreducible character of
$\sigma $
-stable irreducible character of
![]() $G^F$
. Moreover, every
$G^F$
. Moreover, every
![]() $\sigma $
-stable irreducible character of
$\sigma $
-stable irreducible character of
![]() $G^F$
is of this form.
$G^F$
is of this form.
Let
![]() $(\mu _+,\mu _-)$
be the 2-partition defining the quadratic-unipotent character
$(\mu _+,\mu _-)$
be the 2-partition defining the quadratic-unipotent character
![]() $\chi _0$
. Let
$\chi _0$
. Let
![]() $m_+$
and
$m_+$
and
![]() $m_-$
be the nonnegative integers such that
$m_-$
be the nonnegative integers such that
![]() $(m_+,m_+-1,\ldots ,1,0)$
and
$(m_+,m_+-1,\ldots ,1,0)$
and
![]() $(m_-,m_--1,\ldots ,1,0)$
are the 2-cores of
$(m_-,m_--1,\ldots ,1,0)$
are the 2-cores of
![]() $\mu _+$
and
$\mu _+$
and
![]() $\mu _-$
, respectively. Write
$\mu _-$
, respectively. Write
Proposition 3.4.4. [Reference ShuShu22, Corollary 11.1.2]
With the notations in the above theorem, the
![]() $\sigma $
-stable irreducible character
$\sigma $
-stable irreducible character
![]() $\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
extends to a uniform function on
$\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
extends to a uniform function on
![]() $G^F\sigma $
if and only if
$G^F\sigma $
if and only if
![]() $m\le 1$
. Moreover, the extensions of these characters (up to a sign) form a basis of the vector space of all uniform functions on
$m\le 1$
. Moreover, the extensions of these characters (up to a sign) form a basis of the vector space of all uniform functions on
![]() $G^F\sigma $
.
$G^F\sigma $
.
3.4.5
In the rest of this section, we will restrict ourselves to the special case where
![]() $M=L_I$
is a
$M=L_I$
is a
![]() $\sigma $
-stable standard Levi subgroup. Then we have
$\sigma $
-stable standard Levi subgroup. Then we have
![]() $\epsilon _G=\epsilon _M$
,
$\epsilon _G=\epsilon _M$
,
![]() $M_0^F\cong \operatorname {\mathrm {GL}}_{n_0}(q)$
,
$M_0^F\cong \operatorname {\mathrm {GL}}_{n_0}(q)$
,
![]() $M_1^F\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}(q)\times \operatorname {\mathrm {GL}}_{n_i}(q))$
,
$M_1^F\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}(q)\times \operatorname {\mathrm {GL}}_{n_i}(q))$
,
![]() $W_1\cong \prod _i(\mathfrak {S}_{n_i}\times \mathfrak {S}_{n_i})$
, and
$W_1\cong \prod _i(\mathfrak {S}_{n_i}\times \mathfrak {S}_{n_i})$
, and
![]() $W_1^{\sigma }\cong \prod _i\mathfrak {S}_{n_i}$
. The action of F on
$W_1^{\sigma }\cong \prod _i\mathfrak {S}_{n_i}$
. The action of F on
![]() $W_1$
is trivial. A
$W_1$
is trivial. A
![]() $\sigma $
-stable linear character of
$\sigma $
-stable linear character of
![]() $M_1^F$
is of the form
$M_1^F$
is of the form
![]() $(\theta _i,\theta _i{\!}^{-1})_i$
, where
$(\theta _i,\theta _i{\!}^{-1})_i$
, where
![]() $\theta _i$
is a linear character of
$\theta _i$
is a linear character of
![]() $\operatorname {\mathrm {GL}}_{n_i}(q)$
for each i. Then
$\operatorname {\mathrm {GL}}_{n_i}(q)$
for each i. Then
![]() $\mathbf {1}\boxtimes \eta \boxtimes \theta $
is a regular linear character of
$\mathbf {1}\boxtimes \eta \boxtimes \theta $
is a regular linear character of
![]() $M_{00}^F\times M_1^F$
if and only if
$M_{00}^F\times M_1^F$
if and only if
![]() $\theta $
is regular in the following sense.
$\theta $
is regular in the following sense.
Definition 3.4.5. We say that a
![]() $\sigma $
-stable linear character
$\sigma $
-stable linear character
![]() $\theta $
of
$\theta $
of
![]() $M_1^F$
is regular if
$M_1^F$
is regular if
![]() $\theta _i\ne \theta _j^{\pm 1}$
whenever
$\theta _i\ne \theta _j^{\pm 1}$
whenever
![]() $i\ne j$
and
$i\ne j$
and
![]() $\theta _i^2\ne \mathbf {1}$
for all i. The set of
$\theta _i^2\ne \mathbf {1}$
for all i. The set of
![]() $\sigma $
-stable regular linear characters of
$\sigma $
-stable regular linear characters of
![]() $M_1^F$
is denoted by
$M_1^F$
is denoted by
![]() $\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
.
$\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
.
We will give a decomposition formula expressing the extension of
![]() $R^G_M(\chi _1\boxtimes \chi _0)$
to
$R^G_M(\chi _1\boxtimes \chi _0)$
to
![]() $G^F\sigma $
as a linear combination of generalised Deligne-Lusztig characters when
$G^F\sigma $
as a linear combination of generalised Deligne-Lusztig characters when
![]() $m\le 1$
. Therefore, we assume
$m\le 1$
. Therefore, we assume
![]() $m\le 1$
in what follows.
$m\le 1$
in what follows.
3.4.6
The set
![]() $\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
is in bijection with
$\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
is in bijection with
![]() $\prod _i\mathcal {P}(n_i)$
, which is then in bijection with
$\prod _i\mathcal {P}(n_i)$
, which is then in bijection with
![]() $\operatorname {\mathrm {Irr}}(W_1^{\sigma })$
. We define a bijection
$\operatorname {\mathrm {Irr}}(W_1^{\sigma })$
. We define a bijection
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{Irr}}(W^{\sigma}_1)&\smash{\begin{array}{c}\sim\\[-1em] \longrightarrow\end{array}}\operatorname{\mathrm{Irr}}(W_1)^{\sigma}\\ \varphi&\longmapsto\{\varphi\} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{Irr}}(W^{\sigma}_1)&\smash{\begin{array}{c}\sim\\[-1em] \longrightarrow\end{array}}\operatorname{\mathrm{Irr}}(W_1)^{\sigma}\\ \varphi&\longmapsto\{\varphi\} \end{aligned} \end{align} $$
as the composition of these two natural bijections.
Write
![]() $N_{\pm }=(n_{\pm }-m_{\pm }(m_{\pm }+1)/2)/2$
and so
$N_{\pm }=(n_{\pm }-m_{\pm }(m_{\pm }+1)/2)/2$
and so
![]() $n_0=m+2N_++2N_-$
. There exists a unique pair
$n_0=m+2N_++2N_-$
. There exists a unique pair
![]() $(h_1,h_2)\in \mathbb {N}\times \mathbb {Z}$
such that
$(h_1,h_2)\in \mathbb {N}\times \mathbb {Z}$
such that
 $$ \begin{align} \begin{aligned} m_+&=\sup\{h_1+h_2,-h_1-h_2-1\},\\ m_-&=\sup\{h_1-h_2,h_2-h_1-1\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} m_+&=\sup\{h_1+h_2,-h_1-h_2-1\},\\ m_-&=\sup\{h_1-h_2,h_2-h_1-1\}. \end{aligned} \end{align} $$
Note that exchanging
![]() $\mu _+$
and
$\mu _+$
and
![]() $\mu _-$
changes
$\mu _-$
changes
![]() $(h_1,h_2)$
into
$(h_1,h_2)$
into
![]() $(h_1,-h_2)$
. More explicitly, if n is even, then
$(h_1,-h_2)$
. More explicitly, if n is even, then
![]() $m=m_+=m_-=0$
, and so
$m=m_+=m_-=0$
, and so
![]() $h_1=h_2=0$
, and if n is odd, then
$h_1=h_2=0$
, and if n is odd, then
![]() $m=1$
, in which case
$m=1$
, in which case
![]() $h_1$
is always equal to
$h_1$
is always equal to
![]() $0$
while
$0$
while
![]() $h_2=1$
if
$h_2=1$
if
![]() $m_+=1$
and
$m_+=1$
and
![]() $h_2=-1$
if
$h_2=-1$
if
![]() $m_-=1$
. Therefore,
$m_-=1$
. Therefore,
![]() $h_1$
is redundant, and we will write
$h_1$
is redundant, and we will write
![]() $\epsilon =h_2$
.
$\epsilon =h_2$
.
Fix some integers
![]() $r_+>l(\mu _+)$
and
$r_+>l(\mu _+)$
and
![]() $r_->l(\mu _-)$
satisfying the following:
$r_->l(\mu _-)$
satisfying the following:
Assumption.
-
○
 $r_+$
and
$r_+$
and
 $r_-$
are odd if
$r_-$
are odd if
 $\epsilon =0$
;
$\epsilon =0$
; -
○
 $r_+$
is even if and only if
$r_+$
is even if and only if
 $n_+$
is odd,
$n_+$
is odd,
 $r_-$
is even if and only if
$r_-$
is even if and only if
 $n_-$
is odd, if
$n_-$
is odd, if
 $\epsilon =\pm 1$
.
$\epsilon =\pm 1$
.
(See [Reference ShuShu22, Remark 9.4.8].) Note that the parity of
![]() $\epsilon $
only depends on that of n. Let
$\epsilon $
only depends on that of n. Let
![]() $(\alpha _+,\beta _+)_{r_+}$
and
$(\alpha _+,\beta _+)_{r_+}$
and
![]() $(\alpha _-,\beta _-)_{r_-}$
be the
$(\alpha _-,\beta _-)_{r_-}$
be the
![]() $2$
-quotients of
$2$
-quotients of
![]() $\mu _+$
and
$\mu _+$
and
![]() $\mu _-$
, respectively (see §2.2.2). The
$\mu _-$
, respectively (see §2.2.2). The
![]() $2$
-partition
$2$
-partition
![]() $(\alpha _+,\beta _+)_{r_+}$
(resp.
$(\alpha _+,\beta _+)_{r_+}$
(resp.
![]() $(\alpha _-,\beta _-)_{r_-}$
) determines an irreducible character of
$(\alpha _-,\beta _-)_{r_-}$
) determines an irreducible character of
![]() $\mathfrak {W}_{N_+}$
(resp.
$\mathfrak {W}_{N_+}$
(resp.
![]() $\mathfrak {W}_{N_-}$
), denoted by
$\mathfrak {W}_{N_-}$
), denoted by
![]() $\varphi _+$
(resp.
$\varphi _+$
(resp.
![]() $\varphi _-$
). Then with the fixed
$\varphi _-$
). Then with the fixed
![]() $r_+$
and
$r_+$
and
![]() $r_-$
, the
$r_-$
, the
![]() $2$
-partitions
$2$
-partitions
![]() $(\mu _+,\mu _-)$
are in bijection with the data
$(\mu _+,\mu _-)$
are in bijection with the data
![]() $(h_1,h_2,\varphi _+,\varphi _-)$
, or rather
$(h_1,h_2,\varphi _+,\varphi _-)$
, or rather
![]() $(\epsilon ,\varphi _+,\varphi _-)$
, via the quotient-core decomposition.
$(\epsilon ,\varphi _+,\varphi _-)$
, via the quotient-core decomposition.
3.4.7
To simplify, we will write
![]() $\mathfrak {W}_+=\mathfrak {W}_{N_+}$
and
$\mathfrak {W}_+=\mathfrak {W}_{N_+}$
and
![]() $\mathfrak {W}_-=\mathfrak {W}_{N_-}$
. Recall that
$\mathfrak {W}_-=\mathfrak {W}_{N_-}$
. Recall that
![]() $W_0$
is the Weyl group of
$W_0$
is the Weyl group of
![]() $M_0$
. Since
$M_0$
. Since
![]() $W_0^{\sigma }\cong \mathfrak {W}_{N_++N_-}$
, we will regard
$W_0^{\sigma }\cong \mathfrak {W}_{N_++N_-}$
, we will regard
![]() $\mathfrak {W}_+\times \mathfrak {W}_-$
as a subgroup of
$\mathfrak {W}_+\times \mathfrak {W}_-$
as a subgroup of
![]() $W_0^{\sigma }$
in a natural way. Write
$W_0^{\sigma }$
in a natural way. Write
![]() $T=T_0\times T_1$
, with
$T=T_0\times T_1$
, with
![]() $T_0\subset M_0$
and
$T_0\subset M_0$
and
![]() $T_1\subset M_1$
. To each
$T_1\subset M_1$
. To each
![]() $\mathbf {w}=(w_+,w_-)\in \mathfrak {W}_+\times \mathfrak {W}_-$
is associated an F-stable and
$\mathbf {w}=(w_+,w_-)\in \mathfrak {W}_+\times \mathfrak {W}_-$
is associated an F-stable and
![]() $\sigma $
-stable maximal torus
$\sigma $
-stable maximal torus
![]() $T_{\mathbf {w}}\subset M_0$
, in such a way that
$T_{\mathbf {w}}\subset M_0$
, in such a way that
![]() $T_0$
is associated to
$T_0$
is associated to
![]() $1\in \mathfrak {W}_+\times \mathfrak {W}_-$
. There is an isomorphism
$1\in \mathfrak {W}_+\times \mathfrak {W}_-$
. There is an isomorphism
![]() $T_{\mathbf {w}}\cong T_{w_+}\times T_{w-}\times \operatorname {\mathrm {GL}}_{m}$
, where
$T_{\mathbf {w}}\cong T_{w_+}\times T_{w-}\times \operatorname {\mathrm {GL}}_{m}$
, where
![]() $T_{w_{\pm }}$
is isomorphic to
$T_{w_{\pm }}$
is isomorphic to
![]() $(k^{\ast })^{2N_{\pm }}$
equipped with the Frobenius twisted by
$(k^{\ast })^{2N_{\pm }}$
equipped with the Frobenius twisted by
![]() $w_{\pm }$
. To each
$w_{\pm }$
. To each
![]() $w_1\in W_1^{\sigma }$
is associated an F-stable and
$w_1\in W_1^{\sigma }$
is associated an F-stable and
![]() $\sigma $
-stable maximal torus
$\sigma $
-stable maximal torus
![]() $T_{w_1}$
of
$T_{w_1}$
of
![]() $M_1$
, in such a way that
$M_1$
, in such a way that
![]() $T_1$
is associated to
$T_1$
is associated to
![]() $1\in W_1^{\sigma }$
. Then
$1\in W_1^{\sigma }$
. Then
![]() $T_{w_1,\mathbf {w}}:=T_{w_1}\times T_{\mathbf {w}}$
is an F-stable and
$T_{w_1,\mathbf {w}}:=T_{w_1}\times T_{\mathbf {w}}$
is an F-stable and
![]() $\sigma $
-stable maximal torus of M. Given
$\sigma $
-stable maximal torus of M. Given
![]() $\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
and
$\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
and
![]() $\epsilon $
, we can define a
$\epsilon $
, we can define a
![]() $\sigma $
-stable linear character
$\sigma $
-stable linear character
![]() $\theta _{w_1,\mathbf {w}}$
of
$\theta _{w_1,\mathbf {w}}$
of
![]() $T_{w_1,\mathbf {w}}^F$
for any
$T_{w_1,\mathbf {w}}^F$
for any
![]() $w_1\in W_1^{\sigma }$
and
$w_1\in W_1^{\sigma }$
and
![]() $\mathbf {w}\in \mathfrak {W}_+\times \mathfrak {W}_-$
in the following manner. The component of
$\mathbf {w}\in \mathfrak {W}_+\times \mathfrak {W}_-$
in the following manner. The component of
![]() $\theta _{w_1,\mathbf {w}}$
on
$\theta _{w_1,\mathbf {w}}$
on
![]() $T_{w_1}^F$
is simply the restriction of
$T_{w_1}^F$
is simply the restriction of
![]() $\theta $
to
$\theta $
to
![]() $T_{w_1}^F$
. The component of
$T_{w_1}^F$
. The component of
![]() $\theta _{w_1,\mathbf {w}}$
on
$\theta _{w_1,\mathbf {w}}$
on
![]() $T_{w_+}^F$
is the trivial character
$T_{w_+}^F$
is the trivial character
![]() $\mathbf {1}$
. The component of
$\mathbf {1}$
. The component of
![]() $\theta _{w_1,\mathbf {w}}$
on
$\theta _{w_1,\mathbf {w}}$
on
![]() $T_{w-}^F$
is the order 2 character
$T_{w-}^F$
is the order 2 character
![]() $\eta $
of
$\eta $
of
![]() $\mathbb {F}_q^{\ast }$
composed with the product of norm maps. If
$\mathbb {F}_q^{\ast }$
composed with the product of norm maps. If
![]() $\epsilon =1$
, then we require that the component on
$\epsilon =1$
, then we require that the component on
![]() $\operatorname {\mathrm {GL}}_m(q)$
is
$\operatorname {\mathrm {GL}}_m(q)$
is
![]() $\mathbf {1}$
, and if
$\mathbf {1}$
, and if
![]() $\epsilon =-1$
, then we require that the same component is
$\epsilon =-1$
, then we require that the same component is
![]() $\eta $
. Now
$\eta $
. Now
![]() $\theta _{w_1,\mathbf {w}}$
extends to
$\theta _{w_1,\mathbf {w}}$
extends to
![]() $T_{w_1,\mathbf {w}}^F\!<\!\sigma \!>\!$
, and we denote by
$T_{w_1,\mathbf {w}}^F\!<\!\sigma \!>\!$
, and we denote by
![]() $\tilde {\theta }_{w_1,\mathbf {w}}$
the extension which gives
$\tilde {\theta }_{w_1,\mathbf {w}}$
the extension which gives
![]() $1$
at
$1$
at
![]() $\sigma $
.
$\sigma $
.
Remark 3.4.6. We can indeed require that
![]() $\tilde {\theta }_{w_1,\mathbf {w}}$
takes value
$\tilde {\theta }_{w_1,\mathbf {w}}$
takes value
![]() $1$
at
$1$
at
![]() $\sigma $
. To define an extension
$\sigma $
. To define an extension
![]() $\tilde {\theta }_{w_1,\mathbf {w}}$
is to define the action of
$\tilde {\theta }_{w_1,\mathbf {w}}$
is to define the action of
![]() $\sigma $
on the given 1-dimensional representation
$\sigma $
on the given 1-dimensional representation
![]() $\rho $
corresponding to
$\rho $
corresponding to
![]() $\theta _{w_1,\mathbf {w}}$
. Denote by
$\theta _{w_1,\mathbf {w}}$
. Denote by
![]() $\tilde {\rho }(\sigma )$
this action of
$\tilde {\rho }(\sigma )$
this action of
![]() $\sigma $
. In order for it to be well defined, it must satisfy
$\sigma $
. In order for it to be well defined, it must satisfy
![]() $\tilde {\rho }(\sigma )^2=\rho (\sigma ^2)$
. It is easy to check that this condition also suffices. Now if n is odd or if
$\tilde {\rho }(\sigma )^2=\rho (\sigma ^2)$
. It is easy to check that this condition also suffices. Now if n is odd or if ![]() , then
, then
![]() $\sigma ^2=1$
, and so we can obviously put
$\sigma ^2=1$
, and so we can obviously put
![]() $\tilde {\rho }(\sigma )=1$
. If
$\tilde {\rho }(\sigma )=1$
. If ![]() and
and
![]() $\sigma ^2=-1$
, we check that
$\sigma ^2=-1$
, we check that
![]() $\rho (-1)=1$
, and so the same definition of
$\rho (-1)=1$
, and so the same definition of
![]() $\tilde {\rho }(\sigma )$
works in this case as well.
$\tilde {\rho }(\sigma )$
works in this case as well.
Theorem 3.4.7 [Reference ShuShu22, Theorem 11.1.1]
Let
![]() $\chi $
be the
$\chi $
be the
![]() $\sigma $
-stable irreducible character
$\sigma $
-stable irreducible character
![]() $R^G_M(\chi _1\boxtimes \chi _0)$
and let
$R^G_M(\chi _1\boxtimes \chi _0)$
and let
![]() $\tilde {\chi }$
be an extension of
$\tilde {\chi }$
be an extension of
![]() $\chi $
to
$\chi $
to
![]() $\bar {G}^F$
. Suppose that
$\bar {G}^F$
. Suppose that
![]() $\chi _1$
is defined by
$\chi _1$
is defined by
![]() $\theta \in \operatorname {\mathrm {Irr}}^{\sigma }_{\operatorname {\mathrm {reg}}}(M_1^F)$
and
$\theta \in \operatorname {\mathrm {Irr}}^{\sigma }_{\operatorname {\mathrm {reg}}}(M_1^F)$
and
![]() $\{\varphi \}\in \operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
, and that
$\{\varphi \}\in \operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
, and that
![]() $\chi _0$
is defined by a 2-partition which determines the data
$\chi _0$
is defined by a 2-partition which determines the data
![]() $N_+$
,
$N_+$
,
![]() $N_-$
and
$N_-$
and
![]() $(\epsilon ,\varphi _+,\varphi _-)$
. Then for some choice of the extension
$(\epsilon ,\varphi _+,\varphi _-)$
. Then for some choice of the extension
![]() $\tilde {\varphi }$
, the following equality holds up to a sign,
$\tilde {\varphi }$
, the following equality holds up to a sign,
 $$ \begin{align} \tilde{\chi}|_{G^F\sigma}=|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|^{-1}\!\!\!\!\!\!\!\!\sum_{\substack{(w_+,w_-,w_1)\\\in\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}}}\!\!\!\!\!\!\!\!\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)R^{G\sigma}_{T_{w_1,\mathbf{w}}\sigma}\tilde{\theta}_{w_1,\mathbf{w}}. \end{align} $$
$$ \begin{align} \tilde{\chi}|_{G^F\sigma}=|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|^{-1}\!\!\!\!\!\!\!\!\sum_{\substack{(w_+,w_-,w_1)\\\in\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}}}\!\!\!\!\!\!\!\!\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)R^{G\sigma}_{T_{w_1,\mathbf{w}}\sigma}\tilde{\theta}_{w_1,\mathbf{w}}. \end{align} $$
Remark 3.4.8. Since the action of F on
![]() $W_1$
is trivial, the extension
$W_1$
is trivial, the extension
![]() $\tilde {\varphi }$
can, in fact, be chosen to be the trivial one (i.e.,
$\tilde {\varphi }$
can, in fact, be chosen to be the trivial one (i.e.,
![]() $\tilde {\varphi }(w_1F)=\varphi (w_1)$
).
$\tilde {\varphi }(w_1F)=\varphi (w_1)$
).
3.5 Types
We introduce some combinatorial data called types that are used to describe
![]() $\sigma $
-stable irreducible characters of
$\sigma $
-stable irreducible characters of
![]() $G(q)$
.
$G(q)$
.
3.5.1
Types are data of the form
where
![]() $\boldsymbol{\omega} _+$
and
$\boldsymbol{\omega} _+$
and
![]() $\boldsymbol{\omega} _-$
are 2-partitions, and
$\boldsymbol{\omega} _-$
are 2-partitions, and
![]() $(\omega _i)$
is an unordered sequence of nontrivial partitions, the length of which could be
$(\omega _i)$
is an unordered sequence of nontrivial partitions, the length of which could be
![]() $0$
. We will often write
$0$
. We will often write
![]() $\boldsymbol{\omega} _{\ast }=(\omega _i)_{1\le i\le l}$
and
$\boldsymbol{\omega} _{\ast }=(\omega _i)_{1\le i\le l}$
and
![]() $\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-\boldsymbol{\omega} _{\ast }$
for brevity. Such data can equally be written as
$\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-\boldsymbol{\omega} _{\ast }$
for brevity. Such data can equally be written as
![]() $\boldsymbol{\omega} _+\boldsymbol{\omega} _-(m_{\lambda })_{\lambda \in \mathcal {P}}$
, where
$\boldsymbol{\omega} _+\boldsymbol{\omega} _-(m_{\lambda })_{\lambda \in \mathcal {P}}$
, where
![]() $m_{\lambda }$
is the multiplicity of
$m_{\lambda }$
is the multiplicity of
![]() $\lambda $
in the sequence
$\lambda $
in the sequence
![]() $\boldsymbol{\omega} _{\ast }$
. Two types
$\boldsymbol{\omega} _{\ast }$
. Two types
![]() $\boldsymbol{\omega} _+\boldsymbol{\omega} _-(m_{\lambda })$
and
$\boldsymbol{\omega} _+\boldsymbol{\omega} _-(m_{\lambda })$
and
![]() $\boldsymbol{\omega} ^{\prime }_+\boldsymbol{\omega} ^{\prime }_-(m^{\prime }_{\lambda })$
are regarded as the same if and only if
$\boldsymbol{\omega} ^{\prime }_+\boldsymbol{\omega} ^{\prime }_-(m^{\prime }_{\lambda })$
are regarded as the same if and only if
![]() $\boldsymbol{\omega} _+=\boldsymbol{\omega} _+'$
,
$\boldsymbol{\omega} _+=\boldsymbol{\omega} _+'$
,
![]() $\boldsymbol{\omega} _-=\boldsymbol{\omega} _-'$
and
$\boldsymbol{\omega} _-=\boldsymbol{\omega} _-'$
and
![]() $m_{\lambda }=m^{\prime }_{\lambda }$
for all
$m_{\lambda }=m^{\prime }_{\lambda }$
for all
![]() $\lambda \in \mathcal {P}$
. The size of a type is
$\lambda \in \mathcal {P}$
. The size of a type is
![]() $|\boldsymbol{\omega} |:=|\boldsymbol{\omega} _+|+|\boldsymbol{\omega} _-|+\sum _i|\boldsymbol{\omega} _i|.$
The set of types of size a will be denoted by
$|\boldsymbol{\omega} |:=|\boldsymbol{\omega} _+|+|\boldsymbol{\omega} _-|+\sum _i|\boldsymbol{\omega} _i|.$
The set of types of size a will be denoted by
![]() $\mathfrak {T}(a)$
, and we will write
$\mathfrak {T}(a)$
, and we will write
![]() $\mathfrak {T}=\sqcup _{a\in \mathbb {Z}_{\ge 0}}\mathfrak {T}(a)$
. For any
$\mathfrak {T}=\sqcup _{a\in \mathbb {Z}_{\ge 0}}\mathfrak {T}(a)$
. For any
![]() $\boldsymbol{\omega} \in \mathfrak {T}$
, we will write
$\boldsymbol{\omega} \in \mathfrak {T}$
, we will write
![]() $\boldsymbol{\Lambda }(\boldsymbol{\omega} )=\boldsymbol{\Lambda }(\boldsymbol{\omega} _+)\boldsymbol{\Lambda }(\boldsymbol{\omega} _-)\boldsymbol{\omega} _{\ast }$
(recall that
$\boldsymbol{\Lambda }(\boldsymbol{\omega} )=\boldsymbol{\Lambda }(\boldsymbol{\omega} _+)\boldsymbol{\Lambda }(\boldsymbol{\omega} _-)\boldsymbol{\omega} _{\ast }$
(recall that
![]() $\boldsymbol{\Lambda} (-)$
means the symbol corresponding to a given 2-partition). Denote by
$\boldsymbol{\Lambda} (-)$
means the symbol corresponding to a given 2-partition). Denote by
![]() $\tilde {\mathfrak {T}}$
the set of ordered types (i.e., the data
$\tilde {\mathfrak {T}}$
the set of ordered types (i.e., the data
![]() $\boldsymbol{\omega} _+\boldsymbol{\omega} _-(\omega _i)$
with
$\boldsymbol{\omega} _+\boldsymbol{\omega} _-(\omega _i)$
with
![]() $(\omega _i)$
being an ordered sequence). There is an obvious map from
$(\omega _i)$
being an ordered sequence). There is an obvious map from
![]() $\tilde {\mathfrak {T}}$
to
$\tilde {\mathfrak {T}}$
to
![]() $\mathfrak {T}$
; therefore, anything that can be defined for elements of
$\mathfrak {T}$
; therefore, anything that can be defined for elements of
![]() $\mathfrak {T}$
is naturally defined for elements of
$\mathfrak {T}$
is naturally defined for elements of
![]() $\tilde {\mathfrak {T}}$
. Given
$\tilde {\mathfrak {T}}$
. Given
![]() $\boldsymbol{\alpha} =\boldsymbol{\alpha} _+\boldsymbol{\alpha} _-(\alpha _i)_{1\le i\le l_1}$
,
$\boldsymbol{\alpha} =\boldsymbol{\alpha} _+\boldsymbol{\alpha} _-(\alpha _i)_{1\le i\le l_1}$
,
![]() $\boldsymbol{\beta} =\boldsymbol{\beta} _+\boldsymbol{\beta} _-(\beta _i)_{1\le i\le l_2}\in \tilde {\mathfrak {T}}$
, we write
$\boldsymbol{\beta} =\boldsymbol{\beta} _+\boldsymbol{\beta} _-(\beta _i)_{1\le i\le l_2}\in \tilde {\mathfrak {T}}$
, we write
![]() $\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
, if
$\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
, if
![]() $l_1=l_2=l$
and for each
$l_1=l_2=l$
and for each
![]() $1\le i\le l$
, we have
$1\le i\le l$
, we have
![]() $|\alpha _i|=|\beta _i|$
, and moreover,
$|\alpha _i|=|\beta _i|$
, and moreover,
![]() $|\boldsymbol{\alpha} _+|=|\boldsymbol{\beta} _+|$
and
$|\boldsymbol{\alpha} _+|=|\boldsymbol{\beta} _+|$
and
![]() $|\boldsymbol{\alpha} _-|=|\boldsymbol{\beta} _-|$
. A type
$|\boldsymbol{\alpha} _-|=|\boldsymbol{\beta} _-|$
. A type
![]() $\boldsymbol{\omega} $
(ordered or unordered) can be augmented by
$\boldsymbol{\omega} $
(ordered or unordered) can be augmented by
![]() $\epsilon \in \{-1,0,1\}$
and the resulting data written as
$\epsilon \in \{-1,0,1\}$
and the resulting data written as
![]() $\epsilon \boldsymbol{\omega} $
. Define
$\epsilon \boldsymbol{\omega} $
. Define
![]() $|\epsilon \boldsymbol{\omega} |:=|\boldsymbol{\omega} |$
.
$|\epsilon \boldsymbol{\omega} |:=|\boldsymbol{\omega} |$
.
We will denote by
![]() $\mathfrak {T}^{\circ }$
the set of unordered sequences
$\mathfrak {T}^{\circ }$
the set of unordered sequences
![]() $\lambda _+\lambda _-(\lambda _i)_{1\le i\le l}$
, defined in a way similar to types except that
$\lambda _+\lambda _-(\lambda _i)_{1\le i\le l}$
, defined in a way similar to types except that
![]() $\lambda _+$
and
$\lambda _+$
and
![]() $\lambda _-$
are partitions. We may also write such a sequence as
$\lambda _-$
are partitions. We may also write such a sequence as
![]() $\lambda _+\lambda _-\boldsymbol{\lambda} _{\ast }$
, with
$\lambda _+\lambda _-\boldsymbol{\lambda} _{\ast }$
, with
![]() $\boldsymbol{\lambda} _{\ast }=(\lambda _i)$
. The ordered version
$\boldsymbol{\lambda} _{\ast }=(\lambda _i)$
. The ordered version
![]() $\tilde {\mathfrak {T}}^{\circ }$
of these data can be defined in an obvious way. Define
$\tilde {\mathfrak {T}}^{\circ }$
of these data can be defined in an obvious way. Define
![]() $|\boldsymbol{\lambda} |:=|\lambda _+|+|\lambda _-|+\sum _i|\lambda _i|$
.
$|\boldsymbol{\lambda} |:=|\lambda _+|+|\lambda _-|+\sum _i|\lambda _i|$
.
The subset
![]() $\{\boldsymbol{\omega} \in \mathfrak {T}\mid \boldsymbol{\omega} _+=\boldsymbol{\omega} _-=\varnothing \}$
will be denoted by
$\{\boldsymbol{\omega} \in \mathfrak {T}\mid \boldsymbol{\omega} _+=\boldsymbol{\omega} _-=\varnothing \}$
will be denoted by
![]() $\mathfrak {T}_{\ast }$
. We may also regard it as a subset of
$\mathfrak {T}_{\ast }$
. We may also regard it as a subset of
![]() $\mathfrak {T}^{\circ }$
, so that
$\mathfrak {T}^{\circ }$
, so that
![]() $\mathfrak {T}_{\ast }=\mathfrak {T}\cap \mathfrak {T}^{\circ }$
. Thus, for any
$\mathfrak {T}_{\ast }=\mathfrak {T}\cap \mathfrak {T}^{\circ }$
. Thus, for any
![]() $\boldsymbol{\alpha} \in \mathfrak {T}_{\ast }$
, the size
$\boldsymbol{\alpha} \in \mathfrak {T}_{\ast }$
, the size
![]() $|\boldsymbol{\alpha} |$
is automatically defined, and we will denote by
$|\boldsymbol{\alpha} |$
is automatically defined, and we will denote by
![]() $l(\boldsymbol{\alpha} )$
its length. For any
$l(\boldsymbol{\alpha} )$
its length. For any
![]() $\boldsymbol{\alpha} =(m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
, define
$\boldsymbol{\alpha} =(m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
, define
and
If
![]() $\boldsymbol {\alpha }$
is a 2-partition, then we define
$\boldsymbol {\alpha }$
is a 2-partition, then we define
![]() $\{\boldsymbol {\alpha }\}_1$
to be the partition with 2-core
$\{\boldsymbol {\alpha }\}_1$
to be the partition with 2-core
![]() $(1)$
and 2-quotient
$(1)$
and 2-quotient
![]() $\boldsymbol{\alpha} $
and define
$\boldsymbol{\alpha} $
and define
![]() $\{\boldsymbol {\alpha }\}_0$
to be the partition with trivial 2-core and 2-quotient
$\{\boldsymbol {\alpha }\}_0$
to be the partition with trivial 2-core and 2-quotient
![]() $\boldsymbol{\alpha} $
. For any
$\boldsymbol{\alpha} $
. For any
![]() $\boldsymbol{\alpha} =(m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
, define
$\boldsymbol{\alpha} =(m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
, define
![]() $\boldsymbol{\alpha} ^2:=(2m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
. Define a natural map
$\boldsymbol{\alpha} ^2:=(2m_{\lambda })_{\lambda \in \mathcal {P}}\in \mathfrak {T}_{\ast }$
. Define a natural map
 $$ \begin{align} \begin{aligned} \{~\}:\{-1,0,1\}\times\mathfrak{T}&\longrightarrow\mathfrak{T}^{\circ}\\ \epsilon\boldsymbol\omega&\longmapsto \lambda_+\lambda_-\boldsymbol\lambda_{\ast}=\{\epsilon\boldsymbol\omega\} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \{~\}:\{-1,0,1\}\times\mathfrak{T}&\longrightarrow\mathfrak{T}^{\circ}\\ \epsilon\boldsymbol\omega&\longmapsto \lambda_+\lambda_-\boldsymbol\lambda_{\ast}=\{\epsilon\boldsymbol\omega\} \end{aligned} \end{align} $$
as follows. The partition
![]() $\lambda _{\pm }$
has
$\lambda _{\pm }$
has
![]() $\omega _{\pm }$
as the 2-quotient and has trivial 2-core except when
$\omega _{\pm }$
as the 2-quotient and has trivial 2-core except when
![]() $\epsilon =+1$
and
$\epsilon =+1$
and
![]() $\lambda _{+}=\{\boldsymbol{\omega} _+\}_1$
, or when
$\lambda _{+}=\{\boldsymbol{\omega} _+\}_1$
, or when
![]() $\epsilon =-1$
and
$\epsilon =-1$
and
![]() $\lambda _{-}=\{\boldsymbol{\omega} _-\}_1$
. We require that
$\lambda _{-}=\{\boldsymbol{\omega} _-\}_1$
. We require that
![]() $\boldsymbol{\lambda} _{\ast }=\boldsymbol{\omega} _{\ast }^2$
.
$\boldsymbol{\lambda} _{\ast }=\boldsymbol{\omega} _{\ast }^2$
.
We define a natural map
as follows. Let
![]() $\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-\boldsymbol{\omega} _{\ast }\in \mathfrak {T}$
. Regarding
$\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-\boldsymbol{\omega} _{\ast }\in \mathfrak {T}$
. Regarding
![]() $\mathcal {P}^2$
as signed partitions, it sends each part of
$\mathcal {P}^2$
as signed partitions, it sends each part of
![]() $\omega _i$
to a positively signed part with the same size and keeps the sign and size of each part of
$\omega _i$
to a positively signed part with the same size and keeps the sign and size of each part of
![]() $\boldsymbol{\omega} _+$
and
$\boldsymbol{\omega} _+$
and
![]() $\boldsymbol{\omega} _-$
. The union of these signed parts is the image of
$\boldsymbol{\omega} _-$
. The union of these signed parts is the image of
![]() $[~]$
and is denoted by
$[~]$
and is denoted by
![]() $[\boldsymbol{\omega} ]$
.
$[\boldsymbol{\omega} ]$
.
Denote by
![]() $\tilde {\mathfrak {T}}_s$
the subset of
$\tilde {\mathfrak {T}}_s$
the subset of
![]() $\tilde {\mathfrak {T}}$
consisting of elements of the form
$\tilde {\mathfrak {T}}$
consisting of elements of the form
where
![]() $m_+=|\boldsymbol{\omega} _+|$
,
$m_+=|\boldsymbol{\omega} _+|$
,
![]() $m_-=|\boldsymbol{\omega} _-|$
and
$m_-=|\boldsymbol{\omega} _-|$
and
![]() $m_i=|\omega _i|$
. Equivalently, the elements of
$m_i=|\omega _i|$
. Equivalently, the elements of
![]() $\tilde {\mathfrak {T}}_s$
can be written as a sequence of integers:
$\tilde {\mathfrak {T}}_s$
can be written as a sequence of integers:
![]() $\boldsymbol{\omega} =m_+m_-(m_i)_i$
and
$\boldsymbol{\omega} =m_+m_-(m_i)_i$
and
![]() $\boldsymbol{\omega} _{\ast }=(m_i)_i$
. We define its dual type by
$\boldsymbol{\omega} _{\ast }=(m_i)_i$
. We define its dual type by
Define the surjective map
by
![]() $\tilde {S}(\boldsymbol{\omega} ):=|\boldsymbol{\omega} _+||\boldsymbol{\omega} _-|(|\omega _i|)_i$
. If
$\tilde {S}(\boldsymbol{\omega} ):=|\boldsymbol{\omega} _+||\boldsymbol{\omega} _-|(|\omega _i|)_i$
. If
![]() $\boldsymbol{\omega} \in \tilde {\mathfrak {T}}_s$
, then we will denote by
$\boldsymbol{\omega} \in \tilde {\mathfrak {T}}_s$
, then we will denote by
![]() $\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
the inverse image of
$\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
the inverse image of
![]() $\boldsymbol{\omega} $
under
$\boldsymbol{\omega} $
under
![]() $\tilde {S}$
. Two ordered types
$\tilde {S}$
. Two ordered types
![]() $\boldsymbol{\alpha} $
and
$\boldsymbol{\alpha} $
and
![]() $\boldsymbol{\beta} $
satisfy
$\boldsymbol{\beta} $
satisfy
![]() $\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
if and only if they lie in the same
$\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
if and only if they lie in the same
![]() $\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
for some
$\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
for some
![]() $\boldsymbol{\omega} \in \tilde {\mathfrak {T}}_s$
. The unordered version of S and
$\boldsymbol{\omega} \in \tilde {\mathfrak {T}}_s$
. The unordered version of S and
![]() $\mathfrak {T}_s$
can be similarly defined.
$\mathfrak {T}_s$
can be similarly defined.
3.5.2
The relevance of types is as follows. The group
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
in Theorem 3.4.7 is isomorphic to
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
in Theorem 3.4.7 is isomorphic to
![]() $\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
for some integers
$\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
for some integers
![]() $n_i$
and l. The irreducible characters and the conjugacy classes of this group are both parametrised by
$n_i$
and l. The irreducible characters and the conjugacy classes of this group are both parametrised by
![]() $\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
, where
$\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
, where
![]() $\boldsymbol{\omega} =N_+N_-(n_i)_i$
. Therefore, the characters
$\boldsymbol{\omega} =N_+N_-(n_i)_i$
. Therefore, the characters
![]() $(\varphi _+,\varphi _-,\varphi )$
and the conjugacy class of
$(\varphi _+,\varphi _-,\varphi )$
and the conjugacy class of
![]() $(w_1,\mathbf {w})$
as in Theorem 3.4.7 can be represented by an ordered type. In view of Lemma 3.2.1, if
$(w_1,\mathbf {w})$
as in Theorem 3.4.7 can be represented by an ordered type. In view of Lemma 3.2.1, if
![]() $t\in (T^{\sigma })^{\circ }$
(and
$t\in (T^{\sigma })^{\circ }$
(and
![]() $N_-=0$
if n is even), then the
$N_-=0$
if n is even), then the
![]() $C_G(t\sigma )^{\circ F}$
-conjugacy classes of the F-stable maximal tori of
$C_G(t\sigma )^{\circ F}$
-conjugacy classes of the F-stable maximal tori of
![]() $C_G(t\sigma )^{\circ }$
are also paremetrised by
$C_G(t\sigma )^{\circ }$
are also paremetrised by
![]() $\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
. A semi-simple conjugacy class
$\tilde {\mathfrak {T}}(\boldsymbol{\omega} )$
. A semi-simple conjugacy class
![]() $C\subset G\sigma $
is determined by an N-tuple of elements of
$C\subset G\sigma $
is determined by an N-tuple of elements of ![]() ; thus, we define the type of C to be the element of
; thus, we define the type of C to be the element of
![]() $\mathfrak {T}_s$
encoding the multiplicities of ‘eigenvalues’, with
$\mathfrak {T}_s$
encoding the multiplicities of ‘eigenvalues’, with
![]() $m_+$
being the multiplicity of
$m_+$
being the multiplicity of
![]() $1$
and
$1$
and
![]() $m_-$
that of
$m_-$
that of
![]() $\mathfrak {i}$
.
$\mathfrak {i}$
.
Let
![]() $\chi \in \operatorname {\mathrm {Irr}}(\operatorname {\mathrm {GL}}_n(q))^{\sigma }$
. Then there exists some Levi subgroup M such that
$\chi \in \operatorname {\mathrm {Irr}}(\operatorname {\mathrm {GL}}_n(q))^{\sigma }$
. Then there exists some Levi subgroup M such that
![]() $\chi =\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
as in Theorem 3.4.3. Denote by
$\chi =\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
as in Theorem 3.4.3. Denote by
![]() $\operatorname {\mathrm {Irr}}_{st}^{\sigma }\subset \operatorname {\mathrm {Irr}}(\operatorname {\mathrm {GL}}_n(q))^{\sigma }$
the subset of characters such that M can be chosen to be a standard Levi subgroup. Define a map
$\operatorname {\mathrm {Irr}}_{st}^{\sigma }\subset \operatorname {\mathrm {Irr}}(\operatorname {\mathrm {GL}}_n(q))^{\sigma }$
the subset of characters such that M can be chosen to be a standard Levi subgroup. Define a map
as follows. We first fix a choice of M and a realisation of
![]() $\chi $
as an induction:
$\chi $
as an induction:
![]() $\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
. Let
$\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
. Let
![]() $(\lambda _+,\lambda _-)$
be the 2-partition determined by the quadratic-unipotent part
$(\lambda _+,\lambda _-)$
be the 2-partition determined by the quadratic-unipotent part
![]() $\chi _0$
. The character
$\chi _0$
. The character
![]() $\chi _1$
of
$\chi _1$
of
![]() $M_1^F$
is determined by some
$M_1^F$
is determined by some
![]() $\varphi _1\in \operatorname {\mathrm {Irr}}(W_1)$
, which can be represented by a sequence of partitions
$\varphi _1\in \operatorname {\mathrm {Irr}}(W_1)$
, which can be represented by a sequence of partitions
![]() $\boldsymbol{\lambda} _{\ast }\in \mathfrak {T}_{\ast }$
, since
$\boldsymbol{\lambda} _{\ast }\in \mathfrak {T}_{\ast }$
, since
![]() $W_1$
is a product of symmetric groups. Now
$W_1$
is a product of symmetric groups. Now
![]() $\lambda _+\lambda _-\boldsymbol{\lambda} _{\ast }$
lies in
$\lambda _+\lambda _-\boldsymbol{\lambda} _{\ast }$
lies in
![]() $\mathfrak {T}^{\circ }$
. This is the desired
$\mathfrak {T}^{\circ }$
. This is the desired
![]() $\pi _{\circ }(\chi )$
. Note that
$\pi _{\circ }(\chi )$
. Note that
![]() $\varphi _1$
, in fact, lies in
$\varphi _1$
, in fact, lies in
![]() $\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
, and so the multiplicity of any partition
$\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
, and so the multiplicity of any partition
![]() $\lambda $
in
$\lambda $
in
![]() $\boldsymbol{\lambda} _{\ast }$
is an even number. Define a map
$\boldsymbol{\lambda} _{\ast }$
is an even number. Define a map
Let
![]() $(\epsilon ,\varphi _+,\varphi _-)$
be determined by
$(\epsilon ,\varphi _+,\varphi _-)$
be determined by
![]() $\chi _0$
as in §3.4.6 and let
$\chi _0$
as in §3.4.6 and let
![]() $\varphi \in \operatorname {\mathrm {Irr}}(W_1^{\sigma })$
be the inverse image of
$\varphi \in \operatorname {\mathrm {Irr}}(W_1^{\sigma })$
be the inverse image of
![]() $\varphi _1$
under the bijection (3.4.6.1). Now
$\varphi _1$
under the bijection (3.4.6.1). Now
![]() $(\varphi _+,\varphi _-,\varphi )$
is an irreducible character of
$(\varphi _+,\varphi _-,\varphi )$
is an irreducible character of
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
, and so gives an element
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
, and so gives an element
![]() $\boldsymbol{\omega} \in \mathfrak {T}$
. We then define
$\boldsymbol{\omega} \in \mathfrak {T}$
. We then define
![]() $\pi _{\sigma }(\chi )=\epsilon \boldsymbol{\omega} $
. In §3.4.6, we have described a bijection between the data
$\pi _{\sigma }(\chi )=\epsilon \boldsymbol{\omega} $
. In §3.4.6, we have described a bijection between the data
![]() $(\epsilon ,\varphi _+,\varphi _-)$
and
$(\epsilon ,\varphi _+,\varphi _-)$
and
![]() $\mathcal {P}^2(n_0)$
, and a bijection
$\mathcal {P}^2(n_0)$
, and a bijection
![]() $\{~\}:\operatorname {\mathrm {Irr}}(W^{\sigma }_1)\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
. The map (3.5.1.3) should be thought of as sending
$\{~\}:\operatorname {\mathrm {Irr}}(W^{\sigma }_1)\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\operatorname {\mathrm {Irr}}(W_1)^{\sigma }$
. The map (3.5.1.3) should be thought of as sending
![]() $(\epsilon ,\varphi _+,\varphi _-,\varphi )$
to the character of the Weyl group of
$(\epsilon ,\varphi _+,\varphi _-,\varphi )$
to the character of the Weyl group of
![]() $M_{00}\times M_1$
that underlies
$M_{00}\times M_1$
that underlies
![]() $R^G_M(\chi _1\boxtimes \chi _0)$
. Now we have a commutative diagram
$R^G_M(\chi _1\boxtimes \chi _0)$
. Now we have a commutative diagram

Define
Its elements are called
![]() $\sigma $
-stable characters of type
$\sigma $
-stable characters of type
![]() $\boldsymbol{\lambda} $
and type
$\boldsymbol{\lambda} $
and type
![]() $\epsilon \boldsymbol{\omega} $
, respectively. Note that
$\epsilon \boldsymbol{\omega} $
, respectively. Note that
![]() $\operatorname {\mathrm {Irr}}^{\sigma }_{\boldsymbol{\lambda} }$
is empty unless each partition in
$\operatorname {\mathrm {Irr}}^{\sigma }_{\boldsymbol{\lambda} }$
is empty unless each partition in
![]() $\boldsymbol{\lambda} _{\ast }$
has even multiplicity.
$\boldsymbol{\lambda} _{\ast }$
has even multiplicity.
By definition, all
![]() $\sigma $
-stable characters of the same type can be obtained from a common M as in Theorem 3.4.3, but with different
$\sigma $
-stable characters of the same type can be obtained from a common M as in Theorem 3.4.3, but with different
![]() $\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
. Observe that the quadratic-unipotent part of a character is completely determined by its type. Therefore, we have a surjective map
$\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
. Observe that the quadratic-unipotent part of a character is completely determined by its type. Therefore, we have a surjective map
The cardinality of the fibre of this map is equal to
![]() $2^{l(\boldsymbol{\omega} _{\ast })}N(\boldsymbol{\omega} _{\ast })$
. If we write
$2^{l(\boldsymbol{\omega} _{\ast })}N(\boldsymbol{\omega} _{\ast })$
. If we write
![]() $\theta =(\theta _i)_{1\le i\le l}$
, with
$\theta =(\theta _i)_{1\le i\le l}$
, with
![]() $l=l(\boldsymbol{\omega} _{\ast })$
, then the factor 2 comes from the permutation
$l=l(\boldsymbol{\omega} _{\ast })$
, then the factor 2 comes from the permutation
![]() $\theta _i\leftrightarrow \theta _i^{-1}$
, and the factor
$\theta _i\leftrightarrow \theta _i^{-1}$
, and the factor
![]() $m_{\lambda }!$
of
$m_{\lambda }!$
of
![]() $N(\boldsymbol{\omega} _{\ast })$
comes from the permutation of those
$N(\boldsymbol{\omega} _{\ast })$
comes from the permutation of those
![]() $\theta _i$
corresponding to the same
$\theta _i$
corresponding to the same
![]() $\lambda $
.
$\lambda $
.
We also have an explanation of the map
![]() $[~]$
(3.5.1.4). Recall (§3.4.7) that the group
$[~]$
(3.5.1.4). Recall (§3.4.7) that the group
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
is naturally a subgroup of
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
is naturally a subgroup of
![]() $W_0^{\sigma }\times W_1^{\sigma }$
, which is contained in
$W_0^{\sigma }\times W_1^{\sigma }$
, which is contained in
![]() $W^{\sigma }$
. It is easy to see that
$W^{\sigma }$
. It is easy to see that
![]() $[~]$
is just the map between conjugacy classes induced by the inclusion
$[~]$
is just the map between conjugacy classes induced by the inclusion
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }\rightarrow W^{\sigma }$
. Alternatively, by Lemma 3.2.1, the Weyl group
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }\rightarrow W^{\sigma }$
. Alternatively, by Lemma 3.2.1, the Weyl group
![]() $W'$
of the centraliser of a semi-simple element
$W'$
of the centraliser of a semi-simple element
![]() $C_G(t\sigma )^{\circ }$
is isomorphic to
$C_G(t\sigma )^{\circ }$
is isomorphic to
![]() $\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
for some integers
$\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
for some integers
![]() $n_i$
and l (assuming
$n_i$
and l (assuming
![]() $N_-=0$
if n is even). Corollary 2.5.7 gives an injective map
$N_-=0$
if n is even). Corollary 2.5.7 gives an injective map
![]() $W'\rightarrow W^{\sigma }$
. Again, the map induced between conjugacy classes is just
$W'\rightarrow W^{\sigma }$
. Again, the map induced between conjugacy classes is just
![]() $[~]$
.
$[~]$
.
Finally, the set
![]() $B_{\tau }$
that we introduced in §3.3.3 to compute the Deligne-Lusztig characters has an alternative description in terms of types.
$B_{\tau }$
that we introduced in §3.3.3 to compute the Deligne-Lusztig characters has an alternative description in terms of types.
Lemma 3.5.1. Let
![]() $s\sigma \in T^F\sigma $
be a semi-simple element. Let
$s\sigma \in T^F\sigma $
be a semi-simple element. Let
![]() $W'$
be the Weyl group of
$W'$
be the Weyl group of
![]() $C_G(s\sigma )^{\circ }$
defined by
$C_G(s\sigma )^{\circ }$
defined by
![]() $(T^{\sigma })^{\circ }$
. Suppose that there is an isomorphism
$(T^{\sigma })^{\circ }$
. Suppose that there is an isomorphism
![]() $W'\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
so that its conjugacy classes are parametrised by
$W'\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\mathfrak {W}_{N_+}\times \mathfrak {W}_{N_-}\times \prod _{1\le i\le l}\mathfrak {S}_{n_i}$
so that its conjugacy classes are parametrised by
![]() $\tilde {\mathfrak {T}}(\boldsymbol{\beta} )$
, with
$\tilde {\mathfrak {T}}(\boldsymbol{\beta} )$
, with
![]() $\boldsymbol{\beta} =N_+N_-(n_i)_{1\le i\le l}\in \tilde {\mathfrak {T}}_s$
(and
$\boldsymbol{\beta} =N_+N_-(n_i)_{1\le i\le l}\in \tilde {\mathfrak {T}}_s$
(and
![]() $N_-=0$
if n is even). Let
$N_-=0$
if n is even). Let
![]() $\tau \in W^{\sigma }$
and represent its conjugacy class by a 2-partition
$\tau \in W^{\sigma }$
and represent its conjugacy class by a 2-partition
![]() $\boldsymbol{\tau} $
. Then
$\boldsymbol{\tau} $
. Then
Proof. This is simply unwinding the definitions.
4
 $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-Character varieties
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-Character varieties
In this section, we work over an algebraically closed field ![]() with
with ![]() .
.
4.1 Definition of
 $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties
4.1.1
Let
![]() $p':\tilde {\Sigma }'\rightarrow \Sigma '$
be a branched double covering of compact Riemann surfaces and let
$p':\tilde {\Sigma }'\rightarrow \Sigma '$
be a branched double covering of compact Riemann surfaces and let
![]() $\mathcal {R}\subset \Sigma '$
be the ramification locus. Put
$\mathcal {R}\subset \Sigma '$
be the ramification locus. Put
![]() $\Sigma =\Sigma '\setminus \mathcal {R}$
and
$\Sigma =\Sigma '\setminus \mathcal {R}$
and
![]() $\tilde {\Sigma }=\tilde {\Sigma }'\setminus p^{\prime -1}(\mathcal {R})$
and denote by
$\tilde {\Sigma }=\tilde {\Sigma }'\setminus p^{\prime -1}(\mathcal {R})$
and denote by
![]() $p:\tilde {\Sigma }\rightarrow \Sigma $
the restriction of
$p:\tilde {\Sigma }\rightarrow \Sigma $
the restriction of
![]() $p'$
. Fix a base point
$p'$
. Fix a base point
![]() $x\in \Sigma $
and let
$x\in \Sigma $
and let
![]() $\tilde {x}\in p^{-1}(x)$
be the base point of
$\tilde {x}\in p^{-1}(x)$
be the base point of
![]() $\tilde {\Sigma }$
. We will write
$\tilde {\Sigma }$
. We will write
![]() $\pi _1(\Sigma )=\pi _1(\Sigma ,x)$
and
$\pi _1(\Sigma )=\pi _1(\Sigma ,x)$
and
![]() $\pi _1(\tilde {\Sigma })=\pi _1(\tilde {\Sigma },\tilde {x} )$
. The representation variety
$\pi _1(\tilde {\Sigma })=\pi _1(\tilde {\Sigma },\tilde {x} )$
. The representation variety
![]() $\operatorname {\mathrm {Rep}}(\Sigma )$
is defined as the space of homomorphisms
$\operatorname {\mathrm {Rep}}(\Sigma )$
is defined as the space of homomorphisms
![]() $\rho $
that make the following diagram commute:
$\rho $
that make the following diagram commute:

where
![]() $q_1$
is the quotient by
$q_1$
is the quotient by
![]() $\pi _1(\tilde {\Sigma })$
and
$\pi _1(\tilde {\Sigma })$
and
![]() $q_2$
is the quotient by the identity component G. The character variety
$q_2$
is the quotient by the identity component G. The character variety
![]() $\operatorname {\mathrm {Ch}}(\Sigma )$
is defined as the categorical quotient of
$\operatorname {\mathrm {Ch}}(\Sigma )$
is defined as the categorical quotient of
![]() $\operatorname {\mathrm {Rep}}(\Sigma )$
for the conjugation action of G on
$\operatorname {\mathrm {Rep}}(\Sigma )$
for the conjugation action of G on
![]() $G\!<\!\sigma \!>\!$
. This is the
$G\!<\!\sigma \!>\!$
. This is the
![]() $G\!<\!\sigma {>}$
-character variety.
$G\!<\!\sigma {>}$
-character variety.
4.1.2
Denote by g the genus of
![]() $\Sigma '$
. By Riemann-Hurwitz formula, there is an even number of branch points. Let
$\Sigma '$
. By Riemann-Hurwitz formula, there is an even number of branch points. Let
![]() $2k=|\mathcal {R}|$
be the cardinality and write
$2k=|\mathcal {R}|$
be the cardinality and write
![]() $\mathcal {R}=\{x_j\}_{1\le j\le 2k}$
. We may choose the generators
$\mathcal {R}=\{x_j\}_{1\le j\le 2k}$
. We may choose the generators
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
,
$\beta _i$
,
![]() $1\le i\le g$
, and
$1\le i\le g$
, and
![]() $\gamma _j$
,
$\gamma _j$
,
![]() $1\le j\le 2k$
, of
$1\le j\le 2k$
, of
![]() $\pi _1(X)$
that satisfy the relation
$\pi _1(X)$
that satisfy the relation
 $$ \begin{align} \prod_{i=1}^g[\alpha_i,\beta_i]\prod_{j=1}^{2k}\gamma_j=1. \end{align} $$
$$ \begin{align} \prod_{i=1}^g[\alpha_i,\beta_i]\prod_{j=1}^{2k}\gamma_j=1. \end{align} $$
The generators
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
,
$\beta _i$
,
![]() $1\le i\le g$
, are the images of some elements of
$1\le i\le g$
, are the images of some elements of
![]() $\pi _1(\tilde {\Sigma })$
, while
$\pi _1(\tilde {\Sigma })$
, while
![]() $\gamma _j$
,
$\gamma _j$
,
![]() $1\le j\le 2k$
, being small loops around the
$1\le j\le 2k$
, being small loops around the
![]() $x_j$
’s, lie in
$x_j$
’s, lie in
![]() $\pi _1(\Sigma )\setminus \pi _1(\tilde {\Sigma })$
. Let
$\pi _1(\Sigma )\setminus \pi _1(\tilde {\Sigma })$
. Let
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a tuple of semi-simple G-conjugacy classes contained in the connected component
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
be a tuple of semi-simple G-conjugacy classes contained in the connected component
![]() $G\sigma $
. We define the subvariety
$G\sigma $
. We define the subvariety
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}}(\Sigma )\subset \operatorname {\mathrm {Rep}}(\Sigma )$
as consisting of
$\operatorname {\mathrm {Rep}}_{\mathcal {C}}(\Sigma )\subset \operatorname {\mathrm {Rep}}(\Sigma )$
as consisting of
![]() $\rho \in \operatorname {\mathrm {Rep}}(\Sigma )$
such that
$\rho \in \operatorname {\mathrm {Rep}}(\Sigma )$
such that
![]() $\rho (\gamma _j)\in C_j$
for all j. Then we define
$\rho (\gamma _j)\in C_j$
for all j. Then we define
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}(\Sigma ):=\operatorname {\mathrm {Rep}}_{\mathcal {C}}(\Sigma )\!/\mkern -2mu/\mkern -2mu G$
. The representation variety has the following presentation:
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}(\Sigma ):=\operatorname {\mathrm {Rep}}_{\mathcal {C}}(\Sigma )\!/\mkern -2mu/\mkern -2mu G$
. The representation variety has the following presentation:
 $$ \begin{align} \operatorname{\mathrm{Rep}}_{\mathcal{C}}(\Sigma)=\{(A_i,B_i)_i(X_j)_j\in G^{2g}\times \prod_{j=1}^{2k} C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Rep}}_{\mathcal{C}}(\Sigma)=\{(A_i,B_i)_i(X_j)_j\in G^{2g}\times \prod_{j=1}^{2k} C_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\}. \end{align} $$
4.1.3
There is a bijection between the semi-simple conjugacy classes in ![]() and those in
and those in ![]() , sending the class of
, sending the class of
![]() $t\sigma $
to that of
$t\sigma $
to that of
![]() $t\sigma $
, with the
$t\sigma $
, with the
![]() $\sigma $
in
$\sigma $
in ![]() interpreted in the appropriate sense. If
interpreted in the appropriate sense. If
![]() $\mathcal {C}$
is a tuple of semi-simple conjugacy classes in
$\mathcal {C}$
is a tuple of semi-simple conjugacy classes in ![]() , then we define a tuple
, then we define a tuple
![]() $\mathcal {C}^{\ast }$
of conjugacy classes in
$\mathcal {C}^{\ast }$
of conjugacy classes in ![]() by applying this bijection componentwise.
by applying this bijection componentwise.
It is not difficult to see that the ![]() -character variety
-character variety
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is isomorphic to the
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is isomorphic to the ![]() -character variety
-character variety
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}^{\ast }}$
. Therefore, if n is even, we may, and will, only work with
$\operatorname {\mathrm {Ch}}_{\mathcal {C}^{\ast }}$
. Therefore, if n is even, we may, and will, only work with ![]() -character varieties.
-character varieties.
4.2 Generic conjugacy classes
4.2.1
Let
![]() $\mathcal {C}=(C_j)_{j}$
be a
$\mathcal {C}=(C_j)_{j}$
be a
![]() $2k$
-tuple of semi-simple conjugacy classes contained in
$2k$
-tuple of semi-simple conjugacy classes contained in
![]() $G\sigma $
. According to §3.1.3, each class
$G\sigma $
. According to §3.1.3, each class
![]() $C_j$
has a representative
$C_j$
has a representative
![]() $t_j\sigma \in (T^{\sigma })^{\circ }\sigma $
. The following definition is a special case of [Reference ShuShu23, Definition 3.3], as is explained in [Reference ShuShu23, §4.4].
$t_j\sigma \in (T^{\sigma })^{\circ }\sigma $
. The following definition is a special case of [Reference ShuShu23, Definition 3.3], as is explained in [Reference ShuShu23, §4.4].
Each
![]() $t_j$
is given by an N-tuple
$t_j$
is given by an N-tuple
![]() $(a_{j,1},\ldots ,a_{j,N})$
with each
$(a_{j,1},\ldots ,a_{j,N})$
with each ![]() . Write
. Write
![]() $\Lambda =\{1,\ldots ,N\}$
. For any j, any subset
$\Lambda =\{1,\ldots ,N\}$
. For any j, any subset
![]() $\mathbf {A}\subset \Lambda $
and any
$\mathbf {A}\subset \Lambda $
and any
![]() $|\mathbf {A}|$
-tuple of signs
$|\mathbf {A}|$
-tuple of signs
![]() $\smash {\mathbf {e}=(e_{\gamma })_{\gamma \in \mathbf {A}}}$
,
$\smash {\mathbf {e}=(e_{\gamma })_{\gamma \in \mathbf {A}}}$
,
![]() $e_{\gamma }\in \{\pm 1\}$
, write
$e_{\gamma }\in \{\pm 1\}$
, write
![]() $\smash {[\mathbf {A},\mathbf {e}]_j=\prod _{\gamma \in \mathbf {A}}a_{j,\gamma }^{2e_{\gamma }}}$
. We say that
$\smash {[\mathbf {A},\mathbf {e}]_j=\prod _{\gamma \in \mathbf {A}}a_{j,\gamma }^{2e_{\gamma }}}$
. We say that
![]() $\mathcal {C}$
is generic if for any
$\mathcal {C}$
is generic if for any
![]() $1\le N' \le N$
, any
$1\le N' \le N$
, any
![]() $2k$
-tuple
$2k$
-tuple
![]() $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
of subsets of
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
of subsets of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
, and any
$|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
, and any
![]() $2k$
-tuple of
$2k$
-tuple of
![]() $N'$
-tuples
$N'$
-tuples
![]() $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
of signs, we have
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
of signs, we have
We say that
![]() $\mathcal {C}$
is strongly generic if for any
$\mathcal {C}$
is strongly generic if for any
![]() $N'$
,
$N'$
,
![]() $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
, and
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
, and
![]() $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
as above, we have
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
as above, we have
4.2.2
Generic conjugacy classes in the finite group
![]() $G(q)\!<\!\sigma \!>\!$
can be defined in the same way, but only for some particular conjugacy classes.
$G(q)\!<\!\sigma \!>\!$
can be defined in the same way, but only for some particular conjugacy classes.
Let
![]() $\mathcal {C}=(C_j)_{j}$
be a
$\mathcal {C}=(C_j)_{j}$
be a
![]() $2k$
-tuple of semi-simple
$2k$
-tuple of semi-simple
![]() $G(q)$
-conjugacy classes contained in
$G(q)$
-conjugacy classes contained in
![]() $G(q)\sigma $
. Assume that for each
$G(q)\sigma $
. Assume that for each
![]() $1\le j\le 2k$
, the G-conjugacy class containing
$1\le j\le 2k$
, the G-conjugacy class containing
![]() $C_j$
has a representative
$C_j$
has a representative
![]() $t_j\sigma \in (T^{\sigma })^{\circ F}\sigma $
; that is,
$t_j\sigma \in (T^{\sigma })^{\circ F}\sigma $
; that is,
![]() $t_j$
is determined by an N-tuple
$t_j$
is determined by an N-tuple
![]() $(a_{j,1},\ldots ,a_{j,N})$
with each
$(a_{j,1},\ldots ,a_{j,N})$
with each
![]() $a_{j,\gamma }\in \mathbb {F}_q^{\ast }$
. Note that we do not require
$a_{j,\gamma }\in \mathbb {F}_q^{\ast }$
. Note that we do not require
![]() $C_j$
itself to have a representative of this form. As is explained in §3.2.1, this is a very restrictive condition on the conjugacy classes. Generic condition can be defined only for these conjugacy classes.
$C_j$
itself to have a representative of this form. As is explained in §3.2.1, this is a very restrictive condition on the conjugacy classes. Generic condition can be defined only for these conjugacy classes.
With the same notations as in the previous paragraph, we say that
![]() $\mathcal {C}$
is generic (resp. strongly generic) if for any
$\mathcal {C}$
is generic (resp. strongly generic) if for any
![]() $1\le N' \le N$
,
$1\le N' \le N$
,
![]() $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
, and
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
, and
![]() $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
, we have
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
, we have
Lemma 4.2.1. Let
![]() $(C_j)_{1\le j\le 2k}$
be a generic tuple of semi-simple conjugacy classes contained in
$(C_j)_{1\le j\le 2k}$
be a generic tuple of semi-simple conjugacy classes contained in
![]() $G\sigma $
, with each
$G\sigma $
, with each
![]() $C_j$
given by an N-tuple
$C_j$
given by an N-tuple
![]() $(a_{j,1},\ldots ,a_{j,N})$
as in §3.1.3. Let
$(a_{j,1},\ldots ,a_{j,N})$
as in §3.1.3. Let
![]() $N'$
,
$N'$
,
![]() $N"\in \{1,\ldots ,N\}$
. Let
$N"\in \{1,\ldots ,N\}$
. Let
![]() $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
and
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
and
![]() $(\mathbf {A}^{\prime }_1,\ldots ,\mathbf {A}^{\prime }_{2k})$
be two
$(\mathbf {A}^{\prime }_1,\ldots ,\mathbf {A}^{\prime }_{2k})$
be two
![]() $2k$
-tuples of subsets of
$2k$
-tuples of subsets of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
,
$|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
,
![]() $|\mathbf {A}^{\prime }_1|=\cdots =|\mathbf {A}^{\prime }_{2k}|=N"$
and for any
$|\mathbf {A}^{\prime }_1|=\cdots =|\mathbf {A}^{\prime }_{2k}|=N"$
and for any
![]() $1\le j\le 2k$
,
$1\le j\le 2k$
,
![]() $\mathbf {A}_j\cap \mathbf {A}^{\prime }_j=\emptyset $
. Let
$\mathbf {A}_j\cap \mathbf {A}^{\prime }_j=\emptyset $
. Let
![]() $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
(resp.
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
(resp.
![]() $(\mathbf {e}^{\prime 1},\ldots ,\mathbf {e}^{\prime 2k})$
) be a
$(\mathbf {e}^{\prime 1},\ldots ,\mathbf {e}^{\prime 2k})$
) be a
![]() $2k$
-tuple of
$2k$
-tuple of
![]() $N'$
-tuples (resp.
$N'$
-tuples (resp.
![]() $N"$
-tuples) of signs. Then
$N"$
-tuples) of signs. Then
Proof. Suppose
with
![]() $\epsilon =\pm 1$
. For each j, put
$\epsilon =\pm 1$
. For each j, put
![]() $\tilde {\mathbf {A}}_j=\mathbf {A}_j\sqcup \mathbf {A}^{\prime }_j$
. For each j, define a
$\tilde {\mathbf {A}}_j=\mathbf {A}_j\sqcup \mathbf {A}^{\prime }_j$
. For each j, define a
![]() $(N'+N")$
-tuple of signs
$(N'+N")$
-tuple of signs
![]() $\tilde {\mathbf {e}}^j$
by
$\tilde {\mathbf {e}}^j$
by
![]() $\tilde {e}^j_{\gamma }=e^j_{\gamma }$
if
$\tilde {e}^j_{\gamma }=e^j_{\gamma }$
if
![]() $\gamma \in \mathbf {A}_j$
, and
$\gamma \in \mathbf {A}_j$
, and
![]() $\tilde {e}^j_{\gamma }=-\epsilon e^{\prime j}_{\gamma }$
if
$\tilde {e}^j_{\gamma }=-\epsilon e^{\prime j}_{\gamma }$
if
![]() $\gamma \in \mathbf {A}^{\prime }_j$
. Then
$\gamma \in \mathbf {A}^{\prime }_j$
. Then
which is a contradiction.
4.2.3
Here we introduce another constraint on the tuple
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
of semi-simple conjugacy classes.
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
of semi-simple conjugacy classes.
-
(CCL). We say that a semi-simple conjugacy class
 $C\subset G\sigma $
satisfies (CCL) if it has no ‘eigenvalue’ equal to
$C\subset G\sigma $
satisfies (CCL) if it has no ‘eigenvalue’ equal to
 $\pm \mathfrak {i}$
. We say that
$\pm \mathfrak {i}$
. We say that
 $\mathcal {C}$
satisfies (CCL) if
$\mathcal {C}$
satisfies (CCL) if
 $C_j$
satisfies (CCL) for all j.
$C_j$
satisfies (CCL) for all j.
In view of Lemma 3.2.1, that a semi-simple conjugacy class in
![]() $G\sigma $
satisfies (CCL) essentially means that it has a representative
$G\sigma $
satisfies (CCL) essentially means that it has a representative
![]() $t\sigma \in (T^{\sigma })^{\circ }\sigma $
such that
$t\sigma \in (T^{\sigma })^{\circ }\sigma $
such that
![]() $C_{G}(t\sigma )^{\circ }$
is a Levi subgroup of
$C_{G}(t\sigma )^{\circ }$
is a Levi subgroup of
![]() $C_{G}(\sigma )^{\circ }$
. The exceptional case is when the multiplicity of
$C_{G}(\sigma )^{\circ }$
. The exceptional case is when the multiplicity of
![]() $\mathfrak {i}$
among the ‘eigenvalues’ is equal to one, and n is even, since
$\mathfrak {i}$
among the ‘eigenvalues’ is equal to one, and n is even, since
![]() $\operatorname {\mathrm {SO}}_2\cong \mathbb {G}_m$
.
$\operatorname {\mathrm {SO}}_2\cong \mathbb {G}_m$
.
Our main results in §7 will assume the (CCL) property.
4.3 The R-model
It is a general fact that
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is defined over a finite-type subring of
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is defined over a finite-type subring of
![]() $\mathbb {C}$
. But we want to be specific about the base ring so that when passing to finite fields, the conjugacy classes remain generic.
$\mathbb {C}$
. But we want to be specific about the base ring so that when passing to finite fields, the conjugacy classes remain generic.
4.3.1
The conjugacy classes
![]() $(C_j)_j$
are represented by some N-tuples of complex numbers (cf. §3.1.3)
$(C_j)_j$
are represented by some N-tuples of complex numbers (cf. §3.1.3)
satisfying
-
(i)
 $a^j_r\notin \{a^j_s,(a^j_s)^{-1},-a^j_s,-(a^j_s)^{-1}\}$
for any j and any
$a^j_r\notin \{a^j_s,(a^j_s)^{-1},-a^j_s,-(a^j_s)^{-1}\}$
for any j and any
 $r\ne s$
;
$r\ne s$
; -
(ii)
 $(a^j_r)^4\ne 1$
for any j and r;
$(a^j_r)^4\ne 1$
for any j and r; -
(iii)
 $[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}^{2k},\mathbf {e}^{2k}]_{2k}\ne 1$
, for any integers
$[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}^{2k},\mathbf {e}^{2k}]_{2k}\ne 1$
, for any integers
 $N'$
with
$N'$
with
 $1\le N'\le N$
, any
$1\le N'\le N$
, any
 $2k$
-tuple of subsets
$2k$
-tuple of subsets
 $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
of
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
of
 $\{1,\ldots ,N\}$
, such that
$\{1,\ldots ,N\}$
, such that
 $|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
, and any
$|\mathbf {A}_1|=\cdots =|\mathbf {A}_{2k}|=N'$
, and any
 $2k$
-tuple of
$2k$
-tuple of
 $N'$
-tuples of signs
$N'$
-tuples of signs
 $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
(cf. §4.2.1).
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
(cf. §4.2.1).
Denote by
![]() $R_0$
the subring of
$R_0$
the subring of
![]() $\mathbb {C}$
generated by
$\mathbb {C}$
generated by
![]() $\{(a^j_r)^{\pm 1}\mid \text {all }r,j\}$
and
$\{(a^j_r)^{\pm 1}\mid \text {all }r,j\}$
and
![]() $\mathfrak {i}$
if any
$\mathfrak {i}$
if any
![]() $\mathbf {E}^j$
contains
$\mathbf {E}^j$
contains
![]() $\mathfrak {i}$
. Let
$\mathfrak {i}$
. Let
![]() $S\subset R_0$
be the multiplicative subset generated by
$S\subset R_0$
be the multiplicative subset generated by
-
(i)
 $(a^j_{r})^2-(a^j_{s})^2$
and
$(a^j_{r})^2-(a^j_{s})^2$
and
 $(a^j_{r})^2-(a^j_{s})^{-2}$
for any j and
$(a^j_{r})^2-(a^j_{s})^{-2}$
for any j and
 $r\ne s$
;
$r\ne s$
; -
(ii)
 $(a^j_{r})^4-1$
for any j and r;
$(a^j_{r})^4-1$
for any j and r; -
(iii)
 $[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}^{2k},\mathbf {e}^{2k}]_{2k}-1$
, for any
$[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}^{2k},\mathbf {e}^{2k}]_{2k}-1$
, for any
 $N'$
,
$N'$
,
 $(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
and
$(\mathbf {A}_1,\ldots ,\mathbf {A}_{2k})$
and
 $(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
as above.
$(\mathbf {e}^1,\ldots ,\mathbf {e}^{2k})$
as above.
Define the ring of generic eigenvalues as
![]() $R:=S^{-1}R_0$
. We will see below that the character variety is defined over R.
$R:=S^{-1}R_0$
. We will see below that the character variety is defined over R.
Let
![]() $\boldsymbol{\mu} ^j=m^j_+m^j_-(m^j_r)\in \mathfrak {T}_s$
be the type of
$\boldsymbol{\mu} ^j=m^j_+m^j_-(m^j_r)\in \mathfrak {T}_s$
be the type of
![]() $C_j$
, so that
$C_j$
, so that
![]() $l_j=l(\boldsymbol{\mu} _{\ast }^j)$
. Write
$l_j=l(\boldsymbol{\mu} _{\ast }^j)$
. Write
![]() $n^j_-=2m^j_-$
and write
$n^j_-=2m^j_-$
and write
![]() $n^j_+=2m^j_+$
or
$n^j_+=2m^j_+$
or
![]() $n^j_+=2m^j_++1$
according to the parity of n.
$n^j_+=2m^j_++1$
according to the parity of n.
4.3.2
Let
![]() $\mathcal {A}^{\prime }_0$
be the polynomial ring over R with
$\mathcal {A}^{\prime }_0$
be the polynomial ring over R with
![]() $n^2(2g+2k)$
indeterminates. These indeterminates should be thought of as the entries of some
$n^2(2g+2k)$
indeterminates. These indeterminates should be thought of as the entries of some
![]() $n\times n$
matrices
$n\times n$
matrices
![]() $A_1,B_1,\ldots A_g,B_g,X_1,\ldots X_{2k}$
. Let
$A_1,B_1,\ldots A_g,B_g,X_1,\ldots X_{2k}$
. Let
![]() $\mathcal {A}_0$
be the localisation of
$\mathcal {A}_0$
be the localisation of
![]() $\mathcal {A}^{\prime }_0$
at the determinants
$\mathcal {A}^{\prime }_0$
at the determinants
![]() $\det A_i$
,
$\det A_i$
,
![]() $\det B_i$
,
$\det B_i$
,
![]() $\det X_j$
,
$\det X_j$
,
![]() $1\le i\le g$
,
$1\le i\le g$
,
![]() $1\le j\le 2k$
. Let
$1\le j\le 2k$
. Let
![]() $I_0\subset \mathcal {A}_0$
be the ideal generated by
$I_0\subset \mathcal {A}_0$
be the ideal generated by
-
(i) The entries of
 $[A_1,B_1]\cdots [A_g,B_g]X_1\sigma \cdots X_{2k}\sigma -\operatorname {\mathrm {Id}}$
(note that
$[A_1,B_1]\cdots [A_g,B_g]X_1\sigma \cdots X_{2k}\sigma -\operatorname {\mathrm {Id}}$
(note that
 $X_1\sigma X_2\sigma =X_1\sigma (X_2)$
and
$X_1\sigma X_2\sigma =X_1\sigma (X_2)$
and
 $\sigma $
is defined over
$\sigma $
is defined over
 $\mathbb {Z}$
);
$\mathbb {Z}$
); -
(ii) For all
 $1\le j\le 2k$
, the entries of (4.3.2.1)
$1\le j\le 2k$
, the entries of (4.3.2.1) $$ \begin{align} ((X_j\sigma(X_j))^2-\operatorname{\mathrm{Id}})\prod_{r=1}^{l_j}(X_j\sigma(X_j)-(a^j_r)^2\operatorname{\mathrm{Id}})(X_j\sigma(X_j)-(a_r^j)^{-2}\operatorname{\mathrm{Id}}); \end{align} $$
$$ \begin{align} ((X_j\sigma(X_j))^2-\operatorname{\mathrm{Id}})\prod_{r=1}^{l_j}(X_j\sigma(X_j)-(a^j_r)^2\operatorname{\mathrm{Id}})(X_j\sigma(X_j)-(a_r^j)^{-2}\operatorname{\mathrm{Id}}); \end{align} $$
-
(iii) For all
 $1\le j\le 2k$
, the entries of the coefficients of the following polynomial in an auxiliary variable t: (4.3.2.2)
$1\le j\le 2k$
, the entries of the coefficients of the following polynomial in an auxiliary variable t: (4.3.2.2) $$ \begin{align} \det(t\operatorname{\mathrm{Id}}-X_j\sigma(X_j))-(t-1)^{n^j_+}(t+1)^{n^j_-}\prod_r^{l_j}(t-(a^j_r)^2)^{m^j_r}\prod_r^{l_j}(t-(a^j_r)^{-2})^{m^j_r}. \end{align} $$
$$ \begin{align} \det(t\operatorname{\mathrm{Id}}-X_j\sigma(X_j))-(t-1)^{n^j_+}(t+1)^{n^j_-}\prod_r^{l_j}(t-(a^j_r)^2)^{m^j_r}\prod_r^{l_j}(t-(a^j_r)^{-2})^{m^j_r}. \end{align} $$
Define
![]() $\mathcal {A}:=\mathcal {A}_0/\sqrt {I_0}$
. By Lemma 3.1.1, the relations (ii) and (iii) guarantee that the base change to
$\mathcal {A}:=\mathcal {A}_0/\sqrt {I_0}$
. By Lemma 3.1.1, the relations (ii) and (iii) guarantee that the base change to
![]() $\mathbb {C}$
recovers the complex representation variety with the correct conjugacy classes. Then
$\mathbb {C}$
recovers the complex representation variety with the correct conjugacy classes. Then
![]() $\mathbf {Rep}_{\mathcal {C}}:=\operatorname {\mathrm {Spec}}\mathcal {A}$
is the R-model of
$\mathbf {Rep}_{\mathcal {C}}:=\operatorname {\mathrm {Spec}}\mathcal {A}$
is the R-model of
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
. Let G act on
$\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
. Let G act on
![]() $A_i$
and
$A_i$
and
![]() $B_i$
,
$B_i$
,
![]() $1\le i\le g$
, by conjugation, and act on
$1\le i\le g$
, by conjugation, and act on
![]() $X_j$
,
$X_j$
,
![]() $1\le j\le 2k$
, by the
$1\le j\le 2k$
, by the
![]() $\sigma $
-twisted conjugation. Then
$\sigma $
-twisted conjugation. Then
![]() $\mathbf {Ch}_{\mathcal {C}}:=\operatorname {\mathrm {Spec}}\mathcal {A}^{G(R)}$
is the R-model of
$\mathbf {Ch}_{\mathcal {C}}:=\operatorname {\mathrm {Spec}}\mathcal {A}^{G(R)}$
is the R-model of
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
, since taking invariants commutes with flat base change ([Reference SeshadriSes77, §I.2 Lemma 2]).
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
, since taking invariants commutes with flat base change ([Reference SeshadriSes77, §I.2 Lemma 2]).
4.3.3
Let
![]() $\phi :R\rightarrow \mathbb {F}_q$
be any ring homomorphism and let
$\phi :R\rightarrow \mathbb {F}_q$
be any ring homomorphism and let
![]() $\bar {\phi }:R\rightarrow \bar {\mathbb {F}}_q$
be its composition with
$\bar {\phi }:R\rightarrow \bar {\mathbb {F}}_q$
be its composition with
![]() $\mathbb {F}_q\hookrightarrow \bar {\mathbb {F}}_q$
. Regard
$\mathbb {F}_q\hookrightarrow \bar {\mathbb {F}}_q$
. Regard
![]() $G=\operatorname {\mathrm {GL}}_n$
as an algebraic group over
$G=\operatorname {\mathrm {GL}}_n$
as an algebraic group over
![]() $\bar {\mathbb {F}}_q$
. For each
$\bar {\mathbb {F}}_q$
. For each
![]() $1\le j\le 2k$
, denote by
$1\le j\le 2k$
, denote by
![]() $C_j^{\phi }$
the subvariety of G over
$C_j^{\phi }$
the subvariety of G over
![]() $\mathbb {F}_q$
defined by §4.3.2 (ii), (iii). Similarly, denote by
$\mathbb {F}_q$
defined by §4.3.2 (ii), (iii). Similarly, denote by
![]() $C_j^{\bar {\phi }}$
the subvariety of G over
$C_j^{\bar {\phi }}$
the subvariety of G over
![]() $\bar {\mathbb {F}}_q$
. We may regard
$\bar {\mathbb {F}}_q$
. We may regard
![]() $C_j^{\bar {\phi }}$
as a semi-simple conjugacy class contained in
$C_j^{\bar {\phi }}$
as a semi-simple conjugacy class contained in
![]() $G\sigma $
. We have
$G\sigma $
. We have
![]() $C_j^{\phi }\otimes _{\mathbb {F}_q}\bar {\mathbb {F}}_q \cong C_j^{\bar {\phi }}$
. Each class
$C_j^{\phi }\otimes _{\mathbb {F}_q}\bar {\mathbb {F}}_q \cong C_j^{\bar {\phi }}$
. Each class
![]() $C_j^{\bar {\phi }}$
has the same type as the original complex conjugacy class and has ‘eigenvalues’ (cf. §3.1.3)
$C_j^{\bar {\phi }}$
has the same type as the original complex conjugacy class and has ‘eigenvalues’ (cf. §3.1.3)
![]() $\phi (a^j_i)$
(resp.
$\phi (a^j_i)$
(resp.
![]() $1$
, resp.
$1$
, resp.
![]() $\phi (\mathfrak {i})$
) of multiplicity
$\phi (\mathfrak {i})$
) of multiplicity
![]() $\mu ^j_i$
(resp
$\mu ^j_i$
(resp
![]() $\mu ^j_+$
, resp.
$\mu ^j_+$
, resp.
![]() $\mu ^j_-$
) in the corresponding conjugacy class. In particular,
$\mu ^j_-$
) in the corresponding conjugacy class. In particular,
![]() $C_j^{\bar {\phi }}$
has a representative in
$C_j^{\bar {\phi }}$
has a representative in
![]() $(T^{\sigma })^{\circ F}\sigma $
. Denote by
$(T^{\sigma })^{\circ F}\sigma $
. Denote by
![]() $\operatorname {\mathrm {Rep}}^{\phi }_{\mathcal {C}}$
and
$\operatorname {\mathrm {Rep}}^{\phi }_{\mathcal {C}}$
and
![]() $\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}$
the varieties over
$\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}$
the varieties over
![]() $\mathbb {F}_q$
and
$\mathbb {F}_q$
and
![]() $\bar {\mathbb {F}}_q$
, respectively, obtained by base change from
$\bar {\mathbb {F}}_q$
, respectively, obtained by base change from
![]() $\mathbf {Rep}_{\mathcal {C}}$
– and similarly for
$\mathbf {Rep}_{\mathcal {C}}$
– and similarly for
![]() $\mathbf {Ch}_{\mathcal {C}}$
. The variety
$\mathbf {Ch}_{\mathcal {C}}$
. The variety
![]() $\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}$
is defined by the same equation as (4.1.2.2), but over
$\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}$
is defined by the same equation as (4.1.2.2), but over
![]() $\bar {\mathbb {F}}_q$
. Then
$\bar {\mathbb {F}}_q$
. Then
![]() $\operatorname {\mathrm {Rep}}^{\phi }_{\mathcal {C}}(\mathbb {F}_q)$
can be identified with
$\operatorname {\mathrm {Rep}}^{\phi }_{\mathcal {C}}(\mathbb {F}_q)$
can be identified with
![]() $\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}(\bar {\mathbb {F}}_q)^F$
:
$\operatorname {\mathrm {Rep}}^{\bar {\phi }}_{\mathcal {C}}(\bar {\mathbb {F}}_q)^F$
:
 $$ \begin{align} \operatorname{\mathrm{Rep}}^{\phi}_{\mathcal{C}}(\mathbb{F}_q)=\{(A_i,B_i)(X_j)\in G(q)^{2g}\times \prod^{2k}_{j=1} C_j^{\phi}(\mathbb{F}_q)\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Rep}}^{\phi}_{\mathcal{C}}(\mathbb{F}_q)=\{(A_i,B_i)(X_j)\in G(q)^{2g}\times \prod^{2k}_{j=1} C_j^{\phi}(\mathbb{F}_q)\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X_j=1\}, \end{align} $$
where
![]() $C_j^{\phi }(\mathbb {F}_q)=C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F$
is considered as contained in
$C_j^{\phi }(\mathbb {F}_q)=C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F$
is considered as contained in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
.
$\operatorname {\mathrm {GL}}_n\sigma $
.
Notation 4.3.1. For each j, choose
![]() $s_j\in C_j$
and define
$s_j\in C_j$
and define
Different choices of the
![]() $s_j$
’s give isomorphic
$s_j$
’s give isomorphic
![]() $\mathbf {A}(\mathcal {C})$
. Its direct factors are either the trivial group or the 2-element group
$\mathbf {A}(\mathcal {C})$
. Its direct factors are either the trivial group or the 2-element group
![]() $\boldsymbol{\mu} _2$
.
$\boldsymbol{\mu} _2$
.
Notation 4.3.2. Recall §3.2.1 that
![]() $\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F}$
is, in general, not a single
$\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F}$
is, in general, not a single
![]() $G(q)$
-conjugacy classes. Denote by
$G(q)$
-conjugacy classes. Denote by
![]() $C_{j,+}$
the
$C_{j,+}$
the
![]() $G(q)$
-conjugacy class contained in
$G(q)$
-conjugacy class contained in
![]() $\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)}$
which has a representative in
$\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)}$
which has a representative in
![]() $(T^{\sigma })^{\circ F}$
and by
$(T^{\sigma })^{\circ F}$
and by
![]() $C_{j,-}$
the other class if
$C_{j,-}$
the other class if
![]() $\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F}$
is not a single
$\smash {C_j^{\bar \phi }(\bar {\mathbb {F}}_q)^F}$
is not a single
![]() $G(q)$
-conjugacy class. For a given
$G(q)$
-conjugacy class. For a given
![]() $2k$
-tuple
$2k$
-tuple
![]() $\mathcal {C}^{\bar \phi }=(C_j^{\bar \phi })$
of semi-simple conjugacy classes in
$\mathcal {C}^{\bar \phi }=(C_j^{\bar \phi })$
of semi-simple conjugacy classes in
![]() $G\sigma $
and any
$G\sigma $
and any
![]() $\mathbf {e}=(e_j)\in \mathbf {A}(\mathcal {C})$
, we will denote by
$\mathbf {e}=(e_j)\in \mathbf {A}(\mathcal {C})$
, we will denote by
![]() $\mathcal {C}_{\mathbf {e}}=(C_{j,e_j})$
the
$\mathcal {C}_{\mathbf {e}}=(C_{j,e_j})$
the
![]() $2k$
-tuple of
$2k$
-tuple of
![]() $G(q)$
-conjugacy classes contained in
$G(q)$
-conjugacy classes contained in
![]() $\mathcal {C}^{\bar \phi }$
. If
$\mathcal {C}^{\bar \phi }$
. If
![]() $\mathscr {C}$
is a tuple of conjugacy classes of the form
$\mathscr {C}$
is a tuple of conjugacy classes of the form
![]() $\mathcal {C}_{\mathbf {e}}$
, we define
$\mathcal {C}_{\mathbf {e}}$
, we define
![]() $\operatorname {\mathrm {sgn}}\mathscr {C}=\prod _je_j$
.
$\operatorname {\mathrm {sgn}}\mathscr {C}=\prod _je_j$
.
In the following Proposition, we fix the generic tuple of conjugacy classes and omit the subscript
![]() $\mathcal {C}$
. By the definition of the base ring R, the tuple
$\mathcal {C}$
. By the definition of the base ring R, the tuple
![]() $\mathcal {C}^{\bar {\phi }}$
is also generic.
$\mathcal {C}^{\bar {\phi }}$
is also generic.
Proposition 4.3.3. We have the following formula:
Proof. By [Reference SeshadriSes77, §II.4 Theorem 3], there is a natural bijection of sets
Since
![]() $\mathcal {C}^{\bar \phi }$
is generic, each element of
$\mathcal {C}^{\bar \phi }$
is generic, each element of
![]() $\operatorname {\mathrm {Rep}}^{\bar \phi }(\bar {\mathbb {F}}_q)$
is an irreducible
$\operatorname {\mathrm {Rep}}^{\bar \phi }(\bar {\mathbb {F}}_q)$
is an irreducible
![]() $G\!<\!\sigma {>}$
-representation according to [Reference ShuShu23, Proposition 3.8]. By [Reference ShuShu23, Proposition 4.4], irreducible
$G\!<\!\sigma {>}$
-representation according to [Reference ShuShu23, Proposition 3.8]. By [Reference ShuShu23, Proposition 4.4], irreducible
![]() $G\!<\!\sigma {>}$
-representations have finite abelian stabilisers; thus, every
$G\!<\!\sigma {>}$
-representations have finite abelian stabilisers; thus, every
![]() $G(\bar {\mathbb {F}}_q)$
-orbit is closed. We then have a natural bijection of sets
$G(\bar {\mathbb {F}}_q)$
-orbit is closed. We then have a natural bijection of sets
![]() $(\operatorname {\mathrm {Rep}}^{\bar {\phi }}\!/\mkern -2mu/\mkern -2mu G)(\bar {\mathbb {F}}_q)\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}} \operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)/G(\bar {\mathbb {F}}_q)$
. Therefore,
$(\operatorname {\mathrm {Rep}}^{\bar {\phi }}\!/\mkern -2mu/\mkern -2mu G)(\bar {\mathbb {F}}_q)\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}} \operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)/G(\bar {\mathbb {F}}_q)$
. Therefore,
(i.e., the set of F-stable G-orbits). Since G is connected, each F-stable
![]() $G(\bar {\mathbb {F}}_q)$
-orbit in
$G(\bar {\mathbb {F}}_q)$
-orbit in
![]() $\operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)$
must contain some F-stable point by the Lang-Steinberg theorem. We will prove that the number of F-stable points in each such orbit is exactly
$\operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)$
must contain some F-stable point by the Lang-Steinberg theorem. We will prove that the number of F-stable points in each such orbit is exactly
![]() $|G(\mathbb {F}_q)|$
.
$|G(\mathbb {F}_q)|$
.
Let O be an F-stable
![]() $G(\bar {\mathbb {F}}_q)$
-orbit in
$G(\bar {\mathbb {F}}_q)$
-orbit in
![]() $\operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)$
. Then
$\operatorname {\mathrm {Rep}}^{\bar {\phi }}(\bar {\mathbb {F}}_q)$
. Then
![]() $O^F$
splits into some
$O^F$
splits into some
![]() $G(\mathbb {F}_q)$
-orbits according to the stabliliser in G of some F-stable point, say
$G(\mathbb {F}_q)$
-orbits according to the stabliliser in G of some F-stable point, say
![]() $x\in O^F$
. By [Reference ShuShu23, Proposition 4.4] again, the stabiliser is a finite abelian group H. The number of
$x\in O^F$
. By [Reference ShuShu23, Proposition 4.4] again, the stabiliser is a finite abelian group H. The number of
![]() $G(\mathbb {F}_q)$
-orbits in
$G(\mathbb {F}_q)$
-orbits in
![]() $O^F$
is equal to the number of F-conjugacy classes in H.
$O^F$
is equal to the number of F-conjugacy classes in H.
Since H is abelian, each F-conjugacy class of it is of the form
![]() $\{h_0hF(h)^{-1}\mid h\in H\}$
for some
$\{h_0hF(h)^{-1}\mid h\in H\}$
for some
![]() $h_0\in H$
. Again, because H is abelian, the map
$h_0\in H$
. Again, because H is abelian, the map
![]() $h\mapsto hF(h)^{-1}$
is a group homomorphism, with kernel
$h\mapsto hF(h)^{-1}$
is a group homomorphism, with kernel
![]() $K=\{h\in H\mid F(h)=h\}$
. Denote by I the image of this homomorphism. Then the F-conjugacy classes in H are the cosets
$K=\{h\in H\mid F(h)=h\}$
. Denote by I the image of this homomorphism. Then the F-conjugacy classes in H are the cosets
![]() $h_0I$
; therefore, there are
$h_0I$
; therefore, there are
![]() $|H|/|I|=|K|$
of them.
$|H|/|I|=|K|$
of them.
That is, the number of
![]() $G(\mathbb {F}_q)$
-orbits in O is
$G(\mathbb {F}_q)$
-orbits in O is
![]() $|K|$
. However, x has K as its stabiliser in
$|K|$
. However, x has K as its stabiliser in
![]() $G(\mathbb {F}_q)$
, so the cardinality of the
$G(\mathbb {F}_q)$
, so the cardinality of the
![]() $G(\mathbb {F}_q)$
-orbit containing x is
$G(\mathbb {F}_q)$
-orbit containing x is
![]() $|G(\mathbb {F}_q)|/|K|$
. If for some
$|G(\mathbb {F}_q)|/|K|$
. If for some
![]() $g\in G(\bar {\mathbb {F}}_q)$
,
$g\in G(\bar {\mathbb {F}}_q)$
,
![]() $g.x$
is an F-stable point contained in another
$g.x$
is an F-stable point contained in another
![]() $G(\mathbb {F}_q)$
-orbit, then its stabiliser in
$G(\mathbb {F}_q)$
-orbit, then its stabiliser in
![]() $G(\mathbb {F}_q)$
is just
$G(\mathbb {F}_q)$
is just
![]() $gKg^{-1}$
. Indeed, we have
$gKg^{-1}$
. Indeed, we have
![]() $g^{-1}F(g)\in \operatorname {\mathrm {Stab}}_G(x)=H$
. Thus, for any
$g^{-1}F(g)\in \operatorname {\mathrm {Stab}}_G(x)=H$
. Thus, for any
![]() $k\in K$
,
$k\in K$
,
Thus, all
![]() $G(\mathbb {F}_q)$
-orbits in O have cardinality
$G(\mathbb {F}_q)$
-orbits in O have cardinality
![]() $|G(\mathbb {F}_q)|/|K|$
. We conclude that
$|G(\mathbb {F}_q)|/|K|$
. We conclude that
![]() $|O(\mathbb {F}_q)|=|G(\mathbb {F}_q)|$
, which is independent of O. Therefore,
$|O(\mathbb {F}_q)|=|G(\mathbb {F}_q)|$
, which is independent of O. Therefore,
5 Computation of linear characters
In this section, we fix an odd prime power q. The base field is ![]() .
.
5.1 A constraint on types
5.1.1
Theorem 3.4.7 concerns only those irreducible characters of
![]() $G(q)$
that are induced from
$G(q)$
that are induced from
![]() $\sigma $
-stable standard Levi subgroups. We want to show that these characters suffice.
$\sigma $
-stable standard Levi subgroups. We want to show that these characters suffice.
Lemma 5.1.1. Let
![]() $(C_1,\ldots ,C_{2k})$
be a tuple of semi-simple conjugacy classes in
$(C_1,\ldots ,C_{2k})$
be a tuple of semi-simple conjugacy classes in
![]() $G(q)\sigma $
such that for each
$G(q)\sigma $
such that for each
![]() $1\le j\le 2k$
, the G-conjugacy class containing
$1\le j\le 2k$
, the G-conjugacy class containing
![]() $C_j$
has a representative
$C_j$
has a representative
![]() $s_j\sigma \in (T^{\sigma })^{\circ F}\sigma $
. Let M be a
$s_j\sigma \in (T^{\sigma })^{\circ F}\sigma $
. Let M be a
![]() $\sigma $
-stable and F-stable Levi factor of a
$\sigma $
-stable and F-stable Levi factor of a
![]() $\sigma $
-stable parabolic subgroup of G. Suppose that
$\sigma $
-stable parabolic subgroup of G. Suppose that
![]() $(C_j)_j$
is strongly generic and that for all j,
$(C_j)_j$
is strongly generic and that for all j,
![]() $C_j\cap M\sigma \ne \emptyset $
. Then M is
$C_j\cap M\sigma \ne \emptyset $
. Then M is
![]() $G(q)$
-conjugate to a
$G(q)$
-conjugate to a
![]() $\sigma $
-stable standard Levi subgroup.
$\sigma $
-stable standard Levi subgroup.
Proof. We may assume that
![]() $M=L_{I,w}$
for some
$M=L_{I,w}$
for some
![]() $\sigma $
-stable I and some
$\sigma $
-stable I and some
![]() $w\in W_G(L_I)^{\sigma }$
(see §2.6.3 and §3.2.2). There exists
$w\in W_G(L_I)^{\sigma }$
(see §2.6.3 and §3.2.2). There exists
![]() $\dot {w}\in (G^{\sigma })^{\circ }$
representing w and
$\dot {w}\in (G^{\sigma })^{\circ }$
representing w and
![]() $g\in (G^{\sigma })^{\circ }$
such that
$g\in (G^{\sigma })^{\circ }$
such that
![]() $g^{-1}F(g)=\dot {w}$
. Then
$g^{-1}F(g)=\dot {w}$
. Then
![]() $L_{I,w}=gL_Ig^{-1}$
.
$L_{I,w}=gL_Ig^{-1}$
.
For each j, let
![]() $t_j\sigma \in C_j\cap M\sigma $
. For any j,
$t_j\sigma \in C_j\cap M\sigma $
. For any j,
![]() $g^{-1}t_j\sigma g$
lies in
$g^{-1}t_j\sigma g$
lies in
![]() $L_I\sigma $
. By Proposition 2.5.1, for each j, there exists
$L_I\sigma $
. By Proposition 2.5.1, for each j, there exists
![]() $l_j\in L_I$
such that
$l_j\in L_I$
such that
![]() $l_jg^{-1}t_j\sigma gl_j^{-1}$
lies in
$l_jg^{-1}t_j\sigma gl_j^{-1}$
lies in
![]() $(T^{\sigma })^{\circ }\sigma $
, and moreover, for each j, there exists
$(T^{\sigma })^{\circ }\sigma $
, and moreover, for each j, there exists
![]() $w_j\in W^{\sigma }$
and
$w_j\in W^{\sigma }$
and
![]() $z_j\in (T^{\sigma })^{\circ }\cap [T,\sigma ]$
such that
$z_j\in (T^{\sigma })^{\circ }\cap [T,\sigma ]$
such that
For any connected reductive algebraic group H, denote by
the natural surjection, identifying
![]() $H/[H,H]\cong Z_H^{\circ }/(Z_H^{\circ }\cap [H,H])$
. For
$H/[H,H]\cong Z_H^{\circ }/(Z_H^{\circ }\cap [H,H])$
. For
![]() $H=\operatorname {\mathrm {GL}}_n$
, this is the determinant. We have
$H=\operatorname {\mathrm {GL}}_n$
, this is the determinant. We have
Since
![]() $s_j$
lies in
$s_j$
lies in
![]() $(T^{\sigma })^{\circ }$
,
$(T^{\sigma })^{\circ }$
,
![]() $z_j\sigma $
commutes with
$z_j\sigma $
commutes with
![]() $w_js_jw_j^{-1}$
for all j. Since
$w_js_jw_j^{-1}$
for all j. Since
![]() $z_j$
lies in
$z_j$
lies in
![]() $[T,\sigma ]$
,
$[T,\sigma ]$
,
![]() $(z_j\sigma )^2=\sigma ^2$
. Note also that
$(z_j\sigma )^2=\sigma ^2$
. Note also that
![]() $\sigma ^2=1$
by definition. We deduce that
$\sigma ^2=1$
by definition. We deduce that
 $$ \begin{align} \mathbf{D}_{L_I}\big(\prod_{j=1}^{2k}(g^{-1}t_j\sigma g)^2\big)=\mathbf{D}_{L_I}\big(\prod_{j=1}^{2k}(w_js_j^2w_j^{-1})\big), \end{align} $$
$$ \begin{align} \mathbf{D}_{L_I}\big(\prod_{j=1}^{2k}(g^{-1}t_j\sigma g)^2\big)=\mathbf{D}_{L_I}\big(\prod_{j=1}^{2k}(w_js_j^2w_j^{-1})\big), \end{align} $$
and we denote by l this element of
![]() $Z_{L_I}^{\circ }/(Z_{L_I}^{\circ }\cap [L_I,L_I])$
.
$Z_{L_I}^{\circ }/(Z_{L_I}^{\circ }\cap [L_I,L_I])$
.
Let us choose an isomorphism
![]() $L_I\cong \operatorname {\mathrm {GL}}_{n_0}\times \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
, which induces
$L_I\cong \operatorname {\mathrm {GL}}_{n_0}\times \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
, which induces
The action of
![]() $\sigma $
on the factor
$\sigma $
on the factor ![]() corresponding to each i sends
corresponding to each i sends
![]() $(x,y)$
to
$(x,y)$
to
![]() $(y^{-1},x^{-1})$
, and on the first factor sends x to
$(y^{-1},x^{-1})$
, and on the first factor sends x to
![]() $x^{-1}$
. From the right-hand side of (5.1.1.1), we see that l is in fact a
$x^{-1}$
. From the right-hand side of (5.1.1.1), we see that l is in fact a
![]() $\sigma $
-stable element for this action. Thus, we can write
$\sigma $
-stable element for this action. Thus, we can write
![]() $l=(l_0,(l_i,l_i^{-1}))$
under the above isomorphism, where
$l=(l_0,(l_i,l_i^{-1}))$
under the above isomorphism, where
![]() $l_0$
, in fact, equals to
$l_0$
, in fact, equals to
![]() $1$
.
$1$
.
In view of the right-hand side of (5.1.1.1), each
![]() $l_i$
is of the form
$l_i$
is of the form
![]() $[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}_{2k},\mathbf {e}^{2k}]_{2k}$
(see §4.2.2 for the notations). We can then apply Lemma 4.2.1 and conclude that
$[\mathbf {A}_1,\mathbf {e}^1]_1\cdots [\mathbf {A}_{2k},\mathbf {e}^{2k}]_{2k}$
(see §4.2.2 for the notations). We can then apply Lemma 4.2.1 and conclude that
![]() $l_i\ne l_j^{\pm 1}$
whenever
$l_i\ne l_j^{\pm 1}$
whenever
![]() $i\ne j$
. Moreover, every
$i\ne j$
. Moreover, every
![]() $l_i$
lies in
$l_i$
lies in
![]() $\mathbb {F}_q$
. However, the left-hand side of (5.1.1.1) shows that l is an
$\mathbb {F}_q$
. However, the left-hand side of (5.1.1.1) shows that l is an
![]() $F_w$
-stable element (see (2.6.3.1)). The action of a (signed) cycle in w on
$F_w$
-stable element (see (2.6.3.1)). The action of a (signed) cycle in w on
![]() $L_I$
is given by (3.2.2.1). It is easy to see that if there is some cycle of size larger than
$L_I$
is given by (3.2.2.1). It is easy to see that if there is some cycle of size larger than
![]() $1$
, then
$1$
, then
![]() $l_i=l_j$
for some
$l_i=l_j$
for some
![]() $i\ne j$
, which is a contradiction. Finally, if there is some negative cycle of size
$i\ne j$
, which is a contradiction. Finally, if there is some negative cycle of size
![]() $1$
, then the corresponding factor
$1$
, then the corresponding factor
![]() $l_i$
satisfies
$l_i$
satisfies
![]() $l_i=l_i^q=l_i^{-1}$
and so must be equal to
$l_i=l_i^q=l_i^{-1}$
and so must be equal to
![]() $\pm 1$
. This possibility is ruled out by the assumption (4.2.1.2). We conclude that
$\pm 1$
. This possibility is ruled out by the assumption (4.2.1.2). We conclude that
![]() $w=1$
.
$w=1$
.
By Theorem 3.4.3, each
![]() $\sigma $
-stable irreducible character of
$\sigma $
-stable irreducible character of
![]() $G(q)$
is of the form
$G(q)$
is of the form
![]() $\chi =\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
for some F-stable and
$\chi =\epsilon _G\epsilon _M R^G_M(\chi _1\boxtimes \chi _0)$
for some F-stable and
![]() $\sigma $
-stable Levi factor M of some
$\sigma $
-stable Levi factor M of some
![]() $\sigma $
-stable parabolic subgroup. By Theorem 3.4.7, the extension
$\sigma $
-stable parabolic subgroup. By Theorem 3.4.7, the extension
![]() $\tilde {\chi }$
of
$\tilde {\chi }$
of
![]() $\chi $
to
$\chi $
to
![]() $G(q)\sigma $
is a linear combination of inductions from the twisted maximal tori in
$G(q)\sigma $
is a linear combination of inductions from the twisted maximal tori in
![]() $M\sigma $
, assuming that such an extension is a uniform function. By Proposition 3.3.1, if
$M\sigma $
, assuming that such an extension is a uniform function. By Proposition 3.3.1, if
![]() $C_j\cap M\sigma =\emptyset $
, then
$C_j\cap M\sigma =\emptyset $
, then
![]() $\tilde {\chi }(C_j)=0$
. The above lemma then implies that only those
$\tilde {\chi }(C_j)=0$
. The above lemma then implies that only those
![]() $\chi $
with M being a standard Levi subgroup can have an extension
$\chi $
with M being a standard Levi subgroup can have an extension
![]() $\tilde {\chi }$
that is nonvanishing on all
$\tilde {\chi }$
that is nonvanishing on all
![]() $C_j$
, as long as
$C_j$
, as long as
![]() $\mathcal {C}$
is a strongly generic tuple of semi-simple conjugacy classes.
$\mathcal {C}$
is a strongly generic tuple of semi-simple conjugacy classes.
5.2 Möbius inversion functions
The results in this subsection will only be used in §5.4.
5.2.1
Let m be a positive integer and let I be a set of cardinality
![]() $x>m$
. Denote by
$x>m$
. Denote by
![]() $\Pi $
the set of the partitions of
$\Pi $
the set of the partitions of
![]() $\mathbb {I}(m)=\{1,\ldots ,m\}$
. It is a partially ordered set. Two partitions satisfy
$\mathbb {I}(m)=\{1,\ldots ,m\}$
. It is a partially ordered set. Two partitions satisfy
![]() $P_1\prec P_2$
if
$P_1\prec P_2$
if
![]() $P_2$
refines
$P_2$
refines
![]() $P_1$
. Denote by
$P_1$
. Denote by
![]() $P_0$
the partition into m parts, each consisting of a single element. Then
$P_0$
the partition into m parts, each consisting of a single element. Then
![]() $P_0$
is the maximal element. Each
$P_0$
is the maximal element. Each
![]() $P\in \Pi $
can be written as a collection of disjoint subsets
$P\in \Pi $
can be written as a collection of disjoint subsets
![]() $p_1\cdots p_l$
of
$p_1\cdots p_l$
of
![]() $\mathbb {I}(m)$
. Each
$\mathbb {I}(m)$
. Each
![]() $p_i$
is called a part of P and l is called the length of P, denoted by
$p_i$
is called a part of P and l is called the length of P, denoted by
![]() $l(P)$
. For any
$l(P)$
. For any
![]() $P\in \Pi $
, denote by
$P\in \Pi $
, denote by
![]() $(I^m)_{P}$
the subset of
$(I^m)_{P}$
the subset of
![]() $I^m$
consisting of the elements
$I^m$
consisting of the elements
![]() $(i_r)_{1\le r\le m}$
such that
$(i_r)_{1\le r\le m}$
such that
![]() $i_r=i_s$
whenever r and s are in the same part of P. Denote by
$i_r=i_s$
whenever r and s are in the same part of P. Denote by
![]() $(I^m)_{P,\operatorname {\mathrm {reg}}}$
the set of the elements
$(I^m)_{P,\operatorname {\mathrm {reg}}}$
the set of the elements
![]() $(i_r)$
of
$(i_r)$
of
![]() $(I^m)_{P}$
such that
$(I^m)_{P}$
such that
![]() $i_r\ne i_s$
whenever r and s are not in the same part of P. Obviously,
$i_r\ne i_s$
whenever r and s are not in the same part of P. Obviously,
for any
![]() $P_2\in \Pi $
. A
$P_2\in \Pi $
. A
![]() $\bar {\mathbb {Q}}_{\ell }$
-valued function f defined on the set of the subsets of
$\bar {\mathbb {Q}}_{\ell }$
-valued function f defined on the set of the subsets of
![]() $I^m$
is called additive if
$I^m$
is called additive if
![]() $f(U\cup V)=f(U)+f(V)$
for any two disjoint subsets U and V. Given such a function f, we can define two functions F and
$f(U\cup V)=f(U)+f(V)$
for any two disjoint subsets U and V. Given such a function f, we can define two functions F and
![]() $F'$
on
$F'$
on
![]() $\Pi $
by
$\Pi $
by
Then
By the Möbius inversion formula, we have
where
![]() $\mu (P_1,P_2)$
is the Möbius inversion function for the partially ordered set
$\mu (P_1,P_2)$
is the Möbius inversion function for the partially ordered set
![]() $\Pi $
.
$\Pi $
.
Define
![]() $c_{P}(x):=|(I^m)_{P}|$
,
$c_{P}(x):=|(I^m)_{P}|$
,
![]() $c^{\prime }_{P}(x):=|(I^m)_{P,reg}|$
. We have
$c^{\prime }_{P}(x):=|(I^m)_{P,reg}|$
. We have
![]() $c_{P}(x)=(x)^{l(P)}$
and
$c_{P}(x)=(x)^{l(P)}$
and
These are the functions defined by counting elements, and so are additive. Inserting these expressions into the Möbius inversion formula, we have a polynomial identity in x that is valid for all large enough x. Specialising this equality at
![]() $x=-1$
, we get
$x=-1$
, we get
5.2.2
Let I, m and
![]() $\Pi $
be as above. Let
$\Pi $
be as above. Let
![]() $I^{\ast }$
be a set in bijection with I, and we fix a bijection between them. For any
$I^{\ast }$
be a set in bijection with I, and we fix a bijection between them. For any
![]() $i\in I$
, let
$i\in I$
, let
![]() $i^{\ast }$
denote the element of
$i^{\ast }$
denote the element of
![]() $I^{\ast }$
corresponding to i under the given bijection. Write
$I^{\ast }$
corresponding to i under the given bijection. Write
![]() $\bar {I}=I\sqcup I^{\ast }$
. For any i,
$\bar {I}=I\sqcup I^{\ast }$
. For any i,
![]() $i'\in \bar {I}$
, we write
$i'\in \bar {I}$
, we write
![]() $[i]=[i']$
if
$[i]=[i']$
if
![]() $i'\in \{i,i^{\ast }\}$
. For any
$i'\in \{i,i^{\ast }\}$
. For any
![]() $P\in \Pi $
, denote by
$P\in \Pi $
, denote by
![]() $(\bar {I}^m)_P$
the subsets of elements
$(\bar {I}^m)_P$
the subsets of elements
![]() $(i_r)_{1\le r\le m}$
,
$(i_r)_{1\le r\le m}$
,
![]() $i_r\in \bar {I}$
, such that
$i_r\in \bar {I}$
, such that
![]() $[i_r]=[i_s]$
whenever r and s are in the same part of P. Denote by
$[i_r]=[i_s]$
whenever r and s are in the same part of P. Denote by
![]() $(\bar {I}^m)_{P,\operatorname {\mathrm {reg}}}$
the set of the elements
$(\bar {I}^m)_{P,\operatorname {\mathrm {reg}}}$
the set of the elements
![]() $(i_r)$
of
$(i_r)$
of
![]() $(\bar {I}^m)_P$
such that
$(\bar {I}^m)_P$
such that
![]() $[i_r]\ne [i_s]$
whenever r and s are not in the same part of P. We say that an element of
$[i_r]\ne [i_s]$
whenever r and s are not in the same part of P. We say that an element of
![]() $\bar {I}^m$
is regular if it is regular with respect to the maximal partition
$\bar {I}^m$
is regular if it is regular with respect to the maximal partition
![]() $P_0$
. Obviously,
$P_0$
. Obviously,
for any
![]() $P_2\in \Pi $
.
$P_2\in \Pi $
.
Now, put
![]() $\bar {I}=\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{1,\eta \}$
and
$\bar {I}=\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{1,\eta \}$
and
![]() $\tilde {I}=(\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{1,\eta \})/\!\sim $
for the equivalence relation
$\tilde {I}=(\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{1,\eta \})/\!\sim $
for the equivalence relation
![]() $\sim $
that identifies
$\sim $
that identifies
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{-1}$
. For each equivalence class, we choose a representative and denote by I the set of these representatives, and so for any
$\alpha ^{-1}$
. For each equivalence class, we choose a representative and denote by I the set of these representatives, and so for any
![]() $\alpha \in I$
,
$\alpha \in I$
,
![]() $\alpha ^{\ast }=\alpha ^{-1}$
. Let
$\alpha ^{\ast }=\alpha ^{-1}$
. Let
![]() $(a_i)_{1\le i\le m}$
be an m-tuple of elements of
$(a_i)_{1\le i\le m}$
be an m-tuple of elements of
![]() $\mathbb {F}_q^{\ast }$
. Define an additive function on the set of the subsets of
$\mathbb {F}_q^{\ast }$
. Define an additive function on the set of the subsets of
![]() $\bar {I}^m$
by
$\bar {I}^m$
by
 $$ \begin{align*}f(J):=\sum_{(\alpha_i)_{1\le i\le m}\in J}\prod_{1\le i\le m}\alpha_i(a^2_i),\end{align*} $$
$$ \begin{align*}f(J):=\sum_{(\alpha_i)_{1\le i\le m}\in J}\prod_{1\le i\le m}\alpha_i(a^2_i),\end{align*} $$
for
![]() $J\subset \bar {I}^m$
. We define the functions on
$J\subset \bar {I}^m$
. We define the functions on
![]() $\Pi $
:
$\Pi $
:
Then,
5.2.3
Let s be a positive integer. Let
![]() $(a_i)_{1\le i\le s}$
be an s-tuple of elements of
$(a_i)_{1\le i\le s}$
be an s-tuple of elements of
![]() $\mathbb {F}_q^{\ast }$
such that
$\mathbb {F}_q^{\ast }$
such that
![]() $\prod _{1\le i\le s}a_i^{2e_i}\ne 1$
for any
$\prod _{1\le i\le s}a_i^{2e_i}\ne 1$
for any
![]() $(e_i)_{1\le i\le s}\in \boldsymbol{\mu} _2^s$
.
$(e_i)_{1\le i\le s}\in \boldsymbol{\mu} _2^s$
.
Lemma 5.2.1. With the notations of §5.2.2, we have the identity
 $$ \begin{align*} \sum_{\alpha\in I}~\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}~\prod_{1\le i\le s}\alpha(a^{2e_i}_i)=-2^s. \end{align*} $$
$$ \begin{align*} \sum_{\alpha\in I}~\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}~\prod_{1\le i\le s}\alpha(a^{2e_i}_i)=-2^s. \end{align*} $$
Proof. Observe that
 $$ \begin{align*} \sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha^{-1}(\prod_{1\le i\le s}a^{2e_i}_i)=\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{-2e_i}_i)=\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{2e_i}_i), \end{align*} $$
$$ \begin{align*} \sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha^{-1}(\prod_{1\le i\le s}a^{2e_i}_i)=\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{-2e_i}_i)=\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{2e_i}_i), \end{align*} $$
so the desired quantity is equal to
 $$ \begin{align*}\frac{1}{2}\sum_{\alpha\in \bar{I}}~\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{2e_i}_i).\end{align*} $$
$$ \begin{align*}\frac{1}{2}\sum_{\alpha\in \bar{I}}~\sum_{(e_i)_{1\le i\le s}\in\boldsymbol\mu_2^s}\alpha(\prod_{1\le i\le s}a^{2e_i}_i).\end{align*} $$
Since
![]() $\prod _{1\le i\le s}a_i^{2e_i}\ne 1$
, we have
$\prod _{1\le i\le s}a_i^{2e_i}\ne 1$
, we have
 $$ \begin{align*}0=\sum_{\alpha\in\operatorname{\mathrm{Irr}}(\mathbb{F}_q^{\ast})}\alpha(\prod_{1\le i\le s}a_i^{2e_i})=\sum_{\alpha\in\bar{I}}\alpha(\prod_{1\le i\le s}a_i^{2e_i})+2;\end{align*} $$
$$ \begin{align*}0=\sum_{\alpha\in\operatorname{\mathrm{Irr}}(\mathbb{F}_q^{\ast})}\alpha(\prod_{1\le i\le s}a_i^{2e_i})=\sum_{\alpha\in\bar{I}}\alpha(\prod_{1\le i\le s}a_i^{2e_i})+2;\end{align*} $$
that is,
We get
![]() $\frac {1}{2}2^s\cdot (-2)=-2^s$
.
$\frac {1}{2}2^s\cdot (-2)=-2^s$
.
We use the above lemma to compute
![]() $F(P_1)$
in (5.2.2.1).
$F(P_1)$
in (5.2.2.1).
Lemma 5.2.2. We have
![]() $F(P_1)=(-1)^{l(P_1)}2^m$
.
$F(P_1)=(-1)^{l(P_1)}2^m$
.
Proof. Write
![]() $P_1=p_1\cdots p_l$
with
$P_1=p_1\cdots p_l$
with
![]() $l=l(P_1)$
. For each
$l=l(P_1)$
. For each
![]() $k\in \{1,\ldots ,l\}$
, denote by
$k\in \{1,\ldots ,l\}$
, denote by
![]() $\bar {I}^{p_k}$
the components of
$\bar {I}^{p_k}$
the components of
![]() $\bar {I}^m$
indexed by the elements of
$\bar {I}^m$
indexed by the elements of
![]() $p_k$
and denote by
$p_k$
and denote by
![]() $(\bar {I}^{p_k})_0$
the subset consisting of
$(\bar {I}^{p_k})_0$
the subset consisting of
![]() $(i_r)_{r\in p_k}$
satisfying
$(i_r)_{r\in p_k}$
satisfying
![]() $[i_r]=[i_{r'}]$
for any r,
$[i_r]=[i_{r'}]$
for any r,
![]() $r'\in p_k$
. Since
$r'\in p_k$
. Since
![]() $(\bar {I}^m)_{P_1}=\prod _k(\bar {I}^{p_k})_0$
, we have
$(\bar {I}^m)_{P_1}=\prod _k(\bar {I}^{p_k})_0$
, we have
 $$ \begin{align*}F(P_1)=\sum_{(\alpha_i)_{1\le i\le m}\in (\bar{I}^m)_{P_1}}\prod_{1\le i\le m}\alpha_i(a^2_i)=\prod_{k=1}^l\sum_{(\alpha_i)_{i\in p_k}\in (\bar{I}^{p_k})_0}\prod_{i\in p_k}\alpha_i(a^2_i).\end{align*} $$
$$ \begin{align*}F(P_1)=\sum_{(\alpha_i)_{1\le i\le m}\in (\bar{I}^m)_{P_1}}\prod_{1\le i\le m}\alpha_i(a^2_i)=\prod_{k=1}^l\sum_{(\alpha_i)_{i\in p_k}\in (\bar{I}^{p_k})_0}\prod_{i\in p_k}\alpha_i(a^2_i).\end{align*} $$
Note that
 $$ \begin{align*}\sum_{(\alpha_i)_{i\in p_k}\in (\bar{I}^{p_k})_0}\prod_{i\in p_k}\alpha_i(a^2_i)=\sum_{\alpha\in I}~\sum_{(e_i)_{i\in p_k}\in\boldsymbol\mu_2^{p_k}}~\prod_{i\in p_k}\alpha^{e_i}(a^{2}_i),\end{align*} $$
$$ \begin{align*}\sum_{(\alpha_i)_{i\in p_k}\in (\bar{I}^{p_k})_0}\prod_{i\in p_k}\alpha_i(a^2_i)=\sum_{\alpha\in I}~\sum_{(e_i)_{i\in p_k}\in\boldsymbol\mu_2^{p_k}}~\prod_{i\in p_k}\alpha^{e_i}(a^{2}_i),\end{align*} $$
which is equal to
![]() $-2^{|p_k|}$
by Lemma 5.2.1. It then only remains to take the product over k.
$-2^{|p_k|}$
by Lemma 5.2.1. It then only remains to take the product over k.
5.3 A formula for linear characters
5.3.1
Let ![]() be the torus with components indexed by
be the torus with components indexed by
Let F be the Frobenius of T sending t to
![]() $t^q$
. Let
$t^q$
. Let
![]() $w_+$
(resp.
$w_+$
(resp.
![]() $w_-$
) be the automorphism of T that permutes its factors according to (2.3.3.2) (resp. (2.3.3.3)). Write
$w_-$
) be the automorphism of T that permutes its factors according to (2.3.3.2) (resp. (2.3.3.3)). Write
![]() $F_+=\operatorname {\mathrm {ad}} w_+\circ F$
and
$F_+=\operatorname {\mathrm {ad}} w_+\circ F$
and
![]() $F_-=\operatorname {\mathrm {ad}} w_-\circ F$
. These are Frobenius endomorphisms of T such that
$F_-=\operatorname {\mathrm {ad}} w_-\circ F$
. These are Frobenius endomorphisms of T such that
![]() $T^{F_+}\cong \mathbb {F}^{\ast }_{q^m}\times \mathbb {F}^{\ast }_{q^m}$
and
$T^{F_+}\cong \mathbb {F}^{\ast }_{q^m}\times \mathbb {F}^{\ast }_{q^m}$
and
![]() $T^{F_-}\cong \mathbb {F}^{\ast }_{q^{2m}}$
.
$T^{F_-}\cong \mathbb {F}^{\ast }_{q^{2m}}$
.
Lemma 5.3.1. Let
and let
Suppose that
![]() $ut$
lies in
$ut$
lies in
![]() $T^{F_+}$
or in
$T^{F_+}$
or in
![]() $T^{F_-}$
. Then
$T^{F_-}$
. Then
-
(i)
 $u_{i+1}^2=u_i^2$
for all i;
$u_{i+1}^2=u_i^2$
for all i; -
(ii)
 $u_i^4=1$
for all i if
$u_i^4=1$
for all i if
 $ut\in T^{F_-}$
;
$ut\in T^{F_-}$
; -
(iii)
 $\prod _i^mt_i^2=\prod _{i=1}^mt_1^{2q^{i-1}}$
and,
$\prod _i^mt_i^2=\prod _{i=1}^mt_1^{2q^{i-1}}$
and,  $$ \begin{align*}\begin{cases} t_1^{1+q+\cdots+q^{m-1}}\in\mathbb{F}_q^{\ast} & \text{ if } ut\in T^{F_+};\\ t_1^{1+q+\cdots+q^{m-1}}\in\mathbb{F}_q^{\ast} & \text{ if } ut\in T^{F_-} \text{ and } u_i^2=1;\\ t_1^{2(1+q+\cdots+q^{m-1})}\in\mathbb{F}_q^{\ast}\setminus(\mathbb{F}_q^{\ast})^2 & \text{ if } ut\in T^{F_-} \text{ and } u_i^2=-1. \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} t_1^{1+q+\cdots+q^{m-1}}\in\mathbb{F}_q^{\ast} & \text{ if } ut\in T^{F_+};\\ t_1^{1+q+\cdots+q^{m-1}}\in\mathbb{F}_q^{\ast} & \text{ if } ut\in T^{F_-} \text{ and } u_i^2=1;\\ t_1^{2(1+q+\cdots+q^{m-1})}\in\mathbb{F}_q^{\ast}\setminus(\mathbb{F}_q^{\ast})^2 & \text{ if } ut\in T^{F_-} \text{ and } u_i^2=-1. \end{cases} \end{align*} $$
Proof. By the assumption on u, we have
![]() $u_i^q=u_i$
for all i. Therefore,
$u_i^q=u_i$
for all i. Therefore,
and so
![]() $u_{i+1}^2=u_i^2$
.
$u_{i+1}^2=u_i^2$
.
Suppose
![]() $ut\in T^{F_+}$
. Then
$ut\in T^{F_+}$
. Then
![]() $t_1^{q^m}u_1=t_1u_1$
, and so
$t_1^{q^m}u_1=t_1u_1$
, and so
![]() $t_1^{q^m-1}=1$
. This proves the first part of (iii).
$t_1^{q^m-1}=1$
. This proves the first part of (iii).
Now suppose
![]() $ut\in T^{F_-}$
. Since
$ut\in T^{F_-}$
. Since
we deduce that
![]() $u_1^4=1$
and
$u_1^4=1$
and
The proof of part (i) shows that
![]() $t_{i+1}^2=t_i^{2q}$
. Applying the norm map to
$t_{i+1}^2=t_i^{2q}$
. Applying the norm map to
![]() $ut$
, we deduce that
$ut$
, we deduce that
 $$ \begin{align*}\prod_{i=1}^mt_1^{2q^{i-1}}=\prod_{i=1}^mt_i^2\in\mathbb{F}_q^{\ast}. \end{align*} $$
$$ \begin{align*}\prod_{i=1}^mt_1^{2q^{i-1}}=\prod_{i=1}^mt_i^2\in\mathbb{F}_q^{\ast}. \end{align*} $$
Write
![]() $x=\prod _{i=1}^mt_1^{q^{i-1}}$
. Then
$x=\prod _{i=1}^mt_1^{q^{i-1}}$
. Then
![]() $x^2\in \mathbb {F}_q^{\ast }$
, while (5.3.1.1) means that
$x^2\in \mathbb {F}_q^{\ast }$
, while (5.3.1.1) means that
![]() $x^{q-1}=u_1^2$
, whence the assertions.
$x^{q-1}=u_1^2$
, whence the assertions.
Let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in \operatorname {\mathrm {Irr}}(\mathbb {F}_q^{\ast })$
. We regard
$\beta \in \operatorname {\mathrm {Irr}}(\mathbb {F}_q^{\ast })$
. We regard
![]() $\alpha $
as an element of
$\alpha $
as an element of
![]() $\operatorname {\mathrm {Irr}}(\mathbb {F}_{q^m}^{\ast })$
via the norm map. Then
$\operatorname {\mathrm {Irr}}(\mathbb {F}_{q^m}^{\ast })$
via the norm map. Then
![]() $\alpha $
defines an irreducible character
$\alpha $
defines an irreducible character
![]() $(\alpha ,\alpha ^{-1})$
of
$(\alpha ,\alpha ^{-1})$
of
![]() $T^{F_+}\cong \mathbb {F}^{\ast }_{q^m}\times \mathbb {F}^{\ast }_{q^m}$
, denoted by
$T^{F_+}\cong \mathbb {F}^{\ast }_{q^m}\times \mathbb {F}^{\ast }_{q^m}$
, denoted by
![]() $\theta _{\alpha }$
. We regard
$\theta _{\alpha }$
. We regard
![]() $\beta $
as an element of
$\beta $
as an element of
![]() $\operatorname {\mathrm {Irr}}(\mathbb {F}_{q^{2m}}^{\ast })$
via the norm map. Then
$\operatorname {\mathrm {Irr}}(\mathbb {F}_{q^{2m}}^{\ast })$
via the norm map. Then
![]() $\beta $
defines an irreducible character of
$\beta $
defines an irreducible character of
![]() $T^{F_-}\cong \mathbb {F}^{\ast }_{q^{2m}}$
, denoted by
$T^{F_-}\cong \mathbb {F}^{\ast }_{q^{2m}}$
, denoted by
![]() $\theta ^{\prime }_{\beta }$
.
$\theta ^{\prime }_{\beta }$
.
Lemma 5.3.2. With the same notations as in Lemma 5.3.1, we have
-
(i)
 $\theta _{\alpha }(ut)=\alpha (\prod _i^mu_i^2)$
if
$\theta _{\alpha }(ut)=\alpha (\prod _i^mu_i^2)$
if
 $ut\in T^{F_+}$
;
$ut\in T^{F_+}$
; -
(ii)
 $\theta ^{\prime }_{\beta }(ut)=\beta (\prod _i^mt_i^2)=\beta (t_1^{2(1+q+\cdots +q^{m-1})})$
if
$\theta ^{\prime }_{\beta }(ut)=\beta (\prod _i^mt_i^2)=\beta (t_1^{2(1+q+\cdots +q^{m-1})})$
if
 $ut\in T^{F_-}$
.
$ut\in T^{F_-}$
.
Proof. Obvious.
5.3.2
Let
![]() $w\in W^{\sigma }$
. Then there exists
$w\in W^{\sigma }$
. Then there exists
![]() $\dot {w}\in (G^{\sigma })^{\circ }$
representing w. Let
$\dot {w}\in (G^{\sigma })^{\circ }$
representing w. Let
![]() $g\in (G^{\sigma })^{\circ }$
be such that
$g\in (G^{\sigma })^{\circ }$
be such that
![]() $g^{-1}F(g)=\dot {w}$
and put
$g^{-1}F(g)=\dot {w}$
and put
![]() $T_w=gTg^{-1}$
. Suppose
$T_w=gTg^{-1}$
. Suppose
![]() $n=2N+1$
. We can write
$n=2N+1$
. We can write
as in §2.3.3. Then
![]() $\tau $
is a product of cycles:
$\tau $
is a product of cycles:
![]() $\tau =\prod _{i\in \Lambda }c_{I_i}$
, where
$\tau =\prod _{i\in \Lambda }c_{I_i}$
, where
![]() $\Lambda $
is just a set indexing the cycles. The set
$\Lambda $
is just a set indexing the cycles. The set
![]() $\Lambda $
is divided into two parts:
$\Lambda $
is divided into two parts:
![]() $\Lambda _+$
and
$\Lambda _+$
and
![]() $\Lambda _-$
so that
$\Lambda _-$
so that
![]() $\bar {e}_i=-1$
if and only if
$\bar {e}_i=-1$
if and only if
![]() $i\in \Lambda _-$
(see §2.3.3). The size of
$i\in \Lambda _-$
(see §2.3.3). The size of
![]() $I_i$
is denoted by
$I_i$
is denoted by
![]() $\tau _i$
so that
$\tau _i$
so that
![]() $((\tau _i)_{i\in \Lambda _+},(\tau _i)_{i\in \Lambda _-})$
is the 2-partition corresponding to the conjugacy class of w. Now
$((\tau _i)_{i\in \Lambda _+},(\tau _i)_{i\in \Lambda _-})$
is the 2-partition corresponding to the conjugacy class of w. Now
For each
![]() $i\in \Lambda _+$
, let
$i\in \Lambda _+$
, let
![]() $\alpha _i\in \operatorname {\mathrm {Irr}}(\mathbb {F}_q^{\ast })$
and for each
$\alpha _i\in \operatorname {\mathrm {Irr}}(\mathbb {F}_q^{\ast })$
and for each
![]() $i\in \Lambda _-$
, let
$i\in \Lambda _-$
, let
![]() $\beta _i=\mathbf {1}$
or
$\beta _i=\mathbf {1}$
or
![]() $\eta $
. Let
$\eta $
. Let
![]() $\theta _0=\mathbf {1}$
or
$\theta _0=\mathbf {1}$
or
![]() $\eta $
considered as associated to the first component under the above isomorphism. Put
$\eta $
considered as associated to the first component under the above isomorphism. Put
 $$ \begin{align} \epsilon(\theta_0)= \begin{cases} 1 & \text{ if } \theta_0=\mathbf{1},\\ -1 & \text{ if } \theta_0=\eta. \end{cases} \end{align} $$
$$ \begin{align} \epsilon(\theta_0)= \begin{cases} 1 & \text{ if } \theta_0=\mathbf{1},\\ -1 & \text{ if } \theta_0=\eta. \end{cases} \end{align} $$
The characters
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
and
$\beta _i$
and
![]() $\theta _0$
are not necessarily distinct. Under the above isomorphism, we regard
$\theta _0$
are not necessarily distinct. Under the above isomorphism, we regard
as a character of
![]() $T^{F_w}$
via the norm maps. Then
$T^{F_w}$
via the norm maps. Then
![]() $\theta $
is obviously a
$\theta $
is obviously a
![]() $\sigma $
-stable character and so can be extended to a character of
$\sigma $
-stable character and so can be extended to a character of
![]() $T^{F_w}\!<\!\sigma \!>\!$
, denoted by
$T^{F_w}\!<\!\sigma \!>\!$
, denoted by
![]() $\tilde {\theta }$
. We require that
$\tilde {\theta }$
. We require that
![]() $\tilde {\theta }$
takes value
$\tilde {\theta }$
takes value
![]() $1$
at
$1$
at
![]() $\sigma $
. Define
$\sigma $
. Define
![]() $\epsilon (\theta ):=\epsilon (\theta _0)$
if n is odd.
$\epsilon (\theta ):=\epsilon (\theta _0)$
if n is odd.
Lemma 5.3.3. Let
![]() $\theta =(\theta _0,(\alpha _i,\alpha _i^{-1})_{i\in \Lambda _+},(\beta _i)_{i\in \Lambda _-})$
be the character of
$\theta =(\theta _0,(\alpha _i,\alpha _i^{-1})_{i\in \Lambda _+},(\beta _i)_{i\in \Lambda _-})$
be the character of
![]() $T^{F_w}$
as above and let
$T^{F_w}$
as above and let
Suppose that there exists
![]() $h\in G(q)$
such that
$h\in G(q)$
such that
![]() $hs'\sigma h^{-1}\in T_w\sigma $
. Then the following assertions hold.
$hs'\sigma h^{-1}\in T_w\sigma $
. Then the following assertions hold.
(i). The element
![]() $g^{-1}hs'\sigma h^{-1}g$
can be written as
$g^{-1}hs'\sigma h^{-1}g$
can be written as
![]() $st\sigma $
, where
$st\sigma $
, where
and
satisfies
![]() $a_{\gamma }=a^{\prime e_{\gamma }}_{\rho ^{-1}(\gamma )}$
,
$a_{\gamma }=a^{\prime e_{\gamma }}_{\rho ^{-1}(\gamma )}$
,
![]() $1\le \gamma \le N$
, for some permutation
$1\le \gamma \le N$
, for some permutation
![]() $\rho $
of
$\rho $
of
![]() $\{1,\ldots ,N\}$
and some N-tuple of signs
$\{1,\ldots ,N\}$
and some N-tuple of signs
![]() $(e_1,\ldots ,e_N)$
.
$(e_1,\ldots ,e_N)$
.
(ii). Define
and
The set
![]() $\Lambda _-^{\circ }$
is well defined according to Lemma 5.3.1. Then we have
$\Lambda _-^{\circ }$
is well defined according to Lemma 5.3.1. Then we have
 $$ \begin{align*}\tilde{\theta}(st\sigma)=\theta_0(c)\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^2_{\gamma})\prod_{i\in\Lambda_-^{\circ\circ}}(-1)\prod_{i\in\Lambda_-^{\circ}}\epsilon(\theta_0).\end{align*} $$
$$ \begin{align*}\tilde{\theta}(st\sigma)=\theta_0(c)\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^2_{\gamma})\prod_{i\in\Lambda_-^{\circ\circ}}(-1)\prod_{i\in\Lambda_-^{\circ}}\epsilon(\theta_0).\end{align*} $$
Proof. Put
![]() $x=g^{-1}h$
. That
$x=g^{-1}h$
. That
![]() $xs'\sigma x^{-1}\in T\sigma $
implies that
$xs'\sigma x^{-1}\in T\sigma $
implies that
![]() $x=\xi l$
with
$x=\xi l$
with
![]() $\xi \in N_G(T\sigma )$
and
$\xi \in N_G(T\sigma )$
and
![]() $l\in C_G(s'\sigma )^{\circ }$
by Lemma 3.3.5. Write
$l\in C_G(s'\sigma )^{\circ }$
by Lemma 3.3.5. Write
![]() $\xi $
as
$\xi $
as
![]() $t'\dot {v}$
, with
$t'\dot {v}$
, with
![]() $t'\in T$
and
$t'\in T$
and
![]() $\dot {v}$
fixed by
$\dot {v}$
fixed by
![]() $\sigma $
. Such
$\sigma $
. Such
![]() $\dot {v}$
exists since
$\dot {v}$
exists since
![]() $\sigma $
is quasi-central. Write
$\sigma $
is quasi-central. Write
for some
![]() $a_i\in \mathbb {F}_q^{\ast }$
,
$a_i\in \mathbb {F}_q^{\ast }$
,
![]() $1\le i\le N$
and write
$1\le i\le N$
and write
for some ![]() ,
,
![]() $1\le i\le 2N+1$
. Then
$1\le i\le 2N+1$
. Then
Put
![]() $t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_N,t_{N+1},t_N,\ldots ,t_1)$
, with
$t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_N,t_{N+1},t_N,\ldots ,t_1)$
, with
![]() $t_i=t^{\prime }_it^{\prime }_{2N+2-i}$
,
$t_i=t^{\prime }_it^{\prime }_{2N+2-i}$
,
![]() $1\le i\le N+1$
. Then
$1\le i\le N+1$
. Then
Let v be the image of
![]() $\dot {v}$
under the natural map
$\dot {v}$
under the natural map
![]() $N_G(T\sigma )\rightarrow W^{\sigma }$
(see Lemma 3.3.4). Then v can be written as
$N_G(T\sigma )\rightarrow W^{\sigma }$
(see Lemma 3.3.4). Then v can be written as
![]() $((e_1,\ldots ,e_N),\rho )$
under the isomorphism
$((e_1,\ldots ,e_N),\rho )$
under the isomorphism
![]() $W^{\sigma }\cong (\mathbb {Z}/2\mathbb {Z})^N\rtimes \mathfrak {S}_N$
. In fact,
$W^{\sigma }\cong (\mathbb {Z}/2\mathbb {Z})^N\rtimes \mathfrak {S}_N$
. In fact,
![]() $\rho $
and
$\rho $
and
![]() $(e_1,\ldots ,e_N)$
are the desired permutation and N-tuple of signs.
$(e_1,\ldots ,e_N)$
are the desired permutation and N-tuple of signs.
To compute
![]() $\theta (st)=\tilde {\theta }(st\sigma )$
, we apply Lemma 5.3.1 and Lemma 5.3.2 to each cycle in
$\theta (st)=\tilde {\theta }(st\sigma )$
, we apply Lemma 5.3.1 and Lemma 5.3.2 to each cycle in
![]() $\tau $
and get
$\tau $
and get
It remains to tackle the entry
![]() $t_{N+1}c$
of
$t_{N+1}c$
of
![]() $st$
. From the equality
$st$
. From the equality
![]() $g^{-1}hs'\sigma h^{-1}g=st\sigma $
, we see that
$g^{-1}hs'\sigma h^{-1}g=st\sigma $
, we see that
![]() $st$
is
$st$
is
![]() $F_w$
-stable, and so
$F_w$
-stable, and so
![]() $t_{N+1}c\in \mathbb {F}_q$
. Since we have required that
$t_{N+1}c\in \mathbb {F}_q$
. Since we have required that
![]() $\theta _0$
is either
$\theta _0$
is either
![]() $\mathbf {1}$
or
$\mathbf {1}$
or
![]() $\eta $
, it suffices to determine whether
$\eta $
, it suffices to determine whether
![]() $t_{N+1}c$
lies in
$t_{N+1}c$
lies in
![]() $(\mathbb {F}_q^{\ast })^2$
. We are going to compute
$(\mathbb {F}_q^{\ast })^2$
. We are going to compute
![]() $\det (ts)$
in two different ways. On the one hand,
$\det (ts)$
in two different ways. On the one hand,

where the equivalences ![]() and
and ![]() follow from the first and the second part of Lemma 5.3.1 (iii). On the other hand,
follow from the first and the second part of Lemma 5.3.1 (iii). On the other hand,
 $$ \begin{align*} \det(st)&=\det(g^{-1}hs'\sigma(h)^{-1}g)\\ &=\det(hs'\sigma(h^{-1}))\\ &=\det(h^2s')\\ &\equiv \det(s')=c\quad\mod(\mathbb{F}_q^{\ast})^2. \end{align*} $$
$$ \begin{align*} \det(st)&=\det(g^{-1}hs'\sigma(h)^{-1}g)\\ &=\det(hs'\sigma(h^{-1}))\\ &=\det(h^2s')\\ &\equiv \det(s')=c\quad\mod(\mathbb{F}_q^{\ast})^2. \end{align*} $$
Comparing the two expressions for
![]() $\det (st)$
, and using Lemma 5.3.1 (iii) and Lemma 5.3.2 (ii), we deduce that
$\det (st)$
, and using Lemma 5.3.1 (iii) and Lemma 5.3.2 (ii), we deduce that
and so
Corollary 5.3.4. With the same assumptions as in Lemma 5.3.3, we assume further that
![]() $a_{\gamma }^2\ne -1$
for all
$a_{\gamma }^2\ne -1$
for all
![]() $1\le \gamma \le N$
. Then
$1\le \gamma \le N$
. Then
 $$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\theta_0(c)\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma}).\end{align*} $$
$$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\theta_0(c)\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma}).\end{align*} $$
Proof. Clear.
Remark 5.3.5. If n is even, then the same arguments show that
 $$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma})\prod_{i\in\Lambda_-^{\circ\circ}}(-1),\end{align*} $$
$$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma})\prod_{i\in\Lambda_-^{\circ\circ}}(-1),\end{align*} $$
where each term in this expression is defined in a way similar to the odd dimensional case. And if we assume
![]() $a_{\gamma }^2\ne -1$
for all
$a_{\gamma }^2\ne -1$
for all
![]() $\gamma $
, then
$\gamma $
, then
 $$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma}).\end{align*} $$
$$ \begin{align*}\tilde{\theta}(g^{-1}hs'\sigma h^{-1}g)=\prod_{i\in\Lambda_+}\alpha_i(\prod_{\gamma\in I_i}a^{2}_{\gamma}).\end{align*} $$
5.4 Sum of linear characters
5.4.1
Let
![]() $M=L_I$
be a
$M=L_I$
be a
![]() $\sigma $
-stable standard Levi subgroup. As before, we write
$\sigma $
-stable standard Levi subgroup. As before, we write
![]() $M=M_0\times M_1$
, where
$M=M_0\times M_1$
, where
![]() $M_0=\operatorname {\mathrm {GL}}_{n_0}$
and
$M_0=\operatorname {\mathrm {GL}}_{n_0}$
and
![]() $M_1=\prod _{i=1}^l(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
for some integers l,
$M_1=\prod _{i=1}^l(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
for some integers l,
![]() $n_0$
, and
$n_0$
, and
![]() $n_i$
. Let
$n_i$
. Let
![]() $N_+$
and
$N_+$
and
![]() $N_-$
be some nonnegative integers such that
$N_-$
be some nonnegative integers such that
![]() $N_++N_-=[n_0/2]$
, and write
$N_++N_-=[n_0/2]$
, and write
![]() $\mathfrak {W}_+:=\mathfrak {W}_{N_+}$
,
$\mathfrak {W}_+:=\mathfrak {W}_{N_+}$
,
![]() $\mathfrak {W}_-:=\mathfrak {W}_{N_-}$
. For each
$\mathfrak {W}_-:=\mathfrak {W}_{N_-}$
. For each
![]() $j\in \{1,\ldots 2k\}$
, let
$j\in \{1,\ldots 2k\}$
, let
To each
![]() $w_j$
is associated an F-stable and
$w_j$
is associated an F-stable and
![]() $\sigma $
-stable maximal torus
$\sigma $
-stable maximal torus
![]() $T_{w_j}\subset M$
as in §3.4.6. Recall that
$T_{w_j}\subset M$
as in §3.4.6. Recall that
![]() $\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
is the set of
$\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
is the set of
![]() $\sigma $
-stable regular linear characters of
$\sigma $
-stable regular linear characters of
![]() $M_1^F$
in the sense of Definition 3.4.5. Write
$M_1^F$
in the sense of Definition 3.4.5. Write
![]() $\bar {I}:=\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{\mathbf {1},\eta \}$
. Then the elements of
$\bar {I}:=\operatorname {\mathrm {Irr}}(\mathbb {F}^{\ast }_q)\setminus \{\mathbf {1},\eta \}$
. Then the elements of
![]() $\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
are exactly the regular elements of
$\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
are exactly the regular elements of
![]() $\bar {I}^l$
in the sense of §5.2.2. Given
$\bar {I}^l$
in the sense of §5.2.2. Given
![]() $\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
and
$\theta \in \operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
and
![]() $\epsilon \in \{-1,0,+1\}$
, the procedure of §3.4.6 gives a
$\epsilon \in \{-1,0,+1\}$
, the procedure of §3.4.6 gives a
![]() $\sigma $
-stable linear character of
$\sigma $
-stable linear character of
![]() $T_{w_j}^F$
for each j, which is denoted by
$T_{w_j}^F$
for each j, which is denoted by
![]() $\theta _j$
. And we denote by
$\theta _j$
. And we denote by
![]() $\tilde {\theta }_j$
its extension to
$\tilde {\theta }_j$
its extension to
![]() $T_{w_j}^F\!<\!\sigma \!>\!$
, which equals to
$T_{w_j}^F\!<\!\sigma \!>\!$
, which equals to
![]() $1$
at
$1$
at
![]() $\sigma $
. If n is odd, then
$\sigma $
. If n is odd, then
![]() $\epsilon (\theta _j)=\epsilon $
by the definition of
$\epsilon (\theta _j)=\epsilon $
by the definition of
![]() $\theta _j$
.
$\theta _j$
.
Let
![]() $\mathcal {C}=(C_1,\ldots ,C_{2k})$
be a tuple of semi-simple conjugacy classes in
$\mathcal {C}=(C_1,\ldots ,C_{2k})$
be a tuple of semi-simple conjugacy classes in
![]() $G(q)\sigma $
with representatives
$G(q)\sigma $
with representatives
![]() $s_j\sigma $
of the form (5.3.2.2). For each j, regard
$s_j\sigma $
of the form (5.3.2.2). For each j, regard
![]() $s_j\sigma $
as the
$s_j\sigma $
as the
![]() $s'\sigma $
in Lemma 5.3.3. Then let
$s'\sigma $
in Lemma 5.3.3. Then let
![]() $c_j$
and
$c_j$
and
![]() $h_j$
be associated to
$h_j$
be associated to
![]() $s_j\sigma $
and
$s_j\sigma $
and
![]() $w_j$
in the way c and h were associated to
$w_j$
in the way c and h were associated to
![]() $s'\sigma $
and w. Similarly, let
$s'\sigma $
and w. Similarly, let
![]() $\Lambda _j$
,
$\Lambda _j$
,
![]() $\Lambda _{j,+}$
,
$\Lambda _{j,+}$
,
![]() $\Lambda _{j,-}$
, and
$\Lambda _{j,-}$
, and
![]() $I_{j,i}$
with i running over
$I_{j,i}$
with i running over
![]() $\Lambda _j$
, be defined like
$\Lambda _j$
, be defined like
![]() $\Lambda $
,
$\Lambda $
,
![]() $\Lambda _+$
,
$\Lambda _+$
,
![]() $\Lambda _-$
, and
$\Lambda _-$
, and
![]() $I_i$
, respectively. For each j, we can write
$I_i$
, respectively. For each j, we can write
for some characters
![]() $\theta _{j,0}$
,
$\theta _{j,0}$
,
![]() $\alpha _{j,i}$
and
$\alpha _{j,i}$
and
![]() $\beta _{j,i}$
of
$\beta _{j,i}$
of
![]() $\mathbb {F}_q^{\ast }$
. The characters
$\mathbb {F}_q^{\ast }$
. The characters
![]() $\theta _{j,0}$
’s are the same for all j and only depend on
$\theta _{j,0}$
’s are the same for all j and only depend on
![]() $\epsilon $
by definition. Thus, we will write
$\epsilon $
by definition. Thus, we will write
![]() $\theta _0$
instead of
$\theta _0$
instead of
![]() $\theta _{j,0}$
.
$\theta _{j,0}$
.
Lemma 5.4.1. With the above notations, put (cf. Notation 4.3.2)
 $$ \begin{align} \Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}= \begin{cases} -1 & \text{if } \epsilon=- \text{ and } \operatorname{\mathrm{sgn}}\mathcal{C}=-1;\\ 1 & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}= \begin{cases} -1 & \text{if } \epsilon=- \text{ and } \operatorname{\mathrm{sgn}}\mathcal{C}=-1;\\ 1 & \text{otherwise}. \end{cases} \end{align} $$
Suppose that
![]() $\mathcal {C}$
is strongly generic and satisfies (CCL). We have
$\mathcal {C}$
is strongly generic and satisfies (CCL). We have
 $$ \begin{align} \sum_{\theta\in\operatorname{\mathrm{Irr}}_{\operatorname{\mathrm{reg}}}^{\sigma}(M_1^F)}\prod^{2k}_{j=1}\tilde{\theta}_j(h_js_j\sigma h_j^{-1})=(-2)^ll!\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}. \end{align} $$
$$ \begin{align} \sum_{\theta\in\operatorname{\mathrm{Irr}}_{\operatorname{\mathrm{reg}}}^{\sigma}(M_1^F)}\prod^{2k}_{j=1}\tilde{\theta}_j(h_js_j\sigma h_j^{-1})=(-2)^ll!\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}. \end{align} $$
Proof. We will assume
![]() $\epsilon \ne 0$
. The case
$\epsilon \ne 0$
. The case
![]() $\epsilon =0$
follows from similar arguments. Under (CCL), we are in the situation of Corollary 5.3.4, and so for each j we have,
$\epsilon =0$
follows from similar arguments. Under (CCL), we are in the situation of Corollary 5.3.4, and so for each j we have,
 $$ \begin{align*}\tilde{\theta}_j(h_js_j\sigma h^{-1}_j)=\theta_{0}(c_j)\prod_{i\in\Lambda_{j,+}}\alpha_{j,i}(\prod_{\gamma\in I_{j,i}}a^{2}_{j,\gamma}),\end{align*} $$
$$ \begin{align*}\tilde{\theta}_j(h_js_j\sigma h^{-1}_j)=\theta_{0}(c_j)\prod_{i\in\Lambda_{j,+}}\alpha_{j,i}(\prod_{\gamma\in I_{j,i}}a^{2}_{j,\gamma}),\end{align*} $$
where
![]() $a_{j,\gamma }$
is defined like
$a_{j,\gamma }$
is defined like
![]() $a_{\gamma }$
in Lemma 5.3.3. Obviously,
$a_{\gamma }$
in Lemma 5.3.3. Obviously,
 $$ \begin{align*}\prod_{j}^{2k}\theta_0(c_j)=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}},\end{align*} $$
$$ \begin{align*}\prod_{j}^{2k}\theta_0(c_j)=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}},\end{align*} $$
and for any j and
![]() $i\in \Lambda _{j,+}$
, we have
$i\in \Lambda _{j,+}$
, we have
![]() $\alpha _{j,i}(\prod _{\gamma \in I_{j,i}}a^{2}_{j,\gamma })=1$
if
$\alpha _{j,i}(\prod _{\gamma \in I_{j,i}}a^{2}_{j,\gamma })=1$
if
![]() $\alpha _{j,i}=\mathbf {1}$
or
$\alpha _{j,i}=\mathbf {1}$
or
![]() $\eta $
. We will only need to consider the remaining terms.
$\eta $
. We will only need to consider the remaining terms.
Recall that
![]() $\theta $
is defined by a set
$\theta $
is defined by a set
![]() $\{\theta _1,\ldots ,\theta _l\}$
of distinct characters of
$\{\theta _1,\ldots ,\theta _l\}$
of distinct characters of
![]() $\mathbb {F}_q^{\ast }$
. For each
$\mathbb {F}_q^{\ast }$
. For each
![]() $r\in \{1,\ldots ,l\}$
and each j, put
$r\in \{1,\ldots ,l\}$
and each j, put
 $$ \begin{align*}I_{j,r}:=\bigsqcup_{\{i\in\Lambda_{j,+}\mid \alpha_{j,i}=\theta_r\}}I_{j,i},\end{align*} $$
$$ \begin{align*}I_{j,r}:=\bigsqcup_{\{i\in\Lambda_{j,+}\mid \alpha_{j,i}=\theta_r\}}I_{j,i},\end{align*} $$
and for each r,
 $$ \begin{align*}a_r:=\prod_{j=1}^{2k}\prod_{\gamma\in I_{j,r}}a_{j,\gamma}.\end{align*} $$
$$ \begin{align*}a_r:=\prod_{j=1}^{2k}\prod_{\gamma\in I_{j,r}}a_{j,\gamma}.\end{align*} $$
Then,
 $$ \begin{align*}\prod_{j=1}^{2k}\prod_{i\in\Lambda_{j,+}}\alpha_{j,i}(\prod_{\gamma\in I_{j,i}}a^{2}_{j,\gamma})=\prod_{r=1}^{l}\theta_r(a_r^2).\end{align*} $$
$$ \begin{align*}\prod_{j=1}^{2k}\prod_{i\in\Lambda_{j,+}}\alpha_{j,i}(\prod_{\gamma\in I_{j,i}}a^{2}_{j,\gamma})=\prod_{r=1}^{l}\theta_r(a_r^2).\end{align*} $$
Therefore,
 $$ \begin{align*}\sum_{\theta\in\operatorname{\mathrm{Irr}}^{\sigma}_{\operatorname{\mathrm{reg}}}(M_1^F)}\prod^{2k}_{j=1}\tilde{\theta}_j(h_js_j\sigma h_j^{-1})=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}\sum_{\substack{(\theta_1,\ldots,\theta_l)\\ \text{regular}}}\prod^l_{r=1}\theta_r(a_r^2). \end{align*} $$
$$ \begin{align*}\sum_{\theta\in\operatorname{\mathrm{Irr}}^{\sigma}_{\operatorname{\mathrm{reg}}}(M_1^F)}\prod^{2k}_{j=1}\tilde{\theta}_j(h_js_j\sigma h_j^{-1})=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}\sum_{\substack{(\theta_1,\ldots,\theta_l)\\ \text{regular}}}\prod^l_{r=1}\theta_r(a_r^2). \end{align*} $$
Using (5.2.2.1) and Lemma 5.2.2, we get
 $$ \begin{align*}\sum_{\substack{(\theta_1,\ldots,\theta_l)\\ \text{regular}}}\prod^l_{r=1}\theta_r(a_r^2)=\sum_{P_1\prec P_0}\mu(P_1,P_0)(-1)^{l(P_1)}2^l, \end{align*} $$
$$ \begin{align*}\sum_{\substack{(\theta_1,\ldots,\theta_l)\\ \text{regular}}}\prod^l_{r=1}\theta_r(a_r^2)=\sum_{P_1\prec P_0}\mu(P_1,P_0)(-1)^{l(P_1)}2^l, \end{align*} $$
which is equal to
![]() $(-2)^ll!$
by (5.2.1.2).
$(-2)^ll!$
by (5.2.1.2).
6 Symmetric functions associated to wreath products
6.1 Ring of symmetric functions
6.1.1
For
![]() $k\in \{0,1\}$
, let
$k\in \{0,1\}$
, let
![]() $\mathbf {x}^{(k)}=(x^{(k)}_1,x^{(k)}_2,\cdots )$
be an infinite series of variables. Denote by
$\mathbf {x}^{(k)}=(x^{(k)}_1,x^{(k)}_2,\cdots )$
be an infinite series of variables. Denote by
![]() $\mathbf {x}=(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
all of these variables. For any commutative ring with unity R, denote by
$\mathbf {x}=(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
all of these variables. For any commutative ring with unity R, denote by
![]() $\mathbf {Sym}_R[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
the ring of symmetric functions in two variables (symmetric in each
$\mathbf {Sym}_R[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
the ring of symmetric functions in two variables (symmetric in each
![]() $\mathbf {x}^{(k)}$
) with coefficents in R. We will always assume that
$\mathbf {x}^{(k)}$
) with coefficents in R. We will always assume that
![]() $\mathbb {Q}$
is contained in R. The usual choice of R will be the fields
$\mathbb {Q}$
is contained in R. The usual choice of R will be the fields
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbb {Q}(z)$
and
$\mathbb {Q}(z)$
and
![]() $\mathbb {Q}(z,w)$
(i.e., the function fields in variables z and w). If the base field is
$\mathbb {Q}(z,w)$
(i.e., the function fields in variables z and w). If the base field is
![]() $\mathbb {Q}(z,w)$
, then we write
$\mathbb {Q}(z,w)$
, then we write
![]() $\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]=\mathbf {Sym}_{\mathbb {Q}(z,w)}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, and similarly for
$\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]=\mathbf {Sym}_{\mathbb {Q}(z,w)}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, and similarly for
![]() $\mathbb {Q}(z)$
. We will omit the subscript R if there is no confusion with the base ring. For any
$\mathbb {Q}(z)$
. We will omit the subscript R if there is no confusion with the base ring. For any
![]() $r\in \mathbb {Z}_{>0}$
, put
$r\in \mathbb {Z}_{>0}$
, put
 $$ \begin{align} \begin{aligned} p^{(0)}_r(\mathbf{x}):=p_r(\mathbf{x}^{(0)})+p_r(\mathbf{x}^{(1)}),\\ p^{(1)}_r(\mathbf{x}):=p_r(\mathbf{x}^{(0)})-p_r(\mathbf{x}^{(1)}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p^{(0)}_r(\mathbf{x}):=p_r(\mathbf{x}^{(0)})+p_r(\mathbf{x}^{(1)}),\\ p^{(1)}_r(\mathbf{x}):=p_r(\mathbf{x}^{(0)})-p_r(\mathbf{x}^{(1)}), \end{aligned} \end{align} $$
where
![]() $p_r(\mathbf {x}^{(k)})$
is the usual power sum in
$p_r(\mathbf {x}^{(k)})$
is the usual power sum in
![]() $\mathbf {x}^{(k)}$
. Put
$\mathbf {x}^{(k)}$
. Put
![]() $p_0^{(k)}(\mathbf {x})=1$
for both values of k. For a 2-partition
$p_0^{(k)}(\mathbf {x})=1$
for both values of k. For a 2-partition
![]() $\boldsymbol {\lambda }=(\lambda ^{(0)},\lambda ^{(1)})$
, with each partition
$\boldsymbol {\lambda }=(\lambda ^{(0)},\lambda ^{(1)})$
, with each partition
![]() $\lambda ^{(k)}$
written as
$\lambda ^{(k)}$
written as
![]() $\lambda ^{(k)}_1\ge \lambda ^{(k)}_2\ge \cdots $
, the power sum in
$\lambda ^{(k)}_1\ge \lambda ^{(k)}_2\ge \cdots $
, the power sum in
![]() $\mathbf {x}$
is defined by
$\mathbf {x}$
is defined by
The Schur function, monomial symmetric function and the complete symmetric function are respectively defined by
 $$ \begin{align*} s_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &s_{\lambda^{(0)}}(\mathbf{x}^{(0)})s_{\lambda^{(1)}}(\mathbf{x}^{(1)}),\\ m_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &m_{\lambda^{(0)}}(\mathbf{x}^{(0)})m_{\lambda^{(1)}}(\mathbf{x}^{(1)}),\\ h_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &h_{\lambda^{(0)}}(\mathbf{x}^{(0)})h_{\lambda^{(1)}}(\mathbf{x}^{(1)}), \end{align*} $$
$$ \begin{align*} s_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &s_{\lambda^{(0)}}(\mathbf{x}^{(0)})s_{\lambda^{(1)}}(\mathbf{x}^{(1)}),\\ m_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &m_{\lambda^{(0)}}(\mathbf{x}^{(0)})m_{\lambda^{(1)}}(\mathbf{x}^{(1)}),\\ h_{\boldsymbol{\lambda}}(\mathbf{x}):=\ &h_{\lambda^{(0)}}(\mathbf{x}^{(0)})h_{\lambda^{(1)}}(\mathbf{x}^{(1)}), \end{align*} $$
where
![]() $s_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
,
$s_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
,
![]() $m_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
,
$m_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
,
![]() $h_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
are the usual Schur functions, monomial symmetric functions and complete symmetric functions associated to partitions. The usual results on
$h_{\lambda ^{(k)}}(\mathbf {x}^{(k)})$
are the usual Schur functions, monomial symmetric functions and complete symmetric functions associated to partitions. The usual results on
![]() $\mathbf {Sym}[\mathbf {x}^{(0)}]$
and
$\mathbf {Sym}[\mathbf {x}^{(0)}]$
and
![]() $\mathbf {Sym}[\mathbf {x}^{(1)}]$
imply that each family of the symmetric functions above, with
$\mathbf {Sym}[\mathbf {x}^{(1)}]$
imply that each family of the symmetric functions above, with
![]() $\boldsymbol {\lambda }$
running through all 2-partitions, forms a basis of
$\boldsymbol {\lambda }$
running through all 2-partitions, forms a basis of
![]() $\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
$\mathbf {Sym}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
In [Reference ShojiSho01], Shoji defined two families of symmetric functions
![]() $\{P_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}_{\boldsymbol{\Lambda} }$
and
$\{P_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}_{\boldsymbol{\Lambda} }$
and
![]() $\{Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}_{\boldsymbol{\Lambda} }$
in
$\{Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}_{\boldsymbol{\Lambda} }$
in
![]() $\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
. Each of these two families of functions forms a basis of
$\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
. Each of these two families of functions forms a basis of
![]() $\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, and they are both called Hall-Littlewood functions.
$\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, and they are both called Hall-Littlewood functions.
Remark 6.1.1. In [Reference ShojiSho01], Shoji works with reflection groups
![]() $(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
with r not necessarily equal to
$(\mathbb {Z}/r\mathbb {Z})^n\rtimes \mathfrak {S}_n$
with r not necessarily equal to
![]() $2$
. In this general setting, he defines the symmetric functions
$2$
. In this general setting, he defines the symmetric functions
![]() $P^{\pm }_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
$P^{\pm }_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
![]() $Q^{\pm }_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
depending on a sign. When
$Q^{\pm }_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
depending on a sign. When
![]() $n=2$
, they degenerate into
$n=2$
, they degenerate into
![]() $P_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
$P_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
![]() $Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
.
$Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
.
6.1.2
For any partition
![]() $\lambda =(1^{m_1},2^{m_2},\ldots )$
, define
$\lambda =(1^{m_1},2^{m_2},\ldots )$
, define
![]() $\mathfrak {z}_{\lambda }=\prod _ii^{m_i}m_i!$
. For any 2-partition
$\mathfrak {z}_{\lambda }=\prod _ii^{m_i}m_i!$
. For any 2-partition
![]() $\boldsymbol {\lambda }=(\lambda ^{(0)},\lambda ^{(1)})$
, define
$\boldsymbol {\lambda }=(\lambda ^{(0)},\lambda ^{(1)})$
, define
![]() $\mathfrak {z}_{\boldsymbol {\lambda }}=2^{l(\boldsymbol {\lambda })}\mathfrak {z}_{\lambda ^{(0)}}\mathfrak {z}_{\lambda ^{(1)}}$
.
$\mathfrak {z}_{\boldsymbol {\lambda }}=2^{l(\boldsymbol {\lambda })}\mathfrak {z}_{\lambda ^{(0)}}\mathfrak {z}_{\lambda ^{(1)}}$
.
According to [Reference MacdonaldMac95, Chapter I, Appendix B], we have
 $$ \begin{align} p_{\boldsymbol{\beta}}(\mathbf{x})&=\sum_{\boldsymbol{\alpha}\in\mathcal{P}_{n,2}}\chi^{\boldsymbol{\alpha}}_{\boldsymbol{\beta}}~s_{\boldsymbol{\alpha}}(\mathbf{x}); \end{align} $$
$$ \begin{align} p_{\boldsymbol{\beta}}(\mathbf{x})&=\sum_{\boldsymbol{\alpha}\in\mathcal{P}_{n,2}}\chi^{\boldsymbol{\alpha}}_{\boldsymbol{\beta}}~s_{\boldsymbol{\alpha}}(\mathbf{x}); \end{align} $$
 $$ \begin{align} s_{\boldsymbol{\lambda}}(\mathbf{x})&=\sum_{\boldsymbol{\tau}}\frac{1}{\mathfrak{z}_{\boldsymbol{\tau}}}\chi^{\boldsymbol{\lambda}}_{\boldsymbol{\tau}}~p_{\boldsymbol{\tau}}(\mathbf{x}), \end{align} $$
$$ \begin{align} s_{\boldsymbol{\lambda}}(\mathbf{x})&=\sum_{\boldsymbol{\tau}}\frac{1}{\mathfrak{z}_{\boldsymbol{\tau}}}\chi^{\boldsymbol{\lambda}}_{\boldsymbol{\tau}}~p_{\boldsymbol{\tau}}(\mathbf{x}), \end{align} $$
where
![]() $\chi ^{\boldsymbol {\alpha }}_{\boldsymbol {\beta }}$
is the value of the character of
$\chi ^{\boldsymbol {\alpha }}_{\boldsymbol {\beta }}$
is the value of the character of
![]() $(\mathbb {Z}/2\mathbb {Z})^m\rtimes \mathfrak {S}_m$
(
$(\mathbb {Z}/2\mathbb {Z})^m\rtimes \mathfrak {S}_m$
(
![]() $m=|\boldsymbol {\alpha }|=|\boldsymbol {\beta }|$
) of class
$m=|\boldsymbol {\alpha }|=|\boldsymbol {\beta }|$
) of class
![]() $\boldsymbol {\alpha }$
at an element of class
$\boldsymbol {\alpha }$
at an element of class
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
The Kostka-Foulkes polynomials are the entries of the transition matrix
and the modified Kostka-Foulkes polynomials are defined by
with
![]() $\boldsymbol {\Lambda }=\boldsymbol {\Lambda }(\boldsymbol {\alpha })$
.
$\boldsymbol {\Lambda }=\boldsymbol {\Lambda }(\boldsymbol {\alpha })$
.
The transformed Hall-Littlewood function is defined by
and the modified Hall-Littlewood function is defined by
6.2 Orthogonality
6.2.1 Plethysm
Let
![]() $\mathbb {K}$
denote the base field, which will be
$\mathbb {K}$
denote the base field, which will be
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbb {Q}(z)$
or
$\mathbb {Q}(z)$
or
![]() $\mathbb {Q}(z,w)$
, depending on the circumstance. Let R be a
$\mathbb {Q}(z,w)$
, depending on the circumstance. Let R be a
![]() $\lambda $
-ring containing
$\lambda $
-ring containing
![]() $\mathbb {K}$
. Then the ring
$\mathbb {K}$
. Then the ring
![]() $\mathbf {Sym}_R[\mathbf {x}^{(0)}]$
of symmetric functions over R has a natural
$\mathbf {Sym}_R[\mathbf {x}^{(0)}]$
of symmetric functions over R has a natural
![]() $\lambda $
-ring structure
$\lambda $
-ring structure
![]() $\{p_n\}_{n\in \mathbb {Z}_{>0}}$
with
$\{p_n\}_{n\in \mathbb {Z}_{>0}}$
with
![]() $p_n$
sending
$p_n$
sending
![]() $p_1(\mathbf {x}^{(0)})$
to
$p_1(\mathbf {x}^{(0)})$
to
![]() $p_n(\mathbf {x}^{(0)})$
and acting on the coefficients according to the
$p_n(\mathbf {x}^{(0)})$
and acting on the coefficients according to the
![]() $\lambda $
-ring structure of R. If we take
$\lambda $
-ring structure of R. If we take
![]() $R=\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)}]$
, then
$R=\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)}]$
, then
![]() $\mathbf {Sym}_R[\mathbf {x}^{(1)}]\cong \mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
acquires a natural
$\mathbf {Sym}_R[\mathbf {x}^{(1)}]\cong \mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
acquires a natural
![]() $\lambda $
-ring structure, and
$\lambda $
-ring structure, and
![]() $p_n$
sends
$p_n$
sends
![]() $p_1(\mathbf {x}^{(1)})$
to
$p_1(\mathbf {x}^{(1)})$
to
![]() $p_n(\mathbf {x}^{(1)})$
. If
$p_n(\mathbf {x}^{(1)})$
. If
![]() $\mathbb {K}$
contains the indeterminates z or w, then
$\mathbb {K}$
contains the indeterminates z or w, then
![]() $p_n$
sends them to the n’th power. By abuse of notation, we will write
$p_n$
sends them to the n’th power. By abuse of notation, we will write
![]() $\mathbf {x}^{(k)}=p_1(\mathbf {x}^{(k)})$
.
$\mathbf {x}^{(k)}=p_1(\mathbf {x}^{(k)})$
.
Let A be a
![]() $\lambda $
-ring containg
$\lambda $
-ring containg
![]() $\mathbb {K}$
as a
$\mathbb {K}$
as a
![]() $\lambda $
-subring. Given any elements
$\lambda $
-subring. Given any elements
![]() $f_0$
and
$f_0$
and
![]() $f_1$
of A, there is a unique
$f_1$
of A, there is a unique
![]() $\lambda $
-ring homomorphism
$\lambda $
-ring homomorphism
![]() $\varphi _{f_0,f_1}:\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]\rightarrow A$
sending
$\varphi _{f_0,f_1}:\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]\rightarrow A$
sending
![]() $\mathbf {x}^{(0)}$
to
$\mathbf {x}^{(0)}$
to
![]() $f_0$
and
$f_0$
and
![]() $\mathbf {x}^{(1)}$
to
$\mathbf {x}^{(1)}$
to
![]() $f_1$
. For any
$f_1$
. For any
![]() $F\in \mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, its image under this map is denoted by
$F\in \mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, its image under this map is denoted by
![]() $F[f_0,f_1]$
. Concretely, by expressing F as a polynomial
$F[f_0,f_1]$
. Concretely, by expressing F as a polynomial
![]() $f(p_n(\mathbf {x}^{(0)}),p_m(\mathbf {x}^{(1)})\mid n,m\in \mathbb {Z}_{>0})$
, one defines
$f(p_n(\mathbf {x}^{(0)}),p_m(\mathbf {x}^{(1)})\mid n,m\in \mathbb {Z}_{>0})$
, one defines
![]() $F[f_0,f_1]:=f(p_n(f_0),p_m(f_1)\mid n,m\in \mathbb {Z}_{>0})$
. This is the plethystic substitution for F. For example, if
$F[f_0,f_1]:=f(p_n(f_0),p_m(f_1)\mid n,m\in \mathbb {Z}_{>0})$
. This is the plethystic substitution for F. For example, if
![]() $F=s_{\alpha }(\mathbf {x}^{(0)})$
is the usual Schur symmetric function in
$F=s_{\alpha }(\mathbf {x}^{(0)})$
is the usual Schur symmetric function in
![]() $\mathbf {x}^{(0)}$
for some partition
$\mathbf {x}^{(0)}$
for some partition
![]() $\alpha $
, and
$\alpha $
, and
![]() $A=\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, then
$A=\mathbf {Sym}_{\mathbb {K}}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
, then
![]() $F[\mathbf {x}^{(1)},\mathbf {x}^{(0)}]=s_{\alpha }(\mathbf {x}^{(1)})$
.
$F[\mathbf {x}^{(1)},\mathbf {x}^{(0)}]=s_{\alpha }(\mathbf {x}^{(1)})$
.
In what follows, we will often write the variables of a symmetric function in a column vector:
 $$ \begin{align} u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )=u(\mathbf{x})\in\mathbf{Sym}[\mathbf{x}^{(0)},\mathbf{x}^{(1)}]. \end{align} $$
$$ \begin{align} u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )=u(\mathbf{x})\in\mathbf{Sym}[\mathbf{x}^{(0)},\mathbf{x}^{(1)}]. \end{align} $$
Then
![]() $\mathbf {x}^t$
is a row vector. The expression
$\mathbf {x}^t$
is a row vector. The expression
 $$ \begin{align} u( \left( \begin{array}{cc} a & b\\ c & d \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )= u[\begin{bmatrix} a\mathbf{x}^{(0)}+b\mathbf{x}^{(1)}\\ c\mathbf{x}^{(0)}+d\mathbf{x}^{(1)} \end{bmatrix}] \end{align} $$
$$ \begin{align} u( \left( \begin{array}{cc} a & b\\ c & d \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )= u[\begin{bmatrix} a\mathbf{x}^{(0)}+b\mathbf{x}^{(1)}\\ c\mathbf{x}^{(0)}+d\mathbf{x}^{(1)} \end{bmatrix}] \end{align} $$
is the plethystic substitution by
![]() $f_0=a\mathbf {x}^{(0)}+b\mathbf {x}^{(1)}$
and
$f_0=a\mathbf {x}^{(0)}+b\mathbf {x}^{(1)}$
and
![]() $f_1=c\mathbf {x}^{(0)}+d\mathbf {x}^{(1)}$
.
$f_1=c\mathbf {x}^{(0)}+d\mathbf {x}^{(1)}$
.
The following identity will be useful: for any partition
![]() $\alpha $
,
$\alpha $
,
where
![]() $\alpha ^{\ast }$
is the dual partition of
$\alpha ^{\ast }$
is the dual partition of
![]() $\alpha $
.
$\alpha $
.
6.2.2
The Hall inner product on
![]() $\mathbf {Sym}[\mathbf {x}^{(0)}]$
is defined by
$\mathbf {Sym}[\mathbf {x}^{(0)}]$
is defined by
for any partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
. It is known that
$\mu $
. It is known that
The plethystic exponential is defined by
 $$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^{(0)}]=\sum_{n\in\mathbb{Z}_{\ge0}}h_n(\mathbf{x}^{(0)})=\prod_i\frac{1}{1-x^{(0)}_i}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^{(0)}]=\sum_{n\in\mathbb{Z}_{\ge0}}h_n(\mathbf{x}^{(0)})=\prod_i\frac{1}{1-x^{(0)}_i}. \end{align} $$
It satisfies
![]() $\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}+\mathbf {x}^{(1)}]=\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}]\cdot \operatorname {\mathrm {Exp}}[\mathbf {x}^{(1)}]$
. Let
$\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}+\mathbf {x}^{(1)}]=\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}]\cdot \operatorname {\mathrm {Exp}}[\mathbf {x}^{(1)}]$
. Let
![]() $\{u_{\lambda }\}_{\lambda \in \mathcal {P}}$
and
$\{u_{\lambda }\}_{\lambda \in \mathcal {P}}$
and
![]() $\{v_{\lambda }\}_{\lambda \in \mathcal {P}}$
be two families of symmetric functions such that for any
$\{v_{\lambda }\}_{\lambda \in \mathcal {P}}$
be two families of symmetric functions such that for any
![]() $n\in \mathbb {Z}_{>0}$
, each of
$n\in \mathbb {Z}_{>0}$
, each of
![]() $\{u_{\lambda }\}_{\lambda \in \mathcal {P}_n}$
and
$\{u_{\lambda }\}_{\lambda \in \mathcal {P}_n}$
and
![]() $\{v_{\lambda }\}_{\lambda \in \mathcal {P}_n}$
is a basis of the homogenous degree n subspace of
$\{v_{\lambda }\}_{\lambda \in \mathcal {P}_n}$
is a basis of the homogenous degree n subspace of
![]() $\mathbf {Sym}[\mathbf {x}^{(0)}]$
. Then the following conditions are equivalent:
$\mathbf {Sym}[\mathbf {x}^{(0)}]$
. Then the following conditions are equivalent:
-
○
 $\langle u_{\lambda },v_{\mu }\rangle =\delta _{\lambda ,\mu }$
for any
$\langle u_{\lambda },v_{\mu }\rangle =\delta _{\lambda ,\mu }$
for any
 $\lambda $
,
$\lambda $
,
 $\mu $
;
$\mu $
; -
○
 $\sum _{\lambda }u_{\lambda }(\mathbf {x}^{(0)})v_{\lambda }(\mathbf {x}^{(1)})=\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}\mathbf {x}^{(1)}]$
,
$\sum _{\lambda }u_{\lambda }(\mathbf {x}^{(0)})v_{\lambda }(\mathbf {x}^{(1)})=\operatorname {\mathrm {Exp}}[\mathbf {x}^{(0)}\mathbf {x}^{(1)}]$
,
where the bracket means the plethystic substitution, and
![]() $\mathbf {x}^{(0)}\mathbf {x}^{(1)}$
is the family of variables
$\mathbf {x}^{(0)}\mathbf {x}^{(1)}$
is the family of variables
![]() $(x^{(0)}_ix^{(1)}_j)_{i,j}$
.
$(x^{(0)}_ix^{(1)}_j)_{i,j}$
.
6.2.3
The Hall inner product on
![]() $\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
is defined by
$\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
is defined by
for all 2-partitions
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
. By [Reference ShojiSho01, Proposition 2.5], we have
$\boldsymbol {\beta }$
. By [Reference ShojiSho01, Proposition 2.5], we have
The z-inner product on
![]() $\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
is defined by
$\mathbf {Sym}_z[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
is defined by
 $$ \begin{align*}\left\langle F[\mathbf{x}],G[\mathbf{x}]\right\rangle_{z}:=\left\langle F[\mathbf{x}],G[ \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]\right\rangle \end{align*} $$
$$ \begin{align*}\left\langle F[\mathbf{x}],G[\mathbf{x}]\right\rangle_{z}:=\left\langle F[\mathbf{x}],G[ \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]\right\rangle \end{align*} $$
for any F,
![]() $G\in \mathbf {Sym}_{z}[\mathbf {x}]$
. Thus, if
$G\in \mathbf {Sym}_{z}[\mathbf {x}]$
. Thus, if
![]() $u_{\boldsymbol{\alpha} }(\mathbf {x},z)$
and
$u_{\boldsymbol{\alpha} }(\mathbf {x},z)$
and
![]() $v_{\boldsymbol{\alpha} }(\mathbf {x},z)$
are dual basis under the z-inner product, then
$v_{\boldsymbol{\alpha} }(\mathbf {x},z)$
are dual basis under the z-inner product, then
 $$ \begin{align*}\operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\sum_{\boldsymbol{\alpha}}u_{\boldsymbol\alpha}(\mathbf{x};z)v_{\boldsymbol{\alpha}}(\mathbf{y};z). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\sum_{\boldsymbol{\alpha}}u_{\boldsymbol\alpha}(\mathbf{x};z)v_{\boldsymbol{\alpha}}(\mathbf{y};z). \end{align*} $$
We have an explicit expression
 $$ \begin{align*} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\ &\prod_{i,j}\frac{1-z\mathbf{x}^{(1)}_i\mathbf{y}^{(0)}_j}{1-\mathbf{x}^{(0)}_i\mathbf{y}^{(0)}_j}\prod_{i,j}\frac{1-z\mathbf{x}^{(0)}_i\mathbf{y}^{(1)}_j}{1-\mathbf{x}^{(1)}_i\mathbf{y}^{(1)}_j}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\ &\prod_{i,j}\frac{1-z\mathbf{x}^{(1)}_i\mathbf{y}^{(0)}_j}{1-\mathbf{x}^{(0)}_i\mathbf{y}^{(0)}_j}\prod_{i,j}\frac{1-z\mathbf{x}^{(0)}_i\mathbf{y}^{(1)}_j}{1-\mathbf{x}^{(1)}_i\mathbf{y}^{(1)}_j}. \end{align*} $$
This is exactly the generating function
![]() $\Omega (\mathbf {x},\mathbf {y},t)$
in [Reference ShojiSho01, Proposition 2.5].
$\Omega (\mathbf {x},\mathbf {y},t)$
in [Reference ShojiSho01, Proposition 2.5].
6.2.4
The Hall-Littlewood symmetric functions
![]() $P_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
$P_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
and
![]() $Q_{\boldsymbol {\Lambda }'}(\mathbf {x};z)$
form dual basis with respect to the z-inner product.
$Q_{\boldsymbol {\Lambda }'}(\mathbf {x};z)$
form dual basis with respect to the z-inner product.
Theorem 6.2.1 ([Reference ShojiSho01] Corollary 4.6)
There exists a block diagonal matrix
![]() $b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z)$
, with each block corresponding to a similarity class, such that
$b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z)$
, with each block corresponding to a similarity class, such that
 $$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]&=\sum_{\boldsymbol{\Lambda},\boldsymbol{\Lambda}'} b_{\boldsymbol{\Lambda},\boldsymbol{\Lambda}'}(z)P_{\boldsymbol{\Lambda}}(\mathbf{x};z)P_{\boldsymbol{\Lambda}'}(\mathbf{y};z), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]&=\sum_{\boldsymbol{\Lambda},\boldsymbol{\Lambda}'} b_{\boldsymbol{\Lambda},\boldsymbol{\Lambda}'}(z)P_{\boldsymbol{\Lambda}}(\mathbf{x};z)P_{\boldsymbol{\Lambda}'}(\mathbf{y};z), \end{align} $$
 $$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]&=\sum_{\boldsymbol{\Lambda}}P_{\boldsymbol{\Lambda}}(\mathbf{x};z)Q_{\boldsymbol{\Lambda}}(\mathbf{y};z). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]&=\sum_{\boldsymbol{\Lambda}}P_{\boldsymbol{\Lambda}}(\mathbf{x};z)Q_{\boldsymbol{\Lambda}}(\mathbf{y};z). \end{align} $$
Remark 6.2.2. In general,
![]() $Q_{\boldsymbol {\Lambda }}(\mathbf {y};z)$
is a linear combination of
$Q_{\boldsymbol {\Lambda }}(\mathbf {y};z)$
is a linear combination of
![]() $P_{\boldsymbol {\Lambda }'}(\mathbf {y};z)$
with coefficients
$P_{\boldsymbol {\Lambda }'}(\mathbf {y};z)$
with coefficients
![]() $b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z)$
. The minimal element
$b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z)$
. The minimal element
![]() $\boldsymbol {\Lambda }_0=\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)$
with
$\boldsymbol {\Lambda }_0=\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)$
with
![]() $\boldsymbol {\alpha }_0=(\varnothing ,(1^m))$
is alone in its similarity class. If we write
$\boldsymbol {\alpha }_0=(\varnothing ,(1^m))$
is alone in its similarity class. If we write
![]() $b_{\boldsymbol {\Lambda }_0}(z):=b_{\boldsymbol {\Lambda }_0,\boldsymbol {\Lambda }_0}(z)$
, then
$b_{\boldsymbol {\Lambda }_0}(z):=b_{\boldsymbol {\Lambda }_0,\boldsymbol {\Lambda }_0}(z)$
, then
We may also write
![]() $b_{\boldsymbol {\alpha }_0}(z)=b_{\boldsymbol {\Lambda }_0}(z)$
.
$b_{\boldsymbol {\alpha }_0}(z)=b_{\boldsymbol {\Lambda }_0}(z)$
.
Lemma 6.2.3. We have
-
(i)
 $Q_{\boldsymbol {\Lambda }}( \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} ,z)= \bar {H}_{\boldsymbol {\Lambda }}( \left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right ) \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} ,z)$
$Q_{\boldsymbol {\Lambda }}( \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} ,z)= \bar {H}_{\boldsymbol {\Lambda }}( \left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right ) \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} ,z)$
for any
 $\boldsymbol {\Lambda }$
;
$\boldsymbol {\Lambda }$
; -
(ii)
 $ h_{\boldsymbol {\alpha }_0^{\ast }}( \left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right )^{-1} \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} )= (-1)^mz^{-a(\boldsymbol {\alpha }_0)-m}b_{\boldsymbol {\alpha }_0}(z^{-1})^{-1}\tilde {H}_{\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)}(\mathbf {x};z) $
$ h_{\boldsymbol {\alpha }_0^{\ast }}( \left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right )^{-1} \begin {bmatrix} \mathbf {x}^{(0)}\\ \mathbf {x}^{(1)} \end {bmatrix} )= (-1)^mz^{-a(\boldsymbol {\alpha }_0)-m}b_{\boldsymbol {\alpha }_0}(z^{-1})^{-1}\tilde {H}_{\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)}(\mathbf {x};z) $
for
 $\boldsymbol{\alpha} _0=(\varnothing ,(1^m))$
.
$\boldsymbol{\alpha} _0=(\varnothing ,(1^m))$
.
Proof. From the definition of the transformed Hall-Littlewood functions and the orthogonality of the Schur functions, we see that
and so
 $$ \begin{align*}\operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\sum_{\boldsymbol{\Lambda}}P_{\boldsymbol{\Lambda}}(\mathbf{x};z)\bar{H}_{\boldsymbol{\Lambda}}(\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y};z). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Exp}}[\mathbf{x}^t\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y}]=\sum_{\boldsymbol{\Lambda}}P_{\boldsymbol{\Lambda}}(\mathbf{x};z)\bar{H}_{\boldsymbol{\Lambda}}(\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)\mathbf{y};z). \end{align*} $$
This shows that the right-hand side of (i) gives a dual basis of
![]() $\{P_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}$
for the z-inner product and so must coincide with
$\{P_{\boldsymbol {\Lambda }}(\mathbf {x};z)\}$
for the z-inner product and so must coincide with
![]() $Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
.
$Q_{\boldsymbol {\Lambda }}(\mathbf {x};z)$
.
To prove (b), we calculate

Equality ![]() follows from the equality
follows from the equality
![]() $\tilde {H}_{\boldsymbol {\Lambda }_0}(\mathbf {x};z)=z^{a(\boldsymbol {\alpha }_0)}\bar {H}_{\boldsymbol {\Lambda }_0}(\mathbf {x};z^{-1})$
and part (i) of the lemma. Equality
$\tilde {H}_{\boldsymbol {\Lambda }_0}(\mathbf {x};z)=z^{a(\boldsymbol {\alpha }_0)}\bar {H}_{\boldsymbol {\Lambda }_0}(\mathbf {x};z^{-1})$
and part (i) of the lemma. Equality ![]() uses Remark 6.2.2. In equality
uses Remark 6.2.2. In equality ![]() , we have used the second statement about
, we have used the second statement about
![]() $P_{\boldsymbol {\Lambda }}$
in [Reference ShojiSho01, Theorem 4.4]. In equality
$P_{\boldsymbol {\Lambda }}$
in [Reference ShojiSho01, Theorem 4.4]. In equality ![]() , we denote by
, we denote by
![]() $s_{(1^m)}$
the usual Schur function associated to partitions. In equality
$s_{(1^m)}$
the usual Schur function associated to partitions. In equality ![]() , we use (6.2.1.3).
, we use (6.2.1.3).
6.3 Digression – Green functions
For
![]() $\boldsymbol {\Lambda }_0=\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)$
, define the Green function by
$\boldsymbol {\Lambda }_0=\boldsymbol {\Lambda }(\boldsymbol {\alpha }_0)$
, define the Green function by
where
![]() $\chi ^{\boldsymbol {\gamma }}_{\boldsymbol {\beta }}$
is the value of the character
$\chi ^{\boldsymbol {\gamma }}_{\boldsymbol {\beta }}$
is the value of the character
![]() $\chi ^{\boldsymbol {\gamma }}\in \operatorname {\mathrm {Irr}}(\mathfrak {W}_m)$
on the conjugacy class corresponding to
$\chi ^{\boldsymbol {\gamma }}\in \operatorname {\mathrm {Irr}}(\mathfrak {W}_m)$
on the conjugacy class corresponding to
![]() $\boldsymbol{\beta} $
. Let H be
$\boldsymbol{\beta} $
. Let H be
![]() $\operatorname {\mathrm {Sp}}_{2m}$
or
$\operatorname {\mathrm {Sp}}_{2m}$
or
![]() $\operatorname {\mathrm {SO}}_{2m+1}$
over
$\operatorname {\mathrm {SO}}_{2m+1}$
over
![]() $\bar {\mathbb {F}}_q$
, equipped with a split Frobenius F. As in §3.3.1, we denote by
$\bar {\mathbb {F}}_q$
, equipped with a split Frobenius F. As in §3.3.1, we denote by
![]() $W_H$
the Weyl group of H defined by a fixed maximal torus
$W_H$
the Weyl group of H defined by a fixed maximal torus
![]() $T_H$
, and we have an F-stable maximal torus
$T_H$
, and we have an F-stable maximal torus
![]() $T_w$
for each
$T_w$
for each
![]() $w\in W_H$
. The purpose of this subsection is to explain the equality
$w\in W_H$
. The purpose of this subsection is to explain the equality
where the left-hand side is the Green function defined by (3.3.1.1) evaluated at the identity,
![]() $\boldsymbol{\beta} $
is the 2-partition corresponding to the conjugacy class of w, and z is specialised to the prime power q.
$\boldsymbol{\beta} $
is the 2-partition corresponding to the conjugacy class of w, and z is specialised to the prime power q.
This equality is known but not explicitly mentioned in [Reference ShojiSho01].
6.3.1
Let
![]() $b(z)$
be the matrix
$b(z)$
be the matrix
![]() $(b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z))$
as in Theorem 6.2.1. Denote by
$(b_{\boldsymbol {\Lambda },\boldsymbol {\Lambda }'}(z))$
as in Theorem 6.2.1. Denote by
![]() $H(q)$
the finite group
$H(q)$
the finite group
![]() $H^F$
. Define
$H^F$
. Define
where T is the diagonal matrix with entries
![]() $q^{a(\boldsymbol {\alpha })}$
. Let
$q^{a(\boldsymbol {\alpha })}$
. Let
![]() $\tilde {K}(z)$
be the matrix of modified Kostka-Foulkes polynomials (see (6.1.2.4)). By [Reference ShojiSho01, Theorem 5.4], the matrices
$\tilde {K}(z)$
be the matrix of modified Kostka-Foulkes polynomials (see (6.1.2.4)). By [Reference ShojiSho01, Theorem 5.4], the matrices
![]() $P:=\tilde {K}(q)$
satisfy the following matrix equation:
$P:=\tilde {K}(q)$
satisfy the following matrix equation:
The matrix
![]() $\Xi $
is determined by the inner products of Green functions of classical groups, which are known. The matrix
$\Xi $
is determined by the inner products of Green functions of classical groups, which are known. The matrix
![]() $\tilde {\Pi }$
is a block diagonal matrix with nonsingular blocks. The matrix P is a lower triangular block matrix with each diagonal block being the scalar
$\tilde {\Pi }$
is a block diagonal matrix with nonsingular blocks. The matrix P is a lower triangular block matrix with each diagonal block being the scalar
![]() $q^{a(\boldsymbol {\alpha })}$
, with
$q^{a(\boldsymbol {\alpha })}$
, with
![]() $\boldsymbol{\alpha} \in \mathcal {P}^2(m)$
. The polynomials
$\boldsymbol{\alpha} \in \mathcal {P}^2(m)$
. The polynomials
![]() $\tilde {K}_{\boldsymbol {\beta },\boldsymbol {\alpha }}(q)$
are uniquely determined as the entries of P satisfying the above equation.
$\tilde {K}_{\boldsymbol {\beta },\boldsymbol {\alpha }}(q)$
are uniquely determined as the entries of P satisfying the above equation.
Remark 6.3.1 ([Reference ShojiSho01, Theorem 5.4] states that these matrices satisfy [Reference ShojiSho01, (1.5.2)]
For Coxeter groups, this is equivalent to [Reference ShojiSho01, (1.4.2)], since the complex conjugate of an irreducible character coincides with itself.
6.3.2
Let
![]() $\chi \in \operatorname {\mathrm {Irr}}(W_H)$
and let
$\chi \in \operatorname {\mathrm {Irr}}(W_H)$
and let
![]() $(C,\phi )$
be the pair corresponding to
$(C,\phi )$
be the pair corresponding to
![]() $\chi $
under the Springer correspondence (2.4.1.1). Put
$\chi $
under the Springer correspondence (2.4.1.1). Put
 $$ \begin{align*}Q_{\chi}:=\frac{1}{|W_H|}\sum_{w\in W_H}\chi(w)Q_{T_w}^H.\end{align*} $$
$$ \begin{align*}Q_{\chi}:=\frac{1}{|W_H|}\sum_{w\in W_H}\chi(w)Q_{T_w}^H.\end{align*} $$
Then
![]() $Q_{\chi }$
coincides with the characteristic function of the intersection cohomology complex
$Q_{\chi }$
coincides with the characteristic function of the intersection cohomology complex
![]() $\textbf {IC}(\bar {C},\mathcal {L}_{\phi })$
, where
$\textbf {IC}(\bar {C},\mathcal {L}_{\phi })$
, where
![]() $\mathcal {L}_{\phi }$
is the simple H-equivariant local system on C corresponding to
$\mathcal {L}_{\phi }$
is the simple H-equivariant local system on C corresponding to
![]() $\phi $
(see [Reference ShojiSho87, (5.2)]). Let
$\phi $
(see [Reference ShojiSho87, (5.2)]). Let
![]() $I_0$
be a finite set that is in bijection with the image of (2.4.1.1), equipped with the total order induced from symbols. If
$I_0$
be a finite set that is in bijection with the image of (2.4.1.1), equipped with the total order induced from symbols. If
![]() $\chi $
corresponds to
$\chi $
corresponds to
![]() $i\in I_0$
, then we may write
$i\in I_0$
, then we may write
![]() $Q_i=Q_{\chi }$
. For any
$Q_i=Q_{\chi }$
. For any
![]() $(C,\phi )=i\in I_0$
, define the
$(C,\phi )=i\in I_0$
, define the
![]() $H^F$
-invariant function
$H^F$
-invariant function
![]() $\psi _i$
on
$\psi _i$
on
![]() $H^F_u$
as the characteristic function of
$H^F_u$
as the characteristic function of
![]() $\mathcal {L}_{\phi }$
(for a given isomorphism
$\mathcal {L}_{\phi }$
(for a given isomorphism
![]() $F^{\ast }\mathcal {L}_{\phi }\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\mathcal {L}_{\phi }$
). By [Reference ShojiSho87, Theorem 5.3], there exists a square matrix P with entries in
$F^{\ast }\mathcal {L}_{\phi }\smash {\begin {array}{c}\sim \\[-1em] \rightarrow \end {array}}\mathcal {L}_{\phi }$
). By [Reference ShojiSho87, Theorem 5.3], there exists a square matrix P with entries in
![]() $\bar {\mathbb {Q}}_{\ell }$
satisfying
$\bar {\mathbb {Q}}_{\ell }$
satisfying
 $$ \begin{align} Q_i=\sum_{j\in I_0}P_{ij}\psi_j. \end{align} $$
$$ \begin{align} Q_i=\sum_{j\in I_0}P_{ij}\psi_j. \end{align} $$
Beware that this matrix P is the transpose of the P in [Reference ShojiSho87]. Since
![]() $Q_i$
is supported on the closure of C, the matrix P is block lower triangular. By taking the inner products of functions on the unipotent part
$Q_i$
is supported on the closure of C, the matrix P is block lower triangular. By taking the inner products of functions on the unipotent part
![]() $H^F_u$
, we get the following matrix equation for P:
$H^F_u$
, we get the following matrix equation for P:
as [Reference ShojiSho87, (5.6)]. This equation (i.e., entries of
![]() $\boldsymbol{\Lambda} $
and
$\boldsymbol{\Lambda} $
and
![]() $\boldsymbol{\Pi} $
) only differs by a scalar from the equation (6.3.1.1). The solution is unique, and so the entries of this P are also equal to the modified Kostka-Foulkes polynomials
$\boldsymbol{\Pi} $
) only differs by a scalar from the equation (6.3.1.1). The solution is unique, and so the entries of this P are also equal to the modified Kostka-Foulkes polynomials
![]() $\tilde {K}_{\boldsymbol {\beta },\boldsymbol {\alpha }}(q)$
. Finally, observe that if
$\tilde {K}_{\boldsymbol {\beta },\boldsymbol {\alpha }}(q)$
. Finally, observe that if
![]() $C=\{1\}$
, then
$C=\{1\}$
, then
![]() $\phi $
must be the trivial character. Thus,
$\phi $
must be the trivial character. Thus,
where
![]() $i_0$
is the minimal element corresponding to
$i_0$
is the minimal element corresponding to
![]() $(C=\{1\},\phi =\mathbf {1})$
. Combined with the definition of
$(C=\{1\},\phi =\mathbf {1})$
. Combined with the definition of
![]() $Q_{\chi }$
, this implies (6.3.0.2).
$Q_{\chi }$
, this implies (6.3.0.2).
6.3.3
From [Reference ShojiSho01, (1.1.1),(1.4.1)], one sees that
![]() $\tilde {\Pi }_{\boldsymbol {\Lambda }_0,\boldsymbol {\Lambda }_0}=1$
; that is,
$\tilde {\Pi }_{\boldsymbol {\Lambda }_0,\boldsymbol {\Lambda }_0}=1$
; that is,
For
![]() $\operatorname {\mathrm {GL}}_n(q)$
, it is known that (see [Reference MacdonaldMac95, (2.6), (2.7)])
$\operatorname {\mathrm {GL}}_n(q)$
, it is known that (see [Reference MacdonaldMac95, (2.6), (2.7)])
where for any partition
![]() $\lambda $
, the function
$\lambda $
, the function
![]() $b_{\lambda }(z)$
is defined by
$b_{\lambda }(z)$
is defined by
![]() $b_{\lambda }(z)P_{\lambda }(\mathbf {x},z)=Q_{\lambda }(\mathbf {x},z)$
(i.e., the difference between the two Hall-Littlewood symmetric functions associated to the partition
$b_{\lambda }(z)P_{\lambda }(\mathbf {x},z)=Q_{\lambda }(\mathbf {x},z)$
(i.e., the difference between the two Hall-Littlewood symmetric functions associated to the partition
![]() $\lambda $
).
$\lambda $
).
6.4 Symmetric functions associated to types
6.4.1
For any symmetric function
![]() $u(\mathbf {x}^{(0)})\in \mathbf {Sym}[\mathbf {x}^{(0)}]$
, we define
$u(\mathbf {x}^{(0)})\in \mathbf {Sym}[\mathbf {x}^{(0)}]$
, we define
 $$ \begin{align*}u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} ):=u[\mathbf{x}^{(0)}+\mathbf{x}^{(1)}]\in\mathbf{Sym}[\mathbf{x}^{(0)},\mathbf{x}^{(1)}]. \end{align*} $$
$$ \begin{align*}u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} ):=u[\mathbf{x}^{(0)}+\mathbf{x}^{(1)}]\in\mathbf{Sym}[\mathbf{x}^{(0)},\mathbf{x}^{(1)}]. \end{align*} $$
We have
 $$ \begin{align*}u[ \left( \begin{array}{cc} a & b\\ c & d \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} ]=u[(a+c)\mathbf{x}^{(0)}+(b+d)\mathbf{x}^{(1)}].\end{align*} $$
$$ \begin{align*}u[ \left( \begin{array}{cc} a & b\\ c & d \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} ]=u[(a+c)\mathbf{x}^{(0)}+(b+d)\mathbf{x}^{(1)}].\end{align*} $$
In particular,
 $$ \begin{align*} u( \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )&=u[(1-z)(\mathbf{x}^{(0)}+\mathbf{x}^{(1)})],\\ u( \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )&=u[\frac{\mathbf{x}^{(0)}+\mathbf{x}^{(1)}}{1-z}]. \end{align*} $$
$$ \begin{align*} u( \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )&=u[(1-z)(\mathbf{x}^{(0)}+\mathbf{x}^{(1)})],\\ u( \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix} )&=u[\frac{\mathbf{x}^{(0)}+\mathbf{x}^{(1)}}{1-z}]. \end{align*} $$
We will write
 $$ \begin{align} \mathbf{P}=\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \end{align} $$
$$ \begin{align} \mathbf{P}=\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \end{align} $$
in what follows.
6.4.2
For any
![]() $\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-(\omega _i)\in \mathfrak {T}$
, we define the Schur symmetric function associated to
$\boldsymbol{\omega} =\boldsymbol{\omega} _+\boldsymbol{\omega} _-(\omega _i)\in \mathfrak {T}$
, we define the Schur symmetric function associated to
![]() $\boldsymbol{\omega} $
as
$\boldsymbol{\omega} $
as
Regarding
![]() $\mathfrak {T}_{\ast }$
as a subset of
$\mathfrak {T}_{\ast }$
as a subset of
![]() $\mathfrak {T}$
, this definition also makes sense for
$\mathfrak {T}$
, this definition also makes sense for
![]() $\boldsymbol{\omega} \in \mathfrak {T}_{\ast }$
. Monomial symmetric functions, complete symmetric functions and power sum symmetric functions can be similarly defined. Define
$\boldsymbol{\omega} \in \mathfrak {T}_{\ast }$
. Monomial symmetric functions, complete symmetric functions and power sum symmetric functions can be similarly defined. Define
where
![]() $P_{\omega _i}(\mathbf {x},z)$
is the Hall-Littlewood function defined in [Reference MacdonaldMac95, Chapter III], and similarly for
$P_{\omega _i}(\mathbf {x},z)$
is the Hall-Littlewood function defined in [Reference MacdonaldMac95, Chapter III], and similarly for
![]() $Q_{\boldsymbol {\Lambda }(\omega )}(\mathbf {x},z)$
. Note that for any partition
$Q_{\boldsymbol {\Lambda }(\omega )}(\mathbf {x},z)$
. Note that for any partition
![]() $\lambda $
, we have
$\lambda $
, we have
This implies, in particular, that
![]() $p_{\boldsymbol{\omega} }(\mathbf {x})=p_{[\boldsymbol{\omega} ]}(\mathbf {x})$
.
$p_{\boldsymbol{\omega} }(\mathbf {x})=p_{[\boldsymbol{\omega} ]}(\mathbf {x})$
.
6.4.3
For any
![]() $\boldsymbol{\omega} \in \mathfrak {T}$
, define
$\boldsymbol{\omega} \in \mathfrak {T}$
, define
![]() $\mathfrak {z}_{\boldsymbol{\omega} }:=\mathfrak {z}_{\boldsymbol{\omega} _+}\mathfrak {z}_{\boldsymbol{\omega} _-}\prod _i\mathfrak {z}_{\omega _i}$
. Define
$\mathfrak {z}_{\boldsymbol{\omega} }:=\mathfrak {z}_{\boldsymbol{\omega} _+}\mathfrak {z}_{\boldsymbol{\omega} _-}\prod _i\mathfrak {z}_{\omega _i}$
. Define
We may write
![]() $a(\boldsymbol{\omega} ):=a(\boldsymbol {\Lambda }(\boldsymbol{\omega} ))$
. For any
$a(\boldsymbol{\omega} ):=a(\boldsymbol {\Lambda }(\boldsymbol{\omega} ))$
. For any
![]() $\boldsymbol{\lambda} =\lambda _+\lambda _-(\lambda _i)\in \mathfrak {T}^{\circ }$
, define
$\boldsymbol{\lambda} =\lambda _+\lambda _-(\lambda _i)\in \mathfrak {T}^{\circ }$
, define
In particular, for
![]() $\boldsymbol{\alpha} \in \mathfrak {T}_{\ast }$
, we have
$\boldsymbol{\alpha} \in \mathfrak {T}_{\ast }$
, we have
![]() $a(\boldsymbol{\alpha} )=n(\boldsymbol{\alpha} )$
. For
$a(\boldsymbol{\alpha} )=n(\boldsymbol{\alpha} )$
. For
![]() $\boldsymbol{\omega} =(\varnothing ,(1)^{m_+})(\varnothing ,(1^{m_-}))((1^{m_i}))_i\in \mathfrak {T}_s$
, define (see Remark 6.2.2 and §6.3.3)
$\boldsymbol{\omega} =(\varnothing ,(1)^{m_+})(\varnothing ,(1^{m_-}))((1^{m_i}))_i\in \mathfrak {T}_s$
, define (see Remark 6.2.2 and §6.3.3)
6.4.4
For any
![]() $\boldsymbol{\alpha} $
,
$\boldsymbol{\alpha} $
,
![]() $\boldsymbol{\beta} \in \tilde {\mathfrak {T}}$
, if
$\boldsymbol{\beta} \in \tilde {\mathfrak {T}}$
, if
![]() $\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
, define
$\boldsymbol{\alpha} \thickapprox \boldsymbol{\beta} $
, define
![]() $\chi ^{\boldsymbol{\alpha} }_{\boldsymbol{\beta} }:=\chi ^{\boldsymbol{\alpha} _+}_{\boldsymbol{\beta} _+}\chi ^{\boldsymbol{\alpha} _-}_{\boldsymbol{\beta} _-}\prod _i\chi ^{\alpha _i}_{\beta _i}$
; otherwise, we put
$\chi ^{\boldsymbol{\alpha} }_{\boldsymbol{\beta} }:=\chi ^{\boldsymbol{\alpha} _+}_{\boldsymbol{\beta} _+}\chi ^{\boldsymbol{\alpha} _-}_{\boldsymbol{\beta} _-}\prod _i\chi ^{\alpha _i}_{\beta _i}$
; otherwise, we put
![]() $\chi ^{\boldsymbol{\alpha} }_{\boldsymbol{\beta} }=0$
. With these definitions, we have
$\chi ^{\boldsymbol{\alpha} }_{\boldsymbol{\beta} }=0$
. With these definitions, we have
 $$ \begin{align} \begin{aligned} p_{\boldsymbol\beta}(\mathbf{x})&=\sum_{\boldsymbol\alpha}\chi^{\boldsymbol\alpha}_{\boldsymbol\beta}~s_{\boldsymbol\alpha}(\mathbf{x});\\ s_{\boldsymbol\lambda}(\mathbf{x})&=\sum_{\boldsymbol\tau}\frac{1}{\mathfrak{z}_{\boldsymbol\tau}}\chi^{\boldsymbol\lambda}_{\boldsymbol\tau}~p_{\boldsymbol\tau}(\mathbf{x}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p_{\boldsymbol\beta}(\mathbf{x})&=\sum_{\boldsymbol\alpha}\chi^{\boldsymbol\alpha}_{\boldsymbol\beta}~s_{\boldsymbol\alpha}(\mathbf{x});\\ s_{\boldsymbol\lambda}(\mathbf{x})&=\sum_{\boldsymbol\tau}\frac{1}{\mathfrak{z}_{\boldsymbol\tau}}\chi^{\boldsymbol\lambda}_{\boldsymbol\tau}~p_{\boldsymbol\tau}(\mathbf{x}). \end{aligned} \end{align} $$
Remark 6.4.1. One needs to be careful with the summations in these expressions. For example, in the first equation,
![]() $\boldsymbol{\alpha} $
runs over the ordered types
$\boldsymbol{\alpha} $
runs over the ordered types
![]() $\tilde {\mathfrak {T}}$
. Although the symmetric functions are independent of the ordering in the types.
$\tilde {\mathfrak {T}}$
. Although the symmetric functions are independent of the ordering in the types.
Define
and put
![]() $K_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z)=0$
otherwise. We then have
$K_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z)=0$
otherwise. We then have
Define
![]() $\tilde {K}_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z)=z^{a(\boldsymbol{\alpha} )}K_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z^{-1})$
.
$\tilde {K}_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z)=z^{a(\boldsymbol{\alpha} )}K_{\boldsymbol{\beta} ,\boldsymbol{\alpha} }(z^{-1})$
.
With the obvious definitions, we have the following identities for types:
In the first equality,
![]() $\boldsymbol{\alpha} $
lies in
$\boldsymbol{\alpha} $
lies in
![]() $\tilde {\mathfrak {T}}_s$
.
$\tilde {\mathfrak {T}}_s$
.
6.4.5
Lemma 6.2.3 (ii) can also be stated for types.
Corollary 6.4.2. Let
![]() $\boldsymbol{\beta} \in \mathfrak {T}_s$
. Then the following identity holds:
$\boldsymbol{\beta} \in \mathfrak {T}_s$
. Then the following identity holds:
Proof. This follows from Lemma 6.2.3 and [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11, Lemma 2.3.6].
Lemma 6.4.3. Let
![]() $\boldsymbol{\alpha} \in \tilde {\mathfrak {T}}$
and
$\boldsymbol{\alpha} \in \tilde {\mathfrak {T}}$
and
![]() $\boldsymbol{\beta} \in \tilde {\mathfrak {T}}_s$
. Then
$\boldsymbol{\beta} \in \tilde {\mathfrak {T}}_s$
. Then
 $$ \begin{align*}\langle s_{\boldsymbol\alpha}(\mathbf{x}),\tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol\beta)}(\mathbf{x},z)\rangle=\sum_{\boldsymbol\tau\in\tilde{\mathfrak{T}}}\frac{\mathfrak{z}_{[\boldsymbol\tau]}\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}}{\mathfrak{z}_{\boldsymbol\tau}}\sum_{\substack{\boldsymbol\nu\in\tilde{\mathfrak{T}}\\ [\boldsymbol\nu]=[\boldsymbol\tau] }}\frac{Q^{\boldsymbol{\Lambda}(\boldsymbol\beta)}_{\boldsymbol\nu}(z)}{\mathfrak{z}_{\boldsymbol\nu}}.\end{align*} $$
$$ \begin{align*}\langle s_{\boldsymbol\alpha}(\mathbf{x}),\tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol\beta)}(\mathbf{x},z)\rangle=\sum_{\boldsymbol\tau\in\tilde{\mathfrak{T}}}\frac{\mathfrak{z}_{[\boldsymbol\tau]}\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}}{\mathfrak{z}_{\boldsymbol\tau}}\sum_{\substack{\boldsymbol\nu\in\tilde{\mathfrak{T}}\\ [\boldsymbol\nu]=[\boldsymbol\tau] }}\frac{Q^{\boldsymbol{\Lambda}(\boldsymbol\beta)}_{\boldsymbol\nu}(z)}{\mathfrak{z}_{\boldsymbol\nu}}.\end{align*} $$
Remark 6.4.4. The inner product only depends on the corresponding unordered types.
Proof. We use the transition matrices
 $$ \begin{align*}s_{\boldsymbol\alpha}(\mathbf{x})=\sum_{\boldsymbol\tau}\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}\frac{p_{\boldsymbol\tau}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\tau}}\end{align*} $$
$$ \begin{align*}s_{\boldsymbol\alpha}(\mathbf{x})=\sum_{\boldsymbol\tau}\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}\frac{p_{\boldsymbol\tau}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\tau}}\end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol\beta)}(\mathbf{x},z) =\ &\sum_{\boldsymbol\tau}\tilde{K}_{\boldsymbol\tau,\boldsymbol\beta}(z)s_{\boldsymbol\tau}(\mathbf{x})\\ =\ &\sum_{\boldsymbol\tau}\sum_{\boldsymbol\nu}\chi^{\boldsymbol\tau}_{\boldsymbol\nu}\tilde{K}_{\boldsymbol\tau,\boldsymbol\beta}(z)\frac{p_{\boldsymbol\nu}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\nu}}\\ =\ &\sum_{\boldsymbol\nu}Q^{\boldsymbol{\Lambda}(\boldsymbol\beta)}_{\boldsymbol\nu}(z)\frac{p_{\boldsymbol\nu}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\nu}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol\beta)}(\mathbf{x},z) =\ &\sum_{\boldsymbol\tau}\tilde{K}_{\boldsymbol\tau,\boldsymbol\beta}(z)s_{\boldsymbol\tau}(\mathbf{x})\\ =\ &\sum_{\boldsymbol\tau}\sum_{\boldsymbol\nu}\chi^{\boldsymbol\tau}_{\boldsymbol\nu}\tilde{K}_{\boldsymbol\tau,\boldsymbol\beta}(z)\frac{p_{\boldsymbol\nu}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\nu}}\\ =\ &\sum_{\boldsymbol\nu}Q^{\boldsymbol{\Lambda}(\boldsymbol\beta)}_{\boldsymbol\nu}(z)\frac{p_{\boldsymbol\nu}(\mathbf{x})}{\mathfrak{z}_{\boldsymbol\nu}}. \end{aligned} \end{align*} $$
The result follows by taking the inner product, noting that
7 Computation of E-polynomials
7.1 A combinatorial formula for irreducible characters
7.1.1
Let us first give a combinatorial expression for the value of an irreducible character at a semi-simple element. Let
![]() $\chi $
be a
$\chi $
be a
![]() $\sigma $
-stable irreducible character of
$\sigma $
-stable irreducible character of
![]() $G(q)$
, which is induced from some
$G(q)$
, which is induced from some
![]() $\sigma $
-stable standard Levi subgroup
$\sigma $
-stable standard Levi subgroup
![]() $M=M_0\times M_1$
as in Theorem 3.4.3. Denote its extension to
$M=M_0\times M_1$
as in Theorem 3.4.3. Denote its extension to
![]() $G(q)\!<\!\sigma \!>\!$
by
$G(q)\!<\!\sigma \!>\!$
by
![]() $\tilde {\chi }$
. If
$\tilde {\chi }$
. If
![]() $\tilde {\chi }$
is uniform, then it can be written as a linear combination of generalised Deligne-Lusztig characters:
$\tilde {\chi }$
is uniform, then it can be written as a linear combination of generalised Deligne-Lusztig characters:
 $$ \begin{align} \tilde{\chi}|_{G^F\sigma}=|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|^{-1}\!\!\!\!\!\!\!\!\sum_{\substack{\tau=(w_+,w_-,w_1)\\\in\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}}}\!\!\!\!\!\!\!\!\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)R^{G\sigma}_{T_{w_1,\mathbf{w}}\sigma}\tilde{\theta}_{w_1,\mathbf{w}} \end{align} $$
$$ \begin{align} \tilde{\chi}|_{G^F\sigma}=|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|^{-1}\!\!\!\!\!\!\!\!\sum_{\substack{\tau=(w_+,w_-,w_1)\\\in\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}}}\!\!\!\!\!\!\!\!\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)R^{G\sigma}_{T_{w_1,\mathbf{w}}\sigma}\tilde{\theta}_{w_1,\mathbf{w}} \end{align} $$
by Theorem 3.4.7. We will write
![]() $T_{\tau }=T_{w_1,\mathbf {w}}$
and
$T_{\tau }=T_{w_1,\mathbf {w}}$
and
![]() $\theta _{\tau }=\theta _{w_1,\mathbf {w}}$
. Suppose that
$\theta _{\tau }=\theta _{w_1,\mathbf {w}}$
. Suppose that
![]() $\chi $
is of type
$\chi $
is of type
![]() $\epsilon \boldsymbol{\alpha} $
. As is explained in §3.5.2, the irreducible character
$\epsilon \boldsymbol{\alpha} $
. As is explained in §3.5.2, the irreducible character
![]() $(\varphi _+,\varphi _-,\varphi )$
of
$(\varphi _+,\varphi _-,\varphi )$
of
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
corresponds to a unique ordered type, the unordered version of which is exactly
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
corresponds to a unique ordered type, the unordered version of which is exactly
![]() $\boldsymbol{\alpha} $
, with the ordering provided by a specific choice of isomorphism
$\boldsymbol{\alpha} $
, with the ordering provided by a specific choice of isomorphism
![]() $M_1\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
. In this subsection, we fix such an isomorphism and so
$M_1\cong \prod _i(\operatorname {\mathrm {GL}}_{n_i}\times \operatorname {\mathrm {GL}}_{n_i})$
. In this subsection, we fix such an isomorphism and so
![]() $\boldsymbol{\alpha} $
will be regarded as an element of
$\boldsymbol{\alpha} $
will be regarded as an element of
![]() $\tilde {\mathfrak {T}}$
. The sum over
$\tilde {\mathfrak {T}}$
. The sum over
![]() $\tau $
only depends on its conjugacy class, which we denote by
$\tau $
only depends on its conjugacy class, which we denote by
![]() $\mathcal {O}(\tau )$
. Note that the conjugacy classes of
$\mathcal {O}(\tau )$
. Note that the conjugacy classes of
![]() $\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
are parametrised by a subset of
$\mathfrak {W}_+\times \mathfrak {W}_-\times W_1^{\sigma }$
are parametrised by a subset of
![]() $\tilde {\mathfrak {T}}$
. The type of
$\tilde {\mathfrak {T}}$
. The type of
![]() $\mathcal {O}(\tau )$
will be denoted by
$\mathcal {O}(\tau )$
will be denoted by
![]() $\boldsymbol{\tau} $
. We have
$\boldsymbol{\tau} $
. We have
 $$ \begin{align} \frac{|\mathcal{O}(\tau)|}{|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|}=\frac{1}{\mathfrak{z}_{\boldsymbol\tau}},\quad\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)=\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}. \end{align} $$
$$ \begin{align} \frac{|\mathcal{O}(\tau)|}{|\mathfrak{W}_+\times\mathfrak{W}_-\times W_1^{\sigma}|}=\frac{1}{\mathfrak{z}_{\boldsymbol\tau}},\quad\varphi_+(w_+)\varphi_-(w_-)\tilde{\varphi}(w_1F)=\chi^{\boldsymbol\alpha}_{\boldsymbol\tau}. \end{align} $$
We will therefore replace
![]() $\sum _{\tau }(-)\text { by }\sum _{\mathcal {O}(\tau )}|\mathcal {O}(\tau )|\cdot (-)$
. However, for each
$\sum _{\tau }(-)\text { by }\sum _{\mathcal {O}(\tau )}|\mathcal {O}(\tau )|\cdot (-)$
. However, for each
![]() $\boldsymbol{\tau} $
, we will choose a
$\boldsymbol{\tau} $
, we will choose a
![]() $\tau $
representing it so that
$\tau $
representing it so that
![]() $T_{\tau }$
and
$T_{\tau }$
and
![]() $\theta _{\tau }$
have definite meanings.
$\theta _{\tau }$
have definite meanings.
If
![]() $s\sigma \in T^F\sigma $
is a semi-simple element, then the character formula (3.3.2.1) reads
$s\sigma \in T^F\sigma $
is a semi-simple element, then the character formula (3.3.2.1) reads
 $$ \begin{align} R^{G\sigma}_{T_{\tau}\sigma}\tilde{\theta}_{\tau}(s\sigma)=\frac{|(T_{\tau}^{\sigma})^{\circ F}|}{|T_{\tau}^F|\cdot|C_G(s\sigma)^{\circ F}|}\sum_{\{h\in G^{F}\mid hs\sigma h^{-1}\in T_{\tau}\sigma\}}Q^{C_G(s\sigma)^{\circ}}_{C_{h^{-1}T_{\tau}h}(s\sigma)^{\circ}}(1)\tilde{\theta}_{\tau}(hs\sigma h^{-1}). \end{align} $$
$$ \begin{align} R^{G\sigma}_{T_{\tau}\sigma}\tilde{\theta}_{\tau}(s\sigma)=\frac{|(T_{\tau}^{\sigma})^{\circ F}|}{|T_{\tau}^F|\cdot|C_G(s\sigma)^{\circ F}|}\sum_{\{h\in G^{F}\mid hs\sigma h^{-1}\in T_{\tau}\sigma\}}Q^{C_G(s\sigma)^{\circ}}_{C_{h^{-1}T_{\tau}h}(s\sigma)^{\circ}}(1)\tilde{\theta}_{\tau}(hs\sigma h^{-1}). \end{align} $$
Denote by
![]() $\boldsymbol{\beta} \in \tilde {\mathfrak {T}}_s$
the type of the conjugacy class of
$\boldsymbol{\beta} \in \tilde {\mathfrak {T}}_s$
the type of the conjugacy class of
![]() $s\sigma $
, which we assume to satisfy (CCL). Recall that the
$s\sigma $
, which we assume to satisfy (CCL). Recall that the
![]() $C_{G}(s\sigma )^{\circ F}$
-conjugacy classes of the F-stable maximal tori of
$C_{G}(s\sigma )^{\circ F}$
-conjugacy classes of the F-stable maximal tori of
![]() $C_{G}(s\sigma )^{\circ }$
are also parametrised by a subset of
$C_{G}(s\sigma )^{\circ }$
are also parametrised by a subset of
![]() $\tilde {\mathfrak {T}}$
. If
$\tilde {\mathfrak {T}}$
. If
![]() $C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
is of type
$C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }$
is of type
![]() $\boldsymbol{\nu} \in \tilde {\mathfrak {T}}$
, we have
$\boldsymbol{\nu} \in \tilde {\mathfrak {T}}$
, we have
![]() $\mathcal {Q}^{\boldsymbol{\Lambda }(\boldsymbol{\beta} )}_{\boldsymbol{\nu} }(q)=Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }}(1)$
, according to (6.3.0.2), together with the analogous known identity for Green functions of
$\mathcal {Q}^{\boldsymbol{\Lambda }(\boldsymbol{\beta} )}_{\boldsymbol{\nu} }(q)=Q^{C_G(s\sigma )^{\circ }}_{C_{h^{-1}T_{\tau }h}(s\sigma )^{\circ }}(1)$
, according to (6.3.0.2), together with the analogous known identity for Green functions of
![]() $\operatorname {\mathrm {GL}}_n(q)$
.
$\operatorname {\mathrm {GL}}_n(q)$
.
Let
![]() $A_{\tau }^F$
and
$A_{\tau }^F$
and
![]() $B_{\tau }$
be as in 3.3.3. Combining (7.1.1.1) and (7.1.1.3) gives
$B_{\tau }$
be as in 3.3.3. Combining (7.1.1.1) and (7.1.1.3) gives

Equality ![]() uses the surjective map
uses the surjective map
![]() $A^F_{\tau }\rightarrow B_{\tau }$
. Note that
$A^F_{\tau }\rightarrow B_{\tau }$
. Note that
![]() $\theta _{\tau }$
depends on
$\theta _{\tau }$
depends on
![]() $\epsilon $
.
$\epsilon $
.
7.1.2
Now we work in the context of §5.4.1. We will write
![]() $\operatorname {\mathrm {Irr}}^{\sigma }_{\operatorname {\mathrm {reg}}}=\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
(see Definition 3.4.5). For each j, let
$\operatorname {\mathrm {Irr}}^{\sigma }_{\operatorname {\mathrm {reg}}}=\operatorname {\mathrm {Irr}}_{\operatorname {\mathrm {reg}}}^{\sigma }(M_1^F)$
(see Definition 3.4.5). For each j, let
![]() $\boldsymbol{\beta} _j$
be the type of the semi-simple conjugacy class
$\boldsymbol{\beta} _j$
be the type of the semi-simple conjugacy class
![]() $C_j$
. Recall that
$C_j$
. Recall that
![]() $\operatorname {\mathrm {Irr}}^{\sigma }_{\epsilon \boldsymbol{\omega} }$
is the set of
$\operatorname {\mathrm {Irr}}^{\sigma }_{\epsilon \boldsymbol{\omega} }$
is the set of
![]() $\sigma $
-stable irreducible characters of type
$\sigma $
-stable irreducible characters of type
![]() $\epsilon \boldsymbol{\omega} $
.
$\epsilon \boldsymbol{\omega} $
.
Lemma 7.1.1. We have
 $$ \begin{align*}\sum_{\chi\in\operatorname{\mathrm{Irr}}^{\sigma}_{\epsilon\boldsymbol\omega}}\prod^{2k}_{j=1}\tilde{\chi}(C_{j})=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}\prod^{2k}_{j=1}\langle s_{\boldsymbol\omega}(\mathbf{x}_j),\tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol{\beta}_j)}(\mathbf{x}_j,q)\rangle,\end{align*} $$
$$ \begin{align*}\sum_{\chi\in\operatorname{\mathrm{Irr}}^{\sigma}_{\epsilon\boldsymbol\omega}}\prod^{2k}_{j=1}\tilde{\chi}(C_{j})=\Delta_{\epsilon,\operatorname{\mathrm{sgn}}\mathcal{C}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}\prod^{2k}_{j=1}\langle s_{\boldsymbol\omega}(\mathbf{x}_j),\tilde{H}_{\boldsymbol{\Lambda}(\boldsymbol{\beta}_j)}(\mathbf{x}_j,q)\rangle,\end{align*} $$
where for each j,
![]() $\mathbf {x}_j=(\mathbf {x}^{(0)}_j,\mathbf {x}^{(1)}_j)$
is an independent family of variables.
$\mathbf {x}_j=(\mathbf {x}^{(0)}_j,\mathbf {x}^{(1)}_j)$
is an independent family of variables.
Proof. We calculate

In equality ![]() , we have applied (7.1.1.4) to each
, we have applied (7.1.1.4) to each
![]() $\tilde {\chi }(C_j)$
. The factor
$\tilde {\chi }(C_j)$
. The factor
![]() $2^{l(\boldsymbol{\omega} _{\ast })}N(\boldsymbol{\omega} _{\ast })$
comes from the surjective map (3.5.2.5). In equality
$2^{l(\boldsymbol{\omega} _{\ast })}N(\boldsymbol{\omega} _{\ast })$
comes from the surjective map (3.5.2.5). In equality ![]() , we have used Lemma 5.4.1. We have
, we have used Lemma 5.4.1. We have ![]() because the summation over
because the summation over
![]() $h_j$
is independent of
$h_j$
is independent of
![]() $h_j$
, which produces a factor
$h_j$
, which produces a factor
 $$ \begin{align*} \frac{|(T^{\sigma}_{\tau_j})^{\circ F}|}{|T_{\tau_j}^F|\cdot|C_G(s_j\sigma)^{\circ F}|}\mathfrak{z}_{[\boldsymbol\tau_j]}\mathfrak{z}_{\boldsymbol\nu_j}^{-1} \end{align*} $$
$$ \begin{align*} \frac{|(T^{\sigma}_{\tau_j})^{\circ F}|}{|T_{\tau_j}^F|\cdot|C_G(s_j\sigma)^{\circ F}|}\mathfrak{z}_{[\boldsymbol\tau_j]}\mathfrak{z}_{\boldsymbol\nu_j}^{-1} \end{align*} $$
by Proposition 3.3.6, if
![]() $A^F_{\boldsymbol{\tau} _j,\boldsymbol{\nu} _j}$
is nonempty. If some
$A^F_{\boldsymbol{\tau} _j,\boldsymbol{\nu} _j}$
is nonempty. If some
![]() $A^F_{\boldsymbol{\tau} _j,\boldsymbol{\nu} _j}$
is empty, then by Lemma 3.5.1, we must have
$A^F_{\boldsymbol{\tau} _j,\boldsymbol{\nu} _j}$
is empty, then by Lemma 3.5.1, we must have
![]() $[\boldsymbol{\nu} _j]\ne [\boldsymbol{\tau} _j]$
. Therefore, we impose
$[\boldsymbol{\nu} _j]\ne [\boldsymbol{\tau} _j]$
. Therefore, we impose
![]() $[\boldsymbol{\nu} _j]=[\boldsymbol{\tau} _j]$
in the summation. Equality
$[\boldsymbol{\nu} _j]=[\boldsymbol{\tau} _j]$
in the summation. Equality ![]() uses Lemma 6.4.3.
uses Lemma 6.4.3.
7.2 Some notations
7.2.1
Recall the Hook polynomial
![]() $H_{\lambda }(z)$
defined for any partition
$H_{\lambda }(z)$
defined for any partition
![]() $\lambda $
:
$\lambda $
:
where
![]() $\lambda $
is regarded as a Young diagram and x runs over the boxes in the diagram, and
$\lambda $
is regarded as a Young diagram and x runs over the boxes in the diagram, and
![]() $h(x)$
is the hook length. If we denote by
$h(x)$
is the hook length. If we denote by
![]() $\lambda ^{\ast }$
the dual partition of
$\lambda ^{\ast }$
the dual partition of
![]() $\lambda $
, then
$\lambda $
, then
For any
![]() $\boldsymbol{\lambda} =\lambda _+\lambda _-(\lambda _i)\in \mathfrak {T}^{\circ }$
, put
$\boldsymbol{\lambda} =\lambda _+\lambda _-(\lambda _i)\in \mathfrak {T}^{\circ }$
, put
![]() $H_{\boldsymbol{\lambda} }(z):=H_{\lambda _+}(z)H_{\lambda _-}(z)\prod _iH_{\lambda _i}(z)$
. Regarding
$H_{\boldsymbol{\lambda} }(z):=H_{\lambda _+}(z)H_{\lambda _-}(z)\prod _iH_{\lambda _i}(z)$
. Regarding
![]() $\mathfrak {T}_{\ast }$
as a subset of
$\mathfrak {T}_{\ast }$
as a subset of
![]() $\mathfrak {T}^{\circ }$
,
$\mathfrak {T}^{\circ }$
,
![]() $H_{\boldsymbol{\lambda} }(z)$
also makes sense for
$H_{\boldsymbol{\lambda} }(z)$
also makes sense for
![]() $\boldsymbol{\lambda} \in \mathfrak {T}_{\ast }$
. Then for
$\boldsymbol{\lambda} \in \mathfrak {T}_{\ast }$
. Then for
![]() $\chi \in \operatorname {\mathrm {Irr}}_{\boldsymbol{\lambda} }^{\sigma }$
, we have ([Reference MacdonaldMac95, Chapter IV, §6 (6.7)])
$\chi \in \operatorname {\mathrm {Irr}}_{\boldsymbol{\lambda} }^{\sigma }$
, we have ([Reference MacdonaldMac95, Chapter IV, §6 (6.7)])
Remark 7.2.1. The equation ([Reference MacdonaldMac95, Chapter IV, §6 (6.7)]) literally reads
with
![]() $\boldsymbol{\lambda} ^{\ast }=\lambda _+^{\ast }\lambda _-^{\ast }(\lambda _i^{\ast })$
. The difference from (7.2.1.3) is due to a different parametrisation of the unipotent characters of
$\boldsymbol{\lambda} ^{\ast }=\lambda _+^{\ast }\lambda _-^{\ast }(\lambda _i^{\ast })$
. The difference from (7.2.1.3) is due to a different parametrisation of the unipotent characters of
![]() $\operatorname {\mathrm {GL}}_n(q)$
by partitions.
$\operatorname {\mathrm {GL}}_n(q)$
by partitions.
7.2.2
According to [Reference ShuShu23, Theorem 4.6], the dimension of the character variety is given by

In ![]() , we have used (2.4.2.1) and the fact that if H is a connected reductive group over
, we have used (2.4.2.1) and the fact that if H is a connected reductive group over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathcal {B}$
is the flag variety of H, then
$\mathcal {B}$
is the flag variety of H, then
![]() $\dim H=2\dim \mathcal {B}+\operatorname {\mathrm {rk}} H$
.
$\dim H=2\dim \mathcal {B}+\operatorname {\mathrm {rk}} H$
.
7.2.3
Define the infinite series as follows:
 $$ \begin{align*} \Omega_{1}(z):=\ &\sum_{\boldsymbol{\alpha}\in\mathcal{P}^2}z^{k|\boldsymbol\alpha|}z^{(1-g-k)|\{\boldsymbol{\alpha}\}_1|}(H_{\{\boldsymbol{\alpha}\}_1}(z)z^{-n(\{\boldsymbol{\alpha}\}_1)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol{\alpha}}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}_j\\ \mathbf{x}^{(1)}_j \end{bmatrix}],\\ \Omega_{0}(z):=\ &\sum_{\boldsymbol{\alpha}\in\mathcal{P}^2}z^{k|\boldsymbol\alpha|}z^{(1-g-k)|\{\boldsymbol{\alpha}\}_0|}(H_{\{\boldsymbol{\alpha}\}_0}(z)z^{-n(\{\boldsymbol{\alpha}\}_0)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol{\alpha}}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}_j\\ \mathbf{x}^{(1)}_j \end{bmatrix}],\\ \Omega_{\ast}(z): =\ &\sum_{\alpha\in\mathcal{P}}z^{(2-2g-k)|\alpha|}(H_{\alpha}(z)^2z^{-2n(\alpha)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\alpha}[\frac{\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j}{1-z}], \end{align*} $$
$$ \begin{align*} \Omega_{1}(z):=\ &\sum_{\boldsymbol{\alpha}\in\mathcal{P}^2}z^{k|\boldsymbol\alpha|}z^{(1-g-k)|\{\boldsymbol{\alpha}\}_1|}(H_{\{\boldsymbol{\alpha}\}_1}(z)z^{-n(\{\boldsymbol{\alpha}\}_1)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol{\alpha}}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}_j\\ \mathbf{x}^{(1)}_j \end{bmatrix}],\\ \Omega_{0}(z):=\ &\sum_{\boldsymbol{\alpha}\in\mathcal{P}^2}z^{k|\boldsymbol\alpha|}z^{(1-g-k)|\{\boldsymbol{\alpha}\}_0|}(H_{\{\boldsymbol{\alpha}\}_0}(z)z^{-n(\{\boldsymbol{\alpha}\}_0)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol{\alpha}}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} \mathbf{x}^{(0)}_j\\ \mathbf{x}^{(1)}_j \end{bmatrix}],\\ \Omega_{\ast}(z): =\ &\sum_{\alpha\in\mathcal{P}}z^{(2-2g-k)|\alpha|}(H_{\alpha}(z)^2z^{-2n(\alpha)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\alpha}[\frac{\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j}{1-z}], \end{align*} $$
where the bracket means plethystic substitution.
7.3 The formulas for E-polynomials
7.3.1
Recall that for each
![]() $1\le j\le 2k$
, we let
$1\le j\le 2k$
, we let
![]() $\boldsymbol{\beta} _j$
denote the type of the semi-simple conjugacy class
$\boldsymbol{\beta} _j$
denote the type of the semi-simple conjugacy class
![]() $C_j$
.
$C_j$
.
Theorem 7.3.1. Suppose that
![]() $\mathcal {C}$
is strongly generic and satisfies (CCL). Then with the notations above, we have
$\mathcal {C}$
is strongly generic and satisfies (CCL). Then with the notations above, we have
 $$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &~q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is odd;} \end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &~q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is odd;} \end{align} $$
 $$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &~q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_{0}^2}{\Omega_{\ast}(q)},\prod^{2k}_{j=1} h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is even.} \end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &~q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_{0}^2}{\Omega_{\ast}(q)},\prod^{2k}_{j=1} h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle,\text{ if } n \text{ is even.} \end{align} $$
Proof. Proposition 4.3.3, equation (4.3.3.1) and Proposition 2.7.1 now give (cf. Notation 4.3.1 and Notation 4.3.2)
 $$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\mathbf{e}=(e_j)\in \mathbf{A}(\mathcal{C})}\sum_{\chi\in\operatorname{\mathrm{Irr}}(G^F)^{\sigma}} \left(\frac{|G^F|}{\chi(1)}\right)^{2g-2}\prod_{j=1}^{2k}\frac{|C_{j,e_j}|\tilde{\chi}(C_{j,e_j})}{\chi(1)}\nonumber\\ =\ &\sum_{\mathbf{e}=(e_j)\in\mathbf{A}(\mathcal{C})}\sum_{|\epsilon\boldsymbol\omega|=N}\frac{|G^F|^{2g-2}\prod^{2k}_{j=1}|C_{j,e_j}|}{\chi(1)^{2g+2k-2}}\sum_{\chi\in\operatorname{\mathrm{Irr}}^{\sigma}_{\epsilon\boldsymbol\omega}}\prod^{2k}_{j=1}\tilde{\chi}(C_{j,e_j}). \end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\mathbf{e}=(e_j)\in \mathbf{A}(\mathcal{C})}\sum_{\chi\in\operatorname{\mathrm{Irr}}(G^F)^{\sigma}} \left(\frac{|G^F|}{\chi(1)}\right)^{2g-2}\prod_{j=1}^{2k}\frac{|C_{j,e_j}|\tilde{\chi}(C_{j,e_j})}{\chi(1)}\nonumber\\ =\ &\sum_{\mathbf{e}=(e_j)\in\mathbf{A}(\mathcal{C})}\sum_{|\epsilon\boldsymbol\omega|=N}\frac{|G^F|^{2g-2}\prod^{2k}_{j=1}|C_{j,e_j}|}{\chi(1)^{2g+2k-2}}\sum_{\chi\in\operatorname{\mathrm{Irr}}^{\sigma}_{\epsilon\boldsymbol\omega}}\prod^{2k}_{j=1}\tilde{\chi}(C_{j,e_j}). \end{align} $$
In the second equality, we have used the fact that irreducible characters of the same type have the same degree (see (7.2.1.3) and (3.5.2.3)). We have also used Lemma 5.1.1 to restrict the summation to a small subset of
![]() $\operatorname {\mathrm {Irr}}(G^F)^{\sigma }$
. This formula holds for any generic tuple of conjugacy classes.
$\operatorname {\mathrm {Irr}}(G^F)^{\sigma }$
. This formula holds for any generic tuple of conjugacy classes.
We will only give the proof for n odd. The even n case is completely analogous. Since we assume
![]() $\mathcal {C}$
to satisfy (CCL), in the odd n case, we have
$\mathcal {C}$
to satisfy (CCL), in the odd n case, we have
![]() $\mathbf {A}(\mathcal {C})\cong \{\pm 1\}^{2k}$
, whereas in the even n case, the group
$\mathbf {A}(\mathcal {C})\cong \{\pm 1\}^{2k}$
, whereas in the even n case, the group
![]() $\mathbf {A}(\mathcal {C})$
is trivial. We calculate
$\mathbf {A}(\mathcal {C})$
is trivial. We calculate

We have the factor
![]() $2^{2k}$
in
$2^{2k}$
in ![]() because
because
 $$ \begin{align} \sum_{\mathbf{e}=(e_j)\in\{\pm\}^{2k}}\Delta_{\epsilon,\mathcal{C}_{\mathbf{e}}}= \begin{cases} 2^{2k} & \text{if } \epsilon=+,\\ 0 & \text{if }\epsilon=-, \end{cases} \end{align} $$
$$ \begin{align} \sum_{\mathbf{e}=(e_j)\in\{\pm\}^{2k}}\Delta_{\epsilon,\mathcal{C}_{\mathbf{e}}}= \begin{cases} 2^{2k} & \text{if } \epsilon=+,\\ 0 & \text{if }\epsilon=-, \end{cases} \end{align} $$
and the sum can be taken over the entire
![]() $\mathfrak {T}$
because if
$\mathfrak {T}$
because if
![]() $\boldsymbol{\omega} $
was not of size N, then the inner product of symmetric functions would vanish. Equality
$\boldsymbol{\omega} $
was not of size N, then the inner product of symmetric functions would vanish. Equality ![]() uses (7.2.1.3).
uses (7.2.1.3).
Equations (6.3.3.1) and (6.3.3.2) show that
where the factor
![]() $1/2$
comes from the two connected components of the orthogonal group. Combined with Corollary 6.4.2, this shows
$1/2$
comes from the two connected components of the orthogonal group. Combined with Corollary 6.4.2, this shows
where we have specialised the variable z in (6.4.1.1) to q.
Note that for any symmetric functions
![]() $u(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
and
$u(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
and
![]() $v(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
, we have
$v(\mathbf {x}^{(0)},\mathbf {x}^{(1)})$
, we have
 $$ \begin{align*}\left\langle u(\mathbf{P}\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}),v(\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix})\right\rangle = \left\langle u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}), v(\mathbf{P}\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}) \right\rangle.\end{align*} $$
$$ \begin{align*}\left\langle u(\mathbf{P}\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}),v(\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix})\right\rangle = \left\langle u( \begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}), v(\mathbf{P}\begin{bmatrix} \mathbf{x}^{(0)}\\ \mathbf{x}^{(1)} \end{bmatrix}) \right\rangle.\end{align*} $$
This can be checked on the basis of power sums. We will thus move
![]() $\mathbf {P}$
to the left-hand side of the inner product.
$\mathbf {P}$
to the left-hand side of the inner product.
Rewrite the left-hand side of the inner product (7.3.1.4) as follows:
 $$ \begin{align*} &q^{-k(|\boldsymbol\omega_+|+|\boldsymbol\omega_-|+\sum_i|\omega_i|+1)}\sum_{\boldsymbol\omega\in\mathfrak{T}} \frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(1-g)|\{\boldsymbol\omega\}|}(H_{\{\boldsymbol\omega\}} (q)q^{-n(\{\boldsymbol\omega\})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega}(\mathbf{P}\mathbf{x}_j)\\ =\ &~~\left(\sum_{\boldsymbol\omega_+\in\mathcal{P}^2}q^{k|\boldsymbol\omega_+|}q^{(1-g-k)|\{\boldsymbol\omega_+\}_1|} (H_{\{\boldsymbol\omega_+\}_1}(q)q^{-n(\{\boldsymbol\omega_+\}_1)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega_+} (\mathbf{P}\mathbf{x}_j)\right)\\ &\cdot\left(\sum_{\boldsymbol\omega_-\in\mathcal{P}^2}q^{k|\boldsymbol\omega_-|} q^{(1-g-k)|\{\boldsymbol\omega_-\}_0|}(H_{\{\boldsymbol\omega_-\}_0}(q)q^{-n(\{\boldsymbol\omega_-\}_0)})^{2g+2k-2} \prod^{2k}_{j=1}s_{\boldsymbol\omega_-}(\mathbf{P}\mathbf{x}_j)\right)\\ &\cdot\left(\sum_{\boldsymbol\omega_{\ast}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(2-2g-k) |\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2}\prod^{2k}_{j=1} s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j)\right). \end{align*} $$
$$ \begin{align*} &q^{-k(|\boldsymbol\omega_+|+|\boldsymbol\omega_-|+\sum_i|\omega_i|+1)}\sum_{\boldsymbol\omega\in\mathfrak{T}} \frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(1-g)|\{\boldsymbol\omega\}|}(H_{\{\boldsymbol\omega\}} (q)q^{-n(\{\boldsymbol\omega\})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega}(\mathbf{P}\mathbf{x}_j)\\ =\ &~~\left(\sum_{\boldsymbol\omega_+\in\mathcal{P}^2}q^{k|\boldsymbol\omega_+|}q^{(1-g-k)|\{\boldsymbol\omega_+\}_1|} (H_{\{\boldsymbol\omega_+\}_1}(q)q^{-n(\{\boldsymbol\omega_+\}_1)})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega_+} (\mathbf{P}\mathbf{x}_j)\right)\\ &\cdot\left(\sum_{\boldsymbol\omega_-\in\mathcal{P}^2}q^{k|\boldsymbol\omega_-|} q^{(1-g-k)|\{\boldsymbol\omega_-\}_0|}(H_{\{\boldsymbol\omega_-\}_0}(q)q^{-n(\{\boldsymbol\omega_-\}_0)})^{2g+2k-2} \prod^{2k}_{j=1}s_{\boldsymbol\omega_-}(\mathbf{P}\mathbf{x}_j)\right)\\ &\cdot\left(\sum_{\boldsymbol\omega_{\ast}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(2-2g-k) |\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2}\prod^{2k}_{j=1} s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j)\right). \end{align*} $$
By definition,
 $$ \begin{align} \frac{1}{\Omega_{\ast}(q)}=\ &\sum_{m\ge 0}(-1)^m\!\!\!\!\sum_{\substack{\boldsymbol\omega_{\ast}=(m_{\lambda})_{\lambda}\in\mathfrak{T}_{\ast}\\ l(\boldsymbol\omega_{\ast})=m}}\frac{m!}{\prod_{\lambda}m_{\lambda}!} q^{(2-2g-k)|\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2} \prod^{2k}_{j=1}s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j)\nonumber\\ =\ &\sum_{\boldsymbol\omega_{\ast}\in\mathfrak{T}_{\ast}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(2-2g-k)|\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j), \end{align} $$
$$ \begin{align} \frac{1}{\Omega_{\ast}(q)}=\ &\sum_{m\ge 0}(-1)^m\!\!\!\!\sum_{\substack{\boldsymbol\omega_{\ast}=(m_{\lambda})_{\lambda}\in\mathfrak{T}_{\ast}\\ l(\boldsymbol\omega_{\ast})=m}}\frac{m!}{\prod_{\lambda}m_{\lambda}!} q^{(2-2g-k)|\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2} \prod^{2k}_{j=1}s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j)\nonumber\\ =\ &\sum_{\boldsymbol\omega_{\ast}\in\mathfrak{T}_{\ast}}\frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(2-2g-k)|\boldsymbol\omega_{\ast}|}(H_{\boldsymbol\omega_{\ast}}(q)^2q^{-2n(\boldsymbol\omega_{\ast})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega_{\ast}}(\mathbf{P}\mathbf{x}_j), \end{align} $$
whence
 $$ \begin{align*} &q^{-k(|\boldsymbol\omega_+|+|\boldsymbol\omega_-|+\sum_i|\omega_i|+1)}\sum_{\boldsymbol\omega\in\mathfrak{T}} \frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(1-g)|\{\boldsymbol\omega\}|}(H_{\{\boldsymbol\omega\}}(q) q^{-n(\{\boldsymbol\omega\})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega}(\mathbf{P}\mathbf{x}_j)\\ =\ &\frac{\Omega_1(q)\Omega_0(q)}{\Omega_{\ast}(q)}. \end{align*} $$
$$ \begin{align*} &q^{-k(|\boldsymbol\omega_+|+|\boldsymbol\omega_-|+\sum_i|\omega_i|+1)}\sum_{\boldsymbol\omega\in\mathfrak{T}} \frac{K(\boldsymbol\omega_{\ast})}{N(\boldsymbol\omega_{\ast})}q^{(1-g)|\{\boldsymbol\omega\}|}(H_{\{\boldsymbol\omega\}}(q) q^{-n(\{\boldsymbol\omega\})})^{2g+2k-2}\prod^{2k}_{j=1}s_{\boldsymbol\omega}(\mathbf{P}\mathbf{x}_j)\\ =\ &\frac{\Omega_1(q)\Omega_0(q)}{\Omega_{\ast}(q)}. \end{align*} $$
Therefore,
 $$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)| =q^{\frac{1}{2}\left(n^2(2g+2k-2)-2kN\right)- \sum^{2k}_{j=1}a(\boldsymbol\beta_j)}\cdot\left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)},\prod^{2k}_{j=1} h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle. \end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)| =q^{\frac{1}{2}\left(n^2(2g+2k-2)-2kN\right)- \sum^{2k}_{j=1}a(\boldsymbol\beta_j)}\cdot\left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)},\prod^{2k}_{j=1} h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle. \end{align} $$
Finally, we use §7.2.2.
7.4 Connected components
Here we give some explicit computations of E-polynomials in the case
![]() $n=2$
and
$n=2$
and
![]() $n=3$
using (7.3.1.3) and the character tables [Reference ShuShu22, Table 1,2,3,4,5]. Unlike Theorem 7.3.1, which assumes (CCL), we only assume genericity of conjugacy classes. This allows conjugacy classes with nonconnected centralisers when n is even. These computations lead to a conjecture on the number of connected components of
$n=3$
using (7.3.1.3) and the character tables [Reference ShuShu22, Table 1,2,3,4,5]. Unlike Theorem 7.3.1, which assumes (CCL), we only assume genericity of conjugacy classes. This allows conjugacy classes with nonconnected centralisers when n is even. These computations lead to a conjecture on the number of connected components of
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
.
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
.
7.4.1
 $G=\operatorname {\mathrm {GL}}_2$
$G=\operatorname {\mathrm {GL}}_2$
Suppose that
![]() $g=1$
and
$g=1$
and
![]() $2k=2$
. Let
$2k=2$
. Let
![]() $C_2$
be the conjugacy class of
$C_2$
be the conjugacy class of
![]() $\sigma $
and let
$\sigma $
and let
![]() $C_1$
be the conjugacy class of
$C_1$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a,a^{-1})\sigma $
, with
$\operatorname {\mathrm {diag}}(a,a^{-1})\sigma $
, with
![]() $a^q=a$
and
$a^q=a$
and
![]() $a^4\ne 1$
, such that
$a^4\ne 1$
, such that
![]() $\mathcal {C}=(C_1,C_2)$
is generic. The counting formula gives
$\mathcal {C}=(C_1,C_2)$
is generic. The counting formula gives
 $$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_2)}{\chi(1)^2}\\ =\ &2q^4-2q^3-2q+2. \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_2)}{\chi(1)^2}\\ =\ &2q^4-2q^3-2q+2. \end{align*} $$
Now let
![]() $C_{2,+}$
be the conjugacy class of
$C_{2,+}$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
. Since its centraliser is not connected, there is another
$\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
. Since its centraliser is not connected, there is another
![]() $G(q)$
-conjugacy class
$G(q)$
-conjugacy class
![]() $C_{2,-}$
that is G-conjugate to
$C_{2,-}$
that is G-conjugate to
![]() $\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
. The counting formula gives
$\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
. The counting formula gives
 $$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\left(\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_{2,+})}{\chi(1)^2}+\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_{2,-})}{\chi(1)^2}\right)\\ =\ &q^6-3q^4+4q^3-3q^2+1. \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\left(\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_{2,+})}{\chi(1)^2}+\frac{|C_1||C_2|\tilde{\chi}(C_1)\tilde{\chi}(C_{2,-})}{\chi(1)^2}\right)\\ =\ &q^6-3q^4+4q^3-3q^2+1. \end{align*} $$
Suppose that
![]() $g=1$
and
$g=1$
and
![]() $2k=4$
. For
$2k=4$
. For
![]() $j\in \{1,2\}$
, let
$j\in \{1,2\}$
, let
![]() $C_j$
be the conjugacy class of
$C_j$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a_j,a_j^{-1})\sigma $
, with
$\operatorname {\mathrm {diag}}(a_j,a_j^{-1})\sigma $
, with
![]() $a_j^q=a_j$
and
$a_j^q=a_j$
and
![]() $a_j^4\ne 1$
, and let
$a_j^4\ne 1$
, and let
![]() $C_{3,+}$
and
$C_{3,+}$
and
![]() $C_{4,+}$
be the conjugacy class of
$C_{4,+}$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
such that
$\operatorname {\mathrm {diag}}(\mathfrak {i},-\mathfrak {i})\sigma $
such that
![]() $(C_1,C_2,C_{3,+},C_{4,+})$
is generic. The counting formula gives
$(C_1,C_2,C_{3,+},C_{4,+})$
is generic. The counting formula gives
 $$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\sum_{(e_3,e_4)\in\{\pm\}^2}\frac{|C_1||C_2||C_{3,e_3}||C_{4,e_4}|}{\chi(1)^4}\tilde{\chi}(C_1)\tilde{\chi}(C_2)\tilde{\chi}(C_{3,e_3})\tilde{\chi}(C_{4,e_4})\\ =\ &q^{12}-4q^{10}+3q^8+16q^7-32q^6+16q^5+3q^4-4q^2+1. \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)|=\ &\sum_{\chi}\sum_{(e_3,e_4)\in\{\pm\}^2}\frac{|C_1||C_2||C_{3,e_3}||C_{4,e_4}|}{\chi(1)^4}\tilde{\chi}(C_1)\tilde{\chi}(C_2)\tilde{\chi}(C_{3,e_3})\tilde{\chi}(C_{4,e_4})\\ =\ &q^{12}-4q^{10}+3q^8+16q^7-32q^6+16q^5+3q^4-4q^2+1. \end{align*} $$
7.4.2
 $G=\operatorname {\mathrm {GL}}_3$
$G=\operatorname {\mathrm {GL}}_3$
Suppose that
![]() $g=0$
and
$g=0$
and
![]() $2k=4$
. For any
$2k=4$
. For any
![]() $j\in \{1,2,3,4\}$
, let
$j\in \{1,2,3,4\}$
, let
![]() $C_{j,+}$
be the conjugacy class of
$C_{j,+}$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a_j,1,a_j^{-1})\sigma $
, with
$\operatorname {\mathrm {diag}}(a_j,1,a_j^{-1})\sigma $
, with
![]() $a_j^q=a_j$
and
$a_j^q=a_j$
and
![]() $a_j^4\ne 1$
, such that
$a_j^4\ne 1$
, such that
![]() $\mathcal {C}=(C_{1,+},C_{2,+},C_{3,+},C_{4,+})$
is generic. Let
$\mathcal {C}=(C_{1,+},C_{2,+},C_{3,+},C_{4,+})$
is generic. Let
![]() $c\in \mathbb {F}^{\ast }_q\setminus (\mathbb {F}_q^{\ast })^2$
and let
$c\in \mathbb {F}^{\ast }_q\setminus (\mathbb {F}_q^{\ast })^2$
and let
![]() $C_{j,-}$
be the conjugacy class of
$C_{j,-}$
be the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a_j,c,a_j^{-1})\sigma $
for each j. Now the counting formula gives
$\operatorname {\mathrm {diag}}(a_j,c,a_j^{-1})\sigma $
for each j. Now the counting formula gives
 $$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)| =\ &\sum_{(e_j)\in\{\pm\}^4}\sum_{\chi}\left(\frac{|G(q)|}{\chi(1)}\right)^2 \prod_j\frac{|C_{j,e_j}|}{|G(q)|}\prod_j\tilde{\chi}(C_{j,e_j})\\ =\ &q^{14}+2q^{13}+q^{12}-2q^{11}-3q^{10}-2q^9-15q^8+36q^7\\ &-15q^6-2q^5-3q^4-2q^3+q^2+2q+1. \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Ch}}_{\mathcal{C}}(\mathbb{F}_q)| =\ &\sum_{(e_j)\in\{\pm\}^4}\sum_{\chi}\left(\frac{|G(q)|}{\chi(1)}\right)^2 \prod_j\frac{|C_{j,e_j}|}{|G(q)|}\prod_j\tilde{\chi}(C_{j,e_j})\\ =\ &q^{14}+2q^{13}+q^{12}-2q^{11}-3q^{10}-2q^9-15q^8+36q^7\\ &-15q^6-2q^5-3q^4-2q^3+q^2+2q+1. \end{align*} $$
Then we keep
![]() $C_{1,\pm }$
,
$C_{1,\pm }$
,
![]() $C_{2,\pm }$
and
$C_{2,\pm }$
and
![]() $C_{3,\pm }$
as above but put
$C_{3,\pm }$
as above but put
![]() $C_{4,\pm }$
to be the conjugacy classes of
$C_{4,\pm }$
to be the conjugacy classes of
![]() $\sigma $
and
$\sigma $
and
![]() $\operatorname {\mathrm {diag}}(1,c,1)\sigma $
. The same counting formula gives
$\operatorname {\mathrm {diag}}(1,c,1)\sigma $
. The same counting formula gives
7.4.3
Observing the leading coefficients in the E-polynomials, we find that some of the character varieties have two connected components, while others are connected. The isomorphism (B.1.2.1) and Remark B.1.1 in the appendix show that in the case
![]() $n=2$
, the variety
$n=2$
, the variety
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is connected exactly when a conjugacy class has nonconnected centraliser. Note that when n is odd, a semi-simple class in
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is connected exactly when a conjugacy class has nonconnected centraliser. Note that when n is odd, a semi-simple class in
![]() $\operatorname {\mathrm {GL}}_n\sigma $
always has nonconnected centraliser.
$\operatorname {\mathrm {GL}}_n\sigma $
always has nonconnected centraliser.
Conjecture 7.4.1. Let
![]() $\mathcal {C}$
be a tuple of semi-simple conjugacy classes in
$\mathcal {C}$
be a tuple of semi-simple conjugacy classes in
![]() $G\sigma $
that is not necessarily generic. Suppose that the character variety
$G\sigma $
that is not necessarily generic. Suppose that the character variety
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is nonempty. Then it has two connected components if and only if every conjugacy class in
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is nonempty. Then it has two connected components if and only if every conjugacy class in
![]() $\mathcal {C}$
contains elements with connected centraliser, and is connected otherwise.
$\mathcal {C}$
contains elements with connected centraliser, and is connected otherwise.
8 Proof of the main theorem
The goal of this section is to prove that our formula for the E-polynomial given by Theorem 7.3.1 agrees with the
![]() $t=-1$
specialisation of Conjecture 1.7. We also show that Conjecture 1.7 implies Conjecture 1.10.
$t=-1$
specialisation of Conjecture 1.7. We also show that Conjecture 1.7 implies Conjecture 1.10.
8.1 Macdonald polynomials
8.1.1
We begin by collecting some basic facts about the Macdonald polynomials.
Definition 8.1.1. Let
![]() $N\in \mathbb {Z}_{\ge 0}$
. The Macdonald polynomials are a family of symmetric functions
$N\in \mathbb {Z}_{\ge 0}$
. The Macdonald polynomials are a family of symmetric functions
that are uniquely determined by the following properties:
-
(i)
 $H_{\lambda }[(1-z)\mathbf {x}^{(0)};z,w]\in \mathbb {Q}(z,w)\{ s_{\mu }(\mathbf {x}^{(0)}):\mu \ge \lambda \}$
;
$H_{\lambda }[(1-z)\mathbf {x}^{(0)};z,w]\in \mathbb {Q}(z,w)\{ s_{\mu }(\mathbf {x}^{(0)}):\mu \ge \lambda \}$
; -
(ii)
 $H_{\lambda }[(1-w)\mathbf {x}^{(0)};z,w]\in \mathbb {Q}(z,w)\{ s_{\mu }(\mathbf {x}^{(0)}):\mu \ge \lambda ^{\ast }\}$
;
$H_{\lambda }[(1-w)\mathbf {x}^{(0)};z,w]\in \mathbb {Q}(z,w)\{ s_{\mu }(\mathbf {x}^{(0)}):\mu \ge \lambda ^{\ast }\}$
; -
(iii)
 $\langle H_{\lambda }(\mathbf {x}^{(0)};z,w),s_{(n)}(\mathbf {x}^{(0)})\rangle =1$
,
$\langle H_{\lambda }(\mathbf {x}^{(0)};z,w),s_{(n)}(\mathbf {x}^{(0)})\rangle =1$
,
where
![]() $\mathbb {Q}(z,w)\{-\}$
signifies the vector space over
$\mathbb {Q}(z,w)\{-\}$
signifies the vector space over
![]() $\mathbb {Q}(z,w)$
spanned by the indicated elements.
$\mathbb {Q}(z,w)$
spanned by the indicated elements.
The
![]() $z,w$
-inner product on
$z,w$
-inner product on
![]() $\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)}]$
is defined by
$\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)}]$
is defined by
for any F,
![]() $G\in \mathbf {Sym}_{z,w}[\mathbf {x}^{(0)}]$
. The Macdonald polynomials are orthogonal with respect to the
$G\in \mathbf {Sym}_{z,w}[\mathbf {x}^{(0)}]$
. The Macdonald polynomials are orthogonal with respect to the
![]() $z,w$
-inner product. Let
$z,w$
-inner product. Let
be the self-pairing of Macdonald polynomials. It has an explicit expression (See [Reference HaimanHai03, Corollary 5.4.8].)
where x runs over the boxes in the Young diagram of
![]() $\lambda $
,
$\lambda $
,
![]() $a(x)$
and
$a(x)$
and
![]() $l(x)$
denote the arm-length and leg-length, respectively. We will need a deformation of
$l(x)$
denote the arm-length and leg-length, respectively. We will need a deformation of
![]() $N_{\lambda }(z,w)$
defined by
$N_{\lambda }(z,w)$
defined by
Remark 8.1.2. We have
 $$ \begin{align*} H_{\lambda}(\mathbf{x}^{(0)};w,z)7&=H_{\lambda^{\ast}}(\mathbf{x}^{(0)};z,w),\\ N_{\lambda}(w,z)&=N_{\lambda^{\ast}}(z,w),\\ N_{\lambda}(zw,w^2,z^2)&=N_{\lambda^{\ast}}(zw,z^2,w^2). \end{align*} $$
$$ \begin{align*} H_{\lambda}(\mathbf{x}^{(0)};w,z)7&=H_{\lambda^{\ast}}(\mathbf{x}^{(0)};z,w),\\ N_{\lambda}(w,z)&=N_{\lambda^{\ast}}(z,w),\\ N_{\lambda}(zw,w^2,z^2)&=N_{\lambda^{\ast}}(zw,z^2,w^2). \end{align*} $$
Lemma 8.1.3. For any
![]() $\lambda \in \mathcal {P}$
, we have
$\lambda \in \mathcal {P}$
, we have
 $$ \begin{align*}H_{\lambda}(\mathbf{x}^{(0)};z,z^{-1})=\frac{s_{\lambda}[\frac{\mathbf{x}^{(0)}}{1-z}]}{s_{\lambda}[\frac{1}{1-z}]}. \end{align*} $$
$$ \begin{align*}H_{\lambda}(\mathbf{x}^{(0)};z,z^{-1})=\frac{s_{\lambda}[\frac{\mathbf{x}^{(0)}}{1-z}]}{s_{\lambda}[\frac{1}{1-z}]}. \end{align*} $$
Lemma 8.1.4. For any
![]() $\lambda \in \mathcal {P}$
, write
$\lambda \in \mathcal {P}$
, write
 $$ \begin{align*}f_{\lambda}(z)=\frac{1}{s_{\lambda}[\frac{1}{1-z}]}.\end{align*} $$
$$ \begin{align*}f_{\lambda}(z)=\frac{1}{s_{\lambda}[\frac{1}{1-z}]}.\end{align*} $$
Then we have
The proofs of the above two lemmas are simple. We will state and prove the corresponding results for wreath Macdonald polynomials below. We will also need the following:
Proposition 8.1.5 [Reference HaimanHai03, Proposition 3.3.2]
Let
![]() $H_{\lambda }(z)$
be the hook polynomial (7.2.1.1). Then
$H_{\lambda }(z)$
be the hook polynomial (7.2.1.1). Then
8.2 Wreath Macdonald polynomials
Wreath Macdonald polynomials can be defined for
![]() $(\mathbb {Z}/r\mathbb {Z})^N\rtimes \mathfrak {S}_N$
for any
$(\mathbb {Z}/r\mathbb {Z})^N\rtimes \mathfrak {S}_N$
for any
![]() $r>1$
. We will only need the case
$r>1$
. We will only need the case
![]() $r=2$
and will therefore work in the ring
$r=2$
and will therefore work in the ring
![]() $\mathbf {Sym}:=\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
$\mathbf {Sym}:=\mathbf {Sym}_{z,w}[\mathbf {x}^{(0)},\mathbf {x}^{(1)}]$
.
8.2.1
Recall that a partition is uniquely determined by its 2-core and 2-quotient. Given a 2-core, then the dominance partial order on
![]() $\mathcal {P}$
induces an order on the set of 2-partitions, regarded as the 2-quotient of those partitions with the given 2-core. Different 2-cores may give different orders. There are only finitely many different such induced orders.
$\mathcal {P}$
induces an order on the set of 2-partitions, regarded as the 2-quotient of those partitions with the given 2-core. Different 2-cores may give different orders. There are only finitely many different such induced orders.
Recall that
![]() $\mathbf {x}$
is regarded as a column of variables.
$\mathbf {x}$
is regarded as a column of variables.
Definition 8.2.1. Let
![]() $N\in \mathbb {Z}_{\ge 0}$
. Fix a 2-core and thus an order on
$N\in \mathbb {Z}_{\ge 0}$
. Fix a 2-core and thus an order on
![]() $\mathcal {P}^2(N)$
. The wreath Macdonald polynomials are a family of symmetric functions
$\mathcal {P}^2(N)$
. The wreath Macdonald polynomials are a family of symmetric functions
that are uniquely determined by the following properties:
-
(i)
 $\tilde {H}_{\boldsymbol{\alpha} }(\left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right )\mathbf {x};z,w)\in \mathbb {Q}(z,w)\{ s_{\boldsymbol{\beta} }(\mathbf {x}):\boldsymbol{\beta} \ge \boldsymbol{\alpha} \}$
;
$\tilde {H}_{\boldsymbol{\alpha} }(\left ( \begin {array}{cc} 1 & -z\\ -z & 1 \end {array} \right )\mathbf {x};z,w)\in \mathbb {Q}(z,w)\{ s_{\boldsymbol{\beta} }(\mathbf {x}):\boldsymbol{\beta} \ge \boldsymbol{\alpha} \}$
; -
(ii)
 $\tilde {H}_{\boldsymbol{\alpha} }(\left ( \begin {array}{cc} 1 & -w\\ -w & 1 \end {array} \right )\mathbf {x};z,w)\in \mathbb {Q}(z,w)\{ s_{\boldsymbol{\beta} }(\mathbf {x}):\boldsymbol{\beta} \ge \boldsymbol{\alpha} ^{\ast }\}$
;
$\tilde {H}_{\boldsymbol{\alpha} }(\left ( \begin {array}{cc} 1 & -w\\ -w & 1 \end {array} \right )\mathbf {x};z,w)\in \mathbb {Q}(z,w)\{ s_{\boldsymbol{\beta} }(\mathbf {x}):\boldsymbol{\beta} \ge \boldsymbol{\alpha} ^{\ast }\}$
; -
(iii)
 $\langle \tilde {H}_{\boldsymbol{\alpha} }(\mathbf {x};z,w),s_{((n),\varnothing )}(\mathbf {x})\rangle =1$
.
$\langle \tilde {H}_{\boldsymbol{\alpha} }(\mathbf {x};z,w),s_{((n),\varnothing )}(\mathbf {x})\rangle =1$
.
The first two conditions in the definition are called triangularity conditions, and the last one is called the normalisation condition.
Theorem 8.2.2 ([Reference HaimanHai03, Conjecture 7.2.19],[Reference Bezrukavnikov and FinkelbergBF14, Corollary 1.2])
Wreath Macdonald polynomials exist, and they are Schur-positive.
Remark 8.2.3. The Schur positivity for wreath Macdonald polynomials means that the coefficients in the Schur basis are Laurent polynomials instead of polynomials. We will see examples of this in Appendix A.
8.2.2
We define the
![]() $z,w$
-inner product on
$z,w$
-inner product on
![]() $\mathbf {Sym}$
by
$\mathbf {Sym}$
by
 $$ \begin{align*}\left\langle F[\mathbf{x}],G[\mathbf{x}]\right\rangle_{z,w}:=\left\langle F[\mathbf{x}],G[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right) \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \left( \begin{array}{cc} 1 & -w\\ -w & 1 \end{array} \right)\mathbf{x}]\right\rangle \end{align*} $$
$$ \begin{align*}\left\langle F[\mathbf{x}],G[\mathbf{x}]\right\rangle_{z,w}:=\left\langle F[\mathbf{x}],G[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right) \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \left( \begin{array}{cc} 1 & -w\\ -w & 1 \end{array} \right)\mathbf{x}]\right\rangle \end{align*} $$
for any F,
![]() $G\in \mathbf {Sym}$
. This inner product is symmetric in F and G. Observe that
$G\in \mathbf {Sym}$
. This inner product is symmetric in F and G. Observe that
 $$ \begin{align*}s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right)\mathbf{x}]=(-1)^{|\boldsymbol\alpha|}s_{\boldsymbol\alpha^{\ast}}(\mathbf{x}).\end{align*} $$
$$ \begin{align*}s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right)\mathbf{x}]=(-1)^{|\boldsymbol\alpha|}s_{\boldsymbol\alpha^{\ast}}(\mathbf{x}).\end{align*} $$
The wreath Macdonald polynomials are orthogonal with respect to this inner product. Let
be the self-pairing of wreath Macdonald polynomials.
According to Orr and Shimozono [Reference Orr and ShimozonoOS20], the self-pairing
![]() $\tilde {N}_{\boldsymbol{\alpha} }(z,w)$
can be written as
$\tilde {N}_{\boldsymbol{\alpha} }(z,w)$
can be written as
where for
![]() $e=0$
or
$e=0$
or
![]() $1$
,
$1$
,
 $$ \begin{align*}\tilde{N}^{\cot}_{\boldsymbol\alpha}(z,w)=\!\!\!\prod_{\substack{x\in\{\boldsymbol\alpha\}_e\\h(x)\equiv0\ \ \quad\mod 2}}\!\!\!(z^{a(x)+1}-w^{l(x)})(z^{a(x)}-w^{l(x)+1}) \end{align*} $$
$$ \begin{align*}\tilde{N}^{\cot}_{\boldsymbol\alpha}(z,w)=\!\!\!\prod_{\substack{x\in\{\boldsymbol\alpha\}_e\\h(x)\equiv0\ \ \quad\mod 2}}\!\!\!(z^{a(x)+1}-w^{l(x)})(z^{a(x)}-w^{l(x)+1}) \end{align*} $$
is the contribution from the cotangent bundle of the Hilbert scheme along the
![]() $\mathbb {Z}/2\mathbb {Z}$
-fixed point locus, and
$\mathbb {Z}/2\mathbb {Z}$
-fixed point locus, and
![]() $\tilde {N}^{\nabla }_{\boldsymbol{\alpha} }(z,w)$
is a complicated term involving a ‘wreath-
$\tilde {N}^{\nabla }_{\boldsymbol{\alpha} }(z,w)$
is a complicated term involving a ‘wreath-
![]() $\nabla $
’ operator. We define the deformation
$\nabla $
’ operator. We define the deformation
 $$ \begin{align*}\tilde{N}^{cot}_{\boldsymbol\alpha}(u,z,w):=\!\!\!\prod_{\substack{x\in\{\boldsymbol\alpha\}_e\\h(x)\equiv0\ \ \quad\mod 2}}\!\!\!(z^{a(x)+1}-uw^{l(x)})(z^{a(x)}-u^{-1}w^{l(x)+1}) \end{align*} $$
$$ \begin{align*}\tilde{N}^{cot}_{\boldsymbol\alpha}(u,z,w):=\!\!\!\prod_{\substack{x\in\{\boldsymbol\alpha\}_e\\h(x)\equiv0\ \ \quad\mod 2}}\!\!\!(z^{a(x)+1}-uw^{l(x)})(z^{a(x)}-u^{-1}w^{l(x)+1}) \end{align*} $$
in agreement with (8.1.1.2), and then
(i.e., the ‘wreath-
![]() $\nabla $
’ term is not deformed).
$\nabla $
’ term is not deformed).
Remark 8.2.4. We have
 $$ \begin{align*} \tilde{H}_{\boldsymbol\alpha}(\mathbf{x};w,z)=\ &\tilde{H}_{\boldsymbol\alpha^{\ast}}(\mathbf{x};z,w),\\ \tilde{N}_{\boldsymbol\alpha}(w,z)=\ &\tilde{N}_{\boldsymbol\alpha^{\ast}}(z,w),\\ \tilde{N}_{\boldsymbol\alpha}(zw,w^2,z^2)=\ &\tilde{N}_{\boldsymbol\alpha^{\ast}}(zw,z^2,w^2). \end{align*} $$
$$ \begin{align*} \tilde{H}_{\boldsymbol\alpha}(\mathbf{x};w,z)=\ &\tilde{H}_{\boldsymbol\alpha^{\ast}}(\mathbf{x};z,w),\\ \tilde{N}_{\boldsymbol\alpha}(w,z)=\ &\tilde{N}_{\boldsymbol\alpha^{\ast}}(z,w),\\ \tilde{N}_{\boldsymbol\alpha}(zw,w^2,z^2)=\ &\tilde{N}_{\boldsymbol\alpha^{\ast}}(zw,z^2,w^2). \end{align*} $$
8.2.3
In this paragraph, we work with a fixed 2-core, which can be either
![]() $(0)$
or
$(0)$
or
![]() $(1)$
.
$(1)$
.
Lemma 8.2.5. For any
![]() $\boldsymbol{\alpha} \in \mathcal {P}^2$
, we have
$\boldsymbol{\alpha} \in \mathcal {P}^2$
, we have
 $$ \begin{align*}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1})=\frac{s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]}{s_{\alpha^{(0)}}[\frac{1}{1-z^2}]s_{\alpha^{(1)}}[\frac{z}{1-z^2}]}. \end{align*} $$
$$ \begin{align*}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1})=\frac{s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]}{s_{\alpha^{(0)}}[\frac{1}{1-z^2}]s_{\alpha^{(1)}}[\frac{z}{1-z^2}]}. \end{align*} $$
Note that this expression has nothing to do with the given 2-core.
Proof. The first two conditions in Definition 8.2.1 imply that
 $$ \begin{align*}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1})=f(z)s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]\end{align*} $$
$$ \begin{align*}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1})=f(z)s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}]\end{align*} $$
for some
![]() $f(z)\in \mathbb {Q}(z)$
. Taking the inner product with
$f(z)\in \mathbb {Q}(z)$
. Taking the inner product with
![]() $s_{((n),\varnothing )}(\mathbf {x})=h_{((n),\varnothing )}(\mathbf {x})$
is equivalent to setting
$s_{((n),\varnothing )}(\mathbf {x})=h_{((n),\varnothing )}(\mathbf {x})$
is equivalent to setting
![]() $\mathbf {x}^{(0)}=1$
and
$\mathbf {x}^{(0)}=1$
and
![]() $\mathbf {x}^{(1)}=0$
. Therefore, condition (iii) of Definition 8.2.1 gives
$\mathbf {x}^{(1)}=0$
. Therefore, condition (iii) of Definition 8.2.1 gives
 $$ \begin{align*}f(z)s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} 1\\ 0 \end{bmatrix}]=1,\end{align*} $$
$$ \begin{align*}f(z)s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1} \begin{bmatrix} 1\\ 0 \end{bmatrix}]=1,\end{align*} $$
whence the lemma.
Lemma 8.2.6. For any
![]() $\boldsymbol{\alpha} \in \mathcal {P}^2$
, write
$\boldsymbol{\alpha} \in \mathcal {P}^2$
, write
 $$ \begin{align*}f_{\boldsymbol\alpha}(z)=\frac{1}{{s_{\alpha^{(0)}}[\frac{1}{1-z^2}]s_{\alpha^{(1)}}[\frac{z}{1-z^2}]}}.\end{align*} $$
$$ \begin{align*}f_{\boldsymbol\alpha}(z)=\frac{1}{{s_{\alpha^{(0)}}[\frac{1}{1-z^2}]s_{\alpha^{(1)}}[\frac{z}{1-z^2}]}}.\end{align*} $$
Then we have
Proof. Using the previous lemma, we calculate
 $$ \begin{align*} &\left\langle \tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1}),\tilde{H}_{\boldsymbol\alpha}[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right) \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \left( \begin{array}{cc} 1 & -z^{-1}\\ -z^{-1} & 1 \end{array} \right)\mathbf{x};z,w]\right\rangle \\ =\ &\langle f(z)s_{\boldsymbol\alpha}(\mathbf{x}),f(z)s_{\boldsymbol\alpha}[\frac{\mathbf{x}}{z}]\rangle \\ =\ &z^{-|\boldsymbol\alpha|}f_{\boldsymbol\alpha}(z)^2.\\[-34pt] \end{align*} $$
$$ \begin{align*} &\left\langle \tilde{H}_{\boldsymbol\alpha}(\mathbf{x};z,z^{-1}),\tilde{H}_{\boldsymbol\alpha}[\left( \begin{array}{cc} 0 & -1\\ -1 & 0 \end{array} \right) \left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right) \left( \begin{array}{cc} 1 & -z^{-1}\\ -z^{-1} & 1 \end{array} \right)\mathbf{x};z,w]\right\rangle \\ =\ &\langle f(z)s_{\boldsymbol\alpha}(\mathbf{x}),f(z)s_{\boldsymbol\alpha}[\frac{\mathbf{x}}{z}]\rangle \\ =\ &z^{-|\boldsymbol\alpha|}f_{\boldsymbol\alpha}(z)^2.\\[-34pt] \end{align*} $$
8.3 Proof of the main theorem
8.3.1
Recall the symmetric functions defined in §1.8 and §7.2.3.
Lemma 8.3.1. We have
 $$ \begin{align*} \Omega_1(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_1(z),\\ \Omega_0(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_0(z),\\ \Omega_{\ast}(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_{\ast}(z).\\ \end{align*} $$
$$ \begin{align*} \Omega_1(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_1(z),\\ \Omega_0(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_0(z),\\ \Omega_{\ast}(\sqrt{z},\frac{1}{\sqrt{z}})&=\Omega_{\ast}(z).\\ \end{align*} $$
Proof. Let us compute
![]() $\Omega _1(\sqrt {z},\frac {1}{\sqrt {z}})$
. By Lemma 8.2.5 and Lemma 8.2.6, we get
$\Omega _1(\sqrt {z},\frac {1}{\sqrt {z}})$
. By Lemma 8.2.5 and Lemma 8.2.6, we get
 $$ \begin{align} \frac{\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z,z^{-1})}{\tilde{N}_{\boldsymbol\alpha}(z,z^{-1})\tilde{N}_{\boldsymbol\alpha}(1,z,z^{-1})^{k-1}}=z^{k|\boldsymbol\alpha|}\prod_{j=1}^{2k}s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}_j]. \end{align} $$
$$ \begin{align} \frac{\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z,z^{-1})}{\tilde{N}_{\boldsymbol\alpha}(z,z^{-1})\tilde{N}_{\boldsymbol\alpha}(1,z,z^{-1})^{k-1}}=z^{k|\boldsymbol\alpha|}\prod_{j=1}^{2k}s_{\boldsymbol\alpha}[\left( \begin{array}{cc} 1 & -z\\ -z & 1 \end{array} \right)^{-1}\mathbf{x}_j]. \end{align} $$
By Lemma 8.1.4 and Proposition 8.1.5, we have
whence the equality for
![]() $\Omega _1$
. The proof for
$\Omega _1$
. The proof for
![]() $\Omega _0$
is similar. For
$\Omega _0$
is similar. For
![]() $\Omega _{\ast }$
, we use Lemma 8.1.3 and Lemma 8.1.4.
$\Omega _{\ast }$
, we use Lemma 8.1.3 and Lemma 8.1.4.
The following proposition finishes the proof of Theorem 1.11.
Proposition 8.3.2. The following equality holds:
Proof. By Theorem 7.3.1, we have
 $$ \begin{align*}H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,-1)=q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle\end{align*} $$
$$ \begin{align*}H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,-1)=q^{\frac{1}{2}d} \left\langle\frac{\Omega(q)_1\Omega(q)_{0}}{\Omega_{\ast}(q)}, \prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}(\mathbf{x}_j)\right\rangle\end{align*} $$
if n is odd. Then the proposition follows from Lemma 8.3.1. The case of even n is similar.
Proof. By the definitions of
![]() $\Omega _e$
,
$\Omega _e$
,
![]() $e=0$
,
$e=0$
,
![]() $1$
, and
$1$
, and
![]() $\Omega _{\ast }$
in §1.7, and Remark 8.1.2 and Remark 8.2.4, we have
$\Omega _{\ast }$
in §1.7, and Remark 8.1.2 and Remark 8.2.4, we have
Then we see that
The proposition follows.
Corollary 8.3.4. The E-polynomial
![]() $E(q)$
of
$E(q)$
of
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
satisfies
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
satisfies
Proof. Use Theorem 1.11 and the above proposition.
This proves Theorem 1.12.
Appendix A Wreath Macdonald polynomials of degrees 1 and 2
Here we give explicit expressions of Macdonald polynomials of degree 2 and wreath Macdonald polynomials of degrees 1 and 2. They will be used in the computation of the mixed Hodge polynomials of
![]() $\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties in the appendices that follow. The reader will also observe some key features of wreath Macdonald polynomials.
$\operatorname {\mathrm {GL}}_n\!<\!\sigma {>}$
-character varieties in the appendices that follow. The reader will also observe some key features of wreath Macdonald polynomials.
A.1 Young diagrams
A.1.1
Young diagrams of the partitions of
![]() $2$
,
$2$
,
![]() $3$
,
$3$
,
![]() $4$
and
$4$
and
![]() $5$
are given below. The boxes defining their 2-quotients are indicated by ‘
$5$
are given below. The boxes defining their 2-quotients are indicated by ‘
![]() $\bullet $
’, and the second row of each table gives the corresponding 2-quotients. (See Remark 2.2.1 for our convention on 2-quotient.) The partitions are ordered in such a way that a partition sits on the left of another if it is larger under the dominance order. We see that the 2-cores
$\bullet $
’, and the second row of each table gives the corresponding 2-quotients. (See Remark 2.2.1 for our convention on 2-quotient.) The partitions are ordered in such a way that a partition sits on the left of another if it is larger under the dominance order. We see that the 2-cores
![]() $(0)$
and
$(0)$
and
![]() $(1)$
induce the same order on the set of 2-partitions of size
$(1)$
induce the same order on the set of 2-partitions of size
![]() $1$
, but different orders on the set of 2-partitions of size 2.
$1$
, but different orders on the set of 2-partitions of size 2.

A.2 Expressions
A.2.1
The wreath Macdonald polynomials of size
![]() $1$
can be directly computed using the definition. We find the following:
$1$
can be directly computed using the definition. We find the following:
Similarly, we can compute the Macdonald polynomials of degree 2:
The
![]() $z,w$
-inner products of these wreath Macdonald polynomials are given by
$z,w$
-inner products of these wreath Macdonald polynomials are given by
And those of Macdonald polynomials are given by
Note that these
![]() $z,w$
-inner products differ from the corresponding products of wreath Macdonald polynomials by
$z,w$
-inner products differ from the corresponding products of wreath Macdonald polynomials by
![]() $(z-1)(1-w)$
.
$(z-1)(1-w)$
.
We will need to compute the Hall inner products of the (wreath) Macdonald polynomials against the complete symmetric functions. It suffices to notice
A.2.2
We list below the wreath Macdonald polynomials of size 2 and their self-pairings. Observe that the coefficients can be a Laurent polynomial, and that in the self-pairings, there are ‘wreath-
![]() $\nabla $
’ terms.
$\nabla $
’ terms.
2-core
![]() $=(0)$
:
$=(0)$
:
2-core
![]() $(1)$
:
$(1)$
:
The self-pairings are given by the same formulae as in the case of 2-core
![]() $(0)$
, except that
$(0)$
, except that
![]() $\tilde {N}_{((2),\varnothing )}$
and
$\tilde {N}_{((2),\varnothing )}$
and
![]() $\tilde {N}_{((1^2),\varnothing )}$
should be exchanged.
$\tilde {N}_{((1^2),\varnothing )}$
should be exchanged.
Appendix B Conjectural mixed Hodge polynomial;
 $n=1$
and
$n=1$
and
 $n=2$
$n=2$
Our formula for the E-polynomial suggests that a two-parameter series
![]() $\Omega _{e}(z,w)$
,
$\Omega _{e}(z,w)$
,
![]() $e=0$
or
$e=0$
or
![]() $1$
, should roughly be of this form (See (8.3.1.1) and (8.3.1.2)):
$1$
, should roughly be of this form (See (8.3.1.1) and (8.3.1.2)):
 $$ \begin{align*}\sum_{\boldsymbol\alpha\in\mathcal{P}^2}\frac{N_{\{\boldsymbol\alpha\}_1}(z^2,w^2)^{g+k-1}}{\tilde{N}_{\boldsymbol\alpha}(z^2,w^2)^k}\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z^2,w^2).\end{align*} $$
$$ \begin{align*}\sum_{\boldsymbol\alpha\in\mathcal{P}^2}\frac{N_{\{\boldsymbol\alpha\}_1}(z^2,w^2)^{g+k-1}}{\tilde{N}_{\boldsymbol\alpha}(z^2,w^2)^k}\prod_{j=1}^{2k}\tilde{H}_{\boldsymbol\alpha}(\mathbf{x}_j;z^2,w^2).\end{align*} $$
But the E-polynomial is unable to distinguish a self-pairing from its deformed version. The computations in this appendix suggest that there should be
![]() $g+k-1$
deformed self-pairings in the numerator and
$g+k-1$
deformed self-pairings in the numerator and
![]() $k-1$
deformed self-pairings in the denominator, with the remaining one undeformed. This explains our definition in §1.7.
$k-1$
deformed self-pairings in the denominator, with the remaining one undeformed. This explains our definition in §1.7.
We work with arbitrary g and
![]() $k>0$
.
$k>0$
.
B.1 Character varieties with
 $n=1$
and
$n=1$
and
 $n=2$
$n=2$
We first give explicit descriptions of the character varieties when
![]() $n=1$
and
$n=1$
and
![]() $n=2$
.
$n=2$
.
B.1.1
When
![]() $n=1$
,
$n=1$
,
![]() $\operatorname {\mathrm {GL}}_1\!<\!\sigma \!>\!$
is just the multiplicative group with
$\operatorname {\mathrm {GL}}_1\!<\!\sigma \!>\!$
is just the multiplicative group with
![]() $\sigma $
acting as the inversion. In this case, there is only one conjugacy class contained in
$\sigma $
acting as the inversion. In this case, there is only one conjugacy class contained in
![]() $\operatorname {\mathrm {GL}}_1\sigma $
: the connected component itself. By definition, the tuple of conjugacy classes
$\operatorname {\mathrm {GL}}_1\sigma $
: the connected component itself. By definition, the tuple of conjugacy classes
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
with each
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
with each
![]() $C_j=\operatorname {\mathrm {GL}}_1\sigma $
is generic, since there is no proper parabolic subgroup except the trivial one. We claim that
$C_j=\operatorname {\mathrm {GL}}_1\sigma $
is generic, since there is no proper parabolic subgroup except the trivial one. We claim that
The defining equation of the character variety reads
 $$ \begin{align*}1=\prod_i^g[A_i,B_i]\prod_j^{2k}X_j\sigma=X_1X_2^{-1}X_3X_4^{-1}\cdots X_{2k-1}X_{2k}^{-1}\end{align*} $$
$$ \begin{align*}1=\prod_i^g[A_i,B_i]\prod_j^{2k}X_j\sigma=X_1X_2^{-1}X_3X_4^{-1}\cdots X_{2k-1}X_{2k}^{-1}\end{align*} $$
with all
![]() $A_i$
,
$A_i$
,
![]() $B_i$
and
$B_i$
and
![]() $X_j$
lying in
$X_j$
lying in
![]() $\mathbb {G}_m$
. The conjugation action of
$\mathbb {G}_m$
. The conjugation action of
![]() $t\in \mathbb {G}_m$
on the coordinates is given by
$t\in \mathbb {G}_m$
on the coordinates is given by
The quotient is a
![]() $(2g+2k-2)$
-dimensional torus.
$(2g+2k-2)$
-dimensional torus.
B.1.2
Now let
![]() $n=2$
. We will give a relation between
$n=2$
. We will give a relation between
![]() $\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties and
$\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties and
![]() $\operatorname {\mathrm {GL}}_2$
-character varieties.
$\operatorname {\mathrm {GL}}_2$
-character varieties.
The centraliser of
![]() $\sigma $
in
$\sigma $
in
![]() $\operatorname {\mathrm {GL}}_2$
is
$\operatorname {\mathrm {GL}}_2$
is
![]() $\operatorname {\mathrm {SL}}_2$
. Therefore, the
$\operatorname {\mathrm {SL}}_2$
. Therefore, the
![]() $\operatorname {\mathrm {GL}}_2$
-conjugacy class of
$\operatorname {\mathrm {GL}}_2$
-conjugacy class of
![]() $\sigma $
is the variety
$\sigma $
is the variety
![]() $\mathbb {G}_m\sigma $
, where elements of
$\mathbb {G}_m\sigma $
, where elements of
![]() $\mathbb {G}_m$
are regarded as scalar matrices. In fact, we can see that each conjugacy class
$\mathbb {G}_m$
are regarded as scalar matrices. In fact, we can see that each conjugacy class
![]() $C\subset \operatorname {\mathrm {GL}}_2\sigma $
is of the form
$C\subset \operatorname {\mathrm {GL}}_2\sigma $
is of the form
![]() $\mathbb {G}_mC'\sigma $
, for some
$\mathbb {G}_mC'\sigma $
, for some
![]() $\operatorname {\mathrm {SL}}_2$
-conjugacy class
$\operatorname {\mathrm {SL}}_2$
-conjugacy class
![]() $C'\subset \operatorname {\mathrm {SL}}_2$
. The semi-simple conjugacy classes in
$C'\subset \operatorname {\mathrm {SL}}_2$
. The semi-simple conjugacy classes in
![]() $\operatorname {\mathrm {GL}}_2\sigma $
have representatives of the form
$\operatorname {\mathrm {GL}}_2\sigma $
have representatives of the form
We require that
![]() $a^2\ne -1$
. Then there are two possibilities. Either
$a^2\ne -1$
. Then there are two possibilities. Either
![]() $s\sigma $
is conjugate to
$s\sigma $
is conjugate to
![]() $\sigma $
, or
$\sigma $
, or
![]() $a^4\ne 1$
, in which case
$a^4\ne 1$
, in which case
These two kinds of conjugacy classes in
![]() $\operatorname {\mathrm {GL}}_2\sigma $
correspond to the conjugacy classes of
$\operatorname {\mathrm {GL}}_2\sigma $
correspond to the conjugacy classes of
![]() $1$
and of
$1$
and of
![]() $\operatorname {\mathrm {diag}}(a,a^{-1})$
in
$\operatorname {\mathrm {diag}}(a,a^{-1})$
in
![]() $\operatorname {\mathrm {SL}}_2$
, respectively.
$\operatorname {\mathrm {SL}}_2$
, respectively.
The inverse image of a conjugacy class
![]() $C\subset \operatorname {\mathrm {GL}}_2\sigma $
under the double covering
$C\subset \operatorname {\mathrm {GL}}_2\sigma $
under the double covering
![]() $\mathbb {G}_m\times \operatorname {\mathrm {SL}}_2\rightarrow \operatorname {\mathrm {GL}}_2\cong \operatorname {\mathrm {GL}}_2\sigma $
is
$\mathbb {G}_m\times \operatorname {\mathrm {SL}}_2\rightarrow \operatorname {\mathrm {GL}}_2\cong \operatorname {\mathrm {GL}}_2\sigma $
is
![]() $(\mathbb {G}_m\times C')\sqcup (\mathbb {G}_m\times -C')$
for some conjugacy class
$(\mathbb {G}_m\times C')\sqcup (\mathbb {G}_m\times -C')$
for some conjugacy class
![]() $C'\subset \operatorname {\mathrm {SL}}_2$
. Given a tuple of semi-simple conjugacy classes
$C'\subset \operatorname {\mathrm {SL}}_2$
. Given a tuple of semi-simple conjugacy classes
![]() $\mathcal {C}=(C_j)_{1\le j\le 2k}$
in
$\mathcal {C}=(C_j)_{1\le j\le 2k}$
in
![]() $\operatorname {\mathrm {GL}}_2\sigma $
, we denote by
$\operatorname {\mathrm {GL}}_2\sigma $
, we denote by
![]() $\mathcal {C}'=(C^{\prime }_j)_{1\le j\le 2k}$
a tuple of conjugacy classes of
$\mathcal {C}'=(C^{\prime }_j)_{1\le j\le 2k}$
a tuple of conjugacy classes of
![]() $\operatorname {\mathrm {SL}}_2$
that gives
$\operatorname {\mathrm {SL}}_2$
that gives
![]() $\mathcal {C}$
in the above fashion. Note that each
$\mathcal {C}$
in the above fashion. Note that each
![]() $\operatorname {\mathrm {SL}}_2$
-conjugacy class is also a
$\operatorname {\mathrm {SL}}_2$
-conjugacy class is also a
![]() $\operatorname {\mathrm {GL}}_2$
-conjugacy class. Thus, it makes sense to consider the varieties:
$\operatorname {\mathrm {GL}}_2$
-conjugacy class. Thus, it makes sense to consider the varieties:
 $$ \begin{align*}\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^{\pm}:=\left\{(A_i,B_i)_i\times (X^{\prime}_j)_j\in \operatorname{\mathrm{GL}}_2^{2g}\times \prod_{j=1}^{2k} C^{\prime}_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X^{\prime}_j=\pm1\right\},\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^{\pm}:=\left\{(A_i,B_i)_i\times (X^{\prime}_j)_j\in \operatorname{\mathrm{GL}}_2^{2g}\times \prod_{j=1}^{2k} C^{\prime}_j\mid\prod_{i=1}^g[A_i,B_i]\prod_{j=1}^{2k}X^{\prime}_j=\pm1\right\},\end{align*} $$
and
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }:=\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^{\pm }\!/\mkern -2mu/\mkern -2mu\operatorname {\mathrm {GL}}_2$
. Define the
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }:=\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^{\pm }\!/\mkern -2mu/\mkern -2mu\operatorname {\mathrm {GL}}_2$
. Define the
![]() $(2k-1)$
-dimensional tori:
$(2k-1)$
-dimensional tori:
We have an isomorphism:
 $$ \begin{align*} (\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^+\times T^+)\sqcup(\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^-\times T^-)&\smash{\begin{array}{c}\sim\\[-1em] \longrightarrow\end{array}}\operatorname{\mathrm{Rep}}_{\mathcal{C}}\\ (A_i,B_i)_i(X^{\prime}_j)_j(t_j)_j&\longmapsto(A_i,B_i)_i(t_jX^{\prime}_j\sigma)_j. \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^+\times T^+)\sqcup(\operatorname{\mathrm{Rep}}_{\mathcal{C}'}^-\times T^-)&\smash{\begin{array}{c}\sim\\[-1em] \longrightarrow\end{array}}\operatorname{\mathrm{Rep}}_{\mathcal{C}}\\ (A_i,B_i)_i(X^{\prime}_j)_j(t_j)_j&\longmapsto(A_i,B_i)_i(t_jX^{\prime}_j\sigma)_j. \end{align*} $$
Indeed, if
![]() $(A_i,B_i)_i(X_j)_j$
lies in
$(A_i,B_i)_i(X_j)_j$
lies in
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
, then each
$\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
, then each
![]() $X_j$
can be written as
$X_j$
can be written as
![]() $t_jX^{\prime }_j\sigma $
for a unique
$t_jX^{\prime }_j\sigma $
for a unique
![]() $X^{\prime }_j\in C^{\prime }_j$
and a
$X^{\prime }_j\in C^{\prime }_j$
and a
![]() $t_j\in \mathbb {G}_m$
, and we have
$t_j\in \mathbb {G}_m$
, and we have
Since
![]() $\operatorname {\mathrm {SL}}_2\cap \mathbb {G}_m=\{\pm 1\}$
, the tuple
$\operatorname {\mathrm {SL}}_2\cap \mathbb {G}_m=\{\pm 1\}$
, the tuple
![]() $(A_i,B_i)_i(X^{\prime }_j)_j(t_j)_j$
lies in
$(A_i,B_i)_i(X^{\prime }_j)_j(t_j)_j$
lies in
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^+\times T^+\sqcup \operatorname {\mathrm {Rep}}_{\mathcal {C}'}^-\times T^-$
. This isomorphism is equivariant for the conjugation action of
$\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^+\times T^+\sqcup \operatorname {\mathrm {Rep}}_{\mathcal {C}'}^-\times T^-$
. This isomorphism is equivariant for the conjugation action of
![]() $\operatorname {\mathrm {GL}}_2$
on
$\operatorname {\mathrm {GL}}_2$
on
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
and the following action on
$\operatorname {\mathrm {Rep}}_{\mathcal {C}}$
and the following action on
![]() $\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^{\pm }\times T^{\pm }$
:
$\operatorname {\mathrm {Rep}}_{\mathcal {C}'}^{\pm }\times T^{\pm }$
:
Therefore, the quotient by
![]() $\operatorname {\mathrm {GL}}_2$
is isomorphic to
$\operatorname {\mathrm {GL}}_2$
is isomorphic to
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }\times \mathbb {G}_m^{2k-2}$
. We conclude that there is an isomorphism
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }\times \mathbb {G}_m^{2k-2}$
. We conclude that there is an isomorphism
If
![]() $\mathcal {C}$
is generic, then it follows from the definition of generic conjugacy classes in
$\mathcal {C}$
is generic, then it follows from the definition of generic conjugacy classes in
![]() $\operatorname {\mathrm {GL}}_2\sigma $
that both of
$\operatorname {\mathrm {GL}}_2\sigma $
that both of
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }$
have generic conjugacy classes.
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^{\pm }$
have generic conjugacy classes.
Remark B.1.1. If
![]() $C_j$
is the conjugacy class of
$C_j$
is the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a_j,a_j^{-1})\sigma $
for some
$\operatorname {\mathrm {diag}}(a_j,a_j^{-1})\sigma $
for some
![]() $a_j^2=-1$
, then
$a_j^2=-1$
, then
![]() $C^{\prime }_j=-C^{\prime }_j$
and (B.1.2.1) is no longer an isomorphism, but a double covering with the action of
$C^{\prime }_j=-C^{\prime }_j$
and (B.1.2.1) is no longer an isomorphism, but a double covering with the action of
![]() $\mathbb {Z}/2\mathbb {Z}$
permuting the two connected components. It follows that
$\mathbb {Z}/2\mathbb {Z}$
permuting the two connected components. It follows that
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is connected.
$\operatorname {\mathrm {Ch}}_{\mathcal {C}}$
is connected.
B.2 Mixed Hodge polynomials with
 $n=1$
and
$n=1$
and
 $n=2$
$n=2$
B.2.1
By §B.1.1, we have
and so
by [Reference Hausel and Rodriguez-VillegasHRV08, Example 2.1.11] and the Künneth isomorphism for mixed Hodge structures. However, according to Conjecture 1.7, we have
 $$ \begin{align*}H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,t)=(t\sqrt{q})^{2(g+k-1)}\left\langle\frac{\Omega_{1}\Omega_{0}}{\Omega_{\ast}},\prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}\right\rangle.\end{align*} $$
$$ \begin{align*}H_c(\operatorname{\mathrm{Ch}}_{\mathcal{C}};q,t)=(t\sqrt{q})^{2(g+k-1)}\left\langle\frac{\Omega_{1}\Omega_{0}}{\Omega_{\ast}},\prod^{2k}_{j=1}h_{\boldsymbol\beta^{\ast}_j}\right\rangle.\end{align*} $$
Now
![]() $h_{\boldsymbol{\beta} ^{\ast }_j}$
has degree 0; therefore, only the constant term on the left-hand side of the inner product contributes. The constant terms of
$h_{\boldsymbol{\beta} ^{\ast }_j}$
has degree 0; therefore, only the constant term on the left-hand side of the inner product contributes. The constant terms of
![]() $\Omega _{\ast }$
and
$\Omega _{\ast }$
and
![]() $\Omega _0$
are 1. As for
$\Omega _0$
are 1. As for
![]() $\Omega _1$
, we first note that
$\Omega _1$
, we first note that
![]() $\tilde {N}_{\boldsymbol{\alpha} }=1$
for
$\tilde {N}_{\boldsymbol{\alpha} }=1$
for
![]() $\boldsymbol{\alpha} =(\varnothing ,\varnothing )$
. Since
$\boldsymbol{\alpha} =(\varnothing ,\varnothing )$
. Since
![]() $\{\boldsymbol{\alpha} \}_1=(1)$
, we have
$\{\boldsymbol{\alpha} \}_1=(1)$
, we have
![]() $N_{\{\boldsymbol{\alpha} \}_1}(zw,z^2,w^2)=(z-w)^2$
. We find
$N_{\{\boldsymbol{\alpha} \}_1}(zw,z^2,w^2)=(z-w)^2$
. We find
which is the correct mixed Hodge polynomial.
B.2.2
Now we consider the case
![]() $n=2$
. We are unable to compute the mixed Hodge polynomial of arbitrary
$n=2$
. We are unable to compute the mixed Hodge polynomial of arbitrary
![]() $\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties. Instead, we use (B.1.2.1)
$\operatorname {\mathrm {GL}}_2\!<\!\sigma {>}$
-character varieties. Instead, we use (B.1.2.1)
and show that under this isomorphism, Conjecture 1.7 and Conjecture 1.1 predict the same mixed Hodge polynomial. In fact, we will show that they give the same rational function in z and w before setting
![]() $z=-t\sqrt {q}$
and
$z=-t\sqrt {q}$
and
![]() $w=\sqrt {q}^{-1}$
.
$w=\sqrt {q}^{-1}$
.
By Conjecture 1.1, the two character varieties
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+$
and
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+$
and
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^-$
have identical mixed Hodge polynomials. Therefore, we only need to consider
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^-$
have identical mixed Hodge polynomials. Therefore, we only need to consider
![]() $\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+\times \mathbb {G}_m^{2k-2}$
and then multiply the result by
$\operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+\times \mathbb {G}_m^{2k-2}$
and then multiply the result by
![]() $2$
. Now we compute
$2$
. Now we compute
following the procedure of [Reference Hausel, Letellier and Rodriguez-VillegasHLRV11, §2.3.3]. We get a sum of four terms:
 $$ \begin{align*} \mathbb{H}_2:=\ &\frac{[(z^3-w)(z-w)]^{2g}}{(z^4-1)(z^2-w^2)}\prod_{j=1}^{2k}H_{(2)}(\mathbf{x}_j;z^2,w^2),\\ \mathbb{H}_{(1^2)}:=\ &\frac{[(z-w^3)(z-w)]^{2g}}{(z^2-w^2)(1-w^4)}\prod_{j=1}^{2k}H_{(1^2)}(\mathbf{x}_j;z^2,w^2),\\ \mathbb{H}_1:=\ &-\frac{1}{2}\frac{(z-w)^{4g}}{(z^2-1)(1-w^2)}\prod_{j=1}^{2k}H_{(1)}(\mathbf{x}_j;z^2,w^2)^2,\\ \mathbb{H}_1':=\ &-\frac{1}{2}\frac{(z^2-w^2)^{2g}}{(z^2+1)(1+w^2)}\prod_{j=1}^{2k}H_{(1)}(\mathbf{x}_j^2;z^4,w^4). \end{align*} $$
$$ \begin{align*} \mathbb{H}_2:=\ &\frac{[(z^3-w)(z-w)]^{2g}}{(z^4-1)(z^2-w^2)}\prod_{j=1}^{2k}H_{(2)}(\mathbf{x}_j;z^2,w^2),\\ \mathbb{H}_{(1^2)}:=\ &\frac{[(z-w^3)(z-w)]^{2g}}{(z^2-w^2)(1-w^4)}\prod_{j=1}^{2k}H_{(1^2)}(\mathbf{x}_j;z^2,w^2),\\ \mathbb{H}_1:=\ &-\frac{1}{2}\frac{(z-w)^{4g}}{(z^2-1)(1-w^2)}\prod_{j=1}^{2k}H_{(1)}(\mathbf{x}_j;z^2,w^2)^2,\\ \mathbb{H}_1':=\ &-\frac{1}{2}\frac{(z^2-w^2)^{2g}}{(z^2+1)(1+w^2)}\prod_{j=1}^{2k}H_{(1)}(\mathbf{x}_j^2;z^4,w^4). \end{align*} $$
In fact, the rational functions in front of the Macdonald polynomials were computed in [Reference Hausel and Rodriguez-VillegasHRV08, §4.3]. From
we see that it is orthogonal to
![]() $h_1^2=s_{(2)}+s_{(1^2)}$
, the symmetric function representing the regular semi-simple conjugacy class. According to the definition of the generic condition for
$h_1^2=s_{(2)}+s_{(1^2)}$
, the symmetric function representing the regular semi-simple conjugacy class. According to the definition of the generic condition for
![]() $\mathcal {C}$
(not that for
$\mathcal {C}$
(not that for
![]() $\mathcal {C}'$
), and the relation between
$\mathcal {C}'$
), and the relation between
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {C}'$
, there exists at least one regular semi-simple conjugacy class among
$\mathcal {C}'$
, there exists at least one regular semi-simple conjugacy class among
![]() $\mathcal {C}'$
. Therefore, the term
$\mathcal {C}'$
. Therefore, the term
![]() $\mathbb {H}_1'$
must vanish after taking the inner product.
$\mathbb {H}_1'$
must vanish after taking the inner product.
Then we compute
 $$ \begin{align*}\frac{\Omega_{0}(z,w)^2}{\Omega_{\ast}(z,w)}. \end{align*} $$
$$ \begin{align*}\frac{\Omega_{0}(z,w)^2}{\Omega_{\ast}(z,w)}. \end{align*} $$
Write
 $$ \begin{align*} \mathbf{H}_{((1),\varnothing)}:=\ &\frac{(z^3-w)^{2g}(z-w)^{2(g+k-1)}}{(z^4-1)(z^2-w^2)}\prod_{j=1}^{2k}\tilde{H}_{((1),\varnothing)}(\mathbf{x}_j;z^2,w^2),\\ \mathbf{H}_{(\varnothing,(1))}:=\ &\frac{(z-w^3)^{2g}(z-w)^{2(g+k-1)}}{(z^2-w^2)(1-w^4)}\prod_{j=1}^{2k}\tilde{H}_{(\varnothing,(1))}(\mathbf{x}_j;z^2,w^2),\\ \mathbf{H}_1:=\ &\frac{(z-w)^{2(2g+k-1)}}{(z^2-1)(1-w^2)}\prod_{j=1}^{2k}\tilde{H}_{(1)}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2), \end{align*} $$
$$ \begin{align*} \mathbf{H}_{((1),\varnothing)}:=\ &\frac{(z^3-w)^{2g}(z-w)^{2(g+k-1)}}{(z^4-1)(z^2-w^2)}\prod_{j=1}^{2k}\tilde{H}_{((1),\varnothing)}(\mathbf{x}_j;z^2,w^2),\\ \mathbf{H}_{(\varnothing,(1))}:=\ &\frac{(z-w^3)^{2g}(z-w)^{2(g+k-1)}}{(z^2-w^2)(1-w^4)}\prod_{j=1}^{2k}\tilde{H}_{(\varnothing,(1))}(\mathbf{x}_j;z^2,w^2),\\ \mathbf{H}_1:=\ &\frac{(z-w)^{2(2g+k-1)}}{(z^2-1)(1-w^2)}\prod_{j=1}^{2k}\tilde{H}_{(1)}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2), \end{align*} $$
and
Then
 $$ \begin{align*} \Omega_0^2&=1+2U+\text{higher degree terms},\\ \frac{1}{\Omega_{\ast}}&=1-U'+\text{higher degree terms}, \end{align*} $$
$$ \begin{align*} \Omega_0^2&=1+2U+\text{higher degree terms},\\ \frac{1}{\Omega_{\ast}}&=1-U'+\text{higher degree terms}, \end{align*} $$
The contribution of the torus
![]() $\mathbb {G}_m^{2k-2}$
is
$\mathbb {G}_m^{2k-2}$
is
![]() $(z-w)^{2k-2}$
. (Strictly speaking, there is an extra factor
$(z-w)^{2k-2}$
. (Strictly speaking, there is an extra factor
![]() $(t\sqrt {q})^{2k-2}$
, but this will be balanced by the difference between
$(t\sqrt {q})^{2k-2}$
, but this will be balanced by the difference between
![]() $\dim \operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+$
and
$\dim \operatorname {\mathrm {Ch}}_{\mathcal {C}'}^+$
and
![]() $\dim \operatorname {\mathrm {Ch}}_{\mathcal {C}}$
.) Now we can readily see that
$\dim \operatorname {\mathrm {Ch}}_{\mathcal {C}}$
.) Now we can readily see that
![]() $(z-w)^{2k-2}\mathbb {H}_2$
and
$(z-w)^{2k-2}\mathbb {H}_2$
and
![]() $\mathbf {H}_{((1),\varnothing )}$
have the same rational function in front of the Macdonald polynomials. The same conclusion holds when matching the functions:
$\mathbf {H}_{((1),\varnothing )}$
have the same rational function in front of the Macdonald polynomials. The same conclusion holds when matching the functions:
 $$ \begin{align*} (z-w)^{2k-2}\mathbb{H}_{(1^2)}&\longleftrightarrow\mathbf{H}_{(\varnothing,(1))}\\ -2(z-w)^{2k-2}\mathbb{H}_1&\longleftrightarrow\mathbf{H}_1. \end{align*} $$
$$ \begin{align*} (z-w)^{2k-2}\mathbb{H}_{(1^2)}&\longleftrightarrow\mathbf{H}_{(\varnothing,(1))}\\ -2(z-w)^{2k-2}\mathbb{H}_1&\longleftrightarrow\mathbf{H}_1. \end{align*} $$
According to §A.2.1, under the correspondences
 $$ \begin{align*} H_{(2)}(\mathbf{z}_j;z^2,w^2)&\longleftrightarrow\tilde{H}_{((1),\varnothing)}(\mathbf{x}_j;z^2,w^2),\\ H_{(1^2)}(\mathbf{z}_j;z^2,w^2)&\longleftrightarrow\tilde{H}_{(\varnothing,(1))}(\mathbf{x}_j;z^2,w^2),\\ H_{(1)}(\mathbf{z}_j;z^2,w^2)^2&\longleftrightarrow\tilde{H}_{(1)}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2),\\ h_2(\mathbf{z}_j)&\longleftrightarrow h_{((1),\varnothing)}(\mathbf{x}_j),\\ h_{(1^2)}(\mathbf{z}_j)&\longleftrightarrow h_1(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j), \end{align*} $$
$$ \begin{align*} H_{(2)}(\mathbf{z}_j;z^2,w^2)&\longleftrightarrow\tilde{H}_{((1),\varnothing)}(\mathbf{x}_j;z^2,w^2),\\ H_{(1^2)}(\mathbf{z}_j;z^2,w^2)&\longleftrightarrow\tilde{H}_{(\varnothing,(1))}(\mathbf{x}_j;z^2,w^2),\\ H_{(1)}(\mathbf{z}_j;z^2,w^2)^2&\longleftrightarrow\tilde{H}_{(1)}(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j;z^2,w^2),\\ h_2(\mathbf{z}_j)&\longleftrightarrow h_{((1),\varnothing)}(\mathbf{x}_j),\\ h_{(1^2)}(\mathbf{z}_j)&\longleftrightarrow h_1(\mathbf{x}^{(0)}_j+\mathbf{x}^{(1)}_j), \end{align*} $$
the inner products are preserved. Therefore, we get the same functions in z and w.
Appendix C Conjectural mixed Hodge polynomial;
 $n=4$
and
$n=4$
and
 $n=5$
$n=5$
We give two sample computations of the rational function
![]() $\mathbb {H}_{\mathbf {B}}(z,w)$
in Conjecture 1.7. We will see that they indeed satisfy part (i) of Conjecture 1.7. These are the simplest cases where the deformed self-pairings of wreath Macdonald polynomials of degree 2 and 2-core
$\mathbb {H}_{\mathbf {B}}(z,w)$
in Conjecture 1.7. We will see that they indeed satisfy part (i) of Conjecture 1.7. These are the simplest cases where the deformed self-pairings of wreath Macdonald polynomials of degree 2 and 2-core
![]() $(0)$
or
$(0)$
or
![]() $(1)$
appear. We will see the contributions of the ‘wreath-
$(1)$
appear. We will see the contributions of the ‘wreath-
![]() $\nabla $
’ terms, which are absent if
$\nabla $
’ terms, which are absent if
![]() $n<4$
. This is our evidence that the ‘wreath-
$n<4$
. This is our evidence that the ‘wreath-
![]() $\nabla $
’ terms should not be deformed (see §8.2.2).
$\nabla $
’ terms should not be deformed (see §8.2.2).
C.1
 $n=4$
,
$n=4$
,
 $g=0$
,
$g=0$
,
 $k=2$
$k=2$
There are four conjugacy classes:
![]() $\mathcal {C}=(C_1,C_2,C_3,C_4)$
. We assume that
$\mathcal {C}=(C_1,C_2,C_3,C_4)$
. We assume that
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are regular, and
$C_2$
are regular, and
![]() $C_3$
and
$C_3$
and
![]() $C_4$
are the conjugacy class of
$C_4$
are the conjugacy class of
![]() $\sigma $
.
$\sigma $
.
 $$ \begin{align*} &\mathbb{H}_{\mathbf{B}}(z,w)\\ =\ &-16\frac{(z^3-w)^2(z-w)^2(z^2+1)}{(z^2-1)^2(z^2-w^2)(1-w^2)} -16\frac{(z-w^3)^2(z-w)^2(1+w^2)}{(1-w^2)^2(z^2-w^2)(z^2-1)} +64\frac{(z-w)^4}{(z^2-1)^2(1-w^2)^2}\\ &-32\frac{(z-w)^4(1+z^2)}{(z^2-1)^2(z^2-w^2)(1-w^2)} -32\frac{(z-w)^4(1+w^2)}{(1-w^2)^2(z^2-w^2)(z^2-1)}\\ &+4\frac{(z-w)^4(z^2+1)^2}{(z^2-1)^2(z^2-w^2)^2} +4\frac{(z-w)^4(1+w^2)^2}{(1-w^2)^2(z^2-w^2)^2} +8\frac{(z-w)^4(z^2+1)(1+w^2)}{(z^2-1)(1-w^2)(z^2-w^2)^2}\\ &+2\frac{(z^5-w)^2(z-w)^2(z^4+1)(z^2+1)^2}{(z^6-w^2)(z^2-w^2)(z^2-1)^2}+2\frac{(z-w^5)^2(z-w)^2(1+w^4)(1+w^2)^2}{(z^2-w^6)(z^2-w^2)(1-w^2)^2}\\ &+2z^4\frac{(z-w)^4(z^2+w^2)(z^2+1)^3}{(z^6-w^2)(z^2-w^2)^2(z^2-1)} +2w^4\frac{(z-w)^4(z^2+w^2)(1+w^2)^3}{(z^2-w^6)(z^2-w^2)^2(1-w^2)}\\ &+8\frac{(z^3-w^3)^2(z-w)^2(z^2+1)(1+w^2)}{(z^2-w^2)^2(z^2-1)(1-w^2)}\\ =\ &~2\,w^8-4\,w^7\,z+4\,w^6\,z^2+8\,w^6-4\,w^5\,z^3-16\,w^5\,z\\ &+4\,w^4\,z^4+16\,w^4\,z^2+12\,w^4-4\,w^3\,z^5-16\,w^3\,z^3-32\,w^3\,z\\ &+4\,w^2\,z^6+16\,w^2\,z^4+40\,w^2\,z^2+8\,w^2-4\,w\,z^7-16\,w\,z^5-32\,w\,z^3-16\,w\,z\\ &+2\,z^8+8\,z^6+12\,z^4+8\,z^2. \end{align*} $$
$$ \begin{align*} &\mathbb{H}_{\mathbf{B}}(z,w)\\ =\ &-16\frac{(z^3-w)^2(z-w)^2(z^2+1)}{(z^2-1)^2(z^2-w^2)(1-w^2)} -16\frac{(z-w^3)^2(z-w)^2(1+w^2)}{(1-w^2)^2(z^2-w^2)(z^2-1)} +64\frac{(z-w)^4}{(z^2-1)^2(1-w^2)^2}\\ &-32\frac{(z-w)^4(1+z^2)}{(z^2-1)^2(z^2-w^2)(1-w^2)} -32\frac{(z-w)^4(1+w^2)}{(1-w^2)^2(z^2-w^2)(z^2-1)}\\ &+4\frac{(z-w)^4(z^2+1)^2}{(z^2-1)^2(z^2-w^2)^2} +4\frac{(z-w)^4(1+w^2)^2}{(1-w^2)^2(z^2-w^2)^2} +8\frac{(z-w)^4(z^2+1)(1+w^2)}{(z^2-1)(1-w^2)(z^2-w^2)^2}\\ &+2\frac{(z^5-w)^2(z-w)^2(z^4+1)(z^2+1)^2}{(z^6-w^2)(z^2-w^2)(z^2-1)^2}+2\frac{(z-w^5)^2(z-w)^2(1+w^4)(1+w^2)^2}{(z^2-w^6)(z^2-w^2)(1-w^2)^2}\\ &+2z^4\frac{(z-w)^4(z^2+w^2)(z^2+1)^3}{(z^6-w^2)(z^2-w^2)^2(z^2-1)} +2w^4\frac{(z-w)^4(z^2+w^2)(1+w^2)^3}{(z^2-w^6)(z^2-w^2)^2(1-w^2)}\\ &+8\frac{(z^3-w^3)^2(z-w)^2(z^2+1)(1+w^2)}{(z^2-w^2)^2(z^2-1)(1-w^2)}\\ =\ &~2\,w^8-4\,w^7\,z+4\,w^6\,z^2+8\,w^6-4\,w^5\,z^3-16\,w^5\,z\\ &+4\,w^4\,z^4+16\,w^4\,z^2+12\,w^4-4\,w^3\,z^5-16\,w^3\,z^3-32\,w^3\,z\\ &+4\,w^2\,z^6+16\,w^2\,z^4+40\,w^2\,z^2+8\,w^2-4\,w\,z^7-16\,w\,z^5-32\,w\,z^3-16\,w\,z\\ &+2\,z^8+8\,z^6+12\,z^4+8\,z^2. \end{align*} $$
C.2
 $n=5$
,
$n=5$
,
 $g=0$
,
$g=0$
,
 $k=2$
$k=2$
There are four conjugacy classes:
![]() $\mathcal {C}=(C_1,C_2,C_3,C_4)$
. We assume that
$\mathcal {C}=(C_1,C_2,C_3,C_4)$
. We assume that
![]() $C_1$
is regular,
$C_1$
is regular,
![]() $C_3$
and
$C_3$
and
![]() $C_4$
are the conjugacy classes of
$C_4$
are the conjugacy classes of
![]() $\sigma $
, and
$\sigma $
, and
![]() $C_2$
is the conjugacy class of
$C_2$
is the conjugacy class of
![]() $\operatorname {\mathrm {diag}}(a,1,1,a^{-1})\sigma $
with some
$\operatorname {\mathrm {diag}}(a,1,1,a^{-1})\sigma $
with some
![]() $a^4\ne 1$
.
$a^4\ne 1$
.
 $$ \begin{align*} &\mathbb{H}_{\mathbf{B}}(z,w)\\ =\ &-4\frac{(z-w)^4\left((z^5-w)^2+(z-w)^2\right)(3+z^2)}{(z^2-1)^2(1-w^2)(z^2-w^2)} -4\frac{(z-w)^4\left((z-w^5)^2+(z-w)^2\right)(3+w^2)}{(z^2-1)(1-w^2)^2(z^2-w^2)}\\ &+4\frac{(z-w)^4(z^5-w)^2(1+z^2)}{(z^2-1)^2(z^2-w^2)^2} +4\frac{(z-w)^4(z-w^5)^2(1+w^2)}{(z^2-w^2)^2(1-w^2)^2}\\ &+2\frac{(z-w)^4\left((z-w^5)^2+(z^5-w)^2\right)(2+z^2+w^2)}{(z^2-1)(z^2-w^2)^2(1-w^2)}+32\frac{(z-w)^6}{(z^2-1)^2(1-w^2)^2}\\ &-8\frac{(z-w)^4(z^3-w)^2(1+z^2)}{(z^2-w^2)(z^2-1)^2(1-w^2)} -8\frac{(z-w)^4(z-w^3)^2(1+w^2)}{(z^2-w^2)(z^2-1)(1-w^2)^2}\\ &+\frac{(z-w)^2(z^5-w)^2\left((z^9-w)^2+(z-w)^2\right)(1+z^2)(1+z^4)}{(z^6-w^2)(z^2-1)^2(z^2-w^2)}\\ &+\frac{(z-w)^2(z-w^5)^2\left((z-w^9)^2+(z-w)^2\right)(1+w^2)(1+w^4)}{(z^2-w^6)(z^2-w^2)(1-w^2)^2}\\ &+z^4\frac{(1+z^2)(z-w)^4\left((1+z^2)(z^2+w^2)(z^3-w^3)^2+z^2(1+z^2+w^2+z^4)(z-w)^2\right)}{(z^6-w^2)(z^2-1)(z^2-w^2)^2}\\ &+w^4\frac{(1+w^2)(z-w)^4\left((1+w^2)(z^2+w^2)(z^3-w^3)^2+w^2(1+z^2+w^2+w^4)(z-w)^2\right)}{(z^2-w^6)(z^2-w^2)^2(1-w^2)}\\ &+2\frac{(z-w)^4\left((2+z^2+w^2)(z^5-w^5)^2+(1+z^2)(1+w^2)(z^3-w^3)^2\right)}{(z^2-w^2)^2(1-w^2)(z^2-1)}. \end{align*} $$
$$ \begin{align*} &\mathbb{H}_{\mathbf{B}}(z,w)\\ =\ &-4\frac{(z-w)^4\left((z^5-w)^2+(z-w)^2\right)(3+z^2)}{(z^2-1)^2(1-w^2)(z^2-w^2)} -4\frac{(z-w)^4\left((z-w^5)^2+(z-w)^2\right)(3+w^2)}{(z^2-1)(1-w^2)^2(z^2-w^2)}\\ &+4\frac{(z-w)^4(z^5-w)^2(1+z^2)}{(z^2-1)^2(z^2-w^2)^2} +4\frac{(z-w)^4(z-w^5)^2(1+w^2)}{(z^2-w^2)^2(1-w^2)^2}\\ &+2\frac{(z-w)^4\left((z-w^5)^2+(z^5-w)^2\right)(2+z^2+w^2)}{(z^2-1)(z^2-w^2)^2(1-w^2)}+32\frac{(z-w)^6}{(z^2-1)^2(1-w^2)^2}\\ &-8\frac{(z-w)^4(z^3-w)^2(1+z^2)}{(z^2-w^2)(z^2-1)^2(1-w^2)} -8\frac{(z-w)^4(z-w^3)^2(1+w^2)}{(z^2-w^2)(z^2-1)(1-w^2)^2}\\ &+\frac{(z-w)^2(z^5-w)^2\left((z^9-w)^2+(z-w)^2\right)(1+z^2)(1+z^4)}{(z^6-w^2)(z^2-1)^2(z^2-w^2)}\\ &+\frac{(z-w)^2(z-w^5)^2\left((z-w^9)^2+(z-w)^2\right)(1+w^2)(1+w^4)}{(z^2-w^6)(z^2-w^2)(1-w^2)^2}\\ &+z^4\frac{(1+z^2)(z-w)^4\left((1+z^2)(z^2+w^2)(z^3-w^3)^2+z^2(1+z^2+w^2+z^4)(z-w)^2\right)}{(z^6-w^2)(z^2-1)(z^2-w^2)^2}\\ &+w^4\frac{(1+w^2)(z-w)^4\left((1+w^2)(z^2+w^2)(z^3-w^3)^2+w^2(1+z^2+w^2+w^4)(z-w)^2\right)}{(z^2-w^6)(z^2-w^2)^2(1-w^2)}\\ &+2\frac{(z-w)^4\left((2+z^2+w^2)(z^5-w^5)^2+(1+z^2)(1+w^2)(z^3-w^3)^2\right)}{(z^2-w^2)^2(1-w^2)(z^2-1)}. \end{align*} $$
The result is a polynomial:
 $\mathbb {H}_{\mathbf {B}}(z,w)=w^{24}-2\, w^{23}\,z+2\,w^{22}\,z^2+3\,w^{22}-2\,w^{21}\, z^3-6\,w^{21}\,z+2\,w^{20}\,z^4+6\,w^{20}\,z^2+6\,w^{20}-2\,w^{19}\,z^5-6\,w^{19}\,z^3-14\,w^{19}\, z+2\,w^{18}\,z^6+6\,w^{18}\,z^4+17\,w^{18}\,z^2+10\,w^{18}-2\,w^{17}\,z^7-6\,w^{17}\,z^5-18\,w^{17}\, z^3-26\,w^{17}\,z+2\,w^{16}\,z^8+6\,w^{16}\,z^6+18\,w^{16}\,z^4+35\,w^{16}\,z^2+14\,w^{16}-2\,w^{15}\, z^9-6\,w^{15}\,z^7-18\,w^{15}\,z^5-38\,w^{15}\,z^3-42\,w^{15}\,z+2\,w^{14}\,z^{10}+6\,w^{14}\,z^8+18\, w^{14}\,z^6+38\,w^{14}\,z^4+63\,w^{14}\,z^2+18\,w^{14}-2\,w^{13}\,z^{11}-6\,w^{13}\,z^9-18\,w^{13}\, z^7-38\,w^{13}\,z^5-72\,w^{13}\,z^3-62\,w^{13}\,z+2\,w^{12}\,z^{12}+6\,w^{12}\,z^{10}+18\,w^{12}\, z^8+38\,w^{12}\,z^6+75\,w^{12}\,z^4+101\,w^{12}\,z^2+22\,w^{12}-2\,w^{11}\,z^{13}-6\,w^{11}\, z^{11}-18\,w^{11}\,z^9-38\,w^{11}\,z^7-76\,w^{11}\,z^5-120\,w^{11}\,z^3-84\,w^{11}\,z+2\,w^{10}\, z^{14}+6\,w^{10}\,z^{12}+18\,w^{10}\,z^{10}+38\,w^{10}\,z^8+76\,w^{10}\,z^6+129\,w^{10}\,z^4+148\, w^{10}\,z^2+26\,w^{10}-2\,w^9\,z^{15}-6\,w^9\,z^{13}-18\,w^9\,z^{11}-38\,w^9\,z^9-76\,w^9\,z^7-132\, w^9\,z^5-186\,w^9\,z^3-108\,w^9\,z+2\,w^8\,z^{16}+6\,w^8\,z^{14}+18\,w^8\,z^{12}+38\,w^8\,z^{10}+76\, w^8\,z^8+132\,w^8\,z^6+207\,w^8\,z^4+204\,w^8\,z^2+28\,w^8-2\,w^7\,z^{17}-6\,w^7\,z^{15}-18\,w^7\,z^{13}-38\, w^7\,z^{11}-76\,w^7\,z^9-132\,w^7\,z^7-216\,w^7\,z^5-270\,w^7\,z^3-124\,w^7\,z+2\,w^6\,z^{18}+6\,w^6\,z^{16}+18\, w^6\,z^{14}+38\,w^6\,z^{12}+76\,w^6\,z^{10}+132\,w^6\,z^8+218\,w^6\,z^6+306\,w^6\,z^4+245\,w^6\,z^2+23\,w^6-2\, w^5\,z^{19}-6\,w^5\,z^{17}-18\,w^5\,z^{15}-38\,w^5\,z^{13}-76\,w^5\,z^{11}-132\,w^5\,z^9-216\,w^5\,z^7-316\, w^5\,z^5-326\,w^5\,z^3-110\,w^5\,z+2\,w^4\,z^{20}+6\,w^4\,z^{18}+18\,w^4\,z^{16}+38\,w^4\,z^{14}+75\,w^4\, z^{12}+129\,w^4\,z^{10}+207\,w^4\,z^8+306\,w^4\,z^6+354\,w^4\,z^4+228\,w^4\,z^2+11\,w^4-2\,w^3\,z^{21}-6\, w^3\,z^{19}-18\,w^3\,z^{17}-38\,w^3\,z^{15}-72\,w^3\,z^{13}-120\,w^3\,z^{11}-186\,w^3\,z^9-270\,w^3\,z^7-326\, w^3\,z^5-282\,w^3\,z^3-44\,w^3\,z+2\,w^2\,z^{22}+6\,w^2\,z^{20}+17\,w^2\,z^{18}+35\,w^2\,z^{16}+63\,w^2\, z^{14}+101\,w^2\,z^{12}+148\,w^2\,z^{10}+204\,w^2\,z^8+245\,w^2\,z^6+228\,w^2\,z^4+66\,w^2\,z^2+w^2-2\,w\, z^{23}-6\,w\,z^{21}-14\,w\,z^{19}-26\,w\,z^{17}-42\,w\,z^{15}-62\,w\,z^{13}-84\,w\,z^{11}-108\,w\,z^9-124\,w\, z^7-110\,w\,z^5-44\,w\,z^3-2\,w\,z+z^{24}+3\,z^{22}+6\,z^{20}+10\,z^{18}+14\,z^{16}+18\,z^{14}+22\,z^{12}+26\, z^{10}+28\,z^8+23\,z^6+11\,z^4+z^2.$
$\mathbb {H}_{\mathbf {B}}(z,w)=w^{24}-2\, w^{23}\,z+2\,w^{22}\,z^2+3\,w^{22}-2\,w^{21}\, z^3-6\,w^{21}\,z+2\,w^{20}\,z^4+6\,w^{20}\,z^2+6\,w^{20}-2\,w^{19}\,z^5-6\,w^{19}\,z^3-14\,w^{19}\, z+2\,w^{18}\,z^6+6\,w^{18}\,z^4+17\,w^{18}\,z^2+10\,w^{18}-2\,w^{17}\,z^7-6\,w^{17}\,z^5-18\,w^{17}\, z^3-26\,w^{17}\,z+2\,w^{16}\,z^8+6\,w^{16}\,z^6+18\,w^{16}\,z^4+35\,w^{16}\,z^2+14\,w^{16}-2\,w^{15}\, z^9-6\,w^{15}\,z^7-18\,w^{15}\,z^5-38\,w^{15}\,z^3-42\,w^{15}\,z+2\,w^{14}\,z^{10}+6\,w^{14}\,z^8+18\, w^{14}\,z^6+38\,w^{14}\,z^4+63\,w^{14}\,z^2+18\,w^{14}-2\,w^{13}\,z^{11}-6\,w^{13}\,z^9-18\,w^{13}\, z^7-38\,w^{13}\,z^5-72\,w^{13}\,z^3-62\,w^{13}\,z+2\,w^{12}\,z^{12}+6\,w^{12}\,z^{10}+18\,w^{12}\, z^8+38\,w^{12}\,z^6+75\,w^{12}\,z^4+101\,w^{12}\,z^2+22\,w^{12}-2\,w^{11}\,z^{13}-6\,w^{11}\, z^{11}-18\,w^{11}\,z^9-38\,w^{11}\,z^7-76\,w^{11}\,z^5-120\,w^{11}\,z^3-84\,w^{11}\,z+2\,w^{10}\, z^{14}+6\,w^{10}\,z^{12}+18\,w^{10}\,z^{10}+38\,w^{10}\,z^8+76\,w^{10}\,z^6+129\,w^{10}\,z^4+148\, w^{10}\,z^2+26\,w^{10}-2\,w^9\,z^{15}-6\,w^9\,z^{13}-18\,w^9\,z^{11}-38\,w^9\,z^9-76\,w^9\,z^7-132\, w^9\,z^5-186\,w^9\,z^3-108\,w^9\,z+2\,w^8\,z^{16}+6\,w^8\,z^{14}+18\,w^8\,z^{12}+38\,w^8\,z^{10}+76\, w^8\,z^8+132\,w^8\,z^6+207\,w^8\,z^4+204\,w^8\,z^2+28\,w^8-2\,w^7\,z^{17}-6\,w^7\,z^{15}-18\,w^7\,z^{13}-38\, w^7\,z^{11}-76\,w^7\,z^9-132\,w^7\,z^7-216\,w^7\,z^5-270\,w^7\,z^3-124\,w^7\,z+2\,w^6\,z^{18}+6\,w^6\,z^{16}+18\, w^6\,z^{14}+38\,w^6\,z^{12}+76\,w^6\,z^{10}+132\,w^6\,z^8+218\,w^6\,z^6+306\,w^6\,z^4+245\,w^6\,z^2+23\,w^6-2\, w^5\,z^{19}-6\,w^5\,z^{17}-18\,w^5\,z^{15}-38\,w^5\,z^{13}-76\,w^5\,z^{11}-132\,w^5\,z^9-216\,w^5\,z^7-316\, w^5\,z^5-326\,w^5\,z^3-110\,w^5\,z+2\,w^4\,z^{20}+6\,w^4\,z^{18}+18\,w^4\,z^{16}+38\,w^4\,z^{14}+75\,w^4\, z^{12}+129\,w^4\,z^{10}+207\,w^4\,z^8+306\,w^4\,z^6+354\,w^4\,z^4+228\,w^4\,z^2+11\,w^4-2\,w^3\,z^{21}-6\, w^3\,z^{19}-18\,w^3\,z^{17}-38\,w^3\,z^{15}-72\,w^3\,z^{13}-120\,w^3\,z^{11}-186\,w^3\,z^9-270\,w^3\,z^7-326\, w^3\,z^5-282\,w^3\,z^3-44\,w^3\,z+2\,w^2\,z^{22}+6\,w^2\,z^{20}+17\,w^2\,z^{18}+35\,w^2\,z^{16}+63\,w^2\, z^{14}+101\,w^2\,z^{12}+148\,w^2\,z^{10}+204\,w^2\,z^8+245\,w^2\,z^6+228\,w^2\,z^4+66\,w^2\,z^2+w^2-2\,w\, z^{23}-6\,w\,z^{21}-14\,w\,z^{19}-26\,w\,z^{17}-42\,w\,z^{15}-62\,w\,z^{13}-84\,w\,z^{11}-108\,w\,z^9-124\,w\, z^7-110\,w\,z^5-44\,w\,z^3-2\,w\,z+z^{24}+3\,z^{22}+6\,z^{20}+10\,z^{18}+14\,z^{16}+18\,z^{14}+22\,z^{12}+26\, z^{10}+28\,z^8+23\,z^6+11\,z^4+z^2.$
Acknowledgements
A good part of this article was prepared at Université de Paris as part of my thesis. The possibility of this work was suggested by Pierre Deligne to Fernando Rodriguez-Villegas in a private letter, which was then passed to my advisor Emmanuel Letellier. I thank them for sharing this idea. I thank Florent Schaffhauser and my advisor for some discussions. I thank Jean Michel and Philip Boalch for answering some questions. I thank François Digne for carefully reading and giving many comments on an earlier version of the article at the stage of thesis. I have also benefited from some results collected in the preprint [Reference CambòCam17] of Cambò. I thank Mark Shimozono and Daniel Orr for bringing to my attention wreath Macdonald polynomials and answering some questions. I thank the referee for pointing out many typos and giving some suggestions. Part of this article was prepared when I was unemployed at home. I thank my family for their support.
Competing interest
The authors have no competing interest to declare.
Financial support
None.