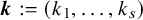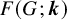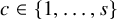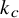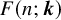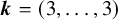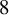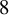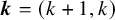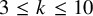Exact solutions to the Erdős-Rothschild problem

Abstract

Let $\boldsymbol {k} := (k_1,\ldots ,k_s)$ be a sequence of natural numbers. For a graph G, let $F(G;\boldsymbol {k})$ denote the number of colourings of the edges of G with colours $1,\dots ,s$ such that, for every $c \in \{1,\dots ,s\}$, the edges of colour c contain no clique of order $k_c$. Write $F(n;\boldsymbol {k})$ to denote the maximum of $F(G;\boldsymbol {k})$ over all graphs G on n vertices. There are currently very few known exact (or asymptotic) results for this problem, posed by Erdős and Rothschild in 1974. We prove some new exact results for $n \to \infty $:

1. (i) A sufficient condition on $\boldsymbol {k}$ which guarantees that every extremal graph is a complete multipartite graph, which systematically recovers all existing exact results.

2. (ii) Addressing the original question of Erdős and Rothschild, in the case $\boldsymbol {k}=(3,\ldots ,3)$ of length $7$, the unique extremal graph is the complete balanced $8$-partite graph, with colourings coming from Hadamard matrices of order $8$.

3. (iii) In the case $\boldsymbol {k}=(k+1,k)$, for which the sufficient condition in (i) does not hold, for $3 \leq k \leq 10$, the unique extremal graph is complete k-partite with one part of size less than k and the other parts as equal in size as possible.

1. Introduction

Let a nonincreasing sequence $\boldsymbol {k} = (k_1,\ldots ,k_s) \in \mathbb {N}^s$ of natural numbers be given. By an s-edge-colouring (or colouring for brevity) of a graph $G=(V,E)$ we mean a function $\chi :E\to [s]$ , where we denote $[s]:=\{1,\dots ,s\}$ . Note that colourings do not have to be proper; that is, adjacent edges can have the same colour. A colouring $\chi $ of G is called $\boldsymbol {k}$ -valid if, for every $c\in [s]$ , the colour-c subgraph $\chi ^{-1}(c)$ contains no copy of $K_{k_c}$ , the complete graph of order $k_c$ . Write $F(G; \boldsymbol {k})$ for the number of $\boldsymbol {k}$ -valid colourings of G. This paper concerns the parameter

$$ \begin{align*}F(n;\boldsymbol{k}) := \max_{G: v(G)=n}F(G;\boldsymbol{k}), \end{align*} $$

the maximum value of $F(G;\boldsymbol {k})$ for an n-vertex graph G, and the $\boldsymbol {k}$ -extremal graphs (i.e., those graphs which attain this maximum). We always assume $s \geq 2$ and $k_s \geq 3$ for otherwise the problem is trivial or reduces to one with shorter $\boldsymbol {k}$ . Determining $F(n;\boldsymbol {k})$ in the case $\boldsymbol {k}=(3,3)$ was originally studied by Erdős and Rothschild [4, 5], and hence, it is called the Erdős-Rothschild problem. It is, in general, wide open. The following summarises all of the cases where $F(n;\boldsymbol {k})$ is known (in one case only asymptotically). Write $(k;s)$ for the tuple $(k,\ldots ,k)$ of length s.

Theorem 1.1. There exists $n_0(k)>0$ such that the following hold for all integers $n \geq n_0$ .

(*) These graphs are known to be asymptotically extremal only: they achieve the right exponent in $F(n;\boldsymbol {k})$ . Here, $T_{\alpha ,\beta }(n)$ denotes the complete partite graph with parts of size $\alpha n, \alpha n, (\frac {1}{4}-\alpha )n, (\frac {1}{4}-\alpha )n, \beta n, \beta n, (\frac {1}{4}-\beta )n, (\frac {1}{4}-\beta )n$ , and $T^{\prime }_{\alpha ,\beta }(n)$ denotes the complete partite graph with parts of size $\frac {n}{4},\frac {n}{4},\alpha n, \alpha n, \beta n, \beta n, (\frac {1}{4}-\alpha -\beta )n, (\frac {1}{4}-\alpha -\beta )n$ .

The constants $C_{3,4},C_{3,6},C_{4,4}$ can be determined, and generally depend on the remainder when n is divided by some small integer; for example, $C_{3,4}$ equals $(2^{14}\cdot 3)^{1/3}$ if $n \equiv 2\ (\mod 4)$ and equals $36$ otherwise. Note that for $\boldsymbol {k} = (k;s)$ , the trivial lower bound for $F(n;\boldsymbol {k})$ is $s^{t_{k-1}(n)}$ , given by taking every s-edge-colouring of the largest $K_k$ -free graph on n vertices – namely, the Turán graph $T_{k-1}(n)$ , the complete partite graph with $k-1$ parts of size as equal as possible (with $t_{k-1}(n) := e(T_{k-1}(n))$ ). This trivial lower bound is, in fact, sharp for $s=2,3$ , but $F(n;\boldsymbol {k})$ is exponentially larger for $s \geq 4$ , as was shown in [1]. As is evident from the table, these cases have been much harder to resolve and there are only four pairs $(k;s)$ where the solution is known. We refer the reader to [10] for a more detailed history of the problem and its variants. This paper is the third in a series (comprising also [11] with Yilma and [10]) concerning the relationship between the Erdős-Rothschild problem and a finite combinatorial optimisation problem, which we now state.

Problem $\mathbf {Q^*}$ : Given a sequence $\boldsymbol {k} := (k_1,\ldots ,k_s) \in \mathbb {N}^s$ of natural numbers, determine

(1.1)

the maximum value of

(1.2) $$ \begin{align} q(\phi,\boldsymbol{\alpha}) := 2\sum_{1 \leq i < j \leq r} \alpha_i \alpha_j \log_2 |\phi(ij)| \end{align} $$

over the set of feasible solutions – that is, triples $(r,\phi ,\boldsymbol {\alpha })$ such that $r \in \mathbb {N}$ and

• ○ $\phi \in \Phi _2(r;\boldsymbol {k})$ , where $\Phi _2(r;\boldsymbol {k})$ is the set of all functions $\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$ such that

  $$\begin{align*}\phi^{-1}(c) := \left\{ ij \in \binom{[r]}{2} : c \in \phi(ij) \right\} \end{align*}$$
  is $K_{k_c}$ -free for every colour $c \in [s]$ and $|\phi (ij)|\ge 2$ for all $ij\in \binom {[r]}{2}$ ;

• ○ $\boldsymbol {\alpha } = (\alpha _1,\ldots ,\alpha _r) \in \Delta ^r$ , where $\Delta ^r$ is the set of all $\boldsymbol {\alpha } \in \mathbb {R}^r$ with $\alpha _i> 0$ for all $i \in [r]$ , and $\alpha _1 + \ldots + \alpha _r = 1$ .

We may assume that $r < R(\boldsymbol {k})$ , where $R(\boldsymbol {k})$ is the Ramsey number of $\boldsymbol k$ (i.e., the minimum R such that $K_R$ admits no $\boldsymbol k$ -valid s-edge-colouring). Note that the maximum in (1.1) is attained, since $q(\phi ,\cdot )$ is continuous for each of the finitely many pairs $(r,\phi )$ , and with the weaker restrictions $\alpha _i\geq 0$ for every i and $\boldsymbol {\alpha }$ is a (nonempty) compact space. (If the maximum is obtained at $(r,\phi ,\boldsymbol {\alpha })$ with some $\alpha _i=0$ , then we can simply remove i to obtain a solution with smaller r.) We call $\phi \in \Phi _2(r;\boldsymbol {k})$ a colour pattern and $\boldsymbol {\alpha } \in \Delta ^r$ a vertex weighting. A triple $(r,\phi ,\boldsymbol {\alpha })$ is called optimal if it attains the maximum; that is, and $q(r,\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$ . Let be the set of optimal triples $(r,\phi ,\boldsymbol {\alpha })$ . Also let

and

In [10] and [11], we considered Problems $Q_0,Q_1,Q_2$ which are as Problem $Q^*$ except we relax $\alpha _i>0$ to $\alpha _i \geq 0$ and Problem $Q_t$ considers feasible $\phi \in \Phi _t(r;\boldsymbol {k})$ , where

$$ \begin{align*}\Phi_t(r;\boldsymbol{k}) := \left\{ \phi: \binom{[r]}{2} \to 2^{[s]} : \phi^{-1}(c) \text{ is }K_{k_c}\text{-free } \forall c \in [s], |\phi(ij)| \geq t \ \forall ij \in \binom{[r]}{2}\right\} \end{align*} $$

(and $q(\phi ,\boldsymbol {\alpha })$ only sums over pairs $ij$ with $\phi (ij) \neq \emptyset $ ). It is not hard to show that the optimal value of each problem is the same. Clearly, Problem $Q^*$ has the smallest feasible set. However, we will sometimes consider also for $t=0,1$ the set of triples $(r,\phi ,\boldsymbol {\alpha })$ with $\boldsymbol {\alpha } \in \Delta ^r$ and $\phi \in \Phi _t(r;\boldsymbol {k})$ which attain the maximum value. We write $\| \boldsymbol {a}-\boldsymbol {b}\|_1 := \sum _i|a_i-b_i|$ for the $\ell ^1$ -distance between finite tuples $\boldsymbol {a}$ and $\boldsymbol {b}$ of real numbers (where in the sum we add trailing $0$ ’s to make $\boldsymbol {a},\boldsymbol {b}$ equal length). In this paper, we always take $\log $ to the base $2$ ; from now on, we omit any subscript. We define $\mathbb {N} := \{1,2,3,\ldots \}$ .

The goal of this series of works has been to verify the following meta-conjecture:

• To solve the Erdős-Rothschild problem, it suffices to solve Problem $Q^*$ .

The main result of the present paper is that to determine $F(n;\boldsymbol {k})$ exactly, it suffices to solve the optimisation problem, when $\boldsymbol {k}$ satisfies a certain condition. This improves the main result of our previous paper [10] which had ‘approximately’ in place of ‘exactly’ – we use the results of [10] as a crucial tool in the present paper. In [11], we proved with Yilma that for every $n \in \mathbb {N}$ , at least one of the $\boldsymbol {k}$ -extremal graphs of order n is complete multipartite, and that

(1.3) $$ \begin{align} F(n;\boldsymbol{k}) = 2^{Q(\boldsymbol{k})\binom{n}{2}+o(n^2)}, \quad\text{ so }F(\boldsymbol{k})=Q(\boldsymbol{k}),\text{ where }\quad F(\boldsymbol{k}) := \lim_{n\to\infty}\frac{\log_2 F(n;\boldsymbol{k})}{\binom{n}{2}}. \end{align} $$

In [10], we proved a stability theorem for $\boldsymbol {k}$ satisfying a certain condition which we call the extension property. This is a property of optimal solutions that says an infinitesimal part added onto such a solution in an optimal way must look like a clone of an existing part.

Definition 1.2 (Clones and extension property)

Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . Given $r \in \mathbb {N}$ and $\phi \in \Phi _0(r;\boldsymbol {k})$ , say that $i \in [r]$ is

• ○ a clone of $j \in [r]\setminus \{ i \}$ (under $\phi $ ) if $\phi (ik) = \phi (jk)$ for all $k \in [r] \setminus \{ i,j\}$ and $|\phi (ij)| \leq 1$ ;

• ○ a strong clone of j if additionally $\phi (ij) = \emptyset $ .

We say that $\boldsymbol {k}$ has

• ○ the extension property if, for every and $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$ such that $\phi |_{\binom {[r^*]}{2}} = \phi ^*$ and $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$ , where

  $$ \begin{align*}\mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) := \sum_{\substack{i \in [r^*]\\ \phi(\{i,r^*+1\}) \neq \emptyset}}\alpha^*_i\log|\phi(\{ i,r^*+1 \})|,\end{align*} $$
  there exists $j \in [r^*]$ such that $r^*+1$ is a clone of j under $\phi $ ;

• ○ the strong extension property if, in fact, $r^*+1$ is a strong clone of j.

The strong extension property holds in all but one of the cases where the problem has been solved (this was proved in [10] apart from in the case $(3;6)$ which we include in the present paper).

Lemma 1.3. Every $\boldsymbol {k}$ in Theorem 1.1 apart from $(3;5)$ has the strong extension property.

The stability theorem says that whenever $\boldsymbol {k}$ has the extension property, every almost extremal graph – that is, G on n vertices such that $F(G;\boldsymbol {k})=F(n;\boldsymbol {k})\cdot 2^{o(n^2)}$ – looks like the blow-up of an optimal solution to Problem $Q^*$ . (For a definition of a $(\delta ,d)$ -regular pair, see Section 2.1.)

Theorem 1.4 (Stability [10, Theorem 1.4])

Let $s \in \mathbb {N}$ and suppose that $\boldsymbol {k} \in \mathbb {N}^s$ with $k_1\geq \ldots \geq k_s$ has the extension property. Then for all $\delta> 0$ , there exist $n_0 \in \mathbb {N}$ and ${\varepsilon }> 0$ such that the following holds. Let G be a graph on $n \geq n_0$ vertices such that

$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$

Then, for at least $(1-2^{-{\varepsilon } n^2})\cdot F(G;\boldsymbol {k})$ colourings $\chi : E(G) \rightarrow [s]$ which are $\boldsymbol {k}$ -valid, there are and a partition $Y_1 \cup \ldots \cup Y_{r^*} = V(G)$ such that the following hold.

1. (i) For all $i \in [r^*]$ , we have that $|\,|Y_i| - \alpha ^*_in\,| < 1$ .

2. (ii) for all $c \in \phi ^*(ij)$ and $ij \in \binom {[r^*]}{2}$ , we have that $\chi ^{-1}(c)[Y_i,Y_j]$ is $(\delta ,|\phi ^*(ij)|^{-1})$ -regular. In particular, $e_G(Y_i,Y_j) \geq (1-s\delta )|Y_i||Y_j|$ .

3. (iii) Suppose $\sum _{i \in [r^*]}e(G[Y_i])> \delta n^2$ . Then $\boldsymbol {k}$ does not have the strong extension property, and all but at most $\delta n^2$ edges in $\bigcup _{i \in [r^*]}G[Y_i]$ are coloured with $1$ under $\chi $ . Moreover, if $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$ is such that at least $\delta n^2$ edges need to be removed from $G[Y_i]$ to make it $K_{\ell _i}$ -free, then $\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$ .

The following corollary is a simple consequence of Theorem 1.4 and shows that when $\boldsymbol {k}$ has the strong extension property, every asymptotically extremal graph is close to complete partite.

Corollary 1.5 (Stability for the strong extension property [10, Corollary 1.5])

Let $s \in \mathbb {N}$ and suppose that $\boldsymbol {k} \in \mathbb {N}^s$ with $k_1\geq \ldots \geq k_s$ has the strong extension property. Then for all $\delta> 0$ , there exist $n_0 \in \mathbb {N}$ and ${\varepsilon }> 0$ such that the following holds. Let G be a graph on $n \geq n_0$ vertices such that

$$ \begin{align*}\frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k}) - {\varepsilon}. \end{align*} $$

Then there are and a partition V(G) = $V_1 \cup \ldots \cup V_{r^*}$ with $\left |\,|V_i|-\alpha ^*_i n \,\right | < 1$ for all $i \in [r^*]$ such that the number of adjacencies in G that need to be changed to obtain $K[V_1,\ldots ,V_{r^*}]$ is at most $\delta n^2$ . Moreover, for at least $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) \boldsymbol {k}$ -valid s-edge-colourings $\chi $ of G, there exists such that $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $ and $\chi ^{-1}(c)[V_i,V_j]$ is $(\delta ,|\phi ^*(ij)|^{-1})$ -regular for all $ij \in \binom {[r^*]}{2}$ and $c \in \phi ^*(ij)$ .

1.1. A general exact result

Our first main result is an exact version of Corollary 1.5 – that is, an exact result for $\boldsymbol {k}$ with the strong extension property. One consequence of this result is that for such $\boldsymbol {k}$ , every large $\boldsymbol {k}$ -extremal graph is complete partite.

Indeed, we prove that every large $\boldsymbol {k}$ -extremal graph $G^*$ is a complete $r^*$ -partite graph, whose classes $X_1,\ldots , X_{r^*}$ are approximately $\boldsymbol {\alpha }^*$ -weighted, for some . Moreover, almost every $\boldsymbol {k}$ -valid colouring $\chi $ of $G^*$ is perfect (with respect to $(\phi ;X_1,\ldots ,X_{r^*})$ ), which means that there is a pattern for some $\boldsymbol {\alpha }$ close to $\boldsymbol {\alpha }^*$ so that every edge e between $X_i$ and $X_j$ in $G^*$ satisfies $\chi (e) \in \phi (ij)$ .

Theorem 1.6 (Exactness for the strong extension property)

Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ have the strong extension property. Then for all ${\varepsilon }> 0$ , there exist $\delta>0$ and $n_0 \in \mathbb {N}$ such that whenever G is a $\boldsymbol {k}$ -extremal graph on $n \geq n_0$ vertices, the following hold.

1. (i) G is a complete multipartite graph; more precisely, there exist and $\boldsymbol {\beta } \in \Delta ^{r^*}$ with $\| \boldsymbol {\alpha }^*-\boldsymbol {\beta }\|_1 < {\varepsilon }$ such that $G = K(X_1,\ldots ,X_{r^*})$ , where $|X_i| = \beta _i n$ for all $i \in [r^*]$ ;

2. (ii) for at least $(1-2^{-\delta n})\cdot F(G;\boldsymbol {k}) \boldsymbol {k}$ -valid colourings $\chi $ of G, there is with $\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 < {\varepsilon }$ and such $\chi $ is perfect with respect to $(\phi ;X_1,\ldots ,X_{r^*})$ .

We show that by solving a further optimisation problem (which is not too difficult in all known cases), one can determine $F(n;\boldsymbol {k})$ up to a multiplicative error of $1+o(1)$ and also determine the extremal graphs – whenever the solution(s) of Problem $Q^*$ are known. Thus, for $\boldsymbol {k}$ with the strong extension property, it is true that ‘to solve the Erdős-Rothschild problem, it suffices to solve Problem $Q^*$ ’. Theorem 1.6 allows us to systematically recover all known exact results for the Erdős-Rothschild problem.

Problem 1.7 (Perfect colouring problem)

Let and $n \in \mathbb {N}$ . Maximise

subject to $\boldsymbol {m} \in P_{r^*}(n)$ , where $P_{r^*}(n)$ is the set of $\boldsymbol {m} \in \mathbb {N}^{r^*}$ with $\|\boldsymbol {m}\|_1 = n$ and $m_1\geq \ldots \geq m_{r^*}$ .

Notice that $\mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m})$ is essentially the number of perfect colourings of a complete $r^*$ -partite graph $K_{\boldsymbol {m}}$ with vertex classes of size $m_1,\ldots ,m_{r^*}$ (with some overcounting due to, for example, distinct $\phi ,\phi '$ with $\phi (ij)\cap \phi '(ij) \neq \emptyset $ for all $ij \in \binom {[r^*]}{2}$ ). However, being able to solve the perfect colouring problem may not a priori allow one to precisely determine the $\boldsymbol {k}$ -extremal graphs. Indeed, since not every colouring of G is perfect, a graph with the maximal number of perfect colourings may not be $\boldsymbol {k}$ -extremal if there is another graph with only slightly fewer. For this reason, we make the following definition.

Definition 1.8 (Solubility of $\boldsymbol {k}$ )

Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . We say that $\boldsymbol {k}$ is soluble if there exist $c> 0$ and $n_0 \in \mathbb {N}$ , such that for all $n \geq n_0$ , there are and $\boldsymbol {m}^* \in P_{r^*}(n)$ such that for all , we have

$$ \begin{align*}\mathrm{perf}_{r^*,\boldsymbol{\alpha}^*}(\boldsymbol{m}^*)> (1+c)\mathrm{perf}_{r',\boldsymbol{\alpha}'}(\boldsymbol{m}) \end{align*} $$

for all $\boldsymbol {m} \in P_{r'}(n)$ for which $(r^*,\boldsymbol {\alpha }^*,\boldsymbol {m}^*)$ is distinct from $(r',\boldsymbol {\alpha }',\boldsymbol {m})$ . We say that $\boldsymbol {m}^*$ is the supersolution to $\boldsymbol {k}$ at n and write $\mathrm {perf}(\boldsymbol {m}^*) := \mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m}^*)$ .

Theorem 1.6(i) implies that every $\boldsymbol {k}$ -extremal graph G on $n \geq n_0$ vertices is such that there is some $\boldsymbol {m} \in \mathbb {N}^{r^*}$ with $\|\boldsymbol {m}-\boldsymbol {\alpha }^*n\|_1 < {\varepsilon } n$ so that $G \cong K_{m_1,\ldots ,m_{r^*}}$ . If $\boldsymbol {k}$ is soluble, then Theorem 1.6(ii) implies that for all large n and all $m_1+\ldots +m_{r^*}=n$ , we have $F(K_{m_1^*,\ldots ,m_{r^*}^*},n)> F(K_{m_1,\ldots ,m_{r^*}},n)$ , where $\boldsymbol {m}^*$ is the supersolution at n and $(m_1,\ldots ,m_{r^*}) \neq (m_1^*,\ldots ,m_{r^*}^*)$ . This gives the following corollary:

Corollary 1.9 (Perfect exactness for the strong extension property)

Let $s \in \mathbb {N}$ and let $\boldsymbol {k} \in \mathbb {N}^s$ be soluble and have the strong extension property. Then

$$ \begin{align*}F(n;\boldsymbol{k}) = (1+o(1)) \cdot \mathrm{perf}(\boldsymbol{m}^*_n)\quad\text{as }n \to \infty, \end{align*} $$

and there exists $n_0 \in \mathbb {N}$ such that for all $n \geq n_0$ , the unique $\boldsymbol {k}$ -extremal graph on n vertices is $K_{\boldsymbol {m}_n^*}$ , where $\boldsymbol {m}^*_n$ is the supersolution to $\boldsymbol {k}$ at n.

Proposition 1.10. Every exact result in Theorem 1.1 (that is, except the case $(3;5)$ ) follows from Corollary 1.9.

1.2. The triangle problem

Our second main result concerns the case $\boldsymbol {k}=(3;s)$ (Erdős and Rothschild’s original problem was $s=2$ ). Previously, $F(n;\boldsymbol {k})$ had been determined for $s=2,3,4,6$ and asymptotically for $s=5$ . We solve the problem for $s=7$ and use the same method to give a new proof for $s=6$ .

Theorem 1.11. There exists $n_0>0$ such that for every $n \geq n_0$ , the Turán graph $T_8(n)$ is the unique $(3;6)$ -extremal graph, and the unique $(3;7)$ -extremal graph.

In fact, our results imply that

$$ \begin{align*}F(n;(3;6)) = (C_j+o(1))\cdot (4^3 3^4)^{t_8(n)/7}\quad\text{and}\quad F(n;(3;7)) = (C+o(1))\cdot 4^{t_8(n)}, \end{align*} $$

where C is a constant and $C_j$ is a constant depending only on the remainder j when n is divided by $8$ . These constants can be explicitly determined if desired.

A key component in our proof is our general exact result, Corollary 1.9, which reduces the task to solving Problem $Q^*$ . For other cases of $\boldsymbol {k}$ , Problem $Q^*$ has been solved by considering a linear relaxation, with variables which are essentially graph densities, and linear constraints which replace combinatorial constraints such as being $K_k$ -free by the associated density bound given by Turán’s theorem. However, the solutions to this relaxation generally do not correspond to feasible solutions to Problem $Q^*$ , so additional constraints are needed. The main new ingredient is a lemma about the density of the union of two dense triangle-free graphs (Lemma 3.3), which may be of independent interest. This allows us to introduce a new constraint which yields a meaningful solution.

In the known cases of the triangle problem, the perfect colourings of extremal graphs are closely related to Hadamard matrices. A Hadamard matrix H of order n is an $n \times n$ matrix with entries in $\{ -1,+1 \}$ such that $HH^\intercal = nI_n$ . A Hadamard matrix of order n exists only if $n=1,2$ or n is divisble by $4$ ; that this is sufficient was conjectured by Hadamard in 1893 [7]. This conjecture remains open – at the time of writing, the smallest multiple of $4$ for which order there is no known Hadamard matrix is $4\times 167$ . It is, however, easy to construct arbitrarily large Hadamard matrices by using smaller ones as building blocks. For example, Sylvester (see, for example, [13]) observed that if H is a Hadamard matrix, then so is $\left (\begin {smallmatrix} H & H\\ H & -H \end {smallmatrix}\right )$ . Hadamard matrices have the largest absolute value of the determinant among all complex square matrices with entries of absolute value at most one (see, for example, [7]).

The connection to Problem $Q^*(3;s)$ is that there is a decomposition of the multigraph $2t K_{4t}$ into copies of $K_{2t,2t}$ if and only if a Hadamard matrix of order $4t$ exists (and the locations of the copies can be read off the matrix); see [3] or Lemma 3.6 for a proof. It is plausible that in an optimal $(2r,\phi ,\boldsymbol {\alpha })$ , every $\phi ^{-1}(c) \cong K_{r,r}$ , and $\boldsymbol {\alpha }$ is uniform (and also plausible that the number of vertices in an optimal solution is even). If also $|\phi (ij)|=p$ for all pairs $ij$ , then such a solution exists if and only if $p K_{2r}$ has a decomposition into copies of $K_{r,r}$ . Comparing edge counts, the number of copies is $s=p\binom {2r}{2}/r^2=p(2r-1)/r$ . So $p = tr$ for some integer t, since r and $2r-1$ are coprime for $r \geq 2$ . If $t=1$ , then $r=2\ell $ for some integer $\ell $ , since otherwise there is no decomposition due to the nonexistence of the corresponding Hadamard matrix. So , where $|\phi _{4\ell -1}(ij)|=2\ell $ for all $ij$ and $\boldsymbol {u}$ is uniform. For $i=1,2,3$ , , where $\phi _{4\ell -1}^{-i}$ is obtained from $\phi _{4\ell -1}$ by removing i colours. Also, , where $\phi _{4\ell -5}^{+4-i}$ is obtained from $\phi _{4\ell -5}$ by duplicating $4-i$ colours.

This suggests the following problem, which would probably be very difficult to resolve.

Problem 1.12. Are the following true for sufficiently large n: For all $\ell \geq 2$ , is the unique $(3;4\ell -1)$ -extremal graph $T_{4\ell }(n)$ ? For all $\ell \geq 2$ , is $T_{4(\ell -1)}(n)$ or $T_{4\ell }(n)$ one of the $(3;4\ell -1-i)$ -extremal graphs for all $i=1,2,3$ ?

All existing results fit the pattern described (see Subsection 3.4).

1.3. The two colour problem

Having proved a general exact result for the case when $\boldsymbol {k}$ has the strong extension property, we now investigate what happens when $\boldsymbol {k}$ has the extension property but not the strong extension property (we will say that such $\boldsymbol {k}$ have the weak extension property). This appears to be much more difficult. The reason for this is the possible presence of small parts in a complete multipartite extremal graph (when $\boldsymbol {k}$ has the strong extension property, no part has size $o(n)$ (see Lemma 2.2(i))). In a perfect colouring, only the neighbourhood into a large part is controlled, and we have a priori no information about colourings between small parts. However, it could be the case that this part of the colouring is forced by the perfect colouring in the rest of the graph, and thus, the number of small parts can also be controlled.

In our final theorem, we consider the simplest case when $\boldsymbol {k}$ has the weak extension property – namely, $\boldsymbol {k} = (k+1,k)$ for $k \geq 3$ . For small k, we determine the (unique) $(k+1,k)$ -extremal graph, which turns out to have a part of size $O(k)$ , and the size of this part depends on the value of n modulo $k-1$ . The proof is already fairly involved and relies heavily on a strong stability theorem for complete partite graphs (Theorem 2.12), which is the main ingredient in the proof of Theorem 1.6. Similar arguments could probably be used to determine the $(k+\ell ,k)$ -extremal graph for (very) small $\ell $ and small k, which we discuss further in Section 6.

Theorem 1.13. For all integers $k \geq 3$ , there exists $n_0>0$ such that for all integers $n \geq n_0$ , we have

$$ \begin{align*}F(n;k+1,k) = O_k(1) \cdot 2^{t_{k-1}(n)}, \end{align*} $$

and every $(k+1,k)$ -extremal graph is complete k-partite, with one part of size at most $2(k-1)$ and the other part sizes all within $2(k-1)$ of each other. Moreover, the constant $O_k(1)$ is at least $2$ .

(Recall that the results of [1] imply that $F(n;k+1,k) \geq F(n;k,k) = 2^{t_{k-1}(n)}$ .) We conjecture that the $O_k(1)$ multiplicative constant has a special form.

Conjecture 1.14. For all integers $k \geq 3$ and $0 \leq j \leq k-1$ , there exists $n_0>0$ such that the following holds for all integers $n \geq n_0$ . Let

$$ \begin{align*}f(k,j,\ell) := \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1 \end{cases} \end{align*} $$

and let $\ell ^*$ be such that $\max _{0 \leq \ell \leq k-1}f(k,j,\ell ) = f(k,j,\ell ^*)$ . Then $\ell ^*$ is unique, and whenever $n \equiv j (\mod k-1)$ ,

$$ \begin{align*}F(n;k+1,k) = (1+o(1))\cdot f(k,j,\ell^*) \cdot 2^{t_{k-1}(n)}. \end{align*} $$

Moreover, the unique $(k+1,k)$ -extremal graph on n vertices is complete k-partite, with one part of size $\ell ^*$ and the other parts as equal as possible.

Given Theorem 1.13, it is easy to prove this conjecture for small k, using computer assistance to test each of the possible extremal graphs.

Theorem 1.15. Conjecture 1.14 holds for $3 \leq k \leq 10$ .

For example, $F(n;4,3) = (2+o(1)) \cdot 2^{t_2(n)}$ when n is even and $F(n;4,3) = (\frac {9}{4}+o(1))\cdot 2^{t_2(n)}$ when n is odd; in both cases, the unique extremal graph has parts of size $2,\lfloor \frac {n-2}{2}\rfloor ,\lceil \frac {n-2}{2}\rceil $ .

1.4. Organisation of the paper

In Section 2, we prove Theorem 1.6, which follows from Theorem 2.12, a strong stability theorem for complete partite graphs. Section 3 solves Problem $Q^*$ in the case when $s=7$ and $k=3$ . Section 4 contains the proofs of Proposition 1.10 and Theorem 1.11, which follow easily by combining Theorem 1.6 and solving Problem $Q^*$ in the relevant cases. In Section 5, we use the full strength of Theorem 2.12 to prove Theorems 1.13 and 1.15. Section 6 contains some concluding remarks and directions for future research.

There are five python programs used in the paper to check various numerical claims (6check.py, 6config.py, 7ext.py, dcheck.py and smallpart.py), which are all written in Python 3. They are included in the ancillary folder of the arXiv version of this paper [9].

2. A general exact result

The aim of this section is to use Theorem 1.4 to prove Theorem 1.6, a strengthening of Corollary 1.5 for $\boldsymbol {k}$ with the strong extension property.

This section is organised as follows. In Subsection 2.1, we collect some tools that we will need, including some lemmas on optimal solutions from [11] and [10], as well as standard regularity tools. In Subsection 2.2, we define increasingly strict properties of colourings with respect to a partition. The main result of Subsection 2.3 is Theorem 2.12, a version of our stability result (Theorem 1.4) for complete multipartite graphs. The new part of this theorem is the last part which says that if every vertex has large contribution to the number of valid colourings, then there are many ‘perfect’ colourings which follow a colour pattern exactly. In Subsection 2.4, we prove Theorem 1.6.

2.1. Tools

The following are tools concerning Problem $Q^*$ from the previous papers in this series. Given a triple $(r,\phi ,\boldsymbol {\alpha })$ , we have

$$ \begin{align*}q(\phi,\boldsymbol{\alpha}) = \sum_{i \in [r]}\alpha_i q_i(\phi,\boldsymbol{\alpha})\quad\text{where}\quad q_i(\phi,\boldsymbol{\alpha}) := \sum_{\substack{j \in [r] \setminus \{ i \}\\ \phi(ij)\neq\emptyset}}\alpha_j\log|\phi(ij)| \end{align*} $$

is the normalised contribution of vertex i to the sum $q(\phi ,\boldsymbol {\alpha })$ .

Proposition 2.1. Let $s,r \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . The following hold.

1. (i) [11, Proposition 11] Let $\phi \in \Phi _0(r;\boldsymbol {k})$ and $\boldsymbol {\alpha },\boldsymbol {\beta } \in \Delta ^r$ . Then

   $$ \begin{align*}|q(\phi,\boldsymbol{\alpha})-q(\phi,\boldsymbol{\beta})| < 2\left(\log s\right)\|\boldsymbol{\alpha}-\boldsymbol{\beta}\|_1. \end{align*} $$

2. (ii) [10, Proposition 2.1] Let . For every $i \in [r]$ with $\alpha _i> 0$ , we have that $ q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k}) $ .

3. (iii) [10, Lemma 2.5] Let and suppose $k_1 \geq \ldots \geq k_s$ . Then $r^* \geq k_2-1$ and $\phi ^{-1}(c)$ is maximally $K_{k_c}$ -free for all $c \in [s]$ .

Lemma 2.2. Let $s \in \mathbb {N}$ and suppose that $\boldsymbol {k} \in \mathbb {N}^s$ has the extension property, where $k_1 \geq \ldots \geq k_s$ . Then the following hold.

1. (i) [10, Lemma 2.8] There exists $\mu> 0$ such that $\alpha _i^*> \mu $ for all and $i \in [r^*]$ .

2. (ii) [10, Lemma 2.9] There exists ${\varepsilon }> 0$ such that the following holds. Let and let $\phi ' \in \Phi _0(r^*+1,\boldsymbol {k})$ be such that $\phi '|_{\binom {[r^*]}{2}} = \phi ^*$ and $ \mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) \geq Q(\boldsymbol {k}) -{\varepsilon } $ . Then there exists $j \in [r^*]$ such that $r^*+1$ is a clone of j under $\phi '$ . If $\boldsymbol {k}$ has the strong extension property, then $r^*+1$ is a strong clone.

3. (iii) [10, Lemma 2.10(iii)] Let and $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$ be such that $\phi |_{\binom {[r^*]}{2}}=\phi ^*$ and $r^*+1$ is a clone of $i \in [r^*]$ under $\phi $ . Then $\phi (\{ i,r^*+1 \}) \subseteq \{ 1 \}$ .

We need various lemmas concerning Szemerédi’s regularity, starting with the following definitions.

Definition 2.3 (Edge density, regularity of pairs and partitions)

Given a graph G and disjoint nonempty sets $A,B \subseteq V(G)$ , we define the edge density between A and B to be

$$ \begin{align*}d_G(A,B) := \frac{e_G(A,B)}{|A||B|}, \end{align*} $$

where $e_G(A,B)$ is the number of edges in G with one vertex in A and one vertex in B. Given ${\varepsilon },d> 0$ , the pair $(A,B)$ is called

• ○ ${\varepsilon }$ -regular if for every $X \subseteq A$ and $Y \subseteq B$ with $|X| \geq {\varepsilon }|A|$ and $|Y| \geq {\varepsilon }|B|$ , we have that $|d_G(X,Y) - d_G(A,B)| \leq {\varepsilon }$ .

• ○ $({\varepsilon }, d)$ -regular if it is ${\varepsilon }$ -regular and $d_G(A,B) = d \pm {\varepsilon }$ (i.e., $d-{\varepsilon }\leq d_G(A,B)\leq d+{\varepsilon }$ ),

• ○ $({\varepsilon },\geq \! d)$ -regular if it is ${\varepsilon }$ -regular and $d_G(A,B) \geq d-{\varepsilon }$ .

Lemma 2.4 (Embedding Lemma [8, Theorem 2.1])

For every $\eta>0$ and integer $k \geq 2$ , there exist ${\varepsilon }>0$ and $m_0 \in \mathbb {N}$ such that the following holds. Suppose that G is a graph with a partition $V(G) = V_1 \cup \ldots \cup V_k$ such that $|V_i| \geq m_0$ for all $i \in [k]$ , and every pair $(V_i,V_j)$ for $1 \leq i < j \leq k$ is $({\varepsilon },\geq \eta )$ -regular. Then G contains $K_k$ .

Proposition 2.5 [10, Proposition 4.4]

Let $A,B$ be disjoint sets of vertices, $s \in \mathbb {N}$ and ${\varepsilon }> 0$ satisfying $1/|A|,1/|B| \ll {\varepsilon } \ll 1/s$ . Let $G_1,\ldots ,G_s$ be pairwise edge-disjoint subgraphs of $K[A,B]$ . Suppose that not all of $G_1,\ldots ,G_s$ are $({\varepsilon },s^{-1})$ -regular graphs. Then there exist $c \in [s]$ and $X \subseteq A$ , $Y \subseteq B$ with $|X| = \lceil {\varepsilon }|A|\rceil $ and $|Y| = \lceil {\varepsilon } |B| \rceil $ such that

$$ \begin{align*}d_{G_c}(X,Y) \leq \frac{1}{s}\left( 1 - \frac{{\varepsilon}}{2}\right). \end{align*} $$

Proposition 2.6. Let $(A,B)$ be an $({\varepsilon }, d)$ -regular pair and let $(A',B')$ be a pair such that $|A' \bigtriangleup A| \leq \alpha |A'|$ and $|B' \bigtriangleup B| \leq \alpha |B'|$ for some $0 \leq \alpha \leq 1$ . Then $(A',B')$ is an $({\varepsilon }+7\sqrt {\alpha }, d)$ -regular pair.

Proposition 2.7 (see, for example, [8])

Let ${\varepsilon },\delta $ be such that $0 < 2\delta \leq {\varepsilon } < 1$ . Suppose that $(X,Y)$ is a $\delta $ -regular pair, and let $X' \subseteq X$ and $Y' \subseteq Y$ . If

$$ \begin{align*}\min \left\{ \frac{|X'|}{|X|} , \frac{|Y'|}{|Y|} \right\} \geq \frac{\delta}{{\varepsilon}}, \end{align*} $$

then $(X',Y')$ is ${\varepsilon }$ -regular.

The following estimate will be useful when counting colourings; it can be proved by looking at the tail of the binomial distribution.

Proposition 2.8 (see, for example, [10, Corollary 4.8])

Let $n,k \in \mathbb {N}$ and $\delta \in \mathbb {R}$ , where $0 < 1/n \ll \delta \ll 1/k$ . Then

$$ \begin{align*}\sum_{i=0}^{\lfloor (k^{-1}-\delta) n \rfloor}\binom{n}{i} (k-1)^{n-i} \leq e^{-\delta^2k n/3} \cdot k^n. \end{align*} $$

Finally, we need the following simple fact.

Proposition 2.9 (see, for example, [10, Claim 2.5.1])

Let $k \in \mathbb {N}$ and let H be maximally $K_k$ -free. Then every $x \in V(H)$ lies in a copy of $K_{k-1}$ if and only if $|V(H)| \geq k-1$ .

2.2. Hierarchy of colourings

We will now define three types of colouring, each stricter than the last – namely, good, locally good and perfect. Each type is defined with respect to a partition of the graph. Theorem 1.4 states that almost every valid colouring of a near-extremal graph G is ‘good’ with respect to a partition weighted like an optimal vertex weighting. Our aim in Theorem 1.6 is to prove that almost all of these colourings are in fact ‘perfect’. We achieve this via the property of being ‘locally good’, where a colouring is such if, looking at a single colour between a pair in a partition, we see a regular graph of the right density, and furthermore, the coloured neighbourhood of a vertex or pair of vertices in every part has the right size.

Given a partition $X_1,\ldots ,X_p$ of a set S, we say that a partition $Y_1, \ldots , Y_r$ of S is a coarsening of $X_1,\ldots , X_p$ if for all $i \in [p]$ , there is a $j \in [r]$ such that $X_i \subseteq Y_j$ .

Definition 2.10 ( $\delta $ -good, ( $\gamma ,\delta )$ -locally good, $(\gamma ,\delta )$ -perfect)

Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . Let G be a complete m-partite graph with vertex partition $X_1,\ldots ,X_m$ . Let $\phi \in \Phi _0(r;\boldsymbol {k})$ , let $Y_0,Y_1,\ldots ,Y_r$ be a coarsening of $X_1,\ldots ,X_m$ (where we allow $Y_0$ to be empty), let $\mathcal {Y} := (Y_1,\ldots ,Y_{r})$ , and let $\delta ,\gamma> 0$ . We say that a $\boldsymbol {k}$ -valid colouring $\chi $ of G is

• ○ $\delta $ -good with respect to $(\phi; \mathcal {Y})$ if the following hold.

  • – For all $ij \in \binom {[r]}{2}$ and $c \in \phi (ij)$ , we have that $\chi ^{-1}(c)[Y_i,Y_j]$ is $(\delta ,|\phi (ij)|^{-1})$ -regular.

  • – $ \sum _{i \in [r]}|\, e_G(Y_i) - |\chi ^{-1}(1)[Y_i]| \,| < \delta n^2$ .

  Write $\mathcal {G}_\delta (G;\phi ,\mathcal {Y})$ for the set of these colourings.

• ○ $(\gamma ,\delta )$ -locally good with respect to $(\phi; \mathcal {Y})$ if the following hold.

  • – $\chi $ is $\delta $ -good with respect to $(\phi ;\mathcal {Y})$ .

  For all $x \in V(G)$ , there exists $i=i_x \in [r]$ such that

  • – For all $j \in [r]\setminus \{ i \}$ , parts $X \subseteq Y_j$ (so $X=X_t$ for some $t \in [m]$ ) and $c \in \phi (ij)$ , we have $|\chi ^{-1}(c)[x,X]|=|\phi (ij)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$ , where $\ell _j$ is the number of parts inside $Y_j$ . In particular, $|\chi ^{-1}(c)[x,Y_j]| = (|\phi (ij)|^{-1}\pm \delta )|Y_j|$ .

  • – $d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$ .

  • – For all $i' \in [r]\setminus \{i\}$ , we have $d_G(x,Y_{i'}) \geq (1-\gamma )|Y_{i'}|$ .

  For all distinct $y,z \in V(G)$ , $j \in [r]\setminus \{i_y,i_z\}$ and parts $X \subseteq Y_j$ , we have

  • – $|N_{\chi ^{-1}(c_y)}(y,X) \cap N_{\chi ^{-1}(c_z)}(z,X)| = |\phi (i_yj)|^{-1}|\phi (i_zj)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$ for all $c_y \in \phi (i_yj)$ and $c_z \in \phi (i_zj)$ .

  Write $\mathcal {LG}_{\gamma ,\delta }(G; \phi ,\mathcal {Y})$ for the set of these colourings.

• ○ $(\gamma ,\delta )$ -perfect with respect to $(\phi; \mathcal {Y})$ if

  • – $\chi $ is $(\gamma ,\delta )$ -locally good with respect to $(\phi ;\mathcal {Y})$ .

  • – For all $x \in V(G)$ , there exists $i \in [r]$ such that for all $j \in [r]$ and $y \in N_G(x,Y_j)$ , we have $\chi (xy) = 1$ if $j=i$ , and $\chi (xy) \in \phi (ij)$ otherwise.

  Write $\mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$ for the set of these colourings.

Note that if $\gamma ' \geq \gamma $ and $\delta ' \geq \delta $ , then a $\delta $ -good colouring is also $\delta '$ -good; a $(\gamma ,\delta )$ -locally good colouring is also $(\gamma ',\delta ')$ -locally good, and a $(\gamma ,\delta )$ -perfect colouring is also $(\gamma ',\delta ')$ -perfect.

It is a fairly straightforward consequence of Lemma 2.4 (the Embedding Lemma) that if a colouring is $(\gamma ,\delta )$ -locally good with respect to $(\phi ;\mathcal {Y})$ and no member of $\mathcal {Y}$ is too small, then it is $(\gamma ,\delta )$ -perfect.

Lemma 2.11. Let $s,r \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ , where $k_1 \geq \ldots \geq k_s$ and $r \geq k_2-1$ , and let $\mu> 0$ . Then there exist $n_0 \in \mathbb {N}$ and $\delta> 0$ such that the following hold. Let G be a complete partite graph on $n \geq n_0$ vertices with parts $X_1,\ldots ,X_m$ , and let $Y_0,\ldots ,Y_r$ be a partition of $V(G)$ which is a coarsening of $X_1,\ldots ,X_m$ . Let $\mathcal {Y} := (Y_1,\ldots ,Y_{r})$ and assume that $|Y_i| \geq \mu n$ for all $i \in [r]$ . Let $\phi \in \Phi _0(r;\boldsymbol {k})$ be such that $\phi ^{-1}(c)$ is maximally $K_{k_c}$ -free for all $c \in [s]$ . Then, for all $\gamma> 0$ ,

$$ \begin{align*}\mathcal{LG}_{\gamma,\delta}(G;\phi,\mathcal{Y}) = \mathcal{P}_{\gamma,\delta}(G;\phi,\mathcal{Y}). \end{align*} $$

Proof. Let ${\varepsilon }> 0,m_0 \in \mathbb {N}$ be the output of Lemma 2.4 applied with $s^{-1},k_c$ playing the roles of $\eta ,k$ for every $c \in [s]$ . Let $n_0 := 2s^2 m_0/\mu $ and $\delta := {\varepsilon }^2$ . By decreasing ${\varepsilon }$ and increasing $m_0$ if necessary, we may assume that $\delta \ll \mu $ .

Certainly, $\mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y}) \supseteq \mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$ by definition. Suppose that there exists $\chi \in \mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$ such that the $(\gamma ,\delta )$ -perfect condition fails at some $x \in V(G)$ . Since $\chi $ is $(\gamma ,\delta )$ -locally good, there exists $i \in [r]$ such that for all $j \in [r]\setminus \{ i \}$ , we have that $|\chi ^{-1}(c)[x,Y_j]|=(|\phi (ij)|^{-1} \pm \delta )|Y_j|$ and $d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$ . We will show that for all $j \in [r]\setminus \{ i \}$ and $y \in N_G(x,Y_j)$ , we have $\chi (xy) \in \phi (ij)$ , and for all $y \in N_G(x,Y_i)$ , we have $\chi (xy) = 1$ .

Suppose first that there exists $j \in [r]\setminus \{ i \}$ and $y \in N_G(x,Y_j)$ such that $\chi (xy) =: c \notin \phi (ij)$ . Let $k := k_{c}$ and $J := \chi ^{-1}(c)$ . Now, $\phi ^{-1}(c)$ is maximally $K_{k}$ -free. Since $ij \notin \phi ^{-1}(c)$ , we have that $\phi ^{-1}(c) \cup \{ ij \}$ contains a copy of $K_{k}$ . So there exist $i_3,\ldots ,i_k \in [r]\setminus \{ i,j \}$ such that $i_1,\ldots ,i_k$ span a copy of $K_k$ in $\phi ^{-1}(c)$ , where $i_1 := i$ and $i_2 := j$ .

Since $\chi $ is $(\gamma ,\delta )$ -locally good, for all $\ell =3,\ldots ,k$ , we have, by the pairs condition, taking the union over all parts $X \subseteq Y_{i_\ell }$ , that

$$ \begin{align*}|N_J(x,Y_{i_\ell}) \cap N_J(y,Y_{i_\ell})| \geq (|\phi(ii_\ell)|^{-1}|\phi(ji_\ell)|^{-1} - \delta)|Y_{i_\ell}| \geq \frac{|Y_{i_\ell}|}{2s^2} \geq \frac{\mu n}{2s^2} \geq m_0. \end{align*} $$

Let $U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$ . Proposition 2.5 implies that $J[U_\ell ,U_{\ell '}]$ is a $(\sqrt {\delta },\geq \! s^{-1})$ -regular pair for all distinct $\ell ,\ell ' \in \{ 3,\ldots , k \}$ . Lemma 2.4 implies that J contains a copy of $K_{k-2}$ . Together with $x,y$ , we obtain a copy of $K_k$ in $\chi ^{-1}(c)$ , a contradiction.

Suppose instead that there is some $y \in N_G(x,Y_i)$ such that $\chi (xy) =: c \neq 1$ . Let $k := k_c$ and $J := \chi ^{-1}(c)$ . Since $r \geq k_2-1 \geq k-1$ , Proposition 2.9 implies that i lies in a copy of $K_{k-1}$ in the graph $\phi ^{-1}(c)$ . Let $i_1 := i$ and let $i_2,\ldots ,i_{k-1}$ be the other vertices in this copy. As before, setting $U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$ for all $\ell \in [2,k-1]$ , we have that $J[U_2,\ldots ,U_{k-1}]$ contains a copy of $K_{k-2}$ . Together with $x,y$ , this gives a copy of $K_k$ in J, a contradiction.

2.3. Stability for complete multipartite graphs

Given a graph G, a subgraph H of G, and an s-edge-colouring $\chi $ of H, we say that $\overline {\chi }$ is an extension of $\chi $ if $\overline {\chi }$ is an s-edge-colouring of G such that $\overline {\chi }|_{H} = \chi $ .

Theorem 2.12 (Stability for complete multipartite graphs)

Let $s \in \mathbb {N}$ and suppose that $\boldsymbol {k} \in \mathbb {N}^s$ with $k_1 \geq \ldots \geq k_s$ has the extension property. Then for all $\delta> 0$ , there exist $n_0 \in \mathbb {N}$ and ${\varepsilon } \in \mathbb {R}$ with $0 < {\varepsilon } < \delta $ such that the following holds. Let $m \in \mathbb {N}$ and $G = K(X_1,\ldots ,X_m)$ be a complete m-partite graph on $n \geq n_0$ vertices such that

$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$

Then for at least $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$ -edge-colourings $\chi $ of G which are $\boldsymbol {k}$ -valid, there are with $r^* \leq m$ and a coarsening $Z_0,\ldots ,Z_{r^*}$ of $X_1,\ldots ,X_m$ such that the following hold.

1. (i) $\sum _{i \in [r^*]}|\,|Z_i|-\alpha _i^*n\,| < \delta n$ , and $\chi $ is $\delta $ -good with respect to $(\phi ^*; Z_1,\ldots ,Z_{r^*})$ .

2. (ii) If, for all $i \in [r^*]$ , $\ell _i$ is the number of $X_j$ in $Z_i$ , then $\ell _1 = \ldots = \ell _{r^*} = 1$ ; or $\boldsymbol {k}$ does not have the strong extension property and $\ell _1 + \ldots + \ell _{r^*} \leq k_1-1$ .

Furthermore, if we have

(2.1) $$ \begin{align} \begin{aligned} &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{aligned} \end{align} $$

then there are at least $(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k}) s$ -edge-colourings $\chi $ of G for which there are and $Z_0,\ldots ,Z_{r^*}$ as above such that $\chi $ is $(0,\delta )$ -perfect with respect to $(\phi ^*; Z_1,\ldots ,Z_{r^*})$ .

Proof. For brevity, write $Q := Q(\boldsymbol {k})$ , $R := R(\boldsymbol {k})$ , $F(G) := F(G;\boldsymbol {k})$ , and abbreviate similarly elsewhere. Lemma 2.2(i) implies that there exists $\mu> 0$ such that for all , we have that $\alpha _i^*> \mu $ for all $i \in [r^*]$ . Applying Lemma 2.2(ii) gives the constant ${\varepsilon }_0$ . We may assume that $\delta \ll {\varepsilon }_0,\mu ,1/R$ since a smaller $\delta $ yields a stronger conclusion. Apply Lemma 2.4 with $(2s)^{-1},k_c$ playing the roles of $\eta ,k$ for all $c \in [s]$ to obtain $m_0 \in \mathbb {N}$ and ${\varepsilon }'> 0$ such that its conclusions hold. Choose constants $\delta _0,\ldots ,\delta _5 \in \mathbb {R}$ such that $0 < \delta _0 \ll \ldots \ll \delta _5 \ll \delta $ . We may assume that ${\varepsilon }' \geq 3\sqrt {\delta }_1$ . Apply Theorem 1.4 with $\delta _0$ playing the role of $\delta $ to obtain $n_0 \in \mathbb {N}$ and ${\varepsilon }> 0$ . Without loss of generality, we may assume that $0 < 1/n_0 \ll {\varepsilon } \ll \delta _0$ and

(2.2) $$ \begin{align} \sqrt{\delta_1}\mu n_0 \geq 2m_0. \end{align} $$

We may further assume that the conclusion of Lemma 2.11 holds with $s,\boldsymbol {k},\mu /2$ playing the roles of inputs $s,\boldsymbol {k},\mu $ , and with outputs $n_0 \in \mathbb {N}, \delta _5> 0$ . Thus, our constants form the hierarchy

(2.3) $$ \begin{align} 0 < 1/n_0 \ll {\varepsilon} \ll \delta_0 \ll \ldots \ll \delta_5 \ll \delta \ll {\varepsilon}_0,\mu,1/R. \end{align} $$

Let $G = K(X_1,\ldots ,X_m)$ be a complete m-partite graph on $n \geq n_0$ vertices such that $\log F(G) \geq (Q-{\varepsilon })\binom {n}{2}$ . Note that $m < R$ (or $F(G)=0$ ). Let also

(2.4) $$ \begin{align} Y_0 := \bigcup_{i \in [m] : |X_i| \leq \delta_1^4 n}X_i. \end{align} $$

Given , let $\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ be the set of partitions $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*})$ of $V(G)\setminus Y_0$ such that $Y_0,\ldots ,Y_{r^*}$ is a coarsening of $X_1,\ldots ,X_m$ , and

$$ \begin{align*}\sum_{i \in [r^*]}|\,|Y_i|-\alpha_i^*n\,| < \delta_1^2n. \end{align*} $$

(We do not yet know that $\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ is nonempty.)

Given $\eta>0$ , let $\mathcal {G}_{\eta }(G)$ be the set of $\boldsymbol {k}$ -valid colourings $\chi $ of G for which there exist and $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ such that $\chi \in \mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$ . Call the elements of $\mathcal {G}_{\eta }(G) \eta $ -good. Given $\eta _1,\eta _2$ , let $\mathcal {LG}_{\eta _1,\eta _2}(G)$ and $\mathcal {P}_{\eta _1,\eta _2}(G)$ be as $\mathcal {G}_{\eta }(G)$ but with $\mathcal {LG}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$ and $\mathcal {P}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$ replacing $\mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$ , respectively.

Claim 2.12.1. We have the following:

1. (i) $|\mathcal {G}_{\delta _1}(G)| \geq (1-2^{-{\varepsilon } n^2})\cdot F(G)$ .

2. (ii) For all , $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ and $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$ , let $t_i$ be the number of $X_j$ in $Y_i$ for all $i \in [r^*]$ . Then either $t_1 = \ldots = t_{r^*} = 1$ ; or $\boldsymbol {k}$ does not have the strong extension property and $t_1+\ldots +t_{r^*} \leq k_1-1$ .

Proof of Claim

By Theorem 1.4 applied to G with parameter $\delta _0$ , we have that there are at least $(1-2^{-{\varepsilon } n^2}) \cdot F(G)$ colourings $\chi : E(G) \rightarrow [s]$ which are $\boldsymbol {k}$ -valid and for which there is some and a partition $V_1 \cup \ldots \cup V_{r^*} = V(G)$ such that

• ○ For all $i \in [r^*]$ , we have $|\,|V_i|-\alpha ^*_i n\,| \leq 1$ .

• ○ $\chi $ is $\delta _0$ -good with respect to $(\phi ^*;V_1,\ldots ,V_{r^*})$ .

• ○ Suppose $\sum _{i \in [r^*]}e(G[V_i])> \delta _0 n^2$ . Then $\boldsymbol {k}$ does not have the strong extension property, and all but at most $\delta _0 n^2$ edges in $\bigcup _{i \in [r^*]}G[V_i]$ are coloured with $1$ under $\chi $ . Moreover, if $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$ is such that at least $\delta _0|V_i|^2$ edges need to be removed from $G[V_i]$ to make it $K_{\ell _i}$ -free, then $\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$ .

We will show that every such $\chi $ lies in $\mathcal {G}_{\delta _1}(G)$ , which implies the first part of the claim. Fix $\chi $ and its associated $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$ and $V_1,\ldots , V_{r^*}$ (recall that both $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$ and the partition $V_1\cup \ldots \cup V_{r^*}$ may be different for different $\chi $ ). For all $ij \in \binom {[r^*]}{2}$ , the $\delta _0$ -goodness of $\chi $ implies that

$$ \begin{align*}e_G(V_i,V_j) \geq \sum_{c \in \phi^*(ij)}|\chi^{-1}(c)[V_i,V_j]| \geq \sum_{c \in \phi^*(ij)}(|\phi^*(ij)|^{-1} - \delta_0)|V_i||V_j| \geq (1-s\delta_0)|V_i||V_j|, \end{align*} $$

so $e_{\overline {G}}(V_i,V_j) \leq s\delta _0n^2$ . Suppose that $X_k$ , some $k \in [m]$ , is such that $|X_k \cap V_i|> \sqrt {s\delta _0}n$ . Then, for every $j \in [m]\setminus \{k\}$ ,

$$ \begin{align*}|X_k \cap V_j| = \frac{e_{\overline{G}[X_k]}(V_i,V_j)}{|X_k \cap V_i|} \leq \frac{e_{\overline{G}}(V_i,V_j)}{|X_k \cap V_i|} < \sqrt{s\delta_0}n. \end{align*} $$

So for all $k \in [m]$ with $|X_k|> \delta _1^4n > R\sqrt {s\delta _0}n$ , there is a unique $i_k \in [r^*]$ such that $|X_k \cap V_{i_k}|> \sqrt {s\delta _0}n$ . For all $i \in [r^*]$ , let

$$ \begin{align*}Y_i := \bigcup_{k \in [m] : i_k = i}X_k. \end{align*} $$

Recall that we already defined $Y_0$ in (2.4). Then $Y_0,\ldots ,Y_{r^*}$ is a coarsening of $X_1,\ldots ,X_m$ , and $|X_j| \leq \delta _1^4 n$ if and only if $X_j \subseteq Y_0$ . For all $i \in [r^*]$ , we have that

(2.5) $$ \begin{align} |Y_i \bigtriangleup V_i| &\leq |Y_0| + \sum_{k \in [m]: i_k \neq i}|X_k \cap V_i| + \sum_{k \in [m]: i_k = i}|X_k \setminus V_i| \leq m\delta_1^4n + 2Rm\sqrt{s\delta_0}n \leq \delta_1^3 n \end{align} $$

and

(2.6) $$ \begin{align} \sum_{i \in [r^*]}|\,|Y_i| - \alpha^*_in \,| \leq \sum_{i \in [r^*]}\left(|\, |V_i| - |Y_i|\, | + |\,|V_i|-\alpha^*_i n\,| \right) \leq R\delta_1^3 n + R < \delta_1^{2} n, \end{align} $$

so $(Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha ^*})$ . Moreover, for all $i \in [r^*]$ , we have

(2.7) $$ \begin{align} |Y_i| \geq (\alpha^*_i - \delta^2_1)n-1 \geq \frac{\mu n}{2}. \end{align} $$

It remains to prove that $\chi $ is $\delta _1$ -good with respect to $(\phi ^*;Y_1,\ldots ,Y_{r^*})$ . Proposition 2.6 and (2.5) imply that for all $ij \in \binom {[r^*]}{2}$ and all $c \in \phi ^*(ij)$ , we have that $\chi ^{-1}(c)[Y_i,Y_j]$ is a $(\delta _1,|\phi ^*(ij)|^{-1})$ -regular pair. Moreover,

$$ \begin{align*} \phantom{=}& \sum_{i \in [r^*]}|\, e_G(Y_i) - |\chi^{-1}(1)[Y_i]| \,| \leq \sum_{i \in [r^*]}|\, e_G(V_i) - |\chi^{-1}(1)[V_i]| \,| + \sum_{i \in [r^*]}|Y_i \triangle V_i|^2\\ &\stackrel{({2.5})}{\leq} \delta_0 n^2 + R\delta_1^6 n^2 < \delta_1^5 n^2. \end{align*} $$

Thus, $\chi \in \mathcal {G}_{\delta _1}(G)$ . This completes the proof of the first part of the claim.

For the second part, fix , $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ and $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$ . For each $i \in [r^*]$ , let $t_i$ be the number of parts $X_j$ which lie in $Y_i$ . Then $t_i$ is at most the number of parts $X_j$ which have intersection at least $\sqrt {s\delta _0}n$ with $V_i$ . Suppose first that $\sum _{i \in [r^*]}e_G(V_i) \leq \delta _0 n^2$ . If $t_i \geq 2$ for some $i \in [r^*]$ , then $e_G(V_i) \geq s\delta _0 n^2$ , a contradiction. So $t_1 = \ldots = t_{r^*} = 1$ .

Suppose now that $\sum _{i \in [r^*]}e_G(V_i)> \delta _0 n^2$ . Then by Theorem 1.4(iii), $\boldsymbol {k}$ does not have the strong extension property. Since $G[V_i]$ is a complete multipartite graph containing at least $t_i$ parts of size at least $\sqrt {s\delta _0}n$ , we have that at least $s\delta _0 n^2> \delta _0|V_i|^2$ edges need to be removed from $G[V_i]$ to make it $K_{t_i}$ -free. Thus, $t_1+\ldots +t_{r^*} \leq k_1-1$ , proving the second part of the claim.

This proves parts (i) and (ii) of Theorem 2.12. Namely, take any $\chi \in \mathcal {G}_{\delta _1}(G) \neq \emptyset $ . Let and $\mathcal {Y} := (Z_0,\ldots ,Z_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ witness $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$ . Then they satisfy items (i) and (ii) of Theorem 2.12.

Suppose now that (2.1) holds, but

(2.8) $$ \begin{align} |\mathcal{G}_{\delta_1}(G) \setminus \mathcal{LG}_{\delta_4,\delta_5}(G)|> 2^{-\delta_2 n} \cdot F(G). \end{align} $$

For most of the next part of the proof, we will establish a contradiction to this assumption. (Recall that, by Lemma 2.11, a direct contradiction to the statement of the theorem would replace $\mathcal {LG}_{\delta _4,\delta _5}(G)$ by $\mathcal {LG}_{0,\delta _5}(G)$ .)

For every , Lemma 2.1(iii) implies that $(\phi ^*)^{-1}(c)$ is maximally $K_{k_c}$ -free for all $c \in [s]$ , and that $r^* \geq k_2-1$ . Lemma 2.11 and (2.7) imply that for every $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ , we have that $\mathcal {P}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y}) = \mathcal {LG}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y})$ . So

(2.9) $$ \begin{align} \mathcal{LG}_{\delta_4,\delta_5}(G) = \mathcal{P}_{\delta_4,\delta_5}(G). \end{align} $$

Given $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ and $x \in V(G)$ , write $\mathcal {Y}-x$ to denote the partition $(Y_1\setminus \{x\},\ldots ,Y_{r^*}\setminus \{x\})$ and define $\mathcal {Y}-y-z$ similarly.

Claim 2.12.2. At least one of the following hold.

There exist $x \in V(G)$ and a $\boldsymbol {k}$ -valid s-edge-colouring $\chi $ of $G-x$ such that the following two statements hold.

1. (i) $\chi \in \mathcal {G}_{2\delta _1}(G-x;\phi ^*,\mathcal {Y}-x)$ , for some and $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ .

2. (ii) There is a set $\mathrm {Ext}(\chi )$ of at least $2^{(Q-\delta _3)n} \boldsymbol {k}$ -valid extensions $\overline {\chi }$ of $\chi $ to G such that $\overline {\chi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$ but $\overline {\chi }$ is not $(\delta _4,\delta _5)$ -locally good with respect to $(\phi ^*;Y_1,\ldots ,Y_{r^*})$ at x.

There exist $zy \in \binom {V(G)}{2}$ and a $\boldsymbol {k}$ -valid s-edge-colouring $\xi $ of $G-z-y$ such that the following two statements hold.

1. (iii) $\xi \in \mathcal {G}_{2\delta _1}(G-z-y;\phi ^*,\mathcal {Y}-z-y)$ , for some and $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ .

2. (iv) There is a set $\mathrm {Ext}(\xi )$ of at least $2^{(Q-\delta _3)(n+n-1)} \boldsymbol {k}$ -valid extensions $\overline {\xi }$ of $\xi $ to G such that $\overline {\xi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$ but $\overline {\xi }$ is not $(\delta _4,\delta _5)$ -locally good with respect to $(\phi ^*;Y_1,\ldots ,Y_{r^*})$ at $z,y$ .

Proof of Claim

Suppose first that for at least half of the colourings in $\mathcal {G}_{\delta _1}(G)\setminus \mathcal {LG}_{\delta _4,\delta _5}(G)$ , the locally good condition fails at some vertex (rather than only at pairs). We will show that there exists an x satisfying (i) and (ii). By (2.8) and (2.9), there is some $x \in V(G)$ such that there are at least $\frac {1}{2}\cdot \frac {1}{n} \cdot 2^{-\delta _2 n} \cdot F(G) \geq 2^{-2\delta _2 n} \cdot F(G)$ valid colourings $\chi $ which are $\delta _1$ -good (with respect to some optimal solution and partition) but for which the $(\delta _4,\delta _5)$ -locally good condition fails at x (for all optimal solutions and partitions). Call this set of colourings $\mathcal {L}_x(G)$ .

We have $\log F(G-x) \geq \log (s^{-n}\cdot F(G)) \geq (Q-{\varepsilon })\binom {n}{2} - n\log s \geq (Q-2{\varepsilon })\binom {n-1}{2}$ , so a version of Claim 2.12.1(i) applied to $G-x$ implies that

$$ \begin{align*}|\mathcal{G}_{2\delta_1}(G-x)| \geq (1-2^{-2{\varepsilon} (n-1)^2})\cdot F(G-x). \end{align*} $$

Suppose that x does not satisfy Claim 2.12.2. Then for each $\boldsymbol {k}$ -valid colouring $\chi $ of $G-x$ , either it does not lie in $\mathcal {G}_{2\delta _1}(G-x)$ or it does lie in $\mathcal {G}_{2\delta _1}(G-x)$ but has at most $2^{(Q-\delta _3)n} \boldsymbol {k}$ -valid extensions which lie in $\mathcal {L}_x(G)$ . We have that

$$ \begin{align*} 2^{-2\delta_2n}\cdot F(G) &\leq |\mathcal{L}_x(G)| \leq |\mathcal{G}_{2\delta_1}(G-x)| \cdot 2^{(Q-\delta_3)n} + (F(G-x)-|\mathcal{G}_{2\delta_1}(G-x)|) \cdot s^n\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3)n} + s^{n} \cdot 2^{-2{\varepsilon} (n-1)^2}F(G-x)\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3/2)n}, \end{align*} $$

and so

$$ \begin{align*}\log F(G) - \log F(G-x) \leq (Q - \delta_3/2 + 2\delta_2)n \leq (Q-\delta_3/3)n < (Q-{\varepsilon})n, \end{align*} $$

a contradiction to (2.1).

Thus, we may assume that at least half the good but not locally good colourings fail due to the pair condition. Again, there is a pair $y,z$ of distinct vertices that appear in at least $2^{-2\delta _2 n}\cdot F(G)$ such colourings, and an identical argument gives the required $\xi $ , satisfying (iii) and (iv).

Suppose there exist $x,\chi $ as in Claim 2.12.2(i) and (ii). So there are and $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ and $\mathrm {Ext}(\chi )$ as in Claim 2.12.2. Define $\boldsymbol {\beta } := (\beta _1,\ldots ,\beta _{r^*})$ by setting $\beta _i := |Y_i|/n$ for all $i \in [r^*]$ . Then (2.6) implies that

(2.10) $$ \begin{align} \|\boldsymbol{\beta} - \boldsymbol{\alpha}^*\|_1 < \delta_1^2. \end{align} $$

Note that $\mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G;\phi ^*,\mathcal {Y})$ . For every $\overline {\chi } \in \mathrm {Ext}(\chi )$ , define $\phi = \phi (\overline {\chi }) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$ by setting

$$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2}; \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[x,Y_j]| \geq \sqrt{\delta_1} |Y_{j}| \} &\mbox{if } i = r^*+1, j \in [r^*]. \\ \end{cases} \end{align*} $$

Fix the pattern $\phi $ that appears for the largest number of extensions $\overline {\chi } \in \mathrm {Ext}(\chi )$ , and let $\mathrm {Ext}_{\phi }(\chi )$ be the set of these $\overline {\chi }$ . By Claim 2.12.2(ii),

(2.11) $$ \begin{align} |\mathrm{Ext}_{\phi}(\chi)| \geq 2^{-sr^*} \cdot |\mathrm{Ext}(\chi)| \geq 2^{(Q-2\delta_3)n}. \end{align} $$

Claim 2.12.3. $\phi \in \Phi _0(r^*+1,\boldsymbol {k})$ .

Proof of Claim

Suppose not. Then there is some $c \in [s]$ such that $\phi ^{-1}(c)$ contains a copy of $K_{k_c}$ . Since $\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$ is the restriction of $\phi $ to $\binom {[r^*]}{2}$ , the vertex $r^*+1$ must lie in this copy. Let $z_1,\ldots ,z_{k_c-1}$ be the other vertices. Let $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$ be arbitrary. For each $k \in [k_c-1]$ , let $Z_k := \{ y \in Y_{z_k} : \overline {\chi }(xy) = c \}$ . Then, by the definition of $\phi $ , we have

(2.12) $$ \begin{align} |Z_k|> \sqrt{\delta_1}|Y_{z_k}| \stackrel{({2.2})}{\geq} m_0. \end{align} $$

Let $kk' \in \binom {[k_c-1]}{2}$ . Now, $\overline {\chi }^{-1}(c)[Y_{z_k},Y_{z_{k'}}]$ is $(3\delta _1,\geq \!\! s^{-1})$ -regular since $\overline {\chi } \in \mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G; \phi ^*,\mathcal {Y})$ . Therefore,

$$ \begin{align*}d(\overline{\chi}^{-1}(c)[Z_k,Z_{k'}]) \geq d(\chi^{-1}(c)[Y_{z_k},Y_{z_{k'}}]) - 3\delta_1 \geq |\phi^*(z_kz_{k'})|^{-1} - 6\delta_1 \geq 1/(2s). \end{align*} $$

Now Proposition 2.7 implies that $\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$ is $3\sqrt {\delta _1}$ -regular. Therefore, $\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$ is $(3\sqrt {\delta _1},\geq \!\!1/(2s))$ -regular. Now (2.12) and Lemma 2.4 imply that $\chi ^{-1}(c)[Z_1,\ldots ,Z_{k_c-1}]$ contains a copy of $K_{k_c-1}$ . Together with x, this gives a c-coloured copy of $K_{k_c}$ in $\overline {\chi }$ , contradicting the fact that $\overline {\chi }$ is $\boldsymbol {k}$ -valid.

Next we will show that there is some $i \in [r^*]$ such that $r^*+1$ is a clone of i under $\phi $ . Suppose for a contradiction that this is not the case. Thus, by our choice of ${\varepsilon }_0$ , we have $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) \leq Q-{\varepsilon }_0$ . Then, using (a version of) Proposition 2.1(i) and Lemma 2.2(ii),

(2.13) $$ \begin{align} \frac{1}{n}\log\prod_{j \in [r^*]}|\phi(\{j,r^*+1\})|^{|Y_j|} &= \mathop{\mathrm{ext}}(\phi,\boldsymbol{\beta}) \leq \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) + \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 \cdot \log s\\ \nonumber &\stackrel{({2.10})}{<} Q - {\varepsilon}_0 + \delta_1^2\log s \leq Q - {\varepsilon}_0/2. \end{align} $$

The number of possible patterns $\phi $ on $r^*+1$ vertices which are extensions of $\phi ^*$ is at most $2^{sr^*}$ , and, by definition, the number of edges with endpoint x which are not coloured according to $\phi $ is at most $s\sqrt {\delta _1}n$ . Therefore, the total number of $\boldsymbol {k}$ -valid extensions $\overline {\chi } \in \mathrm {Ext}(\chi )$ of $\chi $ to G is at most

(2.14) $$ \begin{align} 2^{sr^*} \cdot \binom{n}{\leq s\sqrt{\delta_1}n} \cdot s^{s\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{|Y_j|} \stackrel{({2.4}),({2.13})}{\leq} 2^{(Q-{\varepsilon}_0/3)n} < 2^{(Q-2\delta_3)n}. \end{align} $$

So certainly there are at most this number of extensions which lie in $\mathrm {Ext}_{\phi }(\chi )$ , contradicting (2.11).

Therefore, we may assume that there is some $i^* \in [r^*]$ such that $r^*+1$ is a clone of $i^*$ under $\phi $ . Thus, we have

(2.15) $$ \begin{align} \phi(\{ j,r^*+1 \}) = \phi^*(i^*j) \ \text{ for all } \ j \in [r^*]\setminus \{ i^*\} \ \text{ and } \ \phi(\{ i^*,r^*+1 \}) \subseteq \{ 1 \}, \end{align} $$

where the last inclusion follows from Lemma 2.2(iii).

Claim 2.12.4. We have the following for all $\overline {\chi } \in \mathrm {Ext}_\phi (\chi )$ :

1. (i) There exist $j^* \in [r^*]\setminus \{ i^* \}$ , a part $X \subseteq Y_{j^*}$ and $c \in \phi ^*(i^*j^*)$ such that $|\overline {\chi }^{-1}(c)[x,X]| \neq |\phi (i^*j^*)|^{-1}|X| \pm \frac {\delta _5}{\ell _{j^*}}|Y_{j^*}|$ .

2. (ii) If there exists $h \in [r^*]$ such that the part X of G containing x lies in $Y_{h}$ , and $|X|> \delta _4|Y_{h}|$ , then $i^* = h$ .

Proof of Claim

Define $\ell \in \{ 0,\ldots , r^* \}$ as follows. If there is $i' \in [r^*]$ such that $d_G(x,Y_{i'}) < (1-\delta _4)|Y_{i'}|$ (noting that there can be at most one such $i'$ ), let $\ell := i'$ . If there is no such $i'$ , let $\ell :=0$ . Let X be the part of G which contains x.

Case 1: $\ell = 0$ .

Suppose that (i) is false. Since $\overline {\chi }$ is not $(\delta _4,\delta _5)$ -locally good at x, we must have that $d_G(x,Y_{i^*}) - |\overline {\chi }^{-1}(1)[x,Y_{i^*}]|> \delta _5 |Y_{i^*}|$ . By (2.15) and the definition of $\phi $ , we have that

(2.16) $$ \begin{align} d_G(x,Y_{i^*}) - |\overline{\chi}^{-1}(1)[x,Y_{i^*}]| &= \sum_{c \in \{ 2,\ldots, s \}}|\overline{\chi}^{-1}(c)[x,Y_{i^*}]| < (s-1)\sqrt{\delta_1}|Y_{i^*}| < \delta_5 |Y_{i^*}|, \end{align} $$

a contradiction. For (ii), let $X \subseteq Y_h$ be the part of G containing x and suppose $h \in [r^*]$ . Then $|Y_h|-|X|=d_G(x,Y_h) \geq (1-\delta _4)|Y_h|$ . So in this case, $|X| \leq \delta _4|Y_h|$ and (ii) is vacuous.

Case 2: $\ell \in [r^*]$ .

We will first show that (ii) holds. Note that $h=\ell $ since $X \subseteq Y_h$ and $x\in X$ is not adjacent to the whole of $Y_\ell $ . If $Y_{h} = X$ , then $N_G(x,Y_{h}) = \emptyset $ so $\phi (\{ r^*+1,h \}) = \emptyset $ . So (2.15) implies that $h = i^*$ , as required.

Otherwise, $Y_{h} \neq X$ . Suppose that $i^* \neq h$ . Then $|\phi ^*(i^*h)| \geq 2$ , and so

$$ \begin{align*} \frac{1}{n}\left( \log \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{d_G(x,Y_j)}\right) &\stackrel{({2.15})}{=} \frac{1}{n}\sum_{j \in [r^*]\setminus \{ i^* \}} |Y_j\setminus X| \log|\phi^*(i^*j)|\\ &= \sum_{j \in [r^*]\setminus \{ i^*,h \}}\beta_j \log|\phi^*(i^*j)| + \left(\beta_h -\frac{|X|}{n}\right) \log|\phi^*(i^*h)|\\ &\leq q_{i^*}(\phi^*,\boldsymbol{\alpha}^*) + \left( \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 - \frac{|X|}{n}\right)\log s\\ &\stackrel{({2.10})}{\leq} Q + (\delta_1^2 - \delta_4^2)\log s < Q - 4\delta_3, \end{align*} $$

where the penultimate inequality follows from Proposition 2.1(ii). Combining this with a very similar calculation to (2.14) implies that the total number of $\boldsymbol {k}$ -valid extensions $\overline {\chi } \in \mathrm {Ext}(\chi )$ of $\chi $ to G is less than $2^{(Q-2\delta _3)n}$ , contradicting (2.11). Therefore, $i^*=h$ , proving (ii). The proof of (i) now proceeds exactly as in Case 1.

Claim 2.12.4(i) implies that for every $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$ , there exist $j^* \in [r^*]\setminus \{i^*\}$ , a part $X \subseteq Y_{j^*}$ and $c^* \in \phi ^*(i^*j^*)$ such that, by averaging,

(2.17) $$ \begin{align} |\overline{\chi}^{-1}(c^*)[x,X]| \leq |\phi^*(i^*j^*)|^{-1}|X|-\frac{\delta_5}{s\ell_{j^*}}|Y_{j^*}|. \end{align} $$

In particular, since $\ell _{j^*} \leq k_1 < R$ , we have $|X| \geq \delta _5|Y_{j^*}|/(s \cdot R) \geq (\delta _5)^2|Y_{j^*}|$ . The number of ways of adding edges coloured with $\phi ^*$ between x and X with this reduced density (choosing the set of colour- $c^*$ neighbours, and then colouring every other edge with any available colour other than $c^*$ ) is at most

$$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i^*j^*)|^{-1}|X|-\frac{\delta_5}{s\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i^*j^*)|-1)^{|X|-k}\\ &\leq e^{-\delta_5^2|X|/3(s^2R^2)} \cdot |\phi^*(i^*j^*)|^{|X|} \stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot |\phi^*(i^*j^*)|^{|X|}, \end{align*} $$

where the first inequality is a consequence of Lemma 2.8. Using Proposition 2.1(ii), we have that

(2.18) $$ \begin{align} q_{i^*}(\phi^*,\boldsymbol{\beta}) \leq Q + \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 (2\log s) \stackrel{({2.10})}{\leq} Q+2\delta_1^2\log s. \end{align} $$

Now, we can generate every $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$ from $\chi $ by doing the following. For each $j \in [r^*]$ , choose at most $\sqrt {\delta _1}|Y_j|$ vertices $y \in N_G(x,Y_j)$ and colour $xy$ arbitrarily. Arbitrarily colour all edges $xy_0$ where $y_0 \in Y_0$ . Then choose $j^*,X,c^*$ as above and colour every uncoloured edge (with endpoint x) according to $\phi $ so that (2.17) holds (with a small adjustment to account for the $\sqrt {\delta _1}|Y_j|$ edges that have already been coloured). That this will indeed generate every $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$ is a consequence of the definition of $\phi $ and Claim 2.12.4. Therefore,

$$ \begin{align*} |\mathrm{Ext}_{\phi}(\chi)| &\leq \binom{n}{\leq \sqrt{\delta_1}n} \cdot s^{\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot e^{-\delta_5^5 n} \cdot \prod_{j \in [r^*]\setminus \{ i^*\}} |\phi^*(i^*j)|^{|Y_j|}\\ &\stackrel{({2.4}),({2.18})}{\leq} 2^{-\delta_5^6 n} \cdot 2^{(Q+2\delta_1^2 \log s)n} < 2^{(Q-2\delta_3)n}, \end{align*} $$

contradicting (2.11). So our assumption that there are $x,\chi $ as in Claim 2.12.2(i) and (ii) is false.

Thus, there must be $z,y,\xi $ such that Claim 2.12.2(iii) and (iv) hold. So there are and $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ and $\mathrm {Ext}(\xi )$ as in Claim 2.12.2. Again, we define colour patterns $\phi _y, \phi _z$ in analogy with $\phi $ to be the pair of patterns that appear together for the greatest number of extensions $\overline {\xi } \in \mathrm {Ext}(\xi )$ , and we write $\mathrm { Ext}_{\phi _y,\phi _z}(\xi )$ for the set of extensions $\overline {\xi } \in \mathrm {Ext}(\xi )$ with this pair of patterns. Again, by Claim 2.12.2(iii),

(2.19) $$ \begin{align} |\mathrm{Ext}_{\phi_y,\phi_z}(\xi)| \geq 2^{(Q-2\delta_3)(n+n-1)}. \end{align} $$

Similarly to Claim 2.12.3, we have $\phi _y,\phi _z \in \Phi _0(r^*+1;\boldsymbol {k})$ . Applying Lemma 2.2(ii), we have that there are $i_y, i_z \in [r^*]$ such that in $\phi _y,\phi _z$ , respectively, the vertex $r^*+1$ is a clone of $i_y,i_z$ . And, in particular, $\phi _y(\{i_y,r^*+1\}) \subseteq \{1\}$ and $\phi _z(\{i_z,r^*+1\}) \subseteq \{1\}$ . The analogue of Claim 2.12.4(i) for pairs holds in the same way; that is, there exist $j^* \in [r^*]\setminus \{i_y,i_z\}$ , a part $X \subseteq Y_{j^*}$ , $c_y \in \phi _y(i_yj^*)$ and $c_z \in \phi _z(i_zj^*)$ such that

$$ \begin{align*}|N_{\xi^{-1}(c_y)}(y,X) \cap N_{\xi^{-1}(c_z)}(z,X)| \neq |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| \pm \frac{\delta_5}{\ell_{j^*}}|Y_{j^*}|. \end{align*} $$

It remains to show that this implies there are few extensions of $\chi $ to G. By averaging, there are $c_y^* \in \phi ^*(i_yj^*)$ and $c_z^* \in \phi ^*(i_zj^*)$ such that

$$ \begin{align*}|N_{\xi^{-1}(c_y^*)}(y,X) \cap N_{\xi^{-1}(c_z^*)}(z,X)| < |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| - \frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|. \end{align*} $$

The number of ways of adding edges coloured with $\phi ^*$ between $y,z$ and X with this reduced density (choosing the set of v such that $yv$ is coloured $c_y^*$ and $zv$ is coloured $c_z^*$ , and then colouring every other $yu,zu$ with any pair other than $c_y^*,c_z^*$ ) is at most

$$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X|-\frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i_yj^*)||\phi^*(i_zj^*)|-1)^{|X|-k} \cdot s\\ &\hspace{4cm}\stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot (|\phi^*(i_yj^*)||\phi^*(i_zj^*)|)^{|X|}. \end{align*} $$

Repeating the calculations in the single vertex case, we see that $|\mathrm {Ext}_{\phi _y,\phi _z}(\xi )| < 2^{(Q-2\delta _3)(n+n-1)}$ , contradicting 2.19).

Thus, our assumption (2.8) is false. Therefore, combining its negation with Claim 2.12.1, we see that

$$ \begin{align*} |\mathcal{P}_{\delta_4,\delta_5}(G)| \geq |\mathcal{G}_{\delta_1}(G)| - 2^{-\delta_2 n} \cdot F(G) \geq (1-2^{-{\varepsilon} n}) \cdot F(G). \end{align*} $$

Let $\chi \in \mathcal {P}_{\delta _4,\delta _5}(G)$ . Then there exists and $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$ such that $\chi $ is $(\delta _4,\delta _5)$ -perfect with respect to $(\phi ^*;Y_1,\ldots ,Y_{r^*})$ . So for all $x \in V(G) \setminus Y_0$ , there exists $i(x) \in [r^*]$ such that for all $j \in [r^*]$ and $b \in N_G(x,Y_j)$ , we have $\chi (xb) = 1$ if $j = i(x)$ , and $\chi (xb) \in \phi ^*(i(x)j)$ otherwise. Moreover, (the proof of) the second part of Claim 2.12.4 implies that, if there exists $h(x) \in [r^*]$ such that the part X of G containing x lies in $Y_{h(x)}$ , and $|X|> \delta _4|Y_{h(x)}|$ , then $i(x) = h(x)$ .

Now, define a new partition $Z_0,\ldots ,Z_{r^*}$ of $V(G)$ by setting, for all $i \in [r^*]$ ,

$$ \begin{align*}Z_i := \{ x \in V(G) : i(x) = i \text{ and }x \in X \subseteq Y_{h(x)} \text{ with }|X| \geq \delta_4|Y_{h(x)}| \} \quad\text{and}\quad Z_0 := V(G) \setminus \textstyle\bigcup_{i \in [r^*]}Z_i. \end{align*} $$

Then $Z_0,\ldots ,Z_{r^*}$ is a coarsening of $X_1,\ldots ,X_m$ , and $\chi $ is $(0,\delta _5)$ -perfect with respect to $(\phi ^*;Z_1,\ldots ,Z_{r^*})$ by definition. Moreover, for all $i \in [r^*]$ , $Z_i \subseteq Y_i$ , and $|Y_i \setminus Z_i| \leq R\delta _4|Y_i|$ . So

$$ \begin{align*}\sum_{i \in [r^*]}|\, |Z_i| - \alpha^*_in\, | \leq \sum_{i \in [r^*]}(|Y_i| - |Z_i|) + \sum_{i \in [r^*]}|\, |Y_i| - \alpha^*_in \,| \leq R\delta_4 n + \delta_1^2 n < \delta n, \end{align*} $$

as required. Finally, let $\ell _i$ be the number of $X_j$ in $Z_i$ . Then $\ell _i \leq t_i$ for all $i \in [r^*]$ . The second part of Claim 2.12.1 yields the desired conclusion.

Note that the statement of Theorem 2.12 can be made much simpler in the case when $\boldsymbol {k}$ has the strong extension property as in this case we have that and the partitions $Z_0,\ldots ,Z_{r^*}$ are identical for all of the at least $(1-2^{-{\varepsilon } n^2})F(G;\boldsymbol {k})$ colourings specified in the theorem. Indeed, suppose that and its associated partition $Z_0,\ldots ,Z_{r^*}$ are outputs of Theorem 2.12 for some specified colouring. Then each $Z_1,\ldots ,Z_{r^*}$ is a part of G by Theorem 2.12(ii). Part (i) implies that for each $i \in [r^*]$ , we have that $|Z_i| \geq \alpha ^*_i n - \delta n \geq \mu n/2$ . Furthermore, $|Z_0| \leq \delta n \ll \mu n/2$ . So, provided $\delta $ is chosen to be smaller than $\mu /2$ , the structure of G itself determines $(r^*,\boldsymbol {\alpha }^*)$ and $Z_0,\ldots ,Z_{r^*}$ . Thus, we have the following corollary, which will be used to prove Theorem 1.6.

Corollary 2.13. Let $s \in \mathbb {N}$ and suppose that $\boldsymbol {k} \in \mathbb {N}^s$ has the strong extension property. Then for all $\delta> 0$ , there exist $n_0 \in \mathbb {N}$ and ${\varepsilon } \in \mathbb {R}$ with $0 < {\varepsilon } < \delta $ such that the following holds. Let $m \in \mathbb {N}$ and $G = K(X_1,\ldots ,X_m)$ be a complete m-partite graph on $n \geq n_0$ vertices such that $|X_1| \geq \ldots \geq |X_m|$ and

$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$

Then the following hold.

1. (i) There is with $r^* \leq m$ such that $ \sum _{i \in [r^*]}|\,|X_i|-\alpha _i^*n\,| < \delta n $ .

2. (ii) For at least $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$ -edge-colourings $\chi $ of G which are $\boldsymbol {k}$ -valid, there is such that $\chi $ is $\delta $ -good with respect to $(\phi ^*; X_1,\ldots ,X_{r^*})$ .

3. (iii) Furthermore, if we have

   (2.20) $$ \begin{align} \nonumber &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{align} $$
   then for at least $(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k})$ valid s-edge-colourings $\chi $ of G, there is with $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $ such that $\chi $ is $(0,\delta )$ -perfect with respect to $(\phi ^*; X_1,\ldots ,X_{r^*})$ .

2.4. The proof of Theorem 1.6

The next observation is a simple but key ingredient of our proof, which allows us to only consider complete multipartite graphs. If there were a $\boldsymbol {k}$ -extremal graph H which is not complete multipartite, one can use symmetrisation to obtain from H a new graph $H'$ which is complete multipartite (Theorem 1 in [11]). By symmetrisation, we mean replacing a vertex u with a copy, or twin, of $v \notin N_H(u)$ . Crucially, we can do this in such a way that we end up with a part containing a single vertex (which is connected to every other vertex).

Lemma 2.14. Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . Let G be a $\boldsymbol {k}$ -extremal graph which is not complete multipartite. Then there exists a $\boldsymbol {k}$ -extremal graph $G'$ which is complete multipartite and has a part of size one.

Proof. Since G is not complete multipartite, there exist distinct nonadjacent vertices $u,v \in V(G)$ such that $N_G(u) \neq N_G(v)$ . For any graph H, let $\chi (H)$ be the set of $\boldsymbol {k}$ -valid colourings of H. For each $\chi \in \chi (G-u-v)$ , let $\chi _u, \chi _v$ denote the number of valid extensions of $\chi $ to $G-v$ and $G-u$ , respectively. Since u and v are nonadjacent,

$$ \begin{align*}F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u\chi_v. \end{align*} $$

Let $G_u$ denote the graph obtained from G by replacing v by a twin of u. Define $G_v$ similarly. The operation of passing from G to $G_u$ or $G_v$ is a symmetrisation. We have

$$ \begin{align*}F(G_u;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u^2 \ \text{ and } \ F(G_v;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_v^2. \end{align*} $$

Then

$$ \begin{align*}0 \geq F(G_u;\boldsymbol{k}) + F(G_v;\boldsymbol{k}) - 2F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)} (\chi_u - \chi_v)^2 \geq 0. \end{align*} $$

Therefore, $G_u$ and $G_v$ are both $\boldsymbol {k}$ -extremal.

Let $\mathcal {G}$ be the directed graph whose vertex set contains all n-vertex graphs (up to isomorphism) that can be obtained from G by a sequence of symmetrisations and add a directed edge from H to $H' \neq H$ if $H'\cong H_u$ for some vertex u. Note that H has outdegree equal to $0$ in $\mathcal {G}$ if and only if H is complete multipartite. By [11, Theorem 3], there is at least one sequence of symmetrisations which leads to a ( $\boldsymbol {k}$ -extremal) complete partite graph H; among all choices, pick one such that the number m of parts in H is as small as possible. We may assume that every part has size at least two, or we are done. Let $H^-$ be an inneighbour of H in $\mathcal {G}$ . Observe that $H^-$ is not complete multipartite since it does not have $0$ outdegree. Then there exists $x \in V(H^-)$ such that $H^--x$ is a complete m-partite graph with parts $V_1,\ldots ,V_m$ .

Claim 2.14.1. x has at least one neighbour in each of $V_1,\ldots , V_m$ in $H^-$ .

Proof of Claim

Suppose for a contradiction that x does not have a neighbour in $V_1$ , say. Since $H^-$ is not complete multipartite, without loss of generality, there is $y \in V_2$ such that $xy \notin E(H^-)$ . Replace every $u \in V_2 \setminus \{ y \}$ with a twin of y to obtain a graph J with vertex partition $\{ x \}, V_1,\ldots , V_m$ , such that $J-x \cong K(V_1,\ldots ,V_m)$ , and $xz \notin E(J)$ for all $z \in V_1 \cup V_2$ . This is a sequence of symmetrisations, so there is an oriented path from $H^-$ to J in $\mathcal {G}$ (and, in particular, $J \in V(\mathcal {G})$ ). Now, given $v_1 \in V_1$ and $v_2 \in V_2$ , we have $xv_1,xv_2 \notin E(J)$ but $v_1v_2 \in E(J)$ . Therefore, we can replace $V_1 \cup V_2$ with a set X of $|V_1|+|V_2|$ twins of x to obtain a new graph $J'$ , which has vertex partition $X, V_3,\ldots ,V_m$ , and $J'-X \cong K(V_3,\ldots ,V_m)$ . Again, $J' \in V(\mathcal {G})$ .

Suppose that $x \in V(J)$ is such that $xw \notin E(J)$ for some $w \in V_3 \cup \ldots \cup V_m$ . Then $xw \notin E(J')$ for all $x \in X$ . Replace every $x \in X$ with a twin of w to obtain a complete $(m-2)$ -partite graph which is a vertex in $\mathcal {G}$ . Otherwise, $x \in V(J)$ is adjacent in J to all of $V_3 \cup \ldots \cup V_m$ , and so $J'$ is a complete $(m-1)$ -partite graph which is a vertex in $\mathcal {G}$ . In both cases, we obtain a contradiction to the choice of m. This proves the claim.

Therefore, x has a neighbour in each of $V_1,\ldots ,V_m$ . Then, for each $i \in [m]$ , $V_i$ has partition $A_i,B_i$ , where $xa \in E(H^-)$ for all $a \in A_i$ , and $xb \notin E(H^-)$ for all $b \in B_i$ ; and $A_i \neq \emptyset $ . Observe that every $A_i$ is a set of twins, and $B_i$ is a set of twins. For each $i \in [m]$ , replace $B_i$ by a set of $|B_i|$ twins of $a \in A_i$ . Thus, obtain a graph $H' \cong K(\{ x \}, V_1,\ldots ,V_m)$ which is a vertex of $\mathcal {G}$ , as required.

Lemma 2.15. Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}^s$ . Then, for all ${\varepsilon },\gamma> 0$ , there exist $\eta> 0$ and $n_0 \in \mathbb {N}$ such that the following holds for all graphs G on $n \geq n_0$ vertices with $\log F(G;\boldsymbol {k}) \geq (Q(\boldsymbol {k})-\eta )\binom {n}{2}$ . For every $x \in V(G)$ such that G contains at least $\gamma n$ twins of x, we have that

(2.21) $$ \begin{align}\log F(G; \boldsymbol{k}) \geq (Q(\boldsymbol{k})-{\varepsilon})n + \log F(G-x; \boldsymbol{k}). \end{align} $$

Proof. As before, we omit $\boldsymbol {k}$ from our notation where it is clear from the context, so, for example, $F(H) := F(H;\boldsymbol {k})$ . Choose constants $\delta ,\eta $ such that $0 < \eta \ll \delta \ll \gamma ,{\varepsilon }$ . By (1.3), we can choose $n_0$ to be such that whenever $N \geq n_0/2$ , we have that

(2.22) $$ \begin{align} (Q - \eta)\binom{N}{2} \leq \log F(N) \leq (Q + \eta)\binom{N}{2}. \end{align} $$

Without loss of generality, we may suppose that $1/n_0 \ll \eta $ . Let G be a graph on $n \geq n_0$ vertices. Suppose that there is some $x \in V(G)$ which does not satisfy (2.21). Let $T \subseteq V(G)$ be the set of twins of x (including x). Let $\chi (G-T)$ be the set of $\boldsymbol {k}$ -valid colourings of $G-T$ and let $c(\chi ,x)$ be the number of extensions of $\chi $ to $G - (T \setminus \{ x \})$ . For each $\chi \in \chi (G-T)$ , since every pair of vertices of X are twins, we have that $c(\chi ,x) \equiv c_\chi $ for all $x \in T$ . Therefore, if we list the vertices of T as $x_1,\ldots ,x_{|T|}$ , and let $t \in [\,|T|\,]$ , we have that

(2.23) $$ \begin{align} F(G-x_1-\ldots-x_t) = \sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t}. \end{align} $$

Choose t with $1 \leq t \leq |T|$ to be maximal such that

(2.24) $$ \begin{align} \log F(G-x_1-\ldots-x_{i-1}) < (Q-{\varepsilon})n + \log F(G-x_1 - \ldots - x_i) \end{align} $$

for all $i \in [t]$ . (Since (2.21) does not hold, $t:=1$ satisfies the inequality). Suppose $t < |T|$ . By the Cauchy-Schwarz inequality,

$$ \begin{align*} F(G-x_1-\ldots - x_t)^2 &= \left(\sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t} \right)^2 \leq \left(\sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t-1} \right) \left( \sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t+1} \right)\\ &\stackrel{({2.26})}{=} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_{t-1})\\ &\stackrel{({2.24})}{<} 2^{(Q-{\varepsilon})n} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_t). \end{align*} $$

So $F(G-x_1-\ldots -x_t) < 2^{(Q-{\varepsilon })n} \cdot F(G-x_1-\ldots -x_{t+1})$ . Thus, (2.24) holds for $t+1$ which is a contradiction to the maximality of t. So $t=|T|$ . Therefore, inductively, for all nonempty $T' \subseteq T$ ,

$$ \begin{align*}\log F(G) \leq (Q-{\varepsilon})|T'|n + \log F(G-T'). \end{align*} $$

Choose $T' \subseteq T$ with $|T'| = \lceil \delta n\rceil $ . Then

$$ \begin{align*} \log F(G) &\leq (Q-{\varepsilon})|T'|n + \log F(G-T') \stackrel{({2.22})}{\leq} Q|T'|n -{\varepsilon} \delta n^2 + (Q+\eta)\binom{n-|T'|}{2}\\ &\leq Q\binom{n}{2} + (-{\varepsilon} \delta + \eta +Q\delta^2)n^2 < Q\binom{n}{2} + (\eta + \delta^2 \log s - {\varepsilon} \delta )n^2\\ &< (Q-\eta)\binom{n}{2}, \end{align*} $$

a contradiction to (2.22).

We will now prove Theorem 1.6. The idea is that if there is an extremal graph G not satisfying the conclusion of the theorem, there must be a complete partite extremal graph $G'$ with an induced subgraph satisfying the conclusion of the theorem which is almost the whole of $G'$ . We can either set $G'=G$ or symmetrise to obtain $G'$ (Lemma 2.14), and the required structure of $G'$ follows from Theorem 2.12. In a typical colouring, of which there are many by Theorem 2.12, every exceptional vertex (not in the good induced subgraph) has deficient contribution to $F(G')$ , which is a consequence of the strong extension property. We can form a new graph by replacing each exceptional vertex by a twin of a good vertex to obtain a graph with more valid colourings than $G'$ , which is the required contradiction.

Proof of Theorem 1.6

Again, we omit $\boldsymbol {k}$ from our notation where possible. Let ${\varepsilon }> 0$ . Let $\mu> 0$ be the constant obtained from Lemma 2.2(i) and let ${\varepsilon }_0$ be the constant obtained from Lemma 2.2(ii). Without loss of generality, we may assume that $0 < {\varepsilon }_0 \ll \mu ,{\varepsilon },1/R,1/s$ . Choose $\delta _4,\delta _3,\delta _2,\delta _1>0$ in this order such that $\delta _3$ is at most the output of Corollary 2.13 with input $\delta _4$ , and similarly, $\delta _2$ from $\delta _3$ , and $\delta _1$ from $\delta _2^2$ . Further, let $n_0$ be at least the integer output of all of these applications. By increasing $n_0$ and decreasing $\delta _1,\ldots ,\delta _4$ , we may assume that $0<1/n_0 \ll \delta _1 \ll \ldots \ll \delta _4 \ll {\varepsilon }_0$ and for all $n \geq n_0$ , by (1.3),

(2.25) $$ \begin{align} \left(Q - \delta_1 \right)\binom{n}{2} \leq \log F(n) \leq \left(Q + \delta_1 \right)\binom{n}{2} \end{align} $$

and that Lemma 2.15 applied with $\delta _3,\mu /2$ playing the roles of ${\varepsilon },\gamma $ , respectively, has output $n_1 \leq n_0$ and $\eta> 2\delta _1$ . Altogether, we have the hierarchy

(2.26) $$ \begin{align} 0 < 1/n_0 \ll \delta_1 \ll \delta_2 \ll \delta_3 \ll \delta_4 \ll {\varepsilon}_0 \ll {\varepsilon},\mu,1/R,1/s. \end{align} $$

We first prove part (i). Towards a contradiction, let G be a $\boldsymbol {k}$ -extremal graph on $n \geq 2n_0$ vertices such that either

1. (a) G is not complete multipartite; or

2. (b) there is some $m \in \mathbb {N}$ and $\boldsymbol {\alpha } \in \Delta ^m$ such that $G \cong K_{\alpha _1n,\ldots ,\alpha _mn}$ , but there is no with $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 < \delta _3 < {\varepsilon }$ .

If (a) holds, apply Lemma 2.14 to obtain a $\boldsymbol {k}$ -extremal graph $G'$ on n vertices which is complete m-partite with vertex partition $X_1,\ldots ,X_{m}$ , where $|X_{1}| \geq \ldots \geq |X_m| = 1$ . Observe that $m < R$ . If (b) holds, set $G' := G$ . In both cases, apply Corollary 2.13 with parameter $\delta _2^2$ to $G'$ . Part (i) implies that there exists with $r^* \leq m$ such that, defining $Y_i := X_i$ for $i \in [r^*]$ and $Y_0$ to be the union of the remaining parts of G, we have

(2.27) $$ \begin{align} \sum_{i \in [r^*]}|\,|Y_i|-\alpha_i^*n\,| < \delta_2^2n < \delta_2 n. \end{align} $$

Together with Proposition 2.1(ii), we have that $|Y_i| \geq \mu n/2$ for all $i \in [r^*]$ . So if either (a) or (b) holds, we have $m> r^*$ . Corollary 2.13 implies that each of $Y_1,\ldots ,Y_{r^*}$ is a part of $G'$ (but $Y_0$ may contain several parts). We have that $Y_0,\ldots ,Y_{r^*}$ is a partition of $V(G)$ , and $0 < |Y_0| < R\delta _2^2 n < \delta _2 n$ . From now on, we make no distinction between cases (a) and (b) and only use this fact about the size of $Y_0$ . Let

$$ \begin{align*}H := G'[Y_1 \cup \ldots \cup Y_{r^*}] \cong K[Y_1,\ldots,Y_{r^*}] \end{align*} $$

be the core of $G'$ , and let $N := |V(H)|$ . So

(2.28) $$ \begin{align} 0 < n - N = |Y_0| < R\delta_2^2 n < \delta_2 n. \end{align} $$

Every $\boldsymbol {k}$ -valid colouring of $G'$ can be obtained by extending a $\boldsymbol {k}$ -valid colouring of H, so $F(H) \geq F(G') \cdot s^{-|Y_0|n}$ . Therefore,

(2.29) $$ \begin{align} \nonumber \log F(H) &\stackrel{({2.27})}{\geq} \log F(G') - R\delta_2^2 \log s \cdot n^2 \stackrel{({2.25})}{\geq} \left(Q - \delta_1 \right) \binom{n}{2} - R\delta_2^2 \log s \cdot n^2\\ &\stackrel{({2.28})}{\geq} (Q-\delta_2)\binom{N}{2}. \end{align} $$

Apply Corollary 2.13 to H to see that $|\mathcal {G}(H)| \geq (1-2^{-\delta _3 N^2})\cdot F(H)$ , where (recalling Definition 2.10)

Define $\boldsymbol {\beta } \in \Delta ^{r^*}$ by setting $\beta _i := |Y_i|/N$ for all $i \in [r^*]$ . So (2.27) implies that for all $\boldsymbol {\alpha }$ with $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$ ,

(2.30) $$ \begin{align} \|\boldsymbol{\beta} - \boldsymbol{\alpha}\|_1 < 2\delta_2^2 + \delta_4 \leq 2\delta_4. \end{align} $$

Let $\mathcal {B}(H)$ be the set of $\boldsymbol {k}$ -valid colourings of H not in $\mathcal {G}(H)$ . For each $\chi \in \mathcal {G}(H)$ and $v \in Y_0$ , do the following. Let $\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$ be the pattern of $\chi $ (that is, there is $\boldsymbol {\alpha }$ , which depends on $\chi $ , with and $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$ and ) such that $\chi \in \mathcal {G}_{\delta _4}(H;\phi ^*,Y_1,\ldots ,Y_{r^*})$ . For each valid extension $\overline {\chi }$ of $\chi $ to $G'[V(H) \cup \{ v \}]$ and every $i\in [s]$ , define $\phi = \phi (\overline {\chi },v) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$ by setting

$$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2} \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[v,Y_i]| \geq \sqrt{\delta_4} |Y_i| \} &\mbox{if } i \in [r^*], j = r^*+1. \\ \end{cases} \end{align*} $$

Fix the $\phi $ that appears for the largest number of extensions $\overline {\chi }$ over all $\chi \in \mathcal {G}(H)$ and all $v \in Y_0$ .

Claim 2.15.1. $\phi \in \Phi _0(r^*+1,\boldsymbol {k})$ .

Proof. This is almost identical to Claim 2.12.3 so we omit the proof.

Proposition 2.1(i) implies that

(2.31) $$ \begin{align} q(\phi^*,\boldsymbol{\beta}) \geq q(\phi^*,\boldsymbol{\alpha}) - 2\log s \|\boldsymbol{\beta}-\boldsymbol{\alpha}\|_1 \stackrel{({2.30})}{\geq} Q - 4(\log s)\delta_4. \end{align} $$

Since every $v \in Y_0$ is incident to the whole of $Y_1 \cup \ldots \cup Y_{r^*}$ in $G'$ and $s\sqrt {\delta _4}<1$ , we have that $\phi (\{ i,r^*+1 \}) \neq \emptyset $ for all $i \in [r^*]$ . Thus, $r^*+1$ is not a strong clone of any vertex in $[r^*]$ under $\phi $ . Therefore, applying Lemma 2.2(ii) for the second inequality,

(2.32) $$ \begin{align} \mathop{\mathrm{ext}}(\phi,\boldsymbol{\beta}) &\leq& \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}) + \log s \cdot \|\boldsymbol{\beta}-\boldsymbol{\alpha}\|_1 \stackrel{({2.30})}{<} Q - {\varepsilon}_0 + 4(\log s)\delta_4 < Q - \frac{{\varepsilon}_0}{2}. \end{align} $$

Similarly to the derivation of (2.14), we can now bound the number of extensions of $\chi $ . Indeed, by our choice of $\phi $ , for any $\chi \in \mathcal {G}(H)$ and any $v \in Y_0$ , the number of ways to extend $\chi $ to a valid colouring $\overline {\chi }$ of $G'[V(H) \cup \{ v \}]$ is at most

$$ \begin{align*} &\phantom{\leq} 2^{sr^*} \cdot \prod_{i \in [r^*]}|\phi(\{ i,r^*+1 \})|^{\beta_i N} \cdot \binom{N}{\leq s\sqrt{\delta_4} N} \cdot s^{sr^*\sqrt{\delta_4} n} \stackrel{({2.32})}{\leq} 2^{(Q-{\varepsilon}_0/3)N}. \end{align*} $$

Here, the first term is the number of possible patterns $\phi $ , the second term is the maximum number of extensions given the $\phi $ that appears most often, and the third and fourth terms are an upper bound on the number of ways to choose and colour those edges with uncommon colours. Now we can give an upper bound for the number of valid colourings of $G'$ as follows: Any valid colouring of $G'$ is either an extension of $\chi \in \mathcal {G}(H)$ (where we must additionally colour the edges between the $n-N$ vertices of $Y_0$ and H, and the edges induced by $Y_0$ ) or an extension of $\chi \in \mathcal {B}(H)$ . We have

(2.33) $$ \begin{align} F(G') &\leq \sum_{\chi \in \mathcal{G}(H)} \left( s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \right) + \sum_{\chi \in \mathcal{B}(H)}s^{(n-N)n}\\ \nonumber &\leq s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2} F(H) \cdot s^{(n-N)n}\\ \nonumber &\hspace{-9pt}\stackrel{({2.28})}{\leq} 2^{(Q - {\varepsilon}_0/3 + \delta_2 \log s) N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2/2} \cdot F(H)\\ \nonumber &\leq 2^{(Q-{\varepsilon}_0/4)N(n-N)} \cdot F(H). \end{align} $$

We will now form a new graph on n vertices which shares the same core H, but $Y_0$ is replaced by $n-N$ clones of some vertex in another part.

By (2.31), for any ,

$$ \begin{align*}Q - 4(\log s)\delta_4 \leq q(\phi^*,\boldsymbol{\beta}) = \sum_{i \in [r^*]}\beta_i q_i(\phi^*,\boldsymbol{\beta}). \end{align*} $$

So, by averaging, there exists $i^* \in [r^*]$ such that

(2.34) $$ \begin{align} q_{i^*}(\phi^*,\boldsymbol{\beta}) \geq Q - 4(\log s)\delta_4. \end{align} $$

Let $H' := K[W_1,\ldots ,W_{r^*}]$ , where $W_j = Y_j$ for $j \in [r^*]\setminus \{ i^* \}$ , and $W_{i^*} := Y_{i^*} \cup Y_0$ . Every colouring that follows $\phi ^*$ is valid. Thus,

$$ \begin{align*} \log F(H') &\geq \log\left( \prod_{ij \in \binom{[r^*]}{2}}|\phi^*(ij)|^{|Y_i||Y_j|} \cdot \prod_{k \in [r^*]\setminus\{i^*\}}|\phi^*(i^*k)|^{|Y_0||Y_k|} \right)\\ &= N^2 \cdot q(\phi^*,\boldsymbol{\beta})/2 + (n-N)N \cdot q_{i^*}(\phi^*,\boldsymbol{\beta})/2 \geq nN(Q-4(\log s)\delta_4)/2\\ &\geq (Q-\sqrt{\delta_4}/2)\binom{n}{2} \stackrel{({2.25})}{\geq} F(H) + (Q-\sqrt{\delta_4})N(n-N), \end{align*} $$

which, together with $n-N>0$ and (2.33), implies that $\log F(H')> \log F(G')$ , a contradiction to the $\boldsymbol {k}$ -extremality of $G'$ , and hence G. This completes the proof of part (i).

We have proved that $G \cong K[Y_1,\ldots ,Y_{r^*}]$ such that $\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 < \delta _2$ . Now Lemma 2.15 and our choice of parameters implies that, for all $x \in V(G)$ ,

$$ \begin{align*}\log F(G) \geq (Q-\delta_3)n + \log F(G-x). \end{align*} $$

Note that $F(G) \leq s^n \cdot F(G-x)$ , so, by (2.25), $\log F(G-x) \geq (Q-2\delta _1)\binom {n-1}{2}$ . The hypotheses of Lemma 2.15 still hold for $G-x$ , so, for all $y \in V(G)\setminus \{x\}$ ,

$$ \begin{align*}\log F(G) \geq (Q-\delta_3)n + \log F(G-x) \geq (Q-\delta_3)(n+n-1) + \log F(G-x-y). \end{align*} $$

By Corollary 2.13, there is a set $\mathcal {G}$ of at least $(1-2^{-\delta _3 n})\cdot F(n) \boldsymbol {k}$ -valid colourings $\chi : E(G) \rightarrow [s]$ for which there exists with $\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 \leq \delta _4$ and such that $\chi $ is $(0,\delta _4)$ -perfect with respect to $(\phi ,Y_1,\ldots ,Y_{r^*})$ .

Proof of Corollary 1.9

Suppose that $\boldsymbol {k}$ is soluble. Let c be the constant implied by solubility and let $0 < {\varepsilon } \ll c$ . Let $\delta ,n_0$ be the output of Theorem 1.6 applied with parameter ${\varepsilon }$ . We may assume that $1/n_0 \ll \delta \ll {\varepsilon }$ . Let $n \geq n_0$ and let G be an n-vertex $\boldsymbol {k}$ -extremal graph. Theorem 1.6 implies that G is a complete $r^*$ -partite graph for some $r^* \in \mathbb {N}$ , where, writing $\boldsymbol {\beta } \in \Delta ^{r^*}$ for the vector of the part ratios of G, we have $\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 \leq {\varepsilon }$ for some . Let $\boldsymbol {d}^*$ be the supersolution of n with $\mathrm {perf}(\boldsymbol {d}^*) = \mathrm {perf}_{r,\boldsymbol {\alpha }}(\boldsymbol {d}^*)$ for some . Suppose for a contradiction that $\boldsymbol {\beta } n \neq \boldsymbol {d}^*$ .

The number of perfect colourings of G is at least $(1-2^{-\delta n})F(G;\boldsymbol {k})$ . Then

$$ \begin{align*}F(K_{\boldsymbol{d}^*}) \geq \mathrm{perf}(\boldsymbol{d}^*) \geq (1+c) \cdot \mathrm{perf}_{r^*,\boldsymbol{\alpha}^*}(\boldsymbol{\beta} n) \geq (1+c)\cdot (1-2^{-\delta n})F(G)> F(G), \end{align*} $$

contradicting the $\boldsymbol {k}$ -extremality of G.

3. Forbidden triangles in seven colours

In this section, we solve Problem $Q^*$ in the case $\boldsymbol {k}=(3;7)$ .

Theorem 3.1. Let $\boldsymbol {k}:=(3;7)$ . Then every has $r=8$ , $\boldsymbol {\alpha }$ uniform, $|\phi (ij)|=4$ for all $ij \in \binom {[8]}{2}$ and $\phi ^{-1}(c) \cong K_{4,4}$ for all $c \in [7]$ .

We also solve it in the case $\boldsymbol {k}=(3;6)$ . Recall that $F(n;\boldsymbol {k})$ was already determined exactly in this case in [2].

Theorem 3.2. Let $\boldsymbol {k}:=(3;6)$ . Then every has $r=8$ , $\boldsymbol {\alpha }$ uniform, $|\phi (ij)|\in \{3,4\}$ for all $ij \in \binom {[8]}{2}$ , $\{ij: |\phi (ij)|=3\} \cong K_{4,4}$ and $\phi ^{-1}(c) \cong K_{4,4}$ for all $c \in [6]$ .

3.1. The union of dense triangle-free graphs

The key new idea is the following lemma, a $2$ -coloured version of Mantel’s theorem, that allows us to add a new constraint to the linear relaxation of the optimisation problem. The constraint ensures that the union of any two colour graphs $R := \phi ^{-1}(c), B := \phi ^{-1}(c')$ has density at most $\frac {3}{4}$ whenever the individual graphs have large density. This is attained by two complete balanced bipartite graphs whose overlap is minimal. The trivial bound for the density of $R \cup B$ is $\frac {4}{5}$ . Indeed, $R \cup B$ is $K_6$ -free; otherwise, it would contain a monochromatic triangle, so this claim follows from Turán’s theorem. However, if $R \cup B$ has density $\frac {4}{5}$ , then each of $R,B$ has density $\frac {2}{5}$ , coming from the unique red-blue colouring of $K_5$ without monochromatic triangles. The lemma states that if the sum of densities of $R,B$ is larger, closer to the maximum of $\frac {1}{2}+\frac {1}{2}$ , then $R \cup B$ has a density significantly smaller than $\frac {4}{5}$ .

Lemma 3.3. Let $(a,b)$ be $(\frac {19}{25},\frac {89}{100})$ or $(\frac {3}{4},\frac {19}{20})$ . Let $R,B$ be two triangle-free graphs on the same vertex set of size n with $|R|+|B| \geq b n^2/2$ . Then $|R \cup B| \leq a n^2/2 + o(n^2)$ .

Proof. Let n be a sufficiently large integer. Let R and B be two triangle-free graphs with vertex set $[n]$ . We will sometimes denote their edge sets as R and B, respectively, too. Write $R \cup B$ for the set of edges that lie in at least one of $R,B$ (a simple graph), and $R+B$ for the multiset union of $R,B$ (a multigraph). Suppose that $d(R+B)> b$ and $d(R \cup B)>a$ , where $d(E):=|E|/\binom {n}{2}$ is the edge density of a set E of edges. Let $Y \subseteq [n]$ be a maximal set with the property that Y has a partition $Y_1\cup \ldots \cup Y_t$ into sets of size $5$ where $(R \cup B)[Y_i]\cong K_5$ for all $i \in [t]$ . Since there is a unique $2$ -edge-colouring of $K_5$ which avoids monochromatic triangles, we can label the vertices in each $Y_i$ as $y^i_{1},\ldots ,y^i_{5}$ where $y^i_{j}y^i_{j+1} \in B$ for all $j \in [5]$ , where $y^i_{6}:=y^i_{1}$ , and every other pair is in R (so there are no double edges). Let $X \subseteq \overline {Y} := [n]\setminus Y$ be a maximal set with the property that X has a partition $X_1 \cup \ldots \cup X_s$ into pairs where $(R \cap B)[X_i]\cong K_2$ for all $i \in [s]$ . Write $|Y|=yn$ , $|X|=xn$ and $Z:=[n]\setminus (X \cup Y)$ .

We claim that

(3.1) $$ \begin{align} \nonumber &0 \leq d(R+B) - b \leq 2q(x,y) + o(1)\quad\text{where}\\ &q(x,y) := \frac{x^2}{2}+\frac{3}{4}\cdot\frac{(1-x-y)^2}{2}+x(1-x-y)+\frac{4}{5}\cdot\frac{y^2}{2}+\frac{4}{5}\cdot y(1-y) - \frac{b}{2}. \end{align} $$

This is a consequence of the following observations on the densities of R and B in various subsets of the vertex set. For a graph G with disjoint $U,U' \subseteq V(G)$ , we write $d_G(U) := |E(G[U])|/\binom {|U|}{2}$ and $d_G(U,U') := |E(G[U,U'])|/(|U||U'|)$ .

1. (i) $d_R(X) \leq \frac {1}{2}+o(1)$ by Turán’s theorem (or rather Mantel’s theorem), since R is triangle-free. Similarly for $d_B(X)$ .

2. (ii) $d_{R+B}(Z) \leq \frac {3}{4}+o(1)$ by Turán’s theorem, since $R,B$ are disjoint on Z and so $R+B=R \cup B$ is $K_5$ -free, so $d_{R+B}(Z)=d_{R \cup B}(Z) \leq \frac {3}{4}+o(1)$ .

3. (iii) $d_{R+B}(X,Z) \leq 1$ . If not, by averaging, there is $j \in [s]$ with $e_{R+B}(X_j,Z)>2|Z|$ , so without loss of generality, there is $v \in Z$ such that v sends a red edge to both vertices in $X_j$ , a contradiction.

Thus, (3.1) holds for $y=o(1)$ . So for the rest of the derivation, we may suppose $y=\Omega (1)$ .

1. (iv) $d_{R+B}(Y) \leq \frac {4}{5}+o(1)$ . If not, by averaging, there are distinct $i,j \in [t]$ such that

   $$ \begin{align*}e_{R+B}(Y_i,Y_j) \geq \frac{(\frac{4}{5}+\Omega(1))\binom{yn}{2} - 10\cdot yn/5}{\binom{yn/5}{2}}> 20 \end{align*} $$
   (if $d_{R+B}(Y)> \frac {4}{5}+c$ , then this holds already for $yn>\frac {1}{c}-1$ ). Then, without loss of generality, $d_{R+B}(y^j_{1},Y_i) \geq 5$ . There is at least one double edge, say $y^j_{1}y^i_{1}$ , for otherwise $(R\cup B)[Y_i \cup \{y^j_{1}\}]\cong K_6$ . Then $y^j_{1}$ sends no blue edges to $\{y^i_{2},y^i_{5}\}$ , and at most one red edge. Similarly, $y^j_{1}$ sends no red edges to $\{y^i_{3},y^i_{4}\}$ , and at most one blue edge. Thus, in fact, $d_{R+B}(y^j_{1},Y_i) \leq 4$ , a contradiction.

2. (v) For all $W \subseteq X \cup Z$ , $d_R(Y,W) \leq \frac {2}{5}$ . If not, by averaging, there is $i \in [t]$ and $v\in W$ such that $d_R(v,Y_i) \geq 3$ which yields a red triangle containing v and two vertices in $Y_i$ . Similarly for $d_B(Y,W)$ .

This proves that (3.1) holds, using in order (i)–(v) for each term, bounding the density of $R+B$ in, respectively, $X,Z,(X,Z),Y,(Y,X \cup Z)$ .

We obtain a similar polynomial upper bound for the density of $R\cup B$ . We claim that

$$ \begin{align*} &0 \leq d(R \cup B) - a \leq 2p(x,y) + o(1)\quad\text{where} \end{align*} $$

(3.2) $$ \begin{align} p(x,y) &:= \frac{4}{5}\cdot\frac{y^2}{2}+ \frac{4}{5}(1-x-y)y + \frac{3}{4}\cdot\frac{(1-y)^2}{2} + \frac{7}{10} xy - \frac{a}{2}\\ \nonumber &= -\frac{y}{40}(4x+y-2) - \frac{1}{2}\left(a-\frac{3}{4}\right). \end{align} $$

This follows from some more observations.

1. (vi) $d_{R \cup B}(\overline {Y}) \leq \frac {3}{4}+o(1)$ by Turán’s theorem, since $(R \cup B)[\overline {Y}]$ is $K_5$ -free.

2. (vii) $d_{R \cup B}(Y,X) \leq \frac {7}{10}$ . If not, then by averaging, there is $i \in [t]$ and $j \in [s]$ such that $e(R \cup B)[Y_i,X_j]> \frac {7}{10}\cdot 5 \cdot 2 = 7$ . For ease of notation, write $1,\dots ,5$ for the vertices of $Y_i$ , with blue edges forming the cycle $12,23,34,45,51$ and red edges forming the cycle $13,35,52,24,41$ , and write $X_j=\{x,y\}$ , where $xy$ is both red and blue. Each of $x,y$ has at most two neighbours in $[5]$ of any one colour, and therefore exactly two or we are done. For blue, these neighbours are a subset of one of $\{1,3\},\{2,4\},\{3,5\},\{4,1\},\{5,2\}$ , and for red a subset of $\{1,5\},\{3,2\},\{5,4\},\{2,1\},\{4,3\}$ . We have that $N_B(x),N_B(y)$ are disjoint, as are $N_R(x),N_R(y)$ . Also, each of $N_B(x),N_R(x)$ are disjoint, as are $N_B(y),N_R(y)$ , since otherwise there are at most $7 R \cup B$ -edges between $\{x,y\}$ and $\{1,\ldots ,5\}$ , a contradiction. Without loss of generality, suppose $N_B(x)=\{1,3\}$ . Then $N_R(x) = \{5,4\}$ and $N_B(y)\in \{\{2,4\},\{5,2\}\}$ . For either possibility, there is no choice of $N_R(y)$ which satisfies the disjointness conditions.

Again, (3.2) holds using (iv)–(vii) in order for each term, bounding the density of $R \cup B$ in, respectively, $Y,(Z,Y),X \cup Z, (X,Y)$ . This proves the claim.

Claim 3.3.1. The regions $P:= \{(x,y) \in [0,1]^2: p(x,y) \geq 0\}$ and $Q := \{(x,y) \in [0,1]^2: q(x,y) \geq 0\}$ intersect only when $y=0$ .

Proof of Claim

Write

$$ \begin{align*} p_x(y) &:=40p(x,y) = -y^2 - 2y(2x-1) - 5(4a - 3)\quad\text{and}\\ q_x(y) &:=40q(x,y)= -y^2 - 2y(5x-1) +5(-x^2+2x+3-4b), \end{align*} $$

which are both quadratic functions of y with negative $y^2$ coefficient. Note that their discriminants are

$$ \begin{align*} \mathrm{disc}(p_x) &= 4(2x-1)^2-20(4a-3)\quad\text{and}\\ \mathrm{disc}(q_x) &= 4\left(5x-1\right)^2+20\left(-x^2+2x-3-4b\right)= 80\left(x^2+\frac{4}{5}-b\right)\\ &= 80\left(\left(x-\frac{3}{10}\right)\left(x+\frac{3}{10}\right)+\frac{89}{100}-b\right). \end{align*} $$

Thus, if $\mathrm {disc}(q_x) \geq 0$ , the largest root $y_x$ of $q_x$ is

$$ \begin{align*}-5x+1+2\sqrt{5}\cdot \sqrt{x^2+\frac{4}{5}-b}. \end{align*} $$

Suppose first that $(a,b)=(\frac {19}{25},\frac {89}{100})$ . We claim that $x < \frac {3}{10}$ for all $(x,y) \in P$ . For this, note that $\mathrm {disc}(p_{\frac {3}{10}})<0$ , so $p_{\frac {3}{10}}$ has no real roots, and therefore, $p_{\frac {3}{10}}(y)<0$ for all $y \in [0,1]$ . Since $p(x,y)$ is decreasing in $x \geq 0$ , we have that $p(x,y)=\frac {1}{40}p_x(y)<0$ for all $x \in [\frac {3}{10},1]$ and $y \in [0,1]$ , as required. However, we claim that $x\geq \frac {3}{10}$ for all $(x,y) \in Q$ . Indeed, if $x \in [0,\frac {3}{10})$ , we have $\mathrm {disc}(q_x)<0$ and so again, $q(x,y)=q_x(y)<0$ for all $y \in [0,1]$ . Thus, P and Q are disjoint in this case.

Suppose secondly that $(a,b)=(\frac {3}{4},\frac {19}{20})$ . We claim that $x \leq \frac {1}{2}$ for all $(x,y) \in P$ with $y \neq 0$ . Indeed, $p_x(y)=-y(y+4x-2)$ , so we have $y+4x-2 \leq 0$ for $y \in (0,1]$ , so $x \leq \frac {1}{2}$ . However, we claim that $x>\frac {1}{2}$ for all $(x,y) \in Q$ . Indeed, let $x \in [0,\frac {1}{2}]$ . If $\mathrm {disc}(q_x)<0$ , then, since the coefficient of $y^2$ is negative, $(x,y)<0$ for all $y \in [0,1]$ . Otherwise, the largest root $y_x$ of $q_x$ exists, and it is at least $0$ only if $5x^2-10x+4\leq 0$ , which is false for all $x \in [0,\frac {1}{2}]$ . So $y_x$ is negative, and we see that $q_x(y)<q_x(y_x) = 0$ for all $y \in (y_x,1]$ . Thus, $x> \frac {1}{2}$ for all $(x,y) \in Q$ , as required. This completes the proof of the claim.

The statement of the lemma then follows easily from the claim, noting that for any $(x,y) \in P \cap Q$ , we have $y=0$ and $p(x,0)=\frac {1}{2}(\frac {3}{4}-a) \leq 0$ .

3.2. Solving Problem $Q^*$ via a linear relaxation

We define a further optimisation problem.

Problem $\mathbf {L}$ : Given a sequence $\boldsymbol {k}:=(k_1,\ldots ,k_s)\in \mathbb {N}^s$ of natural numbers, determine $ \ell ^{\mathrm {max}}(\boldsymbol {k}) := \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d}) $ , the maximum value of

$$ \begin{align*}\ell(\boldsymbol{d}) := \sum_{2 \leq t \leq s}\log t \cdot d_t \end{align*} $$

over the set $D(\boldsymbol {k})$ of $(s-1)$ -tuples $\boldsymbol {d}=(d_2,\ldots ,d_s)$ such that $0 \leq d_t \leq 1$ for all $2 \leq t \leq s$ , and $\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$ .

We say that $\boldsymbol {d}$ which is feasible for Problem L is realisable if there is some with

(3.3) $$ \begin{align} d_t=2\sum_{ij \in \binom{[r]}{2}:|\phi(ij)|=t}\alpha_i \alpha_j\quad \text{for all }2 \leq t \leq s \end{align} $$

and call such a feasible triple a realisation (of $\boldsymbol {d}$ ).

We have the following, which is proved by applying Turán’s theorem to blow-ups (defined below). It implies that, in certain special cases, to solve Problem $Q^*$ , it suffices to solve Problem L.

Lemma 3.4 ([10, Lemma 5.1])

Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}$ . Then $Q(\boldsymbol {k}) \leq \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$ . Moreover, the following is true. Suppose that at least one optimal solution $\boldsymbol {d}$ to Problem L is realisable. Then $\max _{\boldsymbol {d}\in D(\boldsymbol {k})}\ell (\boldsymbol {d})=Q(\boldsymbol {k})$ and is the set of all , which are realisations of some optimal $\boldsymbol {d}$ .

We wish to add more constraints to Problem L. Indeed, without additional constraints, Problem L only yields realisable solutions in some very special cases – for example, $\boldsymbol {k}=(k,k)$ or $\boldsymbol {k}=(k,k,k)$ . A constraint is valid if every $\boldsymbol {d}$ which has a realisation must satisfy the constraint. We use I for a set of constraints, each of the type $\sum _{2 \leq f \leq s}a_f d_f \leq b$ for some $a_2,\ldots ,a_s,b \in \mathbb {R}$ . Let Problem $(L,I)$ be Problem L with the constraints in I added to it and let $\ell ^{\mathrm {max}}_I(\boldsymbol {k})$ be the optimal solution of Problem $(L,I)$ . We will still discuss realisable solutions $\boldsymbol {d}$ and realisations of $\boldsymbol {d}$ for Problem $(L,I)$ without referring to I when it is clear from the context.

The two types of constraints that we consider are as follows.

Universal constraints. Let $\mathcal {A}$ be a set of subsets of $\binom {[s]}{\geq 2}$ . Let $i_2,\ldots ,i_s \geq 0$ be such that for each $2 \leq f \leq s$ and $S \in \binom {[s]}{f}$ , the number of $A \in \mathcal {A}$ for which $S \in A$ is at least $i_f$ .

Next, given and $A \subseteq \binom {[s]}{\geq 2}$ , let $H^n_A(\phi ,\boldsymbol {\alpha })$ be the ‘blow-up’ graph on n vertices with vertex classes $X_1,\ldots ,X_r$ , where $|\,|X_i|-\alpha _i n\,| \leq 1$ for all $i \in [r]$ and $xy$ is an edge for $x \in X_i$ , $y \in X_j$ if and only if $\phi (ij) \in A$ . Suppose that $d(H^n_A(\phi ,\boldsymbol {\alpha })) \leq c_A+o_n(1)$ for all $A \in \mathcal {A}$ and all . Then

$$ \begin{align*}i_2 d_{2}+\ldots + i_s d_{s} \leq \sum_{A \in \mathcal{A}}c_A \end{align*} $$

is a valid constraint. Indeed, $\sum _{A \in \mathcal {A}}e(H^{n}_A(\phi ,\boldsymbol {\alpha })) \geq (i_2d_{2}+\ldots +i_sd_{s})\frac {n^2}{2}+O(n)$ .

For example, the basic constraint $\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$ is a universal constraint, coming from $\mathcal {A} := \{A_1,\ldots ,A_s\}$ and $c_{A_t} := 1-\frac {1}{k_t-1}$ , where $A_t := \{S \in \binom {[s]}{\geq 2}: t \in S\}$ , noting that each $S \in \binom {[s]}{f}$ lies in $A_g$ if and only if $g \in S$ , so $i_f :=f$ .

A special case of universal constraint arises when $H_{\mathcal {A}}(\phi ) := \{ij \in \binom {[r]}{2}: \phi (ij) \in A \text { for some }A \in \mathcal {A}\}$ is $K_k$ -free for every . Then $H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha }) := \bigcup _{A \in \mathcal {A}}H_A^n(\phi ,\boldsymbol {\alpha })$ is always $K_k$ -free, so Turán’s theorem implies that $d(H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha })) \leq 1-\frac {1}{k-1}$ . If $\mathcal {A} := \{\binom {[s]}{t}: t \in T\}$ for some $T \subseteq \{2,\ldots ,s\}$ , then $i_f=1$ when $f \in T$ and $0$ otherwise, so we have

$$ \begin{align*}\sum_{t \in T}d_t \leq 1-\frac{1}{k-1}. \end{align*} $$

We have the following observations from [10].

1. (A) Suppose there is equality in this constraint. Then there is a partition of $[r]$ into parts $A_1,\ldots ,A_{k-1}$ such that $\sum _{i \in A_{i'}}\alpha _{i}=\frac {1}{k-1}$ for all $i' \in [k-1]$ , and $ij \in H_{\mathcal {A}}(\phi )$ if and only if $i,j$ lie in different parts $A_{i'},A_{j'}$ .

2. (B) If $S \subseteq [r]$ has $|S| \leq k$ , then $2\sum _{ij \in \binom {S}{2}}\alpha _i\alpha _j \leq \left (1-\frac {1}{k-1}\right )\sum _{i \in S}\alpha _i$ with equality if and only if $\alpha _i=\alpha _j$ for all $ij \in \binom {S}{2}$ .

Existential constraints. Let I be a set of valid constraints. Suppose that there is some which is the realisation of some feasible $\boldsymbol {d}^*$ , and a constraint $a_2d_2+\ldots +a_sd_s \leq b$ , and let $I'$ be obtained from adding this constraint to I. Suppose that Problem L with constraints $I'$ has optimal value $\ell ^{\mathrm {max}}_{I'}(\boldsymbol {k})< \ell (\boldsymbol {d}^*)$ . Then

$$ \begin{align*}a_2d_2 + \ldots + a_sd_s \geq b\quad\text{i.e.}\quad -a_2d_2-\ldots-a_sd_s \leq -b \end{align*} $$

is a valid constraint. Indeed, no optimal solution of Problem $Q^*$ is a realisation of $\boldsymbol {d}$ that satisfies the new constraint, so it cannot hold.

Lemma 3.5. Let $s \in \mathbb {N}$ and $\boldsymbol {k} \in \mathbb {N}$ . Let I be a set of valid constraints from Problem L and let $\ell ^{\mathrm {max}}_I(\boldsymbol {k})$ be the optimal value. Then $Q(\boldsymbol {k}) \leq \ell ^{\mathrm {max}}_I(\boldsymbol {k})$ . Moreover, the following is true. Suppose that at least one optimal solution $\boldsymbol {d}$ to Problem L with constraints I is realisable. Then $\ell ^{\mathrm {max}}_I(\boldsymbol {k})=Q(\boldsymbol {k})$ and is the set of all which are realisations of some optimal $\boldsymbol {d}$ .

Figure 1 Hadamard matrices of order $2,4,8$ , which are unique up to equivalence. Here, black represents $1$ and white represents $-1$ .

3.3. The proof of Theorem 3.1

First we see why a particular density vector $\boldsymbol {d}$ for the $(3;4t-1)$ -problem must give rise to a realisation corresponding to the Hadamard matrix $H_{4t}$ .

Lemma 3.6. Let $t \geq 1$ be an integer and let $\boldsymbol {k}=(3;4t-1)$ . Suppose that $\boldsymbol {d} = (d_2,\ldots ,d_{4t-1})$ with $d_{2t}=1-\frac {1}{4t}$ and all other entries zero is realisable and let be a realisation. Then $r=4t$ , $\boldsymbol {\alpha }$ is uniform, and every $\phi ^{-1}(c) \cong K_{2t,2t}$ . Moreover, there is a Hadamard matrix $H_{4t}$ of order $4t$ whose columns are labelled $0,1,\ldots ,4t-1$ and rows are labelled $1,2,\ldots ,4t$ , normalised so that Column $0$ consists of $1$ -entries, and such that the vertex classes of $\phi ^{-1}(c)$ are given respectively by the set of row indices of the $1$ -entries, and of the $-1$ -entries, in Column c in $H_{4t}$ .

Proof. By Turán’s theorem, $|\phi ^{-1}(c)| \leq \lfloor r^2/4\rfloor $ . Also, $\boldsymbol {d}$ is such that only $d_{2t}$ is nonzero, so $|\phi (ij)|=2t$ for all $ij \in \binom {[r]}{2}$ . So $(4t-1)\lfloor r^2/4\rfloor \geq \sum _{c \in [4t-1]}|\phi ^{-1}(c)|=2t\binom {r}{2}$ . Solving this yields $r\leq 4t$ . However, $1-\frac {1}{4t} = d_{2t} = 2\sum _{ij \in \binom {[r]}{2}}\alpha _i\alpha _j$ , so Observation (B) implies that $r \geq 4t$ . Thus, $r=4t$ and $|\phi ^{-1}(c)|=(4t)^2/4$ for all $c \in [4t-1]$ , and $\boldsymbol {\alpha }$ is uniform. So the graphs $\phi ^{-1}(1),\ldots ,\phi ^{-1}(4t-1)$ , each one isomorphic to $K_{2t,2t}$ , decompose $2tK_{4t}$ , the complete multigraph on $4t$ vertices with every multiplicity equal to $2t$ . That such a decomposition exists, and its connection to Hadamard matrices follows from an observation of de Caen, Gregory and Pritikin [3], as follows. Let $G_1,\ldots ,G_{4t-1}$ be copies of $K_{2t,2t}$ which decompose $2tK_{4t}$ . Construct a $4t\times 4t$ matrix H with the leftmost column consisting of all $1$ -s and the j-th next column with $1$ -s in the rows corresponding to one part of $G_j$ and $-1$ -s in the remaining rows. For distinct $i,i'$ , the number of $j \in [4t-1]$ such that $H_{ij}H_{i'j}=-1$ is exactly the number of $\phi ^{-1}(j)$ containing $ii'$ , which is $2t$ . Clearly, $H_{i0}H_{i'0}=1$ . Thus, for distinct rows $\boldsymbol {h},\boldsymbol {h}'$ of H, we have that the scalar product $\boldsymbol {h}.\boldsymbol {h}'=2t(-1)+2t(1)=0$ , so the rows are pairwise orthogonal. Since the sum of the squares of entries in each row $\boldsymbol {h}$ is $4t$ , we see that the collection of $\frac {1}{\sqrt {4t}}\boldsymbol {h}$ over rows $\boldsymbol {h}$ is an orthonormal basis of $\mathbb {R}^{4t}$ , and hence, $HH^\intercal = 4tI_{4t}$ , so H is a Hadamard matrix.

Remark 3.7. For completeness, we give the other direction of the proof in [3]: that a decomposition can be read off a Hadamard matrix. Let H be a Hadamard matrix of order $4t$ with columns labelled $0,\ldots ,4t-1$ and rows labelled $1,\ldots ,4t$ . First note that we can flip the signs of all entries in a given row to get a new Hadamard matrix. Thus, we can obtain from H a Hadamard matrix whose first column (of index $0$ ) is $(1,\ldots ,1)^\intercal $ . Since $\frac {1}{\sqrt {4t}}H$ is an orthogonal matrix, every pair of columns are orthogonal (and similarly for rows). So comparing every column with Column $0$ , we see that every other column contains exactly $2t 1$ -entries. Take any two rows $\boldsymbol {h}, \boldsymbol {h}'$ with row indices $1 \leq i < i' \leq 4t$ , respectively, and let $\ell _{ij}$ be the number of columns j where $H_{ij} \neq H_{i'j}$ . Since rows are pairwise orthogonal, we have $0 = \boldsymbol {h}.\boldsymbol {h}' = -\ell _{ij}+(4t-\ell _{ij})=4t-2\ell _{ij}$ , so $\ell _{ij}=2t$ . Now for each column $1 \leq j \leq 4t-1$ , let $G_j$ be the copy of $K_{2t,2t}$ on vertex set $[4t]$ with vertex classes $A_j,B_j$ , where $A_j$ consists of those rows $1 \leq i \leq 4t$ , where $H_{ij}=1$ . Given any pair $gh \in \binom {[4t]}{2}$ , the number of $G_j$ where $gh$ is an edge is $\ell _{gh}=2t$ . Thus, $G_1,\ldots ,G_{4t-1}$ decompose $2tK_{4t}$ .

In the next lemma, we solve Problem L for $(3;6)$ and $(3;7)$ using our new tool Lemma 3.3.

Lemma 3.8. Let $\boldsymbol {k}=(3;s)$ .

1. (i) Let $s=6$ . Then $Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$ . Moreover, if $\boldsymbol {d}$ is realisable and satisfies $\ell (\boldsymbol {d})= \frac {1}{2}\log 3 + \frac {3}{4}$ , then $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$ .

2. (ii) Let $s=7$ . Then $Q(\boldsymbol {k})\leq \frac {7}{4}$ . Moreover, if $\boldsymbol {d}$ is realisable and satisfies $\ell (\boldsymbol {d})=\frac {7}{4}$ , then $\boldsymbol {d}=(0,0,\frac {7}{8},0,0,0)$ .

Proof. By Lemma 3.5, it suffices to find a set I of valid constraints for Problem L such that $\ell _I^{\mathrm {max}}(\boldsymbol {k})$ is at most the required value. We first prove (ii). Note that

(3.4) $$ \begin{align} d_2+\ldots + d_7 \leq 1 \end{align} $$

is a valid constraint. (In fact, we could replace $1$ by $1-\frac {1}{R(3;7)-1}$ , which is a special case of the universal constraints discussed earlier.) For each colour $i \in [7]$ , let $A_i := \{B \in \binom {[7]}{\geq 2}: i \in B\}$ and for each pair $ij \in \binom {[7]}{2}$ of colours, let $A_{ij} := A_i \cup A_j$ , and let $\mathcal {A} := \{A_{ij}:ij \in \binom {[7]}{2}\}$ . Then

(3.5) $$ \begin{align} |\mathcal{A}|=\binom{7}{2} \text{ and } (i_2,\ldots,i_7)=(11,15,18,20,21,21) \end{align} $$

since $i_f=\binom {7}{2}-\binom {7-f}{2}$ for each $2 \leq f \leq 7$ . Let be arbitrary and let $n \in \mathbb {N}$ be large. For brevity, write $H^n_i(\phi ,\boldsymbol {\alpha })$ for $H^n_{A_i}(\phi ,\boldsymbol {\alpha })$ and $H^n_{ij}(\phi ,\boldsymbol {\alpha })$ for $H^n_{A_{ij}}(\phi ,\boldsymbol {\alpha })$ . Then $H^n_i(\phi ,\boldsymbol {\alpha })$ and $H^n_j(\phi ,\boldsymbol {\alpha })$ are triangle-free since $\phi ^{-1}(i)$ and $\phi ^{-1}(j)$ are. Clearly, $H^n_{ij}(\phi ,\boldsymbol {\alpha })=H^n_i(\phi ,\boldsymbol {\alpha }) \cup H^n_j(\phi ,\boldsymbol {\alpha })$ .

Let $(8,\phi ^*,\boldsymbol {u})$ be a feasible solution from Remark 3.7 for $t=2$ , so $\boldsymbol {u}$ is uniform, $|\phi ^*|\equiv 8$ and $q(\phi ^*,\boldsymbol {u}) = \frac {7}{4}$ . First consider the constraint set $I_1$ consisting of (3.4) and the single constraint $2d_2+\ldots +7d_7 \leq \frac {339}{100}$ . Multiply (3.4) by $\log \frac {81}{64}$ and the new constraint by $\log \frac {4}{3}$ , and add these together. (These multipliers come from the (unique) solution to the dual linear program.) Then each $d_f$ on the left-hand side has coefficient at least $\log f$ (its coefficient in the objective function), and thus, $\ell ^{\mathrm {max}}_{I_1}(\boldsymbol {k})$ is at most the right-hand side, which is $\frac {39}{50}+\frac {61}{100}\log 3 < \frac {7}{4}=q(\phi ^*,\boldsymbol {\alpha }^*)$ . Thus,

(3.6) $$ \begin{align} 2d_2+\ldots+7d_7 \geq \frac{339}{100} \end{align} $$

is a valid (existential) constraint. Suppose there are $ij \in \binom {[7]}{2}$ and with $d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \leq \frac {89}{100}-\Omega _n(1)$ . Let $\boldsymbol {d}$ be such that $(r,\phi ,\boldsymbol {\alpha })$ is a realisation of $\boldsymbol {d}$ . Since every $d(H^n_{i'}(\phi ,\boldsymbol {\alpha })) \leq \frac {1}{2}+o_n(1)$ , we have

$$ \begin{align*}\nonumber 2d_2+\ldots + 7d_7 + o_n(1) = \binom{n}{2}^{-1}\sum_{i' \in [7]}d(H^n_{i'}(\phi,\boldsymbol{\alpha})) \leq \frac{5}{2}+\frac{89}{100}-\Omega_n(1) = \frac{339}{100}-\Omega_n(1), \end{align*} $$

a contradiction. Thus, Lemma 3.3 implies that $e(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {19}{25}n^2/2$ for every $ij$ and $(r,\phi ,\boldsymbol {\alpha })$ . With $\mathcal {A}$ defined before (3.5), we have by the above that

(3.7) $$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{19}{25} \end{align} $$

is a valid (universal) constraint. Consider the constraint set $I_2$ consisting of the valid constraint (3.7) and the new constraint $2d_2+\ldots + 7d_7 \leq \frac {69}{20}$ . Multiply (3.7) by $\log \frac {32}{27}$ and the new constraint by $\frac {1}{3}\log \frac {9}{8}$ , and add these together. Then each $d_f$ on the left-hand side has coefficient at least $\log f$ , and thus, $\ell ^{\mathrm {max}}_{I_2}(\boldsymbol {k})$ is at most the right-hand side, which is $\frac {129}{100}+\frac {29}{100}\log 3 < \frac {7}{4}$ . So

(3.8) $$ \begin{align} 2d_2+\ldots + 7d_7 \geq \frac{69}{20} \end{align} $$

is a valid constraint. As above, this implies that for every $ij \in \binom {[7]}{2}$ and , which is a realisation of some $\boldsymbol {d}$ , we have $d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \geq \frac {69}{20}-\frac {5}{2} + o_n(1) = \frac {19}{20}+o_n(1)$ . Thus, Lemma 3.3 implies that $d(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {3}{4}+o_n(1)$ for every $ij$ . So

(3.9) $$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{3}{4} \end{align} $$

is a valid constraint. Finally, consider the constraint set $I_3$ consisting of the two valid constraints: (3.9) and $2d_2+\ldots +7d_7 \leq \frac {7}{2}$ , the original universal constraint in Problem L. Multiply the original constraint by $\frac {1}{7}\log \frac {343}{128}$ and (3.9) by $\frac {1}{21}\log \frac {128}{49}$ , and add these together. Then each $d_f$ on the left-hand side has coefficient at least $\log f$ , and thus, $\ell ^{\mathrm {max}}_{I_3}(\boldsymbol {k})$ is at most the right-hand side, which is $\frac {7}{4}$ . Moreover, the coefficient of $d_f$ is strictly greater than $\log f$ unless $f=4$ , so every optimal solution has $d_f=0$ for all $f \neq 4$ . Thus, the unique optimiser has $4d_4 = \frac {7}{2}$ , and all other entries equal to $0$ . This completes the proof of (ii).

The same argument works for $s=6$ to prove (i). Here, $(i_2,\ldots ,i_6)=(9,12,14,15,15)$ . Again, $d_1+\ldots +d_6 \leq 1$ is a valid constraint. We see that $2d_2+\ldots +6d_6 \geq \frac {289}{100}$ is a valid constraint, since its negation alone implies that $\ell (\boldsymbol {d}) = \sum _{2 \leq f \leq s} fd_f \cdot \frac {\log f}{f} \leq \frac {289}{100}\cdot \frac {\log 3}{3} \leq \frac {1}{2}\log 3 +\frac {3}{4}$ . From this, the sum of densities of any pair of colour graphs is at most $\frac {289}{100}-4\cdot \frac {1}{2}=\frac {89}{100}$ , and so Lemma 3.3 implies that their union has density at most $\frac {19}{25}$ . Thus,

(3.10) $$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq \binom{6}{2}\frac{19}{25} \end{align} $$

is a valid constraint. This implies that

(3.11) $$ \begin{align} 2d_2+\ldots+6d_6 \geq \frac{59}{20} \end{align} $$

is a valid constraint. Indeed, if we add $\frac {1}{3}\log \frac {9}{8}$ times (3.10) plus $4-\frac {7}{3}\log 3$ times the negation of (3.11), we see $\ell (\boldsymbol {d}) \leq \frac {2}{5}+\frac {43}{60}\log 3 < \frac {1}{2}\log 3 + \frac {3}{4}$ . Now the sum of densities of any pair of colour graphs is at most $\frac {59}{20}-4\cdot \frac {1}{2}=\frac {19}{20}$ , and so Lemma 3.3 implies that their union has density at most $\frac {3}{4}$ . Thus,

(3.12) $$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq\binom{6}{2}\frac{3}{4} \end{align} $$

is a valid constraint. Finally, we consider Problem L with the set of two valid constraints: (3.12) and $2d_2+\ldots +6d_6 \leq 3$ , the original universal constraint in Problem L. Multiply (3.12) by $\frac {1}{3}\log \frac {9}{8}$ and the original constraint by $4-\frac {7}{3}$ and add these together to see that each $d_f$ on the left-hand side has coefficient at least $\log f$ , and is strictly greater than $\log f$ only for $f=2,5,6$ , and the right-hand side is $\frac {1}{2}\log 3+\frac {3}{4}$ . Thus, the unique optimal solution is $\ell ^{\mathrm {max}}_I(\boldsymbol {k})=\frac {1}{2}\log 3 + \frac {3}{4}$ , and the unique optimiser has $d_2=d_5=d_6=0$ and is therefore $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$ .

Proof of Theorem 3.1

This follows immediately from Lemmas 3.6 and 3.8.

Proof of Theorem 3.2

We need to show that every is as described. Lemma 3.8(i) implies that $Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$ , and that, if there is equality, any optimal $(r,\phi ,\boldsymbol {\alpha })$ is the realisation of $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$ . Since $\|\boldsymbol {d}\|_1 = \frac {7}{8}$ , Observation (B) implies that $r \geq 8$ . Suppose that $|\phi (1i)|=4$ for $i=2,3,4,5$ . Then for all distinct $i,i' \in \{2,3,4,5\}$ , we have $\phi (1i) \neq \phi (1i')$ , otherwise $|\phi (ii')|\leq 2$ (or there would be a monochromatic triangle). Let $\psi (ii'):=\{j \in [6]: j \notin \phi (1i) \cap \phi (1i')\}$ . Then $\phi (ii') \subseteq \psi (ii')$ . We use a computer to obtain all $\binom {15}{4}$ possible $\phi (12),\ldots ,\phi (15)$ and corresponding $\{\psi (ii')\}$ . Then check each triple $ii'i"$ : suppose $\psi (ii'),\psi (i'i"),\psi (i"i')$ share an element j. If they each have size three, we have a contradiction since we must delete j from at least one of these sets so we end up with a $\phi $ -set of size two. If one has size $4$ and two have size $3$ , then we must delete j from the set of size $4$ (that is, the corresponding $\phi $ -sets all have size at most $3$ ). After checking all triples, the resulting sets are still supersets of $\phi (ii')$ for distinct $i,i'=2,3,4,5$ . In every case, the sets are of the form $ \{abc, def, xyuv, xyuv',xy'uv,xy'uv'\}$ , where $\{a,b,c,d,e,f\}=[6], \{x,y,y'\}=\{a,b,c\}, \{u,v,v'\}=\{d,e,f\}$ . So without loss of generality, the resulting sets are $\{123\},\{456\},\{1245\},\{1246\},\{1345\},\{1346\}$ . Sets $1,3,4$ of sizes $3,4,4$ , respectively, all contain $1,2$ , so without loss of generality, we can reduce to

$$ \begin{align*}\{123\},\{456\},\{145\},\{246\},\{1345\},\{1346\}. \end{align*} $$

But now, sets $2,4,6$ of sizes $3,3,4$ , respectively, all contain $4,6$ , which is a contradiction because deleting one copy of each gives a $\phi $ -set of size at most two. Thus, we have eliminated all possible cases. We implemented the above in python (6check.py). Thus, when $r \geq 8$ , for each $i \in [r]$ , there is a set $X_i \subseteq [r]\setminus \{i\}$ of size at most $3$ such that $|\phi (ij)|=4$ if and only if $j \in X_i$ . Therefore, $2\cdot 6\lfloor \frac {r^2}{4}\rfloor \geq 2\sum _{c \in [6]}|\phi ^{-1}(c)| \geq r\cdot (12+3(r-4)) = 3r^2$ . Thus, r is even, every $|X_i|=3$ , and $\phi ^{-1}(c) \cong K_{\frac {r}{2},\frac {r}{2}}$ for all $c \in [6]$ .

For $c \in [6]$ , let $A_c,B_c$ be the vertex classes of $\phi ^{-1}(c)$ . Let $A=(a_{ij})$ be an $r \times 6$ matrix with $\pm 1$ entries, where the c-th column represents $\phi ^{-1}(c)$ , with $a_{jc}=1$ if $j \in A_c$ and $a_{jc}=-1$ if $j \in B_c$ . By relabelling classes, without loss of generality, the r-th row of A is $(1,1,1,1,1,1)$ . Notice that $|\phi (ij)|$ is the number of columns $c \in [6]$ where $a_{jc}$ and $a_{ic}$ differ. So $|\phi (rj)|$ is the number of entries equal to $-1$ in the j-th row. But $|\phi (rj)|=3$ for all but $3$ rows j.

If $r \geq 10$ , then $|\phi (rj)|=3$ for at least $r-1-3 \geq 6$ other rows j. Each of these rows, without loss of generality $j=1,2,3,4,5,6$ , therefore contains exactly $3$ entries equal to $-1$ . By parity, no pair of these rows can differ in exactly three places. Thus, $|\phi (ij)| \neq 3$ , and hence, $|\phi (ij)|=4$ for all $ij\in \binom {[6]}{2}$ , so, for example, $|X_1| \geq 5$ , a contradiction.

Recalling that $r \geq 8$ and r is even, we must have $r=8$ . For $\ell =3,4$ , let $G_\ell := \{ij \in \binom {[8]}{2}: |\phi (ij)|=\ell \}$ . Since also $\|\boldsymbol {d}\|_1=\frac {7}{8}$ , $\boldsymbol {\alpha }$ is uniform. One can check via computer (6config.py) that whenever $\phi ^{-1}(c) \cong K_{4,4}$ for all $c \in [6]$ are such that every edge multiplicity is $3$ or $4$ , then $G_3 \cong K_{4,4}$ and $G_4 \cong K_4 \cup K_4$ . (To reduce computations, first we assume all $\phi ^{-1}(c)$ are distinct. Next, if they are not, one needs at least $3=\log 8$ copies of $K_{4,4}$ to cover every edge of $K_8$ at least once, so at least five such graphs are required to cover every edge at least three times. So it remains to check the cases where $\phi ^{-1}(1),\phi ^{-1}(2)$ are identical and the other colour graphs are distinct.) Given this structure, $3G_3 \cup 4G_4$ has a decomposition into $6$ copies of $K_{4,4}$ if and only if $4K_8$ has a decomposition into $7$ copies of $K_{4,4}$ . Thus, the columns of A are among the $7$ rightmost columns of a normalised order- $8$ Hadamard matrix H (up to permutation of rows and/or negation of rows).

3.4. Hadamard matrices and the triangle problem

Figure 2 shows how the known extremal graphs for the triangle problem relate to Hadamard matrices. For $s \in [7]\setminus \{5\}$ , these are all unique, and for $s=5$ , there is an infinite family of asymptotically extremal graphs, of which two are drawn here. Index the columns of the above matrices by $0,1,\ldots $ . For each $c \in [s]$ , $\phi ^{-1}(c)$ is a complete balanced bipartite graph whose vertex classes are given by the set of row indices of the white squares, and of the black squares, in Column c. Some columns are repeated, denoted by $\times \ell $ , and some are removed, denoted by $-$ . Taking r to be the order of the matrix, and $\boldsymbol {u} \in \Delta ^r$ to be uniform, we have the optimal solution $(r,\phi ,\boldsymbol {u})$ .

Figure 2 Extremal graphs for $(3;s)$ for $2 \leq s \leq 7$ .

4. Applications of Theorem 1.6

Here, we discuss the perfect colouring problem (Problem 1.7), where we have part sizes that maximise the number of perfect colourings. This was implicitly done in previous works (and is trivial in some cases). Let $r \in \mathbb {N}$ and let $H \subseteq K_r$ be regular. Suppose that every has $r^*=r$ , $\boldsymbol {\alpha }^* = \boldsymbol {u}_r$ uniform and furthermore, there is $M_{\phi ^*} \cong H$ such that $|\phi ^*(ij)|=t_1$ for all $ij \in M_{\phi ^*}$ and $|\phi ^*(ij)|=t_2$ for all $ij \in \binom {[r]}{2}\setminus M_{\phi ^*}$ , where $0 \leq t_1-t_2 \leq 1$ . Then we denote $\mathrm {perf}(\boldsymbol {m}) := \mathrm {perf}_{r,\boldsymbol {u}_r}(\boldsymbol {m})$ .

By symmetry, for some explicit integer $C=C(H)$ , we have that

$$ \begin{align*}\mathrm{perf}(\boldsymbol{m}) = C\cdot \sum_{J \cong H}f(\boldsymbol{m},J),\quad\text{where } f(\boldsymbol{m},J) := \prod_{ij \in J}t_1^{m_im_j}\prod_{i'j'\notin J}t_2^{m_{i'}m_{j'}}, \end{align*} $$

where the sum is over all copies J of H in $K_r$ . Let $\boldsymbol {m}':=(m_1-1,m_2,\ldots ,m_{r-1},m_r+1)$ . Write $m_{J(i)} := \sum _{j \in N_J(i)}m_j$ . Then

$$ \begin{align*} C^{-1}\mathrm{perf}(\boldsymbol{m}') &= \sum_{\substack{J: \{1,r\} \notin J\\ J \cong H}}g_{\mathrm{out}}(\boldsymbol{m},J)f(\boldsymbol{m},J)+ \sum_{\substack{J: \{1,r\} \in J\\ J \cong H}}g_{\mathrm{in}}(\boldsymbol{m},J) f(\boldsymbol{m},J), \end{align*} $$

where

(4.1) $$ \begin{align} g_{\mathrm{out}}(\boldsymbol{m},J) &:= \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r-1}\quad\text{and}\quad g_{\mathrm{in}}(\boldsymbol{m},J) := \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r}t_1^{-1}. \end{align} $$

Indeed, if we let $n:= m_1+\ldots +m_r$ and $\boldsymbol {m}":=(m_1-1,m_2,\ldots ,m_r)$ , then $\mathrm {perf}(\boldsymbol {m})/\mathrm {perf}(\boldsymbol {m}") = t_1^{m_{J(1)}}\cdot t_2^{n-m_{J(1)}-m_1}$ . Now combine this with the analogous formula for $\mathrm {perf}(\boldsymbol {m}')/\mathrm {perf}(\boldsymbol {m}")$ , where, for example, the power of $t_1$ is $\sum _{j \in N_J(r)}m_j'$ , which is $m_{J(r)}$ if $\{1,r\} \notin J$ and $m_{J(r)}-1$ otherwise.

Proof of Proposition 1.10

Recall that we consider only nonincreasing sequences $\boldsymbol {m}$ . In each case, letting r be the (unique) number of vertices in every solution in , we will show that whenever $m_1-m_r \geq 2$ , we have $g_{\mathrm {out}}(\boldsymbol {m},J) \geq 1.01$ , say, for all copies J of H with $\{1,r\} \notin J$ and $g_{\mathrm {in}}(\boldsymbol {m},J) \geq 1.01$ for all J with $\{1,r\} \in J$ . Thus, we have $\frac {1}{1.01}\cdot \mathrm {perf}(\boldsymbol {m}') \geq C\cdot \sum _{J \cong H}f(\boldsymbol {m},J) = \mathrm {perf}(\boldsymbol {m})$ . This implies that the unique supersolution to the perfect colouring problem for n is $\boldsymbol {m}^* = (m_1^*,\ldots ,m_r^*)$ , where $\|\boldsymbol {m}^*\|_1=n$ and $m_1^*-m_r^* \leq 1$ , and the perfect colouring problem is soluble with constant $c:= 0.01$ . If $\boldsymbol {k}$ has the strong extension property, Corollary 1.9 implies that for all sufficiently large n, the unique $\boldsymbol {k}$ -extremal graph on n vertices is $K_{m_1^*,\ldots ,m_r^*} \cong T_r(n)$ .

All $\boldsymbol {k}$ from Theorem 1.1 apart from $(3;5)$ have the strong extension property by Lemma 1.3. Indeed, we showed in [10, Theorem 1.7] that each $\boldsymbol {k}$ among $(k;2), (k;3), (3;4), (4;4)$ has the strong extension property for integers $k \geq 3$ and described the optimal solutions [10, Table 2]. Write $g_{\mathrm {in}}$ and $g_{\mathrm {out}}$ when $\boldsymbol {m},J$ are fixed or clear from the context. Suppose $\boldsymbol {k} := (k;s)$ is one of $(k;2),(k;3),(4;4)$ . Then every has $\boldsymbol {\alpha }$ uniform and $\phi $ only takes one value t. Then for all $\boldsymbol {m}$ with $m_1-m_r \geq 2$ , $g_{\mathrm {in}} = g_{\mathrm {out}} = t^{m_1-m_r-1} \geq t \geq 2$ , as required.

Now suppose $\boldsymbol {k} := (3;4)$ . In the above discussion, $r=4$ , $H \cong K_{2,2}$ , so $(t_1,t_2)=(3,2)$ . Let J be a copy of H. If $\{1,4\}\notin J$ , then $J(1)=J(4)=\{2,3\}$ while if $\{1,4\} \in J$ , then $J(1)=\{i,4\}$ and $J(4)=\{j,1\}$ , where $\{i,j\}=\{2,3\}$ . Let $\boldsymbol {m}=(m_1,\ldots ,m_4)$ be such that $m_1-m_4 \geq 2$ . Here, $g_{\mathrm {out}} = 2^{m_1-m_4-1} \geq 2$ and $g_{\mathrm {in}} = 3^{m_1-m_4-1}\left (\frac {2}{3}\right )^{m_i-m_j}$ . If $m_i - m_j \leq 1$ , then this is at least $2$ ; otherwise, $2 \leq m_i-m_j \leq m_1-m_4$ and it is at least $\frac {4}{3}$ .

Suppose finally that $\boldsymbol {k}=(3;6)$ . Here, Theorem 3.2 implies that $r=8$ and H is the disjoint union of two copies of $K_4$ . So $(t_1,t_2)=(4,3)$ . Let J be a copy of H. If $\{1,8\} \in J$ , then $m_{J(1)}-m_{J(8)} = m_8-m_1$ , so $g_{\mathrm {in}} = 4^{m_1-m_8-1} \geq 4$ . It remains to check $g_{\mathrm {out}}$ . So suppose that $\{1,8\} \notin J$ . Then $J(1), J(8)$ are disjoint sets of size three, and $3m_8 \leq m_{J(1)},m_{J(8)} \leq 3m_1$ . Thus, there is an integer $0 \leq j \leq 6(m_1-m_8)$ such that $ m_{J(1)}-m_{J(8)} = 3(m_1-m_8) - j $ . So

$$ \begin{align*}g_{\mathrm{out}} = \left(\frac{81}{64}\right)^{m_1-m_8} \cdot \left(\frac{4}{3}\right)^j \cdot \frac{1}{3}. \end{align*} $$

If $m_1-m_8 \geq 5$ , then $g_{\mathrm {out}} \geq 1.08$ , as required. If $m_1-m_8=4$ and $j \geq 1$ , then $g_{\mathrm {out}} \geq 1.14$ . If $m_1-m_8=3$ and $j\geq 2$ , then $g_{\mathrm {out}} \geq 1.2$ , and if $m_1-m_8=2$ and $j\geq 3$ , then $g_{\mathrm {out}} \geq 1.2$ . There are only a few remaining possibilities – namely, writing $\boldsymbol {m}=(m_1,\ldots ,m_1)+\boldsymbol {b}$ ,

In all cases, we compare by direct calculation to $\boldsymbol {\overline {m}} := (m_1,\ldots ,m_1)+\boldsymbol {b}'$ , where $\boldsymbol {b}'$ has its sum of entries equal to that of $\boldsymbol {b}$ , and all entries are as equal as possible. Indeed,

$$ \begin{align*}\frac{\mathrm{perf}(\boldsymbol{\overline{m}})}{\mathrm{perf}(\boldsymbol{m})} = \frac{\sum_{A' \cup B' = [8]}\prod_{ij \in \binom{A'}{2}}4^{b_i'b_j'} \prod_{ij \in \binom{B'}{2}}4^{b_i'b_j'} \prod_{i \in A', j \in B'}3^{b_i'b_j'}}{\sum_{A \cup B = [8]}\prod_{ij \in \binom{A}{2}}4^{b_ib_j} \prod_{ij \in \binom{B}{2}}4^{b_ib_j} \prod_{i \in A, j \in B}3^{b_ib_j}} \end{align*} $$

depends only on $\boldsymbol {b},\boldsymbol {b}'$ . We did this calculation in python (dcheck.py). In all cases, the ratio is at least $9$ . As before, this implies that the unique supersolution has all entries as equal as possible.

Finally, we need to check that $(3;6)$ has the strong extension property. So let $9$ be a new vertex and let $\phi '$ be an extension of $\phi $ with the property that

$$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{3}{4}+\frac{1}{2}\log 3, \quad\text{that is,}\quad t_1 \ldots t_8 = 2^{6}3^4, \end{align*} $$

where $t_i := \max \{|\phi '(i9)|,1\}$ . Since each $\phi ^{-1}(c) \cong K_{4,4}$ and $\phi ^{\prime -1}(c)$ is triangle-free, in this graph, $9$ has at most $4$ neighbours, and $\phi ^{\prime -1}(c) \subseteq K_{5,4}$ . Let $G_c$ be the copy of $K_{5,4}$ containing $\phi ^{\prime -1}(c)$ , such that $G_c-\{9\} \cong K_{4,4}$ , so we obtain $G_c$ from $\phi ^{-1}(c)$ by adding $9$ to one of the two vertex classes of $\phi ^{-1}(c)$ . One can easily check all such attachments using a computer, trying each of the $2^6$ choices (we implemented this using python (7ext.py)). This reveals that $\{G_c:c \in [6]\}$ has $\prod _{i \in [8]}|\{c \in [6]: i9 \in G_c\}|= 2^6 3^4$ if and only if $\phi ^{-1}(c) \equiv K_{5,4}$ , and there is some $i \in [8]$ such that $9$ lies in exactly the same vertex class as i in each $\phi ^{-1}(c)$ ; that is, $9$ is a strong clone of i (in other words, $9$ corresponds to a copy of an existing row in the $\pm 1$ -matrix representing the optimal solution). Thus, $\phi ^{\prime -1}(c) = G_c$ . We have proved that $(3;6)$ has the strong extension property.

Therefore, we can apply Theorem 1.6 with Theorem 3.2 to see that $T_8(n)$ is the unique extremal graph for sufficiently large n. Moreover, letting $0 \leq j \leq 7$ be such that $n=8N+j$ for $N \in \mathbb {N}$ , we see that the unique supersolution $\boldsymbol {m}$ has j terms equal to $N+1$ and $8-j$ equal to N, and $\mathrm {perf}(\boldsymbol {m})$ equals $C_j' \cdot 4^{12N} \cdot 3^{16N}$ , where $C_j'$ is a constant depending only on j, which can be determined by calculating , by counting certain distinct Hadamard matrices (see the end of the proof of Theorem 1.11). This gives the claimed value of $F(n;(3;6))$ .

Proof of Theorem 1.11

Let $\boldsymbol {k}:=(3;7)$ . By Theorem 3.1, every element of is of the form $(8,\phi ,\boldsymbol {u})$ , where $\boldsymbol {u}$ is uniform and $|\phi (ij)|=4$ for all $ij \in \binom {[8]}{2}$ .

We need to show that $\boldsymbol {k}$ has the strong extension property. So let $9$ be a new vertex and let $\phi '$ be an extension of $\phi $ with the property that

$$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{7}{4} \quad\text{i.e.}\quad t_1 \ldots t_8 = 2^{14}, \end{align*} $$

where $t_i := \max \{|\phi '(i9)|,1\}$ . So every $t_i$ equals $1$ , $2$ , or $4$ , and, in fact, the multiset of values is either $\{4,4,4,4,4,4,4,1\}$ or $\{4,4,4,4,4,4,2,2\}$ . Since each $\phi ^{-1}(c) \cong K_{4,4}$ and $\phi ^{\prime -1}(c)$ is triangle-free, in this graph, $9$ has at most $4$ neighbours, and $\phi ^{\prime -1}(c) \subseteq K_{5,4}$ . Let $G_c$ be the copy of $K_{5,4}$ containing $\phi ^{\prime -1}(c)$ , such that $G_c-\{9\} \cong K_{4,4}$ , so we obtain $G_c$ from $\phi ^{-1}(c)$ by adding $9$ to one of the two vertex classes of $\phi ^{-1}(c)$ . One can easily check all such attachments using a computer, trying each of the $2^7$ choices (we implemented this using python (7ext.py)). This reveals that $\{G_c:c \in [7]\}$ has $\prod _{i \in [8]}|\{c \in [7]: i9 \in G_c\}|= 2^{14}$ if and only if $\phi ^{-1}(c) \equiv K_{5,4}$ and there is some $i \in [8]$ such that $9$ lies in exactly the same vertex class as i in each $\phi ^{-1}(c)$ ; that is, $9$ is a strong clone of i (in other words, $9$ corresponds to a copy of an existing row in the Hadamard matrix representing the optimal solution). Thus, $\boldsymbol {k}$ has the strong extension property.

Since $|\phi |$ only takes the value $4$ , the same argument as at the beginning of the proof of Proposition 1.10 implies that the perfect colouring problem is soluble (with constant $c:= 4$ ) and for all integers n, the unique supersolution $\boldsymbol {m}_n=(m_{n,1},\ldots ,m_{n,8})$ of the perfect colouring problem has $|m_{n,i}-m_{n,j}| \leq 1$ for all $ij$ . Corollary 1.9 implies that the unique extremal graph is $K_{\boldsymbol {m}_n}(n) \cong T_8(n)$ . Let C be the number of Hadamard matrices with first column and last row consisting of $1$ -s. Then $F(n;\boldsymbol {k}) = (C+o(1))\cdot 4^{t_8(n)}$ . Note that one can calculate C if desired. Indeed, two Hadamard matrices are equivalent if one can be obtained from the other by a sequence of permutations and/or negations of rows and/or columns. It is known that, up to equivalence, there is one Hadamard matrix H of order $8$ . So C is the number of distinct matrices that can be obtained from H by permuting the first $7$ rows and the last $7$ columns and making the first column and the last row consist of all $1$ -s.

5. The $(k+1,k)$ -extremal graphs

In this section, we consider the simplest case when $\boldsymbol {k}$ has the weak extension property – namely, $\boldsymbol {k} = (k+1,k)$ for $k \geq 3$ . For small k, we determine the $(k+1,k)$ -extremal graph, which turns out to have a part of size $O(k)$ , and the size of this part depends on the value of n modulo $k-1$ . The proof relies heavily on Theorem 2.12, the full strength of which we have not yet required.

Definition 5.1. For all integers $k \geq 3$ and $n \geq 4$ ,

• ○ for $q \geq 2$ , let $\mathcal {J}_q(n)$ be the family of complete k-partite graphs with parts of size $m_1 \geq \ldots \geq m_{k-1} \geq \ell $ where $m_1-m_{k-1} \leq q$ , $2 \leq \ell \leq q$ and $m_1+\ldots +m_{k-1}+\ell =n$ ;

• ○ let $\mathcal {J}_q^*(n)$ be the set of graphs in $\mathcal {J}_q(n)$ which are $(k+1,k)$ -extremal;

• ○ for $\ell \geq 1$ , let $J^\ell (n)$ denote the complete k-partite graph with parts of size $m_1 \geq \ldots \geq m_{k-1} \geq \ell $ where $m_1-m_{k-1} \leq 1$ and $m_1+\ldots + m_{k-1}+\ell =n$ .

In this section, we prove the following theorem, which includes Theorem 1.13.

Theorem 5.2. For all integers $k \geq 3$ , there exists $n_0>0$ such that for all $n>n_0$ , every n-vertex $(k+1,k)$ -extremal graph is in $\mathcal {J}_{2(k-1)}(n)$ . Moreover, $F(n;k+1,k) = O_k(1) \cdot 2^{t_{k-1}(n)}$ , where the factor $O_k(1)$ is at least $2$ .

Recall from (1.3) that $F(k+1,k)=Q(k+1,k)$ . It is easy to solve Problem $Q^*$ for $s=2$ colours (see [10, Lemma 1.8]): the unique solution is $(k-1,\phi ,\boldsymbol {u})$ where $\boldsymbol {u}$ is uniform and $\phi (ij)=[2]$ for all $ij$ . Thus, when k is fixed and $n \to \infty $ ,

$$ \begin{align*}Q(k+1,k) = \textstyle{\frac{k-2}{k-1}}\quad\text{and}\quad \log F(n;k+1,k) = \left(\textstyle{\frac{k-2}{k-1}}+o(1)\right)\binom{n}{2}. \end{align*} $$

So, while (1.3) determines $ \log F(n;k+1,k)/\binom {n}{2}$ asymptotically, Theorem 5.2 determines $F(n;k+1,k)$ up to a multiplicative constant.

The next proposition is numerical.

Proposition 5.3. Let $k \geq 3$ and $0 \leq j \leq k-2$ be integers. Given $m_1 \geq \ldots \geq m_{k-1} \geq \ell $ , let $\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$ and

$$ \begin{align*} h(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( 2^{-m_1}+ \ldots +2^{-m_{k-1}}\right)^{\ell},\\ h^*(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( \sum_{i \in [k-1]}2^{-m_i} - \sum_{ii' \in \binom{[k-1]}{2}}2^{-m_i-m_{i'}}\right)^{\ell}. \end{align*} $$

Let

$$ \begin{align*}f(k,j,\ell) := \frac{h(\boldsymbol{m}^*;\ell)}{2^{t_{k-1}(n)}}\quad\text{and}\quad f(k,j) := \max_{0 \leq \ell \leq k-1}f(k,j,\ell), \end{align*} $$

where $m^*_1 \geq \ldots \geq m^*_{k-1} \geq \ell $ , $m^*_1 - m^*_{k-1} \leq 1$ and $m^*_1+\ldots + m^*_{k-1}+\ell =n$ (so $m^*_1,\ldots ,m^*_{k-1},\ell $ are the part sizes of $J^\ell (n)$ ). Let $\boldsymbol {m}^*:=(m^*_1,\ldots ,m^*_{k-1})$ .

1. (i) Let $n \equiv j\ (\mod k-1)$ with $0 \leq j < k-1$ and $n \geq k^3$ . Consider the following way of colouring $J \in \mathcal {J}_{n}(n)$ with parts of size $m_1 \geq \ldots \geq m_{k-1} \geq \ell $ : for each x in the $\ell $ -part, pick $i_x \in [k-1]$ and colour every edge between x and the $m_{i_x}$ -part with colour $1$ . All other edges are coloured arbitrarily. The number of colourings is between $h^*(\boldsymbol {m};\ell )$ and $h(\boldsymbol {m};\ell )$ .

2. (ii) If $0 \leq \ell \leq k-1$ , then

   $$ \begin{align*}f(k,j,\ell) = \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1. \end{cases} \end{align*} $$

3. (iii) Let $n \equiv j \ (\mod k-1)$ with $n \geq k^3$ . For $3 \leq k \leq 10$ , the maximum of $h(\boldsymbol {m};\ell )$ over all (part sizes of) $J \in \mathcal {J}_{2(k-1)}(n)$ is attained by $J^{\ell (k,j)}(n)$ , where $\ell (k,j)$ is the $(k,j)$ -th entry in the table below, and the value is separated from the value for any other $J \in \mathcal {J}_{2(k-1)}(n)$ by a factor $1+\Omega (1)$ .

   

4. (iv) For all $0 \leq j \leq k-2$ , we have $f(k,j) \geq \max \{(k+1)^2/8,2\}$ .

Proof sketch

For (i), the assertion about h is clear. Further, h overcounts those colourings with all colour- $1$ edges to at least two other parts. By a Bonferroni-type inequality, $h^*$ is a lower bound.

Let us turn to the remaining claims. Take any admissible $(\boldsymbol {m};\ell )$ . Define the integer b by $n =b(k-1)+j$ and $0 \leq j < k-1$ . Define $b_i := m_i-b$ . Then $b_1 - b_{k-1} \leq 2(k-1)$ . Moreover, $b_1+\ldots + b_{k-1} + \ell = \sum _i m_i - (k-1)b + \ell = n - (k-1)b = j$ . Then

(5.1) $$ \begin{align} h(\boldsymbol{m};\ell) = 2^{\binom{k-1}{2}b^2+(k-2)bj} \cdot 2^{\ell\sum_{i}b_i} \left( 2^{-b_1}+\ldots + 2^{-b_{k-1}}\right)^\ell \prod_{ii'} 2^{b_ib_{i'}}. \end{align} $$

First, we prove (iii). For this, one needs to compare the values of

(5.2) $$ \begin{align} \tilde{h}(\boldsymbol{b};\ell) := 2^{\ell\sum_{i}b_i}(2^{-b_1}+\ldots+2^{-b_{k-1}})^\ell \prod_{ii'}2^{b_ib_{i'}} \end{align} $$

among all tuples $\boldsymbol {b} := (b_1,\ldots ,b_{k-1})$ and $\ell $ with sum j and $|b_i-b_{i'}|,\ell \leq 2(k-1)$ . We implemented this in python (smallpart.py), and the optimal value of $\ell $ (which is indeed unique) for $3 \leq k \leq 10$ was recorded in the table. In all cases, we also had $b_1-b_{k-1} \leq 1$ , so the optimal $m_1,\ldots ,m_{k-1}$ are as equal as possible. Thus, the maximum is attained by some $J^\ell (n)$ . For future reference, we note that we could have defined $b_i$ by subtracting any $b' \leq b$ from $m_i$ , and then to compare values of $h(\boldsymbol {b};\ell )$ , one must compare values of $\tilde {h}(\boldsymbol {b};\ell )$ over tuples $\boldsymbol {b}$ with sum $j+(k-1)(b-b')$ .

Note that

$$ \begin{align*}t_{k-1}(n) =t_{k-1}((k-1)b+j) =\binom{k-1}{2}b^2+(k-2)bj+\binom{j}{2}. \end{align*} $$

For $0 \leq \ell \leq j$ , (5.1) implies that the function $f(k,j,\ell )$ equals $2^{-\binom {j}{2}}\cdot \tilde {h}((1,\ldots ,1,0,\dots ,0);\ell )$ where there are $j-\ell $ entries of value $1$ . For $j < \ell \leq k-1$ , it equals $2^{-\binom {j}{2}}\cdot \tilde {h}((0,\ldots ,0,-1,\ldots ,-1);\ell )$ where there are $\ell -j$ entries of value $-1$ . This proves (ii).

For (iv), we bound $f(k,j,2)$ from below. For $j \geq 2$ , we have

$$ \begin{align*}f(k,j,2) = \frac{1}{2}\cdot (k-j/2)^2 \geq \frac{1}{2} \cdot (k-(k-2)/2)^2 = \frac{(k+2)^2}{8}. \end{align*} $$

We have $f(k,0,2) = (k+1)^2/8$ and $f(k,1,2) = k^2/4$ . For $k \geq 11$ (i.e., not in the table), the smallest of these is $(k+1)^2/8 \geq 18$ .

The next lemma states that whenever every vertex and pair of vertices in a near-extremal complete partite graph, G has almost optimal contribution to $F(G;\boldsymbol {k})$ , then G is only optimal if it lies in $\mathcal {J}_{2(k-1)}(n)$ .

Lemma 5.4. There exist ${\varepsilon }> 0$ and $n_0 \in \mathbb {N}$ such that the following holds. Let G be a graph on $n \geq n_0$ vertices which is complete multipartite, and such that $\log F(G;k+1,k) \geq \left (\frac {k-2}{k-1}-{\varepsilon }\right )\binom {n}{2}$ and

(5.3) $$ \begin{align} &\log F(G;k+1,k) - \log F(G-x;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})n\quad\forall \ x \in V(G),\\ \nonumber &\log F(G;k+1,k) - \log F(G-y-z;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})(n+n-1)\\ \nonumber &\hspace{6cm}\forall\text{ distinct }y,z \in V(G). \end{align} $$

If $G \not \in \mathcal {J}_{2(k-1)}(n)$ , then there is a graph $G'$ of order n with $F(G';k+1,k)> F(G;k+1,k)$ .

Proof. As it is easy to show (or see [10, Lemma 1.8]), $(k+1,k)$ has the extension property. Let $0 < \delta ' \ll \delta $ . Let $n_0,{\varepsilon }>0$ be the parameters returned by Theorem 2.12 applied with parameter $\delta '$ . We may assume that $0 < 1/n_0 \ll {\varepsilon } \ll \delta '$ . Let G be a graph on $n \geq n_0$ vertices as in the lemma. Let $X_1,\ldots ,X_t$ be the partition of $V(G)$ , where $|X_1| \geq \ldots \geq |X_t|$ . By Theorem 2.12, there is a set $\mathcal {P}$ of at least $(1-2^{-{\varepsilon } n})F(G;k+1,k)$ valid colourings of G such that, for each $\chi \in \mathcal {P}$ , the following hold.

1. (i) There is a coarsening $Z_0,Z_1,\ldots ,Z_{k-1}$ of $X_1,\ldots ,X_t$ such that $\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| < \delta 'n$ .

2. (ii) Each of $Z_1,\ldots ,Z_{k-2}$ is a part of G, and $Z_{k-1}$ contains at most two parts of G.

3. (iii) For all $x \in V(G)$ , there is $i(x) \in [k-1]$ , so that we have $\chi (xy) = 1$ for all $y \in N_G(x) \cap Z_{i(x)}$ , and for all $j \in [k-1]\setminus \{i(x)\}$ , it holds that

   (5.4) $$ \begin{align} |\chi^{-1}(c)[x,X]|=\textstyle{\frac{1}{2}}|X|\pm\delta'|Z_j|\quad\text{for all }c \in [2] \text{ and parts }X \subseteq Z_j. \end{align} $$
   Moreover, for all $j \in [k-1]$ and distinct $y,z \in V(G)$ with $i(y)=i(z) \neq j$ , it holds that
   (5.5) $$ \begin{align} |N_{\chi^{-1}(c)}(y,X) \cap N_{\chi^{-1}(c')}(z,X)| = \textstyle{\frac{1}{4}}|X| \pm \delta'|Z_j|\quad\text{for all }c,c' \in [2]\text{ and parts }X \subseteq Z_j. \end{align} $$
   Also, if $x \in Z_i$ for $i \in [k-1]$ , then $i(x) = i$ .

Fix $\chi ^* \in \mathcal {P}$ and choose $Z_0,\ldots ,Z_{k-1}$ and $i : V(G) \mapsto [k-1]$ as above. (Recall that these may be different for different colourings.) If there is a part in $Z_{k-1}$ of size at most $\delta n$ , move it into $Z_0$ . Then (i) holds with parameter $2\delta $ , (iii) holds with parameter $\delta '$ , every part in $Z_{k-1}$ has size at least $\delta n$ , and all but one part in $Z_0$ has size at most $\delta 'n$ . Let $p^* \leq 2$ be the number of parts in $Z_{k-1}$ and $q^*$ the number of parts in $Z_{0}$ (which both depend on $\chi ^*$ ).

Claim 5.4.1. Suppose that $Z_0 \neq \emptyset $ . Then $Z_{k-1}$ contains exactly one part. Moreover, if $x,x' \in Z_0$ lie in different parts of G, then for all $\chi \in \mathcal {P}$ , we have $\chi (xx') = 2$ and $i(x) \neq i(x')$ . In particular, $Z_0$ contains at most $k-1$ parts.

Proof of Claim

Let $\{ B_{p'} : p' \in [p^*] \}$ be the part(s) of G contained in $Z_{k-1}$ . Suppose first that $p^*=2$ and $q^* \geq 1$ . Let $x \in Z_0$ and $\chi \in \mathcal {P}$ be arbitrary. Then $\chi (xv)=1$ for all $v \in Z_{i(x)}$ , and for each $i \in [k-1]\setminus \{i(x)\}$ , the vertex and pair locally good conditions (5.4) and (5.5) hold. Without loss of generality, assume $|B_1| \geq |B_2|$ . Thus, for example, $|B_1| \geq n/(2k)$ and $|B_2| \geq \delta n$ . By (5.4), there is $y \in B_2$ such that $\chi (xy)=1$ (when $i(x) \neq k-1$ , since if $i(x)=k-1$ , this is obvious). Since $i(y)=k-1$ , we also have $\chi (yz)=1$ for every $z \in B_1$ . Let $J := \chi ^{-1}(1)$ . For $i \in [k-2]$ , let $A_i := N_J(x,Z_i) \cap N_J(y,Z_i)$ and let $A_{k-1} := N_J(x,B_1) \cap N_J(y,B_1)$ . Then (5.5) implies that $|A_i| \geq (\frac {1}{4}-\delta ')|Z_i| \geq |Z_i|/5 \geq n/(5k)$ for all $i \in [k-2]$ . Also, by (5.4), $|A_{k-1}| = |N_J(x,B_1)| \geq (\frac {1}{2}-\delta ')|B_1| \geq |Z_{k-1}|/5 \geq n/(5k)$ . Lemma 2.6 implies that $J[A_i,A_j]$ is $(\sqrt {\delta '},\frac {1}{2})$ -regular for all distinct $i,j \in [k-1]$ . By Lemma 2.4, J contains a $K_{k-1}$ with one vertex in each of $A_1,\ldots ,A_{k-1}$ . Together with $x,y$ , this gives rise to a $1$ -coloured copy of $K_{k+1}$ in G, a contradiction. So if $p^*=2$ , then $q^* = 0$ .

Suppose now that $p^*=1$ and let $x,x' \in Z_0$ lie in different parts of G. Similar arguments to those above show that $x,x'$ form the $2$ -element set in a copy of the k-partite graph $K_{1,\ldots ,1,2}$ in $\chi ^{-1}(1)$ . Therefore, (since the edge between them must have some colour) $\chi (xx') = 2$ , as required. Suppose now, for a contradiction, that $i(x) = i(x')$ . Without loss of generality, suppose their common value is $1$ . Then $U_i := N_{\chi ^{-1}(2)}(x,Z_i) \cap N_{\chi ^{-1}(2)}(x',Z_i)$ satisfies $|U_i| = (\textstyle {\frac {1}{4}} \pm \sqrt {\delta '})|Z_i|$ for all $2 \leq i \leq k-1$ . By Proposition 2.7, $\chi ^{-1}(2)[U_i,U_{i'}]$ is $((\delta ')^{1/3},\frac {1}{2})$ -regular for all distinct $2 \leq i,i' \leq k-1$ . By Lemma 2.4, there are $z_i \in U_i$ for $2 \leq i \leq k-1$ such that $x,x',z_2,\ldots ,z_{k-1}$ form a copy of $K_{k}$ in $\chi ^{-1}(2)$ , a contradiction. Thus, $i(x) \neq i(x')$ . This completes the proof of the claim.

The total number of parts is $t = k-2+p^*+q^*$ . Suppose that $t=k-1$ . Then G is $K_k$ -free. Thus, every $2$ -edge colouring is $(k,k+1)$ -valid and so $|\mathcal {P}| \leq 2^{t_{k-1}(n)}$ , and hence, $F(G;\boldsymbol {k}) \leq (1-2^{-{\varepsilon } n})^{-1}\cdot 2^{t_{k-1}(n)}$ .

Suppose $t \geq k$ and every part of G has size at least $\delta n$ . Then every $\chi \in \mathcal {P}$ has the same associated coarsening $Z_1=X_1,\ldots ,Z_{k-2}=X_{k-2},Z_{k-1}=X_{k-1} \cup X_k$ in order to satisfy $\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| \leq \delta ' n$ . The number of perfect colourings is the same as if $X_{k-1},X_k$ were merged into a single part since edges between these parts are coloured with $1$ , so

$$ \begin{align*}|\mathcal{P}| \leq 2^{t_{k-1}(n)},\quad\text{so again}\quad F(G;\boldsymbol{k}) \leq (1+o(1)) \cdot 2^{t_{k-1}(n)}. \end{align*} $$

We will see later, due to Proposition 5.3, that there is $G'$ with $|\mathcal {P}(G')| \geq 1.9|\mathcal {P}(G)|$ .

So from now on, we will assume that $t \geq k$ and there are $q \geq 1$ parts of size less than $\delta n$ . Claim 5.4.1 implies that these parts lie in $Z_0$ so $p^*=1$ and $q^*=q=t-(k-1)$ . Thus, we have $|X_i| < \delta n$ for all $i \geq k$ , so also $|X_1| \geq \ldots \geq |X_{k-1}| \geq \frac {n}{k-1}-(k-1)\delta n$ . We will say that $X_1,\ldots ,X_{k-1}$ are the large parts, of sizes $m_1,\ldots ,m_{k-1}$ , respectively, and $L_1,\ldots ,L_q$ are the small parts, of sizes $\ell _1,\ldots ,\ell _q$ , respectively. Also, let $m := m_1+\ldots + m_{k-1}$ and $\ell := \ell _1 + \ldots + \ell _q$ , and $\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$ and $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _q)$ . For some colourings $\chi $ , one of the $L_i$ may be a part of $Z_{k-1}$ , while in others, all $L_i$ will be parts of $Z_0$ . Suppose there are $\chi $ and i such that $Z_{k-1}=X_{k-1} \cup L_i$ . Then Claim 5.4.1 implies that $q=0$ , so then $t=k$ . So for all $\chi $ , either $(Z_{k-1},Z_0)=(X_{k-1} \cup L_i,\emptyset )$ or $(Z_{k-1},Z_0)=(X_{k-1},L_i)$ . We may assume that we always have the second partition, as the number of perfect colourings is a function of $(Z_1,\ldots ,Z_{k-1},Z_0)$ and there are more choices with the second. Thus, we may assume that each perfect colouring $\chi $ gives rise to the same partition $(Z_1,\ldots ,Z_{k-1},Z_0)=(X_1,\ldots ,X_{k-1},L_1 \cup \ldots \cup L_q)$ , where $q \leq k-1$ .

Let $P_q(k-1)$ be the set of ordered partitions of $[k-1]$ into q parts (some of which may be empty) with the following property. Suppose that exactly a different values appear in $\boldsymbol {\ell }$ , so $\ell _1 = \ldots = \ell _{i_1}> \ell _{i_1+1} = \ldots = \ell _{i_2} > \ldots > \ell _{i_{a-1}+1} = \ldots = \ell _q$ for some $a \in [q]$ . For each unordered partition $\{I_1,\ldots ,I_q\}$ , labelled so that $\min \{I_1\}<\ldots < \min \{I_q\}$ , and any permutation $\sigma : [q]\to [q]$ that has $\sigma (i_{s-1}+1)< \ldots < \sigma (i_{s})$ for all $1 \leq s \leq a+1$ (where $i_0:=0$ and $i_{a+1}:=q$ ), we put $(I_{\sigma (1)},\ldots ,I_{\sigma (q)})$ into $P_q(k-1)$ . So if $\ell _1>\ldots >\ell _q$ , then $P_q(k-1)$ consists of all ordered partitions of $[k-1]$ into q parts, while if $\ell _1=\ldots =\ell _q$ , then for each unordered partition, it contains exactly one ordering.

Every colouring in $\mathcal {P}(G)$ is obtained as follows: First, colour edges between pairs in $Z_1,\ldots ,Z_{k-1}$ arbitrarily and colour edges between the $L_i$ with colour $2$ . By Claim 5.4.1, $i(x) \neq i(x')$ for $x,x'$ in different small parts, so choose $(I_1,\ldots ,I_q) \in P_q(k-1)$ so that $i(x) \in I_j$ for all x in $L_j$ . Now for each $j\in [q]$ and x in $L_j$ , colour all edges between x and $Z_{i(x)}$ with colour $1$ and all edges between x and the remaining $Z_i$ arbitrarily. The number of choices in this colouring procedure is at most

$$ \begin{align*} f(\boldsymbol{m};\boldsymbol{\ell}) := &\prod_{ij\in\binom{[k-1]}{2}}2^{m_im_j}\cdot 2^{m\ell}\cdot g(\boldsymbol{m};\boldsymbol{\ell}), \quad\text{where}\quad g(\boldsymbol{m};\boldsymbol{\ell}) := \sum_{\substack{(I_1,\ldots,I_q)\\\in P_q(k-1)}}\prod_{j \in [q]}\left(\sum_{i' \in I_j}2^{-m_{i'}}\right)^{\ell_j}.\\ \end{align*} $$

We have $|\mathcal {P}(G)| \leq f(\boldsymbol {m};\boldsymbol {\ell })$ and would like an almost matching lower bound. Every colouring from the procedure above is valid so we need to check which colourings have been counted more than once. Suppose $\chi $ is a perfect colouring arising from two different choices. Let $(I_1,\ldots ,I_q)$ and $(I_1',\ldots ,I_q')$ be the respective choices of partitions, which are necessarily different. So there are $i \in [q]$ and $s \in [k-1]$ such that $s \in I_i'\setminus I_i$ . But then in $\chi $ every edge between $L_i$ and $\bigcup _{i'\in I_i \cup \{s\}}Z_{i'}$ is coloured with colour $1$ . In other words, the number of choices for colours of edges between $L_i$ and $Z_1\cup \ldots \cup Z_{k-1}$ has decreased by a multiplicative factor of $2^{m_s\ell _i}$ . The number of such colourings is therefore at most

$$ \begin{align*} f(\boldsymbol{m};\boldsymbol{\ell}) \cdot q \cdot (k-1) \cdot 2^{-m_{k-1}\ell_q} \leq 2^{-n/k}\cdot f(\boldsymbol{m};\boldsymbol{\ell}). \end{align*} $$

Thus,

(5.6) $$ \begin{align} (1-2^{-n/k})f(\boldsymbol{m};\boldsymbol{\ell}) \leq |\mathcal{P}(G)| \leq f(\boldsymbol{m};\boldsymbol{\ell}). \end{align} $$

Now we can state that we are done in the case $t=k-1$ and the case $t=k$ , and every part has size at least $\delta n$ . Indeed, the previous inequality, the fact that $ f(\boldsymbol {m};(\ell )) = h(\boldsymbol {m};\ell ) $ and Proposition 5.3 imply that

(5.7) $$ \begin{align} F(n;k+1,k) \geq (2+o(1))\cdot 2^{t_{k-1}(n)}. \end{align} $$

Moreover, for $3 \leq k \leq 10$ , among graphs in $\mathcal {J}_{2(k-1)}(n)$ , the unique graph with the largest number of valid colourings is $J^{\ell (k,j)}(n)$ , where $\ell (k,j)$ is in the table in Proposition 5.3(iii).

We return to the only remaining case when $t \geq k$ and there is at least one part of size less than $\delta n$ . Write $f(\boldsymbol {m};\ell )$ and $g(\boldsymbol {m};\ell )$ for $f(\boldsymbol {m};(\ell ))$ , $g(\boldsymbol {m};(\ell ))$ , respectively. In the next series of claims, we will compare $|\mathcal {P}(G)| = (1+o(1)) f(\boldsymbol {m};\boldsymbol {\ell })$ with $|\mathcal {P}(G')| = (1+o(1)) f(\boldsymbol {m}';\boldsymbol {\ell }')$ , where $G'$ is another complete partite graph with slightly different part sizes $\boldsymbol {m}',\boldsymbol {\ell }'$ , in order to gradually pin down what $\boldsymbol {m}$ and $\boldsymbol {\ell }$ must be. The first of these claims states that merging small parts does not decrease the number of perfect colourings. (This is not yet sufficient for us to conclude that extremal graphs always have a single small part, as for this, the number of perfect colourings would need to increase by a factor $1+\Omega (1)$ .)

Claim 5.4.2. If $q \geq 2$ , then $g(\boldsymbol {m};\ell ) \geq g(\boldsymbol {m};\ell _1,\ldots ,\ell _q) + 2^{-m_{k-1}\ell }$ , so $f(\boldsymbol {m};\ell )\geq f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$ .

Proof of Claim

If we obtain $G'$ from G by merging $L_1,\ldots ,L_q$ to obtain a single part L, then the number of perfect colourings increases. Indeed, let $x \in L_1$ and $y \in L_2$ , say. In G, the number of valid choices of $(i(x),i(y))$ is strictly less than the number in $G'$ , since $i(x) \neq i(y)$ in G, while there is no such restriction in $G'$ . More precisely, the $(I_1,\ldots ,I_q)$ term in g corresponds to all the colourings that come from choosing $i(x) \in I_i$ for all $i \in [q]$ and $x \in L_i$ . In $G'$ , we can choose $i(x)=k-1$ for all $x \in L$ , giving the new term $2^{-m_{k-1}\ell }$ .

In the next three claims, we assume that G has one small part of size $\ell $ . Write $m_1\geq \ldots \geq m_{k-1}$ for its other parts and let $a_i := m_i-m_{k-1}$ for all $i \in [k-1]$ . By (5.6), as in the proof of Proposition 5.3, to compare the number of perfect colourings of G with another complete partite graph $G'$ with a single small part of size $\ell '$ and large parts of size $m_1',\ldots ,m_{k-1}'$ , it suffices to compare their associated functions $\tilde {h}(\boldsymbol {a};\ell ),\tilde {h}(\boldsymbol {a}',\ell ')$ defined in (5.2), where $\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$ , and $\boldsymbol {a}'=(a_1',\ldots ,a_{k-1}')$ is chosen so that $\sum _i a_i +\ell = \sum _i a_i' + \ell '$ . (Note that in Proposition 5.3, we defined $b_i := m_i-\lfloor \frac {n}{k-1}\rfloor $ , whereas here it is convenient to define $a_i = m_i-m_{k-1}$ so that $a_1 \geq \ldots \geq a_{k-1}=0$ .) The next claim concludes the proof in the case when $\ell $ is large and not every $a_1,\ldots ,a_{k-2}$ is comparable with $\ell $ .

Claim 5.4.3. Suppose $q=1$ . If $a_{k-2} \leq (\ell -1)/2$ and $\ell \geq \min \{13,2k-2\}$ , then there exists an n-vertex graph $G'$ with $|\mathcal {P}(G')|> 1.01|\mathcal {P}(G)|$ .

Proof of Claim

Subtract $1$ from $\ell $ and add $1$ to $a_{k-2}$ , letting $\boldsymbol {a}^{(1)} := (a_1,\ldots ,a_{k-2}+1,a_{k-1})$ . We let $G'$ be the complete partite graph with large parts of size $(m_{k-1},\ldots ,m_{k-1})+\boldsymbol {a}^{(1)}$ and one small part of size $\ell -1$ . Then

(5.8) $$ \begin{align} (1+o(1))\frac{|\mathcal{P}(G')|}{|\mathcal{P}(G)|} = \frac{\tilde{h}(\boldsymbol{a}^{(1)};\ell-1)}{\tilde{h}(\boldsymbol{a};\ell)} = \frac{2^{\ell-a_{k-2}-1}(2^{-a_1}+\ldots + \frac{1}{2}\cdot2^{-a_{k-2}} + 1)^{\ell-1}}{(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}}. \end{align} $$

Now, for $y>0$ and $0 < x \leq 1$ , let

$$ \begin{align*}f(x,y) := \frac{(y+\frac{x}{2}+1)^{\ell-1}}{(y+x+1)^\ell},\quad\text{then}\quad \frac{\partial f}{\partial x} = -\frac{2(y+\frac{x}{2}+1)^{\ell}((\ell+1)(y+1)+x)}{(y+x+1)^{\ell+1}(2(y+1)+x)^2}, \end{align*} $$

so f is decreasing in x, and hence, $f(x,y) \geq f(1,y) = (y+\frac {3}{2})^{\ell -1}/(y+2)^\ell $ . Also,

$$ \begin{align*}\frac{\partial f(1,y)}{\partial y}= -\frac{(y-\frac{\ell}{2}+2)(y+\frac{3}{2})^{\ell-2}}{(y+2)^{\ell+1}} \end{align*} $$

so $f(1,y)$ is increasing from $y=0$ to $y=\frac {\ell }{2}-2 \geq k-3$ . Thus, for $0 \leq y \leq k-3$ , we have $f(1,y) \geq f(1,0) = (\frac {3}{2})^{\ell -1}/2^\ell = \frac {1}{2}\left (\frac {3}{4}\right )^{\ell -1}$ . Since $2^{-a_1}+\ldots +2^{-a_{k-3}} \leq k-3$ , and $\ell \geq 13$ , we see that (5.8) is at least

$$ \begin{align*}2^{\ell-a_{k-2}-1} \cdot \frac{1}{2}\left(\frac{3}{4}\right)^{\ell-1} \geq \frac{1}{2}\left(\frac{\sqrt{2}\cdot 3}{4}\right)^{\ell-1}> 1.013, \end{align*} $$

completing the proof of the claim.

Claim 5.4.4. Suppose $q=1$ . If $a_{k-2} \geq \ell /2$ and $\ell \geq \max \{14,2k-2\}$ , then there exists an n-vertex graph $G'$ with $|\mathcal {P}(G')|> 1.05|\mathcal {P}(G)|$ .

Proof of Claim

Let $A := \{a_1,\ldots ,a_{k-2},\ell \}$ and $b := \sum _{u \in A}u$ . Then, recalling $a_{k-1}=0$ ,

$$ \begin{align*} \tilde{h}(\boldsymbol{a};\ell) \stackrel{({5.2})}{=} \prod_{uu' \in \binom{A}{2}}2^{uu'}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq 2^{t_{k-1}(b)}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}. \end{align*} $$

Note that

$$ \begin{align*}t_{k-1}(n) = t_{k-1}((k-1)m_{k-1}+b)=\binom{k-1}{2}m_{k-1}^2+(k-2)m_{k-1}b+t_{k-1}(b). \end{align*} $$

Thus, $(1+o(1))|\mathcal {P}(G)| = h(\boldsymbol {m};\ell ) \leq 2^{t_{k-1}(n)}\cdot (2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell }$ . But

$$ \begin{align*}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq ((k-2)2^{-a_{k-2}}+1)^{\ell} \leq \left(\left(\frac{\ell}{2}-1\right)\cdot2^{-\ell/2}+1\right)^\ell. \end{align*} $$

This is less than $1.9$ for $\ell \geq 14$ . Equation (5.7) implies the existence of $G'$ with $|\mathcal {P}(G')| = (2+o(1))\cdot 2^{t_{k-1}(n)}$ , and further, $2/1.9> 1.052$ .

The next claim implies that $a_1$ , and hence, all of $a_1,\ldots ,a_{k-1}$ cannot be much bigger than $\ell $ .

Claim 5.4.5. Suppose $q=1$ . If $a_1 \geq \ell +2$ , then there is an n-vertex graph $G'$ with $|\mathcal {P}(G')|> 1.9|\mathcal {P}(G)|$ .

Proof of Claim

Suppose that $a_1 \geq \ell +2$ . Let $\boldsymbol {a}^{(2)} := (a_1-1,a_2,\ldots ,a_{k-2},a_{k-1}+1)$ . Then, recalling $a_{k-1}=0$ ,

$$ \begin{align*}\frac{\tilde{h}(\boldsymbol{a}^{(2)};\ell)}{\tilde{h}(\boldsymbol{a};\ell)} = 2^{a_1-1}\left(\frac{2\cdot 2^{-a_1}+2^{-a_2}+\ldots +2^{-a_{k-2}}+\frac{1}{2}\cdot 2^{-a_{k-1}}}{2^{-a_1}+\ldots + 2^{-a_{k-1}}}\right)^\ell \geq 2^{a_1-1-\ell} \geq 2, \end{align*} $$

since we can lower bound the numerator by $\frac {1}{2}\sum _{i \in [k-1]}2^{-a_i}$ .

Claim 5.4.6. There is a positive function p of k such that the following holds. If $a_1,\ldots ,a_{k-1},\ell = O_k(1)$ and $q \geq 2$ , then the graph $G'$ obtained by merging $L_1,\ldots ,L_q$ has $|\mathcal {P}(G')|>(1+p(k))|\mathcal {P}(G)|$ .

Proof of Claim

It suffices to show that there is $a=a(k)$ such that $f(\boldsymbol {m};\ell ) \geq (1+a)f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$ . We have $g(\boldsymbol {m};\boldsymbol {\ell }) = 2^{-m_{k-1}\ell }g(\boldsymbol {a};\boldsymbol {\ell })$ , where $\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$ satisfies $a_i=m_i-m_{k-1}$ , so $0 \leq a_i = O_k(1)$ for all i. Since also $\ell = O_k(1)$ , we have $g(\boldsymbol {a};\boldsymbol {\ell })=p_0(k)$ for some positive function $p_0$ of k. We have $g(\boldsymbol {a};\ell )\geq g(\boldsymbol {a};\boldsymbol {\ell }) + 1$ by Claim 5.4.2, so

$$ \begin{align*}\frac{f(\boldsymbol{m};\ell)}{f(\boldsymbol{m};\ell_1,\ldots,\ell_q)} = \frac{g(\boldsymbol{m};\ell)}{g(\boldsymbol{m};\ell_1,\ldots,\ell_q)} \geq \frac{p_0(k)+1}{p_0(k)}, \end{align*} $$

as required.

Claim 5.4.7. If $q=1$ and $\ell =1$ and $k \geq 4$ , then the graph $G'$ obtained by moving one vertex from $Z_1$ to $L=L_1$ has $|\mathcal {P}(G')|>1.9|\mathcal {P}(G)|$ .

Proof of Claim

Let $\boldsymbol {a}^{(3)}:= (a_1-1,a_2,\ldots ,a_{k-1})$ . Then

$$ \begin{align*} \frac{\tilde{h}(\boldsymbol{a}^{(3)};2)}{\tilde{h}(\boldsymbol{a};1)} &\geq \frac{2^{a_1-2}\left(2\cdot 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}\right)^2}{ 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}} \geq 2^{-1} + 2^{a_1-a_1-2}+\ldots + 2^{a_1-a_{k-1}-2}\\ &\geq \frac{1}{2}+\frac{k-1}{4} \geq \frac{5}{4}, \end{align*} $$

where the second inequality follows by expanding $(2^{-a_1}+\sum _{i \in [k-1]}2^{-a_i})^2$ .

To complete the proof of Lemma 5.4, assume that $G \notin \mathcal {J}_{2(k-1)}(n)$ . We will find an n-vertex graph $G'$ with $F(G';k+1,k)>F(G;k+1,k)$ . Let $m_1,\ldots ,m_{k-1}$ be the large parts and $\ell _1,\ldots ,\ell _q$ be the small parts of G. Let $a_i := m_i-m_{k-1}$ for all $i \in [k-1]$ . Obtain $G_0$ by merging $L_1,\ldots ,L_q$ and let $\ell := \ell _1+\ldots +\ell _q$ .

By Claim 5.4.2, we have that $|\mathcal {P}(G_0)| \geq (1+o(1))|\mathcal {P}(G)|$ . Suppose $\ell \geq \max \{14,2k-2\}$ . Then Claims 5.4.3 and 5.4.4 imply that there is an n-vertex graph $G'$ such that $|\mathcal {P}(G)|<(1+o(1))|\mathcal {P}(G_0)|<(1+o(1))\frac {1}{1.01}\cdot |\mathcal {P}(G')|$ , as required. Thus, we may suppose instead that $\ell < \max \{14,2k-2\}$ .

Suppose further that $a_1 \geq \ell +2$ . Then Claim 5.4.5 implies that there is an n-vertex graph $G'$ such that $|\mathcal {P}(G)| < (1+o(1))|\mathcal {P}(G_0)| < \frac {1}{1.8}\cdot |\mathcal {P}(G')|$ . So we may suppose that $\max \{14,2k-2\} \geq \ell +1 \geq a_1 \geq \ldots \geq a_{k-2} \geq a_{k-1}=0$ .

Suppose $q \geq 2$ . Then Claim 5.4.6 implies that $|\mathcal {P}(G_0)|>(1+p(k))|\mathcal {P}(G)|$ for some positive function p. So we may suppose that $q=1$ . Suppose now $\ell =1$ . Claim 5.4.7 furnishes us with the required $G'$ when $k \geq 4$ .

If $k \geq 8$ , then we have that $14 \leq 2k-2$ and of course $k \geq 4$ , so, in fact, Claim 5.4.7 implies that $q=1$ , $\ell \geq 2$ and $2k-2 \geq \ell ,a_1,\ldots ,a_{k-1}$ , which is a contradiction since $G \notin \mathcal {J}_{2(k-1)}(n)$ . Thus, we have $k \leq 7$ and $14 \geq \ell ,a_1,\ldots ,a_{k-1}$ . Here, one can use the same program as in the proof of Proposition 5.3(iii) with tweaked parameters to obtain that in every case there is $G'$ with large part differences $a_1',\ldots ,a_{k-1}'$ such that $a_1' \leq 1$ and $\ell '$ is as in the table there, such that $\tilde {h}(\boldsymbol {a}';\ell ')> \tilde {h}(\boldsymbol {a};\ell ) + \Omega (1)$ , since $G \neq G'$ .

We derive Theorem 5.2 from Lemma 5.4 using the same approach as [12].

Proof of Theorem 5.2

We want to show that

(5.9) $$ \begin{align} |\mathcal{P}(J)| = O_k(1) \cdot 2^{t_{k-1}(n)}\quad\text{for all } J \in \mathcal{J}_{2(k-1)}(n), \end{align} $$

which implies the same equality holds for $F(J;k+1,k)$ by the arguments in the proof of Lemma 5.4. For this, start with $T_{k-1}(n)$ with vertex partition $Y_1,\ldots ,Y_{k-1},Y_k=\emptyset $ . Consider moves where each time we move one vertex between parts. One can obtain J in $O(k^2)$ moves, between large parts or from a large part to the small part $Y_k$ . Each move changes F by a multiplicative factor of $O_k(1)$ (we already did the calculations in Claims 5.4.5 and 5.4.7). This proves (5.9).

Apply Lemma 5.4 to obtain ${\varepsilon },n_0$ . We may assume that $1/n_0 \ll {\varepsilon } \ll 1$ . Let $N := n_0^2$ . Let G be a $(k+1,k)$ -extremal graph on $n \geq N$ vertices. Suppose, for a contradiction, that $G \not \in \mathcal {J}_{2(k-1)}(n)$ . Let $G_n := G$ . If $G_n$ is not a complete multipartite graph, apply Lemma 2.14 to obtain a graph $H_n$ on n vertices which is $(k+1,k)$ -extremal and complete multipartite, with a part of size $1$ and let $G_n := H_n$ . Observe that in both cases, $G_n \not \in \mathcal {J}_{2(k-1)}(n)$ . We iteratively apply the following procedure. Let $G_m$ be the current graph on $m \geq n_0+2$ vertices with $\log F(G_m;k+1,k) \geq \left ( \frac {k-2}{k-1}-{\varepsilon } \right )\binom {m}{2}$ and apply Lemma 5.4. If (5.3) fails for some $x \in V(G_m)$ , we let $G_{m-1} := G_m-x$ , decrease m by $1$ , and repeat. Similarly, if (5.3) fails for some pair $y,z \in V(G_m)$ , we let $G_{m-2} := G_m-y-z$ , decrease m by $2$ , and repeat. Note that

$$ \begin{align*}\log F(G_{m-1};k+1,k) \geq \log F(G_m;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)m \geq \left(\frac{k-2}{k-1}-2{\varepsilon} \right)\left(\binom{m}{2}-m\right). \end{align*} $$

If (5.3) holds for all $x \in V(G)$ and pairs $y,z \in V(G)$ , but $G_{m} \not \in \mathcal {J}_{2(k-1)}(m)$ , then we replace $G_m$ by the graph $G'$ returned by Lemma 5.4 and repeat the step (without decreasing m). Recall that $G'$ has strictly more valid colourings than $G_m$ . Note that for every m for which $G_m$ is defined, we have

$$ \begin{align*}\log F(G_m;k+1,k) \geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$

It follows that we never reach $m \leq n_0$ for otherwise, when this happens for the first time, we get that

$$ \begin{align*} \log F(G_m;k+1,k) &\geq \left(\frac{k-2}{k-1}-{\varepsilon}\right)\binom{n}{2} - \left(\frac{k-2}{k-1}-2{\varepsilon}\right)\left(\binom{n+1}{2}-\binom{m+1}{2}\right)\\ &\geq {\varepsilon}\binom{n}{2} + \left( \frac{k-2}{k-1}-2{\varepsilon} \right)\binom{m}{2}> \binom{m}{2} \end{align*} $$

(i.e., $F(m;k+1,k)> 2^{\binom {m}{2}}$ ), a contradiction. Thus, we stop for some $m \geq n_0+2$ , with $G_m \in \mathcal {J}_{2(k-1)}(m)$ . We cannot have $m=n$ , for otherwise, any $J_n \in \mathcal {J}_{2(k-1)}(n)$ has more colourings than G by Lemma 5.4. So $m \leq n-1$ . Almost every colouring of $G_m := J_m \in \mathcal {J}_{2(k-1)}(m)$ is perfect. Thus,

$$ \begin{align*} 1+\log |\mathcal{P}(J_m)| &> \log F(J_m;k+1,k)\\ &\geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$

Since $t_{k-1}(\ell )-t_{k-1}(\ell -1)=\lfloor \frac {k-2}{k-1}\ell \rfloor $ , (5.9) implies that there is some constant $C_k>0$ such that $|\mathcal {P}(J_\ell )| \geq C_k \cdot 2^{\frac {k-2}{k-1}\ell -1}|\mathcal {P}(J_{\ell -1})|$ for all $\ell \geq n_0$ and all $J_\ell \in \mathcal {J}_{2(k-1)}(\ell )$ , $J_{\ell -1}\in \mathcal {J}_{2(k-1)}(\ell -1)$ . Thus,

$$ \begin{align*}\log F(G;k+1,k) \geq \log|\mathcal{P}(J_n)| \geq \frac{k-2}{k-1}\left(n+\ldots + (m+1)\right) + (C_k-1)(n-m) + \log|\mathcal{P}(J_m)|. \end{align*} $$

Together with the previous displayed equation, this is a contradiction to $m \leq n-1$ . Thus, ${G \in \mathcal {J}_{2(k-1)}(n)}$ .

6. Concluding remarks

6.1. The uniform problem

Consider $\boldsymbol {k}=(k;s)$ . In this paper, we obtained an exact result for $(3;7)$ and a new proof for $(3;6)$ . For general $(k;s)$ , it seems reasonable to expect every $(r,\phi ,\boldsymbol {\alpha })$ to be such that $(k-1)|r$ , $\boldsymbol {\alpha }$ is uniform and every $\phi ^{-1}(c) \cong T_{k-1}(r)$ . If this were so, then for distinct $c,c'\in [s]$ , $\phi ^{-1}(c) \cup \phi ^{-1}(c')$ would have at most $(k-1)^2$ parts. This would give rise to a constraint in Problem L which is the analogue of (3.9) – namely,

$$ \begin{align*}(s-1+s-2)d_2 + (s-1+s-2+s-3)d_3 + \ldots + (s-1+s-2+\ldots + s-s)d_s \leq \binom{s}{2}\frac{(k-1)^2-1}{(k-1)^2}. \end{align*} $$

Perhaps this constraint is always valid. As in the case $(3;s)$ , it alone does not seem enough to give a realisable solution for $s \geq 8$ , but for $(5;4)$ and $(5;5)$ , it does give rise to a realisable solution, with $\boldsymbol {d} = (0,\frac {3}{4},\frac {3}{16})$ and $(0,0,\frac {15}{16},0)$ , respectively. The corresponding solution to Problem $Q^*$ has $r=16$ , and colourings come from $\mathbb {F}^2_4$ . Thus, we make the following conjecture.

Conjecture 6.1. There exists $n_0>0$ such that for all $n \geq n_0$ , $T_{16}(n)$ is the unique $(5;4)$ -extremal graph, and the unique $(5;5)$ -extremal graph.

Its proof would probably follow from the following analogue of Lemma 3.3, for b not too small.

Problem 6.2. Find $b>0$ as large as possible such that the following holds for all sufficiently large n. Let $R,B$ be two $K_5$ -free graphs on the same vertex set of size n with $|R|+|B| \geq (\frac {3}{2}-b) n^2/2$ . Then $|R \cup B| \leq \frac {15}{16} n^2/2 + o(n^2)$ .

Suppose $R,B$ are $K_k$ -free graphs on the same vertex set of size n, with $|R|,|B| \geq (\frac {k-2}{k-1}-d)n^2/2$ and $|R \cup B| = (\frac {(k-1)^2-1}{(k-1)^2}+d')n^2/2$ . The strong stability theorem of Füredi [6] implies that at most $dn^2/2$ edges need to be removed from each of $R,B$ to make them $(k-1)$ -partite. Thus, removing at most $dn^2$ edges from $R \cup B$ yields a $(k-1)^2$ -partite graph, so $d' \leq 2d$ . We need $d=\Omega (1)$ and $d'=o(1)$ ; for example, we proved $(d,d')=(\frac {1}{40},o(1))$ in Lemma 3.3.

To prove Lemma 3.3, of which Problem 6.2 is an analogue, we used the fact that $R(3,3)-1 - (3-1)^2=1$ , whereas $R(4,4)-1-(4-1)^2 = 8$ and $26 \leq R(5,5)-1-(5-1)^2 \leq 31$ . Thus, there could be many clique sizes larger than $(k-1)^2$ present in $R \cup B$ , and moreover, they could have many different red/blue colourings. Therefore, the proof method of Lemma 3.3 seems unlikely to generalise.

6.2. The two colour problem

Solving the two colour problem completely seems difficult. Recall that $\boldsymbol {k}=(k,\ell )$ has the weak extension property but not the strong extension property, so our stability theorem Theorem 1.4 applies – which shows there is a large family of almost extremal graphs – but our exact theorem Theorem 1.6 does not. The method we used to prove Theorem 1.13 about $\boldsymbol {k}=(k+1,k)$ could be used to prove further two colour results, but the number of possible coloured graph structures one needs to consider in an analogue of Lemma 5.4 increases with $k-\ell $ .

It seems plausible that the $(5,3)$ -extremal graph may be $T_4(n)$ , with $F(n;(5,3)) = (3+o(1))\cdot 2^{t_2(n)}$ , where almost all valid colourings come from taking one of the $\binom {4}{2}/2$ part-respecting bipartitions and allowing every cross-edge to be either colour, while edges within one part are given colour $1$ . Perhaps for $\boldsymbol {k}=(\ell (k-1)+1,k)$ , the $\boldsymbol {k}$ -extremal graph is $T_{\ell (k-1)}(n)$ , with $F(n;\boldsymbol {k})=(\frac {1}{(k-1)!}\binom {\ell (k-1)}{\ell ,\ldots ,\ell }+o(1)) \cdot 2^{t_{\ell (k-1)}(n)}$ , and for $\boldsymbol {k}=(\ell (k-1)+j,k)$ for $j=2,\ldots ,k-1$ , extremal graphs contain at least one small part.