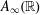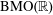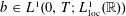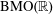Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Canto, Javier
2021.
Sharp Reverse Hölder Inequality for $$C_p$$ Weights and Applications.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 4,
p.
4165.
Ambrosio, Luigi
Nicolussi Golo, Sebastiano
and
Serra Cassano, Francesco
2023.
Classical flows of vector fields with exponential or sub-exponential summability.
Journal of Differential Equations,
Vol. 372,
Issue. ,
p.
458.
Hu, Pingxu
Tao, Jin
and
Yang, Dachun
2023.
New John–Nirenberg–Campanato‐type spaces related to both maximal functions and their commutators.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 5,
p.
5937.