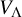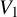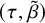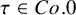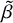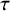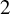1 Introduction
The classification of strongly regular holomorphic vertex operator algebras (abbreviated as VOA) of central charge
![]() $24$
with nontrivial weight one space is basically completed. It has been shown that there are exactly
$24$
with nontrivial weight one space is basically completed. It has been shown that there are exactly
![]() $70$
strongly regular holomorphic VOAs of CFT-type with central charge
$70$
strongly regular holomorphic VOAs of CFT-type with central charge
![]() $24$
and nonzero weight one space and their VOA structures are uniquely determined by the Lie algebra structures of their weight one spaces. Moreover, the possible Lie algebra structures for their weight one subspaces have been given in Schellekens’ list [Reference Schellekens45]. The main tool is the so-called orbifold construction [Reference Carnahan and Miyamoto6; Reference Dolan, Goddard and Montague10; Reference van Ekeren, Möller and Scheithauer17; Reference Frenkel, Lepowsky and Meurman19; Reference McRae36; Reference Miyamoto37; Reference Miyamoto38]. Nevertheless, their constructions and the uniqueness proofs were done by case by case analysis [Reference Dong9; Reference Dolan, Goddard and Montague10; Reference Dong and Mason13; Reference van Ekeren, Möller and Scheithauer17; Reference van Ekeren, Möller and Scheithauer18; Reference Frenkel, Lepowsky and Meurman19; Reference Kawasetsu, Lam and Lin22; Reference Lam24; Reference Lam and Lin26; Reference Lam and Shimakura27; Reference Lam and Shimakura28; Reference Lam and Shimakura29; Reference Lam and Shimakura30; Reference Lam and Shimakura31; Reference Lam and Shimakura32; Reference Lam and Shimakura33; Reference Miyamoto37; Reference Sagaki and Shimakura42]. A simplified and uniform construction and proof of uniqueness is somehow expected. Recently, it is proved in [Reference van Ekeren, Lam, Möller and Shimakura16] (see also [Reference Chigira, Lam and Miyamoto7]) that for any holomorphic VOA of central charge
$24$
and nonzero weight one space and their VOA structures are uniquely determined by the Lie algebra structures of their weight one spaces. Moreover, the possible Lie algebra structures for their weight one subspaces have been given in Schellekens’ list [Reference Schellekens45]. The main tool is the so-called orbifold construction [Reference Carnahan and Miyamoto6; Reference Dolan, Goddard and Montague10; Reference van Ekeren, Möller and Scheithauer17; Reference Frenkel, Lepowsky and Meurman19; Reference McRae36; Reference Miyamoto37; Reference Miyamoto38]. Nevertheless, their constructions and the uniqueness proofs were done by case by case analysis [Reference Dong9; Reference Dolan, Goddard and Montague10; Reference Dong and Mason13; Reference van Ekeren, Möller and Scheithauer17; Reference van Ekeren, Möller and Scheithauer18; Reference Frenkel, Lepowsky and Meurman19; Reference Kawasetsu, Lam and Lin22; Reference Lam24; Reference Lam and Lin26; Reference Lam and Shimakura27; Reference Lam and Shimakura28; Reference Lam and Shimakura29; Reference Lam and Shimakura30; Reference Lam and Shimakura31; Reference Lam and Shimakura32; Reference Lam and Shimakura33; Reference Miyamoto37; Reference Sagaki and Shimakura42]. A simplified and uniform construction and proof of uniqueness is somehow expected. Recently, it is proved in [Reference van Ekeren, Lam, Möller and Shimakura16] (see also [Reference Chigira, Lam and Miyamoto7]) that for any holomorphic VOA of central charge
![]() $24$
with a semisimple weight one Lie algebra, the VOA obtained by the orbifold construction by an inner automorphism g defined by a W-element is always isomorphic to the Leech lattice VOA
$24$
with a semisimple weight one Lie algebra, the VOA obtained by the orbifold construction by an inner automorphism g defined by a W-element is always isomorphic to the Leech lattice VOA
![]() $V_\Lambda $
(see Definition 2.1 for the definition of a W-element). By taking its reverse automorphism
$V_\Lambda $
(see Definition 2.1 for the definition of a W-element). By taking its reverse automorphism
![]() $\tilde {g}$
of
$\tilde {g}$
of
![]() $V_{\Lambda }$
, there is a direct orbifold construction from the Leech lattice VOA
$V_{\Lambda }$
, there is a direct orbifold construction from the Leech lattice VOA
![]() $V_{\Lambda }$
to V. As a consequence, a relatively simpler proof for the Schellekens’ list is obtained [Reference van Ekeren, Lam, Möller and Shimakura16].
$V_{\Lambda }$
to V. As a consequence, a relatively simpler proof for the Schellekens’ list is obtained [Reference van Ekeren, Lam, Möller and Shimakura16].
Möller and Scheithauer [Reference Möller and Scheithauer39] considered a special class of automorphisms in
![]() $\mathrm {Aut}(V_\Lambda )$
, called generalized deep holes. They established a bijection between the algebraic conjugacy classes of generalized deep holes
$\mathrm {Aut}(V_\Lambda )$
, called generalized deep holes. They established a bijection between the algebraic conjugacy classes of generalized deep holes
![]() $g\in \mathrm {Aut}(V_\Lambda )$
with
$g\in \mathrm {Aut}(V_\Lambda )$
with
![]() $\mathrm {rank} (V_\Lambda ^g)_1>0$
and the isomorphism classes of strongly regular, holomorphic VOA V of central charge
$\mathrm {rank} (V_\Lambda ^g)_1>0$
and the isomorphism classes of strongly regular, holomorphic VOA V of central charge
![]() $24$
with
$24$
with
![]() $V_1\neq 0$
[Reference Möller and Scheithauer39, Theorem 6.6]. They also obtained a classification of generalized deep holes of the Leech lattice VOA, which provides a new proof for the classification of holomorphic VOA of central charge 24 with nontrivial weight one spaces. Next, let us recall the notion of generalized deep holes from [Reference Möller and Scheithauer39]. Let V be a strongly regular holomorphic VOA of central charge
$V_1\neq 0$
[Reference Möller and Scheithauer39, Theorem 6.6]. They also obtained a classification of generalized deep holes of the Leech lattice VOA, which provides a new proof for the classification of holomorphic VOA of central charge 24 with nontrivial weight one spaces. Next, let us recall the notion of generalized deep holes from [Reference Möller and Scheithauer39]. Let V be a strongly regular holomorphic VOA of central charge
![]() $24$
. Let g be an automorphism of V of finite order
$24$
. Let g be an automorphism of V of finite order
![]() $n>1$
. If the conformal weight of the unique irreducible g-twisted module is in
$n>1$
. If the conformal weight of the unique irreducible g-twisted module is in
![]() $\frac {1}{n}{\mathbb Z}$
, then g is said to be of type
$\frac {1}{n}{\mathbb Z}$
, then g is said to be of type
![]() $0$
. In this case, one can construct a holomorphic VOA
$0$
. In this case, one can construct a holomorphic VOA
![]() $V^{[g]}$
using the orbifold construction by g and V. It is proved in [Reference Möller and Scheithauer39, Theorem 5.3] that the dimension of the weight one subspace of
$V^{[g]}$
using the orbifold construction by g and V. It is proved in [Reference Möller and Scheithauer39, Theorem 5.3] that the dimension of the weight one subspace of
![]() $V^{[g]}$
is given by the formula
$V^{[g]}$
is given by the formula
where
![]() $c_n(d) \in {\mathbb Q}$
are defined by
$c_n(d) \in {\mathbb Q}$
are defined by
![]() $\sum _{d|n}c_n(d)\cdot GCD(t,d) =n/t$
for all
$\sum _{d|n}c_n(d)\cdot GCD(t,d) =n/t$
for all
![]() $t | n$
. The rest term
$t | n$
. The rest term
![]() $R(g)$
is non-negative and can be described explicitly by the dimensions of the weight spaces of the irreducible
$R(g)$
is non-negative and can be described explicitly by the dimensions of the weight spaces of the irreducible
![]() $V^g$
-modules of weight less than one.
$V^g$
-modules of weight less than one.
Möller and Scheithauer [Reference Möller and Scheithauer39] called an automorphism
![]() $g\in \mathrm {Aut}(V)$
a generalized deep hole of V if g is of type
$g\in \mathrm {Aut}(V)$
a generalized deep hole of V if g is of type
![]() $0$
and
$0$
and
-
1. the upper bound in the dimension formula is attained (i.e.,
 $R(g)=0$
or
$R(g)=0$
or
 $ \dim (V^{[g]})_1= 24 + \sum _{d|n}c_n(d) \dim (V^{g^d})_1$
),
$ \dim (V^{[g]})_1= 24 + \sum _{d|n}c_n(d) \dim (V^{g^d})_1$
), -
2.
 $\mathrm {rank}(V^{[g]})_1 = \mathrm {rank}(V^g)_1$
.
$\mathrm {rank}(V^{[g]})_1 = \mathrm {rank}(V^g)_1$
.
If
![]() $V= V_\Lambda $
is the Leech lattice VOA, the rank condition (2) is equivalent to the fact that
$V= V_\Lambda $
is the Leech lattice VOA, the rank condition (2) is equivalent to the fact that
![]() $(V_\Lambda ^g)_1$
is a Cartan subalgebra of
$(V_\Lambda ^g)_1$
is a Cartan subalgebra of
![]() $(V^{[g]})_1$
. It turns out that the reverse automorphism
$(V^{[g]})_1$
. It turns out that the reverse automorphism
![]() $\tilde {g}\in \mathrm { Aut}(V_{\Lambda })$
associated with the inner automorphism defined by a W-element is a generalized deep hole. Moreover, it is proved that any generalized deep hole g of the Leech lattice VOA with
$\tilde {g}\in \mathrm { Aut}(V_{\Lambda })$
associated with the inner automorphism defined by a W-element is a generalized deep hole. Moreover, it is proved that any generalized deep hole g of the Leech lattice VOA with
![]() $\mathrm {rank}(V^g_\Lambda )_1> 0$
is conjugate to the reverse automorphism of an inner automorphism defined by a W-element of
$\mathrm {rank}(V^g_\Lambda )_1> 0$
is conjugate to the reverse automorphism of an inner automorphism defined by a W-element of
![]() $V = V_\Lambda ^{[g]}$
(see the proof of [Reference Möller and Scheithauer39, Theorem 6.6]). Therefore, without loss of generality, we may assume that a generalized deep hole g of the Leech lattice VOA with
$V = V_\Lambda ^{[g]}$
(see the proof of [Reference Möller and Scheithauer39, Theorem 6.6]). Therefore, without loss of generality, we may assume that a generalized deep hole g of the Leech lattice VOA with
![]() $\mathrm {rank}(V^g_\Lambda )_1> 0$
is a reverse automorphism of an inner automorphism defined by a W-element of a holomorphic VOA V with
$\mathrm {rank}(V^g_\Lambda )_1> 0$
is a reverse automorphism of an inner automorphism defined by a W-element of a holomorphic VOA V with
![]() $V_1\neq 0$
.
$V_1\neq 0$
.
As it is well-known, a deep hole of a lattice L is an element v of
![]() ${\mathbb R} L$
such that a distance
${\mathbb R} L$
such that a distance
![]() $\min \{ |\!|\alpha -v|\!|\mid \alpha \in L\}$
from L is the largest (covering radius) among elements v in
$\min \{ |\!|\alpha -v|\!|\mid \alpha \in L\}$
from L is the largest (covering radius) among elements v in
![]() ${\mathbb R} L$
and so it has a geometrical meaning. Furthermore, deep holes of the Leech lattice
${\mathbb R} L$
and so it has a geometrical meaning. Furthermore, deep holes of the Leech lattice
![]() $\Lambda $
have many interesting geometrical and algebraic meanings. Therefore, it is natural to expect some geometrical properties for generalized deep holes.
$\Lambda $
have many interesting geometrical and algebraic meanings. Therefore, it is natural to expect some geometrical properties for generalized deep holes.
Recall that any automorphism
![]() $\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$
can be written as
$\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$
can be written as
where
![]() $\tau \in Co.0=O(\Lambda )$
,
$\tau \in Co.0=O(\Lambda )$
,
![]() $\beta \in {\mathbb R}\Lambda ^{\tau }$
and
$\beta \in {\mathbb R}\Lambda ^{\tau }$
and
![]() $\widehat {\tau }$
denotes a standard lift of
$\widehat {\tau }$
denotes a standard lift of
![]() $\tau $
in
$\tau $
in
![]() $O(\widehat {\Lambda })$
[Reference Borcherds2; 14]. In this paper, we will show that a holomorphic VOA of central charge
$O(\widehat {\Lambda })$
[Reference Borcherds2; 14]. In this paper, we will show that a holomorphic VOA of central charge
![]() $24$
with non-abelian weight one Lie algebra naturally defines a pair
$24$
with non-abelian weight one Lie algebra naturally defines a pair
![]() $(\tau , \tilde {\beta })$
, where
$(\tau , \tilde {\beta })$
, where
![]() $\tau \in Co.0$
is the same isometry as defined by a reverse automorphism
$\tau \in Co.0$
is the same isometry as defined by a reverse automorphism
![]() $\tilde {g}\in \mathrm {Aut}(V_\Lambda )$
and
$\tilde {g}\in \mathrm {Aut}(V_\Lambda )$
and
![]() $\tilde {\beta }$
is a (
$\tilde {\beta }$
is a (
![]() $\tau $
-invariant) deep hole of the Leech lattice related to
$\tau $
-invariant) deep hole of the Leech lattice related to
![]() $\beta $
. In particular, a generalized deep hole of the Leech lattice VOA defines a ‘true’ deep hole of the Leech lattice. It provides a new combinatorial approach towards the classification of holomorphic VOAs of central charge
$\beta $
. In particular, a generalized deep hole of the Leech lattice VOA defines a ‘true’ deep hole of the Leech lattice. It provides a new combinatorial approach towards the classification of holomorphic VOAs of central charge
![]() $24$
.
$24$
.
Let L be an even lattice. We use
![]() $O(L)$
to denote the isometry group of L. The dual lattice of L is denoted by
$O(L)$
to denote the isometry group of L. The dual lattice of L is denoted by
![]() $L^*$
(i.e.,
$L^*$
(i.e.,
![]() $L^*=\{x\in {\mathbb Q}\otimes _{\mathbb Z} L\mid \langle x, L\rangle \subset {\mathbb Z}\}$
). The discriminant group
$L^*=\{x\in {\mathbb Q}\otimes _{\mathbb Z} L\mid \langle x, L\rangle \subset {\mathbb Z}\}$
). The discriminant group
![]() $\mathcal {D}(L)$
is the quotient group
$\mathcal {D}(L)$
is the quotient group
![]() $L^*/L$
. For
$L^*/L$
. For
![]() $ \tau \in O(L)$
, we denote the fixed point sublattice by
$ \tau \in O(L)$
, we denote the fixed point sublattice by
![]() $L^\tau $
. We also define the coinvariant lattice
$L^\tau $
. We also define the coinvariant lattice
![]() $L_\tau =\{ x\in L \mid \langle x, L^\tau \rangle =0\}$
. The key observation is that there is a ‘duality’ associated with the fixed point sublattice
$L_\tau =\{ x\in L \mid \langle x, L^\tau \rangle =0\}$
. The key observation is that there is a ‘duality’ associated with the fixed point sublattice
![]() $\Lambda ^\tau $
which changes the level; we call it
$\Lambda ^\tau $
which changes the level; we call it
![]() $\ell $
-duality.
$\ell $
-duality.
Main Theorem 1 (see Theorem 4.2)
If
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
is a generalized deep hole, then there is an isometry:
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
is a generalized deep hole, then there is an isometry:
where
![]() $\ell =|\widehat {\tau }|$
.
$\ell =|\widehat {\tau }|$
.
Using this
![]() $\ell $
-duality
$\ell $
-duality
![]() $\varphi $
(extended to
$\varphi $
(extended to
![]() ${\mathbb C}\Lambda ^{\tau }$
), it is easy to show that
${\mathbb C}\Lambda ^{\tau }$
), it is easy to show that
![]() $\langle \varphi _{\tau }(\sqrt {\ell }\beta ), \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in 2{\mathbb Z}$
and its neighbor lattice
$\langle \varphi _{\tau }(\sqrt {\ell }\beta ), \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in 2{\mathbb Z}$
and its neighbor lattice
![]() $N=\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )}+ {\mathbb Z}\varphi _{\tau }(\sqrt {\ell }\beta )$
define a Niemeier lattice with
$N=\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )}+ {\mathbb Z}\varphi _{\tau }(\sqrt {\ell }\beta )$
define a Niemeier lattice with
![]() $N\ncong \Lambda $
, where
$N\ncong \Lambda $
, where
![]() $\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )} = \{ x\in \Lambda \mid \langle x, \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in {\mathbb Z}\}$
.
$\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )} = \{ x\in \Lambda \mid \langle x, \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in {\mathbb Z}\}$
.
Let
![]() $V=(V_{\Lambda })^{[\tilde {g}]}$
be the VOA obtained by the orbifold construction from
$V=(V_{\Lambda })^{[\tilde {g}]}$
be the VOA obtained by the orbifold construction from
![]() $V_{\Lambda }$
by
$V_{\Lambda }$
by
![]() $\tilde {g}$
. Let
$\tilde {g}$
. Let
![]() $\mathcal{H}$
be a Cartan subalgebra of
$\mathcal{H}$
be a Cartan subalgebra of
![]() $V_1$
and let
$V_1$
and let
![]() $M(\mathcal{H})$
be the Heisenberg subVOA of V generated by
$M(\mathcal{H})$
be the Heisenberg subVOA of V generated by
![]() $\mathcal{H}$
. Then there is an even lattice L such that the double commutant
$\mathcal{H}$
. Then there is an even lattice L such that the double commutant
![]() $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$
of
$\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$
of
![]() $M(\mathcal{H})$
in V is isomorphic to the lattice VOA
$M(\mathcal{H})$
in V is isomorphic to the lattice VOA
![]() $V_L$
. The lattice L (or
$V_L$
. The lattice L (or
![]() $L^*$
) encoded the information of the root system of
$L^*$
) encoded the information of the root system of
![]() $V_1$
.
$V_1$
.
Main Theorem 2 (see Theorem 4.9)
Via
![]() $\ell $
-duality, we have
$\ell $
-duality, we have
![]() $ N^{\tau }\cong \sqrt {\ell }\varphi _{\tau }(L^{\ast })$
.
$ N^{\tau }\cong \sqrt {\ell }\varphi _{\tau }(L^{\ast })$
.
In addition, we prove the following theorem.
Main Theorem 3 (see Theorem 5.1 and Proposition 6.1)
Let
![]() $\varphi $
be the isometry defined in the Main Theorem 1. Then we can choose
$\varphi $
be the isometry defined in the Main Theorem 1. Then we can choose
![]() $\beta \in {\mathbb C}\Lambda ^{\tau }$
such that
$\beta \in {\mathbb C}\Lambda ^{\tau }$
such that
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
and
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
and
![]() $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
is a deep hole of
$\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
is a deep hole of
![]() $\Lambda $
of squared length
$\Lambda $
of squared length
![]() $2$
.
$2$
.
The classification of generalized deep holes is thus equivalent to the classification of the pairs
![]() $(\tau , \tilde {\beta })$
with
$(\tau , \tilde {\beta })$
with
![]() $\tau \in O(\Lambda )$
and
$\tau \in O(\Lambda )$
and
![]() $\tilde {\beta }$
a
$\tilde {\beta }$
a
![]() $\tau $
-invariant deep hole of squared length
$\tau $
-invariant deep hole of squared length
![]() $2$
satisfying certain conditions and up to some equivalence.
$2$
satisfying certain conditions and up to some equivalence.
Let
![]() $\mathcal{T}$
be the set of pairs
$\mathcal{T}$
be the set of pairs
![]() $(\tau , \tilde {\beta })$
satisfying certain conditions (see Section 7, (C1)–(C3)). We define a relation
$(\tau , \tilde {\beta })$
satisfying certain conditions (see Section 7, (C1)–(C3)). We define a relation
![]() $\sim $
on
$\sim $
on
![]() $\mathcal{T}$
as follows:
$\mathcal{T}$
as follows:
![]() $(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$
if and only if
$(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$
if and only if
-
(1)
 $\tilde {\beta }$
and
$\tilde {\beta }$
and
 $\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
$\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
 $\Lambda $
(i.e., there are
$\Lambda $
(i.e., there are
 $\sigma \in O(\Lambda )$
and
$\sigma \in O(\Lambda )$
and
 $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
 $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
,
$\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
, -
(2)
 $\tau $
is conjugate to
$\tau $
is conjugate to
 $\sigma ^{-1} \tau ' \sigma $
in
$\sigma ^{-1} \tau ' \sigma $
in
 $O(N)$
.
$O(N)$
.
The following is another main theorem of this article.
Main Theorem 4 (see Theorem 7.1)
There is a one-to-one correspondence between the set of isomorphism classes of holomorphic VOA V of central charge
![]() $24$
having non-abelian
$24$
having non-abelian
![]() $V_1$
and the set
$V_1$
and the set
![]() $\mathcal{T}/\sim $
of equivalence classes of pairs
$\mathcal{T}/\sim $
of equivalence classes of pairs
![]() $(\tau , \tilde {\beta })$
by
$(\tau , \tilde {\beta })$
by
![]() $\sim $
.
$\sim $
.
Since a deep hole of the Leech lattice determines a unique Niemeier lattice, up to isometry and there are only
![]() $23$
Niemeier lattices with nontrivial root system, it is straightforward to list all possible choices for
$23$
Niemeier lattices with nontrivial root system, it is straightforward to list all possible choices for
![]() $(\tau , \tilde {\beta })$
and to determine the corresponding Lie algebra structures for
$(\tau , \tilde {\beta })$
and to determine the corresponding Lie algebra structures for
![]() $V_1$
. Therefore, one can complete the classification of holomorphic VOAs of central charge 24 with non-abelian
$V_1$
. Therefore, one can complete the classification of holomorphic VOAs of central charge 24 with non-abelian
![]() $V_1$
by a purely combinatorial method. Indeed, we will provide an explanation for an observation of Höhn, which relates the weight one Lie algebras of holomorphic VOAs of central charge
$V_1$
by a purely combinatorial method. Indeed, we will provide an explanation for an observation of Höhn, which relates the weight one Lie algebras of holomorphic VOAs of central charge
![]() $24$
to certain codewords associated with the glue codes of Niemeier lattices [Reference Höhn21, Theorem 3.1 and Table 3] (see Section 8 for details).
$24$
to certain codewords associated with the glue codes of Niemeier lattices [Reference Höhn21, Theorem 3.1 and Table 3] (see Section 8 for details).
2 Some previous results
We first recall several results from [Reference Chigira, Lam and Miyamoto7]. Let V be a holomorphic VOA of central charge 24 with
![]() $V_1\not =0$
. Suppose
$V_1\not =0$
. Suppose
![]() $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
is a semisimple Lie algebra. We use
$V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
is a semisimple Lie algebra. We use
![]() $k_j$
(resp.
$k_j$
(resp.
![]() $h^{\vee }_j$
and
$h^{\vee }_j$
and
![]() $r_j$
) to denote the level (resp. the dual Coxeter number and the lace number) of
$r_j$
) to denote the level (resp. the dual Coxeter number and the lace number) of
![]() $\mathcal{G}_j$
,
$\mathcal{G}_j$
,
![]() $j=1, \dots , t$
. Let
$j=1, \dots , t$
. Let
![]() $\mathcal{H}$
be a Cartan subalgebra of
$\mathcal{H}$
be a Cartan subalgebra of
![]() $V_1$
and let
$V_1$
and let
![]() $M(\mathcal{H})$
be the Heisenberg subVOA generated by
$M(\mathcal{H})$
be the Heisenberg subVOA generated by
![]() $\mathcal{H}$
. For a subVOA
$\mathcal{H}$
. For a subVOA
![]() $U\subset V$
, the commutant subalgebra of U in V is defined by
$U\subset V$
, the commutant subalgebra of U in V is defined by
It is easy to see that the double commutant
![]() $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$
is isomorphic to a lattice VOA
$\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$
is isomorphic to a lattice VOA
![]() $V_L$
for an even lattice
$V_L$
for an even lattice
![]() $L\subseteq \mathcal{H}$
.
$L\subseteq \mathcal{H}$
.
Definition 2.1. Let
![]() $\rho _j$
be a Weyl vector of
$\rho _j$
be a Weyl vector of
![]() $\mathcal{G}_{j,k_j}$
and set
$\mathcal{G}_{j,k_j}$
and set
![]() $\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$
, which we call a W-element.
$\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$
, which we call a W-element.
Next, we recall some standard notations for lattice VOAs from [Reference Frenkel, Lepowsky and Meurman19]. Let L be a positive-definite even lattice and
![]() $\mathfrak {h}={\mathbb C}\otimes _{\mathbb Z} L$
. Let
$\mathfrak {h}={\mathbb C}\otimes _{\mathbb Z} L$
. Let
![]() $M(\mathfrak {h})$
be the Heisenberg VOA associated with
$M(\mathfrak {h})$
be the Heisenberg VOA associated with
![]() $\mathfrak {h}$
and let
$\mathfrak {h}$
and let
![]() ${\mathbb C}\{L\}=\bigoplus _{\alpha \in L}{\mathbb C} e^\alpha $
be the twisted group algebra such that
${\mathbb C}\{L\}=\bigoplus _{\alpha \in L}{\mathbb C} e^\alpha $
be the twisted group algebra such that
![]() $e^\alpha e^\beta =(-1)^{\langle \alpha , \beta \rangle }e^{\beta }e^{\alpha }$
, for
$e^\alpha e^\beta =(-1)^{\langle \alpha , \beta \rangle }e^{\beta }e^{\alpha }$
, for
![]() $\alpha ,\beta \in L$
. The lattice VOA
$\alpha ,\beta \in L$
. The lattice VOA
![]() $V_L$
is given by
$V_L$
is given by
![]() $V_L= M(\mathfrak {h}) \otimes {\mathbb C}\{L\}$
. For any coset
$V_L= M(\mathfrak {h}) \otimes {\mathbb C}\{L\}$
. For any coset
![]() $\lambda +L\in \mathcal {D}(L)=L^*/L$
, denote
$\lambda +L\in \mathcal {D}(L)=L^*/L$
, denote
![]() $V_{\lambda +L}=M(\mathfrak {h})\otimes \mathrm {Span}_{\mathbb C}\{e^\alpha \mid \alpha \in \lambda +L\}$
. Then
$V_{\lambda +L}=M(\mathfrak {h})\otimes \mathrm {Span}_{\mathbb C}\{e^\alpha \mid \alpha \in \lambda +L\}$
. Then
![]() $V_{\lambda +L}$
has an irreducible
$V_{\lambda +L}$
has an irreducible
![]() $V_L$
-module structure [Reference Frenkel, Lepowsky and Meurman19]. Moreover,
$V_L$
-module structure [Reference Frenkel, Lepowsky and Meurman19]. Moreover,
![]() $\{ V_{\lambda +L}\mid \lambda +L\in \mathcal {D}(L)\}$
is a set of all inequivalent irreducible modules for
$\{ V_{\lambda +L}\mid \lambda +L\in \mathcal {D}(L)\}$
is a set of all inequivalent irreducible modules for
![]() $V_L$
[Reference Dong9].
$V_L$
[Reference Dong9].
Let
![]() $U=U(0)=\mathrm {Comm}(M(\mathcal{H}),V)$
. Then
$U=U(0)=\mathrm {Comm}(M(\mathcal{H}),V)$
. Then
![]() $U\otimes V_L\subset V$
is a subVOA of the same central charge. From the property of lattice VOA, we have a decomposition
$U\otimes V_L\subset V$
is a subVOA of the same central charge. From the property of lattice VOA, we have a decomposition
where
![]() $U(\delta )$
are
$U(\delta )$
are
![]() $U(0)$
-modules and
$U(0)$
-modules and
![]() $M(\mathcal{H})e^{\delta }$
are
$M(\mathcal{H})e^{\delta }$
are
![]() $M(\mathcal{H})$
-modules. Since V is holomorphic, all irreducible modules of
$M(\mathcal{H})$
-modules. Since V is holomorphic, all irreducible modules of
![]() $V_L$
appear in V [Reference Krauel and Miyamoto23]; thus,
$V_L$
appear in V [Reference Krauel and Miyamoto23]; thus,
![]() $U(\delta )\not =0$
for every
$U(\delta )\not =0$
for every
![]() $\delta \in L^{\ast }$
.
$\delta \in L^{\ast }$
.
Set
![]() $g=\exp (2\pi i\alpha (0))$
, where
$g=\exp (2\pi i\alpha (0))$
, where
![]() $\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$
. In [Reference Chigira, Lam and Miyamoto7] (see also [Reference van Ekeren, Lam, Möller and Shimakura16]), it is proved the VOA
$\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$
. In [Reference Chigira, Lam and Miyamoto7] (see also [Reference van Ekeren, Lam, Möller and Shimakura16]), it is proved the VOA
![]() $V^{[g]}$
obtained by the orbifold construction from V by g is isomorphic to the Leech lattice VOA (i.e.,
$V^{[g]}$
obtained by the orbifold construction from V by g is isomorphic to the Leech lattice VOA (i.e.,
![]() $V^{[g]}\cong V_{\Lambda }$
). Namely, the integer weights submodule
$V^{[g]}\cong V_{\Lambda }$
). Namely, the integer weights submodule
![]() $T^1_{{\mathbb Z}}$
of the simple g-twisted V-module
$T^1_{{\mathbb Z}}$
of the simple g-twisted V-module
![]() $T^1$
is nonzero and
$T^1$
is nonzero and
![]() $V^g\oplus T^1_{{\mathbb Z}}\oplus \cdots \oplus (T^1_{{\mathbb Z}})^{\boxtimes (|g|-1)} \cong V_{\Lambda }$
.
$V^g\oplus T^1_{{\mathbb Z}}\oplus \cdots \oplus (T^1_{{\mathbb Z}})^{\boxtimes (|g|-1)} \cong V_{\Lambda }$
.
In this case, there is an automorphism
![]() $\tilde {g}$
of
$\tilde {g}$
of
![]() $V_{\Lambda }$
acting on
$V_{\Lambda }$
acting on
![]() $(T^1_{{\mathbb Z}})^{\boxtimes m}$
as
$(T^1_{{\mathbb Z}})^{\boxtimes m}$
as
![]() $e^{2\pi i m/n}$
,
$e^{2\pi i m/n}$
,
![]() $n=|g|$
. Moreover, the orbifold construction from
$n=|g|$
. Moreover, the orbifold construction from
![]() $V_{\Lambda }$
by the automorphism
$V_{\Lambda }$
by the automorphism
![]() $\tilde {g}$
gives V (i.e.,
$\tilde {g}$
gives V (i.e.,
![]() $V_{\Lambda }^{[\tilde {g}]}\cong V$
). That
$V_{\Lambda }^{[\tilde {g}]}\cong V$
). That
![]() $\tilde {g} \in \mathrm {Aut}(V^{[g]})$
is called the reverse automorphism of g.
$\tilde {g} \in \mathrm {Aut}(V^{[g]})$
is called the reverse automorphism of g.
Since
![]() $\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$
, we have
$\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$
, we have
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
for some
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
for some
![]() $\tau \in O(\Lambda )=Co.0$
and
$\tau \in O(\Lambda )=Co.0$
and
![]() $\beta \in {\mathbb C}\Lambda $
[Reference Borcherds2; Reference Dong and Nagatomo14]. By choosing a suitable (standard) lift
$\beta \in {\mathbb C}\Lambda $
[Reference Borcherds2; Reference Dong and Nagatomo14]. By choosing a suitable (standard) lift
![]() $\widehat {\tau }$
of
$\widehat {\tau }$
of
![]() $\tau $
, we may choose
$\tau $
, we may choose
![]() $\beta \in {\mathbb C}\Lambda ^{\tau }$
[Reference van Ekeren, Möller and Scheithauer17; Reference Lam and Shimakura27]. Recall that a lift
$\beta \in {\mathbb C}\Lambda ^{\tau }$
[Reference van Ekeren, Möller and Scheithauer17; Reference Lam and Shimakura27]. Recall that a lift
![]() $\widehat {\tau }$
of
$\widehat {\tau }$
of
![]() $\tau \in O(\Lambda )$
is called a standard lift if
$\tau \in O(\Lambda )$
is called a standard lift if
![]() $\widehat {\tau } (e^\alpha )= e^\alpha $
for any
$\widehat {\tau } (e^\alpha )= e^\alpha $
for any
![]() $\alpha \in \Lambda ^\tau $
(see for example [Reference van Ekeren, Möller and Scheithauer17]).
$\alpha \in \Lambda ^\tau $
(see for example [Reference van Ekeren, Möller and Scheithauer17]).
Remark 2.2. By the definition of W-element, it is clear that the order of g on
![]() $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
is
$V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
is
![]() $\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$
; indeed, one can show that
$\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$
; indeed, one can show that
![]() $|g|=\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$
on V [Reference van Ekeren, Lam, Möller and Shimakura16, Proposition 5.1].
$|g|=\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$
on V [Reference van Ekeren, Lam, Möller and Shimakura16, Proposition 5.1].
Set
![]() $n=|g|=|\tilde {g}|$
and let
$n=|g|=|\tilde {g}|$
and let
![]() $K_0,N_0\in {\mathbb Z}$
with
$K_0,N_0\in {\mathbb Z}$
with
![]() $\mathrm {GCD}(K_0,N_0)=1$
such that
$\mathrm {GCD}(K_0,N_0)=1$
such that
![]() $\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$
. As we have shown in [Reference Chigira, Lam and Miyamoto7],
$\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$
. As we have shown in [Reference Chigira, Lam and Miyamoto7],
![]() $n=|\tau |N_0$
and
$n=|\tau |N_0$
and
![]() $N_0|h^{\vee }_j$
; thus,
$N_0|h^{\vee }_j$
; thus,
![]() $|\tau |=\mathrm {LCM}(\{r_ih_j^{\vee }/N_0\mid j \})$
.
$|\tau |=\mathrm {LCM}(\{r_ih_j^{\vee }/N_0\mid j \})$
.
It is also proved in [Reference Chigira, Lam and Miyamoto7, Proposition 4.2] that
![]() $k_i/h_i^{\vee }=\frac {K_0-N_0}{N_0}$
; therefore, we have
$k_i/h_i^{\vee }=\frac {K_0-N_0}{N_0}$
; therefore, we have
 $$\begin{align*}\frac{2}{r_ik_i}=\frac{2}{r_ih^{\vee}_i}\frac{N_0}{K_0-N_0}= \frac{2}{(K_0-N_0)r_ih^{\vee}/N_0} \end{align*}$$
$$\begin{align*}\frac{2}{r_ik_i}=\frac{2}{r_ih^{\vee}_i}\frac{N_0}{K_0-N_0}= \frac{2}{(K_0-N_0)r_ih^{\vee}/N_0} \end{align*}$$
and
As a consequence, we have the following result.
Lemma 2.3.
![]() $\mathrm {LCM}(\{r_ik_i\mid i\}) =(K_0-N_0)|\tau |$
.
$\mathrm {LCM}(\{r_ik_i\mid i\}) =(K_0-N_0)|\tau |$
.
Next we recall an important result from [Reference Chigira, Lam and Miyamoto7].
Proposition 2.4 [Reference Chigira, Lam and Miyamoto7, Propositions 3.25 and 4.3]
We have
![]() $N_0\alpha \in L^{\ast }$
. Moreover,
$N_0\alpha \in L^{\ast }$
. Moreover,
and
![]() $\mathcal{H}+\mathrm {Comm}(M(\mathcal{H}),V)_1$
is a Cartan subalgebra of the weight one Lie algebra of
$\mathcal{H}+\mathrm {Comm}(M(\mathcal{H}),V)_1$
is a Cartan subalgebra of the weight one Lie algebra of
![]() $V^{[g]}\cong V_\Lambda $
.
$V^{[g]}\cong V_\Lambda $
.
Since
![]() $U(jN_0\alpha )\otimes e^{jN_0\alpha }\in V$
,
$U(jN_0\alpha )\otimes e^{jN_0\alpha }\in V$
,
![]() $U(jN_0\alpha )$
appears in
$U(jN_0\alpha )$
appears in
![]() $g^{-jN_0}$
-twisted V-module and so we may choose
$g^{-jN_0}$
-twisted V-module and so we may choose
![]() $\beta $
and
$\beta $
and
![]() $\widehat {\tau }$
so that
$\widehat {\tau }$
so that
![]() $\langle \beta ,\alpha \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$
and
$\langle \beta ,\alpha \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$
and
![]() $\widehat {\tau }$
acts on
$\widehat {\tau }$
acts on
![]() $U(jN_0\alpha )$
as a multiple by
$U(jN_0\alpha )$
as a multiple by
![]() $e^{-2\pi ij/|\tau |}$
.
$e^{-2\pi ij/|\tau |}$
.
As we discussed, a W-element of a holomorphic VOA of central charge
![]() $24$
with a semisimple weight one Lie algebra defines an automorphism
$24$
with a semisimple weight one Lie algebra defines an automorphism
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
for some
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
for some
![]() $\tau \in \mathrm { Aut}(\Lambda )=Co.0$
and
$\tau \in \mathrm { Aut}(\Lambda )=Co.0$
and
![]() $\beta \in {\mathbb C}\Lambda ^{\tau }$
such that
$\beta \in {\mathbb C}\Lambda ^{\tau }$
such that
![]() $V= V_\Lambda ^{[\tilde {g}]}$
. One main question is to determine the isometry
$V= V_\Lambda ^{[\tilde {g}]}$
. One main question is to determine the isometry
![]() $\tau \in Co.0$
arising in this manner.
$\tau \in Co.0$
arising in this manner.
Denote
 $$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg | \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\ \mbox{ automorphism of an orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg | \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\ \mbox{ automorphism of an orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$
In Section 6, we will show that
![]() $\mathcal{P} \subset \mathcal{P}_0 = \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$
. The main idea is to analyze the conformal weights of the irreducible
$\mathcal{P} \subset \mathcal{P}_0 = \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$
. The main idea is to analyze the conformal weights of the irreducible
![]() $\widehat {\tau }$
-twisted modules and
$\widehat {\tau }$
-twisted modules and
![]() $\tilde {g}$
-twisted modules.
$\tilde {g}$
-twisted modules.
3 Irreducible twisted modules for lattice VOAs
First, we review some basic properties of the irreducible twisted modules for lattice VOAs. Let P be an even unimodular lattice. Let
![]() $\tau \in O(P)$
be of order n and
$\tau \in O(P)$
be of order n and
![]() $\widehat {\tau } \in O(\hat {P})$
a standard lift of
$\widehat {\tau } \in O(\hat {P})$
a standard lift of
![]() $\tau $
. We use
$\tau $
. We use
![]() $\pi =\pi _{\tau }: P \to (P^{\tau })^*$
to denote the natural projection. More precisely,
$\pi =\pi _{\tau }: P \to (P^{\tau })^*$
to denote the natural projection. More precisely,
 $$ \begin{align} \pi(x)=\pi_\tau(x) =\frac{1}{n} \sum_{i=0}^{n-1} \tau^i (x). \end{align} $$
$$ \begin{align} \pi(x)=\pi_\tau(x) =\frac{1}{n} \sum_{i=0}^{n-1} \tau^i (x). \end{align} $$
By [Reference Dong, Li and Mason12],
![]() $V_P$
has a unique irreducible
$V_P$
has a unique irreducible
![]() $\widehat {\tau }$
-twisted
$\widehat {\tau }$
-twisted
![]() $V_P$
-module, up to isomorphism. Such a module
$V_P$
-module, up to isomorphism. Such a module
![]() $V_P[\widehat {\tau }]$
was constructed in [Reference Dong and Lepowsky11] explicitly; as a vector space,
$V_P[\widehat {\tau }]$
was constructed in [Reference Dong and Lepowsky11] explicitly; as a vector space,
where
![]() $M(1)[\tau ]$
is the ‘
$M(1)[\tau ]$
is the ‘
![]() $\tau $
-twisted’ free bosonic space,
$\tau $
-twisted’ free bosonic space,
![]() ${\mathbb C}[\pi (P)]$
is the group algebra of
${\mathbb C}[\pi (P)]$
is the group algebra of
![]() $\pi (P)$
and T is an irreducible module for a certain “
$\pi (P)$
and T is an irreducible module for a certain “
![]() $\tau $
-twisted” central extension of P (see [Reference Lepowsky35, Propositions 6.1 and 6.2] and [Reference Dong and Lepowsky11, Remark 4.2] for detail). Recall that
$\tau $
-twisted” central extension of P (see [Reference Lepowsky35, Propositions 6.1 and 6.2] and [Reference Dong and Lepowsky11, Remark 4.2] for detail). Recall that
and that the conformal weight
![]() $\phi (\tau )$
of T is given by
$\phi (\tau )$
of T is given by
 $$ \begin{align} \phi(\tau):=\frac{1}{4n^2}\sum_{j=1}^{n-1}j(n-j)\dim \mathfrak{h}_{(j)}, \end{align} $$
$$ \begin{align} \phi(\tau):=\frac{1}{4n^2}\sum_{j=1}^{n-1}j(n-j)\dim \mathfrak{h}_{(j)}, \end{align} $$
where
![]() $\mathfrak {h}_{(j)}=\{x\in \mathfrak {h}\mid \tau (x)=\exp ((j/n)2\pi \sqrt {-1})x\}$
. Note that
$\mathfrak {h}_{(j)}=\{x\in \mathfrak {h}\mid \tau (x)=\exp ((j/n)2\pi \sqrt {-1})x\}$
. Note that
![]() $M(1)[\tau ]$
is spanned by vectors of the form
$M(1)[\tau ]$
is spanned by vectors of the form
where
![]() $m_i\in (1/n){\mathbb Z}_{>0}$
and
$m_i\in (1/n){\mathbb Z}_{>0}$
and
![]() $x_i\in \mathfrak {h}_{(nm_i)}$
for
$x_i\in \mathfrak {h}_{(nm_i)}$
for
![]() $1\le i\le s$
.
$1\le i\le s$
.
In addition, the conformal weight of
![]() $x_1(-m_1)\dots x_s(-m_s)\otimes e^\alpha \otimes t\in V_P[\widehat {\tau }]$
is given by
$x_1(-m_1)\dots x_s(-m_s)\otimes e^\alpha \otimes t\in V_P[\widehat {\tau }]$
is given by
 $$ \begin{align*}\sum_{i=1}^s m_i+\frac{(\alpha|\alpha)}{2}+\phi(\tau), \end{align*} $$
$$ \begin{align*}\sum_{i=1}^s m_i+\frac{(\alpha|\alpha)}{2}+\phi(\tau), \end{align*} $$
where
![]() $x_1(-m_1)\dots x_s(-m_s)\in M(1)[\tau ]$
,
$x_1(-m_1)\dots x_s(-m_s)\in M(1)[\tau ]$
,
![]() $e^\alpha \in {\mathbb C}[\pi (P)]$
and
$e^\alpha \in {\mathbb C}[\pi (P)]$
and
![]() $t\in T$
. Note that
$t\in T$
. Note that
![]() $m_i\in (1/n){\mathbb Z}_{>0}$
and that the conformal weight of
$m_i\in (1/n){\mathbb Z}_{>0}$
and that the conformal weight of
![]() $V_P[\widehat {\tau }]$
is
$V_P[\widehat {\tau }]$
is
![]() $\phi (\tau )$
.
$\phi (\tau )$
.
Since
![]() $\sum _{j=1}^{n-1} j(n-j)= n(n^2-1)/6$
, we have
$\sum _{j=1}^{n-1} j(n-j)= n(n^2-1)/6$
, we have
 $$\begin{align*}\phi(\tau)=\frac{1}{24}\sum_{i=1}^d a_i\frac{(n_i^2-1)}{n_i} =\frac{1}{24}\{\sum a_in_i-\sum_{i=1}^d \frac{a_i}{n_i}\}= 1-\frac{1}{24}\sum_{i=1}^d\frac{a_i}{n_i} \end{align*}$$
$$\begin{align*}\phi(\tau)=\frac{1}{24}\sum_{i=1}^d a_i\frac{(n_i^2-1)}{n_i} =\frac{1}{24}\{\sum a_in_i-\sum_{i=1}^d \frac{a_i}{n_i}\}= 1-\frac{1}{24}\sum_{i=1}^d\frac{a_i}{n_i} \end{align*}$$
if
![]() $\tau \in O(P)$
has the frame shape
$\tau \in O(P)$
has the frame shape
![]() $\prod _{j=1}^d n_j^{a_j}$
by (3.2).
$\prod _{j=1}^d n_j^{a_j}$
by (3.2).
Remark 3.1. Let
![]() $v\in {\mathbb Q}\otimes _{\mathbb Z} P^\tau \subset \mathfrak {h}_{(0)}$
. Then
$v\in {\mathbb Q}\otimes _{\mathbb Z} P^\tau \subset \mathfrak {h}_{(0)}$
. Then
![]() $\exp (2\pi i v(0))$
has finite order on
$\exp (2\pi i v(0))$
has finite order on
![]() $V_P$
and commutes with
$V_P$
and commutes with
![]() $\widehat {\tau }$
. Set
$\widehat {\tau }$
. Set
![]() $g= \widehat {\tau } \exp (2\pi i v(0))$
. Then the unique irreducible g-twisted module for
$g= \widehat {\tau } \exp (2\pi i v(0))$
. Then the unique irreducible g-twisted module for
![]() $V_P$
is given by
$V_P$
is given by
as a vector space [Reference Bakalov and Kac4]. In this case, the conformal weight of
![]() $V_P[g]$
is given by
$V_P[g]$
is given by
4 Leech lattice and
 $\ell $
-duality
$\ell $
-duality
Let
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism associated with an orbifold construction defined by a W-element of a holomorphic VOA V of central charge
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism associated with an orbifold construction defined by a W-element of a holomorphic VOA V of central charge
![]() $24$
. In this section, we will consider and study several lattices associated with
$24$
. In this section, we will consider and study several lattices associated with
![]() $\tilde {g}$
and try to study their relations to the root system of the weight one Lie algebra
$\tilde {g}$
and try to study their relations to the root system of the weight one Lie algebra
![]() $V_1$
. We first observe that the fixed point sublattice
$V_1$
. We first observe that the fixed point sublattice
![]() $\Lambda ^\tau $
satisfies some duality property, which we call
$\Lambda ^\tau $
satisfies some duality property, which we call
![]() $\ell $
-duality. Using
$\ell $
-duality. Using
![]() $\ell $
-duality, we will associate a Niemeier lattice N with
$\ell $
-duality, we will associate a Niemeier lattice N with
![]() $\tilde {g}$
. We will study the relationships between N and the root system of
$\tilde {g}$
. We will study the relationships between N and the root system of
![]() $V_1$
. We will also relate the Coxeter number of N to the order of
$V_1$
. We will also relate the Coxeter number of N to the order of
![]() $|\tilde {g}|$
. For simplicity, we assume that
$|\tilde {g}|$
. For simplicity, we assume that
![]() $\tau \in \mathcal{P}_0= \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$
in this section. In Section 6, we will show that
$\tau \in \mathcal{P}_0= \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$
in this section. In Section 6, we will show that
![]() $\tau $
is indeed contained in
$\tau $
is indeed contained in
![]() $P_0$
.
$P_0$
.
4.1
 $\ell $
-duality
$\ell $
-duality
In this subsection, we study the properties of the lattice
![]() $\Lambda ^\tau $
for
$\Lambda ^\tau $
for
Lemma 4.1. For
![]() $\tau \in \mathcal{P}_0$
, we have
$\tau \in \mathcal{P}_0$
, we have
![]() $\det (\Lambda ^{\tau })=\ell ^{\mathrm {rank}(\Lambda ^{\tau })/2}$
.
$\det (\Lambda ^{\tau })=\ell ^{\mathrm {rank}(\Lambda ^{\tau })/2}$
.
Proof. For
![]() $\tau \in \mathcal{P}_0$
, it is easy to check that
$\tau \in \mathcal{P}_0$
, it is easy to check that
![]() $(1-\tau ) (\Lambda ^*_\tau )=\Lambda _\tau $
. It follows that
$(1-\tau ) (\Lambda ^*_\tau )=\Lambda _\tau $
. It follows that
![]() $\det (\Lambda ^{\tau })=\det (\Lambda _\tau )=\prod m^{a_m}$
, where
$\det (\Lambda ^{\tau })=\det (\Lambda _\tau )=\prod m^{a_m}$
, where
![]() $\prod m^{a_m}$
is the frame shape of
$\prod m^{a_m}$
is the frame shape of
![]() $\tau $
. The result then follows by a direct calculation (cf. Table 1 in Section 6).
$\tau $
. The result then follows by a direct calculation (cf. Table 1 in Section 6).
Table 1 Conjugacy classes of
![]() $\tau \in Co.0$
with
$\tau \in Co.0$
with
![]() $\dim\, \Lambda ^\tau \geq 4$
.
$\dim\, \Lambda ^\tau \geq 4$
.

Below is one of our key observations. This fact is probably well-known to the experts and it also holds for some other isometries in
![]() $Co.0$
(e.g.,
$Co.0$
(e.g.,
![]() $14B$
).
$14B$
).
Theorem 4.2. If
![]() $\tau \in \mathcal{P}_0$
, then there is an isometry
$\tau \in \mathcal{P}_0$
, then there is an isometry
where
![]() $\ell =|\widehat {\tau }|$
.
$\ell =|\widehat {\tau }|$
.
Remark 4.3. It is known that
![]() $\ell =|\tau |$
or
$\ell =|\tau |$
or
![]() $2|\tau |$
and
$2|\tau |$
and
![]() $\ell =2|\tau |$
if and only if
$\ell =2|\tau |$
if and only if
![]() $<\tau>$
contains a
$<\tau>$
contains a
![]() $2C$
-element, see [Reference Borcherds2].
$2C$
-element, see [Reference Borcherds2].
In [Reference Harada and Lang20], Harada and Lang have determined the structure of
![]() $\Lambda ^{\tau }$
for
$\Lambda ^{\tau }$
for
![]() $\tau \in Co.0$
. In particular, the Gram matrix for the lattice
$\tau \in Co.0$
. In particular, the Gram matrix for the lattice
![]() $\Lambda ^\tau $
has been given explicitly. It is straightforward to check that Theorem 4.2 holds for
$\Lambda ^\tau $
has been given explicitly. It is straightforward to check that Theorem 4.2 holds for
Note that the Gram matrix of the dual lattice
![]() $L^*$
is equal to the inverse of the Gram matrix of L. Therefore, it suffices to check that the Gram matrix of
$L^*$
is equal to the inverse of the Gram matrix of L. Therefore, it suffices to check that the Gram matrix of
![]() $\Lambda ^\tau $
is equal to
$\Lambda ^\tau $
is equal to
![]() $\ell $
times the Gram matrix of
$\ell $
times the Gram matrix of
![]() $(\Lambda ^\tau )^*$
for any
$(\Lambda ^\tau )^*$
for any
![]() $\tau \in \mathcal{P}_0$
.
$\tau \in \mathcal{P}_0$
.
Remark 4.4. Let
![]() $\widehat {\tau }$
be a standard lift of
$\widehat {\tau }$
be a standard lift of
![]() $\tau $
in
$\tau $
in
![]() $\mathrm {Aut}(V_\Lambda )$
and let
$\mathrm {Aut}(V_\Lambda )$
and let
![]() $\phi (\tau )$
be the conformal weight of the irreducible
$\phi (\tau )$
be the conformal weight of the irreducible
![]() $\widehat {\tau }$
-twisted module of
$\widehat {\tau }$
-twisted module of
![]() $V_\Lambda $
. By direct calculations, it is straightforward to verify that for any
$V_\Lambda $
. By direct calculations, it is straightforward to verify that for any
![]() $\tau \in \mathcal{P}_0$
, we have
$\tau \in \mathcal{P}_0$
, we have
In other words,
![]() $\widehat {\tau ^m}$
is of type
$\widehat {\tau ^m}$
is of type
![]() $0$
for any
$0$
for any
![]() $\tau \in \mathcal{P}_0$
and
$\tau \in \mathcal{P}_0$
and
![]() $m \in {\mathbb Z}$
as defined in [Reference van Ekeren, Möller and Scheithauer17].
$m \in {\mathbb Z}$
as defined in [Reference van Ekeren, Möller and Scheithauer17].
4.2 Reverse automorphisms and associated Niemeier lattices
From now on, we assume that
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
is the reverse automorphism associated with an orbifold construction defined by a W-element and assume that
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
is the reverse automorphism associated with an orbifold construction defined by a W-element and assume that
![]() $\tau \in \mathcal{P}_0$
and
$\tau \in \mathcal{P}_0$
and
![]() $\tau (\beta )=\beta $
.
$\tau (\beta )=\beta $
.
First, we discuss some relations between the lattice L discussed in Section 2 and the fixed point sublattice
![]() $\Lambda ^\tau $
of the Leech lattice.
$\Lambda ^\tau $
of the Leech lattice.
Notation 4.5. Let X be an even lattice and let
![]() $\beta \in {\mathbb Q} \otimes _{\mathbb Z} X$
. Denote
$\beta \in {\mathbb Q} \otimes _{\mathbb Z} X$
. Denote
Suppose that
![]() $\langle \beta ,\beta \rangle =2k/n$
for some positive integers k and n with
$\langle \beta ,\beta \rangle =2k/n$
for some positive integers k and n with
![]() $GCD(k,n)=1$
. Let
$GCD(k,n)=1$
. Let
![]() $\bar {X}=\{x\in X\mid \langle x,n \beta \rangle \in {\mathbb Z}\}$
. For
$\bar {X}=\{x\in X\mid \langle x,n \beta \rangle \in {\mathbb Z}\}$
. For
![]() $x\in \bar {X}$
, we define
$x\in \bar {X}$
, we define
![]() $x_{[\beta ]} = x- m\beta $
if
$x_{[\beta ]} = x- m\beta $
if
![]() $\langle x, n\beta \rangle \equiv mk \mod n$
,
$\langle x, n\beta \rangle \equiv mk \mod n$
,
![]() $0\leq m\leq n-1$
and
$0\leq m\leq n-1$
and
![]() $\bar {X}_{[\beta ]} = \{ x_{[\beta ]}\mid x \in \bar {X}\}$
. Then
$\bar {X}_{[\beta ]} = \{ x_{[\beta ]}\mid x \in \bar {X}\}$
. Then
![]() $\bar {X}_{[\beta ]}$
is also an even lattice and
$\bar {X}_{[\beta ]}$
is also an even lattice and
![]() $\det (\bar {X})=\det (\bar {X}_{[\beta ]})$
.
$\det (\bar {X})=\det (\bar {X}_{[\beta ]})$
.
Recall that
![]() $\langle \alpha , \alpha \rangle =2K_0/N_0$
and
$\langle \alpha , \alpha \rangle =2K_0/N_0$
and
![]() $N_0\alpha \in L^*$
for a W-element
$N_0\alpha \in L^*$
for a W-element
![]() $\alpha $
(cf. Proposition 2.4). Thus, we have
$\alpha $
(cf. Proposition 2.4). Thus, we have
![]() $\bar {L}=L$
. Since
$\bar {L}=L$
. Since
![]() $V^{[g]}\cong V_\Lambda $
, we have
$V^{[g]}\cong V_\Lambda $
, we have
![]() $V^g \cong (V_\Lambda )^{\tilde {g}}$
and
$V^g \cong (V_\Lambda )^{\tilde {g}}$
and
It implies
![]() $L_\alpha \cong \Lambda ^\tau _\beta $
. Moreover,
$L_\alpha \cong \Lambda ^\tau _\beta $
. Moreover,
![]() $\Lambda ^\tau = L_{[\alpha ]}+ {\mathbb Z} N_0\alpha $
.
$\Lambda ^\tau = L_{[\alpha ]}+ {\mathbb Z} N_0\alpha $
.
Now consider the irreducible
![]() $\tilde {g}$
-twisted module
$\tilde {g}$
-twisted module
Since
![]() $(V_\Lambda [\tilde {g}])_{\mathbb Z} \neq 0$
and
$(V_\Lambda [\tilde {g}])_{\mathbb Z} \neq 0$
and
![]() $\phi (\tau )=1-1/|\widehat {\tau }|$
for
$\phi (\tau )=1-1/|\widehat {\tau }|$
for
![]() $\tau \in \mathcal{P}_0$
, there exists
$\tau \in \mathcal{P}_0$
, there exists
![]() $\beta '\in -\beta +(\Lambda ^\tau )^*$
such that
$\beta '\in -\beta +(\Lambda ^\tau )^*$
such that
![]() $\langle \beta ', \beta '\rangle / 2\equiv 1/|\widehat {\tau }| \mod {\mathbb Z}$
. Without loss of generality, we may assume
$\langle \beta ', \beta '\rangle / 2\equiv 1/|\widehat {\tau }| \mod {\mathbb Z}$
. Without loss of generality, we may assume
![]() $\beta = -\beta '$
. In this case,
$\beta = -\beta '$
. In this case,
![]() $\beta \in L^*$
. By a general result (cf. [Reference Höhn21; Reference Lam25]), we also have
$\beta \in L^*$
. By a general result (cf. [Reference Höhn21; Reference Lam25]), we also have
(1)
![]() $(\mathcal {D}(L), q)\cong (\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), -q')$
as quadratic spaces;
$(\mathcal {D}(L), q)\cong (\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), -q')$
as quadratic spaces;
(2)
![]() $\det (L) = \det (\Lambda ^\tau ) \times |\tau |^2$
.
$\det (L) = \det (\Lambda ^\tau ) \times |\tau |^2$
.
The quadratic space structure of
![]() $(\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), q')$
has also been determined in [Reference Lam25]. In particular, it has proved that the exponent of
$(\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), q')$
has also been determined in [Reference Lam25]. In particular, it has proved that the exponent of
![]() $L^*/L$
is
$L^*/L$
is
![]() $\ell =|\widehat {\tau }|$
and
$\ell =|\widehat {\tau }|$
and
![]() $q(L^*)\subset \frac {1}{\ell }{\mathbb Z}$
. Thus, we have the following lemma.
$q(L^*)\subset \frac {1}{\ell }{\mathbb Z}$
. Thus, we have the following lemma.
Lemma 4.6. We have
![]() $\ell \beta \in L$
and
$\ell \beta \in L$
and
![]() $L = \Lambda _\beta ^\tau + {\mathbb Z} \ell \beta $
. Moreover,
$L = \Lambda _\beta ^\tau + {\mathbb Z} \ell \beta $
. Moreover,
![]() $\sqrt {\ell } L^*$
is an even lattice.
$\sqrt {\ell } L^*$
is an even lattice.
By Theorem 4.2, there is an isometry
![]() $\varphi =\varphi _\tau : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $
with
$\varphi =\varphi _\tau : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $
with
![]() $\ell =|\widehat {\tau }|$
and it induces an isometry from
$\ell =|\widehat {\tau }|$
and it induces an isometry from
![]() ${\mathbb C} \Lambda ^{\tau } \to {\mathbb C} \Lambda ^{\tau }$
.
${\mathbb C} \Lambda ^{\tau } \to {\mathbb C} \Lambda ^{\tau }$
.
Definition 4.7. Set
![]() $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
and
$\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
and
![]() $N= \Lambda ^{[\tilde {\beta }]} := \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
.
$N= \Lambda ^{[\tilde {\beta }]} := \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
.
By our assumption,
![]() $\langle \tilde {\beta }, \tilde {\beta }\rangle \in 2{\mathbb Z}$
and N is an even unimodular lattice.
$\langle \tilde {\beta }, \tilde {\beta }\rangle \in 2{\mathbb Z}$
and N is an even unimodular lattice.
Theorem 4.8. Let
![]() $n=|g|=|\tilde {g}|$
. Suppose
$n=|g|=|\tilde {g}|$
. Suppose
![]() $m\varphi (\sqrt {\ell }\beta )\in \Lambda $
. Then we have
$m\varphi (\sqrt {\ell }\beta )\in \Lambda $
. Then we have
![]() $n|m$
. Moreover,
$n|m$
. Moreover,
![]() $[ \Lambda ^{[\tilde {\beta }]}: \Lambda _{\tilde {\beta }}]=n$
.
$[ \Lambda ^{[\tilde {\beta }]}: \Lambda _{\tilde {\beta }}]=n$
.
Proof. If
![]() $m\varphi (\sqrt {\ell }\beta )\in \Lambda $
, then
$m\varphi (\sqrt {\ell }\beta )\in \Lambda $
, then
![]() $m\varphi (\sqrt {\ell }\beta )\in \Lambda ^{\tau }=\varphi (\sqrt {\ell }(\Lambda ^{\tau })^*)$
, which is equivalent to
$m\varphi (\sqrt {\ell }\beta )\in \Lambda ^{\tau }=\varphi (\sqrt {\ell }(\Lambda ^{\tau })^*)$
, which is equivalent to
![]() $m\sqrt {\ell }\beta \in \sqrt {\ell }(\Lambda ^{\tau })^{\ast }$
(or equivalently,
$m\sqrt {\ell }\beta \in \sqrt {\ell }(\Lambda ^{\tau })^{\ast }$
(or equivalently,
![]() $m\beta \in (\Lambda ^{\tau })^{\ast }$
).
$m\beta \in (\Lambda ^{\tau })^{\ast }$
).
Since
![]() $[\Lambda ^\tau : \Lambda ^\tau _\beta ]=n ( = [ (\Lambda ^\tau _\beta )^* : (\Lambda ^\tau )^*]) $
and
$[\Lambda ^\tau : \Lambda ^\tau _\beta ]=n ( = [ (\Lambda ^\tau _\beta )^* : (\Lambda ^\tau )^*]) $
and
![]() $(\Lambda ^\tau _\beta )^* = (\Lambda ^\tau )^* +{\mathbb Z} \beta $
,
$(\Lambda ^\tau _\beta )^* = (\Lambda ^\tau )^* +{\mathbb Z} \beta $
,
![]() $m\beta \in (\Lambda ^{\tau })^{\ast }$
implies n divides m.
$m\beta \in (\Lambda ^{\tau })^{\ast }$
implies n divides m.
For the second statement, it suffices to show
![]() $n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $
. Let
$n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $
. Let
![]() $k=|\tau |$
. Then
$k=|\tau |$
. Then
![]() $\widehat {\tau }^k = \exp (2\pi i\delta (0))$
for some
$\widehat {\tau }^k = \exp (2\pi i\delta (0))$
for some
![]() $\delta \in {\mathbb C} \Lambda ^\tau $
. Since
$\delta \in {\mathbb C} \Lambda ^\tau $
. Since
![]() $n=|\tau | N_0=kN_0$
and
$n=|\tau | N_0=kN_0$
and
![]() $\tilde {g}^n= \widehat {\tau }^n\exp (2\pi i\beta (0))^n=1$
, we have
$\tilde {g}^n= \widehat {\tau }^n\exp (2\pi i\beta (0))^n=1$
, we have
![]() $n\beta -N_0 \delta \in \Lambda ^\tau $
.
$n\beta -N_0 \delta \in \Lambda ^\tau $
.
As
![]() $\widehat {\tau }$
is a standard lift,
$\widehat {\tau }$
is a standard lift,
![]() $\widehat {\tau }(e^\gamma )=e^\gamma $
for any
$\widehat {\tau }(e^\gamma )=e^\gamma $
for any
![]() $\gamma \in \Lambda ^\tau $
. Thus,
$\gamma \in \Lambda ^\tau $
. Thus,
![]() $\langle \delta , \Lambda ^\tau \rangle \subset {\mathbb Z}$
and
$\langle \delta , \Lambda ^\tau \rangle \subset {\mathbb Z}$
and
![]() $\delta \in (\Lambda ^\tau )^*$
. By using the isometry
$\delta \in (\Lambda ^\tau )^*$
. By using the isometry
![]() $\varphi $
, we have
$\varphi $
, we have
![]() $n\sqrt {\ell } \varphi (\beta ) - N_0 \sqrt {\ell } \varphi (\delta ) \in \sqrt {\ell } \varphi (\Lambda ^\tau ) < \sqrt {\ell } \varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $
. Since
$n\sqrt {\ell } \varphi (\beta ) - N_0 \sqrt {\ell } \varphi (\delta ) \in \sqrt {\ell } \varphi (\Lambda ^\tau ) < \sqrt {\ell } \varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $
. Since
![]() $\delta \in (\Lambda ^\tau )^*$
, we have
$\delta \in (\Lambda ^\tau )^*$
, we have
![]() $\sqrt {\ell } \varphi (\delta ) \in \Lambda ^\tau $
and
$\sqrt {\ell } \varphi (\delta ) \in \Lambda ^\tau $
and
![]() $n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $
as desired.
$n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $
as desired.
Theorem 4.9. Let
![]() $N= \Lambda ^{[\tilde {\beta }]} = \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
. Then
$N= \Lambda ^{[\tilde {\beta }]} = \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
. Then
![]() $\varphi $
induces an isometry from
$\varphi $
induces an isometry from
![]() $\sqrt {\ell }L^*$
to
$\sqrt {\ell }L^*$
to
![]() $N^\tau $
. In particular, we have
$N^\tau $
. In particular, we have
![]() $N^\tau \cong \sqrt {\ell }L^*$
.
$N^\tau \cong \sqrt {\ell }L^*$
.
Proof. Since
![]() $\tau $
fixes
$\tau $
fixes
![]() $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
, we may assume that
$\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
, we may assume that
![]() $\tau $
acts on
$\tau $
acts on
![]() $N=\Lambda ^{[\tilde {\beta }]}$
and
$N=\Lambda ^{[\tilde {\beta }]}$
and
![]() $N^\tau = \Lambda ^\tau _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$
. Note also that
$N^\tau = \Lambda ^\tau _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$
. Note also that
![]() $\langle \beta , \beta \rangle \in (2/\ell ) {\mathbb Z}$
.
$\langle \beta , \beta \rangle \in (2/\ell ) {\mathbb Z}$
.
By Lemma 4.6, we have
![]() $L= \Lambda _\beta ^\tau +{\mathbb Z} \ell \beta $
. Thus,
$L= \Lambda _\beta ^\tau +{\mathbb Z} \ell \beta $
. Thus,
 $$ \begin{align*} L^* & = \{ x\in (\Lambda_\beta^\tau)^*\mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ &= \{ x\in (\Lambda^\tau)^*+{\mathbb Z} \beta \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ & = < \{ x\in (\Lambda^\tau)^* \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}, \beta>. \end{align*} $$
$$ \begin{align*} L^* & = \{ x\in (\Lambda_\beta^\tau)^*\mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ &= \{ x\in (\Lambda^\tau)^*+{\mathbb Z} \beta \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ & = < \{ x\in (\Lambda^\tau)^* \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}, \beta>. \end{align*} $$
Then
 $$ \begin{align*} \sqrt{\ell} \varphi(L^*) & = < \{ \sqrt{\ell} \varphi(x) \in \sqrt{\ell} \varphi(\Lambda^\tau)^*\mid \langle \sqrt{\ell} \varphi(x) , \sqrt{\ell} \varphi(\beta) \rangle \in {\mathbb Z}\}, \sqrt{\ell} \varphi( \beta)>\\ &=< \{ y\in \Lambda^\tau \mid \langle y, \tilde{\beta} \rangle \in {\mathbb Z}\} , \tilde{\beta}>\\ &= \Lambda^\tau_{\tilde{\beta}} +{\mathbb Z} \tilde{\beta} = N^\tau \end{align*} $$
$$ \begin{align*} \sqrt{\ell} \varphi(L^*) & = < \{ \sqrt{\ell} \varphi(x) \in \sqrt{\ell} \varphi(\Lambda^\tau)^*\mid \langle \sqrt{\ell} \varphi(x) , \sqrt{\ell} \varphi(\beta) \rangle \in {\mathbb Z}\}, \sqrt{\ell} \varphi( \beta)>\\ &=< \{ y\in \Lambda^\tau \mid \langle y, \tilde{\beta} \rangle \in {\mathbb Z}\} , \tilde{\beta}>\\ &= \Lambda^\tau_{\tilde{\beta}} +{\mathbb Z} \tilde{\beta} = N^\tau \end{align*} $$
as desired.
Lemma 4.10. Under the above conditions, we have
![]() $\Lambda ^{[\varphi (\sqrt {\ell }\beta )]}\not \cong \Lambda $
.
$\Lambda ^{[\varphi (\sqrt {\ell }\beta )]}\not \cong \Lambda $
.
Proof. Since
![]() $\tau $
fixes
$\tau $
fixes
![]() $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
, we may assume that
$\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
, we may assume that
![]() $\tau $
acts on
$\tau $
acts on
![]() $N=\Lambda ^{[\tilde {\beta }]}$
. Then
$N=\Lambda ^{[\tilde {\beta }]}$
. Then
![]() $\tau $
induces an isometry
$\tau $
induces an isometry
![]() $\tau '$
of
$\tau '$
of
![]() $N=\Lambda ^{[\tilde {\beta }]}$
.
$N=\Lambda ^{[\tilde {\beta }]}$
.
Suppose
![]() $N \cong \Lambda $
. Since all elements in
$N \cong \Lambda $
. Since all elements in
![]() $O(\Lambda )$
are determined by its frame shape up to conjugate, we may assume
$O(\Lambda )$
are determined by its frame shape up to conjugate, we may assume
![]() $\tau '$
is conjugate to
$\tau '$
is conjugate to
![]() $\tau $
. In particular,
$\tau $
. In particular,
![]() $N^{\tau '}$
is isometric to
$N^{\tau '}$
is isometric to
![]() $\Lambda ^{\tau }$
and so
$\Lambda ^{\tau }$
and so
![]() $\sqrt {\ell }(N^{\tau '})^{\ast } \cong N^{\tau '}$
. By Theorem 4.9,
$\sqrt {\ell }(N^{\tau '})^{\ast } \cong N^{\tau '}$
. By Theorem 4.9,
![]() $N^{\tau '}\cong \sqrt {\ell }L^{\ast }$
and so
$N^{\tau '}\cong \sqrt {\ell }L^{\ast }$
and so
![]() $(N^{\tau })^{\ast }= \frac {1}{\sqrt {\ell }}L$
. Then
$(N^{\tau })^{\ast }= \frac {1}{\sqrt {\ell }}L$
. Then
![]() $\Lambda ^{\tau } \cong \sqrt {\ell }(\Lambda ^{\tau })^{\ast }\cong \sqrt {\ell }(N^{\tau '})^{\ast }\cong L$
. It is not possible since
$\Lambda ^{\tau } \cong \sqrt {\ell }(\Lambda ^{\tau })^{\ast }\cong \sqrt {\ell }(N^{\tau '})^{\ast }\cong L$
. It is not possible since
![]() $\det (L)=\det (\Lambda ^{\tau }). |\tau |^2$
.
$\det (L)=\det (\Lambda ^{\tau }). |\tau |^2$
.
As a consequence of the above lemma and Theorem 4.8, we have the following lemma.
Lemma 4.11. Let h be the Coxeter number of
![]() $N= \Lambda ^{[\varphi (\sqrt {\ell }\beta )]}$
and
$N= \Lambda ^{[\varphi (\sqrt {\ell }\beta )]}$
and
![]() $n= |g|=|\tilde {g}|$
. Then we have
$n= |g|=|\tilde {g}|$
. Then we have
![]() $n \geq h$
.
$n \geq h$
.
4.3 Roots of
 $V_1$
$V_1$
Next we study the structure of the root lattice of
![]() $V_1$
. Let
$V_1$
. Let
![]() $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
. If
$V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$
. If
![]() $u\in L^*$
is a root of
$u\in L^*$
is a root of
![]() $\mathcal{G}_j$
, then
$\mathcal{G}_j$
, then
 $$\begin{align*}\langle u,u\rangle= \begin{cases} \frac{2}{k_j} & \text{ if } u \text{ is a long root,}\\ \frac{2}{r_{j}k_j} & \text{ if } u \text{ is a short root.} \end{cases} \end{align*}$$
$$\begin{align*}\langle u,u\rangle= \begin{cases} \frac{2}{k_j} & \text{ if } u \text{ is a long root,}\\ \frac{2}{r_{j}k_j} & \text{ if } u \text{ is a short root.} \end{cases} \end{align*}$$
As a corollary of
![]() $\ell $
-duality, we have the following:
$\ell $
-duality, we have the following:
Lemma 4.12.
![]() $|\tau |(K_0-N_0)$
divides
$|\tau |(K_0-N_0)$
divides
![]() $\ell $
.
$\ell $
.
Proof. Let
![]() $ e^u \otimes t \in \mathcal{G}_{j,k_j}$
be a short root vector. Then
$ e^u \otimes t \in \mathcal{G}_{j,k_j}$
be a short root vector. Then
![]() $\langle u,u\rangle =\frac {2}{r_jk_j}$
and we have
$\langle u,u\rangle =\frac {2}{r_jk_j}$
and we have
 $$ \begin{align*}\langle u,u\rangle=\frac{2}{r_jk_j}=\frac{2}{r_jh_j^{\vee}} \times \frac{h_j^{\vee}}{k_j} =\frac{2}{r_jh_j^{\vee}}\times \frac{N_0}{K_0-N_0}.\end{align*} $$
$$ \begin{align*}\langle u,u\rangle=\frac{2}{r_jk_j}=\frac{2}{r_jh_j^{\vee}} \times \frac{h_j^{\vee}}{k_j} =\frac{2}{r_jh_j^{\vee}}\times \frac{N_0}{K_0-N_0}.\end{align*} $$
Since
![]() $\langle u,u\rangle \in \frac {{\mathbb Z}}{\ell }$
and
$\langle u,u\rangle \in \frac {{\mathbb Z}}{\ell }$
and
![]() $\mathrm {LCM}(\{r_jh_j^{\vee }/N_0:j\})=|\tau |$
, we have that
$\mathrm {LCM}(\{r_jh_j^{\vee }/N_0:j\})=|\tau |$
, we have that
![]() $K_0-N_0$
divides
$K_0-N_0$
divides
![]() $\ell /|\tau |$
.
$\ell /|\tau |$
.
Remark 4.13. Let
![]() $ e^u \otimes t \in \mathcal{G}_{j,k_j}$
be a root vector associated with a simple short root. Then
$ e^u \otimes t \in \mathcal{G}_{j,k_j}$
be a root vector associated with a simple short root. Then
![]() $\langle \alpha ,u\rangle =\frac {1}{r_jh_j^\vee }$
and
$\langle \alpha ,u\rangle =\frac {1}{r_jh_j^\vee }$
and
![]() $e^u\otimes t$
belongs to
$e^u\otimes t$
belongs to
![]() $\tilde {g}^{s_j}$
-twisted modules, where
$\tilde {g}^{s_j}$
-twisted modules, where
![]() $s_jr_jh^{\vee }_j=n$
. More precisely, it belongs to
$s_jr_jh^{\vee }_j=n$
. More precisely, it belongs to
![]() $s_j$
-power of
$s_j$
-power of
![]() $\tilde {g}$
-twisted module
$\tilde {g}$
-twisted module
![]() $T^1$
by fusion products.
$T^1$
by fusion products.
Lemma 4.14. Suppose there is j such that
![]() $r_jh^{\vee }_j=n=|\tau |N_0$
. Then there is a root
$r_jh^{\vee }_j=n=|\tau |N_0$
. Then there is a root
![]() $u\in L^*$
of
$u\in L^*$
of
![]() $\mathcal{G}_j$
such that
$\mathcal{G}_j$
such that
![]() $\langle u, u\rangle =2/\ell $
.
$\langle u, u\rangle =2/\ell $
.
Proof. Let u be a simple short root of
![]() $\mathcal{G}_j$
. Since
$\mathcal{G}_j$
. Since
![]() $r_jh^{\vee }_j=n=|\tau |N_0$
, we have
$r_jh^{\vee }_j=n=|\tau |N_0$
, we have
![]() $\langle u, u\rangle = \frac {2}{|\tau |(K_0-N_0)}$
and
$\langle u, u\rangle = \frac {2}{|\tau |(K_0-N_0)}$
and
![]() $e^u \otimes t \in T^1_1$
. It implies
$e^u \otimes t \in T^1_1$
. It implies
![]() $\langle u,u\rangle /2 \in 1/\ell +{\mathbb Z}$
. Note also that
$\langle u,u\rangle /2 \in 1/\ell +{\mathbb Z}$
. Note also that
![]() $\ell / |\tau |= 1$
or
$\ell / |\tau |= 1$
or
![]() $2$
and
$2$
and
![]() $ |\tau |(K_0-N_0)$
divides
$ |\tau |(K_0-N_0)$
divides
![]() $\ell $
. Therefore,
$\ell $
. Therefore,
![]() $\ell = |\tau |(K_0-N_0)$
and
$\ell = |\tau |(K_0-N_0)$
and
![]() $\langle u,u\rangle =2/\ell $
.
$\langle u,u\rangle =2/\ell $
.
Definition 4.15. We call a root
![]() $\delta $
of
$\delta $
of
![]() $V_1$
satisfying
$V_1$
satisfying
![]() $\langle \delta ,\delta \rangle =\frac {2}{\ell }$
a shortest root and call a simple component
$\langle \delta ,\delta \rangle =\frac {2}{\ell }$
a shortest root and call a simple component
![]() $\mathcal{G}_j$
of
$\mathcal{G}_j$
of
![]() $V_1$
containing a shortest root a full component. Note that a shortest root exists if
$V_1$
containing a shortest root a full component. Note that a shortest root exists if
![]() $r_jh_j^{\vee }=n$
for some j.
$r_jh_j^{\vee }=n$
for some j.
5 Deep holes
Let V be a holomorphic VOA of central charge
![]() $24$
and
$24$
and
![]() $\alpha $
a W-element of
$\alpha $
a W-element of
![]() $V_1$
. Let
$V_1$
. Let
![]() $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
and let
$g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
and let
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism of g, where
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism of g, where
![]() $\beta \in {\mathbb C}\Lambda ^{\tau }$
.
$\beta \in {\mathbb C}\Lambda ^{\tau }$
.
In this section, we assume that
![]() $\tau \in \mathcal{P}_0$
and try to relate the automorphism
$\tau \in \mathcal{P}_0$
and try to relate the automorphism
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i \beta (0)\in \mathrm {Aut}(V_\Lambda )$
to a deep hole of the Leech lattice. In Section 6, we will prove that
$\tilde {g}=\widehat {\tau }\exp (2\pi i \beta (0)\in \mathrm {Aut}(V_\Lambda )$
to a deep hole of the Leech lattice. In Section 6, we will prove that
![]() $\tau \in \mathcal{P}_0$
.
$\tau \in \mathcal{P}_0$
.
Since
![]() $\tau \in \mathcal{P}_0$
, there is an isometry
$\tau \in \mathcal{P}_0$
, there is an isometry
![]() $\varphi : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $
. Set
$\varphi : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $
. Set
![]() $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
and
$\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$
and
![]() $N=\Lambda ^{[\tilde {\beta }]}= \Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
. Note that
$N=\Lambda ^{[\tilde {\beta }]}= \Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
. Note that
![]() $\langle \beta ,\beta \rangle \in 2{\mathbb Z}/\ell $
and
$\langle \beta ,\beta \rangle \in 2{\mathbb Z}/\ell $
and
![]() $\langle \tilde {\beta },\tilde {\beta }\rangle \in 2{\mathbb Z}$
. Moreover, the root sublattice R of N is nonzero by Lemma 4.10.
$\langle \tilde {\beta },\tilde {\beta }\rangle \in 2{\mathbb Z}$
. Moreover, the root sublattice R of N is nonzero by Lemma 4.10.
One of the main aims in this paper is to prove the following theorem.
Theorem 5.1. The vector
![]() $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
is a deep hole of
$\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
is a deep hole of
![]() $\Lambda $
.
$\Lambda $
.
5.1 Coinvariant sublattices
 $\Lambda _\tau $
and
$\Lambda _\tau $
and
 $N_\tau $
$N_\tau $
In this subsection, we will discuss another main observation of this article, which is related to the structure of the coinvariant sublattice
![]() $N_\tau =\{ x\in N \mid \langle x, N^\tau \rangle =0\}$
.
$N_\tau =\{ x\in N \mid \langle x, N^\tau \rangle =0\}$
.
Since
![]() $\tau $
fixes
$\tau $
fixes
![]() $\tilde {\beta }=\varphi (\sqrt {\ell } \beta )$
, we have
$\tilde {\beta }=\varphi (\sqrt {\ell } \beta )$
, we have
![]() $(\Lambda _{\tilde {\beta }})_\tau =\Lambda _{\tau }$
and
$(\Lambda _{\tilde {\beta }})_\tau =\Lambda _{\tau }$
and
![]() $N_\tau> \Lambda _\tau $
. Moreover,
$N_\tau> \Lambda _\tau $
. Moreover,
![]() $[N_\tau : \Lambda _{\tau }]=|\tau |$
because
$[N_\tau : \Lambda _{\tau }]=|\tau |$
because
![]() $\det (N_\tau )=\det (N^\tau ) =\det (\Lambda ^\tau )/ |\tau |^2=\det (\Lambda _\tau )/ |\tau |^2$
. For
$\det (N_\tau )=\det (N^\tau ) =\det (\Lambda ^\tau )/ |\tau |^2=\det (\Lambda _\tau )/ |\tau |^2$
. For
![]() $\tau \in \mathcal{P}_0$
, we note that
$\tau \in \mathcal{P}_0$
, we note that
![]() $\Lambda _\tau \cong L_B(c)$
as defined in Appendix A.
$\Lambda _\tau \cong L_B(c)$
as defined in Appendix A.
Lemma 5.2. For
![]() $\tau \in \mathcal{P}_0\setminus \{2C\}$
, we have
$\tau \in \mathcal{P}_0\setminus \{2C\}$
, we have
![]() $N_\tau \cong L_A(C)$
, where
$N_\tau \cong L_A(C)$
, where
![]() $C=\langle c\rangle $
is defined as in Table 2 in Appendix A.
$C=\langle c\rangle $
is defined as in Table 2 in Appendix A.
Proof. It follows from the fact that
![]() $\Lambda _{\tau } \cong L_B(C)$
and
$\Lambda _{\tau } \cong L_B(C)$
and
![]() $\mathcal {D}(\Lambda _{\tau })$
has only one nonzero singular element of order
$\mathcal {D}(\Lambda _{\tau })$
has only one nonzero singular element of order
![]() $|\tau |$
, up to isometry if
$|\tau |$
, up to isometry if
![]() $\tau \in \mathcal{P}_0\setminus \{2C\}$
(see Appendix A).
$\tau \in \mathcal{P}_0\setminus \{2C\}$
(see Appendix A).
Next, we consider the case when
![]() $\tau =2C$
. In this case,
$\tau =2C$
. In this case,
![]() $\Lambda _{\tau }\cong \sqrt {2}D_{12}^+$
. We use the standard model for root lattices of type D – that is,
$\Lambda _{\tau }\cong \sqrt {2}D_{12}^+$
. We use the standard model for root lattices of type D – that is,
 $$\begin{align*}D_{12}=\left \{ (x_1, \cdots, x_{12})\in {\mathbb Z}^{12}\mid \sum_{i=1}^{12} x_i =0\quad \mod 2\right\} \end{align*}$$
$$\begin{align*}D_{12}=\left \{ (x_1, \cdots, x_{12})\in {\mathbb Z}^{12}\mid \sum_{i=1}^{12} x_i =0\quad \mod 2\right\} \end{align*}$$
and
![]() $D_{12}^+ = \mathrm {Span}_{\mathbb Z}\{D_{12}, \frac {1}2 (1, \cdots , 1) \}$
. Note that
$D_{12}^+ = \mathrm {Span}_{\mathbb Z}\{D_{12}, \frac {1}2 (1, \cdots , 1) \}$
. Note that
![]() $D_{12}^+$
is an odd lattice.
$D_{12}^+$
is an odd lattice.
Lemma 5.3. For
![]() $\tau \in 2C$
, there are two classes of nonzero singular elements, up to isometry; they correspond to vectors of the form
$\tau \in 2C$
, there are two classes of nonzero singular elements, up to isometry; they correspond to vectors of the form
![]() $\sqrt {2}(1,0, \cdots , 0)$
and
$\sqrt {2}(1,0, \cdots , 0)$
and
![]() $\frac {\sqrt {2}}{2}(1^4 0^8)$
, respectively. There are two index
$\frac {\sqrt {2}}{2}(1^4 0^8)$
, respectively. There are two index
![]() $2$
overlattices of
$2$
overlattices of
![]() $\Lambda _{\tau }$
. They are isometric to
$\Lambda _{\tau }$
. They are isometric to
![]() $L_A(1^{12})\cong \sqrt {2}D_{12}^*$
or the overlattice
$L_A(1^{12})\cong \sqrt {2}D_{12}^*$
or the overlattice
![]() $\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$
, which has the root sublattice
$\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$
, which has the root sublattice
![]() $A_1^4$
.
$A_1^4$
.
Let
![]() $X=\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$
. Then
$X=\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$
. Then
 $$ \begin{align*} X^* &= \{ \alpha\in \frac{\sqrt{2}}{2} D_{12}^+\mid \langle \alpha, \frac{\sqrt{2}}{2}(1^4 0^8)\rangle \in {\mathbb Z} \}\\ & = \frac{\sqrt{2}}{2} \mathrm{Span}_{\mathbb Z}\{D_{4}+D_8, \frac{1}2(1^4 0^8) \}\cong \frac{\sqrt{2}}{2} ({\mathbb Z}^4+D_8). \end{align*} $$
$$ \begin{align*} X^* &= \{ \alpha\in \frac{\sqrt{2}}{2} D_{12}^+\mid \langle \alpha, \frac{\sqrt{2}}{2}(1^4 0^8)\rangle \in {\mathbb Z} \}\\ & = \frac{\sqrt{2}}{2} \mathrm{Span}_{\mathbb Z}\{D_{4}+D_8, \frac{1}2(1^4 0^8) \}\cong \frac{\sqrt{2}}{2} ({\mathbb Z}^4+D_8). \end{align*} $$
Therefore,
![]() $2X^* \cong A_1^4 + \sqrt {2}D_8$
. Then the quadratic form of
$2X^* \cong A_1^4 + \sqrt {2}D_8$
. Then the quadratic form of
![]() $2X^*$
is not isometric to L, which is not possible, and hence, we have the following lemma.
$2X^*$
is not isometric to L, which is not possible, and hence, we have the following lemma.
Lemma 5.4. For
![]() $\tau \in 2C$
,
$\tau \in 2C$
,
![]() $N_\tau \cong L_A(1^{12})\cong \sqrt {2}D_{12}^*$
.
$N_\tau \cong L_A(1^{12})\cong \sqrt {2}D_{12}^*$
.
As a consequence, for any
![]() $\tau \in \mathcal{P}_0$
,
$\tau \in \mathcal{P}_0$
,
![]() $N_\tau \cong L_A(c)$
as described in Appendix A. We also note that
$N_\tau \cong L_A(c)$
as described in Appendix A. We also note that
![]() $\tau $
acts on
$\tau $
acts on
![]() $L_A(c)$
as
$L_A(c)$
as
![]() $g_{\Delta ,c}$
defined in (A.4). In particular,
$g_{\Delta ,c}$
defined in (A.4). In particular,
![]() $\tau $
is contained in the Weyl group of R.
$\tau $
is contained in the Weyl group of R.
Remark 5.5. If the frame shape of
![]() $\tau $
is
$\tau $
is
![]() $\prod k^{m_k}$
, then
$\prod k^{m_k}$
, then
![]() $N_{\tau }$
contains
$N_{\tau }$
contains
![]() $\oplus A_{k-1}^{m_k}$
and
$\oplus A_{k-1}^{m_k}$
and
![]() $\tau $
acts on
$\tau $
acts on
![]() $\oplus A_{k-1}^{m_k}$
as a product of the Coxeter elements. In particular,
$\oplus A_{k-1}^{m_k}$
as a product of the Coxeter elements. In particular,
![]() $\tau $
preserves any irreducible component of the root system of N.
$\tau $
preserves any irreducible component of the root system of N.
Corollary 5.6. If
![]() $N_0=1$
, then the Coxeter number of N is greater than or equal to
$N_0=1$
, then the Coxeter number of N is greater than or equal to
![]() $|\tau |$
.
$|\tau |$
.
Proof. For
![]() $\tau \in \mathcal{P}_0$
, it is easy to check that the frame shape of
$\tau \in \mathcal{P}_0$
, it is easy to check that the frame shape of
![]() $\tau $
contains a positive power of
$\tau $
contains a positive power of
![]() $|\tau |$
. Therefore,
$|\tau |$
. Therefore,
![]() $N_{\tau }$
contains a root system
$N_{\tau }$
contains a root system
![]() $A_{|\tau |-1}$
whose Coxeter number is
$A_{|\tau |-1}$
whose Coxeter number is
![]() $|\tau |$
.
$|\tau |$
.
5.2 Affine root system and shortest roots
One important fact that we will prove is the following:
Lemma 5.7. Let
![]() $\beta \in {\mathbb C}\Lambda $
. Set
$\beta \in {\mathbb C}\Lambda $
. Set
![]() $S=\{ \lambda \in \Lambda \mid \langle \lambda -\beta ,\lambda -\beta \rangle =2\}$
. If
$S=\{ \lambda \in \Lambda \mid \langle \lambda -\beta ,\lambda -\beta \rangle =2\}$
. If
![]() $\tilde {S} =\{\lambda -\beta \mid \lambda \in S \}$
contains an affine fundamental root system, then
$\tilde {S} =\{\lambda -\beta \mid \lambda \in S \}$
contains an affine fundamental root system, then
![]() $\beta $
is a deep hole.
$\beta $
is a deep hole.
Proof. For
![]() $\lambda \in \Lambda $
, let
$\lambda \in \Lambda $
, let
![]() $\lambda ^* = (\lambda , 1, \frac {\langle \lambda ,\lambda \rangle }{2}-1)\in \Lambda +\Pi _{1,1}$
, which is called a Leech root. Set
$\lambda ^* = (\lambda , 1, \frac {\langle \lambda ,\lambda \rangle }{2}-1)\in \Lambda +\Pi _{1,1}$
, which is called a Leech root. Set
![]() $\hat {\beta }= (\beta ,1,\frac {\langle \beta ,\beta \rangle }{2})\in {\mathbb Q} (\Lambda + \Pi _{1,1})$
. Note that
$\hat {\beta }= (\beta ,1,\frac {\langle \beta ,\beta \rangle }{2})\in {\mathbb Q} (\Lambda + \Pi _{1,1})$
. Note that
![]() $\hat {\beta }$
is an isotropic vector. Then
$\hat {\beta }$
is an isotropic vector. Then
![]() $\lambda ^*-\hat {\beta } = (\lambda -\beta , 0 , \frac {\langle \lambda ,\lambda \rangle }{2}-1-\frac {\langle \beta ,\beta \rangle }{2})$
and we have
$\lambda ^*-\hat {\beta } = (\lambda -\beta , 0 , \frac {\langle \lambda ,\lambda \rangle }{2}-1-\frac {\langle \beta ,\beta \rangle }{2})$
and we have
Thus,
![]() $\langle \lambda -\beta ,\lambda -\beta \rangle =2$
if and only if
$\langle \lambda -\beta ,\lambda -\beta \rangle =2$
if and only if
![]() $\langle \lambda ^*, \hat {\beta } \rangle =0$
.
$\langle \lambda ^*, \hat {\beta } \rangle =0$
.
Suppose that
![]() $\beta $
is not a deep hole. Then there is a
$\beta $
is not a deep hole. Then there is a
![]() $\delta \in \Lambda $
such that
$\delta \in \Lambda $
such that
![]() $\langle \delta -\beta ,\delta -\beta \rangle <2$
. In this case,
$\langle \delta -\beta ,\delta -\beta \rangle <2$
. In this case,
![]() $\langle \delta ^*, \hat {\beta } \rangle>0$
. Since
$\langle \delta ^*, \hat {\beta } \rangle>0$
. Since
![]() $\delta ^{\ast }\not \in \{\lambda ^{\ast }\mid \lambda \in S\}$
and the minimal squared norm of
$\delta ^{\ast }\not \in \{\lambda ^{\ast }\mid \lambda \in S\}$
and the minimal squared norm of
![]() $\Lambda $
is
$\Lambda $
is
![]() $4$
,
$4$
,
![]() $\langle \delta ^{\ast },\lambda ^{\ast }\rangle \leq 0$
for all
$\langle \delta ^{\ast },\lambda ^{\ast }\rangle \leq 0$
for all
![]() $\lambda \in S$
. However, since
$\lambda \in S$
. However, since
![]() $\tilde {S}$
contains an affine fundamental root system, there exists a subset
$\tilde {S}$
contains an affine fundamental root system, there exists a subset
![]() $S'\subset S$
and positive real numbers
$S'\subset S$
and positive real numbers
![]() $n_{\lambda }\in {\mathbb R}_{\geq 0}$
such that
$n_{\lambda }\in {\mathbb R}_{\geq 0}$
such that
![]() $\sum _{\lambda \in S'}n_{\lambda }\lambda = m \beta $
, where
$\sum _{\lambda \in S'}n_{\lambda }\lambda = m \beta $
, where
![]() $m=\sum _{\lambda \in S'} n_{\lambda }$
. By direct calculations, we have
$m=\sum _{\lambda \in S'} n_{\lambda }$
. By direct calculations, we have
 $$ \begin{align*} \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right) &= \sum_{\lambda\in S'}n_{\lambda} \frac{\langle\lambda, \lambda\rangle -\langle \lambda-\beta, \lambda -\beta\rangle}2\\ & = \sum_{\lambda\in S'}n_{\lambda} \left( \langle\lambda, \beta\rangle -\frac{\langle \beta,\beta\rangle}2\right) =\frac{m\langle \beta, \beta\rangle}2. \end{align*} $$
$$ \begin{align*} \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right) &= \sum_{\lambda\in S'}n_{\lambda} \frac{\langle\lambda, \lambda\rangle -\langle \lambda-\beta, \lambda -\beta\rangle}2\\ & = \sum_{\lambda\in S'}n_{\lambda} \left( \langle\lambda, \beta\rangle -\frac{\langle \beta,\beta\rangle}2\right) =\frac{m\langle \beta, \beta\rangle}2. \end{align*} $$
Thus, we also have
 $$\begin{align*}\sum_{\lambda\in S'}n_{\lambda}\lambda^*= \left ( \sum_{\lambda\in S'}n_{\lambda}\lambda, \sum_{\lambda\in S'}n_{\lambda}, \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right)\right)= m \hat{\beta}, \end{align*}$$
$$\begin{align*}\sum_{\lambda\in S'}n_{\lambda}\lambda^*= \left ( \sum_{\lambda\in S'}n_{\lambda}\lambda, \sum_{\lambda\in S'}n_{\lambda}, \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right)\right)= m \hat{\beta}, \end{align*}$$
but it implies
![]() $\langle \delta ^{\ast }, \hat {\beta }\rangle \leq 0$
, which is a contradiction.
$\langle \delta ^{\ast }, \hat {\beta }\rangle \leq 0$
, which is a contradiction.
Therefore, in order to prove Theorem 5.1, it is enough to show that the Coxeter number h of N is greater than or equal to
![]() $n=|g|$
, since
$n=|g|$
, since
![]() $R_1=\{\lambda -\tilde {\beta }\mid \langle \lambda -\tilde {\beta }, \lambda -\tilde {\beta }\rangle =2, \lambda \in \Lambda _{\tilde {\beta }} \}$
will contain an affine fundamental root system in this case.
$R_1=\{\lambda -\tilde {\beta }\mid \langle \lambda -\tilde {\beta }, \lambda -\tilde {\beta }\rangle =2, \lambda \in \Lambda _{\tilde {\beta }} \}$
will contain an affine fundamental root system in this case.
5.3 Existence of shortest roots
The purpose of this subsection is to show the following proposition.
Proposition 5.8. There is a root
![]() $\delta $
of
$\delta $
of
![]() $V_1$
such that
$V_1$
such that
![]() $\langle \delta ,\delta \rangle =\frac {2}{\ell }$
.
$\langle \delta ,\delta \rangle =\frac {2}{\ell }$
.
Proof. By Lemma 4.14, it suffices to show that there is j such that
![]() $r_jh_j^\vee =n$
.
$r_jh_j^\vee =n$
.
Recall that
![]() $\mathrm {LCM}(r_jh^{\vee }_j \mid j)=n$
. If
$\mathrm {LCM}(r_jh^{\vee }_j \mid j)=n$
. If
![]() $|\tau |$
is a prime power or
$|\tau |$
is a prime power or
![]() $V_1$
is simple, then there is j such that
$V_1$
is simple, then there is j such that
![]() $r_jh_j^{\vee }=n$
. Therefore, we may assume that
$r_jh_j^{\vee }=n$
. Therefore, we may assume that
![]() $|\tau |$
is not a prime power and
$|\tau |$
is not a prime power and
![]() $\mathrm {rank}(V_1)>4$
; that is,
$\mathrm {rank}(V_1)>4$
; that is,
![]() $\tau $
is
$\tau $
is
![]() $6E=1^22^23^26^2$
or
$6E=1^22^23^26^2$
or
![]() $6G=2^36^3$
and
$6G=2^36^3$
and
![]() $\mathrm {rank}(V_1)=8$
or
$\mathrm {rank}(V_1)=8$
or
![]() $6$
. We have already shown
$6$
. We have already shown
![]() $N_0| h_j^\vee $
for all j. By Corollary 5.6, we may also assume
$N_0| h_j^\vee $
for all j. By Corollary 5.6, we may also assume
![]() $N_0\not =1$
. Suppose there is no j such that
$N_0\not =1$
. Suppose there is no j such that
![]() $r_jh_j^\vee =n=6N_0$
. Then there exist k and l such that
$r_jh_j^\vee =n=6N_0$
. Then there exist k and l such that
![]() $r_kh_k^{\vee }=3N_0$
and
$r_kh_k^{\vee }=3N_0$
and
![]() $r_lh_l^\vee =2N_0$
. If one of
$r_lh_l^\vee =2N_0$
. If one of
![]() $\mathcal{G}_j$
is of type
$\mathcal{G}_j$
is of type
![]() $G_2$
, then
$G_2$
, then
![]() $N_0=4$
and there is also a component
$N_0=4$
and there is also a component
![]() $\mathcal{G}_i$
such that
$\mathcal{G}_i$
such that
![]() $r_ih_i^{\vee }=8$
; that is,
$r_ih_i^{\vee }=8$
; that is,
![]() $\mathcal{G}_i=A_7$
, or
$\mathcal{G}_i=A_7$
, or
![]() $C_3$
. Another possible component is
$C_3$
. Another possible component is
![]() $A_3$
. Therefore, possible choices for
$A_3$
. Therefore, possible choices for
![]() $\tau $
and
$\tau $
and
![]() $V_1$
are
$V_1$
are
![]() $\tau =6E$
and
$\tau =6E$
and
![]() $V_1=G_2C_3^2$
, or
$V_1=G_2C_3^2$
, or
![]() $G_2C_3A_3$
. However, since
$G_2C_3A_3$
. However, since
![]() $\dim V_1=120\not =14+2\times 21$
nor
$\dim V_1=120\not =14+2\times 21$
nor
![]() $14+21+15$
, we have a contradiction. Therefore, there is no component of type
$14+21+15$
, we have a contradiction. Therefore, there is no component of type
![]() $G_2$
. In order to get
$G_2$
. In order to get
![]() $r_kh_k^{\vee }=3N_0$
,
$r_kh_k^{\vee }=3N_0$
,
![]() $r_k=1$
,
$r_k=1$
,
![]() $h_k^\vee =3N_0$
and
$h_k^\vee =3N_0$
and
![]() $V_1$
contains a component of type
$V_1$
contains a component of type
![]() $A_{3N_0-1}$
. Since
$A_{3N_0-1}$
. Since
![]() $N_0\not =1$
,
$N_0\not =1$
,
![]() $\mathrm {rank}(V_1)\leq 8$
and
$\mathrm {rank}(V_1)\leq 8$
and
![]() $V_1$
has a component with
$V_1$
has a component with
![]() $r_ih_i^\vee =2N_0$
, we have
$r_ih_i^\vee =2N_0$
, we have
![]() $N_0=2$
and
$N_0=2$
and
![]() $V_1=A_3+A_5$
(i.e.,
$V_1=A_3+A_5$
(i.e.,
![]() $\mathrm {rank}(V_1)=8$
and
$\mathrm {rank}(V_1)=8$
and
![]() $\tau =6E$
). However,
$\tau =6E$
). However,
![]() $\dim V_1=72\not =15+35$
, which is a contradiction. This completes the proof of Proposition 5.8.
$\dim V_1=72\not =15+35$
, which is a contradiction. This completes the proof of Proposition 5.8.
As a corollary,
![]() $(\Lambda _{\tilde {\beta }}-\tilde {\beta })_2 \not =\emptyset $
and so we may choose
$(\Lambda _{\tilde {\beta }}-\tilde {\beta })_2 \not =\emptyset $
and so we may choose
![]() $\beta $
so that
$\beta $
so that
![]() $\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. In particular,
$\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. In particular,
![]() $\tilde {\beta }$
has squared length
$\tilde {\beta }$
has squared length
![]() $2$
.
$2$
.
5.4 Proof of Theorem 5.1 (part 2)
Notation 5.9. For an even lattice K, we use
![]() $R(K)$
to denote the sublattice generated by
$R(K)$
to denote the sublattice generated by
![]() $K_2=\{a\in K\mid \langle a,a\rangle =2\}$
. A component lattice of
$K_2=\{a\in K\mid \langle a,a\rangle =2\}$
. A component lattice of
![]() $R(K)$
means a sublattice generated by an irreducible component of the roots in
$R(K)$
means a sublattice generated by an irreducible component of the roots in
![]() $K_2$
.
$K_2$
.
Lemma 5.10. Let
![]() $X\subseteq R(N^{\tau })$
be a component lattice and let
$X\subseteq R(N^{\tau })$
be a component lattice and let
![]() $\tilde {X}\subseteq R(N)$
be a component lattice containing X. If
$\tilde {X}\subseteq R(N)$
be a component lattice containing X. If
![]() $X\not =\tilde {X}$
, then
$X\not =\tilde {X}$
, then
![]() $\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$
or
$\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$
or
![]() $\tau $
acts on
$\tau $
acts on
![]() $\tilde {X}$
trivially.
$\tilde {X}$
trivially.
Proof. If
![]() $\tilde {X}\not =X$
and
$\tilde {X}\not =X$
and
![]() $\tau $
does not act on
$\tau $
does not act on
![]() $\tilde {X}$
trivially, then there are
$\tilde {X}$
trivially, then there are
![]() $\mu _1\in X$
and
$\mu _1\in X$
and
![]() $\mu _2\in \tilde {X}-\tilde {X}^{\tau }$
such that
$\mu _2\in \tilde {X}-\tilde {X}^{\tau }$
such that
![]() $\langle \mu _1,\mu _2\rangle =-1$
. Since
$\langle \mu _1,\mu _2\rangle =-1$
. Since
![]() $\mu _2\not \in N^{\tau }$
and
$\mu _2\not \in N^{\tau }$
and
![]() $\mathrm {rank}(R(N_{\tau }))=\mathrm {rank}(N_{\tau })$
(see Remark 5.5), there is a
$\mathrm {rank}(R(N_{\tau }))=\mathrm {rank}(N_{\tau })$
(see Remark 5.5), there is a
![]() $\mu _3\in R(N_{\tau })$
such that
$\mu _3\in R(N_{\tau })$
such that
![]() $\langle \mu _2,\mu _3\rangle =-1$
. Since
$\langle \mu _2,\mu _3\rangle =-1$
. Since
![]() $\mu _3\in \tilde {X}$
,
$\mu _3\in \tilde {X}$
,
![]() $\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$
, as we desired.
$\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$
, as we desired.
Now let’s start the proof of Theorem 5.1. As we explained, it is enough to show that the Coxeter number of N is greater than or equal to n.
Suppose Theorem 5.1 is false and let V be a counterexample. By Proposition 5.8, there is a simple component
![]() $\mathcal{G}_j$
of
$\mathcal{G}_j$
of
![]() $V_1$
such that
$V_1$
such that
![]() $r_jh^{\vee }_j=n$
and we may choose
$r_jh^{\vee }_j=n$
and we may choose
![]() $\langle \tilde {\beta },\tilde {\beta }\rangle =2$
, or equivalently,
$\langle \tilde {\beta },\tilde {\beta }\rangle =2$
, or equivalently,
![]() $\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. Suppose there is a full component
$\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. Suppose there is a full component
![]() $\mathcal{G}_j$
which is simply laced and let
$\mathcal{G}_j$
which is simply laced and let
![]() $L_j$
be its root lattice. Then
$L_j$
be its root lattice. Then
![]() $\sqrt {\ell }\phi (L_j)\subseteq R^{\tau }$
and so
$\sqrt {\ell }\phi (L_j)\subseteq R^{\tau }$
and so
![]() $h\geq n$
, which is a contradiction.
$h\geq n$
, which is a contradiction.
Therefore, there are no simply laced full components in
![]() $V_1$
and
$V_1$
and
![]() $\mathrm {GCD}(6,|\tau |)\not =1$
since the lacing number divides
$\mathrm {GCD}(6,|\tau |)\not =1$
since the lacing number divides
![]() $|\tau |$
. We also have
$|\tau |$
. We also have
![]() $N_0\not =1$
by Corollary 5.6. Furthermore, if
$N_0\not =1$
by Corollary 5.6. Furthermore, if
![]() $\mathrm {rank}(V_1)=4$
, then we have shown
$\mathrm {rank}(V_1)=4$
, then we have shown
![]() $N_0=1$
in [Reference Chigira, Lam and Miyamoto7] and we have a contradiction. Therefore, we may assume
$N_0=1$
in [Reference Chigira, Lam and Miyamoto7] and we have a contradiction. Therefore, we may assume
![]() $|\tau |=2,3,4,6,8$
. We will need a few lemmas.
$|\tau |=2,3,4,6,8$
. We will need a few lemmas.
Lemma 5.11. If
![]() $|\tau |=2$
, then
$|\tau |=2$
, then
![]() $N_0$
is odd.
$N_0$
is odd.
Proof. Suppose
![]() $N_0$
is even. Then
$N_0$
is even. Then
![]() $K_0$
is odd since
$K_0$
is odd since
![]() $\mathrm {GCD}(K_0,N_0)=1$
. Since
$\mathrm {GCD}(K_0,N_0)=1$
. Since
![]() $K_0-N_0=1$
or
$K_0-N_0=1$
or
![]() $2$
,
$2$
,
![]() $K_0=N_0+1$
. Since
$K_0=N_0+1$
. Since
![]() $|\tau |=2$
, there are no components of type
$|\tau |=2$
, there are no components of type
![]() $G_2$
. Moreover,
$G_2$
. Moreover,
![]() $N_0$
is even and
$N_0$
is even and
![]() $n/N_0=2$
; thus,
$n/N_0=2$
; thus,
![]() $4|n$
and there are no full components of type B and F. Therefore, the only full components of
$4|n$
and there are no full components of type B and F. Therefore, the only full components of
![]() $V_1$
are of type
$V_1$
are of type
![]() $C_{N_0-1,1}$
. Since
$C_{N_0-1,1}$
. Since
![]() $N_0$
divides the dual Coxeter numbers, the other components are of the type
$N_0$
divides the dual Coxeter numbers, the other components are of the type
![]() $A_{N_0-1}$
or
$A_{N_0-1}$
or
![]() $D_{N_0/2+1}$
. Recall that
$D_{N_0/2+1}$
. Recall that
![]() $\mathrm {rank}(\Lambda ^\tau )=12$
or
$\mathrm {rank}(\Lambda ^\tau )=12$
or
![]() $16$
and
$16$
and
![]() $N_0$
is even. By a direct calculation, it is easy to verify that the possible cases are only
$N_0$
is even. By a direct calculation, it is easy to verify that the possible cases are only
![]() $V_1=C_{3,1}^a A_{3,1}^b$
(
$V_1=C_{3,1}^a A_{3,1}^b$
(
![]() $N_0=4$
) with
$N_0=4$
) with
![]() $a+b=4$
and
$a+b=4$
and
![]() $C_7D_5$
(
$C_7D_5$
(
![]() $N_0=8$
). Since
$N_0=8$
). Since
![]() $\dim V_1=24(N_0+1)$
, none of them is possible. Note that
$\dim V_1=24(N_0+1)$
, none of them is possible. Note that
![]() $\dim C_3=21, \dim A_3=15, \dim C_7=105$
and
$\dim C_3=21, \dim A_3=15, \dim C_7=105$
and
![]() $ \dim D_5=45$
.
$ \dim D_5=45$
.
Lemma 5.12. Let V be a counterexample of Theorem 5.1. Then
![]() $\tau $
and
$\tau $
and
![]() $(V_1, N_0)$
will be one of the following:
$(V_1, N_0)$
will be one of the following:
-
(1)
 $\tau =2A=1^82^8$
and
$\tau =2A=1^82^8$
and
 $(V_1, N_0)=(C_{4}^4,5), (C_6^2B_4,7), (C_8F_4^2, 9), (C_{10}B_6, 11)$
;
$(V_1, N_0)=(C_{4}^4,5), (C_6^2B_4,7), (C_8F_4^2, 9), (C_{10}B_6, 11)$
; -
(2)
 $\tau =2C=2^{12}$
and
$\tau =2C=2^{12}$
and
 $(V_1, N_0)=(B_2^6, 5), (C_4A_4^2,5), (B_3^4,5), (B_4^3,7), (F_4A_8, 9)$
,
$(V_1, N_0)=(B_2^6, 5), (C_4A_4^2,5), (B_3^4,5), (B_4^3,7), (F_4A_8, 9)$
,
 $(B_6^2,11)$
,
$(B_6^2,11)$
,
 $(B_{12},23)$
;
$(B_{12},23)$
; -
(3)
 $\tau =4F=1^42^24^2$
and
$\tau =4F=1^42^24^2$
and
 $(V_1, N_0)=(C_{7}A_{3}, 4)$
;
$(V_1, N_0)=(C_{7}A_{3}, 4)$
; -
(4)
 $\tau =6E=1^22^23^26^2$
and
$\tau =6E=1^22^23^26^2$
and
 $(V_1, N_0)=(C_5G_2A_1,2)$
;
$(V_1, N_0)=(C_5G_2A_1,2)$
; -
(5)
 $\tau =6G=2^36^3$
and
$\tau =6G=2^36^3$
and
 $(V_1, N_0)=(F_{4}A_{2},3)$
.
$(V_1, N_0)=(F_{4}A_{2},3)$
.
Proof. Without loss of generality, we may assume that
![]() $\mathcal{G}_1$
is a full component.
$\mathcal{G}_1$
is a full component.
Case 1: If
![]() $\mathcal{G}_1=F_4$
, then
$\mathcal{G}_1=F_4$
, then
![]() $\dim F_4=52$
and
$\dim F_4=52$
and
![]() $n=18$
and so the possible choices for
$n=18$
and so the possible choices for
![]() $(\tau , \mathrm {rank}\Lambda ^{\tau },\dim V_1)$
are
$(\tau , \mathrm {rank}\Lambda ^{\tau },\dim V_1)$
are
![]() $(2A,16,240), (2C,12,132)$
,
$(2A,16,240), (2C,12,132)$
,
![]() $(6G,6,60), (6E,8,72)$
, and the possible choices for
$(6G,6,60), (6E,8,72)$
, and the possible choices for
![]() $(\mathcal{G}_j, \dim \mathcal{G}_j)$
are
$(\mathcal{G}_j, \dim \mathcal{G}_j)$
are
![]() $(F_4,52)$
,
$(F_4,52)$
,
![]() $(C_8,136)$
,
$(C_8,136)$
,
![]() $(A_8, 80)$
and
$(A_8, 80)$
and
![]() $(A_2,8)$
. Hence the possible cases are
$(A_2,8)$
. Hence the possible cases are
![]() $\tau =2A$
and
$\tau =2A$
and
![]() $V_1=F_4^2C_8$
;
$V_1=F_4^2C_8$
;
![]() $\tau =2C$
and
$\tau =2C$
and
![]() $V_1=F_4A_8$
; and
$V_1=F_4A_8$
; and
![]() $\tau =6G$
and
$\tau =6G$
and
![]() $V_1=F_4 A_2$
.
$V_1=F_4 A_2$
.
From now on, we may assume that there are no full components of type
![]() $F_4$
.
$F_4$
.
Case 2: If
![]() $\mathcal{G}_1=G_2$
, then
$\mathcal{G}_1=G_2$
, then
![]() $n=12$
and
$n=12$
and
![]() $|\tau |=3 (N_0=4, \dim V_1=120)$
or
$|\tau |=3 (N_0=4, \dim V_1=120)$
or
![]() $|\tau |=6$
(
$|\tau |=6$
(
![]() $N_0=2, \dim V_1=72$
or
$N_0=2, \dim V_1=72$
or
![]() $60$
). If
$60$
). If
![]() $|\tau |=3$
, then
$|\tau |=3$
, then
![]() $\tau =3B$
,
$\tau =3B$
,
![]() $4|h^\vee _i$
,
$4|h^\vee _i$
,
![]() $h_i^\vee < 12$
and
$h_i^\vee < 12$
and
![]() $\mathrm {rank}(\Lambda ^\tau )=12$
. Then
$\mathrm {rank}(\Lambda ^\tau )=12$
. Then
![]() $V_1=G_2^a+A_3^b$
and
$V_1=G_2^a+A_3^b$
and
![]() $2a+3b=12, \dim V_1=14a+15b=120$
, which has no solution. If
$2a+3b=12, \dim V_1=14a+15b=120$
, which has no solution. If
![]() $|\tau |=6$
, then
$|\tau |=6$
, then
![]() $V_1=G_2^a+C_5^b+A_1^c+A_3^d+A_5^e$
. Since
$V_1=G_2^a+C_5^b+A_1^c+A_3^d+A_5^e$
. Since
![]() $\dim (V_1)=60$
or
$\dim (V_1)=60$
or
![]() $72$
and
$72$
and
![]() $\mathrm {rank}(V_1) (=2a+5b+c+3d+5e) =6$
or
$\mathrm {rank}(V_1) (=2a+5b+c+3d+5e) =6$
or
![]() $8$
, the only solution is
$8$
, the only solution is
![]() $V_1=C_5G_2A_1$
.
$V_1=C_5G_2A_1$
.
From now on, we may assume that all full components are of type
![]() $C_m$
or of type
$C_m$
or of type
![]() $B_m$
.
$B_m$
.
Case 3: If
![]() $\mathcal{G}_1=C_8$
, then
$\mathcal{G}_1=C_8$
, then
![]() $n=18$
and
$n=18$
and
![]() $|\tau |=2$
or
$|\tau |=2$
or
![]() $6$
.
$6$
.
(3.1) If
![]() $|\tau |=2$
, then
$|\tau |=2$
, then
![]() $N_0=9$
, and so possible components are
$N_0=9$
, and so possible components are
![]() $C_8, B_5, A_8$
; thus,
$C_8, B_5, A_8$
; thus,
![]() $V_1=C_8^2$
or
$V_1=C_8^2$
or
![]() $C_8A_8$
but
$C_8A_8$
but
![]() $\dim (V_1)=24K_0=240$
. Neither one is possible.
$\dim (V_1)=24K_0=240$
. Neither one is possible.
(3.2) If
![]() $|\tau |=6$
, then
$|\tau |=6$
, then
![]() $N_0=3$
and
$N_0=3$
and
![]() $V_1=C_8$
, but
$V_1=C_8$
, but
![]() $\dim V_1=96\not =\dim C_8$
, a contradiction.
$\dim V_1=96\not =\dim C_8$
, a contradiction.
Case 4: If
![]() $\mathcal{G}_1=C_{2m}$
and
$\mathcal{G}_1=C_{2m}$
and
![]() $0<m\not =4$
, then
$0<m\not =4$
, then
![]() $n=2(2m+1)$
. First, we show that
$n=2(2m+1)$
. First, we show that
![]() $m<7$
. Suppose
$m<7$
. Suppose
![]() $m\geq 7$
. Then
$m\geq 7$
. Then
![]() $\mathrm {rank}(V_1)\geq \mathrm {rank}(C_{2m})\geq 14$
and so
$\mathrm {rank}(V_1)\geq \mathrm {rank}(C_{2m})\geq 14$
and so
![]() $\tau =2A$
and
$\tau =2A$
and
![]() $N_0=2m+1$
and
$N_0=2m+1$
and
![]() $m=7$
or
$m=7$
or
![]() $8$
. In this case,
$8$
. In this case,
![]() $\dim V_1=24(2m+2)$
and
$\dim V_1=24(2m+2)$
and
![]() $\dim C_{2m}=2m(4m+1)$
. If
$\dim C_{2m}=2m(4m+1)$
. If
![]() $m=7$
, then there are no components
$m=7$
, then there are no components
![]() $\mathcal{G}_j$
of rank 2 (or less than 2) with
$\mathcal{G}_j$
of rank 2 (or less than 2) with
![]() $h_j^\vee $
divisible by
$h_j^\vee $
divisible by
![]() $N_0=15$
. So,
$N_0=15$
. So,
![]() $m=8$
and
$m=8$
and
![]() $V_1=C_{16}$
; however,
$V_1=C_{16}$
; however,
![]() $\dim V_1=24(N_0+1)=24\times 18\not = \dim C_{16}=16\times 33$
.
$\dim V_1=24(N_0+1)=24\times 18\not = \dim C_{16}=16\times 33$
.
For
![]() $m<7$
and
$m<7$
and
![]() $m\neq 4$
, we have
$m\neq 4$
, we have
![]() $(2m+1,3)=1$
,
$(2m+1,3)=1$
,
![]() $N_0=2m+1$
and
$N_0=2m+1$
and
![]() $|\tau |=2$
. So, the possible components of
$|\tau |=2$
. So, the possible components of
![]() $V_1$
are
$V_1$
are
![]() $C_{2m}, A_{2m}, B_{m+1}$
. Since
$C_{2m}, A_{2m}, B_{m+1}$
. Since
![]() $K_0-N_0=1$
for
$K_0-N_0=1$
for
![]() $\tau =2A$
and
$\tau =2A$
and
![]() $K_0-N_0=2$
for
$K_0-N_0=2$
for
![]() $\tau =2C$
,
$\tau =2C$
,
![]() $\dim V_1=24(2m+2)$
for
$\dim V_1=24(2m+2)$
for
![]() $\tau =2A$
and
$\tau =2A$
and
![]() $\dim V_1=12(2m+3)$
for
$\dim V_1=12(2m+3)$
for
![]() $\tau =2C$
. If
$\tau =2C$
. If
![]() $\tau =2A$
, then by solving the relation
$\tau =2A$
, then by solving the relation
![]() $2ma+2mb+(m+1)c=16$
and
$2ma+2mb+(m+1)c=16$
and
![]() $2m(4m+1)a+2m(2m+2)b+(m+1)(2m+3)c=24(2m+2)$
and
$2m(4m+1)a+2m(2m+2)b+(m+1)(2m+3)c=24(2m+2)$
and
![]() $a>0$
and
$a>0$
and
![]() $b,c\geq 0$
, we have
$b,c\geq 0$
, we have
![]() $V_1=C_{10}B_6, C_6^2B_4, C_4^4$
.
$V_1=C_{10}B_6, C_6^2B_4, C_4^4$
.
If
![]() $\tau =2C$
, then by solving the relation
$\tau =2C$
, then by solving the relation
![]() $2ma+2mb+(m+1)c=12$
and
$2ma+2mb+(m+1)c=12$
and
![]() $2m(4m+1)a+2m(2m+2)b+(m+1)2m+3)=12(2m+3)$
, we have
$2m(4m+1)a+2m(2m+2)b+(m+1)2m+3)=12(2m+3)$
, we have
![]() $V_1=C_{4}A_{4}^2$
or
$V_1=C_{4}A_{4}^2$
or
![]() $C_{2}^6$
.
$C_{2}^6$
.
We next assume
![]() $\mathcal{G}_1=C_{2m+1}$
. Then since
$\mathcal{G}_1=C_{2m+1}$
. Then since
![]() $2m+2$
is even,
$2m+2$
is even,
![]() $|\tau |\not =2$
.
$|\tau |\not =2$
.
Case 5: If
![]() $\mathcal{G}_1=C_3$
, then
$\mathcal{G}_1=C_3$
, then
![]() $n=8$
and
$n=8$
and
![]() $|\tau |=4$
and
$|\tau |=4$
and
![]() $N_0=2$
and
$N_0=2$
and
![]() $\mathcal{G}$
is a direct sum of
$\mathcal{G}$
is a direct sum of
![]() $C_3$
or
$C_3$
or
![]() $A_1$
, or
$A_1$
, or
![]() $A_3$
. Since
$A_3$
. Since
![]() $\dim C_3=21$
,
$\dim C_3=21$
,
![]() $\dim A_3=15$
,
$\dim A_3=15$
,
![]() $\dim A_1=3$
and
$\dim A_1=3$
and
![]() $\mathrm {rank}(V_1)=10$
, it is impossible to have
$\mathrm {rank}(V_1)=10$
, it is impossible to have
![]() $\dim V_1=72$
, and we have a contradiction.
$\dim V_1=72$
, and we have a contradiction.
Case 6: If
![]() $\mathcal{G}_1=C_5$
, then
$\mathcal{G}_1=C_5$
, then
![]() $n=12$
and
$n=12$
and
![]() $(\tau ,N_0)=(4F,3),(6,2)$
. If
$(\tau ,N_0)=(4F,3),(6,2)$
. If
![]() $\tau =4F$
, then the other possible components are
$\tau =4F$
, then the other possible components are
![]() $A_2, D_4, A_5, C_2$
since there is no component of type
$A_2, D_4, A_5, C_2$
since there is no component of type
![]() $G_2$
. Since
$G_2$
. Since
![]() $\mathrm {rank}(V_1)=10$
is even, it has another component of type
$\mathrm {rank}(V_1)=10$
is even, it has another component of type
![]() $C_5$
or
$C_5$
or
![]() $A_5$
, but since
$A_5$
, but since
![]() $\dim V_1=96$
,
$\dim V_1=96$
,
![]() $\dim C_5=55$
, and
$\dim C_5=55$
, and
![]() $\dim A_5=35$
, we have a contradiction. If
$\dim A_5=35$
, we have a contradiction. If
![]() $|\tau |=6$
, then
$|\tau |=6$
, then
![]() $\mathrm {rank}(V_1)=8$
or
$\mathrm {rank}(V_1)=8$
or
![]() $6$
and possible components are
$6$
and possible components are
![]() $A_1, A_3$
. Since
$A_1, A_3$
. Since
![]() $\dim V_1=72$
or
$\dim V_1=72$
or
![]() $60$
and
$60$
and
![]() $\dim A_1=3$
,
$\dim A_1=3$
,
![]() $\dim A_3=15$
, we have a contradiction.
$\dim A_3=15$
, we have a contradiction.
Case 7: If
![]() $\mathcal{G}_1=C_7$
, then
$\mathcal{G}_1=C_7$
, then
![]() $n=16$
and
$n=16$
and
![]() $(\tau ,N_0)=(4F,4),(8,2)$
. If
$(\tau ,N_0)=(4F,4),(8,2)$
. If
![]() $N_0=2$
, then
$N_0=2$
, then
![]() $\dim V_1=72$
and
$\dim V_1=72$
and
![]() $\dim C_7=105$
, a contradiction. If
$\dim C_7=105$
, a contradiction. If
![]() $\tau =4F$
, then
$\tau =4F$
, then
![]() $N_0=4$
, and the only solution is
$N_0=4$
, and the only solution is
![]() $V_1=C_7A_3$
.
$V_1=C_7A_3$
.
Case 8: If
![]() $\mathcal{G}_1=C_{2m+1}$
and
$\mathcal{G}_1=C_{2m+1}$
and
![]() $m\geq 4$
, then
$m\geq 4$
, then
![]() $\mathrm {rank}(V_1)\geq 2m+1\geq 9$
and so
$\mathrm {rank}(V_1)\geq 2m+1\geq 9$
and so
![]() $\mathcal{G}_1=C_9$
. However, since
$\mathcal{G}_1=C_9$
. However, since
![]() $\mathrm {rank}(V_1)=10$
and
$\mathrm {rank}(V_1)=10$
and
![]() $N_0=5$
, we have a contradiction.
$N_0=5$
, we have a contradiction.
Case 9: We may assume that all full components are of type B. Say,
![]() $\mathcal{G}_1=B_m$
, then
$\mathcal{G}_1=B_m$
, then
![]() $n=2(2m-1)$
. Since
$n=2(2m-1)$
. Since
![]() $2m-1$
is odd,
$2m-1$
is odd,
![]() $|\tau |=2, 6$
.
$|\tau |=2, 6$
.
If
![]() $|\tau |=6$
, then
$|\tau |=6$
, then
![]() $N_0=1/3(2m-1)$
and
$N_0=1/3(2m-1)$
and
![]() $m\leq 8$
. Since
$m\leq 8$
. Since
![]() $N_0\neq 1$
is odd, the only possible values for
$N_0\neq 1$
is odd, the only possible values for
![]() $(N_0,m)$
are
$(N_0,m)$
are
![]() $(3,5)$
and
$(3,5)$
and
![]() $(5,8)$
. If
$(5,8)$
. If
![]() $\tau =6G$
, then
$\tau =6G$
, then
![]() $\mathrm {rank} V_1=6$
and
$\mathrm {rank} V_1=6$
and
![]() $(N_0, m)=(3,5)$
. The only possible choice for
$(N_0, m)=(3,5)$
. The only possible choice for
![]() $V_1$
is
$V_1$
is
![]() $B_5+A_1$
, but since the Coxeter number of
$B_5+A_1$
, but since the Coxeter number of
![]() $A_1$
does not divide
$A_1$
does not divide
![]() $3$
, we have a contradiction. If
$3$
, we have a contradiction. If
![]() $\tau =6E$
, then
$\tau =6E$
, then
![]() $\mathrm {rank} V_1=8$
, and the possible choice of
$\mathrm {rank} V_1=8$
, and the possible choice of
![]() $V_1$
is
$V_1$
is
![]() $B_8$
. Since
$B_8$
. Since
![]() $2C\not \in <6E>$
,
$2C\not \in <6E>$
,
![]() $K_0=N_0+1=4$
and
$K_0=N_0+1=4$
and
![]() $\dim V_1=24K_0=96\not =\dim B_8=8\times 17$
, which is a contradiction.
$\dim V_1=24K_0=96\not =\dim B_8=8\times 17$
, which is a contradiction.
Therefore, we have
![]() $|\tau |=2$
and
$|\tau |=2$
and
![]() $N_0=2m-1$
. Since
$N_0=2m-1$
. Since
![]() $2m-1$
is odd, the non-full components are all of type
$2m-1$
is odd, the non-full components are all of type
![]() $A_{2m-2}$
and so
$A_{2m-2}$
and so
![]() $V_1=B_m^{\otimes a}\oplus A_{2m-2}^{\otimes b}$
. We note
$V_1=B_m^{\otimes a}\oplus A_{2m-2}^{\otimes b}$
. We note
![]() $\dim B_m=m(2m+1)$
and
$\dim B_m=m(2m+1)$
and
![]() $\dim A_{2m-2}=4m(m-1)$
. If
$\dim A_{2m-2}=4m(m-1)$
. If
![]() $K_0=2m$
, then
$K_0=2m$
, then
![]() $am+b(2m-2)=16$
and
$am+b(2m-2)=16$
and
![]() $\dim V_1=48m=am(2m+1)+4bm(m-1)$
. It is easy to see that there is no solution for
$\dim V_1=48m=am(2m+1)+4bm(m-1)$
. It is easy to see that there is no solution for
![]() $a\in {\mathbb Z}_{> 0}$
and
$a\in {\mathbb Z}_{> 0}$
and
![]() $b\in {\mathbb Z}_{\geq 0}$
. Hence,
$b\in {\mathbb Z}_{\geq 0}$
. Hence,
![]() $K_0-N_0=2$
and
$K_0-N_0=2$
and
![]() $\tau =2C$
. In this case,
$\tau =2C$
. In this case,
![]() $am+b(2m-2)=12$
and
$am+b(2m-2)=12$
and
![]() $\dim V_1=12(2m+1)=am(2m+1)+4bm(m-1)$
. The solutions are
$\dim V_1=12(2m+1)=am(2m+1)+4bm(m-1)$
. The solutions are
![]() $b=0$
and
$b=0$
and
![]() $am=12$
; therefore,
$am=12$
; therefore,
![]() $V_1=B_2^6, B_3^4, B_4^3, B_6^2$
, or
$V_1=B_2^6, B_3^4, B_4^3, B_6^2$
, or
![]() $B_{12}$
, as we desired.
$B_{12}$
, as we desired.
This completes the proof of Lemma 5.12.
We will show that none of the Lie algebras in the list of Lemma 5.12 satisfy the desired condition, and we will get a contradiction.
First, we note that
![]() $V_1$
contains a full component of type
$V_1$
contains a full component of type
![]() $C_m$
or
$C_m$
or
![]() $F_4$
unless
$F_4$
unless
![]() $\tau =2C$
.
$\tau =2C$
.
5.4.1 The case
 $\tau \not =2C$
$\tau \not =2C$
We note the short root lattice of
![]() $C_m$
is
$C_m$
is
![]() $D_m$
. Namely, if
$D_m$
. Namely, if
![]() $C_m$
is a full component of
$C_m$
is a full component of
![]() $V_1$
, then
$V_1$
, then
![]() $D_m$
is a sublattice of
$D_m$
is a sublattice of
![]() $N^{\tau }$
. Let X be a component of the root lattice
$N^{\tau }$
. Let X be a component of the root lattice
![]() $R(N)$
of N containing the above
$R(N)$
of N containing the above
![]() $D_m$
. For
$D_m$
. For
![]() $m\geq 4$
, a lattice containing
$m\geq 4$
, a lattice containing
![]() $D_m$
is of type D or E; that is, X is of type D or E. Recall that
$D_m$
is of type D or E; that is, X is of type D or E. Recall that
![]() $n=r_jh_j^{\vee }=2(m+1)$
for
$n=r_jh_j^{\vee }=2(m+1)$
for
![]() $C_m$
and the Coxeter numbers of
$C_m$
and the Coxeter numbers of
![]() $D_m$
and
$D_m$
and
![]() $E_k$
are
$E_k$
are
![]() $2(m-1)$
and
$2(m-1)$
and
![]() $12$
,
$12$
,
![]() $18$
and
$18$
and
![]() $30$
. Since V is a counterexample, the Coxeter number of N is strictly less than n, and the possible choice of X is
$30$
. Since V is a counterexample, the Coxeter number of N is strictly less than n, and the possible choice of X is
![]() $D_m$
or
$D_m$
or
![]() $D_{m+1}$
.
$D_{m+1}$
.
Lemma 5.13. If
![]() $X=D_{m+1}$
, then
$X=D_{m+1}$
, then
![]() $\tau $
acts on X trivially. In particular, if
$\tau $
acts on X trivially. In particular, if
![]() $V_1$
is a direct sum of full components, then
$V_1$
is a direct sum of full components, then
![]() $X=D_m$
.
$X=D_m$
.
If
![]() $\tau =2A$
, then the list of lemma 5.12 says that
$\tau =2A$
, then the list of lemma 5.12 says that
![]() $V_1$
is a direct sum of full components. Therefore, if
$V_1$
is a direct sum of full components. Therefore, if
![]() $C_m$
is a full component, then
$C_m$
is a full component, then
![]() $D_m$
is a connected component of
$D_m$
is a connected component of
![]() $R(N)$
. Therefore, the possible cases are as follows:
$R(N)$
. Therefore, the possible cases are as follows:

It contradicts the fact that
![]() $N_\tau =L_A(1^8)$
.
$N_\tau =L_A(1^8)$
.
If
![]() $\tau =4F$
, then
$\tau =4F$
, then
![]() $R(N)$
contains
$R(N)$
contains
![]() $D_7 A_3^4A_1^2$
. The possible choice of
$D_7 A_3^4A_1^2$
. The possible choice of
![]() $R(N)$
is
$R(N)$
is
![]() $D_7E_6A_{11}$
or
$D_7E_6A_{11}$
or
![]() $D_8^3$
, but neither of them contains
$D_8^3$
, but neither of them contains
![]() $D_7A_3^4A_1^2$
, which is a contradiction.
$D_7A_3^4A_1^2$
, which is a contradiction.
If
![]() $\tau =6E$
, then
$\tau =6E$
, then
![]() $R(N)$
contains
$R(N)$
contains
![]() $D_5A_2A_5^2A_2^2A_1^2$
. The possible choice of
$D_5A_2A_5^2A_2^2A_1^2$
. The possible choice of
![]() $R(N)$
is
$R(N)$
is
![]() $D_5^2A_7^2$
or
$D_5^2A_7^2$
or
![]() $D_6^4$
or
$D_6^4$
or
![]() $D_6A_9^2$
, but none of them contains
$D_6A_9^2$
, but none of them contains
![]() $D_5A_5^2A_2^3A_1^2$
, which is a contradiction.
$D_5A_5^2A_2^3A_1^2$
, which is a contradiction.
If
![]() $\tau =6G=2^36^3$
, then
$\tau =6G=2^36^3$
, then
![]() $n=18$
and
$n=18$
and
![]() $V_1=F_{4,6}A_{2,2}$
. Hence, X contains
$V_1=F_{4,6}A_{2,2}$
. Hence, X contains
![]() $D_4A_5^3A_1^3$
. Since
$D_4A_5^3A_1^3$
. Since
![]() $h<18$
, the possible choice of
$h<18$
, the possible choice of
![]() $R(N)$
is
$R(N)$
is
![]() $D_4^6, D_5^2A_7^2, D_6A_9^2, D_6^4, E_6^4, A_{11}D_7E_6, D_8^3$
,
$D_4^6, D_5^2A_7^2, D_6A_9^2, D_6^4, E_6^4, A_{11}D_7E_6, D_8^3$
,
![]() $D_9A_{15}$
. However, none of them contains
$D_9A_{15}$
. However, none of them contains
![]() $D_4A_5^3A_1^3$
, which is a contradiction.
$D_4A_5^3A_1^3$
, which is a contradiction.
5.4.2 The case
 $\tau =2C$
$\tau =2C$
By the previous lemma,
![]() $V_1=B_2^6, C_4A_4^2, B_3^4,B_4^3, F_4A_8, B_6^2,$
or
$V_1=B_2^6, C_4A_4^2, B_3^4,B_4^3, F_4A_8, B_6^2,$
or
![]() $ B_{12}$
. Since
$ B_{12}$
. Since
![]() $\tau =2C$
, we have
$\tau =2C$
, we have
![]() $\ell =4$
. Since
$\ell =4$
. Since
![]() $v+v^{\tau }\in \Lambda ^{\tau }$
and
$v+v^{\tau }\in \Lambda ^{\tau }$
and
![]() $\{\frac {v+v^{\tau }}{2} \mid v\in \Lambda \}=\pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
and
$\{\frac {v+v^{\tau }}{2} \mid v\in \Lambda \}=\pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
and
![]() $\sqrt {\ell }\phi ( (\Lambda ^{\tau })^{\ast })=\Lambda ^\tau $
, we have
$\sqrt {\ell }\phi ( (\Lambda ^{\tau })^{\ast })=\Lambda ^\tau $
, we have
![]() $2(\Lambda ^{\tau })^{\ast }=\Lambda ^\tau $
; that is, we can take
$2(\Lambda ^{\tau })^{\ast }=\Lambda ^\tau $
; that is, we can take
![]() $\phi =1$
and
$\phi =1$
and
![]() $\tilde {\beta }=2\beta $
.
$\tilde {\beta }=2\beta $
.
By the reverse construction, there is a Niemeier lattice P such that
Since
![]() $N_0\not =1$
,
$N_0\not =1$
,
![]() $P\not =\Lambda $
. Set
$P\not =\Lambda $
. Set
![]() $\widehat {\tau }^2=\exp (2\pi i\delta (0))$
, which has order
$\widehat {\tau }^2=\exp (2\pi i\delta (0))$
, which has order
![]() $2$
. Therefore,
$2$
. Therefore,
Since
![]() $N_0$
is odd,
$N_0$
is odd,
![]() $(\widehat {\tau }\exp (2\pi i\beta (0)))^{2N_0}=\exp (\delta +2N_0\beta )=1$
, there is a
$(\widehat {\tau }\exp (2\pi i\beta (0)))^{2N_0}=\exp (\delta +2N_0\beta )=1$
, there is a
![]() $\mu \in \Lambda ^{\tau }$
such that
$\mu \in \Lambda ^{\tau }$
such that
![]() $\delta =2N_0\beta +\mu $
and so
$\delta =2N_0\beta +\mu $
and so
![]() $V_P=(V_{\Lambda })^{[\exp (2\pi i (N_0+1)\tilde {\beta }(0)]}$
. Note also that
$V_P=(V_{\Lambda })^{[\exp (2\pi i (N_0+1)\tilde {\beta }(0)]}$
. Note also that
![]() $V= V_P^{[\widetilde {g}]}$
and
$V= V_P^{[\widetilde {g}]}$
and
![]() $\widetilde {g}$
acts on
$\widetilde {g}$
acts on
![]() $V_P$
with order
$V_P$
with order
![]() $2$
.
$2$
.
Case
![]() $V_1=B_m^{12/m}$
:
$V_1=B_m^{12/m}$
:
We first note that all components have level
![]() $2$
and
$2$
and
![]() $V^{\exp (2\pi iN_0\alpha )}=(V_P)^{\widetilde {g}}$
; thus,
$V^{\exp (2\pi iN_0\alpha )}=(V_P)^{\widetilde {g}}$
; thus,
![]() $V_P$
contains the Lie subalgebras generated by the long roots. Since the long roots of
$V_P$
contains the Lie subalgebras generated by the long roots. Since the long roots of
![]() $B_{m}$
are of the type
$B_{m}$
are of the type
![]() $D_{m}$
,
$D_{m}$
,
![]() $(V_P)_1$
contains a Lie subalgebra of type
$(V_P)_1$
contains a Lie subalgebra of type
![]() $D_{m,2}^{\oplus (12/m)} $
and the fixed point sublattice
$D_{m,2}^{\oplus (12/m)} $
and the fixed point sublattice
![]() $P^\tau \supseteq \sqrt {2} D_{m}^{\oplus 12/m}$
. Then P must contain
$P^\tau \supseteq \sqrt {2} D_{m}^{\oplus 12/m}$
. Then P must contain
![]() $D_{m,1}^{\oplus 24/m}$
as a sublattice. Since
$D_{m,1}^{\oplus 24/m}$
as a sublattice. Since
![]() $N_0=2m-1$
and
$N_0=2m-1$
and
![]() $|\widetilde {g}^2|=N_0$
, the Coxeter number of P is less than or equal to
$|\widetilde {g}^2|=N_0$
, the Coxeter number of P is less than or equal to
![]() $2m-1$
and thus the root system of P is
$2m-1$
and thus the root system of P is
![]() $D_{m}^{\oplus 24/m}$
. Since
$D_{m}^{\oplus 24/m}$
. Since
![]() $2m-1$
is odd and
$2m-1$
is odd and
![]() $2\delta \in \Lambda $
, there is
$2\delta \in \Lambda $
, there is
![]() $\mu \in \Lambda $
such that
$\mu \in \Lambda $
such that
![]() $\delta =2(2m-1)\beta +\mu $
and
$\delta =2(2m-1)\beta +\mu $
and
![]() $4(2m-1)\beta \in \Lambda $
. Thus, we have
$4(2m-1)\beta \in \Lambda $
. Thus, we have
![]() $V_P=(V_{\Lambda })^{[4\beta ]}$
; that is, every element
$V_P=(V_{\Lambda })^{[4\beta ]}$
; that is, every element
![]() $\mu \in P$
is written
$\mu \in P$
is written
![]() $\mu =\mu _1+4s \beta $
with
$\mu =\mu _1+4s \beta $
with
![]() $\langle \mu _1,4\beta \rangle \in {\mathbb Z}$
(i.e.,
$\langle \mu _1,4\beta \rangle \in {\mathbb Z}$
(i.e.,
![]() $\mu _1\in \Lambda _{4\beta }$
). Since
$\mu _1\in \Lambda _{4\beta }$
). Since
![]() $\langle 4\beta ,2\beta \rangle \in {\mathbb Z}$
,
$\langle 4\beta ,2\beta \rangle \in {\mathbb Z}$
,
![]() $\mu _1\in \Lambda _{2\beta }$
if
$\mu _1\in \Lambda _{2\beta }$
if
![]() $\langle \mu ,2\beta \rangle \in {\mathbb Z}$
(that is,
$\langle \mu ,2\beta \rangle \in {\mathbb Z}$
(that is,
![]() $\mu \in \Lambda _{2\beta }$
).
$\mu \in \Lambda _{2\beta }$
).
Since
![]() $V_P=V^{[\widetilde {g}]}$
can be constructed by a
$V_P=V^{[\widetilde {g}]}$
can be constructed by a
![]() ${\mathbb Z}_2$
-orbifold construction, we have
${\mathbb Z}_2$
-orbifold construction, we have
by the same argument as in Theorem 4.9.
For each
![]() $B_m\subseteq V_1$
, we have a fundamental root system
$B_m\subseteq V_1$
, we have a fundamental root system
![]() $d_1,...,d_{m-1}, d_m$
with long roots
$d_1,...,d_{m-1}, d_m$
with long roots
![]() $d_j (j= 1, \dots , m-1)$
(i.e,
$d_j (j= 1, \dots , m-1)$
(i.e,
![]() $\langle d_j,\alpha \rangle =\frac {1}{2m-1}$
for
$\langle d_j,\alpha \rangle =\frac {1}{2m-1}$
for
![]() $j= 1, \dots , m-1$
and
$j= 1, \dots , m-1$
and
![]() $\langle d_m,\alpha \rangle =\frac {1}{2(2m-1)}$
). Without loss of generality, we may assume
$\langle d_m,\alpha \rangle =\frac {1}{2(2m-1)}$
). Without loss of generality, we may assume
![]() $d_m=\beta $
, which is a short root. Note also that
$d_m=\beta $
, which is a short root. Note also that
![]() $\tilde {d}_m=d_{m-1} +2d_m$
is also a long root and
$\tilde {d}_m=d_{m-1} +2d_m$
is also a long root and
![]() $\{d_1,...,d_{m-1}, \tilde {d}_m\}$
forms a fundamental root system for the long roots. Therefore, in P, we have a root sublattice of type
$\{d_1,...,d_{m-1}, \tilde {d}_m\}$
forms a fundamental root system for the long roots. Therefore, in P, we have a root sublattice of type
![]() $D_m^2$
with the fundamental system
$D_m^2$
with the fundamental system
![]() $\{a_1,\dots ,a_m\}$
and
$\{a_1,\dots ,a_m\}$
and
![]() $\{b_1,\dots ,b_m\}$
,
$\{b_1,\dots ,b_m\}$
,
 $$ \begin{align*}\begin{array}{rclrcl} a_1- \cdots - &a_{m-2}&-a_{m-1},\qquad &b_1-\cdots - &b_{m-2}& -b_{m-1} \cr & | & & &|& \cr &a_m& & &b_m& \cr \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{rclrcl} a_1- \cdots - &a_{m-2}&-a_{m-1},\qquad &b_1-\cdots - &b_{m-2}& -b_{m-1} \cr & | & & &|& \cr &a_m& & &b_m& \cr \end{array}\end{align*} $$
such that
![]() $\tau $
permutes
$\tau $
permutes
![]() $a_i$
and
$a_i$
and
![]() $b_i$
and
$b_i$
and
![]() $\frac {a_i+b_i}{2}=d_i$
for
$\frac {a_i+b_i}{2}=d_i$
for
![]() $i=1,...,m-1$
and
$i=1,...,m-1$
and
![]() $\frac {a_m+b_m}{2}=2\beta +d_{m-1}=2\beta +\frac {a_{m-1}+b_{m-1}}{2}$
. Therefore,
$\frac {a_m+b_m}{2}=2\beta +d_{m-1}=2\beta +\frac {a_{m-1}+b_{m-1}}{2}$
. Therefore,
![]() $2\beta =\frac {a_m-a_{m-1}+b_m-b_{m-1}}{2}$
and
$2\beta =\frac {a_m-a_{m-1}+b_m-b_{m-1}}{2}$
and
![]() $ \langle 2\beta , a_i \rangle \in {\mathbb Z}, \langle 2\beta , b_i\rangle \in {\mathbb Z}$
for all
$ \langle 2\beta , a_i \rangle \in {\mathbb Z}, \langle 2\beta , b_i\rangle \in {\mathbb Z}$
for all
![]() $i=1,...,m$
; that is,
$i=1,...,m$
; that is,
![]() $R(P)\subseteq N=\Lambda ^{[2\beta ]}$
. Since
$R(P)\subseteq N=\Lambda ^{[2\beta ]}$
. Since
![]() $2\beta \in N$
and has norm
$2\beta \in N$
and has norm
![]() $2$
, N contains
$2$
, N contains
![]() $D_{2m}$
and so the Coxeter number of N is greater than or equal to
$D_{2m}$
and so the Coxeter number of N is greater than or equal to
![]() $2(2m-1)$
, which contradicts the choice of V.
$2(2m-1)$
, which contradicts the choice of V.
Case
![]() $V_1=C_{4,2}A_{4,2}^2$
:
$V_1=C_{4,2}A_{4,2}^2$
:
Since
![]() $V_1= C_{4,2}A_{4,2}^2$
and
$V_1= C_{4,2}A_{4,2}^2$
and
![]() $\det (L)=2^{10}4^2$
,
$\det (L)=2^{10}4^2$
,
![]() $L=\sqrt {2}(D_4+E_8)$
and
$L=\sqrt {2}(D_4+E_8)$
and
![]() $N^\tau \cong D_4+\sqrt {2}E_8$
in this case. In particular,
$N^\tau \cong D_4+\sqrt {2}E_8$
in this case. In particular,
![]() $N^\tau $
contains a root sublattice of type
$N^\tau $
contains a root sublattice of type
![]() $D_4$
. Therefore, the possible types for N are
$D_4$
. Therefore, the possible types for N are
![]() $D_4^6$
,
$D_4^6$
,
![]() $D_4A_5^4$
and
$D_4A_5^4$
and
![]() $D_5^2 A_7^2$
. However, the lattices orthogonal to a sublattice of the type
$D_5^2 A_7^2$
. However, the lattices orthogonal to a sublattice of the type
![]() $D_4+\sqrt {2}E_8$
do not contain
$D_4+\sqrt {2}E_8$
do not contain
![]() $L_A(1^{12})$
.
$L_A(1^{12})$
.
Case
![]() $V_1=F_{4,2}A_{8,2}$
:
$V_1=F_{4,2}A_{8,2}$
:
In this case,
![]() $n=18$
and
$n=18$
and
![]() $N_0=9$
.
$N_0=9$
.
Let
![]() $a_1, a_2, b_3, b_4$
be the fundamental roots for
$a_1, a_2, b_3, b_4$
be the fundamental roots for
![]() $F_4$
such that
$F_4$
such that
![]() $a_1, a_2$
are short roots. We may assume
$a_1, a_2$
are short roots. We may assume
![]() $\beta =a_1$
. Since
$\beta =a_1$
. Since
![]() $|\tau |=2$
, there is a Niemeier lattice P such that
$|\tau |=2$
, there is a Niemeier lattice P such that
![]() $V_P=(V_{\Lambda })^{[\tilde {g}^2]}$
, which is also equal to
$V_P=(V_{\Lambda })^{[\tilde {g}^2]}$
, which is also equal to
![]() $V^{[9\alpha ]}$
. Set
$V^{[9\alpha ]}$
. Set
![]() $s=g^9=\exp (2\pi i 9\alpha (0))$
. Then
$s=g^9=\exp (2\pi i 9\alpha (0))$
. Then
![]() $(F_{4,2}A_{8,2})^{<s>}$
contains
$(F_{4,2}A_{8,2})^{<s>}$
contains
![]() $B_{4,2}A_{8,2}$
and the Coxeter number of P is less than or equal to
$B_{4,2}A_{8,2}$
and the Coxeter number of P is less than or equal to
![]() $N_0=9$
. Therefore, the root system of P is
$N_0=9$
. Therefore, the root system of P is
![]() $A_8^3$
. Since
$A_8^3$
. Since
![]() $V=V_P^{[\tilde {g}]}$
,
$V=V_P^{[\tilde {g}]}$
,
![]() $\tau $
acts on one
$\tau $
acts on one
![]() $A_8$
as a diagram automorphism and permutes the other two
$A_8$
as a diagram automorphism and permutes the other two
![]() $A_8$
’s.
$A_8$
’s.
Since
![]() $N_0=9$
is odd, we have
$N_0=9$
is odd, we have
![]() $P=\Lambda _{4\beta }+{\mathbb Z} 4\beta $
and
$P=\Lambda _{4\beta }+{\mathbb Z} 4\beta $
and
![]() $ \tilde {\beta }=2\beta $
by the similar argument as in the case
$ \tilde {\beta }=2\beta $
by the similar argument as in the case
![]() $V_1=B_m^{12/m}$
. By the choice of
$V_1=B_m^{12/m}$
. By the choice of
![]() $\beta $
, the two
$\beta $
, the two
![]() $A_8$
’s permuted by
$A_8$
’s permuted by
![]() $\tau $
is orthogonal to
$\tau $
is orthogonal to
![]() $\beta $
; hence,
$\beta $
; hence,
![]() $N=\Lambda ^{[\tilde {\beta }]}=\Lambda _{2\beta }+{\mathbb Z} 2\beta $
contains
$N=\Lambda ^{[\tilde {\beta }]}=\Lambda _{2\beta }+{\mathbb Z} 2\beta $
contains
![]() $A_8^2$
.
$A_8^2$
.
Since
![]() $F_4$
is a full component, N also contains
$F_4$
is a full component, N also contains
![]() $D_4$
as a root sublattice, which is orthogonal to the above
$D_4$
as a root sublattice, which is orthogonal to the above
![]() $A_8^2$
. Therefore,
$A_8^2$
. Therefore,
![]() $N \supset D_4+A_8+A_8$
. Moreover, the Coxeter number of N is strictly less than
$N \supset D_4+A_8+A_8$
. Moreover, the Coxeter number of N is strictly less than
![]() $n=18$
by our assumption. Then N has the type
$n=18$
by our assumption. Then N has the type
![]() $A_9^2 D_6$
. In this case,
$A_9^2 D_6$
. In this case,
![]() $N_\tau $
, the sublattice orthogonal to
$N_\tau $
, the sublattice orthogonal to
![]() $D_4+ \sqrt {2}A_8$
, does not contain a root sublattice of the type
$D_4+ \sqrt {2}A_8$
, does not contain a root sublattice of the type
![]() $A_1^{12}$
, and we have a contradiction.
$A_1^{12}$
, and we have a contradiction.
This completes the proof of Theorem 5.1.□
Remark 5.14. Since
![]() $\tilde {\beta }$
is a deep hole, it follows that
$\tilde {\beta }$
is a deep hole, it follows that
![]() $[N:\Lambda _{\tilde {\beta }}]=h$
, the Coxeter number of N. Moreover, we have
$[N:\Lambda _{\tilde {\beta }}]=h$
, the Coxeter number of N. Moreover, we have
![]() $[N:\Lambda _{\tilde {\beta }}]=|g|=|\tilde {g}|$
by Theorem 4.8. Thus,
$[N:\Lambda _{\tilde {\beta }}]=|g|=|\tilde {g}|$
by Theorem 4.8. Thus,
![]() $h=|g|=|\tilde {g}|$
. Note that
$h=|g|=|\tilde {g}|$
. Note that
![]() $|\tau |$
divides
$|\tau |$
divides
![]() $|\tilde {g}|$
, and hence,
$|\tilde {g}|$
, and hence,
![]() $|\tau |$
divides h, also.
$|\tau |$
divides h, also.
6 Classification of
 $\tau $
$\tau $
In this section, we will show that
![]() $\tau \in Co.0$
defined by W-elements of holomorphic VOAs of central charge 24 are contained in
$\tau \in Co.0$
defined by W-elements of holomorphic VOAs of central charge 24 are contained in
Combining the results in Sections 3–5, one can associated a pair of
![]() $\tau \in \mathcal{P}_0$
and a
$\tau \in \mathcal{P}_0$
and a
![]() $\tau $
-invariant deep hole
$\tau $
-invariant deep hole
![]() $\tilde {\beta }$
with any holomorphic VOA V of central charge
$\tilde {\beta }$
with any holomorphic VOA V of central charge
![]() $24$
with non-abelian weight one Lie algebra
$24$
with non-abelian weight one Lie algebra
![]() $V_1$
. Set
$V_1$
. Set
 $$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg| \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\[3pt] \mbox{automorphism of some orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg| \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\[3pt] \mbox{automorphism of some orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$
The main result of this section is the following.
Proposition 6.1.
![]() $\mathcal{P}\subseteq \mathcal{P}_0$
.
$\mathcal{P}\subseteq \mathcal{P}_0$
.
Since
![]() $\dim ((V_{\Lambda })^{[\tilde {g}]})_1>24$
, it is easy to see that
$\dim ((V_{\Lambda })^{[\tilde {g}]})_1>24$
, it is easy to see that
![]() $\mathrm {rank}(\Lambda ^\tau ) \geq 4$
and
$\mathrm {rank}(\Lambda ^\tau ) \geq 4$
and
![]() $|\tau |\leq 15$
. Therefore,
$|\tau |\leq 15$
. Therefore,
![]() $\tau $
is in one of the conjugacy classes in Table 1 (cf. [Reference Chigira, Lam and Miyamoto7]).
$\tau $
is in one of the conjugacy classes in Table 1 (cf. [Reference Chigira, Lam and Miyamoto7]).
First, we treat the cases when
![]() $\mathrm {rank}(V_1)= 4$
, which will eliminate many cases with
$\mathrm {rank}(V_1)= 4$
, which will eliminate many cases with
![]() $\dim \Lambda ^\tau =4$
.
$\dim \Lambda ^\tau =4$
.
Lemma 6.2. If
![]() $\mathrm {rank}(V_1)= 4$
, then
$\mathrm {rank}(V_1)= 4$
, then
![]() $\tau \in \mathcal{P}_0$
.
$\tau \in \mathcal{P}_0$
.
Proof. Suppose
![]() $\mathrm {rank}(V_1) = 4$
. By [Reference Dong and Mason13], we know that
$\mathrm {rank}(V_1) = 4$
. By [Reference Dong and Mason13], we know that
![]() $\dim V_1>24$
and
$\dim V_1>24$
and
![]() $h_j^{\vee }/k_j=(\dim V_1-24)/24$
for any component
$h_j^{\vee }/k_j=(\dim V_1-24)/24$
for any component
![]() $\mathcal{G}_j$
; thus,
$\mathcal{G}_j$
; thus,
![]() $V_1$
must be of the type
$V_1$
must be of the type
![]() $B_{4,14}, C_{4,10}, D_{4,36}$
or
$B_{4,14}, C_{4,10}, D_{4,36}$
or
![]() $G_{2,24}^{\oplus 2}$
and
$G_{2,24}^{\oplus 2}$
and
![]() $|\tau |=14,10,6,12$
, respectively. In these cases,
$|\tau |=14,10,6,12$
, respectively. In these cases,
![]() $N_0=1$
. If
$N_0=1$
. If
![]() $|\tau |=14$
, we have
$|\tau |=14$
, we have
![]() $\tau =14B$
. Then
$\tau =14B$
. Then
![]() $\ell =14$
and
$\ell =14$
and
![]() $\det (\Lambda ^\tau )= {14}^2$
. In this case,
$\det (\Lambda ^\tau )= {14}^2$
. In this case,
![]() $\det (L) =14^4$
and
$\det (L) =14^4$
and
![]() $\det (\sqrt {14} L^*)=1$
, which is not possible since
$\det (\sqrt {14} L^*)=1$
, which is not possible since
![]() $\sqrt {14} L^*$
is even (see Section 4.2). If
$\sqrt {14} L^*$
is even (see Section 4.2). If
![]() $|\tau |=10$
, then
$|\tau |=10$
, then
![]() $V_1=C_{4,10}$
and
$V_1=C_{4,10}$
and
![]() $N_0=1$
and so there are
$N_0=1$
and so there are
![]() $\mu \in L^{\ast }$
such that
$\mu \in L^{\ast }$
such that
![]() $\langle \alpha ,\mu \rangle \equiv 1/10$
and
$\langle \alpha ,\mu \rangle \equiv 1/10$
and
![]() $1/5 \pmod {{\mathbb Z}}$
. Therefore, since we may choose
$1/5 \pmod {{\mathbb Z}}$
. Therefore, since we may choose
![]() $\beta $
from
$\beta $
from
![]() $L^{\ast }$
, both of
$L^{\ast }$
, both of
![]() $\tau $
and
$\tau $
and
![]() $\tau ^2$
are of type zero and
$\tau ^2$
are of type zero and
![]() $\phi (\tau )<1$
and
$\phi (\tau )<1$
and
![]() $\phi (\tau ^2)<1$
, which implies
$\phi (\tau ^2)<1$
, which implies
![]() $\tau =10F$
and
$\tau =10F$
and
![]() $\tau \in \mathcal{P}_0$
. If
$\tau \in \mathcal{P}_0$
. If
![]() $|\tau |=6$
,
$|\tau |=6$
,
![]() $V_1=D_{4,36}$
and so there is
$V_1=D_{4,36}$
and so there is
![]() $\mu \in L^{\ast }$
such that
$\mu \in L^{\ast }$
such that
![]() $\langle \tau ,\mu \rangle \equiv 1/6 \pmod {{\mathbb Z}}$
and
$\langle \tau ,\mu \rangle \equiv 1/6 \pmod {{\mathbb Z}}$
and
![]() $\phi (\tau )<1$
. Therefore,
$\phi (\tau )<1$
. Therefore,
![]() $\tau =6I$
and
$\tau =6I$
and
![]() $N_0=1$
. Since
$N_0=1$
. Since
![]() $6\beta \in \Lambda ^{\tau }$
which has the Gram matrix
$6\beta \in \Lambda ^{\tau }$
which has the Gram matrix
![]() $6I_4$
,
$6I_4$
,
![]() $\langle \beta ,\beta \rangle \in 2{\mathbb Z}/12$
. However,
$\langle \beta ,\beta \rangle \in 2{\mathbb Z}/12$
. However,
![]() $\phi (6I)=1/36$
; thus,
$\phi (6I)=1/36$
; thus,
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
is not type zero, and we have a contradiction.
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
is not type zero, and we have a contradiction.
From now on, we may assume
![]() $\dim V^{\langle \tau \rangle }> 4$
.
$\dim V^{\langle \tau \rangle }> 4$
.
Lemma 6.3.
![]() $\tau \not \in 3D$
.
$\tau \not \in 3D$
.
Proof. Recall that
![]() $\Lambda ^{3D}\cong \sqrt {3}E_8$
(cf. [Reference Harada and Lang20]). If
$\Lambda ^{3D}\cong \sqrt {3}E_8$
(cf. [Reference Harada and Lang20]). If
![]() $\mathrm {GCD}(N_0,3)=1$
, then
$\mathrm {GCD}(N_0,3)=1$
, then
![]() $3N_0\beta \in \Lambda ^{3D}$
and so
$3N_0\beta \in \Lambda ^{3D}$
and so
![]() $\langle \beta ,\beta \rangle \in 6{\mathbb Z}/9N_0^2=2{\mathbb Z}/3N_0^2$
, which contradicts
$\langle \beta ,\beta \rangle \in 6{\mathbb Z}/9N_0^2=2{\mathbb Z}/3N_0^2$
, which contradicts
![]() $\phi (3D)+\frac {\langle \beta ,\beta \rangle }{2} \in 1-1/9+\frac{\mathbb{Z}}{3N_0^2}\subset {\mathbb Z}$
. Therefore,
$\phi (3D)+\frac {\langle \beta ,\beta \rangle }{2} \in 1-1/9+\frac{\mathbb{Z}}{3N_0^2}\subset {\mathbb Z}$
. Therefore,
![]() $3|N_0$
. Since
$3|N_0$
. Since
![]() $\dim {\mathbb C}\Lambda ^{3D}=8$
,
$\dim {\mathbb C}\Lambda ^{3D}=8$
,
![]() $N_0|h^{\vee }_j$
for all j and
$N_0|h^{\vee }_j$
for all j and
![]() $|g|=N_0|\tau |=\mathrm {LCM}(\{r_jh_j^\vee \})$
, the only possible case is
$|g|=N_0|\tau |=\mathrm {LCM}(\{r_jh_j^\vee \})$
, the only possible case is
![]() $N_0=3$
and
$N_0=3$
and
![]() $V_1=A_8$
. Since
$V_1=A_8$
. Since
![]() $K_0/N_0=\langle \alpha ,\alpha \rangle /2= \dim V_1/(\dim V_1-24)$
, we have
$K_0/N_0=\langle \alpha ,\alpha \rangle /2= \dim V_1/(\dim V_1-24)$
, we have
![]() $K_0/3= 80/56=10/7$
, which is not possible.
$K_0/3= 80/56=10/7$
, which is not possible.
Suppose Proposition 6.1 is false and let V be a counterexample such that
![]() $k=\mathrm {rank}(V_1)$
is maximal among all counterexamples. We also choose V so that
$k=\mathrm {rank}(V_1)$
is maximal among all counterexamples. We also choose V so that
![]() $\mathrm {Comm}(M(\mathcal{H}),V)$
is largest among all counterexamples with
$\mathrm {Comm}(M(\mathcal{H}),V)$
is largest among all counterexamples with
![]() $\mathrm {rank}(V_1)=k$
.
$\mathrm {rank}(V_1)=k$
.
Let
![]() $\alpha $
be a W-element of
$\alpha $
be a W-element of
![]() $V_1$
and set
$V_1$
and set
![]() $g=\exp (2\pi i\alpha (0))$
. As we discussed, the orbifold construction from V by g gives
$g=\exp (2\pi i\alpha (0))$
. As we discussed, the orbifold construction from V by g gives
![]() $V_{\Lambda }$
. Let
$V_{\Lambda }$
. Let
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
be the reverse automorphism of g corresponding to the above orbifold construction. Since V is a counterexample,
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
be the reverse automorphism of g corresponding to the above orbifold construction. Since V is a counterexample,
![]() $\tau \not \in \mathcal{P}_0$
.
$\tau \not \in \mathcal{P}_0$
.
If m divides
![]() $|\tau |$
and
$|\tau |$
and
![]() $m\not =1$
, then we have
$m\not =1$
, then we have
by Proposition 2.4. Therefore,
![]() $V^{[g^m]}$
is not a counterexample for any
$V^{[g^m]}$
is not a counterexample for any
![]() $1\not =m \mid |\tau |$
. Let L be an even lattice such that
$1\not =m \mid |\tau |$
. Let L be an even lattice such that
![]() $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)\cong V_L$
, where
$\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)\cong V_L$
, where
![]() $\mathcal{H}$
is a Cartan subalgebra of
$\mathcal{H}$
is a Cartan subalgebra of
![]() $V_1=\mathfrak {g}_{1, k_1} \oplus \cdots \oplus \mathfrak {g}_{r,k_r}$
. Let
$V_1=\mathfrak {g}_{1, k_1} \oplus \cdots \oplus \mathfrak {g}_{r,k_r}$
. Let
![]() $\alpha =\sum _{i=1}^{r} \rho _i/h_i^\vee $
be a W-element of
$\alpha =\sum _{i=1}^{r} \rho _i/h_i^\vee $
be a W-element of
![]() $V_1$
. Suppose
$V_1$
. Suppose
![]() $\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$
with
$\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$
with
![]() $K_0,N_0\in {\mathbb Z}$
and
$K_0,N_0\in {\mathbb Z}$
and
![]() $\mathrm {GCD}(K_0,N_0)=1$
.
$\mathrm {GCD}(K_0,N_0)=1$
.
Now consider the VOA
![]() $V^{[g^{N_0}]}$
obtained by the orbifold construction from V by
$V^{[g^{N_0}]}$
obtained by the orbifold construction from V by
![]() $g^{N_0}=\exp (2\pi iN_0\alpha (0))$
. Then
$g^{N_0}=\exp (2\pi iN_0\alpha (0))$
. Then
![]() $V^{[g^{N_0}]}$
also contains an abelian Lie subalgebra
$V^{[g^{N_0}]}$
also contains an abelian Lie subalgebra
![]() $\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$
of rank 24. By viewing it as a Cartan subalgebra of
$\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$
of rank 24. By viewing it as a Cartan subalgebra of
![]() $(V^{[g^{N_0}]})_1$
, there is an even unimodular lattice P of rank
$(V^{[g^{N_0}]})_1$
, there is an even unimodular lattice P of rank
![]() $24$
such that
$24$
such that
![]() $V^{[g^{N_0}]} \cong V_P$
. Furthermore, there is
$V^{[g^{N_0}]} \cong V_P$
. Furthermore, there is
![]() $\mu \in {\mathbb C}\Lambda ^{\tau }$
such that
$\mu \in {\mathbb C}\Lambda ^{\tau }$
such that
![]() $(V_{\Lambda })^{[\exp (2\pi i\mu (0))]}=V_P$
since
$(V_{\Lambda })^{[\exp (2\pi i\mu (0))]}=V_P$
since
![]() $(V^{[g^{N_0}]})^{[g]}=V_{\Lambda }$
. In particular,
$(V^{[g^{N_0}]})^{[g]}=V_{\Lambda }$
. In particular,
![]() $\tau $
fixes
$\tau $
fixes
![]() $\mu $
, and we may view
$\mu $
, and we may view
![]() $\tau $
as an isometry of P.
$\tau $
as an isometry of P.
Remark 6.4. Let
![]() $\tilde {g}'\in \mathrm {Aut}(V_P)$
be the reverse automorphism of
$\tilde {g}'\in \mathrm {Aut}(V_P)$
be the reverse automorphism of
![]() $g^{N_0}\in \mathrm {Aut}(V)$
. By our choice,
$g^{N_0}\in \mathrm {Aut}(V)$
. By our choice,
![]() $\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$
is a Cartan subalgebra of
$\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$
is a Cartan subalgebra of
![]() $V_P$
, and thus, there is a
$V_P$
, and thus, there is a
![]() $\delta \in {\mathbb C} P^{\tau }$
and a standard lift
$\delta \in {\mathbb C} P^{\tau }$
and a standard lift
![]() $\widehat {\tau }'$
of
$\widehat {\tau }'$
of
![]() $\tau $
such that
$\tau $
such that
![]() $\tilde {g}'=\widehat {\tau }'\exp (2\pi i\delta (0))$
and
$\tilde {g}'=\widehat {\tau }'\exp (2\pi i\delta (0))$
and
![]() $\langle N_0\alpha ,\delta \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
. Then
$\langle N_0\alpha ,\delta \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
. Then
![]() $V=(V_P)^{[\widehat {\tau }'\exp (2\pi i\delta (0))]}$
and the actions of
$V=(V_P)^{[\widehat {\tau }'\exp (2\pi i\delta (0))]}$
and the actions of
![]() $\widehat {\tau }$
and
$\widehat {\tau }$
and
![]() $\widehat {\tau }'$
on
$\widehat {\tau }'$
on
![]() $U(jN_0\alpha )$
are the same; namely, they both act on
$U(jN_0\alpha )$
are the same; namely, they both act on
![]() $U(jN_0\alpha )$
as a multiple by a scalar
$U(jN_0\alpha )$
as a multiple by a scalar
![]() $e^{-2\pi ij/|\tau |}$
.
$e^{-2\pi ij/|\tau |}$
.
Since
![]() $N_0\alpha \in L^{\ast }$
,
$N_0\alpha \in L^{\ast }$
,
![]() $V^{<g^{N_0}>}$
contains
$V^{<g^{N_0}>}$
contains
![]() $V_L$
and
$V_L$
and
![]() $L\subseteq \mathcal{H}={\mathbb C}\Lambda ^{\tau }$
. We may also view
$L\subseteq \mathcal{H}={\mathbb C}\Lambda ^{\tau }$
. We may also view
![]() $V_L$
as a subspace of
$V_L$
as a subspace of
![]() $V_P^{<\widehat {\tau }' \exp (2\pi i\delta (0))>}$
. As a conclusion, we have the following.
$V_P^{<\widehat {\tau }' \exp (2\pi i\delta (0))>}$
. As a conclusion, we have the following.
Theorem 6.5. The VOA
![]() $V^{[e^{2\pi i N_0\alpha (0)}]}$
is isomorphic to a lattice VOA
$V^{[e^{2\pi i N_0\alpha (0)}]}$
is isomorphic to a lattice VOA
![]() $V_P$
for an even unimodular lattice P of rank
$V_P$
for an even unimodular lattice P of rank
![]() $24$
. Furthermore,
$24$
. Furthermore,
![]() $P^{\tau }=L+{\mathbb Z} N_0\alpha $
and
$P^{\tau }=L+{\mathbb Z} N_0\alpha $
and
![]() $|g^{N_0}|= |\tau |$
.
$|g^{N_0}|= |\tau |$
.
As we have shown in Theorem 6.5,
![]() $V^{[\exp (2\pi iN_0\alpha (0)]}$
is a Niemeier lattice VOA
$V^{[\exp (2\pi iN_0\alpha (0)]}$
is a Niemeier lattice VOA
![]() $V_P$
and there is
$V_P$
and there is
![]() $\delta \in {\mathbb C} P^{\tau }$
such that
$\delta \in {\mathbb C} P^{\tau }$
such that
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
is the reverse automorphism of
$\widehat {\tau }\exp (2\pi i\delta (0))$
is the reverse automorphism of
![]() $\exp (2\pi iN_0\alpha (0))$
.
$\exp (2\pi iN_0\alpha (0))$
.
Lemma 6.6. By taking a suitable standard lift
![]() $\widehat {\tau }$
of
$\widehat {\tau }$
of
![]() $\tau $
, we may assume
$\tau $
, we may assume
![]() $\delta \in L^{\ast }$
.
$\delta \in L^{\ast }$
.
Proof. By the definition of W-element, there is
![]() $\mu \in L^{\ast }$
such that
$\mu \in L^{\ast }$
such that
![]() $\langle \alpha ,\mu \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$
. Therefore,
$\langle \alpha ,\mu \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$
. Therefore,
![]() $\delta -\mu \in (P^{\tau })^{\ast }$
and there is
$\delta -\mu \in (P^{\tau })^{\ast }$
and there is
![]() $\xi \in P$
such that
$\xi \in P$
such that
![]() $\pi (\xi )=\delta -\mu $
. Set
$\pi (\xi )=\delta -\mu $
. Set
![]() $\xi =\xi '+\pi (\xi )$
with
$\xi =\xi '+\pi (\xi )$
with
![]() $\xi '\in \mathcal{H}^{\perp }$
. Since
$\xi '\in \mathcal{H}^{\perp }$
. Since
![]() $\exp (2\pi i\xi (0))=1$
and
$\exp (2\pi i\xi (0))=1$
and
![]() $\tau $
acts on
$\tau $
acts on
![]() $(\mathcal{H})^{\perp }$
fixed point freely, there is
$(\mathcal{H})^{\perp }$
fixed point freely, there is
![]() $\tilde {h}\in \mathcal{H}^{\perp }$
such that
$\tilde {h}\in \mathcal{H}^{\perp }$
such that
 $$ \begin{align*}\begin{array}{l} \exp(2\pi i\tilde{h}(0))^{-1}(\widehat{\tau}\exp(2\pi i\delta(0))\exp(2\pi i\tilde{h}(0) =\exp(2\pi i\tilde{h}(0))^{-1}\widehat{\tau} \exp(2\pi i\tilde{h}(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\xi'(0))\exp(2\pi i\delta(0)) =\widehat{\tau}\exp(2\pi i\xi(0))\exp(-2\pi i\pi(\xi)(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\mu(0)). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} \exp(2\pi i\tilde{h}(0))^{-1}(\widehat{\tau}\exp(2\pi i\delta(0))\exp(2\pi i\tilde{h}(0) =\exp(2\pi i\tilde{h}(0))^{-1}\widehat{\tau} \exp(2\pi i\tilde{h}(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\xi'(0))\exp(2\pi i\delta(0)) =\widehat{\tau}\exp(2\pi i\xi(0))\exp(-2\pi i\pi(\xi)(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\mu(0)). \end{array}\end{align*} $$
Therefore,
![]() $\widehat {\tau }\exp (2\pi i\delta (0))=\widehat {\tau } \exp (\mu (0))\exp (\pi \xi (0))$
is conjugate to
$\widehat {\tau }\exp (2\pi i\delta (0))=\widehat {\tau } \exp (\mu (0))\exp (\pi \xi (0))$
is conjugate to
![]() $\widehat {\tau }\exp (2\pi i\mu (0)$
. Replacing
$\widehat {\tau }\exp (2\pi i\mu (0)$
. Replacing
![]() $\widehat {\tau }$
by
$\widehat {\tau }$
by
![]() $\exp (2\pi i\tilde {h}(0))^{-1}(\widehat {\tau }\exp (2\pi i\delta (0))\exp (2\pi i\tilde {h}(0))$
, we may assume
$\exp (2\pi i\tilde {h}(0))^{-1}(\widehat {\tau }\exp (2\pi i\delta (0))\exp (2\pi i\tilde {h}(0))$
, we may assume
![]() $\delta \in L^{\ast }$
.
$\delta \in L^{\ast }$
.
By Theorem 6.5, we have
![]() $P^{\tau }=L+{\mathbb Z} N_0\alpha $
and
$P^{\tau }=L+{\mathbb Z} N_0\alpha $
and
![]() $rN_0\alpha \in L$
if and only if
$rN_0\alpha \in L$
if and only if
![]() $|\tau |$
divides r and
$|\tau |$
divides r and
![]() $\langle \delta , N_0\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
. Therefore,
$\langle \delta , N_0\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
. Therefore,
![]() $m\delta \not \in \pi (P)$
if
$m\delta \not \in \pi (P)$
if
![]() $|\tau |\not | m$
. Hence, if
$|\tau |\not | m$
. Hence, if
![]() $|\tau |\not | m$
, then the lowest weight of
$|\tau |\not | m$
, then the lowest weight of
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module is greater than
$\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module is greater than
![]() $\phi (\tau )$
. Therefore, we have the following:
$\phi (\tau )$
. Therefore, we have the following:
Lemma 6.7. If
![]() $\phi (\tau ^m)\geq 1$
, then
$\phi (\tau ^m)\geq 1$
, then
![]() $\widehat {\tau }^m\exp (2\pi im\delta (0))$
-twisted module does not contain a weight one element.
$\widehat {\tau }^m\exp (2\pi im\delta (0))$
-twisted module does not contain a weight one element.
Lemma 6.8.
![]() $<\tau>$
does not contain
$<\tau>$
does not contain
![]() $-2A, 3C, 5C$
.
$-2A, 3C, 5C$
.
Proof. Let m be a divisor of
![]() $|\tau |$
. Suppose
$|\tau |$
. Suppose
![]() $|\tau ^m|=p$
is a prime and
$|\tau ^m|=p$
is a prime and
![]() $\phi (\tau ^m)\geq 1$
.
$\phi (\tau ^m)\geq 1$
.
Let
![]() $\tilde {V}:=V^{[g^{pN_0}]}$
. From the property of orbifold construction and the choice of
$\tilde {V}:=V^{[g^{pN_0}]}$
. From the property of orbifold construction and the choice of
![]() $\widehat {\tau }'$
and
$\widehat {\tau }'$
and
![]() $\delta $
, we have
$\delta $
, we have
![]() $\tilde {V}=(V_P)^{[(\widehat {\tau }')^m\exp (2\pi im\delta (0))]}$
. From Corollary 4.9 in [Reference Chigira, Lam and Miyamoto7],
$\tilde {V}=(V_P)^{[(\widehat {\tau }')^m\exp (2\pi im\delta (0))]}$
. From Corollary 4.9 in [Reference Chigira, Lam and Miyamoto7],
![]() $\tau \not =-2A, 3C, 5C$
and so
$\tau \not =-2A, 3C, 5C$
and so
![]() $m\not =1$
and
$m\not =1$
and
![]() $\tilde {V}$
is not a counterexample.
$\tilde {V}$
is not a counterexample.
Let
![]() $\tilde {\alpha }$
be a W-element of
$\tilde {\alpha }$
be a W-element of
![]() $\tilde {V}_1$
and
$\tilde {V}_1$
and
![]() $\widehat {\sigma }\exp (2\pi i\mu (0))$
the reverse automorphism of
$\widehat {\sigma }\exp (2\pi i\mu (0))$
the reverse automorphism of
![]() $\exp (2\pi i\tilde {\alpha }(0))$
. Then
$\exp (2\pi i\tilde {\alpha }(0))$
. Then
![]() $\sigma \in \mathcal{P}_0$
, and we can use the results in Sections 3
$\sigma \in \mathcal{P}_0$
, and we can use the results in Sections 3
![]() $\sim $
5.
$\sim $
5.
Next, we will show that
![]() ${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$
. As we explained in Section 2,
${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$
. As we explained in Section 2,
![]() $\mathcal{H}+\oplus _{j=0}^{m-1}U(jpN_0\alpha )$
is a Cartan subalgebra of
$\mathcal{H}+\oplus _{j=0}^{m-1}U(jpN_0\alpha )$
is a Cartan subalgebra of
![]() $\tilde {V}_1$
. Since
$\tilde {V}_1$
. Since
![]() $\langle \delta ,\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
,
$\langle \delta ,\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$
,
![]() $\widehat {\tau '}$
acts on
$\widehat {\tau '}$
acts on
![]() $U(jN_0\alpha )$
as a multiple by a scalar
$U(jN_0\alpha )$
as a multiple by a scalar
![]() $e^{-2\pi ij/|\tau |}$
for all
$e^{-2\pi ij/|\tau |}$
for all
![]() $j\in {\mathbb Z}$
. In particular,
$j\in {\mathbb Z}$
. In particular,
![]() ${\mathbb C} P^{\tau ^m}=\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jpN_0\alpha )_1$
and so
${\mathbb C} P^{\tau ^m}=\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jpN_0\alpha )_1$
and so
![]() ${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$
.
${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$
.
We next show that if the order p of
![]() $\tau ^m$
is an odd prime, we have
$\tau ^m$
is an odd prime, we have
![]() $|\widehat {\sigma }|=p$
, and if the order of
$|\widehat {\sigma }|=p$
, and if the order of
![]() $\tau ^m$
is
$\tau ^m$
is
![]() $2$
, we have
$2$
, we have
![]() $|\widehat {\sigma }|=2$
or
$|\widehat {\sigma }|=2$
or
![]() $4$
.
$4$
.
Since
![]() $\phi (\tau ^m)\geq 1$
,
$\phi (\tau ^m)\geq 1$
,
![]() $\widehat {\tau '}^m\exp (2\pi im\delta (0))$
-twisted module contains no weight one element and so we have
$\widehat {\tau '}^m\exp (2\pi im\delta (0))$
-twisted module contains no weight one element and so we have
Since
![]() $|\tau ^m|=p$
is a prime, the root vectors of
$|\tau ^m|=p$
is a prime, the root vectors of
![]() $(V_P)^{<\widehat {\tau '}^m\exp (2\pi im\delta (0))>}_1$
are given by
$(V_P)^{<\widehat {\tau '}^m\exp (2\pi im\delta (0))>}_1$
are given by
(1)
![]() $e^{\mu }$
with
$e^{\mu }$
with
![]() $\mu \in P^{\tau }$
or
$\mu \in P^{\tau }$
or
(2)
![]() $e^{\mu }+\cdots +(\widehat {\tau '}\exp (2\pi im\delta (0)))^{p-1}(e^{\mu })$
with
$e^{\mu }+\cdots +(\widehat {\tau '}\exp (2\pi im\delta (0)))^{p-1}(e^{\mu })$
with
![]() $\mu \in P$
. In this case, it corresponds to the root associated with
$\mu \in P$
. In this case, it corresponds to the root associated with
![]() $\pi (\mu )\in (P^\tau )^*$
and
$\pi (\mu )\in (P^\tau )^*$
and
![]() $\langle \pi (\mu ), \pi (\mu ) \rangle =2/\tilde {r}_j\tilde {k}_j$
. Note also that
$\langle \pi (\mu ), \pi (\mu ) \rangle =2/\tilde {r}_j\tilde {k}_j$
. Note also that
 $$\begin{align*}\langle \pi(\mu), \pi(\mu) \rangle = \langle \pi(\mu), \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle = \langle \mu, \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle \in {\mathbb Z}/p. \end{align*}$$
$$\begin{align*}\langle \pi(\mu), \pi(\mu) \rangle = \langle \pi(\mu), \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle = \langle \mu, \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle \in {\mathbb Z}/p. \end{align*}$$
Therefore, if p is an odd prime, then
![]() $\tilde {r}_j\tilde {k}_j=1$
or p, and if
$\tilde {r}_j\tilde {k}_j=1$
or p, and if
![]() $p=2$
, then
$p=2$
, then
![]() $\tilde {r}_j\tilde {k}_j=1,2,4$
.
$\tilde {r}_j\tilde {k}_j=1,2,4$
.
However, since
![]() $\sigma \in \mathcal{P}_0$
, we have shown
$\sigma \in \mathcal{P}_0$
, we have shown
![]() $|\widehat {\sigma }|=\mathrm {LCM}(\{\tilde {r}_j\tilde {k}_j\mid j\})$
. If
$|\widehat {\sigma }|=\mathrm {LCM}(\{\tilde {r}_j\tilde {k}_j\mid j\})$
. If
![]() $\tilde {r}_j\tilde {k}_j=1$
for all j, then we can easily get a contradiction since
$\tilde {r}_j\tilde {k}_j=1$
for all j, then we can easily get a contradiction since
![]() $\mathrm {rank}(\widetilde {V}_1)=8, 6, 4$
, respectively.
$\mathrm {rank}(\widetilde {V}_1)=8, 6, 4$
, respectively.
Hence, if the order p of
![]() $\tau ^m$
is an odd prime, we have
$\tau ^m$
is an odd prime, we have
![]() $|\widehat {\sigma }|=p$
, and if the order of
$|\widehat {\sigma }|=p$
, and if the order of
![]() $\tau ^m$
is
$\tau ^m$
is
![]() $2$
, we have
$2$
, we have
![]() $|\widehat {\sigma }|=2$
or
$|\widehat {\sigma }|=2$
or
![]() $4$
. From the choice of
$4$
. From the choice of
![]() $\sigma $
, we have
$\sigma $
, we have
![]() $\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=\mathrm {rank}({\mathbb C}\Lambda ^{\tau ^m})$
. Therefore, if
$\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=\mathrm {rank}({\mathbb C}\Lambda ^{\tau ^m})$
. Therefore, if
![]() $\tau ^m=-2A, then \dim \Lambda ^{-2A}=8$
, but there is no
$\tau ^m=-2A, then \dim \Lambda ^{-2A}=8$
, but there is no
![]() $\sigma \in \mathcal{P}_0$
of order
$\sigma \in \mathcal{P}_0$
of order
![]() $2$
or
$2$
or
![]() $4$
such that
$4$
such that
![]() $\Lambda ^{\sigma }=8$
. If
$\Lambda ^{\sigma }=8$
. If
![]() $\tau ^m=3C$
, then
$\tau ^m=3C$
, then
![]() $\mathrm {rank} \Lambda ^{3C}=6$
, but there is no
$\mathrm {rank} \Lambda ^{3C}=6$
, but there is no
![]() $\sigma \in \mathcal{P}_0$
of order
$\sigma \in \mathcal{P}_0$
of order
![]() $3$
with
$3$
with
![]() $\mathrm {rank} \Lambda ^{\sigma }=6$
. If
$\mathrm {rank} \Lambda ^{\sigma }=6$
. If
![]() $\tau =5C$
, then
$\tau =5C$
, then
![]() $\mathrm {rank} \Lambda ^{5C}=4$
, but there is no
$\mathrm {rank} \Lambda ^{5C}=4$
, but there is no
![]() $\sigma \in \mathcal{P}_0$
of order
$\sigma \in \mathcal{P}_0$
of order
![]() $5$
with
$5$
with
![]() $\mathrm {rank} \Lambda ^{\sigma }=4$
.
$\mathrm {rank} \Lambda ^{\sigma }=4$
.
Lemma 6.9.
![]() $\tau \not \in -4C$
.
$\tau \not \in -4C$
.
Proof. Suppose
![]() $\tau \in -4C$
. We note
$\tau \in -4C$
. We note
![]() $V=(V_P)^{[\widehat {\tau }\exp (2\pi i\delta (0))]}$
. Since
$V=(V_P)^{[\widehat {\tau }\exp (2\pi i\delta (0))]}$
. Since
![]() $\phi (\tau )\geq 1$
,
$\phi (\tau )\geq 1$
,
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module does not contain elements of weight one. Recall that
$\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module does not contain elements of weight one. Recall that
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
is the reverse automorphism of
$\widehat {\tau }\exp (2\pi i\delta (0))$
is the reverse automorphism of
![]() $\exp (2\pi iN_0\alpha (0))$
; the above statement means that there is no root
$\exp (2\pi iN_0\alpha (0))$
; the above statement means that there is no root
![]() $\mu \in V_1$
such that
$\mu \in V_1$
such that
![]() $|\tau |\langle \mu ,N_0\alpha \rangle =1$
. Since
$|\tau |\langle \mu ,N_0\alpha \rangle =1$
. Since
![]() $|\tau |=4$
,
$|\tau |=4$
,
![]() $\mathrm {LCM}(\{r_jh^{\vee }_j/N_0\mid j\})$
divides
$\mathrm {LCM}(\{r_jh^{\vee }_j/N_0\mid j\})$
divides
![]() $2$
, which contradicts
$2$
, which contradicts
![]() $\mathrm {LCM}(\{ r_jh^{\vee }_j/N_0 \mid j\})=|\tau |$
.
$\mathrm {LCM}(\{ r_jh^{\vee }_j/N_0 \mid j\})=|\tau |$
.
Therefore, the remaining possibilities of
![]() $\tau \not \in \mathcal{P}_0$
are
$\tau \not \in \mathcal{P}_0$
are
![]() $4D, 4F, -6C$
. Then since
$4D, 4F, -6C$
. Then since
![]() $4D^2=2A, 4F^2=2C, (-6C)^2=3B, (-6C)^3=2A$
, nontrivial powers of
$4D^2=2A, 4F^2=2C, (-6C)^2=3B, (-6C)^3=2A$
, nontrivial powers of
![]() $\tau $
are in
$\tau $
are in
![]() $\mathcal{P}_0$
.
$\mathcal{P}_0$
.
Furthermore,
![]() $\phi (4D)=1-1/8$
,
$\phi (4D)=1-1/8$
,
![]() $\phi (4F)=1/16$
,
$\phi (4F)=1/16$
,
![]() $\phi (-6C)=1$
. Namely,
$\phi (-6C)=1$
. Namely,
![]() $\widehat {\tau }$
is not of type zero or
$\widehat {\tau }$
is not of type zero or
![]() $\phi (\tau )=1$
.
$\phi (\tau )=1$
.
We note that since
![]() $V=V_{\Lambda }^{[\widehat {\tau }\exp (2\pi i\beta (0))]}$
,
$V=V_{\Lambda }^{[\widehat {\tau }\exp (2\pi i\beta (0))]}$
,
![]() $\tilde {V}=V^{[\widetilde {g}^m]}$
is a holomorphic VOA for any
$\tilde {V}=V^{[\widetilde {g}^m]}$
is a holomorphic VOA for any
![]() $m||\tau |$
. Assume
$m||\tau |$
. Assume
![]() $m\not =1$
. Unfortunately,
$m\not =1$
. Unfortunately,
![]() $\widetilde {g}^m$
is not necessary to be a reverse automorphism for an automorphism defined by W-element in
$\widetilde {g}^m$
is not necessary to be a reverse automorphism for an automorphism defined by W-element in
![]() $\tilde {V}$
. Let
$\tilde {V}$
. Let
![]() $\tilde {\alpha }$
be a W-element of
$\tilde {\alpha }$
be a W-element of
![]() $\tilde {V}_1$
and
$\tilde {V}_1$
and
![]() $\widehat {\sigma }\exp (2\pi i\mu (0))$
be a reverse automorphism of
$\widehat {\sigma }\exp (2\pi i\mu (0))$
be a reverse automorphism of
![]() $\exp (2\pi i\tilde {\alpha }(0))$
.
$\exp (2\pi i\tilde {\alpha }(0))$
.
Lemma 6.10. Let
![]() $1\not =m||\tau |$
. If
$1\not =m||\tau |$
. If
![]() $\tau ^m=2A,2C,3B$
, then
$\tau ^m=2A,2C,3B$
, then
![]() $\sigma $
is conjugate to
$\sigma $
is conjugate to
![]() $\tau ^m$
.
$\tau ^m$
.
Proof. If
![]() $\tau ^m=2A,2C,3B$
, then
$\tau ^m=2A,2C,3B$
, then
![]() $\tilde {V}:=V_P^{[\widehat {\tau }^m\exp (2\pi im\delta (0))]}$
is not a counterexample. Let
$\tilde {V}:=V_P^{[\widehat {\tau }^m\exp (2\pi im\delta (0))]}$
is not a counterexample. Let
![]() $\tilde {\alpha }$
be a W-element of
$\tilde {\alpha }$
be a W-element of
![]() $\tilde {V}_1$
and
$\tilde {V}_1$
and
![]() $\widehat {\sigma }\exp (2\pi i\mu (0))$
a reverse automorphism for
$\widehat {\sigma }\exp (2\pi i\mu (0))$
a reverse automorphism for
![]() $\exp (2\pi i\tilde {\alpha }(0))$
. In particular,
$\exp (2\pi i\tilde {\alpha }(0))$
. In particular,
![]() $\sigma \in \mathcal{P}_0$
.
$\sigma \in \mathcal{P}_0$
.
As we have shown,
![]() $\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=\mathrm {rank} \tilde {V}_1=\mathrm {rank} ({\mathbb C}\Lambda )^{\sigma }$
. Let
$\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=\mathrm {rank} \tilde {V}_1=\mathrm {rank} ({\mathbb C}\Lambda )^{\sigma }$
. Let
![]() $\tilde {\mathcal{H}}$
be a Cartan subalgebra of
$\tilde {\mathcal{H}}$
be a Cartan subalgebra of
![]() $\tilde {V}$
and set
$\tilde {V}$
and set
![]() $\mathrm {Comm}(\mathrm {Comm}(\tilde {\mathcal{H}},\tilde {V}),\tilde {V})=V_{\tilde {L}}$
with an even lattice
$\mathrm {Comm}(\mathrm {Comm}(\tilde {\mathcal{H}},\tilde {V}),\tilde {V})=V_{\tilde {L}}$
with an even lattice
![]() $\tilde {L}$
.
$\tilde {L}$
.
Since
![]() $\sigma \in \mathcal{P}_0$
,
$\sigma \in \mathcal{P}_0$
,
![]() $\sqrt {|\widehat {\sigma }|}(\tilde {L})^{\ast }$
is an even lattice by Lemma 5.1. However, since
$\sqrt {|\widehat {\sigma }|}(\tilde {L})^{\ast }$
is an even lattice by Lemma 5.1. However, since
![]() $\tau ^m\in \mathcal{P}_0$
and
$\tau ^m\in \mathcal{P}_0$
and
![]() ${\tilde {V}=(V_P)^{[\widehat {\tau }^m\exp (2m\pi i\delta (0))]}}$
, we have
${\tilde {V}=(V_P)^{[\widehat {\tau }^m\exp (2m\pi i\delta (0))]}}$
, we have
![]() $\phi (\tau ^m)=1-\frac {1}{|\widehat {\tau }^m|}$
and
$\phi (\tau ^m)=1-\frac {1}{|\widehat {\tau }^m|}$
and
![]() $e^{m\delta }\otimes t\in \tilde {V}$
with
$e^{m\delta }\otimes t\in \tilde {V}$
with
![]() $\mathrm {wt}(e^{m\delta })\equiv \frac {1}{|\widehat {\tau }^m|} \pmod {{\mathbb Z}}$
. Therefore,
$\mathrm {wt}(e^{m\delta })\equiv \frac {1}{|\widehat {\tau }^m|} \pmod {{\mathbb Z}}$
. Therefore,
![]() $|\widehat {\tau }^m|$
has to divide
$|\widehat {\tau }^m|$
has to divide
![]() $|\widehat {\sigma }|$
.
$|\widehat {\sigma }|$
.
If
![]() $\tau ^m=2A$
, then
$\tau ^m=2A$
, then
![]() $\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=16$
and
$\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=16$
and
![]() $\sigma =2A$
. If
$\sigma =2A$
. If
![]() $\tau ^m=2C$
, then
$\tau ^m=2C$
, then
![]() $\mathrm {rank}({\mathbb C}\Lambda )^{\sigma }=12$
and so
$\mathrm {rank}({\mathbb C}\Lambda )^{\sigma }=12$
and so
![]() $\sigma =2C$
or
$\sigma =2C$
or
![]() $3B$
. If
$3B$
. If
![]() $\sigma =3B$
, then
$\sigma =3B$
, then
![]() $|\widehat {\sigma }|=3$
is not a multiple of
$|\widehat {\sigma }|=3$
is not a multiple of
![]() $|\widehat {\tau ^m}|=2$
. If
$|\widehat {\tau ^m}|=2$
. If
![]() $\tau ^m=3B$
, then
$\tau ^m=3B$
, then
![]() $\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=12$
and so
$\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=12$
and so
![]() $\sigma =2C$
or
$\sigma =2C$
or
![]() $3B$
. Since
$3B$
. Since
![]() $|\widehat {\tau }^m|=3$
does not divide
$|\widehat {\tau }^m|=3$
does not divide
![]() $|\widehat {\sigma }|=4$
if
$|\widehat {\sigma }|=4$
if
![]() $\sigma =2C$
. Hence,
$\sigma =2C$
. Hence,
![]() $\sigma =3B$
.
$\sigma =3B$
.
As a corollary, for
![]() $\mu \in L^{\ast }$
, if
$\mu \in L^{\ast }$
, if
![]() $\langle \mu , N_0\alpha \rangle \in \frac {{\mathbb Z}}{m}$
, then
$\langle \mu , N_0\alpha \rangle \in \frac {{\mathbb Z}}{m}$
, then
![]() $S(\mu )\otimes e^{\mu } \in V^{[|\tau |g/m]}$
and so we have
$S(\mu )\otimes e^{\mu } \in V^{[|\tau |g/m]}$
and so we have
![]() $|\widehat {\tau }^m|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$
.
$|\widehat {\tau }^m|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$
.
Lemma 6.11.
![]() $\tau \not =-6C$
.
$\tau \not =-6C$
.
Proof. Since
![]() $\phi (-6C)=1$
,
$\phi (-6C)=1$
,
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module does not contain weight one elements. Therefore,
$\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module does not contain weight one elements. Therefore,
![]() $r_jh^{\vee }_j/N_0=2$
or
$r_jh^{\vee }_j/N_0=2$
or
![]() $3$
and both have to appear. Recall that
$3$
and both have to appear. Recall that
![]() $(-6G)^3=2A$
and
$(-6G)^3=2A$
and
![]() $(-6G)^2=3B$
. If
$(-6G)^2=3B$
. If
![]() $ r_jh^{\vee }_j/N_0=2$
, then
$ r_jh^{\vee }_j/N_0=2$
, then
![]() $\exp (2\pi iN_0\alpha (0))^3$
fixes all elements in
$\exp (2\pi iN_0\alpha (0))^3$
fixes all elements in
![]() $\mathcal{G}_j$
and so
$\mathcal{G}_j$
and so
![]() $\sqrt {3}L_j^{\ast }$
is an even lattice since
$\sqrt {3}L_j^{\ast }$
is an even lattice since
![]() $2A\in \mathcal{P}_0$
, where
$2A\in \mathcal{P}_0$
, where
![]() $L_j^{\ast }$
is the co-root lattice of
$L_j^{\ast }$
is the co-root lattice of
![]() $\mathcal{G}_j$
. If
$\mathcal{G}_j$
. If
![]() $r_jh^{\vee }_j/N_0=3$
, then
$r_jh^{\vee }_j/N_0=3$
, then
![]() $\exp (2\pi iN_0\alpha (0))^2$
fixes all elements in
$\exp (2\pi iN_0\alpha (0))^2$
fixes all elements in
![]() $\mathcal{G}_j$
and so
$\mathcal{G}_j$
and so
![]() $\sqrt {2}L_j^{\ast }$
is an even lattice. Therefore,
$\sqrt {2}L_j^{\ast }$
is an even lattice. Therefore,
![]() $\sqrt {6}L^{\ast }$
is an even lattice and
$\sqrt {6}L^{\ast }$
is an even lattice and
![]() $K_0-N_0=1$
and
$K_0-N_0=1$
and
![]() $h_j^{\vee }=k_jN_0$
. If
$h_j^{\vee }=k_jN_0$
. If
![]() $N_0=1$
, then
$N_0=1$
, then
![]() $r_jh^{\vee }_j=2$
and
$r_jh^{\vee }_j=2$
and
![]() $3$
and so
$3$
and so
![]() $\mathcal{G}_j=A_1$
or
$\mathcal{G}_j=A_1$
or
![]() $A_2$
, which contradicts to
$A_2$
, which contradicts to
![]() $\dim V_1>24$
since
$\dim V_1>24$
since
![]() $\mathrm {rank} V_1=6$
. If
$\mathrm {rank} V_1=6$
. If
![]() $N_0=2$
,
$N_0=2$
,
![]() $r_jh^{\vee }_j=4$
and
$r_jh^{\vee }_j=4$
and
![]() $6$
and so
$6$
and so
![]() $\mathcal{G}_1=A_3$
and
$\mathcal{G}_1=A_3$
and
![]() $\mathcal{G}_2=A_5$
, which contradicts
$\mathcal{G}_2=A_5$
, which contradicts
![]() $\mathrm {rank} V_1=6$
. If
$\mathrm {rank} V_1=6$
. If
![]() $N_0=3$
, then one of
$N_0=3$
, then one of
![]() $r_2h_2^{\vee }=9$
and so
$r_2h_2^{\vee }=9$
and so
![]() $\mathcal{G}_2=A_8$
, which contradicts
$\mathcal{G}_2=A_8$
, which contradicts
![]() $\mathrm {rank} V_1=6$
. If
$\mathrm {rank} V_1=6$
. If
![]() $N_0=4$
, then one of
$N_0=4$
, then one of
![]() $r_1h_1^{\vee }=8$
and
$r_1h_1^{\vee }=8$
and
![]() $\mathcal{G}_2=G_2$
. So,
$\mathcal{G}_2=G_2$
. So,
![]() $\mathcal{G}_1=A_7,C_3,D_5$
. Since
$\mathcal{G}_1=A_7,C_3,D_5$
. Since
![]() $\mathrm {rank} V_1=6$
and
$\mathrm {rank} V_1=6$
and
![]() $\mathcal{G}_j\not =A_1$
, we have a contradiction. If
$\mathcal{G}_j\not =A_1$
, we have a contradiction. If
![]() $N_0>4$
,
$N_0>4$
,
![]() $r_1h_2^{\vee }\geq 10$
and
$r_1h_2^{\vee }\geq 10$
and
![]() $r_2h_2^{\vee }\geq 15$
, which contradicts
$r_2h_2^{\vee }\geq 15$
, which contradicts
![]() $\mathrm {rank} V_1=6$
.
$\mathrm {rank} V_1=6$
.
So the remaining cases are
![]() $\tau =4D$
or
$\tau =4D$
or
![]() $4F$
. Recall that a short root in
$4F$
. Recall that a short root in
![]() $\mathcal{G}_j$
is called a shortest root if
$\mathcal{G}_j$
is called a shortest root if
![]() $r_jh_j^\vee = \mathrm {LCM}(r_ih_i^{\vee }|i)= |\tau | N_0$
(or equivalently,
$r_jh_j^\vee = \mathrm {LCM}(r_ih_i^{\vee }|i)= |\tau | N_0$
(or equivalently,
![]() $r_jk_j=\mathrm {LCM}(r_ik_i|i)$
). Since
$r_jk_j=\mathrm {LCM}(r_ik_i|i)$
). Since
![]() $|\tau |=4$
and
$|\tau |=4$
and
![]() $\mathrm {LCM}(r_ih_i^{\vee }/N_0\mid i)=|\tau |=4$
, there is a shortest root. Say,
$\mathrm {LCM}(r_ih_i^{\vee }/N_0\mid i)=|\tau |=4$
, there is a shortest root. Say,
![]() $\mathcal{G}_1$
contains a shortest root.
$\mathcal{G}_1$
contains a shortest root.
Lemma 6.12. If
![]() $\tau =4D$
or
$\tau =4D$
or
![]() $4F$
, then
$4F$
, then
![]() $\exp (2N_0\pi i\alpha (0))^2$
fixes a root vector associated with a shortest root.
$\exp (2N_0\pi i\alpha (0))^2$
fixes a root vector associated with a shortest root.
Proof. Since
![]() $\mathrm {LCM}(\{r_jh_j^{\vee }/N_0\mid i\}=|\tau |$
and
$\mathrm {LCM}(\{r_jh_j^{\vee }/N_0\mid i\}=|\tau |$
and
![]() $h_j^\vee $
is divisible by
$h_j^\vee $
is divisible by
![]() $N_0$
,
$N_0$
,
![]() $r_j$
divides
$r_j$
divides
![]() $|\tau |$
. Therefore,
$|\tau |$
. Therefore,
![]() $\mathcal{G}_j\not =G_2$
.
$\mathcal{G}_j\not =G_2$
.
If
![]() $\mathcal{G}_1\not \cong B_m$
, then there is a shortest root which is a sum of two shortest roots in the fundamental root system, and thus
$\mathcal{G}_1\not \cong B_m$
, then there is a shortest root which is a sum of two shortest roots in the fundamental root system, and thus
![]() $\exp (2N_0\pi i\alpha (0))^2$
fixes a root vector associated with a shortest root in
$\exp (2N_0\pi i\alpha (0))^2$
fixes a root vector associated with a shortest root in
![]() $\mathcal{G}_1$
. So we may assume
$\mathcal{G}_1$
. So we may assume
![]() $\mathcal{G}_1=B_m$
; however,
$\mathcal{G}_1=B_m$
; however,
![]() $r_1h_1^{\vee }=2(2m-1)$
in this case, which contradicts that
$r_1h_1^{\vee }=2(2m-1)$
in this case, which contradicts that
![]() $|\tau |=4$
divides
$|\tau |=4$
divides
![]() $r_1h_1^\vee $
.
$r_1h_1^\vee $
.
Lemma 6.13.
![]() $\tau \not =4D$
nor
$\tau \not =4D$
nor
![]() $4F$
.
$4F$
.
Proof. Suppose false. Set
![]() $\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$
. We may view that
$\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$
. We may view that
![]() $\hat{\tau} $
is an automorphism of
$\hat{\tau} $
is an automorphism of
![]() $\tilde {V}$
of order
$\tilde {V}$
of order
![]() $2$
. Let
$2$
. Let
![]() $\tilde {\mathcal{H}}$
be a Cartan subalgebra of
$\tilde {\mathcal{H}}$
be a Cartan subalgebra of
![]() $\tilde {V}_1$
. Then there is an even lattice
$\tilde {V}_1$
. Then there is an even lattice
![]() $\tilde {L}$
such that
$\tilde {L}$
such that
![]() $\mathrm {Comm}(\mathrm {Comm}(M(\tilde {\mathcal{H}}),\tilde {V}),\tilde {V})\cong V_{\tilde {L}}$
. Let
$\mathrm {Comm}(\mathrm {Comm}(M(\tilde {\mathcal{H}}),\tilde {V}),\tilde {V})\cong V_{\tilde {L}}$
. Let
![]() $\tilde {\alpha }$
be a W-element of
$\tilde {\alpha }$
be a W-element of
![]() $\tilde {V}_1$
and
$\tilde {V}_1$
and
![]() $\widehat {\sigma }\exp (2\pi i\xi (0))$
the reverse automorphism of
$\widehat {\sigma }\exp (2\pi i\xi (0))$
the reverse automorphism of
![]() $\exp (2\pi i\tilde {\alpha }(0))$
. Since
$\exp (2\pi i\tilde {\alpha }(0))$
. Since
![]() $4D^2=2A$
and
$4D^2=2A$
and
![]() $4F^2=2C$
, we have
$4F^2=2C$
, we have
![]() $\sigma =2A$
and
$\sigma =2A$
and
![]() $2C$
, respectively, by the same argument as in the proof of Lemma 6.10.
$2C$
, respectively, by the same argument as in the proof of Lemma 6.10.
Since
![]() $\tilde {V}^{[\exp (2\pi i\alpha (0)]}=V_{\Lambda }$
, there is no root orthogonal to
$\tilde {V}^{[\exp (2\pi i\alpha (0)]}=V_{\Lambda }$
, there is no root orthogonal to
![]() $\alpha $
in
$\alpha $
in
![]() $\tilde {V}$
. Therefore, we can define positive roots by the condition
$\tilde {V}$
. Therefore, we can define positive roots by the condition
![]() $\langle \mu ,\alpha \rangle>0$
. Note that
$\langle \mu ,\alpha \rangle>0$
. Note that
![]() $\alpha $
is fixed by
$\alpha $
is fixed by
![]() $\tau $
. Therefore, if
$\tau $
. Therefore, if
![]() $\mu $
is a positive root, then so is
$\mu $
is a positive root, then so is
![]() $\tau ^i(\mu )$
for any i. By Lemma 6.12, there is a shortest root
$\tau ^i(\mu )$
for any i. By Lemma 6.12, there is a shortest root
![]() $\mu \in L^{\ast }$
such that
$\mu \in L^{\ast }$
such that
![]() $s\otimes e^{\mu }\in V^{<\exp (2\pi iN_0\alpha (0))^2>}\subseteq \tilde {V}=V^{[\exp (4\pi i N_0\alpha (0))]}$
.
$s\otimes e^{\mu }\in V^{<\exp (2\pi iN_0\alpha (0))^2>}\subseteq \tilde {V}=V^{[\exp (4\pi i N_0\alpha (0))]}$
.
Since
![]() $\tau $
has positive frame shape, we may choose
$\tau $
has positive frame shape, we may choose
![]() $\delta $
in
$\delta $
in
![]() $L^{\ast }$
. Note that
$L^{\ast }$
. Note that
![]() $\phi (\tau )=1-\frac {1}{2\ell }$
for
$\phi (\tau )=1-\frac {1}{2\ell }$
for
![]() $\tau \in 4C$
or
$\tau \in 4C$
or
![]() $4D$
. If
$4D$
. If
![]() $\langle \delta , \delta \rangle /2\in \frac {1}{\ell }{\mathbb Z}$
, then the irreducible
$\langle \delta , \delta \rangle /2\in \frac {1}{\ell }{\mathbb Z}$
, then the irreducible
![]() $\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module has no subspaces with integral weights, which is not possible. Therefore, it suffices to show that
$\widehat {\tau }\exp (2\pi i\delta (0))$
-twisted module has no subspaces with integral weights, which is not possible. Therefore, it suffices to show that
![]() $\sqrt {\ell }L^{\ast }$
is an even lattice, or equivalently,
$\sqrt {\ell }L^{\ast }$
is an even lattice, or equivalently,
![]() $\ell \langle \mu ,\mu \rangle \in 2{\mathbb Z}$
since
$\ell \langle \mu ,\mu \rangle \in 2{\mathbb Z}$
since
![]() $\mu $
is a shortest root. Without loss of generality, we may assume
$\mu $
is a shortest root. Without loss of generality, we may assume
![]() $\langle \mu ,\alpha \rangle>0$
. Then we have one of the following two cases: (1)
$\langle \mu ,\alpha \rangle>0$
. Then we have one of the following two cases: (1)
![]() $\mu $
is still a root in
$\mu $
is still a root in
![]() $\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$
or (2)
$\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$
or (2)
![]() $s\otimes e^{\mu }=s'\otimes e^{\mu '}+\tau (s')\otimes e^{\tau (\mu ')}$
with a positive root
$s\otimes e^{\mu }=s'\otimes e^{\mu '}+\tau (s')\otimes e^{\tau (\mu ')}$
with a positive root
![]() $\mu '\in {\mathbb C}\Lambda ^{<\tau ^2>}$
and
$\mu '\in {\mathbb C}\Lambda ^{<\tau ^2>}$
and
![]() $\mu =\frac {\mu '+\tau (\mu ')}{2}$
. In particular,
$\mu =\frac {\mu '+\tau (\mu ')}{2}$
. In particular,
![]() $\mu '+\tau (\mu ')$
is not a root. Note that
$\mu '+\tau (\mu ')$
is not a root. Note that
![]() $\mu '$
and
$\mu '$
and
![]() $\tau (\mu ')$
are both positive roots of the same length, and hence,
$\tau (\mu ')$
are both positive roots of the same length, and hence,
![]() $\frac {2\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle } = 0, -1$
or
$\frac {2\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle } = 0, -1$
or
![]() $2$
, but
$2$
, but
![]() $-1$
is not possible since
$-1$
is not possible since
![]() $\mu '+\tau (\mu ')$
is not a root. We have
$\mu '+\tau (\mu ')$
is not a root. We have
![]() $t=\frac {\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle }\in {\mathbb Z}$
.
$t=\frac {\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle }\in {\mathbb Z}$
.
By Lemma 6.10,
![]() $\tau ^2$
is conjugate to
$\tau ^2$
is conjugate to
![]() $\sigma $
, and thus,
$\sigma $
, and thus,
![]() $|\widehat {\tau }|=2|\widehat {\sigma }|$
. Since
$|\widehat {\tau }|=2|\widehat {\sigma }|$
. Since
![]() $\tilde {V}$
is not a counterexample,
$\tilde {V}$
is not a counterexample,
![]() $\sigma \in \mathcal{P}_0$
and so
$\sigma \in \mathcal{P}_0$
and so
![]() $|\widehat {\sigma }|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$
for the case (1) and
$|\widehat {\sigma }|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$
for the case (1) and
![]() $|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$
for the case (2). For the case (1),
$|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$
for the case (2). For the case (1),
![]() $\ell \langle \mu ,\mu \rangle \in 4{\mathbb Z}$
. For the case (2),
$\ell \langle \mu ,\mu \rangle \in 4{\mathbb Z}$
. For the case (2),
![]() $|\widehat {\sigma }|\langle \tau (\mu '),\mu '\rangle =t|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$
. Then we have
$|\widehat {\sigma }|\langle \tau (\mu '),\mu '\rangle =t|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$
. Then we have
![]() $\ell \langle \mu ,\mu \rangle = 2|\widehat {\sigma }| \langle \frac {\mu '+\tau (\mu ')}{2}, \frac {\mu '+\tau (\mu ')}{2} \rangle =|\widehat {\sigma }|\langle \mu '+\tau (\mu '), \mu '\rangle \in 2{\mathbb Z}$
as desired.
$\ell \langle \mu ,\mu \rangle = 2|\widehat {\sigma }| \langle \frac {\mu '+\tau (\mu ')}{2}, \frac {\mu '+\tau (\mu ')}{2} \rangle =|\widehat {\sigma }|\langle \mu '+\tau (\mu '), \mu '\rangle \in 2{\mathbb Z}$
as desired.
This completes the proof of
![]() $\mathcal{P}\subseteq \mathcal{P}_0$
.
$\mathcal{P}\subseteq \mathcal{P}_0$
.
7 Reverse construction
As we have already shown, one can define a pair of
![]() $\tau \in \mathcal{P}_0$
and a
$\tau \in \mathcal{P}_0$
and a
![]() $\tau $
-invariant deep hole
$\tau $
-invariant deep hole
![]() $\tilde {\beta }$
for any holomorphic VOA V of central charge
$\tilde {\beta }$
for any holomorphic VOA V of central charge
![]() $24$
with non-abelian
$24$
with non-abelian
![]() $V_1$
by choosing a W-element
$V_1$
by choosing a W-element
![]() $\alpha $
of
$\alpha $
of
![]() $V_1$
and considering the reverse automorphism
$V_1$
and considering the reverse automorphism
![]() $\tilde {g}\in \mathrm {Aut}(V_\Lambda )$
of
$\tilde {g}\in \mathrm {Aut}(V_\Lambda )$
of
![]() $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
. The pair
$g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
. The pair
![]() $(\tau , \tilde {\beta })$
satisfies the following conditions:
$(\tau , \tilde {\beta })$
satisfies the following conditions:
-
(C1)
 $\tau \in \mathcal{P}_0$
(Proposition 6.1) and
$\tau \in \mathcal{P}_0$
(Proposition 6.1) and
 $\tilde {\beta }$
is a
$\tilde {\beta }$
is a
 $\tau $
-invariant deep hole of Leech lattice
$\tau $
-invariant deep hole of Leech lattice
 $\Lambda $
with
$\Lambda $
with
 $\langle \tilde {\beta },\tilde {\beta }\rangle =2$
(Theorem 5.1);
$\langle \tilde {\beta },\tilde {\beta }\rangle =2$
(Theorem 5.1); -
(C2) the Coxeter number h of
 $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
is divisible by
$N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
is divisible by
 $|\tau |$
(Remark 5.14);
$|\tau |$
(Remark 5.14); -
(C3)
 $N_{\tau }=L_A(c_{\tau })$
with
$N_{\tau }=L_A(c_{\tau })$
with
 $c_{\tau }$
as defined in Appendix (Lemmas 5.2 and 5.4),
$c_{\tau }$
as defined in Appendix (Lemmas 5.2 and 5.4),
where
![]() $\Lambda _{\tilde {\beta }}=\{\lambda \in \Lambda \mid \langle \lambda , \tilde {\beta }\rangle \in {\mathbb Z}\}$
and
$\Lambda _{\tilde {\beta }}=\{\lambda \in \Lambda \mid \langle \lambda , \tilde {\beta }\rangle \in {\mathbb Z}\}$
and
![]() $N_{\tau }$
denotes an orthogonal complement of
$N_{\tau }$
denotes an orthogonal complement of
![]() $N^{\tau }$
in N. We also use the same notation
$N^{\tau }$
in N. We also use the same notation
![]() $\tau $
to denote the isometry of N induced from
$\tau $
to denote the isometry of N induced from
![]() $\tau $
on
$\tau $
on
![]() $\Lambda $
.
$\Lambda $
.
Let
![]() $\mathcal{T}$
be the set of pairs satisfying the conditions (C1) to (C3). In this section, we will study the reverse construction. Take a pair
$\mathcal{T}$
be the set of pairs satisfying the conditions (C1) to (C3). In this section, we will study the reverse construction. Take a pair
![]() $(\tau , \tilde {\beta })\in \mathcal{T}$
. Assume that
$(\tau , \tilde {\beta })\in \mathcal{T}$
. Assume that
![]() $\tau $
has the frame shape
$\tau $
has the frame shape
![]() $\prod m^{a_m}$
. Then
$\prod m^{a_m}$
. Then
![]() $N_\tau> \oplus _{m\neq 1} A_{m-1}^{a_m}$
, and the conformal weight of the
$N_\tau> \oplus _{m\neq 1} A_{m-1}^{a_m}$
, and the conformal weight of the
![]() $\widehat {\tau }$
-twisted module of
$\widehat {\tau }$
-twisted module of
![]() $V_\Lambda $
is given by
$V_\Lambda $
is given by
![]() $\phi (\tau )=1-\frac {1}{\ell }$
, where
$\phi (\tau )=1-\frac {1}{\ell }$
, where
![]() $\ell =|\widehat {\tau }|$
.
$\ell =|\widehat {\tau }|$
.
Let
![]() $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and define
$\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and define
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
. Note that
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
. Note that
![]() $\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. Set
$\langle \beta ,\beta \rangle =\frac {2}{\ell }$
. Set
![]() $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
and let h be the Coxeter number of N. Since
$N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
and let h be the Coxeter number of N. Since
![]() $-\tilde {\beta }$
is a deep hole of
$-\tilde {\beta }$
is a deep hole of
![]() $\Lambda $
,
$\Lambda $
,
![]() $N^{(1)}$
contains an affine fundamental root system of rank
$N^{(1)}$
contains an affine fundamental root system of rank
![]() $24$
and
$24$
and
![]() $N=\oplus _{k=0}^{h-1} N^{(k)}$
, where
$N=\oplus _{k=0}^{h-1} N^{(k)}$
, where
![]() $N^{(k)}=\Lambda _{\tilde {\beta }}-k\tilde {\beta }$
.
$N^{(k)}=\Lambda _{\tilde {\beta }}-k\tilde {\beta }$
.
We may assume that
![]() $ \widehat {\tau }^{|\tau |} =\exp (2\pi i \delta (0))$
for some
$ \widehat {\tau }^{|\tau |} =\exp (2\pi i \delta (0))$
for some
![]() $\delta $
fixed by
$\delta $
fixed by
![]() $\tau $
and take
$\tau $
and take
![]() $\delta =0$
if
$\delta =0$
if
![]() $\widehat {\tau }^{|\tau |} =1$
. For
$\widehat {\tau }^{|\tau |} =1$
. For
![]() $i\equiv k \mod 2|\tau |$
, the irreducible
$i\equiv k \mod 2|\tau |$
, the irreducible
![]() $\tilde {g}^k$
-twisted modules are as follows:
$\tilde {g}^k$
-twisted modules are as follows:
 $$\begin{align*}T^k =V_\Lambda[\tilde{g}^k]= \begin{cases} {\mathbb C}[-k\beta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } 0 \leq i < |\tau|, \\ {\mathbb C}[-k\beta + \delta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } |\tau| \leq i < 2|\tau| \\ \end{cases} \end{align*}$$
$$\begin{align*}T^k =V_\Lambda[\tilde{g}^k]= \begin{cases} {\mathbb C}[-k\beta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } 0 \leq i < |\tau|, \\ {\mathbb C}[-k\beta + \delta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } |\tau| \leq i < 2|\tau| \\ \end{cases} \end{align*}$$
(see [Reference Lepowsky35, Propositions 6.1 and 6.2] and [Reference Dong and Lepowsky11, Remark 4.2] for detail). In particular,
![]() $T^1$
contains a weight one element
$T^1$
contains a weight one element
![]() $e^{\beta }\otimes t$
with
$e^{\beta }\otimes t$
with
![]() $t\in T_\tau $
, which is the lowest weight element of
$t\in T_\tau $
, which is the lowest weight element of
![]() $T^1$
, and so
$T^1$
, and so
![]() $T^1_{{\mathbb Z}}\not =0$
and the orbifold construction gives a holomorphic VOA
$T^1_{{\mathbb Z}}\not =0$
and the orbifold construction gives a holomorphic VOA
![]() $V:=V^{[\tilde {g}]}$
of central charge
$V:=V^{[\tilde {g}]}$
of central charge
![]() $24$
, and
$24$
, and
![]() $V_1$
is non-abelian since
$V_1$
is non-abelian since
![]() $V_1$
contains a root vector
$V_1$
contains a root vector
![]() $e^{\beta }\otimes t$
.
$e^{\beta }\otimes t$
.
One of the main purposes of this section is to determine an equivalent relation
![]() $\sim $
on
$\sim $
on
![]() $\mathcal{T}$
so that two pairs
$\mathcal{T}$
so that two pairs
![]() $(\tau , \tilde {\beta })$
and
$(\tau , \tilde {\beta })$
and
![]() $(\tau ', \tilde {\beta }')$
define isomorphic VOAs if and only if
$(\tau ', \tilde {\beta }')$
define isomorphic VOAs if and only if
![]() $(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$
. It is clear that
$(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$
. It is clear that
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
are conjugates in
$\tau '$
are conjugates in
![]() $O(\Lambda )$
and
$O(\Lambda )$
and
![]() $\tilde {\beta }$
and
$\tilde {\beta }$
and
![]() $\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
$\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
![]() $\Lambda $
if
$\Lambda $
if
![]() $(\tau , \tilde {\beta })$
and
$(\tau , \tilde {\beta })$
and
![]() $(\tau ', \tilde {\beta }')$
define isomorphic VOAs.
$(\tau ', \tilde {\beta }')$
define isomorphic VOAs.
For two equivalent deep holes
![]() $\tilde {\beta }$
and
$\tilde {\beta }$
and
![]() $\tilde {\beta }'$
, there are
$\tilde {\beta }'$
, there are
![]() $\sigma \in O(\Lambda )$
and
$\sigma \in O(\Lambda )$
and
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
. Since
$\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
. Since
![]() $\tilde {\beta }'$
is
$\tilde {\beta }'$
is
![]() $\tau '$
-invariant,
$\tau '$
-invariant,
![]() $\tilde {\beta }-\lambda $
is
$\tilde {\beta }-\lambda $
is
![]() $\sigma ^{-1} \tau ' \sigma $
-invariant. Moreover,
$\sigma ^{-1} \tau ' \sigma $
-invariant. Moreover,
![]() $\langle \tilde {\beta }, \lambda \rangle \in {\mathbb Z}$
since
$\langle \tilde {\beta }, \lambda \rangle \in {\mathbb Z}$
since
![]() $\langle \tilde {\beta }, \tilde {\beta }\rangle = \langle \tilde {\beta }', \tilde {\beta }'\rangle =2$
. In this case,
$\langle \tilde {\beta }, \tilde {\beta }\rangle = \langle \tilde {\beta }', \tilde {\beta }'\rangle =2$
. In this case,
![]() $\Lambda _{\tilde {\beta }} +\tilde {\beta } = \Lambda _{\tilde {\beta }-\lambda } +(\tilde {\beta }-\lambda )$
. Therefore, up to the action of
$\Lambda _{\tilde {\beta }} +\tilde {\beta } = \Lambda _{\tilde {\beta }-\lambda } +(\tilde {\beta }-\lambda )$
. Therefore, up to the action of
![]() $O(\Lambda )$
, we may identify
$O(\Lambda )$
, we may identify
![]() $N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$
with
$N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$
with
![]() $N' =\Lambda _{\tilde {\beta }'} +{\mathbb Z} \tilde {\beta }'$
. We define an equivalent relation on
$N' =\Lambda _{\tilde {\beta }'} +{\mathbb Z} \tilde {\beta }'$
. We define an equivalent relation on
![]() $\mathcal{T}$
as follows:
$\mathcal{T}$
as follows:
![]() $(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$
if and only if
$(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$
if and only if
-
(1)
 $\tilde {\beta }$
and
$\tilde {\beta }$
and
 $\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
$\tilde {\beta }'$
are equivalent deep holes of the Leech lattice
 $\Lambda $
(i.e., there are
$\Lambda $
(i.e., there are
 $\sigma \in O(\Lambda )$
and
$\sigma \in O(\Lambda )$
and
 $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
 $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
);
$\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$
); -
(2)
 $\tau $
is conjugate to
$\tau $
is conjugate to
 $\sigma ^{-1} \tau ' \sigma $
in
$\sigma ^{-1} \tau ' \sigma $
in
 $O(N)$
.
$O(N)$
.
Note that
![]() $ (\sigma ^{-1} \tau ' \sigma ,\tilde {\beta }-\lambda )\in \mathcal{T}$
and
$ (\sigma ^{-1} \tau ' \sigma ,\tilde {\beta }-\lambda )\in \mathcal{T}$
and
![]() $N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }= \Lambda _{\tilde {\beta }-\lambda } +{\mathbb Z}(\tilde {\beta }-\lambda )$
. Moreover,
$N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }= \Lambda _{\tilde {\beta }-\lambda } +{\mathbb Z}(\tilde {\beta }-\lambda )$
. Moreover,
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
are conjugate in
$\tau '$
are conjugate in
![]() $O(\Lambda )$
since they have the same frame shape by (2).
$O(\Lambda )$
since they have the same frame shape by (2).
We will prove the following main theorem.
Theorem 7.1. There is a one-to-one correspondence between the set of isomorphism classes of holomorphic VOA V of central charge
![]() $24$
having non-abelian
$24$
having non-abelian
![]() $V_1$
and the set
$V_1$
and the set
![]() $\mathcal{T}/\sim $
of equivalence classes of pairs
$\mathcal{T}/\sim $
of equivalence classes of pairs
![]() $(\tau , \tilde {\beta })$
by
$(\tau , \tilde {\beta })$
by
![]() $\sim $
.
$\sim $
.
7.1 W-element and the automorphism
 $\tilde {g}$
$\tilde {g}$
Let
![]() $(\tau , \tilde {\beta })\in \mathcal{T}$
. Set
$(\tau , \tilde {\beta })\in \mathcal{T}$
. Set
![]() $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and define
$\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and define
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
. Let
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
. Let
![]() $V=V_\Lambda ^{[\tilde {g}]}$
be the holomorphic VOA obtained by the orbifold construction from
$V=V_\Lambda ^{[\tilde {g}]}$
be the holomorphic VOA obtained by the orbifold construction from
![]() $V_\Lambda $
and
$V_\Lambda $
and
![]() $\tilde {g}$
. We will show that there is a W-element
$\tilde {g}$
. We will show that there is a W-element
![]() $\alpha $
of
$\alpha $
of
![]() $V_1$
such that
$V_1$
such that
![]() $\tilde {g}$
can be viewed as a reverse automorphism of
$\tilde {g}$
can be viewed as a reverse automorphism of
![]() $\exp (2\pi i \alpha (0)) \in \mathrm {Aut}(V)$
.
$\exp (2\pi i \alpha (0)) \in \mathrm {Aut}(V)$
.
First, we will prove the following theorem.
Theorem 7.2. Let h be the Coxeter number of
![]() $N=\Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
. Then
$N=\Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$
. Then
![]() $|\tilde {g}|=h$
.
$|\tilde {g}|=h$
.
We need several lemmas.
Lemma 7.3.
![]() $s\beta \in \pi (\Lambda )$
if and only if
$s\beta \in \pi (\Lambda )$
if and only if
![]() $h|s$
.
$h|s$
.
Proof. Since
![]() $\sqrt {\ell }\varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $
, we have
$\sqrt {\ell }\varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $
, we have
![]() $s\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
if and only if
$s\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
if and only if
![]() $s\tilde {\beta }\in \Lambda ^{\tau }$
, if and only if
$s\tilde {\beta }\in \Lambda ^{\tau }$
, if and only if
![]() $h|s$
.
$h|s$
.
Lemma 7.4. We have
![]() $\tilde {g}^{2h}=1$
. Furthermore,
$\tilde {g}^{2h}=1$
. Furthermore,
![]() $\tilde {g}^h=1$
if
$\tilde {g}^h=1$
if
![]() $2C\not \in <\tau>$
.
$2C\not \in <\tau>$
.
Proof. By (C3) and
![]() $\tau \in \mathcal{P}_0$
,
$\tau \in \mathcal{P}_0$
,
![]() $N_{\tau }$
contains a root sublattice
$N_{\tau }$
contains a root sublattice
![]() $S\cong A_{|\tau |-1}$
. For a root
$S\cong A_{|\tau |-1}$
. For a root
![]() $\mu $
of S, there is
$\mu $
of S, there is
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $m\in {\mathbb Z}$
such that
$m\in {\mathbb Z}$
such that
![]() $\mu =\lambda +m\tilde {\beta } \in N_{\tau }\subseteq {\mathbb C}\Lambda _{\tau }$
. Then
$\mu =\lambda +m\tilde {\beta } \in N_{\tau }\subseteq {\mathbb C}\Lambda _{\tau }$
. Then
 $$\begin{align*}0=\sum_{i=0}^{|\tau|-1} \tau^i \mu = \sum_{i=0}^{|\tau|-1} \tau^i \lambda +|\tau|m\tilde{\beta} \in \Lambda^\tau. \end{align*}$$
$$\begin{align*}0=\sum_{i=0}^{|\tau|-1} \tau^i \mu = \sum_{i=0}^{|\tau|-1} \tau^i \lambda +|\tau|m\tilde{\beta} \in \Lambda^\tau. \end{align*}$$
Since h is the smallest positive integer satisfying
![]() $h\tilde {\beta }\in \Lambda ^{\tau }$
and
$h\tilde {\beta }\in \Lambda ^{\tau }$
and
![]() $\tau $
is fixed point free on S with order
$\tau $
is fixed point free on S with order
![]() $|\tau |$
, we have
$|\tau |$
, we have
![]() $m=h/|\tau |$
. Moreover, we also have
$m=h/|\tau |$
. Moreover, we also have
![]() $\frac {h}{|\tau |}\tilde {\beta }\in \pi (\Lambda )\in (\Lambda ^{\tau })^{\ast }$
and so
$\frac {h}{|\tau |}\tilde {\beta }\in \pi (\Lambda )\in (\Lambda ^{\tau })^{\ast }$
and so
![]() $\langle \frac {h\tilde {\beta }}{|\tau |}, \Lambda ^{\tau }\rangle \subseteq {\mathbb Z}$
. Hence,
$\langle \frac {h\tilde {\beta }}{|\tau |}, \Lambda ^{\tau }\rangle \subseteq {\mathbb Z}$
. Hence,
![]() ${\mathbb Z} \supseteq \frac {h}{|\tau |}\langle \sqrt {\ell }\varphi (\beta ), \sqrt {\ell }\varphi ((\Lambda ^{\tau })^{\ast })\rangle =\langle \frac {h\ell }{|\tau |}\beta ,(\Lambda ^{\tau })^{\ast }\rangle $
and so
${\mathbb Z} \supseteq \frac {h}{|\tau |}\langle \sqrt {\ell }\varphi (\beta ), \sqrt {\ell }\varphi ((\Lambda ^{\tau })^{\ast })\rangle =\langle \frac {h\ell }{|\tau |}\beta ,(\Lambda ^{\tau })^{\ast }\rangle $
and so
![]() $\frac {\ell }{|\tau |}h\beta \in \Lambda $
, which means
$\frac {\ell }{|\tau |}h\beta \in \Lambda $
, which means
![]() $(\exp (2\pi \beta (0))^{\frac {\ell h}{|\tau |}}=1$
. In particular, if
$(\exp (2\pi \beta (0))^{\frac {\ell h}{|\tau |}}=1$
. In particular, if
![]() $2C\not \in <\tau>$
, then
$2C\not \in <\tau>$
, then
![]() $\ell =|\tau |$
and
$\ell =|\tau |$
and
![]() $\exp (2\pi i\beta (0))^h=1$
.
$\exp (2\pi i\beta (0))^h=1$
.
From now on, we may assume
![]() $\tau =2C, 6G, 10F$
. In particular,
$\tau =2C, 6G, 10F$
. In particular,
![]() $|\tau |=2s$
for some
$|\tau |=2s$
for some
![]() $s=1,3$
or
$s=1,3$
or
![]() $5$
. Note that
$5$
. Note that
![]() $\sigma =\tau ^s$
is a
$\sigma =\tau ^s$
is a
![]() $2C$
-element.
$2C$
-element.
Lemma 7.5. Let
![]() $\tau \in 2C, 6G$
or
$\tau \in 2C, 6G$
or
![]() $10F$
. Let
$10F$
. Let
![]() $\tilde {\beta }$
be a
$\tilde {\beta }$
be a
![]() $\tau $
-invariant deep hole satisfying (C1)–(C3). Let h be the Coxeter number of
$\tau $
-invariant deep hole satisfying (C1)–(C3). Let h be the Coxeter number of
![]() $N=\Lambda _{\beta } +{\mathbb Z}\beta $
. Then
$N=\Lambda _{\beta } +{\mathbb Z}\beta $
. Then
![]() $h/|\tau |$
is odd.
$h/|\tau |$
is odd.
Proof. By our assumptions,
![]() $N_\tau \cong L_A(c_\tau )$
as defined in the Appendix; namely,
$N_\tau \cong L_A(c_\tau )$
as defined in the Appendix; namely,
as a full rank sublattice if the frame shape of
![]() $\tau $
is
$\tau $
is
![]() $ \prod m_i^{a_i}$
. Moreover,
$ \prod m_i^{a_i}$
. Moreover,
Since there are only
![]() $16$
Niemeier lattices whose Coxeter number is even, it is straightforward to determine all Niemeier lattices N such that
$16$
Niemeier lattices whose Coxeter number is even, it is straightforward to determine all Niemeier lattices N such that
![]() $L_A(c_\tau )\subset N$
as a direct summand. Indeed,
$L_A(c_\tau )\subset N$
as a direct summand. Indeed,
![]() $R(N)=A_1^{24}, D_4^6, A_5^4D_4$
,
$R(N)=A_1^{24}, D_4^6, A_5^4D_4$
,
![]() $D_6^4, A_9^2D_6$
,
$D_6^4, A_9^2D_6$
,
![]() $D_8^3$
,
$D_8^3$
,
![]() $A_{17}E_7$
,
$A_{17}E_7$
,
![]() $D_{12}^2$
, or
$D_{12}^2$
, or
![]() $D_{24}$
if
$D_{24}$
if
![]() $\tau \in 2C$
;
$\tau \in 2C$
;
![]() $R(N)= A_5^4D_4$
or
$R(N)= A_5^4D_4$
or
![]() $A_{17}E_7$
if
$A_{17}E_7$
if
![]() $\tau \in 6G$
;
$\tau \in 6G$
;
![]() $R(N)= A_9^2D_6$
if
$R(N)= A_9^2D_6$
if
![]() $\tau \in 10F$
.
$\tau \in 10F$
.
It turns out that
![]() $h/|\tau |$
is odd for all possible cases.
$h/|\tau |$
is odd for all possible cases.
The following lemma can be verified easily using the definition of
![]() $A_{m-1}$
.
$A_{m-1}$
.
Lemma 7.6. Let
![]() $m=2s$
be an even integer and let
$m=2s$
be an even integer and let
![]() $\tau $
be a Coxeter element in
$\tau $
be a Coxeter element in
![]() $\mathrm {Weyl}(A_{m-1})$
. Then the
$\mathrm {Weyl}(A_{m-1})$
. Then the
![]() $(-1)$
-eigenlattice of
$(-1)$
-eigenlattice of
![]() $\tau ^s$
on
$\tau ^s$
on
![]() $A_{m-1}$
is isometric to
$A_{m-1}$
is isometric to
![]() $A_1^s= {\mathbb Z} x_1\oplus \cdots \oplus {\mathbb Z} x_s$
. Moreover, the vector
$A_1^s= {\mathbb Z} x_1\oplus \cdots \oplus {\mathbb Z} x_s$
. Moreover, the vector
![]() $\frac {1}2( x_1+\cdots + x_s)\in s\gamma +A_{m-1}$
, where
$\frac {1}2( x_1+\cdots + x_s)\in s\gamma +A_{m-1}$
, where
![]() $\gamma + A_{m-1}$
is a generator of
$\gamma + A_{m-1}$
is a generator of
![]() $A_{m-1}^*/A_{m-1}$
.
$A_{m-1}^*/A_{m-1}$
.
Lemma 7.7. For
![]() $\tau =2C, 6G, 10F$
and
$\tau =2C, 6G, 10F$
and
![]() $v,u\in \Lambda ^{\tau }$
,
$v,u\in \Lambda ^{\tau }$
,
![]() $\langle v,u\rangle \in 2{\mathbb Z}$
.
$\langle v,u\rangle \in 2{\mathbb Z}$
.
Proof. We note
![]() $\Lambda ^{\tau }\subseteq \Lambda ^{\sigma }$
. Since
$\Lambda ^{\tau }\subseteq \Lambda ^{\sigma }$
. Since
![]() $\ell (\sigma )=4$
,
$\ell (\sigma )=4$
,
![]() $\Lambda ^{\sigma }=2(\Lambda ^{\sigma })^{\ast }$
. Hence,
$\Lambda ^{\sigma }=2(\Lambda ^{\sigma })^{\ast }$
. Hence,
![]() $\frac {v}{2}\in (\Lambda ^{\sigma })^{\ast }$
and
$\frac {v}{2}\in (\Lambda ^{\sigma })^{\ast }$
and
![]() $\langle v,u\rangle = 2\langle \frac {v}{2},u\rangle \in 2{\mathbb Z}$
.
$\langle v,u\rangle = 2\langle \frac {v}{2},u\rangle \in 2{\mathbb Z}$
.
Now now on, we set
![]() $p=h/|\tau |$
, which is an odd integer.
$p=h/|\tau |$
, which is an odd integer.
Proposition 7.8. For
![]() $\tau =2C, 6G, 10F$
and
$\tau =2C, 6G, 10F$
and
![]() $v\in (\Lambda _{\tilde {\beta }}+sp\tilde {\beta })^{\tau }$
, we have
$v\in (\Lambda _{\tilde {\beta }}+sp\tilde {\beta })^{\tau }$
, we have
![]() $\langle v,v\rangle \equiv 2 \pmod {4}$
.
$\langle v,v\rangle \equiv 2 \pmod {4}$
.
Proof. We first note that
![]() $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
forms an affine fundamental system of roots of N. Choose a fundamental root system X from
$(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
forms an affine fundamental system of roots of N. Choose a fundamental root system X from
![]() $\Lambda _{\tilde {\beta }}+{\mathbb Z}\tilde {\beta }$
such that
$\Lambda _{\tilde {\beta }}+{\mathbb Z}\tilde {\beta }$
such that
![]() $\tilde {\beta }\in X$
. Let
$\tilde {\beta }\in X$
. Let
![]() $\rho $
be the corresponding Weyl vector and consider
$\rho $
be the corresponding Weyl vector and consider
![]() $\xi =\exp (2\pi i\rho (0)/h)\in \mathrm {Aut}(V_N)$
.
$\xi =\exp (2\pi i\rho (0)/h)\in \mathrm {Aut}(V_N)$
.
Although
![]() $\tau $
does not fix X,
$\tau $
does not fix X,
![]() $\tau $
preserves
$\tau $
preserves
![]() $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
and
$(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
and
![]() $\xi $
acts on
$\xi $
acts on
![]() $\{e^\alpha \mid \alpha \in (\Lambda _{\tilde {\beta }}+\tilde {\beta })_2 \}$
with the same eigenvalue; hence, the commutator
$\{e^\alpha \mid \alpha \in (\Lambda _{\tilde {\beta }}+\tilde {\beta })_2 \}$
with the same eigenvalue; hence, the commutator
![]() $[\tau , \xi ]=1$
. Therefore, we can induce
$[\tau , \xi ]=1$
. Therefore, we can induce
![]() $\tau $
to an automorphism of
$\tau $
to an automorphism of
![]() $(V_N)^{[\xi ^j]}$
for any j. As it is well-known,
$(V_N)^{[\xi ^j]}$
for any j. As it is well-known,
![]() $(V_N)^{[\xi ]}\cong V_{\Lambda }$
. Now consider the VOA obtained by the orbifold construction using
$(V_N)^{[\xi ]}\cong V_{\Lambda }$
. Now consider the VOA obtained by the orbifold construction using
![]() $V_N$
and
$V_N$
and
![]() $\xi ^2$
. Then
$\xi ^2$
. Then
![]() $(V_N)^{[\xi ^{2}]} \cong V_M$
for some Niemeier lattice M and the Coxeter number of M is
$(V_N)^{[\xi ^{2}]} \cong V_M$
for some Niemeier lattice M and the Coxeter number of M is
![]() $2$
(i.e.,
$2$
(i.e.,
![]() $R(M)=A_1^{24}$
). It is clear that
$R(M)=A_1^{24}$
). It is clear that
By Lemma 7.6, it is easy to check that
Then
![]() $(\Lambda _{\tilde {\beta }} + sp\tilde {\beta })^\tau < M^\tau < M^{\tau ^s}= (L_A(c_{2C}))^\perp $
.
$(\Lambda _{\tilde {\beta }} + sp\tilde {\beta })^\tau < M^\tau < M^{\tau ^s}= (L_A(c_{2C}))^\perp $
.
Therefore, it suffices to check for the case
![]() $\tau \in 2C$
and
$\tau \in 2C$
and
![]() $N\cong N(A_1^{24})$
. In this case, we may assume N contains
$N\cong N(A_1^{24})$
. In this case, we may assume N contains
![]() $A_1^{24}=\oplus _{i=1}^{24} {\mathbb Z} x_i$
and
$A_1^{24}=\oplus _{i=1}^{24} {\mathbb Z} x_i$
and
![]() $N/(A_1^{24})$
is the binary Golay code
$N/(A_1^{24})$
is the binary Golay code
![]() $G_{24}$
of length
$G_{24}$
of length
![]() $24$
and
$24$
and
![]() $\tau (x_i)=x_i$
for
$\tau (x_i)=x_i$
for
![]() $i=1,...,12$
and
$i=1,...,12$
and
![]() $\tau (x_i)=-x_i$
for
$\tau (x_i)=-x_i$
for
![]() $i=13,...,24$
. We may also assume
$i=13,...,24$
. We may also assume
![]() $\tilde {\beta }=x_1$
. By (C3),
$\tilde {\beta }=x_1$
. By (C3),
![]() $N_{\tau }=<x_{13},...,x_{24}, \frac {x_{13}+...+x_{24}}{2}>$
. Then
$N_{\tau }=<x_{13},...,x_{24}, \frac {x_{13}+...+x_{24}}{2}>$
. Then
![]() $\{13,...,24\}$
is a dodecad of
$\{13,...,24\}$
is a dodecad of
![]() $G_{24}$
, and so
$G_{24}$
, and so
![]() $N^{\tau }=(N_{\tau })^{\perp }=<x_1,...,x_{12}, \frac {x_1+...+x_{12}}{2}>$
.
$N^{\tau }=(N_{\tau })^{\perp }=<x_1,...,x_{12}, \frac {x_1+...+x_{12}}{2}>$
.
For a Weyl vector
![]() $\rho $
of N, we may choose
$\rho $
of N, we may choose
![]() $x_i$
such that
$x_i$
such that
![]() $\exp (2\pi i\rho (0)/2)(x_i)=\sqrt {-1}x_i$
, and so
$\exp (2\pi i\rho (0)/2)(x_i)=\sqrt {-1}x_i$
, and so
![]() $\exp (2\pi i\rho (0)/2)(\frac {x_i+...+x_{12}}{2})=\sqrt {-1}^{12}(\frac {x_i+...+x_{12}}{2})=(\frac {x_i+...+x_{12}}{2})$
. Namely,
$\exp (2\pi i\rho (0)/2)(\frac {x_i+...+x_{12}}{2})=\sqrt {-1}^{12}(\frac {x_i+...+x_{12}}{2})=(\frac {x_i+...+x_{12}}{2})$
. Namely,
We note
![]() $\langle \frac {x_1+...+x_{12}}{2}, \frac {x_1+...+x_{12}}{2}\rangle +2\langle \beta , \frac {x_1+...+x_{12}}{2}\rangle =6+2\equiv 0 \pmod {4}$
and
$\langle \frac {x_1+...+x_{12}}{2}, \frac {x_1+...+x_{12}}{2}\rangle +2\langle \beta , \frac {x_1+...+x_{12}}{2}\rangle =6+2\equiv 0 \pmod {4}$
and
![]() $\langle x_1+x_i, x_1+x_i\rangle +2\langle \beta , x_1+x_i\rangle =4+4 \equiv 0 \pmod {4}$
. Since
$\langle x_1+x_i, x_1+x_i\rangle +2\langle \beta , x_1+x_i\rangle =4+4 \equiv 0 \pmod {4}$
. Since
![]() $(\Lambda _{x_1})^{\tau }$
is spanned by such elements and
$(\Lambda _{x_1})^{\tau }$
is spanned by such elements and
![]() $\Lambda _{x_1}$
is self orthogonal modulo
$\Lambda _{x_1}$
is self orthogonal modulo
![]() $2$
,
$2$
,
![]() $\langle v,v\rangle \equiv 2 \pmod {4}$
for all
$\langle v,v\rangle \equiv 2 \pmod {4}$
for all
![]() $v\in \Lambda _{\tilde {\beta }}+\tilde {\beta }$
, as we desired.
$v\in \Lambda _{\tilde {\beta }}+\tilde {\beta }$
, as we desired.
We come back to the proof of Theorem 7.2. We still assume
![]() $\tau =2C, 6G$
or
$\tau =2C, 6G$
or
![]() $10F$
and
$10F$
and
![]() $s,p$
are odd. The main idea is to study the possibilities of weights in
$s,p$
are odd. The main idea is to study the possibilities of weights in
![]() $T^1$
modulo
$T^1$
modulo
![]() ${\mathbb Z}$
. Recall that
${\mathbb Z}$
. Recall that
and the weights of
![]() $M(1)[\tau ]\otimes T_{\tau }$
are in
$M(1)[\tau ]\otimes T_{\tau }$
are in
![]() $1-\frac {1}{\ell }+\frac {1}{|\tau |} {\mathbb Z}$
. Therefore, we will focus on the set
$1-\frac {1}{\ell }+\frac {1}{|\tau |} {\mathbb Z}$
. Therefore, we will focus on the set
![]() $-\beta +(\Lambda ^{\tau })^*$
.
$-\beta +(\Lambda ^{\tau })^*$
.
Since
![]() $\Lambda _{\tilde {\beta }}+p\tilde {\beta }$
contains a root
$\Lambda _{\tilde {\beta }}+p\tilde {\beta }$
contains a root
![]() $\mu $
in
$\mu $
in
![]() $N_{\tau }$
,
$N_{\tau }$
,
![]() $p\tilde {\beta }\in \pi (\Lambda )$
as we explained and we have
$p\tilde {\beta }\in \pi (\Lambda )$
as we explained and we have
![]() $|\Lambda ^\tau /\Lambda _{\tilde {\beta }}^\tau |=| (\Lambda _{\tilde {\beta }}^\tau )^*/ (\Lambda ^\tau )^*|= p$
. For
$|\Lambda ^\tau /\Lambda _{\tilde {\beta }}^\tau |=| (\Lambda _{\tilde {\beta }}^\tau )^*/ (\Lambda ^\tau )^*|= p$
. For
![]() $\lambda \in \Lambda $
, set
$\lambda \in \Lambda $
, set
![]() $\mu =\sqrt {\ell }\varphi (\pi (\lambda ))\in \Lambda ^{\tau }$
. We assume
$\mu =\sqrt {\ell }\varphi (\pi (\lambda ))\in \Lambda ^{\tau }$
. We assume
![]() $\langle \mu , \tilde {\beta }\rangle =\frac {t}{p}$
; that is,
$\langle \mu , \tilde {\beta }\rangle =\frac {t}{p}$
; that is,
![]() $\langle \pi (\lambda ),\beta \rangle =\frac {t}{4sp}$
. Since
$\langle \pi (\lambda ),\beta \rangle =\frac {t}{4sp}$
. Since
![]() $p\mu \in \Lambda ^{\tau }_{\tilde {\beta }}$
,
$p\mu \in \Lambda ^{\tau }_{\tilde {\beta }}$
,
and
![]() $\langle p \mu ,p\mu \rangle +2t\equiv 0 \mod 4$
by Proposition 7.8. Since p is odd, we have
$\langle p \mu ,p\mu \rangle +2t\equiv 0 \mod 4$
by Proposition 7.8. Since p is odd, we have
![]() $\langle \mu , \mu \rangle +2t=4m$
for some
$\langle \mu , \mu \rangle +2t=4m$
for some
![]() $m\in {\mathbb Z}$
; namely,
$m\in {\mathbb Z}$
; namely,
![]() $\langle \pi (\lambda ),\pi (\lambda )\rangle =\frac {4m-2t}{4s}$
. Hence,
$\langle \pi (\lambda ),\pi (\lambda )\rangle =\frac {4m-2t}{4s}$
. Hence,
and so
![]() $\mathrm {wt}(e^{\pi (\lambda )+\beta })=\frac {2mp+t(1-p)+p}{4sp}$
. Since
$\mathrm {wt}(e^{\pi (\lambda )+\beta })=\frac {2mp+t(1-p)+p}{4sp}$
. Since
![]() $2mp+t(1-p)+p$
is always odd, the possible weights modulo
$2mp+t(1-p)+p$
is always odd, the possible weights modulo
![]() ${\mathbb Z}$
are
${\mathbb Z}$
are
![]() $\frac {\mbox {odd}}{4ps}$
; that is, there are
$\frac {\mbox {odd}}{4ps}$
; that is, there are
![]() $h=2sp$
distinct weights modulo
$h=2sp$
distinct weights modulo
![]() ${\mathbb Z}$
at most. That means
${\mathbb Z}$
at most. That means
![]() $|\tilde {g}|\leq h$
, and this completes the proof of Proposition 7.2.
$|\tilde {g}|\leq h$
, and this completes the proof of Proposition 7.2.
![]() $\square $
$\square $
We next show that if we start the orbifold construction from V by using a W-element, we will come back to the original
![]() $(\tau , \tilde {\beta })$
and N.
$(\tau , \tilde {\beta })$
and N.
Let
![]() $V=V_\Lambda ^{[\tilde {g}]}$
. Then we have
$V=V_\Lambda ^{[\tilde {g}]}$
. Then we have
 $$ \begin{align*}V=\bigoplus_{j=0}^{|\tilde{g}|-1} (T^j_{{\mathbb Z}})^{<\tilde{g}>}.\end{align*} $$
$$ \begin{align*}V=\bigoplus_{j=0}^{|\tilde{g}|-1} (T^j_{{\mathbb Z}})^{<\tilde{g}>}.\end{align*} $$
Define L by
![]() $\mathrm {Comm}(\mathrm {Comm}(\mathcal{H}),V),V)\cong V_L$
. Since V is holomorphic, as a
$\mathrm {Comm}(\mathrm {Comm}(\mathcal{H}),V),V)\cong V_L$
. Since V is holomorphic, as a
![]() $V_L$
-module, V contains a submodule isomorphic to
$V_L$
-module, V contains a submodule isomorphic to
![]() $V_{L+\mu }$
for all
$V_{L+\mu }$
for all
![]() $\mu \in L^{\ast }$
.
$\mu \in L^{\ast }$
.
Note that
![]() $\tilde {g}^{|\tau |} =\exp (2\pi i (\delta + |\tau |\beta )(0))$
is an inner automorphism. Then
$\tilde {g}^{|\tau |} =\exp (2\pi i (\delta + |\tau |\beta )(0))$
is an inner automorphism. Then
 $$ \begin{align} L=\bigcup_{j=0}^{|\tilde{g}|/ |\tau| -1} j(\delta +|\tau|\beta)+\Lambda_\beta^\tau. \end{align} $$
$$ \begin{align} L=\bigcup_{j=0}^{|\tilde{g}|/ |\tau| -1} j(\delta +|\tau|\beta)+\Lambda_\beta^\tau. \end{align} $$
Recall that
![]() $|\tilde {g}|=h$
and then
$|\tilde {g}|=h$
and then
![]() $ (h/|\tau |) (\delta +|\tau |\beta ) \in \Lambda _\beta ^\tau $
. Since
$ (h/|\tau |) (\delta +|\tau |\beta ) \in \Lambda _\beta ^\tau $
. Since
![]() $p=h/|\tau |$
is odd and
$p=h/|\tau |$
is odd and
![]() $2\delta \in \Lambda ^\tau $
, we have
$2\delta \in \Lambda ^\tau $
, we have
![]() $\delta \equiv h\tilde {\beta } \mod \Lambda _\beta ^\tau $
.
$\delta \equiv h\tilde {\beta } \mod \Lambda _\beta ^\tau $
.
Proposition 7.9.
![]() $\sqrt {\ell } L^{\ast } \cong \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$
.
$\sqrt {\ell } L^{\ast } \cong \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$
.
Proof. Set
![]() $p=h/|\tau |=2k+1$
. Then
$p=h/|\tau |=2k+1$
. Then
![]() $(\delta +|\tau |\beta ) +\Lambda ^\tau _{\beta } = (k+1)\ell \beta + \Lambda ^\tau _{\beta }$
. Since
$(\delta +|\tau |\beta ) +\Lambda ^\tau _{\beta } = (k+1)\ell \beta + \Lambda ^\tau _{\beta }$
. Since
![]() $2h\beta =(2k+1)\ell \beta \in \Lambda ^\tau $
,
$2h\beta =(2k+1)\ell \beta \in \Lambda ^\tau $
,
![]() $ L= \bigcup _{j=0}^{2k} j(k+1)\ell \beta +\Lambda _\beta ^\tau =\Lambda ^\tau _{\beta }+{\mathbb Z} \ell \beta $
. By the same argument as in Theorem 4.9, we have
$ L= \bigcup _{j=0}^{2k} j(k+1)\ell \beta +\Lambda _\beta ^\tau =\Lambda ^\tau _{\beta }+{\mathbb Z} \ell \beta $
. By the same argument as in Theorem 4.9, we have
![]() $\sqrt {\ell }L^* = \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$
.
$\sqrt {\ell }L^* = \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$
.
Lemma 7.10.
![]() $\mathrm {Comm}_V (\mathcal{H}) = V_{\Lambda _\tau }^{\widehat {\tau }}$
.
$\mathrm {Comm}_V (\mathcal{H}) = V_{\Lambda _\tau }^{\widehat {\tau }}$
.
Proof. Suppose false. Then there exists
![]() $ 0<j< |\tilde {g}|=h$
such that
$ 0<j< |\tilde {g}|=h$
such that
![]() $V_{\Lambda _\beta ^\tau } $
appears as a submodule of
$V_{\Lambda _\beta ^\tau } $
appears as a submodule of
![]() $T^j_{\mathbb Z}$
. It implies
$T^j_{\mathbb Z}$
. It implies
![]() $j\beta \in (\Lambda ^\tau )^*$
. It contradicts that h is the smallest integer such that
$j\beta \in (\Lambda ^\tau )^*$
. It contradicts that h is the smallest integer such that
![]() $h\tilde {\beta }\in \Lambda ^\tau $
(or equivalently,
$h\tilde {\beta }\in \Lambda ^\tau $
(or equivalently,
![]() $h\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
).
$h\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$
).
As a corollary, we have the following:
Lemma 7.11.
![]() $\mathrm {rank}(V_1)=\mathrm {rank}(\Lambda ^{\tau })$
.
$\mathrm {rank}(V_1)=\mathrm {rank}(\Lambda ^{\tau })$
.
Proof. Since
![]() $\mathcal{H}\subseteq V_{\Lambda }^{<\tilde {g}>}$
, we may assume
$\mathcal{H}\subseteq V_{\Lambda }^{<\tilde {g}>}$
, we may assume
![]() $\mathcal{H}\subseteq V_1$
. By the lemma above, we have
$\mathcal{H}\subseteq V_1$
. By the lemma above, we have
![]() $\mathrm {Comm}_V (\mathcal{H})\cap V_1= 0$
.
$\mathrm {Comm}_V (\mathcal{H})\cap V_1= 0$
.
As we have shown,
![]() $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
is a fundamental affine root system
$(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$
is a fundamental affine root system
![]() $\tilde {X}$
of
$\tilde {X}$
of
![]() $R(N)$
. Note that
$R(N)$
. Note that
![]() $\tilde {\beta }\in \tilde {X}$
by our convention. Let
$\tilde {\beta }\in \tilde {X}$
by our convention. Let
![]() $\rho $
be a Weyl vector of X. Then
$\rho $
be a Weyl vector of X. Then
![]() $\exp (2\pi i\rho (0)/h)$
is an automorphism of N of order h and
$\exp (2\pi i\rho (0)/h)$
is an automorphism of N of order h and
![]() $N_{\rho /h}=\Lambda _{\tilde {\beta }}$
. If v is an extended root in
$N_{\rho /h}=\Lambda _{\tilde {\beta }}$
. If v is an extended root in
![]() $\Lambda _{\tilde {\beta }}+\tilde {\beta }$
, then
$\Lambda _{\tilde {\beta }}+\tilde {\beta }$
, then
![]() $\langle v,\rho \rangle =-(h-1)$
. Therefore,
$\langle v,\rho \rangle =-(h-1)$
. Therefore,
![]() $\rho ^{\perp }\subseteq \Lambda _{\tilde {\beta }}= \{x\in N\mid \langle \rho , x\rangle \in h{\mathbb Z}\}$
. Furthermore, for any
$\rho ^{\perp }\subseteq \Lambda _{\tilde {\beta }}= \{x\in N\mid \langle \rho , x\rangle \in h{\mathbb Z}\}$
. Furthermore, for any
![]() $w\in R(N)\cap N^{(k)}$
,
$w\in R(N)\cap N^{(k)}$
,
![]() $\langle \rho ,w\rangle \cong k \pmod {h}$
.
$\langle \rho ,w\rangle \cong k \pmod {h}$
.
Set
![]() $\alpha =\sqrt {\ell }\varphi ^{-1}(\pi (\rho )/h)$
. Then
$\alpha =\sqrt {\ell }\varphi ^{-1}(\pi (\rho )/h)$
. Then
More generally,
![]() $\langle \alpha ,L^{\ast }\rangle =\langle \varphi ^{-1}(\pi (\rho )/h), \varphi ^{-1}(N^{\tau })\rangle =\frac {1}{h}\langle \rho , N^{\tau }\rangle < \frac {{\mathbb Z}}{h}$
. Since
$\langle \alpha ,L^{\ast }\rangle =\langle \varphi ^{-1}(\pi (\rho )/h), \varphi ^{-1}(N^{\tau })\rangle =\frac {1}{h}\langle \rho , N^{\tau }\rangle < \frac {{\mathbb Z}}{h}$
. Since
![]() $\mathcal{H}$
is a Cartan subalgebra of
$\mathcal{H}$
is a Cartan subalgebra of
![]() $V_1$
and
$V_1$
and
![]() $V_1$
contains a root vector associated with
$V_1$
contains a root vector associated with
![]() $\beta $
(i.e., a weight one element
$\beta $
(i.e., a weight one element
![]() $e^{\beta }\otimes T_\tau \in T^1$
with
$e^{\beta }\otimes T_\tau \in T^1$
with
![]() $\langle \beta ,\beta \rangle =\frac {2}{\ell }$
). As we have shown in the previous sections, the isometry in
$\langle \beta ,\beta \rangle =\frac {2}{\ell }$
). As we have shown in the previous sections, the isometry in
![]() $Co.0$
determined by the reverse automorphism defined by a W-element of
$Co.0$
determined by the reverse automorphism defined by a W-element of
![]() $V_1$
is
$V_1$
is
![]() $\tau $
itself and
$\tau $
itself and
![]() $\beta $
is one of shortest roots of
$\beta $
is one of shortest roots of
![]() $V_1$
.
$V_1$
.
Lemma 7.12. Let
![]() $\gamma $
be a root of
$\gamma $
be a root of
![]() $V_1$
. Then
$V_1$
. Then
![]() $\langle \alpha , \gamma \rangle \neq 0$
.
$\langle \alpha , \gamma \rangle \neq 0$
.
Proof. Since
![]() $\rho ^{\perp }\cap N^{\tau } \subseteq \Lambda ^{\tau }$
, we have
$\rho ^{\perp }\cap N^{\tau } \subseteq \Lambda ^{\tau }$
, we have
![]() $\alpha ^{\perp }\cap L^{\ast }\subseteq \pi (\Lambda )$
and we have the desired result.
$\alpha ^{\perp }\cap L^{\ast }\subseteq \pi (\Lambda )$
and we have the desired result.
In other words,
![]() $\alpha $
is a regular element in
$\alpha $
is a regular element in
![]() $\mathcal{H}$
, and we can define a positive root
$\mathcal{H}$
, and we can define a positive root
![]() $\mu $
by
$\mu $
by
![]() $\langle \mu ,\alpha \rangle>0$
. Note that there is a correspondence between
$\langle \mu ,\alpha \rangle>0$
. Note that there is a correspondence between
![]() $L^*$
and
$L^*$
and
![]() $N^{\tau }$
through the map
$N^{\tau }$
through the map
![]() $\sqrt {\ell } \varphi _\tau $
. Since
$\sqrt {\ell } \varphi _\tau $
. Since
![]() $\langle \rho , v\rangle \in {\mathbb Z}$
for all
$\langle \rho , v\rangle \in {\mathbb Z}$
for all
![]() $v\in N$
,
$v\in N$
,
![]() $\langle \alpha , \mu \rangle \in \frac {1}h {\mathbb Z}$
for all
$\langle \alpha , \mu \rangle \in \frac {1}h {\mathbb Z}$
for all
![]() $\mu \in L^{\ast }$
. Since
$\mu \in L^{\ast }$
. Since
![]() $\langle \alpha ,\beta \rangle =\frac {1}{h}$
, we may assume
$\langle \alpha ,\beta \rangle =\frac {1}{h}$
, we may assume
![]() $\beta $
is a simple short root of a full component. Therefore, there is a W-element
$\beta $
is a simple short root of a full component. Therefore, there is a W-element
![]() $\widetilde {\alpha }$
such that
$\widetilde {\alpha }$
such that
![]() $\langle \widetilde {\alpha },\beta \rangle =\frac {1}{h}$
. In this case,
$\langle \widetilde {\alpha },\beta \rangle =\frac {1}{h}$
. In this case,
![]() $\widehat {\tau }\exp (2\pi i\beta (0))$
is a reverse automorphism of
$\widehat {\tau }\exp (2\pi i\beta (0))$
is a reverse automorphism of
![]() $V_\Lambda $
for
$V_\Lambda $
for
![]() $\exp (2\pi i\widetilde {\alpha }(0))$
, and we can recover the pair
$\exp (2\pi i\widetilde {\alpha }(0))$
, and we can recover the pair
![]() $(\tau , \tilde {\beta })$
and a Niemeier lattice
$(\tau , \tilde {\beta })$
and a Niemeier lattice
![]() $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
.
$N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$
.
7.2 The relation
 $\sim $
$\sim $
Next we will study the relation
![]() $\sim $
on
$\sim $
on
![]() $\mathcal{T}$
. Let
$\mathcal{T}$
. Let
![]() $(\tau , \tilde {\beta })$
and
$(\tau , \tilde {\beta })$
and
![]() $(\tau ', \tilde {\beta }')$
be two pairs in
$(\tau ', \tilde {\beta }')$
be two pairs in
![]() $\mathcal{T}$
. Suppose
$\mathcal{T}$
. Suppose
![]() $(\tau , \tilde {\beta }) \sim (\tau ', \tilde {\beta }')$
. As we mentioned, up to the action of
$(\tau , \tilde {\beta }) \sim (\tau ', \tilde {\beta }')$
. As we mentioned, up to the action of
![]() $O(\Lambda )$
, one can assume
$O(\Lambda )$
, one can assume
![]() $N=N'$
and
$N=N'$
and
![]() $\tilde {\beta }'= \tilde {\beta }-\lambda $
for some
$\tilde {\beta }'= \tilde {\beta }-\lambda $
for some
![]() $\lambda \in \Lambda _{\tilde {\beta }}$
.
$\lambda \in \Lambda _{\tilde {\beta }}$
.
Lemma 7.13. Suppose
![]() $\tilde {\beta }'= \tilde {\beta }-\lambda $
is also fixed by
$\tilde {\beta }'= \tilde {\beta }-\lambda $
is also fixed by
![]() $\tau $
. Then the VOAs defined by
$\tau $
. Then the VOAs defined by
![]() $(\tau , \tilde {\beta })$
and
$(\tau , \tilde {\beta })$
and
![]() $(\tau ,\tilde {\beta }')$
are isomorphic.
$(\tau ,\tilde {\beta }')$
are isomorphic.
Proof. By our assumption,
![]() $\lambda \in \Lambda ^\tau $
, and thus,
$\lambda \in \Lambda ^\tau $
, and thus,
![]() $\bar {\lambda }=\frac {1}{\sqrt {\ell }} \varphi ^{-1}(\lambda )\in (\Lambda ^\tau )^*$
. Then
$\bar {\lambda }=\frac {1}{\sqrt {\ell }} \varphi ^{-1}(\lambda )\in (\Lambda ^\tau )^*$
. Then
![]() $\widehat {\tau }\exp (2\pi i(\beta -\bar {\lambda })(0))=\tilde {g}\exp (-2\pi i \bar {\lambda }(0))$
is conjugate to
$\widehat {\tau }\exp (2\pi i(\beta -\bar {\lambda })(0))=\tilde {g}\exp (-2\pi i \bar {\lambda }(0))$
is conjugate to
![]() $\tilde {g}$
by [Reference Lam and Shimakura27, Lemma 4.5 [Reference Borcherds2]]. Therefore, they define isomorphic VOAs by orbifold constructions.
$\tilde {g}$
by [Reference Lam and Shimakura27, Lemma 4.5 [Reference Borcherds2]]. Therefore, they define isomorphic VOAs by orbifold constructions.
In other words, the choice of
![]() $\tilde {\beta }$
is somewhat ambiguous, and we can choose any
$\tilde {\beta }$
is somewhat ambiguous, and we can choose any
![]() $\tau $
-invariant root in the affine fundamental root system as the starting point.
$\tau $
-invariant root in the affine fundamental root system as the starting point.
Proposition 7.14. If
![]() $(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$
, then the VOAs obtained by the orbifold constructions from
$(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$
, then the VOAs obtained by the orbifold constructions from
![]() $V_\Lambda $
associated with
$V_\Lambda $
associated with
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
and
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$
and
![]() $\tilde {g}'=\widehat {\tau '}\exp (2\pi i\beta '(0))$
are isomorphic, where
$\tilde {g}'=\widehat {\tau '}\exp (2\pi i\beta '(0))$
are isomorphic, where
![]() $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and
$\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$
and
![]() $\beta '=\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta }')$
.
$\beta '=\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta }')$
.
Proof. Up to the action of
![]() $O(\Lambda )$
, one may assume
$O(\Lambda )$
, one may assume
![]() $N=N'$
and
$N=N'$
and
![]() $\tilde {\beta }'= \tilde {\beta }-\lambda $
for some
$\tilde {\beta }'= \tilde {\beta }-\lambda $
for some
![]() $\lambda \in \Lambda _{\tilde {\beta }}$
. Since
$\lambda \in \Lambda _{\tilde {\beta }}$
. Since
![]() $\tau $
is conjugate to
$\tau $
is conjugate to
![]() $\tau '$
in
$\tau '$
in
![]() $O(N)$
, there is a
$O(N)$
, there is a
![]() $\mu \in O(N)$
such that
$\mu \in O(N)$
such that
![]() $\tau = \mu \tau ' \mu ^{-1}$
. Then
$\tau = \mu \tau ' \mu ^{-1}$
. Then
![]() $\mu \tilde {\beta }'$
is fixed by
$\mu \tilde {\beta }'$
is fixed by
![]() $\tau $
. Note that h is still the smallest integer such that
$\tau $
. Note that h is still the smallest integer such that
![]() $h\mu \tilde {\beta }' \in \Lambda ^{\tau }$
. Since
$h\mu \tilde {\beta }' \in \Lambda ^{\tau }$
. Since
![]() $N= \cup _{j=1}^{h-1}(\Lambda _{\tilde {\beta }}+j\tilde {\beta })$
,
$N= \cup _{j=1}^{h-1}(\Lambda _{\tilde {\beta }}+j\tilde {\beta })$
,
![]() $\mu \tilde {\beta }' \in (\Lambda _{\tilde {\beta }}+k\tilde {\beta })$
for some k with
$\mu \tilde {\beta }' \in (\Lambda _{\tilde {\beta }}+k\tilde {\beta })$
for some k with
![]() $(k,h)=1$
. Therefore,
$(k,h)=1$
. Therefore,
![]() $<\tilde {g}^k> = <\tilde {g}>$
and
$<\tilde {g}^k> = <\tilde {g}>$
and
![]() $V^{[\tilde {g}]}\cong V^{[\tilde {g}^k]}$
.
$V^{[\tilde {g}]}\cong V^{[\tilde {g}^k]}$
.
Recall that
![]() $N_\tau \cong L_A(c_\tau )>R=\oplus A_{m_i-1}^{a_i}$
and
$N_\tau \cong L_A(c_\tau )>R=\oplus A_{m_i-1}^{a_i}$
and
![]() $\tau $
acts on
$\tau $
acts on
![]() $N_\tau $
as a Coxeter element of the root system R. Therefore, for
$N_\tau $
as a Coxeter element of the root system R. Therefore, for
![]() $ (k, |\tau |)=1$
,
$ (k, |\tau |)=1$
,
![]() $\tau $
is conjugate to
$\tau $
is conjugate to
![]() $\tau ^k$
by an element
$\tau ^k$
by an element
![]() $s\in Weyl(R)$
. In this case,
$s\in Weyl(R)$
. In this case,
![]() $s\mu \tilde {\beta }' =\mu \tilde {\beta }'$
and
$s\mu \tilde {\beta }' =\mu \tilde {\beta }'$
and
![]() $s\tau s^{-1} =\tau ^k$
. Therefore,
$s\tau s^{-1} =\tau ^k$
. Therefore,
![]() $(\tau , \mu \tilde {\beta }')$
and
$(\tau , \mu \tilde {\beta }')$
and
![]() $(\tau ^k,\mu \tilde {\beta }')$
define isomorphic VOAs. Moreover, by Lemma 7.13, the VOAs obtained by the orbifold constructions from
$(\tau ^k,\mu \tilde {\beta }')$
define isomorphic VOAs. Moreover, by Lemma 7.13, the VOAs obtained by the orbifold constructions from
![]() $V_\Lambda $
associated with
$V_\Lambda $
associated with
![]() $\tilde {g}^k=\widehat {\tau }^k\exp (2\pi i k\beta (0))$
and
$\tilde {g}^k=\widehat {\tau }^k\exp (2\pi i k\beta (0))$
and
![]() $\widehat {\tau }^k\exp (2\pi i \mu \beta '(0))$
are isomorphic, and we have the desired result.
$\widehat {\tau }^k\exp (2\pi i \mu \beta '(0))$
are isomorphic, and we have the desired result.
Therefore, there is a one-to-one correspondence between the set of isomorphic classes of holomorphic VOA V of central charge
![]() $24$
with non-abelian
$24$
with non-abelian
![]() $V_1$
and the set of equivalent classes
$V_1$
and the set of equivalent classes
![]() $(\sim )$
of pairs
$(\sim )$
of pairs
![]() $(\tau , \tilde {\beta })$
with
$(\tau , \tilde {\beta })$
with
![]() $\tau \in \mathcal{P}_0$
and
$\tau \in \mathcal{P}_0$
and
![]() $\tau $
-invariant deep hole
$\tau $
-invariant deep hole
![]() $\tilde {\beta }$
of
$\tilde {\beta }$
of
![]() $\Lambda $
satisfying the conditions in Theorem 7.1.
$\Lambda $
satisfying the conditions in Theorem 7.1.
Remark 7.15. Since there is a correspondence between deep holes, up to equivalence, and Niemeier lattices, each pair in
![]() $\mathcal{T}$
will define a unique pair
$\mathcal{T}$
will define a unique pair
![]() $(N, \tau )$
, where N is a Niemeier lattice with
$(N, \tau )$
, where N is a Niemeier lattice with
![]() $R(N)\neq \emptyset $
and
$R(N)\neq \emptyset $
and
![]() $\tau \in O(N)$
with a positive frame shape. Therefore, the classification of holomorphic VOAs of central charge
$\tau \in O(N)$
with a positive frame shape. Therefore, the classification of holomorphic VOAs of central charge
![]() $24$
with non-abelian weight one Lie algebras can also be reduced to a classification of the possible pairs of
$24$
with non-abelian weight one Lie algebras can also be reduced to a classification of the possible pairs of
![]() $(N, \tau )$
, up to some equivalence.
$(N, \tau )$
, up to some equivalence.
8 Höhn’s observation and Lie algebra structure of
 $V_1$
$V_1$
In [Reference Höhn21], Höhn observed that there is an interesting bijection between certain equivalence classes of cyclic subgroups of the glue codes of the Niemeier lattices with roots and the Lie algebra structures of the weight one subspace of a holomorphic vertex operator algebras of central charge
![]() $24$
corresponding to the
$24$
corresponding to the
![]() $69$
semisimple cases in Schellekens’ list. In this section, we will provide an explanation for Höhn’s observation using our main theorem. In particular, we will give a pure combinatorial classification of holomorphic vertex operator algebras of central charge
$69$
semisimple cases in Schellekens’ list. In this section, we will provide an explanation for Höhn’s observation using our main theorem. In particular, we will give a pure combinatorial classification of holomorphic vertex operator algebras of central charge
![]() $24$
with nontrivial weight one spaces. Indeed, the orbit lattice
$24$
with nontrivial weight one spaces. Indeed, the orbit lattice
![]() $N(Z)$
described by Höhn is essentially the lattice
$N(Z)$
described by Höhn is essentially the lattice
![]() $L= \sqrt {\ell }(N^\tau )^*$
, and the glue vector v is the vector
$L= \sqrt {\ell }(N^\tau )^*$
, and the glue vector v is the vector
![]() $\lambda _c$
as we defined in the appendix. The rescaling of the levels of the Lie algebras are handled uniformly using the
$\lambda _c$
as we defined in the appendix. The rescaling of the levels of the Lie algebras are handled uniformly using the
![]() $\ell $
-duality map
$\ell $
-duality map
![]() $\sqrt {\ell } \varphi _{\tau }$
.
$\sqrt {\ell } \varphi _{\tau }$
.
8.1 Roots of
 $V_1$
and
$V_1$
and
 $N^\tau $
$N^\tau $
First, we study the relationship between the root system of
![]() $V_1$
and the lattice
$V_1$
and the lattice
![]() $N^\tau \cong \sqrt {\ell }L^*$
. Recall from [Reference Dong and Wang15] that
$N^\tau \cong \sqrt {\ell }L^*$
. Recall from [Reference Dong and Wang15] that
 $$ \begin{align} L_{\mathfrak{g}_i}(k_i,0)= \bigoplus_{j\in Q_i/k_iQ^i_{l} } V_{\sqrt{k_i}Q^i_{l} + \frac{1}{\sqrt{k_i}} \beta_j} \otimes M^{0, \beta_j}, \end{align} $$
$$ \begin{align} L_{\mathfrak{g}_i}(k_i,0)= \bigoplus_{j\in Q_i/k_iQ^i_{l} } V_{\sqrt{k_i}Q^i_{l} + \frac{1}{\sqrt{k_i}} \beta_j} \otimes M^{0, \beta_j}, \end{align} $$
where
![]() $Q^i$
and
$Q^i$
and
![]() $Q^i_{l}$
denote the root lattice and the long root lattice of
$Q^i_{l}$
denote the root lattice and the long root lattice of
![]() $\mathfrak {g}_i$
, respectively, and
$\mathfrak {g}_i$
, respectively, and
![]() $\beta _j$
is a representative of
$\beta _j$
is a representative of
![]() $j\in Q^i/k_iQ^i_{l}$
.
$j\in Q^i/k_iQ^i_{l}$
.
By (8.1), the roots of the Lie algebra
![]() $V_1=\bigoplus _{i=1}^t\mathfrak {g}_i$
can be represented by elements in
$V_1=\bigoplus _{i=1}^t\mathfrak {g}_i$
can be represented by elements in
![]() $L^*$
. Indeed, we can view them as roots of the lattice
$L^*$
. Indeed, we can view them as roots of the lattice
![]() $\sqrt {\ell }L^*$
.
$\sqrt {\ell }L^*$
.
First, we recall the definition for the root system of an even lattice K (cf. [Reference Scharlau and Blaschke43; 44]).
Definition 8.1. A vector
![]() $v\in K$
is primitive if the sublattice spanned by v is a direct summand of L. A primitive vector v is called a root if
$v\in K$
is primitive if the sublattice spanned by v is a direct summand of L. A primitive vector v is called a root if
![]() $2\langle v, K\rangle /\langle v,v\rangle \subset {\mathbb Z}$
. The set of roots
$2\langle v, K\rangle /\langle v,v\rangle \subset {\mathbb Z}$
. The set of roots
is called the root system of K.
Definition 8.2. Let K be an even lattice. The level
![]() $\ell $
of K is the smallest positive integer
$\ell $
of K is the smallest positive integer
![]() $\ell $
such that
$\ell $
such that
![]() $\sqrt {\ell }K^*$
is still even.
$\sqrt {\ell }K^*$
is still even.
As in [Reference Scharlau and Blaschke43], we denote the scaled root system as follows.

We also consider the reduced discriminant group of an arbitrary scaled root system R, which is a subgroup of the discriminant group of the sublattice generated by R (see [Reference Scharlau and Blaschke43, Definition 2.1]). For an irreducible root system
![]() $^\alpha \! X$
of type A, D or E, the reduced discriminant group of
$^\alpha \! X$
of type A, D or E, the reduced discriminant group of
![]() $^\alpha \! X$
is simply the discriminant group
$^\alpha \! X$
is simply the discriminant group
![]() $\mathcal {D}(X)$
.
$\mathcal {D}(X)$
.
For non-simply laced root systems, the corresponding root lattices and reduced discriminant groups are as follows.

For explicit description of the reduced discriminant groups for the root systems of
![]() ${^\alpha }\!B_n$
and
${^\alpha }\!B_n$
and
![]() ${^\alpha }\!C_n$
, we use the following standard model for their root lattices; namely,
${^\alpha }\!C_n$
, we use the following standard model for their root lattices; namely,
 $$\begin{align*}{^\alpha}\!B_n = \bigoplus_{i=1}^n {\mathbb Z} e_i, \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$
$$\begin{align*}{^\alpha}\!B_n = \bigoplus_{i=1}^n {\mathbb Z} e_i, \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$
roots:
![]() $e_i$
of norm
$e_i$
of norm
![]() $\alpha $
and
$\alpha $
and
![]() $\pm e_i\pm e_j$
of norm
$\pm e_i\pm e_j$
of norm
![]() $2\alpha $
; and
$2\alpha $
; and
 $$\begin{align*}{^\alpha}\!C_n = \{ \sum_{i=1}^n x_i e_i \mid \sum_{i=1}^n x_i \equiv 0\quad \mod 2\} \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$
$$\begin{align*}{^\alpha}\!C_n = \{ \sum_{i=1}^n x_i e_i \mid \sum_{i=1}^n x_i \equiv 0\quad \mod 2\} \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$
roots:
![]() $\pm e_i\pm e_j$
of norm
$\pm e_i\pm e_j$
of norm
![]() $2\alpha $
and
$2\alpha $
and
![]() $2e_i$
of norm
$2e_i$
of norm
![]() $2\alpha $
.
$2\alpha $
.
The reduced discriminant group of
![]() $^{\alpha }\! B_n$
is
$^{\alpha }\! B_n$
is
![]() $0$
if
$0$
if
![]() $\alpha $
is odd, and the reduced discriminant group of R is given by
$\alpha $
is odd, and the reduced discriminant group of R is given by
![]() $\langle \bar {g} \rangle \cong {\mathbb Z}_2$
where
$\langle \bar {g} \rangle \cong {\mathbb Z}_2$
where
 $$\begin{align*}\begin{cases} g=\frac{1}2 (e_1+\cdots +e_n) & \text{ if } R= ^{2\alpha}\!\! B_n, \\ g= e_1 & \text{ if } R= ^{\alpha}\!\! C_n. \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} g=\frac{1}2 (e_1+\cdots +e_n) & \text{ if } R= ^{2\alpha}\!\! B_n, \\ g= e_1 & \text{ if } R= ^{\alpha}\!\! C_n. \end{cases} \end{align*}$$
Remark 8.3 (see [Reference Scharlau and Blaschke43])
An element
![]() $v\in K$
is a root if and only if
$v\in K$
is a root if and only if
![]() $v\in \langle v,v\rangle /2\cdot K^*$
and v is primitive in K. In particular,
$v\in \langle v,v\rangle /2\cdot K^*$
and v is primitive in K. In particular,
![]() $\langle v,v\rangle /2$
divides the exponent of
$\langle v,v\rangle /2$
divides the exponent of
![]() $\mathcal {D}(K)=K^*/K$
.
$\mathcal {D}(K)=K^*/K$
.
Lemma 8.4. Let
![]() $v\in K$
such that
$v\in K$
such that
![]() $v\in \langle v,v\rangle /2\cdot K^*$
. Assume that
$v\in \langle v,v\rangle /2\cdot K^*$
. Assume that
![]() $v/n\in K$
for some
$v/n\in K$
for some
![]() $n\in {\mathbb Z}$
with
$n\in {\mathbb Z}$
with
![]() $n>1$
. Then
$n>1$
. Then
![]() $n=2$
. Moreover,
$n=2$
. Moreover,
![]() $\frac {v}2$
is a root and
$\frac {v}2$
is a root and
![]() $K= {\mathbb Z}(\frac {v}2) \perp (K\cap \langle v\rangle ^\perp )$
.
$K= {\mathbb Z}(\frac {v}2) \perp (K\cap \langle v\rangle ^\perp )$
.
Proof. Since
![]() $v/n\in K$
and
$v/n\in K$
and
![]() $v\in \langle v,v\rangle /2\cdot K^*$
, we have
$v\in \langle v,v\rangle /2\cdot K^*$
, we have
hence,
![]() $n=2$
. Then
$n=2$
. Then
![]() $\frac {v}2$
is primitive in K and
$\frac {v}2$
is primitive in K and
![]() $\frac {2\langle v/2,x\rangle }{\langle v/2,v/2\rangle } = \frac {4\langle v,x\rangle }{\langle v,v\rangle }\in {\mathbb Z}$
for any
$\frac {2\langle v/2,x\rangle }{\langle v/2,v/2\rangle } = \frac {4\langle v,x\rangle }{\langle v,v\rangle }\in {\mathbb Z}$
for any
![]() $x\in K$
; hence, it is a root.
$x\in K$
; hence, it is a root.
Let
![]() $p_v: K \to ({\mathbb Z} \frac {v}2)^*$
be the natural projection. For any
$p_v: K \to ({\mathbb Z} \frac {v}2)^*$
be the natural projection. For any
![]() $x\in K$
,
$x\in K$
,
![]() $p_v(x) = r_x v$
for some
$p_v(x) = r_x v$
for some
![]() $r_x\in {\mathbb Q}$
. Then
$r_x\in {\mathbb Q}$
. Then
![]() $ \frac {2\langle v,x\rangle }{\langle v,v\rangle } = \frac {2\langle v,r_xv\rangle }{\langle v,v\rangle } =2r_x\in {\mathbb Z}$
. That means
$ \frac {2\langle v,x\rangle }{\langle v,v\rangle } = \frac {2\langle v,r_xv\rangle }{\langle v,v\rangle } =2r_x\in {\mathbb Z}$
. That means
![]() $r_x\in \frac {1}2 {\mathbb Z}$
and
$r_x\in \frac {1}2 {\mathbb Z}$
and
![]() $p_v(K)= {\mathbb Z}(\frac {v}2)$
as desired.
$p_v(K)= {\mathbb Z}(\frac {v}2)$
as desired.
The following results can be found in [Reference Scharlau and Blaschke43].
Theorem 8.5. Let K be an integral lattice and R a root system contained in K. Let
![]() $\mathcal {K} = K/ (\langle R\rangle \perp (R^\perp \cap K))$
be the glue code of K over R. Then the elements of R are actually roots of K if and only if
$\mathcal {K} = K/ (\langle R\rangle \perp (R^\perp \cap K))$
be the glue code of K over R. Then the elements of R are actually roots of K if and only if
![]() $\mathcal {K}$
is contained in the reduced discriminant group of R. Furthermore, K contains no elements of the form
$\mathcal {K}$
is contained in the reduced discriminant group of R. Furthermore, K contains no elements of the form
![]() $e/2$
, where e is a basis vector of an
$e/2$
, where e is a basis vector of an
![]() $A_1$
-component.
$A_1$
-component.
Recall that
![]() $\ell $
is divisible by
$\ell $
is divisible by
![]() $|\tau |(K_0-N_0)=\mathrm {LCM} (\{r_ik_i\}_{i=1}^t)$
by Lemmas 2.3 and 4.12.
$|\tau |(K_0-N_0)=\mathrm {LCM} (\{r_ik_i\}_{i=1}^t)$
by Lemmas 2.3 and 4.12.
Lemma 8.6. Let
![]() $\beta $
be a root of
$\beta $
be a root of
![]() $\mathfrak {g}_{i,k_i}$
and
$\mathfrak {g}_{i,k_i}$
and
![]() $M=\sqrt {\ell }L^*$
. Then
$M=\sqrt {\ell }L^*$
. Then
 $$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta \in \frac{\langle v,v\rangle }{2} M^*. \end{align*}$$
$$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta \in \frac{\langle v,v\rangle }{2} M^*. \end{align*}$$
In particular,
![]() $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
is a root of M if it is primitive in M or
$v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
is a root of M if it is primitive in M or
![]() ${\mathbb Z}(v/2)$
is an orthogonal summand of M.
${\mathbb Z}(v/2)$
is an orthogonal summand of M.
Proof. Let
![]() $M=\sqrt {\ell }L^*$
and
$M=\sqrt {\ell }L^*$
and
![]() $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
. Then
$v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
. Then
![]() $M^* =\frac {1}{\sqrt {\ell }} L$
and
$M^* =\frac {1}{\sqrt {\ell }} L$
and
 $$\begin{align*}\frac{\langle v,v\rangle }{2}= \begin{cases} \frac{\ell}{r_ik_i} & \text{ if }\beta\text{ is a short root,}\\ \frac{\ell}{k_i} & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$
$$\begin{align*}\frac{\langle v,v\rangle }{2}= \begin{cases} \frac{\ell}{r_ik_i} & \text{ if }\beta\text{ is a short root,}\\ \frac{\ell}{k_i} & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$
Therefore,
 $$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta= \begin{cases} \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} (r_i\beta)& \text{ if }\beta\text{ is a short root,}\\ \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} \beta & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$
$$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta= \begin{cases} \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} (r_i\beta)& \text{ if }\beta\text{ is a short root,}\\ \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} \beta & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$
Since
![]() $L> \sqrt {k_i}Q^i_{l}$
and
$L> \sqrt {k_i}Q^i_{l}$
and
![]() $r_i\beta \in Q^i_{l}$
(resp.
$r_i\beta \in Q^i_{l}$
(resp.
![]() $\beta \in Q^i_{l}$
) if
$\beta \in Q^i_{l}$
) if
![]() $\beta $
is a short root (resp., a long root),
$\beta $
is a short root (resp., a long root),
![]() $v \in \frac {\langle v,v\rangle }{2} M^*$
as desired.
$v \in \frac {\langle v,v\rangle }{2} M^*$
as desired.
Lemma 8.7. Let
![]() $\mathfrak {g}_{i,k_i}$
be a simple Lie subalgebra of
$\mathfrak {g}_{i,k_i}$
be a simple Lie subalgebra of
![]() $V_1$
. Suppose there is a root
$V_1$
. Suppose there is a root
![]() $\beta $
of
$\beta $
of
![]() $\mathfrak {g}_{i,k_i}$
such that
$\mathfrak {g}_{i,k_i}$
such that
![]() $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
is not a root of
$v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $
is not a root of
![]() $N^\tau $
. Then
$N^\tau $
. Then
![]() $\beta $
is a long root, and the long root lattice of
$\beta $
is a long root, and the long root lattice of
![]() $\mathfrak {g}_i$
is of the type
$\mathfrak {g}_i$
is of the type
![]() $A_1^r$
, where
$A_1^r$
, where
![]() $r=\mathrm {rank}(\mathfrak {g}_i)$
. In particular,
$r=\mathrm {rank}(\mathfrak {g}_i)$
. In particular,
![]() $\mathfrak {g}_i$
is of type
$\mathfrak {g}_i$
is of type
![]() $A_1$
or
$A_1$
or
![]() $C_r$
.
$C_r$
.
Proof. Without loss of generality, we may assume
![]() $\mathrm {rank}(V_1)>1$
. By Lemma 8.6,
$\mathrm {rank}(V_1)>1$
. By Lemma 8.6,
![]() ${\mathbb Z}(v/2)$
is an orthogonal summand of
${\mathbb Z}(v/2)$
is an orthogonal summand of
![]() $N^\tau $
. Suppose
$N^\tau $
. Suppose
![]() $\beta $
is a short root. Then for any short root
$\beta $
is a short root. Then for any short root
![]() $\beta '$
,
$\beta '$
,
![]() $v'=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta '$
is not a root of
$v'=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta '$
is not a root of
![]() $N^\tau $
. Therefore,
$N^\tau $
. Therefore,
![]() $\frac {\sqrt {\ell }}{2\sqrt {k_i}} Q_i \cong \sqrt {s} A_1^r$
; however,
$\frac {\sqrt {\ell }}{2\sqrt {k_i}} Q_i \cong \sqrt {s} A_1^r$
; however,
![]() ${\mathbb Z} \frac {\sqrt {\ell }}{2\sqrt {k_i}} \alpha $
is not an orthogonal summand of
${\mathbb Z} \frac {\sqrt {\ell }}{2\sqrt {k_i}} \alpha $
is not an orthogonal summand of
![]() $\sqrt {s} A_1^r$
for any long root
$\sqrt {s} A_1^r$
for any long root
![]() $\alpha $
. Therefore,
$\alpha $
. Therefore,
![]() $\beta $
is a long root and the long root lattice is of type
$\beta $
is a long root and the long root lattice is of type
![]() $A_1^r$
.
$A_1^r$
.
By the lemmas above, the lattice
![]() $N^\tau =\sqrt {\ell }L^*$
contains the information of the (scaled) root system of
$N^\tau =\sqrt {\ell }L^*$
contains the information of the (scaled) root system of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
8.2 Orbit diagrams and Lie algebra structures of
 $V_1$
$V_1$
Let V be a holomorphic VOA of central charge
![]() $24$
and
$24$
and
![]() $\alpha $
a W-element of
$\alpha $
a W-element of
![]() $V_1$
. Let
$V_1$
. Let
![]() $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
and let
$g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$
and let
![]() $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism of g, where
$\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$
be the reverse automorphism of g, where
![]() $\beta \in {\mathbb C}\Lambda ^{\tau }$
. Let
$\beta \in {\mathbb C}\Lambda ^{\tau }$
. Let
![]() $\varphi _{\tau }: \sqrt {\ell }(\Lambda ^\tau )^* \to \Lambda ^\tau $
be the isometry described in Theorem 4.2. Recall that the vector
$\varphi _{\tau }: \sqrt {\ell }(\Lambda ^\tau )^* \to \Lambda ^\tau $
be the isometry described in Theorem 4.2. Recall that the vector
![]() $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
is a deep hole of
$\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$
is a deep hole of
![]() $\Lambda $
and
$\Lambda $
and
![]() $N=\Lambda ^{[\tilde {\beta }]} \ncong \Lambda $
. Moreover, the Coxeter number h of N is equal to
$N=\Lambda ^{[\tilde {\beta }]} \ncong \Lambda $
. Moreover, the Coxeter number h of N is equal to
![]() $n=\mathrm {LCM}(r_ih_i^\vee )$
and
$n=\mathrm {LCM}(r_ih_i^\vee )$
and
![]() $N^\tau \cong \sqrt {\ell }L^*$
.
$N^\tau \cong \sqrt {\ell }L^*$
.
Let R be the set of roots in N and set
![]() $ R_k=\{\mu \in -k\tilde {\beta }+ \Lambda _{\tilde {\beta }} \mid \langle \mu , \mu \rangle =2 \}. $
Then
$ R_k=\{\mu \in -k\tilde {\beta }+ \Lambda _{\tilde {\beta }} \mid \langle \mu , \mu \rangle =2 \}. $
Then
![]() $R= \cup _{k=1}^{h-1} R_k$
. Since the Leech lattice does not contain a root,
$R= \cup _{k=1}^{h-1} R_k$
. Since the Leech lattice does not contain a root,
![]() $\langle \mu , \nu \rangle \leq 0$
for
$\langle \mu , \nu \rangle \leq 0$
for
![]() $\mu , \nu \in R_k$
with
$\mu , \nu \in R_k$
with
![]() $\mu \neq \nu $
for each k. Indeed,
$\mu \neq \nu $
for each k. Indeed,
![]() $\langle \mu , \nu \rangle =0$
or
$\langle \mu , \nu \rangle =0$
or
![]() $-1$
for any
$-1$
for any
![]() $\mu , \nu \in R_k$
with
$\mu , \nu \in R_k$
with
![]() $\mu \neq \nu $
.
$\mu \neq \nu $
.
One can associate a (simply laced) Dynkin diagram with
![]() $R_k$
for each k. Namely, the nodes are labeled by elements of
$R_k$
for each k. Namely, the nodes are labeled by elements of
![]() $R_k$
, and two nodes x and y are connected if and only if
$R_k$
, and two nodes x and y are connected if and only if
![]() $\langle x, y\rangle =-1$
. By abuse of notations, we often use
$\langle x, y\rangle =-1$
. By abuse of notations, we often use
![]() $R_k$
to denote both the Dynkin diagram and the subset of roots. Note that
$R_k$
to denote both the Dynkin diagram and the subset of roots. Note that
![]() $\tau $
acts on
$\tau $
acts on
![]() $R_k$
for each k and acts as a diagram automorphism associated with the diagram defined by
$R_k$
for each k and acts as a diagram automorphism associated with the diagram defined by
![]() $R_k$
.
$R_k$
.
Since
![]() $\tilde {\beta }$
is a deep hole of the Leech lattice
$\tilde {\beta }$
is a deep hole of the Leech lattice
![]() $\Lambda $
,
$\Lambda $
,
![]() $R_1$
is a disjoint union of the affine diagrams associated with the root system of N. Moreover,
$R_1$
is a disjoint union of the affine diagrams associated with the root system of N. Moreover,
![]() $\tau $
acts on
$\tau $
acts on
![]() $R_1$
. Since
$R_1$
. Since
![]() $N_\tau \cong L_A(c)$
and
$N_\tau \cong L_A(c)$
and
![]() $\tau $
acts as
$\tau $
acts as
![]() $g_{\Delta ,c}$
on a root sublattice of
$g_{\Delta ,c}$
on a root sublattice of
![]() $N_\tau $
,
$N_\tau $
,
![]() $\tau \in \mathrm {Weyl}(R)$
and preserves all irreducible components of
$\tau \in \mathrm {Weyl}(R)$
and preserves all irreducible components of
![]() $R(N)$
. Note also that
$R(N)$
. Note also that
![]() $g_{\Delta ,c}$
induces an isometry in
$g_{\Delta ,c}$
induces an isometry in
![]() $O(\Lambda )$
if and only if
$O(\Lambda )$
if and only if
![]() $\lambda _c\in N$
[Reference Betsumiya, Lam and Shimakura5]. Therefore, the vector
$\lambda _c\in N$
[Reference Betsumiya, Lam and Shimakura5]. Therefore, the vector
![]() $\lambda _c$
corresponds to a codeword of the glue code
$\lambda _c$
corresponds to a codeword of the glue code
![]() $N/R$
. In particular,
$N/R$
. In particular,
![]() $P_{Q_i}(\lambda _c)\in (Q_i)^*$
for every irreducible root sublattice
$P_{Q_i}(\lambda _c)\in (Q_i)^*$
for every irreducible root sublattice
![]() $Q_i$
of N. Note also that
$Q_i$
of N. Note also that
![]() $\tau $
has a positive frame when viewing as an isometry of N.
$\tau $
has a positive frame when viewing as an isometry of N.
Therefore, for each irreducible component, we can consider the quotient diagram as follows: we identify an orbit of nodes as one node, and two nodes are connected if the nodes in the corresponding orbits are connected. By removing the node associated with the extended node, one obtains a usual Dynkin diagram (see Table 2).
Table 2 Diagram automorphisms of affine diagrams.

Note that the fixed sublattice is the (scaled) root lattice of the quotient diagram. A fixed node (or fixed simple root) corresponds to a simple short root of a full component.
Remark 8.8. Let
![]() $\mathcal{G}_i$
be a simple Lie subalgebra of
$\mathcal{G}_i$
be a simple Lie subalgebra of
![]() $V_1$
with
$V_1$
with
![]() $r_ih_i^\vee =n=h$
. Then
$r_ih_i^\vee =n=h$
. Then
![]() $\ell =r_ik_i$
and
$\ell =r_ik_i$
and
![]() $k_i/h_i^\vee = \ell /h$
. Therefore, the level
$k_i/h_i^\vee = \ell /h$
. Therefore, the level
![]() $k_j$
of the simple Lie subalgebra
$k_j$
of the simple Lie subalgebra
![]() $\mathcal{G}_j$
is given by
$\mathcal{G}_j$
is given by
![]() $k_j= \ell h^\vee _j/h$
for any j. Note also that the short roots of
$k_j= \ell h^\vee _j/h$
for any j. Note also that the short roots of
![]() $\mathcal{G}_i$
will correspond to an irreducible (connected) component
$\mathcal{G}_i$
will correspond to an irreducible (connected) component
![]() $S_i$
of
$S_i$
of
![]() $N^\tau _2$
. Moreover,
$N^\tau _2$
. Moreover,
![]() $S_i\cap R_1$
corresponds to the simple short roots of
$S_i\cap R_1$
corresponds to the simple short roots of
![]() $\mathcal{G}_i$
. Therefore,
$\mathcal{G}_i$
. Therefore,
![]() $S_i$
and
$S_i$
and
![]() $S_i\cap R_1$
determines the type of
$S_i\cap R_1$
determines the type of
![]() $\mathcal{G}_i$
uniquely.
$\mathcal{G}_i$
uniquely.
Remark 8.9. In [Reference Möller and Scheithauer40], a notion of generalized hole diagrams is introduced. It was shown that a generalized hole diagram determines a generalized deep hole up to conjugacy and that there are exactly
![]() $70$
such diagrams. This notion of generalized hole diagrams essentially corresponds to the diagram associated with simple short roots of the full components (i.e., elements in
$70$
such diagrams. This notion of generalized hole diagrams essentially corresponds to the diagram associated with simple short roots of the full components (i.e., elements in
![]() $R_1\cap N^\tau _2$
).
$R_1\cap N^\tau _2$
).
8.3 Possible pairs for
 $(N, \tau )$
$(N, \tau )$
Next, we will discuss the possible choices for the pair
![]() $(N, \tau )$
for each
$(N, \tau )$
for each
![]() $\tau \in \mathcal{P}_0$
.
$\tau \in \mathcal{P}_0$
.
8.3.1
 $\tau \in 2A$
$\tau \in 2A$
For
![]() $\tau \in 2A$
of
$\tau \in 2A$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=|\tau |=2$
. In this case,
$\ell =|\widehat {\tau }|=|\tau |=2$
. In this case,
![]() $\Lambda _\tau \cong \sqrt {2}E_8$
. Let
$\Lambda _\tau \cong \sqrt {2}E_8$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $2$
and
$2$
and
![]() $ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^8, \frac {1}2 (\alpha _1 +\cdots +\alpha _8)\}$
, where
$ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^8, \frac {1}2 (\alpha _1 +\cdots +\alpha _8)\}$
, where
![]() ${\mathbb Z} \alpha _1 +\cdots +{\mathbb Z}\alpha _8\cong A_1^8$
. The vector
${\mathbb Z} \alpha _1 +\cdots +{\mathbb Z}\alpha _8\cong A_1^8$
. The vector
![]() $v= \frac {1}2 (\alpha _1 +\cdots +\alpha _8)$
corresponds to a codeword
$v= \frac {1}2 (\alpha _1 +\cdots +\alpha _8)$
corresponds to a codeword
![]() $c\in N/R$
. The possible choices for
$c\in N/R$
. The possible choices for
![]() $(N, \tau )$
, the codeword c and the corresponding root systems and Lie algebra structures for
$(N, \tau )$
, the codeword c and the corresponding root systems and Lie algebra structures for
![]() $V_1$
are listed in Table 3.
$V_1$
are listed in Table 3.
Table 3
![]() $({N}{,}\tau )$
for the case
$({N}{,}\tau )$
for the case
![]() $2A$
.
$2A$
.

8.3.2
 $\tau \in 3B$
$\tau \in 3B$
For
![]() $\tau \in 3B$
of
$\tau \in 3B$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=|\tau |=3$
. In this case,
$\ell =|\widehat {\tau }|=|\tau |=3$
. In this case,
![]() $\Lambda _\tau \cong K_{12}$
is the Coxeter-Todd lattice of rank
$\Lambda _\tau \cong K_{12}$
is the Coxeter-Todd lattice of rank
![]() $12$
. Let
$12$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $3$
and
$3$
and
![]() $N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_2^6, (\gamma _1, \dots , \gamma _6)\}$
, where
$N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_2^6, (\gamma _1, \dots , \gamma _6)\}$
, where
![]() $\gamma _i +A_2$
is a generator of
$\gamma _i +A_2$
is a generator of
![]() $A_2^*/A_2$
for each i. The vector
$A_2^*/A_2$
for each i. The vector
![]() $(\gamma _1, \dots , \gamma _6)$
corresponds to a codeword
$(\gamma _1, \dots , \gamma _6)$
corresponds to a codeword
![]() $c\in N/R$
. The possible choices for
$c\in N/R$
. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures for
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures for
![]() $V_1$
are listed in Table 4.
$V_1$
are listed in Table 4.
Table 4
![]() $(N,\tau )$
for the case
$(N,\tau )$
for the case
![]() $3B$
.
$3B$
.

8.3.3
 $\tau \in 5B$
$\tau \in 5B$
For
![]() $\tau \in 5B$
of
$\tau \in 5B$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=|\tau |=5$
and the Coxeter number of
$\ell =|\widehat {\tau }|=|\tau |=5$
and the Coxeter number of
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
is divisible by
![]() $5$
. In this case,
$5$
. In this case,
![]() $N_\tau \cong \mathrm {Span}_{\mathbb Z}\{ A_4^4, (\gamma _1, \gamma _2, \gamma _3, \gamma _4)\}$
, where
$N_\tau \cong \mathrm {Span}_{\mathbb Z}\{ A_4^4, (\gamma _1, \gamma _2, \gamma _3, \gamma _4)\}$
, where
![]() $\gamma _i +A_4$
is a generator of
$\gamma _i +A_4$
is a generator of
![]() $A_4^*/A_4$
for each i. Again, the vector
$A_4^*/A_4$
for each i. Again, the vector
![]() $(\gamma _1, \gamma _2, \gamma _3, \gamma _4)$
corresponds to a codeword
$(\gamma _1, \gamma _2, \gamma _3, \gamma _4)$
corresponds to a codeword
![]() $c\in N/R$
. That means
$c\in N/R$
. That means
![]() $5=|\tau |$
divides
$5=|\tau |$
divides
![]() $|N/R|$
also. The possible choices for
$|N/R|$
also. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 5.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 5.
Table 5
![]() $(N,\tau )$
for the case
$(N,\tau )$
for the case
![]() $5B$
.
$5B$
.

8.3.4
 $\tau \in 7B$
$\tau \in 7B$
For
![]() $\tau \in 7B$
of
$\tau \in 7B$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=7$
. Let
$\ell =|\widehat {\tau }|=7$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $7$
and
$7$
and
![]() $N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_6^3, (\gamma _1,\gamma _2, \gamma _3)\}$
, where
$N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_6^3, (\gamma _1,\gamma _2, \gamma _3)\}$
, where
![]() $\gamma _i +A_6$
is a generator of
$\gamma _i +A_6$
is a generator of
![]() $A_6^*/A_6$
for each i. The vector
$A_6^*/A_6$
for each i. The vector
![]() $(\gamma _1,\gamma _2, \gamma _3)$
corresponds to a codeword
$(\gamma _1,\gamma _2, \gamma _3)$
corresponds to a codeword
![]() $c\in N/R$
. The possible choices for
$c\in N/R$
. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 6.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 6.
Table 6
![]() $(N,\tau )$
for the case
$(N,\tau )$
for the case
![]() $7B$
.
$7B$
.

8.3.5
 $\tau \in 2C$
$\tau \in 2C$
For
![]() $\tau \in 2C$
of
$\tau \in 2C$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=2|\tau |=4$
. Let
$\ell =|\widehat {\tau }|=2|\tau |=4$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $2$
and
$2$
and
![]() $ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^{12}, \frac {1}2(\alpha ,\dots , \alpha )\}, $
where
$ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^{12}, \frac {1}2(\alpha ,\dots , \alpha )\}, $
where
![]() ${\mathbb Z}\alpha \cong A_1$
. The vector
${\mathbb Z}\alpha \cong A_1$
. The vector
![]() $\frac {1}2(\alpha ,\dots , \alpha )$
again corresponds to a codeword
$\frac {1}2(\alpha ,\dots , \alpha )$
again corresponds to a codeword
![]() $c\in N/R$
. The possible choices for
$c\in N/R$
. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 7.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 7.
Table 7
![]() $(N, \tau )$
for the case
$(N, \tau )$
for the case
![]() $2C$
.
$2C$
.

8.3.6
 $\tau \in 4C$
$\tau \in 4C$
For
![]() $\tau \in 4C$
of
$\tau \in 4C$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=|\tau |=4$
. Let
$\ell =|\widehat {\tau }|=|\tau |=4$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $4$
and the coinvariant lattice
$4$
and the coinvariant lattice
where
![]() $\lambda = 1/2(1,1,1,-3)\in A_3^*$
and
$\lambda = 1/2(1,1,1,-3)\in A_3^*$
and
![]() ${\mathbb Z}\alpha = A_1$
. Note that
${\mathbb Z}\alpha = A_1$
. Note that
![]() $N^\tau $
contains
$N^\tau $
contains
![]() $A_3^4 A_1^2$
as an index
$A_3^4 A_1^2$
as an index
![]() $4$
sublattice. The possible choices for
$4$
sublattice. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 8.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 8.
Table 8
![]() $(N, \tau )$
for the case
$(N, \tau )$
for the case
![]() $4C$
.
$4C$
.

8.3.7
 $\tau \in 6E$
$\tau \in 6E$
For
![]() $\tau \in 6E$
of
$\tau \in 6E$
of
![]() $O(\Lambda )$
, we have
$O(\Lambda )$
, we have
![]() $\ell =|\widehat {\tau }|=6$
. Let
$\ell =|\widehat {\tau }|=6$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $6$
and the coinvariant sublattice
$6$
and the coinvariant sublattice
where
![]() $\beta = \frac {1}6(1^5, -5)\in A_5^*$
,
$\beta = \frac {1}6(1^5, -5)\in A_5^*$
,
![]() $\gamma = \frac {1}3 (1,1,-2)\in A_3^*$
and
$\gamma = \frac {1}3 (1,1,-2)\in A_3^*$
and
![]() $\langle \alpha , \alpha \rangle =2$
. Note that
$\langle \alpha , \alpha \rangle =2$
. Note that
![]() $N^\tau $
is an index
$N^\tau $
is an index
![]() $6$
sublattice of
$6$
sublattice of
![]() $E_8\perp E_8$
. The possible choices for
$E_8\perp E_8$
. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 9.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 9.
Table 9
![]() $(N, \tau )$
for the case
$(N, \tau )$
for the case
![]() $6E$
.
$6E$
.

8.3.8
 $\tau \in 8E$
$\tau \in 8E$
For
![]() $\tau \in 8E$
,
$\tau \in 8E$
,
![]() $\ell =|\widehat {\tau }|=8$
. Let
$\ell =|\widehat {\tau }|=8$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $8$
and the coinvariant lattice
$8$
and the coinvariant lattice
![]() $N_\tau $
is an index
$N_\tau $
is an index
![]() $8$
over-lattice of the lattice
$8$
over-lattice of the lattice
![]() $A_7^2A_3A_1$
. More precisely,
$A_7^2A_3A_1$
. More precisely,
where
![]() $\gamma _3=\frac {1}8 (3^5, -5^3)$
,
$\gamma _3=\frac {1}8 (3^5, -5^3)$
,
![]() $\gamma _1=\frac {1}8 (1^7, -7)$
are in
$\gamma _1=\frac {1}8 (1^7, -7)$
are in
![]() $A_7^*$
,
$A_7^*$
,
![]() $\beta \in \frac {1}2(1,1,1)\in A_3^* $
and
$\beta \in \frac {1}2(1,1,1)\in A_3^* $
and
![]() $\alpha =\frac {1}2 (1,1)\in A_1^*$
.
$\alpha =\frac {1}2 (1,1)\in A_1^*$
.
The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 9.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in Table 9.

8.3.9
 $\tau \in 6G$
$\tau \in 6G$
For
![]() $\tau \in 6G$
,
$\tau \in 6G$
,
![]() $\ell =|\widehat {\tau }| =12$
. Let
$\ell =|\widehat {\tau }| =12$
. Let
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
. Then the Coxeter number of N is divisible by
![]() $6$
and
$6$
and
![]() $N_\tau $
contains
$N_\tau $
contains
![]() $A_5^3 A_1^3$
as an index
$A_5^3 A_1^3$
as an index
![]() $6$
sublattice. The possible choices for
$6$
sublattice. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in the following table.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in the following table.

8.3.10
 $\tau \in 10F$
$\tau \in 10F$
For
![]() $\tau \in 10F$
,
$\tau \in 10F$
,
![]() $\ell =|\widehat {\tau }|=20$
. The Coxeter number of
$\ell =|\widehat {\tau }|=20$
. The Coxeter number of
![]() $N=\Lambda ^{[ \tilde {\beta }] }$
is divisible by
$N=\Lambda ^{[ \tilde {\beta }] }$
is divisible by
![]() $10$
and
$10$
and
![]() $N_\tau $
contains
$N_\tau $
contains
![]() $A_9^2 A_1^2$
as an index
$A_9^2 A_1^2$
as an index
![]() $10$
sublattice. The possible choices for
$10$
sublattice. The possible choices for
![]() $(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in the following table.
$(N, \tau )$
, c and the corresponding root systems and Lie algebra structures are listed in the following table.

Remark 8.10. Since
![]() $N_\tau = L_A(c)$
with c as a codeword of the glue code
$N_\tau = L_A(c)$
with c as a codeword of the glue code
![]() $N/R$
, we can recover the same information as in [Reference Höhn21, Table 3]. In particular, there are exactly
$N/R$
, we can recover the same information as in [Reference Höhn21, Table 3]. In particular, there are exactly
![]() $46$
possible Lie algebra structures for
$46$
possible Lie algebra structures for
![]() $V_1$
if
$V_1$
if
![]() $0 < \mathrm{rank}(V_1) < 24$
. This gives an alternative proof for the Schellekens list.
$0 < \mathrm{rank}(V_1) < 24$
. This gives an alternative proof for the Schellekens list.
A Properties of the lattice
 $\Lambda _{\tau} $
for
$\Lambda _{\tau} $
for
 $\tau \in \mathcal{P}_0$
$\tau \in \mathcal{P}_0$
In this appendix, we review some properties of the coinvariant sublattice
![]() $\Lambda _\tau $
for
$\Lambda _\tau $
for
![]() $\tau \in \mathcal{P}_0$
. Let
$\tau \in \mathcal{P}_0$
. Let
![]() $\Lambda $
be the Leech lattice and let
$\Lambda $
be the Leech lattice and let
Let
![]() $\Lambda _\tau $
be the coinvariant lattice of
$\Lambda _\tau $
be the coinvariant lattice of
![]() $\tau $
. Then
$\tau $
. Then
![]() $\tau $
is fixed-point free on
$\tau $
is fixed-point free on
![]() $\Lambda _\tau $
.
$\Lambda _\tau $
.
The following can be verified by MAGMA.
Lemma A.1. Let
![]() $\tau \in \mathcal{P}_0$
. Then
$\tau \in \mathcal{P}_0$
. Then
-
1.
 $(1-\tau )\Lambda _{\tau }^*=\Lambda _\tau $
.
$(1-\tau )\Lambda _{\tau }^*=\Lambda _\tau $
. -
2. The quotient group
 $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts faithfully on
$C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts faithfully on
 $\mathcal {D}(\Lambda _\tau )$
.
$\mathcal {D}(\Lambda _\tau )$
.
For
![]() $\tau \in \mathcal{P}_0$
, the coinvariant lattice
$\tau \in \mathcal{P}_0$
, the coinvariant lattice
![]() $\Lambda _\tau $
can be constructed by the so-called generalized ‘Construction B’. First, we review the construction.
$\Lambda _\tau $
can be constructed by the so-called generalized ‘Construction B’. First, we review the construction.
Generalized ‘Construction B’
Let
![]() $R_i (1\le i\le t)$
be a copy of the root lattice of type
$R_i (1\le i\le t)$
be a copy of the root lattice of type
![]() $A_{k_i-1}$
, where
$A_{k_i-1}$
, where
![]() $k_i\in {\mathbb Z}_{\ge 1}$
for
$k_i\in {\mathbb Z}_{\ge 1}$
for
![]() $1\le i\le t$
. Let
$1\le i\le t$
. Let
![]() $R=R_1\perp R_2\perp \dots \perp R_t$
. Then
$R=R_1\perp R_2\perp \dots \perp R_t$
. Then
![]() $\mathcal {D}(R_i)\cong {\mathbb Z}_{k_i}$
and
$\mathcal {D}(R_i)\cong {\mathbb Z}_{k_i}$
and
![]() $\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
. Let
$\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
. Let
![]() $\nu :R^*\to R^*/R=\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
be the canonical surjective map. For a subgroup C of
$\nu :R^*\to R^*/R=\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
be the canonical surjective map. For a subgroup C of
![]() $\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, let
$\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, let
![]() $L_A(C)$
denote the lattice defined by
$L_A(C)$
denote the lattice defined by
we call
![]() $L_A(C)$
the lattice constructed by Construction A from C. Note that
$L_A(C)$
the lattice constructed by Construction A from C. Note that
![]() $L_A(\{\mathbf {0}\})=R$
, where
$L_A(\{\mathbf {0}\})=R$
, where
![]() $\mathbf {0}$
is the identity element of
$\mathbf {0}$
is the identity element of
![]() $\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
.
$\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
.
We now fix a base
![]() $\Delta _i$
of the root system of
$\Delta _i$
of the root system of
![]() $R_i$
, which is of type
$R_i$
, which is of type
![]() $A_{k_i-1}$
. Then
$A_{k_i-1}$
. Then
![]() $\Delta =\bigcup _{i=1}^t\Delta _i$
is a base of the root system of R. For
$\Delta =\bigcup _{i=1}^t\Delta _i$
is a base of the root system of R. For
![]() $x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, denote
$x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, denote
where
![]() $x_i$
is regarded as an element of
$x_i$
is regarded as an element of
![]() $\{0,\dots ,k_i-1\}$
and
$\{0,\dots ,k_i-1\}$
and
![]() $\{\lambda _{j}^i\mid 1\le j\le k_i-1\}$
is the set of fundamental weights in
$\{\lambda _{j}^i\mid 1\le j\le k_i-1\}$
is the set of fundamental weights in
![]() $R_i^*$
with respect to
$R_i^*$
with respect to
![]() $\Delta _i$
. The following lemma is immediate from the definition of
$\Delta _i$
. The following lemma is immediate from the definition of
![]() $L_A(C)$
.
$L_A(C)$
.
Lemma A.2. For a generating set
![]() $\mathcal {C}$
of C, the set
$\mathcal {C}$
of C, the set
![]() $\{\lambda _c\mid c\in \mathcal {C}\}$
and R generate
$\{\lambda _c\mid c\in \mathcal {C}\}$
and R generate
![]() $L_A(C)$
as a lattice.
$L_A(C)$
as a lattice.
Set
where
![]() $\rho _{\Delta _i}$
is the Weyl vector of
$\rho _{\Delta _i}$
is the Weyl vector of
![]() $R_i$
with respect to
$R_i$
with respect to
![]() $\Delta _i$
.
$\Delta _i$
.
Define
![]() $ L_B(C)=\{\alpha \in L_A(C)\mid (\alpha |\chi _\Delta )\in {\mathbb Z}\} $
; we call
$ L_B(C)=\{\alpha \in L_A(C)\mid (\alpha |\chi _\Delta )\in {\mathbb Z}\} $
; we call
![]() $L_B(C)$
the lattice constructed by Construction B from C.
$L_B(C)$
the lattice constructed by Construction B from C.
Remark A.3. Up to isometry,
![]() $L_B(C)$
does not depend on the choice of a base
$L_B(C)$
does not depend on the choice of a base
![]() $\Delta $
.
$\Delta $
.
By definitions, it is easy to show the following results (see [Reference Lam and Shimakura34]).
Lemma A.4. Let
![]() $x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
. Then
$x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
. Then
![]() $(\lambda _x|\lambda _x)\in 2{\mathbb Z}$
if and only if
$(\lambda _x|\lambda _x)\in 2{\mathbb Z}$
if and only if
![]() $(\lambda _x|\chi _\Delta )\in {\mathbb Z}$
.
$(\lambda _x|\chi _\Delta )\in {\mathbb Z}$
.
Set
![]() $n=\mathrm {LCM}(\{k_1,\dots ,k_t\})$
.
$n=\mathrm {LCM}(\{k_1,\dots ,k_t\})$
.
Lemma A.5.
![]() $|L_A(C):L_B(C)|=n$
if and only if
$|L_A(C):L_B(C)|=n$
if and only if
![]() $\chi _\Delta \in (1/n)L_A(C)^*$
.
$\chi _\Delta \in (1/n)L_A(C)^*$
.
Next, we consider some isometry of R. Recall that
![]() $R_i\cong A_{k_i-1}$
is a root lattice of type
$R_i\cong A_{k_i-1}$
is a root lattice of type
![]() $A_{k_i-1}$
. Let
$A_{k_i-1}$
. Let
![]() $\Delta _i=\{\alpha ^i_1, \dots , \alpha ^i_{k_i-1}\}$
be a set of simple roots and let
$\Delta _i=\{\alpha ^i_1, \dots , \alpha ^i_{k_i-1}\}$
be a set of simple roots and let
![]() $ \alpha ^i_0=-\sum _{j=1}^{k_i-1} \alpha ^i_{j}$
be the negative of the highest root. Then the map
$ \alpha ^i_0=-\sum _{j=1}^{k_i-1} \alpha ^i_{j}$
be the negative of the highest root. Then the map
![]() $g_{\Delta _i}(\alpha ^i_j)=\alpha ^i_{j+1}$
if
$g_{\Delta _i}(\alpha ^i_j)=\alpha ^i_{j+1}$
if
![]() $1\le j\le k_i-2$
and
$1\le j\le k_i-2$
and
![]() $g_\Delta (\alpha ^i_{k_i-1})=\alpha ^i_0$
defines an isometry on
$g_\Delta (\alpha ^i_{k_i-1})=\alpha ^i_0$
defines an isometry on
![]() $R_i$
, which is a Coxeter element of the Weyl group of
$R_i$
, which is a Coxeter element of the Weyl group of
![]() $R_i$
. In particular,
$R_i$
. In particular,
![]() $g_{\Delta _i}$
acts on
$g_{\Delta _i}$
acts on
![]() $\tilde {\Delta }_i=\Delta _i \cup \{\alpha ^i_0\}$
as a cyclic permutation of order
$\tilde {\Delta }_i=\Delta _i \cup \{\alpha ^i_0\}$
as a cyclic permutation of order
![]() $k_i$
.
$k_i$
.
For
![]() $e=(e_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, set
$e=(e_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$
, set
Lemma A.6.
![]() $g_{\Delta ,e}\in O(L_B(C))$
if and only if
$g_{\Delta ,e}\in O(L_B(C))$
if and only if
![]() $\lambda _e\in L_A(C)^*$
.
$\lambda _e\in L_A(C)^*$
.
Proof. By definition, it is easy to see that
 $$ \begin{align} g_\Delta(\lambda_j)=\lambda_j-\sum_{i=1}^j\alpha_i,\quad g_{\Delta}(\rho_{\Delta})=\rho_{\Delta}-k\lambda_{1}. \end{align} $$
$$ \begin{align} g_\Delta(\lambda_j)=\lambda_j-\sum_{i=1}^j\alpha_i,\quad g_{\Delta}(\rho_{\Delta})=\rho_{\Delta}-k\lambda_{1}. \end{align} $$
Then we have
![]() $ g_{\Delta ,e}(\chi _\Delta )\in \chi _\Delta +(e_1\lambda _1^1,\dots ,e_t\lambda _1^t)+R=\chi _\Delta +\lambda _e+R. $
By the definition of
$ g_{\Delta ,e}(\chi _\Delta )\in \chi _\Delta +(e_1\lambda _1^1,\dots ,e_t\lambda _1^t)+R=\chi _\Delta +\lambda _e+R. $
By the definition of
![]() $L_B(C)$
,
$L_B(C)$
,
![]() $g_{\Delta ,e}\in O(L_B(C))$
if and only if
$g_{\Delta ,e}\in O(L_B(C))$
if and only if
![]() $\lambda _e\in L_A(C)^*$
.
$\lambda _e\in L_A(C)^*$
.
Lemma A.7. The isometry
![]() $g_{\Delta ,e}$
is fixed-point free and of order n if and only if
$g_{\Delta ,e}$
is fixed-point free and of order n if and only if
![]() $\gcd (e_i,k_i)=1$
for all
$\gcd (e_i,k_i)=1$
for all
![]() $1\le i\le t$
$1\le i\le t$
It turns out that the coinvariant lattice
![]() $\Lambda _\tau $
for
$\Lambda _\tau $
for
![]() $\tau \in \mathcal{P}_0$
can be constructed as
$\tau \in \mathcal{P}_0$
can be constructed as
![]() $L_B(C)$
with C generated by a single glue vector c. Moreover,
$L_B(C)$
with C generated by a single glue vector c. Moreover,
![]() $\tau $
can be identified with
$\tau $
can be identified with
![]() $g_{\Delta ,c}$
as defined above.
$g_{\Delta ,c}$
as defined above.
Proposition A.8 [Reference Betsumiya, Lam and Shimakura5]
For any
![]() $\tau \in \mathcal{P}_0$
, the coinvariant lattice
$\tau \in \mathcal{P}_0$
, the coinvariant lattice
![]() $\Lambda _\tau $
of the Leech lattice can be constructed as
$\Lambda _\tau $
of the Leech lattice can be constructed as
![]() $L_B(C)$
with C generated by a single glue vector c. Moreover,
$L_B(C)$
with C generated by a single glue vector c. Moreover,
![]() $\tau |_{L_B(C)}=g_{\Delta ,c}$
as defined above.
$\tau |_{L_B(C)}=g_{\Delta ,c}$
as defined above.
Some properties of
![]() $\Lambda _\tau $
are summarized in Table 10; the structures of
$\Lambda _\tau $
are summarized in Table 10; the structures of
![]() $O(\Lambda _g)$
and
$O(\Lambda _g)$
and
![]() $C_{O(\Lambda _g)}(g)$
are computed by using MAGMA. The symbol
$C_{O(\Lambda _g)}(g)$
are computed by using MAGMA. The symbol
![]() $\prod {a_i}^{b_i}$
for
$\prod {a_i}^{b_i}$
for
![]() $\Lambda _\tau ^*/\Lambda _\tau $
means the abelian group
$\Lambda _\tau ^*/\Lambda _\tau $
means the abelian group
![]() $\bigoplus ({\mathbb Z}/a_i{\mathbb Z})^{b_i}$
. For the notations of groups, see [Reference Conway, Curtis, Norton, Parker and Wilson1].
$\bigoplus ({\mathbb Z}/a_i{\mathbb Z})^{b_i}$
. For the notations of groups, see [Reference Conway, Curtis, Norton, Parker and Wilson1].
Table 10 Coinvariant lattices
![]() $\Lambda _\tau $
for
$\Lambda _\tau $
for
![]() $\tau \in \mathcal{P}_0$
.
$\tau \in \mathcal{P}_0$
.

For
![]() $\tau \in O(\Lambda )$
and
$\tau \in O(\Lambda )$
and
![]() $k\in {\mathbb Z}_{>0}$
, set
$k\in {\mathbb Z}_{>0}$
, set
where
![]() $o(\lambda +\Lambda _\tau )$
is the order of
$o(\lambda +\Lambda _\tau )$
is the order of
![]() $\lambda +\Lambda _\tau $
in
$\lambda +\Lambda _\tau $
in
![]() $\mathcal {D}(\Lambda _\tau )$
. The following lemmas can be verified by using MAGMA [Reference Betsumiya, Lam and Shimakura5].
$\mathcal {D}(\Lambda _\tau )$
. The following lemmas can be verified by using MAGMA [Reference Betsumiya, Lam and Shimakura5].
Lemma A.9. Let
![]() $\tau $
be an isometry of
$\tau $
be an isometry of
![]() $\Lambda $
whose conjugacy class is
$\Lambda $
whose conjugacy class is
![]() $2A$
,
$2A$
,
![]() $3B$
,
$3B$
,
![]() $5B$
or
$5B$
or
![]() $7B$
. Then
$7B$
. Then
![]() $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on the set of all nonzero singular elements.
$C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on the set of all nonzero singular elements.
Lemma A.10. Let
![]() $\tau $
be an isometry of
$\tau $
be an isometry of
![]() $\Lambda $
whose conjugacy class is
$\Lambda $
whose conjugacy class is
![]() $4C$
,
$4C$
,
![]() $6E$
or
$6E$
or
![]() $8E$
. Let k be a divisor of
$8E$
. Let k be a divisor of
![]() $|\tau |$
. Then
$|\tau |$
. Then
![]() $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on
$C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on
![]() $\mathcal {L}_{\tau ,k}$
.
$\mathcal {L}_{\tau ,k}$
.
Lemma A.11. Let
![]() $\tau $
be an isometry of
$\tau $
be an isometry of
![]() $\Lambda $
whose conjugacy class is
$\Lambda $
whose conjugacy class is
![]() $6G$
or
$6G$
or
![]() $10F$
. Then the group
$10F$
. Then the group
![]() $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on
$C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $
acts transitively on
![]() $\mathcal {L}_{\tau , \, |\tau |/2}$
.
$\mathcal {L}_{\tau , \, |\tau |/2}$
.
Competing interest
The authors have no competing interest to declare.
Financial support
C. H. Lam was partially supported by grant AS-IA-107-M02 of Academia Sinica and MoST grant 110-2115-M-001-011-MY3 of Taiwan. M. Miyamoto was partially supported by the Grants-in-Aids for Scientific Research, No.18K18708, The Ministry of Education, Science and Culture, Japan.